12.3—
Control Mechanisms
Having identified possible control points it becomes necessary to determine the mechanism of control. Over a relatively long time scale control may be achieved by changing the amount of an enzyme but over a short time scale control is likely to be achieved by changing the activity of the enzyme.
12.3.1—
Control by Product Inhibition
Every enzyme has a certain affinity for its products and if the enzyme has a high affinity for its product then product inhibition will be pronounced. It appears likely that this form of control is restricted to some synthetic routes and to minor metabolic sequences.
12.3.2—
Control by Negative Feedback
The discovery of negative feedback in metabolic systems appears to have been made by Dische in 1940 who noted that 3-phosphoglycerate inhibits the phosphorylation of glucose in red cells and he proposed that this inhibition might play a regulatory function in glucose metabolism. His paper did not receive the attention it deserved and the idea of feedback had to be rediscovered.
In 1955 Roberts and his coworkers published the result of their extensive studies of the metabolism of E. coli grown on a medium containing 14 C-glucose. They found that the addition of one of a number of amino acids (known to be products of specific synthetic pathways) to the growth medium resulted in the virtually complete inhibition of incorporation of 14 C into that amino acid.
In 1956 Umbarger reported that isoleucine inhibited threonine deaminase—an enzyme which initiates the set of reactions leading to isoleucine biosynthesis. In the same year Yates and Pardee observed that cytidine monophosphate inhibits aspartate transcarbamylase—the first reaction of the pathway leading to the biosynthesis of the pyrimidines. These results offered a biochemical explanation for the end-product inhibition observed by Roberts with intact bacteria.
In 1959 Sir Hans Krebs introduced the first symposium to be held on metabolic control. Ideas on the regulation of carbohydrate and amino acid metabolism were discussed and the general ideas of feedback formulated. Control by negative feedback is an engineering concept and familiar examples include governers of steam engines, thermostats and automatic volume control in amplifiers. The limitations of the analogy between electrical feedback amplifiers and metabolic reactions have been stressed by Britton-Chance. However,
as with other terminology developed for use with metabolic control systems (see discussion of allosteric enzymes) the tendency has been to dispense with rigorous definitions and the general definition of negative feedback is 'increased output decreases the input'.
12.3.3—
Patterns of Control
The most frequently observed pattern of control is when the end. product of a metabolic sequence inhibits the first reaction belonging to that sequence. For example serine can be formed by the reaction sequence shown in Fig. 12.3.
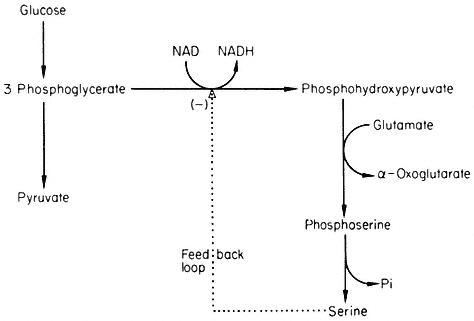
Figure 12.3
Reactions involved in the biosynthesis of serine.
Serine inhibits 3-phosphoglycerate dehydrogenase and so controls its own biosynthesis. This simple mechanism is effective, presumably because a relatively small amount of the flux through the glycolytic pathway is directed towards serine and thus variations in the rate of serine production will not seriously perturb the glycolytic flux.
12.3.4—
Control of Branched Pathways
Inhibition of the first step in a metabolic pathway by an end-product leads to special problems in the case of branched biosynthetic pathways. Consider the sequence
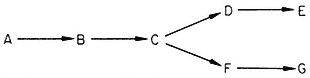
It the first common step (A® B) is inhibited by either or both end-products, then an excess of one could inhibit the step A® B and lead to a deficiency of the
other end-product. Nature has evolved several mechanisms which avoid, to varying degrees, these difficulties. Stadtman (1970) has classified these mechanisms; here we discuss a few examples which have been studied in plants.
12.3.4.1—
The Aspartate Family
The formation of some amino acids from aspartate is outlined in Fig. 12.4 together with feedback controls which have been demonstrated.
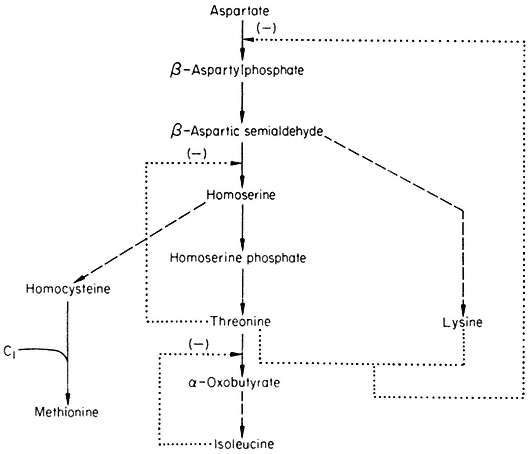
Figure 12.4
Reactions involved in the biosynthesis of the aspartate family of amino acids.
® Single step reaction; ---® multi-step reaction; --® feed back loop.
Aspartokinase which catalyses the first reaction of the pathway is inhibited by lysine and threonine in a concerted or synergistic manner. The term concerted feedback inhibition has been used by Stadtman to describe cases of inhibition by two end products when the single end products produce no inhibition. The term synergistic inhibition is used when the total inhibition is much greater than the sum of their independent effects. The aspartokinase from plants appears to be inhibited by low concentrations of lysine but not by low concentrations of threonine—when both are present a much greater inhibition is observed. Although this effect would seem best to fit Stadtman's definition of synergistic inhibition it has been called concerted inhibition. Whatever the terminology, this mechanism does not involve methionine and is thus only a partial solution to the control of the branched pathway. The non-involvement of methionine means that in conditions where threonine and lysine
accumulate they will tend to inhibit the synthesis of methionine—even in situations where methionine may be in short supply. This imperfection is compounded by the feedback inhibition of homoserine dehydrogenase by threonine which further reduces the flow of intermediates available for the biosynthesis of methionine.
These imperfections in the control mechanism can be invoked to explain the effect of amino acids on the growth of Lemna minor (Table 12.1).
| ||||||||||||||||||||||||||||
The relatively small inhibition observed with lysine can be interpreted in terms of inhibition of aspartokinase (but see section on metabolic interlock ). The inhibition produced by threonine is consistent with the inhibition of homoserine dehydrogenase which would prevent the flow of carbon to methionine. The inhibition produced by homoserine is difficult to explain since as far as known it does not inhibit any of the enzymes involved. Furthermore in some plants e.g. peas, homoserine is produced in large quantities and transported in the phoem. The inhibition produced by isoleucine is consistent with a control pattern known as sequential inhibition. Isoleucine has been shown to inhibit threonine deaminase which would be expected to lead to an accumulation of threonine which in turn inhibits homoserine dehydrogenase and so reduces the flow of carbon to methionine. The inhibition produced by methionine is difficult to explain in terms of the reactions shown in Fig. 12.4. The pronounced inhibition observed with lysine and threonine is consistent with their synergistic effects on aspartokinase producing a reduction in the flow of carbon to methionine, which is reinforced by the inhibition of homoserine dehydrogenase
by threonine. Aspartic acid and isoleucine are unable to reduce the inhibition but methionine and homoserine are able to do so, presumably by supplying methionine directly or indirectly.
12.3.4.2—
Aromatic Biosynthesis
The control of aromatic amino acid biosynthesis has been extensively studied in fungi and bacteria and it is clear that nature has evolved many solutions to the problem of control in branched pathways. Some of the solutions which have been demonstrated in higher plants are shown in Fig. 12.5.
12.3.4.3—
Enzyme Multiplicity
In this control mechanism the first common step is catalysed by two or more enzymes which are under feedback control by compounds formed after the branching point. Four examples are given in Fig. 12.5, the control of chorismate mutase being particularly complicated. Three isozymes have been demonstrated in plants (Woodin & Nishioka, 1973); CM1 and CM3 are inhibited by phenylalanine and activated by tryptophane. CM1 and CM2 are inhibited by caffeic acid and chlorogenic acid whilst CM3 is inhibited by ferulic acid.
12.3.4.4—
Enzyme Aggregation
A number of fungi possess an aggregate of the five enzymes necessary for the conversion of 3-deoxy-D -heptulosonate-7-phosphate to enolpyruvyl-shikimate-5-phosphate. In Neurospora the five enzymes form a complex (M.W. 230,000) coded by the arom gene cluster. This large complex has not been demonstrated in higher plants, but a bifunctional enzyme consisting of dehydroquinase and shikimate dehydrogenase has been isolated (Boudet, 1971). Neurospora contains two dehydroquinases, the one in the aggregate is involved in an anabolic sequence, the other maps outside the arom cluster and is thought to function as a component of a catabolic sequence. The physiological significance of the multienzyme cluster could be to separate the degradative and synthetic routes. This could be achieved if the dehydroquinic acid which is formed in the aggregate is not released as a free product. This idea has become known as metabolic channelling and in a number of cases it has been shown that metabolites involved in channelling do not leave the enzyme surface. For example fungi possess a bifunctional enzyme consisting of carbamyl phosphate synthetase and aspartate transcarbamylase.
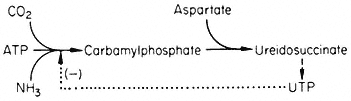
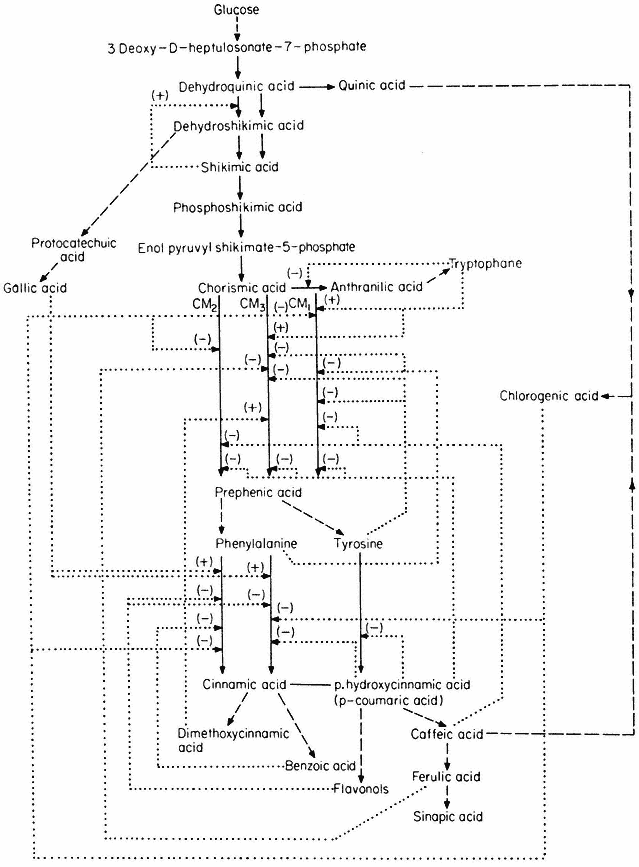
Figure 12.5
Reactions involved in the biosynthesis of aromatic compounds.
® Single step reactions; --® multi-step reactions; --® feed back loop.
When the bifunctional enzyme is synthesizing ureidosuccinate from 14 CO2 , the addition of carbamyl phosphate does not dilute the incorporation of 14 C into ureidosuccinate, showing that carbamyl phosphate formed by the double enzyme does not equilibrate with free carbamyl phosphate.
Higher plants contain two dehydroquinases one forming a bifunctional association with shikimate dehydrogenase, the other being activated by shikimic
acid. Such a system involving a specific regulation of isoenzymes and molecular compartmentalization may function to control the partitioning of dehydroquinic acid between the pathways to phenolcarboxylic acids and aromatic amino acids.
12.3.5—
Metabolic Interlock
The reactions and feedback loops shown in Fig. 12.5 give some idea of the complexity of control within a metabolic pathway. When the feedback loops of other metabolic pathways are taken into consideration it seems highly likely that the control must be interlocked. As an example, consider the reactions involved in the biosynthesis of methionine. In Fig. 12.4, this is shown as the addition of a C1 group to homocysteine. The synthesis of this C1 group is shown in Fig. 12.6.
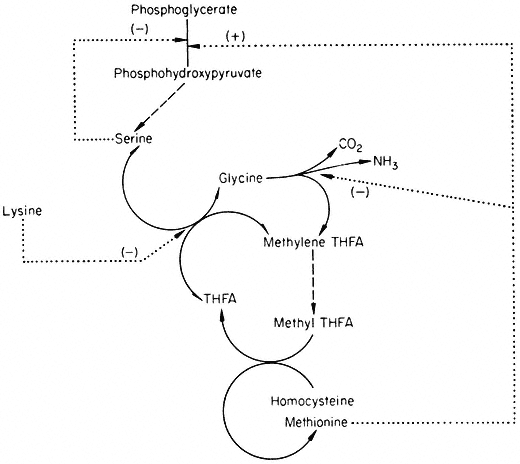
Figure 12.6
Reactions involved in the biosynthesis of methionine.
® Single step reaction; ---® multi-step reaction; . . .® feed back loop.
The active C1 group is generated in the serine hydroxymethyl transferase reaction as methylene tetrahydrofolate. After reduction to methyl THFA the methyl group is transferred to homocysteine to form methionine. Homocysteine is derived from the aspartate family (cf. Fig. 12.4) and so is lysine. The metabolism of the aspartate family and the serine glycine family are thus interlocked via lysine, which inhibits both aspartokinase and serine hydroxymethyl transferase.
12.3.6—
Enzymes as Control Elements
Until the discovery of feedback inhibition in 1956 enzymes were considered as biological catalysts and most enzymologists were concerned with the properties of the active site. When it became apparent that enzyme activity was under the control of specific metabolites, which were structurally unlike the active site, it became necessary to postulate a control site to which metabolites could bind and modulate the activity of the enzyme. Recognizing the lack of structural similarity between the substrate and the effector the term allosteric site was introduced (Monod, Changeux & Jacob, 1963). Subsequently Monod, Wyman and Changeux (1965) noted that many regulatory enzymes with specific allosteric sites exhibit cooperative-type kinetics and they developed a concerted transition hypothesis to explain the observed kinetics. Many workers assume that any enzyme showing sigmoidal kinetics is an allosteric enzyme and some workers imply that the mechanism of activation of all allosteric enzymes follows the mechanism postulated by Monod et al., (1965). The purist may object but the original precise definition has been replaced by a broader but less precise usage.
12.3.6.1—
Allosteric Enzymes
Before 1956, the kinetics of numerous enzymes were shown to follow the rate law of Michaelis and Menten giving a hyperbolic plot of v against S . An examination of enzymes which were known to be subject to feedback regulation showed that in some cases the relationship between v and S was sigmoid. In other cases the addition of a feedback inhibitor led to a change from a hyperbolic to a sigmoid relationship.
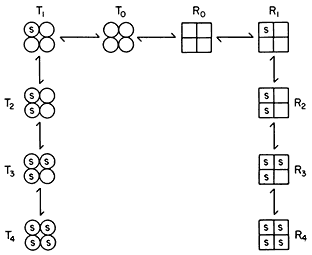
Figure 12.7
Illustration of the Monod model of an allosteric enzyme.
Monod et al., (1965) proposed a simple model to account for the observed kinetics in which they took account of the observation that allosteric enzymes are composed of subunits. They assumed that the protein subunits were arranged in such a way that they occupy equivalent positions so that the enzyme must have at least one axis of symmetry. They further assumed two interconvertible states—R and T—each maintaining the symmetry principle. A simple illustration of the model is given in Fig. 12.7 based on the symbols used by Koshland (1970). The reader is referred to the original article by Monod et al., (1965) for the derivation of the rate law. However a consideration of the illustration leads to a basic understanding of the underlying causes of sigmoid kinetics. Two types of allosteric behaviour may be distinguished—one the variable K system in which the two states of the enzyme have different affinities for the substrate, the other, the variable V system in which the R state is catalytically more active (Fig. 12.8).
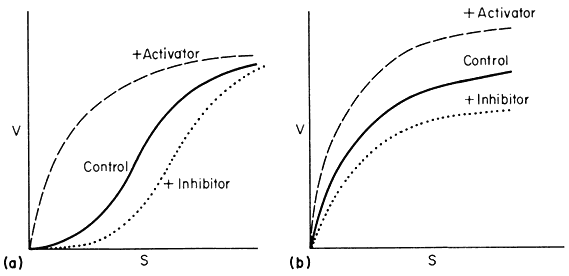
Figure 12.8
Relationship between v and s.
(A) a variable K system; (B) a variable V system.
Variable K Systems
In the variable K system, the R form is assumed to have a higher affinity for S than the T form of the enzyme. If in the absence of ligands, the equilibrium favours the T form then increasing concentrations of S will shift the equilibrium towards the R state giving sigmoid v against S plots. Another way of looking at this situation is to imagine that the interconversion of the R and T forms can be blocked and the enzyme isolated as the R or T form. The T form would give a normal Michaelis-Menten curve with a high Km(T ) and the R form would also give a Michaelis-Menten curve but with a low Km(R ) . Allowing R and T to be interconvertible allows Km to vary.
If an activator binds preferentially to the R state it will tend to put the enzyme entirely in the R state and so remove the sigmoidicity of the v against S plot. Similarly if an inhibitor binds preferentially to the T form it will increase the sigmoidicity.
Variable V Systems
In the variable V system the R form is assumed to be catalytically more active than the T form though both forms have the same affinity for the substrate so that the v/S plot is hyperbolic in the presence or absence of activators and inhibitors. An activator is assumed to have a greater affinity for the R form than for the T form whilst the reverse holds for an inhibitor.
12.3.6.2—
Alternative Models for Allosteric Enzymes
This superficial consideration of the Monod model concentrates on only one aspect of the model–the two configurational states. This limited aspect gives a qualitative explanation of' sigmoid kinetics described by the equation:
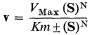
where N = 2.
To explain higher order reactions the Monod model includes some highly restrictive assumptions which produce mathematical simplicity but are nevertheless based on the fundamental properties of protein structure.
An alternative model proposed by Koshland (1970) assumes an induced fit so that the protein subunit undergoes a conformational change when it binds a ligand. A simple sequential model may be illustrated:

This simple model is not a necessary part of the induced fit model (which in fact suggests a diversity of forms of association between enzyme and ligand—25 for a tetrameric protein). Nevertheless it simplifies the mathematical treatment and in many cases provides a close fit to experimental values.
12.3.6.3—
Kinetic Constants for Allosteric Enzymes
When an electronic engineer constructs a control circuit he needs to know the characteristics of the components—the amplification factor, grid bias, etc. Similarly if we wish to understand the control of a system we need to know the characteristics of its components, that is, the kinetic constants of the enzymes. Clearly a variable K system cannot be defined by a Km value nevertheless the same operation value can be used, that is the concentration of substrate producing half maximum velocity which is in this case designated S0.5 . More generally the term (X0.5 ) is used to designate the ligand concentration at half saturation.
The constant N is operationally the order of the reaction, its physical meaning may relate to the number of substrate binding sites on the enzyme or to the degree of cooperativity of binding. Whatever the meaning of N it can be estimated by means of a Hill plot (Fig. 12.9). Another kinetic term, Rs is the ratio between the 90% and 10% saturation values. Rs will be 81 for all curves following Michaelis-Menten kinetics and less than 81 for cases of positive cooperativity–a few cases of negative cooperativity are known and these give Rs values greater than 81.
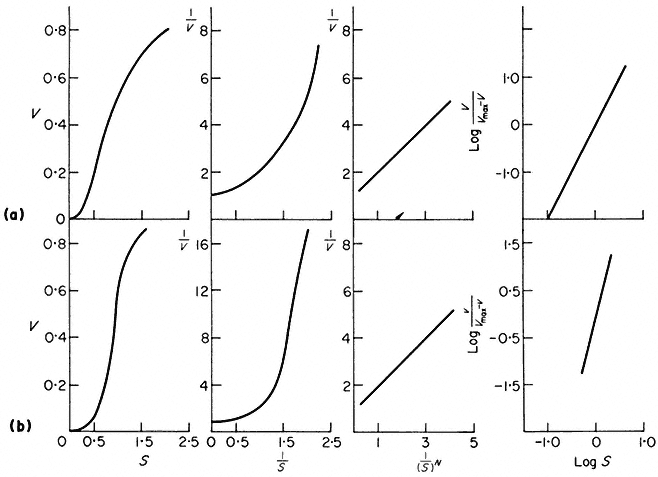
Figure 12.9
Kinetic data for an enzyme with variable 'K' properties.
The curves are drawn assuming
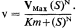
Valve characteristics define the properties of the valve but do not determine the function of the valve–the function of the valve is determined by the circuit in which it operates, in one circuit it may function as a cathode follower, in another as an amplifier. Similarly, the kinetic constants of a control enzyme do not determine its role in metabolic organization. The properties of an enzyme in a metabolic pathway are modified by its association with other enzymes. The study of control in metabolic pathways relates enzymology to physiology and illustrates the somewhat unfashionable view that the whole is more than the sum of the parts.