The Brackets

Having given up on trying to gain insights into the mechanism of radiation, Dirac turned to the more formal side of Heisenberg's scheme, first to the new quantum rule. Since Heisenberg presented this rule as deducible from the high-frequency limit of Kramers's dispersion formula, Dirac naturally went back to the Kramers-Heisenberg paper for a full derivation. On the one hand, he found that Heisenberg's new product already appeared in the dispersion formulae for the incoherent case (see (220) of part B).^[45]

On the other hand, he knew well that in Hamiltonian dynamics the first-order perturbation P₁ of a quantity P₀ (like the electric moment that was responsible for classical dispersion) could be expressed in the form

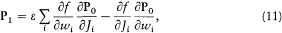
wherein e f is the generating function of the first-order canonical transformation connecting old and new action-angle variables. He probably had learned this from Whittaker's Analytical dynamics , or from Fowler's lectures, which used this type of expression in the perturbative treatment of the Stark effect, and in the classical dispersion formula leading to the Kramers-Heisenberg formulae (see (202) of part B). Poisson brackets also occurred in several of Dirac's early manuscripts, even though he might not have remembered that they were named so. Now, according to the Kramers-Heisenberg procedure for translating from the classical dispersion formula, the Poisson bracket had to be translated into a commutator.^[46]

[44] irac 1925g, 652.

[45] Kramers and Heisenberg 1925.

[46] Whittaker 1904, 302 of the 1960 ed. for the Poisson brackets in perturbation theory; see Dirac's notes and Thomas's more detailed notes on Fowler lectures, AHQP. Poisson brackets (without the name) appeared in Dirac [1924?b] and in the manuscript kept with Darwin's letter (see n. 38 above).

This explanation of Dirac's first important discovery in the new quantum mechanics is not unfounded reconstruction; it may be surmised from a rough calculation found on a back page of a recycled manuscript. The following transcription is the closest possible.^[47]

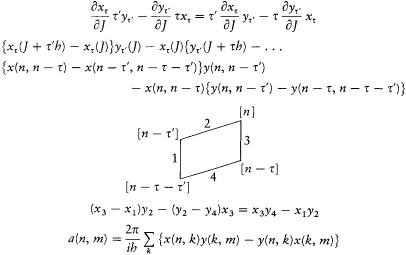
The diagram was obviously taken from the Kramers-Heisenberg paper. In fact, the whole calculation is very similar to that of Kramers and Heisenberg (which is discussed in the equations (214-220) of part B). The second line results from the prescription^[48]

The factor 2p /ih in the expression of a (n, m ) enables us to reestablish its meaning as the quantum amplitude "corresponding" to the harmonic n - m of the classical bracket

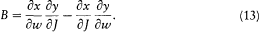
Indeed, if

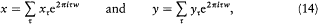
[47] Back page of Dirac [1925c]. Mehra and Rechenberg 1982d discuss Dirac's back-page calculation.

[48] I remind the reader that Dt is defined by Dt f(J )=f (J+t h)-f (J ) and that xt (J ) "corresponds" to a quantum amplitude x (n', n ") with n' - n"=t . The choice of n ' is directed by considerations of symmetry (for Kramers and Heisenberg) or by the desire to make matrix products appear in the final formula (m Dirac's case). The diagram is m Kramers and Heisenberg 1925, 694.

then

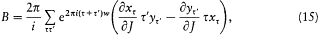
where the quantity in parentheses is the exact starting point of Dirac's note. Finally, the h in 2p /ih comes from the translation rule (12).

Most important, Dirac's discovery of the relation between commutators and Poisson brackets appears to have been based on Kramers's procedure of symbolic translation. Therefore, it was directly connected with the previous sharpening of the correspondence principle. Here lies the secret of Dirac's revelation of a structural analogy between old and new mechanics—one more significant than Heisenberg's formal transposition of classical dynamic equations.

In his final paper, however, Dirac adopted a different presentation of the relation between classical and quantum brackets. There he used the correspondence principle backward, from the commutator to the Poisson bracket, and in its narrower but safer acceptance as an asymptotic convergence of quantum relations toward classical ones. The resulting calculation looks artificial, since it is nothing but the original one, read from bottom to top:^[49]

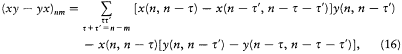
which is asymptotically equal to

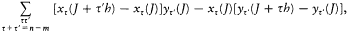
of

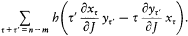
The latter expression is, as we saw, ih/2p times a Fourier coefficient of the Poisson bracket^[50]

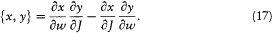
[49] Dirac 1925g, 647-648.

[50] Dirac used the notation [x, y ] instead of {x, y } for the Poisson brackets. In order to avoid confusion, I will conform to the modern usage, which reserves [x, y ] for the commutator.

As immediately noticed by Dirac, the first attractive feature of the Poisson brackets is their canonical invariance: for any choice q, p of the canonical coordinated, they can be expressed as

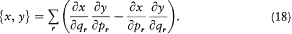
Moreover, they have the same simple algebraic properties as commutators: antisymmetry, bilinearity, distributivity, and Jacobi's identity, which respectively read:

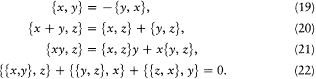
All of this suggested to Dirac the following assumption:^[51] "The difference between the Heisenberg product of two quantities is equal to ih/2p times their Poisson bracket expression. In symbols,

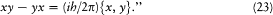
In the case of a canonical pair q, p , this rule gave

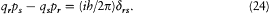
In this way Dirac reached the canonical form of the new quantum rule independently of Born and Jordan, and in a more profound way, one showing the intimate structural analogy between classical and quantum mechanics. He concluded: "The correspondence between the quantum and classical theories lies not so much in the limited agreement when 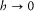as in the fact that the mathematical operations on the two theories obey in many cases the same laws." What Heisenberg had judged to be an "essential difficulty" of his new scheme, the noncommutativity of the quantum product, Dirac viewed as having a natural classical counterpart in the Poisson bracket algebra. As Dirac could not have failed to notice, it also had antecedents, even geometrically meaningful ones, in the algebra of quaternions or in Baker's symbols. This prompted him to develop a "quantum algebra," abandoning commutativity but saving associativity and distributivity.^[52]

[51] Dirac 1925g, 648.

[52] Ibid., 649, italicized by Dirac; Heisenberg 1925c, 883.

For the sake of homogeneity of quantum operations, Dirac required every classical operation to have a counterpart in the quantum algebra. Consequently, he introduced a "quantum differentiation" d/dv , with the characteristic property that

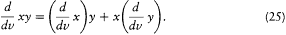
Linear realizations of this property, he showed, could always be expressed under the form

For example, the partial derivatives of Hamilton's equations could be represented as commutators in the equations

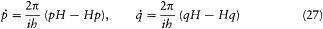
resulting from the corresponding classical equations

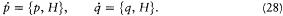
In this elegant manner Dirac dispensed with the awkward mixture of differential and algebraic operations that was being developed with great pain in Göttingen. As Fowler wrote to Bohr: "I think it is a very strong point of Dirac's that the only differential coefficients you need in mechanics are really all Poisson brackets, and that the direct redefinition of the Poisson brackets is better than the invention of formal differential coefficients."^[53]