Chapter XII
Queer Numbers

In July 1925 there came to Cambridge a visitor who thought differently about the power of the correspondence principle and had just drawn from it the first elements of a new mechanics. In fact Heisenberg lectured on "Term zoology and Zeeman botanics" at an informal club of young physicists created by Kapitza. The title of this talk referred to the multimodel approach of multiplet theory (see part B, on pp. 205-207). We do not know for sure whether Heisenberg mentioned his more recent inspiration or whether Dirac was present. However, Fowler almost certainly heard of the new kinematics in private conversations, and asked to be kept informed.^[40]

Poisson Resurrected

In late August Dirac received from Fowler the proofs of Heisenberg's seminal paper. Even before he was able to judge the relevance of the new scheme, he tried his favorite game, finding a relativistic extension. While this premature attempt fell short, it revealed what Dirac considered to be the essence of Heisenberg's new ideas. First there was a substitution of "Heisenberg's product" for the ordinary product, then an endeavor to maintain as much as possible of the structure of classical dynamics: "The

[40] "Minutes of the Kapitza Club," AHQP, entry of 28 July 1925. In Dirac 1977, Dirac remembered having heard Heisenberg's talk, in contradiction of his earlier statement in Dirac [1962]. The source of Heisenberg's talk was Heisenberg 1925b. See Kragh 1990, 14, 317 n. 1.

main point in the present dynamics is that when we have to choose a quantum coefficient, we do so in such a way as to make as many classical relations as possible still true between the quantum quantities."^[41]

Another characteristic of Heisenberg's paper, the organic relation between the new kinematics and the structure of the emitted radiation, initially diverted Dirac's attention from more essential features of the theory. In his tentative relativistic extension, he invoked the unidirectional character of the emitted radiation to justify the introduction of the atomic momentum in the labeling of stationary states. In another manuscript he tried to explain the absence of radiation in the fundamental state by introducing a new distinction between two types of "virtual oscillators." The "i -type" with an amplitude q = a e^iwt was unable to radiate by itself, if only the general expression of radiated energy was assumed to be A ² + B² , where A and B are defined by

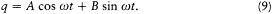
Not to radiate, the fundamental state had to be a pure i -oscillator; the possibility of emission in the other states was then to be attached to a corruption of the i -oscillators by "j -oscillators," with an amplitude be^jwt , wherein j = — i .^[42]

As Dirac quickly realized, this strange idea had every chance to be irrelevant, since it connected subsets of virtual oscillators to definite levels, in the naive fashion

which is not compatible with Heisenberg's product. The manuscript ends with the words: "We cannot, however, put xy (n ) = x (n )y (n ), so that coordinates associated with a stationary state can have only a very restricted meaning."^[43]

The title and introduction of the above-mentioned manuscript, "Virtual oscillators," clearly indicates that Dirac originally interpreted Heisenberg's new scheme as a modification of the BKS theory. In this modification the distinction between positive and negative oscillators was erased, but an alternative distinction, that between i - and j -oscillators, was needed to give some insight into the mechanism of radiation. Heisenberg's own

[41] Heisenberg 1925c; Dirac [1925d], [1925e], undated but almost certainly written before the discovery of the connection between Poisson brackets and commutators. The quotation is from the second manuscript.

[42] Dirac [1925f].

[43] Ibid.

emphasis on radiation properties—the only observable things—probably suggested this misinterpretation. Nevertheless, his careful elimination of the term "virtual oscillator" indicated a fundamental departure from the BKS approach: radiation properties could no longer be connected with a given stationary state, as reflected by the interlocked character of quantum products. After his failed distinction between i - and j -oscillators Dirac also emphasized this impossibility: "The components of a varying quantum quantity are so interlocked . . . that it is impossible to associate the sum of certain of them with a given state."^[44]

The Brackets

Having given up on trying to gain insights into the mechanism of radiation, Dirac turned to the more formal side of Heisenberg's scheme, first to the new quantum rule. Since Heisenberg presented this rule as deducible from the high-frequency limit of Kramers's dispersion formula, Dirac naturally went back to the Kramers-Heisenberg paper for a full derivation. On the one hand, he found that Heisenberg's new product already appeared in the dispersion formulae for the incoherent case (see (220) of part B).^[45]

On the other hand, he knew well that in Hamiltonian dynamics the first-order perturbation P₁ of a quantity P₀ (like the electric moment that was responsible for classical dispersion) could be expressed in the form

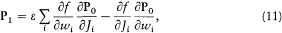
wherein e f is the generating function of the first-order canonical transformation connecting old and new action-angle variables. He probably had learned this from Whittaker's Analytical dynamics , or from Fowler's lectures, which used this type of expression in the perturbative treatment of the Stark effect, and in the classical dispersion formula leading to the Kramers-Heisenberg formulae (see (202) of part B). Poisson brackets also occurred in several of Dirac's early manuscripts, even though he might not have remembered that they were named so. Now, according to the Kramers-Heisenberg procedure for translating from the classical dispersion formula, the Poisson bracket had to be translated into a commutator.^[46]

[44] irac 1925g, 652.

[45] Kramers and Heisenberg 1925.

[46] Whittaker 1904, 302 of the 1960 ed. for the Poisson brackets in perturbation theory; see Dirac's notes and Thomas's more detailed notes on Fowler lectures, AHQP. Poisson brackets (without the name) appeared in Dirac [1924?b] and in the manuscript kept with Darwin's letter (see n. 38 above).

This explanation of Dirac's first important discovery in the new quantum mechanics is not unfounded reconstruction; it may be surmised from a rough calculation found on a back page of a recycled manuscript. The following transcription is the closest possible.^[47]

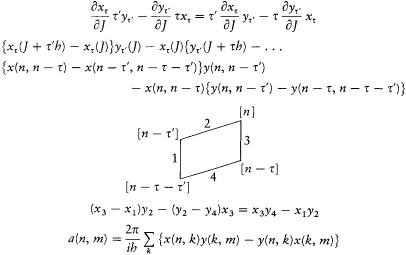
The diagram was obviously taken from the Kramers-Heisenberg paper. In fact, the whole calculation is very similar to that of Kramers and Heisenberg (which is discussed in the equations (214-220) of part B). The second line results from the prescription^[48]

The factor 2p /ih in the expression of a (n, m ) enables us to reestablish its meaning as the quantum amplitude "corresponding" to the harmonic n - m of the classical bracket

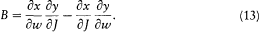
Indeed, if

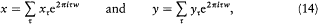
[47] Back page of Dirac [1925c]. Mehra and Rechenberg 1982d discuss Dirac's back-page calculation.

[48] I remind the reader that Dt is defined by Dt f(J )=f (J+t h)-f (J ) and that xt (J ) "corresponds" to a quantum amplitude x (n', n ") with n' - n"=t . The choice of n ' is directed by considerations of symmetry (for Kramers and Heisenberg) or by the desire to make matrix products appear in the final formula (m Dirac's case). The diagram is m Kramers and Heisenberg 1925, 694.

then

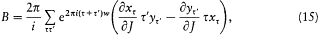
where the quantity in parentheses is the exact starting point of Dirac's note. Finally, the h in 2p /ih comes from the translation rule (12).

Most important, Dirac's discovery of the relation between commutators and Poisson brackets appears to have been based on Kramers's procedure of symbolic translation. Therefore, it was directly connected with the previous sharpening of the correspondence principle. Here lies the secret of Dirac's revelation of a structural analogy between old and new mechanics—one more significant than Heisenberg's formal transposition of classical dynamic equations.

In his final paper, however, Dirac adopted a different presentation of the relation between classical and quantum brackets. There he used the correspondence principle backward, from the commutator to the Poisson bracket, and in its narrower but safer acceptance as an asymptotic convergence of quantum relations toward classical ones. The resulting calculation looks artificial, since it is nothing but the original one, read from bottom to top:^[49]

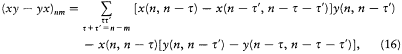
which is asymptotically equal to

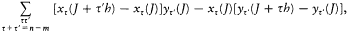
of

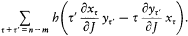
The latter expression is, as we saw, ih/2p times a Fourier coefficient of the Poisson bracket^[50]

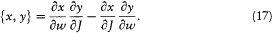
[49] Dirac 1925g, 647-648.

[50] Dirac used the notation [x, y ] instead of {x, y } for the Poisson brackets. In order to avoid confusion, I will conform to the modern usage, which reserves [x, y ] for the commutator.

As immediately noticed by Dirac, the first attractive feature of the Poisson brackets is their canonical invariance: for any choice q, p of the canonical coordinated, they can be expressed as

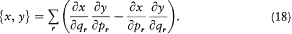
Moreover, they have the same simple algebraic properties as commutators: antisymmetry, bilinearity, distributivity, and Jacobi's identity, which respectively read:

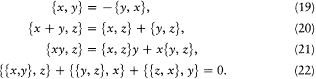
All of this suggested to Dirac the following assumption:^[51] "The difference between the Heisenberg product of two quantities is equal to ih/2p times their Poisson bracket expression. In symbols,

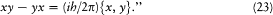
In the case of a canonical pair q, p , this rule gave

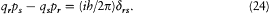
In this way Dirac reached the canonical form of the new quantum rule independently of Born and Jordan, and in a more profound way, one showing the intimate structural analogy between classical and quantum mechanics. He concluded: "The correspondence between the quantum and classical theories lies not so much in the limited agreement when as in the fact that the mathematical operations on the two theories obey in many cases the same laws." What Heisenberg had judged to be an "essential difficulty" of his new scheme, the noncommutativity of the quantum product, Dirac viewed as having a natural classical counterpart in the Poisson bracket algebra. As Dirac could not have failed to notice, it also had antecedents, even geometrically meaningful ones, in the algebra of quaternions or in Baker's symbols. This prompted him to develop a "quantum algebra," abandoning commutativity but saving associativity and distributivity.^[52]

[51] Dirac 1925g, 648.

[52] Ibid., 649, italicized by Dirac; Heisenberg 1925c, 883.

For the sake of homogeneity of quantum operations, Dirac required every classical operation to have a counterpart in the quantum algebra. Consequently, he introduced a "quantum differentiation" d/dv , with the characteristic property that

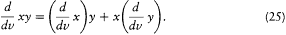
Linear realizations of this property, he showed, could always be expressed under the form

For example, the partial derivatives of Hamilton's equations could be represented as commutators in the equations

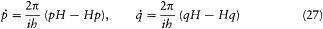
resulting from the corresponding classical equations

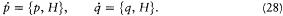
In this elegant manner Dirac dispensed with the awkward mixture of differential and algebraic operations that was being developed with great pain in Göttingen. As Fowler wrote to Bohr: "I think it is a very strong point of Dirac's that the only differential coefficients you need in mechanics are really all Poisson brackets, and that the direct redefinition of the Poisson brackets is better than the invention of formal differential coefficients."^[53]

Action-Angle Variables

On the basis of the extended analogy between classical and quantum mechanics, Dirac hoped to be able to transpose classical methods of resolution of dynamic problems. One method, the introduction of new canonical variables, received an immediate counterpart through the canonical criterion: The variables Q, P shall be canonical if and only if

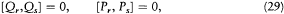
[53] Dirac 1925g, 645; Fowler to Bohr, 22 Feb. 1926, AHQP; see also penetrating comments in Birtwistle 1928, 77.

For systems that were multiperiodic at the classical level, there would presumably be something like quantum action-angle variables (which Dirac rather called uniformizing variables).^[54]

In a first exploration of this notion, Dirac found it convenient to introduce the canonical variables (similar to the modern creators and annihilators)

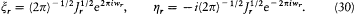
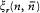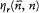In the light of the correspondence principle he requested that the corresponding quantum variables have vanishing matrix elements, except for the elements and with 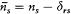. This condition implies the identities

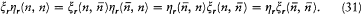
In order to be canonical the variables have to verify another identity:

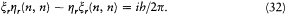
Hence,

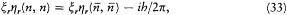
and

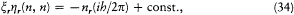
wherein the constant must be taken to be zero in order that all amplitudes may vanish when .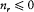

Granted that the classical relation

still holds at the quantum level, the (diagonal) values of the action variables are restricted to J_r = n _r h. Implicitly assuming the classical expression of the energy in terms of the J 's, Dirac commented: "This is just the ordinary rule for quantising the stationary states, so that in this case [when relation (35) is true] the frequencies of the system are the same as those given by Bohr's theory." This was too simple to be true, as we shall presently see. Nevertheless, the general tendency to adapt classical methods in the new mechanics proved to be very productive in Dirac's subsequent work.^[55]

"The fundamental equation of quantum mechanics" was received in early November 1925 by the editors of the Proceedings of the Royal Society

[54] Dirac 1925g, 651-653.

[55] Ibid., 653.

and was hurried to publication by Fowler. The introduction expressed Dirac's personal view of quantum mechanics:

Heisenberg puts forward a new theory, which suggests that it is not the equations of classical mechanics that are in any way at fault, but that the mathematical operations by which physical results are deduced from them require modification. All the information supplied by the classical theory can thus be made use of in the new theory.

Dirac contrasted this outlook with the one associated with the correspondence principle, which confined the validity of classical equations to the asymptotic case of high quantum numbers and to "certain other special cases." In reality the discovery of the connection between commutators and Poisson brackets was inspired by the conception of correspondence as formal translation earlier developed by Kramers, Born, and Heisenberg under Bohr's guidance. The concomitant formal analogy between classical and quantum mechanics was, though Dirac did not know it, the most perfect expression of the "general tendency" expressed in the latest form of the correspondence principle.^[56]

The Canonical Method

How did Dirac's conception differ from that developed in Göttingen? Before seeing Dirac's fundamental paper, Born, Heisenberg, and Jordan had already been aware of the connection between Poisson brackets and commutators. As Kramers communicated to the Dutch Academy in November 1925, Pauli had encountered this relation in the same way as Dirac had, through the classical dispersion formula. However, once the "three men" knew the fundamental equations of quantum mechanics, they stopped referring to their classical origin. They felt that they had in hand an essentially new and self-contained theory, which should be developed from its own axioms with the suitable tools of matrix theory. Instead, Dirac tried his best to transpose the classical methods of solution and apply them to quantum problems. The correspondence between the two theories, he believed, was not limited to the form of the fundamental equations; it concerned mathematical structures , in the modern sense of the word.^[57]

From this perspective, the transformation theory of Hamiltonian dynamics and the action-angle variables, suitably adapted, were likely to be

[56] Ibid., 642.

[57] Kramers 1925c, 376. According to Kragh 1990, 21, 319, J. C. Slater also discovered the connection between Poisson brackets and commutators, and used it to develop quantum formalism in an unpublished work.

useful in the new theory. As Dirac explained at the Solvay congress of 1927, the operator 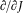of the Hamilton-Jacobi theory even anticipated the interlocked character of stationary states in matrix theory, since it connected two infinitely close orbits, in the same way as matrices connected two stationary states.^[58]

The analogy, as profound as it might be, was full of traps. As Heisenberg wrote to Dirac in December 1925, quantum mechanics, did not simply result from a reinterpretation of the equations of classical mechanics. The very concept of motion had to be changed. Moreover, the formal correspondence between the two mechanics was not as close as Dirac imagined. One could not simply identify all Poisson brackets with commutators without getting into trouble. For instance, the commutator [q² , p ² ] could be evaluated in two contradictory ways, through an algebraic reduction in terms of the commutator [q, p ]:

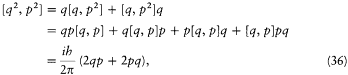
or directly through the corresponding Poisson brackets:

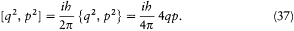
Fortunately, the correspondence still held for canonical pairs, which was all that Dirac needed for his developments.^[59]

Heisenberg also reproached Dirac with a more important overestimation of the classical analogy. Contrary to the assumption made at the end of "The fundamental equations," the expression H (J ) of the Hamiltonian in terms of action variables could not be simply adapted from the classical theory; the quantum-mechanical spectrum of multiperiodic systems had to differ, in general, from that given by the Bohr-Sommerfeld theory. Indeed, as a consequence of the noncommutativity of quantum variables, the quantum-mechanical expression of the original configuration variables (q, p ) in terms of the action-angle variables (w, J ) generally differs from the classical one; so does the expression of H as an implicit function of (w, J ) through (q, p ). For instance, for a rotator the action variable is the

[58] P. Dirac, manuscript notes for the Solvay congress of 1927, AHQP, and Electrons et photons , proceedings of the Solvay congress of October 1927 (Paris, 1928), 182.

[59] Heisenberg to Dirac, 1 Dec. 1925, AHQP (Berkeley copy), quoted in Dirac 1977, 128.

angular momentum J around the axis; as a function of this variable, the classical Hamiltonian is ½aJ² while the quantum-mechanical one is ½aaJ ( + 1).^[60]

These limitations did not discourage Dirac. In his subsequent papers he adapted more correctly the technique of canonical transformations and action-angle variables, taking properly into account the modifications required by noncommutativity. His general strategy was to find the explicit form of a classical transformation, say 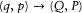, and then modify this expression in such a way that (Q, P ) would remain canonical in the quantum-mechanical sense [Q, P ] = ih /2p , and so on. Take for instance the transformation from plane Cartesian coordinates and momenta to polar coordinates and momenta. Classically,

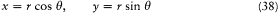
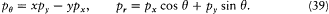
Quantum-mechanically, the latter relation must be modified to

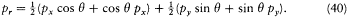
With this type of consideration, Dirac solved the hydrogen atom, discussed the composition of angular momenta in atoms with several electrons—imitating the classical procedure of "the elimination of the nodes" in celestial mechanics—and even derived the Compton scattering probability (his result being that later obtained from the Klein-Gordon equation). With the exception of the latter result, which was almost the only one not available from the old quantum theory, similar progress had been made in the Göttingen group, but by three or four men instead of one, and only with a great amount of heavy mathematics and some hints from Hilbert and Courant.^[61]

Quantum Algebra

Dirac's successful adaptation of the canonical methods of classical dynamics depended much on his conception of "quantum algebra." Several of the symbolic operations which he performed on quantum variables were, indeed, meaningless from the point of view of Göttingen's authorities. For instance, as Jordan explained in a letter to Dirac, there could be

[60] Dirac 1925g, 653; Heisenberg to Dirac, 23 Nov. 1925, quoted in Dirac 1977, 127-128.

[61] Dirac 1926a. Pauli's method (Pauli 1926b), based on Lenz's invariant vector (s × v + e r/r where s is the angular momentum), was equally ingenious but perhaps less general. Dirac 1926b; Dirac 1926c. With the methods of Bohr's theory Breit 1926 obtained the same scattering formula around the same rime.

no matrix (even a continuous one) representing an angle variable, since there is no conjugate operator to operators like the action variables, which have a discrete spectrum and no accumulation point.^[62]

q-Numbers

In "The fundamental equations" Dirac had adopted Heisenberg's original definition of quantum variables as arrays of ordinary numbers, and also the interpretation of the polarization matrix as giving radiation intensities. In his next article he adopted a more abstract stance. The quantum variables were "magnitudes of a kind that one cannot specify explicitly." They had to be defined only by the fundamental equations which they obeyed, while their representation in terms of infinite matrices, if any existed , had to be deduced from these equations. To capture the essence of his position in one word, Dirac introduced the "q -numbers," which were defined by their algebraic properties alone: they could be added and multiplied as in a ring; only some of them commuted with all other q -numbers, in which case they were called "c -numbers." Apparently, c stood for "classical," while q stood for "quantum"; but later Dirac suggested that they respectively stood for "commutative" and "queer."^[63]

In a spectacular illustration of his strategy, Dirac subsequently derived the existence of a matrix representation for most q -numbers in the case of multiperiodic systems.^[64] He first modified his definition of quantum action-angle variables in such a way that they no longer presupposed matrices. Just as in the classical theory, (w, J ) would be action-angle variables if and only if the Hamiltonian was a function of J only, and any q -number (save the multiple-valued ones) could be expressed in the form^[65]

Consider now two q -numbers x and y and their product xy . We have

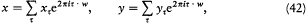
[62] Jordan to Dirac, 14 Apr. 1927, AHQP.

[63] Dirac [1926d], 5; Dirac 1926a, 562; Dirac 1977, 129.

[64] Dirac 1926a, 567-569.

and

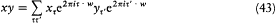
or

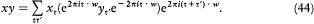
In order to transform the latter expression we first prove the identity

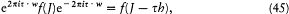
which is valid for any function f expressible as a power series of J . The relation of commutation

implies

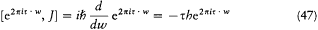
or

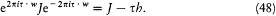
Equating the n^th powers of the two members of the latter equation produces

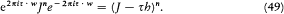
Then, linearly superposing powers of J and composing the results justifies the identity (45) for power series.

The expression (44) for the product xy now becomes

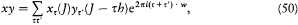
or

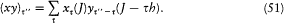
For the sake of transparency change the notation Ct (J ) into C (J, J -t h). Then

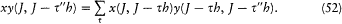
This symbolic relation, noticed Dirac, becomes a matrix product as soon as the J 's are given c -number values nh (i.e., J_r= n_r h). Therefore, any q -number may be represented by a matrix q_mn , wherein n and m refer

to two possible values of the action variables J . The action-variables J themselves and the energy H (J ) are represented by diagonal matrices with diagonal elements corresponding to J = nh . Naturally, the different values of J are assumed to characterize stationary states in Bohr's sense.

Thus defined, the matrices do not yet exhibit the time dependence implied by the fundamental relation

Dirac remedied this by studying the time derivative of the quantum Fourier exponentials:

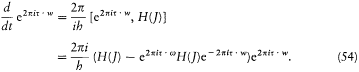
Through the identity (45) this transforms into

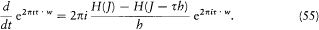
Taking the derivative of a q -number with respect to time therefore amounts to multiplying its C (J, J -t h) by 2p i times the Bohr frequency D t H/h. In this magic way Dirac recovered Heisenberg's matrix form and Bohr's frequency condition.^[66]

Dirac still had to show that the polarization matrix in this scheme provided transition probabilities, as originally asserted by Heisenberg. He did this in the following manner. The harmonic development of the quantum electric polarization P is essentially ambiguous, for it can be written in two equally justified forms:

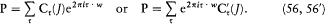
According to identity (45), however, the coefficients Ct and 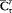are related by

This shows that Ct (J ) is naturally connected to two stationary states, J = nh , and J = (n -t )h , whereas it was connected only to one stationary state in the classical Fourier development. This suggests, in conformity with Bohr's postulates, that radiation is related to a transition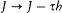

[66] Dirac 1926a, 567.

between two stationary states and that the matrix C (J, J -t h) represents the amplitude of the oscillations connected with this transition.^[67]

This reasoning of Dirac's reflected a strategy reminiscent of Eddington's principle of identification. It first introduced abstract entities defined only by their mutual relations, the q -numbers, then developed the formal consequences of these relations in such a way as to suggest an identification of their physical meaning. There were, however, some differences. According to Eddington, the primitive relations were dictated by the mind, whereas Dirac obtained them through the classical analogy or, better, through some kind of "extensive abstraction" of the structure of Hamiltonian dynamics. Moreover, the identification of observable quantities was not completely dictated by the mind; it relied on Bohr's postulates and also on the privileging of action-angle variables, which was a remnant of the old form of the correspondence principle.

A Mathematical Digression

The essence of Dirac's approach was to leave the properties of q -numbers open to the needs of future developments that might occur in quantum mechanics. Nevertheless, his interest in the purely mathematical side of his theory led him to introduce supplementary axioms that would enrich the algebra of q -numbers and make it closer to the algebras which he already knew, namely, quaternions and Baker's symbols. For instance, he occasionally admitted that all q -numbers had inverses, and he excluded divisors of zero (i.e., numbers such that qq ' = 0 with 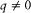and 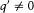). In a mathematical paper of 1926 he added another axiom that was supposed to be necessary for a proper definition of q -number functions: for any two q -numbers x and y there had to exist a q -number b such that y = bxb^-1 .^[68]

As Léon Brillouin noted in a letter to Dirac, none of these axioms was suited to quantum variables. An operator introduced by Pauli in 1926, the spin-raising operator S₊ = S_x + iS _y , furnishes a simple counterexample to the two first axioms. It divides zero since 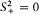, and it cannot be inverted since a relation S_+q = 1 leads to an absurdity once multiplied by S₊ on the left. Finally, if the last axiom were true, any two quantum variables would have the same spectrum—patently untrue. The algebraic

[67] Dirac 1926c, 406.

[68] Dirac 1926a, 562 for the first two properties; Dirac 1926e, 413.

properties of q -numbers, Brillouin concluded, could not differ from those of arbitrary matrices.^[69]

Fortunately, Dirac's attempts to axiomatize the q -numbers did not interfere with their practical use. Despite Brillouin's claim, the q -numbers proved to be more general than Heisenberg's original matrices, since they could cover both discrete and continuous spectra and allowed quantum angle variables that had no matrix representation, and since their applicability was not limited to stationary systems, as exemplified in the calculation of the Compton effect. Above all, Dirac wanted flexibility:

One can safely assume that a q -number exists that satisfies certain conditions whenever these conditions do not lead to an inconsistency, since by a q -number one means only a dummy symbol appearing in the analysis satisfying these conditions. . . . One is thus led to consider that the domain of all q -numbers is elastic, and is liable at any time to be extended by fresh assumptions of the existence of q -numbers satisfying certain conditions, and that when one says that all quantum numbers satisfy certain conditions, one means it to apply only to the existing domain of q -numbers, and not to exclude the possibility of a later extension of the domain to q -numbers that do not satisfy the condition.^[70]

Dirac thus set forth a general program by which arbitrary physical situations might be analyzed with q -numbers, the properties of the q -numbers being tailored to fit the physical situations as well as the fundamental equations.

Stagnation

In May 1926 Dirac put together in his dissertation the first fruits of his conception of quantum mechanics. By then he had found nearly all that could be learned from the q -number adaptation of the method of uniformizing variables. There were obvious signs that the magic of this method was being exhausted. Even a problem that was simply treated on the basis of the old quantum theory, the H-atom, received a fairly complicated treatment within the q -number theory, regardless of the high mathematical skills deployed. The very problem that motivated Heisenberg's discovery of matrix mechanics, the calculation of the intensities of hydrogen lines, was no more accessible to Dirac than it was to the Göttingen group.

[69] Brillouin to Dirac, March 1926, original unlocated, discussed in Dirac 1977, 130; see also Brillouin 1926, 154 n.

[70] Dirac [1926d], 24.

In general (with the questionable exception of the Compton effect), Dirac's methods could not be used to treat more problems than the old quantum theory, precisely because they were nothing but a noncommutative reformulation—should we say complication?—of the methods of this theory.

There was a more fundamental obstacle which Dirac disclosed in the late spring of 1926, either before or right after his first use of the Schrödinger equation: if, in the spirit of Heisenberg's theory, matrices refer only to observable processes, there cannot be any action-angle representation of them in the case of atoms with more than one electron. Let indeed m and n be two similar quantum numbers referring to two electrons in a given atom. According to a natural extension of Heisenberg's observability principle, stationary states differing only by a permutation of m and n should be identified, since there is no observable difference between the transitions 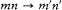and 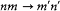. Consider now the Fourier exponential e²p i(2t · w) corresponding to the transition 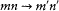. Then the Fourier exponential e² p i(2t · w) corresponds to a transition 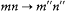, with

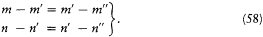
If m'n ' is to be identified with n'm ', one might as well have written

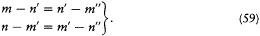
Here comes the absurdity: the values of m"n " deduced from each system cannot refer to the same stationary state since they are neither identical nor related through a permutation. With this ingenious argument Dirac closed a first chapter of his involvement in the history of quantum mechanics.^[71]

Summary

In the fall of 1925, Dirac scrutinized Heisenberg's fundamental papers and perceived three essential elements: the new quantum product, the endeavor to maintain as many classical relations as possible, and the direct connection between the quantum amplitudes and the properties of the emitted radiation. Misled by the latter point, Dirac originally interpreted Heisenberg's theory as a modification of the BKS theory and tried to draw

[71] Dirac 1926f, 668.

from it a new conception of virtual oscillators. But he quickly abandoned this line of thought and addressed a more fruitful question: Where did Heisenberg's new quantum rule come from? In his paper, Heisenberg pointed to the possibility of deducing his quantum rule from the high-frequency limit of Kramers's dispersion formula. Consequently, Dirac went back to the Kramers-Heisenberg paper (or to Fowler's account of it) and observed that the dispersion formula was the symbolic translation of a Poisson bracket (Poisson brackets are differential expressions involving two dynamic quantities: they appear when considering infinitesimal transformations in Hamiltonian mechanics, and they enjoy remarkably simple algebraic properties). Together with Heisenberg's remark, this led him to postulate that quantum mechanics was obtained by expressing the fundamental equations of mechanics in terms of Poisson brackets, and by replacing the brackets by purely algebraic expressions, the commutators (divided by ih /2p ).

This conception implied a deep structural analogy between classical and quantum mechanics, from which Dirac drew maximum profit. First of all, his "fundamental equations" were expressed in a very homogeneous form, one involving only algebraic operations (except for time differentiation), whereas the mechanics developed in Göttingen awkwardly mixed algebraic and differential operations (with respect to matrix coordinates!). On the practical side, Dirac imagined a quantum-mechanical analogue of the canonical methods for solving mechanical problems, particularly an analogue of the powerful technique of action-angle variables. This led him, within a semester, to results comparable, and sometimes superior, to those obtained in Göttingen. At the end of 1925 (a little after Pauli) he solved the hydrogen atom, and, soon after, he derived the algebra of angular momenta and made a relativistic calculation of Compton scattering probabilities.

The superiority of Dirac's method lay in his personal appraisal of the classical analogy in the new mechanics. While Göttingen's physicists judged that this analogy had been integrated, once for all, into the foundation of the theory, Dirac believed that it could still be used profitably in the development of the theory. Accordingly, Dirac exaggerated the analogy between classical and quantum mechanics. He initially underplayed the revolutionary character of quantum mechanics and asserted that only the physical interpretation, but not the equations of classical mechanics, was at fault. Heisenberg corrected him: the revolution affected the very concept of motion (kinematics); furthermore, the formal analogy between the two mechanics was not quite as close as Dirac first thought. One could not,

without contradiction, replace all Poisson brackets of the classical theory with commutators, and the energy expression in terms of action variables was not the same in the classical and the quantum cases, contrary to what Dirac suggested in his first paper on quantum mechanics. But to Dirac these were only points of rigor, which did not affect his general view or strategy.

The success of Dirac's adaptation of classical methods depended on another unique aspect of his approach, namely his notion of quantum algebra. In an Eddingtonian manner, Dirac formulated the fundamental equations of quantum mechanics in a purely abstract way, without having formerly interpreted the symbols entering these equations. The symbols, or "q -numbers," were defined only by their mutual relations, which for him constituted a "quantum algebra." The physical interpretation of these symbols occurred in two steps. The introduction of a quantum analogue of action-angle variables first suggested a matrix representation of the symbols; then the matrices were identified with collections of transition amplitudes, as suggested by some formal properties and a touch of "correspondence." This strategy was reminiscent of Whitehead's extensive abstraction, insofar as the relations defining the symbols were abstracted from ordinary mechanics; and it was akin to Eddington's principle of identification insofar as it purported to deduce the interpretation of the symbols from their formal properties. Dirac's symbols, however, in contrast with Whitehead's geometric objects, were not interpreted on the basis of their empirical origin; and contrary to Eddington's symbols of the world, they could not be interpreted without comparing the theory with an already interpreted theory of the same phenomena, Bohr's old quantum theory.

Dirac did some purely mathematical work on the quantum algebra, in the course of which he ventured to subject q -numbers to axioms similar to those found in Baker's Principles and Kelland and Tait's Quaternions . Some of these axioms did not suit quantum mechanics, as quickly noticed by Jordan and Brillouin. But Dirac already knew that the guilty axioms were not necessary to his practical calculations. In general, he wished to maintain a certain flexibility in his notion of q -number: the algebra had to be adapted to the needs of the developing theory. Also he did not require rigorous mathematical definitions of the objects he was manipulating; it was sufficient for him that the symbolic operations performed on these objects would not lead to contradiction.

By the spring of 1926 Dirac's progress had amazed all his colleagues; yet it seemed to have reached a peak. The method of transposing classical methods indeed had a defect: essentially, it could only solve problems that

had a solvable counterpart in the old quantum theory based on classical orbits. To make it worse, through a very ingenious argument Dirac proved that action-angle variables could not exist for quantum-mechanical systems containing two or more indistinguishable particles (this case includes all atoms beyond hydrogen!). A new method had to be found to solve the fundamental equations of quantum mechanics.