Parallax Cases

The issue of the negligibility or otherwise of what is discounted takes us to some more complicated cases, such as the various assumptions made by different astronomers in different contexts about parallax. We can distinguish between three main types of case. First, there is the assumption that in relation to the sphere of the fixed stars, the earth may be treated as a point: it is of negligible size, and so it does not matter, in this context, that an observer is not at the centre of the earth, but on its surface, at some distance from that centre.^[79] This assumption is set out in Euclid's Phaenomena , for instance, and in the elementary textbook of Cleomedes.^[80] It also figures in Syntaxis book 1 chapter 6, where, moreover, Ptolemy offers a particularly clear statement of the grounds to justify it: the fact that the configurations of the constellations remain unchanged from whatever point on the earth they are observed indicates the very great distance of the stars.^[81]

A second and far more controversial assumption is that made in

[79] Similarly, from an early stage, neither the existence of mountains and valleys nor the appearance that the setting or rising sun presents of being cut off by a straight line at the horizon was allowed to count against the conclusion that the earth is generally spherical in shape: see, for example, Aristotle Cael. 294a1ff., Mete. 1.3.340b33ff., and cf. Theon 124.7ff.

[80] Euclid Phaenomena Proposition 1, 10.12ff., Cleomedes 1.11.102.23ff., 106.9ff.; cf. Theon 120.3ff., Proclus Hyp. 2.26.26ff., 28.13f., and already in Diocles On Burning Mirrors paras. 18ff., Toomer 1976, p. 38 and commentary p. 145.

Aristarchus' heliocentric theory, as reported by Archimedes, namely, that not just the earth but the circle in which the earth moves around the sun is as a point in relation to the sphere of the fixed stars (see Figure 2).^[82] Archimedes' own comment is that that is, strictly speaking, impossible, since a point has zero magnitude and the fixed stars would then be at infinite distance^[83] (a similar point applies, of course, to the first type of parallax case as well). What Aristarchus needs is not that the stars be infinitely, only that they be indefinitely, far away.

The interesting feature is that he evidently incorporated this into his assumptions , in part in order to meet a possible objection to heliocentricity. If the earth moves in a circle around the sun (rather than the sun around the earth) there should be, one might think, observable differences in the shapes of the constellations as viewed from different points in the earth's orbit—from the points representing the spring and autumn equinoxes, for instance, at opposite ends of the same diameter of the orbit. Yet no such variation was observed; indeed, stellar parallax was not confirmed until well into the nineteenth century, with the work of Bessel and others around 1835. Aristarchus seems to have appreciated that this otherwise very damaging objection to heliocentricity was no objection at all provided that the stars are sufficiently far away. If the diameter of the earth's orbit around the sun is negligible in comparison to the diameter of the sphere of the fixed stars, then you would not expect observable variations in the relative positions of the stars, certainly not within the limits of ancient techniques of observation. Unlike Ptolemy's discussion of the size of the earth in Syntaxis 1.6, the assumption in the form adopted by Aristarchus was not itself justified by reference to independently observable phenomena; there was no way in which it could be. Rather, this reveals precisely what has to be accepted among the assumptions in order for an apparent objection from the side of the phenomena not to be the objection it seems. No doubt Aristarchus could have argued that the

[82] Archimedes Aren. 1.4 (HS) 2.218.7ff.

[83] Aren. 1.6 (HS) 2.218.18ff.

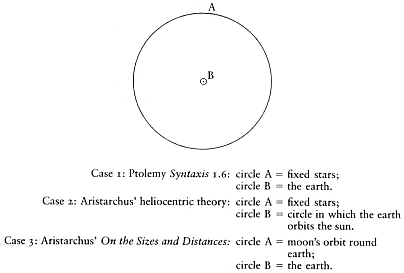
Figure 2
Three cases of discounted parallax. In each case circle B is treated as a point.

inability to confirm an assumption directly does not make it untrue—and Copernicus would have said the same.^[84]

The third type of case again comes from Aristarchus, this time from the extant treatise On the Sizes and Distances of the Sun and Moon . The second hypothesis set out there is that the earth is as a point, not in relation to the sphere of the fixed stars, but in relation to the moon's orbit .^[85] In this form the assumption involves discounting lunar paral-

[84] Cf. Copernicus De revolutionibus orbium coelestium (Rev. ) 1.6. Already those Pythagoreans who treated the earth as one of the planets (see above at n. 12) had argued, according to Aristotle, that there is no difficulty in supposing that the phenomena would be the same as they would be if the earth were at the centre—even though they denied that. "For there is nothing to show, even on the current view, that we are distant half the earth's diameter [viz. from the centre]," Aristotle Cael. 293b25ff., 29f.

[85] Aristarchus Hypothesis 2 (352.5f. Heath).

lax—as if the position of the observer on the surface of the earth makes no difference to observations of the moon. Yet of course it does. The contrast with the careful and complex discussions in the Syntaxis where Ptolemy attempts to determine the allowance that has to be made for lunar parallax^[86] is striking and points up the difficulty that the second hypothesis in Aristarchus' treatise presents, indeed, its complete unacceptability if we are concerned with trying to establish the actual size of the moon and its actual distance from the earth.

Yet we should not be misled by one possible way of taking the title of Aristarchus' treatise (On the Sizes and Distances  . . . ) into thinking that that was his aim. Both the hypotheses and the results militate

[86] See especially Ptolemy Syntaxis 5.11–12, 18–19 (H) 1.401.2ff., 442, 444.2ff.: at 5.11 (H) 1.401.6ff., Ptolemy begins by recalling from 4.1 (H) 1.266.1ff. that the earth does not bear the ratio of a point to the distance of the moon's sphere. With Ptolemy's discussions of lunar parallax we may compare Toomer's proposed reconstruction of the procedures Hipparchus used to determine the distances of the sun and moon (Toomer 1974–75). According to this, Hipparchus took first a minimum, then a maximum, figure for solar parallax, in order to arrive at upper and lower limits for the distance of the moon, expressed in terms of earth radii. First he assumed solar parallax to be zero: using differences in the magnitude of a solar eclipse observed near the Hellespont and at Alexandria, he computed a minimum distance for the moon (71 earth radii). Then Hipparchus took a maximum figure for solar parallax (7') and computed from this the sun's minimum distance and the corresponding maximum distance for the moon (67 1/3 radii in the mean: here Toomer draws on and develops an analysis put forward by Swerdlow 1969). As Toomer emphasised, 1974–75, p. 140, if this reconstruction is correct, one striking feature of Hipparchus' workings would be "the complete honesty with which [he] reveals his discrepant results," namely, that the "maximum distance" obtained by the second method turns out to be smaller than the "minimum distance" obtained by the first. There are, as Toomer also stressed, considerable difficulties in interpreting the meagre and at points conflicting reports in Ptolemy and Pappus on which this reconstruction is based. Both sources, however, agree that Hipparchus took a lower limit for solar parallax of zero. As Ptolemy puts it, Syntaxis 5.11 (H) 1.402.19f., "at one time he assumes that the sun has no perceptible parallax, at another that it has a sufficiently large parallax [viz. to be observed]," and as Pappus reports in his Commentary on Books 5 and 6 of the Syntaxis 67.21ff. Rome: "So Hipparchus . . . assumed in the first book of On Sizes and Distances that the earth has the ratio of a point and centre to the sun (i.e., to the sun's sphere)."

against such a view. First, his results all take the form of ratios or proportions, giving upper and lower limits for the relative sizes and distances on the basis of the assumptions as set out; no absolute figures are presented.^[87] Then, the hypotheses include several that Aristarchus undoubtedly knew to be well wide of the mark. That appears to be the most likely explanation of the notorious sixth hypothesis, that the moon subtends an angle of 2° to the eye;^[88] where 1/2° was the usual ancient approximation and is indeed the figure we can attribute to Aristarchus on the basis of a report in Archimedes.^[89] Again, the fourth hypothesis simply assumes, with no attempt at justification, that the moon is at 87° to the sun when it appears to be halved.^[90] Again, the

[87] For example, Aristarchus Proposition 7 (376.2ff. Heath) ("The distance of the sun from the earth is greater than 18 times, but less than 20 times, the distance of the moon from the earth") and Proposition 18 (410.12ff. Heath) ("The ratio of the earth to the moon is greater than 1259712 to 79507, but less than 216000 to 6859").

[88] Aristarchus Hypothesis 6 (352.14f. Heath) ("That the moon subtends one-fifteenth part of a sign of the zodiac"). The interpretation of this hypothesis has been much debated: see for example Heath 1913, pp. 311ff.; Wasserstein 1962; Neugebauer 1972/1983, p. 366, 1975, vol. 2, pp. 634ff., who concludes, p. 643, "The fact that Aristarchus does not make the obvious transition from the diameters of sun and moon to the distances, measured in earth radii, supports our conclusion that [the Sixth Hypothesis] is not to be taken as a valid observational datum. . . . I think this analysis leads to the conclusion that Aristarchus' treatise on the sizes and distances is a purely mathematical exercise which has as little to do with practical astronomy as Archimedes' 'Sandreckoner' in which he demonstrates the capability of mathematics of giving numerically definite estimates even for such questions as the ratio of the volume of the universe to the volume of a grain of sand."

[89] Archimedes Aren. 1.10 (HS) 2.222.6ff. reports that Aristarchus "discovered that the sun's apparent diameter is 1/720th part of the zodiac circle," and the equivalence of the apparent diameters of the sun and moon is shown in Aristarchus' treatise in Proposition 8 (382.1ff. Heath) and indeed assumed from the beginning (cf. Neugebauer 1975, vol. 2, p. 635). After reporting Aristarchus' value for the diameter of the sun, Archimedes himself goes on to describe how he used a dioptra to obtain upper and lower limits for this, namely, 1/164th and 1/200th of a right angle, that is, between under 33¢ and 27': see Shapiro 1975.

[90] In Hypothesis 4 (352.10f. Heath) this is stated in the form: "when the moon appears to us halved, its distance from the sun is then less than a quadrant by 1/30th of a quadrant."

fifth takes it that the breadth of the earth's shadow, viz., at the moon, is two moons.^[91] Moreover, the second hypothesis itself not only discounts lunar parallax but takes the moon to move in a simple circle with the earth as centre—and no serious Greek astronomer had thought that since before Eudoxus.

Such a set of hypotheses would, of course, be an unmitigated disaster in any attempt to arrive at concrete determinations of the actual sizes and distances of the moon and sun. What Aristarchus is doing, rather, is exploring the geometry of the problems. Given certain assumptions—and it will not matter, for the sake of the geometry, that some of the values are a little, and others wildly, inaccurate—what follows? The study is certainly relevant to astronomy, in particular because it shows how one could obtain actual solutions to the astronomical parameters, that is, it offers one set of answers to the question of the premises, or data, needed in order to arrive at such solutions. Yet it remains itself essentially a study of the geometry of the problems.^[92]