Chapter Six—
Idealisations and Elisions
In the last chapter I discussed both the positive and the negative features of the use of measurement and the search for quantitative exactness in ancient science. This final chapter will be devoted to further aspects of the problem of the match expected between data and theory, between explanandum and explanation. An element of simplification and idealisation is present in all science: it is only by ignoring certain features of what is given that the underlying relationships governing the phenomena can be revealed. Again, a theory is not held to be refuted when what is predicted on its basis is found to disagree, within certain limits, with observed results. The questions we may pose are: What kinds of simplification did ancient scientists allow themselves? What phenomena did they permit themselves to discount and what constraints did they recognise on that discounting? According to a still highly influential view, that of Duhem,[1] the ancient slogan of "saving the phenomena" involved, in astronomy, precisely the production of mathematical theories from which the positions of the heavenly bodies could be predicted independently of any physical considerations. The theories were purely calculating devices; they had nothing to do with any underlying physical realities. Whatever the constraints on the theory from the side
[1] Duhem 1908, 1954b. Aspects of Duhem's interpretation of the ancient evidence are criticised in G. E. R. Lloyd 1978b. See further below at nn. 93ff.
of the match between predicted and observed positions, there were no constraints at least from the side of the physics of the question, since that was of no concern.
The Development of the Notion of Explanation
The validity of that interpretation of areas of ancient inquiry will be examined in due time, but certain preliminary remarks should first be made on the development of the notion of explanation itself. In a sense myths too, as I noted in Chapter 1, provide explanations—of a sort—of the subjects they deal with, but only in a sense, and only attenuated explanations. The myths in question range from major quasi-cosmological statements about the origin of the universe or of man's place in it, through particular aetiological accounts, down to "just-so" stories about "how the leopard got his spots." In interpreting these the first important point is a sociological one, namely, the context of delivery. Anthropologists themselves took some time fully to come to terms with the problems of context and intentionality in their material. Many stories do not record what adults seriously believe, only what adults habitually say in response to—and maybe in the hope of blocking—a certain kind of inquisitive questioning, from children, for example, or even from anthropologists. It is not as if we seriously believe that babies are brought by storks or found under gooseberry bushes. It is not as if many of us believe that the century plant does actually bloom only once in a hundred years.[2]
But apart from the question of whether such stories are claimed to be true , the extent to which they are or contain explanations is problematic. They may contain the equivalent of explanations, that is, the answers to "how," "why," or "what" questions. But in two ways especially, they are likely to be defective. First, the problem may not be made explicit, and, secondly, the proposed solution may consist of a set
[2] Cf. in the 1970 edition of the Encyclopaedia Britannica, s.v. "century plant": "The century plant is a name given to Agave americana from the erroneous supposition that it flowers only when 100 years old."
of arbitrary assertions, the range of applicability of which is left quite indeterminate. This applies not only to tales told to children (under what circumstances storks bring babies is not discussed) but also to quasi-cosmological myths, about the origin of the world, or of humans or animals, or about how fire came to be used or skills discovered. Under what circumstances Marduk split the primeval water goddess Tiamat to make the sky with its celestial waters on the one side and Apsu, the deep, and Esharra, the "great abode," on the other, just does not occur as a question:[3] no more does why the stones thrown by Deucalion and Pyrrha became men and women.[4] That this happened is simply asserted, and it is understood that this was an exceptional occasion with a special outcome. But why thrown stones do not usually metamorphose is not an issue, though it is known that they do not. That very way of querying the story presupposes a framework of natural causation that became self-conscious and explicit only with difficulty and with time—even though that realisation could and did build on what was, in a sense, already common knowledge, or at least commonly assumed.[5]
The emergence of what can begin to be called fully fledged explanations of classes of natural phenomena is an important new development, though a hesitant one, in early Greek philosophy, with the practice of such explanations preceding the theory. The sequence of ideas that Aristotle reports in De caelo 2.13 about the shape and position of
[3] Enuma Elis Tablet 4.135ff., Pritchard 1969, p. 67. Compare the translation in Lambert 1975, p. 55: "Bel [i.e., Marduk] rested, surveying the corpse, / To divide the lump by a clever scheme. / He split her into two like a dried fish, / One half of her he set up and stretched out as the heavens. / He stretched a skin and appointed a watch, / With the instruction not to let her waters escape. / He crossed over the heavens, surveyed the celestial parts, / And adjusted them to match the Apsû, Nudimmud's [i.e., Ea's] abode. / Bel measured the shape of the Apsû, / And set up Esharra, a replica of the Eshgalla. / In Eshgalla, Esharra which he had built, and the heavens, / He settled in their shrines Anu, Enlil, and Ea."
[4] Pindar Olympian 9.41ff., Apollodorus Bibliotheca 1.7.2ff., Hyginus Fabulae 153, Ovid Metamorphoses 1.395ff. (where it is worth recalling the parenthesis, v. 400: quis hoc credat, nisi sit pro teste vetustas ?).
[5] Cf. G. E. R. Lloyd 1979, pp. 49ff.
the earth and on the question of why it does not move illustrates both the advances and the limitations of pre-Socratic natural philosophical accounts, even if it is evidence that must be used with caution.[6] For one thing, it was Aristotle who chose to present these ideas as a sequence of replies to the same set of questions, and that may well distort the original context in which they were proposed. Even so, although it would be quite wrong to represent later theories as progressively more sophisticated (let alone truer or in some sense more correct) than earlier ones, some of the constraints on what counts as an answer appear to be grasped more fully as time goes on.
Three features are worth remarking very briefly. First, there is the phenomenon of the regression of the explanandum . A common suggestion was that the earth does not move because it is supported on something, such as water (according to Thales) or air (as in Anaximenes).[7] That resolved one difficulty by raising another: what keeps the water, or the air, itself in place—a point that was evidently appreciated by Aristotle and may already have been by Anaximander.[8]
Secondly, in Anaximander's suggestion—that the earth does not move because it is equally balanced on all sides and there is no reason, then, for it to move in one direction rather than in any other[9] —we
[6] Aristotle Cael. 2.13.293a15–296a23.
[7] Aristotle Cael. 294a28ff. (Thales), 294b13ff. (on Anaximenes, Anaxagoras, and Democritus, who are said to appeal to the flatness of the earth as the explanation of its being at rest: it does not cleave the air beneath it, but settles on it like a lid).
[8] See Aristotle Cael. 294a32ff. It seems likely from the evidence in Aristotle Ph. 204b24ff., together with Simplicius In Ph. 479.32ff., that Anaximander arrived at his cosmological principle, the Boundless, in part by reflecting on the difficulties presented by any view—such as Thales' doctrine of water—that started from a single determinate substance. If so it is possible—though of course far from certain—that a similar line of reasoning led Anaximander to his radically different solution to the problem of the earth being at rest, in which he appealed not to any underlying support but to its being "equally balanced" on all sides (see next note). The proponents of the view that the earth does not move because it rests on air like a lid appear to have argued that the air itself cannot move for lack of room, Cael. 294b19ff., 25ff.
[9] Cael. 295b10ff., cf. Hippolytus Refutatio Omnium Haeresium (Haer. ) 1.6.3.
have an example of suspending some of the commonly assumed data. A clod of earth, as Aristotle was prosaically to insist, moves in a certain direction, "downwards." Aristotle, with a spherical earth, defined that as towards the centre of the universe, deemed to coincide with the centre of the earth.[10] That answer was not available to Anaximander, who thought the earth flat.[11] But then in his case that truth about pieces of earth has to be assumed not to apply to the earth as a whole, for his suggestion to be an answer to the problem of why the earth does not move.
Thirdly, we find in the same chapter an example of the denial of the data that are supposed to generate the problem. The full motivation of the suggestion that Aristotle ascribes to certain Pythagoreans, namely, that the earth is like a planet,[12] is unclear and controversial, but the effect of the suggestion is to make the earth move in space. The question "Why does the earth not move?" thus gets answered by denying the assumed fact: "But it does move"—though we evidently have another case of the regression of the explanandum, since how it moves and how, on the hypothesis of its movement, other phenomena are to be accounted for involve a series of other problems a stage further back.
These first attempts to resolve questions concerning the position of the earth may look indistinguishable from myths, or at least subject to criticisms that are similar in kind to those I made of the types of
[10] See above, Chap. 4 at n. 79.
[11] See pseudo-Plutarch Stromateis 2, Hippolytus Haer. 1.6.3, Aetius 3.10.2.
[12] Cael. 293a21ff.: the earth is one of the "stars" and makes night and day as it travels round the centre in a circle. At the centre itself is the Central Fire, and Aristotle reports that the Pythagoreans held that fire is more honourable than earth and so occupies this honourable position (Cael. 293a30ff.). The Pythagoreans further postulated an invisible "counter-earth" and held that this and maybe other invisible bodies accounted for eclipses of the moon being more frequent than those of the sun (that is, presumably, as seen at any given position on earth) (Cael. 293b23ff.). Aristotle himself criticises them for introducing the counter-earth merely to bring the number of the heavenly bodies up to the perfect number ten (Metaph. 986a8ff.) and for forcing the appearances to fit their own preconceived opinions (Cael. 293a25ff.).
explanations that are offered in myths. But apart from the well-known point that the philosophers' accounts are naturalistic ones,[13] they are in principle subject to open challenge. A new suggestion on an old topic implicitly claims superiority to others in the field and has, accordingly, to give an account of itself. It is in that crucible of debate on contested issues that clearer working notions of what will count as an explanation, and of what an explanation should be, come to be elaborated.
For the first more explicit discussions of that topic we have to wait until Plato, though several of the Hippocratic writers made, rather more incidentally, important contributions to the understanding of such distinctions as that between causal and merely coincidental factors.[14] Two of the key ideas for which Plato himself appears to have been responsible are, first, the explicit distinction between necessary condition and cause or explanation, and, secondly, the more general contrast between essence and accident. The first distinction is made in the Phaedo , where reference to what is true merely of the material conditions of a situation (without which, to be sure, it would not be the situation it is) is contrasted with reference to the
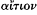
[13] Cf. Farrington's much-quoted dictum 1944–49/1961, p. 37: "What Thales did was to leave Marduk out."
in terms of what a thing is for or the good it serves—that is, that explanation must be teleological—was fraught with significance for the future, and we shall be returning to it later.[16]
The second, more general distinction between essence and accident is crucial for the theory of Forms but is present already in the Socratic search for definitions. The Euthyphro puts it that definition is directed at the
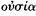
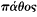
These points are all very familiar. My aim in recalling them is simply to stress the moral they convey, that an explanation—in science or anywhere else—must focus on certain aspects of the phenomena in preference to others (causes, not preconditions) and to the exclusion of yet others (that is, must focus on the essential, not the accidental).
Mathematics and Physics in Plato and Aristotle
Further pressure positively to discard certain features of the phenomena comes from the side of the model of mathematical knowledge—it, too, prominent in Plato. The nature of mathematical truths and of the objects that mathematics studies had become, already by Aristotle's time, topics of intense controversy.[18] Where Platonism construes mathematics as to do with separate intelligible objects and
[16] See below, pp. 319ff.
[17] Plato Euthphr . 11a.
[18] In Metaphysics M and N especially, Aristotle engages in sustained debate with Plato, with Pythagorean positions, and with those of his own contemporaries Xenocrates and Speusippus. See Annas 1976 and the papers collected in Graeser, ed., 1987, especially.
accepts and insists that the truths of geometry, for instance, are never unqualifiedly instantiated in physical objects (the diagram on the blackboard, for example), Aristotle argued that mathematics had no separate entities as its objects: mathematics studies certain features of physical objects taken in abstraction from certain others, namely, the features that make them the physical objects they are.[19] Mathematical truths are, then, truths about the mathematical properties of physical objects. Indeed, it has recently been argued, with some force and sophistication,[20] that Aristotle does not merely not deny , he even requires that there are physical straight lines that fully and perfectly instantiate the geometrical truths about straight lines. It is true that the line drawn in chalk on the blackboard will not do as an example, nor even its outer edge, but, then, it would be wise to say that they are not straight lines. The truths about straight lines will nevertheless be instantiated in any of a number of straight lines that are present in any physical object.[21] That interpretation is disputed, but at least it can be agreed that there is no need for Aristotle to say that in principle it is impossible for physical objects to instantiate mathematical truths; they certainly will not fail to instantiate truths of arithmetic,[22] and he certainly has some perfect spheres—in the heavens.
Whatever the disagreements between Plato and Aristotle in the philosophy of mathematics, both held that mathematics is exact, and that point is fundamental, even though it requires as a gloss that pure mathematics also has to admit approximations in certain contexts (for the values of surds, for example).[23] But in a bid for exactness, applied
[19] See especially Physics 2.2.193b22ff., 24ff., 194a9ff.
[20] See Lear 1982: contrast I. Mueller 1970/1979 and 1982a, pp. 70ff.; Annas 1976, pp. 29ff.; and cf. Annas 1987; Hussey 1983, pp. 176ff.
[21] Cf. Lear 1982, pp. 175ff., 180f. The possibility that some early Greek definitions of a straight line are based on or derived from the physical law of the rectilinear propagation of a ray of light is discussed by Mugler 1957 and 1958.
[22] On Aristotle's philosophy of arithmetic, see Lear 1982, pp. 183f.; J. Barnes 1985; Mignucci 1987. Aristotle himself does not, however, draw attention to differences between arithmetic and geometry in the relevant connection.
[23] Cf. Archimedes' extraction of a value for p in his Dimensio circuli . InPtolemy's Syntaxis , for instance, approximations are certainly just as prominent in the purely mathematical parts of his calculations as they are in the adjustments made to observational data: cf. G. E. R. Lloyd 1982, pp. 153–59.
mathematics too will discard, even for the Aristotelian, some, at least, of the physical aspects of the phenomena.[24] Although the precise conditions under which the procedure called abstraction,
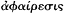
"Saving the Phenomena"
After these rather cursory preliminaries concerning the philosophical background, we may now turn to our principal concern, the kinds of idealisations found in the ancient inquiry into nature. We are told by Simplicius that Plato set as a problem the saving of the apparent wanderings of the planets, by means of regular, orderly—we are to understand, circular—motions.[27] But the question of the conditions un-
[24] Thus at Metaph. 1078a14ff., harmonics and optics study their objects not as sight or as sound, but as lines and numbers, and, he adds, "similarly with mechanics," though at Ph. 194a11ff., optics, for instance, is contrasted in turn with geometry as concerned with a mathematical line but not as mathematical but as physical. The more that is discarded, the more exact the study is: see APo. 87a31ff., Metaph. 982a25ff.
[25] On Aristotelian abstraction see, for example, Philippe 1948; I. Mueller 1970/1979, pp. 98ff.; Lear 1982 (who gives a sophisticated formal analysis of the qua operator as a predicate filter); and cf. Cleary 1985; Annas 1987; Mignucci 1987.
[26] See APr. 49b34ff., APo. 76b39ff., Metaph. 1078a17ff., cf. 1089a21ff.; see Lear 1982, pp. 171ff.
[27] Simplicius In Cael. 488.18ff., 492.31ff. (the latter passage specifies circular motions explicitly). In the first text Simplicius gives Sosigenes as his authority and he has just referred to Sosigenes' use of Eudemus' History of Astronomy . But who first formulated the problem for astronomy in exactly these terms is unclear: neither Plato nor Aristotle speaks of "saving" the "phenomena" as such, though Aristotle, for instance, refers to saving a "hypothesis" at Cael. 306a29f.
der which it could be considered that certain phenomena had been saved —or that an adequate account had been given—is an issue not just for the Platonic or Platonising tradition, and not just for astronomy.[28] We find a variety of expressions used in a number of contexts: saving the phenomena or appearances (
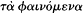

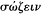
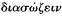
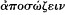
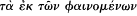
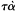
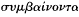
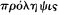
[28] Since Duhem 1908 the literature on the topic of saving the phenomena has been prolific: see especially Mittelstrass 1962, 1979, Wasserstein 1962, Krafft 1965, Sambursky 1965, G. E. R. Lloyd 1978b, and, most recently, A. M. Smith 1981 and 1982. Although in his 1981 paper Smith categorises the metaphysical assumptions in the background too readily and too loosely as Platonic, he draws attention both to the role of the prior selection of the salvanda ("what needed saving was what was deemed salvageable," p. 80) and to that of implicit appeals to the principles of uniformity and economy in the "salvations" proposed. Once the anomalies that provided the main problem had been shown to be explicable in terms of uniformities or regularities, they could be considered not exceptions to, but evidence of, order ("Anomaly was not so much a traducing as a token of real order," p. 99).
[29] E.g. Proclus Hyp. 5.178.13ff.
[30] E.g. Proclus Hyp. 5.156.23f.
[31] E.g. Philoponus De opificio mundi 3.3.115.22ff.
[32] Often what is to be "saved" (in the sense of "accounted for") is an (apparent) irregularity, as for instance at Simplicius In Cael. 509.18f., cf. 507.10ff., In Ph. 292.17f., 21ff. But sometimes what is to be "saved" (in the sense, rather, of "preserved" or "maintained") is a regularity , as for example at Proclus Hyp. 2.30.22ff.
[33] As, for instance, at Simplicius In Ph. 240.24f.
[34] Simplicius In Ph. 93.28f.
ever, many of the explicit references to such slogans (generally in late authors) are vague and leave the requirements on the "saving" indeterminate;[36] our best policy is, rather, to study the actual practice of Greek investigators at work, and we may start with some fairly straightforward cases from the exact sciences.
Harmonics
Take, first, harmonics. I mentioned before[37] that the apocryphal stories about Pythagoras' discovery of the numerical expressions of the principal concords contain many fantastic elements, not least that the results reported for the tests that he is supposed to have undertaken cannot, in several cases, have been obtained in practice.[38] Yet the stories are again important for our inquiry here, since they convey a clear, if implicit, grasp of the principle of varying the conditions of a test in order to isolate the relevant factors producing the result. Pythagoras, in one story, passes a smithy and—if we are to believe our sources[39] —hears hammers striking concords. He first asks the smiths
[36] Pace Sambursky 1965, p. 5. It is clear from Theon (e.g., 175.1ff.), and from Proclus (e.g., Hyp. 2.34.11ff., 38.10ff.) especially, that in astronomy more than one mathematical model may provide a basis for some "saving" of certain phenomena. Yet Theon makes it plain that he is not satisfied with any but the true natural/physical account (177.21ff., 188.8ff., see G. E. R. Lloyd 1978b, pp. 217ff.), and Proclus too demands, so far as possible, true explanations of astronomical phenomena (Hyp. 7.238.13ff.) and claims that Plato had grasped these (cf. In Ti. 3.96.31f., and for other evidence of realist assumptions in Proclus' astronomy, see G. E. R. Lloyd 1978b, pp. 208–11).
[37] See above, Chap. 5 at n. 213.
[38] See Burkert 1972, p. 375 and n. 23, on the impossibilities involved in some of the alleged experiments discussed already by Mersenne. Ptolemy Harm. 1.8 (16.32ff. D.) notes some of the difficulties in some of the trials that purported to reveal the principal concords.
to exchange hammers, but that does not make any difference to the sounds the hammers make. So it is not the strength of the smith that counts. He then weighs the hammers and—according to our sources—obtains his result—even though this is impossible: the note will vary with the anvil, not the hammer.[40]
Those who actually engaged in the study of harmonics (as opposed to merely fantasising about the discoveries of Pythagoras) disagreed about how much of the phenomena to discount, and the epistemological debate, extensively reported in Porphyry especially,[41] is sometimes conducted in rather simplistic terms, as if it were a matter merely of deciding whether reason or perception is the ultimate criterion.[42] At
[40] The story of Hippasus constructing bronze disks to yield the harmonies is closer to what is possible: see schol. Phd. 108d, and cf. Raasted's discussion, 1979, mentioned above, Chap. 5 n. 212, relating this to the story of the hammers.
[41] In Harm. 25.3ff. D.; cf. Ptolemy Harm. 1.8 (19.16ff. D.).
[42] See, e.g., Ptolemais of Cyrene, quoted by Porphyry In Harm. 25.9ff. D., where three groups are distinguished: (1) those who "preferred" reason; (2) those "instrumentalists" who preferred perception; and (3) those who used both. Some of the "Pythagoreans" are here categorised as belonging to the first group, though Pythagoras and his "successors" are in group 3 (cf. Didymus in Porphyry In Harm. 26.15ff. D., who suggests that the Pythagoreans preferred reason but used perception with regard to the starting-point of the inquiry only, and cf. Porphyry's own opinion concerning the Pythagoreans at In Harm. 9.1ff., 15ff., 33.5ff. D.). As Barker has pointed out, e.g., 1981b, pp. 10f. and 16, many of those who were said to value reason more highly than perception did not totally reject the latter (cf. Aristoxenus at Harm. 2.33 and Didymus in Porphyry In Harm. 28.12ff. D., who point out that while the geometer can take what is not straight as straight, the musician cannot take what is not a fourth as a fourth). The point was often, rather, that perception cannot make fine discriminations. Nor can it settle the dispute as to whether or not the octave, fifth, and fourth are exactly six tones, three-and-a-half tones, and two-and-a-half tones, respectively, nor the question of whether or not either the tone or the semitone can be divided exactly into two equal intervals.
In one of the opposing traditions, that of Aristoxenus, the claim was that the unit of measurement must be something identifiable by perception. Thus Aristoxenus defines the tone as the difference between the fifth and the fourth, both concords immediately apprehensible to perception—whereas to thePythagoreans the tone may, rather, be defined mathematically as the difference between sounds whose "speeds" stand in a ratio of 9:8. Whilst for the Pythagoreans musical relations are to be expressed as ratios between numbers, for Aristoxenus musical intervals are construed on the model of line segments and their interrelations investigated quasi-geometrically: cf. Barker 1978b, p. 4, 1981b, p. 3.
Each of these two major traditions faced its own corresponding difficulties or anomalies. Aristoxenus found it impossible, in practice, to carry through his programme of founding music theory on the basis solely of an appeal to what can be heard, on the principle that "what [the voice] cannot produce and [the ear] cannot discriminate must be excluded" from the sphere of useful and practically possible musical intervals (Harm. 1.14). In particular the principle of concordance, on which his theory relies, will not allow the construction of intervals smaller than the semitone (though he attempts to discuss these, e.g., at Harm. 1.21) (cf. Barker 1978a, pp. 15f.). Conversely, as I point out in my text, one problem for the Pythagoreans was that since 8:3 is neither multiplicate nor superparticular, they were led to ignore or deny that the interval of the octave plus a fourth is a concord—and similarly with the double octave plus a fourth.
For Ptolemy and Porphyry, who distance themselves from both the earlier Pythagoreans and from the Aristoxeneans, the chief problems connected with perception are identified as: (1) that different observers obtain different results (e.g., Porphyry In Harm. 18.12ff. D.); (2) that instruments may be unreliable (e.g., Ptolemy Harm. 1.8 [16.32ff. D.], Porphyry In Harm. 119.13ff. D., Ptolemy Harm. 2.12 [66.6ff. D.]); and (3) that perception cannot give the exact measure of very small intervals (e.g., Ptolemy Harm. 1.1 [4.13ff. D.], 1.10 [21.25ff. D., 24.20ff. D.], Porphyry In Harm. 20.12ff., 129.18ff. D., and cf. 75.25ff. D., quoting the pseudo-Aristotelian De audibilibus , and 80.22ff. D., reporting Aristoxenus). More generally the "rough-and-ready" character of perception is often referred to, e.g., Porphyry In Harm. 16.13ff., 17.6ff., 18.9ff., 19.2ff., 21ff. D.
one extreme there were those who sought to reduce the subject to number theory: some, we are told, maintained that since 8:3 is neither a multiplicate ratio (like 2:1 or 4:1) nor superparticular (like 3:2 and 4:3),[43] the interval of an octave plus a fourth cannot be a concord, even if it sounds like one.[44] Yet to that Theophrastus pertinently remarked
[43] A superparticular, or epimoric, ratio is defined as n + 1 : n , where n is a positive integer greater than 1.
[44] See, for example, the discussion in Ptolemy Harm. 1.5f. (11.5ff., 13.1ff. D.), and in Porphyry In Harm. 95.25ff., 105.12ff., 124.4ff. D., and cf. Barker 1981b, pp. 9ff.
that what is heard is not a number , even if concords are expressible numerically.[45]
Whatever their other disagreements, and there were plenty of these, the main practitioners—Aristoxenus, Ptolemy, and Porphyry, for instance—agreed in taking harmonics to be concerned with certain audible phenomena, not just with mathematical relations or number theory. Even in the mathematical, Pythagorean tradition represented by such a work as the Euclidean Sectio canonis , the main concords—octave, fifth, and fourth—are assumed as given to perception.[46] Aristoxenus takes harmonics to deal with the principles of melody, especially the theory of scales and keys,[47] and Ptolemy specifies that it is concerned with the differences in the pitch of sounds.[48] But even for an Aristoxenus or a Ptolemy, aspects of the audible phenomena are to be discounted.[49] The subject matter does not include the volume or magnitude of the note, nor its timbre or quality.[50] Again, it is indifferent to the investigator whether he studies wind or stringed instruments. If he is investigating pitch on the monochord, for example, the thickness of the string, its material, and its tension are all irrelevant (though he knows, of course, that if these are altered, so too will be the pitch of the note);[51] the only data he is concerned with are the lengths that correspond to certain notes.
[45] An extensive quotation from Theophrastus' lost work On Music is given by Porphyry In Harm. 61.22ff. D., discussed by Barker 1977. See in particular 62.9ff. D.
[46] See Barker 1981b, pp. 7, 10f., and 16.
[47] Aristoxenus Harm. 1.1.
[48] Ptolemy Harm. 1.1 (3.1f. D.).
[49] Here, as elsewhere, a distinction may be drawn between discounting some aspects of the phenomena as irrelevant (as is the case with the magnitude of the note) and the discounting of others because the investigator assumes an ideal situation (where again we may contrast, for example, Ptolemy's recognition of the importance, for his purposes, of securing an ideal string, Harm. 1.8 [17.7ff. D.], cf. n. 51 below, with the assumption of an ideal string in, for instance, the Euclidean Sectio canonis ).
[51] The effects of variations in the thickness, humidity, density, and evennessof strings are discussed, for example, by Ptolemy Harm. 1.8 (17.7ff., 27ff., D.), 1.11 (26.15ff. D.), Porphyry In Harm. 121.2ff., 133.28ff. D., Nicomachus Harm. 6.246.22ff., cf. Barker 1981b, p. 8.
Optics
In theoretical[52] optics, too, there were disagreements about such physical issues as whether the visual ray departed from the eye or travelled to it from the object seen,[53] and whether light was a movement,
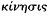
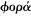
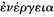
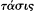
[55] At Optics 2.50ff., 37.4ff. Lejeune, Ptolemy insists, against Euclid, that the visible flux is a continuum: cf. also Optics 2.48, 35.18ff., 36.5ff. L.
[56] Euclid Optics Definition 3, 2.7ff., Propositions 1, 3, and 9, 2.22ff., 4.26ff., 16.7ff., and cf. Theon's Opticorum recensio (Opt.Rec. ) introduction 146.18ff. The interpretation of Optics Proposition 3 especially is, however, disputed: see Brownson 1981, p. 174.
[57] There were, however, those who denied this assumption and held that geometrical magnitudes are made up of indivisibles, notably, in the Hellenistic period, the Epicureans, and cf. also the pseudo-Aristotelian treatise On Indivisible Lines: see, most recently, Sedley 1976b.
[58] This is the issue in Euclid Optics Proposition 3, 4.26ff., especially.
can be considered as a point, the vertex of the visual cone.[60] Moreover, we have good grounds for supposing that the second of these assumptions was clearly recognised by some as an idealisation —since on certain occasions the fact that vision takes place not from a point but from a certain area was acknowledged. Archimedes, in particular, provides a sophisticated discussion of the allowance that has to be made for this in the context of his determination of the angular diameter of the sun in the Sand-Reckoner .[61]
Statics and Hydrostatics
As a third example we may take statics. Although here Archimedes does not state all his assumptions, he evidently discounts, for the purposes of his investigation of the lever, such factors as the possible variation in the material constitution of an actual metal bar and, more
[61] Archimedes Aren. 1.10 (HS) 2.222.3ff., on which see, for example, Lejeune 1947–48, Shapiro 1975, pp. 82f. Cf. also the discussion of binocular vision in Ptolemy Optics 2.27ff. (26.18ff. L.), and 3.25ff. (102.13ff. L.) with Lejeune 1948, pp. 130ff., 145ff.
importantly, that the movement of a bar about a fulcrum will be accompanied by friction.[62] Similarly, in hydrostatics he stipulates explicitly that the fluid be perfectly homogeneous and totally inelastic.[63] Moreover, in his investigation, in the second book of On Floating Bodies , of the conditions of stability of segments of paraboloids of revolution of varying shapes and of varying specific gravities in a fluid, he assumes that he may talk, ideally, of the centres of gravity of plane segments of geometrical figures, as well as of the paraboloids themselves.[64]
These are, as I noted, on the whole comparatively straightforward cases, and they are, of course, among the most commonly cited examples of the successes of Greek science. There has, to be sure, been much, rather laboured, discussion of the possible circularity of the argument in Archimedes' statics—of the relationship between the first postulate, which states that "equal weights at equal distances are in equilibrium,"[65] and the law of the lever subsequently demonstrated, on its basis, in propositions 6 and 7 of book 1 of On the Equilibrium of Planes .[66] Yet to the charge of circularity it might be countered that of course the law of the lever is in some sense presupposed at the beginning, but that is no objection: there is no vicious circularity but, rather, a quite unproblematic, indeed unavoidable, mutual entailment here between postulates and subsequent propositions.[67] That point aside, the type of idealisation involved in the studies we have consid-
[62] Archimedes' assumptions are set out in the first book of De planorum aequilibriis (Aequil. ) (HS) 2.124.3ff.
[63] Archimedes Fluit. 1 Postulate (HS) 2.318.2ff.
[64] Archimedes Fluit. , e.g., 2.2 (HS) 2.350.11ff., 27ff., cf. 1 Postulate 2 (HS) 2.336.14ff., 1.8 (HS) 2.338.26ff., 1.9 (HS) 2.342.15ff., Aequil. 1 Postulates 4f. (HS) 2.124.13ff., 16ff. As to whether the postulates in Aequil. and Fluit. can be thought of as defining implicitly the notion of centre of gravity, see Stein 1931, but contrast Suppes 1981, pp. 207ff., cf. also Schmidt 1975.
[65] Archimedes Aequil. 1 Postulate 1 (HS) 2.124.3f.
[66] Aequil. 1.6 (HS) 2.132.14ff. (for commensurable magnitudes), 1.7 (HS) 2.136.18ff. (for incommensurable ones), on which see Mach 1893, pp. 13f., cf. 1960, pp. 19f.; Duhem 1905–6, vol. 1, pp. 9ff.; contrast Knorr 1978b, p. 185; Suppes 1981, p. 212 n. 3.
[67] Cf. the discussions of Knorr and Suppes cited in the last note.
ered so far is uncontroversial, indeed, not just uncontroversial but the fundamental factor on which the advances in understanding that were made depended. It is only by thinking away some of the features of the phenomenal situation that the underlying, mathematically expressible relations can be revealed.
Dynamics
We can go further: it was partly because of a failure to think away sufficient of the factors in the phenomenal situation that the ancients, Aristotelians and anti-Aristotelians alike, failed to arrive at satisfactory resolutions to the problems in the field we identify as dynamics. Aristotle himself, for instance, argues , as we saw in Chapter 5, that motion must be through a medium; in some of the texts setting out the proportionalities of natural motion he has the express purpose of disproving the void.[68] Philoponus attacked the Aristotelian position on the role of the medium and maintained that it acts purely as a resistance to the moving object.[69] Yet Philoponus, like Aristotle, assumed that weight is one of the factors that determine the speed of a freely falling object and, moreover, not only that it does so in a plenum but also that it would do so in a void.[70] But if you take as your explanandum, or as one of your explananda, motion through a medium , this is bound to prove a major stumbling block to analysis, if only because of the difficulty, indeed the impossibility, of quantifying the factor that corresponds to the density of the medium—a problem that is expressly remarked on by Philoponus.[71]
[68] Aristotle Ph. 4.8.215a31ff., b12ff.; see above, Chap. 5, pp. 217ff.
[69] Philoponus In Ph. 647.9ff., 681.10ff., 682.29ff., especially, and cf. above, Chap. 5 at n. 29.
[70] Philoponus denies that an actual continuous void exists in nature: see Sedley 1982a and forthcoming, Furley 1982. We may contrast the position of the Epicureans, who both asserted the void and maintained that in the void heavy and light atoms move with equal speed "as quick as thought," Epicurus Ep. Hdt. 10.61, cf. 48, and cf. Furley 1967, pp. 121ff.
[71] Philoponus In Ph. 683.1ff., see above, Chap. 5 n. 33.
Astronomy
It would be easy to conclude, on the basis of some of the examples considered so far, that the problem with ancient science is more often too little abstraction than too much . Yet that would be premature. If we turn to astronomy, we see how much more complicated the issue is. Early on in the development of Greek astronomical model-building we find what appears to be a striking example of discounting part of the known data. According to Simplicius,[72] the differences in the apparent brightness of particular planets had already been taken, in Eudoxus' day, to indicate that the distance of each planet from the earth is not constant. Simplicius reports that Eudoxus and Callippus failed to deal with the problem and, indeed, that other astronomers down to Autolycus of Pitane also did—not that Autolycus himself was successful in resolving the difficulty.[73] There was, of course, no way in which such varia-
[72] See In Cael. 504.17ff., where Simplicius gives an extended quotation from Sosigenes.
[73] In Cael. 504.17ff., 20ff., 22ff. As with so many other matters relating to the interpretation of Eudoxus' theory, we are in no position to say with any confidence what his view on the difficulty may have been. Indeed, the very nature of his theory is disputed, for although the evidence provided by Aristotle and Simplicius deals purely with its mathematical characteristics and both sources are silent on the question of Eudoxus' views on the underlying physical realities, the opinion that Eudoxus was quite unconcerned with the latter question is based on no more than that argument from silence. Against what used to be the prevailing scholarly view, Wright 1973–74 has recently argued that some of the mathematical complexities of Eudoxus' theory can only be understood if he had in mind also the physical realities that correspond to the mathematical spheres he postulated. So far as Autolycus goes, neither of his extant treatises, On the Moving Sphere and On Risings and Settings , deals with the problem of the variations in the distances of the planets, sun, and moon, a problem first successfully resolved by the eccentric-epicycle model elaborated by Apollonius: this belongs to the late third century B.C. , even though features of the model go back to the fourth. The notion of the circum-solar (and therefore epicyclic) movement of the lower planets, Venus and Mercury, is often ascribed to Heraclides of Pontus, though the evidence for this is weak (see Neugebauer 1975, vol. 3, pp. 694ff.). More definitely, some of the Pythagoreans, as we have seen, are reported to have adopted a non-geocentric theory, and Polemarchus, a contemporary of Eudoxus, appears to know, since he rejects, eccentricity (see next note).
tions in the distance of a given planet could be accommodated within a theory based on combinations of concentric spheres, with the earth at the centre of the system. Yet it appears that Polemarchus of Cyzicus, for one, recognised the difficulty but, not being prepared to sacrifice the assumption that the earth is at the centre, chose deliberately to ignore it, representing the variation in distance as "imperceptible."[74]
Better still than such instances where we depend on secondary reports, we have some fairly explicit texts in Ptolemy that both show that he is aware of some of the problems and give some insight into how he hoped to overcome them. In Syntaxis book 9 chapter 2, he sets out the main difficulties that any account of the movement of the planets faces. He appeals to these difficulties as his excuse for allowing himself certain moves or devices. One that he mentions is that he will have to make certain primary assumptions that "do not stem from any readily apparent principle," though they are assumptions arrived at from continuous trial and application.[75] His introduction of the equant, or centre of uniform motion, distinct from both the centre of the earth and the centre of the deferent circle, would be one example of such an assumption, though he does not specify it as such here.
The first device he refers to is even more interesting for our concerns. This is the use of certain assumptions he describes as "paradoxical" or "counter to reason,"
emplify: "as when we carry out our proofs—to make them more easy to follow—as if the circles described by the movements in the spheres are bare [widthless] circles, and as if they are all in the same plane, namely, that of the ecliptic."[76] Now, he recognises both that the circles are not, in fact, widthless and that they are not in the plane of the ecliptic. Yet for the sake of his first analysis of planetary motion Ptolemy isolates their longitudinal movements (their motion along the ecliptic) and focuses on them to the exclusion of any consideration of their movements in latitude (that is, north and south of the ecliptic). That achieves a formidable simplification of the problems. Yet it is one for which Ptolemy has a twofold justification. First, as he tells us in 9.2 when commenting on such procedures in general, there can be no objection to them where no appreciable difference, no
Secondly, and more importantly, even though he discounts movements in latitude in his initial discussion of the models of the planets in book 9, he returns to that very problem in book 13, where he modifies the models in an attempt to account for the observed deviations from the ecliptic. There is no question, then, of his simply ignoring the difficulties presented by movement in latitude or of his forgetting that he introduced the simplification in book 9. On the contrary, it is clear that what he borrows for the sake of argument there he pays back in full in book 13.[78]
[77] Ptolemy Syntaxis 9.2 (H) 2.212.10; cf. above, Chap. 5 n. 203, citing other texts from both astronomy and harmonics in which he appeals to a similar principle.
[78] Syntaxis 13.1–5 (H) 2.524.6ff., deals with the problems of the latitudinal movements of the planets. In this context Ptolemy justifies the compli-cated nature of the devices he employs by claiming that they are the simplest possible and by arguing that "simplicity" in regard to heavenly things should not be assessed by the criteria drawn from our ordinary experience of simplicity. Rather, their simplicity should be judged "from the unchangeableness of the natures in heaven itself and of their movements. For thus all would appear simple, and more so than those things that seem so with us, since it is unthinkable that there is any labour or difficulty in their revolutions"; Syntaxis 13.2 (H) 2.532.12ff., 534.1–6. Reverting to the issue mentioned in 9.2, he claims at 13.1 (H) 2.525.3ff. that the devices he introduces to deal with the latitudinal movements make no appreciable difference to longitudinal positions.
Parallax Cases
The issue of the negligibility or otherwise of what is discounted takes us to some more complicated cases, such as the various assumptions made by different astronomers in different contexts about parallax. We can distinguish between three main types of case. First, there is the assumption that in relation to the sphere of the fixed stars, the earth may be treated as a point: it is of negligible size, and so it does not matter, in this context, that an observer is not at the centre of the earth, but on its surface, at some distance from that centre.[79] This assumption is set out in Euclid's Phaenomena , for instance, and in the elementary textbook of Cleomedes.[80] It also figures in Syntaxis book 1 chapter 6, where, moreover, Ptolemy offers a particularly clear statement of the grounds to justify it: the fact that the configurations of the constellations remain unchanged from whatever point on the earth they are observed indicates the very great distance of the stars.[81]
A second and far more controversial assumption is that made in
[79] Similarly, from an early stage, neither the existence of mountains and valleys nor the appearance that the setting or rising sun presents of being cut off by a straight line at the horizon was allowed to count against the conclusion that the earth is generally spherical in shape: see, for example, Aristotle Cael. 294a1ff., Mete. 1.3.340b33ff., and cf. Theon 124.7ff.
[80] Euclid Phaenomena Proposition 1, 10.12ff., Cleomedes 1.11.102.23ff., 106.9ff.; cf. Theon 120.3ff., Proclus Hyp. 2.26.26ff., 28.13f., and already in Diocles On Burning Mirrors paras. 18ff., Toomer 1976, p. 38 and commentary p. 145.
Aristarchus' heliocentric theory, as reported by Archimedes, namely, that not just the earth but the circle in which the earth moves around the sun is as a point in relation to the sphere of the fixed stars (see Figure 2).[82] Archimedes' own comment is that that is, strictly speaking, impossible, since a point has zero magnitude and the fixed stars would then be at infinite distance[83] (a similar point applies, of course, to the first type of parallax case as well). What Aristarchus needs is not that the stars be infinitely, only that they be indefinitely, far away.
The interesting feature is that he evidently incorporated this into his assumptions , in part in order to meet a possible objection to heliocentricity. If the earth moves in a circle around the sun (rather than the sun around the earth) there should be, one might think, observable differences in the shapes of the constellations as viewed from different points in the earth's orbit—from the points representing the spring and autumn equinoxes, for instance, at opposite ends of the same diameter of the orbit. Yet no such variation was observed; indeed, stellar parallax was not confirmed until well into the nineteenth century, with the work of Bessel and others around 1835. Aristarchus seems to have appreciated that this otherwise very damaging objection to heliocentricity was no objection at all provided that the stars are sufficiently far away. If the diameter of the earth's orbit around the sun is negligible in comparison to the diameter of the sphere of the fixed stars, then you would not expect observable variations in the relative positions of the stars, certainly not within the limits of ancient techniques of observation. Unlike Ptolemy's discussion of the size of the earth in Syntaxis 1.6, the assumption in the form adopted by Aristarchus was not itself justified by reference to independently observable phenomena; there was no way in which it could be. Rather, this reveals precisely what has to be accepted among the assumptions in order for an apparent objection from the side of the phenomena not to be the objection it seems. No doubt Aristarchus could have argued that the
[82] Archimedes Aren. 1.4 (HS) 2.218.7ff.
[83] Aren. 1.6 (HS) 2.218.18ff.
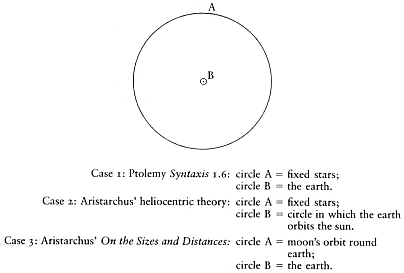
Figure 2
Three cases of discounted parallax. In each case circle B is treated as a point.
inability to confirm an assumption directly does not make it untrue—and Copernicus would have said the same.[84]
The third type of case again comes from Aristarchus, this time from the extant treatise On the Sizes and Distances of the Sun and Moon . The second hypothesis set out there is that the earth is as a point, not in relation to the sphere of the fixed stars, but in relation to the moon's orbit .[85] In this form the assumption involves discounting lunar paral-
[84] Cf. Copernicus De revolutionibus orbium coelestium (Rev. ) 1.6. Already those Pythagoreans who treated the earth as one of the planets (see above at n. 12) had argued, according to Aristotle, that there is no difficulty in supposing that the phenomena would be the same as they would be if the earth were at the centre—even though they denied that. "For there is nothing to show, even on the current view, that we are distant half the earth's diameter [viz. from the centre]," Aristotle Cael. 293b25ff., 29f.
[85] Aristarchus Hypothesis 2 (352.5f. Heath).
lax—as if the position of the observer on the surface of the earth makes no difference to observations of the moon. Yet of course it does. The contrast with the careful and complex discussions in the Syntaxis where Ptolemy attempts to determine the allowance that has to be made for lunar parallax[86] is striking and points up the difficulty that the second hypothesis in Aristarchus' treatise presents, indeed, its complete unacceptability if we are concerned with trying to establish the actual size of the moon and its actual distance from the earth.
Yet we should not be misled by one possible way of taking the title of Aristarchus' treatise (On the Sizes and Distances . . . ) into thinking that that was his aim. Both the hypotheses and the results militate
[86] See especially Ptolemy Syntaxis 5.11–12, 18–19 (H) 1.401.2ff., 442, 444.2ff.: at 5.11 (H) 1.401.6ff., Ptolemy begins by recalling from 4.1 (H) 1.266.1ff. that the earth does not bear the ratio of a point to the distance of the moon's sphere. With Ptolemy's discussions of lunar parallax we may compare Toomer's proposed reconstruction of the procedures Hipparchus used to determine the distances of the sun and moon (Toomer 1974–75). According to this, Hipparchus took first a minimum, then a maximum, figure for solar parallax, in order to arrive at upper and lower limits for the distance of the moon, expressed in terms of earth radii. First he assumed solar parallax to be zero: using differences in the magnitude of a solar eclipse observed near the Hellespont and at Alexandria, he computed a minimum distance for the moon (71 earth radii). Then Hipparchus took a maximum figure for solar parallax (7') and computed from this the sun's minimum distance and the corresponding maximum distance for the moon (67 1/3 radii in the mean: here Toomer draws on and develops an analysis put forward by Swerdlow 1969). As Toomer emphasised, 1974–75, p. 140, if this reconstruction is correct, one striking feature of Hipparchus' workings would be "the complete honesty with which [he] reveals his discrepant results," namely, that the "maximum distance" obtained by the second method turns out to be smaller than the "minimum distance" obtained by the first. There are, as Toomer also stressed, considerable difficulties in interpreting the meagre and at points conflicting reports in Ptolemy and Pappus on which this reconstruction is based. Both sources, however, agree that Hipparchus took a lower limit for solar parallax of zero. As Ptolemy puts it, Syntaxis 5.11 (H) 1.402.19f., "at one time he assumes that the sun has no perceptible parallax, at another that it has a sufficiently large parallax [viz. to be observed]," and as Pappus reports in his Commentary on Books 5 and 6 of the Syntaxis 67.21ff. Rome: "So Hipparchus . . . assumed in the first book of On Sizes and Distances that the earth has the ratio of a point and centre to the sun (i.e., to the sun's sphere)."
against such a view. First, his results all take the form of ratios or proportions, giving upper and lower limits for the relative sizes and distances on the basis of the assumptions as set out; no absolute figures are presented.[87] Then, the hypotheses include several that Aristarchus undoubtedly knew to be well wide of the mark. That appears to be the most likely explanation of the notorious sixth hypothesis, that the moon subtends an angle of 2° to the eye;[88] where 1/2° was the usual ancient approximation and is indeed the figure we can attribute to Aristarchus on the basis of a report in Archimedes.[89] Again, the fourth hypothesis simply assumes, with no attempt at justification, that the moon is at 87° to the sun when it appears to be halved.[90] Again, the
[87] For example, Aristarchus Proposition 7 (376.2ff. Heath) ("The distance of the sun from the earth is greater than 18 times, but less than 20 times, the distance of the moon from the earth") and Proposition 18 (410.12ff. Heath) ("The ratio of the earth to the moon is greater than 1259712 to 79507, but less than 216000 to 6859").
[88] Aristarchus Hypothesis 6 (352.14f. Heath) ("That the moon subtends one-fifteenth part of a sign of the zodiac"). The interpretation of this hypothesis has been much debated: see for example Heath 1913, pp. 311ff.; Wasserstein 1962; Neugebauer 1972/1983, p. 366, 1975, vol. 2, pp. 634ff., who concludes, p. 643, "The fact that Aristarchus does not make the obvious transition from the diameters of sun and moon to the distances, measured in earth radii, supports our conclusion that [the Sixth Hypothesis] is not to be taken as a valid observational datum. . . . I think this analysis leads to the conclusion that Aristarchus' treatise on the sizes and distances is a purely mathematical exercise which has as little to do with practical astronomy as Archimedes' 'Sandreckoner' in which he demonstrates the capability of mathematics of giving numerically definite estimates even for such questions as the ratio of the volume of the universe to the volume of a grain of sand."
[89] Archimedes Aren. 1.10 (HS) 2.222.6ff. reports that Aristarchus "discovered that the sun's apparent diameter is 1/720th part of the zodiac circle," and the equivalence of the apparent diameters of the sun and moon is shown in Aristarchus' treatise in Proposition 8 (382.1ff. Heath) and indeed assumed from the beginning (cf. Neugebauer 1975, vol. 2, p. 635). After reporting Aristarchus' value for the diameter of the sun, Archimedes himself goes on to describe how he used a dioptra to obtain upper and lower limits for this, namely, 1/164th and 1/200th of a right angle, that is, between under 33¢ and 27': see Shapiro 1975.
[90] In Hypothesis 4 (352.10f. Heath) this is stated in the form: "when the moon appears to us halved, its distance from the sun is then less than a quadrant by 1/30th of a quadrant."
fifth takes it that the breadth of the earth's shadow, viz., at the moon, is two moons.[91] Moreover, the second hypothesis itself not only discounts lunar parallax but takes the moon to move in a simple circle with the earth as centre—and no serious Greek astronomer had thought that since before Eudoxus.
Such a set of hypotheses would, of course, be an unmitigated disaster in any attempt to arrive at concrete determinations of the actual sizes and distances of the moon and sun. What Aristarchus is doing, rather, is exploring the geometry of the problems. Given certain assumptions—and it will not matter, for the sake of the geometry, that some of the values are a little, and others wildly, inaccurate—what follows? The study is certainly relevant to astronomy, in particular because it shows how one could obtain actual solutions to the astronomical parameters, that is, it offers one set of answers to the question of the premises, or data, needed in order to arrive at such solutions. Yet it remains itself essentially a study of the geometry of the problems.[92]
The Aims and Assumptions of Greek Astronomers
As this last example shows, certain types of simplifying assumption involve not so much discounting a value that can—with greater or less justification—be deemed to be negligible, as a veritable mutation of the problem. Once certain of the known empirical data are suspended, the study becomes one of pure geometry and does not offer to solve, though it remains relevant to, the astronomical problems themselves. Now, it is just such a shift that Duhem and his followers saw as typical of the dominant strand in Greek astronomy: a lack of concern with the physics of the problems in favour of a preoccupation with the mathematics, the construction of models that are purely calculating devices with nothing to do with any underlying physical realities.[93] It is
[91] Hypothesis 5 (352.13 Heath).
[92] Cf. Neugebauer 1975, vol. 2, p. 643, quoted above, n. 88.
[93] In his 1908, e.g., pp. 120, 281, 284 especially, Duhem drew a fundamental contrast between two views on astronomical hypotheses. On the one hand, they might be treated as "simple mathematical fictions," "pure concep-tions," where there is no question of their being "true" or even "probable," where "true" is glossed as "in conformity with the nature of things." On the other, they might also be held to describe "concrete bodies" and "movements that are actually accomplished." Duhem is in no doubt that the former represents the position of the major Greek astronomers and commentators: cf. Wasserstein 1962, p. 54, and contrast G. E. R. Lloyd 1978b.
indeed undeniable that there are instances (Aristarchus' treatise is one) where the problems are treated, at least for the time, as problems of geometry. There is certainly a tradition of the investigation of the mathematics relevant and useful to astronomy that exists side by side with astronomy itself—a tradition that goes back to Autolycus' work On the Moving Sphere .[94] But that cannot be said to vindicate the line of interpretation that Duhem advocated. What that line of interpretation itself discounts, or at least seriously underestimates, is an equally undeniable concern with more than just the mathematics of the problems in much—indeed, in my opinion, most—ancient Greek astronomy.
In what are admittedly complex issues,[95] the chief objection to Duhem can most easily be illustrated in relation to Ptolemy himself.
[94] Autolycus is represented as active around 330 B.C. : see Mogenet 1950, pp. 5ff.; Neugebauer 1975, vol. 2, pp. 573, 750f.; Aujac 1979, pp. 8ff. On Autolycus and the tradition he represents, see also I. Mueller 1980, pp. 106ff.
[95] The major difficulty we face is that for several important astronomers, such as Apollonius, we have no direct evidence, and for others, such as Hipparchus, only secondary reports of doubtful reliability. Thus Theon 188.15ff. does not—pace Duhem 1908, pp. 119f.; cf. G. E. R. Lloyd 1978b, pp. 217ff.—characterise Hipparchus as indifferent to physics. On the contrary, he represents him as adopting the epicyclic hypothesis in preference to the eccentric one not for purely mathematical reasons, but on general and cosmological grounds: "it is more plausible that all the heavenly bodies should lie symmetrically with regard to the centre of the universe and be joined together similarly." (Moreover, Theon is not only a naive realist himself, but represents Greek astronomy as a whole as founded on the study of nature, contrasting it with Babylonian, Chaldaean, and Egyptian astronomy in just this regard, 177.20ff.). While the positions of Eudoxus and Callippus on this issue are a matter of conjecture (see above, n. 73), it is clear that Aristotle demanded a physically unified system in Metaph.L 8.1073b38ff. As for our single most important and most comprehensive source, Ptolemy, both the Planetary Hypotheses (Plan.Hyp .) and the Syntaxis make it abundantly clear, in my view, that his strategic intention was to provide not just a mathematical, but also a physical account of the phenomena.
First, the treatise known as the Planetary Hypotheses provides incontestable evidence that he aimed for a physical account of astronomical phenomena. There he discusses the nature and relations of the spheres on which the heavenly bodies move. The circles that govern the movements of the planets, sun, and moon are conceived as strips of spheres.[96] He even engages with the problems of celestial dynamics, that is, with what makes the heavenly bodies move or the forces at work, when he suggests that we should suppose that each of the planets possesses its own vital force: they move because they are alive.[97]
But the case does not rest with that work. Within the Syntaxis itself, the very rejection of heliocentricity or, rather, the rejection of the ascription of any movement to the earth shows that, for all the concentration on the mathematics of the problems in that treatise, the whole discussion is set firmly in the framework of certain physical assumptions.[98] There can be no question of the earth moving, in Ptolemy's view, primarily because of the (apparent) absence of the expected physical effects of its movement on the earth's surface. If the earth rotated, for instance, you would expect the violence of that motion to have visible effects around us. Clouds, or missiles travelling through the air, could, he says, never move eastwards, for they would always be anticipated by the motion of the earth itself.[99]
[96] Ptolemy Plan.Hyp. 2.4 (H) 113.12ff., and 2.6 (H) 117.8ff. especially.
[97] See Plan.Hyp. 2.5 (H) 116.20ff., and 2.7 (H) 119.18ff.
[99] See Syntaxis 1.7 (H) 1.24.14ff. The defence against this objection, that the air moves with the earth, is itself countered by Ptolemy at 1.25.15ff. with the argument that composite objects in the air would still always seem to beleft behind by the movement of earth and air together, while if those objects too were carried round "united" with the air, they would never appear to have any independent eastward or westward motion. Earlier in the same chapter, 1.21.14ff., Ptolemy had invoked the Aristotelian doctrine that heavy objects naturally move towards, and rest at, the centre. To the argument from the violence of the supposed rotation of the earth, Copernicus Rev. 1.8 countered by referring to the difficulties involved in the incredibly swift motion that, on the Ptolemaic view, the heavens themselves were supposed to make in their diurnal revolution. But for Ptolemy that merely reinforced the belief in the exceptional nature of the substance of which the heavens were made.
To return to the chief point with which we are concerned here, namely, the nature of and constraints on the idealisations that Greek astronomers allowed themselves. Ptolemy, at least, certainly does not permit himself any general escape clause. In every or almost every case where he introduces an idealisation or a simplification, he has to exercise his judgement concerning the magnitude and character of the discounting. So far as his primary assumptions go, he claimed, as we saw, that he adopts something "paradoxical" only when the consequences fall within the limits of negligible difference. Elsewhere he often justifies the approximations he makes on the grounds of the specific problems encountered in securing reliable data.[100] Although we may often question his judgement and may sometimes even suspect his bona fides , he does not proceed as if he could allow himself any arbitrary adjustment he liked—that is, what he could cheerfully agree to be such—an adjustment that would have the effect of turning his discussion into a purely hypothetical, mathematical exercise. The constraints on that discussion come both from the physics of the situation (on the issue of the movement of the earth) and from the astronomical data as secured, as well as may be, by observation.
There is, however, one notable, indeed notorious, instance that looks, and to some extent is, an exception to what is still the general rule. This is the famous case of the discrepancy between what his theory predicts and what is observed on the question of the angular diameter of the moon. It follows from Ptolemy's lunar model that the maximum distance of the moon from the earth is nearly twice the
[100] See above, Chap. 5 at nn. 84–91.
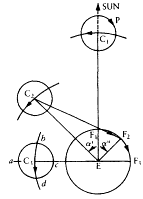
Figure 3
Ptolemy's model to explain the moon's second anomaly.
The moon's epicycle, centre C, moves round a centre (F)
which itself describes a circle round the earth (E). F moves
round E with the same angular velocity as, but in the contrary
sense to, the movement of C round E. At position (1) (syzygy)
the model is equivalent to a simple epicycle model. At
position (3) (quadrature), when the moon is at apogee or perigree
on the epicycle (that is, at a or at c ) the model is again equivalent
to a simple epicycle model so far as the moon's angular
distance from the sun in concerned. But at position (3),
when the moon is at b or d , midway between apogee and
perigee on the epicycle, the effect of the new model is to
increase the apparent diameter of the epicycle.
Derived from G. E. R. Lloyd, Greek Science after Aristotle , fig. 27.
minimum distance (see Figure 3).[101] The angular diameter of the moon should, in turn, vary roughly by a similar amount, a factor of 2. Yet it patently does not. Nor does the evidence in the Syntaxis suggest that Ptolemy thought that it did. It is true that he gives specific values only for the maximum and minimum apparent diameter at syzygy (not for the maximum at quadrature),[102] but those he offers are of the right
[101] Taking the distance from the earth (the centre of the ecliptic) and the centre of the moon's epicycle (R = EC, in the diagram) as usual as 60 parts, Ptolemy estimated the radius of the epicycle (r = C1 P in the diagram) as 5; 15p expressed sexagesimally (i.e., 5 15/60ths) and the eccentricity (e = EF in the diagram) as 10; 19p, Syntaxis 5.4 (H) 1.366.15ff. Maximum geocentric distance, at syzygy, i.e., R + r , will then be 65; 15p. Minimum geocentric distance, at quadrature, i.e., R – 2e – r , will be 34; 7p, only slightly over half the value for the maximum. Cf. Neugebauer 1952/1957, pp. 194ff., 1975, vol. 1, pp. 86ff., cf. Pedersen 1974, pp. 192ff.
[102] The modification that Ptolemy introduced to Hipparchus' lunar model was to suppose that the centre of the deferent circle (F in the diagram) itself moves in a circle round the earth (E) at the same angular velocity as, but in thecontrary sense to, the movement of the centre of the epicycle (C) round the earth: angle a = angle a in the diagram. The effect of this modification on the geocentric distance of the moon, and so on its apparent diameter, is at a maximum at quadrature, but decreases to zero at syzygy (conjunction or opposition): in the latter case the difference between apogee and perigee corresponds simply to the epicycle's diameter.
order of magnitude, a minimum of 31' 20" and a maximum at perigree at syzygy of 35' 20".[103] Moreover, and to complicate matters further, the Planetary Hypotheses tackles the problem of how the spheres of the heavenly bodies nest into one another, where it is assumed that the maximum distance of one body corresponds to the minimum distance of the one above it, and there Ptolemy clearly accepts the geometrical consequences of his epicycle-eccentric model in the Syntaxis as correct.[104] So far from being embarrassed by those consequences, he takes them as the basis of his calculations of the absolute distances of the moon and other bodies.
Here, then, we have a major discrepancy between the theory and the data of observation, and Ptolemy's lack of embarrassment just increases ours, since it looks as if he has simply discarded part of the phenomena quite arbitrarily. That he has discarded part of his data is clear. That it is quite arbitrary is more debatable. We have to recall that the theory worked extremely well as a theory of the longitudinal positions of the moon, where it represented a quite marked improvement on Hipparchus' lunar model, which itself gave tolerably serviceable results.[105] As regards the lack of appreciable variation in the apparent size of the moon, how—without recourse to desperate expedients—Ptolemy thought he could get round the difficulty we do not know.[106] But he may not have despaired—presumably he did not despair—of
[103] See Syntaxis 5.14 (H) 1.421.3ff., 6.5 (H) 1.479.14ff. In his comments on the hypotheses in Aristarchus' On the Sizes and Distances , Pappus attributes the same figures to Ptolemy, apparently as if they were his definitive values: Collectio 6.37.71 (2.556.17ff. Hultsch).
[104] See Plan.Hyp. 1 part 2 chap. 3, Goldstein 1967, pp. 7f., and cf. Plan.Hyp. 2.16 (138.14ff. H.).
[105] On the superiority of Ptolemy's final lunar model, in Syntaxis 5.5 (H) 1.367.3ff., to its predecessors, see Petersen 1969 and Gingerich 1980, pp. 256ff.
[106] Thus there is no suggestion that Ptolemy wavered in his belief in the constancy of the radius of the moon's epicycle, though this possibility has been canvassed in the case of Hipparchus; see Neugebauer 1975, vol. 1, pp. 315f.
some explanation being possible. In his view, we may assume, the difficulty presented by this phenomenon was not great enough to justify his abandoning the model as a whole.
As we have noted before, until such time as a superior model is available, any scientist would be justified in continuing to maintain, in the face of prima facie counter-evidence, a theory that had shown its ability to account for at least part of the phenomena, though every scientist should in principle, to be sure, be especially self-critical on the question of when the strength of the counter-evidence is such as to make a new model imperative.[107] Yet the price Ptolemy has paid in this case is clear: the elision of part of the data is here no mere temporary
[107] This raises, of course, one of the most hotly contested topics in recent philosophy of science, namely, the rationality of different responses to anomalies or counter-examples in scientific research programmes. The issues have been debated in connection especially with Kuhn's ideas on the generation of "crisis" in normal, puzzle-solving, science, and with those of Lakatos on the relation between the "hard core" of a scientific research programme ("irrefutable" by the methodological decision of its proponents) and its "protective belt" of auxiliary hypotheses (where anomalies may abound and the programme still remain "progressive"—defined in terms of increasing content) and where Lakatos distinguishes between different types of ad hoc procedure, including the strategies he dubbed "monster-barring," "exception-barring," and "monster-adjustment" (this last defined as turning a counter-example, in the light of a new theory, into an example). See most notably Kuhn 1962/1970, and 1977; Lakatos 1976, 1978a, e.g., p. 48, p. 63 n. 3; Laudan 1977, 1981a; Newton-Smith 1981; and Hacking 1983. Ptolemy's astronomy as a whole, which has been much discussed in relation to Copernicus especially (Kuhn 1957; Lakatos 1978a, chap. 4, pp. 168ff.), represents, from an ancient perspective, the most elaborate and fully developed research programme in ancient science—and it was one that was to prove extremely durable. The example of the variation in the angular diameter of the moon shows that, on occasion, Ptolemy, confronted with an anomaly, offered no adjustment but simply passed it by in silence. When the general problem of the apparent complexity of his devices is explicitly raised as a problem , in Syntaxis 13.2 (H) 2.532.12ff., his response, as we have seen, n. 78, is to claim that he has attempted to use, so far as possible, the simplest hypotheses, but then also to argue that "simplicity" in regard to heavenly things should not be judged by our ordinary criteria of simplicity. At this, the point where the question of the viability of the system as a whole comes, perhaps, closest to the surface, there is an uncomfortable tension between simplicity invoked as a criterion to judge between theories, and the axiomatic assertion that the movements of the heavenly bodies are simple, however complicated they may appear to us.
simplification for the sake of argument, but represents a limitation on the viability of the model itself.
Conclusions for the Exact Sciences
Our survey, to date, of some of the main types of simplification and idealisation in Greek science has been drastically selective, but some points have, I hope, emerged sufficiently clearly. The move to discount some of the phenomena in question is associated with some of the most notable successes of Greek science. On occasion, to one looking back with the benefits of hindsight, it seems as if the problem in ancient science is too little abstraction from the complexities of the phenomenal situation, rather than too much, though there was—there is—no way of telling in advance when this may be the case. Some attention, at least, is paid by Ptolemy, for one, to the conditions under which simplification is possible, though he provides no exact rules, only rough-and-ready practical guidelines, with his appeal to a vague, certainly unquantified, notion of "negligible difference." That already indicates some awareness of the problem of discounting parts of the phenomena to leave in play only what is readily explicable. While this was often a sensible policy, it could also prove all too facile a manoeuvre, when recalcitrant data that are central to a problem are simply ignored and when there is no question of their being reintroducible, in principle, at a later stage, with the theory remaining intact.
The Life Sciences:
Teleology
Thus far we have taken our examples from the exact sciences, but comparable moves can be documented also in other areas of ancient speculative thought with results that must provoke further reflection on the aims and methods of ancient investigators. Teleology offers a general rubric under which we can discuss some especially striking examples from various areas of the life sciences.[108] From the time of
[108] On the pre-Platonic background see especially Theiler 1924, Solmsen 1963, Balme 1965; cf. Sorabji 1980a.
Plato, at least, the notion that the world as a whole is well-ordered, the product of divine design, is one of the most powerful motive forces in ancient science, though it remained a far from unanimous, indeed a much contested, view.[109] The question we may raise in this regard is whether or how far teleological accounts were secured at a cost of discarding part of the phenomena in a way that is broadly comparable with the elisions we have studied from the exact sciences.
In the first developed statement of a teleological cosmology, in Plato's Timaeus —and often thereafter—it is explicity recognised that other factors besides the good have to be taken into account. Plato's Demiurge and the workings of reason are confronted with the factor of necessity, exemplified by the concomitance of material properties, as when the hardness of bone necessary to protect the head is inseparable from a heaviness that weighs it down and makes for insensitivity.[110] The human race would have been longer-lived but less intelligent if the head had been covered by a thicker layer of bone: as it is, unable to secure both long life and intelligence, god sacrifices the former, lesser end to insure for humans, as far as possible, a noble and intelligent, if shorter, life. In Aristotle, too, the final cause is often contrasted with what he too calls necessity—that is, simple, not conditional, necessity[111] —again associated with the material properties of things. Some
[109] Teleological explanation was, of course, denied, both before and after Aristotle, by the atomists especially.
[110] Plato Ti. 74e ff. On the role of necessity and of what Plato calls the "wandering cause" (Ti. 48a7) in the Timaeus , see especially A. E. Taylor 1928, pp. 299f.; Vlastos 1939/1965, 1975a; Morrow 1950/1965; Alt 1978.
[111] As we have noted before, Chap. 3 at n. 149, Aristotle distinguishes between several different types or modes of necessity in passages in the Organon, the Metaphysics , and the physical and biological works, and the interpretation of his distinctions and the question of their consistency have been the subject of protracted recent debate. Apart from (1) necessity in the sense of the compulsory or the violent, and (2) absolute or unqualified necessity relating to "eternal" things, including both (2a) the eternal heavenly bodies, and (2b) the (timeless) truths of mathematics, two further types of necessity are of particular concern to the natural philosopher. (3) "Conditional" or "hypothetical" necessity is explained in terms of the material conditions necessary for an end to be realised; thus for a house to be built, matter of a particular kind must be available; for an axe to be able to cut, it must be of suitable material. But this isin turn contrasted with (4) the necessary consequences of the natures of things or of their being as they are. While (3), conditional necessity, works with the final cause, as the necessary condition for the realisation of some good, (4) is sometimes contrasted with the good. The distinction is drawn at PA 642a31ff. in connection with the example of respiration, where (4) is illustrated by the necessary behaviour of the hot substance moving in and out and of the air flowing in. Again, at PA 677a11ff., discussing bile, Aristotle contrasts those residues that nature is able to turn to some advantage with those where this is not the case. At PA 662b23ff., 663b22ff., for instance, he had pointed out that in the case of horns, surplus earthy matter is made to serve the purposes of self-defence and attack, but bile itself is not "for the sake of something" but arises merely as the consequence of other things that are for some good (PA 677a16ff.). Again at GA 5.1.778b10ff., 16ff., when he contrasts what arises merely in the process of generation or formation with what is contained in the essence of an animal and is for the sake of some good, he distinguishes the necessity for an animal to have an eye (where that characteristic belongs to the essence of the animal in question) and the necessity for it to have an eye of a particular kind (the result merely of the natural processes of formation). Cf., for example, APo. 94b27ff., Ph. 2.8.198b10ff., GC 337a34ff., PA 1.1.639b21ff., 642a1ff., Metaph. 1015a20ff. The issues are controversial, but among the most important recent studies are Balme 1965, 1987; Kullmann 1974a, 1979; Preus 1975; Gotthelf 1976–77; Nussbaum 1978, pp. 59ff.; Sorabji 1980a; Waterlow 1982a; Lennox 1981, 1985; Leszl 1982; Cooper 1982, 1987; Furley 1985.
things are so because they have to be so, or happen to be—the colour of the eyes, for instance—not for the sake of some end.[112]
Since teleology does not apply without exception in Plato or Aristotle,[113] there is no need for failures of the good to be denied —though both philosophers will insist that the Demiurge or nature has secured
[113] The limits of teleological explanation are also discussed in Theophrastus' Metaphysics: see above, Chap. 3 at nn. 161ff.
the best possible results, within the constraints of necessity.[114] Failures need not simply be elided, since they can be laid at the door of necessity or the recalcitrance of matter, even though for Plato, and to some extent for Aristotle, that risks amounting to a concession that they are, in that respect at least, beyond explanation, since a proper explanation, by definition, will be in terms of the good.[115]
Moreover, the normative role of the concept of nature in Aristotle, in the zoological treatises especially, deserves remarking. His official and explicit statement, many times repeated, is that nature corresponds to what happens always or for the most part.[116] In practice, however, "natural" is sometimes reserved not for what happens usually, but for what is quite exceptional.[117] This is the case, for instance, where we are told that in humans alone the natural parts are fully "according to nature": in humans alone the "upper" part is directed to
[114] See, e.g., Plato Ti. 30a, Aristotle Ph. 259a10ff., 260b21f., GC 336b27f., among a very large number of other texts. Similar themes often recur, of course, in both later philosophy and science, as, most notably, in the Stoic doctrine of providence and in Proclus, both in his commentaries on Plato (e.g., In Ti. 1.370.13ff.) and in Hyp. (e.g., 1.4.20ff.). Cf. also on Galen, below at nn. 126ff.
[116] See especially Ph. 2.8.198b10ff., 34ff., 199b23ff., on which see most recently Furley 1985.
the "upper" part of the universe, and the right side is most rightsided.[118] Here what Aristotle describes as "natural" is what he deems to be best, where he uses the human species as the norm by which the rest of the animal kingdom is to be judged. By that standard all other animals fall short. Yet the ideal they fall short of is still referred to as what is "according to nature" or "natural," despite the fact that this picks out not what happens always nor even for the most part, but what is true of humans alone.
Many of the parts and functions of the lower animals are thus evaluated from the point of view of those of higher species, especially of the supreme species, humans. The heuristic value of this idea is clear. It enables Aristotle to recognise, for example, that in the so-called bloodless animals there is an analogous fluid that performs the same functions as blood,[119] or, again, that there are analogues to the heart, in his view the control centre of the vital functions.[120] Yet, equally clearly, he is led to make some very dubious value judgements. He speaks repeatedly of the parts of certain animals, or of whole species, as deformed or maimed , using the very same terms,[121] such as
[118] See especially PA 656a10ff., IA 706a16ff., 20ff., b9f., HA 494a26ff., 33ff.
[119] See especially HA 489a20ff., PA 645b8ff., 648a1ff., 19ff., 678a8f., GA 728a20f.
[120] What is analogous to the heart exists in lower groups of animals not only as the receptacle for what is analogous to blood (e.g., PA 665b11ff.), but also as the centre of perception, imagination, and locomotion in those animals that have them and indeed of life in general (e.g., Juv. 469b3ff., PA 647a30f., 678b1ff., De Motu Animalium 703a14ff., GA 735a22ff., 738b16f., 741b15ff., 742b35ff., 781a20ff.).
[121] See, for example, PA 684a32ff. (on lobsters), IA 714a6ff. (on flatfish), PA 695b2ff. (on fish in general), and other texts discussed in G. E. R. Lloyd 1983a, pp. 40f.
[122] HA 533a2ff., but cf. HA 491b27ff. and De An. 425a10f. Compare also PA 657a22ff. on the seal's "ears."
the
Similar tendencies are particularly prominent in Galen. The whole of his treatise On the Use of Parts and many other extended passages in other works are devoted to establishing and illustrating the thesis that nature does nothing in vain, which he often, indeed generally, construes as not just a general but an exceptionless rule: every part has a purpose, and nature is perfect.[126] But the tension this thesis sets up can be seen in his anatomy, his physiology, and his pathology.
[123] IA 714b8ff., 10ff., 14ff. Cf. also PA 683b18ff.: the testacea, having their head downwards, are said to be "upside down," as also are the plants, in that they take in food through their roots (cf. PA 686b31ff., IA 705b2ff., 706b5ff.).
[124] "Upper" is defined functionally in relation to the intake and distribution of food. See PA 686b2ff., 20ff., 689b25ff., 695a8ff. At IA 710b12ff. infants are said to be dwarf-like in comparison with adults.
[125] As we have noted before (Chap. 1 n. 160), Aristotle explicitly states at PA 645a15ff., 21ff., that all natural things, and especially all animals, have some share of the admirable and the beautiful—and this insures that all are accordingly and to that extent worthy of investigation. Yet the shares are evidently unequal, and while in principle there need be no reason why downgrading in regard to a creature higher in the hierarchy should entail downgrading as a subject of study, it follows from Aristotle's insistence on the physicist's concern with the final cause (and the good) that the extent to which they are manifested in any given subject matter has direct repercussions on how worthwhile the investigation of that subject matter is, at least under that heading. Moreover, in practice, in the zoological treatises, although there are exceptions, the attention Aristotle devotes to the various kinds of animals broadly reflects, even if it is not to be precisely correlated with, his view of their position in the overall hierarchy.
[126] The strong thesis—that there is no possible improvement to the work of nature—appears, for example, in UP 1.5 (H) 1.6.18ff., (K) 3.9.4ff., 3.10 (H) 1.177.20ff., (K) 3.242.5ff., 3.16 (H) 1.190.10ff., (K) 3.259.3ff., and 5.5(H) 1.267.12ff., (K) 3.364.17ff. (where the Erasistrateans are rebuked for failing to demonstrate how nature is worthy of praise in detail—by considering each organ in turn). Elsewhere, however, Galen recognises that nature cannot achieve perfection (see below [at n. 139]) and must weigh the balance of advantage (e.g., UP 5.4 (H) 1.260.1ff., (K) 3.354.17ff.).
Thus, developing a common Greek idea,[127] Galen represents apes as caricatures of human beings.[128] Yet, as is well known, he often uses apes—as others had done before him—as the basis of his anatomical descriptions of humans; his account of the muscles, for example, explicity derives from his dissections of apes.[129] From the point of view of transferring conclusions to human anatomy, the ape had better be as close to us as possible.[130] Yet so far from some of Galen's great admiration for humans extending to the ape, he calls the ape ridiculous: it has a ridiculous soul and so also a ridiculous body.[131] Yet why, if nature does nothing in vain, it plays such jokes, is not explained—and similar points apply also, regrettably, to Galen's account of the human female.[132]
[127] See, for example, Aristotle Top. 117b17ff., cf. Archilochus 81, 83, Semonides 7.71ff., Plato Hp.Ma. 289a–b, cf. Vegetti 1983, pp. 59ff.
[128] See, for example, UP 1.22 (H) 1.58.18ff., (K) 3.79.18ff., 3.8 (H) 1.152.21ff., (K) 3.208.15ff., 3.16 (H) 1.194.11ff.,(K) 3.264.9ff., 11.2 (H) 2.117.14ff., (K) 3.848.8ff., 15.8 (H) 2.367.15ff., (K) 4.252.5ff., AA 4.1 (K) 2.416.3ff.
[129] See, for example, AA 4.2 (K) 2.423.5ff., 5.9 (K) 2.526.4ff. and cf. 1.2 (K) 2.222.2ff., 3.5 (K) 2.384.12ff., 6.1 (K) 2.532.5ff., 6.3 (K) 2.548.2ff.
[130] Galen recognises, indeed, that different species of apes resemble humans to different degrees, and he recommends using those that are most like man, with short jaws and small canines: AA 1.2 (K) 2.222.5ff., 223.9ff., 6.1 (K) 2.532.5–535.15 (specifying apes with an upright gait, a thumb in the hand, and a temporal muscle like that in humans), UP 11.2 (H) 2.114.17ff., (K) 3.844.7ff.
[131] See UP 13.11 (H) 2.273.8ff., 23ff., (K) 4.126.1ff., 15ff., in addition to the passages cited above in n. 128.
Elsewhere—in, for example, his account of the blood-vascular system—we can see the heuristic value of the principle that each part serves a purpose, yet his identification of purposes is selective. Thus he infers that blood is transferred from the right to the left side of the heart, in the adult, through pores in the septum separating the ventricles. He does not claim that these pores can be seen, though pits in the septum suggest their beginnings.[133] But they are necessary to account for blood in the arterial system.[134] However, he knows very well that in the embryo there is a direct route for the blood between the two atria, namely, through the foramen ovale, and he also knows that this closes after birth.[135]Why it should close should be a problem, since if it had remained open nature would not have needed the interventricular pores. Yet Galen quite fails to discuss this, merely remarking how marvellous it is that the foramen closes after birth and asserting that it would be of no use in the adult.[136] It is enormously to his credit that he realises that the communications in the embryo heart differ from those in the child once born, and it is to his credit too that
[133] Nat.Fac. 3.15 (H) 3.251.27ff., (K) 2.207.17ff.
[135] See especially UP 6.21 (H) 1.371.4ff., (K) 3.510.2ff., 15.6 (H) 2.360.19ff., 361.12ff., (K) 4.242.18ff., 243.18ff., AA 12.5 (pp. 118ff. D.). Galen also clearly knows of the ductus arteriosus, the communication, in the foetal heart, between the pulmonary artery and the aorta, e.g., AA 12.5 (pp. 118ff. D.), 13.10 (p. 179 D.), cf. (K) 2.828.10ff.
[136] See UP 6.21 (H) 1.374.4ff., (K) 3.514.2ff., and 15.6 (H) 2.362.1ff., (K) 4.244.14ff.
he does not fudge the function of the foramen ovale, of which he provides the first extant description.[137] Thus there is no question of his attempting to deny that the foramen exists or that it acts as a foramen. Nevertheless, it is striking that his thinking is sufficiently compartmentalised for the difficulty I have mentioned not to have occurred to him.
Finally, a far more massive elision is involved in his treatment of diseases, where we may recall some of the problems raised in Chapter 1. How, we may ask, does an out-and-out teleologist account for diseases? Here, if anywhere, there is evidence of a failure of the good.[138] One argument that was available, and that Galen duly uses, is that nature can only achieve as good results as the material she has to work with will allow.[139] Left to herself, Galen says, nature would have made us immortal.[140] He also argues that residues, for example, are formed as the necessary by-products of other physiological processes that are essential to secure some good, and, again, that potentially damaging bile is needed to counteract the potentially damaging phlegmatic residues:[141] one thing leads to another. He asserts that when the animal is healthy, there is no danger, but adds that nature foresaw that it would be easy for excessive residues to be purged from the stomach by vomiting—a remedy long used by Greek doctors.[142] Nature evidently needs a helping hand; but Galen still fails to confront the question of the break-down of the system in ill-health. What good does that do?
[137] Whether Galen himself was the discoverer is not clear and has been doubted principally on the inconclusive grounds that he makes no claims in that direction (see May 1968, vol. 1, p. 331 n. 102, with references to earlier literature).
[139] See, for example, UP 3.10 (H) 1.175.3ff., (K) 3.238.11ff., 5.4 (H) 1.260.5ff., (K) 3.355.4ff., 17.1 (H) 2.446.11ff., 19ff., (K) 4.358.14ff., 359.6ff.
[140] UP 14.2 (H) 2.285.7ff., (K) 4.143.5ff., cf. also 5.4 (H) 1.260.7ff., 13ff., (K) 3.355.5ff., 11ff.
[141] See UP 5.3 (H) 1.255.6ff., 257.4ff., (K) 3.348.4ff., 350.16ff., and 5.4 (H) 1.258.26ff., 259.6ff., 263.20ff., (K) 3.353.7ff., 15ff., 359.17ff., especially.
[142] UP 5.4 (H) 1.259.11ff., 262.17ff., 263.1ff., (K) 3.354.3ff., 358.9ff., 18ff.
None, obviously; it is simply the necessary consequence of the materials we are made of. But the problem is that that factor had been appealed to before, to account for how we come to have residues in health. Why those potentially damaging residues should get out of control, why there is a disruption of the status quo in the body, is left unexplained, at least unexplained in teleological terms.
The thesis that nature always acts for the good can only be sustained by resolutely focusing on some parts of the phenomena to the exclusion of others that had also to be reckoned as part of common knowledge. The failure of the animal kingdom to be humans is not allowed to count as counter-evidence even to the weaker, qualified Aristotelian version of the thesis, for many animals, as degenerate or deformed, are not fully "natural." Nor are evident inconveniences in the anatomy or the physiological processes of humans allowed to tell against the stronger, Galenic position, and no more are diseases. It is not that teleology as such is mistaken in principle. On the contrary, in many areas and on many questions it proved itself in the ancient world—as it was also to do later—a marvellously powerful heuristic tool. Yet the negative features of its use, as a device for exclusion, for foreclosure, are manifest.
To try to understand this dominant—though, it should be repeated, far from universal—trend in ancient science, it may be helpful to recall our earlier discussions of the extent to which Greek scientists offered accounts that did not merely differ from but directly rivalled and aimed to supersede traditional mythical and religious beliefs and attitudes.[143] While many ancient scientists had no intention of incorporating a moral message in their work, many others had and did. Even where that was not the primary motivation of their inquiry, it was sometimes an adjunct to it. Ptolemy not only draws personal comfort from the order revealed by astronomy, he claims (following Plato) that it improves men's characters,[144] and that the same is true also of the
[143] Cf. above, Chap. 1, pp. 46ff.
study of harmonics.[145] But the revelation of order is not, of course, by itself bad science. The nub of the question is what kind of order, and how—with what scruples—secured. The double bind on the teleologists was that the greater the potential strength of the moral message concerning the beauty and goodness of nature, the more had to be set aside and either ignored completely or set down to necessity and to the recalcitrance of matter. The most striking examples of the difficulty arise in connection with claims made in the life sciences, but the exact sciences too exemplify the point,[146] and even where the good is not at issue, there were hesitations and waverings on the limits of permissible, and those of necessary, idealisations.
[145] See especially Harm. 3.4ff. (94.24ff. D.), on which see E. A. Lippmann 1964, chap. 2. The more general idea that harmonics reveals and demonstrates the orderliness and rationality of the works of nature (e.g., Harm. 1.2 [5.19ff. D.]) is echoed also by Porphyry In Harm. 24.22ff. D. Again, the notion of the moral value of music has the authority of Plato, e.g., Ti. 47c–d, cf. 80a–b, R. 522a. At Harm. 2.31–32, Aristoxenus mentions the view that the study of harmonics can make you a better person, but there expresses his own reservations on the topic.
The Value and Effect of Science in the Ancient World
These case-studies have raised a number of extremely general issues in the interpretation of ancient Greek science, and we may, in conclusion—and at the risk of still further sweeping generalisations—broach as a final topic the question of some of its values and effects. From the point of view of the ancient world it is worth asking what difference science made. The question relates to their point of view, since from ours parts of the answer, concerning what difference their science made, must be clear. From the Renaissance on, the myths and realities of Greek science have been enormously influential: myths, because the ancients' ideas have often been distorted when invoked on either side of later disputes, whether to be idealised or to be reviled; realities, because not everything that Greek science has been taken to stand for is mere fantasy, in particular not certain key methodological notions, including those of the value of empirical research, of the application of mathematics to the understanding of the physical world, and of an axiomatic deductive system. The repercussions both of those myths and of those realities have been immense, even though it goes without saying that not every idea influential in the rise of modern science has an ancient antecedent, real or mythical—in particular not our intense preoccupation with the possibility that science, by being applied, may provide the key to material progress and prosperity (an idea only modestly represented in the ancient world).[147] Moreover, when translated into modern terms and given an institutional framework as a result partly of that preoccupation, what were mere aspirations towards understanding and control in the ancient world have certainly been transformed in the process of their very actualisation.
[147] While the idea of the past advance of civilisation from a state of primitivism can be exemplified readily enough in poetry, in history, and in philosophy (the evidence is collected and discussed by Edelstein 1967b and by Dodds 1973 especially), the notion of future progress tends to find expression primarily in the context of the spiritual, not the material. Aristotle, for instance, occasionally states that nearly all possible discoveries and knowledge have been secured already (see Politics 1264a1ff., Metaph. 981b20ff.).
The blunter and in some ways harder question I proposed concerned the ancients themselves. There the inquiry into nature was generally an activity confined to a tiny elite and intelligible to not many more. Natural science, and even mathematics, established only very limited bridgeheads in what passed for moderately general education. Long after the correct explanation of eclipses was available, ordinary soldiers—and some of their generals—were still capable of being frightened by them, as the debacle of the Athenian retreat from Syracuse illustrates.[148] Moreover, in that instance, those ordinary soldiers were nevertheless able, at least according to the story in Plutarch, to win their freedom, in some cases, by reciting passages from Euripides.[149]
Even among the literate elite themselves, the gap between those who were capable of independent research and those who merely knew something about it was very great, as the immensely learned, but at points quite uncritical and confused, Pliny illustrates.[150] Introductory or elementary textbooks came to be produced in mathematics, astronomy, and medicine, but in late antiquity this increasingly had the negative effect of defining the outer limits of what there was to know, as much as the positive one of increasing the chance of what was within those limits being preserved.[151] Medicine, to be sure, was al-
[148] Thucydides 7.50; cf. Plutarch Nicias 23, which claims that while many understood that solar eclipses were caused by the moon, they had no explanation for lunar eclipses. Among well-known earlier texts that express some consternation at solar eclipses are Archilochus 74 and Pindar Paean 9.
[149] Nicias 29.
[150] Aspects of this in connection with the botanical and pharmacological sections in HN are discussed in G. E. R. Lloyd 1983a, part 3, chap. 3, pp. 135ff. Cf. Green 1954; Vegetti 1983, pp. 91ff.
[151] Thus in astronomy the phenomenon of the precession of the equinoxes, which had been discovered by Hipparchus and was the subject of a careful discussion in Ptolemy, was either ignored completely or flatly denied by later writers: see, for example, Proclus In Ti. 3.125.15ff., Hyp. 5.136.4ff., 7.234.7ff., Philoponus De opificio mundi 3.4.117.12ff. While Galen prides himself on his use of proof more geometrico , he expresses some diffidence in offering a geometrical demonstration of some optical phenomena in UP 10.12ff. (H) 2.93.5ff., (K) 3.812.14ff., putting it in 10.14 (H) 2.109.8ff., (K) 3.835.17ff., that most people would rather suffer anything than have to do geometry, and claiming that he has omitted many proofs that require astronomy,geometry, music, and so on from his works so that they will not be utterly hated by doctors, (H) 2.110.9ff., (K) 3.837.7ff.
ways of exceptional general interest.[152] The other main area that involves the inquiry concerning nature where knowledge and interest extended beyond a small minority was astrology, which must be granted an important positive role in keeping some scientific knowledge alive, since, as we remarked before, some of the same framework of theory underpinned it as underpinned the study of planetary motions in themselves.[153]
Much of the otherwise reasonably well-educated or well-read public remained very largely ignorant of advanced natural science. There were particular discoveries—such as that of the vast size of the universe in comparison with the earth—that might have had important repercussions on common assumptions, but they did not, or did not to any great extent, even when they were not totally ignored.[154] The day when science could shake the whole foundation of the belief in the privileged place of man in the universe was not yet. The ancients themselves often maintained the belief in some form, and they tended rather to be fortified in it by their scientific studies.[155]
[152] Yet the shrinking of medical knowledge can be illustrated in connection with the production of medical encyclopedias in late antiquity. In the mid-fourth century, Oribasius, encouraged as he tells us by the emperor Julian, collected "all that is most important from all the best doctors" in a comprehensive Medical Collection in seventy books (see Coll.Med.Reliq. 1 praef. 2, CMG 6.1.1.4.7f.). But Paul of Aegina, in the seventh century, referring to Oribasius' work in the proem to his own treatise, says that it is too bulky and offers his own shorter compendium: CMG 9.1 praef. 4.6ff.
[153] See above, Chap. 1, pp. 45f.
[154] On ancient views of the dimensions of the universe, see Préaux 1968, 1973, pp. 202ff. especially. There were, to be sure, those who denied that the universe is finite, but when, for example, infinite worlds were located beyond our heavens, that idea was not necessarily, and not even often, combined with any definite notions of the dimensions of our world: cf. Furley 1981a. One writer who did, however, draw out some of the implications of the minuteness of the earth in comparison with the sphere of the fixed stars is Seneca, for example at Quaestiones Naturales 1 praef. 11–13.
[155] This is especially true of zoological and anatomical studies such as those of Aristotle and Galen which we have considered, in which man is treated as the supreme animal.
One general moral was, however, quite widely learned. Natural scientific explanations appeared to have enough success to justify the general claim that natural phenomena have naturalistic explanations. Yet even here bad examples (such as the quite speculative and largely imaginary theories of thunder and lightning) were cited as often as good ones (such as eclipses), and it is notable that those who used this argument in late antiquity were more often philosophers—such as the Epicureans[156] —than those who actually engaged extensively in advanced scientific research. Meanwhile, more sinisterly, those successes of science, especially the demonstration of the orderliness of heavenly motions, were also appealed to, as early as Plato, in order to support a particular view of the moral governance of the cosmos, itself invoked—in Plato's case—as justification for drastic measures of social control directed against atheists and dissidents of every kind.[157] More generally, whenever the order revealed in nature could be represented as hierarchical, this provided grist to authoritarian mills.[158]
As seen by the average theatre-goer, those who studied nature were figures of fun, in Aristophanes' day, in Plautus'—and in Molière's.[159] Natural science was thus assimilated to any other kind of mumbo-jumbo or wonder-work, including to some more traditional modes of
[156] Yet, for the Epicureans, inquiry ceased when some explanation was available: see above, Chap. 3 n. 239.
[157] In Laws 10, the various types of atheists, who include those who attempted materialist cosmologies based on the denial that soul is prior to body, are made subject to penalties that are set out at 907d ff. The mildest of these—for anyone who does not heed warnings to reform and is convicted of impiety—is imprisonment, but death is prescribed in many cases.
[158] As Aristotle puts it at Metaph. 1075a16ff., "everything is ordered together in a way, but not in the same way," and he uses the example of a household and the distinction between slave and free to illustrate how different places are occupied by different kinds of being. Cf. Politics 1256b15ff., where plants are said to be for the sake of animals, and the other animals for humans, and the extended argument in Politics 1.1–5, especially 1253b14ff., 1254a17ff., maintaining that the distinction between the function of ruling and of being ruled—and so also that between master and slave—is natural.
[159] Aristophanes' targets range over a wide spectrum, including not just the new learning (represented in different ways by Socrates and by Euripides) but also more traditional modes: prophecy and divination are often his butt (e.g., Pax 1045ff., Av. 961ff.) and temple-medicine is at Plutus 665ff.
special wisdom such as prophecy or divination. Furthermore, although some ancient natural scientists were keen to differentiate themselves from rivals, whether from divination, from philosophy, or from within science itself, others, as we have seen, sought, rather, to associate their activity to moral philosophy (astronomy is good for the soul) or even to religion,[160] as when Galen talks about the study of the parts of animals in terms drawn from the mystery religions and speaks of his own book on that subject as a hymn to nature and, indeed, superior to ordinary hymns.[161] In part this simply reflects the modalities of the expression of the theoretical motivation of scientific research (which was not the only possible motivation; there were other, practical ones as well, especially in medicine).[162] But while to assimilate science to moral
[162] The possible practical applications of the knowledge gained from anatomical dissection, for instance, are emphasised by Galen in AA 2.2–3 in texts discussed above, Chap. 3 at nn. 229ff.
philosophy, to the pious worship of nature, even to prophecy, might make it more prestigious, even more comprehensible to a certain audience, this also masked certain differences between science and other modes of wisdom. Anatomical research might be described by Galen as an initiation into the mysteries of nature, but in many respects it was unlike any other initiation: it was harder work, and the results obtained were subject to a different kind of scrutiny and verification. Ptolemy too might hope that studying examples of heavenly order might make you more orderly in everyday life. But, again, that heavenly order was to be revealed only by distinct and rather rigorous methods.
Much of the ancient inquiry concerning nature was formalised common knowledge, and much was fantastic speculation. But some of it was neither, as we can see from such examples as the proofs of the sphericity of the earth, or of Archimedes' principle, or of the role of the valves of the heart, or by such discoveries as that of the precession of the equinoxes, or the nervous system, or the diagnostic value of the pulse. To express an allegiance to the principles of engaging in research and of securing a comprehensive and reliable data base, to the need to put theories to the test, to expose and root out unexamined assumptions, to withhold judgement where the evidence was insufficient, to acknowledge your own mistakes and uncertainty—all this was often no more than a matter of paying lip-service to high-sounding ideals. But if this was to bluff (and as we have seen, it often was), it was a bluff that could be called, and we have also seen how, on occasion, it was called, and how the ideals were at least sometimes lived up to and the promises they implied fulfilled.
For all the more or less ill-informed, at the limit actually malicious, confusion of science with some other kinds of wisdom—a confusion to some extent fed by the scientists themselves—it was, as those very scientists were, to judge from their practice, well aware, a wisdom with a difference. It was a wisdom committed to different procedures of discovery and of the justification of belief—even if the full force of those differences was hardly generally appreciated, and even if the full demonstration of its potential had to wait until modern times. It was more vulnerable than other modes of wisdom, since in principle it incorporated within itself an invitation to challenge its results (it gave
hostages to its opponents); at the same time it was more secure, insofar as parts of those challenges could be withstood successfully. It played for higher stakes, and sometimes won, even if not as often as it claimed. The distinction between science and myth, between the new wisdom and the old, was often a fine one, and the failures of ancient science to practise what it preached are frequent; yet what it preached was different from myth, and not just more of the same, more myth. The rhetoric of rationality was powerful and cunning rhetoric, yet it was exceptional rhetoric, not so much in that it claimed not to be rhetoric at all (for any rhetoric may aim to conceal itself), as in supplying the wherewithal for its own unmasking—even if some of its exponents did not notice that the mask was still in place. If many of the new wise men were short on delivery, they were long on aspiration, and the aspirations were of a kind that were, in time, to produce extraordinary delivery.
Meanwhile, however, the fact that in its beginnings, science was often explicitly concerned, if sometimes rather naively, with the moral dimension of the activity of science itself reminds us, if we need reminding, that it originated in no merely intellectualist debate. Indeed, its offering an alternative world view, in the widest sense an alternative morality, was central to some of its confrontations with traditional wisdom, though the fact that science may and to some extent must incorporate such values was rather to be lost sight of in the aftermath of the scientific revolution and has only gradually come to be recognised once more in recent times. There is a moral for us today, too, in the point that, again from its very beginnings, we can detect some tension in disciplines that professed that they must give a public account of themselves but that, to a greater or lesser degree, were bound to remain specialised, if not exclusive, studies. We have had many occasions to point to the mystifications of the ancient inquiry into nature, but of course that is a feature that is still with us today, and one whose threat has increased immeasurably with the increasing remoteness and specialisations of science—as one might say of the massive superstructures that have been erected on or, rather, built over the foundations laid by some ancient visionaries.