APPENDIX

Symbols and Machine Computation

Chapter 5 of this book presented a brief discussion of the tokening of symbols in computers. More specifically, it did two things: (1) it gave a brief examination of how the semiotic categories described in the Semiotic Analysis of chapter 4 can apply to things in computers, and (2) it distinguished these categories from an implicitly functionalist usage of the words 'symbol' and 'semantics' found in the works of some writers dealing with the computer paradigm. Chapter 5 offered only a cursory discussion of symbols in computers, as the main point there was simply to convince the reader of the facts that (a ) symbols (in the usual semiotic sense of that term) are indeed present in production-model computers, and (b ) most of our talk about "symbols in computers" is best cashed out precisely in terms of these semiotic categories. This appendix, by contrast, offers more of a full-dress examination of how the Semiotic Analysis might be applied to symbols in computers. In light of the distinctions made in chapter 4, this analysis can be broken down into the following four questions:

(1) The Marker Question: In what sense(s) and under what conditions can computers be said to store marker tokens?

(2) The Signifier Question: In what sense(s) and under what conditions can the marker tokens in computers be said to be signifiers (i.e., to have semantic properties)?

(3) The Counter Question: In what sense(s) and under what conditions can arrangements of marker tokens in computers be said to be syntactic arrangements?

(4) The System Question: In what sense(s) and under what conditions can the regularities of computer state changes be said to be governed by syntactic or formal rules?

The basic forms that answers to these questions may take have already been laid out in the technical locutions developed in chapter 4. These provide schemata for talking about how anything can be a marker, a signifier, or a counter. What remains is to fill in the details of how computers can contain such entities.

An object is said to be a marker, a signifier, or a counter by virtue of its relationships with conventions and intentions . It is the existence of marker-, signifier-, and counter-establishing conventions that render an object interpretable as a marker, signifier, or counter, and the possibility of such conventions that render it interpretable-in-principle as a marker, signifier, or counter. It is by virtue of authoring intentions that an object is said to be intended as a marker, signifier, or counter; and an object is said to be interpreted as a marker, signifier, or counter by virtue of the way it is construed or interpreted by someone who apprehends it. These modalities, moreover, are applicable to objects of any conventionally determined type. Notably, larger units of language games, such as proofs of theorems, are subject to the same distinctions: a series of marker tokens can only count as a token proof if there is a language game which involves proofs, and whose criteria for being a proof are met by the series of marker tokens. If computer state changes are to be viewed in terms of formal rules, one must therefore also ask how their having a description that involves formal rules is dependent upon conventions and intentions.

This appendix will separate the questions that deal with convention from those that deal with intention . The discussion of convention will examine conventions by which the contents of storage devices in computers count as marker tokens, how those marker tokens are conventionally associated with semantic interpretations, and how their arrangements count (by convention) as syntactic arrangements. The section on intention will discuss the ways in which the states of the computer are further involved in networks of human intentions—notably, those of computer designers, programmers, and users.

A.1—
The Design Process and Semiotics

Computers come into relationship with conventions and intentions at two junctures: in the design of hardware and software by engineers and programmers, and in the use of computers by end-users. Both the design process and the user's understanding of the computer must be articulated in terms of tasks the computer is to perform—tasks such as the evaluation of mathematical functions, the storage and editing of text, the statistical analysis of data, the proof of logical theorems, etc. Such an understanding of what computers do presumes that computers are in some sense "symbol manipulators." But neither designers nor endusers are usually concerned with questions about just how the things they are dealing with can be said to be symbols, or how the processes can be said to count as analyses or proofs. From the design standpoint, one begins with some set of tasks one wishes to automate—the evaluation of some set of mathematical functions, for example—and then sets out to design a system that is appropriate to that task. This involves (a ) determining what sorts of things need to be represented, (b ) deciding upon a way of representing those things, (c ) determining what processes and relationships between those things need to be captured, and then

(d ) designing hardware or software that will manipulate the representations in a way that mirrors the relationships between the things represented and tracks the processes which they undergo.

The design process thus proceeds "top-down" from an informally specified task, and from there to a more rigorous description of the task, thence to a system of representations and functions, down to the "functional architecture" of the program or the machine, which is in turn realized through the hardware. The semiotic questions to which we need answers, on the other hand, require us to proceed "bottom up" from the hardware through functional architecture to the levels at which the machine may be said to be storing markers, counters, and signifiers and performing operations such as evaluating functions. The designer is concerned with questions about what system of representations and functions will allow the computer to perform certain tasks. But we are concerned with the more basic question of how and in what senses what the computer does can be said to involve representations and formal operations in the first place.

The discussion here will thus proceed in very much the opposite direction from the design process. Whereas the design process proceeds from the assumption that one can unproblematically speak of computer representations and operations and seeks the right functional architecture, we shall begin by assuming that it is unproblematic that computer hardware and software are functionally describable and that this description forms a level of analysis distinct from the description of the computer in physical terms (since the same functional architecture can be realized through different components). We shall then ask how and in what senses the objects picked out by the functional description can further serve as the basis for the tokening of markers, signifiers, and counters, and how the functionally characterized state changes can be deemed to be rule-governed processes.

A.2—
The Functional Level

Digital computers are functionally specifiable devices . That is, the workings of a digital computer can be seen wholly in terms of the interrelationships of its components and relations to inputs and outputs. Each of the components, moreover, is itself a digital device—i.e., one that is capable of being in some integral number of mutually exclusive states, and is always in one of those states whenever the computer system is in operation. (Most production model computers are composed of binary digital devices—i.e., devices capable of exactly two stable states.) The state of the entire computer at any time t is a function of the states of its many components. We shall follow Turing (1936) in referring to this overall state of the machine as its "complete configuration." The complete configuration of a machine may be viewed as an ordered n -tuple of the states of its n components.

It should perhaps be noted at least in passing that viewing the computer as a digital device requires a certain amount both of abstraction and of idealization from its physical description. One abstracts away from properties of the machine that are irrelevant to its functional description (e.g., its weight and color); but one also performs a more important abstraction in treating as equivalent phenomena that may be different for the physicist's purposes (slightly different volt-

age levels that do not affect the behavior of a circuit, differences in timing that are fine-grained compared to the clock speed of the machine, etc.). One idealizes the behavior of the computer by making certain background assumptions that may not always be true in vivo—for example, that electric current of the proper voltage is running through the machine. Change the voltage or cut off the power supply, and of course the functional description no longer describes the actual behavior of the machine. When one treats the "proper" background conditions as given, one is making an idealization, albeit an innocent one. Similar idealizations are necessary for most if not all nomic descriptions in the sciences.

Many of the components of a digital computer are devices with inputs and outputs. To take an example, an electronic AND-gate circuit has two or more input leads and one output lead. Each lead has an active or "on" state (characterized by some physical property, such as a high voltage level) and an inactive or "off" state. The circuit, moreover, is so designed that the output lead will be active just in case every input lead is active. The AND-gate is functionally specifiable in the sense that the state of the output lead may be viewed as a function of the states of the input leads. (This is a use of the term 'function' in the strict mathematical sense.) One may represent the functional configuration of the AND-gate by way of a table showing the state the output lead will be in for each configuration of input leads:

In a similar fashion, the entire computer may be characterized by a function table—called the machine table for that computer—which specifies, for each complete configuration, what the next states of the various components will be. In a relatively few cases, the computer will be completely deterministic, and its function table will specify, for each complete configuration, the next state of every component. (This is the case, for example, with the machine Turing describes.) In most cases, however, the computer will have input devices, and these will include transducers whose states are partially determined by environmental conditions to which they are designed to respond. In these cases, the machine table maps from complete configurations to equivalence classes of complete configurations, where complete configurations in the same equivalence class are identical except for the states of input transducers. (Alternatively, it maps from ordered pairs [complete configuration, input configuration] to complete configurations.)

It is possible for computers and other functionally specifiable devices to have isomorphic machine tables and yet be built from different components. To use the simple example of the AND-gate, such a circuit can be realized in many ways. It can be built from vacuum tubes, for example, or from transistors. The result-

ing circuits are different physically because they are made from different components, but are math-functionally equivalent, because the mappings from inputs to outputs are isomorphic. In similar fashion, two computers can be math-functionally equivalent even if they differ in physical structure, so long as they share a machine table. Descriptions at the math-functional level are thus not reducible to physical descriptions, since there are many ways that a given math-functional description can be realized.

The functional level of description thus involves a significant abstraction from the various levels of physical description, since it picks out equivalence classes of objects by virtue of the interrelationships of their component parts while abstracting from the physical nature of those parts. Yet functional description picks out real relationships between components which are physical particulars, and what it picks out does not depend on convention. To get from physical description to functional description, one need only abstract; no interpretation is necessary.^[1]

An individual object may be subject to more than one functional description, and thus may be describable as being a computer of more than one type. (Similarly, if one is creatively inclined, it is possible to find a way of describing any collection of objects as a system of digital devices—with the consequence that any collection of objects has a description as a computer.) Computers can, moreover, be subject to multiple functional descriptions in ways which are connected to the intentions of the designers and programmers . A program running on a computer causes it to function in particular ways, and the way a computer works by virtue of running a particular program may itself be described by a function table. Such a table will not be inconsistent with the machine table for that computer, but will not involve some of the complete configurations that appear in the machine table at all and will treat others as equivalent. The resulting table, moreover, may very well be isomorphic to the machine table for some other computer, in which case the program run on the first computer may be said to emulate the second. The functionally describable system of relationships set up by such a program is sometimes called a virtual machine because the first computer functions like the second while running the program.

The term functional architecture will here be used to denote any functionally describable system of interrelationships in a computer, be they those realized through a program or those of the hardware of the system. (This is probably the most prevalent use of the expression 'functional architecture', but it is worth noting that some writers [notably Pylyshyn 1980, 1984] reserve the expression 'functional architecture' for the functionally described hardware . Here the broader use will be adopted, since from a functional standpoint there is nothing of unique interest about the hardware used in computers. If a distinction need be made, one may simply qualify the expression with the words 'hardware' or 'program'.)

A.3—
Functional Architecture and Semiotics

The components picked out by the functional description also play roles in the way the computer is used. Some of them are used for storage of symbolic repre-

sentations. Others are used to manipulate such representations in a way that is useful for the evaluation of mathematical and logical functions and the manipulation of symbol strings. Those used for storage are relevant to the discussion of computer markers, signifiers, and counters. Those used in programs that govern the state changes the computer is to undergo are relevant to the System Question.

It is important to note, however, that while the functional architecture of the computer may render it suitable for the storage of markers, signifiers, and counters, there is nothing about functional architecture in and of itself that makes what is in computer storage a marker, signifier, or counter. The functional architecture is indeed designed so as to accommodate representations, and the operations the computer is built to perform are designed so that the changes in representations that they induce will be interpretable as derivations in accordance with syntactically based rules. But it is only by virtue of conventions and intentions that the storage locations picked out by functional description and realized through physical parts of the machine can count as storing marker tokens. And the reason for this is perfectly straightforward: an object is only said to be a marker by virtue of its relationships to conventions and intentions.

It is useful for purposes of analysis to treat each level of convention as characteristic of a particular level of analysis. At the marker level, marker conventions allow things picked out by functional description to count as marker tokens. Once one has a set of marker conventions, one can then adopt syntactic conventions and construe arrangements of them as syntactic arrangements (at the counter level ) and adopt semantic conventions linking markers with interpretations (the signifier level ). Finally, once one has adopted syntactic conventions for expressions, one can apply conventions that allow one to interpret the state changes induced by a program or a hardware function as governed by syntactically based rules (the system level ). The resulting hierarchy may be represented by a diagram (see fig. A1).

Several features of this model are worthy of emphasis. First, there is a fundamental difference between the physical and functional levels, on the one hand, and all of the higher levels on the other: namely, the former do not involve convention, and the latter do. Indeed, each level above the functional level is reached by way of an additional set of conventions. A second important feature of this analysis is its treatment of the relationship between the signifier, counter, and system levels. Here the signifier and counter levels are treated as being parallel and independent . The reason for this is simple: there are semantic conventions that are not dependent upon syntax and syntactic conventions that are not dependent upon semantics. This does not mean that no semantic conventions presume any notion of syntax, or vice versa. (The meanings of complex words are sometimes a function of the syntactic arrangements of bound and unbound morphemes, for example, and the meanings of sentences a function of the meanings of the words.) What it does mean is that there is no absolute priority between syntactic and semantic conventions. There is, however, a priority relationship between the counter and system levels: in order for a succession of computer states to be interpretable as in accordance with a formal rule, it must be the case that the individual states be interpretable as counter tokens. (Otherwise there is

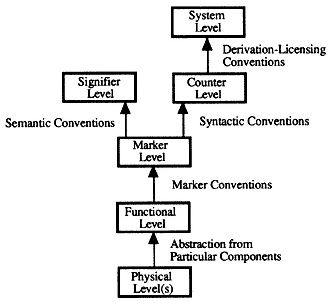
Figure A1

no syntactic structure to them on the basis of which the rules can be applied.) But the reverse does not hold: one can very well interpret a series of computer states as a series of syntactically structured entities without interpreting the series as something licensed by formal rules.

The structure of this model seems clearly licensed by the semiotics developed in chapter 4. The relationships and priorities it picks out are those relevant to computer semiotics. For other purposes—such as those of the system designer—they admittedly might prove irrelevant or even confusing. To answer the questions of how and in what senses computers can store and manipulate symbols, however, one must proceed upwards from the level of functional architecture and ask how conventions make storage locations interpretable as bearing marker tokens, and how these in turn are interpretable as signifiers and counters. One may then ask how computer processes involving these conventionally determined entities are interpretable as involving formal rules. Having answered these questions about the role of convention in the semiotics of computer storage, we may then ask how the things that are interpretable in these ways are related to actual human intentions.

A.4—
Markers in Computers

How, then, are the storage locations that are picked out by functional description and realized in actual computers through particular hardware components to count as markers? The question is best approached through examining a par-

adigm example. Consider the devices employed for circuit storage in production-model computers. The circuit storage of production-model computers generally consists of a series of bistable circuits or flip-flops . These circuits have two output leads (generally designated by the numerals 0 and 1), and have an internal configuration such that exactly one of the output leads will be at some particular higher voltage level (e.g., +10V relative to ground) and the other at some other, lower level (e.g., -10V). The state of the circuit is determined by which output is at the high voltage level: if the 0-output is at +10V, the circuit may be said to be in its 0-state, and if the 1-output is at +10V, it may be said to be in its 1-state.^[2]

It is important to note, however, that describing a circuit in digital terms—namely, as having a "1-state" and a "0-state"—is not tantamount to describing it as storing numerals or numbers . The digital description of a circuit is an abstraction from its many possible physical states, an abstraction that picks out two equivalence classes of physical states. In the case of the bistable circuit, the equivalence classes are picked out both architecturally (by the behavior of the circuit in and of itself) and functionally (by its relationship to the rest of the machine). Architecturally, the structure of the circuit is such that there are some states that are stable and some that are not. The stable states fall into two clusters: those that involve voltages very close to +10V at the 0 output and those that involve voltages very close to +10V at the 1 output. The states within each of these clusters may be treated as equivalent, and any state within the one cluster may be called a "0-state" and any state within the other cluster a "1-state." If the computer system has been properly engineered, these same equivalence classes will also be those picked out by the functional description of the computer—i.e., it will be differences in the digital state of the circuit, and only such differences, that will have an effect on how it influences other components of the system. There will be cases in which the state of that circuit will help determine the next state of the overall system, but only those differences picked out by the digital description (and not, for example, minor differences in voltage level at the outputs) will make a difference in the behavior of the overall machine. The labels '0-state' and '1-state', however, are just convenient labeling conventions we have chosen to provide, and signify no special relationship to particular numerals or numbers. (We might as well have called them the "cat-state" and the "dog-state" or the "Isaac-state" and the "Ishmael-state.")

Other digital storage media function in an analogous fashion. In each case there are atomic storage locations that are ordered and capable of some integral number of discrete states. In the case of magnetic disks and tape, for example, the storage locations are regions of the disk or tape, and the physical property that determines the state of a location is the magnetic flux density at that location. In the case of paper cards and tape, the storage locations are again regions of the card or the tape, but the physical property that determines the state of the location is the presence or absence of a perforation at that location. In each of these cases, one may call one of the two possible states of each location the "0-state" and the other the "1-state." Similar descriptions can be given for other media, such as magnetic cores and holographic disks.

While neither the internal structure of the storage location nor its functional

role makes it count as being or storing a marker token, there are conventions whereby either the states of single atomic storage locations or patterns of states found across series of such locations can serve as the criteria for conventional types. One could, for example, adopt a convention for the tokening of markers in individual flip-flops. The convention would set up two marker types: the criterion for one would be the circuit's being in its 1-state, and the criterion for the other would be the circuit's being in its 0-state.

Such a convention would be of very limited use, however, since it would limit one to two marker types. One can obtain a more flexible convention by typifying markers according to the pattern of digital states across a series of atomic storage locations. A string of n storage locations, each of which is capable of i different states, can hold any of iⁿ different digital patterns . In production-model computers, bistable circuits in memory generally function in groups—most often in groups of eight, sixteen, or thirty-two—and the most elegant way of understanding the coding schemes used with computers involves treating groups or sequences of atomic storage units as storage locations for markers. The criteria for marker types are patterns or sequences of 0-states and 1-states present across the series of circuits making up the group. The further conventions by which computer states can count as representations of numbers, text, etc., involve assignments of interpretations to states typified by such digital patterns .

This way of describing the patterns in storage has several important advantages. First, it provides a way of seeing that the same pattern can literally be present in two very different storage media. Second, as a result of this, if digital patterns are used as criteria for marker types, the typification of markers can be independent of the nature of the storage medium—i.e., the same marker types can be used whether one is dealing with bistable circuits, magnetic tape or disk, paper tape or cards, holographic disks, etc. So long as a storage medium is composed of atomic units that have a digital description, series of atomic units can hold a digital pattern, and a convention may be employed whereby objects possessing digital pattern P_i are interpretable as tokens of marker type M_j . One may, moreover, adopt a canonical notation for digital patterns which can be used to represent them regardless of what medium they are present in. In the case of binary patterns, the numerals 0 and 1 may be used, and the pattern represented by a concatenation of these numerals: for example, 00001111, 101, etc. These sequences of token numerals are representations of patterns. The individual numerals do not represent anything in particular, and the pattern itself is not composed of numerals or numbers, though a sequence of numerals is itself an object in which such a pattern is present.

While any binary pattern whatsoever can serve as the criterion for a marker type (and hence any object possessing a binary pattern is interpretable-in-principle as a marker token whose type is typified by that pattern), only a very small subset of such patterns is actually employed in the design, programming, and use of a computer. In general, computers are designed with several basic kinds of operations in mind—notably, logical operations, mathematical computations, and operations upon text and other symbol strings—and the designers usually decide upon efficient ways of storing text and representing mathematical and boolean values. Efficiency may require that different computer operations work upon

strings of different lengths—e.g., one might use a sixteen-bit storage location to represent an integer, but employ a larger location to represent a floating-point number. The design process will thus characteristically involve developing conventions for several sets of marker types. Some of these will be fixed-length types—e.g., sixteen-bit patterns for integers, thirty-two-bit patterns for floating points, sixty-four-bit patterns for machine language instructions—while other types may be defined by a rule that allows for strings of variable length.^[3] (A LISP machine, for example, would be designed to work with LISP files which are conceived of as lists, which are among other things concatenations of markers. A list, moreover, can be of any length.) Additional conventions may be supplied by the programmer, whose program may require data structures that use fixed-length strings of lengths other than those used for general machine functions or variable-length strings that are governed by rules other than those directly accommodated by the design of the machine. (A LISP interpreter, for example, may be run on a computer that is not itself a LISP machine.) It is in virtue of such conventions that a pattern across a storage location may be said to be interpretable as a marker token.

A.5—
Computer Signifiers

Like other markers, those in computers can be used to bear semantic values if there are conventions linking marker types to semantic interpretations. There are two basic kinds of conventions that link marker tokens in computers with semantic interpretations. Conventions of the first kind, which will here be called representation schemes, associate marker types with semantic interpretations: for example, with the boolean values true and false, with integers, or with floating point numbers. The second kind, which will here be called coding schemes, do not associate marker types directly with semantic interpretations, but rather associate marker types with other marker types. The ASCII code, for example, associates the alphanumerics and other graphemic characters with computer marker types typified by binary strings. Although a coding scheme does not itself involve any direct association of marker types with semantic interpretations,^[4] it indirectly allows for the representation in the code alphabet (e.g., in the set of marker types used for ASCII coding) of anything that may be represented in the source alphabet (e.g., the set of graphemic characters used in written English).^[5]

Consider the kind of representation scheme often employed for the representation of integers in computer storage. Such schemes generally employ fixed-length storage locations to store representations of integers. Contemporary computers tend to use sixteen-bit or thirty-two-bit locations, but for ease of notation let us discuss a convention which employs an eight-bit location. Each eight-bit storage location is a series of eight binary storage units, each of which is either in its 0-state or its 1-state. The eight-place series of binary locations carries a binary pattern of length eight. There are 2⁸ or 256 such patterns, and this set of patterns can provide the criteria for 256 marker types. A number of notational conventions are employed to indicate such patterns, and generally are treated as equivalent. The most perspicuous way to note a marker type is to use the string

of 0s and 1s which serves as the canonical representation of the binary pattern characteristic of that type. Other notations, however, are possible, and may be advantageous for reasons of brevity. A representation of a binary pattern may also be read as a representation, in base-2 notation, of an integer, and the pattern can be more briefly noted by the decimal or hexadecimal (base-16) notation for that same integer. (Thus the binary pattern whose canonical notation is 11110000 might also be noted by the decimal string 240 or by the hexadecimal string $F0.)^[6]

The most commonly used representation schemes for the integers also exploit the relationship between the notation for the pattern present across a series of binary storage locations and the base-2 notation for integers: since the canonical representations of binary strings can also serve as representations of integers in base-2 notation, it is convenient for an interpretation scheme to assign to a string of binary digits the integer that string would represent if interpreted under base-2 conventions. However, since there are both positive and negative integers, one of the digits of the string is used to indicate the sign of the number. Here, then, is a sample convention for the interpretation of markers typified by eight-digit binary strings as representations of integers:

(1) If the first digit of the canonical representation of the string is a 0, take the remaining seven digits and interpret them as a representation of an integer in base-2 notation; this is the number the marker represents under this convention.

(2) If the first digit of the canonical representation of the string is a 1, take the remaining seven digits and interpret them as a representation of an integer in base-2 notation; multiply this number by -1; the resulting number is the number the marker represents under this convention.

While computers are often thought of primarily as "number crunchers," and while the bulk of computation done by production-model computers may well be numerical, representation schemes can be devised which will link computer marker types with any interpretations one might like. A series of binary storage locations n bits long can hold any of 2ⁿ binary patterns. If these binary patterns are used as the criteria for a set of marker types, these marker types can then be associated, via signifier conventions, with as many as 2ⁿ interpretations. For example, the boolean values true and false can be represented in a single binary storage location, with a 1-state indicating one value and a 0-state the other. Similarly, if one wished to be able to represent the twelve apostles, the set of sixteen four-unit binary patterns would provide criteria for enough marker types to ground an unambiguous representation scheme, even if one included Judas and Paul. One would simply employ a convention, for example, whereby the marker type typified by the binary pattern 0000 would stand for Peter, 0001 for Andrew, etc.

Computer markers can also be used to store meaningful data in a way that does not depend upon conventions that directly associate computer marker types with semantic interpretations. A second sort of convention—a coding scheme —takes marker types that are already employed in meaningful language games (e.g.,

the graphemic characters used for inscriptions of natural languages) and associates them with marker types in a "code alphabet" such as a set of marker types typified by binary patterns. The ASCII coding scheme is probably the most familiar example of a scheme that associates computer markers with markers of other types. The scheme takes marker types characterized by seven-bit binary patterns and associates them with a set of graphemic symbols which includes the upper- and lower-case letters, the numerals, punctuation symbols, and a number of additional frequently used graphemes, plus several less familiar types used to represent the backspace, spacebar, and return keys found on a computer keyboard. Unlike the mapping involved in the representational scheme for the integers, the mapping involved in the ASCII convention is most easily expressed not by a rule that maps marker types onto interpretations, but by a table that associates binary patterns with the graphemes with which they are paired under the convention.

The encoding of text under the ASCII convention is fairly straightforward. A file containing text is simply a sequence of storage locations, each of which bears a pattern that renders it interpretable as a marker suitable to the ASCII convention.^[7] But the convention for ASCII coding is a convention for the coded representation of text —a convention whereby sequences of binary strings can encode sequences of graphemes. The purpose of the "encoding," moreover, is not to make the message unreadable, but rather to make it suitable for storage in a computer, and hence to make it readable through the mediating operations of the machine. It is thus reasonable to view an ASCII file produced by a word processing program as containing text in a natural language, albeit in a notational form that differs from written language. It is not natural language text by virtue of consisting of seven-digit binary patterns, of course; rather, it is natural language text because there are conventions for the graphemic representation of linguistic items and further conventions for the translation of these graphemic representations into ASCII notation. A properly encoded message retains its imputed semantic value, and does not lose it just by virtue of the encoding. The explanation of how the marker type may be said to be associated with an interpretation, however, is slightly more complex in the case of symbols in a code, because there are two levels of convention involved: (1) the coding conventions associating items in the source alphabet with items in the code alphabet (e.g., the ASCII code), and (2) the semantic conventions associating items in the source alphabet (e.g., strings of graphemes) with interpretations. (One might, of course, view phonemically based written language in a similar fashion—i.e., as involving coding conventions associating phonemes with graphemes and semantic conventions associating strings of phonemes with interpretations.)

A.6—
The Counter Question

The syntactic properties of computer markers depend in similar fashion upon the web of conventions and intentions of designers, programmers, and users. Since computer storage locations are arranged in series, there can be sequences of markers in storage. Some language games involve syntactic patterns whose criteria pick out equivalence classes of marker sequences. Insofar as a marker

token fits into one of the slots of such a pattern, it may be called a counter in that language game. The kinds of "fit," moreover, are the four modalities of chapter 4. In the case of computer storage, there can be several different sources for the relevant conventions and intentions. In pure cases of coding, such as ASCII files containing text, the coded sequence inherits the syntactic properties of the uncoded sequence. In the case of more structured representations such as records containing multiple fields, the conventions are those of the programmer who designed the representation structures. Finally, in some cases, such as parsing programs and theorem provers, the syntactic structures are picked out by more flexible rules. The computer can be made to be "sensitive" to syntactic structure—i.e., can be so designed that its operations covary with the presence and absence of a particular structure—but the computer cannot literally be said to recognize syntactic structure.

A.6.1—
Coding and Inherited Syntax

The storage of text in computer storage media is often accomplished through the use of a coding scheme. When this is the case, the text file is stored in a series of storage locations, each of which holds a marker of a type appropriate to the coding scheme that is being employed. The file is thus a series of tokens from the "code alphabet," each of which is associated by the coding scheme with some type in the "source alphabet." In many cases, there is an almost exact correspondence between the series of markers in computer storage and the series of graphemes that would appear in a printed representation of the same text.^[8]

Graphemic characters are used in language games that have syntactic structures. Notably, they are used for writing text in a natural language. This means that there are conventions whereby strings of graphemes can count as written tokens of words, sentences, assertions, etc. Token sentences in natural languages have syntactic structures, and this is true independently of whether the sentences are spoken or written. And so a token string of graphemes can (by virtue of conventions) count as having a syntactic structure. Encoding the string of graphemes by substituting for each the binary string it is associated with by the ASCII convention preserves both the ordering of the marker tokens and the syntactic properties that they have by virtue of being written language. If a coding scheme is used for encoding text, the coded message preserves the syntactic properties of the original.

Here, then, is one way that markers in computers can be said to have syntactic properties: if (a ) there are conventions setting up a one-to-one coding scheme whereby a set C of computer markers are used to encode some other set M of markers, and (b ) there is a language game G which uses markers from M , and (c ) G is syntactically structured. In such cases, strings of markers in the computer preserve the syntactic structures of G .^[9] In this sense, all of the syntactic features of natural language can be preserved in computer storage in precisely the way that they can be preserved in printed text.

To most of these features, however, the computer is likely to be little more sensitive than is a printed book. Research in artificial intelligence has made some inroads into sentence parsing, but the average computer does not have a sentence

parser. Nor does it need one in order to store coded natural language text, any more than a book needs a parser in order to contain written sentences. The computer's insensitivity to grammatical features of text it stores places limits on what it can do with that text—e.g., its ability to respond to questions or requests for deductions—but does not impair its ability to store syntactically structured text.

A.6.2—
Structured Representations

Computer design and programming can and does make use of syntactic structures to which the computer is sensitive as well. In programming, for example, it is common to create complex representational structures by combining simpler ones. Suppose, for example, that a researcher in the social sciences is engaged in an experiment in which he uses a questionnaire with fifty true-false questions. He wishes to store the results of the questionnaire in a data base and then run several statistical analysis programs on his data, and wishes to index the answers from each questionnaire by the Social Security number of the participant. An efficient and intuitively appealing way of organizing the data is to think of the information from each questionnaire as one record, and the entire data base as a series of records. Each record holds an encoded social security number and fifty representations of answers to questions.

Such a record could be stored by means of a complex marker structured in the following way: (1) a series of nine seven-bit locations holding the ASCII encodings of the digits of the Social Security number, followed by (2) a series of fifty one-bit locations holding representations of the boolean values true (represented by a 1-state) and false (represented by a 0-state). What has just been articulated is a convention for a complex data type. The convention specifies not only the coding and representational schemes to be employed, but the syntactic structure of the record as well. And this sort of syntactic structure the programmer would assure that his program was sensitive to, since he wants to be able to have access to different kinds of information and wants to be able to perform different operations on different kinds of information.

A.6.3—
Rule-Governed Syntactic Structures

A slightly more complex example along similar lines could be provided by a program such as a parser or a theorem prover. Here, however, the syntactically structured types are not set up in terms of fixed-length representational structures, but are articulated in terms of rules governing classes of concatenations of markers. A program designed to generate derivations in the sentential calculus, for example, might check a representation of a proposition to see if it fit any of a number of syntactically structured patterns such as the following:

[negation sign],[wff]

[wff],[implication sign],[wff]

[wff],[disjunction sign],[wff]

[wff],[conjunction sign],[wff]

Checking a string of markers against such templates might involve a fairly complicated test procedure, especially since the operation might have to be recursive to determine whether a given substring is a wff . The aim of such a procedure, however, is simply to provide a means of determining when a representation is of one of the syntactic types relevant to derivations in the propositional calculus. And it is important to distinguish the ability to determine whether the syntactic structure is present from the fact that it is present. A computer marker string can have a syntactic structure just by virtue of being associated with some syntactically structured human language game, as in the case of stored text, without the computer being sensitive to the syntax. It is, however, possible in some cases to make the computer sensitive to the syntax—namely, in those cases where the syntactic class can be picked out by a rule that operates upon marker concatenations.

A.6.4—
The Nature of the Computer's Syntactic "Sensitivity"

But just what does the computer's "sensitivity" to syntactic structure amount to? In this sort of case, a computer may be said to be "sensitive to" a syntactic pattern P just in case (1) there is a functionally describable operation provided by the hardware or the programming which (2) takes marker strings as input and (3) whose output depends precisely upon whether the input string can be construed as having pattern P . What this most assuredly does not involve is any understanding of syntax on the part of the computer. The computer's "sensitivity to syntax" is a matter of computer operations on marker strings tracking conventionally sanctioned syntactic construals of those strings. The computer does not recognize syntactic patterns as syntactic patterns. To recognize something, it would have to be a cognizer; and to construe patterns as syntactic, it would have to be privy to the conventions of a language game. It may well be that it is logically possible for there to be computers which were also cognizers and could share our conventions; but it is not necessary to posit such things about actual computers in order to explain what they already do. For this all one need see is that the functional architecture of the computer and the programs it runs can be so designed that computer operations will be in a relationship of causal covariance with syntactic patterns licensed by (human) conventions.

A.7—
Formal Rules and the System Question

Thus far the discussion of computer semiotics has been confined almost exclusively to questions about symbol tokens . And what has been said about the way these are related to conventions is very similar to what might have been said about printed text on a blackboard or a page of a book. Yet computers differ from blackboards and books in one very important respect: whereas blackboards, books, and computers can all serve as media for storing symbols, computers can also in some sense manipulate symbols, while blackboards and books cannot. Moreover, the manipulations may be construed as corresponding to formal rules. To see how this is so, it is useful to separate two issues: first, how individual functions performed by either circuitry or software can be viewed as cor-

responding to formal rules; second, how the machine table of the entire computer may be viewed in such a fashion.

First, consider a program that is designed to evaluate mathematical functions such as integrals. The designer of the program presumably will know a number of techniques for integrating different sorts of expressions—indeed, the familiar methods for integration involve a piecemeal set of rules for expressions with different syntactic forms. What the designer does is to find an efficient way of encoding a wide range of expressions that will preserve the syntactic features relevant to the integration methods, and then write a set of procedures corresponding to the different integration techniques. Each procedure will contain two parts: a section which tests a marker string supplied to the program to see if it has the right syntactic form for that integration technique, and a section which generates a new marker string if the result of the test is positive. The new marker string should correspond, under the designer's coding conventions, to the result of integrating the expression encoded by the string sent to the program.

How does what the procedure does end up counting as a derivation in accordance with a formal rule? It does so because (1) the procedure generates a new marker string only if the input string is within an equivalence class whose members are interpretable^[10] as being of a syntactic type T (i.e., only if it is of the right counter type), (2) the output string it generates is interpretable as being of a syntactic type U , and (3) there is a language game L containing a syntactically based rule whereby expressions of type T license the derivation of expressions of type U . There is thus an analogy between aspects of the language game on the one hand—namely, (a ) the derivation-licensing rules, (b ) the expressions already derived, and (c ) those expressions whose derivation is licensed on the basis of (a ) and (b )—and aspects of computer procedures: namely, (a ́) the hardware or software that performs the operation, (b ́) input strings that cause the hardware or software to perform its operation, and (c ́) the output strings produced as a result.

A.7.1—
Causality, Functional Architecture, and Formal Rules

The computer operation, however, has two aspects: causal and symbolic. And it is essential that the two aspects be distinguished . For the causal propensities of any computer operation can be described in purely functional terms (i.e., as a function to and from equivalence classes of digital patterns) without any mention of symbols or syntax. Understanding the operations of the computer function in syntactic terms involves the imputation of symbolic status to what is in the computer, and this involves convention. It is, of course, the task of the designers of hardware and software to make the functional architecture that is to perform manipulations of symbols correspond to formal rules. It may additionally be the case that all functions performable by a computer can be interpreted as rule-based counter manipulations. But the fact that a physical process has a functional description no more makes it the application of a syntactic rule than the fact that a storage location is picked out by a functional description of a computer makes the state of that location the tokening of a marker. Functional description simply does not suffice for syntax, because syntax requires convention as well.

A computer function is thus interpretable as a derivation in accordance with a formal rule if three conditions hold. First, there must be a functionally describable, causal covariation between inputs and outputs for that function. Second, those inputs and outputs must be interpretable in terms of syntactic categories. And third, there must be formal rules available under which counters of the types that cause the function to produce an output would also license the derivation of counters of the types produced by the function in response to such input.

It is absolutely essential to note that there is no mention here of the computer dealing with syntax as syntax . Rather, the functional architecture is designed in such a fashion that the causal covariations will track syntactic relationships. It is thus misleading at best to say that a computer "knows" or "deals with" syntax but not semantics. Functional architecture can support state changes that track the formal relationships used in syntactic derivation techniques. But it can in similar fashion support both static data structures and state changes that track semantic relationships. There may be a large difference in degree between what syntactic features can be supported and what semantic features can, but the computer's relationships to syntax and semantics are quite parallel: it is said to involve each only by virtue of conventions.

We should thus be very careful to make the distinction between saying that state changes happen in accordance with a rule (i.e., in a fashion interpretable as licensed by such a rule) and saying that they involve the application of a rule. Computers do not apply rules. Or even if there were some computer that was part of our linguistic community and could make semiotic conventions, this would be something more than what we are talking about when we say, in general, that computer state changes are "rule-governed." Here we merely mean that computer storage locations are interpretable as counters, and that the computer operations that change the states of computer components are interpretable as functions to and from equivalence classes of counters, and that such functions may be expressed in the form of syntactically based rules.

A.7.2—
The Machine Table and Formal Rules

It is not only small, local computer functions that may be viewed as rule-governed in the sense articulated above. The entire machine may also be described in such a fashion. The entire computer, after all, is characterized by its machine table, which is a function table from complete configurations to equivalence classes of complete configurations. Seldom are there explicit syntactic conventions for interpreting the complete configuration of a machine as a syntactically structured marker string, but one could create such conventions. (Turing [1936], for example, gives such conventions for describing the machine state of the machine he describes.) The complete configuration, after all, is an ordered n -tuple of the machine's n constituent components. If one employs a marker convention that would link each possible component state with a marker type, each complete configuration is interpretable as a string of markers. Once this has been established, it is simple to prove that the machine may be regarded as "rule-governed." Simply take each complete configuration to be the sole member of a syntactic

class (i.e., a counter type). For each complete configuration, there is a set of complete configurations which can be the next state. (The members of a class differ only with respect to the states of input transducers.) Each of these next states has an interpretation as a counter. To view the machine as rule-governed, one need only view each mapping from a complete configuration C to its set of possible successors as the function table for a rule which licenses the derivation of any of the counters corresponding to the successors whenever the counter corresponding to C is tokened by the machine.

A.8—
Computers and Intentions

This brings to a close the discussion of conventions associating the states of computer storage conventions with semantic interpretations. There is little difficulty in seeing that marker tokens in computers are often interpretable under widely employed conventions as having semantic values. Given the representation scheme for integers outlined above, for example, any series of storage units possessing an eight-unit binary pattern is straightforwardly interpretable as a representation of some integer under that convention in much the same way that a sequence of numerals is interpretable as a representation of some integer. The role of intentions and actual interpretations in the semantics of computer markers, however, is not so straightforward as it is in the case of inscriptions. The reason for this is that someone who sets out to inscribe a meaningful message has some sort of awareness of the marker token he is authoring and has at least implicit knowledge of the semantic convention under which the marker token is to count as a signifier of a given sort, while the computer user may be quite unaware of the coding and representation conventions through which he stores his data, and almost certainly lacks any direct access to the storage media and the marker tokens found therein. With the possible exceptions of perforated tapes and cards, computer storage media store markers in forms that human perceptual faculties are ill suited to perceive. Circuits and disks are generally hidden from the user, and even when they are not, his eyes and ears and fingers cannot perceive voltage levels or flux densities. In addition, the user is quite unlikely to have any explicit knowledge of the conventions for marker tokening. The average user of a word processor has a dim understanding that what he has typed at the keyboard ends up "in the computer" or "on the disk," but probably has no knowledge of the coding conventions employed, the marker types they use, or the physical properties through which the marker tokens are realized in circuit memory and disk segments.

There is, in effect, a kind of division of duties between the designers and programmers of the computer, on the one hand, and the users, on the other. The design of hardware and software is generally pursued with the understanding that the computer will be used in tasks that involve certain kinds of representation, and the functions that are built into the hardware and software are designed so that they will manipulate marker tokens in ways that track meaningful relationships between the things that the markers are to be used to represent. If, for example, one wishes to build a circuit or write a program which performs computer addition (i.e., which takes pairs of representations of numbers and returns

a representation of their sum), one must know how the numbers are to be represented, since the choice of a representation scheme will have consequences for how the circuit or the program must be designed. Indeed, one needs a clear idea of what representational scheme one is going to employ in order to write any program that is to induce state changes that track meaningful relationships, be it a theorem prover, a language simulator, a numerical analysis program, or a chess program.

To these conventions the average computer user is usually oblivious. He has direct access only to input devices, such as the keyboard on which he types, and output devices such as monitors and printers, through which he has access to graphic and graphemic representations of data stored in the computer. If, for example, he is entering and editing text through a word processing program, he may very well think of himself as typing words of written English on a roll of "virtual paper" that scrolls past on his monitor. He may be completely ignorant of how text storage is accomplished in the computer; indeed, the question may never occur to him. He does, however, perform actions which he intends to result in there being some kind of linguistic representations—text, in effect—"in the computer," however vague or misguided his beliefs about how that is achieved.

These two difficulties—the lack of direct access to marker tokens and the user's ignorance of marker conventions—complicate the question of how things in computers can be intended as and interpreted as marker tokens. What may be said of things that are interpretable as marker tokens and caused by a computer user will depend on what kind of access the user has to the markers and what kind of understanding he has of the conventions, and these factors are subject to a great deal of variability. At one extreme, there are some marker tokens which are interpretable under conventions as markers, counters, and signifiers, but really are never authored or apprehended at all. At the opposite extreme, a computer engineer using a program that allows him to sample and alter the states of specific storage locations has very reliable if not direct access and knows the conventions he is working with. In his case, the fact that his access is mediated by software and hardware does not seem all that significant. But what about the user of a word processing program, for example, who is untutored in programming and computer science? Are the things that get into storage as a result of his actions intended as marker tokens? Are the things in storage that result in text appearing on his monitor interpreted as marker tokens?

The answer to this question can be yes so long as one allows that the user's relatively vague intention that his actions at the keyboard count as "typing something into the computer" can connect his actions with marker conventions of which he does not know the specifics. This suggestion is in some sense parallel to Burge's insistence that the use of a word in a natural language ties one's utterances and even one's beliefs to the standard meaning of the word, even when one does not have a full grasp of that meaning. The suggestion here is similar: the intentions involved in "typing text into a computer" involve assumptions to the effect that (1) there is marker tokening going on, (2) this corresponds in a fairly straightforward way to the kind of tokening that goes on when one types on paper, and (3) the marker tokening is connected in regular ways to keystrokes on the input side and output in graphemes on paper or a monitor.

One may make a similar case to the effect that under certain conditions the apprehension of graphic or graphemic representations on paper or monitors may also amount to the apprehension (with varying degrees of directness) of marker tokens in storage. The example of the electrical engineer using a program that displays representations of binary strings found in storage locations is the clearest case of someone interpreting the contents of a storage location as a marker of a certain sort, but some case can be made for anyone who thinks of the output as "coming from the computer" and believes that it was "in the computer" in the form of marker tokens.

If this analysis is right, then in cases like word processing, the computer user's intentions alone are sufficient for determining what the markers created as a result of his actions (e.g., his typing on a keyboard) are intended as . Recall the definition of authoring intentions for signifiers:

(S2): An object X may be said to be intended (by S) to signify (mean, refer to) Y iff

(1) X was produced by some language-user S ,

(2) S intended X to be a marker of some type T ,

(3) S believed that there are conventions whereby T -tokens may be used to signify Y , and

(4) S intended X to signify Y by virtue of being a T -token.

The definition allows some degree of latitude in the extent to which S must be cognizant of either the marker or signifier conventions that are relevant to his inscription or utterance. People can intend to use words meaningfully, for example, even if they are unsure, confused, or even mistaken about how they are spelled or pronounced. They can also intend to use a word meaningfully even if they are unsure, confused, or mistaken about the semantic value(s) the word carries under standard semantic conventions. (A foreigner who mixed up the English words 'dog' and 'cat' might intend to express the belief that the cat is on the mat by saying, "The dog is on the mat." His utterance would not, however, be interpretable under English conventions as an expression of the belief that the cat is on the mat.) Similarly, a user of a word processor has some understanding that he is "typing text into the computer" even though he may be unaware of just what that amounts to, or even have erroneous beliefs about what is involved. (He might believe, for example, that tiny letters are being inscribed in ink somewhere inside the machine.)

In general, explicating the exact ways in which particular marker tokens in computer storage may be said to be meaningful representations will involve tracing out the web of human conventions and intentions that have played a role in the etiology of those particular tokens. In particular, one must attend to the representation and coding schemes intended by the programmers and engineers on the one hand and the authoring intentions of the user on the other. Carrying out such an explication will generally prove significantly more involved than carry-

ing out an explication of the meaningfulness of an inscription or utterance—in part because there are more people's intentions to take into account, and in part because there are more processes mediating the symbol user's access to the symbols. In principle, however, there is no problem in saying of markers in computer storage that they have semantic properties under any of the four modalities outlined in chapter 4.