TWO
The Ontology, Physicomathematics, and Psychology of Imaging in the Early Writings of Descartes
Chronicling Descartes's life and thought before 1630 is not an easy task. Early biographers like Pierre Borel and Adrien Baillet[1] not infrequently invented plausible and plausibly timed accounts of events and travels—plausible in the sense, for example, that the curious, well-to-do scion of a family that had achieved some distinction in the provinces (Rennes) might have found his way, or at least wanted to find his way, to certain places and events. The dates and the factuality of many events are therefore uncertain. Even the chronology of his early compositions is often unconfirmable, and those that have come down to us are for the most part fragmentary and undated.
Until his death in Sweden in February 1650, Descartes preserved several notebooks from this early period (as attested by the Stockholm inventory made at his death; see AT X 5-12), but none of the originals has survived. Even if they were extant there would still be uncertainties about the dating of individual entries, since some were started from both ends (turning the notebook upside down) and divided by topic. The notes that survive were copied (many by Cottfried Wilhelm Leibniz or at his behest) according to principles of selection that we can only guess at, so that it is often impossible to know with certainty from which notebooks and categories they derive.[2] Moreover, from the entire period preceding Le Monde (which Descartes began ca. 1630) there are just three surviving works complete or extensive enough to merit reading as integral: "De solidorum ele-mentis," a short (14 pages in AT) treatise on the regular geometric solids;
[1] Pierre Borel, Vitae Renati Cartesii, summi philosophi, Compendium (Paris, 1656); and Adrien Baillet, Vie de Monsieur Descartes, 2 vols. (Paris, 1691).
[2] But see the brilliant reconstruction in Henri Gouhier, Les Premières pensées de Descartes: Contribution à l'histoire de l'anti-Renaissance (Paris: J. Vrin, 1958), 11-18.
Regulae ad directionem ingenii (111 pages), which although unfinished has long been recognized as of capital importance in reconstructing the development of Descartes's thought; and Compendium musicae (53 pages), a treatment of the principles of musical rhythm, consonance, and dissonance. The first work, despite its brevity, is a significant document in the history of mathematics, but it has been ascribed variously to both the early and the late 1620s and so is not a suitable first exhibit for establishing Descartes's earliest intellectual concerns. The Regulae , although it is of key importance in this study, has also been rendered chronologically uncertain by disputes over dating.[3] The Compendium musicae, however, is both complete and precisely dated; Descartes presented it to Isaac Beeckman[4] as a gift on New Year's Day, 1619.
A. COMPENDIUM MUSICAE: IMAGINATION AND MUSICAL PERCEPTION
The Compendium begins with various reflections. "The end [of music] is that it please, and that it move in us various affections." "The means to the end, or the affections of sound, are two principal ones: namely differences in the ratio of duration or time, and in the ratio of the intensity with regard to acute [= sharp] and grave [= flat]. For the quality of sound itself, from what body and in what way it comes out more pleasing, is treated by physicists." "And so, because of all things it [= the human voice] is most in conformity to our spirits, it appears to make the human voice most pleasing to us. Thus perhaps [the voice] of a closest friend is more pleasing
[3] The composition of the Regulae was until recently thought to have taken place in or around 1628. Jean-Paul Weber, La Constitution du texte des "Regulae" (Paris: Société d'édition d'enseignment supérieur, 1964), changed the terms of debate by arguing for a complex layering of the work that has to be unraveled by using contradictions and tensions to distinguish between parts and to reconstruct their sequence of composition; in addition, he claimed that the last two paragraphs of Rule 4, the so-called Rule 4-B, were where Descartes started the project in October or early November 1619. The Weber thesis has struck even some of its supporters as oversubtle. John A. Schuster has reduced the number of strata to basically three: first, a concern with universal mathematics that predated November 1619 (the topic of 4-B, mentioned nowhere else in the Regulae, at least not under that name); second, an elaboration of method in the period 1619-1621 (corresponding to the rest of the first eight rules); and, finally, a return to heuristic questions and a problem-solving mathematics in the later 1620s (reflected from the middle of Rule 8 to the end of the extant work). See Schuster, "Descartes' Mathesis Universalis: 1619-28," in Descartes: Philosophy, Mathematics and Physics, ed. Stephen Gaukroger (Brighton, Sussex: Harvester Press/Totowa, N.J.: Barnes and Noble Books, 1980), esp. 41 and 81n.4. Jean-Luc Marion, Sur L'Ontologie grise de Descartes: Science cartési-enne et savoir aristotelicien dans les Regulae (Paris: J. Vrin, 1975), criticizes the Weber thesis on the grounds that what seem to Weber to be contradictions often are not, and he offers in response a generally coherentist reading of the Regulae that dissolves many of the "contradictions" that were supposed to reveal different layers. Frederick Van de Pitte, "Descartes' Ma-thesis Universalis," Archiv für Geschichte der Philosophie 61 (1979): 154-174, makes the case that Weber misunderstood the precise character of mathesis universalis and so falsely distinguished mathematics and method (a similar point might be addressed, with qualification, to Schuster). Although my work addresses the Weber thesis only occasionally and indirectly, I can say here that I find it highly unlikely that any part of the Regulae was composed before the early 1620s, and I think it is conceivable that Descartes abandoned it as late as the early 1630s. My reading of the Regulae is, like Marion's, basically coherentist, but by placing it in the context of Descartes's understanding of imagination, I believe that we can see more clearly the kinds of tensions and perhaps even contradictions that do mark it.
than that of an enemy, from the sympathy and antipathy of affections: for the same reason from which people say that the skin of a sheep used for a drumhead becomes silent if it happens that a wolf's skin resounds in another drum" (AT X 89-90).
In the last remark one is immediately struck by the distinctly unCar-tesian tone of sympathy and antipathy used as principles of explanation. The passage has led some critics to depreciate the importance of the Compendium and others to interpret it as Descartes's implicitly polemical dismissal of a kind of ancient and medieval occultism, which is left, slightingly, to those who deal with matter and its qualities (the physicists) rather than to mathematicians.[5] This interpretation has the advantage of making the passage more recognizably Cartesian but commits the fallacy of assuming that the twenty-two-year-old Descartes was in essential respects the philosopher of the Meditations. As shall become evident shortly, other notes from around t620 suggest that explanations in terms of sympathies would not have seemed prima facie inconceivable to the young Descartes. Even more important, however, is that those who wish to read the Compendium as a step in the Cartesian project of mathematizing nature overlook (or dismiss) his characterization of the study of mathematical ratios as a means to understanding an end, the end of music, which is to arouse affections in the soul.
That the work is chiefly an investigation into ratios or proportions is not in doubt, but the framework in which their investigation makes sense is not that of the abstract mathematization of nature. This is made clearer by the eight postulates, which immediately follow the remarks just quoted.
1. All senses are capable of a certain delight.
2. For this delight there is required a certain proportion of the object with
[4] Beeckman (1588-1637) and Descartes met in Holland in October 1618, apparently while both were inspecting a poster announcing a problem in mathematics. Beeckman, who had just received his medical degree and had begun teaching school, was interested in approaching the physical sciences with techniques that were experimental, mathematical, and above all picturable. See Klaas van Berkel, Isaac Beeckman (1588-1637) en de mechanisering van bet wereldbeeld, Nieuwe Nederlandse Bijdragen tot de Geschiedenis der Geneeskunde en der Natuurwetenschappen, no. 9 (Amsterdam: Rodopi, 1983), chaps. 4, 7; see also pp. 317-319.
[5] See René Descartes, Abrégi de rausique, suivi des "Eclaircissements physiques sur la musique de Descartes" du R. P Nicolas Poisson, trans, and ed. Pascal Dumont (Paris: Méridiens Klinck-sieck. 1990), 17, 147n.4.
its sense. Whence it happens, for example, that the din of muskets or thunder does not seem suitable to music: because, namely, it hurts the ears, just as the very great brilliance of the sun [hurts] eyes directed toward it.
3. The object must be such that it does not befall sense too difficultly and confusedly. Whence it happens that, for example, a certain very complicated figure, even if it be regular, as is the mater[6] in the astrolabe, does not please sight as much as another that is made of more equal lines, such as the astrolabe's fete usually is. The reason of this is that sense is more satisfied in the latter than in the former, where there are many things that it does not perceive distinctly enough.
4. That object in which there is less difference of parts is more easily perceived by sense.
5. We call less different from one another the parts of a whole object between which there is greater proportion.
6. That proportion must be arithmetic, not geometric.[7] The reason is that there are not so many things in it to be noticed, since the differences are everywhere equal, and therefore sense is not so fatigued, so that it perceives everything in it distinctly. Example: the proportion of [these] lines [fig. l] is more easily distinguished by the eyes than of those [fig. 2], because, in the first, one only has to notice the unit as the difference of each line; but, in the second, the parts ab and bc, which are incommensurable, and therefore, as I judge, they can in no way be perfectly known simultaneously by sense, but only in an orderly relation to arithmetic proportion: in other words, should one notice, for example, two parts in ab, three of which exist in bc It is plain that here sense is constantly deceived.[8]
[6] In the planispheric astrolabe, which was used by astronomers and navigators for taking the altitudes of celestial bodies, the mater was a plate engraved with crisscrossing circles of altitude, while the rete was a rotatable circular ring of the stars, "often beautifully designed in fretwork cut from a sheet of metal, with named pointers to show the positions of the brighter stars relative to one another and to a zodiacal circle showing the sun's position for every day of the year." S.v. 'astrolabe', Encyclopaedia Britannica (Chicago: Encyclopaedia Britannica, 1967), 2:640.
[7] A series of numbers, or of lines having those numbers as measure, constitutes an arithmetic proportion if the series increases (or decreases) by a fixed amount; thus 2, 5, 8, 11, 14 are in arithmetic proportion because the series increases each time by 3. A series constitutes a geometric proportion if each successive element is derived by multiplying the preceding one by a fixed number; thus 2, 6, 18, 54, 162 are in geometric proportion because each element is three times the preceding one.
[8] AT notes that the concluding sentence of postulate 6 is present in two Latin manuscript copies and in the Latin text published in 1650, but not in the French translation of 1668 prepared by Nicholas Poisson, who had at hand Descartes's original MS. It is not necessary, at any rate, to interpret the sentence as a reason for doubting the reliability of the senses in general. Rather, it indicates a tendency of the senses to "read" the proportions of things as simpler or more commensurate than they actually are; this tendency produces a need for the intervention of higher powers of mind to establish the true ratios, as will become clear from what follows.
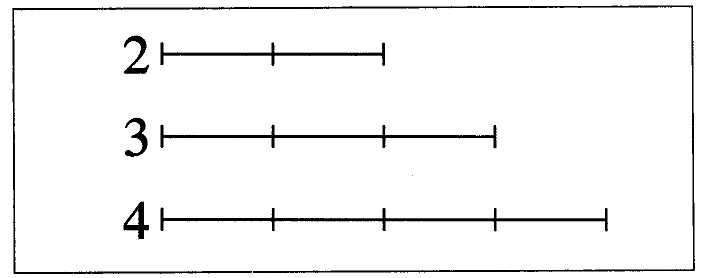
Fig. 1. The three line segments can be easily compared because
each contains a whole number of units.
Fig. 2. The middle line segment is not commensurable with the other two,
so that a visual comparison of the parts is more difficult.
7. Among objects of sense the most pleasing to the soul is not that which is most easily perceived by sense, nor that which is perceived with most difficulty; but that which is not so easy, so that the natural desire by which the sense is drawn to the objects not be completely satisfied, nor so difficult that it tire sense.
8. Finally it is to be noted that in all things variety is most pleasing. (AT X 91-92)
It has been said that if one is searching for the originality of the Compendium musicae, one will not find it in these postulates, for the doctrine of sensation being itself a kind of proportion (or based on proportion, logos ) goes back at least to Aristotle.[9] One might mention also Aquinas, for
[9] See Descartes, Abrégée de musique, 16. The particular passage in Aristotle noted as one that "everyone recopied for centuries" is De anima, bk. 3, chap. 2,426a27-426b7.
whom "beauty consists in due proportion, for the senses delight in things duly proportioned, as in what is like them—because the sense too is a sort of ratio, as is every cognitive power."[10] The doctrine is not intrinsically Aristotelian-Scholastic, for Pythagoreanism and Platonism likewise understood sensation, or at least its most perfect forms, as having a basis in proportionality or even as being proportion.[11]
Indeed, the convergence of different philosophical traditions on this basic point is a reason for thinking that, regardless of what specific works Descartes read or did not read, the doctrine could not have been unknown to him. (This is especially true since the doctrine is a staple of traditional musical theory, with which Descartes shows a more than passing acquaintance.) Plato's writings, especially the Republic and the Timaeus, give an account of the cosmos as proportionally structured. The divided line of Book 6 of the Republic presents what could be called an ontology of pro-portionalized imaging that grounds an epistemology of proportionalized imaging, in which the Forms are imaged in the Mathematicals, the Mathe-maticals in the objects of the physical world, and the objects of the physical world in shadows and reflections—and between each major category there obtain strictly proportional relations. In Aristotle the operations of the senses with respect to their objects are frequently said to be proportional to the operation of the intellect with respect to its objects. Although Plato gives somewhat more emphasis to ontological imaging than to proportions, and Aristotle emphasizes the proportionalities without explicitly addressing the possible resemblance of the sensible species to an intelligible species, both thinkers provide adequate space for reflecting on the overall importance of resemblance and proportionalities in the process of moving from sensation to intellection. This is a contextual topography that opens up the significance of Descartes's Compendium rausicae more re-vealingly than does the search for Descartes's putative originality in the history of musical theory (a "reduction to mathematical abstractions," for example).
My initial thesis is this: It was precisely in pursuing the question of the proportionalities of the senses and the other cognitive powers that Descartes became a philosopher. He began this pursuit not because he already had in mind a mathematical method but rather because he suspected that proportionality was the fundamental principle of knowing and that it reflected the way the cosmos was structured. The underlying theory of such proportionality is what Descartes eventually called mathesis universalis : a theory expressible not just in the abstractions of intellect but also, and equally well, or perhaps even better, in the figuration of extension, whether according to sense or according to imagination.
[10] Summa, theologiae, I,q. 5, art. 4, ad 1
[11] For example, in Augustine's De musica. See Summers, Judgment of Sense, 67-69.
The Compendium musicae shows that by late 1618 Descartes had already taken at least the first steps toward working out a theory of the communication of proportions from the external world to the senses. It attempts to demonstrate that the rhythms and tones of music are subject to a logic inherent in the senses in general and in the sense of hearing in particular, a logic (from logos, one of whose meanings in Greek is 'ratio' or 'proportion') of arithmetic proportion. Both rhythm and tone are governed by relations that can be expressed in terms that are arithmetically increased or decreased through the addition or subtraction of a unit. The doctrine of the Compendium is therefore a particular application of the principles enunciated in the postulates, which are understood as applying to all sensation. This does not in itself imply a radical reduction to mathematics any more than it does for Aristotle or Plato. Rather, because sound, like all other sensibles, reflects the order and measure of the world, it implicitly contains and reflects the principles that Descartes educes and represents through mathematics. The specific qualities of sound are in no way eliminated; they are rather understood to necessarily carry with them a proportional structure that can be, and is, communicated from thing to thing, and from thing to mind.
The basic mathematics of consonance and dissonance has been recognized at least since Pythagoras. Descartes's specific contribution with respect to this mathematical tradition in the Compendium is to show that the consonant tonal relationships can be discovered in, and represented by, the arithmetic proportionalities of a single string (line) divided into five parts by first bisecting the whole string, next bisecting the rightmost of the two segments, then the leftmost of these two and finally the leftmost of this last division (see fig. 3).[12] According to the principles enunciated in the postulates, these tones, because of the simplicity of their relationships, are precisely those that are most suited to the sense of hearing and the most easily perceived. The sense of hearing is so constituted that the tones based on an arithmetic division of the string are perceived as simplest in their relationships to one another. The theory of these simplest relationships, which the Compendium presents, is the fundamental theory that Descartes believes should guide intelligent musical composition toward the end of music, the delight of the senses.
A corollary of the standard thesis that Descartes abstractly mathematized musical theory is that he subjectivized musical perception. But the
[12] See AT X 98-105. This division and its novelty in the tradition of musical theory are discussed by Johannes Lohmann, "Descartes' 'Compendium musicae' und die Entstehung des neuzeitlichen Bewußtseins," Archiv für Musikwissenschaft 36, no. 2 (1979): 81-104, and H. F. Cohen, Quantifying Music: The Science of Music at the First Stage of the Scientific Revolution, 1580-1650, University of Western Ontario Series in Philosophy of Science, no. 23 (Dordrecht: D. Reidel, 1984). esp. 161-179.

Fig. 3. Descartes's division of a line by successive bisectioning gives rise to ratios of the principal consonances. Point C bisects AB; D bisects CB; Ebisects CD; and F bisects CE. AC produces the octave above AB; AC and AD yield a fifth; AD and AB produce a fourth; AC and AE yield a major third. These proportions are based on the numbers 2, 3, and 5 or their multiples; the process of bisection makes this visually comprehensible. All the relationships dependent on the last bisection at F lead to dissonances. As a result of this technique of division, all the consonances are simply imaged by a single line.
corollary is as questionable as the thesis. It is indeed true that, from 1630 on, Descartes described the pleasure taken in music as depending on the peculiarities of individual history and taste, but such testimony cannot decide what Descartes thought in 1618.[13] The method and doctrine of the Compendium are predicated on the real existence of proportions in tone and rhythm, the real correlation of such proportions to the satisfactions of hearing and the soul, and the real ability of the human psyche to detect, at first implicitly and eventually with knowledge, the presence of these proportions, whether in the sounds of nature or in musical compositions. If there is such a "preestablished harmony," then it should not be surprising that the human ear might have a natural sympathy for the human voice (presumably human beings would try even in speaking to produce tones pleasing to their own ears and thus to the ears of those with souls and organs similarly attuned) and a natural antipathy for sounds not in accordance with the natural proportions. The recognition of such proportions
[13] See, for example, AT I 128 (letter to Mersenne, 4 March 1630). Even at this later date Descartes makes a distinction: although "everyone knows that the fifth is sweeter than the fourth," what pleases more, or is found more agreeable, may be something different. This apparently corresponds to the distinction the Compendium's postulates make between what is perceived most easily and what is most pleasing. In any case, Descartes's so-called subjectivization of aesthetics occurs after a decisive shift in his thought away from the cognitive value of sensible proportions. One should also note that the Compendium's postulates 6 through 8 imply that the satisfactions of music, which are proper to the soul rather than to physical organs, are not to be settled on the level of what is satisfying to the sense. Sense per se is pleased by the simplest arithmetic proportions; they are not always to be found in good music (end of post. 6), however, because the purpose of music is not to satisfy immediately and completely the natural desire of the sense or to frustrate sense by complexity, but to present the soul with an intermediate difficulty in knowing (post. 7). When all is said and done, the soul is satisfied not by simplicity but by variety (post. 8). This gives a glimpse into Descartes's earliest anthropological psychology: the human soul is constituted so as to take delight in difficulties, at least so long as the difficulties can be overcome. It is therefore of the nature of the human soul to solve problems.
constitutes the foundation of Descartes's theory. The theory is expressed in the mathematics of proportions, but this mathematics is precisely what is detected or perceived in the sensation of sound, in its aisthesis. In this precise sense, the Compendium musicae is the foundation of the mathematical aesthetics of sound.
In this study, the particular question to be asked is how imagination enters into this mathematical aesthetics. In the course of the Compendium, Descartes talks frequently about the senses and perception, but only occasionally about imagination. The imagination words occur infrequently, ordinarily without any great intrinsic significance. For example, the adjective imaginarius is used as synonymous with 'fanciful' or 'merely fictional', and the verb imaginor occurs in the sense of 'depict' or 'conceive'.[14] But the imagination does figure importantly in the section following the postulates: "On the number or time in sound that is to be observed." After noting that musical tempi are divided into double and triple times, Descartes explains how we perceive them.
This division is marked by percussion or beat, as they call it, which occurs in order to aid our imagination; by means of which we might more easily be able to perceive all the parts of the song and enjoy [them] by means of the proportion that must be in them. Such proportion is most often observed in the parts of a song so that it might aid our apprehension thus, that while we are hearing the last [part] we still remember the time of the first one and of the rest of the song; this happens, [for example] if the whole song consists of 8 or 16 or 32 or 64, etc., parts, that is, when all the divisions proceed in double proportion. For then, when we hear the first two members, we conceive them as one; when [we hear] the third member, we further conjoin that with the first ones, so that there occurs triple proportion; thereafter, when we hear the fourth, we join that with the third so that we conceive [them] as one; thereupon we again conjoin the two first with the latter two so that we conceive these four simultaneously as one. And thus our imagination proceeds all the way to the end, where at last it conceives the entire song as one thing fused out of many equal members. (AT X 94)
Perception, apprehension, memory, imagination, and conception all enter into the mental process described in this paragraph, and we might suspect that the young Descartes was not necessarily using these terms very precisely. 'Imagination' and 'conception', for example, appear to be synonymous. However, we have noted earlier that Descartes allows precisely this synonymy in Rule 12, probably ten years later, which makes it more likely that it reflects a constant in Descartes's understanding of the two terms before 1630.[15]
[14] AT X: 109 and 102, respectively.
[15] In chap. l, above. All theories dating the Regulae agree that the composition of Rule 12 was relatively late.
The discussion begins and ends with imaginatio. Rhythm aids imagination by marking divisions so that they might be perceived; the proportionality among the parts of the song produces "delectation," enjoyment, and aids apprehension by enabling us to remember what came before as we hear what comes next. How does this happen? By continually recursive acts of conceiving, each synthesizing the new part with all the preceding and expressing it in relation to the others by means of a unit of time. Accordingly, rhythm, just like tone, is governed by arithmetic proportion. But, in contrast with tone, this proportion is expressed not all at once or in a short musical phrase but throughout the entire song, so that sense by itself or even with the aid of short-term memory will not be able to perceive the proportions. It is imagination that performs the task of synthesizing the individual deliverances of the sense, of the individual units that mark the rhythm. "And thus our imagination proceeds all the way to the end, where at last it conceives the entire song as one thing fused out of many equal members." That is, apprehension and delectation come about by imagination's progressively, proportionately synthesizing one thing to another.
Imagination is portrayed here as an extraordinarily active power that is responsible for the ability to perceive the complex unity of sounds as a whole rather than as simply a congeries of unconnected tones. In the passage it is also the primary agent of cognition, of the grasping by mind (apprehension). It is an agent: that is, imagination does the work of conceiving/synthesizing; an agent of cognition: that is, the imagination is not simply projecting visual (or auditory) images but recognizing something not directly perceived by the sense, the proportions in the song taken as an entirety. Moreover, the memory required for this synthesis and cognition appears to be a by-product of the process as it takes place from moment to moment, from musical part to musical part.
By late 1618, Descartes conceived imagination as a synthetic conceptive power operating on sensation, a power that gathers or collects the various parts or moments that are successively presented and then conceives them as unified by the determinate proportional relationships they bear to one another. The notion of proportionality will be discussed presently, under the aspect of the relation of imagination to the mathematics of proportion. Here we might remark that imagination comes up first not in the visual realm but in the auditory, which suggests that Descartes was already thinking of the power of imagination as transcending the specific character of any single sense. It is precisely imagination's character of being presentative, synthetic, and memorative that seems to interest him, rather than any merely representational use. This character rests on proportionality or, to use the Greek equivalent, analogy.
There is in the Compendium no comparable explanation of imagination's
functions in the case of tone, the other basic component of the aesthetics of music, but this should not be surprising. Rhythm ordinarily extends in an equable way throughout an entire song (or throughout each of its major units), so that the synthetic activity of conceiving rhythm creates a complex unity by iteration and temporal projection/retention, a complex that nevertheless falls into one of two classes, either double or triple time. With tone there is less need for an extended synthesis (putting aside the loose regularity determined by the key or mode of a passage), since the relationships of primary importance exist between tones sounded in immediate succession or even simultaneously. These immediate relationships are already proportioned to the sense of hearing and its pleasures, so the synthetic functioning of imagination is less urgent for properly appreciating them. Moreover, there is a greater variety of melodic effects than two, and to explain all of them would require a greater complication in the investigation both of the ways in which the soul is moved and of how the proportions expressed in one harmony or phrase are related backward and forward to the other parts of the song. At the end of the Compendium, Descartes in fact notes with respect to the variety of grades and proportions of tone that
from these and similar [items] various things might be deduced about their nature, but it would be long. And it would also follow that I should treat separately about the individual motions of the soul that can be excited by music and should show by means of what grades, consonances, tempi, and so forth, these ought to be excited; but I would exceed the purpose of the compendium.[16] (AT X 140)
Descartes's purpose was not to exhaust the theory of music but to set down its principles. In such a context the account of imagination's work presented in the section on rhythm should not be taken as a feature of accidental interest but as a process essential to cognition through the senses.
B. THE "COGITATIONES PRIVATAE": THE TWO-IMAGINATIONS NOTE
The relation between imagination and proportion is developed further in the "Cogitationes privatae," notes copied from one of Descartes's early notebooks (dated 1619-1621) by Leibniz and first published in 1859.[17] It may be only an artifact of Leibniz's selection, but it is surprising how many of them deal with imagination and images either directly or indirectly.
[16] 'Compendium' in fact implies a brevity and economy that is nevertheless comprehensive.
[17] In Oeuvres inédits de Descartes, ed. Louis Alexandre comte Foucher de Careil, 2 vols. (Paris: Ladrange et Durand, 1859-1860), 1:2-57.
These notes present an epistemology based on the figuration of resemblances, within an ontological hierarchy of body and spirit. That is, the different powers of the mind or soul put the human being into touch with higher things by way of their resemblance to lower ones. The fundamental instrument of this ascent from low to high is imaginative analogy and proportion.
Consider again a note already quoted in the introduction.
As imagination uses figures to conceive bodies, so intellect uses certain sensible bodies to figure spiritual things, like wind, [and] light: whence, philosophizing, we can by cognition raise the mind higher in the sublime.[18] It can seem amazing, why pregnant meanings [are] in the writings of poets more than of philosophers. The reason is that poets write through enthusiasm and the force of imagination: there are particles [or seeds] of science in us, as in flintstone, that are educed by philosophers through reason, [but] that through imagination are shaken loose by poets and shine out more. (AT X 217)
Not only does this note (which henceforth will be called "the two-imaginations note") try to ground the principle of analogy by use of an analogy—an approach not likely to be chosen by a Descartes who is supposed to believe in the primacy of the direct intellectual intuition of elemental truths and the rigorous deduction of new truths from such foundations—even more important, it also presents imagination in a twofold significance central to Descartes's early conception. The first part of the note treats imagination as the power of making corporeal things conceivable through figures and images; intellect in turn uses the corporeal things as figures of even higher, spiritual (or intelligible)[19] things. In this context, imagination proper is a lower cognitive power functioning by means of figures and images that allow an understanding of bodies. Yet the second part of the note suggests, de facto if not de dicto, that there is an intellectual imagination more directly in touch with the highest things than is reason (ratio): the imagination of the poet, which ascends more easily to spiritual heights than does the plodding, discursive reason of the philosopher.
The rest of this section and the several sections following focus on ramifications of the two-imaginations note and related ones. In essence I argue that elaborating the background and scope of the note is key to understanding the basic principles of the "Cogitationes privatae."
[18] It is not clear whether this entry should be broken into two paragraphs (at "Mirum videri possit"); for a discussion, see Gouhier, Les Premières pensées, 79-80.
[19] The choice between 'spiritual' and 'intelligible' is not a matter of indifference. In his earliest writings Descartes tended to refer to the highest things and powers as spiritual. In the Regulae the pair 'material'/'spiritual' is used alongside the more Cartesian 'corporeal'/'intelligible'. 'Spiritual' is ordinarily used in the early writings in a broad sense that embraces 'intelligible'.
Two very strong, possibly crippling preliminary objections might point out (l) that the note could be an idiosyncrasy, perhaps a mere jotting without further consequence, and (2) that since the "Cogitationes privatae" are Leibniz's culling of Descartes's notes, any unity to be found is more likely to be due to the mind of the former than of the latter. As for the first objection, the immediately following notes pursue further the question of using images and symbols for the sake of knowing both physical and extra-physical things. A particularly unCartesian note is the other private cogitation already quoted in full in the introduction: "The cognition of natural things by human beings [occurs] solely through the similitude of those things that fall under sense: and indeed we judge that person to have more truly philosophized who will have more successfully assimilated the thing sought to what is cognized by sense" (AT X 218-219). Another seems to explicate the intent of the two-imaginations note by giving examples of how "sensible things [are] apt for conceiving Olympian things": wind signifies spirit, motion in time signifies life, and so on. Notes like this might well provide clues for interpreting some of the more elusive moments of Descartes's early intellectual career, for example, the three dreams of 10-11 November 1619[20] But even more significant is that these notes help explain the principle Descartes was following in the physical and mathematical notes that apparently formed the major part of the "Cogitationes privatae." Moreover, the two-imaginations note not only helps clarify the relevance of cogitations that otherwise seem to stand in isolation (like a reflection on the art of memory and adversions to that aspect of the human soul called ingenium) but also points ahead to problems faced in the Regulae ad directionem ingenii. Therefore, in response to the second objection, even if Leibniz's selection is responsible for the appearance of a greater unity than existed in the original, that original unity, however much looser, would nevertheless be Descartes's doing.
To return to the interpretation, then: The two-imaginations note sketches out a power of mind or soul, imagination in the usual, corporeal sense, that uses figures to conceive bodies, and another, analogous power of intellect, what I have termed 'intellectual imagination', that takes bodies and uses them to conceive or figure spiritual things. Both are cognitive, the one directed toward bodies, the other toward spiritualia, spiritual matters. Both are active and synthetic, insofar as the figuration of a body requires that the body be seen as represented by an (perhaps complex) image, whereas the figuration of higher things requires a body to be seen as the analogical image of something spiritual. The most basic similarity of
[20] See Gouhier, Les Premières pensées, 84-85. According to Baillet, the narrative of the dream was contained in the section of the "Cogitationes privatae" notebook rifled "Olym-pica." See Baillet, Vie, 1:81-86, which is reproduced in AT X 181-188.
the two is precisely marked out by the fundamental analogy: as figures are to bodies, so are bodies to spiritualia. Ordinary imagination relates figures to bodies, intellect in its imaginative mode relates bodies to spirit, and so it seems reasonable to conclude that imagination stands to intellect according to the same proportion. This implies that there is not an infinite gap between any of the pairs figures and bodies, bodies and spiritual realities, imagination and intellect; all have the ability to mirror a set of common relationships.
C. IMAGINING AND THE PROPORTIONAL MATHEMATICS OF RESEMBLANCE
What is involved in conceiving bodies? The first clause of the two-imagina-tions note says imagination uses figures to conceive bodies. How does the object (the body) stand in relation to the figure? There is nothing in the passage to suggest that the object is originally constructed by imagination or sense; that is, there is no hint here of a Kantian position, or of a generalization of the hearing processes described in the Compendium rausicae so that they apply to vision. If what is originally given to the ear in the Compendium is tone and beat, out of which melody and rhythm are constructed, there ought to be something else that is given to the eye, but what that might be is not identified. However, since hearing is a temporal process, whereas vision is seemingly instantaneous, there is no objection in principle to saying that the visible body is what is originally given. In any case, the process of imagination described in the two-imaginations note begins only once the object is already in the possession of sense.
The clause therefore suggests that seeing or otherwise sensing an object or body is not understanding, but only the starting point for understanding, because understanding requires the act of imagination/conception. If the experience of the thing as originally given is to become understanding, imagination must come into play. Imagination has the power of using figures. How are these figures formed and used? The answer is implicitly given in large part by other notes of the "Cogitationes privatae," especially the mathematical and physicomathematical ones (see Sec. D, below), but in principle the procedure is not much different from the Compendium musicae's use of line segments to represent musical consonances. The repeatedly bisected string of the Compendium can be presented in imagination or on paper, or it can be instantiated in a real musical string. To bring some regularity into usage and simultaneously to shed light on the relationships, we can say that for imagination proper to work there must be (1) an object to be understood, (2) a figure, and (3) an act of the mind seeing the object in the perspective of the figure. In a simple musical case the object might be a string of a given length at a fixed
tension; the figure could be the imaginative conception of a line segment repeatedly bisected; the act of the mind would be to conceive the object as variously stopped in accordance with the divisions of the imagined segment. But then the imagined segment stands not just for the real string but for the whole set of harmonic relationships that the musical theorist knows about. The imagined figure is a dynamic presentation, a presentation for the sake of manifold use; and in this sense one could add that the act of conception is pragmatically oriented.
Obviously this analysis calls for some further clarification. First, given this type of position Descartes cannot very well accept his later dualistic metaphysics, where there is no necessary resemblance between the ideas of the thinking soul and the extended world. Moreover, Descartes does not at this stage of his career use the vocabulary of the later position, so that it is at least somewhat misleading to call the figures that help conceive the bodies and the bodies that figure spiritual things ideas. For now, let us note that the ideas of the later philosophy have a representative function. It is their very nature to point to something beyond themselves; this aspect is dubbed the objective reality of the ideas in the Third Meditation. There the question immediately arises whether, and how closely, ideas resemble their proper objects; indeed, the hyperbolic doubt of the Meditations thrives on the worry that the resemblance is far less than perfect. Here in the "Cogitationes privatae" there is no presumption that the figures or bodies need to represent anything perfectly, and therefore it is doubtful that one should even think of the relation primarily in terms of representation. It is more appropriate to think of it as symbolic, provided that the symbol not be taken as a mere sign.
What is a symbol? Eytmologically it is something thrown together (a parallel Latinate term would therefore be conject ). It is said that the Greek word originally denoted the parts of a coin, seal, or tile that had been broken to provide holders of the parts with an unreplicable mark of a solemn transaction; the symbols needed to be reassembled to complete the transaction. The symbol was therefore a sign of the whole, a mark of it, and it was also a part of the whole and shared in its character. Each part existed because of the whole and in relation to it. Moreover, the part was a symbol not because it externally represented something else but rather because it participated in a nature common to the other part and the whole.
Representation as commonly conceived is governed chiefly by the question of external signing or pointing, whereas the symbol is part of the same reality and has some resemblance to the other parts relevant to a transaction. The symbolic resides in what may be called the partial presence of the absent or distant whole.
Let us look more closely at what the two-imaginations passage has to say and suggest about the presence of the absent. What the first clause ap-
pears to say is this: we see or experience an object, a body; but having an object in sensation is not in any way to understand it. How do we come to understand or conceive it? By imagination, which uses figures (presumably modeled according to some aspect or aspects of the body) as the way to conception and knowledge. Imagination is therefore not construed here as the act of originally representing the object as object to perception, but rather as a way of (re)construing or (re)grasping that object in the presence of the object, which is either direct presence (sensed) or remembered presence.
Imagination is a way of (re)grasping the object, either in direct (sensed) or remembered presence. We use a figure to conceive a rock when we consider the outline of its shape or even when we simplify the outline to the nearest regular geometrical figure it resembles. To approximate the space taken up by the rock, we can imagine a parallelepiped, or a sphere, or a spheroid that renders the volume in a rough-and-ready way; to measure it more precisely, we can imagine it as, say, divided into tens or hundreds or thousands of identical cubes (a thousand cubic centimeters, for example). Similarly we can conceive of a certain direction as an axis and mentally place the rock along it, thereby getting a line (and, implicitly, a measure) that can represent it for some limited purpose. The figure or line derived in this way resembles at least some part or aspect of the thing, however minimally, and it is imagined as standing for this part. It is a symbol, and potentially a representamen, through which the mind (re)grasps the object symbolized.
One need not restrict this process of figuration to the geometry of the object, however. The hardness and the color of the rock, for example, can be figured in both a literal and an extended sense. In the simplest kind of case we could conceive a hard, gray rock insofar as it is able to scratch basalt or insofar as its hue is a particular shade. Such simple cases suggest that we are imaging/grasping the thing in implicit, but potentially systematic, comparison with similar things. We can classify the hardness of minerals by scratch tests using a large number of standard samples, or arrange colors along different scales (within a Newtonian spectrum, or in the CIE color triangle, or according to the Munsell color-chip catalog, with respect to the colors' brightnesses, hues, or other salient characteristics). This kind of figuration presupposes that we have previous experience, reflection, even experimentation, some of which (the scratch test, for example) will involve a more invasive activity than simply measuring or sketching an outline (whether this is done in the mind or on paper). In principle, however, all figuration requires activity—the minimum of which is like conceiving figures mentally or sizing up an object in a glance.
This interpretation has already gone considerably beyond the direct evidence of the note, though, as we shall see, not beyond the evidence of the
"Cogitationes privatae," the Compendium musicae, and, ultimately, the Regulae . This excursus has brought us to the point where we can more precisely characterize differences from Descartes's later works. In Discourse 4 of Dioptrics (published in 1637 as one of the three essays prefaced with the Discourse on the Method ) as well as in the first chapter of Le Monde (written ca. 1630-1633), Descartes argued that there was no necessary resemblance between images or ideas in the mind and the objects from which the images come (AT VI 109-114, XI 3-6). In the Meditations the questions of resemblance were summarized in the problematic of the objective reality of ideas—that is, their representative function—which our natures incline us to accept as showing things the way they truly are. But this is not the problem situation of the "Cogitationes privatae." Indeed, the question of the relationship between how things appear to us (in subjectivity, to use post-Cartesian parlance) and how they are in themselves (objectively) is absent. The figures, the bodies, and even the spiritualia are understood as things in and of the world. A circle, a star, and a spirit can certainly all be conceived in the mind, but even more important is that they are extra-mental existences that can be used to exemplify or figure one another. Descartes is not concerned in his earliest writings with whether the shape that consciousness registers in looking at a star is the star's shape in reality, but rather with how the mind can take a figure and use it to help conceive the star. The operative assumption is not that the "idea in the mind" intimately resembles the thing in the world but that the two things are different with relevant samenesses; both difference and sameness are determined analogically and proportionally. 'Conception' here is the grasping of the thing in question. The cognitive ability of the soul is understood not according to the authority or veridical character of its passive or receptive powers (including sensation) but according to the activity performed with what it already possesses.
It is not appropriate, therefore, to formulate the activity described in the two-imaginations note as representation. The logic of representation has the representing thing, the representamen, stand for and in place of the represented. Although using a circle or a prolate spheroid to figure a rock has a representative aspect, it is not merely or even essentially a representation. This is clear by recalling a fundamental problem for episte-mological representationalism: the subject has access to not the objects of the world but the representations of them in consciousness. Consciousness is the plane on which the objects are projected, without any clear warrant that the things projected there have been rendered accurately according to a reliable process. The situation of the knower is thus uni-planar, restricted to the plane of consciousness. The situation of the two-imaginations note, however, is biplanar. To conceive corporeal things, we use figures; that is, there is first the plane of corporeal objects, to which
we already have access, and then there is the plane of images and figures, to which we also have access and which we can freely vary, either on paper or in our imaginations. The first plane is viewed in comparison to, or rather through, the second. A further difference is that in the uniplanar situation the homunculus problem can be avoided only by putting consciousness in the plane of the appearances, whereas by its very nature the biplanar situation cultivates a movable consciousness that can attend to one plane, or another, or even to whatever may be between for example, in figuring out the relationship and solving problems between planes.
This biplanar situation makes very little sense in standard Cartesian terms, but it is perfectly intelligible in a Scholastic-Aristotelian framework. As was explained in chapter 1, the doctrine of the internal senses holds that there are internal powers of sensibility, the internal or inward senses, that prepare and manipulate the phantasm that is considered essential for all thinking. In particular, the common sense is presented with an image composed of the proper and the common sensibles, that is, with an image produced from all the senses—in more modern terms, we could call it the composite sensation or even the composite percept—and, in turn, from this and/or from remembered images as well, the cooperating internal senses, including imagination and cogitation, produce the phantasm that is necessary for the intellective powers to operate. In simplified terms, the corporeal object perceived is in common sense, whereas the figure through which we conceive it is in phantasia. We are thus in possession of both the object and the figure: each is present in its own field or plane, and there is an awareness or consciousness that pertains to each plane but also transcends each.
This brings us to a clearer distinction between the uniplanar situation of representation and the biplanar situation of imagination. Representations, it is presumed, are ultimately caused by states of affairs in the world, but we have no access to those states of affairs except through the representations—and that only by way of inferences about what kinds of connections between world and mind could produce those representations. In the biplanar situation of body and image, in contrast, we have direct access to both, and we can view the body directly through the medium of the image. It is not even essential in this biplanar framework that we be currently sensing the body, for through another of the internal senses, memory, we are able to preserve and recall direct images of the body that, held in one plane, can be figured in another.[21]
[21] We need not do the biplanar viewing directly, since we can temporarily allow the perceived or remembered body to drop from our attention while we figure out relations in the image. For example, we might picture a pasture as a square and, after measuring the sides, sit down with paper and pencil to calculate the area of the imagined square to obtain the pasture's area. The employment of memory doubtless raises the question of whether or not memory images appear in the same plane as the figuring images. It is at least conceivable that the planes are different, but even if they are the same, it is possible to retain a nontrivial sense of biplanarity in that one moves back and forth between the frame of the figuring and the frame of the remembering—as it were, like moving between different windows of a multitasking computer program.
The Compendium musicae's portrayal of the perception of rhythm implicitly illustrates how this biplanarity works: successive notes are heard and please the sense more or less according to the proportions between them; then the imagination begins its work of figuring out the rhythm or the harmony of the whole song. It does this by successive acts of integration of the notes into a projected whole. After the first two notes one probably cannot yet know whether the rhythm is in double or triple meter, but already at that point the imagination conjectures a whole. Because music is spread out in time and because in comparison to vision so much more constructive activity seems to be required to get even fairly simple aural objects, the Compendium's example needs some adjustment to be applicable to vision. As everyone having even a little acquaintance with Descartes's later writings knows, the paradigmatic metaphor for the soul's activity is seeing. Vision appears quite early on to have displaced hearing in his conception of imaginative knowing.
Even with the shift to the paradigm of vision, however, Descartes retained his understanding of imagination as an activity. The figuration presented in the two-imaginations note is work, an accomplishment, whether it is done by corporeal imagination or imaginative intellection. Here again the Compendium provides a clue about how and why this work takes place. Sensation has a natural affinity for certain rhythms and musical intervals, whereas the soul as a whole takes maximum pleasure not in what is simplest or most complicated but rather in what presents a solvable challenge to its powers of imaginative discrimination and judgment. Descartes always recognized his penchant for solving puzzles and figuring out problems he put to himself.[22] If there is in human beings a natural desire to know and a corresponding pleasure in knowing, and if nearly all knowing presents itself first in the form of a question or problem that has to be sorted out and solved—a notion that one already finds in Aristotle[23] —then it would seem likely that the soul should in general take pleasure in solving problems. In each case it would begin with a power, an external or internal
[22] See AT X 214. Just two entries earlier, in what is the second note of the whole "Cogirationes privatae," Descartes remarks, "as a youth, whenever ingenious discoveries were presented, I asked myself whether I could discover [them] for myself, even without having read the author: from which I gradually noticed that I was using fixed rules [certis regulis ]" (AT X 214). See also the Regulae, AT X 403.
[23] See Metaphysics, 982b12-983a21.
sense, that receives what it is given in accordance with its natural affinities for some things rather than others and then would reconfigure this given according to the corporeal imagination (or, in the case of spiritual things, the intellectual imagination) in order to get hold of a solution, that is, in order to know. The original reception and retention takes place in one plane, the reconfiguration in another.
The notion of these two planes helps clarify some important features. In analogy to microscopes and telescopes, which have an object lens on the side of the object being viewed and an ocular lens for the viewer's eye, we can call the plane of reception/retention the object plane, where the soul is given the original object and its relevant context, and the plane of reconfiguration the ocular plane, where the work of the imagination proper takes place. It is precisely these planes as contexts that now take on thematic importance.
The object exists or appears as part of a context, for example a stone lying loose on a sandy beach. If I now image this as a large sphere on a one-inch-thick bed of tiny spheres jumbled together, I have mimicked the immediate experiential context and can use it as a kind of template that configures the rock and its situation. The important thing to notice is that within each plane there can take place certain events and transformations independent of any that might take place in the other, yet many of which can be mimicked reciprocally. For instance, another stone might be washed up on the beach (I can figure this as a second large sphere being pushed onto the bed of tiny spheres); or the sphere might be rolled in a way that traces an S-curve among the tiny spheres (obviously corresponding to a similar path traced by the real stone). Each plane has a degree of autonomy and certain principles according to which it operates; in fact, it is these principles that make for the autonomy. Each of the planes also has a degree of openness to innovations, although these are not unlimited. For example, I could imagine the sand as occupied by a group of sunbathers in addition to the nearby stone: I would thus be bringing the sun and human beings and their comportments into the beach situation. I could perhaps mimick these with cartoon or stick figures in my ocular plane refiguration, but beyond a certain limit there is no point in carrying this further. I might instead become interested in the question of how the tiny spheres would move if a sinkhole developed, and in what way they might carry the large sphere along with them. With a computer visualization and some simple dynamical rules I might well be able to develop a tolerable model of real sinkhole behavior (and building the computer model amounts to opening a third plane).
I could try to set up an analogous situation on a real beach with a more or less spherical rock and perform experiments, but only if I saw some reason to do this. In every case there would be a certain limit beyond which it
would become difficult or even pointless to continue developing the context and situation of one plane so that it corresponds to the other.
What makes a plane a plane, then, is that there is a situation of relevancy that is or can be transformed according to certain principles. In a very basic sense we could say that the situation of the rock on the beach is all the processes and activities that take place in a short span of time. This looks like the "real-world" situation. But the real-world situation is itself labile, for a geologist might see the appropriate situation as involving millennia or even millions of years. Thus there is always a temporal and sparial situation of a real-world object. The apparently relevant time and space may be expanded or contracted, and the relations of the object with other things may change depending on the focus of attention. In the case of the plane in which I figure the beach with spheres, the time is the vaguely definable one of present concern, and the place might be called a subset of imagined three-dimensional Euclidean geometry. But the principles according to which processes and comportments take place in this time and place would depend on the rules of transformation and the intrinsic powers of the imagination to conceive and reconfigure the time and place.
The advantage that the plane of imaginative geometry has over the real-world plane is that its possibilities are less unpredictable; they are in fact autarchic, defined by the imaginer in principle. If certain rules are followed, or if the situation conforms to basic powers of the imagination, it is more controllable than the real-world situation. Such a situation would be maximally achieved, for example, if I imagined a universe in which all particles were of the same size and shape (spheres) that obeyed well-defined rules of movement (linear) and collision (perfectly elastic, conserving momentum). In such a case, one would not need to make constant ad hoc interventions or decisions to maintain an ongoing process: the initial rules and situation would take care of all that followed.
The reader will recognize that I have in effect developed the notion of a model. That was not the primary intention, but in fact the notion of a model is derivative from the possibility of biplanar viewing, seeing one thing and its situation in terms of another. A model is a formalized and multi-dimensional analogy, whereas biplanar viewing is simply a way of getting a "visual" fix on something.[24] One needs to get a fix before one can model. One thing that should be clear by now is that there is no intrinsic reason why one of the planes should or must always be the real world. For example, the mathematical realm of an equation can be pictured as (viewed in terms of) a geometrical curve, and vice versa. It should be evident as well that if one can get a fix on something in one plane (the object plane) in
[24] This difference corresponds roughly to that between analogy and metaphor and tends to support the cognitive primacy of metaphor.
terms of another plane (an ocular plane that happens to be simpler), then the relative simplicity of that ocular plane may ease the difficulties of finding answers to questions that come up in the object plane. All that is required is that certain things and relationships in one be figured in the other. Ordinarily this would mean that certain proportions be maintained, even if not in an immediately recognizable form. Furthermore, it is also evident that if B is an ocular plane figuring object plane A, then in turn plane B can become an object plane with respect to new ocular plane C, and that if some proportionality is maintained in each transition, then C can serve as an ocular plane, directly or indirectly, for plane A.
The reader may think that we have generated a mountainous apparatus to explain a simple point that Descartes was getting at. More significant, he or she may already guess that the ultimate outcome and support of this biplanar figuring is a strict analogy between the material universe (geometric space) and the space of the imagination to be found in the later Descartes. But it is necessary to make the general case about the concept of biplanarity because the imaginative figuring of the early Descartes, even when it figures in a strictly geometric sense concerning physical questions, proceeds with a much greater flexibility than it did later on, and it displays a marked preference for ad hoc solutions that respect the particular context of the problem and therefore the essential relativity of the planes that I have emphasized. Furthermore, the fundamental notion of extension in the later Descartes will take on a different significance when it is conceived in terms of a biplanarity established, in the manner of Le Monde, between the realm of physical extension and the realm of the imagination (the fable that begins in chapter 6 of that work). This in turn will have an effect on the way in which we conceive the positions achieved in the writings published in Descartes's lifetime.
Although some of the issues related to the intellectual imagination must be postponed until the final section of this chapter, we have already seen enough to recognize that nothing in principle prevents the method of biplanar figuring from being extended to spiritual and intellectual matters. For the technique is based, not on the materiality or extensionality of imagination, but on the ability of relations in one plane to be analogically and proportionally figured in another plane. That is, as long as there are "mirrorable" relations in a plane, no matter what the nature of the entities in that plane or the rules of mirroring, those entities and relations can to that degree be imaged by figures and bodies. The method is therefore ontologically based: not in terms of substances and essences, but rather in terms of relations, relations that can in most cases be presented in the very clear and rigorously delimitable terms of mathematics. Thus the ontological basis is that of similarity between various things, possibly even between all things; the ontological basis is psychologically and epistemologically
imaged in corporeal and intellectual imagination; and the way in which these relations are presented gives rise to determinate and often mathematically solvable problems.
If we limit ourselves simply to the realm of the corporeal, we can derive from these considerations a comprehensive technique or method of solving problems of this realm. This seems to have been the point of the note quoted earlier in which Descartes said that the goal of natural explanation is to accommodate explanations to what is known by sense (AT X 218-219). Such a bald assertion could never have been uttered by the older Descartes. The note links all natural things to sense by way of similarity, a similarity that pervades all nature and sense and that allows the "assimilation" of one kind of natural knowledge to another.[25] It is probably not coincidental that in Leibniz's selection there is just a single note (about the perfection of the acts of animals suggesting their lack of free will) between this and the beginning of the series of notes about natural scientific and mathematical topics, a series that continues right up to the end of Leibniz's selection. Even if they were not contiguous in the original notebook, the physicomathematical notes apply in fact what the preceding "figuring" notes develop in principle. It is in light of the technique of figuring, then, that we can appreciate one of the earliest stages of Descartes's thinking about method.
D. THE PHYSICOMATHEMATICAL NOTES OF THE "COGITATIONES PRIVATAE"
Shortly after their first meeting, Isaac Beeckman recorded in his journal that Descartes considered him the only person he had met who accurately joined physics with mathematics, a compliment that Beeckman reciprocated (AT X 52). Beeckman was in the habit of giving marginal titles to his
[25] Consider the cogitatio privata that reads "Una est in rebus activa vis, amor, charitas, harmonia" (AT X 218), "One [and the same] is in things active power, love, charity, harmony." The usual renderings into English and French construe this along the lines of "There is only one active force in things: love, charity, harmony," but the Latin word order supports construing vis as part of the concluding series. Despite amor's being a masculine noun ordinarily requiring unus, the weight of the three feminines makes a distributive construal of una to all four permissible; and on the usual reading, the three concluding nouns dangle. The aphorism would therefore be not primarily about the active force in things hut about the fundamental ontological identity in things of active power, love, charity, and harmony, although according to distinctions of reason they appear to be different. When taken in this manner the sequence is a strongly ascending order: from the ordinary power in (physical) things to the yearning, erotic love of the animate to selfless, spiritual love and, finally, to the dynamic equilibrium of all things in the cosmos. The whole universe is thus united in a continuous web of relational powers stretching across the entirety of creation, from ordinary things to things of the spirit.
journal entries; this one he labeled "Physicomathematici paucissimi," the very few physicomathematicians. Since then the rubric has been not uncommonly used to designate the method and kind of natural science that Descartes practiced early in his career. In brief, physicomathematics is the application of a geometric analysis to problems conceived according to a mechanical and more or less corpuscular understanding of natural things and events, like the motion of a body subject to uniform acceleration or the path followed and the pressure exerted in a water-filled container by a particle of water at the upper surface.
Here I shall not offer an interpretation of this physicomathematics as an episode in the history of modern physics or in the development of its conceptual apparatus, or even in comparison with the later physics of Descartes.[26] Instead, I begin by noting that these two problems were recorded both in Descartes's notebook and in Beeckman's Journal, that they are just two of a large number of similar problems raised in the notebook, and that what they have in common is a method of using ingenious geometrical figuration to arrive at solutions, or solutions in principle, of physical problems. I remark further that these notes are in essential continuity with the technique of representing musical consonances by a line divided into proportional parts, yet with an increasingly sophisticated development of the figures, the proportions, and the operations used for deriving problem solutions.
So, for example, the first physicomathematical problem in the "Cogitationes privatae," much discussed in the literature since early in this century, is that of a falling stone, subject to uniform acceleration in a vacuum.[27]
It happened to me a few days ago to make the acquaintance of a most ingenious man, who proposed to me this question:
"A stone," he said, "descends from A to B in one hour; it is, however, attracted by the earth by a force constantly the same, and it does not lose from its speed what has been impressed on it by prior attraction. For what is moved in a vacuum is always moved," he considered. What is sought: Win what time a given space is traversed."
[26] Such analyses can be found in Gaston Milhaud, Descartes savant (Paris: Alcan, 1921); E. J. Dijksterhuis, The Mechanization of the World Picture: Pythagoras to Newton, trans. C. Dikshoorn (Oxford: Clarendon Press, 1961; reprinted Princeton: Princeton University Press, 1986); John A. Schuster, "Descartes and the Scientific Revolution, 1618-1634: An Interpretation" (Ph.D. diss., Princeton University, 1977), esp. 50-159; Schuster, "Descartes' Mathesis Universalis "; William R. Shea, The Magic of Numbers and Motion: The Sdentific Career of René Descartes (Canton, Mass.: Science History Publications, 1991), 15-22; and Daniel Garber, Descartes' Metaphysical Physics (Chicago: University of Chicago Press, 1992), 9-12.
[27] See, for example, Milhaud, Descartes savant, 26-31; Alexandre Koyré, Galileo Studies, trans. John Mepham (Atlantic Highlands, N.J.: Humanities Press, 1978; French original 1939), 79-94; and Shea, Magic of Numbers and Motion, 15-27.
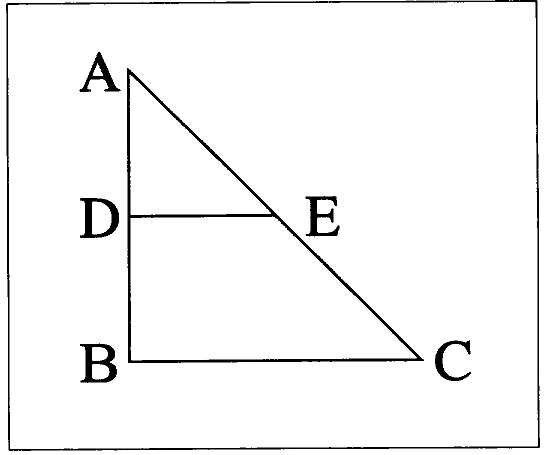
Fig. 4. The figure that Descartes used to "solve" the falling body problem.
I solved the question. In a right isosceles triangle [fig. 4], the space ABC represents <the motion=;[28] the inequality of the space from point A to base BC,the inequality of the motion. Therefore AD is traversed in a time that ADE represents; DB in the time that DEBC represents: where it is to be noted that less space represents a slower motion. But AED is a third part of DEBC: ergo it traverses AD three times slower than DB. (AT X 219)
It has long been recognized that Descartes's "solution" is wrong and that it suffers from conceptual ambiguities. It does not carefully distinguish between distance, speed, and time: first the areas are said to represent motion, that is, speed; next they are taken to represent times; then they are taken to correspond to degrees of slowness rather than speed. Descartes concludes that the rock traverses AD three times slower than DB, which is the same as to say that if AD is traversed in one unit of time then the successive equal distance of fall DB will take l/3 (0.333) unit. The correct, Galilean answer, which we derive algebraically from the relation d = 1/2 at2 (where d is distance, a acceleration, and t time), is that if AD is tra-
[28] The caret brackets are in AT.
versed in one unit of time, then traversing DB takes another
Beeckman preserved in his Journal a more fully explicated and somewhat less problematic version of this solution and also his own answer, which by modern standards is correct.[29] Beeckman's note on Descartes's solution also mentioned other problems that could be solved by figurate reasoning. The one that immediately follows the falling body problem is a variant of it in which the attractive force (and so also the acceleration) is constantly increasing; according to Descartes's techniques, says Beeckman, the solution requires a three-dimensional figure (a pyramid) appropriately subdivided into sections. This entry in the Journal also briefly considers the problem of compound interest.
One imagines it to increase in individual moments, and asks what is owed at this or that time: for this problem is solved using proportions divided by a triangle; but the line ab must not be divided into arithmetic parts, that is, equal parts, but in geometrical, or proportional. All of which I could prove most evidently from my [= Descartes's] geometric algebra, but it would be too long. (AT X 78)
This compound interest problem appears, in its turn, in the "Cogita-tiones privatae," as does also the variant of the falling body problem that postulates an increasing force of attraction; the note about the latter acknowledges that its solution would require a pyramid. It is immediately followed by two entries that make a methodological generalization.
Yet as I lay down the foundations of this science, motion everywhere equal [= constant, unaccelerated motion] will be represented by a line, or by a rectangular surface, or a parallelogram, or a parallelepiped; what is increased by one cause, by means of a triangle; by two, a pyramid, as above; by three, by means of other figures.
From these things an infinite number of questions are solved. (AT X 220)
In the continuation of this last note and the notes that follow, Descartes states problems and describes the kinds of curves that would be used in solving them: for example, at what point the speed of a rock falling in air stops increasing, the compound interest problem, whether the curvature of a chain hanging slack between two supports describes a conic section, why an object hurled from an arm moving circularly around a pivot point begins to move straight ahead when it is released, and many others. Although Descartes does not attempt actual solutions or sketch figures in
[29] Beeckman solved the problem by letting the area of the figure stand for time; see AT X 58-61. Compare AT X 75-78 for the fuller account of Descartes's solution that Beeck-man recorded in his Journal.
most of these notes, it is clear that he had already considered many in detail and that he had recognized some specific difficulties they raised. Concerning the compound interest problem, he appears to have gone beyond the solution outlined in Beeckman's Journal for he recognizes that constructing "the line of proportions" in the geometrical figure requires using a curve known as the quadratrix, which "arises from two motions not subordinated to one another, [one] circular and [the other] straight" (AT X 223).
E. THE UNIVERSAL SCIENCE OF PROPORTION
The question of the quadratix and the kind of "line of proportions" its construction requires in fact puts us fight in the middle of the central problematic of Descartes's mathematics: proportionality. One of the main problems—one should probably call it the main problem—Descartes pursued throughout his career as a mathematician was the technique of constructing geometric proportionals. The construction of these proportionals had long been recognized as an issue in musical theory and was taken up in detail by the one author to whom Descartes acknowledges a debt in the Compendium, Gioseffo Zarlino.[30] The classic construction techniques of the ancient Greek mathematicians, employing ruler and compass, are in general not sufficient for producing an arbitrarily chosen number of geometric proportionals.[31] The mathematician Eratosthenes, however, took an important step in the development of more complicated, nonclassical devices for constructions by inventing the mesolabe, a set of interconnected triangles with pivoting arms that are able to slide in a rectangular framework. The mesolabe can be used to find two mean proportionals between two given line segments, which enabled Eratosthenes to duplicate the cube (i.e., to construct a cube double the size of a given cube). It also
[30] In Zarlino's Istituzioni harmoniche (Venice, 1558), 113-114, and Dimostrazioni harmoniche (Venice, 1571), 163-168; cited by Shea, Magic of Numbers and Motion, 38-40.
[31] Using just ruler and compass one can always find a point that determines a singte geometric mean proportional c between two lengths a and b. One can therefore also take this new line and find the mean proportionals between it and the other two (between a and c find d, between c and b find e ), thus acquiring three mean proportionals, d, c, and e, between the original lines; dividing each successive pair of these five lines yields four more mean proportionals, for a total of seven between the original two lines; dividing again produces a total of fifteen, etc. (i.e., one can use this technique to find l, 3, 7, 15, 31, 63, and in general 2 - 1 mean proportionals between the two original lengths). But one cannot in general construct an arbitrary number of geometric proportionals between two lengths. By contrast, for any counting number n one can divide the interval between two lines into n equal segments; that is, any arbitrary number of arithmetic mean proportionals can be found using ordinary techniques of construction.
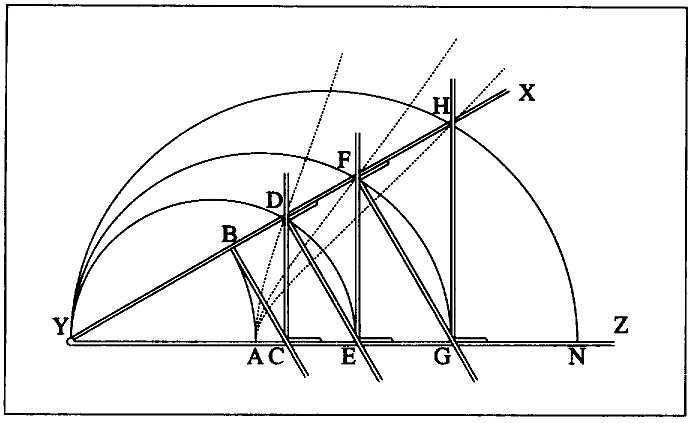
Fig. 5. Descartes's proportional compass. YX and YZ are joined by a pivot at Y; ruler BC (which can be made as long as necessary on side C) is rigidly attached to YX at a right angle; ruler CD has a sliding attachment that keeps it perpendicular to YZ; as do also EF and GH; similarly, DE and FG have sliding attachments to keep them perpendicular to YX. As the compass is pivoted open, the point of intersection between BC and YZ, that is, C, moves to the right, and the ruler BC pushes CD along YZ, CD pushes DE along YX, and so forth; when the compass is closed, all the rulers are pulled back toward Y.
can be used for dividing an octave into twelve equal semitones, for which purpose Zarlino mentions it.[32]
Apparently stimulated by the usefulness of the mesolabe, in early 1619 Descartes began to devise other mechanical instruments for solving complex geometrical problems. In particular, he made a geometrical compass that could in principle be used to find any number of geometric proportionals between two given lengths. The only limit was a practical one: how many rotating and sliding rulers could be manageably combined in a network of pivots and grooves. The construction of the instrument, pictured in figure 5, begins with two principal rulers, YX and YZ, pivoted at Y. These rulers are machined with grooves that allow the transverse rulers like BC
[32] After dividing the interval between a string and its midpoint into three geometrically proportional segments using the mesolabe, one then divides these three proportionally using just ruler and compasses (this produces six intervals between the original two lines), then divides each of these six again by a single proportional (yielding twelve intervals, the semitones of a musical octave).
and CD to slide as the compass is opened (that is, as angle XYZ is enlarged) or closed (XYZ gets smaller). These transverse rulers are attached in the following way.
First, BC is rigidly affixed to the upper ruler YX at B ; these two rulers always remain perpendicular to one another at this point. When XYZ is opened, point C will move progressively to the right along YZ . If we make rulers YX, YZ , and BC as long as we need and please, then as XYZ is opened very wide (so that YX and YZ are nearly perpendicular to one another) the point C will move toward the right to infinity, until finally BC becomes parallel to YZ when YX turns perpendicular to YZ.
So much for the first of the transverse rulers. The second transverse ruler, CD , represented in the figure as L-shaped, is fitted to the other rulers so that it will be pushed to the right by BC as the compass is opened and pulled back to the left as the compass is closed; as this happens, CD always remains perpendicular to YZ. Unlike the first transverse ruler, which is permanently attached at point B, CD and all the rest of the transverse rulers slide along either YX or YZ;C, D, E, F, G, and H are all moving points that move right or left according to whether the instrument is opened or closed, while the short leg of each transverse ruler keeps it perpendicular to either YX or YZ.
Thus the two principal rulers and the transverse rulers, as many as one likes (though here there are just six transverse rulers), are mechanically interlinked so that increasing or decreasing the principal angle XYZ causes the points C, D, E, and so on, to begin sliding; the transverse rulers push and pull one another into new positions as a network. For it all to function in a real instrument there would need to be appropriately tooled linkages: for example, a slot along the bottom of BC in which a button pivot attached to CD at C would slide as BC pushed or pulled on CD . In a similar fashion, DE will be attached to CD at D so that the ruler CD pushes or pulls DE to make the short leg of DE (at D ) slide along YX and the point E move to the right or the left along YZ. EF, FG, and GH will be attached and work in a similar way. With a routing tool and button pivots one could fairly easily construct a working version of such a compass. There is no limit in theory to the number of transverse rulers that can be used, but practically the instrument would soon grow bulky and stiff in its operation if one used too many.
The theoretical key to this compass's usefulness is that the interlocking rulers form triangles that are geometrically similar to one another. If one takes any two triangles formed by the various parts of the compass, one will find equal corresponding angles, and this assures that the lengths of the corresponding sides will maintain a strict proportion to one another. So, for example, in the triangles YBC and YFG , the angles at Y are equal, the right angles at B and F are equal, and the angles at C and G are equal;
therefore YB/YF = YC/YG = BC/FG. Triangle YBC is also similar to CBD, which is similar to DCE, which is similar to EDF , which is similar to FEG , which is similar to GFH ; YBC is similar to YCD, YEF , and YGH as well.
Because of these similarities we can set up a long series of proportions that hold between the ruler lengths. It is a simple exercise to see that HG/GF = GF/FE = FE/ED = ED/DC = DC/CB = CY/YB ; and even simpler that YB/YC = YC/YD = YD/YE = YE/YF = YF/YG = YG/YH. The compass is in effect a machine for generating series of line segments in constant, continuing proportion. So, for example, we can see that YC is the geometric mean proportional between YB and YD (since, from the beginning of the second equation string just given, YB/YC = YC/YD ; the geometric mean proportional between two numbers or lengths a and b is the number or length x such that a/x = x/b or, equivalently, such that x2 = ab ). YD is the geometric mean between YC and YE ; YE is the mean between YD and YF ; and so forth.
Now if we stipulate that YB is going to be our unit length, so that YB = l, we get 1/YC = YC/YD, which is equivalent to YD = YC2 . In the second equation string of the second sentence in the preceding paragraph, we have the equality YC/YD = YD/YE ; since we just showed that YD = YC 2 , we can substitute YC 2 for YD : YC/YC 2 = YC[2] /YE. Multiplying both sides of this equation by YC and by YE , then reducing it to simplest form, we get YE = YC[3] . Similarly, since YD / YE = YE / YF , we can substitute and work the equation to show that YF = YC[4] ; from YE/YF = YF/YG, we can reason that YG = YC[5] , and finally YF/YG = YG/YH lets us conclude that YH = YC 6 . If in theory or reality we build a compass with n transverse rulers, we can in a similar way find a line length that is equal to YCn for any positive integer n.
One of the things this compass does, then, is to raise the quantity c represented by the length YC to any power we like—or, more accurately, it raises it to all powers simultaneously, since YC, YD, YE, YF, YG, YH, and so on, represent the first, second, third, fourth, fifth, sixth, and so on, powers at the same time. Notice that to get all these powers one only needs to make YB the unit measure and open the compass until YC is of the desired length c ; one can then read the powers off of the principal rulers, with the lengths corresponding to odd-numbered powers lying along YZ and even-numbered powers along YX Inversely, one can take any number k , open the compass so that YD = k and have the square root represented by YC ; or open the compass so that YE = k and have YC be the cube root of k ; or open it until YF = k and have YC be the fourth (quartic) root of k ; and so forth. So the compass also extracts roots of any degree.
The last use of the compass to point out here—one that is a strict consequence of the preceding—is that it will display simultaneously any arbitrary number of geometric mean proportionals between two numbers/ lengths (presuming, of course, that we can add on transverse rulers at will).
Between YB and YG the compass displays the four mean proportionals YC, YD, YE , and YF ; between YB and YH it displays five (with YG added to the previous list). So given any two numbers a and b , set the scale on all the rulers so that YB = a (a scale, of course, just sets a basic proportion that will hold throughout all the terms of a problem or representation, as in a scale drawing),[33] expand the compass so that, say, YH = b , and one will have the five geometric mean proportionals.
Later, as is evidenced by the Geometry of 1637, Descartes continued his studies of this and related compasses, studies that were crucial for developing his version of what we call analytic geometry. The fundamental point is that if one takes YZ as fixed in place, it in effect becomes the equivalent of the x -axis of Cartesian coordinates in two dimensions, and the points of intersection between the transverse rulers and the upper principal ruler, that is, points B, D, F , and H , all trace out curves as the YX arm is rotated counterclockwise. These are the dotted lines of figure 5. Any such curve traced by the moving points of intersection of this compass is describable as an algebraic polynomial.[34]
In effect, these polynomial curves can be used geometrically to construct solutions to problems of proportion, even without the direct use of the compass. Contrariwise, the compass, with pencils attached to the moving points, can be used to trace polynomial curves. All the motions are rigidly interconnected and interdependent: the motion of any part of the device produces a determinate motion in every other part. This device and others like it, plus Descartes's researches into questions of how the procedures of sliding and rotating could be generalized mathematically to generate curves and figures for solving problems, are to be found in the last pages of the "Cogitationes privatae." For example, he conceives of a device for producing conic section curves by imagining a line capable of sliding through a fixed point while it simultaneously rotates around an axis; if the line is imagined to be a pen tracing out a curve on a fixed paper plane, the geometrical device becomes a practical one, an instrument for drawing conic sections. Such imagining provides the principle according to which a technician might devise corresponding practical machines. This technique of imagining the determinate configuration and motions of ideal machines occurs also in Descartes's work of the later 1620s, in particular in his search for devices to grind optical lenses.
Although we shall not follow these developments of Descartes's mathe-
[33] As we shall note presently, fixing the scale exactly, which is quivalent to determining he unit measure, is not always a solvable problem.
[34] An algebraic polynomial has the form a nx + an-1x + . . . + a2x + a1x + a0 , where n is a positive integer greater than or equal to o and all the terms aI are rational numbers (equivalently, one can restrict all the terms ai to integer values).
matics further, the crucial point is that Descartes's "analytic geometry" was derived from his examination of proportionality; it was driven by his discovery of an equivalence between (on the one hand) numerical/algebraic approaches and (on the other) geometric construction by the continuous, rigidly interlocked motions of mechanical instruments. Any algebraic problem, it seemed, could be embodied in a machine or compass, and any machine or compass could be used to generate what we would recognize as an algebraic polynomial in one unknown. These machines are perfectly describable by a mathematics using only rational numbers and therefore quite concretely and determinately imaginable.
At the end of the previous section and the beginning of this one, I mentioned a curve called the quadratrix. The quadratrix, Descartes realized, was the curve necessary for solving problems of compound interest. Its significance in the present context is that it cannot be generated by the kind of interlocking machines and compasses I have been describing. In figure 6, let OD and OC be our mutually perpendicular reference (coordinate) axes, fixed rigidly in place. Take a line segment OA and attach it by a pivot at O (this segment will rotate around O once we set the machine into operation). Take another line segment BC and attach it to OD so that it can slide up and down OD while remaining perpendicular to axis OD and parallel to axis OC . The machine will start working at time t0 with OA lying along OD and BC intersecting OD at A . We begin the motions by putting OA into clockwise rotation around O at a uniform speed and letting BC slide at a uniform speed downward along OD. We want to coordinate the rotation of OA and the downward slide of BC so that at the moment when BC reaches O (and therefore lies along OC ) the entire rotating segment OA will coincide with BC and OC . This device constructs the quadratrix as the line traced out by the moving point of intersection of OA and BG In figure 5, it is the curve marked by the points B, E, F, G, H . By attaching a pencil at this moving point of intersection we could actually draw the curve with an accuracy limited only by technical ingenuity.
What differentiates this "machine" from the proportional compass and other rigidly interlinked instruments is that it is not a single machine at all but two independent machines in need of coordination. The catch is that the coordination cannot take place by means of an interlinked system of pivots, sliding rulers, gears, or the like, connected in a way to assure that the two lines move uniformly and also coincide at exactly the right moment Such coordination can be achieved only approximately, and although there will always be ways to improve the approximation, it is impossible to give a solution that is general and exact.
With purely pragmatic goals supported by a sufficiently powerful technology, the lack of an ideal solution is a minor problem. One can still gain "control" over theoretical and practical problems apart from 100 percent
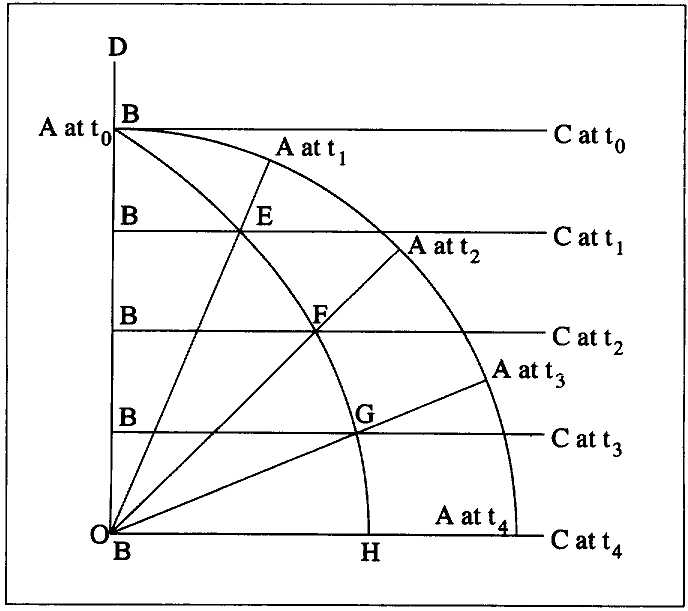
Fig. 6. Segment OA is pivoted at O and set rotating clockwise at a uniform rate; its positions at times t0 , t1 , t2 , t3 , and t4 are pictured. Simultaneously segment BC slides down axis OD at a uniform rate; its positions at times to through t4 are pictured. The two motions are coordinated so that OA falls along axis OC precisely at the moment (t4 ) when BC reaches it; at that moment OA, BC, and OC coincide. The quadratrix is the curve traced out by the moving point of intersection of OA and BC, indicated by the curve BEFGH.
accuracy and generality. The techniques of biplanar figuring would continue to be useful. But Descartes does not seem to have been interested in purely practical control without a theoretical certainty to back it up. The reasons are probably relatively simple. First, without knowledge of the exact solution, one cannot know how accurate a merely practical solution is. This is not to deny that in particular cases one can determine what the accurate solution would be: for example, there are simple techniques for constructing a limitless number of individual points of the quadratrix. Yet one loses thereby the economy that the general solution provides, and, even more important, one loses a careful and comprehensible understand-
ing of the relationships involved (i.e., one loses sight of the truth of the matter and its true cause or causes). In the solution of a single problem the resulting imprecision might matter little, but if the problem is part of a series of interconnected problems the uncertainties could quickly pile up in an indeterminate way, thus adding further uncertainties to any overall solution. Second, if a mechanical construction is impossible, the question arises whether this kind of motion is possible at all, that is, whether it could really occur in nature. God, of course, could bring it about, but not by ordinary, natural means.
Eventually, in the period leading up to the composition of the Geometry , the last of the essays accompanying the Discourse on the Method , Descartes became interested in the problem of systematically describing in algebraic terms the curves produced by the kinds of machines he had imagined in his youth. In the earlier period we can see traces of this interest, but it is not well developed. Although at the very end of the "Cogitationes privatae" he presents arguments about how algebraic equations of the fourth degree can be reduced to third-degree problems, he does not, surprisingly, call attention to any connections between his geometrical and his algebraic investigations. Their interrelationships are explicit in the Geometry , however; indeed, these interrelationships are its essential teaching.
Precisely when Descartes moved on to examine the essential structures of the interrelationship of algebra and geometric curves is a matter of debate. Looking at things from the longer perspective provided by the Geometry, one can nevertheless generalize: The kinds of machines Descartes conceived in the "Cogitationes privatae" can be used to trace out curves that are describable as analytic polynomials (i.e., curves that correspond to algebraic polynomials having whole number coefficients). In principle such curves are the result of raising a variable number (length) to a power (i.e., multiplying the variable length by itself the number of times indicated by the power, resulting in a "power length"), multiplying the result by a whole number (i.e., adding the power length to itself a whole number of times), and finally adding to or subtracting from one another all the resulting terms (lengths).[35] As a result, there is a translatability from a variable geometry into analytic polynomials and back, a translatability that provides powerful techniques for mathematical problem solving. A simple example: to solve an equation like x[5] = 4 one can in effect find four geometrical mean proportionals between a line of length 1 and another of length 4; contrariwise, to find solutions to geometrical problems, in particular those that require the construction of new line segments, one can translate the relationships into algebraic terms, perform successive
[35] As we shall see in chapter 3, this is the kind of mathematics presented in the uncompleted second part of the Regulae ad directionem ingenii.
operations on the equations to isolate the solution for an unknown, and then reproduce the geometrical analogs of these operations using geometrical figures and appropriate construction machines.
Things become more complicated when one allows irrational coefficients in the equations, that is, when the givens of the geometrical problem do not have a common measure, and more complicated still when the equations one is dealing with are no longer representable by a finite algebraic polynomial. The quadratrix is an example of the last, as are also the trigonometric functions (sines, cosines, tangents, etc.). One should realize, however, that the issue is not simply one of constructibility, since, for example, one can easily construct segments representing the trigonometric values for a given angle using just a ruler and a compass; likewise one can find as many points of the quadratrix as one likes using just these simple tools. The issue is rather whether the whole curve can be smoothly, continuously constructed by a constant motion that embraces every possibility, not just for a finite number of values or even for a potentially infinite number selected one by one.
In the letter to Beeckman of 26 March 1619, Descartes explained the goal he was pursuing with these and related researches.
And assuredly, as I shall lay bare to you what I am laboring at, I do not desire to propound a Llullian Ars brevis but a completely new science, by which might be solved generally all questions that can be put forward in any genus of quantity, continuous as well as discrete. But each according to its nature: for, as in Arithmetic, some questions are solved by rational numbers, some only by surd [= irrational] numbers, others finally can indeed be imagined but not solved: so I hope that I shall demonstrate that, in continuous quantity, some problems can be solved with straight or circular lines alone; others cannot be solved except with curved lines, but which arise from one single motion, and therefore can be drawn by the new compasses, which I consider no less certain and Geometrical than the common ones with which circles are drawn; others, finally, cannot be solved except by means of curved lines generated by different motions that are not subordinated to one another, which are certainly only imaginary: such a [curved] line is the quadratrix, [which is] well known enough. And I think that nothing can be imagined that cannot be solved at least by these lines; but I hope that I shall demonstrate which questions can be solved in this way or that and not another: so that almost nothing will remain to be discovered in Geometry. The work is virtually infinite, and not for one person alone. [It is] incredibly ambitious; but I have glimpsed through the obscure chaos of this science some sort of light, by the help of which I think every darkness, however dense, can be dispelled. (AT X 156-158; my emphasis)
Descartes's hope, as he spells it out here, is born of having conceived a science of quantity more general than either geometry or arithmetic. The former deals in magnitudes like length, width, and volume, which can take
on any value whatever, the latter in number, which is in essence based on the discrete elements of order. As any Aristotelian might have observed, these are both species of quantity, of the "how much." Thus his object is to develop a kind of mathematics that deals not with one or the other but with quantity per se. In arithmetic, problems can be divided according to the kinds of numbers that arise: the simplest problems are solved by counting numbers and the results of the four basic arithmetic operations (division, in particular, gives rise to the rational numbers); the next level of complexity is in problems that require surds, that is, irrational numbers that result from the four basic operations plus the taking of roots of any degree; the last is imaginary only, by which Descartes means not imaginary numbers in the modern sense[36] but rather solutions that require numbers that cannot be directly expressed by either arithmetic or root-taking operations (and so cannot be derived from the motions of rigidly interconnected machines) but are nevertheless determinate. For example, calculating the circumference of a circle requires the use of a number, pi , which is neither rational nor surd, yet it is quite determinately imagined as the ratio of the circumference of a circle to its diameter.
The problem of proportions was at the center of the mathematics of Descartes in large part because it appeared to him the key to arriving at a general method of solving problems. The construction of proportions falls into a general scheme that divides problems into those that can be solved by arithmetic proportions (rational numbers), those that can be solved by geometrical proportions (analytic, which means the solutions can be represented by a polynomial having rational coefficients), and those that can only be imagined (having transcendental solutions) hut not generally or mechanically solved. The criterion here is that classes one and two are both constructible and imaginable, whereas class three is only imaginable.
It is sufficiently clear, then, that exploring the power and scope of imagination was at the root of Descartes's early mathematics and science. The fundamental categories of the science of quantity were determined in accordance with imaginability, both the kind that is mechanically constructible
[36] That is, by taking the square root of a negative number. Although Descartes is sometimes credited with having in this passage initiated the modern usage of 'imaginary number' (see Gino Loria, "L'Enigma del numeri immaginari attraverso i secoli," Scientia 21 (1917): 105), it is clear that he is not referring to square roots of negative numbers but indicating imaginable but mechanically unconstructible solutions. AT agrees that Descartes is not referring to modern imaginary numbers but then suggests that he is thinking of solutions to equations higher than degree four (AT X 157). This seems doubtful to me, since equations of degree five and higher do not produce solutions different in kind from equations of lower degree, though perhaps the practical difficulties of solving higher-degree equations led Descartes to suggest this third kind of quantity (general techniques for solving equations of the first four degrees had been invented by the middle of the sixteenth century, and it was discovered later that there can be no general techniques for degree five and higher).
and the looser kind that is picturable but not constructible. There is a corollary: The realm of the corporeal is only a special case of the imaginable; the imagination in its most general form is more capacious and more powerful than the world that is merely given. One can imaginatively conceive what cannot be corporeally implemented.
F. DREAMS, AND IMAGES OF THE SPIRIT
The two-imaginations note begins with the power of corporeal imagination to figure physical things; it ascends to the use of physical things to figure what is higher. Intellect uses bodies, that is, the ordinary things of this world, to figure spiritual things. It is clear that there is license for taking 'figuration' in an extended sense even at the level of the corporeal imagination (i.e., imagination is not confined to pure geometry) and that the process of figuration is repeated at the spiritual level—presumably in a way analogous to the lower-level process. What this figuration by means of bodies is like is illuminated by another of the private cogitations.
Sensible things [are] apt for conceiving Olympian things: wind signifies spirit; motion in time, life; light, cognition; heat, love; instantaneous activity, creation. All corporeal forms act through harmony. More things [are] cold than dry, and humid rather than hot, because otherwise the active would have quickly carried off triumph, and the world would not have long endured. (AT X 218)
This note seems to present a quite precise symbology for the higher things; one could imagine extending the list to yield a "key" for spiritual interpretation. But this is probably going too far, and it overlooks that the key to interpreting the symbols must be the analogy of participation. Creation is a kind of act, so insofar as a corporeal activity is also an act it can symbolize creation; but among corporeal actions the most appropriate symbol would be one that acts in an instant (since creation, in Christian theology, happens outside of time and is the beginning of time). Similarly for the others; either the analogical resemblance appears to be based in a natural and obviously shared characteristic, as in figuring knowledge by light, or there is some event or set of events that establishes the rightness of the symbol (wind for spirit derives from the tradition of spirit as pneuma and the coming of the Holy Spirit at Pentecost—an event that would also justify fire as a symbol).[37]
[37] Of course, some symbols are obvious only because of established convention, and historically based symbols will be meaningful only to those who share the history. But this is not really an objection to symbology per se. If the world is pervaded by analogy and resemblance, there are many ways to get from one thing to another, since resemblances and analogies are manifold, and every thing and every act participate in natures or forms that they share with other things and acts.
The Olympian things here are spirit, life, cognition, love, creation; taking a cue from the first member of the list, we can call them spiritualia. What the note implies is that sensible things stand in certain definite correspondences with spiritualia and therefore can be used (by the poet or the ingenious philosopher) to illuminate the latter. Henri Gouhier has brought this and related notes into connection with the section "Olyrm pica" of the vanished notebook C, which section included, according to Baillet, the narration of three dreams that Descartes experienced on the night of 10-11 November 1619.[38] In the first dream Descartes was walking to some unspecified place when he began to meet with a series of hindrances: weakness on his right side, turbulent and opposing winds, and encounters with acquaintances who wanted to speak with him. When he awoke from this dream he prayed for deliverance from the evil things it foreboded and then considered the good and evil of the world for nearly two hours before falling asleep a second time. The second "dream" was a noise like thunder that frightened him out of sleep, whereupon he saw scintillating lights that by closing and opening his eyes he interpreted favorably according to "reasons taken from his philosophy." He fell asleep once more in a feeling of calm and had a third dream, centered on the appearance and disappearance of two books, a dictionary and a collection of poetry. Descartes said that he began interpreting while he was still dreaming and continued after awakening. The dictionary, he thought, represented the sciences taken all together, and the collection of the poets "marked in particular, and in a more distinct manner, philosophy and wisdom joined together" (AT X 184). Baillet continues:
He did not believe that one ought to be so very astonished to see that the Poets, even those who only amuse, are full of sentences of more gravity, more sensed, and better expressed than those found in the writings of the Philosophers. He attributed this marvel to the divinity of Enthusiasm and to the force of Imagination, which makes the seeds of wisdom (which are found in the spirit of all men, like the sparks of fire in stone) emerge with much more facility and even much more brilliance than Reason can do in the Philosophers.
Already the editors of the Adam and Tannery edition remarked that this passage contains a nearly verbatim translation of the two-imaginations note from the "Cogitationes privatae," and Gouhier interpreted it as a commentary on the dreams. One can easily agree with Gouhier's contention that it is not a key to the interpretation of dreams that Descartes was searching for (since he of course knew there are dreams that fantasy alone produces, without relation to truth) but rather a magnificent generalization
[38] The narration begins: "X. November 1619, when I was full of enthusiasm and was uncovering the foundations of a wonderful science etc." See AT X 179-188.
in answer to the question, "Is there not a necessity that spiritual things be translated by sensible images? Not only in dreams, but in the Bible, in nature itself insofar as it expresses the perfection of the Creator." One can also agree with Gouhier that this is Descartes as man of the Renaissance rather than as father of modern philosophy.[39] Yet it is not at all clear that we can dismiss this line of thought as a youthful, enthusiastic indiscretion of which he later repented, for it is an intimate part of his early philosophy and closely connected to themes that persisted into maturer years. At the very least we might wonder what turned Descartes from philosopher of the Renaissance to philosopher of modernity.
There is in fact a theme in the "Cogitationes privatae" that can help us identify a common basis for the two imaginations: discovery in accordance with the seeds or sparks of truth in the human soul. It becomes evident from a review of cogitations about the soul, its powers, and its inclinations. Descartes remarks that when he was young he would often try to see whether just by hearing about a new discovery he could replicate it for himself and that little by little he noticed that he was using certain rules (AT X 214). Most books, he notes, reveal their entire message in a few lines and a few figures, the rest merely fills up paper (AT X 214). "For all ingenia determinate limits are prescribed that they cannot transcend. If some cannot use principles for discovery because of a defect of ingenium, they can nevertheless know the true reward of the sciences, which suffices them for carrying out true judgments in the estimation of things" (AT X 215). He calls vices "diseases of the soul" and notes that they are harder to diagnose than diseases of the body, because although we have often experienced the proper health of the body, we have never experienced the health of the mind (AT X 215). He notes his inclination to sleep and eat when he is sad or when danger is imminent, whereas joy inclines him to neither (AT X 215). The two-imaginations note is followed by a reflection that "the sayings of the wise can be reduced to a certain very few general rules" (AT X 217), and it is preceded by this:
There are certain parts in all ingenia that, when even lightly touched, excite strong affects: thus a boy with a strong spirit, having been scolded, will not cry but get angry; another will cry. If it is said that many and great calamities have happened, we will be saddened; if it is added that some evil person was the cause, we will get angry. The passage from passion to passion [occurs] through neighboring ones; often, however, the passage from contraries is more robust, as when at a joyful party there is suddenly announced a sad event. (AT X 217)
[39] Gouhier, Les Premieres pensées, 84-86. For a different view of the dreams, as a hyper-rationalist fiction, see Richard Kennington, "Descartes' 'Olympica,'" Social Research 28, no. (Summer 1961): 171-204.
In each human being there are not just seeds of truth but also seeds of natural tendencies to affective responses, though the latter are more variable from person to person than the seeds and outgrowths of truth. This reflection puts us back in the conceptual universe of the Compendium musicae , which was based on the postulate of typical affective responses to tones more or less in accord with the organs of hearing. Descartes's concern here is the native endowment of the human being, each person's ingenium. The cognitively relevant seeds of truth are in each human being, but they blaze out in the higher imagination of poets, which is only ploddingly approached by philosophers.
According to the Olympian things note, all corporeal forms work by harmony. This picks up a theme of the immediately preceding note: In things, active force, love, charity, harmony are one.[40] The action of bodies takes place harmoniously by virtue of their forms. There is a balance in the cosmos so that the hot, corresponding to love, does not immediately overwhelm the cold. This is as far from conventional materialism as one can imagine, and alien to any mechanism that works chiefly by collisions, pushes, and pulls. This kind of action or causality is based on harmony, and, since harmony is harmonious because of the observance of proportions, then it can ultimately be figured mathematically, even if exactitude is not feasible. That this thought is cosmological in at least the physical sense is clear from the sentence that follows, which, using terms drawn from Aristotle's physics, implies that the elements and their qualities had to be in a certain proportion so that the world could endure: too much heat and dryness would lead to excessive activity that, presumably, would turn the world into a mere incoherency of overexcited, too rapidly moving elements.
One must be careful, however, not to read too much of the mathematical into such passages. The tendency of most Descartes interpreters is to follow the suggestion of the Discourse and to presume that the young Descartes, seeing that arithmetic and geometry were the most certain of sciences, proceeded to extend a method derived from these to the rest of knowledge. That is to miss something crucially distinctive. For the young Descartes, the power of mathematics is essentially its ability to symbolize relations and to express proportionalities, and this ability is grounded in the analogical structure of the cosmos. Thus the science of nature is not so much intrinsically mathematical as harmoniously proportionate, a harmony and proportion that is by its nature expressible in both geometric and arithmetic language. In a sense, each thing reflects other things, each relationship is expressible in manifold ways.
What natural science should do is pithily expressed in a private cogitation
[40] See footnote 25 for a discussion of the translation of "una est in rebus activa vis, amor, charitas, harmonia."
I have already cited twice: "The cognition of natural things by human beings [occurs] solely through the similitude of those things that fall under sense: and indeed we judge that person to have more truly philosophized who will have more successfully assimilated the thing sought to what is cognized by sense" (AT X 218-219). Certainly mathematics can be of use in this process of assimilation, but its power is not unique. Mathematics is deeply enmeshed in the ontological and psychological powers of figuration; its advantage as a mode of figuration is that it is perfectly expressible in the realm of the material and sensible.
G. IMAGES, MEMORYART, AND THE SECRETS OF METHOD
The relation between mathematics, physics, and imagination in the earliest stage of Descartes's work, then, depends on the analogical/proportional character of the world that allows imagination to figure one kind of thing by using another and to discover truths comprehensive of a class of things by manipulating and transforming an imaginative representation of them. Put generally, imagination serves as the agent of intelligent perception, the foundation of physics and mathematics, and the chief faculty for rising to spiritual truths.
It should not be surprising, then, that imagination and proportion also served as the core of an early reflection on the method and unity of the sciences in another of the "Cogitationes privatae," which proposes two approaches to a "true art of memory."
On reading through Schenckel's profitable trifles (in the book De arte memoria)[41] I readily thought that everything I have discovered had been embraced by imagination. It occurs by the leading back [reductio] of things to causes: when all those things are finally led back to a single one, there will be no need of memory for any science. For whoever understands causes, will easily form anew in the brain the altogether vanished phantasms by the impression of the cause. This is the true art of memory and it is plain contrary to the art of that sorry fellow [Schenckel]. Not because his [art] lacks effect, but because it requires the whole space[42] that ought to be occupied by better
[41] AT identifies this "profitable trifle" as Lambert Thomas Schenckel's De memoria (1595); see AT X 251. According to Paolo Rossi, this work was reprinted in Schenckel's 1610 omnibus collection of various memory treatises, titled Gazophylacium ; see Rossi, Clavis Universalis: Arti della memoria e logica combinatoria da Lullo a Leibniz, 2d ed. (Bologna: I1 Mulino, 1983), 149. I have consulted [Johann] Lambertus Schenckelius Dusilvius, Gazophylacium artis memoriae, published in Variorum de arte memoriae, tractatus sex, 2 vols. in one (Frankfurt: J. H. Ellinger, 1678), 1:1-182.
[42] 'Space' is Frances A. Yates's suggestion; see Yates, The Art of Memory (Chicago: University of Chicago Press, 1966), 373. The word is actually chartam, paper, sheet, or tablet. Schenckel's art employs the "space" of the imagination, not external, material aids.
things and consists in an order that is not right; the [right] order is that the images be formed from one another as interdependent. He omits this (whether advisedly I do not know), which is the key to the whole mystery.
I have excogitated another mode: If from the images of not unconnected things there are learned additionally [addiscantur] new images common to all, or at least if out of all of them at the same time there comes to be one image, not only would there be a relation to the closest, but also to the others: so that should the fifth relate to the first by means of a spear thrown on the ground, the middle one [would be related] by stairs from which they descend, the second one by an arrow projected at it, and the third by some similar rationale, in accordance with the reason of signification either real or fictitious.[43] (AT X 230)
Both Paolo Rossi and Frances Yates quote this passage in their books on the art of memory;[44] Rossi, in particular, uses it to show that the memory art was instrumental in shaping Descartes's conception of method. It would be going too far afield to give an account of what was involved in this art and its long tradition going back to ancient Greece and Rome. It must suffice to remark that it was based on creating image-symbols for what was to be remembered and then putting these in determinate memory places.[45] For example, one chose a familiar space, say, a Roman basilica or a theater, and then located within it, in an easily reproducible order, vivid and significant images that could be recollected in sequence whenever one needed to remember. The images could be direct or merely mnemonic, either conventional or personal.[46] One could, alternatively, detach the art from any particular space and instead create emblematic images (Justice blindfolded, holding a sword and scales, is a conventionalized remnant of such emblems). Or, using even greater abstraction, one could practice the art by combining routinized symbols, a technique that Schenckel prefers. At any rate, Schenckel's work is a fairly ample account of the art of memory based on the physiology of the brain and on the
[43] The last clause reads, Net tertia simili aliquâ ratione in rationem significationis vel verae vel fictitiae."
[44] Rossi, Clavis Universalis, 175; and Yates, Art of Memory, 373-374.
[45] The use of actual or fictional places for the images led to the alternative name for this technique, local memory. This spatial localization of images was not universally advocated, however; Schenckel's method, for instance, does not crucially depend on it. See Yates, Art of Memory ; Mary J. Carruthers, The Book of Memory: A Study of Memory in Medieval Culture, Cambridge Studies in Medieval Literature, no. 10 (Cambridge: Cambridge University Press, 1990); and Janet Coleman, Ancient and Medieval Memories: Studies in the Reconstruction of the Past (Cambridge: Cambridge University Press, 1992).
[46] Yates repeatedly makes the point that, in most versions of the art, vividness required creating the images for oneself, although medieval and Renaissance proponents often provided conventionalized symbols and emblems. By direct image, I mean, e.g., the image of Socrates talking used to remember what he said to Glaucon; by mnemonic, e.g., the image of Socrates used to stand for wisdom.
psychology of the internal senses as these were understood in the Middle Ages and the Renaissance. The techniques he teaches are supposed to be applicable to anything that needs remembering, including all sciences.
Yates remarks that the first, causal approach that Descartes offers as an alternative to Schenckel is innovative, whereas the mnemonic devices employed in the second are quite traditional. The first in essence eliminates the need for memory: one impresses the cause in imagination, and this produces the entire sequence of all the related images or phantasms. The mind in possession of causes is therefore in virtual possession of all the phantasms that derive from them. The second alternative depends on finding an image that is common to all others, so that one need not even go outside the realm of images (to causes). In this second mode the images all stand in a determinate, interdependent relationship that can be recalled to mind by symbols like the hurled spear (for the most distant relation of first to fifth) and the stairs (which bring us from the first to the middle level). This conception of ordering phantasms could easily be translated into terms of sequences ordered by proportion.
It is not hard to see how Descartes might have believed that he had found a way to unite both these methods, the causal and the proportionate. The kinds of devices he imagined consisting of interconnected, moving lines effect an outcome in principle that can be causally translated to real machines in the physical world; all these motions and effects are interconnected by proportional relationships. All complex proportions, in turn, are constructible from simple proportions that are subject to geometrical complication; the acts of geometrical complication are, in their turn, imitable by the arithmetic operations of addition, subtraction, multiplication, division, raising to powers, and taking roots. The art that takes advantage of these imaginable, proportionate operations is the true one, because it depends not at all on the arbitrariness and memorization of the classic art of memory, but instead only on the easily imaginable, easily replicable principles of mathematical proportion. At the very least, Descartes must have thought, the human mind's powers are sufficiently commensurable with the nature of the cosmos that it can embrace the overarching principles of harmony that pervade it in constellations of proportionally interrelated images (the second method of the Schenckel note); but even better would be a way that allowed the mind to pass from image to image according to the active causes that govern the cosmos.
In this light, it is easy to give an explanation of Descartes's progress in the sciences in the course of the decade from 1618, when he composed the Compendium musicae, to the late 1620s, when he gave up work on the Regulae ad directionem ingenii. During this period the chief disciplines of Descartes's theoretical attention were harmony, mechanics, optics, and mathematics. Rather than interpret this work merely as a progressive mathemati-
zation of the sciences of nature, we note instead that musical harmony is a special but obvious case of the fundamental cosmic harmony that unites all the things of the world, a harmony that makes them all expressive and knowable in accordance with the human faculties that are attuned to them. His investigation of music is simultaneously an exploration of harmony, that is, of proportionalities, and of their communication and intrinsic communicability. In this light Descartes's study of mathematics is really not what modern historiography has made of it, an early version of analytic geometry, but rather a comprehensive elaboration of the principles of proportion that support the relatedness of all things. The study of mechanics is not simply the first stage in the mechanization of the world but even more the study of the dynamics of physical objects as they stand to one another in a network governed by proportional relations and proportional motions. The study of light, as we shall see shortly, also fits within the schema of harmony and proportion, for optics is a study of the fundamental power of the communication of the proportional states of things to one another and to the human being endowed with sensitive and cognitive powers.
At the center of all these investigations is the power of proportionalizing imagination. It is no accident that this power is the not-so-hidden center of the work that is a culmination of this project, as well as a transition to the later philosophy: the Regulae ad directionem ingenii.