Weighing
So far I have concentrated exclusively on the exact sciences. But one simple measuring technique used in a wide variety of contexts was weighing ,[116] and this will now take us further afield, including into what we call the life sciences. Heavy and light were often cited as, or among, the differentiae of natural substances in both physics and physiology, but we must be careful, since they are sometimes understood in purely qualitative terms, on a par with wet and dry, or sweet, salty, and bitter.[117] Thus when in certain contexts in his mineralogical work On Stones Theophrastus differentiates varieties of pumice or of
[115] Lejeune 1940–46, p. 97, suggests that the second difference was applied to the middle range in the tables and that Ptolemy extrapolated from these to the (generally less accurate) results claimed for the extreme cases of angles of incidence for 10° and (especially) 80°. On the other hand, provided we assume, as in the cases Ptolemy discusses, that the incident ray from the eye passes from the less dense to the denser medium, the generalisations he sets out at 5.34.245.1ff. L, are unobjectionable, namely, that where i ' is greater than i , (1) i' : i > r' : r , (2) i' : r' > i : r , and (3) (i' - i) : i > (r' - r ) : r .
[116] Written evidence for standardised weights in Greece goes back to the Mycenaean period: see Chadwick 1973, pp. 54–58. Moreover, the archaeological record provides evidence for the standardisation of weights in the ancient Near East and the Indus valley at a much earlier date: see Hemmy 1931; F. G. Skinner 1954, pp. 779ff.
[117] Thus at GC 329b18ff. (cf., e.g., GC 326a7f., 329a10ff.), Aristotle lists heavy and light along with hot and cold, dry and wet, hard and soft, viscous and brittle, rough and smooth, dense and rare, among the tangible contrarieties. Moreover, when taken as definable in terms of a natural tendency to move in a certain direction (up/down), heavy and light run counter to the stipulation, in the Categories 5b11ff., that quantities have no contraries. However, at Metaph. 1052b18–31 Aristotle includes weight with length, breadth, depth, and speed among examples of what can be measured, where it meets the criterion that there must be units or standards of measurement by which weight can be determined.
metal-bearing ore by "heaviness,"[118] no actual quantities are mentioned. "Pumices," he says, "differ from one another in colour, density, and heaviness. They differ in colour inasmuch as the pumice from the Sicilian lava-flow is black, while in density and heaviness it is quite like a millstone. For pumice of this kind does indeed exist, heavy and dense and more valuable in use than the other kind. This pumice from the lava-flow is a better abrasive than the kind which is light [in weight] and white in colour, although that which comes actually from the sea is the best abrasive of all."[119]
Elsewhere, however, direct reference is made to weighing to distinguish heavier and lighter kinds of the same substance. The Hippocratic treatise On Airs Waters Places is much preoccupied with the differences in the waters that occur in different places, distinguishing those that are "hot" and "cold," "hard" and "soft," stagnant and free-running, turbid and pure and bright, as well as—frequently—those that are "heavy" and those that are "light."[120] The opening chapter
[119] Theophrastus Lap. 22. Cf. Lap. 39: "There are also many kinds of stones extracted from mines. Of these some contain gold and silver, though only the silver is clearly perceptible: they are rather heavy and strong-smelling. . . . There is also another stone like charcoal in colour, but heavy." At Lap. 46 the quantities of metals in gold alloys are said to be determinable by the use of the touchstone.
suggests that here we are dealing not just with vague general impressions, but with something measurable, for there we are told that waters "vary both in taste and 'on the balance.'"[121]
Measurement is also clearly involved in Archimedes' famous hydrostatical investigations. The story of how he detected the adulteration of
a gold crown by observing that it displaced more water than the equivalent weight of pure gold may well be inaccurate in the form in which we have it from Vitruvius.[122] But the extant treatise On Floating Bodies shows that he had a clear working conception of—even if he does not explicitly formulate—what we call specific gravity.[123] In book 1, chapters 3ff., he distinguishes between solids that are "equal in weight" (
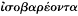
Further evidence from the medical writers shows that they referred readily enough to weighing and measuring in particular contexts. For instance, in their pharmacology, the proportions of the ingredients in compound drugs, and the dose to be used, are often—though certainly far from invariably—specified by weight or otherwise by exact quantity, that is, by dry or liquid measure.[126] Thus On the Diseases of
[122] Vitruvius 9 praef. 9ff.
[123] The Arabic writer Al Khazini ascribes to Archimedes a device that could be used to determine relative specific gravities of different metals when weighed in water, in the Book of the Balance of Wisdom 4.1, on which see, for example, Knorr 1982b.
[124] De corporibus fluitantibus (Fluit. ) 1.3ff. (HS) 2.320.32ff.
[126] Already much earlier in Egyptian pharmacology, quantities are sometimes specified (as, for example, in para. 2 of the Papyrus Ebers: "to expel diseases in the belly: Another [remedy] for the belly, when it is ill: cumin 1/2 ro,goosefat 4 ro, milk 20 ro, are boiled, strained and taken. Another: figs 4 ro, sebesten 4 ro, sweet beer 20 ro, likewise" [Ebbell 1937, p. 30]), though this is not invariably the case (cf. para. 3 of the Papyrus Ebers: "another: wine, honey, colocynth, are strained and taken in one day" [Ebbell 1937, p. 31]). F. L. Griffith 1898, pp. 5ff., commenting on the prescriptions in the Petrie papyri, noted that the "quantities to be used are often left to the discretion of the practitioner to determine; but where necessary the amount is specified, though in round terms, by measure and not by weight," and he went on to argue that "a great advance was made when weight was substituted for measure, as in the Greek medical works." As we shall see, however, there is still plenty of indeterminacy in Hippocratic prescriptions too, as well as in those of later periods. On the measures used in the Ebers Papyrus, see Ebers 1890; for a comparison between Greek and ancient Near Eastern pharmacological recipes, see Goltz 1974, Harig 1975, 1977, 1980, Harig and Kollesch 1977. On the possibility of the deliberate withholding of information concerning quantities for reasons of secrecy, see, for example, Goody 1977, pp. 137f.
Women book 1 gives this prescription to promote parturition: "one obol of dittany, one obol of myrrh, two obols of anis, one obol of nitre: pound these till they are smooth, pour on them a cyathus of sweet wine and two cyathi of hot water; give to the patient to drink and wash her in warm water."[127] Many similar examples could be given—though
so too can others where the quantity of one or more of the ingredients, or the dose, is not specified exactly,[128] and after the Hippocratics, references to the problems of the standardisation of weights and measures and of correlating those used in different parts of the Greco-Roman world appear in the pharmacological sections of such writers as Celsus, Scribonius Largus, and Galen,[129] while tables of weights and measures begin to become common in specialist metrological writings.[130]
[129] See, for example, Celsus Med. 5.17.1c, CML 1.194.5ff.; Scribonius Largus praef. 15.5.23ff.; Galen (K) 13.435.1ff., 616.1ff., 789.2ff., 893.4ff. Cf. also Pliny HN 21.185 (though at 22.117–18 Pliny says that it is not possible to weigh out the powers of drugs "scruple by scruple," and at 29.24f. remarks that Mithridates' antidote that contains fifty-four ingredients no two of which have the same weight is clearly the product of ostentatious boasting).
[130] The remains of Greek and Roman metrological writings have been collected by Hultsch 1864 and 1866. The treatise devoted to weights and mea-sures in the Galenic corpus, (K) 19.748.1–781.3, is spurious, as is some of the corresponding material in the works of Hero: see Hultsch 1882, pp. 7ff.
A twofold contrast suggests itself. On the one hand, the simpler notion, found already in Empedocles' element theory,[131] that a compound consists of certain proportions of the constituent substances may be contrasted with the more precise idea that the quantities of the constituents are to be determined by weight .[132] Yet on the other, despite the progress made towards exact quantitative specification, that progress was still very incomplete. Moreover, quantitative specification when we find it—even when all the relevant quantities are stated—was often no more than window-dressing.
In interpreting this evidence we have to bear in mind, first, that the ingredients used are not chemically pure substances, and, secondly, that ancient doctors are frequently urged to modify the drug and the dosages in relation to particular patients .[133] Thirdly, as we noted in Chapter 3, some early medical writers insist that medicine, though a genuine techne , art or skill, cannot be made an exact study,[134] and
[131] Empedocles frr. 96 and 98.
[132] Apart from in the pharmacological contexts we have considered, the specification of the weights and measures of ingredients is common also in the extant Greek chemical and alchemical texts. See, for example, from the Leyden Papyrus X, pagina 1a.21ff. and 25ff. (Leemans 1885, p. 205); pag. 8a.28ff. (p. 225); pag. 11a.8ff. (p. 233); 24ff. (p. 235); Halleux 1981, nos. 4, 5, 56, 81, and 83; and Berthelot and Ruelle 1888, part 1.13.10ff., 2.31.7ff., part 4.19.1ff., 2.285.6ff. Cf. also Preisendanz 1973–74, P. 12.193ff., 2 p. 71. Although the reactions of various natural substances to fire were often remarked on, for example by Aristotle (cf. above, n. 52) and by Theophrastus, especially Lap. 9–17, no ancient scientist thought to make systematic observations of the weights of substances before and after combustion. Vitruvius 2.5.3, however, does note that in the manufacture of quicklime "about a third" of the weight of the stone is lost.
[133] See, for example, Vict. 1.2 (L) 6.470.7, 14ff.; Mul. 2.192 (L) 8.372.7ff.; cf., e.g., Pliny HN 25.150. Alternatively the dose is to be modified in accordance with the strength of the disease, as, e.g., at Mul. 1.78 (L) 8.184.17. It may also be noted that the problem of the identification of the active ingredients in compound drugs is further complicated when beliefs about their interactions, including their "sympathies" and "antipathies," have to be taken into account: cf. Pliny HN 22.106. Cf. Müri 1950, p. 189; Harig 1974, pp. 64ff., 83ff., 133ff., and 1980.
[134] Cf. above, Chap. 3 at nn. 89–103, on texts in VM, Morb. 1, Loc.Hom. and Vict. 3, especially.
some object specifically to appeals to such a procedure as weighing. When the writer of On Ancient Medicine protests that exactness in the control of diet is difficult to achieve, he says that "one should aim at some measure,"[135] but he then goes on: "but as a measure you will find neither number nor weight by referring to which you will know what is exact, and no other measure than the feeling of the body."[136] The treatise On Sterile Women , too, writes that treatment should be adapted to the particular patient, having regard to her condition and strength, which are not a matter of weighing ,
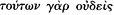
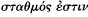
To these pharmacological cases we can add an admittedly limited number of other examples from medical writers at different periods where quantitative reasoning is in play in various physiological or pathological contexts. In the general description of the climatic and
[137] Steril. 230 (L) 8.444.1f.
[138] Cf. above, Chap. 3 at nn. 26ff., on the dogmatic claims to certain knowledge in such treatises as De arte , and below at nn. 150ff. on Hippocratic numerology.
epidemiological conditions encountered that is set out in the Constitution in Epidemics book 3, it is remarked, at one point, that the urine discharged was out of proportion to the fluid drunk, though here no specific quantities are mentioned.[139] In one of the case-histories in Epidemics book 7, however, we are told that a patient discharged more than a chous[140] of fresh blood in his stool and then, after a short while, a further third of a chous of coagulated globlets.[141] Specifications of the quantities of the lochial discharge or of the menses are also sometimes given in the gynaecological and the embryological treatises—though in several cases the quantities reported appear fanciful.[142]
Then Erasistratus, in a remarkable experiment recorded in Anonymus Londinensis,[143] tried to prove that animals emit invisible effluvia, by keeping a bird in a closed vessel without food for a period and then weighing the bird and its visible excreta. Comparing this with the original weight, he found, we are told, that there had been a "great loss of weight"—another case where, in our source at any rate, an observed difference in weight is remarked without any actual weights being reported.[144]
[139] Epid. 3.10 (L) 3.90.7f., cf., e.g., Morb. 4.42 (L) 7.564.4ff.
[140] A chous is estimated as between 2.52 and 3.96 litres in OCD .
[141] Epid. 7.10 (L) 5.380.20ff.; cf., e.g., 7.3 (L) 5.370.23ff., 372.1ff., where the exceptional quantities of milk consumed by a particular patient are specified; Epid. 5.14 (L) 5.214.1ff., 5.18 (L) 5.218.10; 5.50 (L) 5.236.16.
[142] See Mul. 1.6 (L) 8.30.8ff.: menses of two Attic cotylae "or a little more or less," i.e., c. 0.45 litres (cf. Aristotle, who claimed generally that female humans produce more menses than any other animal, e.g., HA 521a26f., and estimated the discharge of a cow in heat as "about half a cotyle or a little less," HA 573a5ff.; and contrast Soranus Gyn. 1.20, CMG 4.14.4, who gives a maximum figure for menstruation as two cotylae but who then devotes two chapters to pointing out how the quantity and duration may vary, 1.21–22, CMG 4.14.6ff., 15.1ff.). Mul. 1.72 (L) 8.152.3ff., Nat.Puer. 18 (L) 7.502.3ff.: the lochial discharge is one and a half Attic cotylae "at first" "or a little more" (Nat.Puer. adds "or a little less"). For discussion of these figures, see Bourgey 1953, p. 178 and n. 2; R. Joly 1970, p. 62 n. 2; Lonie 1981a, pp. 190ff.
[143] Anon. Lond. 33.43ff.; see von Staden 1975, pp. 179ff., and forthcoming. Further tests involving the weighing of fresh and "high" meat, and of a bladder empty and full of air, are reported in other contexts in Anon. Lond. at 31.10ff., 34ff. (purporting to present an Empiricist view), 32.22ff.
[144] It appears from a report in Galen UP 7.8 (H) 1.392.25ff., (K)3.540.8ff., that Erasistratus attempted to distinguish between different types of "air" by their "thinness" and "thickness," claiming that the air from burning coals is "thinner" than "pure" air, but Galen records no measurement in this connection.
Galen, especially, uses quantitative arguments on several occasions. In On the Use of Parts he remarks generally on the proportionalities between the fluids and solids taken into the body and those discharged or lost,[145] and elsewhere he specifies actual amounts of, for example, pus expectorated.[146] In On the Natural Faculties the difference in size between, on the one hand, the vena cava (together with the right auricle) and, on the other, the pulmonary artery is cited among the arguments to support the conclusion that some blood must pass directly from the right ventricle to the left through invisible pores in the septum, though—unlike Harvey—Galen does not attempt to measure the quantities or flow of blood exactly or even approximately.[147] Most notably of all, perhaps, a quantitative argument is adduced in the refutation of Lycus' view that urine is the residue from the nourishment of the kidneys.[148] That cannot be the case, Galen claims, if one considers the amounts discharged, which in exceptional cases may be as much as three or four choes.[149] If that is produced from nourishing the
[145] See UP 4.13 (H) 1.223.10ff., (K) 3.304.7ff. (where the quantity of drink consumed is proportional to the urine discharged), and UP 16.14 (H) 2.433.4ff., (K) 4.340.2ff. (where the nourishment taken in is equal to the material lost from the body).
[146] E.g., (K) 8.321.15ff. Cf. also (K) 11.227.9ff., blood expectorated up to two cotylae.
[147] De naturalibus facultatibus (Nat.Fac. ) 3.15 (H) 3.252.13ff., (K) 2.208.11ff. Cf. UP 6.17 (H) 1.362.7ff., (K) 3.497.9ff., where Galen reverses the explanation, putting it that there is good reason for the vena cava to be larger than the pulmonary artery, since blood is taken over from the right ventricle to the left through the interventricular pores.
[148] Nat.Fac. 1.17 (H) 3.152.17ff., (K) 2.70.10ff., on which see Temkin 1961, and cf. Temkin 1973, pp. 153f.
[149] Nat.Fac. 1.17 (H) 3.153.23ff., (K) 2.72.4ff.; cf. also (H) 3.153.13ff., (K) 2.71.12ff. Altman and Dittmer 1972–74, vol. 3, p. 1496, give a normal figure, for a 70 kg body, of 1.4 litres, with upper and lower limits of 2.94 and 0.49 litres. Galen's "three choes" is clearly more than five times the normal figure and more than twice the upper limit.
kidneys, one would expect even greater amounts of residue from the nourishment of the other principal viscera, where there is no sign of this.