Six—
The Paradigm Extended:
On Motion , Theorem 4 and Problem 4
Contemporary textbooks in astronomy or physics attribute three laws governing planetary motion to the work of Kepler: the first law states that a planet moves in an elliptical path about the sun located at a focus of the ellipse; the second law states that a line joining the sun and a planet sweeps out equal areas in equal times; and the third law states that the period of a planet about the sun is proportional to the three-halves power of the transverse axis of the elliptical orbit. In Theorem 1 of On Motion , Newton demonstrates that the second law is valid for any central force; in Problem 3 he demonstrates that, given the first law, it follows that the force will be inversely proportional to the square of the distance; and in Theorem 4, he demonstrates the third law.
Theorem 4—
The Three-Halves Power Law
Theorem 4. Supposing that the centripetal force is reciprocally proportional to the square of the distance from the center, the squares of the periodic times in ellipses are as the cubes of their transverse axes .
Figure 6.1 is based on the diagram that accompanies the theorem in the tract On Motion . In the following, I consider each line of Newton's demonstration of the theorem in detail.
[A] Let AB be the transverse axis of an ellipse , PD the other axis , L the latus rectum, S one of the foci ;
Thus, AB is the major axis and PD is the minor axis. Newton employed the Apollonian definition of the latus rectum L , which states that the latus rectum L is in the same ratio to the minor diameter PD as the minor diameter PD is to the major diameter AB (i.e., L : PD :: PD : AB or L / PD = PD / AB
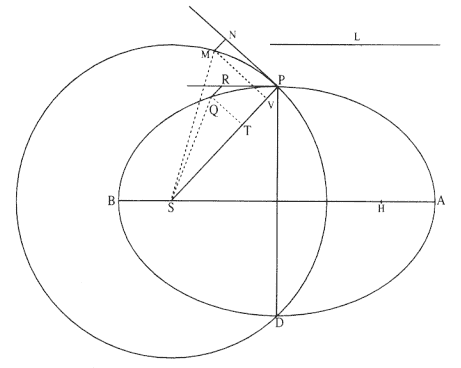
Figure 6.1
Based on Newton's diagram for Theorem 4.
or L = PD2 / AB ). From the definition of an ellipse, the distance (SP + PH ) is a constant equal to the principal axis AB . In this construction SP = PH , therefore AB = 2SP and thus L = PD2 / 2SP , a relationship that will be employed in the following.
[B] let the circle PMD be described with S as the center and SP as the radius .
Thus, the circle PMD has a radius SP and its diameter, 2SP , is equal to the major axis of the ellipse, AB .
[C] And at the same time let two orbiting bodies describe an elliptical arc PQ and the circular arc PM, with the centripetal force directed to the focus S.
It will be demonstrated next that the period of the body orbiting on the circle is equal to the period of the body orbiting on the ellipse when the diameter of the circle is equal to the transverse axis of the ellipse.
[D] Let PR and PN be tangent to the ellipse and circle at the point P. Parallel to PS draw QR and MN meeting those tangents at R and N.
The deviation QR measures the elliptical departure from the tangential inertial motion along PR (see fig. 6.2), and the deviation MN measures the
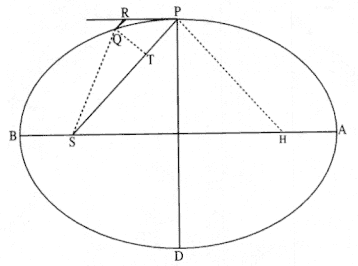
Figure 6.2
The ellipse abstracted from the general diagram for Problem 4.
circular departure from the tangential inertial motion along PN (see fig. 6.3). Both are employed in the linear dynamics ratio as a measure of the force.
[E] But let the figures PQR and PMN be indefinitely small, so that (by the scholium to Problem 3) there results L × QR = QT2and 2SP × MN = MV2 .
In the scholium to Problem 3, Newton demonstrates that the ratio QT2 / QR approaches the latus rectum L of the ellipse as the point Q approaches the point P , or ultimately L × QR = QT2 . For a circle, the major axis, the minor axis, and the latus rectum are all equal to the diameter, 2SP . Thus, for the circle, L = MV2 / MN = 2SP or 2SP × MN = MV2 .
[F] On account of their common distance SP from the center S and therefore equal centripetal forces , MN and QR are equal .
The centripetal force depends only upon the distance SP , which is the same for the common point P on both orbits (see fig. 6.1). Thus, for a given time, the displacements MN and QR are equal because the forces are equal.
[G] Consequently QT2is to MV2as L to 2SP, and so QT to MV as the mean proportional between L and 2SP;
Taking QT2 = L × QR and MV2 = 2SP × MN from [E], QT2 / MV 2 = L × QR / 2SP × MN = L / 2SP , since MN = QR from [F]. Thus, QT2 / MV2 = L / 2SP , or what is equivalent, QT / MV is the mean proportional between L and 2SP .
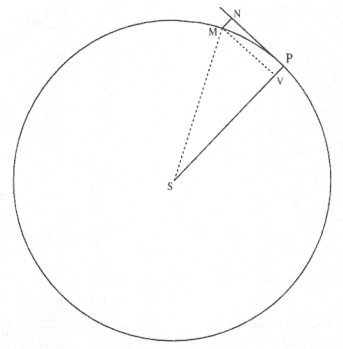
Figure 6.3
The circle abstracted from the general diagram for Problem 4.
[H] [that is , PD to 2SP]
From [G], QT2 / MV2 = L /(2SP ). From [A], L = (PD 2 / AB ) and AB = (2SP ), therefore L = PD2 / (2SP ). Thus, L / (2SP ) = PD2 / (2SP )2 . Therefore, QT / MV = PD / (2SP ).
[I] for this reason the area SPQ is to the area SPM as the total area of the ellipse to the total area of the circle .
The area of the ellipse equals p (AB / 2) (PD / 2) = (1/4)pAB × PD , and the area of the circle equals pSP 2 . Hence, the ratio of areas = AB × PD /4SP2 = PD /2SP because AB = 2SP from line [B]. The ratio of the triangular areas SPQ = (1/2)SP × QT and SPM = (1/2) SP × MV reduces to QT / MV , which from line [H], is as PD / 2SP . Thus areas (SPQ / SPM ) = PD / 2SP = areas (ellipse / circle).
[J] But the parts of the areas generated at individual moments are as the areas SPQ and SPM, and hence as the total areas ,
The incremental areas of the circle DAC and the ellipse DAE are in the same ratio as the total areas given in [I] (i.e., DAC /DA E = AC / AE ).
[K] and consequently when multiplied by the number of moments they will likewise turn out equal to the total areas .
The total areas equal the sums of the N incremental areas or A = SDA = NDA . Thus, DAC / DAE = (NC DAC ) / (NED AE ) = AC / A E .
[L] Revolutions on ellipses, therefore, are accomplished at the same time as those on circles whose diameters are equal to the transverse axes of the ellipses .
From line [K], the number of moments N must be equal (i.e., NC = NE ). Moreover, the number of moments to sweep out the total area equals the period T divided by the size of the equal time increment D t (i.e., N = T /D t ). Thus, NC / NE = (TC /Dt ) / (TE /Dt ) = TC /T E or TC = TE .
[M] The squares of the periodic times in circles (by Corollary 5 of Theorem 2) are as the cubes of their diameters. And hence also in ellipses. Which was to be proven .
In the 1687 edition, Newton proves this result (Kepler's third law) directly from the limiting relationship given in the scholium to Problem 3 (i.e., QR / QT2® L ) without using the concentric circle employed here in On Motion (1684).
When Newton published the 1687 edition of the Principia , which builds directly upon On Motion , he adds a third book devoted to the analysis of the actual observations of celestial phenomena. Thus, he brings to life rather abstract mathematical demonstrations of the nature of gravitational force by comparing them to the actual data compiled by astronomers. In the following, Newton adds a scholium to the theorem just discussed, Theorem 4, that suggests one way in which the measurements of the periods of the planets can be used to determine the dimensions of their orbits.
Scholium
Hence in the celestial system from the periodic times of the planets we come to know the proportions of the transverse axes of their orbits. We shall assume one axis, from which others will be given.
The assumed axis usually will be the diameter of the earth's orbit. Then, using Theorem 4, the ratio of the other axes will be known from their observed periods.
[Scholium] When the axes have been given, however, the orbits will be determined in this way. Let S be the position of the sun, or one focus of the ellipse ; A, B, C, D positions of the planets found by observation; and Q the transverse axis of the ellipse. With center A and radius Q – AS let the circle FG be described, and the other focus of the ellipse will be in its circumference . [See fig. 6.4.]
The points A, B, C , and D all lie on the planetary ellipse. It is a property of an ellipse (see [2-E] in Problem 3) that the sum of the distances from any point on the ellipse to the foci is a constant equal to the length of the
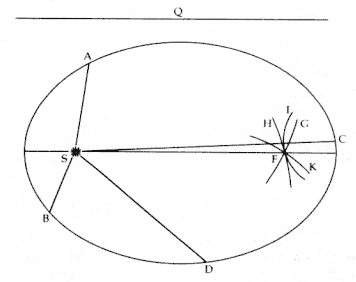
Figure 6.4
The first diagram for the scholium to Theorem 4.
transverse axis, Q . Thus AS + AF = Q or AF = Q – AS . Thus, the circle FG of radius Q – AS about the point A will intersect the transverse axis at the focus F .
[Scholium] Likewise, with centers B, C, D, etc., and intervals Q – BS, Q – CS, Q – DS, etc., let any number of other circles be described, and that other focus will be in all their circumferences and hence at the common intersection of all of them. If all of the intersections do not coincide, a mean point for the focus must be taken. The advantage of this procedure is that as many observations as possible may be made to elicit a single conclusion, and they may be expeditiously compared with one another .
The transverse axis Q and the positions A, B, C, D , etc., are only known approximately. Thus, the various circles will not intersect at a single point. If all the points are known with equal accuracy, however, then the mean point for F could be defined as the simple arithmetic mean.[1]
[Scholium] Halley has shown, however, how to find the individual positions A, B, C, D, etc., of a planet from pairs of observations, once the great orbit of the earth is known.[2]If that great orbit is not yet considered to be exactly enough determined, then by knowing it approximately, the orbit of any other planet, like Mars, will be determined more closely. Then from the orbit of the earth, the orbit of the planet will be determined more accurately by far than before. And so in turn, until the intersections of the circles in the focus of each orbit concur exactly enough .
By this method we may determine the orbits of the earth, Mars, Jupiter, and Saturn; but for the orbits of Venus and Mercury, do the following .
Figure 6.5
The second diagram for the scholium to Theorem 4.
The method Newton describes employs pairs of solar oppositions to fix the position and relative sizes of the planetary radii. Since the two inner planets, Venus and Mercury, can never be in opposition to the sun, then another method, such as the following, must be used for them.
[Scholium] From observations made in the greatest digression of the planets from the sun, let tangents of the orbits be obtained. To such a tangent KL let the perpendicular SL be dropped from the sun, and with center L and radius half the axis of the ellipse let the circle KM be described; the center of the ellipse will be in its circumference . [See fig. 6.5.]
Whiteside suggests that Newton may here assume that his reader would know an equivalent proposition from Apollonius to demonstrate that the center of the ellipse would lie on such a circle.[3]
[Scholium] and thus when several circles of this kind are described, it will be found at the intersection of all of them. Then, when the dimensions of the orbits are known, the lengths of these planets will be determined more exactly from their passage through the disc of the sun .
This technique only gives proportions relative to an assumed size of the earth's orbit. The reference here is to the determination of the absolute size of the distance from the sun to the earth by observations of the transits of Mercury and Venus across the solar disc. Halley had traveled to the island of St. Helena (latitude 16°S) in October of 1677 to observe a transit of Mercury, and he may have called Newton's attention to the possible use of such observations during his famous visit to Cambridge in August of 1684.[4]
Problem 4—
Given an Inverse Square Force, Find the Resulting Conic Section
In Problem 3, the elliptical orbit and focal force center were given, and the force function was found to be inversely proportional to the square of
the distance. In Problem 4, the force function is given as inversely proportional to the square of the distance and the orbit is to be determined. Newton considers a body projected at a given point, with a given speed, acted upon by an inverse square force whose absolute value (gravitational constant) is given. From the solution to Problem 3, it is known that one possible orbit under such conditions is that of an ellipse with the center of force at a focus of the ellipse. Newton begins with the assumption that the body is moving in such an ellipse. Moreover, he assumes the existence of an auxiliary circular orbit that is centered on the focus of the ellipse.[5] He then proceeds to determine all the relevant parameters of the initial ellipse from the given elements of the problem. Having done so, he then allows the initial speed of the body to increase and demonstrates that the initial elliptical path becomes a parabolic path and then a hyperbolic path. Newton makes no explicit claim that this solution provides a demonstration that the conic sections exhaust all possible types of motion under the action of an inverse square force (i.e., that it is a solution of the inverse problem). But others saw the possibility of such a solution in his demonstration of Problem 4, which also appears as Proposition 17 in the Principia . As Bertoloni Meli points out, support came from both the English mathematician John Keill and the continental mathematician Leonhard Euler.
In 1716 Keill claimed that Proposition 17 [Problem 4] contained a demonstration of the inverse theorem. In his reply through his student Johann Kruse, however, Johann Bernoulli objected that Proposition 17 [Problem 4] assumes the result rather than proving it. Surprisingly Johann Bernoulli's most talented pupil and possibly the most gifted mathematician of the Enlightenment sided with Keill: Leonhard Euler, in his 1736 Mechanica , claimed that the inverse problem of central forces could be solved on the basis of Proposition 17 [Problem 4].[6]
The composite nature of the solution, however, is such that it has been the subject of considerable controversy, and the debate still continues.[7]
I give the statement of the problem and then follow it with a line-by-line analysis of Newton's demonstration of the solution. Figure 6.6 is based on Newton's diagram for Problem 4.
Problem 4. Supposing that the centripetal force be made reciprocally proportional to the square of the distance from its center, and that the absolute quantity of that force is known; there is required an ellipse which a body will describe, when released from a given position with a given speed along a given straight line .
[A] Let the centripetal force directed to point S be that which makes the body P orbit in a circle pq described with center S and any radius Sp.
The body p moves in a reference circle pq of radius Sp about the center of force S . For a given "absolute quantity of force" (i.e., a given force con-
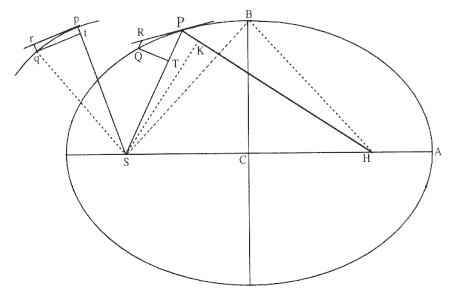
Figure 6.6
Based on Newton's diagram for Problem 4.
stant) there exists a particular constant tangential speed for which the body p will move uniformly in a circle, as has been demonstrated in Theorem 2. In what follows, Newton assumes that the proper set of initial conditions has been met and he will relate various aspects of this constant uniform circular motion to the more general conic motion of the orbit PQ (see fig. 6.6).
[B] Let the body P be released from the position P along line PR, and soon after let it deflect under the compulsion of the centripetal force into the ellipse PQ. The straight line PR, therefore, will touch this at P.
This description of the elements of the diagram constitute Newton's standard method of analysis of direct problems. The line PR represents the tangential linear displacement the body would have made had no force acted on it. The possibility of elliptical motion under an inverse square centripetal force has been demonstrated in Problem 3, and here Newton assumed that the proper set of initial conditions had been met for the body P to move on an ellipse. Moreover, from Theorem 1, the motion will be such that the radius will sweep out equal areas in equal times because the force is directed to a fixed center. Newton was aware that other initial conditions will produce other motions than elliptical ones, and he addressed those alternate motions in what follows.
[C] In the same way let the straight line pr touch the circle at p,
The tangent is defined for the reference circle.
[D] and let PR be to pr as the initial speed of the body P sent out to the uniform speed of the body p.
The implicit assumption is made that the tangential displacements PR and pr take place in equal times. If vp is the projection speed at P and vp is the uniform circular speed at p , then the displacements PR and pr are equal to the product of the speed and the time, or are proportional to those speeds in the same time t (i.e., PR / pr = v pt / vp t = vp /vp ).
[E] Let RQ and rq be drawn parallel to SP and Sp, the latter meeting the circle at q, the former the ellipse at Q,
The deviations QR and qr are the first elements required for the respective linear dynamics ratios.
[F] and let the perpendiculars QT and qt be drawn from Q and q to SP and Sp.
The perpendiculars QT and qt are the second elements required for the respective linear dynamics ratios.
[G] RQ is to rq as the centripetal force at P is to the centripetal force at p:
For a given time, the force F p is proportional to the deviation QR and the force Fp is proportional to the deviation qr , as has been discussed in detail in the previous problem solutions.
[H] that is, as Sp2to SP2 , and hence that ratio is given .
From the statement of the problem, Fp / F p = (C / SP2 ) / (C /Sp2 ) = Sp2 / SP2 , where C is a constant set by the given absolute value of the force. Since the ratio of the displacements RQ /rq is given in [D] by the initial projection speed, and since that ratio equals the ratio of the forces [from line [G]], then ratio Sp2 / SP 2 is also given, and it equals QR / qr .
[I] The ratio QT to qt is also given .
The ratio of the areas, (QT × SP ) / (qt × Sp ), is equal to the ratio of the times (Theorem 1: Kepler's law of equal areas in equal times). Since the times are equal, then (QT × SP ) = (qt × Sp ), or QT / qt = Sp / SP , and the ratio QT / qt is thus given (because the ratio Sp / SP is given in line [H]).
[J] From this latter ratio doubled let the given ratio QR to qr be taken away, and there will remain the given ratio of QT2 / QR to qt2 / qr,
Divide the square of the given ratio of (QT / qt )2 by the given ratio of (QR / qr ), and there results the given ratio of (QT2 / QR ) / (qt2 / qr ).
[K] that is (by the scholium to Problem 3 ) the ratio of the latus rectum of the ellipse to the diameter of the circle;
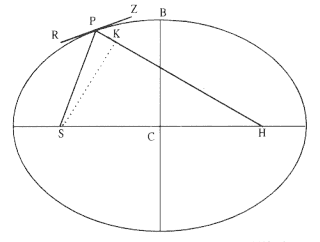
Figure 6.7
Angle RPS equals angle ZPH , and thus angle RPH is the
supplement of angle RPS .
That is, (QT2 / QR ) / (qt2 / qr ) = L / Sp . The scholium to Problem 3 states that the limiting value for the ratio QT2 / QR for an ellipse as Q®P is the latus rectum, L . Thus, since the ratio in line [J] is known, the ratio of LE for the ellipse to LC for the circle is known. The latus rectum LC for the circle, however, is its diameter Sp . (From the definition, L = (minor diameter)2 / (major diameter); for a circle the two diameters are equal; thus, LC = diameter.)
[L] and therefore the latus rectum of the ellipse is given. Let that be L.
Thus, since the diameter of the circle Sp is given, the latus rectum L of the ellipse is known (i.e., from [K] L / Sp = (QT2 / QR ) / (qt2 / qr ), where the final ratio is given from line [J]).
[M] In addition, the focus of the ellipse S is given .
The focal point S is given in the opening statement in line [A].
[N] Let angle RPH be the complement of angle RPS to two right angles [i.e., angle RPH is the supplement of angle RPS],
From figure 6.7, angle RPH + angle HPZ = 180°. From the properties of conics (Apollonius, Proposition 48, Book 3) the angles RPS and ZPH that are made by the tangent and focal lines are equal.[8] Thus, the angle RPH = 180° – ZPH = 180° – RPS , or angle RPH is the supplement of angle RPS .
[O] and there will be given in position the line PH in which the other focus H is located .
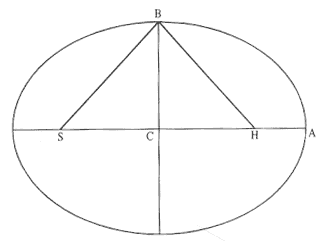
Figure 6.8
The focal distances SC and CH are equal, and thus SH can be
given as 2CH .
The angle RPS is known from the projection velocity. From line [P] the angle SPH is known; it is 180° – 2RPS . Thus, the direction of the line on which the second focus H is located is known relative to the line SP , or as Newton puts it, "There will be given in position the line PH ." The distance PH , however, is not yet known. Lines [P] to [V] are required to determine the length of PH and thus to locate the second focus H .
[P] After the perpendicular SK is let down to PH and the semi-minor axis BC is erected, there is SP2 – 2KP × PH + PH2 = SH2
This result is found in Euclid, Book 2, Proposition 13.[9] (Otherwise, from the law of cosines, SH2 = SP2 – 2SP × PH × cos(angle SPH ) + PH2 . From figure 6.7, cos (angle SPH ) = KP / SP . Thus, SP2 – 2KP × PH + PH2 = SH2 .)
[Q] SH2 = 4BH2 – 4BC2
From figure 6.8, SH = SC + CH = 2CH or SH2 = 4CH2 . From the right triangle BCH , one has CH2 = BH2 – BC2 . Thus, 4CH2 = 4(BH2 – BC2 ) or SH2 = 4BH2 – 4BC2 .
[R] 4BH2 – 4BC2 = (SP + PH)2 – L × (SP + PH)
From the definition of an ellipse, (SP + PH ) = 2AC = 2BH , thus 4BH2 = (SP + PH )2 . From the definition of the latus rectum , L = 2BC 2 / AC , thus 4BC 2 = L × 2AC = L × (SP + PH )2 . Thus, 4BH2 – 4BC2 = (SP + PH )2 – L × (SP + PH ) as given above.
[S] (SP + PH)2 – [L × (SP + PH)] = (SP2 + 2SP × PH + PH2 ) – [L × (SP + PH)].
Simply expand the square, (SP + PH )2 = (SP2 + 2SP × PH + PH2 ).
[T] To each side add 2KP × PH + L × (SP + PH) – SP2 – PH2and there will result L × (SP + PH) = 2SP × PH + 2KP × PH,
Starting at line [P], SP 2 – 2KP × PH + PH2 has been shown to be equal at line [S] to (SP2 + 2SP × PH + PH2 ) – L × (SP + PH ), which upon cancellation and rearrangement becomes L × (SP + PH ) = 2SP × PH + 2KP × PH .
[U] or (SP + PH) to PH as (2SP + 2KP) to L.
Dividing both sides by L × PH , one has (SP + PH ) / PH = (2SP + 2KP ) / L
[V] From which the other focus H is given .
The direction of the line PH was determined in line [P]. The length of PH was determined by the ratio in line [U], because the elements, SP, L , and KP are given. (KP = SP cos (SPH ), where the angle SPH is given in line [P].) Thus, the direction and distance of PH relative to S is determined, and therefore the second focus H is known.
[W] Given the foci, however, along with the transverse axis SP + PH, the ellipse is given. As was to be proven .
Knowledge of the position of both foci and the distance (SP + PH ) permits construction of the ellipse. A simple demonstration is accomplished by putting a tack at each of the foci and joining them with a loose string of length (SP + PH ). When a pencil is moved so that the string remains taut, the ellipse is drawn.
[X] This argument holds when the figure is an ellipse. But it can happen that a body moves in a parabola or a hyperbola .
The initial conditions set in line [B] restricted the motion to an ellipse, but in [X] Newton demonstrates that the motion under an inverse square force could also be a parabola or a hyperbola (i.e., any conic section). In doing so, he permits the projection speed vp of the body P to take on greater values than the specific value that produced elliptical motion at a given point under an inverse square centripetal force with a given force constant. He demonstrates that the resulting motion will be one of the conic sections.
[Y] But if the speed of a body is so great that the latus rectum L is equal to 2SP + 2KP, [then ] the figure will be a parabola having its focus at the point S and all its diameters parallel to the line PH.
As the second focus H recedes to infinity, the figure becomes a parabola. From line [N ], as PH increases without limit, (SP + PH ) / PH® 1 or the latus rectum L approaches (2SP + 2PK ).
[Z] But if the body is released at an even greater speed, [then ] it will be moved in a hyperbola having one focus at the point S, the other at the point H taken on the opposite side of the point P, and its transverse axis equal to the difference of the lines PS and PH.
The second focus H , having receded to infinity, now approaches the other focus S from the opposite side of the general point P .
Newton did not address the full question of the uniqueness of this solution to Problem 4 (i.e., do the three conic sections exhaust all the possible solutions for motion under an inverse square force?). Perhaps he thought the affirmative answer self-evident, since for every initial speed, angle of projection, and value of force constant, a unique conic is defined: an ellipse, a parabola, or a hyperbola.[10] Moreover, the subject of the uniqueness of the solution was not discussed in the revised solution to Problem 4 that appeared as Proposition 17 in the 1687 edition of the Principia . In Propositions 11, 12, and 13, however, he presented the solutions for the direct problems of each of the conic orbits: an ellipse, a hyperbola, and a parabola. In the 1687 edition, he included the following corollary to Proposition 13, which directly assumed uniqueness.
Corollary. From the last three propositions it follows that if any body P should depart from Position P along any straight line Pr, with any velocity, and is at the same time acted upon by a centripetal force that is reciprocally proportional to the square of the distance from the center, this body will be moved in one of the sections of conics having a focus at the center of forces; and conversely .
In the 1713 edition, however, he added a statement to the corollary in Proposition 13 that was intended to address and to justify the assumption of uniqueness. (See chapter 10 for a discussion of that revised corollary.) That demonstration is important because, if established, the solution to the direct problem in combination with this solution serves as a solution to the inverse problem. Following Newton, it has been demonstrated to the satisfaction of the most demanding of mathematicians that the conic sections are the unique set of solutions for motion under an inverse square force. In On Motion and in the 1687 edition of the Principia , however, Newton is satisfied with a much more intuitive demonstration of uniqueness.
In the scholium to Theorem 4, Newton discussed the theorem's application to the computation of the relative size of planetary orbits from the observation of planetary periods. In the scholium to Problem 4, he applies his techniques developed in Problem 4 to the determination of orbits of comets. Again, he applies the ideal mathematical world of the tract to the actual observational world of the heavens. The topic of comets caused Newton much concern. In a letter to Halley, written more than a year after sending the following scholium on comets, Newton states that "in Autumn
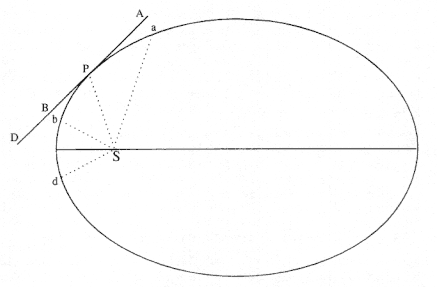
Figure 6.9
The diagram for the scholium to Problem 4.
last I spent two months in calculations to no purpose for want of a good method." Not until Newton replaces the linear approximation discussed next with a parabolic approximation for the elliptical path does the "good method" appear as Proposition 41 of Book Three of the 1687 Principia .
Scholium
Now indeed with the help of this problem when it has been solved, it is possible to define the orbits of comets, and from that the times of their revolutions, and from a comparison of the magnitude of their orbits, eccentricities, [perihelia ], inclinations to the ecliptic plane and their nodes, to know whether the same comet returns to us frequently.
The most celebrated example of a returning comet is the comet of 1682, which Halley correctly identified as the return of the comet of 1531 and 1607 (a period of 75 or 76 years) and which he correctly predicted to return in 1758 (after his death).
[Scholium] To be sure, from the four observations of the comet's position, according to the hypothesis that a comet moves in a straight line, its rectilinear path must be determined. Let that [path ] be APBD, and let A, P, B, D be positions of the comet on that path at the times of observations, and let S be the position of the sun. Imagine that with the speed at which it regularly traverses the straight line AD, the comet is released from one of its positions P, and, soon forced by centripetal force, it is deflected from the straight path and goes off into the ellipse Pbda. [See fig. 6.9.][11]
By the time of this analysis of 1684, Newton had come to accept the universality of the gravitational force (i.e., that the force derived in Problem 3 for planetary motion also applied to all celestial bodies, such as comets). Previously there had been a question in Newton's mind concerning the curved nature of cometary paths. The rectilinear hypothesis (that is, comets move in straight lines), however, is simply an approximation: one that will be replaced by a more sophisticated method in the Principia .[12]
[Scholium] This ellipse must be determined as in the problem above. In it let a , P, b, d be positions of the comet at the times of observations. Let the longitudes and latitudes of these positions from the earth be known. As much as the observed longitudes and latitudes are greater or less than these, let new longitudes and latitudes be taken greater or less than the observed ones. From these new [measurements ] let the rectilinear path of the comet again be found, and from that the elliptical path as before. And the four new positions on the elliptical path, having been augmented or diminished by previous errors now will agree sufficiently precisely with the observations .
In the determination of the elliptical orbit in Problem 4 above, one must assume a value for the magnitude of the gravitational force (see the statement of the problem). Moreover, it is not clear how one is to know that the new position will produce convergence with the actual path of the comet. Clearly, Newton is struggling with the procedure.
[Scholium] But if perchance palpable errors should still remain, it is possible for the entire task to be repeated. And, so that the computations may not be annoying to the astronomers, it will suffice to determine all these things by a geometrical procedure .
There then follows another paragraph in which Newton discusses the difficulty in assigning areas proportional to the times. Whiteside observes that the method outlined in this scholium is a "makeshift construction . . . more optimistic of a chance success than solidly reasoned."[13] In fact, the entire subject of the motion of comets was a challenge. Newton claimed that "this discussion about comets is the most difficult in the whole book."[14] This challenge continued to receive his attention and would eventually be met in the Principia .
In Book Three of the Principia Newton will consider many more such observational problems. The following is an example taken from the 1687 Principia in which Newton discusses the application of the theorems from Book One to the phenomena discussed in Book Three. In On Motion , and in its extension into Book One of the Principia , Newton has discussed the ideal case of a single planet orbiting about a single stationary center of force in the sun. In the following proposition from Book Three he discusses the influence of adjacent planets upon their mutual motion (that is, a three-body versus a two-body problem). Now Newton is less a mathematician and more of a practical astronomer. He must call into action estimates of the relative masses of the sun and planets as well as their relative
distances. He calls on demonstrations in Propositions 66 and 67 in Book One concerning motion about the center of mass to relate the ideal mathematical problem with a fixed center of force to the actual problem of the sun and planet moving about their center of mass.
Book Three
Proposition 13
Theorem 13
Book Three. Proposition 13. Planets move in ellipses having a focus in the center of the sun, and with radii having been constructed to that center they describe areas proportional to the times .
We have talked above about these motions from the phenomena. Now that we have understood the principles of motions, from these [principles ] we infer celestial motions a priori. Since the weights of the Planets toward the sun are reciprocally as the squares of the distances from the center of the sun; if the sun were at rest and the other Planets were not acting on each other, [then ] their orbits would be elliptical having the sun in a common focus and areas would be described proportional to the times (by Propositions 1 and 11 and Corollary 1 Proposition 13 Book One [Theorem 1 and Problem 3 in On Motion ]). But the actions of the Planets reciprocally on each other are very small (so that they might be able to be neglected ), and they disturb the motions of the Planets in ellipses around the sun in motion less (by Proposition 66, Book One ) than if those motions were being performed around the sun at rest .
Indeed, the action of Jupiter upon Saturn must not be altogether neglected. For the gravity toward Jupiter is to the gravity toward the sun (the distances being equal ) as 1 to 1,100 ;
Modern values of the masses of the sun and Jupiter give a ratio of 1 to 1,047, which compares to Newton's value of 1 to 1,100 (a value that appears as 1,067 in the revised Principia ), values which Newton obtained using Kepler's third law (Theorem 4) and measurements of the periods of their satellites (Venus for the sun, its moons for Jupiter).[15]
[Proposition 13] and therefore in the conjunction of Jupiter and Saturn, since the distance of Saturn from Jupiter is to the distance of Saturn from the sun, almost as 4 to 9;
Modern value of the semi-major axis of Jupiter is 5.203 AU, for Saturn it is 9.539 AU, and thus the distance between Jupiter and Saturn at conjunction is the difference, or 4.336 AU. Thus, the ratio of distances is 4.336 to 9.539 or, as Newton states, 4 to 9.
[Proposition 13] the gravity of Saturn toward Jupiter will be to the gravity of Saturn toward the sun as 81 to 16 × 1,100; or 1 to about 217 .
The gravitational force is directly proportional to the mass and inversely proportional to the square of the distance. Thus, the force on Saturn due to Jupiter is as 1/42 and that due to the sun as 1,100/92 , or a ratio of (1/16) / (1,100/81) = 81/(16 × 1,100) = 1/217.
[Proposition 13] Yet the whole error in the motion of Saturn around the sun, arising from so great a gravity toward Jupiter, can be avoided by constructing a focus of the orbit of Saturn in a common center of gravity of Jupiter and the sun (by Proposition 67, Book One) and hence when the error is greatest it hardly exceeds two minutes. But in the conjunction of Jupiter and Saturn, the accelerative gravities of the sun toward Saturn, of Jupiter toward Saturn, and of Jupiter toward the sun, are almost as 16, 81, and 16 × 81 × 2,360/25 or 122,342 ,
Using modern notation, the forces between two masses can be expressed as
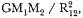
[Proposition 13] and thus the differences of gravities of gravities of the sun toward Saturn, and of Jupiter toward Saturn, is to the gravity of Jupiter toward the sun as 65 to 122,342 or as 1 to 1,867. But the greatest power of Saturn to disturb the motion of Jupiter is proportional to this difference: and hence the perturbation of the orbit of Jupiter is far less than that of Saturn's. The perturbations of the remaining orbits are even far less .
Thus, does Newton the mathematician and Newton the practical astronomer relate the demonstrations of the theorems and solutions of abstract problems to the observations of the motion of celestial bodies. The applications and examples are increased in the editions of the Principia that follow the tract On Motion . The demonstration of a universal gravitational force that depends upon the inverse square of the distance is to be found in the heavens as well as in the pages of the Principia .
Conclusion
Following his receipt in London of Newton's tract On Motion in November of 1664, Halley returned to Cambridge to consult with Newton once again. He found Newton occupied with the task of rewriting the work in more detail. That project would eventually require two years to complete. Under Halley's personal encouragement, careful editorial eye, and financial support, it would ultimately result in publication as the first edition of the Principia in 1687. Upon his return to London, Halley reported to the Royal Society at its meeting on 10 December 1684, about his interchange with Newton and of his intent to have the tract entered in the Register of the
Society, which it was. It was not until two years later, however, at the meeting of the Royal Society on 21 April 1686, that Halley announced that the work was almost ready for the press. At the following meeting, on 28 April 1686, he presented the manuscript of Book One to the society. He delivered Book One to the printer that same month, but it was not until March of the following year that Halley delivered Books Two and Three to the printer.[16] On 5 July 1687, Halley wrote to Newton about the details of the final publication figures and to announce, "I have at length brought your Book to an end."[17]