PART 1
RATIONALIZATION OF KNOWLEDGE

1
The Mathematical Philosophy

By Tore Frängsmyr

There are two distinct opinions regarding the status of science in the 18th century. One dismisses the period as an uninteresting interval between the breakthroughs of the 17th century and the expanding industrialism of the 19th. The opposing view holds that the 18th century was the time when all the important work of the previous century bore fruit.

The dismissers argue that nothing really new emerged in the 18th century. "By many historians the century has been deplored for allegedly producing science that was boring, unoriginal, lacking in rigour and overspeculative." It has been castigated as "comparatively undistinguished in its science"; if its science is included in its reputation, the siècle des lumières cannot be freed from "an element of dullness."^[1]

In direct opposition to these nay-sayers, other historians have identified much of the intellectual life of the 18th century with the fostering of its heritage from the scientific revolution. The Enlightenment thus climaxes the development of early modern science.^[2] The most recent general assessment of the role of science in the Enlightenment gives particular weight to the century's efforts to consolidate and organize what it had received. "The creation of the new scientific disciplines was probably the most important contribution of the Enlightenment to the modernization of science, and one that we might easily overlook. It marks the Enlightenment as a period of

[1] G.S. Rousseau and Roy Porter, eds. The ferment of knowledge: Studies in the historiography of eighteenth-century science (Cambridge: Cambridge University Press, 1980), introduction.

[2] Preserved Smith, A history of modern culture , 2 vols. (New York: H. Holt and Co., 1930–4), 33–5.

transition between the old and the new."^[3] That careful and informed students of the 18th century have reached diametrically opposed evaluations of its science is largely a consequence of their differing ideas about what counts as science. In this volume we sidestep the difficulty by restricting our attention to the working out of a particular method, or, as it might better be called in many instances, of an appeal to a slogan. That slogan, as Galileo formulated it, holds that "the book of nature is written in the language of mathematics."^[4]

In the 18th century, this proposition inspired the work of the most productive mathematicians and underlay the program of the most ambitious philosophers, who proposed to extend it beyond the book of nature to the books of man—that is, to all exercises of human reason.^[5] The languages of reason and nature were thereby to agree. We see two phases in the 18th-century elaboration of this proposition. Until about 1760, "mathematics" was applied to the general exercise of reason (as opposed to mathematics itself and the quantified parts of astronomy and physics) more as a symbol and slogan than as a useful tool. In this first phase the philosophy of Leibniz's epigone, Christian Wolff, is exemplary. In the last third of the century, however, the equation of reason with mathematics inspired instrumentalist and quantitative approaches to a wide range of problems in various sciences, arts, and technologies. We take the activities of this quantifying spirit to have been progressive, in the sense that under its inspiration the achievements of the scientific revolution were extended and reinterpreted in a way that made possible rapid advance in mathematics, physical sciences, and statistics (conceived as the sciences of the state) in the early 19th century.

In what follows, Wolff's method is seen as representative of the process by which reason was "naturalized" during the first half of the 18th century. The purpose is to provide both an introduction and a contrast to the applications of the quantifying spirit later in the century that form the subject matter of the other essays in this volume.

[3] Thomas L. Hankins, Science and the Enlightenment (Cambridge: Cambridge University Press, 1985), 5.

[4] Smith, A history of modern culture .

[5] Ibid., 118.

Universal Mathematics

Leibniz wanted not only to see the world as a machine with a "static structure of matter in geometrical and mechanical relation"; he also wanted to give exact mathematical expression to all the processes and changes that took place in the world. Through the infinitesimal calculus he found a constant law that remained valid for an infinite number of processes and changes. The elements constituting the universe, nature, and human life were not particles of matter, but forces and motions. Each element or individual substance—Leibniz called them "monads"—was complete in itself, a microworld or a mirror of the universe, and yet intimately related to all other individuals in a system of pre-established harmony. The mathematical system came by its harmony naturally.

Given this structure of the world it was natural for Leibniz to take another step: to organize human knowledge in a mathematical pattern. Drawing both on the Lullian tradition that sought a universal language and on his own mathematical work, Leibniz wanted to create a mathesis universalis or ars characteristica , which would represent, combine, and produce all possible knowledge. This language would serve not only as a philosophical method but also as the key to a true encyclopedia. In the mathesis universalis , each human concept or idea corresponded to a different symbol or combination of symbols. By combining these symbols according to mathematically defined rules, Wolff's method could produce long lists of new truths and confirm old ones. The new language became for Leibniz both a means of communication and a new kind of logic, a way to formulate statements and an instrument of reason.^[6]

The most influential philosopher in the Leibnizian tradition was Christian Wolff. Wolff was not an original thinker. Instead, he took the foundation of his system from his teacher Leibniz, systematized it, and put it within the grasp of any educated person. Because of his

[6] Louis Couturat and L. Leau, Histoire de la langue universelle (Paris: Librairie Hachette, 1903); Louis Couturat, La logique de Leibniz d'après des documents inédits (Paris: F. Alcan, 1901), esp. chaps. 2–4; cf. C.I. Lewis and C.H. Langford, Symbolic logic (New York: The Century Company, 1932), 5ff.

firm insistence on the rationalism that was characteristic of his "mathematical method," Wolff came to be regarded as a philosopher of the Enlightenment. Mathematics held symbolic value as the driving force behind the progress of science, and also the progress of reason and free thought. As Newton had given the universe a mathematical structure, so Wolff aimed to subsume human and society within a vast mathematical system. He pushed his mathematical method into every possible area: philosophy and science, theology and ethics, politics and public finance.

Wolff's "Rational Thoughts"

Many historians of philosophy have described Wolff as one of the most influential philosophers of his time, without, however, paying much attention to his ideas. He has been called "the master of the Enlightenment in Germany," and even outside Germany; Diderot sang Wolff's praises in his Encyclopédie . Paul Hazard made Wolff "the intellectual leader of Germany" and a general-purpose sage admired by all nations. Lewis White Beck portrays Wolff as a rationalist in the Enlightenment spirit: "Wolff is the best German representative of a general movement of thought towards deism, utilitarianism and free thought that was sweeping over Europe as a whole."^[7]

These characterizations of Wolff and his influence claim both too much and too little. Too much, because terms like "rationalism" and "mathematics" did not necessarily imply Enlightenment, nor did Wolff's philosophy. It was the form of mathematics that interested him, its way of pursuing an argument to its proof. The characterizations claim too little because the association of Wolff's brand of rationalization with the Enlightenment neglects the vast effort at systematization of all knowledge inherited from Leibniz and the 17th century.

[7] Paul Hazard, European thought in the eighteenth century (London: Hollis, 1954), 40; Lewis White Beck, Early German philosophy: Kant and his predecessors (Cambridge, Mass.: Belknap Press, 1969), 256–76. Cf. Tore Frängsmyr, "Christian Wolff's mathematical method and its impact on the eighteenth century," Journal of the history of ideas , 36 (1975), 863–8.

Wolff turned to the connection between mathematics and philosophy early in his career. He obtained his doctorate in 1703 with a dissertation on ethics based on mathematical foundations. He soon came into contact with Leibniz, who nominated him for election to the Academy of Sciences in Berlin. In 1707 Wolff became professor of mathematics at Halle and later assumed the chair of philosophy. In Wolff's work the one subject cannot be distinguished from the other. As a mathematician he hardly made an original contribution, but his diligence yielded bulky volumes summarizing the contemporary state of knowledge—for instance, his Anfangsgründe aller mathematischen Wissenschaften (6 vols., 1710) and Elementa matheseos universae (5 vols., 1713–5).

Wolff announced his own particular specialty—the application of mathematics to philosophy—in his Ratio praelectionum Wolfianarum in mathesin et philosophiam universam (1718). This line of work culminated in a book in German with the monumental title Vernünfftige Gedancken von Gott, der Welt und der Seele des Menschen, auch allen Dingen überhaupt (1720). The book, usually known as his "German metaphysics," sets out Wolff's philosophy virtually in its entirety; it brought him wider renown and prefigured a whole literary genre during the 18th century. Wolff himself published a series of Vernünfftige Gedancken on various topics; elsewhere philosophers followed his lead and published "rational thoughts" on one subject after another.^[8]

Wolff's stature as a liberal theologian has also contributed to his reputation as a rationalist philosopher of the Enlightenment. In Halle, the dominant theology was the conservative strain of Pietism developed by August Hermann Francke, which sought renewal within the Church. Competition came from influential orthodox

[8] Hans Werner Arndt, "Rationalismus und Empirismus in der Erkenntnislehre," in Werner Schneider, ed., Christian Wolff, 1679–1754: Interpretationen zur seiner Philosophie und deren Wirkung (Hamburg: F. Meiner, 1983), 31–47. The same collection contains six articles about Wolff's influence, among them Notker Hammerstein, "Christian Wolff und die Universitäten: Zur Wirkungsgeschichte des Wolffinanismus im 18. Jahrhundert," 266–77. See also Beck's chapter "A generation of epigoni," in Early German philosophy , 276–305, and Tore Frängsmyr, Wolffianismens genombrott i Uppsala (Universitet; Stockholm: Almqvist & Wiksell, 1972), with an English summary: "The emergence of Wolffianism at Uppsala University, 1720–1760."

pastors and from a group of "transitional theologians," who attempted the feat of mixing orthodoxy, Pietism, and rationalism.

Wolff found himself at odds with this eclectic combination. In 1721 he delivered a formal address on the teaching of Confucius, Oratio de sinarum philosophia practica , which emphasized its strict morality.^[9] By studying human nature, but without invoking divine revelation, Confucius had attained a lofty moral position. From this Wolff argued that morality could be comprehended by reason alone. Here he linked up with the deism that had been spreading steadily since the mid-17th century and that often saw in Confucianism the confirmation of its ideas. Wolff's address contained nothing new or sensational, but under the circumstances it was taken as a challenge. The Pietists retaliated by accusing Wolff of atheism; condemnatory sermons echoed in the churches and protests ascended to higher levels; the highly regarded theologian Johann Franz Buddeus, orthodox but favorably disposed to the Pietists, wrote an indictment of Wolff's views. The campaign finally succeeded in 1723, when Frederik Wilhelm I banished Wolff from Halle. Wolff retreated to Marburg, a little university town in the landgraviate of Hessen, an environment more conducive to his reputation. Within a few years he was being hailed as the greatest mathematician and philosopher of his age; students on their grand tours included a stop in Marburg to attend his lectures; scientific academies and universities throughout Europe wooed him. He began to write in Latin, which permitted access to a wider international audience. The 1730s saw the appearance of the great classical works, Philosophia prima sive ontologia (1730), Cosmologia generalis (1731), Psychologia empirica (1732), Psychologia rationalis (1734), Theologia naturalis (2 vols., 1736–7), and Philosophia practica universalis (2 vols., 1738–9). Again, they contained little new, but developed and refined Wolff's ideas in different philosophical disciplines and generated popularity, renown, and followers for their author.^[10]

[9] Wolff's Oratio de sinarum philosophia is now published in a Latin-German parallel edition, Rede über die praktische Philosophie der Chinesen , ed. Michael Albrecht (Hamburg: Meiner, 1985), with a 100-page introduction. See also Beck, Early German philosophy , 258ff.

[10] Anton Bissinger, Die Struktur der Gotteserkenntnis (Bonn: H. Bouvier, 1970).

Wolff's reputation as a rationalist and freethinker derived more from his banishment than from his writings. His position was enhanced when Frederick the Great ascended the throne of Prussia and decreed that salvation was everyone's responsibility. One of Frederick's first acts was to recall Wolff to Halle and to shower him with honors. Wolff assumed positions as professor of law, vice-chancellor of the university, privy councillor, and, in three years, chancellor. In 1745 he was ennobled as baron von Wolff. The summons from Frederick the Great, prince of Enlightenment, confirmed Wolff's status as an Enlightenment philosopher.

The Mathematical Method

The characteristic aspect of Wolff's philosophical teaching was its strictly logical construction. He had a manic capacity for arranging and systematizing everything, step by step, clearly and paradigmatically, accurately and in detail. He worked from the principles of contradiction (principium contradictionis ) and of sufficient reason (principium rationis sufficientis ). He regarded the principle of contradiction as the first law of philosophy from which all other propositions could be derived. With the principle one could decide whether something was possible; that is, everything that might be held to have sufficient reason. Philosophy was the science of the possible, with the task of showing how and why things are possible.^[11]

In working out his science, the philosopher had to observe certain rules. No principles could be employed unless adequately proved, and no new ones allowed unless derived from proven principles. No departure could be made from the meaning that words had generally acquired, and if new words or concepts were required, they had to be accurately defined. Intrinsically different objects and phenomena had to be given different names. Starting with axioms, clear definitions, and distinctions, deductive methods would link truths with one another and thus reach irrefutable conclusions. In this way results

[11] Vernünfftige Gedancken von den Kräfften des menschlichen Verstandes (Halle: Renger, 1723; 7th ed., 1733), 1. Cf. Cogitationes rationales (Frankfurt and Leipzig: Renger, 1730), 1.

obtained in philosophy would be as reliable as those in mathematics. In none of this did Wolff go beyond Leibniz, or, for that matter, Aristotle, Thomas Aquinas (whose influence he acknowledged), Descartes, Spinoza, or Tschirnhausen, whose Medicina mentis he had studied in detail. The mathematical method nevertheless became known as Wolffian, because Wolff systematized it as never before. In his hands it became an all-purpose means for establishing truth in any sphere.^[12]

Wolff's epistemology is quite simple. Human knowledge outside Christian revelation can be acquired in three ways: by experience (historical knowledge), by reason (mathematical knowledge), or by a combination of the two (philosophical knowledge). The last of these three methods is preferable; the other two have value only to the extent that they can be of use to philosophy. Our senses awaken our most general concepts, which are innate in our consciousness, and provide many fresh ideas; reason clarifies them and puts them into context. Thus every philosophical discipline has both empirical and rational components. For Wolff, philosophy came to mean the same thing as science, as the German term for philosophy, "Welt-Weis-sheit," suggests.

Mathematics is not a part of Wolff's philosophy. Instead, it serves as an instrument of knowledge in its own right—a method, a means rather than an end. Mathematics, in both form and inherent logic, provides a model for all areas of human knowledge. From this point of view, the mathematical method was identified with the philosophical one, and assumed a central role in the scheme of all Wolffian philosophers, even if they did not all see mathematics in the same subtle light as Wolff did. For the imitators, in fact, mathematics at times meant little more than computation.^[13]

Wolff held dear the idea of a system of knowledge. Knowledge was not merely a sudden insight or an idea, but arose from step-by-step deduction leading to reliable conclusions. The complex, reliable system therefore became an emblem of Wolff's entire philosophy—

[12] Philosophia rationalis sive Logica , 2d ed. (Frankfurt and Leipzig: Renger, 1732), 53–71; the "Discursus preliminaris" is the best explanation of Wolff's goal.

[13] Ibid., 28–52, "De partibus philosophiae."

both theoretical (logic, metaphysics, psychology, natural theology, physics, and technology) and practical (law, ethics, economics, and politics).^[14]

For Wolff, mathematics was the method and philosophy the content . This distinction is essential to an appreciation of his philosophy and its place in 18th-century thought.

For and Against Enlightenment

Wolff's working life falls into two periods. In the first he was active at Halle, wrote in his native German, formulated a more popular philosophy, and spoke so freely on religious matters that he was accused of atheism and banished. In the second period he lived in Marburg, wrote books in Latin, put forward a more theoretical philosophy explicitly addressed to the world of learning, and appeared in religious matters as an orthodox and unrelenting apologist. The watershed came somewhere around 1730. In the earlier phase he followed the precepts of the Enlightenment; in the latter he opposed them.

Wolff's German books aimed at a larger public are characteristic of his enlightened period. They have a pronounced practical and utilitarian tone and allot philosophy a "liberating" role, fully comparable to later manifestos of the French Enlightenment. Good examples are plentiful in his Vernünfftige Gedancken von der Menschen Thun und Lassen, zu Beförderung ihrer Glückseligkeit (1720). A critical indication of his popular, liberal position was his vacillation between physicotheology and teleology, two doctrines not easily distinguished and therefore often confused. Physicotheology rested on the ingenious organization of the natural world in general, but it often singled out particular features in nature as evidence of a creator behind the order. This search for an all-ordering God behind the exquisite subtlety of nature could justify, and even motivate, all scientific research. Where order served as a fundamental principle in physi-

[14] Carl Günther Ludovici, Kurtzer Entwurff einer vollständiger Historie der Wolffischen Philosophie (Leipzig: J.G. Löwe, 1736), 113ff. Cf. Bissinger, Die Struktur , 49f.

cotheology, so intention emerged as essential in teleology. If everything fulfills a definite purpose, there must be at least an implicit ordering principle—a God who intended the order. Many physicotheologists came to confuse proofs based on general order and those based on intent, and to subsume teleology under physicotheology. In either case, a "popular" proof of the existence of a divine creator was secured.

To see Wolff as a great representative of physicotheology, however, is to overplay his hand. Wolff attacked both the physicotheological and teleological approaches.^[15] He recognized the legitimacy of demonstrating divine intent in nature, but demanded a prior proof of God's existence and of the creation of the world as a free divine act. Wolff's method required that the theoretical foundation be established first. Yet a few years later, Wolff appeared as a full-fledged physicotheologist in his great work Vernünfftige Gedancken von der Absichten der natürlichen Dinge (1723). Had his views suddenly changed? No, he had distinguished between two sets of readers—academic and popular. Wolff's major works in Latin do not feature physicotheology. In a foreword to a translation of Nieuwentyt's well-known book on physicotheology (1731), he referred to his own work in German and underlined that it was intended for readers who did not speak the languages of the erudite. Whatever he said, in practice he inferred God's perfection from the usual inventory of the natural scientist. He described the cosmos and all its bodies, the sun and the fixed stars, the earth and the planets; he dealt with air and winds, different kinds of precipitation, rainbows, lightning, and thunder. The quantitative philosopher will want to know that his evidence includes "the number of heavenly bodies."^[16]

In sum, although Wolff demanded strict standards of logical proof in his mathematical method, he allowed himself to break the rules when addressing an unlearned audience. The end justified the means,

[15] Ratio praelectionum Wolfianarum in mathesin et philosophiam universam (Halle: Renger, 1718), 153-8.

[16] Wolff's preface reprinted in Gesammelte kleine philosophische Schrifften (Halle: Renger, 1736), 515f. Cf. Bissinger, Die Struktur , 232f.

for the religious objective was all-important. He made an even more significant adjustment in his major work Theologia naturalis , an extended exercise in apologetics, rapidly becoming his specialty. He devoted more than 350 pages to demonstrating the false steps and absurd notions of atheism.^[17] He did not confine his attack to unbelievers but also took up cudgels against every conceivable kind of philosophical freethinker: atheists, fatalists, deists, naturalists, anthropomorphists, materialists, paganists, Manichæans, Spinozists, and Epicureans. Just as he had previously used the mathematical method to lend positive support to philosophy or theology, he now used it to expose and exclude those who were not orthodox. Fourteen years earlier he had been banished and accused of atheism; now Wolff attacked those who adopted the viewpoint he had then espoused. Yet he held fast throughout these sea-changes to his mathematical method and philosophical rationalism.

Weighing in the Balance

Which side of Wolff attracted his contemporaries—the mathematical-rationalist or the teleological-apologetic? The answer must be that many accepted both sides, viewing them as two parts of the same entity. The mathematical method tied them together, and became the guiding principle for Wolff's pupils, even for those most inclined to apologetics.^[18]

One of the first of these pupils was Ludwig Philipp Thümmig, appointed professor in Kassel on the master's recommendation. His extensive Institutiones philosophiae Wolfianae (2 vols., 1725–6) differed little from Wolff's own account, and functioned as an authoritative source for later Wolffians. Another pupil, regarded as even more significant, was Georg Bernhard Bilfinger, professor of philosophy first at Tübingen, then at St. Petersburg, and again at Tübingen. His

[17] "De atheismo aliisque agnatis erroribus," Theologia naturalis II (Frankfurt and Leipzig: Renger, 1737), 369–726.

[18] Max Wundt, Die deutsche Schulphilosophie im Zeitalter der Aufklärung (1945; new ed., Hildesheim: G. Olms, 1964), 199–230, and Beck, Early German philosophy , 276–305.

Dilucidationes philosophiae de Deo, anima humana, mundo et generalibus rerum affectionibus (1725) followed up, in title and contents, Wolff's Vernünfftige Gedancken von Gott, der Welt und der Seele des Menschen . Bilfinger emphasized the twin foundation stones of reason and experience, and stood ready to point out correspondences between natural science and Christian faith. Alexander Gottlieb Baumgarten, first in Halle, then at Frankfurt, wished above all to apply Wolff's philosophy to aesthetics. His well-balanced Metaphysics (1739), extremely faithful to Wolffian systematics, amounted to a reference book or compendium of Wolffian doctrine. In Leipzig, Johann Christian Gottsched and Carl Günther Ludovici wrote historical works on Wolff but were not themselves leading philosophers. Israel Theophil Canz at Tübingen did much to inject the doctrine into theology, as did Jacob Carpov at Jena, who sought to prove divine revelation using Wolff's teleological method. Important expositions of the mathematical method were also offered by Friedrich Christian Baumeister at Gölitz and Georg Heinrich Ribov at Göttingen.

Outside Germany Wolffianism found adherents in England, France, the Netherlands, Switzerland, and Scandinavia. In Denmark, Wolff's doctrines exerted influence through a number of mathematicians and philosophers: Christian Hee, who stayed for a time with Wolff at Marburg; Friedrich Christian Eilschow; and, above all, Jens Kraft, eminent as both a mathematician and a philosopher, who published a series of textbooks in imitation of Wolff. In Sweden, too, mathematicians introduced Wolff's ideas, which spread to the Swedish university at Åbo (Turku) in Finland.^[19]

In Sweden

The tendency of Wolff's disciples to tread confidently in their master's footsteps, to accept both his philosophical and his theological views, and to tie them together via the mathematical method, was muted in Sweden by resistance to the casual combination of philosophy and theology. Sweden's true introduction to Wolff came through

[19] Frängsmyr, Wolffianismens genombrott , 11–44.

the efforts of the mathematicians Anders Celsius and Samuel Klingenstierna, whose reputation at Uppsala University recommended their opinions to many students. In a manual of arithmetic (1727), Celsius spoke warmly of the existence of the mathematical method and also of its importance to other disciplines.^[20] By the following year, in a pro gradu dissertation on the existence of the soul or the intelligence, Celsius completely embraced the philosophy of Wolff. He praised not only Wolff's method but also followed the master in setting out his dissertation in traditional Euclidean form, with short propositions under such headings as axioma, theorema, definitio, observatio, demonstratio , and scholion . The dissertation argues that the soul can be proved to exist by means of Wolff's philosophical laws, and Wolff himself is called "the greatest philosopher of our time," philosophus nostra aetate summus .^[21]

Several theses reminiscent of Celsius' approach appeared over the next few years, all of them loud in praise of the mathematical method and bearing the imprint of the mathematical form favored by Wolff. Early in June 1729, the brothers Erik, Nils, and Johan Gottschalk Wallerius and their close friend Olof Hammaræus performed as respondents to four Wolffian dissertations. Presented first pro exercitio , two years later all four dissertations were defended pro gradu , under Celsius and Klingenstierna as tutors. Several of the dissertations describe the mathematical method without employing it; one stresses that certain philosophical knowledge is impossible without it. Jacob Friedrich Müller, professor of philosophy at Giessen, was quoted in support of this statement, although, unknown to the author, Müller had just defected to the camp of Wolff's denigrators.^[22]

Other dissertations under Celsius follow the same pattern. One deals with the subject of "incomprehensible books," which provided

[20] Celsius, Arithmetica eller räkne-konst (Uppsala, 1727), preface.

[21] De existentia mentis , pres. J.J. Hermansson, resp. A. Celsius (Uppsala, 1728), 7.

[22] De natura et utilitate scientificae , pres. S. Klingenstierna, resp. J.G. Wallerius (Stockholm, 1731), 4, 7, 10. Cf. De demonstratione , pres. E. Alstrin, resp. E. Wallerius (Stockholm, 1729). All these dissertations appear in Frängsmyr, Wolffianismens genombrott , chap. 3, 64–87.

the opportunity to laud Wolff as an example of lucidity and intelligibility.^[23] Evidence suggests that Celsius was behind the most detailed presentation of Wolff's philosophy, a dissertation in two parts (1731–2) on the subject of "how to attain worldly happiness through philosophy." The subject may appear novel, but the theme is familiar. The philosophy that can promote profit and happiness is contained in logic and mathematics. Hence the mathematical method is superior to earlier instruments and Wolff is the greatest of philosophers, outshining lesser lights like Plato, Aristotle, and Descartes. With Wolff's method, the author "brushes aside the weapons of atheism and defends the truths of the Christian religion." Ad pleniorem scientiam , the dissertation demonstrates that mathematics and physics are of fundamental importance to all other sciences, technology and mechanics, medicine, law, economics, and military subjects such as fortification and pyrotechnics.^[24]

Samuel Klingenstierna had already earned a name for himself as a mathematical genius when he set off to study abroad in 1727. He went first to Marburg to hear the much admired Wolff. It is recorded that the pupil much impressed the teacher. When the chair of mathematics at Uppsala became vacant, Klingenstierna applied for it. Because Marburg was within the native state of King Fredrik I of Sweden, Wolff had access to the king and recommended Klingenstierna in the strongest terms. Appointed to the post in 1728, Klingenstierna did not take up his professorship until 1731, when he returned to Sweden with newly purchased books and fresh reports on the fashionable new philosophy. His were popular lectures, and students sought him as tutor for their doctoral theses. These theses are filled with quite simple Wolffian propositions about the excellence of the mathematical method or the role of contingency in the creation of the world, and frequently make reference to Wolff and Bilfinger. Mathematics thus linked up with philosophy, notably in Klingenstierna's seminars in philosophiam naturalem .^[25]

[23] De obscuritate librorum , pres. A. Celsius, resp. O.J. Petræus (Uppsala, 1731), 11.

[24] De felicitate civili per philosophiam comparanda , pres. A. Celsius, resp. J. Råfelt (Uppsala, 1732), passim. Quotations from and references to Wolff abound.

[25] Uppsala University, Catalogus lectionum publicarum (1731).

But enthusiasm for Wolff and the use of mathematics in philosophy went too far. Alert theologians, worried by the excessive spread of rationalism, castigated Wolff as "heathen and atheistic." In 1732 the chancellor of Uppsala, Gustaf Cronhielm, warned professors against dealing too casually with the new philosophy inspired by Wolff. The professors responded with promises to be careful and to protect their young students. Two years later the tone of admonition grew sharper. The chancellor decreed that professors should not preside at theses outside their own disciplines, a rebuke directed particularly at the professors of mathematics, who had been so ready to interpret the Wolffian philosophy. A year later, students were required to give a declaration of faith when enrolling at the university, to guard the purity of the doctrine. Such censorship and official criticism encouraged attacks on Wolff. His opponents asserted that mathematics and philosophy did not belong among the fundamental sciences; they saw all questions as ultimately teleological in nature. Philosophy, they insisted, should stick to its time-honored role as the handmaiden of faith.^[26]

The situation soon changed radically. Cronhielm was succeeded as chancellor by Gustaf Bonde, known for his deep interest in mysticism, alchemy, and Platonic mathematics. An admirer of physicotheology and of Wolff, he later published three volumes of "reflections on the wonders of God in nature." On a visit to Uppsala University in 1738, Bonde stressed the desirability of teaching the younger generation theologia naturalis as a timely defense against "atheists and indifferentists." The new chancellor thus recommended what the old one had forbidden. Bonde went even further when he engineered an offer to Wolff of the most highly regarded professorship in the university (which Wolff declined). Bonde's permissiveness sanctioned latent interests among the faculty. Petrus Ullén, professor of philosophy, became the first important figure in this new phase. By the time of his death in 1747, he had presided over a hundred theses, a third of which were Wolffian through and through. Ullén was no original

[26] The university chancellor's letter reprinted in Claes Annerstedt, Upsala Universitets historia , app. 3 (Uppsala: Almqvist & Wiksell, 1910), 198.

thinker. He praised mathematics for its ability to clarify and present problems in easily grasped diagrams and figures, and he insisted on the importance of the Wolffian philosophy to theology. He vehemently attacked all tendencies toward deism or "indifferentism"; true to the later Wolff, he used rationalism as a defense of orthodoxy and against the ideas of the Enlightenment.^[27]

An even louder champion of Wolffianism was Nils Wallerius, who started out as a mathematician and physicist, continued as a philosopher, and ended up as a theologian. He succeeded Ullén as professor of philosophy in 1746. Within the compass of philosophy he included logic, metaphysics, psychology, and natural theology, all slavishly arranged in accordance with Wolff's system. The mathematical method was fundamental in all philosophy, but mathematics must yield to theology, lest it lead to materialism and atheism. Wallerius shared the concern of both philosophers and theologians over theologia polemica —the struggle against Enlightenment philosophy. In 1755 Wallerius received a new chair in theology devoted to uncovering and combatting heretics. The new professor was to repudiate all freethinkers, "such as atheists, naturalists, deists, anti-scripturalists, indifferentists and other unbelievers."^[28] Wallerius warmed to the task: Moravian Brethren, Socinians, pantheists, and mystics, too—here he named Jakob Böhme, Paracelsus, Robert Fludd, and Johann Conrad Dippel—fell under his flail. In an essay on the repulsiveness and wickedness of materialism, Wallerius ranted at the ancient atomists Democritus, Epicurus, and Lucretius and their modern successors Thomas Hobbes and Pierre Bayle. "O stupida ingenia, sive mente ac ratione ," you are so blind that you cannot imagine anything beyond the bounds of the material.^[29] In 1756, Julien Offray de La Mettrie, the leading contemporary materialist, came in for particularly severe criticism.^[30] Wallerius decried the deists from Locke to Hume as

[27] Frängsmyr, Wolffianismens genombrott , 110–29.

[28] Wallerius's program printed in Annerstedt, Upsala Universitets historia , app. 3, 417f.

[29] Diss. mala et incommoda materialismi sistens , pres. N. Wallerius, resp. C.P. Eurenius (Uppsala, 1754), 4, 7, 11.

[30] Diss. sistens particulam primam vindiciarum religionis contra D:num De La Mettrie , pres. N. Wallerius, resp. G. Nordén (Uppsala, 1756–65), vi, 76.

"naturalists"—Wallerius' favorite epithet for his opponents—and Voltaire as "the greatest fraud of the day."^[31]

Wallerius' guiding ambition was to reconcile mathematics, philosophy, and theology. At hand were all the necessary tools: a professional graps of mathematics, philosophy, and theology; a passion for system; and Wolff's method. His eminent elogist in the Royal Swedish Academy of Sciences, Torbern Bergman, showed restrained appreciation of Wallerius' contribution, and a like opinion was expressed in another contemporary biography: "Had he lived fifty years earlier and in a more scholastic era, his memory would have been even more illustrious."^[32]

By Kant

Wolff's use of mathematics usually made the best impression on those who knew the least mathematics. During the late 1740s, in a celebrated dispute between the supporters of Newton and those of Wolff, Pierre Louis Moreau de Maupertuis was the main adversary of the Wolffians. The most telling attack on Wolff came from Kant, however, who as usual went right to the core and challenged the mathematical method itself.

The Berlin Academy had posed the question of whether metaphysical truth could be equated with mathematical truth and, if it could not, what sort of truth it then was. Kant replied with the treatise, Untersuchung über die Deutlichkeit der Gründsätze der natürlichen Theologie und der Moral (1762, published in 1764), which struck a decisive blow to Wolff's philosophical teachings.^[33]

Kant had been influenced by Wolff's philosophy, but had never

[31] Nils Wallerius, Proenotiones theologicae , 6 vols. (Uppsala, 1756), e.g., 13f.

[32] Upsala Ärkestifts Herdaminne, 1 (Uppsala), 426–7; Torbern Bergman, Åminnelse-tal öfver Nils Wallerius (Stockholm: L. Salvius, 1756), 24.

[33] Reprinted in Kant's Gesammelte Schriften (Berlin: G. Reimer, 1902– ), 2. Cf. G.G. Fülleborn, Zur Geschichte der mathematischen Methode in der deutschen Philosophie , in Beyträge zur Geschichte der Philosophie, 5 (Züllichau and Freystadt: F. Fromann, 1795), 108–30; Giorgio Tonelli, "Der Streit über die mathematischen Methode in der Philosophie in der ersten Hälfte des 18. Jahrhunderts und die Entstehung von Kants Schrift über die 'Deutlichkeit'," Archiv für Philosophie, 9 (1959), 37–66; Hans-Jürgen Engfer, "Zur Bedeutung Wolffs für die Methodendiskussion der deutschen Aufklärungsphilosophie: Analytische und syntetische Methode bei Wolff und beim vorkritischen Kant," in W. Schneider, ed., Christian Wolff , 48–65.

followed it slavishly. The treatise of 1762 marked his rejection of the mathematical ideal in philosophy. In it Kant draws his well-known distinction between analytic and synthetic propositions, and concludes that metaphysics is not synthetic like mathematics but rather analytic. The synthetic structures of mathematics cannot be transferred to philosophy and its "mathematical method," for philosophy, unlike mathematics, does not have at its disposal definitions and axioms from which to proceed methodically. Application of the mathematical method to the field of philosophy had thus given rise to errors and mistakes: no dogma in philosophy could be likened to the definitions and axioms of mathematics.

Kant's criticism swept away the very foundations of Wolff's influence. Wolff's mathematical method depended on the possibility of applying procedures of mathematical proof to all philosophical and theological questions. Now Kant argued that the basic structures of mathematics and philosophy were different. Wolff's system crumbled.^[34]

Several conclusions emerge. Wolffian thinking became a fashionable philosophy in the first half of the 18th century, and its exponents and detractors both saw the mathematical method as the essential element of his doctrine. It is important to distinguish between form and content in our analysis of the Wolffian mathematical method, and to recognize that Wolff's philosophy fulfilled different functions in different situations. While "rationalism" and "mathematical method" were popular rhetorical flourishes in the 18th century, they also stood for a well-defined means of attaining certain intellectual objectives. Both friends and enemies of the Enlightenment appropriated that method, since mathematics as a method of proof promised results in all areas of human knowledge. That it collapsed so readily under Kant's attack reflected that Wolff's mathematical method had already proved inadequate: it failed to provide tools for revamping critical philosophy, or for creating instrumentalist science, or for solving practical problems facing the bureaucratic states of the late 18th century. The form and content of mathematics itself, however, would continue to speak to these needs.

[34] Cf. Raffaele Ciafardone, "Von der Kritik an Wolff zum vorkritischen Kant: Wolff-Kritik bei Rüdiger und Crusius," and Norbert Hinske, "Wolffs Stellung in der deutschen Aufklärung," in ibid., 289–305, 306–20, resp.

2
The Broken Circle

By Gunnar Broberg

The word "quantitative" applies to natural history during the second half of the 18th century in two distinct but related ways: as characteristic of the object and of the method of study. As for object, the sheer number of known and estimated forms forced new approaches to the storage and retrieval of information; as for method, these new approaches were instrumentalist and, in the dominant system of Linnæus, mathematical. These features—the overwhelming flow of information and the determination to inventory and survey it for useful purposes—characterize much of the learned activity of the late Enlightenment. In what follows, I first bring Ernst Cassirer's opposition between l'esprit de système and l'esprit systématique to bear, and indicate the scope of the problem of order faced by the encyclopedists of the Enlightenment. I then turn to natural history, reporting the inflation of information and some of the problems of keeping it together. Finally, I look at the paradoxes of natural history at the turn of the century.

Encyclopedism and Order

The classificatory project of 18th-century natural history runs parallel to and was in many ways inspired by the development of the encyclopedic enterprise of the same period. Natural historians and encyclopedists shared similar ambitions for totality, coherence, and order. Both camps had to ask the same questions: How much is there in the world to know? Is it proper to measure all the riches of creation? If so, by what "method" should they be described? Is there a correspondence between what we can know and the fundamental nature of things? Parallel to the rapid increase of information

came the epistemological shake-up of the early Enlightenment. Natural history as well as general encyclopedism moved from the finite world of the baroque to the infinite world of modern times.^[1] If "encyclopedia" means "the circle of knowledge," the circle was broken during the latter part of the 18th century. Natural history opened out similarly.

In following this development we shall find it useful to adopt a distinction d'Alembert employed in his introduction to La grande encyclopédie . By esprit de système he meant the old a priori physics connected with scholasticism, rationalism, and deduction, the sort of thing that Christian von Wolff did in the first half of the 18th century.^[2]Esprit systématique was connected with experiments, empiricist ideals, and a readiness to go down the toilsome path from the Lockean world; travelers on this journey had to accept a demarcation between what we can know and what we cannot know, between physics and metaphysics, and to try not to mingle both sides. But that is what often happened. As Cassirer wrote in The philosophy of Enlightenment : "This difference in mode of thinking [between esprit de système and esprit systématique ] does not mean a radical transformation, it amounts merely to a shifting of emphasis. This emphasis is constantly moving from the general to the particular, from principles to phenomena. But the basic assumptions remain. . ., the self-confidence of reason is nowhere shaken. The rationalistic postulate of uniformity dominates the mind of this age."^[3]

The 18th century manifested its rationalism in encyclopedias. Natural history helped to determine their structure. The Linnæan encyclopedia had one of its roots in the religious idea of Creation as the Book of Nature opened to the naturalist-reader. The same ambition to take possession of what had been discovered, indeed conquered, characterized both the Systema naturae and the great French

[1] Marjorie Nicolson, The breaking of the circle: Studies in the effect of the "new science" upon seventeenth-century poetry , rev. ed. (New York: Columbia University Press, 1960).

[2] See Tore Frängsmyr, chap. 1 in this volume.

[3] Ernst Cassirer, The philosophy of the Enlightenment (Princeton: Princeton University Press, 1951), 22f.

Encyclopédie . It was not mere coincidence that d'Alembert's and Diderot's great work began at the same time that Georges Louis Buffon's Histoire naturelle and the geodetic survey of France started. In his Discours préliminaire , d'Alembert alluded—and most appropriately—to the new success of natural history.^[4] Each side could profit from the other. Linnæan natural history, with its clear structure, universal language, and simplicity, made a good model for encyclopedias. Its rationality and practicality gave it entrée everywhere.

According to Zedler's magnificent Grosses vollständiges Universal-Lexicon aller Wissenschaften und Künste (1732–54), an encyclopedia is "a total idea of all sciences, which the ancients brought together so as to show the relationship they have to one another."^[5] Zedler settled for something less. Both he and Ephraim Chambers, the author of the Cyclopedia (1728), arranged their works not systematically but alphabetically, though, to be sure, not without long discussions about the systematic aspect: "It may be even said, that if the system be an improvement upon the Dictionary, the Dictionary is some advantage to the System; and that this is perhaps the only way wherein the whole circle, or body of knowledge, with all its parts and dependencies, can well be delivered." Chambers, who was influenced by Locke and Newton, went on to explain the perfection that characterizes a classical work in contrast to a modern one. The classic had so little to compare itself to that it could devote all its attention to order and its own perfection, whereas the latter—"since experiments are endless"—will never reach so far. "To have philosophy complete, we should have the order, precision and distinctness of the old; and the matter and copia of the new."^[6] Chambers opposed order to abundance of material.

The opposition Chambers developed was connected with the decline of rationalistic systems of sciences in the Leibniz-Wolff

[4] Jean Le Rond d'Alembert, Inledning till Encyclopedien (Stockholm: Carmina, 1981), 84.

[5] Johann Heinrich Zedler, Grosses vollständiges Universal-Lexicon aller Wissenschaften und Künste , 64 vols. and 4 supplements (Halle and Leipzig: J.H. Zedler, 1732–54), 8 (1734), 1138.

[6] Ephraim Chambers, Cyclopedia , ed. Rees (London, 1778; original ed., London: J. & J. Knapton, 1728), "Preface," xxii.

tradition, which were especially important in Germany from 1720 to 1765.^[7] These often extremely elaborate maps of knowledge lost much of their appeal when examined in the light of English empiricist and French sensualistic epistemology, more precisely the French Encyclopédie and later Kant's criticism. The Encyclopédie has often been taken as the starting point for a new concept of knowledge because of its antimetaphysics, its updated information, its optimism, its democratic call for action, and many more things, including its empiricism.

The Encyclopédie was a joint adventure with many collaborators and two principal editors, Diderot and d'Alembert, who did not agree about everything. D'Alembert's famous Discours préliminaire stressed the "order and connection of human knowledge," the inner order and harmony of the sciences, and the possibility of making a uniform system of encyclopedic knowledge. It was not clear, however, how he supposed the tree of knowledge to grow—did logical division or historical development control the branching? His ideals were those of a geometer, believing in a regular universe and operating with axioms and principles. "If somebody could survey the whole universe from one standpoint, it would be seen as consisting of one single fact and one single truth."^[8] Alphabetical order does not necessarily invalidate coherence, since cross-references could link the various subject matters from a synthetic point of view. How well these combinations in the end corresponded to the tree of knowledge was problematic.

Diderot's article "Encyclopédie" (1755) gave a truer picture of the purposes of the Encyclopédie . It responded to accusations that the first volumes did not have the coherence promised in d'Alembert's essay: "It is impossible to improve the arbitrariness of this great original profusion. The universe presents us only with individual things, infinite in number and with almost no fixed and determined division [among them]; none of them can be called the first or the last; everything is connected to everything else by insensible gradations." Later

[7] Giorgio Tonelli, "The problem of the classification of the sciences in Kant's time," Rivista critica di storia della filosofia, 38 (1975), 243–94.

[8] D'Alembert, Inledning , 57.

Diderot insisted on the value of irregular articles. "The formation of an encyclopedia is like the foundation of a great city." He compared encyclopedic order with a machine, the parts of which fit together, but which can also be assembled in a completely new way.^[9] Rather than being the organized accumulation of the total stock of human knowledge, the cross-referenced Encyclopédie would be an open-ended conversation among members of a cité scientifique .

Diderot's dynamism would become even more pointed in the Rève d'Alembert , in which he defended poetry against geometry.^[10] That did not mean total hostility toward all "systems," only metaphysical and deductive ones; acceptable systems should act as heuristic devices and hypotheses and as pedagogical tools. When Diderot defended this openness in contrast to closed systems, he also defended the alphabetical arrangement, which predominated thereafter. This arrangement represented an important step toward secularization of knowledge and agnosticism toward taxonomies of knowledge. To quote a recent interpretation: "As the zero degree of taxonomy, alphabetical order authorizes all reading strategies; in this respect it could be considered an emblem of the Enlightenment."^[11]

The encyclopedic business thrived on this tension between knowledge and information. The first edition of Encyclopedia Britannica (1768–71) was more weighted toward information, whereas the success of the Brockhaus Conversationslexicon provoked charges of superficiality.^[12] Hegel used the same word as Kant did for natural history works, Aggregaten, to describe the state of contemporary

[9] Diderot, "Encyclopédie," Oeuvres complètes, 7 (Paris: Hermann, 1976), 174–262, quotations on 210, 218.

[10] John Pappas, "L'esprit de finesse contre l'esprit de géométrie: Un débat entre Diderot et d'Alembert," Studies on Voltaire and the eighteenth century, 89 (1972), 1229–53.

[11] Charles Porset, "Figures de l'encyclopédie," in Christiane Mervaud and Sylvain Menant, eds., Le siècle de Voltaire. Hommage à René Pomeau (Oxford: Voltaire Foundation, 1987), 719–33, on 719.

[12] See also the mild contempt in the commentary of the Swedish classicist Adolf Törneros (ca. 1820): "Lexica, e.g., Conversations-Lexica, are like grocery stores [krambodar], where everybody can fetch his temporary or minute [timmeliga eller minuteliga] needs, like snuff for two pence." Aphorism 84, in Brev och dagboksanteckningar , ed. Nils Afzelius (Stockholm: A. Bonnier, 1962), 27.

encyclopedias. To Hegel, an encyclopedia should be a summarized introduction to scientific knowledge. An heroic attempt to combine these different traditions, literally identified with the heritage from Francis Bacon and Plato, is found in the "General introduction" to the Encyclopedia metropolitana (1817). The objective is no less than a reconstruction of "the circle of knowledge in its harmony" to provide that "unity of design and of elucidation, the want of which we have most deeply felt in other works of similar kind, where the desired information is divided into innumerable fragments scattered over many volumes, like a mirror broken on the ground, presenting instead of one, a thousand images, but none entire."^[13] But the future belonged to fragments and to Brockhaus's Aggregaten .

Whatever its organization, an encyclopedia required supplements to stay current.^[14] A popular work could be updated, commented on, and augmented; but in principle an encyclopedia should stand unaltered. The editors of the Encyclopédie failed in their initial plans to translate Chambers' Cyclopedia . Too much had to be altered or added. A two-volume Supplement to Chambers' work was published in London in 1753. About the same time a new series of supplements began to complete the already published sixty-four volumes of Zedler's Lexicon, and Felice's Encyclopédie, ou Dictionaire universel raisoné des connaissances humaines , received six volumes of supplements in 1775–6. Four supplementary volumes completed d'Alembert's and Diderot's great work in 1776–7. This constant adding made an encyclopedia something like a journal. Diderot wrote to the point. "An encyclopedia is a rapid and disinterested exposition of mankind's discoveries in all places, of all types, and in all times, without any judgment about people. Journals are only a passing account of books and authors."^[15] Still, the comparison was possible,

[13] Samuel Taylor Coleridge, "On the science of method," Encyclopoedia metropolitana (London: B. Fellowes, 1817–45), 1 , 42.

[14] See examples listed in Giorgio Tonelli, A short-title list of subject dictionaries of the sixteenth, seventeenth, and eighteenth centuries as aids in the history of ideas , Warburg Institute, Surveys, 4 (London: Warburg Institute, 1971).

[15] Diderot, "Encyclopédie," 241.

and in a sense the encyclopedia and the newspaper were getting closer to one another.

The increase of information that perplexed encyclopedists also vexed lexicographers. In his Plan for an English dictionary (1747), Dr. Johnson declared it to be his purpose to "fix" the language once and for all, because "all change is of itself evil." By the time his Dictionary appeared in 1755, Johnson had shifted his position. He now thought that "fixing" the language was as futile an effort as "embalming" it.^[16] In the interim he had put in much hard work to collect words and to define them, work similar to what natural historians tried to do in the species jungle. He too had to deal with the problematic relation between words and things. "I am not yet so lost in lexicography as to forget that words are the daughters of earth, and that things are the sons of heaven." Thus he inclined to accept Locke's criticism of essentialism, although as a lexicographer he could not be happy about the instability of meanings. "Definition is, indeed, not the province of man; everything is set above or below our faculties," he sighed on another occasion.^[17] The lexicographer had to make the best of the situation, and describe words, not define them; and so Johnson proceeded.

Emanuel Swedenborg also had something to say about the growing awareness of never-ending knowledge. In an undated note from the middle of the century he wrote: "I was allowed to enter a library where there was a great number of books. . . . In the inner parts of still more libraries were books written by adherents of the old churches and still farther were books from the oldest. . . . The libraries had many departments according to the training of the students. There were also many other libraries in heaven, but not public ones. Further on there were still more libraries likewise divided into

[16] Cf. James H. Sledd and Gwin J. Kolb, Dr. Johnson's dictionary (Chicago: University of Chicago Press, 1935); Tom McArthur, Worlds of reference (London: Cambridge University Press, 1986).

[17] Johnson, quoted in James McLaverty, "From definitions to explanations. Locke's influence on Johnson's Dictionary," Journal of the history of ideas (1986), 277–94, on 291. "Preface to the dictionary," in Howard D. Weinbrot, ed., New aspects of lexicography (London and Amsterdam; Carbondale: Southern Illinois University Press, 1972), 73–94.

departments. They were as many as there are research areas."^[18] We meet the famous spiritualist and one-time scientist, the inspiration of Borges' story of the libraries of Babel and of Eco's monastery; we recognize the principle of plenitude, and also of order. The multitude is overwhelming, but chaotic only to those who have not found—like Swedenborg and his fellow countryman Linnæus—the general patterns of reality.

The relation between order and plenitude is a constant problem in librarianship. A survey of German Sachkatalogen from the 17th to the 19th centuries shows a change from hierarchical systems to alphabetism. Gabriel Naudé, who introduced the concepts of systematic and alphabetic catalogues in the early 1600s, compared a library to an army. Strict order must rule in both. During the second half of the 18th century the Göttingen school of librarianship dominated. Its head, professor of medicine Georg Matthiae, stressed the necessity of arranging the library into "classes" according to a "natural" system. The systematic catalogue should be given priority over an alphabetic one since the coherence of books provides the basis of a scientific arrangement; considerations of size, form, and so on, mark the simple and unscientific librarian. Some disagreed: "Pure arrangement of books by their sciences is almost impossible and by no means necessary. The place a book stands is of no importance."^[19] The librarian's main problem was to find room for new books on old shelves; but, like natural historians, librarians wanted to raise their professional status by invoking order, classification, and science. The reverse analogy also held. Linnæus once wrote: "Gardens are like living libraries of plants." The garden and the library shared the same problem: growing knowledge had made systems cumbersome.^[20]

[18] Emanuel Swedenborg, Diarium spirituale , ed. J.F.I. Tafel (London: W. Newbery, 1844), no. 5999.

[19] Quoted in Harald Kleinschmidt, "Von System zur Ordnung. Bermerkungen zu Bewertungen von Sachkatalogen vornehmlich im 18. und 19. Jahrhundert," Libri, 37:2 (1987), 113.

[20] Linnæus, Demonstrationes plantarum in horto upsaliensi (Uppsala, 1753), sect. 1. In what follows, I treat questions similar to those addressed by Michel Foucault in Les mots et les choses (Paris: Gallimard, 1966) and by Wolf Lepenies in Das Ende der Naturgeschichte (Munich: C. Hanser, 1977): both contrast the classifying episteme of natural history with the new biology. The emphasis here is on the dynamics of fact accumulation and on the interplay between two models of knowledge handling—the encyclopedia and taxonomy in natural history. Recently Vernon Pratt has argued that the 18th-century obsession with taxonomy should be interpreted as a fascination with the order of nature as such rather than with animals and plants per se: "System-building in the 18th century," in J.D. North and J.J. Roche, eds., The light of nature (Dordrecht, 1985). As Pratt himself admits, he risks overemphasizing the point. The system-builders—John Ray, Tournefort, Michel Adanson, and Linnæus—were indeed trying "to articulate the order of nature," but we should not undervalue the fact that they were scientists working in the Baconian tradition. Certainly they would not recognize themselves in the mirror of modern historiography.

The Challenge of Plenitude

The plenitude of being was a constant cause for religious as well as scientific amazement. John Ray's famous The wisdom of God manifested in the works of creation (1691) opens by quoting Psalm 104:24—"How manifold are thy works, O Lord! In wisdom hast thou made them all"—and continues by changing the exclamation into a question. Ray called attention to the number of stars and planets, then calculated the number of animals. His estimate that there are 2,000 insect species in Britain alone, and 20,000 in the whole world, must have seemed very bold at the time, and likewise the figure 40,000 to 45,000 for all plants and animals together. He also discussed the proportions between the number of species, showing that the less perfect genera contain more species than the more perfect, a matter he went on to explain with many insights into the interplay of nature. To him, as to many of his contemporaries, the microscope had proved the plenitude of creation. We should note a typical 17th-century conceit: the greater the number of variations, the greater the glory of Man, since the Lord made them for human pleasure. As Ray put it: "another reason why so many kinds of creatures were made, might be to exercise the contemplative Faculty of Man; which is nothing so much pleas'd as in the variety of objects."^[21]

Compare Ray's numbers with the estimates given by Pieter van Musschenbroek half a century later. Following Hermann Boerhaave's lead, Musschenbroek reckoned the number of plant species at 13,000. He allowed 5 insect species to each plant. This made 65,000 insects

[21] John Ray, The wisdom of God manifested in the works of the Creation (London: Samuel Smith, 1691), chap. 1. Cf. William T. Stearn, "John Wilkins, John Ray and Carl Linnæus," Royal Society of London, Notes and records, 40:2 (1986), 101–23.

and (he guessed) 72,500 species in the entire animal kingdom—or, rather, twice that many, since each animal serves as food for another. Suddenly, the number has reached 145,000, and, again, the figures should be doubled since so little of the earth had been explored. We have in all 291,000 species, magnificent proof of the skill of the creator. Musschenbroek referred to Antony van Leeuwenhoek, to Henry Baker's book on microscopy, and to René Antoine Réaumur's entomology. It may be objected that Musschenbroek, a professor of physics, reasoned too much like a mathematician to win the confidence of the natural historian. Still, both had recourse to physicotheology.^[22]

At first, Linnæus probably did not estimate nature's multitude as extravagantly as had Ray. He inherited the task of describing the 6,000 species in Caspar Bauhin's Pinax (1623) from his predecessors, Olof Rudbeck, father and son, who planned to publish pictures of every known plant. (Their project was stopped by the great fire in Uppsala in 1702.) Anyone shouldering such a task would try to keep the numbers down. According to Linnæus, botanists should be able to remember at least all genera. Hence this second Adam, as Albrecht von Haller called him, must have believed it possible to survey nature taxonomically. In his Oratio de telluris habitabilis incremento (1743), he supposed that in the beginning the world was a paradise island containing all species.^[23] The only thing that had happened since then was the constant increase of individuals—and land.

The number of new discoveries during the 1740s forced Linnæus to change his mind. He had to fit these novelties into the context of his already published textbooks. The characters of the fresh-water polyps and the corallines, and later different fungi, seemed to contradict the taxonomical borderlines of nature. Critics labeled the

[22] Pieter [Petrus] van Musschenbroek, Oratio de sapientia divina (Leiden: S. Luchtmans, 1744). Cf. Maria Roosenbom, "Petrus van Musschenbroek's 'Oratio de sapientia divina,'" in P. Smith and J.Ch.V. ter Laage, eds., Essays in biohistory [presented to] Frans Verdoorn (Utrecht: International Association for Plant Taxonomy, 1970), 177–94.

[23] Tore Frängsmyr, "Linnæus as a geologist," in Tore Frängsmyr, ed., Linnæus, The man and his work (Berkeley: University of California Press, 1983), 110–55. Formally the Oratio is an exposition of sect. 134 of Fundamenta botanica (1736) on the fixity of species. "We count today as many species as were created in the beginning."

sexual system scholastic and artificial and contrary to the notion of nature's great chain. As an answer, Linnæus sketched an evolutionary hypothesis in Genera plantarum (1764), which also expressed his views about the natural system of plants. The more Linnæus peeked into the secret depths of nature, the more he found intricate connections. He now preferred the concept of mappa naturae over the simple hierarchical arrangement of the scala naturae.^[24]

Still more material flooded into Linnæus' study. The Systema naturae expanded from twelve folio pages in the first edition to almost 2,000 pages in the twelfth. He classified some 7,700 plants, 6,200 animals, and 450 mineral species. Altogether Linnæus' nature contained no more than 15,000 species, but that, as he knew, was but a beginning. Systema naturae goes from God to gravel, aiming at nothing less than a complete inventory or encyclopedia of the world. To Linnæus, nature's multitude must have been both a wonderful ongoing revelation and a terrible curse. He must have been one of the greatest optimists of all time. His library, now in the Linnæan Society of London, is filled with volumes of additions scrawled in the margins of his books.

Did Linnæus ever indicate the possible "size" of nature's kingdoms? Perhaps. In the fifth edition of Genera plantarum (1754), he introduced the idea of an alphabet or letters of the botanical language. These 26 letters combined two at a time were to cover all parts of the flower with the help of four "certain and mechanical principles," namely number, position, figure, and relative position. By a combination of these characters, botanists could give a good description of the genera, which in difficult cases should be checked by the concept of "habitus," the over-all impression of the plant. The largest possible number of genera is 26 × 26 × 4 or 2,684. Linnæus' evolutionary hypothesis of 1764 seems to end up in a similar number. At the beginning God created the "natural orders," which Linnæus elsewhere counted as 58. The next level, of the genera, came into existence by "mixing" the orders two by two: 58 × 58 makes 3,364

[24] See Gunnar Broberg, "Linné's systematics and the new natural history discoveries," in John Weinstock, ed., Contemporary perspectives on Linnæus (Lanham: University Press of America, 1985), 153–81.

natural genera. The third step, another multiplication by 58, gives us the number of possible species "mixed" by nature. There is also a fourth step, when "casus" or change mixes the species, which constantly happens and to such an extent that the botanist should not bother about all the resultant "varieties." Thus, the successive unfolding of types is caused by God, nature, and chance. The orders and the genera deserve special study. To keep up with the rest will be almost impossible. Here Linnæus seems to have retreated from his earlier optimism about human possibilities.^[25] If his reasoning seems odd, consider this from his fellow Swede Christopher Polhem, the great technical innovator. A descriptive name can be constructed by using letters in a prescribed order. For instance, an initial "p" could mean man, a "b" animal, "k" grass, while vowels might stand for the different senses, "a" for sight, "e" for hearing, "i" for smell. Further letters could indicate medical effects. With this system, Polhem guaranteed 1,406,250 possibilities; "more differences should not exist." If they do, it would be easy to add one or more variables or letters.^[26]

Linnæus' critic, Buffon, had to face the same problems. At the outset of his series on birds, he admitted a problem in acquiring all existing species. He and his collaborators worked for twenty years, constantly enlarging the collections of the Cabinet du Roi but never approaching completeness. Still, he could offer three times as many species of birds as were found in the tenth edition of Systema naturae (1758). (These figures depended on species definition and are not strictly comparable.) There are two competing strains in Buffon's writing: his early fascination with individuality in nature and his later encyclopedic ambitions. These tensions are even more obvious in the writings of Linnæus' second major French critic, Michel Adanson. Adanson faulted Linnæus for, among other things, grossly

[25] Genera plantarum , 6th ed. (Stockholm: L. Salvius, 1764), unpaginated. Cf. C.E.B. Bremekamp, "Linné's views on the hierarchy of the taxonomic groups," Acta botanica nederlandica, 2 (1953), 242–53. Linnæus' cortex-medulla theory probably put limits to possible change, since he considered the medulla as solely responsible for producing new properties.

[26] Christopher Polhem, Efterlämnade skrifter , 4 vols. (Uppsala: Almqvist & Wiksell, 1947–54), 4 , 333–51.

underestimating the number of species of coquillages in Senegal.^[27] We will return to Adanson. Here he exemplifies awareness of nature's tropical abundance, while Buffon represents the contention that this abundance cannot be counted.

Linnæus and Buffon both received credit in an unusually unbiased way in Haller's preface to the German translation of the Histoire naturelle (1750). In view of his old quarrel with Linnæus about who was the better naturalist and who had collected more plants, this sympathetic judgment might seem surprising. It may be explained by the message of the essay, that is, the blessings of hypotheses for the progress of science. "Laws in botany are arbitrary," Haller stated, "but they have done us an unbelievable service. Now we can distinguish ten thousand plants more easily than the Ancients did their six hundred." Linnæus' new theory performed the greatest service. At present, botany was advancing its lead over all sciences. "Not only is it nearest to completion, and has little by little determined the nature of almost all its classes and resemblances; it has [also] spread its laws throughout the entire Kingdom of Nature. Zoologists and mineralogists have received their laws from it and accepted them as the Romans did from the Areopagus." This last allusion is not a poor piece of flattery. Haller certified that botany would soon be finished, that all the work of collecting material and its description would be brought to their happy end. Success was guaranteed by the model he gave for natural history research: just as a land surveyor begins a map by determining some locations without the positions of places in between, the natural historian starts off with an initial sketch, which later knowledge will fill. The analogy is typical for an era of geographical exploration. It hardly implies the notion of an infinite or a dynamic nature, but rather only the hope of completing the process of exploration.^[28]

[27] Michel Adanson, Histoire naturelle du Sénégal (Paris: C.-J.-B. Bauche, 1757), xxvii.

[28] Haller, quoted in John Lyon and Philip R. Sloan, eds., From natural history to the history of nature. Readings from Buffon and his critics (Notre Dame: University of Notre Dame Press, 1981), 297ff.

A similar promise of prompt success (if only governments and princes would offer enough financial support) appeared in an article with the upbeat title, "Have we still to hope for a complete system of nature?" The author, entomologist Johan Samuel Schröter, did so hope, provided natural historians adopted his rules. In Schröter's scheme, only one person should be responsible for each major natural group and should be endowed with dictatorial powers to suppress quarrels among naturalists. Schröter held that only a group of specialists in natural history, and not a single person alone, could fulfill the Linnæan task. Other necessary preconditions were "ability, leisure, and money."^[29]

The most ambitious attempt of the 18th century to secure exact figures for the contents of the natural world, however, was made by Eberhard Zimmermann in his book, Geographische Geschichte des Menschen und der allgemein vierfüssigen Thiere (1778–83). Zimmermann combined macroscopic information from the explorers with inspiration from the microscopists' overfilled world. As professor of mathematics—he taught Gauss at Braunschweig University—he excelled in calculations about the size of the known world in relation to the number of known animals.^[30] These ratios show an impressive knowledge of zoological detail but also have strong similarities with the more unrealistic parts of political arithmetic as well as with Musschenbroek's calculations. Zimmermann vigorously pursued the Linnæan project, and equally vigorously attacked Buffon's "complete ataxia." But Zimmermann's calculations made the works of the Lord too manifold for the grasp of His creatures.

Zimmermann began small, with minerals, whose maximum number he put at 750. The variety of plants is much greater; recent estimates reached to almost 30,000 known species, only a fraction of the total quantity, which Zimmermann by various calculations raised

[29] Johan Samuel Schröter, "Haben wir noch ein vollständiges System der Natur zu hoffen," Berlinische Sammlungen, 2:1 (1770), 249–71, 3:1 (1770), 353–75, quotation on 263.

[30] On Zimmermann, see F.S. Bodenheimer, "Zimmermann's Specimen zoologiae geographiae quadrupedum," Archives internationales d'histoire des sciences, Oct–Dec 1955, 251–7.

to 175,000. He showed even more interest in the number of animals. Erxleben, Schreiber, Johann Friedrich Blumenbach, and others had set the quantity of known species at 10,000. Following Roesel von Rosenhoff and Linnæus (Pandora insectorum, 1758), Zimmermann proposed that there must be at least five insect species specialized on each plant species. Immediately we have 175,000 × 5 or 875,000 insect species of which only 51,000 had been described; entomologists had work to do. Nature abounds with parasitic and intestinal worms, with polyzoa and infusoria, and the sea is crammed with life to an extent almost impossible to grasp. "Who can follow the flying fish?" Probably the variety of sea organisms is two or three times that of land organisms. Zimmermann provided for invisible organisms, small and pellucid, on which the insects feed, and also for atmospherical fauna. Bearing all this in mind, he reached seven million species of animals, perhaps more. Then there are the innumerable specimens of each species. In the universe our planet is just a small spot unknown even to the inhabitants of Jupiter. And yet it has such multitude and magnificence! Zimmermann ended his essay with "a paean of thanks" to the Creator, the traditional natural-theological envoi . Following the natural-philosophical tradition as well, he offered calculations of the number of mammals undiscovered in different parts of the world, but despite the obvious interest of these estimates for the history of biogeography we leave them out.^[31]

This account of Zimmermann's work sums up several of the features of late Enlightenment natural history. He enthusiastically accepted the Linnæan project of species-hunting. Several times he appealed to princes for support for its completion. He was also intoxicated by the idea of nature's plenitude. As Ray did a century earlier, he compared the plenitude of this world with the plenitude of the universe. But we must note the enormous difference in the numbers they gave. And Zimmermann turned the whole architecture of the chain of being upside down. Whereas Ray (and Linnæus in Oratio , 1743) claimed that the ratios between nature's kingdoms were such

[31] Eberhard August Wilhelm Zimmermann, Geographische Geschichte des Menschen und der allgemein vierfüssigen Thiere , 3 vols., 3 (Leipzig: Weygand, 1783), 48.

that the lowest—the mineral—was more numerous than the vegetable, the vegetable more than the animal, Zimmermann proudly formulated a different and "remarkable law: the total of types of organized bodies increases with the degree of sensation and life."^[32] Throughout Zimmermann supported the idea of the chain of being, but obviously that notion was collapsing—so to speak—under its own weight. Zimmermann's discussion reflected many of the components of 18th-century natural history, but his figures neither fit the Linnæan project nor supported the single-line chain of being. His account did not visibly change the direction of natural history, but it forced two themes to the surface: the dramatic growth of numbers and the pessimistic prospects for complete knowledge.

So much for external problems; the Linnæan system has internal ones as well. It was fundamentally mathematical in a very simple way, based on the numerical principles of the sexual system as well as on zoological taxonomy. The naturalist counted stamens and pistils, teeth and nipples, toes, scales, antennas, everything. Among other advantages, mathematics afforded brevity and exactness. Linnæus was in every respect an economical man, who had to budget both time and space for his enormous undertaking to map the whole natural world. Without the Linnæan reforms the natural historian would not have been successful in surveying nature; with them, however, nature might appear to be one long list of numbers.

It was reasonable to question the validity of the criteria. Buffon did, in his famous criticism of Linnæus in the "Premier discours" of the Histoire naturelle in Buffon (1749).^[33] There Buffon argued that species as well as higher taxa are simply constructions of the taxonomist, while nature by contrast only consists of individuals. For Buffon, the counting of stamens and pistils has nothing to do with the true study of nature. He found no room for mathematics in natural history, the more remarkable considering his background in

[32] Ibid., 22.

[33] Buffon, "De la manière d'etudier et traiter l'histoire naturelle," in Buffon, Oeuvres philosophiques , ed. Jean Piveteau (Paris: PUF, 1954), 7. See also Wolf Lepenies, Das Ende der Naturgeschichte , and Philip R. Sloan, "The Buffon-Linnæus controversy," Isis, 57 (1976), 356–75.

that discipline. Nor did he use numbers to reason about nature's continuity. Indeed, he did not stress continuity in his writings as strongly as is generally thought. He of course made references to the great chain of being; but he rejected the idea of animal reason and opposed linking human and animal via the ape as a link to man. At bottom, however, what makes Linnæan taxonomy impossible in Buffon's eyes is that the number of natural "groups" must be infinitely great, since the only natural entity is the individual. The only way to treat nature, the only "method" or plan in the Histoire naturelle , is to accept subjectivity and to arrange descriptions according to how we normally get to know the animals.

In many ways Buffon adhered to the observer tradition, as did the master entomologist Réaumur, who advocated a similar concentration on the individual in contrast to more or less complete taxonomic surveys. Since we never will know everything, Réaumur wrote, we should not regret that some thousands of insects do not figure in our inventories. Instead, we should concentrate on the truly interesting wasps and butterflies. Observations rather than coherent systems are what matter.^[34]

In another line of attack, Linnæan mathematics was met with more mathematics. Adanson attacked the essentialistic and scholastic elements in Linnæan taxonomy and recommended an overall statistical evaluation of the plant's character, a method appropriate for modern computers.^[35] It is uncertain how far he himself used his method. It is not only extremely time consuming, it also stands in strong contrast to his predilection for completeness and universality. Thus Adanson's suggestions, although in many ways interesting, were a dead end in practice. Practical taxonomy could function only in connection with some sort of essentialism, while nominalism seemed to belong more to philosophy.

[34] René-Antoine Ferchault de Réaumur, Mémoires pour servir à l'histoire des insectes, 1 (Paris: Imprimerie Royale, 1734), preface. In reference to the contrast between "observers" and "taxonomists," see Jacques Roger, "The living world," in G. Rousseau and R. Porter, eds., The ferment of knowledge (Cambridge: Cambridge University Press, 1980), 255–83.

[35] See Peter H.A. Sneath, "Mathematics and classification from Adanson to the present," in Adanson. The bicentennial of Michel Adanson's 'Famille des plantes' , 2 vols. (Pittsburgh: Hunt Botanical Library, 1963–4), 2, 471–98.

The philosophical core of these objections and of 18th-century natural history in general was the idea of the great chain of being. In his thematic study, Lovejoy singles out the species problem, the interest in missing links, and the studies of the microscopists, all of which involved philosophical problems such as continuity and causality. By the end of the century, the idea had suffered many changes. Lovejoy emphasizes what he calls the temporalization of the chain, brought about by the study of fossils.^[36] More might well have been said about continuity . In general, both philosophers and natural historians adhered to the Cartesian-Leibnizian idea of continuity without any leaps or bounds.^[37] Action by contact keeps the world together and makes it go around. The Newtonian model of a void universe operating by distant forces did not appeal to natural historians. If there is continuity along the whole chain, then it should be possible to use the same classificatory devices and characters to judge all organisms. But, as Charles Bonnet objected, humans lack the right perspective and must satisfy themselves with "classifying classes," with specializing within fairly broad limits.^[38] Linnæus could stretch his scheme through botany only with difficulty—the sexual system was hardly useful for the cryptogams—and new principles were invoked for the other kingdoms of nature. Natural historians could see only fragments of the great chain before it twisted or disappeared from sight.

The related problem of plenitude , so beautifully demonstrated by the observations of the microscopists, also meant continuity along the

[36] Arthur O. Lovejoy, The great chain of being (Cambridge, Mass.: Harvard University Press, 1936); chaps. 6–9. See also A. Vartanian, "Trembley's polyp, La Mettrie, and eighteenth-century French materialism," Journal of the history of ideas, 11 (1950), 259–86; Herbert Thienemann, "Der Stufenfolge der Dinge," Zoologische Annalen, 6 (1910); Philip C. Ritterbush, Overtures to biology. The speculations of eighteenth-century naturalists (New Haven: Yale University Press, 1964); William T. Bynum, "The great chain of being forty years after," History of science, 13:1 (1975), 1–28.

[37] Francesca Rigotti, "Biology and society in the age of Enlightenment," Journal of the history of ideas, 47 (1986), 215–34.

[38] See Lorin Anderson, Charles Bonnet and the order of the known (Dordrecht and Boston: D. Reidel, 1982).

chain. Its main impact on classification, however, was the implication that God created an unlimited number of individuals rather than "types" or species. The vast numbers that came into being through the laws of generation were studied by Leeuwenhoek and other animal demographers.^[39] How to impose limits on this continuity? The question was similar to Zeno's paradox and, if taken seriously, could have led to taxonomy's suicide. The 18th-century natural historian had to deny the physicotheological premises that underpinned his work. To be sure, some very straightforward observations could strengthen him in his denial. As Voltaire wondered shrewdly, why is there no link between animals with two feet and with four? Johann Hermann, in his admirable Tabula affinitatum animalium (1783) (affinity had become the new catchword for genetic, evolutionary, or taxonomic relationship), emphasized symmetry in the animal world. To him, the chain was not linear but rather like a net with many intermediary and vacant steps. The number of possible types between two species of bug became almost impossible to estimate. Working with only ten variables, he found 10,172,640 possible varieties. Where, then, is the species limit? His conclusion seems to be that, apart from the possibility of an innumerable quantity of species on other planets, about which we know nothing, the Creator must have condensed his unlimited multiplying ability into a limited number of multifaceted species.^[40] As a solution of the plenitude dilemma,

[39] See Clifford Dobell, Antony van Leeuwenhoek and his "little animals" (London and New York: Staples Press, 1932); also Marjorie Hope Nicolson, The microscope and English imagination (Northampton, Mass.: Smith College, 1935). Leeuwenhoek calculated the number of sperm in the milt of a single cod to be no less than 150,000,000,000, a figure 13 times greater than the possible number of humans on the earth; a second calculation raised the proportion to 30:1. These investigations made a great impression on Réaumur, Buffon, and Bonnet. Cf. Frank G. Egerton, "Leeuwenhoek as a founder of animal demography," Journal of the history of ideas, 1 (1968), 1–22. Such counting was connected with utilitarian ambitions: for Wolff's extensive experiments on increasing grain number, see Günter Mühlpfordt, "Physiologie, Biologie und Agronomie im nationalistischen Wissenschaftssystem Christian Wolffs," Martin-Luther-Universität Halle-Wittemberg, Wissenschaftliche Beiträge , 1932:6, 472–91. On checks on the growth of any one species, see Clarence Glacken, Traces on the Rhodian shore (Berkeley: University of California Press, 1967), esp. 508–12.

[40] Johann Hermann, Tabula affinitatum animalium (Strasbourg: J.G. Treuttel, 1783), 19–24.

Hermann's suggestions seemed good enough. But they were purely defensive and conjectural.

Kant's criticism of Linnæan natural history also deals with the problems of continuity and plenitude. Either we work from logical entities as Linnæus did in Systema naturae , or we work with categories like time and space, that is, with Naturbeschreibung or Naturgeschichte based on geography. The Linnæan method did not attend to geographical dispersion. Kant sharpened his view: "The systems of Nature so far proposed should more correctly be called Aggregates of Nature; for a system presupposes the idea of the whole , from which the multiplicity of things can be derived. Really we have no Systema naturae . In our present systems, things are just placed together."^[41] This criticism, delivered in a lecture in 1756, was sooner or later bound to affect the ethos of natural history.

We conclude this section with two examples of pessimism, or rather modesty, on the part of late 18th-century epistemologists. The Swedish-Finnish chemist Jacob Gadolin observed that scholars stumble and fumble through the unknown regions of knowledge hoping to find a chain like the Linnæan method to follow. "If every country had its Linnæus, there would be no end of discoveries since Nature is an unfathomable treasure." So far optimism—but as Adam after the Fall was to experience, "the more we open our eyes the more we see that we are naked."^[42] Gadolin combined epistemological skepticism with traditional biblical pessimism. Again in a combination of religion and chemistry, Joseph Priestley confessed that for himself he found it impossible "to produce a work that shall be anything like complete ." "In completing one discovery we never fail to get an imperfect knowledge of others, of which we could have no idea before; so we cannot solve one doubt without creating several new ones." "The greater is the circle of light, the greater is the boundary

[41] Immanuel Kant, "Physikalische Geographie" (1756), in Gesammelte Schriften, 9 (Berlin: G. Reimer, 1923), 159ff. Cf. James L. Larson, "Linné and Kant," in Ragnar Granit, ed., Utur stubbotan rot (Stockholm: Norstedt, 1978), 99–107; Lepenies, Das Ende der Naturgeschichte .

[42] Jacob Gadolin, Tal om gränsorne imellan det vi uti naturen känne, och det vi ännu icke hunnit fatta (Stockholm, 1761), 17f.

of the darkness by which it is confined."^[43] The awareness of this truth is the other side of the belief in progress.

The Broken Circle

The success of natural history was overwhelming. With well-founded enthusiasm, Sir James Edward Smith in 1788 pushed to inaugurate a new society entirely devoted to this study, which came to life as the Linnæan Society of London. He wrote: "He who determines with certainty a single species of the minutest moss or meanest insect, adds so far to the genral stock of human knowledge, which is more than can be said of many a celebrated name."^[44] Smith had good reasons for thinking that his initiative would be well received, since more and more scholars worked in naming and surveying the living world. Linnæan natural history had conquered rival systems and spread into other areas as well. A common, international scientific language thus developed. Internationalism in botany was promoted further by trade in seeds and dried specimens and by the travels of natural historians. Traveling scientists, Linnæan apostles, Blumenbachian headhunters, the Cook company, explorers, adventurers, artists, collectors, all brought home a rich harvest from the field.

Natural history became interesting to the general public also as a part of a new aesthetic appreciation of nature. The growth of gardens and museums demonstrated the institutional strength of natural history. Curators naturally wanted to increase the size of their holdings. Next to salaries, the botanical garden and the library made heaviest demands on university budgets.^[45] Visits to famous gardens were

[43] Joseph Priestley, Experiments and observations I–III (Birmingham, 1790), xviii–xix.

[44] J.E. Smith, "Introductory discourse on the rise and progress of natural history," Linnæan Society of London, Transactions, 1 (1788), 1–55. Cf. Roy Porter, "The new taste for nature in the eighteenth century," The Linnoean, 4:1 (1988), 14–30; David E. Allen, The naturalist in Britain: A social history (London: A. Lane, 1976); Blanche Henrey, British botanical and horticultural literature before 1800 , 3 vols. (London and New York: Oxford University Press, 1975).

[45] See William T. Stearn, "Botanical gardens and botanical literature in the eighteenth century," Catalogue of botanical books in the collection of Rachel McMasters Hunt, 2 (Pittsburgh: Hunt Botanical Library, 1961), xlii–cxl.

mandatory for the traveler. At the end of the 18th century, Kew Garden had grown to an important promoter of the new tastes in England. To Kew and to the President of the Royal Society, Joseph Banks, came endless material from the colonies.^[46] Museums, no longer chambers of curiosities but institutions serving the scientific public, were entering the modern era. In France the Jardin du Roi was reorganized after the Revolution into the Muséum d'Histoire Naturelle according to a modified Linnæan plan.^[47]

Among the modifications was abandonment of the hope of a complete inventory of nature. Rather than showing the full divine order, the naturalist collectors wanted to outdo competitors in the size of their herbaria. The competitive element in collecting became increasingly obvious, but it was a race without a finish line. When Carl Peter Thunberg, successor to Linnaeus at Uppsala, had his Botanicum built around 1800, his architect provided herbarium space for only 15,000 specimens. Soon the windows in the beautiful main hall would be blocked with the cases of specimens that marked Thunberg's proficiency in the collecting game. In writing he devoted himself to mere description of small units and did not try to put together the big jigsaw puzzle. Thunberg's admirable industry is obvious from his series of dissertations on Nova plantarum genera (fifteen parts) and his Museum naturalium academiae upsaliensis (twenty-nine parts including appendices). His colleague, the entomologist Schönherr, wrote sixteen volumes totaling 5,000 pages on the insect-group cucurlionides . The dream for completeness survived only in completeness in detail. Its form could be labeled "descriptionism," a pure registration of facts.^[48]

[46] Lucile H. Brockway, Science and colonial expansion. The role of the British Royal Botanic Gardens (New York: Academic Press, 1979).

[47] Friedrich Klemm, Geschichte der naturwissenschaftlichen und technischen Museen , Deutsches Museum, Abhandlungen und Berichte, 41:2 (Munich: VDI-Verlag, 1973); Yngve Löwegren, Naturaliekabinett i Sverige under 1700-talet (Uppsala: Almqvist & Wiksell, 1932).

[48] For descriptionism, see J.L. Heilbron, "Fin-de-siècle physics," in C.G. Bernhard et al., eds., Science, technology and society in the time of Alfred Nobel (Oxford: Pergamon Press, 1982), 51–73.

In the early 19th century, probably only Robert Brown could handle the whole of botany. The last person able to treat all of nature was Alexander von Humboldt, who discovered several hundred plant species along the slopes of Chimborazzo in a few months (1800).^[49] The mass of little details struck some people as ridiculous. The philosopher Lichtenberg predicted the advent of "a Linnaeus of sand."^[50] Coleridge complained that despite all the work by the botanists there was "little more than an enormous nomenclature, a huge catalogue, bien arrangé , yearly and monthly augmented in various editions, each with its own scheme of technical memory and its own conveniences of references!"^[51]

The new situation called forth a variety of means of publication: a growing number of sumptuous books for the connoisseur, textbooks for the tyros, handbooks for the collectors, journals for specialists. It also produced a number of bibliographies by Haller, by Boehmer, by

[49] Alexander von Humboldt, Aus meinem Leben (Munich: Beck, 1987), 170ff., letter to Wildenow, February 21, 1801: he was now completely convinced "that we do not know more than three-fifths of the plant species." According to J.C. Loudon, the total number of vegetable species known in 1820 was 44,000, of which 38,000 had been described. "It is now (1829) believed that there may be from 100,000 to 200,000 species of plants. Such is the progress of discovery and of ideas," he added proudly. At the end of the 19th century, M.A.J. Möbius counted 415,600 species so far described, which should be compared to the 4,162 of Systema naturae (1758). Compare the growth of knowledge in an unusually well researched animal group: in 1758, 564 species of birds were known (Systema naturae , 10th ed.); in 1760, 1,500 (Brisson, Ornithologia ); in 1790, 2,951 (Latham, Index ornithologicus ); in 1812, 3,779 (Illiger, Tabellarische übersicht ); in 1841, 6000 (Gray, British Museum Catalogue ); and in 1909, 18,939 species (Sharpe, Hand-list of the genera and species of birds ); statistics from Erwin Stresemann, Die Entwicklung der Ornithologie (Berlin: F.W. Peters, 1951), 271. The Natural History Museum of Sweden today holds at least 15,000,000 specimens, and in 1980 the British Museum's entomological department alone housed 22,500,000. But according to a recent estimate, there might be 30,000,000 to 40,000,000 species of insects in the world, a multitude nobody can survey; see E.O. Wilson, Science, 13 December 1985. The question of nature's multitude has become an issue in the debate over conservation. Cf. S.J. Gould: "I'm just very confused by the whole debate. How can you be confident about an issue when the base level datum, which is the number of species out there that are threatened, is so unknown that estimates are ranging from two million to 30 or 40 million?" (interview in Dialogue , 1987:4, 16f.). For more recent estimates, see Biodiversity , 29 Feb 1988.

[50] Dietrich von Engelhardt, Historisches Bewusstsein in der Naturwissenschaften: Von der Aufklärung bis zum Positivismus (Munich: Alber, 1979), 79.

[51] Coleridge, "On the science of method," 15. Quoted in Collison, Encyclopedias , 261.

Jonas Dryander (on Bank's library), by Joseph Reuss, and so on. A new genre arose, the natural-history dictionary . With its alphabetical arrangement, it aped the encyclopedias: facts, in the Lockean sense, would speak for themselves. Considering their number, these dictionaries must have meant good business for the publishers; considering the size of some of them, they did have something to summarize. They are a proof of the success and the failure of 18th-century natural history.

The compilers of dictionaries had two banks to rob: Systema naturae and Buffon's Histoire naturelle , changed into smaller coin and arranged alphabetically. The reader got Linnaeus' exactness and Buffon's fine writing, both science and literature, in such extravagant works as Houttyun's Natuurkyke historie of uitvoerige beschryving der dieren, planten en mineralen , published in thirty-seven volumes (1761–85), and Valmont de Bomare's Dictionaire raisoné universel d'histoire naturelle (1760– ), in fifteen volumes, at least five editions, and a Danish translation (Den almindelige naturhistorie i form af et dictionaire (1767– ). There was also Friedrich Heinrich Martini's Allgemeine Geschichte der Natur in alfabetischer Ordnung (1774– ), which built on Bomare's Dictionaire and invited its readers to participate in making a new edition by filling out pages left blank for the purpose. The new edition would not be complete, of course; in natural history, Martini said, "complete is a harmonious sound without meaning." There were still more dictionaries: the anonymous Manuel du naturaliste (Paris, 1770); W.F. Martyn's A new dictionary of natural history ; Philip Miller's very handsome The gardener's and botanist's dictionary (1731, 8th edition 1768); and Lamarck's botanical chunk of the Encyclopédie méthodique . A somewhat earlier, similar trend has been noted in geography.^[52]

Both Linnaeus and Adanson had considered the possibility of making dictionaries. Through his patron Carl Gustav Tessin, Linnaeus had the help of a copyist to compile a Dictionnaire portatif d'histoire

[52] Numa Broc, La géographie des philosophes géographes et voyageurs français au XVIIIe siècle (Lille: Université de Lille III, 1972), 347ff.

naturelle . He began in 1757, but abandoned the project two or three years later. It fell victim to his fear that nothing can be omitted. Nothing, in any event, is left of the manuscript.^[53] In a Memorial printed in 1775, Adanson summarized what he had accomplished so far—the description of 300 species of mammals, 2,000 of birds, and so on, in all some 17,000 animals, 10,000 plants, and 8,000 to 10,000 minerals. He proposed grand and encyclopedic ventures, a new nomenclature, a universal language, a plan to cover all natural history in three "orbes," the first to contain 40,000 species. Nothing, however, came of these plans; and to cope with economic realities he had to work in the dictionary business. To the Supplément à l'Encyclopédie Adanson contributed about 450 articles, and among his huge piles of manuscripts there is much material intended for alphabetical publication.^[54] In their unsuccessful way both Adanson and Linnaeus tried to balance two interests: scientific order and communicable information.

There were other strategies to make natural history scientifically meaningful. Georg Forster returning from the Cook expedition wanted to combine Linnæan formalism and Buffon's individualism, as in his famous monograph on the breadfruit tree.^[55] Robinet preferred to concentrate not on the species level but on the type.^[56] That was also the way chosen by the idealistic morphologists, by Goethe, Etienne Geoffroy Saint-Hilaire, and Sir Richard Owen, and in Sweden by the mycologist Elias Magnus Fries and the algologist Agardh. Or one could adjust the size of taxonomic groups to make them easier to handle. That seems to have been the reason why Alphonse-Laurent de Jussieu recognized one hundred families of plants, none of which had more than one hundred genera.^[57] Then

[53] Linnaeus, Svenska arbeten , ed. Evald Ährling, 2 vols. (Stockholm, 1878–80) 1 , 20, 25, 26, 33, 45.

[54] See Adanson. The bicentennial , 64–74; also "Plan & tableau de mes ouvrages," in François Rozier, Observations sur la physique, 5 (Paris, 1775), 257–74.

[55] Cf. Ludwig Uhlig, Georg Forster. Einheit und Mannigfaltigkeit in seiner geistlichen Welt (Tübingen: M. Niemeyer, 1965), 45–55.

[56] On Robinet, see Lovejoy, The great chain of being , chap. 9.

[57] Cf. Frans A. Stafleu, Linnoeus and the Linnoeans (Utrecht: A. Oosthoek, 1971), 325–32.

there was Humboldtian science, which took not the species or genus as subject of study but the plant community as such.^[58]

The widening scope of the natural history project split it into such specialties as ornithology, entomology, and mycology.^[59] The new public for natural history, professors as well as amateurs, wanted information to suit diversified tastes. Thus, as a result of the widening fragmentation of the subject and the dissolution of the chain of being, a new science was invented. "Biology" was inaugurated in the very year 1800 by Jean Baptiste Lamarck, a critic of the concept of the great chain but also one of the most prominent pursuers of the natural history project.

Finally, we must note a change of metaphors. Both natural history and encyclopedism had experienced the increase of quantity , of boundless, unmeasurable information. The encyclopedic enterprise, aiming at order, totality, and coherence, had exchanged the esprit systématique for the esprit de système . In natural history, epistemological criticism and awareness of nature's richness had made the great chain of being succumb to its own weight. The metaphors of "chain" and "scale," both very popular during the 18th century, gave way to metaphors less apt for classification, such as "map" or "net," used by, among others, Linnaeus, Haller, and Hermann.^[60] The geographical imagery recurs in Adanson's "orbe." In a similar manner, d'Alembert used the older metaphors "circle of knowledge" and "tree" in elucidating the concept of encyclopedia, while Diderot preferred "growing city" and "machine." The critics (Kant, Hegel, Törneros) spoke of the modern encyclopedia as an "aggregate" or a "grocery store." There is a clear progression from symbols appropriate to a traditional classification to symbols suited for an open-ended collection. The systematic "encyclopedia" in the old sense of "whole circle of knowledge" was breaking up. This broken circle is one aspect of the

[58] Malcolm Nicolson, "Alexander von Humboldt, Humboldtian science and the origin of the study of vegetation," History of science, 25 (1987), 167–94.

[59] On specialization in this period, see Paul Farber, The emergence of ornithology as a scientific discipline (Dordrecht: D. Reidel, 1982), chaps. 7–8.

[60] See P.F. Stevens, "Metaphors and typology in the development of botanical systematics, 1690–1960, or the art of putting new wine in old bottles," Taxon, 33:2 (1984), 174ff.

critical work of the Enlightenment. It might be possible to argue that such a shift reflects a general development during the second half of the century from a "geometrical" to an "arithmetical" mentality, when systems and stable structures mattered less than quick, irregular information.

3
Systematics and the Geometrical Spirit

By John E. Lesch

During the latter 18th century European thinkers embraced a systematic model of order with an enthusiasm and conviction unprecedented before and unmatched since. Systematics—the classification of objects into groups according to degrees of identity and difference, and rationalized description and nomenclature—largely constituted the scientific study of the three kingdoms of nature: animal, vegetable and mineral. Drawing upon a century and a half of groping and hesitant effort by naturalists, Linnæus had succeeded in standardizing names and the process of naming, clarifying and simplifying the criteria of classification, and including the known objects of each kingdom in a simple, coherent, and comprehensive arrangement. Systematics dominated the study of the three kingdoms in the latter 18th century, to the disadvantage of anatomical, physiological, and microscopical approaches. Although most obviously successful in natural history, the systematic model may be found in many other domains. Late Enlightenment thinkers classified, or sought standards of description and naming, for objects as diverse as chemicals, diseases, the vital properties or anatomical elements of organisms, algebraic curves and surfaces, machines, and medicinal drugs. Whether we view these activities as the result of a diffusion of the model from one or a few sources—most probably natural history—or as the synchronous expressions of an underlying disposition, the systematic model formed a major modality of late Enlightenment thought.

The chapter begins by identifying the fundamental characteristics of the model by examination of one of its earliest and most prestigious exemplars, systematic botany, and determining in what sense the model participated in a more general geometrical spirit. It then

surveys the model's manifestations in other areas of thought, emphasizing mineralogy, chemistry, and medicine, and ends by suggesting that the success of the systematic model, and its decline in the early 19th century, must be understood in relation to its coherence with other elements of late Enlightenment culture.

The Systematic Model

Systematic botany emerged as a fully developed science in the first half of the 18th century, as the culmination of a gradual development of concepts and methods over the preceding two hundred years. The stimulus of Renaissance humanism and naturalism in art, the growing popularity of natural history as a leisure pastime, and increasing exploration of the various habitats of European flora as well as the findings of European explorers in Asia, Africa, and America brought rapid increases in the numbers of known plants. A six-to-tenfold increase can be recorded between 1550 and 1623, when 6,000 species were listed in a leading textbook. By 1690, the number had more than tripled again, rising to 19,000.^[1]

From around 1600 problems of botanical nomenclature and classification became acute. Writers on botany recognized that creation of a standardized, uniform, and accurate system of naming, describing, and grouping plants was fundamental to the construction of a science of botany. Until such a system existed, the rapidly expanding knowledge of plants would yield more embarrassment than glory. By the time that Linnæus began his scientific career in the 1730s, many of the materials and methods of systematic botany were already in existence. It was only through Linnæus' work, however, that an authoritative system of nearly universal appeal emerged.^[2] In Linnæus' Systema naturae (1735–67, thirteen editions), Critica botanica (1737), Philosophia botanica (1751), Species plantarum (1753), and

[1] A.G. Morton, History of botanical science (London and New York: Academic Press, 1981), 115–286. On numbers of plant species, see also Gunnar Broberg, chap. 2 in this volume.

[2] W.T. Stearn, "Introduction" In Carl Linnæus, Species plantarum. A facsimile of the first edition 1753 , 2 vols. (London: The Ray Society, 1957), 1 , 1–176, esp. 3.

other writings, botanists were at last in possession of a comprehensive, rationalized language upon which to found their science.^[3]

The result was the relatively sudden appearance, around the middle of the 18th century, of a dogmatic confidence that the correct approach to botany had been found. Although particular points of Linnæus' classificatory schemes were questioned or modified, his methods of nomenclature and description had been generally adopted by botanists by the time of his death in 1778. Linnæus' work not only consolidated earlier developments in systematic botany, it also defined its future tasks. The search for new species and genera, their naming and systematic placement, became the main aim of botany, to the relative neglect of plant anatomy and physiology.

Linnæus' botany was a project of rationalization, an effort to create a set of concepts and procedures that would bring uniformity, consistency, and coherence to the representation of a clearly defined domain of natural objects. "Minerals grow, plants grow and live, animals grow, live, and have feeling," wrote Linnæus in the Systema naturae , thus marking off in epigrammatic style the three kingdoms to be organized.^[4] The essential tasks of the organizing system were to describe, to name, and to classify every object within its kingdom by uniform and consistent principles. In the Systema naturae Linnæus wrote that "the first step in wisdom is to know the things themselves; this notion consists in having a true idea of the objects; objects are distinguished and known by classifying them methodically and giving them names. Therefore, classification and name-giving will be the foundation of our science."^[5]

[3] Frans A. Stafleu, Taxonomic literature: A selective guide to botanical publications with dates, commentaries, and types (Utrecht: International Bureau for Plant Taxonomy and Nomenclature, 1967), 275–90; William T. Stearn, "Linnæan classification, nomenclature, and method," in Wilfrid Blunt, ed., The compleat naturalist: A life of Linnæus (New York: Viking Press, 1971), 242–49; Gunnar Eriksson, "Linnæus the botanist," in Tore Frängsmyr, ed., Linnæus: The man and his work (Berkeley: University of California Press, 1983), 63–109.

[4] Carolus Linnæus, Systema naturae 1735. Facsimile of the first edition , ed. and transl. M.S.J. Engel-Ledeboer and H. Engel (Nieuwkoop, Holland: B. de Graaf, 1964), 19 (quoted); Julius Sachs, History of botany 1530–1860 (Oxford: Clarendon Press, 1890), 7–9; Stearn, "Introduction," 3.

[5] Linnæus, Systema naturae , 19, 22–4. In practice Linnæus sometimes allowed his sense of affinities to overcome the rigid application of his criteria. See Stearn, "Linnæan classification," 244. On consistency as a criterion of systems, see Michel Adanson, Familles des plantes , 2 vols. (Paris: Vincent, 1763), 1 , xli. Daudin contrasts Linnæus' truly systematic approach, in which the number of categories is universally and necessarily limited to five (class, order, genus, species, variety), with "a simple 'synopsis,' in which the number of successive dichotomies vary at will from one section to another," Henri Daudin, De Linné à Jussieu: Méthodes de classification et idée de série en botanique et en zoologie (Paris: Librairie Felix Alcan, 1926), 38.

In the Critica botanica and Philosophia botanica , Linnæus laid down in aphoristic form detailed rules for describing, naming, and classifying plants. His binomial nomenclature for designating genus and species placed the plant within a logically integrated system. Binomials had been used in a haphazard way before Linnæus to define more or less isolated groups, but in the Linnæan system they became instruments of a rationalizing project to impose unity, consistency, and logical order on the whole field of botany.

Also central to Linnæus' botanical work was his sexual system of classification, the fundamental features of which were abstraction, numeration, and artificiality. Abstraction, because Linnæus proceeded by setting aside as irrelevant all but a few select qualities of the plant. The essence of plants, Linnæus said, consists in sexual reproduction or fructification. The essence of fructification consists in the flower and fruit, and the essence of the flower consists in the stamen and pistil. The essence of the stamen consists in anthers, the essence of the pistil consists in the stigma. Thus did Linnæus justify the narrowing of classificatory critieria to a part of a part of the plant. As W.T. Stearn and James L. Larson have remarked, Linnæus' thinking was informed by Aristotelian logic, and Linnæus drew an analogy between logical and natural forms. Yet it is founded also on a close study of particulars. Linnæus went well beyond his predecessors in distinguishing and naming the organs of fructification.^[6]

Having distilled the essence of the plant by abstraction, Linnæus classified it by numeration. The sexual system, in Stearn's words, is

[6] Linnæus, Systema naturae , 22–4; J.L. Larson, Reason and experience: The representation of natural order in the work of Carl von Linné (Berkeley: University of California Press, 1971), 2–3, 149; Stearn, "Introduction," 2–3. See also V.H. Heywood, "Linnæus—the conflict between science and scholasticism," in John Weinstock, ed., Contemporary perspectives on Linnæus (New York: University Press of America, 1985), 1–15.

"a basically simple but ingenious arithmetical system, whereby the genera are grouped into twenty-four classes according to the number of stamens (together with their relative lengths, their distinctness or fusion, their occurrence in the same flower as the pistil or their separation in unisexual flowers, or their apparent absence), while division into orders within each class is determined by number of pistils"^[7] (fig. 3.1). Such a system gives a privileged place to the numerical or spatial qualities of its objects, and to the visual sense. In the Systema naturae Linnæus refers to his science as one of "describing and picturing," and defines a naturalist as one who distinguishes and names the parts of natural bodies by sight.^[8]

Abstraction and numeration gave the sexual system a clarity and simplicity that translated into ease of use and certainty of identification. These advantages came at a price, however, namely the divergence that opened up between the classifications so constituted and those based on a less sharply defined but more intuitively satisfying grouping of the vegetable kingdom that resulted from simultaneous consideration of multiple characteristics. Julius von Sachs argued that the major aims of systematic botany from the late 16th century to Linnæus were to arrive at a natural grouping of plants and to identify the groups by a few easily recognizable marks. Linnæus was, in Sachs' view, the first to recognize that these two aims were incompatible. Linnæus sketched the elements of a natural system—an outline that became the basis of later attempts by others—but devoted his major effort to a classification, based on the sexual system, that was avowedly artificial. Even his use of the parts of the flower, justified by the flower's functional importance, contained an irony, since just those aspects of the parts used as criteria—number and connection—are functionally irrelevant.^[9]

Paying the price of artificiality proved a good investment for systematic botany. In the Systema naturae Linnæus compared tables of

[7] Stearn, "Introduction," 22–6.

[8] Linnæus, Systema naturae , 19.

[9] Linnæus, Systema naturae , 22–4; Stearn, "Introduction," 24–6; Sachs, History of botany , 7–9, 82–3. Linnæus considered his genera to be less artificial or conventional than his classes or orders. Cf. Daudin, De Linné à Jussieu , 34–48.

classification to maps. They were like maps in abstracting from a complex reality, in representing degrees of proximity and distance of a sort, and, above all, in their utility. The sexual system's clarity, simplicity, and ease of use opened up botany to the contributions of amateurs. The very step that constituted systematic botany as a science made it more, not less, accessible to popular participation. In this case, at least, it appears that the simplification effected by a successful effort of rationalization facilitated a real, although subordinate, role for the nonexpert.^[10]

In all of this the formal qualities of Linnæus' science are evident. Linnæus' formalism is expressed in his insistence on explicit rules, especially in the Critica botanica and Philosophia botanica , and their consistent application in the systematic works. It is found in the analogy of logical and natural forms that is implicit in the very idea of a system of nature and explicit in the parallel Linnæus drew between the hierarchies of logical and systematic categories. It is embodied in the a priori habit of mind that led Linnæus to embrace an artificial system placing clarity of concept over empirical intuition, and that may have led him to the sexual system in the first place. It is, finally, most obvious in his presentation, which is methodical, concise, impersonal, and—to some—arid. The formality of the Linnæan system was facilitated and reinforced by its atemporality. Time did not appear in the Linnæan scheme because within it species were constant, while each natural group had as its basis a common type, which, like a Platonic form, was beyond the reach of temporal change.^[11]

Linnæus' system was universal by intention and also in effect. In ways not yet systematically studied, botanists in the 18th century

[10] Linnæus, Systema naturae , 19; Stearn, "Introduction," 3; Blunt, The compleat naturalist , 183–92; and Stearn, "Linnæan classification," 244

[11] Linnæus, Systema naturae , 18, 22; Sachs, History of botany , 7–9; Stearn, "Introduction," 2–3, 17, 24–26; Larson, Reason and experience , 149–50. The epistemological issues raised by the analogy of logical and natural categories, and by the problematic status of systematics in relation to mathematical physics, were taken up by Kant in the Critique of judgment . See Ernst Cassirer, "Das Problem der Klassifikation und der Systematik der Naturformen" in Cassirer, Das Erkenntnis problem in der Philosophie und Wissenschaft der neueren Zeit von Hegels Tod bis zur Gegenwart (1832–1932), 4 (Stuttgart: W. Kohlhammer, 1957), 127–44.

formed an international community, corresponding, exchanging specimens and visits, and struggling toward a common scientific language. Publishing in Latin, and developing his system through an extensive network of international correspondents, Linnæus achieved widespread acceptance. By his death in 1778, the binomial system of nomenclature was universal and the sexual system in general use.^[12]

Related to the universalism of Linnæus' system was its ease of generalization. It was readily—almost promiscuously—transferable from one domain of objects to another. Nowhere is this better illustrated than in Linnæus himself, whom Sachs rightly compared to a "classifying, coordinating, and subordinating machine." Besides plants, he provided systematic arrangements for animals, minerals, and diseases. In the Bibliotheca botanica (1736) he classified botanists, in the process nicely revealing the relative value and place he assigned to the various components of the science (fig. 3.2).^[13]

The universality of these qualities of the systematic model may be seen in counterpoint in the work of one of Linnæus' major critics, the French botanist Michel Adanson. Confronted for the first time by a tropical flora during his six-year service in Senegal with the Compagnie des Indes, Adanson brought back to France a conviction of the inadequacy of the Linnean and every other system. In place of "systems," Linnæan or otherwise, which based classification on one or a few parts of the plant defined at the outset, Adanson proposed the "natural method." The botanist was first to consider "the ensemble of all the parts of plants," including roots, twigs, and fruits as well as flowers, insofar as these could be studied in their number, figure, situation, relative proportion, and symmetry. Affinities were to be determined by subsets of common features arrived at empirically and open to revision by new experience. In his Familles des plantes (1763), Adanson elaborated the principles of the natural method and applied it to the formation of fifty-eight families of plants.^[14]

[12] Stearn, "Introduction," 2–3.

[13] Sachs, History of botany , 89–91; Sten Lindroth, "The two faces of Linnæus," in T. Frängsmyr, ed., Linnæus , 1–62 (22–4); Linnæus, Bibliotheca botanica (Amsterdam, 1736).

[14] Michael Adanson, Familles des plantes, 1 , esp. clv. On Adanson, see Morton, History of botanical science , 301–14; Frans A. Stafleu, "Adanson and the 'Familles des plantes,'" in Adanson: The bicentennial of Michel Adanson's 'Familles des plantes' , 2 vols. (Pittsburgh: The Hunt Botanical Library, Carnegie Institute of Technology, 1963), 1 , 123–264, and Linnæus and the Linnoeans: The spreading of their ideas in systematic botany, 1735–1789 (Utrecht: Oosthoek, 1971), 310–39. An instructive comparison of "system" and "method" is given by Michel Foucault, The order of things: An archeology of the human sciences (New York: Vintage Press, 1973; translation of Les mots et les choses , 1966), 128–45.

Adanson gave the first full theoretical statement and justification of the method by which a natural arrangement of plants could be constructed. Despite his thoroughness, however, Adanson was not successful in his aim to displace the Linnæan system. That achievement fell to his younger contemporary and associate Antoine-Laurent de Jussieu, who benefited not only from the teachings of his uncle Bernard and of Adanson, but also from detailed study of the many new plants yielded by voyages of exploration, and from his adoption of the popular Linnean binomials. It was largely through A.-L. de Jussieu's Genera plantarum (1789) and other writings that the natural method gained ascendency in systematic botany in the early 19th century.^[15]

Although the differences between natural and artificial systems loomed large to their protagonists, on most points the two approaches shared the general features of the systematic model. Adanson's project was one of rationalization that stressed comprehensiveness, internal consistency, and disciplined use of language. Adanson insisted that his method was comprehensive—or, as he put it, "universal"—in that he strove to include all plants, tropical as well as temperate and glacial. Consistency, too, was to be sought in steady adherence to the more empirical rules of the natural method. Even Adanson's rejection of binomial nomenclature resulted from his commitment to principles of the priority and stability of names, in opposition to the precedence given by Linnæus to their significance.^[16]

[15] Linnæus' attempt at a natural arrangement—the Methodi naturalis fragmenta —first appeared as part of his Classes plantarum (1738). See Morton, History of botanical science , 301–14; Stafleu, Linnæus , 310–39; and Stearn, "Linnæan classification," 244. Stafleu notes common features in the views of Linnæus and advocates of the natural method. See "Adanson and the 'Familles des plantes,'" esp. 155, 166, 167, 229, 236.

[16] Adanson, Familles des plantes, 1 , clii-cliii, cxci-cxcii. On Adanson and nomenclature, see Stafleu, Linnoeus , 311; and "Adanson and the 'Familles des plantes,'" 187.

Adanson, like Linnæus, abstracted from the totality of the plant's features criteria for defining degrees of identity and difference. The two botanists differed not on the goal of abstraction but on the tactics used to obtain it. Where Linnæus' procedure was a priori and essentialist, at least at the level of classes and orders, Adanson's was inductive or "experimental," first looking at all features, then narrowing to a subset. The two naturalists also converged in their emphasis on numerically or spatially definable traits and the associated precedence of the visual sense. Here Adanson was, if anything, more explicit than Linnæus, remarking that botany "distinguishes plants only by their relations of quantity, whether numerical or discrete, or continuous, which gives us the extent of their surface or their size, their figure, their solidity."^[17]

On one point—simplicity, or ease of mastery and use—Linnæus' system had a seeming advantage. Adanson conceded as much and also that artificial systems had increased the popularity of botany and the numbers of botanical publications. But he complained that the result was merely superficiality, the spoiling of the most penetrating minds, and the production of quantities of catalogues on Linnæan principles. Most important, Adanson regarded artificial systems as incapable of bringing a permanent end to the confusion and uncertainty of botany. Certainty, stability—in short, a true system based on true principles—would come to botany only through the slower, more empirical, but ultimately more reliable procedures of the natural method.^[18]

In its insistence on explicit rules, its positing of a hierarchy of systematic categories implicitly analogous to logical ones, and its methodical, precise, and impersonal form of presentation, Adanson's natural method can be described as formalistic. The categories of Adanson's method, like those of Linnæus' system, are untouched by

[17] Morton, History of botanical science , 303, 306–8; Adanson, Familles des plantes, 1 , cc–cci (quote).

[18] Adanson, Familles des plantes, 1 , xli–xlii, clii–cliv, cxci–cxcv. Adanson sounded an Enlightenment theme when he appealed to nature as a source of truth in opposition to "the old prejudice in favor of systems and the ideas on which they are based." Ibid., clvii.

time or change.^[19] Where Adanson's formalism departed from that of Linnæus was in his clear break with essentialism and with Linnæus' a priori habits of mind. Like Linnæus, Adanson intended his method to be universally adopted. But the success of the Linnæan system, Adanson's rejection of binomials, and his lack of an institutional teaching position doomed the Familles des plantes to an oblivion from which it had to be rescued by Henri Baillon in the following century. Only through its adoption and extension by A.-L. de Jussieu did Adanson's method achieve a delayed acceptance and play a role in the formation of modern systematics.^[20]

A collaborator of Diderot and d'Alembert, described by Stafleu as plus encyclopédiste que les encyclopédistes , Adanson conceived a vast work that would extend the natural method to other parts of natural history, physics, chemistry, ethnology, philology, and related subjects. Although never brought to fruition, the project expresses Adanson's conviction of the compatibility of his method with the systematic model.^[21]

In one respect, at least, Adanson's natural method had an advantage over artificial systems that added a significant quality to the systematic model. Having identified the general features of a family, the Adansonian botanist could predict that other members of the group as yet unknown would have numbers of features in common. No such predictive quality could be relied upon for artificial systems. Besides its value for systematics, predictiveness enhanced the utility of the method, particularly at a time when voyages of exploration were bringing new plants to Europe in ever greater numbers. For example, plants of medicinal value might be found among the newly discovered specimens belonging to families already known to include medically useful plants.^[22]

[19] Morton, History of botanical science , 309–11.

[20] Stafleu, Linnæus , 311, and "Adanson and the 'Familles des plantes,'" 126–7, 187.

[21] Stafleu, "Adanson and the 'Familles des plantes,'" 136, 197; Jean-Paul Nicolas, "Adanson, the Man," in Adanson: The bicentennial, 1 , 1–121, esp. 35–6, 65–78.

[22] Adanson, Familles des plantes, 1 , lxxiii–lxxx, cxcv–cxcvi; Morton, History of botanical science , 306; Stafleu, Linnoeus , 330; and "Adanson and the 'Familles des plantes,'" 161, 196. When, in the first decades of the 19th century, Paris pharmacists turned to the chemical analysis of medicinal plants, they incorporated the botanists' prediction into their research program. See John E. Lesch, Science and medicine in France: The emergence of experimental physiology 1790–1855 (Cambridge, Mass.: Harvard University Press, 1984), 125–44.

The Model and the Geometrical Spirit

The systematic model was one expression of the geometrical spirit of the late Enlightenment. In its most general sense the geometrical spirit may be identified with analysis, a term and concept placed by Ernst Cassirer at the center of Enlightenment thought. In its first meaning analysis is indeed mathematical—or "geometrical" in 18th-century usage—referring especially to algebra. Enlightenment thinkers, however, allowed the term a wider formulation that gave it nearly unlimited applicability. In this formulation, "analysis" refers to a double movement of analysis and synthesis by which the phenomena of a field are reduced to their elements, and then restructured into a true whole that can be known by reason because, in Cassirer's words, reason "can reproduce it in its totality and in the ordered sequence of its individual elements." As Cassirer remarks further, for the Enlightenment "to 'know' a manifold of experience is to place its component parts in such a relationship to one another that, starting from a given point, we can run through them according to a constant and general rule." For Michel Foucault, too, analysis represents a universal method of classical thought that includes but is not confined to its mathematical expression in algebra. Systematics, in this view, is made possible by analysis in the form of a system of signs, and is a nonmathematical expression of the quest for a mathesis or universal science of measurement and order.^[23] The kinship of the systematic model with mathematics is therefore not a question of derivation or a direct modeling of systematics on one or another field of mathematics, but of the sharing of a generalized method of analysis and of the qualities that make such a method possible.

The most obvious of these are abstraction and numeration. Just as the mathematical sciences confined their treatment of the physical

[23] Ernst Cassirer, The philosophy of the Enlightenment , transl. Fritz C.A. Koelln and James P. Pettegrove (Boston: Beacon Press, 1955; original German edition 1932), 13–6, 23–4; and Foucault, The order of things , 46–77.

world to its numerable or measurable qualities of extension and motion, so did Linnæan and Adansonian systematics reduce the plant to the number, form, connection, and spatial arrangement of its characters. The formal qualities of Linnæus' and Adanson's approaches—their insistence on explicit rules, their methodical, impersonal, and economical presentation, and, in the case of Linnæus, a priori thinking subordinating the empirical to the conceptual clarity of the artificial—all have clear analogues in mathematics, as do the certainty and simplicity each system offered its users.

Adanson grasped the connection clearly. Insisting that botany was a science not merely of names but also of facts, he added that "we even believe that we find in it an immediate relationship with geometry." This relationship consisted not only in the exclusive use of characters subject to number and measure but also in the botanist's ability to pose questions analogous to "the most sublime geometry" in difficulty and instructiveness. "Find the most sensible point that establishes the line of separation or of definition between the family of the Scabiosa and that of the honeysuckle," or "Find a known genus of plants (natural or artificial, it does not matter) which occupies an accurate middle point between the family of dogbane and that of borage." Properly constructed, such questions would yield conclusions on the possibilities "that would be as evident and as well-demonstrated as the truths of the best geometry." In this way, too, the botanist would be able to estimate how many families or genera were lacking between two distant families or genera whose intermediaries were unknown, "presumptions which, if they would not have all the precision of mathematics, nevertheless would yield large views, and would furnish new means of extending our knowledge in botany." While admitting that absolute perfection in a botanical system—which he equated with "the necessary exactitude, which characterizes mathematical perfection"—was not possible, he nevertheless credited the families determined by the natural method with bringing to botany all the certitude, stability, comprehensiveness, concision, ease of use, and utility of which it was capable.^[24]

[24] Adanson, Familles des plantes, 1, cxci–cxcii, cc–cci. Underlying Adanson's presumption of the existence of unknown intermediaries between known families and genera was his commitment to the idea of a progression that connects "in a continuous series the families that resemble one another the most, and in each family, the genera that have the most general relationships." Cf. Adanson, Familles des plantes, 1, clxxxviii; Stafleu, Linnoeus , 328; and "Adanson and the 'Familles des plantes,'" 194. On the idea of series in botany and zoology, see Daudin, De Linné à Jussieu , esp. 79–187.

Another who saw systematics as an extension of the mathematical way of thinking to the ordering of empirical objects was Johann Heinrich Lambert. Much of his life work was an effort to reshape science and philosophy in the image of mathematics and to assure for those fields of knowledge the exactness and certitude of their exemplar. Lambert treated the problem of order and its measure not in relation to natural history or any domain of particulars, but abstractly as a problem of knowledge in general.^[25] Mathematics, he pointed out, had been most successfully applied where the objects of knowledge could be construed as homogeneous entities, because only such entities could be added, subtracted, and related to one another as more and less. In its formation of generic names and the abstract ideas derived from them, language often lost sight of the homogeneities on which the names and ideas were originally based. The result was conceptual confusion and failure in communication. Where homogeneities could be defined, however, "mathematics shows us that. . .they present ideas that are simple, very knowable, and exempt from logomachy. And this is what is necessary for a clear and well-arranged system."^[26]

According to Lambert, the degree of order of a given arrangement may often be calculated as a proper fraction. In the simplest case, a linear succession of objects, each of which is assigned a rank or value, absolute order is rank order. The degree of disorder that results from displacement of one object from this absolute order is taken as the product of the number of places the object is displaced and the value

[25] Johann Heinrich Lambert, "Essai de taxéometrie, ou sur la mesure de l'ordre," Akademie der Wissenschaften, Berlin, Nouveau mémoires , 1770, 327–42 and 1773, 347–68. See Christoph J. Scriba, s.v. "Lambert, Johann Heinrich" Dictionary of scientific biography (DSB) , 7, 595–600; Colloque international et interdisciplinaire Jean-Henri Lambert (Paris: Editions Ophyrs, 1979); and Gereon Wolters, Basis und Deduktion: Studien zur Entstehung und Bedeutung der Theorie der axiomatischen Methode bei J.H. Lambert (1728–1777) (Berlin: Walter de Gruyter, 1980).

[26] Lambert, "Essai de taxéometrie," 327–9.

of the object displaced. Similar calculations of degrees of order may be carried out in the more complex case of systems of classification. Lambert gives the example of a well-arranged library in which the books are classified first according to the sciences, next according to their age, their format, their binding, and so on. If each book satisfies all conditions, the library will be absolutely well-arranged. Its order will then be unity. It cannot be greater, but can admit of fractions.^[27] Suppose that there are n books and that each book must satisfy three conditions, a,b,c . The product n(a + b + c) = 1. But suppose an arrangement in which all books satisfy a , while of the other two conditions m books satisfy b and c, p books satisfy only b , q books satisfy only c , and r books satisfy neither b nor c . Then the degree of order of this arrangement would be expressed as the fraction:

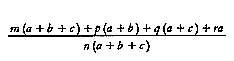
What such a calculation measures is the degree to which a given classificatory system conforms to a set of explicitly defined, consistent criteria. It does not touch the fit of the scheme with nature, and Lambert, who was no naturalist, did not discuss the specific problems of botany or any other particular field. Nevertheless, Lambert's conviction that systematics could be treated as an extension of mathematics, and his implicit commitment to the wide applicability of the systematic model, do indicate once more the confluence of that model and the late Enlightenment's ambition to establish a general science of order.

Considered in a wider perspective, mathematics and the systematic model may also be associated as instruments of a movement of rationalization that was pervasive in the late Enlightenment. This movement found literary expression in numerous encyclopedias and dictionaries, of which the Encyclopédie was only the most famous.^[28] It appeared in government in forms as diverse as attempts to monitor

[27] Ibid., 329–37.

[28] Stearn, "Introduction," 11–2.

and improve public health through statistics, formulation of the metric system, and the shaping of armies as tools of the absolutist state. It entered the empirical sciences as an effort to classify their objects and reform their nomenclatures. Often its actions, especially in the sciences, were driven by pedagogy, as professors sought to order their subjects for presentation to students. Everywhere rationalization harnessed the geometrical spirit that, in different ways, informed both mathematics and the systematic model.

The development of systematic botany and of the fields for which it came to serve as a model was conditioned by material and social factors that remain to be investigated in detail. By the mid-18th century botany had long since achieved its intellectual independence of medicine, although—as the case of Linnæus indicates—important institutional links were preserved. Exploration and empire now provided the richest opportunities and resources for botanists and zoologists. Like early Christians spreading their creed over Roman roads, 18th-century naturalists were moved by their own sort of zeal to the far-flung corners of European colonial and commercial empires, and brought or sent back the specimens that gave substance to the systematists' projects. Adanson's experience in Senegal is an excellent case in point. Mineralogy owed much to the increasing need for technical expertise in mining and metallurgy, and chemistry was stimulated by its ever-closer association with pharmacy and industry. Nosology, of course, was an integral part of medical theory. The stimulus afforded by the high popularity of natural history among the educated classes must not be overlooked. Linnæus' productive stay in Holland from 1735 to 1738 was largely supported by the patronage of a wealthy banker, George Clifford. The mineralogist, Jean Baptiste Louis Romé de l'Isle, too, long derived his sole financial support from wealthy patrons with amateur interests in natural history. Another mineralogist, René Just Haüy, was himself an amateur botanist. And the medical profession, historically sensitive to areas of science invested with prestige by the lay public, could not fail to be affected by the popular prestige accorded the natural history disciplines.^[29]

[29] Stearn, "Introduction," 8–10; Blunt, The compleat naturalist , 102–8, 116–8.

The need for rationalization was felt most acutely in fields untouched by the great synthesis of Newton and the continental mathematicians. The mathematicians had provided a new basis for sciences—including astronomy, optics, and mechanics—that had already acquired mathematical form. In other fields, for which the conceptual structure was less secure or coherent, the order of the day was the gradual establishment of foundations. For some of these, such as electricity and magnetism, the path led from discursive theorizing and experimental manipulation to mathematization.^[30] For others, including chemistry and medicine as well as natural history, the systematic model of order was decisive. Where electricity and magnetism had to deal with specialized physical phenomena, the latter fields had to contend with an ever increasing quantity of diverse specimens.^[31]

Mineralogy

The pervasiveness of the model's influence between 1760 and 1810 is well exemplified in mineralogy, chemistry, and medicine. Spurred by the practical needs of mining and metallurgy and the curiosity of naturalists, mineralogy was an active field in the latter 18th century. Linnæus included a scheme for the mineral kingdom in the Systema naturae . His example was decisive both in his implicit commitment to the existence of mineral species, and in his use of crystalline form as classificatory criterion. The formal parallel between crystalline forms and the sexual parts of plants was strengthened by the analogy he perceived between the chemical formation of crystals

[30] J.L. Heilbron, Electricity in the 17th and 18th centuries: A study of early modern physics (Berkeley: University of California Press, 1979).

[31] "If the multiplicity of objects to be described has been the true source of this useful method, and if it was on account of this multiplicity that Linnæus believed he had to imagine a new and short method to characterize these objects, should not all the natural sciences, in which the facts and observations multiply in such a way that they require the presentation of immense details, follow the same path and adopt the same descriptive system?" Antoine Fourcroy, s.v. "Caractères," Encyclopédie méthodique: Chimie, pharmacie et metallurgie , 6 vols. (Paris, 1786–1815), 2 (1792), 784–5.

and the reproduction of living things, an analogy that assured constancy of species in the mineral as in the plant or animal kingdoms. Linnæus distinguished each mineral genus by a basic geometrical figure, and the species within each genus by truncation of the edges or angles of the generic figure. In keeping with his general practice, he assigned each species a genus-species binomial.

Linnæus' system entirely subordinated physical and chemical properties of minerals to the geometrical form of the crystal. In part this may be attributed to the weakness of contemporary chemical analysis and to the absence of quantitative techniques for the measurement of physical properties like hardness. Far more determinative, however, was the compatibility of crystalline form with the requirements of Linnæus' systematic model. Just as the sexual system abstracted from the plant just those visible qualities that could be expressed in numbers or spatial relationships, so did crystalline form abstract from the mineral visible external characters that could be numerically or geometrically defined.^[32]

Linnæus' mineral scheme did not enjoy the success of the sexual system. Mauskopf has identified three distinct approaches to mineral classification in the last quarter of the 18th century, based on chemical analysis, groups of external characteristics, and crystal form. All three recognized the need to know chemical composition. Given the state of chemistry at the time, however, chemical criteria were very difficult to apply. The other two approaches looked for characteristics other than the chemical that would still express degrees of essential identities and differences.^[33]

In 1774 Abraham Werner, a professor of mineralogy at the mining school of Freiberg, published a work entitled On the external characters of minerals . Aiming to produce a practical handbook for the miner and naturalist, Werner made use of readily accessible mineral characteristics like color, shape, hardness, and texture. He did not

[32] John G. Burke, Origins of the science of crystals (Berkeley and Los Angeles: University of California Press, 1966), esp. 52–77; Seymour H. Mauskopf, "Crystals and compounds: Molecular structure and composition in 19th-century French science," American Philosophical Society, Transactions, 66:3 (1976), 7–20.

[33] Mauskopf, "Crystals," 14.

group his species in higher categories, but did restate the Linnæan concept of primary forms of crystals, and pointed out that certain forms were related and could be derived from one another by truncation.^[34]

More theoretical, and more directly in the Linnæan tradition, was the work of the French crystallographers Romé de l'Isle and Haüy. Both came to mineral classification by way of crystallography. In his Essai de cristallographie of 1772 and his revised and expanded Cristallographie of 1784, Romé de l'Isle attempted a comprehensive classification of crystals based on the theory that there were a limited number of primitive crystalline forms. In his theory, the diversity of forms observed in nature arose from variations on the primitive ones induced by different conditions of solution or by varying proportions of the constituent chemical principles. The Cristallographie incorporated steps toward a quantitative science of crystals, including use of the contact goniometer and statement of the fundamental law of constant interfacial angles.^[35]

Linnæus had not drawn a hard-and-fast line between the kingdoms of living things and minerals. He had therefore not felt a need to justify mineral taxonomy. As the line between organic and inorganic was more and more sharply drawn, however, the need for justification and explicit methodological discussion became inescapable. Prompted by an essay of Louis Daubenton that denied the existence of mineral species, Romé de l'Isle made explicit his commitment to their reality, distinctness, and fixity. In Des caractères extérieurs des mineraux (1784), he argued that invariable laws of chemical affinity assured the same fixity for mineral species that reproduction did for organic ones. In practice, however, he relied on more accessible external features—crystal form, hardness, density—that he presumed to be the direct expression of uniform chemical composition.^[36]

[34] Ibid.; Burke, Origins , 59–62.

[35] Mauskopf, "Crystals," 9–11; Burke, Origins , 62–7, 69–77; R. Hooykaas, s.v. "Romé de l'Isle," DSB, 11 , 520–4. See also R. Hooykaas, La naissance de la cristallographie en France au XVIIIe siècle (Paris: Palais de la Découverte, 1953).

[36] Mauskopf, "Crystals," 16–8; Burke, Origins , 71–7.

Haüy is said to have come to crystallography from botany, seeking a mineral analogue to botanical regularities of form. If so, the botanical inspiration did not immediately extend to questions of mineral taxonomy, for in the Essai d'une théorie sur la structure des cristaux of 1784 Haüy denied the relevance of crystal form to mineral classification. The Essai introduced the concept of the molécule constituente (later termed the molécule intégrante ), a theoretical entity understood as the smallest molecule of a crystal that displayed a characteristic chemical composition and geometrical form. In his emphasis on the geometry of the molécule intégrante and its relationship to the geometry of macroscopic crystals, and in his insistence on the agreement of theoretical and measured results, Haüy took a decisive step in the mathematization of crystallography and attracted the patronage of Laplace. He also provided an original basis for mineral taxonomy.^[37]

In a paper of 1793, Haüy defined the mineral species in chemical terms, remarking that just as in botany it is reproduction that assures uniformity in the species, so in mineralogy it is the nature and proportions of the combined chemical principles that guarantee specific identity. In this sense, Haüy argued, chemistry is well suited to accomplish one of the two main purposes of method, that is, classification. For the other purpose—the ready recognition and naming of bodies—chemistry is ill adapted, however, if only because chemical analysis often requires long and laborious procedures that use up all or part of the specimen. Seldom can species be grouped into genera by a single character that is easy to recognize. Thus classification in mineralogy does not compare favorably with that in botany, "where the characters, always drawn from the figure of the organs, that is to say, from a modification that is plainly visible (qui parle aux yeux ) follow a simple, uniform course, and have the merit of offering a picture in which a small number of colors suffice to give a rich and varied expression." In botany, unlike mineralogy, the same means serve the ends of both classification and recognition. A useful

[37] Mauskopf, "Crystals," 18–9; Burke, Origins , 108–13; R. Hooykaas, s.v. "Haüy, René Just," in DSB, 6 , 181–2; Roger Hahn, chap. 13 in this volume.

mineralogical method therefore involves much more groping than is the case in botany.^[38]

In Haüy's major work of the early 19th century, the molécule intégrante figures in the chemical composition and geometrical form that defined mineral species. The molécule intégrante was, however, a theoretical entity. In practice the results of crystallography and chemistry sometimes diverged. Bodies grouped together by crystallography might be separated by chemistry, and vice versa. Some of this dissonance might be accounted for, Haüy argued, by the imperfection of current chemical analysis or by impurities in the mineral samples. So far as species determination was concerned, however, crystal structure offered the more certain guide: "Only for geometry are all minerals pure." Crystal form, more accessible and less ambiguous than chemical composition, dominated Haüy's determination of species, while his genera, orders, and classes were decided by chemical composition^[39] (fig. 3.3).

The practical difficulties resulting from the use of both chemical and crystallographic criteria in mineral classification are reflected in Haüy's struggles with nomenclature. His ideal was a binomial based on the new chemistry by Lavoisier and his circle. The state of the art did not make the ideal possible. In practice, therefore, the unavoidable mix of chemical and crystallographical criteria blurred the clarity of Haüy's nomenclature, which remained only partially rationalized.^[40]

[38] René Just Haüy, "Mémoire sur les méthodes minerologiques," Annales de chimie, 18 (1793), 225–40, on 237 (quote).

[39] Haüy, Traité de mineralogie , 5 vols. (Paris: Conseil des Mines, 1801), and Tableau comparatif des résultats de la crystallographie et de l'analyse chimique relativement à la classification des mineraux (Paris: Courcier, 1809), i-xxxv, on xv. In the Tableau comparatif , Haüy once more showed that he had a close eye on the practice of botanists, calling crystals "the flowers of minerals," comparing crystalline structure to the organization of living things, and citing A.-L. de Jussieu as a model in the presentation of classificatory results. He also justified measures taken to enhance the unity and simplicity of his systematic methods by appeal to l'esprit géométrique. Tableau comparatif , xvii-xix, xxv. For a more detailed discussion of Haüy's double method of classification, see R. Hooykaas, "The species concept in 18th-century mineralogy," Archives internationales d'historire des sciences, 18 (1952), 45–55.

[40] R. Hooykaas, "Haüy," DSB , 181–2.

Chemistry

In mineralogy the two modalities of the geometrical spirit—systematics and mathematics—intersected at Haüy's theory of crystal structure. A similar convergence and intersection may be seen in chemistry, though with a difference. Whereas in mineralogy the point of contact between systematics and mathematics lay in criteria of classification, in chemistry it was most pronounced in the establishment of rationalized nomenclature. The chemists' reform of their system of naming was inspired by algebra, legitimized by philosophy, and modeled on botany.

By the third quarter of the 18th century, pressure was mounting for reforms in the language of chemistry. A growing list of substances, of which the newly isolated atmospheric gases formed only a part, raised the problem of how names should be formulated. Criticism of the dominant phlogiston theory highlighted the potential theoretical content of chemical names. The views of the philosopher Condillac, for whom a science was a well-made language based on the natural order of mental processes and on exact correspondences between words and things, were gaining increasing currency among French savants.

Only after Linnæan systematics became available as a model and was so perceived by chemists was substantial progress made. The initiative came from Linnæus' student, the professor of chemistry at the University of Uppsala, Torbern Bergman. Bergman was disturbed by the lack of system and order in chemical names. A name might be based on the appearance or properties of a substance, its place of discovery or occurrence, the name of its discoverer, or its alchemical association with the planets. As new substances became known to chemists, they were assigned names ad hoc. The resulting confusion and imprecision of language made it difficult for aspiring chemists to master their subject and for established chemists to communicate with colleagues. In the 1770s Bergman set out to formulate a binomial system that would do for chemistry what Linnæus had done for botany.^[41]

[41] Maurice P. Crosland, Historical studies in the language of chemistry (Cambridge, Mass.: Harvard University Press, 1962), 139–52; Douglas McKie, Antoine Lavoisier: Scientist, economist, social reformer (New York: Schuman, 1952), 263.

Bergman's project gained a positive reception from the French chemist Guyton de Morveau. In a paper of 1782, Guyton cited the rapid increase in the number of known substances in the preceding twenty years as a major motive for reform. Another motive came from theoretical changes in chemistry as a result of Lavoisier's studies of combustion and the overthrow of the phlogiston theory. In the 1780s Lavoisier's theory was accepted by major scientists, including the physicist Laplace and the chemists Berthollet, Guyton de Morveau, Antoine Fourcroy, and Joseph Black. With the ensuing controversies, the problem of nomenclature became still more acute, since the terminology embodied theoretical views.^[42]

In France, Lavoisier, Guyton de Morveau, Berthollet, and Fourcroy joined to suggest appropriate reforms. One of the central pieces of the resulting Méthode de nomenclature chimique , which appeared in 1787, was an article by Lavoisier explaining the principles on which the proposed reforms were based. Lavoisier's interest in precise language and nomenclature was based in part on his impression of the contrast between the systematic, logical exposition of mathematical physics and the confusion and disorder of chemistry. He had also been impressed with Condillac's writings. Citing Condillac, Lavoisier emphasized the need for control of chemical reasoning by consistent reference to observation and experiment, a requirement closely connected with the reform of nomenclature. In Lavoisier's view there was to be an exact correspondence between a fact, the idea of the fact, and the word used to express the idea.^[43]

Lavoisier and his collaborators tried to arrive at a list of simple substances, that is, of bodies they could not decompose by any existing means of chemical analysis. The total of these substances came to

[42] Crosland, Historical studies , 153–76.

[43] Guyton de Morveau et al., Méthode de nomenclature chimique (Paris, 1787), 1–25; Antoine-Laurent Lavoisier, Elements of chemistry, in a new systematic order, containing all the modern discoveries (New York: Dover, 1965), xiii-xxxvi; Crosland, Historical studies , 153–92. On Condillac, see Isabel Knight, The geometric spirit: The Abbé de Condillac and the French Enlightenment (New Haven: Yale University Press, 1968), and Robin Rider, chap. 4 in this volume.

fifty-five. Most already had well-known names, which the reformers decided to keep unless they gave rise to confusion. If so, or if the substance was new, a new name would be given, usually derived from Greek and expressing the substance's most general properties. An example was hydrogen, so called because it was one of the constituents of water. To deal with the great many bodies composed of two simple substances, it was necessary to establish a classification. Here the binomial nomenclature modeled on botany took effect. The acids, which Lavoisier thought of as composed of oxygen plus one other simple substance, are a good example. Sulfuric acid is the combination of sulfur with oxygen. The similar acid containing less oxygen was called sulfurous acid . The metallic calces, which Lavoisier had shown to be compounds of metals and oxygen, had the generic name oxide and specific names derived from the names of the metals. The reforming chemists listed the simple substances, and gave a classification of their compounds with examples, in an expansive tableau de la nomenclature chimique . The result was a revolution in the language of chemistry that made the chemical name of a substance a direct expression of its elementary composition.^[44]

Underlying Lavoisier's theory of acids was his prior commitment to the existence of a systematic order for chemicals analogous to those already established for the plant and animal kingdoms. Four-croy made this commitment explicit. Writing in the Encyclopédie méthodique , he praised the Linnæan method for establishing the characters by which natural objects are recognized and described, for expressing these characters in concise phrases in which words represent precise ideas, and for reducing the description (tableau ) of immense numbers of objects to a single comprehensive framework. Fourcroy recalled that when he began to teach chemistry his mind was full of the language and descriptions of Linnaeus, and at the same time weighed down with the immense quantity of chemical properties and experiments that he found in the existing literature. The reform of chemical nomenclature in which Fourcroy had

[44] Méthode de nomenclature chimique , 26–100 (table follows p. 100); Lavoisier, Elements , xxv–xxviii.

participated had been conceived and executed in a spirit "analogous to that which had directed Linnaeus," and "we therefore find in modern chemical nomenclature a course similar to that adopted in natural history." Chemical compounds could be arranged in classes, orders, genera, and kinds (sortes ) on the basis of their principal and common properties characterized simply and concisely. In the article "axiomes chimiques ," Fourcroy presented such a scheme, which included 34 genera of salts estimated to total some 240 species. Evidently prompted by Lavoisier's naming of oxygen, Fourcroy suggested that the three species making up the genus alkalis are all formed by combinations of nitrogen with other substances, and that nitrogen or azote should therefore be called alcaligène . Lavoisier and Fourcroy were soon proved wrong in their theories of acids and alkalis, but both theories testify to the strength of the impulse to establish clear generic categories for chemistry.^[45]

Medicine

If the role of the systematic model in chemistry was centered on the problem of nomenclature, its influence in medicine was most clearly perceptible in questions of definition, description, and classification of disease. The desire to bring order to a large and ill-integrated body of knowledge, disillusionment with the results of mechanistic or chemical physiology in practical therapeutics, and a need to overcome the opposite extreme of radical skepticism, were among the factors behind the development of nosology, as medical systematics came to be called.

[45] Encyclopédie méthodique, chimie, pharmacie, metallurgie, 2 , articles "Alkalis," "Axiomes chimiques," and "Caractères," on 20–9, 455–89, 784–5, resp. The formlessness that Fourcroy found in chemistry when he began to teach the subject in the 1770s had also been noted by J.H. Lambert, who pointed to chemistry textbooks as examples of "a very inferior degree of order" in the arrangement of the different parts of a science. Lambert, "Essai de taxéometrie," 337. The importance of generic categories in shaping chemical perception and research is discussed for a particular case in John E. Lesch, "Conceptual change in an empirical science: The discovery of the first alkaloids," Historical studies in the physical sciences, 11 (1981), 305–28.

The beginnings of the systematic model in medicine appear early in the writings of the English physician of the late 17th century, Thomas Sydenham. A friend of Locke and admirer of Francis Bacon, Sydenham called for the setting aside of hypotheses and philosophical systems in favor of "a natural description or history of all diseases." He took the significant step of asserting that as there were species of plants, so too there were species of disease. This implied that diseases were distinct entities, not merely disturbances blending into one another, and that these distinct entities could be systematically grouped or classified. In practice Sydenham concentrated on exact definition and description. He gave concise accounts of smallpox, dysentery, cholera, plague, and other diseases. He was the first to differentiate between measles and scarlet fever, and his description of gout made possible its separation from rheumatism. For Sydenham specificity of disease implied specificity of remedy, and it was this idea, as much as the example of cinchona bark for malaria, that was behind his doctrine of specific medicines.^[46]

The 18th century continued Sydenham's botanical approach while shifting its emphasis from description of individual species to comprehensive classifications using higher taxonomic categories. The first such effort was made by François Boissier de Sauvages, a professor at the medical school of Montpellier familiar with contemporary botany. Sauvages' Treatise on the classes of diseases of 1731 arranged its objects in classes, orders, and genera as well as species. His major work carried the instructive title Methodical nosology, in which diseases are arranged by classes according to the system of Sydenham and the order of the botanists . Like Sydenham, Sauvages distrusted contemporary physiological theories and rejected the idea that a classification of diseases could be based on knowledge of their

[46] Knud Faber, Nosography in modern internal medicine (New York: Hoeber, 1923), 5–49; Lester S. King, The medical world of the 18th century (Huntington, N.Y.: Krieger), 193–226; Michel Foucault, The birth of the clinic. An archeology of medical perception (New York: Pantheon Books, 1973), 3–21; and Sergio Moravia, "Philosophie et médecine en France à la fin du XVIIIe siècle," Studies on Voltaire and the 18th century, 89 (1972), 1089–1151, esp. 1129–38. On Sydenham, see also The works of Thomas Sydenham , 2 vols. (London: The Sydenham Society, 1848–50), 1 , 3–24.

underlying causes. He insisted that classification be based instead on study of directly observable symptoms. Species definition depended largely on designation of the various circumstances in which symptoms might appear. Species proliferated accordingly, finally reaching 2,400, divided into 315 genera, 44 orders, and 10 classes.^[47]

Sauvages set the pattern for the nosology of the latter 18th century. Linnaeus had been a medical student when Sauvages' first book appeared in 1731. Subsequently the two men corresponded, became friends, and influenced one another. When he became professor of medicine at Uppsala, Linnaeus based his lectures on Sauvages' nosological system. In 1763, the year that Sauvages' Methodical nosology appeared, Linnaeus published his own work on Genera morborum . Given the long-standing botanical association of nosology, the increasing success and prestige of Linnaeus' botanical system after midcentury no doubt strengthened the appeal of the nosological approach to medicine. There is a clustering of nosological treatises in the 1760s and 1770s. Vogel published at Göttingen in 1764; Cullen, at Edinburgh in 1772; Macbride, at Dublin in 1775; Sagar, at Vienna in 1776; and Vitel, at Lyons in 1778. All of these works followed Sauvages in departing from Sydenham's original emphasis within the systematic program. Rather than seeking new, more accurate descriptions of disease, the nosologists of the latter 18th century took existing descriptions and tried to catalogue and group them, usually on the basis of symptoms.^[48]

The nosologists' insistence on observable symptoms as criteria of classification reveals in several ways the kinship of their enterprise with contemporaneous systematic endeavors in other fields. It is analogous to the use of visible external characters in botany and

[47] François Boissier de Sauvages, Nouvelles classes de maladies, qui dans un ordre semblable à celui des botanistes, comprennent les genres et les especes de toutes les maladies, avec leurs signes et leurs indications (Avignon, 1731), and Nosologia methodica sistens morborum classes, genera et species juxta Sydenhami mentem et botanicorum ordinem , 2 vols. (Amsterdam: De Tournes, 1763). See also King, The medical world , 205–14.

[48] Linnaeus, Genera morborum, in auditorum usum (Uppsala, 1763); Fredrik Berg, "Linnés systema morborum," Uppsala Universitets Årsskrift , 1957:3, 1–132; King, The medical world , 198–204; Faber, Nosography , 25–6.

mineralogy and appears consonant with their empiricist philosophical posture. It is also artificial, not in the sense of limiting the numbers of external characteristics to be considered, but in the sense of ruling out, at least for the moment, consideration of the structural and functional processes underlying disease.

The Paris clinical school of the early 19th century would challenge what it took to be the superficiality of this approach and insist that diseases be studied in anatomical depth, in the structural changes they produced in the organs and tissues of the body. The transition can be seen in the work of the Paris physician Philippe Pinel. Pinel's Nosographie philosophique, ou la méthode de l'analyse appliquée à la médicine , first appeared in 1798, and went through six editions in two decades (fig. 3.4). On the surface it is a work of the 18th century. To be sure, Pinel was critical of the "overloaded tables" and "arbitrary and vacillating" classifications of his predecessors. He granted, however, that there was an "absolute necessity" for some such method to save physicians from uncertainty, perplexities, risk, and precipitous decisions, and to save patients from mistakes. Pinel accepted the validity of the systematic model for medicine, and attempted to describe and classify the full range of known diseases.

In making his nosography "philosophical" and in citing the "method of analysis," he referred to the same views of Condillac that had helped motivate Lavoisier's reform of chemical nomenclature and Haüy's revision of the language of mineralogy. He declared that he would replace the earlier medical motto, "Given a disease, find the remedy," with a new motto of his own: "Given a disease, determine its true character, and the rank that it must occupy in a nosological table." Viewed more closely, however, Pinel's approach does not exactly correspond to that of his predecessors:

We must make every effort [he wrote] to introduce into medicine the method now followed in all the other parts of natural history, that is, a severe exactitude in descriptions, precision and uniformity in nomenclature, a wise reserve in rising to general views without giving reality to abstract terms, and a simple, regular classification founded invariably on the relation of the structure or organic functions of the parts.

The last crucial phrase separates Pinel's work from the nosologies of the 18th century. For Pinel a valid classification had to be based not only on symptoms but also on pathological anatomy. The class of inflammations—to give only one example—Pinel divided into orders on the basis not of symptoms but of the kind of membrane that was attacked. The result was a system greatly simplified by comparison with earlier nosologies. It included 5 classes, 80 genera, and fewer than 200 species of disease. As Pinel's Nosography went through successive editions, the classificatory scheme itself became less and less prominent. With the last edition of 1818, the 18th-century tradition of nosology came to an end.^[49]

The varied expressions of the systematic model in mineralogy, chemistry, and medicine only begin to indicate the omnipresence and diversity of its applications in the late Enlightenment. Some idea of this variety may be gained from a brief look at several of the model's less predictable incarnations, in mathematics, physics, mechanics, the theory of machines, physiology, anatomy, and materia medica.

Varia

If the geometrical spirit is found in systematics, the systematic spirit is also found in geometry, more precisely in analytic geometry. The field that joined algebraic analysis and geometry for the benefit of each was the subject of intense activity in the first half of the 18th century. The study of curves was taken up first primarily as a means to determine the roots of equations. Increasingly curves came to be of interest in themselves, however; and by midcentury they had become a candidate for systematization. Leonhard Euler's Introductio in analysin infinitorum (1748) and Gabriel Cramer's Introduction à l'analyse des lignes courbes algébriques (1750) were largely successful, though different, efforts to meet the need for systematic order acknowledged by both.^[50]

[49] Phillippe Pinel, Nosographie philosophique, ou la méthode de l'analyse appliquée à la é;decine , 6th ed. (Paris: J.A. Brosson, 1818), iv–xviii; Faber, Nosography , 28–30; King, The medical world , 224–6.

[50] Pierre Speziali, Gabriel Cramer (1740–1752) et ses correspondents (Paris: Palais de la Découverte, 1958), 14–6; Phillip S. Jones, s.v. "Cramer, Gabriel," DSB, 3 , 459–62; Pierre Speziali, "Leonard Euler et Gabriel Cramer," in Leonhard Euler 1707–1783. Beiträge zu Leben und Werk (Basel: Birkhäser, 1983), 421–34; Carl B. Boyer, History of analytic geometry (New York: Scripta Mathematica, 1956), 180–91.

Cramer's treatise, described by Speziali as "a true encyclopedia of algebraic curves," was well received in the latter 18th century and remained a classic text well into the 19th. Although Cramer conceded that the ancients had formulated useful particular propositions about curves, he gave modern mathematics high marks for its method, its art of deducing from a single universal principle a great number of truths, submitting them to general rules, and connecting them so as to stimulate new discoveries. Algebra, the "universal key of mathematics," provided the mathematician with "an ingenious means of reducing problems to the simplest and easiest calculation that the question proposed can admit."^[51] And the key to algebra was the curve. A proper distribution of curves into orders, classes, genera, and species would serve mathematicians as a "well-arranged arsenal," enabling them to choose without hesitation the arms that might serve in the resolution of a proposed problem. Cramer credited Newton, whose Enumeratio linearum tertii ordinis had first appeared in 1704, with opening the way to such a classification.^[52]

Cramer defines the order of algebraic curves "according to the degrees of their equations. . . . Thus one may form, for each order of lines, a general equation that represents all the possible lines of this order." To do so, Cramer makes use of J.P. de Gua de Malves' analytic triangle, a modified version of Newton's parallelogram arrangement of the terms of algebraic equations. The analytic triangle gives the different terms of a general equation of a given degree on a horizontal line, starting with a degree zero (a ) at the bottom, then degree one (by, cx ), degree two (dy^[2] , exy, fx^[2] ) and so on.^[53]

[51] Speziali, Cramer , 17–8; Boyer, History of analytic geometry , 193–6; Gabriel Cramer, Introduction à l'analyse des lignes courbes algébriques (Geneva: Les Frères Cramer & Cl. Philibert, 1750), vi–vii; Moritz Cantor, Vorlesungen über Geschichte der Mathematik, 2d ed., 4 vols. (Leipzig: Teubner, 1907–13), 3 , 605–9, 823–41.

[52] Cramer, Introduction , vii–ix; W.W. Rouse Ball, "On Newton's classification of cubic curves," London Mathematical Society, Proceedings, 22 (1890–91), 104–43; Boyer, History of analytic geometry , 138–40, 146–7; and D.T. Whiteside, ed., The mathematical papers of Isaac Newton , 8 vols. (Cambridge: Cambridge University Press, 1967–81), 1 , 155–212; 2 , 10–88; 4 , 346–405; and 7 , 565–655.

[53] Using the triangle Cramer derives the formula v^[2] /2 + 3v /s for the number of coefficients of the general equation of degree v , and concludes from this that a curve of order v can be made to pass through v /2 + 3v /2 points. The demonstration leads him into presentation of a rule for solving v linear equations in v unknowns. This rule, together with a paradox developed out of the same formula, had its own subsequent history. See Cramer, Introduction , xi, xiii–xiv, 52–70, esp. 52–60; Jones, "Cramer," 460–1.

The subdivision of the first five orders of curves into their classes and genera is accomplished via the number, nature, and position of the infinite branches of each type of curve. The second order contains three classes: the ellipse, of which the circle is one species; the hyperbola; and the parabola. In essentials, Cramer follows Newton's Enumeratio in his division of third-order curves into four classes and fourteen genera. His fourth order has nine classes, based on the number and the hyperbolic or parabolic character of the infinite branches of its curves. For example, the eighth class contains the curves that have six hyperbolic branches. This class contains three genera: those curves that have only two, nonparallel asymptotes; those that have three asymptotes, of which two are parallel; and those that have three nonparallel asymptotes. The fifth order has eleven classes, defined by procedures similar to those for the fourth order (fig. 3.5).^[54]

Cramer's classification, although comprehensive for its subject, was confined to plane curves. In the 1770s several mathematicians, including Euler, Joseph Louis Lagrange, and Gaspard Monge, began to take analytic geometry into three dimensions. From the outset of his epoch-making work in this field, Monge had as one of his concerns the groupings of its objects. In his Feuilles d'analyse (1795 and 1801) he discussed some twenty families of surfaces defined by their mode of generation.^[55]

The Feuilles d'analyse first appeared as notes to Monge's course at the Ecole polytechnique, where as professor he was responsible for solid analytic geometry. Finding himself without a satisfactory

[54] Cramer, Introduction , 352–99.

[55] Gaspard Monge, Feuilles d'analyse appliquée à la géométrie (Paris, 1795); René Taton, "Une correspondance mathématique inédite de Monge," Revue scientifique , 85 (1947), 963–89, esp. 979–82; Taton, s.v. "Monge, Gaspard," DSB, 9, 469–78; and L'Oeuvre scientifique de Monge (Paris: Presses Universitaires de France, 1951), 209–20; Boyer, History of analytic geometry , 204–25.

textbook, he was compelled to put his results in systematic order. Similar pedagogical challenges created by the new Ecoles helped motivate other efforts at systematization and rationalization during the Revolution and the First Empire. In these efforts, the full systematic model in its Linnæan form, with logically nested categories—especially the canonical five, class, order, genus, species, variety—and binomial nomenclature, was frequently replaced by other arrangements more or less improvised for the matter at hand. Natural history categories might or might not be used, rationalized nomenclature might or might not be a goal, and other qualities of the full model such as numeration or formalism might be present in different degrees. What these undertakings did consistently have in common with the full systematic model were its emphasis on rationalization and method, its aim for comprehensiveness, and its promise of utility.

The work of Etienne Barruel, an examiner in physics at the Ecole polytechnique, is a case in point. As its title advertises, Barruel's textbook, Physics reduced to systematic tables (1799), offered students a complete summary of current physics in tabular form. Apart from brief prefatory remarks, the entire volume consists of thirty-eight tables, most in large fold-out format.^[56]

Barruel defined physics "properly speaking" as the science that considers the properties of natural bodies, in contrast to natural history, which studies their varieties, organization, and so on, and chemistry, which considers their combination. "In the methodical order that I have adopted," Barruel wrote, "a science that has for its object the properties of bodies, cannot be subject to any other division than that of these same properties." Accordingly the first table, labeled tableau général de la physique , lists twenty-one fundamental physical properties, divided into two major groups. The first group comprises properties "that affect bodies in a constant manner" (extension, impenetrability, mobility, inertia, gravity). The second is constituted by properties "that affect bodies in a variable manner" (porosity, sonority, affinity, caloricity, electricity, elasticity, solidity,

[56] Etienne Barruel, La physique réduite en tableaux raisonnée, ou programme du cours de physique fait à l'Ecole polytechnique (Paris: Baudouin, an VII).

liquidity, gaseousness, capillarity, hygrometricity, meteoricity, crystallizability, light, magnetism, galvanism). Barruel subdivides the first group into "constant and essential" properties such as extension and impenetrability, and "constant and non-essential" properties, made up of gravity alone. He subdivides the second major group into "variable properties that belong to all bodies in general," such as porosity and affinity, and "variable properties that belong only to certain bodies," for example hygrometricity and light.^[57]

The tableau général characterizes each property in one or two lines. For example, hygrometricity is the property by virtue of which liquids capable of wetting bodies enter their pores. Light is the property by virtue of which bodies excite a vivid impression in the organ of sight. At least one additional table is devoted to each property, elaborating on such points as its manner and circumstances of appearance, the laws to which it is subject, its relation to the senses, or instruments that may make use of it. Light, to give a single example, is the subject of seven tables. The initial division is made according to whether light reaches the eye directly, after reflection, or after refraction. Among the later subdivisions under refraction is a table that considers light in relation to instruments including telescopes and microscopes, subdivided in turn into their kinds.^[58]

Except for its initial division of physics according to the properties of bodies, Barruel's text does not have the form of a classification of objects of the same general type (plants, animals, minerals, chemicals, algebraic curves, etc.) according to a determined set of categories. Instead it offers an arrangement of the different aspects of knowledge about what Barruel took to be single things (here properties, such as light) in a table formed by successive dichotomizations. No rule limits the number of dichotomies, and the kinds of criteria by which they are made may vary substantially within the same table. Barruel

[57] Barruel, La physique , 3, and table 1. In a second edition of 1806, Barruel added an introduction that expanded on the characterizations of properties. A revised tableau général redefined the major divisions of properties as physical and chemical. He also revised the content of the tables and changed their order, although the total number remained the same.

[58] Barruel, La physique , table 1, 27–33.

does not attempt a rationalized system of names, and indeed he derides reliance on "a simple nomenclature" for its aridity. Barruel's was nevertheless a project of systematization and rationalization, and he remarked that "it is to be desired that the elements of all sciences were accompanied by similar tables."^[59]

One who heeded Barruel's call was Gaspard Prony. In 1800, when he published his Mécanique philosophique , Prony could draw upon five years of teaching experience at Ecole polytechnique. The title deliberately imitated Antoine Fourcroy's Philosophie chimique (1792), for, like Fourcroy, Prony intended to present a synoptic view of his science systematically organized on the basis of an analysis of its elements. Every even-numbered page contained formulas, definitions, and brief discussion. Each facing odd-numbered page was divided into four columns, the first defining the letters in the formulas, the second listing items defined in the text, the third and fourth stating theorems and problems. As far as possible, Prony eliminated demonstrations and "intermediate calculations" in favor of a concise presentation of results.^[60]

Prony's procedure embodied a double movement of analysis and synthesis. He began with a complex mass of material—his lectures, current knowledge of mechanics in all its detail—and analyzed it into its matériaux primitifs , its simplest, most fundamental propositions or elements. Out of these he then constructed the complex structure of the science of mechanics, but in such a way that its components were grouped so that their relations were transparent. In this effort of

[59] Barruel, La physique , 3–4.

[60] In five major divisions of the text he covered preliminary notions, including elementary concepts of mechanics; the mechanics of solid bodies, statics and dynamics; the mechanics of fluid bodies, hydrostatics and hydrodynamics; the application of mechanics to machines and engineering problems; and "transcendental mechanics," general propositions such as the principle of virtual velocities or the principle of least action. Gaspard Clair François Marie Riche, baron de Prony, Mécanique philosophique, ou analyse raisonnée des diverse parties de la science d'équilibre et du mouvement (Paris: Imprimerie de la République, an VIII). Fourcroy's work, Philosophie chimique, ou vérités fondamentales de la chimie moderne, disposées dans un nouvel ordre (Paris, 1792), was based on Fourcroy's article, "Axiomes chimiques" for the Encyclopédie méthodique , which in turn was directly inspired by Linnæan systematics. Cf. W.A. Smeaton, s.v. "Fourcroy, Antoine François de," DSB, 5 , 89–93.

systematization, in his implicit commitment to a sensationalist theory of knowledge, and in his remarks on science as a well-made language, Prony revealed his links with the encyclopedic tradition and the philosophy of Condillac as well as the kinship of his work with other systematic endeavors.^[61]

Mechanics of a more immediately practical sort was the subject of Jean-Nicolas-Pierre Hachette's Traité élémentaire des machines (1811). A colleague of Barruel and Prony and student of Monge, Hachette taught a course on machines for engineers at the Ecole polytechnique. The Traité was based on these lectures and on the ideas of Monge, who treated the theory of machines as a branch of descriptive geometry.^[62]

Hachette limited his treatment to machines that transform motion of one type into motion of another type. The types could be exhaustively enumerated: continuous circular, alternating circular, continuous rectilinear, and alternating rectilinear. These four types of motion make six when taken two at a time; and to these six combinations may be added the four that result when each movement reproduces itself. Hachette concluded, therefore, that there are ten different series of elementary machines.^[63] Part of his table of elementary machines is reproduced here (fig. 3.6). Each machine is represented by a picture in a small box. The table presents the ten series of machines in numbered horizontal ranks; capital letters placed above the vertical columns allow a brief designation of each box. So, for example, the box 3^a D designates a machine (the windmill) of the third series, which changes continuous rectilinear movement (wind) into continuous circular movement (the mill). Two series, the second and eighth, are empty, for no known machines changed continuous rectilinear into alternating rectilinear motion, or alternating rectilinear motion into itself.^[64]

[61] Prony, Mécanique philosophique , i–iv, citing Barruel's La physique as a model.

[62] Jean-Nicolas-Pierre Hachette, Traité élémentaire des machines (Paris: J. Klosterman fils, 1811), x; Taton, "Monge," 477.

[63] Hachette counts each pair of different motions as defining a single kind of machine, even though in these six cases the order, and thus the source of motion and the receiver of motion, may be reversed, and although he concedes that this reversal rarely occurs in the same machine. Hachette, Traité , 4–5, 7–8.

[64] Hachette, Traité , 6–8, 261–9.

The inclusion of two empty series in the table reveals in a graphic way the a priori and arithmetically determined character of Hachette's systematization. He identifies an exhaustive set of possibilities, subdivides them, and distributes existing machines into the preexisting categories. Once again, mathematics intersects the systematic model in criteria of classification.

Prompted in part by the same pedagogical needs that moved Monge, Prony, and Hachette, physiologists and anatomists analyzed and reanalyzed the human body into its functional and structural elements, classified these elements, and provided them with rationalized nomenclature. Xavier Bichat, who taught surgery at the Hôtel-Dieu in Paris, ordered the vital properties into which he analyzed the phenomena peculiar to living things into classes, genera, species, and varieties, and associated the divisions with the elementary tissues yielded by his anatomical analysis. Bichat published his work in a series of textbooks. So, too, did the professors of medicine, François Chaussier and Charles Louis Dumas, who were determined to provide their students with a rationalized nomenclature and classification of the parts of the human body.^[65]

Physicians and pharmacists disturbed by radical criticism of traditional materia medica and drug therapy turned to the systematic model as the key to rationalization of knowledge of medicines. Pharmacists had an especially strong motive for reform, since the legitimacy of the body of esoteric knowledge on which their claim to a professional status comparable to that of physicians and surgeons was being threatened. From the 1780s on, systematic arrangements of the materia medica proliferated, especially in France, where differing

[65] William R. Albury, "Experiment and explanation in the physiology of Bichat and Magendie," Studies in history of biology, 1 (1977), 47–131; Lesch, Science and medicine in France , 62–8; François Chaussier, Tableau synoptique des muscles de l'homme (Paris: T. Barrois le jeune, 1797), and Exposition sommaire de la structure et des differentes parties de l'encéphale ou cerveau suivant la méthode adoptée à l'Ecole, de médecine de Paris (Paris: Théophile Barrois, 1807), and Planches anatomiques à l'usage des jeunes gens qui se destinent à l'étude de la chirurgie, de la peinture et de la sculpture. . .avec des notes et explications suivant la nomenclature méthodique de l'anatomie et des tables synonymiques , 2d ed. (Paris: Pancoucke, 1823); Charles Louis Dumas, Système méthodique de nomenclature et de classification des muscles du corps humain (Montpellier: Bonnariq, Avignon et Migueyron, an V).

versions were published by Antoine Fourcroy, Xavier Bichat, C.J.A. Schwilgué, Jean Alibert, and Jean Baptiste Barbier.^[66]

Conclusions

The diversity of its applications places in clear relief both the ease with which the systematic model could be brought to bear on different subject matters and its prestige and pervasiveness among late Enlightenment thinkers as a way of ordering knowledge or experience. The systematic model rode a wave of enthusiasm that carried it above and beyond its connections to any particular field of inquiry. Its successes may be readily catalogued. They are not so easily explained, although several conclusions may be ventured on the basis of the preceding analysis.

In several cases, the adoption of rationalized nomenclature or the systematic grouping of the objects of a field in hierarchical categories was the result of a direct modeling on systematic botany, and not simply the expression of a more fundamental impulse of which botany itself was one manifestation. As Foucault pointed out, botany enjoyed epistemological precedence in the classical age, if only because the externality of the significant characters of plants lent itself most easily to specification of degrees of identity and difference according to visible marks. The role of the botanical model is also suggested by the temporal priority of systematic botany, which had emerged full-fledged by the middle of the 18th century. Tentative efforts for parallel reforms in medicine, mineralogy, and chemistry are visible before consolidation of Linnæan botany, but it was only after this consolidation that substantial movement took place in other fields. The serious botanical interests evident in the early careers of such key figures as Sauvages in medicine and Haüy in mineralogy, and the involvement of Linnæus himself in the systematics of minerals and diseases, lend further support to the view that systematic botany served as a model for other fields.

[66] Lesch, Science and medicine in France , 130–5, 145–8.

Utilization of the model was not mechanical and uniform. Each field seized on those aspects that promised to meet its own most pressing requirements. For chemists it was above all the possibility of a rationalized and radically simplified nomenclature that appealed. For mineralogists and physicians it was the concept of species, the emphasis on exact description, and the promise of a comprehensive ordering of data that counted most. For all of these fields, and for others such as analytic geometry, mechanics, the theory of machines, physiology, anatomy, and materia medica, the rationalization made possible by the systematic model was in part motivated by, and often served the needs of teaching.

The place and importance of the systematic model in the late Enlightenment was enhanced by its resonance with other elements of the time. The kinship and—on occasion—the intersection of the model with mathematics as modalities of the geometrical spirit have been mentioned. Systematics and mathematics were also associated in the prevailing epistemology, best represented by Condillac. Condillac's name and ideas reappeared again and again in applications of the systematic model to fields as diverse as chemistry, mineralogy, nosology, and anatomy. Although his inspiration came from algebra, Condillac's stress on science as a well-made language helped to motivate and sanction attempts to construct rationalized systems of nomenclature. His emphasis on the epistemological priority of sensations validated the use of externally observable features as criteria of classification. And his notion of analysis underlined the importance of seeking the elementary constituents out of which any larger whole was constituted.

In their efforts to systematize and rationalize all knowledge within their chosen domains, proponents of the systematic model moved easily with the broader currents of the encyclopedic movement. As W.T. Stearn has noted, Linnæus was a born encyclopedist in the extent of his knowledge of particulars, in the clarity and concision of his expression, in his industry, perseverance, and talent for methodological organization, and in his attention to utility. Adanson not only contributed to the Encyclopédie , but conceived vast encyclopedic ambitions of his own. Systematic efforts in particular subject areas

were easily subsumed under the more comprehensive task of organizing all knowledge, as the articles on special fields within the Encyclopédie méthodique make plain.^[67]

By the time that Bichat published his books on physiology and anatomy around 1800, the model's prestige and influence were already beginning their decline. Bichat himself was moving away from his taxonomy of vital properties and toward a more strictly experimental approach to physiology. While they continued to do systematics, botanists and zoologists—the latter led by Cuvier—turned increasingly to more natural systems that embraced structural and functional aspects of the organism, and to anatomical and physiological studies in their own right. While classification and nomenclature of minerals continued to be active issues well into the 19th century, the center of interest in mineralogy shifted to chemical composition and physical properties. Inorganic chemists, with rational nomenclature firmly established, moved on to new problems: proximate and elementary analysis, atomic theory, electrochemistry, and so on. Nosology was displaced by pathological anatomy.

No doubt the model proved less appropriate and productive outside botany and zoology than within them. This is clear enough in retrospect, since evolutionary community of descent provides a natural basis for hierarchical grouping of plants and animals that does not exist for minerals, chemical compounds, or diseases. To some extent the model was eclipsed by its very success. At least this was the case in botany and chemistry, where the establishment of rationalized nomenclature and classification enabled botanists and inorganic chemists to carry out more effective studies of other problems in their fields. Where these foundations were not in place, the systematic model could find new life. The appearance of burgeoning numbers of new organic compounds from the 1820s provoked fresh preoccupation with problems of naming and grouping in chemistry. To these problems the model could and did respond, with substantial consequences for chemical theory.^[68]

[67] Stearn, "Introduction," 11–2.

[68] N.W. Fisher, "Organic classification before Kekulé," Ambix, 20 (1973), 106–31; and 21 (1974), 29–52.

That is not the whole story, however. The very extravagance with which the systematic model was embraced between 1750 and 1810 suggests that more was involved in its success than its appropriateness for particular sciences at a determinate stage of their development, and more involved in its demise than the evolution of those sciences to a higher stage. The resonances of the systematic model with applied mathematics as a modality of the geometrical spirit, with sensationalist epistemology, with the encyclopedic movement, and with the rationalizing endeavors of the absolutist state, suggest the coherence of systematics with general and characteristic features of the culture of the late 18th century.

4
Measure of Ideas, Rule of Language: Mathematics and Language in the 18th Century

By Robin E. Rider

In the 18th century mathematics both shone as an example and served as an instrument of enlightenment: it was at once rational, universal, certain, precise, unambiguous. Many 18th-century authors hoped that the same could shortly be said of common language. Toward that end they sought to infuse language with rationality and to render it universal; to guarantee its certainty, increase its precision, strip it of ambiguity. Some sought to convert into mechanical processes both the derivation of words and their transmission. Throughout their struggles with the inadequacy of existing languages and the complexity of creating new ones, language reformers were guided by mathematics.

By the second half of the 18th century the close connection between the content of thought and its form of expression was a familiar philosophical refrain.^[1] In his Diversions of Purley , for example, John Horne Tooke carefully re-examined a century's worth of views on the intimate connection between language and thought, then pushed the philosophical commonplace one step further. For Tooke, the operations of the mind were none other than the operations of language—hence, language is thought.^[2]

[1] Many authors echoed John Locke: "Though therefore it be the Mind that makes the Collection, 'tis the Name which is, as it were, the Knot, that ties them fast together." An essay concerning human understanding (London: Basset, 1690), 205. Cf. Hans Aarsleff, Study of language in England, 1780–1860 (Princeton: Princeton University Press, 1967), 51; Murray Cohen, Sensible words. Linguistic practice in England, 1640–1785 (Baltimore: Johns Hopkins University Press, 1977).

[2] John Horne Tooke, The diversions of Purley , 2d ed., 2 vols. (London: Johnson and Hunter, 1798–1815), 1 .

Growing appreciation of the link between language and thought and renewed concern for the quality of thought gave rise to new laments about the inadequacies of existing languages and their unhappy consequences. Authors in the Age of Enlightenment followed a century-old lead in condemning the arbitrary assignment of words to things. Tooke, for instance, recalled Francis Bacon, who had likened words to a Tartar's bow: they "shoot back upon the understanding of the wisest, and mightily entangle and pervert the judgment."^[3]

Language studies in the 18th century also addressed questions of syntax—the structure of phrases and sentences—and what was called universal or general grammar. The latter was defined in the Encyclopédie as the "invariable and universal rule that must serve as the foundation for the particular construction of any given language." General grammar thus rested on the premise that all languages follow "the laws of logical analysis of thought; and these laws are invariably the same everywhere and always." Or, more pointedly, "a sane logic is the foundation of grammar."^[4]

An Instrument of Analysis

Armed with the view of language as a species of logic, and mindful of the power of language to deceive or mislead, writers on language in the latter part of the 18th century looked for ways to harness language in the service of enlightenment. For many,

[3] Likewise John Wilkins, with others in the early Royal Society, had called for the "unmasking [of] many wild errors, that shelter themselves under the disguise of affected phrases." Bacon and Wilkins as quoted in Tooke, Diversions of Purley, 1 , 31–3.

[4] Encyclopédie, 7 (1757), s.v. "Grammaire." This view derived from a precept underlying the Port-Royal grammar and logic texts of the late 17th century—that language reflects the processes of rational thought. On the shift in emphasis from the lexical to the syntactic, see Cohen, Sensible words , 26, 41, 51–2, 60, and Stephen K. Land, From signs to propositions. The concept of form in eighteenth-century semantic theory (London: Longman, 1974). On the evolution of general grammar in the 18th century, see Aarsleff, The study of language in England , 14–5; James Knowlson, Universal language schemes in England and France 1600–1800 (Toronto: University of Toronto Press, 1975), 147; and Cohen, Sensible words , 101–2.

mathematics, the embodiment of enlightened values, served as a guide. Mathematics was eminently rational to 18th-century eyes; its symbols and results were truly international; its reasoning was at once powerful and certain. More than that, at the heart of 18th-century mathematics stood analysis, and the method of analysis enjoyed privileged status among the philosophes . Small wonder that, in an age that prized the rational and the universal, mathematics—that sharp and sure instrument of reason—offered inspiration and example to the reformers of language.

The privileged status accorded to the philosophical method of analysis during the Enlightenment helped to focus attention upon its manifestation in mathematics, and in particular upon algebra as a powerful instrument of analysis,^[5] especially in the hands of a master. Few could rival the mastery of Leonhard Euler. In Condorcet's view, Euler "sensed that algebraic analysis was the most comprehensive and certain instrument one can employ in all sciences, and he sought to render its usage general. This revolution. . .earned [Euler] the unique honor of having as many disciples as Europe has mathematicians."^[6] The power of the Eulerian formulation of infinitestimal analysis provided dramatic confirmation of the mathematical potential of algebra and lent credence to the view of algebra as the fundamental language of mathematics.

Algebraic analysis found a vigorous advocate in Etienne Bonnot de Condillac, whose treatises on philosophical analysis, language, and mathematics explicitly invoked mathematics as a model for the perfection of language. Condillac's treatise on logic rejected prevailing approaches to logic and deprecated the grand philosophical systèmes of the 17th century. What was needed for building knowledge, Condillac argued, was not "to imagine ourselves a system," but instead to

[5] See Robin E. Rider, Mathematics in the Enlightenment: A study of algebra, 1685–1800 (Ph.D. dissertation, University of California, Berkeley, 1980; DAI , 42/01A, 351), esp. chaps. 3 and 9. Cf. John Fauvel and Jeremy Gray, eds., The history of mathematics: A reader (London: Macmillan, 1987) on style and formalism in 18th-century mathematics.

[6] Marie Jean Antoine Nicolas Caritat, marquis de Condorcet, "Discours sur les sciences mathématiques," in Condorcet, Oeuvres , ed. A. Condorcet O'Connor and M.F. Arago, 12 vols. (Paris, 1847–49), 1 , 453–81, on 467.

"attend to what nature teaches us." And what nature teaches us is to analyze: "analysis is the only method by which accurate knowledge is to be acquired."^[7]

Condillac offered graphic examples of analysis at work. When you order a copy of a sample dress, seamstresses "will naturally perceive that it is necessary to take [the sample] apart and remake the pattern of each part." When you throw open a window and look at a landscape, you take the scene apart by focusing on first one object, then another. "We make this decomposition only because an instant is not sufficient for us to study all those objects. But we only decompose in order to recompose." Analysis for Condillac is thus nothing more than observing "in a successive order the qualities of an object, so as to give them in the mind the simultaneous order in which they exist."^[8]

Condillac threw open a window on our thought processes themselves. "To see distinctly all that at once offers itself in my mind, I must decompose it, as I have decomposed what offered itself to my sight; I must analyse my thoughts." In his enthusiasm, he contended that analysis, which some called the method of invention, "has made all discoveries": "by the medium of analysis we become capable of creating arts and sciences." He thus echoed Voltaire's dictum—"Let us make an exact analysis of things"—which served as a motto for the Enlightenment. It was clear to Condillac that seamstresses knew more than philosophers, who used synthesis, not analysis, to wrap up the truth "in a heap of vague notions, opinions, errors" and who "strayed prodigiously, when they forsook analysis" for the "tenebrous method" of synthesis.^[9]

In his depiction of language as an instrument of reason, Condillac also renewed the critique of existing languages and their unhappy effects on thought. In an oft-quoted passage, he attacked philoso-

[7] Etienne Bonnot de Condillac, The logic of Condillac , edited and with a preface by Daniel N. Robinson (Washington: University Publications of America, 1977), 7–8, based on Joseph Neef's English translation (published in 1809) of La logique (1780), part of the course of study Condillac devised for Ferdinand, duke (and later) prince of Parma, whom Condillac served as tutor during the years 1758–67.

[8] Ibid., 13, 10, 11.

[9] Ibid., 11, 13, 67, 76, 73.

phers as "subtle, singular, mysterious, visionary, unintelligible, [who] often seemed to be afraid of not being obscure enough, and affected to cover with a veil their real or pretended knowledge. Therefore, the language of philosophy has been nothing else but a jargon of gibberish for many centuries past." The tirade continued, "The art of misapplying words was for us the art of reasoning: arbitrary, frivolous, ridiculous, absurd, it had all the vices of disordered imaginations."^[10]

Analysis, that lever of the mind, offered Condillac a solution to the problem of language: "To speak so that we may be understood, we must conceive and express our ideas in the analytical order which decomposes and recomposes each thought." The result will necessarily be "clearness and precision." Condillac then took the argument one step further: "The art of reasoning is in truth only a well constructed language." He rejected the remedy, often proposed, of "seeking in words their essential qualities"; instead, he exhorted us to seek in words only "what we placed in them, the relation of things to us, and those relations which they bear to each other." Nature displays to us a natural order; by our analysis of nature we perceive and recreate that order in our mind. Language should reflect a natural taxonomy that corresponds to the "order of our ideas." Condillac concluded that a well-constructed language is nothing other than an analytical method.^[11]

Condillac was captivated by the power and achievement of the 18th-century brand of mathematical analysis and set out to facilitate analytical thought in metaphysics by studying algebra—the fundamental language of mathematical analysis. In his treatise on logic, Condillac insisted that no distinction need be drawn between mathematical analysis and logical or metaphysical analysis, "because in all of them [analysis] leads from the known to the unknown, by reasoning; that is, by a series of judgments which are included in each other." For Condillac, the advantage of mathematical analysis consists strictly in

[10] Ibid., 64, 69.

[11] Ibid., 46, 12, 67, 66. On the connection between language and taxonomy, see M.M. Slaughter, Universal languages and scientific taxonomy in the seventeenth century (Cambridge: Cambridge University Press, 1982).

the fact "that it speaks there the most simple language"—and that most simple language is algebra.^[12]

For Condillac the mathematical advances of the late 17th and especially the 18th century offered a powerful argument in favor of algebra as the language of mathematics. Algebra constituted "very striking proof that the progress of the sciences depends solely on the progress of languages; and that correct languages alone could give analysis that degree of simplicity and precision of which it is susceptible." Further, he called attention to the central role played by Euler and Joseph Louis Lagrange in putting mathematical analysis in algebraic form: they "are great mathematicians, because they are great analysists [sic ]. They excellently write algebra, a language in which good writers are most scarce, because it is the most correct." Condillac put the point forcefully. Algebra "is a language, and cannot be any thing else." It is "a language which could not be badly constructed"; this in turn means that mathematicians who couched their analysis in algebraic language are able thereby to "speak with precision."^[13]

Condillac maintained that languages are in and of themselves analytical instruments, which ought to lay bare the relations and analogies of our ideas. Most languages, in Condillac's view, were too blunt, too imprecise. But in algebra, conceived as the rules by which equations and their components could be manipulated and transformed, the language (and the analytical method) corresponded exactly to the analogies existing among mathematical ideas. As he explained it, "One goes from identity to identity until the conclusion that resolves the question, in other words, from identical equation to identical equation until the final equation." Condillac's explanation of the chain of identities sounds a good deal like a passage from d'Alembert's Preliminary discourse to the Encyclopédie : "Thus, the chain of connection of several geometrical [mathematical] truths can be regarded as more or less different and more or less complicated

[12] Condillac, Logic , 77, 80. Cf. La langue des calculs , which appeared first as vol. 23 of his Oeuvres , 23 vols. (Paris, an VI [1798]), and was reprinted in Oeuvres philosophiques , ed. Georges Le Roy, 3 vols. (Paris, 1947–51).

[13] Condillac, Logic , 82, 75, 82, 62; cf. La langue des calculs .

translations of the same proposition and often of the same hypothesis." D'Alembert was describing a series of mathematical propositions deduced one from the other: "It is almost as if one were trying to express this proposition by means of a language whose nature was being imperceptibly altered, so that the proposition was successively expressed in different ways representing the different states through which the language had passed. Each of these states would be recognized in the one immediately neighboring it; but in a more remote state we would no longer make it out, although it would still be dependent upon those states which preceded it and designed to transmit the same ideas."^[14]

Condillac's enthusiasm for algebra went beyond a recommendation to study its method: he provided a sort of elementary algebra textbook in the work La langue des calculs . In line with the interest, common during the second half of the 18th century, in the origin of language, Condillac attempted in this work to trace the origin of algebra, that most excellent of languages. He traced the development of calculating from finger-counting to words to letters and symbols. Familiar numerical expressions like 1, 10, and 100 were not introduced until well into the book, since, according to Condillac, the use of numerals followed the use of letters and symbols in the historical development of calculating. The remainder of La langue des calculs explained the basic operations of calculating with letters and numbers. Condillac confined his exposition to the canons by which algebraic and arithemtic quantities were to be expressed and manipulated. In stopping short of the solution of polynomial equations or their application in solving problems, he showed himself to be concerned primarily with algebra as the expression of relations among mathematical entities and as the means to make those relations reveal new facts.

Condillac's intent in writing La langue des calculs was not to add another volume to the lengthening shelf of elementary algebra textbooks in the 18th century, nor can his rational reconstruction of the

[14] Condillac, quoted in Knowlson, Universal language schemes , 171. D'Alembert, Preliminary discourse to the Encyclopedia of Diderot , transl. Richard N. Schwab with Walter E. Rex (Indianapolis, 1963), 28.

birth of calculating be considered a serious addition to the historiography of mathematics. Nor should his work be read as a recommendation that all thought be "mathematicized" or "algebraicized." In our attempts to reform languages, we should not wield recklessly the instrument of algebra, but instead should attend to the lessons of mathematics as we devise new tools. Condillac called attention to algebra precisely because the chain of reasoning in a series of identities "is more easily perceived, when we express ourselves with algebraical signs." He issued a call to action: "If, therefore, any sciences are not very exact, it is not because we do not talk algebra in them; it is, because their languages are not correct. . . . All the sciences would be exact, if we knew how to speak the language of every one."^[15] His work thus represents an important example of the confluence of two deep philosophical currents in the 18th century: advocacy of the method of analysis in all domains of thought and the desire to perfect language. In both aspects Condillac was strongly influenced by what he knew of mathematics.

Artificial Languages

In the last third of the 18th century, perceived flaws in existing languages called forth a spate of proposals for artificial ones free from flaws—and the very profusion of existing languages, like antiquated social structures and inconsistent systems of weights and measures, cried out for rationalization. To answer this call, several authors proposed a "pasigraphy," from the Greek terms for "universal" and "writing"—a set of rational, universal symbols each person could read in his or her own language. Consider the artificial language proposed by György Kalmár in his Praecepta grammatica atque specimina linguae philosophicae sive universalis, ad omnevitae genus adcommodatae .^[16] The fact that Kalmár thought it necessary to publish his proposal in Latin, German, and Italian editions in the space of just two

[15] Condillac, Logic , 81, 72.

[16] Published in Berlin and Leipzig in 1772. Cf. Kalmár, Precetti di grammatica (Rome, 1773) and Grammaticalische Regeln (Vienna, 1774).

years testified to the need, as he saw it, for a universal mode of communication. Clearly, his native Hungarian would not suffice; nor, he thought, would other existing languages. All were crippled by grammatical irregularities and orthographic confusion. For his new language, Kalmár constructed both a general, rational grammar and a new set of 400 primitive characters. Kalmár's familiarity with Hungarian as well as other languages helped him to construct a general language capable of accommodating "the details, and even the anomalies, of all existing languages."^[17]

Two more examples, taken from opposing camps in the political turmoil of the 1790s, illustrate further the broad appeal of the rationalization of grammar and the invention of a language all nations might share. In 1795 Jean Delormel presented to the National Convention in Paris his project for a new and universal language. Shortly thereafter Joseph de Maimieux, a nobleman who had fled to Germany and no friend of the Convention, published his own pasigraphy. Both Delormel and de Maimieux intended their schemes to further the objectives of rationalization and universal communication; both drew inspiration and justification from the esprit géometrique .

Delormel recognized that "extraordinary epochs" offer the opportunity, impossible in normal circumstances, to realize "interesting projects." He presented his own proposal during just such an epoch, at a moment ripe for disseminating "the principles of equality." Delormel's proposal included a binomial classification of substantives by genera and species. In tune with the call for rationalization, Delormel coupled the taxonomy with a system for the regular formation of derivative words; no longer would language need to submit to the tyranny and caprice of usage. As a reviewer of Delormel's scheme commented in 1797, "changes on words are to be rung with all the regularity of a multiplication-table."^[18] Such comments doubtless

[17] As noted by the polymath Johann Heinrich Lambert, himself the inventor of a symbolic logic, in a letter to de Francheville (1 Mar 1772), quoted by Kalmár, Precetti , 110.

[18] Jean Delormel, Projet d'une langue universelle, présentée à la Convention nationale (Paris: Chez l'auteur, an III), 1, 3. The critic in the Monthly review , Sep-Dec 1797, 562, is quoted by Knowlson, Universal language schemes , 150.

pleased Delormel, who considered the analogy to numeration to be a prime reason for the simplicity of his scheme.

His system prescribed ten vowels, according to the spirit of the day, and twice that number of consonants. The thicket of synonyms was cleared away, replaced by seven degrees of comparison. Delormel measured the advantages to be gained: where ordinary dictionaries contained 30,000 words, he claimed that one-tenth that number would suffice in his project. More than that, he proclaimed that his new language would promote the "central unity" of the Republic and, by uniting savants of different nations, would spur the progress of science. "Enlightenment brings together men of all sorts, and this language, by facilitating communication, will propagate enlightenment."^[19]

Joseph de Maimieux also billed his pasigraphy as offering all the advantages of a rational scheme of knowledge expressed in a universal form. And, he claimed, an enthusiastic audience awaited. One exuberant disciple would later honor the all-encompassing nature of de Maimieux's scheme by dubbing him a second Leibniz. De Maimieux likened pasigraphy to numerals in arithmetic, lines of music, and "characters of chemistry" — "equally intelligible from Petersburg to Malta, Madrid to Peru, London and Paris to Philadelphia or the isle de Bourbon."^[20] He devised twelve characters, some of which were mirror images of one another; twelve grammatical rules universally applicable and permitting no exceptions; and three sets of tables. These sets of tables corresponded to the three species of pasigraphic words: those of three, four, or five characters respectively. Words of three characters constituted what de Maimieux called the Indicule . In the Indicule , the first character specified the relevant column (out of twelve columns); the second specified the tranche (six for each column); and the third, the line (one of six) within a given tranche . The Indicule , together with the Petit

[19] Delormel, Projet , 4, 7, 9–10, 48, 50.

[20] Joseph de Maimieux, Pasigraphie. . .ou. . . premiers élémens du nouvel art-science d'écrire et d'imprimer (Paris, 1797), 2, 20, which had a German translation (Paris, 1797) and new French edition as Pasigraphie et pasilalie (Paris, 1801). See Biographie universelle , 85 vols. (Paris: Michaud frères, 1811–62), s.v. "Maimieux."

Nomenclateur (for words of four characters) and the Grand Nomenclateur (for words of five characters), made up the second part of the Maimieux's pasigraphy. Each page of the tables contained scores of French words, arrayed according to de Maimieux's outline of knowledge.

He claimed much for this scheme. Unlike the "alphabetic chaos" of standard dictionaries, "the pasigraphic order is a natural order." Every word in the system could express "thought, state, action, or passion by means of a progressive analytic development, but without any analytic appareil ." The twelve grammatical rules governed declension, modification, conjugation, and enunciation, and, de Maimieux puffed, yielded up great logical and grammatical riches. The tables of the Indicule, Petit Nomenclateur , and Grand Nomenclateur also provided a mappemonde intellectuel of visual, analytic, and mnemonic convenience.^[21]

Although the printer might have complained about having to cast a new font of type (which might never be used again), de Maimieux was fortified by enthusiasm. The relative complexity of concepts would be evident at a glance, measured by the number of characters used in a given word; nature and knowledge could be surveyed with ease from an armchair. De Maimieux proclaimed his lowered expectations, at least by comparison to those held by Wilkins and others in the creation of universal characters in the late 17th century. De Maimieux aimed, not at a representation of truth, but at a handy chart to facilitate communication across linguistic boundaries.

The coordinates in this mappemonde covered varied lexical terrain. Column 9 of the Indicule concerned simple aspects of "science, grammaire, calcul." At the 6th tranche , line 1, de Maimieux put "Plus, au plus, de plus"; four lines down he placed "Beaucoup, bien, très, fort."^[22] Cadre 6, column 6 of the Petit Nomenclateur listed civil acts, including privilège, procès-verbal , and confronter ; more lively were the inhabitants of cadre 3, column 6, tranche 4: "Rhinoceros, girafe, onagre, zèbre, buffle, cerf, daim, rène, chamois, gazelle,

[21] Ibid., 5, 22, 32.

[22] Ibid., 2e Partie, 6.

grisbock, chevreuil, cabri, vigogne, musc, élan, original." In the Grand Nomenclateur de Maimieux mapped out more complex concepts, with columns for such diverse categories as Dieu, etre, esprit; astres, signes, élémens; insouciance; actes religieux; meubles; arts chymiques . He paid tribute to the reigning confusion of measures and money by supplying an additional four-page alphabetic, multilingual list of available units.

De Maimieux thus borrowed from the encyclopedic spirit of the age, reckoned with the profusion of measures and tongues, marshaled concepts of universal grammar, and hammered his system into a numerical matrix. By analogy to latitude and longitude, de Maimieux's characters could lead a reader straight to the location of the idea in the "topographic map of the domain of thought."^[23] De Maimieux followed this with a Carte générale pasigraphique in 1808. Containing some 8,000 words, the tableau of 1808 was nearly as complete as the original version, but multiplied pasigraphic confusion by its incompatibility with its predecessor.^[24]

Both de Maimieux and his defenders resorted to mathematical terms in describing the merits of his pasigraphies. De Maimieux saw his system as "a sort of general glossomètre which will give the measure of the richness of each language [and] rectify the inexactitudes of translations, in applying to languages a common scale."^[25] One of his disciples went so far as to describe algebra as "that pasigraphy of quantities."^[26]

De Maimieux's pasigraphy is a multidimensional variant on proposals in the 17th and 18th centuries for numerical dictionaries—polyglot dictionaries with numbered entries. All these proposals built upon what was seen as the universal intelligibility of Arabic numerals.^[27] As Robert Boyle had written in the mid-17th century,

[23] De Maimieux's preface to his Epître familière (1802), quoted by Knowlson, Universal language schemes , 153. Cf. ibid., 156, 160, 260, and Armand-Charles-Daniels, comte de Firmas-Périès, Pasitélégraphie (Stuttgart: Metzler, 1811), 21.

[24] Michaud, Biographie universelle , s.v. "Maimieux."

[25] Firmas-Périès, Pasitélégraphie , 28, quoting de Maimieux.

[26] Ibid., 27, quoting Charles Dalberg.

[27] See the discussion of universal language proposals leading to that of Leibniz, in Louis Couturat, La logique de Leibniz d'après des documents inédits (Hildesheim: Olms, 1969; reprint of 1901 edition), 51–3.

"Since our arithmetical characters are understood by all the nations of Europe the same way, though every several people express that comprehension with its own particular language I conceive no impossibility that opposes the doing that in words, that we see already done in numbers."^[28] The idea that mathematical concepts, especially the concepts of number and their representation by Arabic numerals, were universally comprehensible, held persistent appeal to those who aimed at universal, rational languages. In 1801, for example, Zalkind Hourwitz proposed a Polygraphie that relied on the assignment of a number to each word in a basic polyglot dictionary. The same number thus served to designate words with the same meaning in several languages.^[29] As the subtitle of his book indicates, Hourwitz intended polygraphy to facilitate the art of communication across national boundaries. Not long afterward Jacques de Cambry did likewise, explicitly invoking the blessings of numeracy in his Manuel interprète de correspondance, on Vocabulaires polyglottes alphabétiques et numériques en tableaux .^[30] His mappemonde encompassed not merely Francophones, but also speakers and writers of Italian, Spanish, German, English, Dutch, and the ever-vexing "Celto-breton."

Mechanical Communication

In the final decade of the 18th century, French revolutionary expansionism lent special urgency to the problem of long-distance communication.^[31] The logistic necessity of swift and sure communi-

[28] Boyle to S. Hartlib (1647), in Boyle, Works, 1, 22, quoted in Knowlson, Universal language schemes , 21.

[29] Zalkind Hourwitz, Polygraphie: ou, L'art de correspondre, à l'aide d'un dictionnaire, dans toutes les langues, même dans celles dont on ne possède pas seulement les lettres alphabétiques (Paris: Chez l'auteur, an IX). Cf. Knowlson, Universal language schemes , 259, on Montmignon, La clef de toutes les langues. Biographie universelle , s.v. "Montmignon," refers to the "numérotage des mots."

[30] Paris: Mme Johanneau, 1805.

[31] A number of solutions to the problem had already been tried. Aeschylus' account of the Persian wars, for example, described signal torches; beacons warned England of the approach of the Spanish Armada; the future King James II devised a system of signal flags for communication at sea. Thomas Northmore, writing in the 1790s, called the telegraph "new only in name": A quadruplet of inventions [etc.], 2d ed. (Exeter: Trewman and Son, 1799; 1st ed. 1796), 7.

cation with allied military units on distant fronts called for a language simple enough to be transmitted over many miles. Here was an obvious and practical instance of the importance, as proclaimed by philosophers, for a simple, clear, expressive, unequivocal language. In most of the late 18th-century proposals for an optical or military telegraph, the preferred means of transmission were mechanical; the elements of the message were geometrical or numerical.

The first telegraph to attract international attention was the invention of Claude Chappe. Chappe began by exploring the possibility of electrical telegraphy.^[32] In 1790 he abandoned the electrical for the mechanical as a means of transmitting language and built a prototype optical telegraph. By 1791 he had extended its range to 15 kilometers. Revolutionary crowds, however, feared telegraphy as a royalist instrument and tore down Chappe's Parisian stations.^[33]

The apparatus consisted of a 1-foot pole atop a tower or tall building, a 14-foot crossbar pivoting at the center, a 6-foot arm at each end of the crossbar, control wires by which an operator could manipulate the arms, and lanterns on the arms for nighttime operation. The crossbar could be positioned either horizontally or vertically; the arms then pivoted around the ends of the crossbar. Each arm could assume seven different positions with respect to the crossbar. Each possible position was assigned a number.

With the help of a friend familiar with diplomatic codes, Chappe formulated a manual of nearly 10,000 words. As in the numerical dictionaries,^[34] each word corresponded to a number. The positions of

[32] Cf. T.K. Derry and Trevor I. Williams, A short history of technology from the earliest times to A.D. 1900 (New York: Oxford University Press, 1961), 623–4; Keith Dawson, "Electromagnetic telegraphy: Early ideas, proposals and apparatus," History of technology, 1, (1976), 113–42; Shelby T. McCloy, French inventions of the eighteenth century (Lexington: University of Kentucky Press, 1952), 41. For an account of the claims of Christoph Ludwig Hoffmann, see Hans Walter Wichert, "Ein Vorschlag zur optischen Telegraphie aus Westfalen ausdem Jahre 1782," Technikgeschichte, 51:2 (1984), 86–93.

[33] K.T. Rowland, Eighteenth-century inventions (Newton Abbot: David and Charles; New York: Barnes and Noble, 1974), 154; McCloy, Inventions, 42–3.

[34] See, for example, Jacques Cambry, Manuel interprète de correspondance, ou vocabulaires polyglottes alphabétiques et numériques en tableaux (Paris: Johanneau, 1805), plus other examples cited by Firmas-Périès, Pasitélégraphie, 22–4.

the arms signaled first the page number and then the numbered word on that page. Eventually Chappe added two more code books—one containing phrases and another containing place names. Operators would then transmit sets of three signals: the first indicated which code book to use; the second, the page number; and the third, the number of the word on the page. The scheme thus resembled Hourwitz's numerical dictionary and de Maimieux's matrix of knowledge. As a reviewer commented, Chappe had coupled his mechanical apparatus with an analysis of language: "The table of characters . . . is a tachygraphic method. . . fruit of [Chappe's] long and laborious meditations."^[35] In the interest of enhancing its tachygraphic possibilities, a member of the Chappe organization later suggested the use of two-person teams, one to dictate in a sort of numerical shorthand what he saw on the distant tower, the other to record the information.

Through the good offices of his brother, a deputy in the Legislative Assembly, Chappe's system came to the attention of the Assembly's committee on public instruction. After the demise of the Assembly, its successor, the National Convention, was persuaded in April 1793 to order a test "in order to determine the utility of the telegraph" and to consider the use in war of such a "rapid messenger of thought." The commissaires appointed by the Convention—Lakanal, Arbogast, and Daunou—were joined by "several celebrated savants and artists" on the day of the test.^[36] They were apparently impressed: Lakanal's official report on the merit of Chappe's telegraph envisioned its "great utility . . . especially in wars on land and at sea, where prompt communication and rapid awareness of maneuvers can have a great influence on success."^[37] The positive report led to Chappe's appointment as official ingénieur-télégraphe and, more telling, a high-priority claim on scarce supplies with which to construct a full-scale telegraph system. In September 1794 public enthusiasm was

[35] Lakanal, Rapport sur le thélégraphe [sic] du citoyen Chappe (Paris: Imprimerie nationale, n.d.), 2.

[36] Lakanal, Rapport sur le télégraphe (Paris: Imprimerie nationale, an III), 3; Rapport sur le thélégraphe (n.d.), 2.

[37] Lakanal, Rapport sur le thélégraphe (n.d.), 1–2.

buoyed (and suspicions about Chappe's loyalties presumably quelled) when the newly constructed telegraph line carried to the capital news of the capture of Condé. A year later the Directory authorized continued support of Chappe's venture, and in 1798 a second line (connecting Paris and Strasbourg) was completed. Eventually the system consisted of eight principal lines and covered some 3,000 miles.^[38]

News of the successful deployment of Chappe's system spread quickly. The first printed version of the "alphabet Chappe" appeared anonymously in Leipzig in 1794; periodicals carried accounts of the bullétin télégraphique reporting the capture of Condé a second edition of Chappe's Beschreibung und Abbildung des Telegraphen appeared in 1795. The need for an optical telegraph was widely felt. From 1794, for example, committees of the Patriotic Society of Hamburg had discussed the development of a telegraph system to replace the cumbersome apparatus of messenger boats, observers, and towers used to regulate shipping traffic between Hamburg and Cuxhaven. The Society's secretary, Friedrich Johann Lorenz Meyer, also noted the military potential of a telegraph system. On a visit to Paris in 1796, Meyer witnessed a demonstration of Chappe's optical telegraph, and carried the news of its success back to Hamburg, where a select committee was convened to study its merits. Their cost-benefit analysis argued against establishing a Chappe-style system in Hamburg, on grounds both of cost (estimated at 20,000 marks) and of poor visibility in the northern German climate.^[39]

[38] McCloy, Inventions, 44–5; Rowland, Eighteenth-century inventions, 154; Derry and Williams, Short history, 622; Henri Gachot, Le télégraphe optique de Claude Chappe. Strasbourg-Metz-Paris et ses embranchements (Saverne: Imprimerie et Edition Savernoises, 1967), 44.

[39] Henry E. Lowood, Patriotism, profit, and the promotion of science in the German Enlightenment: The economic and scientific societies, 1760-1815 (Ph.D. dissertation, University of California, Berkeley, 1987; DAI 49/06A, 1563), 177–8. Cf. Friedrich Johann Lorenz Meyer, Ueber Telegraphie und über Errichtung e. telegraph. Correspondenz zwischen Hamburg und Kuxhaven (Hamburg, 1798), as cited in Gesamtverzeichnis der deutschsprachigen Schrifttums (GV): 1700–1910 , 160 vols. (Munich: Saur, 1979–87), s.v. "Meyer." Meyer also promoted the use in Hamburg of the French metric system: Lowood, Patriotism, profit, and the promotion of science, 178–9.

The issue of the optical telegraph also engaged the attention of savants and royalty elsewhere in the German states. In Berlin, the academician and chemist Franz Karl Achard demonstrated his version of the telegraph to Friedrich Wilhelm II in 1795, successfully sending such meaningful messages as "The King is loved by his subjects just as much as he is feared by his enemies." As reward for his efforts, Achard received a substantial bonus of 500 Reichstaler, equal to one-third of his annual salary at the Berlin Academy.^[40]

Another savant inspired to imitate or improve upon Chappe's invention was the Swedish academician and natural philosopher Abraham Niklas Edelcrantz. He seized on its military possibilities: "In case of war," a telegraph would afford the possibility of "quick communication for discussion between several armies or divisions of the same army."^[41] Edelcrantz began his investigations in September 1794 with variants on Chappe's design of crossbars and pivoting arms. He then switched to a lattice of ten "holes" or windows with shades visible in daylight and lanterns behind them at night. This arrangement permitted 1,024 different signals. The first trials of the Swedish telegraph took place between Stockholm and Drotningholm on 30 October and 1 November 1794. Demonstrations of the system the following year were conducted in "the presence of the king, the regent, and the whole royal court."^[42]

Like Chappe, Edelcrantz compiled a codebook, which he called a telegraphische Chiffren-Tabelle . It contained short words, syllables, and a few phrases, each corresponding to a three-digit number.^[43] Each

[40] Karl Hufbauer, The formation of the German chemical community (1720–1795) (Berkeley, Los Angeles, London: University of California Press, 1982), 206. See also Allgemeine deutsche biographie, s.v. "Achard"; Dieter Herbarth Die Entwicklung der optischen Telegrafie in Preussen (Cologne: Rheinland-Vert., 1978); Volker Aschoff, "Franz Karl Achard und die optische Telegraphie," Technikgeschichte, 144 (1977), 246–54.

[41] Abraham Niklas Edelcrantz, Abhandlung über Telegraphen und ein Versuch zu einer neuen Einrichtung derselben, transl. J.J.F. Plagemann (Hamburg: Meyn und Mahncke, 1802), 82 fn. First published in Swedish (1796); translated into French as Traité des télégraphes, transl. Hector B. (Paris: C.F. Patris, an IX [1801]).

[42] Edelcrantz, Abhandlung, 22–3, 25, 26–8; quotation on 87.

[43] Throughout his discussion of the Chiffren-Tabelle (and also in his assessment of competing systems), Edelcrantz showed himself to be well acquainted with combinatorial mathematics. This was just at the time that Karl Friedrich Hindenburg and his colleagues were issuing their Sammlung combinatorisch-analytischer Abhandlungen, 2 vols. (Leipzig, 1796–1800). Cf. Robin E. Rider, A bibliography of early modern algebra, 1500–1800 (Berkeley: Office for History of Science and Technology, 1982).

number designated one of the 1024 signals possible with the ten-window lattice. Edelcrantz saw his codebook as the basis for a universal language: "A cipher-table or dictionary explaining signs for all languages should be made to go along with this language-instrument, which can be completely portable."^[44]

Thomas Northmore, inspired by what he knew of Polybius' telegraph, also linked his proposal for a Nocturnal or Diurnal Telegraph (which used reflecting lamps moved by a winch) with an account of his new universal character. He proclaimed the "ground-work of the whole super-structure" to be "that if the same numerical figure be made to represent the same word in all languages, an universal medium is immediately obtained." "Diversity of idioms" would prove no obstacle in Northmore's simplified language, which required as a "constant companion" only a "small pocket numerical dictionary," containing some 5,000 to 6,000 "select words."^[45]

One of de Maimieux's royalist disciples likewise saw the connection between universal language and telegraphy. The comte de Firmas-Périès, who served in the army of the prince de Condé, recognized the versatility of de Maimieux's pasigraphy and reformulated it for use in telegraphy. Firmas-Périès' mechanical semaphore system, which he labeled "pasitelegraphy," converted de Maimieux's latitude and longitude indicators to arrangements of wooden "hands" on a large clock face operated by chains and pulleys à la Vaucanson.^[46] To decipher the message, the operator turned to de Maimieux's tables of words (and knowledge).

Reports concerning the French telegraph, including one retrieved from the pocket of a French prisoner in 1794, also inspired English inventors, including John Gamble, chaplain of the staff of H.R.H.

[44] Edelcrantz, Abhandlung, 86 fn., with a manuscript annotation "Pasiphrasie."

[45] Northmore, A quadruplet of inventions, 10, 17–8, 23–4. Northmore carried the mathematical imagery further by alluding (on p. 26) to algebraic powers as analogous to the sign he used for plural words. For his account of earlier examples of numerical universal characters, ibid., 27.

[46] Firmas-Périès, Pasitélégraphie, preface, 348–9, 355; Biographie universelle, s.v. "Firmas-Périès." Cf. Knowlson, Universal language schemes, 160.

Frederick, Duke of York and Albany. As would Edelcrantz, Gamble analyzed "the different modes which have been, or may be adopted for the purpose of distant communication"—this at the request of the Duke.^[47] Gamble recognized the need for a "figurative language" adequate for communication and capable of quick transmission, and settled on a portable apparatus of five shutters ("lever boards"), which in various combinations denoted the letters of the alphabet. The use of lamps behind the shutters looked promising for nighttime transmissions.^[48] The Admiralty implemented Gamble's suggestion on a series of "telegraph hills" between London and Deal as early as 1796 and found that a short message could be relayed in a minute's time. Like the other systems of the late 18th century, the Admiralty telegraph was quick (though labor-intensive) and promptly proved its value for the transmission of military intelligence.^[49]

The efficiency of mechanical-optical telegraph systems itself came under scrutiny in Edelcrantz' study. He treated the visibility of signals at a distance like a problem in exact experimental physics, and assessed the accuracy of contemporary telescopes, threshold values for the angular diameter of an object visible at a given distance, and differential effects of color and humidity on visibility. The analysis was informed by Edelcrantz' familiarity with contemporary work on experimental optics, meteorology, and other branches of 18th-century physics. Indeed, Edelcrantz saw the possibility that a network of telegraph operators and stations, suitably equipped with an array of scientific instruments, might also advance the cause of science: "Every telegraph is a real Observatory, which can become an

[47] From the subtitle of his Observations on telegraphic experiments (London, 1795?). Cf. Gamble, An essay on the different modes of communication by signals (London: S. Gosnell for W. Miller, 1797), 69, 71.

[48] Gamble, Observations , 77, 13–5. On the difficulties of using lamps, see Gamble, An essay , 114.

[49] Derry and Williams, Short history , 622–3. Cf. Edelcrantz, Abhandlung , 89, and figures 35–42; McCloy, Inventions , 48; Tom W. Holmes, The semaphore: The story of the Admiralty-to-Portsmouth shutter telegraph and semaphore lines 1796 to 1847 (Ilfracombe, Devon, 1983). McCloy also describes a system devised by Richard Lovell Edgeworth as early as 1767 and put into operation in Ireland circa 1797 to contend with the threat of a French invasion. On Gamble's difficulties with the Admiralty, see Gamble, An essay , 89–91.

astronomical one, with the appropriate instruments and the understanding of the director, and science would be enriched with new discoveries."^[50]

Signs and Thought

The larger problem of the connection between signs and thought once again claimed the attention of philosophers and linguists in the last third of the 18th century. In his history of universal language schemes, Knowlson has identified some of the reasons for this renewed interest. Studies of the origin of languages and of general grammar helped to stimulate thinking on the subject by focusing on the evolution of nomenclature and the logical significance of syntactical structure. What Knowlson calls a "general climate of rationalization," as demonstrated by the design of new systems of schools and of weights and measures, promoted the search for a new and rational language. Political events and trends also played their part. Hopes that a rationally constructed language would break down political and cultural barriers were fed by republican aspirations to extend the realm of liberté, égalité , and fraternité . The reconstruction of chemical language, and its happy consequences for the science of chemistry, lent an optimistic note. Condillac's views of language also attracted more attention at the end of the century as editors prepared a complete edition of his writings. It would include the first appearance in print of La langue des calculs , left unfinished at Condillac's death in 1780.^[51]

A series of essays in the memoirs of the Berlin Academy evinces the widespread interest in "the reciprocal influence of reason on language and language on reason" (the phrase comes from the title of Sulzer's memoir of 1767). In his essay of 1774, for example, Dieudonné Thiébault argued in favor of a universal language, rejecting Johann Gottfried Herder's contention that such a language would be nearly useless. Thiébault envisioned a language with a limited number

[50] Ibid., 85.

[51] Knowlson, Universal language schemes , 149, 161–3, 172–3, quotation on 163.

of base words or concepts, a uniform system of derivation, and a regularization of grammatical relations. Such a language would provide, he claimed, "at once the best book of logic and metaphysics." Castillon took up a similar question at the end of the century, in his "Mémoire touchant l'influence des signes sur la formation des idées."^[52]

Anne-Robert-Jacques Turgot, well acquainted with attempts to rationalize activities of the French state, also concerned himself with the connections of language, logic, and mathematics. He suggested that "The study of language, if well done, would perhaps be the best of logics," since language served as both the "expression" and the "measure" of thought. Language exemplified Turgot's view of progress as passage through various states of perfection, each state accompanied by new symbols. For Turgot, as his biographer Frank Manuel has explained, the language of mathematics could serve as "an impregnable barrier against retrogression"—"the armor of numbers and equations" in defense of reason. Turgot's protégé Condorcet also envisioned a philosophical language, clad in algebraic notation, applicable to all of knowledge and assured, by virtue of its mathematical foundation, of precision.^[53]

Among those who thought that the whole matter of language and its relation to thought bore reexamination were the idéologues , who, building upon the ideas of Condillac, Turgot, and Condorcet, launched a thorough review of the question of signs and thought. Idéologie (the term was introduced by Destutt de Tracy) tackled the analysis of sensations and ideas, and drew upon the 18th-century discussion of general grammar and logic. The Institut national de France, and in particular its Classe des sciences morales et politiques,

[52] Sulzer, in Akademie der Wissenschaften, Berlin, Mémoires , 1767, 413–40; Thiébault, "Observations générales sur la grammaire et les langues," ibid., Nouveaux mémoires , 1774, 520–2; Castillon, ibid., Mémoires , 1799–1800, Classe de philosophie speculative, 3–28.

[53] Turgot, Réflexions sur les langues , quoted in Frank Manuel, Prophets of Paris , 30; ibid., 332–3, quotation from Manuel on 43; Keith Michael Baker, Condorcet: From natural philosophy to social mathematics (Chicago: University of Chicago Press, 1975). For Condorcet's view of Condillac, see Baker, "Un 'éloge' officieux de Condorcet: Sa notice historique et critique sur Condillac," Revue de synthèse, 88:47–8 (1967), 227–51.

proved to be a hotbed of Idéologie , and its members debated vigorously the connection between signs and thought. To encourage consideration of this issue, the Classe set as its first prize question, "To determine the influence of signs on the formation of ideas."^[54]

Among the entries was an essay by P.F. Lancelin. His work received honorable mention, and in expanded form was subsequently published under the title Introduction à l'analyse des sciences, ou de la génération, des fondemens, et des instruments de nos connoissances.^[55] As the title page announced, Lancelin aimed at nothing less than the perfection of human reason. He saw language as the lever of the mind and the perfection of language as the best mechanism for assuring the reign of reason and for avoiding error and prejudice.^[56] The mechanical metaphor is worth noting. As an Ingénieur-constructeur de la Marine française, Lancelin was a product of the technical training establishment in France, and his "analysis of the sciences" bears the stamp of his training, which saluted the military virtues of mathematics and mechanics. Lancelin's intent was to take apart the human mind in the same way an engineer takes apart a machine.^[57]

The influence of Condillac is also evident. Like Condillac, Lancelin reduced the art of thinking to the use and analysis of a well-constructed language—"a language based on good observations, correct ideas, and exact facts"—and sought to reveal the development of the human mind by examining "the exact formation of mathematical languages." Language was an analytical method; properly used, it would enable the mind to soar like "an eagle over the whole globe of human knowledge." For Lancelin, as for Condillac, algebra—the language of mathematics—was just such an analytic method and as such deserved careful attention, since a method that delivers exactitude in one sphere of human knowledge will do so in all.^[58]

[54] Cf. Knowlson, 174–5.

[55] In 3 vols. (Paris: Imprimerie de Bossange, Masson et Besson [etc.], an IX).

[56] Lancelin, Introduction, 1 , xxxv.

[57] Ibid., xvi, xviii.

[58] Ibid., xxx, vi, xxxviii, xxxvi, xxi, xxii, 284. See, for comparison, the words of J.-J. Rossignol, "Que l'Arithmétique nous fait aller à pied, que la Géométrie nous fait voyager à cheval et que l'Algèbre nous donne des ailes pour planer dans les airs," in his Collection complète (1804), 94.

Lancelin shared in the general Enlightenment enthusiasm for mathematics and professed the common faith in the correctness and certainty of mathematical reasoning. But in order to conclude that the method that gives us exact knowledge in the realm of mathematics can do so in other realms of thought, Lancelin had to consider why mathematics works at all. Mathematics deals with what Lancelin called "measurable ideas"—those formed by successive addition or repetition of identical elements. The restriction to measurable ideas clearly enhances the certainty of mathematical reasoning, Lancelin argued, but it is not the sole cause for that certainty. At least as important as a guarantee of correct reasoning is the art of mathematical signs. Or, turning the argument around, differences of opinion outside mathematics are to be blamed as much on the inexactitude of signs as on the inexact formulation of the ideas they represent.^[59]

In an attempt to improve signs and thus thought, Lancelin built upon Condillac's contention that propositions, judgments, and equations are all essentially the same—that is, expressions of the formation of complex ideas out of simple elements. He concluded that ordinary sentences can usefully be translated into a sort of algebra. He offered as example the statement "gold is yellow, heavy, meltable, and malleable," which he transformed into the "equation" O = a + b + c + d , where O denotes gold, a denotes yellow, b denotes heavy, and so on. By a liberal use of algebra, the language of mathematical analysis, Lancelin thought he could facilitate the application of analysis outside the normal realm of mathematics.^[60]

Nor did Lancelin stop there. He advanced an ambitious plan for representing "in a series of synoptic tables the ideas and languages of all peoples." His idea for tables of knowledge and nature was scarcely novel.^[61] What is noteworthy, however, is the way the suggestion flowed directly from his ideas about the perfectibility of language and the privileged nature of mathematical reasoning. The whole discussion was embedded in an extravagant reform program that also

[59] Lancelin, Introduction, 1 , 90, xxxv.

[60] Ibid., xxxiii, 224. Cf. 285–95, and the plate opposite 280.

[61] Ibid., 297, xxxiii; cf. table at end of vol. 2. See also Slaughter, Universal languages and scientific taxonomy .

included the perfection of naval engineering, a complete overhaul of the French educational system, a new approach to solar astronomy, and an "experimental physics of the soul," in which the "thinking force" could be measured and expressed in an analytic formula.^[62] However ambitious and impractical his plans, it is evident that they were shaped by his faith in mathematics.

A more sober and critical approach was taken by Baron Joseph Marie de Gerando in his prize-winning essay for the competition sponsored by the Institut national. In considering the relation of signs and thought, de Gerando compared analysis and synthesis in both mathematics and metaphysics, argued for the privileged nature of mathematical knowledge, and presented a careful critique of proposals for a philosophical language and an algebra of thought. His essay, published in four thick volumes, constituted a thorough reexamination of ideas on language and mathematics from the mid-17th century to the end of the 18th century.

Like so many of the authors whom he discussed, de Gerando deplored the abuse of words and urged that we hasten to discover a remedy. He thus granted the desirability of reforming language, but did not see flaws in language as the root of all wrong thinking. Instead, he blamed the imperfections of language on imperfect thought.^[63]

He then compared the methods of analysis and synthesis in both philosophical and mathematical contexts and decided in favor of analysis (although not with the same determined enthusiasm as had Condillac). De Gerando was especially interested in the "prodigious successes" of algebra, which seemed to offer the greatest hope to those who sought to perfect all abstract sciences, because the use of algebra permits us both to display the relations between quantities and to eliminate extraneous information. His analysis focused on the advantage of algebra over ordinary calculation or over reasoning using words, the praiseworthy character of the signs used in algebra, and

[62] Lancelin, Introduction, 1 , xlv, and the conclusion of section III.

[63] De Gerando, Des signes et de l'art de penser considérés dans leurs rapports mutuels , 4 vols. (Paris: Goujon fils, Fuchs, Henrichs, an VIII), 4, 43, 238, 240, 242, 252.

the connection between algebraic signs and the nature of the ideas they represent.^[64]

De Gerando also drew attention to a particular feature of algebraic calculations: there is no need at the outset, as there is in arithmetic, to determine an idea before establishing its relations to other quantities. By using signs for unknown and known quantities alike, "we are not stopped by our own ignorance." In citing the virtues of algebraic analysis, he quoted Laplace: "Such is the fecundity of analysis, that it suffices to translate particular truths into this universal language, in order to see how to proceed from these expressions to a host of new and unexpected truths. . . . Thus the geometers of this century, convinced of its superiority, have applied themselves to extending its domain and pushing back its boundaries."^[65]

De Gerando's enthusiasm for mathematics in general, and for algebraic analysis in particular, was qualified by his recognition of the privileged character of mathematical ideas. He divided all ideas into four categories, of which the most straightforward and least problematic was the class of "ideas of simple modes." This class is roughly equivalent to Lancelin's category of measurable ideas. The properties and advantages of "la langue du calcul," recalling Condillac's phrase, were to be seen as a "privilege" of such simple ideas: the essential identity of the elements of such ideas means that both the nature of the elements and their mode of combination are already determined. Thus mathematicians reason only on clearly conceived and unequivocal notions.^[66]

De Gerando then undertook an evaluation of schemes proposed for philosophical or universal languages in the hopes of demonstrating which reforms are desirable and which are feasible. He defined the desiderata for an artificial language—analogy of signs to ideas, analogies of signs among themselves, simplicity of the whole system as well as of its details, neat and precise distinctions between signs, and "a sufficient abundance" of signs—and described the general categories into which all philosophical languages can be divided.

[64] Ibid., 2 , 211–2, quotation on 212. Cf. 218–9.

[65] Ibid., 2 , 218–9, 215, 213–4; Laplace quoted in ibid., 4 , 217.

[66] Ibid., 2 , 198, 203; 4 , 215.

Using these categories, and working from a thoughtful analysis of mathematical reasoning itself, he set up criteria for the evaluation of universal and philosophical languages. The conclusion was a gloomy one. He found—sometimes by use of numerical assessments of the set of base concepts or the complexity of the character systems—that such language proposals necessarily fell far short of the desired ends. Thus, for each category, including the pasigraphies of the 1790s, he found it impossible to satisfy the necessary conditions with which he began. (De Maimieux's pasigraphy came in for special criticism because it forced the distribution of ideas to conform to a scheme requiring equal numbers of division or subdivisions, regardless of content.) Hence the goal of a truly philosophical language, however desirable, was an impossible dream.^[67]

De Gerando also traced the attempts to create an algebra of thought from Ramon Lull and Athanasius Kircher through Leibniz to Lambert and other 18th-century proponents of symbolic logic. Here, too, de Gerando offered a careful and ultimately pessimistic critique, warning that a true algebra of thought will require a large number of primitive ideas to be capable of handling more than very simple and general propositions. Indeed, the number of primitive ideas and symbols required will be prohibitively large. Unlike Lancelin, with his boundless enthusiasm for mathematics, de Gerando cautioned against confusing the "method of reasoning of geometers with the mechanical processes of their calculs ." Although geometers and metaphysicians share the same method of reasoning, he argued, we cannot assume that the virtues of mathematical algebra—"the simplicity of forms and the speed of execution"—will follow from an uncritical application of its procedures to metaphysics.^[68] He thus invoked the privileged character of mathematics in order to discount the likelihood that its procedures can be applied uncritically in realms of thought outside mathematics.

Although mathematics was an instructive and inspirational guide, the path chosen by 18th-century language reformers was steep and

[67] Ibid., 4 , 44, 80–1, 352, 353–5, 412, 435–6.

[68] Ibid., 4 , 448–9, 450, 451.

rocky. The efforts to construct artificial, universal languages made some progress toward rationalization, especially in replacing idiosyncracies of existing languages by means of new, regular schemes of word derivation. Most of these schemes were informed by at least the rudiments of combinatorics, and it was hoped that by pursuing the analogy to numbers language reformers would approach the precision and transparency characteristic of mathematical language. Establishment of a set of base words and categories capable of expanding to encompass all of human knowledge proved more difficult. Also elusive was the conversion of language into an instrument of discovery as effective and certain as mathematical reasoning.

Mechanicians of language, with their optical telegraph systems, were more successful. Taking inspiration from military need and encouragement from governmental coffers, they took account of combinatorics in constructing signaling apparatus, devised clear and unequivocal codes, and treated as essentially interchangeable words, numbers, and geometrical patterns. Using such systems, trained operators were able to transmit messages rapidly and without distortion over long distances. However, military exigencies, which called for the codebooks to remain secret, blocked hopes that telegraphic cipher-tables might serve as a universal language, at least in times of war.

Whether they met with success, as in the optical telegraph, or failure, as in the universal language schemes, efforts in the 18th century to invoke mathematics in the consideration of language were frequently self-conscious. Condillac, Lancelin, de Gerando, Gamble, Meyer, and Edelcrantz all took seriously the task of evaluating the possibility of achieving their objectives. Condillac, although he did not recommend the algebraicization of all fields of knowledge, still thought it wise to study algebra as the best available example of a well-made language. Lancelin's faith in mathematics, which exceeded Condillac's, led him to argue that it was practical to remake language in the image of mathematics. De Gerando's assessment was more careful and conservative. Edelcrantz and Gamble also looked for mathematical measures of the functioning of telegraph systems

and applied considerations drawn from mechanics and experimental physics in their appraisals.

Of the 18th-century attempts to employ mathematics in the construction of language, only the optical telegraph achieved practical success. The quest for a universal or philosophical language modeled on mathematics was an uphill struggle; indeed, in de Gerando's opinion, it was assured of failure. That language reformers were so determined to ground their projects in mathematical terms, whatever the outlook for success, is yet another measure of the pervasive appeal of mathematics in the late Enlightenment.