Orbit-Killers in the Zeeman Jungle

In 1918, while writing the third part of "On the quantum theory of line spectra," Bohr gave some thought to a notorious anomaly of the atomic theory. According to the correspondence principle, the only possible effect of a weak magnetic field on a spectral line was a triplet splitting, as a result of the correspondence of the quantum spectrum with the Fourier spectrum of the classical electronic motion, which would be subjected to Larmor's precession in such a field. This triplet structure was observed in the case of hydrogen and helium (although a better spectral resolution would have given different results). Alas, in the case of other atoms, many lines were known to split into more complex patterns. More specifically, an anomalous pattern appeared whenever the unperturbed lines belonged to narrow doublets or triplets (forming the so-called "complex structure" of spectra). And it disappeared—that is to say, the normal Zeeman triplets reappeared—as soon as the magnetic splitting became much larger than

[145] Bohr [1923f], [507]-[509]. See also Bohr 1923e; BCW 4: [576]-[578].

[146] Pauli to Sommerfeld, 6 June 1923, PB , no. 37; Kramers 1923b, 557.

the complex structure, as F. Paschen and E. Back had observed for the first time in 1912.^[147]

Bohr concluded: "These [anomalous Zeeman] effects which clearly have intimate connection with the unknown mechanism responsible for the doubling of the lines can obviously not be explained on the basis of the general considerations mentioned above [Larmor theorem and correspondence principle]." He further alluded to a possible connection of this anomaly with the absence of paramagnetism for many elements despite a nonvanishing magnetic moment (in the ring model). The natural way out was to admit a violation of Larmor's theorem, and a violation of ordinary mechanics for the interactions responsible for the complex structure and the anomalous magnetic effects.^[148]

In the same text of 1918 Bohr attributed the complex structure to an interaction between the atomic core and outer electrons, and gave an a priori reason to expect a failure of ordinary mechanics in this interaction: the corresponding perturbation of the core could not be calculated on the basis of ordinary mechanics because a core made of electron rings was mechanically unstable. When, in September 1922, Bohr finally made up his mind to publish this text (as the third part of "On the quantum theory of line spectra"), he mentioned in an appendix that the latter argument remained valid after the abandonment of the ring model, because the atomic core was still mechanically unstable (as explicitly proved by Kramers in the case of a heliumlike core).^[149]

As a corollary of the above discussion, from Bohr's point of view (at least) the complex structure and anomalous Zeeman effect could not be the source of the crisis of the quantum theory which arose in the winter 1922-23. Since 1918 he had been aware of the central difficulty connected with anomalous Zeeman splitting: if the correspondence principle were true, there could be no question of an explanation of this effect as long as the validity of ordinary mechanics in stationary states was maintained.

[147] See Forman 1968; also Mehra and Rechenberg 1982a. In the modern terminology the complex structure is generally called fine structure, since there is no essential difference between the fine-structure splitting in hydrogen and the complex structure in higher elements: both are relativistic effects mostly due to spin-orbit (and spin-spin) coupling. The spin-orbit coupling energy is a rapidly increasing function of the charge number (about (a Z) E₀ , if a is the fine-structure constant (a = e /hc ), and E₀ the fundamental energy of the outer electron). This explains why the fine structures of hydrogen and helium were the only ones which were not enough resolved to give an observable (anomalous) Zeeman splitting of their components (for a history of the latter point see Jensen 1985). As we shall presently see, in the old quantum theory the fine structure of hydrogen and the complex structure of higher elements were thought to be of different origins.

[148] Bohr 1922b (written m 1918), 111.

[149] Ibid., 105; Ibid., appendix (September 1922), 114.

In his eyes, the real source of the crisis of 1922-23 was the failure of the helium model, for this failure occurred precisely where he expected a major success, one able to serve as a paradigm of his second atomic theory.

Bohr's initial belief that the helium orbits were immune to a breakdown of ordinary mechanics was supported by two considerations: an empirical one, namely, that the corresponding Zeeman patterns were normal at the available precision; and a theoretical one, namely, that in excited helium, the inner system, a single electron on a quasi-circular orbit, was obviously stable. Therefore, Bohr expected troubles to start only with lithium, and from his point of view that would have affected only the finer details of the orbital motion, ones irrelevant to atomic building.^[150]

For some other specialists, like Sommerfeld and Landé, the anomalous Zeeman effect seems to have played a more important part in the recognition of a crisis in the quantum theory. However, they did not conclude that the Bohr-Sommerfeld theory was impotent in the realm of such problems until, in 1921-22, explicit, quantitative models of the Zeeman effect showed a necessary departure from Larmor's theorem. Bohr's earlier proof of a necessary breakdown of Larmor's theorem in higher atoms had little chance to convince them, since it rested on a not fully understood correspondence principle. They had no taste for Bohr's "philosophy" and were more attracted by the "number mysteries" (Sommerfeld) of atomic spectra, especially by the striking regularities of anomalous Zeeman patterns.^[151]

By late 1922, the gap between what Bohr could prove on the basis of the general assumptions of his quantum theory and what model-builders could simulate had considerably widened. The successful but eccentric models of the anomalous multiplets contributed to the feeling of crisis. On the positive side, Bohr and Pauli hoped that these models could perhaps serve as indicators of the extent and nature of the breakdown of classical concepts in the quantum theory. In 1925, while a new quantum mechanics was about to be born, Pauli judged this intuition to have been largely confirmed:

How deep the failure of known theoretical principles is, appears most clearly in the multiplet structure of spectra. While during the past few years physicists were able to derive empirical regularities of an astonishing simplicity and beauty, and of a very considerable generality, one cannot do justice to the simplicity of these regularities within the framework of the usual principles of the quantum

[150] See Bohr 1922b, 105, 117n..

[151] Sommerfeld 1920a. See Forman 1970.

theory. It even seems that one must renounce the practice of attributing to the electrons in the stationary states trajectories that are uniquely defined in the sense of ordinary kinematics.^[152]

In the following I will retrace the events that led Pauli to this questioning of ordinary kinematics.

Number Mysteries

In his Berlin lecture of April 1920, Bohr expounded his ideas on the nature of the magnetic anomalies. He emphasized the role of the correspondence principle in his conclusion about the failure of Larmor's theorem and manifested his belief that the complex structure of spectra and the anomalous Zeeman patterns had a common origin, to be found in a nonmechanical coupling between atomic core and outer electrons. As a result of this coupling, the motion of the outer electrons had to "possess a somewhat more complicated character than that of a simple central motion." Bohr also recalled Voigt's old theory of the Zeeman and Paschen-Back effects of the yellow sodium doublet, a simple model based on three coupled oscillators. This model, Bohr suggested, could be to the final quantum theory of the anomalous Zeeman effect what Lorentz's model had been to the Debye-Sommerfeld theory of the normal Zeeman effect. ^[153]

Meanwhile, Sommerfeld was trying to express the empirical data on complex structure and Zeeman multiplets in quantum-theoretical language. More specifically, he wanted to find a system of spectral terms and selection rules from which these data would derive. In the spring of 1920, this led him, in the case of the complex structure, to the "inner quantum number" i . To a given n_k term in the Rydberg scheme (n for the principal quantum number, k for the azimuthal one) corresponded a multiplet, whose terms were labeled i , according to the following table:

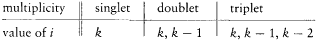
The selection rules were

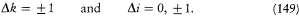
[152] Pauli 1926a, 167.

[153] Bohr 1920b, 58-59.

Even though he alluded to a "hidden rotation," Sommerfeld left the precise origin of the inner quantum number open.^[154]

A few months later Landè gave a similar treatment of the anomalous Zeeman patterns. In the presence of a (weak) magnetic field, a given (n, k, i )-term with the energy E₀ had to give rise to a multiplet with the energies

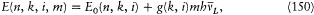
where 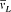is the Larmor frequency, m is the "magnetic quantum number," and g is the so-called Landé factor, which was always given as a simple rational fraction composed of k and i . For instance, g = 1 in the singlet case, and g = 2i /(2k - 1) in the doublet case. Any departure of g from unity directly implied a violation of Larmor's theorem. In analogy with the normal Zeeman effect Landé submitted the magnetic quantum number m to the selection rule

In the singlet and triplet case m was an integer restricted by 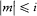. But, very strangely, it took the following half-integral values in the doublet case:

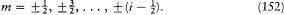
This normalization was the only one compatible with the selection rule Dm = 0, ± 1 and the symmetry of all Zeeman multiplets with respect to the unperturbed term.^[155]

If one believed that the magnetic quantum number had something to do with a precession around the magnetic axis, Landé commented, the selection rule D m = 0, ± 1 was the only one compatible with the correspondence principle (however, Sommerfeld preferred the rule Dm = 0, ± 2,

the values of m being twice Landé's). The same principle, or Rubinowicz's considerations on the angular momentum of radiation, suggested to Landé an interpretation of i as the total angular momentum of the atom. Bohr of course approved the reasoning and specified the type of motion to be associated with i (or j in Bohr's notation): a uniform precession of the plane of the outer electron orbit around the vector i.^[156]

In the meantime, Sommerfeld followed Bohr's suggestion for a quantum-theoretical version (Umdeutung ) of Voigt's spectrum, which promised to give, in the case of doublets, a generalization of Landé's formula that would apply for arbitrary magnetic fields. That is to say, he found a system of term energies and selection rules corresponding to this spectrum. For the splitting of a k -term in an arbitrary (small or large) magnetic field B, he derived

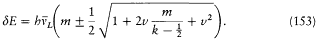
In this expression m takes the half-integral values ±½, 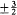, . . . , ±(i - ½, 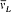is the Larmor frequency e B/4pmc , and 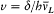, wherein d is the doublet width. The selection rules are Dm = 0, ± 1 and D (±) = 0. For small fields (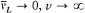), this gives

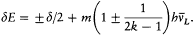
The first term yields the doublet in absence of field, and the second one reproduces Landé's expression (150) for the anomalous Zeeman effect of a doublet (since 1 ± 1/(2k - 1) = 2i /(2k - 1), with i = k , k - 1). In the large field limit (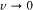), the general formula (153) reduces to

where m ±½ takes all integral values between - k and k . This reproduces the normal Zeeman pattern, in conformity with the Paschen-Back effect.^[157]

Heisenberg's Rumpf Model

In late 1921, a young student of Sommerfeld in Munich, Werner Heisenberg, managed to find a simple quantum-theoretical model that repro-

[156] Landé 1921a, 240. See, e.g., Bohr [1923f], [546]-[549].

[157] Sommerfeld 1922.

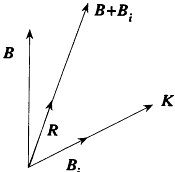
Figure 22.
Diagram for Heisenberg's Rumpf  model.

duced all regularities expressed in Landé's and Sommerfeld's formulae and even predicted new ones for the case of triplets. In the case of doublets in alkali atoms, to which I will limit my account, Heisenberg's model was based on the following assumptions:^[158]

1. The atomic core borrows (on average) from the outer electron an angular momentum R = ½ (in units h /2p ), leaving a momentum K = k - ½ the outer electron.^[159]

2. The rotating core (or Rumpf ) orients itself in a direction parallel or antiparallel to the total magnetic field B + B_i , wherein B is the external field, and B_i the magnetic field created (on average) by the outer electron at the place of the core (see fig. 22).^[160]

3. The angle between the angular momentum K of the outer electron and the external field (if any) is quantized according to K · B = mB , where m takes half-integral values (in units h /2p ).^[161]

[158] Heisenberg 1921. See Cassidy 1979.

[159] In a manuscript entitled "Memorabilia" (BMSS, 1917 or 1918) Bohr has written, "possibility of an explanation of anomalous Zeeman effect by assuming that in a magnetic field the total angular momentum round axis (equal to entire multiple of h /2p ) is divided in fractions between outer and inner electron," as probably suggested by the appearance of simple rational fractions (with the so-called "Runge denominator") in the expression of magnetic energy shifts.

[160] Heisenberg assumed that K and B, shared the same direction, even though the orbital picture of the outer electron leads to opposite directions.

4. The term shift of the atomic system is given by the model's magnetic energy, as determined by the ordinary theory of magnetic interactions.

This magnetic energy is

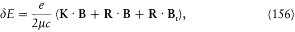
if m is the mass of the electron. Assumptions (1) and (2) lead to

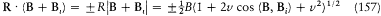
with v = B_i /B . The field B _i , created by the orbital motion of the outer electron, is parallel to the orbital momentum K , which implies

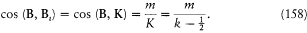
Assumption (3) and the formulae (156) and (157) finally give

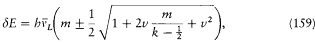
in agreement with the Voigt-Sommerfeld formula (153).

The success was great, but the method questionable, as Heisenberg himself commented in a first private report of his result to Pauli: "Success sanctifies means." From the point of view of the quantum theory of multi-periodic systems, the assumption (4) was the only conservative one: it maintained the classical expression for magnetic energies and the classical value (e /2m c) of the gyromagnetic factor for the core and the outer electron. The assumptions (1) and (3) departed from the usual quantization rules since they both involved half-integral quantum numbers, and since assumption (3) deliberately omitted the contribution of the core in the spatial quantization of the total angular momentum ("passivity of the Rumpf "). Further, the empirically known range of m , given by |m | < i , received no explanation.^[162]

Another major offense to general principles was contained in assumption (2): if classical mechanics applied to the motion in the stationary states of the Rumpf model, the equations of motions had to be

[162] Heisenberg to Pauli, 19 Nov. 1921, PB , no. 16.

for the total angular momentum J = R + K , and

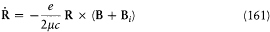
for the angular momentum of the core. The first equation implies a precession of J around B, while the second, if assumption (2) is to be true, implies the permanence of R . These two conditions are clearly incompatible.

In spite of general admiration for Heisenberg's ingenuity, no major theoretician could accept the transgressions of general principles contained in the work, save for Sommerfeld, the leader of what Heisenberg called the seminar of Atommystik. In his GÖttingen lectures, Bohr judged Heisenberg's paper "very promising" but found the involved assumptions "difficult to justify," which for Bohr meant perfectly intolerable. Bohr certainly admitted that any successful model of the anomalous Zeeman effect had to depart from the general assumptions of the Bohr-Sommerfeld theory. But he could not accept violations of rules that pertained to the corroborated part of the quantum theory. Accordingly, he judged Heisenberg's major sin to be his recourse to half-integral values of the azimuthal quantum number k (K in Heisenberg's notation). This conflicted both with the correspondence principle, according to which k had to correspond to the advance of the outer loops of the outer electron, and with the permanence of k , which was part of the foundation on which the building (Aufbau ) of atoms took place.^[163]

To Pauli and Landé, Heisenberg's worst offenses were the "passivity of the core" implied by assumption (3) and the violation of the theorem concerning the motion of angular momentum. In general, Pauli judged severely the opportunistic trend of Heisenberg's works in this period: "He [Heisenberg] is very unphilosophical, he does not care about a clear elaboration of the fundamental assumptions and of their relation to the previous theories." ^[164]

Sturm und Zwang in Copenhagen

From September 1922, Pauli spent a year in Copenhagen, and helped Bohr to explore, among other things, the mysteries of the anomalous Zeeman

[163] "Atomrnystik" is in Heisenberg to Pauli, 19 Nov. 1921, PB , no. 16; Bohr [1922c], [391]; Bohr 1923e; BCW 4: [647]n.

[164] Pauli's position was inferred from Heisenberg to Pauli, 25 Nov. 1921, PB , no. 17, and 17 Dec. 1921, PB , no. 18; Landé 1922: in this article Landé managed to do without the passivity of the core; Pauli to Bohr, 11 Feb. 1924, PB , no. 73.

effect. He first tried his best to find a multiperiodic model of this effect: one that would necessarily involve some extramechanical property of the core but that would nevertheless retain the regular quantum theory of multiperiodic systems with integral quantum numbers. As Bohr put it in March 1923, after the failure of Pauli's attempt, "It was a desperate attempt to remain true to the integral quantum numbers; we hoped to find in the very paradoxes an indication of the path along which one should search for a solution of the anomalous Zeeman effect."^[165]

Confronted with this failure, Bohr was pressed to locate the precise type of departure from ordinary mechanics needed to account for the success of Heisenberg's model. To this end he proposed the notion of unmechanischer Zwang , a form of nonmechanical stress occurring in the interaction between the atomic core and outer electrons. In order to be fundamental, this notion had to be independent of particular models, and of the specific labeling of multiplet terms favored by Sommerfeld and Landé. Thus Bohr reasoned in terms of the a priori statistical weights of the n_k states, for they had a direct empirical meaning, as the total number of terms in a magnetic field corresponding to a given value of n and k .^[166]

Consider the case of alkali doublets. On the one hand, the multiplicity associated with n_k had to be 2(2k - 1), because, according to Landé, there were 2k choices of m corresponding to i = k , and 2k - 2 choices of m corresponding to i = k - 1. On the other hand, for a vanishing coupling between core and outer electron, the statistical weight of the core had to be one in order to account for the diamagnetism of the corresponding noble gas;^[167] and the multiplicity of the outer electron would be that given by the Sommerfeld atom: 2k (Bohr and Sommerfeld excluded the value m = 0 on the grounds that the corresponding orbit is adiabatically connected to an orbit passing through the nucleus).^[168] The resulting total

[165] Bohr to Landé, 3 Mar. 1923, AHQP. At the end of 1922 Pauli sent a manuscript to Pauli containing an analysis of the anomalous Zeeman effect with integral quantum numbers only (see Heisenberg to Sommerfeld, 4 Jan. 1923, AHQP), but he soon surrendered to Heisenberg's objections (see Heisenberg to Pauli, 21 Feb. 1923, PB ) and admitted with Bohr a half-integral j .

[166] See the excellent account m Serwer 1977.

[167] Indeed, the absence of paramagnetism implies a vanishing net magnetic moment of the atom, and therefore no magnetic splitting of its energy. This result seemed to be at variance with Bohr's second atomic theory, which gave a unit angular momentum to all noble gases (due to the heliumlike K-shell, the other shells being saturated and symmetrical). Bohr avoided the contradiction by admitting a violation of ordinary mechanics already m the diamagnetic behavior of noble gases (cf. n. 148).

[168] Interestingly, the exclusion of m = 0 led to the correct number of Zeeman components for the levels of the hydrogen atom: to a n_k level in the Sommerfeld atom corresponds a definite value of J = k - ½ m the modern theory, which gives 2J + 1 = 2k magnetic sublevels.

multiplicity was thus 1 × 2k = 2k . This result was incompatible with the existence of a multiperiodic model of the interaction between core and electron, since in such a model an adiabatic variation of the coupling strength would have conserved the total statistical weight of an n_k term. ^[169]

In March 1923 Bohr concluded:

The coupling of the series electron to the atomic core is subject to a stress [Zwang ] which is not analogous to the effect of an external field, but which forces the atomic core to adopt two different orientations in the atom, instead of the single orientation possible in a constant external field, while, at the same time, as a result of the same stress, in the atomic assemblage the outer electron can only assume 2k - 1 orientations in an external field instead of 2k .^[170]

This way of splitting the multiplicity 2(2k - 1) into two factors was of course suggested by Heisenberg's Rumpf model. However, as Bohr and Pauli noticed, it explained why the S-states (k = 1) of alkali atoms were singlets instead of doublets, a fact for which Heisenberg had no satisfactory explanation. Indeed, in this case Heisenberg's model still gives two orientations for the Rumpf in the outer electron's field, and therefore a doublet (in absence of external field). Instead Bohr's Zwang gives the multiplicity 2(2k - 1) = 2, to be attributed to a singlet with double magnetic splitting. ^[171]

More fundamentally, Bohr's Zwang was in perfect harmony with his previous analysis of the origins of the failure of the helium atom. In both cases the stability of the relevant dynamic structure eluded ordinary mechanics and requested a nonmechanical stress. This lack of mechanical stability implied a violation of the adiabatic theorem, which in turn created a gap in the definition of energy (in the helium case) or in the definition of statistical weights (in the alkali doublet case).

Altogether, Bohr did not think that the anomalous Zeeman effect made the situation worse than it already was as a result of the failure of the helium atom. He concluded without any sign of a disturbance: "Under these circumstances [the necessity of an unmechanical Zwang ], we must presume that the coupling between the series electrons and the atomic core cannot be directly described according to the quantization rules of multi-periodic systems." Pauli reacted quite differently, identifying this failure of general principles as a personal failure, as appears in one of his letters to Landé (May 1923): "I am very depressed that I have not been able to

[169] Bohr 1923e, 274-277; Bohr [1923f], [525]-[530].

[170] Bohr 1923e, 276.

[171] Ibid., 279.

find a satisfactory explanation of these dumbfoundingly simple regularities [of the anomalous Zeeman effect] in terms of a model.^[172]

Double Magnetism and Vector Model

In reality, in spite of the lack of a proper model, Pauli had made great progress toward the identification of the necessary nonmechanical features of a possible model of the anomalous Zeeman effect, as he reported in the same letter to Landé. His approach started from the Paschen-Back effect. In this case the correspondence between the observed spectrum and a mechanical model was likely to be more transparent, for at least two reasons: the normal Zeeman splitting was observed, and the coupling between the core and the outer electron was negligible. For the Paschen-Back splitting of doublets, Sommerfeld and Heisenberg had

obtained (formula 155)

and the selection rulesDm = 0, ± 1; Dm_r = 0. The half-integral m and m_r respectively gave the angular momentum of the outer electron and of the Rumpf along B (in this approximation B and B + B_i are used interchangeably).

In order to comply with Bohr's requirement of integral k , Pauli introduced a quantum number m_k representing the component of the orbital momentum along B , and taking the 2k - 1 values 0, ±1, ± 2, . . ., ± (k - 1) (in conformity with Bohr's Zwang ), and wrote

which gives the same spectrum as Heisenberg's formula, provided that the selection rules are Dm_r = 0, and Dm_k = 0, ± 1, in conformity with the orbital interpretation of m_k . According to Heisenberg's Rumpf model, more generally according to Landé's interpretation of m = m_k + m_r as the projection of the total angular momentum along B , m _r had to measure the angular momentum of the core (along B ). Consequently, the factor 2 in front of m_r in Pauli's formula meant a double magnetism of the core.^[173]

Pauli found another indication of this double magnetism in a study by Landé of the Zeeman effects of the higher multiplets (quadruplets,

[172] Ibid., 276; Pauli to Landé, 23 May 1923, PB , no. 35. For the reasons and effects of Pauli's depressed mood, see Heilbron 1983.

[173] Pauli to Landé, 23 May 1923, PB , no. 35. To m_k and m _r correspond, respectively, m_L and m _s in the modern spectroscopic notation, the electronic spin playing the role of the atomic core.

quintets, etc.) discovered by Catalán in 1922. Quite remarkably, Landé discovered a synthetic formula for a "Landé factor" applicable to the magnetic splitting of any multiplet:

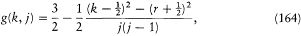
here written with the Bohr-Pauli normalization: k = 1, 2, . . ., n ; r = 0 (singlet), ½ (doublet), 1 (triplet) . . .; and (for k > r ) j = k - r , k - r + 1, . . ., k + r - 1, k + r (as would be suitable for an angular momentum obtained by composition of k and r ).^[174]

In his paper Landé also pointed to the similarity of this formula to the one resulting from a simple model, the so-called "vector model," in which the angular momentum K of the outer electron was coupled with the angular momentum, R , of the bare core, and with an angular momentum R ' borrowed by the core from the outer electron in the manner of Heisenberg. Whereas Heisenberg always took R ' = ½ (with R = 0 in the case of doublets, and R = ½ in the case of triplets), Landé had to take R ' = R for any multiplet.^[175]

From Pauli's viewpoint, the latter identity between intrinsic core momentum and borrowed momentum meant nothing but a double magnetism of the core. His version of the vector model^[176] was based on this double magnetism. Unlike Heisenberg's Rumpf model, the new model saved the equations of mechanics, including

and

[175] Landé 1923a, 197-205.

[176] Pauli first described his version of the vector model in Pauli to Landé, 23 May 1923, PB , no. 35. A more detailed formulation is in Landé 1923b, also in Pauli 1924. Landé 1923b also gave a formula for multiplet splitting in the absence of an external field. I will not discuss this formula since it played a less important role in the identification of the necessary departures from the quantum theory of multiperiodic systems. See, e.g., Pauli 1926a, 229-231.

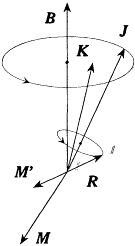
Figure 23.
Diagram for the Landé-Pauli vector model.

where M and M ' are respectively the magnetic moments of the atom and of the core (see fig. 23). However, the latter moment is given, according to Pauli's assumption of double magnetism, by

and the total magnetic moment by

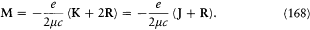
The part of the magnetic energy depending on the external field B is

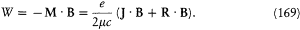
According to equation (165) the scalar product J · B is stationary. The product R · B is not, but, according to (166), if the field B is small (B << B_i ), R rotates around J much faster than J rotates around B . Consequently the following identities hold approximately for the temporal average :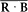

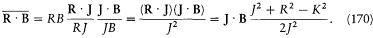
Using this expression, the temporal average 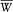of the perturbing energy (169) becomes

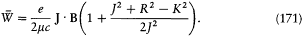
The quantization of this model gives integral values to J , R , and K , and also to the projection m of J along B (in units h /2p ). The quantum-theoretical value of the magnetic energy shift is therefore (according to the first-order perturbation theory)

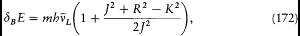
which gives the Landé factor

to be compared to Landé's empirical formula (164),

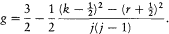
Even a translation of the quantum numbers by ½ could not reestablish the agreement. One also had to perform the substitution

The theoretical g was related to the empirical one, Pauli commented, by

the "substitution of a derivative to a difference." Indeed,

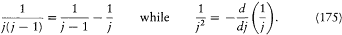
Pauli repeated this consideration in a letter to Sommerfeld of July 1923, with the comment: "This seems to point to something unmechanical." To Landé he also wrote: "I am convinced that in the anomalous Zeeman effect there is no multiperiodic model and that something essentially new must be done."^[177]

Being in a depressed mood, Pauli did not want to publish the above considerations, which were of a mostly negative character. Under Bohr's pressure, however, he consented to the publishing of the part of his reasonings which could be formulated without reference to any model. This included the formula (162) for the Paschen-Back effect, now introduced as the simplest possible empirical formula employing the selection rules Dm_k = 0, ± 1 (with the corresponding rule of polarization) and Dm _r = 0. He also provided a new and ingenious derivation of the Landé factors in weak fields on the basis of the following assumption: "The sum of the

[177] Pauli to Landé, 23 May 1923, PB , no. 35; pauli to Sommerfeld, 19 July 1923, PB , no. 40; Pauli to Landé, 17 Aug. 1923, PB , no. 42.

energy values of all stationary states that belong to given values of m and k [and n of course] remains a linear function of the field intensity during the whole transition from weak field to strong field."^[178]

This "sum rule" had first been introduced by Heisenberg in order to justify his dual quantization of the Rumpf . Not only did it lack a fundamental proof, but it was incompatible with the vector model, a further sign of "something unmechanical." In a letter sent along with this paper, Pauli commented to Sommerfeld: "As you will see, I was so intimidated that I have carefully avoided even the term 'angular momentum'." However, he promptly confessed: "I would never have reached the given representation of the spectral terms in strong fields if I had not been guided by model representations."^[179]

Ambiguous Momenta

In the following months Pauli kept thinking about the extent of the breakdown of classical concepts. In a letter to Landé of October 1923, he rewrote Landé's empirical formula for the g-factor as

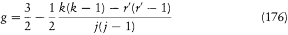
with r ' = r + 1. "You see," he commented, "the formula could hardly be more symmetrical." Of course, this form depended on the normalization of the quantum numbers, which differed from the one originally favored by Landé on semiempirical grounds. Nevertheless, Pauli believed his choice to be the more fundamental, for it still made k an integer and maintained the symmetry of the distribution of the values of j around k . This led him to the following suggestion: "You see that every momentum is represented not by a single number but by a pair of numbers. In a certain sense the momenta seem to be double-valued [zweideutig ]."^[180]

Pauli further related the ambiguity of the angular momenta r and j to Bohr's unmechanical Zwang : "The violation of the conservation of statistical weights [as expressed in Bohr's Zwang ] during the coupling results

[178] Pauli 1923a, 155.

[179] Pauli to Sommerfeld, 19 July 1923, PB , no. 40. In 1924 Paul, published a detailed account of his vector model, with the following motivation: being multiperiodic, this model is subject to the adiabatic theorem and therefore allows a derivation of the correspondence between the quantum numbers m a weak field and those in a strong field (Pauli 1924).

[180] Pauli to Landé, 23 Sept. 1923, PB , no. 46. In Pauli 1924, 372n, Pauli redefined the quantum numbers in the manner adopted m Sommerfeld 1923a, 1923b, 1924 (with different notations and purposes). The new numbers are obtained by subtracting one unit from k, r ', j , and they are exactly the ones now m use (L , S , and J ).

from the atomic core reacting either with one momentum value or with the other." The ambiguity of k was far more puzzling, since it contradicted Bohr's use of a well-defined k as a foundation of his second atomic theory. Pauli nevertheless found further support for this heresy in a remarkable property of X-ray spectra, brought to light by Coster and Wentzel in 1921.^[181]

The complex structure of these spectra appeared to be made of two alternating types of doublets, a relativistic one given by Sommerfeld's formula (with proper re-scaling) and a screening type calculated by replacing, in the hydrogenlike system, the Coulomb potential by a different spherically symmetric potential. Globally, the terms of the X-ray spectrum were well represented by the Bohr-Coster formula:

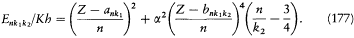
Strangely enough, two different quantum numbers, k₁ and k ₂ , were needed to express the screening parameters (a and b ) and the relativistic correction (compare with formula (38)). To Pauli this suggested an ambiguity of the azimuthal quantum number and of its orbital origin. None of the kinematic characteristics of Bohr's theory seemed to survive in atoms with several electrons. ^[182]

A New Quantum Principle in Gottingen

In conformity with his Rumpf model, Heisenberg preferred a half-integral k to an ambiguous k . However, he welcomed Pauli's suggestion of an ambiguous j and managed to integrate it in a revolutionary program just started by his new adviser Max Born.

Born's call for a revolution in quantum theory was not new. It was first expressed in a letter to Pauli of 1919, under the following interesting circumstances. The young prodigy had just published an in-depth criticism of Weyl's unified theory of gravitation and electricity. Among other technical reproaches, he wrote:

There is a physical-conceptual objection that should not be forgotten. In Weyl's theory we constantly operate with the field strength in the interior of the electron. For a physicist the field strength is only defined as a force on a test body;

[181] Pauli to Landé, 23 Sept. 1923, PB , no. 46.

[182] Pauli alluded to this duality of k in his letter to Landé, ibid.: "This conception [dual k ] also seems to be in better agreement with the facts regarding Röntgen spectra." A thorough discussion of this point is in Pauli 1926a, 204-205; the original X-ray doublet formulae are in Sommerfeld and Wentzel 1921 and Bohr and Coster 1923.

and since there are no smaller test bodies than the electron itself, the concept of the electric field strength in a mathematical point seems to be an empty meaningless fiction. One should stick to introducing only those quantities in physics that are observable in principle.^[183]

Pleased by this Machian statement, Born immediately extended it to atomic theory and even dreamed of a completely discrete world, perhaps one based on an analogy with the main object of his past researches, crystal lattices. In his reply to Pauli's letter he wrote:

I have especially been interested by your remark at the end, that you regard the application of the continuum theory to the interior of the electron as meaningless, because one is there dealing with things which are unobservable in principle. I have pursued exactly this idea for some time. . .. The way out of all quantum difficulties must be sought by starting from entirely fundamental points of view. One is not allowed to carry over the concept of space-time as a four-dimensional continuum from the macroscopic world of experience into the atomistic world; the latter evidently demands another type of number-manifold to give an adequate picture [Bild]. . .. Although I am not yet old, I am already too old and burdened to arrive at the solution. That is your task; according to what I have heard about you, to solve such problems is your calling.^[184]

However, when Pauli collaborated with Born in 1921-22, it was not in an attempt to overthrow space-time concepts but rather to improve the mechanics of electronic orbits. In the meantime, Born had learned to appreciate the qualities of the Bohr-Sommerfeld theory, in spite of the persistent difficulties with the radiation problem. For a short while he was even more optimistic than Bohr about the ability of this theory to represent atomic structure and spectra. When, in early 1923, the helium atom resisted such a treatment, Born quickly returned to his original extremist standpoint. In the summer of the same year he declared that "not only new physical assumptions would be needed but that the entire system of concepts would have to be restructured in its foundations. " On the contrary Bohr believed, as already mentioned, that the basic principles of the quantum theory could very well accommodate the failure of classical mechanics in the stationary states. And he kindly reproached Born for his extreme attitude. ^[185]

[183] Pauli 1919, 749-750. For the roots of Pauli's operationalism see Hendry 1984.

[184] Born to Pauli, 23 Dec. 1919, PB , no. 4.

[185] Born 1922, 542. See Bohr to Born, 2 May 1923, BCW 4: [673]: "However, I do not see this difficulty quite m the same light as you indicate."

The Born-Pauli formalism, or any calculation of energy spectra in the Bohr-Sommerfeld theory, rested on the more or less tacit assumption that the anticlassical character of radiation processes did not contaminate the Coulomb interaction between atomic constituents. Once confronted with the impossibility of proper quantum-theoretical models for helium and anomalous Zeeman patterns, Born adopted the opposite assumption. As a heuristic principle, he assumed that the discrete character of radiation processes implied by the relation D E = hv had a counterpart in nonradiative interactions. This took him back to the "number manifold" of 1919, with the new leitmotiv "discretization of atomic physics." In the future theory, the continuous electronic orbits of the Bohr atom would naturally disappear; in general, unobservable quantities would disappear, as he had argued during his early exchange with Pauli.^[186]

With the help of Pauli's idea of a dual j , in October 1923 Heisenberg gave a first boost to Born's new program. The first assumption of the new theory read: "The model representations have only a symbolic meaning; they are the classical analogue of the 'discrete' quantum theory." In this way Heisenberg could deny a direct physical meaning to previous atomic models, but he nevertheless extracted from them a symbolic content, to be integrated into a new, completely discrete theory. In other words, he was trying to design for Pauli a proper mechanical version of the correspondence principle—that is to say, a formal analogy between classical mechanics (without radiation) and a new discontinuous mechanics.^[187]

In the case of the anomalous Zeeman effect, Heisenberg gave the specific correspondence between the Landé-Pauli vector model and its discrete version, in terms of a "new quantum principle" inspired by Born's idea of a structural analogy between mechanical and electrodynamic interactions.^[188] Just as radiation energies were expressed in terms of differences (hv = DE ), the true energies E of the stationary states had to be given by a finite difference of a certain function F . More specifically, Heisenberg took

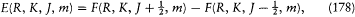
with

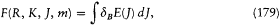
[186] Born 1924, 379; Heisenberg to Pauli, 9 Oct. 1923, PB , no. 47.

[187] Heisenberg to Pauli, 9 Oct. 1923, PB , no. 47.

[188] Ibid.; Heisenberg 1924. Presumably discouraged by Bohr's and Pauli's comments, Heisenberg sent his paper for publication only in June 1924.

where d_B E is the energy value (172) given by the vector model

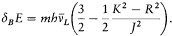
This choice reproduced Landé's empirical formula (164), in Landé's original half-integral normalization (R =r +1/2, K =k -1/2, J =j -1/2). Obviously, Heisenberg had been inspired by Pauli's remark (175), that

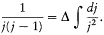
By the time Heisenberg finally published these considerations, he and Landé had extracted from empirical data the "branching rule," according to which an ion with angular momentum J gave rise, by addition of an electron with a given (sufficiently high) value of K, to two multiplets corresponding to R =J +1/2 and R =J -1/2. This gave immediate support to the new quantum principle, according to which the spectroscopic value J of the angular momentum of the ion corresponded to two values of J in the vector model, J +1/2 and J -1/2. In return, this principle permitted a formal generalization of Bohr's principle of the permanence of quantum numbers to the angular momentum of the atomic rest (the rest being what is left of an atom after removing one electron): the quantum number R of a given element was equal to the quantum number J of the normal state of the previous element. For instance, in the case of calcium and sodium, the fundamental state of sodium is a singlet state, with K =1/2, R = 1, and J = 1 (k = 1, r = 1/2, j = 3/2 in the Bohr-Pauli normalization); according to Heisenberg, J = 1 should be replaced by the couple of values, J = (1/2, 3/2), which gives rise to R = 1/2, 3/2 for calcium; these values correspond to the observed singlets and triplets.^[189]

Bohr was not as pleased by this accomplishment as Heisenberg expected. Bohr wrote to Heisenberg that "he would welcome his proposed solution if only he could grasp sufficiently the formal as well as the physi-

[189] Landé and Heisenberg 1924; Heisenberg 1924, 300-301. In the example of sodium and calcium, Heisenberg's branching rule simply corresponds to the composition of the spins of the last two bound electrons, which determines the multiplicity of the complex structure as long as the coupling is of the L · S type. However, in other cases (multiplets "hoherer Stufe" for which the single-ionized atom is not in a S state, or "normal" multiplets the coupling of which is not of the L · S type), Heisenberg's rule did not give the correct multiplet grouping of terms; it lust gave the correct values of the total angular momentum. In determining these values, the order of composition of the partial angular momentum is irrelevant, so that one may compose, in the modern terminology, the orbital momentum of one electron with that obtained by composing the spin of this electron with the total angular momentum of the rest of the electrons (this kind of composition generally differs from that prescribed by L · S or j · j coupling). See Pauli 1926a, 260.

cal side." Pauli was even more critical: "I consider [Heisenberg's theory] to be an ugly theory. For, in spite of radical assumptions, it does not provide an explanation of the half-integral quantum numbers and of the failure of Larmor's theorem [the double magnetism of the core]." He nevertheless approved something fundamental in Heisenberg's strategy, as appears in a letter to Bohr of February 1924:

To me the most important question is: To what extent one can speak of well-defined trajectories of the electrons in the stationary states. I do not think that this can be posited as obvious at all, especially with regard to your considerations about the balance of statistical weights in the coupling [leading to the Zwang ]. In my opinion Heisenberg hits the truth precisely when he doubts that it is possible to speak of determinate trajectories.

Indeed, Heisenberg regarded his new quantum principle as something general. Not only the vector model but also all orbital models became purely symbolic. In Landé's terms, they were "Ersatz-models" that had nothing to do with the real, yet unknown nature of motion inside atoms.^[190]

A Relativistic Conception

In his antimodel war, Pauli was even more radical than Heisenberg. To him a "symbolic model" was still too much of a model. He believed that even the orbital meaning of the azimuthal quantum number (through the correspondence principle) was lost forever, as he wrote in his letter to Bohr of February 1924: "Against the point of view which you were still holding last fall, I now believe that even for the quantum number k (not only j ) essential features of the true laws cannot be reproduced by the theory of multiperiodic systems." As indicated above, Pauli had derived this judgment from the appearance of k (k - 1) in his expression of the Landé factor, and from the ambiguity of k in the X-ray doublet spectra. There was also, as he explained in the above letter, the persistent lack of any explanation of the Zwang on the outer electrons 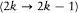on the basis of a multiperiodic model.^[191]

At this point some remarks should be made about the nature of the disagreement between Bohr and Pauli. I have insisted that from an early period Bohr did not attribute to the electronic orbits of his theory more than a "formal value," since, as he agreed with Campbell in 1921, they

[190] Bohr to Heisenberg, 31 Jan. 1924, AHQP; Pauli to Landé, 14 Dec. 1923, PB , no. 51; Pauli to Bohr, 21 Feb. 1924, PB , no. 56; Landé 1923c.

[191] Pauli to Bohr, 21 Feb. 1924, PB , no. 56.

could not be considered to be the sources of the radiation emitted by atoms according to ordinary electrodynamics. Moreover, as explained in "On the quantum theory of line spectra" (1918) and repeated in "The fundamental postulates" (1923), this type of model could be operational only in the limit for which the Coulomb interaction can be separated from the radiative interaction.^[192]

Nevertheless, when Heisenberg spoke of a "symbolic" character of the electronic orbits, and Pauli of the nonexistence of these orbits, they went further than Bohr: they believed that the idea of definite orbits was not even relevant to an approximate determination of stationary states through ordinary mechanics or any extension of it. In Pauli's opinion, Bohr was wrong to retain classical concepts while he gave up classical laws . In a letter of 1923 to Eddington he alleged that this was the source of all quantum paradoxes. A proper quantum theory, he believed, had to start from an entirely new set of concepts.^[193]

As the encyclopedist of relativity, Pauli found the strongest argument against orbits in the relativistic explanation of optical doublets given by Landé (and, independently, by Millikan and Bowen) in April 1924. In December :1924 he declared to Bohr: "The relativistic doublet formula seems to me to show without any doubt that not only the dynamic concept of force but also the classical theory's kinematic concept of motion will have to be profoundly modified." According to the experiments made by Millikan and Bowen, the doublet spectrum of highly ionized atoms (which lies in the far UV region) appeared to be very similar to that given by the X-ray emission from atoms with an incomplete internal shell. In fact both types of spectra could be described by a formula of the type (177) (up to a sign difference), if only j was identified with k₂ , and k with k₁ (with the proper normalization), in harmony with the selection rules Dk₁ =± 1 and Dk₂ = 0, ±1. This suggested an extrapolation of the relativistic interpretation of X-ray doublets to optical doublets, but again only at the expense of employing the strange ambiguity of the azimuthal quantum number noticed by Pauli in the X-ray case.^[194]

There was an important reason, Pauli continued, to favor the relativistic explanation of doublets over the one based on the concept of a magnetic core (Neigungsgesichtspunkt in Pauli's terminology), both in the optical and in the X-ray case. This reason had been found by Landé in the

[192] See p. 157; p. 122; Bohr 1923b, trans., 10.

[193] Pauli to Eddington, 20 Sept. 1923, PB , no. 45.

[194] Pauli to Bohr, 12 Dec. 1923, PB , no. 74; also Pauli to Landé, 24 Nov. 1924, PB , no. 71; Landé 1924a, 1924b; Millikan and Bowen 1924a, 1924b, 1924c. See Pauli 1926a, 210-212.

Z-dependence of the width of doublets, where Z is here the effective charge number perceived by the emitting electron. In the X-ray case, the relativistic correction implied by Sommerfeld's formula is proportional to Z⁴ , as experimentally verified. Instead, the magnetic-core model gives a Z³ dependence, since the corresponding perturbation is due to the magnetic field created by the outer electron, which behaves like

in the simple case of a circular orbit (the velocity v is proportional to Z, and the radius a is inversely proportional to Z).^[195]

In the optical case, a nontrivial Z-dependence occurs only in the case of dipping orbits. If, for simplicity, we limit ourselves to deeply dipping orbits, the relativistic correction is most important in the part of the orbit which is closest to the nucleus. Calling Z_i and t_i /t₀ the charge number perceived and the fraction of time spent by the electron in this inner part, the corresponding energy-shift is proportional to 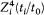. Since, in a Kepler orbit, the time of revolution is proportional to Z^-2 , the relativistic doublet width must be proportional to 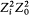where Z₀ is the effective charge number corresponding to the outer part of the orbit. Now, in the magnetic-core model this width behaves like the magnetic field created by the inner part of the orbit:

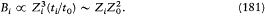
Here again spectral data confirmed the relativistic conception.