The Response of the People

The Academy of Sciences resumed its existence late in 1795 as the principal part of the new Institut de France, a government monopoly of the most learned new republicans. On 4 April 1796, the Institut took over the metric project through a commission composed of the reborn academicians Berthollet, Borda, Brisson, Coulomb, Delambre, Haüy, Laplace, Legendre, Méchain, Monge, and Prony. They had developed skill in the political as well as the technical aspects of their charge. Laplace proposed the convening of an international body of savants to check and accept the prototypes of the new units. "You realize [Laplace wrote Delambre] that all this is only a formality, to

[72] Berthaut, Ingénieurs, 1 , 165; Bigourdan, Système métrique , 135–45; Méchain and Delambre, Base, 1 , 66–80; Méchain to Delambre, 20 brumaire an VI (22 October 1797), ibid., 83.

[73] Méchain and Delambre, Base, 1 , 84–90; Delambre, Rapport , 6, 53–4; Berthaut, Carte, 1 , 123–4.

enable them to consider the system on their own, to do away with national envy, and to make them adopt the measures." Borda opposed the meeting; Napoleon supported it; the Directory ordered it.^[74] The irrepressible Talleyrand, now minister of foreign affairs, issued the invitations, and had the satisfaction this time of omitting Britain altogether.

The international committee of experts convened appropriately in a military setting, in the Dépôt de la Marine, on 28 November 1798, having waited in Paris for a few months for Delambre and Méchain to remeasure a baseline. These patient experts represented client states and friendly powers, to wit: the Bavarian, Cisalpine, Helvetian, Ligurian, and Roman Republics, and Denmark, Sardinia, Spain, and Tuscany. The meeting divided into three working committees, one to control the weight of the kilogram, a second to compare the scales used in the work with the old toise, and the third—composed of four members calculating independently—to deduce the length of the meter from the cornucopia of measurements made by Méchain and Delambre. Their calculations fixed the definitive meter over-precisely at 443.295936 lignes of the toise de Peru taken at 17.6°C, some 0.144 lignes shorter than the provisional meter by then distributed throughout France. (The difference was meaningless for commerce, since it amounted to one foot in a kilometer.) Independent observers had nothing but praise for Borda's circle and for the care with which the units of volume and weight were deduced from the meter and the density of water.^[75]

The Danish delegate retained enough independence to observe that although Méchain and Delambre had been as precise as was humanly possible, "it cannot be assumed that the determination of the meter is so absolutely and completely borrowed from nature that there is no doubt at all about its final accuracy." No echo of this

[74] Hellman, "Legendre," 333–5; Crosland, in Bugge, Science , 197; Laplace to Delambre, 29 Jan 1798, in Yves Laissus, "Deux lettres de Laplace," Revue d'histoire des sciences, 14 (1961), 285–96, on 287–8.

[75] Crosland, in Bugge, Science , 197–200; Bugge, ibid., 205–11; Méchain and Delambre, Base, 1 , 92–4. Praise for the circle: Bugge, Science , 204; Delambre, Rapport , 232–3, quoting F.X. von Zach.

discordant and irrelevant observation was heard in the speeches on 22 June 1799, when the joint committees formally presented the prototype standards to the people. In accepting them, the president of the upper legislative body, the Conseil des anciens, observed that it was a work of genius to have found an inviolable base of measurement in nature; "that, citizens, is the immortal service that the National Institute has rendered to the French Republic, or rather, the benefit that it offers to the entire human race."^[76] It remained only to convince the race to accept the benefit.

Resistance

The experts returned to their countries encouraged to propagate the metric system at home for the improvement of commerce and the tightening of ties to France. The sort of pressure they were under appears from a hint earlier given by the Convention's Committee of Public Instruction to a newly liberated territory. The Committee pointed to the great "advantage it would be to the union just established between the French and Batavian republics to spread the system of uniform and decimal measures beyond French territory." The Cisalpine Republic, consisting of Lombardy and Emilia-Romagna, also felt the pressure early.^[77] Annexed territory, such as the Département du Mont-Tonnerre carved out of the Rhineland, felt a heavier hand. By a decree of 18 June 1801, the Département would be obliged to use the metric system exclusively; all old weights and measures found in shops and all meter sticks on which former units of length were indicated would be confiscated.^[78]

In friendly but not subject territory the system was recommended for its combination of abstract science and practical utility. "We [in the Kingdom of Sardinia] are obliged to the nation that has

[76] Bugge, Science , 204, and in Crosland, "'Nature' and measurement," 305–8; P.C.L. Baudin, "Réponse," in Méchain and Delambre, Base, 3 , 652. The president of the lower legislative body, the Conseil des cinq cents, spoke similarly; ibid., 3 , 649.

[77] Quoted by Laissus, "Deux lettres," 288.

[78] Tables de comparaison entre les mesures anciennes en usage dans le Département du Mont-Tonnerre et les nouvelles mesures républicaines (Mayence: Pfeipfer, an X), xxxii.

sustained with unexampled courage the most terrible political upheavals for having put forth, in the very midst of a frightful tumult, the most abstract speculations of mathematicians as a rule for every-day transactions." "Nature and not France brings [the new measures] to us [Spaniards]. Let us accept them following our natural ally with whom we have so many commercial relations. . . .It behooves Spain [because it helped Méchain] to set other nations the example of adopting these units."^[79]

None of this cajoling or commanding had much immediate effect. Even in France, where the new units were to oust the old in land transactions on 1 vendémiaire an X (23 September 1801), the people declined to benefit from the republican measures created ostensibly in their interest.^[80] One of the orators at the presentation of the prototypes in July 1799 had imagined the satisfaction a peasant would feel in computing his holdings in square meters. "The field that supports my children is such and such a fraction of the globe. In that proportion I am a co-owner of the world."^[81] In practice the peasant and his surveyor, builder, and draper refused to give up their toise sticks. So brutish a rejection of the natural and the rational perplexed the savants. "There is no respect in which the reform of weights and measures has not been advantageous," declared the president of the Agricultural Society of Paris (Société d'agriculture de Paris) in 1809, "and, consequently, if reason always was listened to, the success of the reform would have been complete."^[82]

Alas, the meter had only complicated ordinary life. Artisans brought home their measures in familiar units and sat up all night converting them into meters, and into a crowd of irrelevant decimals, in order to write estimates and contracts in the obligatory figures.

[79] Capelli, Rapports , 5; Gabriel Ciscár, Memoria elemental sobre les nuevos pesos y medidas decimales fundados en la naturaleza (Madrid: Imprenta real, 1800), on 33–4.

[80] François Gattey, Eléments du nouveau systême métrique, suivis des Tables de rapports des anciennes mesures agraires avec les nouvelles (Paris: Bailey and Rondonneau, an X), 65. Cf. Bugge, Science , 205, and Maurice Crosland, "The congress on definitive metric standards, 1798–1799: The first international scientific congress?" Isis , 60 (1969), 226–31, on 229–31.

[81] Quoted by Crosland, "'Nature' and measurement," 285.

[82] L. C[hessiron], "Mesures," in Nouveau cours complet d'agriculture théorique et pratique, 8 (Paris: Delerville, 1809), 291–314, on 299–300.

Why did they not measure in meters to begin with and enjoy "the happy effects of the most useful of the gifts that scientists have been able to make to society"?^[83] Because they were creatures of habit, vain, traditional, pious, ignorant, and ungrateful.^[84] And also canny and suspicious. According to a British metrologist, who had it from a French merchant, consumers opposed the new units on the theory that they would be an advantage to shopkeepers, and shopkeepers opposed them for fear that consumers would be able to figure out true costs. The government hoped that a play with words would overcome suspicion. On 4 November 1800, it allowed the use of old words for multiples of the new measures, for example, "toise" for "two meters," "pinte métrique" for "litre," and so on. The reformers thought the concession damaging and absurd: if the people could use Greek words like "chirurgien" and "apothécaire," why not "kilogramme"?^[85]

Because the people did not like change and cared nothing for system. So stubborn and irrational were they that in 1812 the imperial government sacrificed the jewel of the reform, the key to democracy, that is, reckoning by tens. Two laws, of 12 February and 28 March of that year, indicate the state of affairs. The first ordered that the official system be taught in all schools throughout the empire, that it alone be used in public administration, markets, and commercial transactions. The second destroyed the official system by introducing "common measures" ("mesures usuelles") divided by twos and threes: a toise of 2 meters divided into 6 pieds; an aune of 1.2 meters divisible into halves, quarters, eighths, and sixteenths, and also into thirds, sixths, and twelfths; and similarly for weights and coins. Our British metrologist enjoyed the spectacle: "Thus, after twenty years of

[83] Ibid., 292.

[84] Concocted from compliments in ibid.; Méchain and Delambre, Base, 3 , 651 (text of 1799); Ciscár, Memoria , 38–9; Jean Guillaume Garnier, Traité d'arithmétique , 4th edn. (Paris: Houdin, 1818), 281.

[85] P. Kelly, Metrology; or, an exposition of weights and measures, chiefly those of Great Britain and France (London: Lockington et al., 1816), 25–6; Gattey, Eléments , 9–10; Chessiron, "Mesures," 296. The convenience of halves and doubles of the fundamental units was widely urged as an advantage of the reform, e.g., in Journal de physique, 47 (messidor an VI [1798]), 59, 60.

trouble, mystery, and litigation, no advances are made, except that of having one common standard."^[86] Otherwise confusion had only been compounded: the puzzled citizen had the provisional meter of 1795, the definitive of 1799, the compromised names of 1801, the common system of 1812, and, unofficially and omnipresent, the ancient units of the Kings of France. It is easy to change governments, not hard to reform currency, but almost impossible to alter the most common weights and measures. "Nothing has a greater tendency to grow worse, or more obstinately resists improvement." One took the long view. "This new metric system, all of whose parts fit together so simply, will no doubt triumph in the end over the obstacles that habit still opposes to its general adoption," so reads a text of 1820, "especially if it continues to be obligatory."^[87]

Spread

A gauge of the rate of penetration of the new units is the pattern of their use in books requiring specification of units, like atlases, compendia of architectural drawings, and manuals of surveying, building, and engineering. Although such works employing old units exclusively were published into the 19th century,^[88] the common pattern up to around 1815 was to present measurements and calculations in both meters and toises and their multiples. A good indication for the early years is the collection of architectural designs awarded prizes by the Institut de France and other government bodies between 1795 and 1803. Forty of these designs have units: three use toises only, two use meters only, and the balance uses both. Before 1800 toises have priority when both scales are present; after

[86] Kelly, Metrology , xiii; ibid., 27–30, for text of the laws of 1812.

[87] Respectively, Kelly, Metrology , xvi, and Louis Puissant, Traité de topographie, d'arpentage et de nivellement , 2nd edn. (Paris: Courcier, 1820), 245 (1820).

[88] See, for example, Charles-François Viel, De la construction des édifices publics sans l'emploi du fer (Paris: Perronneau, 1803); L. Ducrest, Vues nouvelles sur les courans d'eau, la navigation intérieure et la marine (Paris: Perronneau, 1803); Molard, Description , 1; J.Ch. Krafft, Recueil d'architecture civile (Paris: Bance ainé et al., 1812); Bernard Forest de Belidor, La science des ingénieurs, dans la conduite des travaux de fortification et d'architecture civile , ed. C.L.M.H. Navier (Paris: Firmin Didot, 1813).

1800, meters.^[89] A collection of plans for large structures published in 1823 shows a very considerable change: of seventy-six plates with scales, two have toises only, eleven have both, and sixty-three meters only; and the old measures occur exclusively in one section of the collection, on stone bridges.^[90] The obvious extrapolation does not hold, however; a set of 105 house plans published in 1843 under the promising title Paris moderne suggests that builders of private dwellings then still preferred to express themselves in the measures of the old regime. About 30 percent of the plans use toises only; another 30 percent, meters only; and 40 percent, both. All the plans are dated, the earliest to 1815; the strongest showing of the toise against the meter occurs not at the beginning, but in the period 1835–9. The meter takes over after 1840, the year in which the metric system at last became obligatory in France.^[91]

Up-to-date technical manuals show the same equivocation as architectural drawings. An authoritative indicator is the huge treatise on the building arts (four volumes in five of text, three of plates) published between 1805 and 1816 by Jean-Baptiste Rondelet, chief architect of the church of Sainte-Geneviève and architectural consultant to the government. Rodelet's plates strongly favor the old measures; his text appears to be the work of a schizophrenic. The earliest volume (1805) uses pieds, pouces, and lignes and also metric units, sometimes converted but often not, in tables and in calculations; at one point it gives dimensions in meters and computes in toises.^[92] In the volumes published in 1812, Rondelet usually proffers all dimensions in both the old and new style, but without the advantage of decimal notation: for example, "31 pieds 3/7 (10 mètres 209 millimètres)."

[89] Projets d'architecture et autres productions de cet art qui ont merité les grands prix accordés par l'Académie, par l'Institut national de France, et par des Jury du choix des artistes ou de gouvernment (Paris: Detourelle, 1806).

[90] Louis Bruyère, Etudes relatives à l'art des constructions (Paris: Bance ainé et al., 1823).

[91] Louis Marie Normand and G.E. Lemmonier and Paris moderne, ou choix de maisons de campagne et constructions rurales des environs de Paris , 3 vols. (Liège: d'Avanzo, 1843), and several other editions; Bouchard, Prieur , 313. The obligation was laid down in a law of 4 July 1837; it took effect on 1 January 1840.

[92] Jean Baptiste Rondelet, Traité théorique et pratique de l'art de bâtir (Paris: chez l'auteur, 1805–16), 3, 57, 66–7, 83 ff., 102, 164, 179–83, 269 ff., 388–96.

His preference for the old appears from his way of obtaining specific gravity, which he understands as the weight in grams of a cubic centimeter of a substance. He measures the weight of a sample, in air and in water, in onces and gros, deduces the weight of a cubic pied, and converts to the metric system. The preference for the old units persists into the last volumes, published in 1816. Then—after 1,839 pages of schizophrenic computations, the last of which provides the cost of old bricks in old money—Rondelet introduces some "notions about metric measures."^[93] It is instructive that this instruction precedes a recomputation of costs in metric measures and decimalized currency. The relative ease of such computations was the great benefit that the reformers had advertised.

From about 1810 many technical manuals by professors and government officials used metric measures exclusively. For example, the professor of mathematics at the Ecole impériale militaire, Louis Puissant, and Pierre Pommiés, professor at the Lycée Napoléon, both influential teachers of surveying and geodesy, used meters exclusively and without explanation in many textbooks beginning in 1807.^[94] Jean-Nicholas Hachette, professor at the Ecole polytechnique, brought the metric system into the preface of his textbook on machines, without comment, as the only satisfactory way "to express their effect in numbers." The chemist Jean-Antoine Chaptal, one-time minister of the interior and long-time educational reformer, naturally used nothing but modern measures in his survey of the state of French industry after the fall of Napoleon. Still there are hints of backsliding where least expected. The official surveyors of France might have worked exclusively in meters and understood the higher geodesy; but the local land measurer often enough made do with old units and little geometry into the reign of Louis Philippe. A manual for such measurers, "especially people who have not studied geometry," was published in 1833 by an inspector of the cadastral survey. It contains an explanation of the metric system, an injunction

[93] Ibid., 1 , 99, 101–2, 158–60; 4 , 583–604, 609–44.

[94] Puissant, Traité de topographie , 139, 154, and Michel Pommiés, Manuel de l'ingénieur du cadastre (Paris: Impr. impériale, 1808), 166–9, illustrate the type.

to use it, and tables for the easy conversion of old local measures into meters, "and vice versa."^[95]

As it spread, the metric system did help to realize the reformers' ambition to improve the numeracy of Europeans. In the Ancien Régime, despite its baroque abundance of metrological units, most people had need only for a single system; during the Empire, because of the government's policy of driving the meter home, more and more citizens had to learn how to convert one set of measures into another. If the first advance of European "Rechenhaftigkeit"—"the inclination, habit, and ability to resolve the world into numbers and to bring these numbers together into an artificial system of income and outgo"—may be likened to literacy in one language, the domestication of the metric system made reckoners bilingual.^[96]

The early treatises on metric calculations propagated not only decimal arithmetic, including the concept of place, but also the idea of significant figures and the operation of rounding off. An Exposition abrégée du nouveau système , published in the provinces in 1802 or 1803, may stand for the genre. It explains that the many decimals generated during conversion are artifacts of multiplication and division, and demands that they be dropped from the final answer.^[97] Rounding off, says Rondelet, in his belated account of metric computations, is essential to the new system. Rounding off might in practice mean only rounding up, as readers of an Arithmétique pratique of 1800, which recommends changing 0.7411440 to 0.75, learned to do; a practice that would favor shopkeepers, who could round up each of their many small transactions.^[98] Even arithmetic may have its social bias. The utility of metric conversions in teaching numeracy

[95] J.A. Chaptal, De l'industrie Françoise , 2 vols. (Paris: Renouard, 1819); A. Lefevre, Guide practique et mémoratif de l'arpenteur, particulièrement destiné aux personnes qui n'ont point étudié la géométrie (Paris: Bachelier, 1833), i-vi, 15–21.

[96] Quote from Werner Sombart, Der Bourgeois. Zur Geistesgeschichte des modernen Wirtschaftsmenschen (Munich: Duncker and Humblot, 1913), 164.

[97] Exposition abrégée , 23–4, 29–30. See also the contemporary Tables de comparaison , xiv–xxix; Capelli, Rapports , 49–57.

[98] Rondelet, Traité, 4:2 (1816), 610–3; Adrien Poittier, Arithmétique pratique et démontrée, pour réduire les anciennes mesures en nouvelles (Paris: Bernard and Moutardier, nivôse an VIII), 146–52. Gattey, Eléments , 32–3, rounds up only if the part dropped is >> 0.5 of the last figure kept.

appears further from popular textbooks of arithmetic that use such computations as exercises. This practice persisted long after the universal adoption of the metric system in France.^[99]

According to the president of the Paris Agricultural Society, the great majority of people who could read and write in 1810 knew nothing more of arithmetic than addition and subtraction. He had a prescription for correcting this innumeracy and a vision of the happy consequences. "If decimal calculations could be introduced into primary schools along with the use of the new measures, not only would the housewife be able to make all the computations she requires, but also the worker could measure without difficulty and, by adding the use of the rule and compass for tracing geometrical figures,he would be able to draw all his plans himself, and the farmer would have no problem with surveying."^[100] This grand project has been realized in large measure. The male academic and quantitative spirit of the late Enlightenment found a fertile if capricious partner in La belle Marianne , the spirit of revolutionary France.

[99] See, for example S.F. Lacroix, Traité élémentaire d'arithmétique, à l'usage de l'Ecole centrale des quatres nations , 2d edn. (Paris: Courcier, 1805), 115–46; Garnier, Traité, 1 , 263–75, 281–93; and, for the later period, A. Thinon, Leçons sur le système métrique et sur les applications usuelles de l'arithmétique (Paris: Dezobry and Magdelleine, 1860), 131.

[100] Chessiron, "Mesures," 8 , 293.

Fig. 1.1
Besides the strict mathematical method, which was intended only
for the learned reader, Wolff also used the physicotheological method 
for a popular audience. According to the latter method, everything in 
nature must be both perfect and useful. Demonstrating or proving 
this thesis became a rationale for 18th-century natural history. The 
scientist should look for "greatness in small things" (maxima in minimis), 
which phrase served as the motto for Friedrich Christian Lesser's 
Insectotheology (Frankfurt, 1740). The study of nature reveals the
infinite diligence of the wasps and the ants, the beauty and strange 
development of the butterfly, the artfulness of the spider, the utility of the 
silkworm—these and other features of nature provided inspiration 
for 18th-century research and speculation.

Fig. 1
Albrecht von Haller called Linnæus "the second Adam." He appears in this role
in a vignette for the eleventh edition of Systema naturae (ed. Lange, Haller, 1760). As
 Adam, Linnæus is sitting naked, naming all the animals (cf. Genesis 2:19). Paradise is 
crowded with animals and plants, monkeys climbing the trees, whales swimming in 
the sea; everything is at peace. The fall is yet to come. The figure in the middle is Diana 
polymammae, symbol of Nature and its generative force. Linnæus—with "his" flower
 Linnea borealis at his feet—is urging numbers and names, Numeros et nomina, 
from Diana. He is Nature's bookkeeper.

Fig. 2
This instructive vignette, from Charles Bonnet, Oeuvres d'histoire naturelle, 4 
(Neufchâtel, 1781), depicts man at the top of the scale of nature. As man belongs 
to both the material and the spiritual world, he keeps hishead in the clouds. On 
lower steps of the scale follow the monkey, the lion and the dog, the eagle, fish,
lizards, corals, and so on. Everything in nature is thus to be understood 
both in hierarchy and in continuity.

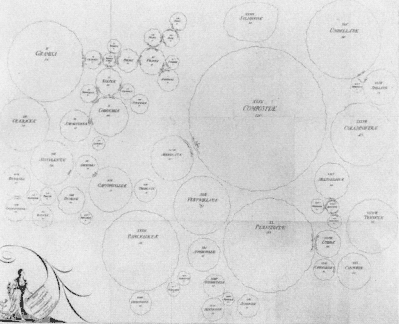
Fig. 3
In private lectures Linnæus discussed the possibility of arranging 
natural orders linearly. With so many uncertainties in establishing these 
orders and with so many more plants still to discover, however, such an 
arrangement must wait. This map, believed to be based on a drawing by
Linnæus, shows continuity between some groups, as well as gaps requiring 
more knowledge: Linnæus, Praelectiones in ordines naturales plantarum, 
ed. P.D. Gieseke (Hamburg, 1792), facing p. 623.

Fig. 3.1
Illustration of the Linnæan sexual system, from William Withering, A botanical arrangement 
of all the vegetables growing in Great Britain (1776). See chapter 3, page 77.

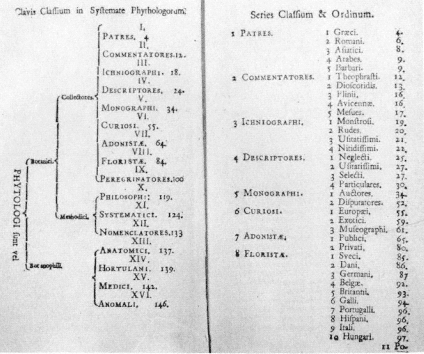
Fig. 3.2
Linnæus' classification of botanists, from his Bibliotheca 
botanica (1736). See chapter 3, page 79.

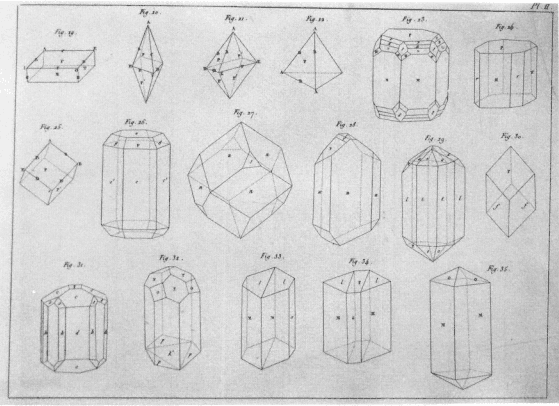
Fig. 3.3
René Just Haüy's geometrical forms of crystals, from his Tableau comparatif des résultats
de la cristallographie et de l'analyse chimique relativement à la classification des
 minéraux (1809). See chapter 3, page 92.

Fig. 3.4
Classification of nervous disorders showing orders, genera, species, and 
varieties, from Philippe Pinel, Nosographie philosohique, 6th ed. (1818). 
See chapter 3, page 99.

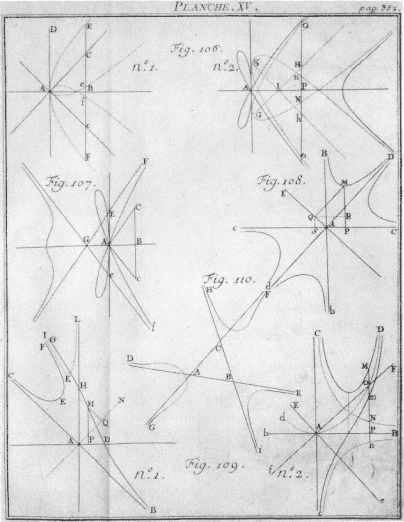
Fig. 3.5
Illustration of curves classified by Gabriel Cramer in his Introduction 
à l'analyse des lignes courbes algébriques (1750). See chapter 3, page 102.

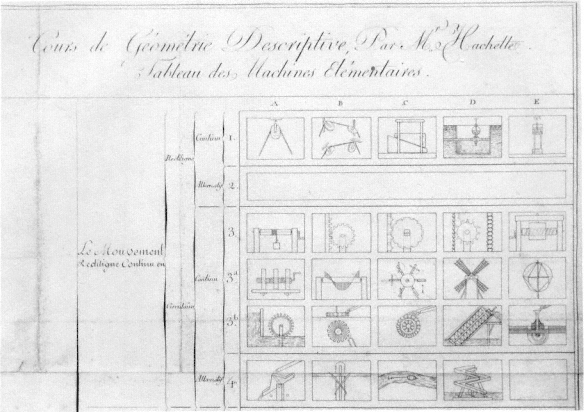
Fig. 3.6
Portion of Jean Nicolas Pierre Hachette's classification of simple machines, from 
his Traité élémentaire des machines (1811). See chapter 3, page 106.

Fig. 6.1
The repeating circle, from Jacques Cassini, Pierre François Méchain, and 
Adrien-Marie Legendre, Exposé des opérations faites en France [1791]. By 
courtesy, National Land Survey (Lantmäteriverket), Gävle.

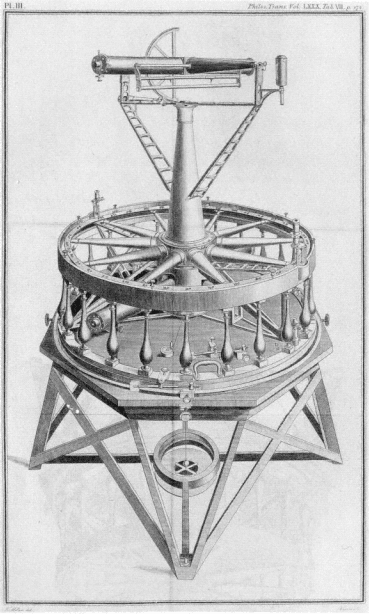
Fig. 6.2
According to William Roy, "It is a brass circle, three feet in diameter, 
and may be called a theodolet [theodolite], rendered exremely perfect." 
From Roy's "Account of the trigonometrical operation" in the 
Philosophical transactions for 1790.

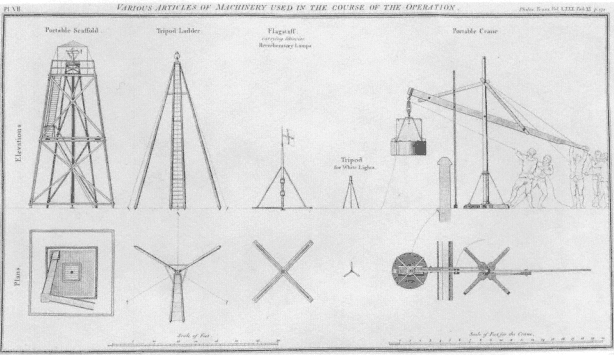
Fig. 6.3
The theodolite was used with a portable scaffold and crane in the high-tech military surveying 
operations of the late 18th century. From Roy's "Account of the trigonometrical operation" (1790).

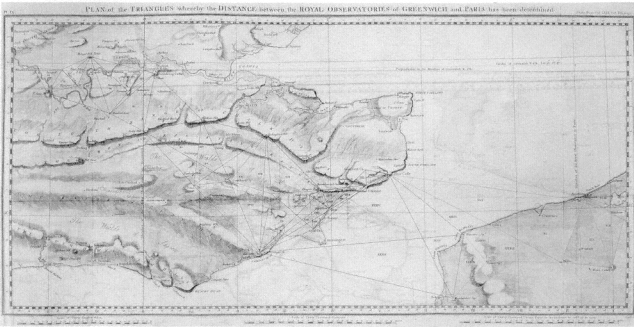
Fig. 6.4
The cross-channel connection, from Roy's "Account of the trigonometrical operation" (1790).

Fig. 8.1
The close connection between economics, technology, and chemistry in 
"die ganze Historie vom Kiess," from F.J. Henckel, Pyrotologia (1725). Instruments
in the small buildings illustrate the role of chemistry in the production
of sulfur, vitriol, and arsenic from pyrites.

Fig. 8.2
Ädelfors mine in Sweden as seen in 1767 by G. Jars. From his Voyages métallurgiques, 2 (1780).

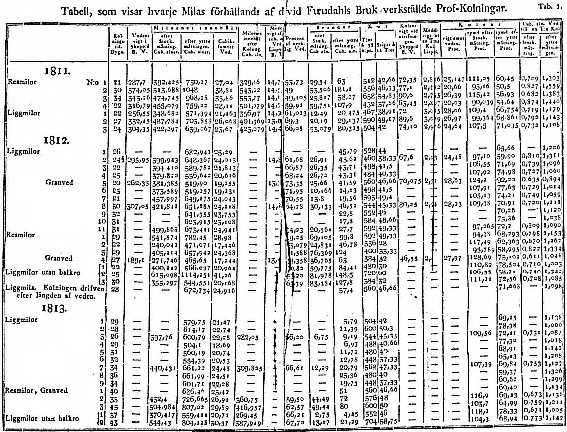
Fig. 10.1
Tabular display of experiments in charcoal-burning in Dalecarlia, from 
Carl David af Uhr, Berättelse om kolnings-försök  åren 1811, 1812 och 1813.

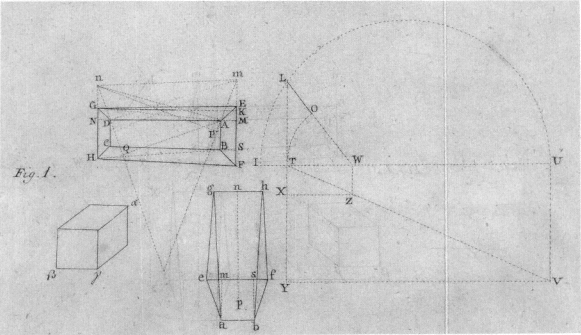
Fig. 10.2
Illustrations for Zacharias Plantin's studies of the volume of rhombic sledges of charcoal, 
from the  Kungl. Vetenskapsakademiens Handlingar  for 1778 and 1784.

Fig. 10.3
Systematic display of data from Johann Eric Norberg's study (1772–3) of human muscle power,
from the Kungl. Vetenskapsakademiens Handlingar for 1799.

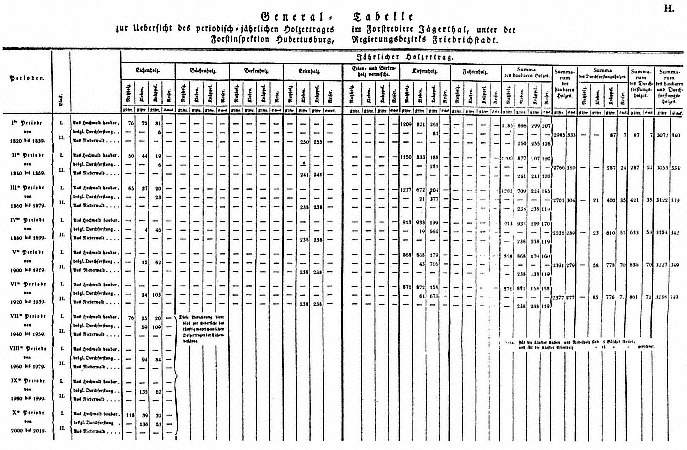
Fig. 11.1
Georg Hartig's 200-year plan for the Jägerthal forest district, from his Neue Instructionen (1819). 
By courtesy, Department of Special Collections, Yale University.

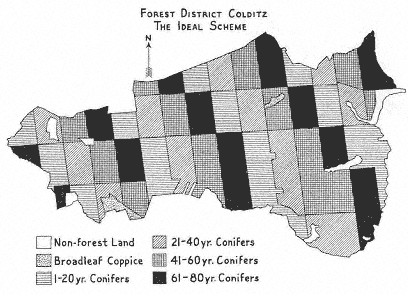
Fig. 11.2
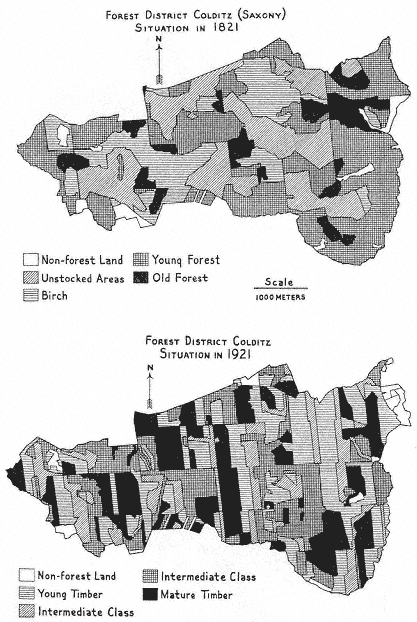
Transformation of the Colditz forest district after 100 years of managements 
according to Cotta's ideal scheme. From Heske, German forestry. 
By courtesy, Stanford University Libraries.