Helium

In the fall of 1916 Bohr and Kramers started extensive perturbative calculations of the classical orbits of the helium atom's two electrons. The spectrum of this atom had long been known to consist in two non-combining series spectra named ortho- and para-helium spectra. Transitions between the two types of terms never occurred, even in the presence of strong electric fields, so that physicists believed for a while that o-He and p-He were two different elements.^[107]

In his first calculations with Kramers, Bohr investigated both coplanar and perpendicularly oriented orbits for the two electrons, and found, in the coplanar case, two simple classes of periodic motions that seemed

[105] ohr 1922a. On Ehrenfest's friendship with Bohr see Klein 1986.

[106] Bohr [1921d], [1922c].

[107] See Rud Nielsen's introduction to BCW 4, on [36]-[39], and Mehra and Rechenberg 1982a, 398. In modern quantum mechanics, the o-He and p-He spectra respectively correspond to the values S = 1 and S = 0 of the total spin, and the noncombination of the two spectra corresponds to the selection rule DS = 0.

likely to correspond to the o- and p-helium spectra.^[108] Nevertheless, a quantitative determination of the terms and of the ionization potential appeared to be far out of reach. The subsequent extension of the Bohr theory to multiperiodic systems did not ease the task: the classical three-body system was not multiperiodic, and the well-known difficulty of the corresponding celestial problem suggested that the helium problem would be at least as difficult. In 1919, however, Alfred Landé, an ambitious student of Sommerfeld's, jumped over these obstacles and proposed a simple multiperiodic model to which he could apply Sommerfeld's quantum rules.^[109]

According to Landé, the inner orbiting electron could be replaced (for given values of the principal quantum numbers) with a rigid rotator making a constant angle with the angular momentum of the outer electron. This was a plausible approximation if the outer orbit was much larger than the inner, which should at least be the case for highly excited states. Then the quantization of the total angular momentum j , assuming unit angular momentum of the inner electron and a momentum k for the outer electron, gave (in units h /2p ):

the two extreme values corresponding to coplanar orbits, and the middle one to almost perpendicular orbital planes (see fig. 18).^[110]

Having excluded (for no good reason) the case j = k - 1, Landé could show that the quantized coplanar orbits fitted well with the o-He spectrum, while the perpendicular orbits fitted well with the p-He spectrum. He also identified the normal state as the stationary state corresponding to the lowest term in the o-He spectrum, since this state had the lowest energy. Even for this normal state Landé and Sommerfeld assumed the distinction between inner and outer orbits to be valid, which gave two concentric one-quantum (n = 1) orbits, in opposition to Bohr's earlier ring model (see fig. 19).

In the same year 1919 Franck and Knipping (also Horton and Davies) applied the Franck-Hertz technique of accelerated electrons to the first precise determination of the ionization potential of the helium atom (this

[108] In the first class of motion the shape of the inner orbit was invariable, while in the second class the eccentricity of the inner orbit changed periodically under the perturbing influence of the outer electron. See Bohr 1922b (written m 1918), 105; Bohr to Landé, 26 June 1919, AHQP; and numerous helium calculations by Bohr or Kramers in BMSS.

[109] Landé 1919a. See Forman 1970.

[110] Landé developed his rather intricated procedures in Landé 1919b, 1920. For a clear account of Landé's method, see Bohr 1921d, [123]-[124].

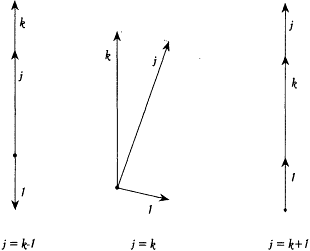
Figure 18.
Diagram for Landé's composition of a unit angular momentum with the momentum k.

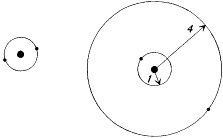
Figure 19.
Two planar models for helium, with n = 1 for both electrons: 
the ring model (left), and the Landé-Sommerfeld model (right).

energy was not accessible to optical measurements since the corresponding frequency lies in the far UV region). They found 25.5 V instead of the 30 V predicted by Landé and Sommerfeld (the ring model also gave about 30 v). This brought them to suspect that the normal helium state belonged to the p-He terms and that the state corresponding to the lowest o-term was only metastable. The two conjectures were soon supported by the following reasoning, due to Franck and Reiche.^[111]

In 1914 Paschen had observed that the 10830 Å line of the o-He spectrum was a resonance line of the absorption spectrum obtained after the helium sample had been subjected to an electric discharge. On the one

[111] Franck and Knipping 1919, 1920; Horton and Davies 1919.

hand, in Landé's interpretation of the helium spectrum, this line had to correspond to a transition from a two-quantum (n = 2) state of the outer electron. On the other hand, in Bohr's theory the large absorption and scattering (the frequency of the scattered light being the same as that of the absorbed light) characteristic of resonance lines were interpreted as due to transitions between a nondecaying stationary state (generally the normal state) and another excited state. Consequently, the two-quantum (n = 2) state of the o-He spectrum had to be metastable, and the one-quantum (n = 1) state of o-He had to be forbidden for some unknown reason. The normal state could now only belong to the p-He terms (see fig. 20).^[112]

Bohr approved Franck and Reiche's clever analysis. He also congratulated Landé for his successful classification of the helium terms but criticized the roughness of the underlying model. He believed that his and Kramers's approach, being more true to the general principles of quantum theory, would be the only one able to provide quantitative results and a proper identification of the normal state. The strategy to be followed was clear but not easily executable. One first had to extract continuous classes of multiperiodic motions from among the motions of the exact orbital model; then one had to quantize the motions in each class with the help of Bohr's golden rule (100); finally, selection rules had to be established on the basis of the correspondence principle.^[113]

Concerning the possible continuous classes of multiperiodic motions, Bohr and Kramers somewhat revised their original opinion (perhaps in reaction to Landé's connection of the p-He spectrum with perpendicular orbits). In 1920 they believed, until Born and Heisenberg proved the contrary, that there were only two such classes (once the class of symmetrical ring motions had been excluded), one corresponding to mutually perturbed concentric, circular, and coplanar orbits, the other corresponding to mutually perturbed perpendicular, circular orbits (the angle between the two orbits being affected by the perturbation). They also believed, until Born and Heisenberg proved the contrary of this as well, that these two classes were not connected by a continuous set of multiperiodic solutions. In this way they could explain very simply the existence of two separate series spectra and why they did not combine. Indeed, in the generalization to non-multiperiodic systems, the correspondence principle suggested a

[112] See Franck and Reiche 1920. With his new vacuum spectrograph (for the extreme ultraviolet) T. Lyman soon detected the p-He spectral line (585 Å) corresponding to the transition from n = 2 to n = 1 (Lyman 1922).

[113] Bohr to Franck, 18 Oct. 1920, BCW 3:[644]-[645]; Bohr to Landé, 24 Feb. 1920, BCW 4:[719]-[720]; Bohr [1921d], [132]-[133]. This manuscript contains, m its second paragraph ("Helium," [122]-[139]), the most detailed description of Bohr's and Kramers's ideas on helium by late 1921. Bohr 1922b, appendix (September 1922), [180]-[181].

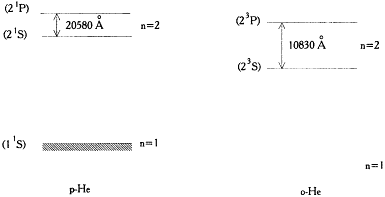
Figure 20.
Helium levels according to Franck and Reiche 
(the modern notation is given in parentheses).

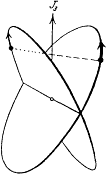
Figure 21.
The Bohr-Kemble model of the helium 
atom (from Born 1925, 331). J₃  denotes 
the total angular momentum.

correspondence between the topological structure (connectedness) of the space of classical motions and the connectivity (defined by the possibility of quantum transitions) of stationary states. In this respect, Bohr commented, Landé's model was necessarily wrong, since all resulting motions belonged to a unique continuous multiperiodic class.^[114]

Among the multiperiodic motions of the orbital model Bohr still had to determine the one corresponding to the normal state, which was of course the most important task from the point of view of atomic building. There were three candidates for which the two electrons were in a one-quantum (n = 1) state: the old ring state, the Landé-Sommerfeld planar concentric state, and an intersecting state belonging to the p-He class (fig. 21). Bohr

[114] Bohr [1921d], [122]-[139]; Bohr [1922c], [379]-[387]; Bohr [1921d], [124].

and Kramers first proved that the second candidate was mechanically excluded. Indeed, according to classical mechanics, the radial action variable corresponding to the motion of the outer electron in a Coulomb potential modified by the inner electron always exceeds the quantum of action if the inner electron is on a one-quantum orbit. This makes the one-quantum quantization of the motion of the outer electron impossible. It might be worth noticing that this mechanical type of exclusion already had an antecedent, namely, the exclusion of the value k = 0 in the Sommerfeld atom, on the ground that the corresponding orbit would cross the nucleus.^[115]

To exclude the old ring state Bohr appealed to the correspondence principle, exactly in the same way as in the exclusion of transitions between o- and p-He states. The ring motion was not continuously related to the class of coplanar concentric motions and could therefore not be obtained by the radiative decay of stationary states corresponding to the latter motions. As Bohr put it in his Göttingen lectures, in order to form a ring atom from an o-He state, "one must so to speak demand a readiness on the part of the outer electron to come to an understanding with the inner electron." And such understanding presupposed some kind of continuity, as in Bohr's early meditations on language.^[116]

At the very best, the one-quantum ring motion could have resulted from a simultaneous binding of the two electrons through a succession of larger ring motions with decreasing radius. But this was a very unrealistic way to form helium atoms. Here we have the key of Bohr's above-discussed exclusion of "configurations of polyhedral symmetry": such configurations could not be continuously related to earlier dissymmetric steps in the formation of the atom, at least if one could believe in the analogy with helium, the simplest atom with more than one electron.^[117]

Having excluded the two planar candidates for the normal state of helium, one was left with the intersecting motion, obtained from the simple model of two intersecting one-quantum circular orbits by mutual perturbation. For the total angular momentum to be h /2p , the angle between the planes of the orbits has to be 120°. On the basis of this model (which was also proposed by Kemble on different grounds) Kramers calculated the ionization potential of the helium atom, taking the inverse of the charge number of the nucleus, 1/Z , as a perturbation parameter (for large Z the mutual perturbation of the two electrons can be neglected). To first order in 1/Z the result was 4V below the experimental value. When Bohr lectured in Göttingen in June 1922, he still hoped that the dis-

[115] Bohr [1920c], [64]; Bohr [1921d], [133]-[134].

[116] Bohr [1922c], [386].

[117] Bohr [1921d], [135], [137]-[138].

crepancy resulted from the large value ½ of the perturbation parameter. If this were true, the quantum theory, with the help of the correspondence principle, would account for all known empirical properties of helium.^[118]