Preferred Citation: . The Oceans, Their Physics, Chemistry, and General Biology. New York: Prentice-Hall, c1942 1942. http://ark.cdlib.org/ark:/13030/kt167nb66r/
 | The Oceans Their Physics, Chemistry, and General BiologyH. U. SverdrupProfessor of Oceanography, University of California |
Preferred Citation: . The Oceans, Their Physics, Chemistry, and General Biology. New York: Prentice-Hall, c1942 1942. http://ark.cdlib.org/ark:/13030/kt167nb66r/
Copyright, 1942, by PRENTICE-HALL, INC. 70 Fifth Avenue, New York
ALL RIGHTS RESERVED. NO PART OF THIS BOOK MAY BE REPRODUCED IN ANY FORM, BY MIMEOGRAPH OR ANY OTHER MEANS, WITHOUT PERMISSION IN WRITING FROM THE PUBLISHERS.
PRINTED IN THE UNITED STATES OF AMERICA
Preface
Four years ago when we started the preparation of this book, we hoped to give a survey of well-established oceanographic knowledge, but it soon became apparent that the book could not be brought up to date without summarizing and synthesizing the wealth of information that has been acquired within the past dozen years, as well as the many new ideas that have been advanced. Consequently, the book has grown far beyond its originally planned scope, and the presentation has become colored by the personal concepts of the authors. Discussion of many topics, such as the absorption of radiation in the sea, the relations of organisms to the chemical composition of sea water, or the productivity of the sea, has led to tentative conclusions that are perhaps presented here as better substantiated than is actually the case. At the risk of premature generalizations we have, however, preferred definite statements to mere enumeration o uncorrelated observations and conflicting interpretations, believing that the treatment selected would be more stimulating.
The book is intended to provide a good deal of factual information, but above all it should be an aid to the beginner and specialist alike in the coordination of the various fields of oceanography. The lists of literature at the ends of chapters are not intended to be exhaustive, but will serve as guides to recent publications. When possible, reference is made to books containing comprehensive bibliographies rather than to original papers.
We are much indebted to our colleagues at the Scripps Institution of Oceanography for their numerous helpful suggestions and their constructive criticism of many parts of the book. We are also obliged to Mr. John A. Fleming, Director of the Department of Terrestrial Magnetism, Carnegie Institution of Washington, for permitting free use of unpublished data from the last cruise of the Carnegie.
We extend our thanks to Dr. L. Lek for assistance in carrying out a large number of computations, to Mr. E. C. La Fond for preparation of most of the graphs and charts, to the American Association of Petroleum Geologists and the G. M. Manufacturing Company of New York for use of illustrations published by them, and to the University of Chicago Press for use of the Goode Base Maps. Miss Ruth Ragan has rendered invaluable assistance in correcting and checking manuscript and proofs and in compiling the bibliographies.
The Authors.
Contents
| Chapter | Page |
|---|---|
| Preface | v |
| I. Introduction | 1 |
| II. The Earth and the Ocean Basins Figure and size of the earth. Distribution of water and land. Relief of the sea floor. Major features of topography. Terminology of submarine topography. Bottom configuration of the oceans. Bottom configuration of the Arctic and Antarctic regions. Bottom configuration of adjacent seas. Submarine canyons. Shorelines. Bibliography. | 8 |
| III. Physical Properties of Sea Water Salinity and chlorinity. Units of temperature, salinity, and pressure, and their ranges in the sea. Density of sea water. Thermal properties of sea water. Colligative and other properties of sea water. Properties of sea ice. Transmission of sound. Absorption of radiation. Eddy conductivity, diffusivity, and viscosity. Bibliography. | 47 |
| IV. General Distribution of Temperature, Salinity, and Density The heat budget of the earth as a whole. The heat budget of the oceans. Evaporation from the sea. Salinity and temperature of the surface layer. Theory of the periodic variations of temperature at subsurface depths. Distribution of density. Subsurface distribution of temperature and salinity. The water masses of the oceans. Basins. Bibliography. | 98 |
| V. Theory of Distribution of Variables in the Sea Scalar fields. Relation between the distribution of properties and the currents in the sea. Distribution of conservative concentrations in the sea. Distribution of nonconservative concentrations. The Principle of dynamic equilibrium. Bibliography. | 153 |
― viii ―
VI. Chemistry of Sea WaterConstancy of composition. Units used in chemical oceanography. Composition of sea water. Elements present in sea water. Preparation of artificial sea water. Dissolved gases in sea water. The carbon dioxide system. Solubility of salts in sea water. The oxidation-reduction potential of sea water. Inorganic agencies affecting the composition of sea water. Geochemistry of the ocean waters. Bibliography. | 165 |
| VII. Organisms and the Composition of Sea Water Chemical composition of marine organisms. Interrelations between elements whose distribution is affected by biological activity. Distribution of phosphate, nitrogen compounds, and silicate in the oceans. Factors influencing the distribution of nutrient elements. Compounds of carbon, nitrogen, phosphorus, and silicon in the sea. Bibliography. | 228 |
| VIII. The Sea as a Biological Environment Physical and chemical characteristics of the marine environment. Other characteristics of the environment. Classification of the marine environment. General character of populations of the primary biotic divisions. Development of life in the sea. Bibliography. | 267 |
| IX. Populations of the Sea Plant Groups of the Sea: Thallophyta; Blue-green algae (Myxophyceae) ; Green algae (Chlorophyceae) ; Brown algae (Phaeophyceae) ; Red algae (Rhodophyceae) ; Yellow-green algae; The higher plants in the sea. The Animal Population of the Sea: Synopsis of the more important systematic groups of marine animals; Reproduction and life cycles in marine animals. Bibliography. | 286 |
| X. Observations and Collections at Sea Oceanographic Vessels and Their Facilities: Vessels; Winches; Wire ropes and accessory fittings; Shipboard laboratories. Observations and Collections: Positions at sea; Sonic soundings; Wire soundings; Bottom-sampling devices; Temperature measurements; Water-sampling devices; Treatment and analysis of serial observations; Observations of tides; Deep-sea anchoring. Current Measurements: Drift methods; Flow methods; Current meters; Analysis of records of currents. Collection and Analysis of Biological Samples: Collection of benthic organisms; Collection of nekton; Collection of plankton; Interpretation of plankton observations. Bibliography. | 331 |
| XI. Geneeral Character of Ocean Currents | 389 |
| XII. Statics and Kinematics Statics: Units and dimensions; The fields of gravity, pressure, and mass; Significance of Sigma-T surfaces; Stability. Kinematics: Vector fields; The field of motion and the equation of continuity; Representations of the field of motion in the sea. Bibliography. | 400 |
| XIII. Dynamics of Ocean Currents The hydrodynamic equations. Currents related to the field of pressure. Friction. Wind currents. Conclusions as to currents on the basis of tonguelike distribution of properties. Thermodynamics of ocean currents. Bibliography. | 431 |
― ix ―
XIV. Waves and TidesIntroduction. Surface waves. Long waves. Tides. Tidal currents. Effect of friction on tides and tidal currents. The semidiurnal tide of the Atlantic Ocean. Internal waves. Bibliography. | 516 |
| XV. The Water Masses and Currents of the Oceans Antarctic Circumpolar Ocean. The South Atlantic Ocean. The equatorial region of the Atlantic Ocean. The adjacent seas of the North Atlantic Ocean. The North Atlantic Ocean. Adjacent seas of the Indian Ocean. The Indian Ocean. The South Pacific Ocean. The equatorial region of the Pacific Ocean. The North Pacific Ocean. The adjacent seas of the North Pacific Ocean. The water masses of the oceans: A summary. The deep-water circulation of the oceans. Bibliography. | 605 |
| XVI. Phytoplankton in Relation to Physical-Chemical Properties of the Environment Methods of Flotation. Factors of Phytoplankton Production: I: Direct primary factors of reproduction and growth; Direct and indirect secondary factors influencing population density. Factors of Phytoplankton Production: 11: Photosynthesis of phyto-plankton; Plant nutrients and vertical circulation of water; Horizontal ocean currents; Temperature. Bibliography. | 762 |
| XVII. Animals in Relation to Physical-Chemical Properties of the Environment Ecological Groups and Some of Their Adjustments and Conditions of Life: Benthos, animals of the sea floor; Nekton, the swimming animals; Zooplankton, the floating animals. Relations to the Physical-Chemical Properties of the Environment: Light; Salinity; Temperature; Ocean currents; Oxygen. Bibliography. | 799 |
| XVIII. Interrelations of Marine Organisms Natural Associations of Organisms. Nutritional Relationships: The significance of micro-plants; The significance of micro-animals; Plankton and filter feeders; Detritus feeders and scavengers; Littoral browsers; Preying animals. Biological Factors Influencing Movements and Concentration of Organisms: Phytoplankton-zooplankton; Nekton; Benthos. Marine Bacteria and Their Role in the Biological and Chemical Cycles in the Sea: Structure and reproduction; Bacterial modes of life; The nitrogen cycle ; Phosphorus, carbon, and sulphur cycles; Bacteria and bottom deposits; Distribution of bacteria in the sea. Bibliography. | 879 |
| XIX. Organic Production in the Sea Phytoplankton production. Zooplankton production. Commercial production. The production in different regions. Bibliography. | 925 |
― x ―
XX. Marine SedimentationIntroduction. Constituents of Marine Sediments. Transportation of Sedimentary Debris: Transportation of sediment to the sea; Transportation of sediment in the sea. Mass Properties of Marine Sediments. Classification of Recent Marine Sediments. Distribution of Pelagic Sediments. Mass Properties of Deep-Sea Sediments. The Environment of Deposition. Calcium Carbonate: Factors which determine accumulation and deposition of calcareous material; The distribution of calcium carbonate. Organic Matter: Quantity and character of organic matter in marine sediments; Distribution of organic matter. Shallow-Water and Nearshore Sediments. Elements Concentrated on the Sea Bottom and Authigenic Minerals. Rates of Sedimentation. Summary of Factors Determining Character of Marine Sediments. Bibliography. | 946 |
| Appendix. Tables for Computing Geopotential Distances Between Isobaric Surfaces Contents. Symbols and definitions. Explanation. Bibliography. | 1051 |
| Index | 1061 |
I. Introduction
Oceanography embraces all studies pertaining to the sea and integrates the knowledge gained in the marine sciences that deal with such subjects as the ocean boundaries and bottom topography, the physics and chemistry of sea water, the types of currents, and the many phases of marine biology. The close interrelation and mutual dependence of the single marine sciences have long been recognized. Thus, the first report, in 1902, of the administration of the International Council for the Study of the Sea, states:
… it was seen from the beginning that the study of the physical conditions, of the chemical nature of the ocean waters, of the currents, etc., was of the greatest importance for the investigation of the problems connected with life, that on the other hand, the study of the floating organisms had particular worth for the solution of hydrographic problems, and consequently that a sharp line should never be drawn between these two main divisions….
The same idea is expressed even more clearly in the prospectus which in 1908 accompanied the first number of the Internationale Revue der gesamten Hydrobiologie und Hydrographie:
Above all, the editors recognize the necessity of a synthesis of our biological and hydrographic-geological knowledge of the waters. These two spheres of investigation are inseparable, since the water, whether as river, lake, or sea, is never a factor in the shaping of the earth without being also a medium for life, and, on the other hand, is never a medium for life without at the same time having an important influence in the shaping of the earth's surface.
As the biology of the waters has now passed from the description of what is found therein to inquire into the causes and origins of the animal and plant life and the phenomena accompanying it, the absolute necessity has arisen for the biologist to really understand the nature of the separate waters, their physics and chemistry as well as their form and the history of their bed.
Since 1900, great advances have been made within all of the marine sciences, and the contacts between the special fields have become more and more intimate. The development is due partly to improved technique and partly to the application to the phenomena in nature of theoretical research and results of laboratory studies.
At the beginning of the twentieth century the distribution of land and sea was known with the exception of parts of the Arctic and the Antarctic, but now most coast lines are charted. The introduction of radio time signals has made possible the exact determination of longitudes and, thus, the correction of minor errors that previously could not be avoided. About twenty-five years ago, knowledge of the submarine topography was very scant, except in shallow-water areas of importance to navigation, where detailed soundings with lead and line could be made rapidly. Since a single sounding in deep water, say 6000 m or more, required several hours, however, such soundings were few and far between, and it was generally considered that the deep-sea bottom was a flat, monotonous plain devoid of rugged relief. In 1911, Fessenden made the first attempts to determine depths by sonic methods, and from about 1920 sonic depth finders have been in use with which soundings can be taken in a few seconds from a vessel running full speed. This new method has in a few years completely altered our concept of the topography of the ocean bottom. Basins and ridges, troughs and peaks have been discovered, and in many areas a bottom topography has been found as rugged as the topography of any mountain landscape.
The increased knowledge of the character of the bottom topography has greatly facilitated the understanding of the flow of the bottom water, and has helped toward explaining observed differences of hydrographic conditions in neighboring areas. Such differences, on the other hand, have been used for determining the height of barriers separating different basins in areas in which few soundings had been made.
Knowledge of bottom sediments has been advanced partly by the introduction of refined physical and chemical methods for the study of the fine-grained inorganic materials and partly by improved methods of obtaining long cores of bottom deposits and specimens of solid rock. The presence of stratification in core specimens from the open ocean has stimulated great interest in the processes controlling the character of the sediments and the rate of sedimentation. These advances have led to the rapid development of the science of submarine geology, which deals with the topographic features of the sea bottom, the agencies that have been active in the development of these features, the types and distribution of sediments, and the processes of sedimentation. The foundation for submarine geology was laid by Sir John Murray, who, with various co-workers, discussed the bottom samples of the Challenger Expedition, 1873–1876, and examined virtually all bottom samples collected prior to his death in 1914. The recent rapid development of interest and the application of new techniques is due mainly to American scientists such as Piggott, Revelle, Shepard, Stetson, and Vaughan, and to the German workers, Correns and Pratje.
Numerous problems within submarine geology cannot be studied properly without knowledge of the nature of ocean currents, the physics and chemistry of the sea water, the general character of the organisms that contribute to the marine sediments, and the transformative activities of the bacteria in the sediments. Thus, submarine geology is dependent upon the results of nearly every other marine science.
Within physical oceanography the study of waves and tides stands in a separate class, because theoretical investigations preceded the accumulation of information as to the exact character of the phenomena. Thus, the theory of surface waves was developed by Gerstner as early as 1802 and was improved by Stokes in 1847. In this early work, however, the water was considered to be an ideal fluid, and many results were more mathematically beautiful than practically applicable, but during the last decades studies, particularly by H. Jeffreys, have partly filled the gap between theory and observation.
Theories of tides were developed by Newton (1642–1727) and Lagrange (1736–1813). Lagrange's formulation of the problems is still valid, but the mathematical difficulties of the theory have not yet been overcome. In recent years notable advances toward the understanding of the tides have been made by the staff of the Liverpool Tidal Institute, headed by Proudman, which has solved fundamental problems for ocean basins of analytically defined geometrical shape, and by the Austrian School, notably Defant and Sterneck, which has used the principles of hydrodynamics in the studies of tides in bays of irregular form. American workers in the U. S. Coast and Geodetic Survey have made notable contributions in the analysis of observed tides and the prediction of tides in coastal areas.
A third type of waves, internal waves or boundary waves, was discussed by Stokes in 1847. The theory treated only the case of waves at the boundary of two ideal fluids of different density, but in 1904 it was successfully applied by Ekman to explain the phenomenon of “dead water.” Subsequent observations indicated that other types of internal waves, generally of tidal periods, were present in the open ocean, and the study of these was greatly furthered by Fjeldstad's theory, which was advanced in 1933 and which deals with internal waves in a liquid whose density increases continuously with depth.
The physical properties of sea water can conveniently be divided into two groups: those that are independent of the ocean currents and of such impurities as suspended particles of inorganic or organic origin—for example, density, specific heat, osmotic pressure, and others; and those that depend upon currents and suspended particles—for example, eddy viscosity, conductivity, diffusion, and transparency. The properties in the first group were accurately determined at the beginning of the century,
The general physical theories of ocean currents were developed at the beginning of the present century, notably by Scandinavian oceanographers. Helland-Hansen applied V. Bjerknes' theorem of circulation in a nonhomogenous fluid to the ocean, and Ekman developed the theory of wind-driven currents. The practical application of the Bjerknes theorem was made possible largely through the ingenuity of Fridtjof Nansen, who, about the year 1900, achieved increased accuracy of temperature and salinity determinations. Rossby and his collaborators in the United States have applied results from fluid mechanics to the dynamical problems of the sea. It cannot be foreseen to what extent these new ideas will modify the concepts of the dynamics of ocean currents, but Rossby's work has given new impetus to the theoretical and practical examination of the phenomena. The application of his and of the earlier theories has become increasingly important, owing to the rapid accumulation of temperature and salinity observations and of current measurements.
In the field of physical oceanography, the greater part of the theoretical and practical work can be conducted with little or no attention to results in other marine sciences. Occasionally, conclusions are tested by examining distributions of properties that are influenced by biological activity—for instance, the dissolved oxygen content—but often studies in physical oceanography can be carried out independently. For this reason several oceanographic institutions, such as the Institut für Meereskunde of the University of Berlin, and the Division for Oceanography at the Geophysical Institute, Bergen, Norway, are devoted to research within physical oceanography only, and for this same reason the International Association of Physical Oceanography exists as part of the International Union of Geodesy and Geophysics, and separate from other branches of oceanography. The linking of physical oceanography to the geophysical sciences is logical. Many problems, particularly those related to the dynamics of the atmosphere and the sea, are so similar in meteorology and physical oceanography that the theoretical approach is nearly identical, and the field dealing with the interaction between
Although physical oceanography is to a great extent independent of the other marine sciences, its results are used extensively in marine biology and submarine geology. In marine biology it is necessary to know the physical and chemical characteristics of the medium in which the organisms live, the types of currents that may regulate the distribution of the organisms, the vertical motion that carries subsurface waters rich in plant nutrients toward the surface, the depth to which light penetrates, and so on. In submarine geology, knowledge of the large-scale ocean currents is needed for the study of dispersal of fine material brought into the sea by rivers; and information as to the currents at the bottom, their velocity, and their state of turbulence is required for an understanding of the character of sediments found in different localities and of the processes of sedimentation. Because of this wide application it is desirable that the physical oceanographer be acquainted with problems in other marine sciences in order to make his own conclusions better understood and more available to workers in other fields.
In the field of chemistry, the major constituents of the salts that are dissolved in sea water were accurately determined in the 1880's by Dittmar, and around 1900 the empirical relations between chlorinity, salinity, and density were established by Knudsen. These relations are of such importance to physical oceanography that the chemical methods for determining density are considered as necessary tools in that field. Later determinations of the major constituents have introduced only small changes in the early results, but refined methods of analysis have led to the detection of more and more elements in sea water, and in many instances have made possible accurate measurements of the amounts of these minor constituents.
In recent years, notable advances have been achieved in the development of rapid methods for determining the biologically important plant nutrients, and in this field the contacts between marine biology and the chemistry of sea water are so intimate that it is difficult to indicate where the biology stops and the chemistry begins. Concepts and results in physical chemistry have been especially useful in explaining the biologically important carbon dioxide system in the sea water. Important contributions have been made by Harvey, Atkins, and Cooper in Great Britain; Moberg, Rakestraw, and Thompson in the United States; by Wattenberg in Germany, and by Buch in Finland.
Early biological observations were naturally concerned mainly with the larger animals and plants obtainable by simple methods of collecting. This was true even as late as 1839, when Edward Forbes pioneered in the study of marine organisms in relation to their physical environment. It was then generally thought that life could not exist at great depths
The realization that life is possible at all depths was of great biological interest, but the discovery of a community of floating microscopic organisms inhabiting the upper water strata was a vastly more significant one, as far as the economy of the sea is concerned. The use of townet and microscope in the study of this ubiquitous multitude of tiny drifting plants and animals of the sea was begun by Johannes Müller about 1846. In 1887 Victor Hensen applied the name plankton to this community and initiated the first quantitative studies. The discovery of plankton made possible an approach to the understanding of the economy of the sea as a whole, for it is the prolific production of this community of organisms that supports the larger forms of life and that is responsible for variations in the distribution of certain chemical elements in the sea.
Most of the older marine biological studies were of necessity chiefly exploratory and descriptive in nature, for only through systematic description and cataloguing of the myriads of forms could a foundation for future work be laid and tools for analysis provided. The descriptive studies must continue, but, as the taxonomic groups become defined and their structure becomes known, the need for such work diminishes and, especially in the better-known areas of the ocean, the emphasis has already shifted to questions of interrelations of the organisms with each other and with the inanimate environment. Near the close of the last century and at the beginning of the present, this point of view was given much impetus by many workers, among whom may be mentioned Brandt, Hjort, Gran, Johnstone, Lohmann, Johannes Schmidt, and Steuer in Europe, and Agassiz, Bigelow, Fraser, Kofoid, and Ritter in America. It is this view which has been carried forward to the present time.
The pressing need for elucidation of the many biological phenomena of the sea has been a motivating force not only in inspiring the application of known aspects of physical and chemical oceanography, but also in stimulating studies of such problems as penetration of light, viscosity, osmotic pressure, the carbon dioxide system, and especially researches on the biologically important elements. Conversely, the distribution and fluctuations of these elements are explicable only through the assistance of biological observations.
During the last decades, for which the trend in oceanographic research has been briefly reviewed, the knowledge of the oceans has been greatly increased. Prior to about 1900, deep-sea observations had been accumulated mainly on large-scale expeditions, foremost among which stands the expedition that represents the beginning of oceanography, the British
A comprehensive review of the present status of oceanographic exploration and information on the location, history, and facilities of every establishment engaged in marine research was compiled by T. W. Vaughan and published in 1937 by the National Academy of Sciences under the title International Aspects of Oceanography. This book, together with H. B. Bigelow's Oceanography, Its Scope, Problems, and Economic Importance, published by the National Academy in 1931, summarizes the present facilities for oceanographic research and the aims toward which the work is directed. The development of the exploration of the sea is described in such books as Sir John Murray's Summary of the Scientific Results of the “Challenger” Expedition of 1873–1876, Murray and Hjort's Depths of the Ocean, and Herdman's Founders of Oceanography.
Our knowledge of the oceans is still fragmentary and inadequate. In the Pacific and Indian Oceans, large regions exist from which absolutely no information is available, and from most areas only general conditions in certain seasons of the year are known. Expeditions are needed for filling in gaps and for carrying out systematic exploration of regions from which only scattered data are available. The need is even greater for systematic work at sea by well-equipped oceanographic stations that will represent many of the marine sciences, so that findings in different fields can be correlated. Only through such correlation can the marine sciences become the unified science of Oceanography that was visualized at the time the International Council for the Study of the Sea was established.
II. The Earth and the Ocean Basins
Figure and Size of the Earth
As a first approximation the earth may be considered as a sphere, but, according to accurate observations, its figure is more closely represented by an ellipse of rotation—that is, an oblate spheroid, the shorter axis being the axis of rotation. The figure of the earth has been defined by various empirical equations, the constants of which are based on observations and are subject to modification as the number of observations increases and their accuracy is improved. The geometrical figures defined by these equations cannot exactly represent the shape of the earth because of the asymmetrical distribution of the water and land masses.
To define the position of a point on the earth's surface, a system of coordinates is needed, and as such the terms latitude, longitude, and elevation or depth are used. The first two are expressed by angular coordinates and the third is expressed by the vertical distance, stated in suitable linear units, above or below a reference level that is generally closely related to mean sea level. The latitude of any point is the angle between the local plumb line and the equatorial plane. Because the earth can be considered as having the form of a spheroid, and as the plumb line, for all practical purposes, is perpendicular to the surface of the spheroid, any plane parallel to the Equator cuts the surface of the spheroid in a circle, and all points on this circle have the same latitude. These circles are called parallels of latitude. The latitude is measured in degrees, minutes, and seconds north and south of the Equator. The linear distance corresponding to a difference of one degree of latitude would be the same everywhere upon the surface of a sphere, but on the surface of the earth the distance represented by a unit of latitude increases by about 1 per cent between the Equator and the Poles. At the Equator, 1 degree of latitude is equivalent to 110,567.2 m, and at the Poles it is 111,699.3 m. In table 1 are given the percentages of the earth's surface between different parallels of latitude.
The line in which the earth's surface is intersected by a plane normal to the equatorial plane and passing through the axis of rotation is known as a meridian. The angle between two meridian planes through two
| Latitude | % | Cumulative % |
|---|---|---|
| 0°– 5° | 8.68 | 8.68 |
| 5–10 | 8.62 | 17.30 |
| 10–15 | 8.48 | 25.78 |
| 15–20 | 8.30 | 34.08 |
| 20–25 | 8.04 | 42.12 |
| 25–30 | 7.72 | 49.84 |
| 30–35 | 7.36 | 57.20 |
| 35–40 | 6.92 | 64.12 |
| 40–45 | 6.44 | 70.56 |
| 45–50 | 5.92 | 76.48 |
| 50–55 | 5.33 | 81.81 |
| 55–60 | 4.71 | 86.52 |
| 60–65 | 4.05 | 90.57 |
| 65–70 | 3.36 | 93.93 |
| 70–75 | 2.64 | 96.57 |
| 75–80 | l.90 | 98.47 |
| 80–85 | 1.15 | 99.62 |
| 85–90 | 0.38 | 100.00 |
| Equatorial radius, a.................... 6378.388 km |
| Polar radius, b......................... 6356.912 km |
| Difference (a − b)................ 21.476 km |
| Area of surface......................... 510,100,934 km2 |
| Volume of geoid......................... 1,083,319,780,000 km3 |
The distance between points on the earth's surface and the area represented by a given zone cannot be correctly represented unless the size of the earth is known. The values for the equatorial and polar radii are given in table 2, with other data concerning the size of the earth that can be computed from these values. The values for the equatorial and polar radii are those for sea level. The land masses are elevations upon the geometrical figure of the earth, and the sea bottoms represent depressions.
Measurements of depressions below sea level, to be strictly comparable, should be referred to the ideal sea level; that is, to a sea surface which is everywhere normal to the plumb line. In the open ocean the deviations from the ideal sea level rarely exceed 1 or 2 m. The errors that are introduced by referring soundings to the actual sea surface are insignificant in deep water, where the errors of measurement are many times greater. In coastal areas where shoal depths represent a hazard to navigation and where soundings can be made with great accuracy, the
Mean low water. United States (Atlantic Coast), Argentina, Norway, Sweden.
Mean lower low water. United States (Pacific Coast).
Mean low water springs. Great Britain, Italy, Germany, Denmark, Brazil, Chile.
Mean monthly lowest low water springs. Netherlands.
Lowest low water springs. Brazil, Portugal.
Indian spring low water. India, Argentina, Japan.
Mean semi-annual lowest low water. Netherlands East Indies.
Lowest low water. France, Spain, Norway, Greece.
International low water. Argentina.
The mean of the heights of low-water spring tides is known as the low water springs. International low water is 50 per cent lower, reckoned from mean sea level, than low water springs. Indian spring low water depends upon component tides found by harmonic analysis. Other terms are defined elsewhere (p. 562).
The topographic features of the earth's surface can be shown in their proper relationships only upon globes that closely approximate the actual shape of the earth, but for practical purposes projections that can be printed on flat sheets must be used. It is possible to project a small portion of the earth's surface on a flat plane without appreciable distortion of the relative positions. However, for the oceans or for the surface of the earth as a whole, most types of map projections give a grossly exaggerated representation of the shape and size of certain portions of the earth's surface. The most familiar type of projection is that developed by Mercator, which represents the meridians as straight, parallel lines. Although it is satisfactory for small areas and for the lower latitudes, the size and shape of features in high latitudes are greatly distorted because the linear scale is inversely proportional to the cosine of the latitude. In the presentation of oceanographic materials, this exaggeration is most undesirable and, consequently, projections should be used on which the true shape and size of the earth's features can be more closely approximated.
Numerous types of projections have been developed by cartographers. In some instances, these are geometrical projections of the surface of the geoid on a plane surface that can be flattened out, while in others the essential coordinates, the parallels of latitude, and the meridians have been constructed on certain mathematical principles. Maps and charts
In order to show the oceans with the least possible distortion of size and shape, the world maps used in this volume are based on an interrupted projection developed by J. P. Goode. Comparison with a globe will show that the major outlines of the oceans are not distorted and that the margins of the oceans are clearly represented. This projection has the additional advantage of being “equal-area”; that is, that areas scaled from the map are proportional to their true areas on the surface of the earth. To show the relationships between the various parts of the oceans in high latitudes, polar projections are used, and for smaller areas Mercator and other types of projections have been employed.
Distribution of Water and Land
The continental land masses extend in a north-south direction, with the greatest percentage of land in the Northern Hemisphere (table 3), and there is a more or less antipodal arrangement of land- and water-covered areas. The North Polar Sea surrounding the North Pole is opposite to the continent of Antarctica, which is centered on the South Pole, and the continental land masses represented by Europe, Asia, and part of Africa are antipodal to the great oceanic area of the South Pacific. The ocean waters are continuous around Antarctica and extend northward in three large “gulfs” between the continents, on the basis of which three oceans are recognized. The Atlantic Ocean extends from Antarctica northward and includes the North Polar Sea. It is separated from the Pacific Ocean by the line forming the shortest distance from Cape Horn (70°W) to the South Shetland Islands, and the boundary between the Atlantic and the Indian Oceans is placed at the meridian of the Cape of Good Hope (20°E). The boundary between the Pacific and the Indian Oceans follows the line from the Malay Peninsula through Sumatra, Java, Timor, Australia (Cape Londonderry), and Tasmania, and follows the meridian of 147°E to Antarctica. In the north the limit between the Atlantic and the Pacific Oceans is placed in Bering Strait, which is only 58 km wide and has a maximum depth of 55 m. Unless otherwise stated, the oceans as defined above are considered to include the semi-enclosed adjacent seas that connect with them.
Generally speaking, only three oceans are recognized, but it is sometimes desirable to make a further division. The waters surrounding
The nomenclature applied to subdivisions of the oceans is very confused. Generic names designating certain types of features, such as sea, gulf, and bay, are used somewhat indiscriminately and hence have little physiographic significance. For example, the term sea is used in connection with inland salt lakes, such as the Caspian Sea, with relatively isolated bodies of the ocean, such as the Mediterranean Sea, with less isolated areas, such as the Caribbean Sea, and even for some areas with no land boundaries, such as the Sargasso Sea in the western North Atlantic.
Several systems for naming parts of the oceans are employed in oceanographic, work. In certain instances the boundaries are selected arbitrarily by drawing straight or curved lines on the map where there are no land features which constitute natural boundaries. Such a system is followed by the International Hydrographic Bureau (1937). Wüst (1936) has suggested that the submarine ridges that are present at depths of about 4000 m be used to delimit the various parts of the oceans, and that the names now applied to the basins with depths greater than 4000 m be used to designate the areas above them. The general location of such boundaries may be seen in chart I. Oceanography is concerned not only with the form of the oceans as shown on a surface chart, but also with the distribution of properties and living organisms and the nature of the currents. Therefore, a system of nomenclature which indicates the relationships that exist in the sea would be very useful. Wüst's system, based on the ocean bottom topography, meets this purpose for the deep water but not for the upper layers. To formulate “natural regions” of the oceans, other workers, notably Schott (1926, 1935), have attempted to bring together not only geographic and topographic relationships, but also the distribution of properties and organisms, the climatic conditions, and currents. In the discussion of the distribution of organisms, fig. 220 (p. 804) shows how the oceans are subdivided upon the basis of the fauna1 distribution alone, and in the discussion of the water masses of the oceans, fig. 209 (p. 740) shows a subdivision based upon the characteristic temperature and salinity relations of the various regions. A comparison of such charts shows that, although there are certain boundaries which fall in approximately the same localities, there are many regions in which it is not possible to reconcile limits established in different ways.
In table 3 are given the areas of land and water between parallels of latitude five degrees apart. For the whole earth, the ocean waters cover
| Latitude (°) | Northern Hemisphere | Southern Hemisphere | ||||||
|---|---|---|---|---|---|---|---|---|
| Water (106 km2) | Land (106 km2) | Water (%) | Land (%) | Water (106 km2) | Land (106 km2) | Water (%) | Land (%) | |
| 90–85 | 0.979 | ....... | 100.0 | .... | ....... | 0.978 | .... | 100.0 |
| 85–80 | 2.545 | 0.384 | 85.2 | 12.8 | ....... | 2.929 | .... | 100.0 |
| 80–75 | 3.742 | 1.112 | 77.1 | 22.9 | 0.522 | 4.332 | 10.7 | 89.3 |
| 75–70 | 4.414 | 2.326 | 65.5 | 34.5 | 2.604 | 4.136 | 38.6 | 61.4 |
| 70–65 | 2.456 | 6.116 | 28.7 | 71.3 | 6.816 | 1.756 | 79.5 | 20.5 |
| 65–60 | 3.123 | 7.210 | 31.2 | 69.8 | 10.301 | 0.032 | 99.7 | 0.3 |
| 60–55 | 5.399 | 6.613 | 45.0 | 55.0 | 12.006 | 0.006 | 99.9 | 0.1 |
| 55–50 | 5.529 | 8.066 | 40.7 | 59.3 | 13.388 | 0.207 | 98.5 | 1.5 |
| 50–45 | 6.612 | 8.458 | 43.8 | 56.2 | 14.693 | 0.377 | 97.5 | 2.5 |
| 45–40 | 8.411 | 8.016 | 51.2 | 48.8 | 15.833 | 0.594 | 96.4 | 3.6 |
| 40–35 | 10.029 | 7.627 | 56.8 | 43.2 | 16.483 | 1.173 | 93.4 | 6.6 |
| 35–30 | 10.806 | 7.943 | 57.7 | 42.3 | 15.782 | 2.967 | 84.2 | 15.8 |
| 30–25 | 11.747 | 7.952 | 59.6 | 40.4 | 15.438 | 4.261 | 78.4 | 21.6 |
| 25–20 | 13.354 | 7.145 | 65.2 | 34.8 | 15.450 | 5.049 | 75.4 | 24.6 |
| 20–15 | 14.981 | 6.164 | 70.8 | 29.2 | 16.147 | 4.998 | 76.4 | 23.6 |
| 15–10 | 16.553 | 5.080 | 76.5 | 23.5 | 17.211 | 4.422 | 79.6 | 20.4 |
| 10–5 | 16.628 | 5.332 | 75.7 | 24.3 | 16.898 | 5.062 | 76.9 | 23.1 |
| 5–0 | 17.387 | 4.737 | 78.6 | 21.4 | 16.792 | 5.332 | 75.9 | 24.1 |
| 90–0° | 154.695 | 100.281 | 60.7 | 39.3 | 206.364 | 48.611 | 80.9 | 19.1 |
| All oceans and seas................................. 361.059 × 106 km2, 70.8% | ||||||||
| All land...........:.................................. 148.892 × 106km2, 29.2% | ||||||||
In table 4 are given the areas, volumes, and mean depths of the oceans and of certain mediterranean and marginal seas that together constitute the adjacent seas. The data are from Kossinna (1921), and in most instances the designated areas are readily recognized, but for details concerning the boundaries the original reference should be consulted. The Arctic Mediterranean includes the North Polar Sea, the waters of the Canadian Archipelago, Baffin Bay, and the Norwegian Sea, and is therefore separated from the open Atlantic by the line joining Labrador and Greenland in Davis Strait and running through Greenland, Iceland, Faeroe Islands, Scotland, and England, and across the English
Additional data on the areas of the adjacent seas of the Atlantic Ocean are given by Stocks (1938). Littlehales (1932) gives slightly different values for the areas of the oceans.
Relief of the Sea Floor
From the oceanographic point of view the chief interest in the topography of the sea floor is that it forms the lower and lateral boundaries of water. The presence of land barriers or submarine ridges that impede a free flow of water introduces special characteristics in the pattern of circulation and in the distribution of properties and organisms. Furthermore, as will be shown in chapter XX, the nature of the sediments in any area is closely related to the surrounding topography. On the other hand, the geomorphologist or physiographer is concerned primarily with the distribution and dimensions of certain types of topographic features that occur on the submerged portion of the earth's crust. As 71 per cent of the earth's surface is water-covered, knowledge of the major features of the earth's relief will be fragmentary if based only upon those structures that can be seen on land. During the geological history of the earth which covers a span of some thousands of million years, areas now exposed above sea level have at one or more periods been covered by the sea, and parts of the now submerged surface have been above sea level. Many problems in historical geology are therefore dependent upon knowledge concerning the configuration of the sea floor surrounding the continents and the form of the deep-ocean bottom.
Although valuable work in the open ocean has been carried on by scientific organizations, by far the greater proportion of our knowledge of submarine topography is based on soundings taken by or for national agencies in the preparation or improvement of navigational charts. In the United States the U. S. Coast and Geodetic Survey prepares charts for the waters bounding the United States and its possessions, and the Hydrographic Office of the U. S. Navy carries out similar work on the high seas and in foreign waters. The earlier hydrographic work was limited largely to the mapping of coast lines and to soundings in depths less than about 100 fathoms, where hazards to the safe operation of vessels might occur, but deep-sea soundings received a great impetus when surveys were made prior to the laying of the transoceanic cables in the latter part of the nineteenth century. Up to and including the time of the voyage of the Challenger, 1873–1876, all soundings were made with hemp ropes, which made the process a long and tedious undertaking,
| Body | Area (106 km2) | Volume (106 km3) | Mean depth (m) |
|---|---|---|---|
| Atlantic Ocean excluding adjacent seas | 82.441 | 323.613 | 3926 |
| Pacific Ocean excluding adjacent seas | 165.246 | 707.555 | 4282 |
| Indian Ocean excluding adjacent seas | 73.443 | 291.030 | 3963 |
| All oceans (excluding adjacent seas) | 321.130 | 1322.198 | 4117 |
| Aretic Mediterranean | 14.090 | 16.980 | 1205 |
| American Mediterranean | 4.319 | 9.573 | 2216 |
| Mediterranean Sea and Black Sea | 2.966 | 4.238 | 1429 |
| Asiatic Mediterranean | 8.143 | 9.873 | 1212 |
| Large mediterranean seas | 29.518 | 40.664 | 1378 |
| Baltic Sea | 0.422 | 0.023 | 55 |
| Hudson Bay | 1.232 | 0.158 | 128 |
| Red Sea | 0.438 | 0.215 | 491 |
| Persian Gulf | 0.239 | 0.006 | 25 |
| Small mediterranean seas | 2.331 | 0.402 | 172 |
| All mediterranean seas | 31.849 | 41.066 | 1289 |
| North Sea | 0.575 | 0.054 | 94 |
| English Channel | 0.075 | 0.004 | 54 |
| Irish Sea | 0.103 | 0.006 | 60 |
| Gulf of St. Lawrence | 0.238 | 0.030 | 127 |
| Andaman Sea | 0.798 | 0.694 | 870 |
| Bering Sea | 2.268 | 3.259 | 1437 |
| Okhotsk Sea | 1.528 | 1.279 | 838 |
| Japan Sea | 1.008 | 1.361 | 1350 |
| East China Sea | 1.249 | 0.235 | 188 |
| Gulf of California | 0.162 | 0.132 | 813 |
| Bass Strait | 0.075 | 0.005 | 70 |
| Marginal seas | 8.079 | 7.059 | 874 |
| All adjacent seas | 39.928 | 48.125 | 1205 |
| Atlantic Ocean | 106.463 | 354.679 | 3332 |
| Pacific Ocean, including adjacent seas | 179.679 | 723.699 | 4028 |
| Indian Ocean | 74.917 | 291.945 | 3897 |
| All oceans (including adjacent seas) | 361.059 | 1370.323 | 3795 |
Because of their practical importance and the ease with which they could be obtained, the number of soundings in depths less than a few hundred meters accumulated rapidly during the nineteenth century, but in 1895 there existed only 7000 soundings from depths greater than about 2000 m, and of these only about 550 were from depths greater than 5500 m (Bencker, 1930). These data were used by Murray in preparing the bathymetric charts accompanying the reports of the Challenger Expedition.
During the next twenty-five years the number of deep-sea soundings increased slowly, but the introduction of sonic-sounding equipment after 1920 has completely changed the picture. Devices for measuring the depth by timing the interval for a sound impulse to travel to the sea bottom and back again (only a few seconds even in deep water) are used in surveying work and are now standard equipment on many coastwise and oceanic vessels. The development of automatic echo-sounding devices (chapter X) not only made depth measurements simple but, by making accurate bathymetric charts available, introduced another aid in navigation, since passage over irregularities of the sea floor may be used to check positions. This development has necessitated extending accurate surveys into deeper water and, hence, farther from shore. Along the coasts of the United States the bottom is now being charted in detail to depths of about 4000 m. With sonic methods, if the appropriate apparatus is available, it is no more trouble to sound in great depths than it is in shoal waters, and, since many naval vessels and transoceanic commercial vessels make systematic records of their observations, the soundings in the deep sea are now accumulating more rapidly than they can be plotted.
The most common method of representing submarine topography is to enter upon a chart showing the coast lines the numerical values of the soundings at the localities in which they were obtained. Charts issued by the national hydrographic services of the English-speaking countries give depths in fathoms or, if harbor charts, in feet (1 fathom = 6 ft = 1.8288 m). Those issued by other countries generally use meters, although still other units are employed by certain European countries.
Because it is generally impossible to enter all soundings, and as numerical values alone do not give any graphic representation of the topography, contours of equal depths (isobaths) are drawn in those regions in which the number of soundings or the purpose of the chart makes it desirable. On navigational charts, contours are generally restricted to shallow areas where soundings are also shown, but, for certain regions that have been carefully examined, charts are now issued with contours entered to depths as great as 2000 fathoms (for example, U. S.
The accuracy with which submarine topography can be portrayed depends upon the number of soundings available and upon the accuracy with which the positions of the soundings were determined. Topographic maps of land surfaces are based on essentially similar data; namely, elevations of accurately located points, but the surveyor has one great advantage over the hydrographer. The surveyor is able to see the area under examination and thereby distribute his observation points in such a manner that the more essential features of the topography are accurately portrayed. The hydrographer, on the other hand, must construct the topography of the sea floor from a number of more or less random soundings. Sonic sounding methods and the introduction of more accurate means of locating positions at sea (see Veatch and Smith, 1939) have made it feasible to obtain adequate data for constructing moderately accurate charts or models of parts of the sea floor. This is particularly true of the coastal waters of the United States. Veatch and Smith have prepared contour maps of the eastern seaboard based on the investigations of the U. S. Coast and Geodetic Survey, and Shepard and Emery (1941) have made use of similar data from the Pacific Coast, where over 1,300,000 soundings were available.
In some instances it is preferable to represent the bottom configuration by vertical profiles or by relief models, but, because of the difference in magnitude of the vertical and horizontal dimensions of the oceans, it is generally necessary to exaggerate the vertical scale. The average depth of the ocean is about 3800 m, and the vertical relief of the ocean floor is therefore of the order of a few kilometers, whereas the horizontal distances may be of the order of thousands of kilometers. Hence such distorted representations give a false impression of the steepness of submarine slopes. If profiles are drawn to natural scale, the ocean waters form a shallow band with barely perceptible undulations of the bottom. Examples of undistorted profiles are given by Johnstone (1928).
In fig. 1 are shown two representations of a profile of the sea bottom in the South Atlantic based on the observations of the Meteor (Stocks and Wüst, 1935). The upper section (A) is constructed from thirteen wire soundings, and is comparable in detail to most of the profiles that could be prepared before the introduction of sonic methods. The lower section (B) is based upon over 1300 sonic soundings that were taken by the Meteor along the same route, shown in the map at the bottom part of the figure (C), where the depth contours are from chart I. The increasing complexity of the known topography of the sea bottom resulting
The water surface coincides, for all practical purposes, with the surface of the geoid, and the sea bottom, if “flat,” would be parallel to the sea surface. Irregularities of the sea floor therefore represent departures from this surface, which is convex outward. Only in small features with steep slopes are depressions actually concave outward.
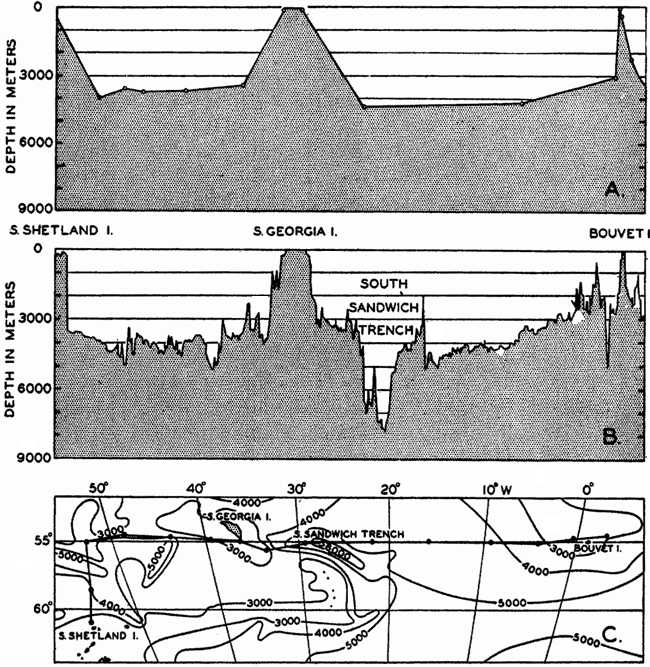
Bottom topography in the South Atlantic Ocean. (A) Profile of the bottom between the South Shetland Islands and Bouvet Island based on 13 wire soundings. (B) Profile over the same course constructed from over 1300 sonic soundings (Meteor). (C) Bottom configuration as shown in Chart I and the track of the Meteor. Vertical exaggeration in (A) and (B) about 200:1. (In part, after Stocks and Wüst, 1935.)
The greatest depths so far discovered are in the Pacific Ocean, where, in the Philippines Trench and the Japan Trench, soundings greater than 10,000 m have been obtained. In the Philippines Trench the German vessel Emden obtained a sonic sounding of 10,540 m, which, however, is considered to be about 200 m too great. The Dutch vessel Willebrord
Representations of submarine topography are usually referred to sea level, and particular interest has always been attached to those regions in which great depths are found. The greater detail with which the sea floor can now be mapped has emphasized the importance of relative relief; that is, the form and magnitude of elevations or depressions with respect to their general surroundings. In later pages it will be shown that there are two primary levels of reference on the earth's crust, one slightly above sea level, corresponding to the land masses, and a second at depths between 4000 and 5000 m, corresponding to the great oceanic basins. In comparing topographic features on land with those on the sea floor it is essential to consider them with reference to these levels.
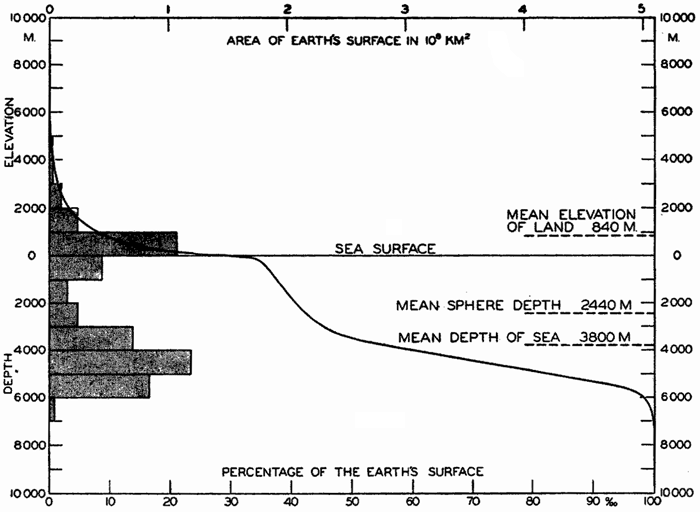
Hypsographic curve showing the area of the earth's solid surface above any given level of elevation or depth. At the left in the figure is the frequency distribution of elevations and depths for 1000-meter intervals.
One method of presenting the character of the relief of the earth's crust is by means of a hypsographic curve showing the area of the earth's solid surface above any given contour of elevation or depth. The hypsographic curve in fig. 2 is from Kossinna (1921). Although added data
The hypsographic curve of the earth's crust should not be interpreted as an average profile of the land surface and sea bottom, because it represents merely the summation of areas between certain levels without respect to their location or to the relation of elevations and depressions. Actually, the highest mountains are commonly near the continental coasts, large areas of low-lying land are located in the central parts of the continents, and the greatest depths are found near the continental masses, and not in the middle of the oceanic depressions. Entered in fig. 2 are the percentages of elevations and depressions for 1000-m intervals. These show two maxima, one just above sea level and a second between depths of 4000 and 5000 m. The significance of these maxima is discussed later (p. 23).
In table 5 are given the percentage areas of the depth zones in the three oceans, and for all oceans with and without adjacent seas. It will be noted that the shelf (0–200 m) represents a prominent feature in the Atlantic Ocean, which is also the shallowest of the oceans. By combining data in tables 4 and 5 the absolute areas of the depth zones may be computed. The hypsographic curve in fig. 2 is based on the values for all oceans, including adjacent seas.
During the geological history of the earth, great changes have occurred in the relief of the land and sea bottom. The exact nature and extent of these vertical movements is beyond the scope of the present discussion, but it should be noted that changes in relative sea level of the order of 100 m, which are readily accounted for by the withdrawal and addition of water during glacial and interglacial periods, would expose and inundate relatively large areas.
The continental shelf is generally considered to extend to depths of 100 fathoms, or 200 m, but Shepard (1939) found that the limit should be somewhat less than this; namely, between 60 and 80 fathoms (110 and
| Depth interval (m) | Including adjacent seas | Excluding adjacent seas | ||||||
|---|---|---|---|---|---|---|---|---|
| Atlantic | Pacific | Indian | All oceans | Atlantic | Pacific | Indian | All oceans | |
| 0–200 | 13.3 | 5.7 | 4.2 | 7.6 | 5.6 | 1.7 | 3.2 | 3.1 |
| 200–1000 | 7.1 | 3.1 | 3.1 | 4.3 | 4.0 | 2.2 | 2.7 | 2.8 |
| 1000–2000 | 5.3 | 3.9 | 3.4 | 4.2 | 3.6 | 3.4 | 3.1 | 3.4 |
| 2000–3000 | 8.8 | 5.2 | 7.4 | 6.8 | 7.6 | 5.0 | 7.4 | 6.2 |
| 3000–4000 | 18.5 | 18.5 | 24.0 | 19.6 | 19.4 | 19.1 | 24.4 | 20.4 |
| 4000–5000 | 25.8 | 35.2 | 38.1 | 33.0 | 32.4 | 37.7 | 38.9 | 36.6 |
| 5000–6000 | 20.6 | 26.6 | 19.4 | 23.3 | 26.6 | 28.8 | 19.9 | 26.2 |
| 6000–7000 | 0.6 | 1.6 | 0.4 | 1.1 | 0.8 | 1.8 | 0.4 | 1.2 |
| >7000 | .... | 0.2 | .... | 0.1 | .... | 0.3 | .... | 0.1 |
From the above values it may be seen that the average slope of the shelf is of the order of 2 fathoms per mile, or 0.2 per cent. This corresponds to a slope angle of about 7ʹ. Although there is a general seaward slope of the shelf, it is by no means an even-graded profile. As mentioned above, there may be terraces, ridges, hills, and depressions, and in many areas there are steep-walled canyons cutting across it. Shelf irregularities are most conspicuous off glaciated coasts, and were caused by the ice during a glacial period when this zone was exposed to glacial erosion (Shepard, 1931).
On land the slope is often more significant than the absolute range in elevation. According to Littlehales (1932) the smallest slope that the human eye can detect is 17ʹ. Therefore, except for the minor irregularities, the continental shelf would in general appear flat.
From an examination of 500 profiles, Shepard (1941) found that the inclination of the continental slope varied with the character of the coast. Continental slopes off mountainous coasts have, on the average, a slope of about 6 per cent (3°30ʹ), whereas off coasts with wide, well-drained coastal plains the slopes are about 3.5 per cent (2°0ʹ).
The submerged slopes of volcanic islands are similar to the exposed slopes of volcanic mountains, and may be as great as 50° (Kuenen, 1935). In large submarine canyons the walls are as rugged and precipitous as those of the Grand Canyon of Arizona (fig. 8, p. 40). Fault scarps above and below sea level show comparable slopes.
The average slopes of the deep-sea floor are small. Krümmel (Littlehales, 1932) found that in the North Atlantic the mean slopes varied between about 20ʹ and 40ʹ, but these are averages, or were obtained by dividing the difference in elevation by the distance between two points. Where the distances are great or when the number of soundings is small, the slopes obtained in this way do not give a true representation of the relief. The increased data now available have revealed irregularities comparable in ruggedness to the larger topographic features on land.
Major Features of Topography
The discussion of the bottom topography of the oceans will be restricted to a brief consideration of the large-scale topographic features that are represented on small charts with large contour intervals. In regions where many soundings have been obtained, it has been found that the sea bottom may be virtually as irregular as the land surface, but such details can be shown only on large-scale charts with small contour intervals, and are not included in this volume.
Submarine geology is concerned with the topography of the sea floor, the composition and physical character of the sedimentary and igneous materials that are found on the ocean bottom, and the processes involved in the development of topographic relief. The field is a relatively new one which has received great impetus from the development of sonic sounding methods that made it possible to obtain accurate maps of the sea floor, and from the development of geophysical methods (measurement and interpretation of gravity anomalies, of the earth's magnetic field, and of the path and velocity of earthquake and artificial seismic waves) that yielded estimates of the character and thickness of the materials forming the crust of the earth. However, there is yet no agreement concerning the processes involved in the geological history of the ocean basins, and the various hypotheses will not be discussed here. General reviews of the problems will be found in Johnstone (1928), Bucher (1933), Kuenen (1935), and Gutenberg (1939). A symposium on the geophysical exploration of the sea bottom (Field et al, 1938) covers many of the developments.
The distribution of elevations and depressions on the earth's crust (fig. 2) shows that there are large portions with elevations between sea level and 1000 m, and with depths between 4000 m and 5000 m. According to Bucher (1933) the larger, lower ones are related to the character of the earth's crust, while the upper ones are the result of subaerial erosion and sedimentation. The question then arises as to the extent to which the topography of the ocean bottom with reference to a depth of about 4500 m corresponds to that of the land with reference to sea level or a slightly higher level. According to Bucher, the large-scale features are essentially similar, and elevations and depressions of comparable dimensions are found both on land and on the ocean bottom. Although the major features are comparable, the details are quite different, because erosion, which plays such an all-important role in the creation of sharp relief and in the ultimate destruction of elevations on land, is virtually absent in the sea. In the sea the most effective agents of erosion are the surface waves, and these tend to produce flat-topped features that are restricted to shallow depths, since the velocity of the water particles in such waves decreases rapidly with increasing depth (p. 528). Other processes which may contribute to erosion of the sea floor are discussed in chapter XX and in the section dealing with the origin of submarine canyons (p. 41). Deposition is the characteristic process that modifies the topography of the sea bottom. Sedimentary debris accumulates in depressions, while there is little or no accumulation on topographic highs, which are devoid of fine-grained sediment and are subject to erosion if near the surface or in localities of exceptionally strong currents.
Bucher (1933) has stated that there are essentially two types of large-scale topographic features on the land and on the ocean bottom: (1) those of approximately equidimensional lateral extent, to which he applies the names swells and basins, and (2) those of elongate form, generally with steeper sides, to which he applies the names welts and furrows. On the ocean bottom the elongate welts and furrows appear to be the more common, and there is a considerable range in the size of such structures. There is a tendency for the large welts on the sea bottom to be parallel to the continental coasts, so that the oceans are divided into elongate troughs. Transverse ridges in turn subdivide these major depressions into a series of basins that are separated from one another to a greater or lesser degree. This ridge and basin topography is clearly shown by the bottom of the Atlantic Ocean and the Indian Ocean and in the western part of the Pacific Ocean, but does not appear to be so conspicuous a feature in the main part of the Pacific.
Within the smaller welts and furrows, the steepest slopes, the highest elevations, and the greatest depths are found. The welts and furrows are commonly close together, with arced outlines, and are characteristically found near the continents. The deep furrows are generally on the convex
Terminology of Submarine Topography
The terms applied to features of submarine topography will be classified according to the origin of the features rather than according to their size, although the latter procedure is the common one (for example, Niblack, 1928, Littlehales, 1932). The features of submarine relief may be grouped in two main categories, depending upon whether they have gained their characteristic form through diastrophic activity (crustal movements) or through erosion or deposition. The primary large-scale process involved in the development of relief must be diastrophic, but in many cases the characteristic feature is produced by erosion or deposition. No distinction will be made here between features that have been formed below the sea surface and those that may possibly owe their origin to subaerial erosion or deposition. As pointed out before, deposition in the sea tends to fill in the depressions and thus to level out the minor irregularities of the bottom, and, with the exception of those cases in which organisms play an important role (for example, in the formation of coral reefs), little or no deposition takes place on topographic highs.
There has been much discussion as to the processes that have led to the formation of the continental and insular shelves. Some authors maintain that they are wave-built (depositional); others consider that they are wave-cut (erosional), or that they are a combination of both processes (Johnson, 1919; Shepard, 1939). Geophysical studies on the two sides of the North Atlantic (Bucher, 1940) indicate that the shelves are composed of great prism-shaped accumulations of sedimentary rock that at the outer edge of the shelf bordering the eastern United States are 4000 m thick. To what extent these features resulted from the slow accumulation and sinking of the crust and to what extent violent diastrophic movements have been involved has not yet been decided. The characteristic form of the shelf and of isolated flat-topped banks and shoals, and other features of the shallow bottom indicate that wave erosion and transportation by currents have played an important part
The terms used to designate certain types of topographic features, their French and German equivalents, and their definitions, which are given below, correspond to those suggested by the International Hydrographic Bureau (Niblack, 1928). Unfortunately, there is still considerable confusion in the use of certain terms, particularly those which apply to the larger features of the topography. Sometimes several different descriptive terms have been applied to the same structure, and in other instances the same term is applied to features of vastly different size and probably of different origin. A committee of the International Association of Physical Oceanography (Vaughan et al, 1940) attempted to clarify many of the problems relating to the terminology, but much confusion still prevails. In order to designate any individual feature, the descriptive term is prefixed by a specific name. The specific names attached to large-scale features are generally geographical, but those assigned to such features as banks, shoals, seamounts, canyons, and sometimes deeps are often those of vessels or individuals associated with their discovery or mapping.
Features Resulting from Crustal Deformation
Elevations. The large-scale elevations of the ocean bottom are termed ridges, rises, or swells.
Ridge (F, Dorsale; G, Rücken). A long and narrow elevation with sides steeper than those of a rise.
Rise (F, Seuil; G, Schwelle). A long and broad elevation which rises gently from the ocean bottom.
Isolated mountain-like structures rising from the ocean bottom are known as seamounts. Where the ridges are curved, and particularly if parts of them rise above sea level, they are sometimes termed arcs. The broad top of a rise is termed a plateau. The expression sill is applied to a submerged elevation separating two basins. The sill depth is the greatest depth at which there is free, horizontal communication between the basins.
Depressions. The terms trough, trench, and basin are those most commonly applied to the large-scale depressions on the ocean bottom.
Trough (F, Dépression; G, Mulde). A long, broad depression with gently sloping sides.
Trench (F, Fossé; G, Graben). A long and narrow depression with relatively steep sides.
Basin (F, Bassin; G, Becken). A large depression of more or less circular or oval form.
The terms defined above are used rather loosely and are applied to features of a wide range in size.
For those parts of a depression which exceed 6000 m in depth, the term deep (F, Fosse; G, Tief) is used. As originally suggested by Murray, the term designated areas where the depths exceeded 3000 fathoms (5486 m), but it is now generally restricted to those depressions of greater depth (Vaughan et al, 1940). The term depth (F, Profondeur; G, Tiefe), prefixed by the name of the vessel concerned, may be used to designate the greatest sounding obtained in any given deep.
Features Resulting from Erosion, Deposition, and Biological Activity
As pointed out above, the features in this category have been produced by erosion of, or deposition upon, structures which may be primarily of diastrophic origin. The most prominent types of features in this group are the shelf and the slope.
Shelf. The zone extending from the line of permanent immersion to the depth, usually about 120 m, where there is a marked or rather steep descent toward the great depths. Continental Shelf (F, Plateau continental; G, Kontinental-Schelff) is applied to the feature bordering the continents, while Insular Shelf (F, Socle; G, Insel-schelff) is used for the feature surrounding islands.
Slope. The declivity from the outer edge of the shelf into deeper water. Continental Slope (F, Talus continental; G, Kontinental-Abfall) and Insular Slope (F, Talus insulaire; G, Inselabfall) are applied to the slopes bordering continents or islands.
The following terms are applied to the upper parts of elevations which show the effects of erosion or deposition.
Bank (F, Banc; G, Bank). A more or less flat-topped elevation over which the depth of water is relatively small, but which is sufficient for surface navigation.
Shoal (F, Haut-fond; G, Untiefe or Sandgrund). A detached elevation with such depths that it is a danger to surface navigation and which is not composed of rock or coral.
Reef (F, Récif; G, Riff). A rocky or coral elevation (generally elongate) which is dangerous to surface navigation. It may extend above the surface.
A variety of names has been applied to the steep-walled fissures that penetrate the slope and cut across the shelf. The most commonly used terms are canyon and valley, but gully, gorge, and mock-valley are also applied to these features.
In addition to the terms given above, many expressions are employed in descriptions of submarine topography with the same meanings that they have when used for land topography.
Bottom Configuration of the Oceans
The major features of the topography of the ocean bottom are of such large dimensions that they are readily shown on a chart with contour intervals 1000 m apart. Such a representation is given in chart I, where the contours are entered for 1000-m intervals between 3000 m and 7000 m. The areas with depths less than 3000 m represent a rather small part of the sea floor, and the complex nature of the contours for depths less than this would confuse rather than add to the value of a chart of this kind. The topography is based upon the most recent charts available, and primarily upon the bathymetric chart prepared by the International Hydrographic Bureau in 1939 (Vaughan et al, 1940). Other sources that may be consulted for details concerning the configuration of the ocean floor are listed on page 29. It will be noted that the complexity of the topography varies in different regions. This difference must be attributed, in part, at least, to the variable amount of data available, because in those regions where the soundings are widely spaced the contours will be smooth and rounded, whereas in those areas where there are numerous soundings the contours are more complex and irregular. The Atlantic Ocean, the central part of the North Pacific Ocean, the Northern Indian Ocean, and the area surrounding Antarctica are fairly well sounded, but in many other regions, such as the North Polar Sea and the Southern Indian and South Pacific Oceans, the observations are very sparse. The increase in the complexity of the known topographic features that follows the accumulation of more depth measurements can be seen by comparing recent bathymetric charts with those published in the early years of the present century. The status of bathymetric knowledge in 1937 is shown by a series of charts in Vaughan et al (1937).
As stated above, the topography of the ocean bottom is characterized by depressions and elongated ridges. Some of these features are of very
A longitudinal ridge, the Indian Ridge, is present in the Indian Ocean and extends from India to Antarctica, but differs from the one in the Atlantic Ocean in that it is wider and does not extend so near the surface. In the Pacific Ocean the longitudinal elevations are not so conspicuous; however, the West Pacific Ridge, which is actually composed of several shorter ridges, can be traced from Japan to Antarctica, and is continuous at depths less than 4000 m except for breaks at 11°N, 10°S, and 53°S. A second elevation extends from Central America to the south and west, reaching Antarctica in the longitude of New Zealand. This East Pacific Ridge is continuous at depths less than 4000 m and separates the central depression from the deep basins bordering Central and South America and the Pacific Antarctic Basin. The effect of these major elevations on the distribution of bottom-water temperatures is shown in fig. 211, p. 749.
Within the major depressions or troughs which are bordered by the continents and the longitudinal ridges are transverse ridges that separate to a greater or lesser degree a number of basins. Wüst (Vaughan et al, 1940) has suggested that the 4000-m contour be used as the boundary in designating basins, but this is a purely arbitrary delimitation that places undue emphasis upon the absolute depth rather than upon the relative relief, which in many instances is of greater significance. For example, the Mediterranean Sea Basin is virtually excluded from such a classification, although it is a deep, isolated basin, much of it extending more than 3000 m below the sill in the Strait of Gibraltar. In the tabulation accompanying chart I are listed the names for the major parts of the oceanic depressions which Wüst has termed basins; namely, those parts which have depths exceeding 4000 m. Certain individual basins are clearly
In the tabulation of the basins given on chart I are listed some of the more prominent deeps; namely, those features where the depths exceed 6000 m. Some deeps are located more or less centrally in the large basins; for example, Wharton Deep, Byrd Deep, and the numerous deeps in the central part of the North Pacific, but these rarely exceed 7000 m in depth. On the other hand, numerous deeps of elongate character are located near and parallel to continental coasts, island arcs, or submarine ridges which correspond to the furrows discussed on p. 23. These marginal deeps, to which the term trench or sometimes trough is applied, are the features within which the greatest depths are found, in nearly all cases exceeding 8000 m. Only one such trench is found in the Indian Ocean; namely, the Sunda Trench. In the Atlantic are to be found the Romanche Trench, the South Sandwich Trench, and the Puerto Rico and Cayman Troughs. The greatest number are in the western part of the Pacific Ocean, although there is a chain of such features paralleling the mountainous coast of parts of Central and South America. As stated before, the regions in which these deep trenches occur are sites of volcanic and seismic activity. The complex topography of the East Indian Archipelago, which has been described by Kuenen (1935), is shown schematically in fig. 208, p. 736.
For a detailed description of the features of the sea bottom the reader should consult Littlehales (1932). Vaughan (1938) has described the topography of the Southern Hemisphere. There is much information of value in the large report by Vaughan and others (1940), which also contains the small-scale bathymetric chart prepared by the International Hydrographic Bureau on a Mercator projection, a special chart of the North Pacific prepared by the U. S. Hydrographic Office, and an excellent, detailed chart of the Caribbean Sea region prepared by the same agency. The standard charts on the bathymetry of the oceans are those in the series known as the Carte Générale Bathymétrique des Océans, published by the International Hydrographic Bureau at Monaco. These charts comprise twenty-four sheets which are revised from time to time
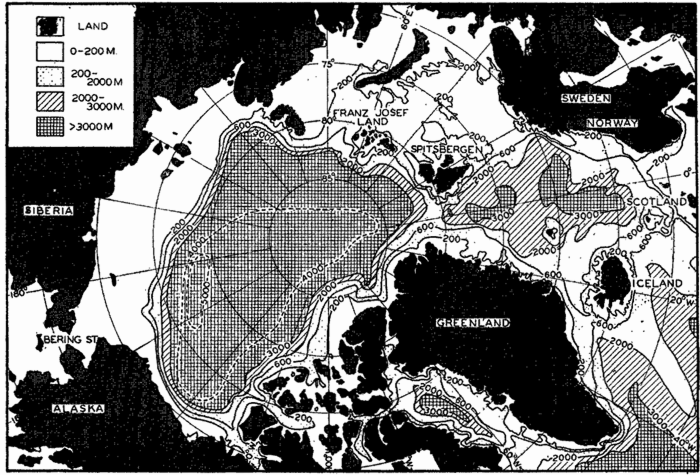
Polar projection of the Arctic regions showing the generalized topography of the sea bottom. (Cherevichny's soundings of 1941 not included.)
Bottom Configuration of the Arctic and Antarctic Regions
Fig. 3 has been prepared to show the submarine topography of the North Polar regions, which cannot be properly visualized from the interrupted projection used in chart I. The figure is based on a chart by Stocks (1938) and incorporates all of the available data. Because of the larger scale it is possible to show the contours for the shallower depths that form such a large part of this area. The conspicuous topographic
Very little is known of the topography of the North Polar Basin, and the form of the contours is largely hypothetical. Soundings greater than 3000 m are fairly numerous to the north of Europe, and there are some to the north of Alaska. A line of soundings also extends from the Pole and parallels the east coast of Greenland. These soundings were obtained by the Russian expedition which landed on the ice from planes and, in 1937–1938, drifted with the pack ice until picked up off the east coast of Greenland. Within 100 km of the Pole, this party obtained a sounding of 4300 m. The 5000-m contour is inserted on the basis of a single sounding of 5440 m obtained in 1927 by Sir Hubert Wilkins, who flew out by plane from Alaska, landed on the ice, and measured the depth with a portable sonic sounding instrument. The correctness of this sounding appears doubtful, however. In April, 1941, the Russian aviator Cherevichny, who landed on the ice in three different localities to the north of Wrangel Island and spent from three and a half to six days in each place, obtained much smaller depths (unpublished data communicated through the American Russian Institute, San Francisco, California). Cherevichny's soundings are as follows:
| Latitude, north | Longitude | Depth, m |
|---|---|---|
| 81°02ʹ | 180°00ʹE | 2647 |
| 78 30 | 176 40 E | 1856 |
| 80 00 | 170 00 W | 3430 |
These soundings were not available when the bathymetric chart of the Arctic region (fig. 3) was prepared.
The more or less elliptical North Polar Basin is connected with the Norwegian Basin by a fairly deep channel between Greenland and Spitsbergen, in which the sill depth is about 1500 m (table 6). The Norwegian Basin, in which there are two depressions with depths exceeding 3000 m, is separated from the open Atlantic by a ridge extending from Greenland to Scotland, from which Iceland and the Faeroe Islands rise above sea level. The sill depths in Denmark Strait, between Greenland and Iceland, and over the Wyville Thomson Ridge, between the Faeroes and Scotland, are about 500 m. Rising from the floor of the Norwegian Basin is an isolated elevation that extends above the surface as Jan Mayen Island.
Another depression of considerable magnitude that does not appear on chart I is in Baffin Basin between Baffin Island and Greenland, where the depths exceed 2000 m. This basin is separated from the open Atlantic by a ridge in Davis Strait between Baffin Island and Greenland, where the sill depth is about 700 m.
Interesting topographic features which are well developed in the Arctic regions are the “troughs” that cut across the shelf. These U-shaped furrows were apparently cut by glaciers at a period when the sea surface stood at a lower level. One such trough extends around the southern tip of Norway, and others may be traced by the irregularities of the 200-m contour to the north of Russia and between the islands of the Canadian Archipelago. Nansen (1928), in a discussion of the topography of the North Polar Basin, has described these features.
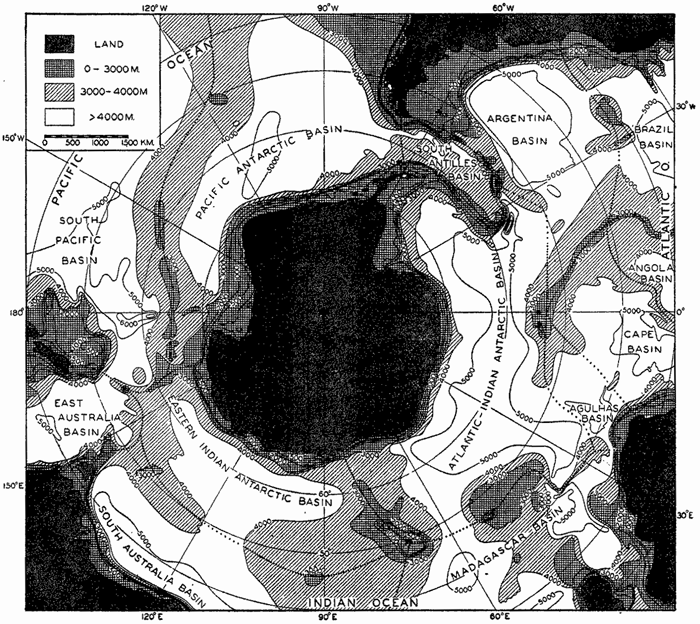
Polar projection showing the generalized sea-bottom topography of the Antarctic regions. Depths less than 4000 m shaded. Heavy dotted lines show the location of the elevations which separate the various basins. Contours at depths of 3000 m and more Correspond to those in chart I.
Fig. 4 is a polar projection of the Antarctic regions which shows the relationships between the major features of the submarine topography that cannot be visualized from chart I. The topography is based on the same data used for the preparation of chart I supplemented from other sources. All major depressions are also shown in the world map, but it has been possible to enter in this figure the contours above 3000 m. There are many striking differences between the topography of the North
The deep basins extend close to the continent of Antarctica, and the slopes are relatively steep. Joining South America to Antarctica is the South Antilles Arc, upon which are located South Georgia, South Sandwich, South Orkney, and South Shetland Islands. The ridge is continuous at 4000 m, and at 3000 m there are only relatively narrow openings. The Atlantic Ridge does not extend as far south as Antarctica, but is terminated in the vicinity of Bouvet Island. The ridge to the south of Africa and Madagascar is known as the Crozet Ridge, after the island of that name that rises from it. Forming a part of the Indian Ridge is the conspicuous elevation surrounding Kerguelen Island known as the Kerguelen Ridge. The ridge extending from Australia to Antarctica supports Macquarie Island and is known as the Macquarie Ridge. The importance of these ridges in determining the distribution of properties and the character of the circulation around Antarctica is discussed in chapter XV, p. 610 et seq. The greatest depths found in the region shown in fig. 4 are in the Byrd Deep to the south of New Zealand and in the South Sandwich Trench on the convex side of the South Antilles Arc.
Bottom Configuration of Adjacent Seas
It is beyond the scope of this volume to present charts or descriptions of the many marginal and adjacent seas. In table 4 are listed the area, volume, and mean depth of some of these features. The adjacent seas of the Arctic regions are shown in fig. 3, and in figs. 5 and 6 are shown the generalized topographies of the European and American Mediterraneans. Details of the topography of other marginal areas are presented elsewhere. The degree of isolation—namely, the extent to which free exchange of water with the adjacent ocean is impeded by the presence of land or submarine barriers—plays an important role in determining the characteristic distribution of properties in such regions (see chapters IV and XV).
The European Mediterranean, which comprises the Mediterranean Sea, the Black Sea, and the waters connecting them (namely, the Dardanelles, the Sea of Marmora, and the Bosporus) forms an intercontinental sea bordered by Europe, Asia, and Africa. The Mediterranean Sea occupies a deep, elongated, irregular depression with an east-west trend, and the Black Sea occupies a small and topographically simpler depression offset to the north. The Black Sea Basin, with depths exceeding 2200 m, is virtually isolated from the Mediterranean Sea proper, the connection
Generalized bottom topography of the European Mediterranean. The larger basins are (I) Algiers-Provençal, (II) Tyrrhenian, (III) Ionian, (IV) Levantine, and (V) Black Sea Basin.
The generalized topography of the European Mediterranean is shown in fig. 5, which is based on a chart prepared by Stocks (1938). The Black Sea Basin (V) is of more or less elliptical form except in the north, where there are irregular shallow seas of which the largest is the Sea of Azov, east of the Crimean Peninsula. The connection with the Mediterranean Sea is through the Bosporus, the Sea of Marmora, and the Dardanelles into the Aegean Sea, where the irregular topography is reflected in the large number of islands. The Mediterranean Sea Basin is subdivided by a series of transverse ridges with a north-south trend, parts of which extend above sea level. The primary division into the western and eastern depressions is effected by a ridge extending from Europe to Africa—namely, Italy, Sicily, and the submerged part of the elevation between these land areas and Africa. The sill depth in the strait between Sicily and Tunis is about 400 m. The Western Mediterranean, in turn, is subdivided into the Algiers-Provençal Basin (I) and the Tyrrhenian Basin (II) by the ridge extending from northwestern Italy to Tunis, from which Corsica and Sardinia rise above the sea surface. The Eastern Mediterranean is subdivided into two major depressions: the Ionian Basin (III), in which maximum depths of 4600 m are found,
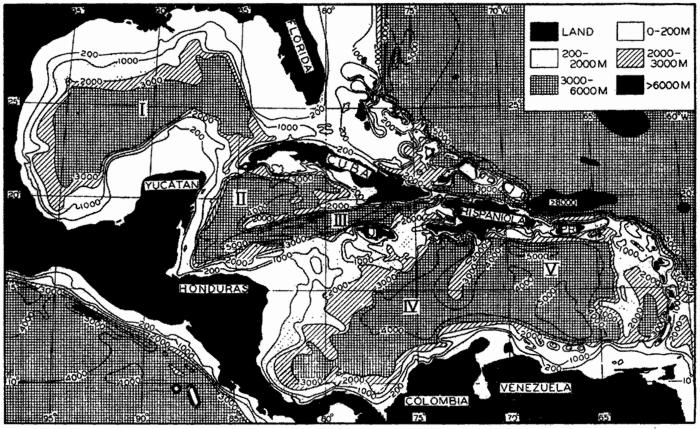
Generalized bottom topography of the American Mediterranean. The larger basins are (I) Mexico Basin; (II) Cayman Basin and (III) Cayman Trough, in the Western Caribbean; (IV) Colombia Basin and (V) Venezuela Basin, in the Eastern Caribbean. The greatest known depth in the Atlantic Ocean, 8750 m, is located in the Puerto Rico Trough to the north of Puerto Rico.
The American Mediterranean encompasses the partially isolated basins of the wide gulf bordered by North, Central, and South America which are separated from the open Atlantic by ridges, parts of which rise above sea level. The generalized topography of the region is shown in fig. 6, which is based on a chart by Stocks (1938). The chief difference between the European Mediterranean and the American Mediterranean is that the latter has numerous shallow and several deep connections with the open Atlantic. The topography of the American Mediterranean is extremely rugged, with deep trenches adjacent to steep-sided ridges, many of which rise above sea level. This is particularly true in the central and southern parts of the region, which are areas of pronounced gravity anomaly, volcanism, and strong seismic disturbances (Field et al, 1938). Bordering the low-lying coast of the Gulf of Mexico, off part of Honduras and Nicaragua, and surrounding the Bahama Islands are extensive shelves. The slopes leading down to deep water are in general rather steep, particularly between Cuba and Jamaica and along the
The American Mediterranean is subdivided into two major depressions, the Gulf of Mexico and the Caribbean Sea, by a ridge between Yucatan and Cuba, and by the island of Cuba. The sill depth in the Yucatan Channel is less than 1600 m. The Mexico Basin (I) is a relatively simple depression lacking the irregularities that characterize the topography of the Caribbean region. Maximum depths of nearly 4000 m are found in the western part of the basin. The Caribbean region is separated into two major basins, the Western and the Eastern Caribbean, by the Jamaica Rise, which extends from Honduras to Hispaniola and from which Jamaica rises above the surface. The Western Caribbean is in turn divided into Yucatan Basin (II) and the Cayman Trough (III) by the Cayman Ridge, which extends westward from the southern extremity of Cuba. The Cayman Trough is the deepest depression in the American Mediterranean, and within the Bartlett Deep to the south of Cuba the U.S.S. S-21 obtained a maximum sounding of 7200 m. The Windward Passage between Cuba and Hispaniola appears to be a continuation of the depression forming the Cayman Trough. The greatest saddle depth between the Western and Eastern Carribbean is located in the passage between Jamaica and Hispaniola, where it is about 1200 m. The Eastern Caribbean is partially divided into two basins by the Beata Ridge, which extends south and west from Hispaniola toward South America. The western portion of the depression is known as the Colombia Basin (IV) and the eastern as the Venezuela Basin (V). The Aves Swell separates a small basin with depths greater than 3000 m in the eastern part of the Venezuela Basin, which is called the Grenada Trough.
The terminology to be applied to the features of the American Mediterranean is discussed by Vaughan in the report by Vaughan et al (1940), which also includes an excellent bathymetric chart of the Caribbean region prepared by the U. S. Hydrographic Office. The currents and distribution of properties in this area are described in chapter XV, p. 637.
| Basin | Max. depth (m) | Adjacent deep depression | Surface feature | Location of sill | Sill depth (m) | Max. depth — sill depth (m) |
|---|---|---|---|---|---|---|
| Arctic Mediterranean Region | ||||||
| North Polar Basin | 5400 | North Pacific | Bering Strait | Siberia-Alaska | 55 | .... |
| Norwegian Basin | Greenland-Spitsbergen | 1500 | 3900 | |||
| Norwegian Basin | 3700 | North Atlantic | Denmark Strait | Greenland-Iceland | 500 | 3200 |
| North Atlantic | Faeroe Is.-Scotland | 500 | 3200 | |||
| Baffin Basin | 2200 | North Atlantic | Davis Strait | Baffin Is.-Greenland | 700 | 1500 |
| European Mediterranean Region | ||||||
| Western Mediterranean Basin | 3700 | North Atlantic | Strait of Gibraltar | Gibraltar-Morocco | 320 | 3400 |
| Eastern Mediterranean Basin | 4600 | Western Mediter-ranean | Sicily-Tunis | 400 | 4200 | |
| Black Sea Basin | 2200 | Eastern Mediter-ranean | Bosporus | 40 | ||
| Dardanelles | 70 | 2200 | ||||
| American Mediterranean Region | ||||||
| Eastern Caribbean Basin | 5500 | North Atlantic | Anegada and Jungfern Passages | Virgin Is.-Lesser Antilles | 1600 | 3900 |
| Western Caribbean Basin | 7200 | North Atlantic | Windward Passage | Cuba-Hispaniola | 1600 | 5600 |
| Eastern Caribbean | Jamaica Channel | Jamaica-Hispaniola | 1200 | .... | ||
| Mexico Basin | 3900 | Western Caribbean | Yucatan Channel | Yucatan-Cuba | 1600 | 2300 |
| North Atlantic | Strait of Florida | Florida-Bahama Is | 800 | .... | ||
| Other Regions | ||||||
| Japan Sea Basin | 3700 | Philippines Basin | Tsushima Strait | Korea-Japan | 150 | 3550 |
| Red Sea Basin | 2800 | Indian Ocean | Strait of Bab-el-Mandeb | Somaliland-Arabia | 100 | 2700 |
| Baltic Sea Basin | 300 | North Atlantic | Danish Sounds | Danish Is.-Germany | 20 | 280 |
Isolated basins are of great interest from an oceanographic point of view, and in table 6 are brought together some of the data relating to the larger basins in adjacent seas. This tabulation does not include the basins in the East Indian Archipelago, which are discussed elsewhere (table 87, p. 738). The maximum depth within each basin and the greatest sill depth at which there is horizontal communication with the adjacent basins are listed as well as the difference between the greatest depth in the basin and the sill depth. The latter value corresponds to the depth of the “lake” that would be formed if the water level were lowered to the greatest sill depth. It will be seen that most of the basins listed are without horizontal communication through vertical distances of 3000 to 4000 m, and that in the Yucatan Basin the greatest depth is 5600 m below the sill. In great contrast to these deep basins is the Baltic Sea (average depth, 55 m), where depths greater than 300 m are restricted to small, isolated depressions and where the sill depth is only 20 m.
In fig. 7 is shown the topography of the area off the coast of Southern California. This coastal area is one of considerable interest in that it is physiographically similar to the adjacent land area and apparently represents a down-warped portion of the continent. The continental shelf is relatively narrow, and offshore is a series of basins and ridges upon which several islands are located. In the southern part the real continental slope leading down to the oceanic abyss is approximately 150 miles from the coast. This is not shown in the map. Several small canyons are also depicted in the figure.
Submarine Canyons
For many years it has been known that there were furrows cutting across the shelf in certain regions, but only since it became possible to obtain large numbers of accurately located soundings of the shelf and slope were such features found to be numerous and widespread. Variously termed canyons, valleys, mock-valleys, and gullies by different authors, they have stimulated a great deal of interest among geologists, and a large literature has been built up dealing with the character and mode of formation of these canyons. The data concerning the topography of the canyons have largely been obtained by national agencies engaged in the careful mapping of nearshore areas. Such data have been used by Veatch and Smith (1939) and by Shepard and Emery (1941) to prepare general and detailed topographic charts of the canyons off the east and west coasts of the United States. Stetson (1936) has carried out independent observations on the east coast, and Shepard
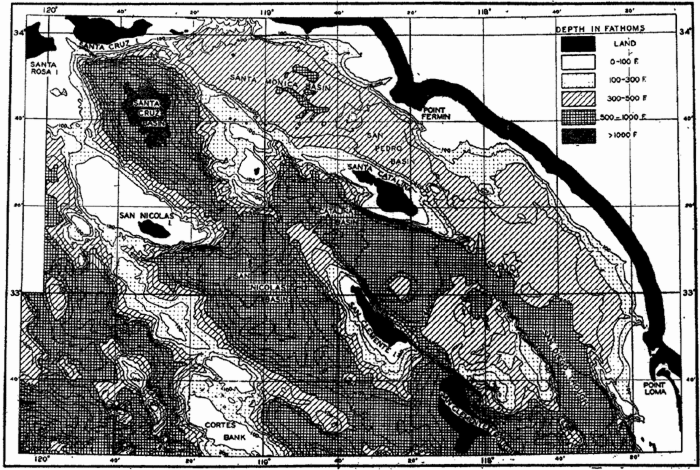
Topography of a part of the very irregular sea bottom off the coast of southern California where there is a basin and ridge topography very similar to that on the adjacent land. Depths in fathoms (after Revelle and Shepard, 1939).
Although the terms listed above have been used more or less synonymously, the size and general character of the canyons vary greatly. Some of them off the mouths of rivers, such as the Hudson (fig. 9), Congo, and Indus Canyons, have depressions that can be traced across the shelf and even into the mouths of the rivers. Some canyons extend across the shelf, but others—for example, many of those shown in the charts prepared by Veatch and Smith—are limited to gashes in the continental slope and do not cut far across the shelf. The upper parts of the canyons are generally found to be steep-walled, V-shaped in profile, with the bottom sloping continuously outward (fig. 8). Some are winding, and many show a dendritic pattern, having smaller tributary canyons. In size they vary from small gullies to vast structures of the same dimensions as the Grand Canyon of the Colorado River (fig. 8).
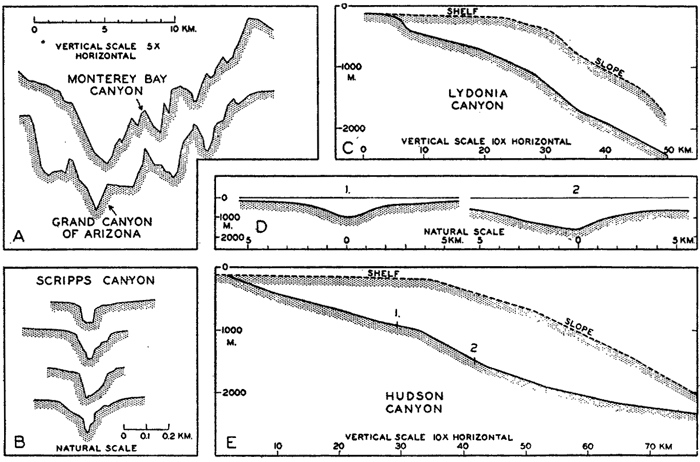
Profiles of submarine canyons. (A) Transverse profile of the submarine canyon in Monterey Bay compared to a profile of the Grand Canyon of the Colorado River in Arizona (cf. fig. 10). (B) Transverse profiles of a small, steep-walled canyon off the southern California coast. (C) Longitudinal profiles of the Lydonia Canyon and the adjacent shelf and slope. (D) and (E) Transverse and longitudinal profiles of the Hudson Canyon, showing the relation to the adjacent shelf and slope. The locations of the transverse sections (D) are shown on the longitudinal profile. Note the vertical exaggeration in certain of the diagrams and the differences in horizontal scales (A and B after Shepard, 1938; C, D, and E after Veatch and Smith, 1939).
The steep walls of the canyons are generally free of unconsolidated sediment, and in those canyons where special investigations have been made the walls appear to be generally of sedimentary rock; in a few cases (for example, Monterey Canyon off the California coast, fig. 10) the canyons are cut into granite that is overlain by sedimentary rock. The sediments in the bottom of the canyons are generally coarser than those on the adjacent shelves, and in some of them cobbles and gravel have been found.
The following agencies have been advanced as possible causes for the formation of the canyons:
Diastrophism.
Erosion by submarine currents. Daly (1936) advanced the theory that “density currents” produced by suspension of much fine-grained sediment may have flowed down the slope and cut the canyons, particularly during intervals of lowered sea level during the glacial periods. Density currents occur in reservoirs, but there is no evidence of their existence in the sea, where the density stratification of the water impedes vertical flow.
Spring sapping. Johnson (1939), in a thorough review of the literature concerning the character and origin of submarine canyons, develops the hypothesis that solution and erosion resulting from the outflow of underground water might contribute to the formation of the canyons.
Mudflows and landslides. Mudflows are known to occur in the canyons (Shepard and Emery, 1941) and are agents which tend to keep the canyons clear of unconsolidated debris, but it is doubtful whether they are capable of eroding rock.
Tsunamis or earthquake waves (p. 544). Bucher (1946) pointed out that most of the currents that might be found in canyons are of relatively low velocity and are therefore incapable of active erosion of rock. As a possible explanation of the submarine origin of the canyons he suggested that the rapid currents associated with earthquake waves set up in the sea by violent seismic motion of the sea bottom might be effective agents.
Subaerial erosion. The five explanations listed above are compatible with the formation of the canyons below the sea surface. Because of their many resemblances to river-cut canyons on land, many investigators, notably Shepard, believe that the canyons must have had a subaerial origin. However, there is no accepted geological theory that would account for the world-wide exposure of the shelf and slope within relatively recent geological time. To overcome this difficulty, Shepard has suggested that during the ice ages the amount of water removed from the ocean and deposited as ice caps may have been much greater than ordinarily believed (p. 25).
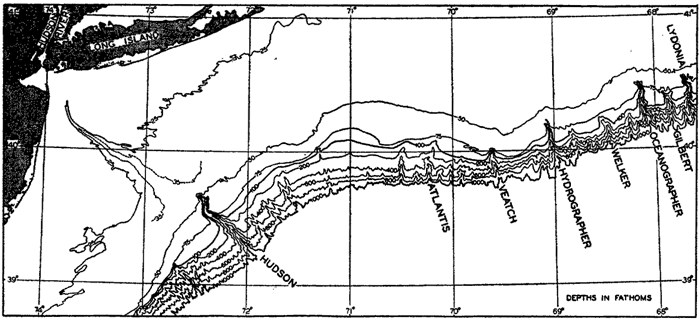
Topography of the shelf and slope off part of the eastern coast of the United States showing different types of submarine canyons. The Hudson Canyon can be traced far across the shelf; others, such as the Lydonia, Oceanographer, and Hydrographer Canyons, cut into the outer margin of the shelf, while others are restricted to the slope itself. Depth contours in fathoms. (Simplified from chart in Veatch and Smith, 1939.)
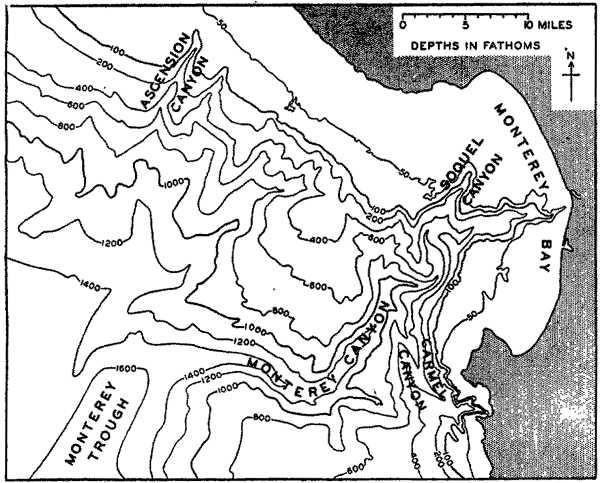
Monterey Canyon off the coast of California.
Shepard (Shepard and Emery, 1941) has carefully evaluated the arguments in favor of and opposed to these various hypotheses concerning the origin of submarine canyons, and he concludes that no single hypothesis yet advanced can account for their characteristic features. Problems also exist concerning the processes which remove the sedimentary debris that must be swept into the canyons from the shelf. Mudflows and transportation by currents are known to be operative, but their effectiveness has not yet been determined.
Shorelines
The study of the development of shorelines has been carried out by geologists and physiographers who have classified the different types of coasts largely upon the basis of the extent to which erosion and deposition have affected the coastal configuration. Johnson (1919, 1925) has described the characteristic features of the coast and shallow-water zone, and these and other sources should be consulted in order to appreciate the complex nature of the transition zone between land and sea, where the effects of erosion and deposition, both subaerial and marine, must be
The classification of shorelines has been treated by Johnson (1919) and Shepard (1937). Shepard's primary classification is based upon a consideration of the following factors:
Primary or youthful coasts with configurations due mainly to nonmarine agencies.
Those shaped by terrestrial erosion agencies and drowned by deglaciation or down-warping.
Those shaped by terrestrial depositional agencies such as rivers, glaciers, and wind.
Those shaped by volcanic explosions or lava flows.
Those shaped by diastrophic activity.
Secondary or mature coasts with configurations primarily the result of marine agencies.
Those shaped by marine erosion.
Those shaped by marine deposition.
The beach is defined as the zone extending from the upper and landward limit of effective wave action to low-tide level. Consequently, the beach represents the real transition zone between land and sea, since it is covered and exposed intermittently by the waves and tides. The characteristics of beaches depend so much upon the nature of the source material composing their sediments and the effects of the erosion, transportation, and deposition by waves and currents that they can be more profitably discussed in the chapter on marine sedimentation. The upper part of the beach is covered only during periods of high waves, particularly when storms coincide with high spring tides. The slope of the beach is largely determined by the texture of the sediments (p. 1018), but the extent of the beach will depend upon the range in tide. The terminology applied to the various parts of the beach and the adjacent regions is shown in fig. 11, taken from a report by the Beach Erosion Board (U. S. Beach Erosion Board, 1933).
Beaches composed of unconsolidated material are characteristically regions of instability. Every wave disturbs more or less of the smaller sedimentary particles, and the character of the waves will determine whether or not there is a net removal or accretion of sediment in any
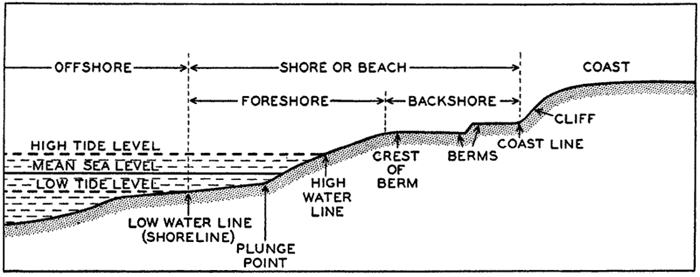
Terminology applied to various parts of the beach profile. Berms are small impermanent terraces which are formed by deposition during calm weather and by erosion during storms. The plunge point is the variable zone where the waves break, hence its location depends on the height of the waves and the stage of the tide.
Although subject to short-period disturbances, the beach in general represents an equilibrium condition, despite the slow erosion of the coast or the permanent deposition that may be taking place. If the normal interplay of waves and currents is impeded in any way, as by the building of piers, breakwaters, or jetties, the character of the beach may be entirely changed. In some instances, highly undesirable erosion of the coast may result, and in others equally undesirable deposition may result. These changes will proceed until a new equilibrium is established that may render the value of the structure worthless for the purpose for which it was originally intended. The construction of breakwaters, jetties, sea walls or groins, and similar structures on an open coast should be undertaken only after a careful investigation of the character and source of the sedimentary material, the prevailing currents, the strength and direction of the waves, and other factors that determine the equilibrium form of the beach. The Beach Erosion Board of the U. S. Army, Corps of Engineers, as well as various private organizations, are engaged in studies of this type.
Bibliography
Bencker, H.1930. “The bathymetric soundings of the oceans” . Hydrographic Review, v. 7, no. 2, p. 64–97, 1930. Monaco.
Bucher, Walter H.1933. The deformation of the earth's crust. Princeton Univ. Press, 518 pp., 1933.
Bucher, Walter H.1940. “Submarine valleys and related geologic problems of the North Atlantic” . Geol. Soc. Amer., Bull., v. 51, p. 489–512, 1940.
Daly, Reginald A.1934. The changing world of the ice age. New Haven, Yale Univ. Press, 271 pp., 1934.
Daly, Reginald A.1936. “Origin of submarine “canyons.”” Amer. Jour. Sci., v. 31, p. 401–420, 1936.
Field, Richard M., et al.1938. “Symposium on the geophysical exploration of the ocean bottom arranged by the American Geophysical Union” . Amer. Philos. Soc., Proc., v. 79, p. 1–144, 1938.
Fowle, Frederick E.1933. “Smithsonian physical tables” . Smithsonian Misc. Coll, v. 88, 682 pp., 1933.
Gutenberg, Beno, ed. 1939. “Internal constitution of the earth” . v. 7 of Physics of the Earth. (Nat. Research Council.) New York, McGraw-Hill, 413 pp., 1939.
International Hydrographic Bureau. 1937. “Limits of oceans and seas” . Internat. Hydrogr. Bur., Spec. Pub. no. 23, 2d ed., 25 pp., 1937.
Johnson, Douglas W.1919. Shore processes and shoreline development. New York, Wiley & Sons, 584 pp., 1919.
Johnson, Douglas W.1925. The New England-Acadian shoreline, New York, Wiley & sons, 608 pp., 1925.
Johnson, Douglas W.1939. The origin of submarine canyons. New York, Columbia Univ. Press, 126 pp., 1939.
Johnstone, James. 1928. An introduction to oceanography. Liverpool, University Press, 368 pp., 1928.
Kossinna, Erwin. 1921. Die Tiefen des Weltmeeres. Berlin Univ., Institut f. Meereskunde, Veröff., N. F., A. Geogr.-naturwiss. Reihe, Heft 9, 70 pp., 1921.
Kuenen, Ph. H., 1935. “Geological interpretation of the bathymetrical results. Snellius Exped. in the eastern part of the Netherlands East Indies 1929–1930” , v. 5, Geological Results, pt. 1, 123 pp. and charts, 1935. Utrecht.
Littlehales, G. W.1932. “The configuration of the oceanic basins” . p. 13–46 in Physics of the Earth, v. 5, Oceanography. Nat. Research Council, Bull. no. 85, 1932. Washington, D. C.
Nansen, Fridtjof. 1928. “The oceanographic problems of the still unknown Arctic regions” . p. 3–14 in: Problems of Polar Research. Amer. Geogr. Soc., Spec. Pub. no. 7, 479 pp., 1928. New York.
Niblack, A. P.1928. “Terminology of submarine relief” . Hydrographic Review, v. 5, no. 2, p. 1–23, 1928. Monaco.
Raisz, Erwin. 1938. General cartography. New York, McGraw-Hill. 370 pp., 1938.
Revelle, Roger, and F. P. Shepard. 1939. “Sediments off the California coast” . p. 245–282 in: Recent Marine Sediments, A symposium. Amer. Assn. Petrol. Geol.736 pp., 1939. Tulsa.
Schott, G.1926. Geographie des Atlantischen Ozeans. Hamburg, C. Boysen, 368 pp., 1926.
Schott, G.1935. Geographie des Indischen und Stillen Ozeans. Hamburg, C. Boysen, 413 pp., 1935.
Shepard, Francis P.1931. “Glacial troughs of the continental shelf” . Jour. Geol., v. 39, p. 345–360, 1931.
Shepard, Francis P.1933. “Geological misconceptions concerning the oceans” . Science, v. 78, p. 406–408, 1933.
Shepard, Francis P.1937. “Revised classification of marine shorelines” . Jour. Geol., v. 45, p. 602–624, 1937.
Shepard, Francis P.1938. “Submarine canyons off the California coast” . Calif. Jour. Mines and Geol., Report 24, State Mineralogist, p. 298–310, 1938.
Shepard, Francis P.1939. “Near-shore sediments—hemipelagic deposits” . p. 219–229 in: Recent Marine Sediments, A symposium. Amer. Assn. Petrol. Geol., 736 pp., 1939. Tulsa.
Shepard, Francis P.1941. Unpublished data.
Shepard, F. P., and K. O. Emery. 1941. “Submarine topography off the California coast: canyons and tectonic interpretations” . Geol. Soc. Amer., Spec. Paper, no. 31, 171 pp., 4 charts, 1941.
Shepard, F. P., and E. C. La Fond. 1940. “Sand movements along the Scripps Institution pier” . Amer. Jour. Sci., v. 238, p. 272–285, 1940.
Stetson, Henry C.1936. “Geology and paleontology of the Georges Bank canyons” . Geol. Soc. Amer., Bull., v. 47, p. 339–366, 1936.
Stocks, Theodor. 1938. “Morphologie des Atlantischen Ozeans. Statistik der Tiefenstufen des Atlantischen Ozeans” . Deutsche Atlantische Exped., Meteor, 1925–1927, Wiss. Erg., Bd. 3, 1. Teil, 2. Lief., p. 35–151, 1938.
Stocks, Theodor, and G. Wüst. 1935. “Die Tiefenverhältnisse des offenen Atlantischen Ozeans” . Deutsche Atlantischen Exped. Meteor, 1925–1927, Wiss. Erg., Bd. 3, Teil 1, l., Lief., 31 pp., 1935.
U. S. Beach Erosion Board. 1933. Interim report. April 15, 1933.
van Riel, P. M.1934. “The bottom configuration in relation to the flow of the bottom water” . Snellius Exped. in the eastern part of the Netherlands East Indies 1929–1930, v. 2, Oceanographic results, pt. 2, chap. 2, 62 pp., 1934. Utrecht.
Vaughan, Thomas Wayland. 1938. Recent additions to knowledge of the bottom configuration of the southern oceans. Congrès Internat. de Géographie, Amsterdam, 1938, Comptes rendus, IIb, Océanographie, p. 160–174, 1938.
Vaughan, T. W., et al.1937. “International aspects of oceanography” . Washington, D. C., Nat. Acad. Sci., 225 pp., 1937.
Vaughan, T. W., et al.1940. “Report of the Committee on the criteria and nomenclature of the major divisions of the ocean bottom” . Union Géod. et Géophys. Internat., Assn. d'Océanographie phys., Pub. sci., no. 8, 124 pp., 1940. Liverpool.
Veatch, A. C., and P. A. Smith. 1939. “Atlantic submarine valleys of the United States and the Congo Submarine Valley” . Geol. Soc. Amer., Spec. Pap. no. 7, 101 pp., 1939.
Wüst, Georg. 1936. “Die Gliederung des Weltmeeres” . Hydrographic Review, v. 13, no. 2, p. 46–56, 1936. Monaco.
III. Physical Properties of Sea Water
The properties of pure water are unique in comparison with those of other liquids, and the nature of our physical environment—that is, the characteristics of the oceans, the atmosphere, and the land—is in many ways dependent upon the peculiar properties of water. The “fitness” of water for the manifold needs of living organisms has been pointed out by physiologists and ecologists (for example, Henderson, 1913, Bayliss, 1927). Table 7 shows some of the characteristics which are important in this respect for both fresh water and sea water.
The unique character of water is further emphasized by the fact that, according to studies on related compounds, pure water should freeze at about − 150°C and boil at − 100°C. The chemical constitution of water offers no explanation for these anomalies and certain other deviations from the theoretical properties. However, it has been found that liquid water is not made up of individual H2O molecules but that it is polymerized—that is, multiple groups containing one, two, or three elementary H2O molecules may exist. These are referred to as monohydrol, dihydrol, and trihydrol. The relative proportions of the three forms depend upon the temperature, the immediate past history of the water, and other factors. The degree of polymerization decreases with increasing temperature. The existence of the water polymers is helpful in explaining certain of the peculiar properties of water such as the high melting and boiling points. The degree of polymerization has been thought to have certain physiological effects (Barnes and Jahn, 1934).
The discovery of isotopes of hydrogen and oxygen has modified our conception of “pure” water. All naturally occurring water contains small but variable amounts of heavy hydrogen (deuterium) and heavy oxygen. These modify the density and other properties, but, since their concentrations are extremely small, the effect is slight. As the understanding of this problem increases, it may become desirable to define more exactly certain physical units that are based on the properties of water, such as the liter and calorie, by taking into account the isotopic composition of water. The amounts of the heavy isotopes vary somewhat, depending upon the source of the water. Wirth, Thompson, and Utterback (1935) found that distilled water prepared from sea-water samples was, on the average, 1.4 × 10−6 greater in density than distilled tap water. Sea water from areas of great dilution showed a somewhat smaller anomaly—namely, 0.2 to 0.5 × 10−6 in density. Samples from the depths of the ocean were higher than the average. Swartout and Dole (1939) found that the density of water distilled from a sea-water sample was 1.7 × 10−6 greater than that prepared from Lake Michigan water. They also found that the ratio between hydrogen and deuterium in sea water was about 7000:1. Rain water, and consequently fresh water, has a lower proportion of the heavy isotopes than sea water, since a certain fractionation takes place in the process of evaporation. The field of isotope study is relatively new, and as yet little is known about the distribution or significance of the isotopes. Their variability is apparently rather small and consequently will not significantly affect the magnitude of the properties to be discussed.
| Property | Comparison with other substances | Importance in physical-biological environment |
|---|---|---|
| Heat capacity | Highest of all solids and liquids except liquid NH3 | Prevents extreme ranges in temperature |
| Heat transfer by water movements is very large | ||
| Tends to maintain uniform body temperatures | ||
| Latent heat of fusion | Highest except NH3 | Thermostatic effect at freezing point owing to absorption or release of latent heat |
| Latent heat of evaporation | Highest of all substances | Large latent heat of evaporation extremely important in heat and water transfer of atmosphere |
| Thermal expansion | Temperature of maximum density decreases with increasing salinity. For pure water it is at 4°C | Fresh water and dilute sea water have their maximum density at temperatures above the freezing point. This property plays an important part in controlling temperature distribution and vertical circulation in lakes |
| Surface tension | Highest of all liquids | Important in physiology of the cell |
| Controls certain surface phenomena and drop formation and behavior | ||
| Dissolving power | In general dissolves more substances and in greater quantities than any other liquid | Obvious implications in both physical and biological phenomena |
| Dielectric constant | Pure water has the highest of all liquids | Of utmost importance in behavior of inorganic dissolved substances because of resulting high dissociation |
| Electrolytic dissociation | Very small | A neutral substance, yet contains both H+ and OH− ions |
| Transparency | Relatively great | Absorption of radiant energy is large in infra red and ultraviolet. In visible portion of energy spectrum there is relatively little selective absorption, hence is “colorless.” Characteristic absorption important in physical and biological phenomena |
| Conduction of heat | Highest of all liquids | Although important on small scale, as in living cells, the molecular processes are far outweighed by eddy conduction (see text) |
Information as to the physical properties of distilled water is found in comprehensive handbooks (for example, Dorsey, 1940) or in the International Critical Tables. A number of these physical properties depend upon two variables, temperature and pressure, but in the case of sea water a third variable has to be considered; namely, the salinity of the water, which will be defined and discussed below. Some of the properties, such as compressibility, thermal expansion, and refractive index, are only slightly altered by the presence of dissolved salts, but other properties that are constant in the case of distilled water, such as freezing point and temperature of maximum density, are dependent on salinity in the case of sea water. Furthermore, the presence of dissolved salts adds a few new characteristics to sea water, such as osmotic pressure. General surveys of the physical properties of sea water have been given by Krümmel (1907), Matthews (1923), Harvey (1928), Johnstone (1928), and Thompson (1932).
Another important aspect of the physical characteristics that has to be considered when dealing with water as it occurs in nature, regardless of whether fresh water or sea water is concerned, is that several important processes are greatly modified by the presence of minute suspended particles or by the state of motion. Thus, the absorption of light in lakes or in the sea is entirely different from the absorption of light in distilled water or in “pure” sea water, because the waters encountered in nature always contain suspended matter that causes increased scattering of the light and consequently increased absorption in layers of similar thickness. The processes of heat conduction, chemical diffusion, and transfer of momentum from one layer to another are so completely altered in moving water that, for water under natural conditions, the coefficients which have been determined under laboratory conditions must be replaced by corresponding “eddy” coefficients that depend
Salinity and Chlorinity
In the chapter on chemical oceanography the composition of the dissolved constituents in sea water is considered in detail. Our present interest is only in the more abundant substances whose concentration will affect the physical properties. It has been found that, regardless of the absolute concentration, the relative proportions of the different major constituents are virtually constant, except in regions of high dilution (low salinity), where minor deviations may occur. From this rule it follows that any one of the major constituents may be used as a measure of the others and of the total amount of salt, and that water samples having the same total salt content, regardless of their source, are virtually identical in their physical properties.
Owing to the complexity of sea water, it is impossible by direct chemical analysis to determine the total quantity of dissolved solids in a given sample. Furthermore, it is impossible to obtain reproducible results by evaporating sea water to dryness and weighing the residue, because certain of the materials present, chiefly chloride, are lost in the last stages of drying. These difficulties can be avoided by following a technique yielding reproducible results which, although they do not represent the total quantity of dissolved solids, do represent a quantity of slightly smaller numerical value that is closely related and by definition is called the salinity of the water. This technique was established by an International Commission (Forch, Knudsen, and Sörensen, 1902), and on the basis of its work the salinity is defined as the total amount of solid material in grams contained in one kilogram of sea water when all the carbonate has been converted to oxide, the bromine and iodine replaced by chlorine, and 'all organic matter completely oxidized.
The determination of salinity by the method of the International Commission is rarely if ever carried out at the present time because it is too difficult and slow, but, owing to the constant composition of the dissolved solids, the determination of any of the elements present in relatively large quantity can be used as a measure of the other elements and of the salinity. Chloride ions make up approximately 55 per cent of the dissolved solids and can be determined with ease and accuracy by titration with silver nitrate, using potassium chromate as indicator.
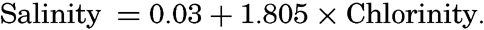
Chlorinity. In the titration with silver nitrate, bromides and iodides are precipitated together with the chlorides, but in the computation it is assumed that they are chlorides. Chlorinity was therefore originally defined as the total amount of chlorine, bromine, and iodine in grams contained in one kilogram of sea water, assuming that the bromine and the iodine had been replaced by chlorine. This definition introduces a chlorine-equivalent that is dependent upon the atomic weights used in preparing the standard solutions. Since the time of the work of the International Commission, there have been changes in the atomic weights, and the relation between salinity and chlorinity as defined above is no longer strictly true. In order to retain this relationship and to avoid apparent changes in the chlorinity of sea water it has fortunately been possible to redefine chlorinity so that it is independent of changes in atomic weights.
The primary standard used in the determination of chlorinity is so-called “Normal Water” (Eau de mer normale), prepared by the Hydrographical Laboratories in Copenhagen, Denmark, and distributed to all oceanographic institutions. Some of these institutions made their own secondary standards by means of the Normal Water. As a result of world conditions the preparation of Normal Water has temporarily been taken over by the Woods Hole Oceanographic Institution.
Normal Water is sea water whose chlorinity has been adjusted to about 19.4 ‰ and accurately determined by either direct or indirect comparisons with the original standard prepared in 1902. Hence, the chlorinities of all batches have been independent of changes in the atomic weights. A new primary standard (Urnormal-1937), prepared in 1937, will be used to establish the chlorinity of future batches of Normal Water for general distribution (Jacobsen and Knudsen, 1940). Comparison with earlier series of Normal Water showed the chlorinity of the new standard to be 19.381 ‰. As a more absolute method should be available with which to check future Normal Water preparations, the 1937 primary standard was analyzed, using extremely pure “atomic weight silver.” The equivalent amount of silver necessary to precipitate the halides was determined and the ratio of chlorinity to silver was found to be 0.3285233. On this basis a new definition of chlorinity was
The ratio of chlorine to silver, using the 1940 atomic weights (Ag = 107.880 and Cl = 35.457), is 0.3286707. Hence the ratio of chlorine-equivalent to the chlorinity is:
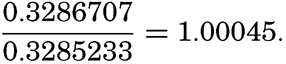
When dealing with the chemistry of sea water, other substances are generally determined and reported on a volume basis, wherefore it is convenient to introduce chlorosity (Cl) (Intern. Assn. Phys. Oceanogr., 1939), which is the property corresponding to the chlorinity expressed as grams per 20°-liter (p. 169). Chlorosity is obtained by multiplying the chlorinity of a water sample by its density at 20°. Table 8 gives the corresponding values of chlorosity for chlorinities between 15.00 and 21.00 ‰.
Methods for Obtaining Salinity, Other than Titration with Silver Nitrate. The salinity can also be determined from the density of a water sample at a given temperature or by measuring either the electrical conductivity or the refractive index, both of which depend upon the salinity. The character of these properties will be dealt with below, but their application to salinity determinations will be briefly discussed here.
Determinations of density are appropriately included under methods for obtaining salinity, because such determinations are generally made at
| Chlorinity, ‰ | 15.00 | 16.00 | 17.00 | 18.00 | 19.00 | 20.00 | 21.00 |
| Chlorosity, g/L | 15.28 | 16.32 | 17.37 | 18.41 | 19.46 | 20.51 | 21.57 |
| .28 | .32 | .37 | .41 | .46 | .51 | .57 |
Measurements of the electrical conductivity have been employed on board the Carnegie and by the U. S. Coast Guard as the routine method for obtaining salinities. Owing to the relatively high concentration of the ions and the effect that temperature has upon the conductivity, the apparatus and the technique employed are rather complicated (Wenner, Smith, and Soule, 1930; Soule, 1932). These instruments are standardized empirically, using sea-water samples of known salinity (determined by silver nitrate titrations against Normal Water), and the values for the unknown samples are obtained by interpolation. In order to obtain
According to Thomas, Thompson, and Utterback (1934) the Grinnel Jones conductivity bridge may be used with Washburn pipette-type cells, the constants of which are determined with standard potassium chloride solutions.
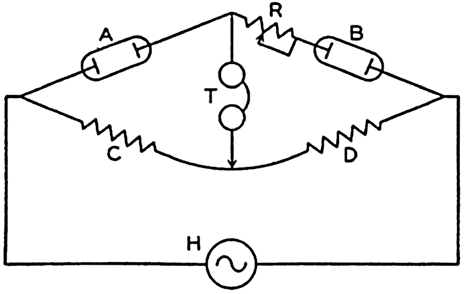
Circuit used in measurements of the electrical conductivity as a means of obtaining the salinity of sea water. Symbols are explained in the text.
The refractive index of sea water, which will be discussed later (p. 70) in greater detail, varies only slightly within the ranges of temperature and salinity encountered in the sea, but, in an interferometer, differences in refractive index can be measured with extreme accuracy. At a given temperature such differences depend only upon the salinity, and special types of interferometers have therefore been developed for indirect determinations of salinity, using water of known salinity as a standard. Monochromatic light must be used because the refractive index varies with the wave length. This method of determining salinity has not been widely used.
Units of Temperature, Salinity, and Pressure, and Their Ranges in the Sea
In oceanography the temperature is measured in degrees centigrade. The thermometers used are described on p. 347. The accuracy of the measurements is about ± 0.02°C. Salinity is given as grams per kilogram of sea water; that is, in parts per thousand, or per mille, for which the symbol ‰ is used. An accuracy of ±0.02 ‰ is required. Pressure (p. 170) is measured in atmospheres or in units of the c.g.s. system. An atmosphere is defined as the pressure exerted per square centimeter by a
In the oceans the temperature ranges from about −2° to +30°C. The lower limit is determined by the formation of ice, and the upper limit is determined by processes of radiation and exchange of heat with the atmosphere (p. 127). In landlocked areas the surface temperature may be higher, but in the open ocean it rarely exceeds 30°C.
The salinity in the oceans is generally between 33 ‰ and 37 ‰. The surface salinity in high latitudes, in regions of high rainfall, or where there is dilution by rivers may be considerably less, and in certain semi-enclosed areas, such as the Gulf of Bothnia, the salinity may approach zero. In isolated seas in intermediate latitudes, such as the Red Sea, where evaporation is excessive, salinities may reach 40 ‰ or more. As the range in the open oceans is rather small, it is sometimes convenient to use a salinity of 35 ‰ as an average for all oceans. In the chapter on the chemistry of sea water the tabulations are made for water of 19.00 ‰ chlorinity; that is, 34.325 ‰ salinity.
In dealing with the pressure in the oceans, the atmospheric pressure is always neglected and the pressure at the sea surface is entered as zero. Since the pressure is essentially a function of depth and the numerical value in decibars nearly equals the depth in meters, the range in pressure will be from zero at the sea surface to over 10,000 decibars in the deepest part of the ocean.
Owing to the character of the distribution of temperature and salinity in the oceans, some relationships exist between these conditions and the pressure. The temperature of the deep and bottom water of the oceans is always low, varying between 4° and − 1°C, so that high pressures are associated with low temperatures. Similarly, the salinity of deep and bottom water varies within narrow limits, 34.6 ‰ to 35‰, and high pressures are therefore associated with salinities between these limits.
Density of Sea Water
The density of any substance is defined as the mass per unit volume. Thus, in the c.g.s. system, density is stated in grams per cubic centimeter. The specific gravity is defined as the ratio of the density to that of distilled water at a given temperature and under atmospheric pressure. In the c.g.s. system the density of distilled water at 4°C is equal to unity. In oceanography, specific gravities are now always referred to distilled water at 4°C and are therefore numerically identical with densities. In oceanography the term density is generally used, although, strictly speaking, specific gravity is always considered.
The density of sea water depends upon three variables: temperature, salinity, and pressure. These are indicated by designating the density by the symbol ρs,ϑ,p, but, when dealing with numerical values, space is saved by introducing σs,ϑ,p which is defined in the following manner:
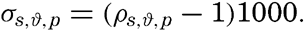
The density of a sea-water sample at the temperature and pressure at which is was collected, ρs,ϑ,p is called the density in situ, and is generally expressed as σs,ϑ,p. At atmospheric pressure and temperature ϑ°C, the corresponding quantity is simply written σt, and at 0° it is written σ0. The symbol ϑ will be used for temperature except when writing σt, where, following common practice, t stands for temperature.
At atmospheric pressure and at temperature of 0°C the density is a function of the salinity only, or, as a simple relationship exists between salinity and chlorinity, the density can be considered a function of chlorinity. The International Commission, which determined the relation between salinity and chlorinity and developed the standard technique for determinations of chlorinity by titration, also determined the density of sea water at 0° with a high degree of accuracy, using pycnometers. From these determinations the following relation between (σ0 and chlorinity was derived:
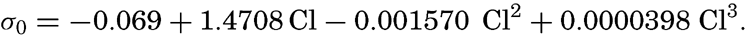
In order to find the density of sea water at other temperatures and pressures, the effects of thermal expansion and compressibility on the density must be known. The coefficient of thermal expansion has been determined in the laboratory under atmospheric pressure, and
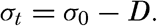
The effect on the density of the compressibility of sea water of different salinities and at different temperatures and pressures was examined by Ekman (1908), who established a complicated empirical formula for the mean compressibility between pressures 0 and p decibars (quoted in V. Bjerknes and Sandström, 1910). From this formula, correction terms have been computed which, added to the value of σt, give the corresponding value σs,ϑ,p for any value of pressure.
Computation of Density and Specific Volume in Situ. Tables from which the density in situ, ρs,ϑ,p could be obtained directly from the temperature, salinity, and pressure with sufficiently close intervals in the three variables would fill many large volumes, but by means of various artifices convenient tables have been prepared. Following the procedure of Bjerknes and Sandström (1910), one can write
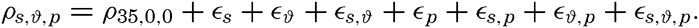
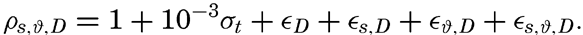
Instead of the density, ρs,ϑ,p, its reciprocal value, the specific volume in situ, αs,ϑ,p is generally used in dynamic oceanography. In order to avoid writing a large number of decimals, the specific volume is commonly expressed as an anomaly, δ, defined in the following way:
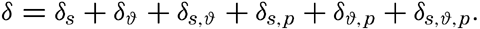
The value of Δs,ϑ, = δs + δϑ + δs, ϑ is easily obtained from σt because
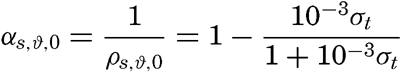
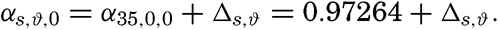
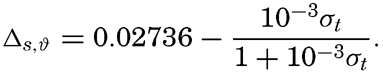
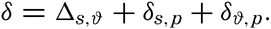
The procedure that is followed in calculating the density or specific volume in situ can be summarized as follows. For a given water sample the temperature, salinity, and depth at which it was collected must be known. For reasons stated elsewhere it can be assumed that the numerical value of the pressure in decibars is the same as that of the depth in meters. From the temperature and salinity the value σt is obtained from Knudsen's Tables or from graphs or tables prepared from this source, (McEwen, 1929; Matthews, 1932). With the values of σt temperature, salinity, and pressure the specific volume anomaly is computed by means of the tables given in the appendix. If the absolute value of the specific volume is required, the anomaly must be added to
Another set of tables for computing the specific volume in situ has been prepared by Matthews (1938), who, in our notations, defines the anomaly as δ′ = αs,ϑ,p − α34,85,0,p. Thus, he refers the anomalies to water of salinity 34.85 ‰, for which σ0 = 28.00. The difference, δ − δ′ = α34,85,0,p − α35,0,p, depends upon the pressure:

Use of Knudsen's Hydrographical Tables. A certain point concerning the use of Knudsen's Hydrographical Tables should be kept in mind. Although they have been shown to hold very well over the normal range of the concentration of sea water, they are not necessarily valid for highly diluted or concentrated sea water. The tables are based on the careful examination of a series of samples collected from various regions. The dilute samples used were taken in the Baltic Sea, where dilution sometimes reduces the chlorinity to about 1 ‰, and where the river water that is mainly responsible for the dilution contains relatively large quantities of dissolved solids. This is shown by the fact that the equation relating salinity to chlorinity shows a salinity of 0.03 ‰ for zero chlorinity, and according to Lyman and Fleming (1940) the total dissolved solids corresponding to this figure are probably of the order of 0.07 ‰. Thus, empirically, the salinity of sea water can be expressed by an equation of the type
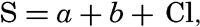
Thermal Properties of Sea Water
Thermal Expansion. The coefficient of thermal expansion, e, defined by e = (l/αs,ϑ,p)(∂αs,ϑ,p/∂ϑ), is obtained, at atmospheric pressure, from the terms for D in Knudsen's Hydrographical Tables, and at higher pressures from Ekman's tables or formulae (p. 57). The coefficient for sea water is greater than that for pure water and increases with increasing pressure. A few numerical values are given in table 9, in which negative values indicate contraction with increasing temperature.
| Pressure (decibars) | Salinity ‰. | Temperature (°C) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| −2 | 0 | 5 | 10 | 15 | 20 | 25 | 30 | ||
| 0………… | 0 | −105 | − 67 | 17 | 88 | 151 | 207 | 257 | 303 |
| 10 | − 65 | − 30 | 46 | 112 | 170 | 222 | 270 | 315 | |
| 20 | − 27 | 4 | 75 | 135 | 189 | 237 | 282 | 324 | |
| 30 | 7 | 36 | 101 | 157 | 206 | 250 | 292 | 332 | |
| 35 | 23 | 51 | 114 | 167 | 214 | 257 | 297 | 334 | |
| 2,000………… | 35 | 80 | 105 | 157 | 202 | 241 | 278 | ||
| 40 | 94 | 118 | 168 | 210 | 248 | 283 | |||
| 4,000………… | 35 | 132 | 152 | 196 | 233 | 266 | |||
| 40 | 144 | 162 | 204 | 240 | 272 | ||||
| 6,000………… | 34.85 | 177 | 194 | 230 | |||||
| 8,000………… | 34.85 | …… | 231 | 246 | |||||
| 10,000………… | 34.85 | …… | 276 | 287 | |||||
Thermal Conductivity. In water in which the temperature varies in space, heat is conducted from regions of higher to regions of lower
Specific Heat. The specific heat is the number of calories required to increase the temperature of 1 g of a substance 1°C. When studying liquids, the specific heat at constant pressure, cp, is the property usually measured, but in certain problems the specific heat at constant volume, cv must be known.
The specific heat of sea water of different chlorinities was investigated by Thoulet and Chevallier, whose results have been recalculated and presented in different ways. Krümmel (1907) gives the following values for the specific heat at 17.5°C and atmospheric pressure:
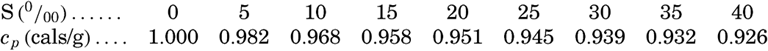
Kuwahara (1939) gives an empirical equation for the specific heat at 0°C and atmospheric pressure:
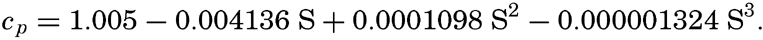
It will be noted that the specific heat decreases with increasing salinity, but it has been pointed out by Krümmel that the effect is somewhat larger than might be expected from the composition of the solution, and the problem merits reinvestigation. The effects of temperature and pressure have not been measured, but it has been assumed that they are the same as those for pure water. Ekman (1914) gives the following values showing the effect of temperature on the specific heat of water of S = 34.85 ‰ at atmospheric pressure:
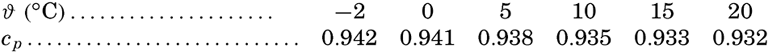
The effect of pressure on the specific heat has been computed by Ekman (1914) from the equation
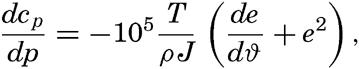
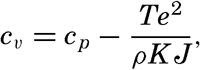
| θ (°C) | p (decibars) | ||||
|---|---|---|---|---|---|
| 2000 | 4000 | 6000 | 8000 | 10,000 | |
| − 2………… | 0.0171 | 0.0315 | 0.0435 | ||
| 0………… | 0.0159 | 0.0291 | 0.0401 | 0.0492 | 0.0566 |
| 5………… | 0.0136 | 0.0248 | 0.0340 | 0.0416 | 0.0479 |
| 10………… | 0.0120 | 0.0220 | |||
| 15………… | 0.0110 | 0.0203 | |||
| 20………… | 0.0105 | ||||
Latent Heat of Evaporation. The latent heat of evaporation of pure water is defined as the amount of heat in gram calories needed for evaporating 1 g of water, or as the amount of heat needed for producing 1 g of water vapor of the same temperature as the water. Only in the latter form is the definition applicable to sea water. The latent heat of evaporation of sea water has not been examined, but it is generally assumed that the difference between that and pure water is insignificant; therefore, between temperatures of 0° and 30°C, the formula
Adiabatic Temperature Changes. When a fluid is compressed, without gain or loss of heat to the surroundings, work is performed on the system and there is a rise in temperature. Conversely, if expansion takes place, the liquid itself gives up energy, which is reflected in a drop in temperature. Such adiabatic temperature changes are well known and important in the atmosphere. Sea water is compressible, and the effects of adiabatic processes, although small, must be taken into account when studying the vertical distribution of temperature in the great depths of the oceans and in deep isolated basins where the adiabatic heating may lead to a temperature increase toward the bottom (for example, p. 739). Adiabatic cooling is of immediate practical concern when water samples are taken with thermally insulated water bottles and the temperature of the water sample is determined after it has been raised to the surface (p. 355)
| Depth (m) | Temperature (°C) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| −2 | 0 | 2 | 4 | 6 | 8 | 10 | 15 | 20 | |
| 0. | 0.016 | 0.035 | 0.053 | 0.078 | 0.087 | 0.103 | 0.118 | 0.155 | 0.190 |
| 1,000. | 0.036 | 0.054 | 0.071 | 0.087 | 0.103 | 0.118 | 0.132 | 0.166 | 0.199 |
| 2,000. | 0.056 | 0.073 | 0.089 | 0.104 | 0.118 | 0.132 | 0.146 | 0.177 | 0.207 |
| 3,000. | 0.075 | 0.091 | 0.106 | 0.120 | 0.133 | 0.146 | 0.159 | 0.188 | |
| 4,000. | 0.093 | 0.108 | 0.122 | 0.135 | 0.147 | 0.159 | 0.170 | 0.197 | |
| 5,000. | 0.110 | 0.124 | 0.137 | 0.149 | |||||
| 6,000. | 0.120 | 0.140 | 0.152 | 0.163 | |||||
| 7,000. | …… | 0.155 | 0.165 | 0.175 | |||||
| 8,000. | …… | 0.169 | 0.178 | 0.187 | |||||
| 9,000. | …… | 0.182 | 0.191 | 0.198 | |||||
| 10,000. | …… | 0.194 | 0.202 | 0.209 | |||||
Any adiabatic effect is related to changes in pressure, but in the sea the pressure can be considered proportional to the depth, and adiabatic temperature changes can be given as changes per unit of depth instead of per unit of pressure. According to Lord Kelvin, the change in temperature for each centimeter of vertical displacement is
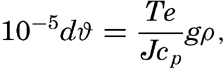
| Depth (m) | Temperature, ϑm (°C) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| − 2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1,000…… | 2.6 | 3.5 | 4.4 | 5.3 | 6.2 | 7.0 | 7.8 | 8.6 | 9.5 | 10.2 | 11.0 | 11.7 | 12.4 |
| 2,000…… | 7.2 | 8.9 | 10.7 | 12.4 | 14.1 | 15.7 | 17.2 | 18.8 | 20.4 | 21.9 | 23.3 | 24.8 | 26.2 |
| 3,000…… | 13.6 | 16.1 | 18.7 | 21.2 | 23.6 | 25.9 | 28.2 | 30.5 | 32.7 | 34.9 | 37.1 | 39.2 | 41.2 |
| 4,000…… | 21.7 | 25.0 | 28.4 | 31.6 | 34.7 | 37.7 | 40.6 | 43.5 | 46.3 | 49.1 | 51.9 | 54.6 | 57.2 |
| 5,000…… | 31.5 | 35.5 | 39.6 | 43.4 | 47.2 | 50.9 | 54.4 | ||||||
| 6,000…… | 42.8 | 47.5 | 52.2 | 56.7 | 61.1 | 65.3 | 69.4 | ||||||
| 7,000…… | …… | …… | 66.2 | 71.3 | 76.2 | 80.9 | 85.5 | ||||||
| 8,000…… | …… | …… | 81.5 | 87.1 | 92.5 | 97.7 | 102.7 | ||||||
| 9,000…… | …… | …… | 98.1 | 104.1 | 109.9 | 115.6 | 121.0 | ||||||
| 10,000…… | 115.7 | 122.1 | 128.3 | 134.4 | 140.2 | ||||||||
The temperature that a water sample would attain if raised adiabatically to the sea surface has been called the potential temperature (Helland-Hansen, 1912b) and has been designated Θ. Thus, Θ = ϑm − Δϑ, where ϑm, is the temperature in situ and Δϑ is the amount by which the temperature would decrease adiabatically if the sample were raised to the surface. The potential temperature can be obtained from a table of the adiabatic gradients by step-wise computations. Such computations are long and tedious, but Helland-Hansen (1930) has prepared a, convenient table for Δϑ which has been reproduced in table 12. The table is based on a salinity of 34.85 ‰ (σ0 = 28.0) and is applicable in general to the deep ocean areas, because in these the salinity does not differ much from 34.85 ‰ and because the effect of salinity on the adiabatic processes is small. It may be seen that if water of 2°C is raised adiabatically from 8000 m to the surface, Δϑ = 0.925°, and therefore the potential temperature of that water is 1.075°. The adiabatic cooling of water of different
Colligative and Other Properties of Sea Water
Colligative Properties. The colligative properties—namely, vapor-pressure lowering, freezing-point depression, boiling-point elevation, and osmotic pressure—are unique properties of solutions. If the magnitude of any one of them is known for a solution under a given set of conditions, the others may readily be computed. Solutions of the complexity and concentration of sea water do not obey the generalized theories of the colligative properties, but in all cases the departures from the theoretical values are proportional.
| Salinity (V%) | Temperature, ϑm (°C) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | |
| 30.0…… | 3.5 | 5.3 | 7.0 | 8.7 | 10.3 | 11.8 | 13.2 | 14.7 | 16.1 | 17.6 | 18.9 | 20.3 |
| 32.0…… | 3.9 | 5.7 | 7.3 | 9.0 | 10.6 | 12.1 | 13.5 | 15.0 | 16.4 | 17.8 | 19.1 | 20.5 |
| 34.0…… | 4.3 | 6.0 | 7.7 | 9.4 | 10.9 | 12.4 | 13.8 | 15.3 | 16.6 | 18.0 | 19.3 | 20.7 |
| 36.0…… | 4.7 | 6.4 | 8.1 | 9.7 | 11.2 | 12.7 | 14.1 | 15.5 | 16.9 | 18.3 | 19.6 | 20.9 |
| 38.0…… | 5.1 | 6.8' | 8.4 | 10.0 | 11.6 | 13.0 | 14.4 | 15.8 | 17.2 | 18.5 | 19.8 | 21.1 |
| Depth (m) | Temperature, ϑm (°C) | ||
|---|---|---|---|
| 12 | 13 | 14 | |
| 1000…………………… | 14.4 | 15.1 | 15.8 |
| 2000…………………… | 30.0 | 31.4 | 32.7 |
| 3000…………………… | 46.6 | 48.6 | 50.6 |
| 4000…………………… | 64.2 | 66.7 | 69.2 |
Only the depression of the freezing point for sea water of different chlorinities has been determined experimentally (Knudsen, 1903; Miyake,
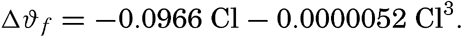
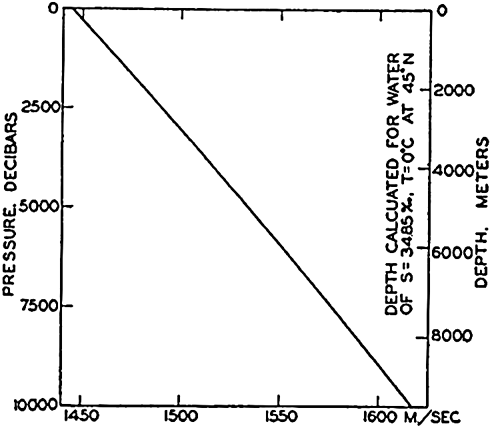
Osmotic pressure, vapor pressure relative to that of pure water, freezing point, and temperature of maximum density as functions of chlorinity and salinity.
The vapor pressure of sea water of any chlorinity referred to distilled water at the same temperature can be computed from the following equation (Witting, 1908):
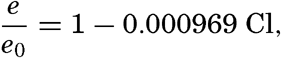
The osmotic pressure can be calculated from the freezing-point depression by means of the equation derived by Stenius (Thompson, 1932):
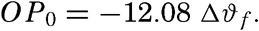
The osmotic pressure at any temperature may then be computed:
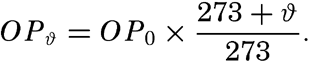
It will be noted that the freezing-point depression and, therefore, the other colligative properties are not linear functions of the chlorinity, because chlorinity is reported as grams per kilogram of sea water and not as grams per kilogram of solvent water, in which case a linear relationship should be expected. In agreement with this expectation, Lyman and Fleming (1940) found that the freezing-point depression could be written in the form
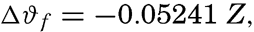
The magnitude of the colligative properties depends upon the concentration of ions in the solution and upon their activity. According to present concepts the major constituents of sea water exist as ions whose concentrations may be computed from data in table 35 (p. 173). Within the normal range of sea water the gram-ionic concentration per kilogram of solvent water may be obtained from the following expression:
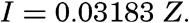
Maximum Density. Pure water has its maximum density at a temperature of very nearly 4°, but for sea water the temperature of maximum density decreases with increasing salinity, and at salinities greater than 24.70‰ is below the freezing point. At a salinity of 24.70 ‰, the temperature of maximum density coincides with the freezing point: ϑf = −1.332°. Consequently, the density of sea water of salinity greater than 24.70 ‰ increases continuously when such water is cooled to its freezing point. The temperature of maximum density is shown in fig. 13 as a function of salinity and chlorinity.
| p (bars) | Temperature (°C) | ||||||
|---|---|---|---|---|---|---|---|
| 0 | 5 | 10 | 15 | 20 | 25 | 30 | |
| 0 | 4659 | 4531 | 4427 | 4345 | 4281 | 4233 | 4197 |
| 100 | 4582 | 4458 | 4357 | 4278 | |||
| 200 | 4508 | 4388 | 4291 | ||||
| 400 | 4368 | 4256 | |||||
| 1000 | 4009 | 3916 | |||||
Compressibility. Ekman (1908) has derived an empirical equation for the mean compressibility of sea water between pressures 0 and p bars (p. 57), as defined by αs,ϑ,p = αs,ϑ,0 (1 − kp). Numerical values are given in table 15, where the bar has been used as pressure unit.
The true compressibility of sea water is described by means of a coefficient that represents the proportional change in specific volume if the hydrostatic pressure is increased by one unit of pressure: K = (− l/α)(dα/dp). The true compressibility can be calculated from the mean compressibility, which was tabulated by Ekman, using the equation
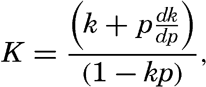
Viscosity. When the velocity of moving water varies in space, frictional stresses are present. The frictional stress which is exerted on a
| Salinity (%) | Temperature (°C) | ||||||
|---|---|---|---|---|---|---|---|
| 0 | 5 | 10 | 15 | 20 | 25 | 30 | |
| 0………… | 17.9 | 15.2 | 13.1 | 11.4 | 10.1 | 8.9 | 8.0 |
| 10………… | 18.2 | 15.5 | 13.4 | 11.7 | 10.3 | 9.1 | 8.2 |
| 20………… | 18.5 | 15.8 | 13.6 | 11.9 | 10.5 | 9.3 | 8.4 |
| 30………… | 18.8 | 16.0 | 13.8 | 12.1 | 10.7 | 9.5 | 8.6 |
| 35………… | 18.9 | 16.1 | 13.9 | 12.2 | 10.9 | 9.6 | 8.7 |
The viscosity that has been discussed so far is valid only if the motion is laminar, but, as stated above, turbulent motion prevails in the sea, and an “eddy” coefficient must be introduced which is many times larger (p. 91).
Diffusion. In a solution in which the concentration of a dissolved substance varies in space, the amount of that substance which per second diffuses through a surface of area 1 cm2 is proportional to the change in concentration per centimeter along a line normal to that surface (dM/dt = −δ dc/dn). The coefficient of proportionality (δ) is called the coefficient of diffusion; for water it is equal to about 2 × 10−5, depending upon the character of the solute, and is nearly independent of temperature. Within the range of concentrations encountered in the sea the coefficient is also nearly independent of the salinity.
What was stated about the coefficient of thermal conductivity in the sea applies also to the coefficient of diffusion. Where turbulent motion prevails, it is necessary to introduce an “eddy” coefficient that is many times larger and that is mainly dependent on the state of motion.
Surface Tension. The surface tension of sea water is slightly greater than that of pure water at the same temperature. Krümmel (1907) carried out experimental observations from which he derived an empirical equation relating the surface tension to the temperature and salt content. This equation was revised by Fleming and Revelle (1939) to take into account the more recent values for pure water. The revised expression has the form
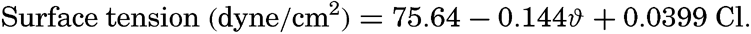
Refractive Index. The refractive index increases with increasing salinity and decreasing temperature. The problem of determining the relationship between these variables, and the types of equipment to be used, has been discussed by a number of authors (for example, Utterback, Thompson, and Thomas, 1934; Bein, Hirsekorn, and Möller, 1935; Miyake, 1939). Since the index varies with the wave length of light, a standard must be selected, usually the D line of sodium.
Utterback, Thompson, and Thomas determined at a number of temperatures the refractive index of ocean-water samples that had been diluted with distilled water. They found that the refractive index could be represented by expressions of the following type:
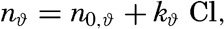
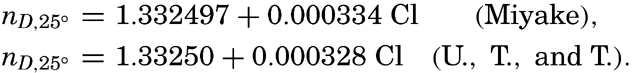
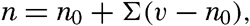
Electrical Conductivity. Thomas, Thompson, and Utterback (1934), and Bein, Hirsekorn, and Möller (1935) have studied conductivity as a function of chlorinity and temperature and have given tables for the specific conductance in reciprocal ohms per cubic centimeter for a wide range in conditions.
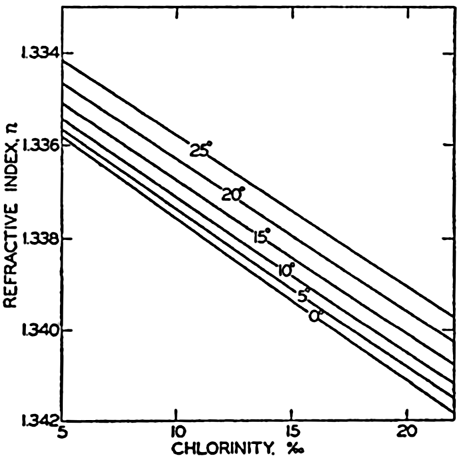
Refractive index of sea water as a function of temperature and chlorinity.
The results of the investigations of Thomas, Thompson, and Utterback are expressed at temperatures of 0, 5, 10, 15, 20, and 25°. Their results are shown graphically in fig. 15. The values for the low chlorinities were obtained by diluting ocean water with distilled water, and hence the density and other properties will not correspond exactly to those of water of the same chlorinity, as represented in Knudsen's Hydrographical Tables.
Properties of Sea Ice
The processes of freezing and the chemical properties of ice formed from sea water in high latitudes are discussed elsewhere. The physical properties of sea ice, like those of the water, depend upon the salt content, which in turn is a function of the rate of freezing, age, thermal history, and so forth. The salts in sea ice (p. 217) do not differ greatly in composition from those in the water, as they are generally present in brine that is enclosed in small cells. Therefore, within practical limits, the terms chlorinity and salinity of sea ice have the same meaning as for the water, although the salts are not uniformly distributed in the ice.
The freezing point of sea water, as was pointed out previously, represents the initial freezing point at which ice is in equilibrium with sea water of the indicated chlorinity. If the ice and sea water are in a closed system, as when brine is enclosed in cells in the ice, a further reduction of temperature is necessary to cause additional ice to separate.
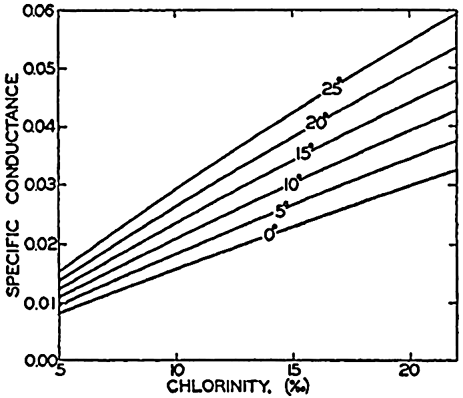
Specific conductance, reciprocal ohms/cm3, of sea water as a function of temperature and chlorinity.
Another variable which markedly affects certain physical properties of sea ice is the gas content. The gases normally occur as small “bubbles” in the ice, and the quantity is generally large in ice that has frozen rapidly, in which case bubbles represent gases originally in solution in the water, or in old ice that has undergone partial thawing and been refrozen, in which case atmospheric air is trapped in the ice.
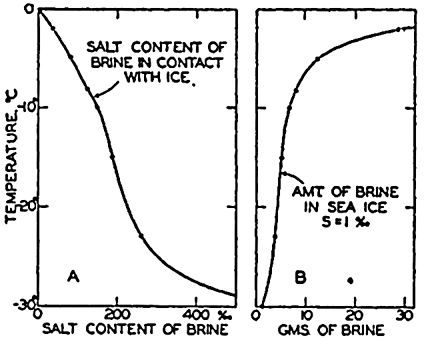
(A) Salt content of the enclosed brine in equilibrium with sea ice at different temperatures. (B) Amount of brine in 1 kg of sea ice of salinity 1 ‰ at different temperatures.
In the following discussion the numerical values relating to the properties of sea ice are quoted from the work of Malmgren (1927), unless otherwise noted. The corresponding values for pure ice represent physical constants for gas- and salt-free ice, and are taken from Barnes (1928).
Pure ice at 0° has a density of 0.91676, whereas pure water at the same temperature has a density of 0.9998674. The density of sea ice
The specific heat of pure ice depends upon its temperature and varies within narrow limits, but that of sea ice is a much more variable property, depending upon the salt or brine content and the temperature. Changing the temperature of sea ice will generally involve either melting or freezing, and the amount of heat required will depend upon the salinity of the ice, as shown in table 17. It should be noted that the specific heat of pure ice is less than half that of pure water. Near the initial freezing point, the extremely high specific heat of ice of high salinity is, of course, due to the formation of ice from the enclosed brine or its melting.
| Salinity ‰ | Temperature (°C) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| −2° | −4° | −6° | −8° | −10° | −12° | −14° | −16° | −18° | −20° | −22° | |
| 0………… | 0.48 | 0.48 | 0.48 | 0.48 | 0.48 | 0.47 | 0.47 | 0.47 | 0.47 | 0.47 | 0.46 |
| 2………… | 2.47 | 1.00 | 0.73 | 0.63 | 0.57 | 0.55 | 0.54 | 0.53 | 0.53 | 0.52 | 0.52 |
| 4………… | 4.63 | 1.50 | 0.96 | 0.76 | 0.64 | 0.59 | 0.57 | 0.57 | 0.56 | 0.55 | 0.54 |
| 6………… | 6.70 | 1.99 | 1.20 | 0.88 | 0.71 | 0.64 | 0.61 | 0.60 | 0.58 | 0.57 | 0.56 |
| 8………… | 8.76 | 2.49 | 1.43 | 1.01 | 0.78 | 0.68 | 0.64 | 0.64 | 0.61 | 0.60 | 0.58 |
| 10………… | 10.83 | 2.99 | 1.66 | 1.14 | 0.85 | 0.73 | 0.68 | 0.67 | 0.64 | 0.62 | 0.60 |
| 15………… | 16.01 | 4.24 | 2.24 | 1.46 | 1.02 | 0.85 | 0.77 | 0.76 | 0.71 | 0.68 | 0.65 |
The latent heat of fusion of pure ice at 0°C and at atmospheric pressure is 79.67 calories per gram. As the melting of sea ice does not occur at a fixed temperature on account of the presence of the salts, it is impossible to designate the latent heat in the usual way. Malmgren gives the heat required to melt 1 g of ice of given salinity that was initially at the indicated temperature (table 18). It may readily be seen that the presence of salts reduces the apparent latent heat.
The vapor pressure of sea ice has not been investigated, but it cannot depart very much from that of pure ice, which has the following values:
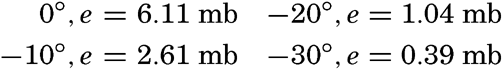
The latent heat of evaporation of pure ice is variable. It has been found that under certain conditions the ice can volatilize directly to vapor without going through the liquid stage, in which case the latent heat of evaporation is about 600 calories per gram. If the evaporation
| Temperature (°C) | Salinity (‰) | ||||||
|---|---|---|---|---|---|---|---|
| 0 | 2 | 4 | 6 | 8 | 10 | 15 | |
| −1………… | 80 | 72 | 63 | 55 | 46 | 37 | 16 |
| −2………… | 81 | 77 | 72 | 68 | 63 | 59 | 48 |
For pure ice the coefficient of thermal expansion (e) per one degree is about 1.7 × 10−4, where e = (l/α)(dα/dϑ). The coefficient is independent of temperature. The thermal expansion of sea ice is a function of its temperature and salinity and shows a considerable range over both positive and negative values, as shown in table 19, where negative values indicate expansion on cooling, positive values contraction on cooling. This anomalous behavior is again related to the salt or brine content because any change in temperature leads to the formation or melting of a certain amount of ice. Thus, the processes in sea ice are a combination of the sudden change in volume associated with the ice ⇌ water transformation and the thermal expansion of the brine and the ice. According to table 19, sea ice of high salinity expands rapidly as it is cooled below the initial freezing point. The coefficient decreases at lower temperatures but is always negative. On the other hand, ice of low salinity first expands and then contracts as its temperature is lowered.
The coefficient of thermal conductivity of pure ice is about 0.005, which is approximately three times as great as that of pure water at 0°. Malmgren carried out a number of measurements in the Arctic ice fields and found that the conductivity was greatly affected by the character of the ice, particularly by the gas content (that is, the porosity) of the ice. Under natural conditions, porosity is greater near the surface than in the deeper portions of the ice. On the average, the coefficient of thermal conductivity near the surface was about 1.5 × 10−3, at 0.5 m it was 4.0 × 10−3, and below 1.0 m it approached the value of pure ice given above—namely, 5.0 × 10−3.
Transmission of Sound
Water is a very efficient medium for the transmission of sound, which travels more rapidly and with much less absorption of energy through water than through air. This characteristic has made possible the development of submarine acoustic methods that are of tremendous value in navigation. The most familiar use is in echo sounding, where the time required for an impulse to travel to the sea floor and back to the vessel is used as a measure of the depth. Horizontal sound transmission is used in radio-acoustic range finding, which is employed by surveying vessels in order to determine their location accurately when carrying on sounding operations out of sight of land. The position of the vessel is determined by measuring the time intervals required for the impulse of a bomb explosion to travel to two or more submarine sound detectors (hydrophones) at known locations, usually near shore. Sound transmission from subsurface bells has also been used as a navigational aid near lighthouses. Ultrasonic impulses (frequency above the range audible to the human ear) are largely directional, and many attempts have been made to develop instruments for locating icebergs and other navigational hazards in the path of a vessel. The practical aspects of this problem and the types of equipment used are too numerous to consider in this discussion, and reference is made to the Hydrographic Review (Monaco) as an excellent source of material on these problems.
| Salinity (‰) | Temperature (°C) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −2 | −4 | −6 | −8 | −10 | −12 | −14 | −16 | −18 | −20 | −22 | ||
| 2………… | −22.10 | −4.12 | −1.06 | 0.16 | 0.83 | 1.13 | 1.23 | 1.27 | 1.33 | 1.38 | 1.44 | |
| 4………… | −45.89 | −9.92 | −3.81 | −1.37 | −0.02 | 0.57 | 0.78 | 0.85 | 0.96 | 1.07 | 1.88 | |
| 6………… | −69.67 | −15.73 | −6.55 | −2.90 | −0.88 | 0.00 | 0.33 | 0.43 | 0.60 | 0.76 | 0.93 | |
| 8………… | −93.46 | −21.53 | −9.30 | −4.43 | −1.73 | −0.57 | −0.13 | 0.02 | 0.23 | 0.45 | 0.67 | |
| 10………… | −117.25 | −27.34 | −12.05 | −5.95 | −2.59 | −1.13 | −0.59 | −0.40 | −0.13 | 0.14 | 0.42 | |
| 15………… | −176.72 | −41.85 | −18.92 | −9.78 | −4.73 | −2.54 | −1.72 | −1.45 | −1.04 | −0.63 | −0.22 | |
The velocity of sound in sea water is independent of the wave length except for impulses resulting from the detonation of relatively large amounts of explosives. Initially the impulse from such explosions may travel about 30 per cent faster than normal, apparently because of the tremendous energy involved.
The velocity of sound in a liquid may be computed from the elasticity and density:
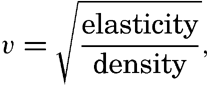
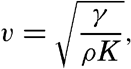
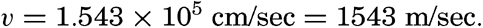
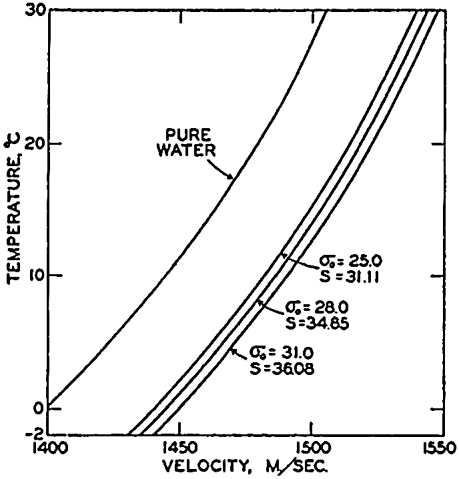
Velocity of sound in pure water and in sea water at atmospheric pressure as a function of temperature and salinity.
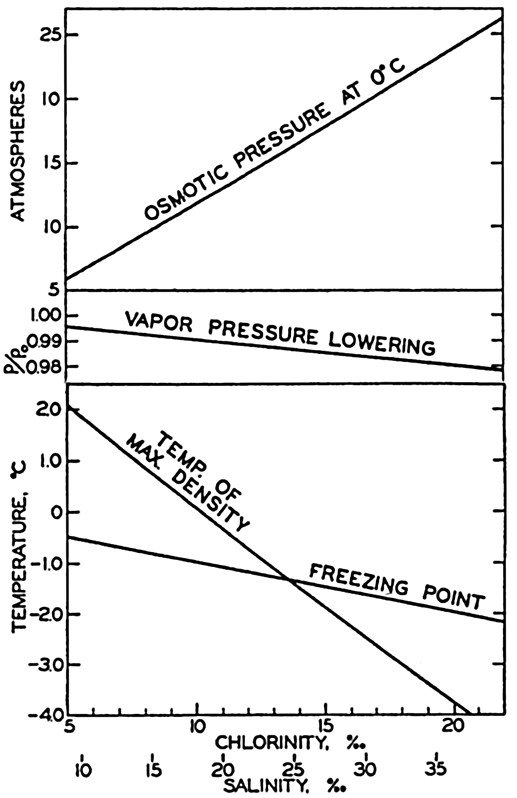
Effect of pressure upon the velocity of sound in sea water of salinity 34.85 ‰ at 0°.
If the velocity of the sound is known, it is possible to determine the wavelength of sound of different frequencies from the equation λ = υ/n, where λ is the wave length, υ is the velocity, and n is the frequency (table 20). Frequencies between about 25 and 10,000 vibrations per second are easily detected by the human ear, and the maximum sensitivity is at about 1000 per second. Ultrasonic waves of frequencies above those audible to the human ear have certain desirable properties that make them valuable in submarine acoustics, but, as will be shown later, their effective range is much less because their absorption is greater. The effective range has been increased by constructing sound emitters which for small wave lengths give a directional beam, somewhat
| Air | Sea water | Sea water | |
|---|---|---|---|
| ϑ = 20°, | S = 34.85 ‰ | S = 34.85 ‰ | |
| Frequency | p = 1 atm | ϑ = 0°, p = 1 atm | ϑ = 20°, p = 1 atm |
| v = 346 rn/sec | v = 1445.2 m/sec | v = 1518.5 m/sec | |
| wave length, λ (m) | wave length, λ (m) | wave length, λ (m) | |
| 10 | 35.6 | 144.5 | 151.8 |
| 100 | 3.56 | 14.45 | 15.18 |
| 1,000 | 0.36 | 1.44 | 1.52 |
| 10,000 | 0.036 | 0.144 | 0.152 |
| 40,000 | 0.009 | 0.036 | 0.038 |
| 100,000 | 0.0036 | 0.0144 | 0.0152 |
In the absence of appreciable absorption and refraction the intensity of sound varies inversely as the square of the distance from the source. Owing to the viscosity of the water, a certain amount of the kinetic energy of the sound waves is converted into heat, and hence there is an absorption of sound somewhat analogous to that of light. The problem of absorption of sound in sea water has been discussed by Langevin (1924). The sound intensity of a plane sound wave decreases exponentially from I0, to Ix, by passage through a distance x. Therefore
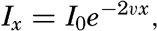
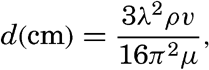
The velocity with which a sound wave travels through the water varies considerably with depth. Hence a “beam” of ultrasonic waves may be refracted when transmitted in a quasi-horizontal direction. Generally the velocity decreases with increasing depth in the upper layers and the beam is bent downward. Studies made by the U. S. Coast and Geodetic Survey (Swainson, 1936) have shown that a sound impulse may travel directly to the hydrophone, or may reach the hydrophone after having been reflected one or more times at the surface and the bottom. In many cases it was possible to distinguish several different “rays” which were received after different intervals. The direct transmission could be obtained only at distances less than 20 km and when the depth to the bottom was about 2000 m. The velocity of the direct wave impulse corresponded to that computed from the temperature and salinity, but those wave impulses which were reflected showed an apparent “horizontal” velocity less than the theoretical because of the longer paths traveled. This empirical horizontal velocity depends upon the distance between the vessel and the hydrophone, the depth to the bottom, the bottom profile, the physical properties of the water, and so forth.
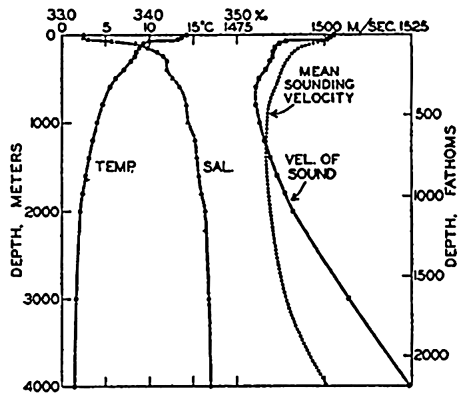
Vertical distributions of temperature and salinity off southern California at 32°57′N and 122°07′W, the computed velocity of sound, and the mean sounding velocity.
As stated previously, the vertical velocity is a function of the depth and the distribution of temperature and salinity. Most sonic depth-finding instruments are adjusted for a constant “sounding velocity,” usually 800 to 820 fathoms per second (1463 to 1500 m/sec). In certain cases it is desirable to correct the readings to true depths. This can be done if the distributions of temperature and salinity are known. For different areas of the oceans and for different depths, the British Admiralty Tables contain “mean sounding velocities”; that is, mean velocities from the surface to the stated depth. In general, these first decrease somewhat with depth, because the effect of decreasing temperature dominates, but at greater depths they increase again as the pressure
Absorption of Radiation
Absorption Coefficients of Distilled Water and of Pure Sea Water. In water the intensity of parallel beams of radiation of wave length λ decreases in the direction of the beams, the decrease in a layer of infinitesimal thickness being proportional to the energy, I, and to the thickness of the layer:
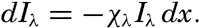
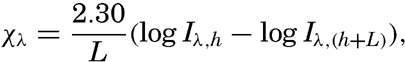
The decrease of intensity of radiation passing through a layer of water depends not only upon the amount of radiation that is truly absorbed—that is, converted into another form of energy—but also upon the amount that is scattered laterally. In “pure” water the scattering takes place against the water molecules, and the effect of scattering is related to the molecular structure of the water (p. 47). However, when the absorption in pure water is measured, the effect of scattering is not separated but is included in the absorption coefficient, which varies greatly with wave length.
A great number of measurements of the absorption coefficients in pure water have been conducted, but the results by different investigators do not agree (Dorsey, 1940). Thus, at a wave length of .48 μ
| Hüfner and Albrecht, 1891.................................0.048 |
| Ewan, 1895...............................................0.030 |
| Aschkinass, 1895..........................................0.020 |
| Sawyer, 1931.............................................0.015 |
From the table it is evident that water is very transparent for radiation of wave lengths between 0.4 μ and 0.6 μ; that is, for visible rays in the violet, blue, green, and yellow parts of the spectrum. It is less transparent for orange and red light, and in the infrared the transparency is practically nil (fig. 21), because, if the absorption coefficient per meter equals 100, 99.5 per cent of the radiation is absorbed in a layer of thickness 5.3 cm.
| Wave length in μ | Absorption coefficient per meter | Wave length in μ | Absorption coefficient per meter | Wave length in μ | Absorption coefficient per meter | Wave length in μ | Absorption coefficient per meter |
|---|---|---|---|---|---|---|---|
| .32 | 0.58 | .52 | 0.019 | .85 | 4.12 | 1.60 | 800 |
| .34 | 0.38 | .54 | 0.024 | .90 | 6.55 | 1.70 | 730 |
| .36 | 0.28 | .56 | 0.030 | .95 | 28.8 | 1.80 | 1700 |
| .38 | 0.148 | .58 | 0.055 | 1.00 | 39.7 | 1.90 | 7300 |
| .40 | 0.072 | .60 | 0.125 | 1.05 | 17.7 | 2.00 | 8500 |
| .42 | 0.041 | .62 | 0.178 | 1.10 | 20.3 | 2.10 | 3900 |
| .44 | 0.023 | .65 | 0.210 | 1.20 | 123.2 | 2.20 | 2100 |
| .46 | 0.015 | .70 | 0.84 | 1.30 | 150 | 2.30 | 2400 |
| .48 | 0.015 | .75 | 2.72 | 1.40 | 1600 | 2.40 | 4200 |
| .50 | 0.016 | .80 | 2.40 | 1.60 | 1940 | 2.50 | 8500 |
Collins has compared the absorption in distilled water to that in salt solutions, and from his results it can be concluded that the dissolved salts in concentrations occurring in sea water exert a negligible effect on the absorption coefficient. The maximum effect appears to be about 1.3 per cent, and the uncertainty of the observed values is greater than
It has also been concluded that the effect of temperature on absorption, which has been established in the case of distilled water, is applicable to uncontaminated sea water. The effect of temperature changes is to increase the absorption in certain parts of the infrared by about 0.5 per cent for every temperature increase of 1°C, but over a large part of the spectrum the temperature effect is much smaller. When dealing with sea water the effect can be neglected.
Extinction Coefficients in the Sea. In oceanography the greater interest is attached to the rate at which downward-traveling radiation decreases. The rate of decrease can be defined by means of a coefficient similar to the absorption coefficient:
The first crude measurements of absorption in the visible part of the spectrum were made by lowering a white disc of standard size (30 cm), the Secchi disc, and observing the depth at which the disc disappeared from sight. Comparisons with recent exact measurements by other methods have shown that in the English Channel the extinction coefficient of visible rays can roughly be attained from the formula κ = 1.7/D, where D is the maximum depth of visibility in meters, as determined by the Secchi disc (Poole and Atkins, 1929).
The next step in the investigation of the absorption of radiation in sea water was made by subsurface exposure of photographic plates enclosed in watertight containers. Such experiments, which were conducted by Helland-Hansen (1912a) on the Michael Sars Expedition by exposing panchromatic plates at different depths in the vicinity of the Azores, showed that photographic plates were blackened at very great depths.
In other experiments colored filters were used, which showed that the red portion of the spectrum was rapidly absorbed, whereas the green and blue rays penetrated to much greater depths. Quantitative results as to the absorption at different wave lengths were obtained by using spectro- photometers (Knudsen, 1922), but the methods were laborious and not sensitive enough to be used at great depths.
The introduction in recent years of photoelectric cells has made possible rapid and accurate determinations of extinction coefficients in different parts of the spectrum. A number of different instruments have been and still are in use, but a standardized technique has been proposed by a committee of the International Council for the Exploration of the Sea (Atkins et al, 1938). Because of the wide variation in absorption at different wave lengths, efforts have been directed toward measuring exactly the absorption in narrow spectral bands. The determinations are accomplished by lowering stepwise a photoelectric or photronic cell enclosed in a watertight container and provided with suitably colored filters, and by observing on deck the photoelectric current by means of a sensitive galvanometer or a suitable bridge circuit. The measurements must be made at constant incident light either on clear, sunny days or on days when the sky is uniformly overcast, because the rapid variations in incident light that occur on days with scattered clouds will naturally lead to erroneous results as to the absorption. To determine the percentage amount of radiation that reaches a certain depth, it is necessary to make simultaneous readings of the incident radiation on board ship. For the different precautions that have to be taken, reference is made to papers listed in the bibliography, particularly to Atkins et al (1938).
These methods give information as to the absorption in layers of definite thickness. Instruments for measurements of the transparency of sea water at given depths and of the scattering of light have been designed by H. Pettersson (1936b) and have been used for determining relative values. It has been demonstrated, particularly, that at boundary surfaces sharp variations in transparency and scattering occur. The study of the absorption of radiation in the sea is in rapid progress, and several of the following generalizations are therefore presented with reservations.
The main results as to the character of the extinction coefficient in the sea of radiation of different wave lengths can be well illustrated
| Type of water | Wave length in μ | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| .46 | .48 | .515 | .53 | .565 | .60 | .66 | .80 | 1.00 | |
| Pure water | .015 | .015 | .018 | .021 | .033 | .125 | .280 | 2.40 | 39.7 |
| Oceanic water lowest | .038 | .026 | .035 | .038 | .074 | .199 | |||
| Oceanic water average | 086 | .076 | .078 | .084 | .l08 | .272 | |||
| Oceanic water highest | .160 | .154 | .143 | .140 | .167 | .333 | |||
| Coastal water lowest | .224 | .230 | .192 | .169 | .375 | .477 | |||
| Coastal water average | .362 | .334 | .276 | .269 | .437 | .623 | |||
| Coastal water highest | .510 | .454 | .398 | .348 | .489 | .760 | |||
The transparency of the water for radiation of different wave lengths can be expressed by means of the percentage amounts of radiation which penetrate a 1-m layer. These percentage amounts are given in table 23, from which it is seen that the greatest transparency of the clearest oceanic water is at a wave length of 0.48 μ—that is, in the blue part of the spectrum—whereas the greatest transparency of coastal water is at wave lengths 0.53 μ or higher—that is, in the green or green-yellow part of the spectrum. It is also seen that 97.5 per cent of radiation of wave length 0.48 μ passes through 1 m of the clearest oceanic water, but only 63.5 per cent of radiation of the same wave length passes through 1 m of turbid coastal water.
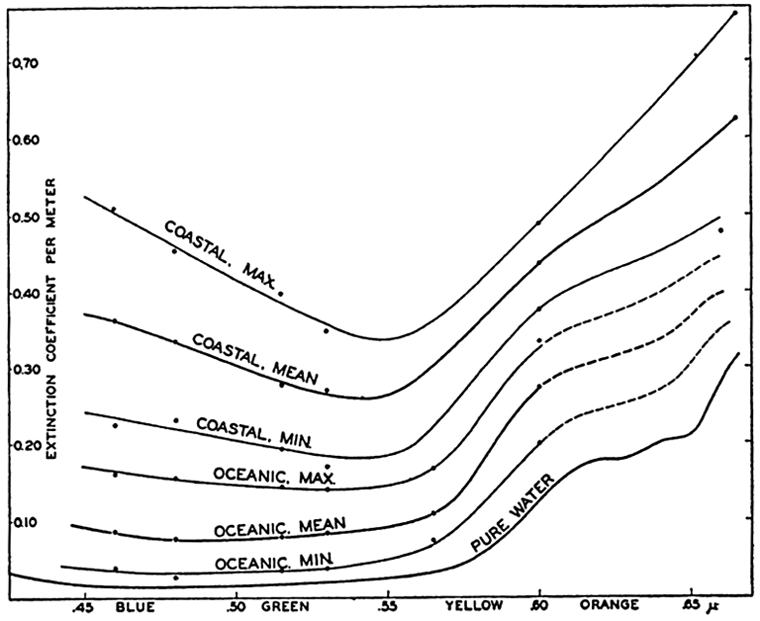
Extinction coefficients of radiation of different wave lengths in pure water and in different types of sea water.
The great difference between the mean and the maximum values of the extinction coefficients shows that the absorption of sea water varies within very wide limits. In the example presented in table 22 the percentage variations are about the same in coastal and oceanic water, and the maximum values in the oceanic water approach the minimum values in the coastal water. In any given locality, great variations also occur in a vertical direction, layers of low absorption alternating with layers of high absorption, and this feature further complicates the actual conditions.
Similar results have been obtained by other investigators from such widely different areas as in the English Channel (Poole and Atkins, 1929;
| Type of water | Wave length (μ) | ||||||
|---|---|---|---|---|---|---|---|
| .46 | .48 | .515 | .53 | .565 | .60 | .66 | |
| Pure water | 98.5 | 98.5 | 98.2 | 97.9 | 96.8 | 88.3 | 75.9 |
| Oceanic water lowest | 96.4 | 97.5 | 96.6 | 96.3 | 92.9 | 81.8 | |
| Oceanic water average | 91.8 | 92.7 | 92.5 | 91.8 | 89.8 | 75.9 | |
| Oceanic water highest | 85.1 | 85.7 | 86.7 | 86.9 | 84.5 | 71.6 | |
| Coastal water lowest | 80.0 | 79.4 | 82.6 | 84.5 | 68.7 | 62.0 | |
| Coastal water average | 69.7 | 71.6 | 75.9 | 76.4 | 64.6 | 53.6 | |
| Coastal water highest | 60.0 | 63.5 | 67.1 | 70.6 | 61.4 | 46.7 | |
Influence of the Altitude of the Sun Upon the Extinction Coefficient. The extinction coefficient is a measure of the reduction of intensity on a, vertical distance and depends, therefore, upon the obliquity of the rays. The obliquity of the incident rays is reduced, however, by refraction when entering the water from the air and by the effect of scattering. When the sun's rays pass the water surface, the angle of refraction increases from zero with the sun in zenith to 48.5 degrees with the sun at the horizon, and therefore the most oblique rays penetrating into the water form an angle of less than 48 degrees with the vertical. Owing to the scattering and the sifting out by absorption of the most oblique rays, the radiation that penetrates to moderate depths will become nearly vertical, and the measured extinction coefficients will be independent, within wide limits, of the altitude of the sun. The reduction of the obliquity of the incident radiation has been directly demonstrated by Johnson and Liljequist (1938). Conditions at very. low sun have not been examined, but it is probable that at low sun the extinction coefficients are increased, and this increase may have bearing
The Scattering of Radiation in the Sea The Scattering of Radiation has been examined both directly by means of Pettersson's scattering meter (p. 83) and by measuring the relative intensities of downward- and upward-traveling radiation or vertical and horizontal radiation. Jorgensen and Utterback (1939) found that in coastal waters the intensity of the upward-traveling radiation ranged for the short wave lengths from 1 to 3 per cent of that of the downward-traveling radiation, and for the long wave lengths from 0.5 to 2 per cent. In oceanic water Utterback (1936) found ratios between 1 and 2 per cent at the shorter wave lengths. Clarke (1936) found considerably higher values in shallow coastal waters, but similar values in the deep basin of the Gulf of Maine.
The relative intensities of horizontal and vertical radiation have been measured by Clarke off the east coast of the United States and by Poole and Atkins in the English Channel. The greatest value found by Clarke was 17 per cent, but Poole and Atkins (1929) have reported an average value of 50 per cent for the horizontal radiation down to a depth of 25 m in the English Channel. The conclusion that can be drawn from these experiments is that the subsurface illumination becomes more and more diffuse with increasing depth, particularly in coastal waters, but that the directional character of the radiation is lost only slowly. This conclusion is particularly true in clear oceanic water, where Helland-Hansen (1912a) found that the vertical radiation was distinctly more intense than the horizontal at a depth of 500 m. (p. 82).
Cause of the Great Extinction Coefficients in the Sea. The great extinction coefficients in the sea as compared to those of absolutely pure water are as a rule ascribed to the presence of minute particles which cause scattering and reflection of the radiation and which themselves absorb radiation. If such particles are small compared to the wave length, λ, of the radiation, the scattering will be proportional, according to Lord Rayleigh, to λ−4, and the effect therefore at wave length, say, .46 μ will be 2.86 times greater than at wave length .60 μ. This selective effect leads to a shift toward longer wave lengths in the region of minimum absorption.
Clarke and James (1939) found that the increased absorption in oceanic water was chiefly caused by suspensoids that could be removed by means of a “fine” Berkefeld filter, and that these suspensoids were largely nonselective in their effect. Utterback's data (1936) indicated, on the other hand, that the increased absorption in oceanic water is at least in part due to selective scattering, because at short wave lengths the extinction coefficients were increased more, above those of pure water, than at longer wave lengths (table 22). Kalle (1938) is of the
The increase of the absorption coefficients in coastal waters appears to be due in part to another process. Clarke and James (1939) conclude from their examination that in coastal water both suspensoid and “filter-passing” materials are effective in increasing the absorption, and that each exerts a highly selective action, with greatest absorption at the shorter wave lengths. These great absorptions at the shorter wave lengths are demonstrated by Utterback's measurements (table 22). Clarke does not discuss the nature of the “ filter-passing” material, but Kalle (1938) has shown that in sea water water-soluble pigments of yellow color are present. These pigments appear to be related to the humic acids, but their chemical composition has not been thoroughly examined, for which reason Kalle calls them “yellow substance.” This yellow substance seems to occur in greatest abundance in coastal areas, but Kalle has demonstrated its presence in the open ocean as well and believes that it represents a fairly stable metabolic product related to the phytoplankton of the sea. The selective absorption 'of this yellow substance may then be responsible, in part, for the character of the absorption in coastal water and for shift of the band of minimum absorption toward longer wave lengths.
It has not been possible anywhere to demonstrate any direct influence of phytoplankton populations on the absorption, but very dense populations may cut down the transparency. At present it appears that the major increase of absorption of sea water over that of pure water is due to two factors: the presence of minute suspended particles, and the presence of dissolved “yellow substance.” The former factor dominates in oceanic waters, and the latter is particularly important in coastal waters.
The Color of the Sea. The color of the sea, as it appears to an observer ashore or on board a vessel, varies from a deep blue to an intense green, and is in certain circumstances brown or brown-red. The blue waters are typical of the open oceans, particularly in middle and lower latitudes, whereas the green water is more common in coastal areas, and the brown or “red” water is observed in coastal regions only.
The color of the sea has been examined by means of a Secchi disk (p. 82) by observing the color that the water appears to have when seen against the white submerged surface of the disc. This color is recorded according to a specially prepared color scale, the “ Forel scale” (Krümmel, 1907). The method is a rough one and the scale is not adapted for
Kalle has critically reviewed earlier theories as to the causes of the color of the sea and arrives at conclusions that appear to be consistent with all available observations. The blue color is explained, in agreement with earlier theories, as a result of scattering against the water molecules themselves, or against suspended minute particles smaller than the shortest visible wave lengths. The blue color of the water is therefore comparable to the blue color of the sky. The transition from blue to green cannot be explained, however, as a result of scattering, and Kalle concludes that this transition is due to the above-mentioned “ yellow substance,” pointing out that the combination of the yellow color and the “natural” blue of the water leads to a scale of green colors as observed at sea. Fluorescence may contribute to the coloring but appears to be of minor importance.
The color of suspended larger particles, if present in great abundance, can give color to the sea. In this case the color is not determined by the optical properties of the water or by dissolved matter, but by the colors of the suspended inorganic or organic particles, and the water is appropriately called “ discolored.” Discoloration can be observed when large quantities of finely suspended mineral particles are carried into the sea after heavy rainfall, or when very large populations, several million cells per liter, of certain species of algae or dinoflagellates are present very near the surface. Thus, the “red water” (often more brown than red) which is quite frequently observed in many areas and after which the Red Sea and the Vermilion Sea (Gulf of California) have been named is due to abundance of certain algae (in the Red Sea, Trichodesmium erythraeum) or dinoflagellates. The discoloration, beautiful examples of which have been given by Gunther (1936), is, however, a phenomenon of the typical coastal waters, the green colors being frequent in waters near the coast or at sea in high latitudes, and the blues charac teristic of the open ocean in middle and lower latitudes (fig. 214, p, 784).
Eddy Conductivity, Diffusivity, and Viscosity
In the preceding discussion it has been repeatedly stated that the coefficients of heat conduction, diffusion, and viscosity that have been dealt with so far are applicable only if the water is at rest or in laminar flow. By laminar flow is understood a state in which sheets (laminae) of liquids move in an orderly manner such that random local fluctuations of velocity do not occur. However, the molecules of the liquid, including those of dissolved substances, move at random, and, owing to this
In nature, laminar flow is rarely or never encountered, but, instead, turbulent flow, or turbulence, prevails. By turbulent flow is understood a state in which random motion of smaller or larger masses of the fluid is superimposed upon some simple pattern of flow. The character of the turbulence depends upon a number of factors, such as the average velocity of the flow, the average velocity gradients, and the boundaries of the system. Under these conditions the exchange between adjacent moving layers is not limited to the interchange of molecules, but masses of different dimensions also pass from one layer to another, carrying with them their characteristic properties. As a consequence, a snapshot of the instantaneous distribution of velocity, temperature, salinity, and other variables in the sea would show a most complicated pattern, but so far no means have been developed for establishing this picture. Measurements by sensitive current meters have demonstrated that in a given locality the velocity fluctuates from second to second, but in most cases observations of ocean currents give information as to mean velocities for time intervals that may vary from a few minutes to twenty-four hours or more. Similarly, special measurements have demonstrated that the details of the temperature distribution are very complicated, but in general observations are made at such great distances apart that only the major features of the temperature distribution are obtained. Inasmuch as it is impossible to observe the instantaneous distribution in space of temperature, salinity, and velocity, it follows that the corresponding gradients cannot be determined and that no basis exists for application to the processes in the sea of the coefficients of thermal conductivity, diffusion, and viscosity that have been determined in the laboratory. Since only certain average gradients can be determined, another approach has to be made when dealing with the processes in the sea. In order to illustrate this approach, let us first consider the viscosity.
In the case of laminar flow the coefficient of viscosity, μ, is defined by the equation τs = μdv/dn where τs is the shearing stress exerted on a surface of unit area, and dv/dn is the shear normal to that surface.
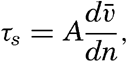
The definition of the eddy viscosity in the above manner appears purely formalistic, but it is based on the concept that masses which leave one layer carry with them the momentum corresponding to the average velocity in that layer, and that by impact they attain the momentum corresponding to the average velocity of their new surroundings before again leaving them (p. 472). Thus, A is an expression for the transfer of momentum of mean motion. This transfer is much increased by the turbulence, as is evident from the fact that the eddy viscosity is many times greater than the molecular viscosity.
The eddy viscosity can be determined only by examination of the effect on the mean motion. This effect is discussed on pp. 492 and 577, but a few points will be mentioned here. It has been found practical to distinguish between two types of turbulence in the sea—vertical and lateral, In the case of vertical turbulence the effective exchange of masses is related to comparatively slight random motion in a vertical direction or, if the term “eddy motion” is used, to small eddies in a vertical plane. Actually, the eddies are oriented at random, but only their vertical components produce any effect on the mean motion. The corresponding eddy viscosity has been found to vary between 1 and 1000 c.g.s. units, thus being one thousand to one million times greater than the molecular viscosity of water. In the case of lateral turbulence the effective exchange of masses is due to the existence of large quasi-horizontal eddies, The corresponding eddy viscosity depends upon dimensions of the system under consideration and has been found to vary between 106 and 108 c.g.s. units.
The distinction between vertical and lateral turbulence is particularly significant where the density of the water increases with depth, because such an increase influences the two types of turbulence in a different manner. Where the density of the sea water increases with depth (disregarding the effect of pressure), vertical random motion is impeded by
With regard to the eddy conductivity, similar reasoning is applicable. When dealing with eddy viscosity it was assumed that the exchange of mass leads to a transfer of momentum from one layer to another, which is expressed by means of A. Correspondingly, when dealing with eddy conductivity, one can assume that the transfer of heat through any surface is proportional to the exchange of mass through the surface, as expressed by A, and to the gradient of the observed temperatures, −d /dn; that is, dQ/dt = −rA d
/dn; that is, dQ/dt = −rA d /dn, where r is a factor that depends upon the specific heat of the fluid and upon the manner in which the heat contents of the moving masses are given off to the surroundings. When dealing with homogeneous water, it is assumed that a large mass which is transferred to a new level breaks down at that level into smaller and smaller elements, and that equalization of temperature ultimately takes place by molecular heat conduction between the small elements and the surroundings. If such is the case, both the difference in momentum and the difference in heat content are leveled off, and the proportionality factor, r, is equal to the specific heat of the liquid. Since the specific heat of water is nearly unity, the numerical values of eddy conductivity and eddy viscosity are practically equal. However, where stable stratification prevails, the elements, being lighter or heavier than their surroundings, may return to their original level before completion of temperature equalization, but equalization of momentum may have been accomplished by collision. In this case, the factor of proportionality, r, will be smaller than the specific heat of the liquid; that is, in the sea, r is smaller than unity, and the eddy conductivity is smaller than the eddy viscosity. Thus, stable stratification reduces the vertical eddy conductivity even more than it reduces the vertical eddy viscosity. Taylor (1931) has presented the above reasoning in mathematical language (p. 476).
/dn, where r is a factor that depends upon the specific heat of the fluid and upon the manner in which the heat contents of the moving masses are given off to the surroundings. When dealing with homogeneous water, it is assumed that a large mass which is transferred to a new level breaks down at that level into smaller and smaller elements, and that equalization of temperature ultimately takes place by molecular heat conduction between the small elements and the surroundings. If such is the case, both the difference in momentum and the difference in heat content are leveled off, and the proportionality factor, r, is equal to the specific heat of the liquid. Since the specific heat of water is nearly unity, the numerical values of eddy conductivity and eddy viscosity are practically equal. However, where stable stratification prevails, the elements, being lighter or heavier than their surroundings, may return to their original level before completion of temperature equalization, but equalization of momentum may have been accomplished by collision. In this case, the factor of proportionality, r, will be smaller than the specific heat of the liquid; that is, in the sea, r is smaller than unity, and the eddy conductivity is smaller than the eddy viscosity. Thus, stable stratification reduces the vertical eddy conductivity even more than it reduces the vertical eddy viscosity. Taylor (1931) has presented the above reasoning in mathematical language (p. 476).
The discussion has so far been limited to a consideration of the vertical eddy conductivity, but lateral eddy conductivity due to lateral turbulence has also to be introduced. The numerical value of lateral
Numerical values of the coefficients of eddy conductivity can be derived only from a study of the effect of mixing processes on the observed distribution of temperature. Methods of such determinations and numerical values are presented on pp. 483 and 484. The results have confirmed the above conclusions and have also demonstrated that the eddy conductivity varies within wide limits. In the upper layers of the sea, where stable stratification prevails, the vertical coefficient of eddy viscosity varies between 1 and 1000, whereas the corresponding eddy conductivity is smaller and varies between 0.01 and 100; in homogeneous water, however, no difference has been established (p. 485). In the cases in which the lateral coefficients of viscosity and conductivity have been examined, nearly equal numerical values have been found in agreement with the conclusion that the stability of the stratification does not influence the lateral turbulence.
The transfer of salinity or other concentration is similar to the heat transfer. The eddy diffusivity is also proportional to the exchange of mass as expressed by A, the factor of proportionality being a pure number. In sea water of uniform density r = 1, but in the case of stable stratification, when complete equalization of concentration does not take place, r < 1; that is, the vertical eddy diffusivity is smaller than A and equals the eddy conductivity. This conclusion has also been confirmed by observations (p. 484).
Bibliography
Atkins, W. R. G., G. L. Clarke, H. Pettersson, H. H. Poole, C. L. Utterback, and A. Ångström.1938. “Measurement of submarine daylight. Conseil Perm” . Intenat. p. 1'Explor. de la Mer, Journal du Conseil, v. 13, p. 37–57, 1938.
Barnes, H. T.1928. Ice engineering. Renouf Pub. Co., Montreal. 364 pp., 1928.
Barnes, T. C., and Theo. L. Jahn. 1934. “Properties of water of biological interest” . Quart. Rev. Biol., v. 9, p. 292–341, 1934.
Bayliss, W. M.1927. Principles of general physiology. 4th ed.Longmans, Green and Co., Ltd., London. 882 pp., 1927.
Bein, Willy, Heinz-Günther Hirsekorn, and Lotte Möller. 1935. Konstan-tenbestimmungen des Meerwassers und Ergebnisse über Wasserkörper. Berlin, Universität. Institut f. Meereskunde, Veröff., N.F., A. Geogr.-naturwiss. Reihe, Heft 28, pp. 240, 1935.
Bergmann, Ludwig. 1939. Ultrasonics and their scientific and technical applications. Trans. from the German by H. S. Hatfield. John Wiley and Sons, New York. 264 pp., 1939.
Bjerknes, V., and J. W. Sandström.1910. Dynamic meteorology and hydrography. Pt. I, Statics. Carnegie Inst. Washington, Pub. no. 88, 146 pp. + tables.1910.
Clarke, George L.1933. “Observations on the penetration of daylight into mid-Atlantic and coastal waters” . Biol. Bull., v. 65, p. 317–37, 1933.
Clarke, George L.1936. Light penetration in the western North Atlantic and its application to biological problems. Conseil Perm. Intern, p. l'Explor. de la Mer, Rapp. et Proc.-Verb., v. 101, pt. 2, no. 3, 14 pp., 1936.
Clarke, George L., and Harry R. James. 1939. “Laboratory analysis of the selective absorption of light by sea water” . Optical Soc. Amer., Jour., v. 29, p. 43–55, 1939.
Cummings, N. W.1932. “A sinker method for the determination of specific gravities” . Scripps Inst. Oceanogr., Univ. Calif., Bull., tech. ser., v. 3, p. 101–18, 1932.
Dietrich, G.1939. “Die Absorption der Strahlung im reinen Wasser und im reinen Meerwasser” . Ann. d. Hydrogr. u. Mar. Meteor., Bd. 67, S.411–17, 1939.
Dorsey, N. Ernest. 1940. “Properties of ordinary water-substance” . Amer. Chem. Soc., Monograph Ser. No. 81. Reinhold Pub. Corp., New York. 673 pp., 1940.
Ekman, V. W.1908. Die Zusammendrückbarkeit des Meerwassers. Conseil Perm. Intern, p. l'Explor. de la Mer, Pub. de Circonstance, No. 43, 47 pp., 1908.
Ekman, V. W.1914. Der adiabatische Temperaturgradient im Meere. Ann. d. Hydrogr. u. Mar. Meteor., Bd. 42, S.340–44, 1914.
Fleming, R. H., and Roger Revelle. 1939. “Physical processes in the ocean. P. 48–141 in Recent marine sediments, A symposium” . Parker D. Trask, Ed. Amer. Assn. Petroleum Geol., Tulsa, Okla. 736 pp., 1939.
Forch, C., Martin Knudsen, und S. P. L. Sörensen. 1902. “Berichte über die Konstantenbestimmungen zur Aufstellung der hydrographischen Tabellen. D. Kgl. Danske Vidensk. Selsk. Skrifter, 6” . Raekke, naturvidensk. og mathem., Afd XII.1, 151 pp., 1902.
Gunther, E. R.1936. A report on oceanographical investigations in the Peru coastal current. Discovery Repts., v. 13, p. 107–276, 1936.
Hartmann, G. K., and Alfred B. Focke. 1940. “Absorption of supersonic waves in water and in aqueous solutions” . Phys. Rev., v. 57, p. 221–25, 1940.
Harvey, H. W.1928. Biological chemistry and physics of sea water. Cambridge Univ. Press, London, 194 pp., 1928.
Heck, N. H., and Jerry H. Service. 1924. “Velocity of sound in sea water” . U. S. Coast and Geod. Surv., Spec. Pub. no. 108, 27 pp., 1924.
Helland-Hansen, B.1912a. Physical oceanography. Ch. 5, p. 210–306 in Murray and Hjort, Depths of the ocean. Macmillan and Co., London, 821 pp., 1912.
Helland-Hansen, B.1912b. “The ocean waters, An introduction to physical oceanography” . Intern. Rev. d. Hydrobiol., Suppl. to Bd. Ill, Ser. 1, H. 2, 84 pp., 1912. Leipzig.
Helland-Hansen, B.1930. “Physical oceanography and meteorology. Michael Sars North Atlantic Deep-Sea Exped.” , 1910, Rept. Sci. Results, v. 1, art. 2, 217 pp., 1930.
Henderson, L. J.1913. The fitness of the environment. Macmillan Co., New York, 317 pp., 1913.
Hesselberg, Th., and H. U. Sverdrup. 1914. “Die Stabilitätsverhältnisse des Seewassers bei vertikalen Verschiebungen” . Bergens Museums Aarbok, no. 14, 17 pp., 1914–15.
Hydrographic Review. Published by the International Hydrographic Bureau, Monaco, v. 1-, 1923 to date.
International Association of Physical Oceanography (Assn. d'Océanogr. Phys.) Union Géod. et Géophys, Intern. 1939. Report of the Committee on Chemical Methods and Units. Presented at 7th General Assembly, Washington, D. C., 1939. Publication Scientifique. In press.
International critical tables of numerical data, physics, chemistry and technology. Published for Nat. Research Council by McGraw-Hill Co., New York. 7 volumes, 1926–1930.
Jacobsen, J. P., and Martin Knudsen. 1940. Urnormal 1937 or primary standard sea-water 1937. Union GÉod. et Geophys. Intern., Assn. d'Océan-ographie, Pub. sci., no. 7, 38 pp., Liverpool, 1940.
Johnson, Nils G., and G. Liljequist. 1938. “On the angular distribution of submarine daylight and on the total submarine illumination” . Svenska Hydrogr.-Biologiska Kommiss. Skrifter. N.S., Hydrografi no. 14, 15 pp., 1938.
Johnstone, James. 1928. An introduction to oceanography. Univ. Press, Liverpool. 368 pp., 1928.
Jorgensen, Wilhelm, and C. L. Utterback. 1939. “Periodic changes in spectral scattering and spectral transmission of daylight in tidal water” . Jour. Marine Research, v. 2, p. 30–37, 1939.
Kalle, K.1938. “Zum Problem der Meereswasserfarbe” . Ann. d. Hydrogr. und Mar. Meteor., Bd. 66, S.1–13, 1938.
Knudsen, Martin. 1901. Hydrographical tables. G. E. C. Gad, Copenhagen, 63 pp., 1901.
Knudsen, Martin. 1903. Gefrierpunkttabelle für Meerwasser. Conseil Perm. Intern, p. l'Explor. de la Mer, Pub. de Circonstance, no. 5, p. 11–13, 1903.
Knudsen, Martin. 1922On measurement of the penetration of light into the sea. Conseil Perm. Intern, p. l'Explor. de la Mer, Pub. de Circonstance, no. 76, 16 pp., 1922.
Krümmel, Otto. 1907. “Handbuch der Ozeanographie: Bd. 1” , Die raümlich, chemischen und physikalischen Verhältnisse des Meeres. J. Engelhorn. Stuttgart. 526 pp., 1907.
Kuwahara, Susumu. 1939. “Velocity of sound in sea water and calculation of the velocity for use in sonic sounding” . Hydrogr. Rev., v. 16, no. 2, p. 123–40, 1939. Monaco.
Langevin, P.1924. “The employment of ultra-sonic waves for echo sounding” . Hydrogr. Rev., v. 2, no. 1, p. 57–91, 1924. Monaco.
Lyman, John, and Richard H. Fleming. 1940. “Composition of sea water” . Jour. Marine Research, v. 3, p. 134–46, 1940.
Malmgren, Finn. 1927. “On the properties of sea-ice” . Norwegian North Polar Exped. with the Maud 1918–1925, Sci. Results, v. 1, no. 5, 67 pp., 1927.
Matthews, Donald J.1923. Physical oceanography, v. 3, p. 665–692 in A dictionary of applied physics, Sir Richard Glazebrook, Ed. Macmillan and Co., London, 1923.
Matthews, Donald J.1927. Tables of the velocity of sound in pure water and sea water for use in echo-sounding and sound-ranging. British Admiralty, Hydrogr. Dept., H.D. no. 282, 29 pp., 1927.
Matthews, Donald J.1932. Tables of the determination of density of sea water under normal pressure, Sigma-t. Conseil Perm. Intern, p. l'Explor. de la Mer. Copenhagen. 59 pp., 1932.
Matthews, Donald J.1938. Tables for calculating the specific volume of sea water under pressure. Conseil Perm. Intern, p. lExpl. de la Mer. Copenhagen. 67 pp., 1938.
McEwen, Geo. F.1929. “Tables to facilitate dynamic computations of ocean currents according to the Bjerknes circulation theory” . Scripps Inst. Oceanogr., Univ. Calif. Mimeographed, 1929. La Jolla.
Miyake, Y.1939a. “Chemical studies of the western Pacific Ocean. III. Freezing point, osmotic pressure, boiling point and vapour pressure of sea water” . Chem. Soc. Japan, Bull., v. 14, no. 3, p. 58–62, 1939.
Miyake, Y.1939b. “Chemical studies of the western Pacific Ocean. IV. The refractive index of sea water” . Chem. Soc. Japan, v. 14, no. 6, p. 239–42, 1939.
Nansen, Fridtjof. 1900. “On hydrometers and the surface tension of liquids” . Norwegian North Polar Exped. 1893–1896, Sci. Results, v. 3, no. 10, 88 pp., 1900.
Pettersson, Hans. 1936a. Das Licht im Meer. Bioklim. Beiblätter, Heft 1, 11 pp., 1936.
Pettersson, Hans. 1936b. The transparency of sea water. Conseil Perm. Intern. p. l'Explor. de la Mer, Rapp. et Proce.-Verb., v. 101, pt. 2, no. 6, 7 pp., 1936.
Pettersson, Hans and Otto. 1929. “Methods for determination of the density and salinity of sea water” . Svenska Hydrogr.-Biologiska Kommiss. Skrifter. N.S., Hydrografi no. 3, p. 1–4, 1929.
Poole, H. H.1936. The photo-electric measurement of submarine illumination in offshore waters. Conseil Perm. Intern, p. l'Explor. de la Mer, Rapp. et Proc.-Verb., v. 101, pt. 2, no. 2, 12 pp., 1936.
Poole, H. H., and W. R. G. Atkins. 1929. “Photo-electric measurements of submarine illumination throughout the year” . Marine Biol. Assn. U. K., Jour., v. 16, p. 297–324, 1929. Plymouth.
Schmidt, Wilhelm. 1917. “Wirkungen der ungeordneten Bewegung im Wasser der Meere und Seen” . Ann. d. Hydrogr. u. Mar. Meteor., Bd. 45, S. 367–81, 431–45, 1917.
Soule, Floyd M.1932. Oceanographic instruments and methods. Physics of the earth, v. 5, Oceanography, p. 411–441. Nat. Research Council, Bull. no. 85, 1932.
Sund, Oscar. 1929. An oceanographical slide rule. A new apparatus for calculating oceanographical data. Conseil Perm. Intern, p. l'Explor. de la Mer, Jour, du Conseil, v. 4, p. 93–98, 1929.
Sverdrup, H. U.1933. Vereinfachtes Verfahren zur Berechnung der Druckund Massenverteilung im Meere. Geofysiske Publikasjoner, v. 10, no. 1, 9 pp., 1933. Oslo.
Swainson, O. W.1936. “Velocity and ray paths of sound waves in sea water” . U. S. Coast and Geod. Surv., Field Engineers Bull. no. 10, 64 pp., 1936.
Swartout, J. A., and Malcolm Dole. 1939. “The protium-deuterium ratio and the atomic weight of hydrogen” . Amer. Chem. Soc., Jour., v. 61, p. 2025–29, 1939.
Taylor, G. I.1931. Internal waves and turbulence in a fluid of variable density, Conseil Perm. Intern, p. l'Explor. de la Mer, Rapp. et Proc.-Verb., v. 76, p. 35–42, 1931.
Thomas, B. D., T. G. Thompson, and C, L. Utterback. 1934. The electrical conductivity of sea water. Conseil Perm. Intern, p. l'Explor. de la Mer, Jour, du Conseil, v. 9, p. 28–35, 1934.
Thompson, T. G.1932. “The physical properties of sea water” . Physics of the earth, v. 5, Oceanography, p. 63–94. Nat. Research Council, Bull. no. 85, 1932.
Utterback, C. L.1936, Spectral bands of submarine solar radiation in the North Pacific and adjacent inshore waters. Conseil Perm. Intern, p. l'Explor. de la Mer, Rapp. et Proc.-Verb., v. 101, pt. 2, no. 4, 15 pp., 1936.
Utterback, C. L., T. G. Thompson, and B. D. Thomas. 1934. Refractivity-chlorinity-temperature relationships of ocean waters. Conseil Perm. Intern, p. l'Explor. de la Mer, Jour, du Conseil, v. 9, p. 35–38, 1934.
Wenner, P., Edward H. Smith, and Floyd M. Soule. 1930. “Apparatus for the determination aboard ship of the salinity of sea water by the electrical conductivity method” . Jour. Research, U. S. Bur. Standards, v. 5, p. 711–32, 1930.
Wirth, H. E., T. G. Thompson, and C. L. Utterback. 1935. “Distribution of isotopic water in the sea” . Amer. Chem. Soc., Jour,, v. 57, p. 400–04, 1935.
Witting, R.1908. “Untersuchungen zur Kenntnis der Wasserbewegungen und der Wasserumsetzung in den Finnland umgebenden Meeren” . Finländische Hydrogr.-Biologische Untersuchungen, no. 2, 246 pp., 1908. Cf. p. 173.
Young, R. T., Jr., and R. D. Gordon. 1939. “Report on the penetration of light in the Pacific Ocean off the coast of southern California” . Scripps Inst. Oceanogr., Univ. Calif., Bull., tech. ser., v. 4, p. 197–218, 1939.
IV. General Distribution of Temperature, Salinity, and Density
The Heat Budget of the Earth as a Whole
For the earth as a whole, the total amount of heat that is received during one year from the sun at the limit of the atmosphere must exactly balance the total amount that in the same period is lost by reflection and by radiation into space. Otherwise, the temperature of the atmosphere and the oceans would change. The radiation from the hot sun is called short-wave radiation, because the wave lengths which reach the limit of the earth's atmosphere lie roughly between 0.38 μ and 2.5 μ, whereas the dark-heat radiation which is emitted by all objects at ordinary temperatures is called long-wave radiation, being of wave lengths between 5 μ and 20 μ. The part of the short-wave radiation that is reflected is of no importance to the heat budget of the earth, and therefore the amount of short-wave radiation that is absorbed by the atmosphere, the oceans, and the land must exactly balance the long-wave radiation into space from the entire system. A small part of the heat that the atmosphere receives is transformed into kinetic energy which by friction is transformed back again to heat and ultimately lost into space by radiation. Thus, the transformation of heat to kinetic energy does not lead to any net gain of heat but serves to maintain the circulations of the atmosphere and the oceans.
As is customary procedure, the amounts of heat will be given in gram calories and not in units of work such as ergs or joules. The conversion factors are: 1 gram calorie = 4.183 × 107 ergs = 4.183 joules.
In lower latitudes, heat received by radiation is greater than heat lost by back radiation and reflection, whereas in higher latitudes the gain is less than the loss. Table 24 contains values of heat received and lost by processes of radiation and reflection in different latitudes. The third column, containing the differences between the two quantities, shows that there is an annual net gain of heat in the equatorial regions and a net loss in the polar regions. The mean annual temperatures in different latitudes on the earth remain unchanged from one year to another, showing that within the atmosphere and the oceans there must be a transport of heat from lower to higher latitudes which exactly equals the difference
The transport of heat from lower to higher latitudes takes place partly by air currents (winds) and partly by ocean currents. In meteorological literature it is generally assumed that the transport by ocean currents is negligible (Bjerknes et al, 1932), although the question has not been thoroughly examined. It can be shown that the assumption is correct when dealing with averages for the whole earth, but in some regions the transport by ocean currents is of considerable importance.
| Latitude (°) | Heat received (g cal/cm2/min) | Heat lost (g cal/cm2/min) | Surplus or deficit (g cal/cm2/min) | Heat transport across parallels of latitude (1016 g cal/min) | Heat transport across every centimeter of parallels of latitude (107 g cal/cm/min) |
|---|---|---|---|---|---|
| 0 | 0.339 | 0.300 | 0.039 | 0.00 | 0.00 |
| 10 | 0.334 | 0.299 | 0.035 | 1.59 | 0.40 |
| 20 | 0.320 | 0.294 | 0.026 | 2.94 | 0.78 |
| 30 | 0.297 | 0.283 | 0.014 | 3.58 | 1.07 |
| 40 | 0.267 | 0.272 | −0.005 | 3.96 | 1.30 |
| 50 | 0.232 | 0.258 | −0.026 | 3.34 | 1.32 |
| 60 | 0.193 | 0.245 | −0.052 | 2.40 | 1.20 |
| 70 | 0.160 | 0.231 | −0.071 | 1.20 | 0.88 |
| 80 | 0.144 | 0.220 | −0.076 | 0.32 | 0.46 |
| 90 | 0.140 | 0.220 | −0.080 | 0.00 | 0.00 |
The amount of heat transported in a north-south direction by a unit volume of ocean water is equal to cρϑvN, where c represents the specific heat, ρ the density, ϑ the temperature of the water, and vN the north-south component of velocity. The total transport through a certain section of the sea can be found by integration, but for the sake of simplicity
 ρTN, where
ρTN, where 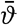 represents the average temperature of the water and ρTN represents the mass of water passing north through the section in unit time. If the section is taken across an ocean, the mass transport to the north, ρTN, must equal the mass transport to the south, ρTS, but the heat transport may differ because the temperature of the water transported in one direction may be higher or lower than that of the water which is transported in the opposite direction. If these temperatures are designated by ϑN and ϑS, the net transport of heat will be c(ϑN − ϑS)ρT, where ρT now means the transport to the north and the south. As an example, we can apply these considerations to the North Atlantic Ocean along the parallel of 55°N. In the eastern Atlantic about 10 million m3/sec of warm water flow toward the north, and in the western Atlantic an equal volume of cold water is carried south by the Labrador Current and by the flow of the deep water (p. 684). With ϑN − ϑS = 5°, c = 1, ρ = 1, and T = 10 × 106 m3/sec, we find that the heat transport toward the north through latitude 55° in the Atlantic Ocean is about 0.3 × 1016 g cal/min. The total heat transport across the parallel of 55°N is about 3 × 1016 g cal/min; hence in the North Atlantic the fraction carried by the ocean currents is appreciable.
represents the average temperature of the water and ρTN represents the mass of water passing north through the section in unit time. If the section is taken across an ocean, the mass transport to the north, ρTN, must equal the mass transport to the south, ρTS, but the heat transport may differ because the temperature of the water transported in one direction may be higher or lower than that of the water which is transported in the opposite direction. If these temperatures are designated by ϑN and ϑS, the net transport of heat will be c(ϑN − ϑS)ρT, where ρT now means the transport to the north and the south. As an example, we can apply these considerations to the North Atlantic Ocean along the parallel of 55°N. In the eastern Atlantic about 10 million m3/sec of warm water flow toward the north, and in the western Atlantic an equal volume of cold water is carried south by the Labrador Current and by the flow of the deep water (p. 684). With ϑN − ϑS = 5°, c = 1, ρ = 1, and T = 10 × 106 m3/sec, we find that the heat transport toward the north through latitude 55° in the Atlantic Ocean is about 0.3 × 1016 g cal/min. The total heat transport across the parallel of 55°N is about 3 × 1016 g cal/min; hence in the North Atlantic the fraction carried by the ocean currents is appreciable.This example represents an outstanding case of poleward transport of heat by ocean currents. In the Pacific Ocean a transport of comparable magnitude probably takes place in latitudes 30°N to 40°N, but in the southern oceans the north-south circulation and the corresponding temperature contrasts between currents flowing toward or away from the higher latitudes are smaller than those in the northern oceans. A detailed study of the transport of heat by ocean currents has not been made, but it seems certain that by far the major transport of heat is taken care of by the atmosphere.
The Heat Budget of the Oceans
The above consideration applies to the entire system formed by the atmosphere and the oceans, but for the oceans alone we encounter an entirely different picture. On an average, the gain of heat must exactly balance the loss, but the processes involved are not limited to those of radiation, as is evident from the list at the bottom of page 101.
These processes will be discussed in detail, but it can already be stated that of the processes of heating only the first one is important, and the heat budget of the oceans as a whole can therefore be written
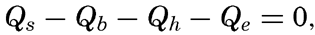
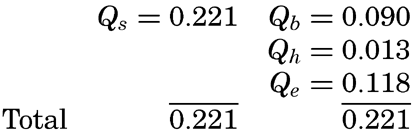
If a specific region is considered, it must be taken into account that heat may be brought into or out of that region by ocean currents or by processes of mixing, and that during short time intervals a certain amount of heat may be used for changing the temperature of the water. The complete equation for the heat balance of any part of the ocean in a given time interval is, therefore,
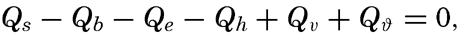
Radiation from the Sun and the Sky. The short-wave radiation that reaches the sea surface comes partly directly from the sun and partly from the sky as reflected or scattered radiation. The amount of radiation energy which is absorbed per unit volume in the sea depends upon the amount of energy that reaches the sea surface, the reflection from the sea surface, and the absorption coefficients for total energy. The incoming radiation depends mainly upon the altitude of the sun, the absorption in the atmosphere, and the cloudiness. With a clear sky and a high sun, about 85 per cent of the radiation comes directly from the sun and about 15 per cent from the sky, but with a low sun the proportion from the sky is greater, reaching about 40 per cent of the total with the sun 10 degrees above the horizon.
| Processes of Heating of the Ocean Water | Processes of Cooling of the Ocean Water |
|---|---|
|
|
The incoming energy from the sun is cut down when passing through the atmosphere, partly through absorption by water vapor and carbon dioxide in the air and partly through scattering against the air molecules or very fine dust. The total effect of absorption and scattering in the atmosphere depends upon the thickness of the air mass through which the sun's rays pass, as expressed by the equation
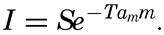
The sun's radiation on a horizontal surface is obtained by multiplication with sin h, where h is the sun's altitude. To this amount must be added the diffuse sky radiation in order to obtain the total radiation on a horizontal surface. Instruments are in use for recording the total radiation and for recording separately the radiation from the sun and from the sky.
When the sun is obscured by clouds, the radiation comes from the sky and the clouds and, on an average, can be represented by the formula Q = Q0(1 − 0.071 C), where the cloudiness C is given on the scale 0 to 10, and where Q0 represents the total incoming radiation with a clear sky. This formula is applicable, however, only to average conditions. If the sun shines through scattered clouds, the radiation may be greater than with a clear sky, owing to the reflection from the clouds, and on a completely overcast dark and rainy day the incoming radiation may be cut down to less than 10 per cent of that on a clear day. Table 25 contains the average monthly amounts of incoming radiation, expressed in g cal/cm2/min, which reach a horizontal surface in the indicated localities (computed from Kimball, 1928). The differences between the parts of the oceans in the same latitudes are mainly due to differences in cloudiness.
Few direct measurements of radiation are available from the oceans, and when dealing with the incoming radiation it is necessary to consider average values which can be computed from empirical formulae. Mosby (1936) has established such a formula by means of which monthly or annual mean values of the incoming radiation on a horizontal surface can be computed if the corresponding average altitude of the sun and the average cloudiness are known:
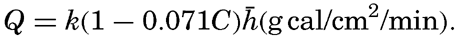
 is the average altitude of the sun. The factor k depends upon the transparency of the atmosphere and appears to vary somewhat with latitude, being 0.023 at the Equator, 0.024 in lat. 40°, and 0.027 in lat. 70°. Mosby's formula is not valid at h > 60°, but gives correct results if, at high altitudes of the sun, the true altitude is replaced by a reduced altitude as follows: The values computed by means of this formula agree within a few per cent with those derived by Kimball in an entirely different manner (table 25).
is the average altitude of the sun. The factor k depends upon the transparency of the atmosphere and appears to vary somewhat with latitude, being 0.023 at the Equator, 0.024 in lat. 40°, and 0.027 in lat. 70°. Mosby's formula is not valid at h > 60°, but gives correct results if, at high altitudes of the sun, the true altitude is replaced by a reduced altitude as follows: The values computed by means of this formula agree within a few per cent with those derived by Kimball in an entirely different manner (table 25).| Locality | Month | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Latitude | Longitude | Jan. | Feb. | Mar. | Apr. | May | June | July | Aug. | Sept. | Oct. | Nov. | Dec. |
| 60°N | 7°E- 56°W | .002 | .053 | .125 | .207 | .272 | .292 | .267 | .212 | .147 | .074 | .006 | 0 |
| 60 N | 135–170 W | .005 | .078 | .155 | .208 | .269 | .260 | .242 | .185 | .127 | .077 | .015 | 0 |
| 52 N | 10 W | .048 | .089 | .148 | .219 | .258 | .267 | .251 | .211 | .160 | .104 | .062 | .041 |
| 52 N | 129 W | .053 | .091 | .135 | .185 | .246 | .250 | .230 | .214 | .158 | .097 | .058 | .039 |
| 42 N | 66 -70W | .094 | .138 | .212 | .272 | .306 | .329 | .302 | .267 | .230 | .174 | .115 | .086 |
| 42 N | 124 W | .100 | .151 | .210 | .286 | .331 | .360 | .320 | .274 | .231 | .174 | .113 | .092 |
| 30 N | 65–77 W | .146 | .165 | .238 | .285 | .317 | .310 | .301 | .282 | .239 | .188 | .169 | .142 |
| 30 N | 128 -130 E | .141 | .153 | .199 | .241 | .258 | .238 | .256 | .260 | .219 | .178 | .153 | .135 |
| 10 N | 61–69 W | .254 | .276 | .299 | .305 | .272 | .276 | .285 | .292 | .287 | .269 | .248 | .239 |
| 10 N | 116 E- 80 W | .226 | .257 | .292 | .278 | .255 | .239 | .240 | .242 | .247 | .237 | .224 | .219 |
| 0 | 7–12 E | .239 | .248 | .244 | .230 | .210 | .196 | .188 | .194 | .220 | .240 | .239 | .235 |
| 0 | 48 W & 170 E | .261 | .265 | .282 | .297 | .309 | .300 | .300 | .340 | .366 | .362 | .339 | .278 |
| 10 S | 14 E; 36- 38 W | .329 | .328 | .301 | .254 | .219 | .206 | .232 | .278 | .312 | .324 | .317 | .320 |
| 10 S | 72 -171 E | .290 | .308 | .315 | .289 | .266 | .253 | .269 | .306 | .332 | .313 | .301 | .303 |
| 30 S | 17 and 116 E | .452 | .406 | .340 | .254 | .186 | .148 | .166 | .214 | .274 | .362 | .401 | .430 |
| 30 S | 110 W | .380 | .330 | .260 | .209 | .162 | .130 | .145 | .176 | .237 | .321 | .340 | .390 |
| 42 S | 73 W; 147 E | .343 | .297 | .223 | .154 | .104 | .085 | .092 | .135 | .187 | .264 | .310 | .348 |
| 52 S | 58 W | .289 | .237 | .167 | .112 | .062 | .039 | .049 | .097 | .150 | .222 | .273 | .302 |
| 60 S | 45 W | .213 | .171 | .105 | .056 | .011 | 0 | .003 | .054 | .111 | .156 | .204 | .221 |
| True altitude (°) | 60 | 65 | 70 | 75 | 80 | 85 | 90 |
| Reduced altitude (°) | 60 | 62 | 64 | 66 | 68 | 69 | 70 |
Part of the incoming radiation is lost by reflection from the sea surface, the loss depending upon the altitude of the sun. When computing the loss, the direct radiation from the sun and the scattered radiation from the sky must be considered separately. With the sun 90°, 60°, 30° and 10° above the horizon, the reflected amounts of the direct solar radiation are, according to Schmidt (1915), 2.0 per cent, 2.1 per cent, 6.0 per cent, and 34.8 per cent respectively. For diffuse radiation from the sky and from clouds Schmidt computes a reflection of 17 per cent. Measurements by Powell and Clarke (1936) gave values on clear days in agreement with the above, but on overcast days when all radiation reaching the sea surface was diffuse, the observed reflection was about 8 per cent. If the fractions of the total radiation from the sun and the sky on a clear day are designated p and q, respectively, and if the corresponding percentages reflected are designated m and n, the percentage of the total incoming radiation that is reflected on a clear day is r = mp + nq. Thus, on an overcast day, when all incoming radiation is diffuse, r = 8 per cent. Table 26 contains approximate values of r at different altitudes of the sun on a clear day.
| Altitude of the sun (°) | 5 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
| Percentage reflected | 40 | 25 | 12 | 6 | 4 | 3 | 3 | 3 | 3 | 3 |
The values in the table are applicable only if the sea surface is smooth. In the presence of waves the reflection loss at a low sun is somewhat increased and will be of particular importance in high latitudes. The amount of radiation which under stated conditions penetrates the sea surface is obtained by subtracting the reflection loss from the total incoming radiation.
Absorption of Radiation Energy in the Sea. The radiation that penetrates the surface is absorbed in the sea water. The amounts absorbed within given layers of water can be derived by measuring with
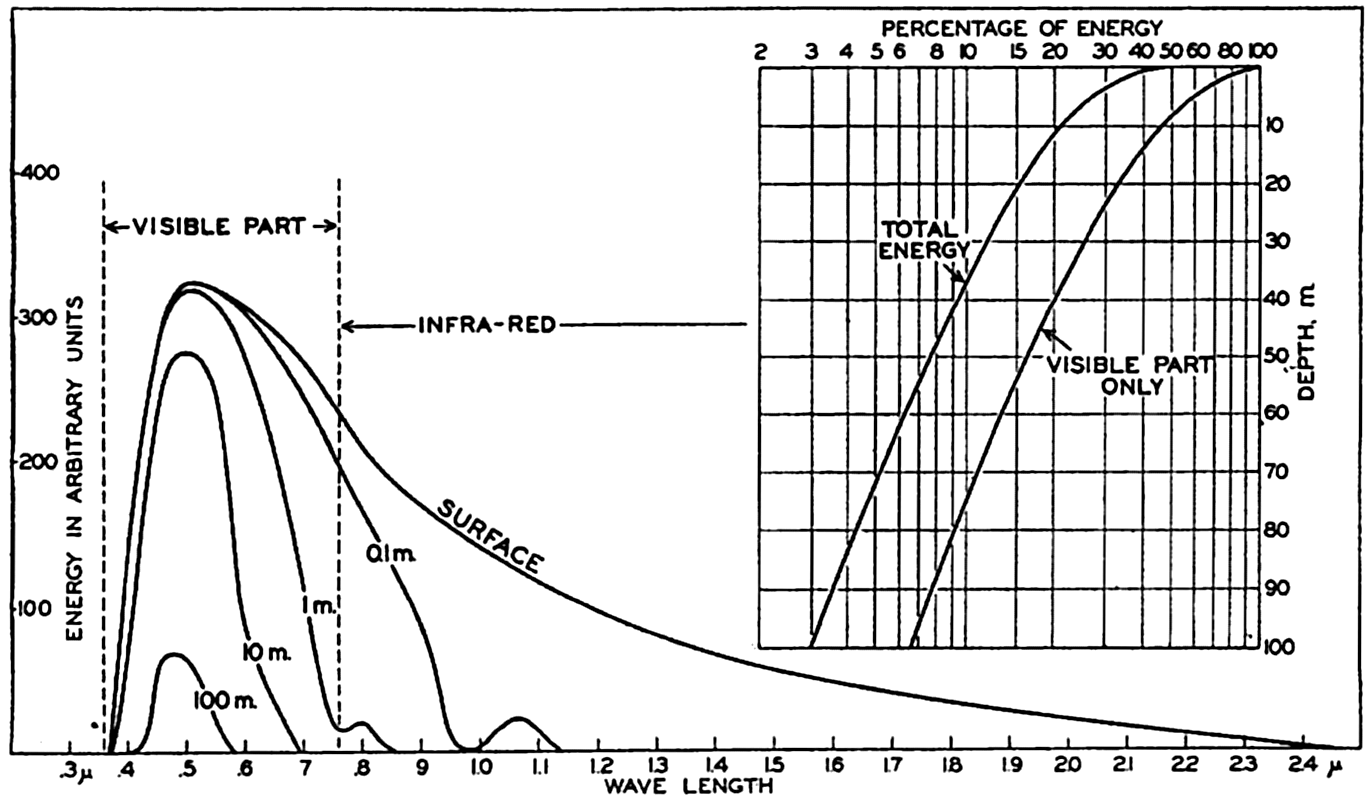
Schematic representation of the energy spectrum of the radiation from the sun and the sky which penetrates the sea surface, and of the energy spectra in pure water at depths of 0.1, 1, 10, and 100 m. Inset: Percentages of total energy and of energy in the visible part of the spectrum reaching different depths.
The spectrum of the energy that penetrates the sea surface is represented approximately by the upper curve in fig. 21, which also shows the energy spectra at different depths in pure water. The total energy at any given depth is proportional to the area enclosed between the base line and the curves showing the energy spectrum. In the inserted diagram the total energy, expressed as percentage of the energy penetrating the surface, as well as the corresponding percentages of the energy in the visible part of the spectrum, is plotted against depth. The figure shows that pure water is transparent for visible radiation only.
For sea water the percentage of the total energy reaching various depths has been computed for the clearest oceanic water, for average
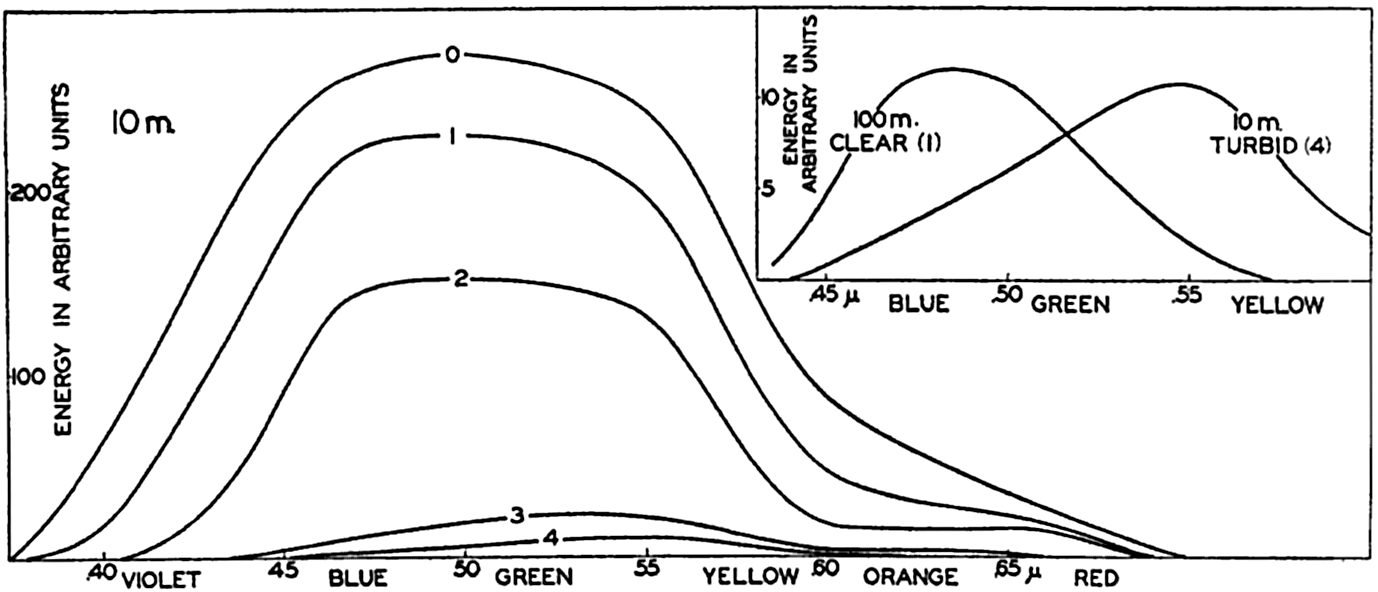
Energy spectra at a depth of 10 m in different types of water. Curves marked 0, 1, 2, 3, and 4 represent energy spectra in pure water, clear oceanic, average oceanic, average coastal, and turbid coastal sea water, respectively. Inset: Energy spectra at a depth of 100 m in clear oceanic water and at 10 m in turbid coastal water.
The absorption of energy is illustrated in fig. 22, which shows the energy spectra in different types of water at a depth of 10 m. At this depth the maximum energy in the clearest water is found in the blue-green portion of the spectrum, whereas in the turbid coastal water the maximum has been displaced toward the greenish-yellow part. This displacement is further illustrated by the inserted curve in the upper right-hand corner of the figure, which shows the energy spectra at 100 m in the clearest water and at 10 m in the most turbid water.
Extinction coefficients of total energy have been computed and are entered in table 27. These extinction coefficients are very high in the upper 1 m but decrease rapidly, at greater depth approaching the minimum extinction coefficients characteristic of the types of water dealt with. The smallest values given in the table can be considered valid at greater depths as well.
| Percentage amounts of incident energy | Extinction coefficients per meter | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Depth | Pure sea water | Oceanic water | Coastal water | Interval of depth (m) | Pure sea water | Oceanic water | Coastal water | ||||
| Clearest | Average | Average | Turbid | Clearest | Average | Average | Turbid | ||||
| 0 | 100 | 100 | 100 | 100 | 100 | 0–1 | .944 | .975 | 1.080 | 1.318 | 1.385 |
| 1 | 38.9 | 37.7 | 35.2 | 26.7 | 22.8 | 1–2 | .143 | .176 | .230 | .450 | .547 |
| 2 | 33.7 | 31.6 | 28.0 | 17.0 | 13.2 | 2–5 | .062 | .095 | .159 | .351 | .452 |
| 5 | 28.0 | 23.7 | 17.3 | 5.95 | 3.41 | 5–10 | .048 | .076 | .120 | .318 | .405 |
| 10 | 22.0 | 16.1 | 9.50 | 1.21 | 0.449 | 10–20 | .033 | .054 | .094 | .292 | .368 |
| 20 | 15.8 | 9.35 | 3.72 | 0.064 | 0.012 | 20–50 | .024 | .042 | .083 | ||
| 50 | 7.64 | 2.69 | 0.311 | 50–100 | .018 | .036 | |||||
| 100 | 3.04 | 0.452 | 0.0057 | ||||||||
In fig. 23 the curves marked 0, 1, 2, 3, and 4 represent the percentage amounts of energy which reach different levels between the surface and 10 m, according to the data in table 27. The three curves marked Capri, Trieste, and Venice represent results of measurements in the Mediterranean according to Vercelli (1937), and four other curves represent observed values in lakes according to Birge and Juday (1929). The agreement of the character of the curves indicates that reliable values as to the absorption of energy in the sea can be obtained by means of computations based on observed extinction coefficients.
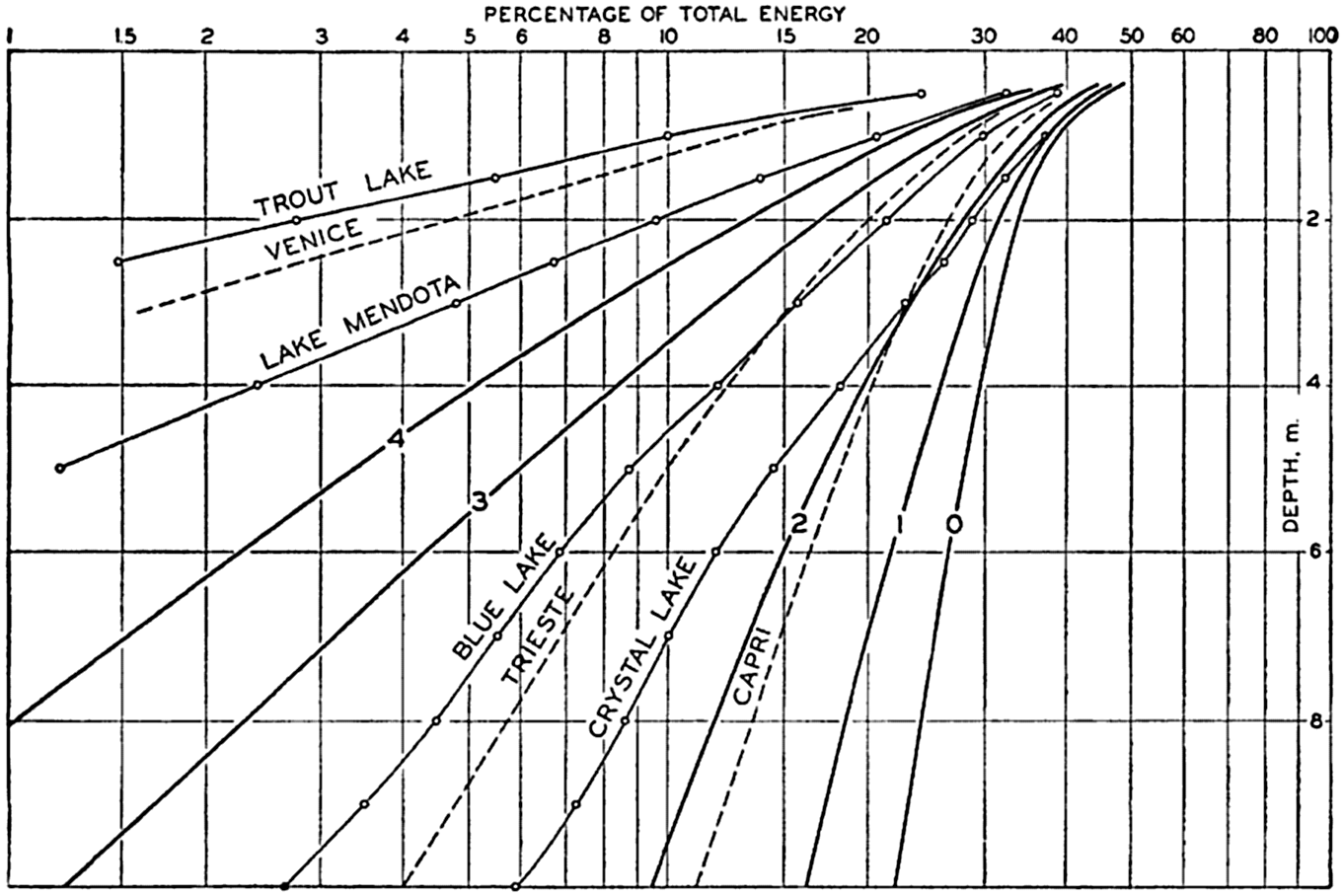
Percentages of total energy reaching different depths in pure water, clear oceanic, average oceanic, average coastal, and turbid coastal sea water (curves 0, 1, 2, 3, and 4), computed from extinction coefficients, and corresponding directly to observed values in four lakes and at three localities in the Mediterranean.
An idea of the heating due to absorption of radiation can be secured by computing the increase of temperature at different depths which results from a penetration of 1000 g cal/cm2 through the surface. The results are shown in table 28, which serves to emphasize that the greater part of the energy is absorbed near the surface, particularly in turbid water. If no other processes took place, the temperature between the surface and 1 m would increase in the clearest water by 6.24°, and in the most turbid water by 7.72°. Between 20 and 21 m the corresponding values would be 0.04° and 0.0003°.
The temperature changes recorded in table 28 show no similarity to those actually occurring in the open oceans, where processes of mixing entirely mask the direct effect of absorption, but in some small, landlocked
| Interval of depth (m) | Oceanic water | Coastal water | ||
|---|---|---|---|---|
| Clearest | Average | Average | Turbid | |
| 0–1 | 6.24 | 6.48 | 7.32 | 7.72 |
| 1–2 | 0.610 | 0.720 | 0.970 | 0.960 |
| 5–6 | .236 | .282 | .164 | .120 |
| 10–11 | .104 | .096 | .030 | .0140 |
| 20–21 | .040 | .030 | .0016 | .0003 |
| 50–51 | .0096 | .0024 | .0534 | .0715 |
| 100–101 | .0016 | .0411 | ||
Fig. 24 shows the vertical distribution of temperature on June 30 and July 15 in a basin that was examined by Gaarder and Spärck. The days in the period between the stated dates were clear and no rain fell. According to Kimball (1928) the diurnal amount of incoming short-wave radiation was about 740 g cal/cm2/day, or about 11,100 g cal/cm2 for
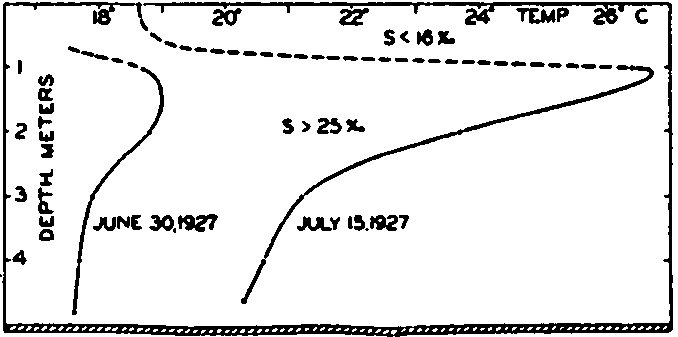
Vertical distribution of temperature in a Norwegian oyster basin on June 30 and July 15, 1927.
Conduction of Heat Through the Ocean Bottom. It has been estimated that the flow of heat through the bottom of the sea amounts to between 50 and 80 g cal/cm2/year (Helland-Hansen, 1930). This amount represents less than one ten-thousandth part of the radiation received at the surface and can generally be neglected when dealing with the heat budget of the oceans. In a few basins, where the deep water is nearly stagnant and where no conduction of heat takes place from above or from the sides, the amount of heat conducted through the bottom may conceivably play a part in determining the distribution of temperature, but so far no such case is known with certainty (p. 739).
Transformation of Kinetic Energy into Heat. The kinetic energy transmitted to the sea by the stress of the wind on the surface and by part of the tidal energy is dissipated by friction and transformed into heat. The energy transmitted by the wind can be estimated at about one ten-thousandth part of the radiation received at the surface and can be neglected. In shallow coastal waters with strong tidal currents the dissipation of tidal energy is so great, however, that it may become of some local importance. Thus, in the Irish Channel, according to Taylor (1919), the dissipation amounts to about 0.002 g cal/cm2/min, or 1050 g cal/cm2/year. The average depth can be taken as about 50 mn, or 5000 cm, and, if the same water remained in the Irish Channel a full year,
Heating due to chemical processes can be completely disregarded.
The convection of sensible heat and the condensation of water vapor will be dealt with in the discussion concerning the exchange of heat and water with the atmosphere.
Effective Back Radiation from the Sea Surface. The sea surface emits long-wave heat radiation, radiating nearly like a black body, the energy of the outgoing radiation being proportional to the fourth power of the absolute temperature of the surface. At the same time the sea surface receives long-wave radiation from the atmosphere, mainly from the water vapor. A small part of this incoming long-wave radiation is reflected from the sea surface, but the greater portion is absorbed in a small fraction of a centimeter of water, because the absorption coefficients are enormous at long wave lengths. The effective back radiation from the sea surface is represented by the difference between the “temperature radiation” of the surface and the long-wave radiation from the atmosphere, and this effective radiation depends mainly upon the temperature of the sea surface and the water-vapor content of the atmosphere. According to Ångström (1920), the latter is proportional to the local vapor pressure, which can be computed from the relative humidity if the air temperature is known. Over the oceans the air temperature deviates so little from the sea-surface temperature that the vapor pressure can be obtained with sufficient accuracy from the sea-surface temperature and the relative humidity of the air at a short distance above the surface.
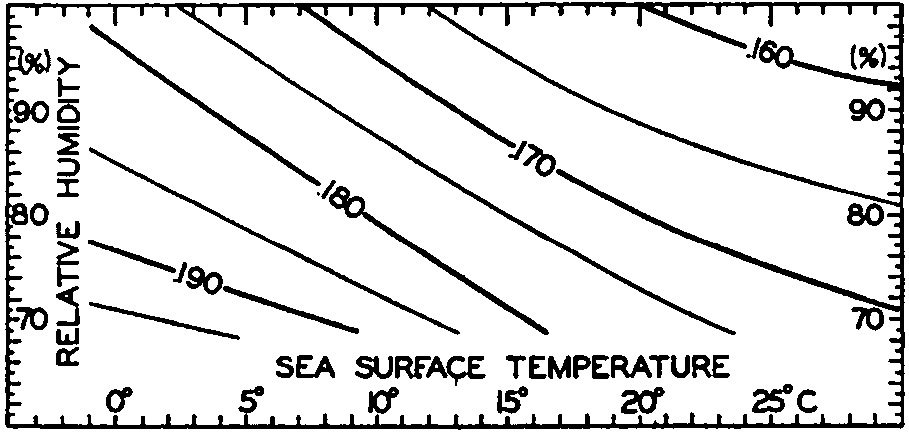
Effective back radiation in gm cal/cm2/min from the sea surface to a clear sky. Represented as a function of sea-surface temperature and relative humidity of the air at a height of a few meters.
Ångström (1920) has published a table that summarizes results of observations of effective radiation against a clear sky from a black body of different temperatures and at different vapor pressures. Fig. 25 has been prepared by means of this table, taking into account the small difference between the radiation of a black body and that of a water surface. The figure shows the effective radiation as a function of sea-surface temperature and of relative humidities between 100 per cent and 70 per cent, but the values that can be read off from the graph may be 10 per cent in error, owing to the scanty information upon which the curves are based. It brings out the interesting fact, however, that, owing to the increased radiation from the atmosphere at higher temperatures (higher vapor pressures), the effective back radiation decreases slowly with increasing temperature. At a temperature of 0°C and a relative humidity of 80 per cent, the effective back radiation is 0.188 g cal/cm2/min, and at a temperature of 25° and the same relative humidity it is 0.167 g cal/cm2/min. At a given temperature the effective radiation decreases with increasing humidity, owing to the increased back radiation from the atmosphere. Thus, at a surface temperature of 15° the effective radiation is about 0.180 g cal/cm2/min at a relative humidity of 70 percent, and about 0.163 g cal/cm2/min at a relative humidity of 100 percent.
The values of the effective back radiation at higher temperatures, as obtained by extrapolation of Ångström's data (fig. 25) are greater than those computed from Brunt#x0027;s empirical formula,
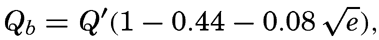
The diurnal and annual variations of the sea-surface temperatures and of the relative humidity of the air over the oceans are small, and the effective back radiation at a clear sky is therefore nearly independent of the time of the day and of the season of the year, in contrast to the incoming short-wave radiation from the sun and the sky, which is subjected to very large diurnal and seasonal variations.
In the presence of clouds the effective back radiation is cut down because the radiation from the atmosphere is increased. The empirical relation can be written
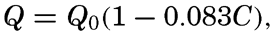
The annual incoming short-wave radiation from the sun and the sky is greater in all latitudes than the outgoing effective back radiation. According to Mosby (1936) the average annual surplus of incoming radiation between latitudes 0 and 10°N is about 0.170 g cal/cm2/min, and between 60° and 70°N about 0.040 g cal/cm2/min. The surplus of radiation must be given off to the atmosphere, and the exchange of heat and water vapor with the atmosphere is therefore equally as important as the processes of radiation in regulating the ocean temperatures and salinities.
The characteristics of the oceans in respect to radiation are very favorable to man. The water surface reflects only a small fraction of the incoming radiation, and the greater part of the radiation energy is absorbed in the water, distributed by processes of mixing over a layer of considerable thickness, and given off to the atmosphere during periods when the air is colder than the sea surface. The oceans therefore exercise a thermostatic control on climate. Conditions are completely changed, however, if the temperature of the sea surface decreases to the freezing point so that further loss of heat from the sea leads to formation of ice, because, when water passes this critical temperature, its thermostatic characteristics are altered in a very unfavorable direction. Sea ice, which soon attains a gray-white appearance owing to enclosed air bubbles, reflects 50 per cent or more of the incoming radiation, and if it is covered by rime or snow the reflection loss increases to 65 per cent, or even to 80 per cent from fresh, dry snow. The snow surface, on the other hand, radiates nearly like a black body, and consequently the heat budget related to processes of radiation, instead of rendering a surplus as it does over the open ocean, shows a deficit until the temperature of the ice surface has been lowered so much that the decreased loss by effective back radiation balances the small fraction of the incoming radiation that is absorbed. The immediate result of freezing is therefore a general lowering of the surface temperature of the ice and a rapid increase of the thickness of the ice. The air that comes in contact with the ice is cooled, and, as this cold air spreads, more ice is formed. Thus, a small lowering of the temperature of the water in high latitudes followed by freezing may lead to a rapid drop of the air temperature and
Exchange of Heat between the Atmosphere and the Sea. The amount of heat that in unit time is carried away from the sea surface through a unit area is equal to
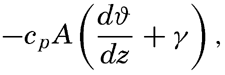
Detailed and accurate temperature measurements in the lowest meters of air over the ocean have not yet been made, because the hull and masts of a vessel disturb the normal distribution of temperature to such an extent that values observed at different levels on board a vessel are not representative of the undisturbed conditions. The few measurements that have been attempted indicate, however, that the general distribution as outlined above is encountered.
The sea surface must be warmer than the air at a small distance above the surface if heat is to be conducted from the sea to the air. When such conditions prevail, the air is heated from below, the stratification of the air becomes unstable, and the turbulence of the air becomes intense (p. 92). If the sea surface is very much warmer than the air, as may be
It has been found (p. 128) that on an average the sea surface is slightly warmer than the overlying air and therefore loses heat by conduction. So far, no detailed studies have been made, but Ångström has estimated that only about 10 per cent of the total heat surplus is given off to the atmosphere by conduction and that 90 per cent is used for evaporation. Other estimates indicate that these figures are approximately correct (p. 117). Thus, evaporation is of much greater importance to the heat balance of the oceans than is the transfer of sensible heat. Evaporation will therefore be dealt with in greater detail.
Evaporation from the Sea
The Process of Evaporation. The vapor tension at a flat surface of pure water depends on the temperature of the water. The salinity decreases the tension slightly, the empirical relation between vapor tension and salinity being (p. 66)
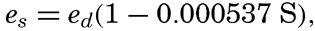
Air in which the vapor tension is less than that over water of the same temperature is undersaturated with moisture, and air in which the vapor tension exactly equals that over a water surface of the same temperature is saturated with moisture. In absolutely pure air the vapor pressure can be above the saturation value, but generally the air contains “nuclei” on which the vapor is condensed when the vapor tension reaches the value corresponding to that over water of the same temperature. Under these conditions the vapor tension in the air cannot be further increased, and in meteorology one therefore uses the
| Temperature (°C) | Vapor pressure (mb) | Temperature (°C) | Vapor pressure (mb) |
|---|---|---|---|
| −2 | 5.19 | 18 | 20.26 |
| −1 | 5.57 | 19 | 21.57 |
| 0 | 5.99 | 20 | 22.96 |
| 1 | 6.44 | 21 | 24.42 |
| 2 | 6.92 | 22 | 25.96 |
| 3 | 7.43 | 23 | 27.59 |
| 4 | 7.98 | 24 | 29.30 |
| 5 | 8.56 | 25 | 31.12 |
| 6 | 9.17 | 26 | 33.01 |
| 7 | 9.83 | 27 | 35.02 |
| 8 | 10.52 | 28 | 37.13 |
| 9 | 11.26 | 29 | 39.33 |
| 10 | 12.05 | 30 | 41.68 |
| 11 | 12.88 | 31 | 44.13 |
| 12 | 13.76 | 32 | 46.71 |
| 13 | 14.70 | ||
| 14 | 15.69 | ||
| 15 | 16.74 | ||
| 16 | 17.85 | ||
| 17 | 19.02 |
In discussing the process of evaporation it is more rational to consider not the vapor pressure but the specific humidity, f—that is, the mass of water vapor per unit mass of air. The amount of water vapor, F, which per second is transported upward through a surface of cross section 1 cm2 is, then, – Adf/dz, where A is the eddy conductivity and – df/dz is the vertical gradient of the specific humidity, which is positive when the specific humidity decreases with height. If the vapor pressure, e, is introduced, the equation becomes approximately
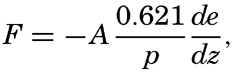
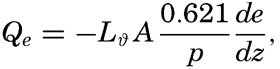
The ratio between the amounts of heat given off to the atmosphere as sensible heat (p. 114) and used for evaporation is
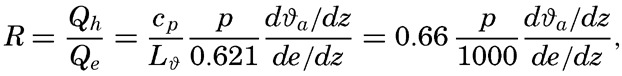
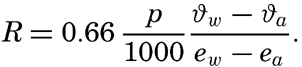
Values of the ratio R can be computed from climatological charts of the oceans, but a comprehensive study has not been made. Calculations based on data contained in the Atlas of Climatic Charts of the Oceans, published by the U. S. Weather Bureau (1938), show that the ratio varies from one part of the ocean to the other. As a rule, the ratio is small in low latitudes, where it remains nearly constant throughout the year, but is greater in middle latitudes, where it reaches values up to 0.5 in winter and in some areas drops to –0.2 in summer. A negative value indicates that heat is conducted from the atmosphere to the sea. On an average, the value for all oceans appears to lie at about 0.1, meaning that about 10 per cent of the heat surplus that the oceans receive by radiation processes is given off as sensible heat, whereas about 90 per cent is used for evaporation (p. 115).
There are certain points regarding the character of the evaporation which need to be emphasized. If the water is warmer than the air, the vapor pressure at the sea surface remains greater than that in the air, and evaporation can always take place and will be greatly facilitated in these circumstances because the turbulence of the air will be fully developed owing to the unstable stratification of the very lowest layers (p. 92). It must therefore be expected that the greatest evaporation occurs when cold air flows over warm water. If the air is much colder
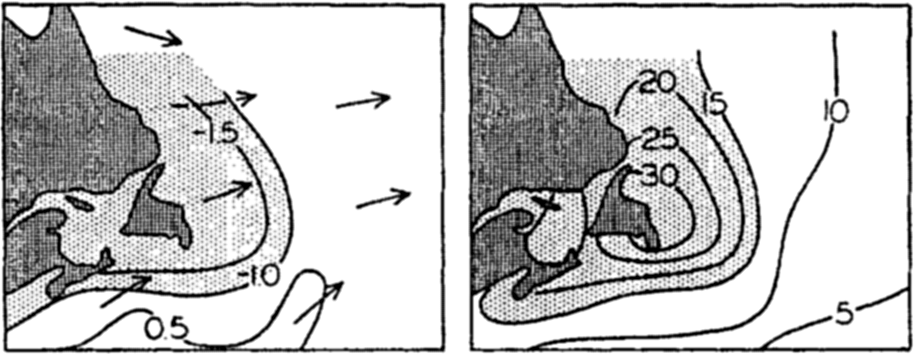
Left: The difference, air minus sea-surface temperature, and the prevailing wind-direction over the Grand Banks of Newfoundland in March, April, and May. Right: Percentage frequency of fog in the same months.
When the sea surface is colder than the air, evaporation can take place only if the air is not saturated with water vapor. In this case turbulence is reduced and evaporation must stop when the vapor content of the lowest layer of the atmosphere has reached such a value that the vapor pressure equals that at the sea surface. If warm, moist air passes over a colder sea surface, the direction of transport will be reversed and condensation will take place on the sea surface in such a way that heat is brought to the surface and not carried away from it. Owing to the fact that this process can take place only when the air is warmer than the sea and that then turbulence is greatly reduced, one can expect that condensation of water vapor on the sea will not be of great importance, but it should be borne in mind that this process can and does take place when conditions are right. In these circumstances, contact with the sea and conduction lower the air temperature to the dew point for a considerable distance above the sea surface. Condensation takes place in the air and fog is formed, “advection” fog that is commonly encountered over the sea. The relation between the frequency of fog or mist and the difference between sea-surface and air temperatures are well illustrated by charts in the Atlas of Climatic Charts of the Oceans (1938). As an example, fig. 26 shows the frequency of fog, the difference between air and sea-surface temperature, and the prevailing wind direction over the Grand Banks of Newfoundland in March, April, and May. It can be concluded that in spring, when the water is colder than the air, no
In middle and higher latitudes the sea surface in winter is mostly warmer than the air, and hence one must expect the evaporation then to be at its maximum. This conclusion appears contrary to common experience that evaporation from heated water is greater than that from cold water, but the contradiction is only apparent, because greatest evaporation always occurs when a water surface is warmer than the air above it, which is exactly what happens in winter.
Observations and Computations of Evaporation. Present knowledge of the amount of evaporation from the different parts of the oceans is derived partly from observations and partly from computations based on consideration of the heat balance.
Observations have been made by means of pans on board ship, but such observations give values of the evaporation from the sea surface that are too high, partly because the wind velocity is higher at the level of the pan than at the sea surface, and partly because the difference between vapor pressure in the air and that of the evaporating surface is greater at the pan than at the sea surface. Analyzing the decrease of the wind velocity and the increase of the vapor pressure between the average level of pans used on shipboard and a level a few centimeters above the sea surface, Wüst (1936) arrived at the conclusion that the measured values had to be multiplied by 0.53 in order to represent the evaporation from the sea surface.
In computing the evaporation on the basis of the heat balance, one has to begin with the equation (p. 101)
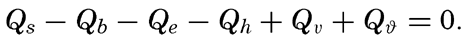
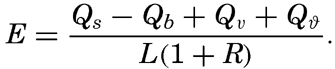
A second method for computing the evaporation from the oceans has been suggested by Sverdrup (1937), who, on the basis of results in fluid mechanics as to the turbulence of the air over a rough surface, established a formula for the evaporation, using in part constants that had been determined by laboratory experiments and in part constants that were obtained from the character of the variation of vapor pressure with
The exact formulae are not well suited for numerical computation, but at wind velocities between 4 and 12 m/sec, the mean annual evaporation in centimeters can be found approximately from the simple relation
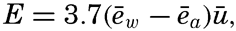
Average Annual Evaporation from the Oceans. On the basis of pan measurements conducted in different parts of the ocean, Wüst (1936) found that the average evaporation from all oceans amounts to 93 cm/year, and he considers this value correct within 10 to 15 per cent. W. Schmidt (1915) computed the evaporation by means of the preceding equation for E, in which the terms Qϑ and Qv can be omitted in considering the oceans as a whole. Schmidt introduced high values of R, and on the basis of the available data as to incoming radiation and back radiation he found a total evaporation of 76 cm/year. A revision based on more recent measurements of radiation (Mosby, 1936) and use of R = 0.1 resulted in a value of 106 cm/year. The latter value represents an upper limit, and may be 10 to 15 per cent too high, whence it appears that Wüst's result is nearly correct.
It is of interest in this connection to give some figures regarding the relation between evaporation and precipitation over the oceans, the land areas, and the whole earth (according to Wüst, 1936). The total evaporation from the oceans amounts to 334,000 km3/year, of which 297,000 km3 returns to the sea in the form of precipitation, and the difference, 37,000 km3, must be supplied by run-off, since the salinity of the oceans remains unchanged. The total amount of precipitation falling on the land is 99,000 km3, of which amount a little over one third, 37,000 km3, is supplied by evaporation from the oceans and 62,000 km3 is supplied by evaporation from inland water areas or directly from the moist soil. For the sake of comparison it may be mentioned that the capacity of Lake Mead, above Boulder Dam, is 45 km3.
Evaporation in Different Latitudes and Longitudes. From pan observations at sea, Wüst has derived average values of the evaporation from the different oceans in different latitudes (table 30, p. 123). By means of the energy equation one can compute similar annual values, assuming that the net transport of heat by ocean currents can be neglected. Such a computation has been carried out for the Atlantic
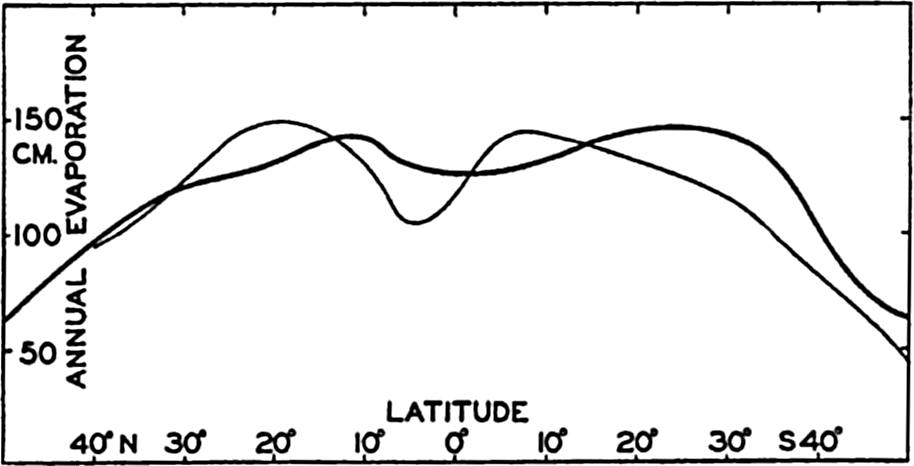
Annual evaporation from the Atlantic Ocean between latitudes 50°N and 50°S. Thin curve based on observations (Wüst, 1936) and heavy curve on computations, using the energy equation.
It appears that the average annual values of the evaporation in different latitudes are well established, but the evaporation also varies from the eastern to the western parts of the oceans and with the seasons. These variations are of great importance to the circulation of the atmosphere, because the supply of water vapor that later on condenses and gives off its latent heat represents a large portion of the supply of energy. So far, none of the details are known, but it is possible that approximate values of the evaporation from different parts of the ocean and in different seasons can be found by means of the method proposed by Sverdrup (1937) and used by Jacobs (1942).
Annual Variation of Evaporation. The character of the annual variation of evaporation can be examined by means of the energy equation (Sverdrup, 1940):
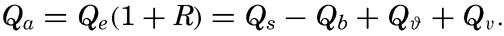
The quantity Qϑ can be computed if the annual variation of temperature due to processes of heating and cooling is known at all depths where such annual variations occur. The annual variation of temperature at the surface has been examined, but only few data are available from subsurface depths, the most reliable being those which have been compiled by Helland-Hansen (1930) from an area in the eastern North Atlantic with its center in 47°N and 12°W (p. 132). The radiation income in that area can be obtained from Kimball#x0027;s data (1928), the back radiation can be found by means of the diagram in fig. 25, and the transport by currents, Qv, can be neglected. In fig. 28A are represented the annual variation of the net surplus of radiation, Qr, the annual variation of the amount of heat used for changing the temperature of the water, Qϑ, and the difference between these two amounts, Qa, which represents the total amount of heat given off to the atmosphere. The greater part of the last amount is used for evaporation, and the curve marked Qa represents, therefore, approximately the annual variation of the evaporation, which shows a maximum in the fall and early winter, a secondary minimum in February, followed by a secondary maximum in March, and a low minimum in summer. In June and July no evaporation takes place. The total evaporation during the year is about 80 cm.
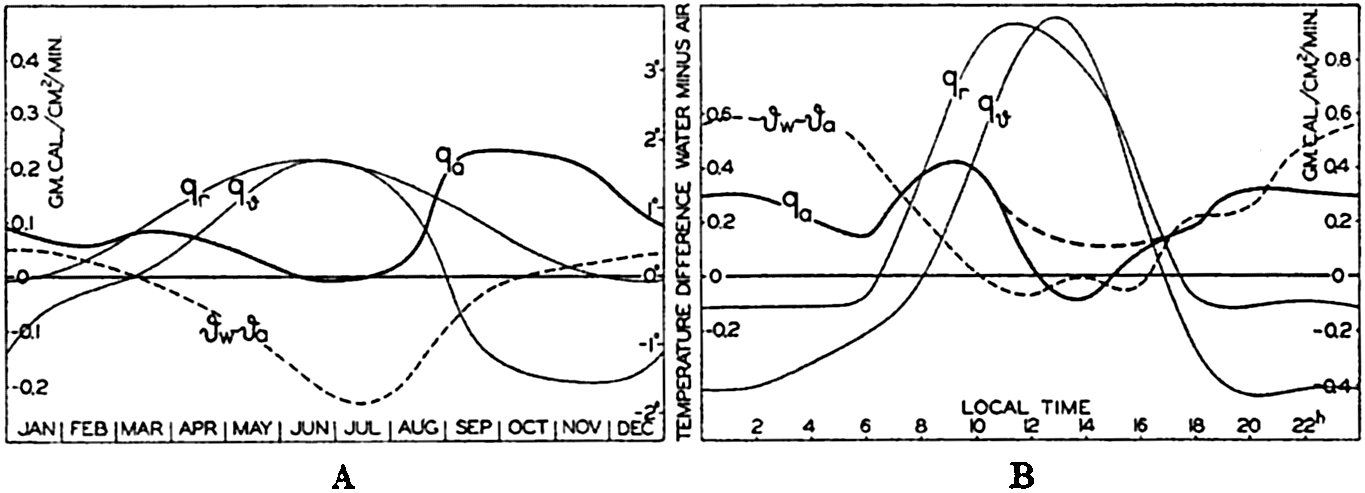
(A) Annual variation in the total amount of heat, qa, given off to the atmosphere in an area of the North Atlantic (about 47°N, 12°W). (B) Corresponding diurnal variation near the Equator in the Atlantic Ocean. (For explanation of symbols, see text.)
This example illustrates a method of approach that may be applied, but so far the necessary data for a more complete study are lacking. The result that the evaporation is at a minimum in summer and at a maximum in fall and early winter is in agreement with the conclusions that were drawn when discussing the process of evaporation in general.
| Latitude | Atlantic Ocean | Indian Ocean | Pacific Ocean | All Oceans | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S (‰) | E (cm/yr) | P (cm/yr) | E – P (cm/yr) | S (‰) | E (cm/yr) | P (cm/yr) | E – P (cm/yr) | S (‰) | E (cm/yr) | P (cm/yr) | E – P (cm/yr) | S (‰) | E (cm/yr) | P (cm/yr) | E – P (cm/yr) | |
| 40°N | 35.80 | 94 | 76 | 18 | 33.64 | 94 | 93 | 1 | 34.54 | 94 | 93 | 1 | ||||
| 35 | 36.46 | 107 | 64 | 43 | 34.10 | 106 | 79 | 27 | 35.05 | 106 | 79 | 27 | ||||
| 30 | 36.79 | 121 | 54 | 67 | 34.77 | 116 | 65 | 51 | 35.56 | 120 | 65 | 55 | ||||
| 25 | 36.87 | 140 | 42 | 98 | 35.00 | 127 | 55 | 72 | 35.79 | 129 | 55 | 74 | ||||
| 20 | 36.47 | 149 | 40 | 110 | (35.05) | (125) | (74) | (51) | 34.88 | 130 | 62 | 68 | 35.44 | 133 | 65 | 68 |
| 15 | 35.92 | 145 | 62 | 83 | (35.07) | (125) | (73) | (52) | 34.67 | 128 | 82 | 46 | 35.09 | 130 | 82 | 48 |
| 10 | 35.62 | 132 | 101 | 31 | (34.92) | (125) | (88) | (37) | 34.29 | 123 | 127 | − 4 | 34.72 | 129 | 127 | 2 |
| 5 | 34.98 | 105 | 144 | − 39 | (34.82) | (125) | (107) | (18) | 34.29 | 102 | (177) | (-75) | 34.54 | 110 | 177 | − 67 |
| 0 | 35.67 | 116 | 96 | 20 | 35.14 | 125 | 131 | − 6 | 34.85 | 116 | 98 | 18 | 35.08 | 119 | 102 | 17 |
| 5°S | 35.77 | 141 | 42 | 99 | 34.93 | 121 | 167 | − 46 | 35.11 | 131 | 91 | 40 | 35.20 | 124 | 91 | 33 |
| 10 | 36.45 | 143 | 22 | 121 | 34.57 | 99 | 156 | − 57 | 35.38 | 131 | 96 | 35 | 35.34 | 130 | 96 | 34 |
| 15 | 36.79 | 138 | 19 | 119 | 34.75 | 121 | 83 | 38 | 35.57 | 125 | 85 | 40 | 35.54 | 134 | 85 | 49 |
| 20 | 36.54 | 132 | 30 | 102 | 35.15 | 143 | 59 | 84 | 35.70 | 121 | 70 | 51 | 35.69 | 134 | 70 | 64 |
| 25 | 36.20 | 124 | 40 | 84 | 35.45 | 145 | 46 | 99 | 35.62 | 116 | 61 | 55 | 35.69 | 124 | 62 | 62 |
| 30 | 35.72 | 116 | 45 | 71 | 35.89 | 134 | 58 | 76 | 35.40 | 110 | 64 | 46 | 35.62 | 111 | 64 | 47 |
| 35 | 35.35 | 99 | 55 | 44 | 35.60 | 121 | 60 | 61 | 35.00 | 97 | 64 | 33 | 35.32 | 99 | 64 | 35 |
| 40 | 34.65 | 81 | 72 | 9 | 35.10 | 83 | 73 | 10 | 34.61 | 81 | 84 | − 3 | 34.79 | 81 | 84 | − 3 |
| 45 | 34.19 | 64 | 73 | − 9 | 34.25 | 64 | 79 | − 15 | 34.32 | 64 | 85 | − 21 | 34.14 | 64 | 85 | − 21 |
| 50 | 33.94 | 43 | 72 | − 29 | 33.87 | 43 | 79 | − 36 | 34.16 | 43 | 84 | − 41 | 33.99 | 43 | 84 | − 41 |
Diurnal Variation of Evaporation. The diurnal variation of evaporation can be examined in a similar manner, but at the present time suitable data are available only at four Meteor stations near the Equator in the Atlantic Ocean (Defant, 1932; Kuhlbrodt and Reger, 1938). In fig. 28B the curves marked Qr and Qϑ correspond to the similar curves in fig. 28A, and the difference between these, Qa, shows the amount of heat lost during twenty-four hours, which is approximately proportional to the evaporation. The diurnal variation of evaporation in the Tropics appears to have considerable similarity to the annual variation in middle latitudes, and is characterized by a double period with maxima in the late forenoon and the early part of the night and minima at sunrise and in the early afternoon hours. It is possible that the afternoon minimum appears exaggerated, owing to uncertainties as to the absolute values of Qr and Qϑ. The total diurnal evaporation was 0.5 cm, but the sky was nearly clear on the four days that were examined and the average diurnal value is therefore smaller. The double diurnal period of evaporation appears to be characteristic of the Tropics, but in middle latitudes a single period with maximum values during the night probably dominates.
Salinity and Temperature of the Surface Layer
The Surface Salinity. In all oceans the surface salinity varies with latitude in a similar manner. It is at a minimum near the Equator, teaches a maximum in about latitudes 20°N and 20°S, and again decreases toward high latitudes.
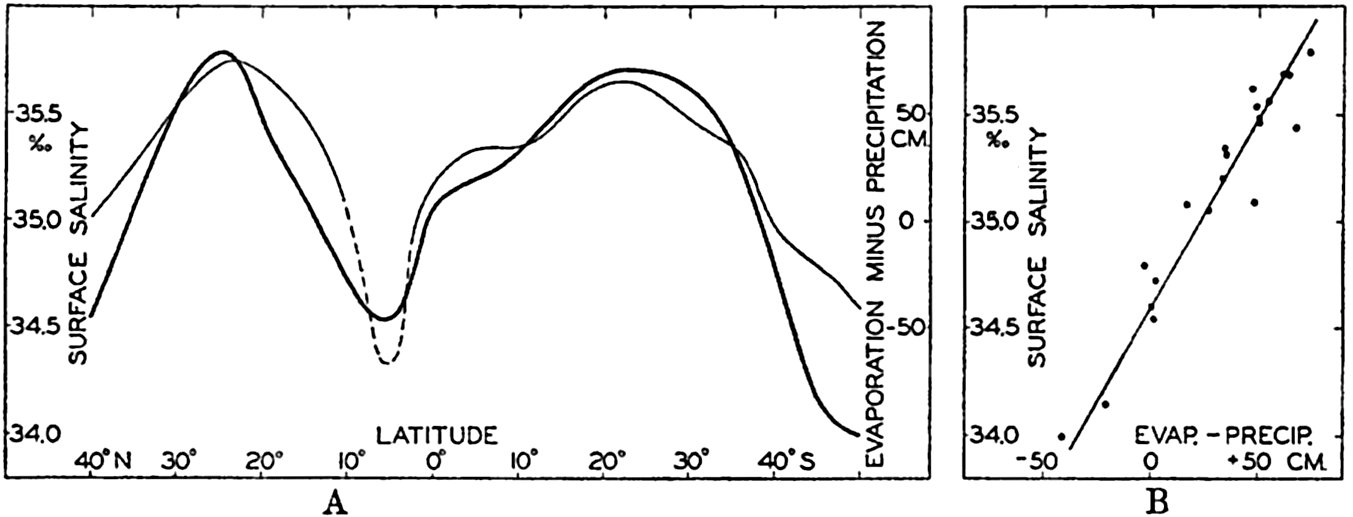
(A) Average values for all oceans of surface salinity and the difference, evaporation minus precipitation, plotted against latitude. (B) Corresponding values of surface salinity and the difference, evaporation minus precipitation, plotted against each other (according to Wüst, 1936).
Table 30 contains average values of the surface salinity, the evaporation, the precipitation, and the difference between the last quantities for the three major oceans and for all combined, according to Wüst (1936).
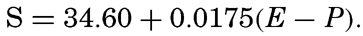
Wüst points out that such an empirical relationship is found because the surface salinity is mainly determined by three processes: decrease of salinity by precipitation, increase of salinity by evaporation, and change of salinity by processes of mixing. If the surface waters are mixed with water of a constant salinity, and if this constant salinity is represented by S0, the change of salinity due to mixing must be proportional to S0 – S, where S is the surface salinity. The change of salinity due to processes of evaporation and precipitation must be proportional to the difference (E – P). The local change of the surface salinity must be zero; that is,
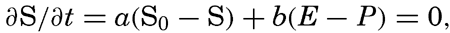
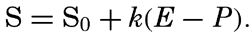
As this simple formula has been established empirically, it must be concluded that the surface water is generally mixed with water of a salinity which, on an average, is 34.6 ‰. This value represents approximately the average value of the salinity at a depth of 400 to 600 m, and it appears therefore that vertical mixing is of great importance to the general distribution of surface salinity. This concept is confirmed by the fact that the standard value of the salinity differs for the different oceans. For the North Atlantic and the North Pacific, Wüst obtains similar relationships, but the constant term, S0, has the value 35.30 ‰ in the North Atlantic and 33.70 ‰ in the North Pacific Ocean. The corresponding average values of the salinity at a depth of 600 m are 35.5 ‰ and 34.0 ‰, respectively. For the South Atlantic and the South Pacific Oceans, Wüst finds S0 = 34.50 ‰ and 34.64 ‰, respectively, and the average salinity at 600 m in both oceans is about 34.5 ‰. In these considerations the effect of ocean currents on the distribution of surface salinity has been neglected, and the simple relations obtained indicate that transport by ocean currents is of minor importance as far as average conditions are concerned. The difference between evaporation and precipitation, E – P, on the other hand, is of primary importance, and,
The distribution of surface salinity of the different oceans is shown in chart VI, in which the general features that have been discussed are recognized, but the details are so closely related to the manner in which the water masses are formed and to the types of currents that they cannot be dealt with here.
Periodic Variations of the Surface Salinity. Over a large area, variations in surface salinity depend mainly upon variations in the difference between evaporation and precipitation. From Böhnecke#x0027;s monthly charts (1938) of the surface salinity of the North Atlantic Ocean, mean monthly values have been computed for an area extending between latitudes 18° and 42°N, omitting the coastal areas in order to avoid complications due to shifts of coastal currents. The results of this computation (fig. 30) show the highest average surface salinity, 36.70‰ in March, and the lowest, 36.59 ‰, in November. The variations from one month to another are irregular, but on the whole the salinity is somewhat higher in spring than it is in the fall.
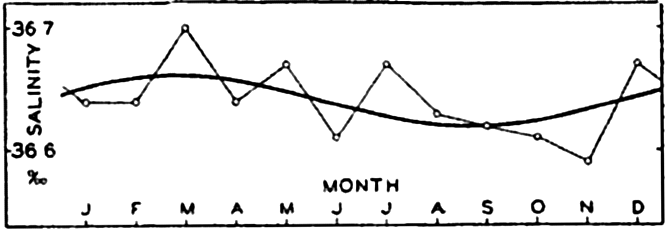
Annual variation of surface salinity in the North Atlantic Ocean between latitudes 18°N and 42°N.
Harmonic analysis leads to the result
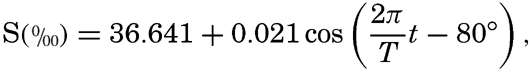
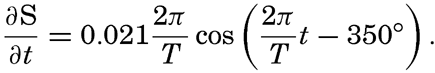
More complicated conditions are encountered in the northwestern part of the Atlantic Ocean, where, according to G. Neumann (1940),
From the open ocean no data are available as to the diurnal variation of the salinity of the surface waters, but it may be safely assumed that such a variation is small, because neither the precipitation nor the evaporation can be expected to show any considerable diurnal variation.
| North latitude | Atlantic Ocean | Indian Ocean | Pacific Ocean | South latitude | Atlantic Ocean | Indian Ocean | Pacific Ocean |
|---|---|---|---|---|---|---|---|
| 70°–60° | 5.60 | ...... | ...... | 70°–60° | − 1.30 | − 1.50 | − 1.30 |
| 60–50 | 8.66 | 5.74 | 60–50 | 1.76 | 1.63 | 5.00 | |
| 50–40 | 13.16 | 9.99 | 50–40 | 8.68 | 8.67 | 11.16 | |
| 40–30 | 20.40 | ...... | 18.62 | 40–30 | 16.90 | 17.00 | 16.98 |
| 30–20 | 24.16 | 26.14 | 23.38 | 30–20 | 21.20 | 22.53 | 21.53 |
| 20–10 | 25.81 | 27.23 | 26.42 | 20–10 | 23.16 | 25.85 | 25.11 |
| 10–0 | 26.66 | 27.88 | 27.20 | 10–0 | 25.18 | 27.41 | 26.01 |
Surface Temperature. The genera1 distribution of surface temperature cannot be treated in a manner similar to that employed by Wüst when dealing with the salinity, because the factors controlling the surface temperature are far more complicated. The discussion must be confined to presentation of empirical data and a few general remarks.
Table 31 contains the average temperatures of the oceans in different latitudes according to Krümmel (1907), except in the case of the Atlantic Ocean, for which new data have been compiled by Böhnecke (1938). In all oceans the highest values of the surface temperature are found somewhat to the north of the Equator, and this feature is probably related to the character of the atmospheric circulation in the two hemispheres. The region of the highest temperature, the thermal Equator, shifts with the season, but in only a few areas is it displaced to the Southern Hemisphere at any season. The larger displacements (Schott, 1935, and Böhnecke, 1938) are all in regions in which the surface currents change
The average distribution of the surface temperature of the oceans in February and August is shown in charts II and III. Again the distribution is so closely related to the formation of the different water masses and the character of the currents that a discussion of the details must be postponed.
Difference Between Air and Sea-Surface Temperatures. It was pointed out that in all latitudes the ice-free oceans received a surplus of radiation, and that therefore in all latitudes heat is given off from the ocean to the atmosphere in the form of sensible heat or latent heat of water vapor. The sea-surface temperature must therefore, on an average, be higher than the air temperature. Observations at sea have shown that such is the case, and from careful determinations of air temperatures over the oceans it has furthermore been concluded that the difference, air minus sea-surface temperature, is greater than that derived from routine ships' observations. In order to obtain an exact value, it is necessary to measure the air temperature on the windward side of the vessel at a locality where no eddies prevail, but where the air reaches the thermometer without having passed over any part of the vessel. For measurements of the temperature a ventilated thermometer must be used. According to the Meteor observations (Kuhlbrodt and Reger, 1938) the air temperature over the South Atlantic Ocean between latitudes 55°S and 20°N is on an average 0.8 degree lower than that of the surface, whereas in the same region the atlas of oceanographic and meteorological observations published by the Netherlands Meteorological Institute gives an average difference of only 0.1 degree. The reason for this discrepancy is that the air temperatures as determined on commercial vessels are on an average about 0.7 degree too high because of the ships' heat. The result as to the average value of the difference, υw – υa, is in good agreement with results obtained on other expeditions when special precautions were taken for obtaining correct air temperatures. Present atlases of air and sea-surface temperatures have been prepared from the directly observed values on board commercial vessels without application of a correction to the air temperatures. This correction is so small that it is of minor importance when the atlases are used for climatological studies, but in any studies that require knowledge of the exact difference between air- and sea-surface temperatures it is necessary to be aware of the systematic error in the air temperature.
The difference of 0.8 degree between air and surface temperatures, as derived from the Meteor observations, is based on measurements of air temperature at a height of 8 m above sea level. At the very sea surface the air temperature must coincide with that of the water, and consequently the air temperature decreases within the layers directly above the sea. The most rapid decrease takes place, however, very close to the sea surface, and at distances greater than a few meters the decrease is so slow that it is immaterial whether the temperature is measured at 6, 8, or 10 m above the surface. The height at which the air temperature has been observed on board a ship exercises a minor influence, therefore, upon the accuracy of the result, and discrepancies due to differences in the height of observations are negligible compared to the errors due to inadequate exposure of the thermometer.
The statement that the air temperature is lower than the water temperature is correct only when dealing with average conditions. In any locality the difference, υw – υa, generally varies during the year in such a manner that in winter the air temperature is much lower than the sea-surface temperature, whereas in summer the difference is reduced or the sign is reversed. The difference also varies from one region to another according to the character of the circulation of the atmosphere and of the ocean currents. These variations are of great importance to the local heat budget of the sea because the exchange of heat and vapor between the atmosphere and the ocean depends greatly upon the temperature difference.
It was shown that the amount of heat given off from the ocean to the surface is, in general, great in winter and probably negligible in summer. Owing to this annual variation in the heat exchange, one must expect that in winter the air over the oceans is much warmer than the air over the continents but in summer the reverse conditions should be expected. That such is true is evident from a computation of the average temperature of the air between latitudes 20°N and 80°N along the meridian of 120°E, which runs entirely over land, and along the meridian of 20°W, which runs entirely over the ocean (von Hann, 1915, p. 146). In January the average temperature along the “land meridian” of 120°E is −15.9 degrees C, but along the “water meridian” of 20°W it is 6.3 degrees. In July the corresponding values are 19.4 and 14.6 degrees, respectively. Thus, in January the air temperature between 20°N and 80°N over the water meridian is 22.2 degrees higher than that over the land meridian, whereas in July it is 4.8 degrees lower. The mean annual temperature is 7.0 degrees higher along the water meridian.
Annual Variation of Surface Temperature. The annual variation of surface temperature in any region depends upon a number of factors, foremost among which are the variation during the year of the radiation income, the character of the ocean currents, and of the prevailing
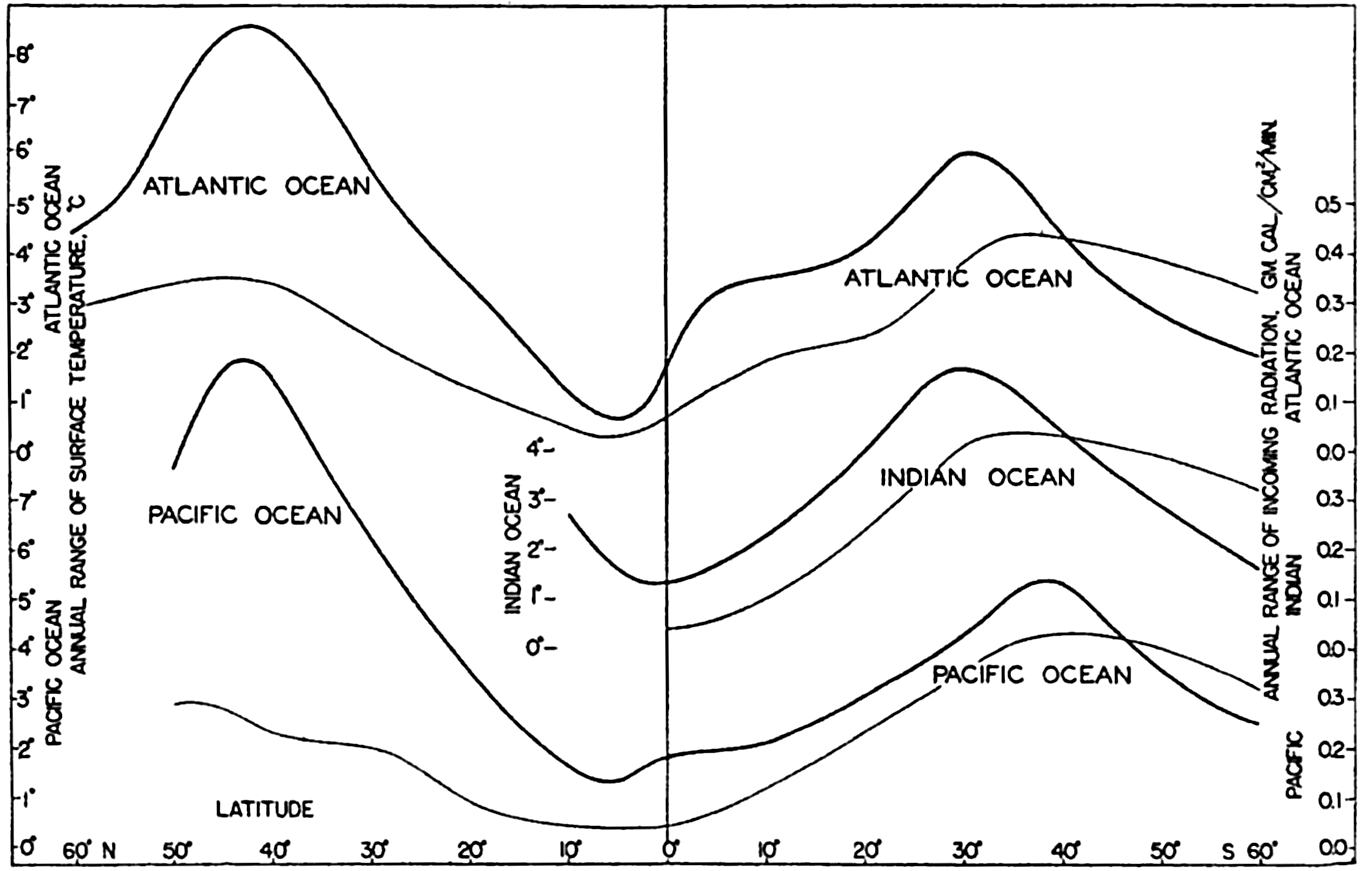
Average annual ranges of surface temperature in the different oceans plotted against latitude (heavy curves) and corresponding ranges in the radiation income (thin curves).
Annual Variation of Temperature in the Surface Layers. At subsurface depths the variation of temperature depends upon four factors: (1) variation of the amount of heat that is directly absorbed at different depths, (2) the effect of heat conduction, (3) variation in the currents related to lateral displacement of water masses, and (4) the effect of vertical motion. The annual variation of temperature at subsurface depths cannot be dealt with in a general manner, owing to lack of data, but it is again possible to point out some outstanding characteristics, using two examples from the Pacific and one from the Atlantic Ocean. The effects of all four of the important factors are illustrated in fig. 32A, which shows the annual variation of temperature at the surface and at depths of 25, 50, and 100 m at Monterey Bay, California (Skogsberg, 1936). Skogsberg divides the year into three periods: the period of the Davidson Current, lasting from the middle of November to the middle of February; the period of upwelling, between the middle of February and the end of July; and the oceanic period, from the end of July to the middle of November. The California Current off Monterey Bay during the greater part of the year is directed to the south, but during winter, from the middle of November to the middle of February, an inshore flow to the north, the Davidson Current, is present (p. 724). The water of this inshore flow is characterized by relatively high and uniform temperature and appears in the annual variation of temperature as warm water at subsurface depths. The upper homogeneous layer is relatively thick, as is evident from the fact that the temperature is nearly the same at 25 m as it is at the surface, and that at 50 m it is only slightly lower. At the end of February the California Current again reaches to the coast and, under the influence of the prevailing northwesterly winds, an overturn of the upper layers
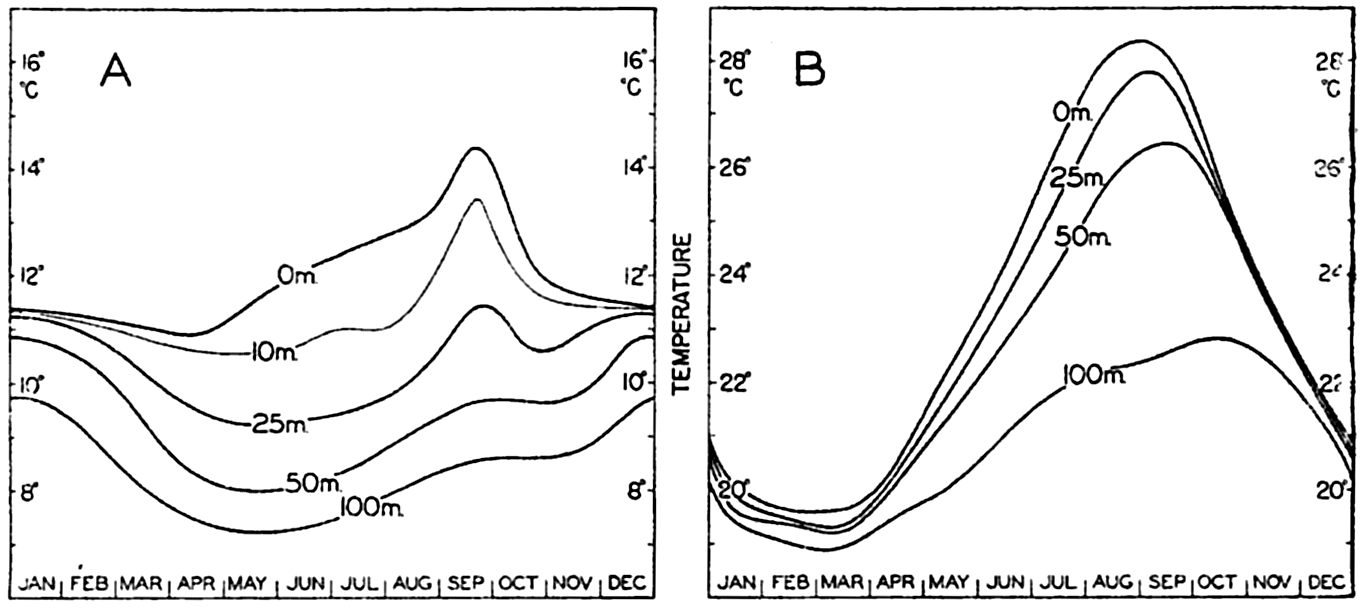
(A) Annual variation of temperature at different depths in Monterey Bay, California. (B) Annual variation of temperature at different depths in the Kuroshio off the South Coast of Japan.
The annual variation of temperature in the Kuroshio off the south coast of Japan (Koenuma, 1939), as shown in fig. 32B, gives an entirely different picture. The annual variation has the same character at all depths between the surface and 100 m, with a minimum in late winter and a maximum in late summer or early fall, but the range of the variation decreases with depth, and the time of maximum temperature occurs later with increasing depth. From the course of the curves it may be concluded that the annual variation is due to heating and cooling near the surface and is transmitted to greater depths by processes of conduction (p. 136). This appears to be correct, but the heating and cooling is only partly caused by variations in the net radiation, and it also depends on excessive cooling in winter by cold and dry winds blowing toward the sea (Sverdrup, 1940).
In order to be certain that observed temperature variations are related to processes of heating and cooling only, it is necessary to examine whether the water in a given locality is of the same character throughout the year. For this purpose Helland-Hansen (1930) developed a method that is applicable in areas in which it is possible to establish a definite relation between temperature and salinity (p. 142). He assumed that any temperature value above or below that determined by the temperature-salinity relation can be considered as resulting from heating or cooling of the water, and he used the method within three areas in the eastern North Atlantic. Fig. 33 shows the curves which he determined for an area off the Bay of Biscay with its center in approximately 47°N and 12°W. The character of the curves, the reduction of the range, and the displacement of the times of maxima clearly show that one has to deal with heat conduction. In this case the variation in the heat content
These examples serve to illustrate different types of annual variation of temperature that may be encountered in different localities and also to stress the fact that conclusions as to the temperature variations associated with processes of local heating are valid only if the data are such that the influences of shifting currents and vertical motion can be eliminated.
Diurnal Variation of Surface Temperature. The range of the diurnal variation of surface temperature of the sea is not more, on an average, than 0.2 to 0.3 degree. Earlier observations gave somewhat higher values, particularly in the Tropics, but new, careful measurements and reexamination of earlier data in which doubtful observations have been eliminated have shown that the range of diurnal variation is quite small. Meinardus (Kuhlbrodt and Reger, 1938, p. 301–302) summarizes his examination of a large number of data by stating, “in general, the diurnal variation of water temperature in lower latitudes can be represented by a sine curve with extreme values between 2:30h and 3h and between 14:30h and 15h, and a range of 0.3° to 0.4°. In higher latitudes the extreme values come later and the range is even smaller.” The Meteor observations give ranges of only 0.2 to 0.3 degree in the Tropics. The Meteor data and the Challenger data, which have been discussed by Wegemann (1920), both show that close to the Equator the diurnal variation of surface temperature is somewhat unsymmetrical, the temperature increasing rapidly after sunrise and decreasing slowly after sunset, but at greater distances from the Equator the curve becomes somewhat more symmetrical.
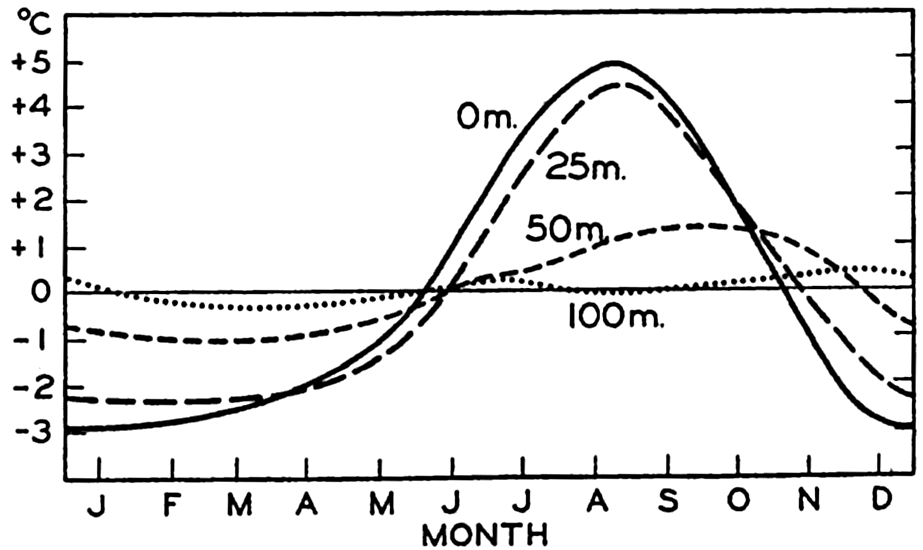
Annual variation of temperature at different depth off the Bay of Biscay in approximately 47°N and 12°W.
The changes through the year of the range of diurnal variation of surface temperature have been examined in some coastal areas. At forty-four stations around the British Isles, Dickson (see Wegemann, 1920) found that on an average the diurnal range varied between 0.20 degree in December and 0.69 degree in May. At individual stations both the mean annual range and the variation of the range from month to month were dependent upon the exposure of the locality and the depth of the water at which the measurements were made. This annual variation in range is closely related to the annual variation in the diurnal amount of net heat received by processes of radiation.
| Temperature range, °C | |||
|---|---|---|---|
| Wind and cloudiness | Average | Maximum | Minimum |
| 1. Moderate of fresh breeze | |||
| a. Sky Overcast | 0.39 | 0.6 | 0.0 |
| b. Sky clear | 0.71 | 1.1 | 0.3 |
| 2. Calm or very light breeze | |||
| a. Sky overcast | 0.93 | 1.4 | 0.6 |
| b. Sky clear | 1.59 | 1.9 | 1.2 |
The range of the diurnal variation of temperature depends upon the cloudiness and the wind velocity. From observations in the Tropics, Schott (Krümmel, 1907) found the mean and extreme values that are shown in table 32. Similar results but higher numerical values were found by Wegemann from the Challenger data. In both cases the numerical values may be somewhat in error, but the character of the influence of cloudiness and wind is quite evident. With a clear sky the range of the diurnal variation is great, but with great cloudiness it is small, at calm or light breeze it is great, and at moderate or high wind it is small. The effect of cloudiness is explained by the decrease of the diurnal amplitude of the incoming radiation with increasing cloudiness. The effect of the wind is somewhat more complicated, but the main feature is that at high wind velocities the wave motion produces a thorough mixing in the surface layers and the heat which is absorbed in the upper meters is distributed over a thick layer, leading to a small range of the temperature, whereas in calm weather a corresponding intensive mixing does not take place, the heat is not distributed over a thick layer, and consequently the range of the temperature near the surface is much greater.
Diurnal Variation of Temperature in the Upper Layers. Knowledge as to the diurnal variation of temperature at depths below the surface is very scanty. It can be assumed that the depth at which the diurnal variation is perceptible will depend greatly upon the stratification of the water. A sharp increase of density at a short distance below the free-water surface will limit the conduction of heat (p. 477) to such an extent that a diurnal variation of temperature will be present above the boundary surface only.
On the Meteor expedition, hourly temperature observations were made at the surface and at a depth of 50 m at a few stations in the Tropics where an upper homogeneous layer was present which had a thickness of 70 m. Defant (1932) has shown that in these cases the diurnal oscillation of temperature at subsurface depths is in agreement with the laws that have been derived on the assumption of a constant heat conductivity (p. 136). At 50 m the amplitude of the diurnal variation was reduced to less than two tenths of the amplitude at the surface, and the maximum occurred about 6.5 hours later.
The diurnal variation of sea temperature in general is so small that it is of little importance to the physical and biological processes in the sea, but knowledge of the small variations is essential to the study of the diurnal exchange of heat between the atmosphere and the sea (p. 124). The data which are available for this purpose, however, are very inadequate at the present time.
Theory of the Periodic Variations of Temperature at Subsurface Depths
Subsurface temperature variations due to processes of heat conduction can be studied by means of the equation (p. 159)

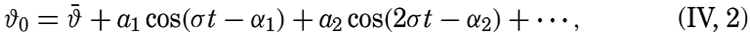
Then
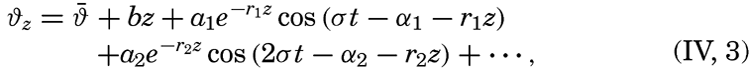
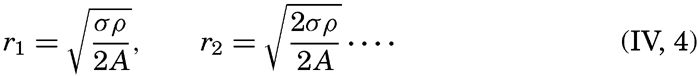
Defant (1932) has shown that at the Meteor anchor station no. 288 in latitude 12°38′N, longitude 47°36′W, the diurnal variation of temperature in the upper homogeneous layer indicated a constant eddy conductivity. The amplitudes of the diurnal term at the surface and at 50 m were 0.093 and 0.017 degree, respectively, and the phase difference was 6.5 hours. With ρ = 1.024, and T = 24 hours, he obtained from both the decrease of the amplitude and the difference in phase angle A = 320 g/cm/sec.
In cases in which the annual variation of temperature has been examined, the decrease of amplitude and change of phase give different values of A, indicating that A is not independent of depth and time, as assumed when performing the integration. Fjeldstad (1933) has developed a method for computing the eddy conductivity if it changes with depth, provided that the periodic temperature variations are known at a number of depths between the surface and a depth, h, at which they are supposed to vanish. He arrives at the formula

Fjeldstad has applied the method to the annual temperature variations off the Bay of Biscay, which have been determined by Helland-Hansen (p. 132). He found, with ρ = 1.025,
| Depth (m) | 0 | 25 | 50 | 100 |
| Amplitude, a1, °C | 3.78 | 3.24 | 1.24 | 0.23 |
| Phase angle, a1 | 225.1° | 235.2° | 254.7° | 289.3° |
| Eddy conductivity, g/cm/sec | 16.4 | 3.2 | 2.1 | 3.8 |
Several features show, however, that the observed temperature variations cannot be accounted for by assuming that the eddy conductivity varies with depth only, and variations with seasons also must be considered. Fjeldstad has examined this question and finds that the conductivity reaches a maximum in spring when the stability is at a minimum, but the values remain small throughout the year.
Fjeldstad#x0027;s method can also be applied to the annual variation of temperature in the Kuroshio, which has been discussed by Koenuma (1939) (fig. 32B, p. 131). It is necessary, however, to make the reservation
| Depth (m) | 0 | 25 | 50 | 100 | 200 |
| Amplitude, a1, °C | 4.26 | 3.97 | 3.49 | 2.09 | 0.71 |
| Amplitude, a2, °C | 0.58 | 0.49 | 0.44 | 0.39 | 0.14 |
| Phase angle, a1 | 250.2° | 253.5° | 258.7° | 271.8° | 289.3° |
| Phase angle, a2 | 71.4° | 81.0° | 100.0° | 135.5° | 152.6° |
| Eddy conductivity, A1, g/cm/sec | 78 | 34 | 23 | 22 | 29 |
| Eddy conductivity, A2, g/cm/sec | 58 | 43 | 39 | 32 | 26 |
Both the annual and the semiannual periods have been used for computing the eddy conductivity, and the agreement between the values of A derived from them must be considered satisfactory, in view of the small amplitudes of the semiannual variation. The numerical values decrease with depth, but are much greater than off the Bay of Biscay, as might be expected, because the high velocity of the Kuroshio must lead to intense turbulence. A possible annual variation of the eddy conductivity has not been examined.
In the Kuroshio region, where the velocity of the current is great and the turbulence correspondingly intense, the annual variation of temperature becomes perceptible to a depth of about 300 m, but in the Bay of Biscay it is very small at 100 m. It can therefore safely be concluded that below a depth of 300 m the temperature of the ocean is not subject to any annual variation.
The eddy conductivity off the Bay of Biscay and in the Kuroshio region is much smaller than that in the upper homogeneous layer near the Equator. The difference can be ascribed to the facts that in the former localities the density increases with depth and that the eddy conductivity is greatly reduced where this takes place (p. 477).
Distribution of Density
The distribution of the density of the ocean waters is characterized by two features. In a vertical direction the stratification is generally stable (p. 416), and in a horizontal direction differences in density can exist only in the presence of currents. The general distribution of density is therefore closely related to the character of the currents, but for the present purposes it is sufficient to emphasize the point that in every ocean region water of a certain density which sinks from the sea surface tends to sink to and spread at depths where that density is found.
Since the density of sea water depends on its temperature and salinity, all processes that alter the temperature or the salinity influence the density. At the surface the density is decreased by heating, addition
In the open oceans the temperature of the surface water in lower and middle latitudes is so high that the density of the water remains low even in regions where excess evaporation causes high salinities. In these latitudes convection currents are limited to a relatively thin layer near the surface and do not lead to the formation of deep or bottom water. Such formation takes place mainly in high latitudes where, however, the excess of precipitation in most regions prevents the development of convection currents that reach great depths. This excess of precipitation is so great that deep and bottom water is formed only in two cases: (1) if water of high salinity which has been carried into high latitudes by currents is cooled, and (2) if relatively high-salinity water freezes.
The first conditions are encountered in the North Atlantic Ocean where water of the Gulf Stream system, the salinity of which has been raised in lower latitudes by excessive evaporation, is carried into high latitudes. In the Irminger Sea, between Iceland and Greenland, and in the Labrador Sea this water is partly mixed with cold water of low salinity which flows out from the Polar Sea (p. 682). This mixed water has a relatively high salinity, and, when cooled in winter, convection currents that may reach from the surface to the bottom develop before any formation of ice begins. In this manner deep and bottom water is formed which has a high salinity and a temperature which lies several degrees above the freezing point of the water (table 82, p. 683). A similar process takes place in the Norwegian Sea, but there deep and bottom water is formed at a temperature that deviates only slightly from the freezing temperatures (p. 657).
In the Arctic the second process is of minor importance. There the salinity of the surface layers is very low in the regions where freezing occurs, mainly because of the enormous masses of fresh water that are carried into the sea by the Siberian rivers. Close to the Antarctic
In some isolated adjacent seas the evaporation may be so intense that a moderate cooling leads to the formation of bottom water. This is the case in the Mediterranean Sea and the Red Sea, and to some extent in the inner part of the Gulf of California, in which the bottom water has a high temperature and salinity and is formed by winter cooling of water whose salinity has been increased greatly by evaporation. Where such seas are in communication with the open oceans, deep water flows out over the sill, mixes with the water masses of the ocean, and spreads out at an intermediate depth corresponding to its density (pp. 670 and 693).
In general, the water of the greatest density is formed in high latitudes, and because this water sinks and fills all ocean basins, the deep and bottom water of all oceans is cold. Only in a few isolated basins in middle latitudes is relatively warm deep and bottom water encountered. When spreading out from the regions of formation the bottom water receives small amounts of heat from the interior of the earth, but this heat is carried away by eddy conduction and currents, and its effect on the temperature distribution is imperceptible.
Sinking of surface water is not limited to regions in which water of particularly high density is formed, but occurs also wherever converging currents (convergences) are present, the sinking water spreading at intermediate depths according to its density. In general, the density of the upper layers increases from the Tropics toward the Poles, and water that sinks at a convergence in a high latitude therefore spreads at a greater depth than water that sinks at a convergence in middle latitudes.
The most conspicuous convergence is the Antarctic Convergence, which can be traced all around the Antarctic Continent (fig. 158, p. 606). The water that sinks at this convergence has a low salinity, but it also has a low temperature and consequently a relatively high density. This water, the Antarctic Intermediate Water, spreads directly over the deep water and is present in all southern oceans at depths between 1200 and
In middle and lower latitudes two more convergences are found, the Subtropical and the Tropical Convergences. These are not so well defined as the Antarctic Convergence, but must be considered more as regions in which converging currents are present. The Subtropical Convergence is located in latitudes in which the density of the upper layers increases rapidly toward the Poles. The sinking water therefore has a higher density the farther it is removed from the Equator and will spread out at the greater depths.
In the Tropics the density of the surface water is so low that, regardless of how intense a convergence is, water from the surface cannot sink to any appreciable depth but spreads out at a short distance below the surface. A sharp boundary surface develops between this light top layer and the denser water at some greater depth.
In order to account for the general features of the density distribution in the sea, emphasis has been placed on descending motion of surface water, but regions evidently must exist in which ascending motion prevails, because the amount of water that rises toward the surface must exactly equal the amount that sinks. Ascending motion occurs in regions of diverging currents (divergences), which may be present anywhere in the sea but which are particularly conspicuous along the western coasts of the continents, where prevailing winds carry the surface waters away from the coasts. There, the upwelling of subsurface water takes place, which will be described when dealing with specific areas. The upwelling brings water of greater density and lower temperature toward the surface and exercises therefore a widespread influence upon conditions off coasts where the process takes place, but the water rises from depths of less than a few hundred meters. Ascending motion takes place on a large scale around the Antarctic Continent, particularly to the south of the Atlantic Ocean, where rising deep water replaces water that contributes to the formation of the Antarctic bottom water and also replaces water that sinks at the Antarctic Convergence.
It is evident from these considerations that in middle and low latitudes the vertical distribution of density to some extent reflects the horizontal distribution at or near the surface between the Equator and the Poles. It is also evident that, in general, the deeper water in any vertical column is composed of water from different source regions and was once present in the surface somewhere in a higher latitude. Such generalizations are subject, however, to modifications within different ocean areas, owing to the character of the currents, and these modifications will be discussed when dealing with the different oceans.
Subsurface Distribution of Temperature and Salinity
The general distribution of temperature is closely related to that of the density. In high latitudes the temperature is low from the surface to the bottom. The bottom and deep waters that spread out from high latitudes retain their low temperature, but in middle and lower latitudes a warm top layer is present the thickness of which depends partly on the processes of heating and cooling at the surface and partly on the character of the ocean currents. This upper layer of warm water is separated from the deep water by a transition layer within which the temperature decreases rapidly with depth. From analogy with the atmosphere, Defant (1928) has applied the terms troposphere and stratosphere to two different parts of the ocean. Troposphere is applied to the upper layer of relatively high temperature that is found in middle and lower latitudes and within which strong currents are present, and stratosphere to the nearly uniform masses of cold deep and bottom water. This distinction is often a useful one, particularly when dealing with conditions in lower latitudes, but it must be borne in mind that the terms are based on an imperfect analogy with atmospheric conditions and that only some of the characteristics of the atmospheric stratosphere find their counterparts in the sea.
So far we have mainly considered an ideal ocean extending to high northerly and high southerly latitudes. Actually, conditions may be complicated by communication with large basins that contribute to the formation of deep water, such as the Mediterranean Sea, but these cases will be dealt with specifically when we consider the different regions. Conditions will be modified in other directions in the Indian and Pacific Oceans, which are in direct communication with only one of the polar regions, and these modifications will also be taken up later. Here it must be emphasized that the general distribution of temperature is closely related to the distribution of density, which again is controlled by external factors influencing the surface density and the type of deep-sea circulation.
The general distribution of salinity is more complicated than that of temperature. Within the oceanic stratosphere the salinity is very uniform, but within the troposphere it varies greatly, being mainly related to the excess of evaporation over precipitation. The distribution of surface salinity, which was discussed on pp. 124 and 125 is, in general, characteristic of the distribution within the troposphere, as is evident from the vertical section in figs. 210 and 212, which will be dealt with in detail later on.
The Water Masses of the Oceans
TheT-S Diagram. Water masses can be classified on the basis of their temperature-salinity characteristics, but density cannot be used
The corresponding temperature and salinity values in a water column are found to arrange themselves according to depth. The depths of the observed values can be entered along the T-S curve, which then will also give information as to variation of temperature and salinity with depth.
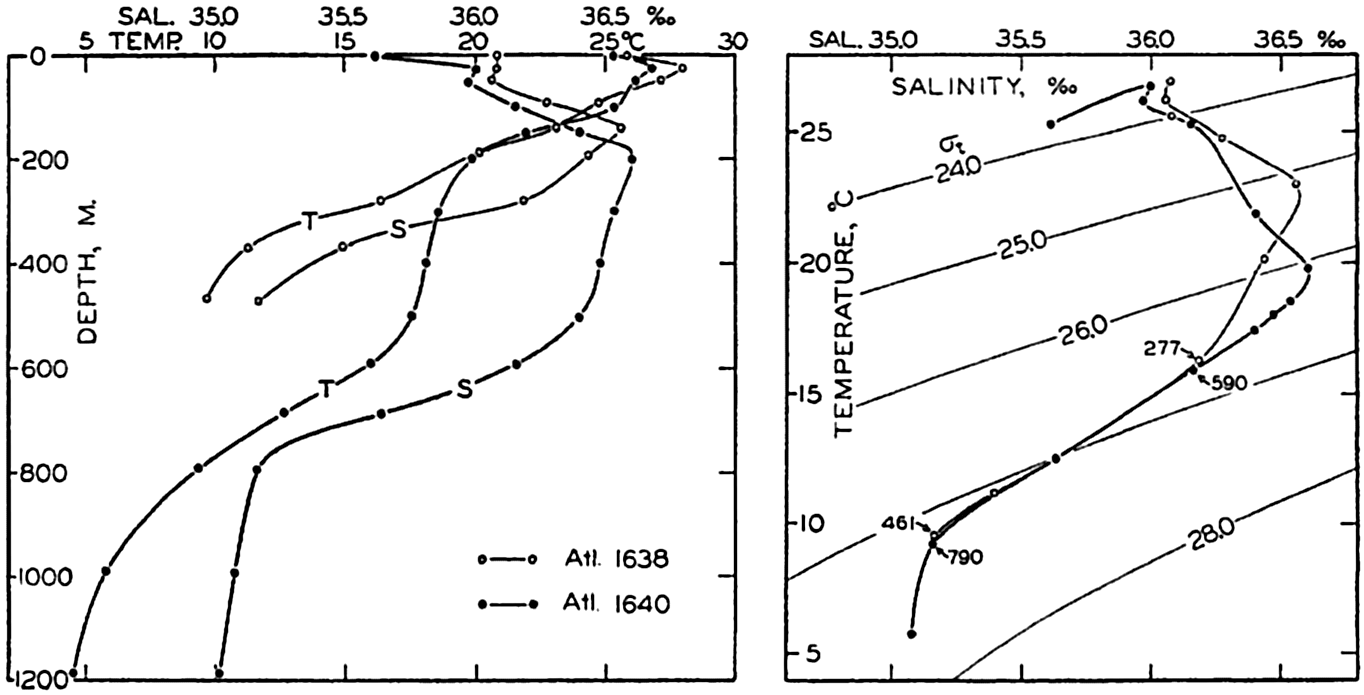
Left: Temperature and salinity at Atlantis stations 1638 and 1640 in the Gulf Stream off Onslow Bay plotted against depth. Right: The same data plotted in a T-S diagram in which σt-curves have been entered.
Since the density of the water at atmospheric pressure, which is expressed by means of σt (p. 56), depends only on temperature and salinity, curves of equal values of σt can be plotted in the T-S diagram. If a sufficiently large scale is used, the exact σt value corresponding to any combination of temperature and salinity can be read off and, if a small scale is used, as is commonly the case, approximate values can be obtained. The slope of the observed T-S curve relative to the σt curves gives immediately an idea of the stability of the stratification (p. 417).
A T-S diagram is shown on the right in fig. 34. On the left in the same figure the observed temperatures and salinities at the Atlantis stations 1638 and 1640 in the Gulf Stream off Onslow Bay are plotted
The T-S diagram has become one of the most valuable tools in physical oceanography. By means of this diagram characteristic features of the temperature-salinity distribution are conveniently represented and anomalies in the distribution are easily recognized. The diagram is also widely used for detecting possible errors in the determination of temperature or salinity (p. 358).
Water Masses and Their Formation. Following Helland-Hansen's original suggestion, a water mass is defined by a T-S curve, but in exceptional cases it may be defined by a single point in a T-S diagram; that is, by means of a single temperature and a single salinity value. These exceptional cases are encountered in basins where homogeneous water is present over a wide range of depth. A water type, on the other hand, is defined by means of single temperature and salinity values, but a given water type is generally present along a surface in the sea and has no thickness. Only in the exceptional cases that were referred to are the terms “water type” and “water mass” interchangeable, but in oceanographic literature the terms have been used loosely and without the distinction that has been introduced here.
In many areas the T-S curves are straight lines or can be considered as composed of several pieces of straight lines. Elementary considerations show that a linear relation between temperature and salinity must result if the water types that can be defined by the end points of the straight line mix in different proportions. Similarly, a curved T-S relation may result from the mixing of three different types of water. Fig. 35 illustrates in two simple cases how progressive mixing alters the temperature-salinity relation. These considerations are of a formalistic nature, but have in many instances led to the concept that certain water types exist and that the T-S relations that are observed represent the end results of mixing between the types. This concept presupposes that the water types (often referred to as water masses) are continually renewed, because, if that were not the case, processes of mixing would ultimately lead to the formation of homogeneous water. It is possible, however, to account for the character of the T-S curves in the ocean by considering other processes.
In the first place it should be observed that a water mass of uniform temperature and salinity is rarely formed in the open ocean. In high latitudes, where convection currents in winter may reach to the bottom, most of the deep and bottom water will not be uniform, because in some
Diagrammatic representation of results of vertical mixing of water types. To the left the results of mixing are shown by temperatures and salinities as functions of depth, and to the right are shown in three T-S diagrams the initial water types (1) and the T-S relations produced by progressive mixing (2 and 3).
However, a similar T-S relationship can be established by different processes, as illustrated in the lower part of fig. 36. It is here assumed that two water types, a and b, are formed at the surface and sink along their characteristic σt surfaces. It is furthermore assumed that at subsurface depths mixing takes place between these two water types, whereas near the surface external processes influence the distribution of temperature and salinity so that there the different curves cross each other. In these circumstances one obtains a T-S relation at subsurface depths that is similar to the one found in the previous example, but along the sea surface an entirely different T-S relation may exist. The processes of mixing, in this case, must take place across σt surfaces in order to establish the T-S relation, but at subsurface depths mixing along σt surfaces is not excluded. At present it is impossible to decide what processes are of the greater importance.
Upper: Schematic representation of the formation of a water mass by sinking along σt surfaces (which coincide with the parallel temperature and salinity surfaces) in a region of convergence. The diagram to the right demonstrates that the vertical T-S relation of the water mass agrees with the horizontal T-S relation at the surface in the region of convergence. Lower: Schematic representation of the formation of a water mass by sinking of water types at two convergences and by subsequent mixing. The diagram to the right illustrates that in this case the vertical T-S relation of the water mass need not agree with the horizontal T-S relation at the surface between the convergences.
The point to bear in mind is that the waters of the oceans all attained their original characteristics when the water was in contact with the atmosphere or subject to heating by absorption of radiation in the surface layers, and that in course of time these characteristics may become greatly changed by mixing. This mixing can either be lateral—that
An example of lateral mixing between water masses is found off the coast of California (Sverdrup and Fleming, 1941), where the water which flows north close to the coast has a T-S relation that differs greatly from that of the water flowing south at some distance from the coast (fig. 199, p. 713). Between these two water masses are found waters of an intermediate character which could not possibly have been formed by vertical mixing and which must have been formed by lateral mixing, probably along σt surfaces. An example of modification of a water mass by vertical mixing is found in the South Atlantic, where the Antarctic intermediate water flows north. This water, near its origin, is characterized by a low salinity minimum, but the greater the distance from the Antarctic Convergence the less pronounced is this minimum (fig. 210, p. 748). The change probably cannot be accounted for by lateral mixing, but Defant (1936) has shown that it can be fully explained as a result of vertical mixing.
Wüst (1935) has introduced a different method for the study of the spreading out and mixing of water types, the “Kernschicht-methode,” which can be translated “the core method.” By the “core” of a layer of water is understood that part of the layer within which temperature or salinity, or both, reach extreme values. Thus, in the Atlantic Ocean, the water that flows out from the Mediterranean has a very high salinity and can be traced over large portions of the Atlantic Ocean by means of a secondary salinity maximum which decreases in intensity with increasing distance from the Strait of Gibraltar. The layer of salinity maximum is considered as the core of the layer in which the Mediterranean water spreads, and the decrease of the salinity within the core is explained as the result of processes of mixing. In this case a certain water type, the Mediterranean water, enters the Atlantic Ocean and loses its characteristic values, owing to the mixing, but can be traced over long distances. The spreading of the water can also be described by means of a T-S curve, one end point of which represents the temperature and salinity at the source region and the other end point of which represents the temperature and salinity in the region where the last trace of this particular water disappears. Having defined such a T-S curve, one can directly read off from the curve the percentage amount of the original water type that is found in any locality. The core method has proved very successful in the Atlantic Ocean and is particularly applicable in cases in which a well-defined water type spreads out from a source region.
Basins
Oceanographically a basin is defined as a depression that is filled with sea water and that is partially separated by land or submarine
Basins with Outflow Across the Sill. In nearly closed basins in the semiarid regions of lower latitudes, evaporation greatly exceeds precipitation and run-off, and the salinity of the surface water is increased above that of the adjacent open ocean. The evaporation is at a maximum in winter when the surface temperature is simultaneously lowered under the influence of cold continental winds. In winter the surface density is therefore increased so much that vertical convection currents are developed which, in some years when extreme conditions exist, may reach to the greatest depth and bring about renewal of the bottom water. The basin water which is formed in this manner, owing to its very high salinity, will be of greater density than the water at the same depth outside the sill, and must therefore flow out over the sill, following the bottom slope. At some higher level the oceanic water must flow into the basin, partly to compensate for the outflow and partly to compensate for the excess of evaporation over precipitation and run-off. The Mediterranean Sea, the Red Sea, and the inner part of the Gulf of California represent examples of such basins.
In basins of this character the basin water is always characterised by high salinity and generally by high oxygen content. The amounts of inflow and outflow depend upon the difference between evaporation and precipitation and run-off, and the volumes of in- and outflowing water are many times greater than the excess of evaporation. Under stationary conditions the total amount of water which in a given time, Ti, flows into a region must equal the sum of the outflow, Tu, and the difference, D, between evaporation over precipitation and run-off in the same time: Ti = Tu + D. Simultaneously, the amounts of salt carried by the in- and outflowing currents must be equal. In the first approximation (p. 426) 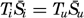 where
where 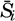 is the average salinity of the inflowing water and
is the average salinity of the inflowing water and 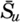 is the average salinity of the outflowing water. From these relations one obtains
is the average salinity of the outflowing water. From these relations one obtains
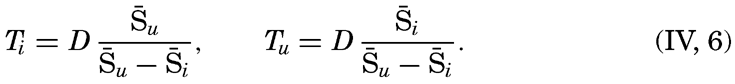
The above considerations are valid only if the entrance is sufficiently wide or deep to permit both inflow and outflow. The Gulf of Kara-Bugaz, on the Caspian Sea, represents an example of a basin which is in such restricted communication with a larger body of water that outflow is practically impossible. This gulf is separated from the Caspian Sea by a 60-mile-long bar and has a shallow entrance which is only a few hundred meters wide. The outflow of the saline deep water is so greatly impeded that, owing to excess evaporation, the salinity of that water in 1902 was 164 ‰ as compared with 12.7 ‰ for the Caspian Sea as a whole.
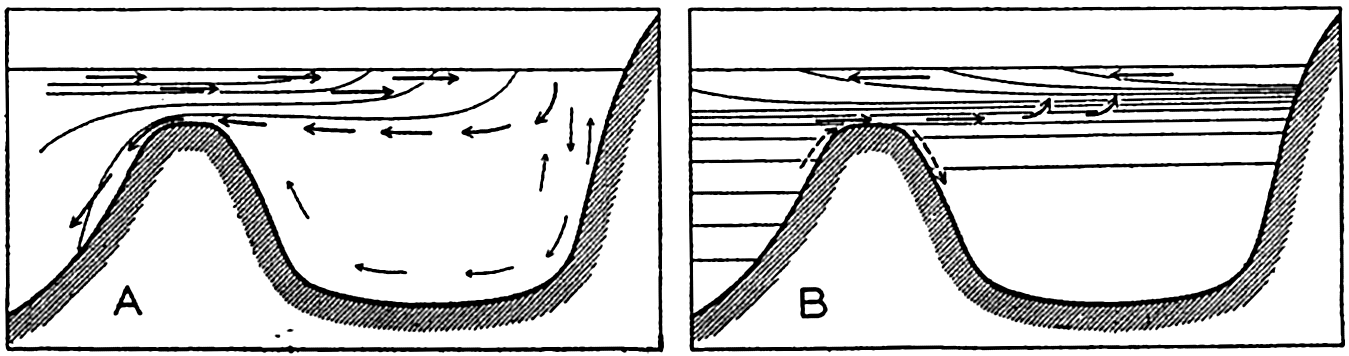
(A) Basin with local formation of basin water and outflow across the sill. (B) Basin with surface outflow of water of low density and occasional renewal of the basin water by inflow of dense water across the sill.
Conditions are encountered which vary from this extreme case to cases in which the excess evaporation for the entire year is zero, but in which seasonal changes may be large enough to permit occasional development of vertical convection currents reaching to the bottom. The essential features to be emphasized is that in basins of this type renewal of the basin water takes place by vertical convection currents which develop in the basin itself and may reach from surface to bottom. Therefore, the water at and below the sill depth has a higher density than the water at sill depth outside the basin, and is not stagnant.
Basins with Inflow Across the Sill. In the nearly closed basins in higher latitudes, precipitation and run-off exceed evaporation. In such basins a surface layer of low salinity and correspondingly low density is developed. Because of the excess of precipitation and run-off there must be a surface outflow of relatively fresh water, and in order to maintain the salt balance there must be an inflow of more saline water.
The exchange of water with the outside sea is small because the difference, 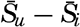 , is great. If the difference is so great that the ratio
, is great. If the difference is so great that the ratio 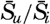 is small compared to unity, the relations that are represented by equation (IV, 6) are reduced to
is small compared to unity, the relations that are represented by equation (IV, 6) are reduced to
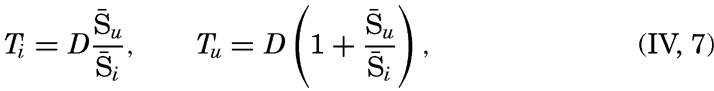
In basins of this type, stagnant water is often found because renewal of the basin water takes place only if the inflowing water is of greater density than the basin water. Outside the sill the density of the water generally increases much more rapidly with depth than it does inside the sill. Renewal of the basin water takes place if the outside water masses are raised so much that the water which flows in across the sill is of such high density that it sinks toward the bottom of the basin. Fig. 37 shows schematically the character of the exchange with the outside and the renewal of the basin water in the two types of basins.
The rapidity of the renewal of the deep water in the basin depends upon the steepness of the vertical density gradient at the sill depth. If this gradient is steep, an occasional large disturbance fills the basin below sill depth with water of great density, and subsequent disturbances must be as great or greater in order to bring about renewal of the basin water. In extreme cases renewal takes place only by major catastrophes. In the intervals between such catastrophes the basin water may become stagnant, because in the upper layers of stable stratification vertical mixing is insignificant. Some mixing takes place, however, which, between major disturbances, reduces the density of the basin water so much that complete renewal can take place when a new catastrophe occurs.
On the other hand, if the density gradient at the sill depth is small, the outside deep water is brought over the sill by any minor disturbance, and stagnation is prevented by intermittent intrusion of outside deep water, and also by vertical mixing, which is more effective owing to the small density gradient.
The water which sinks at sill depth is heated adiabatically, and the basin water is therefore of nearly constant potential temperature. The effective sill depth—that is, the depth at which the potential temperature in the outside water equals that in the basin—is lower on an average than the actual depth of the sill (table 87, p. 738), and the smaller the density gradient in the outside water, the greater is the difference between the effective and the actual sill depth. Great density gradients, if present, are always found near the surface, and a basin with inflow at
The sill depth has bearing also on the direction of flow across the sill, and this direction does not therefore depend exclusively on an excess or a deficit of evaporation, which was used to facilitate the discussion. At small sill depths an excess or deficit of evaporation determines the character of the exchange, but at great sill depths inflow across the sill develops in most instances. Oceanic water flows freely in and out of the basin at some distance above the sill depth, but at the sill depth the average flow is directed, as a rule, into the basin, because the density of the basin water remains lower than that of the outside water, owing to more effective vertical mixing in a restricted region. The main in- and outflow takes place, however, at lesser depths, the water often flowing in through one entrance and out through another. The basins of the American Mediterranean Sea serve as examples (p. 639).
In large basins in high latitudes, such as the Norwegian Sea and Baffin Bay, deep water is formed locally, owing to freezing or excessive cooling of high-salinity water, although precipitation exceeds evaporation. In such basins, which might be listed as a third type, stagnating water is not found.
Bibliography
Ångström, Anders. 1920. Applications of heat radiation measurements to the problems of the evaporation from lakes and the heat convection at their surfaces. Geografiska Annaler, H. 3, 16 pp. Stockholm. 1920.
Birge, E. A., and C. Juday. 1929. “Transmission of solar radiation by the waters of inland lakes” . Wisconsin Acad. Sci., Arts, and Letters, Trans., v. 24, p. 509–80, 1929.
Bjerknes, V., J. Bjerknes, H. Solberg, T. Bergeron. 1932. Physikalische Hydrodynamik. Berlin. Julius Springer, 797 pp., 1932.
Böhnecke, G.1938. “Temperatur, Salzgehalt und Dichte an der Oberfläche des Atlantischen Ozeans. Deutsche Atlantische Exped. Meteor” . Meteor1925–1927, Wiss. Erg., Bd. 5, 2 Lief., 62 pp., 1938.
Bowen, I. S.1926. “The ratio of heat losses by conduction and by evaporation from any water surface” . Phys. Rev., v. 27, p. 779–787, 1926.
Defant, Albert. 1928. Die systematische Erforschung des Weltmeeres. Gesellsch. f. Erdkunde, Zeitschrift, Jubiläums Sonderband, p. 459–505, Berlin, 1928.
Defant, Albert. 1932. “Die Gezeiten und inneren Gezeitenwellen des Atlantischen Ozeans. Deutsche Atlantische Exped. Meteor” . Meteor 1925–1927, Wiss. Erg., Bd. 7, 1 Teil, p. 1–318, 1932.
Defant, Albert. 1936. “Ausbreitungs- und Vermischungsvorgänge im Antarktischen Bodenstrom und im Subantarktischen Zwischenwasser. Deutsches Atlantische Exped” . Meteor1925–1927, Wiss. Erg., Bd. 6, 2 Teil, Lief. 2, p. 55–96, 1936.
Fjeldstad, J.1933. “Wärmeleitung im Meere” . Geofysiske Publikasjoner, v. 10, no. 7, 20 pp., 1933. Oslo.
Fleming, R. H., and Roger Revelle. 1939. Physical processes in the ocean. P. 48–141 in: Recent Marine Sediments, A symposium. Tulsa. Amer. Assn. Petrol. Geol. 1939.
Gaarder, T., and R. Spärck. 1932. Hydrographisch-biochemische Untersuchungen in norwegischen Austern-Pollen. Bergens Museums Aarbok 1932, Naturvidenskapeligrekke, Nr. 1, p. 5–144, 1932.
Helland-Hansen, B.1916. Nogen hydrografiske metoder. Skand. Naturforsker möte, Kristiania (Oslo). 1916.
Helland-Hansen, B.1930. “Physical oceanography and meteorology. Michael Sars North Atlantic Deep-Sea Exped.” , 1910, Rept. Sci. Results, v. 1, art. 2, 217 pp., 1930.
Iselin, C. O'D.1939. “The influence of vertical and lateral turbulence on the characteristics of the waters at mid-depths” . Nat. Research Council, Amer. Geophys. Un., Trans., p. 414–17, 1939.
Jacobs, W. C.1942. “On the energy exchange between sea and atmosphere” . Jour. Marine Research, v. 5, 37–66, 1942.
Kimball, Herbert H.1928. “Amount of solar radiation that reaches the surface of the earth on the land and on the sea, and methods by which it is measured” . Monthly Wea. Rev., v. 56, p. 393–99, 1928.
Koenuma, K.1939. “On the hydrography of southwestern part of the North Pacific and the Kuroshio” . Imper. Marine Observ., Memoirs, v. 7, p. 41–114, 1939 Kobe.
Krümmel, Otto. 1907. “Handbuch der Ozeanographie. Bd. 1. Stuttgart” . J. Engelhorn, 526 pp., 1907.
Kuhlbrodt, Erich, and Joseph Reger. 1938. “Die meteorologischen Beobachtungen. Methoden, Beobachtungsmaterial und Ergebnisse. Deutsche Atlantische Exped.” . Meteor1925–1927, Wiss. Erg., Bd. 14, p. 215–345, 1938.
McEwen, George P.1938. “Some energy relations between the sea surface and the atmosphere” . Jour. Marine Research, v. 1, p. 217–38, 1938.
Millar, F. Graham. 1937. Evaporation from free water surfaces. Canadian Meteorol. Memoirs, v. 1, p. 41–65, 1937. Ottawa.
Montgomery, R. B.1940. Observations of vertical humidity distribution above the ocean surface and their relation to evaporation. Papers in Physical Oceanogr. and Meteorol. v. 7, no. 4, 30 pp., 1940. Cambridge and Woods Hole.
Mosby, Hökon. 1936. “Verdunstung und Strahlung auf dem Meere” . Ann. d. Hydrogr. u. Mar. Meteor., Bd. 64, p. 281–86, 1936.
Netherlands Meteorological Institute. Atlas of oceanographic and meteorological observations.
Neumann, Gerhard. 1940. “Die ozeanographischen Verhältnisse an der Meeresoberfläche im Golfstromsektor nördlich und nordwestlich der Azoren. Ann. d. Hydrogr. u. Mar. Meteor.” , Beiheft zum Juniheft, 1. Lief., 87 pp., 1940.
Powell, Wilson M., and G. L. Clarke. 1936. “The reflection and absorption of daylight at the surface of the ocean” . Optical Soc. Amer., Jour., v. 26, p. 111–120, 1936.
Schmidt, Wilhelm. 1915. Strahlung und Verdunstung an freien Wasserflächen; ein Beitrag zum Wärmehaushalt des Weltmeers und zum Wasserhaushalt der Erde. Ann. d. Hydrogr. u. Mar. Meteor., Bd. 43, p. 111–24, 1915.
Schott, G.1935. Geographie des Indischen und Stillen Ozeans. Hamburg, C. Boysen, 413 pp., 1935.
Skogsberg, Tage. 1936. “Hydrography of Monterey Bay” , California. Thermal conditions, 1929–1933. Amer. Phil. Soc., Trans., N.S., v. 29, p. 1–152, 1936.
Ström, K. M.1936. Land locked waters. Hydrography and bottom deposits in badly ventilated Norwegian fjords with remarks upon sedimentation
Sverdrup, H. U.1929. “The waters on the North-Siberian Shelf” . Norwegian North Polar Exped. with the Maud1918–1925, Sci. Results, v. 4, no. 2, 131 + 75 pp., 1929.
Sverdrup, H. U.1937. “On the evaporation from the oceans” . Jour. Marine Research, v. 1, p. 3–14, 1937.
Sverdrup, H. U.1940. “On the annual and diurnal variation of the evaporation from the oceans” . Jour. Marine Research, v. 3, p. 93–104, 1940.
Sverdrup, H. U., and R. H. Fleming. 1941. “The waters off the coast of southern California” , March to July, 1937. Scripps Inst. Oceanogr., Univ. Calif., Bull., V. 4, p. 261–378, 1941.
Taylor, G. I.1919. “Tidal friction in the Irish Sea. Roy. Soc.” , Philos. Trans., Series A, v. 220, p. 1 ff., 1919. London.
U. S. Weather Bureau. 1938. Atlas of climatic charts of the oceans. W. B. no. 1247, 130 pp., 1938. Washington, D. C.
Vercelli, Francesco. 1937. La propagazione delle radiazioni solar nelle acque marine. La Laguna di Venezia, v. 1, parte II, tomo V, 102 pp., 1937. Venice.
von Hann, Julius. 1915. Lehrbuch der Meteorologie. 3rd ed., Leipzig. Tauchnitz. 847 pp., 1915.
Wegemann, G.1920. Der tägliche Gang der Temperatur der Meere und seine monatliche Veränderlichkeit. Wiss. Meeresuntersuch., N.F., Bd. 19, Abt. Kiel, Abh. 2. Kiel. 1920.
Wüst, Georg. 1935. “Die Stratosphäre. Deutsche Atlantische Exped. Meteor 1925–1927” , Wiss. Erg., Bd. 6, 1 Teil, 2. Lief, 288 pp., 1935.
Wüst, Georg. 1936. Oberflächensalzgehalt, Verdunstung und Niederschlag auf dem Weltmeere. Festschrift Norbert Krebs (Länderkundliche Forschung), p. 347–59. Stuttgart. 1936.
V. Theory of Distribution of Variables in the Sea
Scalar Fields
It cannot be too strongly emphasized that the ocean is three-dimensional and that the distribution of properties or the type of motion must be represented in space. For this purpose a convenient system of coordinates is needed. Any point in the ocean can be designated by means of its geographic latitude and longitude and its depth below sea level, but if one deals with a small area one may consider the surface of the earth within that area as flat, and can introduce ordinary rectangular coordinates with the horizontal axes at sea level and the vertical axis positive downward. By “sea level” is meant not the actual sea level but an ideal sea level, which is defined as a surface along which no component of gravity acts. The difference between the actual and the ideal sea level will be further explained when dealing with the distribution of pressure (p. 406).
The location in the ocean space of any given surface is completely determined if in every latitude and longitude one knows the depth of the surface below the ideal sea level. In a chart this surface can be represented by means of lines of equal depth below sea level (isobaths), which together render it picture of the topography of the surface. Thus, the topography of the sea bottom is shown by isobaths drawn at selected intervals of depth.
The quantities that must be considered when dealing with the sea are either scalars or vectors. A scalar quantity is a physical quantity whose measure is completely described by a number, that depends on the selected system of units. Pressure, temperature, salinity, density, and oxygen content can be mentioned as examples of scalar quantities. A vector is a physical quantity that is completely described by magnitude and direction. The velocity of a particle, the acceleration of a particle, and the forces acting on a particle are examples of vectors.
The magnitude of a vector, such as the numerical value of the velocity of a particle, is a scalar quantity. A vector can be represented by means of its components along the axes of a coordinate system, and these components are scalar quantities.
A continuous fluid is characterized, at every point in the space which it occupies, by a number of different properties. The space distribution of one particular property is called the field of that property. The field is called a scalar field if the property is a scalar quantity, and a vector field if the quantity is a vector. In the ocean there are scalar fields such as the pressure field, the temperature field, and the density field, and there are vector fields such as the velocity field, the acceleration field, and so on.
The term field was first applied to a vector field in order to describe the distribution of electromagnetic forces. Every student of physics has seen the magnetic field of force demonstrated by means of iron filings placed on a card above a magnet, but this experiment brings out only certain characteristics of the field. It shows the direction of the magnetic forces in one single plane, but it does not show the space distribution or the magnitude of the force of the field.
A scalar field is completely represented by means of equiscalar surfaces—that is, surfaces along which the scalar quantity has the same numerical value. The temperature field in the ocean, for instance, would be completely described if one knew exactly the form of the isothermal surfaces, and, similarly, the pressure field would be fully represented if one knew the form of the isobaric surfaces. However, it is impracticable to prepare space models that show the actual configuration of isothermal surfaces or other equiscalar surfaces in the ocean, and it would be impossible to publish such representations. For practical purposes one must select other forms of representation. One widely used method is to show the lines of intersection between equiscalar surfaces and the coordinate surfaces. A chart showing the distribution of temperature at sea level is an example of such representation. In this case the sea level represents one of the principal coordinate surfaces, and the isotherms represent the lines at which the surfaces of equal temperature in the sea intersect the sea surface. Similarly, a chart showing the distribution of temperature at a depth of 1000 m shows the lines along which the isothermal surfaces intersect the 1000-m surface, whereas the temperature distribution in a vertical section shows the lines along which the isothermal surfaces intersect the vertical plane that is under consideration.
A series of horizontal charts of isotherms in surfaces at different distances below sea level give a representation of the temperature field in the ocean, and a series of vertical sections showing isotherms give another representation of the same field.
On the other hand, one can make use of an entirely different method of representation. Instead of showing the lines along which the isothermal surfaces intersect a coordinate surface, one can represent the isothermal surface itself and can show the lines along which the coordinate surfaces at different distances below sea level intersect that surface. Such a
These topographic charts would represent charts of absolute topography, because it is assumed that the depths below the ideal sea level are known. This ideal sea level, however, is a fictitious level that cannot be determined by observations, and all measurements have to be made from the actual sea level. In practice, therefore, the topography of a surface in the ocean will not represent the absolute topography but a relative topography referred to the unknown shape of the actual sea surface. In many instances one need not take the difference between absolute and relative topography into account, because it generally amounts to less than 1 m. For instance, it can be neglected when one deals with isothermal surfaces, because the change in temperature on a fraction of a meter is generally negligible. When dealing with the isobaric surfaces, on the other hand, as will be explained in detail when discussing the field of pressure, one must discriminate sharply between absolute and relative topographies.
These matters have been set forth explicitly, because it is essential to bear in mind that one must always consider distribution in space, which can be fully described by means of equiscalar surfaces. These, however, may have highly complicated forms.
The mathematical definition of an equiscalar surface can be written
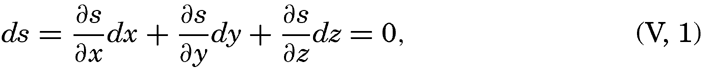
In a vertical section in the x-z plane the equiscalar curves are similarly defined by

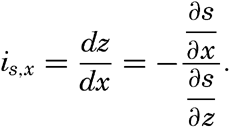
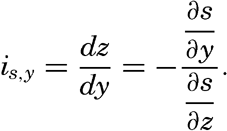
So far, the discussion has dealt with equiscalar surfaces in general. In practice, one may select these surfaces so that there is a constant difference between the value of the variable at any two surfaces. These surfaces are called standard equiscalar surfaces. In the case of temperature, the isothermal surfaces might be selected for every one degree of temperature; in the case of salinity, the isohaline surfaces might be selected for every 0.1 ‰, and so on. These surfaces would divide the space into thin layers characterized by a constant difference of the quantity at the two boundary surfaces of every layer. Such layers are called equiscalar sheets. It should be noted that the scalar is not constant within this sheet but has a constant average value. It is evident that the thickness of these sheets represents the rate at which the scalar varies in a direction at right angles to the equiscalar surfaces. Where the sheets are thin the variation is great, but where the sheets are thick the variation is small. The rate of variation can be represented by means of a vector whose direction is normal to the equiscalar surface and whose magnitude is inversely proportional to the thickness of the sheet. The vector representing the rate of decrease is generally called the gradient (temperature gradient, pressure gradient), and the vector representing the rate of increase is called the ascendant. If the scalar is called s, then the gradient, G, and the ascendant, A, are defined by the equations
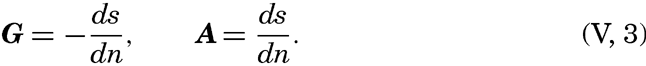
If the field is represented by means of a sufficient number of surfaces, these surfaces will completely define the gradients and ascendants that are characteristic of the distribution. Thus, the special vector fields of gradients and ascendants are entirely described by means of systems of equiscalar surfaces, but other vector fields cannot be described in that manner. Vector fields will be dealt with in chapter XII.
Relation between the Distribution of Properties and the Currents in the Sea
Consider any scalar quantity, s (temperature, salinity, pressure, oxygen content, and so on), the distribution of which is continuous in space and time, so that it can be represented as a function of time and the three space coordinates, s = f(t,x,y,z). Let us assume that this scalar quantity can be considered a property of the individual particles of the fluid. A particle in motion after a time dt will be in a new locality,
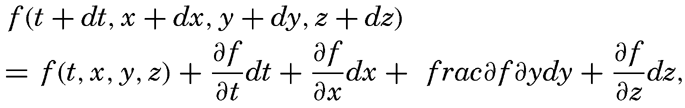
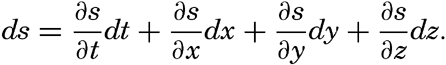
Dividing by dt and considering that dx/dt, dy/dt and dz/dt represent the components of the velocity, one obtains
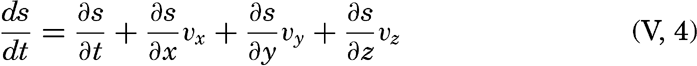
A few important points can be brought out by means of the above equation: (1) the distribution of any scalar quantity is stationary—that is, independent of time if the local change is zero (∂s/∂ t = 0); (2) the advection terms disappear if there is no motion or if the field is uniform—that is, if either vx = vy = vz = 0 or ∂ s/∂ x = ∂ s/∂ y = ∂ s/∂ z = 0; (3) when the individual change is zero (ds/dt = 0), the local change is equal to the advection but is of opposite sign; (4) if the field of a property is stationary (∂ s/∂ t = 0) and if, further, the individual time change is zero (ds/dt = 0), equation (V, 4) is reduced to
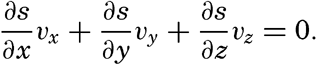
Distribution of Conservative Concentrations in the Sea
The discussion has so far been of a purely formalistic nature. If one goes a step further and considers the processes that maintain or tend
The processes that tend to modify the concentrations can be divided into two groups: external processes, which are active only at the boundary surfaces of the fluid, and internal processes, which are active anywhere in the fluid. The external processes are of importance in determining the concentrations at the boundaries, and the internal processes, together with the boundary values, determine the distribution throughout the fluid.
By conservative concentrations are meant concentrations that are altered locally, except at the boundaries, by processes of diffusion and advection only. Heat content and salinity are two outstanding examples of conservative concentrations. Consider a cube the surfaces of which are of unit area and are normal to the coordinate axes. Through the two surfaces that are normal to the x axis, diffusion leads to a transport in unit time of (Ax/ρ)1(∂ s/∂ x)1 and (Ax/ρ)2(∂ s/∂ x)2, respectively, where both the coefficient, Ax, and the derivative, ∂ s/∂ x, may vary in the x direction. The coefficient of diffusion enters here in the “kinematic” form (p. 470) as A / ρ, where A is the eddy diffusivity, because concentrations have been defined as amounts per unit volume. The difference per unit length of these transports, ∂/∂ x[(Ax/ρ)(∂ s/∂ x)], represents the net change of concentration in the unit volume due to diffusion. In the presence of a current in the x direction, there will also be a net change of concentration due to advection. The concentration that a current of velocity, vx, transports through a unit surface in unit time is equal to svx, and, if this transport changes in the direction of flow, the concentration per unit volume is altered by —∂(svx)/∂ x. Similar considerations are applicable to transport through the other surfaces of the cube, and the combined local change of concentration, therefore, is the sum of terms representing diffusion and advection:
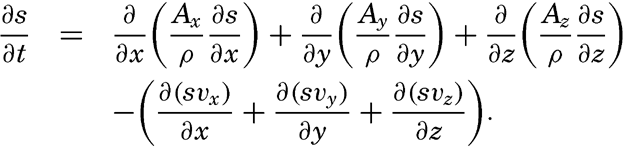
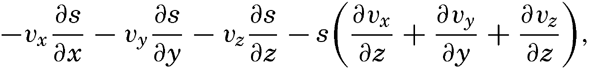
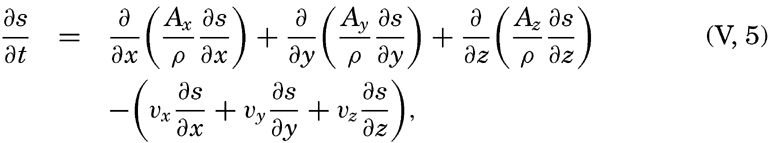
Taking equation (V, 4) into consideration, one obtains
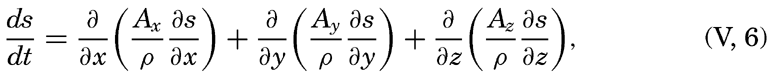
In practice these equations must be greatly simplified. Consider, for example, a two-dimensional system in which the velocity is directed along the x axis, in which diffusion in the x direction can be neglected, and in which it can be assumed that the coefficient of vertical diffusion, A / ρ, is constant. For such a system the condition for a stationary distribution of s, (∂ s/∂ t = 0), is reduced to

As another example, consider a uniform field for which ∂ s/∂ t=ds/dt and assume that Ax = Ay = 0. The above equations are then reduced to

Other simplifications of the equations can be made, depending upon the nature of the problem under consideration (Montgomery, 1939, Sverdrup, 1939).
Distribution of Nonconservative Concentrations
By nonconservative concentrations are meant primarily concentrations whose distributions are influenced by biological processes besides
The local time change of concentration due to biological processes will be called R. Adding this quantity at the right-hand side of equation (V, 5) one can state
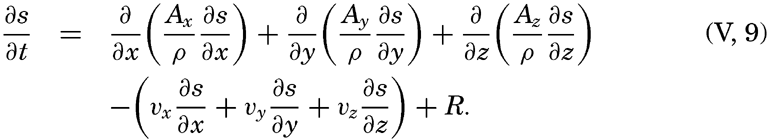
The Principle of Dynamic Equilibrium
Experience shows that in a large body of water comparable, say, to the body of water in the Mediterranean Sea, the average conditions do not change from one year to another. The average distribution of temperature remains unaltered year after year, and the same is true as to the average salinity, oxygen content, and contents of minor constituents. If time intervals longer than a year are considered, say ten-year periods, it is probable that even the average number of different species of organisms remains unaltered, provided that the nonaquatic animal, man, does not upset conditions by exterminating certain species and depleting the stock of others. These unchanging conditions represent a state of delicate dynamic equilibrium between factors that always tend to alter the picture in different directions.
In dealing with conservative concentrations, diffusion and advection are at balance except at the sea surface, where external processes contribute toward maintaining the concentration at a certain level. This was illustrated when discussing the general distribution of surface salinity (p. 125), which was shown to depend on two terms, one that represents the external processes of evaporation and precipitation, and one that represents the internal processes of diffusion and advection. Similarly, the surface temperature depends upon heating and cooling by processes of radiation and by exchange with the atmosphere and upon conduction and advection of heat.
In a study of the subsurface distribution of temperature and salinity, it is not necessary to know the processes that maintain the surface values, but it is sufficient to determine these values empirically. If this could be done and if the processes of diffusion and the currents were known, the general distribution of temperature and salinity could be computed. Conversely, if these distributions were known, information as to diffusion and currents could be obtained. In oceanography only the latter method of approach has been employed.
When nonconservative concentrations are dealt with, the principle of a dynamic equilibrium implies that the effects of diffusion, advection, and biological processes cancel. Of the nonconservative concentrations, only the dissolved gases are greatly influenced by the contact with the atmosphere, and other nonconservative concentrations are practically unaltered by external processes.
Application of the principle of dynamic equilibrium can be illustrated by considering the distribution of oxygen. Below the euphotic zone, biological processes that influence the oxygen content always lead to a consumption of oxygen, and the processes of diffusion and advection therefore must lead to a replenishment that exactly balances the consumption. No further conclusions can be drawn. This obvious consideration has been overlooked, however, and some authors have interpreted a layer of minimum oxygen content as a layer of minimum replenishment (Wüst, 1935), while others have considered it a layer of maximum consumption (Wattenberg, 1938).
Conclusions as to the rapidity of consumption (and replenishment) could be drawn from the known distribution of oxygen only if the consumption depended upon the absolute content of oxygen, but the consumption appears to be independent of the oxygen content until this has been reduced to nearly nil (ZoBell, 1940). When all oxygen has been removed, consumption and replenishment must both be zero, and even this obvious conclusion should not be overlooked.
In certain instances a relation may exist between the oxygen distribution and the character of the current. Assume that a nearly horizontal internal boundary exists which separates currents flowing in opposite directions, that diffusion takes place in a vertical direction only, and that the coefficient of diffusion is independent of z. When dynamic equilibrium exists, equation (V, 9) is then reduced to

Similar reasoning is valid when dealing with compounds that are removed from the water by organisms for building up their tissues and are returned to solution as metabolic products or by decomposition of organic tissues. A balance is maintained, but in many cases it is not correct to speak of “replenishment” by advection and diffusion, as in the case of oxygen, because the biological processes may lead to a net replenishment, in which case the physical processes must take care of a corresponding removal. Thus, in the deeper layers phosphates and nitrates are added to the water by decomposition of organic matter and removed by diffusion and advection.
When dealing with populations, similar considerations enter. It must be emphasized especially that the number of organisms present in unit volume of water gives no information as to the processes that operate toward changing the number. A small population of diatoms, say, may divide very rapidly without increasing in number, owing to the presence of grazers that consume diatoms. On the other hand, a large population of diatoms may not indicate a rapid production of organic matter, because further growth may be impossible owing to lack of nutrient salts in the water. The terms “population” and “production” have to be clearly defined and kept separate. (“Population” represents concentration, whereas “production” represents one of the processes that alter the concentration.
Another warning appears to be appropriate—namely, a warning against confusion between individual and local changes (p. 157). From the fact that a local population remains unaltered, it cannot be concluded that the population within the water which passes the locality of observation also remains constant—that is, that the individual time change is zero. Similarly, if a sudden change in population is observed in a given locality, it cannot be concluded that the processes which have been active in that locality have led to a rapid growth, because it is equally possible that a new water mass of other characteristics is passing the locality.
If the external influences were clear, if processes of diffusion and advection were known, and if biological and organic chemical processes were fully understood, the distribution of all concentrations could be accounted for. It would then be possible not only to explain the average distribution but also to account for all periodic and apparently random changes. This is the distant goal, but when working toward it one must be fully aware of the limitations of the different methods of approach.
Thus, complete description of the oxygen distribution below the euphotic zone is theoretically possible if the oxygen content in the surface
The dynamic equilibrium, the importance of which has been stressed, exists only insofar as average conditions within a large body of water and over a considerable length of time are concerned. During any part of the day or year the external or internal processes may be subject to periodic or random variation such that at a given moment no equilibrium exists (∂ s/∂ t ≢ 0). At the surface, heating periodically exceeds cooling, and cooling periodically exceeds heating, as a result of which the surface temperature is subjected to diurnal and annual variations that by processes of conduction are transmitted to greater depths. It is possible that longer periods exist which are related to periodic changes in the energy received from the sun, but these long-period variations are of small amplitudes. In many areas, shifts of currents lead to local changes of the temperature which are periodic in character if the shifts are associated with the seasons, or nonperiodic if they are related to apparently random events. In the discussion of the annual variation of temperature (p. 131) the effect of these different processes was illustrated. Similar reasoning is applicable to periodic and random variations of salinity and also to variations of nonconservative properties.
From what has been stated it is evident that in the discussion of the distribution of concentrations in the sea it is as yet impossible to apply a method of deduction based on knowledge of all processes involved in maintaining the distribution. Instead, one has to follow a winding course, discuss processes and their effects whenever possible, discuss actual distributions if such have been determined, and either interpret these distributions by means of knowledge gained from other sources as to acting processes or draw conclusions as to these processes from the distribution. In some instances the processes that maintain the boundary values can be dealt with at considerable length, but otherwise the observed boundary values have to be accepted without attempts at explanation. In all cases, however, it is essential to bear in mind that one is dealing with concentrations in a continuous medium and that general considerations as set forth here are always applicable.
Bibliography
Defant, Albert. 1929. Stabile Lagerung ozeanischer Wasserkörper und dazu gehörige Stromsysteme. Berlin Universität, Institut f. Meereskunde, Veröff., N.F., A. Geogr.-naturwiss, Reihe, Heft, 19, 33 pp., 1929.VI. Chemistry of Sea Water
If suspended solid material of either organic or inorganic origin is excluded, sea water may be considered as an aqueous solution containing a variety of dissolved solids and gases. Determination of the chemical nature and concentrations of the dissolved substances is difficult for the following reasons: (1) some of the dissolved substances, such as chloride and sodium ions, are present in very high concentrations, while others, certain metals for instance, are present in such minute quantities that they have not been detected in sea water, although they have been found in marine organisms or salt deposits; (2) two of the major constituents, sodium and potassium, are extremely difficult to determine accurately; (3) it is virtually impossible in some cases to separate related substances such as phosphate and arsenate, calcium and strontium, and chloride, bromide, and iodide. In these cases the combined elements are determined together and usually reported as if they represented only one; that is, calcium and strontium are often calculated as “calcium,” and chloride, bromide, and iodide as “chloride.”
Because of the complex nature of the dissolved materials in sea water a specially developed technique is usually required to determine the concentration of any constituent. The standard methods for the quantitative analysis of solutions which are given in textbooks generally cannot be applied to sea water without adequate checks on their accuracy. This is particularly true when dealing with elements present in extremely low concentrations, because the elements occurring as impurities in the reagents may be in amounts many times those found in the water.
Constancy of Composition
It has been found that, regardless of the absolute concentration of the total solids, the ratios between the more abundant substances are virtually constant. The importance of this result cannot be overemphasized, as upon it depends the validity of the chlorinity:salinity:density relationships and, hence, the accuracy of all conclusions based on the distribution of density where the latter is determined by chemical or indirect physical methods such as electrical conductivity or refractive index.
The relative uniformity in the composition of the sea water was established by the investigations of Forchhammer, Natterer, and Dittmar. Although Forchhammer analyzed a large number of samples, his investigations were not complete because he did not determine certain of the abundant elements. Natterer made more detailed analyses, but it was Dittmar who laid the solid foundation for the present knowledge of the composition of sea water.
Dittmar (1884) made careful determinations on 77 water samples, representative of all oceans, which had been collected on the voyage around the world of H.M.S. Challenger. He determined the halides, sulphate, magnesium, calcium, and potassium. On composite samples he found the ratio of bromine to chlorine and estimated the carbonate. From the sums of the chemical equivalents of the negative and positive ions, he calculated the sodium by difference. This procedure was followed because he was unable to achieve satisfactory direct determinations for sodium. The results of Dittmar's work showed that there were no significant regional differences in the relative composition of sea water; consequently his average values could be used to represent the ratios between the major dissolved constituents. In table 33 are given Dittmar's average values in the units in use at the present time and referred to a chlorinity of 19.00 ‰. The percentages of the various ions are also shown.
| Ion | Original values | Recalculated, 1940 atomic weights | 1940 values | |||
|---|---|---|---|---|---|---|
| Cl = 19 ‰ | % | Cl = 19 ‰ | % | Cl = 19 ‰ | % | |
| C1− | 18.971 | 55.29 | 18.971 | 55.26 | 18.980 | 55.04 |
| Br− | 0.065 | 0.19 | 0.065 | 0.19 | 0.065 | 0.19 |
| SO4− | 2.639 | 7.69 | 2.635 | 7.68 | 2.649 | 7.68 |
| CO3− | 0.071 | 0.21 | 0.071 | 0.21 | …… | …… |
| HCO3− | …… | …… | …… | …… | 0.140 | 0.41 |
| F− | …… | …… | …… | …… | 0.001 | 0.00 |
| H3BO3 | …… | …… | …… | …… | 0.026 | 0.07 |
| Mg++ | 1.278 | 3.72 | 1.292 | 3.76 | 1.272 | 3.69 |
| Ca++ | 0.411 | 1.20 | 0.411 | 1.20 | 0.400 | 1.16 |
| Sr++ | 0.013 | 0.04 | ||||
| K+ | 0.379 | 1.10 | 0.385 | 1.12 | 0.380 | 1.10 |
| Na+ | 10.497 | 30.59 | 10.498 | 30.58 | 10.556 | 30.61 |
| Total | 34.311 | 34.328 | 34.482 | |||
Since 1884 the modification of atomic weights has affected the numerical results reported by Dittmar. Corrections for these changes may be made (Lyman and Fleming, 1940) as shown in the “recalculated” values in table 33. In the latter tabulation the sodium has been recalculated by Difference.
It is interesting to compare Dittmar's results with those obtained by modern methods of analysis as shown in the last columns of the table. The sources of these data are indicated in table 35. It is immediately seen that there are small differences for most of the elements determined by Dittmar and that certain other ions have been added to the list of major constituents. The bound carbon dioxide is reported as bicarbonate ion instead of as carbonate, strontium is given by itself instead of in combination with calcium, and fluoride and boric acid have been added.
The close agreement between the results of Dittmar and those obtained recently is remarkable when we consider the complexity of the problem and the great advance in knowledge of analytical chemistry. However, although the differences are small, they are significant, and hence the importance of Dittmar's work is that it showed the constancy of the ratios between the major constituents, and not that it led to accurate numerical values of these ratios.
In table 33 the composition is shown by referring the substances to a standard concentration, C1 = 19.00 ‰, and by means of the ratios between the different ions and the total dissolved solids. In most instances it is preferable to use a third method; namely, to give the ratios between the various substances and the chlorinity or the chlorosity (p. 52), and these ratios are known as C1-ratios and chlorosity factors, respectively. The Cl-ratio is the amount of any ion or substance per unit (gram) of chlorinity, and is obtained by dividing the concentration in grams per kilogram by the chlorinity, or the concentration in grams per 20°-liter by the chlorosity. Multiplication of the C1-ratio by a given chlorinity or corresponding chlorosity will give the concentrations as grams per kilogram or per liter, respectively. Concentrations in milligram-atom units are always on a liter basis, and, if divided by the chlorosity, yield the ratios that are called chlorosity factors. It may be noted that a chlorosity factor multiplied by chlorinity yields the concentration in milligram-atoms per kilogram.
The uniformity of relative composition in the oceans is the result of circulation and mixing. These operations are continuous, and tend to eliminate regional differences in composition, whatever the cause. Disturbing agencies bring about changes that are small compared to the bulk of the substances present and consequently will not materially affect the relative concentration of the major constituents. Further-more, many of the disturbing processes that tend to modify the relative composition are reversible. For example, the secretion of calcium
The constancy of composition is, as already emphasized, of the greatest importance. Not only is it the basis of the chlorinity:salinity:density relationships, but it also affords a means of estimating the concentrations of all of the major constituents when the concentration of any one of them is known. Furthermore, results of studies on the composition or the physical properties of sea water in any locality are generally applicable to the water in any other part of the oceans.
Except in special areas, such as in the Baltic Sea, the Black Sea, and off the mouths of large rivers, it is not necessary to consider that the water represents special local types with properties that differ from those of sea water in general. Nevertheless, it should be remembered that the composition is not absolutely constant even for the major constituents listed in table 33. Various factors which will be discussed in detail later are always operating and always tend to modify the relative abundances. Rivers introduce dissolved material in proportions that are markedly different from those in the sea, and they also introduce sedimentary material that reacts in various ways with the dissolved constituents. The formation and melting of sea ice may bring about a modified distribution of the dissolved substances.
Thus far, comment has been largely restricted to those constituents of sea water that are present in large, or at least relatively constant, proportions. If we consider those elements which are present in small quantities and which are utilized by marine organisms, the concept of constant composition is no longer generally valid, because the concentrations of these elements vary widely, particularly near the surface. A great part of the work in chemical oceanography is now devoted to determining the space and time variations in variable constituents, and much thought is directed toward the solution of the problems related to the processes that control the observed distribution.
Units Used in Chemical Oceanography
In chemical oceanography most of the numerical results are expressed as concentrations—that is, as the amounts of various constituents in a certain quantity of sea water. Obviously many different combinations
Only two units are to be used for expressing the quantity of sea water: either (1) the kilogram or (2) the amount of water which at 20° C. and pressure one atmosphere occupies the volume of one liter. The latter unit is designated as L20, but in this discussion it will be indicated as L. The system in which the constituents are reported as the amounts present per liter is designated as the “preferred” one, with an alternative for the abundant substances that may be reported as grams per kilogram of sea water. Salinity and chlorinity are always reported as grams per kilogram of sea water. It should be understood that the proposed system applies only to the reporting of analytical data in the literature. Any suitable units may be adopted for the discussion of special problems.
For expressing the amounts of the dissolved constituents, two types of units are proposed: (1) physical units of mass, volume, or pressure, and (2) units based upon the number of atoms of the designated element, which may be present as ions or molecules either singly or in combination with other elements. In certain cases the number of chemical equivalents is acceptable.
The mass units most commonly used are those of the metric system and bear the following relations to each other:
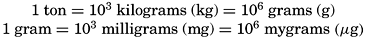
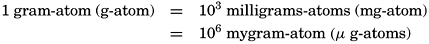
In certain cases (for example, alkalinity and hydrogen-ion concentration) it is desirable to report the concentration in terms of chemical equivalents. The units shall then be
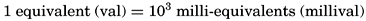
For expressing the partial pressure of gases dissolved in sea water the basic pressure unit is the “physical atmosphere” (p. 55):
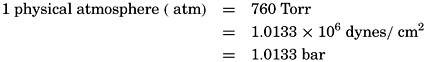
Volume units are all based upon the true liter—that is, the volume of 1 kg of distilled water at 4°C. When volume units are used, the temperature and pressure should be stated. The quantities of dissolved gases, when expressed as milliliters (ml), should be those for 0°C and a pressure of 1 atmosphere, that is, NTP.
The centigrade scale is to be used for reporting temperatures.
The units to be used in reporting data, proposed by the International Association of Physical Oceanography, are given in table 34. It should be noted that all units are based upon the amount of a designated element that may be present either singly (for example, oxygen or calcium) or in combination with other elements (for example, phosphate-phosphorus).
Because the 20° liter is the standard volume unit for expressing the quantity of sea water, glassware should be calibrated for this temperature, and, if practicable, measurements and chemical determinations should be made at or near this temperature. If the sea-water samples are not at 20°, it may be necessary to apply certain corrections. Full descriptions of the methods for making such corrections and tables to facilitate the transformation are included in the Report of the International Association of Physical Oceanography. In most cases the accuracy of the methods of analysis for the elements present in small amounts do not justify such corrections.
As already stated, it is frequently desirable to express the relative concentrations as Cl-ratios or chlorosity factors (p. 167). These relationships may be used to calculate the quantity of the major elements present in water of known chlorinity or to check variations in composition which may be brought about by natural agencies, pollution by sewage and industrial wastes, or by other agencies.
Composition of Sea Water
So far, the discussion of the composition of sea water has been based mainly on the results of the fundamental investigations of Dittmar. Since his time our knowledge of the composition of sea water has increased tremendously. Improved methods of analysis have been developed and consequently more accurate values can be obtained. Tests have also been developed for the detection and determination of elements other than those previously discussed. Particular efforts have been devoted to the study of the so-called plant nutrients—that is, those elements
| Designated substance | Abbreviation | Units (p = preferred, a = alternative) | |||
|---|---|---|---|---|---|
|
|
| ‰ | ||
| Ammonia-nitrogen | Ammonia-N | p | |||
| Argon | Argon | p | |||
| Arsenate-arsenic | Arsenate-As | p | |||
| Arsenite-arsenic | Arsenite-As | p | |||
| Borate-boron | Borate-B | p | |||
| Calcium | Ca | p | a | ||
| Carbon dioxide | Carbon dioxide-C | p | |||
| CO2 | a | ||||
| Chlorinity | Cl | p | |||
| Copper | Cu | p | |||
| Iron | Fe | p | |||
| Magnesium | Mg | p | a | ||
| Manganese | Mn | p | |||
| Nitrate-nitrogen | Nitrate-N | p | |||
| Nitrite-nitrogen | Nitrite-N | p | |||
| Nitrogen (gas) | N2 | p | a | ||
| Oxygen (gas) | O2 | p | a | ||
| Phosphate-phosphorus | Phosphate-P | p | |||
| Potassium | K | p | a | ||
| Radioactive substances | p | ||||
| Salinity | S | p | |||
| Silicate-silicon | Silicate-Si | p | |||
| Sodium | Na | p | a | ||
| Sulphate | Sulphate-S | p | |||
| SO4 | a | ||||
| Hydrogen sulphide | Sulphide-S | p | |||
| H2S | a | ||||
Hence, in order to prepare a tabulation of the composition of sea water it is necessary to combine the results of numerous workers who have examined samples from different sources. All available data were collected by Thompson and Robinson (1932), and additional references will be found in the following discussion. In some cases the information is extensive, but for other elements only a few determinations have been made on water from a single locality. We shall first examine the quantities of the major elements—that is, those which bear a virtually constant relationship to the chlorinity.
In table 35 is given a compilation of the major ions that make up over 99.9 per cent of the known dissolved solid constituents of sea water. The sources of these data have been discussed by Lyman and Fleming (1940). The concentrations of the various ions are shown for water of 19.00 ‰ chlorinity, and also the Cl-ratios. The quantities are also expressed in terms of chemical equivalents per kilogram for water of 19.00 ‰ chlorinity and as milligram-atoms per 20° liter. Chlorosity factors are given for units of milligram-atoms. The carbon dioxide has been reported as bicarbonate. This method is not strictly accurate, because the bound carbon dioxide content of sea water is variable, but, as will be shown in the discussion of the carbon dioxide system, the sum of the chemical equivalents of carbonate and bicarbonate is virtually constant for any chlorinity.
It is immediately seen that the sum of the halides (chloride, bromide, and fluoride) by weight is greater than the chlorinity. The amount of iodide is negligible. Even if the bromide is calculated as chloride, and if the fluoride is disregarded because it does not take part in the chlorinity determination, the chloride equivalent is 1.00045 times greater than the chlorinity. The reasons for this apparent discrepancy have been discussed on page 52.
Lyman and Fleming (1940) obtained the following empirical equation for the dissolved solids as represented in table 35:
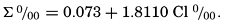
From this it will be seen that in water of 19.00 ‰ chlorinity the total dissolved solids are 34.4816 ‰, but, according to the equation used to calculate the salinity from the chlorinity (p. 51), the salinity is 34.325 ‰. Thus, the total amount of dissolved solids is greater than the salinity. If, on the other hand, the salinity is calculated from the total solids, using the definition for the former quantity—that is, by converting the bicarbonate to oxide and converting the bromide to chloride—we obtain the salinity “by definition” as 34.324 ‰. This agreement must be considered as more or less accidental, as there are many uncertainties in the analytical data. Confidence in the values is strengthened, however, by the fact that the sodium: chlorinity ratio as reported by Robinson and Knapman (1941) agrees exactly with the value that Lyman and Fleming (1940) found by difference. Although the table represents the most probable figures for the composition of the major dissolved constituents, it is subject to change as additional data become available.
| Ion | ‰ | Cl-ratio, g per unit Cl | Equivalent per kg of sea water | mg-atoms per liter | Chlorosity factor, mg-atoms per unit Cl | Authority |
|---|---|---|---|---|---|---|
Total dissolved solids = 34.4816 ‰ Sum of constituents (HCO3− as O−, and Br− as Cl−) = 34.324 ‰ Salinity (S ‰ = 0.030 + 1.805 Cl ‰) = 34.325 ‰ aRatio for millival/kg = 0.1205 bRatio for boron/Cl = 0.000240 cBoric acid undissociated dSodium calculated by difference in sum of equivalents | ||||||
| Chloride, Cl− | 18.9799 | 0.99894 | 0.5353 | 548.30 | 28.173 | Dittmar (1884), Jacobsen and Knudsen (1940) |
| Sulphate, SO4− | 2.6486 | 0.1394 | 0.0551 | (SO4-S) 38.24 | 1.451 | Thompson, Johnston, and Wirth (1931) |
| Bicarbonate, HC03− | 0.1397 | 0.00735[a] | 0.0023 | (HCO3−C) 2.34 | 0.120 | Revelle (1936) |
| Bromide, Br− | 0.0646 | 0.00340 | 0.0008 | 0.83 | 0.0426 | Dittmar (1884) |
| Fluoride, F− | 0.0013 | 0.00007 | 0.0001 | 0.07 | 0.0036 | Thompson and Taylor (1933) |
| Boric acid,c H3BO3 | 0.0260 | 0.00137[b] | [c] | (H3BO3-B)0.43 | 0.0221 | Harding and Moberg (1934), Igelsrud, Thompson, and Zwicker (1938) |
| _______ | ||||||
| Total | 0.5936 | |||||
| Sodium,[d] Na+ | 10.5561 | 0.5556 | 0.4590 | 470.15 | 24.153 | By difference, and Robinson and Knapman (1941) |
| Magnesium, Mg++ | 1.2720 | 0.06695 | 0.1046 | 53.57 | 2.752 | Thompson and Wright (1930) |
| Calcium, Ca++ | 0.4001 | 0.02106 | 0.0200 | 10.24 | 0.5262 | Kirk and Moberg (1933); Thompson and Wright (1930) |
| Potassium, K+ | 0.3800 | 0.02000 | 0.0097 | 9.96 | 0.5113 | Thompson and Robinson (1932) |
| Strontium, Sr++ | 0.0133 | 0.00070 | 0.0003 | 0.15 | 0.0077 | Webb (1938) |
| _______ | ||||||
| Total | 0.5936 | |||||
The data in table 35 apply more specifically to surface water than to deep water. Both bicarbonate ion and calcium will be slightly higher in deeper water. Furthermore, some of the other compounds not included in this tabulation, such as nitrate and silicate, may be present in sufficient quantities to disturb the balance of the anions and cations shown in the table. The Cl-ratios should therefore be considered more as indices than as absolute values. However, in no case will the ratios vary by more than a unit or two in the last decimal place when the water under investigation is from the open sea. Under abnormal conditions, as in highly diluted water, larger departures may be found. By definition the salinity is not zero at zero chlorinity; hence the ratios of certain elements would be expected to approach infinity at very high dilutions when the diluting water contained substances other than halides. Therefore, in studies in areas of highly diluted water the character of the river water should be taken into account. As pollution problems frequently occur in such areas, it will be necessary to determine the normal ratios for different dilutions for a specific zone before any conclusions can be drawn as to the nature or extent of the pollution.
Elements Present in Sea Water
Thus far, only the major constituents of sea water have been considered. In table 36 are entered all elements that are known to occur in sea water as dissolved solids, except hydrogen and oxygen. They are not given as ions in this case but as the amounts of the individual elements which occur in water of chlorinity 19.00 ‰. The elements are arranged in the order of their abundance. In the first column they are reported as milligrams per kilogram, and in the second as milligram-atoms per liter. For convenience, the 1940 atomic weights and their reciprocals have been included. These constants are necessary when converting weight units to gram-atom units, and vice versa. The values for the major elements correspond to those given in previous tables and, in general, are valid for surface water. For many of the elements ranges in concentration have been indicated. No doubt ranges should be shown for others, but the lack of sufficient observations or uncertainty as to the reliability of reported data leaves these problems unsettled. For many of the elements that are present in very low concentrations there are only one or two determinations available, and in some cases only indirect estimates have been made. Hence, in these cases the indicated values can represent only the order of magnitude of the quantities present. Omitting the six most abundant elements, only carbon (CO2 components), silicon,
Forty-four elements are listed in table 36, and if we add hydrogen, oxygen, and the inert gases neon, helium, and argon, we obtain a total of forty-nine elements that are known to occur in sea water. Further investigations will undoubtedly demonstrate the presence of others. Certain problems of the origin and concentration of the dissolved solids relative to their concentration in the earth's crust will be discussed later.
The following brief discussion is limited to those elements that either occur in relatively large amounts or whose distribution has been shown to be affected by biological activity. For elements in the latter group additional data are given in chapter VII. In table 36 references are given for those elements not discussed in the text. A comprehensive discussion is given by Thompson and Robinson (1932), and other results are reported by Goldschmidt (1937) and Wattenberg (1938). The elements are considered in the order in which they appear in the table.
Chlorine, present as chloride ion, is the most abundant ion and makes up about 55 per cent by weight of the dissolved material. It is rarely measured except in combination with other halides in the chlorinity determination. The bromide and iodide are then computed as if they were chloride. It should be kept in mind that the ratio of the chlorine equivalent of the halides to the chlorinity is 1.00045 (p. 52). The chlorinity is of the greatest importance, not only as the basis of density computations, but also as the standard to which those substances present in major amounts are referred.
Sodium is the most abundant cation in sea water, but it is rarely determined directly, owing to the technical difficulties involved in the determination of the alkali metals. The average ratio to chlorinity, 0.5556, as obtained by Robinson and Knapman (1941) agrees exactly with the value that Lyman and Fleming (1940) calculated by difference. It is somewhat higher than the average of 0.5509 given by Thompson and Robinson (1932), but is in fair agreement with the ratio 0.5549 obtained by Webb (1939) by direct analysis. The sodium: chlorinity ratio may be modified near river mouths.
Magnesium content of sea water has been investigated rather carefully, particularly by Thompson and Wright (1930). The magnesium is usually determined by a special modification of the magnesium-ammonium-phosphate method. The ratio of magnesium to chlorinity is very uniform.
| Element | mg/kg Cl = 19.00 ‰ | mg-atoms/L Cl = 19.00 ‰ | Atomic weight (1940) | 1/atomic weight | Authority |
|---|---|---|---|---|---|
| Chlorine | 18980 | 548.30 | 35.457 | 0.02820 | |
| Sodium | 10561 | 470.15 | 22.997 | 0.04348 | |
| Magnesium | 1272 | 53.57 | 24.32 | 0.04112 | |
| Sulphur | 884 | 28.24 | 32.06 | 0.03119 | |
| Calcium | 400 | 10.24 | 40.08 | 0.02495 | |
| Potassium | 380 | 9.96 | 39.096 | 0.02558 | |
| Bromine | 65 | 0.83 | 79.916 | 0.01251 | |
| Carbon | 28 | 2.34 | 12.01 | 0.08326 | |
| Strontium | 13 | 0.15 | 87.63 | 0.01141 | |
| Boron | 4.6 | 0.43 | 10.82 | 0.09242 | |
| Silicon | 0.02 –4.0 | 0.0007 –0.14 | 28.06 | 0.03564 | |
| Fluorine | 1.4 | 0.07 | 19.00 | 0.05263 | |
| Nitrogen (comp.) | 0.01 –0.7 | 0.001 –0.05 | 14.008 | 0.07139 | |
| Aluminum | 0.5 | 0.02 | 26.97 | 0.03708 | |
| Rubidium | 0.2 | 0.002 | 85.48 | 0.01170 | |
| Lithium | 0.1 | 0.014 | 6.940 | 0.14409 | |
| Phosphorus | 0.001–0.10 | 0.00003–0.003 | 30.98 | 0.03228 | |
| Barium | 0.05 | 0.0004 | 137.36 | 0.00728 | |
| Iodine | 0.05 | 0.0004 | 126.92 | 0.00788 | |
| Arsenic | 0.01–0.02 | 0.00015–0.0003 | 74.91 | 0.01335 | |
| Iron | 0.002–0.02 | 0.00003–0.0003 | 55.85 | 0.01791 | |
| Manganese | 0.001–0.01 | 0.00002–0.0002 | 54.93 | 0.01820 | |
| Copper | 0.001–0.01 | 0.00002–0.0002 | 63.57 | 0.01573 | |
| Zinc | 0.005 | 0.00008 | 65.38 | 0.01530 | Atkins (1936) |
| Lead | 0.004 | 0.00002 | 207.21 | 0.00483 | Boury (1938) |
| Selenium | 0.004 | 0.00005 | 78.96 | 0.01266 | Goldschmidt and Strock (1935) |
― 177 ― Cesium | 0.002 | 0.00002 | 132.91 | 0.00752 | Wattenberg (1938) |
| Uranium | 0.0015 | 0.00001 | 238.07 | 0.00420 | Föyn et al (1939) |
| Molybdenum | 0.0005 | 0.000005 | 95.95 | 0.01042 | Ernst and Hoermann (1936) |
| Thorium | <0.0005 | <0.000002 | 232.12 | 0.00431 | Föyn et al (1939) |
| Cerium | 0.0004 | 0.000003 | 140.13 | 0.00714 | Goldschmidt (1937) |
| Silver | 0.0003 | 0.000003 | 107.880 | 0.00927 | Haber (1928) |
| Vanadium | 0.0003 | 0.000006 | 50.95 | 0.01963 | Ernst and Hoermann (1936) |
| Lanthanum | 0.0003 | 0.000002 | 138.92 | 0.00720 | Goldschmidt (1937) |
| Yttrium | 0.0003 | 0.000003 | 88.92 | 0.01125 | Goldschmidt (1937) |
| Nickel | 0.0001 | 0.000002 | 58.69 | 0.01704 | Ernst and Hoermann (1936) |
| Scandium | 0.00004 | 0.0000009 | 45.10 | 0.02217 | Goldschmidt (1937) |
| Mercury | 0.00003 | 0.0000001 | 200.61 | 0.00498 | Goldschmidt (1937) |
| Gold | 0.000006 | 0.00000002 | 197.2 | 0.00507 | Haber (1928) |
| Radium | 0.2 – 3 × 10−10 | 0.8 – 12 × 10−13 | 226.05 | 0.00442 | Evans, Kip, and Moberg (1938) |
| Cadmium | Fox and Ramage (1931) | ||||
| Chromium | Webb (1937) | ||||
| Cobalt | Thompson and Robinson (1932) | ||||
| Tin | Thompson and Robinson (1932) |
Sulphur is present in sea water as sulphate ion, and is in this form usually determined by precipitation as barium sulphate. An extensive study of the sulphate distribution has been made by Thompson, Johnston, and Wirth (1931). Under stagnant conditions occurring in certain isolated basins, and in and near bottom sediments, a part of the sulphate may be converted to sulphide ion. Considerable quantities of sulphide occur in the Black Sea and in certain Norwegian fjords, and its presence has been reported in many localities. The sulphate: chlorinity ratio may also be modified by dilution with river water, which is generally relatively high in sulphate. Processes of freezing and melting may possibly affect the relative concentration (p. 216).
Calcium is present in much smaller quantities than either sodium or magnesium, but its distribution in the ocean has been studied much more thoroughly, mainly because calcium is a major constituent of many skeletal remains found in marine sediments. By deposition of such remains calcium is permanently removed from the water, but this removal does not necessarily imply that the calcium concentration is decreasing, because a large supply is maintained by the river waters flowing into the sea. Detectable differences in the calcium: chlorinity ratio have been observed. In the Baltic, Gripenberg (1937a) has shown that the type of river water which has diluted the sea water can be determined from that ratio. Furthermore, Moberg and Revelle (1937) have demonstrated the existence of vertical differences in the calcium: chlorinity ratio which they attribute to the removal of calcium in the surface layers through biological activity. Interest in the concentration of calcium has also centered around the question of the solubility of calcium carbonate in sea water and the factors that control precipitation and solution. In certain areas calcium carbonate is apparently precipitated inorganically, and in other regions it apparently passes into solution. In addition to these problems, knowledge of the calcium concentration is important in an understanding of the carbon dioxide system in the sea, which will be discussed later. The quantity of calcium is usually determined by precipitation as the oxalate under carefully controlled conditions and subsequent titration with potassium permanganate. One such method has been described by Kirk and Moberg (1933).
Webb has pointed out that in this method for the estimation of calcium the strontium will be carried down, and hence the calcium figure will be too high by the equivalent amount of strontium. As the ratio calcium: strontium is apparently constant, Webb suggests that the “calcium” shall be taken to mean the calcium after the strontium and barium have been replaced by calcium. Since the barium is negligible in this case, the values of “calcium” will be given directly by volumetric methods, but when the quantities are determined by weighing, corrections
Potassium is the fourth most abundant cation and is present in amounts of only a few per cent of that of sodium. The potassium is rarely determined directly, but apparently it bears a very constant relationship to the chlorinity (Thompson and Robinson, 1932). However, the content of potassium may be modified by biological agencies, since some organisms, particularly the large algae, concentrate potassium to a marked degree. The ratio of the potassium to chlorinity may also be modified by dilution with river water. The potassium may react with the colloidal and clay particles brought to the sea by rivers and run-off, and consequently this agency may influence the ratio. Certain minerals formed on the sea bottom, such as glauconite, contain potassium.
Bromine shows a very constant ratio to the chlorinity and is apparently all present as bromide ion.
Discussion of the concentration of carbon in sea water is complicated by the fact that it occurs not only in the form of carbonic acid and its salts but also in appreciable amounts as a constituent of organic material, either living or dead. The detrital organic material may be either particulate or in solution. The solubility of carbon dioxide depends upon the temperature and salinity of the water, and exchange of carbon dioxide with the atmosphere takes place at the surface. Photosynthesis in the surface layers reduces the amount of carbon dioxide in the water, and respiration increases the concentration. Consequently, the quantities of carbon present as either free carbon dioxide, bicarbonate, or carbonate will show a considerable range. These problems will be discussed in the sections dealing with the carbon dioxide system in the sea. The quantity of carbon given in table 36 was calculated on the assumption that only bicarbonate ions were present. The organic carbon, which is probably of the order of 2 to 3 mg/L (0.15 to 0.25 mg-atoms/L), was not included. The methods by which the different carbon dioxide components and the particulate and dissolved organic carbon may be determined are discussed later.
Strontium has not been investigated in detail, as it is extremely difficult to determine quantitatively. In determinations of calcium by means of the oxalate precipitation, the strontium is carried down with the calcium, and consequently the ratio of calcium: chlorinity usually reported for sea water represents the calcium plus strontium reported as calcium. Strontium is a constituent of the calcareous skeletons of certain organisms.
Boron occurs in sea water in a surprisingly high concentration and bears a constant relationship to the chlorinity. Apparently it is present as undissociated boric acid. There has been considerable uncertainty as to the form in which boron occurs, but the method of determination is standardized against boric acid and the values can at least be expressed as equivalent to a certain concentration of boric acid. The determination of boric acid in sea water is based on titration with very dilute sodium hydroxide in the presence of mannitol. Methods have been described by Harding and Moberg (1934) and by Igelsrud, Thompson, and Zwicker (1938). The amount of boron present in sea water is of interest in the carbonate equilibria and in this connection will be discussed later. Boron is concentrated by certain marine organisms.
Silicon has been studied extensively because it is utilized by diatoms and other silica-secreting organisms. According to a tabulation by Thompson and Robinson (1932), the silicate-silicon varies by more than one hundredfold—namely, from 0.0007 to 0.11 mg-atoms/L (0.02 to 3.0 mg/L). Clowes (1938) found values slightly exceeding .14 mg-atoms/L (4.0 mg/L) in the deep waters of the Antarctic. Surface samples are usually low, owing to the development of silica-secreting organisms, but a progressive increase in silicate takes place with depth, which is ascribed to the dissolving of soluble silicates. However, there is always the possibility that the water contains silicon in some compound present in colloidal form. River water contains a high content of silicon, both in solution and as colloidal particles. Diatom and radiolarian oozes contain the siliceous remains of organisms that have developed near the surface and settled to the bottom after their death. Although siliceous deposits of organic origin cover large areas, most of the siliceous skeletal remains dissolve after the death of the organisms. Silicon present as soluble silicate is determined colorimetrically. The method has been described by Thompson and Houlton (1933) and by Wattenberg (1937). Because of the rapidity with which water samples are contaminated by silicate that dissolves from the glass, the analyses should be made soon after the water samples are collected. Waxed containers are sometimes recommended, and it is always desirable to use “aged” bottles that have been thoroughly leached with sea water. Tourky and Bangham (1936) tested the reaction between the molybdate reagent and colloidal silica and found that the color development was not proportional to the amount of silicon present. Treatment of the colloidal silica with alkali prior to analysis yielded correct values. Experiments with sea water indicated that colloidal silica may pass into true solution on ageing.
Fluorine is present in oceanic sea water in concentrations slightly above 1 mg/L. It is present as fluoride and, according to the work of Thompson and Taylor (1933), bears a constant ratio to the chlorinity.
The method of determination is described by these authors. Little is known concerning the role of fluorine in the sea.
Nitrogen occurs in sea water both in compounds of various kinds and as free dissolved nitrogen gas. As it is an essential constituent of living matter, nitrogen is found in organic compounds both in organisms and in particulate and dissolved organic material in amounts between 0.1 and 10.0 μg-atoms/L (p. 254). In addition, it is present as nitrate, nitrite, and ammonia. In routine observations only the inorganic nitrogen compounds are determined. Nitrate- and nitrite-nitrogen are determined colorimetrically, and the ammonia either colorimetrically (Robinson and Wirth, 1934) or by micro-titration after distillation (Krogh, 1934).
The nitrate method originally described by Harvey (1926) is given by Wattenberg (1937). Rakestraw (1936) and Wattenberg describe the procedure for the determination of nitrite. Since the inorganic nitrogen compounds are subject to change after the water samples have been collected, analyses must be run within a few hours. Even the addition of preservatives may not prevent changes in the NH3 and NO2, indicating that purely chemical transformations may be involved. Ammonia tends to disappear in storage, and nitrite sometimes decreases, but at other times shows an increase. The nitrate, which is more abundant, does not show such relatively large changes.
Because of their relatively low concentrations and their utilization by organisms, the inorganic nitrogen compounds show a wide range in values:
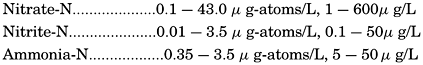
Nitrogen compounds are carried to the sea by rivers and by precipitation. The greater part of these are supposed to have been fixed by electrical discharges in the atmosphere. Possibly a certain amount of the fixed nitrogen in the sea is liberated as free nitrogen and returned to the atmosphere. Bottom sediments contain a small percentage of organic nitrogen in resistant organic detritus, and a part of this is
Aluminum is present in sea water in very small amounts. The colloidal clay particles which are carried to the sea contain a large percentage of aluminum, and hence analyses of water samples collected near shore may show the presence of aluminum, but it is not necessarily all in solution. The value given in table 36 is the average quantity reported by Haendler and Thompson (1939). Their values range between 0.006 and 0.065 mg-atoms/L (0.16 and 1.8 mg/L) with an average of 0.02 mg-atoms/L (0.54 mg/L).
Although earlier workers (Thompson and Robinson, 1932) were unable to detect rubidium in sea water, Goldschmidt (1937) has reported about 0.002 mg-atoms/L (0.2 mg/L).
Lithium content of sea water has been investigated by Thomas and Thompson (1933), who found 0.014 mg-atoms/L (0.1 mg/L).
Phosphorus, which is present in sea water as phosphate ions, is another of the essential constituents of living organisms, and its distribution in the sea is markedly affected by organic agencies. In addition to the nitrogen and silicon compounds, phosphate-phosphorus has been considered as one of the substances that may limit production of plant life. The inorganic phosphorus concentration varies from virtually zero at the surface, under certain conditions, to approximately 0.003 mg-atoms/L (0.090 mg/L) at subsurface levels when values are corrected for salt error. There is frequently a subsurface maximum similar to that in the distribution of nitrate-nitrogen. Phosphorus removed from the surface layers by phytoplankton is largely returned to solution on the death and decomposition of the organisms. It is supplied by rivers, and some is removed from the sea, as a small quantity is present in most marine sediments. In certain shallow areas, phosphatic concretions are found that contains a rather high concentration of phosphorus. The mode of origin of these concretions is not yet known. It has been suggested that in many regions the water is supersaturated in respect to tricalcium phosphate which, therefore, may be deposited inorganically (Dietz, Emery, and Shepard, 1942).
Phosphate phosphorous is determined colorimetrically. The method has been described by Robinson and Wirth (1935) and Wattenberg (1937). Cooper (1938a) has discussed the magnitude of the salt error. Phosphate analyses are frequently carried out as routine observations, and our knowledge of the distribution of phosphate in the ocean is fairly comprehensive. The rather scant knowledge we have concerning the
The amount of barium in sea water has been reported by Goldschmidt (1937) as 0.0004 mg-atoms/L (0.05 mg/L). This is lower than the values reported by Thompson and Robinson (1932). Barium occurs in marine organisms and it is a constituent of most marine sediments. In certain localities the deposits contain large amounts of barium sulphate in the form of concretions and nodules. The mode of formation of these structures is not yet understood.
The distribution and concentration of iodine in the sea has received a great deal of attention because of its important role in the physiology of man and terrestrial animals. Marine products are an important source of iodine-rich foods, The form in which iodine occurs in sea water is not yet clearly understood, but at least part of it is present as iodide and iodate. It is concentrated to a marked degree by marine plants, and for many years sea weeds have been used as a commercial source of iodine. The distribution and determination of iodine in sea water and marine organisms have been discussed by Closs (1931) and Reith (1930).
Arsenic content of sea water has been investigated by Rakestraw and Lutz (1933), who report values ranging from 0.15 to 0.3 μg-atoms/L (9 to 22 μg/L). This wide range is attributed to the fact that organisms may utilize arsenic in place of phosphorus. It is known to be a constituent of the tissues of many marine forms. The exact form in which arsenic occurs in sea water is not yet known.
Iron is an essential constituent of plants and has been considered as one of the substances that may limit the amount of plant production in the sea. Investigations show that at least part of the iron is not present in true solution, as it can be removed by ultrafiltration. Cooper (1937b) has pointed out that the amount of iron in true solution as ferric or ferrous salts is probably less than 2 μg/L, whereas the total iron present is generally about ten times this quantity. The amount present in the plankton may be as much as 16 per cent of the total iron of the water. Harvey (1937) considers that diatoms are able to adsorb and utilize colloidal iron. Iron is brought to the sea in relatively large quantities in the colloidal clay particles, and consequently considerable amounts of iron are found in the marine sediments. In many instances the iron content of the sediments is even higher than should be expected, indicating addition of iron through physical, chemical, or organic agencies. In inshore areas near the source of supply the total iron content of the water is sometimes much higher than that found in the open ocean. Methods for the determination of iron in sea water in its various forms have been described by Thompson and Bremner (1935a and b), Cooper (1935), and Rakestraw, Mahnke, and Beach (1936).
Manganese is apparently subject to concentration by marine organisms. Thompson and Wilson (1935) have reported values between 0.02 and 0.2 mg-atoms/L (1 and 10 mg/L). The value cited by Goldschmidt (1937) is 4 mg/L. Interest in manganese has been aroused by the occurrence of manganese nodules which are widely distributed in certain types of marine sediments, particularly in the Pacific Ocean.
The quantity of copper present in sea water probably lies between 0.02 and 0.2 μg-atoms/L (1 to 10 μg/L) (Marks, 1938, Wattenberg, 1938). Copper is an essential constituent of many marine organisms and it is also considered a factor in the life history of oysters, as a relatively high copper content of the water is apparently necessary for proper development of the larvae.
Much interest is attached to the content of radioactive elements in sea water, because deep-sea sediments are high in radium, compared to igneous rocks, and it is considered that the enrichment must be due to precipitation from the water of radium or its precursors. The radium content of sea water has been studied by many investigators, using various techniques, but it is only recently that methods have been sufficiently refined to yield trustworthy results. Studies by Evans, Kip, and Moberg (1938) and by Pettersson and Rona (Föyn et al, 1939) show that the radium content, measured by the radon emanation technique, varies between about 0.2 and 3.0 × 10−13 ‰ in sea water of salinity approximately 35 ‰. The low values are found in the surface layers, and it is suggested that organisms are responsible for a selective removal of this element. Both groups of workers found that organisms concentrate the radium about one hundredfold in their soft tissues. Calcareous structures show an increase in the radium:calcium ratio over that in the water. The maximum value listed above—namely 3.0 × 10−13 ‰— was found in water in contact with the sediments (Evans, Kip, and Moberg, 1938), and generally the radium content of the deeper waters is about 1 × 10−13 ‰.
Pettersson and co-workers (Föyn et al, 1939) have emphasized the importance of searching for the radioactive precursors of radium, as this element has the relatively short half-life period of only 1690 years. Of these elements uranium and ionium are probably the most; important, but thus far only uranium has been examined. Karlik (Föyn et al 1939) has analyzed a number of samples from various parts of the oceans and obtained for oceanic water a mean value of 1.5 × 10−6 ‰. Surface waters have a somewhat lower content than those from greater depths, but Karlik does not consider that the data are sufficiently adequate to show any differential removal. Studies of the dilute waters of the Baltic Sea showed that the uranium content was a function of the salinity.
Föyn and Rona (Föyn et al) have sought for thorium in sea water, but have been unable to detect it by the most refined methods. By examining
The radium content of marine sediments and the theories concerning the deposition of radium and its precursors are discussed in the chapter on marine sedimentation.
Preparation of Artificial Sea Water
It is impossible to prepare solutions that exactly duplicate the properties of sea water because (1) the ions (salts) in which the elements occur in sea water are not always known, (2) elements that occur in sea water in small amounts are present as contaminants in other compounds in quantities which may far exceed those that should be added, and (3) many of the salts which must be added in fairly large amounts are hygroscopic or contain water of crystallization and are difficult to weigh accurately. The latter difficulty may be partially avoided by preparing concentrated solutions of these salts, determining their concentration by chemical analysis, and adding the required volume of the solution.
Although it would be of great interest to prepare solutions duplicating all the physical and chemical properties of sea water, it is generally not essential. In studies of certain of the physical-chemical properties, it is sufficient to add to the solution only the more abundant ions. In other instances—for example, when chemical methods are to be standardized—only one element or ion need be accurately known and other ions only approximately. Furthermore, in experiments with marine plants the major elements may not have to be closely controlled, but it will generally be necessary to know the concentrations of the biologically essential elements that are normally present in small amounts. If possible, natural sea water should always be used in physical or biological studies, but in the latter case it is sometimes desirable to enrich the water with certain of the plant nutrients (p. 235). Rogers (1938) has discussed various “modified ” types of solutions that are used in experiments on marine animals.
In table 37 are given three suggested formulae for preparing solutions approximating the composition of sea water. They have been adjusted to yield solutions of 19.00 ‰ chlorinity. The recipe of McClendon et al (1917), which has been used quite extensively, contains the nitrogen, phosphorus, and silicon needed by marine plants. Additional elements may be necessary but are probably always present as impurities. The formulae of Brujewicz (Subow, 1931) and of Lyman and FIeming (1940) contain only the major elements. The last-mentioned recipe corresponds to the composition of sea water given in table 35. The other formulae have not been adjusted to the composition presented in earlier sections of
| McClendon et al (1917) | Brujewicz (Subow, 1931) | Lyman and Fleming (1940) | |||
|---|---|---|---|---|---|
| Salt | g/kg | Salt | g/kg | Salt | g/kg |
| NaCl | 26.726 | NaCl | 26.518 | NaCl | 23.476 |
| MgCl2 | 2.260 | MgCl2 | 2.447 | MgCl2 | 4.981 |
| MgSO4 | 3.248 | MgSO4 | 3.305 | Na2SO4 | 3.917 |
| CaCl2 | 1.153 | CaCl2 | 1.141 | CaCl2 | 1.102 |
| KCl | 0.721 | KCl | 0.725 | KCl | 0.664 |
| NaHCO3 | 0.198 | NaHCO3 | 0.202 | NaHCO3 | 0.192 |
| NaBr | 0.058 | NaBr | 0.083 | KBr | 0.096 |
| H3BO3 | 0.058 | H3BO3 | 0.026 | ||
| Na2SiO3 | 0.0024 | SrCl2 | 0.024 | ||
| Na2Si4O9 | 0.0015 | NaF | 0.003 | ||
| H3PO4 | 0.0002 | ||||
| Al2Cl6 | 0.013 | ||||
| NH3 | 0.002 | ||||
| LiNO3 | 0.0013 | ||||
| Total | 34.4406 | 34.421 | 34.481 | ||
| Water to 1,000.0000 | Water to 1,000.000 | Water to 1,000.000 | |||
Dissolved Gases in Sea Water
All of the atmospheric gases are found in solution in sea water. In addition to nitrogen and oxygen, the most abundant gases in the air, carbon dioxide is present in large quantities in sea water, chiefly combined as carbonates and bicarbonates. Of the rarer gases, ammonia, argon, helium, and neon have been reported in sea water, and hydrogen is undoubtedly present in minute quantities. In the absence of dissolved oxygen, hydrogen sulphide may be present, and it is possible that in stagnating water other products of putrefactive decomposition, such as methane, may occur.
Because of its importance in biological processes the dissolved oxygen distribution in the oceans has been examined intensively. Besides being an index to the biological history of the water, the general character of the distribution of oxygen in the deeper water is helpful in studies of currents and of mixing processes. The carbon dioxide distribution is of equal biological importance; its discussion begins on p. 192. Nitrogen has not been studied very widely, as it is apparently chemically inert. Argon is also inert, and is sometimes included with the nitrogen when the
Determination of Dissolved Gases. The content of dissolved oxygen is usually determined by the Winkler method, which depends upon the oxidation of manganous hydroxide by the dissolved oxygen. When acid is added, the oxidized manganese reacts with potassium iodide and sets free iodine, in amounts equivalent to the original dissolved oxygen content, which is determined by titration with sodium thiosulphate. The Winkler method is simple and extremely accurate if certain precautions are observed in handling the water samples and reagents (Thompson and Robinson, 1939).
Problems relating to the determination of carbon dioxide are discussed on p. 192.
Dissolved nitrogen cannot be determined by direct chemical methods, and hence gasometric techniques must be used. In general, the sea-water sample is acidified and all the gases are driven off by boiling or by applying a vacuum. The carbon dioxide is then absorbed in alkali, and the oxygen is absorbed in alkaline pyrogallol. The residual gas is sometimes considered as “atmospheric nitrogen,” although actually there are other gases, principally argon, mixed with it. Rakestraw and Emmel (1937) developed a method for determining the dissolved oxygen and nitrogen content of sea water by first extracting the gases and removing the carbon dioxide, then absorbing the oxygen on phosphorus and the nitrogen on molten lithium. The oxygen contents determined in this way agreed with direct Winkler analyses. The nitrogen determinations on saturated water samples showed results consistently lower than the saturation values according to Fox (1907); further studies (Rakestraw and Emmel, 1938b) indicate that Fox's tables are slightly in error. The gases remaining after the extraction of nitrogen are considered as “argon.”
The presence of hydrogen sulphide can be detected by its characteristic odor. A method for its determination has been described by Gaarder (1916). Although commonly referred to as hydrogen sulphide, a part, at least, will not be present as free gas but as sulphide or bisulphide of some base. A hydrogen sulphide system somewhat comparable to the carbon dioxide system must exist, but it has not yet been investigated.
The determination of ammonia is discussed in the section dealing with nitrogen compounds.
The units to be used in reporting the concentrations of dissolved gases are mg-atoms/L or (ml of gas at NTP)/L.
In some cases it is of interest to know the excess or deficiency of the concentration with respect to water of the same temperature and salinity in equilibrium with the normal dry atmosphere. The saturation values for oxygen and nitrogen are given in tables 38 and 39. If the saturation
| Chlorinity (‰) | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|
| Salinity (‰) | 27.11 | 28.91 | 30.72 | 32.52 | 34.33 | 36.11 |
| Temperature (°C) | ||||||
| –2 | 9.01 | 8.89 | 8.76 | 8.64 | 8.52 | 8.39 |
| 0 | 8.55 | 8.43 | 8.32 | 8.20 | 8.08 | 7.97 |
| 5 | 7.56 | 7.46 | 7.36 | 7.26 | 7.16 | 7.07 |
| 10 | 6.77 | 6.69 | 6.60 | 6.52 | 6.44 | 6.35 |
| 15 | 6.14 | 6.07 | 6.00 | 5.93 | 5.86 | 5.79 |
| 20 | 5.63 | 5.56 | 5.50 | 5.44 | 5.38 | 5.31 |
| 25 | 5.17 | 5.12 | 5.06 | 5.00 | 4.95 | 4.86 |
| 30 | 4.74 | 4.68 | 4.63 | 4.58 | 4.52 | 4.46 |
| * mg-atoms of oxygen per liter = 0.08931 × ml/L. | ||||||
| Chlorinity (‰) | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
|---|---|---|---|---|---|---|---|
| Salinity (‰) | 27.11 | 28.91 | 30.72 | 32.52 | 34.33 | 36.11 | 37.94 |
| Temperature (°C) | |||||||
| 0 | 15.22 | 15.02 | 14.82 | 14.61 | 14.40 | 14.21 | 14.01 |
| 5 | 13.43 | 13.26 | 13.10 | 12.94 | 12.78 | 12.62 | 12.45 |
| 10 | 12.15 | 12.00 | 11.86 | 11.71 | 11.56 | 11.42 | 11.27 |
| 15 | 11.04 | 10.92 | 10.79 | 10.66 | 10.53 | 10.39 | 10.26 |
| 20 | 10.08 | 9.98 | 9.87 | 9.76 | 9.65 | 9.54 | 9.43 |
| 25 | 9.30 | 9.21 | 9.11 | 9.02 | 8.92 | 8.82 | 8.73 |
| 28 | 8.89 | 8.84 | 8.72 | 8.62 | 8.53 | 8.44 | 8.35 |
| * mg-atoms of nitrogen per liter = 0.08929 × ml/L. | |||||||
The dissolved oxygen in the sea varies between zero and 0.75 mg-atoms/L (about 8.5 ml/L), although in areas of low temperature and intense photosynthesis the content may exceed this upper limit. Nitrogen, which is apparently unaffected by biological processes, varies between 0.75 and 1.3 mg-atoms/L (8.4 and 14.5 ml/L). The total
Factors Controlling the Distribution of Dissolved Gases. The following general factors control the distribution of dissolved gases in the oceans: (1) temperature and salinity, which determine the concentrations when the water is at the surface and in equilibrium with the atmosphere, (2) biological activity, which markedly affects the concentrations of oxygen and carbon dioxide, (3) currents and mixing processes, which tend to modify the effects of biological activity through mass movement and eddy diffusion.
Water in contact with the atmosphere will tend to reach equilibrium either by giving up or absorbing the individual gases until the water is just saturated. Although the zone of contact is a thin one, convective movements due to cooling, evaporation, or wind action may bring a layer of considerable thickness into equilibrium with the atmosphere. According to Henry's law the concentration, m, of a gas in a liquid is related to the partial pressure, p, of the gas and to the character of the gas and the liquid: m = csp. The numerical value of cs, the coefficient of saturation (absorption), depends upon the units for expressing the concentration of the gas in the solution and its pressure, and upon the chemical character of the gas and the temperature and salinity of the water.
| Gas | Percent of volume or pressure | Partial pressure, Torr |
|---|---|---|
| Nitrogen | 78.03 | 593.02 |
| Oxygen | 20.99 | 159.52 |
| Argon | 0.94 | 7.144 |
| Carbon | 0.03 | 0.228 |
| Hydrogen, | 0.01 | 0.088 |
| 100.00 | 760.000 |
With the exception of water vapor the relative composition of the atmosphere can be considered for practical purposes as constant (table 40). This does not strictly apply to carbon dioxide, relatively slight changes in the partial pressure of which have a pronounced effect upon
The solubilities of those gases, such as oxygen and nitrogen, which do not react chemically with the water or its dissolved salts decrease with increasing temperature and salinity. The solubilities of oxygen and nitrogen in sea water of different salinities over the normal range of temperature were investigated by Fox (1907, 1909). Fox's values for oxygen are still the accepted standards, but his data for nitrogen have been superseded by those of Rakestraw and Emmel (1938b). The solubility of carbon dioxide is greater than that of oxygen and nitrogen because it reacts with the water. Part of the carbon dioxide is present as free CO2 and H2CO3, but in sea water by far the greater part is present as carbonates and bicarbonate, and for the same partial pressure the total CO2 content of sea water is much greater than that of distilled water or neutral salt solutions. The content of free CO2 and H2CO3 decreases with increasing temperature and salinity. Argon is sometimes included with the “atmospheric nitrogen,” and, because its solubility differs from that of nitrogen, the values of the saturation coefficients will be slightly modified. Little is known concerning the other gases in sea water; however, both hydrogen sulphide and ammonia are very soluble gases and their saturation values can play no important part in their distribution.
In table 41 are given values of the saturation coefficients (absorption coefficients) for oxygen, nitrogen, and carbon dioxide in fresh and sea water at different temperatures. The values for oxygen are from Fox (1909), as are also the values for nitrogen in distilled water. The other nitrogen values are from Rakestraw and Emmel(1938b). The values for carbon dioxide (Buch et al, 1932) correspond to the total CO2 in water of zero alkalinity or to the free CO2 and H2CO3 in sea water. It is seen that carbon dioxide is much more soluble than the other two gases and that oxygen is about twice as soluble as nitrogen.
From table 41 it is seen that within the range of chlorinity normally encountered in the oceans the temperature is the most important property influencing the solubility (see also tables 38, 39).
In studies of the distribution of dissolved gases in the sea it is generally assumed that, whatever the location of a water particle, at some time it has been at the surface and in equilibrium with the air. In their studies of the dissolved nitrogen content Rakestraw and Emmel (1938a) have found that the water is virtually saturated (referred to a normal atmosphere), regardless of depth; therefore this assumption appears valid and also indicates that biological activity involving either fixation or production of nitrogen cannot be sufficient to affect significantly the concentration of this gas in the water. As the waters of the oceans appear to have been saturated with oxygen and carbon dioxide at some stage in their history when they were at the surface, the differences between the saturation values (computed from the temperatures and salinities) and the observed contents are measures of the changes which have been effected by biological agencies. The factors influencing the distribution of carbon dioxide are discussed in the following sections, and the distribution of dissolved oxygen will be considered in many places in the ensuing chapters.
| Temperature | 0° | 12° | 24° | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Chlorinity (‰) | O2 | N2 | CO2 | O2 | N2 | CO2 | O2 | N2 | CO2 | |||||||||
| ml/L | mg-atoms O/L | ml/L | mg-atoms N/L | ml/L | mg-atoms C/L | ml/L | mg-atoms O/L | ml/L | mg-atoms N/L | ml/L | mg-atoms C/L | ml/L | mg-atoms O/L | ml/L | mg-atoms N/L | ml/L | mg-atoms C/L | |
aFox (1909). | ||||||||||||||||||
bDistilled water, Fox (1909); sea water, Rakestraw and Emmel (1938b). | ||||||||||||||||||
cBuch et al (1932), after Bohr. Concentrations represent amounts of free CO2 and H2CO3. | ||||||||||||||||||
| 0 | 49.24 | 4.40 | 23.00 | 2.06 | 1715 | 77.0 | 36.75 | 3.28 | 17.80 | 1.59 | 1118 | 50.2 | 29.38 | 2.62 | 14.63 | 1.31 | 782 | 35.1 |
| 16 | 40.1 | 3.60 | 15.02 | 1.73 | 1489 | 66.8 | 30.6 | 2.75 | 11.56 | 1.33 | 980 | 44.0 | 24.8 | 2.22 | 9.36 | 1.08 | 695 | 31.2 |
| 20 | 38.0 | 3.40 | 14.21 | 1.64 | 1438 | 64.5 | 29.1 | 2.61 | 10.99 | 1.26 | 947 | 42.5 | 23.6 | 2.12 | 8.96 | 1.03 | 677 | 30.4 |
The Carbon Dioxide System
Although an extensive literature exists concerning the carbon dioxide system in sea water, publications prior to about 1929 are now chiefly of historic interest. The solution of the problems involved awaited not only the development of suitable analytical methods for the determination of the total carbon dioxide and the various forms in which it is present in sea water, but also the development of the theory and methods for studying the hydrogen ion concentration and certain general theories in physical chemistry. In the brief discussion to follow, only the salient features of the contemporary theories will be presented. These may be adequate for many purposes, but the investigations are not yet closed. Methods of analysis require further refinements, and in many cases fundamental constants must be more accurately determined.
Early investigators studying the carbon dioxide in sea water attempted to apply methods similar to those used for fresh water, where the carbon dioxide is largely present as free carbon dioxide that can be driven off by boiling, by applying a vacuum, or by bubbling through the water a stream of CO2-free gas. The use of such methods on sea water gave variable and conflicting results. It was later found that in order to drive off all the CO2 a strong acid must be added to the water, indicating that at least part of the carbon dioxide was present as the carbonate or bicarbonate of some basic cation. Methods were then developed for the determination of the total carbon dioxide and also for measuring the quantity present as carbonate and bicarbonate ions. It is now considered that the CO2 can exist in the following forms in sea water and that under any given set of conditions equilibria will prevail:
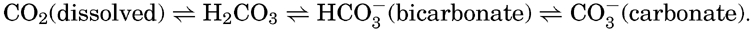
From the foregoing discussion it can be seen that the total CO2 in sea water does not follow Henry's law for the solution of gases in inert solutions. Nevertheless, the partial pressure of the carbon dioxide in sea water in contact with the atmosphere will tend to establish equilibrium with that in the air. If the pressure is increased the amount in solution will be greater, and if it is reduced the quantity of CO2 will decrease. The quantity present in a sample of water in equilibrium with a given carbon dioxide pressure will depend on the concentration of carbon dioxide bound base and the temperature and salinity of the water sample. If these factors are kept constant, the partial pressure of CO2 can be used as a measure of the total carbon dioxide content of the water.
Hydrogen Ion Concentration (pH) of Sea Water. Sea water is normally alkaline. Since both the H+ and OH− ions play parts in the equilibria, any understanding of the carbon dioxide system requires knowledge of their concentrations. Pure distilled water dissociates into hydrogen and hydroxyl ions:
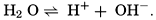
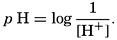 . Thus, a neutral solution has a pH of approximately 7, an acid solution a pH less than 7, and an alkaline solution a pH greater than 7. It should be noted that a unit change in pH corresponds to a tenfold change in the hydrogen ion and hydroxyl ion concentrations.
. Thus, a neutral solution has a pH of approximately 7, an acid solution a pH less than 7, and an alkaline solution a pH greater than 7. It should be noted that a unit change in pH corresponds to a tenfold change in the hydrogen ion and hydroxyl ion concentrations.The hydrogen ion concentration, or pH, of a solution may be determined in various ways, but all are essentially either electrometric or
Certain organic compounds classed as indicators have the property of changing color over a given range of hydrogen ion concentration. So-called bicolor indicators have one color when in an “acid” solution and another color when in an “alkaline” solution. For any indicator the color change takes place over a definite range in pH, and, at the hydrogen ion concentration that is numerically equal to the dissociation constant of the indicator, equal quantities of both color phases are present in the solution. The range in pH for which various indicators can be used is described by Clark (1928), who also gives in detail the methods for preparing the indicators. For sea water, cresol red and phenol red are generally used, as they cover the pH range normally found in the sea. When working in high pH ranges, bromthymol blue is commonly used.
Three important properties of pH indicators must be known before they can be applied to sea water: the dissociation constant of the indicator, the effect of temperature upon this value, and the salt error. The presence of neutral ions in the solution has a pronounced effect upon the color and, hence, upon the apparent pH as determined by indicators. This is known as the salt error. In general, neutral salts increase the apparent dissociation constant of the indicator, and therefore give low pH readings. In practice a carefully controlled quantity of an indicator solution is added to a sample of sea water, and either the color developed is compared to a set of tubes containing the equivalent quantity of indicator in solutions of known pH or the sample is examined in a bicolorimeter. The accepted colorimetric technique used for determining the pH of sea-water samples and the correction to be applied for salt error and temperature effects are described by Buch (1937) and by Buch and Nynäs (1939). Because of the effects of changes in temperature and pressure upon the dissociation constants of carbonic acid (p. 200) the measured pH of a sea-water sample will differ from the pH in situ. The magnitude of the temperature correction is given by Buch (1937), and the effect of pressure upon the pH has been studied by Buch and Gripenberg (see Buch et al, 1932).
The pH encountered in the sea is between about 7.5 and 8.4. That is, the hydrogen ion concentration ranges from 32 × 10−9 to 4 × 10−9
Alkalinity and Carbon Dioxide Components. The total amount of carbon dioxide in sea water, present either as free gas or bound, may be determined gasometrically after a strong acid has been added to the water to break up the carbonate compounds. Such a method has been described by Greenberg, Moberg, and Allen (1932). In order to determine the carbon dioxide components—namely, the amounts present as carbonic acid (including the free CO2), bicarbonate, and carbonate—titrations must be made. For a given sample of sea water the amount of a strong acid (usually HCl about 0.01 normal) necessary to reduce the pH to about 4.5 is independent of the total CO2. This amount of acid is required to set free the weak acids whose anions have been bound against basic cations. It is therefore not only a measure of the quantity of anions of weak acids in the sample, but also of the cations balanced against them. This quantity, when expressed as the number of milliequivalents of hydrogen ions (mg-atoms of H+) necessary to set free the ions of weak acids in a volume of water which at 20° has a volume of 1 L, is known as the alkalinity. This quantity has also been referred to as the titratable base, excess base, titration alkalinity, and buffer capacity. The term alkalinity has been adopted as the standard designation by the International Association of Physical Oceanography (1939). It should be noted that the term as here defined has no relation to the hydroxyl ion concentration or to the fact that sea water is normally alkaline.
A number of methods have been suggested for determining the alkalinity, and these have been summarised by Thompson and Robinson (1932) and Gripenberg (1937b). In general, they follow one of two techniques. Either the titration is carried out in the presence of the carbon dioxide, in which case the end point is taken at about 4.5, or the carbon dioxide is driven off. In the latter case a higher pH, about
The alkalinity bears a fairly constant relation to the chlorinity. The alkalinity: chlorosity factor for surface water has been determined by a number of workers and found to be close to 0.120 when the alkalinity is expressed in terms of milligram-atoms. The designation specific alkalinity that has been used in some cases is obtained by dividing the alkalinity, as mg-atoms/L, by the chlorinity, in g/kg, but such a mixed ratio should not be used. In water from greater depths the ratio may be somewhat higher than that given above, approaching an upper limit of 0.125 near the sea floor (Wattenberg, 1933). In brackish water the ratio may be increased tremendously if the river water is high in bound carbonate compounds. When the alkalinity: chlorosity factor is to be used as an index in studies of industrial pollution, the “normal” change in the ratio with concentration must first be established in samples of sea water diluted with unpolluted river water. Observations by Moberg and Revelle (1937) and by Wattenberg (1936) have shown that in oceanic water the increase in the Ca:Cl factor with depth is equivalent to the rise in the alkalinity:Cl factor. This indicates that changes in the alkalinity and calcium are of common origin—namely, precipitation or solution of CaCO3. Further material concerning the regional variations in the alkalinity: chlorosity factor is given on p. 208.
Because variations in the alkalinity: chlorosity factor in oceanic water are associated with corresponding changes in the calcium: chlorosity factor, the calcium content of the water may be computed from the alkalinity by the following expression:
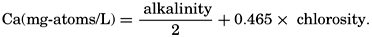
It may be seen that the alkalinity: chlorosity factor of 0.1205 is the same as the HCO3−:Cl factor given in table 35, when the bicarbonate is expressed as milligram-atoms of carbon per liter. The reason for this identity is that, in preparing the table, it was assumed that the pH of the water was such that only bicarbonate ions were present and, hence, would be equivalent to the alkalinity.
In discussions of the carbon dioxide system in sea water, the concentrations of the components have commonly been given in millimoles per liter. These are numerically identical with concentrations given as mg-atoms/L of carbon.
Salts of weak acids containing the following elements are known to occur in sea water: carbon, boron, phosphorus, arsenic, and silicon. Of these, salts of carbonic and boric acid only are present in sufficient concentrations to affect the magnitude of the alkalinity. For the present, we shall neglect the boric acid, which does not affect the alkalinity determination and which has to be considered in the carbonate system only at higher pH's. The alkalinity may then be taken as a measure of the concentration of bicarbonate and carbonate ions, and
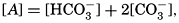
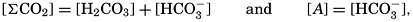
Studies of the carbon dioxide system based on measurements made by these methods have been reported by Greenberg, Moberg, and Allen (1932) and Moberg, Greenberg, Revelle, and Allen (1934). In fig. 38 are shown vertical distribution curves for the carbon dioxide components, total carbon dioxide calculated from the titrations and by direct gasometric measurements, and the alkalinity at a station off the coast of southern California. The total CO2 obtained by the two methods agrees very well and shows a general increase with depth. In the upper layers there is an appreciable amount of CO3−, but this decreases to zero at 200 m, and below this level H2CO3 occurs in quantities which increase with depth. The alkalinity is indicated for the upper 200 m, below which it corresponds, of course, to the curve showing the amount of HCO3−. The increase of alkalinity with depth may be partly due to the biological precipitation of CaCO3 in the upper layers, but in this area it is principally associated with the increasing salinity.
We shall now proceed to a discussion of the laws governing the equilibria between the various carbon dioxide components, the alkalinity,
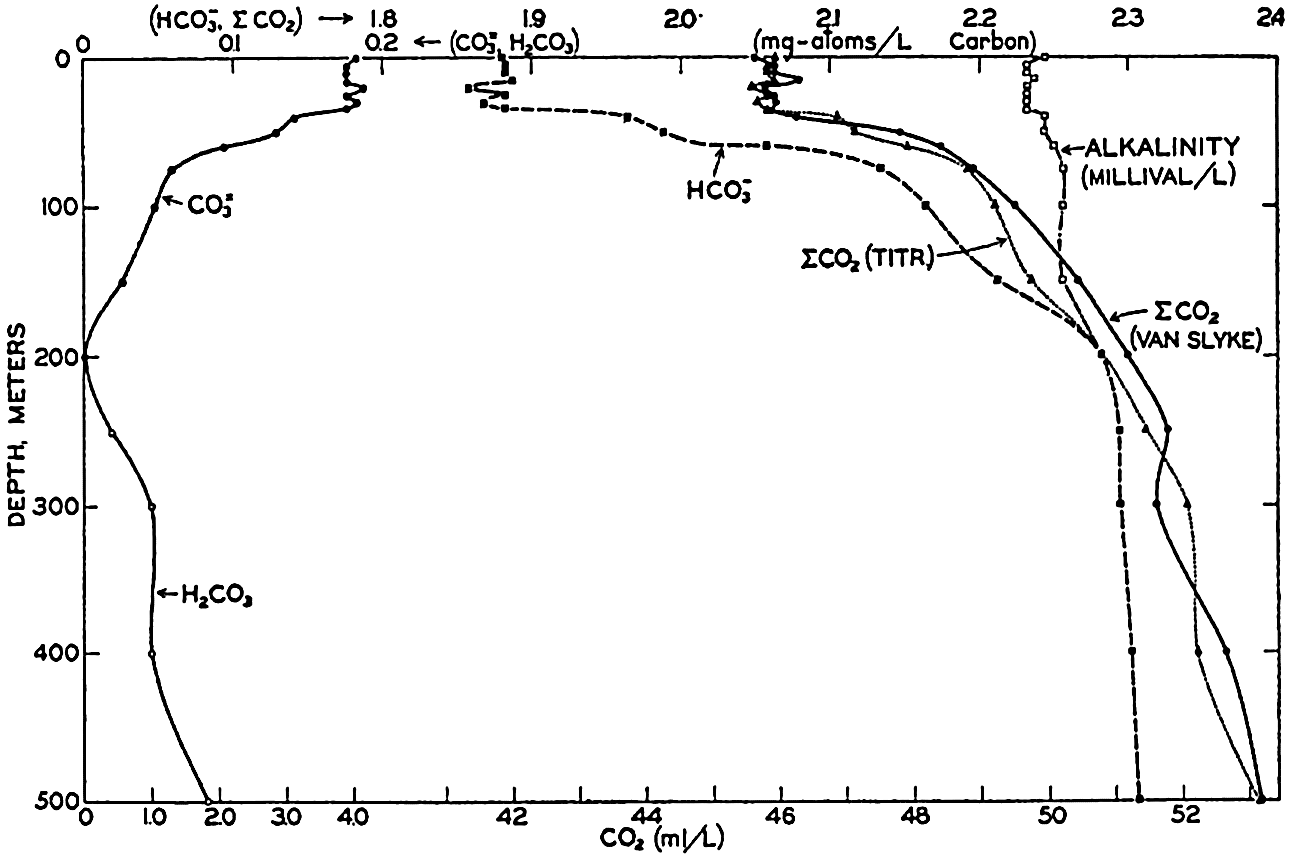
Vertical distribution of the alkalinity and carbon dioxide components off southern California.
If we indicate the portion of the base (alkalinity) directly bound to the carbon dioxide components as ACO2, the relationship may be written (Buch, 1933a,b)
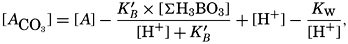
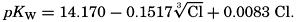
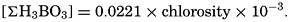
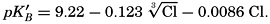
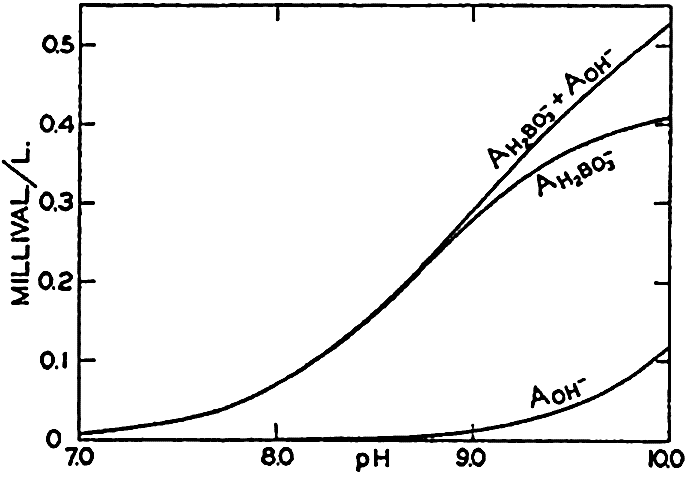
Concentrations of hydroxidebound (AOH−) and borate-bound (AH2BO3−) base as a function of pH in water of Cl = 19.00 ‰ at 20°C.
The equation for the first dissociation constant of carbonic acid is
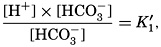
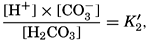
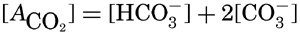
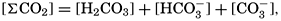
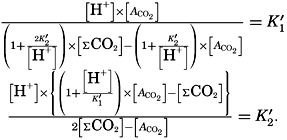
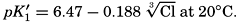
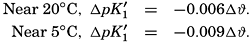
The effect of hydrostatic pressure, as expressed by means of the depth Δz in meters, on the first dissociation constant is
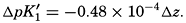
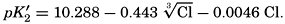
Over the normal range of chlorinity in sea water a simpler expression is adequate—namely,
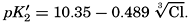
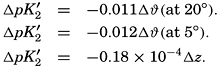
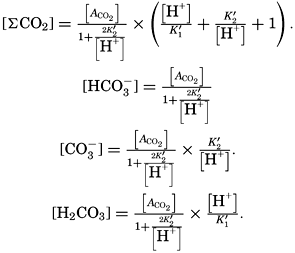
The partial pressure of carbon dioxide is related to the amount of free CO2 + H2CO3 (indicated as H2CO3; see p. 190) in the solution:
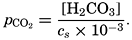
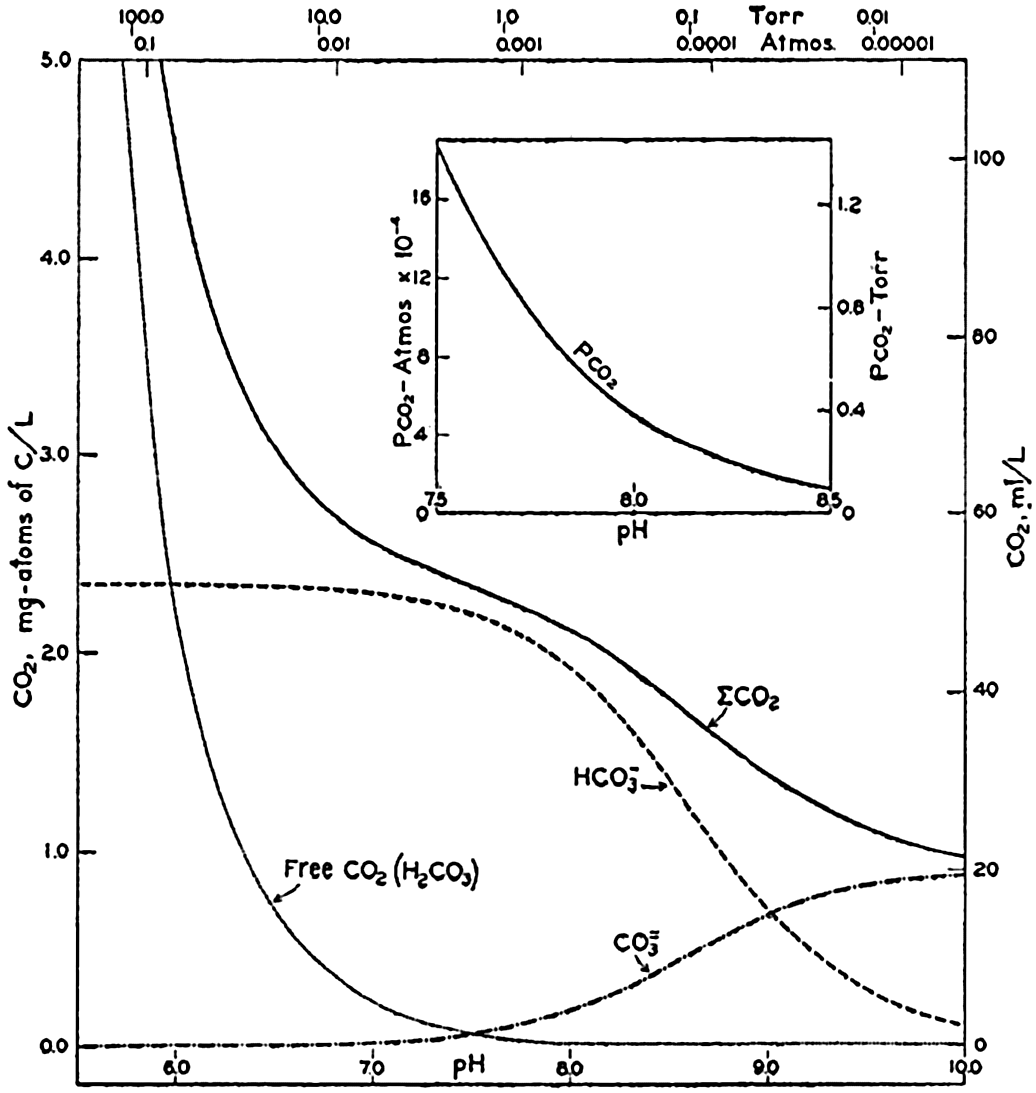
Carbon dioxide components in sea water of Cl = 19.00 ‰ at 20°C as a function of pH and the partial pressure of carbon dioxide.
In fig. 41 are shown curves for cs at different temperatures and chlorinities, where they represent the amount of H2CO3, in milligram atoms of carbon per liter of sea water, in solution under the designated conditions when the partial pressure of CO2 is 1 physical atmosphere (760 Torr). At 20° and 19 ‰ Cl, cs, is 34.2. That is, a partial pressure of one atmosphere of CO2 would be in equilibrium with a solution containing 34.2 milligram-atoms of carbon as free CO2 + H2CO3. The data are from Buch et al (1932).
The variations in pco2 with the other components is shown in fig. 40. The range is from less than 0.01 to greater than 100 Torr (0.1 × 10−4 to 1000 × 10−4 atm). The relationship over the pH range normally encountered in sea water is shown in the inset diagram in fig. 40. Between pH 7.5 and 8.3, pco2 decreases from 1.4 to 0.15 Torr (18.0 to 2.0 × 10−4 atm). The average partial pressure of CO2 in the air is about 0.23 Torr; hence surface sea water of Cl = 19.0 ‰ at 20° will have a pH of 8.2 if it is in equilibrium with the atmosphere.
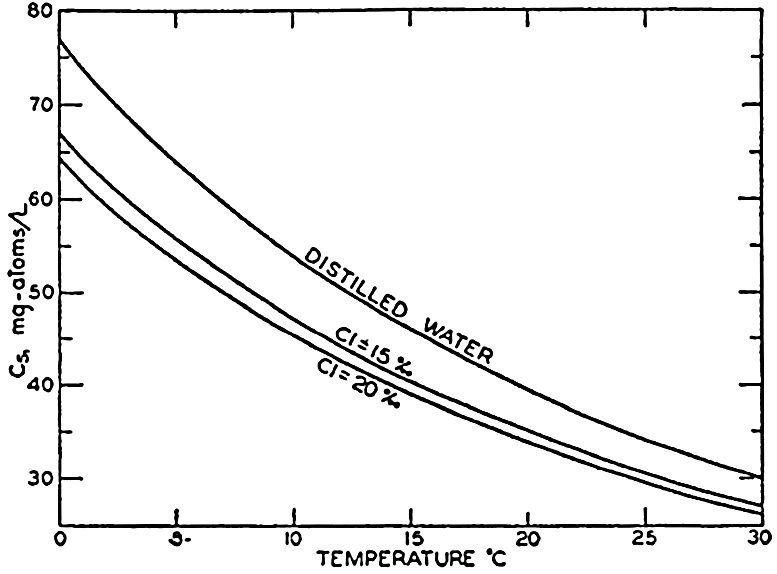
Absorption coefficient (cs) of carbon dioxide in sea water as a function of temperature and chlorinity.
Sea water is a very favorable medium for the development of photosynthetic organisms. It not only contains an abundant supply of Co2, but removal or addition of considerable amounts results in no marked changes of the partial pressure of CO2 and the pH of the solution, both of which are properties of importance in the biological environment (p. 268). If the CO2 available for photosynthesis is assumed to be H2CO3 + ½HCO3−, 0.48 mg-atoms of carbon per liter may be removed from water of Cl = 19 ‰ with an increase of the pH from 7.5 to only 8.5. In distilled water or in an inert salt solution of zero akalinity initially at pH 7.5, the total CO2 would be about one seventh of that amount.
Buffer Action of Sea Water. If a small quantity of a strong acid or base is added to pure water, there are tremendous changes in the numbers of H+ and OH− ions present, but the changes are small if the acid or base is added to a solution containing a weak acid and its salts or a weak base and its salts. This repression of the change in pH is known as buffer action, and such solutions are called buffer solutions. Sea water contains carbonic and boric acids and their salts and is, therefore, a buffer solution. Let us consider only the carbonate system. Carbonate and bicarbonate salts of strong bases, such as occur in sea water, tend to hydrolyze, and there are always both H+ and OH− ions in the solution. If an acid is added, carbonate is converted to bicarbonate and the bicarbonate to carbonic acid, but, as the latter is a weak acid (only slightly dissociated), relatively few additional hydrogen ions are set free. Similarly, if a strong base is added, the amount of carbonate increases, but the OH− ions formed in the hydrolysis of the carbonate increase only slightly. The buffering effect is greatest when the hydrogen
Cycle of CO2 Between Sea and Atmosphere. Investigations of the partial pressure of CO2 in the ocean and the atmosphere have been made by Krogh (1904) and Buch (1939a,b). The following internal changes will increase or decrease the pCO2 in the surface layer:
| Increase pco2 | Decrease pco2 |
|---|---|
| 1. Rise in temperature | 1. Decrease in temperature |
| 2. Rise in salinity (evaporation) | 2. Decrease in salinity |
| 3. Respiration | 3. Photosynthesis |
| 4. Precipitation of CaCO3 | 4. Solution of CaCO3 |
| 5. Deep water brought to surface |
The partial pressure of CO2 in the surface water can be computed with sufficient accuracy when the temperature, salinity, alkalinity, and pH are known, but, before a better understanding of the CO2 exchange between the sea and the atmosphere can be obtained, a far more comprehensive study of the partial pressure of the atmospheric CO2 must be made. Buch (1939b) has reported a number of direct observations on the CO2 content of the air which indicate that polar air is relatively low in CO2 (pCO2 = 0.23 Torr), compared to continental and tropical air (pCO2 = 0.25 Torr). It has been suggested that in low latitudes the air is enriched with CO2 from the ocean and that the general atmospheric circulation carries the CO2 into high latitudes. There it again dissolves in the sea water, which in time brings it back toward the Equator.
Activity of Ions in Sea Water. The apparent first and second dissociation constants of carbonic acid and the first dissociation constant of boric acid in sea water are larger than in distilled water and increase with increasing salinity. That is, the strength of these acids appears to be greater in solutions containing salts. These phenomena can be accounted for on the theory of activity introduced by Lewis and Randall (1923) and developed mathematically by Debye and Hückel. In a solution containing a mixture of electrolytes, such as sea water, there is a mutual interference of the ions, so that their activity or ability to participate independently in some reaction is much reduced. Most chemical determinations measure the total concentration of some ion and not its activity; however, certain physical measurements show the activity. For example, electromotive force determinations involve the activity of the hydrogen and other ions. Similarly, the measurement of the vapor pressure of a solution of a nonvolatile compound is an indication of the activity of the solvent. The activity will be less than that of the pure solvent under similar conditions. The partial pressure of dissolved gases is a measure of their activity.
The activity coefficient γ is related to the activity α of an ion as in the following example:
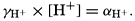
In the studies of the carbon dioxide system in sea water, the total CO2, alkalinity, and carbon dioxide components are measured chemically, and hence the values represent the stoichiometric values and not the activities. On the other hand, the hydrogen ion concentration is determined colorimetrically or electrometrically, and these methods yield the activity of hydrogen ions directly. Therefore, in the equations relating the CO2 components αH+ could have been inserted instead of [H+]. The dissociation constants have been referred to as apparent dissociation constants, in contrast to the thermodynamic constants that would be obtained at infinite dilution, where the activity coefficients (γ) are unity. The apparent dissociation constants are indicated by the symbol prime (′)—for example, K′2. For carbonic acid the thermodynamic second dissociation constant can be written
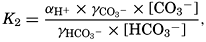
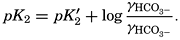
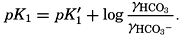
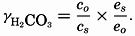
From the empirical equations relating pK′1 and pK′2 to the temperature and chlorinity, we know that at 20° and zero chlorinity the thermodynamic values are pK1 = 6.47 and pK2 = 10.288, and, at 19.00 ‰ Cl, pK'1 = 5.97 and pK'2 = 9.02. By substituting these values and γH2CO3

Empirical equations have been presented which relate pK′1 and pK′2 to the cube root of the chlorinity. It has been shown (Buch et al, 1932, Moberg et al, 1934) that these equations are generally valid for salt solutions other than sea water if the ionic strength is used instead of chlorinity as a measure of concentration. The ionic strength (μ) of a solution is obtained by first multiplying the concentration of each individual type of ion, in moles per kilogram of solvent water, by the square of its valence, and then taking half the sum of these products (Lewis and Randall, 1923, p. 373). Lyman and Fleming (1940) have shown that the ionic strength of sea water in the normal range of concentration may be computed from the expression
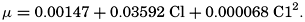
Solubility of CaCO3. The solubility of an electrolyte, such as calcium carbonate, may be expressed by a solubility product. The solubility product is identical with the ionic product (if concentrations are expressed as moles per liter) when the solution is in equilibrium with the solid salt and, therefore, saturated. The value of the solubility product depends upon temperature, the concentration of other ions (salinity), and the hydrostatic pressure. If, under a given set of conditions, the ionic product is less than the solubility product, the solution is undersaturated; if the ionic product is greater the solution is supersaturated, and if suitable nuclei are present, precipitation will proceed until the ionic product equals the solubility product.
The solubility product of CaCO3(KCaCO3) in distilled water at 20° is 5.0 × 10−9. In sea water of chlorinity 19.00 ‰ and at the same temperature, the calcium content is 10.23 mg-atoms/L, and at pH 8.2 the carbonate ion concentration is 0.26 mg-atoms/L of carbon. Therefore the ionic product is
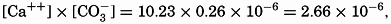
It is therefore necessary to determine empirically the concentrations of Ca++ and CO−3 that can exist in contact with solid CaCO3. Working at 30° and increasing the CO−3 content by lowering the total CO2, Revelle and Fleming (1934) obtained precipitation of CaCO3 as aragonite needles and spherulites. The calcium content of the solution was determined directly, and the CO−3 was calculated from measurements of the pH, alkalinity, and chlorinity. The average of three experiments gave K'CaCO3 = 2.4 × 10−6 at 30°C. Wattenberg has carried out a number of studies on the solubility of calcium carbonate in sea water. His general procedure was to add CaCO3 crystals to sea water, and in some instances to increase the pCO2 The sea-water samples were then placed in sealed flasks and agitated until equilibrium was established. The calcium content of the water was calculated from the alkalinity measurements (p. 196), and the CO3 was obtained with the aid of pH determinations. Wattenberg and Timmerman (1936) give the following values for the apparent solubility product in sea water of Cl = 18.5 to 19.5 ‰:
| Temperature, °C | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 |
| K′CaCO3 | 8.1 | 7.9 | 7.4 | 6.8 | 6.2 | 5.5 | 4.7 | 3.8 × 10−7 |
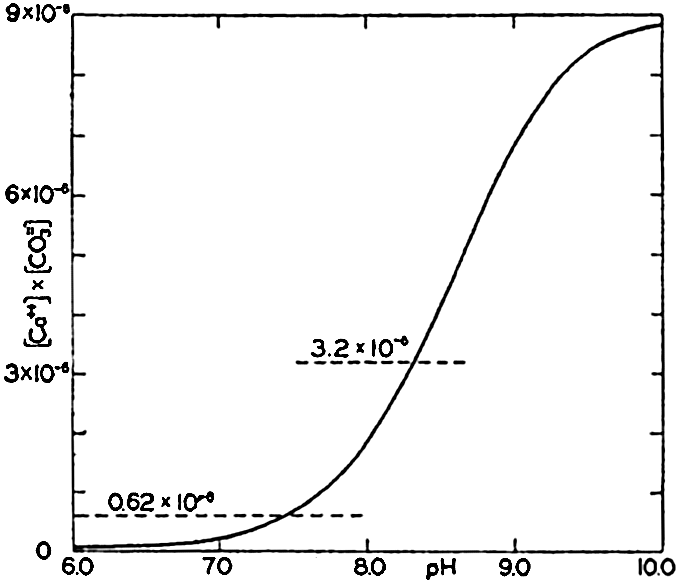
Ionic product [Ca++l × [CO3−] in sea water of Cl = 19.00 ‰ at 20°C as a function of pH. The horizontal lines indicate the solubility product according to Wattenberg (0.62 × 10−6 and according to Revelle and Fleming (3.2 × 10−6).
At 30° Wattenberg's value is only one fifth of that obtained by Revelle and Fleming. No satisfactory explanation of this difference has yet been offered. In fig. 42 the ionic product in sea water of Cl = 19.00 ‰ at 20° is plotted against pH. The value of K'CaCO3, for this temperature obtained by Wattenberg—namely, 0.62 × l0−6—would indicate that supersaturation exists at all pH's above about 7.5. Surface water in equilibrium with the atmosphere has a pH of about 8.2 and would be
Smith (1940) has investigated the calcium carbonate deposition that takes place in the shallow waters overlying the Bahama Banks. He found the alkalinity to be much reduced, and from measurements he computed the ionic product, [Ca++] × [CO3−]. Minimum values of the product that he considers approach the solubility product were found to fall between the values of Revelle and Fleming and those of Wattenberg.
According to Wattenberg (1936), K'CaCO3 at 20° changes with the chlorinity in the following way:
| Cl, ‰ | 0 | 5 | 10 | 15 | 20 |
| K′CaCO3 | 0.05 | 1.8 | 4.0 | 5.0 | 6.2 × 10−7 |
That is, in sea water the apparent solubility product of CaCO3 increases with chlorinity and decreases with temperature.
Revelle (1934) and Wattenberg (1936) consider that hydrostatic pressure has no significant effect upon the value of K'CaCO3. However, it should be remembered that, because of changes in the dissociation constants of carbonic acid, pressure does modify the relative amounts of HCO3 and CO−3 in the water. Hence, water that is saturated at the surface will be slightly undersaturated if subjected to hydrostatic pressure, even if the total CO2 and calcium contents remain unaltered. Conversely, bottom water saturated with CaCO3 will be supersaturated when brought to the surface.
Although our knowledge of the values of K′CaCO3 under different conditions is incomplete and uncertain, it is possible to show the effect of changes in the conditions upon the ionic product, thus obtaining an understanding of those agencies that will favor precipitation or solution. Revelle (1934) has shown that, in surface water, increase of the salinity and the temperature, and decrease of the pco2—that is, the total CO2 content—all tend to increase the ionic product and therefore favor precipitation. The salinity effect is relatively small, and hence areas of high or rising temperature and of active photosynthesis will be those where precipitation of CaCO3 is most likely to occur. Opposite conditions will favor solution.
In the deep water the range in temperature and salinity is small, and therefore the variations in pCO2 will have the most pronounced effect. According to Wattenberg's studies (1933) the deep waters of the Atlantic Ocean are virtually saturated with calcium carbonate. Areas overlying red clay show slight undersaturation, and those overlying calcareous deposits (globigerina ooze) show either saturation or slight supersaturation.
Certain types of calcareous sedimentary material, both recent and fossil, do not show any evidence of organic origin. These are sometimes considered to be “chemical” deposits. In certain areas, microorganisms undoubtedly play an important part in establishing conditions that result in the incidental precipitation of carbonates. In tropical seas, this process may occur in shoal-water areas, coral reefs, lagoons, and mangrove swamps (Field, 1932). Although microorganisms can produce conditions favoring the precipitation of calcium carbonate, it is considered that they are effective agents in this process only in and on the sediments in the environments listed above. Smith (1940) has found that over the Great Bahama Bank CaCO3 is precipitated, under conditions of heating and excessive evaporation, on nuclei supplied by the sediments. The finely divided CaCO3 in certain deep-sea sediments is thought to arise from the break-down of the shells of foraminifera (p. 982) and not from precipitation in situ.
Distribution of Alkalinity, pH, and Carbon Dioxide Components. In the preceding discussion it has been assumed that the alkalinity: chlorosity factor is constant, and the value 0.1205 (milliequivalents per unit Cl) has been used in computations. This is in agreement with the average of a large number of observations made by Wattenberg (1933) in the Atlantic Ocean and those reported by Revelle (1936) for the upper layers of the Pacific Ocean. Wattenberg's value is commonly given as the specific alkalinity—namely, as milliequivalents per unit chlorinity, in which case it is 0.123. A number of different methods (p. 195) have been employed for measuring alkalinity, but there is no definite proof that they all yield similar values. Hence, it is difficult to compare the results obtained from various parts of the oceans by different workers. However, the findings of Wattenberg (1933), Mitchell and Rakestraw (1933), and Revelle (1936) all show that there is a somewhat higher alka1inity:chlorosity factor in the deeper water than there is in the surface layers. The increase in the factor usually amounts to about 0.005. Wattenberg examined a number of water samples collected immediately over the bottom, and in these he found an even larger factor. The low values in the surface waters are ascribed to removal of calcium carbonate by organisms possessing calcareous skeletons. Smith (1940) has suggested that, at least in certain localities, there may be inorganic precipitation if suitable nuclei are present when
The pH of sea water in contact with the air will vary between about 8.1 and 8.3, depending upon the temperature and salinity of the water and the partial pressure of carbon dioxide in the atmosphere. In areas of great dilution lower values may occur. At subsurface levels, where exchange of carbon dioxide with the atmosphere is impossible, the pH will vary with the extent to which the CO2 content of the water is modified by biological activity. In the euphotic zone, higher pH's are usually found; below this they decrease to a minimum corresponding in general to the layer of minimum oxygen content, and then increase again toward the bottom. Although variations in the salinity affect the pH, the predominant factor is the total carbon dioxide content or its partial pressure.
Unfortunately, differences in technique and in the constants used in arriving at pH's from colorimetric measurements make it difficult to compare the results of different workers. The most extensive studies made on the distribution of pH in the oceans are those of the Meteor (Wattenberg, 1933) in the Atlantic Ocean and those of the Carnegie in the Pacific Ocean. The distributions of pH and dissolved oxygen along a longitudinal profile in the eastern Atlantic Ocean are shown in fig. 43. The rather close similarity of the isolines can easily be seen, and similar patterns would be given by the partial pressure and total CO2 content, although in this case the relations would be inverse ones. The temperature

Distribution of pH and dissolved oxygen in the eastern part of the Atlantic Ocean. The locations of the sections are shown in the map on the left-hand side. The vertical and horizontal scales are different in the two sections. (After Wattenberg.)
Solubility of Salts in Sea Water
The solubility of calcium carbonate in sea water has been examined in some detail, but relatively little is known about the other constituents. Because of the complex nature of sea water and the effect of other ions upon the activity of any one, the solubility product of a single salt in distilled water cannot be applied to sea water. Cooper (1937b) considers that most of the iron in sea water is not in true solution, but is present in some colloidal form, as the solubility product for the hydroxide is
Thompson and his co-workers (for example, Igelsrud and Thompson, 1936) have carried out extensive phase-rule studies of solutions containing some of the salts in sea water, but so far they have not extended their investigations to natural water.
Some indication of the great solubility of the major constituents is afforded by data on the separation of salts when sea water is frozen (p. 217). Somewhat similar data may be obtained from the evaporation studies by Usiglio (Thompson and Robinson, 1932), which again bring out the fact that sea water is far from saturated with most of the constituents.
| Salt | K Distilled water | K' Sea water S = 35 ‰, ϑ = 20° | Ionic product Cl = 19.0 ‰, ϑ = 20° pH = 8.2 |
|---|---|---|---|
| CaCO3 | 0.5 × 10− 3 | 50 × 10− 3 | 270 × 10− 3 |
| MgCO33H2O | 0.1 × 10− 4 | 3.1 × 10− 4 | 0.14 × 10− 4 |
| SrCO3 | 0.3 × 10− 9 | 500 × 10− 9 | 39 × 10− 9 |
| Mg(OH)2 | 1 × 10− 11 | 5 × 10− 11 | 0.02 × 10− 11 |
The Oxidation-Reduction Potential of Sea Water
The oxidation-reduction potential is a measure of the ability of one chemical system to oxidize a second. It is generally expressed in volts relative to the normal hydrogen electrode. Those substances or solutions having high potentiaIs are able to oxidize those with lower potentials. Although considerable work has been done on the oxidation-reduction potentials in living organisms, little is known about the conditions prevailing in the water. The potential in sea water has been considered
The oxidation-reduction potential of the environment is important to organisms. So-called aerobic bacteria thrive at a higher potential than micro-aerophiles, and anaerobic bacteria can exist only when the potential is low. Hence, in stagnant water and muds where there is no oxygen and the potential is low, only anaerobic forms can exist. The potential is also of geological importance, as the character of certain of the constituents of the sediments will be determined by the prevailing “oxidizing” or “reducing” conditions (p. 996).
Inorganic Agencies Affecting the Composition of Sea Water
The factors that may modify the absolute and the relative concen, trations of the substances in sea water are exchange with the atmosphere-inflow of river water, freezing and melting of sea ice, and biological activity. Biological processes and their effects upon the distribution of various elements are considered in chapter VII.
Exchange with the Atmosphere. The distribution of salinity in the oceans, and hence the concentrations of the major elements, is maintained by agencies that are described elsewhere, but one point must be considered at this time. Over the sea and along its shores, spray is continually being swept up into the air, and as the spray represents actual particles of sea water with its dissolved salts, this process affords a mechanism for the removal of salts from the sea. A large portion of the spray undoubtedly falls back into the water or is carried down by rain (Köhler, 1921). However, winds blowing toward the land will carry with them their content of salt, which may be deposited on the land directly or carried down by the rain. Observations by Jacobs (1937) on the chloride content of the air near the sea showed concentrations ranging between 0.07 and 0.5 mg of chloride per cubic meter of air. The amount increased with the wind velocity and was greatest with onshore winds.
A considerable proportion of the dissolved material carried to the sea by rivers is “cyclic salt”—that is, salt that has been carried inland by the atmosphere and then deposited or carried down by rain and snow (Clarke, 1924, Knopf, 1931).
Besides the exchange of salts that takes place between the atmosphere and the ocean as described above, there is an exchange of dissolved gases and nitrogen compounds which may modify the quantity of these substances present in sea water that is in contact with the atmosphere. The factors that affect the exchange of gases are described elsewhere. The exchange of water between the atmosphere and oceans was taken up in chapter IV.
Rain water contains relatively high concentrations of nitrogen compounds, which are believed to be formed from the constituents of the atmosphere by electrical discharges; hence the atmosphere supplies to the ocean, either directly through rainfall or indirectly through run-off from the land, a certain amount of fixed nitrogen. Whether this increment in the amount of fixed nitrogen is balanced by deposition of organic nitrogen in sediments or by the liberation of gaseous nitrogen through the decomposition of nitrogen compounds in the sea is not yet known.
Effects of Rivers on the Composition of Sea Water. The run-off from land is but a part of the cycle of leaching. The precipitation on the land contains only the cyclic salts, dissolved atmospheric gases, and nitrogen compounds. This water acts upon the rocks, contributing to the mechanical break-down of the solid material and extracting from them their more soluble constituents. The nature and quantity of the various elements dissolved depends upon the character of the rocks or soils with which the water comes in contact on its way to the sea. Because the leaching is carried out by water of low salt concentration yet relatively high in carbon dioxide compounds, it is capable of dissolving materials that would not pass into solution if they were in contact with sea water. In addition to dissolved material, rivers carry to the sea colloidal and particulate material in tremendous quantities. A considerable part of this debris is dropped to the sea bottom near shore, and much of the finer material coagulates and settles when mixed with sea water. Sea water reacts in various ways with the colloidal and finely dispersed material, and some of these reactions may affect the relative composition of the dissolved constituents. Interaction between the dissolved constituents of sea water and the sedimentary debris may be subdivided as follows: (1) solution of the constituents of the sediment, (2) adsorption on the sediment, (3) ionic exchange, and (4) reactions to form new substances. Little is known concerning the importance of these processes.
From the magnitude of the land area drained by rivers emptying into the sea and from the composition of the salts dissolved in river waters,
| Ion | River water (weighted average) | Sea water | River water (less “cyclic” salts) |
|---|---|---|---|
| CO3− | 35.15 | 0.41 (HCO3−) | 35.13 |
| SO4− | 12.14 | 7.68 | 11.35 |
| Cl− | 5.68 | 55.04 | 0.00 |
| NO3− | 0.90 | ............. | 0.90 |
| Ca++ | 20.39 | 1.15 | 20.27 |
| Mg++ | 3.41 | 3.69 | 3.03 |
| Na+ | 5.79 | 30.62 | 2.63 |
| K+ | 2.12 | 1.10 | 2.02 |
| (Fe,Al)2O3 | 2.75 | ............. | 2.75 |
| SiO2 | 11.67 | ............. | 11.67 |
| Sr++, H3BO3, Br− | ...... | 0.31 | ..... |
| 100.00 | 100.00 | 89.75 |
It is not known whether the addition of dissolved solids brings about progressive changes in the relative composition of the sea salts or whether there is any progressive alteration of the total salt content or salinity. In any event, both processes must be exceedingly slow. The total amount of dissolved solids contributed by the rivers each year is only an infinitesimal fraction, 5.4 × 10−8, of the total dissolved solids in the ocean.
| Sea water … … … … … … … … … … … … … … … | 268.45 | 1 |
| Fresh water.… … … … … … … … … … … … … … | 0.1 | “ |
| Continental ice.… … … … … … … … … … … … … | 4.5 | “ |
| Water vapor.… … … … … … … … … … … … … … | 0.003 | “ |
The average composition of the river water is of interest in considering the effect on the oceans as a whole and over long periods, but particular investigations must be concerned with the effects brought about by individual rivers whose dissolved solids may differ markedly in composition and concentration from the average. Data can be obtained from Clarke (1924) or similar sources; as an illustration, values for several of the large American rivers are given in table 44.
From these examples it can be seen that the composition of individual rivers may differ considerably from the average. Thus, the Columbia River is low in chloride and the Colorado River is high, and the latter river is high in sodium and sulphate and below average in calcium and carbonate. The effect that dilution will have upon the chlorosity factors will therefore depend upon the character of the river water.
Thus far we have considered only the more abundant elements in the river water. Undoubtedly, all elements are carried to the sea either in solution or as finely divided particulate material. The high production of plant and animal life which frequently occurs near the mouths of rivers has sometimes been ascribed to the plant nutrients introduced by the rivers. Riley (1937) has found that the Mississippi
Effects of Formation and Melting of Sea Ice on the Composition of Sea Water. A laboratory study of the freezing of sea water was made by Ringer, whose results have been reported by Krümmel (1907) and Johnstone (1928). In these experiments sea water was cooled in the laboratory, and at various temperatures below the initial freezing point the ice and precipitated salts were separated from the mother liquor. Sea water of salinity 35.0‰ begins to freeze at − 1.91°C (p. 66). At first, pure ice crystals separate, and, as the concentration of the brine is increased, the temperature must be further reduced to bring about the formation of additional ice. As the temperature is lowered and the concentration of the brine is increased, the solubility of certain of the dissolved salts is exceeded. At −8.2° the Na2SO4 begins to separate and continues to do so with further cooling. At −23° the NaCl begins to crystallize. In addition, a certain amount of CaCO3 precipitates. Ringer's analyses of the “ice” (including the ice crystals and the precipitated salts) and the brine when the temperature had been reduced to −30° are as follows:
| Ion | Average | Mississippi River | Columbia River | Colorado River |
|---|---|---|---|---|
| CO3− | 35.15 | 34.98 | 36.15 | 13.02 |
| SO4− | 12.14 | 15.37 | 13.52 | 28.61 |
| Cl− | 5.68 | 6.21 | 2.82 | 19.92 |
| NO3− | 0.90 | 1.60 | 0.49 | .......... |
| Ca++ | 20.39 | 20.50 | 17.87 | 10.35 |
| Mg++ | 3.41 | 5.38 | 4.38 | 3.14 |
| Na+ | 5.79 | }8.33* | 8.12 | 19.75 |
| K+ | 2.12 | 1.95 | 2.17 | |
| (Fe,Al)2O3 | 2.75 | 0.58 | 0.08 | .......... |
| SiO2 | 11.67 | 7.05 | 14.62 | 3.04 |
| Annual contribution of dissolved solids (metric tons) | 100,000,000 | 19,000,000 | 13,416,000 | |
| Salt content (g/l) | 0.166 | 0.0924 | 0.702 | |
| * Sum | ||||
One kilogram of sea water, initial salinity 35.05 ‰, yielded:
| Ice crystals ……………………… | 931.9 | g |
| NeCl crystals … … … … … … … | 20.23 | “ |
| Na2SO4 crystals… …………… | 3.95 | “ |
| CaCO3 crystals.… … … … …… | Trace | |
| Brine… … … … ………………… | 43.95 | “ |
The brine contained 23.31 g of H2O and
| Na+……………… | 1.42 g | Cl−……………… | 7.03 g |
| Mg++……………… | 1.31 “ | Br−……………… | 0.08 “ |
| K+……………… | 0.38 “ | SO4−……………… | 0.03 “ |
| Ca++……………… | 0.39 “ |
From these data it is readily seen that, when the temperature of the ice and brine is lowered to −30°, there are marked differences in the relative composition of the salts in the “ice” and in the brine. If the cooling is continued to −50°, there is further separation of ice and salt crystals, but some very concentrated brine is still present.
From these experiments it would appear that the formation of sea ice might have a pronounced effect upon the relative composition of the salts in the water. The brine from which it formed would be modified in one direction, and, if melting took place in water other than that from which the ice formed, the effect would be in the opposite direction. However, the formation of sea ice in nature is not reproduced by these laboratory experiments. Let us suppose that, in a region where the depth to the bottom is moderate or great, sea water of normal composition is subjected to cooling at the surface. The resulting increase in density gives rise to convection movements that continue until the water at the surface reaches the freezing point, and then ice will begin to form. The brine, being of greater concentration but having virtually the same temperature, will sink and new water will be brought toward the surface and into contact with the ice. At first, isolated, elongated ice crystals are produced, but as the freezing continues these form a matrix in which a certain amount of the brine is mechanically included. The ice crystals themselves are at this stage probably “pure ice.” If the freezing proceeds rapidly, the brine will accumulate in separate cells within the body of the ice and, as the temperature of the ice near the surface is reduced, more ice crystals are formed, the cells decrease in size, and the concentration of the brine in the cells increases (fig. 16, p. 72). This may continue so far that solid salts crystallize in the cells. From this it can be seen that there is not necessarily any relative change in the composition of the dissolved salts in the sea water and in the sea ice (ice crystals plus the enclosed brine).
The salinity of the ice, using the same definition as applied to sea water, has been shown to depend upon the rate of freezing. Malmgren (1927), from the observations made by the Maud Expedition, gives the
| Air temperature (°C) | Salinity of ice (‰) |
| − 16 | 5.64 |
| − 28 | 8.01 |
| − 30 | 8.77 |
| −40 | 10.16 |
The salinities are based upon chlorinity determinations made on samples of the melted ice. The salinity of the surface water was about 30 ‰. The effect of the rate of freezing is also shown by the analyses of samples obtained in April from an ice floe that had started to form the preceding November:
| Distance from surface of ice (cm) | 0 | 6 | 13 | 26 | 45 | 82 | 95 |
| Salinity of ice (‰) | 6.74 | 5.28 | 5.31 | 3.84 | 4.37 | 3.48 | 3.17 |
The lower salt content of the deeper ice is related to the slower rate of formation. When ice is formed with extreme rapidity, its salinity will approach that of the water from which it is produced.
According to Ringer's experiments the cooling of ice containing cells of brine leads to formation of additional ice crystals and, if the temperature is reduced sufficiently, to separation of salt crystals within the ice. With very rapid freezing, brine and salt crystals may accumulate on the surface of the ice, making the surface “wet” at temperatures of −30° to −40°C and greatly increasing the friction against sled runners or skis.
In such rapidly frozen ice the cells containing the brine are large or numerous. If the temperature rises, the ice surrounding thg cells melts and the separated salt crystals are dissolved, but before complete solution has taken place the brine cells may join, permitting the brine to trickle through the ice. Under these conditions some of the solid salts may be left in the ice, and the composition of the water obtained by melting will differ from that of normal sea water. If, on the other hand, the temperature of the ice is raised to 0°C, all salts dissolve, the cells grow so large that the ice becomes porous, all brine trickles down from the portions of the ice above the sea surface, and the exposed old ice becomes fresh and can be used as a source of potable water.
Analyses by Wiese (1930) indicate that the processes that have been described may be effective in changing the relative composition of the salts, He found that the sulphate and alkalinity factors were greater in the ice than in the water and were greater in old ice than in newly frozen ice. This indicates that small amounts of sulphate, probably present as Na22SO4, have remained in the ice during the process of ageing and, probably, that the relative amounts of CaCO3 have changed.
Results of the Maud Expedition, reported by Malmgren (1927) and Sverdrup (1929), are not in agreement with the findings of Wiese. Chlorinities of water obtained by melting ice were systematically higher when determined by titration than when computed by means of Knudsen's Hydrographical Tables from observations of density. This discrepancy was interpreted to mean that the sea ice contains an excess of chlorides, but it may arise from the application of Knudsen's Tables to water that has been diluted by essentially distilled water, as explained on p. 59. The fact that the SO4/Cl ratio was nearly the same in the ice and the sea water (Malmgren, 1927, p. 9) supports the latter explanation and indicates that no changes in relative concentration had resulted from processes of freezing and melting. The problem, however, cannot be considered solved, and it offers opportunities for further laboratory investigations and observations in the field.
Geochemistry of the Ocean Waters
The total quantity of dissolved solids present in the waters of the oceans can be estimated by assuming an average salinity of 35 ‰ and assuming that the volume of the ocean is 1.37 × 109 km3 (p. 15). With a density in situ of 1.04 for the ocean waters, the dissolved solids amount to 5 × 1016 metric tons. This immense quantity of material would form a layer of dried salts 45 m thick over the entire earth, or 153 m thick over the present land area. The amount in tons of any element may be estimated by multiplying the value given in the first column in table 45 by 1.42 × 1012. The figures for the variable elements correspond to the higher values listed in table 36. Obviously the total amounts of even the trace elements are tremendous, and, if methods of extraction were economically feasible, the oceans would serve as an “inexhaustible” source of these substances.
| Element | Sea water S = 35‰ (mg/kg) | Potential “supply” in 600 g of rock (mg/kg of sea water) | Percentage in solution |
|---|---|---|---|
| Silicon | 4 | 165,000 | 0.002 |
| Aluminum | 0.5 | 53,000 | 0.001 |
| Iron | 0.02 | 31,000 | 0.0001 |
| Calcium | 408 | 22,000 | 1.9 |
| Sodium | 10,769 | 17,000 | 65 |
| Potassium | 387 | 15,000 | 2.6 |
| Magnesium | 1,297 | 13,000 | 10 |
| Titanium | ............ | 3,800 | ? |
| Manganese | 0.01 | 560 | 0.002 |
| Phosphorus | 0.1 | 470 | 0.02 |
| Carbon | 28 | 300 | 9 |
| Sulphur | 901 | 300 | 300 |
| Chlorine | 19,353 | 290 | 6700 |
| Strontium | 13 | 250 | 5 |
| Barium | 0.05 | 230 | 0.02 |
| Rubidium | 0.2 | 190 | 0.1 |
| Fluorine | 1.4 | 160 | 0.9 |
| Chromium | p | 120 | ? |
| Zirconium | ............ | 120 | ? |
| Copper | 0.01 | 60 | 0.02 |
| Nickel | 0.0001 | 60 | 0.0002 |
| Vanadium | 0.0003 | 60 | 0.0005 |
| Tungsten | ............ | 41 | ? |
| Lithium | 0.1 | 39 | 0.2 |
| Cerium | 0.0004 | 26 | 0.002 |
| Cobalt | p | 24 | ? |
| Tin | p | 24 | ? |
| Zinc | 0.005 | 24 | 0.02 |
| Yttrium | 0.0003 | 19 | 0.002 |
| Lanthanum | 0.0003 | 11 | 0.003 |
| Lead | 0.004 | 10 | 0.04 |
| Molybdenum | 0.0005 | 9 | 0.005 |
| Thorium | <0.0005 | 6 | 0.01 |
| Cesium | 0.002 | 4 | 0.05 |
| Arsenic | 0.02 | 3 | 0.7 |
| Scandium | 0.00004 | 3 | 0.001 |
| Bromine | 66 | 3 | 2000 |
| Boron | 4.7 | 2 | 240 |
| Uranium | 0.015 | 2 | 0.8 |
| Selenium | 0.004 | 0.4 | 1 |
| Cadmium | p | 0.3 | ? |
| Mercury | 0.00003 | 0.3 | 0.001 |
| Iodine | 0.05 | 0.2 | 25 |
| Silver | 0.0003 | 0.06 | 0.5 |
| Gold | 0.056 | 0.003 | 0.3 |
| Radium | 0.093 | 0.066 | 0.05 |
| p = present | |||
According to present theories, most of the solid material dissolved in the sea originated from the weathering of the crust of the earth. The problem as to the amount of rock weathered has been treated by Goldschmidt (1933) in the following way. For each square centimeter of the surface of the earth there are 278 kg of sea water; therefore, for each square centimeter the ocean water contains very nearly 3 kg of sodium. The average sodium content of igneous rocks is 2.83 per cent, and in sedimentary deposits it is 1.00 per cent. In the process of weathering, a certain amount of the material is leached away, and Goldschmidt estimates that the mass of the sedimentary deposits (Y) is 0.97 of the original igneous rocks (X) that gave rise to them. Therefore,
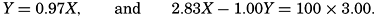
Examination of table 45 shows that the elements may be grouped in three classes, depending upon the percentage in solution: (1) Sulphur, chlorine, bromine, and boron occur in amounts greater than those which could have been supplied by the weathering of the 600 g of rock. Goldschmidt considers that these elements were present in the primeval atmosphere as volatile compounds and that they accumulated in the ocean waters in the earliest times. (2) Calcium, sodium, potassium, magnesium, carbon, strontium, selenium, and iodine, which form relatively soluble compounds, are present in sea water in amounts greater than 1 per cent of the potential supply. (3) The remaining elements, which are present in small amounts.
It is striking that silicon, aluminum, and iron, the most abundant elements in igneous rocks (oxygen is actually the most abundant, but does not have to be considered here), are present in sea water in extremely small amounts. Thus, the relative abundance of the elements in sea water differs markedly from that in the earth's crust. With a few exceptions, all of the elements have been potentially available in much larger amounts than are actually present in solution. The relative composition of river water differs from that of sea water, and, in addition to the dissolved constituents, rivers introduce large quantities of particulate material that would pass into solution if the sea water were unsaturated with respect to these substances. Therefore, it appears that factors operating in the sea itself must control the concentrations of many of the elements that are potentially available in Iarge amounts. These factors are solubility, physical-chemical reactions, and biological activity. Our present knowledge is inadequate to designate which process or processes may control the concentration of a given element. Therefore, the following remarks will merely indicate the character of the factors that may be involved.
Certain elements may be present in such amounts that the solubility of their compounds may limit their concentration. In these eases,
Bibliography
Atkins, W. R. G.1923. The phosphate content of fresh and salt waters in its relationship to the growth of algal plankton. Marine Biol. Assn. U. K., Jour., v. 13, p. 119–50, 1923. Plymouth.
Atkins, W. R. G.1936. “Estimation of zinc in sea water using sodium diethyldithiocarbamate” . Marine Biol. Assn. U. K., Jour., v. 20, p. 625–26, 1936. Plymouth.
Ball, Eric G., and C. C. Stock. 1937. “The pH of sea water as measured with the glass electrode” . Biol. Bull., v. 73, p. 221–26, 1937.
Bein, Willy, H. Hirsekorn, L. Möller. 1935. Konstantenbestimmungen des Meerwassers und Ergebnisse über Wasserkörper. Berlin, Universität, Institut f. Meereskunde, Veröff., N.F., A. Geogr.-naturwiss. Reihe, Heft 28, 240 pp., 1935.
Boury, M.1938. Le plomb dans le milieu marin. L'Office des Pêches maritimes. Revue des Travaux scientifiques, v. 11, p. 157–66, 1938. Paris.
Buch, Kurt. 1933a. Der Borsäuregehalt des Meerwassers und seine Bedeutung bei der Berechnung des Kohlensäuresystems im Meerwasser. Conseil Perm. Internat. p. l'Explor. de la Mer, Rapp. et Proc.-Verb., v. 85, p. 71–75, 1933.
Buch, Kurt. 1933b. “On boric acid in the sea and its influence on the carbonic acid equilibrium” . Conseil Perm. Internat. p. l'Explor. de la Mer, Jour. du Conseil, v. 8, p. 309–25, 1933.
Buch, Kurt. 1937. Die kolorimetrische Bestimmung der Wasserstoffionenkoncentration im Seewasser. pt. 2, p. 27–33 in: Wattenberg, H., Critical review of the methods used for determining nutrient salts and related constituents in salt water. Conseil Perm. Internat. p. l'Explor. de la Mer, Rapp. et Proc.-Verb., v. 103, 1937.
Buch, Kurt. 1938. “New determination of the second dissociation constant of carbonic acid in sea water” , Acta Acad. Aboensis, Math. et Physica, v. 11, no. 5, 18 pp. 1938. Abo, Finland.
Buch, Kurt. 1939a. “Beobachtungen über das Kohlensäuregleichgewicht und über den Kohlensäureaustausch zwischen Atmosphäre und Meer im Nord-Atlantischen Ozean” . Acta Acad. Aboensis, Math. et Physica, v. 11, no. 9, 32 pp., 1939. Abo, Finland.
Buch, Kurt. 1939b. “Kohlensäure in Atmosphäre und Meer an der Grenze zum Arktikum” . Acta Acad. Aboensis, Math. et Physica, v. 11, no. 12, 41 pp., 1939. Abo, Finland.
Buch, Kurt, H. W. Harvey, H. Wattenberg, and S. Gripenberg. 1932. Über das Kohlensäuresystem im Meerwasser. Conseil Perm. Internat. p. l'Explor. de la Mer, Rapp. et Proc.-Verb., v. 79, 70 pp., 1932.
Buch, Kurt, and Ole Nynäs.1939. “Studien Über neuere pH-Methodik mit besonderer Berücksichtigung des Meerwassers” . Acta Acad. Aboensis, Math. et Physica, v. 12, no. 3, 41 pp., 1939. Abo, Finland.
Clark, W. M.1928. The determination of hydrogen ions. 3rd ed., Baltimore, Williams and Wilkins, 717 pp., 1928.
Clarke, F. W.1924. “The data of geochemistry” . 5th ed.U. S. Geol. Survey, Bull.no. 770, 841 pp., 1924. Washington, D. C.
Closs, Karl. 1931. Über das Vorkommen des Jods im Meer und in Meeresorganismen. Morten Johansen, Oslo. 150 pp., 1931.
Clowes, A. J.1938. Phosphate and silicate in the southern oceans. Discovery Repts., v. 19, p. 1–120, 1938.
Cooper, L. H. N.1935. “Iron in the sea and in marine plankton” . Roy. Soc., Proc., Ser. B, v. 118, p. 419–38, 1935. London.
Cooper, L. H. N.1937a. “Oxidation-reduction potential in sea water” . Marine Biol. Assn. U. K., Jour., v. 22, p. 167–76, 1937. Plymouth.
Cooper, L. H. N.1937b. “Some conditions governing the solubility of iron” . Roy. Soc., Proc., Ser. B, v. 124, p. 299–307, 1937. London.
Cooper, L. H. N.1938a. “Salt error in determinations of phosphate in sea water” . Marine Biol. Assn. U. K., Jour., v. 23, p. 171–78, 1938. Plymouth.
Cooper, L. H. N.1938b. “Redefinition of the anomaly of the nitrate-phosphate ratio” . Marine Biol. Assn. U. K., Jour., v. 23, p. 179, 1938. Plymouth.
Dietz, R. S., K. O. Emery, and F. P. Shepard. 1942. “Phosphorite deposits on the sea floor off southern California” . Geol. Soc. Amer., Bull, v. 53, p. 815—48, 1942.
Dittmar, W.1884. Report on researches into the composition of ocean water, collected by H.M.S. Challenger. Challenger Repts., Physics and Chem., v. 1, p. 1–251, 1884.
Dorsey, N. Ernest. 1940. “Properties of ordinary water-substance” . Amer. Chem. Soc., Monograph Ser.No. 81, New York, Reinhold Pub. Corp., 673 pp., 1940.
Ernst, Theodor, and Hans Hoermann. 1936. Bestimmung von Vanadium, Nickel und Molybdän im Meerwasser. Gesellsch. d. Wiss. zu Göttingen.
Evans, R. D., A. F. Kip, and E. G. Moberg. 1938. “The radium and radon content of Pacific Ocean water, life, and sediments” . Amer. Jour. Sci., v. 36, p. 241–59, 1938.
Field, R. M.1932. “Microbiology and the marine limestones” . Geol. Soc. Amer., Bull., v. 43, p. 487–93, 1932.
Fox, C. J. J.1907. On the coefficients of absorption of the atmospheric gases in distilled water and sea water. Conseil Perm. Internat. p. l'Explor. de la Mer, Pub. de Circonstance, no. 41, 27 pp., 1907.
Fox, C. J. J.1909. “On the coefficients of absorption of nitrogen and oxygen in distilled water and sea water and of atmospheric carbonic acid in sea water” . Faraday Soc., Trans., v. 5, p. 68–87, 1909.
Fox, H. Munro, and Hugh Ramage. 1931. “A spectrographic analysis of animal tissues” . Roy, Soc., Proc., Ser. B, v. 108, p. 157–73, 1931. London.
Föyn, Ernst, B. Karlik, H. Pettersson, and E. Rona. 1939. The radioactivity of seawater. Oceanografiska Inst. Göteborg (Göteborgs K. Vetensk… … Handlingar, 5, Ser. B), Meddelanden, N. S., 44 pp., 1939.
Gaarder, T.1916. De vestlandske fjordes hydrografi. I. Surstoffet i fjordene. Bergens Mus. Aarbok, 1915–16.
Goldschmidt, V. M.1933. Grundlagen der quantitativen Geochemie. Fortschritte der Mineral., Kristal. und Petrographie, v. 17, p. 112–56, 1933.
Goldschmidt, V. M.1937. “The principles of distribution of chemical elements in minerals and rocks” . Chem. Soc., Jour., p. 655–73, 1937. London.
Goldschmidt, V. M., and L. W. Strock. 1935. Zur Geochemie des Selens, II. Gesellsch. d. Wiss. zu Göttingen, Math.-Phys. Klasse. Fachgruppe IV, Geol. u. Mineral., N.F., v. 1, p. 123–42, 1935.
Greenberg, D. M., E. G. Moberg, and E. C. Allen. 1932. “Determination of carbon dioxide and titratable base in sea water” . Ind. Eng. Chem., Anal. ed., v. 4, p 309–13, 1932.
Gripenberg, Stina. 1937a. “The calcium content of Baltic water” . Conseil Perm. Internat. p. l'Explor. de la Mer, Jour. du Conseil, v. 12, p. 293–304, 1937.
Gripenberg, Stina. 1937b. “The determination of excess base in seawater” . Internat. Assn. Phys. Oceanogr. (Assn. d'Océanogr. Phys.), Union Géod. et Géophys. Internat., Proc.-Verb., no. 2, p. 150–52, 1937. Liverpool.
Haber, F.1928. Das Goldim Meere. Zeitschr. d. Gesellsch. f. Erdkunde, Suppl. 3, p. 3–12, 1928.
Haendler, H. M., and T. G. Thompson. 1939. “The determination and occurrence of aluminum in sea water” . Jour. Marine Research, v. 2, p. 12–16, 1939.
Harding, M. W., and E. G. Moberg. 1934. Determination and quantity of boron in sea water. Fifth Pacific Sci. Cong., Canada, 1933, Proc., v. 3, p. 2093–95, 1934.
Harvey, H. W.1926. “Nitrates in the sea” . Marine Biol. Assn. U. K., Jour., v. 14, p. 71–88, 1926. Plymouth.
Harvey, H. W.1937. “The supply of iron to diatoms” . Marine Biol. Assn. U. K., Jour., v. 22, p. 205–19, 1937. Plymouth.
Hewitt, L. F.1937. Oxidation-reduction potentials in bacteriology and biochemistry. 4th ed. London County Council, no. 3200, 101 pp., 1937.
Igelsrud, Iver, and T. G. Thompson. 1936. “Equilibria in the saturated solutions of salts occurring in sea water. II” . The quaternary system MgCl2− CaCI2−KC1-H2O at 0° Amer. Chem. Soc., Jour., v. 58, p. 1–13, 1936.
Igelsrud, Iver, T. G. Thompson, and B. M. G. Zwicker. 1938. “The boron content of sea water and of marine organisms” . Amer. Jour. Sci., v. 35, p. 47–63, 1938.
International Assn. Phys. Oceanography. (Assn. d'Océanographie Physique, Union Géodesique et Géophysique Internationale.) Report of the Committee on Chemical Methods and Units. Presented at 7th General Assembly, Washington, D. C., 1939. Publication scientifique. (In press.)
Jacobs, Woodrow C.1937. “Preliminary report on a study of atmospheric chlorides” . Monthly Wea. Review, v. 65, p. 147–51, 1937. Washington, D, C.
Jacobsen, J. P., and Martin Knudsen. 1940. “Urnormal 1937 or primary standard sea-water 1937” . Internat. Assn. Phys. Oceanogr. (Assn. d'Océanogr. Phys., Union Géod. et Géophys. Internat.) Pub. sci. 7, 38 pp., 1940. Liverpool.
Johnstone, James. 1928. An introduction to oceanography. Liverpool, University Press, 368 pp., 1928.
Kirk, P. L., and E. G. Moberg. 1933. “Microdetermination of calcium in sea water” . Ind. Eng. Chem., Anal. ed., v. 5, p. 95–97, 1933.
Knopf, A.1931. “Age of the ocean. Physics of the earth” , v. 4, Age of the earth, pt. 2, p. 65–72. Nat. Res. Council, Bull., no. 80, 1931. Washington, D. C.
Köhler, Hilding. 1921. Zur Kondensation des Wasserdampfes in der Atmosphäre. Geofysiske Publikasjoner, v. 2, no. 1, 15 pp., 1921. Oslo.
Krogh, August. 1904. “On the tension of carbonic acid in natural waters and especially in the sea” . Medd. om Grönland, v. 26, p. 342, 1904.
Krogh, August. 1934. “A method for the determination of ammonia in water and air” . Biol. Bull., v. 67, p. 126–131, 1934.
Krümmel, Otto. 1907. Handbuch der Ozeanographie. Bd. 1. Die räumlichen, chemischen und physikalischen Verhältnisse des Meeres. Stuttgart, J. Engelhorn, 526 pp., 1907.
Lewis, G. N., and Merle Randall. 1923. Thermodynamics and the free energy of chemical substances. N. Y., McGraw-Hill, 653 pp., 1923.
Lyman, John, and R. H. Fleming. 1940. “Composition of sea water” . Jour. Marine Research, v. 3, p. 134–46, 1940.
McClendon, J. F., C. C. Gault, and S. Mulholland. 1917. The hydrogen-ion concentration, CO2− tension, and CO2−content of sea water. Carnegie Inst.Washington, Pub. no. 251, Papers from Dept. Marine Biol., p. 21–69, 1917.
Malmgren, Finn. 1927. “On the properties of sea-ice” . Norwegian North Polar Exped. with the Maud 1918–1925, Sci. Results, v. 1, no. 5, 67 pp., 1927.
Marks, Graham. 1938. “The copper content and copper tolerance of some species of mollusks of the southern California coast” . Biol. Bull., v. 75, p. 224–37, 1938.
Michaelis, L.1930. “Oxidation-reduction potentials” . Phila., Lippincott, 199 pp., 1930.
Mitchell, P. H., and N. W. Rakestraw. 1933. “The buffer capacity of sea water” . Biol. Bull., v. 65, p, 437–451, 1933.
Moberg, E. G., D. M. Greenberg, R. Revelle, and E. C. Allen. 1934. “The buffer mechanism of sea water” . Scripps Inst. Oceanogr., Calif. Univ., tech. ser., v. 3, p. 231–78, 1934.
Moberg, E. G., and R. R. D. Revelle. 1937. “The distribution of dissolved calcium in the North Pacific” . Internat. Assn. Phys. Oceanogr. (Union Géod. et Géophys. Internat., Assn. d'Océanogr. Phys.), Procès-verb., no. 2, p. 153, 1937.
Rakestraw, Norris W.1936. “The occurrence and significance of nitrite in the sea” . Biol. Bull., v. 71, p. 131–67, 1936.
Rakestraw, N. W., and V. M. Emmel. 1937. “The determination of dissolved nitrogen in water” . Ind. Eng. Chem., Anal. ed., v. 9, p. 344–46, 1937.
Rakestraw, N. W., and V. M. Emmel. 1938a. “The relation of dissolved oxygen to nitrogen in some Atlantic waters” . Jour. Marine Research, v. 1, p. 207–16, 1938.
Rakestraw, N. W., and V. M. Emmel. 1938b. “The solubility of nitrogen and argon in sea water” . Jour. Phys. Chem., v. 42, p. 1211–15, 1938.
Rakestraw, N. W., C. E. Herrick, Jr., and W. D, Urry. 1939. “The helium-neon content of sea water and its relation to the oxygen content” . Amer. Chem. Soc., Jour., v. 61, p. 2806–07, 1939.
Rakestraw, N. W., and F. B. Lutz. 1933. “Arsenic in sea water” . Biol. Bull., v. 65, p. 397–401, 1933.
Rakestraw, N. W., H. E. Mahncke, and E. F. Beach. 1936. “Determination of iron in sea water” . Ind. Eng. Chem., Anal. ed., v. 8, p. 136–38, 1936.
Reith, J. F.1930. “Der Jodgehalt von Meerwasser” . Recueil Trav. chim. Pays-Bas, v. 49, p. 142–50, 1930.
Revelle, Roger. 1934. “Physico-chemical factors affecting the solubility of calcium carbonate in sea water” . Jour. Sedim. Petrol., v. 4, p. 103–10, 1934.
Revelle, Roger. 1936. Marine bottom samples collected in the Pacific Ocean by the Carnegie on its seventh cruise. California University, Dissertation, 1936. (Carnegie Inst.Washington, Carnegie Repts. In press.)
Revelle, Roger, and R. H. Fleming. 1934. “The solubility product constant of calcium carbonate in sea water” . Fifth Pacific Sci. Cong., Canada, 1933, Proc., v. 3, p. 2089–92, 1934.
Riley, G. A.1937. “The significance of the Mississippi River drainage for biological conditions in the northern Gulf of Mexico” . Jour. Marine Research, v. 1, p. 60–74, 1937.
Robinson, Rex J., and F. W. Knapman. 1941. “The sodium-chlorinity ratio of ocean waters from the northeast Pacific” . Jour. Marine Research, v. 4, p. 142–152, 1941.
Robinson, Rex J., and H. E. Wirth. 1934. Report on the free ammonia, albuminoid nitrogen and organic nitrogen in the waters of the Puget Sound area, during the summers of 1931 and 1932. Conseil Perm. Internat. p. l'Explor. de la Mer, Journal du Conseil, v. 9, p. 15–27, 1934.
Robinson, Rex J., and H. E. Wirth. 1935. “Photometric investigation of the ceruleomolybdate determination of phosphate in waters” . Ind. Eng. Chem., Anal. ed., v. 7, p. 147–50, 1935.
Rogers, C. G.1938. Textbook of comparative physiology. 2d ed.New Pork, McGraw-Hill, 715 pp., 1938.
Smith, C. L.1940. “The Great Bahama Bank. II. Calcium carbonate precipitation” . Jour. Marine Research, v. 3, p 171–189, 1940.
Ström, K. M.1936. Land-locked waters. Hydrography and bottom deposits in badly ventilated Norwegian fjords with remarks upon sedimentation under anaerobic conditions. Norske Vidensk. Ak. i Oslo, 1. Math.-Naturv. Klasse, no. 7, 85 pp., 1936.
Subow, N. N.1931. “Oceanographical tables. U.S.S.R.” , Oceanogr. Institute, Hydro-meteorol. Com., 208 pp., 1931. Moscow.
Sverdrup, H. U.1929. “The waters on the North-Siberian Shelf. Norwegian North Polar Exped. with the Maud 1918–1925” , Sci. Results, v. 4, no. 2, 206 pp., 1929.
Thomas, Bertram D., and T. G. Thompson. 1933. “Lithium in sea water” . Science, v. 77, p. 547–48, 1933.
Thompson, T. G., and R. W. Bremner. 1935a. “The determination of iron in sea water” . Conseil Perm. Internat. p. l'Explor. de la Mer, Jour. du Conseil, v. 10, p. 33–38, 1935.
Thompson, T. G., and R. W. Bremner. 1935b. The occurrence of iron in the water of the northeast Pacific Ocean. Conseil Perm. Internat. p. l'Explor. de la Mer, Jour. du Conseil, v. 10, p. 39–47, 1935.
Thompson, T. G., and H. G. Houlton. 1933. “Determination of silicon in sea water” . Ind. Eng. Chem., Anal, ed., v. 5, p. 417–21, 1933.
Thompson, T. G., W. R. Johnston, and H, E. Wirth. 1931. The sulfate-chlorinity ratio in ocean water. Conseil Perm. Internat. p. l'Explor. de la Mer, Jour. du Conseil, v. 6, p. 246–51, 1931.
Thompson, T. G., and R. J. Robinson. 1932. Chemistry of the sea. Physics of the earth, v. 5, Oceanography, p. 95–203. Nat. Research Council, Bull., no. 85, 1932. Washington, D. C.
Thompson, T. G., and R. J. Robinson. 1939. “Notes on the determination of dissolved oxygen in sea water” . Jour. Marine Research, v. 2, p. 1–8, 1939.
Thompson, T. G., and H. J. Taylor. 1933. “Determination and occurrence of fluorides in sea water” . Ind. Eng. Chem., Anal. ed., v. 5, p. 87–89, 1933.
Thompson, T. G., and T. L. Wilson. 1935. “The occurrence and determination of manganese in sea water” . Amer. Chem, Soc., Jour., v. 57, p. 233–36, 1935.
Thompson, T. G., and C. C. Wright. 1930. “Ionic ratios of the waters of the North Pacific Ocean” . Amer. Chem. Soc., Jour., v. 52, p. 915–21, 1930.
Tourky, A. R., and D. H. Bangham. 1936. “Colloidal silica in natural waters and the “silicomolybdate” colour test” . Nature, v. 138, p. 587–88, 1936.
Wattenberg, H.1933. “Über die Titrationsalkalinität und den Kalziumkar-bonatgehalt des Meerwassers. Deutsche Atlantische Exped” . Meteor 1925–1927, Wiss. Erg., Bd. 8, 2 Teil, pp. 122–231, 1933.
Wattenberg, H.1936. Kohlensäure und Kalziumkarbonat im Meere. Fortschritte d. Mineral., Kristal. u. Petrographie, v. 20, p. 168–95, 1936.
Wattenberg, H.1937. Critical review of the methods used for determining nutrient salts and related constituents in salt water. 1. Methoden zur Bestimmung von Phosphat, Silikat, Nitrat und Ammoniak im Seewasser. Conseil Perm. Internat. p. l'Explor. de la Mer, Rapp. et Proc.-Verb., v. 103, pt. 1, p. 1–26, 1937.
Wattenberg, H.1938. Zur Chemie des Meerwassers: Über die in Spuren vorkommenden Elemente. Zeitschr. f. anorg. u. allgemeine Chemie, v. 236, p. 339–60, 1938.
Wattenberg, H., and E. Timmermann. 1936. Über die Sättigung des Seewassers an CaCO3, und die anorganogene Bildung von Kalksedimenten. Ann. d. Hydrogr. u. Mar. Meteor., p. 23–31, 1936.
Wattenberg, H., and E. Timmermann. 1938. Die Löslichkeit von Magnesiumkarbonat und Strontium-karbonat in Seewasser. Kieler Meeresforschungen, Bd. 2, p. 81–94, 1938.
Webb, D. A.1937. “Studies on the ultimate composition of biological material. Pt. 2. Spectrographic analyses of marine invertebrates with special reference to the chemical composition of their environment” . Roy. Dublin Soc., Sci., Proc., v. 21, p. 505–39, 1937.
Webb, D. A.1938. “Strontium in sea water and its effect on calcium determinations” , Nature, v. 142, p. 751–52, 1938.
Webb, D. A.1939. “The sodium and potassium content of sea water” . Jour. Exper. Biol., v. 16, p. 178–83, 1939.
Wiese, W.1930. Zur Kenntnis der Salze des Meereises. Ann. d. Hydrogr. u. Mar. Meteor., Jahrg. 58, p. 282–286, 1930.
VII. Organisms and the Composition of Sea Water
Chemical Composition of Marine Organisms
Alterations of the concentration of the dissolved constituents of sea water are brought about by the development and subsequent death and disintegration of organisms. Virtually all of the substances extracted from the water are returned to solution by metabolic processes or by disintegration of the organisms, but the elements removed are returned to solution at some later time and often in some other part of the water column. Hence, the modifications may be in opposite directions at different times and localities. A small fraction of the organic remains accumulates on the sea bottom and is lost to the cycle.
Sea water probably contains in solution all of the chemical elements, although only some fifty have yet been detected. There is a large amount of data on the occurrence of various elements in marine plants and animals, but unfortunately the material is far from complete for any one biological group. Either a few elements only have been determined—such as iodine, for example, which has been thoroughly investigated—or only a portion of the organisms—for example, the skeletal structures—has been analyzed.
Vinogradov (1935, 1937) has compiled the chemical analyses of the lower plants and animals, both aquatic and terrestrial. He reports some sixty of the elements that have been found in one or more species. Webb and Fearon (1937) have tabulated thirty-nine elements that are commonly found and have divided these into two groups according to their apparent importance to living things: (1) eighteen invariable elements, and (2) twenty-one variable elements. These classes are further sub-divided on the basis of the concentration in which the elements are present. Seven elements are listed as contaminants (table 46).
The primary invariable elements are the essential constituents of carbohydrates, lipides (fats), and proteins. Some of the invariable elements classed as secondary or as microconstituents are always present in the lipides and proteins. This list is for plants and animals in general and not for marine forms alone. Comparison of tables 46 and 36 shows that nine elements (starred) detected in organisms have not yet been
| Invariable (18) | Variable (21) | Contaminants | |||
|---|---|---|---|---|---|
| Primary 1–60% | Secondary 0.05–1% | Microconstituents <0.05% | Secondary | Microconstituents | |
* Not yet reported for sea water. | |||||
| Hydrogen | Sodium | Boron | Titanium[*] | Lithium | Helium |
| Carbon | Magnesium | Fluorine | Vanadium | Beryllium[*] | Argon |
| Nitrogen | Sulphur | Silicon | Zinc | Aluminum | Selenium |
| Oxygen | Chlorine | Manganese | Bromine | Chromium[*] | Gold |
| Phosphorus | Potassium | Copper | Cobalt[*] | Mercury | |
| Calcium | Iodine | Nickel | Bismuth[*] | ||
| Iron | Germanium[*] | Thallium[*] | |||
| Arsenic | |||||
| Rubidium | |||||
| Strontium | |||||
| Molybdenum | |||||
| Silver | |||||
| Cadmium[*] | |||||
| Tin[*] | |||||
| Cesium | |||||
| Barium | |||||
| Lead | |||||
The lack of comparable data for the different types of organisms makes it necessary to consider their composition under three headings—namely, organic material (largely carbohydrates, lipides, and proteins), inorganic skeletal structures, and inorganic solutes in the body fluids. Although the proportions of carbohydrates, lipides, and proteins may vary considerably, the composition of any one type is rather constant, so that the average values in table 47 can be used with some confidence. Furthermore, there are numerous determinations of lipides (ether extract) and protein (based on nitrogen determinations), and from these measurements and the loss on ignition the carbohydrate may be computed. Skeletal structures differ so much in composition and in their mass, compared to that of the organic material, that they must be considered separately. Inorganic solutes in the body fluids are considered as a separate class, because they apparently do not differ very much in composition
| Percentage composition | Relative proportions by weight, C = 100 | |||||||
|---|---|---|---|---|---|---|---|---|
| Element | Carbohydrates | Lipides | Proteins | Element | Sea water | Lipides | Proteins | |
| O | 49.38 | 17.90 | 22.4 | C | 100 | 100 | 100 | |
| C | 44.14 | 69.05 | 51.3 | P | 0.05 | 3.1 | 1.4 | |
| H | 6.18 | 10.00 | 6.9 | N | 0.5 | 0.88 | 34.7 | |
| P | 2.13 | 0.7 | S | 3150 | 0.45 | 1.6 | ||
| N | 0.61 | 17.8 | Fe | 0.07 | 0.2 | |||
| S | 0.31 | 0.8 | ||||||
| Fe | 0.1 | |||||||
In table 47 are given the average compositions of the three great classes of organic material (Rogers, 1938) and the relative proportions in which their component elements occur in sea water. The oxygen and hydrogen are not considered, and the values are adjusted to C = 100. The values for C, S, and Fe are from table 36; those for N and P are the average winter values in the English Channel (pp. 252, 258). In the lipides, phosphorus is concentrated, and in the proteins the nitrogen and phosphorus show a great increase with respect to carbon. The fact that sulphur, which is one of the relatively abundant elements in sea water, is a minor constituent of the lipides and proteins in organic material indicates that carbon, here used as the reference element, is itself markedly concentrated. The values given in table 47 are general averages, and those for marine organisms may differ slightly. It should be noted that changes in the proportions of carbohydrates, lipides, and proteins will modify the ratios in which the above-mentioned elements will be removed from the water. Many of the other elements that are concentrated by organisms—for example, iodine, iron, and copper—probably form a part of the organic material or they occur in the skeletal structures, as it is difficult to see how the free ions could be retained in the body fluids
In table 48 are given analyses of certain types of skeletal material. In each case there is some organic matter, which is highest in the lobster carapace, and even in the phosphatic brachiopod shell it forms a large fraction. Of course, there are wide ranges in the proportion of inorganic skeletal structures in the whole organism, and in some cases such structures may be entirely lacking. The first three examples are for calcareous types with CaCO3 predominating, but in some groups MgCO3 forms an important part of the shell. The lobster may be considered as representative of the arthropods in general, although the proportion of organic matter is probably even greater in the small forms. The amount of phosphate is notable in the lobster and even more so in the phosphatic brachiopod shell, which is predominantly calcium phosphate. The sponge spicules are virtually pure hydrated silica and may be taken as representative of the diatom and radiolarian skeletons. The silica, iron, and aluminum in the other analyses probably represent impurities introduced by the presence of clay and sand grains. These analyses cannot be regarded as complete, and further examination will undoubtedly reveal many other elements present in small amounts. It should be noted that chlorine and sodium, the two most abundant elements in sea water, are not shown in any of these analyses. These elements form soluble compounds and hence would not be suitable for skeletal structures. From table 48 it can be seen that the development or re-solution of skeletal structures of marine organisms may be expected to affect the concentrations
| Substance | Foraminifera (Orbitolites marginatis) | Coral (Oculina diffusa) | Calcareous alga (Lithophyllum antillarum) | Lobster (Homarus sp.) | Phosphatic brachiopod (Discinisca lamellosa) | Siliceous sponge (Euplectella speciosa) |
|---|---|---|---|---|---|---|
| Ca | 34.90 | 38.50 | 31.00 | 16.80 | 26.18 | 0.16 |
| Mg | 2.97 | 0.11 | 4.36 | 1.08 | 1.45 | 0.00 |
| CO3 | 59.70 | 58.00 | 62.50 | 22.40 | 7.31 | 0.24 |
| SO4 | 0.68 | 0.52 | 4.43 | 0.00 | ||
| PO4 | tr | tr | tr | 5.45 | 34.55 | 0.00 |
| SiO2 | 0.03 | 0.07 | 0.04 | 0.30 | 0.64 | 88.56 |
| (Al,Fe)2O3 | 0.13 | 0.05 | 0.10 | 0.44 | 0.32 | |
| Organic matter, etc | 2.27 | 3.27 | 1.32 | 53.45 | 25.00 | 10.72 |
The relative concentrations of the elements that are abundant in the body fluids do not differ very much from those in sea water (table 49). Although little is known concerning the less abundant elements, it appears that the inorganic portion of the body fluids can be considered as slightly altered sea water. Therefore, this part of the organism cannot play any appreciable part in modifying the composition of the water. Although the composition and concentration of the inorganic solutes is of no particular importance in the present problem, these features have been studied intensively in problems of osmotic pressure relations (chapter VIII) and in connection with the mechanism of solute and water exchange between aquatic organisms and their environment. These fields have been reviewed by Rogers (1938).
| Element | Sea water | Echinus esculentus (Sea urchin) | Homarus vulgaris (Lobster) | Cancer pagurus (Crab) |
|---|---|---|---|---|
| Cl | 180 | 182 | 156 | 156 |
| Na | 100 | 100 | 100 | 100 |
| Mg | 12.1 | 12.0 | 1.5 | 5.7 |
| S in SO4 | 8.4 | 8.5 | 2.2 | 6.7 |
| Ca | 3.8 | 3.9 | 5.0 | 4.8 |
| K | 3.6 | 3.7 | 4.7 | 4.0 |
Thus far only the various fractions of the organisms have been discussed, and it is of interest to consider the composition of the entire plant or animal. As the plants are the primary “consumers” of inorganic material, it would be desirable to know the composition of such important groups as the diatoms and peridinians, but no complete analyses of these forms have been made. What information we have will be discussed below. The data for animals is also far from complete, but in table 50 are given three examples. The relative compositions have been adjusted to Na = 100, and, for comparison, the constituents of sea water are given in the same way. The relatively high proportions of the elements abundant in sea water which occur in the copepod analysis indicate the presence of considerable sea water in the original sample. As Archidoris possesses internal calcareous structures, the calcium content is high. Consequently the proportions of the elements constituting the organic material are rather low in these two cases. It is immediately obvious, however, that the essential constituents of the organic material, such as carbon, nitrogen, and phosphorus, are very high when compared to their relative concentrations in sea water.
| Element | Calanus (Copepod) Vinogradov, 1938 | Fish[a] (Average) | Archidoris britannica (Nudibranch) McCance & Masters, 1937–38 | Sea water | Concentration factors | ||
|---|---|---|---|---|---|---|---|
| Copepod | Fish | Nudibranch | |||||
aFrom analysis of Jowett and Davies (1938), Clements and Hutchinson (1939). | |||||||
bWinter values, English Channel. | |||||||
cHigher values from table 36. | |||||||
| Cl | 194 | 180 | 180 | 1.1 | 1.0 | ||
| Na | 100 | 100 | 100 | 100 | 1.0 | 1.0 | 1.0 |
| Mg | 5.6 | 36 | 156 | 12.1 | 0.46 | 3.0 | 12.9 |
| S | 25.9 | 259 | 7.1 | 8.4 | 3.1 | 31 | 0.85 |
| Ca | 7.4 | 52 | 262 | 3.8 | 1.9 | 13.7 | 69 |
| K | 53.7 | 383 | 20 | 3.6 | 15 | 109 | 5.5 |
| Br | 1.7 | 0.6 | 3 | ||||
| C | 1113 | ca 4100 | ca 480 | 0.26 | 4,300 | 15,800 | 1,850 |
| Sr | 11 | 0.12 | 92 | ||||
| Si | 1.3 | 0.001[b] | 13,000 | ||||
| F | 69 | 0.01 | 6,900 | ||||
| N | 280 | 1276 | 107 | 0.001[b] | 280,000 | 1,276,000 | 107,000 |
| P | 24.1 | 256 | 6 | 0.0001[b] | 241,000 | 2,560,000 | 60,000 |
| I | 0.04 | 0.0005 | 80 | ||||
| Fe | 1.3 | 1.3 | 0.23 | 0.0002[c] | 6,000 | 6,000 | 1,000 |
| Mn | 0.0008 | 0.0001[c] | 8 | ||||
| Cu | 0.008 | 0.43 | 0.0001[c] | 80 | 4,300 | ||
If the relative amounts of the various elements in these animals are divided by their relative concentrations in sea water, a series of concentration factors, referred to sodium, are obtained. It will be seen that chlorine would give virtually identical results. The concentration factors range from about unity up to over two million for phosphorus in the fish, and in all three cases they are greatest for nitrogen and phosphorus. If it is assumed that the rates of diffusion of all substances and their rates of absorption by the organisms depend only upon the amounts of the ions in the water, then the concentration factors should be a measure of the time required to accumulate them. Those elements having the highest concentration factors would then be the ones that might limit the rate of growth. The data in table 50 indicate that nitrogen and phosphorus may very well be limiting elements in the sea, although it should be remembered that the examples are for animals that must obtain their supply of these elements either directly or indirectly from the plants. If the total carbon in sea water had been used as the reference element, only nitrogen and phosphorus would have significantly larger factors. But it is obvious that carbon is itself concentrated more than one thousandfold with reference to the major elements in sea water. According to table 50 the relative concentration
| Element | Sea water | Diatoms | Peridinians | Copepods | Concentration factors (referred to carbon) | ||
|---|---|---|---|---|---|---|---|
| Diatoms | Peridinians | Copepods | |||||
aWinter values, English Channel. | |||||||
bHigher value, table 36. | |||||||
| C | 100 | 100 | 100 | 100 | 1 | 1 | 1 |
| N | 0.5[a] | 18.2 | 13.8 | 25.0 | 36 | 28 | 50 |
| P | 0.05[a] | 2.7 | 1.7 | 2.2 | 54 | 34 | 44 |
| Fe | 0.07[b] | 9.6 | 3.4 | 0.13 | 137 | 49 | 2 |
| Ca | 1420 | 12.5 | 2.7 | 0.66 | 0.01 | 0.002 | 0.0005 |
| Si | 0.4[a] | 93.0 | 6.6 | 0.13 | 232 | 16 | 0.3 |
In table 51 are given the relative concentrations of certain elements in diatoms, peridinians, and copepods, adjusted to C = 100. The data for the photosynthetic forms are recomputed from Vinogradov (1935), and for copepods are the same as those given in table 50. The concentration factors for nitrogen and phosphorus are about the same in all three forms. In the diatoms, iron is higher, while silicon has the highest factor, which may indicate that these elements also limit the rate of growth. For the peridinians the factors for nitrogen, phosphorus, and iron are nearly the same.
Interrelations Between Elements Whose Distribution Is Affected by Biological Activity
Because the relative composition of organisms living in the sea differs from that of sea water, their growth will tend to modify the composition of the water. The ultimate regeneration of the inorganic substances by biological processes will return the elements to solution, but the net effects will usually be in opposite directions at different times and in different parts of the water column. Tables 50 and 51 show that certain elements present in the water in low concentrations, such as nitrogen, phosphorus, iron, and silicon, are those removed in the largest relative amounts. The distribution of these elements, known as the plant nutrients, is profoundly affected by biological activity, their concentrations are virtually independent of salinity, and they are commonly referred to as nonconservative, in contrast to those elements that bear a constant ratio to the total dissolved solids.
Plants are the most important “consumers” of the inorganic substances. Their activity is restricted to the upper layers of the sea (the euphotic zone), where there is adequate light for them to carry on photosynthesis. In nearshore areas the thickness of the euphotic layer may be only a few meters, and even in the open sea, where the transparency is great, the growth of plants is restricted to the upper few hundred meters (chapter XVI). Animals living below the euphotic layer may remove elements from solution which are necessary for the secretion of skeletal structures, but most of the materials must come directly or indirectly from plants that develop near the surface. The metabolic activities of the plants, animals, and bacteria return the elements to inorganic form. Part of the regeneration must occur in the euphotic layer, but there is a general downward movement of the particulate matter, either living or dead, and, consequently, a continuous transport of the elements away from the surface layer. As described thus far, it
Redfield (1934), following an earlier suggestion by Harvey, showed that regardless of the absolute concentrations a constant ratio exists between the nitrate-nitrogen and phosphate-phosphorus content of sea water, that these elements are apparently removed from the water by organisms in the same proportions in which they occur, and that on the death and decomposition of the organisms they are returned to solution simultaneously. Cooper (1938a) proposed a modified ratio, pointing out that the phosphorus data for sea water used by Redfield had not been corrected for salt error. Fleming (1940) obtained from examination of additional data a slightly different relationship for the N:P in plankton. All these figures are given in table 52, which also shows the relation of carbon to the other two elements in plankton.
| Source | By weight | By atoms | ||||
|---|---|---|---|---|---|---|
| C | N | P | C | N | P | |
| Redfield (1934) Plankton | 53.2 | 8.2 | 1 | |||
| Redfield (1934) Seawater | 9.0 | 1 | 20 | 1 | ||
| Cooper (1938a) Seawater | 6.8 | 1 | 15 | 1 | ||
| Fleming (1940) Phytoplankton | 42 | 7 | 1 | |||
| Fleming (1940) Zooplankton | 40 | 7.4 | 1 | |||
| Fleming—Average: Plankton. | 41 | 7.2 | 1 | 106 | 16 | 1 |
The ratios given above hold very well for the nitrate and phosphate in ocean waters (see fig. 51), but, since they represent the net effect of biological activity, marked deviations from the ratios may be found in individual types of organisms. However, they indicate the order of magnitude of the relationships in marine organisms.
In order to extend the usefulness of these relationships, it is worth while to add the oxygen. As an approximation, it may be assumed that two atoms of oxygen are required for the oxidation of each atom of
In the euphotic layer, for each milligram of phosphorus utilized in photosynthesis, these ratios indicate that the plants will take up 7.2 mg of nitrogen (chiefly nitrate) and 76 ml of CO2 and release the same volume of oxygen. At lower levels, where regeneration is taking place, the consumption of 76 ml of O2 should set free the corresponding amounts of CO2, N, and P. The oxygen saturation value for water of 5° temperature is of the order of 7.0 ml/L; hence it may be seen that, if all of the oxygen has been consumed in subsurface water of approximately this temperature, the NO3-N and PO4-P will be increased by about 50 μg-atoms/L (0.650 mg/L) and 3 μg-atoms/L (0.090 mg/L), respectively. These values are approximately the largest amounts ever encountered in the ocean. If all the waters leaving the surface were saturated with oxygen and completely depleted of nitrate and phosphate, it might be expected that there would be a close agreement in the deeper waters between these substances and the oxygen depletion (difference between the saturation value and the observed content). Such a general relationship exists in waters that have left the surface in lower latitudes, but in higher latitudes water sinking from the surface is saturated with oxygen and contains appreciable amounts of nutrients; hence the relationship between the oxygen depletion and the nutrient content must have the form
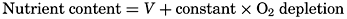
The above comments do not necessarily apply to elements composing hard “inorganic” skeletal structures. Both calcium carbonate and silica are utilized by organisms in the euphotic layer and elsewhere, but the ratios of utilization of Ca, C as CO3, and Si with reference to, say, phosphate-P, depend upon the character of the organisms. As pointed out elsewhere (p. 208), CaCO3 is removed from the surface layers, and the same is true of the SiO2. Although there is generally a depletion of Si in regions where the nitrate-N and phosphate-P are low, the processes of re-solution of calcareous and siliceous structures do not necessarily parallel decomposition and the regeneration of the elements found in the soft parts of the organisms. Therefore, the general distribution of silicon in the sea differs somewhat from that of phosphate and nitrate, and the ratios between Si and N and Si and P are variable.
Locations of vertical sections and stations used to illustrate the distribution of phosphate, nitrate, and silicate, in the oceans.
Distribution of Phosphate, Nitrogen Compounds, and Silicate in the Oceans
The distribution of phosphate in the three oceans may best be shown by means of longitudinal vertical sections whose locations are indicated in fig. 44. The representations are intended to bring out only the major features of the vertical distribution, and for this reason many of the minor irregularities have been omitted. The section in the Atlantic Ocean (fig. 45) is based on data obtained by the Discovery (Deacon, 1933) in the Southern Hemisphere, by the Atlantis (Seiwell, 1935) in the North Atlantic, and by the Meteor (Defant et al, 1936) in the area to the south of Greenland. The section in the Pacific Ocean (fig. 46) has been constructed from Discovery observations in the Antarctic (Clowes, 1938) and from those of the Carnegie (in press). The section in the Indian Ocean (fig. 47) is based on Discovery observations (Clowes, 1938). Examination of these sections and the vertical distribution curves in figs. 48 and 50 shows that in general the distribution of phosphate and nitrate is characterized by four different layers: (1) a surface layer in which the concentration is low and relatively uniform with depth, (2) a layer in which the concentration increases rather rapidly with depth, (3) a layer of maximum concentration that is usually located somewhere between 500 and 1500 m, and (4) a thick bottom layer in which there is relatively little change with depth. Examination of figs. 45, 46, and 47 shows that the surface layer is thickest in mid-latitudes
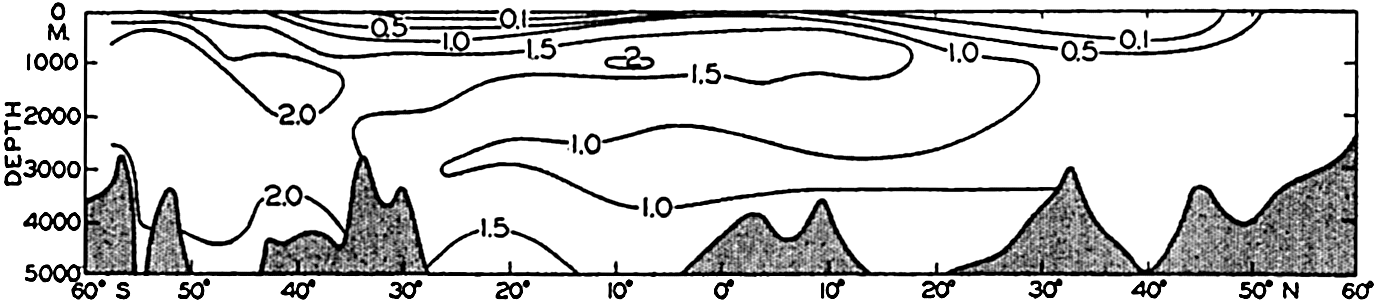
Phosphate distribution in a longitudinal section in the central Atlantic Ocean. Units: μg-atoms of phosphorus per 20° liter.
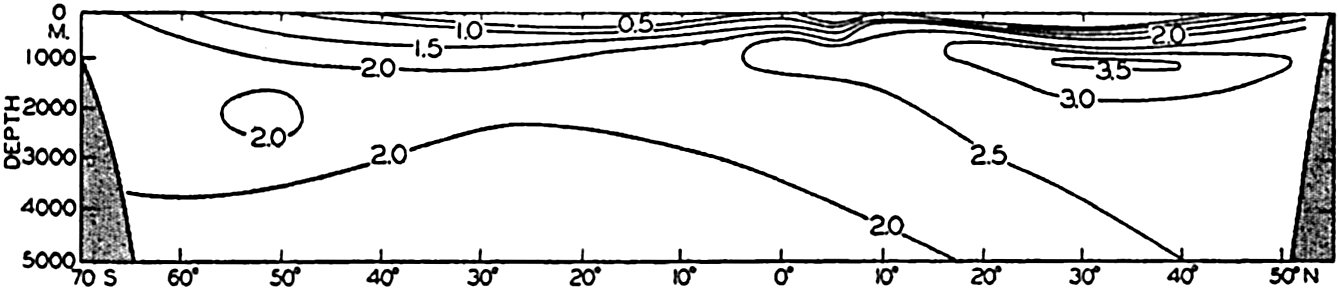
Phosphate distribution in a longitudinal section in the Pacific Ocean. Units: μg-atoms of phosphorus per 20° liter.
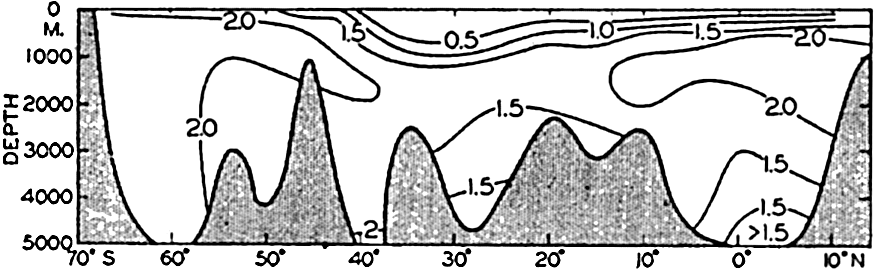
Phosphate distribution in a longitudinal section in the western Indian Ocean. Units: μg-atoms of phosphorus per 20° liter.
In the Atlantic Ocean the highest phosphate content (about 2 μg-atoms/L) is found in an intermediate layer extending northward from the Antarctic and centered at depths of about 1000 m. At all depths of about 1000 m or more there is a gradual decrease in phosphate concentration from south to north. A layer of minimum concentration containing less than 1.0 μg-atoms/L of phosphorus extends southward beneath the layer of maximum content. The phosphate concentration in the Antarctic is about twice that found in the northern part of the ocean. Regional differences in the phosphate distribution in the upper 50 m of the Atlantic Ocean are shown in fig. 217 (p. 787). Such differences are of importance in the distribution of plankton. The variations in a transverse section across the South Atlantic are illustrated in fig. 218 (p. 788), which shows the variable thickness of the surface layer of low phosphate content.
The distribution of phosphate in the Pacific Ocean (fig. 46) has many features that differ from those in the Atlantic Ocean. As might be expected, the conditions in the Antarctic are rather similar. However, the maximum amounts in the Pacific are found not in the Southern Hemisphere, as in the Atlantic, but north of the Equator, where the amounts present are about twice those found in the Antarctic (3.5 μg-atoms/L and about 2.0 μg-atoms/L, respectively). Furthermore, there is no clearly defined layer of minimum phosphate content beneath the maximum. The deeper waters of the Pacific are in general higher in phosphate than those of the Atlantic Ocean. The difference in the character of the distribution in the two oceans is related to the nature
The amounts of phosphate in the Indian Ocean (fig. 47) are greater than those in the Atlantic but somewhat less than those in the Pacific Ocean. The intermediate maximum in southern latitudes corresponds to that in the Atlantic, and the maximum in the equatorial region corresponds to that in the North Pacific, as it is related to the low oxygen content of the water. The minimum layer, at depths of about 3500 m, is clearly defined in all latitudes north of 40°S.
The differences between the phosphate concentrations in the three oceans are brought out in fig. 48, which is based on data collected by the Dana (Thomsen, 1931) on a voyage around the world and by the Atlantis in the western North Atlantic (Rakestraw and Smith, 1937). Observations from six stations (locations shown in fig. 44) in each ocean have been averaged and the values corrected for salt error (p. 182), so that they are somewhat higher than the values given in the sections. Too great emphasis should not be placed on the absolute values, as the purpose of the illustration is only to show the character of the vertical distribution in the three oceans, and to emphasize the higher phosphate content of the Pacific and the Indian Oceans in contrast to that of the Atlantic Ocean. Data from individual stations in moderate and low latitudes usually show a well-defined intermediate maximum.
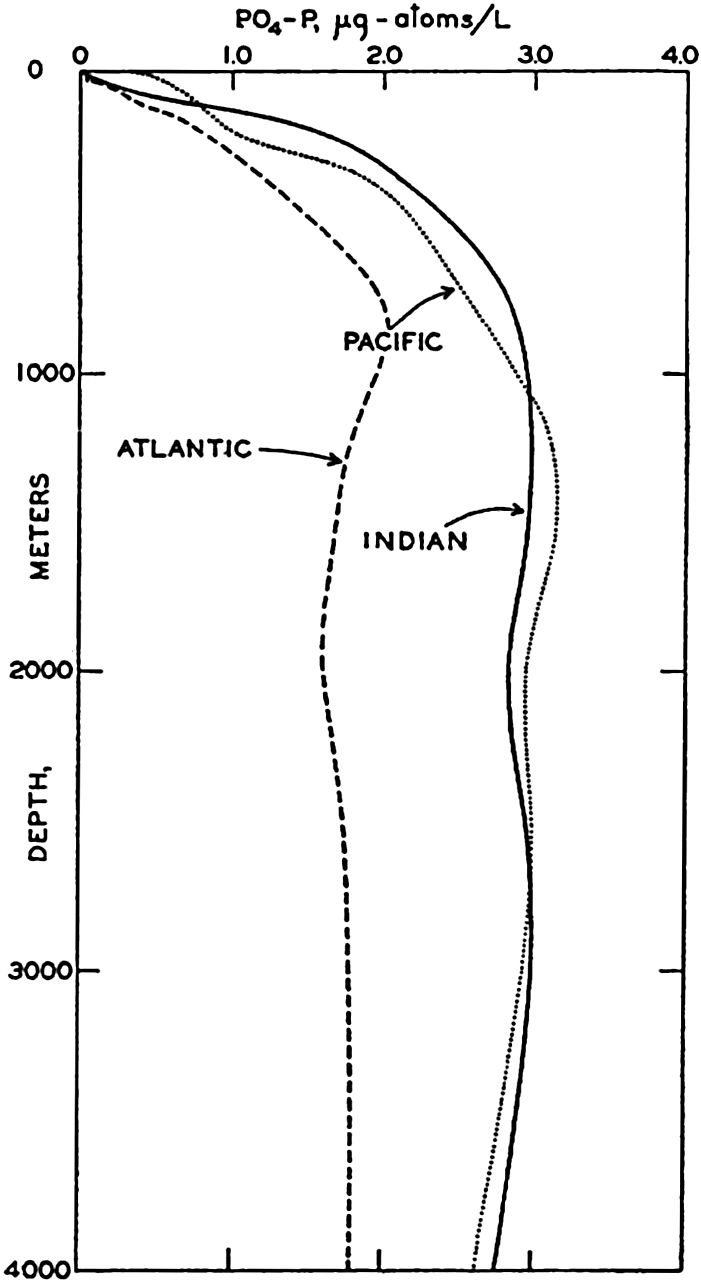
Vertical distribution of phosphate in the Atlantic, Pacific, and Indian Oceans based on data from the stations shown in fig. 44.
The lack of nitrate observations from many parts of the sea makes it impossible to prepare sections comparable to those for phosphate. Considerable data have been collected by the Dana (Thomsen, 1931, 1937), the Discovery (Discovery Reports, 1932; Deacon, 1933), the
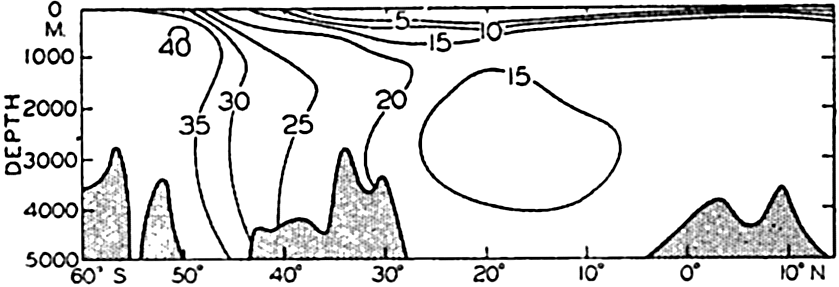
Distribution of nitrate in a longitudinal section in the central Atlantic Ocean. Units: μg-atoms of nitrogen per 20° liter.
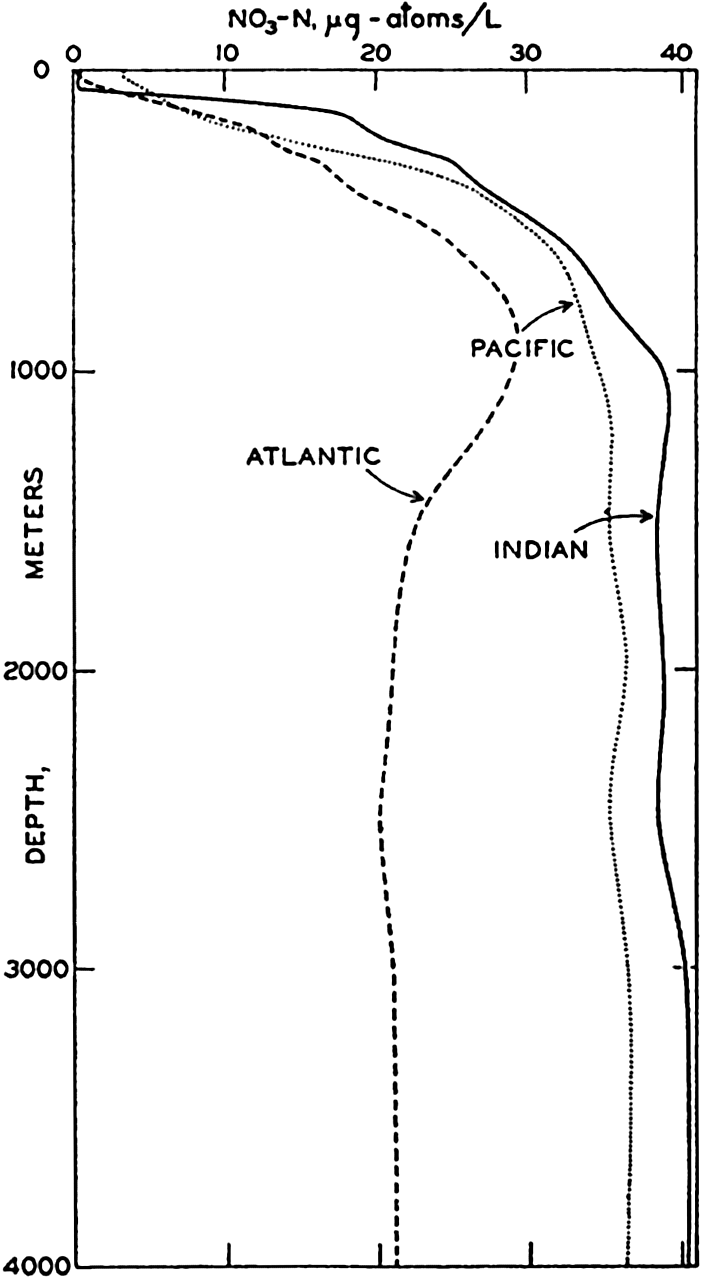
Vertical distribution of nitrate in the Atlantic, Pacific, and Indian Oceans based on data from the stations shown in fig. 44.
Curves for the nitrate distribution in the three oceans based on observations of the Dana and Atlantis and comparable to those shown for phosphate are given in fig. 50. Too much emphasis should not be placed upon the absolute values, but the curves clearly demonstrate the characteristic features of the vertical distribution
It has repeatedly been emphasized that there is a close parallelism between the concentrations of nitrate and phosphate. This relationship has been demonstrated by plotting against each other in fig. 51 the average data for phosphate and nitrate presented in figs. 48 and 50. It is immediately seen that there is a good linear relationship between the two substances. The straight line represents the “normal” ratio of nitrogen to phosphorus of 15:1 atoms proposed by Cooper (1938a). Because of this relationship, it is possible to predict with a fair degree of accuracy the concentration of either nitrate or phosphate when either one is known, and, as pointed out previously (p. 237), a relationship exists between the concentrations of these elements and the oxygen depletion.
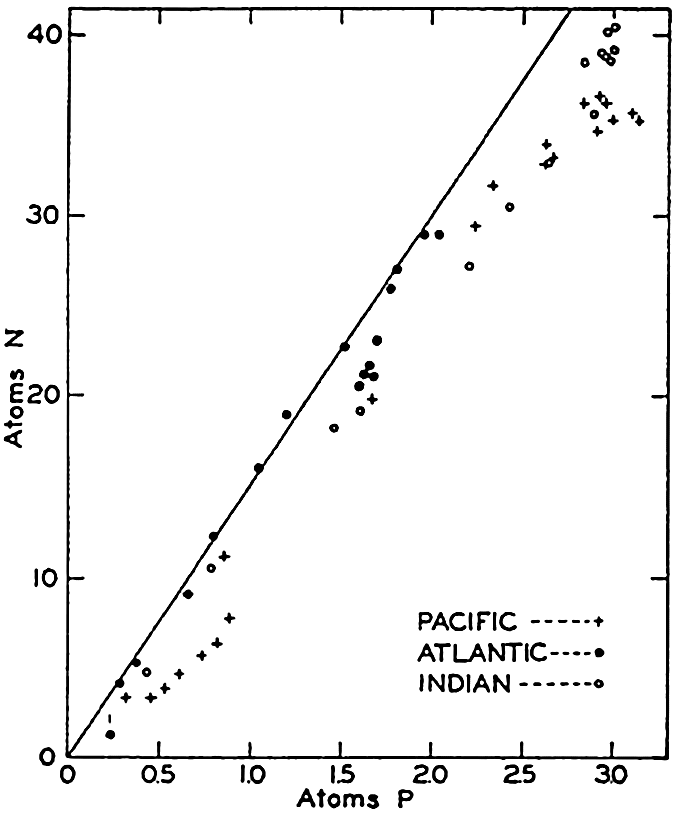
Relation between phosphate and nitrate in the three oceans. Points represent averages for individual depths used in constructing figs. 48 and 50. Straight line represents “normal” ratio proposed by Cooper.
The ranges in the various inorganic forms of nitrogen have been given (p. 181) as
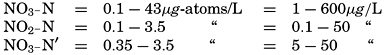
The nitrate is the most abundant form of inorganic nitrogen, and, as shown in fig. 51, the low values occur at and near the surface, the high values in deeper water. The distribution of nitrite and ammonia, which are always in low concentrations, differs from that of nitrate in that the higher values occur in or above the thermocline. Nitrite may also be found near the bottom in shallow water, but it is generally absent from most of the water column. The ammonia content of the deeper waters is relatively uniform and low. Data given by Rakestraw (1936) and by Redfield and Keys (1938) indicate that in deep water, away from shore, the amounts of these substances are small. At one station, half way between Cape Cod and Bermuda, the nitrite was found only at about
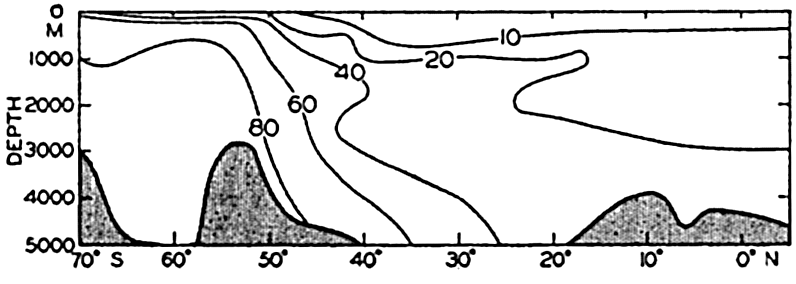
Distribution of silicate in a longitudinal section in the southeastern Atlantic Ocean. Units: μg-atoms of silicon per 20° liter.
The data available on the distribution of silicate in the oceans are even fewer than those for nitrate. The Discovery (Clowes, 1938) has made numerous observations in southern latitudes, and certain of these data have been used in preparing longitudinal sections in the South Atlantic (fig. 52) and in the Indian Ocean (fig. 54). The locations of these sections are shown in fig. 44. The Carnegie obtained numerous observations in the northeastern and central Pacific and there are scattered observations from other regions, but they are inadequate for the preparation of longitudinal sections. In order to bring out similarities and differences in distribution, the silicate sections should be compared with the corresponding phosphate sections (figs. 47 and 53). It is readily seen that the vertical distribution of silicate differs from that of phosphate and nitrate, as there is no marked intermediate maximum and the concentration increases all the way down to the bottom. The reasons for this difference in the pattern of distribution have already been set forth (p. 237). In the Atlantic Ocean (fig. 52) the silicate content of the deeper water is much less in low latitudes than it is in the
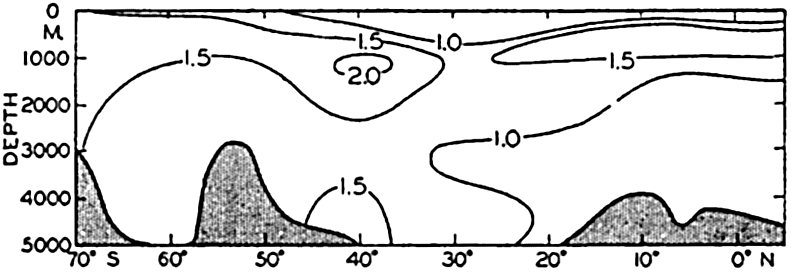
Distribution of phosphate in a longitudinal section in the southeastern Atlantic Ocean. Units: μg-atoms per 20° liter.
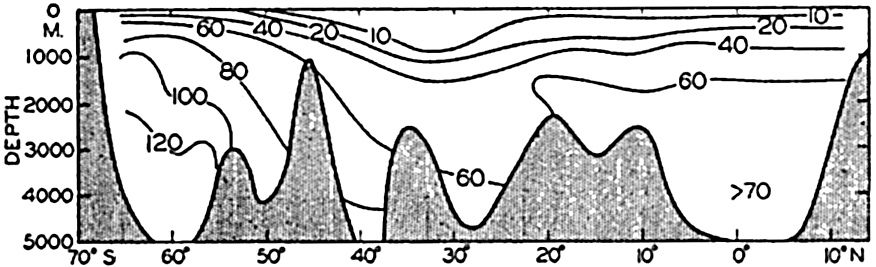
Distribution of silicate in a longitudinal section in the western Indian Ocean. Units: μg-atoms of silicon per 20° liter.
Vertical distribution of silicate at individual localities in the North Pacific, South Atlantic, and Indian Oceans.
In basins, the distributions of the elements discussed above may be quite different from those characteristic of the open sea. As shown in chapter IV, the conditions in basins depend upon the topography, the character of the renewal processes below sill depth, and the dissolved oxygen content (aeration) of the water. In well-aerated basins, where there is inflow at the surface, the nutrient content is usually low. For example, in the Mediterranean Sea the phosphate and nitrate below sill depth are small when compared with the concentrations in the waters of the Atlantic Ocean (Thomsen, 1931). In the western Mediterranean below about 1000 m the contents of phosphate and nitrate are constant in amounts of 0.6 μg-atoms/L and 11 μg-atoms/L, respectively, which are about one half or less of the amounts in the open Atlantic. The dense water that flows out of the Mediterranean over the sill and mixes with the intermediate waters of the North Atlantic is therefore relatively low in nutrient elements and tends to reduce the phosphate and nitrate contents of the waters at intermediate levels in the eastern North Atlantic.
In basins of low oxygen content, such as the Red Sea, the nitrate and phosphate are relatively high for reasons already stated (p. 237). In stagnant Norwegian fjords, where hydrogen sulphide is present in the water, Ström (1936) found the phosphate to be as high as 10 μg-atoms/L.
Factors Influencing the Distribution of Nutrient Elements
The concept of dynamic equilibrium (p. 160) can be applied to the large-scale distributions of phosphate, nitrate, and silicate discussed above. On this assumption the distribution is stationary, the local change is zero, (∂s/∂t = 0), and there must be a balance between the effects of diffusion, advection, and the net effects of biological processes. Although the concept of stationary distribution is applicable to the deeper waters and probably to the upper layers in low latitudes, it is not valid for the upper several hundred meters in localities where seasonal variations are conspicuous.
In the surface layers—that is, in the euphotic zone—biological processes will generally lead to a net utilization of the nutrient elements, and, if the rate of utilization exceeds the rate of supply by diffusion and by advection, the concentrations will decrease. This is the characteristic change that occurs during the spring and summer months in regions where physical conditions limit plant activity during the winter. In such regions the reverse change takes place during the winter, when the supply to the surface layers by diffusion and advection outweighs the utilization and leads to an increase in the nutrient content at and near the surface. Consequently in regions where the temperature, light intensity, and biological or other agencies are unfavorable for plant growth during part of the year, marked seasonal variations may occur in the nutrient distribution in the surface layers. In addition to fluctuations in consumption, the supply of nutrient elements to the surface layers by diffusion and advection may vary during the course of the year. For example, the magnitude of the vertical coefficient of eddy diffusivity, Az, is independent of the gradient in the nutrient concentrations but will be affected by the temperature distribution and the wind conditions. Furthermore, changes due to shifts in currents will affect the distributions, although undoubtedly the most conspicuous effects are those related to vertical advection. In regions of surface convergence, waters low in nutrients may extend for a considerable distance below the euphotic layer. On the other hand, where there is divergence—that is, upwelling—nutrientrich waters are carried upward toward the surface. Divergence may occur in the open ocean, as on the Equator and at the northern boundary of the Equatorial Countercurrent (p. 635), or along continental coasts where the prevailing winds are such that upwelling is induced (p. 501). In coastal areas where upwelling is seasonal or intermittent, the nutrient
Seasonal variations in the silicate content at various depths in Monterey Bay, California. Silicate scale increases downwards.
From the foregoing comments, it is obvious that seasonal variations in the distribution of the biologically affected elements must be interpreted with great care. Fluctuations in concentration cannot be ascribed to biological processes alone unless it can be established on the basis of other data, such as temperature and salinity observations, that the effects of advection and diffusion can be neglected. In certain regions where there are marked differences between the summer and winter concentrations, estimates of organic production have been made from the depletion of nutrients occurring in the upper layers. Such estimates are minimal unless the effects of regeneration and diffusion are taken into account, and will be invalid if advection is an important factor, as in Monterey Bay. No systematic study of the seasonal variations in the distribution of the nutrients in the open ocean has yet been made, but in certain coastal areas a considerable amount of data has been accumulated that will be taken up under the discussion of the individual elements in the following pages.
Compounds of Carbon, Nitrogen, Phosphorus, and Silicon in the Sea
Organic Carbon. The carbon present as carbon dioxide and the salts of carbonic acid, as well as many of the effects of biological activity on the distribution of CO2, have been discussed in chapter VI. Seasonal changes in the CO2 content of the waters of the English Channel have been described by Cooper (1933). The carbon present in sea water in organic combination will now be considered.
The CO2 that is removed from the water by organisms is utilized partly for the secretion of calcareous structures but chiefly for building up organic compounds. Metabolic activity returns most of the organic carbon to solution as CO2, and bacteria and other microorganisms play an important part in the break-down of excretory products and the detrital material resulting from the death and partial disintegration of plants and animals. If dissolved oxygen is present in the water, the end products will be completely oxidized, but in the absence of oxygen anaerobic bacteria may flourish and hydrogen sulphide and other products of putrefactive decomposition may be formed. The latter conditions apparently occur only in and above the sediments in certain areas and in enclosed basins. The CO2 in calcareous structures returns to solution if the skeletal material dissolves. It should be remembered that, as with other elements, the cycle of carbon in the sea is not completely closed, since there is some loss to the sediments in both calcareous material and in resistant organic matter.
Before proceeding to a discussion of the amounts of carbon occurring in organic combination, either in living organisms or in particulate or dissolved compounds of organic origin, it should be pointed out that the division of the organic matter into various fractions is an empirical one. It has been customary to speak of “net plankton”—usually that which can be removed from the water by filtration through a fine net; “nannoplankton”—that which will pass through the ordinary net but which can be removed by centrifuging or passage through filter paper; and “dissolved organic matter”—that which will pass through the filter. Examination of the literature reveals that a variety of methods have been used to separate those fractions, and consequently the results for different fractions are not always comparable. In the following discussion the term “particulate material” will be used to designate all the material, either living or dead, which is caught by a fine filter that will retain particles of about the size of the larger bacteria. It should be kept in mind that the organisms in sea water, the number of bacteria, and even the inorganic constituents involved in bacterial development undergo rather rapid changes after the collection of samples. Therefore, unless the separation into the required fractions is made immediately, or unless suitable preservatives are added, the results obtained for the
Pütter (p. 912) maintained that marine invertebrates obtained nourishment from the dissolved organic matter in the water. This hypothesis was based on observations which indicated that the amount of organic matter in solution was many hundred times greater than that present as plankton and particulate detritus. Further investigation has tended to reduce the difference between the two fractions of organic matter, because the earlier determinations of dissolved organic material were obtained by inaccurate methods. Additional studies summarized by Krogh (1931) and Bond (1933) also indicate that dissolved organic matter cannot be utilized by animals. Although Pütter's hypothesis has lost its original significance, it has stimulated a great deal of interest in the problem of the dissolved organic material and its utilization, and investigations have shown that dissolved organic material, although unused by animals, can be utilized by bacteria (p. 912).
Although the problem has attracted much discussion and speculation, there are very few trustworthy data concerning the amounts of carbon present in particulate or dissolved material in the sea. It is extremely difficult to determine accurately the carbon in small amounts of organic matter, especially in the presence of large quantities of salts. Methods have been proposed for concentrating the particulate material by filtration or precipitation (von Brand, 1935) and for determining the carbon by a microcombustion method. No method is as yet available for concentrating the dissolved organic material and freeing it from the salt; consequently the existing methods are based on wet combustions with strong oxidizing agents such as permanganate or chromate. (Bond, 1933; Krogh and Keys, 1934.) Two difficulties are inherent in the latter type of determination: (1) many of the inorganic salts present in sea water interfere with the oxidation and usually tend to give high values, (2) there is uncertainty as to the completeness of the destruction of the organic compounds. Some organic materials may be completely converted into carbon dioxide, water, and so on, by such a procedure; other compounds are only partially decomposed, and still others are not attacked at all. As the chemical constitution of the dissolved material is not known, it is difficult to evaluate the accuracy of determinations made by such methods. Determinations made by wet combustion give the “oxygen consumed,” and a further uncertainty arises when it is necessary to convert these values into the amounts of organic carbon present in the samples.
The development of marine bacteriology has offered a new approach to the problem of the amount of organic material (both particulate and dissolved) in sea water. If sea water is placed in clean, stoppered bottles and kept in the dark, bacteria will develop in great numbers
The amount of carbon present in oceanic sea water in inorganic compounds is between 2.1 and 2.5 mg-atoms per liter (25 to 30 mg/L), depending upon the salinity, temperature, and effects of biological activity. Krogh (1931, 1934a,b) has summarized the available data on the amount of organic carbon in sea water. In his later work he reports total organic carbon analyses on six water samples from the Atlantic Ocean. Virtually no variation with depth was found, and Krogh considers the average value applicable to all depths and oceans. The average was 0.2 mg-atoms (2.05 mg) of carbon per liter, which is approximately one tenth of the amount present in inorganic form. From estimates of the amount of plankton, Krogh found the dissolved material to be about three hundred times more abundant than the particulate organic matter. These figures apply to the deeper water of the open ocean. Bond (1933) examined the surface layers in nearshore areas of higher production and found rather different values. His original data, obtained by wet combustion, are expressed in terms of oxygen consumed. In order to make them comparable to those of Krogh, it has been assumed that two atoms of oxygen were required to oxidize one atom of carbon. The recomputed minimum, maximum, and average values are given in table 53. Although Bond's values for the dissolved fraction are approximately the same as those of Krogh for the total carbon, they show a considerable range. Furthermore, it will be noted that the particulate material is relatively more abundant and forms between one tenth and one third of the total.
The results of bacteria1 oxygen-consumption studies are difficult to evaluate because of the variety of techniques that have been used.
| Substance | mg-atoms/L of carbon | ||
|---|---|---|---|
| Minimum | Maximum | Average | |
| Net plankton | 0.008 | 0.06 | 0.03 |
| Nannoplankton | 0.005 | 0.11 | 0.03 |
| Dissolved | 0.13 | 0.25 | 0.20 |
| Total organic | 0.143 | 0.42 | 0.26 |
The oxygen consumptions given above were for water from near the surface in areas relatively rich in plankton. Samples from deeper levels consume about one half as much oxygen. As shown previously (p. 236), there are relatively constant ratios between carbon, nitrogen, and phosphorus in the organic material. This fact has been used in certain studies in which the organic nitrogen (determined by the Kjeldahl method) is used as a measure of the amount of organic matter. The relative amounts of organic nitrogen and phosphorus in sea water are in fair agreement with the amounts of carbon given above. The organic nitrogen content of bottom samples (p. 1010) has been widely used as a measure of their content of organic matter. In sediments the ratio of
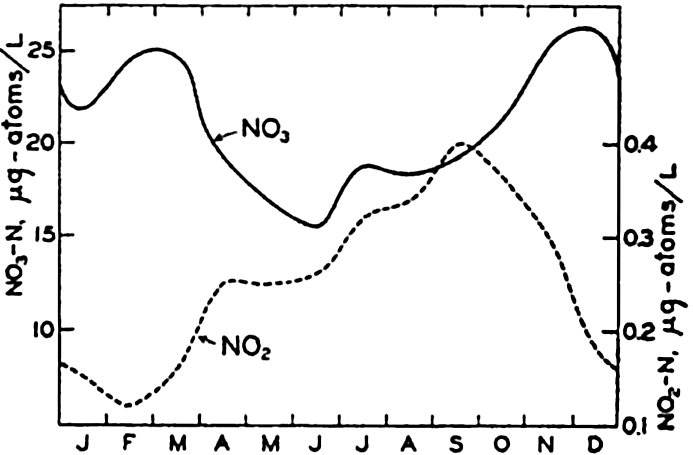
Annual cycle in the nitrate and nitrite content of the surface waters at Friday Harbor, Washington.
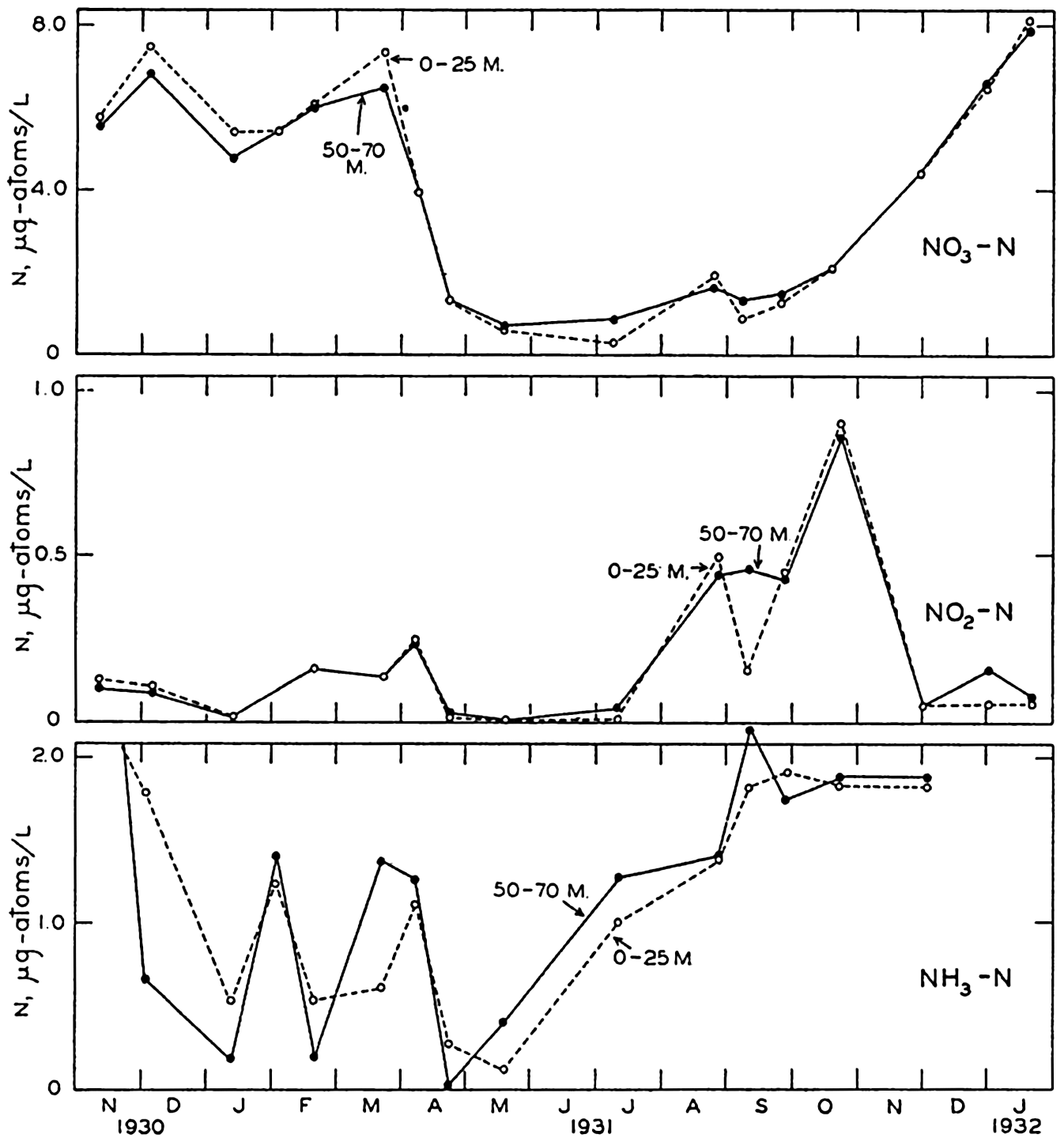
Seasonal variations in nitrate, nitrite, and ammonia in the surface layer (0–25 m) and in the bottom layer (50–70 m) in the English Channel during the period November, 1930, to January, 1932. (After Cooper, 1937b.)
Nitrogen Compounds and Their Seasonal Variation. In certain coastal areas, sufficient data are available to examine the seasonal changes in the distribution of nitrate, nitrite, and ammonia. Only selected cases of seasonal variations will be given, but additional references may be found in the works cited. Phifer and Thompson (1937) give the results of nearly five years' studies of the surface conditions at Friday Harbor, on the San Juan Channel. The averages of the monthly means for NO3 and NO2 for the period 1931 to 1935 are shown in fig. 57. It should be noted
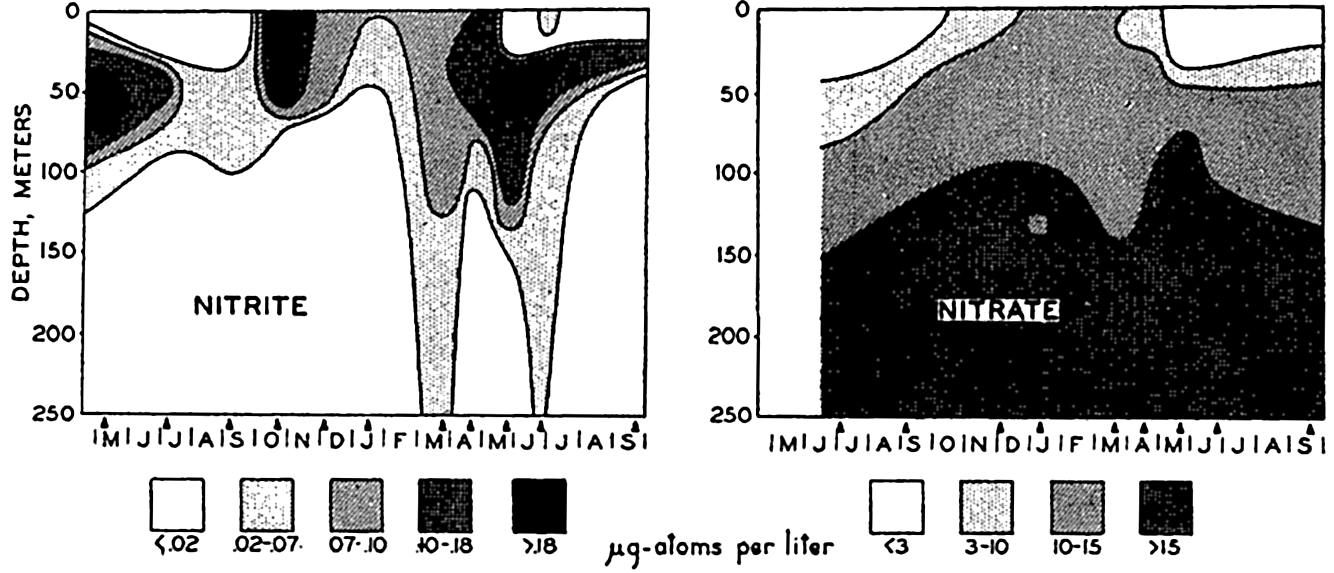
Seasonal variations in the vertical distribution of nitrite and nitrate in the Gulf of Maine during the period May, 1933, to September, 1934. (After Rakestraw, 1936b.)
The nitrogen in particulate organic material may be determined on the separated material which has been concentrated by filtration or
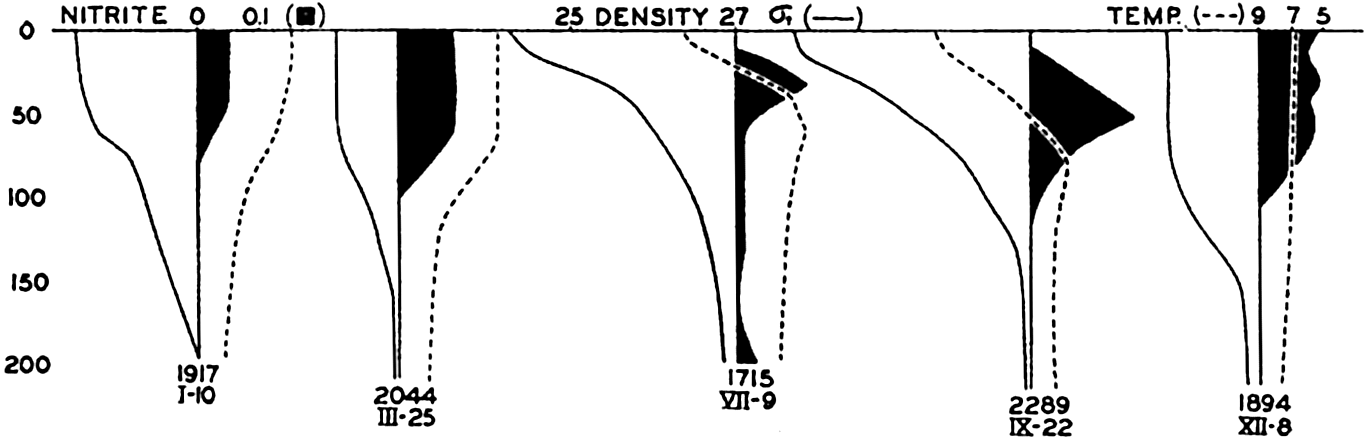
Vertical distribution of nitrite, as related to density (σt) and temperature. (After Rakestraw, 1936.)
The total organic nitrogen, including both particulate and dissolved material, has been investigated by Robinson and Wirth (1934a,b). Kjeldahl analyses on unfiltered oceanic sea water showed about 7.2 μg-atoms/L of organic nitrogen near the surface, about half this amount at intermediate depths, and a slight increase again toward the bottom. In nearshore water the values near the surface were about twice as high as those in the oceanic samples. Moberg and Fleming (1934), using a similar method, found about 10 μg-atoms/L, on an average, of organic nitrogen in the surface layers off southern California and somewhat higher values at greater depths.
Figures 57 and 58 show that at Friday Harbor about 10 μg-atoms/L of NO3-N disappear during the summer, and that the change in the English Channel is approximately the same. As NH3 and NO2 are rarely present in comparable amounts, we must conclude that the nitrogen is in organisms, organic debris, dissolved organic compounds, or in some unrecognized inorganic form.
Interesting experiments by von Brand, Rakestraw, and Renn (1937, 1939) on the regeneration of nitrate from marine plankton in vitro indicate that the formation of ammonia from organic matter probably takes place without the formation of intermediate compounds. The results
These experiments are extremely interesting, although regenerative processes in vitro apparently differ considerably from those in the sea. This result might well be expected from the peculiar laboratory conditions and the fact that the water was enriched with organic material. It may also account for the fact that the NH3 and NO2 reached relatively high values (the same as the NO3), and that during the regeneration the stages of production of NH3, NO2, and NO3 were clearly defined (cf. figs. 57 and 58). Furthermore, it is interesting to note the great increase in the amount of nitrogen present as particulate material that was apparently resistant to the action of the bacteria present. At the end of the experiment, approximately 50 per cent of the nitrogen was in this form. Such a “waste” of nitrogen does not take place in the sea. It is also of interest to note that diatoms would flourish if the medium were placed in the light when either NH3 or NO2 were abundant and before the NO3 had been produced. This supports the theory that marine plants can use any of these inorganic forms bf nitrogen equally well.
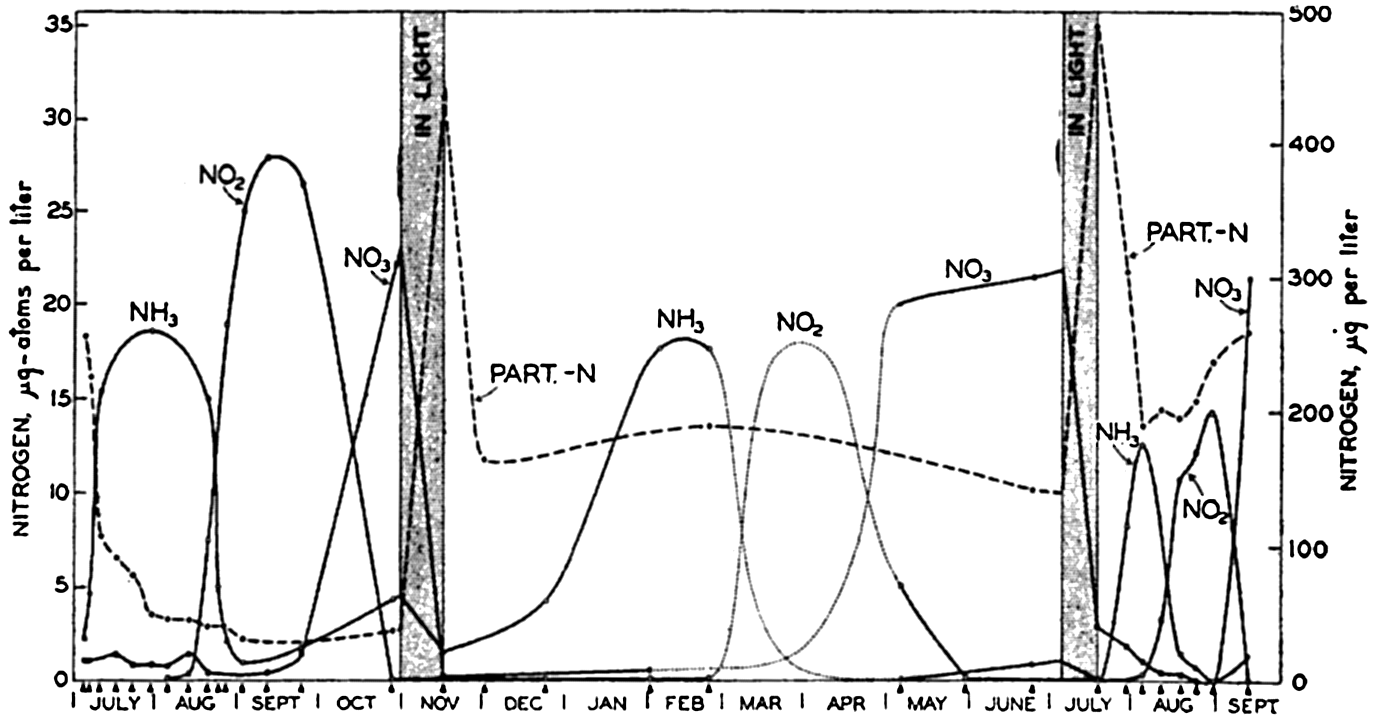
Experiment on the utilization and regeneration of nitrate. When medium was placed in light, it was innoculated with diatoms. Data from von Brand, Rakestraw, and Renn, 1939.
Nitrogen Cycle in the Sea. The chemically bound nitrogen in sea water is known to occur in living organisms, in dissolved and particulate material of organic origin, and as ammonia, nitrite, and nitrate.
Bacteria play important roles in the mineralization of organic nitrogen by acting upon detrital material, excreta, and dissolved organic matter, and in the intertransformation of NH3, NO2, and NO3 (chapter XVIII). Pure culture studies with different species of marine bacteria show that a variety of transformations can be made under laboratory conditions, but these observations must be applied to the sea with caution because the organisms may not be capable of carrying on similar processes in the natural environment. The very large literature bearing on the nitrogen cycle in the sea has been reviewed by Cooper (1937b), who has considered all the various modes of transformation that are possible and from them has selected the more probable ones. In general, it is believed that the nitrogenous material gives rise to ammonia, which in turn is converted to nitrite and then to nitrate. The ammonia may be formed by the hydrolysis of protein material, amino acids, amines, and purine compounds such as urea, or through bacterial action on them.
The oxidation of ammonia to nitrite releases a large amount of energy and hence needs only to be activated in some way. The following agencies have been suggested:
Photochemical oxidation induced by direct sunlight. This reaction was first observed in sea water by ZoBell (1933), but, as pointed out by Cooper, can be effective only within the upper meter or so of water, owing to the rapid absorption of the shorter wave lengths that activate the reaction.
Chemical oxidation by the free oxygen in the water in the presence of surface catalysts. This reaction is of unknown significance.
Bacterial oxidation. Nitrifying bacteria are present in bottom sediments, and forms isolated by Zobell (1935b) converted ammonia to nitrite. However, the conversion occurred at a much higher oxidation-reduction potential than is ordinarily found in the sediments. Studies of the decomposition of marine plankton in vitro show a conversion of ammonia to nitrite, but no nitrifying bacteria could be isolated (von Brand, Rakestraw, and Renn, 1937). Nonetheless, the fact that nitrifying bacteria cannot be readily detected in sea water is not definite proof of their absence. It is well known that many marine bacteria are difficult to culture, and development of new techniques may establish their presence. Carey (1938) has shown that they can be isolated from
― 257 ―water rich in plankton. The presence of nitrite, which can sometimes be detected near the sea bottom, as in the English Channel in certain seasons, may indicate either oxidation of ammonia or reduction of nitrate. Although it has not been established, bacteria are probably the most important agency in the oxidation of ammonia to nitrite.
Oxidation of nitrite to nitrate also releases energy, and, as in the oxidation of ammonia, purely chemical or photochemical processes may be important. Bacteria capable of making the transformation are abundant in sediments, but they are difficult to isolate from the water column. Development of suitable techniques may also clarify this problem. Cooper has pointed out that in sea water saturated with oxygen the nitrate in equilibrium with nitrite will be of a tremendously greater order of magnitude. Hence, the detection of nitrite in the water column may indicate active production of this substance, which is present only as a transitional stage in the regeneration of nitrate. Brandt's hypothesis (p. 768) was based on the discovery of marine bacteria which under laboratory conditions were capable of denitrification. However, it is now considered that under the conditions prevailing in the sea there is little or no loss of fixed nitrogen, although it has been shown that reduction of NO3 to NO2 may occur. This reduction may also be carried out by diatoms, as has been observed in pure-culture experiments (ZoBell, 1935a).
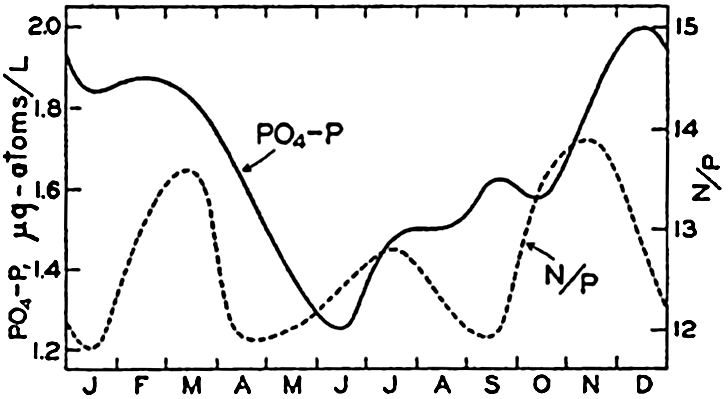
Annual cycle in the phosphate content of the surface waters at Friday Harbor, Washington, and the monthly N/P ratios.
Organic Phosphorus and Seasonal Variations in Phosphate. For certain coastal areas, sufficient data exist to show the nature of the seasonal variations in phosphate. Friday Harbor, the English Channel, and the Gulf of Maine have been selected as examples.
In fig. 62 are presented the averages based on about four years' observations of the monthly mean values for PO4-P at Friday Harbor (Phifer and Thompson, 1937). Highest values occur during the winter, and lowest values during the summer season, when phytoplankton growth has been great. The monthly ratios of N:P are somewhat lower than the normal ratio proposed by Cooper, and their variability during the course of the year indicates that proportionally more nitrate than phosphate is utilized. Neither of these substances can be considered as limiting the amount of phytoplankton produced at this locality. Phosphate data from the English Channel (Cooper, 1938b) for the period November, 1930, to January, 1932, are presented in fig. 63 as
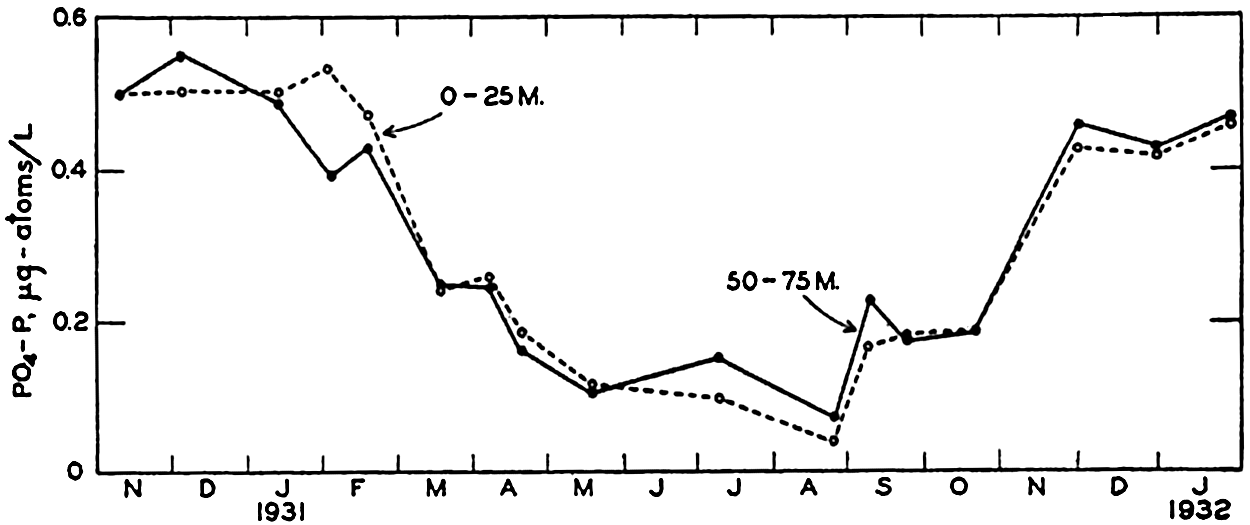
Seasonal variations in the phosphate content of the surface layer (0–25 m) and the bottom layer (50–75 m) in the English Channel during the period November, 1930, to January, 1932.
Cooper (1938b) has assembled phosphate data for the English Channel covering a period of eighteen years. In fig. 64 are entered the winter maxima for the average PO4-P content of the water column near Plymouth. As the phosphate content of the water during the winter is a measure of potential production for the following spring and summer, his data indicate a drop in fertility after 1929 or 1930. The changes are considered to be associated with the circluation, which may undergo random or periodic fluctuations.
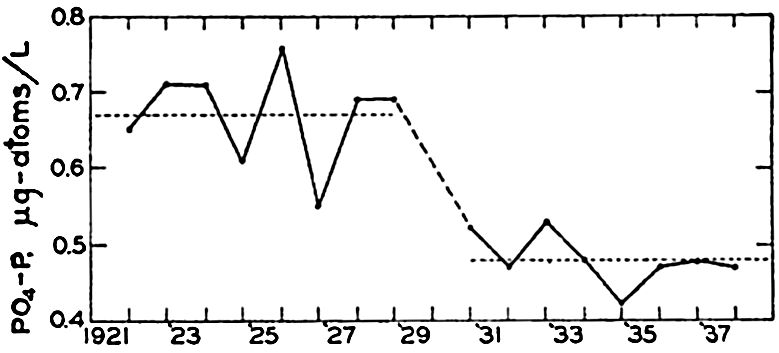
Winter maxima for phosphate in the English Channel for the period 1921–1938.
In the preceding discussion, emphasis has been placed on the cyclic nature of the seasonal variations, and it is obvious that the conditions in any area may not repeat themselves if disturbances, such as shifts in the circulation, bring about changes.
The seasonal variations in the PO4-P and in the various organic phosphorus fractions in the Gulf of Maine have been studied by Redfield, Smith, and Ketchum (1937). During one year, five series of samples were collected at various depths between the surface and the bottom. These
| Form of phosphorus | Interval of depth, meters | μg-atoms/L of phosphorus | ||||
|---|---|---|---|---|---|---|
| May 18, 1935 | Aug. 20, 1935 | Nov. 8, 1935 | Feb. 26, 1936 | May 14, 1935 | ||
| Phosphate | 0–60 | 0.60 | 0.68 | 0.65 | 1.03 | 0.64 |
| 60–120 | 1.11 | 0.91 | 1.08 | 1.02 | 1.25 | |
| 120–180 | 1.31 | 1.22 | 1.25 | 1.11 | 1.51 | |
| 180–240 | 1.61 | 1.39 | 1.22 | 1.51 | 1.60 | |
| Dissolved organic | 0–60 | 0.08 | 0.34 | 0.29 | 0.07 | 0.14 |
| 60–120 | 0.02 | 0.29 | 0.31 | 0.14 | 0.36 | |
| 120–180 | 0.01 | 0.17 | 0.29 | 0.17 | 0.15 | |
| 180–240 | 0.00 | 0.20 | 0.37 | 0.03 | 0.10 | |
| Particulate organic | 0–60 | 0.15 | 0.10 | 0.10 | 0.05 | 0.12 |
| 60–120 | 0.06 | 0.05 | 0.05 | 0.05 | 0.07 | |
| 120–180 | 0.04 | 0.03 | 0.08 | 0.03 | 0.02 | |
| 180–240 | 0.04 | 0.03 | 0.08 | 0.04 | 0.06 | |
| Total (Average for whole water column) | 0–240 | 1.26 | 1.36 | 1.44 | 1.31 | 1.51 |
Earlier work on organic phosphorus in the sea has been summarized by Cooper (1937a), who also reports observations from the English Channel. Cooper points out that many determinations of the total “organic phosphorus” (both particulate and dissolved) probably include arsenite-arsenic that has been oxidized to arsenate when the organic matter was destroyed and that has not been reduced again. Arsenate will give the same reaction as phosphate in the colorimetric estimation, and, because the arsenic present as arsenite will not affect the inorganic phosphate analyses, the determination of “organic phosphorus” will be too high by about 0.2 μg-atoms/L (the concentration of arsenic). In the determinations in the Gulf of Maine this source of error was
The maximum values reported by Redfield et al in the Gulf of Maine for particulate and dissolved organic phosphorus are
Phosphorus Cycle in the Sea. The cycle of phosphorus in the sea is rather similar to that of nitrogen except that only one inorganic form, phosphate, is known to occur. As shown above, phosphorus can be found in organisms, in particulate and dissolved organic compounds, and as phosphate. Probably only the phosphate is utilized by plants, and the dissolved organic fraction, which can originate as a metabolic product and from excreta, and the decomposition of organic material must be intermediate stages in the regeneration of phosphate. The roles that bacteria play are not yet known.
Studies of the decomposition of plankton material in vitro have led to some interesting results. Cooper (1935) added zooplankton and phytoplankton material of known phosphorus content to sea water and determined the rate at which the PO4-P was formed. The PO4 appeared more rapidly in the zooplankton samples than in the diatom material. Furthermore, the PO4 produced in the zooplankton samples was in excess of that originally present as PO4 plus that added in the particulate material. This excess was formed from dissolved organic phosphorus originally present in the water. The PO4 in the diatom experiments never rose to the level of the original PO4 plus that added, even after an interval of about five months. The initial rate of appearance of PO4 was rapid, and in the zooplankton experiments the transformation was nearly complete in about two weeks. The difference in behavior of the plant and animal material cannot yet be accounted for. Seiwell and Seiwell (1938) found that zooplankton decomposition at 22° to 25°C (probably higher than the temperature of Cooper's experiments) was such that the formation of PO4 was most rapid during the first day or two after death. This stage was often followed by a period when the rate of utilization of PO4 by microorganisms in the experiments exceeded that of formation. On the basis of these experiments it is sometimes considered that the PO4 must be regenerated more rapidly than the NO3. However, field evidence offers little support for this theory. Examination
Redfield, Smith, and Ketchum (1937), on the basis of the material summarized in table 54, have calculated the manner in which the various phosphorus compounds vary in the different layers, assuming (1) that all utilization of phosphate takes place in the upper 60 m, (2) that all downward transport of phosphorus is due to the settling of organisms and particulate material, and (3) that the upward transport is all due to eddy diffusion. From their examination it was concluded that decomposition and regeneration took place throughout the column of about 240 m of water.
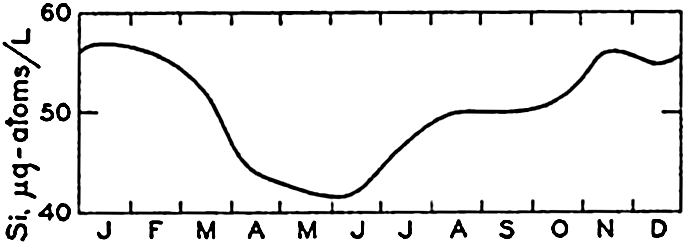
Annual cycle in the silicate content of the surface waters at Friday Harbor, Washington.
Seasonal Variation in Silicate. Observations on the seasonal cycle in silicate-silicon have been carried out in many localities, of which Friday Harbor and the English Channel have been selected as examples. The data presented are comparable to those given for NO3-N and PO4-P. Fig. 65 shows the average monthly values for Friday Harbor based on more than four years' observations. The highest values occur during the winter and the lowest values during the early summer. The range in silicon is 15 μg-atoms/L. The ranges in SiO3-Si, NO3-N, and PO4-P are in the proportions of 20:14.7:1. Data for the English Channel (Cooper, 1933) are shown in fig. 66. It will be noted that the concentration of silicon in the English Channel is much lower than it is at Friday Harbor, being in general only about 1/25 as great. The range in silicon
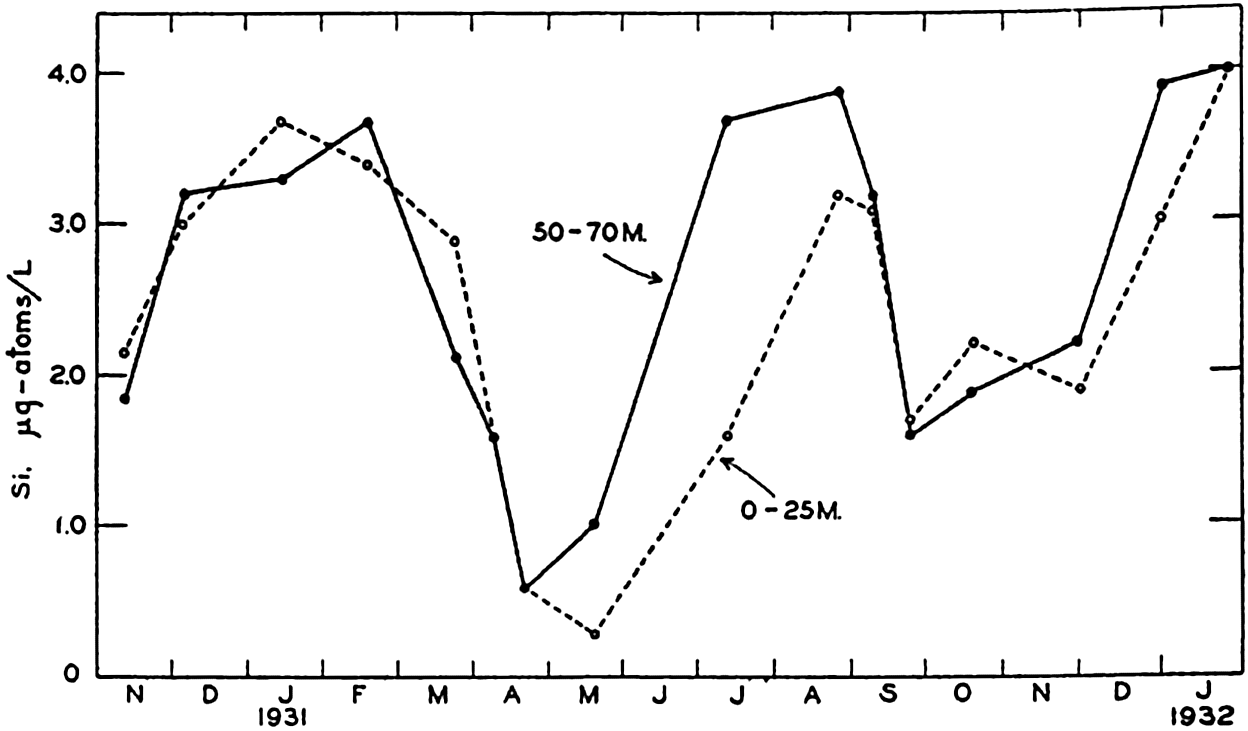
Seasonal variations in the silicate content of the surface layer (0–25 m) and the bottom layer (50–70 m) in the English Channel during the period November, 1930 to January, 1932.
A factor that may complicate the seasonal changes in the silicon concentration in nearshore areas is the amount of siliceous material carried in by river waters, which is generally several times greater than that found in sea water; dilution will therefore tend to raise the concentration of silicate (Hutchinson, 1928).
The Silicon Cycle in the Sea. The depletion of the silicon in the surface layers is the result of biological activity and the sinking of the organisms or of their skeletal remains. The silicon removed from the water by diatoms or other organisms may return to solution after the death of the organism or may be deposited on the sea bottom. Unlike their roles in the cycles of nitrogen and phosphorus, bacteria are probably not directly involved in the re-solution of silicon from skeletal material. The skeletal material that sinks to the bottom forms either a temporary or permanent constituent of the sediments. Siliceous sediments are found in higher latitudes where the bottom material contains a very large proportion of diatom frustules, while in other regions radiolarian skeletons make up a large part of the sediment (chapter XX).
In the English Channel the silicon distribution is more erratic than that of PO4 and of NO3, and there may be large differences in the amounts at various levels. High values often occur near the surface and immediately over the bottom. The high surface values are ascribed to the effects of river water, the high bottom values to the re-solution of skeletal material that has settled there. The accumulation of dissolved silicates at a marked thermocline is also evidence of re-solution of slowly settling debris.
Estimates of plankton production in the English Channel based on the difference between the winter maxima and summer minima in PO4-P, NO3-N, and SiO3-Si (Cooper 1933, 1938b) yield values from the SiO3 data which are approximately 1/15 of those obtained from the other elements. Cooper has attributed the smaller value to the rapidity with which the silicon passes through its cycle. The difference in the amount of silicon utilized in the English Channel and at Friday Harbor was noted above, and the fact that the concentration is reduced in the English Channel to a very low level may indicate that in that locality it does influence the production of diatoms.
King and Davidson (1933) found that the quantity of SiO3-Si in solution affected the growth of diatoms in laboratory cultures. They also followed the changes in dissolved silicon after the death of the diatoms and found that complete solution took place in about five months. Marine phytoplankton were similarly studied, and it was found that samples which were boiled dissolved more slowly than those unboiled. The authors suggest the possible existence of an enzyme that hastens solution.
Bibliography
Barnes, C. A., and T. G. Thompson. 1938. Physical and chemical investigations in Bering Sea and portions of the North Pacific Ocean. Univ. of Washington, Pub. in Oceanogr., v. 3, no. 2, 79 + App. 163 pp., 1938. Seattle.
Bond, R. M.1933. “A contribution to the study of the natural food-cycle in aquatic environments” . Bingham Oceanogr. Coll., Peabody Museum, Bull., v. 4, art. 4, 89 pp., 1933.
Carey, Cornelia L.1938. “The occurrence and distribution of nitrifying bacteria in the sea” . Jour. Marine Research, v. 1, p. 291–304, 1938.
Carnegie Results. Physical and chemical data and results of dynamic computations for Carnegie deep-sea stations, 1928–1929, Tabulated data. Results of Oceanographic and Meteorological Work on Board the Carnegie on Cruise VII, 1928–1929. (In press.) Carnegie Institution of Washington.
Clarke, F. W., and W. C. Wheeler. 1922. “The inorganic constituents of marine invertebrates” . U. S. Geol. Surv., Prof. Paper, no. 124, p. 1–62, 1922.
Clements, F. W., and R. C. Hutchinson. 1939. “The ash constituents of Australian fish” . Australian Jour. Exper. Biol. and Med. Sci., v. 17, p. 89–92, 1939.
Clowes. A. J.1938. “Phosphate and silicate in the southern oceans” . Discovery Repts., v. 19, p. 1–120, 1938.
Cooper, L. H. N.1933. “Chemical constituents of biological importance in the English Channel, November, 1930, to January, 1932” . Marine Biol. Assn. U. K., Jour., v. 18, p. 677–753, 1933. Plymouth.
Cooper, L. H. N.1934. “The determination of phosphorus and nitrogen in plankton” . Marine Biol. Assn. U. K., Jour., v. 19, p. 755–59, 1934. Plymouth.
Cooper, L. H. N.1935. “The rate of liberation of phosphate in sea water by the breakdown of plankton organisms” . Marine Biol. Assn. U. K., Jour., v. 20, p. 197–200, 1935. Plymouth.
Cooper, L. H. N.1937a. ““Organic” phosphorus in sea water from the English Channel” . Marine Biol. Assn. U. K., Jour., v. 21, p. 673–78, 1937. Plymouth.
Cooper, L. H. N.1937b. “The nitrogen cycle in the sea” . Marine Biol. Assn. U. K., Jour., v. 22, p. 183–204, 1937. Plymouth.
Cooper, L. H. N.1938a. “Redefinition of the anomaly of the nitrate-phosphate ratio” . Marine Biol. Assn. U. K., Jour., v. 23, p. 179, 1938. Plymouth.
Cooper, L. H. N.1938b. “Phosphate in the English Channel, 1933–38, with a comparison with earlier years, 1916 and 1923–32” . Marine Biol. Assn. U. K. Jour., v. 23, p. 181–95, 1938. Plymouth.
Deacon, G. E. R.1933. “A general account of the hydrology of the South Atlantic Ocean” . Discovery Repts., v. 7, p. 171–237, 1933.
Defant, A., G. Böhnecke, H. Wattenberg. 1936. “Die ozeanographischen Arbeiten des Vermessungsschiffes Meteor in der Dänemarkstrasse und Irmingersee, Berlin Universität, Institut f. Meereskunde, Veröff., N.F., A. Geogr.-naturwiss” . Reihe, Heft 32, 152 pp., 1936.
Discovery Reports. 1932. “Station list, 1929–1931” . Discovery Repts., v. 4, p. 1–230, 1932.
Fleming, Richard H.1940. “The composition of plankton and units for reporting populations and production” . Sixth Pacific Sci. Congr., Calif., 1939, Proc.v. 3, p. 535–540, 1940.
Gilson, H. C.1937. “The nitrogen cycle, John Murray Exped., 1933–34” , Sci. Repts., v. 2, no. 8, p. 21–81, 1937.
Hutchinson, A. H.1928. “A bio-hydrographical investigation of the sea adjacent to the Fraser River mouth” . Roy. Soc. Can., Trans., v. 22, Sect. 5, p. 293–310, 1928.
Jowett, W. G., and W. Davies. 1938. “A chemical study of some Australian fish” . Australia, Council for Sci. and Industr. Research, Pamphlet 85, 40 pp., 1938.
Keys, Ancel, E. H. Christensen, and A. Krogh. 1935. “The organic metabolism of sea water with special reference to the ultimate food cycle in the sea” . Marine Biol. Assn. U. K., Jour., v. 20, p. 181–96, 1935. Plymouth.
King, E. J., and Viola Davidson. 1933. “The biochemistry of silicic acid. IV. Relation of silica to the growth of phytoplankton” . Biochem. Jour., v. 27, p. 1015–21, 1933.
Krogh, August. 1931. “Dissolved substances as food of aquatic organisms” . Conseil Perm. Internat. p. l'Explor. de la Mer, Rapp. et Proc.-Verb., v. 75, p. 7–36, 1931.
Krogh, August. 1934a. “Conditions of life in the ocean” . Ecol. Monographs, v. 4, p. 421–29, 1934.
Krogh, August. 1934b. “Conditions of life at great depths in the ocean” . Ecol. Monographs, v. 4, p. 430–39, 1934.
Krogh, August, and Ancel Keys. 1934. “Methods for the determination of dissolved organic carbon and nitrogen in sea water” . Biol. Bull., v. 67, p. 132–44, 1934.
McCance, R. A., and M. Masters. 1937–38. “The chemical composition and acid base balance of Archidoris brittanica.” . Marine Biol. Assn., U. K., v. 22, p. 273–79, 1937–38. Plymouth.
Moberg, E. G., and R. H. Fleming. 1934. “The distribution of nitrogen compounds in the sea near southern California” . Fifth Pacific Sci. Congr., Canada, 1933, Proc., v. 3, p. 2085–88, 1934.
Phelps, Austin. 1937. “The variation in the silicate content of the water in Monterey Bay, California, during 1932, 1933, and 1934” . Amer. Phil. Soc., Trans., v. 29, p. 153–88, 1937.
Phifer, Lyman D., and T. G. Thompson. 1937. “Seasonal variations in the surface waters of San Juan Channel during the five-year period, January 1931 to December 30, 1935” . Jour. Marine Research, v. 1, p. 34–53, 1937–38.
Rakestraw, Norris W.1936. “The occurrence and significance of nitrite in the sea” . Biol. Bull., v. 71, p. 133–67, 1936.
Rakestraw, N. W., and H. P. Smith. 1937. “A contribution to the chemistry of the Caribbean and Cayman Seas” . Bingham Oceanogr. Coll., Peabody Museum, Bull., v. 6, art. 1, 41 pp., 1937.
Redfield, A. C.1934. On the proportions of organic derivatives in sea water and their relation to the composition of plankton. p. 176–92 in James Johnstone Memorial Volume, Liverpool, Univ. Press, 348 pp., 1934.
Redfield, A. C., and Ancel Keys. 1938. “The distribution of ammonia in the waters of the Gulf of Maine” . Biol. Bull., v. 74, p. 83–92, 1938.
Redfield, A. C., H. P. Smith, and B. Ketchum. 1937. “The cycle of organic phosphorus in the Gulf of Maine” . Biol. Bull., v. 73, p. 421–43, 1937.
Robertson, J. D.1939. “The inorganic composition of the body fluids of three marine invertebrates” . Jour. Exp. Biol., v, 16, p. 387–97, 1939.
Robinson, R. J., and H. E. Wirth. 1934a. “Report on the free ammonia, albuminoid nitrogen and organic nitrogen in the waters of the Puget Sound area, during the summers of 1931 and 1932” . Conseil Perm. Internat. p. l'Explor. de la Mer, Journal du Conseil, v. 9, p. 15–27, 1934.
Robinson, R. J., and H. E. Wirth. 1934b. “Free ammonia, albuminoid nitrogen and organic nitrogen in the waters of the Pacific Ocean off the coasts of Washington and Vancouver Island. Conseil Perm” . Internat. p. l'Explor. de la Mer, Journal du Conseil, v. 9, p. 187–95, 1934.
Rogers, C. G.1938. Textbook of comparative physiology. 2nd ed.. New York, McGraw-Hill, 715 pp., 1938.
Seiwell, H. R.1935. “The cycle of phosphorus in the western basin of the North Atlantic. I. Phosphate phosphorus” . Papers in Physical Oceanogr. and Meteorol., v. 3, no, 4, 56 pp., 1935.
Seiwell, H. R., and G. E. Seiwell. 1938. “The sinking of decomposing plankton in sea water and its relationship to oxygen consumption and phosphorus liberation” . Amer. Phil. Soc., Proc., v. 78, p. 465–81, 1938.
Ström, K. M.1936. “Land-locked waters. Hydrography and bottom deposits in badly ventilated Norwegian fjords with remarks upon sedimentation under anaerobic conditions” . Norske Vidensk. Ak. i Oslo, 1. Mat.-Naturv. Klasse, no. 7, 85 pp., 1936.
Thompson, T. G., B. D. Thomas, and C. A. Barnes. 1934. Distribution of dissolved oxygen in the North Pacific Ocean. p. 203–34 in James Johnstone Memorial Volume, Liverpool Univ. Press, 348 pp., 1934.
Thomsen, Helge. 1931. “Nitrate and phosphate contents of Mediterranean water” . Danish Oceanogr. Exped. 1908–1910, v. 3, no. 6, 14 pp., 1931.
Thomsen, Helge. 1937. “Hydrographical observations made during the Dana Expedition 1928–1930” . Dana Repts., no. 12, 46 pp., 1937.
Vinogradov, A. P.1935. “Elementary chemical composition of marine organisms. (In Russian) Pt. 1. Laboratoire de Biogeochimie près l'Acad” . des Sci., U.R.S.S., Travaux, v. 3, p. 63–278, 1935. Leningrad.
Vinogradov, A. P.1937. “Elementary chemical composition of marine organisms” . (In Russian) Pt. 2. Laboratoire de Biogeochimie près l'Acad. des Sci., U.R.S.S., Travaux, v. 4, p. 5–225, 1937. Leningrad.
Vinogradov, A. P.1938. “Chemical composition of marine plankton. (In Russian.)” . Inst. Marine Fisheries and Oceanogr. of the U.S.S.R., Trans., v. 7, p. 97–112, 1938. Moscow.
von Brand, Theodor. 1935. “Methods for the determination of nitrogen and carbon in small amounts of plankton” . Biol. Bull., v. 69, p. 221–32, 1935.
von Brand, Theodor. 1937. “Observations upon the nitrogen of the particulate matter in the sea” . Biol. Bull., v. 72, p. 1–6, 1937.
von Brand, Theodor. 1938. “Quantitative determination of nitrogen in the particulate matter of the sea” . Conseil Perm. Internat. p. l'Explor. de la Mer, Journal du Conseil, v. 13, p. 187–96, 1938.
von Brand, Theodor, N. W. Rakestraw, and C. E. Renn. 1937. “The experimental decomposition and regeneration of nitrogenous organic matter in sea water” . Biol. Bull., v. 72, p. 165–75, 1937.
von Brand, Theodor, N. W. Rakestraw, and C. E. Renn. 1939. “Further experiments on the decomposition and regeneration of nitrogenous organic matter in sea water” . Biol. Bull., v. 77, p. 285–96, 1939.
Waksman, S. A., and C. E. Renn. 1936. “Decomposition of organic matter in sea water by bacteria. III. Factors influencing the rate of decomposition” . Biol. Bull., v. 70, p. 472–83, 1936.
Webb, D. A., and W. R. Fearon. 1937. “Studies on the ultimate composition of biological material. Pt. I. Aims, scope and methods” . Roy. Dublin Soc., Sci. Proc., n.s., v. 21, p. 487–504, 1937.
ZoBell, Claude E.1933. “Photochemical nitrification in sea water” . Science, v. 77, p. 27–28, 1933.
ZoBell, Claude E.1935a. “The assimilation of ammonium nitrogen by Nitzschia closterium and other marine phytoplankton” . Nat. Acad. Sci., Proc.v. 21, p. 517–22, 1935.
ZoBell, Claude E.1935b. “Oxidation-reduction potentials and the activity of marine nitrifiers” . Abstract. Jour. Bacter., v. 29, p. 78, 1935.
ZoBell, Claude E.1940. “The effect of oxygen tension on the rate of oxidation of organic matter in sea water by bacteria” . Jour. Marine Research, v. 3, p. 211–23, 1940.
ZoBell, Claude E., and D. Q. Anderson. 1936. “Observations on the multiplication of bacteria in different volumes of stored sea water and the influence of oxygen tension and solid surfaces” . Biol. Bull., v. 71, p. 324–42, 1936.
VIII. The Sea as a Biological Environment
In the foregoing chapters an account has been given of the chemical and physical aspects of the elements that together constitute the inorganic marine environment—namely, (1) the sea water itself, and (2) the ocean floors. The chemical constituents and the physical properties of the sea water, together with their distribution, concentrations, and cyclic changes, the movement of the water, and the nature of the ocean floors are decisive factors in the history and fate of a perplexing array of living things. Herein are held many secrets of racial development, and herein must be sought the understanding of the delicately balanced maintenance of life and of the potentialities of future development.
Marine organisms are to be considered a part of the sea as it exists today. Just as sea water includes the various salts, both conservative and nonconservative (biologically changed), so also it includes the multitude of organisms which are bound to the sea for their existence and which, by origin, are a part of the sea both racially and individually. The organisms, like the saIts, are subject to the natural laws of the sea and are a part of the perpetual cycle of inorganic and organic substances so important in many aspects of oceanography. The changes that are apparent in concentration represent only patterns that are inherent in the phases of the cycle or that result from other causes, such as currents and processes of mixing.
The aquatic environment offers the greatest intimacy between itself and the organisms which it bathes both over the body surface and within open or partially closed cavities as, for example, the internal systems of coelenterates, echinoderms, and tunicates. Because of the stability of the physical characteristics of the sea water and of the composition and concentration of the dissolved salts the organisms, in general, have not developed highly specialized integuments and regulatory systems to protect themselves against sudden and intense environmental changes, as have most land animals. It follows that small changes in the aquatic medium are promptly brought to play upon its population. It should be borne in mind, also, that the organisms themselves, being a part of the dynamic environment, modify particularly its chemical character by withdrawing or adding substances associated with the activities of life.
In subsequent chapters we shall discuss the relation of some of the measurable environmental factors to such phenomena as distribution, propagation, survival, and special adaptations, but first some facts of general application must be considered.
Physical and Chemical Characteristics of the Marine Environment
Water is essential to the maintenance of all life. It constitutes 80 per cent or more by weight of active protoplasm. It is the most efficient of all solvents and carries in solution the necessary gases, oxygen and carbon dioxide, as well as the mineral substances necessary to the growth of plants and animals, and it is itself one of the essential raw materials in the manufacture of foods by plants.
Organisms living in the terrestrial environment have devised means, such as impervious integuments, to conserve water, and the land plants have roots and special vascular systems for transport of water to all growing parts. In the marine environment there is freedom from dessication, except at high-tide levels, and therefore no highly specialized means are provided for conservation of water or for its transport in plants.
Also of biological importance are the high heat capacity of water and its high latent heat of evaporation, both of which obviate the danger that might result from rapid change of temperature in the environmental medium. Owing to the high degree of transparency of water it is possible for the sea to sustain plant life throughout a relatively deep layer, and in animals the development of organs of vision and of orientation has progressed to a marked degree.
Sea water is a buffered solution; that is, changes from acid to alkaline condition, or vice versa, are resisted (p. 195). This property is of vital importance to the marine organisms, mainly for two reasons: (1) an abundant supply of carbon can be available in the form of carbon dioxide for the use of plants in the synthesis of carbohydrates without disturbance to the animal life that may be sensitive to small changes in pH, and (2) in the slightly alkaline habitat the many organisms that construct shells of calcium carbonate (or other calcium salts) can carry on this function much more efficiently than in a neutral solution.
The support offered to the bodies of marine organisms by the specific gravity of the surrounding medium obviates the need of special supporting skeletal structure in many forms. Striking examples of these are the jelly fishes, unarmored molluscs, unarmored dinoflagellates, and even the large marine mammals with their heavy skeletons, which could not survive in their present bulky state except in an aquatic habitat. The hard shells of crabs, clams, snails, and so on, doubtless serve as support, especially in some burrowing and intertidal forms, but these hard parts may be looked upon also as protective and as a framework for attachment of muscles used in digging, creeping, or swimming.
Sea Water and the Body Fluids. Sea water is a most appropriate environment for living cells, since it contains all of the chemical elements essential to the growth and maintenance of plant and animal protoplasm. It has been shown that sea water is a solution of a large number of salts, and it is important here to consider how it is related as an external fluid medium to the “internal medium”—namely, the body fluids (blood, coelomic fluid, and so on) of the organisms. The ratios of the major salts to each other, and usually their total concentration also, are strikingly similar in sea water and in the body fluids of marine invertebrates. The similarity of composition is not confined to marine animals, however, but is also in evidence in modified form in both terrestrial and fresh-water animals, including the lower and higher vertebrates, as is shown in table 55, which is from data compiled by Pantin (1931) and expanded by Dakin (1935).
Osmotic Relationships.It is well known that when solutions of different osmotic pressure are separated by a semipermeable membrane that allows the passage of water but not of the solutes, there is a movement of the water through the membrane into the more concentrated solution. The cell membranes of organisms are just such semipermeable membranes through which a movement of fluids occurs inward or outward, depending upon whether the osmotic pressure of the external medium is less (hypotonic) or greater (hypertonic) than the internal medium. The internal and external media are isotonic when they are of equal osmotic pressure.
The osmotic pressure of a solution can be computed from the freezing-point depression (p. 67). This computation is possible because the salts that increase the osmotic pressure of a solution also depress its freezing point. The freezing-point depression below 0°C has been designated by Δϑ, (p. 67), but will here be abbreviated to Δ. Sea water having a salinity of 35.00 ‰ freezes at − 1.91°, owing to depression by the substances in solution. In other words, the value for Δ is 1.91°. Similarly, we obtain a Δ of 0.56 for human blood with a freezing point of −0.56°C.
On the basis of Δ values, the osmotic relations of the body fluids of marine and fresh-water animals to their external environmental medium are compared in table 56, from data compiled by Dakin (1935), to whose review the reader is directed for much greater detail and historical treatment.
From the few examples in the table it is evident that the body fluids of marine invertebrates are isotonic or nearly so with their fluid environment, whereas in the fresh-water forms the body fluids are hypertonic to the dilute external medium. For this reason the marine environment in its osmotic relations fails to exact of its inhabitants as great an expenditure of energy in maintaining the proper concentration of body fluids as does the fresh-water environment. The exact mechanism whereby the fresh-water animals are independent of the external medium and are able to maintain a homoiosmotic condition (that is, steady value for Δ) in the presence of the hypotonic water is not known (see Δ for the eel Anguilla anguilla in fresh and salt water, table 56). Their existence under these conditions, however, requires a constant expenditure of energy in eliminating, through the kidneys and other excretory organs, the excess water taken in by osmosis. Marine invertebrates are poikilosmotic (Δ changing with that of the external medium) only within rather narrow limits (Dakin, 1935); hence, they, too, must have some regulating mechanism. Except in estuarine conditions, however, the range of salinity in most parts of the sea is perhaps within the limits of poikilosmoticity of the invertebrates living there. For example, the lugworm, Arenicola marina, in Helgoland waters with a Δ1.72 has an internal medium Δ1.7, but in the Baltic Sea with a water of Δ0.77 the same species has a Δ value of 0.75 for the internal medium.
| Date taken or calculated from | Na | K | Ca | Mg | Cl | SO4 | |
|---|---|---|---|---|---|---|---|
| Sea Water | 100 | 3.6 | 3.8 | 12.1 | 180 | 25.2 | |
| Aurelia flavidula (mesogloea) | Macallum (1926) | 100 | 5.2 | 4.1 | 11.4 | 186 | 13.2 |
| Limulus polyphemus | Macallum (1926) | 100 | 5.6 | 4.1 | 11.2 | 187 | 13.4 |
| Aplysia limacina | Bethe (1929) | 100 | 4.0 | 4.4 | 11.0 | 180 | |
| Homarus americanus | Macallum (1926) | 100 | 3.7 | 4.9 | 1.7 | 171 | 6.7 |
| Acanthias vulgaris | Macallum (1926) | 100 | 4.6 | 2.7 | 2.5 | 166 | |
| Carcinus maenas | Bethe (1929) | 100 | 4.8 | 4.5 | 4.8 | 180 | |
| (Cod) Gadus collarus | Macallum (1926) | 100 | 9.5 | 3.93 | 1.41 | 149.7 | |
| (Pollock) Pollachius virens | Macallum (1926) | 100 | 4.33 | 3.10 | 1.46 | 137.8 | |
| Frog | Macallum (1926) | 100 | 11.8 | 3.17 | 0.79 | 135.6 | |
| Dog | Macallum (1926) | 100 | 6.6 | 2.8 | 0.76 | 139.5 |
It should be mentioned here that the teleost (bony) fishes in marine waters are definitely hypotonic and, therefore, in order to keep their body fluids down to the required osmotic pressure for the species, they secrete chloride through the “chloride cells” of the gills (Keys, 1933). This function is a regulation toward a low osmotic pressure of the blood, as opposed to regulation toward a high one as performed by the kidneys of animals in fresh-water environments. That this group of aquatic animals has achieved a marked degree of independence of the osmotic pressure of the external medium is evidenced especially by such forms as the salmon and eel, both of which, though practically homoiosmotic, spend their lives partly in hypotonic and partly in hypertonic environments, The elasmobranchs—namely, the sharks and rays—are isotonic with sea water, but in these the high osmotic pressure of the blood is due not only to the presence of such salts as occur in sea water, but also to high urea content. For further discussion of salinity as an environmental factor, see also p. 839.
Other Characteristics of the Environment
In addition to the chemical and physical properties of sea water, certain other biologically important characteristics are inherent in the marine environment as a whole. These result from the magnitude of the ocean itself, its great depth, and its expanse.
In considering the ocean in its entirety as an environment, we are at first impressed by the wide ranges of living conditions, the salinities varying from those of dilute estuarian waters to concentrations of 37 ‰ or more in the open sea, temperatures from 30°C to freezing point, light intensities from brilliant sunlight at the surface to absolute and perpetual darkness in the deeper layers, and pressures from a single atmosphere at the surface to about 1000 atmospheres in the greatest oceanic deeps.
| Marine Animals | ||
|---|---|---|
| Species | Internal medium Δ°C | External medium Δ°C |
* Dakin includes certain observations from the region of Naples giving the Δ of the sea water as 2.29°. These observations, which are often quoted in the literature, have been omitted here because a Δ of 2.29° corresponds to such a high salinity (43.5 ‰) that it must be in error. The maximum salinity in the western Mediter-ranean is about 39 ‰ and the corresponding Δ is 2.14°. | ||
| Annelida | ||
| Arenicola marina | 1.72 | 1.7 |
| Arenicola marina | 0.77 | 0.75 |
| Mollusca | ||
| Ostrea edulis | 2.23 | 2.11–2.14 |
| Mytilus edulis | 2.26 | 2.11–2.14 |
| Octopus vulgaris | 2.16 | 2.11–2.14 |
| Arthropoda | ||
| Homarus americanus | 1.82 | 1.80 |
| Cancer pagurus | 1.84–1.91 | 1.91 |
| Hyas aranea | 1.83 | 1.80 |
| Limulus polyphemus | 1.90 | 1.82 |
| Tunicata | ||
| Ascidia mentula | 2.08 | 1.98 |
| Teleost fishes | ||
| Pleuronectes platessa | 0.787 | 1.9 |
| Conger vulgaris | 0.77 | 2.14 |
| Gadus aeglefinus | 0.74 | 1.92 |
| Fresh-water Animals | ||
| Mollusca | ||
| Anodonta cygnea | 0.09 | |
| Unio pectorum | 0.15 | |
| Limnaea stagnalis | 0.22–0.23 | 0.02–0.03 |
| Crustacea | ||
| Telphusa fluviatile | 1.17 | |
| Daphnia magna | 0.20–0.67 | |
| Potamobius astacus | 0.80 | |
| Eriocheir sinenais | 1.09 | |
| Astacopsis | 1.1 | |
| Teleost fishes | ||
| Salmo fario | 0.57 | |
| Anguilla anguilla | 0.62 | |
| (in sea water) | 0.73 | 1.87 |
| Barbus fluviatilis | 0.50 | |
| Cyprinus carpio | 0.50 | |
| Anabas tetudineus | 0.64 | |
| Dipnoi fishes | ||
| Epiceratodus fosteri | 0.42 | |
Impressive as these ranges may be, nevertheless very uniform conditions do prevail over extensive areas of the environment, and many organisms may, by reason of the monotony of these extensive areas, be very delicately attuned to the prevailing unvarying conditions. Hence, it follows that faunal areas characterized by specific forms can be recognized. On the other hand, a wide range of conditions may be encountered in more restricted areas, especially in coastal regions. These conditions may be due to the physiographic character of the coastline, depth to bottom, topography and nature of the bottom, inflow of land drainage, meteorological conditions, and so forth. Specially adapted and tolerant forms occur here in profusion, for, as will be shown in later chapters, the shallow depths and varying conditions are frequently favorable to abundant production of primary food.
It must not be overlooked that the gradients of salinity, light, and temperature that exist in the sea are favorable to a number of sensitive animals that possess the ability, through swimming or otherwise, to adjust themselves to optimum conditions.
Depth and Light. Inherent in the vertical range or depth of the open-sea habitat are a number of important features of far-reaching biological effect. Of prime importance is the relatively great vertical range of the euphotic zone available for production of floating microscopic plants. But the gradient of light, both as to quantity and quality, resulting from depth of water also allows adjustment of many animals to the optimum condition with respect to this factor and, indeed, is associated with diurnal migrations of many forms to lighter or darker situations.
Pressure. Pressure in itself does not exclude life from the abyssal regions of the sea, for water is but little compressed and equilibrium exists between the inner and outer pressure affecting the body tissues. However, pressure may limit the vertical range of motile forms, although some eurybathic animals apparently are not seriously affected and are known to make daily vertical wanderings of up to 400 m, corresponding to pressure variations up to 40 atmospheres. Harpooned whales are said to “sound” to a depth of 800 m, and the sperm whales must descend normally to great depths, since the large squids upon which they feed inhabit very deep water.
Water Movements. The sea must be viewed as an environment that for the most part is in constant motion with both regular and irregular patterns of flow. The principal biological benefits derived from the circulation are (1) oxygenation of subsurface water, (2) dispersal of wastes resulting from processes of metabolism, (3) dispersal of plant nutrients and other variable elements essential to plant and animal
Extent of the Marine Environment. That part of the earth which is capable of sustaining life, both plant and animal, is known as the biosphere. The biosphere is subdivided into three principal divisions or habitats known as biocycles. These are the terrestrial, the marine, and the fresh-water biocycles. Each has its characteristic types of ecological features and associations of plants and animals. A few animal species may at times migrate freely from one to another, as is witnessed especially by the salmon or the eel.
The oceans cover some 71 per cent of the earth's surface. Thus, the area of the oceans is about two and one half times the area of the land, but, when considering the space in which life might conceivably exist, account has to be taken of the relative vertical range provided by the two main environments, the terrestrial and the marine. On this basis it is estimated (Hesse, Allee, and Schmidt, 1937) that the marine environment actually provides about three hundred times the inhabitable space provided by the terrestrial and the fresh-water biocycles together; for, whereas the terrestrial environment provides space only in a shallow zone mainly at the immediate surface and to a depth of a few feet at the most, the marine habitat provides livable space for at least some form of life from the surface even to the abyssal depth of several miles. The fresh-water biocycle constitutes only a small fraction of the other two. The aerial portion of the globe is not properly considered a separate biocycle, since entrances into it by birds, insects, and so forth may be considered mainly as temporary journeys.
Owing to the difficulties attendant on the study of the oceans, the marine biocycle is the least known of all.
Classification of the Marine Environment
In order to facilitate a study of the marine environment and its inhabitants, the former may be conveniently divided broadly into primary and secondary biotic divisions based upon physical-chemical attributes or upon the nature of the biota. The boundaries between these biotic divisions, which are diagrammatically shown in fig. 67, are in some instances well defined, but more frequently there is a good deal of overlapping. Thus, although the primary divisions are definitely set off from each other on physical bases, and the typical subdivisions of these habitats can be clearly recognized both biotically and abiotically, yet there are no well-defined boundaries between them.
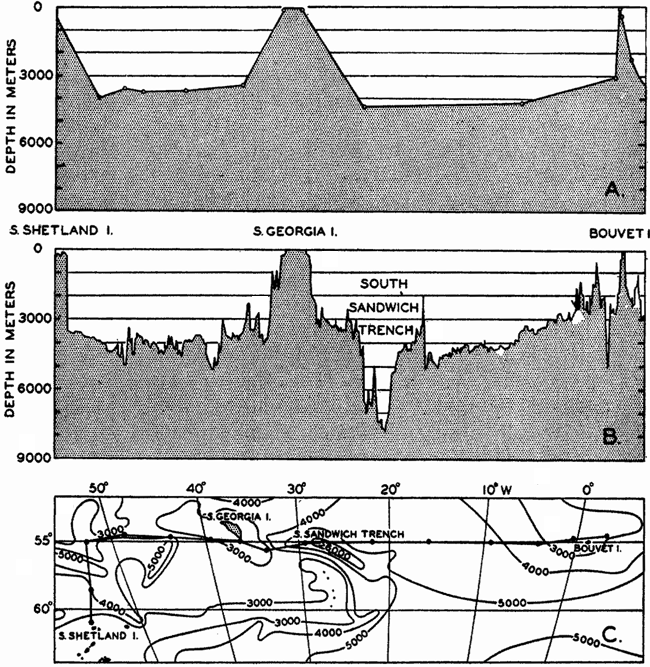
The main divisions of the marine environment.
The two primary divisions of the sea are the benthic and the pelagic. The former includes all of the ocean floor, while the latter includes the whole mass of water.
The Benthic Biotic Environment and Its Subdivisions. This division includes all of the bottom terrain from the wave-washed shore line at flood-tide level to the greatest deeps. It supports a characteristic type of life that not only lives upon but contributes to and markedly modifies the character of the bottom. Ekman (1935) discusses the boundaries of the vertical zones from a zoogeographic standpoint, and we follow mainly the scheme employed in his text.
The benthic division may be subdivided into two main systems—namely, the littoral and the deep-sea systems. The dividing line between these has been set at a depth of about 200 m on the arbitrary supposition that this represents the approximate depth of water at the outer edge of the continental shelf (p. 20), and, roughly, also the depth separating the lighted from the dark portion of the sea. The littoral system is subdivided into the eulittoral and the sublittoral zones. The deep-sea system is divided into an upper (archibenthic) and a lower (abyssal-benthic) zone. The limits of the benthic subdivisions are hard to define, and are variously placed by different authors because uniform boundaries that will fit all requirements cannot be drawn. For general biological studies, the different boundaries must be based on the peculiarities of the endemic plant and animal distribution and should follow the region of most distinct faunal and floral change. The biotic zones thus delineated will be characterized by a more or less clearly defined range of external ecological factors which have given character to the population.
The eulittoral zone extends from the high-tide level to a depth of about 40 to 60 m. The lower border is set roughly at the lowest limit at which the more abundant attached plants can grow. The sublittoral zone extends from this level to a depth of about 200 m, or the edge of the continental shelf. The dividing line between these subdivisions varies greatly between extremes, since it is determined by penetration of light sufficient for photosynthesis. It will be relatively shallow in the higher latitudes and deep in the lower latitudes. In the upper part of the eulittoral zone a relatively well-defined tidal or intertidal zone that is bounded by the high- and low-water extremes of the tide is recognized. Some authors confine the eulittoral zone to this narrow section and consider the sublittoral to begin at the low-tide level (cf. Gislen, 1930). The vertical range of the intertidal zone, though rather well defined for any given area, varies greatly in different sections of the world, for it is determined by the tidal range (see chapter XIV). In the upper reaches of the Bay of Fundy the zone may have a vertical range of over 15 m, while in the Gulf of Mexico it is less than 0.7 m, and in areas like the Mediterranean along the southwest coast of Italy the range is yet smaller, only 10 to 30 cm. On exposed coasts subjected to direct ocean waves and swells the upper range is somewhat extended to include a rather well-defined supratidal spray zone with a sparse population of especially resistant forms among which a few animals, such as the isopod Ligyda, appear to be in the process of becoming terrestrial in habit. Many species of animals are found only in the tidal zone and may be limited vertically in maximum distribution even to certain levels within the zone—for example, Ligyda and the gastropods Littorina scutalata, L. planaxis, Acmaea digitalis, and others found at Monterey Bay only above the 0.76-m tidal level (Hewatt, 1937). Thus, in the tidal zone
The eulittoral zone gives rise to many biotopes, for it is greatly varied as to type of substratum—for example, rocky, sandy, or muddy—and also as to character of shore line and degree of exposure. The overlying water may be slightly or greatly reduced in salinity. These variations are direct, decisive features controlling the type and abundance of sessile littoral forms (cf. Shelford et al, 1935). The plentiful primary food in this zone is derived from both pelagic and attached plants.
Attempts to establish such zones as Fucus zone, Laminarian zone, and so on, based on the depths at which these plants are characteristically attached, has the disadvantage that the plants are very frequently absent along vast stretches of the coast, owing to unfavorable substratum or other ecological factors; nevertheless, such classification may be of useful local application.
Though the boundary between the sublittoral and the deep-sea systems is set at a depth of 200 m, Ekman's compilations based on the fauna indicate that in most regions the boundary may be located between 200 and 400 m. Light and temperature are important factors, and in high latitudes these factors operate together to shift the boundary into shallower water.
The upper division of the deep-sea system is called the archibenthic, a word introduced by Alexander Agassiz, but the term is unfortunate in that it implies the beginning of the benthos from this region. The zone is also called the continental deep-sea zone, but this gives rise to greater confusion, since the term “continental fauna” sometimes used must include also the littoral fauna unless specifically called continental-slope or deep-sea fauna. The archibenthic zone extends from the sublittoral to a depth between 800 and 1100 m.
The abyssal-benthic zone comprises all of the deep-sea benthic system below the archibenthic zone. It is a region of relatively uniform conditions. Temperatures are uniformly low, from 5° to −1°C, and solar light is wanting. There are no seasons, and hence the seasonal biological phenomena associated with the littoral zone are suppressed. Stagnant conditions do not prevail in the open ocean, however, for there is ample circulation to supply well-aerated water resulting from deep vertical movements in the high latitudes (p. 138). No plants are produced, and the extent to which autotrophic bacteria play a part in the manufacture of food is not known. The animals are carnivorous, feeding mainly upon organic detritus which in its initial organic state must have originated
The benthic environment from shore seaward to abyssal depths is covered, to a greater or less degree, by sedimentary deposits that may be classified as terrigenous deposits, organic or pelagic oozes, and red clay. A detailed discussion of the deposits will be found in chapter XX, and the nature of the distribution is shown in fig. 253. As far as the biology of benthic animals is concerned, the most important features of these oozes are their physical consistencies and the amount of digestible organic material they contain. Most deep-sea benthic forms are detritus eaters and mainly dependent, therefore, upon the rain of pelagic organisms that falls to the bottom. The production of pelagic food usually decreases markedly with increasing distance from the coast, and the amount reaching the bottom in areas of very deep water is further reduced by its disintegration while sinking. Hence, the littoral muds are most rich in food, and the red clay at great depths and far from shore is the poorest. This difference is reflected in the number of animals actually collected from different areas (cf. p. 806).
The Pelagic Environment and Its Subdivisions. The pelagic division includes all of the ocean waters covering the benthic division. Horizontally, the pelagic division is subdivided into an open-sea (oceanic) province, and an inshore (neritic) province.
Vertically, the oceanic province has an upper lighted zone and a lower dark zone with no well-marked boundary between the two. For convenience the boundary is arbitrarily set at 200 m, since this would correspond with the arbitrarily set depth for the edge of the continental shelf and at the same time place the littoral system and the neritic province in areas definitely within the lighted portion. Actually, light changes gradually in both quantity and quality from the very surface downward to depths where it is no longer detectable (p. 82), and this depth varies with latitude, season, amount of suspended material, living or dead, and therefore also with distance from shore. These variables of the pelagic environment are of profound importance to the population of the sea, as will be pointed out later.
The outstanding features of the oceanic province are the broad spatial expanses and the great ranges of depth. As distinguished from the neritic province the waters are as a rule very transparent, with little or no detritus of terrestrial origin. These waters are predominantly blue in color and support the blue surface fauna to be discussed more fully in chapter XVII. Although solar light penetrates relatively deeper than in inshore waters, the great depth of the water included in this province results in complete elimination of solar light in the deeper portion
The chemical composition of the offshore water is relatively stable. Salinity is uniformly high, with only small fluctuations in space and time (p. 123), and plant nutrients are frequently relatively low in the upper layer and only slowly replaced.
The vertical border separating the neritic province from the oceanic is set at the edge of the continental shelf; hence all water of depths shallower than 200 m would fall within the neritic province, which accordingly may extend far seaward in instances where the continental shelf is broad, as off the east coast of the United States, or be very narrow, as off the west coast of South America.
Although biologically and chemically the border between the oceanic and the neritic provinces is not strictly definable, yet as we approach the coast the plant and animal life takes on characteristics not found in the typically oceanic province where “blue-sea” forms prevail. The chemical constituents of the sea water in the neritic province are more variable than in the oceanic. Salinities are usually lower, sometimes markedly, and undergo seasonal or sporadic fluctuations such that many of the inhabitants are more or less euryhaline in nature—that is, able to endure wide ranges of salinity. River water may bring in nutrients and may also exert a stabilizing influence on the turbulent motion, being at times, therefore, instrumental in initiating plant growth in the upper layers (p. 789). Plant nutrients, nitrates, phosphorus, and so on are more readily available in the shallower inshore water because of the greater possibility of return by vertical currents after they have been regenerated from the disintegrating organisms on the bottom or in the deeper water (chapter VII). This factor is of the utmost importance to production of diatoms, foremost of the primary food of the sea. Therefore, per unit area of the sea, the neritic province is far more productive than the oceanic province and is consequently the region of greatest importance to marine life in general. Here fish of greatest economic importance are taken, not only because of greater availability, but also because it is their natural habitat.
Other Biotic Units. The above classification of the marine environments is based mainly on broad geographical, physical, chemical, and biological characteristics that circumscribe more or less clearly the separate zones. Within each of these extensive zones we observe many and varied sets of ecological conditions resulting from differences in substratum, proximity to shore, depth and chemical-physical condition of the water, and so forth.
The primary “topographic” unit used in ecological classification of the environment is the biotope, or niche, which is defined as “an area of which the principal habitat conditions and the living forms which are
Biotopes having certain characteristics in common—for example, proximity to the coast or estuarine locality—are united into larger divisions known as biochores.
General Character of Populations of the Primary Biotic Divisions
Under the previous headings we have dealt with the classification of the marine environment. For purposes of future discussion it is desirable at this point to outline briefly a broad, highly practical classification of the marine population inhabiting the above primary biotic divisions, a classification based not on natural phylogenetic or taxonomic relationships, as given on p. 282, but rather on an artificial basis, grouping heterogeneous assortments of organisms depending upon common habits of locomotion and mode of life and upon common ecological distribution.
On these grounds the population of the sea may be divided into three large groups—namely, the benthos, nekton, and plankton, the first belonging to the benthic region and the other two to the pelagic region.
In the benthos (Gr., deep or deep-sea) are included the sessile, creeping, and burrowing organisms found on the bottom of the sea. Representatives of the group extend from the high-tide level down into the abyssal depths. The benthos comprises (1) sessile animals, such as the sponges, barnacles, mussels, oysters, crinoids, corals, hydroids, bryozoa, some of the worms, all of the seaweeds and eel grasses, and many of the diatoms, (2) creeping forms, such as crabs, lobsters, certain copepods, amphipods, and many other crustacea, many protozoa, snails, and some bivalves and fishes, and (3) burrowing forms, including most of the clams and worms, some crustacea, and echinoderms.
The nekton (Gr., swimming) is composed of swimming animals found in the pelagic division. In this group are included most of the adult squids, fishes, and whales—namely, all of the marine animals that are able to migrate freely over considerable distances. Obviously, there are no plants in this general group.
In the plankton (Gr., wanderer) is included all of the floating or drifting life of the pelagic division of the sea. The organisms, both plant and animal, of this division are usually microscopic or relatively small; they float more or less passively with the currents and are therefore at the mercy of prevailing water movements. Many of the animals are able to make some progress in swimming, although their organs of locomotion are relatively weak and ineffective. The plankton is divided into two main divisions, the phytoplankton and the zooplankton. The former comprises all of the floating plants, such as diatoms, dinoflagellates, coccolithophores, and sargassum weeds. In the zooplankton are included (1) myriads of animals that live permanently in a floating state, and (2) countless numbers of helpless larvae and eggs of the animal benthos and nekton. Since the plankton and nekton occupy the same biotic realm and are part of the same community, it is necessary always to remember that the distinction is one based primarily on relative size and speed of swimming, and does not signify a divergence of ecological relationship.
Each of these three ecological groups will be more fully discussed in later chapters.
Development of life in the Sea
Let us review briefly the observations that indicate the relative antiquity of the marine environment as a biological realm. It is not possible to know when life arose in the sea, but the close similarity of the chemical composition of body fluids and sea water has led to the supposition that the sea was already saline at that early time and that, because of the intimacy of primitive organisms with the fluid environment, the elements present entered into the fundamental composition and mode of metabolism of the primitive organisms and are maintained in present-day forms with certain modifications in the proportions of the principal ions, especially magnesium (table 55). These interesting relationships have led to much speculation relative to the development of organisms and the chemical composition of primitive seas, but we cannot enter further upon that phase of the action of the environment. Pearse (1936) has given some reviews and listed literature pertaining to these questions and to the theory of migration of animals from sea to land.
The part played by the sea in the distribution and maintenance of present-day life upon our globe is a vital one. The sea itself is abundantly populated, and no life could exist on land were it not for the perpetual
That the sea is the original environment of animal life is strongly indicated by certain facts that point to the greater age of marine life as compared to terrestrial and fresh-water faunas to which it has seemingly given rise. Evidence pointing to a greater age of marine fauna over the terrestrial and fresh-water faunas is mainly along four lines: (1) general composition of present-day faunas, (2) similarity in the chemical composition of body fluids and sea water, (3) life histories, and (4) paleontological relationships.
(1) The whole animal kingdom is divided into a number of primary divisions, each known as a phylum. Each phylum is composed of animals having certain fundamental morphological similarities not possessed by any animals of other phyla. Thus, a natural, as opposed to artificial, relationship is indicated. Each phylum is then divided into natural but more restricted groups known as classes, and these in turn are followed by other yet lower divisions in the following manner:

Species are formed of individuals, and the morphological features by which each species is characterized are less fundamental and presumably of more recent origin than those characterizing the genera. Similarly, the generic structures are less fundamental than those of families, and so on to the highest division, which is based on structures of great antiquity.
A review of all the higher or major divisions—namely, the phyla and classes of animal life—reveals the striking preponderance of marine groups. All of the seventeen phyla (using the taxonomic ranking of H. S. Pratt, 1935, in Manual of Invertebrate Animals) are represented in the sea, and most, if not all, are believed to have originated there. The following five are exclusively marine: Ctenophora, Echinodermata, Phoronidea, Brachiopoda, Chaetognatha. Some authors recognize fewer than seventeen phyla, but this has only the effect of increasing the preponderance of purely marine classes.
Of the forty-seven classes (where only subphyla were given under phyla, they are here rated as classes) of invertebrates as given by Pratt, twenty-one, or 43.7 per cent, are exclusively marine, and only three, or
These divisions demonstrate the astonishing variety of marine animals, as far as the major phylogenetic groups are concerned. However, the terrestrial environment harbors the greatest number of species, mainly owing to the large number of species of one restricted group, the insects, which are almost totally absent from the sea. The presence in the sea of so many major groups, many of which are restricted to the sea, indicates the great tendency on the part of the marine environment to preserve the groups that have once become evolved.
It should be noted also that, in addition to the remarkable diversity of marine life in the ocean, there is a conspicuous primitive element, as judged by simplicity of structure, in the groups represented. In the sea there is a more complete developmental series of animal life than exists anywhere else, because of which, and also because of the natural and intimate relationships of the organisms to the sea-water medium, the studies issuing from the marine biological laboratories have contributed vastly to information on biological problems dealing with development and maintenance of life.
The relative uniformity of the marine environment has been instrumental not only in preserving the diversity of forms but also in retaining a generally more primitive character as compared with terrestrial and fresh-water animals. It is true that in the sea we do find associated with the lower forms a number of highly developed animals that must be considered marine because of their dependence on the sea. These are the seals, whales, certain reptiles, fishes, and birds. All of these groups, however, have had a large part of their racial development in the terrestrial and fresh-water habitat. They have more recently reverted to the sea and have only secondarily become adapted to it. The teleost fishes, which are believed to have evolved to their present status in fresh water, were originally derived from marine stock.
(2) The relation of body fluids to sea water has already been discussed (p. 269).
(3) A study of the life histories of invertebrates suggests the antiquity of marine life. During the early history of the individuals of some animal groups the larval stages are markedly different in structure and habit from the mature phase. The larval stages, which sometimes resemble the mature stages of other groups or only the larvae of other groups, are thought to reflect a structural similarity to ancestral stock. Whether or not this is a real recapitulation of racial history or only an
There is a tendency for some aggressive animal groups to desert the sea for fresh-water or land habitats. This is shown by the crustaceans, among which there are forms such as the prawn, Eriocheir, which enters fresh water at a young stage but when mature returns to the sea to spawn. The land crabs, Cardisoma, Gecarcinua, and so forth, also go through a free-swimming larval stage in sea water.
(4) It is well known that animal fossils occurring in the oldest known fossiliferous rocks of the earth's crust are mainly marine forms.
Marine animals were abundant and became fossilized in the Cambrian period (500 million years ago), when certain portions of the land now above sea level formed a part of the sea bottom along the coasts of ancient seas. Several invertebrate phyla were already developed, and such forms as trilobites and brachiopods were particularly abundant.
The chief roles of the marine and terrestrial environments in the development of life may be summarized by saying that the great part played by the former is chiefly in the development and maintenance of a wide diversity of lower forms, while in the latter the influence of the more rigorous habitats has produced less diversity of form but a higher type of complexity.
The area where these two great environments meet, the intertidal zone, is in an intermediate position and subject to rapid and marked vicissitudes, and it is from here that much of the migration to land is supposed to have taken place.
Bibliography
Bethe, A.1929. “Ionendurchlassigkeit der Körperfläche von wirbellosen Thieren des Meeres als Ursache der Giftigkeit von Seewasser abnormer Zusammensetzung” . Pflugers Arch., 221, p. 344–362, 1929.
Dakin, W. J.1935. “The aquatic animal and its environment” . Linnean Soc. New South Wales, Proc., v. 60, pts. 1, 2, p. viii–xxxii, 1935.
Ekman, Sven. 1935. “Tiergeographie des Meeres” . Akad. Verlagsgesellsch., Leipzig. 542 pp., 1935.
Gislen, T.1930. Epibiosis of Gullmar Fjord. II. Kristinebergs Zool. Sta. 1877 to 1927, No. 4, p. 1–380, 1930.
Hesse, Richard, W. C. Allee, and K. P. Schmidt1937. Ecological animal geography. An authorized, rewritten edition based on “Tiergeographie auf oekologischer Grundlage,” by Richard Hesse. John Wiley & Sons. New York. 597 pp., 1937.
Hewatt, Willis G.1937. “Ecological studies on selected marine intertidal communities of Monterey Bay, California” . Amer. Midland Naturalist, v. 18, p. 161–206, 1937.
Keys, Ancel. 1933. “The mechanism of adaptation to varying salinity in the common eel and the general problem of osmotic regulation in fishes” . Roy. Soc., Proc., B, v. 112, p. 184–199, 1933. London.
Macallum, A. B.1926. “Paleochemistry of body fluids and tissues” . Physiol. Rev., v. 6, p. 316–357, 1926.
Pantin, C. F. A.1931. “Origin of the body fluids in animals” . Biol. Reviews, v. 6, p. 459–482, 1931. Cambridge, England.
Pearse, A. S.1936. “The migrations of animals from sea to land” . Durham, N. C., Duke Univ. Press, 176 pp., 1936.
Pratt, Henry S.1935. “A manual of the common invertebrate animals exclusive of insects” . Revised. Philadelphia. Blakiston, 854 pp., 1935.
Shelford, V. E., et al.1935. “Some marine biotic communities of the Pacific Coast of North America. Pt. 1. General survey of the communities” . Ecol. Monographs, v. 5, p. 250–332, 1935.
IX. Populations of the Sea
PLANT GROUPS OF THE SEA
In the sea, as on land, the plants are the real producers—that is, the organisms that are capable of elaborating complex organic substances from the simple inorganic compounds dissolved in the water. Without marine plants as synthesizers of primary food, development of marine animal life would be impossible beyond a negligible quantity that might be supported alongshore and in estuaries where particulate organic material of terrestrial origin would find its way into the sea.
A notable feature of marine vegetation is its dearth of variety when compared to the multiplicity of forms characterizing the terrestrial vegetation. Also, the types of plants most important in the production of primary food in the sea are in striking contrast to those constituting the chief synthesizers on land. This marked difference is readily explained, as we shall see, since it is dependent upon the radically different demands made on the plants by the marine environment. The poverty of plant variety in the sea is also in striking contrast to the abundant diversity of marine animal life. It may truly be said that the animal kingdom belongs mainly to the sea, while the terrestrial environment fosters the plants, although the most primitive of the plant groups, the algae, are wonderfully developed in the sea.
Light is of prime importance to all photosynthetic plants, and the possibility for attachment to the substratum is of secondary importance. More will be said about this later, but we must point out here that only in a very small portion of the sea are the two factors, light and suitable substratum for attachment, at the same time operative. This small portion of the sea wherein there may be sufficient light penetration to support attached plants—that is, the eulittoral zone—constitutes about 2 per cent of the sea floor.
Anyone frequenting the seashore is familiar with the covering of brown rockweed, Fucus, the green sea lettuce, Ulva, and a number of other low-growing plants that carpet the rocks in the intertidal zone. These or yet other relatively low-growing or encrusting plants may extend to varying depth below low tide if a suitable substratum for attachment is
The large kelps, such as Nereocystis, Pelagophycus, and Macrocystis, are found typically on rocky reefs some distance from the intertidal zone. Growth may occur on shoal reefs or rocks miles from shore, but the destructive mechanical effect of breaking waves and swells usually prevents any growth of these long-stiped forms in the immediate vicinity of exposed shores or rocks. Hence, the large kelps characteristically form in bands or patches some distance from shore where there is active circulation of water and yet where the danger of abrasion is reduced.
It was pointed out that only a small per cent of the sea floor may be considered to have sufficient light to support attached plants. Although this area may have enough light, it is vastly reduced as a suitable area for attachment of larger plants because of the great coastal stretches of mud, sand, shingle, or other unfavorable features. Therefore the bulk of the material produced by the attached marine plants is relatively small and can support only a small portion of the animal life actually present throughout the vast marine habitat; nevertheless, in more restricted areas along the coasts, attached plants—for example, the eel grasses—may be the chief producers. As a result of this restricted production by the benthic, or attached, plants, the primary food production becomes mainly a function of the unattached floating plants, notably, the diatoms and dinoflagellates, which, though microscopic in size, occur in vast, incalculable numbers.
Accordingly, our study of plant production must be concerned mainly with these floating forms. The means and adjustments by which this extensive community of floating plants—that is, the phytoplankton—is maintained and is related to other forms of life will be dealt with in subsequent chapters. First, however, in order to have a more complete understanding of the whole biological “setup” of the sea, it will be necessary as a point of departure to make a brief review of the various groups that are important to the economy of the sea as a whole.
The entire plant kingdom is divided into four primary divisions: the Thallophyta, Bryophyta, Pteredophyta, and Spermatophyta. Only the first and last of these are represented in the sea.
These primary divisions are each again divided and subdivided into many smaller secondary divisions which are indispensable to the specialist in marine botany, but for our purpose it will suffice to mention these smaller divisions only when they are important to marine economy, or when they have obtained rather widespread inclusion in more or less general literature dealing with the sea.
Only an abridged classification can be given. For a more complete treatment of the systematics the reader can refer to numerous good texts on botany or to publications dealing specifically with the group in which he is interested. A few of these publications are included in the bibliography, and yet others can be traced from those works included.
Thallophyta
Nearly all of the marine plants fall into this botanical division, which is made up of primitive plants in which the body shows little or no differentiation of vegetative organs—that is, no true root, stem, or leaf. Important among these thallus plants are the marine algae and the marine fungi, especially the bacteria. Since bacteria constitute the subject of a more specialized study of the sea, they will be dealt with under a special heading in chapter XVIII.
Most algae are beautifully colored, and sometimes also iridescent. The pigments of the chromatophores intercept solar energy, which is used in the synthesis of organic compounds. The type of pigment or pigment combination occurring in the algae as color manifestations has led to the names commonly used for the classes:
Blue-green algae (Myxophyceae)
Green algae (Chlorophyceae)
Brown algae (Phaeophyceae)
Red algae (Rhodophyceae)
Yellow-green algae (a heterogeneous group variously classified by different authors)
In general, the colors are characteristic of the classes, but other characteristics associated with cell structure and life history are more fundamental in distinguishing the five groups. Each group has a considerable variation in general morphology, some features of which will be pointed out in a review of the classes. The first four, with the exception of some blue-greens, are attached plants, while the yellow-greens are characteristically floating, or planktonic, forms.
Blue-Green Algae (Myxophyceae)
This class contains only small, poorly organized plants, some consisting of only a single cell, while others are multicellular. The blue color of these plants is due to a water-soluble accessory pigment, phycocyanin. In certain inland waters, it has been reported that upon the

Characteristic types of multicellular marine algae. a, Trichodesmium; b, Fucus; c, Alaria; d, Ulva; e, Ectocarpus; f, Sargassum; g, Rhodymenia; h, Polysiphonia; i, Cytosiphon; j, Lithothamnion.
Methods of Reproduction. Reproduction in this group is by asexual fission. This, the most simple method of propagation, consists of single individuals dividing to form two of lesser size, which in turn again divide after growth. In instances involving blue-green algae that form chains of cells, the chains divide into smaller sections known as hormogonia. Fission of the cells in the hormogonia again increases the length of the filaments.
Distribution. The Myxophyceae are of less general importance in the oceans than are the following algal groups. They are widely distributed in fresh and brackish water. In the sea they are most often found in the warmer waters, where they may cause the phenomenon of sliming. A brackish-water form, Nodularia spumigena, native to calm fjords of the north, may at times cause extensive sliming of the waters. In the Gulf of Bothnia, sliming due to this or similar forms may assume considerable proportions.
Green Algae (Chlorophyceae)
As the name indicates, the algae of this class are green in color. The pigments of the chloroplasts include the two types of chlorophyll, a and b, and the various carotinoids. The yellow and orange of the latter pigments are masked by the abundance of the green chlorophyll. In contrast to the chitinous cell wall of the blue-greens, these plants produce walls that are largely cellulose—a carbohydrate as opposed to the nitrogenous product, chitin. Some green algae of the sea—for example, Halimeda of the Siphonales—become incrusted with calcium carbonate, and thus may contribute materially in some places to the formation of lime deposits in warmer seas. The joints of the plant remain uncalcified, and thus allow flexibility in the moving water.
There is great diversity in the morphological features of this class. Common forms are filamentous with septa (Urospora) or without septa (Codium), tubular (Enteromorpha), and sheet-like (Ulva, or sea lettuce) (fig. 68d).
Methods of Reproduction. Common methods of reproduction may be illustrated by the habit of the cosmopolitan Ulva. In sexual reproduction the contents of any of the ordinary cells of the flat two-layered plant may form biciliated bodies called gametes which, upon escaping into the water, unite in pairs and by cellular division grow to form the new plant, known as the sporophyte, but usually passing first through a filamentous stage. Reproduction may also be asexual, in which case any of the common cells of the sporophyte plant may form microscopic quadriciliate zoospores (spores are simple reproductive cells which differ from seeds mainly in that they do not contain any ready-made embryo plant). These zoospores, upon being discharged, grow directly into gametophytes, the plants that produce the gametes.
During the period of reproduction, large swarms of gametes and zoospores may be released, leaving the parent plant colorless and forming a green “bloom” on the waters of quiet bays. For many filter-feeding animals, the floating microscopic reproductive products of these and other algae form a source of food that must not be overlooked in a study of food of littoral animals. In bays, also, these swimming stages of algae, as well as algal slime, contribute to primary film formation that leads to an eventual fouling growth on ships and other submerged structures.
Distribution of Green Algae in the Sea. The green algae are found mainly in the upper littoral zone, especially in the lower half of the tidal zone, and in the immediate subtidal region down to a depth of 10m or more, and therefore in a relatively well-lighted habitat. It is with the green algae that the fresh-water algae are most closely related.
In geographic distribution, green algae are found most abundantly in the warmer seas. Algologists have remarked on the relative scarcity and dwarfed development of the Chlorophyceae in the Arctic Sea.
Brown Algae (Phaeophyceae)
Brown algae belong almost entirely to the sea, only a very few occurring in fresh water. Here are included the conspicuous brown seaweeds, many of which grow to notably large size. The pigments of this class include green chlorophyll, which is masked by the yellow and brown pigments, xanthophyll, carotin, and fucoxanthin.
Plants of this class of algae form the conspicuous offshore growths popularly known as “kelp beds.” They are the giants among the seaweeds, and form the marine forests among whose waving stipes and fronds myriads of neritic fish obtain their food and seek shelter from their aquatic enemies. These, also, are the kelps commonly harvested in many places for the commercial products they yield.
The brown algae possess a great range of size and structure. There are minute, delicate, filamentous branching plants (Ectocarpus, fig. 68e); coarse, hollow, sausage-like chains a foot or more in length (Scytosiphon, fig. 68i); short-stalked forms with broad thalli (Laminaria, Costaria, and Alaria, fig. 68c, some of which become nearly 2 m broad); many branched forms (Fucus, Egregia); and long-stalked giants of the Pacific with long leathery fronds (Macrocystis, Nereocystis, Pelagophycus).
In structure the brown algae are the most advanced of all thallophytes. If we refer only to the more superficial details, Nereocystis
Nereocystis may attain a length of 35 m or more. The plant is anchored to a hard substratum by means of a profusely branched structure known as the holdfast, but there are no true roots. From the holdfast extends the long cylindrical stipe, which is hollow through most of its length and ends distally in a large hollow bulb. This bulb, like the stipe, is filled with gas, giving buoyancy to the plant. Ribbon-like fronds or laminae issue from the distal end of the bulb.
The gross structure and life cycle of Nereocystis. a, sporophyte plant; b, swimming zoospores; c, male and d, female gametophyte plants; e, young sporophyte.
The hollow bulb and stipe maintain the upper portion of the plant near the surface, exposing the fronds to favorable light conditions. In common with other large algae, the parts are tough, flexible, and slippery in order to withstand with least resistance the effect of frequently violent storm waves and strong currents.
Methods of Reproduction. The life cycle of the brown algae includes various types of alternation of generations. Commonly, in the Laminariales, which includes the large kelps, there is an alternation of generations that may be illustrated by the cycle shown in Nereocystis (fig. 69). Here the large, conspicuous sporophyte plant produces a series of sori, or “fruiting areas,” appearing as dark brown patches running longitudinally along the whole length of the fronds. Beginning at the distal end of the frond, these patches are detached at maturity, leaving a broad gap (3 to 10 cm) in the frond. From the mature sori, innumerable ciliated zoospores escape and, upon reaching a suitable substratum, grow to small filamentous plants, the inconspicuous gametophyte stage. Thus the alternation of generations in this form is
In the brown algal group, Fucales, to which Fucus and Sargassum (fig. 68f) belong, the main plant is a sporophyte, but, within the thousands of tiny cup-like conceptacles forming the bladders, gametes are formed like spores. These unite after being discharged free in the water. Thus the alternation of generations is evident only cytologically. In connection with the “spawning” of Fucus, it is interesting to note that it is rhythmic with the tide, taking place after a period of exposure at low tide.
Distribution. The brown algae reach their maximum development in cooler waters, and are therefore typical of the rocky coast of higher latitudes. Sargassum and others of the Fucales are characteristic, however, of tropical or subtropical regions. Tilden (1935) is of the opinion that the Laminariales arose in the North Pacific, while the Fucales had their origin in the South Pacific. Several species or varieties of Sargassum, or “gulfweed,” are found in large quantities in the Sargasso Sea, whence they have drifted and multiplied after being torn loose from coastal areas. They are kept afloat by air bladders and grow vegetatively, propagating by fragmentation, but apparently do not form fruiting bodies. The drifting masses form a characteristic environment with associations including other algal and animal forms of littoral type.
The vertical distribution of brown algae shows many low-growing forms, especially the Fucales, in the rocky intertidal zone. Near the lowest tide level the medium-sized forms with leathery fronds and short limber stipes begin to prevail, and they increase markedly in the next 15 to 20 m of depth, finally diminishing and disappearing below the eulittoral zone.
Intermingled with these short-stiped algae are the giant long-stiped kelps that usually grow most abundantly some distance from the shore and extend to depths of 30 m or more. Macrocystis, one of the giant kelps of the Pacific, is said to reach to the surface from a depth of 80 m off the coast of Chile (Hesse, Allee, and Schmidt, 1937), but in the North Pacific it has its most abundant growth in water of about 15 m. Kelps of this genus are said to be absent from strictly tropical waters and, as a
Mention should also be made of epiphytic forms such as the filamentous Ectocarpus (fig. 68e), which prefers to be attached to other algae growing at various depths.
Red Algae (Rhodophyceae)
Nearly all of the red algae are marine. From the standpoint of color, they are the most striking of all the marine algae, some of them being also highly iridescent. Many of the delicate forms are among the most beautiful macroscopic objects of the sea. The order Gelidiaceae ranks first in importance commercially since certain of its members form the main source of agar.
The pigments of the chromatophores include the usual chlorophylls together with xanthophyll, carotin, and, in addition, the red phycoerythrin and sometimes phycocyanin. The plants may appear red, purple, violet, or, to some degree, brown or green. The deeper-growing species are the more purely red, a fact which is perhaps associated with their ability to synthesize more efficiently in the subdued light of greater depths than are the shallow-water types (Gail, 1922).
Though usually small in size, the red algae show a diversity of form much greater than the brown, and they are also more numerous. All are multicellular, the simplest being filamentous branching forms like Polysiphonia (fig. 68h), which, together with other filamentous algae, are commonly called “sea moss.” The larger flat types may be illustrated by Rhodymenia (fig. 68g), in which the broad frond may attain a considerable length. However, the maximum length of the larger red algae is only about 1 to 2 m.
Methods of Reproduction. The life cycle of some species is very complicated and cannot be amply discussed here. The reader is referred to the works of Kylin and other texts for a more complete treatment. In the higher types there is a regular morphological alternation of generations in which the sporophyte and gametophyte may superficially appear similar. Polysiphonia is commonly used to illustrate the life cycle of red algae. Here three types of plants are produced—namely, a male and a female gametophyte and an asexual tetrasporic plant. The last arises from the carpospores, which occur on the female plant. The carpospores are the products of union of male and female gametes. Upon germination, the tetraspores of the asexual plant give rise, in turn, to the sexual plants.
One of the most remarkable features of reproduction in red algae however, is the complete absence of any ciliated or flagellated swimming spores or gametes. This feature is a notable departure from the rule
Distribution. The Rhodophyceae are widely distributed geographically, but are most abundant in temperate seas. Their vertical distribution indicates that they prefer to grow in subdued light. A few species may be found in the intertidal zone, but the most luxuriant growth is subtidal. They may occur in abundance in depths less favorable to most of the green and the brown algae, and in the Mediterranean they have been reported from depths of 130 m. Thus, from shallow to deep water the general vertical distribution of the algal groups discussed is successively the green, the brown, and the red, with a wide degree of overlapping.
It should be mentioned here that certain red algae (the Nullipores) play an important role in calcium carbonate precipitation in the sea. They have contributed, and still do contribute, greatly to geological formations. Among these are, especially, the coralline algae, of which Lithothamnion (fig. 68i) is a typical example. They are distributed from lat. 73°5′ S to 79°56′ N (Tilden, 1935) and can be observed as copious encrustations on rocks and shells in the littoral zone of every exposed shore.
Yellow-Green Algae
There is considerable disagreement as to the proper grouping and status of divisions within this heterogeneous assemblage of organisms, some of which, as indicated below, are animal in nature. As a matter of convenience in discussing the more important marine members, we shall here employ only names of more or less familiar usage in biology and oceanography. Many of the members included are classified as animals in zoological texts, but in consideration of their holophytic nature (faculties of photosynthesis) it is most convenient for oceanographic studies to include them a priori among the producers. For more detailed treatment of the systematics of the various divisions, the reader is referred to Fritsch (1935) and the relevant works included in the discussions under the separate groups.
In contrast to the algae previously discussed, the members of this assemblage of plants and plantlike animals are primarily floating forms and will be taken up in the order of their importance in the economy of the sea.
Diatoms. The plants here included are all microscopic in size, the larger species viewed individually appearing only as tiny points. Some earlier authors of marine botany included them with the brown algae. A comprehensive treatment of the group is given by Hustedt (1930). In structure they are unicellular, but individuals may form chains or groups of various types. Examples of types representing the common genera are
Characteristic types of diatoms. a, Corethron; b, Nitzschia closterium; c, Planktoniella; e, Coscinodiscus; f, Fragilaria; g, Chaetoceros; h, Thalassiosira; i, Asterionella; j, Biddulphia; k, Ditylum, l, Thalassiothrix; m, Navicula; n, o, Rhizosolenia semispina, summer and winter forms.
Since these plants as a group may be considered the most important in the economy of the sea, it is imperative that we treat them in considerable
The shell structure of diatoms (fig. 71) may be likened to a box with a telescoping lid, because it consists of two nearly equal halves fitted one over the other. The pieces corresponding to the top and bottom of the box are known as the valves, and these are each joined by connecting bands that overlap and together form the girdle. The larger half of the shell is known as the epitheca, and the smaller half, which fits into it, as the hypotheca. The protoplasm lies wholly within the shell, but for exchange of metabolic products it is exposed by a slit (raphae) in the valve of some types and by small pores in others.

The gross structure of a simple diatom (Coscinodiscus). a, valvular view; b, girdle-view section of cell wall.
Reproduction in diatoms. a,b, cell division; c, diminution of size resulting from cell division in three generations.
Diatoms may possess only one or many chromatophores, which may vary in color from yellow to olive-green or brown. Authorities are in poor agreement as to the nature of the pigments present, but there is some indication that the common pigments are masked by the accessory brown pigment diatomin, which may be identical with fucoxanthin of the brown algae. An important product of assimilation is an oil that is frequently visible as droplets within the diatom.
Methods of Reproduction. The most common method of propagation among the diatoms is by simple cell division (fig. 72a). This method has a far-reaching effect on the population in two distinct ways. First, it is conducive to a rapid production of enormous numbers when
Reproduction in diatoms. a, auxospore formation in Thalassiosira aestivalis (after Gran and Angst); b, increase in cell size following auxospore formation in Melosira nummuloides (after Fritsch); c, resting spores in mother cells, Chaetoceros vanhurckii; d, resting spore of Chaetoceros diatema; e, resting spore of Chaetoceros radicans; f, microspores in Ditylum; g, microspores in Chaetoceros didymus (after Gran and Angst).
Diatoms may also produce what are known as microspores (fig. 73b). These were early observed by Murray, Gran, and others. They consist of small protoplasmic spheres occupying the shell, and may escape as biciliated spores. The significance of these bodies is not fully known.
Resting spores of characteristic structure (fig. 73c) are also formed in most pelagic neritic species, especially of the centric types, by the cell contents becoming condensed and surrounded by a heavy, siliceous wall. They may be produced at the initial appearance of unfavorable living conditions, and may drift for some time within the old frustule or sink to the bottom to survive the unfavorable seasons of inadequate nutrients, cold, or of varying salinity so characteristic of many coastal areas. Gran (1912) has reported them from Arctic collections in which they were enclosed in ice.
Winter and summer forms of oceanic diatom species have been reported. These are cases of marked dimorphism in which the coarse winter forms have been looked upon as a means of survival from one favorable season to another. However, the dimorphism may be only an adjustment to changes of viscosity inherent with seasonal temperature changes.
Many diatoms grow normally on the bottom in the littoral zone, where they may or may not be attached by stalks or glide freely over the bottom. These benthic forms produce the heavily shelled types with most exquisite designs. Diatoms may also grow in profusion on other plants and animals. The littoral genus Licmophora frequently occurs on pelagic copepods, and the massed growth of Cocconeis ceticola flourishing on the skin of whales that have spent considerable time in the cold antarctic waters has, by its yellow color, given rise to the name “sulphur-bottom” for the blue whale.
Dinoflagellata. These are frequently spoken of collectively as the dinoflagellates (fig. 74). Space will not permit the amount of discussion that this diverse group of organisms requires for adequate treatment (see Kofoid and Swezy, 1921, Kofoid and Skogsberg, 1928, Fritsch, 1935). It is a group concerning which it is not easy to make generalizations without the danger of introducing errors. The members are of great importance in the economy of the sea. A large number are holophytic and rank second to the diatoms as producers in the marine plankton. They are therefore best studied with the phytoplankton. Others are holozoic or animal-like in nutritional requirements, ingesting particulate food and possessing other characteristics that place them clearly with the animals. Some are saprophytic, living upon dead organic matter. All are important as food to filter- and detritus-feeding animals.
Typically, the dinoflagellates are unicellular, some being armored with plates of cellulose, others unarmored or naked. All possess two flagella for locomotion, an important feature in the holophytic forms, for
Dinoflagellates and other phytoplankton organisms. a, Ceratium tripos; b, Dinophysis; c, Ornithocercus; d,e, Triposolenia, front and side views; f, Peridinium; g, Amphisolenia; h, Goniaulax; i, Ceratium fusus.
Methods of Reproduction. Among the dinoflagellates, reproduction is accomplished mainly by processes of cell division, which in some instances result in a chain of individuals clinging loosely together. Temporary structural variations may normally occur in individual cells at opposite ends of the chain. The progressive size reduction that is
Dinoflagellates are found in all seas, but the greatest development of species is met with in the warmer waters, where a number of very bizarre forms are to be found. Owing to the destructibility of their cellulose plates by bacteria and other agencies, they are not preserved in bottom deposits. Important genera are Ceratium, Peridinium, Dinophysis, Gonyaulax.
Phaeocystis. Phaeocystis is a brown, flagellated plant, neritic in habit, that forms colonies in gelatinous, lobed globules visible to the naked eye. The large numbers produced may at times render the surface water quite brown and become a serious cause of clogging in silk plankton nets. Reproduction is accomplished by formation of flagellated spores that escape from the colonies.
Coccolithophoridae. Among the smallest (5 to 20 microns) of autotropic organisms of the sea are the biflagellated (some marine forms are not flagellated) forms of this group (fig. 74). Usually they are not caught by the ordinary net, through the meshes of which they readily escape, and when caught special care must be taken that their calcareous protecting armor is not dissolved by the preservative, leaving only an indefinable mass. The soft parts are shielded by tiny calcified circular plates or shields of various design and projections called coccoliths, or rhabdoliths. These shields had been found in enormous numbers in marine bottom deposits before the organisms of which they are a part were discovered by the Challenger and identified from their living habitat in the plankton, where they were found entangled in protoplasmic strands of pelagic protozoa or in the stomachs of salps and pteropods. Typically, the coccolithophoridae belong to the open sea, but they may occasionally reproduce in large numbers in coastal waters; at one time, according to Gran (1912) numbers of 5 to 6 million per liter gave the waters of Oslo Fjord a milky appearance. Some also occur in fresh water.
Though minute in size, they are of great importance as food to filter-feeding organisms, and also as contributors to calcareous bottom sediments. They occur in geological formations dating from the Cambrian period. Common genera among these organisms are Coccolithus, Pontasphaera, and Rhabdosphaera.
Halosphaera. Halosphaera is a unicellular, microscopic plant of the order Heterococcales (fig. 74). Earlier authors have included it with the green algae. It occurs at times in vast numbers in the plankton, floating mostly near the surface. Halosphaera virides occurs over the whole Atlantic and is abundant both in the warmer waters of the Gulf Stream system and in high southerly latitudes, where the Discovery investigations in the Antarctic found it second in importance to the diatoms. Meringosphaera of this order also occurs in marine plankton.
According to Gran, Halosphaera is practically the only open-sea form in which the predominantly green color of land plants is to be found. Notwithstanding the vast numbers that are often found, it does not reproduce by the quick method of simple binary fission, as in diatoms, but, after having grown for some time to its maximum size, the cell contents are transformed into a large number of zoospores. These swimming spores escape and through some unknown method are transformed back into tiny globular forms that gradually increase to normal size by successively shedding their weakly silicified investing membranes. Resting spores may also be produced.
Silicoflagellates. These flagellate organisms (fig. 74) deserve mention only briefly, since they do not usually occur in sufficiently large numbers to enter materially into the economy of the sea. However, they are such persistent members of plankton communities from nearly all colder seas that their starlike, open, siliceous shells attract a good deal of interest. Many occur in bottom sediments, and their development is shown in fossil marine deposits. That they contribute at least in a small way to the food of animals is shown by their frequent occurrence in food vacuoles of tintinnids.
The Higher Plants in the Sea
The two intermediate phyla of the plant kingdom—namely, the mosses (Bryophyta) and the ferns (Pteridophyta)—are wanting in the sea. However, the highest of plants, the Spermatophyta, are represented by about thirty species of Angiosperms, or flowering plants. These belong to three genera of the Hydrocharitaceae and six genera of the Potamogetonaceae (Arber, 1920). They have not originated in the sea, but have invaded and colonized it by way of fresh water. Their closest affinities are with widespread fresh-water angiosperms belonging to the same families.
The eel grass Zostera, to show leaves, rhizome, and true roots.
Of outstanding importance among the marine angiosperms is the eel grass, Zostera (fig. 75). Botanically, the plant is not a grass despite the long, slender, and flexible grasslike leaves, which are thus adapted to withstand the force of moving water. Unlike the benthic algae, Zostera and its relatives possess true roots that are attached to an underground stem, or rhizome, forming an anchor in the soft substratum. There are fertile and sterile plants, and, since the plants grow submerged, mostly in depths of 4 or 5 m but also to a depth of 14 m (Petersen, 1918), the flowers are pollinated under water through the agency of currents.
THE ANIMAL POPULATION OF THE SEA
Many different species of distinct animal groups live intermingled in the same faunal area. Some may have identical habits and requirements, but for the most part the separate species or higher ranks have characteristic limitations, and each has its own function in conditioning the whole complex organic environment, thus influencing the type of species forming the association. This will become increasingly clear in considering the interrelations of the organisms (chapter XVIII).
For an adequate understanding of the intricacies of the fauna, it becomes necessary, therefore, to understand the part played by the separate species or groups of species, and, in order to circumscribe and to interpret the geographic and bathymetric distribution of species, their exact identity must be established. Systematic biology—that is, taxonomy—provides the tools for these purposes and is therefore an indispensable aid toward the desired goal. The field of study is so overwhelmingly large, however, that the many species comprising the primary groups must be investigated in special studies and the results of many different specialists must be integrated to provide a picture of the fauna as a whole. Much still remains to be done in this field, for many sections of the oceans have been only superficially investigated.
A full descriptive treatment of the animals of the sea would require several volumes, but it will suffice for our purpose to list or succinctly to review the primary divisions, including only a few of the secondary divisions that in the development of the study of marine biology and oceanography have assumed more or less importance and that are illustrative of the general field.
In the following synopsis, where the number of species is recorded for any group, the figures have been obtained mainly from Pratt (1935) and Hyman (1940). Illustrations are found mainly in chapter XVII.
Synopsis of the More Important Systematic Groups of Marine Animals
A. INVERTEBRATES
PHYLUM PROTOZOA
Protozoa are single-celled organisms microscopic or minute in size. The sea bottom harbors many creeping and attached protozoa of the ameboid or ciliate types, but we shall be concerned mainly with the pelagic forms inhabiting the plankton.
CLASS MASTIGOPHORA
Order Dinoflagellata. In the broadest sense, this group contains both animals and plants, it being a borderline group.
Foremost among the protozoa in the economy of the sea are the dinoflagellates, chiefly because of the capacity of many types to carry on photosynthesis. These holophytic members are considered more fully in the discussion on plants, and for oceanographic studies are properly included in the phytoplankton. It will suffice to mention here only Noctiluca (fig. 225g) as an important representative of the holozoic members, none of which have chromatophores. The soft spherical body of Noctiluca is pale pink in color and bears a conspicuous flexible tentacle. The maximum size is only about 1.5 mm, but, when reproducing in profusion by simple cell division, the countless numbers produced may, by their accumulation, impart a pinkish-red color to considerable areas of surface coastal water, and the masses may be blown into conspicuous windrows or patches resembling “tomato soup.” Noctiluca are voracious feeders, engulfing particulate food such as diatoms and other small organisms. This form is also important as a contributor to the luminescence of the sea.
CLASS SARCODINA
Order Foraminifera. The oceanographic interest of this order (and also, to some extent, of the following order) lies in the skeletal structures produced by its members. In the foraminifera the shells are variously formed, with one or more chambers arranged in a straight line or in a spiral (fig. 225a). Some are provided with many pores for the projection of protoplasmic pseudopodia used in capturing food. The shells are constructed typically of calcium carbonate, but silica and chitin are also used, and in some
Order Radiolaria. These are planktonic organisms whose skeletons are composed mainly of silica, but the Acantharia contain acanthin (strontium sulphate), and all types possess an inner capsule of chitin. The siliceous skeletons are formed in the most intricate and widely divergent patterns in the different species and are the most beautiful of all objects found in the sea (fig. 225e,f). Upon sinking and mingling with the bottom sediments, the skeletons become the type constituents of the siliceous radiolarian oozes found most abundantly covering the ocean floor in the deep tropical waters of the Pacific Ocean (fig. 253). There are about 4400 species, all marine.
CLASS CILIATA
Suborder Tintinnoinea. These protozoans, commonly called tintinnids, are mostly of extremely small size, varying from 20 μ for Tintinnopsis nana to 640 μ for Cymatocylis robusta. Swimming is accomplished by the beating of a whorl of hairlike cilia at the anterior end. Their loricae, or shells, range in shape from tubular to urn-shaped structures that are secreted in a stereotyped fashion by the animal and may or may not include agglomerated foreign material such as bits of sand, diatom shells, and coccoliths (fig. 225c,d). The tintinnids at times are found in vast numbers, especially in coastal water, where they are important feeders on the smallest plankton, the nannoplankton. Their sensitivity to small changes in environmental conditions makes them fluctuate in numbers with seasonal or other changes. There are 692 known species,
PHYLUM PORIFERA
The sponges are multicellular animals, though of simple and loose organization, either with spicules of silica or calcium carbonate imbedded in their bodies for support or with fibrous skeletons made of the horny substance spongin, as in the common commercial sponge. Sponges are all benthic and nearly all marine, only one family occurring in fresh water. In the sea they are to be found in all parts and at all depths, the siliceous forms living largely in the deep sea. Sponges grow attached to the substratum and obtain their food by propelling water through tiny pores in the body wall and filtering out the microorganisms and detritus that may be present. There are about 2500 species, mostly marine.
PHYLUM COELENTERATA
Coelenterata are tubelike primitive forms with a continuous body wall surrounding a simple digestive cavity with but one opening encircled by tentacles used in capturing food. The group shows a remarkable degree of polymorphism; that is, a single species may present a variety of forms reducible either to the sessile polyp or the swimming medusoid type.
Class Hydrozoa. To this class belong the hydroids commonly found growing in little tufts on rocks and sea weeds along the coast. From these branching polyps are budded the small jellyfish or medusae such as Obelia (fig. 79). The Siphonophora, an order of this class, are characteristic of the open sea and are represented by the beautiful blue Velella (“by-the-wind sailer”) (fig. 226b) and Physalia (the “Portuguese man-of-war”), neither of which possesses a sessile stage. They are planktonic colonial medusae, exhibiting the maximum development of polymorphism of all animals. There are about 2700 species of hydrozoa.
Class Scyphozoa. To this class belong the larger medusae with eight notches in the margin of the bell. Here are included the giant jellyfishes, some of which may become 2 m in diameter. A much-suppressed sessile polyp stage is present in the group. The 200 species are entirely marine. Examples: Aurelia, Cyanea.
Class Anthozoa. To this class belong the sea anemones, corals, and alcyonarians. There is no medusoid stage, and many of the polyps are colonial; some, especially the corals, are notable for their precipitation of calcareous skeletal structures, which, through long periods of accumulation, are important in the
― 307 ―building up of coral reefs and similar formations. All 6100 known species of anthozoa are marine.
PHYLUM CTENOPHORA
Ctenophora are small globular or flattened forms of jellylike consistency and with eight meridional rows of fused cilia used in swimming. Some possess a pair of trailing tentacles used in the capturing of food. The abundant globular species are commonly known as “comb jellies” or “sea walnuts” (fig. 226a). There are 80 species, all marine. Numerically important genera are Pleurobrachia and Beroë.
PHYLUM PLATYHELMINTHES
Platyhelminthes are flatworms, a large number of which are found in the sea, either free-living or parasitic.
Class Turbellaria. Nearly all of this class are free-living on the bottom under stones and in crevices, where they move about by means of cilia covering the body.
Class Nemertinea. These are ribbonlike worms sometimes considered as a separate phylum. The benthic species live among rocks, algae, mussels, and so on, or burrow in the bottom, where they capture small organisms by means of a long eversible proboscis. Extraordinary size variations occur, some species being only 5 mm long, while one, Lineus longissimus, may become 25 m in length when extended, and therefore is the longest of the invertebrates; however, its threadlike form contains but little bulk. Fifty-two planktonic species of nemerteans are known, some living at great depths—for example, Pelagonemertes. (Coe, 1926). The planktonic forms are modified, some with caudal and horizontal fins for swimming (fig. 228c). There are about 550 species of nemerteans, of which nearly all are marine.
PHYLUM NEMATHELMINTHES
The thread or round worms occur largely as parasites, but some are found in the plankton, and very large numbers occur in decaying organic detritus on the bottom. There are about 1500 species, many of which are nonmarine.
PHYLUM TROCHELMINTHES
Class Rotatoria (Rotifera). These are tiny benthic or planktonic organisms provided with rings of cilia for swimming and for gathering food. Vast numbers may occur in the neritic plankton during the warmer seasons. There are about 1200 species of rotifers, of which most are fresh-water inhabitants.
PHYLUM BRYOZOA
These colonial animals, known as “sea mats” or “moss animals,” form flexible tufts or thin incrustations over the surface of solid objects both in intertidal and deep waters. Below low tide, many species form rigid, erect, latticed or branched colonies. The individual minute animals have calcareous protective skeletons and possess a ring of ciliated tentacles for gathering microscopic food. There are over 3000 species, about 35 of which are nonmarine.
PHYLUM BRACHIOPODA
Brachiopoda are ancient sessile animals superficially resembling bivalve molluscs, but the hinged calcareous or horny shells are dorsoventrally situated instead of laterally, as in the molluscs, and the animals gather their food by means of delicate ciliated arms attached within the shell. They grow permanently attached to rocks and shells, usually in the littoral zone below low tide. A few live in burrows. All are marine and all are very abundant as fossils in the Paleozoic and Mesozoic rocks. About 120 living and 3500 fossil species are known.
PHYLUM PHORONIDEA
Phoronidea are wormlike animals, living in membranous tubes in the sand and collecting food by means of ciliated tentacles. There are about 12 marine species.
PHYLUM CHAETOGNATHA
Chaetognatha include numerous but small (maxima about 75 mm long) holoplanktonic wormlike animals known as “arrow worms” or “glass worms.” They are highly transparent and provided with eyespots, a caudal fin and one or two pairs of lateral fins, and with strong chitinous jaws and teeth for capture of prey. They occur from the surface to great depths and are distributed far to sea in all latitudes. All 30 known species are marine. Sagitta (fig. 228a) is the most abundant genus.
PHYLUM ANNELIDA
Annelida are true worms with elongated bodies composed of a series of similar segments.
Order Polychaeta. These are marine worms of great abundance provided with many setae and typically with a variety of well-defined head structures such as eyes, tentacles, chitinous jaws, ciliated cirri, and so forth, which are modified in keeping with their habits of life and mode of feeding. They have a wide distribution horizontally and bathymetrically.
Order Oligochaeta. These are earthworms, of which only a very few are marine, living near shore.
Class Echiuroidea. These are fleshy marine worms with only one or two pairs of setae. They are unsegmented or indistinctly segmented in the adult. They live in burrows in the mud and sand of the littoral zone. There are about 20 species.
PHYLUM ARTHROPODA
Arthropoda include animals with a segmented, chitinous exoskeleton and with jointed appendages, variously modified for locomotion, feeding, and other activities.
Class Crustacea. Entomostraca. This group, formerly considered a subclass, is of convenience in designating a large assemblage of small, primitive crustacea belonging to several subclasses and orders distinguished from the higher crustacea, or Malacostraca.
Suborder Cladocera. Only a few occur in the sea. Examples: Podon, Evadne, sometimes important in neritic plankton. Very numerous in fresh water.
Order Ostracoda. This order includes more than 2000 species, mostly marine, living in the plankton and on the bottom (fig. 227b).
Order Cirripedia. These are the barnacles which as adults have calcareous shells and live sessilely in all benthic habitats, especially coastal. Some grow attached to drifting objects or upon whales and other animals, or they may form special floats for suspension. There are about 500 species, all marine.
Order Copepoda. Though small in size (about 0.3 mm to 8 mm in length), the copepods bulk large in the animal substance of the sea, for they are by far the most abundant of all crustaceans and usually constitute about 70 per cent of the zooplankton. There are over 6000 species of copedods, found mostly in the sea, where some 750 species are planktonic and extremely numerous. Many others are benthic or parasitic. The three main suborders of free-living forms are Calanoida (fig. 227c), Cyclopoida (fig. 229d), and Harpacticoida (fig. 229a). The first two are mainly pelagic,
― 310 ―the last benthic. Like other Entomostraca and some Malacostraca, they gather food by means of fine bristles on certain appendages (p. 887).
subclass malacostraca. These are the large crustacea, mostly benthic, many with strong claws and biting mouth appendages.
Order Mysidacea. There are about 300 species, mostly marine, living on or near the bottom.
Order Cumacea. About 400 species of this order are known; nearly all are marine, benthic.
Order Euphausiacea. These are commonly known as “krill,” and in some regions are very abundant in the plankton and near or on the bottom. Some attain a length of about 50 mm, and may at times be the major constituent of the zooplankton. There are 85 known species, all marine. Examples: Euphausia, Meganyctiphanes (fig. 227a).
Order Amphipoda. There are about 3000 species, nearly all marine, in various habitats.
Order Isopoda. Over 3000 species are known; they are mostly marine, living on the bottom and on vegetation or burrowing in wood. Examples: Limnoria, Munnopsis (figs. 77 and 221).
Order Stomatopoda. This order contains about 200 species, all marine, benthic, most common in shallow water of lower latitudes.
Order Decapoda. Decapoda include crabs, lobsters, shrimps. They are widely distributed in both the pelagic and benthic regions. Most of the over 8000 species are marine.
Class Arachnoida. This class is well represented in the sea by a number of marine mites, over 400 species of sea spiders or pycnogonids, and 5 species of Limulus, the king crab. All are benthic.
Class Insecta. Only one insect is submarine during its whole life; a few others live on the foreshore or skip over the surface in search of food. Example: Halobates.
PHYLUM MOLLUSCA
The molluscs are noted particularly for their construction of an infinite variety of calcareous shells encasing the body and for the structural modifications that have taken place in the soft parts known as the foot and the mantle. These modifications are associated with the method of locomotion and capture of food.
Class Amphineura. The chitons are all flat, benthic animals creeping with the aid of a broad, flat foot. There are about 630 species, all marine.
Class Scaphopoda. Tusk shells live in the bottom mud from shallow water to depths of over 5000 m. All 200 known species are marine.
Class Gastropoda. In most types there is a spiral shell, and the foot is used in creeping. In this and the preceding classes a rasplike radula is a characteristic food-gathering organ. Some gastropods are holoplanktonic and may be without shells. These are the marine pteropods and heteropods (about 90 species of each) with the foot modified for swimming (fig. 228d,f). The latter are especially characteristic of the oceanic waters of the lower latitudes. There are about 49,000 species in the class, mostly marine.
Class Pelecypoda. The clams, oysters, and mussels have a hatchet-shaped foot which in many is used for digging. All are benthic, usually sessile or burrowing in mud, rock, or wood. The soft parts are enclosed within hinged shells and the food is conveyed to the mouth by means of ciliary action setting up water currents, sometimes through long siphons. There are about 11,000 species, of which about four fifths are marine.
Class Cephalopoda. In the squids, devilfish, and so forth, the foot is divided to form arms used in capture of prey. In keeping with their active, predacious habits, the eyes are usually well developed, but blind deep-sea forms occur. In Nautilus and related forms there is a well-developed shell. Cephalopods are either benthic or pelagic, some living at great depths. The giant squid, Architeuthis princeps, having a body girth of nearly 1 m and attaining a total length of about 16 m, is the largest of all invertebrates. There are about 400 species, all marine.
PHYLUM ECHINODERMATA
Echinodermata are animals with calcareous plates forming a more or less rigid skeleton, or with scattered plates and spicules embedded in the body wall. Many are provided with spines. All are marine, and all but a few sea cucumbers are benthic.
Class Holothuroidea. The sea cucumbers are mainly benthic. only members of the order Pelagiothurida being planktonic. There are over 650 species, some living in abyssal regions.
Class Asteroidea. The sea stars are among the most conspicuous of shore animals, but they live also at very great depths. About 1100 species are known.
― 312 ―Class Ophuroidea. There are more than 1600 species of brittle stars, with a wide horizontal and bathymetric distribution.
Class Echinoidea. There are about 600 species of sea urchins and sand dollars, a few of which live in deep water.
Class Crinoidea. About 800 species of sea lilies and sea feathers are known, with the center of distribution in the East Indian waters, but they also occur in many other waters. The former live mainly in the deep sea and are anchored by long stalks. The latter occur mainly at shallower depths and are without stalks. The class is a vanishing remnant of a formerly abundant group that has left more than 2000 fossil species.
PHYLUM CHORDATA
Chordata are animals which in some stage of their life have gill slits and a skeletal axis known as a notochord.
Subphylum Tunicata. These are primitive chordates; of about 700 species, all are marine.
Class Larvacea (Appendicularia). These are small planktonic forms, sometimes abundant. Examples: Oikopleura (fig. 228e), Fritillaria.
Class Ascidiacea. These are sessile ascidians such as Ciona and Culeolus.
Class Thaliacea. This class is made up of pelagic tunicates that float singly or in chains; they may be very abundant at the surface in the warmer waters. Examples: Salpa, Doliolum.
Other protochordates are the wormlike Enteropneusta and the fishlike Cephalochorda, both of which are found burrowing in mud and sand.
VERTEBRATES
Subphylum Vertebrata. This group includes animals with vertebrae. All but the classes Aves and Mammalia are cold-blooded.
Class Cyclostomata. The hagfishes and lampreys are fishlike forms but without paired fins. They have a circular sucking mouth without jaws. The former are all marine, while the latter live both in the sea and in fresh water.
Class Elasmobranchii. These primitive fishes—the sharks, rays, and chimaeras with a cartilaginous endoskeleton—have paired fins and a lower jaw. In this group are many large forms such as the giant manta and the whale shark, the largest of all fishes, which becomes about 16 m long. Nearly all are marine.
Class Pisces. This class includes the true fishes, with a bony endoskeleton, paired fins, and an operculum covering the gills. They are characteristically streamlined for great swimming
Class Reptilia. This class is represented in the sea by snakes and turtles. They breathe air and are therefore inhabitants of surface waters. The turtles frequent the shore to deposit their eggs on sandy beaches; the snakes bring forth living young and are therefore less dependent upon the shore. The sea snakes are found in the Indo-West Pacific and in tropical waters of America. They grow to a length of from 1 to 2 m or more and some are very poisonous. The sea turtles occur in tropical and subtropical seas. They have paddlelike limbs for swimming, and some grow to great size. The leathery turtle, for example, which is the largest of the class, may attain a weight of 1000 pounds.
Class Aves. A great number of birds are dependent upon the sea for food. Some of these frequent the land only for nesting and rearing of young. Typical examples are the albatrosses, petrels, cormorants, and auks.
Class Mammalia. These are warm-blooded, air-breathing animals with hair and mammary glands.
Order Carnivora. The marine members of this order are the sea otters and, to a lesser degree, the polar bears. The sea otters occur only in small numbers and only along the west coast of North America, where they were formerly hunted commercially to the very verge of extinction. Recently, under rigid protection, they have recuperated to an encouraging degree. The polar bears are confined to the Arctic region, usually on or near floating ice
Order Pinnipedia. Pinnipedia include seals and walruses, nearly all marine. The limbs are finlike, in adaptation to the aquatic existence. There are three families: (1) Otariidae include the eared seals, sea lions, and fur seals. Small external ears are present and the hind limbs can be rotated forward. (2) Phocidae are the hair seals without external ears and with hind limbs incapable of rotation forward. (3) Odobenidae include the walruses, with greatly elongated canine teeth in the upper jaw. They are confined to the Arctic.
Order Sirenia. Sirenia are heavy-bodied mammals with a flat tail and with forelimbs modified as paddles. Hind limbs are wanting. They live near shores in warm waters,
― 314 ―where they browse upon vegetation. They are not numerous. Examples: sea cows, manatees, and dugongs.Order Cetacea. This order includes whales and dolphins, highly modified for aquatic life by a streamlined body and finlike forelimbs and tail. The hind limbs are wanting.
Suborder Mysticeti. These are the baleen, or whalebone, whales, with a series of long plates of baleen suspended in the mouth (fig. 76a). The frayed ends of these are used in screening out plankton food. Examples: fin whale, humpbacked whale, and blue whale. The last named is the largest of all animals, growing to a maximum length of about 34 m and weighing 294,000 pounds.
a, the blue whale—a whalebone whale; b, the sperm whale—a toothed whale.
Suborder Odontoceti. Odontoceti are the toothed whales. This group includes (1) sperm whales with teeth only in the lower jaw (fig. 76b) and (2) the numerous dolphins and porpoises with teeth in both jaws.
Reproduction and Life Cycles in Marine Animals
In any comprehensive study of oceanography wherein biological activities are implicated or in the study of any population or individual species in relation to environmental factors, it is necessary to take into consideration the nature of the life cycles of the organisms involved. Only thus can the biological activities and the methods whereby the race is maintained through countless numbers of generations be fully understood. The utility of life-cycle studies in such practical fields as economic entomology, parasitology, and fisheries has been abundantly demonstrated. Through a knowledge of the methods of reproduction and through recognition of the various developmental stages of marine animals the investigator has at hand valuable means of aiding the interpretation
It should be pointed out here that, in dealing with the propagation of any individual species in relation to its distribution, we must distinguish broadly between (1) reproductive distribution and (2) sterile distribution. Reproductive distribution is associated with areas where environmental conditions are favorable to maturation, spawning, and larval development. Such areas may be called areas of reproduction, or nursery areas. Sterile distribution is associated with areas in which the submature or adult individuals may live and some spawning may take place, but in which the eggs fail to hatch or the larvae do not survive, so that the area must be restocked periodically by invasion of postlarval stages produced elsewhere.
In a study of the life cycles of marine animals, one is impressed particularly with three facts: (1) the preponderance of animals which, though sessile, creeping, or burrowing in the adult stage, possess a free-swimming period during the early stages of life; (2) the enormous numbers of young that are produced by both pelagic and benthic animals; and (3) the fundamental similarity of the larvae of different invertebrate groups. We shall be concerned only with the first two.
In a superficial survey of populations, it is mainly the larger, more conspicuous adult animals that are seen, yet, from the standpoint of numbers, vastly more starfish, barnacles, clams, crabs, fish, and so on, are represented in the microscopic, feebly swimming larval stages than in the adult stages. Most of these larvae do not survive to assume the adult habit, but, instead, serve as nourishment for other organisms, swimming or sessile, or are in some manner destroyed through action of the physical or chemical environment.
Types of Reproduction. In reproduction, animals are either oviparous or viviparous. The oviparous forms deposit eggs that develop outside the mother's body, while in the viviparous forms the young are nourished by the mother and are born alive in a postembryonic state. An intermediate condition exists in the ovoviviparous forms, where the eggs are incubated and hatched within the body, as in certain sharks, perch, and blennies. The term larviparous is sometimes used to indicate that larval stages are born. An embryo derives its nourishment from the yolk of the egg or directly from the mother, whereas typically a larva is morphologically adapted with mouth and digestive tract for the purpose of seeking its own nourishment. Later it will be seen how important this fact is in the life of many marine animals.
By far the greater number of animals of the sea are oviparous, and it is among these that the extraordinarily large numbers of eggs are
| American oyster | 115,000,000 | Pacific halibut | 3,500,000 |
| Sea hare (Tethys) | 478,000,000 | Cod | 4,400,000 |
| Teredo navalis, more than | 2,000,000 | Sunfish (Mola) | 300,000,000 |
Parental care of eggs and larvae.
It has long been recognized, however, that the exceedingly great number of eggs produced by some species is not directly correlated with the number of adults that are found. The large numbers of eggs and larvae produced are, instead, a measure of the tremendous toll paid by these species in order to assure survival of enough individuals to carry on the race.
In the marine population as a whole, very little parental protection is given to the offspring in the larval stages, and frequently even the eggs are given no care, yet hundreds of examples can be cited wherein varying degrees of protection are afforded the embryonic stages and sometimes the larvae as well. Many of the larger crustacea retain the developing eggs attached by secretions to hairlike structures on the abdominal appendages. Some annelids produce viscid secretions for attaching the eggs to setae or to the body wall, while others retain the young up to a well-developed larval stage in special brood pouches, as in Spirorbis (fig. 77). Many other invertebrates provide brood pouches—for example,
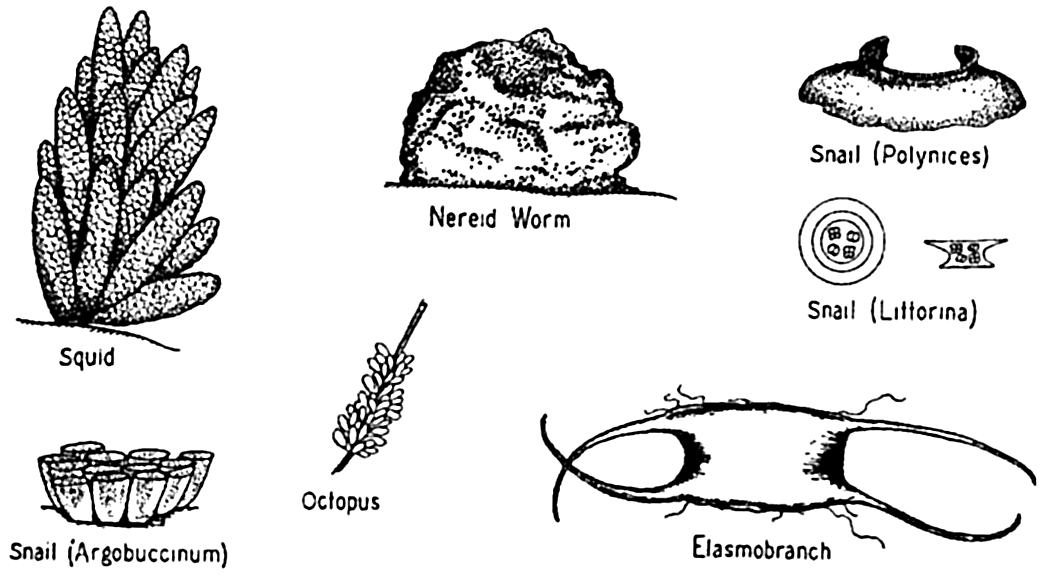
Some types of egg cases for protection of eggs and larvae.
It is clear that in these instances of parental protection the need for large numbers of eggs is somewhat diminished. Nevertheless, when a relatively long, helpless, pelagic stage follows the protected period of incubation, many larvae must still be produced. Thus, for instance, the blue crab, which, though protecting the eggs till the young are hatched, has pelagic larvae and is said to carry over two million eggs (Truitt, 1939). In contrast, Limnoria produces a maximum of only about-twenty-five eggs, but retains these within a pouch until the young are able to burrow into the wood where they were born. Thus they escape the hazardous pelagic life of larvae. In this animal the hazards of a swimming existence are met not by the very young but by submature specimens which by short migrations attempt to establish themselves in less crowded situations prior to breeding (Johnson, 1935). The fact that some animals produce more eggs than others and at the same time offer more parental care must indicate that factors operate to destroy more developing young in one than in the other.
Finally should be mentioned the common method of depositing eggs in masses or protective capsules of various types (fig. 78), thus diminishing loss from excessive dispersal and other hazards of a floating existence during the period of incubation. The capsules are also sometimes
Types of Development. There are two main types of development: (1) direct and (2) indirect. The direct development in oviparous species is associated with eggs of considerable yolk content, such as are found in the fishes, cephalopods, some nemerteans, crustaceans, and others. The newly hatched young are similar to the parent except for size.
Direct development is common among the deep-sea benthic animals, and this habit appears to be an advantageous adaptation. The slowly moving currents of great depths are of less importance in the dispersal of larvae than are the stronger currents of shallow water. The micro-planktonic life so characteristic of surface layers and from which the pelagic larvae of littoral animals directly derive their food has no counter-part in the deep, and hence it is imperative that the young produced be able to feed directly upon the bottom detritus. The possibility of deep-sea larvae swimming from great depths to the surface, where food is plentiful, and later returning to the bottom appears to be impracticable in nature. The young of some mid-depth pelagic forms—for example, Cyclothone among the fishes and Acanthephyra among the prawns—do however live nearer the surface, where food is more plentiful, than where the adults are commonly to be found (Hjort, 1912).
Benthic animals of Arctic and Antarctic regions also commonly possess no pelagic larval stages. Hjort (1912) and Murray (1913) consider this a probable explanation of the great local concentrations of certain boreal and arctic benthic animals, because the direct development results in the young remaining in the area in which they are born. Brief pelagic larval stages following protection during incubation and absence of dispersing currents lead also to local adult concentrations.
The indirect development is associated with a type of egg with little yolk (that is, alecithal), and hence a self-sustaining larva must develop quickly or the organism dies. This type of development is characteristic of marine invertebrates, which usually cast their eggs free in the water or carry them through the incubative period in special brood pouches. Larval stages appear before the full character of the species to which they belong becomes established. Many of these—for example, the pluteus larvae of the Echinoidea and the Ophuroidea—when first discovered were described as distinct kinds of animal, only to be found later to be the young of already well-known species. The locomotor organs of most of the larvae are cilia (see below for exceptions) which by their rhythmic beating propel the animal slowly through the water at a rate just sufficient to keep them in suspension. The great similarity of structure exhibited by the larvae of some groups suggests a common origin for the groups which as adults are structurally very dissimilar.
Typical Life Cycles. The life cycles of many species have not been investigated, but the principal features in the life history of the major groups have been established. We shall here review only the groups of most immediate interest in general oceanographic studies.
In the protozoa, reproduction is mainly by binary fission, whereby the animals divide to form two separate animals, these in turn dividing after growth. Under favorable conditions, this method makes possible a production of great masses of individuals, as is often witnessed in such forms as Noctiluca. Gametes are also formed in this animal as a result of multiple fission. These unite in pairs, but their further development is unknown. In foraminifera, and possibly also in radiolaria, there is a cyclical alternation of generations in which sexual and asexual phases alternate and give rise to morphologically different individuals (Myers, 1936).
In the tintinnids, in which transverse binary fission occurs, the anterior daughter escapes from the lorica, while the posterior daughter retains the old lorica (Kofoid, 1930).
The sponges reproduce asexually by budding or fragmentation, and sexually by union of gametes, the latter resulting in a free-swimming, flagellated larva, the amphiblastula, which, after a period of swimming, settles to the bottom and grows to form the adult sponge. Asexually produced units, known as gemmules, possessing a heavy protective covering are produced by some sponges as a means of survival during adverse periods. Reproduction by formation of gemmules occurs principally among the fresh-water sponges, but some marine forms also produce gemmules.
In the coelenterates, both sexual and asexual reproduction are important features in the life cycle. The union of germ cells results in a free-swimming, ciliated, planula larva about 1 mm long (fig. 80c). The planulae, though lacking the mouth and enteron of typical larvae, may live for a sufficiently long period on yolk food to bring about dispersal of sessile coelenterates such as the corals and anemones. Vaughan (1919) found the pelagic period of corals to be from one day to two or three weeks. Upon settling to a hard bottom the planulae of corals and other Anthozoa develop a mouth and tentacles for feeding, and later the reproductive organs are formed. In some there is also active asexual reproduction by fission and budding. Large coral colonies are thus initiated from a single individual. It is the skeletons of these asexually produced individuals which form the large coral heads, some of which are 3 m or more in diameter and contain many thousands of individual polyps. The length of time required for formation of such colonies has been investigated by Vaughan (1919), who found that a coral colony (Porites asteroides) 50 mm in diameter may be formed in four years.
The remarkable life histories of many jellyfish of the class Hydrozoa offer the examples of alternation of generations that are used in all zoological texts. The jellyfish, or medusa, stage (fig. 79) of such forms as Obelia is either male or female, and the eggs are cast free in the water, where they are fertilized and develop into planula larvae. The planula soon settles on the bottom to form the sessile polyp, or hydroid, stage. From special structures on the polyp, asexually produced buds become separated as swimming medusae, thus completing the cycle. The alternation of sessile and pelagic generations is a factor of great significance in the distribution not only of the hydrozoa such as Obelia, but also of other forms—for instance, the large scyphozoan Aurelia, which, though varying in details of life history, possesses stages similar to those in Obelia. The sessile generation is the chief link instrumental in restricting all stages of such animals to the neritic waters, generally to the proximity of shores and shoals with a suitable substratum of rocks, shells, or larger plants for attachment of the planula larvae. Bigelow (1938) found that in the open sea off Bermuda only about 3 per cent of the medusae caught at a distance of 10 miles from shore were of the type with a fixed stage in their life history. The degree of dispersal is, of course, dependent upon the speed and direction of the water currents prevailing. Some swimming jellyfish—for example, Aglantha digitalis and other members of the order Trachylina—are not dependent upon a sessile stage because daughter medusae develop directly from the pelagic stages.
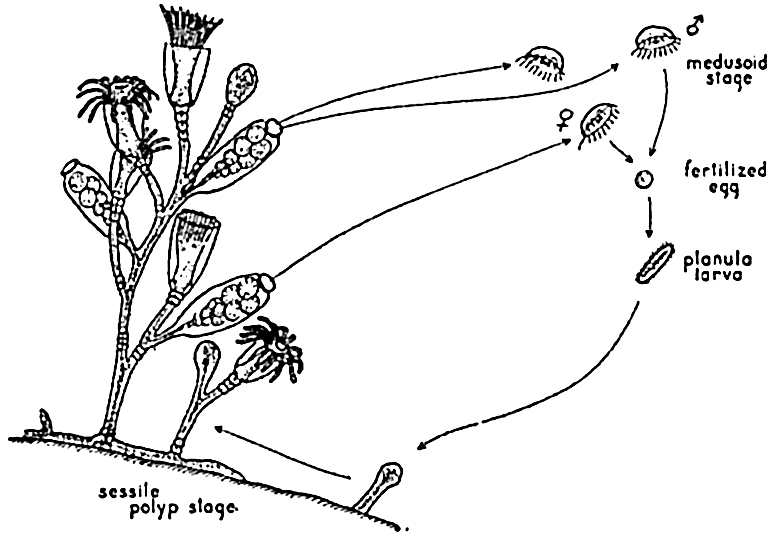
The life cycle of a typical hydrozoan jellyfish, Obelia.
Open-sea colonial coelenterates—for example, Velella or Physalia—are representatives of the “blue-sea fauna.” Their life cycle is adapted to offshore life by elimination of the sessile stage. The planula larva gives rise to a medusiform stage from which the complicated colony arises.
The Ctenophores are all hermaphroditic, and the eggs are usually shed into the water, where, upon fertilization, they grow by direct development into free-swimming larvae. Gastrodes, a parasite in Salpa, produces a typical planula larva.
The great importance of annelids, especially in the littoral benthic fauna, warrants their inclusion in this brief study of life histories. At certain seasons the voracious swimming larvae of annelids are a major
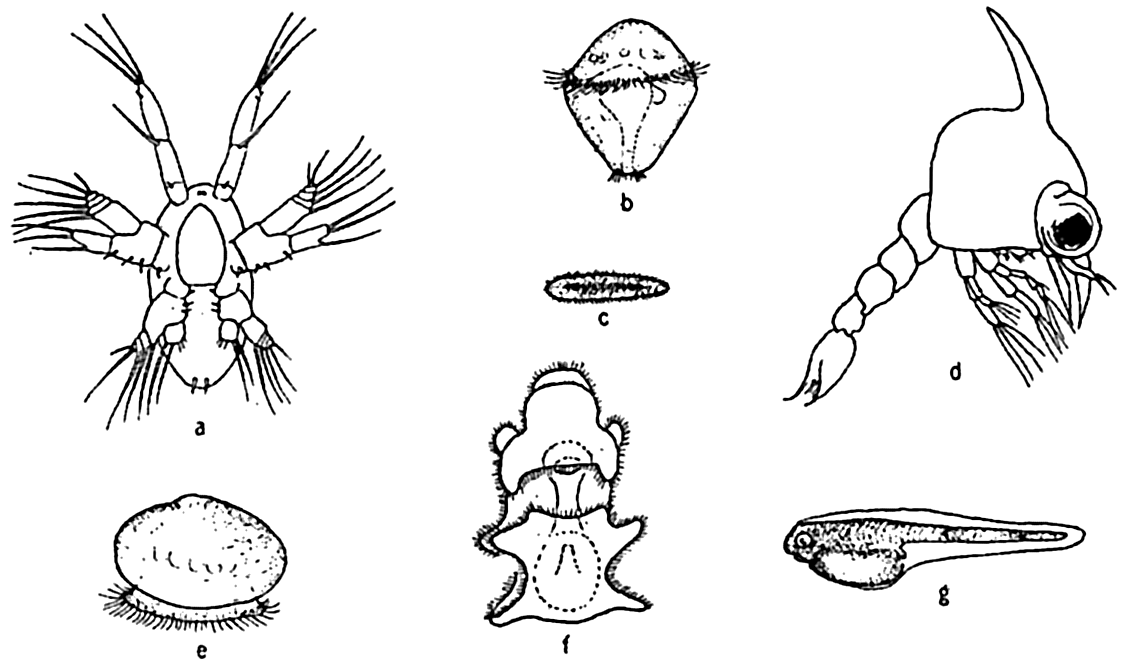
Some characteristic marine larvae. a, nauplius larva of the copepod Labidocera; b, trochophore larva of the annelid Nereis agassizi; c, planula larva of coelenterates; d, zoea larva of the crab Pachygrapsus; e, veliger larva of the clam; f, bipinnaria larva of starfish; g, the cod larva with yolk sac.
The larvae of many benthic annelids enter the plankton only after they have completed their early stages under some means of special protection. For example, in the little tube worm, Spirorbis, and related forms, they develop in a special brood pouch beneath the operculum, while in some Polynoe, or scale worms, they are sheltered by the dorsal, flaplike elytra, and in yet other instances the eggs are deposited in attached or demersal gelatinoid masses (fig. 78), where the developing embryos and larvae enjoy some degree of protection. In Spirorbis the trochophore stage is passed in the brood pouch and the older larvae may assume the sessile habit after only twenty-four to thirty-six hours in the plankton. If a suitable substratum is not available, the pelagic stage is somewhat prolonged. Nereis agassizi spawns the eggs free
The chaetognaths, or arrow worms, are hermaphroditic but not self-fertilizing. The eggs, which are fertilized internally, are shed into the water, where they develop directly into free-swimming larvae not unlike the adults.
Most crustaceans, in which we are particularly interested because of their prominence in some phases of oceanographic studies, pass through several distinct pelagic larval stages. The common initial crustacean larva is the nauplius (fig. 80a), bearing three pairs of appendages used for both swimming and feeding.
In copepods the sexes are separate, in some species the ratio of adult males to females being strikingly unequal at all times, while in other species the inequalities are seasonal, the males being more abundant at the onset of breeding but later diminishing in numbers more rapidly than the females after the breeding season (Damas, 1905, Farran, 1927, Campbell, 1934). The most important of the planktonic copepods spawn the fertilized eggs free in the water, yet many littoral species and some important pelagic species—for instance, Oithona, Paraeuchaeta, and others—carry the eggs in brood sacs through the period of incubation (fig. 77). In both cases the eggs hatch to typical self-sustaining nauplii. Paraeuchaeta is somewhat of an exception, for it develops from a heavily yolked egg and does not feed in the naupliar stage (Nicholls, 1934). In copepods there are normally six successive naupliar stages separated by definite moulting of the chitinous skin. The hard exoskeleton of crustaceans does not grow, and must therefore be shed or moulted periodically as the animal becomes too large for the encasement. In many crustaceans the number of moults may be variable, but in copepods there are a fixed number of stages, each separated by a moult. At the termination of the sixth naupliar stage a complete metamorphosis occurs from which emerges Stage I of six successive copepodid (copepodite) stages. Copepodid Stage VI is the adult, and, during spring reproduction in waters of the latitude of the British Isles, maturity may be reached in a period of about twenty-eight days in Calanus finmarchicus, but it is much delayed in the autumn-winter generation or in populations of more northern waters.
In Calanus finmarchicus, by far the most thoroughly investigated of all pelagic copepods, it has long been known (Gran, 1902, and others) that the animals spend the winter months in the deeper water layers. The breeding of this species occurs in spring and summer in boreal waters, and there are two or more successive generations, each of which, apparently, may bear more than one brood. The generation arising from the first spring spawning appears to mature quickly, spawn, and die. The last generation produced in autumn is a relatively long-lived
The life cycle of Calanus finmarchicus appears to be quite characteristic of other members of that important genus and perhaps of other related genera as well, but very few pelagic copepods have been adequately investigated, and considerable variation can be expected. We shall not enter into the remarkable life histories of the parasitic copepods, but an example of a typically free-living littoral form—that is, Tisbe furcata—is instructive for comparison with Calanus. Tisbe furcata carries the eggs through the incubative period in brood sacs. There are six naupliar and six copepodid stages, as in Calanus but the time required for development from egg to mating maturity may be as little as ten days, and filled egg sacs are carried by females of the new generation in fourteen days after hatching. During maximum production, one female may produce at least seven or eight broods at about five- to eight-day intervals.

Successive generations of Calanus finmarchicus (from Nicholls).
In the euphasiids, another group of outstanding importance in the economy of the sea, the method of reproduction is not unlike that occurring in many copepods, in that usually the eggs are shed in the water, but the succession of generations is not rapid and the life span is of greater length. For Euphausia superba, in Antarctic waters, the time required to reach sexual maturity is estimated by Ruud (1932) to be two years. Some investigations indicate that normally the animals live in the immediate vicinity of the bottom and that during spawning they congregate in swarms and ascend to deposit the eggs in surface-water layers. Here, while slowly sinking, the eggs hatch to typical naupliar larvae, which are followed by successive stages of distinctive larvae, the older of which may return for a time to the surface layers. In
Among most other crustaceans the eggs are carried through incubation attached to appendages or in brood pouches of various types. In heavily yolked eggs, as in the common crab and related forms, the nauplius stage is passed within the egg, and the developmental stage emerging from the egg is known as a zoea larva (fig. 80d), of which there may be several separate stages. The weakly swimming zoea may drift in the plankton for several weeks before changing to the megalopa stage and settling on the bottom. The lobster produces a special type of pelagic larva. the phyllosoma, which, with its leaflike body, is especially adapted to float in the plankton (fig. 229g). In barnacles, the larvae escaping from the mantle cavity within the shell of the sessile adult are typical nauplii which, after living a pelagic existence for a few weeks, are transformed into what are called cypris larvae (fig. 2241). The cypris larvae soon settle to the bottom and, upon attachment to a solid surface, metamorphose to assume the adult state.
In most bivalve (pelecypod) molluscs the sexes are separate, although some are hermaphroditic, and others—for example, certain species of oysters—are unisexual but change their sex alternately from one to the other. This phenomenon is also observed in other marine animals (Coe, 1940). Fertilization of the eggs frequently takes place after the eggs have been shed into the water, but commonly the eggs are retained within the brood pouch formed by the gills, in which case the spermatozoa are taken in through the inhalant siphon with the stream of water that is kept flowing over the gills. A modified trochophore larva is first formed, and from this a later larva, the veliger, results (fig. 80e). After a period of swimming the veliger settles to the bottom.
Gastropods are often hermaphroditic. Fertilization among them is commonly internal, and their eggs are frequently deposited in gelatinous or membranous cases attached to rocks or sea weed. Tiny floating cases containing several eggs are sometimes formed, as in Littorina (fig. 78). The trochophore and part of the veliger stage are passed within the egg case.
Among the echinoderms the sexes are separate and the eggs are usually spawned into the water, where fertilization occurs. Some (Asterina) lay demersal eggs which, because of their viscid nature, adhere to rocks and other objects. In other echinoderms, especially deep-sea and polar species, the eggs are fertilized and retained in brood pouches, where they undergo early development. Development is indirect in all cases, but the forms with most heavily yolked eggs do not have pelagic
The metamorphosis resulting in the adult state is as complete as that experienced by the butterfly, and it is not surprising that, before the parentage of the pelagic larvae was known, they were considered as distinct animals unrelated to the adult (figs. 80f and 224f and j). The characteristic larvae are bipinnaria (sea stars), echinopluteus (sea urchins), ophiopluteus (brittle stars), auricularia (sea cucumbers). The echinoderm larvae are of only moderate interest in the economy of the sea, but great biological interest is attached to the probable significance of some in showing a relationship to the most primitive chordates.
Many fishes—for example the cod, mackerel, halibut, and sardine—shed their eggs into the water, where fertilization takes place and the developing larvae are nourished by the yolk of the floating eggs (fig. 80g). The herring deposits viscid eggs which, upon sinking to the bottom in shallow water, become attached to solid objects. The gobies, blennies, sculpins, and others attach their eggs to solid objects or lay them on the bottom, where the male may stand guard over them until hatched. The grunion buries its eggs in the sand of wave-washed beaches during periods of high spring tide. Here the eggs remain for a period of about two weeks, when the next series of high tides washes them out and stimulates their hatching (Thompson, 1919, Clark, 1925). In sharks and rays, fertilization is internal, and either the young are born alive or the nonbuoyant eggs are deposited in leathery cases known as “mermaids, purses” (fig. 78, p. 317).
The eggs of fishes fall roughly into two groups, depending upon buoyancy: (1) pelagic and (2) demersal. The demersal eggs sink to the bottom or are deposited there; pelagic eggs float freely in the water and hence greater numbers are produced to overcome the losses inherent with this group. Many fisheries investigations are concerned with the occurrence and dispersal of pelagic eggs and the resulting larvae, for from such studies much information is gleaned regarding the spawning habits and areas of many commercially important fishes (p. 861). In general, the development of fishes can be considered as being direct, there being no general metamorphosis of form to the adult morphology. There is frequently, nonetheless, a marked degree of dissimilarity between larvae and adult, and in some there is a distinct metamorphosis. The Leptocephalus larva of the eel, for instance, was once considered a separate species. Many fishes have definite spawning grounds far removed from their feeding habitat, and the remarkable migrations of such fishes as the eel and the salmon are directly associated with reproductive instincts (pp. 811 and 861).
The reproductive habits of certain deep-sea fishes are of special interest as an indication of adaptation to the environment. In the lightless,
The mammals of the sea bring forth living young, which are nursed for a period by the mother. Like those of some fishes, the great migratory movements of whales and seals are associated with wanderings to and from favorable breeding grounds. Growth in whales is extremely rapid; sexual maturity may be reached in two years, and one calf may be produced every other year.
The spawning of many marine animals, especially in boreal waters, is of a spontaneous nature, and vast numbers of individuals spawn within a period of a few days, with the result that in such cases the main spawning period is easily ascertained, since great swarms of eggs or larvae appear suddenly in the plankton and are gradually dispersed by water movements. This feature is especially well illustrated by the oyster, certain sea cucumbers (Cucumaria), nereid worms, and barnacles.
The degree of success of (1) spawning or (2) survival of larvae of successive spawning seasons gives rise to an inequality in numerical strength of year classes of adult or juvenile forms constituting any given population. This inequality is best demonstrated by studies of commercial fishes, investigations of which have been most ardently pursued. However, the same inequality must also occur in the populations of any animals with a normal life span sufficiently long for individuals to live through several reproductive seasons as juveniles and adults.
For purposes of illustration we may consider a species with a life span of several years in which the age of individuals can be accurately determined and in which adequately large and inclusive samples are obtainable for comparison. Now, assume a highly successful spawning and larval survival in a moderate population of this species in the breeding season of 1930, a very poor spawning season in 1931, an average degree of spawning and survival of larvae in 1932, and then another highly successful year in 1933. The 1930 year class will, upon investigation of the whole population in 1931, show up as a disproportionately great number of small, one-year-old individuals in relation to the other age groups in the population. In the next year (1932) the two-year-old individuals of the 1930 spawning are still conspicuous in the population, but the smaller number of one-year-old individuals is evidence of a poor spawning or survival for the 1931 reproductive season. Thus, in 1933 and subsequent years the downward trend of numerical strength of the 1930 and 1931 classes can be traced and compared with other year classes—for example, that of the average year 1932 and of the successful year 1933
From such comparative studies of year classes and with a knowledge of the spawning habits and age groups, means are provided for analysis of probable environmental factors that determine the degree of success of spawning or survival of larvae, because the relative number of individuals entering into any year class must depend mainly on these critical periods. In subsequent years within the normal life span of the species, the reduction of numbers in year classes is not so likely to be of catastrophic nature. It has been pointed out by Hjort et al (1933) that for a given region the average rate of growth of individuals within the different year classes of Norwegian herring is the same for each year class regardless of the relative numerical strength of the classes. This seems to indicate that, in the sea, nature each year provides a sufficiency of food for the survival and growth of the older stages of this fish as represented in the composite commercial catch. The numbers of individuals belonging to the separate year classes may be widely different (as much as 1 to 30), and this difference must then result from some factor or multiplicity of factors operating to destroy the animals during the very early stages of their existence.
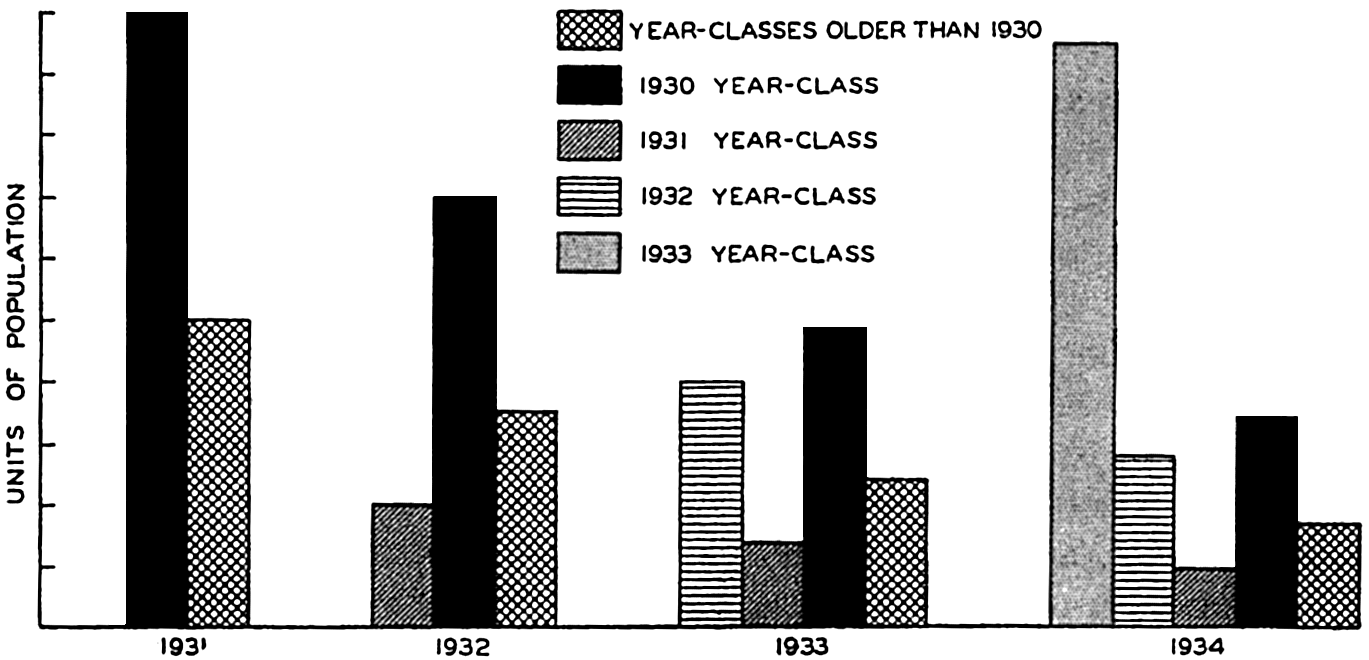
Schematic illustration of changes in year class composition of a population.
Studies of commercially important fish, shellfish, and whales are deeply concerned with analysis of the year classes. For example, in nature there is an equilibrium between the rate at which fish enter the accumulated stock or supply and the rate at which they are withdrawn through natural mortality. Additional removal through fishing exploitation disturbs this equilibrium and may constitute so serious a drain upon the stock that the drain becomes greater than the rate of replenishment and the stock subsequently becomes so depleted that it is no longer
Year-class analyses of the fish population are also utilized as a basis in arriving at forecasts of the most probable abundance of fish in the next year's catch. Illustrative of this are the investigations of the U. S. Bureau of Fisheries into the fluctuations so characteristic of commercial catches of mackerel. Sette (1931et seq) studied the relative abundance of these fish caught with reference to each year class of the population. The numerical strength of the younger year classes entering into the catch provided a basis for calculating the probable yields that these classes would give in the following year under similar conditions of fishing. Such calculations can be significant only when the downward trend in numbers of the dominant year classes is rather regular. In dealing with migratory fishes, the occurrence of sporadic invasions of populations produced elsewhere or with a different range and whose year-class composition is not known must give rise to unexpected changes in the ratio of the year classes occurring in any one range or locality under investigation. The continued success of such commercial fisheries as the mackerel is determined mainly by the numerical strength of the dominant year classes of the population native to the fishing area. In the above investigation it was found that the big year class of 1923 constituted the main bulk of a declining fisheries yield for a period of years until the industry again experienced a sharp upward incline as the contingents of the 1928 successful spawning entered the catch.
Bibliography
Arber, A.1920. Water plants. London. Cambridge Univ. Press.
Bigelow, H. B.1938. “Plankton of the Bermuda Oceanographic Expedition. VIII. Medusae taken during the years 1929 and 1930” . Zoologica, v. 23, p. 99–189, 1938.
Campbell, M. H.1934. “The life history and post embryonic development of the copepods, Calanus tonsus Brady, and Euchaeta japonica Marukawa. Canada” , Biol. Board, Jour., v. 1, p. 1–65, 1934.
Clark, Frances N.1925. “The life history of Leuresthes tenuis, an atherine fish with tide-controlled spawning habits” . Calif. Fish and Game Comm., Fish Bull.no. 10, p. 1–51, 1925.
Coe, W. R.1926. “The pelagic nemerteans” . Harvard Coll., Mus. Comp. Zool., Mem., v. 49, 244 pp., 1926.
Coe, W. R.1940. “Divergent pathways in sexual development” . Science, v. 91, p. 175–82, 1940.
Damas, D.1905. Notes biologiques sur les copepodes de la mer Norvégienne. Conseil Perm. Internat, p. l'Explor. de la Mer, Pub. de Circonstance, no. 22, 23 pp., 1905.
Ellis, B. F. and A. R. Messina. 1940. “A catalogue of foraminifera. New York” . Amer. Mus. Nat. Hist.30,000 pp.1940.
Farran, G. P.1927. “The reproduction of Calanus finmarchicus off the south coast of Ireland. Conseil Perm. Internat. p. l'Explor. de la Mer” , Jour. du Conseil, v. 2, p. 132–43, 1927.
Fritsch, F. E.1935. The structure and reproduction of the algae. Vol. 1, Introduction, Chlorophyceae, Xanthophyceae, Crysophyceae, Bacillariophyceae, Cryptophyceae, Dinophyceae, Chloromonadineae, Euglenineae, colorless Flagellata. New York, Macmillan. 791 pp., 1935.
Gail, F. W.1922. “Photosynthesis in some of the red and brown algae as related to light. Univ. Washington” , Puget Sound Biol. Sta., Pub., v. 3, p. 177–193, 1922. Seattle.
Gran, H. H.1902. Plankton des Norwegischen Nordmeeres von biologischen und hydrografischen Gesichtspunkten behandelt. Norwegian Fishery and Marine Investigations, Rept., v. 2, No. 5, p. 1–222, 1902. Bergen.
Gran, H. H.1912. Pelagic plant life. p. 307–86 in: Murray and Hjort, Depths of the ocean. London, Macmillan. 821 pp., 1912.
Hartge, L. A.1928. “Nereocystis. Univ. Washington” , Puget Sound Biol. Sta., Pub., v. 6, p. 207–37, 1928.
Hesse, Richard, W. C. Allee, and K. P. Schmidt. 1937. Ecological animal geography. An authorized, rewritten edition based on “Tiergeographie auf oekologischer Grundlage” by Richard Hesse. New York. John Wiley & Sons. 597 pp., 1937.
Hjort, J.1912. In: Murray and Hjort, Depths of the ocean. London, Macmillan. 821 pp., 1912.
Hjort, Johan, Gunnar Jahn, and Per Ottestad. 1933. The optimum catch. Hvalrådets Skrifter, No. 7, p. 92–127, 1933. Oslo.
Hustedt, F.1930 et seq. Die Kieselalgen. In: Rabenhorst's Kryptogamen-Flora, v. 7, 1 Teil, 2 Teil, 576 pp., 1930–1933. Leipzig. Akad. verlagsges.
Hyman, Libbie H.1940. The invertebrates: Protozoa through Ctenophora. New York, McGraw-Hill. 726 pp., 1940.
Johnson, Martin W.1935. “Seasonal migrations of the wood-borer Limnoria lignorum (Rathke) at Friday Harbor” , Washington. Biol. Bull., v. 69, p. 427–438, 1935.
Kofoid, C. A.1930. Factors in the evolution of the pelagic Ciliata, the Tintinnoinea. p. 1–39 in: Contributions to Marine Biology, Stanford Univ. Press, 277 pp., 1930.
Kofoid, C. A., and A. S. Campbell. 1929. “A conspectus of the marine and fresh-water Ciliata belonging to the suborder Tintinnoinea, with descriptions of new species principally from the Agassiz Expedition to the eastern tropical Pacific 1904–1905” . Calif. Univ., Pub. Zool., v. 34, 404 pp., 1929.
Kofoid, C. A., and T. Skogsberg. 1928. “The Dinoflagellata: The Dinophysoidae. Report, Albatross Exped. 1904–1905” . Harvard Coll., Mus. Comp. Zool. Mem., v. 51, 766 pp., 1928.
Kofoid, C. A., and Olive Swezy. 1921. “The free-living unarmored Dinoflagellata” . Calif. Univ., Mem., v. 5, 538 pp., 1921.
Lebour, M.1926. “A general survey of larval euphausiids, with a scheme for their identification” . Marine Biol. Assn. U.K., Jour., v. 14, no. 2, p. 519–27, 1926. Plymouth.
Murray, Sir John. 1913. The ocean: A general account of the science of the sea. London, Williams and Norgate, 256 pp., 1913.
Myers, E.1936. “The life cycle of Spirella vivipara Ehrenberg, with notes on morphogenesis, systematics and distribution of the foraminifera” . Roy. Microsc. Soc., Jour., v. 56, p. 120–46, 1936.
Nicholls, A. G.1933. “On the biology of Calanus finmarchicus. I. Reproduction and seasonal distribution in the Clyde Sea area during 1932” . Marine Biol. Assn. U. K., Jour., v. 19, no. 1, p. 83–101, 1933. Plymouth.
Nicholls, A. G.1934. “The developmental stages of Euchaeta norvegica Boeck” . Roy. Soc. Edin., Proc., v. 54, pt. 1, no. 4, p. 31–50, 1934.
Petersen, C. G. Joh. 1918. “The sea bottom and its production of fish food” . Danish Biol. Sta., Rept., v. 25, 62 pp., 1918. Copenhagen.
Pratt, H. S.1935. A manual of the common invertebrate animals exclusive of insects. Revised. Phila., Blakiston, 854 pp., 1935.
Ruud, J. T.1932. On the biology of southern Euphausiidae. Hvalrådets Skrifter, no. 2, 105 pp., 1932. Oslo.
Setchell, W. A.1912. Kelps of the United States and Alaska. U. S. Senate Document 190, Fertilizer resources of the United States, App. K, p. 130–178, 1912.
Sette, O. E.1931. Outlook of mackerel fishery in 1931. U. S. Bureau of Fisheries, Fishery Circularno. 4, 20 pp., 1931, et seq.
Thompson, W. F.1919. “Spawning of the grunion (Leuresthes tenuis)” . Calif. Fish and Game Comm., Fish Bull., no. 3, p. 1–29, 1919.
Thompson, W. F.1937. “The theory of the effect of fishing on the stock of halibut” . Internat. Fisheries Comm., Report no. 12, 22 pp., 1937.
Tilden, J. E.1935. The algae and their life relations, Fundamentals of phycology. Minneapolis, Minn., Univ. Press, 550 pp., 1935.
Truitt, R. V.1939. Our water resources and their conservation. Chesapeake Biol. Laboratory, Contribution no. 27, 103 pp., 1939.
Vaughan, T. W.1919. Corals and the formation of coral reefs. Smithsonian Inst., Report for 1917, p. 189–276, 1919.
Wilson, D. P.1935. Life of the shore and shallow sea. London. Ivor Nicholson and Watson. 150 pp.1935.
X. Observations and Collections at Sea
OCEANOGRAPHIC VESSELS AND THEIR FACILITIES
Vessels
For purposes of oceanographic research, a very sturdy, seaworthy vessel capable of working under practically all weather conditions and of withstanding any storm is required. Vessels engaged in marine investigations can be broadly classified as either oceanic or coastal types, depending largely upon their size and cruising radius, but the two categories are not sharply defined, since large vessels may be used for near-shore investigations and relatively small vessels sometimes extend their operations far out to sea. In the following discussion, vessels and equipment used in coastal surveying and in the study of fisheries problems will not be described, although vessels engaged primarily in such work are sometimes employed in oceanographic investigations. Practically any vessel, small or large, can be used for certain types of investigations, but rarely is any single craft, unless specially designed, suitable for all kinds of oceanographic work. One of the chief requirements of oceanographic vessels operated by private or small organizations is economy of operation. This generally means a relatively small craft with low maintenance cost which can be handled by a small crew. Vessels owned or operated by national agencies, such as the Meteor (Germany), Discovery II (Great Britain), and Willebrord Snellius (Netherlands), are generally fairly large, but in most cases they serve a dual purpose. For example, the Meteor was used as a naval training ship and as a survey vessel, and the Snellius was especially built for surveying work in the Netherlands East Indies.
The following features are desirable in vessels that are to be used in oceanographic research:
Sturdiness and seaworthiness, large cruising radius, and accommodations for laboratory work and the storage of collections.
Low freeboard in order to make possible the handling of instruments near the sea surface and to reduce the wind drift when hove to at stations.
Sails to increase the cruising radius, to provide a safety factor in case of engine breakdown, and to improve the working conditions on board by reducing the roll and vibration when under way. Riding sails to steady the vessel when hove to at stations and to reduce the leeway by keeping the vessel headed into the wind.
Sufficient clear deck space for the installation of winches and for handling bulky equipment such as trawls and dredges.
| Name of vessel | Nationality | Operated by | Type of vessel | Launched | Commissioned for oceanographic work | Overall length, feet | Tonnage | Officers and crew | Scientists | Reference |
|---|---|---|---|---|---|---|---|---|---|---|
aSunk in collision in North Sea, June 23, 1935. | ||||||||||
bDestroyed by explosion and fire at Apia, Samoa, Nov. 29, 1929. | ||||||||||
cWas previously equipped exclusively for work in terrestrial magnetism and atmospheric electricity. | ||||||||||
| R.R.S. Discovery II | Great Britain | Discovery Committee of the Colonial Office | Steel steam vessel (trawler) (special) | 1929 | 1930 | 234 | 2100 (disp.) | 46 | 6 | Ardley and Mackintosh (1936) |
| F. & V.S. Meteor | Germany | Hydrographic Department of the Navy | Steel steam vessel for survey and training (gunbost) | 1915 | 1924 | 233 | 1200 (disp.) | 114 | 10 | Spiess (1932a) |
| H.M.S. Willebrord Snellius | Netherlands | Hydrographic Section, Department of Defense | Steel steam vessel for surveying (gunboat) | 1928 | 1929 | 204 | 1055 (disp.) | 84 | 6 | Pinke (1938) |
| R.R.S. Dana (II)[a] | Denmark | Danis Commission for the Investigation of Sea | Steel steam vessel (trawler) | 1917 | 1921 | 138 | 360 (gross) | 14 | 8 | Schmidt (1929) |
| Armauer Hansen | Norway | Geophysical Institute, Bergen | Wooden auxiliary ketch (special) | 1912 | 1913 | 76 | 57 (gros) | 5 | 6 | Helland-Hansen (1914) |
| Carnegie[b] | U.S.A. | Department of Terrestrial Magnetism, Carnegie Institution of Washington | Wooden auxiliary brigantime (nonmagnetic) | 1909 | 1928[c] | 155 | 568 (disp.) | 17 | 8 | Bauer, Peters, Ault, Fleming (1917) |
| Atlantis | U.S.A. | Woods Hole Ocean ographic Institution | Steel auxiliary ketch (special) | 1930 | 1931 | 142 | 460 (disp.) | 17 | 5 | Iselin (1933) |
| E.W. Scripps | U.S.A. | Scripps Institution of Oceanography, University of California | Wooden auxiliary schooner (yacht) | 1924 | 1938 | 104 | 140 (disp.) | 7 | 6 | Moberg and Lyman (1942) |
| Catalyst | U.S.A. | Oceanographic Laboratories, University of Washington | Wooden motor vessel (special) | 1932 | 1932 | 75 | 94 (gros) | 5 | 9 | Thompson (1936) |
In table 57 are listed certain representative vessels that have been extensively used in oceanographic investigations. Those owned by national agencies are large, over 200 feet long, and carry large crews, while, on the other hand, vessels owned and operated by institutions are generally between 100 and 150 feet long and carry crews of less than twenty. During the nineteenth century the practice of utilizing only large craft in oceanographic work made it impossible for private organizations to engage in independent and systematic investigations. However, Björn Helland-Hansen, of the Geophysical Institute in Norway, convinced that small vessels could be used effectively, had the Armauer Hansen built to conform to his ideas. This small vessel, only 76 feet long, has carried out both intensive and extensive work in the North Atlantic and has ably confirmed Helland-Hansen's thesis. Following his lead, other private institutions have purchased or built small vessels that can be economically operated.
Winches
Winches used in oceanographic investigations vary so widely in construction that it is impossible to describe any standard designs. The type and design of winches depend not only upon the character of the work contemplated but also upon the size of the vessel, the space available for the installation, the length of wire rope to be carried, and the power for operating the winch. Details of construction and installation of the winches on the vessels listed in table 57 may be found in the references cited.
Winches may be classified under three headings, depending almost entirely upon the strength of the wire rope they carry.
Sounding winches are relatively light. They carry single or multistrand wire of small diameter and are designed for sounding and for obtaining bottom samples with light gear. Sometimes they can be used for other types of oceanographic work. An electric powered deep-sea sounding winch is described by Parker (1932).
Hydrographic winches are moderately stout. They carry somewhat heavier wire than the sounding winches and are designed for handling water-sampling devices, thermometers, and plankton nets. Since the introduction of sonic sounding methods, winches especially designed for taking wire soundings are not so common, and hence hydrographic
Heavy winches are strongly built to carry the largest and strongest cables. They are used for dredging, trawling, anchoring in deep water, and for any other work requiring heavy equipment or the ability to withstand a great strain.
The construction of winches depends not only upon the size of wire rope handled, but also upon its length, since those carrying small amounts need not be so large or so strong as those that must handle several thousand meters of wire rope. For investigations in the open sea, winches should carry at least 5000 m of cable, and for studies in the deeps, more than 10,000 m may be required. Winches carrying only a few hundred meters of wire rope can be cheaply built and, if necessary, operated by hand. However, heavy winches and those carrying large amounts of wire are always power driven. Winches may be operated by steam, as on the Discovery II, by gasoline or diesel motors coupled directly to the winch, by the main engine through some suitable mechanism, or by electric motors. Because of its economy of operation and its flexibility, steam is in many ways the most desirable source of power for winches, but it is practical only on steam-driven vessels. Oceanographic winches are now most commonly operated by electric motors. It is essential that all winches, particularly those used in handling water-sampling devices and nets, have a considerable range in speed of lowering and hauling in. They must also be capable of being controlled quickly and accurately so that instruments can be lowered to a predetermined depth and raised to a convenient level above the water for examination or removal from the wire. The maximum rate of haul on the hydrographic winch should be about 200 m/min. If electric motors are used to operate winches, speed control is obtained by the use of rheostats. In certain installations, reduction in speed also reduces the horsepower of the motor, but such designs should be avoided, because heavy loads must be hauled in slowly.
Electric motors mounted on deck must be waterproof, and the winches themselves must be so constructed that they can be readily lubricated and protected from corrosion by salt water. Winches carrying large amounts of wire rope must have drums with extremely staunch flanges; otherwise, the packing of the wire may break the flanges away from the core when the winch is hauling in under tension.
Spreaders of some type are necessary to lay the wire smoothly and evenly on winch drums that carry large amounts of wire rope. If no provision is made for such spreaders, the wire may accumulate unevenly on the drum, causing the strands to break down and, what is more serious, causing the wire to slip down between the underlying coils in such a way that when payed out again it may be badly snarled. Spreaders may be
The hydrographic and sounding winches are customarily placed on deck near the rail, where they can be conveniently operated and where the wire rope will clear obstructions on deck and on the hull. The heavy winch, which is more bulky, must be installed in such a way that it can be strongly supported, can withstand heavy loads, and will not affect the stability of the vessel. On smaller craft it is commonly installed amidships below deck or, sometimes, half sunk below the deck level. The axis of rotation of the heavy winch is generally athwartships.
Wire Ropes and Accessory Fittings
Wire ropes used in oceanographic work must have the following properties:
They must be of strong material so that rope of relatively small diameter can be used, thus reducing the bulk of the winch.
They must be flexible and not liable to kink or unravel.
They must be made of a metal that is resistant to corrosion, and thus long-lived, and free from materials that will contaminate water samples and plankton catches.
Such requirements are best answered by multistrand ropes of stainless steel, but this alloy is expensive, and in practice tinned or galvanized steel ropes are satisfactory. Phosphor-bronze and aluminum-bronze ropes are also used, as they are noncorroding, but they are only about one half as strong as steel and their life is limited because they crystallize with use and lose their strength. Many wire ropes have hemp cores, but these are not so satisfactory as ropes with wire cores, because the hemp may shrink and break when submerged, and it is also liable to rot unless specially treated. High-grade manila rope is about one tenth as strong as steel rope of comparable diameter.
The strength of steel depends upon its composition and treatment and varies from about 50,000 to 400,000 lb/in2. Steels employed in wire ropes are usually of relatively high tensile strength, the tensile strength of the rope increasing with decreasing diameter of the individual wires. The greater strength of a rope made up of smaller but more numerous wires is offset, however, by the greater surface offered for corrosion and by the greater likelihood of the individual wires breaking after a certain amount of wear.
Single-strand wire of the type known as piano or music wire is used for deep-sea sounding and for running taut-wire traverses (p. 342). This wire is of extremely high tensile strength, but is stiff and liable to break if kinked. If no bottom sample is required when sounding at great depths and in taut-wire traverses, the wire is usually cut away, as it is not worth the time required to reel it in again. Piano wire of
The wire ropes used on the hydrographic and heavy winches are generally of either the 7 × 7 or the 7 × 19 types. A 7 × 7 wire rope consists of six strands, each composed of seven individual wires that are wound around a central core strand which itself contains seven wires. A 7 × 19 wire rope is similarly constructed, but each of the seven strands contains nineteen individual wires. The 7 × 19 ropes are slightly heavier than the 7 × 7 type, and the ropes of smaller diameter are considerably stronger, but the small size of the individual wires is a disadvantage. Ropes of the 7 × 7 type with diameters between about one eighth inch and one quarter inch are sufficiently flexible for oceanographic use, but, to obtain the desired flexibility in larger ropes, it is necessary to employ 7 × 19 rope on the heavy winch. In table 58 are given the characteristics of 7 × 7 galvanized steel ropes of the type known as aircraft cord.
For most purposes it is considered that the working load of wire rope should not be more than one fifth of the breaking strength—that is, a safety factor of five. In marine investigations it is sometimes impossible to maintain such a high factor of safety, but, if the anticipated strain is known, the diameter of the wire should be such that the maximum load is never more than half the breaking strength. There is not only the danger of losing valuable equipment, but also the hazard to those on deck if the wire should break near the water surface. Steel has a greater elasticity than bronze, and the safety factor must be somewhat greater when bronze ropes are employed.
When great lengths of wire rope are paid out, the weight of the rope in the water may approach the breaking strength and exceed the safety factor of five, even when there is no gear suspended from the rope. Ropes of the type listed in table 58 exceed the safety factor of five when more than 4000 m of wire are suspended in the water. When taking water samples and temperatures or other observations with light gear where there are no sudden strains upon the rope, the safety factor may be reduced and the work extended to great depths. However, in trawling, dredging, and taking cores of the bottom sediments, and when anchoring in deep water, the equipment must be such that it can withstand a heavy working load in addition to the weight of the wire rope. The increased working strength necessary for observations in deep water is gained by using tapered wire ropes, which are of the smallest diameter
| Diameter | Weight in air per 100 m | Breaking strength | |||
|---|---|---|---|---|---|
| Millimeters | Inch | Kilograms | Pounds | Kilograms | Pounds |
| Data through Courtesy of John A. RoebIing's Sons Co., Trenton, New Jersey. | |||||
| 3.18 | 1/8 | 3.6 | 8.0 | 610 | 1,350 |
| 3.97 | 5/32 | 6.9 | 15.3 | 1,180 | 2,600 |
| 4.76 | 3/16 | 8.6 | 19.0 | 1,450 | 3,200 |
| 5.56 | 7/32 | 12.3 | 27.2 | 2,090 | 4,600 |
| 6.35 | 1/4 | 15.6 | 34.4 | 2,630 | 5,800 |
| 7.94 | 5/16 | 24.9 | 54.8 | 4,200 | 9,200 |
| 9.52 | 3/8 | 34.2 | 75.5 | 5,900 | 13,100 |
| 11.10 | 7/16 | 45.8 | 101.0 | 7,400 | 16,400 |
| 12.70 | 1/2 | 62.6 | 138.0 | 10,200 | 22,500 |
Many preparations are on the market to be used for the preservation of wire ropes. Whether or not any of these are suitable depends upon the manner in which the wire rope is to be used, as those which flake off will contaminate plankton samples and other collections. Relatively frequent application of used crankcase oil is a satisfactory method for preserving steel ropes. The oil is applied before the rope is first placed in the water, and thereafter at intervals, particularly when the rope will not be in service for a long period.
The wire rope used on the hydrographic winch must be smooth and free from kinks or stray broken wires that will prevent the passage of messengers or weights. Where a break or other damage necessitates a join, wire rope may be repaired with a long splice, which does not materially increase the diameter of the wire or decrease the breaking strength. Kinks that form in the wire should never be pulled out, but should be eliminated by untwisting the wire, straightening the strands, and realigning them.
Sheaves are aIways necessary for leading the wire rope outboard. They should be free-running and of such diameter that the wire passing over them will not be cramped or strained. Unless the circumstances
An essential part of the equipment for each winch is a meter wheel (fig. 83) for measuring the amount of rope payed out. A meter wheel is a sheave with a wheel of appropriate circumference fitted with a device that records the number of revolutions. The device is so designed that the difference between two readings of the dials gives directly in meters, fathoms, or feet the amount of wire that is run out or hauled in. For soundings and for obtaining temperatures and water samples the meter wheel must be carefully constructed and checked from time to time for wear. The effective diameter of the wheel is its own diameter plus the diameter of the wire rope. The meter wheel may be mounted on the boom or davit that leads the wire outboard, or it may be built into the spreader on the winch. The latter arrangement is a convenient one because the winch operator can then see the recorder at all times. If the meter wheel itself is in such a location that the dial is not readily seen, recorders operated by a flexible speedometer cord may be mounted in a more convenient place. To avoid slippage of the wire rope over the meter wheel, the angle of contact should be at least 90 degrees.

Meter wheel with dial indicators and stainless steel sheave.
The wire rope is led outboard from the winch through sheaves and finally from a boom or davit extending out over the side of the vessel on the windward side. The lead from the heavy winch must be approximately amidships because, when dredging, the vessel must be maneuvered under sail or power, which is possible only if the wire rope is suspended from a sheave near the middle of the vessel. To avoid striking the side of the vessel the outboard leads should be arranged so that the wire, when hanging vertical, is several feet away from the hull, and to facilitate the handling of gear it is usually necessary to have a working platform extending out from the hull and large enough to accommodate two men. If the wire rope on the heavy winch is used for deep-sea anchoring,
Sudden strains on the wire rope that may be caused by the rolling of the vessel or by fouling equipment on the bottom are a hazard to both the apparatus and the wire. These strains may be equalized somewhat by the use of accumulators, which are usually coil springs mounted with one end secure and the other end attached to the sheave through which the wire rope passes. Accumulators can usually be calibrated so that the extension or compression of the spring may be used to measure the strain on the wire rope. Some types are secured to the outer end of the boom or davit with the meter wheel or a plain sheave attached to the free end, or they may be an integral part of the davit or winch. The strain on the accumulator may be used in deep soundings to determine when the weight strikes the bottom, and in dredging and trawling it should be watched so that sudden strains may be eased by slacking off on the winch. Special devices known as dynamometers may be used to measure the strain on the wire rope.
Shipboard Laboratories
The location of laboratories on shipboard, the amount of space devoted to them, and the facilities installed depend upon the size and nature of the vessel and the types of investigations to be made. The laboratories may be classified as deck laboratories and analytical laboratories. The deck laboratory opens on the deck and is used for storing certain oceanographic equipment. There the reversing thermometers are read, water samples are drawn from the sampling device, and certain preliminary steps are taken in the preservation or preparation of water and plankton samples. The deck laboratory should contain racks in which the water-sampling bottles may be placed as soon as they are removed from the wire rope. These racks should be so arranged that the temperatures can be read and the water samples can be taken out without removing the bottles. Space should be provided for the glass bottles in which the water samples are transported, for certain chemical reagents, and for the solutions required for the preservation of biological material. A bench where records and labels can be prepared is also a great convenience. A large sink with running fresh and salt water is very useful, and the deck should be watertight and provided with drains because water is spilled in filling the glass bottles. Deck laboratories are a great asset on oceanographic vessels, particularly in bad weather and at night, as much more satisfactory work can be done under shelter where there is good illumination.
The analytical laboratories are usually located below decks where there is the most space and where the motion of the vessel is at a minimum.
Vibration transmitted through the vessel from the engines and motors is often more troublesome in the laboratory than the roll or pitch of the vessel, and consequently the engines should be mounted, when practicable, on flexible springs or on cork or rubber. The equipment used in the laboratories will generally be identical with that used on shore, but the benches, storage space, and methods of securing apparatus to the benches must be adapted to work at sea under any conditions. Work benches are usually of such a height that the worker can be seated on a stool or seat that is fixed in place and so arranged that he can brace himself with his legs, thus leaving his hands free. In some cases provisions are made for a bench mounted on gimbals, but the advantages of a relatively level surface are often outweighed by its unsteadiness. All apparatus must have suitable storage compartments in which there is no danger of the apparatus falling out or smashing together in a high sea. Burettes and other instruments, while in use, must be secured to the bench or to permanent burette stands.
The analytical laboratory should be provided with running fresh water and a source of distilled water. The latter may be carried in large bottles or, preferably, in specially installed tin-lined tanks. On a long cruise it may be necessary to provide distilling apparatus. When living organisms are to be investigated, a source of cooled sea water or a cold box is necessary. A cold box is also desirable for preserving water or sediment samples for bacteriological examination.
Laboratory work on shipboard is usually kept to a minimum because of the undesirable working conditions that arise from the cramped space, the motion of the vessel, vibration, and the time required for merely collecting the samples. However, there are certain chemical tests that must be made immediately after the samples are collected, and generally these must be made on board. The methods of analysis are referred to in chapter VI. On longer cruises it may be necessary to do more of the work on board, but in such cases the analyses may be done when the weather conditions are favorable or when the vessel is in port or at anchor. Biological work on board the vessel is limited in character, since most specimens can be preserved for later examination ashore and because vibration and motion of the vessel make the use of microscopes virtually impossible.
Samples of water, organisms, or sediments that are to be examined ashore are usually not stored in the laboratory but must be kept in a place not subject to wide ranges in temperature or to extreme temperatures. High temperatures lead to the disintegration of the rubber washers used on most bottles and thus permit evaporation, which will ruin the specimens. Fluctuating temperatures may loosen the stoppers and lead to evaporation, or may even break the bottles. Freezing temperatures must also be avoided, owing to the danger of breakage.
OBSERVATIONS AND COLLECTIONS
Positions at Sea
The geographical location at which an observation is made must be known. The greater frequency with which observations are now taken makes it necessary to know the locations of sampling very accurately, and hence special methods of determining positions at sea have been developed. Accurate knowledge of locations is particularly necessary in surveying, where the introduction of sonic sounding methods has made it possible to take large numbers of soundings that must be precisely plotted in order to bring out the true configuration of the bottom. The specialized techniques developed by such organizations as the U. S. Coast and Geodetic Survey have not yet been used for general oceanographic work, but the methods may be adopted for the study of special problems.
When in sight of land where recognizable features are accurately located, the position of the vessel may be determined by means of horizontal angles and bearings on shore features. Out of sight of land the position can be determined by astronomic sights or by radio direction-finder bearings. Between positions established in these ways the location at any time is obtained by dead reckoning—namely, from the course steered and the distance run. Such methods are adequate for most oceanographic work, but, where greater accuracy is required, as in offshore surveying, positions found in this way are not commensurate with the accuracy and frequency of soundings. In certain cases an anchored vessel or buoy whose position can be exactly established by repeated astronomic observations is used as a point of reference. Since 1923 the U. S. Coast and Geodetic Survey has experimented with sonic methods of locating positions and has developed them to a high degree of accuracy. In radioacoustic ranging (usually designated as R.A.R.), the surveying vessel drops a depth bomb that is fired by fuse or electricity. The sound of the explosion is picked up by a hydrophone on the vessel and recorded on a chronograph. The impulse of the explosion, which travels in all directions, is picked up by hydrophones attached to shore stations, anchored vessels, or buoys whose positions are accurately known. The hydrophones are connected to radio transmitters, and the sound impulse received at each hydrophone is transmitted by radio to the surveying vessel, where the times of reception are automatically recorded on the chronograph. Since the time required for the transmission and reception of the radio signal is infinitesimal, the period between the bomb explosion and the return of the signal from each hydrophone is that required for the sound impulse to travel through the water from the point of the bomb explosion to the hydrophone. The velocity of sound in water can be computed from the known distribution of temperature and salinity
Taut-wire traverses are also used to determine accurately the distances between anchored buoys when detailed surveys are made out of sight of land. The distances are measured by paying out steel piano wire under controlled tension over an accurate meter wheel from drums which carry over 140 miles of wire. When the distance between a row of anchored buoys 15 or 20 miles long has been measured, the wire is cut and abandoned. With a combination of the methods outlined above, extremely accurate surveys can be made out of sight of land where depths are not too great to make it impossible to anchor the buoys satisfactorily. The methods employed by the Coast and Geodetic Survey have been described by Rudé (1938) and by Veatch and Smith (1939).
Sonic Soundings
Sonic-sounding equipment consists of three essential parts: (1) a source that will emit a sound impulse, (2) an instrument for detecting or recording the outgoing and the returning signals, and (3) a means of measuring the time required for the sound to travel to the sea bottom and for the echo to return to the ship. Sound sources are of two general types: those that emit sound of audible frequency which is nondirectional in water, or those that emit high-frequency vibrations which are nonaudible and are classed as ultrasonic. The audible type is satisfactory for general use, but for sounding in shoal water or over a bottom that is very irregular, directional ultrasonic equipment must be used. Audibletype transmitters usually consist of a diaphragm that is vibrated by an electromagnet, although other devices are employed. The ultra- or supersonic transmitter depends upon the piezoelectric property of quartz crystals which, when subjected to a high voltage, vibrate at high frequency, and, as the process is reversible, the returning echo stimulates a current through the circuit, so that the same device is used as a transmitter and as a sound detector. In the audible-type sonic sounder the outgoing signal and the returning echo are picked up by a submerged microphone called a hydrophone.
Various devices are used to determine the time required for the sound impulse to travel to the bottom and return to the hydrophone. For sounding in deep water the simplest method is to measure the
Wire Soundings
Since the introduction of sonic methods, relatively few wire soundings are taken for the sole purpose of measuring depths. Checks must be made from time to time to see that the sonic equipment is operating successfully, but in most cases wire soundings are now made for the express purpose of obtaining samples of the sea-bottom sediments. The weight of equipment used for collecting bottom samples has increased, and, as a consequence, the piano-wire sounding machines are no longer
An unprotected reversing thermometer for measuring pressure, used in conjunction with a protected reversing thermometer and attached to the sounding wire some 50 m above the weight, is sometimes used as a check on the depth (p. 351).
Bottom-Sampling Devices
Devices used for collecting specimens of the sea-bottom sediments depend upon the character of the deposit, the depth of water, and the strength of the wire rope available. Certain apparatus that is suitable for work in soft, cohesive sediments cannot be used where the bottom material is coarse-grained or where it is rocky. Similarly, other types that can be operated in shallow depths are too heavy for general use in deep water. Methods have been devised for sampling the superficial layers of the sediments, but since the Meteor Expedition, 1925–1927, greater emphasis has been placed upon obtaining core samples. Instruments are now in use that will take cores several meters long, and much thought is being given to the development of instruments that will take even longer samples. Unlike the equipment used in most of the other fields of oceanography, the devices for taking samples of the marine sediments are not standardized. Every investigator uses his own type of bottom sampler, but all samplers are based on certain basic designs. Hough (1939) has listed and described the various types and gives an exhaustive bibliography.
Bottom samplers used for oceanographic work fall into three general categories; dredges (drag buckets), snappers, and coring tubes. Dredges patterned after the naturalist dredge (fig. 89), but constructed of stronger material and with a chain-mesh bag, are used for procuring samples of rock where the sea bottom is covered with rock fragments or where there are outcrops of solid rock. Smaller cylindrical dredges with solid bottoms
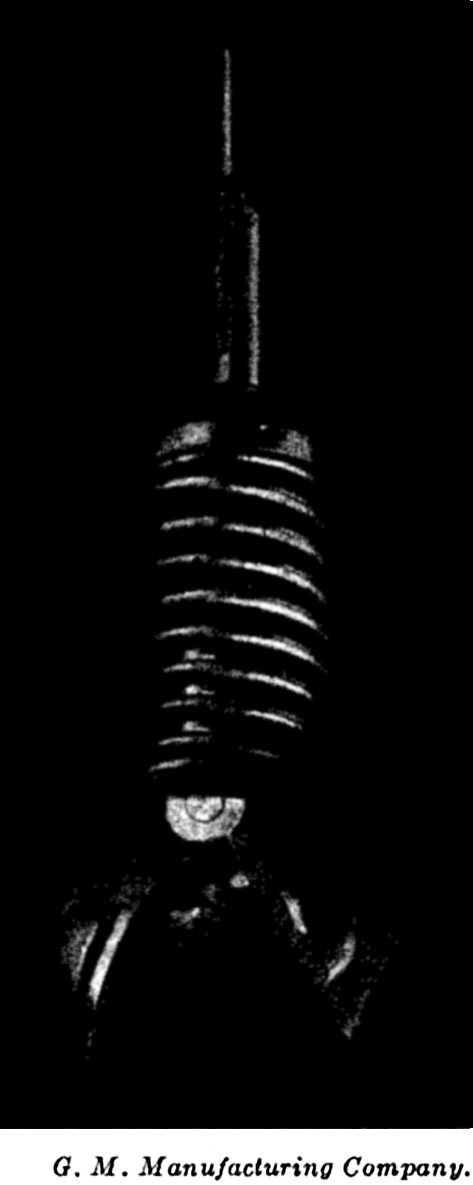
Bottom sampler—snapper type.
Coring devices (fig. 85) are essentially long tubes that are driven into the sediment, either by their own momentum or by the discharge of an explosive. The latter principle is used in the coring instrument developed by Piggot (1936). A momentum-type coring instrument weighing about 600 lb with the weights attached will take cores up to about 5 m in length in soft sediments at depths as great as about 2000 m (Emery and Dietz, 1941). The Piggot coring tube has been used to take cores about 3 m long at depths greater than 4000 m. In coarse-grained deposits the coring tubes are not capable of penetrating more than about 0.5 m.
The momentum-type core sampler is allowed to run out freely when it approaches the bottom. The depth of penetration is determined by the weight of the instrument, the character of the sediment, the diameter of the tube, and the type of cutting nose. The factor that determines the size and type of coring tube which can be used on any wire rope is not the weight of the instrument alone, because the greatest strain is developed when the coring tube is pulled out of the sediment, and this may be several times the weight of the instrument. The Emery-Dietz sampler is constructed of galvanized iron pipe of 2- or 2.5-inch diameter. It is connected through a reducing coupling to a smaller pipe on which the weights are mounted. The reducing coupling is perforated to permit the passage of water, and is sometimes fitted with a ball valve. The cutting nose is sharp, with a slightly smaller internal diameter than the tube itself so as to reduce the internal wall friction and to hold in the inner liner, which further reduces the wall friction and facilitates the removal of the core samples. Inner liners are sheets of metal or celluloid rolled up and inserted in the pipe, or they are glass or metal pipes that are cut open after the sample is taken. In some coring devices a “core catcher” is fitted to the nose of the coring tube to prevent the core from sliding out of the tube after the instrument is raised from the bottom. The depth of penetration of coring tubes is generally considerably greater than the length of the sample obtained. The amount of “compaction” varies between about 25 and 50 per cent, depending upon the characteristics of the coring tube and the type of sediment. The nature of the compaction and the effects that it may have upon the stratification of the sample have been investigated by Emery and Dietz (1941). Smaller instruments based on an original design by Ekman and developed by Trask (Hough, 1939), but of the same general type described above, can be used on fairly light gear and will take samples between 0.5 and 1.0 m in length.
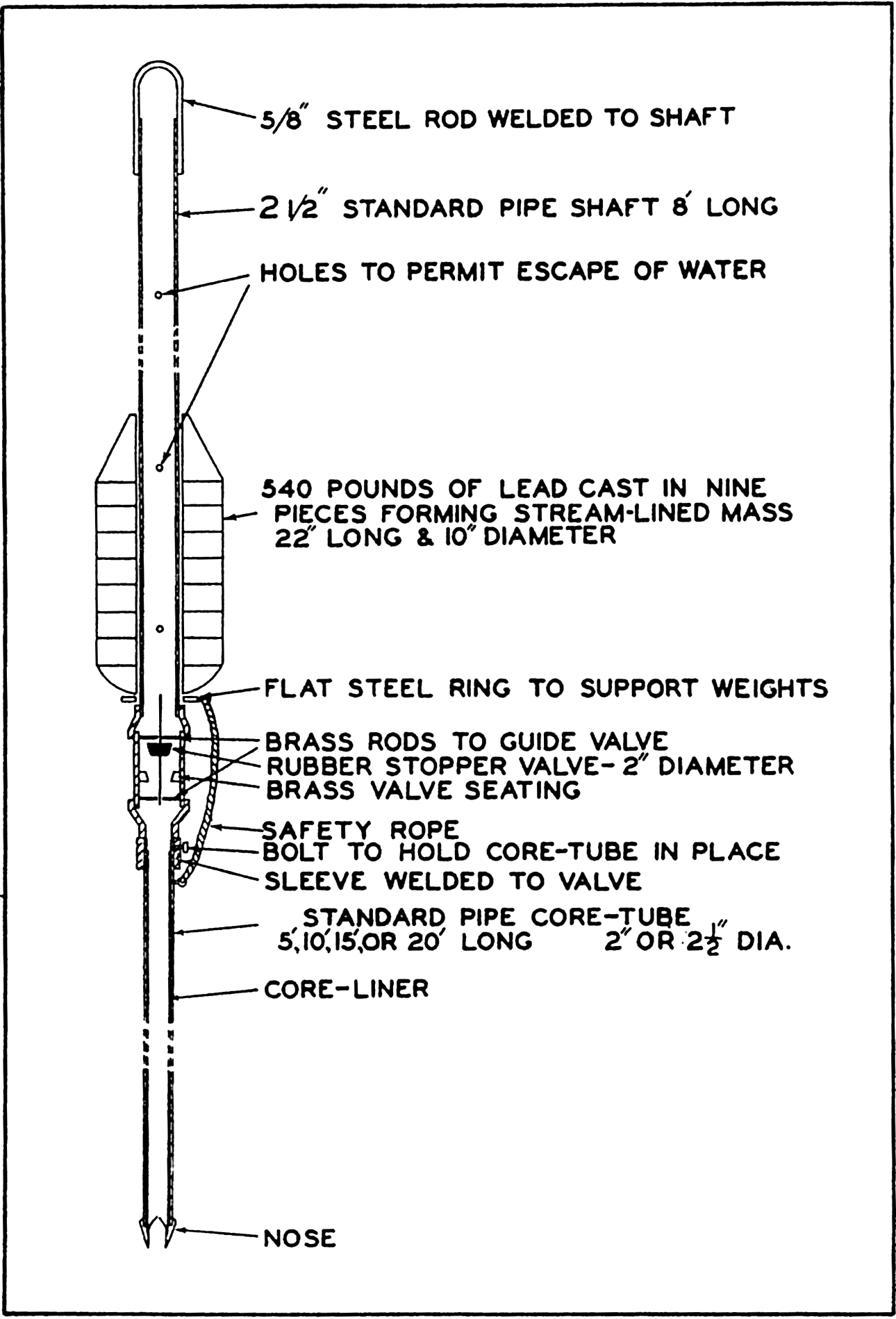
The Emery-Dietz core sampler.
The care and treatment of bottom samples depend to a large extent upon the nature of the examinations that are to be made later (chapter XX). For most purposes it is sufficient to place the specimens in mason jars fitted with rubber washers. No preservative or additional water is necessary. Labels should be placed on the outside of the bottle, since mechanical abrasion and the activities of microorganisms may destroy or render illegible any paper in contact with the sediment sample. Core samples may be cut in sections and carefully placed in bottles, or the entire specimen may be kept in the inner liner.
Temperature Measurements
Three types of temperature-measuring devices are used in oceanographic work. Accurate thermometers of the standard type are employed for measuring the surface temperature when a sample of the surface water is taken with a bucket and for determining the subsurface temperatures when the water sample is taken with a thermally insulated sampling bottle (p. 354). The thermometers used for measuring temperatures at subsurface levels are of the reversing type and are generally mounted upon water-sampling bottles so that temperatures and the water sample for salinity or other chemical and physical tests are obtained at the same level. The third type are temperature-measuring instruments that give a continuous record, such as thermographs, which are employed at shore stations and on board vessels to record the temperature at some fixed level at ot near the sea surface. Many devices have been invented for
The centigrade scale is the standard for the scientific investigation of the sea. A high degree of accuracy is necessary in temperature measurements because of the relatively large effects that temperature has upon the density and other physical properties and because of the extremely small variations in temperature found at great depths. Subsurface temperatures must be accurate to within less than 0.05°C, and under certain circumstances to within 0.01°. Such accuracy can be obtained only with well-made thermometers that have been carefully calibrated and rechecked from time to time. Because of the greater variability of conditions in the surface layers the standards of accuracy there need not be quite so high.
Conventional-type thermometers for surface temperatures or for use with an insulated bottle must have an open scale that is easy to read, with divisions for every tenth of a degree. The scale should preferably be etched upon the glass of the capillary. The thermometer should be of small thermal capacity in order to attain equilibrium rapidly; it should also be checked for calibration errors at a number of points on the scale by comparison with a thermometer of known accuracy, and it should be read
Protected and unprotected reversing thermometers in set position, that is, before reversal. To the right is shown the constricted part of the capillary in set and reversed positions.
Protected Reversing Thermometers. Reversing thermometers (fig. 86) are usually mounted upon the water-sampling bottles (fig. 87), but they may be mounted in reversing frames and used independently. Reversing thermometers were first introduced by Negretti and Zambra (London) in 1874, and since that time have been improved, so that well made instruments are now accurate to within 0.01°C. On the Challenger Expedition, 1873–1876, the subsurface temperatures were measured by means of minimum thermometers, which were the most satisfactory instrument available at that time.
A reversing thermometer is essentially a double-ended thermometer. It is sent down to the required depth in the set position, and in this position it consists of a large reservoir of mercury connected by means of a fine capillary to a smaller bulb at the upper end. Just above the large reservoir the capillary is constricted and branched, with a small arm, and above this the thermometer tube is bent in a loop, from which it continues straight and terminates in the smaller bulb. The thermometer is so constructed that in the set position mercury fills the reservoir, the capillary, and part of the bulb. The amount of mercury above the constriction depends upon the temperature, and, when the thermometer is reversed, by turning through 180 degrees, the mercury column breaks at the point of constriction and runs down, filling the bulb and part of the graduated capillary, and thus indicating the temperature at reversal. The loop in the capillary, which is generally of enlarged diameter, is designed to trap any mercury that is forced past the constriction if the temperature is raised after the thermometer has been reversed. In order to correct the reading for the changes resulting from differences between the temperature at reversal and the surrounding temperature at the time of reading, a small standard-type thermometer, known as the auxiliary thermometer, is mounted alongside the reversing thermometer. The reversing thermometer and the auxiliary thermometer are enclosed in a heavy glass tube that is partially evacuated except for the portion surrounding the reservoir of the reversing thermometer, and this part is filled with mercury to serve as a thermal conductor between the surroundings and the reservoir. Besides protecting
Readings obtained by reversing thermometers must be corrected for the changes due to differences between the temperature at reversal and the temperature at which the thermometer is read, and for calibration errors. An equation developed by Schumacher is commonly used for correction:
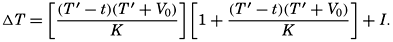
Reversing thermometers are usually used in pairs, most commonly attached to the water-sampling bottles, but they may be mounted in special reversing frames that are either operated by messenger or that have a propeller release. The frames holding the thermometers are brass tubes which have been cut away so that the scale is visible and which are perforated around the reservoir. The ends of the tubes are fitted with coil springs or packed with sponge rubber so that the thermometers are firmly held but are not subject to strains.
Unprotected Reversing Thermometers. Reversing thermometers identical in design with those previously described but having an open protective tube are employed to determine the depths of sampling (fig. 86). Because of the difference in the compressibility of glass and mercury, thermometers subjected to pressure give a fictitious “temperature” reading that is dependent upon the temperature and the pressure. This characteristic is utilized for determining the depth of reversal. Instruments used for this purpose are so designed that the apparent temperature increase due to the hydrostatic pressure is about 0.01°C/m. An unprotected thermometer is always paired with a protected thermometer, by means of which the temperature in situ, Tw, is determined. When Tw, has been obtained by correcting the readings of the protected thermometer, the correction to be added to the reading of the unprotected thermometer, T′u, can be obtained from the equation
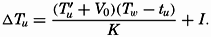
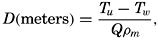
Special Devices. Temperatures measured by the methods mentioned above yield observations at discrete points in space and time. Subsurface observations with reversing thermometers are time consuming and the instruments and equipment are expensive. Many devices have been suggested for obtaining continuous observations at selected levels or as a function of depth. Thermographs are commonly used at shore stations and on vessels to obtain a continuous records at or near the sea surface. The thermometer bulb, usually containing mercury, is mounted on the ship's hull or in one of the intake pipes and connected to the recording mechanism by a fine capillary. The recording mechanism traces the temperature on a paper-covered revolving drum. Records of temperatures obtained by a thermograph should be checked at frequent intervals against temperatures obtained in some other way.
Various types of electrical-resistance thermometers have been designed to be lowered into the water and to give a continuous reading, but have not proved satisfactory. Spilhaus (1938, (1940) has developed an
Water-Sampling Devices
The types of water-sampling devices that will be described are those that are intended for taking samples at subsurface levels for physical and chemical studies. Samples for the enumeration of phytoplankton and for bacteriological examination may be obtained with these instruments, but for such purposes specially designed samplers are more commonly used. A water sampler for collecting at subsurface levels is so designed that it can be closed watertight at any desired depth, and thus the enclosed sample is not contaminated by water at higher levels or lost by leakage after the bottle is brought on board. Because of the great pressures encountered in deep water the sampling bottles are sent down open and then closed at the required depths by means of messengers or propeller releases. To expedite work at sea, water-sampling devices are used in series—that is, with more than one bottle on the wire rope so that samples can be taken at a number of depths on the same cast. As it is essential that temperatures and water samples be taken at the same depths, the water-sampling bottles are fitted with frames in which one or more reversing thermometers are placed. An exception to this is the insulated Pettersson-Nansen bottle, which can be used for the upper few hundred meters (p. 354). Water-sampling devices must be constructed of noncorrosive materials that will reduce contamination of the water samples to a minimum. The bottles are usually made of brass, plated inside with tin or silver or coated with a special lacquer. For removing the water sample they are fitted with a drain cock and an air vent. To be clearly visible when hauling in, the bottles should be painted white. Many types of sampling bottles have been invented, but the rigorous working conditions and the desirable features that have been listed above have reduced the types in general use to only a few of simple but rugged design.
The Nansen reversing water bottle. Left: Before reversing; first messenger approaches releasing mechanism. Middle: Bottle reversing; first messenger has released the second. Right: In reversed position.
Messengers are essential for the operation of many types of oceanographic equipment. Although their size and shape will vary for different types of apparatus, they are essentially weights which are drilled out so that they will slide down the wire rope. In order to remove or attach them they are either hinged or slotted. The speed of travel depends upon the shape and weight of the messenger and upon the wire angle (the angle the wire rope makes with the vertical). With no wire angle the messengers used with the Nansen bottles travel approximately 200 m per minute.
Water-sampling devices are of two general types, depending upon the method of closing, which may be accomplished by means of plug valves or by plates seated in rubber. The Nansen bottle, an example of the first type, is the one most widely used in oceanographic research. The Ekman bottle is of the second type.
The Nansen bottle (fig. 87) is a reversing bottle fitted with two plug valves and holding about 1200 ml. The two valves, one on each end of the brass cylinder, are operated synchronously by means of a connecting rod fastened to the clamp that secures the bottle to the wire rope. When the bottle is lowered, this clamp is at the lower end, and the valves are in the open position so that the water can pass through the bottle. The bottle is held in this position by the release mechanism, which passes around the wire rope, but, when a messenger sent down the rope strikes the release, the bottle falls over and turns through 180 degrees, shuts the valves, which are then held closed by a locking device, and reverses the attached thermometers. After reversing the bottle, the messenger releases another messenger that was attached to the wire clamp before lowering. This second messenger closes the next lower bottle, releasing a third messenger, and so on.
The Ekman bottle, which can also be operated in series, consists of a cylindrical tube and top and bottom plates fitted with rubber gaskets. The moving parts are suspended in a frame attached to the wire rope, and, when the instrument is lowered, the water can pass freely through the cylinder. When struck by a messenger the catch is released and the cylinder turns through 180 degrees, thereby pressing the end plates securely against the cylinder and enclosing the water sample. Reversing thermometers are mounted on the cylinder.
Thermally insulated bottles such as that of Pettersson-Nansen (for illustration, see Murray and Hjort, 1912) consist of several rigidly fixed concentric cylinders each of which is fitted with end plates. When these plates are shut, a series of water samples are isolated one within the other. The outermost cylinder and end plates are constructed of brass and ebonite, the inner ones of brass and celluloid, the cylinders
On the Meteor Expedition a glass-lined sampling bottle with a capacity of 4 l was used to collect large samples with a minimum of contamination. This bottle was attached to the end of the wire rope, the closing mechanism being similar to that used for the insulated bottle. A special mounting that reversed when the bottle was closed was provided for thermometers (Wüst, 1932).
In connection with wire sounding and bottom sampling, it is often desirable to obtain the temperature and the water samples close to the bottom and, as an added check, to obtain the depth by means of an unprotected thermometer. In order to avoid waiting for a messenger to travel all the way to the bottom, possibly one half hour or more, special sampling devices activated by propeller releases are used (Soule, 1932; Parker, 1932). These are usually reversing bottles in which the release pin is attached to a propeller. When the apparatus is being lowered, the propeller holds the pin in place, but, as soon as hauling in is commenced, the propeller rotates and withdraws the pin.
Spilhaus (1940) has devised a multiple sampler consisting of six small valve-closing bottles that can be closed individually at predetermined depths by releases which are activated by the hydrostatic pressure. The instrument was designed to be used in conjunction with the bathythermograph (p. 352) from a vessel while under way.
The general procedure for taking water samples and temperatures by means of Nansen bottles or other serial sampling devices is as follows. In order to keep the wire rope taut and to reduce the wire angle, a stray weight is attached to the end of the wire rope, usually of 50 to 100 lb, depending upon the size of the rope, the depths at which observations are to be taken, and the general working conditions. A certain amount of the wire rope (25 to 50 m) is then payed out so that the weight will not strike the ship when the bottom bottle is being attached or detached, and also to reduce the possibility of damaging the bottle if the weight strikes bottom.
The depth at which samples are to be collected should be planned before the cast is begun. The first bottle, adjusted to the set position, is then attached to the wire rope, the thermometers are checked, and the meter wheel is set at zero. When the wire has been lowered the required
Just before the messenger is released the wire angle should be estimated or measured. Knowledge of the wire angle is useful when determining the depth of sampling, as will be shown later.
Certain accessories are necessary when handling water-sampling bottles. As a safety measure a light line with a harness snap should be attached to the rail. This line is snapped on the bottle before it is handed to the operator on the working platform and is not removed until the bottle is firmly clamped on the wire rope. It is also attached when removing the bottle. To hold the wire rope steady and close to the platform a short line with a large hook should be attached to the platform. The hook is placed on the wire rope when instruments are being attached to it or removed from it. When the vessel is drifting with wind or surface currents, the wire will not hang vertically and will sometimes trail so far away that the wire angle may be as much as 50 or 60 degrees. Under these circumstances the wire rope must be pulled in by means of a boat hook or block and tackle in order to attach the hook.
Because of the larger vertical gradients in the distribution of properties in the upper layers, observations are taken at relatively close intervals near the surface and at increasingly larger intervals at greater depths. The International Association of Physical Oceanography,
TREATMENT AND ANALYSIS OF SERIAL OBSERVATIONS
After a number of temperature observations, salinity determinations, or other analyses have been made, it is necessary to eliminate those values that are in error and to put the data into a convenient form to make them readily comparable with other material of a similar character. The methods by which observations obtained with reversing thermometers are corrected to yield the temperatures in situ and by which the depths of sampling can be computed from the readings of unprotected thermometers have been described on preceding pages. The determination of salinity by chlorinity titration and other methods is discussed in chapter III. In addition, numerous chemical tests and analyses may be made on the water samples by methods listed in chapter VI. After the temperature in situ and the thermometric depths have been calculated, the observational data are generally listed on a summary sheet which shows the following information about each water sample: wire depth of each sampling instrument (the amount of wire rope between the surface and the sampling device), wire angle for each cast, temperature in situ (the corrected protected thermometer reading, or, if two thermometers were attached to the bottle, the average), depth of sampling as computed from the unprotected thermometer (these are usually not attached to each bottle), chlorinity, salinity, and other analyses that have been made.
The next step in the analysis of serial oceanographic observations is to establish the depths of sampling. A considerable amount of personal judgment enters, and this can be improved only by general experience, knowledge of the area in which observations were made, and familiarity with the behavior of individual instruments. The general procedure that must be followed is somewhat as follows: (1) if there was any error in the meter wheel, the necessary corrections must be applied to the meter-wheel readings; (2) if the wire angle was 5 degrees or less, the depths of sampling can be taken as equal to the wire depths as
After the accepted depths have been decided upon, the next step in the analysis of the observations is to plot vertical distribution curves. In one diagram, one of the observed properties may be plotted as a function of depth at a number of stations, or all of the observed properties at a single station may be plotted. From such curves it is often possible to detect those samples that are incorrect because of faulty functioning of the thermometers or because the water-sampling device closed prematurely or leaked when being hauled up. From the vertical distribution curves the following data are taken: (1) the interpolated values at standard depths, and (2) the depths of selected values of a given property at a number of stations. These data are necessary in order to construct vertical sections of the distribution of any property.
Besides the vertical distribution curves, it is common practice to prepare other plots of various kinds which serve either to detect errors or to bring out characteristic features of the data. One of the most common of these is the temperature-salinity curve (T-S curve), in which the corresponding values of temperature and salinity from a single station are plotted in a graph, with temperature and salinity as the coordinates, and are then joined by a curve in order of increasing depth. In any given area the shape of the T-S curve has a fairly definite form, and hence errors in observation may sometimes be detected from such a graph. Many other uses of graphs of this nature are discussed in chapter V. Similar constructions can be used for the other serial data whenever
The interpolated values of temperature and salinity at standard depths are obtained before the density, specific volume anomaly, and other calculations based upon these data are made (see chapter III). As a check upon the correctness of the data, it is often advisable to plot the vertical distribution of density (σι) and the specific volume anomalies for each station as functions of depth.
Various types of distribution diagrams may be prepared from the serial observations, many of which are shown elsewhere in this volume, particularly in chapter XV.
The interpretation of serial oceanographic observations depends so much on the nature of the data, the distribution of observations in space and time, and the characteristic features of the region under investigation that it is impossible to attempt to formulate any “system” of analysis. Only from a knowledge of oceanographic problems and of the significance of the various kinds of data can the most fruitful method of attack be decided upon in any given investigation. The development of new theories and new viewpoints may invalidate earlier conclusions, but the observational data remain valid if they have met the required standards of accuracy.
OBSERVATIONS OF TIDES
Observations of the tides are necessary to establish reference levels for depths and elevations, for reducing soundings to the local reference level (p. 10), for the preparation of tables of predicted tides for use in navigation, and to further the scientific study of tidal phenomena. The rise and fall of the sea surface associated with tidal movements is discussed in chapter XIV, where it is shown that in any locality the range of tide, character of tide, and time of tide with reference to the meridional passage of the moon must be obtained by observation. When adequate data are assembled, the tides at that locality may be predicted with great accuracy.
The essential data are a series of measurements of the elevation of the sea surface at certain time intervals referred to a standard time system, and from these measurements the rise and fall of the sea surface associated with the tide may be plotted as a function of time. In all such studies the elevations must be referred to one or more bench marks, which may or may not be connected with other points of tide observations by accurate leveling. Bench marks are necessary so that the
The simplest device for measuring the rise and fall of the tide on shore is a tide staff. A tide staff is a stout plank that is graduated in feet and tenths of feet or according to the metric system and which is securely fastened to some permanent structure such as a rocky cliff, cement dock, or piling. It must be of sufficient length to extend above the highest tide and below the lowest tide. The graduation must be adjusted with reference to the bench mark, so that if the staff is removed for repairs or replaced, the readings can be referred to a common base. If observations are made every hour, a complete marigram (tide curve) can be constructed, but in many cases observations are made only at certain selected times of the day, or only high and low water are measured. By comparison with the conditions at nearby stations, such random observations are sufficient to determine the character of the local tide. The tide staff is quite accurate in protected water where the waves are small, but on an open coast waves and swells may make it difficult to obtain accurate observations (Rudé, 1928).
In localities where waves cause difficulties, tape gauges are used for visual observations. A float is suspended in a well, commonly a large pipe with small openings below the lowest tide level, and attached to the float is a graduated tape that passes over a pulley, a counterweight being on the other end. The rise and fall of the surface due to waves is largely eliminated, and the tape may then be read with reference to some arbitrary level at appropriate time intervals (Rudé, 1928).
The principle of the tape gauge may be adapted for obtaining a continuous automatic record of the tide level. In the standard automatic gauge used by the U. S. Coast and Geodetic Survey (Rudé, 1928), the float, which is suspended in a well, is attached to a wire that turns a pulley mounted on a threaded rod. As the pulley turns, a carriage with a pencil moves back and forth along the threaded rod that is mounted at right angles to a clockwork-driven roller carrying a sheet of paper. The paper is driven ahead about one inch per hour, and the device thus traces the marigram automatically. Suitable reduction is obtained by varying the size of the pulley and the pitch of the threaded rod. An accurate clock makes a special mark every hour, and a fixed pencil traces a reference line. Short-period waves are largely eliminated because of the damping in the well, but seiches and disturbances of the sea surface lasting several minutes or more are recorded (p. 542). From the marigram the hourly heights and the levels and times of high and low water are easily read off. The standard gauge carries enough paper for one month, but the clocks must be wound once a week, and each day the
The devices so far described can be used only on shore or where some rigid structure extends above the sea surface. Many types of pressure-recording devices for use on the sea bottom have been designed. In some the pressure element only is placed below the sea surface, with the recording device on land; in others, such as those to be used far from shore, the recording device is an integral part of the instrument, which may be placed on the sea floor or anchored and left in position for a week or more. Such open-sea tidal recorders are not beyond the experimental stage. Descriptions of the various types may be found in the Hydrographic Review. The character of the tide over shoals in the open sea may be determined from an anchored ship by means of repeated wire or sonic soundings, if the bottom is flat enough to warrant such observations.
DEEP-SEA ANCHORING
Oceanographic vessels are sometimes anchored in deep water for periods ranging from part of a day to as much as two weeks for the purpose of measuring currents at subsurface levels and for obtaining repeated observations on the vertical distribution of properties at a single locality. Such observations are made to confirm the validity of currents computed from the distribution of density and to obtain measurements of the water movements associated with the tides, internal waves, and other periodic and aperiodic disturbances. Knowledge of the fluctuations in the vertical distribution of properties is valuable in establishing the significance of single sets of observations and in the analysis of the character of internal disturbances.
For the accurate measurement of currents a fixed point of suspension is required, but this condition cannot be fulfilled by a vessel anchored in depths of several thousand meters. Not only does the vessel swing in a relatively large arc, but it also tends to ride up on the cable and then fall away again. In addition, the anchor usually drags somewhat in the soft bottom. So far, it has not proved practical to anchor in deep water with more than one cable. In order to eliminate as far as possible the effect of the vessel's movements on the current measurements, the tension on the cable is noted, detailed records are made of the direction and velocity of the wind and surface currents, and numerous astronomic fixes are taken. The movements of the anchored vessel are generally not significant when making repeated serial observations to
The first vessel to be anchored successfully at great depths was the U.S. Coast and Geodetic Survey steamer Blake, which in 1888–1889, under the command of Lieutenant J. E. Pillsbury, carried out studies of the Gulf Stream (Pillsbury, 1891). The Blake was anchored at thirty-nine localities in depths as great as 4000 m, where currents were measured and subsurface temperatures were determined. Under the direction of Helland-Hansen the Michael Sars and Armauer Hansen have been anchored at great depths in the North Atlantic, and other vessels have since been anchored at great depths elsewhere. The Meteor (Spiess, 1932b), Willebrord Snellius (Perks, in Pinke, 1938), and Atlantis (Seiwell, 1940) have all anchored in depths greater than 4500 m for periods of from several hours to as much as two weeks. The greatest depth in which a vessel has been anchored is about 5500 m, at which depth the Meteor anchored for two days.
Because of the weight of the wire rope suspended in the water, extremely strong hoisting gear and deck fittings are required. The wire ropes are generally tapered multistrand steel ropes of a special nonkinking type. Some have hemp cores for part of their length. The ropes used on the Blake, Meteor, and Snellius had a diameter at the free end of about 3/8 inch, which increased to about 5/8 inch at the winch end. Near the anchor, manila rope, chain, or special cable is used to avoid kinking the wire rope on the bottom. Various types of anchors have been used, either singly or in pairs, which weigh between 400 and 500 lb. The anchors are either of standard patterns with somewhat enlarged flukes or they are of the mushroom type. The weight of the anchors is apparently not very important. The E. W. Scripps has anchored successfully in depths of about 1600 m using a Danforth anchor weighing only 40 lb. The hoisting is usually done with a steamor power-driven capstan head of large diameter, the wire rope being wound under tension on a winch drum. As the strains may exceed several tons, all fittings must be of stout construction. The wire rope is usually led through an accumulator to ease sudden strains, over a dynamometer, through a braking device, and then over a large pulley or roller mounted on the bow. A meter wheel is necessary to measure the amount of rope payed out. The equipment and its use are described in the references already cited.
When anchored in the strong current of the Gulf Stream, the Blake used a scope (ratio between the amount of wire rope payed out and the depth of water) of two or three, but for anchoring in the open sea scopes between 1.1 and 1.6 have been used. The smaller the scope, the less will be the movement of the vessel, but the surface current and the wind and sea will determine the needed scope.
CURRENT MEASUREMENTS
The ocean currents are complicated because, superimposed upon the major currents that transport enormous masses of water, there are irregular eddies that may reach to great depths, wind currents that are confined to the surface layers, and tidal currents or currents associated with internal waves which are present at all depths between the surface and the bottom but which change periodically. In many instances the major currents cannot be directly measured, but conclusions as to their directions and velocities must be based on the application of the laws of hydrodynamics to the observed distribution of density. The methods used in such studies are dealt with in chapter XIII. Here will be discussed only the methods for direct observation, and these can be conveniently classified into two groups: drift methods and flow methods. An excellent summary of all methods and a description of instruments used have been prepared by Thorade (1933).
In scientific literature the velocity of a current is given in centimeters per second (cm/sec) or occasionally in meters per second (m/sec), but in publications on navigation the velocity is stated in knots (nautical miles per hour) or in nautical miles per 24 hours. The term “knots” dates back to the time of the sailing vessels when the speed of the vessel was measured by chip log, log line, and sand glass. Along the log line distances from a zero mark were shown by short strings provided with knots. On the first string was tied one knot, on the second two, and so on. When the chip log was thrown overboard the log line would be pulled out and as the zero mark passed the rail the sand glass was turned. When the sand glass had run down, the log line was stopped and the number of knots on the nearest string were counted. The sand glass and the distances between strings were adjusted to give the speed of the vessel in nautical miles per hour; thus the number of knots gave the speed in this unit—that is, in “knots.”
The direction is always given as the direction toward which the current flows, because a navigator is interested in knowing the direction in which his vessel is carried by the current. The direction is indicated by compass points (for example, NNW, SE), by degrees reckoned from north or south toward east or west (for example, N 60°W, S 30°E) or in degrees from 0° to 360°, counting current towards north as 0° (or 360°) and current towards south as 180°.
Drift Methods
Information as to the general direction of surface currents is obtained from the drift of floating objects such as logs, wreckage from vessels, and fishermen's implements. Thus, glass balls used by Japanese fishermen and wrecked Chinese junks are sometimes found on the west coast
More than a century ago, in order to overcome such uncertainties, drift bottles were introduced. These are weighted down with sand so that they will be nearly immersed, offering only a very small surface for the wind to act on, and they are carefully sealed. They contain cards giving the number of the bottle, which establishes the locality and time of release, and requesting the finder to fill in information as to place and time of finding and to send this information to a central office.
In order further to insure reduction of the direct effect of the wind, drift bottles have sometimes been provided with a kind of drift anchor—for example, a cross-shaped piece of sheet iron suspended about 1 m below the bottle. In other instances, two bottles have been used, one of which has been weighted so much that it is carried by the other, the connecting wire between the bottles being about 1 m long. Still other experiments have been conducted with two bottles, one containing a weak acid which in a given length of time corrodes a metal stopper, thus permitting the sea water to fill the bottle. When this takes place, the bottles sink to the bottom, where they are held by a piece of sheet metal that acts as an anchor. This device has been used in the shallow waters of the North Sea, where bottom trawls are used extensively by fishermen, who recover many of the bottles.
The interpretation of results of drift-bottle experiments presents difficulties. In general, a bottle has not followed a straight course from the place of release to the place of finding, and conclusions as to the probable drift must be guided by knowledge of the temperature and salinity distribution in the surface layers. Fairly accurate estimates of the average speed of the drift can be made if the bottle is picked up from the water, or if a special drift bottle is brought up from the bottom. Bottles that are picked up on frequented beaches can also be used for estimating the speed of the drift. Tait's conclusions (1930) from the
Drift bottles have been used successfully for obtaining information as to surface currents over relatively large ocean areas, such as the equatorial part of the Atlantic Ocean (Defant, 1929, p. 34) and the seas around Japan (Uda, 1935). They have supplied numerous details in more enclosed seas like the English Channel and the North Sea (Fulton, 1897; Carruthers, 1930; Tait, 1930), but have proved less successful off an open coast (Tibby, 1939).
The drift method can also be used for obtaining information as to currents in a shorter time interval. The currents derived from ships' records are determined by this method (p. 428) and give the average surface current in twenty-four hours or multiples of twenty-four hours. From an anchored vessel, say a lightship, the surface current can be determined either by a chip log (Bowditch, 1934, p. 11) or by drift buoys, below which, in general, there is a “current cross” acting as a sea anchor. This type of drift buoy was used on the Challenger. The latter methods give nearly instantaneous values of the surface currents at the place of observation.
Near land the methods can be elaborated in such a manner that the drift of a body can be determined in detail over long distances and long periods. A drifting buoy can be followed by a vessel whose positions can be accurately established by bearings on known landmarks, or the buoy can be provided with a mast and the direction to the buoy can be observed. Its distance from a fixed locality can then be measured by a range finder. Both methods have been used successfully. The latter can also be employed in the open ocean by anchoring one buoy, setting another buoy adrift, and determining the bearing of and the distance to the drifting buoy from a ship that remains as close as possible to the anchored buoy.
Still another drift method has been used with advantage in order to determine the ice drift in shallow waters out of sight of land. The method consists in letting a weight drop so rapidly to the bottom that it sticks in the bottom mud. The time and the length of wire rope payed out are recorded, and then more wire rope is payed out according to the drift of the ice floe to which the vessel is tied up. After a given length of
Flow Methods
From an anchored vessel or float, currents can be measured by stationary instruments past which the current flows, turning a propeller of some type or exerting a pressure that can be determined by various methods. The advantage of these instruments is that observations need not be limited to the currents of the surface layers but can be extended to any depth. The obvious difficulty is to retain the instrument in a fixed locality so that the absolute flow of the water may be measured and not merely the flow relative to a moving instrument. In shallow water a vessel can be anchored so that the motion of the vessel is small enough to be insignificant or of such nature that it can be eliminated. In deep water, current measurements were first made from anchored boats, but in later years the technique of deep-sea anchoring has been advanced (p. 361) to such an extent that vessels like the Meteor, Armauer Hansen, and Atlantis have remained anchored in depths of from 4000 to 5500 m for days and weeks. In other instances, relative currents have been measured from slowly drifting vessels.
Maintaining a vessel at anchor for a long time is expensive, and devices have therefore been developed for anchoring automatic recording current meters that can be left for weeks at a time (p. 370). Measurements of currents very close to the sea bottom cannot be made safely from an anchored vessel, no matter how securely it is kept in position, because an instrument suspended from the vessel cannot be retained at a constant distance from the bottom owing to the motion due to swells and tides. This difficulty was first overcome by Nansen, who lowered a tripod to the sea bottom and suspended a current meter from the top of the tripod. The same method was later used by Stetson (1937), Revelle and Fleming (p. 480), and Revelle and Shepard (in press). The latter suspended three current meters from the top of the tripod and thus were able to obtain simultaneous measurements of currents at three levels within less than 2 m of the bottom.
Current Meters
Current meters differ in design, but all propeller or cup instruments have some device for counting the number of revolutions of the propellers or cups in a given time interval, a vane for orienting the meter in the direction of the current, and a more or less complicated mechanism for recording this direction, either relative to the magnetic meridian (by compass) or relative to some fixed plane (bifilar suspension). Instruments that measure the pressure may not have a vane, because the
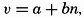
Use of a compass for determining the direction of the current has the disadvantage that near a steel vessel a compass needle will be greatly influenced by the ship's magnetism. The deviation due to the ship's magnetism may be as much as 180°; that is, off the side of a vessel a compass needle may be completely reversed. This deviation, which decreases rapidly with depth, depends upon the heading of the ship, the latitude, and the depth of the current meter. It changes with time because a great part of the ship's magnetism is not permanent. It is a hopeless task to determine this deviation for all headings of the ship and all depths of measurement, and therefore a compass should not be used for observing directions from a steel vessel at depths of less than 50 m. Even from wooden vessels directions by compass have to be carefully examined, particularly if the depth is less than 20 m. For the upper layers, a bifilar suspension is recommended with an arrangement for recording the direction of the current relative to the orientation of the bifilar frame, which again can be determined by means of the ship's heading. A compass instrument can be used near the surface from an anchored boat, particularly if a manila rope is used for anchoring and not a steel rope or an anchor chain.
All propeller and cup instruments suffer from the disadvantage that drifting material may impede the motion of the screw or stop it completely. Instruments designed to be left in position for a long time should be checked at frequent intervals to insure perfect functioning. It should also be borne in mind that jellyfish or similar organisms may be caught on the wire rope and prevent a messenger from passing.
Owing to its simplicity and reliability, the Ekman current meter (Ekman, 1905, 1932) has been and still is widely used. This instrument is described in detail below. The greatest disadvantage of the Ekman meter is that only one instrument can be attached to the wire and that it has to be hauled up to be read after each period in which the propeller
Continuously recording current meters have obvious advantages, but they are complicated and expensive. The recording device may be mechanical, requiring a clockwork that will function reliably in sea water, or electrical, requiring contacts that are insulated from the sea water, or photographic, requiring a watertight chamber which can withstand the pressure and in which the photographic equipment is enclosed. Detailed descriptions of various designs are given by Thorade (1933). Here only a brief summary is given of the most important features of instruments that have been or are in use.
Ekman Current Meters (Ekman, 1905, 1932). The essential parts of this instrument are the propeller, the revolutions of which are recorded on a set of dials, the compass box, with the device for recording the orientation of the meter, and the vane which orients the instrument so that the propeller faces the current (fig. 88). The free swing of the instrument is ensured by mounting it in ball bearings on a vertical axis. The wire for lowering is fastened to the upper end of this axis, and a suitable weight is attached below the axis. The instrument is balanced in water so that the axis is vertical. The carefully balanced propeller, with four to eight thin, light blades, runs inside a strong protective ring but can easily be removed for inspection or transportation. The axis of the propeller runs with tantalum points on agate bearings. Inside the protective ring is a lever that can be operated by messengers. With the lever in its lowest position the propeller is arrested, and in this state the instrument is lowered. When the desired depth is reached, a messenger weight is dropped, pushing the lever up to its middle position and releasing the propeller, the turns of which are recorded on a set of dials. After a number of minutes a second messenger weight is dropped which pushes the lever up to the highest position and stops the propeller. In later types the propeller is also shielded in front when the instrument is lowered in order to prevent fouling of the propeller by such organisms as medusae. This front shield is opened by the first messenger.
The direction of the current is recorded by an ingenious device that is simple and reliable. A tube extends from above the dial box to a

The Ekman current meter. Messenger, dials, and compass box are seen. Propeller is hidden by protective ring.
Ekman Repeating Current Meter (Ekman, 1926). In this instrument the propeller is released and stopped by messengers. When the propeller is stopped, three numbered balls are released from a container. One ball drops down into a compass box, giving the direction of the current at the time the propeller was stopped, and two balls are guided into other slots by the position of dials turned by the propeller. From the slots into which the balls fall, the positions of the dials can be found and thus the number of revolutions of the propeller can be obtained. The messengers are designed to split when they strike the instrument, and the two parts are caught in a container. The operation can be repeated forty-seven times, when the store of numbered balls is exhausted.
Carruthers Residual Current Meter (Thorade, 1933). This instrument is designed for giving the residual current over a long period of time. It has no device for directly recording the revolutions of the cups, but after a certain number of turns a ball is released and drops down into a compass box similar to the compass box of the Ekman meter. The velocity is obtained from the number of balls released. The balls are supplied from a large box containing more than 22,000. At the end of the period of measurement, which may comprise one or more days or even weeks, the number of balls in the slots of the compass box are counted. From these data and the calibration results the average direction and velocity can be found.
Böhnecke Mechanical Recording Current Meter (Thorade, 1933). In this current meter the propeller drives a set of horizontal dials with raised numbers on their vertical rims. A similar dial is attached to the magnet of a compass. A strip of tin foil passes the vertical rims of these dials, being rolled by clockwork from one spool to another. At intervals of five or ten minutes a hammer presses the tin foil against the raised numbers on the rims of the disks, thus recording the positions of the dials, which are turned by the propeller and the magnets of the compass. The instrument can aIso be suspended in a bifilar frame and the direction relative to the orientation of that frame can be recorded. The instrument has not been widely used, probably because it is difficult to find material for the spring in the clockwork, which will be exposed to sea water.
Witting Electrical Recording Current Meter (Witting, 1923). In this instrument the axis of a wheel that is turned by a propeller carries an eccentric disk operating a fork-shaped lever. Through a semiwatertight connection, one part of the fork is brought into a circular box filled with petroleum, where it raises or lowers a magnet. In raised position the magnet is free to swing, and no electrical current passes through the system. In lowered position the frame to which the magnets
Sverdrup-Dahl Electrical Recording Current Meter, Compass Type (Sverdrup And Dahl, 1926; Sverdrup, 1929). This instrument is similar to the Witting current meter except that the contact rings are not enclosed in a semiwatertight box, but are arranged at the top of an inverted brass cylindrical container that serves as a diving bell. Before the instrument is lowered, petroleum is introduced into a vessel in the cylinder. When lowering, the petroleum floats on top and protects the contacts against the sea water, which, with increasing pressure, rises higher and higher. The magnet rests on a pin that is lifted and lowered as the propeller turns. The electric wiring differs somewhat from Witting's, but the record is similar.
Sverdrup-Dahl Electrical Recording Current Meter, Bifilar Type. In this current meter the vane of the instrument turns a sliding contact that rests against a resistance ring rigidly connected with the bifilar suspension. The electric circuit is closed and opened by a key operated by the propeller, remaining closed for about eighty revolutions of the propeller and open for about twenty. The electric contacts are arranged at the top of a “diving bell,” and a recording milliammeter serves as recording instrument. The last-named three instruments require only one insulated conductor, the suspension wire serving as a second conductor.
Ott Electrical Recording Current Meter (Thorade, 1933). In this meter the current velocity is recorded on a chronograph on which a mark is made electromagnetically when the propeller has completed a given number of turns. The direction is not recorded continuously, but by a somewhat complicated arrangement it is shown on a dial whenever the observer on board ship presses a button. All electrical contacts are enclosed in petroleum-filled chambers. Two insulated conductors are required.
Rauschelbach Electrical Recording Current Meter (Rauschelbach, 1929). This instrument is designed for bifilar suspension. The velocity is recorded on a chronograph by contacts made for every
Pettersson Photographic Recording Current Meter (O. Pettersson, 1913, H. Pettersson, 1915). The propeller of this meter is mounted on a vertical axis below a watertight cylindrical chamber. Outside this cylinder the propeller, through a reduction gear, turns a strong magnet which by induction turns a similar magnet in the cylinder. The magnet in the cylinder carries a disk with a transparent division along the rim. The compass carries a smaller disk with transparent division, the two disks being concentric. A short cylinder of soft iron shields the compass magnet from the magnets rotated by the propeller. Every half hour the positions of the two disks are photographed on a film that is advanced by clockwork. The clockwork also turns on and off a small electric bulb, the power for which is supplied by a storage battery. The meter is designed for suspension below a buoy that can be anchored 10 m or more below the sea surface and left for two weeks.
Idrac Photographic Recording Current Meter (Idrac, 1931). The cups of this instrument are mounted on a vertical axis and operate an electric contact which is placed at the top of an inverted cylindrical container similar to that used in the Sverdrup-Dahl meter. When the electric circuit is closed, a lamp is lighted and a mark is made on a film that is advanced at a constant speed by clockwork. The clockwork and the camera are enclosed in a watertight cylinder, and a storage battery is enclosed in a similar cylinder. The current velocity is obtained from the number of marks on the film in one hour. The direction is recorded continuously. Attached to the magnet of the compass is a black disk on which are marked two white concentric circles connected by a white spiral. The spiral rises from the outer to the inner circle in exactly 360 degrees. The camera is mounted above the disk and is provided with a narrow slit through which a very narrow strip of the disk is photographed, the two white circles and the white spiral appearing as points. If the orientation of the meter relative to the magnetic meridian remains constant, all points will produce straight lines on the moving film, but, if the meter turns, only the two circles give straight lines and the spiral gives a curve from which the orientation of the meter—that is, the direction of the current—is obtained.
Winters Photographic Recording Current Meter (Thorade, 1933). The Winters meter is constructed on principles similar to those of the Pettersson meter, but photographs of the counting device and of the position of the compass card are obtained at intervals of five minutes.
Nansen Pendulum Current Meter (Nansen, 1906). This instrument is designed for mounting on a tripod and for measuring very weak currents near the sea bottom. A light pendulum swings above a slightly concave disk which is carried by a magnet and which is covered by graduated waxed paper. At short intervals of time a clockwork lowers the pendulum and a fine stylus attached to its bottom marks the paper, indicating the direction and velocity of the current.
Jacobsen's Bubble Current Meter (Jacobsen, 1909). This current meter is designed for use from such vessels as lightships. It employs no propeller or compass, but measures the magnitude and direction of the deflection of a pendulum relative to the ship from which the pendulum is lowered into the water. Cylinders open at both ends are used as pendulums. The line from the cylinder is fastened to a rod, the orientation of which as to inclination and plane of inclination is observed by a bubble in a segment of a sphere.
Buchanan-Wollaston Mechanical Recording Current Meter (Buchanan-Wollaston 1925, 1930). In this instrument the current velocity is recorded by the pressure exerted by the current against two perforated disks which always remain in a vertical position and which are made to face the current by a vane. The recording unit is enclosed in a watertight cylinder that is mounted horizontally and that turns around a horizontal axis when pressure is applied to the two perforated disks. The turning of the cylinder is recorded, and at intervals of twenty minutes the direction by compass is indicated. The instrument has the advantage that it carries no screw to be clogged by drifting objects, but it is not sensitive to weak currents, since the minimum velocity that can be recorded is about 12 cm/sec.
Analysis of Records of Currents
Different methods of representing surface currents are discussed on pp. 427–430. For currents of a periodic character, it is convenient in most cases to compute the north-south and east-west components of the currents or the components referred to some other coordinate system, say parallel to and at right angles to the coast. The components can readily be subjected to harmonic analysis or to other forms of statistical treatment, subsequent to which the results can be represented in a simple manner (see fig. 145, p. 573). Harmonic analysis has been widely applied and is a very useful tool (see Thorade, 1933).
COLLECTION AND ANALYSIS OF BIOLOGICAL SAMPLES
Biological investigations in any area consist essentially of two parts: (1) descriptive and (2) analytical.
The descriptive part is concerned chiefly with determining the kind of the organisms present and their phylogenetic relationships, and with establishing their geographic and bathymetric distribution. This phase of marine biology was the first to develop historically, and is naturally the first in the investigation of new areas. The relative volume of strictly descriptive work gradually diminishes as the various groups of organisms and their distribution become known, but the application of the results will always be a part of biological studies.
The second, or analytical, phase is concerned above all with the factors operative in the development and distribution of the populations and with the biologic economy of the inhabitants as related to the inorganic and organic factors of the environment. Some of the factors operative in nature can be studied under controlled experiments in the field or in the laboratory, but in any event the information gained must be applied to an interpretation of the complex environmental conditions as they affect the lives of organisms found in the sea. Therefore, the collection of representative samples of plants and animals in nature and the analysis and interpretation of these samples become items of prime importance in order that true correlations can be found.
From the outset it must be realized that at best any sample of organisms collected from the sea is only a minute portion of a population that may occupy a tremendously large area of the sea or only a restricted portion thereof, and that the concentrations are often very irregular. It is only through the collection of numerous samples in various areas and seasons that a true picture of the members of the population—their distribution, life cycles, and interrelations—can be acquired, The nature, size, motility, and habitat of the organisms determine the type of collecting equipment to be used.
Collection of Benthic Organisms
In the intertidal region, only simple equipment is needed, but for collecting in deep water various types of dredges and grabs are used. A dredge (fig. 89b) consists essentially of a heavy rectangular or triangular iron frame to which is attached a baglike fish net of cotton or wire web to retain the organisms. The dredge is dragged on the bottom by means of a wire cable operated from a power winch aboard a slowly movingship. The size of dredges used varies greatly, depending upon the equipment available for their manipulation aboard ship. A practical size for use on a vessel 15 m or more in length and in water of moderate depth has a beam of about 1 m. Only stationary or slowly moving organisms are caught; microscopic forms are included if they are incidentally attached to larger animals and plants or in sediment that has not been completely washed through the meshes of the net during the ascent of the dredge. The
Illustrative of equipment for quantitative collecting of benthic life is the Petersen grab, or bottom sampler, developed by Petersen (1918) for quantitative investigation of benthic animals in relatively shallow waters. It consists of a pair of very heavy metal jaws that are held open during the descent (fig. 89a). When the grab strikes the bottom, the slackened cable releases the tension on a clutch that holds the jaws open, and, when the cable is again drawn tight by the winch aboard ship, the jaws snap shut by their own weight and enclose the material, including the sessile organisms, covering a measured area, usually 0.1 m2, of the bottom over which the open jaws descended. The organisms caught are screened from the bottom sediments, classified, and counted
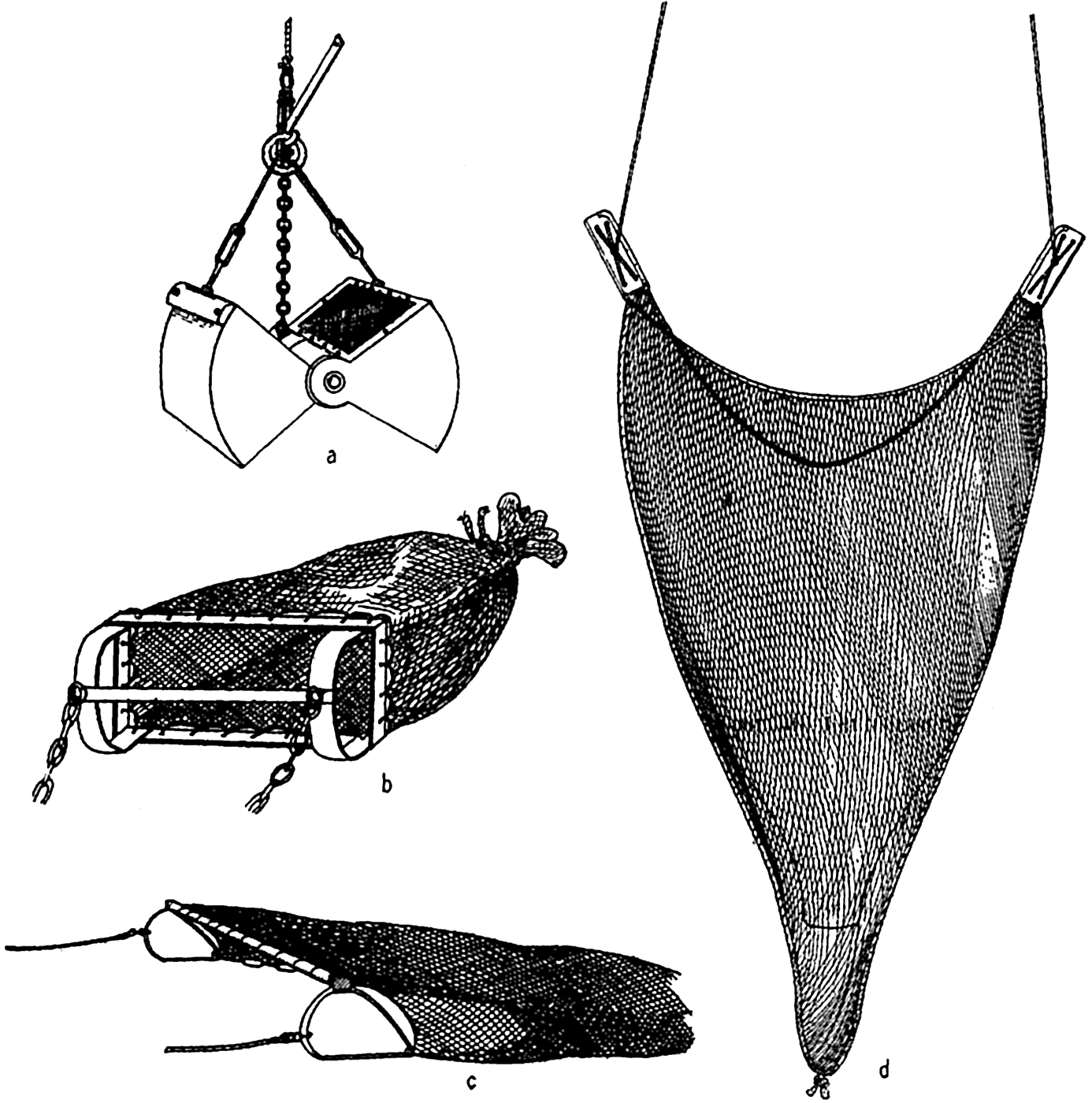
Gear for biological collecting: a, Petersen grab; b, dredge; c, beam-trawl; d, otter-trawl.
Small snappers and coring devices (figs. 84, 85) are useful in collecting quantitative biological samples only of microscopic organisms such as foraminifera and bacteria.
Collection of Nekton
In commercial fishing, diverse methods involving nets, trawls, traps, hooks, and harpoons are used, depending upon the animals sought, but we shall here consider only the trawl, which has been much used in collecting deep-water animals for scientific research. The beam trawl (fig. 89c) is constructed somewhat like the dredge, but the frame does not form digging and scraping edge and it may have a much larger opening, up to 15 m or more; since it is not designed to dig into the bottom, it may be towed at greater speed and thus catch the faster moving animals—shrimps, fishes, and so forth—that live on or near the bottom.
For pelagic trawling the otter trawl is used mostly. The opening to the web sack is kept distended, not by a rigid beam, as in the beam trawl, but by means of otter boards attached to opposite sides of the opening. Upon being towed, these boards are forced apart by the resistance of the water (fig. 89d). The span of the opening may be 20 to 26 m and the net may be 40 m long. A small otter trawl was employed successfully by the Michael Sars in fishing at depths as great as 5160 m.
The ring trawl is essentially a large, relatively coarse plankton net attached to a strong ring of large diameter and provided with a towing bridle (see below).
Collection of Plankton
A great variety of nets and other equipment has been used in obtaining samples of the phyto- and zooplankton. The plankton tow net was apparently first introduced by Johannes Müller in 1846 and has found the widest use of all plankton-collecting devices.
The plankton net consists of a filtering cone attached to a metal ring by which the net is towed through the water. Detailed instructions for cutting patterns for ordinary nets are given by Seiwell (1929). The filtering material forming the net is usually some grade of silk bolting cloth of the type used for sifting flour. It is numbered from 0000 to 25, depending upon the number of meshes per linear inch. The strands are so woven that the aperture size is not readily changed; hence they differ from those in ordinary weaving, where the strands cross each other alternately without a binding turn (fig. 90). The dimensions of the
Enlarged camera lucida drawing to show weave of No. 20 bolting cloth, together with aperture size compared with the size of some common plankton organisms drawn to the same scale. Organisms, horizontal row: Coscinodiscus granii, nauplius Stage III Acartia; early clam larva, Prorocentrum micans Ditylum, Dinophysis, Chaetoceros, Ceratium tripos, Vertical row, down: Favella, nauplius Stage I, Acartia, Stenosomella, Ceratium furca. On cloth: Coscinodiscus wailsii and Rhizosolenia semispina, two unusually large diatoms.
At the cod, or tail, end of the net a detachable jar, vial, or small strainer of some type is placed to receive the concentrated tow.
A continuous plankton recorder has been developed by Hardy (1936) for towing behind a ship while under way at full speed. The machine is essentially a torpedo-shaped tube, circular or rectangular in cross section, and about 1 m long. The front end is provided with a small hole for entrance of water as the machine is hauled forward. This opening leads to a wider tunnel across which a long band of silk gauze is slowly wound from one spool to another and through which the water must pass before its exit by way of a hoIe at the rear end of the tube. The gauze, with the plankton screened from the water, is continuously rolled onto the storage spool. The winding is done by a propeller outside of the machine, and thus the speed at which the band is wound within the machine is controlled by the speed with which the whole machine is drawn through the water and is therefore in direct relation to the
| Silk No. | Meshes per inch | Size of aperture (mm) | Silk No. | Meshes per inch | Size of aperture (mm) |
|---|---|---|---|---|---|
| 0000 | 18 | 1.364 | 10 | 109 | 0.158 |
| 000 | 23 | 1.024 | 11 | 116 | 0.145 |
| 00 | 29 | 0.752 | 12 | 125 | 0.119 |
| 0 | 38 | 0.569 | 13 | 129 | 0.112 |
| 1 | 48 | 0.417 | 14 | 139 | 0.099 |
| 2 | 54 | 0.366 | 15 | 150 | 0.094 |
| 3 | 58 | 0.333 | 16 | 157 | 0.086 |
| 4 | 62 | 0.318 | 17 | 163 | 0.081 |
| 5 | 66 | 0.282 | 18 | 166 | 0.079 |
| 6 | 74 | 0.239 | 19 | 169 | 0.077 |
| 7 | 82 | 0.224 | 20 | 173 | 0.076 |
| 8 | 86 | 0.203 | 21 | 178 | 0.069 |
| 9 | 97 | 0.168 | 25 | 200 | 0.064 |
A smaller and simpler device known as the plankton indicator has been developed (Hardy, 1936) mainly for use by herring fishermen in determining the general type of plankton in the water before casting their nets. It consists of a tube 56 cm long, 8.9 cm in diameter, and with both ends tapering to 3.8-cm openings. Across the lumen of the tube a small disk of bolting cloth is placed for screening out the plankton as the tube is drawn forward through the water at full speed of the boat. The disk can be quickly removed and a clean one inserted, thus allowing frequent direct gross examinations to determine whether patches of phyto- or zooplankton are being traversed (see p. 907).
Zooplankton. Attempts to standardize the nets of various types have led to a comparison of the “catching power” of several common nets as compared to the Hensen egg net, which for basis of comparison is rated as having a catching power of 1.0 (Künne, 1933). In comparison with the Hensen net, the Nansen net was found to have a catching power of 0.87, or, in other words, under comparable conditions quantitatively it caught nearly the same number of animals in the same proportion as the Hensen net. The standard net, which is a modified Nansen net, caught much less, its catching power being only 0.1, while the Helgoland larvae net was rated at 4.1. It should be emphasized that the catching power refers only to the relative capacity of each net to catch the animals
Types of plankton nets, their length, mouth diameter, type of filtering material, and relative catching power (c.p.), as explained in text: a to e drawn to same scale; f to h to a reduced scale. a, Hensen egg net; b, Nansen net open; c, Nansen net closed; d, standard net; e, medium Epstein net; f, Hensen egg net; g, Helgoland larva net; h, large vertical net of stramin.
The truncated nets, illustrated especially by the Hensen egg net and the Apstein net, have a reduced opening at the head end in order to increase the ratio of the filtering area of the net to its mouth area and at the same time, by means of the canvas head piece, to minimize backwash while the net is being towed through the water.
Some nets, illustrated by the Nansen and standard nets, may be closed by means of a messenger that activates a mechanism (fig. 92) releasing the bridle lines and thus causing the strain to fall upon the puckering line, which, at any desired depth, closes off the head end of the net (fig. 91b,c). Thus it is possible to obtain a sample of the plankton population at any subsurface level without contamination by the organisms living in the overlying water layers.
Single nets are sometimes hauled through the water horizontally at the desired depth, or a series of nets may be placed at given intervals on the wire in order to sample several water strata at once. Commonly a net is payed out to a given depth, and, after a period of fishing at this level, it is hoisted successively to a series of higher levels to fish for the same length of time at each before being hauled in, thus obliquely sampling several strata with one net. In the above methods of sampling, it is difficult to obtain an estimate of the amount of water that has been filtered. A more reliable estimate of the amount of water filtered is gained if the net is towed vertically instead of horizontally or obliquely.
In vertical hauls the net, with the cod end tied to a weight suspended by long lines from the top ring, is lowered to the desired depth and then raised vertically, filtering a column of water the length of the course traversed. There is always a considerable amount of backwash, however, resulting from the resistance of the net, especially if it is constructed of fine mesh or has become partially clogged by the plankton. Hence somewhat less water has been filtered than would have gone through an open ring of the diameter of the net mouth. Therefore, when using the area of the net opening as the cross section of the water column filtered, the figures obtained for the number of organisms caught are always minimal ones. As a rule, also, it is not possible to haul the net exactly vertically, since the boat from which it is operated usually drifts more or less, resulting in a haul somewhat longer than the true vertical. There appears to be no sure method of avoiding these types of collecting errors inherent in the use of ordinary nets. Sometimes a recording meter is placed in the mouth of the net so that the water passing into the net activates a small propeller attached to a counting mechanism. When properly calibrated, the number of revolutions of the propeller is taken to indicate the amount of water having passed through the net. From this the number of organisms per unit volume of water, usually per liter or per cubic meter, can be calculated, but, owing to unavoidable irregularities in filtration or analysis, the figures obtained are at best usually only
A tripping mechanism for closing nets and similar apparatus at subsurface levels; back and side views.
Total filtration and exact analysis, of course, will be more nearly realized in sparsely populated waters, while in dense populations or in the presence of gelatinous objects, such as jellyfishes or cast-off appendicularian vestments (“houses”), the errors must become greater. Coarse-meshed nets provided with a water-measuring device represent the most ideal combination for collecting, but they are highly selective and can be used only where such selection is desirable on the basis of size—for example, in the study of large fish eggs or larvae. For a statistical study of the variations in catch of plankton nets the reader is referred to Winsor and Clarke (1940), and the relevant works included in their bibliography.
In an attempt to overcome the uncertainties inherent in net collecting of plankton, various devices (bottles and buckets) have been designed to entrap a definite amount of water together with its plankton population from a definitely known depth. Pumps operated from aboard ship and provided with a long hose, the intake of which can be lowered to the desired depth, have been used successfully, especially in fresh water, for sampling the population at depths down to about 75 m (Birge and Juday, 1922). Known amounts of water from a series of depths can in this way be filtered through fine nets, as the water is delivered from the pump, which is also provided with a water meter. These methods are excellent for some purposes, but are also subject to grave limitations, since they are useful only for inactive or relatively slowly moving organisms, when abundant and rather evenly distributed, such as diatoms, dinoflagellates, protozoa, and sometimes larvae. Fast moving, sparse, and irregularly distributed forms are not likely to be caught with sufficient regularity to give significant data. The ease with which such samples can be taken makes more samplings possible, and this advantage overcomes somewhat the adverse features.
Except for special studies, the zooplankton caught must be preserved in the field. Usually a 4 per cent solution of formaldehyde (preferably neutral) is used for this purpose. The collecting data on the label, placed inside the jar, should include serial number, date, hour, station number, depth sampled, and type of net used and how operated. The laboratory analysis of the samples usually consists of identifying and counting all of the desired species occurring in an aliquot portion of the well-mixed sample. From this is computed the total number of the selected species occurring in the whole sample. Finally, the volume of water filtered by the net in taking the sample having been approximately determined, the population is reported as the number of different
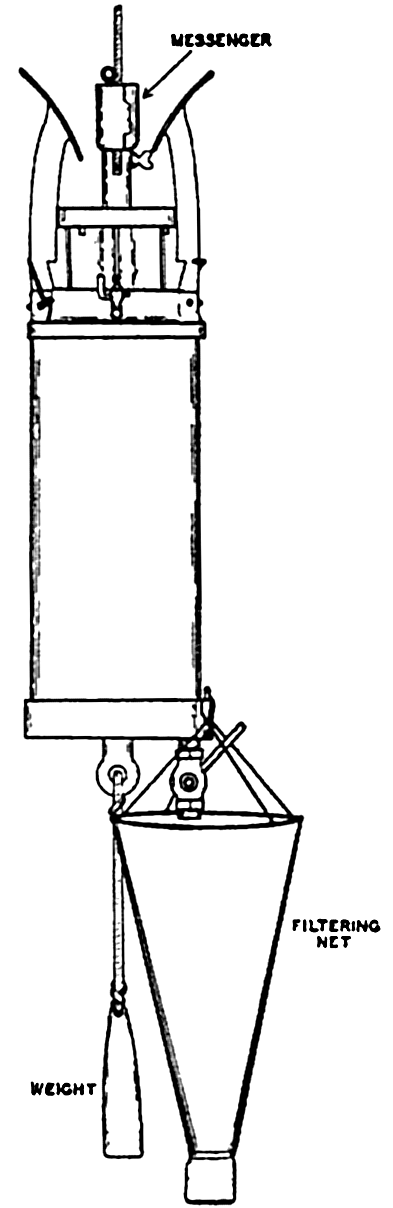
Allen phytoplankton bottle with filtering net in place for emptying.
Phytoplankton. The regular Nansen hydrographic water bottle (fig. 87) is much used for collecting phytoplankton samples, or, if larger samples are desired, the Allen bottle (fig. 93), with a capacity of 5 l, can be used. When the Nansen bottle is employed, samples from certain levels, usually 1, 10, 25, 40, 75, 150 m or more, are tapped off directly into as many citrate bottles, neutral formaldehyde preservative is added, and the bottles are stored for examination in the laboratory. When the collection has been made with an Allen bottle (or similar large collector) at similar depths, the catch is immediately concentrated in a small volume of water (100–150 ml) by filtering through a small net of No. 25 bolting cloth. The sample is then preserved as above for study in the laboratory.
When the sample has not been concentrated in the field, the laboratory analysis consists first of centrifuging a measured portion (say 10 to 50 ml, depending upon the abundance of plankton) of the well-shaken sample. The clear fluid is withdrawn by means of a pipette, and the organisms that have been thrown down in the centrifuge tube are removed, together with the remaining fluid, to a cross-ruled glass slide. They are then covered by a cover slip, and the organisms are identified and enumerated under a compound microscope (Gran, 1932). The numbers obtained form tbe basis for calculating and reporting the
If the sample was concentrated in the field by filtering, an aliquot portion of the concentrated sample is placed in a Sedgwick-Rafter counting cell holding 1.0 ml of the sample, and the organisms are examined and reported as above.
The phytoplankton population may also be conveniently analyzed chemically by extracting the yellow pigments with acetone and reporting the population in numbers of plant-pigment units. In this analysis, the diatoms are filtered from a known quantity of water, and the pigments are then extracted with a measured volume of acetone. The tinted acetone resulting is compared colorimetrically with an arbitrary standard prepared by dissolving 25 mg of potassium chromate and 430 mg of nickel sulphate in 1 l of water. One milliliter of the standard solution is equivalent to one “pigment unit.” For a fuller discussion of this method and of other means of estimating phytoplankton production through utilization of plant nutrients and through oxygen production and consumption, see chapter XIX.
Bacteria. The collection of bacterial samples presents a very special problem, since they must be sterilely taken. In fig. 94 is shown a collecting bottle in the sampling frame with a combination glass and rubber filling tube. This tube is so designed that when the glass section is broken, the rubber part, which is under tension, projects the distal end of the tube, with the intake orifice, at some distance from the bottle and other equipment (ZoBell, 1941). The sea water entering the sterile bottle is thus free from contamination by bacteria that might otherwise be forced in from the surface of the sampling equipment. The frame, with the sampling bottle in place, is attached to the cable, and, at the desired depth, a messenger trips the tube-breaking device. Since the bottles are lowered empty, the depth at which samples can be taken by this means is limited to water pressures that will not break the bottle or force in the stopper. Experiments using rubber bottles to overcome these difficulties are now in progress. Laboratory analysis of the sample collected consists of plating out a known portion of the sample on nutrient material and noting the maximum number of colonies that grow, each
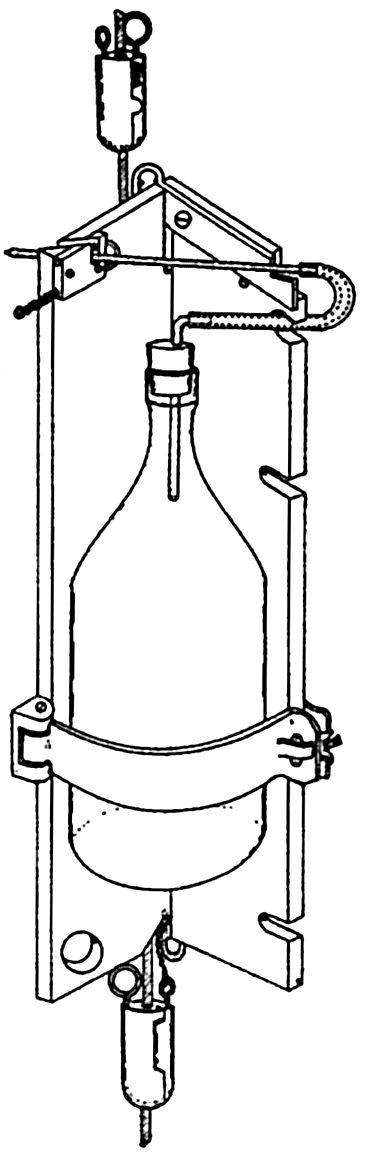
Bacteria sampling bottle in frame attached to cable. The upper messenger breaks the glass intake tube and releases the second messenger when samplers are used in series.
The bacterial population in collected water or mud samples changes very rapidly, making it necessary to plate out the samples as soon as they are obtained in the field in order to obtain the most reliable estimates of the numbers of bacteria in situ. The type of culture medium used is of vital importance in obtaining a growth response from the maximum number of viable bacteria in the sample. Only media made up with sea water are effective (ZoBell, 1941).
The bacteria from bottom sediments are obtained by sterilely removing a sample of the undisturbed material in the center of a core taken with some type of coring device (p. 345).
Interpretation of Plankton Observations
In the interpretation of field observations on plankton, it must be remembered that the different requirements of separate species lead to a more or less complete change of the elements in the population when external factors, especially temperature and nutrients, become altered in the water mass inhabited. When such a biological change takes place within a rather well-defined water mass, whether moving or stationary, we may speak of it as an individual population succession. This must not be confused with a change of population resulting from a sequence of distinct water masses flowing with their distinct populations into a given geographical position where successive series of observations are being made. This type of change may be termed a local sequence. It is frequently not possible to distinguish between these two important types of changes that may occur in the population of an area under investigation, though hydrographic data accompanying biological sampling will aid materially in the interpretation of the biological data by providing information on the nature of residual movements of water. Local sequences in populations are likely to be more sudden than individual population successions, since the latter depend upon biological development rather than upon a simple physical shift of water masses. The former may also at times be slow when neighboring populations become mixed or scattered only through the process of advection or lateral mixing.
An example embracing both local sequence and individual population succession in a population is illustrated by the recent observations of Redfield (1939) on the history of populations of the pteropod Limacina retroversa, its entrance and sojourn in the Gulf of Maine (see also p. 864). A population of small individuals appears in the Gulf in December with inflowing water from the east. Caught in the cyclonic circulation of the Gulf, they gradually decrease in number through mortality or some are
The changes occurring in a population may involve a succession of development stages of a given species. In view of this it should be noted that any biological succession observed may result from two causes. There may be (1) a change in composition of species, owing to different biological responses to physical or chemical changes (that is, rise or fall in temperature or nutrient state of the water) that have occurred within the individual water mass, or (2) a change in the relative maturity of the population, owing simply to the passage of time and to chronologically developed stages in the life history of the individuals of one or more species. A change in the phytoplankton involving a succession of species is well illustrated in boreal water, where in late spring or summer there is commonly a drop in the concentration of diatoms in a predominantly diatom plankton and an accompanying or following increase in dinoflagellates. Here two factors, in particular, are operative in the individual water mass: (1) an increase in temperature (owing to advance of the season), which favors the warmth-loving dinoflagellates, and (2) depletion of plant nutrients by the diatoms to a point suboptimal for their abundant proliferation, but still sufficient for the dinoflagellates, which are able to reduce the nutrients further and through their motility to adjust themselves in some degree with respect to favorable light conditions (see p. 765). The phosphate and nitrate requirements of certain dinoflagellates (Ceratium sp., Peridinium sp., Prorocentrum micans) have been found experimentally to be exceedingly low (Barker, 1935). The maximum rate of division has already been reached with 0.1 parts per million of nitrogen, and this element is probably a limiting factor only at dilutions of 0.01 to 0.001 parts per million.
A biological succession involving the percentage composition of developmental stages of a single dominant species associated with lapse of time is illustrated in studies of the life cycle of Calanus finmarchicus in the relatively slowly flushed waters of the Clyde Sea area (p. 323) where in Loch Striven it was possible (Marshall, Nicholls, and Orr, 1934) to trace the successive developmental stages and broods of Calanus that occur during the seasons.
Bibliography
Ardley, R. A. B., and N. A. Mackintosh. 1936. “The royal research ship Discovery II” . Discovery Repts., v. 13, p. 77–106, 1936.
Barker, H. A.1935. “The culture and physiology of marine dinoflagellates” . Archiv f. Mikrobiol., Bd. 6, 2 Heft, p. 157–181, 1935.
Bauer, L. A., W. J. Peters, J. P. Ault, J. A. Fleming1917. “The magnetic work of the Carnegie, 1909–1916” . Carnegie Inst. Washington, Pub. 175, Researches of the Dept. of Terrestrial Magnetism, v. 3, p. 157–165, 1917.
Birge, E. A., and Chancey Juday. 1922. “The inland lakes of Wisconsin. The plankton. I. Its quantity and chemical composition” . Wisc. Geol. & Nat. Hist. Survey, Bull. no. 64, Sci. Ser., no. 13, p. 1–222, 1922.
Bowditch, Nathaniel. 1934. Instruments and accessories in navigation. p. 11–40 in: American Practical Navigator, no. 9, Washington, D. C., 852 pp.1934.
Brooks, Charles F.1932. Oceanography and meteorology. Physics of the earth, v. 5, Oceanography, p. 457–519, Nat. Research Council, Bull.no. 85, 1932. Washington, D. C.
Buchanan-Wollaston, H. J.1925. “A recording current meter” . Conseil Perm.Internat. p. l’Explor. de la Mer, Pub. de Circonstance, no. 86, 14 pp., 1925.
Buchanan-Wollaston, H. J.1930. “Note on a self-recording current meter” . Conseil Perm. Internat. p. l’Explor. de la Mer, Rapp. et Proc.-Verb., v. 64, p. 33, 34, 1930.
Carruthers, J. N.1930. “Further investigations upon the water movements in the English Channel” . Marine Biol. Assn. U. K., Jour., v. 17, p. 241–275, 1930.
Defant, A.1929. Dynamische Ozeanographie. Naturwissensch. Monographien u. Lehrbücher, Bd. IX, Einführung in die Geophysik III, 222 pp., 1929. Berlin
Ekman, V. W.1905. “Kurze Beschreibung einer Propellerstrommessers” . Conseil Perm. Internat. p. l’Explor. de la Mer, Pub. de Circonstance, no. 24, 4 pp., 1905.
Ekman, V. W.1926. “On a new repeating current-meter” . Conseil Perm. Internat. p. l’Explor. de la Mer, Pub. de Circonstance, no. 91, 27 pp., 1926.
Ekman, V. W.1932. “An improved type of current-meter” . Conseil Perm. Internat. p. l’Explor. de la Mer, Jour. du Conseil, v. 7, p. 3–10, 1932.
Emery, K. O., and R. S. Dietz. 1941. “Gravity coring instrument and mechanics of sediment coring” . Geol. Soc. Amer., Bull.,, v. 52, p. 1685–1714, 1941.
Fulton, T. W.1897. “The surface currents of the North Sea” . Scottish Geogr. Mag., v. 13, p. 636–645, 1897. Edinburgh.
Gran, H. H.1932. “Phytoplankton. Methods and problems” . Conseil Perm. Internat. p. l’Explor. de la Mer, Jour. du Conseil, v. 7, no. 3, p. 343–358, 1932.
Hardy, A. C.1936. “The ecological relations between the herring and the plankton investigated with the plankton indicator” . Pt. I. The object, plan and methods of the investigation. Marine Biol. Assn. U.K., Jour., v. 21, p. 147–177, 1936.
Helland-Hansen, Björn. 1914. “Eine Untersuchungsfahrt im Atlantischen Ozean mit dem Motorschiff Armauer Hansen im Sommer 1913” . Internat. Rev. d. ges. Hydrobiol. u. Hydrogr., Bd. VII, p. 61–83, 1914.
Hough, Jack. 1939. “Bottom-sampling apparatus” . p. 631–664 in Recent Marine Sediments, A Symposium. Tulsa, Okla., A.A.P.G., 736 pp., 1939.
Idrac, P.1931. “Le nouvel enregistrateur de courants sousmarins” . Inst. Océanographique, Ann., v. 10, p. 99–116, 1931. Paris.
Iselin, C. O’D., II1933. “Some phases of modern deep-sea oceanography” . Smithsonian Rept. for 1932, p. 251–67, 1933.
Jacobsen, J. P.1909. “Der Libellenstrommesser” . Conseil Perm. Internat. p. l’Explor. de la Mer, Pub. de Circonstance, no. 51, 20 pp., 1909.
Künne, Cl.1933. “Weitere Untersuchungen zum Vergleich der Fangfähigkeit verschiedener Modelle von vertikal fischenden Plankton-Netzen” . Conseil Perm. Internat. p. l’Explor. de la Mer, Rapp. et Proc.-Verb., v. 83, 36 pp., 1933.
Marshall, S. M., A. G. Nicholls, and A. P. Orr. 1934. “On the biology of Calanus finmarchicus. V. Seasonal distribution, size, weight, and chemical composition in Loch Striven in 1933, and their relation to the phytoplankton” . Marine Biol. Assn. U.K., Jour., v. 19, no. 2, p. 793–828, 1934.
Moberg, E. G., and John Lyman. 1942. “The E. W. Scripps” . Scripps Inst. Oceanogr., Records of Observations, no. 1, p. 3–12, 1942.
Mosby, H.1940. “An oceanographic thermo-sounder” . Union Géod. et Géophys. Intern., Assn. d’Oceanographie Phys., Procés-Verb., no. 3, p. 190–91, 1940.
Murray, Sir John, and Johan Hjort1912. The depths of the ocean. Macmillan, London, 821 pp., 1912.
Nansen, Fridtjof. 1906. “Methods for measuring direction and velocity of currents in the sea” . Conseil Perm. Internat. p. l’Explor. de la Mer, Pub. de Circonstance, no. 34, 42 pp., 1906.
Parker, W. E.1932. “Additional oceanographic instruments. Physics of the Earth, v. 5, Oceanography, p. 442–450” . Nat. Res. Council, 581 pp., 1932.
Petersen, C. G. Joh. 1918. “The sea bottom and its production of fish food. I. Apparatus for investigation of the sea bottom” . Danish Biol. Station. Rept., no. 25, p. 1–6, 1918.
Pettersson, H.1915. “A recording current meter for deep sea work” . Roy. Met. Soc., London, Quart. Jour., v. 41, p. 65–69, 1915.
Pettersson, O.1913. “Photographisch registrierender Tiefenstrommesser für Dauerbeobachtungen” . Ur. Svenska Hydr. Biol. Komm. Skr., v. 5, 8 pp., 1913. Göteborg.
Piggot, Charles S.1936. “Apparatus to secure core samples from the ocean bottom” . Geol. Soc. Amer., Bull., v. 47, p. 675–984, 1936.
Pillsbury, John E.1891. “The Gulf Stream. Methods of the investigation and results of the research” . U. S. Coast and Geod. Surv., Rept. for 1880, Appendix no. 10, p. 461–620, 1891.
Pinke, F.1938. The expeditionary ship and the naval personnel's share. Snellius-Exped. in the eastern part of the Netherlands East-Indies 1929–1930. v. 1, p. 47–78, 1938.
Rauschelbach, H.1929. “Beschreibung eines bifilar aufgehängten, an Bord elektrisch registrierenden Strommessers” . Ann. d. Hydrogr. u. Mar. Meteor., Beiheft, 71 pp, 1929.
Redfield, A. C.1939. “The history of a population of Limacina retroversa during its drift across the Gulf of Maine” . Biol. Bull., v. 76, p. 26–47, 1939.
Revelle, R. R., and F. P. Shepard. 1942. Bottom currents at the California sea floor (to be submitted to Geol. Soc. Amer., Bull.)
Rudé, G. T.1928. “Instructions for tide observations” . U. S. Coast and Geod. Surv., Spec. Pub. no. 139, 78 pp., 1928.
Rudé, G. T.1938. “New methods of marine surveying” . Amer. Phil. Soc., Proc., v. 79, p. 9–25, 1938.
Schmidt, Johs. 1929. “Introduction to the oceanographical reports. Danish Dana-Expeditions 1920–1922 in the North Atlantic and the Gulf of Panama” . Oceanogr. Repts., no. 1, p. 1–20, 1929.
Seiwell, H. R.1929. “Patterns for conical silk plankton-nets of one meter and half-meter diameters” . Conseil Perm. Internat. p. 1’Explor. de la Mer, Jour. du Conseil, v. 4, p. 99–103, 1929.
Seiwell, H. R.1940. “Anchoring ships on the high seas” . U. S. Naval Inst., Proc., v. 66, p. 1733–1740, 1940.
Soule, Floyd M.1932. “Oceanographic instruments and methods. Physics of the Earth, v. 5, Oceanography, p. 411–441” . Nat. Research Council, Bull.no. 85, 581 pp., 1932.
Spiess, H. C. Fritz. 1932a. “Das Forschungsschiff und seine Reise. Deutsche Atlantische Exped” . Meteor 1925–1927, Wiss. Erg., Bd. 1, 442 pp., 1932.
Spiess, H. C. Fritz. 1932b. “Mooring of ships in deep water for the direct measurement of currents” . Hydrogr. Rev., v. 9, no. 1, p. 1–38, 1932.
Spilhaus, Athelstan F.1938. “A bathythermograph” . Jour. Marine Research, v. 1, p. 95–100, 1938.
Spilhaus, Athelstan F.1940. “A detailed study of the surface layers of the ocean in the neighborhood of the Gulf Stream with the aid of rapid measuring hydrographic instruments” . Jour. Marine Research, v. 3, p. 51–75, 1940.
Stetson, H. C.1937. “Current measurements in the Georges Bank canyons” . Nat. Research Council, Amer. Geophys. Union, Trans., p. 216–219, 1937.
Sverdrup, H. U.1929. “The waters on the North Siberian Shelf” . Norwegian North Polar Exped. with the Maud 1918–1925, Sci. Results, v. 4, no. 2, 131 + 75 pp., 1929. Bergen.
Sverdrup, H. U., and Odd Dahl. 1926. “Two oceanographic current recorders designed and used on the Maud Expedition” . Optical Soc. Amer., Jour., v. 12, p. 537–545, 1926.
Tait, J. B.1930. “The water drift in the northern and middle area of the North Sea and in the Faeroe-Shetland Channel. Fishery Board for Scotland” . Sci. Invest, no. 4, 56 pp., 1930. Edinburgh.
Thompson, Thomas G.1936. “The motorship Catalyst—A seagoing laboratory” . Jour. Chem. Education, v. 13, p. 203–209, 1936.
Thorade, Hermann. 1933. Methoden zum Studium der Meeresströmungen. Abderhalden's Handbuch der biologischen Arbeitsmethoden, Abt. II, Teil 3, p. 2865–3095, Berlin1933.
Tibby, R. B.1939. “Report on returns of drift bottles released off southern California, 1937” . Div. Fish and Game of Calif., Bur. Marine, Fisheries, Fish Bull.no. 55, 36 pp., 1939.
Uda, M.1935. “The results of simultaneous oceanographical investigations in the North Pacific Ocean adjacent to Japan made in August, 1933” . Japan, Imperial Fisheries Exper. Sta., Jour., no, 6, 130 pp., 1935.
Veatch,. A. C., and P. A. Smith. 1939. “Atlantic submarine valleys of the United States and the Congo Submarine Valley” . Geol. Soc. Amer., Spec. Paper, no. 7, 101 pp., 1939.
Winsor, C. P., and G. L. Clarke. 1940. “A statistical study of variations in the catch of plankton nets” . Jour. Marine Research, v. 3, p. 1–34, 1940.
Witting, R.1923. “Om en till skeppsbord reporterande strömmätare” . Festsschrift f. Otto Pettersson, p. 90–96, 1923. Helsingfors.
Wüst, Georg. 1932. “Programm, Ausrüstung, Methoden der Serienmessungen” . Deutsche Atlantische Exped. Meteor 1925–1927, Wiss. Erg., Bd. IV, 1 Teil, p. 1–59, 1932.
Wüst, Georg. 1933. “Thermometric measurement of depth” . Hydrogr. Rev., v. 10, no. 2, p. 28–49, 1933.
ZoBell, Claude E.1941. “Studies on marine bacteria. I. The cultural requirements of the heterotrophic aerobes” . Jour. Marine Research, v. 4, p. 42–75, 1941.
XI. General Character of Ocean Currents
The theory of ocean currents will be presented in chapters XII, XIII, and XIV. Here the currents will be discussed nonmathematically, partly as an introduction to the more exact treatment, and partly to facilitate a study of the chapter on water masses and currents of the oceans for those who are not completely familiar with the theories of hydrodynamics. The ocean currents may be conveniently divided into three groups: (1) currents that are related to the distribution of density in the sea, (2) currents that are caused directly by the stress that the wind exerts on the sea surface, and (3) tidal currents and currents associated with internal waves.
To the first class belong the well-known large-scale currents of the oceans, such as the Gulf Stream, the Kuroshio, the Equatorial Currents, the Benguela Current, and others. All of these currents transport great amounts of waters. Their courses at the surface are known from ships' observations (p. 428), and at subsurface depths their character has, in a few localities, been derived from direct measurements of currents from anchored vessels, and in many more localities they have been ascertained from determinations of temperatures and salinities. The methods used for drawing conclusions as to currents from such observations will be discussed below.
The wind drift transports water in one and the same direction over large areas if it blows prevailingly from one direction, but the currents that are associated with tides and internal waves run alternatingly in opposite direction or are rotating. Although tidal currents may attain high velocities, they are of no direct importance to the circulation of the ocean waters.
Currents Related to the Distribution of Density. An explanation of the nature of the currents that are related to the distribution of density in the sea can be based upon a few simple laws of physics. One of these states that the acceleration of a body equals the sum of the forces that act per unit mass of the body. This law, which is applicable to any part of a fluid, implies that, if a body moves with a uniform velocity, the forces that act on the body balance each other. Another law of physics states that within a fluid a force is exerted in the direction
In the oceans the pressure increases downward, and the pressure gradient that is directed against decreasing pressure is therefore directed upward. It is so nearly vertical that it practically balances the acceleration of gravity per unit mass. If it exactly balanced the acceleration of gravity, the isobaric surfaces would coincide with the level surfaces and perfect static equilibrium would exist. Actually, the isobaric surfaces in the ocean slope slightly relative to the level surfaces, but the slope is so small that quasi-static equilibrium exists, meaning that along any vertical the distance between two isobaric surfaces can be found if the density of the water in the interval is known. Let the pressure at the two isobaric surfaces be p1 and p2, respectively, and let the average density along a vertical be  . The corresponding vertical distance between the isobaric surfaces is then h = (p1 − p2)/g
. The corresponding vertical distance between the isobaric surfaces is then h = (p1 − p2)/g , where g is the acceleration of gravity. Therefore the distance is great where the average density of the water is small, and vice versa.
, where g is the acceleration of gravity. Therefore the distance is great where the average density of the water is small, and vice versa.
The small deviations from a state of perfect static equilibrium can be found if the density of the water at different depths is known with great accuracy. From these deviations—that is, from the slopes of the isobaric surfaces—conclusions can be drawn as to the ocean currents, taking the acting forces into account. Along an isobaric surface the pressure gradient is, by definition, zero, and consequently no force related to the distribution of pressure acts along such a surface. If an isobaric surface coincides with a level surface, no component of gravity acts along the surface, and if the water is at rest it will remain at rest. On the other hand, if an isobaric surface slopes relative to a level surface, a component of gravity acts along it, and the water cannot remain at rest. It must move down the sloping surface, but as soon as it is set in motion the effect of the earth's rotation has to be considered.
In order to describe conveniently and precisely the motion of any moving mass on the earth, it is necessary to introduce the deflecting force of the earth's rotation (Corioli's force), which is proportional to the speed at which the mass moves and is directed at right angles to the velocity—to the right in the Northern Hemisphere and to the left in the Southern. The reason for introducing this force is explained on p. 432. Corioli's force is so weak that in nearly all problems of mechanics it can be neglected, because other acting forces are so much greater, but when dealing with the atmosphere and the oceans the weak Corioli's force becomes highly significant, because other forces are small.
With regard to the motion of the water, it can be stated that this motion is no longer accelerated if the component of gravity acting along the isobaric surface is balanced by Corioli's force. The component of gravity is directed down-slope, and Corioli's force must therefore be directed up-slope. Since Corioli's force is directed at right angles to the current, the current follows the contours of the sloping isobaric surface. In the Northern Hemisphere the isobaric surface slopes upward to the right of an observer looking in the direction of the current; in the Southern Hemisphere it slopes upward to the left.
The numerical value of the velocity for a given slope is
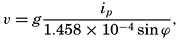
In middle latitudes even the strongest surface currents rarely have velocities above 100 cm/sec (about 2 knots). In latitude 45° the corresponding slope of the sea surface is 1.05 × 10–5; that is, the surface drops or rises about 1 cm in 105 cm (1 km), or about 1 m in 105 m (100 km). Such a gentle slope cannot possibly be observed directly, but the slope of one isobaric surface relative to another can be determined if the density of the water at two neighboring localities is accurately known at a number of depths. The sea surface can always be considered an isobaric surface, and the slope of the sea surface relative to an isobaric surface at any depth below the surface can be determined from the density distribution. If at two neighboring stations A and B the average density between the sea surface and, say, 1000 m is less at A than at B, the distance between an isobaric surface at a depth of about 1000 m and the sea surface, is greater at A than it is at B. Relative to the isobaric surface at about 1000 m, the sea surface slopes downward from A to B. If this relative slope is to be determined with sufficient accuracy, the density must be known to the fifth decimal place, meaning that errors in salinity determinations must not exceed 0.02 ‰ and errors in temperature observations must not exceed 0.02°C. This is one reason for the many efforts to improve the accuracy of salinity and temperature measurements.
From relative slopes relative currents can be computed, but we wish to determine absolute currents. It is therefore necessary to find the absolute slopes of the isobaric surfaces, and valid conclusions as to absolute slope can often be drawn from a careful examination of the vertical and horizontal distribution of temperature and salinity or from consideration
The computations needed for constructing such topographic charts are commonly called dynamic computations. In these computations a vertical distance is expressed by means of the work that is performed or gained in moving a unit mass from one level to another. The work is expressed in the unit dynamic meter, which represents the work performed in lifting a unit mass nearly 1 m. When dynamic meters are used, charts of geopotential (dynamic) topography of isobaric surfaces are prepared. The contours represent lines along which a body can be moved without work having to be performed against gravity, and, if the contours are drawn at equal intervals of dynamic distance, the same work is always performed or gained in moving a unit mass from one contour to another. Within a small area, no perceptible difference exists between the contours expressed in units of dynamic meters or ordinary meters, but over large areas the two types of contours do not coincide, because the acceleration of gravity varies with latitude. The velocity of the current in meters per second is obtained by the formula
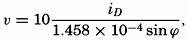
From a chart of the topography of an isobaric surface the corresponding currents are readily obtained on the assumptions that have been made, namely, that the component of gravity acting along the isobaric surface is balanced by Corioli's force. On this assumption the current is directed along the contours. If these are drawn at equal intervals, the slope of the surface is inversely proportional to the horizontal distance
Charts of currents which are constructed in this manner give pictures that are only approximately correct. In the first place, errors may have been introduced by the selection of a reference isobaric surface. These errors are difficult to avoid, because such selection requires not only thorough familiarity with oceanographic data and with the principles of hydrodynamics, but also a certain amount of judgment. In the second place, errors are introduced because the distribution of density changes in the course of time, the implication being that the velocity of any moving water mass is always changing; that is, that accelerations which have been neglected are not quite absent. It can be shown, however, that the velocities computed by neglecting accelerations are rarely more than a few per cent in error (p. 453). More serious are the errors which may be introduced by treating the oceanographic observations as if they were simultaneous. It has been tacitly assumed that simultaneous observations were available from a number of localities, but in general the data to be used have been obtained on a cruise of a single vessel, and the occupation of the stations may have taken weeks or months. For each individual area it is desirable to determine the time interval within which work must be completed in order to avoid serious distortion of the picture of the currents. It can be stated in general, however, that the closer the stations are spaced the shorter must be the period in which they are occupied and that ocean-wide currents can be examined by means of stations which are far apart and which have been occupied in different years and seasons.
In the third place, frictional forces have been neglected. This omission is not a serious matter, because, according to accumulated experience, the influence of friction on currents that are related to the distribution of density is small.
In the fourth place, it has been assumed that the slopes of the isobaric surfaces depend entirely upon the distribution of density and that, in general, one level isobaric surface can be found to which all slopes can be referred. This assumption is not always true. The surface of no motion may slope so much that it does not coincide with any isobaric surface, but the difficulty here is only minor. Within a small region the surface of no motion can be considered level, and by proceeding step by step one can find the slope of the sea surface or of any other isobaric surface relative to the layer of no motion. A more serious difficulty arises when the slope of the sea surface is caused not only by the water masses having different densities, but also by actual piling up of water in some localities and removal of water in others. In landlocked bodies of water, such as the Baltic or the Gulf of Bothnia, piling up of water by wind may lead
So many reservations have been made that it may appear as if the computed currents have little or no relation to the actual currents. Fortunately, however, most of the assumptions made lead only to minor errors, and currents can be correctly represented in the first approximation by means of the slopes of a series of isobaric surfaces relative to one reference surface. In the Straits of Florida an excellent agreement has been obtained between observed and computed currents (fig. 184, p. 674); off the Grand Banks of Newfoundland the computed currents have been used successfully by the International Ice Patrol for predicting the drift of icebergs (p. 668); and in many areas results of computations have been checked against directly observed surface currents or results of drift-bottle experiments. The method that has been outlined has therefore become standard procedure in physical oceanography.
It was stated that in the Northern Hemisphere the current is so directed that the isobaric surfaces slope upward to the right of an observer looking in the direction of flow and that the distances between isobaric surfaces increase with decreasing density. Provided that the level of no motion lies at some distance below the sea surface, one has then the simple rule: In the Northern Hemisphere the lighter water lies on the right-hand side of an observer looking in the direction of the current, and the denser water lies on the left hand. In the Southern Hemisphere the lighter water lies to the left and the denser water to the right.
Inasmuch as the density of the water near the surface is generally more dependent on the temperature than on the salinity, the term “lighter” may be replaced by “warmer,” and “denser” by “colder.” These rules greatly facilitate a rapid survey of the directions of the currents if charts are available showing the distribution of density or of temperature at different depths below the surface or in vertical sections. In general, the distribution of density is represented by σt or by anomalies of specific volume, δ (pp. 56–59).
Greater differences in density in a horizontal direction are found only in the upper layers of the ocean, and hence steep relative slopes of isobaric surfaces are present in the upper layers only. If the deeper and more uniform water masses are moving slowly, it follows that steep absolute slopes and corresponding swift currents are limited to the upper layers. In some areas the currents that are related to the distribution of density are negligible at a depth of 500 m or less (California Current, Equatorial Countercurrents), in others at 1000 or 2000 m (Kuroshio, Gulf Stream),
In general, the flow of the deep water cannot be computed from the distribution of density, mainly because in the deep water the differences in density in a horizontal direction are so small that they cannot as yet be determined with sufficient accuracy. Conclusions as to the motion of the deep water are therefore based directly upon an examination of the distribution of temperature and salinity, and not upon the computations that have been outlined.
The transport of water by the currents can be obtained from the computed velocities or directly from the distribution of density. Computation of transport is often useful for determining a layer of no motion, because the amount of water that is transported into any ocean region must nearly equal the amount that is transported out of the region in the same time. The difference must equal the difference between evaporation on one hand and precipitation and runoff from land on the other hand. This difference is, in general, small compared to the water masses that are transported by currents. Similarly, the net amount of salt carried by currents into any ocean region must be zero, a fact that may be used independently or in conjunction with consideration of the transport of water (p. 457).
In the preceding discussion, no mention has been made of cause and effect. The reason is that any given distribution of density can remain unaltered in course of time only in the presence of currents of the type that has been described. Therefore, all that can be stated is that a mutual relation exists between the distribution of density and the corresponding currents, but it is impossible to tell whether the distribution of density causes the currents or the currents cause the distribution of density. In order to enter upon the causal relationship, it is necessary to consider the factors that influence the distribution of density—namely, the processes of heating and cooling and the effect of the wind. The heating and cooling were discussed in chapter IV, and here emphasis will be placed on the effect of the wind.
Wind Currents and the Secondary Effect of the Wind Toward Producing Ocean Currents. The effect of the wind on the ocean currents is twofold. In the first place, the stress that the wind exerts on the sea surface leads directly to the development of a shallow wind drift; in the second place, the transport of water by the wind drift leads to an altered distribution of density and the development of corresponding currents.
In the case of the wind drift, only frictional forces and Corioli's forces are important. The wind exerts a stress on the sea surface which
It follows that a depth can always be found at which the current flows in a direction exactly opposite to that of the surface current. At this depth the velocity has decreased, on the assumption of a constant eddy viscosity, to a small fraction of its value at the surface, and below this depth the currents are negligible. Ekman therefore calls this depth the depth of frictional resistance. The thickness of the layer above the depth of frictional resistance can roughly be considered equal to the thickness of the layer which under the influence of prevailing winds is stirred up so thoroughly that it is nearly homogeneous. The depth of frictional resistance increases with increasing wind velocity and with decreasing latitude. At the Equator it is theoretically infinite. The relations between depth of frictional resistance, D, wind velocity, W, and latitude, ϕ, are expressed approximately by 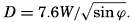 . The depth is obtained in meters when the wind velocity is given in meters per second. Similarly, at the sea surface the velocity of the wind drift is approximately
. The depth is obtained in meters when the wind velocity is given in meters per second. Similarly, at the sea surface the velocity of the wind drift is approximately 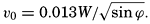 .
.
The total transport due to the wind drift is directed at right angles to the wind, in the Northern Hemisphere to the right and in the Southern Hemisphere to the left. This transport is independent of the character and the numerical value of the eddy viscosity and depends only upon the stress of the wind and the latitude.
The wind drift that has been described can develop only in the open ocean in regions where the wind blows in the same direction and with the same velocity over wide areas. Near coasts and near regions of wind shifts, modifications arise and the secondary effect of the wind becomes important. Consider a wind which in the Northern Hemisphere blows parallel to a coast that is on the right-hand side of an observer
If the coast lies to the left of the wind direction, the light and warm surface water is transported away from the coast and is replaced by denser and colder subsurface water. This process, which is known as upwelling, also leads to an altered distribution of density to which a current flowing in the direction of the wind corresponds. Experience shows that the upwelling is restricted to shallow depths, and its effect can be traced only to depths of 100 to 300 m. The phenomenon of upwelling has been studied extensively, partly because the cold subsurface water that is drawn up to the surface exercises a great influence upon the climates of the coasts where upwelling occurs, and partly because the upwelling water is rich in plant nutrients. Regions of upwelling are therefore regions of high productivity. These relations are dealt with elsewhere, and here it needs only to be emphasized that the upwelling is a direct effect of the wind and that, as a secondary effect, a current develops parallel to the coast and in the direction of the wind.
In the open ocean, analogous conditions are encountered. Where an atmospheric anticyclone is located over the ocean, the prevailing winds tend to transport the light surface water toward the center of the anticyclone. Owing to this transport, an accumulation of light water is maintained near the center of the anticyclone, and corresponding to this distribution of density a current must be present that again flows in the direction of the wind.
From this discussion it is clear that the prevailing winds are of primary importance to the current systems of the oceans. This importance is seen by a comparison of charts showing the prevailing winds and currents, because in many regions the directions closely coincide. There are notable exceptions, however, which are mainly caused by the necessity of the coastal currents to follow the coast lines.
It would be wrong, however, to place too great emphasis on the importance of the winds in maintaining the ocean currents, because in homogeneous water an entirely different system would develop. The
Tidal Currents. In contrast to currents that are related to the distribution of density or to the wind, tidal currents do not bring about a transport of water over large distances. In sounds and narrow straits the tidal currents reverse their direction every six hours where a semidiurnal tide dominates and every twelve hours where a diurnal tide is present. In the open ocean the tidal currents are, in general, rotating, owing to the effect of Corioli's force; that is, from hour to hour the currents change in both direction and velocity. In the Northern Hemisphere the change in direction is clockwise; in the Southern Hemisphere it is counterclockwise. The current completes one rotation in about twelve hours where the tide is semidiurnal and in about twenty-four hours where the tide is diurnal. The net transport of water in twelve or twenty-four hours is therefore zero. Theoretically, the tidal currents should run in the same direction and with the same velocity from the surface to the bottom except in the lowest 20 to 30 m, where they are influenced by bottom friction. The correctness of this conclusion has been verified in shallow waters, but observations sufficient for verification are not available from the deep sea.
The tidal currents vary from one locality to another, depending upon the character of the tide, the depth to the bottom, and the configuration of the coast, but in any given locality they repeat themselves as regularly as the tides to which they are related. In the open ocean, however, they are less readily observed because they are superimposed upon other currents that vary in an irregular manner and that can be eliminated only when long series of observations are available. Information as to tidal currents has primarily been collected from regions in which these currents are of importance to navigation.
From the point of view of the marine biologist the most important aspect of the tidal currents is that they contribute greatly toward the stirring of the water layers, particularly in coastal areas, where the currents can attain velocities up to several knots.
Currents that are related to internal waves are in general of tidal period, but these currents vary in direction and velocity with depth. In the open ocean they can attain much higher velocities than the tidal
The tidal currents are maintained by rhythmic variations in the slopes of the isobaric surface. The rise and fall of the tide, which is caused by the action of the moon and the sun, demonstrates that water is rhythmically piled up (high water) or removed (low water). The sea surface slopes down from a region of high water to one of low water, and all isobaric surfaces below the sea surface slope similarly, but six hours later the direction of the down-slope is reversed. The water particles therefore move under the influence of a periodically varying force, and the corresponding motion is an oscillation comparable to the oscillation of a pendulum, except that Corioli's force makes the particles move in ellipses instead of back and forth along a straight line, where such elliptic orbits are not prevented by boundaries.
Internal waves can be considered as being maintained by rhythmic variations in the distribution of density, which, according to the relation between the distributions of density and pressure, is equivalent to rhythmic variation in the slopes of the isobaric surfaces. In an internal wave, one or more isobaric surfaces at intermediate depth remain level, however, and the slopes of the isobaric surfaces above or below a level surface are in opposite directions. The corresponding currents are also in opposite directions, and, if several internal waves of different periods are present simultaneously, a complicated pattern of currents is found.
From this brief summary it is evident that it is virtually impossible to obtain knowledge of the ocean currents on an entirely empirical basis. If this were to be accomplished, it would be necessary to conduct measurements from anchored vessels at numerous localities for long periods and at many depths. By means of such measurements the different types of periodic currents could be examined, and by averaging they could be eliminated and the other types studied. In many oceanographic problems, however, knowledge of the periodic current is less essential. The currents that transport water over long distances are the important ones. Currents related to the distribution of density can be computed from the more easily observed temperatures and salinities, following the procedure which has been outlined here and which will be discussed in detail in the following chapters, and wind currents can be examined theoretically. Herein lies the value of the application of hydrodynamics to oceanography and the necessity of familiarity with this application if all possible conclusions shall be drawn from the observed distributions.
XII. Statics and Kinematics
STATICS
Units and Dimensions
In the preceding chapters, different units have been introduced without strict definitions, but now it is necessary to define both units and dimensions. The word “dimension” in the English language is used with two different meanings. In everyday language, the term “dimensions of an object” refers to the size of the object, but in physics “dimensions” mean the fundamental categories by means of which physical bodies, properties, or processes are described. In mechanics and hydrodynamics, these fundamental dimensions are mass, length, and time, denoted by M, L, and T. When using the word “dimension” in this sense, no indication of numerical magnitude is implied, but the concept is emphasized that any physical characteristic or property can be described in terms of certain categories, the dimensions. This will be clarified by examples on p. 402.
Fundamental Units. In physics the generally accepted units of mass, length, and time are gram, centimeter, and second; that is, quantities are expressed in the centimeter-gram-second (c.g.s.) system. In oceanography, it is not always practicable to retain these units, because, in order to avoid using large numerical values, it is convenient to measure depth, for instance, in meters and not in centimeters. Similarly, it is often practical to use one metric ton as a unit of mass instead of one gram. The second is retained as the unit of time. A system of units based on meter, ton, and second (the m.t.s. system) was introduced by V. Bjerknes and different collaborators (1910). Compared to the c.g.s. system the new units are 1 m = 102 cm, 1 metric ton = 106 g, 1 sec = 1 sec. For thermal processes, the fundamental unit, 1°C, should be added.
Unfortunately, it is not practical to use even the m.t.s. system consistently. In several cases it is of advantage to adhere to the c.g.s. system in order to make results readily comparable with laboratory results that are expressed in such units, or because the numerical values are more conveniently handled in the c.g.s. system. When measuring horizontal
Derived Units. Units in mechanics other than mass, M, length, L, and time, T, can be expressed by the three dimensions, M, L, and T, and by the unit values adopted for these dimensions. Thus, velocity has the dimension length divided by time, which is written as LT−1 and is expressed in centimeters per second or in meters per second. Velocity, of course, can be expressed in many other units, such as nautical miles per hour (knots), or miles per day, but the dimensions remain unaltered. Acceleration is the time change of a velocity and has the dimensions LT−2. Force is mass times acceleration and has dimensions MLT−2.
Table 60 shows the dimensions of a number of the terms that will be used. Several of the terms in the table have the same dimensions, but the concepts on which the terms are based differ. Work, for instance, is defined as force times distance, whereas kinetic energy is defined as mass times the square of a velocity, but work and kinetic energy both have the dimensions ML2T−2. Similarly, one and the same term can be defined differently, depending upon the concepts that are introduced. Pressure, for instance, can be defined as work per unit volume, ML2T−2L−3 = ML−1T−2, but is more often defined as force per unit area, MLT−2L−2 = ML−1T−2.
| Term | Dimension | Unit in c.g.s. system | Unit in m.t.s. system |
|---|---|---|---|
| Fundamental unit | |||
| Mass | M | g | metric ton = 106 g |
| Length | L | cm | meter = 102 cm |
| Time | T | sec | sec |
| Derived unit | |||
| Velocity | LT−1 | cm/sec | m/sec = 100 cm/sec |
| Acceleration | LT−2 | cm/sec2 | m/sec2 = 100 cm/sec2 |
| Angular velocity | T−1 | 1/sec | 1/sec |
| Momentum | MLT−1 | g cm/sec | ton m/sec = 108 g cm/sec |
| Force | MLT−2 | g cm/sec2 = 1 dyne | ton m/sec2 = 108 dynes |
| Impulse | MLT−1 | g cm/sec | ton m/sec = 108 g cm/sec |
| work | ML2T−2 | g cm2/sec2 = 1 erg | ton m2/sec2 = 1 kilojoule |
| Kinetic energy | ML2T−2 | g cm2/sec2 = 1 erg | ton m2/sec2 = 1 kilojoule |
| Activity (power) | ML2T−3 | g cm2/sec2 = erg/sec | ton m2sec3 = 1 kilowatt |
| Density | ML−3 | g/cm2 | ton/m3 = g/cm3 |
| Specific volume | M−1L3 | cm3/g | m3/ton = cm3/g |
| Pressure | ML−1T−2 | g/cm/sec2 = dyne/cm2 | ton/m/sec2 = 1 centibar |
| Gravity potential | L2T−2 | cm2/sec2 | m2/sec2 = 1 dynamic decimeter |
| Dynamic viscosity | ML−1T−1 | g/cm/sec | ton/m/sec = 104 g/cm/sec |
| Kinematic viscosity | L2T−1 | cm2/sec | m2/sec = 104 cm2/sec |
| Diffusion | L2T−1 | cm2/sec | m2sec = 104 cm2/sec |
In any equation of physics, all terms must have the same dimensions, or, applied to mechanics, in all terms the exponents of the fundamental
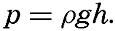
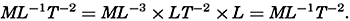
Some of the constants that appear in the equations of physics have dimensions, and their numerical values will therefore depend upon the particular units that have been assigned to the fundamental dimensions, whereas other constants have no dimensions and are therefore independent of the system of units. Density has dimensions ML−3, but the density of pure water at 4° has the numerical value 1 (one) only if the units of mass and length are selected in a special manner (grams and centimeters or metric tons and meters). On the other hand, the specific gravity, which is the density of a body relative to the density of pure water at 4°, has no dimensions (ML−3/ML−3) and is therefore expressed by the same number, regardless of the system of units that is employed.
The Fields of Gravity, Pressure, and Mass
Level Surfaces. Coordinate surfaces of equal geometric depth below the ideal sea surface are useful when considering geometrical features, but in problems of statics or dynamics that involve consideration of the acting forces, they are not always satisfactory. Because the gravitational force represents one of the most important of the acting forces, it is convenient to use as coordinate surfaces the level surfaces, defined as surfaces that are everywhere normal to the force of gravity. It will presently be shown that these surfaces do not coincide with surfaces of equal geometric depth.
It follows from the definition of level surfaces that, if no forces other than gravitational are acting, a mass can be moved along a level surface without expenditure of work and that the amount of work expended or gained by moving a unit mass from one surface to another is independent of the path taken.
The amount of work, W, required for moving a unit mass a distance, h, along the plumb line is
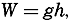
In the following, the sea surface will be considered a level surface. The work required or gained in moving a unit mass from sea level to a point above or below sea level is called the gravity potential, and in the m.t.s. system the unit of gravity potential is thus one dynamic decimeter.
The practical unit of the gravity potential is the dynamic meter, for which the symbol D is used. When dealing with the sea the vertical axis is taken as positive downward. The geopotential of a level surface at the geometrical depth, z, is therefore, in dynamic meters,


The acceleration of gravity varies with latitude and depth, and the geometrical distance between standard level surfaces therefore varies with the coordinates. At the North Pole the geometrical depth of the 1000-dynamic-meter surface is 1017.0 m, but at the Equator the depth is 1022.3 m, because g is greater at the Poles than at the Equator. Thus, level surfaces and surfaces of equal geometric depth do not coincide. Level surfaces slope relative to the surfaces of equal geometric depth, and therefore a component of the acceleration of gravity acts along surfaces of equal geometrical depth.
The topography of the sea bottom is represented by means of isobaths—that is, lines of equal geometrical depth—but it could be presented equally well by means of lines of equal geopotential. The contour lines would then represent the lines of intersection between the level surfaces and the irregular surface of the bottom. These contours would no longer be at equal geometric distances, and hence would differ from the usual topographic chart, but their characteristics would be that the amount of work needed for moving a given mass from one contour to another would be constant. They would also represent the new coast lines if the sea level were lowered without alterations of the topographic features of the bottom, provided the new sea level would assume perfect hydrostatic equilibrium and adjust itself normal to the gravitational force.
Any scalar field can similarly be represented by means of a series of topographic charts of equiscalar surfaces in which the contour lines
The Field of Gravity. The fact that gravity is the resultant of two forces, the attraction of the earth and the centrifugal force due to the earth's rotation, need not be considered, and it is sufficient to define gravity as the force that is derived empirically by pendulum observations. Furthermore, it is not necessary to take into account the minor irregular variations of gravity that detailed surveys reveal, but it is enough to make use of the “normal” value, in meters per second per second, which at sea level can be represented as a function of the latitude, ϕ, by Helmert's formula:
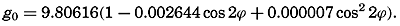
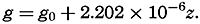
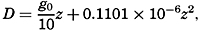
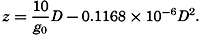
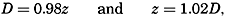
The field of gravity can be completely described by means of a set of equipotential surfaces corresponding to standard intervals of the gravity potential. These are at equal distances if the geopotential is
The Field of Pressure. The distribution of pressure in the sea can be determined by means of the equation of static equilibrium:

The hydrostatic equation will be discussed further in connection with the equations of motion (p. 440). At this time it is enough to emphasize that, as far as conditions in the ocean are concerned, the equation, for all practical purposes, is exact.
Introducing the geopotential expressed in dynamic meters as the vertical coordinate, one has 10dD = gdz. When the pressure is measured in decibars (defined by 1 bar = 106 dynes per square centimeter), the factor k becomes equal to 1/10, and equation (XII, 3) is reduced to
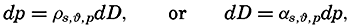
Because ρs, ϕ, pand αs, ϕ, p differ little from unity, a difference in pressure is expressed in decibars by nearly the same number that expresses the difference in geopotential in dynamic meters, or the difference in geometric depth in meters. Approximately,
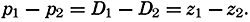
The pressure field can be completely described by means of a system of isobaric surfaces. Using the geopotential as the vertical coordinate, one can present the pressure distribution by a series of charts showing isobars at standard level surfaces or by a series of charts showing the geopotential topography of standard isobaric surfaces. In meteorology, the former manner of representation is generally used on weather maps, in which the pressure distribution at sea level is represented by isobars. In oceanography, on the other hand, it has been found practical to represent the geopotential topography of isobaric surfaces.
The pressure gradient is defined by
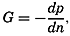
The pressure gradient has two principal components: the vertical, directed normal to the level surfaces, and the horizontal, directed parallel to the level surfaces. When static equilibrium exists, the vertical component, expressed as force per unit mass, is balanced by the acceleration of gravity. This is the statement which is expressed mathematically by means of the equation of hydrostatic equilibrium. In a resting system the horizontal component of the pressure gradient is not balanced by any other force, and therefore the existence of a horizontal pressure gradient indicates that the system is not at rest or cannot remain at rest. The horizontal pressure gradients, therefore, although extremely small, are all-important to the state of motion, whereas the vertical are insignificant in this respect.
It is evident that no motion due to pressure distribution exists or can develop if the isobaric surfaces coincide with level surfaces. In such a state of perfect hydrostatic equilibrium the horizontal pressure gradient vanishes. Such a state would be present if the atmospheric pressure, acting on the sea surface, were constant, if the sea surface coincided with the ideal sea level and if the density of the water depended on pressure only. None of these conditions is fulfilled. The isobaric surfaces are generally inclined relative to the level surfaces, and horizontal pressure gradients are present, forming a field of internal force.
This field of force can also be defined by considering the slopes of isobaric surfaces instead of the horizontal pressure gradients. By definition the pressure gradient along an isobaric surface is zero, but, if this surface does not coincide with a level surface, a component of the acceleration of gravity acts along the isobaric surface and will tend to set the water in motion, or must be balanced by other forces if a steady state of motion is reached. The internal field of force can therefore be represented also by means of the component of the acceleration of gravity along isobaric surfaces (p. 440).
Regardless of the definition of the field of force that is associated with the pressure distribution, for a complete description of this field one must know the absolute isobars at level surfaces or the absolute geopotential contour lines of isobaric surfaces. These demands cannot possibly be met. One reason is that measurements of geopotential distances of isobaric surfaces must be made from the actual sea surface, the topography of which is unknown. It will be shown that all one can do is to determine the pressure field that would be present if the pressure
In order to illustrate this point a fresh-water lake will be considered which is so small that horizontal differences in atmospheric pressure can be disregarded and the acceleration of gravity can be considered constant. Let it first be assumed that the water is homogeneous, meaning that the density is independent of the coordinates. In this case, the distance between any two isobaric surfaces is expressed by the equation

This equation simply states that the geometrical distance between isobaric surfaces is constant, and it defines completely the internal field of pressure. The total field of pressure depends, however, upon the configuration of the free surface of the lake. If no wind blows and if no stress is thus exerted on the free surface of the lake, perfect hydrostatic equilibrium exists, the free surface is a level surface, and, similarly, all other isobaric surfaces coincide with level surfaces. On the other hand, if a wind blows across the lake, the equilibrium will be disturbed, the water level will be lowered at one end of the lake, and water will be piled up against the other end. The free surface will still be an isobaric surface, but it will now be inclined relative to a level surface. The relative field of pressure, however, will remain unaltered as represented by equation (XII, 4), meaning that all other isobaric surfaces will have the same geometric shape as that of the free surface.
One might continue and introduce a number of layers of different density, and one would find that the same reasoning would be applicable. The method is therefore also applicable when one deals with a liquid within which the density changes continually with depth. By means of observations of the density at different depths, one can derive the relative field of pressure and can represent this by means of the topography of the isobaric surfaces relative to some arbitrarily or purposely selected isobaric surface. The relative field of force can be derived from the slopes of the isobaric surface relative to the selected reference surface, but, in order to find the absolute field of pressure and the corresponding absolute field of force, it is necessary to determine the absolute shape of one isobaric surface.
These considerations have been set forth in great detail because it is essential to be fully aware of the difference between the absolute field of pressure and the relative field of pressure, and to know what types of data are needed in order to determine each of these fields.
The Field of Mass. The field of mass in the ocean is generally described by means of the specific volume as expressed by (p. 57)
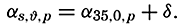
The former field is of a simple character. The surfaces of α35,0,p coincide with the isobaric surfaces, the deviations of which from level surfaces are so small that for practical purposes the surfaces of α35,0,p can be considered as coinciding with level surfaces or with surfaces of equal geometric depth. The field of α35,0,p can therefore be fully described by means of tables giving α35,0,p as a function of pressure and giving the average relationships between pressure, geopotential and geometric depths. Since this field can be considered a constant one, the field of mass is completely described by means of the anomaly of the specific volume, δ, the determination of which was discussed on p. 58.
The field of mass can be represented by means of the topography of anomaly surfaces or by means of horizontal charts or vertical sections in which curves of δ = constant are entered. The latter method is the most common. It should always be borne in mind, however, that the specific volume in situ is equal to the sum of the standard specific volume, α35,0,p at the pressure in situ and the anomaly, δ.
The Relative Field of Pressure. It is impossible to determine the relative field of pressure in the sea by direct observations, using some type of pressure gauge, because an error of only 0.1 m in the depth of a pressure gauge below the sea surface would introduce errors greater than the horizontal differences that should be established. If the field of mass is known, however, the internal field of pressure can be determined from the equation of static equilibrium in one of the forms
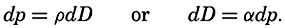
Integration of the latter form gives
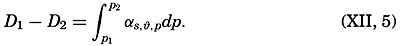
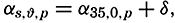
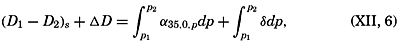
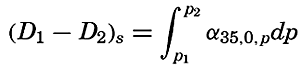

Equation (XII, 6) can be interpreted as expressing that the relative field of pressure is composed of two fields: the standard field and the field of anomalies. The standard field can be determined once and for all, because the standard geopotential distance between isobaric surfaces represents the distance if the salinity of the sea water is constant at 35 ‰ and the temperature is constant at 0°C. The standard geopotential distance decreases with increasing pressure, because the specific volume decreases (density increases) with pressure, as is evident from table 7H in Bjerknes (1910), according to which the standard geopotential distance between the isobaric surfaces 0 and 100 decibars is 97.242 dynamic meters, whereas the corresponding distance between the 5000-and 5100-decibar surfaces is 95.153 dynamic meters.
The standard geopotential distance between any two standard isobaric surfaces is, on the other hand, independent of latitude, but the geometric distance between isobaric surfaces varies with latitude because g varies.
Because in the standard field all isobaric surfaces are parallel relative to each other, this standard field lacks a relative field of horizontal force. The relative field of force, which is associated with the distribution of mass, is completely described by the field of the geopotential anomalies. It follows that a chart showing the topography of one isobaric surface relative to another by means of the geopotential anomalies is equivalent to a chart showing the actual geopotential topography of one isobaric surface relative to another. The practical determination of the relative field of pressure is therefore reduced to computation and representation of the geopotential anomalies, but the absolute pressure field can be found only if one can determine independently the absolute topography of one isobaric surface.
In order to evaluate equation (XII, 7), it is necessary to know the anomaly, δ, as a function of absolute pressure. The anomaly is computed from observations of temperature and salinity, but oceanographic observations give information about the temperature and the salinity at known geometrical depths below the actual sea surface, and not at known pressures. This difficulty can fortunately be overcome by means of an artificial substitution, because at any given depth the numerical value of the absolute pressure expressed in decibars is nearly the same as the numerical value of the depth expressed in meters, as is evident from the following corresponding values:
| Standard sea pressure (decibars) | 1000 | 2000 | 3000 | 4000 | 5000 | 6000 |
| Approximate geometric depth (m) | 990 | 1975 | 2956 | 3933 | 4906 | 5875 |
Thus, the numerical values of geometric depth deviate only 1 or 2 percent from the numerical values of the standard pressure at that depth. This agreement is not accidental, but has been brought about by the selection of the practical unit of pressure, the decibar.
It follows that the temperature at a pressure of 1000 decibars is nearly equal to the temperature at a geometric depth of 990 m, or the temperature at the pressure of 6000 decibars is nearly equal to the temperature at a depth of 5875 m. The vertical temperature gradients in the ocean are small, especially at great depths, and therefore no serious error is introduced if, instead of using the temperature at 990 m when computing δ, one makes use of the temperature at 1000 m, and so on. The difference between anomalies for neighboring stations will be even less affected by this procedure, because within a limited area the vertical temperature gradients will be similar. The introduced error will be nearly the same at both stations, and the difference will be an error of absolutely negligible amount. In practice one can therefore consider the numbers that represent the geometric depth in meters as representing absolute pressure in decibars. If the depth in meters at which either directly observed or interpolated values of temperature and salinity are available is interpreted as representing pressure in decibars, one can compute, by means of the tables in the appendix, the anomaly of specific volume at the given pressure. By multiplying the average anomaly of specific volume between two pressures by the difference in pressure in decibars (which is considered equal to the difference in depth in meters), one obtains the geopotential anomaly of the isobaric sheet in question expressed in dynamic meters. By adding these geopotential anomalies, one can find the corresponding anomaly between any two given pressures. An example of a complete computation is given in table 61.
Certain simple relationships between the field of pressure and the field of mass can be derived by means of the equations for equiscalar surfaces (p. 155) and the hydrostatic equation. In a vertical profile the isobars and the isopycnals are defined by
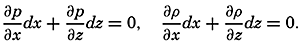
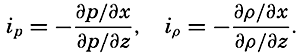
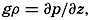
| Meters or decibars | Temp. (°C) | Salinity (‰) | σt | 105Δs,ϕ | 105δs,p | 105δϕ,p | 105δ | ΔD | ΔD(dynamic meter) |
| 0 | 14.22 | 33.25 | 24.81 | 315.0 | 315 | ||||
| 10 | 13.72 | .24 | .91 | 305.5 | 0.3 | 306 | .0310 | .0310 | |
| 25 | .71 | .24 | .91 | 305.5 | 0.7 | 306 | .0459 | .0769 | |
| 50 | .35 | .30 | 25.03 | 294.2 | −0.1 | 1.3 | 296 | .0752 | .1521 |
| 75 | 9.96 | .57 | .86 | 215.2 | −0.2 | 1.6 | 217 | .0641 | .2162 |
| 100 | .38 | .84 | 26.17 | 185.7 | −0.3 | 2.0 | 187 | .0505 | .2667 |
| 150 | 8.82 | .98 | .37 | 166.5 | −0.3 | 2.9 | 169 | .0890 | .3557 |
| 200 | .48 | 34.09 | .51 | 153.5 | −0.3 | 3.7 | 157 | .0815 | .4372 |
| 250 | .30 | .16 | .59 | 145.9 | −0.4 | 4.6 | 150 | .0768 | .5140 |
| 300 | 7.87 | .20 | .69 | 136.4 | −0.5 | 5.2 | 141 | .0728 | .5868 |
| 400 | .07 | .20 | .80 | 125.9 | −0.6 | 6.4 | 132 | .1365 | .7233 |
| 500 | 6.14 | .26 | .97 | 109.8 | −0.7 | 7.2 | 116 | .1240 | .8473 |
| 600 | 5.51 | .35 | 27.12 | 95.6 | −0.8 | 7.9 | 103 | .1095 | .9568 |
| 800 | 4.65 | .42 | .28 | 80.4 | −1.0 | 8.9 | 88 | .1910 | 1.1478 |
| 1000 | 3.99 | .44 | .36 | 72.9 | −1.2 | 9.8 | 82 | 1700 | 1.3178 |
| 1200 | .52 | .52 | .48 | 61.5 | −1.4 | 10.3 | 70 | .1520 | 1.470 |
| 1400 | .07 | .54 | .54 | 55.8 | −1.0 | 10.8 | 66 | .1360 | 1.606 |
| 1600 | 2.69 | .56 | .59 | 51.1 | −1.0 | 10.9 | 61 | .1270 | 1.733 |
| 1800 | .37 | .59 | .64 | 46.3 | −1.0 | 10.8 | 56 | .1170 | 1.850 |
| 2000 | .13 | .64 | .69 | 41.6 | −1.1 | 10.6 | 51 | .1070 | 1.957 |
| 3000 | 1.62 | .68 | .76 | 35.0 | −1.4 | 11.7 | 45 | .4800 | 2.437 |
| 4000 | .50 | .70 | .81 | 30.2 | −1.7 | 14.1 | 43 | .4400 | 2.877 |
one obtains
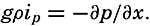
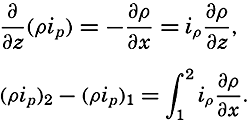
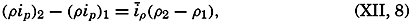
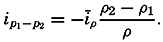

Profiles of isobaric surfaces based on the data from a series of stations in a section must evidently be in agreement with the inclination of the δ curves, as shown in a section and based on the same data, but this obvious rule often receives little or no attention.
Relative Geopotential Topography of Isobaric Surfaces. If simultaneous observations of the vertical distribution of temperature and salinity were available from a number of oceanographic stations within a given area, the relative pressure distribution at the time of the observations could be represented by a series of charts showing the geopotential topography of standard isobaric surfaces relative to one arbitrarily or purposely selected reference surface. From the preceding it is evident that these topographies are completely represented by means of the geopotential anomalies.
In practice, simultaneous observations are not available, but in many instances it is permissible to assume that the time changes of the pressure distribution are so small that observations taken within a given period may be considered simultaneous. The smaller the area, the shorter must be the time interval within which the observations are made. Figs. 110, p. 454 and 204, p. 726, represent examples of geopotential topographies. The conclusions as to currents which can be based on such charts will be considered later.
Charts of geopotential topographies can be prepared in two different ways. By the common method, the anomalies of a given surface relative to the selected reference surface are plotted on a chart and isolines are drawn, following the general rules for presenting scalar quantities. In this manner, relative topographies of a series of isobaric surfaces can be prepared, but the method has the disadvantage that each topography is prepared separately.
By the other method a series of charts of relative topographies is prepared stepwise, taking advantage of the fact that the anomaly of geopotential thickness of an isobaric sheet is proportional to the average
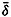 , in the isobaric sheet. Thus, if the thickness of the isobaric sheet is 100 decibars, δDp1p1-100 = 100δ. Consequently, curves of 100δ represent the topography of the surface p = p1 − 100 relative to the surface p = p1, and one can proceed as follows: The topography of the surface ps − 200, where ps is the selected reference surface, is constructed by means of curves of equal values of the specific volume anomaly in the sheet ps to ps − 100. The topography of the surface ps − 200 relative to the surface ps − 100 is constructed by means of the specific volume anomalies in the sheet ps − 100 to ps − 200, and by graphical addition of these two charts (V. Bjerknes and collaborators, 1911) the topography of the surface ps − 200 relative to the surface ps is found. This process can be repeated, and by successive constructions of charts and specific volume anomalies and by graphical additions, the entire fields of mass and pressure can be represented.
, in the isobaric sheet. Thus, if the thickness of the isobaric sheet is 100 decibars, δDp1p1-100 = 100δ. Consequently, curves of 100δ represent the topography of the surface p = p1 − 100 relative to the surface p = p1, and one can proceed as follows: The topography of the surface ps − 200, where ps is the selected reference surface, is constructed by means of curves of equal values of the specific volume anomaly in the sheet ps to ps − 100. The topography of the surface ps − 200 relative to the surface ps − 100 is constructed by means of the specific volume anomalies in the sheet ps − 100 to ps − 200, and by graphical addition of these two charts (V. Bjerknes and collaborators, 1911) the topography of the surface ps − 200 relative to the surface ps is found. This process can be repeated, and by successive constructions of charts and specific volume anomalies and by graphical additions, the entire fields of mass and pressure can be represented.This method is widely used in meteorology, but is not commonly employed in oceanography because, for the most part, the different systems of curves are so nearly parallel to each other that graphical addition is cumbersome. The method is occasionally useful, however, and has the advantage of showing clearly the relationship between the distribution of mass and the distribution of pressure. It especially brings out the geometrical feature that the isohypses of the isobaric surfaces retain their form when passing from one isobaric surface to another only if the anomaly curves are of the same form as the isohypses. This characteristic of the field is of great importance to the dynamics of the system.
Character of the Total Field of Pressure. From the above discussion it is evident that, in the absence of a relative field of pressure, isosteric and isobaric surfaces must coincide. Therefore, if for some reason one isobaric surface, say the free surface, deviates from a level surface, then all isobaric and isosteric surfaces must deviate in a similar manner. Assume that one isobaric surface in the disturbed condition lies at a distance Δh cm below the position in undisturbed conditions. Then all other isobaric surfaces along the same vertical are also displaced the distance Δh from their undisturbed position. The distance Δh is positive downward because the positive z axis points downward. Call the pressure at a given depth at undisturbed conditions p0. Then the pressure at disturbed conditions is pt = p0 − Δp, where Δp = gρΔh and where the displacement Δh can be considered as being due to a deficit or an excess of mass in the water column under consideration.
The above considerations are equally valid if a relative field of pressure exists. The absolute distribution of pressure can always be completely determined from the equation
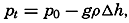
Significance of σt Surfaces
The density of sea water at atmospheric pressure, expressed as σt = (ρs,ϕ,0 − 1) × 103, is often computed and represented in horizontal charts or vertical sections. It is therefore necessary to study the significance of σt surfaces, and in order to do so the following problem will be considered: Can water masses be exchanged between different places in the ocean space without altering the distribution of mass?
The same problem will first be considered for the atmosphere, assuming that this is a perfect, dry gas. In such an atmosphere the potential temperature means the temperature which the air would have if it were brought by an adiabatic process to a standard pressure. The potential temperature, θ, is
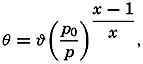
Consider two air masses, one of temperature ϕ1 at pressure p1, and one of temperature ϕ2 at pressure p2. If both have the same potential temperature, it follows that
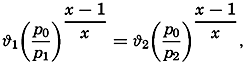
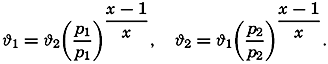
With regard to the ocean, the question to be considered is whether surfaces of similar characteristics can be found there. Let one water mass at the geopotential depth D1 be characterized by salinity S1 and temperature ϕ1, and another water mass at geopotential depth D2 be characterized by salinity S2 and temperature ϕ2. The densities in situ of these small water masses can then be expressed as σs1,ϑ1,D1 and σs2,ϑ2,D2.
Now consider that the mass at the geopotential depth D1 is moved adiabatically to the geopotential depth D2. During this process the temperature of the water mass will change adiabatically from ϕ1 to θ1 and the density in situ will be σs1,θ1,D2. Moving the other water mass adiabatically from D2 to D1 will change its temperature from ϕ2 to θ2. If the two water masses are interchanged, the conditions

The adiabatic change in temperature between the geopotential depths of 200 and 700 dyn meters is 0.09°, and thus θ1 = 13.82, θ2 = 8.01. By means of the Hydrographic Tables of Bjerknes and collaborators, one finds
It should also be observed that the mixing of two water masses that are at the same depth and are of the same density in situ, but of different temperatures and salinities, produces water of a higher density. If, at D = 700 dyn meters, equal parts of water S1 = 36.01 ‰, ϕ1 = 13.82°,
This discussion leads to the conclusion that in the ocean no surfaces exist along which interchange or mixing of water masses can take place without altering the distribution of mass and thus altering the potential energy and the entropy of the system (except in the trivial case that isohaline and isothermal surfaces coincide with level surfaces). There must exist, however, a set of surfaces of such character that the change of potential energy and entropy is at a minimum if interchange and mixing takes place along these surfaces. It is impossible to determine the shape of these surfaces, but the σt surfaces approximately satisfy the conditions. In the preceding example, which represents very extreme conditions, the two water masses were lying nearly on the same σt surface (σt1, = 27.05, σt2 = 26.97).
Thus, in the ocean, the σt surfaces can be considered as being nearly equivalent to the isentropic surfaces in a dry atmosphere, and the σt surfaces may therefore be called quasi-isentropic surfaces. The name implies only that interchange or mixing of water masses along σt surfaces brings about small changes of the potential energy and of the entropy of the body of water.
Stability
The change in a vertical direction of σt is nearly proportional to the vertical stability of the system. Assume that a water mass is displaced vertically upward from the geopotential depth D2 to the geopotential depth D1. The difference between the density of this mass and the surrounding water (see p. 57) will then be
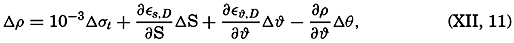
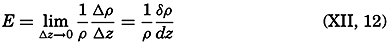
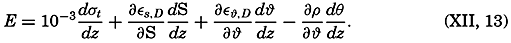

| Depth (m) | Temp. (°C) | Salinity (‰) | σt | 108E | 105(dσt/dz) |
| 0 | 19.2 | 36.87 | 26.42 | ||
| 10 | .31 | .85 | .38 | −440 | −400 |
| 25 | .34 | .83 | .35 | −150 | −200 |
| 50 | .24 | .79 | .34 | −13 | −40 |
| 75 | 18.65 | .79 | .49 | 610 | 600 |
| 100 | .24 | .78 | .58 | 390 | 375 |
| 150 | 17.50 | .56 | .61 | 34 | 60 |
| 200 | 16.45 | .40 | .73 | 270 | 240 |
| 300 | 14.52 | .02 | .88 | 160 | 150 |
| 400 | 13.08 | 35.77 | .99 | 120 | 110 |
| 500 | 11.85 | .64 | 27.13 | 150 | 140 |
| 600 | 10.80 | .54 | .25 | 130 | 120 |
| 800 | 9.09 | .39 | .43 | 100 | 90 |
| 1000 | 8.01 | .37 | .58 | 89 | 75 |
| 1200 | 7.27 | .42 | .74 | 84 | 80 |
| 1400 | 6.40 | .35 | .80 | 48 | 30 |
| 2000 | 4.52 | .15 | .87 | 39 | 12 |
| 3000 | 2.84 | 34.92 | .86 | 11.2 | −1 |
| 4000 | 2.43 | .90 | .87 | 7.6 | 1 |
| 5000 | 2.49 | .90 | .87 | 1.3 | 0 |
Hesselberg and Sverdrup (1914–15) have published tables by means of which the terms of equation (XII, 13) are found, and give an example based on observations in the Atlantic Ocean on May, 1910, in lat. 28°37′N, long. 19°08′W (Helland-Hansen, 1930). This example is reproduced in
Hesselberg and Sverdrup have also computed the order of magnitude of the different terms in equation (XII, 13) and have shown that dσt/dz is an accurate expression of the stability down to a depth of 100 m, but that between 100 and 2000 m the terms containing ε may have to be considered, and that below 2000 m all terms are important. The following practical rules can be given:
Above 100 m the stability is accurately expressed by means of 10−3dσt/dz.
Below 100 m the magnitude of the other terms of the exact equation (XII, 13) should be examined if the numerical value of 10−3dσt/dz is less than 40 × 10−8.
The stability can also be expressed in a manner that is useful when considering the stability of the deep water:
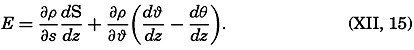

KINEMATICS
Vector Fields
A vector field can be completely represented by means of three sets of charts, one of which shows the scalar field of the magnitude of the vector and two of which show the direction of the vector in horizontal and vertical planes. It can also be fully described by means of three sets of scalar fields representing the components of the vector along the principal coordinate axes (V. Bjerknes and different collaborators, 1911). In oceanography, one is concerned mainly with vectors that are horizontal, such as velocity of ocean currents—that is, two-dimensional vectors.
Representation of a two-dimensional vector field by vectors of indicated direction and magnitude and by vector lines and equiscalar curves.
Vector lines cannot intersect except at singular points or lines, where the magnitude of the vector is zero. Vector lines cannot begin or end within the vector field except at singular points, and vector lines are continuous.
The simplest and most important singularities in a two-dimensional vector field are shown in fig. 96: These are (1) points of divergence (fig. 96A and C) or convergence (fig. 96B and D), at which an infinite number of vector lines meet; (2) neutral points, at which two or more vector lines intersect (the example in fig. 96E shows a neutral point of the first order in which two vector lines intersect—that is, a hyperbolic point); and (3) lines of divergence (fig. 96F) or convergence (fig. 96G), from which an infinite number of vector lines diverge asymptotically or to which an infinite number of vector lines converge asymptotically.
It is not necessary to enter upon all the characteristics of vector fields or upon all the vector operations that can be performed, but two important vector operations must be mentioned.
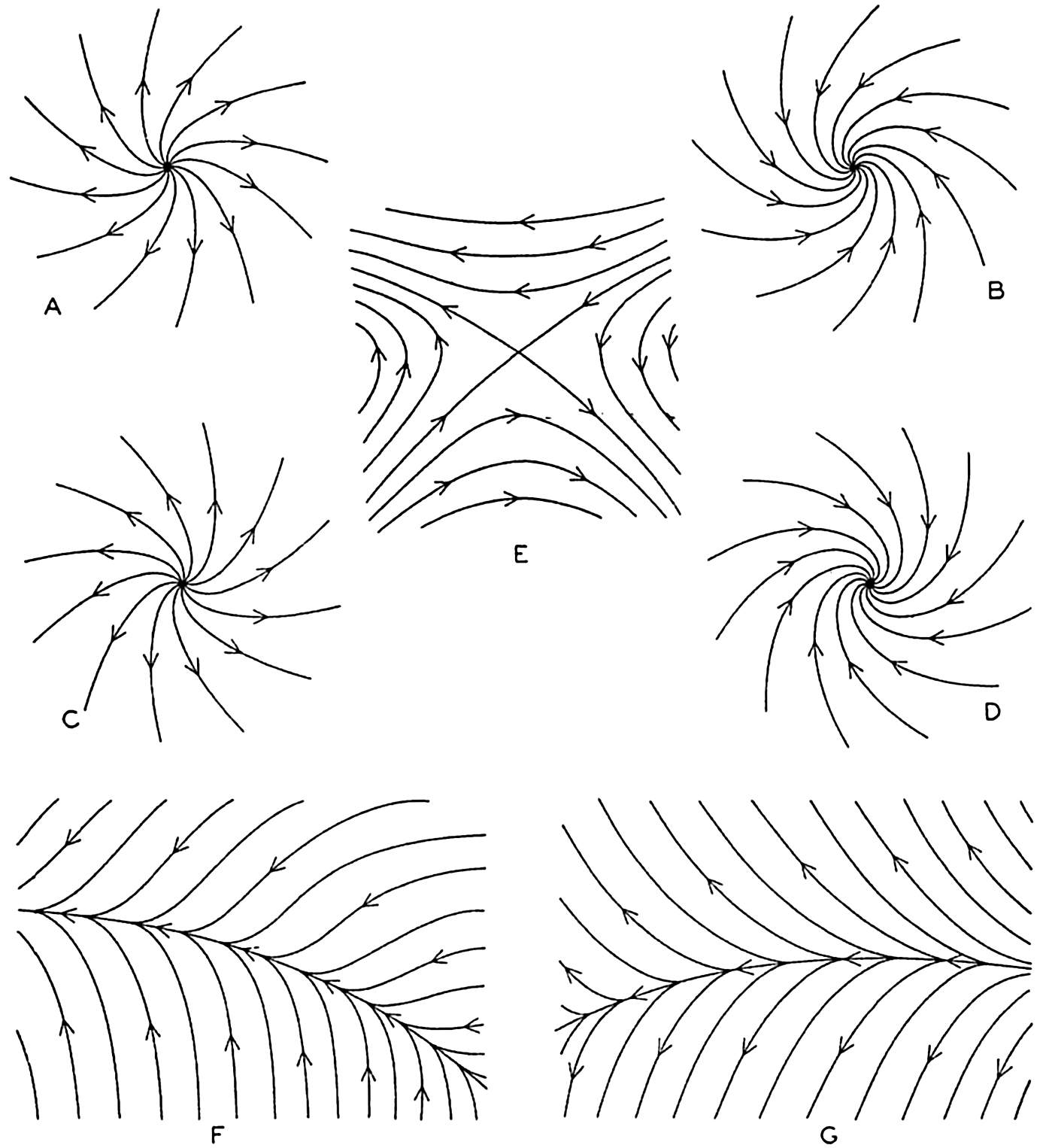
Singularities in a two-dimensional vector field. A and C, points of divergence; B and D, points of convergence; E, neutral point of first order (hyperbolic point); F, line of convergence; and G, line of divergence.
Assume that a vector A has the components Ax, Ay, and Az. The scalar quantity
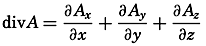
The vector which has the components
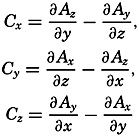
Two representations of a vector that varies in space and time will also be mentioned. A vector that has been observed at a given locality during a certain time interval can be represented by means of a central vector diagram (fig. 97). In this diagram, all vectors are plotted from the same point, and the time of observation is indicated at each vector. Occasionally the end points of the vector are joined by a curve on which the time of observation is indicated and the vectors themselves are omitted. This form of representation is commonly used when dealing with periodic currents such as tidal currents. A central vector diagram is also used extensively in pilot charts to indicate the frequency of winds from given directions. In this case the direction of the wind is shown by an arrow, and the frequency of wind from that direction is shown by the length of the arrow.
Time variation of a vector represented by a central vector diagram (left) and a progressive vector diagram (right).
If it can be assumed that the observations were made in a uniform vector field, a progressive vector diagram is useful. This diagram is constructed by plotting the second vector from the end point of the first, and so on (fig. 97). When dealing with velocity, one can compute the displacement due to the average velocity over a short interval of time. When these displacements are plotted in a progressive vector diagram, the resulting curve will show the trajectory of a particle if the velocity field is of such uniformity that the observed velocity can be considered representative of the velocities in the neighborhood of the place of observation. The vector that can be drawn from the beginning of the first vector to the end of the last shows the total displacement in the entire time interval, and this displacement, divided by the time interval, is the average velocity for the period.
The Field of Motion and the Equation of Continuity
The Field of Motion. Among vector fields the field of motion is of special importance. Several of the characteristics of the field of motion can be dealt with without considering the forces which have brought about or which maintain the motion, and these characteristics form the subject of kinematics.
The velocity of a particle relative to a given coordinate system is defined as ν = dr/dt, where dr is an element of length in the direction in which the particle moves. In a rectangular coordinate system the velocity has the components
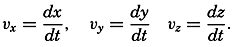
The velocity field can be completely described by the Lagrange or by the Euler method. In the Lagrange method the coordinates of all moving particles are represented as functions of time and of a threefold multitude of parameters that together characterize all the moving particles. From this representation the velocity of each particle, and, thus, the velocity field, can be derived at any time.
The more convenient method by Euler will be employed in the following. This method assumes that the velocity of all particles of the fluid has been defined. On this assumption the velocity field is completely described if the components of the velocity can be represented as functions of the coordinates and of time:
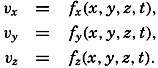
The characteristic difference between the two methods is that Lagrange's method focuses attention on the paths taken by all individual particles, whereas Euler's method focuses attention on the velocity at each point in the coordinate space. In Euler's method it is necessary, however, to consider the motion of the individual particles in order to find the acceleration. After a time dt, a particle that, at the time t, was at the point (x,y,z) and had the velocity components fx(x,y,z,t), and so on, will be at the point (x + dx, y + dy, z + dz), and will have the velocity components fx(x + dx, y+ dy, z + dz, t + dt), and so on. Expanding in Taylor's series, one obtains
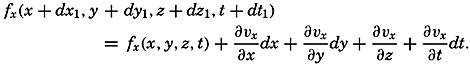
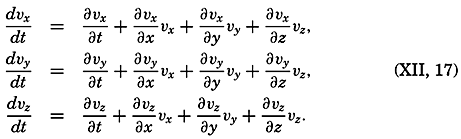
Thus, one has to deal with two time derivatives: the individual time derivative, which represents the acceleration of the individual particles, and the local time derivative, which represents the time change of the velocity at a point in space and is called the local acceleration. The last terms in equation (XII, 17) are often combined and called the field acceleration.
The above development is applicable not only when considering the velocity field, but also when considering any field of a property that varies in space and time (p. 157). The velocity field is stationary when the local time changes are zero:


The Equation of Continuity. Consider a cube of volume dxdydz. The mass of water that in unit time flows in parallel to the x axis is equal to pvxdydz, and the mass that flows out is equal to
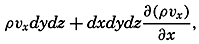
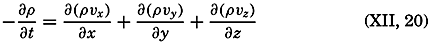
Now:
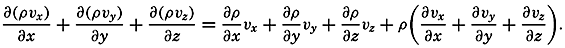
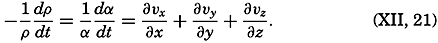
The equation of continuity is not valid in the above form at a boundary surface because no out- or inflow can take place there. In a direction normal to a boundary a particle in that surface must move at the same velocity as the surface itself. If the surface is rigid, no component normal to the surface exists and the velocity must be directed parallel to the surface. The condition

Application of the Equation of Continuity. At the sea surface the kinematic boundary condition must be fulfilled. Designating the vertical displacement of the sea surface relative to a certain level of equilibrium by η, and taking this distance positive downward, because the positive z axis is directed downward, one obtains
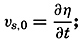
With stationary distribution of mass (∂ρ/∂t = 0) the equation of continuity is reduced to
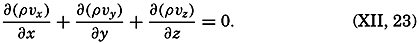
The total transport of mass through a vertical surface of unit width reaching from the surface to the bottom has the components
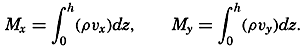
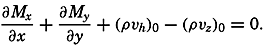

When dealing with conditions near the surface, one can consider the density as constant and can introduce average values of the velocity components 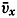 and
and 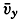 within a top layer of thickness H. With these simplifications, one obtains, putting νz,0 = 0,
within a top layer of thickness H. With these simplifications, one obtains, putting νz,0 = 0,
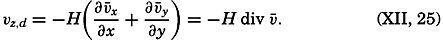
For this purpose, it is of advantage to write the divergence of a two-dimensional vector field in a different form:

The equation of continuity is applicable not only to the field of mass but also to the field of a dissolved substance that is not influenced by biological activity. Let the mass of the substance per unit mass of water be s. Multiplying the equation of continuity by s and integrating from the surface to bottom, one obtains, if the vertical velocity at the surface is zero,
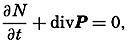
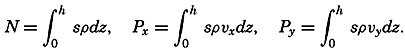

These equations have already been used in simplified form in order to compute the relation between inflow and outflow of basins (p. 147). Other simplifications have been introduced by Knudsen, Witting, and Gehrke (Krümmel, 1911, p. 509–512).
Trajectories (full drawn lines) and stream lines (dashed lines) in a progressive surface wave.
Stream Lines and Trajectories. The vector lines showing the direction of currents at a given time are called the stream lines, or the lines of flow. The paths followed by the moving water particles, on the other hand, are called the trajectories of the particles. Stream lines and trajectories are identical only when the motion is stationary, in which case the stream, lines of the velocity field remain unaltered in time, and a particle remains on the same stream line.
The general difference between stream lines and trajectories can be illustrated by considering the type of motion in a traveling surface wave. The solid lines with arrows in fig. 98 show the stream lines in a cross section of a surface wave that is supposed to move from left to right, passing the point A. When the crest of the wave passes A, the motion of the water particles at A is in the direction of progress, but with decreasing
It is supposed that the speed at which the wave travels is much greater than the velocity of the single water particles that take part in the wave motion. On this assumption a water particle that originally was located below A will never be much removed from this vertical and will return after one wave period to its original position. The trajectories of such particles in this case are circles, the diameters of which decrease with increasing distance from the surface, as shown in the figure. It is evident that the trajectories bear no similarity to the stream lines.
Representations of the Field of Motion in the Sea
Trajectories of the surface water masses of the ocean can be determined by following the drift of floating bodies that are carried by the currents. It is necessary, however, to exercise considerable care when interpreting the available information about drift of bodies, because often the wind has carried the body through the water. Furthermore, in most cases, only the end points of the trajectory are known—that is, the localities where the drift commenced and ended. Results of drift-bottle experiments present an example of incomplete information as to trajectories. As a rule, drift bottles are recovered on beaches, and a reconstruction of the paths taken by the bottles from the places at which they were released may be very hypothetical. The reconstruction may be aided by additional information in the form of knowledge of distribution of surface temperatures and salinities that are related to the currents, or by information obtained from drift bottles that have been picked up at sea. Systematic drift-bottle experiments have been conducted, especially in coastal areas that are of importance to fisheries.
Stream lines of the actual surface or subsurface currents must be based upon a very large number of direct current measurements. Where the velocity is not stationary, simultaneous observations are required. Direct measurements of subsurface currents must be made from anchored vessels, but this procedure is so difficult that no simultaneous measurements that can be used for preparing charts of observed subsurface currents for any area are available.
Numerous observations of surface currents, on the other hand, have been derived from ships' logs. Assume that the position of the vessel at
Determination of surface currents by difference between positions by fixes and dead reckoning.
The data on surface currents obtained from ships' logs cannot be used for construction of a synoptic chart of the currents, because the number of simultaneous observations is far too small. Data for months, quarter years, or seasons have been compiled, however, from many years' observations, although even these are unsatisfactory for presentation of the average conditions because such data are not evenly distributed over large areas but are concentrated along trade routes. In some charts the average direction in different localities is indicated by arrows, and where strong currents prevail the average speed in nautical miles per day is shown by a number. In other charts the surface flow is represented by direction roses in which the number at the center of the rose represents the percentage of no current, the lengths of the different arrows represent the percentage of currents in the direction of the arrows, and the figures at the ends of the arrows represent the average velocity in miles per day of currents in the indicated direction. These charts contain either averages for the year or for groups of months.
On the basis of such charts, average surface currents during seasons or months have in some areas been represented by means of stream lines and equiscalar curves of velocity. The principle advantage of this representation is that it permits a rapid survey of the major features and that it brings out the singularities of the stream lines, although in many instances the interpretation of the data is uncertain and the details of the chart will depend greatly upon personal judgment.
In drawing these stream lines it is necessary to follow the rules concerning vector lines (p. 419). The stream lines cannot intersect, but an infinite number of stream lines can meet in a point of convergence or divergence or can approach asymptotically a line of convergence or diverge asymptotically from a line of divergence.
Stream lines of the surface currents off southeastern Africa in July (after Wilimzik).
As an example, stream lines of the surface flow in July off southeast Africa and to the south and southeast of Madagascar are shown in fig. 100. The figure is based on a chart by Willimzik (1929), but a number of the stream lines in the original chart have been omitted for the sake of simplification. In the chart a number of the characteristic singularities of a vector field are shown. Three hyperbolic points marked A appear, four points of convergence marked B are seen, and a number of lines of convergence marked C and lines of divergence marked D are present. The stream lines do not everywhere run parallel to the coast, and the representation involves the assumption of vertical motion at the coast, where the horizontal velocity, however, must vanish.
The most conspicuous feature is the continuous line of convergence that to the southwest of Madagascar curves south and then runs west, following lat. 35°S. At this line of convergence, the Subtropical Convergence, which can be traced across the entire Indian Ocean and has its counterpart in other oceans, descending motion must take place. Similarly, descending motion must be present at the other lines of convergence, at the points of convergence, and at the east coast of Madagascar, whereas ascending motion must be present along the lines of divergence and along the west coast of Madagascar, where the surface waters flow away from the coast. Velocity curves have been omitted, for which reason the conclusions as to vertical motion remain incomplete (see p. 425). Near the coasts, eddies or countercurrents are indicated, and these phenomena often represent characteristic features of the flow and remain unaltered during long periods.
As has already been stated, representations of surface flow by means of stream lines have been prepared in a few cases only. As a rule, the surface currents are shown by means of arrows. In some instances the representation is based on ships' observation of currents, but in other cases the surface flow has been derived from observed distribution of temperature and salinity, perhaps taking results of drift-bottle experiments into account. The velocity of the currents may not be indicated or may be shown by added numerals, or by the thickness of the arrows. No uniform system has been adopted (see Defant, 1929), because the available data are of such different kinds that in each individual case a form of representation must be selected which presents the available information in the most satisfactory manner. Other examples of surface flow will be given in the section dealing with the currents in specific areas.
Bibliography
Bjerknes, V., and different collaborators. 1910. Dynamic meteorology and hydrography. Pt. I. Statics. Carnegie Inst. Washington, Pub. no. 88, 146 pp. + tables, 1910.
Bjerknes, V., and different collaborators. 1911. Dynamic meteorology and hydrography. Pt. II. Kinematics. Carnegie Inst. Washington, Pub. no. 88, 175 pp., 1911.
Defant, A.. 1929. Dynamische Ozeanographie. Naturwissenschaftliche Monographien und Lehrbücher, Bd. 9, III, 222 pp., 1929. Berlin.
Helland-Hansen, B.. 1930. “Physical oceanography and meteorology. Michael Sars North Atlantic Deep-Sea Exped., 1910” . Rept. Sci. Results, v. 1, art. 2, 217 pp., 1930.
Hesselberg, Th.. 1918. “Über die Stabilitätsverhältnisse bei vertikalen Verschiebungen in der Atmosphäre und im Meer” . Ann. d. Hydr. u. Mar. Meteor., p. 118–29, 1918.
Hesselberg, Th., and H. U. Sverdrup. 1915. Die Stabilitätsverhältnisse des Seewassers bei vertikalen Verschiebungen. Bergens Museums Aarbok 1914–15, No. 15, 16 pp., 1915.
Willimzik, M.1929. “Die Strömungen im subtropischen Konvergenzgebiet des Indischen Ozeans. Berlin, Universität” . Institut f. Meereskunde, Veröff., N. F., A. Geogr.-naturwiss. Reihe, Heft 14, 27 pp., 1929.
XIII. Dynamics of Ocean Currents
Our knowledge of the currents of the ocean would be very scanty if it were based entirely on direct observations, but, fortunately, conclusions as to currents can be drawn from the distribution of readily observed properties such as temperature and salinity. When drawing such conclusions, one must take into account the acting forces and apply the laws of hydrodynamics and thermodynamics as derived from theoretical considerations or from generalizations of experimental results.
For the sake of simplification, one may distinguish between four different methods of approach: (1) computations of currents from the distribution of density as obtained from observations of temperature and salinity, (2) conclusions as to currents caused by wind, (3) considerations of currents that result from differences in heating or cooling, precipitation or evaporation, (4) qualitative inferences as to currents which would account for special features of the observed distribution of such properties as temperature, salinity, and oxygen. Of these four methods of approach the first two are dynamical. The third involves considerations of a thermodynamical nature, and the fourth method is partly kinematic, but neither of these approaches is possible unless the dynamics of the system is understood.
The Hydrodynamic Equations
The Hydrodynamic Equations of Motion in a Fixed and in a Rotating Coordinate System. One of the fundamental laws of mechanics states that the acceleration of a body equals the sum of the forces per unit mass acting on the body. This law is applicable not only to individual bodies but also to every part of a fluid. The hydrodynamic equations of motion express only this simple principle, but, when dealing with a fluid, not only the equations of motion must be satisfied, but also the equation of continuity and the proper dynamic and kinematic boundary conditions.
The hydrodynamic equations of motion as developed by Euler take into account two forces only: an external force acting on a unit mass, and the total pressure gradients per unit mass. If the components of the
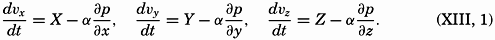
In this form or in the form obtained by substituting equation (XII, 17) for dv/dt, the equations represent the basis of classical hydrodynamics and have been used extensively for the study of many types of fluid motion. The only external force that needs to be considered in these cases is the acceleration of gravity. If the coordinate system is placed with the xy plane coinciding with a level surface, the equation takes an especially simple form, because the horizontal components of the external force vanish and the vertical is equal to g:
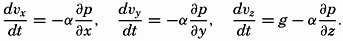
In many problems, friction must be considered, and to each equation a term must be added to represent the components of the frictional force.
The coordinate system used in these cases is rigidly connected with the earth and therefore takes part in the earth's rotation. When, for example, the flow through a pipe is analyzed, the x axis is placed in the direction of the pipe. This procedure is justified on the empirical basis that the observed motion can be correctly described in this manner. This fact, and only this fact, made possible the development of the Galileo-Newton mechanic. Phenomena exist, however, which cannot be adequately described by means of the simple equations of motion if accurate observations are made, as, for instance, the free fall of a body or the exact oscillation of a pendulum. In these cases the discrepancies between theory and observations are not very great, but for the large-scale motions of the atmosphere and the sea the discrepancies become so great that the simple equations fail completely.
The question arises as to whether it is possible to find another coordinate system in which the equations of motion in their simple form will describe the observed phenomena in an empirically correct manner. Experience has shown that this appears always to be possible. In the case that is of special interest here, it is found that the large-scale motion of the ocean waters can be dealt with if it is referred to a coordinate system, the center of which is placed at the center of the earth and the axes of which point toward fixed positions between the stars. Relative to this coordinate system the earth rotates once around its axis in twenty-four sidereal hours, and any coordinate system that is rigidly connected with the earth takes part in this rotation. The motion of a body on the earth relative to this “fixed” coordinate system is, as a rule, called the “absolute motion,” but incorrectly so because this “fixed” coordinate
It is impractical, however, to describe the currents of the sea in terms of “absolute” motion, for the interest centers around the velocities relative to the earth, and the problem is therefore to transform the simple equations of motion in such a manner that the new equations give the motion relative to a coordinate system that rotates with the earth. The transformation would require the development of equations which would otherwise not find use. The interested reader is therefore referred to the complete presentation by V. Bjerknes and collaborators (1933), from which part of the above explanation is taken. The transformation leads to the result that, if the equations of motion shall be valid in a coordinate system that rotates with the earth, it is necessary to add on the right-hand side of the equations the accelerations:
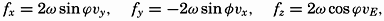
When applying the equations of motion to oceanographic problems, a left-handed coordinate system is used with the positive z axis directed downward. Taking this into account, adding the deflecting force of the earth's rotation, and including an as yet undetermined friction force with components per unit volume Rx, Ry, and Rz, one obtains the equations of motion in the form
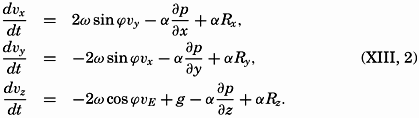
The Deflecting Force of the Earth's Rotation. Many attempts have been made to show directly, without undertaking the complete transformation of the equation of motion, that the rotation of the coordinate system must be taken into account in the above manner. These
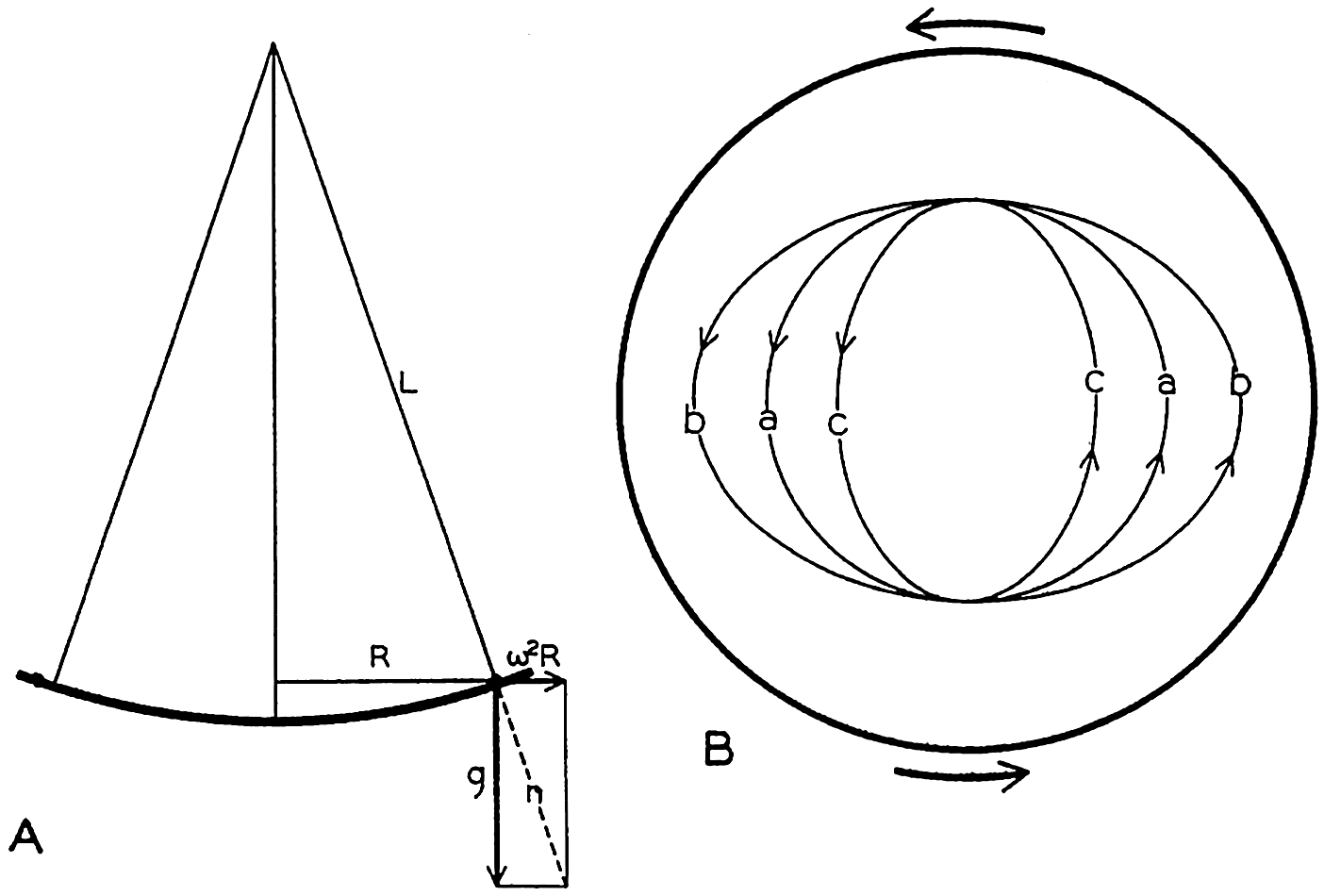
Motion of a body on a rotating disk. (A) Profile of the disk. (B) Different orbits of moving bodies.
Consider a disk that in an “absolute” system rotates at an angular velocity ω. Assume that a uniform gravitational force acts in the direction of the axis of rotation and that the disk has such a shape that the surface is normal to the resultant of the acceleration of gravity and the centrifugal force (fig. 101). Assume, furthermore, that the surface of the disk is absolutely smooth and offers no frictional resistance to any moving body. On these assumptions a body that rotates with the disk will complete one revolution in the time T = 2π/ω. A body that does not move in respect to an outside observer will, on the other hand, when placed on the disk, oscillate back and forth between two extreme distances from the center, R. The rotation of the disk does not affect this motion, since it has been assumed that the surface of the disk is frictionless. The period of the oscillation is easily found because in the first approximation the oscillation can be considered a pendulum motion (fig. 101). The period of oscillation of a pendulum is

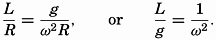
Therefore, T′ = 2π/ω = T, where T is the time in which the disk completes one revolution.
If the observer gives the body a velocity equal to the velocity of the disk at the point at which he places it, the body will travel around with the disk and complete one revolution in the time T = 2π/ω. If the body is given a velocity greater or less than the velocity of the disk (fig. 101b or c), it will describe an ellipse in the same time T.
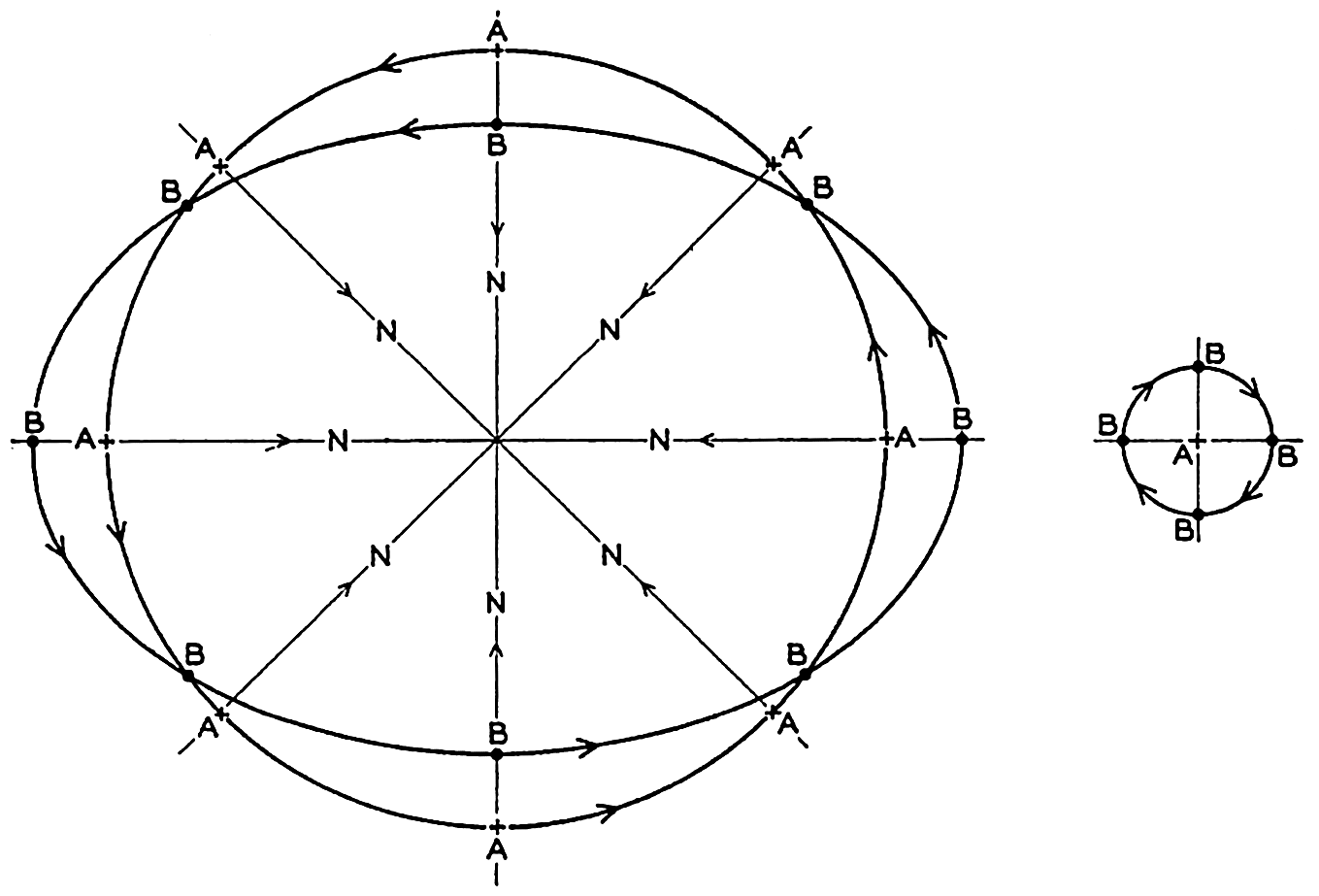
Motion of a body on a rotating disk as seen by an observer who looks down on the disk (left) or by an observer on the disk (right).
So far, the motion has been described relative to a fixed coordinate system. Now consider what an observer on the disk sees. This observer will refer the motion of the body to a coordinate system which, like himself, rotates with the disk and will, for instance, let the positive x axis point toward the center of the disk (fig. 102). Let the direction of the positive x axis be called north. Assume that the body at the time t = 0 was to the north of the observer and traveling faster than the disk. At the time t = T/8 the body will be to the east of the observer, at the time t = T/4 it will be to the south of the observer, at the time t = 3T/8 it will be to the west, and at the time t = T/2 it will again be to the north. To the observer it will therefore appear that the body travels in circles
The apparent angular velocity of the body will be 2ω, and the linear velocity will be 2ωr, where r is the radius of the circle. In order to account for this motion the observer will say that a deflecting force directed toward the center of the circle exists which exactly balances the centrifugal force of the circular motion. The deflecting force must be equal to
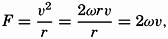
The deflecting force performs no work, because it is always directed at right angles to the velocity. This conclusion is obvious, since the deflecting force is not a physical force but enters in the equations of motion only because the simple equations (XIII, 1) containing the physical forces have been transformed from the fixed coordinate system in which they are valid to a rotating coordinate system. It is a force, however, which, when dealing with relative motion, is just as necessary as any other force for a correct description of the motion, and which to an observer in the rotating system has the same “reality” as other forces.
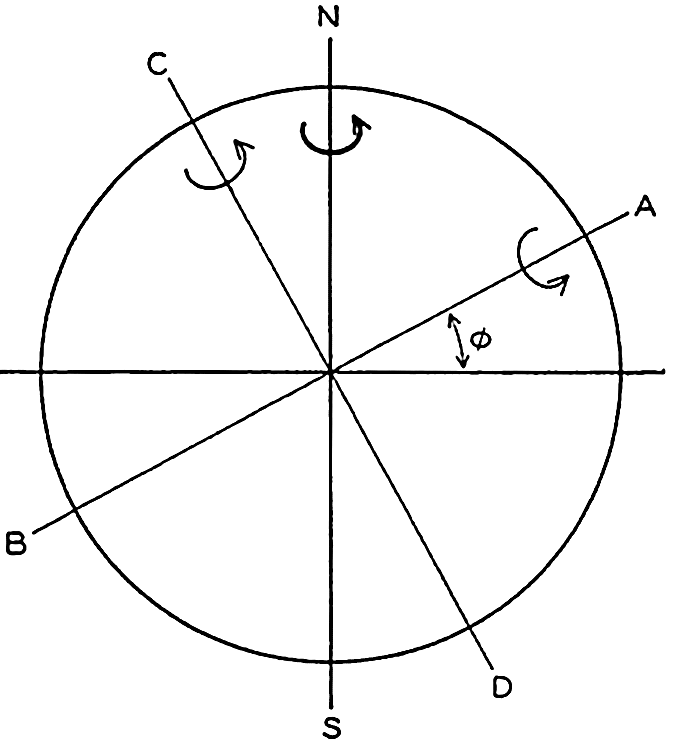
Rotation of the earth around the axis N-S decomposed in rotations around the axes A-B and C-D.
The above reasoning is directly applicable to conditions very near the poles of the earth, because a level surface on the earth is normal to the resultant of the force of gravitational attraction and the centrifugal force due to the earth's rotation.
In order to find what happens at a locality M at an angular distance of ϕ from the Equator (fig. 103), the rotation around the axis N-S can be considered as resulting from two rotations around the axes A-B and C-D. The angular velocities of rotation around these axes are ω sin ϕ and ω cos ϕ, respectively, if ω is the angular velocity of rotation around N-S. The rotation around C-D produces the vertical deflecting force
If no other forces are acting, the deflecting force must be balanced by a centrifugal force which, if the radius of the orbit is called r, is equal to ν2/r. Therefore
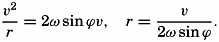
The radius of the orbit remains practically constant if the motion is such that variations in latitude are small, meaning that the particle will move in a circle of radius r. This circle is called the circle of inertia, because this circle, which appears in the relative motion, corresponds approximately to the straight-line inertia movement that characterizes “absolute” motion. In lat. 40° the radius of the circle of inertia is 106 m, 1060 m, and 10.6 km, respectively, if the velocity of the particle is 1 cm/sec, 10 cm/sec, or 100 cm/sec. The angular velocity of the body is 2ω sin ϕ, and the time required for one completion of the circle of inertia is therefore T′ = 2π/2ω sin ϕ. This time is called one half pendulum day, because it equals half the time required for a complete turning of the plane in which a pendulum swings (Foucault's experiment).
The motion in the circle of inertia in the Northern Hemisphere is clockwise, but in the Southern Hemisphere it is counterclockwise. In view of the fact that to an observer who faces the Equator the sun appears in the Northern Hemisphere to travel clockwise across the sky, and in the Southern Hemisphere counterclockwise, Ekman has introduced the term cum sole for describing the direction of motion in the inertia circle in both hemispheres. Similarly, the term contra solem describes rotation in the opposite direction.
It was stated that, when dealing with relative motion, the deflecting force is just as “real” as any other force. It can nevertheless be neglected when dealing with most problems of mechanics because, as a rule, it is very small compared to other forces. For instance, consider an automobile weighing 1500 kg which travels on a flat road in 40°N at constant speed of 75 km/hour (47 miles/hour) when the motor develops 15 kw (20.4 hp). The force per unit mass acting in the direction in which the car travels is then equal to 41.3 dynes/g. As the motion is steady, this force must be balanced by the resultant of the friction against the road and the deflecting force, but the deflecting force per unit mass, f = 2ω sin ϕ ν = 0.02 dyne/g, is less than 1/1000 of the other forces and can be neglected. The physical forces that maintain the motion of the atmosphere and the ocean, on the other hand, are of the same order of magnitude as the deflecting force, which therefore becomes of equal importance.
The effect of the rotation of the earth has been given so much consideration because in most problems the effect of the rotation enters and because the nature of the deflecting force should be thoroughly understood.
Motion in the Circle of Inertia. If the deflecting force of the earth's rotation is the only acting force, the equations of motion are reduced to
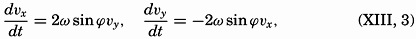
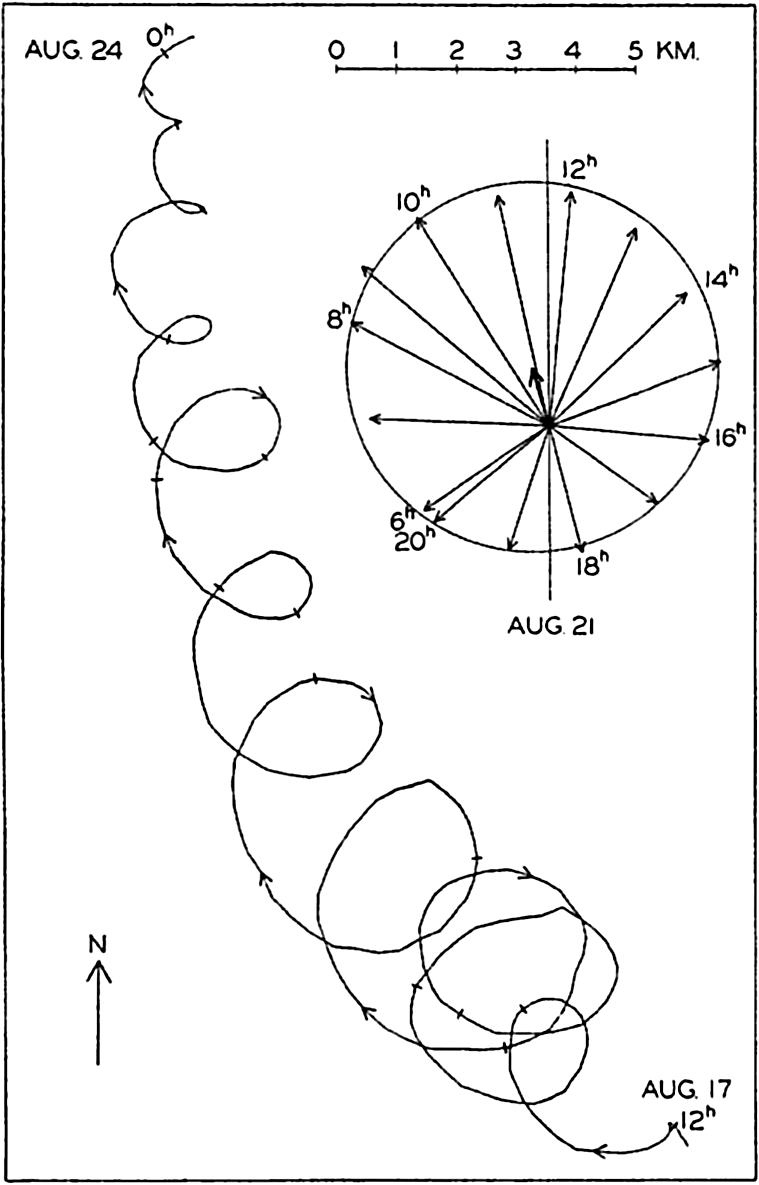
Rotating currents of period one-half pendulum day observed in the Baltic and represented by a progressive vector diagram for the period, Aug. 17 to Aug. 24, 1933, and by a central vector diagram between 6h and 20h on Aug. 21 (according to Gustafson and Kullenberg).
Gustafson and Kullenberg have represented the results of the records in the form of a “progressive vector diagram” (fig. 104), which is prepared
The curve shows a general motion toward the northwest and later toward the north, and superimposed upon this is a turning motion to the right, the amplitude of which first increases and later decreases. This rotation to the right (cum sole) is brought out by means of the inset central vector diagram in which the observed currents between 6h and 20h, August 21, are represented. The end points of the vectors fall nearly on a circle, as should be expected if the rotation is a phenomenon of inertia, but the center of the circle is displaced to the north-northwest, owing to the character of the mean motion.
The period of one rotation was fourteen hours, which corresponds closely to one half pendulum day, the length of which in the latitude of observation is 14h08m, and on an average the periodic motion was very nearly in a circle. It is possible that this superimposed motion can be ascribed to the effect of wind squalls and that the gradual reduction of the radius of the circle of inertia is due either to frictional influence or to a spreading of the original disturbance, but a theoretical examination by Defant suggests that inertia oscillations of this nature are associated with internal waves (p. 596). This was the case at the Altair station in lat. 44°33′N to the north of the Azores, where a rotating current of period 17h was present (Defant, 1940) corresponding very closely to a period of one half pendulum day and varying with depth in the manner found in internal waves. Ekman (1939) believes that the twenty-four-hour oscillations observed by himself and Helland-Hansen (1931) in about latitude 30°N are related to inertia movement.
The measurements that have been mentioned and other observations of currents made in deep water from anchored vessels (Defant, 1932, Lek, 1938) also show oscillating currents of tidal periods, some of which appear to be ordinary tidal currents, whereas others are associated with internal waves of tidal periods. In most instances, only tidal periods dominate and, according to Seiwell (1942), a period of one half pendulum day is not found in numerous oscillations which he has examined. It should perhaps be concluded that, although inertia movements may be found in the sea, it is still doubtful whether such a type of motion is very common. Arguments can be advanced against the general occurrence of movements in the inertia circle (Ekman, 1939).
The Equations of Motion Applied to the Ocean. When applying the equations of motion to the ocean, certain simplifications can be made. The vertical acceleration and the frictional term Rz can always be neglected. Similarly, the term depending upon the vertical component
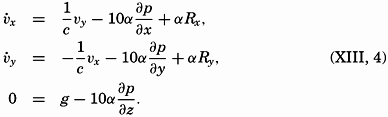
At perfect hydrostatic equilibrium the isobaric surfaces coincide with level surfaces, but this is no longer the case if motion exists. At any given time an isobaric surface is defined by (p. 155)
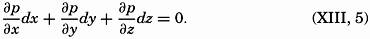
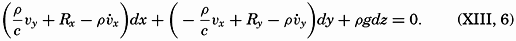
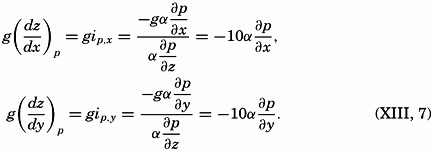
Introducing the geopotential slope defined by iD,x = dD/dx, iD,y = dD/dy, and measuring the geopotential in dynamic meters, dD = gdz/10 (p. 403), one obtains
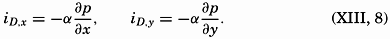
Thus, the geopotential slope in dynamic meters per meter equals the product of the specific volume and the pressure gradient in decibars per meter. These relations will find extensive use.
A dynamic boundary condition must be added to the kinematic boundary condition (p. 424)—namely, that at any boundary surface the pressure must be the same on both sides of the surface. This condition also applies to internal boundaries, separating water of different density, in which case the condition states only that the pressure must vary continuously. The densities and velocities may, however, vary abruptly when passing from one side of the boundary surface to the other. Calling the densities on both sides ρ and ρ′, and the velocities ν and ν′, and omitting the frictional terms and the accelerations, one obtains the dynamic boundary condition in the form
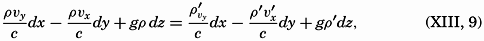
The dynamic energy equation is obtained by considering that the work done by a force is equal to the product of the force and the distance traveled in the direction of the force. Multiplying the equations of horizontal motion by νx and νy, respectively, and adding, one obtains
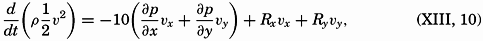
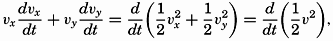
The equation is of small interest because it tells only that the increase of kinetic energy per unit volume equals the work performed per unit volume by the acting forces, but combined with the thermodynamic energy equation it becomes of importance. The complete derivation is given by V. Bjerknes and collaborators (1933), and here only the result for a system which is enclosed by solid boundaries is stated:
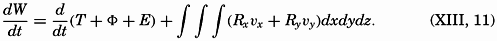
Here, W is the amount of heat added to the system, T is the total kinetic energy of the system, Φ is the potential, and E is the internal energy. If the total energy of the system remains unaltered, the amount of heat added in unit time must equal the work per unit time of the frictional forces. If, on the other hand, no heat is added, the work of the frictional forces must lead to a change of the total energy of the system.
Currents Related to the Field of Pressure
Relative Currents and Slope Currents. The above considerations are all general and are valid regardless of the character of the pressure field. When discussing the latter (p. 413) it was pointed out that the total pressure field could always be considered as composed of two parts: the relative field of pressure due to the field of mass, and the slope field due to actual piled-up masses: pt = p − Δp, where pt is the total pressure and p is the relative pressure, and where the last term represents a correction due to piled-up masses. With the pressure in decibars, Δp = gρΔh/10, where Δh represents the thickness of the removed or added mass in meters, and is positive when mass is removed, because the positive z axis is directed downward.
The total pressure gradient, therefore, has the components
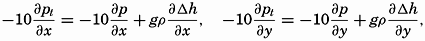
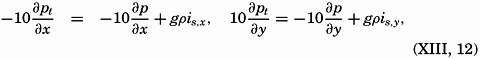
Introducing equation (XIII, 12) in the equation of motion, considering that pt has previously been written p, and omitting the frictional terms, one obtains
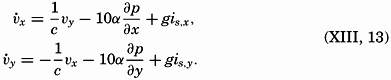
In the first approximation, therefore, writing νx = νp,x + νs,x and νy = νp,y + νs,y, one obtains
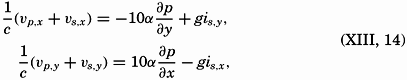
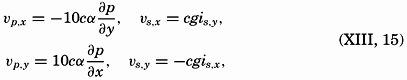
These equations mean that the current can be considered as composed of two parts: one which is dependent on the relative field of pressure and will be called the relative current, and one which depends on the added slope of the free surface and will be called the slope current. Ekman has called the relative current the convection current, but this term, as pointed out by Ekman, is liable to cause confusion because, in meteorology, convection currents mean ascending and descending currents and not horixontal flow.
Of these two types of currents, only the relative current can be derived from observations of density, because only the relative field of pressure can be determined from such observations. Any added slope of the isobaric surfaces due to actual piling up of mass in certain instances can be derived from precise leveling along coasts, but in general it cannot be observed. It is of great importance to bear these facts in mind in order to avoid erroneous conclusions.
The character of the slope current is readily seen. Equations (XIII, 15) state that the velocity is always directed at right angles cum sole relative to the slope. As the slope is independent of the depth, the same therefore applies to the velocity. Thus, if slope currents exist, they are uniform from top to bottom, in contrast to the relative currents, which vary with depth.
In the equations which, on the above assumptions, determine the relative current, the geometric or the geopotential slope of the relative isobaric surfaces can be introduced (p. 440):
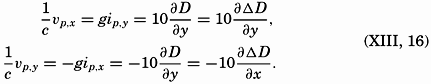
Currents in Stratified Water. Some of the outstanding relationships between the distribution of mass and the velocity field are brought out by considering two water masses of different density, ρ and ρ′, where ρ is greater than ρ′. In the absence of currents, the boundary surface between the two water masses is a level surface, the water mass of lesser density, ρ′, lying above the denser water. On the other hand, if the water of density ρ′ moves at a uniform velocity ν′ and the water of greater density moves at another uniform velocity ν, the boundary must slope. For the sake of simplicity it will be assumed that both water masses move in the direction of the y axis and that the acceleration of gravity g can be considered constant. The dynamic boundary condition (p. 441) then takes the form
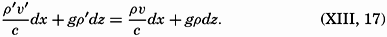
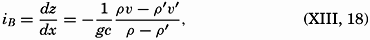

As an extreme case, consider two water masses, one of salinity 34.00 ‰ and temperature 20°, and one of salinity 35.00‰ and temperature 10°, and assume that the velocity of the former is 0.5 m/sec. Neglecting the effect of pressure on density, one obtains
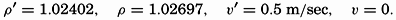
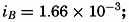
The slopes of the isobaric surfaces are much smaller. Inserting the numerical values in equation (XIII, 19), one obtains
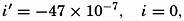
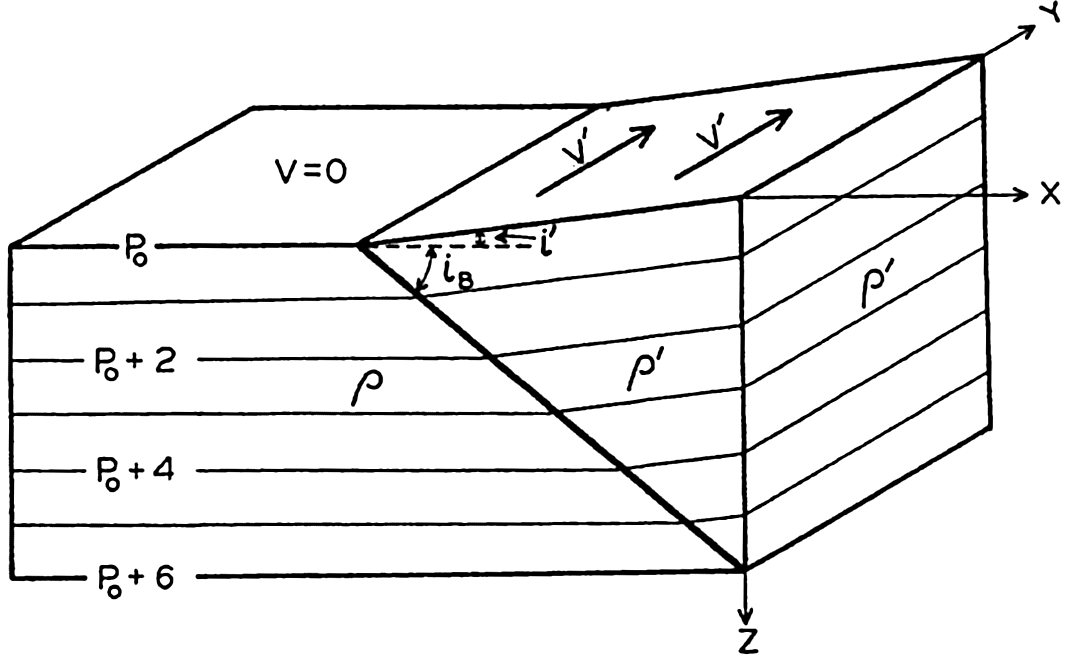
Isobaric surfaces and currents within a wedge of water which extends over resting water of greater density.
As another example, consider the case in which the current in the upper layer is limited to a band L. In this case, perfect static equilibrium must exist in the regions of no currents, and there the boundary between the two water masses must be horizontal, but in the region where the water of low density flows with a velocity ν′, the boundary surface must slope, the steepness of the slope being determined by equation (XIII, 18). These conditions are shown schematically by the block diagram in fig. 106, in which it is supposed that the denser water reaches the surface on the left-hand side of the current. This figure brings out an important relationship between the current and the distribution of mass: The current flows in such a direction that the water of low density is on the right-hand side of the current, and the water of high density is on the left-hand
Other examples could be added (Defant, 1929b), but the two which have been given here demonstrate sufficiently the relation between the currents and the distribution of mass in stratified water.
In the ocean a discontinuous transition from one type of water to another is never found, but in several regions a transition takes place in such a short distance that for practical purposes the layer of transition can be considered as a boundary surface. In such cases, equation (XIII, 18) can be used for computing the relative currents in a direction parallel to the boundary surface. Certain simplifications can be introduced, because ρ and ρ′ always differ so little that (ρν − ρ′ν′) can be replaced by 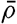 (ν − ν′). Therefore, the relative velocity can be computed by means of the equations
(ν − ν′). Therefore, the relative velocity can be computed by means of the equations
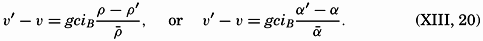
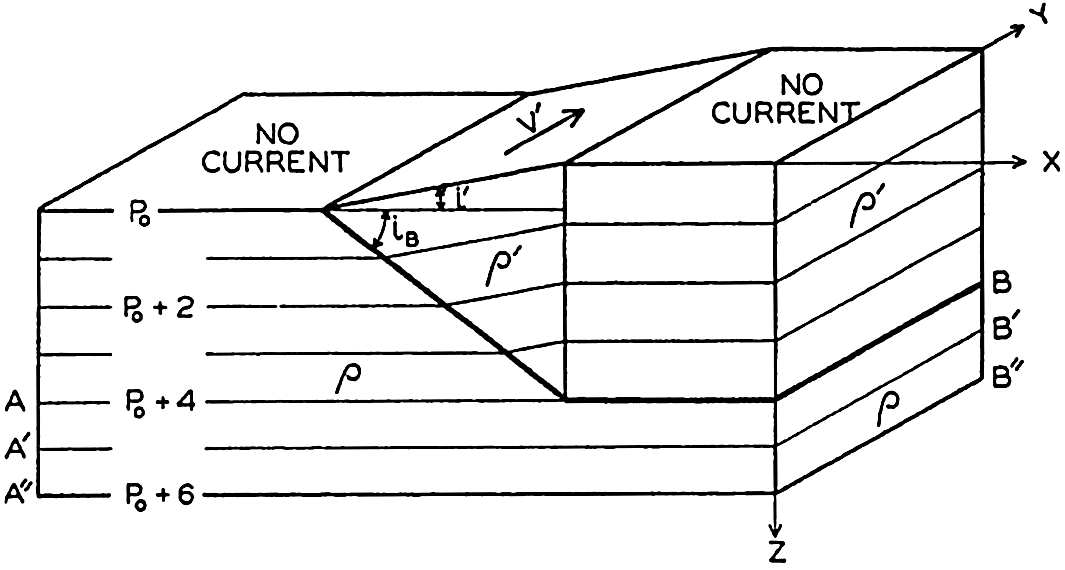
Isobaric surfaces and curreants within water which in part extends as a wedge over resting water of greater density.
The relative slope of the isobaric surfaces (XIII, 19) can also be expressed by means of the slope of a boundary layer:
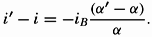
The above equation can be derived in a different manner. In fig. 106, it has been assumed that the isobaric surfaces that lie completely in the
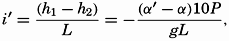
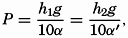
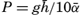 . With this value, one obtains
. With this value, one obtains
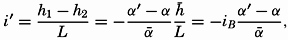
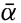 /L equals the slope of the boundary surface.
/L equals the slope of the boundary surface.Where the isobaric surfaces slope, a current must flow in a direction at right angles to the slope, and with such velocity that the component of gravity acting along the slope is balanced by the deflecting force of the earth's rotation:
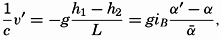
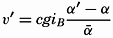

Currents in Water in Which the Density Increases Steadily with Depth. The discussion in the preceding paragraph leads directly to corresponding formulae in the general case in which the density of the water increases steadily with depth. The relative velocity has, as previously, the numerical value ν1 − ν2 = cgip1−p2, where ip1−p2 is the inclination of the isobaric surface p1 relative to the isobaric surface p2.
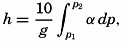
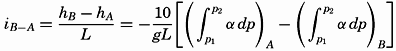
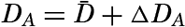 and
and 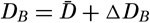 (p. 408), the equation is reduced to
(p. 408), the equation is reduced to
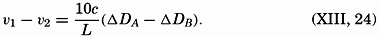
By means of the relations between the field of pressure and the field of mass, which were derived on p. 410, one similarly obtains (Werenskiold, 1937)

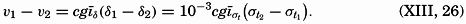
Equations (XIII, 26) are of practical importance because they facilitate a rapid survey of the relative currents at right angles to a section in which the field of mass has been represented by means of the anomalies, δ, or by means of σt curves. The inclination of a curve is positive when the curve slopes downward from left to right, because the positive z axis points downward (see fig. 107). Since “pressure”
In the Northern Hemisphere the current at one depth relative to the current at a greater depth flows away from the reader if, on an average, the δ or σt curves in a vertical section slope downward from left to right in the interval between the two depths, and toward the reader if the curves slope downward from right to left. In the Southern Hemisphere the current flows toward the reader if the curves slope downward from left to right, and away from the reader if the curves slope downward from right to left.
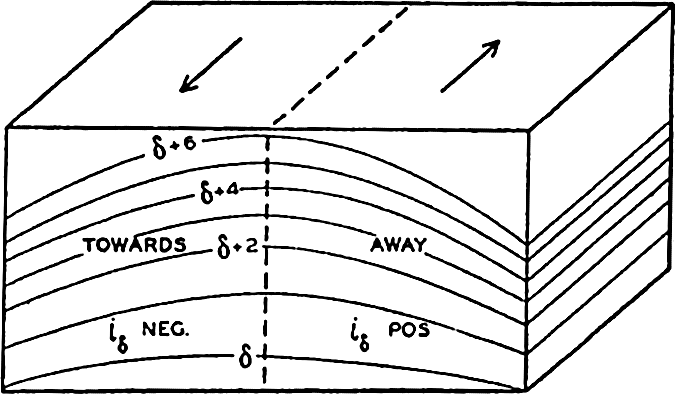
Schematic representation of a field of mass and of the direction of the currents which must be present if the field shall remain stationary (Northern Hemisphere).
These rules make possible an orientation as to the direction of the relative currents by a glance at a δ or σt section and a rapid computation of the approximate velocities.
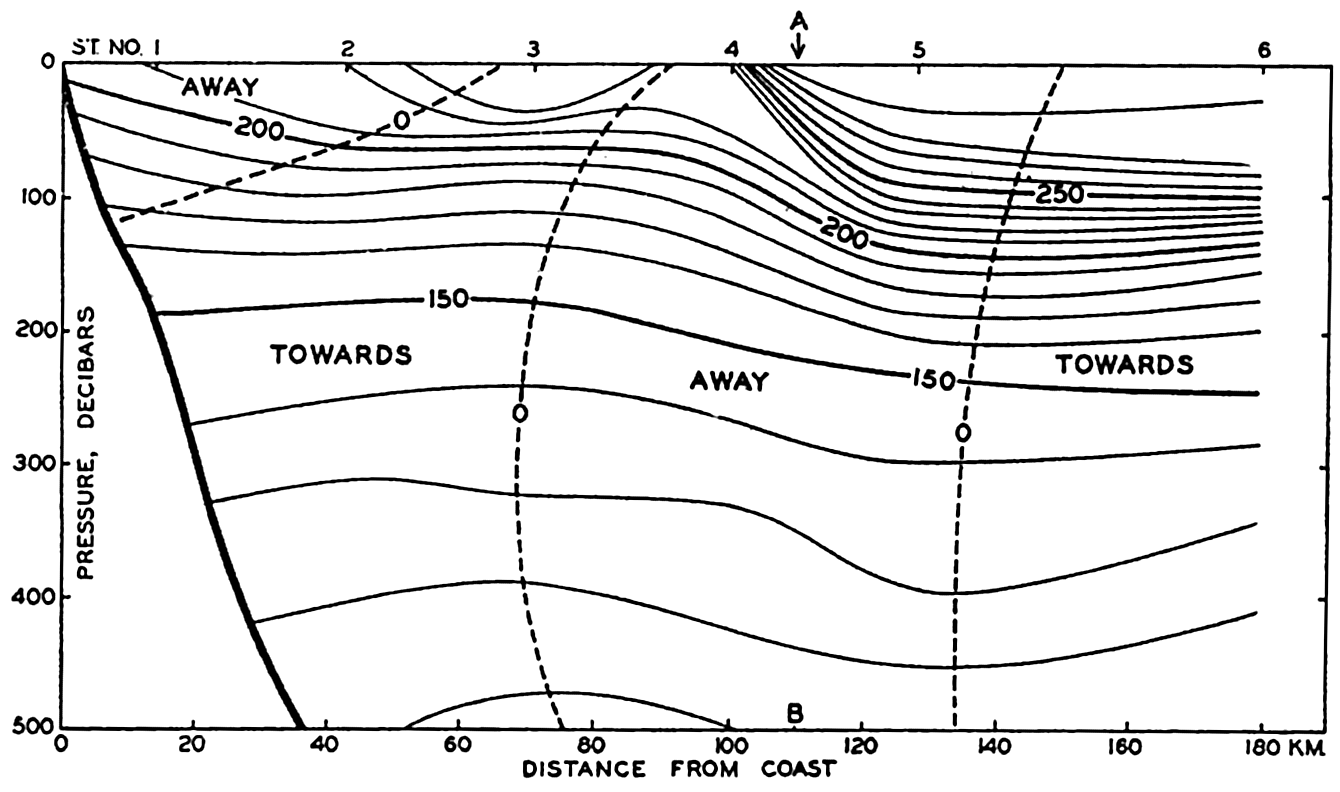
Specific volume anomalies in a vertical section at right angles to the coast of California in lat, 34.5°N, and direction of corresponding currents above 500 decibars.
Fig. 108 gives an example of a section at right angles to the coast of California in lat. 34.5°N. The section runs in the direction northeast-southwest, and the reader looks southeast. In the section, δ curves are entered at intervals of 10 × 10−5. The velocity relative to the
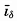 is approximately zero between them and the 500-decibar surface. To the right the relative current is directed toward the reader, and to the left it is also directed toward the reader except within the upper layer. In the middle a strong current is directed away from the reader, toward the southeast. Along the line A-B,
is approximately zero between them and the 500-decibar surface. To the right the relative current is directed toward the reader, and to the left it is also directed toward the reader except within the upper layer. In the middle a strong current is directed away from the reader, toward the southeast. Along the line A-B,
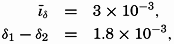
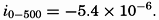
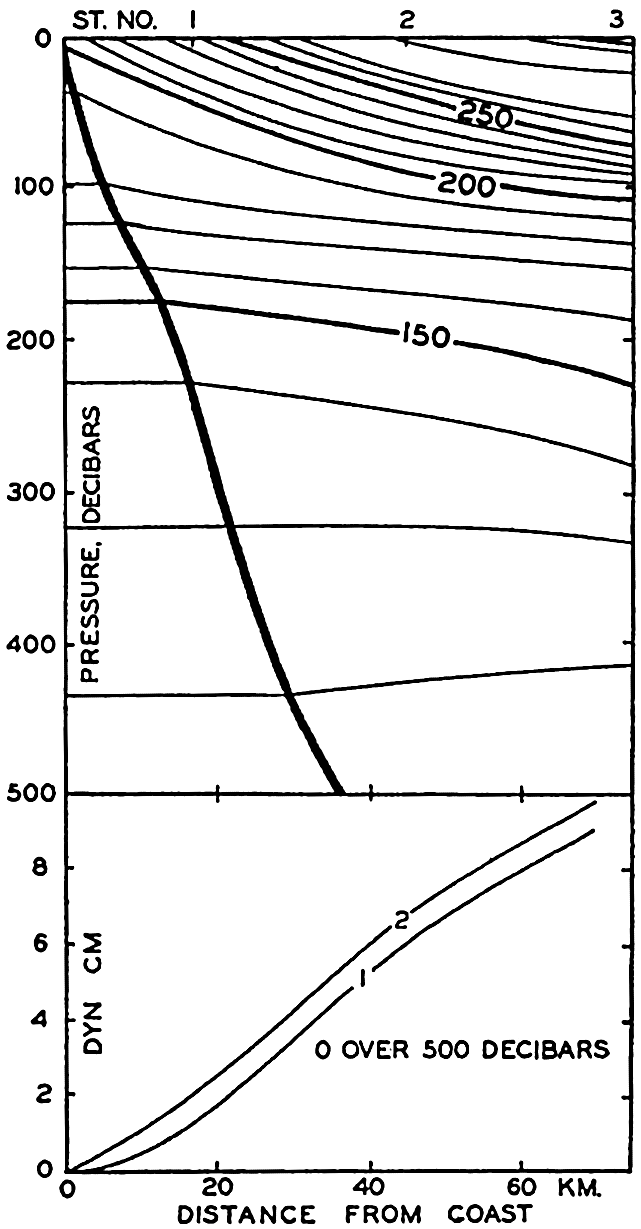
Upper. Specific volume anomalies in a vertical section at right angles to the coast of California in lat. 34.5°N. Lower. Profiles of sea surface computed (1) by continuing the anomaly curves horizontally from the point where they intersect the sea bottom, or (2) by assuming that the slope of the anomaly curves at the bottom determines the slope of the isobaric surface (see text).
Fig. 108 brings out a difficulty that is encountered when dealing with conditions in a section which extends into shallow water. In the figure the δ curves have been drawn to the solid line that represents the contour line of the bottom. Formula (XIII, 26), for computing the slope of the free surface relative to the slope of the 500-decibar surface, is applicable, however, only where the depth to the bottom is greater than 500 m, and loses its meaning if the depth to the bottom is less. The question then arises as to how the inclination of the free surface shall be computed when the depth to the bottom is less than the depth of the standard isobaric surface to which the inclination is referred. At the suggestion of Nansen, Helland-Hansen (1934) introduced a method which is actually based on the assumption that along the bottom both the
A similar method has been proposed by Jacobsen and Jensen (1926), but their formula introduces the additional assumptions that the profile of the bottom of the sea is a straight line and that the δ curves are parallel and at equal distances.
The assumption that the velocity vanishes at the bottom is probably always correct because of the influence of friction, but it is doubtful if the slope of the isobaric surface vanishes. As another approximation, one can apply the equation ip = −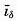 (δ1 − δ2) (p. 412), introducing the slope of the δ surfaces where they cut the bottom and taking the difference δ1 − δ2 along the bottom. In the lower part of fig. 109 the profile of the free surface is shown as computed by means of the two assumptions. The difference in this case is very small and, even under extreme conditions, will never be very significant.
(δ1 − δ2) (p. 412), introducing the slope of the δ surfaces where they cut the bottom and taking the difference δ1 − δ2 along the bottom. In the lower part of fig. 109 the profile of the free surface is shown as computed by means of the two assumptions. The difference in this case is very small and, even under extreme conditions, will never be very significant.
No general rule can be given as to what method should be preferred. One may encounter conditions in which the assumption that the slope of the isobaric surface vanishes at the bottom is justified, and in such cases Helland-Hansen's method should be used, but in other instances, where it may appear improbable that the slope of the isobaric surface is zero near the bottom, the last-mentioned method should be preferred.
Practical Method for Computing Relative Currents. The formulae that have been dealt with in the last chapter are applicable to computation of currents at right angles to a vertical section. In order to derive a method for computing the currents in space, it is necessary only to return to equation (XIII, 16), which states that in the absence of friction and acceleration the velocity must be such that the deflecting force of the earth's rotation balances the component of gravity acting along an isobaric surface. It is now desirable to drop the assumption that the acceleration of gravity can be considered constant and to use the geopotential slope of isobaric surfaces instead of the geometric slope. It follows from equation (XIII, 16) that, on the assumptions made, the direction of the velocity will be normal to the slope of the isobaric surfaces—that is, parallel to the contour lines of the topography of the surfaces. The magnitude of the velocity will be inversely proportional to the distance between the contour lines, the factor of proportionality depending upon the latitude. The whole problem of presenting the
As has already been stated (p. 412), oceanographic observations can give information only as to the relative topographies, and therefore only as to the relative velocities. When using the term “relative velocity,” one should bear in mind that the absolute velocities (referred to the rotating earth) are not obtained by adding a constant value to the relative velocities, but that the value which has to be added in order to obtain the absolute velocities varies from one point to another, depending upon the unknown slope of the isobaric surface that has been used as a reference surface.
The contour lines of the isobaric surfaces represent the stream lines of the relative motion, but they are not, as a rule, identical with trajectories even if the reference surface is sufficiently level so that the computed velocities represent the absolute motion. If such is the case, the contour lines will be trajectories only if the motion is stationary—that is, if ∂ν/∂t = 0 (p. 157). Because it has been assumed that dv/dt = 0, it follows that the conditions
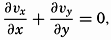
It is also of great importance to remember that equations (XIII, 16) and (XIII, 22) express nothing as to cause or effect. They do not state that the current is present because the distribution of mass is such and such. Nor do they state that the distribution of mass shows certain
The computation of the geopotential distances between isobaric surfaces has already been discussed, and the whole problem of computing ocean currents would therefore be very simple if (1) simultaneous observations of temperature and salinity at different depths were available from a number of stations so that relative topographies could be constructed, (2) accelerations could be neglected, (3) frictional forces could be neglected, and (4) periodic changes in the distribution of mass as related to internal waves (p. 601) were negligible.
Simultaneous observations from a number of stations are never available, and the question therefore arises as to whether charts based on stations that have been occupied within a certain time interval can be considered as approximately representing a synoptic situation. This question can be examined by repeated surveys of the same area. Such surveys have shown that conditions vary in time, but so slowly that the main features of a certain topography are represented correctly by nonsimultaneous observations that have been taken within a reasonably short time interval. Results of repeated surveys are found in the publications of the U. S. Coast Guard presenting the work of the International Ice Patrol off the Grand Banks of Newfoundland, where a small area has been covered in less than a week and where cruises have been repeated at intervals of three to four weeks. In these intervals of time the details of the relative topography have changed greatly, but the main features have changed much more slowly. Similar surveys have been conducted off southern California by the Scripps Institution of Oceanography (Sverdrup and staff, 1942).
Fig. 110 shows the results of two cruises off the coast of southern California in 1940. The upper chart shows the topography of the surface relative to the 500-decibar surface according to observations between April 4 and 14, and the lower chart shows the corresponding topography on April 22 to May 3. The stations upon which the charts are based are shown as dots. The time interval between the cruises was about sixteen days, and, although the main features were similar, the details were greatly changed. Thus, in lat. 33°40′N, long. 120°W, the computed surface current on the first cruise was 36 cm/sec toward N 80°E, whereas on the second cruise it was 14 cm/sec toward S 30°E. In the time interval between the two cruises the average local acceleration was therefore 2.5 × 10−5 cm/sec2 toward S 57°W, but, compared to the acting forces, this is a small quantity. On the first cruise the numerical value of the geopotential slope of the surface was 294 × 10−5 cm/sec2, and on the second it was 117 × 10−5 cm/sec2. The total acceleration is generally of the same order of magnitude as the local acceleration, and was therefore also small. Even in these cases the stream lines of the flow approximately coincided with the contour lines, although the distribution of mass was changing continuously, and the combination of observations taken during ten days led to a somewhat distorted picture of the topography.
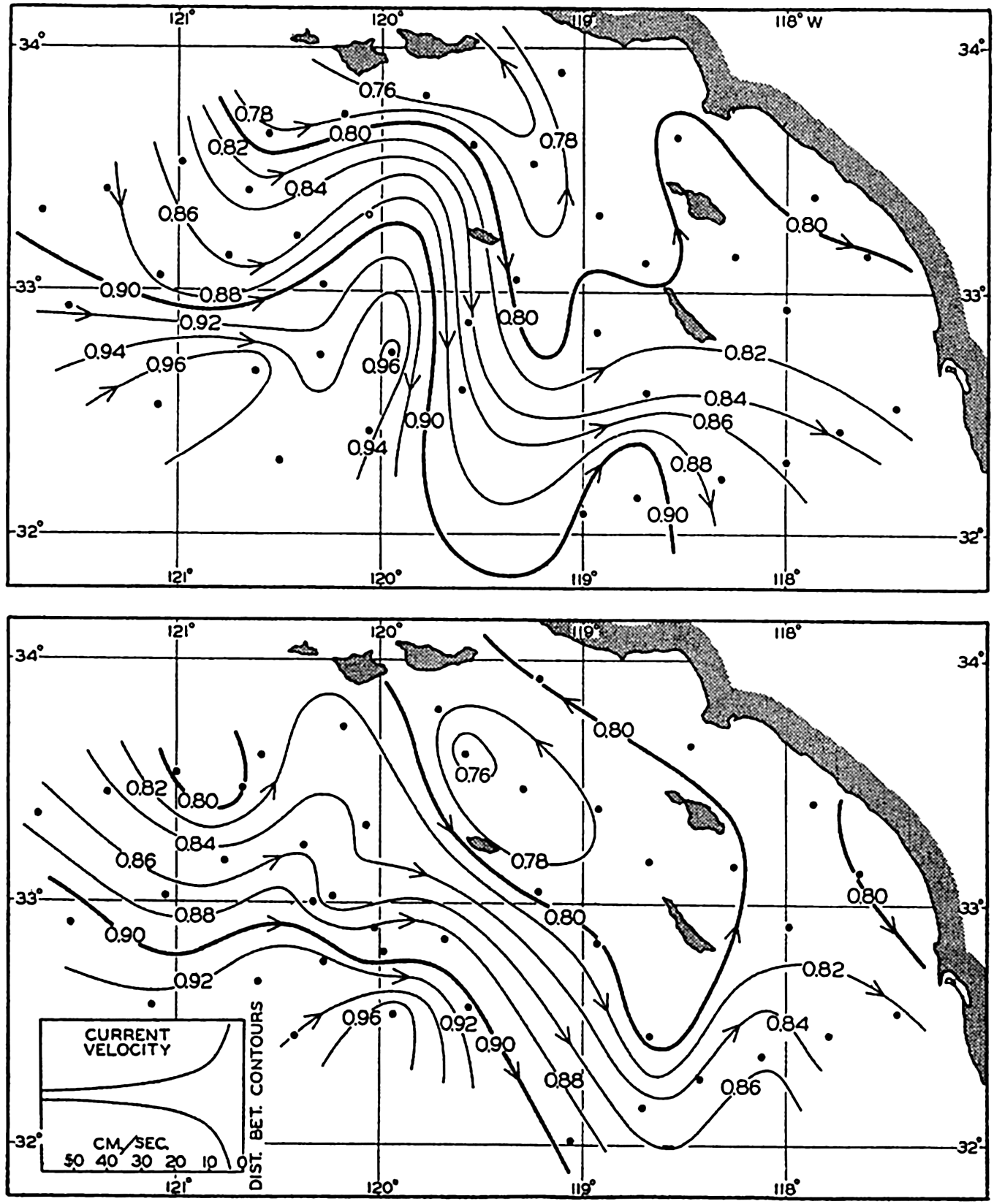
Geopotential topography of the sea surface in dynamic meters referred to the 500-decibar surface according to observations off southern California on April 4 to 14, 1940 (upper), and on April 22 to May 3, 1940 (lower).
As a rule, it can be stated that the smaller the area the more nearly simultaneous must observations be in order to permit conclusions as to currents. On the other hand, when dealing with ocean-wide conditions, observations from different years can be combined.
The second assumption, that the motion is not accelerated, is evidently not fulfilled when dealing with a smaller area within which conditions change rapidly, but, according to the above numerical example, no serious errors are introduced if one is satisfied with an approximate value of velocity. The assumption will be more closely correct when large-scale conditions are considered.
The third assumption, that the frictional forces can be disregarded, must also be approximately correct, as is evident from agreement obtained between computed surface currents and surface currents that are derived from ships' logs or from the results of experimentation with drift bottles. The fourth assumption is nearly correct where the accelerations are small. It can be stated therefore that the computations which have been outlined can be expected to render an approximately correct pictures of the relative velocities that are associated with the distribution of mass.
Absolute Currents Associated with the Field of Mass. In the discussion so far, we have considered only the relative currents associated with the relative field of pressure, but the ultimate goal must be to determine the absolute current. The problem of determining absolute currents can be dealt with in two steps. In the first place, one can consider whether there are reasons to assume that the absolute currents are determined completely by the internal distribution of mass. If this question is answered in the affirmative, one can decide what reference surface should be used in order to find the absolute motion.
The first question can be approached in the following manner: If the distribution of mass remains stationary, the flow must always be parallel to the isopycnals, because, if this condition is not fulfilled, the distribution of mass will be altered by the motion. On the assumptions made, the flow is always parallel to the isobars, and it follows, therefore, that under stationary conditions isopycnals and isobars must be parallel at all levels. It also follows that the isobars and isopycnals at one level must be parallel to those at all other levels (p. 157). This rule is identical with the “law of the parallel solenoids” of Helland-Hansen and Ekman (Ekman, 1923). The absolute motion that must be considered when dealing with distortion of the field of mass depends, however, on the total field, and this total field must evidently have the same geometrical shape as the internal field if the law of the parallel solenoid shall be fulfilled. The total field is composed of the internal and the slope fields (p. 413); consequently, these fields must coincide if the law of the parallel
The study of large-scale conditions in the ocean has shown that over large areas the isotherms and isohalines, and, consequently, the isopycnals, are parallel at different levels and that their direction coincides with the direction of the relative isobars or with the contour lines of the isobaric surfaces. This empirical result strongly supports the view that the large-scale currents are mainly determined by the internal distribution of mass. Even in small areas a similar arrangement is often found, but many exceptions are encountered there which clearly demonstrate that stationary conditions do not exist, and which may be interpreted as indicating that the details of the absolute currents are not determined by the distribution of mass.
The next question that arises is whether it is possible in the ocean to determine a surface along which the velocity is zero, so that absolute velocities are found when the relative motion is referred to this surface. Such a surface need not be an isobaric surface but may have any shape.
One school of oceanographers points out that the deep waters of the oceans are nearly uniform and that in the deep water the isopycnal surfaces are nearly horizontal. It is therefore assumed that in the deep water the isobaric surfaces are also nearly horizontal and that absolute currents are found if the reference level is placed at a sufficiently great depth.
A second school of oceanographers claims that the distribution of oxygen in the ocean must be closely related to the type of motion, and especially that the layer or layers of minimum oxygen content that are found over large areas must represent layers of minimum horizontal motion. Consumption of oxygen takes place at all levels, owing to biological processes, and it is reasoned that minimum oxygen content is found where the replenishment of oxygen by horizontal flow is at a minimum because of weak motion. Rossby (1936a) and Iselin (1936), among others, have drawn attention to the fact, which has been clearly demonstrated by Dietrich (1937a), that this conception may lead to peculiar results concerning the currents. In the Gulf Stream, with the 2000-decibar surface as reference surface, one finds flow in the direction of the Gulf Stream from the sea surface to a depth of 2000 m, whereas, by selecting the oxygen minimum layer as reference surface, one finds that the flow in the direction of the Gulf Stream is limited to the upper layers, while at greater depths the current flows in the opposite direction with velocities that increase toward the bottom. The latter type of flow appears unreasonable, and therefore the oxygen minimum layer in that case cannot be a layer of no motion.
Another argument may also be advanced against assigning dynamic significance to the oxygen minimum layer (Sverdrup, 1938a). As has already been stated with regard to this layer as a layer of minimum motion, it is argued that the low oxygen content is due to a slow replenishment of oxygen by horizontal flow. It must be borne in mind, however, that in the ocean the distribution of oxygen is nearly stationary, meaning that at any point the amount of oxygen which in a given time is brought into a given volume by physical processes, such as diffusion and horizontal flow, must exactly equal the amount which in the same time and volume is consumed because of biological processes. Therefore, if the oxygen minimum layer represents a layer of minimum replenishment, it must also represent a layer of minimum consumption, and this requirement leads to certain conceptions concerning the biological conditions in the ocean which at present appear arbitrary. From this point of view, it does not appear permissible to make use of the oxygen distribution when drawing conclusions as to the character of the currents, although cases exist in which a minimum oxygen layer may lie close to a surface of no motion (p. 161).
A third method has been employed by Defant (1941), who points out that in the Atlantic Ocean the relative distances between isobaric surfaces remain nearly constant within certain intervals of depth. He assumes that a surface of no motion lies within this interval, and arrives in this manner at a consistent picture of the shape of the reference surface in the Atlantic and at results which are in good agreement with those obtained by considering the equation of continuity.
A fourth method is based on the equation of continuity, but this method has so far been little used because it requires comprehensive data. The application can be illustrated by considering the currents of such an ocean as the South Atlantic. It is evident that the net transport of water (p. 465) through any cross section of the South Atlantic between South Africa and South America must be zero, because water cannot permanently be removed from the North Atlantic or be accumulated in that ocean, which is practically a closed bay. In the South Atlantic a surface of no motion must therefore be selected so that the flow to the north above that surface equals the flow to the south below the same surface (p. 465). Similarly, the surface of no motion has to be selected in other regions in such a manner that one arrives at a consistent picture of the currents, taking into account the continuity of the system and the fact that subsurface water masses retain their character over long distances. Examples of such pictures are shown in figs. 187 and 205. Hidaka (1940) has computed absolute currents by another application of the equations of continuity in the form div P = 0, div M = 0 (p. 426). This and similar methods should be more widely used.
Slope Currents. Variations of Sea Level. The fact that over large areas of the open oceans the law of parallel solenoids is nearly fulfilled indicates, as has already been stated, that no large-scale slope currents exist, but the absence of such currents does not exclude the possibility that slope currents may be found within small areas, particularly in coastal regions. It is probable that converging winds may lead to an actual piling up of water in certain areas, and diverging winds to a removal of water from other areas, thus creating slopes that may give rise to currents at all levels between the surface and the bottom. This type of slope current may be more readily developed near coasts, where piling up takes place against the solid boundary. So far, only indirect evidence exists for the occurrence in the open ocean of such slope currents, and this evidence will be dealt with later (p. 678).
Under the discussion of the general character of the distribution of pressure (p. 407) it was mentioned that the absolute topography of the free surface of a lake might be determined by means of very accurate measurements of the water level along the shores of the lake. This method has actually been used for studying the influence of the wind on the slope of the sea surface in such landlocked bodies of water as the Gulf of Bothnia (Palmén and Laurila, 1938). Similarly, it might seem possible to obtain an idea of the absolute topography of the ocean surface by exact leveling along the coasts, but this procedure encounters the difficulty that lines of precision leveling cannot be carried from one continent to the other. Precision leveling along the coasts of the United States has been completed, however, although as yet the interpretation of most of the results appears doubtful.
According to these results (Bowie, 1936) the mean sea level along the coast of the Gulf of Mexico generally drops eastward, but along the Atlantic coast of the United States the mean sea level rises to the north (table 81, p. 677). If friction can be disregarded and if slope currents do not exist, the differences in sea level should be completely accounted for by the differences in the average density of the water off the coast, provided that minor corrections for differences in atmospheric pressure have been applied. A study of the distribution of density (Dietrich, 1937b, Montgomery, 1938) shows that in the Gulf of Mexico the decrease of mean sea level toward the east is in good agreement with the density distribution. However, the rise toward the north along the two coasts cannot be accounted for in this manner. Dietrich (1937b) arrives at the conclusion that the rise along the Atlantic coast is due to frictional influence, and he states that a rise of the mean sea level along a coast in the direction of flow of the main current off the coast must be present where the addition of kinetic energy to the current is less than the destruction of kinetic energy by friction. Ekman (1939), however, expresses doubt as to the correctness of Dietrich's conclusion, and the
On the Pacific coast the mean sea level is horizontal between San Diego and San Francisco. To the north of San Francisco the sea level appears to rise, but this conclusion is based on records of sea level at the mouth of the Columbia River (Fort Stevens), where the outflow of fresh water may account for the higher sea level, and, further to the north, on records of sea level at great distances from the open coast. The rise toward the north is therefore not well established.
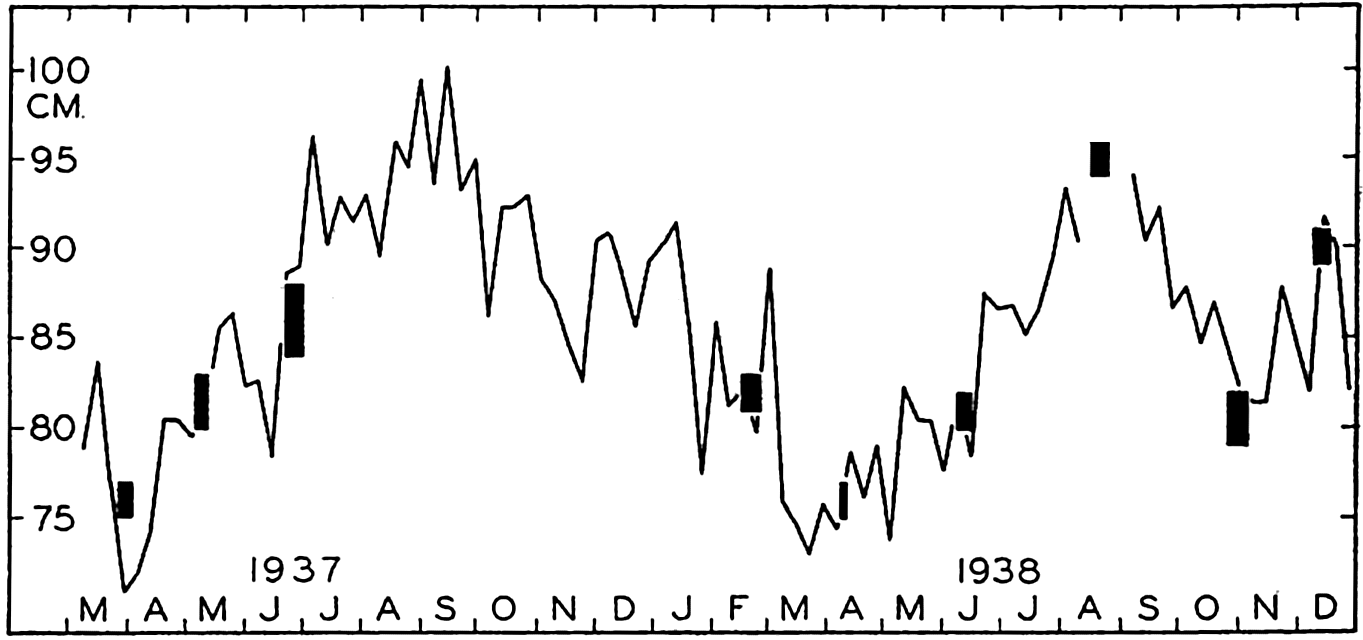
Variations of sea level at La Jolla, California, according to tidal records (curve), and according to observed variations in density above a depth of 500 m (columns).
Sea level on the Pacific coast is about 50 cm higher than on the Atlantic coast, and this difference may perhaps be related to the lower average density of Pacific water.
Variations in the average density of water columns appear capable of accounting for local variations in sea level, as is demonstrated by recent studies of Montgomery (1938) and LaFond (1939). The curve in fig. 111 (LaFond, 1939) shows weekly averages of sea level according to tidal records at La Jolla, California, and the black columns represent the sea level at La Jolla as extrapolated from charts showing the topography of the surface relative to the 500-decibar surface as derived from cruises in 1937 and 1938. The 500-decibar surface was used as reference because near the coast water of uniform density was encountered below a depth of 500 m. Columns have been entered instead of dots because extrapolation of the contour lines as far as the coast is uncertain. The height of the columns gives the probable limits within which sea level on the coast should lie, and the width corresponds to the length in time of the cruises. The agreement between the variations of sea level as
Off a coast near which the density of the coastal water may vary owing to external influences (whereas the density of the oceanic water remains relatively constant), the variations in sea level have direct bearing on the slope of the sea surface toward or away from the coast. Variation in sea level can thus be interpreted in terms of slope of sea surface—that is, in terms of a coastal current. Similarly, if a current flows between an island and a coast, there must be a difference in sea level across the current. Simultaneous registrations of sea level on the island and on the coast may be very helpful in detecting changes of the slope and, thus, in changes in the velocity of the current. For the purpose of detecting such changes, the Woods Hole Oceanographic Institution, with the cooperation of the U. S. Coast and Geodetic Survey, has established a permanent tidal station on Cat Cay, one of the Bimini Islands, which lies on the southeastern side of the Strait of Florida. The records at this station will be compared to those at Key West and Miami, Florida. It can be expected that these studies, which deal with variations in the slope, will amplify the knowledge of the total field of pressure.
Bjerknes' Theorem of Circulation. The general formula for computing ocean currents from the slope of the isobaric surfaces, ν =−gci, was derived by H. Mohn in 1885, but Mohn did not discriminate sharply between the slope due to internal distribution of mass and the slope due to external factors. Furthermore, the oceanographic observations at the time when Mohn presented his theory were not sufficiently accurate for computation of the relative field of pressure. Owing to these circumstances, and also to others depending on certain characteristics of the theory that have recently been explained by Ekman (1939), Mohn's formula received no attention. The corresponding formula for computation of currents associated with the relative distribution of pressure,
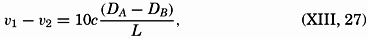
Bjerknes makes use of the term “circulation along a closed curve.” Consider a closed curve that is formed by moving particles of a fluid. The velocity of each particle has a component νs along the curve, and
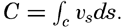 .
.If friction is neglected, the time change of the circulation can easily be found from the equations of motion, because
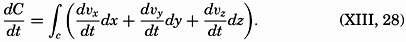
Consider, first, conditions in a coordinate system that is at rest and assume that gravity is the only external force. The integral of the component of gravity along a closed curve is always zero, because it represents the work performed against gravity in moving a particle along a certain path back to the starting point. There remains, therefore, only

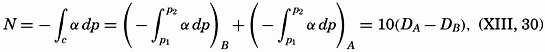
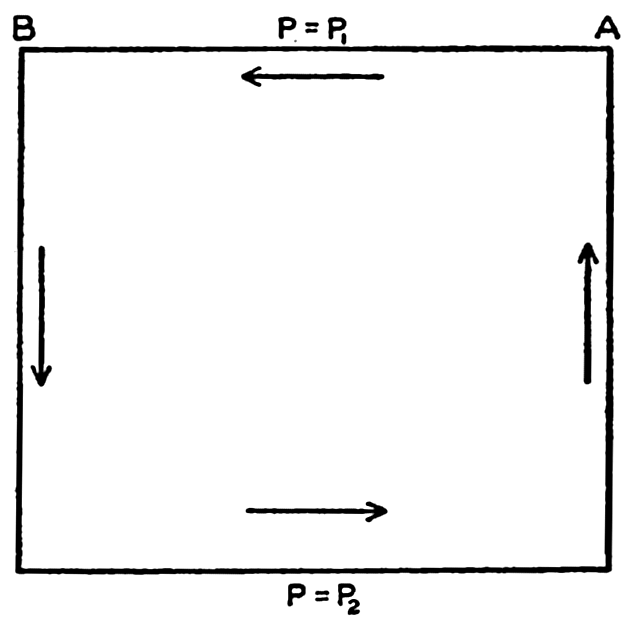
Location in the pressure field of a curve along which the time change of circulation is examined.
If the circulation relative to the earth is considered, the deflecting force has to be taken into account. According to Bjerknes, this is done by writing
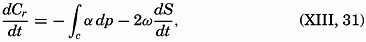
Consider the same curve as before, and assume that the upper line, p = p1, moves at a velocity ν1 at right angles to the line A−B, whereas the lower line, p = p2, moves at a velocity ν2, and let the distance A−B be called L. Then the time change of the projection on the equator plane is
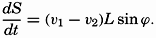
Assume now that the circulation is constant (dC/dt = 0). It then follows that the velocity difference, ν1 − ν2, must be expressed by the equation
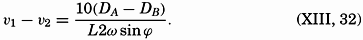
*In the literature, some confusion exists as to the signs in these equations. The above signs are consistent with the coordinates used. The relative velocity is positive; that is, the relative current is directed away from the reader if A lies to the right of B and if DA is greater than DB.
The complete theorem of circulation contains a great deal more than the simple statement expressed by equation (XIII, 32), but so far it has not been possible to make more use in oceanography of Bjerknes' elegant formulation of one of the fundamental laws governing the motion of nonhomogeneous fluids.
Transport by Currents. The volume transport by horizontal currents has the components
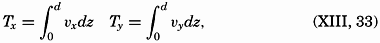
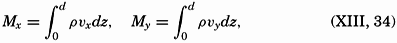
The absolute volume transport can be computed only if the absolute velocities are known, but the volume transport by relative currents can be derived from the distribution of mass. By means of equations (XIII, 16), one obtains
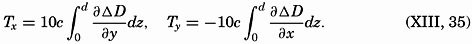

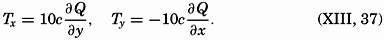
The quantity Q is easily computed, because ΔD is always determined if velocities are to be represented.
It should be observed that in practice the numbers that represent the geometric depths are also considered as representing the pressures in decibars (p. 410). In computing Q the integration is therefore carried to the pressure p decibars and the depth d meters, which are both expressed by the same number, but a small systematic error is thereby introduced. Jakhelln (1936) has examined this error and has shown that the customary procedure leads to Q values that are systematically 1 per cent too small, but this error is negligible.
Curves of equal values of Q can be drawn on a chart, and these curves will bear the same relation to the relative volume transport that the curves of ΔD bear to the relative velocity, provided that the derivations of Q are taken as positive in the direction of decrease. Therefore, the direction of the volume transport above the depth to which the Q values are referred will be parallel to the Q lines, and numerical values will be proportional to the gradient of the Q lines. The factor of proportionality will depend upon the latitude, however; between two Q lines that indicate transport to the north, the transport will increase in the direction of flow, whereas, between two Q lines indicating transport to the south, the transport will decrease in the direction of flow. Taking this fact into account, one can construct curves between which the transport is constant, but these curves will no longer be exactly parallel to the direction of the transport. Within a small area the deviation will be imperceptible, but within a larger area it will be considerable.
Between two stations A and B (A lying to the right), at distance L, the volume transport is
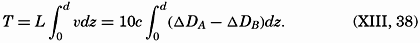
It is not necessary to develop corresponding equations for the mass transport, because this can be derived with sufficient accuracy from the volume transport by multiplication with an average density (Ekman, 1929, 1939; Jakhelln, 1936).
Convenient formulae for the computation of the transport of a coastal current have been developed by Werenskiold (1937) on the assumption that the isosteres rise toward the surface and intersect the surface at some distance from the coast (see fig. 113).
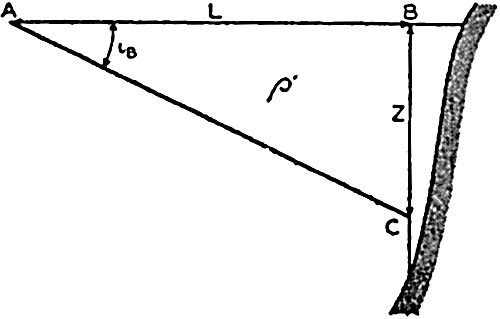
Schematic representation of hydrographic conditions off a coast.
If there are only two layers of homogeneous water, the transport is easily found. If the water of greatest density is at rest, the velocity in the area ABC (fig. 113) is
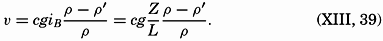
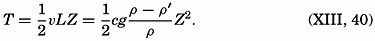
The volume transport apparently has been computed from observations at only the one station at which the depth to the boundary surface is Z, but the assumption that at and beyond the distance L the homogeneous, denser water reaches surfaces is equivalent to assuming that conditions at a second station at or beyond L are known. Owing to this circumstance, it is readily seen that the boundary surface can have any shape, because it has already been shown that the transport between two stations depends only upon the distribution of density at the two stations and is independent of the distribution of density between the stations.
For currents in water within which the density varies continually with depth, Werenskiold arrives at the formula
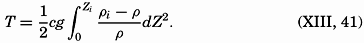
A consideration of computed transport and of the continuity of the system is helpful, under certain conditions, in separating currents flowing one above the other. The average transport through a vertical section that represents the opening to a basin must be zero, because water cannot accumulate in the basin, nor can it continue to flow out of the basin. Observations at stations at the two sides of such a section may, however, show transport in or out if the velocity along the bottom is assumed to be zero. However, this assumption would be wrong, and a depth of no motion must be determined in such a manner that the transport above and below that depth are equal. This depth can be found by plotting the difference ΔDA − ΔDB against depth, computing the average value of the difference between the surface and the bottom, and reading from the curve the depth at which that average value is found. This depth is then the average depth of no motion, and the transports above and below that depth are in opposite directions.
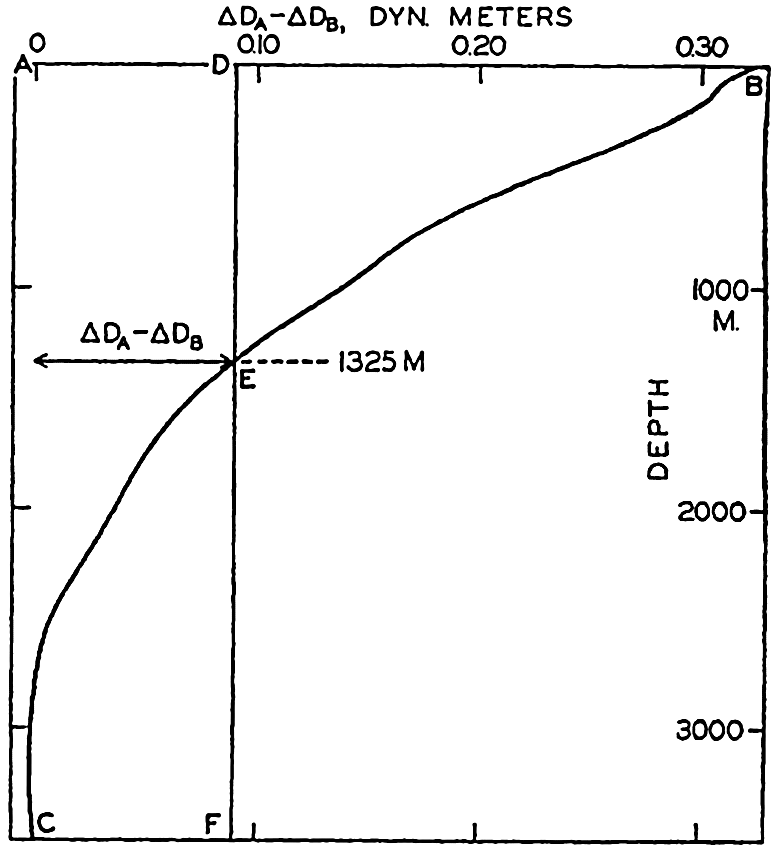
Determination of the depth above and below which the transport between two stations, A and B, is equal.
The procedure is illustrated in fig. 114, in which is plotted the difference ΔDA − ΔDB at Meteor stations 46 off South America and 23 off South Africa, both in about latitude 29°S. Assuming no current at a depth of 3500 m, one would obtain a transport to the north proportional to the area ABC, or equal to 44.5 million m3/sec. Such a transport to the north is impossible, and the velocity must therefore be zero at some other depth. The average value of ΔDA − ΔDB is 0.090 dynamic meters, and this value is found at a depth of 1325 m. If this depth is selected as a depth of no motion, the transport to the north becomes proportional to the area DBE and equal to 20.7 million m3/sec, and below 1325 m the transport is directed to the south, is proportional to the area ECF, and is also equal to 20.7 million m3/sec. The transport above the depth of no motion can be written in the form
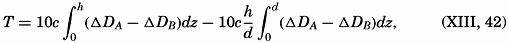
Only the average depth of no motion can be determined in this manner. Generally, the depth of no motion is not constant, but the inclination can be found by studying the distribution of temperature and salinity in the section. It is rational to assume that a surface of no motion coincides with isothermal and isohaline surfaces, and that therefore, in a section, the depth of no motion follows the isotherms and isohalines. On that assumption, one finds that in the example which has been discussed the depth of no motion rises from about 1450 m off South America to about 1200 m off South Africa.
Deflections of a current when passing a ridge, the profile of which is shown at the bottom. Left. Deflection of a current in homogeneous water, due to friction (Ekman). Right. Deflection of a relative current (see fig. 116).
The Influence of Bottom Topography on Ocean Currents. Ekman (1923, 1927, 1932) has examined the effect of the bottom topography on currents, taking into account the rotation of the earth. He arrived at the conclusion that in low latitudes the currents tend to flow east-west, independent of the slope of the bottom, but that in middle and high latitudes the currents tend to follow the bottom contours. These conclusions are verified by experience. Ekman also found that a current will be deflected cum sole when entering shallower water and contra solem when entering deeper water, and that these deflections are independent of the absolute depth to the bottom. The curvature of the stream lines is greatest where the change in slope is greatest, and when crossing a ridge the stream lines will therefore have the form shown in fig. 115, left.
In his examination, Ekman assumed homogeneous water and the presence of a slope current within which the velocities are independent of depth except within a layer that is influenced by bottom friction (p. 499). The effect of the bottom topography on relative currents in non-homogeneous water has not been examined, but qualitatively the character of the modifications is easily seen. Consider first, in the Northern Hemisphere, a relative current which in an ocean of constant depth reaches nearly to the bottom (fig. 116). Within such a current the deepest isopycnic or isosteric surfaces are horizontal, but above the
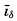 (δ1 − δ2) expresses the relation between the slope of the isobaric surface, ip, and the average slope of the δ surfaces,
(δ1 − δ2) expresses the relation between the slope of the isobaric surface, ip, and the average slope of the δ surfaces, 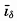 (p. 412). This distribution of mass and pressure is illustrated on the right-hand side of the perspective diagram in fig. 116, where it is supposed that the isosteric surface δ = δ1 coincides with a level surface.
(p. 412). This distribution of mass and pressure is illustrated on the right-hand side of the perspective diagram in fig. 116, where it is supposed that the isosteric surface δ = δ1 coincides with a level surface.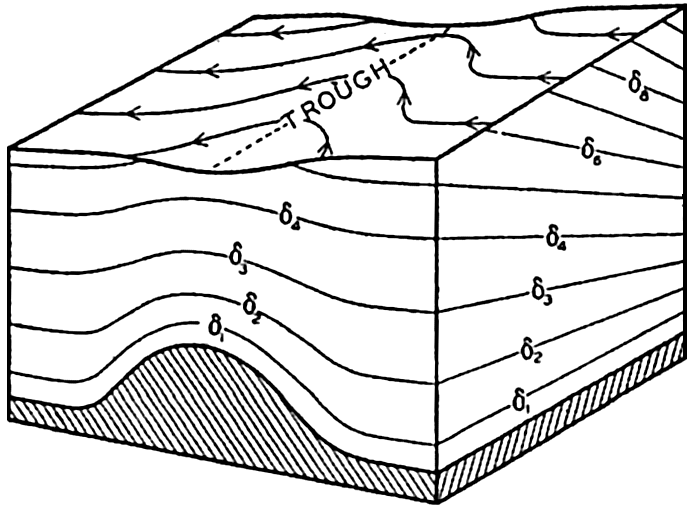
Perspective diagram showing the deformation of the sea surface when a relative current reaching nearly to the bottom crosses a submarine ridge.
When this current approaches a submarine ridge over which the water must flow, the δ surfaces must rise, as shown in the diagram. Accordingly, the distribution of mass is altered in the direction of flow in such a manner that the δ surfaces slope upward when approaching the ridge and downward after passing the ridge. The isobaric surfaces are altered correspondingly and must slope downward when the current approaches the ridge and upward after it has passed; that is, a low-pressure trough develops along the ridge, but this trough rises from left to right relative to an observer who looks in the direction of flow, because the lighter water remains on the right-hand side (fig. 116). Consequently, the isohypses of the isobaric surfaces, which were straight lines over the even bottom, bend to the right when the current approaches the ridge and to the left when it has passed. In the Southern Hemisphere the bends will be in opposite directions, and, in general, a deep current is therefore deflected from its straight course when crossing a ridge, the deflection being to the right in the Northern Hemisphere and to the left in the Southern. The maximum deflection in this case is directly over the ridge, as shown in fig. 115.
In the schematic representation in fig. 116 the δ surfaces at intermediate depths—say, the surfaces marked δ3 and δ4—must evidently show a ridge above the bottom ridge and must at the same time slope from left to right. The σt surfaces must have a similar form. As an example of such influence of the bottom topography on the field of mass, fig. 117 shows the topography of the surface σt = 27.7 in the region where
Topography of the surface σt = 27.7 in the area from the Drake Passage to the east of South Sandwich Islands.
Qualitative examples other than the one shown in fig. 116 can easily be prepared. Thus, the current must flow around a peak rising from the sea bottom, and this flow will result in a widening of the distance between the stream lines above the peak and perhaps in the development of a cyclonic eddy. The discussions by Wüst (1940) and Neumann (1940) of conditions around the Altair dome in the North Atlantic confirm these conclusions.
The above reasoning is purely qualitative. If the quantitative effect of the bottom topography is to be examined, it is necessary to consider that the equation of continuity and the equations of stationary motion and stationary distribution of mass must be satisfied. No quantitative computations have been made, but it can be pointed out that stationary distribution of mass requires that the law of the parallel solenoids be fulfilled (p. 455). Hence the isohypses of all isobaric
Friction
General Consideration of Friction. Two of the fundamental concepts concerning friction in a fluid are (1) that shearing stresses are produced when layers are slipping relative to each other, and (2) that the shearing stresses acting on a unit area are proportional to the rate of shear normal to the surface on which the stress is exerted: τ = μdv/dn. The factor of proportionality, μ, is called the dynamic viscosity of the fluid.
Frictional stresses in the direction of the x axix on two sides of a cube.
Frictional forces per unit volume are equal to the differences between shearing stresses exerted on opposite sides of a cube of unit dimensions. Consider a cube of side length Δz (fig. 118) in a fluid moving only in the direction of the x axis, and let the rate of shear at the upper and lower surfaces of the cube be (dv/dz)1 and (dv/dz)2, respectively. The shearing stress per unit area of the upper surface is then τ1 = (μdv/dz)1, and the total stress acting on the upper surface is
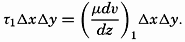
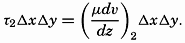
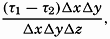

In classical hydrodynamics the dynamic viscosity, μ, is considered a characteristic property of the fluid—namely, the property that resists angular deformation. Being a characteristic property, the magnitude of μ is independent of the state of motion, but it varies, as a rule, with the temperature of the fluid. Within wide limits it is independent of the pressure. The dynamic viscosity has the dimensions ML−1T−1, whereas the kinematic viscosity, defined as ν = μ/ρ, has the dimensions L2T−1. A table of the dynamic viscosity of sea water is given on p. 69.
The derivation of the general frictional terms that must be taken into account when dealing with motion in space is given in the general textbooks on hydrodynamics or fluid mechanics which are listed at the end of this chapter. The complete theory requires the introduction of both shearing and normal stresses, and leads, if μ is considered constant, to the expressions for the frictional terms:
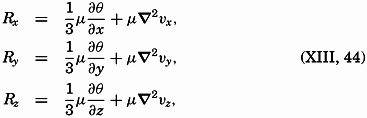
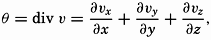
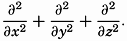 .
.When these terms are added to the equations of motion (XIII, 1), and if the terms depending upon the divergence of the velocity are omitted, one obtains the Navier-Stokes equation of motion (for example, Lamb, 1932), which in greatly simplified form has found application to problems in fluid mechanics. The theory that leads to the development of the Navier-Stokes equation excludes, however, the possibility of local fluctuations in velocity and presupposes that the fluid moves in layers, or laminae. This type of motion is called “laminar flow,” but is probably never encountered in the ocean. The Navier-Stokes equations find, therefore, no application to oceanographic problems and have been mentioned here only as an approach to the problem of fluid resistance
Turbulence. Laminar flow, in which sheets of fluid move in an orderly manner is, as has already been stated, not known to occur in the ocean. The ocean currents are, instead, characterized by numerous eddies of different dimensions by which small fluid masses are constantly carried into regions of different velocity. It is this completely irregular type of motion which is called turbulent flow, and the process by which a rapid exchange of fluid masses is maintained is called turbulence.
The very character of turbulent flow is such that rapid fluctuations of velocity take place in all localities, and no steady state of motion exists if attention is paid to the individual particles of the fluid. It might therefore appear hopeless to arrive at a theory that takes full account of the complicated character of the actual motion, but the problem has, nevertheless, been attacked with considerable success by using statistical methods. The velocity at any given point in space can always be considered as the vector sum of two different velocities: 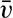 , which represents the average velocity at that point during a long period of time, and ν′ which represents the added “turbulent” velocity. At any given time the actual velocity components can therefore be written
, which represents the average velocity at that point during a long period of time, and ν′ which represents the added “turbulent” velocity. At any given time the actual velocity components can therefore be written
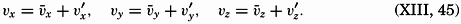
After such a segregation is made, the whole pattern of flow can be considered as composed of two systems, one representing the average flow, which may be steady or accelerated, according to the acting forces, and one representing the irregular turbulent motion, which is superimposed upon the average flow and whose nature is not known at any given time. The former system, the average flow, is of interest when dealing with the ocean currents, but knowledge of the superimposed turbulent flow is necessary for studying the extent to which the turbulent flow modifies the apparent viscosity.
Frictional Stresses Due to Turbulent Motion. It is not possible here to present the complete development of the frictional terms. Interested readers are referred to general textbooks on hydrodynamics or fluid mechanics (for example, Lamb, 1932, Rouse, 1938), but a few important points must be brought out here. Owing to the very character of the turbulent motion, small fluid masses are carried back and forth across any given surface, and a mass coming from a region of high velocity has, when entering a region of low velocity, a momentum which is greater than that of the surrounding particles. If this fluid mass assumes approximately the velocity of the surroundings, it loses momentum, and, similarly, a small fluid mass that comes from a region of low velocity into one of high velocity gains momentum. Thus, where a
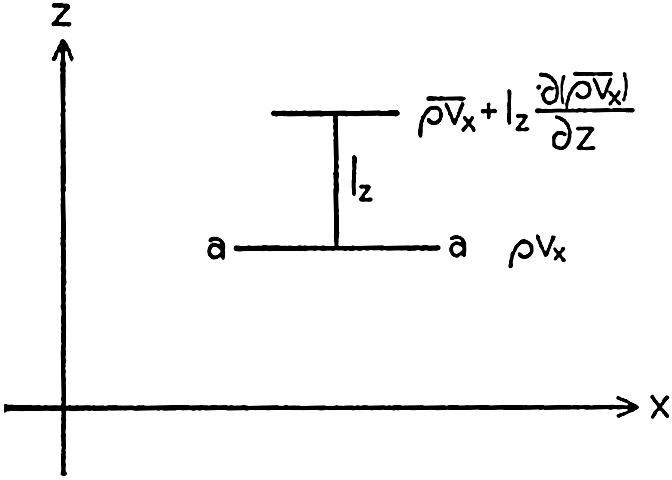
Change of momentum on the vertical distance lz.
Reynolds first derived expressions for the stresses due to momentum transport, and since then the theory of turbulence has been further developed, notably by L. Prandtl, G. I. Taylor, and Th. v. Kármán. The method of attack which so far has found the greatest application to oceanographic problems is based on Prandtl's introduction of the mixing length. Consider that the average flow is in the direction of the x axis and that 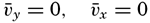 . Then
. Then
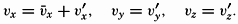
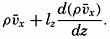
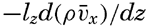 between the average original momentum of the small fluid masses
between the average original momentum of the small fluid masses 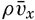 and the average momentum at the locality where exchange takes place. The momentum given off per unit time must be proportional to the average numerical value of the vertical velocity of the small fluid masses, which is
and the average momentum at the locality where exchange takes place. The momentum given off per unit time must be proportional to the average numerical value of the vertical velocity of the small fluid masses, which is 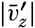 . Therefore, the rate of momentum transport, M, will be
. Therefore, the rate of momentum transport, M, will be


Prandtl's theory also leads to another definition of Az:


The above considerations lead to the result that

Equation (XIII, 50) is similar to the equation τ = μdv/dn (p. 69). The coefficient Az has the same dimensions as the dynamic viscosity μ and is called the eddy viscosity. However, a fundamental difference exists between the two quantities. The dynamic viscosity is independent of the state of motion and is a characteristic property of the fluid, comparable to the elasticity of a solid body, but the eddy viscosity depends upon the state of motion and is not a characteristic physical property of the fluid. The numerical value of the eddy viscosity varies within very wide limits according to the type of motion, and, as far as ocean currents are concerned, only the order of magnitude of Az has been ascertained.
It should be observed that the eddy viscosity can be introduced without paying any attention to the mixing length or any other statistical quantity that describes the character of the turbulence. Because in a
 , where
, where  stands for the mean motion and where A evidently must depend upon the character of the turbulence. This notation was used by Ekman (1905) in his classical discussion of wind currents, in which the eddy viscosity was first introduced analytically under the name “virtual viscosity” when dealing with oceanographic problems.
stands for the mean motion and where A evidently must depend upon the character of the turbulence. This notation was used by Ekman (1905) in his classical discussion of wind currents, in which the eddy viscosity was first introduced analytically under the name “virtual viscosity” when dealing with oceanographic problems.For the sake of completeness, it may be added that the expression for the stress should also contain the term  , but this can always be neglected, because μ is very small compared to A. Oceanographic data give values of A ranging between 1 and 1000 g/cm/sec, whereas μ is about 0.015 (table 16, p. 69).
, but this can always be neglected, because μ is very small compared to A. Oceanographic data give values of A ranging between 1 and 1000 g/cm/sec, whereas μ is about 0.015 (table 16, p. 69).
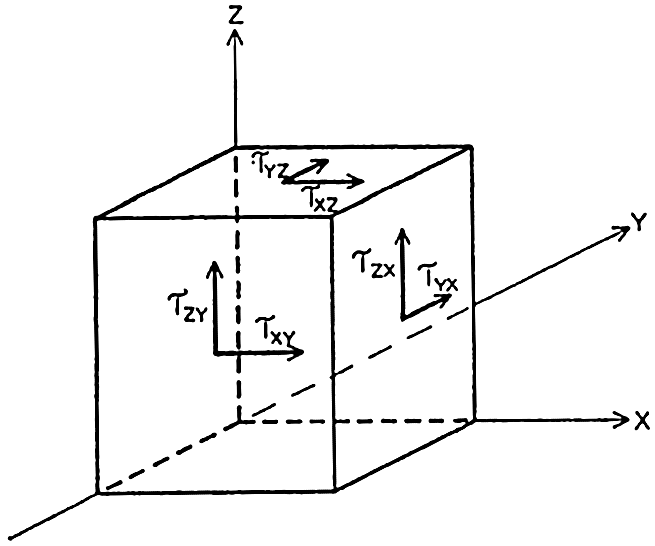
Shearing stresses acting on three sides of a cube.
The discussion of the shearing stresses due to turbulent exchange of momentum can now be extended by dropping the assumption that the motion takes place in the direction of the x axis only, because the reasoning is equally correct if the average velocity has a component in the direction of the y axis. The stress in the direction of the y axis on a surface normal to the z axis, τyz, is

Dropping the assumption that 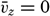 = 0 and that the average velocity does not vary in a horizontal direction leads to the introduction of four new shearing stresses (fig. 120):
= 0 and that the average velocity does not vary in a horizontal direction leads to the introduction of four new shearing stresses (fig. 120):
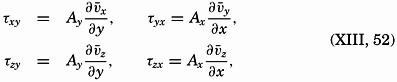
Here the coefficients of eddy viscosity may be defined as before:
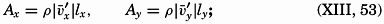
Frictional Forces Due to Turbulent Motion. The frictional force acting in the direction of the x axis is derived from the stresses τxz and τxy (fig. 120):
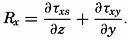
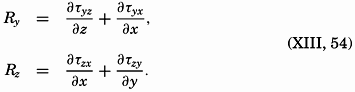
In order to arrive at frictional terms that are of importance when dealing with ocean currents, it will be assumed that (1) only the shearing stresses that have been discussed here are important, (2) the vertical velocity is so small that the gradients of the vertical velocity are negligible, and (3) the horizontal mixing length and the average horizontal turbulent velocities are independent of the direction of motion; that is, Ax = Ay = Ah. Writing simply νx instead of 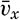 , and so on, one obtains the frictional terms in the form
, and so on, one obtains the frictional terms in the form
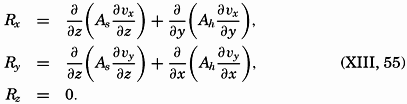
The above derivation is not an exact one, and therefore the equations that define the frictional forces in the ocean represent only approximations that appear satisfactory at the present stage of knowledge of ocean currents. When it becomes desirable to improve these expressions, it will be necessary to consult the treatment of the problem of fluid friction which is given in the textbooks on hydrodynamics or fluid mechanics listed at the end of this chapter.
In applying the expressions for the frictional forces, a further simplification is generally be introduced—namely, that the horizontal frictional forces can be disregarded. The concept of horizontal turbulence, however, has been introduced because horizontal or quasihorizontal turbulence appears to play an important part in large-scale processes of diffusion, although the dynamic significance is not yet clear.
If horizontal turbulence is neglected, the consideration of transport of momentum leads to the frictional terms
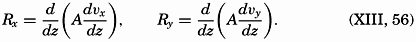
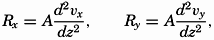
Influence of Stability on Turbulence. No theory has been developed for the state of turbulence which at indifferent equilibrium or at stable stratification characterizes a given pattern of flow, except in the immediate vicinity of a solid boundary surface (p. 480), but it has been demonstrated that the turbulence as expressed by the eddy viscosity decreases with increasing stability. Thus, Fjeldstad (1936) found that he could obtain satisfactory agreement between observed and computed tidal currents in shallow water by assuming that the eddy viscosity was a function not only of the distance from the bottom but of the stability as well. He introduced A = f(z)/(1 + aE), where E is the stability and where the factor a is determined empirically.
The relation between eddy viscosity and eddy diffusion has been examined by Taylor (1931). Taylor's reasoning is based on the fact that, in the presence of turbulence, the kinetic energy of the system can be considered as composed of two parts: the kinetic energy of the mean motion, and the kinetic energy of the superimposed turbulent motion. In homogeneous water the latter is being dissipated by viscosity only, wherefore, if the turbulence remains constant, turbulent energy must enter a unit volume at the same rate at which it is dissipated. Where stable stratification is found (p. 92), part of the turbulent energy is also used for increasing the gravitational potential energy of the system. In this case the rate at which turbulent energy enters a unit volume, T, must equal the sum of the rate at which the potential energy increases, P, and the rate at which energy is dissipated by viscosity, D. It follows that, if the turbulence remains unaltered, one must have T > P.
Taylor shows that the rate at which turbulent energy enters a unit volume equals 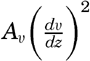 , where Av means the eddy viscosity, and that the rate at which the potential energy increases equals gEAs, where E is the stability (p. 416) and As is the eddy diffusivity. It follows that
, where Av means the eddy viscosity, and that the rate at which the potential energy increases equals gEAs, where E is the stability (p. 416) and As is the eddy diffusivity. It follows that

Taylor tested the correctness of this conclusion by measurements made by Jacobsen (1913) in Danish waters, where Jacobsen found values
According to Taylor's theory, turbulence can always be present, regardless of how great the stability is, but the type of turbulence must be such that the condition (XIII, 57) is fulfilled; that is, the rate at which the Reynolds stresses communicate energy to a region must be greater than the rate at which the potential energy of that region increases. It explains why observations in the ocean mostly give smaller values of As than of Av. A velocity gradient of 0.1 m/sec on 100 m is common where the stability is about 10−6 m−1, and with these values one obtains As < 0.1Av. Within layers of very great stability the velocity gradient is generally also great, but the value of As becomes even smaller than in the above example. Thus, below the Equatorial Countercurrent in the Atlantic the decrease of velocity in a vertical direction is 6.10−3 sec−1, and the stability is about 5.10−5 m−1 (Montgomery, 1939). With these values, one obtains As < 7.10−2 Av, or, if the eddy viscosity were equal to 10 g/cm/sec, the eddy diffusivity would be less than 0.7.
Thus the effect of stability on turbulence is twofold. In the first place, the turbulence is reduced, leading to smaller values of the eddy viscosity, and, in the second place, the type of the turbulence is altered in such a manner that the accompanying eddy diffusivity becomes smaller than the eddy viscosity. The latter change is explained by Jacobsen (1930) by assuming that elements in turbulent motion give off their momentum rapidly to their surroundings, but that other properties are exchanged slowly, and that before equalization has taken place the elements are moved to new surroundings by gravitational forces (p. 92). A possible influence of stability on lateral turbulence has not been examined, but it has been suggested by Parr (1936) that this kind of turbulence increases with increasing stability.
Horizontal Turbulence. The horizontal turbulence needs some further explanation because of the effect of the earth's rotation. Let it be assumed that the field of pressure is such that the deflecting force associated with the mean motion is balanced by the pressure gradient:
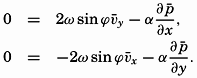
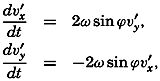
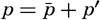 , one finds that the above equations must take the form
, one finds that the above equations must take the form
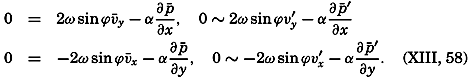
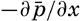 and
and 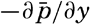 represent the mean pressure gradients, and −∂p′/∂x and −∂p′/∂y represent local pressure gradients associated with the turbulent motion.
represent the mean pressure gradients, and −∂p′/∂x and −∂p′/∂y represent local pressure gradients associated with the turbulent motion.Thus, superimposed upon the average field of pressure must be an irregular field. If the pressure distribution could be represented by means of the absolute geopotential topographies of isobaric surfaces (p. 413), these would show, besides certain major features that would characterize the mean motion, also a number of small “lows” and “highs,” troughs and ridges, which would represent the superimposed irregular pressure field. Detailed surveys during which the oceanographic stations have been spaced at intervals of 20 km or less have revealed that the relative distribution of pressure shows numerous irregularities of such nature. This fact strongly supports the conclusion that the horizontal motion associated with the pressure distribution is far from being uniform, but is characterized by numerous eddies that may have dimensions up to 20 km or more.
Boundary Friction. In oceanography the problem of frictional stresses at boundary surfaces can be dealt with in the same manner as the similar problem in fluid mechanics. Over an absolutely smooth surface
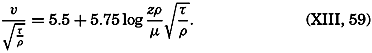
Over a rough surface, different conditions are encountered. Prandtl assumes that over such a surface the turbulent motion extends to the very surface, meaning that the mixing length has a definite value at the surface itself:

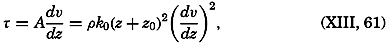
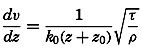

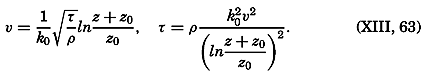
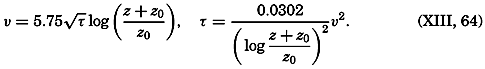
Measurements of the velocity at two distances are needed in order to determine both τ and z0, and measurements at three or more levels are necessary in order to test the validity of the equation. So far, few measurements have been made so close to the bottom that they can be used for testing the application of these results to oceanographic conditions, but one example can be given. On November 15, 1937, Revelle and Fleming (unpublished data) measured tidal currents off the entrance to San Diego Harbor at 126, 51, and 21 cm above the bottom. Table 63 contains the average velocities and the stress at the bottom, if the bottom is assumed to be smooth or rough. Agreement is obtained only if the bottom is considered rough. The roughness length is found to be about 2.0 cm, and with this value the observations consistently give the same stress at the bottom. These observations indicate therefore that the above formulae, with von Kármán's constant, k0 = 0.4, are applicable to the currents directly above the sea bottom. In this case the value of the eddy viscosity would be A = 0.93 (z + z0); that is, at a distance of 1 m above the bottom the eddy viscosity would be 95 g/cm/sec.
| Distance from bottom, cm | 126 | 51 | 21 |
| Average velocity, cm/sec | 26.3 | 21.6 | 15.6 |
| Computed frictional stress, g/cm/sec2} Smooth bottom | 0.87 | 0.71 | 0.46 |
| Computed frictional stress, g/cm/sec2} Rough bottom, z0 = 2.0 cm | 5.8 | 6.2 | 6.0 |
The above results apply to a fluid in a state of indifferent equilibrium. Certain modifications must be introduced if the stratification is stable or unstable, but the character of these modifications is not fully understood. It can be stated only that under stable conditions the velocity profile at some distance from the surface can no longer be represented by a logarithmic law, but is better represented by a power law of the type Vz1/Vz2 = (z1/z2)n. However, very near the surface, the logarithmic law appears to be valid (Sverdrup, 1939b).
At the sea surface, different boundary conditions have to be considered. In the first place, it should be observed that the currents of the sea are always much slower than the air currents, the winds. Therefore the velocity of the air relative to that of the water can always be considered, with sufficient accuracy, equal to the velocity of the wind.
At the sea surface the stress that the wind exerts on the water, τa, must balance the stress that the water exerts on the air:
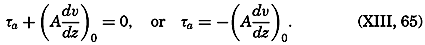
When a current flows parallel to a coast, a lateral stress is exerted, and one may expect a horizontal velocity profile to develop which shows some similarity to the vertical profile near the bottom. The velocity profile must be related to the horizontal eddy viscosity and to the lateral stress, but this relation has not yet been examined.
Numerical Values of the Vertical and Lateral Eddy Viscosity and Eddy Diffusivity. For the determination of the eddy viscosity, Aν., in the ocean, it is necessary to know the frictional forces and the velocity gradients. The frictional forces cannot be determined directly, but may be obtained as the difference between other acting forces. The velocity gradients, however, can be obtained from directly obseryed currents. When dealing with wind currents, theories based on certain assumptions as to the character of the eddy viscosity are helpful (p. 492), and for considering currents close to the bottom, results from fluid mechanics make possible conclusions as to the eddy viscosity from current measurements only (p. 480). The uncertainties of the correct application of theories, the difficulties in making current measurements in the open ocean, and the even greater difficulties in determining the acting forces, all introduce great uncertainties in the numerical values of the eddy viscosity which have so far been determined.
Table 64 contains results of such determinations. The specific methods used cannot be discussed here, but some of them will be mentioned later on. All values are from regions of moderate or strong currents that have been measured with considerable accuracy, or they have been derived from the effect of wind currents on the surface layer. The values range from nearly zero up to 7500 g/cm/sec, but some consistency in the variations can be seen. At the very bottom, small values are always found; at greater distances from the bottom, great values are associated with strong currents and small stability or with strong currents and great stability. On the North Siberian Shelf the eddy viscosity approached a small value in a thin layer of very great stability within which the tidal currents reached their maximum values.
| Locality | Layer | Av in g/cm/sec | Av derived from | Authority |
aW = wind velocity in m/sec. | ||||
bz = distance from bottom in meters. | ||||
cVery great stability. | ||||
dVery strong currents. | ||||
ez = distance from bottom in meters. Formula valid between z = 0.2 and z = 1.3 m. | ||||
| All oceans | surface | [a]Av = 1.02 W3 (W<6m/sec) | homogeneous layer | Thorade, 1914 |
| Av = 4.3 W2 (W >6m/sec) | Thickness of upper | Ekman, 1905 | ||
| North Siberian Shelf | 0 to 60 m | 0−1000 | Tideal currents | Sverdrup, 1926 |
| North Siberian Shelf | 0 to 60 m | 10−400 | Tidal currents | Fjeldstad, 1936 |
| North Siberian Shelf | 0 to 22 m | [b] | Wind currents | Fjeldstad, 1929 |
| North Sea | 0 to 31 m | 75−1720 | Strong tidal currents | Thorade, 1928 |
| Danish waters | 0 to 15 m | [c] 1.9−3.8 | All currents | Jacobsen, 1913 |
| Kuroshio | 0 to 200 m | [d] 680−7500 | All currents | Suda, 1936 |
| Japan Sea | 0 to 200 m | 150−1460 | All currents | Suda, 1936 |
| Off San Diego, Calif | near bottom | [e] 93(z + 0.02) | Tidal currents | Revelle and Fleming, ms. |
By computations that are based on equation (V, 5), p. 159, in a simplified form, the eddy diffusivity, As can be derived from observed time and space variations of temperature, salinity, oxygen content, or other properties. In some cases the currents need not be known, but in other cases only the ratio As/v can be determined, where ν is the velocity of the currents (p. 159). If this velocity can be estimated, an approximate value of As can be found. Temperature, salinity, and oxygen content can be measured much more easily and with greater accuracy than currents, and data for studying the eddy diffusion are therefore more readily obtained. As a consequence, many more determinations of eddy diffusivity have been made, and the results show greater consistency.
Table 65 contains a summary of values derived from observations in different oceans and at different depths between the surface and the bottom. The values range from 0.02 up to 320 g/cm/sec, but by far the greater number of values lie between 3 and 90. The range is therefore smaller than the apparent range of the eddy viscosity. The highest value, 320 g/cm/sec, was found in a homogeneous surface layer, within which one can expect the eddy diffusivity to equal the eddy viscosity. This value is the only one which is as great, probably, as the corresponding eddy viscosity; otherwise, the eddy diffusivity is smaller, in agreement with the fact that generally stable stratification is encountered. From the remarks in the table, it is evident that the eddy diffusivity increases with increasing velocity of the currents and decreases with increasing stability, in agreement with the preceding considerations.
The results of a few determinations of lateral eddy coefficients are given in table 66. The values of the coefficients have been derived by bold assumptions and can be considered as indicating only the order of magnitude. The fact that this order of magnitude depends upon the size of the area from which observations are available probably explains why the value from the California Current is much smaller than the values from the Atlantic Ocean, where conditions within much larger regions have been considered. The latter values, which have been obtained partly from observations at or near the surface and partly from observations at great depth, agree remarkably well. No relation appears between the average velocity of the currents and the eddy coefficients or between the stability and the coefficients. Similarly, from the meager evidence, the eddy viscosity and eddy diffusivity appear to be equal. Therefore, the processes of lateral turbulence seem to be entirely different from those of vertical turbulence, but it should be borne in mind that the study of lateral turbulence in the ocean is at its very beginning.
| Locality | Layer | As in g/cm/sec | Remarks | Authority |
| Equatorial Atlantic Ocean | 0 to 50 m | 320 | Homogeneous water, moderate currents | Defant, 1932 |
| Bay of Biscay | 0 to 100 m | 2–16 | Moderate stability, weak currents | Fjeldstad, 1933 |
| Danish waters | 0 to 15 m | 0.02–0.6 | Great stability, moderate currents | Jacobsen, 1913 |
| Kuroshio | 0 to 200 m | 30–80 | Moderate stability, strong currents | Sverdrup et al, 1942 |
| Kuroshio | 0 to 400 m | 7–90 | Moderate stability, strong currents | Suda, 1936 |
| Japan Sea | 0 to 200 m | 1–17 | Moderate to small stability, moderate currents | Suda, 1936 |
| California Current | 0 to 200 m | 30–40 | Moderate stability, weak currents | McEwen, 1919 |
| Arctic Ocean | 200 to 400 m | 20–50 | Small stability, weak currents | Sverdrup, 1933 |
| South Atlantic Ocean | 400 to 1400 m | 5–10 | Moderate stability, weak currents | Defant, 1936 |
| Equatorial Atlantic Ocean | 600 to 2000 m | 8 | Moderate stability, weak currents | Seiwell, 1935 |
| Caribbean Sea | 500 to 700 m | 2.8 | Moderate stability, weak currents | Seiwell, 1938 |
| South Atlantic Ocean | 3000 m to bottom | 4 | Homogeneous water, weak currents | Defant, 1936 |
| South Atlantic Ocean | Near bottom | 4 | Homogeneous water, weak currents | Wattenberg, 1935 |
| Locality | Layer | Av,h or As,h in g/cm/sec | Remarks | Authority |
| Northwestern North Atlantic Ocean | Surface | As,h 4 × 108 | Strong currents | Neumann, 1940 |
| Atlantic Equatorial Countercurrent | 0 to 200 m | Av,h 7 × 107 | Great stability, moderate currents | Montgomery and Palmén, 1940 |
| 0 to 200 m | As,h 4 × 107 | Montgomery, 1939 | ||
| South Atlantic Ocean | 2500 to 4000 m | As,h 1 × 108 | Small stability, weak currents | Sverdrup, 1939a |
| California Current | 200 to 400 m | As,h 2 × 106 | Moderate stability, weak currents, small area | Severdrup and Fleming, 1941 |
The Energy Equation When Friction Is Taken into Consideration. Because explicit terms for the components of the frictional forces have been introduced, the total power of the frictional forces can be computed. Disregarding the effect of horizontal turbulence, the power of the frictional forces per unit volume is
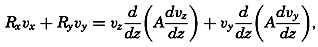
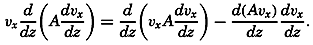
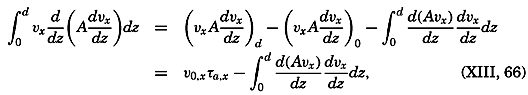
The integral on the right-hand side represents the loss per unit time and unit surface area of kinetic energy due to the vertical turbulence (the dissipation). If A were constant, the integral would be reduced to

The first term on the right-hand side, ν0,τa, represents the power per unit area (ML2T−3 × L−2) which is exerted by the stress of the wind.
The energy equation can now be written in the form
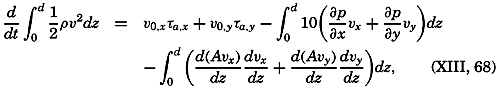
Some general conclusions can be drawn from this equation. In the first place, it is seen that the change of the kinetic energy may be positive or negative; that is, the energy transmitted to the water from the atmosphere may be greater or smaller than the loss due to motion across isobars and dissipation. Furthermore, if the kinetic energy remains unaltered and the stress of the wind is zero, energy must be gained by motion across the isobars; that is, the average motion must be from high to low pressure, because the dissipation is always positive. On the other hand, if the first integral vanishes, the dissipation equals the power of the stress of the wind. The first integral can disappear, either because the term (∂p/∂x)vx + (∂p/∂y)vy is zero at all depths, or because the term is negative at some depths and positive at others. In the former case the motion is parallel to the isobars. Furthermore, if stationary conditions are assumed, the isobars at one level must be parallel to the isobars at another level (p. 455). If the horizontal x axis is placed in the direction of the pressure gradient, the equations of motion are reduced to
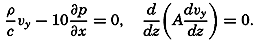
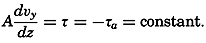
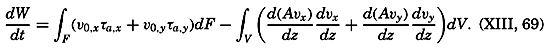
The energy equations have so far received but little attention in oceanographic work, and further theoretical considerations and applications to specific problems appear desirable.
Other conclusions as to the effect of the stress of the wind can be based directly upon an integration of the equations of motion. Consider a closed space in which stationary conditions exist, and assume that the motion is nowhere accelerated. In such a system the transport through any cross section must be zero. Therefore, if the positive x axis is placed in the direction of the wind, one obtains, by multiplying the equations of motion by dxdydz and integrating over the entire volume,
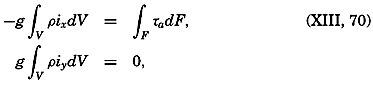

The formula is valid only if the depth to the bottom is so great that the velocity gradient at the bottom is zero, because only on this assumption does the stress at the bottom vanish. If this condition is not fulfilled, one obtains

In nonhomogeneous water, one can write
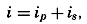
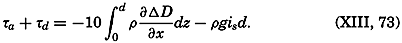
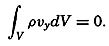
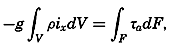
All of the above equations become modified if horizontal stresses and frictional forces related to such stresses are considered, but so far these modifications have not been examined. Rossby (1936a), however, has pointed out that the stress of the wind exerts an anticyclonic torque on the surface of the different oceans and that lateral stresses must provide the balancing cyclonic torque, because the bottom stresses are probably negligible. Studies by Montgomery and Palmén (1940) support this conclusion, but the problem deserves further attention.
Wind Currents
The Stress of the Wind. From laboratory results dealing with flow over smooth and rough surfaces, one may expect that the stress can be expressed by means of equation (XIII, 59), which gives the stress over a smooth surface, or equation (XIII, 63), which gives the stress over a rough surface. The density, ρ, which enters in the formulae is then the density of the air. In order to determine whether the sea surface can be considered smooth or rough and, if it is rough, to determine the value of the roughness length, zo, simultaneous measurements of wind velocities must be made at three or more levels above the sea surface. From such measurements conducted by Wüst (1920), Rossby and Montgomery (1935) concluded that at moderate wind velocities the sea surface has the character of a rough surface with roughness length 0.6 cm. From a general theory of the wind profile in the lower part of the atmosphere, Rossby (1936b) later developed formulae that permit computation of zo from the angle between the surface wind and the gradient wind (corresponding to no friction) or from the ratio between surface-wind velocity and gradient-wind velocity. When applying these formulae to observed values from the ocean, Rossby found that at moderate and strong winds the roughness length is independent of the wind velocity and equal to

A similar expression was derived by Ekman as early as 1905 through study of the slope of the sea surface during a storm in the Baltic in 1872. A. Colding had found that the lines of equal water level were directed nearly perpendicular to the direction of the wind. The sea-level values were obtained from records at stations on the coast, and thus represent the values of the physical sea level. The relation between wind velocity, W, depth, d, and slope, i, could be expressed by the equation

In the case examined by Colding, Ekman assumes that τa + τd = 3/2τa, and obtains, therefore,
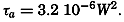
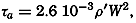
Palmén and Laurila (1938) have made a similar study of the effect of the wind on the sea level in the Gulf of Bothnia during a storm in October, 1936, and obtained
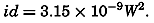
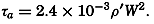
These results, although uncertain, confirm the conclusion that at moderate and strong winds the stress of the wind is proportional to
At low wind velocities, somewhat different conditions appear to prevail. From a study of simultaneous wind measurements at different heights above the sea, Rossby (1936b) concludes that at low wind velocities the sea surface has the character of a smooth surface, because the wind profiles indicate the existence of a laminar sublayer. At low wind velocities the stress should therefore be computed from equation (XIII, 59), which gives values that are about one third of those obtained on the assumption that the surface is rough.
Table 67 shows the values of the stress corresponding to a smooth surface or a rough surface characterized by z0 = 0.6 cm.
| Surface | Wind velocity in m/sec at 15 m | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | |
| “Smooth” | 0.04 | 0.16 | 0.34 | (0.58) | |||||
| “Rough” | (0.11) | (0.45) | (1.01) | 1.81 | 2.83 | 4.09 | 5.56 | 7.25 | 9.20 |
It is evident that, if the sea surface can be considered smooth at wind velocities below 6 to 7 m/sec, the stress of wind velocities below this limit is of little significance, but the above conclusions need to be confirmed by means of many more data. The problem of the stress of the wind still deserves great attention, and it is particularly desirable to obtain more measurements of wind profiles, because results in fluid mechanics can be successfully applied in the study of such profiles.
The theoretical equations for the relations between stress and wind velocity are valid only if the stability of the air is nearly indifferent. Under stable or unstable conditions the wind profiles will be different, and the relationships between wind velocity and stress will be altered (Sverdrup, 1939b). A study of wind profiles at different stabilities of the air is therefore of great interest.
Wind Currents in Homogeneous Water. In 1902, V. Walfrid Ekman published his classical paper on wind currents in which, for the first time, the effect both of the deflecting force of the earth's rotation and of the eddy viscosity was taken into account. Ekman undertook the mathematical analysis at the suggestion of Fridtjof Nansen, who, during the drift of the Fram across the Polar Sea in 1893–1896, had observed that the ice drift deviated 20° to 40° to the right of the wind, and had attributed this deviation to the effect of the earth's rotation. Nansen further reasoned that the direction of the motion of each water layer must deviate to the right of the direction of movement of the overlying water layer in a similar manner, because it is swept on by this layer much like the ice, which covers the surface, is swept on by the wind. Therefore, at some depth the current would run in a direction opposite to that of the surface flow. These conclusions of Nansen's were fully confirmed by the mathematical treatment.
In homogeneous water the equations of motion of a steady state take the form
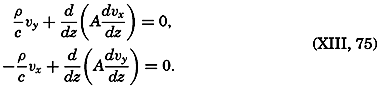
Assuming that the eddy viscosity is independent of depth, one can integrate the equations directly. Writing

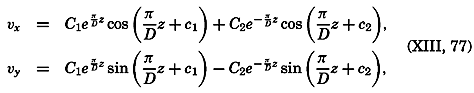
In this form the result is applicable to conditions in the Northern Hemisphere only, because in the Southern Hemisphere sin ϕ is negative, wherefore D is imaginary. In order to obtain a solution that is valid in the Southern Hemisphere, the direction of the position of the y axis must be reversed.
The solution takes the simplest form if the depth to the bottom is so great that one can assume no motion near the bottom, because then
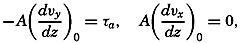
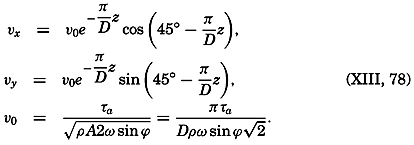
Therefore, the wind current is directed 45° cum sole from the direction of the wind. The angle of deflection increases regularly with depth, so that at the depth z = D the current is directed opposite to the surface current. The velocity decreases regularly with increasing depth, and at z= D is equal to e−x times the surface velocity, or one twenty-third of the value at the surface. By far the more important velocities occur above the depth z = D, and Ekman has therefore called this depth “the depth of frictional resistance.” It should be observed, however, that according to this solution the velocity of the wind current never becomes zero, but approaches zero asymptotically and is practically zero below z = D
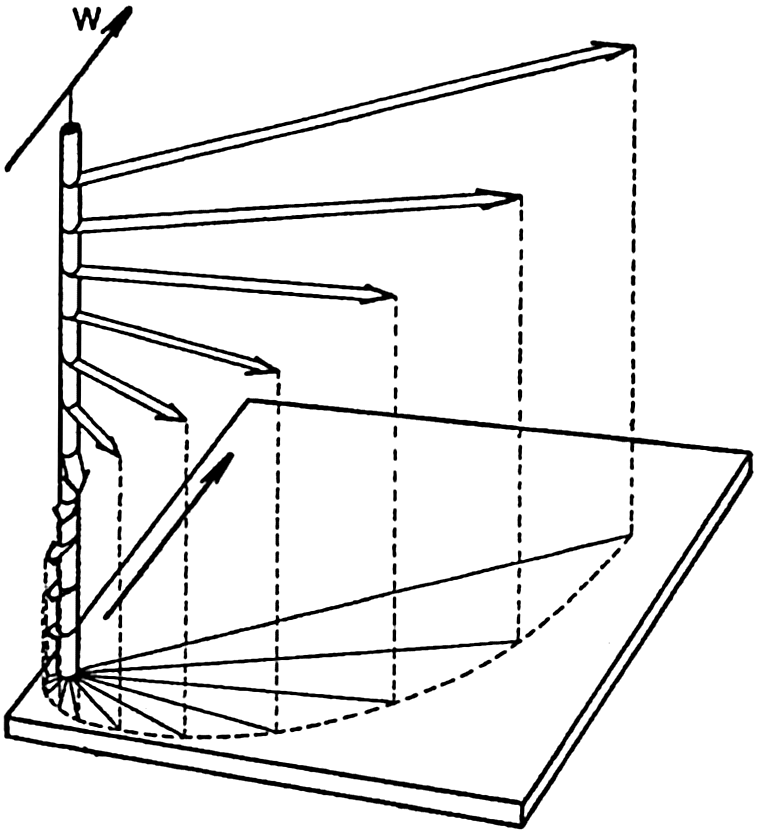
Schematic representation of a wind current in deep water, showing the decrease in velocity and change of direction at regular intervals of depth (the Ekman spiral). W indicates direction of wind.
A schematic representation of the pure wind current is given in fig. 121. The broad arrows represent the velocities at depths of equal intervals. Together they form a spiral staircase, the steps of which rapidly decrease in width as they proceed downward. Projected on a horizontal plane the end points of the vectors lie on a logarithmic spiral.
The average deflection of the wind current from the direction of the wind has been examined (Krümmel, 1911) and found to be about 45° cum sole from the wind direction, independent of latitude, in agreement with Ekman's theory.
The ratio between the velocity of the surface current, which Thorade has called the wind factor, depends upon the stress of the wind and upon the value of the eddy viscosity—that is, upon D. The stress of the wind is proportional to the square of the wind velocity, τa = 3.2 10−6W2 (p. 490), where the wind velocity, W, is measured in centimeters per second. Introducing this value into (XIII, 78), one obtains
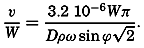



From equations (XIII, 76), (XIII, 80), and (XIII, 81), one obtains (see table 64)
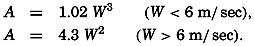
| Wind velocity (m/sec) | 2 | 4 | 6 | 8 | 10 | 15 | 20 |
| A (g/cm/sec) | 8 | 65 | (218) | 375 | 430 | 970 | 1720 |
Rossby (1932) and Rossby and Montgomery (1935) have developed a new theory of the wind currents by introducing an eddy viscosity that
According to Ekman's theory the angle should remain constant at 45°, and the wind factor, according to the empirical results that he made use of, should be equal to 0.025 in lat. 15° and 0.0136 in lat. 60°. Rossby and Montgomery point out that the wind factor depends upon the depth at which the wind current is measured. Their theoretical values apply to the current at the very surface, but wind currents derived from ships' logs will apply to a depth of 2 or 3 m, depending upon the draft of the vessel. At this depth, their theory gives a wind factor in better agreement with Ekman's value, and they show that their theoretical conclusions are in fair agreement with empirical results. However, the introduction of an eddy viscosity that decreases to zero at a lower limit of the wind-stirred layer is justifiable only if no other currents are present. In the presence of other currents, such as tidal currents or currents related to distribution of mass, the eddy viscosity characteristic of the total motion must be introduced, and the variation of this eddy viscosity probably depends more upon the stability of the stratification than upon the geometric distance from the free surface. A theory of the wind currents must take this fact into account, but such a theory cannot be developed until more is known of the actual character of the turbulence. At present, Ekman's classical theory appears to give a satisfactory approximation, especially because no observations are as yet available by means of which the results of a refined theory can be tested.
So far, it has been assumed that the depth of the water is great compared to the depth of frictional resistance. Ekman has also examined the wind currents in shallow water and has determined the constants in equations (XIII, 77) by assuming that at the bottom the velocity is zero. This analysis leads to the result that in shallow water the deflection of the surface current is less than 45° and that the turning with depth is slower. In very shallow water the current flows nearly in the direction of the stress at all depths.
The assumption of an eddy viscosity that is independent of depth is not valid, however, if the water is shallow, because the eddy viscosity must be very small near the bottom (p. 480), regardless of the character of the current. The effect of a decrease of the eddy viscosity toward the bottom is generally that the angle between wind and current becomes greater at all depths and that the current velocities become greater. This effect is illustrated by measurements of wind currents on the North Shelf in lat. 76°35′ N, long. 138°24′ E (Sverdrup, 1929), where the depth to the bottom was 22 m. From these observations, Fjeldstad (1929) found that the eddy viscosity could be represented by the formula
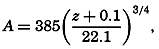
Wind current in shallow water assuming a constant eddy viscosity (dashed curve) or an eddy viscosity which decreases towards the bottom (full-drawn curve). Observed currents indicated by crosses.
The question of the time needed for establishing the assumed stationary conditions has also been examined by Ekman (1905), who has made use of a solution given by Fredholm for the case of a wind that suddenly begins to blow with a velocity which later remains constant. It is found that the motion will asymptotically approach a steady state. At each depth the end points of the velocity vectors, when represented as a function of time, will describe a spiral around the end point of the final velocity vector, the period of oscillation being 12 pendulum hours, corresponding to the period of oscillation by inertia movement (p. 438). The average velocity over 24 hours will be practically stationary from the very beginning, but the oscillations around the mean motion may continue for several days and may appear as damped motion in the circle of inertia.
Wind Currents in Water in Which the Density Increases with Depth. In the equations of motion which govern the wind current, the density enters explicitly, and it might therefore be expected
The rate at which a wind current penetrates toward greater depths will also depend upon the change of density with depth. Where an upper, nearly homogeneous layer of considerable thickness has already been developed by cooling from above and resulting vertical convection, the wind current will, in a short time, reach its normal state. Where a light surface layer has been developed because of heating or, in coastal areas, because of addition of fresh water, the wind current will first stir up the top layer and by mixing processes create a homogeneous top layer. When this layer is formed, the stability will be great at its lower boundary; there the eddy viscosity will be small and a further increase of the thickness of the homogeneous top layer will be effectively impeded, although the thickness may be much less than that of the layer within which normally a wind current should be developed. The further increase must be very slow, but no estimate can be given of the time required for the wind current to penetrate to the depths that it would have reached in homogeneous water. The gradual increase of the homogeneous top layer is shown schematically in fig. 123A.
Effect of wind in producing a homogeneous surface layer demonstrated by showing progressive stages of mixing.
If the wind dies off, heating at the surface may again decrease the density near the surface, but as soon as the wind again starts to blow, a new homogeneous layer is formed near the surface, and consequently two sharp bends in the density curve may be present (fig. 123B).
If conclusions are to be drawn from the thickness of the upper homogeneous layer as to the depth to which wind currents penetrate, cases must be examined in which the wind has blown for a long time from the same direction and with nearly uniform velocity. In middle and high latitudes the wind current will reach its final state more rapidly in winter, when cooling takes place at the surface, than in summer, when heating takes place.
Transport and Energy Equations Applied to Wind Currents. The transport by wind currents across a vertical surface 1 cm wide is obtained by integration of the equations of motion, taking the boundary condition into account. In the open ocean, where the water is deep, the result is
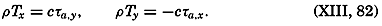
If in homogeneous water the kinetic energy remains constant, the energy equation (XIII, 68) is reduced to
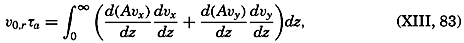
In Ekman's solution 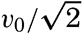 , where ν0 is the velocity of the surface wind current, which deviates 45° from the direction of the wind. Because A is assumed to be constant, one obtains
, where ν0 is the velocity of the surface wind current, which deviates 45° from the direction of the wind. Because A is assumed to be constant, one obtains
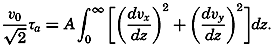
In nonhomogeneous water the complete energy equation has to be considered. The power of the wind stress on the surface must equal the work performed against the pressure gradients and the loss of energy by dissipation due to friction. This is only another way of stating that the wind currents are modified in stratified water, but so far the extent of modification has not been examined.
One of the characteristics of the modifications can be demonstrated as follows. The boundary condition must always be fulfilled (XIII, 65); that is,
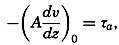
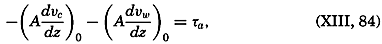
Effect of Friction on Bottom Currents. A current flows along the bottom if the isobaric surfaces are inclined near the bottom, and in this case the effect of friction cannot be neglected. The motion must be zero at the bottom, and directly over the bottom the eddy viscosity must increase rapidly with the distance from the bottom (see p. 480).
The equations of motion can easily be integrated if one assumes that the eddy viscosity is constant and that near the bottom the slope of the isobaric surfaces is independent of the distance from the bottom. The latter assumption implies that in the absence of friction the “gradient velocity,” Vi = − gci, is independent of the distance from the bottom. Placing the center of the coordinate system at the bottom, the positive y axis in the direction of the slope of the isobaric surfaces, and the z axis positive upward, one obtains
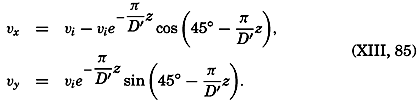
This solution, which was given also by Ekman, corresponds exactly to the solution which represents the wind current, and can be represented in a similar manner (see fig. 121, p. 493). Above the bottom the current first turns to the right and its velocity increases until, above the depth D′, which corresponds to the depth of frictional resistance, it practically attains the constant velocity vi. Projected on a horizontal plane, the end points of the velocity vectors lie on a logarithmic spiral.
This solution gives a first orientation as to the effect of friction near the bottom, but it cannot be expected that the solution will give a
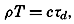
The above considerations are valid if the depth of the water is greater than the thickness of the layer of frictional resistance. In shallow water, modifications are encountered which have been discussed by Ekman on the assumption of a constant eddy viscosity.
Secondary Effect of Wind Toward Producing Currents. Upwelling. In the open ocean the total mass transport by wind is equal to Cτa and is directed normal to the wind regardless of the depth to which the wind current reaches and regardless of the variation with depth of the eddy viscosity. This fact is of the greatest importance, because the transport of surface layers by wind plays a prominent part in the generation and maintenance of ocean currents. Boundary conditions and converging or diverging wind systems must, in certain regions, lead to an accumulation of light surface waters and, in other regions, to a rise of denser water from subsurface depths. Thus, the wind currents lead to an altered distribution of mass and, consequently, to an altered distribution of pressure that can exist only in the presence of relative currents. These processes will be illustrated by a few examples.
Consider in the Northern Hemisphere a coast line along which a wind blows in such a manner that the coast is on the right-hand side of an observer who looks in the direction of the wind (see fig. 124). At some distance from the coast the surface water will be transported to the right of the wind, but at the coast all motion must be parallel to the coast line. Consequently a convergence must be present off the coast leading to an accumulation of light water along the coast. This accumulation creates a relative field of pressure with which must be associated a current running parallel to the coast in the direction of the wind. Thus, the wind produces not only a pure wind current but also
Consider next a wind in the Northern Hemisphere which blows parallel to the coast, with the coast on the left-hand side. In this case the light surface water will be transported away from the coast and must, owing to the continuity of the system, be replaced near the coast by heavier subsurface water. This process is known as upwelling, and is a conspicuous phenomenon along the coasts of Morocco, Southwest Africa, California, and Peru (pp. 702 and 725). The upwelling also leads to changes in the distribution of mass, but now the denser, upwelled water accumulates along the coast and the light surface water is transported away from the coast. This distribution of mass again will give rise to a current that flows in the direction of the wind.
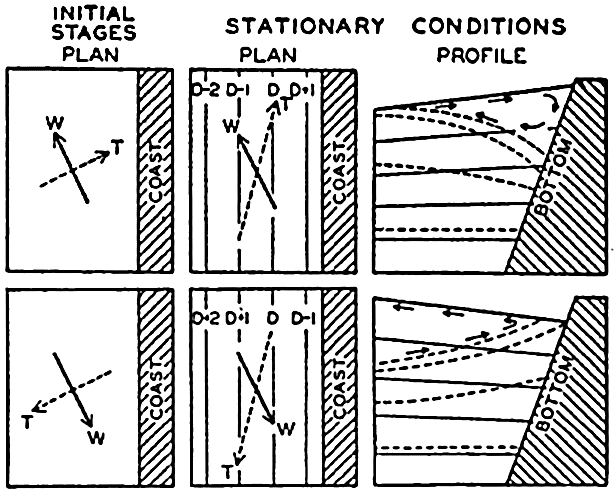
Schematic representation of effect of wind towards producing currents parallel to a coast in the Northern Hemisphere and vertical circulation. W shows wind direction, and T, direction of transport. Contours of sea surface shown by lines marked D, D + 1. … Top figures show sinking near the coast; bottom figures show upwelling.
The qualitative explanation of the upwelling was first suggested by Thorade (1909) and was developed by McEwen (1912). Recent investigations by Gunther (1936), Defant (1936b), Sverdrup (1930, 1938b), and Sverdrup and Fleming (1941) have added to the knowledge of the phenomenon, and have especially shown that water is drawn to the surface from depths not exceeding 200 to 300 m. Deep water does not rise to the surface, but an overturning of the upper layer takes place.
In spite of the added knowledge, it is as yet not possible to discuss quantitatively the process of upwelling or to predict theoretically the velocity and width of the coastal current that develops. It is probable that the tendency of the current is to break up in eddies, and that the forced vertical circulation limits the development of the current. Also, the wind that causes the upwelling does not, as a rule, blow with a steady velocity, and variations of the wind may greatly further the formation of eddies.
Figure 125 demonstrates the effect of winds from different directions on the currents off the coast of southern California in 1938. The charts show the geopotential topography of the sea surface relative to the 500-decibar surface, which in this case can be considered as nearly coinciding with a level surface. Arrows have been entered on the isolines, indicating that these are approximately stream lines of the surface currents.
In the absence of wind, one should expect a flow to the south or southeast, more or less parallel to the coast. In February, 1938 (fig. 125A), winds from the south or southwest had been blowing for some time. The light surface water had been carried toward the coast, and, consequently, a coastal current running north was present and was separated from the general flow to the south by a trough line, which probably represents a line of divergence. This inshore current to the north may not be an effect of the wind only, however, but may represent a countercurrent that develops when variable winds blow (p. 677).
(A) Geopotential topography of the sea surface off southern California relative to the 500-decibar surface in February, 1938, after a period with westerly or southwesterly variable winds. (B) Topography and corresponding currents in June after a period with prevailing northwesterly winds.
In June, 1938 (fig. 125B) northwesterly winds had prevailed for several months and had carried the light surface water out to a distance of about 150 km from the coast, where the swift current followed the boundary between the light offshore water and the denser upwelled water. Within both types of water several eddies appear.
Similar considerations apply to conditions in the open ocean. Take the case of a stationary anticyclone in the Northern Hemisphere. Over the ocean the direction of the wind deviates but little from the direction of the isobars, so that the total transport of the wind will be nearly toward the center of the anticyclone. Light surface water will, therefore, accumulate near the center of the anticyclone, and a distribution of mass will be created that will give rise to a current in the direction of the
Mention has so far been made only of the direction of the wind, but the total transport depends also upon the square of the wind velocity and upon the latitude. In order to find the actual convergence due to wind, it is necessary, therefore, to take into account both the velocity and the latitude. An attempt in this direction has been made by Montgomery (1936), who finds that in the North Atlantic Ocean the region of maximum convergence lies to the south of the anticyclone. Further investigations of this nature are desirable.
Every wind system, whether stationary or moving, will create currents associated with the redistribution of mass due to wind transport. It is possible, furthermore, that within a moving wind system the distribution of mass does not become adjusted to the wind conditions, and that actual piling up or removal of mass may occur such as takes place in partly landlocked seas like the Gulf of Bothnia (p. 490). If this is true, slope currents reaching from the surface to the bottom develop, but they are of a local character and will soon be dissipated. One may thus expect that superimposed on the general currents will be irregular currents due to changing winds and, furthermore, eddies which are characteristic of the currents themselves and independent of wind action. A synoptic picture of the actual currents can therefore be expected to be highly complicated.
Conclusions as to Currents on the Basis of Tonguelike Distribution of Properties
Where horizontal differences in density are so small that differences in computed anomalies of distances between isobaric surfaces become doubtful, conclusions as to currents are often drawn from tonguelike distribution of properties, especially of temperature and salinity. In such cases, it is necessary to distinguish between tongues in a horizontal plane and those in a vertical section.
As a rule a tonguelike distribution in a horizontal plane can be interpreted by means of the dynamic considerations that have been presented. If a tongue of low temperature is present, as shown in fig. 126, one can assume in most cases that the water of the lowest temperature also has the highest density and, in accordance with the rule that in the Northern Hemisphere the water of the highest density must be found on the left-hand side of the current, arrows representing the approximate direction of flow can be entered. In the example shown in fig. 126 the flow to the northwest on the coastal side of the tongue of cold water was confirmed by results of drift-bottle experiments (Sverdrup and Fleming, 1941). Thus, the stream lines tend to follow the contour lines of the tongues.
If the dynamics of the system were not borne in mind, one might assume that the spread of the water would be jetlike and that the axes of the jet currents would coincide with the tongues of low or high temperatures, as indicated by the open arrows in fig. 126. Such an interpretation, however, would neglect the effect of horizontal pressure gradients and therefore would be in disagreement with the character of the acting forces. These conclusions will be somewhat modified by a consideration of the effect of friction, and they may not be valid at the sea surface, where external factors may contribute toward maintaining the temperature distribution.
Tonguelike distribution of temperature at a depth of 50 m off southern California in May, 1937. Solid arrows indicate direction of flow according to the geopotential topography of the sea surface; open arrows show the axes of the tongues.
Consider next a vertical section in which a tonguelike distribution of temperature and salinity appears (fig. 127). In this case the tongue may indicate horizontal flow in the direction of the tongue, and such flow may no longer be in conflict with the dynamics of the system. However, if only horizontal motion occurs, processes of mixing must be of importance to the development of the tongue, because the properties of the mass in a moving volume are changing in the direction of flow, and in the subsurface layers such changes can be due only to mixing (p. 158).
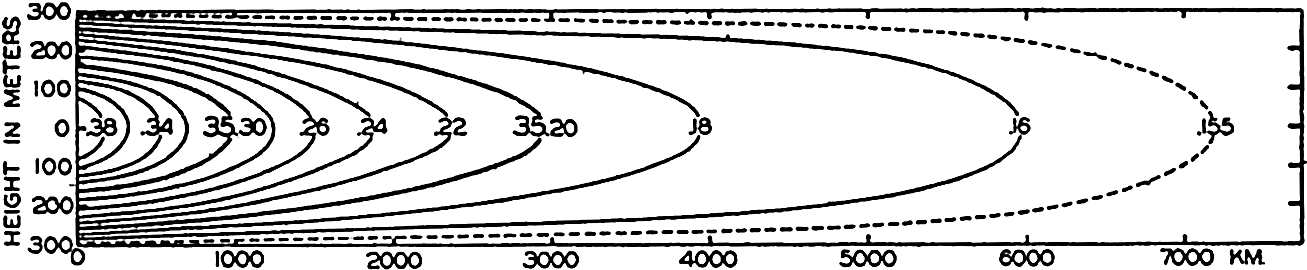
Tonguelike distribution of salinity in a vertical section corresponding to given boundary conditions and given values of velocity and eddy diffusion. See text.
Defant (1929b) and Thorade (1931) have examined analytically the relation between the velocity and the effect of vertical mixing. Under stationary conditions the equation (p. 159)

Equation (XIII, 86) can be solved if A/ρ is supposed to be constant and a number of simple assumptions are introduced. Consider, for instance, a horizontal current of uniform velocity, ν, in a layer of thickness 2h, flowing between z = +h and z = − h (see fig. 127). Assume that at x = 0 the distribution of the property is given by the equation
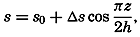
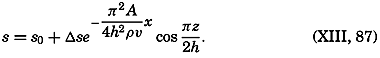
Figure 127 shows an example of such a distribution which has been prepared by Defant after the introduction of numerical values of s0, Δs, and h and by assuming that A/ν = 2. The solution presupposes certain boundary conditions that are not specified here. Transport of the property into the volume must take place through the surface x = 0, and transport out of the volume must take place through the other boundary surfaces. In these circumstances, it is necessary to assume that certain physical processes maintain the constant value s = s0 along the horizontal boundaries.
As shown by Thorade (1931), equation (XIII, 86) can be integrated on many different assumptions, and different types of tongues can be derived. It is particularly interesting to observe that on certain assumptions the tongue is found to curve up or down, although horizontal flow is assumed, and that the axis of the tongue need not coincide with an axis of maximum velocity. In fig. 127, uniform velocity was supposed, but the tonguelike distribution of the property may create the erroneous impression that the velocity is at a maximum along the center line of the tongue. In view of these results, it is necessary to exercise great care when drawing conclusions as to currents from tonguelike distribution.
Defant (1936a) has made use of equation (XIII, 86) in an improved form in order to compute the ratio A/ν directly from oceanographic data. Considering that along the bottom the motion cannot be horizontal, but must follow the slope of the bottom and that, even at some distance from the bottom, the motion may deviate from the horizontal, Defant writes

It has so far been assumed that horizontal mixing can be disregarded, but a tonguelike distribution can equally well be brought about by horizontal and vertical mixing and by horizontal flow and vertical mixing. If a given distribution in a vertical plane is maintained only by processes of mixing in horizontal and vertical directions, equation (XIII, 86) must be replaced by

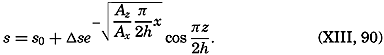
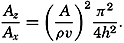
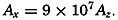
The “core method,” which Wüst has introduced (p. 146) and used successfully in studying the deep-water flow in the Atlantic, does not contain any assumption as to the character of the mixing, and is well suited therefore for giving a qualitative picture of the spreading of certain water types.
Thermodynamics of Ocean Currents
The preceding description of the effect of the wind, especially the discussion of the secondary effect of the wind in producing currents in stratified water, may leave the impression that the wind is all-important to the development of the ocean currents and that thermal processes can be entirely neglected. Such an impression would be very misleading, however. In discussing the secondary effect of the wind, it was repeatedly mentioned that the development of the currents caused by a redistribution of mass by wind transport would be checked partly by mechanical processes and partly by thermal processes. Surface waters that were transported to higher latitudes would be cooled, and thus a limit would be set to the differences in density that could be attained. Upwelling water would be heated when approaching the surface, and at a certain vertical velocity a stationary temperature distribution would be established at which the amount of heat absorbed in a unit volume would exactly balance the amounts lost by eddy conduction and by transport of heat through the volume by vertical motion. The establishment of a stationary temperature distribution within upwelling water would check the effect of upwelling on the horizontal distribution of density.
The above examples serve to emphasize the importance of the thermal processes in the development of the currents, but an exact discussion of the thermodynamics of the ocean is by no means possible. So far, the principles of thermodynamics have found very limited application to oceanographic problems, but this statement does not mean that the thermal processes are unimportant compared to the mechanical.
Thermal Circulation. The term “thermal circulation” will be understood to mean a circulation that is maintained by heating a system in certain regions and by cooling it in other regions. The character of the thermal circulation in the ocean and in the atmosphere has been discussed by V. Bjerknes and collaborators (1933). Their conclusions can be stated as follows: If within a thermal circulation heat shall be transformed into mechanical energy, the heating must take place under higher pressure and the cooling under lower pressure. Such a thermodynamic
In the ocean, “higher pressure” can generally be replaced by “greater depth,” and “lower pressure” by “smaller depth.” Applied to the ocean the theorem can be formulated as follows: If within a thermal circulation heat shall be transformed into mechanical energy, the heating must take place at a greater depth than the cooling.
This theorem was demonstrated experimentally by Sandström previous to its formulation by Bjerknes. In one experiment, Sandström placed a “heater” at a certain level and a “cooler” at a lower level in a vessel filled with water of uniform temperature. The heater consisted of a system of tubes through which warm water could be circulated, and the cooler consisted of a similar system through which cold water could be circulated. When warm and cold water were circulated through the pipes, a system of vertical convection currents developed and continued until the water above the heater had been heated to the temperature of the circulating warm water, and the water below the cooler had been cooled to the temperature of the circulating cold water. When this state had been reached and a stable stratification had been established, with temperature decreasing downward, all motion ceased.
In a second experiment, Sandström placed the cooling system above the heating system. In this case the final state showed a circulation with ascending motion above the heating unit and descending motion below the cooling unit. Thus, a stationary circulation was developed, because the heating took place at greater depth than the cooling.
From these experiments and from Bjerknes' theorem, it is immediately evident that in the oceans conditions are very unfavorable for the development of thermal circulations. Heating and cooling take place mainly at the same level—namely, at the sea surface, where heat is received by radiation from the sun during the day when the sun is high in the sky, or lost by long-wave radiation into space at night or when the sun is so low that the loss is greater than the gain and heat is received or lost by contact with air.
Because heating and cooling take place at the surface, one might expect that no thermal circulation can develop in the sea, but this is not true. Consider a vessel filled with water. Assume that heating at the surface takes place at the left-hand end, and that towards the right-hand end the heating decreases, becoming zero at the middle of the vessel. Beyond the middle, cooling takes place, and reaches its maximum at the other end. Under these conditions the heated water to the left will have a smaller density than the cooled water to the right, and will therefore spread to the right. Owing to the continuity of the system, water must rise near the left end of the vessel and sink near the right
This circulation is quite in agreement with Bjerknes' theorem, because at the surface the water that flows from left to right is being cooled, since it flows from a region where heating dominates into a region where cooling is in excess. During the return flow, which takes place at some depth below the surface, the water is, on the other hand, being warmed by conduction, because it flows from a region of lower temperature to a region of higher temperature. Thus the circulation is such that the heating takes place at a greater depth than the cooling. This circulation, however, cannot become very intensive, particularly because the heating within the return flow must take place by the slow processes of conduction.
If the oceanic circulation is examined in detail, many instances are found in which the vertical circulation caused by the wind is such that the thermal machine runs in reverse, meaning that mechanical energy is transformed into heat, thus checking the further development of the wind circulation. When upwelling takes place, the surface flow will be directed from a region of low temperature to a region of high temperature, and the subsurface flow will be directed from high to low temperature. The thermal machine that is involved will consume energy and thus counteract a too-rapid wind circulation. In the Antarctic the thermal circulation will be directed at the surface from north to south and will counteract the wind circulation, which will be directed from south to north. On the other hand, systems are found within which the thermal effect tends to increase the wind effect and within which the increase of the circulation must be checked by dissipation of kinetic energy.
The Thermohaline Circulation. So far, only thermal circulations have been considered, but it must be borne in mind that the density of the water depends on both its temperature and its salinity, and that in the surface layers the salinity is subject to changes due to evaporation, condensation, precipitation, and addition of fresh water from rivers. In the open ocean the changes in density are determined by the excess or deficit of evaporation over precipitation. These changes in density may be in the same direction as those caused by heating and cooling, or they may be in opposite directions. When examining the circulation that arises because of the external factors influencing the density of the surface waters, one must take changes of both temperature and salinity into account, and must consider not the thermal but the thermohaline circulation. Bjerknes' theorem is then better formulated as follows:
If thermal and haline circulations are separated, it is found that in some instances they work together and that in others they counteract each other. The greatest heating takes place in the equatorial region, where, owing to excess precipitation, the density is also decreased by reduction of the salinity. In the latitudes of the subtropical anticyclones the heating is less, and, in addition, the density of the water is increased by excess evaporation. Between the Equator and the latitudes of the subtropical anticyclones, conditions are therefore favorable for the development of a strong thermohaline circulation. North and south of these latitudes the haline circulation will, however, counteract the thermal, because the density is decreased by excess precipitation but increased by cooling. A weak thermohaline circulation might be expected there.
In the absence of a wind system, one might expect at the surface a slow thermohaline circulation directed from the Equator to the poles and directed at some subsurface depth in the opposite direction. This circulation would be modified by the rotation of the earth and by the form of the ocean basins, but nothing can be said as to the character of the system of currents that would develop under such conditions. It is probable, however, that the existing current system bears no similarity to the one that would result from such a thermohaline circulation, but is mainly dependent upon the character of the prevailing winds and upon the extent to which the circulation maintained by the wind is checked by the thermal conditions. In other words, the wind system tends to bring about a distribution of density that is inconsistent with the effect of heating and cooling, and the actual distribution approaches a balance between the two factors. These two factors—the wind and the process of heating and cooling—are variable, however, in time and space, for which reason a stationary distribution of density with accompanying stationary currents does not exist. Only when average conditions over a long time and a large area are considered can they be regarded as stationary.
Vertical Convection Currents. The thermohaline circulation is of small direct importance to the horizontal current, but is responsible mainly for the development of vertical convection currents. Wherever the density of the surface water is increased so much by cooling or evaporation that it becomes greater than the density of the underlying strata, the surface water must sink and must be replaced by water from some subsurface depth. The vertical currents that arise in this manner are called vertical convection currents. They are irregular in character and
The depth to which vertical convection currents penetrate depends upon the stratification of the water. A mass of surface water, the density of which has been increased by cooling or evaporation, sinks until it meets water of equal density. If mixing with neighboring water masses takes place, it sinks to a lesser depth. When vertical convection currents have been active for some time, an upper layer of homogeneous water is formed, the thickness of which depends upon the original stratification of the water, the intensity of the convection currents, and the time the process has lasted. Thus, an upper homogeneous layer can be formed in two different ways: either by the mechanical stirring due to wind, or by the effect of the thermohaline vertical convection currents.
The vertical convection currents are, as a rule, of greater importance in higher latitudes. In latitudes where an excess of evaporation is found, the heating of the surface is often so great that the decrease of the surface density by heating more than balances the increase by evaporation. In these circumstances the surface salinity will be greater than the salinity at a short distance below the surface. The formation of deep and bottom water by vertical convection currents is dealt with elsewhere (p. 138).
Bibliography
Bjerknes, V., J. Bjerknes, H. Solberg, T. Bergeron. 1933. Physikalische Hydrodynamik. Berlin. Julius Springer. 797 pp., 1933.
Bowie, William. 1936. “The place of geodesy in geophysical research” . Amer. Geophys. Un., Trans., p. 15–20, 1936.
Defant, A.1929a. “Dynamische Ozeanographie” . Einführing in der Geophysik, 3, 222 pp.Berlin. 1929.
Defant, A.1929b. Stabile Lagerung ozeanischer Wasserkörper und dazu gehorige Stromsysteme. Berlin, Universität, Institut f. Meereskunde, Veröff. N.F., A. Geogr.-naturwiss. Reihe, Heft 19, 33 pp., 1929.
Defant, A.1932. “Die Gezeiten und inneren Gezeitenwellen des Atlantischen Ozeans” . Deutsche Atlantische Exped. Meteor1925–1927, Wiss. Erg., Bd. 7, 1 Teil, 318 pp., 1932.
Defant, A.1936a. “Ausbreitungs- und Vermischungsvorgänge im Antarktischen Bodenstrom und im Subantarktischen Zwischenwasser” . Deutsche Atlantische Exped. Meteor1925–1927, Wiss. Erg., Bd. 6, 2 Teil Lief. 2, p. 55–96, 1936.
Defant, A.1936b. “Das Kaltwasserauftriebsgebiet vor der Küste Südwestafrikas” . Länderkundliche Forschung, Festschrift Norbert Krebs zur Vollendung des 60. Lebensjahres dargebracht, p. 52–66, 1936.
Defant, A.1940. “Die ozeanographischen Verhältnisse während der Ankerstation des Altair am Nordrand des Hauptstromstriches des Golfstromsnördlich der Azoren” . Ann. d. Hydrogr. u. Mar. Meteor., November–Beiheft, 4. Lief., 35 pp., 1940.
Defant, A.1941. “Die absolute Topographie des physikalischen Meeresniveaus und der Druckflächen, sowie die Wasserbewegungen im Atlantischen Ozean” . Deutsche Atlantische Exped. Meteor1925–1927, Wiss. Erg., Bd. VI, 2 Teil, 5. Lief., p. 191–260, 1941.
Defant, A., and Bj. Helland-Hansen. 1939. “Bericht über die ozeanographischen Untersuchungen im zentralen und östlichen Teil des Nordatlantischen Ozeans im Frühsommer 1938 (Internationale Golfstrom-Expedition)” . Preuss. Akad. d. Wissenschaften, Abhandl., Jahrg. 1939, Phys.-math. Klasse, Nr. 5, 64 pp., 1939.
Dietrich, Günter. 1937a. “Die dynamische Bezugsfläche, ein Gegenwarts-problem der dynamischen Ozeanographie.” Ann. d. Hydrogr. u. Mar. Meteor., Bd.65, pp. 506–19, 1937.
Dietrich, Günter. 1937b. Die Lage des Meeresoberfläche im Druckfeld von Ozean und Atmosphäre mit besonderer Berücksichtigung des westlichen Nordatlantischen Ozeans und des Golfs von Mexico. Berlin, Universität, Institut f. Meereskunde, Veröff., N. F., A. Geogr.-naturwiss. Reihe, Heft 33, 52 pp., 1937.
Ekman, V. Walfrid. 1902. “Om jordrotationens inverkan på vindströmmar i hafvet.” Nyt. Mag. f. Naturvid., v. 40, 1902. Kristiania.
Ekman, V. Walfrid. 1905. “On the influence of the earth's rotation on ocean currents.” Ark. f. Mat. Astr. och Fysik. K. Sv. Vet. Ak., Stockholm, 1905–06, v. 2, no. 11, 1905.
Ekman, V. Walfrid. 1923. “Über Horizontalzirkulation bei winderzeugten Meeresstromungen” . Arkiv. f. Mat. Astr. o. Fys., v. 17, no. 26, 1923. Stockholm.
Ekman, V. Walfrid. 1927. Meeresströmungen. Handbuch d. physikalischen u. technischen Mechanik, Bd. 5, Lief 1, p. 177–206, 1927.
Ekman, V. Walfrid. 1929. “Über die Strommenge der Konvektiönsstrome im Meere.” Lunds Univ. Arsskr., N. F., Afd. 2, v. 25, nr. 6, Lund u. Leipzig, 1929.
Ekman, V. Walfrid. 1932. “Studien zur Dynamik der Meeresströmungen” . Gerlands Beitr. z. Geophysik, Bd. 36, p. 385–438. Leipzig. 1932.
Ekman, V. Walfrid. 1939. “Neuere Ergebnisse und Probleme zur Theorie der Konvektionsströme im Meere” . Gerlands Beitr. z. Geophysik, Suppl. Bd. 4, Ergebn. d. kosmischen Physik IV, Physik d. Hydro- u. Lithosphäre, 74 pp., 1939. Leipzig.
Ekman, V. Walfrid, and Bj. Helland-Hansen. 1931. “Measurements of ocean currents (Experiments in the North Atlantic).” Kungl. fysiografiska Sallskapet i Lund Förhandlingar, v. 1, no. 1, 1931.
Fjeldstad, J. E.1929. “Ein Beitrag zur Theorie der winderzeugten Meeresströmungen.” Gerlands Beitr. z. Geophysik, Bd. 23, 1929.
Fjeldstad, J. E.1933. Wärmeleitung im Meere.Geofysiske Publikasjoner, v. 10, no. 7, 20 pp., 1933. Oslo.
Fjeldstad, J. E.1936. “Results of tidal observations. Norwegian North Polar Exped. with the Maud 1918–1925.” Sci. Results, v. 4, no. 4, 88 pp., 1936.
Gunther, E. R.1936. “A report on oceanographical investigations in the Peru coastal current” . Discovery Repts., v. 13, p. 109–275, 1936.
Gustafson, T., and B. Kullenberg. 1936. “Untersuchungen von Trägheits-strömungen in der Ostsee.” Sv. Hydr.-Biol. Komm. Skr., Ny Ser. Hydr., no. 13, 28 pp., 1936.
Helland-Hansen, Bj.1934. The Sognefjord section. p. 257–274 in James Johnstone Memorial Volume.Liverpool. Univ. Press, 348 pp., 1934.
Hidaka, K.1940. “Absolute evaluation of ocean currents in dynamical calculations” . Imperial Acad. Japan, Proc., v. 16, p. 391–393, 1940. Tokyo.
Iselin, C. O'D.1936. “A study of the circulation of the western North Atlantic” . Papers in Physical Oceanogr. and Meteor., v. 4, no. 4, 101 pp., 1936.
Jacobsen, J. P.1913. “Beitrag zur Hydrographie der dänischen Gewässer.” Komm. f. Havunders. Medd., Ser. Hydr., v. 2, no. 2, 94 pp., 1913. Copenhagen.
Jacobsen, J. P.1930. “Remarks on the determination of the movement of the water and the intermixing of the watersheets in a vertical direction.” Conseil Perm. Internat. p. l'Explor. de la Mer, Rapp. et Proc.-Verb., v. 64, p. 59–68, 1930.
Jacobsen, J. P., and A. J. C. Jensen. 1926. “Examination of hydrographical measurements from the research vessels Explorer and Dana during the summer of 1924.” Conseil Perm. Internat. p. l'Explor. de la Mer, Rapp. et Proc.-Verb., v. 39, p. 31–84, 1926.
Jakhelln, A.1936. The water transport of gradient currents.Geofysiske Publikasjoner, v. 11, 14 pp., 1936.
Krümmel, O.1911. Handbuch der Ozeanographie. v. 2, Stuttgart, Engelhorn, 764 pp., 1911.
La Fond, Eugene C.1939. “Variations of sea level on the Pacific coast of the United States.” Jour. Marine Research, v. 2, p. 17–29, 1939.
Lamb, H.1932. Hydrodynamics. London. Cambridge Univ. Press. 6th ed., 748 pp., 1932.
Lek, Lodewijk. 1938. Die Ergebnisse der Strom- und Serienmessungen. Snellius Exped. in the eastern part of the Netherlands East-Indies 1929–1930, v. 2, pt. 3, 169 pp., 1938.
McEwen, George F.1912. “The distribution of ocean temperatures along the west coast of North America deduced from Ekman's theory of the upwelling of cold water from the adjacent ocean depths.” Intern. Revue ges. Hydrobiol. u. Hydrogr., Bd. 5, p. 243–286, 1912.
McEwen, George F.1919. “Ocean temperatures, their relation to solar radiation and oceanic circulation.” Scripps Inst. Biol. Res. Misc. Studies in Agric. and Biol., SemicentennialPub. Univ. Calif., 1868–1918, p. 335–421, 1919.
Montgomery, R. B.1936. “Transport of surface water due to the wind system over the North Atlantic.” Papers in Physical Oceanogr. and Meteorol., v. 4, no. 3, p. 23–30, 1936.
Montgomery, R. B.1938. “Fluctuations in monthly sea level on eastern U. S. coast as related to dynamics of western North Atlantic Ocean.” Jour. Marine Research, v. 1, p. 165–185, 1938.
Montgomery, R. B.1939. “Ein Versuch den vertikalen und seitlichen Austausch in der Tiefe der Sprungschicht im äquatorialen Atlantischen Ozean zu bestimmen” . Ann. d. Hydrogr. u. Mar. Meteor., Bd. 67, p. 242–246, 1939.
Montgomery, R. B., and E. Palmén.1940. “Contribution to the question of the Equatorial Counter Current.” Jour. Marine Research, v. 3, p. 112–133, 1940.
Neumann, Gerhard. 1940. “Die ozeanographischen Verhältnisse an der Meeresoberfläche im Golfstromsektor nördlich und nordwestlich der Azoren.” Ann. d. Hydrogr. u. Mar. Meteor., Beiheft sum Juniheft, 1. Lief., 87 pp., 1940.
Palmén, E., and E. Laurila. 1938. “Über die Einwirkung eines Sturmes auf den hydrographischen Zustand im nordlichen Ostseegebiet” . Soc. Sci. Fen. Com. Phys.-Mat., v. 10, no. 1, 53 pp., 1938. Helsingfors.
Parr, A. E.1936. “On the probable relationship between vertical stability and lateral mixing processes.” Conseil Perm. Internat. p. l'Explor. de la Mer, Journal du Conseil, v. 11, p. 308–313, 1936.
Rossby, C.-G.1932. “A generalization of the theory of the mixing length with applications to atmospheric and oceanic turbulence.” Papers in Physical Oceanogr. and Meteorol., v. 1, no. 4, 36 pp., 1932.
Rossby, C.-G.1936a. “Dynamics of steady ocean currents in the light of experimental fluid mechanics.” Papers in Physical Oceanogr. and Meteorol., v. 5, no. 1, 43 pp., 1936.
Rossby, C.-G.1936b. “On the frictional force between air and water and on the occurrence of a laminar boundary layer next to the surface of the sea.” Papers in Physical Oceanogr. and Meteor., v. 4, no. 3, 20 pp., 1936.
Rossby, C.-G., and R. B. Montgomery. 1935. “The layer of frictional influence in wind and ocean currents.” Papers in Physical Oceanogr. and Meteorol., v. 3, no. 3, 101 pp., 1935.
Rouse, Hunter. 1938. Fluid mechanics for hydraulic engineers. New York. McGraw-Hill, 422 p., 1938.
Sandström, J. W., and B. Helland-Hansen. 1903. “Über die Berechung von Meeresströmungen.” Reports on Norwegian Fishery and Marine Investigations. Bd. 2, Nr. 4, 43 pp., 1903. Bergen.
Seiwell, H. R.1935. “The distribution of oxygen in the western basin of the North Atlantic.” Papers in Physical Oceanogr. and Meteorol., v. 3, no. 1, 86 pp., 1935.
Seiwell, H. R.1938. “Application of the distribution of oxygen to the physical oceanography of the Caribbean region.” Papers in Physical Oceanogr. and Meteorol., v. 6, no. 1, 60 pp., 1938.
Seiwell, H. R.1942. “An analysis of vertical oscillations in the southern North Atlantic.” Amer. Phil. Soc., Proc., v. 85, p. 136–158, 1942.
Smith, Edward H.1926. A practical method for determining ocean currents. U. S. Coast Guard, Bull.no. 14, 50 pp., 1926.
Suda, K.1936. “On the dissipation of energy in the density current (2nd paper).” Geophys. Mag., v. 10, p. 131–243, 1926. Tokyo.
Sverdrup, H. U.1926. Dynamic of tides on the North Siberian Shelf. Results from the Maud Expedition.Geofysiske Publikasjoner, v. 4, no. 5, 75 pp., 1926.
Sverdrup, H. U.1929. “The waters on the North Siberian Shelf.” Norwegian North Polar Exped. with the Maud 1918–1925, Sci. Results, v. 4, no. 2, 131 + 175 pp., 1929.
Sverdrup, H. U.1930. “Some oceanographic results of the Carnegie's work in the Pacific–-The Peruvian Current.” Amer. Geophys. Un., Trans., p. 257–264. 1930.
Sverdrup, H. U.1933. “Narrative and oceanography of the Nautilus Expedition, 1931.” Papers in Physical Oceanogr. and Meteorol., v. 2, no. 1, 63 pp., 1933.
Sverdrup, H. U.1938a. “On the explanation of the oxygen minima and maxima in the oceans. Conseil Perm. Internat. p. l'Explor. de la Mer” , Journal du Conseil, v. 13, no. 2, p. 163–172, 1938.
Sverdrup, H. U.1938b. “On the process of upwelling.” Jour. Marine Research, v. 1, p. 155–164, 1938.
Sverdrup, H. U.1939a. “Lateral mixing in the deep water of the South Atlantic Ocean.” Jour. Marine Research, v. 2, p. 195–207, 1939.
Sverdrup, H. U.1939b. “On the influence of stability and instability on the wind profile and the eddy conductivity near the ground.” Fifth Internat. Congr. Applied Mech., Trans., p. 369–372, 1939.
Sverdrup, H. U., and R. H. Fleming. 1941. “The waters off the coast of southern California, March to July, 1937” . Scripps Inst. Oceanogr., Bull., v. 4, p. 261–378, 1941.
Sverdrup, H. U., and Staff. 1942. “Oceanographic observations on the E. W. Scripps cruises of 1938.” Scripps Inst. Oceanogr., Records of Observationsv. 1, no. 1, 63 pp., 1942.
Taylor, G. I.1931. “Internal waves and turbulence in a fluid of variable density. Conseil Perm. Internat. p. l'Explor. de la Mer” , Rapp. et Proc.-Verb., v. 76, p. 35–43, 1931.
Taylor, G. I.1932. “The transport of vorticity and heat through fluids in turbulent motion.” Royal Soc. London, Proc., Ser. A, v. 135, p. 685–701, 1932.
Thorade, H.1909. “Über die Kalifornische Meeresströmung.” Ann. d. Hydrogr. u. Mar. Meteor., Bd. 37, p. 17–34, 63–76, 1909.
Thorade, H.1914. “Die Geschwindigkeit von Triftströmungen und die Ekmansche Theorie.” Ann. d. Hydrogr. u. Mar. Meteor., Bd. 42, p. 379–91, 1914.
Thorade, H.1928. “Gezeitenuntersuchungen in der Deutschem Bucht der Nordsee.” Deutsche Seewarte, Archiv, Bd. 46, Nr. 3, p. 1–85, 1928. Hamburg.
Thorade, H.1931. “Strömung und Zungenförmige Ausbreitung des Wassers.” Gerlands Beitr. z. Geophysik, Bd. 34, p. 57–76, 1931. Leipzig.
Wattenberg, H.1935. “Kalkauflösung und Wasserbewegung am Meeresboden.” Ann. d. Hydrogr. u. Mar. Meteor., Bd. 63, p. 387–391, 1935.
Werenskiold, W.1937. “Die Berechnung von Meeresströmungen.” Ann. d. Hydrogr. u. Mar. Meteor., Bd. 65, p. 68–72, 1937.
Wüst, Georg. 1920. Die Verdunstung auf dem Meere.BerlinUniversität, Institut f. Meereskunde, N. F., A. Geogr.-naturwiss. Reihe, Heft 6, 95 pp., 1920.
Wüst, Georg. 1940. “Das Relief des Azorensockels und des Meeresbödens nordlich und nordwestlich der Azoren.” Ann. d. Hydrogr. u. Mar. Meteor., August-Beiheft, 2. Lief., 19 pp., 1940.
XIV. Waves and Tides
Introduction
The preceding sections have dealt with the types of motion in the ocean that bring about transport of water masses in a definite direction during a considerable length of time. They have also dealt with the random motion, the turbulence, which is superimposed upon the general flow. Besides these types, one has also to consider the oscillating motion characteristic of waves. In general, this motion manifests itself to the observer more by the rise and fall of the sea surface than by the motion of the individual water particles.
Waves have attracted attention since before the beginning of recorded history, and in recent years they have been the subject of extensive theoretical studies. Surveys of our knowledge as to the character of ocean waves have been presented by Cornish (1912, 1934), Krümmel (1911), Patton and Marmer (1932) and by Defant (1929). Lamb (1932) has discussed the hydrodynamic theories of waves, and Thorade (1931) has given a comprehensive review of the theoretical studies of ocean waves and has compiled a long list of literature covering the period from 1687 to 1930.
Our understanding of the waves of the ocean, how they are formed and how they travel, is as yet by no means complete. The reason is, in the first place, that actual observations at sea are so difficult that the characteristics of the waves cannot easily be determined. In the second place, the theories that serve to bring the observed sequence of events in nature into intimate connection with experience gained by other methods of study are still incomplete, particularly because most theories are based on classical hydrodynamics, which deal with wave motion in an idealized fluid. Here will be presented only a brief review of the best-established facts concerning waves and of some of the more outstanding theoretical accomplishments. Readers who wish to gain further insight are referred to some of the above-mentioned books.
In order to classify waves, it is necessary to introduce certain definitions. Wave height, H, is defined as the vertical distance from trough to crest, whereas wave amplitude, a, is one half of that distance (fig. 128).
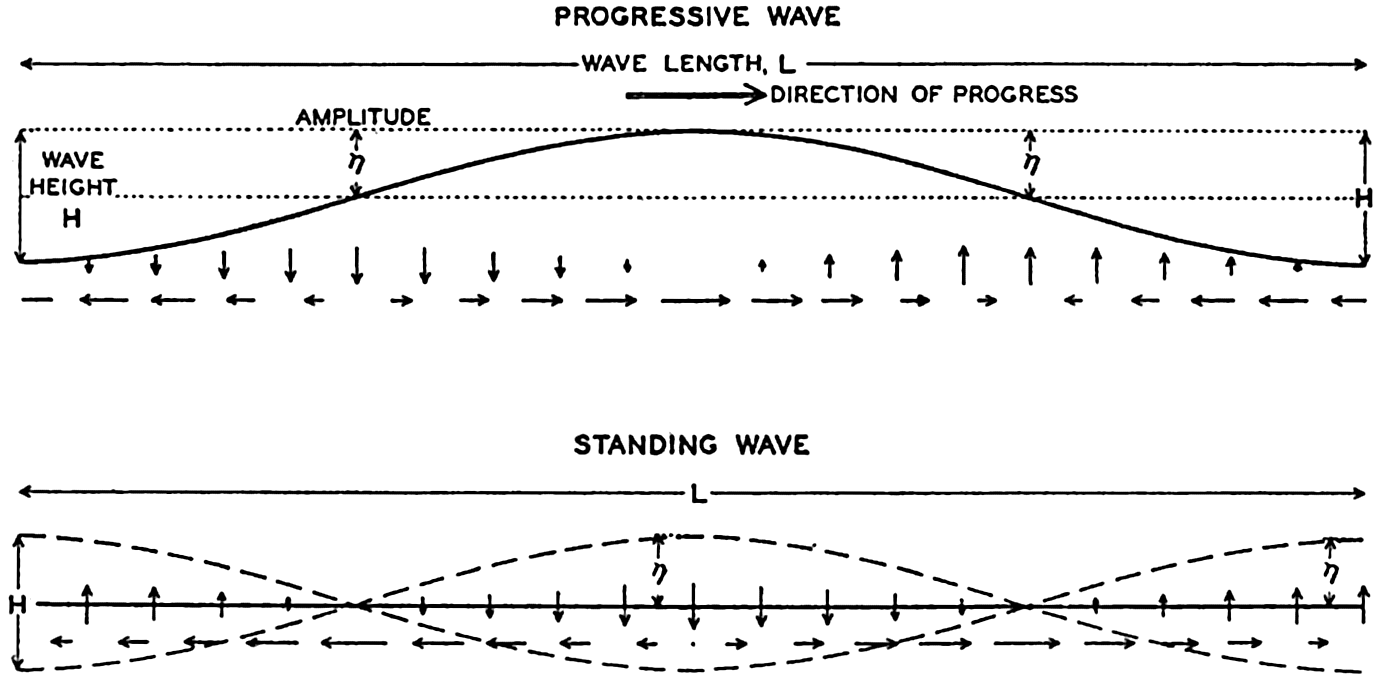
Schematic representation of a progressive and of a standing wave.
For a wave the amplitude of which is small compared to the wave length, the height of the free surface, η, at a given locality can be represented by means of a simple harmonic function,
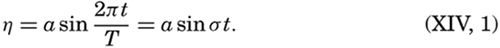
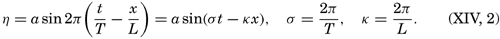
In wave motion, two types of velocity have to be considered: the velocity of progress of the wave itself and the velocity of the individual water particles. The water particles move back and forth, in circles, or
The rise and fall of the free surface can be ascribed to convergence and divergence of the horizontal motion of the water particles. Within a progressive wave (fig. 128, also fig. 98, p. 426) the horizontal flow at the wave crest is in the direction of progress, and at the trough it is opposite to the direction of progress. Convergence therefore takes place between the crest and the trough, and there the surface rises. Within a standing wave (fig. 128) the horizontal velocity is zero at every point at the time when the wave reaches its greatest height. During the following half period the horizontal velocity is directed from the crest to the trough, causing divergence below the crest and convergence below the trough, for which reason the crest will sink and the trough will rise. This process continues until the positions of the crest and of the trough become interchanged, and during the following half period the horizontal motion is reversed. The vertical velocity is always zero halfway between the crest and the trough, where the wave has nodes. The horizontal velocity is always zero at the crests and troughs, where the wave has antinodes or loops. Evidently a vertical wall can be inserted at the antinode without altering the character of the wave, because no horizontal motion exists at the antinode.
From a different point of view, waves can be classified as forced or free waves. A forced wave is a wave that is maintained by a periodic force, and the period of a forced wave must always coincide with the period of the force, regardless of the dimensions of the basin or of frictional influence. A free wave, on the other hand, represents one of the possible oscillations of a body of water if this body is set in motion by a sudden impulse. The period of a free wave depends on the dimensions of the basin and on the effect of friction. Later on, these types will be dealt with more fully.
When ocean waves are concerned, gravity and Corioli's force are the two important forces to be considered. For waves of a few centimeters in length the surface tension of the water has to be taken into account, but such waves are of no consequence in the sea. We shall therefore deal with gravity waves only and shall at first neglect Corioli's force.
A rational division of gravity waves into two classes can be made when considering the relation between wave velocity, wave length, and the depth to the bottom. The wave velocity can with sufficient accuracy be represented by means of the equation of classical hydrodynamics:


If, on the other hand, the depth is small compared to the wave length, tanh 2πh/L can be replaced by 2π;h/L, so that c = 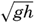 . Thus, if the depth is small compared to the wave length, the velocity of the wave depends only on the depth to the bottom and is independent of the wave length. The latter waves are called long waves, whereas the former, the velocity of which is independent of depth, are called short waves, or surface waves. For water of any given depth the transition takes place within a narrow range of wave lengths, for which reason the classification is a very satisfactory one.
. Thus, if the depth is small compared to the wave length, the velocity of the wave depends only on the depth to the bottom and is independent of the wave length. The latter waves are called long waves, whereas the former, the velocity of which is independent of depth, are called short waves, or surface waves. For water of any given depth the transition takes place within a narrow range of wave lengths, for which reason the classification is a very satisfactory one.
The physical reason for the difference between the surface waves and the long waves has been explained in simple words by H. Jeffreys (Cornish, 1934). Jeffreys points out that within surface waves the individual water particles near the surface move in circular orbits, but that the radii of these orbits, and therefore the velocities, decrease rapidly with depth. Theoretically the diameter of orbits at a depth of one half the wave length is only one twenty-third of the corresponding diameter at the surface. Regardless of the actual depth the character of the wave therefore remains unaltered if the depth to the bottom is greater than that short distance. Direct observations for substantiating this conclusion have not been made, but experience on submarines shows that in deep water a moderate wave motion decreases rapidly with depth and becomes negligible at a short distance below the surface, say at a depth of 30 m.
In shallow water the fact that no vertical motion can exist at the bottom modifies the character of the waves. At the bottom the motion can be only back and forth, and, if the depth is small compared to the wave length, the motion will remain nearly horizontal at all depths. Actually, the orbits of the single water particles will be flat ellipses that become more and more narrow when approaching the bottom, and at the bottom they degenerate into straight lines.
In a sea of variable depth the transition from short to long waves begins when the depth to the bottom becomes less than half the wave length, or where h < ½L. Since L = T2g/2π (p. 525) it is possible to establish a relation between the critical depth at which the transformation begins to take place and the wave period:
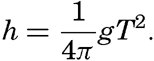
Waves of tidal period, on the other hand, always have the character of long waves. If the rotation of the earth is disregarded, their velocity of progress is equal to 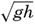 = L/T if h/L is so small that tanh 2πh/L equals 2πh/L. The equation
= L/T if h/L is so small that tanh 2πh/L equals 2πh/L. The equation 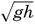 , = L/T can be written
, = L/T can be written
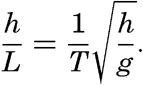
For waves of short periods the rotation of the earth can be disregarded, as can be shown by comparing the accelerations of the moving particles with Corioli's force. If Corioli's force is very small compared to the accelerations, it can be disregarded, because it is then negligible compared to the other forces, the resultant of which represents the accelerations.
Corioli's force is proportional to 2ω sin ϕ ν v, where ν is the horizontal velocity, and the acceleration, dv/dt, is proportional to (2π/T)v. The ratio between Corioli's force and the acceleration due to the wave motion is therefore proportional to (T/2π)2ω sin ϕ or to (T/Te)2 sin ϕ, where Te is the period of rotation of the earth. If the period is measured in hours, one can write (T/Te)2 sin ϕ = (T/12) sin ϕ. Now, 12/sin ϕ is equal to one half pendulum day (p. 437), and it can therefore be stated that the earth's rotation will be of importance to wave motion if the period of the wave approaches the length of one half pendulum day. For ocean surface waves the wave period T is always a very small fraction of half a pendulum day, for which reason the deflecting force is negligible beside the other forces, but long waves may be of tidal period, in which case the period length is of the same order of magnitude as a pendulum day, meaning that the deflecting force is of the same importance as other acting forces. Corioli's force will therefore be introduced when dealing with these waves.
Another noteworthy characteristic of surface waves is that below the depth to which motion of particles is perceptible the pressure remains constant when the waves pass. A pressure gauge placed on the bottom, if the depth were great enough, would not show any effect of surface waves, regardless of their height. The reason is that below the crest of the wave the acceleration is directed downward and will therefore counteract the effect of the acceleration of gravity, but below the trough the acceleration is directed upward and will be added to the acceleration
For waves of long periods the vertical accelerations, on the other hand, can be neglected, because the vertical displacements require a very long time. Consider a surface wave of period 10 sec and height 1 m, and a long wave of semidiurnal tidal period 44,700 sec and height 1 m. The ratio of the average vertical accelerations during the time when a water particle near the surface moves from its lowest to its highest position is inversely proportional to the square of the ratio of the wave periods, or in the wave of tidal period the vertical accelerations are about 5 × 10−8 times the vertical accelerations within the surface wave—that is, they are negligible. Consequently, when a long wave passes, the pressure at any given level is proportional to the height of the water, and a pressure gauge at the bottom gives a true record of the passing wave.
Some of the most outstanding characteristics of ocean surface waves and long waves can be summarized as follows:
| Surface Waves | Long Waves | |
|---|---|---|
| Character of wave. | Progressive, standing, forced or free. | Progressive, standing, forced or free. |
| Velocity of progress. | Dependent on wave length but independent of depth. | Dependent on depth but independent of wave length. |
| Movement of water particles in a vertical plane. | In circles, the radii of which decrease rapidly with increasing distance from the surface. Motion imperceptible at a depth which equals the wave length. In some types of surface waves the motion is in wide ellipses. | In ellipses which are so flat that practically the water particles are oscillating back and forth in a horizontal plane. Horizontal motion independent of depth. |
| Vertical displacement of water particles. | Decreases rapidly with increasing distance from the surface and becomes imperceptible at a depth which equals the wave length. | Decreases linearly from the surface to the bottom. |
| Distribution of pressure. | Below the depth of perceptible motion of the water particles the pressure is not influenced by the wave. | The wave influences the pressure distribution in the same manner at all depths. |
| Influence of the earth's rotation. | Negligible. | Cannot be neglected if the period of the wave approaches the period of the earth's rotation. The velocity of progress of the wave and the movement of the water particles are modified. |
In the following discussion the characteristics of the wave types of the oceans will be dealt with more fully.
Surface Waves
Origin of Surface Waves. It is evident to the most casual observer that surface waves are created by wind, but only recently, in a work by H. Jeffreys, has a successful physical explanation of the process been presented (Defant, 1929, Thorade, 1931). Jeffreys avails himself of the fact that in air in turbulent flow, eddies are formed on the lee side of obstacles. If a strong wind blows against an isolated house, an eddy is formed in the same manner that eddies are formed behind stones in a river. The result is that the wind exerts a pressure on the windward side of the house, but on the lee side there will be suction. Similarly, when the wind blows over a sequence of waves, eddies will be formed on the lee side of the waves, for which reason the pressure of the wind will be greater on the windward slopes than on the slopes that are sheltered by the crests. This condition can prevail, however, only if the waves travel at a velocity that is smaller than the speed of the wind. On the basis of these arguments, Jeffreys finds that waves may increase only if
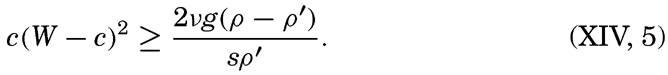
The term on the right-hand side of equation (XIV, 5) is always positive. The product on the left-hand side must therefore always be positive and can exceed the right-hand term only if the wave velocity differs sufficiently both from zero and from the wind velocity. For any given wind velocity, there can be only a limited range of possible wave velocities. It is readily seen that at a given wind velocity the right-hand side of (XIV, 5) is at a maximum when c = ⅓W. Therefore, unless

Equation (XIV, 6) determines the velocity of the weakest wind which can raise any waves, and this weakest wind could be determined if the sheltering coefficient were known. Jeffreys has not been able to make
The velocity of the smallest possible waves should be one third of the limiting wind velocity, or about 37 cm/sec, and according to the theory the corresponding wave length must be 8.8 cm (p. 525). Thus, measurements of the smallest waves can be used for testing the correctness of the theory, but measurement of such small wave lengths is very difficult and no exact observations have been made. Jeffreys finds that the length of the shortest waves observed by him lies in the neighborhood of the theoretical value. On the other hand, Scott Russell reported in 1844 that he had measured surface waves of a length of only 5 cm, and the smallest waves measured by Cornish are only about 2.5 cm long. The problem of the generation of surface waves is therefore not satisfactorily solved, but the approach by Jeffreys is in better agreement with observations than is any previous attempt.
It should be added that if only the forces due to surface tension and gravity are considered, waves should not be formed until the wind velocity passes the limit of 6.7 m/sec, and if only the stress of the wind on the surface and gravity are taken into account, the limiting wind velocity will be about 4.8 m/sec. Experience shows that these values are far too high, and the turbulent character of the wind must therefore be of the greatest importance.
Form and Characteristics. In physics the general picture of surface waves is that of sequences of rhythmic rise and fall which appear to progress along the surface when progressive waves are concerned, or which appear stationary if standing waves are being considered. The actual appearance of the surface of the open sea, however, is mostly in the sharpest contrast to that of rhythmic regularity. If a wind blows, waves of all different sizes are present, varying in form from long, gently sloping ridges to waves of short and sharp crests. Superimposed on the gentler waves, which may or may not run in the direction of the wind, series of deformations of the surface appear which, from the point of view of physics, can be termed “waves” only by stretching the definition.
If the sea surface were characterized by an unbroken series of waves of the same amplitude, a chart of the topography of the surface would contain nothing but a series of straight lines showing the alternating wave
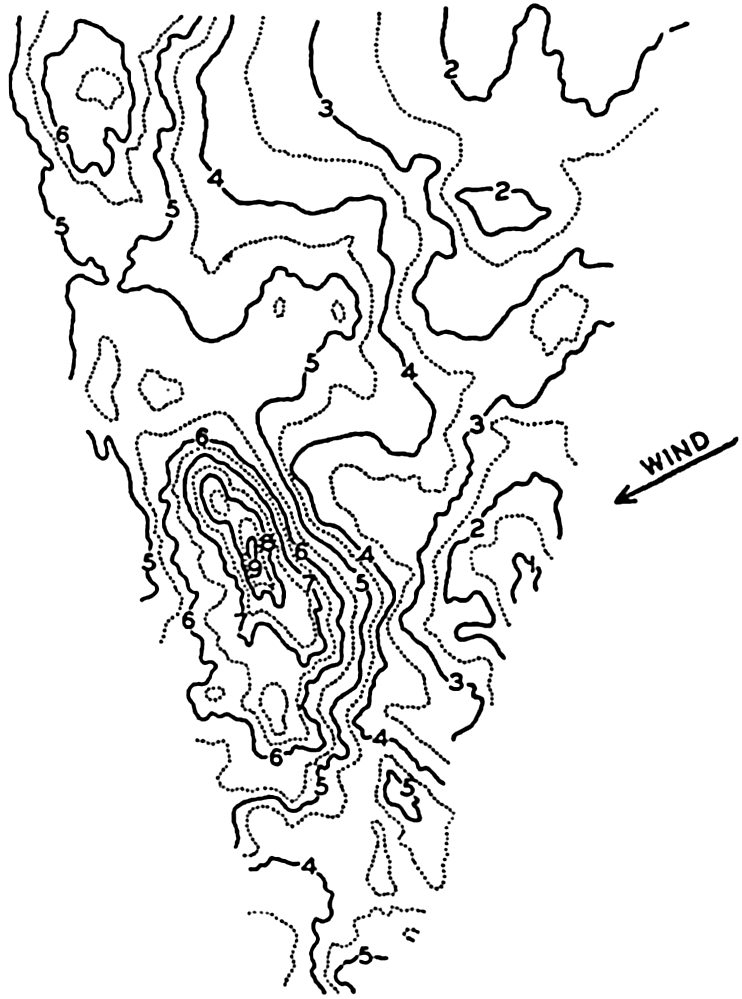
Topography of the sea surface derived from stereophotogrammetric pictures of the sea surface taken on board the Meteor on January 23, 1926, in lat. 59°S, long. 63°4′ W. The state of the sea was recorded as 6, waves as advancing from WSW, wind WSW 7 (Beaufort).
The most striking characteristic of the picture is not a regular sequence of waves but a great irregularity in topography. A relation to the direction of the wind is evident, however, because the wind was blowing at nearly right angles to the prevailing direction of the contour lines of the surface, but, instead of a long wave crest running at right angles to the wind direction, there are two separate heights, one of which is very steep. This irregular appearance, the “cross sea” (Kreuz See) is more common in the open ocean than the swells with long crests, which are more conspicuous near the coast, where series of long waves may roll against the beach in rhythmic sequence.
In spite of the irregular appearance of the sea, it is possible to apply the terms wave period, wave height, and wave length, because some of the waves will be more conspicuous than others and their characteristics can be observed. As has already been stated, the general theory of waves on the surface of the sea leads to a simple formula for the wave velocity:
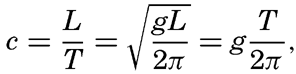
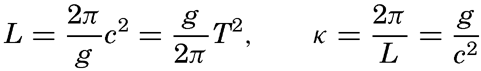
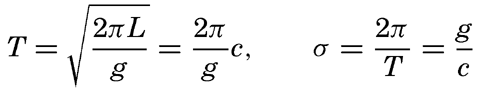
Of the three interrelated quantities, c, T, and L, the wave period T can probably be most easily determined by using the method which was proposed by Cornish (1934) and which consists in recording the time intervals between appearances of a well-defined patch of foam at a sufficient distance from the ship. The same method can be used on the coast, where, in addition, the interval between breakers can be accurately timed. A simple device for recording the movement of a floater on a rotating drum has been used with success at the end of the Scripps Institution of Oceanography pier (Shepard and La Fond, 1940). At sea the wave length is mostly estimated on the basis of the ship's length, but this procedure leads to uncertain results, because it is often difficult to locate both crests of the wave relative to the ship and because of disturbances due to the waves created by the movement of the ship. The most satisfactory measurements are made from a ship that is hove to. Another method consists in letting out a floater as a wave crest passes the stern of the ship and recording both the length of line paid out when the floater reappears on the crest and the angle that the line forms with the heading of the ship. The velocity of the wave can be found by recording the time needed for the wave to run a measured distance along the ship. If the period is also determined, the wave length is found from the simple formula L = cT.
A large number of measurements have been made at sea in order to establish the relationship between the wave period, the wave length, and the wave velocity. Critical examination of the methods employed has been made, especially by Cornish (1912, 1934), and a number of average results have been compiled by different authors. Table 68 contains one of the compilations made by Krümmel, from which it is evident that the observed values are in fair agreement with the theoretical expectation.
The longest wave periods observed at sea rarely exceed the value of 13.5 sec, which Cornish reports from the Bay of Biscay. It has been established, however, that the swell reaching the shore may have much longer periods and correspondingly longer wave lengths and greater velocities of progress. The longest period that Cornish has observed is about 22.5 sec, corresponding to a wave length in deep water of about
The theory of waves leads not only to a relation between velocity of progress and the wave length, but also to results concerning the profile of the wave. These results are based on the concepts of classical hydrodynamics and have been derived from the hydrodynamic equations, omitting friction but taking the boundary conditions into consideration. In an ideal fluid the free surface of the waves, according to Stokes' results of 1847 (Lamb, 1932), very nearly take the shape of a trochoid—that is, the curve which is formed by the motion of a point on a disk when this disk rolls along a level surface. If the amplitude is small compared to the wave length, the trochoid approaches in shape a sine curve, but at great amplitude the crests become narrower and the troughs longer. Gerstner's theory of 1802 leads exactly to the trochoid form, but Stokes has pointed out that this theory is not in complete agreement with the concepts of classical hydrodynamics.
| Region | Wave velocity, m/sec | Wave length, m | Wave period, sec | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Observed | Computed from | Observed | Computed from | Observed | Computed from | ||||
|
|
|
|
|
| ||||
| Atlantic Ocean | |||||||||
| Trade wind region | 11.2 | 10.8 | 10.5 | 65 | 70 | 61 | 5.8 | 6.0 | 6.2 |
| Indian Ocean | |||||||||
| Trade wind region | 12.6 | 13.1 | 13.7 | 96 | 88 | 104 | 7.6 | 7.3 | 6.9 |
| South Atlantic Ocean | |||||||||
| West wind region | 14.0 | 15.5 | 17.1 | 133 | 109 | 163 | 9.5 | 8.6 | 7.8 |
| Indian Ocean | |||||||||
| West wind region | 15.0 | 15.2 | 13.7 | 114 | 125 | 104 | 7.6 | 8.0 | 8.3 |
| China Sea | 11.4 | 11.9 | 12.4 | 79 | 72 | 86 | 6.9 | 6.6 | 6.3 |
| Western Pacific Ocean | 12.4 | 13.6 | 14.7 | 102 | 85 | 121 | 8.2 | 7.5 | 6.9 |
Stokes's results lead to the conclusion that at increasing amplitude the wave form deviates more and more from the trochoid. Studies of the stability of waves by Michell (Lamb, 1932) show that the wave becomes unstable if the angle formed by the crest approaches 120°, and that the smallest ratio of height to length is 1:7 (fig. 130). The velocity of progress of these waves is no longer independent of the height; in the case
Accurate measurements of actual wave profiles would be very desirable in order to examine the correctness of the above-mentioned theoretical conclusions. Such actual measurements can be based on photogrammetric pictures, but so far only a few such pictures have been evaluated. Fig. 131 (Schumacher, 1928) shows two profiles of the wave the topography of which was presented in fig. 129 and two profiles of other waves that were photographed on the Meteor Expedition. In the figure the trochoids are entered as dashed lines, and it is seen that these curves can hardly be considered as fitting the actual profiles with any degree of accuracy.

True dimensions of steepest possible wave, according to Stokes and Michell.
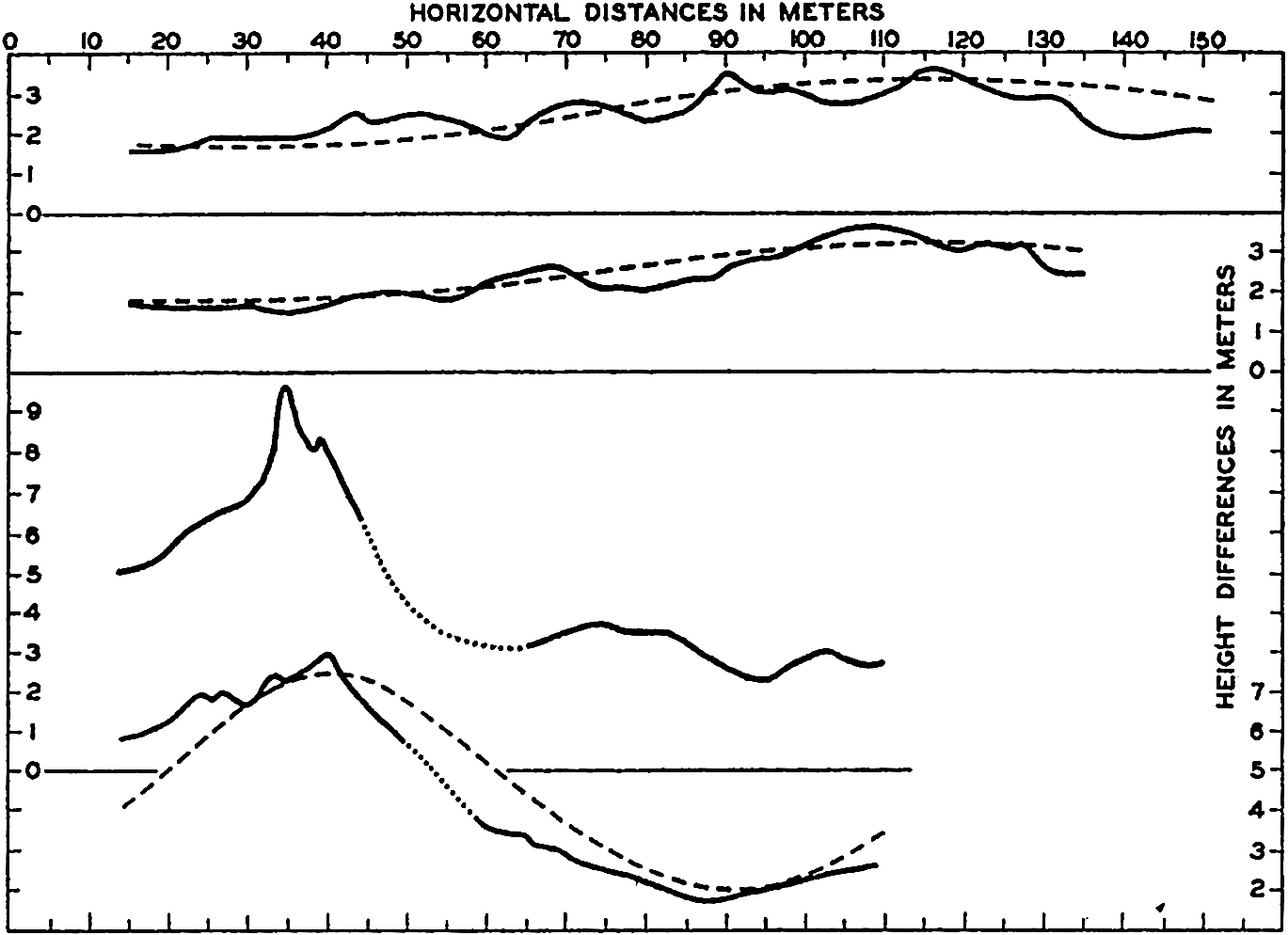
Profiles of waves (vertical scale 5 × horizontal scale) of waves derived from stereophotogrammetric pictures taken on the Meteor. The two lower profiles refer to the wave shown in fig. 129; the two upper profiles refer to waves photographed on July 7, 1926. The waves proceed from right to left. The dashed curves represent trochoids.
The wave theory also leads to certain conclusions concerning the character of motion of individual water particles. In a wave that has
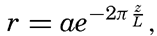
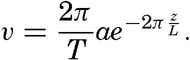
| Wave characteristics | Velocity of particles in cm/sec at stated depths | ||||||
|---|---|---|---|---|---|---|---|
| Period length (sec) | Velocity of progress (cm/sec) | Length (m) | Height (m) | 0 m | 2 m | 20 m | 100 m |
| 2 | 312 | 6.2 | 0.25 | 39 | 5.2 | 0.0 | 0.0 |
| 4 | 624 | 25 | 1.00 | 79 | 49 | 0.5 | 0.0 |
| 6 | 937 | 56 | 2.00 | 105 | 85 | 11.3 | 0.0 |
| 8 | 1249 | 100 | 5.00 | 196 | 173 | 55.6 | 0.4 |
| 10 | 1561 | 156 | 7.00 | 220 | 203 | 99.0 | 4.2 |
| 12 | 1873 | 225 | 10.00 | 211 | 199 | 114.0 | 12.9 |
| 14 | 2185 | 306 | 12.00 | 273 | 262 | 180.0 | 35.0 |
| 16 | 2498 | 396 | 10.00 | 197 | 190 | 143.0 | 40.6 |
| 18 | 2810 | 506 | 8.00 | 140 | 136 | 109.0 | 40.5 |
| 20 | 3122 | 624 | 5.00 | 78 | 76 | 63.0 | 28.4 |
No measurements are available of the actual motion of water particles in waves. Experience in submarines has shown, however, that the wave motion decreases rapidly with increasing depth. Vening Meinesz has availed himself of this fact and has been able to conduct observations of gravity at sea on board a submarine, making use of pendulums, which can be employed only when the motion of the vessel is small.
As a consequence of the decrease of the particle velocity with depth a small transport of water takes place in the direction of progress. A water particle moves in the direction of progress when it is above its mean depth, and in the opposite direction when it is below its mean depth, but, owing to the decrease of velocity with depth, it moves somewhat faster in the direction of progress than in the opposite direction. Consequently, after having completed one revolution in its orbit, the particle does not return to the point from which it started, but is advanced somewhat in the direction of progress, meaning that an actual transport of water takes place in this direction even in the absence of wind (see U.S. Beach Erosion Board, 1941.)
The irregular appearance of the surface is not accounted for by the theories that have been mentioned so far, but a somewhat better understanding of the pattern of waves is obtained when one takes into account the phenomenon of interference. Two surface waves that travel in the same direction can then be represented by the equations

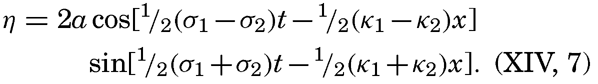
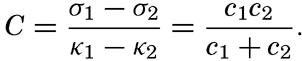
Upper curve: Record of waves at the end of the Scripps Institution pier, showing interference. Middle curve: Computed pattern of wave interference. Lower curve: Example of the ordinary type of records of waves at the Scripps Institution pier, showing very complicated conditions.
The upper curve in fig. 132, which is a reproduction of a record obtained at the end of the Scripps Institution of Oceanography pier, represents an example of interference of waves of nearly the same period length but of different amplitudes. In the middle portion of the figure are shown two sine curves, one of period 9.6 sec and amplitude 0.75 m, and one of period 8.7 sec and amplitude 0.32 m. The heavy curve presents the wave pattern that would result by interference between the two, and it is seen that this corresponds roughly to the observed pattern. The discrepancies are accounted for partly by the fact that the
These considerations help to explain the occurrence of a sequence of high waves followed by a sequence of low ones, but they do not explain the irregular pattern of waves that is called “cross sea.” Progress towards explaining the typical cross sea, however, has been made by H. Jeffreys (Defant 1929). The waves that have been dealt with so far he called long crested, because the crest of the wave is long compared to the wave length. Mathematically speaking, it is assumed that the wave crests are of infinite length (see equation XIV, 2). Jeffreys has introduced the so-called short-crested waves, which can also travel without altering from and therefore belong to the group of waves that are theoretically possible. These waves can be represented by
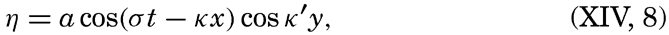
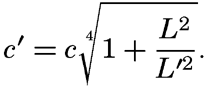
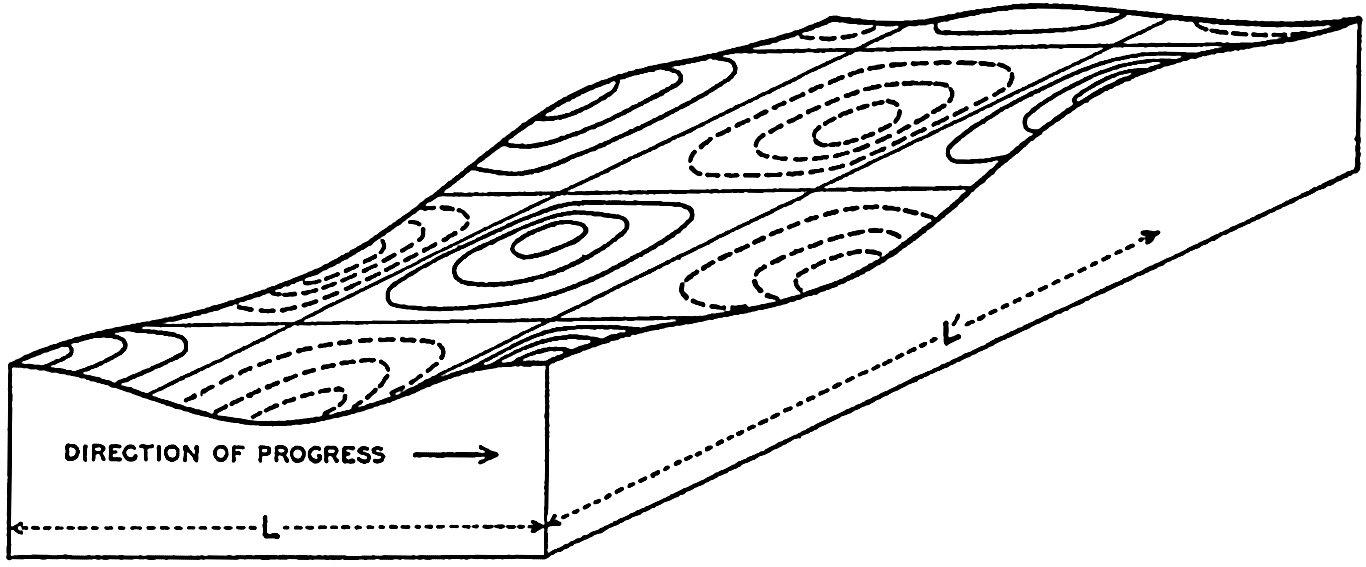
Schematic picture of short-crested waves.
According to Jeffreys, the first waves that are generated by the weakest winds must be long crested, but, when the wind increases in velocity, short-crested waves can be formed. The explanation here is that the
In table 68, only wave velocity, wave length, and wave period are listed, with no information as to the wave height. A large number of measurements of wave heights has been made by different methods which, although uncertain, are considered more accurate than the measurements of wave lengths. The wave height can be found if a location on board ship can be selected at which the tops of the waves appear level with the horizon, in which case the wave height is equal to the eye height of the observer above the water line. Another method is based on the records of a delicate barometer, and still another that gives very accurate results makes use of photogrammetric measurements.
The greatest wave heights observed in most oceans are about 12 m. Cornish gives a very vivid description of waves of such height during a storm that he experienced in the Bay of Biscay in December, 1911. On the day preceding the gale a heavy swell with a period of 11.4 sec and an average height of about 6 m came from the northwest. The wind, which had blown as a breeze from the southwest, changed during the night to west-northwest and increased in the morning to a strong gale with velocities up to 23 m/sec. The period of the waves increased to 13.5 sec, corresponding to a length of 310 m and a velocity of progress of 21 m/sec, while the wave height increased to 12 m. There are many accounts of similar large waves. In a hurricane in the North Atlantic in December, 1922, when the wind velocity probably exceeded 45 m/sec, one of the officers of the Majestic reported waves that averaged more than 20 m in height and reached a maximum height of up to 30 m. It is probable, however, that these great wave heights refer to occasional peaks of water that may shoot up to elevations considerably above the general wave height. In the region of the prevailing westerlies of the Antarctic Ocean, wave heights up to 14 or 15 m have been observed relatively often, but the average wave height lies much below these values.
The observations quoted regarding maximum wave height and wave length all refer to conditions far from land. Near the shore, waves created directly by wind do not reach such heights, but the height will depend upon the stretch of water across which the wind has blown—namely, upon the fetch of the wind. Stevenson (Cornish, 1934) has combined the average data into the simple formula h = ⅓ 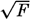 , where h is the greatest observed wave height in meters and F is the fetch of the wind in kilometers. This formula is valid for small bodies of water, and is
, where h is the greatest observed wave height in meters and F is the fetch of the wind in kilometers. This formula is valid for small bodies of water, and is
Growth and Dissipation of Surface Waves. In order to explain some of the phenomena concerned here, it is necessary to consider the energy of the waves. This energy can be computed by considering that it is present partly as potential energy and partly as kinetic energy. The computation leads to the result that for long-crested waves the energy per unit area of the sea surface is approximately equal to ½gρa2, where g is the acceleration of gravity, ρ is the density of the water, and a is the amplitude of the wave. For short-crested waves the energy per unit area of sea surface is approximately one half of this amount.
The energy of the waves is transmitted to them by the wind, and, according to Jeffreys, the processes that lead to the generation of waves are also of fundamental importance to their further development. When the wind velocity increases, the pressure exerted on the windward side of the wave will be greater than that on the lee side. Consequently, the waves will increase in height as their energy increases. The energy considerations do not lead to any limit of height to which the waves can grow, but the wave theory itself as developed by Michell (see p. 527) shows that the height cannot exceed about one seventh of the wave length. Thus, if energy is constantly imparted to the waves by the wind without an increase of the wave length, the crests will break and the sea will become covered with whitecaps. However, the longer the wave, the greater height it can reach and thus the greater amount of energy it can absorb from the wind. The wind is able to produce waves of different length, but the shorter will rapidly reach their maximum height and break, whereas the longer will continue to grow. Jeffreys therefore concludes that, “when the waves have travelled a long distance, with the wind blowing them all the time, the longest waves will tend to predominate, simply because they can store more energy.”
However, there is also a limit to the length that waves can attain, because the velocity of progress of the waves increases with increasing wave length and because the wind cannot impart further energy to the waves if they travel at a speed that is as great as or greater than the wind velocity. At a given wind velocity the longest-possible waves will therefore be those that travel at a velocity somewhat below the wind velocity. According to Cornish the speed of the fully developed waves, on an average, is eight tenths of the speed of the wind, but it should be borne in mind that the observed wind velocity depends upon the height at which it is measured. Information is still lacking as to the relation between the velocity of the wind directly over the sea surface and the velocity of the waves.
It also follows that the greatest wave velocity cannot exceed the velocity of the wind that created the waves, assuming that a surface wave continues to proceed at a constant speed after leaving a region of strong winds. Theories developed by Poisson and Cauchy (Lamb, 1932), however, lead to the conclusion that the wave length and therefore the velocity of progress and the period of a surface wave increase in course of time. The velocity of progress of the swell reaching the coast, according to these theories, should be greater than the velocity of the waves that were directly created by the wind. Krümmel (1911) quotes a single observation that may support these conclusions, whereas Cornish (1934) emphasizes the fact that no breakers have been observed of such period lengths that their velocity of progress in deep water would exceed observed wind velocities. Breakers with a period of 20 sec, corresponding to a velocity of progress of about 30 m/sec, were observed on the coast of the English Channel on December 29, 1898, and Cornish points out that prior to the arrival of these breakers a gale had been reported in mid-Atlantic in which the force of the wind had probably exceeded 35 m/sec, which was about 5 m/sec greater than the speed of the waves. He considers it probable that these waves were formed within the area of the gale and traveled for a long distance at their original speed.

Interference between a long swell and a much shorter wave.
Cornish also points out that in the open ocean the existence of long swells can be obscured if shorter waves of greater height are present at the same time. He illustrates his point by a graph similar to the one shown in fig. 134. It is here assumed that two waves are present: one long swell, curve A, and one wave that has only one third the period of the swell but twice the amplitude, curve B. By interference of these two waves, the surface takes the appearance shown by the heavy curve C. An observer would get the impression in this case that the waves present were of the same period as the shortest waves but of variable height, a phenomenon which is often recorded. The long swell may therefore very well be obscured by shorter waves.
A number of studies have dealt with the relation between the wind velocity and the maximum wave height, and between the steepness of the waves and their velocity of progress. In instances in which the quantities to be correlated have not been directly measured, use is made of the equations (p. 525), which give the theoretical relations between wave velocity, wave length, and wave period.
Cornish's empirical results regarding the highest waves can be summarized as follows:
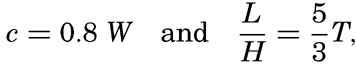
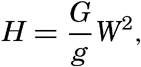
The steepness of the waves is generally expressed by means of the ratio of wave length to wave height, L/H, which is inversely proportional to the steepness but can be used as a measure. Cornish's relations lead to the formula L/H = 0.85 W, but this formula is evidently not valid at wind velocities much below 10 m/sec, because the steepest possible waves have a ratio L/H = 7. Zimmerman's values give L/H = 8.1 W⅓. These two results are in qualitative agreement, because both indicate an increase of the ratio L/H with increasing wind velocity. They are also in agreement with Jeffrey's explanation of the growth of waves, according to which one must expect L/H to be greatest for the longest waves. Schott, on the other hand, found that the ratio L/H decreased with increasing wind velocity, but Krümmel (1911), in discussing a large number of observations by Paris, found the ratio to be constant. The ratio between the length and the height of the waves appears to vary between 10 and 20 m when a fresh wind blows, but in the case of the swell the ratio may lie between 30 and 100. Observations from lakes indicate that there the ratio varies between 10 and 12.
A similar confusion exists regarding the relation between wave velocity and wind velocity. As already stated, Cornish found c = 0.8 W, but from Zimmerman's relation it follows that c = 2.35 W⅔. According to the latter equation the wave velocity is greater than that of the wind up to a wind velocity of 13.2 m/sec, and it is smaller when the wind is above that value, in disagreement with energy considerations, which
All these discrepancies indicate that wave height, wave profile, and velocity of progress are not dependent upon the wind velocity alone at the time of observation, but may also depend upon the length of time the wind has blown, the state of the sea when the wind started blowing, and the dimensions of the area over which the wind blows. Comprehensive observations are needed for clearing up these questions.
It has been mentioned (p. 532) that the wave height depends upon the fetch of the wind, and that for small bodies of water a simple empirical relationship has been established between maximum wave heights and the dimensions of the body. This formula is valid to a distance of 1000 to 1500 kilometers, at which the maximum wave height characteristic of the open ocean, about 12 m, may be reached. The fact that greater wave heights are rarely observed may be due to the circumstance that the wind systems mostly have dimensions smaller than 1500 kilometers, so that in the open ocean the actual fetch of the wind will be, at most, 1500 km, or it may be that a longer fetch of the wind tends more toward increasing the length of the waves than toward increasing their height.
The differences in energy of long-crested and short-crested waves and of large and small waves have to be considered in the discussion of what happens to waves when the wind stops blowing. Owing to the smaller energy per unit area the short-crested waves will be destroyed more rapidly by friction, and the largest of the long-crested waves stand the best chance of surviving for a long time. It is also probable that the dissipation of energy is more rapid within the steeper waves, for which reason the steeper and shorter waves will be destroyed more rapidly than the longer and less steep. Thus, one should expect that, outside of the region in which the wind blows, long-crested swells will become more and more dominating, and at considerable distances from the wind areas only long-crested swells will be present. These conclusions are in good agreement with observed conditions.
Waves Near the Coast. Breakers. When waves approach the coast, a number of things happen. In the first place it is conspicuous that the short-crested cross sea disappears at some distance from the coast and that mainly long-crested rollers reach the beaches. Jeffreys has been able to show that this transformation is associated with the change in form and dissipation of energy that take place when surface waves enter shallow water. One of the characteristic deformations which take place is that, when the depth decreases, originally symmetrical waves become unsymmetrical, the front of the waves becomes steeper, and, finally, the waves break. This effect is more pronounced in the case of the short-crested waves, and the latter will, therefore, break at a greater
Another effect of the decrease of depth is related to a decrease of the wave velocity. The part of the wave that first approaches the coast is slowed down, but the outer portion of the wave still advances with great velocity, wherefore the direction of the wave front is turned, and a wave that approaches the coast at an angle may be turned in such a way that the wave front becomes nearly parallel to the coast.
Still another effect is related to the fact that when approaching shallow coastal waters the waves are transformed into types which are intermediate between surface waves and long waves (p. 519). The waves of long period take on some of the characteristics of long waves at a greater distance from the coast than do those of short period. Consequently the movement of the water particles of the long-period waves will reach to the bottom at a greater distance from the coast, although the height of these waves may be smaller than that of the short-period waves. This circumstance may have considerable bearing on sand movement caused by waves in shallow water.
The breaking of the wave is primarily related to change in the velocity of progress when the wave reaches shallower water (see Defant, 1929). As a consequence of this change, the wave front becomes increasingly steeper until it breaks. Friction may also play a part.
When a wave breaks near the shore, another wave type, known as a wave of translation, may develop. This wave, which was discovered and studied by Russell (Lamb, 1932), is characterized by having only a crest and no trough. The motion of water particles is only in the direction of progress, and the water particles are therefore displaced forward as the wave passes. It is formed when a mass of water is suddenly added to still water, and may therefore be produced as the crest of a breaking wave topples over and crashes down on the water surface in front. This wave type is unimportant in the open sea, but may be prominent on a shallow coast.
Certain phenomena that appear to be associated with breakers are not yet understood. The existence of undertow has not been satisfactorily explained, and is doubted by some observers (Shepard and La Fond, 1939). The rip currents which flow away from the coast through the breakers and which may carry swimmers far out from the beach also have not been fully explained, but it is probable that these currents are associated with surface transport of water against the beach by the waves (Shepard et al, 1941).
The destructive effect of breakers has been the subject of intensive studies, particularly by engineers, but cannot be discussed here. Interested readers are referred to some of the general works that are included in the list of literature.
Long Waves
Standing Waves in Bays. Seiches. In bays, standing waves may develop which are similar to the oscillations in lakes. These waves are known as seiches, and were first studied by Forel (Defant, 1929; Thorade, 1931) in the Lake of Geneva. They are free oscillations of a period that depends upon the horizontal dimensions and the depth of the lake and upon the number of nodes of the standing wave. The wave length will be of the same order of magnitude as the length of the lake, and, as the length of a lake is usually great compared to the depth, the waves will have the character of long waves.
A long wave that proceeds in water of constant depth in the positive or negative x direction must satisfy the equations of motion and continuity in the form (p. 425 and p. 432)
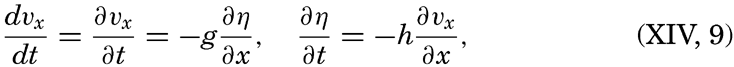
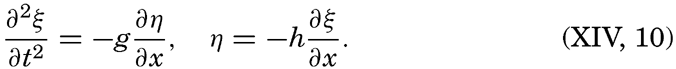
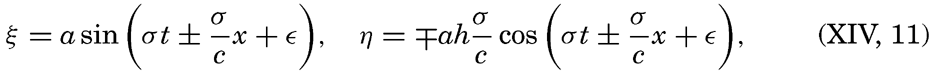
 .
.Equations (XIV, 11) define two waves that progress in opposite directions. The equations of motion are therefore also satisfied by a superposition of two waves that proceed in opposite directions and for which the velocity of progress is c:
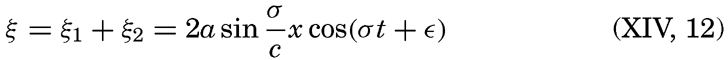
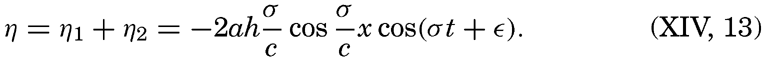
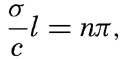
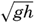 ,
,

It is readily seen that n is the number of nodes of the standing wave. The standing wave of the longest period is the one that has only one node and the period

In applying this very simple theory to actual oscillations of the water in lakes, considerable modifications must be made, because the shape of a lake deviates very much from that of a rectangular basin of constant depth. Crystal (Defant, 1925) has developed the theory of standing waves in basins of different shapes, and more recently Defant (1925) has introduced a convenient method of determining the possible periods of oscillation in lakes by means of a numerical integration of the hydrodynamic equations. Defant's method can be directly applied to lakes or bays of any shape and permits the computation of periods, the relative magnitudes of vertical displacements, and the position of nodal lines. Defant's reasoning as presented in his book of 1929 will be briefly summarized here.
In a basin of variable width b, and variable cross-section area S, the equations of motion and of continuity can be written in the form
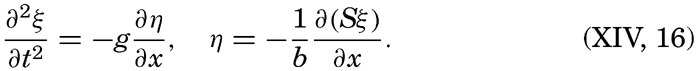
The vertical and horizontal displacements are supposed to vary periodically:
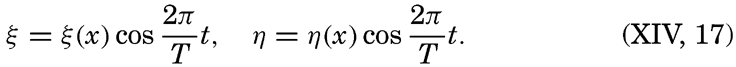
Replacing the differentials in equation (XIV, 16) by the small quantities Δξ and Δη, one obtains
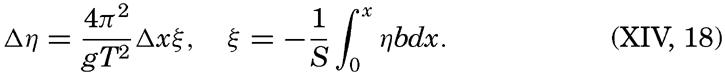
These equations can be used for a stepwise computation of the displacements if it is possible to determine independently an approximate value of the period of the free oscillations. If then one cross section after another is considered, and if these cross sections are placed close together, it can be assumed that the changes of the displacement from one cross section to the next are linear, in which case equation (XIV, 18) can be written
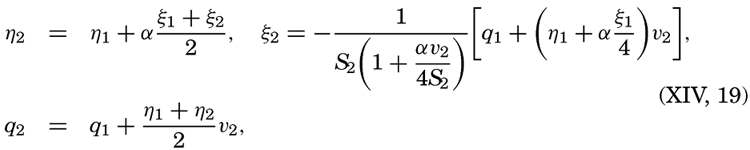
The period T for any given basin can be computed in the following manner. First, an approximate value of T is found by means of formula (XIV, 15), introducing the average depth of the basin. The result is an approximate value of α. At the end of the basin at which the computation begins (x = 0), the horizontal displacement must be zero, and for the vertical displacement an arbitrary value can be selected. In this manner the boundary condition at the one end is fulfilled. By means of equation (XIV, 19), one can now, step by step, compute the displacements for all cross sections of the basin, and, if the approximate period that was derived by means of formula (XIV, 15) is correct for the simplest seiche, the computation must give the value ξ = 0 at the other end of the lake in order to fulfill the boundary condition. The computed value will usually differ from zero, and hence it is necessary to select another value of the period and to repeat the entire computation. If this new value does not lead to a correct result, one has to select a third one, but as a rule it is possible to select the first two values of the period in such a way that the correct one lies between them and can be determined by suitable interpolation. The final result will give relative values of the displacements and the exact locations of the nodal line. In a similar manner, one can find the period of an oscillation with two nodal lines and fix their location. Figure 135 shows the computed displacement of seiches in Garda Lake, according to Defant.
So far, only lakes have been considered. In a bay that is in open communication with a large body of water, horizontal flow can take place through the opening. For a rectangular bay the simplest form of a standing wave will be that which has a nodal line across the opening and

If the opening of the bay is very wide, it is necessary to introduce a correction that increases the period. The increase is 32 per cent, according to Rayleigh (Thorade, 1931), if the width of the bay equals the length, but is reduced to about 10 per cent if the width is one tenth of the length. Actual experimental verification of this theory has not been obtained.
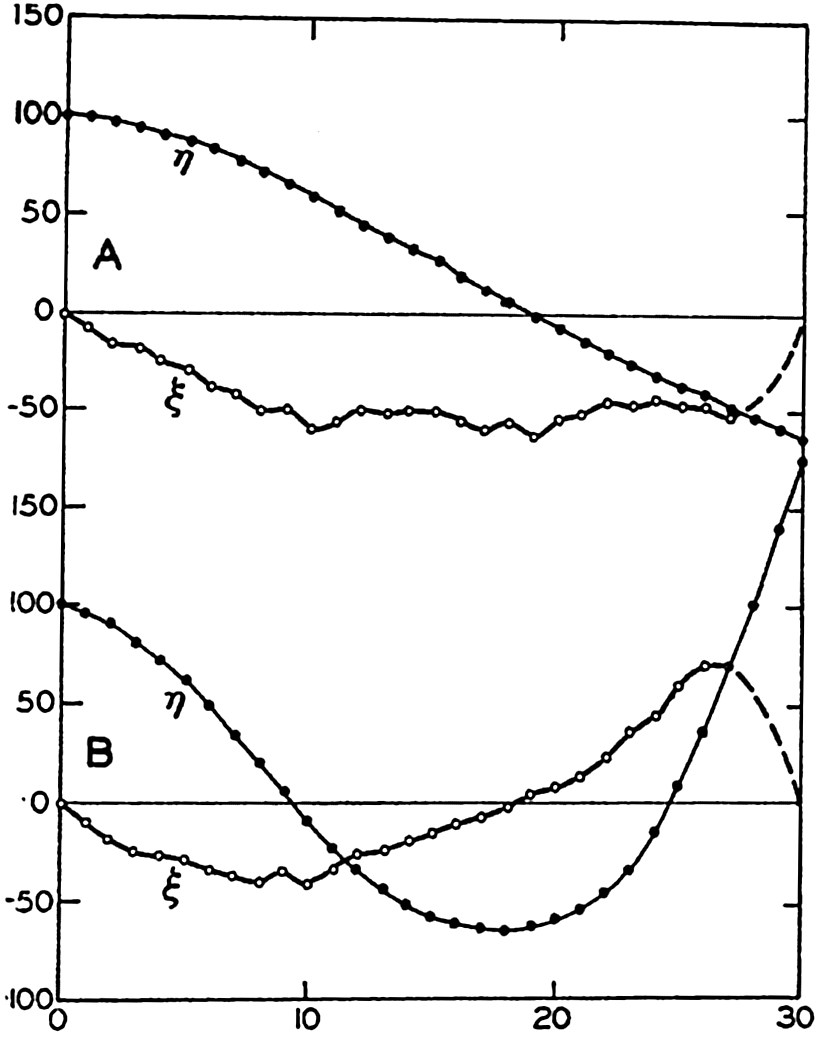
Oscillations of the Garda Lake, according to Defant. Relative values of the vertical and horizontal amplitudes are indicated by η and ξ. Upper curves marked A show the oscillation with one node of period T1 = 39.8 minutes; lower curves marked B show oscillation of two nodes of period T2 = 22.6 minutes.
In a canal that is open at both ends, standing waves can also be present, but these must be such that nodal lines are located at the two openings of the canal. The longest possible period of a standing oscillation is therefore the same as the period of a lake of similar shape, but in a lake antinodes are located at the ends of the lake, whereas in a canal nodes are found at the ends.
The period and the character of the oscillation in bays or canals can be found by Defant's method, taking the proper boundary conditions into account. In a bay the vertical displacement must be equal to zero at the opening, and in a canal it must be equal to zero at both openings.
Seiches occur commonly in bays, as is evident from records of tidal gauges in such localities. Studies of oscillations in bays along the coast of Japan have been conducted by Honda, Terada, Yoshida, and Isitani
The causes of such oscillations are not fully understood. It should be observed, however, that only a small amount of energy is needed for producing standing oscillations in a body of water and for maintaining them. Very weak periodical variations in wind or barometric pressure may therefore produce seiches if these variations are of a period length corresponding to one of the possible free oscillations. It has also been shown by J. Proudman and A. T. Doodson (Defant, 1929) that a sudden change of wind or a rapid variation in pressure may cause oscillations that will gradually die out because of friction.
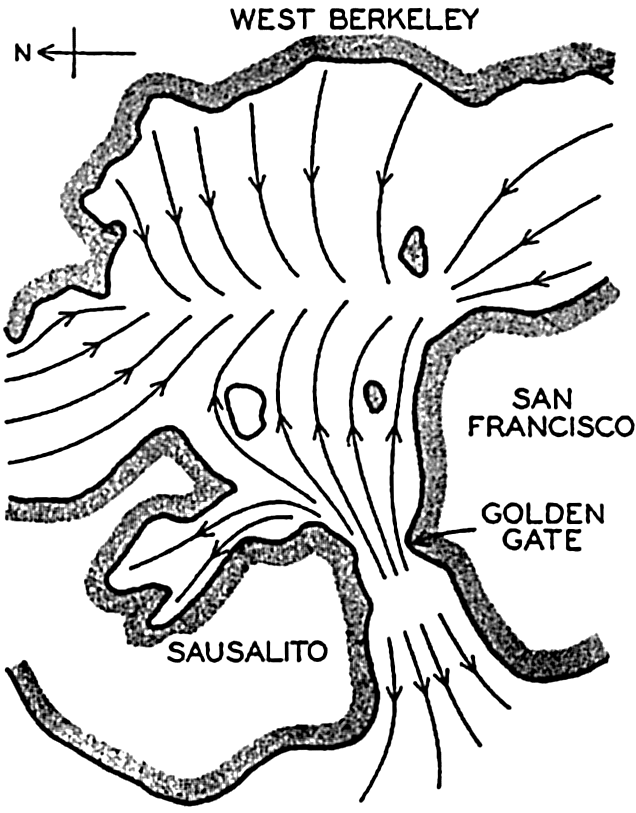
Oscillation with three nodes in San Francisco Bay, according to experiments by Honda, Terada, Yoshida, and Isitani.
Seiches do not appear to be confined only to bays, but occur frequently on practically open coasts. As an example, Patton and Marmer (1932) mention that at Atlantic City, on the open coast of New Jersey, heavy winds will frequently bring about a seiche oscillation with a period of about 15 minutes. They assume that this seiche represents an oscillation of some part of the wide embayment of the coast between Nantucket Island and Cape Hatteras. The theory of such seiches has been developed by Hidaka (1935).
Destructive Waves. The waves that occasionally inundate low-lying coasts and cause enormous damage are considered here, although they are commonly known as “tidal waves.” However, they have nothing in common with the tides, but the name “tidal wave” has become so firmly established in the English language that the popular use will probably be continued in spite of the unfortunate confusion to which it gives rise. The destructive waves known as tidal waves are caused by
Waves in the sea caused by earthquakes are of two different types. In the first place a submarine earthquake may produce longitudinal oscillations that proceed at the velocity of sound waves. When reaching the surface, such longitudinal oscillations will be felt on board a ship as a shock that violently rocks the vessel. The shock may be so severe that the sailors believe their vessel has struck a rock, and several such reported “rocks” were indicated on early charts in waters where recent soundings have shown that the depth to the bottom is several thousand meters. There are many ship reports dealing with shock waves, particularly from regions in which seismological records show that submarine earthquakes are frequent. Explosion waves of this character usually occur as independent phenomena, but occasionally they are accompanied by the release of large amounts of gases that rise toward the surface and may lift the surface up like a dome, thus producing a transverse wave that behaves like any other gravitational wave. Observations of this kind of waves are rare, but it is possible that ships which have been lost at sea have been completely destroyed by such enormous disturbances. A wave of this nature spreads out from the place where it is formed and decreases in amplitude. By the time it reaches the coast, it has usually become so reduced that it does not cause much damage.
Destructive waves caused by earthquakes, dislocation waves, or “tsunamis” are in general associated with submarine landslides which directly create transverse waves. These waves may reach enormous dimensions both in the open sea and near the coasts, and they proceed as ordinary long gravitational waves. Many records exist of such waves which, near their origin, have caused enormous damage by completely inundating low-lying areas and which have subsequently traversed the entire Pacific or Atlantic Ocean. Thus, the great damage caused by the earthquake at Lisbon on November 1, 1755, was mainly due to the gigantic wave which was set up and which continued across the Atlantic Ocean, reaching the West Indies as a “tidal wave” 4 to 6 m high. In Japan, similar earthquake waves have on many occasions brought great destruction and have led to the loss of many lives. As an example, it may be mentioned that in 1703 more than 100,000 persons lost their lives when the coast of Awa was flooded. Among the most discussed waves are those that accompanied the eruption of the volcano Krakatao in the Sunda Strait on August 26 and 27, 1883. Several waves occurred after the different eruptions, and the highest ones caused great devastation on some of the East Indian Islands, where more than 36,000 persons lost their lives and where the waves in certain localities must have reached a
These waves proceed, as already stated, as long gravitational waves and their velocity of progress should therefore, over a uniform bottom, be equal to 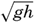 . Where the depth to the bottom is variable, the velocity of progress will be somewhat less than
. Where the depth to the bottom is variable, the velocity of progress will be somewhat less than 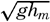 where hm is the average depth, but it has been found that the velocity of progress is smaller than should be expected even if variations in depth are considered. In spite of this circumstance, the study of the rate of propagation of these waves served to give an idea of the average depth of the ocean prior to the time of deep-sea soundings. Thus, in 1856, A. D. Bache computed the average depth of the oceans to be about 4000 m, whereas Laplace had assumed an average depth of about 18,000 m.
where hm is the average depth, but it has been found that the velocity of progress is smaller than should be expected even if variations in depth are considered. In spite of this circumstance, the study of the rate of propagation of these waves served to give an idea of the average depth of the ocean prior to the time of deep-sea soundings. Thus, in 1856, A. D. Bache computed the average depth of the oceans to be about 4000 m, whereas Laplace had assumed an average depth of about 18,000 m.
The period length of tsunamis varies between 15 and 60 minutes (Krümmel, 1911, Gutenberg, 1939). Where the depth to the bottom is 200 m, the velocity of progress of a long wave (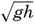 ) is 44.2 m/sec, and with a period length of 30 minutes the wave length is 79.5 km. The corresponding maximum particle velocity is independent of the wave period and equals
) is 44.2 m/sec, and with a period length of 30 minutes the wave length is 79.5 km. The corresponding maximum particle velocity is independent of the wave period and equals 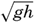 η0/h (p. 565), where η0 is the amplitude of the wave and h is the depth to the bottom. With the above numerical values the maximum particle velocity becomes equal to 0.22η0. The energy of the wave per unit area of the surface is ½gη02, and, thus, equal to that of surface waves or tides of the same amplitude.
η0/h (p. 565), where η0 is the amplitude of the wave and h is the depth to the bottom. With the above numerical values the maximum particle velocity becomes equal to 0.22η0. The energy of the wave per unit area of the surface is ½gη02, and, thus, equal to that of surface waves or tides of the same amplitude.
Destructive “waves” caused by wind are of an entirely different nature. In this case one has to deal, not with the effect of a wave, but instead with inundations which are caused by the ocean waters being swept up against the coast by violent storms. Abnormally high water levels caused by strong winds are frequent on many coasts, but fortunately the sea level rarely rises so much that great damage occurs. The most destructive storm “wave” known in the history of the United States is that which practically destroyed Galveston on September 8, 1900. A West Indian hurricane approached the coast of the Gulf of Mexico, where at Galveston the barometric pressure fell from 996.2 millibars, (29.42 inches) at noon to 964.4 millibars (28.48 inches) at 8:30 P.M. At the same time the wind velocity increased to 45 m/sec (100 miles per hour) at about 6:00 P.M., when the anemometer was broken to pieces. It has been estimated that the average wind velocity between 6:00 and 8:00 P.M. must have been about 55 m/sec, or 120 miles per hour. During the day of September 8 the water rose steadily but slowly until the wind had reached hurricane force, when a much more rapid rise took place. In the evening the water level was nearly 5 m (15 feet) above mean high
The hurricane that on September 21, 1938, struck the coast of New England brought an even higher water level in many localities, but did not cause so much loss of life. At Buzzard's Bay the highest water level ranged from 4 to 5 m above mean low water, and at Fall River it was reported that “the water came up rapidly in a great surge,” rising to about 6 m above normal. More than 600 persons lost their lives in the hurricane, and the property damage was estimated at $250,000,000 to $330,000,000, although only part of this damage was due to destructive waves (Tannehill, 1938).
Tides
The longest waves known in the ocean are those associated with the tidal movement, which manifests itself on the coast by the rhythmic rise and fall of the water and, particularly in sounds and narrow straits, by the regularly changing tidal currents. The wavelike character of the phenomenon is readily recognized by means of an automatic tide gauge, which records the actual sea level as a smooth curve with alternating maxima and minima. It is also recognized in connection with tidal currents in a strait, because these currents show a regularly alternating motion characteristic of waves. The rise and fall of the water and the accompanying currents should therefore be dealt with together, because they are only different manifestations of the same phenomenon. However, for practical reasons, it is of advantage to deal with them separately and, following common usage in English, to refer to the rise and fall of the water as the “tide,” and to the accompanying currents as “tidal currents.”
Since a knowledge of tides is of particular value to navigation, there exists an enormous literature dealing with the phenomenon, partly in the form of theoretical studies, partly in the form of extensive series of observations and discussions of them, and partly in the form of popular treatises. The tidal currents have also been dealt with extensively, although they are less readily observed than the tides and even more difficult to examine theoretically. The literature on tidal currents, however, is also very large. Only a brief outline of the tidal theories and of the character of tides and tidal currents will be presented here. (Reference made to Darwin, 1911; Krümmel, 1911; Marmer, 1932.)
Tide-Producing Forces. Tides are caused by the attraction of the moon and sun. In a given locality the tide is of a complicated character, but any tide can be shown to consist of a number of partial tides, each of which is related to the motion of the earth relative to the moon and the
Considering the moon and the earth only, let the mass of the earth be equal to unity, and the mass of the moon equal to m. The gravitational attraction of the moon at the center of the earth is then proportional to m/r2, where r is the distance from the center of the moon to the center of the earth (fig. 137). This distance remains constant, on an average, and the attraction of the moon on the earth must, therefore, on an average, be balanced by a centrifugal force that is directed away from the moon and is also proportional to m/r2.
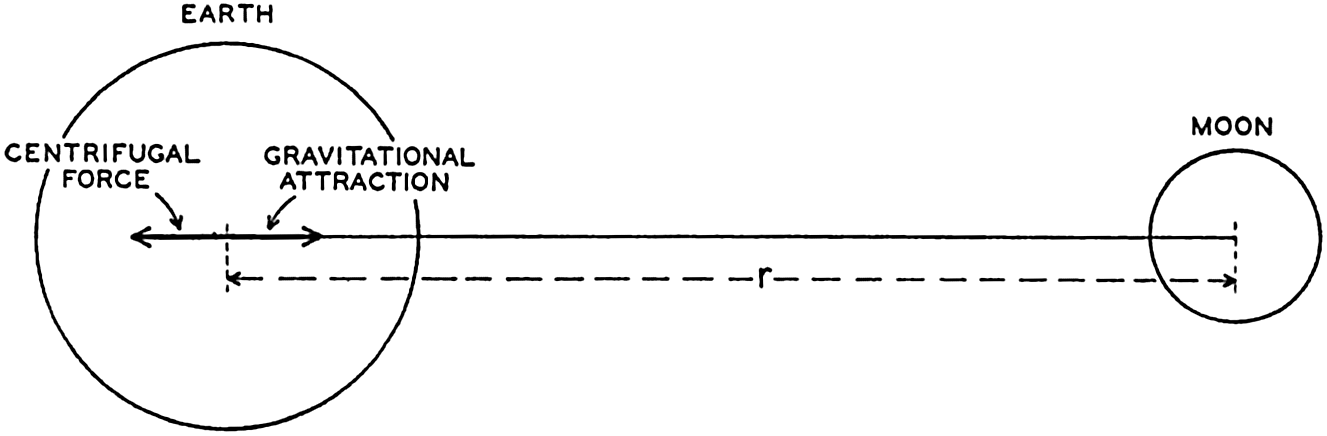
Schematic representation of the gravitational attraction between the earth and the moon and the centrifugal force which balances the attraction.
The centrifugal force acting on any particle on the earth is the same, but the attraction of the moon varies. Consider a point at the surface of the earth lying on the line which joins the centers of the two bodies. At this point the attraction of the moon is proportional to m/(r − ρ)2, where ρ is the radius of the earth. The difference between the attraction of the moon at this point and the centrifugal force is proportional to m/(r − ρ)2 − m/r2, or to 2mρ/r3, because ρ/r is a small quantity. The numerical values are m = 1/81.45, r = 60.34ρ. Owing to this difference the moon's attraction tends to raise the surface of the earth at the point under consideration, but at the same point the attraction of the earth acts and is proportional to 1/ρ2. Thus the ratio between the disturbing force of the moon and the attraction of the earth is equal to 2mρ3/r3 = 1.176 × 10−7. The attraction of the earth, on the other hand, equals the acceleration of gravity, and thus the tide-producing force of the moon is only about 1.176 × 10−7 times the acceleration of gravity; that is, at the point under consideration the acceleration of gravity is reduced by the amount 0.000115 cm/sec2.
Consider next a point at the surface of the earth but opposite to the moon. At this point the attraction of the moon is less than the centrifugal force and is proportional to m/(r + ρ)2. The disturbing force is again found from the difference
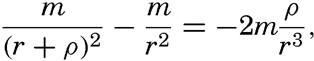
Now take a point at the surface of the earth at right angles to the line joining the centers of the moon and of the earth. At this point the attraction of the moon is of the same magnitude as the attraction at the center of the earth, m/r2, but is directed, in fig. 138, along the line PM. The centrifugal force is parallel, however, to the line EM, and the resultant of these two forces is directed toward the center of the earth and is proportional to mp/r3. In this case the disturbing force leads to an increase in the acceleration of gravity of 0.00058 cm/sec2.
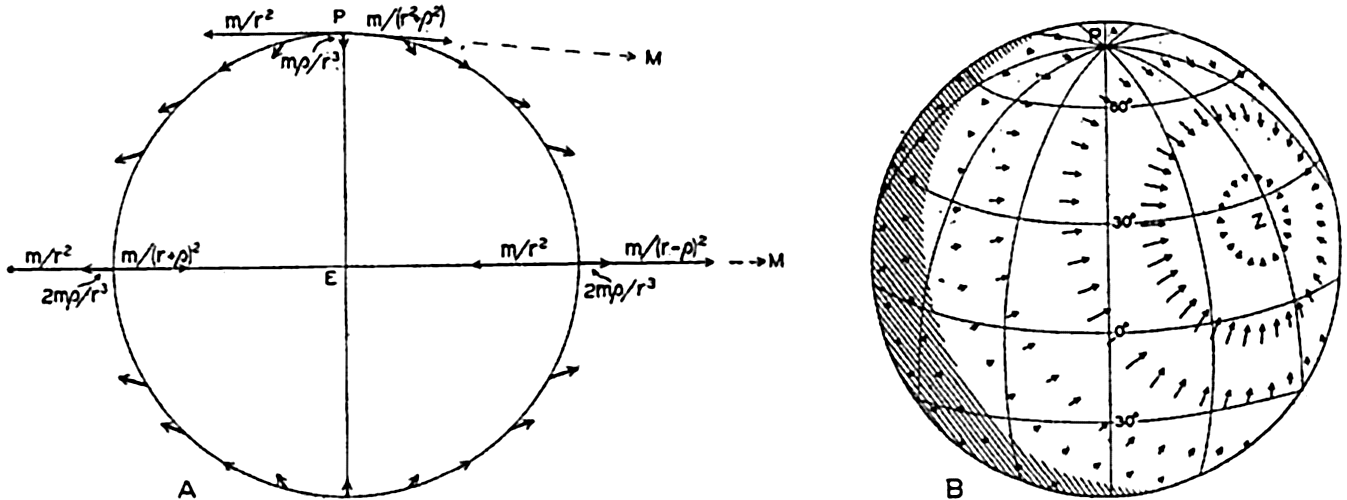
(A) Schematic representation of the tide-producing forces in a plane through the line joining the centers of the earth and the moon. (B) Distribution of horizontal tide-producing forces over the earth (according to G. H. Darwin). The moon is at zenith above the point marked Z.
If a point were selected at random on the surface of the earth, one would find that generally the disturbing force forms an angle with the surface of the earth different from 90° and can therefore be considered as having a vertical component and a horizontal component along the earth's surface (fig. 138). The complete theory leads to the following equations for the vertical and horizontal components of the disturbing forces:
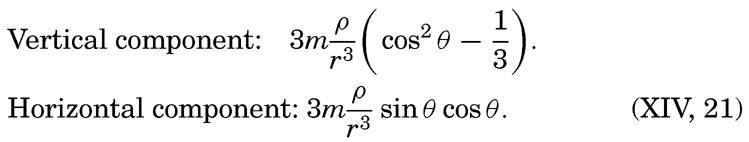
Exactly similar reasoning can be applied if one considers the sun and the earth, but for numerical computations the mass of the sun and the distance between the sun and the earth must be entered. Using the same units as before, one finds that the mass of the sun is equal to 333,400 and that the distance is 23,484p. With these values, one finds that the maximum tide-producing force of the sun is only about 0.46 times that of the moon. The greater distance between the sun and the earth more than balances the effect of the greater mass of the sun.
By considerations of this nature, it is easily shown that no other heavenly body can produce tides on the earth. The closest planets are too small to have any effect, and the large planets are too far away.
The motion of the sun and the moon relative to the earth is so complicated that the system of tide-producing forces changes greatly in the course of time, but the patterns are repeated in regular sequence.
From the graphs in fig. 138 it is seen, for instance, that the field of the moon's tide-producing forces is symmetrical with respect to the poles of the earth if the moon stands above the Equator—that is, when the declination of the moon is zero. In this case, when the earth rotates around its axis, the components of the tide-producing forces will in all latitudes show two equally high maxima and two equally low minima during 24 lunar hours, a period that represents the time interval between two culminations of the moon, or 24.84 solar hours. To an observer on the earth the field of tide-producing forces appears to rotate around the earth in 12 lunar hours. The declination of the moon varies, however, during one month from about 28°S to about 28°N, meaning that at the greatest southern declination the moon passes through zenith in about lat. 28°S, and at the greatest northern declination the moon passes through zenith in about 28°N. In these positions of the moon the field of tide-producing forces is no longer symmetrical with respect to the poles of the earth. At the Equator the two diurnal maxima of the tide-producing forces still remain equal, but in all other latitudes one of the maxima will be less pronounced than the other during a complete revolution of the earth. To an observer on the earth the field appears to be composed of two fields, one that rotates twice in 24 lunar hours, and one that rotates once in the same time. Instead of continuing these reasonings, which would become very involved owing to the many variations in the relative positions of moon, sun, and earth, one can arrive at a complete picture by introducing a series of fictitious heavenly bodies that will each bring about a symmetrical field of tide-producing forces and by considering the total field as composed of all of these partial fields.
Assume first that there is an ideal moon that always remains in the equatorial plane and at any locality passes the upper meridian at intervals
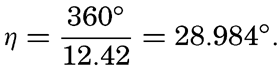
Similarly, one could introduce other fictitious bodies, but the resultant angular velocities of the principal components of the tide-producing forces can all be derived from a small number of characteristic velocities:
The angular velocity of earth relative to the stars, g = 15.0411°.
The angular velocity of the rotation of the moon around the earth, s = 0.5490°.
The angular velocity of the movement of the long axis of the elliptic orbit of the moon, which completes one rotation in 8.85 years, p = 0.0046°.
The angular velocity of the motion of the earth around the sun, e = 0.04107°.
The angular velocities of the different components which together form the actual field of tide-producing forces can be obtained by combinations of these. Thus the angular velocity of the field due to the ideal moon that was first considered is 2(g − s) = 28.984°.
The complete analysis makes it possible to compute coefficients that are related to the intensities of these different partial fields. The significance of these coefficients will be explained. Analysis of tides shows that to these partial fields there are corresponding partial tides that have all received characteristic names and symbols. Table 70 contains the names of the more important semidiurnal, diurnal, and long-period partial tides, their symbols, their periods and angular velocities, and their so-called coefficients.
Thus, the components of the tide-producing forces in a given latitude can be represented by equations of the form
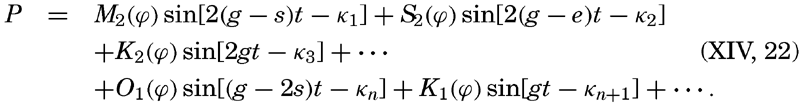
| Name of corresponding partial tide | Symbol | Period in hours | Angular velocity | Coefficient | |
|---|---|---|---|---|---|
| Symbol | In degrees per hour | ||||
| Semidiurnal: | |||||
| Principal lunar | M2 | 12.42 | 2(g − s) | 28.9841 | .4543 |
| Principal solar | S2 | 12.00 | 2(g − e) | 30.0000 | .2120 |
| Larger lunar elliptic | N2 | 12.66 | 2g − 3s + p | 28.4397 | .0880 |
| Luni-solar | K2 | 11.97 | 2g | 30.0821 | .0576 |
| Diurnal: | |||||
| Luni-solar | K1 | 23.93 | g | 15.0411 | .2655 |
| Principal lunar | O1 | 25.82 | g − 2s | 13.9430 | .1886 |
| Principal solar | P1 | 24.07 | g − 2e | 14.9589 | .0880 |
| Long-Period: | |||||
| Lunar fortnightly | Mf | 327.86 | 2s | 1.0980 | .0783 |
| Lunar monthly | Mm | 661.30 | s − p | 0.5444 | .0414 |
| Solar semi-annual | Ssa | 2191.43 | 2e | 0.0821 | .0365 |
Theories of Tides. In the preceding section the tide-producing forces were discussed, but no reference to the actual tides was made except in the content of table 70, in which were listed the partial tides corresponding to the more important tide-producing forces. Two different theories have been advanced as to how these forces can bring about tides, of which the first, the equilibrium theory, is mainly of historical interest and has been replaced by the dynamic theory. The equilibrium theory, which was first developed by Newton, is so often referred to, however, that its principles should be mentioned.
Assume first that the rotation of the earth relative to the moon is such that the same side of the earth always faces the moon. In this case the field of tide-producing forces, which was derived on p. 547 and shown in fig. 138, would remain stationary relative to the earth. The tide-producing forces would lead to a permanent reduction of the acceleration of gravity at the points of the earth nearest to and farthest away
Since the reduction of the acceleration of gravity at the points nearest to and farthest away from the moon is 2mρ/r3, the value of the acceleration of gravity is in the same units: 1/ρ2 − 2mρ/r3. This reduced value is found at a small distance h above the undisturbed surface, where the acceleration of gravity is 1/(ρ + h)2 = 1/ρ2 − 2h/ρ3. Therefore
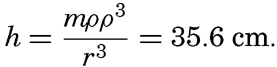
The equilibrium theory assumes that these flood protuberances are actually formed and that the highest portions of the protuberances lie at the points nearest to and farthest away from the moon. However, the earth does not always have the same side turned toward the moon, but rotates relative to the moon once in 24.84 hours. Each flood protuberance therefore appears to travel once around the earth in 24.84 hours, and, because there are two protuberances, the time interval between the passages of flood protuberances will be 12.42 hours. Similar flood protuberances will be caused by the sun and by the irregularity of the motion of the moon and the sun, and the actual tides should appear as the combined result of such a series of protuberances, the heights of which would be proportional to the coefficients in table 70. The obvious criticism that can be directed at this theory is that the movement of a flood protuberance over the surface of the earth cannot take place unless water masses actually change position, but consideration of the movement of the water has been completely disregarded. Other objections to the theory need not be discussed here.
The dynamic theory is based on the fact that only the horizontal tide-producing forces are of importance to the movement of the water. The vertical tide-producing forces are unimportant because they can be considered as consisting of very small periodical variations of the acceleration of gravity. It has previously been shown that the distance between isobaric surfaces in the sea depends upon the acceleration of gravity, and it is evident that variations of the latter must lead to variations of the distances between isobaric surfaces. Where the depth to the bottom is
The general equations of the dynamic theory, which were developed by Lagrange, lead to problems mathematically so difficult that they have not yet been solved so far as the tides of the oceans are concerned. Instead, the application of the dynamic concept has followed two different lines. In the first place, the theory of tides in basins of defined geometrical shape has been developed, particularly by Proudman and Doodson; in the second place, tides in natural basins have been studied mainly by Sterneck and Defant by methods of numerical integration of the hydrodynamic equations. Both methods have helped toward an understanding of the observed phenomena, but here only the latter approach will be dealt with, because it leads to direct comparisons between theoretical results and observed conditions, and because it does not require any lengthy mathematical presentation.
Tides in relatively small bodies of water that are in communication with the open sea have much in common with seiches, and can therefore be discussed in much the same manner. The tides, however, differ from the seiches in the respect that they are forced oscillations of periods which must coincide with the periods of the impulses by which they are maintained, whereas the periods of the free oscillations depend only upon the geometrical shape of the bay.
The similarities and differences between tides and seiches are brought out by considering the oscillations in a long, rectangular bay of constant depth. Any wave in such a bay must fulfil the equations of motion and continuity. It was shown on p. 538 that, when the earth's rotation and friction are neglected, these equations are satisfied by
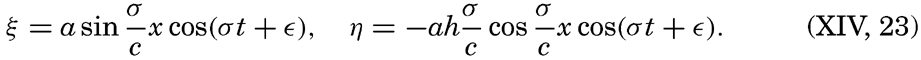
These equations must always hold, and, in addition, certain boundary conditions must be satisfied. These conditions depend upon whether one considers a free oscillation or an oscillation of the same period as an oscillation of the body of water with which the bay communicates, a cooscillation. In the case of a free oscillation in a bay of length l the boundary conditions were x = 0, ξ = 0, and x = l, ξ = 0, and from these


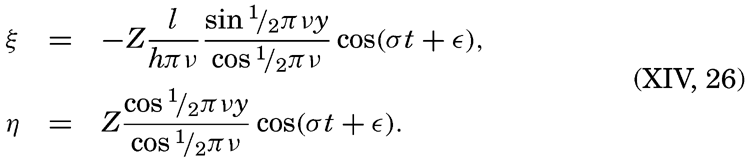
(A) Character of cooscillating tides in bays corresponding to different values of v. (B) Character of independent tides in bays corresponding to different values of v. (According to Defant.)
For the independent tide which is produced directly by the tidal forces, it is necessary to add on the right-hand side of the equation of motion (XIV, 9) a periodic force: x = f cos (σt + ∊). With the boundary conditions x = y = 0, ξ = 0, and x = l, or y = 1, η = 0, one obtains
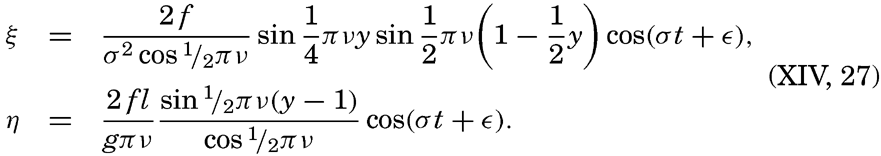
So far, a rectangular bay of constant depth has been considered. For a bay of irregular shape and varying depth, one can start from the equations of motion and continuity in the form (XIV, 16) and can determine the character of the cooscillating and the independent tides by means of a numerical integration similar to the one developed by Defant (p. 539) for determining the free oscillation of the water in a basin (Defant, 1925). In all cases the character of the forced oscillation depends upon the relation of the period of the forced oscillation to that of the free. It can be shown that in general the increase of the range of the tide due to narrowing and shallowing is relatively small, and that very high tides at the ends of bays are, as a rule, a result of resonance.
In the preceding discussion, tide-producing forces have been considered which act in the direction of the long axis of the basin, and it has been assumed that at any given time the force is the same at all cross sections. If the basin is large, it may have to be taken into account that transverse forces exist, causing transverse oscillations, or that at a given time the force varies in the longitudinal direction.
The introduction of friction leads to further complications. In a free oscillation the period is increased by the effect of the friction, but the period of the forced oscillation must always remain equal to that of the force and cannot be altered by friction. The result is that no complete resonance can develop, because the greater the amplitude of the wave becomes, the greater is the effect of friction and the greater the increase of the period of the free oscillation. The ratio v can in these circumstances never remain at the value, 1, 3, 5, …, but can stay near one of these values.
Another effect of friction alters the character of the forced waves. In the absence of friction the cooscillating tide can be considered as a wave in a basin of constant depth which proceeds with constant amplitude and is totally reflected at the closed end of the bay. In the presence of friction the amplitude of the “incoming” wave decreases in the direction of progress, and the reflected wave has therefore a smaller amplitude
Even greater complications arise when the effect of the rotation of the earth is considered. Such consideration is necessary in most cases, since a comparison of the magnitude of the acting forces shows that the deflecting force cannot be neglected when dealing with tidal phenomena, because their period length is of the order of magnitude of a pendulum day (p. 520).
In order to get some idea of the modifications that arise owing to the rotation of the earth, it is necessary to return to the complete equations of motion and to consider not only the vertical and horizontal displacements, but also the horizontal velocities to which no attention has been paid so far. If the depth is constant, if friction is neglected, and if γ = 2ω sin ϕ, the equations of motion and continuity take the form
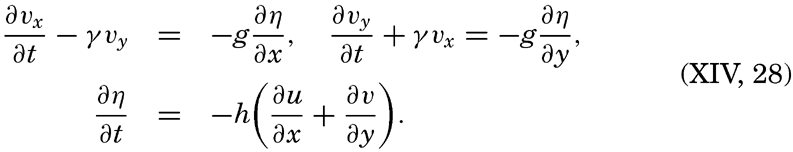
Two solutions of these equations can easily be written. Consider first an infinitely long canal of constant width b. If the x axis is placed in the direction of the canal, the boundary conditions y = 0, vy = 0, and y = b, vy = 0 must be fulfilled, because at the walls of the canal the motion can be in the x direction only. With these boundary conditions, one obtains in the Northern Hemisphere
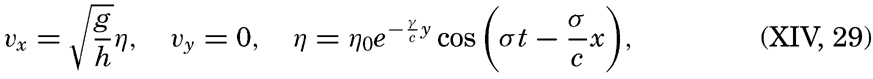
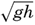 .
.This solution, which was first given by Lord Kelvin (Lamb, 1932), defines a wave, the Kelvin wave, which proceeds in the x direction with the velocity c and is characterized by great amplitudes on the right-hand side and by small amplitudes on the left-hand side. At high water, when the current flows in the direction of progress, the wave crest slopes down from right to left, and the component of gravity acting down that slope is exactly balanced by the deflecting force of the earth's rotation acting in the opposite direction. At low water the directions of the slope and the current are reversed. The forces again balance each other, and the
Another solution, given by Sverdrup (1927), is applicable to a wave that proceeds in an unlimited sea, provided that γ = 2ω sin ϕ can be considered constant:
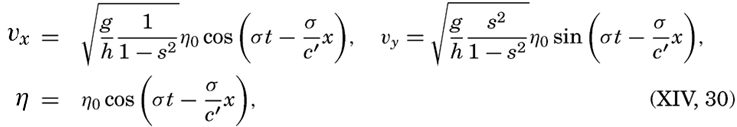

These equations define a wave that has horizontal crests like an ordinary long wave, but a velocity of progress that has been increased in the ratio  . At the same time the motion of the water particles is no longer alternating back and forth, but is rotating, because, in addition to the velocities in the direction of progress (the longitudinal velocities), transverse velocities also exist. The ratio between the maximum longitudinal and transverse velocity is 1/s, and the latter reaches its maximum one fourth of a period after the longitudinal velocity was at its maximum. The character of these currents will be dealt with later, and attention will be focused here on the wave itself.
. At the same time the motion of the water particles is no longer alternating back and forth, but is rotating, because, in addition to the velocities in the direction of progress (the longitudinal velocities), transverse velocities also exist. The ratio between the maximum longitudinal and transverse velocity is 1/s, and the latter reaches its maximum one fourth of a period after the longitudinal velocity was at its maximum. The character of these currents will be dealt with later, and attention will be focused here on the wave itself.
The velocity of progress of the wave becomes infinite when s = 1 and imaginary when s > 1. Now, s = γ/σ = (Tt/12) sin ϕ, where Tt is the period of the tide in hours. Thus, c becomes infinite when Tt = 12/sin ϕ, or, if sin ϕ = 1, when Tt = 12; that is, on a disk which rotates once in 24 hours, waves of this type cannot exist if the period of the wave is greater than half the period of rotation of the disk. Applied to the earth, the meaning is that waves of this type cannot exist if their period is longer than one half pendulum day. This result is not so significant as it appears to be, because the solution is valid only for an unlimited body of water, and on the rotating earth the limitation of the ocean will make impossible a complete development of this wave type. If a wave proceeds in the longitudinal direction of an ocean, the transverse velocities must vanish along the coasts, but may develop at some distance from the coast. The wave must be of an intermediate type between the Kelvin wave and the wave described here, and can be considered as composed of longitudinal and transverse oscillations, the nature of which cannot yet be expressed analytically.
In a narrow sea, transverse oscillations of the sea level will be present even if no conspicuous transverse currents are developed. The periodic
In the absence of transverse oscillations the tide will be zero along a nodal line, but in the presence of transverse oscillations the tide will vanish at a single point only. Points that have high or low water at the same hour can be joined by lines which are called cotidal lines. These cotidal lines all meet at a point where the tide vanishes, which is called an amphidromic point. An amphidromic point can be caused either by the effect of the earth's rotation or by the interference of two tidal waves.
If a standing oscillation exists in a bay, there are no cotidal lines, because high water occurs at the same time everywhere. However, when transverse oscillations are present which differ from the longitudinal by one quarter period, an amphidromic point is developed that lies on the original nodal line (fig. 140). To the right of the center, high water occurs at the time t = 0, to the left at the time t = ½T, and the other cotidal lines are spaced between these. Thus, the rotation of the cotidal lines around an amphidromic point that is caused by the earth's rotation is, in the Northern Hemisphere, counterclockwise (as shown in fig. 140), but it is clockwise in the Southern Hemisphere. This characteristic may be used for deciding whether or not an observed amphidromic point may be due to the rotation of the earth.
The methods of analysis that have been set forth here have been applied mainly by Sterneck and Defant to the tides in “adjacent seas,” such as the North Sea, the Adriatic Sea, the Red Sea, and others. In the case of the North Sea, from which numerous current measurements are available, other methods developed by Proudman and Defant have been used for deriving a complete picture. The considerations have even found application to the Atlantic Ocean, the principal tides of which have been studied by Sterneck and Defant. Their conclusions will be dealt with when the tidal currents are discussed. In the other oceans, application of the dynamic theories presents enormous difficulties and has not been attempted. The above reasonings are purely qualitative, but G. I. Taylor has succeeded in giving an exact solution for a bay of rectangular
A generalization of the observed conditions has been made by R. A. Harris (1894–1907), who divided the oceans into “oscillating areas,” the period of free oscillation of which would be about 12 or 24 lunar hours if they were enclosed by solid boundaries. The areas were selected so that the observed difference in the time of high water at both ends of the area would be approximately 6 or 12 hours. Within each area one or more nodal lines would be present. This division of the oceans into “oscillating areas” brings a surprising consistency in the otherwise confused picture of the tides, but, as pointed out by G. H. Darwin, it can hardly be accepted as a physical explanation because, among other factors, the rotation of the earth has been disregarded.
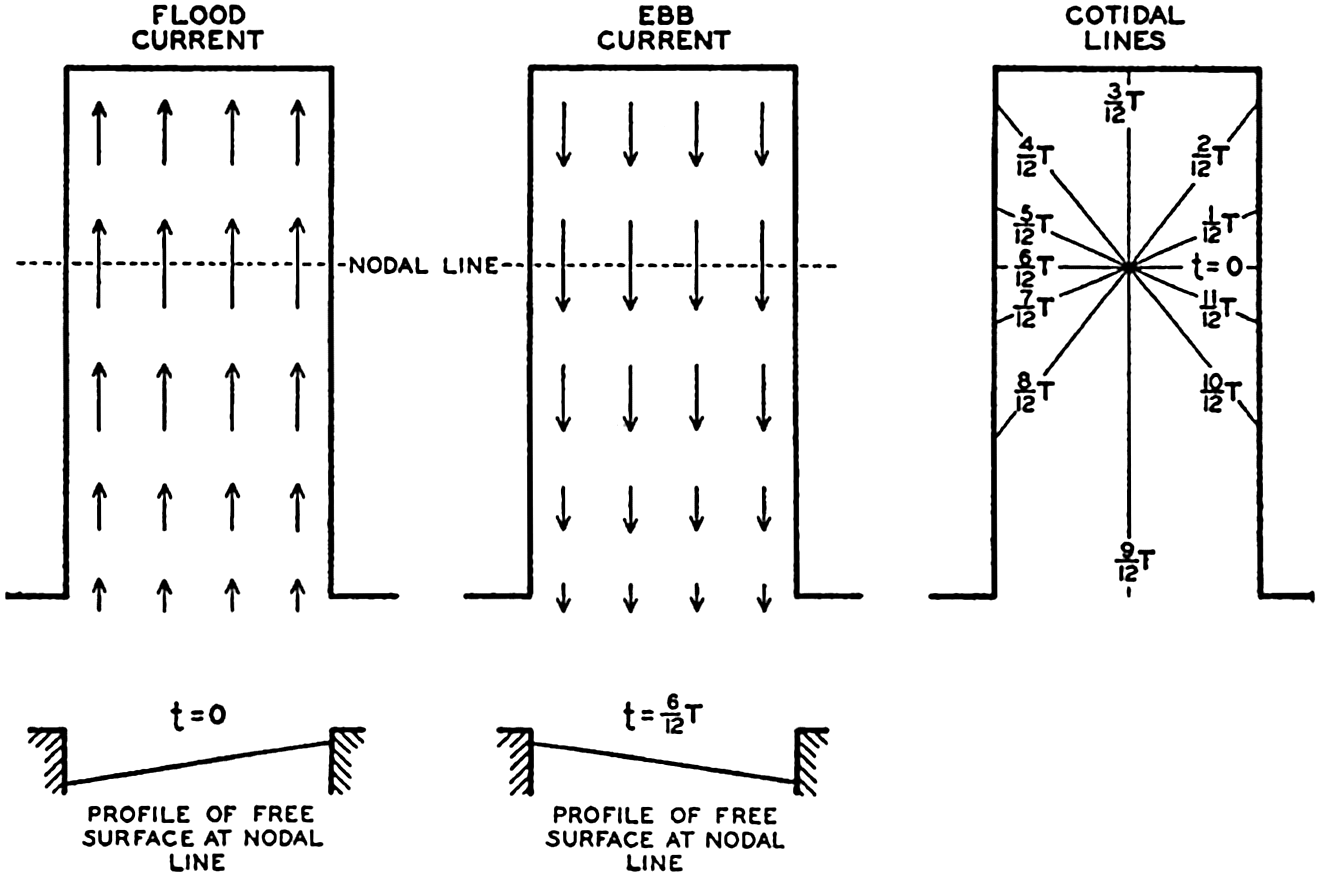
Schematic representation of transverse oscillations in a bay in the Northern Hemisphere leading to the development of an amphidromic point.
The Character of the Tides. The tide-producing forces can be computed with great accuracy, but the response of the oceans to these forces is too complicated to be determined. Experience has shown, however, that the tides can be considered as composed mainly of a series of harmonic oscillations, or partial tides, having the periods of the tide-producing forces. To these terms must be added, in many localities, annual and semiannual terms which are not related to astronomical forces but which are ascribed to the effect of prevailing winds or changes of sea level due to heating and cooling (p. 459). These long-period tides
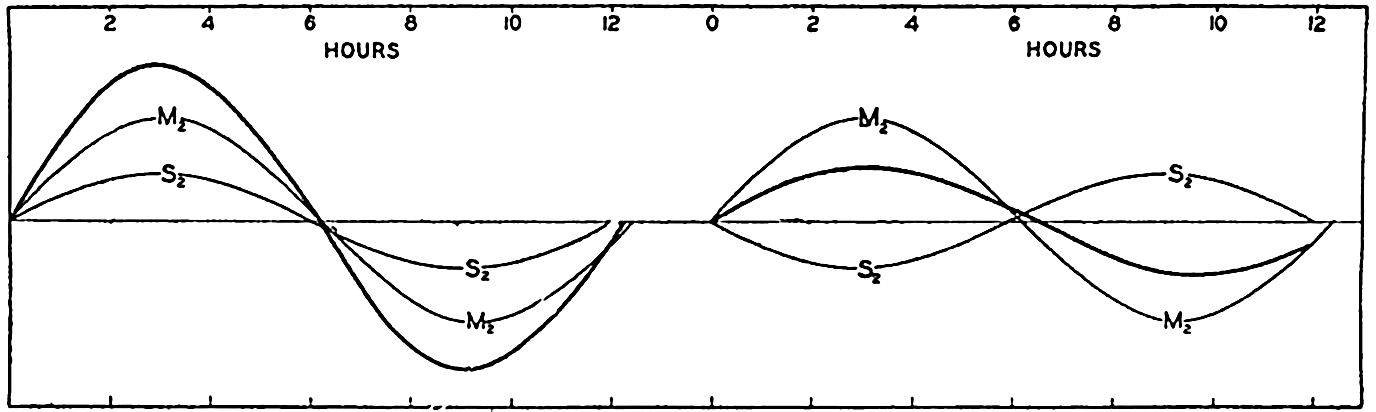
Tide curves at spring tide (left) and neap tide (right).
The most important tide-producing forces are those of nearly semi-diurnal and nearly diurnal period, for which reason the character of the tide in any locality depends mainly upon the relative heights and phase angles of the partial tides corresponding to these forces. Let us first consider the partial tides due to the semidiurnal lunar forces of a period 12.42 hours and to the semidiurnal solar force of a period of 12 hours. The former will give rise to two high waters and two low waters in 24.84 hours (one lunar day), and the latter to two high waters and two low waters in 24 hours (one ordinary day). Thus, the high water due to the moon will be retarded 0.84 hours every day, or about 50 minutes relative to that caused by the sun. After coinciding on a given day, the partial high waters will move apart, to coincide again when the lunar tide has been retarded 12 hours, or after 12/0.84 = 14.3 days. The semidiurnal tide will be great when the two partial tides coincide and small when they counteract each other (fig. 141). The large tides are called spring tides, and the small tides are called neap tides, and in a locality in which the semidiurnal components are dominating, spring and neap tides come at intervals of 14.3 days. Where the tides are of the semidiurnal type, the ratio between the ranges of the lunar and solar partial tides may be fairly close to the theoretical ratio 1:0.47 (table 70 p. 550), in which case the ratio between the ranges of spring and neap tides is fairly close to 1.47:0.53 = 2.77.
If the tides followed the tide-producing forces, the lunar and solar semidiurnal tides would coincide at full and new moon and would be opposite in phase at the quarters of the moon. In most localities the tides lag somewhat behind the tide-producing forces, and spring tides occur a day or two after full moon and a day or two after new moon. The time difference between the meridian passage of full or new moon and the occurrence of the highest high water is called the age of the tide, and is given in days.
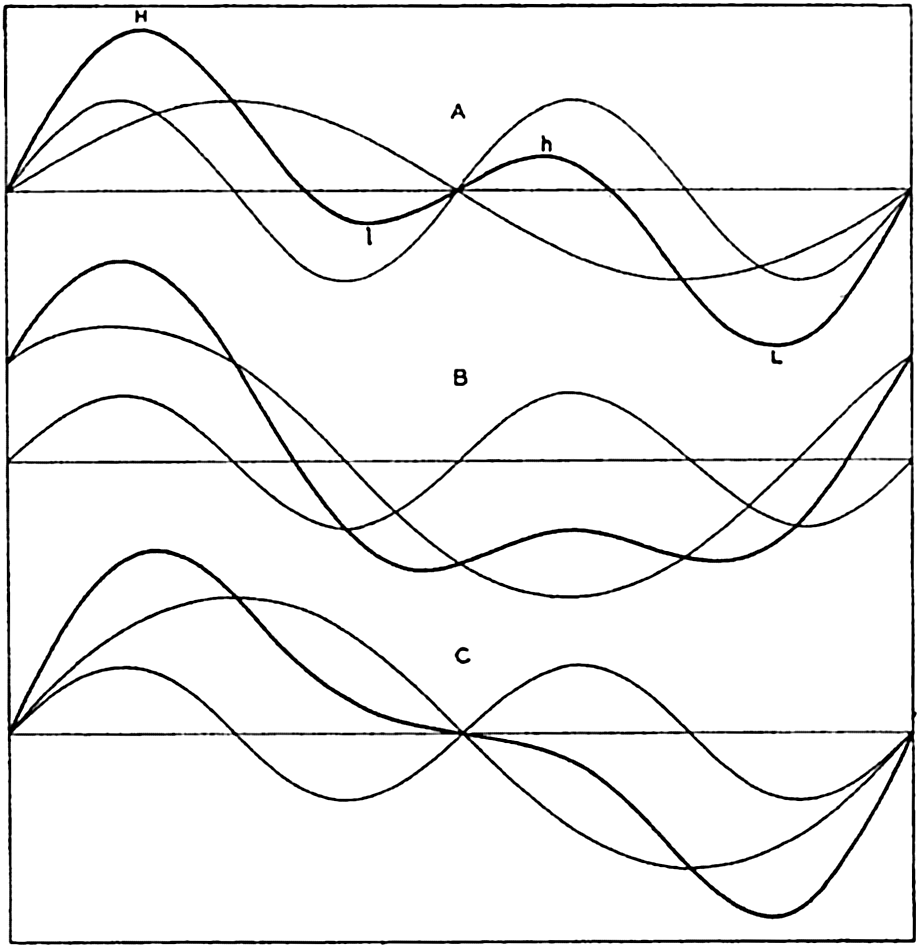
Examples of different types of tides resulting from simultaneous diurnal and semidiurnal tidal components.
The close relation of the tide to the moon is also demonstrated by the fact that, where a semidiurnal tide prevails, high water always comes at nearly the same number of hours after the moon passes through the upper or lower meridian—that is, after the moon is due south or due north. The mean time difference between the meridian passage of the moon and the occurrence of the next high water is called the mean high water lunitidal interval, and is measured in hours.
Diurnal partial tides greatly complicate the picture, because the tide will depend upon the relative magnitudes of the semidiurnal and diurnal components and upon the time at which these components reach their maxima. Figure 142 illustrates a few possible combinations. Figure 142A shows an ordinary “mixed type” of tide in which one of the two high waters of the day is much higher than the other, and one of the
Figure 142B illustrates a case in which the inequality is found in the high waters only, the two low waters being equally low. Figure 142C illustrates a case in which only one high and one low water occur during the day, because the other high and low water melt together into a period of several hours with nearly constant water level. This particular phenomenon is called the “vanishing” tide.
The examples in fig. 142 were constructed by combining diurnal and semidiurnal tides of different heights and different phase angles. It is evident that different combinations lead to other tide curves in which the diurnal inequality of the tide appears more or less pronounced. The diurnal inequality of the tide varies during a month, because the distribution of the moon's tide-producing force over the earth varies with the declination of the moon. The tides that display the greatest diurnal inequalities are called the tropic tides, since they occur when the moon's declination is at its maximum or at its minimum—that is, when the moon is nearly above the Tropic of Cancer or of Capricorn.
Taking partial tides of other periods into account, and considering the fact that the tide-producing forces vary with the distance from the earth of the moon and the sun, one finds that a nearly unlimited number of possible types of tides exists and that, in any given locality, the type of the tide may change considerably during one month. As a rule, however, the tide has the same characteristics at neighboring stations on an open coast. Detailed information as to the character of the tides in different localities is found in several of the books listed at the end of this chapter.
Several terms used for describing the tide have been defined, but a few more must be added. Mean sea level is the plane about which the tide oscillates (Marmer, 1927). It is determined from tidal observations by averaging the tabulated hourly heights of the tide over a period of several years. Mean sea level does not coincide, as a rule, with an equipotential surface, because, where permanent currents are present, the sea surface always slopes at right angles to the current (p. 391). Mean sea level may also rise or drop along a coast, as is evident from results of precision leveling along the Atlantic coast of the United States (p. 677). Daily, weekly, monthly, and yearly sea level can be derived from observations during a day, a week, a month, or a year. For daily sea level, it is necessary to state how the average has been computed (see Marmer, 1927).
Mean high water is the average height of all high waters over several years, and, similarly, mean low water is the average height of all low waters over several years. The half-tide level lies exactly half way between mean high water and mean low water, and differs as a rule from mean sea level. In localities where the tide shows a considerable diurnal inequality, mean higher high water and mean lower low water are computed from the highest and lowest tides of each day.
In bays and in seas which communicate with the ocean through a relatively narrow opening, the tide may differ from that in the ocean, because the shape of the bay or the adjacent sea may favor the development of certain components of the tide. Modifications due to the rotation of the earth may also arise.
The tide in the English Channel represents an example of the latter modification. The tide there has in part the character of a progressive wave which enters the continental shelf from the Atlantic Ocean and which, as it advances, takes the appearance of a Kelvin wave, with small ranges on the left-hand side, the south coast of England, and great ranges on the right-hand side, the northwest coast of France. On the coast of France the Bay of St. Malo is particularly famous for its large tides, because in the inner part of the bay the range of the spring tide is up to 12 m (39 feet). This enormous range is in part attributed to the narrowing of the bay and the shoaling of the bottom.
The largest known tides occur in the Bay of Fundy, where, in Noel Bay, spring-tide ranges up to 15.4 m (50.5 feet) have been measured. However, this tide can be accounted for in a different manner. In the Bay of Fundy, high water occurs nearly simultaneously all around the bay and, furthermore, it has been found that the strongest tidal currents flow into the bay when the water is rising most rapidly, and out of the bay when the water is falling fastest. These features—the increase in the range of the tides toward the end of the bay, the simultaneous occurrence of high and low water all over the bay, and the maximum currents at mean water—all indicate that in the Bay of Fundy one has to deal with a standing wave.
The range of the tide is, however, not zero at the opening of the bay, for which reason the tide must be of the cooscillating type (fig. 139), and the great increase of the range toward the head of the bay must be due to resonance. An exact computation of the period of free oscillations of the waters of the Bay of Fundy has not been undertaken, but according to rough estimates this period lies between 13 and 11.6 hours (Defant, 1925). Such a period means that in the Bay of Fundy the ratio v = Tf/Tc (p. 553) is probably sufficiently close to unity to bring about resonance, but the increase of range toward the end of the bay may also be augmented by the narrowing and the shoaling of the upper part.
The tides in the Bay of Fundy are remarkable because of their great range, but the increase of the range from the opening to the end of the bay is not greater than in some other localities. The tides of the Adriatic Sea have been examined very thoroughly by Defant and Sterneck, who have found that there the cooscillating tide dominates. The longitudinal semidiurnal tide shows a node at a distance from the opening of about three quarters of the length of the sea, and inside the node the range of the semidiurnal tide increases rapidly. On the other hand, the range of the diurnal tides increases regularly from the opening toward the end, and is, at the end, about four times as great as the range at the opening. The range of the Bay of Fundy tide is also increased about fourfold from opening to end, and this increase represents therefore no exceptional case. By studying fig. 139 it is easily seen that the range of the cooscillating tide must increase from the opening to the end of a bay if the ratio v lies between 0 and 2, and that the increase must be the greater the closer v is to unity. In the Adriatic Sea the transverse oscillations due to the earth's rotation have also been studied, and excellent agreement has been obtained between observations and theory. Interested readers are referred to Defant (1925).
Attempts to represent the tides of a large area on charts encounter considerable difficulty, because the character of tides is known from coasts and islands only, and the data can be combined in many different ways. The first comprehensive representation was prepared by Whewell, who in 1833 published a map of the cotidal lines of all oceans (Marmer, 1926). As explained earlier (p. 557), cotidal lines are lines which join points having high water at the same time, referred to Greenwich or some other standard meridian. Later, charts of cotidal lines were prepared for several smaller areas, and for the Atlantic Ocean the cotidal lines of the semidiurnal and the diurnal tides have been plotted separately. Charts dealing with the partial tides are preferable, because the character of the cooscillating and independent partial tide of any body of water depends on the period of that tide. Similarly, charts showing the range of the tide have more rational meaning when they present partial tides, and charts of this nature have been prepared for some adjacent seas. When dealing with tidal ranges, one should use data from well-exposed stations, since the tide in bays and estuaries may be distorted.
Owing to the uncertainty involved in arriving at a general representation of the tides, it is often necessary to interpret the available data in a certain manner in order to arrive at a consistent picture. The most outstanding example of such interpretation is Harris's division of the oceans into “oscillating areas,” which was mentioned on p. 558. However,
Analysis and Prediction of Tides. Any observed tide curve can be represented, as has already been stated, by means of a series of harmonic terms, the periods of which correspond to the periods of the astronomical and meteorological tides (p. 550). This is true regardless of how complicated the tide is. The coefficients of the different terms can at any given localities be determined with great accuracy by means of harmonic analysis if sufficient data are available. Methods employed in harmonic analysis are described by Schureman (1924). Here it will be mentioned only that the harmonic analysis of tidal data is a complicated process, because many periods have to be considered, some of which differ but little in length. Methods have been developed, however, which permit fairly rapid calculations.
The tide curve can be reproduced with a high degree of accuracy if a sufficient number of harmonic terms have been evaluated. These terms can be used for computation of future tides, since the tide is one of the few geophysical phenomena that repeat themselves with nearly astronomical regularity. The process of computation consists in calculating the tide corresponding to each single term, using the empirically determined amplitudes and phase angles and finally adding the terms, thus constructing a predicted tide curve. The calculation and addition is now made by means of specially constructed tide-predicting machines for preparing tide tables. These machines are operated by the U. S. Coast and Geodetic Survey, Washington, D. C., the British Admiralty, London, and the Deutsche Seewarte, Hamburg. The tide tables, which are issued for each year, give advance information as to the time and height of high water and low water of all commercially important ports of the world. In addition, information is given as to the time difference between high water at principal ports and high water in neighboring localities.
A popular description of the tide-predicting machine of the U. S. Coast and Geodetic Survey is given by Marmer (1926), and a technical description is given by Schureman (1924). Experience has shown that the deviations of the actual tides from the predicted values are mostly small and are due to nonperiodic disturbances caused by winds and shifts in currents.
Tidal Currents
Tidal currents represent the motion of the water particles in the progressive or standing tide waves which on coasts and islands are recognized by the rise and fall of the tide. The tidal currents will therefore be of different character in different areas, depending upon the character
In order to discuss the general character of the tidal currents, it is necessary to repeat some of the equations that have been used previously. Disregarding friction and the rotation of the earth, placing the x-axis in the direction of progress of the tide wave, and assuming constant depth, one obtains the equations of motion and continuity in the form
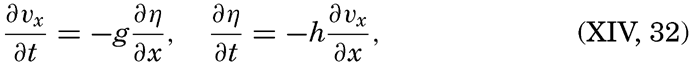
For a progressive wave,

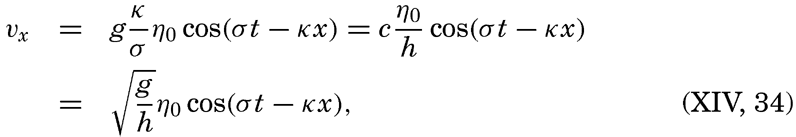
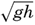 is the velocity of progress of the wave.
is the velocity of progress of the wave.Thus, the velocity reaches its maximum in the direction of progress at high tide (η = η0) and its maximum in the opposite direction at low tide (η = −η0). The tidal current is alternating, changing its direction every half period.
For a standing wave

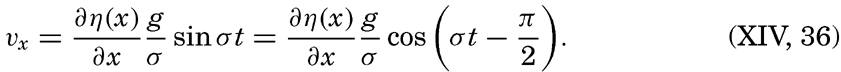
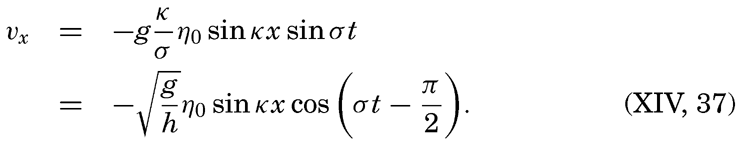
The total horizontal displacement during one half tidal period when the water flows in the same direction, if the maximum tidal current is called V, is
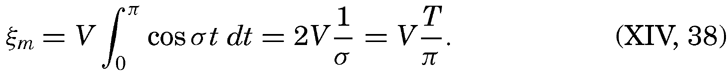
In order to get an idea of the corresponding velocities of the tidal currents and the maximum displacements, we shall consider the tide in a progressive wave of an amplitude (not range) of 100 cm. The corresponding maximum tidal currents in seas of different depths are shown in table 71.
| Semidiurnal tide | Depth (m) | ||||
|---|---|---|---|---|---|
| 100 | 500 | 1000 | 2000 | 4000 | |
| Maximum current {cm/sec | 31.3 | 14.0 | 9.9 | 7.0 | 4.9 |
| {knots | 0.61 | 0.27 | 0.19 | 0.14 | 0.10 |
| Maximum displacement {km | 4.4 | 2.0 | 1.4 | 1.0 | 0.7 |
| {nautical miles | 2.4 | 1.1 | 0.75 | 0.54 | 0.38 |
It appears from this table that in the open ocean the tidal currents cannot reach any appreciable velocities, but measurements demonstrate that the actual velocities are considerably higher than those tabulated, partly because the earth's rotation must be taken into account, and partly for reasons that as yet are unexplained. Before the effect of the earth's rotation is considered, tidal currents in waters of changing depth or changing width will be dealt with.
In a channel of rectangular cross section but variable depth, h, and width, b, the combination of the equations of motion and of continuity can be written (Lamb, 1932, p. 275)
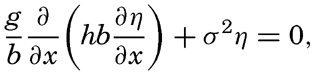
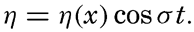
Fleming (1938) has used this equation for studying the tidal currents on a continental shelf related to a standing wave with a node line parallel to the coast. In this case, b is constant, and one obtains
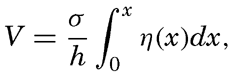
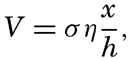
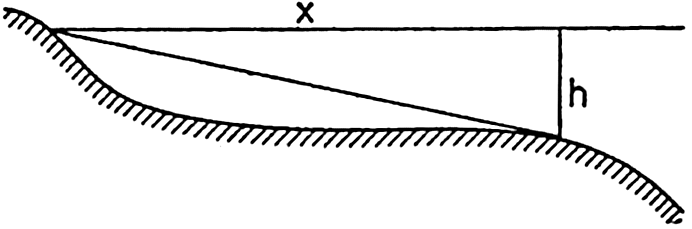
Schematic cross section of a continental shelf showing that the ratio x/h is at a maximum near the border of the shelf.
If the depth is constant, the velocity increases linearly with distance from the coast, but, if the slope of the bottom, x/h, is constant, the velocity is independent of the distance. Generally, the ratio x/h is not constant, and then the tidal currents reach a maximum at the distance x at which x/h is greatest. The profiles of many continental shelves are such that x/h is greatest near the border of the shelf (fig. 143), and the maximum tidal currents may therefore be expected near the border.
These considerations hold true not only in the case of a standing wave, but also, in general, if a transport of water toward the coast takes place during some part of the tidal period and away from the coast during some other part of the tidal period. Therefore they help to clarify some of the characteristics of tidal currents near coasts.
Another question of interest is that of tidal currents where the bottom topography is irregular, showing basins and submarine ridges and peaks. A basin is generally of small dimensions relative to the length of the tide wave (the semidiurnal tide wave is 4200 km long where the depth is 1000 m), and the tidal current, if existing, must therefore be in the same direction in the entire basin during one half tidal period, but such flow would necessitate the presence of ascending and descending motion of considerable velocity at the borders of the basin. If the depth of the basin below the general level of the sea bottom is 1 km and if the width of the area of ascending motion is 10 km, then the average ascending motion would have to be one tenth of the horizontal velocity. This type of flow would be possible in homogeneous
Variation in the width of bodies of water leads to other modifications of the tidal currents. Strong tidal currents through narrow sounds are readily accounted for by the fact that large amounts of water have to flow through these openings during each half tidal period. Consider a bay of surface area A square meters which is in communication with the open sea by an opening whose cross-section area is S square meters. Let the average range of the tide in the bay be 2η0 m. The total volume of water that flows into the bay in the time interval between low and high water is then A × 2η0 m3. The inflow, on the other hand, is equal to 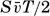 , where
, where 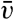 is the average velocity during the half tidal period (T/2) in which inflow takes place. The maximum velocity during that time is π/2 times the average velocity, but the flow is not uniform through the cross section. Observations have shown that in mid-channel the velocity is about one third larger than the average velocity. Therefore, the maximum velocity of the tidal currents in mid-channel is approximately
is the average velocity during the half tidal period (T/2) in which inflow takes place. The maximum velocity during that time is π/2 times the average velocity, but the flow is not uniform through the cross section. Observations have shown that in mid-channel the velocity is about one third larger than the average velocity. Therefore, the maximum velocity of the tidal currents in mid-channel is approximately
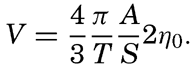
As a schematic example, let us consider a bay that has an area of 100 km2 and is in communication with the open sea through a channel that is only 200 m wide and 50 m deep. Let us assume that the range of the semidiurnal tide in the bay is 2 m. Then, in the time interval between high and low water (6.21 hours, or 22,356 seconds), 2 × 108 m3 of water must flow out through the channel, the cross section of which is 104 m2. The average current must therefore be
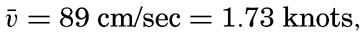
If, in the above example, the opening had been 1 km wide and 100 m deep, the maximum currents at the center of the channel would have been only 0.36 knots. This clearly demonstrates that exceptionally strong tidal currents can be expected only in narrow sounds or inlets. Marmer (1926) has computed the tidal currents at the opening of the Bay of Fundy and found no higher maximum velocities than 1.59 knots, in spite of the tremendous range of the tide at the head of the bay. This result, which is in agreement with observations, clearly shows that strong tidal currents are not encountered at the opening of such bays as the Bay of Fundy, where the cross-section area of the opening is great compared to the surface area of the bay.
The tidal energy can be well illustrated by considering the number of horsepower which can theoretically be developed by tidal currents flowing through a narrow sound connecting a basin with the open sea. The average number of horsepower during one half tidal period, ½T, is equal to gρA2η02/T. With A = 100 km2 and 2η0 = 2 m one obtains 360,000 h.p., but even under the best of conditions only a small fraction of this amount can be actually utilized. Owing to the depth and the width of the opening through which the tidal currents flow, the energy is not concentrated as in a waterfall, but is distributed over a large surface. Furthermore, the tidal power has an intermittent character varying from zero to its maximum value in one quarter tidal period and reaching much higher maximum values at spring tide than at neap tide. This makes utilization on a large scale extremely difficult, but on a small scale tidal power is being used in a few river estuaries. Marmer (1926) computes that theoretically the tides in the Bay of Fundy can produce no less on an average than 200,000,000 h.p., but he adds that by the time the scheme
Neglecting the earth's rotation, the tidal currents are alternating if they are associated with a single standing or progressive tide wave; but if several tide waves are present, interference takes place which may give rise to rotary tidal currents, meaning that the tidal currents regularly change direction and velocity during one tidal period. If the velocities are plotted as vectors from one central point, the end points of the vector will describe a closed curve during one tidal period (fig. 144), and in the absence of other currents the vector sum will be zero.
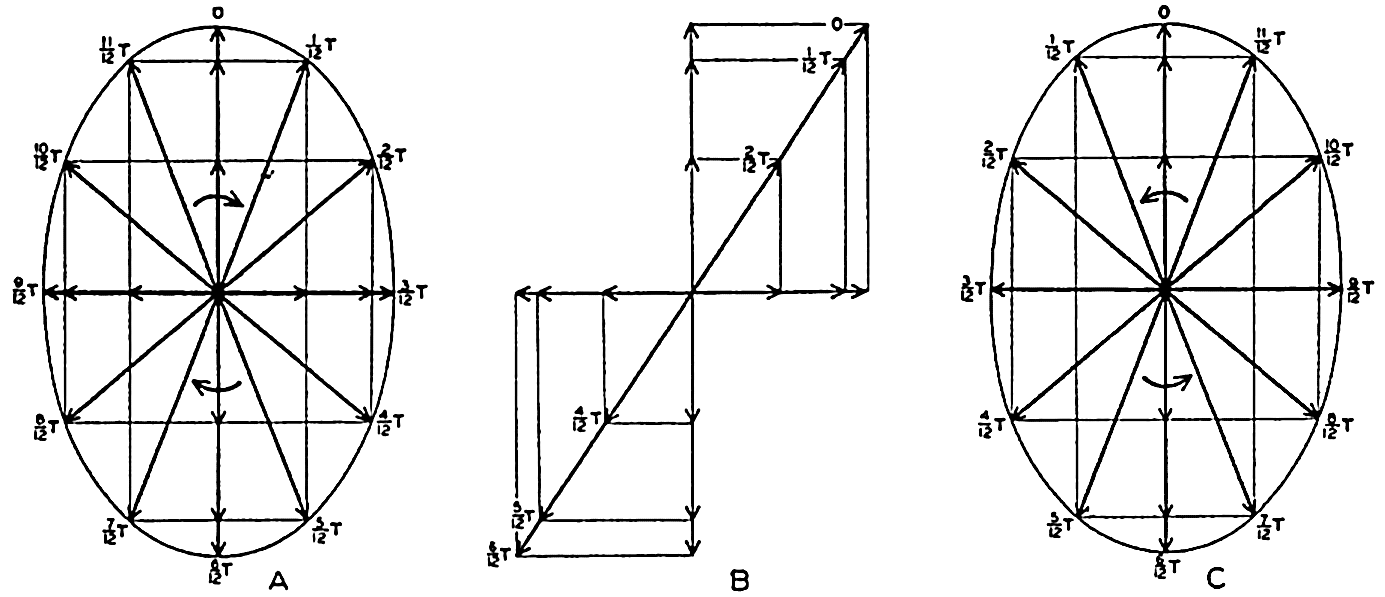
Examples of rotating currents produced by interference of tide waves progressing at right angles to each other and of different phases.
As a simple case, let us consider the interference between two tidal waves which progress along the positive x and y axes. If the depth is constant, the alternating tidal currents corresponding to the two waves are at the point x = y = 0
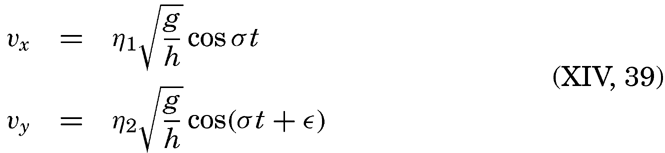
Assume next ∊ = π/2, meaning that the maximum velocity in the direction of the negative y axis is reached one quarter period after the maximum velocity in the positive x direction. The result will be a current which rotates clockwise, the end points of the vectors representing
If ∊ = −π/2, similar reasoning leads to the conclusion that the current will turn counterclockwise as shown in fig. 144C. In general, interference of tide waves leads to rotating currents, the direction of rotation being clockwise or counterclockwise, depending upon the phase difference between the two interfering waves, and the ratio between the axes of the resulting ellipse depending upon the phase difference and the amplitudes of the waves.
Except in narrow sounds the observed tidal currents are mostly rotating. If these currents resulted from interference, one should expect to find clockwise or counterclockwise rotation to be equally frequent, but in the Northern Hemisphere, from which most observations are available, clockwise rotation is by far the more common. This fact indicates that the rotary currents are as a rule not caused by interference but by the effect of the rotation of the earth.
On p. 555 are given the equations of motion and continuity which apply to long waves, taking the rotation of the earth into account. Two integrals of these equations have been given—one by Lord Kelvin, which is applicable to a tidal wave in an infinitely long canal of constant width and depth:
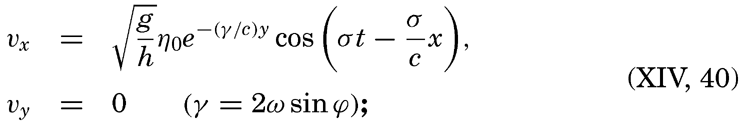
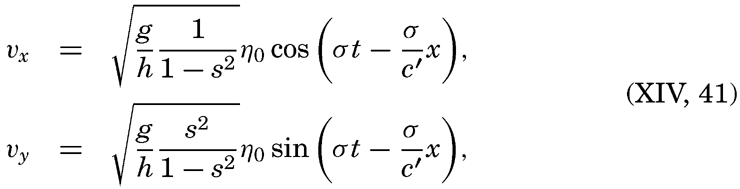
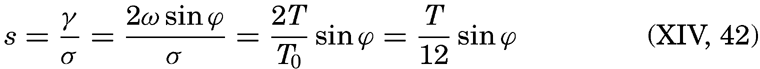
Measurements at lightships have shown that rotating currents occur at a short distance from the coasts, and measurements from vessels anchored in deep water have demonstrated that rotating currents are as a rule present in the open sea. Most of these observations have been made in the Northern Hemisphere where, in nearly all instances, clockwise rotation of the tidal currents has been encountered, whereas a few observations in the Southern Hemisphere have shown counterclockwise rotation. These facts present the best support of the concept that, in general, the rotating tidal currents are due to the effect of the earth's rotation and not to interference, but in some cases interference may complicate the picture. An exact mathematical treatment of the tidal currents of the ocean, however, encounters the same difficulties as the exact development of the dynamic theories of the tides.
As already stated, tidal currents and tides represent two different manifestations of the same phenomenon. When dealing with the tides it was shown that in any locality the tide can be represented by means of a series of harmonic terms having the same periods as the periods of the tide-producing forces. The tidal currents can be represented in a similar manner, but if one deals with rotating currents it is necessary to consider separately two components of the current, say, the N-S and the E-W components. Tidal currents are much more difficult to observe exactly, however, mainly because other types of currents are as a rule superimposed on them, and a great number of data are needed in order to eliminate the superimposed currents and obtain a clear picture of the periodic tidal motion. It can be shown, however, that the tidal currents are closely related to the character of the tide.
It was mentioned that on the Atlantic coast of the United States the tide is of the semidiurnal type, the diurnal components being small. In agreement with this feature it has been found that off the Atlantic coast the tidal currents are also of the semidiurnal type, meaning that during 24 lunar hours the end points of vectors representing the tidal
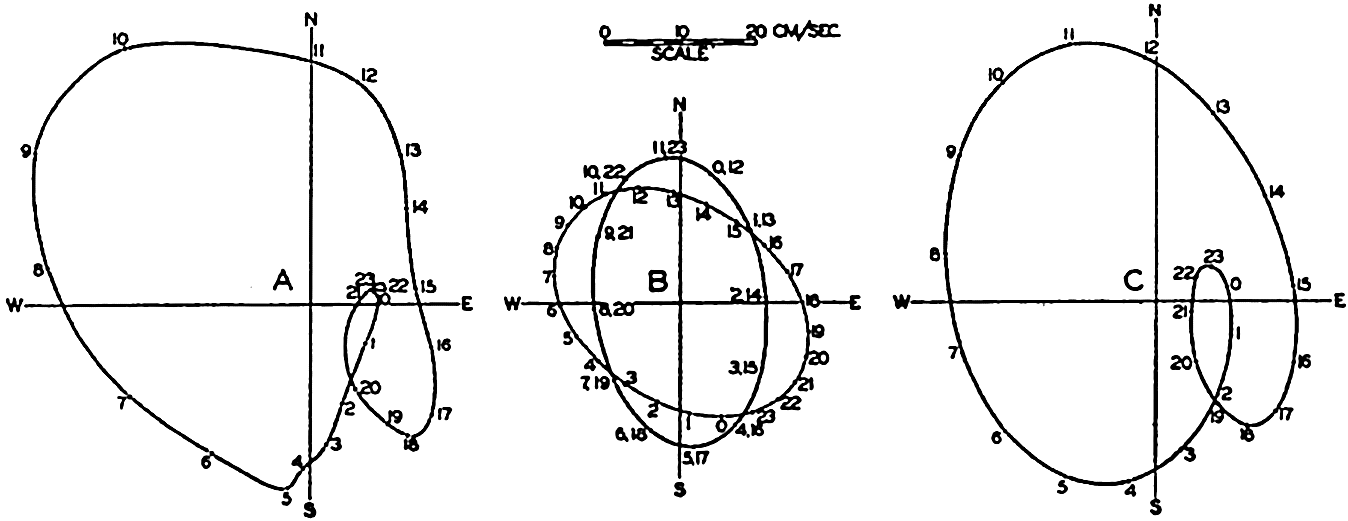
(A) Observed tidal currents at San Francisco light vessel. (B) Semidiurnal and diurnal tidal currents derived from the observations by harmonic analysis. (C) Tidal currents at the San Francisco light vessel computed from the semidiurnal and diurnal currents shown in B.
On the Pacific coast of the United States the tides are of the mixed type and are characterized by a considerable diurnal inequality. Off that coast, complicated tidal currents are present and in course of a lunar day the end points of the vector representing hourly velocities and directions of the tidal flow describe curves that have no similarity to ellipses but that nevertheless result from the combination of several current ellipses corresponding to tides of different periods. In most instances a good approximation to the observed conditions is obtained by combining the different semidiurnal periods to one single period of length 12 lunar hours and the diurnal periods to a single diurnal period of length 24 lunar hours. This is illustrated in fig. 145, in which the left-hand diagram represents the average tidal currents (Marmer, 1926b) during 24 lunar hours at San Francisco light vessel, which is anchored in 31 m of water at a distance of nine nautical miles from the nearest coast. The representation corresponds to those in fig. 144 except that the arrows have been omitted and only the curve joining their end points is shown. The hours marked along this curve represent the lunar hours after the highest high water at San Francisco, the time of that high water being marked 0h. Harmonic analyses of the semidiurnal and diurnal tidal currents leads to the results which are represented in the middle part of the figure. The semidiurnal and diurnal currents both reach about the same maximum velocities, but the semidiurnal rotates twice in 24 lunar hours, whereas the diurnal rotates once. The diagram to the right has been derived by combining the two, and this diagram is sufficiently like the one to the left to demonstrate that the complicated pattern is mainly a
The periods of the tidal currents are in agreement with the periods of the tide, but no general relationship has been established between the velocities of the tidal currents and the height of the tide. The reason is that the velocities of the tidal currents depend not only upon the height of the tide but also upon the depth to the bottom, the slope of the bottom, and the effect of the earth's rotation. Theoretical consideration of all these variables has not yet been possible and observations of currents are too few to permit the establishment of empirical laws.
Effect of Friction on Tides and Tidal Currents
In shallow water the tide and the tidal currents will be modified by the friction to which the waters are subjected when moving over the bottom. This bottom friction influences the currents to a considerable distance from the boundary surface, owing to the turbulent character of the flow (p. 480).
The effect of friction on the tide can be illustrated by considering a co-oscillating tide in a bay of constant depth and width. In the absence of friction the tide will have the character of a standing wave that can be considered composed of two waves traveling in opposite direction, the incoming wave and the reflected wave. In the presence of friction the tide can still be considered as composed of two such waves, but the combination no longer results in a single standing oscillation because the amplitudes of both waves must decrease in their directions of progress. In general, it can be assumed that the amount of energy that is dissipated is always proportional to the total energy of the wave. If this is true, the friction leads to a logarithmic decrease of the amplitude, provided the depth is constant. Assume that the waves progress in the x direction, that the influence of friction begins at x = 0 and that reflection takes place at x = l. On these assumptions the amplitude of the incoming wave will be (Fjeldstad, 1929)
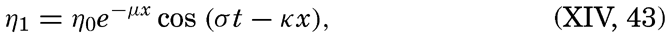
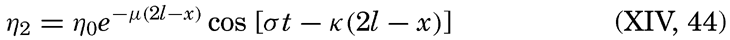
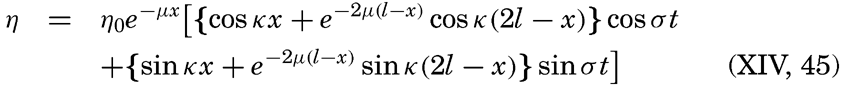
From this equation it follows that the oscillation can be considered as brought about by two standing waves of phase difference π/2 or one quarter of a period (p. 552).
Let us consider a bay the length of which is ⅜ L, where L is the length of the wave in the bay. This means introducing l = ⅜ L, kl = ¾ π, and kx = 2πx/L. Let us furthermore assume that at the opening of the bay the tide can be represented by the equation η0 = Z cos σt, which means that at x = 0 the amplitude is Z and high water occurs at t = 0. In the absence of friction the standing wave in the bay will show a node at a distance of one quarter wave length from the opening, and inside of the node high water will occur at t = 6h if the period of the wave is 12h.
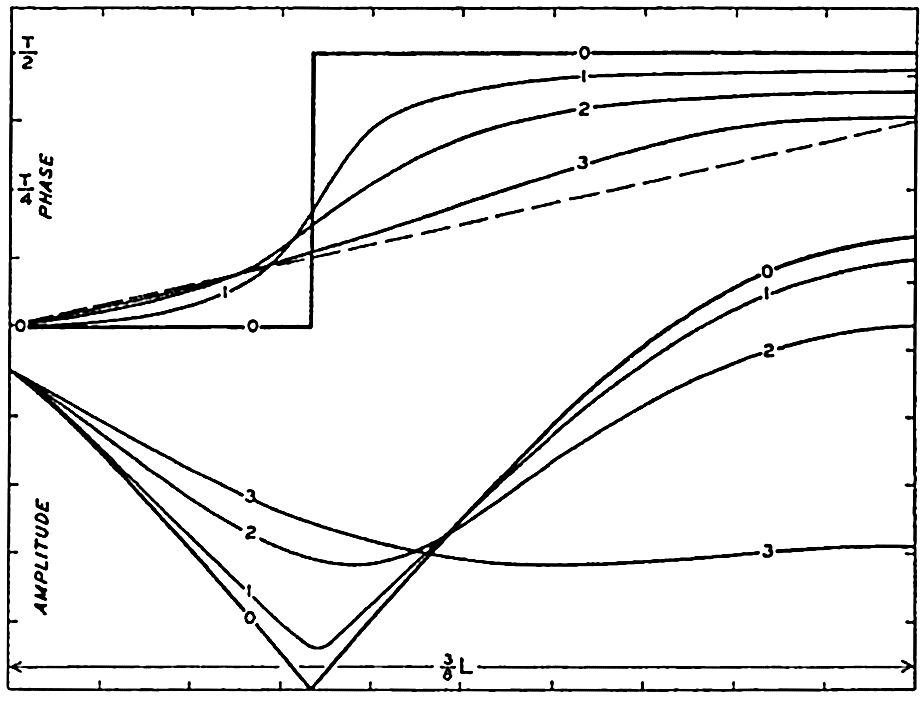
Effect of friction on amplitude and phase of the cooscillating tide in a bay, the length of which is 3/8 of the length of the tide wave.
The variations along the length of the bay of amplitude and phase are shown in fig. 146, by the curves marked 0. The effect of friction will depend upon the value of μ and, in order to illustrate the effect, we introduce three numerical values μ = 8/(15L), μ = 4/(3L), and μ = 4/L, corresponding to a decrease of the amplitude of the tide wave to one half of its value on a distance equal to 1.17 L, 0.52 L, and 0.17 L, respectively. The corresponding variations along the length of the bay of amplitude and phase of the tide are shown in fig. 146 by the curves marked 1, 2, and 3. The dashed line in the upper part of the figure shows the change in phase on three eighths of a wave length of a progressive wave.
By means of fig. 146 three effects of friction are brought out: (1) the node at which the amplitude of the tide is zero disappears and, instead, a region with minimal range is found; (2) the abrupt change of phase disappears and is replaced by a gradual change; (3) the phase difference between the opening and the end of the bay is decreased and approaches
The most striking example of the influence of friction on tides is found on the wide shelf along the Arctic coast of eastern Siberia. There the tide wave reaches the shelf from the north after having entered the Polar Sea through the wide opening between Spitsbergen and Greenland and having crossed the deep portions of the Polar Sea. Between longitudes 150°E and 180°E the width of the North Siberian Shelf exceeds 300 miles and in the greater part of that area the depth of the water is between 20 and 40 meters. The sea is ice-covered nearly throughout the year and, owing to the resistance which the ice offers, the tidal currents are subjected to frictional influences from the ice on top as well as from the bottom. The total effect of friction is therefore so great that on the coast the tide nearly vanishes (Sverdrup, 1927, Fjeldstad, 1929 and 1936). The decrease of the amplitude when approaching the coast is brought out by the data in table 72, which shows the amplitude and phase of the term M2 near the border of the shelf and at two localities on the coast. Of these two localities, Ayon Island lies a little south of Four Pillar Island, but the tide wave reaches Four Pillar Island later because the direction of progress of the wave is altered near the coast owing to the configuration of the bottom (Sverdrup, 1927).
| Locality | Latitude N | Longitude E | M2 | ||
|---|---|---|---|---|---|
| Amplitude (cm) | Phase (degrees) | Difference in phase | |||
| Near border of shelf | 74°33′ | 167°10′ | 13.75 | 158 | 0 |
| Ayon Island | 69 52 | 167 43 | 1.78 | 347 | 189 |
| Four Pillar Island | 70 43 | 162 35 | 0.98 | 60 | 262 |
It is seen that the later the tide the smaller the amplitude is, and it can be readily verified that the logarithm of the amplitude is nearly a linear function of the phase difference, as should be expected if the wave length remained constant, because in that case μx = μLα/2π where α = kx represents the phase difference.
The fact that the tide practically vanishes on the coast shows that when crossing the wide shelf the energy of the incoming tide wave is
In several adjacent seas the effect of friction has been studied by H. Jeffreys, who used a method developed by G. I. Taylor and first applied to conditions in the Irish Sea. The principle is simply that under stationary conditions the net amount of tidal energy which is brought into an area must equal the amount which is lost in the same area by dissipation due to friction. Therefore a determination of the net amount of tidal energy which is brought into an area represents also a determination of the dissipation.
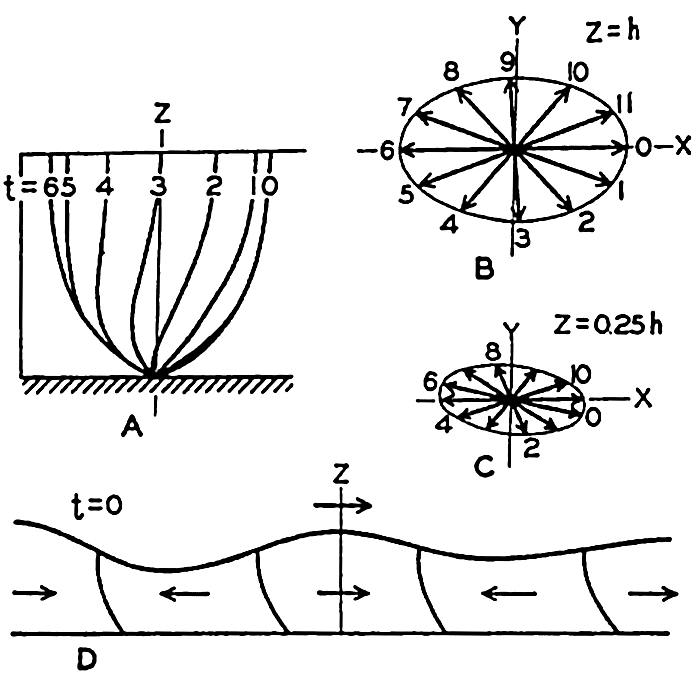
Combined influence of friction and the rotation of the earth on tidal currents in shallow water in the Northern Hemisphere (according to Sverdrup). For explanation, see text.
These studies have found an interesting application. It appears to be established by astronomers that the speed of rotation of the earth is very slowly decreasing, so that during a century the length of the day increases on an average by about one thousandth of a second. This slowing up may be caused by the dissipation of tidal energy, because estimates of the dissipation give values which correspond to the energy needed for bringing about the observed change in the earth's period of rotation.
So far, we have considered the effect of friction on the tides. In order to study theoretically the effect of friction on tidal currents, it is necessary to add the frictional terms (p. 475) in the equations of motion applicable to long gravitational waves (p. 555), and to integrate the equations. Such integration was performed by Sverdrup (1927) on the assumption that only the vertical turbulence need be considered and that the coefficient of eddy viscosity was constant. The boundary conditions were that at the free surface the shearing stresses should be zero and at the bottom the velocity should be zero. The results give some idea about the effect of friction, although the assumption of a constant eddy viscosity is not in agreement with more recent results according to which the eddy viscosity near the bottom increases rapidly with increasing distance from the bottom.
The more important conclusions can be summarized as follows. Near the bottom there exists a “layer of frictional influence” the thickness of which depends upon the ratio s = (2T sin ϕ)/T0 and upon the value of the eddy viscosity, and above which the tidal currents have the
Tidal currents in the North Sea, lat. 58°17′N, long. 2°27′E, depth 80 m, demonstrating the effect of friction when approaching the bottom. Measurements by Helland-Hansen on August 7 and 8, 1906.
Figure 148 shows an example of current measurements in the North Sea which appear to confirm the above conclusions. Other examples are found in Sverdrup's discussion (1927) of current measurements on the North Siberian Shelf, but in several of these cases it was necessary to take into account that the ice offered a resistance to the tidal motion and also that occasionally a nearly discontinuous increase in density at some depth brought complications. In the latter case an approximation could be obtained by introducing two layers of constant eddy viscosity separated by a layer of no eddy viscosity, the latter being the layer of very great stability.
The theoretical treatment of the subject has been expanded by Fjeldstad (1929, 1936) who has found integrals of the equations of wave motion in cases in which the eddy viscosity can be represented as a simple function
(A) Observed variations with depth of tidal currents at different lunar hours, according to measurements by Sverdrup on August 1, 1925, in lat. 76°36′N, long. 138°30′E. (B) Computed variation with depth of tidal currents, assuming an eddy viscosity which increases linearly from the bottom to the surface (according to Fjeldstad).
At the bottom one should expect, from analogies with experimental work in laboratories (p. 479), that the eddy viscosity will be small, having a value which depends upon the roughness of the bottom and the “friction velocity.” Near the bottom the eddy viscosity should increase linearly with increasing distance, the increment being proportional to the friction velocity. At some greater distance from the bottom, stability of the stratification may influence the eddy viscosity, and in very shallow water the eddy viscosity must reach a maximum below the free surface and decrease to a small value at the very surface. In homogeneous shallow water it may be expected, however, that the introduction of an eddy viscosity which increases linearly from the bottom to the surface will give a good approximation because conditions close to the bottom exercise the greatest influence upon the character of the motion and because at some distance from the bottom the value of the eddy viscosity is of minor importance. This is illustrated by the example in fig. 149. To the left are represented the components of the tidal current in the direction of progress of the tide wave, at the time of maximum current at the surface (marked I) and at the five following tidal hours. The curves are based on observations at three depths—0, 12, and 20 m—on
Observations of tidal currents at different distances from the bottom and within the layer of frictional resistance are not available from many localities and the factual information as to the effect of friction on tidal currents is therefore meager. Measurements from the North Sea off the coast of Germany have been discussed by Thorade (1928), who has studied the influence of friction by a different method of attack. In the North Sea the gravitational forces can be directly determined because the slope of the surface due to the tide wave can at any time be derived from tidal observations at coastal stations. Furthermore, Corioli's force and the accelerations can be derived from the current measurements and the frictional forces can therefore be found by means of the equations of wave motion because all other terms in the equations are known. Thorade's results are, in general, in agreement with the conclusions which have been presented, but many details need further examination. It is of particular interest, however, to observe that on an average during one tidal period Thorade finds that the eddy viscosity is very small at the bottom, increases rapidly with increasing distance from the bottom, but decreases again when approaching the surface. The general character of this variation is in agreement with the above considerations as to the variation of the eddy viscosity.
The influence of friction on tidal currents is also evident from studies of the tidal currents in the Dover Straits by J. van Veen (1939). He finds there that the velocity distribution between the surface and the bottom can be represented by means of a function of the form v = az1/n where n equals about 5.2. This implies that the eddy viscosity is approximately proportional to z4.2/5.2, meaning that the increase is somewhat less than that corresponding to a linear law, but no conclusions can be drawn as to the numerical values of the coefficient.
The effect of lateral mixing on tidal currents has so far not been examined, but it is possible that friction arising from lateral turbulence is of importance close to coasts.
The Semidiurnal Tide of the Atlantic Ocean
A number of the theoretical considerations which have been set forth have been applied, particularly by Defant, towards explaining the tides of the Atlantic Ocean. Defant (1932) has dealt with both the semidiurnal and the diurnal tides, but in the following we shall consider mainly the semidiurnal tide.
The Atlantic Ocean and its continuation, the Norwegian Sea and the Polar Sea, can be considered as a long bay which is closed in the north, whereas in the south it is in open communication with the Antarctic Ocean. On the basis of this concept the tides of the Atlantic Ocean can be considered as composed of two parts, a cooscillating tide which is maintained by the tide of the Antarctic Ocean, and a free tide which is maintained by the direct effect of the tide-producing forces. Neglecting the rotation of the earth and the effect of friction, both the cooscillating and the free tide can be computed by means of the method of numerical integration which was presented on p. 539, taking into account that the energy of the part of the tide wave which enters the Norwegian Sea and the Polar Sea is completely dissipated on the shallow shelves of these areas and that for this reason no reflected wave returns from these areas (p. 577). Part of the entire tide wave will be reflected, however, and the resultant picture will have some similarity to that which was discussed when dealing with the effect of friction on the tide (p. 574).
The numerical computations involved are somewhat lengthy but have been carried through by Defant. The result, in agreement with the conclusions presented on p. 575, is that the semidiurnal tide of the Atlantic Ocean can be considered as composed of two standing oscillations having a phase difference of one quarter period or three lunar hours. The computation renders only the variation in amplitude and phase along the middle section of the Atlantic Ocean and, in order to obtain absolute values, it is necessary to introduce observed values from two localities. As such observations Defant selected the tidal data from the Azores in the North Atlantic Ocean and from Tristan da Cunha in the South Atlantic.
A check on the theory is obtained by comparing observed values of the amplitude and the phase of the semidiurnal tide at other islands of the Atlantic Ocean with the computed values, and a further check is possible by comparing theoretical phase angles along the central part of the Atlantic Ocean with those which can be derived from Sterneck's chart of cotidal lines for the diurnal tide. This chart, which is reproduced in fig. 150, is based not only upon data from islands but upon all available data on the coasts. The full-drawn lines in fig. 151 show Defant's computed values of the amplitude and phase of the semidiurnal tide along a line which approximately follows the center of the Atlantic Ocean.
Cotidal lines of the semidiurnal tide in the Atlantic Ocean (Sterneck).
The crosses indicate the amplitude or phase at the island stations, the names of which are shown in the figure, and the dashed line in fig. 151B indicates the change in phase according to Sterneck's map. The agreement between observations and computations is remarkably good, all of the crosses falling nearly on the computed curves. The discrepancy in the northern part of the North Atlantic Ocean between the computed phase and the phase as derived from Sterneck's map can be accounted for by the fact that the location of the amphidromic point to the south of Greenland is admittedly uncertain. The agreement speaks strongly in favor of Defant's concepts, and further evidence for the validity of his computations is obtained by an examination of the tidal currents as
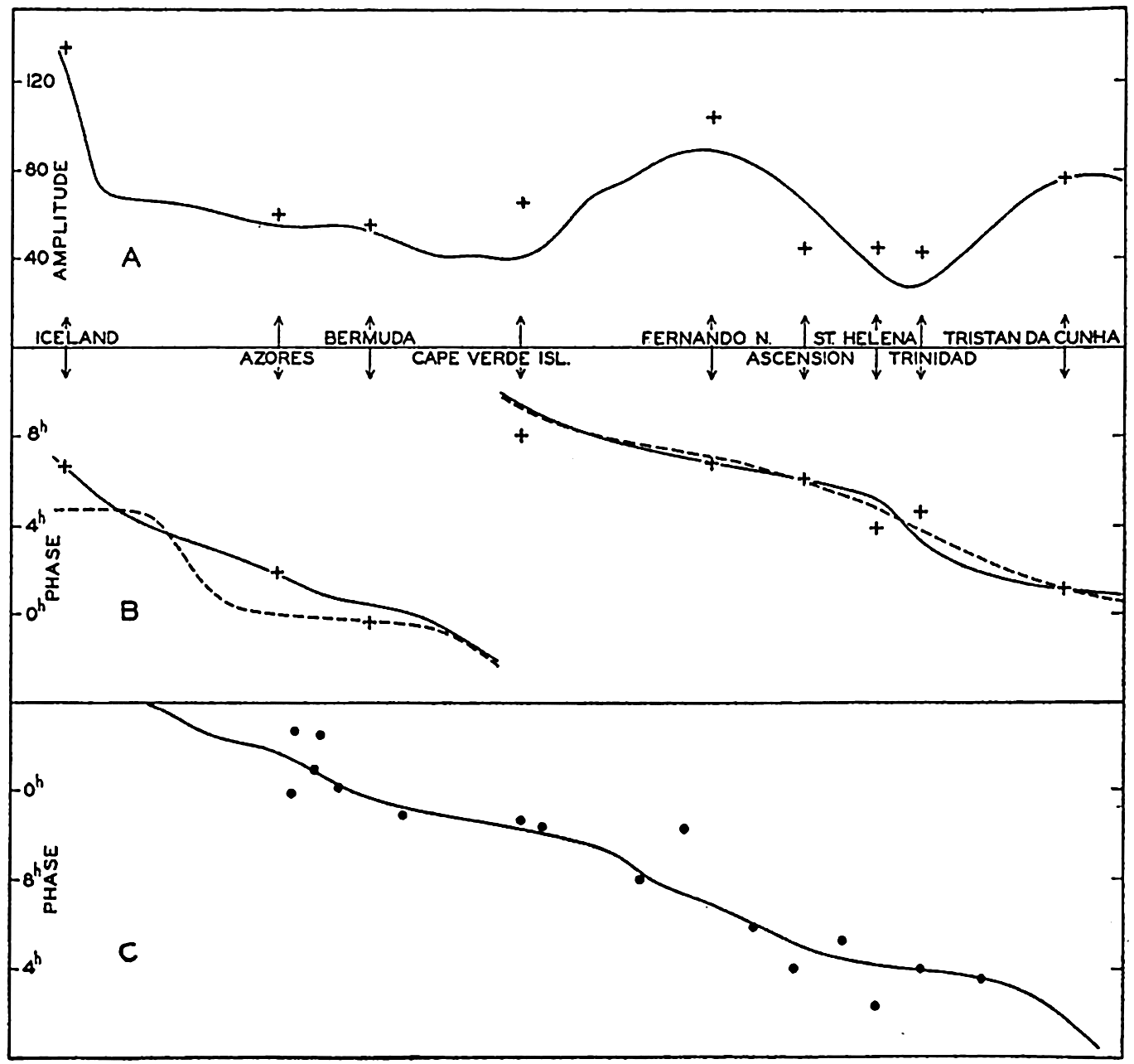
(A) Computed variation of the amplitude of the semidiurnal tide along the central part of the Atlantic Ocean (according to Defant). Crosses indicate observations at islands. (B) Computed variation of the phase of the semidiurnal tide along the central part of the Atlantic Ocean (according to Defant). Crosses represent observations at islands, and dashed lines represent the variation according to Sterneck's map. (C) Computed variation of phase of the semidiurnal tidal currents along the central part of the Atlantic Ocean (according to Defant). Dots represent observed values.
Certain discrepancies are revealed, however, if one compares the observed amplitudes of the tidal currents with the theoretical. Defant points out that the computed and observed velocities show similar variations with latitude if one subtracts from the observed velocities a latitude effect which can be ascribed to the earth's rotation. The latter was neglected when making the computation and must therefore be eliminated from the observed values. The correction which should be applied is due to the fact that on the rotating earth the velocity of the tidal current is
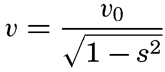
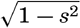 .
.After having done this, Defant finds that the character of the variation of the velocities agrees with the computed velocities, but the observed velocities are between two and three times greater than the computed. The computations give velocities of about 3 cm/sec, whereas the reduced observations give velocities of about 8 cm/sec. Defant suggests that this discrepancy arises because the direction of the tidal currents is not uniform through an entire cross section, as postulated by the theory, but another possible explanation is suggested on p. 595. Whether or not these explanations are accepted, the evidence in favor of Defant's theory is so great that his explanation of the semidiurnal tides of the Atlantic Ocean has to be given weight.
Concerning the character of the tidal currents it should be observed, furthermore, that the current measurements plainly show the effect of the earth's rotation. At all anchor stations the average semidiurnal current between the surface and the greatest depth of observation showed rotating currents, the direction of rotation being cum sole in 55 of 60 cases, including as cum sole four cases in which the current was practically alternating. The ratio between the major and minor axes of the current ellipses was on an average close to the theoretical value s = (T sin ϕ)/12 (p. 571). Thus, in mean latitude 36°18′, the observed ratio between the
Defant also computed the difference between the time of the maximum tidal current at the different anchor stations and the time of high water. He finds that in general high water occurs about one and a half hours before the maximum tidal current towards the north, and points out that this time difference should be zero if one had to deal with a progressive wave, and three hours if one had to deal with a standing wave. The fact that the time difference lies between these two values also shows that the semidiurnal tide of the Atlantic Ocean has neither the character of a progressive wave nor that of a standing wave, but is intermediate and can be regarded as brought about by superposition of several standing waves. It may especially be observed that in the South Atlantic Ocean the wave has nearly the character of a progressive wave, whereas in the North Atlantic Ocean the characteristics of a standing wave are more conspicuous.
The diurnal tide of the Atlantic Ocean is less well-known and Defant confines himself to a more summary treatment, the results of which indicate, however, that similar concepts are applicable in that case as well. It should be particularly pointed out that in the case of the diurnal wave the ratio between the axes of the current ellipses does not increase as rapidly as required by the simple theory on p. 571. According to this theory the current ellipse should degenerate in 30°N to a circle with infinite radius, and beyond 30°N diurnal waves of the simple character considered should no longer be possible. The observations show that the ratio between the axes of the diurnal current ellipses increases very slowly with increasing latitude, indicating that in relation to the diurnal wave the Atlantic Ocean cannot be considered as a wide ocean but as a bay or canal of moderate width. This conclusion may have bearing on future studies of the diurnal tides.
Similar treatment of the tides of other oceans has not yet been attempted and will encounter much greater difficulties. This is particularly true when considering the Pacific Ocean, which is so large that there the free tides must be of much greater importance.
Internal Waves
The waves which have been dealt with so far are characterized by maximum vertical displacements at the surface. For short waves the vertical displacement of the water particles decreases exponentially downwards, and for long waves the vertical displacement decreases linearly with depth, being zero at the bottom (p. 521). These waves will now be called ordinary waves. They are the only ones possible in homogeneous
The theory of the internal waves was first developed by Stokes (Lamb, 1932, p. 370) in the simple case of two layers of different density, and the general theory of progressive internal waves in heterogeneous water was developed by Fjeldstad (1933). Both theories have found application to oceanographic phenomena.
In a fluid consisting of two layers of infinite thickness, one lower layer of density p′ and one upper layer of density p′, waves at the boundary surface between the two layers will have a velocity of progress as given by

When dealing with internal waves in water which has a free surface but consists of two homogeneous layers of different density, the kinematic and dynamic boundary conditions must be fulfilled both at the free surface and at the internal boundary surface, and the equation of continuity must be satisfied. This leads to a quadratic equation for c2 which, for short waves, has the approximate roots
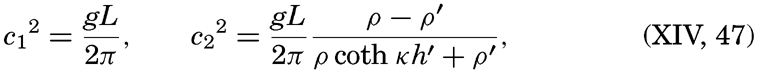
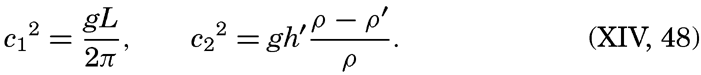
Applied to the ocean, this means that wherever there exists a thin top layer of water of small density, two types of waves are possible: the ordinary surface waves that progress with velocity c1; and the internal waves at the boundary between the light top layer and the heavier water underneath, that progress with velocity c2. Ekman (1904) has availed himself of this conclusion in order to explain the phenomenon known as “dead water.” In the time of the sailing vessels many captains reported that with a light breeze their vessels occasionally appeared to “stick” in the water, behaving sluggishly and making little headway. The experience was particularly common in Arctic waters in the presence of a thin top layer of nearly fresh water produced by melting of ice, and off rivers from which fresh water spread out. Slowly moving steamers have had similar experiences, but when their speed was increased to a few knots the unusual resistance disappeared. According to Ekman's theoretical studies and the results of his numerous experiments, this dead water is due to the fact that a slowly moving vessel may create internal waves at the lower boundary of a thin fresh-water layer the thickness of which is not much less nor much greater than the draft of the vessel. The energy otherwise applied towards overcoming the ordinary resistance of the water will now be used also for generating and maintaining internal waves, for which reason the vessel appears to “stick” in the water. The velocity of progress of internal waves as given by equation (XIV, 48) is, however, small. If the velocity of the vessel is greater than this small value, no internal waves are created and the vessel can proceed normally. With p − p′ = 0.025, nearly corresponding to a layer of fresh water on top of sea water of temperature 10°C and salinity 30 ‰, and with h′ = 400 cm, one obtains c2 = 100 cm/sec = 1.9 knots. These numerical values indicate that at a speed of a few knots no internal waves are created, which is in agreement with the general experience that dead water is not encountered at speeds above a few knots.
The short internal waves that have been dealt with so far may be present anywhere in the ocean, but escape observation on the high seas where the variation of density with depth is less conspicuous. In the open ocean long internal waves exist, however, and these have in recent years received much attention. When dealing with two layers and neglecting the effect of the earth's rotation the velocities of progress of the ordinary long wave and of the internal wave are obtained from the equations
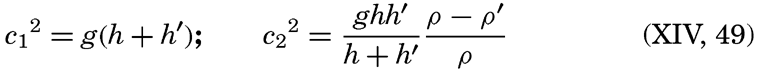
The internal wave is characterized by having its maximum amplitude at the boundary surface. At the free surface the amplitude of the internal wave does not entirely disappear but is reduced to


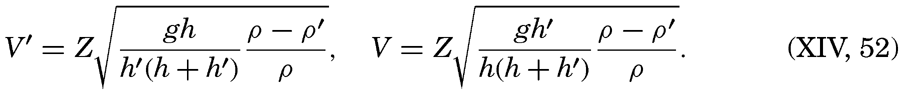

This numerical example shows that internal waves are characterized by large horizontal particle velocities. The corresponding velocity of progress of the internal wave is 78 cm/sec, whereas the ordinary long wave proceeds at a velocity of 4430 cm/sec.
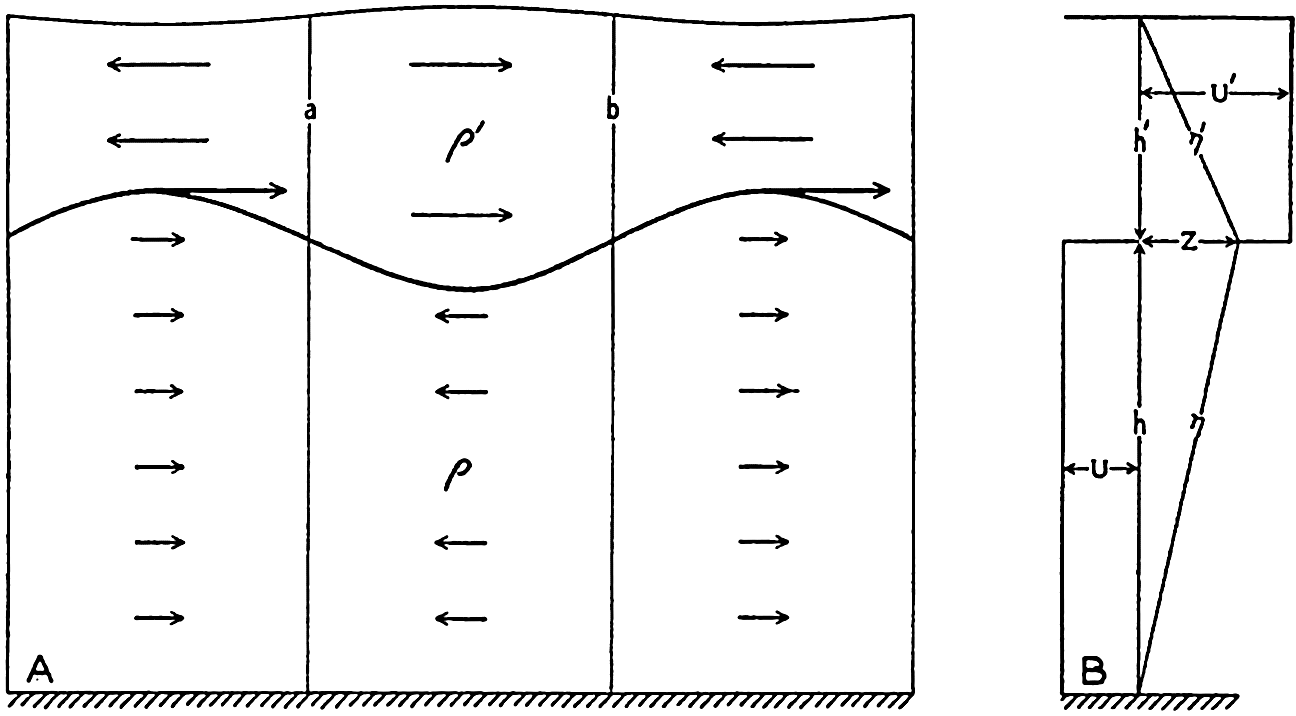
(A) Schematic representation of an internal wave at the boundary between two liquids of densities p and p′. (B) Schematic representation of the variation with depth of the amplitudes of the vertical displacements p and p′, and of the maximum horizontal velocities U′ and U.
The character of the internal wave at the boundary between two liquids of different density is illustrated in fig. 152A, which shows the deformation of the boundary surface and the directions of the horizontal velocities within the two layers. The wave is supposed to progress from left to right. At the line marked a the horizontal currents in the upper layer are divergent, for which reason the lower boundary surface must rise, and the horizontal velocities in the lower layer are convergent, for which reason also the boundary surface must rise. At the line marked b the boundary surface must sink for similar reasons, and the wave must therefore progress from left to right, as stated. In the figure it is also indicated that the vertical displacement of the free surface is opposite in phase to that of the boundary surface, but the displacement of the free surface has been greatly exaggerated. The pressure at the bottom remains constant and equal to the hydrostatic pressure because the vertical accelerations are negligible. The amplitude of the deformation of the free surface can be computed from the hydrostatic equation and the result is as before, η0 = −Z(p − p′)/p.
If several boundary surfaces are present, several internal waves can occur simultaneously, and the greater the number of boundary surfaces, the greater the number of possible internal waves. On the basis of this reasoning, when the density varies continuously with depth one should expect an unlimited number of possible internal waves. That such is the case has been shown by Fjeldstad (1933), who has developed the theory of internal waves in water in which the density is a continuous function of depth. He deals with progressive waves only, and presents a complete
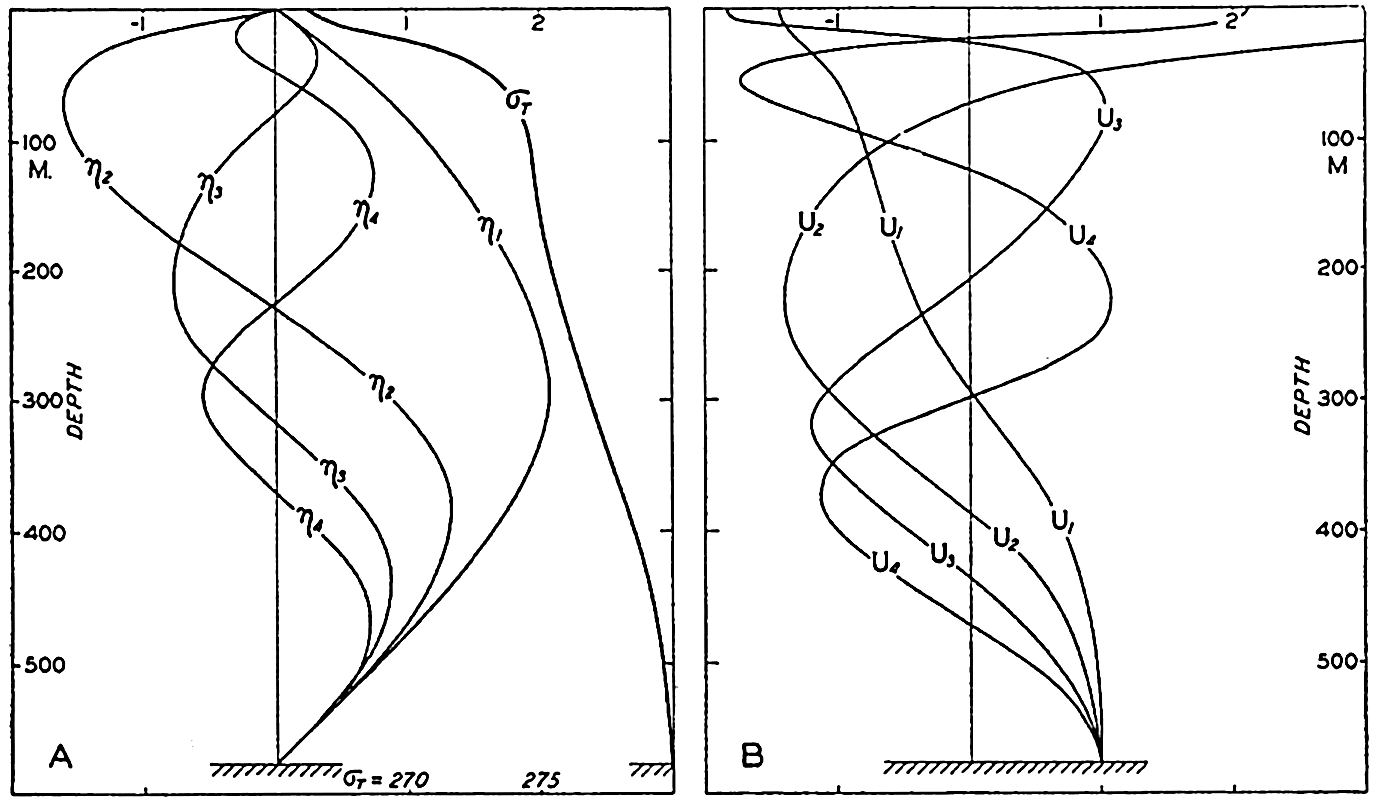
(A) Variation with depth of the vertical displacements corresponding to internal waves of first, second, third, and fourth order at Michael Sars Station 115 (according to Fjeldstad). The density distribution is shown by the curve marked σt. (B) Variation with depth of the amplitudes of the horizontal velocities corresponding to an internal wave of first, second, third, and fourth orders (according to Fjeldstad). Vertical displacements and amplitudes are plotted on an arbitrary scale.
Figure 153A shows Fjeldstad's computed vertical displacements and horizontal velocities as functions of depth for the internal waves of first, second, third, and fourth orders, corresponding to the distribution of density as shown in the same figure, which was observed at Michael Sars station 115 (Helland-Hansen, 1930), where the depth to the bottom was 580 meters. The amplitudes of the accompanying horizontal velocities
Fjeldstad's method also leads to determination of the velocity of progress of waves of different orders, provided that the depth is constant and that the distribution of density remains unaltered in the direction of progress; but the periods of the waves cannot be determined theoretically and must be derived from observation. At Michael Sars station 115 the velocities of progress were c1 = 70 cm/sec, c2 = 39 cm/sec, c3 = 26 cm/sec, and c4 = 19.5 cm/sec; and for a wave of period 24 lunar hours the corresponding wave lengths are 62.5 km, 34.8 km, 23.2 km and 17.4 km, respectively. Evidently, the internal waves are short compared to tide waves. It should be observed that the velocity of progress increases when the difference in density between the upper and lower layers decreases, and also increases with increasing depth to the bottom. In low and middle latitudes the velocity of progress of the first-order wave will, however, rarely exceed 300 cm/sec. For diurnal or semidiurnal waves the corresponding wave lengths are 268 km or 134 km, respectively, and the waves of higher order are correspondingly shorter.
Observations indicating vertical displacements of water masses which may be related to internal waves have been made on numerous occasions when oceanographic observations have been repeated in the same locality at short time intervals. If observations of temperature at different depths are made at, say, hourly intervals, from an anchored vessel or from a vessel which maneuvers in such a manner that its position changes only one or two miles, it is often found that the temperature varies more or less periodically at all depths. Assuming that these variations are due to vertical displacements, one can find the vertical displacements at the different depths if the average temperature distribution is known. If, for instance, the average temperature at 200 m is 12.40° and at 220 m is 12.17°, it may be concluded when a temperature of 12.17° is observed at 200 m that water which under undisturbed conditions should be found at 220 m has been displaced 20 m upwards. If the temperature oscillation at a given depth d is periodic and has an amplitude of A°, the amplitude of the corresponding vertical oscillation is found by dividing the amplitude A° by the average temperature gradient at that depth, (dθ/dz)d. Similar conclusions may be based on observations of salinity and oxygen, and when all these elements have been observed good
If the observations have been carried out during a sufficiently long time, it is possible to find the period length of the oscillations. In a number of cases period lengths have corresponded to tidal period, and it has therefore been concluded that internal waves of tidal periods commonly occur in the ocean. It is not probable that such internal waves are caused directly by the tide-producing forces but it is more nearly probable, as suggested by Defant, that they are caused by the periodic variations of the actual tidal currents which may lead to periodic changes in the inclination of isosteric surfaces in the sea. Besides these internal waves of tidal periods, waves of other periods also exist.
The first observations of short-period variations which indicated the existence of internal waves were discussed by Helland-Hansen and Nansen (1909). On the Michael Sars Expedition to the North Atlantic in 1910, repeated serial observations were made at several stations, and on one occasion simultaneous observations in the Faeroe-Shetland Channel were conducted from the Michael Sars and the Scottish research vessel, the Goldseeker, the two vessels being about 106 km (57 mi) apart. The possible vertical displacements derived from the temperature observations can be well represented by two periodic oscillations of period length 12 and 24 lunar hours. The results of Helland-Hansen's harmonic analysis (1930) of these data are given in table 73. It appears that the oscillations at the two stations were different in respect to the vertical variations of amplitude and phase of the two waves, and in respect to the relative magnitude of the semidiurnal and diurnal oscillations. This might be expected if the oscillations were associated with progressive internal waves. If waves of different order are present, the combined result may be a complicated variation with depth of amplitudes and phase angles (fig. 156, p. 598), and the velocity of progress of such waves is so small, 0.7 to 2.5 km per hour, that different phases must be found at stations which are 106 km apart. Furthermore, the amplitudes may vary along a line at right angles to the direction of progress, owing to the earth's rotation, as in a Kelvin wave (p. 555).
In his discussion Helland-Hansen draws special attention to the fact that the observed variations of temperature may be caused by variations of horizontal currents and not by internal waves. In the Faeroe-Shetland Channel all isothermal surfaces slope considerably, and lateral displacement might therefore give rise to such variations as were recorded. The same reservation must always be made when interpreting oscillations of temperature in a region where a lateral temperature gradient exists.
Recent measurements by Seiwell (1937) have substantiated the view, however, that observed oscillations are due to vertical displacements and not to horizontal movement, because he selected a locality for repeated serial measurements in the region NNW of Bermuda within which, on several of the Atlantis cruises, very small horizontal gradients had been found. On July 12 and 13, 1936, Seiwell (1937) observed very large vertical displacements, reaching total ranges during 24 hours up to 80 m at depths of 500 to 600 m. As an example the observed temperatures at 500 m are shown in fig. 154 where the corresponding vertical displacements are also entered. The latter were computed by dividing the temperature
Variation of temperature (thin curve) at a depth of 500 meters on July 13, 1936, and corresponding vertical displacements (heavy curve). From Seiwell's observations (1937).
| Depth (m) | Semidiurnal vertical displacements | Diurnal vertical displacements | ||||||
|---|---|---|---|---|---|---|---|---|
| Michael Sars 115 | Sc | Michael Sars 115 | Sc | |||||
| Amplitude (m) | Phase (lunar hours) | Amplitude (m) | Phase (lunar hours) | Amplitude (m) | Phase (lunar hours) | Amplitude (m) | Phase (lunar hours) | |
| 100 | 15 | 6.3 | 42 | 0.7 | 18 | 17.0 | 39 | 12.3 |
| 200 | 12 | 8.4 | 58 | 11.2 | 16 | 15.9 | 11 | 14.2 |
| 300 | 24 | 9.3 | 22 | 11.6 | 9 | 17.7 | 8 | 17.7 |
| 400 | 7 | 9.5 | 11 | 9.2 | 10 | 9.0 | 9 | 4.4 |
| 500 | 3 | 6.6 | 24 | 11.1 | 5 | 11.3 | 6 | 5.2 |
| 600 | 24 | 7.3 | 25 | 1.2 | ||||
Harmonic analysis showed that at all levels the major part of the observed oscillations could be represented as the sum of three oscillations of periods 24, 12, and 8 lunar hours. The amplitudes of the harmonic terms varied with depth, but the 24-hour term dominated at all levels and the 8-hour term was smallest at most levels. The facts that in this case horizontal motion cannot account for the observed variations of temperature and that the oscillations were periodic strongly suggest the presence of some kind of wave motion.
| Depth (m) | Semidiurnal waves | Diurnal waves | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Current | Vertical displacement | Current | Vertical displacement | |||||||
| Maximum current towards | Velocity (cm/sec) | Phase (lunar hours) | Amplitude (m) | Phase (lunar hours) | Maximum current towards | Velocity (cm/sec) | Phase (lunar hours) | Amplitude (cm) | Phase (lunar hours) | |
| 0 | N 41°W | 6.8 | 3.5 | |||||||
| 50 | N 30 W | 9.4 | 3.0 | N 12°W | 10.3 | 11.8 | ||||
| 100 | N 72 E | 5.4 | 1.9 | N 33 W | 4.8 | 15.9 | ||||
| 150 | N 67 E | 11.6 | 3.3 | 7 | 3.7 | N 84 W | 9.9 | 6.1 | 4 | 7.4 |
| 200 | N 61 W | 11.1 | 6.8 | 10 | 4.0 | N 63 W | 6.7 | 3.8 | 8 | 16.9 |
| 300 | N 42 W | 9.4 | 6.3 | 7 | 3.6 | N 49 W | 4.7 | 5.4 | 6 | 23.4 |
| 500 | N 51 W | 5.7 | 3.2 | 7 | 3.8 | N 14 W | 11.9 | 17.2 | 6 | 6.4 |
The existence of internal waves is also confirmed by the results of numerous current measurements from vessels anchored in deep water (Ekman and Helland-Hansen, 1931, Defant, 1932, Lek, 1938). Observations from different depths show that currents of tidal periods dominate; but, instead of being uniform from surface to bottom as would be expected if the currents were ordinary tidal currents, the amplitude and the time of maximum current (the phase) vary in a complicated manner with depth, and at some levels the semidiurnal currents are strongest, and at others, the diurnal. This is illustrated by the results of current measurements and repeated serial observations at Meteor anchor station 176 on the Mid-Atlantic Ridge in the South Atlantic Ocean, lat. 21°29.8′S, long. 11°41.5′W
It is evident that extremely complicated currents may be found if several internal waves of different orders, different phases, and different tidal periods are present, and if the currents associated with these waves are superimposed upon the ordinary tidal currents. At first glance it may appear hopeless to separate the latter from the currents of the internal waves of tidal periods, but fortunately these “internal tidal currents” can be eliminated if observations are available from a sufficient number of depths. Because (p. 588)

It follows from equation (XIV, 53) that currents associated with internal waves are eliminated by computing the average currents between the surface and the bottom, provided that observations from a sufficient number of depths are available. Such elimination was attempted by Defant when he derived the tidal currents from observations at anchor stations in the Atlantic Ocean (see p. 584), but the available data were mostly from the upper layers only, and this accounts perhaps for the fact that he found much greater velocities than those corresponding to the range of the tide.
So far, the effect of the earth's rotation and of friction have been neglected. It cannot be expected that Corioli's force alters the variation with depth of amplitude of the internal wave, and Fjeldstad's method should therefore in all cases give correct results as to the relative amplitudes. On the rotating earth the accompanying currents, however, will also be rotating if the period of the internal wave approaches the period of a pendulum day. Transverse currents will accordingly be present, but these must also satisfy equation (XIV, 53) and can therefore be eliminated if observations from many depths are available. The velocity
An internal wave in water consisting of two layers of different density can be considered as an oscillation of the boundary surface. Defant (1940) has shown that on the rotating earth the period of a free oscillation of a boundary surface in the sea approaches the period of the inertia oscillation when the dimensions of the oscillating system are great. In a basin of length l the longest period of the free oscillations is, with the previous notations and neglecting the earth's rotation,
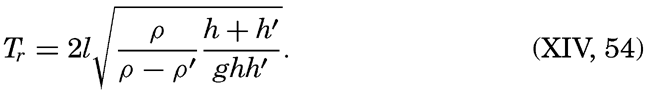
The period of the inertia oscillation is Te = 2π/2ω sin ϕ. Defant obtains the result that on the rotating earth the period of the free oscillation is

As a numerical example values from the Baltic may be introduced, ρ − ρ′ = 2 × 10−3, h′ = 25 m, and h = 35 m. With these values one obtains Tr = 3.75 l (l in meters). If it is required that Te/Tr = 0.1, one obtains in latitude 57°49′, l = 136 km. In a basin of these dimensions, the difference between the periods of the free oscillations and the inertia oscillation would be only 1 per cent, and it seems therefore probable that a disturbance which would develop motion in the inertia circle would set up free oscillations of the boundary surface. A deeper basin or a basin in lower latitudes would have to be of greater dimensions; thus, with ρ − ρ′ = 2 × 10−3, h′ = 500 m, and h = 1500 m, one obtains Tr = 0.736 l, and with Te/Tr = 0.1, one finds that in the latitude 57°49′, l = 692 km, and in latitude 30°,l = 1170 km.
The friction will lead to a dissipation of the energy of the internal wave, and unless the wave is maintained by a periodic disturbance it will gradually die off. The current observations from the Baltic by Gustafson and Kullenberg, which were discussed on page 438 (fig. 104), can be interpreted as inertia oscillations that may be associated with an internal wave and as showing the gradual dissipation of the energy of the wave.
It is evident from this discussion that the internal waves greatly complicate the actual movement of the water masses and lead to the
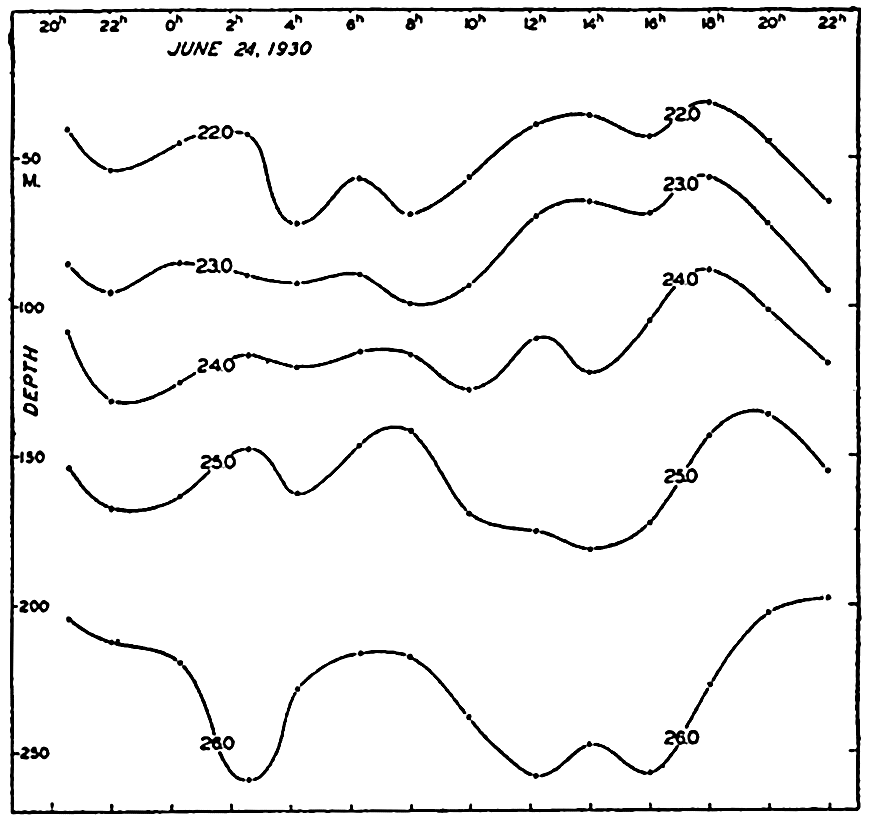
Variation in depth of stated σt values on June 23 and 24, 1930, according to observations of the Snellius Expedition at Station 2534 in lat. 1°47.5′S, long. 126°59.4′E.
An illustration of the application of Fjeldstad's theory is given by Lek (1938) in his discussion of results of current and serial measurements of the Snellius Expedition in the eastern part of the Netherlands East Indies, 1929–1930. On this expedition current measurements were made at a number of anchor stations and at one of these, station 253A, lat. 1°47.5′S, long. 126°59.4′E, very complete observations comprised hourly measurements during 26 hours of currents at 0, 50, 100, 200, 350, and 500 m, and hourly observations of temperature, salinity, and oxygen at seven depths between the surface and 800 m. The depth to the bottom was 1740 m. From the temperature and salinity data the density was computed. In fig. 155 is shown the variation in depth of different σt curves during the period of observation. From this graph one obtains immediately the impression that large vertical oscillations took place, some of which appear to have been of a diurnal, others of a semidiurnal, period. The phases of the oscillations appear to have varied with depth, the vertical oscillation at a depth of about 50 m being opposite in phase to the oscillation at a depth of about 230 m. Hence,
In order to examine the character of these waves, Lek, in cooperation with Fjeldstad, computed the relative amplitudes of the internal waves of first, second, third, and fourth orders by means of the average distribution of density between the surface and the bottom. Consider first the semidiurnal oscillations. It is evident that any observed variation with depth of amplitude and phase can be represented by a sufficiently large number of the theoretical internal waves of different orders, because the absolute values of the theoretical amplitudes and the phase angles of the theoretical displacements can be adjusted to fit the observed data. A certain check on the theory is, however, obtained if the number of the theoretical internal waves is smaller than the number of depths of observations.
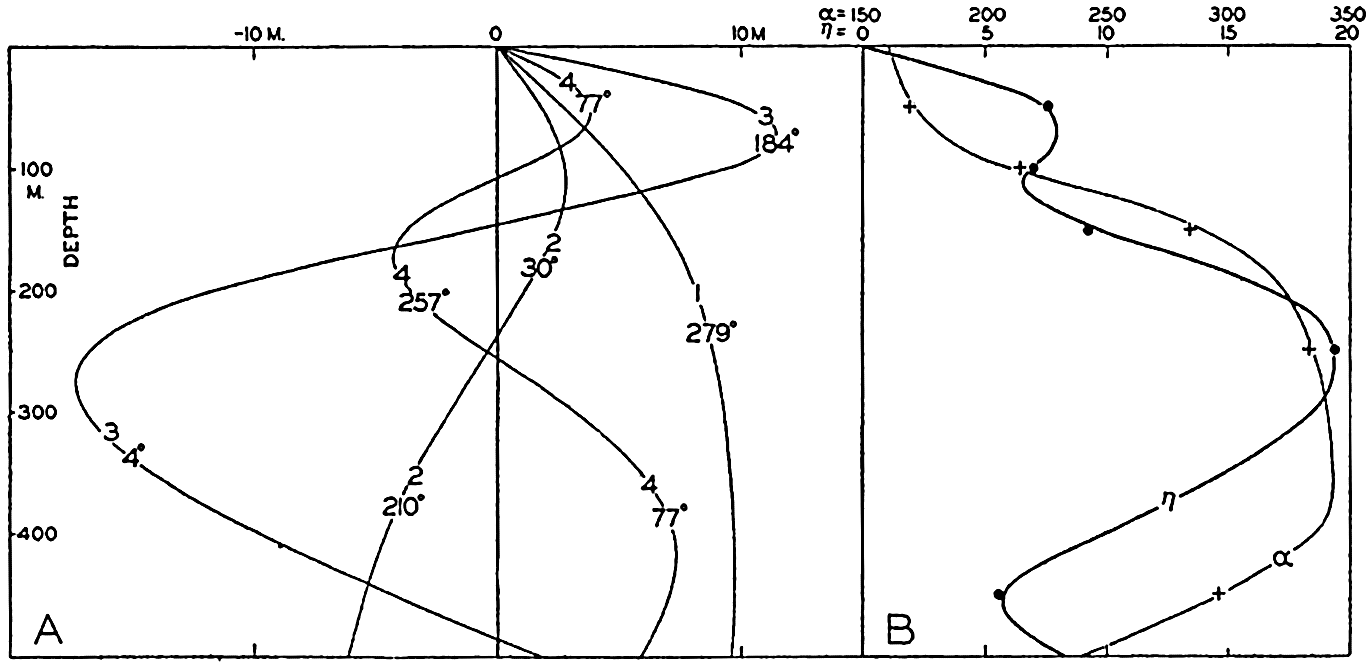
(A) Variation with depth of the amplitudes of internal waves of order 1 to 4 at Snellius Station 253A. The phases of the different waves are shown in the figure. (B) Curves show the variation with depth of amplitude η and phase α, as derived from the curves in (A). Crosses and dots indicate observed values (according to Lek and Fjeldstad).
In the present case observations from five levels were used for determining the amplitudes and phases to be assigned to the internal waves or orders one to four, meaning that an adjustment was made, and that the validity of the theory could be checked to a certain extent by examining how closely the observed values would agree with the theoretical after making such adjustments. Figure 156A shows the adjusted amplitudes and phase angles of the internal waves of order one to four between the surface and 500 m. From this figure it is evident that the wave of third order is dominant. By combining these four waves one obtains
| Depth (m) | Amplitude (cm/sec) | Phase | ||
|---|---|---|---|---|
| Observed | Computed | Observed | Computed | |
| 0 | 21.8 | 31.4 | 144.9° | 126.8° |
| 50 | 21.6 | 15.1 | 120.3 | 139.0 |
| 100 | 13.7 | 15.6 | 247.8 | 247.5 |
| 150 | 14.0 | 19.5 | 237.7 | 247.6 |
| 200 | 14.9 | 13.0 | 228.8 | 225.6 |
| 350 | 9.0 | 0.5 | 260.9 | 202.5 |
| 500 | 7.8 | 6.1 | 2.9 | 352.7 |
These results cannot be considered as conclusive evidence as to the character of the observed displacements, because the numerical values of the theoretical terms have been adjusted to fit the data, but an entirely independent check can be obtained by computing the currents corresponding to the theoretical internal waves and comparing these computed values with the observed ones. When doing this, it should be borne in mind that the theory presupposes the existence of progressive waves, and agreement in phase of computed and observed currents would indicate that the internal waves actually were of the progressive type. It should also be borne in mind that the observed currents include ordinary tidal currents besides those associated with internal waves of tidal periods, and that for this reason certain discrepancies must be expected. The semidiurnal currents were not used as a check on the theory because there were reasons for believing that these were not of the simple progressive type, but the computed and observed diurnal currents which are shown in table 75 are in surprisingly good agreement, particularly when considering the reservations which were made. Lek points out that the greatest discrepancies between computed and observed values occur at a depth of 350 m, where according to the theory the current due to internal waves should nearly vanish, and that therefore the discrepancy may be due to the presence of actual tidal currents. It thus appears that in this case the complicated variations of the currents
Lek and Fjeldstad find the following velocities of progress: c1 = 234 cm/sec, c2 = 116 cm/sec, c3 = 77 cm/sec, c4 = 58 cm/sec. The corresponding lengths of the waves of period 24 lunar hours are 210 km, 104 km, 69 km, and 52 km, respectively.
This example illustrates the numerous complications which may be encountered anywhere in the ocean, and serves to emphasize the fact that many observations of currents over long periods of time are needed in order to obtain information as to the many types of motion present in the sea.
Standing internal waves may be present in bays or basins. The probability of such standing waves is great, because in heterogeneous water in a bay or a basin of a given form a large number of internal waves of different wave lengths are possible, corresponding to waves of different order and corresponding to different period lengths. An intermittent disturbance or a disturbance of tidal period may therefore bring about an oscillation which corresponds to one of the possible free oscillations of the system, particularly because a small amount of energy is needed for creating an internal wave.
In a bay of constant depth and width the periods of oscillation of free standing waves in the presence of two layers are
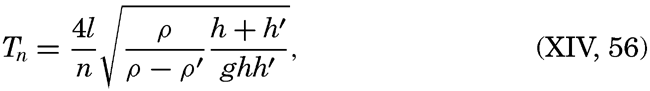
A computation of this nature may give approximately correct results if a distinct boundary surface is present and if the geometrical shape
In conclusion, two effects of internal waves should be emphasized because they have bearing on general oceanographic problems. In the first place the internal waves probably are of importance to the process of mixing. Where internal waves are present, large velocity gradients are often met with which lead to great values of the eddy viscosity. Furthermore, owing to the dissipation of energy by friction, a given water mass will never return exactly to the locality from which it started out, even in the absence of general currents, and consequently an exchange of water in horizontal direction must take place. The intensity of the mixing processes which are maintained by internal waves has not yet been examined, but it is probable that these processes are not negligible.
In the second place, it has been pointed out, particularly by Seiwell (1937), that owing to the existence of internal waves the distribution of mass along any vertical will be subject to periodic variations and, as a consequence, the geopotential height of the free surface relative to a given isobaric surface will vary periodically. This agrees with the statement (p. 588) that when dealing with internal waves on a boundary between two liquids the free surface will also show a wave motion of a small amplitude. The variations in height of the free surface are so small that when dealing with the internal wave they can be disregarded, but when examining results of dynamic computations they cannot be left out of account because these variations are of the same order of magnitude as the horizontal differences in geopotential height which may occur on distances up to 100 km or more. As an illustration, fig. 157 shows the variation of geopotential height of the free surface above the 800-decibar surface as derived from the serial observations at Snellius station 253A. It is seen that during 26 hours the height of the surface varies no less than 14.5 dyn cm. Seiwell has computed that, due to internal waves at Atlantis station 2639 (p. 453) the variations of the
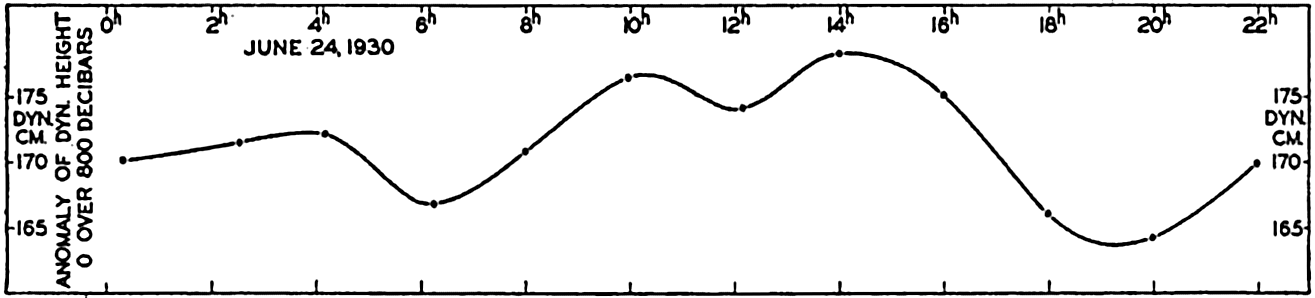
Variation with time of the dynamic height of the surface over the 800-decibar surface at Snellius Station 253A.
Bibliography
Cornish, Vaughan. 1912. Waves of the sea and other water waves. Chicago. Open Court Pub. Co.374 pp.1912.
Cornish, Vaughan. 1934. Ocean waves and kindred geophysical phenomena. Cambridge University Press. 164 pp.1934.
Darwin, G. H.1911. The tides and kindred phenomena in the solar system. 3rd ed.New York. Houghton, Mifflin.1911.
Defant, A.1925. “Gezeitenprobleme des Meeres in Landnähe” . Probleme der kosmischen Physik, VI. Hamburg. 80 pp.1925.
Defant, A.1929. “Dynamische Ozeanographie” . Einführing in der Geophysik. Berlin. III, 222 pp.1929.
Defant, A.1932. Die Gezeiten und inneren Gezeitenwellen des Atlantischen Ozeans. Deutsche Atlantische Exped. Meteor1925–1927, Wiss. Erg., Bd. 7, Heft 1, 318 pp.1932.
Defant, A.1940. “Die ozeanographischen Verhältnisse während der Ankerstation des Altair am Nordrand des Hauptstromstriches des Golfstroms nördlich der Azoren” . Ann. d. Hydrogr. u. Mar. Meteor., November-Beiheft, 4. Lief, 35 pp.1940.
Ekman, V. W.1904. “On dead water. Norwegian North Polar Exped.” , 1893–1896, Sci. Results, v. 5, no. 15, 152 pp.1904.
Ekman, V. W., and B. Helland-Hansen. 1931. Measurements of ocean currents (Experiments in the North Atlantic). Kungl. fysiografisca Sällskapet i Lund Förhandlingar, v. 1, no. 1. 1931.
Fjeldstad, J. E.1929. “Contribution to the dynamics of free progressive tidal waves” . Norwegian North Polar Exped. with the Maud, 1918–1925, Sci. Results, v. 4, no. 3, 80 pp.1929.
Fjeldstad, J. E.1933. Interne Wellen. Geofysiske Publikasjoner, v. 10, no 6, 53 pp.1933. Oslo.
Fjeldstad, J. E.1936. “Results of tidal observations. Norwegian North Polar Exped. with the Maud, 1918–1925” , Sci. Results, v. 4, no. 4, 88 pp.1936.
Fleming, Richard H.1938. “Tides and tidal currents in the Gulf of Panama” . Jour. Marine Research, v. 1, p. 192–206. 1938.
Gaillard, D. D. W.1904. “Wave action in relation to engineering structures” . Prof. Pap. Corps. Engin., U. S. Army, no. 31, Washington, D. C. 1904.
Gutenberg, B.1939. “Tsunamis and earthquakes” . Seismol. Soc. Amer., Bull., v. 29, p. 517–526. 1939.
Harris, Rollin A.1894–1907. “Manual of tides. Parts 1 to 5. Appendices to U. S. Coast and Geod” . Surv., Reports. Washington, D. C.
Helland-Hansen, B.1930. “Physical oceanography and meteorology” . Michael Sars North Atlantic Deep-Sea Exped., 1910, Rept. Sci. Results, v. 1, 115 + 102 pp.1930.
Helland-Hansen, B., and F. Nansen. 1909. “The Norwegian Sea” . Norwegian Fishery and Marine Investigations, Report. v. 2, pt. 1, no. 2, 390 pp. + tables. 1909.
Hidaka, K.1935. “A theory of shelf seiches” . Imperial Marine Observatory, Memoirs, v. 6, p. 9–11. 1935. Kobe, Japan.
Hidaka, K.1939. “Study of ocean waves by stereophotogrammetry (in Japanese)” . Journal of Oceanography (Imperial Marine Observatory, Kobe, Japan), v. 11, no. 4, p. 693–703. 1939.
Krümmel, O.1911. Handbuch der Ozeanographie, v. 2. Stuttgart. 764 pp.1911.
Lamb, H.1932. Hydrodynamics. London. Cambridge University Press. 6th ed., 738 pp.1932.
Lek, Lodewijk. 1938. Die Ergebnisse der Strom- und Serienmessungen. Snellius Exped. in the eastern part of the Netherlands East-Indies, 1929–1930, v. 2, pt. 3, 169 pp.1938.
Marmer, H. A.1926. The tide. New York. D. Appleton. 282 pp.1926.
Marmer, H. A.1926b. “Coastal currents along the Pacific coast of the United States” . U. S. Coast and Geod. Surv., Spec. Pub. 121, 77 pp.1926.
Marmer, H. A.1927. “Tidal datum planes. Washington, D. C. U. S” . Coast and Geod. Surv., Spec. Pub. 135, 142 pp.1927.
Marmer, H. A.1932. Tides and tidal currents. Physics of the earth, v. 5, Oceanography, p. 229–309. National Research Council, Bull. no. 85. Washington, D. C. 1932.
Munk, W. H.1941. “Internal waves in the Gulf of California” . Jour. Marine Research, v. 4, p. 81–91. 1941.
Patton, R. S., and H. A. Marmer. 1932. The waves of the sea. Physics of the earth, v. 5, Oceanography, p. 207–228. National Research Council, Bull. no. 85. Washington, D. C. 1932.
Rossby, C.-G., and R. B. Montgomery. 1935. “The layer of frictional influence in wind and ocean currents” . Papers in Physical Oceanography, v. 3, no. 3, 101 pp.1935.
Schumacher, A.1928. “Die stereogrammetrische Wellenaufnahmen der deutschen Atlantischen Expedition” . p. 105–120 in Ergänzungsheft 3, Zeitschr. f.d. Gesellschaft für Erdkunde zu Berlin. 1928.
Schumacher, A.1939. “Stereophotogrammetrische Wellenaufnahmen” . Deutsche Atlantische Exped, Meteor, 1925–1927, Wiss. Erg., Bd. 7, H. 2, L. 1, 156 pp. and Atlas. Berlin. 1939.
Schureman, P.1924. “A manual of the harmonic analyses and prediction of tides” . U. S. Coast and Geod. Surv., Spec. Pub. 98, 416 pp.1924.
Seiwell, H. R.1937. “Short-period vertical oscillations in the western basin of the North Atlantic” . Papers in Physical Oceanography, v. 5, no. 2, 44 pp.1937.
Shepard, F. P., and E. C. La Fond. 1939. Undertow. Science, v. 89, p. 78–79, 1939.
Shepard, F. P., and E. C. La Fond. 1940. “Sand movements along the Scripps Institution pier” . Amer. Jour. Science, v. 238, p. 272–285. 1940.
Shepard, F. P., K. O. Emery, and E. C. La Fond. 1941. “Rip currents: A process of geological importance” . Jour. Geology, v. 49, p. 337–369. 1941.
Sverdrup, H. U.1927. Dynamic of tides on the North Siberian Shelf. Geofysiske Publikasjoner, v. 4, no. 5, 75 pp.1927. Oslo.
Sverdrup, H. U.1940. “The Gulf of California: Preliminary discussion of the cruise of the E. W. Scripps in February and March, 1939” . Sixth Pacific Sci. Congr., California, 1939, Proc., v. 3, p. 161–166. 1940.
Tannehill, I. R.1938. “Hurricane of September 16 to 22, 1938” . Monthly Weather Rev., v. 66, p. 268–288. 1938.
Thorade, H.1928. “Gezeitenuntersuchungen in der Deutschen Bucht der Nordsee” . Deutsche Seewarte, Archiv. Bd. 46, Nr. 3, 85 pp., 1928. Hamburg.
Thorade, H.1931. Probleme der Wasserwellen. Probleme der kosmischen Physik, XIII and XIV, 219 pp.1931. Hamburg.
U. S. Beach Erosion Board. 1941. “A study of progressive oscillatory waves in water” . Tech. Series, Washington, Govt. Print. Off., no. 1, 39 pp.1941.
van Veen, Joh. 1938. “Water movements in the Straits of Dover” . Conseil Perm. Internat. p. l'Explor. de la Mer, Jour. du. Conseil, v. 13, p. 7–36. 1938.
XV. The Water Masses and Currents of the Oceans
Within any given region, the character of the water masses depends mainly upon three factors—the latitude of the region, the degree of isolation, and the types of currents—the relative importance of which will be brought out in the course of the discussion.
It is rational to deal first with the simpler conditions and gradually to enter upon the more complicated. This can be done by first discussing the Antarctic Ocean, where the latitude effect is easily explained, where the waters are in free communication with those of the major oceans, and where the system of prevailing currents is unusually clear-cut. After a description of conditions within the Antarctic Ocean we shall consider the Atlantic, Indian, and Pacific Oceans, the adjacent seas of these oceans, and in conclusion we shall discuss the deep-water circulation between the large ocean basins.
The Antarctic Circumpolar Ocean
Boundaries and General Characteristics of Water Masses. It is difficult to assign a northern boundary to the Antarctic Ocean because it is in open communication with the three major oceans: the Atlantic, the Indian, and the Pacific Oceans. In some instances the antarctic waters are dealt with as parts of the adjacent oceans and are designated the Atlantic Antarctic Ocean, or the Indian or Pacific Antarctic Ocean, whereas in other instances the antarctic waters must be considered an integral part of all oceans. The latter case, for instance, applies when dealing with the deep-water circulation, which is of such a nature that the intercommunication between different regions must be taken into account. The antarctic waters, on the other hand, can be discussed without entering upon details of the conditions in neighboring oceans, in which case one has to establish oceanographic boundaries between the Antactic Ocean and the neighboring areas.
On the basis of observations of surface temperatures only, it is possible to divide the Antarctic Ocean into two separate regions and to establish its approximate northern boundary. Near the Antarctic Continent the surface temperature is low, but with increasing distance from the coasts it increases slowly until a region is reached within which an increase of two or three degrees takes place in a very short distance.
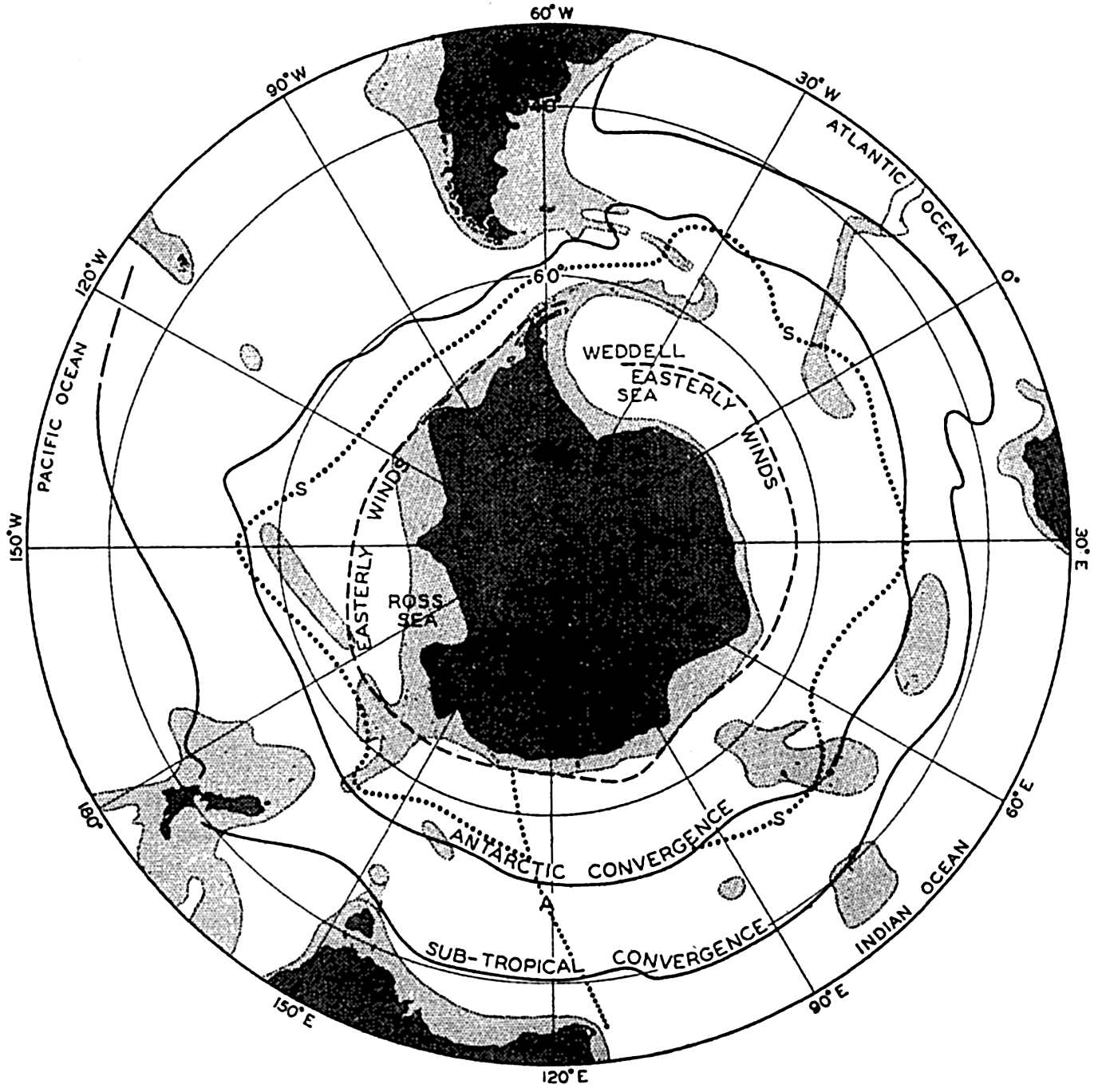
Locations of the Antarctic and Subtropical Convergences. Locations of the vertical sections shown in figures 159 and 160, and limit between westerly and easterly winds (dashed line). Light shading: depths less than 3000 m.
Figure 158 shows the location of the two convergences according to the results of the Discovery Expedition (Deacon, 1937a). The location of the Antarctic Convergence is, in part, dependent upon the distribution of land and sea and upon the bottom topography. The southward displacement of the Antarctic Convergence to the south of Australia and New Zealand can probably be ascribed to the relative narrowness of the passage between these regions and Antarctica, and the similar displacement off South America can be attributed to the southerly location of Drake's Passage separating South America from Graham Land. The bends of the Antarctic Convergence are to a great extent related to the bottom topography. On the western side of the submarine ridges, the more conspicuous of which are indicated in the figure by the 3000-m contour, the convergence is deflected to the north, and on the eastern side to the south. The reason for this relation to the bottom topography was explained when dealing with the currents (p. 466).
The location of the Subtropical Convergence is similarly related to the distribution of land and sea, but appears to be less dependent upon the bottom configuration. It is less well defined than the Antarctic Convergence, and instead of referring to a line of convergence it is, according to Defant (1938) more correct to refer to a region of convergence.
Within the antarctic and subantarctic regions the water masses can be classified according to their temperature-salinity characteristics (p. 141). Such a classification is here conveniently based on a study of the distribution of temperature and salinity in a vertical section running at right angles to the Antarctic Continent. Figure 159 is taken from Deacon's discussion (1937a) and shows the distribution of temperature and salinity along a section running south-southwest from Cape Leeuwin, Western Australia, to the ice edge south of Australia in 63°41'S. The two convergences are indicated which divide the area into the antarctic and subantarctic regions. Within the antarctic region a surface layer of low temperature and low salinity is present. Below this surface layer one recognizes a transition layer which increases in thickness towards the north and within which the temperature rapidly increases to values higher than 2°) and the salinity gradually increases to values higher than 34.5 ‰. Below the transition layer one encounters the Antarctic Circumpolar Wuter, the greater mass of which has a salinity a little above 34.70 ‰ and a temperature between 2° and 0°. Water of similar characteristics is found within the subantarctic region below a depth of about 2000 m. That is, the deep water within the subantarctic region has the same characteristics as the Antarctic Circumpolar Water which rises towards the surface near the Antarctic Continent. At station 887, close to the continent, a salinity of 34.67 ‰ is met with at a depth of 200 m, but at station 879 south of the Subtropical Convergence the
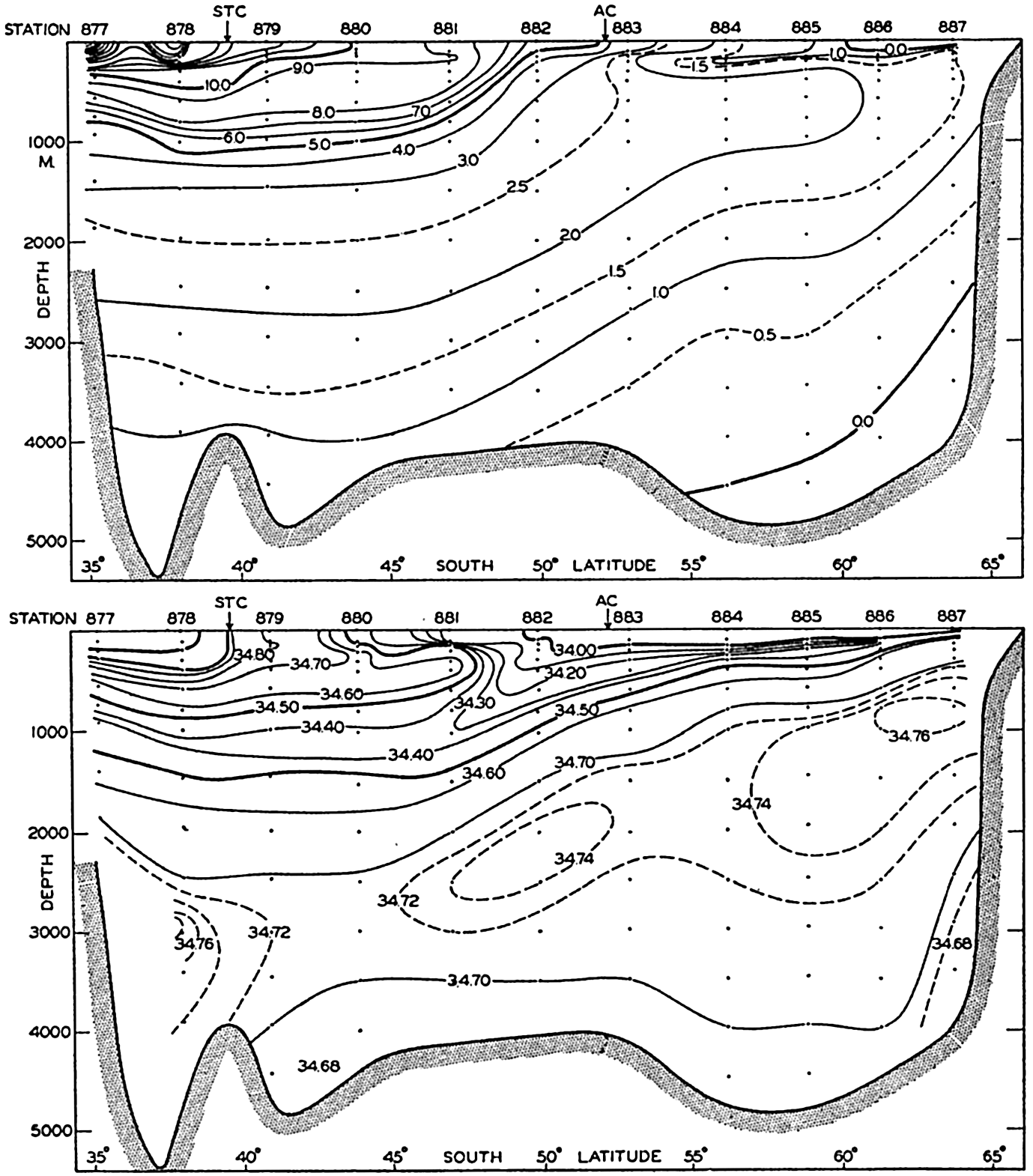
Distribution of temperature and salinity in a vertical section from Cape Leeuwin, Australia, to the Antarctic Continent (after Deacon). Location of section shown by line A in fig. 158.
Within the subantarctic region one can conveniently distinguish between two water masses above the deep water, the Subantarctic Upper Water of a uniform temperature between 8° and 9° and of a relatively high salinity, appearing in the salinity section as a tongue extending towards the south, and the Antarctic Intermediate Water of a temperature between
The Antarctic Surface Water. In winter the southern half of the antarctic region is covered by a thin layer of nearly homogeneous surface water of a thickness of 100 m or less which has a temperature about freezing point and a salinity that varies between 34.0 and 34.5 ‰, the highest value being found in the Weddell Sea. At a station occupied by the Deutschland in the Weddell Sea (lat. 65°32'S, long. 43°‰'W) on August 26, 1912 (Brennecke, 1921), a nearly homogeneous layer was found between the surface and a depth of 100 m having a temperature of −1.83° and a salinity of 34.47 ‰. With increasing distance from the Antarctic Continent the temperature rises to 0° where the Antarctic Convergence is far south, and to about 1° where this convergence is far north.
In summer the salinity at the surface is decreased owing to the melting of ice. By far the greater amount of the radiation surplus of the season is used for melting ice, but a small amount is used for raising the temperature of the water above freezing point. In the vicinity of the pack ice the surface temperature and salinity vary greatly from one locality to another, because the nearly fresh water produced by melting of ice is not immediately mixed with the surrounding or deeper water. In ice-free areas a more thorough mixing takes place, particularly where strong winds are frequent, and there a well-mixed layer may extend to depths of 55 to 85 m. The temperature of this water is a few degrees above freezing, owing to absorption of heat, but below this warmed layer colder water is found. This colder water may have been formed in situ during the preceding winter, but it is also possible that a northward flow of the colder stratum takes place (Mosby, 1934).
On the continental shelves, particularly in the Weddell Sea, the winter cooling and the increase in salinity associated with freezing of ice may extend to the bottom, leading to formation of homogeneous water which, from the surface to the bottom, may have a temperature as low as −1.95° and a salinity as high as 34.70 ‰. The importance of this cold and saline water to the formation of the bottom water will be discussed on page 611.
Antarctic Circumpolar Water. At a short distance below the surface water the Antarctic Circumpolar Water is encountered, which is characterized, in general, by a temperature higher than 0.5° and a salinity slightly above 34.7 ‰. Within this water the temperature generally is at a maximum at a depth of 500 to 600 m, below which it decreases slowly towards the bottom. The salinity is at a maximum at a somewhat greater depth that varies between 700 and 1300 m and below which it decreases towards the bottom. The great uniformity of this water which, all around Antarctica, has nearly the same temperature and the same salinity, is illustrated in fig. 160, which shows a vertical section around Antarctica. The section, the location of which is indicated by the line marked S in fig. 158, has been placed between two transport lines of the circumpolar current (fig. 163, p. 615) and follows therefore approximately the same water mass. Disregarding the surface water, one finds that within this enormous body of water the differences in temperature hardly exceed two degrees, and below a depth of about 800 m the differences in salinity do not exceed 0.1 ‰. It should be observed, however, that if the section had been placed closer to the Antarctic Continent the temperatures and salinities would have been lower, and if it had been placed at greater distances from the continent the temperatures and salinities would have been higher.
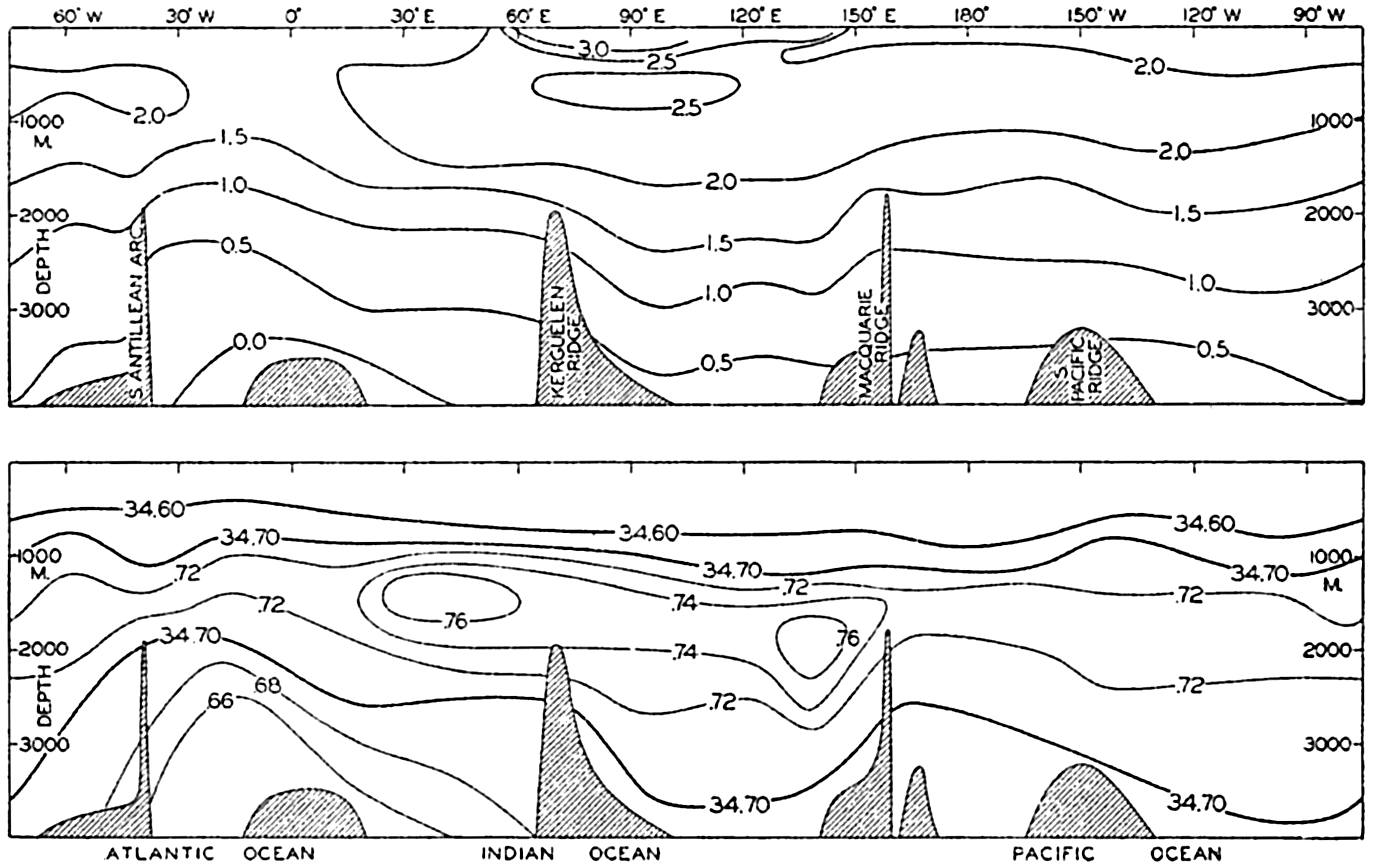
Distribution of temperature and salinity in a vertical section around the Antarctic Continent. Location of section is shown by line S in fig. 158.
The water which enters the Drake Passage from the west (left margin of section), between 1000 and 4000 m, has a salinity a little higher than
The temperature section shows that the water which enters Drake Passage from the west has maximum temperatures only slightly above 2°C and minimum temperatures near the bottom somewhat below 0.5°. Towards the east of the South Antilles Arc the cold bottom water of the Weddell Sea appears, and at higher levels the maximum temperature drops below 2°, probably owing to admixture of this cold water. In long. 10°E the maximum temperature increases and, between long. 60° and 120°E, lies above 2.5°. These high temperatures are due to admixture of relatively warm water from the Atlantic and Indian Oceans. When the water passes into the Pacific area, the maximum temperature again decreases owing to admixture of the colder Pacific Deep Water. The isotherms of 1° and 0.5° do not exactly follow the bottom topography as should be expected if the water crossed the different submarine ridges without mixing taking place, for which reason it appears necessary to assume that processes of mixing exercise some influence upon the distribution of temperature and therefore, also, upon the distribution of salinity.
The Antarctic Bottom Water. The most extreme type of bottom water is found in the Weddell Sea area, where below a depth of about 4000 m the temperature is about −0.4° and the salinity is about 34.66 ‰. This water is probably formed by the mixing in approximately equal parts of water flowing down from the continental shelf and of Antarctic Circumpolar Water (Mosby, 1934). The former has a temperature, on an average, of about −1.9° and a salinity of about 34.62 ‰, whereas the circumpolar water near the Antarctic Continent has a temperature of 0.5° and a salinity of 34.68 ‰. Expressed by means of σi, the densities of these two types of water are 27.89 and 27.84, respectively, and the density of the bottom water is 27.86. The water on the continental shelf, the salinity of which may be increased up to 34.62 ‰ or slightly
According to this explanation, first offered by Brennecke (1921) and later substantiated by Mosby (1934), the freezing of ice on the Antarctic continental shelves is of primary importance to the formation of the Antarctic Bottom Water. On a small scale, cooling of water of relatively high salinity may contribute to the formation of bottom water by a process similar to the one which takes place in the waters around Greenland (see p. 656), but this process appears to be limited to some areas in the Bransfield Strait (Clowes, 1934).
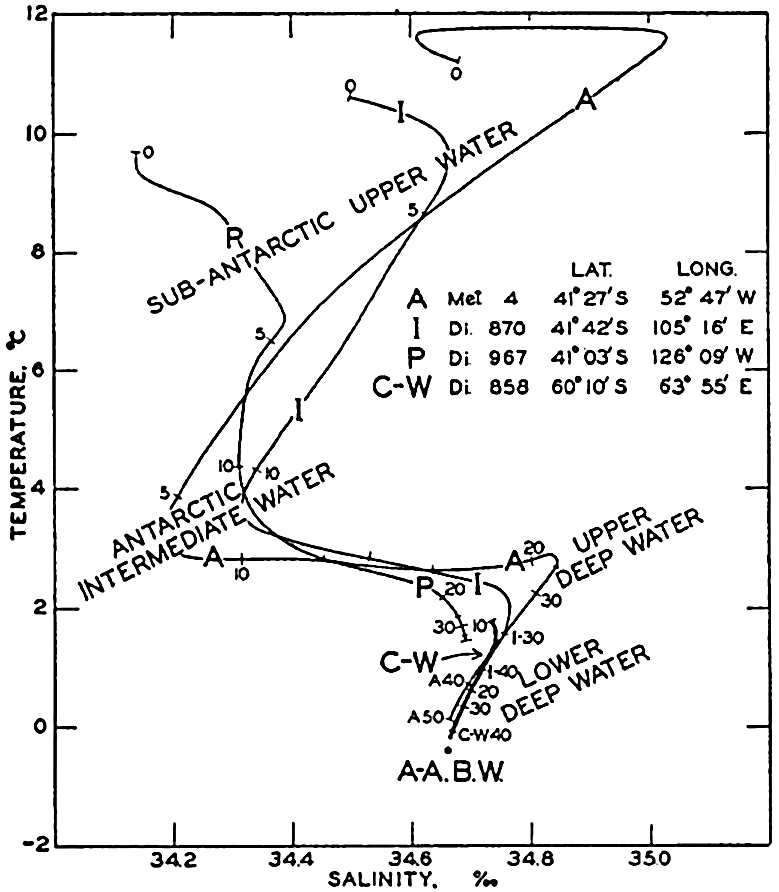
Temperature-salinity curves at three stations in the subantarctic regions in the Atlantic (A), the Indian (I), and the Pacific (P) sectors of the Antarctic Ocean, and at a station within the region of circumpolar water (C-W). Antarctic Bottom Water shown by A-A.B.W.
By far the major part of the Antarctic Bottom Water is formed in the Weddell Sea, as is evident from the section in fig. 160, according to which water of a salinity of 34.66 ‰ is present only between 30°W and 30°E. Intermittently, bottom water is also formed south of the Indian Ocean between long. 30°E and 140°E (Sverdrup, 1940), but no evidence exists for such formation to the south of the Pacific Ocean. These features have bearing on the deep-water circulation of the different oceans and we shall therefore return to them later (p. 745).
The Waters of the Subantarctic Region. These waters differ much more both regionally and in a vertical direction, for which reasons a well-defined classification cannot be undertaken. The curves in the T-S diagram in fig. 161 illustrate the waters present and show that generally one can distinguish between five different water masses, the Subantarctic Upper Water, the Antarctic Intermediate Water, the Upper Deep Water, the Lower Deep Water, and the Bottom Water.
The three curves representing conditions in the subantarctic region are based on observations in the Atlantic, Indian, and Pacific sectors,
Within all areas the upper water is characterized by relatively high temperatures and a salinity maximum at some distance below the surface, the highest salinities occurring in the Atlantic area. The Antarctic Intermediate Water is present in all areas. In the Atlantic it is of somewhat lower salinity and is found at a somewhat lesser depth below the surface, but these features are partly related to the distances of the stations from the Antarctic Convergence. At the stations in the Atlantic and Indian Ocean areas the Upper Deep Water shows a relatively high salinity and high temperature, whereas the Lower Deep Water is of the same character as the Antarctic Circumpolar Water, but is found at a greater depth. In the Pacific Ocean the Upper Deep Water is of lower temperature and lower salinity, but the Lower Deep Water approaches the character of the Antarctic Circumpolar Water.
The reason for these regional differences will be discussed when dealing with the deep-water circulation and it is sufficient here to emphasize that the subantarctic waters differ within the three oceans, whereas the antarctic waters are of similar character all around the Antarctic Continent.
The Currents of The Antarctic Ocean. The more or less permanent currents of the Antarctic Ocean consist principally of two types, the relative currents which are associated with the distribution of mass, and the wind drifts of the surface layers.
The character of the relative currents can be derived from fig. 162 showing the distribution of the specific volume anomalies in the section which was used for demonstrating the character of the water masses (see fig. 159). At any level the water of the smallest specific volume, that is, the greatest density, is found near the Antarctic Continent and, in general, the lines of equal anomaly slope downward from south to north. As a consequence of this distribution of mass, the isobaric surfaces all rise towards the north if the 4000-decibar surface is considered horizontal. This rise towards the north is evident from the upper part of fig. 162, in which are shown the profiles of a series of isobaric surfaces relative to the 4000-decibar surface. The current which is associated with the distribution of mass must be directed away from the reader, that is, from west to east, because in the Southern Hemisphere
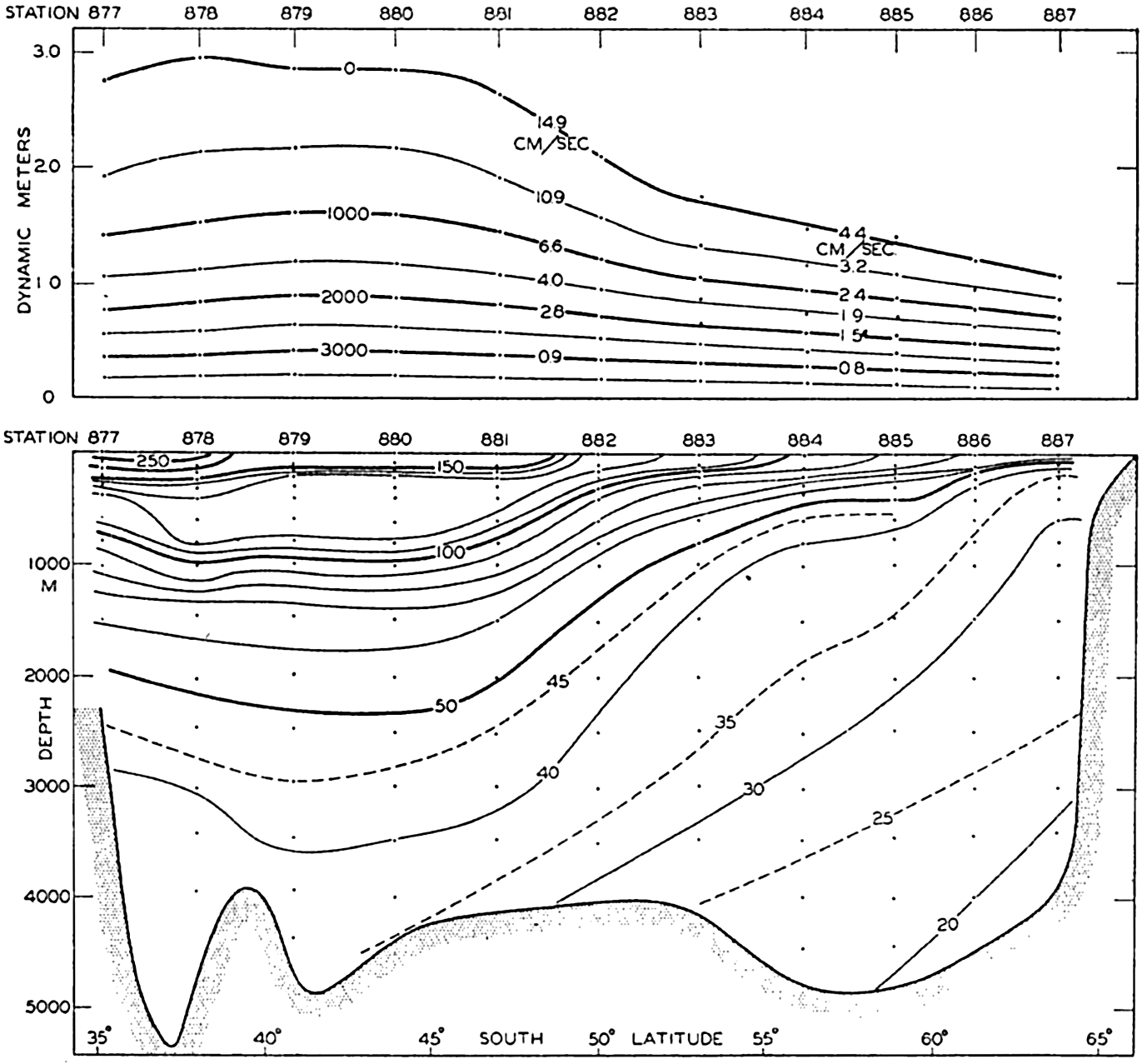
Lower: Distribution of the anomaly of specific volume, 105δ, in a vertical section from Cape Leeuwin, Australia, to the Antarctic Continent (see fig. 158). Upper: Profiles of the isobaric surfaces relative to the 4000-decibar surface.
In general, the current runs from west to east around the Antarctic Continent, but is locally deflected from its course, partly by the distribution of land and sea and partly by the submarine topography. The effect of the submarine topography is evident in Deacon's charts (1937b) of the dynamic topography of the surface or the 600-decibar surface relative to the 3000-decibar surface, and it is also seen from fig. 163, which shows the total volume transport relative to the 3000-decibar surface as computed by means of the data which Deacon has used for his presentation, adding the results from a number of Meteor stations in the South Atlantic. In the figure the volume transport is shown by lines which are approximately in the direction of transport and which have been drawn with such intervals that the transport between two lines equals 20 × 106 m3/sec.
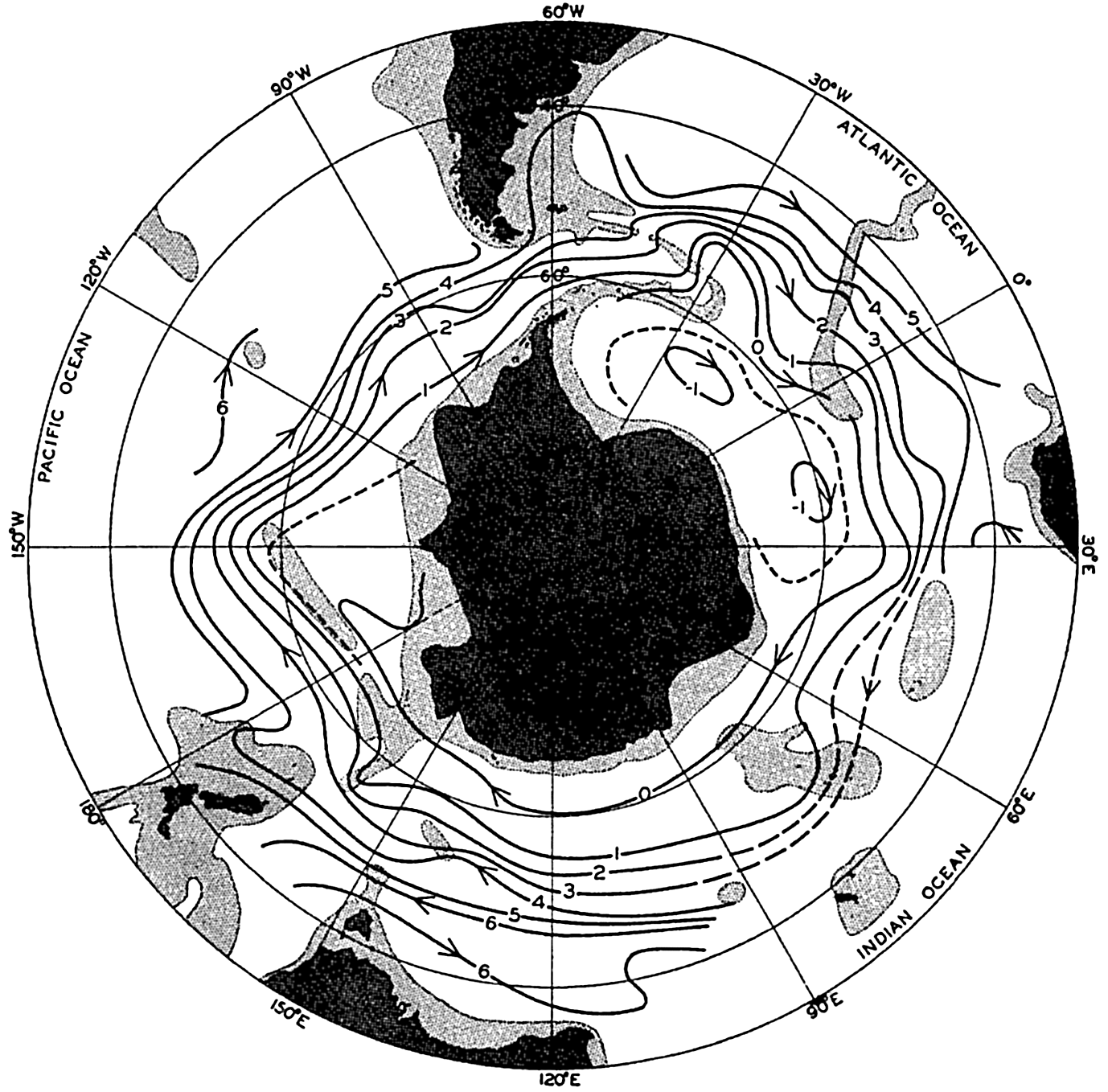
Transport lines around the Antarctic Continent. Between two lines the transport relative to the 3000-decibar surface is about 20 million cubic meters per second.
Following the current around the Antarctic Continent, it is seen that when approaching a submarine ridge the current bends to the left and after having passed the ridge it bends to the right, in accordance with our preceding discussion of the effect on a deep current (p. 466). Having passed through Drake Passage, the Circumpolar Current approaches the South Antilles Arc, where it first bends to the north and then to the south after having crossed the ridge. When the current passes the shallower areas near Bouvet Island between long. 0° and 10°E, the bends to the north and to the south are repeated; when passing the Kerguelen Ridge, similar bends occur but these are less well defined, perhaps owing to the lack of data. South-southwest of New Zealand the current crosses the Macquarie Ridge, bending sharply north and south, between long. 180° and 155°W, runs towards the east-northeast paralleling the South Pacific Ridge, and having passed the eastern extremity of the shallower portion it bends again towards the south. Thus, five distinct ridges or shallower areas are crossed and in each case the water masses are deflected to the left when approaching the ridges or the shallow areas and are deflected to the right after having passed them. These bends show up in part at the surface in the location of the Antarctic Convergence (see p. 607) and some of them appear on charts of the surface currents (see chart VII).
Besides the bends which are associated with the bottom topography, the effects of the distribution of land and sea and of the currents in the adjacent oceans are also seen. The location of the Drake Passage naturally forces the current further south than in any other region, but on the eastern side of South America a branch of the current, the Falkland Current, turns north. Along the east coast of South Africa the Agulhas Stream flows south, partly turning into the Atlantic Ocean but mainly bending around towards the east, and the narrowness of the Circumpolar Current in long. 30°E is probably related to the effect of the Agulhas Stream. When the Circumpolar Current has passed New Zealand, a bend towards the north is evident which corresponds on a small scale to the Falkland Current.
The transport line marked “zero” is not continuous around the Antarctic Continent, but begins in the Weddell Sea area and ends against the coast of the Antarctic Continent in the region of the Ross Sea. This feature indicates that our representation is not entirely correct and that the transport does not take place exactly along the lines which have been entered, because actual lines of equal transport must be closed lines and cannot end against the shores. Some transport must take place across the lines, and the fact that our line “zero” stops against the continent to the west of Drake Passage indicates that in this narrow passage a certain amount of piling up of water takes place and that transport occurs here across the contour lines. Referring the flow to
A flow to the west near the Antarctic Continent is evident only in the Weddell Sea area, where an extensive cyclonic motion occurs to the south of the Circumpolar Current. The water masses which take part in this cyclonic movement, however, are small compared to those of the Circumpolar Current, and their velocities are small.
Within the subantarctic region the current is also directed in general from west to east but only the southern portion of the waters close to the Antarctic Convergence circulates around the Antarctic Continent and forms part of the Circumpolar Current. In the Pacific Ocean the northern portion belongs to the current system of that ocean and must therefore be dealt with again when describing the conditions in the South Pacific. Thus, a strict northern limit of the Antarctic Ocean cannot be established on oceanographic principles, but a boundary region has to be considered which, depending upon the point of view, may be assigned either to the Antarctic Ocean or the adjacent oceans.
The total transport of the Antarctic Circumpolar Current must be greater than is apparent from fig. 163, which shows only the transport relative to the 3000-decibar surface. According to the figure, the transport through Drake Passage is about 90 million m3/sec, whereas Clowes’ computations (1933) gave 110 million above the 3500-decibar surface. It is therefore probable that the absolute transport between the lines in fig. 163 is not 20 million, but at least 25 million m3/sec.
This discussion of the Circumpolar Current is based entirely on the distribution of mass as derived from deep-sea oceanographic observations. The surface currents have been determined independently by means of ships’ records, and show that the flow of the surface water is governed partly by the distribution of mass and partly by the effect of the prevailing winds. Near the Antarctic Continent easterly and southeasterly winds blow away from the large land masses, but between lat. 60° and 40°5 strong westerly winds prevail. The dashed line in fig. 158, p. 606, shows (according to Deacon, 1937a) the approximate boundary between the regimes of the easterly and westerly winds. Correspondingly one finds, as seen on chart VII, westward surface currents prevailing near the border of the Antarctic Continent and eastward surface currents at some distance from the coast. In the Southern Hemisphere the wind drift deviates to the left of the direction of the wind and consequently the eastward surface current shows a
Deacon attributes the Antarctic Convergence to the character of the deep-water circulation. He points out that the convergence is found where the relatively warm but saline deep water rises, and he reasons that within the antarctic region the upper water, being heavier than the warm surface water further north, would sink if it were not prevented by the highly saline deep water. He writes (1937a, p. 23):
As soon, however, as the northward current has passed the point where the deep water climbs steeply towards the surface it is no longer prevented from sinking, and the sections suggest that the antarctic water flows over the steep ascent of the warm deep water like a stream over a waterfall.
Sverdrup (1934), on the other hand, suggests that the convergence is brought about because in the subantarctic region a thermohaline circulation dominates, which would carry the light surface waters to the south, whereas in the antarctic region a wind circulation dominates, which would carry the surface water to the north. It remains to be seen whether either of these explanations is acceptable or whether a combination of them, or perhaps an entirely new point of view, must be introduced.
As a consequence of the divergence and convergence at the surface, a transverse circulation must be present which is superimposed upon the general flow from west to east. Such a transverse circulation is evident from the vertical sections in fig. 159, p. 608, and fig. 210, p. 748. In these, between 45° and 63°5, the deep water seems to climb from a depth of about 3000 meters to within 200 meters of the surface. The deep water does not appear to reach the very surface, but within the entire antarctic region a considerable amount of deep water of high salinity must be added to the surface layer, because otherwise the salinity would be lowered owing to excess of precipitation and the addition of fresh water by the melting of antarctic icebergs. A southward flow of deep water is also required for balancing the transport of the surface water to the north by the prevailing winds. In the section shown in fig. 159, sinking of water near the Antarctic Continent probably does
At the Antarctic Convergence, water of relatively low salinity and low temperature sinks. A small portion of the sinking water appears in some areas to return towards the south at a depth of a few hundred meters, but the greater part continues towards the north, forming the tongues of Antarctic Intermediate Water which in all oceans can be traced to great distances from the antarctic region. It is probable that this water gradually mixes with the underlying deep water and returns to the Antarctic with the deep water (p. 750). Within the subantarctic regions the upper water appears to flow towards the south, but the nature of this flow is not fully understood.
The antarctic water which leaves the surface has a temperature of 2.2° and a salinity of 33.80 ‰ in the Atlantic area (Wüst, 1935). In the Indian Ocean area and to the south of Australia, similar values are found (Sverdrup, 1940) which appear applicable to the Pacific area as well, because the Antarctic Convergence follows the isotherms and isohalines of the sea surface (Deacon, 1937a). Thus, water of temperature 2.2°, salinity 33.80 ‰, and σt = 27.02, represents a water tgpe (p. 143) that is continuously or intermittently formed near the Convergence, where it sinks. When sinking, it is rapidly mixed with surrounding waters and a water mass, the Antarctic Intermediate Water, is formed which mainly spreads towards the north, being characterized at its core by a salinity minimum. Owing to continued mixing, the characteristic T-S relation of the intermediate water changes as the distance from the Convergence increases, and layers of gradual transition are found both above and below the water mass, for which reason no distinct boundaries can be introduced. The best method for following the spreading out of the intermediate water and the results of mixing is the “core method” which was introduced by Wüst (p. 146), who, in the Atlantic Ocean, examined the temperature and salinity at the core of the intermediate water and determined the depth of the core.
On the basis of these considerations one arrives at the schematic picture of the transverse circulation which is shown in the block diagram in fig. 164. In the diagram the formation of bottom water has been taken into account and, furthermore, it is indicated that the deep-water flow towards the Antarctic Continent is strengthened by addition of both intermediate and bottom water. The main features of the transverse circulation are represented by the sinking of cold water near the Antarctic Continent, the climb of the deep water towards the surface, the
The climb of the deep water towards the surface is of great biological importance, because through that process the amount of plant nutrients in the surface layer is being constantly renewed; the enormous numbers of organisms found in the antarctic water is therefore closely related to the type of transverse circulation which is present.
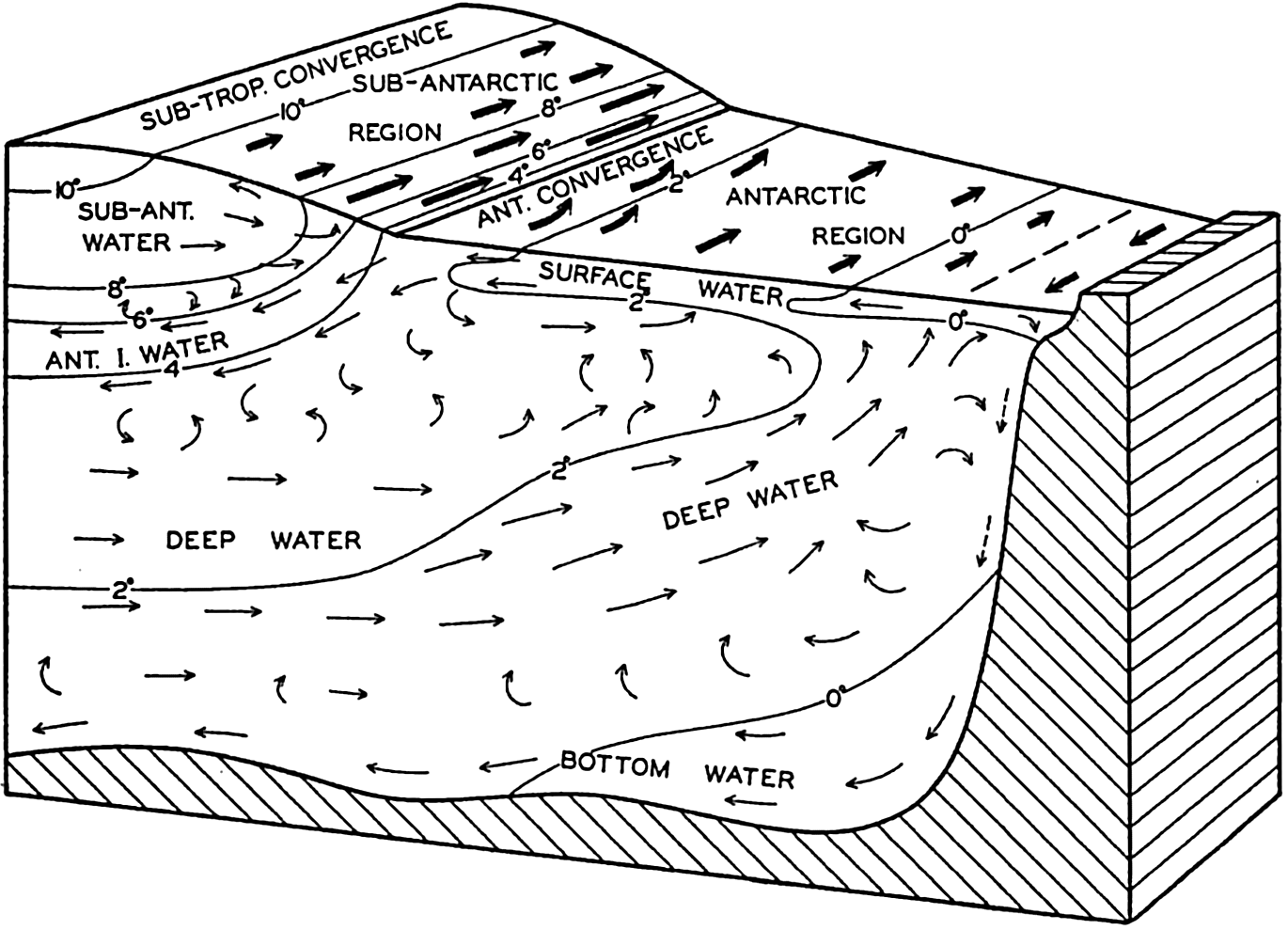
Schematic representation of the currents and water masses of the Antarctic regions and of the distribution of temperature.
From the foregoing it is evident that one cannot consider the Antarctic Circumpolar Water mass as a body of water which circulates around and around the Antarctic Continent without renewal. On the contrary, one has to bear in mind that water from the antarctic region is carried towards the north and out of the region both near the surface and near the bottom, and that deep water from lower latitudes is drawu into the system in order to replace the lost portions. Through external processes, cooling and heating, evaporation and precipitation, freezing and melting of ice, and through processes of mixing, the temperature and salinity in a given locality remains nearly unchanged over a long period, except for such changes as are associated with displacements of the currents. Thus, the stationary distribution of conditions which characterize the entire Antarctic Ocean represents a delicate balance between a number of factors which tend to alter the conditions. On the other hand, an
When one examines the dynamics of the Circumpolar Current, frictional forces have to be taken into consideration. The stress which the wind exerts at the sea surface cannot be balanced by a piling-up of water in the direction of flow (p. 488) because the current is continuous around the earth, and therefore it must be balanced by other frictional stresses. The velocities along the bottom are too small to give rise to bottom friction, and one is therefore led to the conclusion that great stresses exist at the boundaries of the current due to lateral mixing. According to Sverdrup (1939a) such lateral mixing takes place. The torque exerted by these stresses along the quasi-vertical boundary surfaces of the current must balance the torque exerted by the wind on the surface, but so far no attempt has been made at an analysis of the dynamics of the current, taking friction into account.
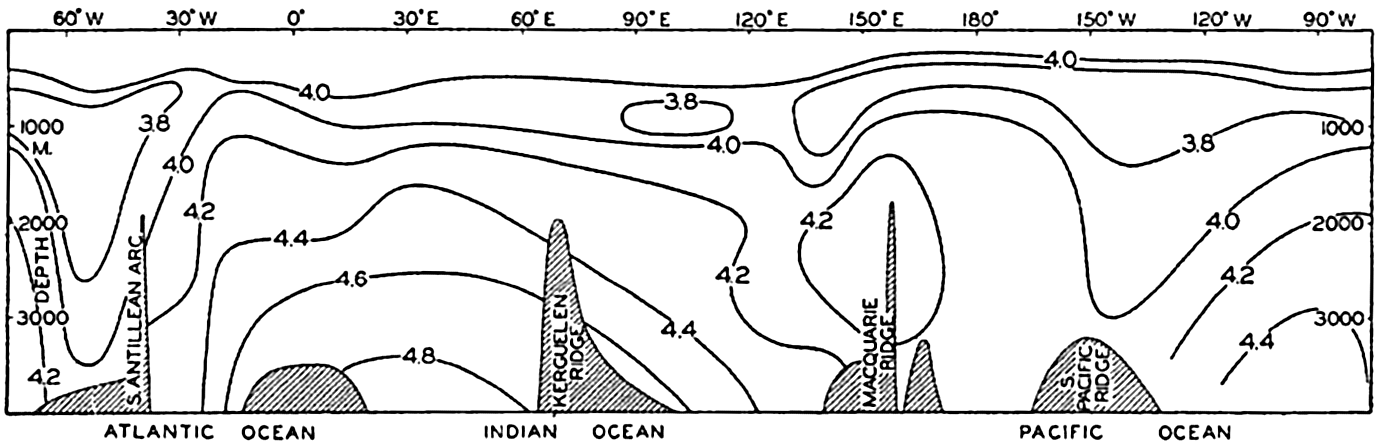
Distribution of oxygen (ml/L) in a vertical section around the Antarctic Continent. Location of section is shown by line S in fig. 158. See also fig. 160.
Oxygen Distribution. The distribution of oxygen around the Antarctic Continent is illustrated by the section in fig. 165, which corresponds to the sections in fig. 160. The water which enters the Drake Passage from the west has a low and uniform oxygen content below a depth of 600 m. A minimum oxygen content of about 3.7 ml/L is found at a depth of about 1200 m, and near the bottom the oxygen content is only slightly higher than 4.0 ml/L. To the east of the South Antilles Arc the oxygen content is considerably higher, evidently because the bottom water of the Weddell Sea contains a relatively large amount of oxygen. In the section, values higher than 4.8 ml/L are shown and the minimum value, which is here encountered above a depth of 1000 m, is only slightly less than 4.0 ml/L. As the water proceeds further towards the east, the oxygen content generally decreases both within the layer of minimum oxygen content and within the deep and bottom water. The decrease, however, is irregular, and more data are needed in order to
The variation of oxygen content in a north-south direction is illustrated in fig. 166, representing the Discovery section to the south of Western Australia, and in the southern parts of the sections in fig. 210, p. 748, and fig. 212, p. 753. In fig. 166 the high oxygen content of the surface waters decreases towards the north, owing to the increasing temperature. The water which sinks at the Antarctic Convergence has a relatively high oxygen content, but the content decreases so rapidly towards the north that no intermediate maximum develops. A layer of minimum oxygen content, within the subantarctic zone, is found at a depth of nearly 2000 m and this layer rises to the south. In the antarctic region, the layer of minimum oxygen content is encountered at a depth of about 600 m. The Antarctic Circumpolar Water has a higher oxygen content than the deep water further north, and the Antarctic Bottom Water which is found near the Antarctic Continent shows the highest oxygen content with values above 4.6 ml/L.
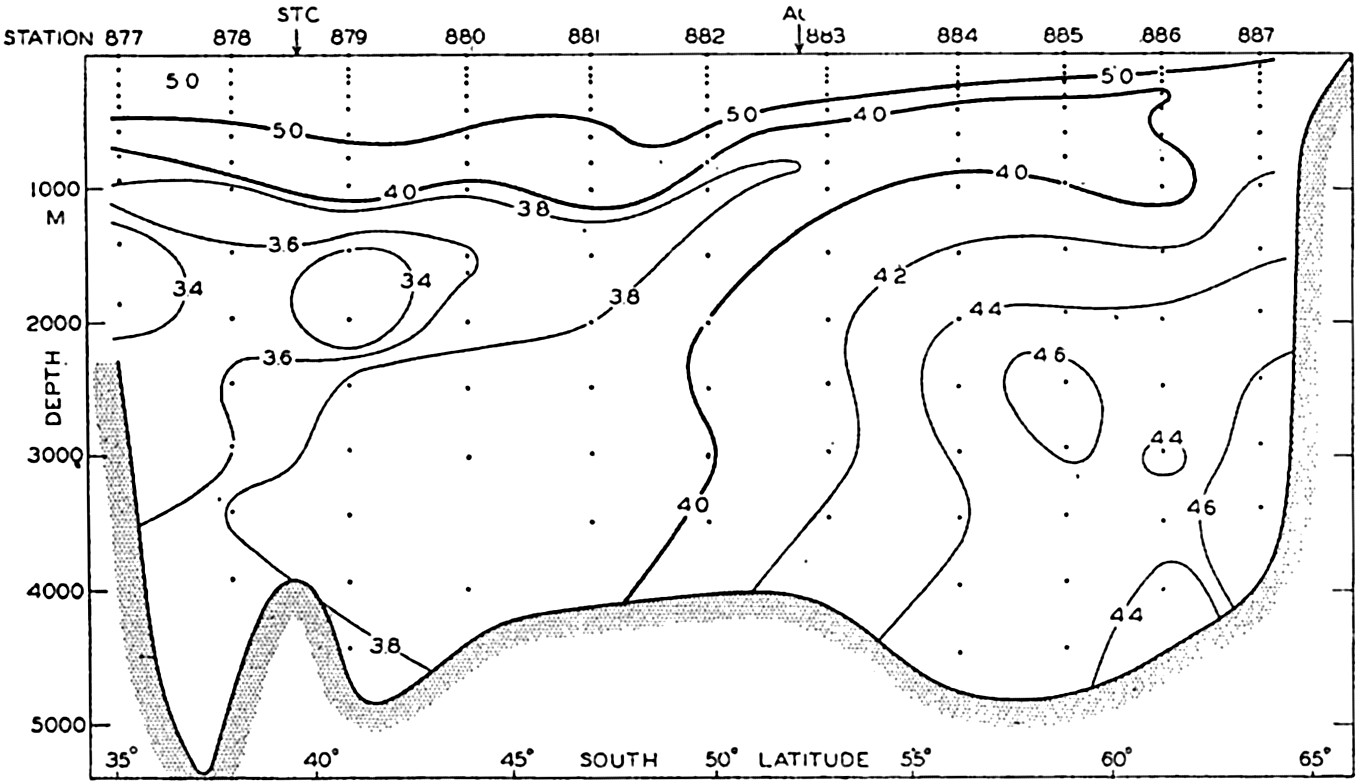
Distribution of oxygen in a vertical section from Cape Leeuwin, Australia, to the Antarctic Continent (after Deacon). Location of section shown by line A in fig. 158. See also figs. 159 and 162.
In the Weddell Sea area which is shown in fig. 210, p. 748, the bottom water has an oxygen content higher than 5.5 ml/L, and close to the continental slope values up to 6.5 are encountered. These high values confirm the conclusion that the greater amount of the Antarctic Bottom Water is formed in the Weddell Sea region. Mosby (1934) points out that the shelf water which contributes to the formation of the bottom water has an oxygen content of about 7 ml/L, whereas the deep water
To the north of the Weddell Sea the Antarctic Intermediate Water is characterized by a maximum of oxygen below which is present a layer of minimum oxygen content which rises towards the south. The deep water shows a higher oxygen content than that in the same latitude to the west of Australia. Within the subantarctic waters, then, regional differences are present not only in temperature and salinity (p. 612) but in oxygen content as well.
Ice and Icebergs. Two forms of ice are encountered in the Antarctic Ocean, sea ice which is formed by freezing of sea water and icebergs which represent broken-off pieces of glaciers. The appearance of both sea ice and icebergs varies widely. Several classifications have been proposed (Transehe, 1928, Smith, 1932, Maurstad, 1935, Zukriegel, 1935) and several codes for reporting ice have been introduced, one of which (Maurstad, 1935) has been adopted by the International Meteorological Organisation. The classification of sea ice deals with forms produced under different conditions of freesing, forms which are due to the tearing apart and packing together of the ice under the action of winds and tides, and forms which result from disintegration and melting of the ice. The classification of icebergs is based on the shape of the bergs, which depends partly upon the type of glacier from which they originate and partly upon the processes of melting and destruction to which they have been subjected.
The great mass of sea ice around the Antarctic Continent is in general described by the somewhat loose term “pack ice,” by which is meant drifting fields of close ice, mainly consisting of relatively flat ice floes, the edges of which are broken and hummocked. The pack ice is kept in motion by winds and currents. The effect of the wind is conspicuous when observations are made from a vessel drifting with the ice, because every change in wind direction and velocity brings about a corresponding change in the drift of the ice. Careful observations of the ice drift were conducted by Brennecke (1921) during the drift of the Deutschland in the Weddell Sea in 1911–1912. He found that the direction of the ice drift deviated on an average 34° from the wind direction and not 45° as required by the Ekman theory of wind currents (p. 493). The discrepancy was explained by Rossby and Montgomery (1935) as due to a layer of shearing motion in the water directly below the ice; but it may be due in part to the resistance offered by the ice, because the wind does not blow uniformly over large areas, wherefore the ice is packed together in some areas and torn asunder in others. The ice resistance
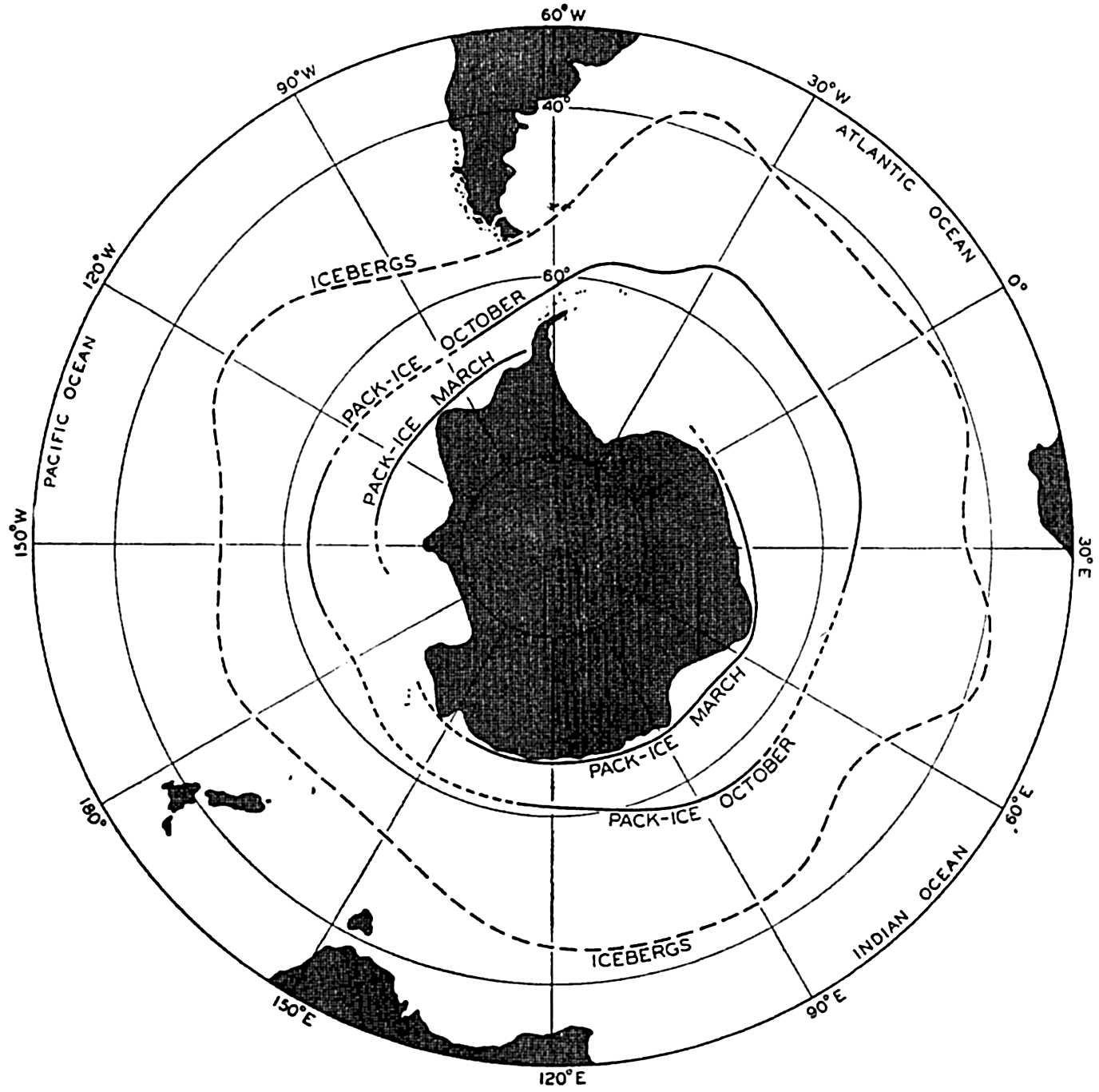
Average northern limits of pack-ice around the Antarctic Continent in March and October (after Mackintosh and Herdman), and average northern limit of icebergs according to British Admiralty Chart No. 1241.
The antarctic pack ice has in all months of the year a well-defined northern boundary beyond which no great amounts of scattered ice are encountered. The northern limits of the ice at the end of the winter (October) and the end of the summer (March) are shown in fig. 167 (Mackintosh and Herdman, 1940). Parts of the antarctic coast are always ice-free in summer, such as the Pacific side of Graham Land, and other parts are often ice-free, such as the coasts to the south of Australia and Africa. The eastern areas of the Weddell Sea and the
The great icebergs of the Antarctic originate mainly from the shelf ice, which represents the direct continuation of the antarctic ice cap where it extends into the shallow waters surrounding the continent. The shelf ice is partly afloat, and when it is pushed far out it breaks off in enormous pieces which may be tens of kilometers wide and up to 100 km long, and may rise 90 m out of the water, which corresponds to a thickness of about 800 m. These giant bergs, which have occasionally been mistaken for islands, drift through the pack ice and often move in an opposite direction to the pack because they are carried by currents and are less influenced by wind. The melting of these bergs takes a long time, for which reason they drift to greater distances from the continent than the sea ice. Figure 167 also shows the average northern boundary of icebergs according to British Admiralty chart No. 1241, but icebergs or remains of icebergs have been reported much further north than is indicated by this average limit. On April 30, 1894, a small piece of floating ice was sighted in lat. 26°30'S, long. 25°40'W, but otherwise remains of icebergs are rarely reported from localities north of 35°s in the Atlantic Ocean, north of 45°5 in the Indian Ocean, and north of 50°5 in the Pacific Ocean.
The South Atlantic Ocean
The three major oceans, the Atlantic, the Indian, and the Pacific, can be considered as deep bays that are in open communication with the Antarctic Ocean to the south but are closed at their northern ends. Of these oceans the Atlantic extends farthest to the north, and several large adjacent seas, the Mediterranean, the Caribbean, the Gulf of Mexico, Baffin Bay, the Norwegian Sea, and the North Polar Sea, exercise characteristic effects on the waters of the North Atlantic. The communication between the North Atlantic Ocean and the Antarctic takes place through the South Atlantic Ocean, which is of nearly constant width and without adjacent seas. This wide and short channel is divided lengthwise by the South Atlantic Ridge, which rises from depths exceeding 5000 m to within 2000 m from the surface. The two deep troughs on either side of the ridge are divided into basins by ridges running more or less in an east-west direction, the most conspicuous of which is the Walfish Ridge which closes the eastern trough off to the south.
The Water Masses of the South Atlantic Ocean. In order to illustrate the character of the water masses in the South Atlantic Ocean, seven Meteor stations have been selected, the locations of which are shown in the inset map in fig. 168. The stations are equally distributed over the entire South Atlantic Ocean between latitudes 41°S and the Equator.
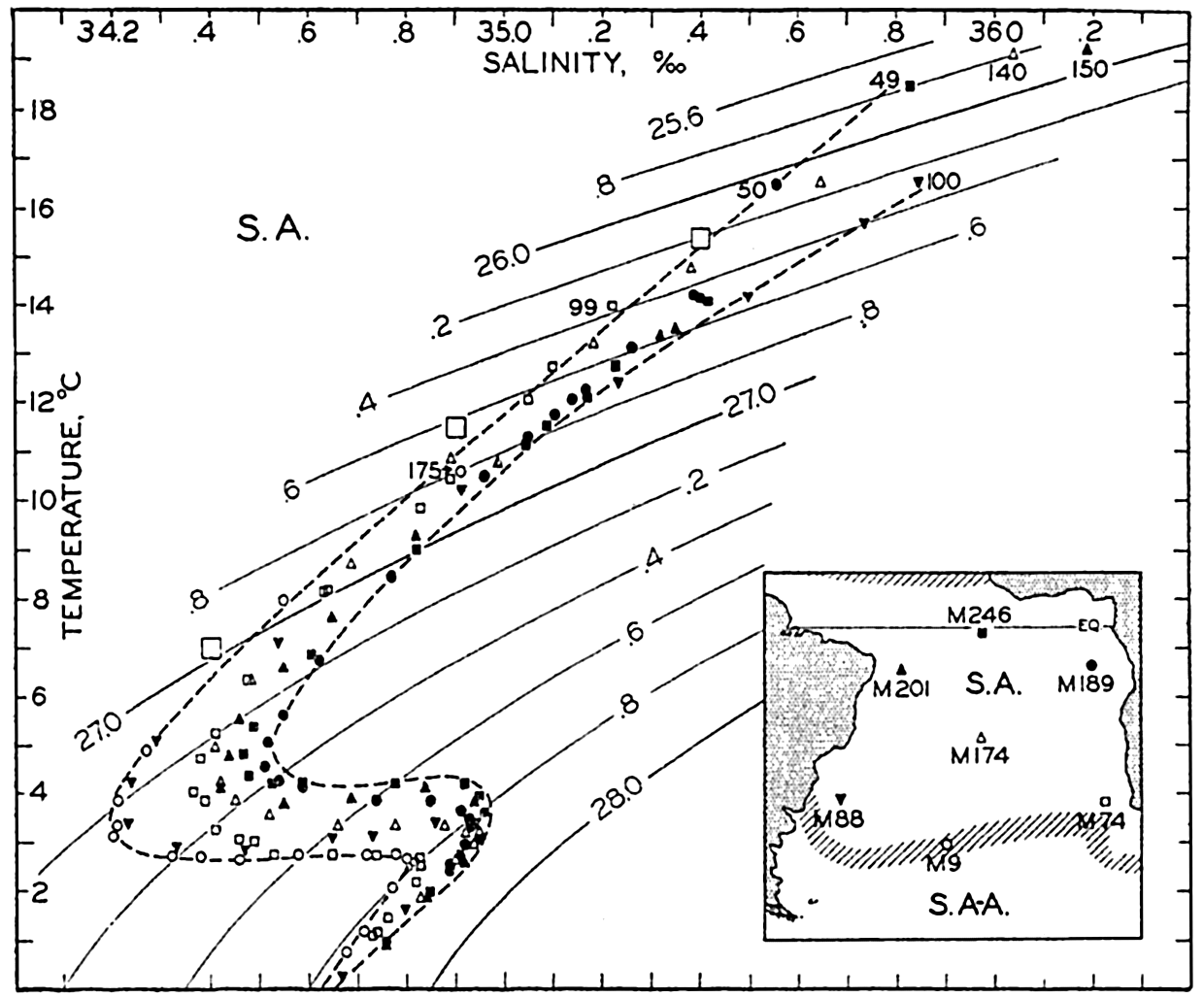
Temperature-salinity relation in the South Atlantic Ocean. Depths of shallowest values are shown. Winter surface values in latitudes 30°S to 40°S indicated by large squares. Inset map shows location of Meteor stations used. S.A. indicates South Atlantic region; S.A-A., subantarctic region.
Below the Central Water the Antarctic Intermediate Water shows up by the characteristic salinity minimum which is found over the greater part of the ocean at a depth of approximately 800 m. The Antarctic Intermediate Water is most typically present at the southern stations and at the stations close to South America, and appears to be considerably mixed with other water masses at the northern stations off the African
The T-S data in fig. 168 give no information as to the vertical extension of the different water masses because indications of depths have been omitted in order to avoid making the presentation too complicated. The vertical extension can be seen from fig. 169, showing the distribution of temperature and salinity in the Meteor profile VII (Wüst and Defant, 1936), which nearly follows the parallel of lat. 22°s. The central water, which is approximately bounded by the isohalines 36 ‰ and 34.65 ‰ is found in a layer which is about 450 m thick; the intermediate water, of salinity less than 34.65 ‰, is about 750 m thick, whereas the deep and bottom water is of greater thickness than the two other water masses together. The figure also demonstrates the presence of a thin layer of surface water which in this particular profile is of high temperature and high salinity. The upper water and the surface layer, as shown in the figure, together comprise the troposphere according to Defant's definition (p. 141). In these layers the strongest currents are encountered.
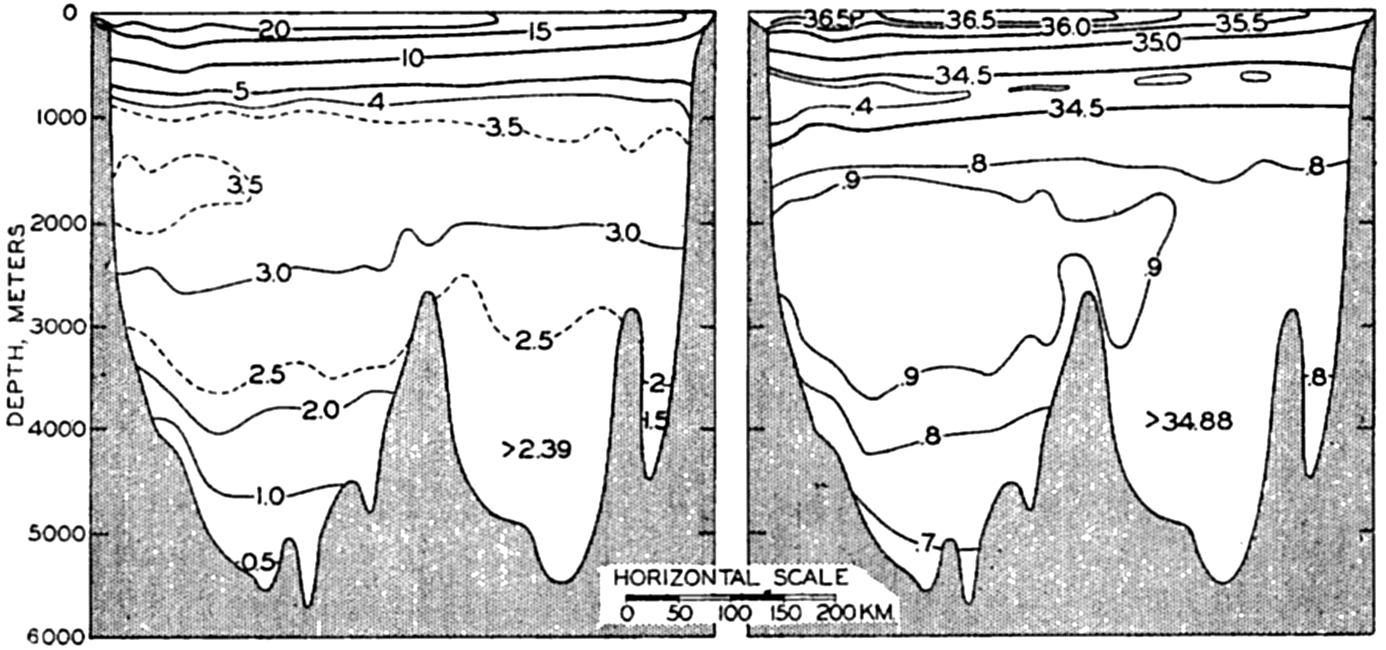
Distribution of temperature and salinity in vertical sections across the South Atlantic Ocean in about latitude 22°s (after Wüst.) Sections are seen from the south.
The Currents of the South Atlantic Ocean. The most outstanding current of the South Atlantic Ocean is the Benguela Current, which flows north along the west coast of South Africa and is particularly conspicuous between the south point of Africa and lat. 17° to 18°S. In agreement with the dynamics of currents in the Southern Hemisphere, the denser water of low temperature is found on the right-hand side of the current, that is, close to the African coast. Under the influence of the prevailing southerly and southeasterly winds the surface layers are carried away from the coast, and upwelling of water from moderate
Proceeding towards the Equator the Benguela Current gradually leaves the coast and continues as the northern portion of the South Equatorial Current, which flows towards the west across the Atlantic Ocean between lat. 0° and 20°S. In the charts showing the distribution of surface temperatures (charts II and III), the tongue of low temperature along the Equator is due not only to the cold waters of the Benguela Current but also to a divergence along the Equator. The South Equatorial Current partly crosses the Equator, continuing into the North Atlantic Ocean, and it partly turns to the left and flows south along the South American coast, where it shows up as a tongue of water of high temperature and high salinity, the Brazil Current. Close to the coast of Argentina a branch of the Falkland Current extends from the south to about latitude 30°S, carrying water of lower temperature and lower salinity. The most conspicuous feature of the currents of the South Atlantic is represented by the counterclockwise gyral with the cold Benguela Current on the eastern side, the warm Brazil Current on the western side, the South Equatorial Current flowing west on the northern side, and the South Atlantic Current flowing east on the southern side. It is a system of shallow currents because the entire circulation takes place above the Antarctic Intermediate Water or within the troposphere, and near the Equator it is probably limited to a depth of less than 200 m.
In agreement with this circulation, the water within the southern and eastern parts of the current system is of somewhat lower salinity than that of the northern and western parts (see fig. 168, p. 626). In the south, admixture of subantarctic water lowers the salinity, but in the north admixture of saline surface water increases the salinity.
A quantitative study of the currents of the South Atlantic Ocean on the basis of the Meteor data (Defant, 1941) leads to results similar to those that have been described here. Defant computed the absolute geopotential topographies of a series of isobaric surfaces by the third method described on p. 457. His conclusions are essentially in agreement with those which can be derived by making use of the equation of continuity (the fourth method, p. 457).
For calculations of the transport through vertical sections between South Africa and South America (p. 465), the Meteor data lead to the result that the transport above a depth of 4000 m is directed towards the north, but this is obviously impossible because the net transport through
| Latitude | Water mass | Current | Transport in million m3/sec toward | |
|---|---|---|---|---|
| North | South | |||
| 30°S | Benguela Current | 16 | ||
| Upper water | Brazil Current | 10 | ||
| Central part of South Atlantic gyral | 7 | 7 | ||
| Intermediate water | 9 | |||
| Deep water | 18 | |||
| Bottom water | 3 | |||
| 0° | Upper water | 6 | ||
| Intermediate water | 2 | |||
| Deep water | 9 | |||
| Bottom water | 1 | |||
The transport through vertical sections in the South Atlantic can be studied in greater detail, and approximate values can be computed for the amounts of the different types of water which are carried to the north and to the south, taking the continuity of the system into account. In table 76 are shown results of such computations, as referred to a section in 30°S. The table also contains values for the transport across the Equator, but these have been obtained in a different manner. The value of a northward transport of about 6 million m3 per second of upper water is mainly based on a comparison between the waters of the Caribbean Sea and the Sargasso Sea, and the values of the northward transports of intermediate and bottom water are estimated.
The approximate correctness of the figures can be checked by considering that the net transport of salt must be zero. A calculation of the net transport of salt requires knowledge of the velocity distribution within the different parts of the current system, but a rough computation which is based on average values confirms the above conclusions. We shall have to return to some of these matters when discussing the deep-water circulation, but here it will be emphasized that a large quantity of South Atlantic Central and Intermediate Water crosses the Equator and enters the North Atlantic Ocean, where it exercises an influence on the character of the waters along the coast of South America and in the Caribbean Sea and in the Gulf of Mexico.
In his discussion of the currents of the South Atlantic, Defant (1941) shows that in lat. 30°S to 45°S the stream lines of the currents are wave-like, the apparent wave length being 850 to 880 km. He points out that according to a theory of Rossby, extended by Haurwitz (1940), stationary wave patterns in a primary current are possible, provided that a relation exists between the velocity and width of the primary current and the wave length of the disturbance. Using this relation and introducing measured values of the width of the current across the South Atlantic and the wave length of the disturbances, Defant obtains a velocity of about 27 cm/sec for the primary current, in good agreement with values derived from the geopotential topography of the sea surface.
The wave pattern must be quasi-stationary because it is derived from observations in different years. Defant suggests that it is related to the topography of the bottom, but if this is true the deflections caused by the bottom topography must be in the opposite direction from those which were described on p. 466 (see fig. 116, p. 467 and fig. 117, p. 468). It is perhaps more likely, as also suggested by Defant, that the wavelike disturbance originates where the Brazil Current and the Falkland Current meet.
Oxygen Distribution. The major features of the oxygen distribution are shown in the longitudinal sections in fig. 43, p. 210, and fig. 210, p. 748. According to these sections the oxygen content of the central water is low near the Equator where, off west Africa, minimum values below 0.5 ml/L are found at a depth of about 350 m. This minimum is less pronounced off the coast of South America, where the minimum values are only slightly below 3 ml/L. The great depletion of oxygen along the African west coast is probably due to the oxidation of remains of organisms which fall towards the bottom from the productive region of the Benguela Current.
On the American side (fig. 210, p. 748), the Antarctic Intermediate Water is characterized by high oxygen content and this water mass can therefore be traced by means of a tongue of maximum oxygen values which extends nearly to the Equator. In the transition layer, below the
The Equatorial Region of the Atlantic Ocean
The Water Masses of the Equatorial Region of the Atlantic Ocean. Between depths of 100–200 m and 600–700 m, the water masses of the equatorial region are mainly of South Atlantic origin, but in the northern parts there is evidence of admixture of large quantities of North Atlantic Central Water which, as will be seen later, at temperatures between 8° and 15°C has a salinity which is nearly 0.5 ‰ higher than that of the South Atlantic Central Water. Figure 170 contains T-S values at selected equatorial stations, the locations of which are given on the inset map, and also shows the characteristic T-S relationships of the central water masses. At the two stations close to the Equator, stations M246 and M259, nearly typical South Atlantic water occurred, but at station M289 in 11°N and 50°W the water contained a considerable admixture of North Atlantic water and the same was true of station M267 in lat. 14°N off the African coast, where North Atlantic water appeared conspicuously at temperatures below 10.5°. At the most northern station, M281 in lat. 19°N, nearly pure North Atlantic water was encountered.
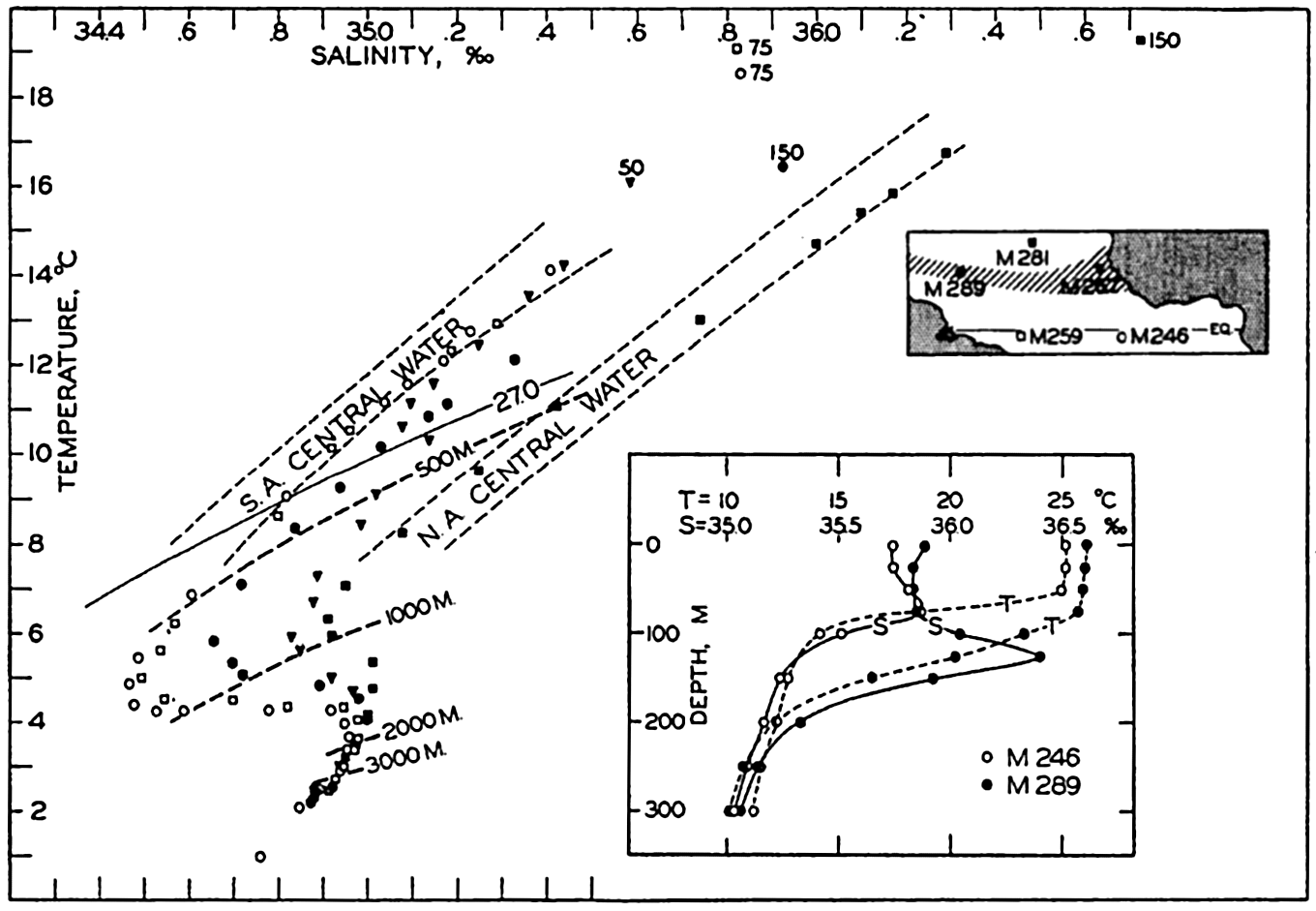
Temperature-salinity relation in the equatorial region of the Atlantic Ocean. Inset map shows location of Meteor stations used, and inset diagram shows vertical distribution of temperature and salinity at Meteor station 246 in 2°40′S, 16°37′W, and at Meteor station 289 in 11°02′N, 49°33′W.
In the figure are entered lines joining the T-S points at the different stations, which represent conditions at depths of 500, 1000, 2000, and 3000 m, and the line σt = 27.0 is shown. At 500 m there is a wide range in the temperature and salinity of the water but the density is practically constant, as is evident from the fact that the 500-m line in the diagram nearly coincides with a σt curve. At 1000 m there is still a considerable spread of temperatures and salinities, but a constant density, whereas at 2000 and 3000 m the variations in temperatures and salinities are nearly within the limits of the accuracy of the observation. The uniformity of the deep water is brought out by the close spacing of the 2000- and 3000-m marks.
In the equatorial region, the water masses which have been dealt with so far are separated from the surface waters by a layer within which the density increases so rapidly with depth that it has the character of a discontinuity layer. The existence of this discontinuity layer is illustrated by the inset diagram in fig. 170, showing the vertical distribution of temperature and salinity at Meteor stations 246 and 289. At the latter station a distinct salinity maximum was present in the discontinuity layer, such as is the case within large areas (Defant, 1936b).
The discontinuity layer is explained mainly as a result of heating of the surface water due to the absorption of radiation from the sun and forced mixing due to wind. The water comes from higher latitudes and has originally a relatively low temperature. As the heating and mixing penetrates to greater and greater depths, the differences in density between the warm surface waters and the colder subsurface strata are concentrated in a thinner and thinner layer within which the stratification becomes more and more stable. When the stratification has become so stable that the layer takes the character of a discontinuity surface, further mixing is inhibited because the eddy conductivity is greatly reduced by the exceedingly great stability (p. 476) and the amounts of heat which are conducted downwards become so small that they are carried away by weak currents. Additional absorption of solar energy is used mainly for evaporation, and the final temperature which is attained will depend upon the rate of evaporation and is therefore determined by the interaction between the atmosphere and the ocean.
The Currents of the Equatorial Region of the Atlantic Ocean. In a given locality the thickness of the upper warm layer depends not only upon the intensity of mixing but also upon the character of the circulation in the top layers, because in the presence of currents the discontinuity surface cannot remain horizontal but must slope (p. 444). On the basis of the Meteor data and all other observations available from
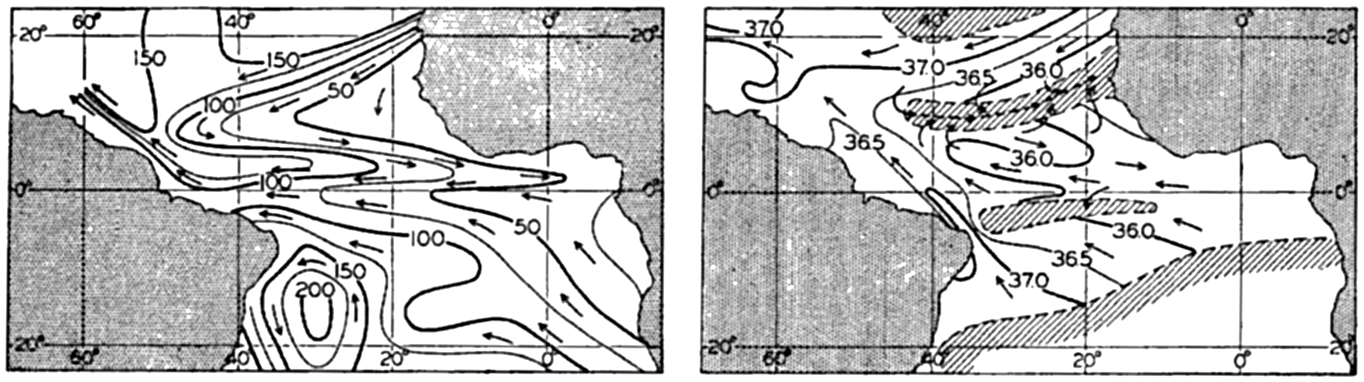
(A) Topography of the discontinuity surface in the Equatorial region of the Atlantic, shown by depth contours in meters, and corresponding currents. (B) Salinity in the layer of maximum salinity below the discontinuity layer and assumed currents. Regions without salinity maximum shaded. (Both representations after Defant.)
Evidently the countercurrent is related to the distribution of mass as demonstrated by the slope of the discontinuity surface. In a profile from south to north the discontinuity surface rises towards the Equator, reaches a maximum elevation at the Equator, and drops towards a minimum in 2° to 3°N latitude, at the northern boundary of the South Equatorial Current. Between 2° to 3°N and 6° to 8°N the discontinuity surface rises towards the north, reaching a second and more pronounced maximum in the latter latitude. This is the region of the countercurrent, and to the north of the second maximum, where the surface slopes downwards again, the North Equatorial Current is found. This distribution of mass was first recognized by means of the Carnegie observations in the Pacific (fig. 198, p. 710). On the basis of these, Sverdrup (1932) suggested that the countercurrent appeared because the trade winds maintaining the equatorial currents are not symmetrical to the Equator, the calm belt between them lying in the Northern Hemisphere, whereas the effect of the rotation of the earth is symmetrical in respect to the Equator.
The dynamics of the countercurrent have recently been discussed by Montgomery (1940) and by Montgomery and Palmén (1940). Montgomery writes:
The trade winds, by continually exerting a westward stress on the sea surface, produce a westward ascent of sea level along the Equator. This slope amounts to about 4 cm per thousand km, and the accompanying pressure gradient extends down to about 150 m in the Atlantic Ocean. The Equatorial Counter Currents are found in the doldrums and apparently result simply as a downslope flow in this zone where the winds maintaining the slope are absent.
The ascent of sea level from east to west is due to a greater accumulation of light surface water along the coasts of South America. Figure 171A shows that such accumulation exists because the thickness of the homogeneous surface layer above the discontinuity surface increases from less than 40 m in the east to about 140 m in the west. Above a depth of 150 m the isosteric surfaces, therefore, slope downwards from east to west, but below 150 m they are practically horizontal. Accordingly, Montgomery and Palmén find that at the Equator the geopotential height of the free surface referred to the 1000-decibar surface is 14 dyn cm greater in the west than in the east, but the 150-decibar surface is parallel to the 1000-decibar surface. The countercurrent is therefore a very shallow current which is confined to the surface layer above the discontinuity.
A swift current which is embedded between water masses moving in the opposite direction must be subject to a considerable retardation owing to friction. A certain amount of energy is therefore needed for maintaining such a current, and this energy is, according to Montgomery and Palmén, derived from the trade winds which maintain the slope of the sea surface. Montgomery and Palmén assume that the retarding friction may be due to lateral mixing with the westward-flowing equatorial currents, and estimate the coefficient of lateral eddy viscosity to be 7 X 107 g/cm/sec. This concept leads to the important conclusion that on both sides of the countercurrent the equatorial currents are subjected to great lateral frictional stresses which are directed opposite to the horizontal stresses exerted by the trade winds on the surface. Similar lateral stresses must be directed opposite to the general flow along the continental boundaries of the two large counterclockwise gyrals of the two
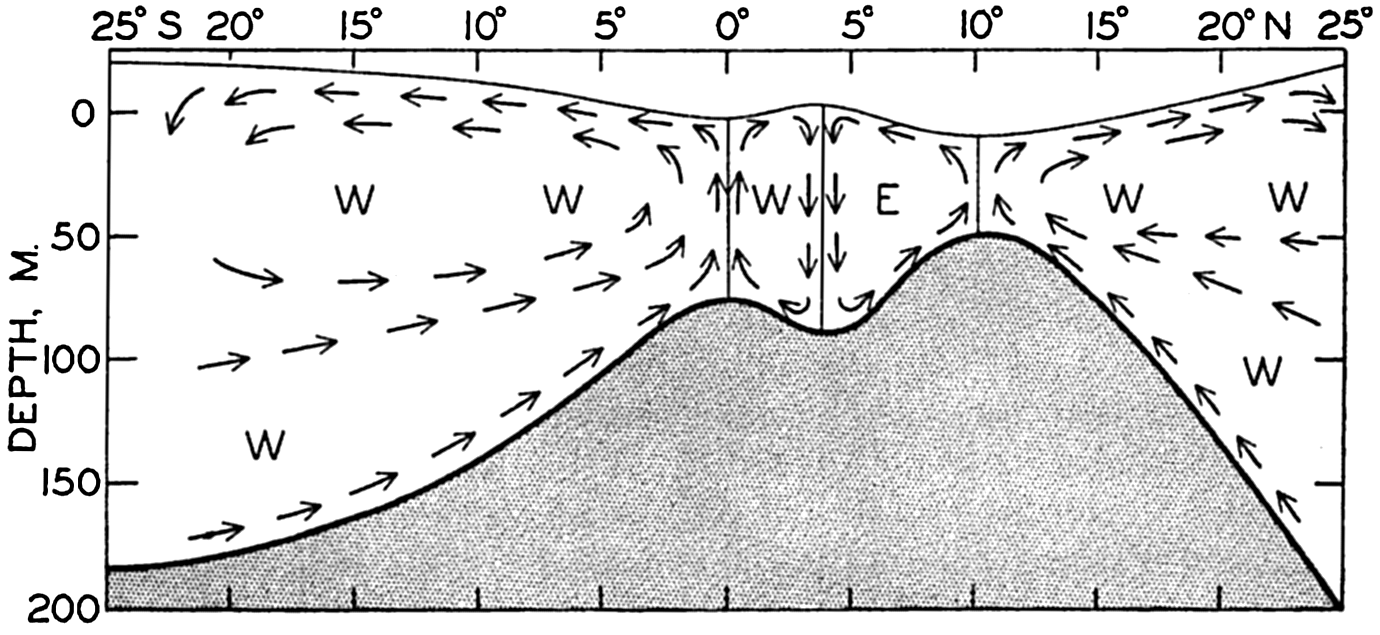
Schematic representation of the vertical circulation within the equatorial region of the Atlantic. The direction of the currents is indicated by the letters W and E. The water below the discontinuity surface, which is supposed to be at rest, is shaded.
Within the countercurrent and the adjacent equatorial currents, the frictional forces must lead to a transport of water across the isolines, that is, to a transverse circulation. This was examined theoretically by Defant (1936b), who considered friction due to vertical mixing, but the conclusions are probably applicable if the friction is due to lateral mixing. Defant's results are shown schematically in fig. 172, according to which four “cells” are present, representing gyrals with horizontal axes, neighboring gyrals rotating in opposite directions. Within the southern cell the water sinks in the region of the Tropical Convergence and rises at the Equator, and within the next cell, located between the Equator and the southern boundary of the countercurrent, the water rises at the Equator and sinks at the boundary of the countercurrent. Within the countercurrent the water rises at the northern and sinks at the southern boundary, and within the northern cell sinking motion takes place at the Tropical Convergence and rising motion at the northern boundary of the countercurrent. The data from the Atlantic Ocean indicate the existence of these cells and the Carnegie section across the Pacific countercurrent (fig. 198, p. 710) demonstrates their presence convincingly. As a consequence of these transverse circulations, the northern boundary of the countercurrent and the Equator represent lines of divergence, whereas
In summer, when the countercurrent is best developed, the effect of the divergence at the Equator appears on the charts of surface temperatures (Böhnecke, 1936) as a tongue of low temperature, but no effect of the divergence at the northern boundary of the countercurrent is visible. The divergences also appear to be of biological importance because the ascending motion maintains a replenishment of nutrients to the surface layers, thus favoring the development of phytoplankton. The tongues of water of high phosphate content and of abundant phytoplankton which extend towards the west from the coast of Africa (see figs. 216 and 217, p. 786) are probably related to the structure of the currents.
In order to study the currents in and below the tropical discontinuity layer, Defant examined the character of the salinity maximum in the discontinuity layer, which is present between lat. 10°S and 20°N except within two narrow bands in about 3°S and 11°N. In fig. 171B the isohalines in the layer of salinity maximum are entered and the areas with and without salinity maxima in the discontinuity layer are indicated (after Defant). Within the discontinuity layer the vertical turbulence must, as already stated, be so much reduced that in this layer the water spread without being mixed with overlying or underlying masses, and the water can therefore move over long distances without losing its characteristics provided no horizontal mixing takes place. In this case the direction of flow must be approximately parallel to the isohalines, and from the chart showing these isohalines it is possible on these assumptions to derive the direction of flow in the discontinuity layer. The arrows in fig. 171B demonstrate the direction of these currents. It should be observed particularly that the belts without salinity maxima appear here as regions of convergence, whereas at the surface they are regions of divergence. This relation is in agreement with the conclusion as to the character of the vertical circulation (fig. 172).
Montgomery (1939) has approached the problem of the subsurface currents near the Equator in an entirely different manner, assuming that the subsurface flow takes place along σt surfaces and that besides the vertical mixing, lateral mixing along σt surfaces determines the distribution of salinity and temperature. He points out that the layer of maximum salinity approximately coincides with the surface σt = 25.5, and has prepared a chart showing that in this surface the isohalines have in general the same form as those in fig. 171B. He furthermore assumes that the principal water motion follows the tongues of low or high salinity, whereas Defant assumes that lines of flow are roughly parallel to the isohalines. The pictures of the current as derived by Defant and
Montgomery points out that the observed distribution of salinity can remain stationary in the presence of the assumed currents if either vertical or lateral mixing dominates. He has computed the possible maximum values of the coefficients and obtained for the vertical one a value which was much greater than is consistent with the great stability of the stratification. If the vertical diffusion is small, the lateral diffusion must determine the character of the salinity distribution. The lateral diffusion was found to be about 4 × 107 cm2/sec, in agreement with the value of the lateral eddy viscosity which was derived by an entirely different method (p. 485). At the present time it is not possible to decide which of the two interpretations is the correct one, but the dynamic consequences of Montgomery's concept appear to fit better into a large-scale picture of the ocean currents.
The chart of the surface currents (chart VII) shows that on an average a transport takes place from the Southern to the Northern Hemisphere in agreement with the conclusions which were based on the Meteor sections between lat. 20°S and 33°S, according to which an average transport to the north of about 8 million m3/sec should take place above a depth of approximately 800 m. It appears that the greater part of this transport, about 6 million m3/sec, takes place within the warm surface layers, for which reason it is probable that this process contributes towards displacing the thermal Equator towards the north. The fact that the surface temperature of the Atlantic Ocean is, in the Southern Hemisphere, lower, but in the Northern Hemisphere higher than that of the Pacific Ocean (see table 31, p. 127), is perhaps related to this transport.
The Adjacent Seas of the North Atlantic Ocean
The water masses and currents of the North Atlantic Ocean can be dealt with more precisely when the waters of the adjacent seas have been discussed, and we shall therefore turn first to the adjacent seas—the Caribbean Sea and the Gulf of Mexico, the Mediterranean and the Black Seas, the Norwegian Sea, the Baltic and the Polar Seas, and the Labrador Sea and Baffin Bay.
The American Mediterranean Sea. The Caribbean Sea and the Gulf of Mexico can be considered together under the name of the American Mediterranean Sea, a name which has been employed particularly by German oceanographers. The Caribbean Sea has the shape of a wide and somewhat irregular channel, the eastern end of which opens towards the tropical part of the North Atlantic (see fig. 6, p. 35). The opening is wide, but is partly closed by the submarine ridge on which the Lesser Antilles lie. In most localities the ridge rises to less than 1000 m below sea level and communication with the open ocean exists,
The water masses of the upper layers enter the Caribbean Sea from the east and show characteristics similar to those of the adjacent North Atlantic waters. Below a thin homogeneous top layer a nearly discontinuous decrease of temperature is found and in most localities a salinity maximum is present within the discontinuity layer. The water masses that enter between the Lesser Antilles show a streaky distribution of salinity, narrow bands of high salinity alternating with bands of low salinity, but these differences are rapidly smoothed out in the Caribbean Sea owing to such intense mixing that the waters flowing through the narrow passages of the Yucatan Channel and the Straits of Florida are of more uniform character.
The upper waters that flow into the Caribbean Sea are mainly of North Atlantic origin but contain a considerable admixture of South Atlantic water. The relative amounts of the two types of water can be approximately determined by a comparison between the temperatures and salinities of the South Atlantic water that crosses the Equator, the waters passing through the Yucatan Channel, and the water from the western Sargasso Sea, the T-S relations of which have been examined by Iselin (1936). Table 77 contains corresponding temperatures and salinities of these three water masses at different σt values. The last column in the table gives the ratio between the amounts of South Atlantic and North Atlantic water that pass through the Yucatan Channel. It is seen that at higher temperatures the current through the Channel carries about one part of South Atlantic and three and one half parts of North Atlantic water. The total transport is about 26 million m3/sec,
Below the upper water a considerable amount of Antarctic Intermediate Water enters the Caribbean Sea, such that the water at the intermediate salinity minimum is mainly of South Atlantic origin, as pointed out by Nielsen (1925) and Parr (1937). The intermediate salinity minimum in the Caribbean Sea decreases in intensity in the direction of flow. In the eastern part of the Caribbean Sea, in about longitude 68°W, the average minimum salinity is 34.73 ‰, whereas in the Yucatan Channel the average minimum salinity is 34.88 ‰. This increase in salinity is, according to Seiwell (1938), mainly due to vertical mixing within the moving water mass.
| Value of σt | A South Atlantic | B West Sargasso Sea | Yucatan Channel | Ratio A/B in Yucatan Channel | |||
|---|---|---|---|---|---|---|---|
| Temp. (°C) | S (‰) | Temp. (°C) | S (‰) | Temp. (°C) | S (‰) | ||
| 26.4 | 15.8 | 35.64 | 18.3 | 36.55 | 17.8 | 36.38 | 1/4 |
| 26.6 | 13.6 | 35.39 | 16.8 | 36.32 | 16.1 | 36.11 | 1/3.5 |
| 26.8 | 11.3 | 35.08 | 14.8 | 35.98 | 13.9 | 35.74 | 1/3 |
| 27.0 | 9.0 | 34.82 | 12.4 | 35.61 | 11.6 | 35.40 | 1/3 |
| 27.2 | 6.0 | 34.52 | 10.0 | 35.29 | 8.7 | 35.03 | 1/2 |
The deeper portion of the American Mediterranean Sea is divided into a series of basins, the most important being the Venezuela and Colombia basins in the eastern Caribbean Sea, the Cayman Trough and the Yucatan Basin in the western Caribbean Sea, and the Mexico Basin in the Gulf of Mexico. The character of the deep water in these basins depends upon their communications with the adjacent parts of the North Atlantic Ocean and upon the intercommunications between the basins. The greatest depth of the sills separating the basins of the eastern Caribbean from the North Atlantic are found in the Anegada and Jungfern Passages, between which lies the small St. Croix Basin. Figure 173 shows the distribution of potential temperature in a section passing from the Atlantic through the Anegada Passage, the St. Croix Basin, and the Jungfern Passage into the Venezuela Basin (Dietrich, 1939). It appears from this distribution that the sill depth of the Anegada Passage is somewhat greater than that of the Jungfern Passage,
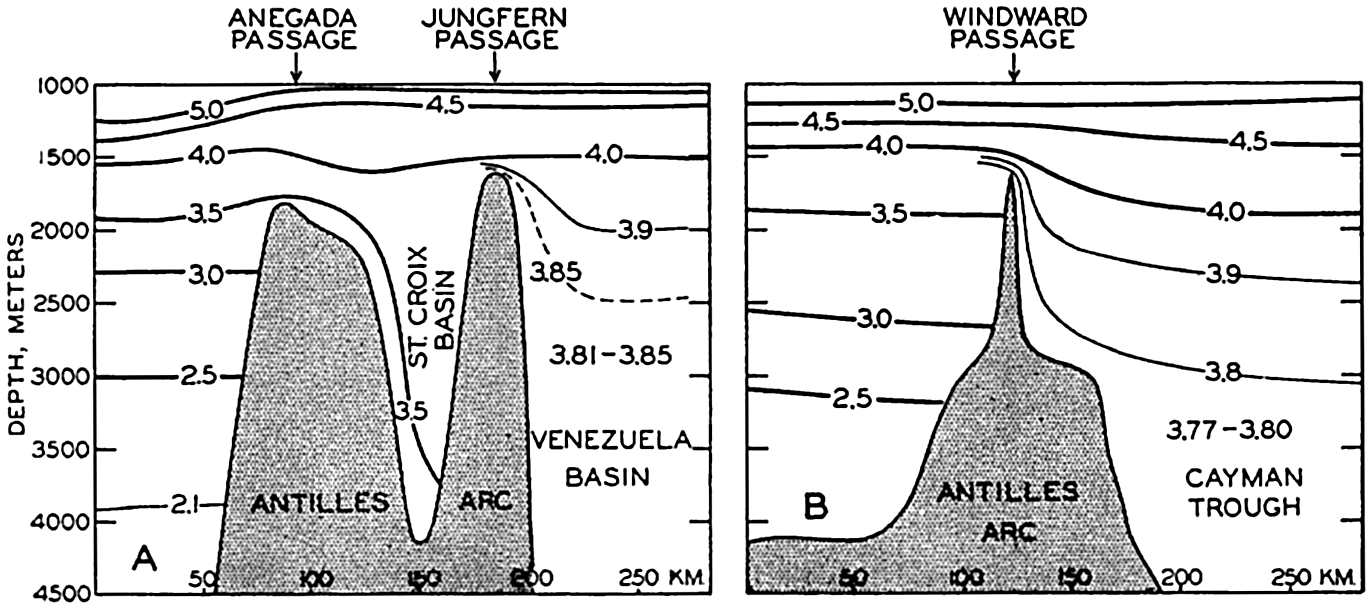
Sill depths between the Atlantic Ocean and the Caribbean Sea according to temperature observations. (A) potential temperature in a vertical section through the Anegada and Jungfern Passages. (B) Potential temperature in a vertical section through the Windward passage (after Dietrich).
The sill depth of the Jamaica Rise, which separates the western Caribbean Sea from the eastern, is less than the sill depth of the Windward Passage. The deep water of Cayman Trough and the Yucatan Basin is therefore renewed through the Windward Passage which, according to the distribution of potential temperature (fig. 173), must have a sill depth of approximately 1600 m. The renewal of the deep water in these basins appears to be even more rapid because the average oxygen content in the Yucatan Basin and the Cayman Trough is, at 2500 m, between 5.5 and 6.0 ml/L.
The deepest connection between the Mexico Basin and the adjacent seas is found in the Yucatan Channel, and the deep water of the Mexico Basin is therefore renewed from the Yucatan Basin by flow across the sill in the Yucatan Channel. The sill depth is not exactly known but is probably somewhat less than the sill depth of the Windward Passage, because the potential temperature of the water in the Mexico Basin is about 3.95° as compared to 3.85° in the Yucatan Basin. The passages to the north of Cuba are much more shallow and no renewal of deep water can take place through them. Even in the case of the Mexico
The different sill depths have not yet been established by means of soundings, and the depths given above are all based on studies of the hydrographic conditions. These can be interpreted in several manners and different values of the sill depths have therefore been arrived at by different authors, but in the above we have followed Dietrich's presentation (1939), which appears to combine the known facts in the most satisfactory manner. Dietrich has also been able to plot the potential temperatures at depths greater than 2500 m, and these show a remarkable regularity in spite of the fact that the greatest differences observed in the single basins do not exceed 0.05°. The arrangement of the potential temperatures further supports the conclusions as to the localities at which inflow of deep water into the basins takes place.
The salinity of the deep water is very uniform. According to Parr (1937) the average salinity is 34.98 ‰ and the deviations from this value are within the probable errors of the salinity determinations.
It is evident from this summary that the American Mediterranean Sea does not exercise any influence upon the deep-water circulation of the Atlantic Ocean, but it may exercise a considerable influence on the circulation in the upper layers.
The surface currents in spring are shown in fig. 174. A strong current passes through the Caribbean Sea, continues with increased speed through the Yucatan Channel, bends sharply to the right, and flows with great velocity out through the Straits of Florida. On the flanks of the main current numerous eddies are present, of which the one in the wide bay between Nicaragua and Colombia and the one between Cuba and Jamaica are particularly conspicuous. In the Gulf of Mexico several large eddies exist, and all of these appear to be semipermanent features, the locations of which are determined by the contours of the coast and the configuration of the bottom.
The presentation of the currents in fig. 174 is based on ships’ observations. When attempting a calculation of currents by means of numerous Atlantis data from the Caribbean Sea, Parr (1937) found that the flow is not directed parallel to the contours of the isobaric surfaces, but between the Lesser Antilles and the Yucatan Channel the current flows uphill. Parr suggested that this feature may be due to piling up of water in front of the narrow Yucatan Channel, caused by the stress exerted on the surface by the prevailing easterly winds. This idea was further examined by Sverdrup (1939b), who concluded that the piling up of the surface water can be fully explained as the effect of winds blowing with an average velocity of about 10 m/sec, which agrees well with the observed values in spring. A further consequence of this piling up is that in the Gulf of Mexico a higher sea level is maintained than along the adjacent coast of
Regardless of the effect of the stress of the wind or the existence of a hydrostatic head, the mass distribution must adjust itself to the major currents that are present. In general, the lighter water is therefore found on the right-hand side of the current and the sea surface rises to the right when looking in the direction of flow. This rise to the right is particularly conspicuous within a swift and narrow current and, in the case of the Florida Current, it has been computed that at the north coast of Cuba sea level must be about 45 cm higher than at Key West, Florida (Dietrich, 1936, Montgomery, 1938). The Florida Current will be further dealt with when discussing the Gulf Stream System of the North Atlantic, but in this place it should be pointed out that, according to Dietrich (1939), the Florida Current is essentially a direct continuation of the current through the Yucatan Channel and that the waters of the Gulf of Mexico mainly form independent eddies and are only to a small extent drawn into the Straits of Florida.
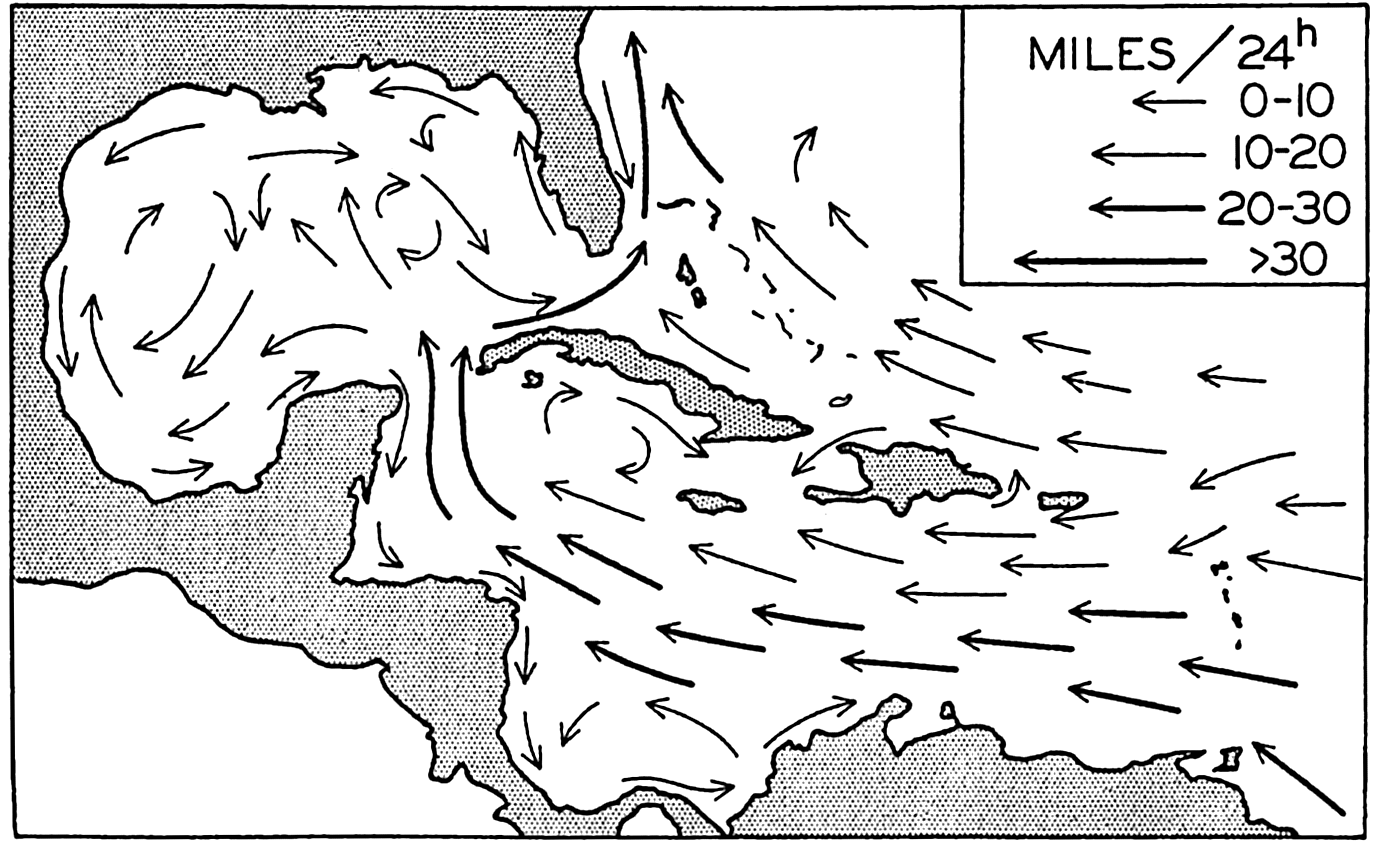
Surface currents in spring in the American Mediterranean Sea (after Dietrich).
The European Mediterranean Sea. From the oceanographic point of view the waters of the Mediterranean Sea are basin water masses which are in communication with the Atlantic Ocean only through the
The Mediterranean proper is divided into a series of deep basins more or less isolated from each other. The most outstanding of these are, in the western Mediterranean, the Algiers-Provençal Basin to the west of Sardinia and Corsica and the Tyrrhenian Basin on the west side of Italy, and, in the eastern Mediterranean, the Ionian Basin to the south of Italy and Greece and the Levantine Basin to the south of Asia Minor (fig. 5, p. 34). The two former basins are separated from the two latter by shallow ridges between Tunisia and Sicily, whereas the two basins in the western Mediterranean Sea and the two basins in the eastern Mediterranean Sea are separated by deep sills.
In the Mediterranean Sea proper (not including the Black Sea), evaporation greatly exceeds precipitation and runoff, and in winter deep water of very high salinity is formed in different places by vertical convection currents. The Mediterranean proper belongs, therefore, to the first type of basin (p. 147), in which deep water of great density is formed with outflow over the sill and inflow at the surface.
The water masses of the Mediterranean are characteristically different from those of the adjacent North Atlantic, because, owing to the isolation, the deep water has a higher temperature. The Atlantic water which flows into the Mediterranean Sea is so rapidly mixed with Mediterranean surface water that it soon loses its Atlantic character. The surface salinity is higher than 37.00 ‰, except where the surface current flows to the east along the north coast of Africa as far east as Tunisia, and in the inner portion of the Adriatic Sea and the Aegean Sea, where there is a considerable addition of river water or surface water from the Black Sea. It is above 39 ‰ to the south of Asia Minor. The surface salinity is subjected to seasonal variations, but these are not known in detail. The surface temperature generally increases from the Strait of Gibraltar to the inner portions, except in winter, when the lowest surface temperatures are found in the most northerly portions, namely off the French and Italian Rivieras and in the inner portions of the Adriatic and Aegean Seas. The seasonal variation in temperature is great, the annual range everywhere exceeding 9° and reaching 13° to 14° off the Riviera and in the northern part of the Adriatic Sea.
Below the surface four different water masses are encountered, including a thick transition layer which separates the intermediate water from
The surface water generally extends to a depth of 100 to 200 m. In the western Mediterranean the lower limit of the surface water is indicated by a temperature minimum, as seen at station 4119, whereas in the eastern Mediterranean the temperature minimum is generally absent and a layer of slow temperature decrease is found instead, as seen at station 4070. The depth of the temperature minimum or the depth of the layer of slow decrease represents the depth to which vertical convection currents ordinarily reach in winter, and the temperature and salinity at the depth of the minimum or in the layer of small decrease correspond to the surface values in winter.
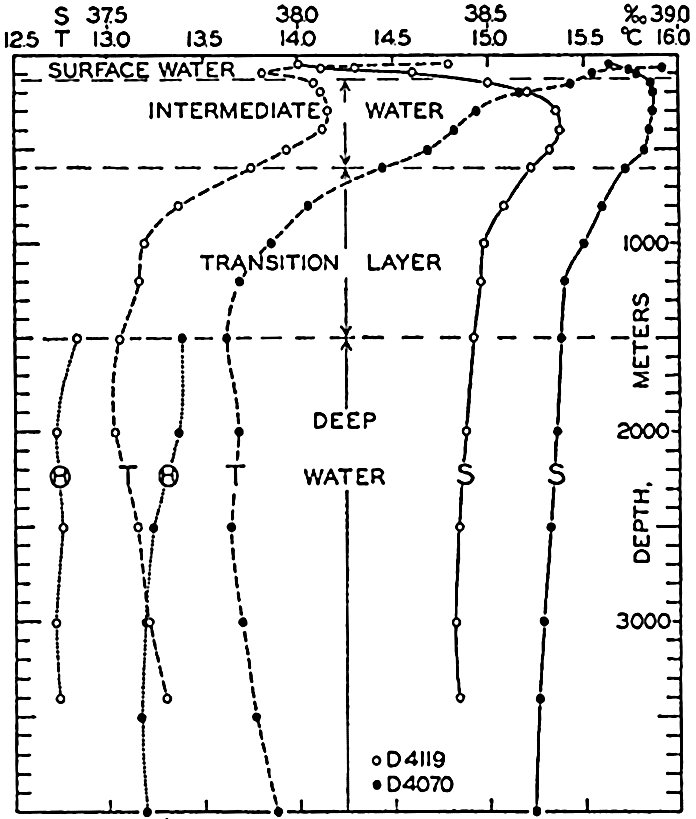
Character of the water masses in the Mediterranean Sea illustrated by curves showing the vertical distribution of temperature (T), salinity (S), and potential temperature (θ) at the Dana stations 4119 in 40°13′N, 12°06′E, and 4070 in 35°40.5'N, 21°54'E.
Below the surface layer one finds, in the greater part of the Mediterranean, an intermediate water which is characterized by a salinity maximum at a depth of 300 to 400 m. In the western sea a temperature maximum is present at nearly the same depth, but in the eastern sea only a second layer of small temperature decrease is found. This intermediate water, according to Nielsen (1912), is formed in the inner part of the Mediterranean, from where it spreads towards the west and finally flows out through the Strait of Gibraltar. At the Thor stations 178 and 160, in about long. 30°E, no subsurface salinity maximum was present but the salinity decreased regularly from the surface. Between 175 and 200 m the temperature remained constant, and this layer of constant temperature represents both the layer to which convection currents reach in winter and the layer of intermediate water which originates in that part of the sea. As this water spreads to the west, the salinity and the temperature at the core decrease owing to mixing processes.
The lower boundary of the intermediate water can be placed, somewhat arbitrarily, at about 600 m, where both temperature and salinity
| Basin | Temperature (°C) | Potential temperature (°C) | Salinity (‰) |
|---|---|---|---|
| Algiers-Provençal | 13.00 | 12.69 | 38.39 |
| Tyrrhenian | 13.10 | 12.79 | 38.44 |
| Ionian | 13.57 | 13.25 | 38.65 |
| Levantine | 13.62 | 13.30 | 38.66 |
These data show that there is an appreciable difference between the western and eastern basins, which are separated by the rise between Tunisia and Sicily.
The deep and bottom water in the different basins is formed in localities in which the intermediate water is lacking and where convection currents in winter can reach from the surface to the bottom. Nielsen shows that the bottom water of the western basins originates mainly from the northern parts of the Balearic and Ligurian Seas, off the French and Italian Rivieras. At the Thor station 37, which was occupied on January 30, 1909, in lat. 41°56′N, long. 6°18′E, nearly uniform density was found between the surface and 2000 m. The average value of σt was 29.04, and the greatest deviations from the average were ±0.04. The temperature at the surface was 12.40°, and the potential temperature at 2000 m was 12.70°, the salinities were 38.24 ‰ and 38.35 ‰, respectively. Even more extreme conditions were observed by Nathansohn
Nielsen believes that the formation of bottom water takes place intermittently and this concept is substantiated by the potential temperatures at station 4070, which were constant at 13.38° between 1500 and 2000 m and at 13.19° below 2500 m, indicating that slightly different water is formed under different conditions (fig. 175). Nielsen furthermore emphasizes that the uniform character of the deep and bottom water in a horizontal direction demonstrates active horizontal movement at great depth.
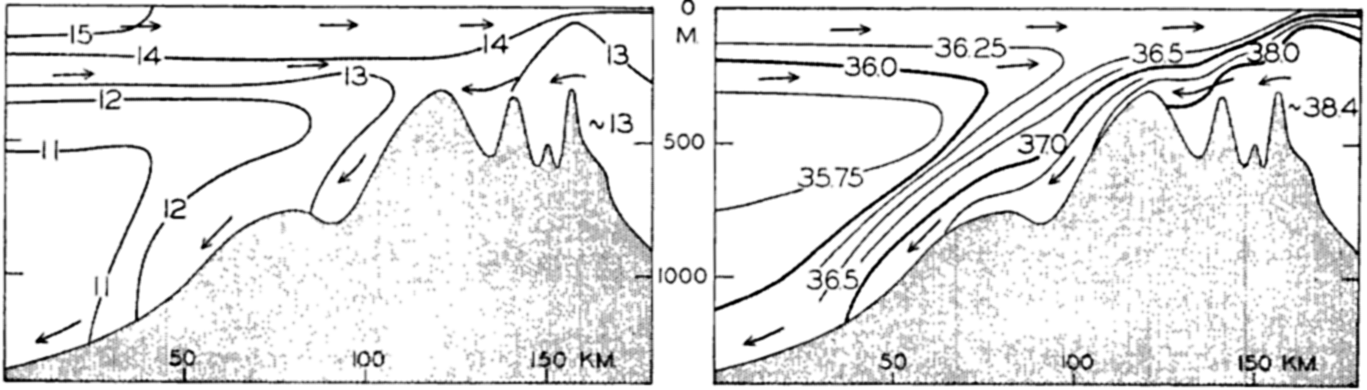
Temperature and salinity in a vertical section through the Strait of Gibraltar.
The water that sinks from the surface in order to renew the deep water must be replaced, and such replacement is accounted for by an inflow of Atlantic water. The exchange of water between the North Atlantic Ocean and the Mediterranean takes place through the Strait of Gibraltar, which is noted for its strong currents. The bottom topography of the Strait is complicated; in its shallow portion two or possibly three ridges are present with sill depths of about 320 m. The character of the water masses passing in and out through the Strait of Gibraltar is illustrated in fig. 176, showing isohalines and isotherms in a longitudinal section through the Strait. The observations used for perparing this section were made in late spring and early summer, in the months of May, June, and July of different years (Schott, 1928, Ramalho and Dentinho, 1931).
In the upper layers Atlantic water of a salinity somewhat higher than 36.00 ‰ and a temperature
The average velocity of the total inflow, according to measurements on Danish expeditions, is approximately 100 cm/sec (2 knots). By means of this value Schott (1915) has computed the inflow to be approximately 1.75 million m3/sec. The outflow can be computed by means of the relations on page 148. Such computations have been made by Nielsen (1912) and Schott (1915), but subsequent data indicate that they have assumed somewhat too high values for the salinity of the outflowing water. From the sections published by Schott in 1928 it appears that the average salinity of the inflowing water should be, in the Strait of Gibraltar, about 36.25 ‰ and that of the outflowing water should be not more than 37.75 ‰. With these values one obtains an outflow of 1.68 million m3/sec and the difference between inflow and outflow, 70,000 m3/sec, represents the excess of evaporation over precipitation and runoff. A fraction of this excess is made up, however, by a net inflow from the Black Sea, amounting to 6500 m3/sec (p. 650).
The exchange of water through the Strait of Gibraltar presents a good example of how water from one region can be transformed by external influences and return as a different type of water, in this case as water of high salinity. The rapidity of the exchange is illustrated by stating that the in- and outflow is sufficient to provide for a complete renewal of the Mediterranean water in about seventy-five years.
Using the figures which Schott gives for precipitation and runoff, one arrives at the water budget of the Mediterranean Sea proper, which is summarized in table 78. From this it appears that the total evaporation amounts to 115,400 m3/sec, corresponding to an annual evaporation of 145 cm, which is in fair agreement with the annual evaporation in these latitudes according to observations and computations (fig. 27, p.121).
This discussion brings out a very characteristic difference between the Mediterranean Sea and the American Mediterranean Sea. The Mediterranean Sea exercises no great influence on the surface currents of the Atlantic Ocean because the amount of water that flows in through the Strait of Gibraltar represents a small fraction of the water masses that are transported by currents of the upper water layers; but the Mediterranean exercises a widespread influence on the deep water of the North Atlantic by adding appreciable quantities of water of high salinity. The American Mediterranean Sea, on the other hand, exercises a great influence upon the currents of the upper layers because large water masses flow into the Caribbean Sea and out of the Gulf of Mexico, and the types of currents are greatly modified by the character of the passages; but the importance of the American Mediterranean Sea to the deep-water circulation is negligible.
| Gains | m3/sec | Losses | m3/sec |
|---|---|---|---|
| Inflow from the Atlantic Ocean | 1,750,000 | Outflow to the Atlantic Ocean | 1,680,000 |
| Inflow from the Black Sea | 12,600 | Outflow to the Black Sea | 6,100 |
| Precipitation | 31,600 | Evaporation | 115,400 |
| Run-off | 7,300 | ||
| 1,801,500 | 1,801,500 |
Within the Mediterranean an exchange of water takes place across the submarine ridge between Tunisia and Sicily that is similar to the exchange through the Strait of Gibraltar. Surface water of Atlantic origin and of salinity about 37.20 ‰ flows towards the west through the channel which cuts the ridge between Tunis and Sicily at a depth of about 400 m. According to Nielsen about 4 per cent of the inflowing water is lost by excess evaporation in the eastern Mediterranean, whereas 96 per cent is carried out again by the intermediate current after the salinity has been increased by about 1.5 parts per mille.
In fig. 177 a schematic picture is given of the surface currents and the flow of the intermediate water (according to Nielsen, 1912). It is seen that both surface currents and intermediate currents have a tendency to circle the different areas in a counterclockwise direction.
The distribution of oxygen confirms the conclusions as to the origin of the different water masses of the Mediterranean and the flow of water.
The surface water, which extends to a depth of 100 to 200 m, shows a high oxygen content. The oxygen content of the intermediate water is relatively high in the eastern Mediterranean where this water is formed, but decreases toward the west, the lowest values being found in the western part of the Mediterranean area, the Balearic Sea. The transition layer between the intermediate and the deep water is characterized by an oxygen minimum that is more conspicuous in the eastern than in the western regions. The deep water has a somewhat higher oxygen content, the highest value being found in the Balearic Sea, where the formation of deep water is probably most rapid. These general features are shown in table 79, which is based upon the Thor and the Dana observations in the summers of 1910 and 1930. For three different areas, the Ionian, Tyrrhenian, and the Balearic Seas, the table contains mean values of temperature, salinity, and oxygen at the layer of salinity maximum, at the layer of oxygen minimum, and below 2000 m. It also gives average depths of the salinity maximum and the oxygen minimum within the different areas. The observations from 1910 and 1930 agree remarkably well in the western Mediterranean, but in the Ionian Sea the oxygen values and the salinity values were on the whole higher in 1930 than in 1910, indicating that in different years the formation of intermediate water may be more or less intense.
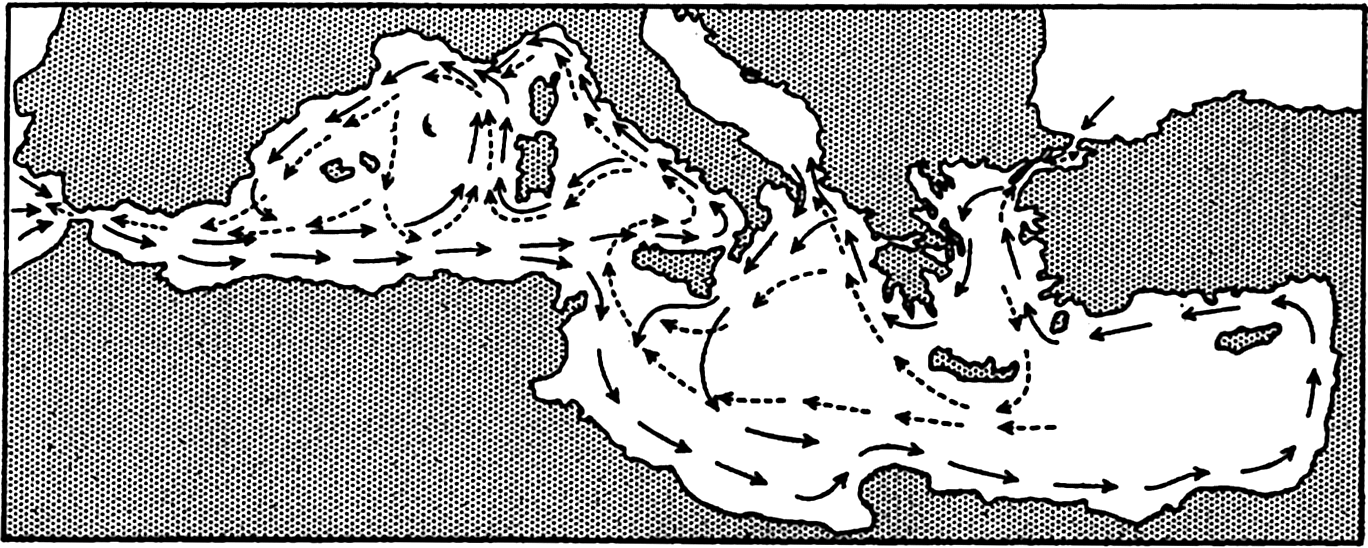
Surface currents (solid arrows) and currents at intermediate depths (dashed arrows) in the Mediterranean Sea (after Nielsen).
The water masses of the Black Sea are entirely different from those of the Mediterranean proper. In the Black Sea precipitation and runoff exceed evaporation, for which reason a surface layer is present of relatively low salinity and correspondingly low density. Vertical mixing tends to reduce the density of the deep water, which therefore has a lower density than that of the water in the Mediterranean Sea proper at the same depth. The character of the waters of the Black Sea is seen from table 80, containing some of the observations at Thor Station 172, about 100 m inside the Bosporus.
Owing to the distribution of density, the surface waters of the Black Sea flow out through the Bosporus and through the Dardanelles, and Mediterranean water flows in along the bottom. Intensive mixing takes place in these narrow straits, and the salinity of the inflowing water is therefore reduced from more than 38.50 ‰ at the entrance of the Dardanelles to between 35.00 and 30.00 ‰ where the bottom current enters the Black Sea at the northern end of the Bosporus. Similarly, the salinity of the outflowing water is increased from about 16.00 ‰ where it enters the Bosporus to nearly 30.00 ‰ where it leaves the Dardanelles. The out- and inflowing water masses are separated by a well-defined layer of transition which oscillates up and down according to the contours of the bottom. The currents through the Bosporus can well be compared to two rivers flowing one above the other in a river bed which has a width of about 4 km (2 miles) and a depth of 40 to 90 m.
| Location | Depth (m) | Temp. (°C) | S (‰) | O2 (ml/L) | |
|---|---|---|---|---|---|
| At salinity maximum | Ionian Sea | 250 | 14.59 | 38.83 | 4.84 |
| Tyrrhenian Sea | 420 | 13.91 | 38.65 | 4.30 | |
| Balearic Sea | 390 | 13.18 | 38.47 | 4.16 | |
| At oxygen minimum | Ionian Sea | 1180 | 13.59 | 38.68 | 4.01 |
| Tyrrhenian Sea | 960 | 13.30 | 38.51 | 4.12 | |
| Balearic Sea | 580 | 13.07 | 38.44 | 4.10 | |
| Below 2000 m | Ionian Sea | 13.67 | 38.64 | 4.14 | |
| Tyrrhenian Sea | 13.23 | 38.41 | 4.25 | ||
| Balearic Sea | 13.06 | 38.39 | 4.55 | ||
Appreciable water masses pass through the Bosporus. According to current measurements and other observations by A. Merz (L. Möller, 1928), the most probable values of the out- and inflow through it are 12,600 m3/sec and 6,100 m3/sec, respectively. (The Mississippi River carries, on an average, 120,000 m3/sec.) The difference between inflow and outflow, 6,500 m3/sec, represents the excess of precipitation and runoff over the evaporation. Precipitation and runoff have been estimated at 7,600 and 10,400 m3/sec, respectively, and the evaporation should therefore amount to 11,500 m3/sec or 354 km3/year. The area of the Black Sea is 420,000 km2 and the above value therefore corresponds to an evaporation of 84 cm per year, in good agreement with observed and computed values for this latitude (p. 121).
For the Black Sea the out- and inflowing water masses are of the same order of magnitude as the difference between precipitation plus
| Depth (m) | Temp. (°C) | S (‰) | σt | O2 (ml/L) | H2S (ml/L) |
|---|---|---|---|---|---|
| 0 | 24.1 | 17.59 | 10.56 | 5.14 | |
| 10 | 24.1 | 17.59 | 10.56 | 5.14 | |
| 25 | 12.73 | 18.22 | 13.54 | 7.40 | |
| 50 | 8.22 | 18.30 | 13.22 | 6.71 | |
| 75 | 7.44 | 18.69 | 14.62 | 5.51 | |
| 100 | 7.61 | 19.65 | 15.33 | 2.33 | |
| 150 | 8.31 | 20.75 | 16.12 | 0.17 | |
| 200 | 8.54 | 21.29 | 16.51 | 0.90 | |
| 300 | 8.68 | 21.71 | 16.82 | 2.34 | |
| 400 | 8.72 | 21.91 | 16.97 | 4.17 | |
| 600 | 8.76 | 22.16 | 17.16 | 4.96 | |
| 800 | 8.80 | 22.21 | 17.19 | 6.06 | |
| 1000 | 8.85 | 22.27 | 17.24 | 6.04 |
The Arctic Mediterranean Sea. Under the name “Arctic Mediterranean Sea” are understood the areas to the north of the Wyville Thomson Ridge between the Orkneys and Faeroe Islands, the Faeroe Islands-Iceland Ridge, and the Iceland-Greenland Ridge. Exchange of water between the Atlantic Ocean and the Arctic Mediterranean Sea takes place across these ridges. In addition, the water masses of the Arctic Mediterranean are in restricted communication with those of the Atlantic through the English Channel and through the narrow sounds to the west of Greenland, and with the waters of the Pacific Ocean through Bering Strait. The Arctic Mediterranean is the largest of all adjacent seas and is subdivided into a number of distinct areas, of which the more important are the Norwegian Sea, the North Sea, the Baltic
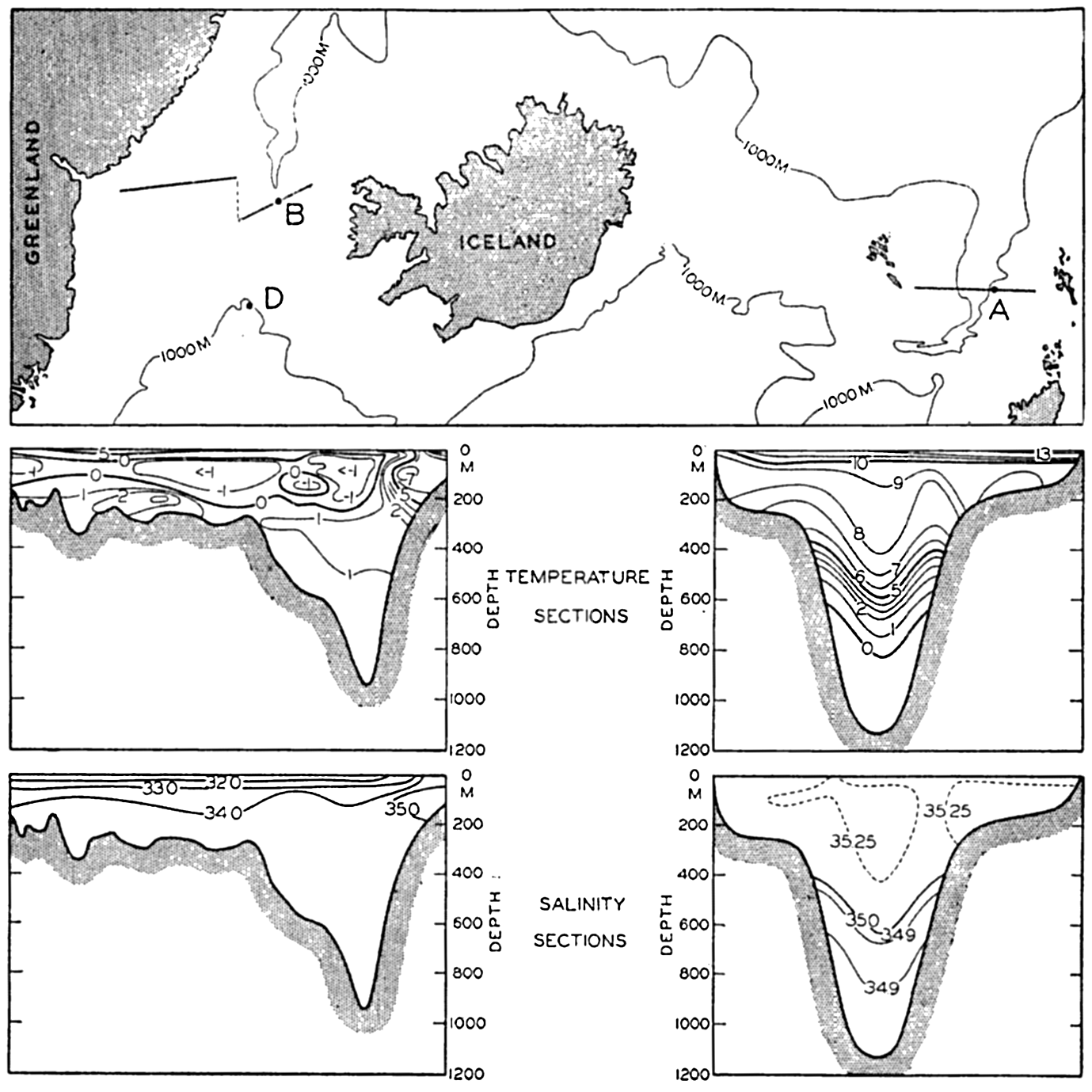
Chart of the important openings between the Atlantic Ocean and the Arctic Mediterranean Sea, and vertical sections showing distribution of temperature and salinity in the Faeroe-Shetland Channel (right) and in the Denmark Strait (left). Stations A, B and D are shown, but station C lies outside of the region covered by the chart.
Much the major exchange of water between the Arctic Mediterranean and the adjacent oceanic regions takes place through the straits between Scotland and Greenland. The character of the exchange is radically different from that between the Atlantic Ocean and the Mediterranean Sea, where inflow of Atlantic water takes place in the upper layers of the Strait of Gibraltar and outflow near the bottom. The opening between the Atlantic Ocean and the Arctic Mediterranean is so wide that the water flows in through the southeastern part of the opening and out through the northwestern. The character of the water masses is illustrated
The great difference between the inflowing Atlantic water masses and the outflowing Arctic water is illustrated in fig. 179. In the main part of the figure, T-S curves are plotted showing the character of the waters at Michael Sars station 106 (A), which was occupied in the Faeroe-Shetland Channel on August 10 and 11, 1910, and at the Heimdal station 47 (B), which was occupied in the channel to the north of the Iceland-Greenland Ridge on July 22, 1933. The inset diagram shows T-S curves which are drawn on a much wider salinity scale, demonstrating the character of the waters at Michael Sars station 106 (A); at Michael Sars station 100 (C), which was occupied to the southwest of the Wyville Thomson Ridge on August 6, 1910; and at the Heimdal station 33 (D), which was occupied to the south of the Iceland-Greenland Ridge on July 17, 1933. The last two stations have been added in order to demonstrate the similarity between the waters in the Faeroe-Shetland Channel above 600 m and the water masses to the south of the Ridge on the entire distance from the Orkneys to Greenland. The inset diagram demonstrates that one has to deal here with exactly the same water mass, but water which to the north of the Wyville Thomson Ridge was found at a depth of 600 m, south of the ridge was present at 1200 m, and to the west of Iceland was present at 800 m.
The similarity of the water masses at Michael Sars station 100 and Heimdal station 33 shows that only part of the Atlantic water flows across the Wyville Thomson Ridge and that part bends towards the west and flows towards Greenland. This current will be dealt with later
On the southern side of the barrier, Atlantic water is present to the greatest depths except along the continental shelf of Greenland, where the Polar Current flows south, but on the northern side of the barrier and below the sill depths the water masses have a uniform salinity of about 34.92 ‰ and a temperature below 0°. This deep water, formed in the Norwegian Sea, has a greater density than the Atlantic water at corresponding depths, but there is no evidence of an outflow of this water across the sills. At the Wyville Thomson Ridge the deep water of the Norwegian Sea does not reach up to the sill depth, whereas at the Iceland-Greenland Ridge it does, as is evident from the Heimdal observations, but no trace of that deep water was present at Heimdal station 33 on the southern side of the ridge (see curve D, fig. 179) nor at any of the Meteor stations in the same region (Defant et al, 1936).
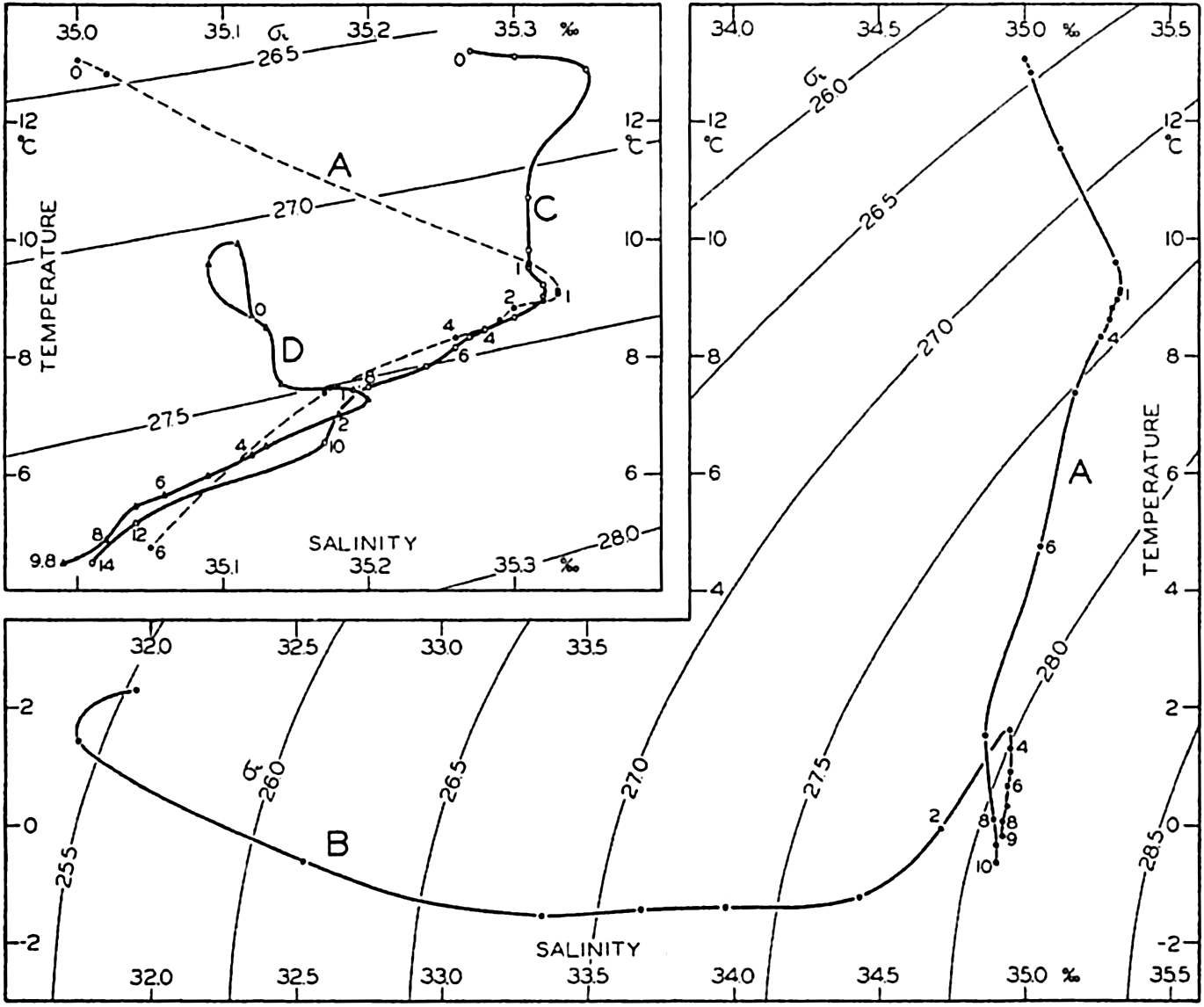
Temperature-salinity relations at stations in the Faeroe-Shetland Channel (A) and in Denmark Strait (B). Inset: Temperature-salinity relations at stations southwest of the Wyville Thomson Ridge (C) and south of the Iceland-Greenland Ridge (D). Depths in hectometers are entered along the curves. Locations of stations A, B, and D are shown in fig. 178.
Helland-Hansen (1934) has computed the volumes of Atlantic water that in May, 1927 and May, 1929, flowed north through a section from lat. 60°40′ on the coast of Norway to lat. 63°20′, long. 4°W, northwest of the Faeroe Islands. He found 2.78 and 3.31 million m3/sec respectively, and the average inflow of Atlantic water may therefore be estimated at about 3 million m3/sec.
In addition to the inflow of Atlantic water, an inflow of Bering Sea water takes place through Bering Strait. On August 1, 1934, the United States Coast Guard Cutter Chelan anchored in Bering Strait and measured currents between the surface and the bottom during 21 hours. From these measurements it was concluded (U. S. Coast Guard, 1936) that the transport inward through Bering Strait was 0.88 million m3/sec, but the average annual transport is probably much smaller because the inflow is less regular and weaker in winter. It does not seem probable that the average inflow during the year exceeds 0.3 million m3/sec.
The Arctic Mediterranean also receives a considerable amount of fresh water in the form of runoff from the great Siberian and Canadian rivers and from excess of precipitation over evaporation. The runoff from the Siberian rivers averages, according to Zubov (1940), about 0.16 million m3/sec. The excess precipitation over the North Sea and the Norwegian Sea can be estimated at about 0.5 m per year, and over the Arctic Sea, where the precipitation is small, at about 0.12 m per year. On this basis one finds a total excess of precipitation of about 0.09 million m3/sec.
The outflow from the Arctic Mediterranean Sea takes place principally through the Denmark Strait, for which reason the water budget of the region can be presented as follows:
| Inflow northwest of Scotland | 3.0 million m3/sec |
| Inflow through Bering Strait | 0.3 million m3/sec |
| Runoff from rivers | 0.16 million m3/sec |
| Excess precipitation | 0.09 million m3/sec |
| Inflow and addition of fresh water | 3.55 million m3/sec |
| Outflow through Denmark Strait | 3.55 million m3/sec |
On the basis of these figures one finds that a complete renewal of the waters of the Arctic Mediterranean Sea would take about 165 years.
A rough check on the relative correctness of the above values can be obtained by considering that the net salt transport into the Arctic Mediterranean must be zero. The average salinity of the inflowing Atlantic water is about 35.30 ‰ and that of the Bering Sea water about 32.00 ‰. Therefore 3.0 × 35.3 + 0.3 × 32.0 = 3.55 SA where SA is the salinity of the outflowing Arctic water. This equation gives SA = 32.5 ‰, in fair agreement with the salinity shown in the section in fig. 178. If the addition of fresh water were 0.1 × 106 m3/sec or 0.4 × 106 m/sec, the salinity of the outflowing water would be 34.0 ‰
The amount of heat given off by the water can also be estimated. The average temperatures of the in- and outflowing waters between Scotland and Greenland can be taken as 8°C and -1°C, respectively, and the average temperature of the water flowing through Bering Strait, the runoff, and the excess precipitation can be taken as 0°C. The total amount of heat given off by the waters in the Arctic Mediterranean Sea is then about 24 × 1012 g cal/sec. It is probable that at least half of this amount is given off where the Atlantic water flows north along the west coast of Norway, or over an area not greater than 2 × 1012 m2. The average amount of heat given off in this area would then be 12 g cal/m2/sec = 0.072 g cal/cm2/min = 103 g cal/c m2/day. This value, although uncertain, serves to demonstrate the important bearing of the Atlantic Current on the climate of the extreme northwestern part of Europe.
From the above discussion of the water, salt, and heat budgets of the Arctic Mediterranean Sea it is evident that the Atlantic water which contributes mostly to the inflow is diluted and cooled off to such an extent that the outflowing water is of entirely different character. We have here another striking example of local factors operating towards changing the inflowing water and producing a new water mass.
The influence of the local factors is more or less conspicuous in the different parts of the Arctic Mediterranean Sea, giving rise to other water masses than those mentioned, and to water masses produced by mixing. Every subdivision of the Arctic Mediterranean has its own characteristic water masses, which will be briefly described.
In the Norwegian Sea, Atlantic water is found off the west coast of Norway, where it flows to the north, losing some of its heat content to the atmosphere and being somewhat diluted by excess precipitation. On the right-hand side of the Atlantic water is the Norwegian coastal water, which has a lower salinity, owing to runoff, and a considerable annual range in surface salinity and temperature. On the left-hand side of the Atlantic water are found water masses which have been formed by mixing between the Atlantic water and the Arctic water which flows south along eastern Greenland. The latter is characterized by low salinity and temperatures below 0°C, as illustrated in the left-hand section in fig. 178. The mixed water in the central and western parts of the Norwegian Sea has a salinity around 34.90 ‰ and at the surface a temperature which varies considerably during the year. In winter the surface layers are cooled, but before reaching freezing point the waters attain a higher density than that of the deeper waters and therefore sink to the bottom. By this process, first described by Nansen (1906), the bottom
The North Sea waters have, in general, salinities between 34.00 ‰ and 35.00 ‰, but Atlantic water of salinity above 35.00 ‰ is found in a tonguelike area to the south of a line from Scotland to the west coast of Norway and in another tonguelike area extending northwest from the English Channel. Norwegian coastal water of salinity as low as 30.00 ‰ is encountered in the northeastern part of the North Sea (Deutsche Seewarte, 1927).
The Baltic Sea, together with the Gulf of Finland and Gulf of Bothnia, represents a region which, oceanographically, has some features in common with the Black Sea. In the Baltic, as in the Black Sea, precipitation and runoff greatly exceed evaporation, for which reason a layer of brackish surface water is formed that flows out through the sounds between Sweden, the Danish Islands, and Jutland. Along the bottoms of these sounds, North Sea water that has been considerably diluted with Baltic water flows in. The sounds are narrow and shallow, for which reason intensive mixing takes place in and directly outside the sounds, and the influence of the Baltic water does not reach to any great distance. In this respect conditions are similar to those in the Black Sea and the Mediterranean, where the influence of the low-salinity water flowing out from the Black Sea is present only in the northern part of the Aegean Sea. There exists, however, one striking difference. The Black Sea has a deep basin filled by stagnant water of relatively high salinity, but in the Baltic only a few small basins exist, the deepest (with a maximum depth of about 210 m) being found off the island of Gotland. In these basins water of higher salinity is found, but the basins are so limited in extent and the difference in salinity between the bottom water and the surface water is so small that renewal of the deep water in the basins can take place, and stagnant water corresponding to that of the Black Sea is not found. Over large portions of the Baltic the salinity of the surface layer is about 7.00 ‰ but it drops, in the inner parts of the Gulfs of Finland and Bothnia, to less than 3.00 ‰, in spring even below 1.00 ‰ (Deutsche Seewarte, 1927). The salinity of the water in the different basins decreases from about 16.00 ‰ in the southern basins to about 12.00 ‰ in the basins further north. The surface temperatures show a large annual variation.
In the North Polar Sea three main water masses are encountered, the Arctic Surface Water, the Atlantic water, and the Arctic Deep Water. The Arctic Surface Water has a low salinity ranging from a few per mille at the mouths of the Siberian rivers to 32 ‰ or 33 ‰ to the north of Spitsbergen. Owing to the low salinity of the surface waters, no deep water is formed in the Arctic Sea itself, but in winter a top layer of homogeneous water is developed. On the North Siberian Shelf at a distance of about 400 km from the coast, the salinity of this homogeneous layer reached, in 1923, its maximum value, 29.67 ‰, in May (Sverdrup, 1929), but at the end of the summer a nearly fresh top layer was formed by the melting of ice, and as a result of admixture of this fresh water the salinity was somewhat reduced down to a depth of about 30 m. The temperature of this upper layer remained at freezing point during the winter and in summer was raised slightly above freezing point. It is probable that an upper layer of similar characteristics is found all over the Polar Sea, as indicated by Nansen's observations in 1893–1896, but data from later Russian expeditions are not yet available.
Below this upper layer and a transition layer is found the Atlantic water, which enters the North Polar Sea north of Spitsbergen as a subsurface flow. In 1931 (Mosby, 1938) water of a salinity of 35.10 ‰ and a temperature between 3° and 4° was found to the north of Spitsbergen in lat. 80°38′ and longitude 13°41′E, between depths of 75 and 400 m. Nansen's observations (1902) showed that this Atlantic water can be traced across the Polar Sea toward the region of the New Siberian Islands, and his observations have recently been confirmed by those which were conducted during the drift of the Sedov in 1937–1940. Zubov (1940) states that both the temperature and the salinity of the Atlantic water were higher in 1937–1940 than they were in 1893–1896. In both instances admixture with Polar water led to a decrease of temperature and salinity in the direction in which the Atlantic water spreads out.
The deep water of the Polar Sea has a uniform salinity of about 34.93 ‰ and uniform temperature of about -0.85°. Nansen observed an increase of the temperature toward the bottom which can be explained as a result of adiabatic heating. This deep water cannot be formed anywhere in the Polar Sea, but it shows great similarity to the deep water in the northern part of the Norwegian Sea. Nansen therefore concluded that the deep water of the Polar Sea was formed in the Norwegian Sea and flowed in across the submarine ridge between Spitsbergen and Greenland, which supposedly has a sill depth of 1200 to 1500 m. These conclusions
The marginal areas of the North Polar Sea, the Barents Sea, the Kara Sea, and the areas between the islands of the Canadian Archipelago show complicated conditions owing to dominating local influences and inflow of different water masses. Atlantic water, for example, flows into the Barents Sea both to the north of Norway, where it branches out in different directions, and to the north of Spitsbergen, where part of the Atlantic water turns south between Northeastland and Franz Josef Land. The different basins in the Barents Sea therefore contain waters of slightly differing characteristics depending upon their origin.
The currents of the Arctic Mediterranean Sea have been repeatedly mentioned in the preceding discussion of the water masses. Later observations have not materially changed the conception of the surface currents of the Norwegian Sea which Helland-Hansen and Nansen presented in 1909. Their picture is reproduced in fig. 180, according to which the two main currents in that region are the Norwegian Current, representing a continuation of the North Atlantic Current, and the East Greenland Current.
The Norwegian Current, a part of the Gulf Stream system (p. 673), is flanked on the left-hand side by a series of whirls, some of which are probably stationary and related to the bottom topography, whereas others may be traveling eddies. Off northern Norway the Norwegian Current branches, one branch continuing into Barents Sea and another turning north toward Spitsbergen and bending around the northwest of the Spitsbergen islands. The waters of this current have a high salinity and a high temperature, the maximum salinity decreasing from about 35.3 ‰ north of Scotland to about 35.0 ‰ off Spitsbergen and the subsurface temperature decreasing from about 8° to less than 4° in the same distance.
The East Greenland Current flows on or directly off the East Greenland shelf, carrying water of low salinity and low temperature. The greater part of the East Greenland Current continues through Denmark Strait between Iceland and Greenland, but one branch, the East Iceland Arctic Current, turns to the east and forms a portion of the counterclock-wise circulation in the southern part of the Norwegian Sea.
No velocities are entered on the figure, but within the Norwegian Current velocities up to 30 cm/sec, or about 0.5 knot, occur and within the East Greenland Current, where the water moves fastest directly off the shelf, velocities of 25 to 35 cm/sec are encountered. These values are based partly upon computation from the distribution of density and partly upon direct current measurements (Helland-Hansen and Nansen 1909, Jackhelln, 1936).
In the North Sea a counterclockwise circulation is also present, as has been demonstrated not only by the distribution of temperature and salinity but also by the results of large-scale experiments with drift bottles. The details of the currents are much more complicated than can be shown in the figure, and several smaller but permanent eddies appear to be present. In the straits between Sweden and Denmark the surface current is directed in general from the Baltic to the North Sea, but along the bottom the water flows into the Baltic. In the Baltic and the adjacent gulfs the currents are so much governed by local wind conditions that no generalization is possible.

Surface currents of the Norwegian. Sea (after Helland-Hansen and Nansen).
The outflowing water from the Baltic continues as a low-salinity current along the south and southwest coast of Norway, as shown in fig. 180. This Norwegian coastal current carries warm water in summer and cold water in winter, the development of the current being greatly influenced by the prevailing wind. A striking example of the advance of cold water masses along the coast in the winter of 1937 is discussed by Eggvin (1940), who traced the movements of a cold-water front by surface thermograph records and oceanographic observations at fixed localities.
In the North Polar Sea the surface currents are also greatly influenced by local winds. An independent current appears to be present only to the north of Spitsbergen and to the northeast of Greenland, where the surface waters flow south to feed the East Greenland Arctic Current. The greater part of the Atlantic water which reaches Spitsbergen as the northern branch of the Norwegian Current submerges below the Arctic surface water and spreads as an intermediate layer over large parts of the Polar Sea.
In the Barents Sea a counterclockwise circulation prevails with relatively warm water of Atlantic origin on the southern side and Arctic water on the northern, and with numerous eddies in the central portion. In the other marginal areas of the Polar Sea—the Kara Sea, the Laptev Sea, the North Siberian Sea, and the Chukotsk Sea—the currents are mainly determined by local winds and, in summer, by the discharge of large quantities of fresh water from the Siberian rivers or the Yukon River, but details of the currents are little known.
The Norwegian Current and its branches are subject to variations which are related to other phenomena. Helland-Hansen and Nansen (1909, 1920) have shown that the surface temperature of the Atlantic water off the Norwegian coast fluctuates considerably from one year to another and that high summer temperatures of the surface water are mostly followed by high air temperatures during the subsequent winter and spring. Besides such minor fluctuations major changes take place that lead to altered conditions over a number of years (Helland-Hansen, 1934). In 1901–1905 and in 1925 and 1927 the maximum salinity of the Atlantic water off western Norway at depths greater than 50 m was between 35.30 ‰ and 35.35 ‰, but in 1929 a maximum salinity of 35.45 ‰ was observed, and in 1928 and 1930 the highest values were 35.43 ‰ and 35.40 ‰ respectively. The temperatures in 1929 were higher than on any previous occasion and, in agreement with this observation, the air temperature in Norway from November, 1929, to April, 1930, was higher, on an average, than in any winter since 1900.
Helland-Hansen found that in 1929 the Atlantic water flowing into the Norwegian Sea was not only warmer and of higher salinity but that the volume was also greater than average. He points out that such an increased inflow must have had far-reaching consequences. Owing to
The causes of the fluctuations which have been described are not known, nor is it known whether these fluctuations are periodic in character, and the same statements apply to fluctuations which occur in other regions of well-defined currents.
The large water masses of the Arctic Mediterranean have a high oxygen content, but within the many minor bodies of water which are in restricted communication with the waters of the Arctic Mediterranean the oxygen content varies within wide limits. In general, the Atlantic water of the Norwegian Current has a high oxygen content, but off the Norwegian coast minimum values somewhat below 5 ml/L have frequently been observed. The deep water of the Norwegian Sea contains large quantities of oxygen, in agreement with the concept that this water is rapidly renewed by vertical convection currents which in late winter extend from the surface to the bottom. At a temperature of -1° values up to 7.2 ml/L have been observed, corresponding to a saturation of 88 per cent. Both the Atlantic water that flows into the Polar Sea to the north of Spitsbergen and the deep water that enters over the Spitsbergen-Greenland Ridge is rich in oxygen, as is evident from the observations by Mosby (1938) and Sverdrup (1933). In the deep water of the Polar Sea to the north of Spitsbergen the highest observed value was 6.73 ml/L at a depth of 3,000 m. On the other hand, in coastal areas where the bottom topography or other local conditions are important, very low oxygen values may be found. On the North Siberian shelf, where occasional intrusion of high-salinity water takes place, low oxygen values occur, probably owing to the consumption of oxygen by the organisms on the bottom of the shallow shelf or to decomposition of organic matter which has accumulated on the bottom. Values as low as 1.56 ml/L were observed at a distance of 5 m from the bottom, where the salinity was
The Labrador Sea and Baffin Bay. The waters of the Labrador Sea are at all depths in free communication with those of the Atlantic Ocean, wherefore the Labrador Sea should be considered not an adjacent sea but a part of the Atlantic. The waters of Baffin Bay, on the other hand, are partly separated from those of the Labrador Sea by the submarine ridge across Davis Strait; but, because of the close relationship between the waters of Baffin Bay and Labrador Sea, and because of the strong influence of similar local factors in both regions, it appears desirable to treat them jointly.
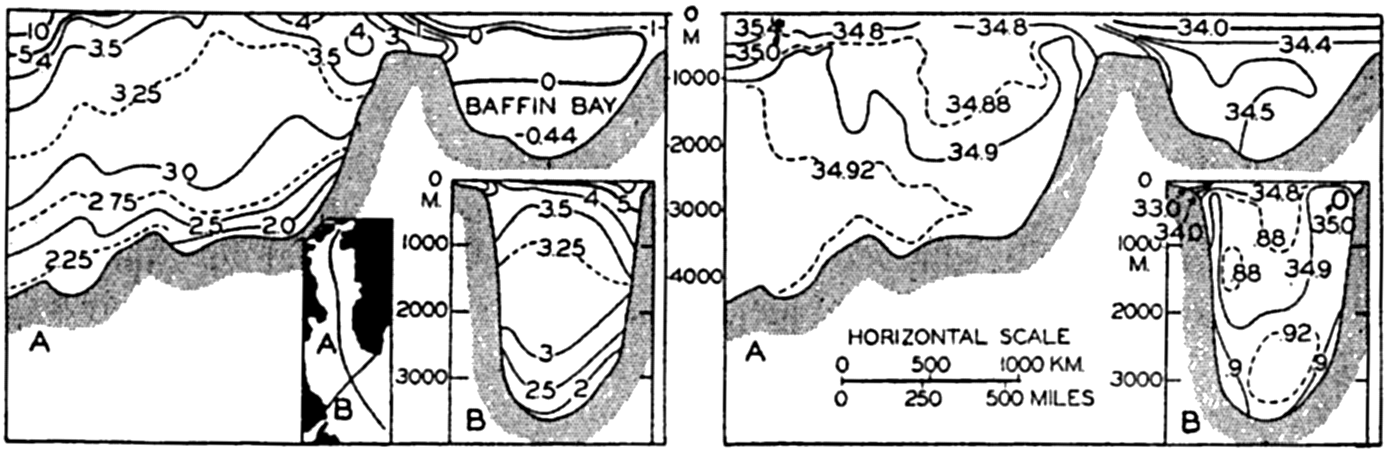
Temperature and salinity distributions in a longitudinal section through the Labrador Sea and Baffin Bay, and in a cross-section from Labrador to Greenland. Location of sections shown in inset map.
The character of the water masses in the Labrador Sea and Baffin Bay is illustrated in fig. 181, based upon diagrams prepared by Smith et al (1937). The distributions of temperature and salinity are shown in a cross section from South Wolf Island off the coast of Labrador to Cape Farewell on Greenland and in a longitudinal section between latitudes 78°N and 55°N. The locations of the sections are indicated on the small inset map.
The cross section from Labrador to Greenland shows a distribution of temperature and salinity having considerable similarity to the distribution found in the Norwegian Sea. On the continental shelf off Labrador (to the left in the figure) is found water of a temperature which is mostly below 0°C and of salinity less than 34.00 ‰, the lowest values being less than 30.00 ‰. This water, which flows south, corresponds in its character to the waters of the East Greenland Current. The greater part of the section shows water of a uniform temperature which, except for a surface layer showing the effect of seasonal heating, is between 4° and 1.7°, by far the greater part of the water having a temperature between 3.5° and 3.0°. The salinity lies between 34.86 ‰ and 34.94 ‰, the
The longitudinal section which has been constructed along the center line of Baffin Bay and Labrador Sea demonstrates, in the first place, the uniform character of the waters of the central part of the Labrador Sea. In the second place, the section shows that the water in the Baffin basin represents a mixture of Labrador Sea water and surface water which has been greatly diluted by excess precipitation. The low temperatures near the bottom indicate an admixture of surface water the salinity of which has been increased in winter by the freezing of ice.
The processes of cooling and of mixing which go on in the Labrador Sea are comparable to those in the Norwegian Sea. The large body of relatively uniform water in the central part of the Labrador Sea is formed by mixing of the two essentially different types of water, the Atlantic water and the Arctic water. In certain areas the mixed water at the surface will have a salinity in the neighborhood of 34.90 ‰ and, when cooled in winter to a temperature of 3° or lower, will sink and renew the deep and bottom water. That is, formation of deep and bottom water takes place in winter by vertical convection currents in the manner which was first described by Nansen when discussing the formation of the bottom water in the Norwegian Sea. The fact that the deep and bottom water has an oxygen content between 6.0 ml/L and 6.5 ml/L strongly supports the concept that this water is formed by vertical convection currents and is being renewed every winter.
In the Baffin basin entirely different conditions are encountered. The temperature and salinity of the bottom water in this basin indicate, as already stated, that here the bottom water represents a mixture of Labrador Sea deep water and surface water of the Baffin Bay region, the salinity of which has been increased sufficiently by freezing to cause the water to sink. It is probable that this sinking of cold surface water is
The surface currents of the Labrador Sea, which have been briefly mentioned, are shown in fig. 182, prepared by means of the charts of Smith et al (1937) and of Kiilerich (1939). These representations are the results of calculations based on the distribution of density. The outstanding features are the West Greenland Current that flows north along the west coast of Greenland and the Labrador Current that flows south off the coast of Labrador. Part of the West Greenland Current turns around when approaching Davis Strait and joins the Labrador Current, whereas part continues into Baffin Bay, where it rapidly loses its character as a warm current. Along the west side of Baffin Bay the Arctic waters flow south, having been partly reinforced by currents carrying Arctic water through the sounds between the islands to the west of Greenland. The central areas of the Labrador Sea and Baffin Bay both appear as areas in which numerous eddies occur, but nothing is known as to the permanency of the details shown in the picture. The similarity between the Labrador Sea and the Norwegian Sea is again striking, but it should be emphasized that, whereas the Norwegian Sea is in communication with the Atlantic Ocean in the upper 600 m only, so that the deep water is shut off, the Labrador Sea is in communication with the Atlantic at all depths and the deep water can freely flow to the south.
Schematic representation of the surface currents in the Labrador Sea.
According to Smith et al (1937) the inflow in the Labrador Sea amounts to 7.5 million m3/sec and the outflow along the coast of Labrador amounts
Ice and Icebergs in the Arctic. The Polar Sea with its adjacent seas, the western portion of the Norwegian Sea, Baffin Bay, and the western portion of the Labrador Sea are covered by sea ice during the greater part of the year, whereas, under the influence of the warm Atlantic water, the west coast of Norway is always ice-free except for occasional freezing over of the inner parts of fjords.
The Arctic pack ice that covers most areas is more broken and piled up than the Antarctic pack ice (p. 623). Large, flat ice floes are rare, but fields of hummocked ice and pressure ridges rising up to five or six meters above the general level of the ice are frequently found. The broken-up and rugged appearance of the Arctic pack ice is ascribed to the action of the wind in conjunction with the restricted freedom of motion of the ice owing to land barriers on all sides.
The wind drift of the ice has been discussed by Nansen (1902) and Sverdrup (1928), who found that the direction of the drift deviated, on an average, 28° and 33°, respectively, from the direction of the wind, instead of 45° as required by Ekman's theory of wind currents. The discrepancy is due to the resistance against motion offered by the ice itself (Sverdrup, 1928, Rossby and Montgomery, 1935) and because this resistance is greatest at the end of the winter when the ice is most closely packed, the deviation of the ice drift from the wind direction is smallest at that time of the year. Similarly the wind factor, that is, the ratio between the velocity of the ice drift and the wind velocity, is smaller at the end of the winter than in summer, varying between 1.4 × 10−2 in April to 2.4 × 10−2 in September.
Under the influence of variable winds the ice is, in all seasons of the year, torn apart in some localities, where lanes of open water are formed,
In winter the average thickness of the Arctic pack ice is probably 3 to 4 m and in summer 2 to 3 m, but under pressure ridges and great hummocks the thickness is greater. Hummocked ice is often found stranded where the depth is 8 to 9 m, and in exceptional localities where strong tidal currents prevail, masses of piled-up ice have been found stranded where the depth was 20 m.
The ice passes through a regular annual cycle. In summer melting takes place during 2 to 3 months, and on an average the upper 1 m of the ice melts. In winter ice forms on the underside of the floes, but the thicker the ice the slower the freezing. The average thickness of the ice depends mainly upon the rapidity of melting in summer and freezing in winter, and is therefore determined by climatic factors. Near shore, river water and warm offshore winds facilitate melting and the development of navigable lanes of open water along the coasts. In recent years the U.S.S.R. has been able to take advantage of such lanes along the north coast of Siberia for establishing shipping connections with the large Siberian rivers. Aerial surveys of ice conditions have preceded the operations and ice breakers have been used where necessary.
Within the greater part of the Polar Sea the ice is moving mainly under the action of the winds, but it is also carried slowly by currents toward the opening between Spitsbergen and Greenland. The speed of the current increases when approaching the opening, and great masses of ice are carried swiftly south by the East Greenland Current. Since 1894 detailed information as to the extent of the sea ice in the Norwegian Sea and in the Barents Sea has been annually compiled and published by the Danish Meteorological Institute.
The icebergs in the Arctic originate from glaciers, particularly on Northern Land, Franz Josef Land, Spitsbergen, and Greenland. No icebergs are encountered in the Polar Sea except near Northern Land,
Many of the icebergs carried south by the East Greenland Current disintegrate before they reach Cape Farewell, the southern cape of Greenland, but others are carried around the south end of Greenland and continue to the north along the west coast. They are joined by other icebergs from the West Greenland glaciers and together with these are finally carried south by the Labrador Current. The icebergs reach farthest south off the Grand Banks of Newfoundland in the months from March to June or July, when they represent a serious menace to shipping. After the Titanic disaster in 1911, the International Ice Patrol was established in order to safeguard the shipping by reporting icebergs and predicting their probable course. The ice patrol is conducted by the United States Coast Guard, the publications of which contain a large amount of information as to the number, distribution, and drift of icebergs in the region of the Grand Banks. Prediction of the ice drift has been based successfully on currents computed from the distribution of density as observed on cruises during which several lines of oceanographic stations have been occupied in about two weeks. This work of the Coast Guard is the outstanding example of practical application of the methods for computing ocean currents (p. 453).
The North Atlantic Ocean
Water Masses of the North Atlantic Ocean. The character of the water masses in the North Atlantic Ocean is illustrated in the T-S diagram in fig. 183. Ten stations scattered over the North Atlantic have been selected, the locations of which are shown in the inset map. Observations from the upper 100 m have been omitted. All stations are located at such distances from the coast that local waters are not considered.
The striking features of the presentation are that in the North Atlantic Ocean one has to deal principally with two typical water masses: the North Atlantic Central Water, characterized by a nearly straight T-S curve between the points T = 8°, S = 35.10‰, and T = 19°, S = 36.70‰; and a deep and bottom water, which is characterized by temperatures between 3.5° and 2.2°, and salinities between 34.97 ‰ and 34.90 ‰. Between these two typical water masses are found other
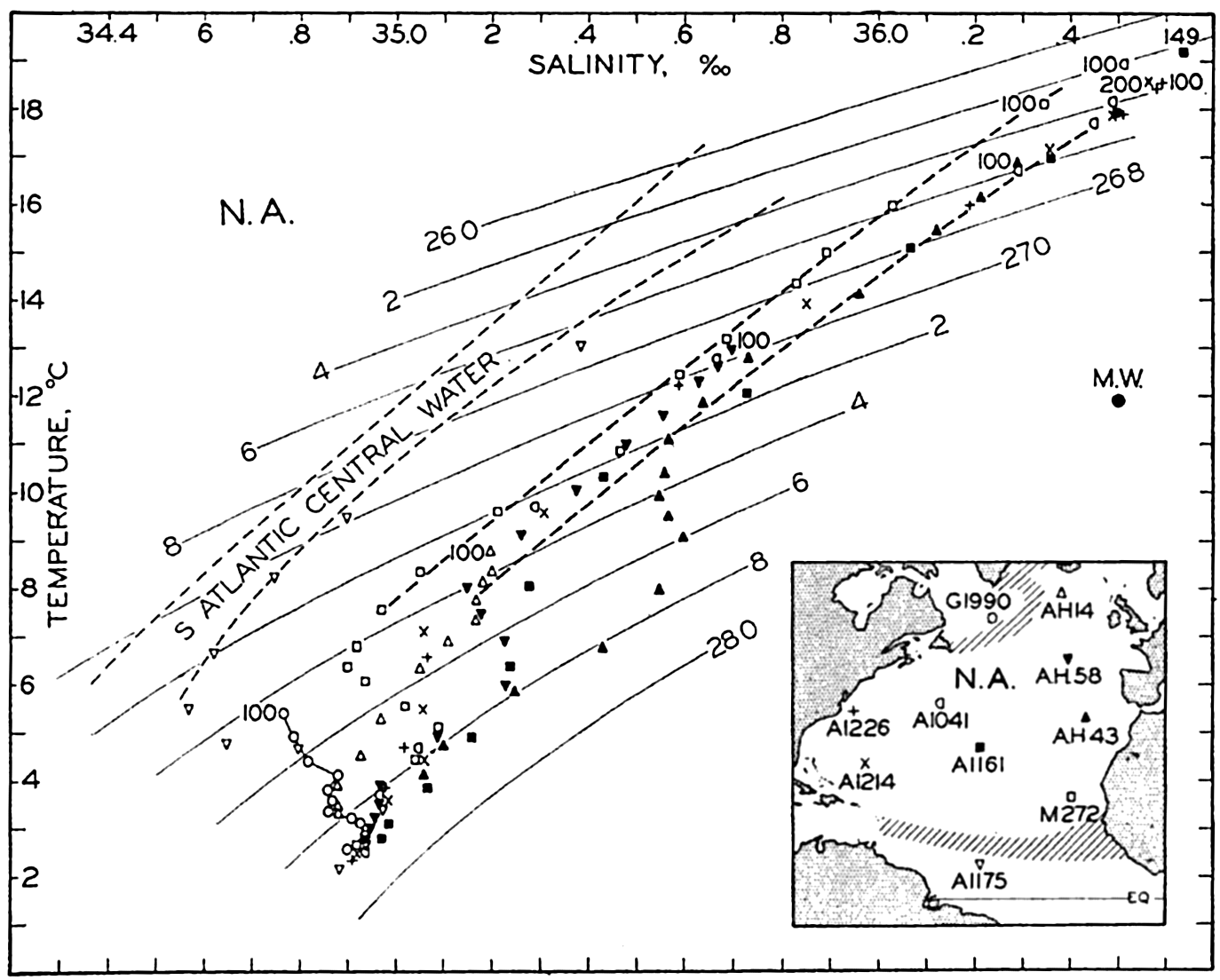
Temperature-salinity relation in the North Atlantic Ocean. The depths of the shallowest values are indicated. Large squares represent winter surface values in the northwestern Atlantic. Inset map shows location of stations. Abbreviations: A = Atlantis, AH = Armauer Hansen, G = General Greene, M = Meteor, N.A. = North Atlantic Central Region, M.W. = Mediterranean Water.
The North Atlantic Central Water evidently spreads over a very large area, because it is typically present at all stations shown in the map except at station G 1990 to the south of Cape Farewell on Greenland, and at station A 1175 in latitude 6°50′N. At station AH 14a, to the south of Iceland, North Atlantic Central Water is found although no water occurs of a temperature above 9°. There is a remarkable agreement between the upper water at such widely separated stations as AH 58 to the west of the Bay of Biscay and A 1226 in the Gulf Stream region to the east of Cape Hatteras. At station A 1175 water of a different character is present, namely upper water which originates in the South Atlantic Ocean and has been carried across the Equator, but this water does not appear to exercise any great influence on the large body of North Atlantic water. The water at station G 1990 to the south of
At intermediate depths, three other types can be pointed out. At station A 1175 Antarctic Intermediate Water is present which has its origin in the South Atlantic Ocean. Upon entering the North Atlantic, this water mixes with the North Atlantic masses and appears to exercise an influence on water which has a σt of approximately 27.4. Another type of intermediate water is present at the two northern stations and is characterized by a salinity of about 34.88 ‰ and a temperature of 3.5°. This water represents the corresponding Arctic Intermediate Water which, however, is formed in small quantities only and exercises a very limited influence outside of the region where it originates.
At three of the stations in the eastern Atlantic, AH 43, AH 58, and M 272, high salinities are found at intermediate depths. These high salinities result from the spreading out of Mediterranean water which, off the Strait of Gibraltar, according to Wüst (1935), has a temperature of 11.9°, a salinity of 36.50‰, and a σt of 27.78. The Mediterranean water, as defined by these values, is indicated in the figure by the point marked MW. The form of the T-S curves clearly indicates that this water spreads in the Atlantic Ocean between the 27.6 and 27.8 σt surfaces. Here again one has to deal with a type of water which has not been formed in the open North Atlantic Ocean but in one of the adjacent seas and which shows up over large areas, as clearly demonstrated by Wüst's charts.
The deep and bottom waters are of a remarkably uniform character all over the Atlantic Ocean, as is evident from the excellent agreement between values of temperature and salinity which have been determined in different regions by different expeditions. The deep water has its origin in the most northern part of the North Atlantic Ocean, but the bottom water is probably somewhat mixed with bottom water of antarctic origin. We shall return to that question when discussing the deep-water circulation.
The large body of North Atlantic Central Water must have been formed in the North Atlantic Ocean. Iselin (1939) has shown that this water has probably attained its characteristic temperatures and salinity when in contact with the atmosphere. Making use of Böhnecke's (1936) charts of surface salinity and surface temperature of the North Atlantic Ocean in late winter, Iselin plotted temperature-salinity values from the surface in a diagram, together with typical T-S curves in mid-ocean. These surface values, which represent the characteristic T-S relation in a horizontal direction, nearly coincide with the vertical T-S curves, and by selecting other corresponding values at the surface one could obtain complete coincidence. This agreement supports the conclusion that the central water mass is formed by sinking of surface water and
The thickness of the North Atlantic Central Water is closely related to the character of the currents in the North Atlantic Ocean. Within a region of a strong current the thickness will be great on the right-hand side of the current and small on the left-hand side, according to the general rule that in the Northern Hemisphere light water is present on the right-hand side of a current.
The Currents of the North Atlantic Ocean. The system of currents in the North Atlantic (chart VII) is dominated by the North Equatorial Current to the south and the Gulf Stream system to the north. The North Equatorial Current flows from east to west in the trade-wind region and is fed by the southeasterly currents off the west coast of North Africa. Corresponding to flow from the northwest, water of relatively high density and low temperature is found off the African coast, as is evident from the charts of surface temperatures (charts II and III). The temperature close to the coast is also lowered by upwelling from moderate depths due to the action of prevailing northwesterly winds, but this upwelling does not exercise influence as widespread as does the corresponding upwelling off the coasts of southwest Africa or, particularly, as does that off the west coasts of North and South America. Details as to the upwelling off northwest Africa are still lacking, but the results of the work of the Meteor in these waters in 1937 (Defant, 1937a) can be expected to give much interesting information.
The wide North Equatorial Current runs, as already stated, from east to west, but does not follow an absolutely straight course. Schumacher (1940) points out that north of 15°N, on most of the monthly charts of the surface currents of the North Atlantic Ocean which he has prepared by means of ships’ observations, the North Equatorial Current bends to the north (to the right) when approaching the mid-Atlantic Ridge and to the south (to the left) after having passed the ridge. Schumacher also draws attention to the fact that on Defant's chart (1936b) of “average currents in the upper layers as derived from the inclination of the discontinuity layer in the troposphere,” these bends are much more conspicuous and that they appear reduced at the surface, probably owing to the superimposed pure wind drift. The maximum deflection to the north occurs directly above the mid-Atlantic Ridge and it seems therefore that the bends are due to the crossing of the ridge,
In the western part of the Atlantic Ocean the North Equatorial Current joins the branch of the South Equatorial Current which has crossed the Equator and which, according to fig. 183, p. 669, carries characteristically different water masses. Mixing takes place between these water masses and the corresponding North Atlantic water, and the waters in the Caribbean Sea are therefore intermediate in character (table 77, p. 639). Thus, the part of the North Equatorial Current which continues into the Caribbean Sea carries water which is mixed with water of South Atlantic origin, whereas the northern branch of the North Equatorial Current which flows along the northern side of the Great Antilles as the Antilles Current carries water which is identical with that of the Sargasso Sea.
The North Equatorial Current terminates in the current through the Yucatan Channel and the Antilles Current. The continuation of these currents represents the beginning of the Gulf Stream system which dominates the circulation of a great part of the North Atlantic Ocean. Following the nomenclature of Iselin (1936), the term “Gulf Stream System” is used to include the whole northward and eastward flow beginning at the Straits of Florida and including the various branches and whirls found in the eastern North Atlantic that can be traced back to the region south of the Newfoundland Banks. This system can be subdivided into the three following parts:
The Florida Current. The northward-moving water from the Straits of Florida to a point off Cape Hatteras where the current ceases to follow the continental slope. The Florida Current can be traced directly back to the Yucatan Channel, as explained on p. 642, because the greater part of the water flowing through this strait continues on the shortest route to the Straits of Florida and a small amount only sweeps into the Gulf of Mexico, later to join the Florida Current. After having passed the Straits of Florida the current is reinforced by the Antilles Current, but the name “Florida Current” is retained as far as to Cape Hatteras.
The Gulf Stream. The mid-sector of the system, from the region where the current first leaves the continental slope off Cape Hatteras to
― 673 ―the region to the east of the Grand Banks in about long. 45°W where the stream begins to fork. This application of the name “Gulf Stream” represents a restriction of the popular term, but such a restriction is necessary in order to introduce clear definitions.The North Atlantic Current. The name is used as a general term covering all the easterly and northerly currents of the North Atlantic from the region to the east of the Grand Banks where the Gulf Stream divides. The branches of the North Atlantic Current are often masked by shallow and variable wind-drift surface movements, which have become commonly known as the North Atlantic Drift.
The terminal branches of the Gulf Stream System are not all well known, but among the major ones are the Irminger Current, which flows towards the west to the south of Iceland, and the Norwegian Current, which enters the Norwegian Sea across the Wyville Thomson Ridge and can be traced ultimately into the Polar Sea (p. 661). Other more irregular branches which turn to the south have been examined by Helland-Hansen and Nansen (1926), who find that they terminate in great whirls off the European coast.
The Florida Current. The energy of the Florida Current appears to be derived directly from the difference in sea level between the Gulf of Mexico and the adjacent Atlantic coast, the observed difference between Cedar Keys and St. Augustine being 19 cm. (p. 642). Assuming that this hydrostatic head accounts for all of the energy, and assuming frictionless flow, Montgomery (1938) finds that the velocity through the Straits of Florida should be 193 cm/sec, which is somewhat higher than the average velocity at the center of the current. The difference in level is probably maintained by the trade winds, and the energy of the Florida Current is therefore derived from the circulation of the atmosphere.
Within the current flowing through the Straits of Florida, the distribution of density must adjust itself in the usual manner; that is, the lighter water must be found on the right-hand side of the current and the denser water on the left-hand side, and the sea surface, instead of coinciding with a level surface, must accordingly rise towards the right-hand side of the current. In the case of the Florida Current this rise amounts to about 45 cm, sea level at the coast of Cuba being about 45 cm higher than at the American mainland (Dietrich, 1936).
The character of the currents in the Straits of Florida was established by the outstanding measurements made in the years 1885 to 1889, by the United States Coast and Geodetic Survey from the survey vessel Blake, commanded by J. E. Pillsbury. Pillsbury's observations of currents, carried out from a vessel anchored in deep water in a swift stream, are among the classical data in physical oceanography, not so much because they give complete information as to the average currents, but mainly because they made possible a convincing demonstration of the
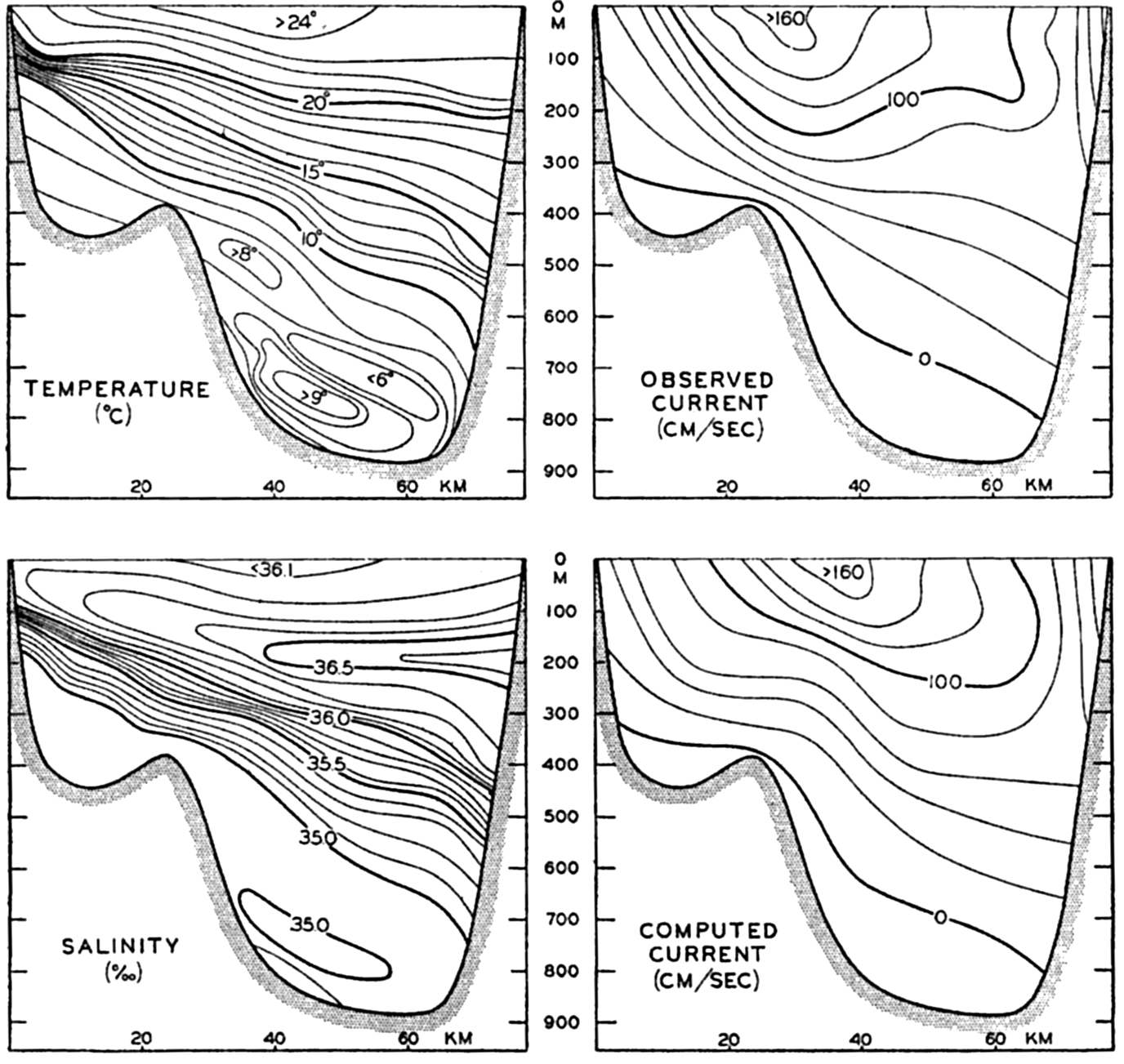
Left: Observed temperatures and salinities in the Straits of Florida. Right: Velocities of the current through the Straits according to direct measurements and according to computations based on the distributions of temperature and salinity (after Wüst).
On the basis of measurements and computations Wüst finds that the average transport of water through the Straits of Florida is 26 million m3/sec. The transport probably shows an annual variation and may differ from year to year, but so far little is known about such fluctuations (Montgomery, 1938, 1941, Iselin, 1940).
In its further course the Florida Current closely follows the continental slope, flowing most swiftly directly along the slope. The shallow coastal waters to the left of the Florida Current remain more or less at rest; often the transition from these waters to the blue waters of the Florida Current is so abrupt that the border of the Florida Current can be seen as a line stretching from horizon to horizon. After emerging from the Straits of Florida, the current is soon joined by the Antilles Current which, according to Wüst (1924), carries about 12 million m3/sec. Owing to the moderate depth to the bottom, the current remains relatively shallow, not more than about 800 m deep, and carries no water colder than 6.5° until it leaves the Blake Plateau in about lat. 33°N. According to Iselin (1936) the current increases steadily in volume by absorption of Sargasso Sea water, and as it leaves the Blake Plateau both the depth and the volume suddenly increase as a result of the joining in of water of a temperature considerably below 8° which comes from the southwestern Sargasso Sea.
The Gulf Stream. The middle portion of the Gulf Stream System, for which the name Gulf Stream is retained, continues as a well-defined and relatively narrow current which, in contrast to the Florida Current, flows at some distance beyond the continental shelf. To the right of the current is the Sargasso Sea water, as previously, but to the left are now found two water masses, the coastal water which covers the shallow shelf areas and the slope water which, at temperatures between 4° and 10°, is very similar to the Gulf Stream water (Iselin, 1936) but at higher temperatures is of lower salinity. Within the upper layers of the slope water great seasonal variations in temperature and salinity occur and, in addition, eddies of Gulf Stream water occasionally intrude.
The surface velocities of the Gulf Stream are very high, the computed values reaching, in lat. 36°N, long. 73°W, more than 120 cm/sec (Iselin, 1936) and in lat. 38°N, long. 69°W, 140 cm/sec (Seiwell, 1939). On the
The dynamics of the Florida Current and the Gulf Stream, particularly the downstream increase in volume as far as Cape Hatteras, is not clearly understood. Rossby (1936) has compared the Florida Current and its continuation, the Gulf Stream, to a wake stream which emerges from the Straits of Florida, and has examined the effect on such a stream of stresses due to lateral mixing. In a wake stream in homogeneous water the momentum transport remains constant whereas the volume (mass) transport increases downstream, the increase being due to inflow from the sides. Expanding the theory to a stratified medium, Rossby finds that a “compensation current” in the direction of flow must develop on the right-hand side of the wake stream, whereas to the left a counter current in the opposite direction must appear, and this picture agrees in general with the pattern of the Gulf Stream and its surroundings. Another important aspect of the theory is that owing to the lateral stresses a transverse circulation should develop, water being absorbed from the oceanic areas to the right of the current and discharged into the countercurrent to the left. Such a mechanism would account for the presence of eddies of Gulf Stream water in the slope current, but Defant (1937b) and Ekman (1939) have warned against immediate acceptance of the theory because several of the necessary assumptions appear not to be fulfilled. Regardless of whether the theory is confirmed or disproven, it has been greatly stimulating, particularly because of its emphasis on the importance of lateral mixing. In this connection the possibility may be mentioned that the developments of the counter current and the transverse circulation may not necessarily be associated
| Locality | Sea level (cm) | Mean | Distance along coast (km) | Slope | |
|---|---|---|---|---|---|
| Avers, 1927 | Rappleye, 1932 | ||||
| St. Augustine, Fla. | 0 | 0 | 0 | 0 | |
| Fernandina, Fla. | |||||
| Brunswick, Ga. | |||||
| 6 × 10−8 | |||||
| Norfolk, Va | 4 | 7 | 6 | 1000 | |
| 35 × 10−8 | |||||
| Cape May, N.J. | 16 | 24 | 20 | 1400 | |
| Atlantic City, N.J. | |||||
| Fort Hamilton, N.J. | |||||
| 13 × 10−8 | |||||
| Boston, Mass. | 25 | 30 | 28 | 2000 | |
| Portland, Me. | |||||
| 12 × 10−88 | |||||
| Halifax, Nova Scotia | — | 35 | 35 | 2600 | |
A satisfactory theory of the Gulf Stream must not only account for the increase in volume transport in the direction of flow and the fact that this increase takes place without evidence of strong inflow from the southeast, but it also must account for another important feature which has been given considerable attention (Dietrich, 1937b) without having been explained satisfactorily (Ekman, 1939). Precise leveling along the American east coast shows that the mean sea level increases towards the north from St. Augustine, Florida, to Halifax, Nova Scotia, the most conspicuous increase taking place directly north of Cape Hatteras. Table 81 summarizes the results of the precise leveling, according to Avers (1927) and Rappleye (1932). In the table the sea level along the coast has been referred to that on the coast of Florida and southern Georgia, values from stations less than 200 km apart having been eombined as averages. The distances along the coast from Florida-Georgia are entered and also the values of the slope of the sea surface. These values are of the same order of magnitude as those derived from
If this upward slope were due to the distribution of mass in the ocean, the average density of the Gulf Stream water off the continental shelf would have to decrease in the direction of flow and the Gulf Stream would have to flow uphill. Dietrich (1937b), however, has shown that along the continental slope the distribution of density does not indicate any rise of the sea surface if the topography of the surface is referred to the oxygen minimum layer, and the same is true if the topography of the sea surface is referred to the 2000-decibar surface. These conclusions are not altered by taking into consideration the small effect of differences in atmospheric pressure. A discrepancy therefore exists between the results of precise leveling and the results of what Dietrich calls oceanographic leveling. It is not surprising that such discrepancies appear because, as explained on p. 407, oceanographic observations can give information only as to the topography of the sea surface relative to some selected surface in the ocean and information as to the absolute topography of the sea surface must be derived from precise leveling along the coasts.
The question now arises whether it is possible to reconcile the different observations and at the same time arrive at transport values which are compatible with the distribution of density. The results of precise leveling are so accurate that the upward slope of the sea surface north of Cape Hatteras must be taken as established. It is also established that this slope of the sea surface is not compensated for by the distribution of mass, as is the case in the Caribbean Sea, for which reason it follows that the water must actually be piled up against the coast. The lack of compensation is understood if one considers that the piling up takes place in the shallow waters along the coast and does not extend to any distance beyond the continental slope. However, a transition must exist from the region of uncompensated piling up of mass to the region where compensation can take place, and it appears reasonable to assume that the transition takes place along the edge of the continental shelf. There the sea level sinks to the value indicated by the oceanographic data and, consequently, a current to the south runs along the continental slope, following approximately the absolute contour lines of the surface. A current to the south must also flow over the shallow portion of the shelf where it flows downhill and where the balance of forces is maintained by the effect of friction.
The transports can be calculated by considering that, owing to the piling up of water along the coast, the actual profiles of the isobaric surfaces slope downwards from the coast towards the outer part of the slope water and then rise because of the distribution of density. If this consideration is correct, the computed transport of Gulf Stream water must come out too high if based on the oceanographic data alone because
This reasoning can be illustrated by certain computations based on the Atlantis section of April 17–23, 1932, using the stations 1231–1225 which have been used extensively by Iselin and Dietrich. It is assumed here that over the shelf the piling up of water leads to the sea level on the coast being 10 cm higher, that the same piling up effect is present at the border of the continental shelf, and that no effect is found beyond a distance of 40 km from the border. Furthermore, it is assumed that beyond that distance the 2000-m level is a level of no motion. On the basis of such assumptions one arrives at the following figures:
| Transport to the southwest of slope water inside of station 1229 | 19 million m3/sec. |
| Transport to the northeast of slope and Gulf Stream water outside of station 1229 | 74 million m3/sec. |
| Net transport to the northeast | 55 million m3/sec. |
According to this computation the net transport of the Gulf Stream is of 55 against 74 million m3/sec if the southward motion of the slope water is disregarded. A net transport of about 55 million m3/sec is in agreement with the previous conclusion (p. 676) that not more than 15 to 20 million m3/sec circulate in the gyral to the right of the Gulf Stream; and if the reasoning is correct, another gyral is present on the left-hand side within which approximately 20 million m3/sec circulate. The slope water on the coastal side of the Gulf Stream is essentially of the same character as the Gulf Stream water, but has a slightly lower salinity owing to admixture with coastal water. The southward motion directly off the continental shelf is not associated with high surface velocities because one has to deal with a “slope current,” and on the assumptions made the velocity of the current is about 10 cm/sec.
Figure 185 gives a schematic picture of the conditions which have been described. The lines provided with arrows represent transport lines, each line corresponding to a transport of about 10 million m3/sec. The two gyrals on both sides of the Gulf Stream are shown and, in addition, an eddy is indicated between the slope-water gyral and the Gulf Stream where the latter is at a greater distance from the coast. Such an eddy, rotating clockwise, has repeatedly been observed to the south of Nova Scotia (Iselin, 1936), but the clockwise rotation has been difficult to explain because the eddy was considered an offshoot of the Gulf Stream. The direction of rotation is better understood, on the other hand, if the eddy is considered as a part of the slope-water gyral. The inset diagram shows a profile of the sea surface along the line A-B. The line marked 1 represents the profile which is obtained from oceanographic observations and the line marked 2 is the profile which is assumed to exist on the basis of these observations and the results of precise leveling.
It remains to account for the piling up of the water masses on the continental shelf. It can be suggested that this piling up is maintained by the prevailing winds over a large area of the North Atlantic Ocean. Southwesterly winds over the northern parts of the North Atlantic may maintain a higher sea level along the northern borders of the ocean and, consequently, a slope of the sea surface along the eastern and western borders.
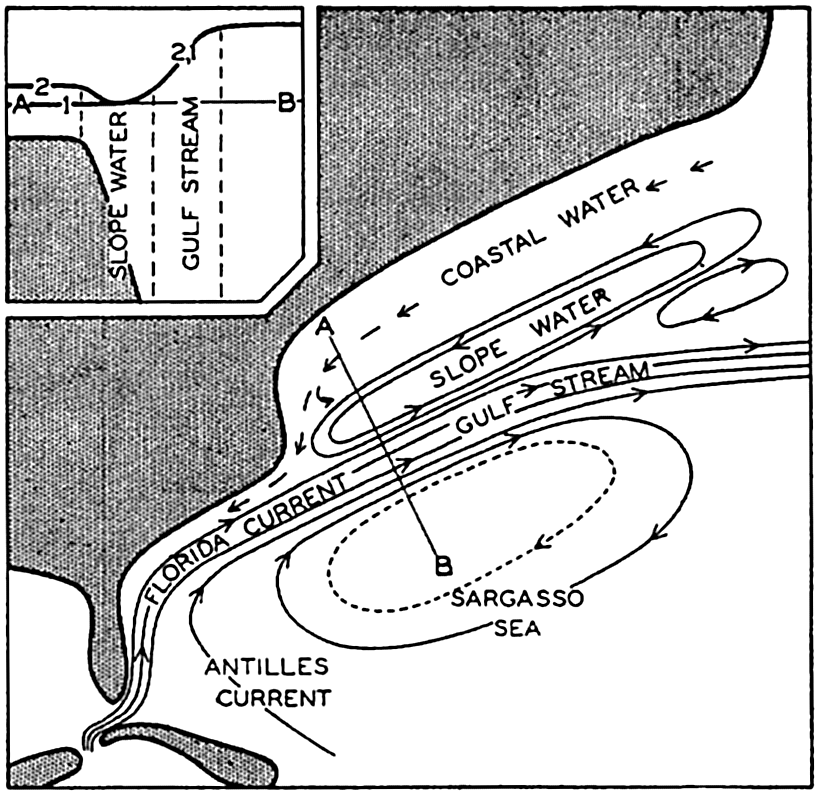
Schematic representation of the character of the Gulf Stream, taking results of precise leveling into account. Inset: Profiles of the sea surface along the line A-B. Profile 1 derived from oceanographic data only; Profile 2, from these data and the results of precise leveling.
The North Atlantic Current. The North Atlantic Current represents the continuation of the Gulf Stream after it leaves the region to the east of the “tail” of the Grand Banks. Beyond this region the Gulf Stream loses its characteristics as a well-defined current and divides into branches that are often separated by countercurrents or eddies. Some of the branches turn south but others continue towards the east across the mid-Atlantic Ridge, being flanked on the northern side by waters of the Labrador Current that have been mixed with Gulf Stream water.
The contrast between the Gulf Stream and the North Atlantic Current to the north of the Azores is illustrated in fig. 186, which shows two temperature profiles on the same scale. To the left in the figure are shown the isotherms in a vertical section from Chesapeake Bay towards Bermuda according to observations at the Atlantis stations 1231–1226. The Gulf Stream is here concentrated within the narrow band in which the isotherms slope steeply downward toward the right. The section to the right in the figure runs north-northwest from the Azores to lat. 48°0N and is based on the observations on board the Altair during the International Gulf Stream Expedition in 1938 (Defant and Helland-Hansen, 1939). In this section the isotherms generally slope downward toward the south, indicating a flow towards the east, but the slope is not uniform and countercurrents or eddies are present between the east-flowing branches of the current. In the section is shown the location of the Altair cone, discovered during the expedition, which probably
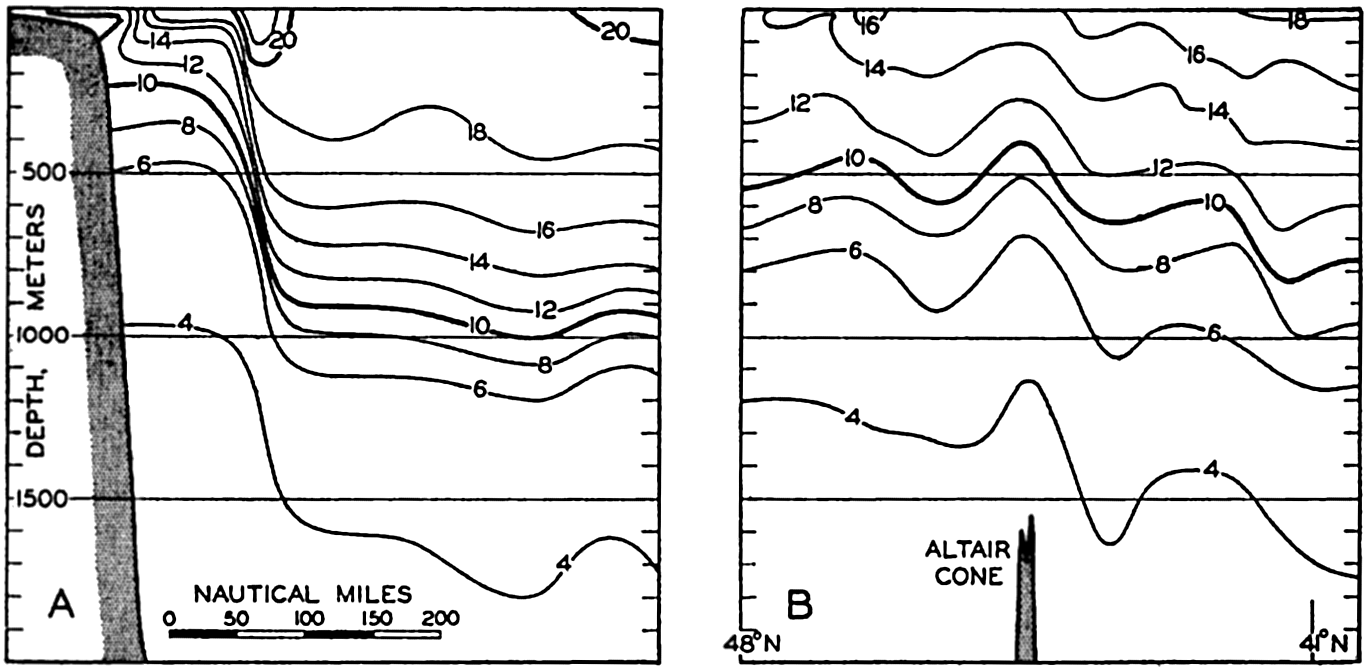
Temperature profiles across the Gulf Stream off Chesapeake Bay and across the North Atlantic Current to the north of the Azores.
The intensive work conducted by the International Gulf Stream Expedition of 1938 (Defant and Helland-Hansen, 1939) clearly shows the complicated details of the oceanographic conditions. Between June 1 and 22, 1938, the German vessel Altair and the Norwegian vessel Armauer Hansen occupied 159 stations in an area of less than 100,000 square miles, and at one station the Altair anchored and made hourly observations of temperature, salinity, and currents at a number of depths between the surface and 800 m for a period of 90 hours. The dense network of stations showed even greater irregularities than one might expect. At 600 m, for example, the temperature varied between approximately 7° and 13°, and differences up to 5° were observed at distances less than 40 miles. Some of the observed features may be due to the influence of the bottom topography and others may be related to traveling disturbances. Regardless of how the features are interpreted, they do show that caution has to be exercised when drawing conclusions from a few scattered observations
A series of stations which were occupied in 1931 by the Atlantis along the mid-Atlantic Ridge in long. 30°W demonstrates that in spite of irregularities one can distinguish between two major branches of the North Atlantic Current. The northern branch flows between lat. 50° and 52°N, at the boundary between the water of the Gulf Stream System and the Subarctic Water, and carries water which represents Gulf Stream water mixed with waters of the Labrador Current. The other branch flows approximately in lat. 45°N and carries undiluted Gulf Stream water. The northern branch continues mainly towards the east-northeast and divides up. Part of the water flows across the Wyville Thomson Ridge into the Norwegian Sea (p. 653) and part turns toward the north and northwest as the Irminger Current that flows along the southern coast of Iceland. A small portion of the water of the Irminger Current bends around the west coast of Iceland (fig. 178, p. 652), but the greater amount turns south and becomes more or less mixed with the waters of the East Greenland Current. The detailed work of the Meteor in the area between Iceland and southeastern Greenland (Defant, 1936c) indicates that many eddies within which this mixing takes place remain in approximately the same locality from one year to another, and the position of the eddies may therefore be related to the configuration of the coast. The last traces of the Gulf Stream water continue around Cape Farewell where, at some distance from the coast, water of salinity above 35.00 ‰ is encountered (fig. 181, p. 663).
In the central part of the Irminger Sea, off southern Greenland, mixing between the North Atlantic water and the Labrador Sea water leads to the formation of Subarctic Water of uniform salinity close to 34.95 ‰ and a temperature which from a depth of a few hundred meters and downwards is nearly 3°C. When the surface layers are cooled in winter to temperatures below 3°, vertical convection currents develop, reaching from the surface to the bottom and leading to renewal of the deep water. Table 82 contains data from two Meteor stations which were occupied in early spring and at which nearly uniform water was present. The oxygen observations have been included in order to show the high oxygen content of the deep water. The intense mixing that takes place in winter in this area and in the Labrador Sea (p. 664) must have important bearing on the productivity of the subarctic waters.
The branch of the North Atlantic Current that crosses the mid-Atlantic Ridge in approximately lat. 45°N turns to the right and continues as an irregular flow toward the south between the Azores and Spain, sending whirls into the Bay of Biscay. No distinct currents exist in this region, as is evident from the discussions of the conditions in the eastern North Atlantic by Helland-Hansen and Nansen (1926), but a diffuse
| Depth (m) | Meteor 121, March 9, 1935 Lat. 56°037′N, Long. 44°054.5′W | Meteor 79, March 30, 1933 Lat. 59°038′N, Long. 40°042.5′W | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Temp. (0°C) | S (‰) | σt | O2 (ml/L) | O2 (%) | Temp. (0°C) | S (‰) | σt | O2 (ml/L) | O2 (%) | |
| 0 | 2.82 | 34.87 | 27.80 | 7.24 | 96 | 4.07 | 34.96 | 27.76 | 6.92 | 95 |
| 50 | 3.01 | 34.90 | 27.81 | 7.26 | 97 | 4.07 | 34.97 | 27.77 | 6.99 | 96 |
| 100 | 3.09 | 34.92 | 27.82 | 7.24 | 97 | 4.06 | 34.96 | 27.77 | 6.81 | 94 |
| 200 | 3.17 | 34.93 | 27.82 | 6.70 | 90 | 3.98 | 34.97 | 27.77 | 6.84 | 94 |
| 800 | 3.26 | 34.96 | 27.83 | 6.98 | 94 | 3.76 | 34.95 | 27.77 | 6.60 | 90 |
| 1000 | 3.20 | 34.95 | 27.83 | 6.96 | 93 | 3.33 | 34.89 | 27.77 | 6.64 | 89 |
| 1500 | 3.17 | 34.93 | 27.82 | 6.99 | 94 | 3.28 | 34.94 | 27.82 | 6.39 | 86 |
| 2000 | 3.23 | 34.93 | 27.82 | — | — | 2.84 | 34.96 | 27.88 | 6.37 | 87 |
Transport. On the basis of the above discussion and numerous computations of transports, fig. 187 has been prepared, giving a schematic picture of the volume transport of the currents which carry North Atlantic Central Water or Subarctic Water. No lines of equal transport are entered but the different branches of the current system are indicated and the approximate volume transport in millions of cubic meters per second is stated. The presentation has been derived by computing the transport of water of temperature higher than 7° between a number of selected stations north of lat. 20°N, and adjusting the figures in order to take the continuity of the system into account. To the northwest of a line which can be drawn roughly between the Straits of Florida and the English Channel it has been assumed that the 2000–decibar surface could be taken as a surface of no motion, but to the southeast of that line it has been assumed in general that the 7° isothermal surface was a surface of no motion. This treatment was necessary because the condition of continuity has to be satisfied and because a reversal of the direction of flow appears to take place below the 7° isothermal surface over large parts of the southeastern area. It is not claimed that the picture in fig. 187 is accurate in details, but it is believed that it gives an approximately correct
The selected surface of no motion has several features in common with the corresponding surface which Defant (1941) arrived at by using the third method discussed on p. 457, without taking the equation of continuity into account. Defant's results as to the prevailing currents differ somewhat, however, from ours, particularly along the north coasts of the Antilles where he finds currents toward the southeast dominating, whereas according to our analysis the currents are directed toward the northwest in agreement with other generally accepted results.
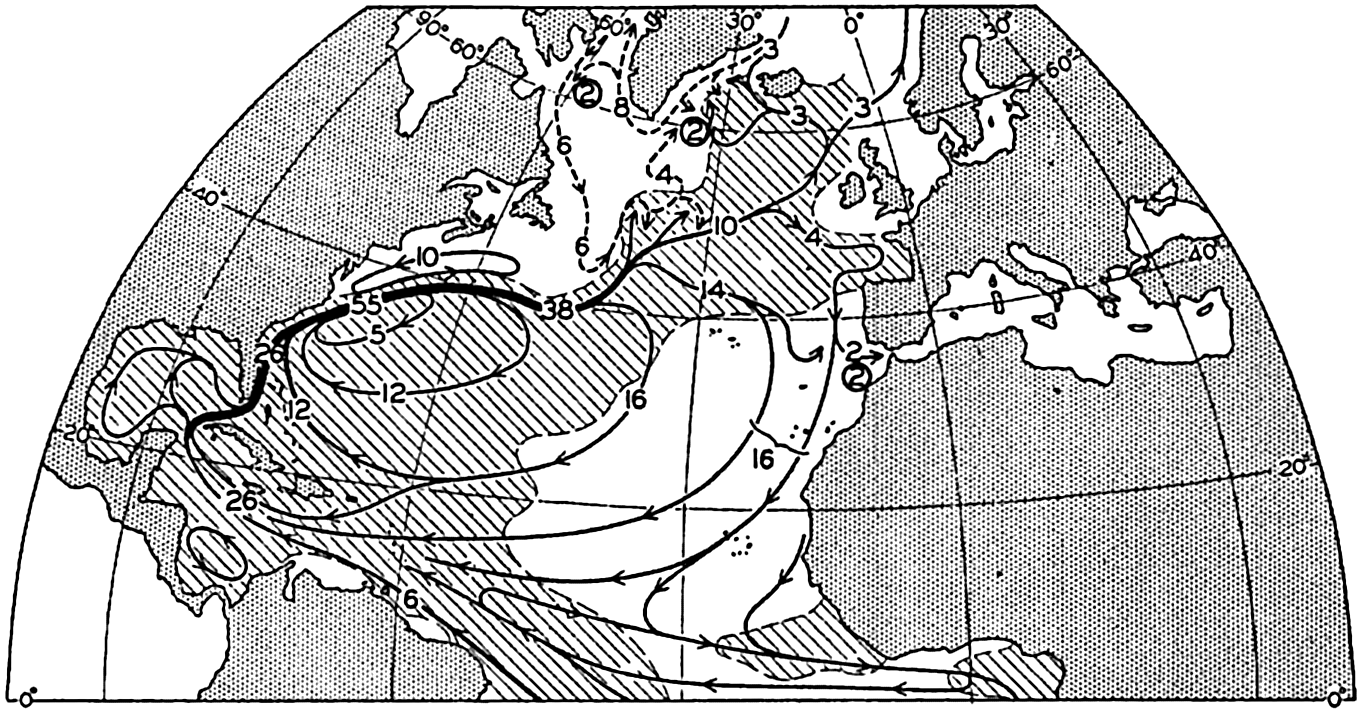
Transport of Central Water and Subarctic Water in the Atlantic Ocean. The lines with arrows indicate the direction of the transport, and the inserted numbers indicate the transported volumes in millions of cubic meters per second. Full-drawn lines show warm currents, dashed lines show cold currents. Areas of positive temperature anomaly are shaded.
The representation in fig. 187 shows the Florida Current and the Gulf Stream as the only well-defined currents of the Atlantic Ocean. It also shows that the greater amount of the waters of the Gulf Stream turns south before reaching the Azores and circulates around the Sargasso Sea.
In the figure the areas are shaded in which the average surface temperature is higher than the general average for that latitude. The shaded portions therefore represent the areas with positive temperature anomalies as referred to the average temperatures of the Atlantic Ocean, and the unshaded portions represent the areas of negative temperature anomalies. As should be expected, water which is transported from lower to higher latitudes is relatively warm, whereas water which is transported from higher to lower latitudes is relatively cold. If the velocity distribution within the different branches of the currents were known it would be possible to compute the net amounts of heat which are carried
Another characteristic of the system of currents is brought out by a comparison between the transports and the temperatures off Chesapeake Bay and to the north of the Azores (fig. 186). The Gulf Stream off Chesapeake Bay transports large volumes of water of temperatures above 16° but the North Atlantic Current to the north of the Azores carries only small amounts of water as warm as 16°. This apparent reduction in temperature must be due to the fact that the warmer waters of the upper layers have been carried south before reaching the Azores, whereas the somewhat colder waters at greater depths have continued toward the east. If such is the case, the law of the parallel solenoids is not fulfilled, owing possibly to cooling in the direction of flow (Parr, 1936).
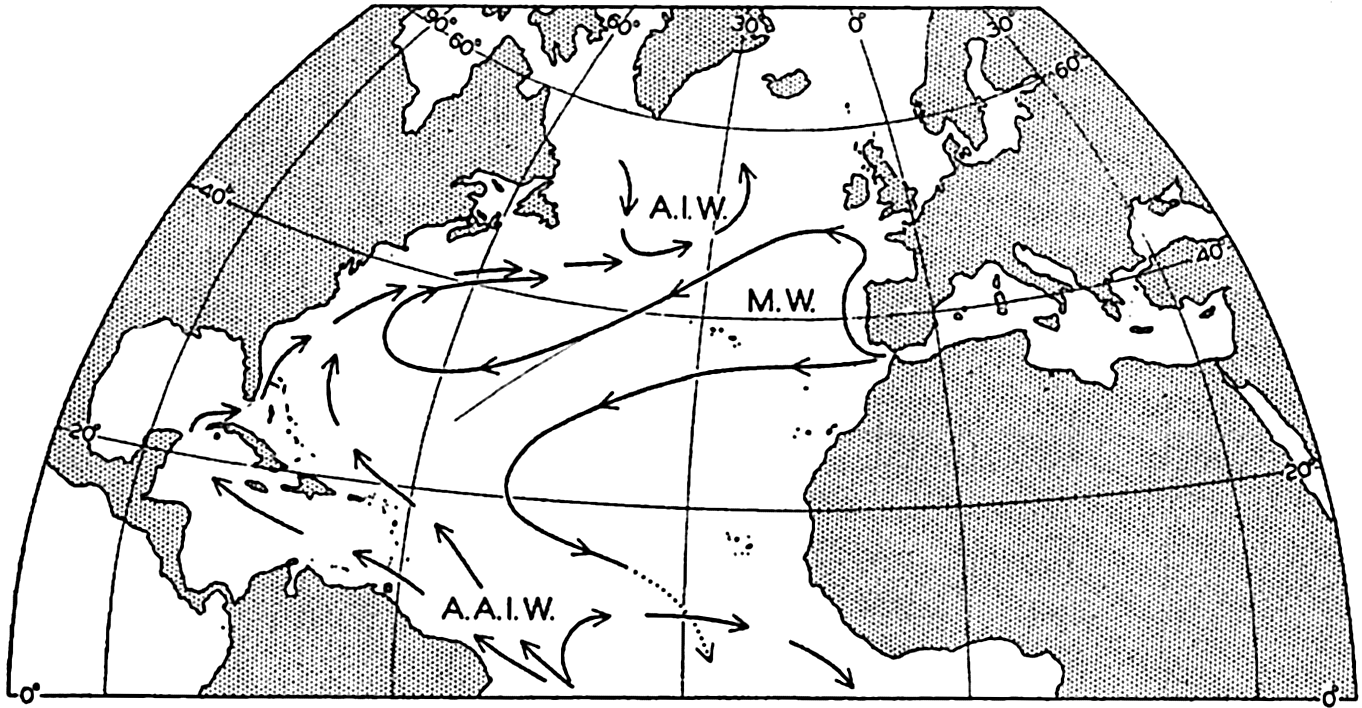
Approximate directions of flow of the intermediate water masses of the North Atlantic. A.I.W., Arctic Intermediate Water; M.W., Mediterranean Water; A.A.I.W., Antarctic Intermediate Water.
As previously mentioned (p. 629), 6 million m3/sec of South Atlantic Upper Water enter the North Atlantic Ocean along the coast of South America. Correspondingly, 6 million m3/sec of North Atlantic water sink in different localities and return to the South Atlantic as a deep-water flow. The three regions where sinking takes place and the amounts of water sinking from the surface are shown by circles and inserted numbers that represent rounded-off values. About 2 million m3/sec sink outside the Strait of Gibraltar and about the same amount sinks in the Labrador Sea. Both of these values are based on fairly accurate data (pp. 647 and 666), wherefore it follows that a similar amount sinks in the third region within which bottom and deep water is being renewed, namely the region to the southeast of southern Greenland.
The direction of flow of the different types of intermediate waters of lower temperature does not always coincide with the direction of flow of the upper water. On the basis of the character of the water and the results of dynamic calculations, fig. 188 has been prepared, giving a tentative picture of the spreading of the Arctic Intermediate Water, the Mediterranean and the Antarctic Intermediate Water. The Arctic Intermediate Water is present in the northern region only. The Mediterranean water partly bends north before turning west and partly spreads directly toward the west. Some of this water turns south and continues across the Equator below the Antarctic Intermediate Water, as indicated by the crossing of the lines of flow. The Antarctic Intermediate Water enters the North Atlantic Ocean along the coast of South America. One branch bends toward the east and south, returning across the Equator, and two other branches continue, one into the Caribbean Sea and the other along the north side of the Antilles. Mixing takes place between the different types of water and the actual pattern of flow or spreading out is therefore far more complicated than is shown. For details it is necessary to refer to the discussions by Wüst (1935) and Iselin (1936).
Oxygen Distribution. The general character of the distribution of oxygen in the North Atlantic is evident from fig. 43, p. 210 and fig. 210, p. 748. The upper layers are rich in oxygen, but at depths between 500 and 900 m an oxygen minimum layer is present except in the northern parts of the ocean. In the minimum layer the lowest values are found in lat. 15°S to 15°N, where on the eastern side of the ocean (shown in fig. 43) values below 1.0 ml/L are observed as compared to minimum values of about 3.0 ml/L on the western side (fig. 210). To the north of 30°N the contrast between the two sides of the ocean is reversed and the lowest values are found on the western side, although they do not drop much below 4.0 ml/L.
Below the oxygen-minimum layer the oxygen content increases rapidly with depth; the deep water of the North Atlantic contains very large amounts of oxygen which decrease somewhat, however, from north to south. In the region where the North Atlantic Deep Water is formed, the oxygen content is at all depths higher than 6.5 ml/L (see table 82, p. 683) and from that area the oxygen content gradually decreases to 5.5 ml/L at the Equator and less than 5 ml/L in 45°S. In the same distance the percentage saturation decreases from about 85 to 75 or 70. The southern part of the Weddell Sea is the only other oceanic area in which water at depths below 2000 m contains as much oxygen as does the deep water of the North Atlantic Ocean.
Adjacent Seas of the Indian Ocean
The Red Sea. Before discussing the water masses and currents of the Indian Ocean it is of advantage to deal with the one important
Extending between lat. 12°N and 30°N, the Red Sea fills a long and narrow basin which at the northern end is closed except for the communication through the Suez Canal and at the southern end is separated from the Gulf of Aden by a shallow sill. The total length of the Red Sea is nearly 1800 km and the width 270 km. Outside the shallow and reef-bound coastal waters the general depth is about 700 m, but the bottom is very irregular and apparently isolated depressions exceeding 2000 m occur in several places. The sill at the southern entrance of the Red Sea lies 140 km inside of the narrow Strait of Bab el Mandeb off Hanish Island, where the greatest depth is only about 100 m. The fairly complete sonic soundings of the John Murray Expedition have failed to reveal any deeper channel (Thompson, 1939b).
The Red Sea is located in a region which is characterized by such an arid climate that evaporation from the water surface greatly exceeds the small precipitation. There is no runoff because no rivers enter the Red Sea. Along the entire length the prevailing winds blow consistently from the north-northwest during half of the year, from May to September, but during the other half of the year, October to April, the north-northwest winds reach only as far south as lat. 22° or 21°N, and south of 20°N the wind direction is reversed, south-southeast winds dominating.
The climatic conditions and the prevailing winds determine the character of the waters in the Red Sea and the exchange of water between the Red Sea and the Gulf of Aden. Owing to the excessive evaporation the surface salinity of the water in the northern part of the Red Sea reaches values between 40 ‰ and 41 ‰. In summer the temperature of the surface water is very high, mostly exceeding 30°, but in winter the temperature is decreased, particularly in the northern end where the average temperature in February is as low as 18°. The lowering of the temperature in winter, together with the intense evaporation in that season, leads to the formation of deep water that fills the entire basin of the Red Sea below the sill depth and has a salinity between 40.5 ‰ and 41.00 ‰ and a temperature between 21.5° and 22°. The formation of this deep water is further facilitated by the character of the currents, which is related to the character of the prevailing winds. According to Barlow (1934), who has examined 6100 direct observations of currents, averaging them by months for the areas 12° to 20°N and 20° to 28°N, the surface current flows toward the north-northwest (into the Red Sea) from November to March and to the south-southeast (out of the Red Sea) from June to September, with transition stages in April, May, and October. During November to March, when the current flows in, the velocity is less in the northern half of the sea where the flow is directed
The oxygen content of the deep water is very low in spite of sinking of surface water in winter. According to Thompson, the oxygen content shows an annual variation, values higher than 2.0 ml/L being observed at the end of the winter, whereas at the end of the summer most values were lower than 1 ml/L. Thompson attributes the low oxygen values and the annual variation to a very rapid consumption of oxygen, which at depths between 350 and 600 m appears to amount to about 2ml/L/year. This rate of oxygen consumption is by far the highest which has been found at such depths, but appears reasonable in view of the very high water temperature (about 22°C). The observations of the John Murray Expedition in September and in April-May both indicate the existence of a region of minimum oxygen content in the central portion of the Red Sea at depths between 300 and 500 m. Thompson attributes this minimum to a vertical rotational movement, which in winter is related to the sinking of surface water in the northern part of the Red Sea and rising of deep water inside of the sill, but which, in summer, in part reverses owing to the piling up of water inside of the sill.
The exchange of water between the Red Sea and the adjacent parts of the ocean takes place through the Suez Canal and through the Strait of Bab el Mandeb. The exchange through the Suez Canal is of no importance to the water and salt budget of the Red Sea but shows some interesting details (Wüst, 1934). Wüst points out that any flow of water through the Suez Canal is greatly complicated by the fact that the canal passes through the Bitter Lakes, the bottoms of which consist of layers of salt which are gradually being dissolved, thus increasing the salinity of the waters in the canal to a concentration above that of the Red Sea or Mediterranean Sea waters. In October-December the salinity at the surface of the canal above the Great Bitter Lake is as high as 50.00 ‰ and at the bottom it is above 55.00 ‰. The flow through the Suez Canal is mainly determined by three factors: (1) the difference
The exchange of water between the Red Sea and the Gulf of Aden is subject, according to Vercelli (1925) and Thompson (1939b), to a distinct annual variation which is related to the change in the direction of the prevailing winds in winter and summer. In winter, when south-southeast winds blow in through the Strait of Bab el Mandeb, the surface layers are carried from the Gulf of Aden into the Red Sea, and at greater depths highly saline Red Sea water flows out across the sill. In summer, when north-northwest winds prevail, the surface flow is directed out of the Red Sea and at some intermediate depths water from the Gulf of Aden flows in, having a lower salinity and a lower temperature than the outflowing surface water. At still greater depths highly saline Red Sea water appears to flow out over the sill, but it is probable that this outflow is much reduced as compared to the outflow in winter. On the basis of direct measurements of currents at anchor stations, Vercelli found that in winter the average inflow amounts to approximately 0.58 million m3/sec, whereas the outflow of Red Sea water amounts to approximately 0.48 million m3/sec. No measurements are available for summer.
Owing to the complicated character of the water exchange in summer, the average salinity of the in- and outflowing water is not known and, furthermore, the excess evaporation from the Red Sea is not well determined, for which reasons a computation of the exchange of water cannot be based on a consideration of the salt balance. Vercelli even thinks it possible that more salt is carried in than out and that the salinity of the Red Sea is increasing. He also points out that owing to the rapid change in salinity through the Strait of Bab el Mandeb, the outflowing tidal currents carry water of higher salinity than the inflowing, such that tidal currents assist in the transport of salt out of the Red Sea. He concludes that in winter the net inflow of 0.1 million m3/sec is nearly twice as great as the net loss of water by evaporation, for which reason the water level in the Red Sea must rise during winter. According to Vercelli the average annual evaporation excess from the Red Sea amounts to about
The final result of this discussion is not very conclusive. As far as the conditions in the Indian Ocean are concerned, the greatest interest is attached to the amount of Red Sea water that flows out over the sill and spreads at an intermediate depth in a manner similar to the spreading of the Mediterranean Sea water in the Atlantic Ocean. According to Vercelli the amount that flows out in winter is, as already stated, 0.48 million m3/sec, but in summer the outflow must be considerably smaller. The average annual amount is therefore probably between 0.3 and 0.4 million m3/sec, that is, approximately one sixth of the amount which flows out through the Strait of Gibraltar. This conclusion is in agreement with the fact that, as presently will be shown, the Red Sea water is of less importance in the Indian Ocean than is the Mediterranean water in the Atlantic Ocean.
The Persian Gulf is so shallow that any exchange of water between it and the adjacent Gulf of Oman is of small significance. The average depth of the Persian Gulf is only 25 m and the maximum depth is about 90 m. It appears to be filled by water of a nearly uniform salinity of about 38.00‰ and some exchange must take place with the waters of the Gulf of Oman, but the character of this exchange has not been examined.
The Indian Ocean
The Water Masses of the Indian Ocean. Oceanographically, the southern limit of the Indian Ocean can be placed in the region of the Subtropical Convergence, according to which definition the Indian Ocean extends to approximately lat. 40°S. The ocean is closed toward the north and all the water masses in the upper layers are therefore such as are characteristic of the middle latitudes and the equatorial regions. No subpolar water mass enters the Indian Ocean. A considerable number of oceanographic stations have recently been occupied in the equatorial areas of the Indian Ocean by the Dana, Snellius, and John Murray Expeditions, but as yet most of the data from the two latter are not available. The Discovery expeditions have occupied many stations along the African east coast and off South Africa, and a few to the south and southwest of Australia, but no accurate observations are available from the entire central and southern part of the Indian Ocean except a few from the Planet Expedition in 1906. Any discussion of the types of water in the Indian Ocean must therefore be of a preliminary character and the classification given here will have to be subject to future corrections.
Within the surface waters the temperature increases rapidly toward the north from the Subtropical Convergence and, in the equatorial regions, it is uniformly high during the greater part of the year, between 25° and 29°. In August lower temperatures, down to 22°, are found along the southeast coast of Arabia and the east coast of Africa as far south as to the Equator, in consequence of the upwelling under the influence of the prevailing southwest monsoon. In February lower temperatures are similarly found in the Gulf of Oman and the Bay of Bengal in consequence of the effect of the northwest monsoon. The salinity of the surface waters shows, to the west of Australia, the common subtropical maximum, and in the equatorial and northern regions is subject to considerable annual variations which are related to the changing monsoons and the annual variation in the precipitation (see chart VI).
At subsurface depths three larger water masses can be shown to exist, the Indian Ocean Central Water and the Indian Ocean Equatorial Water, both of which extend to moderate depths, and the deep water, present below a depth of roughly 2000 m. Transition types are found and, furthermore, two types of water spread at mid-depths, the Antarctic Intermediate Water and the Red Sea Water.
In the inset map in fig. 189 are shown the approximate regions in which the Central Water mass and the Equatorial Water mass are found. Within the area of the Central Water mass seven widely separated stations have been selected, as indicated in the figure. The temperature-salinity relation at these stations is shown in fig. 189 (left), from which it is evident that nearly all the observed temperatures and salinities fall on a straight line between the points T = 8°, S = 34.60‰, and T = 15°, S = 35.50 ‰. A remarkable agreement exists between such widely separated stations as Discovery 427 off Port Elizabeth in South Africa and B.A.E. 75 (Howard, 1940) to the southwest of Australia, and between the latter station and Dana station 3938 to the northwest of Madagascar. The deeper values from Dana station 3938 deviate, however, showing higher salinities that indicate presence of Red Sea water. Traces of this water are also found at Dana station 3960 to the south of Madagascar. The southern limit of the Central Water mass coincides with the approximate location of the Subtropical Convergence. In the region of the convergence the surface temperature and salinity vary rapidly with latitude, and the horizontal T-S relation in that region in certain seasons agrees very well with the vertical T-S relation between depths of approximately 100 m and 800 m within the Central Water mass. It is therefore probable that this water mass has been formed by sinking’ at the Subtropical Convergence. The northern limit of the Central Water mass cannot be determined, owing to lack of observations.
The Equatorial Water of the Indian Ocean is not so well-defined as the Central Water, but at most stations to the north of the Equator a considerable
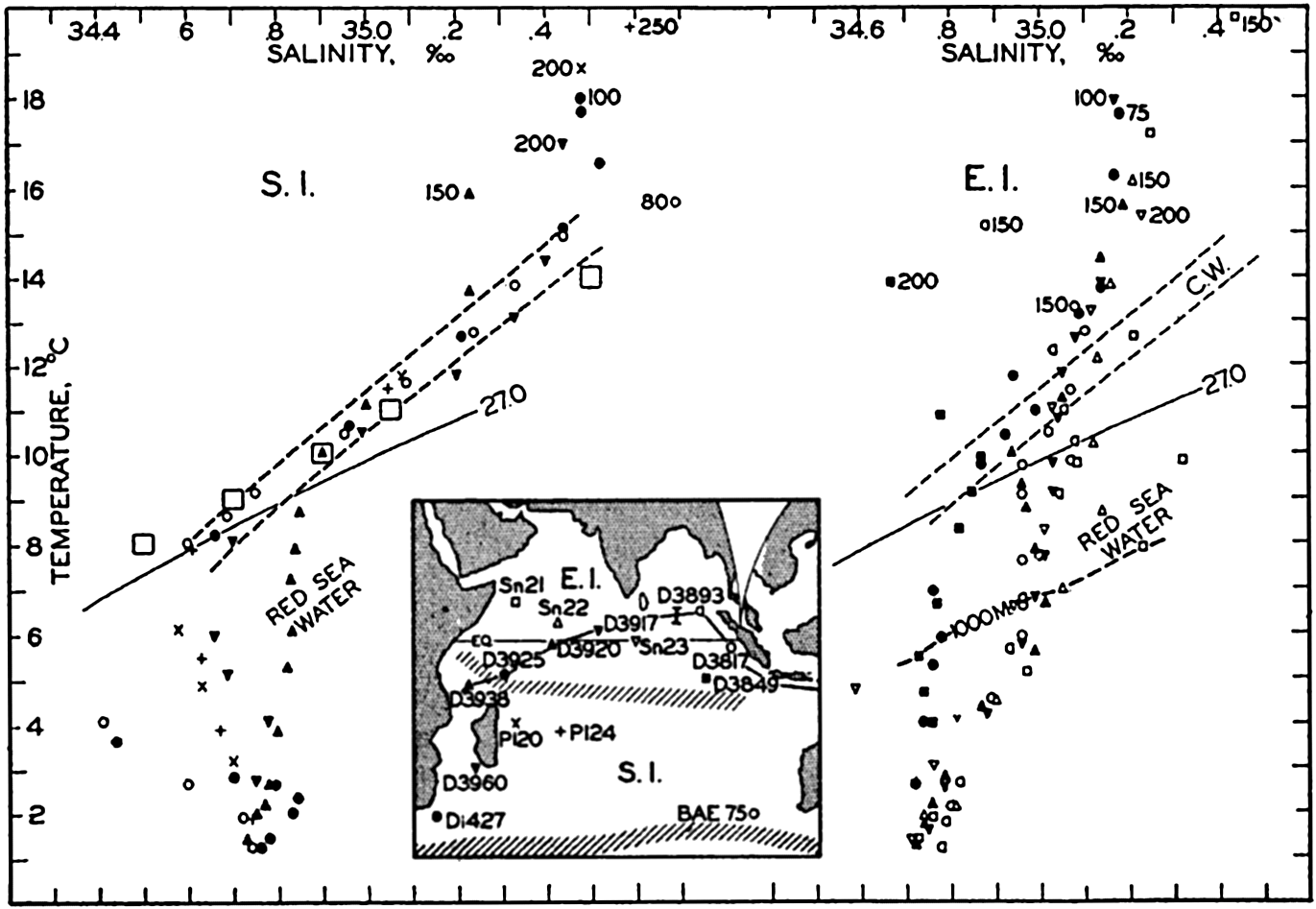
Temperature-salinity relations in the Indian Ocean. The depths of the shallowest values are indicated. Large squares represent winter surface values in the region of the subtropical convergence. Inset map shows locations of stations used and boundaries of water masses. Abbreviations: Sn, Snellius; D, Dana; Di, Discovery; P, Planet; BAE, B.A.N.Z. Expedition; E.I., Equatorial Indian Ocean; S.I.. South Indian Ocean.
The spreading of the Red Sea water in the Indian Ocean is probably similar to that of the Mediterranean water in the Atlantic Ocean, but owing to lack of data it is impossible to carry out a detailed analysis comparable to that of the Mediterranean component made by Wüst (1935). Repeated observations at the same stations in the Gulf of Aden have given very different salinity values, a condition which strongly indicates that the outflow is intermittent. A seasonal variation in the outflow appears to be well established, but great year-to-year differences may also occur and such fluctuations complicate the conditions at greater distances. The best idea of the spreading of the Red Sea water is obtained from a Discovery section parallel to the African east coast, the location of which is shown in the inset map, fig. 192 (p. 697). The distributions of temperature, salinity, and oxygen in this section have been discussed by Clowes and Deacon (1935), from whose paper fig. 190 and fig. 192 have been reproduced. Figure 190 shows the Red Sea water penetrating as a tongue of water of high salinity, which sinks from a depth of about 500 m at station 1588 in lat. 8°N (see fig. 192) to a depth of about 1250 m south of lat. 20°S between southern Madagascar and the mainland. This water has a low oxygen content, as is evident from fig. 192. Clowes and Deacon draw attention to the fact that the oxygen distribution indicates a further penetration of the Red Sea water to the south, such that the last traces of this water may possibly be present in lat. 40°S.
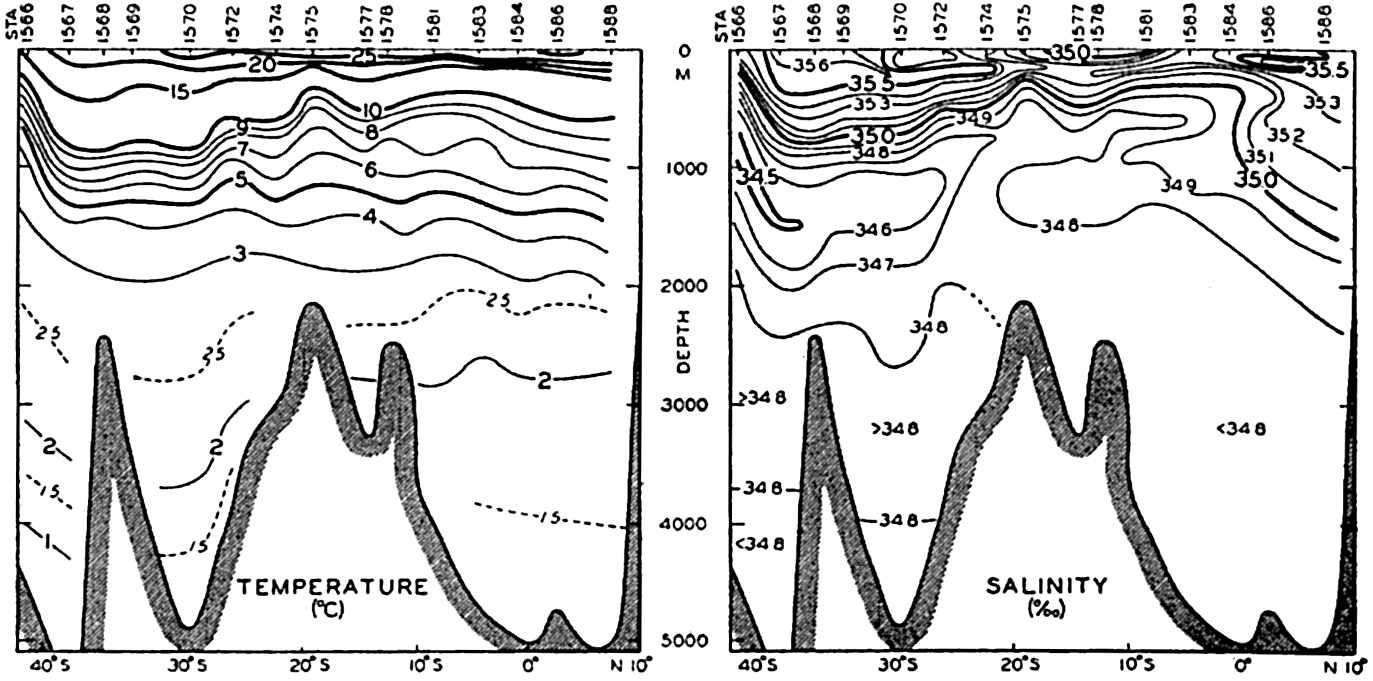
Distribution of temperature and salinity in a vertical section along the east coast of Africa. Location of section shown on inset map in fig. 192. (After Clowes and Deacon.)
The Discovery section off the African east coast is the only longituibeal section that can be constructed in the Indian Ocean by means of redinall
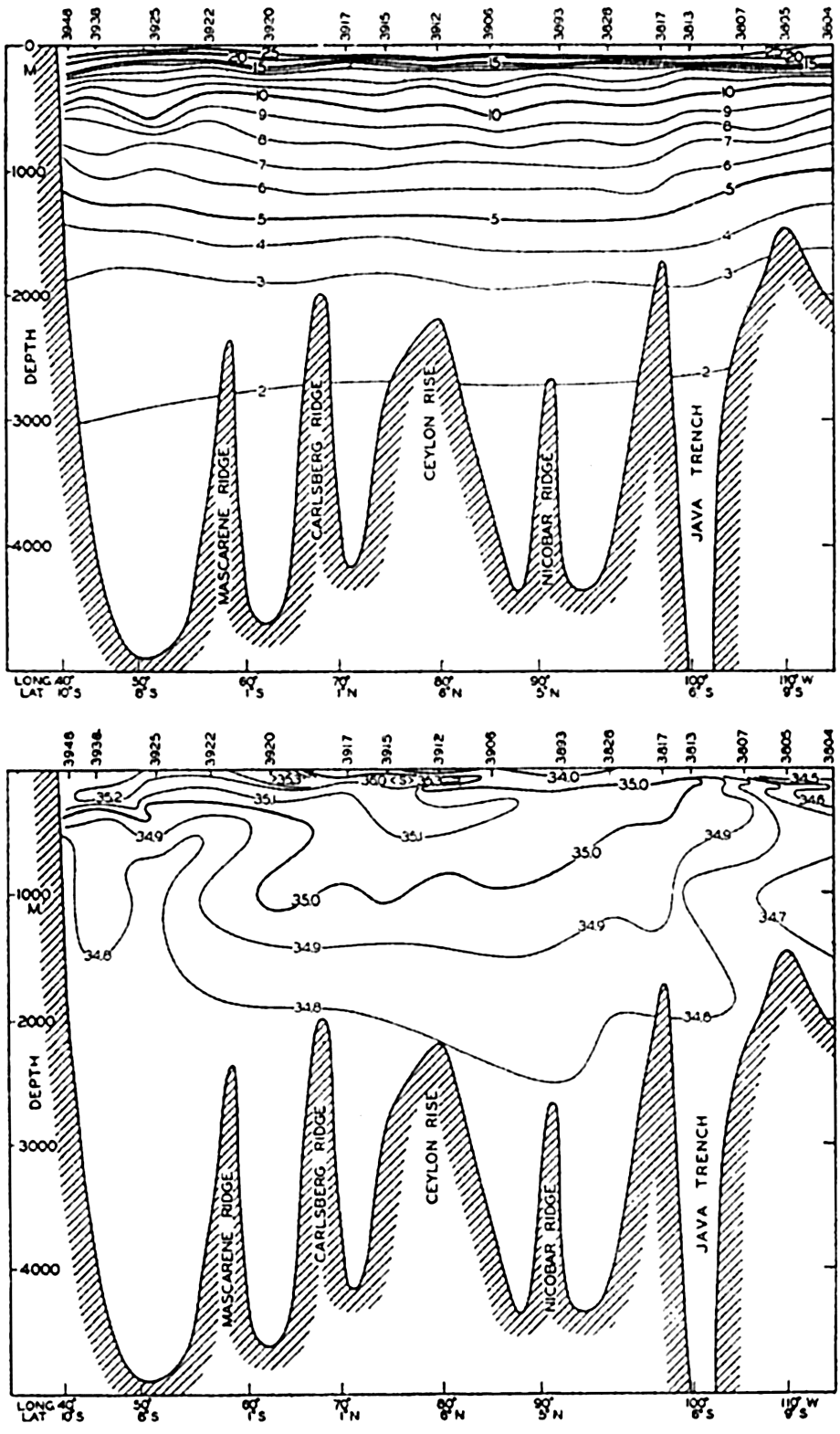
Distribution of temperature and salinity in a vertical nearly east-west section in the equatorial region of the Indian Ocean. Location of section shown by line I on inset map in fig. 189.
An approximately east-west section in the equatorial regions has been constructed by means of Dana observations, using stations along line I in fig. 189. The section follows the coasts of Java and Sumatra, crosses the Bay of Bengal, and runs in a south-southeasterly direction from Ceylon to Cape Delgado on the coast of east Africa in lat. 10°S, lying to
The surface salinity is below 35.00 ‰ except to the west of long. 70°E, but a subsurface salinity maximum is present over a large part of the section, the maximum being found near the upper limit of the sharp thermocline, as was the case in the Atlantic Ocean. In the Indian Ocean this high-salinity surface water appears to come from the Arabian Sea.
Below the salinity maximum the salinity gradually decreases with increasing depth, until the nearly constant value for the deep water of about 34.76‰ is reached between depths of 2500 and 3000 m; but to the right in the section, low-salinity water is present that probably comes from the Pacific Ocean where water of similar characteristics is found (p. 707). The Red Sea water is not very conspicuous. To the extreme left it is shown by the downward bend of the 34.8 isohaline and by the greater distance between the 8° and 7° isotherms.
In the middle part of the section the equatorial water is present, the bulk of which has a temperature below 10° and a salinity less than 35.10‰. This water probably contains some admixture of Red Sea water but mainly it is formed and maintained by slow processes of mixing between the high-salinity water from the Arabian Sea and the deep water; the origin of the latter will be discussed when dealing with the deep-water circulation of the oceans.
The Currents of the Indian Ocean. In the southern part of the Indian Ocean a great anticyclonic system of currents appears to prevail, comparable to the corresponding systems of the South and North Atlantic Ocean except that it is subjected to greater annual variations. Between South Africa and Australia the current is directed in general from west to east. In the southern summer the current bends north before reaching the Australian Continent and is joined by a current which flows from the Pacific to the Indian Ocean to the south of Australia. In winter the current appears to reach to Australia and in part to continue towards the Pacific along the Australian south coast. To the north of 20°S the South Equatorial Current flows from east to west, reaching its greatest velocity
In both seasons of the year part of the South Equatorial Current turns south along the east coast of Africa, feeding the strong Agulhas Stream. To the south of lat. 30°S the Agulhas Stream is a well-defined and narrow current which extends to a distance from the coast of less than 100 km. As is to be expected in a flow towards the south in the Southern Hemisphere, the coldest water is found inshore and the sea surface rises when departing from the coast. Off Port Elizabeth the rise amounts to about 29 cm in a distance of about 110 km (Dietrich, 1936). To the south of South Africa the greater volume of the waters of the Agulhas Stream bends sharply to the south and then toward the east, thus returning to the Indian Ocean by joining the flow from South Africa toward Australia across the southern part of that ocean, but a small portion of the Agulhas Stream water appears to continue into the Atlantic Ocean (Dietrich, 1935). Owing to the reversal of the direction of the main current to the south of Africa, numerous eddies develop, resulting in a highly complicated system of surface currents which probably is subjected to considerable variations during the year and variations from one year to another.
To the north of lat. 10°S the surface currents of the Indian Ocean, which are probably nearly identical with the currents above the tropical discontinuity surface, vary greatly from winter to summer owing to the different character of the prevailing winds. During February and March when the northwest monsoon prevails, the North Equatorial Current is well developed and an Equatorial Countercurrent is present with its axis in approximately 7°S. Along the African east coast between the Gulf of Aden and lat. 5°S the current is directed towards the south. In August–September when the southwest monsoon blows, the North Equatorial Current disappears and is replaced by the Monsoon Current, which flows from west to east. Along the coast of east Africa the current is directed north from lat. 10°S, water of the Equatorial Current crosses the Equator, and considerable upwelling takes place off the Somali coast. The Equatorial Countercurrent does not appear to be present in this season.
At present nothing is known as to the motion of the water below the tropical discontinuity in the northern part of the Indian Ocean. The character of the water, together with the very low oxygen values which are found to the north of the Equator, indicates that no strong currents exist and that only a sluggish flow takes place.
In the southern part of the Indian Ocean the Antarctic Intermediate Water probably flows north, but the flow must be less well-defined than the corresponding flow in the South Atlantic Ocean, because in the Indian Ocean the Antarctic Intermediate Water loses its typical characteristics on a shorter distance from the Antarctic Convergence (Sverdrup, 1940). The probable flow of the deep water will be discussed later on.
The data from the Indian Ocean are too scanty to permit many quantitative calculations as to the amount of water carried by the different branches of the current. The only reliable figure which is available is found in Dietrich's study of the Agulhas Stream, which transports a little more than 20 million m3/sec. A transport map similar to the one for the North Atlantic Ocean cannot be constructed.
Distribution of oxygen (ml/L) in a vertical section along the east coast of Africa. Location of section shown on map. (After Clowes and Deacon.)
Oxygen Distribution. The distribution of oxygen in the Indian Ocean is not known in detail, but some of the characteristic features can be seen from the Discovery and Dana sections in figs. 192 and 193. According to the Discovery section along the African east coast the oxygen content of the Indian Ocean decreases from the south toward the Equator. The Red Sea water is characterized by low oxygen content, but the content increases in the direction in which the Red Sea water spreads, probably due to mixing with the over- and underlying water masses. The Antarctic Intermediate Water is relatively high in oxygen and the same statement applies to the deep water, in which values ranging from 4.4 to 3.6 ml/L are observed. To the north of 20°S an intermediate minimum of oxygen is present at a depth of approximately 200 m. According to the Dana section the oxygen content of the tropical waters
Distribution of oxygen (ml/L) in a vertical nearly east-west section in the equatorial region of the Indian Ocean. Location of section shown by line I on inset map in fig. 189.
The South Pacific Ocean
Water Masses of the South Pacific Ocean. Above the deep water the water masses of the Pacific Ocean are of more complicated character than those of the other oceans. Subantarctic Water is of small significance in the Atlantic and Indian Oceans, but the South American
Temperature-salinity relations within the Subantarctic Water of the South Pacific. The depths of the shallowest values are indicated. Locations of stations and boundaries of water masses are shown on the inset map. Abbreviations: D, Dana; C, Carnegie, Di, Discovery, W.S., William Scoresby, SA-A.S.P., Subantarctic South Pacific; W.S.P. Western South Pacific; E.S.P., Eastern South Pacific.
Turning first to the South Pacific Ocean, one finds to the south of lat. 40°S the Subantarctic Water mass which, in the upper layers, is characterized by a salinity between 34.20 ‰ and 34.40 ‰ and a temperature between 4° and 8°. This is evident from the T-S curves in fig. 194, according to which the water at Dana station 3642 off New Zealand was of the same character as the water at the Discovery station 967 half way between New Zealand and South America. Part of this
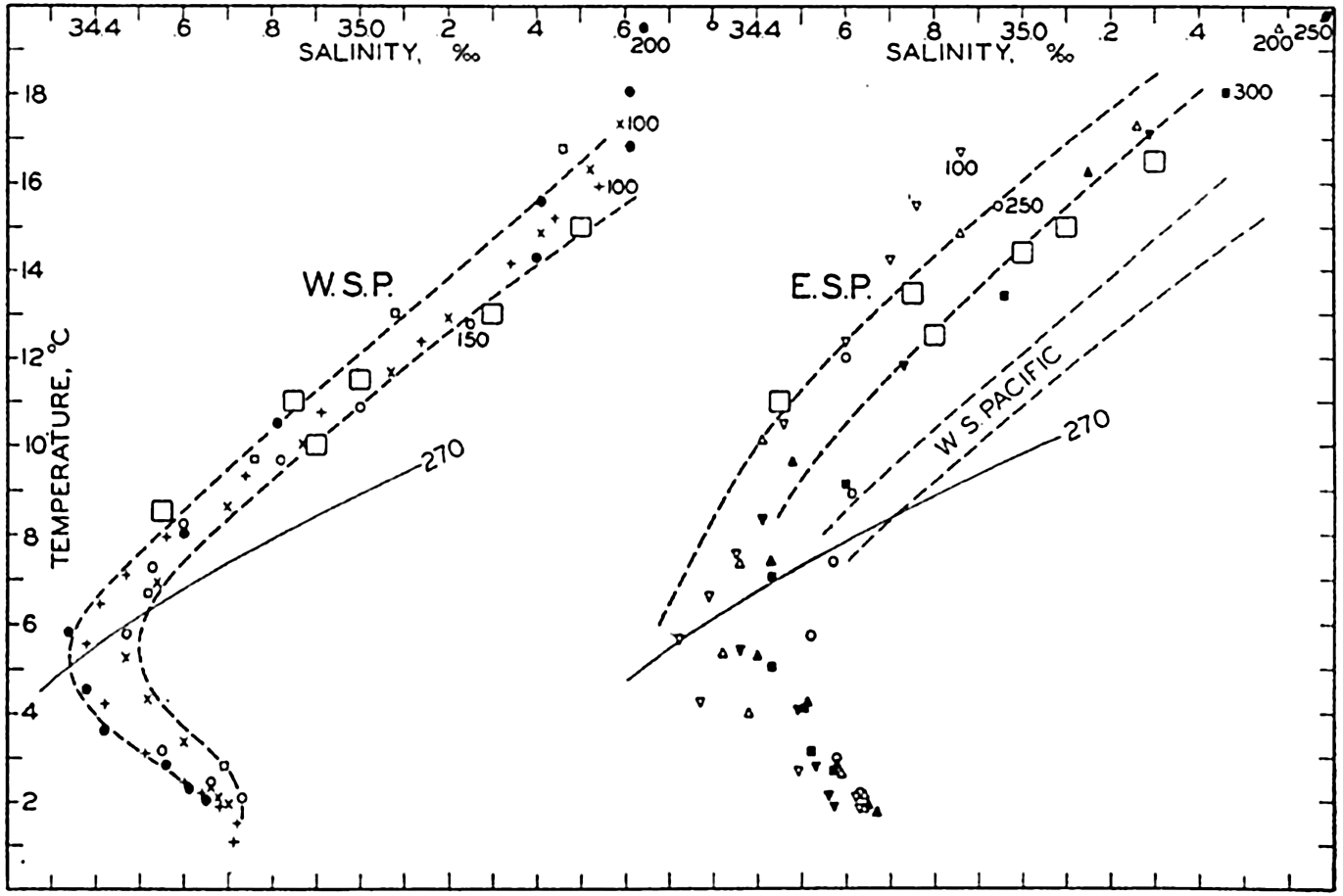
Temperature-salinity relations in the western and eastern South Pacific. The depths of the shallowest values are shown. Squares represent winter surface values in the region of the Subtropical Convergence. Locations of stations used and boundaries of water masses shown on inset map in fig. 194. W.S.P., Western South Pacific; E.S.P., Eastern South Pacific.
In the western part of the South Pacific Ocean a water mass is encountered that is similar to the Central Water of the Indian Ocean. This is evident from fig. 195, in which the corresponding temperature and salinity values at a number of Dana stations are entered, together with those from Discovery station 898 off Tasmania and Planet station 331 in lat. 2°S and long. 152°E. A comparison with fig. 188, p. 685, shows that the Indian Ocean Central Water and the water in the western Pacific are practically identical.
The large squares in the figure show the corresponding values of surface temperatures and salinities in August in lat. 35° to 45°S, long. 150°E to 160°W (according to Schott's charts, 1935). Again a region is found
In the eastern South Pacific the few available data indicate the existence of another water mass which has, between temperatures of 10° and 18°, a salinity nearly 0.50 ‰ lower than that of the western body of water. The definition of this water mass is mainly based on the observations at a number of Carnegie stations, four of which are shown in fig. 195. At Dana station 3580, located in 19°S, 163°W, the water is intermediate in character between the eastern and western masses, and the boundary region between these water masses can therefore be placed approximately along the meridian of 165°W. The squares in fig. 195 (right) show corresponding values of surface temperature and salinity in August in lat. 35° to 40°S and long. 150° to 120° W.
In the South Pacific Ocean we therefore encounter three distinctly different upper water masses: the Subantarctic Water mass, which is more or less uniform to the south of 40°S and which changes its characteristics as it moves north along the coast of South America, and the western and the eastern South Pacific Central Water masses, which are separated from each other by a region of transition in about 165°W. The eastern Central Water mass does not extent north of 10°S but the western may extend nearly to the Equator, as indicated by the observations at Planet station 331. The existence of two characteristically different central water masses indicates that in the South Pacific Ocean the circulation is split up in two large cells, the location of which appears to be related to the prevailing winds. In the southern winter the atmospheric pressure shows two distinct areas of high pressure over the Pacific Ocean, one eastern with its center in approximately lat. 28°S and long. 100°W, and one western which extends partly over the Pacific Ocean with its center over eastern Australia. The surface currents (chart VII), which only in part reflect the circulation in the deeper layers, and in part show the wind drift of surface water, indicate in most seasons the existence of a region of weak and irregular currents in about 160°W which is the approximate region where the transition between the two central water masses takes place.
Below the upper water masses Antarctic Intermediate Water is present, in the east probably to within 10° to 15° from the Equator, and in the west to the Equator. In the South Pacific no salinity maximum is found below the intermediate water, but the salinity increases toward the bottom or remains constant below a depth of 2500 or 3000 m.
Currents of the South Pacific Ocean. The only major current of the South Pacific Ocean which has been examined to some extent is the Peru Current. Following the nomenclature proposed by Gunther (1936), the name Peru Current will be applied to the entire current between the South American Continent and the region of transition
As is evident from the character of the waters (fig. 194), the origin of the Peru Current has to be sought in the subantarctic region, part of the Subantarctic Water which flows towards the west across the Pacific Ocean being deflected towards the north when approaching the American Continent. The total volume of water in the current does not appear to be very great. On the basis of a few Discovery stations it is found that the transport lies somewhere between 10 and 15 million m3/sec, and this figure includes transport of the upper water layers and of Antarctic Intermediate Water. The western limit of the current appears to be diffuse and cannot be well established on the basis of the available data, but it is probable that the current extends to about 900 km from the coast in 35°S. The northern limits, according to Schott (1931), can be placed a little south of the Equator where the flow turns toward the west.
The current being wide and the transport small, the velocities are quite small. This must be true particularly in the case of the Peru Oceanic Current which, however, is little known. The Peru Coastal Current is better known, partly because numerous observations of surface currents and surface temperatures are available off the coasts of Peru and Ecuador between the Equator and 10°S, and partly because of the extensive examination of the coastal waters which was conducted by the R.R.S. William Scoresby in 1931 and which has been discussed in detail by Gunther (1936). Within the Peru Coastal Current upwelling represents a very conspicuous feature. The upwelling is caused by the southerly and south-southeast winds which prevail along the coasts of Chile and Peru and carry the warm and light surface waters away from the coast, resulting in cold water being drawn from moderate depths toward the surface. On the basis of numerous sections close to the coast, Gunther concludes that the upwelling water comes from depths between 40 and 360 m, the average depth being 133 m. The upwelling therefore represents only an overturning of the upper layers and no water from greater depths is ever drawn to the surface.
The process of upwelling will naturally influence the current parallel to the coast because the distribution of density is altered, as explained on p. 500. The William Scoresby observations clearly show that the upwelling is an intermittent process, greatly influenced by local winds, and that reversal of the wind direction frequently leads to subsidence, that is, to re-establishment of the stratification characteristic of the undisturbed conditions.
According to Schott and to Gunther, the most active upwelling occurs in certain regions separated by regions in which the upwelling is less
In early winter, April to June, the shoreward-directed branch of the northern swirl is well developed and carries water of high temperature in toward the coast in latitudes 9° to 12°S. It may even appear as an inshore warm current which brings great destruction to the animal life of the coastal waters. In the discussion of the California Current it will be shown that during the period of upwelling this current is similarly characterized by a series of swirls on the coastal side of the current, whereas from November to February, when there is practically no upwelling, a warm countercurrent flows to the north along the coast.
Close to the coasts of Peru and Chile a subsurface countercurrent flows south, as is evident from the section prepared by Gunther, showing the distribution of salinity between the surface and a depth of 400 m at a distance of approximately 180 km from the coast and between lat. 3° and 36°S. The subsurface current appears to originate at the equatorial end of the section, where it is present at a depth of less than 100 m, but sinks gradually when progressing to the south, being found at nearly 300 m in lat. 36°S. The water of this countercurrent is of the type which has been called Pacific Equatorial Water (p. 706), as is evident from the T-S curves in fig. 194, in which the data from two stations within the countercurrent, stations WS 638 and WS 612, have been plotted. To the north of lat. 25°S, where excessive evaporation increases the salinity, the salinity of the subsurface countercurrent is lower than that of the surface water, whereas to the south of about 25°S the salinity of the countercurrent is higher than that of the surface waters. Consequently, the upwelling brings relatively low-salinity water to the surface off the coast of Peru, but relatively high-salinity water to the surface off
At the northern boundary of the Peru Coastal Current certain characteristic seasonal changes take place. During the northern summer the Peru Coastal Current extends just beyond the Equator where it converges with the Equatorial Countercurrent, the waters of which in summer mainly turn towards the north. In winter this countercurrent is displaced further to the south and part of the warm but low-salinity water of the Countercurrent turns south along the coast of Ecuador, crossing the Equator before converging with the Peru Coastal Current. The warm south-flowing current along the coast is known as El Niño and is a regular phenomenon in February and March, but the southern limit mostly lies only a few degrees to the south of the Equator. Occasionally, major disturbances occur which appear to be related to changes in the atmospheric circulation (Schott, 1931). In disturbed years, such as in 1891 and in 1925, El Niño extends far south along the coast of Peru, reaching occasionally past Callao in 12°S. According to Schott, the duration of El Niño periods in 1925 was as follows:
| Locality | Latitude | Dates | Duration, days |
|---|---|---|---|
| Off Lobitos | 4°20′S | Jan. 20 to April 6 | 76 |
| Off Puerto Chicana | 7°40′S | Jan. 30 to April 2 | 63 |
| Off Callao | 12°20′S | March 12 to March 27 | 15 |
| Off Pisco | 13°40′S | March 16 to March 24 | 8 |
These figures show that the warm surface waters of the equatorial area slowly penetrated to the south, but withdrew much more rapidly, because the time interval between the appearance of the warm water off Lobitos and off Pisco was 44 days, whereas the time interval between the disappearance of the warm water at the two localities was only 13 days. The surface temperature of the water in March, 1925, was nearly 7° above the average, as is evident from the following compilation:
| Locality | Average temperature in March (°C) | Temperature in March, 1925 (°C) |
|---|---|---|
| Lobitos | 22.2 | 27.3 |
| Puerto Chicana | 20.3 | 26.9 |
| Callao | 19.5 | 24.8 |
| Pisco | 19.0 | 22.1 |
Details as to the surface salinity are not available, but normally the surface salinity between 5°S and 15°S is above 35.00 %0, whereas the waters of El Niño have a salinity between 33.00 and 34.00 %0.
The extreme development of El Niño leads to disastrous catastrophes of both oceanographic and meteorological character. The decrease of the temperature of El Niño toward the south indicates that the waters are mixed with the ordinary cold coastal waters, and during this mixing process the organisms in the coastal current, from plankton to fish, are destroyed on a wholesale scale. Dead fish later cover the beaches, where they decompose and befoul both the air and the coastal waters. So much hydrogen sulphide may be released that the paint of ships is blackened, a phenomenon known as the “Callao painter.” More serious is the loss of food to the guano birds, many of which die of disease or starvation or leave their nests, so that the young perish, bringing enormous losses to the guano industry. The meteorological phenomena which accompany El Niño are no less severe. Concurrent with a shift in the currents a shift of the tropical rain belt to the south takes place. In March, 1925, the precipitation at Trujillo in 8°S amounted to 395 mm, as compared to an average precipitation in March of the eight preceding years of only 4.4 mm. In 1941 the rainfall was again excessive, but no details are available. These terrific downpours naturally cause damaging floods and erosion. In the 140 years from 1791 to 1931 twelve years were characterized by excessive rainfall at Piura in lat. 5°S and twenty-one years by moderate rainfall which was, however, greatly in excess of the average. During the remaining nearly one hundred years the rainfall was close to nil. A greater development of El Niño is therefore not an uncommon phenomenon, but the catastrophic developments appear to occur on an average of once in twelve years. The records reveal no periodicity because the interval between two disastrous years varies from one year to thirty-four years.
El Niño is not the only current that brings warm water to the coast of Peru with subsequent destruction of the organisms near the coast. High temperatures off the coast appear to be an annual occurrence in the months of April to June, in about lat. 9° to 12°S, that is, at and to the north of Callao. These high temperatures are due, as pointed out by Gunther, to the greater development of the warm branch of the northern swirl; the water that approaches the coast is in this case offshore oceanic surface water of high temperature and relatively high salinity (p. 703). The disastrous effect on the marine organisms is very much milder than that of El Niño, but otherwise similar in character. It may lead to the killing of plankton and fish and to the migration of guano birds, but is ordinarily observed mainly by reason of a change in the color of the coastal water and development of hydrogen sulphide. Locally, these changes are known by the name of aguaje, also used synonymously with
On leaving the coast the waters of the Peru Current join the waters of the South Equatorial Current, which flows all the way across the Pacific towards the west but is known only as far as surface conditions are concerned. The subsurface data are inadequate for computation of velocities and transports, and it is therefore not possible to give any numerical values. Some features of this current will, however, be dealt with when discussing the currents of the equatorial regions of the Pacific, and it will be shown that the cold water along the Equator does not represent a continuation of the Peru Coastal Current but is due to a divergence along the Equator within the South Equatorial Current.
The other currents of the South Pacific Ocean are even less known, but from the character of the water masses it appears that two current systems exist, the nature of which may be revealed by future exploration. One big gyral appears to be present in the eastern South Pacific; in the western South Pacific annual variations are so great that in many regions the direction of flow becomes reversed, as is the case off the east coast of Australia. No chart of the transport by the current can be prepared.
The Equatorial Region of the Pacific Ocean
Water Masses of the Equatorial Pacific. In the equatorial region of the Pacific and below the tropical discontinuity layer, one finds an Equatorial Water mass of a remarkably uniform character which extends over the entire Pacific Ocean from east to west, as is evident from fig. 196, in which the temperature-salinity values at nine stations have been plotted. This Equatorial Water mass has its greatest north-south extension along the American coast, where it is present between latitudes 18°S and 20°N. Towards the west it appears to become narrower although, as will be shown, Equatorial water is occasionally found near the Hawaiian Islands. For points still further west detailed information is lacking, but at Dana station 3750, close to the Equator in long. 135°E, characteristic Equatorial Water was encountered, as is evident from the figure.
The Equatorial Water is probably formed off the coast of South America by gradual transformation of the Subantarctic Water, as suggested by the T-S curves in fig. 194, and spreads to the north and to the west. In the extreme western part of the Pacific the Dana data indicate that some of this water enters the North Pacific Ocean.
The Pacific Equatorial Water mass is characterized by a nearly straight T-S correlation between T = 15°, S = 35.15 ‰, and T = 8°, S = 35.6 ‰. At a depth of about 800 m where the temperature is about 5.5°, a salinity minimum exists in which the minimum values lie between 34.50 ‰ and 34.58 ‰. Below a depth of 1000 m the T-S
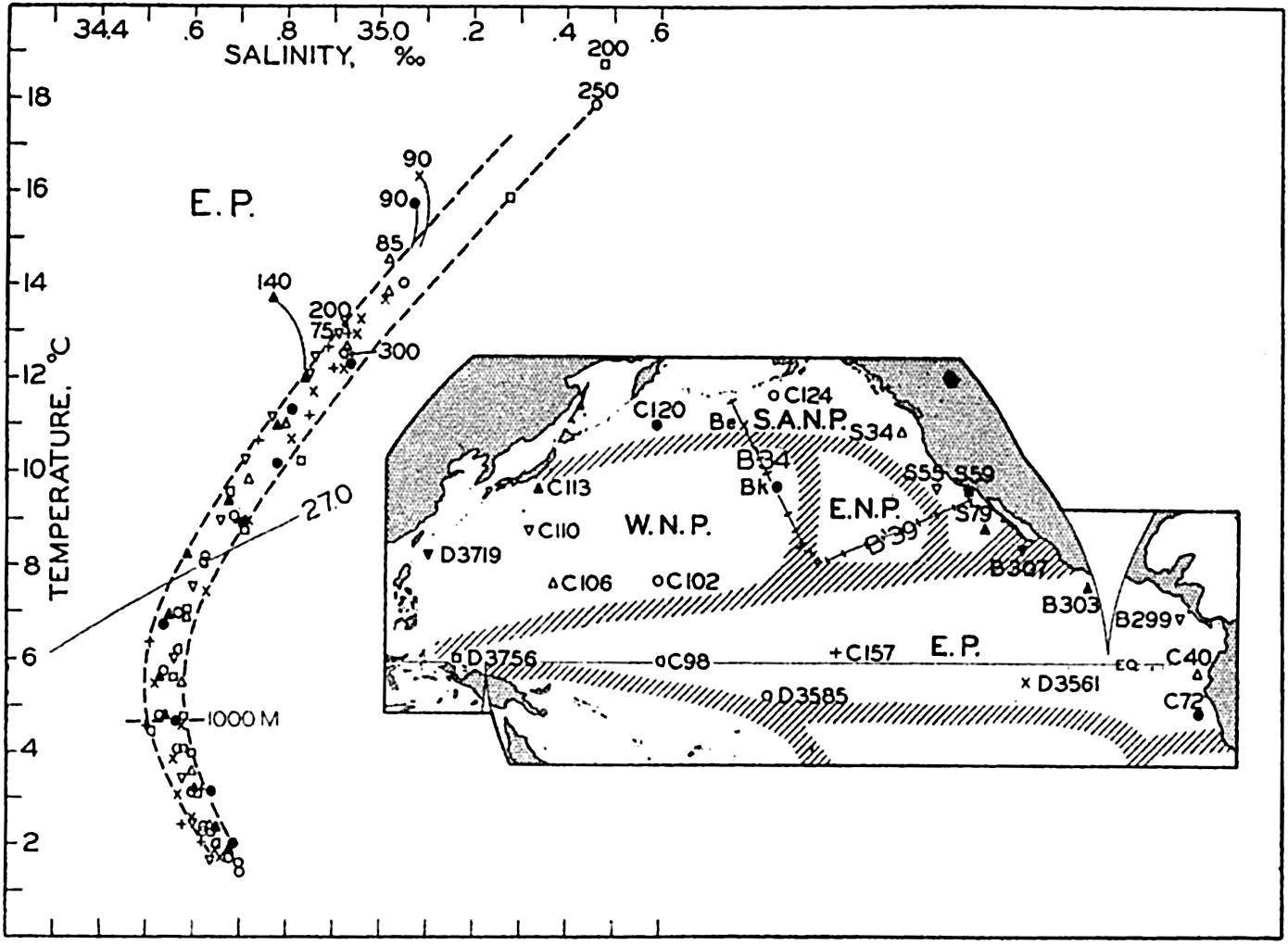
Temperature-salinity relations in the Equatorial Pacific. The depths of the shallowest values are shown. Locations of stations and boundaries of water masses are shown in the inset map. Abbreviation: C, Carnegie, B, Bushnell, S, E. W. Scripps, D, Dana, B34, Bushnell, 1934; B39, Bushnell, 1939; E.P., Equatorial Pacific; W.N.P., Western North Pacific; E.N.P., Eastern North Pacific; S.A.N.P., Subarctic North Pacific.
The water masses near the surface are separated from the Equatorial Water mass by a layer of transition within which the temperature decreases and the density increases so rapidly with depth that in many localities the layer has the character of a discontinuity surface. In or directly above the discontinuity layer a salinity maximum is present over large areas. Within the surface layer the temperature is nearly constant to a depth that varies from as little as 10 or 15 m up to nearly 100 m. These conditions are quite similar to those in the tropical regions of the Atlantic and Indian Oceans, but the scarcity of data makes it impossible to study the upper layers in the equatorial part of the Pacific in such detail as can be done in the Atlantic Ocean. A few general features can, however, be pointed out. In fig. 197, which covers the tropical region of the Pacific Ocean, is shown the approximate depth to the thermocline by means of curves drawn at intervals of 50 m. The
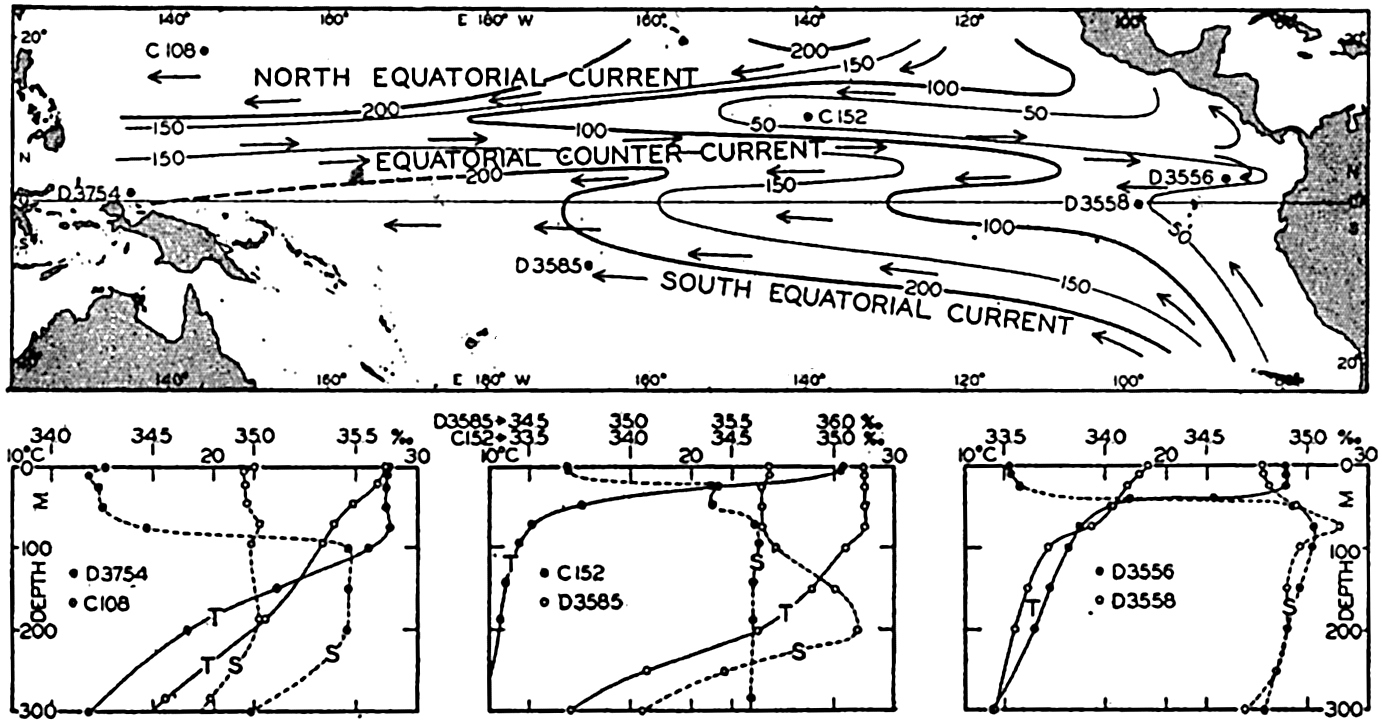
Upper: Topography of the discontinuity surface in the equatorial region of the Pacific and corresponding currents. Lower: Vertical temperature and salinity curves at six stations, the locations of which are shown in the upper figure. C, Carnegie, D, Dana.
Currents of the Equatorial Pacific. The chart of the depth to the thermocline immediately gives an idea of the currents in the upper layers in the tropical region. If the motion of the water below the discontinuity
The Equatorial Countercurrent is remarkably well developed in the Pacific Ocean where, according to charts by Puls (1895), it is present at all seasons of the year, lying always in the Northern Hemisphere but further away from the Equator in the northern summer. In this season the velocities of the current also appear to be higher, reaching values up to 2 knots at the surface. The structure of the water masses was first demonstrated by the Carnegie section in approximately long. 140°W, which was obtained in October, 1929. Figure 198A and 198B show the distribution of temperature and salinity in this section between the surface and 300 m. The figure brings out the great variation in the depth to the thermocline in a north-south direction, and the presence of the surface layer of uniform temperature and the tongues of maximum salinity. In figure 198C is shown the velocity distribution, computed on the assumption of no motion at the 700-decibar surface. These computations are uncertain near the Equator, but the resulting picture is remarkably consistent. In this case the Equatorial Countercurrent lies between 3°N and 10°N, as indicated by the letters stating the direction in which the currents flow.
Montgomery and Palmén (1940) have shown that the Equatorial Countercurrent in the Pacific Ocean, as well as that in the Atlantic Ocean, is maintained by the piling up of the light surface water against the western boundary of the ocean. They have made use of one Dana station, 3558, in long. 99°07′W, and of three Dana stations, 3775, 3756, 3767, in long. 134°44′E, all near the Equator. A comparison between the dynamic heights of the sea surface relative to the 1000-decibar surface shows that in long. 135°E the surface lies 62.6 dyn. cm higher than in long. 99°W, but the difference decreases with increasing depth and the 300-decibar surface is parallel to the 1000-decibar surface. If dynamic centimeters are replaced by centimeters one obtains the result that along the Equator the slope of the sea surface is 4.5 × 10−8. This slope of the surface and the slopes of the isobaric surfaces above the 300-decibar surface can be maintained by an east wind of velocity 4 m/sec, which is lower than the observed velocity of the trades. The stress of wind, therefore, more than accounts for the observed conditions (p. 488). Owing to the slope of the sea surface the Equatorial Countercurrent flows downhill in the calm belt between the trade winds, and the distribution of mass adjusts itself to the presence of the current. The maximum velocity at the surface, as computed from the Carnegie section (fig. 198C) is a little over 50 cm/sec or about 1 knot, in good agreement with values reported from ships.
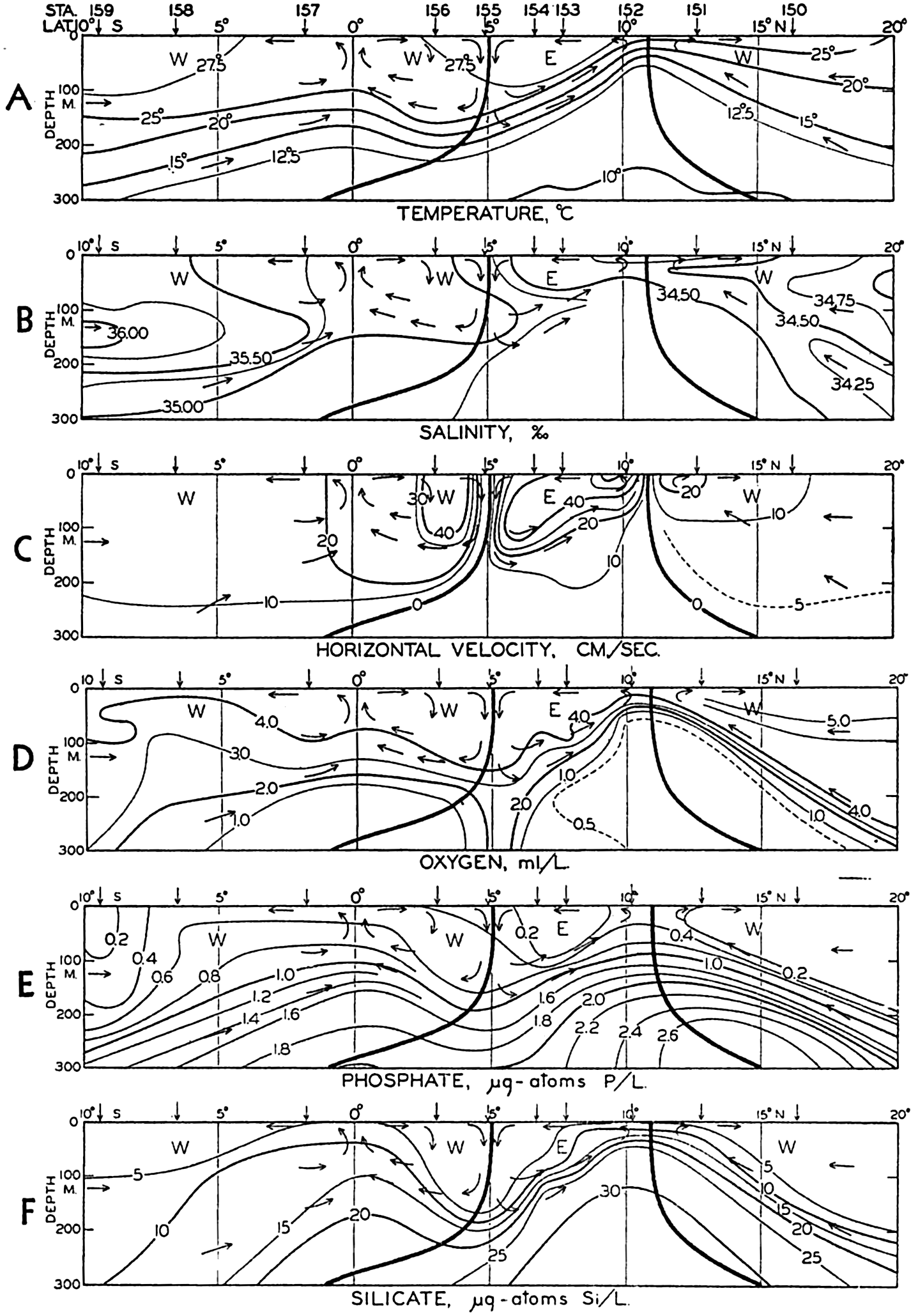
Temperature, salinity, computed velocity, oxygen, phosphate, and silicate in a vertical section between 10°S and 20°N in the Pacific Ocean. According to the Carnegie observations. Arrows indicate direction of north-south flow. E indicates flow to the east; W, flow to the west.
The Carnegie section gives a transport to the east by the Equatorial Countercurrent of approximately 25 million m3/sec; the volume transport of this countercurrent in the Pacific is therefore comparable to that of the Florida Current. The surface observations seem to indicate that the transport is somewhat less in the western part of the ocean and that water is drawn into the current as it crosses the Pacific Ocean.
Within the Equatorial Countercurrent and between that current and the Equator, a distinct transverse circulation is superimposed upon the flow toward the east or the west. The character of this transverse circulation is evident, particularly from the distribution of salinity, oxygen, phosphate, and silicate (figs. 198B, D, E, and F). The arrows shown in the figures have been derived from the distribution of oxygen and have been transferred to the other representations, where they fit equally well with the course of the isolines. Within the Equatorial Countercurrent descending motion takes place at the southern boundary and ascending motion at the northern boundary, and between the Equator and the countercurrent descending motion takes place at the boundary of the countercurrent and ascending motion at the Equator. Thus, two cells appear with divergence at the northern limit of the countercurrent and at the Equator, and with a convergence at the southern boundary of the countercurrent. This system, which appears so clearly in the Carnegie section, is quite similar to the one which Defant (1936b) has derived for the Equatorial Countercurrent in the Atlantic Ocean on the basis of theoretical considerations (fig. 172, p. 635).
Owing to the convergence and the divergences the water does not flow due east or due west; but a spiral motion is superimposed upon the major current, and within the countercurrent this motion carries water from the northern to the southern boundary at the surface and carries water in the opposite direction at depths between 50 and 200 m. Within the Equatorial Current the surface water moves from the Equator toward the countercurrent, but at depths between 100 and 150 m the water moves in the opposite direction. To the north of the Equatorial Countercurrent and to the south of the Equator, subsurface water moves toward the divergences at the surface, and this water must originate from the regions of the Tropical Convergences which lie outside the section under consideration. According to Defant's estimate the maximum
The divergences at the Equator and at the northern boundary of the countercurrent must be expected to be regions of high productivity, because the ascending motion brings water which is rich in plant nutrients into the euphotic zone. The plankton collections made on board the Carnegie when crossing the Equator confirm this expectation (see p. 788). The region in the vicinity and to the west of the Galapagos Islands is known to be abundant in marine life, but observations are not detailed enough to show whether two maxima of abundance of marine life occur, related to the two divergences. From the above discussion it is evident that the equatorial divergence, with all its consequences, is not related to the proximity of land, and that the conditions met with in the Galapagos area and to the west do not simply represent a continuation of the conditions off the coast of Peru, as had previously been assumed.
The character of the Equatorial Countercurrent is complicated both at the origin of the current between New Guinea and the Philippines and at the termination against the American coast. Schott (1939) has shown that large seasonal changes take place to the north of New Guinea. From June to August the South Equatorial Current follows the north coast of this Island and converges sharply with the North Equatorial Current in about lat. 5°N, where the countercurrent begins. From December to February, part of the North Equatorial Current bends completely around off the southern islands of the Philippines, sending one branch toward the southeast along the north coast of New Guinea, and another branch, the countercurrent, toward the east.
Similarly, great seasonal variations occur in the Central American region, as is evident from the data presented on the United States Hydrographic Pilot Charts, but in this region the picture is complicated by numerous eddies, the locations of which appear to vary from one year to another. The only persistent features are that the Equatorial Countercurrent is in most months well developed between lat. 5°N and 6°N and that the greater volume of water transported by the Countercurrent is deflected to the north and northwest, where a strong current prevails off the coast of Central America. Another branch, weaker and much more irregular, turns to the south. In the Gulf of Panama large seasonal changes occur which are associated with the change in the prevailing wind direction (Fleming, 1941).
The North Pacific Ocean
Water Masses of the North Pacific Ocean. In the North Pacific Ocean one encounters a Subarctic Water mass which is characterized in about lat. 50°N by an average temperature between 2° and 4° and by a salinity which at the surface may be as low as 32.00 ‰ but
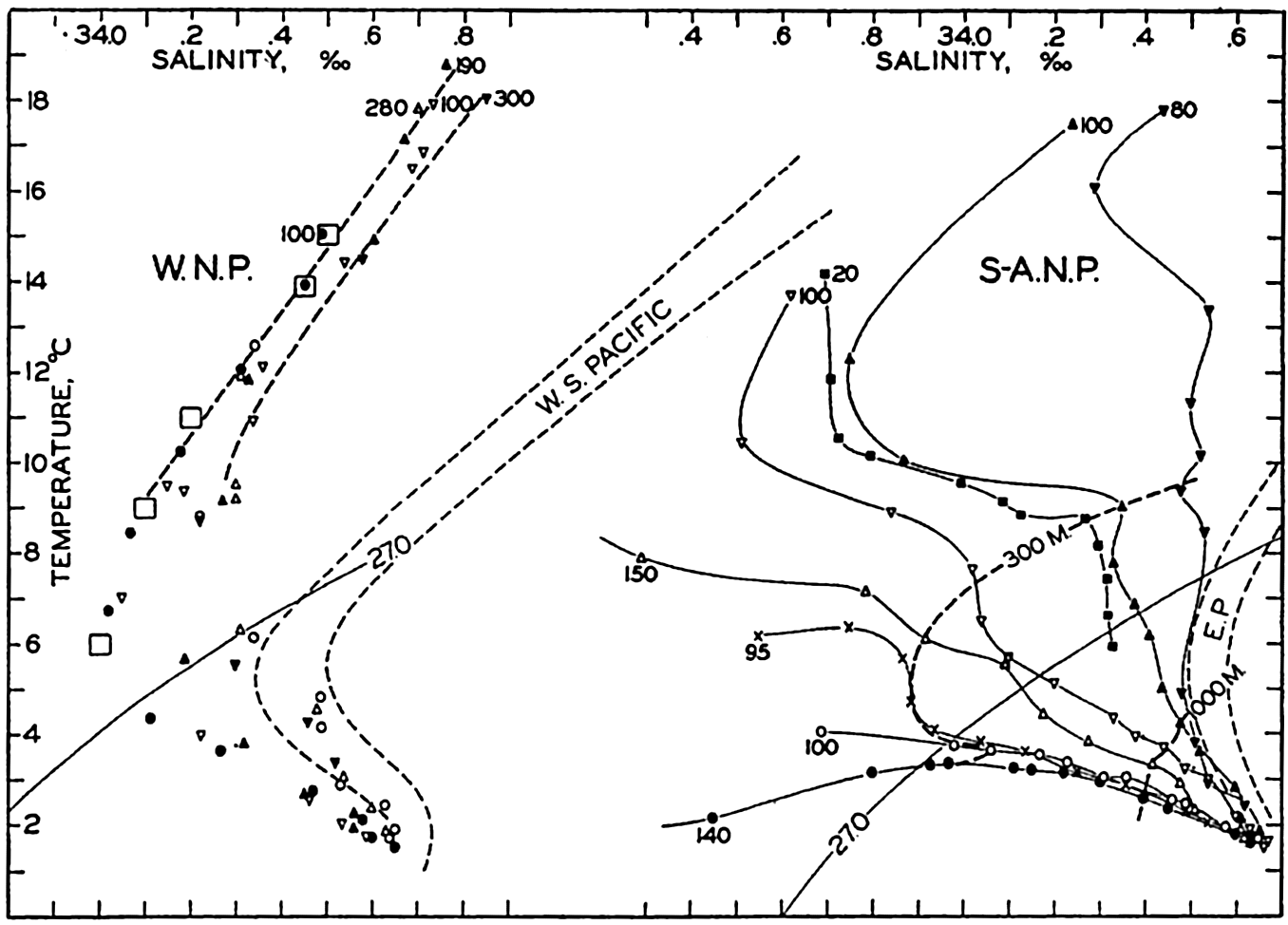
Temperature-salinity relations in the North Pacific Ocean. The areas of the Subarctic and the Western North Pacific waters and the locations of stations are shown in fig. 196. The depths of the shallowest values are entered, and to the left the large squares represent winter surface values near the Subtropical Convergence. W.N.P., Western North Pacific; S-A.N.P., Subarctic North Pacific.
The term Subarctic Water should be applied strictly only to the water to the north of 45°N, but for the sake of convenience the name will be used for the entire North Pacific Subarctic Water mass, the character of which is illustrated to the right in fig. 199. In about lat. 23°N, off the south coast of Lower California, the Subarctic Water converges with the Equatorial Water. At Station B 307 in lat. 22°22′N, nearly pure Equatorial Water was present; at Station S 79 in lat. 25°22′N the water below a depth of 300 m, where a temperature of 9° and a salinity of 34.35‰ was observed, approached the equatorial type. The bend in the T-S curve at that station suggests that an intrusion of Equatorial Water takes place below the depth of 300 m where the bend occurs.
Below 300 m the stations between lat. 22°N and 45°N show T-S curves intermediate in character between those characteristic of the true Subarctic Water of the North Pacific and the Equatorial Water; this fact suggests that the water at these stations is formed by lateral mixing between those two large and well-defined water masses. Such mixing is facilitated by a northward penetration along the coast of water that contains a large component of Equatorial Water (Sverdrup and Fleming, 1941, Tibby, 1941). This penetration is shown in fig. 199 by the T-S curve at station S 59, which lies about 30 km from the coast and at which the water is of more equatorial character than at station 55 in nearly the same latitude but about 550 km from the coast.
In the western North Pacific a well-defined Central Water mass appears to be present, because very similar T-S curves have been obtained from such widely separated localities as Carnegie station 106 in lat. 16°N and long. 152°E and Bushnell station k in lat. 24°N and long. 163°W (fig. 199, left). At Dana station 3719, 21°N and 126°E, and Carnegie station 113, 34°N and 142°E, water of nearly the same character was encountered, but of a slightly higher salinity due perhaps to admixture of Equatorial Water. This Central Water mass covers an area nearly as great as the area of the North Atlantic Ocean, but it does not extend all the way across the Pacific Ocean. It is perhaps formed in latitudes 30°N to 40°N and longitudes 150°E to 160°E, where in February the T-S relation at the surface is similar to the vertical T-S relation of the water mass.
Other observations indicate that between the Hawaiian Islands and the American coast an Eastern Central Water mass occurs, but this is of much smaller extent and is separated from the adjoining water masses by wide areas of transition. In order to demonstrate the character of this water mass, the T-S curves have been plotted from a series of stations between San Diego and the Hawaiian Islands occupied by the Bushnell in 1939, and from a series of stations between Dutch Harbor, Aleutian Islands, and the Hawaiian Islands occupied by the Bushnell in 1934 (fig. 200).
At the two stations closest to the coast of California, Subarctic Water was present of the same character as that shown by the curves in fig. 199. Between stations 309 and 310 a very marked transition took place; at station 309 the water of a temperature of 15° had a salinity of 33.55‰, whereas at station 310 the corresponding salinity was 34.40‰. In the central area between the coast and the Hawaiian Islands the T-S curves show considerable similarity to each other, but the slope of the curves is much greater than the slope of the corresponding curves which characterize the Western Central Water mass. In order to demonstrate this feature the T-S relations of the latter water mass have been indicated in the figure. Close to the Hawaiian Islands station 316 shows considerable
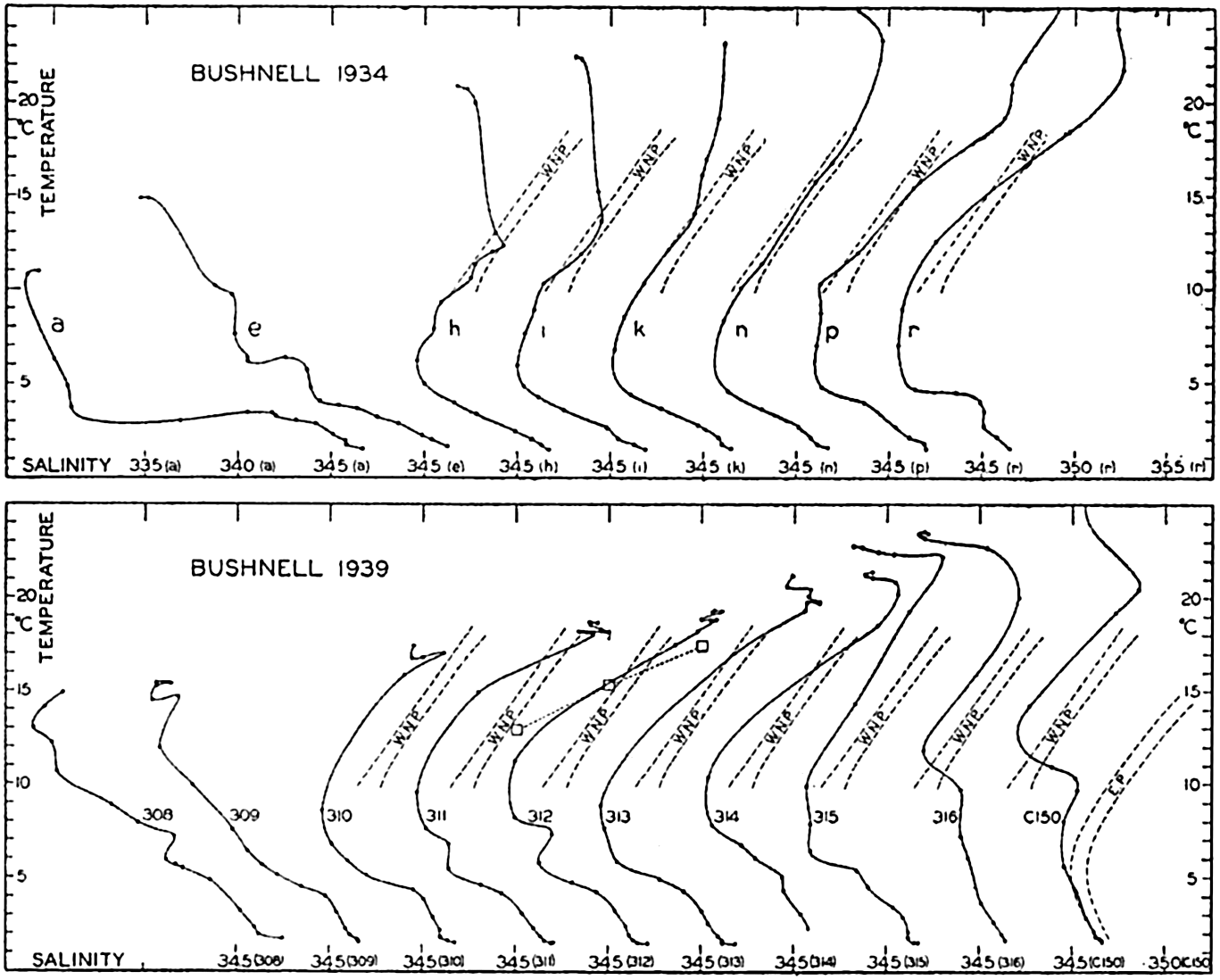
Upper: T-S curves at a number of Bushnell stations of 1934 between the Aleutian and the Hawaiian Islands. Lower: T-S curves at a number of Bushnell stations of 1939 between San Diego, California, and the Hawaiian Islands, and at station Carnegie 150 to the southeast of the Hawaiian Islands. The T-S relations of the Western North Pacific and the Equatorial Pacific are shown. Large squares represent winter surface values in about lat. 40°N, long. 140°W. The stations used are located along B34 and B39 in fig. 196.
Proceeding south from the Aleutian Islands, the northern stations show Subarctic Water, but between stations e and h a transition takes place. At station e Subarctic Water is found, but at station h Western Central Water is present, as is evident from the lines marked WNP in the figure. This same water mass is present at stations i, k, and n, but between stations n and p a new transition takes place, water more similar to the Eastern Central Water being present at stations p and r.
From this description it is evident that in the North Pacific (as in the South Pacific, see p. 701) we encounter three typically different water masses which are separated by regions of transition: the Subarctic Water mass which penetrates toward the south along the west coast of North America and two Central Water masses of which the western occupies the larger area. The existence of these two Central Water masses indicates that in the North Pacific the circulation is also characterized by the presence of two separate gyrals of which the western is the larger. The location of the eastern gyral coincides approximately with the average location of the Pacific high-pressure area, but on an average no corresponding high-pressure area is found over the western Pacific. The development of the western gyral can therefore not be a direct effect of the prevailing winds but may be related to the boundaries of the ocean.
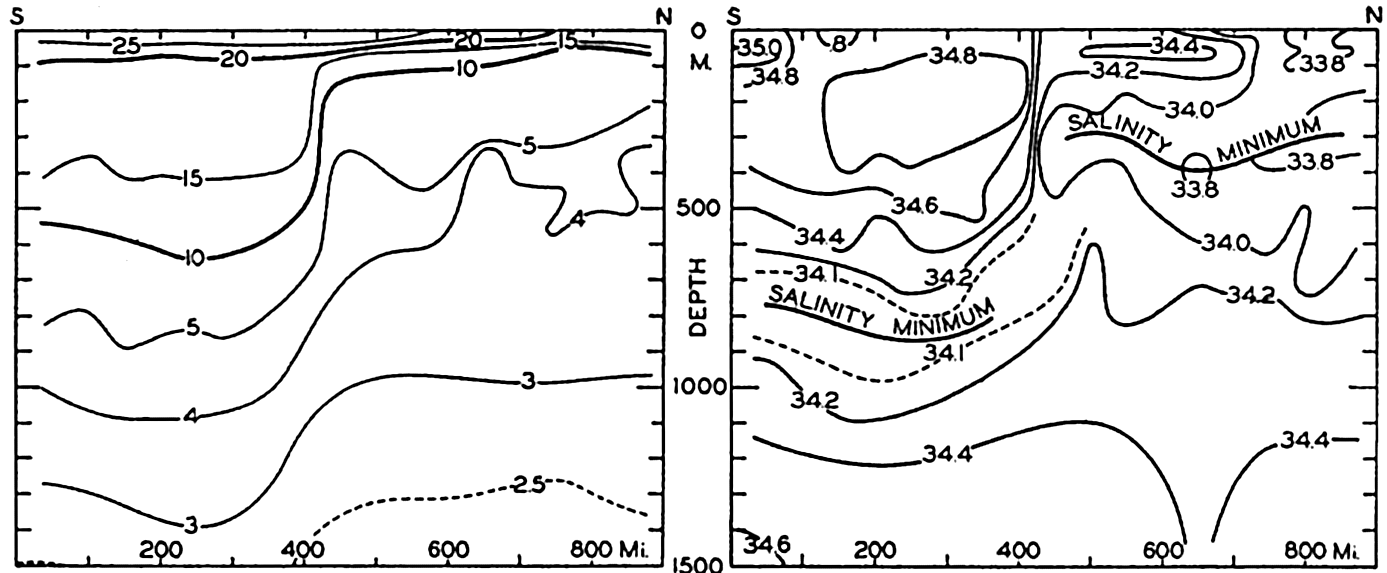
Distribution of temperatures and salinities in a vertical section between lat. 30°28′N, long. 150°04′E, and lat. 42°40′N and 157°00′E. (After Uda.)
In the North Pacific the most complicated hydrographic conditions are encountered in the waters to the northeast of Japan, where the Subarctic Water carried south by the cold Oyashio meets the warm Central Water carried northeast by the Kuroshio. The Kuroshio follows closely along the coast of Japan as far as lat. 35°, where it turns east, sending branches off toward the northeast, where intensive mixing with the waters of the Oyashio takes place. Numerous eddies are present and the different branches of the current are often separated by sharp lines of demarcation, which are visible as “tide rips” on the sea surface (Uda, 1938a).
The sharp transition from one water mass to another is illustrated in fig. 201, showing temperatures and salinities in a vertical section between the points lat. 30°28′N, long. 150°04′E and lat. 42°40′N, long. 157°0′E, about 1000 km from the coast. The waters of the Kuroshio are present to the south of lat. 36°N, where an abrupt transition takes place to waters which, above 200 m, represent Kuroshio water greatly diluted by
Both to the north and to the south of lat. 36°N an Intermediate Water is present, characterized by a salinity minimum. Below the Kuroshio water the salinity minimum is found at a depth of about 800 m, and the lowest salinity values are between 34.00‰ and 34.1‰, whereas below the mixed water to the north of lat. 36°N the salinity minimum is found at a depth of 300 m, the lowest salinities being less than 33.8‰. The oxygen content of the Northern Intermediate Water is considerably higher than that of the Southern.
Intermediate Water is present below the Central Water masses all over the North Pacific Ocean. On the basis of the Carnegie data, the Bushnell data, and the numerous observations on Japanese expeditions in the western part of the Pacific, the somewhat schematic picture in fig. 202 has been prepared, showing the value of the salinity at the minimum layer. Smooth curves have been drawn in the western area in order to bring out the main features, omitting the numerous details which would confuse the presentation. Within the Subarctic Water no salinity minimum is present; the curves have therefore been carried only to the boundary region between the Subarctic Water and the Central Water masses. The depth of the layer of minimum salinity is indicated by a few numerical values. In lat. 10°N two depths have been entered because there the layer of salinity minimum appears to divide, one branch rising toward the surface at the northern limit of the Equatorial Countercurrent, and one branch sinking and approaching the minimum layer of the Equatorial Water mass (see fig. 198). Similarly two depths are entered in lat. 28°N, long. 130°W, because several stations in that region show a double minimum (see fig. 200).
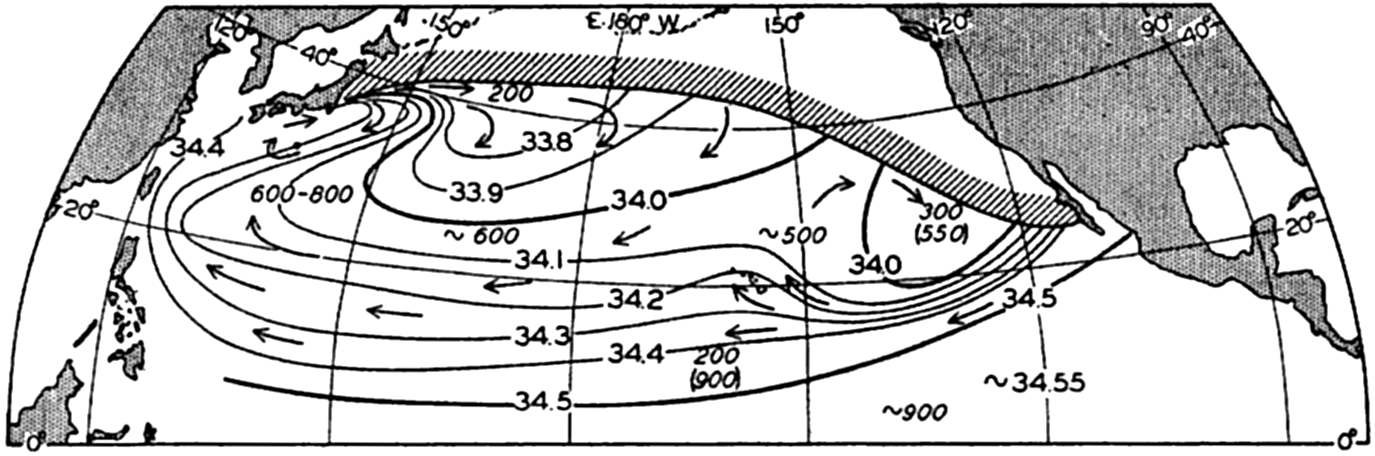
Salinity in the layer of minimum salinity of the North Pacific. The direction of flow is indicated by arrows. The approximate depths (in meters) of the minimum values are shown. Where two minima are present, one of the depths is entered in parenthesis.
In order to understand the distribution of salinity within the minimum layer it is necessary to discuss the probable flow of the water, to which we
Below the Intermediate Water the salinity increases regularly, reaching maximum values of 34.65‰ to 34.67‰ at the bottom. No salinity maximum is present between the minimum layer and the bottom, but in several regions the salinity is constant in the lower 1000 m.
The Currents of the North Pacific Ocean. There is considerable similarity between certain currents of the North Pacific and of the North Atlantic Oceans, but there are also striking differences due mainly to the occurrence of large quantities of Subarctic Water in the North Pacific, as contrasted to the small amounts of that type in the North Atlantic. The Subarctic Water of the Pacific and the currents that carry Subarctic Water are present in the northern and eastern areas and similarity to the North Atlantic is therefore found in the southern and western part of the ocean, where the North Equatorial Currents correspond to each other and where the Kuroshio corresponds to the Florida Current and the Gulf Stream.
The North Equatorial Current of the Pacific Ocean runs from east to west, increasing in volume transport because new water masses join the current from the north. The very beginning of the North Equatorial Current is found where the waters of the Equatorial Countercurrent turn to the north off Central America. To these water masses are later added the waters of the California Current, which have attained a relatively higher temperature and salinity owing to heating and evaporation, and which have been mixed with waters of the tropical region. Between the American coast and the Hawaiian Islands, Eastern North Pacific Water is added to the equatorial flow, and to the west of the Hawaiian Islands a considerable addition of Western North Pacific Water appears to take place. In about long. 160°W the volume transport of the North Equatorial Current above a depth of 1000 m is, according to Carnegie
It is probable that, before reaching the western boundary of the ocean, the Equatorial Current begins to branch off, mainly to the north but partly to the south, feeding the countercurrent. To the east of the Philippine Islands a definite division of the current takes place, one branch turning south along the coast of the island of Mindanao and the larger branch turning north, following closely the east side of the northern Philippine Islands and the island of Formosa. The intensity of the flow to the south varies with the season (p. 712) and so probably does the flow to the north.
After having passed the island of Formosa, the warm waters continue to the northeast between the submarine ridge on which the Riukiu Islands lie and the shallow areas of the China Sea. On reaching lat. 30°N the current bends to the east and then to the northeast, following closely the coast of Japan as far as lat. 35°N. The name Kuroshio is particularly applied to the current between Formosa and lat. 35°N, but in agreement with the nomenclature used when dealing with the currents of the Atlantic, and following Wüst (1936), we shall apply the name “Kuroshio System” to all branches of the current system and shall introduce the following subdivisions:
The Kuroshio. The current running northeast from Formosa to Riukiu and then close to the coast of Japan as far as lat. 35°N.
The Kuroshio Extension. The warm current which represents the direct continuation of the current and flows nearly due east, probably in two branches, and can be traced distinctly to about long. 160°E.
The North Pacific Current. The further continuation of the Kuroshio Extension which flows toward the east, sending branches to the south and reaching probably as far as long. 150°W.
To these three major divisions of the Kuroshio System can also be added the Tsushima Current, the warm current that branches off on the left-hand side of the Kuroshio and enters the Japan Sea following the western coast of Japan to the north, and the Kuroshio Countercurrent, part of a large eddy on the right-hand side of the Kuroshio.
The Kuroshio. The great similarity between the Kuroshio and the Florida Current has been pointed out by Wüst (1936). Wüst compares the Kuroshio between the Riukiu Islands and the continental shelf to the current through the Caribbean Sea and the flow of the Kuroshio across the Riukiu Ridge in lat. 30°N to the flow through the Straits of Florida. This part of the Kuroshio, as well as the current to the south of Shiono-misaki in lat. 33°N, long. 135°W, has been studied by Japanese oceanographers, who have conducted current measurements and have occupied a large number of oceanographic stations. The results have been discussed mainly by Wüst (1936) and Koenuma (1939). According to Koenuma, the current between Formosa and the southern of the Riukiu Islands reaches to a depth of about 700 m and the maximum velocity near the surface is 89 cm/sec. These figures are based on computations, but are in good agreement with direct measurements at one station in the passage. The transport amounts to about 20 million m3/sec. Similar conditions are encountered further north, between the northern of the Riukiu Islands and the continental shelf; here, however, a weak counter current appears to be present on the left-hand side of the main flow. The maximum velocities in this profile are somewhat above 80 cm/sec and the computed transport is 23 million m3/sec.
The profile to the south of Shiono-misaki has been discussed both by Wüst and Koenuma, who do not agree in their interpretation of the measurements, particularly as to the depth of the level of no motion. Wüst assumed that the level of no motion coincides approximately with the 10° isothermal surface, which nearly represents the upper boundary of the Intermediate Water; but this assumption leads to computed velocities which are considerably below the observed ones. Koenuma, on the other hand, assumes that close to the coast the observed velocity of the Intermediate Water, 16 cm/sec to the northeast, is correct, and furthermore assumes that at greater distances from the coast the Intermediate Water flows toward the southwest at a velocity of about 5 cm/sec. These assumptions are based on a number of considerations that appear to be valid. In this manner Koenuma arrives at a computed velocity distribution in good agreement with observations. The Kuroshio runs here very close to the coast with maximum velocities up to 160–180 cm/sec (up to 3½ knots), but extends only to a distance of 140 km from the coast. At greater distances a countercurrent flows to the southwest within which maximum velocities up to 20 cm/sec are encountered, in agreement with ships’ observations. The character of the Kuroshio is here closely related to that of the Florida Current to the south of Cape Hatteras. The transport of the Kuroshio between the coast and its outer limit is greatly increased, but the countercurrent on the right-hand side carries large amounts of water in the opposite direction.
The temperatures of the Kuroshio water are comparable to those of the Florida Current but the salinities are much lower, the maximum salinity in the Kuroshio being slightly less than 35.00‰, whereas the maximum salinity in the Florida Current is about 36.50‰. This difference reflects the general lower salinity of the Pacific as compared to the Atlantic. The temperature of the Kuroshio is subject to a large annual variation (p. 131) related to excessive cooling in winter by cold offshore winds. Off Shiono-misaki the annual range at the surface amounts to nearly 9° and at 100 m the range is still nearly 4.5°.
The Kuroshio Extension. In lat. 35°N, where the Kuroshio leaves the coast of Japan, it divides into two branches; one major branch turns due east and retains its character as a well-defined flow as far as approximately long. 160°E, and one continues toward the northeast as far as lat. 40°N where it bends toward the east. The major branch is evident on charts showing the anomaly of the surface temperature or the difference between air and surface temperatures in winter. According to Schott (1935) a tongue within which this difference is greater than 4°C extends east toward long. 170°E, that is, beyond the eastern limit of the well-defined flow. Between long. 155° and 160°E considerable water masses turn toward the south and southwest, forming part of the Kuroshio countercurrent which runs at a distance of approximately 650 km from the coast as the eastern branch of a large whirl on the right-hand side of the Kuroshio.
According to the vertical sections of temperature and salinity in fig. 201, the Kuroshio Extension is, in long. 153°E, still a narrow current, but continuing toward the east a section in long. 162°E (Uda, 1935) shows that the current has been broken up into a number of branches separated by eddies and countercurrents. The change corresponds to the one which, in the Atlantic Ocean, takes place between the regions to the south of the Grand Banks and to the north of the Azores (see fig. 186, p. 681).
The northern branch of the Kuroshio Extension becomes rapidly mixed with the cold waters of the Oyashio that flow south close to the northeastern coasts of Japan, reaching nearly to 35°N. The extensive work of Japanese oceanographers (Uda, 1935, 1938b) shows that along the boundary between the Kuroshio Extension and the Oyashio numerous eddies develop, within which a thorough mixing of the water masses takes place. From the sections in fig. 201 it is evident that to the north of lat. 36°N the Kuroshio waters, which can be traced to lat. 41°N, have been greatly diluted by the Oyashio water. These processes of mixing gradually form the water mass that is present in the northwestern
The North Pacific Current. Under this name is understood the general eastward flow of warm water to the east of long. 160°E. Details of this flow are not known, but from the Bushnell section of 1934 (fig. 200) it is evident that Kuroshio water crosses long. 170°W, because at a number of Bushnell stations the T-S curves are similar to those of the Kuroshio Water. The greater part of this water appears to turn around toward the south before reaching 150°W, and only a small portion continues and flows south between the Hawaiian Islands and the west coast of North America after having been mixed with waters of different origin. The main part of the North Pacific Current does not, therefore, extend across the Pacific Ocean but turns back toward the west in the longitude of the Hawaiian Islands.
The Aleutian (Subarctic) Current. To the north of the North Pacific Current one finds a marked transition to an entirely different type of water, the Subarctic Water, which also flows toward the east. According to the Bushnell observations the transport of Subarctic Water between the Aleutian Islands and lat. 42°N amounts to about 15 million m3/sec above the 2000-decibar surface. This water mass must have been formed by mixing of Kuroshio and Oyashio water, the temperature of the mixture having been reduced by cooling and the salinity of the upper layer decreased by excessive precipitation. One branch of the Aleutian Current turns north and enters the Bering Sea, following along the northern side of the Aleutian Islands and circling the Bering Sea counter clockwise. In the Bering Sea these waters are further cooled, and flowing south they reach the northern islands of Japan as the cold Oyashio. The amount of water in this gyral is not known, but inflow and outflow from the Bering Sea must be nearly equal, wherefore it follows that the 15 million m3/sec of Subarctic Water which continues east on the southern side of the Aleutian Islands are supplied by the Kuroshio, the waters
Before reaching the American coast the Aleutian Current divides, sending one branch toward the north into the Gulf of Alaska and another branch toward the south along the west coast of the United States. The former branch is part of the counterclockwise gyral in the Gulf of Alaska. It enters the gulf along the American west coast, and since it comes from the south it has the character of a warm current in spite of the fact that it carries Subarctic Water. It therefore exercises an influence on the climatic conditions similar, on a small scale, to that which the North Atlantic and the Norwegian Currents exercise on the climate of northwestern Europe. The major branch, which turns toward the south along the west coast of the United States, is known as the California Current, but before dealing with this it is desirable to discuss the warm-water currents between the Hawaiian Islands and the American West Coast.
The Eastern Gyral in the North Pacific Ocean. The existence of an eastern gyral is recognized mainly by the character of the water masses and by the results of computations based on observations between the Hawaiian Islands and the coast of California and between the Hawaiian Islands and the Aleutian Islands. The study of water masses (fig. 200, p. 715) brought out that a distinctly different water mass was present in the region to the east of the Hawaiian Islands, a mass in part formed at the boundary between the warmer waters and the Subarctic Water between long. 130° and 150°W. Computation of currents and transport, the results of which are shown schematically in fig. 205, p. 727, leads to the conclusion that a clockwise rotating gyral is present in the eastern North Pacific with its center to the northeast of the Hawaiian Islands. It is probable that the location of this gyral changes with the seasons and shifts from year to year, so that occasionally the gyral may lie entirely to the northeast of the Hawaiian Islands, whereas in other circumstances the Hawaiian Islands may lie inside the gyral. If the gyral is displaced considerably to the north, Equatorial Water may reach as far north as to the Hawaiian Islands, as was observed in 1939 at Bushnell station 316 (see fig. 200, p. 715). At the surface the gyral is masked by wind-driven currents.
The existence of this gyral is confirmed by the values of the salinity at the salinity maximum (fig. 202). The high values which are found to the northeast of the Hawaiian Islands must be associated with a flow to the northeast, and the presence of two salinity minima in about lat. 28°N and long. 130°W must be related to the circulation. The upper minimum at which the salinity is about 33.95‰ is probably formed where the Central Water mass spreads over the Subarctic Water; the lower minimum at which the salinity is about 34.10‰ represents the
The California Current. The California Current represents, as already explained, the continuation of the Aleutian Current of the North Pacific. The name is applied to the southward flow between lat. 48° and 23°N, where the Subarctic Water converges with the Equatorial (fig. 199, p. 713). The outer limit of the California Current is represented by the boundary region between the Subarctic Water and the Eastern North Pacific Central Water, and lies in lat. 32°N at a distance of approximately 700 km from the coast, according to the observations by the Carnegie in 1929, the Louisville in 1936, and the Bushnell in 1939. The total volume transport of the California Current above the 1500-decibar surface is probably not more than about 10 million m3/sec, and in view of the great width of the current no high velocities are encountered except within local eddies. As a whole, the current represents a wide body of water which moves sluggishly toward the southeast.
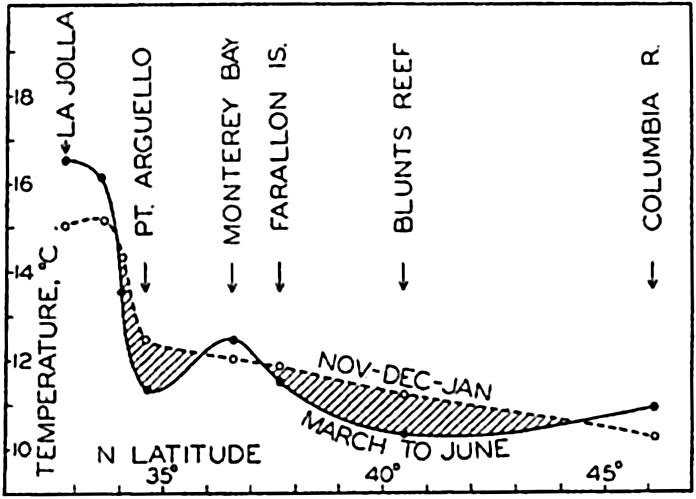
Surface temperatures along the coast of California in March to June and in November to January. In regions of intense upwelling, the average surface temperature is lower in March to June than in December to January.
In spring and early summer the California Current is a counterpart to the Peru Current, several characteristic features of the two currents being strikingly similar. During these months north-northwest winds prevail off the coast of California, giving rise to upwelling that mostly begins in March and continues more or less uninterruptedly until July. Records of surface temperatures show that on the coast the lowest temperatures regularly occur in certain localities separated by regions with higher surface temperatures. This is demonstrated by fig. 203, in which are plotted the surface temperatures between lat. 32°N and 45°N along the American west coast in March to June and in November, December, and January. In the regions of intense upwelling the spring temperatures are lower than the winter temperatures, but in regions of less intense upwelling they are higher.
Recent work of the Scripps Institution of Oceanography shows that from the areas of intense upwelling tongues of water of low temperature extend in a southerly direction away from the coast; these tongues are separated from each other by tongues of higher temperature extending in toward the coast. Within the tongues of higher temperature the flow
To the north of lat. 30°N the two most conspicuous centers of upwelling are located in lat. 35°N and 41°N. The two swirls associated with these centers of upwelling and the alternating movements away from and toward the coast are shown in fig. 204, which is based on observations in May to July, 1939. The coast to the south of 34°N is under the influence of water which returns after having traveled a long distance as surface water, and, correspondingly, the surface temperatures are much higher there than those encountered where the water was recently drawn to the surface (fig. 203). A third region of intense upwelling is found perhaps in about latitude 24°N, on the coast of Lower California (Thorade, 1909).
The upwelling water rises from moderate depths only, probably less than 200 m (Sverdrup and Fleming, 1941), and the phenomenon therefore represents only an overturning of the upper layers such as is the case in other regions which have been examined. According to McEwen (1934) the rate of upwelling is about 20 m a month and on an average the process is therefore a very slow one. It is, however, of the greatest importance to the productivity of the waters off the coast, because the rising water brings nutrient salts into the euphotic zone. The importance of upwelling to the distribution of phytoplankton (p. 785) has been discussed by Sverdrup and Allen (1939).
During the entire season of upwelling a countercurrent that contains considerable quantities of Equatorial Water flows close to the coast at depths below 200 m (Sverdrup and Fleming, 1941). This subsurface countercurrent appears to be analogous to the subsurface countercurrent off the coast of Peru, the existence of which was shown by Gunther (p. 703). In spring and early summer the currents off the coast of California are therefore nearly a mirror image of those off the coast of Peru, but the similarity is found in this season only because the character of the prevailing winds off California changes in summer, whereas off Peru the winds blow from nearly the same direction throughout the year.
Toward the end of the summer the upwelling gradually ceases and the more or less regular pattern of currents flowing away from and toward the coast breaks down into a number of irregular eddies, some of which carry coastal waters far out into the ocean (Johnson, 1939). Other eddies carry oceanic waters in toward the coast, particularly in the regions between the centers of upwelling, as shown by Skogsberg (1936) in his discussion of the waters of Monterey Bay (p. 131).
In the fall upwelling ceases, and in the surface layers a countercurrent develops, the Davidson Current which in November, December, and January runs north along the coast to at least lat. 48°N. In this season the subsurface countercurrent still exists and the main difference between the seasons without and with upwelling is therefore that in the former a countercurrent is present at all depths on the coastal side of the California Current, whereas when upwelling takes place the countercurrent has disappeared in the surface layer where, instead, a number of long-stretched swirls have developed. This difference suggests that in the absence of prevailing winds that cause upwelling, a countercurrent would appear on the coastal side, as is the case in other localities (see p. 677). In the presence of upwelling the overturn of the surface layers destroys the countercurrent above a depth of 200 m and leads to an entirely different pattern of flow.
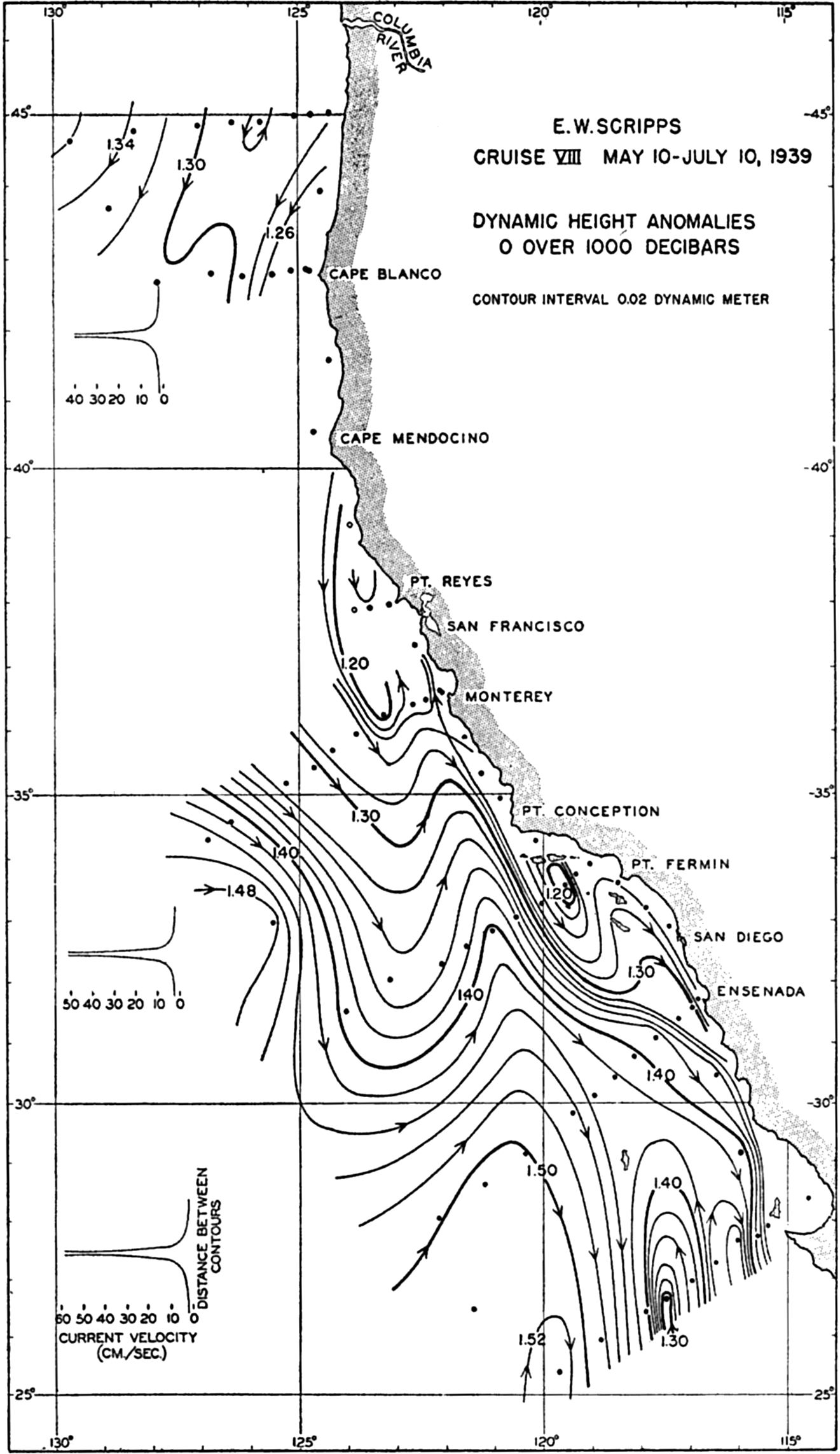
Geopotential topography of the sea surface relative to the 1000-decibar surface off the American west coast in May to July, 1939, showing flow alternating away from and towards the coast.
Transport. On the basis of the values of the volume transport of the different branches of the current system that have been mentioned and others that have been computed, the schematic picture in fig. 205 has been prepared. The lines with arrows give the approximate direction of the transport and the numbers give the volume transport in millions of m3/sec. In this case the transport numbers include the motion of the Upper and the Intermediate Water because the Intermediate Water of the Pacific appears to flow in general in the same direction as the Upper Water (fig. 202). The lines showing the direction of transport are full-drawn where the upper water masses are warm and dashed where they are cold.
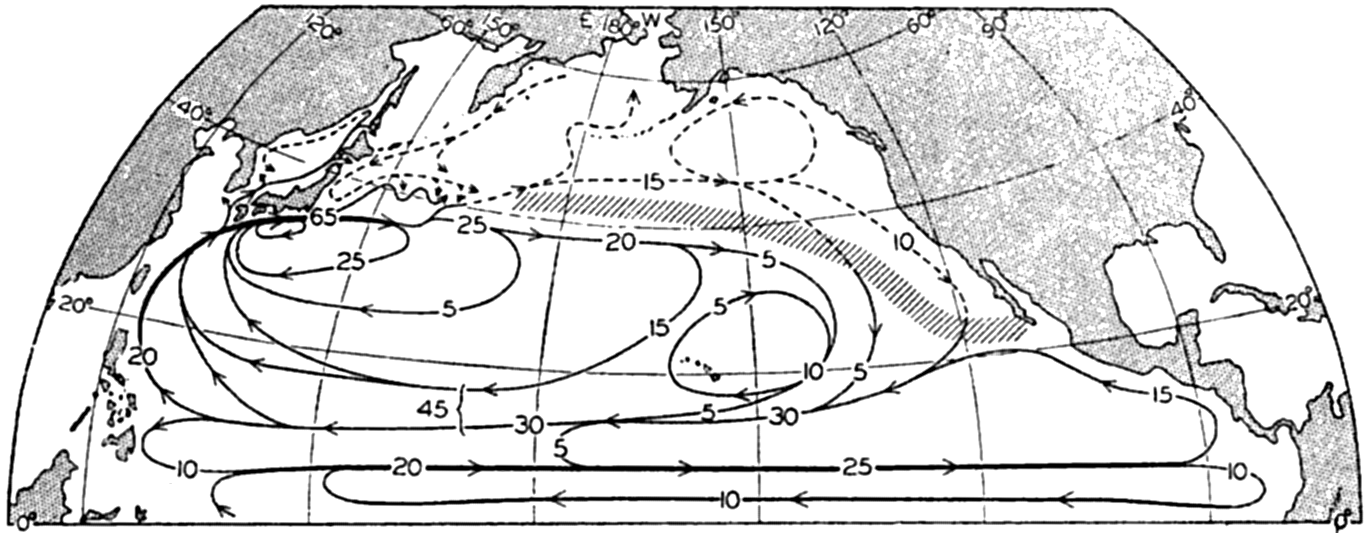
Transport chart of the North Pacific. The lines with arrows indicate the approximate direction of the transport above 1500 meters, and the inserted numbers indicate the transported volumes in millions of cubic meters per second. Dashed lines show cold currents; full-drawn lines show warm currents.
The figure brings out that in the North Pacific Ocean the Equatorial Countercurrent and the Kuroshio are the two outstanding, well-defined currents. Over the greater part of the Pacific Ocean weak or changing currents are present, and the transport numbers that are entered refer therefore to broad cross sections. The figure intends only to bring out
The Oxygen Distribution in the Pacific Ocean. In the South Pacific Ocean no oxygen observations are available from the central and eastern parts except for a few at two Carnegie stations in about lat. 33°S and long. 110°W. On board the William Scoresby oxygen determinations were made in the waters of the Peru Coastal Current, but so far the data have not been published. From the western South Pacific and from the equatorial part of the South Pacific oxygen values are available at a number of Dana and Carnegie stations.
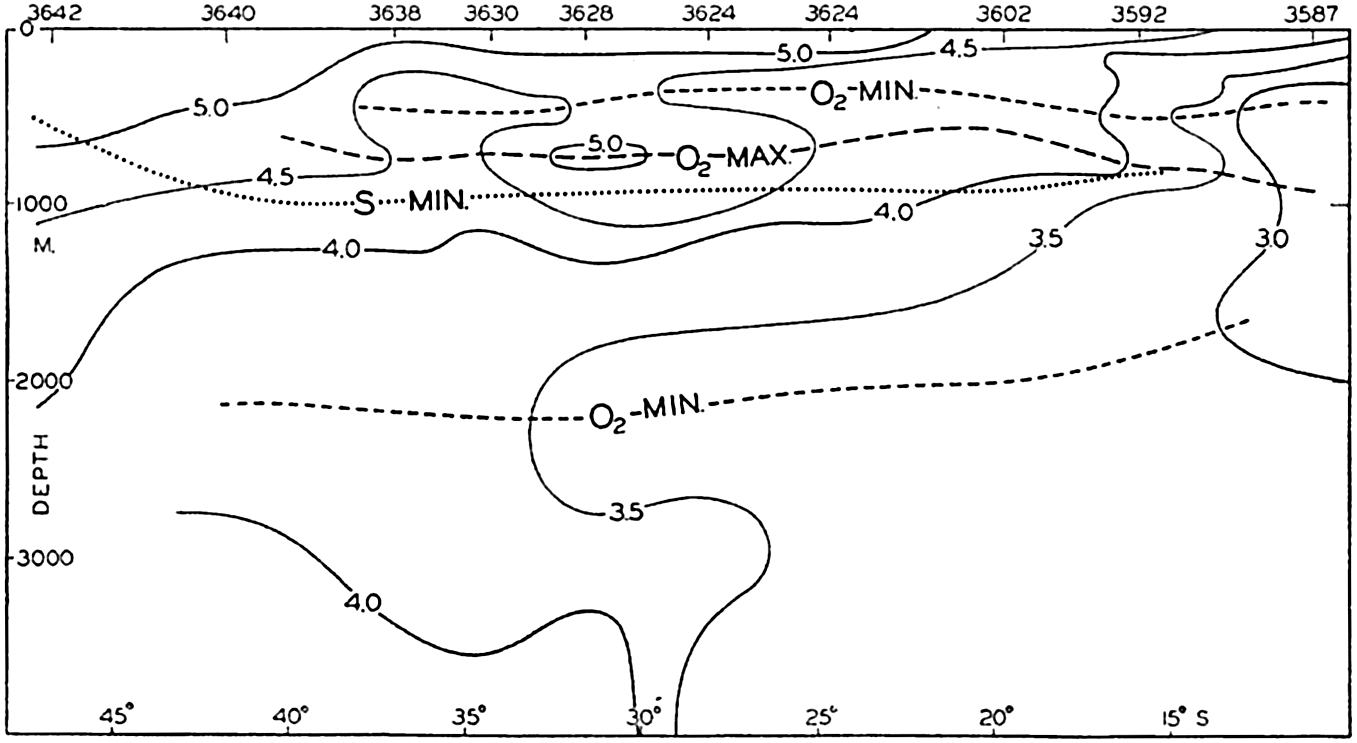
Oxygen distribution (ml/L) in a vertical section along the 180° meridian between latitudes 48°S and 10°S. (According to observations of the Dana.)
Figure 206 shows the distribution of oxygen in a vertical section which nearly follows the meridian of 180° between latitudes 48°S and 10°S. Near the Antarctic the oxygen content of the water is generally high, decreasing more or less regularly from the surface to a depth of about 2000 m, where the content is a little below 4 ml/L. At greater depth a small increase takes place, such that below 2500 m the content is greater than 4 ml/L. To the north of 40°S an oxygen minimum is present at about 400 m, but below this minimum an intermediate maximum is found between 600 and 800 m. This intermediate maximum lies a few hundred meters above the core of the Antarctic Intermediate Water, which is indicated by the line marked S-min. At about 2000 m a second layer of minimum oxygen is found and below this the oxygen content slowly increases toward the bottom. In a horizontal direction an abrupt decrease in the oxygen content takes place at about 15°S. At 11°S the oxygen content is below 3 ml/L between 300 m and 2000 m and a
According to observations at two Carnegie stations in about lat. 33°S and long. 110°W (see Schott, 1935), the oxygen distribution is there quite similar to that found off New Zealand; but from analogy with conditions within the Benguela Current it appears highly probable that the oxygen content of the subsurface waters is low within the Peru Current, particularly within the Peru Coastal Current. At Dana stations 3559, 3560, and 3561, located to the south of the Equator between long. 104° and 117°W, minimum oxygen values as low as 0.09 ml/L were observed at 400 m. This low-oxygen water probably comes from the coast off Peru, indicating that there a minimum oxygen layer is present within which the oxygen content is even lower than that found off the coast of South Africa. Such conditions should be expected because of the great productivity of the Peru coastal waters and, consequently, the great consumption of oxygen at subsurface depths by decomposition of sinking remnants of organisms.
In the North Pacific the oxygen content of the subsurface waters is as a rule lower than in the South Pacific, but a similar contrast exists between west and east, the oxygen content in the eastern areas being lower than in the western. The lowest oxygen values are consistently found 400 or 500 m below the salinity-minimum layer where such a layer is present, and in the Subarctic Waters at a depth of 600 or 800 m. Minimum values higher than 2 ml/L are found only in the extreme western part to the west of long. 160°E and between the Equator and 36°N. Over the greater part of the North Pacific the minimum values are below 1 ml/L, and off the west coasts of Central America and Mexico the content is nearly nil. Below the minimum layer the oxygen content increases toward the bottom, at which values somewhat above 3 ml/L are found in the western part and somewhat below 3 ml/L in the eastern part.
The most striking feature of the oxygen distribution in the North Pacific is the presence of a very large body of water within which the oxygen content is exceedingly small. This body is found off the American coast between lat. 28°N and the Equator; it extends toward the west like a wedge, gradually becoming more and more narrow, and reaches at least past long. 140°W. Close to the coast the layer of oxygen content less than 0.25 ml/L is found between the depths of 200 to 300 m and 1200 m, and according to Carnegie observations it is found in long. 140°W between 100 and 600 m. It is probable, as already stated, that another water mass of equally low oxygen content extends toward the west from the coast of Peru, but the two water masses appear to be separated by a region of slightly higher oxygen content.
The character of the oxygen distribution off the American west coast is illustrated in fig. 207, showing a section which runs parallel to the
A systematic study of the types of organisms which may be found in this oxygen-poor water has not yet been made. A few scattered observations indicate that organisms are found even where the oxygen content is as low as 0.1 ml/L; the further examination of the distribution of such organisms and their adaptation to the extreme conditions represents one of the fascinating biological problems of the Pacific Ocean.
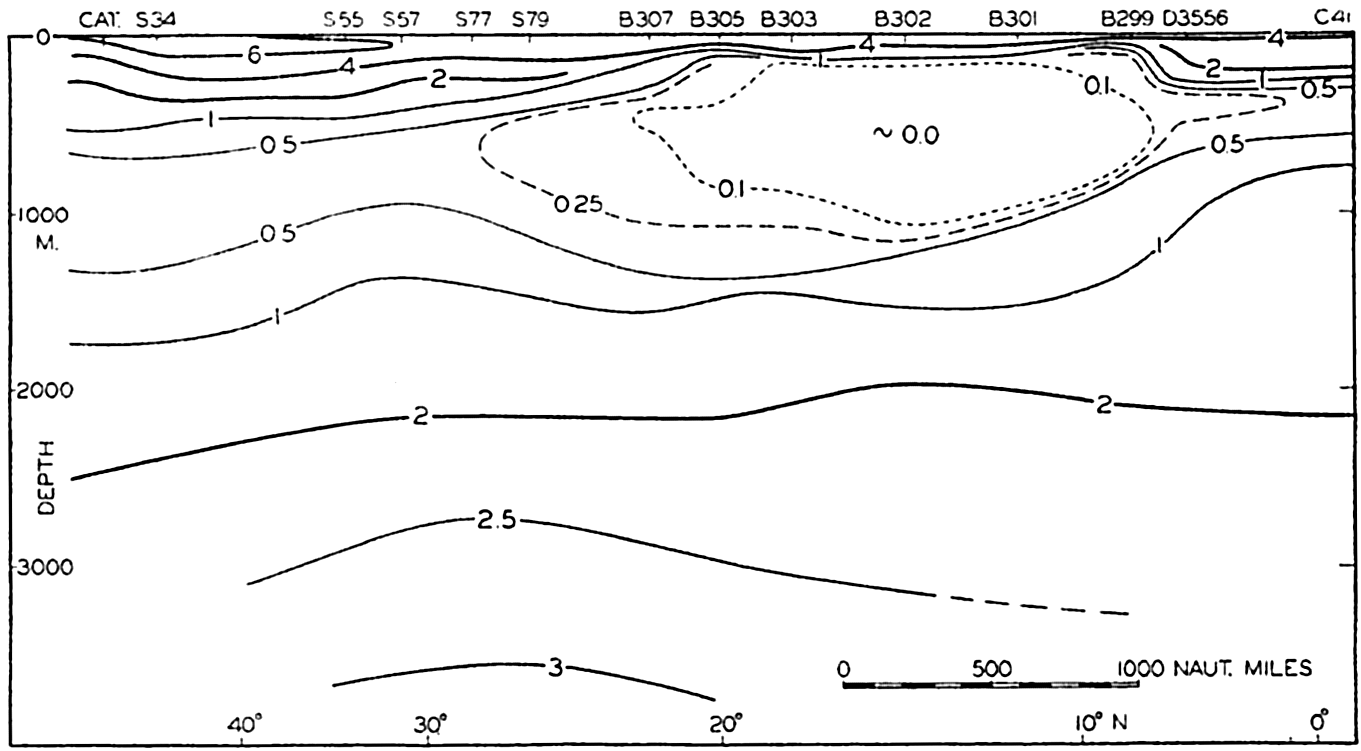
Oxygen distribution (ml/L) in a vertical section along the west coast of North and Central America at a distance of a few hundred miles from the coast (mainly based on observations of E.W. Scripps and Bushnell).
The Adjacent Seas of the North Pacific Ocean
None of the adjacent seas of the North Pacific Ocean exercise any appreciable influence on the water masses of the ocean and it has therefore not been necessary to discuss them until now.
Gulf of California. The Gulf of California lies in a climatic region which is comparable to that in which the Red Sea is located, but hydrographically the Gulf of California is entirely different from the Red Sea, the reason being that the Gulf of California is not separated from the adjacent ocean by a submarine ridge. To 28°30″N the bottom of the Gulf is trough-shaped, with the greatest depth at the opening to the south. The soundings of the E. W. Scripps in 1939 and 1940 have
| Depth (m) | Bushnell 305 March 24, 1939 20°00″N, 108°16′W | E. W. Scripps VII-27 March 4, 1939 26°21″N, 110°46′W | E. W. Scripps VII-53 March 19, 1939 28°46.5″N, 113°08′W | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Temp. (°C) | S (‰) | O2 (ml/L) | Temp. (°C) | S (‰) | O2 (ml/L) | Temp. (°C) | S (‰) | O2 (ml/L) | |
a At 1270 m. | |||||||||
b At 2400 m. | |||||||||
| 0 | 23.78 | 34.88 | 5.06 | 15.95 | 35.22 | 5.37 | 15.80 | 35.12 | 5.43 |
| 25 | 22.00 | 35.02 | 5.20 | 15.45 | .16 | 4.87 | 14.06 | .07 | 4.90 |
| 50 | 17.22 | 34.70 | 1.45 | 15.34 | .15 | 4.90 | 13.81 | .08 | 4.27 |
| 100 | 13.15 | .78 | 0.17 | 13.44 | 34.82 | 0.41 | 13.11 | .01 | 3.13 |
| 200 | 11.50 | .75 | 0.16 | 12.00 | .78 | 0.25 | 12.50 | 34.95 | 2.32 |
| 400 | 8.71 | .55 | 0.10 | 9.60 | .65 | 0.11 | 11.83 | .84 | 1.63 |
| 600 | 6.69 | .52 | 0.07 | 7.26 | .52 | 0.07 | 11.50 | .83 | 1.58 |
| 800 | 5.45 | .52 | 0.09 | 5.54 | .52 | 0.12 | 11.34 | .80 | 1.53 |
| 1000 | 4.70 | .52 | 0.20 | 4.46 | .52 | 0.26 | 11.18 | .79 | 0.96 |
| 1500 | 3.10 | .58 | 1.01 | 2.89 | .61 | 0.84 | (10.98 | .76 | 0.62)[a] |
| 2000 | 2.21 | .63 | 1.84 | 2.52 | .60 | 1.26 | |||
| 2500 | 1.85 | .66 | 2.35 | (2.56 | .62 | 1.28)[b] | |||
| 3000 | 1.82 | .65 | 2.46 | ||||||
The character of the waters in the Gulf is shown in table 83, containing temperature, salinity, and oxygen at three stations: station B 305 in 20°00″N off the entrance to the Gulf, station EWS VII-27 in the middle portion of the Gulf, and station EWS VII-53 in the trench south of Angel de la Guardia. In March, when the stations were occupied, the surface temperatures in the Gulf were lower than those off the entrance, the difference being due to cooling by northwesterly winds and to local upwelling. The salinity, on the other hand, was higher in the Gulf owing to excessive evaporation. Between depths of 100 and 1500 m the waters in the middle portion of the Gulf were nearly identical with those off the entrance. Some differences were found at 2000 m and 2400 m because
During the cruise of the E. W. Scripps in 1939 a number of stations were occupied in the shallow northern portion of the Gulf. The most northern station was located at a distance of about 70 km from the mouth of the Colorado River where the depth to the bottom was 60 m. In this locality the influence of fresh water from the Colorado River was not perceptible, the surface salinity being 35.31 ‰, whereas the highest surface salinity, 35.50 ‰, was observed at the neighboring station only about 35 km to the southeast.
No well-defined exchange of water between the Gulf and the adjacent parts of the Pacific Ocean could be established. It is probable that such an exchange takes place by irregular currents in the upper layers and by a slow inflow of deep water and outflow of surface water.
Bering Sea. In the deeper portions of the Bering Sea the water masses are similar to those in the subarctic region of the North Pacific, as is evident from table 84, showing temperatures, salinities, and oxygen values at stations on the south and the north sides of the Aleutian Islands and at a third station about 240 km to the north of the Aleutian Islands. Below a depth of about 200 m the water masses at these three stations were practically identical. At 200 m the temperature shows a minimum at all stations but, according to the more detailed original observations, the lowest temperatures were found somewhat above 200 m. At the two northern stations an oxygen maximum appeared at the depth of the temperature minimum and at the southern station the oxygen content was high. This situation suggests that the depth of the intermediate temperature minimum represents the depth to which convection currents reach in winter. Such a layer of minimum temperature has been established at a number of stations in the subarctic region and lower temperature values have been observed further toward the west, where winter cooling is more intense.
The shallow shelf areas in the eastern and northern part of the Bering Sea are covered by water of a considerably lowered salinity owing to dilution by runoff from the large Alaskan rivers. The influence of the waters of the Yukon River is particularly conspicuous. In summer warm water of low salinity is found along the northeastern coast of the Bering Sea and this water continues through Bering Strait into the Polar
Some of the water that flows into the Bering Sea around the Aleutian Islands contributes in summer to the current which flows through Bering Strait (see p. 655), but the major amount of water turns around and flows south along the coast of Kamchatka, reaching the northern of the Japanese Islands as the cold Oyashio (Barnes and Thompson, 1938).
| Depth (m) | Station B-a, August 18, 1934, 50°30″N, 175°16″W | Station G-8, June 13, 1933, 52°37″N, 177°20″W | Station C-107, August 21, 1934, 55°04″N, 168°49″W | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Temp. (°C) | S (‰) | O2 (ml/L) | Temp. (°C) | S (‰) | O2 (ml/L) | Temp. (°C) | S (‰) | O2 (ml/L) | |
| 0 | 10.91 | 32.92 | 6.24 | 6.57 | 33.28 | 8.85 | 9.77 | 32.50 | 6.33 |
| 25 | 10.50 | .87 | 6.40 | 4.13 | .33 | 6.82 | 5.52 | .94 | 5.36 |
| 50 | 6.00 | 33.04 | 7.22 | 3.86 | .31 | 5.65 | 4.26 | 33.12 | 4.90 |
| 100 | 3.48 | .12 | 7.10 | 3.54 | .37 | 5.07 | 3.77 | .31 | 4.32 |
| 200 | 3.11 | .75 | 2.60 | 3.25 | .46 | 5.40 | 3.20 | .46 | 4.36 |
| 400 | 3.42 | 34.13 | 0.63 | 3.43 | .87 | 2.08 | 3.44 | .86 | 2.21 |
| 600 | 3.22 | .22 | 0.46 | 3.31 | 34.09 | 1.10 | 3.27 | 34.13 | 0.90 |
| 800 | 2.98 | .34 | 0.44 | 3.11 | .23 | 0.62 | 3.04 | .25 | 0.63 |
| 1000 | 2.74 | .44 | 0.58 | 2.89 | .34 | 0.65 | 2.79 | .38 | 0.52 |
| 1500 | 2.17 | .52 | 0.96 | 2.31 | .49 | 0.74 | |||
| 2000 | 1.88 | .58 | 1.64 | 1.91 | .58 | 1.19 | |||
| 2500 | 1.72 | .59 | 2.20 | 1.70 | .63 | 1.67 | |||
| 3000 | 1.61 | .64 | 2.58 | 1.61 | .65 | 1.81 | |||
Okhotsk Sea. The few data available from the Okhotsk Sea (Krümmel, 1911) show that in winter excessive cooling of the waters takes place such that even in summer the temperature at a depth of 100 to 200 m is as low as −1.4°. The salinity of the water is also low, being about 33.1 ‰. It is probable that the cold intermediate layer of the Okhotsk Sea flows out between the Kurile Islands and contributes to the maintenance of the layer of intermediate temperature minimum in the northwestern part of the Pacific and in the Bering Sea; but there is no evidence that the salinity of the water in the Okhotsk Sea in winter is increased so much by freezing that bottom water is formed, nor does any such formation take place in Bering Sea. One finds, therefore, no region
Japan Sea. The Japan Sea is a basin in which the greatest depth is about 3700 m. The deepest sill is found in the Tsushima Strait between Korea and Japan, where the maximum depth is about 150 m. In the Japan Sea (Suda and Hidaka, 1932, Uda, 1934) above 400 m there exists a striking contrast between the waters along the west coast of Japan and those along the east coast of Korea. A branch of the Kuroshio, the Tsushima Current, flows into the Japan Sea and carries water of high temperature and high salinity toward the north. Branches of the current flow out through the straits between the northern Japanese islands and part of the water continues along the west side of Sakhalin Island, turns around, and flows south after having been cooled and diluted. The contrast between the waters on the east and the west sides of the Japan Sea is shown by the data in table 85. Schott (1935) points out that the cold water along the mainland side cannot come from the Okhotsk Sea through the narrow strait between the Asiatic coast and Sakhalin Island, because the strait at its narrowest is only 6.7 km wide and 12 m deep. The cold water must therefore have been formed in the Japan Sea by excessive cooling in winter and must have been diluted by river water. The water below a depth of about 400 m is of a temperature slightly above 0° and a salinity a little above 34.0 ‰.
| Depth (m) | East side, August, 1930, 41°N, 140°E; sounding, 887 m | West side, July, 1930, 41°N, 132°E; sounding, 3300 m | ||
|---|---|---|---|---|
| Temp. (°C) | S (‰) | Temp. (°C) | S (‰) | |
| 0 | 27.00 | (32.68) | 19.30 | 33.73 |
| 25 | 22.04 | 34.14 | 5.35 | .98 |
| 50 | 17.73 | .36 | 2.58 | 34.00 |
| 100 | 12.45 | .47 | 1.23 | .00 |
| 150 | 9.30 | .30 | 0.74 | .01 |
| 200 | 6.54 | .16 | 0.50 | .02 |
| 400 | 0.91 | .04 | 0.24 | .04 |
| 600 | 0.19 | .03 | 0.18 | .07 |
| 800 | 0.16 | .02 | 0.13 | .11 |
| 1000 | 0.16 | .11 | ||
| 1500 | 0.15 | .06 | ||
On a small scale the Japan Sea is comparable to the Arctic Mediterranean, into which flows a branch of the North Atlantic Current carrying warm water of high salinity which is cooled and diluted so that the outflowing current carries cold water of low salinity. The contrast between the eastern and western sides of the Japan Sea corresponds to the contrast between the eastern and western sides of the Norwegian Sea and also to the contrast between the eastern and western sides of the Labrador Sea. The main difference is that no great outflow of cold water takes place from the Japan Sea; the cold water on the western side is mainly part of an eddy.
Yellow Sea and East China Sea. In both of these the surface salinity is greatly reduced by runoff from rivers, and temperature and salinity alike are subjected to great annual variations. The waters are shallow and the processes that take place have small bearing on conditions at greater distances from the coast.
| depth (m) | Dana 3714, May 20, 1929, 15°22′N, 115°20′E; sounding, 4240 m | Dana 3685, April 4, 1929, 7°22′N, 121°16′N; sounding, 4825 m | ||||||
|---|---|---|---|---|---|---|---|---|
| Temp. (°C) | θ (°C) | S (‰) | O2 (ml/L) | Temp. (°C) | θ (°C) | S ‰ | O2 (ml/L) | |
| 0 | 29.54 | 29.54 | 33.73 | 27.08 | 27.08 | 34.08 | ||
| 50 | 24.07 | 24.06 | 34.04 | 4.57 | 24.37 | 24.36 | .16 | 3.67 |
| 100 | 18.66 | 18.64 | .52 | 2.33 | 20.93 | 20.91 | .31 | 2.17 |
| 200 | 14.46 | 14.43 | .60 | 2.44 | 14.56 | 14.53 | .51 | 1.74 |
| 400 | 9.94 | 9.85 | .48 | 2.23 | 11.47 | 11.41 | .51 | .59 |
| 1000 | 4.38 | 4.30 | .56 | 1.85 | 10.11 | 9.98 | .50 | .43 |
| 1200 | 3.58 | 3.49 | .60 | .83 | .10 | .95 | .49 | .42 |
| 2000 | 2.53 | 2.38 | .58 | .89 | .14 | .88 | .51 | .33 |
| 3000 | .38 | .13 | .63 | 2.47 | .28 | .86 | .51 | .40 |
| 4000 | .44 | .08 | .63 | .50 | .42 | .84 | .49 | .48 |
| 4750 | .56 | .85 | .50 | .46 | ||||
South China Sea. In the South China Sea, between the Philippine Islands and the Asiatic mainland, a basin is found within which the greatest depths exceed 4600 m and which is in communication with the adjacent part of the Pacific Ocean through the passage between the Philippine Islands and Formosa, where the sill depth is between 2500 and 3000 m. Table 86 contains observations of temperature, salinity, oxygen, and computed potential temperatures at a Dana station located
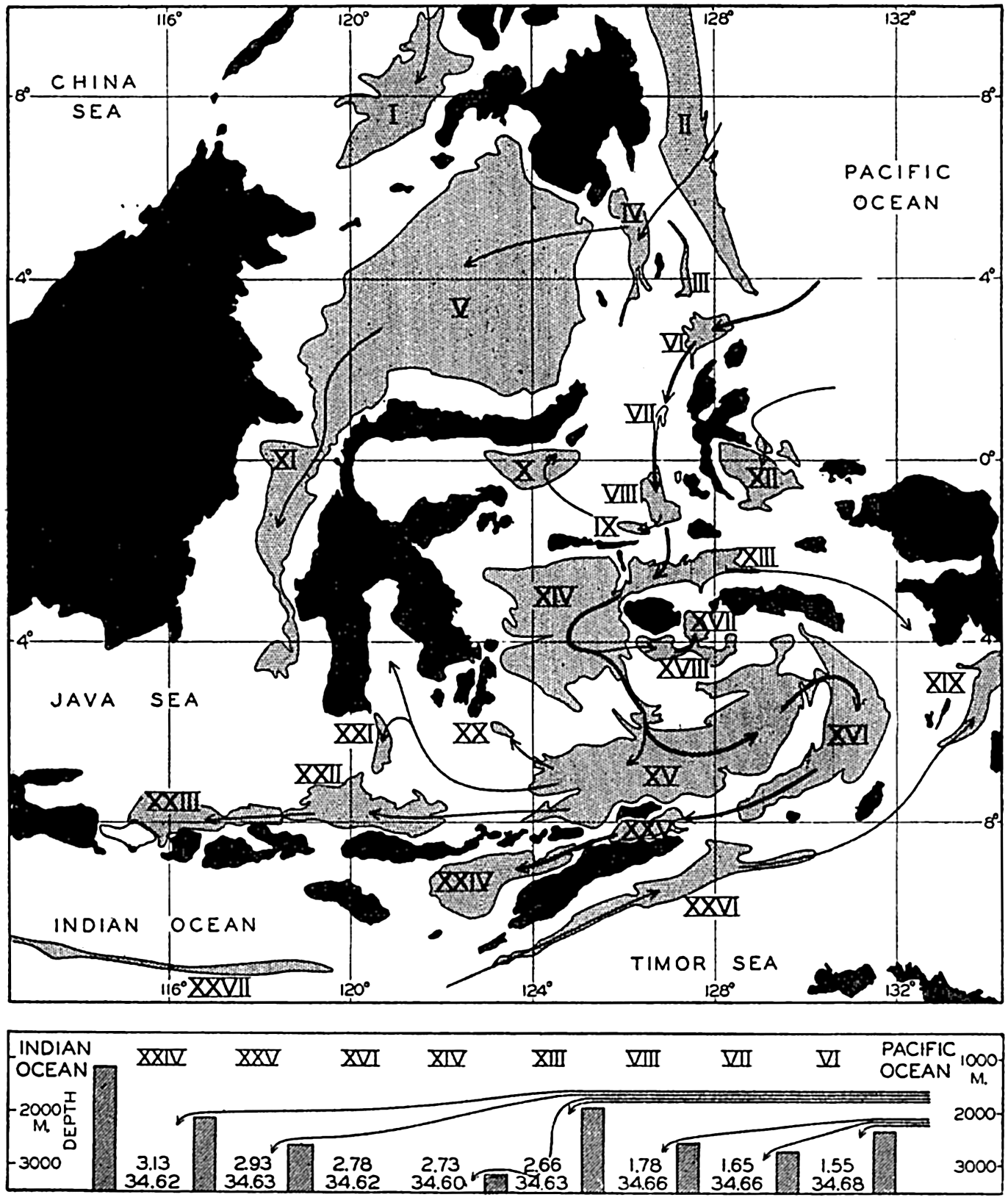
Upper: Basins of the East Indian Archipelago, and direction from which the basin waters are renewed. Lower: Direction of renewal and potential temperature and salinity of the basin waters along the heavy line in the upper figure (according to van Riel).
The Waters of the East Indian Archipelago. Detailed examination of the waters of the East Indian Archipelago has been conducted on the Snellius expedition, and the following summary is based mainly on van Riel's discussions (1932b, 1934, 1938). In fig. 208 are shown the numerous basins which are found in this region of highly complicated bottom topography, also the direction from which the renewal of water in these basins takes place. The names of the basins and their probable sill depths and maximum depths are listed in table 87. The flow of the surface water, according to van Riel (1932b), is also approximately in the direction of the arrows. The high-salinity water, which in the western Pacific is found at depths between 100 and 200 m, flows into the seas between the East Indian Islands, where the thickness of the high-salinity layer decreases in the direction of flow and the maximum salinities are reduced. Between Borneo and Celebes the layer of maximum salinity disappears in about lat. 2°S, but to the west of New Guinea it can be followed to about 8°S. In the southwestern portion of the areas under consideration, then, a region exists without an intermediate salinity maximum and with low-salinity water in the upper layers.
From the arrows in fig. 208 it is evident that the water in the deep basin in the Sulu Sea is renewed from the north by inflow of water from the South China Sea. The sill depth between the South China Sea and the Sulu Basin is probably about 400 m, and the water passing the sill has a potential temperature of about 9.9° and a salinity of about 34.50 ‰. These conditions are illustrated by the observations at Dana station 3685 in the Sulu Sea (table 86), from which it is seen that in the Sulu Sea the temperature increases with depth below 1200 m but the potential temperature decreases slightly except in the lower 1000 m. The oxygen content is somewhat lower than that of the South China Sea, and remains practically constant between 500 and 5000 m.
In all of the other basins shown in fig. 208 except the Timor Trench and the Sunda Trench, renewal of the deep water in the basins takes place from the Pacific Ocean. The potential temperature and the salinity of the water in the different basins is directly related to the manner of renewal and to the type of communication that exists. At the bottom of the figure is shown schematically how the renewal takes place in the series of basins joined by the heavy line in the upper part of the figure. The potential temperatures and the salinities at or directly below the sill depths are entered.
In all basins examined on the Snellius Expedition, a layer of minimum temperature was found a little below the sill depth across which renewal takes place. Below the layer of minimum temperature a small increase toward the bottom was observed, but this increase was in all instances
| Number[*] | Name | Sill depth (m) | Maximum depth (m) | Observed minimum temperature | Salinity of deep water (‰) | |
|---|---|---|---|---|---|---|
| (°C) | Depth (m) | |||||
* Numbers refer to fig. 208. | ||||||
| I | Sulu basin | 400 | 5580 | 10.08 | 1225 | 34.49 |
| II | Mindanao trench | 10500 | 1.56 | 3490 | .63 | |
| III | Talaud trough | 3130 | 3450 | |||
| IV | Sangihe trough | 2050 | 3820 | 2.40 | 2550 | .64 |
| V | Celebes basin | 1400 | 6220 | 3.58 | 2475 | .56 |
| VI | Morotai basin | 2340 | 3890 | 1.81 | 2490 | .65 |
| VII | Ternate trough | 2710 | 3450 | 1.85 | 2761 | .67 |
| VIII | Batjan basin | 2550 | 4810 | 2.06 | 2970 | .66 |
| IX | Mangole basin | 2710 | 3510 | |||
| X | Gorontalo basin | 2700 | 4180 | 2.20 | 2740 | .63 |
| XI | Makassar trough | 2300 | 2540 | 3.59 | 2133 | .58 |
| XII | Halmahera basin | 700 | 2039 | 7.76 | 1839 | .60 |
| XIII | Boeroe basin | 1880 | 5319 | 3.02 | 3240 | .61 |
| XIV | Northern Banda basin | 3130 | 5800 | 3.04 | 2990 | .62 |
| XV | Southern Banda basin | 3130 | 5400 | 3.06 | 2720 | .60 |
| XVI | Weber deep | 3130 | 7440 | 3.07 | 2990 | .61 |
| XVII | Manipa basin | 3100 | 4360 | 3.10 | 3185 | .60 |
| XVIII | Ambalaoe basin | 3130 | 5330 | 3.08 | 3235 | .61 |
| XIX | Aroe basin | 1480 | 3680 | 3.90 | 2240 | .65 |
| XX | Boetoeng trough | 3130 | 4180 | |||
| XXI | Salajar trough | 1350 | 3370 | 3.86 | 1750 | .60 |
| XXII | Flores basin | 2450 | 5130 | 3.22 | 2480 | .61 |
| XXIII | Bali basin | 1590 | 3.58 | 1488 | .61 | |
| XXIV | Sawoe basin | 2100 | 3470 | 3.39 | 2360 | .61 |
| XXV | Wetar basin | 2400 | 3460 | 3.16 | 2500 | .61 |
| XXVI | Timor trench | 1940 | 3310 | 2.67 | 2254 | .71 |
| XXVII | Sunda trench | 7140 | 1.18 | 4230 | .71 | |
The water in the Timor and Sunda Trenches originates from the Indian Ocean, as is evident from the high salinity of the water, 34.71 ‰ in contrast to values between 34.60 ‰ and 34.66 ‰ in all the other basins of the Archipelago.
The classical example on adiabatic increase of the temperature toward the bottom is found in the Mindanao Trench (the Philippines Trench), on the east side of Mindanao, in which a depth in excess of 10,000 m has been recorded. From the somewhat uncertain observations of the Planet in 1907–1908, Schott (1914) concluded that the adiabatic temperature increased toward the bottom and that the stratification was unstable, but Wüst (1929) showed that the observations could be interpreted differently and that indifferent equilibrium probably exists. His conclusion has been confirmed by observations on the Snellius Expedition, according to which the potential temperature actually decreases slightly with depth, whereas the observed differences in salinity are within the limits of the experimental errors. An extract from the Snellius observations in the Mindanao Trench is given in table 88. Thus, stable stratification appears to exist even in the deepest troughs, but a state of indifferent equilibrium is closely approached.
| Depth (m) | Temp. (°C) | θ (°C) | S (‰) |
|---|---|---|---|
| 2,470 | 1.82 | 1.65 | 34.64 |
| 2,970 | 1.66 | 1.44 | .66 |
| 3,470 | 1.58 | 1.31 | .67 |
| 3,970 | 1.59 | 1.26 | .67 |
| 4,450 | 1.64 | 1.25 | .67 |
| 5,450 | 1.78 | 1.26 | .67 |
| 6,450 | 1.92 | 1.25 | .67 |
| 7,450 | 2.08 | 1.24 | .68 |
| 8,450 | 2.23 | 1.22 | .69 |
| 10,035 | 2.48 | 1.16 | .67 |
The Water Masses of the Oceans: A Summary
In figs. 209A and 209B are shown the characters of the water masses that have been discussed, their regions of formation, and their distribution. The chart in fig. 209A and the T-S curves in fig. 209B should together illustrate the concepts that water masses are formed at the sea surface and sink and spread in a manner that depends upon their density in relation to the general distribution of density in the oceans This applies to all water masses except the equatorial water masses of the Indian and Pacific Oceans, which are formed by subsurface processes of mixing.
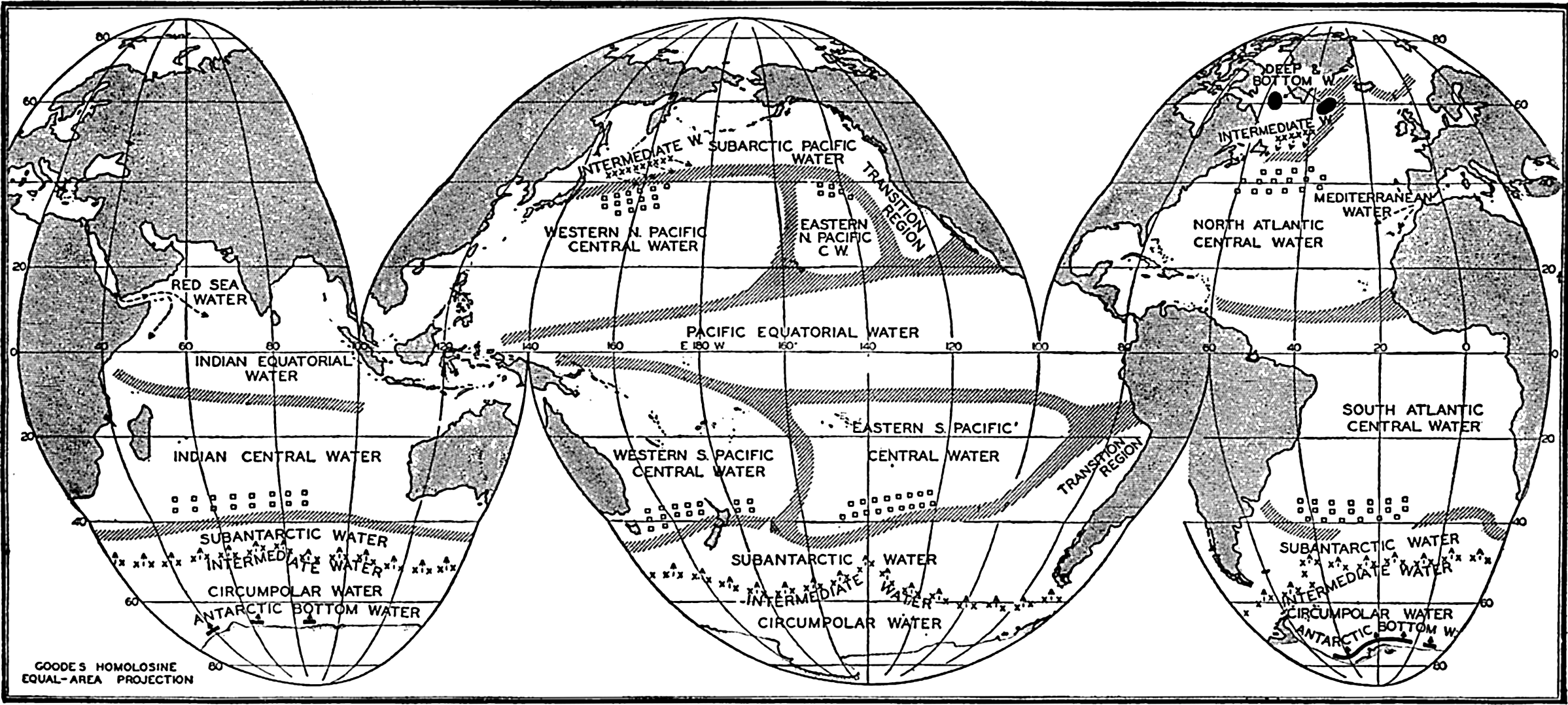
Approximate boundaries of the upper water masses of the ocean. Squares indicate the regions in which the central water masses are formed; crosses indicate the lines along which the antarctic and arctic intermediate waters sink.
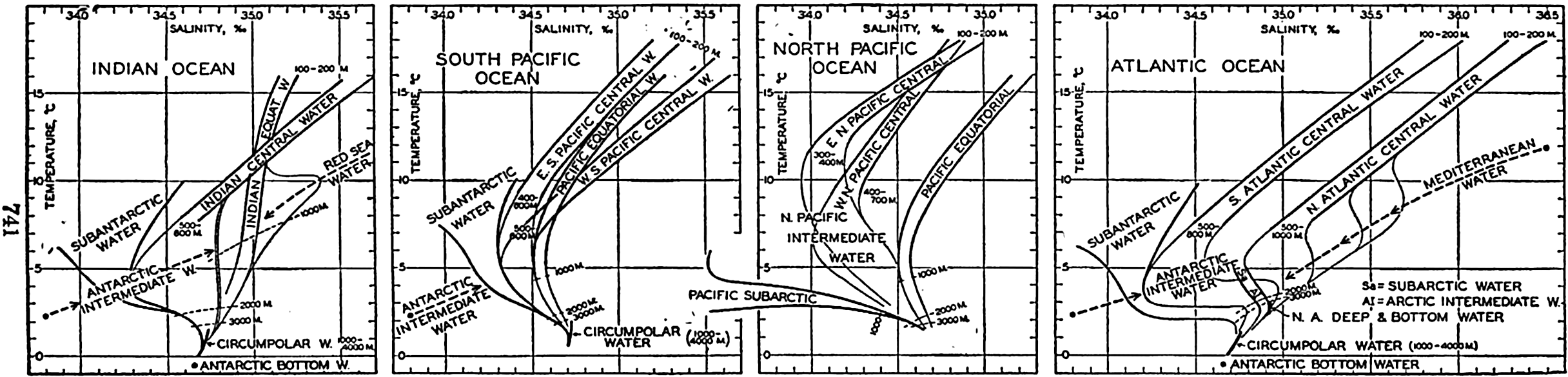
Temperature-salinity relations of the principal water masses of the oceans.
With the exception of two water masses found at intermediate depths and to which we shall return, no water mass is formed at the sea surface in low latitudes, but in all oceans the regions of the subtropical convergences (between 35°S and 40°S and between 35°N and 40°N) are regions where the central water masses originate. This concept is based on the fact that in certain seasons of the year the horizontal T-S relations in these regions are similar to the vertical T-S relations of the different central water masses. These relations are all expressed on a T-S diagram by nearly straight bands, but the slopes vary from one ocean region to another. Table 89 contains the average salinities of the central water masses at different temperatures and the maximum deviations from the averages, according to the curves in fig. 209B. It is seen from the table and the figure that the central water masses of the South Atlantic, the Indian, and the western South Pacific Oceans are very similar, as should be expected, because they are formed in regions in which the external influences, that is, the atmospheric circulation and the processes of heating and cooling, are similar. The corresponding water mass of the eastern South Pacific is of lower salinity, probably because of admixture of the low-salinity Subantarctic Water of the Peru Current. Such admixture may also be responsible for the fact that the Central Water of the western South Pacific has a slightly lower salinity than the Central Waters of the Indian and South Atlantic Oceans.
The Central Waters of the North Atlantic and the North Pacific Oceans are quite different, the former having a very high and the latter a very low salinity. The contrast probably results from the different character of the ocean circulation and from the differences in the amounts of evaporation and precipitation, especially in high latitudes, which are intimately related to the distribution of land and sea.
The central water masses are all of small vertical extension, particularly in the North Pacific Ocean where their thickness over large areas is only 200 to 300 m. In all oceans the greatest thickness of the central water masses is found along the western boundaries; it reaches 900 m in the Sargasso Sea region of the North Atlantic.
In the equatorial part of the Atlantic Ocean the two Central Water masses are separated by a region of transition where the T-S relation is intermediate, but in the Pacific the Central Water masses are separated by a well-defined water mass, the Pacific Equatorial Water. From the T-S curves in fig. 209B it is evident that this water mass is formed in the South Pacific because it is similar to the water masses of that ocean, but it has a higher salinity than any of the water masses of the North Pacific. In the northern part of the Indian Ocean a corresponding Equatorial Water mass is present, which at a temperature of 15° or higher is of the same salinity as that of the Pacific, but at lower temperatures it is of a higher salinity. The higher salinities indicate admixture of Red Sea water, but in general the manner in which the water mass is formed is not clear.
| Temperature (°C) | 8° | 10° | 12° | 14° | 16° |
|---|---|---|---|---|---|
| South Atlantic | 34.64 ± 0.08 | 34.86 ± 0.08 | 35.11 ± 0.08 | 35.37 ± 0.09 | 35.64 ± 0.10 |
| Indian Ocean | 34.65 ± 0.07 | 34.89 ± 0.06 | 35.13 ± 0.07 | 35.37 ± 0.08 | 35.62 ± 0.09 |
| Western South Pacific | 34.58 ± 0.07 | 34.80 ± 0.06 | 35.04 ± 0.08 | 35.30 ± 0.08 | 35.55 ± 0.09 |
| Eastern South Pacific | 34.54 ± 0.07 | 34.70 ± 0.08 | 34.88 ± 0.08 | 35.08 ± 0.08 | |
| North Atlantic | 35.12 ± 0.09 | 35.37 ± 0.09 | 35.63 ± 0.09 | 35.88 ± 0.09 | 36.12 ± 0.09 |
| Western North Pacific | 34.24 ± 0.07 | 34.38 ± 0.06 | 34.52 ± 0.06 | 34.67 ± 0.07 | |
| Eastern North Pacific | 34.11 ± 0.09 | 34.32 ± 0.08 | 34.62 ± 0.08 |
The central and equatorial water masses are covered by a surface layer 100 to 200 m thick, within which the temperature and the salinity of the water vary greatly from one locality to another, depending upon the character of the currents and the exchange with the atmosphere, and within which great seasonal variations occur in middle latitudes. A discussion of the surface layer is not included in this summary. The surface layer, the central water masses, and the upper portions of the equatorial water masses together form the oceanic troposphere (p. 141).
The Subantarctic Water occurs between the central water masses of the southern oceans and the Antarctic Convergence. This water has nearly the same character all around the earth, and is therefore considered as belonging to the waters of the Antarctic Ocean (p. 606). The Subantarctic Water is of low salinity and is probably formed by mixing and vertical circulation in the region between the Subtropical and the Antarctic Convergences. In the North Atlantic the corresponding Subarctic Water is found in a small region only and is of relatively high salinity, but in the North Pacific it is of wide extension and of low salinity. The Subarctic Water must be formed by processes which differ from those that maintain the Subantarctic Water. In the southern oceans the Antarctic Convergence represents a continuous and well-defined southern boundary of the Subantarctic Water, but in the northern oceans the corresponding Arctic Convergence is found in the western parts of the oceans only, and in large areas there exists no marked northern boundary of Subarctic Waters. This contrast between south and north must be related to the differences in the distribution of land and sea and is reflected in the character of the waters. The Subarctic Waters are similar to the corresponding Arctic Intermediate Waters, but the Subantarctic Water is distinctly different in character from the Antarctic Intermediate Water.
Below the central water masses the intermediate waters are found in all oceans. The Antarctic Intermediate Water is the most widespread. This water, in contrast to the central waters, sinks along a well-defined line, and the water which leaves the surface is not a water mass but a water type, which, all around the Antarctic Continent, is characterized by a salinity of 33.8 ‰ and a temperature of 2.2°. After sinking, the water spreads to the north, mainly between the σt surfaces σt = 27.2 and σt = 27.4, and mixes with the over- and underlying waters. In this
In the North Atlantic the corresponding Arctic Intermediate Water is formed to the east of the Grand Banks of Newfoundland, but probably in small quantities because it appears only in a limited area of the north-west Atlantic. In the North Pacific Ocean the Arctic Intermediate Water, on the other hand, is present between lat. 20°N and 43°N, except off the American west coast where the Subarctic Water flows south. This Intermediate Water is probably formed mainly to the northeast of Japan, but it is added to off the American west coast, where at a depth of 500 to 600 m Subarctic Water spreads below the intermediate water that originates further to the west. Correspondingly, two salinity minima are found in that region (fig. 200, p. 715, and fig. 202, p. 717).
Two other intermediate water masses are of importance, namely those formed in the Atlantic and the Indian Oceans by addition of Mediterranean and Red Sea water, respectively. The Mediterranean water that flows out along the bottom of the Strait of Gibraltar has a salinity of 38.1 ‰ and a temperature of 13.0°, but it is rapidly mixed with surrounding Atlantic water and spreads mainly between the σt surfaces σt = 27.6 and σt = 27.8, that is, below the Antarctic Intermediate Water. It can be traced over wide areas by an intermediate salinity maximum. The spreading of the Red Sea water is not so well-defined, but over large parts of the equatorial and western regions of the Indian Ocean the Red Sea water is recognized by a salinity maximum at a σt value of about 27.4.
Below the intermediate water the deep ocean basins are filled by deep and bottom water, the maximum densities of which vary from σt = 27.90 in the North Atlantic to 27.75 in the North Pacific. These water masses are formed in high northerly latitudes in the Atlantic Ocean and in high southerly latitudes close to the Antarctic Continent in the Weddell Sea area, and to the south of the Indian Ocean. The spreading of these water masses will be dealt with in the following discussion of the deep-water circulation of the oceans.
The Deep-water Circulation of the Oceans
In the preceding sections reference has frequently been made to the deep and bottom waters of the different oceans, the character of which is illustrated in figs. 161, 168, 183, 189, 195, 196, and 199.
| Atlantic Ocean, and Atlantic Antarctic Ocean | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Depth (m) | Met 127 | Atl 1223 | Met 279 | ||||||
| March 12, 1935 | April 19, 1932 | March 17, 1927 | |||||||
| 50°27.5′N, 40°14.5′W | 33°19′N, 68°18′W | 19°16′N, 27°27′W | |||||||
| °C | S‰ | O2 | °C | S‰ | O2 | °C | S‰ | O2 | |
| 2000 | 3.32 | 34.92 | 6.30 | 3.62 | 34.97 | 6.08 | 3.54 | 34.98 | 5.07 |
| 2500 | .22 | .93 | .26 | .37 | .97 | .04 | .11 | .96 | .30 |
| 3000 | 2.97 | .93 | .17 | 2.95 | .96 | 5.99 | 2.76 | .94 | .27 |
| 3500 | .63 | .95 | .28 | .61 | .94 | 6.03 | .49 | .92 | .32 |
| 4000 | .38 | .95 | .34 | .45 | .92 | .06 | .39 | .89 | .42 |
| 5000 | — | — | — | .54 | .90 | 5.88 | — | — | — |
| Depth (m) | Met 86 | Met 135 | Met 129 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Dec. 4, 1925 | March 7, 1926 | Feb. 22–23, 1926 | |||||||
| 32°49′S, 40°01′W | 39°46′S, 22°12′E | 58°53′S, 4°54′E | |||||||
| 2000 | 2.97 | 34.77 | 4.71 | 2.68 | 34.76 | 4.70 | −0.26 | 34.67 | 3.37 |
| 2500 | 3.10 | .90 | 5.53 | .54 | .82 | .99 | −0.36 | .67 | .52 |
| 3000 | 2.86 | .92 | .65 | .32 | .81 | 5.14 | −0.42 | .66 | .59 |
| 3500 | .15 | .89 | .46 | 1.93 | .80 | .04 | −0.51 | .65 | .67 |
| 4000 | 0.77 | .69 | 4.88 | .42 | .78 | 4.97 | −0.55 | .64 | .79 |
| Indian Ocean, and Indian Antarctic Ocean | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Depth (m) | Da 3917 | B.A.E. 75 | Di 858 | ||||||
| Dec. 5, 1929 | March 19, 1930 | April 24, 1932 | |||||||
| 1°45′N, 71°05′E | 36°41′S, 114°55′E | 60°10′S, 63°55′E | |||||||
| °C | S‰ | O2 | °C | S‰ | O2 | °C | S‰ | O2 | |
| 2000 | 2.68 | 34.79 | — | 2.70 | 34.60 | — | 0.90 | 34.72 | 4.41 |
| 2500 | .09 | .76 | 3.22 | .28 | .68 | — | .63 | .70 | .51 |
| 3000 | 1.84 | .79 | 2.78 | 1.93 | .72 | — | .34 | .68 | .48 |
| 3500 | .66 | .75 | 3.17 | .59 | .73 | — | .11 | .68 | .66 |
| 4000 | .71 | .74 | .61 | .25 | .74 | — | -0.09 | .67 | .77 |
| Pacific Ocean, and Antarctic Pacific Ocean | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Depth (m) | B | EWS VIII-77 | Da 3745 | ||||||
| Aug. 18, 1934 | July 3, 1939 | July 8, 1929 | |||||||
| 50°30′N, 175°16′W | 28°02′N, 122°08′W | 3°18′N, 129°02′E | |||||||
| °C | S‰ | O2 | °C | S‰ | O2 | °C | S‰ | O2 | |
| 2000 | 1.88 | 34.58 | 1.64 | 2.13 | 34.61 | 1.89 | 2.24 | 34.67 | 2.56 |
| 2500 | .72 | .59 | 2.20 | 1.83 | .63 | 2.44 | 1.86 | .69 | .82 |
| 3000 | .61 | .64 | .58 | .65 | .64 | .72 | .65 | .69 | 3.15 |
| 3500 | .50 | .68 | 3.00 | .55 | .67 | 3.00 | .62 | .70 | .26 |
| 4000 | — | — | — | — | — | — | .57 | .70 | .27 |
| Depth (m) | Da 3561 | Da 3628 | Di 950 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Sept. 24, 1928 | Dec. 15, 1938 | Sept. 7, 1932 | |||||||
| 4°20′S, 116°46′W | 31°25′S, 176°25′W | 59°05′S, 163°46′W | |||||||
| °C | S‰ | O2 | °C | S‰ | O2 | °C | S‰ | O2 | |
| 2000 | 2.30 | 34.63 | 2.53 | 2.42 | 34.60 | 3.32 | 1.70 | 34.73 | 4.27 |
| 2500 | .01 | .64 | .75 | .16 | .64 | .25 | .34 | .73 | .33 |
| 3000 | 1.84 | .65 | .86 | 1.89 | .68 | .75 | .09 | .72 | .37 |
| 3500 | .70 | .66 | .96 | .49 | .72 | 4.27 | 0.91 | .71 | .20 |
| 4000 | .64 | .67 | 3.00 | .22 | .72 | .52 | .87 | .70 | .06 |
| 5000 | — | — | — | .02 | .71 | .55 | — | — | — |
The manner in which the deep and bottom water is formed has been discussed (p. 138), and certain statements as to the deep-water circulation have been made, but so far no general review of the deep-water circulation has been presented. Table 90 has been prepared in order to facilitate such a review. It contains temperatures, salinities and oxygen values of the deep and bottom water at fifteen selected stations, six in the Atlantic, three in the Indian and six in the Pacific Ocean, including the adjacent parts of the Antarctic Ocean. The content of this table will not be dealt with separately but must be examined as the discussion proceeds.
In order to understand the deep-water circulation, one has to bear in mind that deep and bottom waters represent water the density of which became greatly increased when the water was in contact with the atmosphere, and that this water, by sinking and subsequent spreading, fills all deeper portions of the oceans. The most conspicuous formation of water of high density takes place in the subarctic and in the antarctic regions of the Atlantic Ocean. The deep and bottom water in all oceans is derived mainly from these two sources, but is to some extent modified by addition of high-salinity water flowing out across the sills of basins in lower latitudes, particularly from the Mediterranean and the Red Sea.
In the North Atlantic Ocean, North Atlantic Deep and Bottom Waters flow to the south, the flow being reinforced, and the upper deep water being modified, by the high-salinity water flowing out through the Strait of Gibraltar. The newly formed deep and bottom water has a high oxygen content which decreases in the direction of flow. Figure 210 and the values given in table 90 demonstrate the character of these waters and show particularly the increase in salinity at moderate depth caused by addition of Mediterranean water. Antarctic Bottom Water flows in the opposite direction, from south to north, and has been traced beyond the Equator to lat. 35°N (Wüst, 1935). The spreading to the north of the Antarctic Bottom Water is illustrated in fig. 211, showing the potential temperatures below a depth of 4000 m. Owing to admixture of this water the salinity of the bottom water of the North Atlantic decreases toward the south.
The North Atlantic Deep Water crosses the Equator and continues toward the south above the Antarctic Bottom Water. On the other hand, it sinks below the Antarctic Intermediate Water and therefore, in the South Atlantic Ocean, it becomes sandwiched between the Antarctic Intermediate Water and the Antarctic Bottom Water, both of which are of lower salinity. In a vertical section the deep water of the South Atlantic Ocean is therefore characterized by a salinity maximum, but, owing to mixing with the overlying and the underlying water, the absolute value of the salinity at the maximum decreases toward the south.
The bottom water of antarctic origin is colder than the deep water and to the south of about latitude 20°S the Antarctic Intermediate Water is also colder. In a vertical section the deep water therefore shows a temperature maximum and also a decreasing temperature to the south, owing to admixture from above and from below.
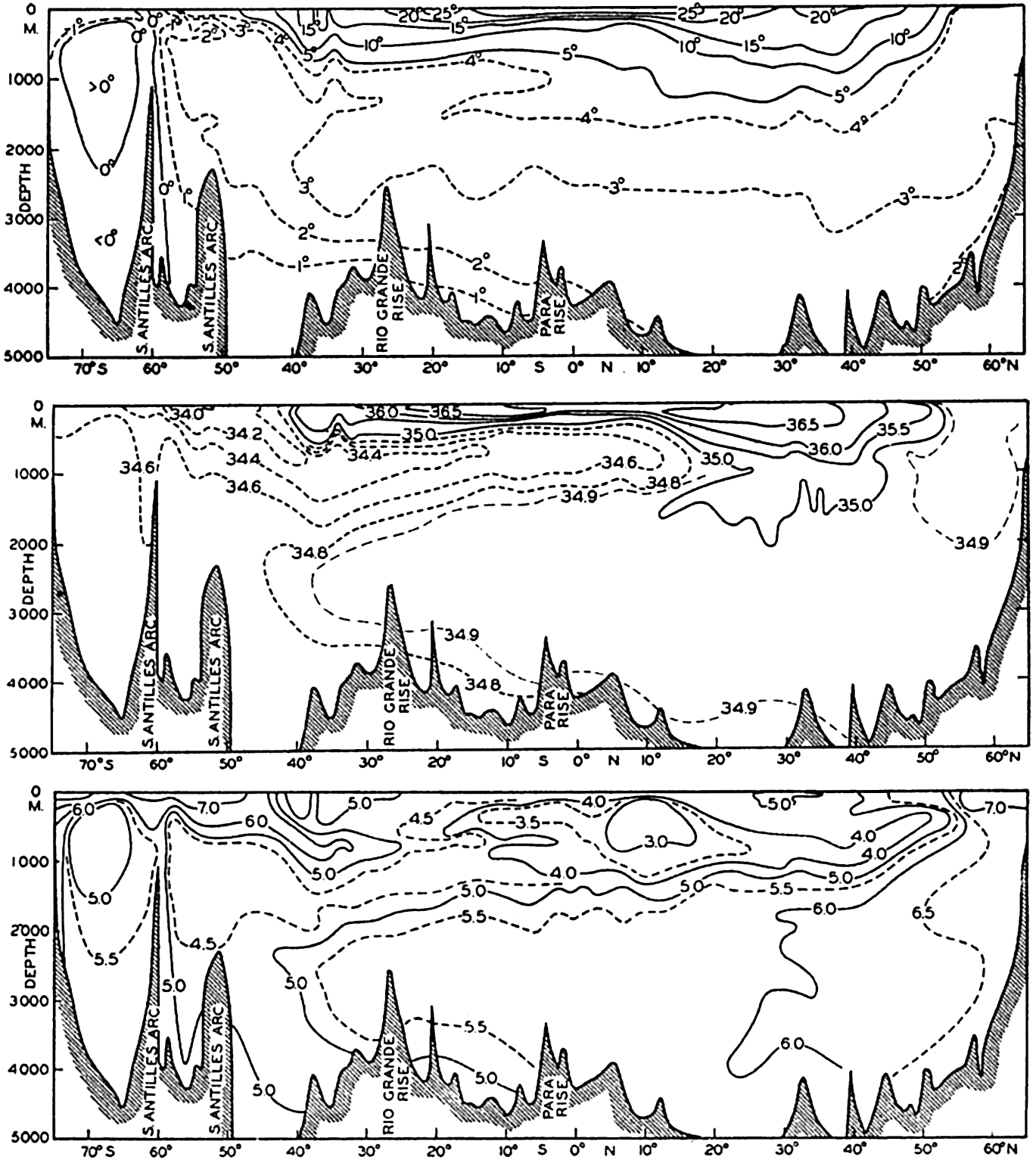
Vertical sections showing distributions of temperature, salinity, and oxygen in the Western Atlantic Ocean (after Wüst).
In the South Atlantic Ocean a large amount of water of antarctic origin, bottom water or intermediate water, returns to the Antarctic after having been mixed with the south-moving deep water. According to the computations which were discussed on pp. 465 and 629, the transport across the Equator of North Atlantic Deep Water amounts to about 9 million m3/sec, whereas between 20° and 30°S the corresponding transport toward the south of deep water is about 18 million m3/sec. If these figures are approximately correct they indicate that 9 million m3 of water of antarctic origin return toward the Antarctic every second. An examination of the salinity in the South Atlantic Ocean at depths below 1600 m confirms this conclusion. At the Equator the average salinity of the North Atlantic Deep Water between 2000 and 3500 m is approximately 34.93 ‰. If this water is mixed with an equal amount of intermediate and bottom water of salinity approximately 34.7 ‰, the salinity will decrease to 34.81 ‰, which approximates the salinity of the deep water in lat. 40°S.
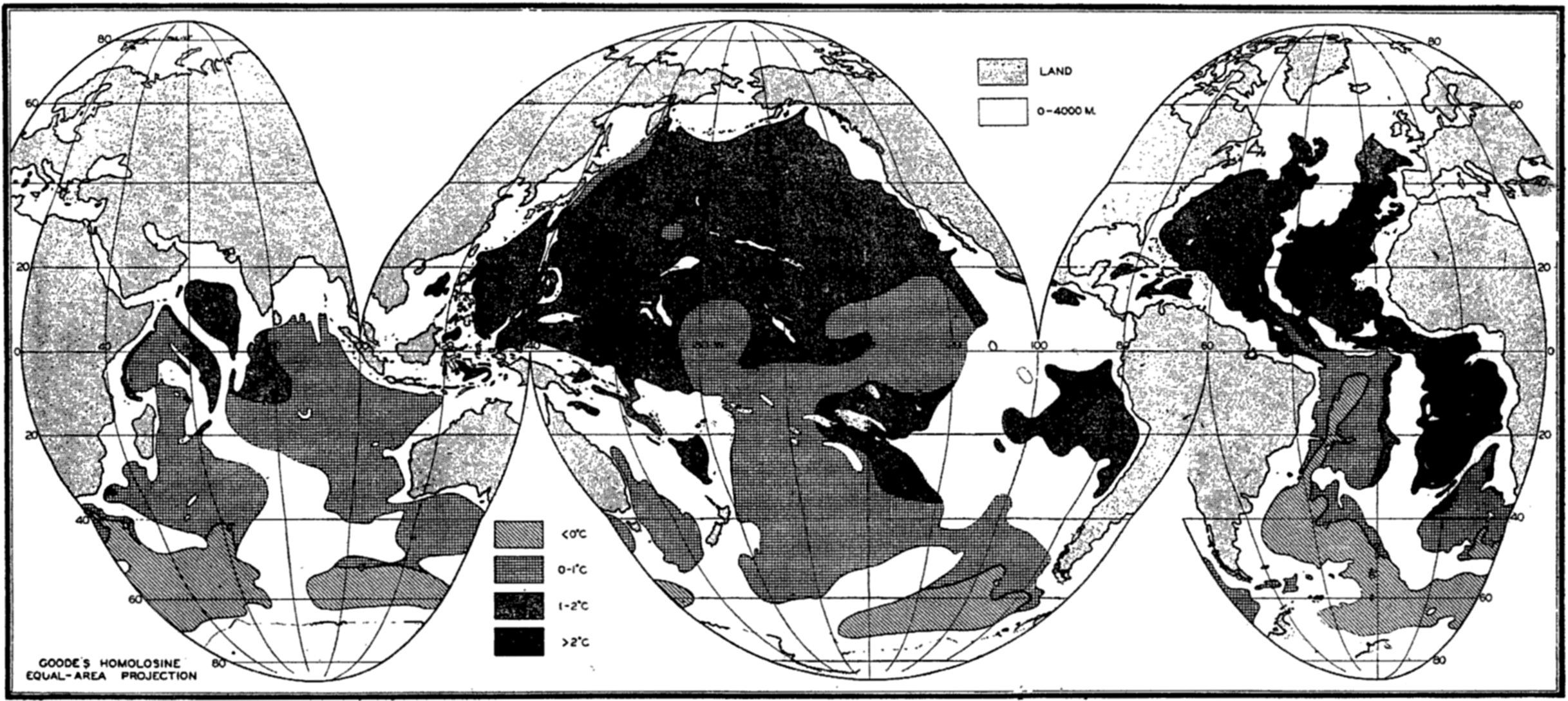
Potential temperature at depths exceeding 4000 meters (after Wüst).
In sum, the deep-water circulation of the Atlantic appears to represent a superposition of two types of circulation: (1) an exchange of water between the North Atlantic and the South Atlantic Ocean which is of such a nature that North Atlantic Deep Water flows south across the Equator, whereas Antarctic Bottom and Intermediate Waters flow north; and (2) a circulation within the South Atlantic Ocean where large quantities of Antarctic Bottom and Intermediate Water mix with the south-flowing deep water and return to the Antarctic. The final result of these processes is that the deep water reaching the Antarctic Ocean from the north is diluted as compared to the deep water of the North Atlantic and is of a lower temperature. This is the water that contributes to the formation of the large body of Antarctic Circumpolar Water flowing around the Antarctic Continent. The oxygen content of Circumpolar Water is lower than that of the North Atlantic Deep Water and the Weddell Sea water, and decreases somewhat toward the east from Weddell Sea toward Drake Passage (see p. 621). The circulation that has been described is present in the western part of the South Atlantic Ocean, but in the eastern part it is impeded by the Walfish Ridge.
In the Indian Ocean there is no large southward transport of deep water across the Equator. The T-S diagram in fig. 189 and the data in table 90 show that to the north of the Equator the deep water contains an admixture of Red Sea Water that maintains a relatively high salinity down to depths exceeding 3000 m, but to the south of the Equator the T-S curves indicate only a slight effect of the Red Sea Water. In the southern part of the Indian Ocean an independent circulation must be present. The deep water from the South Atlantic Ocean continues into the Indian Ocean and is particularly conspicuous in the western part, where maximum salinities of 34.80 ‰ have been observed. This water flows mainly toward the east, being somewhat diluted by admixtures of intermediate and bottom waters. On the other hand, Antarctic Intermediate Water flows north and the bottom temperatures demonstrate that bottom water also moves north (fig. 211); these water masses must return again to the south. It is probable that the intermediate water
From the Indian Ocean the Antarctic Circumpolar Water with its components of Atlantic and Indian Ocean origin enters the Pacific Ocean. The Discovery and Dana observations in the Tasman Sea between Australia and New Zealand, and in the Pacific to the east of New Zealand, show that the salinity of the deep and bottom water has been reduced so much that the maximum values lie between 34.72 ‰ and 34.74 ‰. These maximum salinities are found at depths between 2500 and 4000 m, the salinity of the water close to the bottom being slightly lower. From the region where the deep water enters the Pacific Ocean the salinity decreases both toward the north and toward the east. The Discovery data indicate that below the Antarctic Convergence a core of water of salinity higher than 34.72 ‰ is found, which represents water of the Circumpolar Current; but to the north of this region of maximum salinity, values below 34.70 ‰ prevail, increasing uniformly toward the bottom. The Carnegie and the Dana data similarly show that north of 40°S the highest salinities are found near the bottom. The structure of the water masses of the Pacific differs completely, therefore, from that found in the other oceans, where the highest salinities are encountered in the deep water and not in the bottom water.
This feature can be explained if one assumes that in the South Pacific Ocean there also exists a circulation which is similar to that of the South Atlantic and Indian Oceans, namely, that intermediate and bottom water flow to the north and that a flow of deep water to the south takes place. This north-south circulation is superimposed upon a general flow from west to east. The Pacific Deep Water is, therefore, of Atlantic and Indian origin but has become so much diluted by admixture of intermediate and bottom water that the salinity maximum has disappeared. These conclusions as to the character of the deep-water circulation of the South Pacific are in agreement with the concept of Deacon (1937a), who has shown that the deep water of the Pacific moves toward the south and rises within the Antarctic region in a similar manner to that of the deep water of the Atlantic and Indian Oceans.
The more or less closed systems of the deep-water circulation in the Southern Hemisphere between the Antarctic Ocean and the Equator are
| Depth (m) | Western Pacific | Eastern Pacific | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| S, min. (‰) | S, max. (‰) | S (‰) | Temp. (°C) | O2 (ml/L) | S, min. (‰) | S, max. (‰) | S (‰) | Temp. (°C) | O2 (ml/L) | |
| 2500 | 34.64 | 34.71 | 34.674 | 1.98 | 3.20 | 34.62 | 34.69 | 34.655 | 1.85 | 2.36 |
| 3000 | .68 | .71 | .690 | 1.78 | 3.37 | .64 | .69 | .669 | 1.71 | 2.56 |
| 3500 | .69 | .72 | .698 | 1.64 | 3.48 | .65 | .70 | .677 | 1.56 | 2.94 |
On the other hand, continuity must exist between the South and the North Pacific, for which reason the depths of the North Pacific Ocean are filled by water of the same character as that found in the northern portion of the South Pacific (fig. 212). The most accurate data available indicate that a very small exchange of deep water takes place between the two hemispheres and that a sluggish motion to the north may occur on the western side of the Pacific Ocean, whereas a sluggish motion to the south may occur on the eastern side. A comparison of salinities at the depths of 2500, 3000, and 3500 m in the eastern and western parts of the North Pacific is found in table 91, from which it is seen that the salinity in the eastern part is about 0.02 ‰ lower than that in the western. This
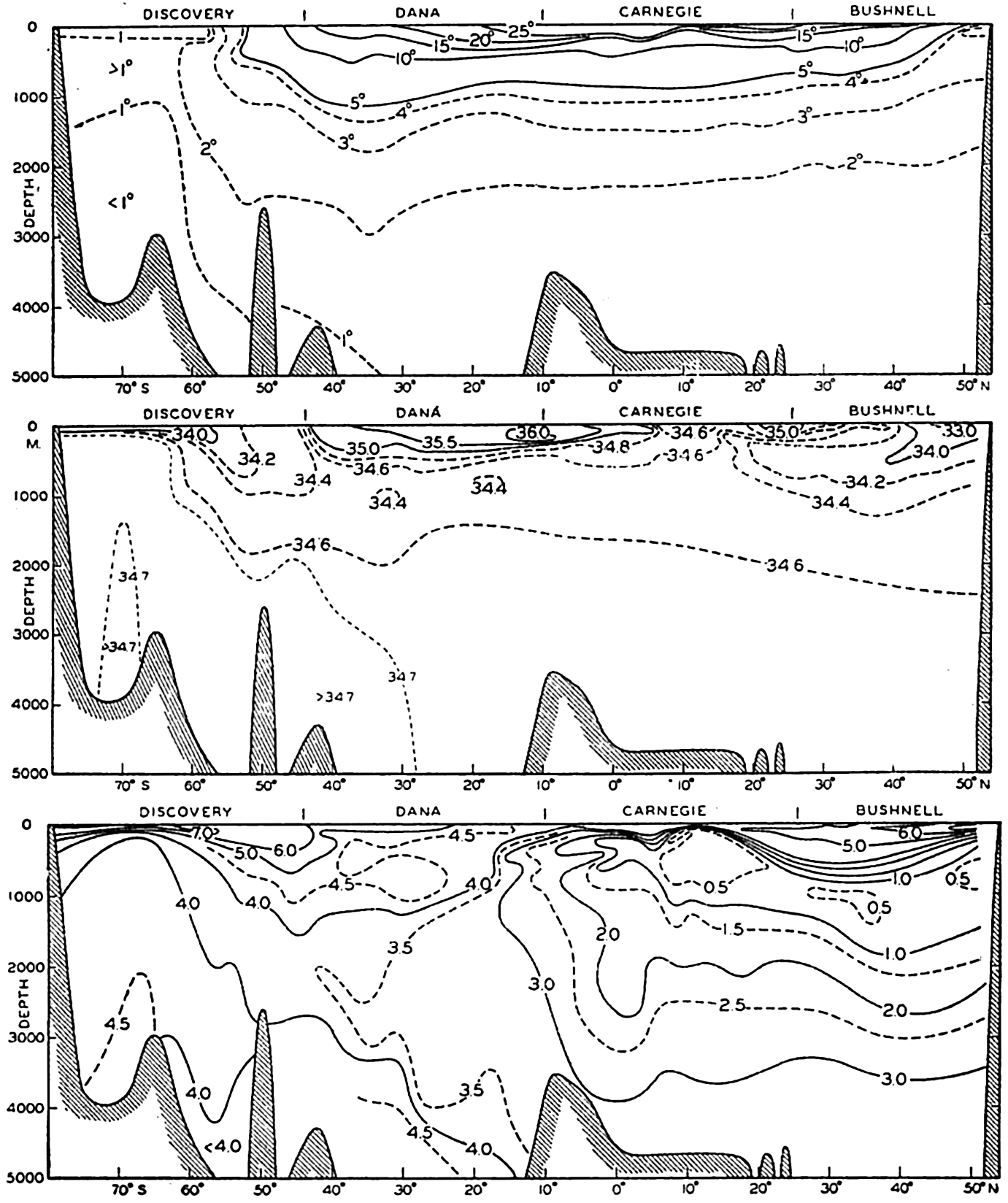
Vertical sections showing distribution of temperature, salinity and oxygen in the Pacific Ocean, approximately along the meridian of 170°W.
In the preceding discussion the term “flow of water” has been used freely, but one has to deal actually with such slow and sluggish motion that the term “flow” can hardly be used, since the average velocities must often be measured in fractions of a centimeter per second.
In conclusion it can be stated that appreciable exchange of deep and bottom water across the Equator takes place in the Atlantic Ocean only. It is rudimentarily present in the Indian Ocean and practically absent in the Pacific. Superimposed upon such an exchange between the hemispheres, independent circulations exist in the three southern oceans, because Antarctic Intermediate and Bottom Water return to the Antarctic as Deep Water. This circulation is well established in the Atlantic Ocean, and in the Indian and Pacific Oceans the existence of such a circulation is derived partly by analogy with the Atlantic Ocean and partly by an examination of the few available precise salinity observations.
The general distributions of oxygen, phosphates, nitrates and silicates discussed in chapter VII are in good agreement with the deep-water circulation that has been outlined. The generally high and uniform content of phosphates, nitrates, and silicates around the Antarctic Continent is consistent with the uniform character of the Circumpolar Water. The low concentration in the North Atlantic is directly related to the exchange of water between the South Atlantic and the North Atlantic. The water that flows into the North Atlantic is mainly central and intermediate water, and the former is low in phosphates, nitrates, and silicates. The net transport of these salts across the Equator must be nearly zero, and the south-flowing deep water of the North Atlantic must therefore have low concentrations. In the South Atlantic the deep water becomes rapidly mixed with Antarctic Intermediate Water and Antarctic Bottom Water, both of which contain so much phosphate, nitrate, and silicate that the contents in the deep water increase as it flows south. The North Pacific Deep Water, on the other hand, contains great amounts of phosphates, nitrates and silicates, in agreement with the concepts that a small exchange of deep water takes place between the South and North Pacific and that in the North Pacific the circulation of
Bibliography
Avers, Henry G.1927. “A study of the variation of mean sea-level from a level surface” . Amer. Geophys. Un., Trans., Nat. Research Council Bull. no. 61, p. 56–58, 1927. Washington, D. C.
Barlow, E. W.1934. “Currents of the Red Sea and the part of the Indian Ocean north of Australia” . Marine Observer, p. 67–68, 110, 150–154, 1934. London.
Barnes, C. A., and T. G. Thompson. 1938. Physical and chemical investigations in Bering Sea and portions of the North Pacific Ocean. University of Washington Pub. in Oceanogr., v. 3, no. 2, 243 pp., 1938. Seattle.
Böhnecke, G.1936. “Atlas: Temperatur, Salzgehalt und Dichte an der Oberfläche des Atlantischen Ozeans” . Deutsche Atlantische Exped. Meteor, 1925–27, Wiss. Erg., Bd. 5, Atlas, vii + 76 pp., 1936.
Brennecke, W.1921. “Die ozeanographischen Arbeiten der Deutschen Antarktischen Expedition 1911–1912 (Deutschland)” . Deutsche Seewarte, Archiv, Bd. 39, Nr. 1, 216 pp., 1921. Hamburg.
Clowes, A. J.1933. “Influence of the Pacific on the circulation in the southwest Atlantic Ocean” . Nature, v. 131, p. 189–91, 1933. London.
Clowes, A. J.1934. “Hydrology of the Bransfield Strait” . Discovery Reports, v. 9, p. 1–64. Cambridge Univ. Press, London, 1934.
Clowes, A. J., and G. E. R. Deacon. 1935. “The deep-water circulation of the Indian Ocean” . Nature, v. 136, p. 936–938, 1935. London.
Deacon, G. E. R.1937a. “The hydrology of the southern ocean” . Discovery Reports, v. 15, p. 1–124, plates I-XLIV, 1937. Cambridge Univ. Press, London, 1937.
Deacon, G. E. R.1937b. “Note on the dynamics of the southern ocean” . Discovery Reports, v. 15, p. 125–152. Cambridge Univ. Press, London, 1937.
Defant, A.1936a. Das Kaltwasserauftriebsgebiet vor der Küste Südwest afrikas. p. 52–66 in Länderkundliche Forschung. Festschrift Norbert Krebs, Stuttgart. 1936.
Defant, A.1936b. “Die Troposphäre” . Deutsche Atlantische Exped. Meteor, 1925–1927, Wiss. Erg., Bd. VI, Teil 1, 3. Lief., p. 289–411, 1936.
Defant, A.1936c. “Bericht uber die ozeanographischen Untersuchungen des Vermessungsschiffes Meteor in der Dänemarkstrasse und in der Irmingersee” . Preuss. Akad. d. Wiss., Sitz., Phys.-Math. Klasse, XIX, p. 13, Taf. 1,2, 1936. Berlin.
Defant, A.1937a. “Die ozeanischen Arbeiten auf der ersten Teilfahrt der Deutschen Nordatlantischen Expedition des Meteor Februar bis Mai 1937” . Ann. d. Hydrogr. u. mar. Meteorol., Beiheft zum Septemberheft, p. 6–14, 1937.
Defant, A.1937b. “C.-G. Rossby, Dynamik stationärer ozeanischer Ströme im Lichte der experimentellen Stromlehre” . Ann. d. Hydrogr. u. mar. Meteor., p. 57–68, 1937.
Defant, A.1938. “Aufbau und Zirkulation des Atlantischen Ozeans” . Preuss. Akad. d. Wiss., Sitz., Phys.-Math. Klasse, XIV, 29 pp., 1938. Berlin.
Defant, A.1941. “Die absolute Topographie des physikalischen Meeresniveaus und der Druckflächen, sowie die Wasserbewegungen im Atlantischen Ozean” . Deutsche Atlantische Exped. Meteor 1925–1927, Wiss. Erg., Bd. VI, 2 Teil, 5. Lief., p. 191–260, 1941.
Defant, A., G. Böhnecke, and H. Wattenberg. 1936. “Die ozeanographischen Arbeiten des Vermessungsschiffes Meteor in der Dänemarkstrasse und Irmingersee” . Berlin Univ., Institut f. Meereskunde, Veröff., N. F., A. Geogr.-naturwiss. Reihe, Heft 32, 152 pp., 1936.
Defant, A., and B. Helland-Hansen. 1939. “Bericht über die ozeanographischen Untersuchungen im zentralen und östlichen Teil des Nordatlantischen Ozeans im Frühsommer 1938 (Internationale Golfstrom-Expedition)” . Preuss. Akad. d. Wiss., Abh., Jahrg. 1939, Phys.-Math. Klasse, Nr. 5, 64 pp., 1939.
Deutsche Seewarte. 1927. “Atlas für Temperatur, Salzgehalt und Dichte der Nordsee und Ostsee” . Hamburg, Deutsche Seewarte, 48 pls., 1927.
Dietrich, Günter. 1935. “Aufbau und Dynamik des südlichen Agulhas-Stromgebietes” . Berlin Univ., Institut f. Meereskunde, Veröff., N. F., A. Geogr.-naturwiss. Reihe, Heft 27, 79 pp., 1935.
Dietrich, Gunter. 1936. “Das “ozeanische Nivellement” und seine Anwendung auf die Golfküste und die atlantische Küste der Vereinigten Staater von Amerika” . Zeitschr. f. Geophysik, Jahrg. 12, Heft 7/8, p. 287–298, 1936.
Dietrich, Gunter. 1937a. “Die dynamische Bezugsfläche, ein Gegenwartsproblem der dynamischen Ozeanographie.” Ann. d. Hydrogr. u. mar. Meteor., Bd. 65, p. 506–19, 1937.
Dietrich, Gunter. 1937b. “I. Die Lage der Meeresoberfläche im Druckfeld von Ozean und Atmosphäre, mit beasonderer Berücksichtigung des westlichen Nordatlantischen Ozeans und des Golfes von Mexiko. II. Uber Bewegung und Herkunft des Golfstromwassers.” Berlin Univ., Institut f. Meereskunde, Veröff., N. F., A. Geogr.-naturwiss. Reihe, Heft 33, 1–51, 52–91, 1937.
Dietrich, Gunter. 1939. “Das Amerikanische Mittelmeer” . Gesellsch. f. Erdkunde zu Berlin, Zeitschr., p. 108–130, 1939.
Eggvin, J.1940. The movements of a cold water front. Fiskeridirektoratets Skrifter, Ser. Havundersokelser (Rept. Norweg. Fishery and Mar. Invest.), v. 6, no. 5, 151 pp., 1940.
Ekman, V. Walfrid. 1939. “Neuere Ergebnisse und Probleme zur Theorie der Konvektionsströme im Meere.” Gerlands Beiträge zur Geophysik, Supplementband 4, Erg. d. Kosmischen Physik IV, Physik der Hydro- und Lithosphäre, 74 pp., 1939. Leipzig.
Fleming, Richard H.1941. “A contribution to the oceanography of the Central American region.” Sixth Pacific Sci. Congr., California, 1939, Proc., v. 3, p. 167–175, 1941.
Gunther, E. R.1936. “A report on oceanographical investigations in the Peru Coastal Current” . Discovery Reports, v. 13, p. 107–276. Cambridge Univ. Press, London, 1936.
Haurwitz, B.1940. “The motion of atmospheric disturbances.” Jour. Marine Research, v. 3, p. 35–50, 1940.
Helland-Hansen, B.1930. “Physical oceanography and meteorology” . Michael Sars North Atlantic Deep-sea Exped., 1910. Rept. Sci. Results, v. 1, 115 + 102 pp., 1930.
Helland-Hansen, B.1934. The Sognefjord Section. Oceanographic observations in the northernmost part of the North Sea and the southern part of the Norwegian Sea. p. 257–274 in James Johnstone Memorial Volume, University Press, Liverpool, 348 pp., 1934.
Helland-Hansen, B.1936. De hydrografiske forhold ved Sydöstgronland ög i Danmarkstredet. p. 61–79 in Iversen, Sydöstgrönland, Jan Mayen. Fiskeridirektoratets Skrifter, Ser. Havundersökelser (Rept. on Norweg. Fishery and Mar. Invest.), v. 5, no. 1, 171 pp., 1936. Bergen.
Helland-Hansen, B., and F. Nansen. 1909. “The Norwegian Sea. Its physical oceanography based upon the Norwegian researches 1900–1904.” Report on Norwegian Fishery and Marine Investigations, v. 2, pt. 1, no. 2, 390 pp. + Suppl., 1909.
Helland-Hansen, B., and F. Nansen. 1920. “Temperature variations in the North Atlantic Ocean and in the atmosphere” . Smithsonian Misc. Coll., v. 70, no. 4, 408 pp., 1920. Washington, D. C.
Helland-Hansen, B., and F. Nansen. 1926. “The eastern North Atlantic” . Geofysiske Publikasjoner, v. 4, no. 2, 76 pp., 1926. Oslo.
Howard, A.1940. “Hydrology, Programme of work and record of observations.” B.A.N.Z. Antarctic Research Exped. 1921–31, Reports, Ser. A, v. 3, Oceanography, Pt. 2, Sec. 2, p. 24–86, 1940.
Iselin, C. O'D.1936. “A study of the circulation of the western North Atlantic” . Papers in Physical Oceanogr. and Meteorol., v. 4, no. 4, 101 pp., 1936.
Iselin, C. O'D.1939. “The influence of vertical and lateral turbulence on the characteristics of the waters at mid-depths” . Amer. Geophys. Un., Trans., 1939, Pt. 3, p. 414–17, 1939.
Iselin, C. O'D.1940. “Preliminary report on long-period variations in the transport of the Gulf Stream System” . Papers in Physical Oceanogr. and Meteorol., v. 8, no. 1, 40 pp., 1940.
Jakhelln, Anton. 1936. “Oceanographic investigations in east Greenland waters in the summers of 1930–1932.” Skrifter om Svalbard og Ishavet, No. 67, 79 pp., 1936.
Johnson, Martin W.1939. “The correlation of water movements and dispersal of pelagic larval stages of certain littoral animals, especially the sand crab, Emerita” . Jour. Marine Research, v. 2, p. 236–45, 1939.
Kiilerich, Alf B.1939. “The Godthaab Expedition 1928. A theoretical treatment of the hydrographical observation material.” Medd. om Grönland. Komm. Vidensk. Undersogelser i Grönland. Bd. 78, no. 5, 149 pp., 1939.
Koenuma, K.1939. “On the hydrography of south-western part of the North Pacific and the Kurosio.” Imper. Marine Observ., Memoirs, v. 7, p. 41–114, 1939. Kobe.
Krümmel, O.1911. Handbuch der Ozeanographie. v. 2, Stuttgart, 764 pp., 1911.
McEwen, George F.1934. “Rate of upwelling in the region of San Diego computed from serial temperatures” . Fifth Pacific Sci. Congr., Canada, 1933, Proc., v. 3, p. 1763, 1934.
Mackintosh, N. A., and H. F. P. Herdman. 1940. “Distribution of the pack-ice in the southern ocean.” Discovery Reports, v. 19, p. 285–296. Cambridge Univ. Press, London, 1940.
Maurstad, H.1935. Atlas of sea ice. Geofysiske Publikasjoner, v. 10, no. 11, 17 pp., x pls., 1935. Oslo.
Möller, Lotte. 1928. “Alfred Merz' Hydrographische Untersuchungen in Bosporus und Dardanellen.” Berlin Univ., Institut f. Meereskunde, Veröff., Heft 18, 284 pp., 1928.
Moller, Lotte. 1929. “Die Zirkulation des Indischen Ozeans. Auf Grund von Temperatur- und Salzgehaltstiefenmessungen und Oberflachenstrom-beobachtungen.” Berlin Univ., Institut f. Meereskunde, Veröff., N. F., A. Geogr.-naturwiss. Reihe, Heft 21, 48 pp., 1929.
Moller, Lotte. 1933. “Zur Frage der Tiefenzirkulation im Indischen Ozean. Ann. d.” Hydrogr. u. Mar. Meteor., p. 233–236, 1933.
Montgomery, R. B.1938. “Fluctuations in monthly sea level on eastern U. S. coast as related to dynamics of western North Atlantic Ocean” . Jour. Marine Research, v. 1, p. 165–85, 1938.
Montgomery, R. B.1939. “Ein Versuch den vertikalen und seitlichen Austausch in der Tiefe der Sprungschicht im äquatorialen Atlantischen Ozean zu bestimmen” . Ann. d. Hydrogr. u. mar. Meteor., Bd. 67, p. 242–246, 1939.
Montgomery, R. B.1940. “The present evidence of the importance of lateral mixing processes in the ocean” . Amer. Met. Soc., Bull., v. 21, p. 87–94, 1940.
Montgomery, R. B.1941. “Transport of the Florida Current off Habana” . Jour. Marine Research, v. 4, p. 198–220, 1941.
Montgomery, R. B., and E. Palmén. 1940. “Contribution to the question of the Equatorial Counter Current” . Jour. Marine Research, v. 3, p. 112–133, 1940.
Mosby, H.1934. “The waters of the Atlantic Antarctic Ocean” . Norwegian Antarctic Exped. 1927–1928 et SQQ., Sci. Results, v. 1, no. 11, 131 pp., Norske Vidensk. Akad., 1934. Oslo.
Mosby, H.1938. “Svalbard waters” . Geofysiske Publikasjoner, v. 12, no. 4, 85 pp., 1938. Oslo.
Nansen, Fridtjof. 1902. “The oceanography of the North Polar Basin” . Norwegian North Polar Exped. 1893–1896, Sci. Results, v. 3, no. 9, 427 pp., 1902. Christiania. Longmans, Green & Co.
Nansen, Fridtjof. 1906. “Northern waters: Captain Roald Amundsen's oceanographic observations in the Arctic Seas in 1901. With a discussion of the bottom waters of the northern seas” . Vid. Selskabets Skrifter, I. Math.-Naturv. Klasse, no. 3, Christiania, 1906.
Neumann, Gerhard. 1940. “Die ozeanographischen Verhältnisse an der Meeresoberfläche im Golfstromsektor nördlich und nordwestlich der Azoren” . Ann. d. Hydrogr. u. mar. Meteor., Beiheft zum Juniheft, 1. Lief., 87 pp., 1940.
Nielsen, J. N.1912. “Hydrography of the Mediterranean and adjacent waters” . Danish Oceanogr. Exped. 1908–1910, Rept., v. 1, p. 77–191, 1912.
Nielsen, J. N.1925. “Golfströmmen” . Geografisk Tidskrift, v. 28, no. 1, 1925. Copenhagen.
Parr, A. E.1936. “On the relationship between dynamic topography and direction of current under the influence of external (climatic) factors” . Conseil Perm. Internat. p. l'Explor. de la Mer, Jour. du Conseil, v. 11, p. 299–307, 1936.
Parr, A. E.1937. “A contribution to the hydrography of the Caribbean and Cayman Seas based upon the observations made by the research ship Atlantis, 1933–34” . Bingham Oceanogr. Collection, Bull., v. 5, art. 4, 110 pp., 1937. New Haven.
Puls, C.1895. “Oberflächentemperaturen und Strömungen des Aquatorial-gürtels des Stillen Ozeans” . Deutsche Seewarte, Archiv, Bd. 18, nr. 1, 38 pp., 1895.
Ramalho, A., and L. Dentinho. 1931. “Contribution a l'étude océanographique du Golfe de Gibraltar” . Conseil Perm. Internat. p. l'Explor. de la Mer, Rapp. et Proc.-Verb., 70, p. 82–115, 1931.
Rappleye, H. S.1932. “The 1929 adjustment of the level net” . Military Engineer, v. 24, no. 138, 1932.
Rossby, C.-G. 1936. “Dynamics of steady ocean currents in the light of experimental fluid mechanics” . Papers in Phys. Oceanogr. and Meteorol., v. 5, no. 1, 43 pp., 1936.
Rossby, C.-G., and R. B. Montgomery. 1935. “The layer of frictional influence in wind and ocean currents” . Papers in Physical Oceanogr. and Meteorol., v. 3, no. 3, 101 pp., 1935.
Schott, Gerhard. 1914. “Adiabatische Temperaturänderung in grossen Meerestiefen” . Ann. d. Hydrogr. u. Mar. Meteorol., p. 321–340, 1914.
Schott, Gerhard. 1915. “Die Gewässer des Mittelmeeres” . Ann. d. Hydrogr. u. Mar. Meteorol., Bd. 43, p. 1–18, 63–79, 1915.
Schott, Gerhard. 1928. “Die Wasserbewegungen im Gebiete der Gilbraltarstrasse” . Conseil Perm. Internat. p. l'Explor. de la Mer, Jour. du Conseil, v. 3, p. 139–175, 1928.
Schott, Gerhard. 1931. “Der Peru-Strom und seine nördlichen Nachbargebiete in normaler und anormaler Ausbildung” . Ann. d. Hydrogr. u. Mar. Meteorol., Bd. 59, p. 161–169, 200–213, 1931.
Schott, Gerhard. 1935. “Geographie des Indischen und Stillen Ozeans” . Hamburg, Verlag von C. Boysen, 413 pp., 1935.
Schott, Gerhard. 1939. “Die äquatorialen Strömungen des westlichen Stillen Ozeans” . Ann. d. Hydrogr. u. Mar. Meteorol., p. 247–257, 1939.
Schumacher, Arnold. 1940. “Monatskarten der Oberflächenströmungen im Nordatlantischen Ozean (5°S bis 50°N)” . Ann. d. Hydrogr. u. Mar. Meteorol., p. 109–123, Taf. 6, 7, 1940.
Seiwell, H. R.1938. “Application of the distribution of oxygen to the physical oceanography of the Caribbean Sea region” . Papers in Physical Oceanogr. and Meteorol., v. 6, no. 1, 60 pp., 1938.
Seiwell, H. R.1939. “The effect of short period variations of temperature and salinity on calculations in dynamic oceanography” . Papers in Physical Oceanogr. and Meteorol., v. 7, no. 3, 32 pp., 1939.
Skogsberg, Tage. 1936. “Hydrography of Monterey Bay, California. Thermal conditions, 1929–1933” . Amer. Phil. Soc., Trans., N.S., v. 29, p. 1–152, 1936. Philadelphia.
Smith, E. H.1932. “Ice in the sea” . Physics of the Earth, v. 5, Oceanography, p. 384–408. Nat. Research Council, Bull.no. 85, 1932. Washington, D. C.
Smith, E. H., F. M. Soule, Olav Mosby. 1937. Marion and General Greene expeditions to Davis Strait and Labrador Sea under the direction of the U. S. Coast Guard 1928–1931–1933–1934–1935. 259 pp., 1937. Washington, D.C.
Soule, Floyd M.1939. “Consideration of the depth of the motionless surface near the Grand Banks of Newfoundland” . Jour. Marine Research, v. 2, p. 169–180, 1939.
Ström, K. M.1936. “Land-locked waters. Hydrography and bottom deposits in badly ventilated Norwegian fjords with remarks upon sedimentation under anaerobic conditions” . Norske Vidensk. Akad. 1. Mat.-Naturv. Klasse, no. 7, 85 pp., 1936. Oslo.
Suda, K., and K. Hidaka. 1932. “The results of oceanographic observations on board R.M.S. Syunpu Maru in the principal part of the Japan Sea in the summer of 1930” . Jour. Oceanography, v. 4, p. 1–174, 1932. Imper. Marine Observ., Kobe, Japan.
Sverdrup, H. U.1928. “The wind-drift of the ice on the North Siberian Shelf” . Norwegian North Polar Exped. with the Maud 1918–1925, Sci. Results. v. 4, no. 1, 46 pp., 1928.
Sverdrup, H. U.1929. “The waters on the North-Siberian Shelf” . Norwegian North Polar Exped. with the Maud 1918–1925, Sci. Results, v. 4, no. 2, 131 + 75 pp., 1929.
Sverdrup, H. U.1932. “Arbeider i luft-og havforskning” . Chr. Michelsens Institutt for Videnskap og Aandsfrihet, Beretninger, v. 2, no. 5, 20 pp., 1932. Bergen.
Sverdrup, H. U.1933. “Narrative and oceanography of the Nautilus Expedition, 1931” . Papers in Physical Oceanogr. and Meteorol., v. 2, no. 1, 63 pp., 1933.
Sverdrup, H. U.1934. “Wie entsteht die Antarktische Konvergenz?” . Ann. d. Hydrogr. u. Mar. Meteor., p. 315–317, 1934.
Sverdrup, H. U.1939a. “Lateral mixing in the deep water of the South Atlantic Ocean” . Jour. Marine Research, v. 2, p. 195–207, 1939.
Sverdrup, H. U.1939b. “Oceanic circulation” . p. 279–293 in Fifth Internat. Congress Applied Mechanics, 1938, Proc.New York, John Wiley & Sons, 748 pp., 1939.
Sverdrup, H. U.1940. “Hydrology, Section 2, Discussion” . B.A.N.Z. Antarctic Research Exped. 1921–31, Reports, Ser. A, v. 3, Oceanography, Pt. 2, Sec. 2, p. 88–126, 1940.
Sverdrup, H. U., and W. E. Allen. 1939. “Distribution of diatoms in relation to the character of water masses and currents off southern California” . Jour. Marine Research, v. 2, p. 131–144, 1939.
Sverdrup, H. U., and R. H. Fleming. 1941. “The waters off the coast of southern California, March to July, 1937” . Scripps Inst. Oceanogr., Bull., v. 4, no. 10, p. 261–378, 1941.
Thompson, E. F.1939a. “Chemical and physical investigations” . The general hydrography of the Red Sea. John Murray Exped. 1933–34, Sci. Repts., v. 2, p. 83–103, 1939.
Thompson, E. F.1939b. “Chemical and physical investigations” . The exchange of water between the Red Sea and the Gulf of Aden over the “sill.” John Murray Exped. 1933–34, Sci. Repts., v. 2, p. 105–119, 1939.
Thomsen, Helge. 1933. “The circulation in the depths of the Indian Ocean” . Conseil Perm. Internat. p. l'Explor. de la Mer, Jour. du Conseil, v. 8, p. 73–79, 1933.
Thomsen, Helge. 1935. “Entstehung und Verbreitung einiger charakteristischer Wassermassen in dem Indischen und südlichen Pazifischen Ozean” . Ann. d. Hydrogr. u. Mar. Meteor., p. 293–305, 1935.
Thorade, H.1909. “Über die Kalifornische Meeresströmung” . Oberflächen-temperaturen und Strömungen an der Westkuste Nordamerikas. Ann. d. Hydrogr. u. Mar. Meteor., p. 17–34, 63–76, 1909.
Tibby, Richard B.1941. “The water masses off the west coast of North America” . Jour. Marine Research, v. 4, p. 112–121, 1941.
Transehe, N. A.1928. “The ice cover of the Arctic Sea, with a genetic classification of sea ice” . p. 91–123 in Problems of Polar Research. Amer. Geogr. Soc., Spec. Pub.no. 7, 479 pp., 1928. New York.
Uda, M.1934. “Hydrographical studies based on simultaneous oceanographical surveys made in the Japan Sea and in its adjacent waters during May and June, 1932” . Records of Oceanographic Works in Japan, v. 6, p. 19–107, 1934. Nat. Research Council, Tokyo.
Uda, M.1935. “The results of simultaneous oceanographical investigations in the North Pacific Ocean adjacent to Japan made in August, 1933” . Japan, Imperial Fisheries Exper. Sta., Jour., no. 6, 130 pp., 1935.
Uda, M.1938a. “Researches on “Siome” or current rip in the seas and oceans” . Geophys. Mag., v. 11, no. 4, p. 307–72, 1938. Central Meteor. Observ., Tokyo.
Uda, M.1938b. “Hydrographical fluctuation in the northeastern sea-region adjacent to Japan of North Pacific Ocean” . Japan, Imper. Fisheries Exper. Sta., Jour., no. 9, p. 64–85 (English abstract, p. 64–66), 1938.
U. S. Coast Guard. 1936. “Report of oceanographic cruise, United States Coast Guard Cutter Chelan, Bering Sea and Bering Strait, 1934, and other related data” . Mimeographed report, Washington, D. C.
van Riel, P. M.1932a. “Einige ozeanographische Beobachtungen in Roten Meer, Golf von Aden und Indischen Ozean” . Ann. d. Hydrogr. u. Mar. Meteor., p. 401–407, 1932.
van Riel, P. M.1932b. “The Snellius Expedition” . Conseil Perm. Internat. p. l'Explor. de la Mer, Jour. du Conseil, v. 7, p. 212–2171932.
van Riel, P. M.1934. “The bottom configuration in relation to the flow of the bottom water” . Snellius Exped. in the eastern part of the Netherlands East Indies 1929–1930, v. 2, ch. 2, Oceanography, 63 pp., 1934.
van Riel, P. M1938. “Influence of bottom configuration on properties of sea water in abyssal layers” . Congrés Intern. d. Geographie, Amsterdam, 1938, v. 2, Travaux de la section IIb, Océanographie. Leiden, 1938.
Vercelli, Francesco. 1925. “Bilancio dello Scambio di acqua fra Mar Rosso e Oceano Indiano” . Campagna idrografico-scientifica nel Mar Rosso R. N. Ammiraglio Magnaghi, 1923–24, Ricerche di oceanografia fisica, Parte 1, Correnti e Mareo, p. 178–183, 1925.
Wüst, Georg. 1924. “Florida- und Antillenstrom” . Berlin Univ., Institut f. Meereskunde, Veröff., N. F., A. Geogr.-naturwiss. Reihe, Heft 12, 48 pp., 1924.
Wüst, Georg. 1929. “Schichtung und Tiefenzirkulation des Pazifischen Ozeans” . Berlin Univ., Institut f. Meereskunde, N. F., A. Geogr.-naturwiss. Reihe, Heft 20, 63 pp., 1929.
Wüst, Georg. 1934. “Salzgehalt und Wasserbewegung im Suezkanal” . Natur-wissenschaften, 22 Jahrg., Heft 36, p. 447–50, 1934.
Wüst, Georg. 1935. “Die Stratosphäre” . Deutsche Atlantische Exped. Meteor 1925–1927, Wiss. Erg., Bd. 6, 1 Teil, 2. Lief., 288 pp., 1935.
Wüst, Georg. 1936. “Kuroshio und Golfstrom” . Berlin Univ., Institut f. Meereskunde, Veröff., N. F., A. Geogr.-naturwiss. Reihe, Heft 29, 69 pp., 1936.
Wüst, Georg. 1940. “Das Relief des Azorensockels und des Meeresbodens nördlich und nordwestlich der Azoren” . Ann. d. Hydrogr. u. Mar. Meteor., August Beiheft, 2. Lief., 19 pp., 1940.
Wüst, G., and A. Defant. 1936. “Schichtung und Zirkulation des Atlantischen Ozeans” . Deutsche Atlantische Exped. Meteor 1925–1927, Wiss. Erg., Bd. VI, Atlas, 103 pls., 1936.
Zubov, N. N.1940. “The drift of the ice-breaker Sedov” . Nature, v. 145, p. 533–39, 1940.
Zukriegel, J.1935. “Cryologia maris” . Travaux Geographiques Tcheques, no. 15, 177 pp., 1935. Prague.
XVI. Phytoplankton in Relation to Physical-Chemical Properties of the Environment
With the phytoplankton are included all of the passively floating plants of the sea (fig. 213). In our review of the systematic position, general structure, and methods of reproduction of the plant population comprising the floating flora of the sea, we noted that the population is composed of an assortment of organisms which, largely for convenience, were grouped under the yellow-green algae. It must be emphasized, however, that the chief components of the phytoplankton are firstly, the diatoms, and secondly, the dinoflagellates. The other autotrophic organisms are of varying importance and consist of coccolithophores, Halosphaera, silicoflagellates, and a few others. The lack of diversity of major groups in the phytoplankton as contrasted with the zooplankton is striking, but this is characteristic of the whole marine flora when compared with the marine fauna. There is no dearth of variety, however, within the restricted group represented by the diatoms and dinoflagellates. Structural variations give rise to large numbers of genera and species, but the number of species occurring in concentrations sufficient to be recorded in nontaxonomic biological surveys of the plankton in any one area is not large; and of these species, fewer yet assume numerical importance. In Puget Sound such a survey (Phifer, 1933) showed 70 species in 24 genera. Among these, 5 species in 5 genera were tychopelagic, having been swept up by currents from their normal habitat on the bottom in the littoral zone. In the Gulf of Maine and the Bay of Fundy, Gran and Braarud (1935) report 78 species of diatoms in 30 genera, and of this number 6 species in 6 genera were tychopelagic. In this region there were also 57 species of dinoflagellates in 11 genera. In warmer seas the number of dinoflagellate species is usually greater. Peters (1932) found that of 55 species of Ceratium occurring in the South Atlantic, 33 were confined to warm water. The phytoplankton may, like the zooplankton, be divided broadly into neritic and oceanic populations.
Among the neritic diatoms there are a great number which form resting spores, and this is in keeping with the greater fluctuations in salinity, temperature, and other environmental details, characteristic of
Photomicrograph of a phytoplankton community.
Oceanic phytoplankton may at times be abundant in the open sea, and densities of 220,000 diatoms per liter have been recorded for the open North Pacific (Allen, 1936), although concentrations are usually much less. The presence of considerable populations of both pelagic and benthic animals in deep-sea and oceanic areas gives ample evidence of offshore production, for it is only the oceanic plants, together with a few others drifting from coastal waters, that constitute the actual source of food for the offshore animals. Lohmann believed that the coastal waters, on the whole, are fifty times more productive than open ocean waters
The vital importance of the phytoplankton organisms as producers of the primary food supply of the sea has repeatedly been emphasized. Let us now examine a little closer some of the adjustments or adaptations required by the floating mode of existence and the factors influencing and controlling multiplication and growth.
METHODS OF FLOTATION
It is clear that if plant life is to exist at all in the offshore waters of more than very moderate depths, it must in some manner be maintained in the upper layers where it can float freely suspended near the surface, for only there can sunlight penetrate sufficiently to meet the requirements of photosynthesis. Once a diatom or any other autotrophic organism requiring light has sunk below this zone, it is doomed to disintegration in the lower layers unless there be prevailing in the area some sort of vertical circulation which will bring it quickly back to the surface. This may occur in some few instances, but there is a strong tendency for water to remain stratified with the lighter layers on top until strong forces overcome this stability (p. 497).
Living protoplasm is heavier than pure water, its specific weight ranging from 1.02 to 1.06, and the shells are even heavier; hence, adaptations are required to prevent or retard sinking. The rate of sinking of a body heavier than water depends upon the ratio of surplus weight to friction. Friction in turn is determined mainly by the surface area. The simplest way to obtain a relatively large surface area is to reduce the absolute size. However, adaptations have gone far beyond this simple limitation to minute size. Special structures, shapes, or other means presently to be considered have evolved to enable the small plants and animals to remain in suspension and thus to populate the vast pelagial expanses of the sea that would otherwise be sterile. Doubtless, the most important adaptation to a pelagic existence in plants is a reduction of absolute size in order to increase the ratio of surface area to volume. In plants the advantage is twofold, for it facilitates not only flotation but also absorption of plant nutrients, which in the sea are in very dilute solutions at best. As a further response to the requirements of this passive floating existence, the plants in most instances also possess structures considered to be special adaptations which aid them in keeping in suspension sufficiently long to grow and reproduce. The characteristic morphological adaptations represent forms which are diametrically opposite to streamline.
Diatoms. Let us first consider the pelagic diatoms, since they are wholly unable by voluntary means to adjust themselves with respect to depth.
The structural adaptations may be divided into four classes (Gran, 1912), and are illustrated in fig. 70, p. 296, depicting diatom types.
Bladder type, in which the cell is relatively large and the cell wall and protoplasm form a thin layer inside the shell or test, and the remainder of the cell is filled with a light cell fluid or sap. Examples are found in species of Coscinodiscus. The shape may approach that of a disc as in Planktoniella, which sinks in a zigzag course, covering a much greater distance than if it were to follow a direct line from the surface to the bottom.
The needle or hair type is long and slender and is typified by Rhizosolenia and Thalassiothrix, which sink slowly when suspended with the long axis horizontal to the pull of gravity but with increased rate when in a vertical position. The cells also may be curved or provided with ends that are beveled in such a manner that they are soon brought back into the horizontal position, once they have been displaced. In this way the sinking is accomplished in great wide circles. The same applies to Nitzschia serriata when in chains with overlapping ends.
The ribbon type is illustrated by Fragillaria and Climacodium. Here the cells are broad and flat and are attached to each other in chains in which the individual cells lie side by side in a single layer. They are not numerous in the sea.
The branched type is illustrated especially by the genus Chaetoceros, and by Corethron. Here a great many spines are grown as projections to resist sinking, and the cells are often in chains and are frequently spiraled for greater effect. They are extremely abundant in the sea.
All of the pelagic species are thin-shelled as compared with the bottom or littoral forms, and some may secrete a coating of light mucus to aid in tiding over unfavorable conditions. There are also summer and winter forms in some species. The summer forms usually have lighter shells, which is in keeping with the reduced viscosity of warmer water.
The specific gravity of diatoms may also be lessened by the presence of oil in the cells. Oil has been noted to accumulate in diatoms late in the vegetative period and, in addition to providing a food reserve, may also result in keeping them afloat while waiting return of conditions favorable for multiplication.
Many diatom species, though conforming in cell structure to either of the above types, also unite the separate cells into chains of various types. This is accomplished by siliceous cements or by mucous pads or threads (fig. 70).
Dinoflagellates. Unlike diatoms, the dinoflagellates are not strictly passive, for they are provided with two minute whiplike flagella which by almost constant undulating motion provide a means of feeble
In some dinoflagellates, for example, Triposolenia spp. and Amphisolenia spp. (fig. 74), an asymmetry is developed, resulting in a deflection of the ends of the antapical horns. During periods of rest or weak swimming, these deflected horns tend to orient the sinking body so that the long axis lies horizontal and thus provides the maximum surface and resistance against passive sinking. In Triposolenia, a descent of about ten times its body length is sufficient to swerve the organism slowly into this advantageous passive position. Here it remains at least momentarily and the frequent alternation of positions leads to a slow wavering descent.
In referring to the asymmetry discussed above, Kofoid (1906) remarks,
Had it appeared as one of the characters of a single species, or even of several, it would be dismissed as one of those usual chance vagaries of structure which so often crop out in the diagnostic features of a species. Its occurrence in the two genera named and suggestions of an analogous structural feature in some other genera of dinoflagellates is indicative of a more profound relationship to the welfare of the organisms in which it appears.
FACTORS OF PHYTOPLANKTON PRODUCTION: I
In the study of plankton, the production is generally understood as being the amount of organic matter produced by the phytoplankton under a unit area of sea surface or in a unit volume of water during a given
The principal factors controlling productivity have been reviewed by Braarud (1935) and we follow his scheme with some modifications in outlining the analysis of the direct and indirect factors. Under the heading of direct factors are included (a) direct primary factors that operate directly on the growth and proliferation of the individual alga, and (b) direct secondary factors that directly affect the population density and, therefore, the total production which is possible in a given period of time.
Direct Primary Factors of Reproduction and Growth
The Energy Factors. In the presence of carbon dioxide and water, plants are able by virtue of their pigments to intercept the sun's radiant energy required by them in the manufacture of compounds of carbon. The chemical change is expressed in simple form by the equation 6CO2 + 6H2O → C6H12O6 + 6O2. This process of carbon assimilation is an endothermic reaction, wherein the energy absorbed is derived from the light and the resultant product contains more energy than was present in the reactants CO2 and H2O. This energy, stored in the complex organic substance of the plant, becomes the source of chemical energy for life processes, directly for those of the plant and of herbivorous animals and indirectly for those of carnivorous animals, and also for the heterotrophic bacteria and other saprophytic forms.
It is important to note that the by-product of carbon assimilation is free oxygen. The process therefore becomes a source of an appreciable portion of the dissolved oxygen in the water and, consequently, is of great moment in the general metabolism of the sea, in the respiration of organisms, and in oxidation of organic and inorganic substances.
Since oxygen is always used in the respiration of the algae, the free supply dissolved in the water is drawn upon for metabolic processes during periods of low light intensity or when the plants have sunk to a depth at which the light intensity is below the minimum required for oxygen production by photosynthesis to balance oxygen consumption by respiration. The depth where light intensity is just sufficient to bring about this balance is known as the compensation depth (cf. p. 779).
Factors of Food Supply. The utilization of carbon dioxide is directly associated with the process of photosynthesis and is briefly discussed above. It is sufficiently abundant in the sea at all times, either as a dissolved gas or as a fixed constituent of the bicarbonates, to meet the requirements of the plants; it is, therefore, apparently never a limiting factor in phytoplankton production in the sea, for as rapidly as it is consumed by the plants a supply becomes available by the hydrolysis of the bicarbonates (p. 192). It has been estimated by Moore (in John-stone, Scott, and Chadwick, 1924) that in the Irish Sea 20,000 to 30,000 tons of carbon dioxide per cubic mile of sea water are passed through the biological cycle annually.
Although carbon dioxide cannot be considered a limiting factor in plant production, it is an item of far-reaching biological significance. In the final analysis the carbon compounds of all living creatures of the sea, from protozoa to the higher animals, come directly from the carbon dioxide in the sea.
Under dissolved nutrient salts we include the mineral salts that have been shown to influence and at times limit or control the production of phytoplankton, namely, the nitrogen and phosphorus, and also, to a more uncertain degree, iron and other trace elements. The control of growth is expressed in Liebig's law of the minimum, which states that growth is limited by the factor that is present in minimal quantity.
In the early studies of phytoplankton, Brandt (1899) suggested that diatom growth must be regulated by the nutrient substances that the diatoms utilize in the lighted waters of the sea. He anticipated the importance of compounds of nitrogen and phosphorus as substances which, according to Liebig's law, might be limiting factors. With the improvements of analytical methods by Atkins and Harvey, it has been shown beyond doubt that Brandt's theory was correct. Various investigators have demonstrated that phytoplankton organisms may assimilate different compounds of nitrogen (cf. p. 915), not only nitrates but also nitrites and ammonia (Schreiber, 1927, Braarud and Föyn, 1931, Harvey, 1933, ZoBell, 1935). Of these, nitrates are the most important, and in waters of temperate and arctic latitudes they accumulate during the winter and form the main nitrogen supply for spring diatom growth (Cooper, 1937).
The utilization of nitrates and phosphates in the synthesis of organic substance proceeds at an approximately parallel rate so that, although both may become markedly reduced by plants, the ratio of the two approaches fifteen atoms of nitrogen to one atom of phosphorus, with some deviation called the “anomaly of the nitrate-phosphate ratio,” perhaps dependent upon stages in the nitrogen cycle, a more rapid bacterial regeneration of phosphates, and the history of the particular body of water. In keeping with this there is an agreement in the ratio
Although the two elements discussed above have been shown to be vital to plant production, yet in nature the diatom population has been known to decrease while these nutrients were still present in sufficient quantity to support production. In these instances the limiting factors must be looked for elsewhere.
Gran (1931) believed that low concentrations or lack of iron might be a factor in limiting plant growth at times, especially for neritic species. From experiments, this seems probable (Harvey, 1937), and Thompson and Bremner (1935) have recorded a reduction in the quantity of iron in sea water coincident with heavy diatom production.
There are still other elements that occur in minute quantities in sea water or as traces in the analysis of plants, but since the status of these in the economy of the plant is as yet uncertain, they will not be dealt with in this general survey. Manganese, for example, has been shown to influence the growth of the diatom Ditylum (Harvey, 1939).
Silicates, used in the formation of the siliceous shells of diatoms and of certain other organisms, show seasonal fluctuations and also vertical distribution correlated with phytoplankton activity (Atkins, 1926, Harvey, 1928). Yet there is no evidence that reduction of silicon ever becomes a limiting factor. However, data from areas especially rich in silicon show a degree of utilization of this element by diatoms that would exceed the total supply available if applied to areas of low silicon (p. 261).
Accessory Growth Factors. It is becoming increasingly evident that the nutritional requirements for a lively diatom growth include substances not referred to in the above consideration. In experimental cultures utilizing artificial sea water, Allen (1914) found that the diatom Thalassiosira gravida would not grow unless small quantities of natural sea water or extracts of the marine alga Ulva were added. The accessory growth substance added with the sea water and the alga is not known. More recently Harvey (1939) has shown that even natural sea water enriched with nitrate, phosphate, and iron may lack the growth substances necessary for the continuous production of the marine diatom Ditylum brightwelli. The experiment indicates also that there are complementary substances, neither of which function well without the other. Some diatoms, for example Nitzschia closterium, apparently do not need the accessory substances although their presence stimulates growth. It is thought that diatoms like Nitzschia may be able by their own activity to make the organic accessory required. The accessory substances are
The above will serve to illustrate in part the complex problems involved in the explanation of phytoplankton nutrition.
Factors Influencing Metabolism. The rate of metabolism is much accelerated with rise in temperature. According to van't Hoff's law the increase is two to three times for each 10° rise in temperature within favorable limits. Very little is known regarding the optimum temperature conditions for the various phytoplankton species. However, it is known that various species may be attuned to a given temperature range. The species with common temperature requirements constitute biological groups which, if cold-water loving, may thrive in the Arctic in summer and in lower latitudes only during colder seasons. The growing season for a cold-water group may thus shift toward the Equator as winter approaches, and that for a warm-water group poleward with the approach of summer.
The salinity of the water is important in maintaining the proper osmotic relationship between the protoplasm of the organism and the water. The extent to which osmotic relationships can vary is dependent upon the species. Very little study has been made on the osmotic relations of diatoms, but the diatom Ditylum apparently does not act as an ordinary osmotic system (Gross, 1940). Some diatoms, especially neritic forms, have a tolerance for a rather wide range of salinity and are known as euryhaline forms, while the oceanic forms are usually stenohaline, that is, capable of enduring only small changes in salinity. Changes in this factor operative mainly in estuarine or in inshore situations. The variations in salinity operate mainly as a selective agency determining the composition or types of species that make up the population rather than on the fertility of the region.
The hydrogen-ion concentration or pH of sea water is generally maintained within narrow limits owing to the buffer effect of the dissolved salts (p. 202), hence its range of variations at most, perhaps, has only a moderate influence as a limiting factor for phytoplankton. However, during periods of high diatom production a marked rise in pH does occur as a result of the rapid utilization of carbonic acid by the plants during photosynthesis. On such occasions an excessive rise might tend to act as a natural check on further proliferation of some species, although this has not been shown for diatoms. Gail (1920) found that growth of the brown benthic alga Fucus evanescens is much inhibited at the high pH
Direct and Indirect Secondary Factors Influencing Population Density
We have already described the methods of reproduction characteristic of the plankton algae. These methods, which involve mainly simple cell division, are highly efficient and under optimal nutritional and metabolic conditions result in building up by geometric progression an excessively dense population. Any factor, then, that disturbs this progression has a far-reaching effect on the total numbers that can be produced in a given period of time.
By way of illustration, Braarud shows in a hypothetical example the difference between two identical populations of 500 cells per liter after nine cell divisions, when one population suffers no loss between successive cell divisions, while the other is assumed to experience a net loss of 10 per cent between the successive divisions. The undisturbed population would have increased at the end of the given time to 256,000 cells per liter, whereas the other at the same time would have only 99,159 cells per liter. The total withdrawal in cells would be only 12,343, but these plus their potentiality to produce yet other cells in the given time would amount to 144,498 cells per liter, in other words, the difference in increase between the two initial populations of 500 cells per liter at the end of nine cell divisions.
Just how much time would elapse during nine cell divisions in nature is dependent upon the living conditions and the species involved. The rate of division is dependent, of course, upon the direct primary factors mentioned above. In culture experiments (Gran, 1933) in the sea at Woods Hole it was found that population increases corresponded to seven divisions in three days for Chaetoceros compressus, six divisions in five days for the oceanic species Rhizosolenia alata, and five to six divisions in three days for other species. It has been estimated by Harvey et al (1935) that diatoms divide at a rate of once each 18 to 36 hours.
In nature, the number of cells lost between successive divisions would not remain constant even when resulting from consumption by a uniform population of filter-feeding animals, for there is some evidence that the rate at which these animals filter water remains the same whether or not the water is thinly or thickly populated with plankton food (p. 901). Harvey et al also show that during periods of abundant food the grazing plankton animals consume more than they are able to digest and void pellets of only partially digested diatoms.
Consumption. Since the phytoplankton is the main pasturage of the sea, it is very heavily drawn upon by the countless numbers of herbivorous plankton animals living within or periodically invading the euphotic zone. This has long been recognized as a foregone conclusion (Hensen, 1887, Lohmann, 1908),
The planktonic copepods are doubtless the chief diatom grazers, and due to their vast numbers they must exact an exceedingly heavy toll. In examining the digestive tracts of copepods, Dakin (1908) found that diatoms were the most abundant organisms present, especially species of Thalassiosira and Coscinodiscus. Species of Peridinium were next in importance. Esterly (1916), in direct examination, also found evidence of phytoplankton grazing, there being included in the digestive tract diatoms, dinoflagellates, and coccolithophores. Lebour (1922), Marshall (1924), and others have also shown that diatoms are important in the diet of copepods.
In addition to the copepods there are also large numbers of other small animals, especially the larval stages of benthic invertebrates, that graze directly upon the phytoplankton. For example, larval annelids are voracious feeders and, when abundant, may diminish materially the diatom population. Lohmann, working at Kiel, calculated that during the course of a year the increase in volume of pelagic plants was 30 per cent daily. Hence, that fraction of the plant population could be consumed daily by grazers without endangering the plant stock, if no other loss occurred.
The unevenness of phytoplankton distribution both in space (horizontally and vertically) and in time may reflect relative intensity of grazing rather than control through nutrient or physical conditions of the water, and actually more organic production may have taken place in areas only moderately rich in plants at any given time (p. 901).
Sinking. Even though diatoms are especially adapted to a floating existence, the suspensory organs and analogous structures usually operate only to retard sinking and not as a complete counter to the constant pull of gravity. Therefore, many individuals of the population tend to sink below the euphotic zone and may be considered as being withdrawn from the reproducing population as completely as if consumed by animals in the euphotic zone, unless before death they are fortuitously returned to the lighted waters by ascending water movements. According to the definition of compensation values (pp. 778 and 779), when the depth to which the plants have sunk is characterized by light with intensity below the “compensation point,” theoretically they would be considered as having become, at least temporarily, nonproducers for the twenty-four hours considered. It is probable, however, that the slowly sinking specimens have an adaptability enabling them to carry on photosynthesis sufficiently to reproduce slowly at a lower illumination than is indicated for experimental cultures at the compensation point. Harvey (1939) found a “physiological state” in Ditylum which indicated an adaptability to
In connection with the velocity of sinking, temperature becomes an important indirect factor influencing production owing to its marked effect on viscosity. A marked discontinuity layer, providing a sharp temperature decrease within the euphotia layer, is an important feature in maintaining the plants in the productive layer, since viscosity is inversely proportional to temperature and the rate of sinking is inversely proportional to viscosity.
Vertical Transport. Some of the points discussed in relation to sinking will be equally applicable in the factor of vertical transport. We learn from the discussion of turbulence (p. 471) that water particles within a water mass are not at rest but may be shifted in various directions. Passive microscopic objects, such as diatoms, caught in these shifts are transported along with the water. But as far as transport is concerned, we are interested here mainly in the vertical component of turbulence. If this vertical component is confined to the transportation of particles up or down within the euphotic layer, its effect on the production will be of no great significance, although it is of importance in maintaining a “seed” supply in the euphotic layer. If, however, the movement involves a transport of water from the productive layer downward into darker layers, it will have a deleterious effect on production in so far as it carries with it a certain portion of the phytoplankton population. This deleterious effect may be partly compensated for by a return of normally sinking plants to the lighted zone by ascending currents, but the time spent below optimum light conditions must constitute a loss.
Indirect Factors. The indirect factors of productivity also belong to the secondary group and operate simultaneously with them, in most instances also with the direct primary factors. Temperature, for instance, modifies the rate of metabolism, while at the same time it regulates the viscosity, and the vertical temperature gradient tends to reduce active turbulence. On the other hand, turbulence, upwelling, or convection currents are essential to the return of nutrients to the euphotic layer; thus the effect on the population is very complicated.
Among the more obvious of indirect factors of productivity may be listed water movements of various kinds, stability of waters within the euphotic layer, discharge of rivers, meteorological conditions, bathymetric conditions, and geographic position. The separate indirect factors exert their influence on productivity through the effect on the direct factors, and also on the other indirect factors. As a result, a complex of forces is constantly at play to increase or to decrease the total production during shorter or longer periods of time.
FACTORS OF PHYTOPLANKTON PRODUCTION: II
The relation of plants to the physical-chemical and biological properties has been touched upon in the foregoing discussion outlining the factors that control phytoplankton production. It remains to enlarge upon and examine more closely how some of these factors operate in nature. This examination will be organized in reference to (a) photosynthesis of phytoplankton, (b) plant nutrients and vertical circulation of water, (c) horizontal ocean currents, and (d) temperature.
Photosynthesis of Phytoplankton
The intensity of light decreases gradually with depth; yet for the purpose of biological investigations it is convenient to consider the sea as divided vertically into three zones with respect to the amount of light that is present. The depths given are approximations and vary with latitude and season.
The euphotic zone, which is abundantly supplied with light sufficient for the photosynthetic processes of plants. This zone extends from the surface to 80 or more meters. All of the eulittoral zone lies within this layer.
The disphotic zone, which is only dimly lighted and extends from about 80 to 200 or more meters. No effective plant production can take place in this zone, and the plants found here have mostly sunk from the layer above.
The aphotic zone, the lightless region below the disphotic zone. In the deep sea it is a very thick layer in which no plants are produced and the animal life consists only of carnivores and detritus feeders.
Until the relationship between rate of photosynthesis and light intensity at different wave lengths is more thoroughly understood than at present, it will be necessary to restrict discussion to the relationship between rate of photosynthesis and total light intensity in the sea as expressed in energy units or in units of illumination.
When using energy units the light intensity is expressed in ergs per unit surface and unit time, for example, ergs/cm2/sec; or in gram calories or joules per unit surface and unit time (1 g cal = 4.18 × 107 ergs, 1 joule = 107 ergs). The penetration of radiant energy in the sea was discussed in chapter IV (p. 104). It was stated there that no direct measurements are available of the energy which under different conditions reaches different depths below the surface, but that these amounts could be computed from observations of the extinction coefficients for radiation of different wave lengths and from the intensity of the radiation of stated wave lengths reaching the sea surface (table 27, figs. 21, 22). In all experiments in which the intensity of light has been examined in conjunction with studies of photosynthesis, the energy at different levels has
In a number of published reports on photosynthesis in the sea, light intensity is expressed in units of illumination, that is, in units based on the power of light to produce visual sensation. Illumination units such as 1 meter-candle = 1 lux = 0.093 foot-candle have been widely used, and it is therefore necessary to explain their relation to the energy units. Because the unit of illumination is directly based on the reaction of the human eye, a mechanical equivalent of the illumination unit can be established only at a specified wave length. At moderate illumination the maximum sensitivity of the human eye lies at a wave length of 0.56 μ, and at this wave length the “luminous equivalent” has been established (Smithsonian Tables, 1933) at
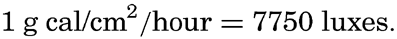
It is not possible to give any table by means of which the energy reaching a certain depth can be converted into units of illumination, because the conversion factors will depend upon the quality of the light. Thus, in turbid coastal water and in the clearest oceanic water the same amount of energy is found at the depths of 10 and 100 m, respectively (table 27), but at 10 m in the coastal water the maximum intensity lies
Table 92 has been prepared in order to show approximately corresponding values of energy and illumination at different depths and in different types of water. For the sake of simplicity the intensity of the radiation penetrating the surface has been selected at 100 g cal/cm2/hour, corresponding approximately to the radiation from sun and sky with the sun at zenith. The illumination at the surface is then about 120,000 luxes. The illumination decreases more slowly with depth than does the energy, but it is realized that the values in the table do not correspond exactly to each other. They give only the approximate relationship and can serve in obtaining a rough estimate of the energy if the illumination is stated, or vice versa.
| Depth (m) | Energy (gm cal/cm2/hour) | Illumination (luxes) | ||||||
|---|---|---|---|---|---|---|---|---|
| Oceanic water | Coastal water | Oceanic water | Coastal water | |||||
| Clearest | Average | Average | Turbid | Clearest | Average | Average | Turbid | |
| 10 | 16.1 | 9.50 | 1.21 | 0.449 | 65,000 | 42,000 | 6800 | 2600 |
| 20 | 9.35 | 3.72 | 0.064 | 0.012 | 42,000 | 20,000 | 380 | 70 |
| 50 | 2.69 | 0.311 | 14,000 | 1,800 | ||||
| 100 | 0.452 | 0.0057 | 2,500 | 33 | ||||
| 150 | 0.076 | 440 | ||||||
The effect of light (somewhat modified by the effect of temperature) on photosynthesis can be illustrated by an experiment in which a series of suitable clear glass bottles are filled with sea water containing a substantial phytoplankton population and are submerged in the day time at various depths in the euphotic zone. It will be found that at a few meters below the surface the oxygen content of the water will increase as a result of the photosynthetic activities of the plants within the bottles.
| Depth range (m) | Temperature (°C) | Condition of bottles | Oxygen after exposure (ml/L) | Change in oxygen (ml/L) | Oxygen produced (ml/L) |
|---|---|---|---|---|---|
* In this experiment the effect of respiration of animals or bacteria within the bottles has not been considered (see p. 780). | |||||
| 0 | 10.75 | covered | 7.11 | −0.71 | |
| exposed | 9.42 | +1.60 | +2.31 | ||
| exposed | 9.44 | +1.62 | +2.33 | ||
| 10–8 | 10.60 | covered | 7.32 | −0.50 | |
| exposed | 8.40 | +0.58 | +1.08 | ||
| exposed | 8.44 | +0.62 | +1.12 | ||
| 20–16 | 10.0 | covered | 7.42 | −0.40 | |
| exposed | 8.07 | +0.25 | +0.65 | ||
| exposed | 8.02 | +0.20 | +0.60 | ||
| 30–24 | 6–9 | covered | 7.61 | −0.21 | |
| exposedxs | 7.81 | −0.01 | +0.20 | ||
| exposed | 7.72 | −0.05 | +0.16 | ||
| 40–32 | 5–6 | covered | 7.54 | −0.28 | |
| exposed | 7.66 | −0.16 | +0.12 | ||
| exposed | 7.71 | −0.11 | +0.17 | ||
| 50–40 | 4–5 | covered | 7.61 | −0.21 | |
| exposed | 7.59 | −0.22 | +0.01 | ||
| exposed | 7.64 | −0.18 | −0.03 | ||
When the temperature decreases with increasing depth, the rate of respiration decreases. As long as the light intensity is so high that it does not limit the rate of photosynthesis, this rate also falls somewhat with falling temperature, but at low light intensities the effect of temperature
The photosynthesis depends on the light intensity, and the light intensity at which oxygen production and oxygen utilization are equal is therefore called the compensation point, or the compensation light intensity. The illumination at this point is “the minimum intensity at which the plant could survive in nature and [is] still too low for any crop increase” (Jenkin, 1937). The more pronounced effect of lowered temperature on the rate of respiration as compared with the effect on the rate of photosynthesis leads to a slight lowering of the compensation point with decreasing temperature, at least in certain higher algae (Spoehr, 1926).
It is obvious that the compensation point is determined by physiological characteristics of the plants and may, therefore, be somewhat different for different species, just as the optimum light intensity is not the same for all species. The compensation point is independent of the time during which photosynthesis and respiration have been measured if the oxygen production per unit time remains proportional to the light intensity and the oxygen consumption per unit time remains constant. On these assumptions, the oxygen production dP in the short time interval dt equals aIdt, where a is a constant and I is the light intensity, and the oxygen consumption dR equals bdt where b is another constant. The compensation point, Ic, is defined by
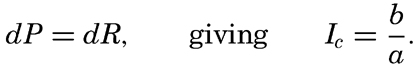
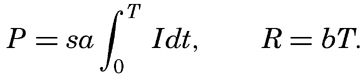
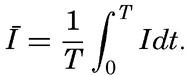
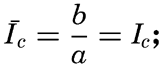
The two factors a and b which have been introduced here are in general not determined, but measurements of the difference between production and consumption are made at different light intensities and the compensation point is found by interpolation. Since the compensation point depends upon the ratio b/a, it follows that it depends on temperature if photosynthesis and respiration are influenced differently by the temperature.
The depth at which the compensation point is found is called the compensation depth. This depth evidently varies with the season of the year, the time of day, the cloudiness, and the character of the water. In the experiment quoted in table 93, the compensation depth lies between 27 m and 44 m. For a given locality one can introduce such terms as daily compensation depth with a clear sky, daily compensation depth with an overcast sky, average annual compensation depth, and so on. With a clear sky the compensation depth will in a given locality reach its maximum value at noon and will rise to the surface shortly before sunset. The average daily compensation depth is less than the compensation depth at noon, except at the North Pole.
The diatoms and many other algae thrive best in somewhat subdued light, but the optimum light intensity is not the same for all species. For example, Schreiber (1927) found the optimum for the diatom Biddulphia mobiliensis to be 1600 luxes, and for the green flagellate Carteria sp. over 3200 luxes. Some diatoms are able to grow in much reduced light. This has been shown in nature by Vanhoeffen for arctic species found growing under the ice in March. From Schreiber's results with Biddulphia we learn that high illumination does not necessarily increase the rate of photosynthesis, since the rate of multiplication was proportional to light intensity only at the intermediate illuminations 200 to 400 luxes. That this is quite generally true is indicated by the habit exhibited by many diatoms of grouping the otherwise scattered chromatophores into knots when exposed to strong light. In this way they afford mutual protection during such periods of unusual exposure as might occur when being swept by ascending currents to the very surface on bright days. This condition whereby the chromatophores are concentrated or collected into a group is known as a systrophe, and was described by Schimper (Karsten, 1905). For the diatom Coscinodiscus excentricus this has been found to occur at a light intensity of about 9.6 g cal/cm2/hour, p. 781. That diatom photosynthesis falls off
Assimilation experiments with raw plankton samples can be carried on only if the diatom population is sufficiently dense that the metabolic activities provide differences in oxygen content and pH values above the limits of experimental error of the method. Experiments with persistent cultures have the advantage that they make possible field-assimilation experiments even at seasons when in nature the phytoplankton is at a minimum. The absence of small planktonic animals and the possible control of bacterial populations in such cultures eliminates a source of error in computing oxygen utilization. On the other hand, the diatoms in persistent cultures may represent selective species with slightly different light optima and may therefore not be typical of the mixed population of raw cultures.
The considerable variation found for the depth of compensation of oxygen production and utilization by phytoplankton results from variations in latitude, season, weather, and turbidity, all of which influence the depth of submarine illumination. Theoretically, it should be possible to determine the depth of optimum diatom production for a given area during the growing season by a study of the vertical distribution of
Not only is the quantity of light a factor to be considered, but so also is the quality. It is well known that as sunlight enters the sea the intensity is reduced, but there is moreover a differential absorption, certain light rays being absorbed before others. The red component of light is removed in the first few meters of water, while the blue light penetrates to much greater depths (p. 106). Therefore, diatoms in nature have their greatest growth at depths where the red component is much reduced; rich growths are found at depths (15 to 20 m) where only blue and green light prevail. A realization of this has led to experiments on the effect of light intensities selectively reduced.
In experimental cultures, using Nitzschia closterium, a diatom much used in culture experiments, Stanbury (1931) concluded that the precise wave length is not so important as the amount of energy transmitted.
Assuming that the total energy in all wave lengths within the visible spectrum provides the best measure of available energy for photosynthesis of diatoms, Jenkin (1937), working in the English Channel, computed the available energy in joules or gram calories at various depths and correlated these values with the amount of oxygen produced by Coscinodiscus excentricus in submerged experimental bottles at the various depths tested. The results indicate that with an energy flux less than 7.5 joules, or 1.8 g cal/cm2/hour, the oxygen production is directly proportional to the energy and the utilization of the available energy is about 7 per cent. With an energy flux greater than the above, the photosynthesis is gradually inhibited. Systrophe takes place at an
In certain sessile shallow-water diatoms adapted to a depth of only a few centimeters the maximum oxygen production occurs at higher energy values, that is, 60 g cal/cm2/hour or 80,000 luxes (Curtis and Juday, 1937).
Diatoms tend to show chromatic adaptation when grown under different components of light, assuming colors that are complementary to those under which they are grown. They thus tend to become yellow-green when grown in red and yellow light, and dark brown in green and blue light. For benthic green algae the red component of light is essential to healthy growth, while brown algae and, especially, red algae characteristic of deep water are adapted to carry on photosynthesis with the red component absent or reduced. We have seen also (p. 295) that, in keeping with this, the order of vertical distribution of the benthic marine algae is greens, browns, and reds, from shallow to deeper water. The quantity of chlorophyll present in these classes of algae is also diminished in the same order (Lubimenko and Tikhouskaia, 1928). The depth at which these benthic algae can grow is also directly correlated with the depth of submarine illumination. In northern latitudes the maximum depth is about 40 to 50 m, whereas in the clear waters of the Mediterranean it is said to be over 100 m. It has been suggested (Klugh, 1930) that certain pigments present in plants growing some distance below the surface may act as photosensitizers to the chlorophyll, enabling it to function with less light intensity.
Plant Nutrients and Vertical Circulation of Water
The inorganic substances required by plants are commonly spoken of as “plant nutrients.” These constitute the raw materials or building blocks out of which the plants, with the aid of sunlight, build up organic compounds entering into their cell structure. The growing plants can obtain these raw materials only from the sea water in which they live. This must therefore be looked upon as a dilute nutrient medium containing all of the elements necessary for plant growth. The concentrations of the nutrient salts are remarkably small; yet a concentration of 1 mg of phosphorus to 10001 of water, for example, is sufficient to produce a vigorous growth of diatoms if other factors are favorable. This is facilitated partly by the very minute size of most phytoplankton organisms and may be illustrated by comparing one plant 1 mm3 in size with a
The mineralized nutrient elements are not uniformly distributed in the sea, however, and they undergo cycles during which there are periods of delay between the available mineralized state and the unavailable organically bound state of the nutrients. This leads to fluctuations in the intensity of plant production both in space and in time. The production of marine phytoplankton is nature's greatest demonstration of hydroponics, or water culture. The operation of the whole system in detail in the sea is different in many respects, however, from the operation of experimental hydroponic tanks. For example, there is a difference in the population; as we have learned, the floating plants of the sea are not specialized with aerial portions for utilization of CO2 and elimination of O2; and roots are not provided for intake of mineral nutrients; neither are there elaborate vascular systems to transport fluids and food. All of the metabolic processes of the marine phytoplankton are carried on within the individual cells which are always submerged beneath the water surface. This universality means that the whole plant must receive light, and the specializations, as already discussed, are along lines designed to maintain the plants in the upper lighted portions of the sea. In the sea the mineral nutrients are not added from without as needed; they have accumulated from the land over eons of time and are stored mainly in the deeper dark-water layers where they are not accessible to autotrophic plants and from whence they must be transported by water movements to replenish the supply periodically exhausted in the productive lighted zone. For discussion of the forces causing this transport see chapter XIII.
It is well known that with return of sunshine and increased temperatures during spring in the temperate and higher latitudes there is a phenomenal outburst of phytoplankton growth in the surface waters. Even the most causal observer is impressed with the brown-green color that is imparted to the waters of coastal areas and over banks during these periods of diatom “bloom.” The production may go on at varying intensities during the summer and frequently becomes augmented again in the autumn. But during the winter months, and sometimes at other seasons as well, there is a dearth of plants and the waters again become deeper blue in color. Similar conspicuous changes in water color occur when one leaves the rich coastal waters and proceeds to the barren open
Brandt's theory that phosphates and nitrates may constitute limiting factors in phytoplankton production has found proof in investigations of subsequent workers (Marshall and Orr, 1927, Schreiber, 1927, Gran, 1930, Hentschel and Wattenberg, 1930, and others). At the initiation of vernal phytoplankton production these salts are relatively abundant in the euphotic layer, but as production proceeds the quantity gradually falls off until it can no longer maintain a large population, and the organisms diminish in number or disappear from the water.
Color of the sea as indicated in per cent of yellow according to the Forel scale (from Schott).
Here Nathansohn's theory forms a complement to Brandt's theory in the explanation of irregularities in distribution and periodic fluctuations in phytoplankton production. (See p. 901 for control through organic factors.) Nathansohn (1906) suggested that the nutrient salts must disappear from the lighted surface layers owing to the fact that they are consumed by the plants and that they must therefore accumulate in the deep sea through sinking of living or dead bodies, both plant and animal, constantly settling towards the bottom. The store of nutrients thus accumulated in the deep water through the dissolution of these bodies is, in time, returned to the euphotic layer through diffusion and vertical circulation of the water.
With improvements of methods in chemical analysis it has, indeed, been shown that usually phosphate concentrations do increase with
The average number of diatoms per liter between the surface and 60 or 70 m, off the California coast. Character of currents is indicated by heavy lines with arrows, and distribution of diatoms is indicated by hatching (modified from Sverdrup and Allen).
Upwelling. The upwelling of subsurface water in which nutrient salts are brought back to the lighted layers is reflected in large diatom production along the California coast (Moberg, 1928, Sverdrup and Allen, 1939; fig. 215), along the western South American coast through the mechanism of the Peruvian Coastal Current (Gunther, 1936), in regions of divergence along the equatorial countercurrents, and along
Not all surface currents show this tendency to unusually rich fertility indicated by the above great coastal populations and the seaward tonguelike extensions. In seeking an explanation we find that the upwelling along the African coast has brought to the surface nutrient-rich water, fertilizing the illuminated euphotic layer. The plants respond with a luxuriant growth, which diminishes in intensity as the nutrients are gradually consumed by the population in the waters as they move to greater and greater distances away from the coast and from the regions of upwelling. Figure 217 shows how closely the distribution of phosphates coincides with the areas shown by direct examination of plankton catches to be fertile in phytoplankton.
The concentration of total plankton (micro- and nannoplankton) in the South Atlantic, surface to 50 m. The numbers on the curves represent thousands of individuals per liter.
The distribution of phosphates as shown in fig. 218, which represents a vertical section from the coast of Africa across the Atlantic to the coast of South America at lat. 9°S, also illustrates how nutrient-rich water is nearer the surface on approaching the African coast. The water with more than 1 μg-atom/L (30 mg/cm3) rises to within about 40 m of the surface, whereas on the South American coast water of nutrient concentration greater than this is not found above about 1000 m. It must be borne in mind that not only phosphates, but also other nutrients needed for plant life that have been regenerated in the deep waters from sinking bodies of organisms produced in the upper layers, are conveyed from the
Regions of Divergence and Convergence. Regions of divergence are defined as those regions where surface water masses of the ocean flow away from each other or away from the coast so that water from the deep must rise, as a feature of upwelling, to replace them. It appears that such areas, whether at the coast or in the open sea, are productive of phytoplankton; this condition is exemplified in the South Atlantic Congo tongue of cold water which extends far out to sea from the region of the Congo River (Hentschel, 1928). Conversely, regions of convergence are areas where surface waters meet and sink. Such areas are relatively barren of plants, the waters having been impoverished by earlier exhaustion of the nutrients.
The hydrographic features of these two types of water movements are discussed on p. 140, and graphically shown in fig. 198, p. 710, for a Carnegie section across the equatorial currents of the Pacific. Here are two parallel regions of divergence between which lies a region of convergence associated with the Equatorial Countercurrent. When the Carnegie plankton volumes from H. W. Graham's analysis (1941) are compared with the hydrography of this section, we find that the relative volumes of general plankton, which must reflect phytoplankton production, show greater concentrations at stations 157 and 151 which lie within the regions of divergence. This is brought out in fig. 219, where the upper diagram shows the relative plankton volumes (precipitated in special bottles) in centimeters per mile of haul, and the lower diagram shows the vertical water movements and selected isolines for phosphate. For greater detail, see fig. 198.
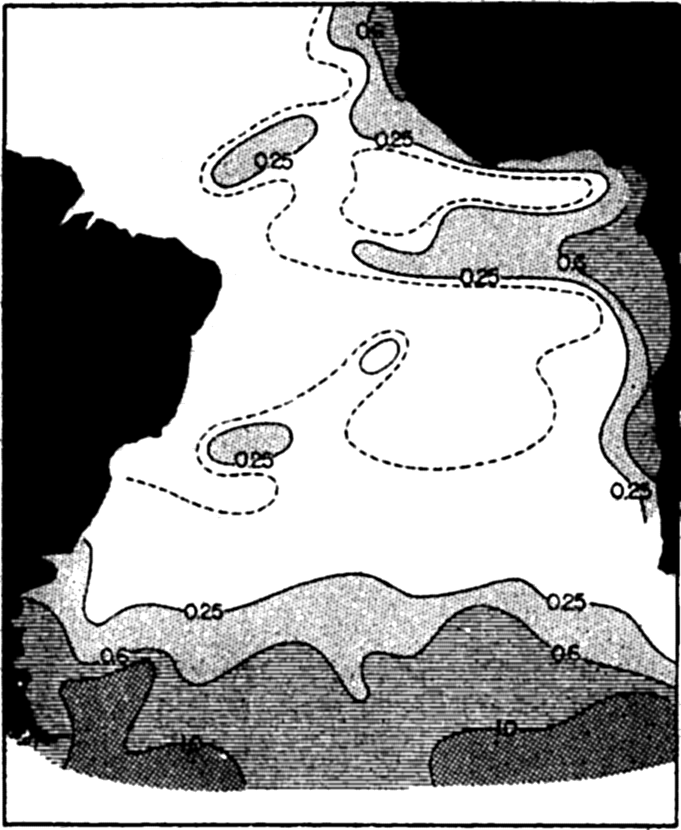
Horizontal distribution of phosphates in the South Atlantic: mg P2O5/m3 (from Wattenberg).
Turbulence. The effect of renewal of plant nutrients from the deeper water as the result of turbulence and accompanying diffusion is demonstrated especially in such areas as the Bay of Fundy and Puget Sound, where strong tidal currents flowing over uneven bottom and through tortuous passages maintain a relatively homogeneous water
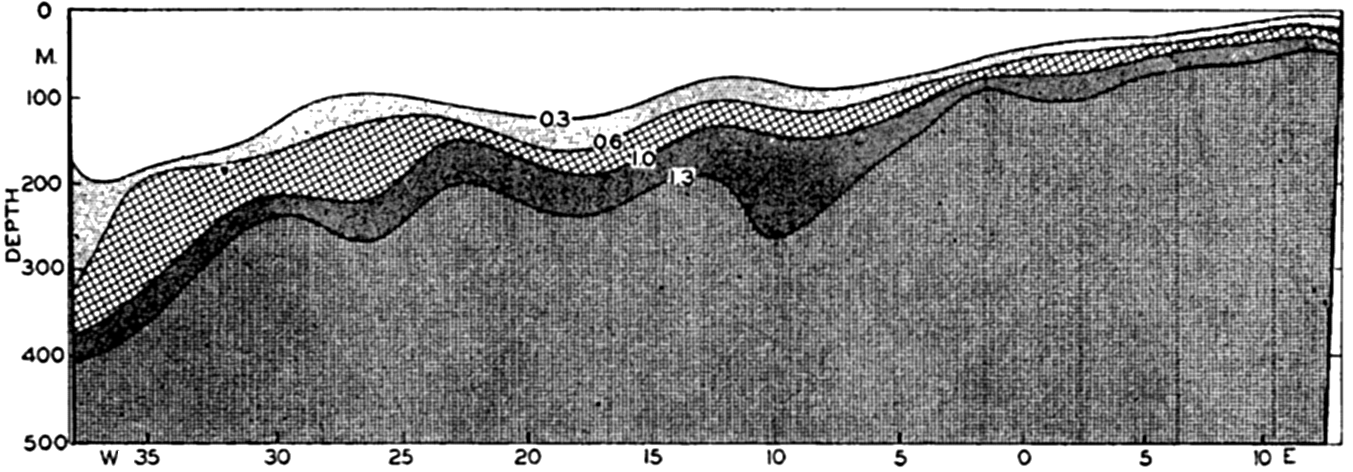
Vertical distribution of phosphates in mg P2O5/m3 at lat. 9°S across the South Atlantic.
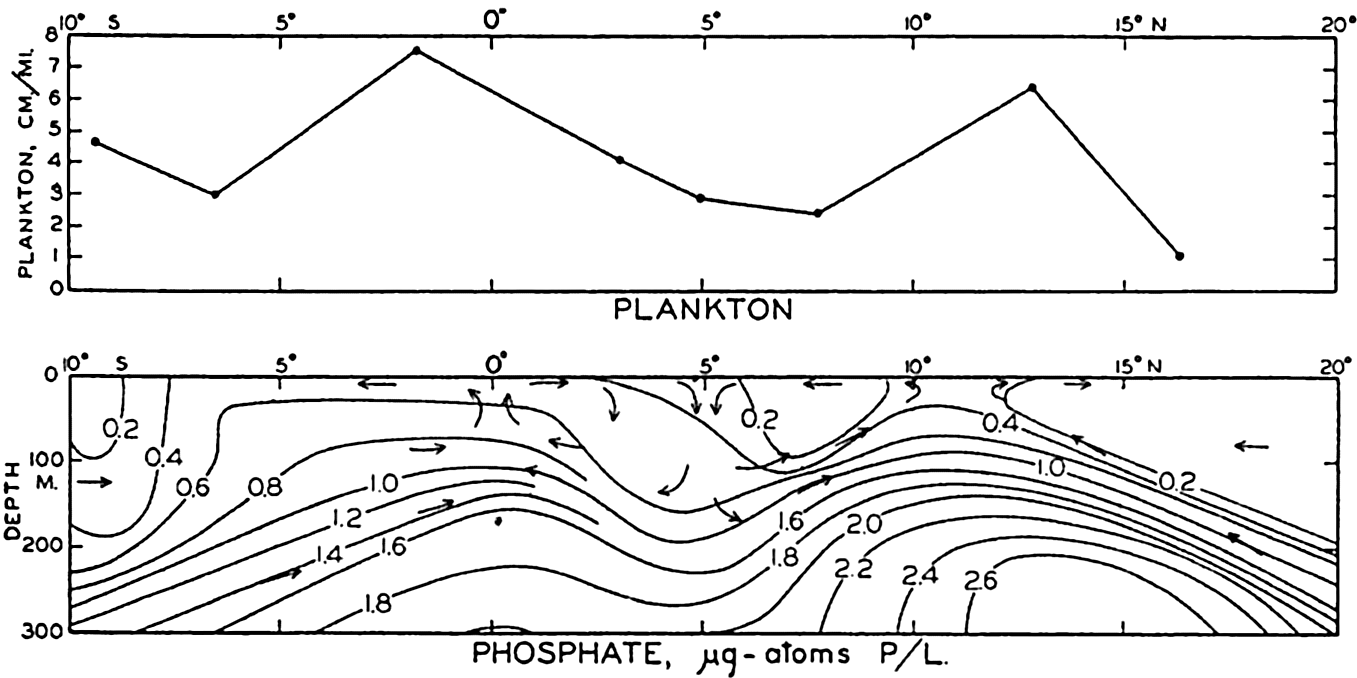
Upper: concentration of plankton in a section across the Pacific Equatorial Countercurrent. Lower: phosphate concentration for the same section.
As far as renewal of plant nutrients is concerned, upwelling and turbulence are similar in that they are more or less continuous throughout the year with some variation resulting from periodic changes in the direction or intensity of the winds (cf. p. 725) or from stabilization resulting
Where turbulence and upwelling are sufficiently vigorous to involve the euphotic layer, there may always be present a ready supply of nutrients to support at least a moderate plankton production. Under such conditions the cessation of production must result from other factors than depletion of nutrients. During the winter season the controlling factors in some latitudes may be the reduction of light or temperature. The cessation of reproduction during a portion of the year may well represent a period of rest induced by a change in conditions, at least for neritic species.
Stabilization. During recent years there has been a realization that for maximum production a certain degree of vertical stability is required within the euphotic layer. In areas of excessive turbulence this stability is wanting, with the result that, although nutrients and other factors may be optimal, only a moderate production of phytoplankton takes place because the descending currents withdraw a portion of the diatom stock into the deeper water where there is not sufficient light for photosynthesis. Ascending currents may bring some of these back to depths of adequate light. The length of time spent below the euphotic layer would then determine the extent of loss, if any, to total production. The complex problem introduced by turbulence may be stated as mainly one of balancing the beneficial factor against the deleterious factor: ascending currents constantly conveying nutrients from deeper water against descending currents withdrawing a portion of the population to suboptimal lighting conditions. The depth of turbulence and the thickness of the euphotic layer are important in this connection. An example of the beneficial effect is seen when comparing areas in the Gulf of Maine and the Bay of Fundy (Bigelow, 1926, Gran and Braarud, 1935). In the open Gulf, marked stratification due to summer heating leads to the exhaustion of nutrients in the euphotic zone with a subsequent drop in phytoplankton production. Over Georges Bank, however, a fairly rich diatom plankton is maintained during the summer owing to the turbulence of water flowing over the bank.
The deleterious effect is illustrated in parts of the Bay of Fundy where, in June, surface areas rich in nutrients, 0.3 μg-atom/L PO4-P (10 mg PO4-P per m3) and up to 4 μg-atoms/L NO3-N (60 mg NO3-N per m3) at a depth of 1 m, resulting from turbulence, were nevertheless poor in plankton because of the combination of turbulence and low transparency. Diatoms were fewer than 500 cells per liter in the most affected areas. The largest populations were found in areas of moderate stratification. Two months later some stabilization had occurred with the advance of summer, but the most turbulent areas still showed high nutrients and a small population of about 7000 or fewer diatoms per
Convection. In regions where there are marked seasonal changes in temperatures between winter and summer, the changes are of great importance not only because of the effect of temperature directly upon the rate of metabolism but also because of its indirect effect in the renewal of nutrients to the surface layers. This method of renewal is characteristic of fresh-water lakes, but is also very important in the sea, especially in the higher latitudes. The phenomenon is, of course, dependent upon the surface waters cooling to a point where their density becomes sufficient to cause them to sink and be replaced by upward movement of lighter and incidentally nutrient-rich waters from below. Similar effects result from pronounced evaporation and must contribute essentially to the maintenance of phytoplankton in the open tropical seas and in isolated seas like the Mediterranean. In areas where vertical circulation results from convection currents, the biological implications are somewhat different than those resulting when nutrient renewal is brought about through the agency of upwelling or turbulence. Except as discussed later, renewal of surface waters by convection is a seasonal rather than a continuous process. The replenishment of elements essential to plants occurs during autumn and winter, with the result that the euphotic layer is richly fertilized in readiness for diatom growth as soon as sufficient sunshine becomes available in spring and as soon as other favorable living conditions are attained. A period of intense growth then ensues, resulting in depletion of nutrients, and since no general renewal can take place until autumn such areas typically experience a marked summer minimum in diatom production following the spring maximum. There is usually a secondary autumnal maximum before the gradually diminishing light reaches a point too low for effective photosynthesis. The regularity of this system may be disturbed by wind-induced turbulence sufficient to cause an upward transport of nutrientladen water from deeper layers, or by fertilization of the surface layers with nutrients brought down from land by rivers. Thus there may be alternating maxima and minima of greater or lesser duration and intensity throughout the whole growing season.
In boreal waters, when the spring production of diatoms has come to a low ebb owing to marked stratification and near exhaustion of nutrients, the role of organic production may be taken over in a diminished degree by the dinoflagellates, especially members of the genus Ceratium. These organisms, owing to their low nutrient requirements and slow rate of growth (daily increase under summer conditions of only 30 to 50 per cent as opposed to 360 per cent in the diatom Chaetoceros curvisetum) can develop at lower nutrient salt concentrations than can diatoms, and they may therefore continue to propagate in impoverished waters.
Horizontal Ocean Currents
As an outcome of the phytoplankton collections taken by the Challenger from the various seas of the world, it appeared that in general no essential differences existed between the pelagic flora of different seas; but later, as a result of the more detailed plankton work of the German Plankton Expedition, Schütt concluded that different ocean currents are inhabited by characteristic types of floating plants.
Cleve (1900) was of the opinion, after studying extensive plankton collections from many separate areas, that plankton species endemic to separate geographic areas (each with its own set of environmental conditions) are transported from these areas by water currents to remote regions, depending upon the hydrographic conditions prevailing. Accordingly, the procedure of investigation should be first, to determine the geographic distribution of the separate species and to learn the conditions of life required by the principal plankton associations. Then, according to the theory, the origin of various water masses could be determined by a biological analysis of the waters to ascertain the type of plankton organisms they support. Cleve recognized a number of plankton communities with dominant types characteristic of separate ocean regions wherein the water has certain uniform characteristics with respect to the physical characters, but the hope of utilizing the diatom plankton types as indicators of water origin has not been fully realized. The nature of the life history of diatom populations, their prompt response by increase or decrease to fluctuating conditions of nutrients and other variable environmental factors, must make them of less value as direct indicators of ocean currents than are the planktonic animals with longer, more tenacious lives. Certain species of Ceratium have proved of special value in characterizing water masses, for example, the fluctuating flow of Arctic and Atlantic waters around Newfoundland (p. 865).
The diatom plankton types of Cleve are of great significance, however, as biological types (p. 793), each with different requirements of life which make them respond in succession to changes of season as living conditions become favorable to their specific needs.
From the strictly biological aspect, we are especially interested in the dispersal of species that is brought about by means of ocean currents. The widespread distribution of most species is evidence in itself of the operation of this type of dispersal. Many species are common to widely separate areas where living conditions are similar during at least a portion of the year. The diatom Asterionella japonica was not recorded from the waters of Romsdalsfjord, Norway, during investigations covering the
It is not uncommon to find small numbers of neritic diatoms that have been carried far seaward with outgoing currents. They may even reproduce for a time by fission but they gradually become abnormal, with weakly silicified shells and diminutive in size; some may form resting spores which drift about. Just what are the oceanic factors that are unfavorable to neritic species is not clearly known. It may be a matter of nutrition or salinity, though, with respect to the latter, many neritic species are doubtless euryhaline.
The most popularly known drift of marine plants is that of the higher alga Sargassum. Although naturally an attached littoral plant, Sargassum may be torn from its moorings along the shore and float far to sea with the currents. Under these conditions it thrives vegetatively but is unable to reproduce except by fragmentation. Its tendency to accumulate in the slowly flowing cyclonic circulation in the North Atlantic has given the name Sargasso Sea to that relatively quiet halistatic area. Commonly, other littoral seaweeds and animals live attached to or among the branches and gas-filled floats of the Sargassum.
Temperature
Because of the close association of temperature with other factors, we have already had numerous occasions to refer to it in the course of discussion. It is certainly one of the most important of physical factors. However, it is not easy to generalize and designate any one factor as being more important than any other in a complex natural environment where all of the numerous known factors operate simultaneously. According to Liebig's law of the minimum, production is limited by the factor occurring in minimal quantity. This factor is obviously not the same for each circumstance. Hence, actually, the factor occurring in minimal quantity, whatever it may be, is temporarily the most important factor. It becomes the so-called “limiting factor” which has been defined as “any of the direct factors which is not optimal at the conditions present in a water mass, viz., without any change of the other factors.”
The rate of metabolism, hence the rate of growth and reproduction of any given species, is regulated by temperature. Just what will be the required range of temperature is dependent upon the species, but the warmest as well as the coldest waters of the sea are able, when other external factors are favorable, to produce a characteristic type of flora
| April, 3°C | Thalassiosira nordenskioeldi |
| Porosira glacialis | |
| Chaetoceros diadema | |
| May, 6°C | Chaetoceros debilis |
| June, 9°C | Chaetoceros compressus |
| August, 12°C | Chaetoceros constrictus |
| Chaetoceros cinctus | |
| Skeletonema costatum |
Neritic species of the higher latitudes are also durothermic with respect to low temperatures during resting stages. These resting stages are very resistant to extreme temperatures and have been found to be viable even though they have spent unfavorable periods frozen solidly in ice.
We may conclude, then, that one great influence of temperature is in determining the character, that is, the composition, of species that will develop in any one region at various periods of the year. In temperate latitudes it is possible, depending on season and other conditions, for both high-latitude and subtropical species to grow provided either that “seed” can be carried in by currents at the proper season or that durothermic resting stages can survive the “off” season and germinate again with return of the growing season.
In this way Cleve's geographical diatom types, namely, arctic, boreal, temperate, and tropical, are explained not as having been produced in and carried from these separate areas but rather as having their metabolic requirements adjusted to temperatures characterizing these regions. During seasons of unfavorable temperatures the stock of separate types is maintained as resting-spores or resistant individuals with potentialities of quick response upon the return of their specific temperature tolerance, the different species succeeding each other in order according to their requirements.
Perhaps one of the most far-reaching influences of temperature is indirect through its effect on the viscosity of the water. We have had frequent need to mention how vitally important it is that the open-sea plants be kept within the euphotic layer. The degree of viscosity or internal friction of the water is vital to passively floating organisms with a specific gravity greater than the water in which they live. Variations
Winter and summer variations which occur in the structure of certain species are attributed to the temperature variations of the seasons in areas where there is great temperature range, but temperature differences in higher and lower latitudes have the same effect, consequently summer forms of high-latitude species may occur in the warmer seas or vice versa. The structural differences are concerned mainly with adaptations leading to a better adjustment to the floating existence. The summer or warm-water forms have thinner shells and are of more slender build. A classical example is given in the diatom Rhizosolenia semispina (fig. 70), wherein a temperate form (semispina) and an arctic form (hebetata), once regarded as separate species, may originate one from the other or wherein opposite ends of a single cell may even show characteristics of both. The form hebetata is now regarded as a primitive resting stage of the form semispina.
In concluding this discussion it should be emphasized that even though the conditions with respect to light, temperature, nutrients, and so forth may be favorable to diatom production, yet no spontaneous population development can take place if previous conditions with respect to any factor have left the water sterile of vegetative plants or of resistant resting spores of species capable of taking advantage of the return of good conditions. This may explain in some instances the dearth of phytoplankton in offshore situations where the great depth of water prohibits the ready return of resting stages common to species of neritic waters. The phenomenal outbursts of diatoms in arctic regions coincident with the spring melting of ice have been explained as probably being associated with the rapid germination of spores that have been locked in the ice and are released through melting. It is known that these regions simulate biological conditions of coastal areas and the population is largely neritic. In investigating oceanographic conditions at a line of stations through Barents Sea from the coast northward to the Arctic ice, Kreps and Verjbinskaya (1930) found in spring that the early vernal flares of diatoms were confined to coastal waters and to waters near the Arctic ice, while between these and at some distance from
The stimulation of phytoplankton growth commonly observed to be coincident with the mixing of two bodies of water with different characteristics may also result from an inoculation of a sparse population living under poor conditions into more favorable waters which have lacked spores suitable to take advantage of the good physical-chemical environment.
Population control through biological factors, such as animal consumption, is discussed in chapter XVII.
Bibliography
Allen, E. J.1914. “On the culture of the plankton diatom Thalassiosira gravida Cleve, in artificial sea water” . Marine Biol. Assn. U. K., Jour., v. 10, p. 417–439, 1914. Plymouth.
Allen, E. J., and E. W. Nelson. 1910. “On the artificial culture of marine plankton organisms” . Marine Biol. Assn. U. K., Jour., v. 8, p. 421–474, 1910.
Allen, W. E.1936. Surface plankton diatoms in the North Pacific Ocean in 1934. Madroño, v. 3, p. 1–3, 1936.
Atkins, W. R. G.1926. “A quantitative consideration of some factors concerned in plant growth in water” . Conseil Perm. Internat. p. l'Explor. de la Mer, Jour. du Conseil, v. 1, p. 99–126, 1926.
Bigelow, Henry B.1926. “Plankton of the offshore waters of the Gulf of Maine” . U. S. Bur. Fisheries, Bull. 40, p. 5–487, 1926.
Braarud, T.1935. The Öst expedition to the Denmark Strait, 1929. II. The phytoplankton and its conditions of growth. Hvalradets Skrifter, no. 10, p. 5–144, 1935. Oslo.
Braarud, T., and B. Föyn. 1931. “Beiträge zur Kenntnis des Stoffwechsels im Meer. Norske Vidensk” . Akad., Avhandl., no. 14, 24 pp., 1931.
Brandt, K.1899. Ueber den Stoffwechsels im Meer. Komm. z. Wissensch. Untersuch. Deutschen Meere in Kiel und d. Biologischen Anstalt auf Helgoland. Wissensch. Meeresuntersuch., N.F., Abt. Kiel, Bd. 4, p. 213–230, 1899.
Clarke, G. L., and R. H. Ostler. 1934. “The penetration of the blue and red components of daylight into Atlantic coastal waters and its relation to phytoplankton metabolism” . Biol. Bull., v. 67, p. 59–75, 1934.
Cleve, P. T.1900. The seasonal distribution of Atlantic plankton organisms Göteborgs Kundl. Vet.-och Vitterhets Samhalles Handlingar, v. 17, 36 pp., 1900.
Cooper, L. H. N.1937. “On the ratio of nitrogen to phosphorus in the sea” . Marine Biol. Assn. U. K., Jour., v. 22, p. 177–183, 1937.
Curtis, J. T., and C. Juday. 1937. “Photosynthesis of algae in Wisconsin Lakes. III. Observations in 1935” . Intern. Rev. d. ges. Hydrobiol. u. Hydrogr., Bd. 35, p. 122–133, 1937.
Dakin, W. J.1908. “Notes on the alimentary canal and food of the Copepoda” . Intern. Rev. d. ges. Hydrobiol. u. Hydrogr., Bd. 1, p. 772–782, 1908.
Esterly, C. O.1916. “The feeding habits and food of pelagic copepods and the question of nutrition by organic substances in solution in the water” . Calif. Univ., Pub. in Zool., v. 16, p. 171–184, 1916.
Gaarder, T., and H. H. Gran. 1927. “Investigation of the production of plankton in the Oslo Fjord. Conseil Perm” . Intern. p. l'Explor. de la Mer, Rapports et Proc.-Verb., v. 42, 48 pp., 1927.
Gail, F. W.1920. “Hydrogen ion concentration and other factors affecting the distribution of Fucus” . Puget Sound Biol. Sta., Pub., v. 2, p. 287–304, 1920. (Univ. of Washington, Oceanographic Laboratories, Seattle.)
Graham, Herbert W.1941. “Plankton production in relation to character of water in the open Pacific” . Jour. Marine Research, v. 4, p. 189–197, 1941.
Gran, H. H.1912. Pelagic plant life. p. 307–386 in Murray and Hjort, Depths of the Ocean. London, Macmillan, 821 pp., 1912.
Gran, H. H.1927. The production of plankton in coastal waters off Bergen, March to April, 1922. Norwegian Fishery and Marine Investigations, v. 3, no. 8, 74 pp., 1927. Bergen.
Gran, H. H.1929. “Investigation of the production of plankton outside the Romsdalsfjord 1926–1927” . Conseil Perm. Internat. p. l'Explor. de la Mer, Rapports et Proc.-Verb., v. 56, 15 pp., 1929.
Gran, H. H.1930. “The spring growth of the plankton at Möre in 1928–29 and at Lofoten in 1929 in relation to its limiting factors” . Norske Vidensk. Akad. i Oslo, Skrifter, 1. Mat.-Naturv. Klasse, no. 5, p. 5–77, 1930.
Gran, H. H.1931. “On the conditions for production of plankton in the sea” . Conseil Perm. Internat. p. l'Explor. de la Mer, Rapp. et Proc.-Verb., v. 75, p. 37–46, 1931.
Gran, H. H.1933. “Studies on the biology and chemistry of the Gulf of Maine. II. Distribution of phytoplankton in August, 1932” . Biol. Bull.v. 64, p. 159–181, 1933.
Gran, H. H., and T. Braarud. 1935. “A quantitative study of the phytoplankton in the Bay of Fundy and the Gulf of Maine (including observations on hydrography, chemistry, and turbidity)” . Biol. Board of Canada, Jour., v. 1, p. 279–467, 1935.
Gran, H. H., and T. G. Thompson. 1930. “The diatoms and the physical and chemical conditions of the sea water of the San Juan Archipelago” . Puget Sound Biol. Sta., Pub., v. 7, p. 169–204, 1930.
Gross, F.1940. “The osmotic relations of the plankton diatom Ditylum brightxswelli (West.)” . Marine Biol. Assn. U. K., Jour., v. 24, p. 381–415, 1940.
Gunther, E. R.1936. “A report on the oceanographical investigations in the Peru coastal current” . Discovery Repts., v. 13, p. 107–276, 1936.
Harvey, H. W.1928. Biological chemistry and physics of sea water. Cambridge Univ. Press, 189 pp., 1928.
Harvey, H. W.1933. “On the rate of diatom growth” . Marine Biol. Assn. U. K., Jour., v. 19, p. 253–276, 1933.
Harvey, H. W.1937. “The supply of iron to diatoms” . Marine Biol. Assn. U. K., Jour., v. 22, p. 205–219, 1937.
Harvey, H. W.1939. “Substances controlling the growth of a diatom” . Marine Biol. Assn. U. K., Jour., v. 23, p. 499–520, 1939.
Harvey, H. W., L. H. N. Cooper, M. V. Lebour, and F. S. Russell. 1935. “Plankton production and its control” . Marine Biol. Assn. U. K., Jour., v. 20, p. 407–442, 1935.
Hensen, Victor. 1887. Über die Bestimmung des Planktons oder des im Meere treibenden Materials an Pflanzen und Thieren. Komm. zur Wissensch. Untersuch. d. Deutschen Meere in Kiel, Fünfter Bericht, XII–XVI Jahrg., p. 1–107, 1887.
Hentschel, E.1928. “Die Grundzüge der Planktonverteilung im Südatlantischen Ozean” . Internat. Rev. d. ges. Hydrobiol. u. Hydrogr., Bd. 21, p. 1–6, 1928.
Hentschel, E., and H. Wattenberg. 1930. “Plankton und Phosphat in der Oberflächenschicht des Südatlantischen Ozeans” . Ann. d. Hydrogr. u. Mar. Meteor., Bd. 58, p. 273–277, 1930.
Jenkin, Penelope M.1937. “Oxygen production by the diatom Coscinodiscus excentricus Ehr. in relation to submarine illumination in the English Channel” . Marine Biol. Assn. U. K., Jour., v. 22, p. 301–342, 1937.
Johnstone, J., A. Scott, and H. C. Chadwick. 1924. The marine plankton. Liverpool, Univ. Press, 194 pp., 1924.
Karsten, G.1905. Das Phytoplankton des Antarktischen Meers nach Material der Deutschen Tiefsee-Expedition 1898–1899. Wiss. Erg. d. Deutschen Tiefsee-Exped. auf dem Dampfer Valdivia 1898–1899, Bd. II, 2 Teil, 136 pp., 1905.
Klugh, A. B.1930. Studies on the photosynthesis of marine algae. No. 1. Photosynthetic rates of Entromorpha linza; Porphyra umbilicalis, and Delesseria sinuosa in red, green, and blue light. Contributions to Canadian Biol. and Fisheries, N.S., v. 6, p. 41–63, 1930.
Kofoid, C. A.1906. “On the significance of the asymmetry in Triposolenia” . Univ. Calif., Pub. Zool., v. 3, p. 127–133, 1906.
Kreps, E., and N. Verjbinskaya. 1930. “Seasonal changes in the phosphate and nitrate content and in hydrogen ion concentration in the Barents Sea” . Conseil Perm. Internat. p. l'Explor. de la Mer, Jour. du Conseil, v. 5, p. 329–346, 1930.
Krogh, A.1934. Conditions of life in the ocean. Ecological Monographs, v. 4, p. 421–429, 1934.
Lebour, Marie V.1922. “The food of plankton organisms” . Marine Biol. Assn. U. K., Jour., v. 12, p. 644–677, 1922.
Lohmann, Hans. 1908. Untersuchungen zur Feststellung des vollständigen Gehaltes des Meeres an Plankton. Komm. z. Wissensch. Untersuch. d. Deutschen Meere in Kiel und d. Biologischen Anstalt auf Helgoland, Wissensch. Meeresuntersuch., N.F., Abt. Kiel, Bd. 10, p. 131–370, 1908.
Lubimenko, V. N., and Z. Tikhouskaia. 1928. “Recherches sur le photosynthèse et l'adaptation chromatique chez les algues marines” . Sebastopol Biol. Sta., Trudy, v. 1, p. 153–190, 1928 (U.S.S.R. Akad. Nauk).
Marshall, Sheina. 1924. “The food of Calanus finmarchicus during 1923” . Marine Biol. Assn. U. K., Jour., v. 13, p. 473–479, 1924.
Marshall, S. M., and A. P. Orr. 1927. “The relation of the plankton to some chemical and physical factors in the Clyde Sea area” . Marine Biol. Assn. U. K., Jour., v. 14, p. 837–868, 1927.
Marshall, S. M., and A. P. Orr. 1928. “The photosynthesis of diatom cultures in the sea” . Marine Biol. Assn. U. K., Jour., v. 15, p. 321–360, 1928.
Moberg, Erik G.1928. “Interrelation between diatoms, their chemical environment, and upwelling water in the sea off the coast of southern California” . Nat. Acad. Sci., Proc., v. 14, p. 511–518, 1928.
Nathansohn, A.1906. Über die Bedeutung vertikaler Wasserbewegungen für die Produktion des Planktons im Meer. Kgl. Sächs. Gesellsch. der Wissensch., Abhandl. d. Math.-Phys. Klasse, Bd. 29, no. 5, 1906.
Ostenfeld, C. H.1909. “Immigration of a plankton diatom into a quite new area within recent years: Biddulphia sinensis in the North Sea waters” . Internat. Rev. d. ges. Hydrobiol. u. Hydrogr., Bd. II, p. 362–374, 1909.
Peters, N.1932. “Die Bevölkerung des Südatlantischen Ozeans mit Ceratien. Deutsche Atlantische Exped. Meteor 1925–1927” , Wiss. Erg., Bd. XII, 1 Teil, p. 1–69, 1932.
Pettersson, H., H. Höglund, and S. Landberg. 1934. Submarine daylight and the photosynthesis of phytoplankton. Oceanografiska Inst. Göteborg
Phifer, L. D.1933. Seasonal distribution and occurrence of planktonic diatoms at Friday Harbor, Washington. Univ. of Washington, Pub. in Oceanogr., v. 1, p. 39–81, 1933.
Schreiber, E.1927. Die Reinkultur von marinen Phytoplankton und deren Bedeutung fur der Produktionsfahigkeit des Meerswassers. Komm. z. Wissensch. Untersuch. der Deutschen Meere in Kiel und d. Biologischen Anstalt auf Helgoland, Wissensch. Meeresuntersuch., N. F., Abt. Helgoland, Bd. 16, p. 1–35, 1927.
Spoehr, H. A.1926. Photosynthesis. New York, Chemical Catalog Co., Inc., 393 pp., 1926.
Stanbury, F. A.1931. “The effect of light of different intensities, reduced selectively and non-selectively, upon the rate of growth of Nitzschia closterium” . Marine Biol. Assn. U. K., Jour., v. 17, p. 633–653, 1931.
Steemann Nielsen, E.1939. “Über die vertikale Verbreitung der Phytoplanktonten im Meere” . Internat. Revue d. ges. Hydrobiol. u. Hydrogr., Bd. 38, p. 421–440, 1939.
Sverdrup, H. U., and W. E. Allen. 1939. “Distribution of diatoms in relation to the character of water masses off southern California in 1938” . Jour. Marine Research, v. 2, p. 131–144, 1939.
Thompson, T. G., and R. W. Bremner. 1935. “The occurrence of iron in waters of the northeast Pacific Ocean” . Conseil Perm. Internat. p. l'Explor. de la Mer, Jour. du Conseil, v. 10, p. 39–47, 1935.
Thompson, T. G., and M. W. Johnson. 1930. “The sea water at the Puget Sound Biological Station from September, 1928, to September, 1929” . Puget Sound Biol. Sta., Pub., v. 7, p. 345–368, 1930.
ZoBell, Claude E.1935. “The assimilation of ammonium nitrogen by Nitzschia closterium and other marine phytoplankton” . Nat. Acad. Sci., Proc., v. 21, p. 517–522, 1935.
XVII. Animals in Relation to Physical-Chemical Properties of the Environment
ECOLOGICAL GROUPS AND SOME OF THEIR ADJUSTMENTS AND CONDITIONS OF LIFE
The study of world distribution of marine animals is the function of marine zoogeography. Its chief aim is the characterization of the animal world of the sea. In causal zoogeography we seek the causes that are or have been operative to bring about the type of animal distribution actually found in present-day faunas, whether benthos, nekton, or plankton.
In the earliest studies attempts were made to establish arbitrary zoogeographic boundaries along lines of latitude, and so forth, but since these have no ecological significance rational faunal boundaries could not result, and it was not until boundaries were drawn to follow certain isotherms that the faunal divisions were also more or less clearly circumscribed. Even this does not necessarily result in rational zoogeographic boundaries because, after all, it is the actual distribution of animals themselves that forms the basis for zoogeographic divisions, since the thermal relations or other factors are not always clear. However, animal distribution (as well as other biological phenomena in the sea) is not haphazard but has resulted from orderly events some of which, although historical, may have lost their continuity, while others are continually operative as single or multiple factors conditioning dispersal, survival, and abundance. Any apparent absence of order results from lack of sufficient information with which to decipher and trace the complicated patterns that result from the inherent nature of the organisms and the factors in the environment. Marine ecology, which is concerned with the organisms in relation to their present-day environmental conditions, is a vital link in the study of zoogeography and many other biological problems of the sea.
The ecological groups to be considered in this division of the present chapter are (a) benthos, the animals of the sea floor; (b) nekton, the swimming animals; (c) zooplankton, the floating animals.
Benthos, Animals of the Sea Floor
Wherever successful dredging operations have been conducted, the ocean floors have been found to be inhabited by benthic animals from the Arctic to the Antarctic and from shore to the greatest depth. However, the number of animals (that is, the concentration per unit area) varies greatly; moreover, the kinds of animals that make up the major portion of the population differ, especially the species, genera and families. Such differences are apparent in the populations of such small topographic units as biotopes, as well as in the larger environmental divisions, and they are the biological criteria for establishing the vertical zones, littoral, archibenthic, and abyssal-benthic, as well as the horizontal faunal areas to be discussed later. It is mainly with the fauna of these larger divisions that we shall deal. For greater detail on the zoogeography of the seas the reader is referred especially to Ekman's text (1935), in which an extensive bibliography is also included.
Animals of the Littoral Zone. The outstanding feature of the littoral zone, especially of the upper or eulittoral zone extending to depths of about 40 to 60 m, is the great diversity and variability of the physical-chemical conditions of habitats. The substratum varies from clean firm rocks to shifting sands and soft muds. Marked salinity gradients sometimes exist, and seasonal and diurnal fluctuations add variety to the life of animals of this zone. Wave and tide actions are highly important, particularly in the shallower portions. Morphologically, the animals are variously modified along special lines associated, for instance, with the type of bottom, degree of exposure, depth, feeding habits. Many of the sessile forms, such as the limpets and chitons of the intertidal zones, are flattened and streamlined the better to withstand the wash and impact of rushing waters. Mussels are securely attached by strong and flexible byssus threads, while adult barnacles, corals, tube worms, and encrusting Bryozoa are rigidly and permanently cemented to rocks, shells, or other solid objects. Less rigidly attached are the hydroids, sponges, and anemones. The sessile or immobile habit so conspicuous in vast numbers of adult marine organisms is highly characteristic of life in the sea. This mode of life is made possible only by the continuous supply of floating microscopic food and the water movements necessary for its production and dispersal (see following chapters).
Among the free-moving bottom forms we find adaptations and habits so varied that all conceivable habitat facies are used. The sea urchin, Strongylocentrotus purpuratus, for example, is able to bore into rocks for protection on exposed coasts. The shells of molluscs are frequently of more sturdy structure when grown on exposed, wave-washed shores. Corals on exposed reefs are massive and compact in comparison to the more fragile and branched types found in lagoons (Vaughan, 1919).
On muddy or soft bottom environments other adaptive modifications result. The shelled animals of these environments build relatively thin, fragile shells as compared with those of animals in exposed or rocky situations. Burrowing bivalves of muddy, sandy bottoms commonly possess an enlarged “foot” useful in digging, and the siphons are elongated to extend above the substratum for intake of water providing food and oxygen. In contrast, the bivalves of hard bottoms may have these structures much reduced, and in more active forms like the scallops, tactile organs and even eyes are developed on the mantle edge. Creeping snails possess a broad foot to aid in gliding over soft mud. Burrowing worms are able to maintain permanent or temporary tubes by means of a mucous or fibrous lining secreted by the animals. Many mud-inhabiting animals are detritus feeders, eating the mud for the organic material it contains or sucking up the detritus that has settled at the mud-and-water interface.
In the littoral zone there is an abundant supply of food for animals. This results directly from favorable conditions for the production of plants, both attached and floating, and from the availability of these plants directly or indirectly to the benthic animals. An appreciable amount of organic material of terrigenous or fresh-water origin must supplement the great quantities produced in this zone. Due to this ready supply of food, the littoral zone produces benthic animals in abundance. The actual concentration is variable, of course, depending upon such local conditions as type of bottom, rate of flow of overlying water, river outflow, and upon meteorological conditions. The last is especially pronounced in intertidal situations, where seasonal rains and freshets may dilute tide pools and exposed flats with devastating results to the more sensitive species. Unusual temperatures during exposure on the foreshore result in great losses (p. 844). Most animals of this zone have a wide range of tolerance to changing conditions, but the selective action of the environment in certain areas may produce a great concentration of the species most suited to the conditions. For example,
Most littoral areas are provided with good circulation, owing to irregular bottom configuration, to the effect of tidal actions and winds, and to seasonal or diurnal convection. However, in some bays the exchange of waters may be sluggish, with the result that the free oxygen is used up by decomposing organic matter—usually abundant in such bays—and that hydrogen sulphide is produced, making for precarious if not fatal living conditions. Extreme cases of this nature are found in certain threshold fjords of Norway, where the mouth of the fjord is partially cut off from the sea by a sill of shallower depth than the inner portion of the fjord and where fresh water from adjacent land drainage may form a thin top layer. These situations offer an excellent example of the effect of physical-chemical circumstances on the success of animal life. Normally in these pools there can be no exchange of water between the ocean and the deeper water of the fjord below the sill depth because the water flowing over the sill is of lower density than the deep water of the fjord. Much of the organic material resulting from the plankton and its dependent life in the upper layers sinks to the bottom and, in decomposing, depletes the oxygen supply of the bottom water. Highly toxic conditions, resulting particularly from production of hydrogen sulphide, make it impossible for benthic aerobic life to inhabit the bottoms of these fjords. In some fjords oysters are cultivated, but they must be kept suspended in racks above the hydrogen-sulphide-charged bottom water. The layer of fresh water insulates the lower water and may make for tropical submarine climate with temperatures rising to 30°C (p. 871). Occasionally unusual circumstances, such as continuous offshore winds, build up an offshore gradient that forces upward the heavier deeper oceanic water outside the sill to a height sufficient for it to flow over the sill into the pool, where it lifts the lighter toxic hydrogen-sulphide-laden waters toward the surface. This water is lethal to the fjord animals, fishes, and invertebrates, which upon death sink to the already organically rich muds of the bottom. These or similar catastrophic circumstances lead to mass fossilization of littoral marine life; and,
Horizontal Distribution of the Littoral Fauna. As a result of faunal studies and compilation of the work of many specialists, Ekman in his Tiergeographie des Meeres (1935) has divided the seas into faunal zones characterized by the species, genera, and families of animals found within the littoral zone of these regions (fig. 220). The animals thus employed include not only the littoral benthos but also pelagic forms that are bound by their life histories to the coastal zones. In such an analysis, the assemblage of species and genera of different animal groups that are confined to or are characteristic of the population of an area is the criterion for establishing the faunal regions. Obviously the number of endemic genera or of higher taxonomic orders is often of greater significance than the number of endemic species in distinguishing a faunal region, for the species are biologically of more recent origin. For example, the Pacific and the Atlantic tropical faunas of America, though now separated by the isthmus of Panama and having only relatively few species in common, show by numerous common genera (33 for certain crabs) and by geminate (closely related) species that these faunas were a continuous fauna in past geologic ages when the two great oceans were connected in this tropical region.
The faunal areas are not sharply defined, of course, and the boundaries are to be considered transition zones the width of which is determined largely by hydrographic features, water temperature being a cardinal determining factor. But other factors also determine the geographical extent of a faunal area. These are especially continental land barriers or broad expanses of deep water such as the East Pacific oceanic barrier (fig. 220). This, owing to its depth, precludes spreading of adult littoral forms through the abyssal zone, and, because of the vast horizontal extent of water between the American shores and the easternmost Polynesian Islands, prevents transport of pelagic larval stages of littoral forms except when these stages are of specially long duration.
Broadly speaking, the littoral fauna may be divided clearly into arctic, tropical, and antarctic. Between these there are gradations giving rise to such divisions as boreal, temperate, or antiboreal Kerguelen fauna. Some of the faunal divisions may also be subdivided into east-west regions; for instance, the tropical fauna, though homogenous in many characteristics—for example, in the formation of coral reefs—may be recognized as consisting of four parts, namely Indo-West Pacific, Pacific Tropical American, Atlantic Tropical American, and the Tropical West African.
Other faunal areas of the sea are given in fig. 220. These areas are again subdivided as the classification is made narrower to meet more local conditions. The Atlantic Boreal is, for example, divided into east and west sections and the Arctic into High and Low Arctic. For additional details and reference to original data, the student is referred to Ekman (1935). Many animals of eurythermic nature may be quite cosmopolitan and the sublittoral fauna may extend beyond the boundaries shown by the eulittoral animals. See also p. 845 for comparison of thermic boundaries to those of certain faunal regions.
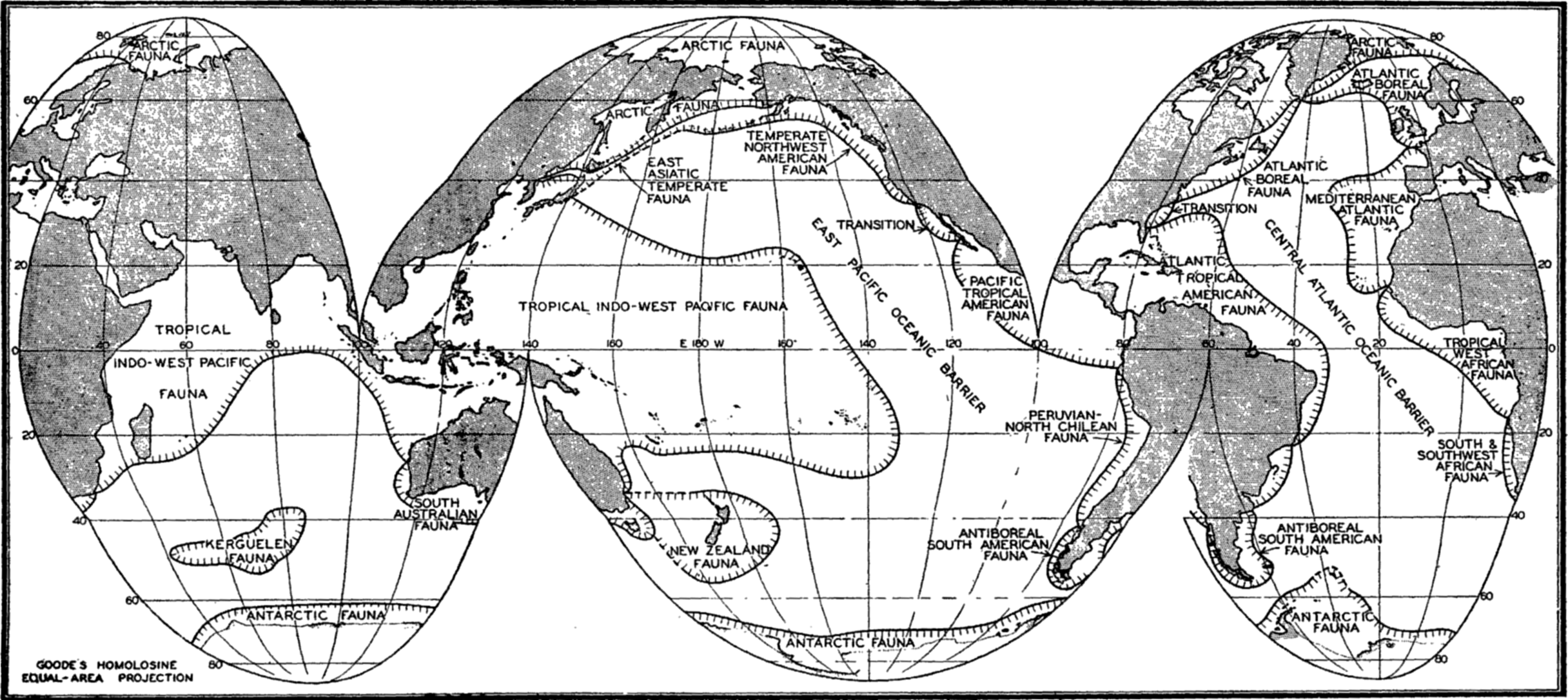
Faunal areas of littoral animals (based on Ekman).
Deep-sea Benthos. In 1843 Edward Forbes, pioneer in marine biology, observed the diminution of the number of animals with increasing depth of water beyond the littoral zone and he established with some hesitation what he called an “azoic zone” covering the deep ocean floor from depths below 300 to 700 m. Before this time, however, in 1819, Sir John Ross reported having found worms in mud brought up from a depth of 1800 m in Baffin Bay, but the idea of life existing in great depths was then so untenable that these and other findings were discredited. It was not until 1860 that positive proof of the existence of animal life in the deep sea was first provided by a broken submarine cable that was brought up for repair from a depth of over 2000 m in the Mediterranean with various bivalve molluscs, gastropods, hydroids, alcyonarians, and worms attached. The dredging operations of the Challenger and other expeditions have definitely shown that benthic animals do live in very great depths, probably in smaller numbers even at the greatest depths, since pressure and cold seem not to be excluding factors. During the Challenger Expedition more than 1500 animal species were discovered below 1000 m and a dredge haul at 6250 m yielded 20 specimens belonging to 10 species. Bottom deposits brought up in sounding tubes from the great deeps contained remains of foraminifera and sponges that probably live at these depths.
The summary in table 94, compiled from Murray (1895) and based on the Challenger observations, will serve to illustrate the vertical distribution of bottom fauna of size sufficiently large to be taken by the apparatus used. The specimens were collected with both dredge and bottom trawl and may therefore include a few not strictly benthic.
All of the animal world below the littoral zone may be spoken of collectively as the deep-sea fauna. Although not many deep-sea collections have been made, the endemic fauna appears to be divisible vertically into two parts, an upper archibenthic fauna (continental deep-sea fauna) and a lower-abyssal fauna, the dividing line between these two being placed at about 1000 m depth.
There is no well-defined border line, of course, between littoral and deep-sea fauna; the border is even less clearly defined between the archibenthic and the abyssal. The natural boundary between faunas is the region of most distinct faunal change. This boundary, however, is influenced by outside factors such as temperature and light, with their
| Zone | Number of stations | Average yield of species at each station | Average yield of individuals at each station |
|---|---|---|---|
| 180 m | 70 | 62.8 | |
| 180 to 900 m | 40 | 51.2 | 150 |
| 900 to 1800 m | 23 | 30.9 | 87 |
| 1800 to 2700 m | 25 | 24.0 | 80 |
| 2700 to 3600 m | 32 | 15.6 | 39 |
| 3600 to 4500 m | 32 | 10.6 | 25.6 |
| 4500 m | 25 | 9.4 | 24 |
Outstanding among the eurybathic forms given by Ekman are:
| Pennatularia | Kophobelemnon setelliferum | 36 to 3600 m |
| Polychaetes | Amphictera gunneri | littoral to 5000 m |
| Cirripeds | Verruca stroemia | littoral to 3000 m |
| Cumacea | Diastylis laevis | 9 to 3980 m |
| Bivalves | Scrobicularia longicallus | 36 to 4400 m |
| Snails | Neptunea islandica | 30 to 3000 m |
| Starfish | Henricia sanguinolenta | 0 to 2450 m |
| Brittle stars | Ophiocten sericeum | 5 to 4500 m |
| Sea urchins | Echinocardium australe | 0 to 4900 m |
| Sea cucumber | Mesothuria intestinalis | 20 to 2000 m |
That much of the animal life in the deep sea is truly endemic, not merely a downward extension of eurybathic forms, is shown by the presence of vast numbers of species and many genera and higher taxonomic orders that are found consistently only in these deeper zones. Important among the characteristically deep-sea forms are the glass sponges, Hexactinellida, with 15 families, 80 genera, and about 400 species; seven families of Pennatularia; the deep-sea Holothuroidea, of the order Elasipoda with four families, over 20 genera, and many species.
Tables 95 and 96, based on summaries of Ekman, depict further the arrangement of certain elements of the faunas of the three major bathymetric zones.
A striking characteristic of the deep-sea fauna is the relatively smaller number of species in proportion to the number of genera. On the basis of the Challenger data Murray (1913) concluded that the ratio of species to genera decreases regularly from coastal to offshore deep water, so that in the deepest zone the ratio of species to genera is 5 to 4, whereas in the shallow coastal water it is 3 to 1. It is a significant fact that whole orders and numerous families of various taxonomic groups are confined to the deep sea or are characteristic of its population.
| Animals | Zones | Number of species |
|---|---|---|
| Littoral, or littoral and archibenthic | 31 | |
| Crinoidea | Littoral to abyssal | 10 |
| (North Atlantic) | Archibenthic | 11 |
| Archibenthic and abyssal, or purely abyssal | 35 | |
| Littoral or mostly so | 13 | |
| Starfish | Littoral to abyssal | 28 |
| (North Atlantic) | Archibenthic or abyssal | 97 |
| Animals | Zones | Number of genera |
|---|---|---|
| Purely littoral | 62 | |
| Littoral and archibenthic | 14 | |
| Tunicata | Littoral to abyssal | 11 |
| Purely archibenthic. | 3 | |
| Archibenthic and abyssal | 4 | |
| Purely abyssal | 13 |
Deep-sea animals of the benthic region are in the main mud-dwelling forms adapted in various ways to this mode of life. A considerable number, typified by the isopod genus Munnopsis (fig. 221) and the shrimp Nematocarcinus, are adapted by elongated appendages to the quiet water and the softest of muds; sponges and hydroids are provided with
Munnopsis typica, a deep-water isopod (redrawn from Sars).
As previously stated, the population of the benthic region of the deep sea is relatively sparse, the animals decreasing numerically with increasing depth, also with distance from shore. The one factor most operative in limiting the abundance of animal life in the deep sea is undoubtedly food. Abyssal animals do indeed live a precarious life with regard to food. It is not surprising that only relatively few animals have been found on bottoms covered with red clay, for most deep-sea animals depend upon the nourishment obtainable directly or indirectly from the bottom oozes and tests show that the red clay is of all bottom deposits the poorest in organic material. Yet even it is not without its quota of marine metazoan life. It has been pointed out that with the intensified adversity of living conditions in abyssal regions, the animals adapted to survive the physical conditions there would be numerous were it not for a shortage of food. Since plants can live only in the lighted upper strata of the sea, it follows that deep-sea animals are either carnivores or detritus feeders, a population utterly dependent upon plant and animal production in the upper water layers and upon the ultimate sinking of dead bodies of these plants and animals to greater depths. Much of the surface production is broken down, however, by bacterial or autolytic action within the upper or intermediate layers and is thus lost to the dependent abyssal life. The direct food of abyssal forms
It is instructive to note that the poverty of animals in deep-sea zones is apparently not a direct result of depth of water but is intimately connected with distance from continental shores. Murray reports that collections made in depths between 1800 and 3650 m near shore yielded per haul an average of 121 specimens belonging to 39 species, whereas collections made in comparable depths further than about 500 km from shore yielded an average of only 21 specimens and 10 species per haul. This strongly indicates a relative shortage of food for benthic animals in the offshore localities. In the preceding chapter it was emphasized that conditions for phytoplankton production are enhanced in coastal waters where the supply of mineral nutrients in the lighted zone can be enriched through vertical circulation extending to a depth sufficient to tap the store of nutrients that accumulate there through the sinking of organisms produced in surface layers. Owing to the movements of such nutrient-enriched surface water, much of its plankton load becomes deposited in the deep inshore waters and thus supplies more food to the deep-sea benthic animals living there than is possible far from shore. Any offshore hydrographic condition that leads to enrichment of the plant nutrients in the surface layers will produce similar results, reflected in the abundance of benthic fauna that can be supported under such waters. This is illustrated by the surprisingly rich deep-sea benthos encountered by the Challenger Expedition in the deep offshore waters of the Antarctic, especially in the Kerguelen region. Murray believed that this exceptional abundance of deep-sea life resulted from offshore extension of coastal conditions owing to floating ice or to greater destruction of plankton life at the junction of waters of separate origin, but study of the now better-known hydrographic features of the Antarctic reveals that these rich accumulations lie under the region of the great Antarctic Convergence (fig. 158, p. 606) and, according to the investigations carried out by the Discovery, the surface waters of this region show possibilities of a rich supply of nutrients and of a great production of phyto- and zooplankton.
From this dependent relationship it becomes obvious that the deep-sea and abyssal fauna could have come into being only after the pelagic life of the sea had become established, or simultaneously with it. Both the pelagic animals and the deep-sea forms are believed to have been derived from the littoral fauna. The many structural modifications and the numerous endemic genera give evidence that the fauna of great depths is, indeed, an ancient one. But in generalizing, we may say that although the deep-sea fauna possesses many bizarre and unusual forms, nevertheless the structural adaptations found in these animals are only
Horizontal Distribution of Deep-sea Benthic Animals. As a rule deep-sea animals in general are widely distributed, but not to such an extent as was formerly believed would be the case owing to the uniform conditions of the deep-sea environment. The abyssal fauna, however, is the most widely distributed of benthic life, the archibenthic being next, and the littoral fauna the least widely distributed. In other words, the horizontal distribution of marine benthic animals increases directly with increasing depth. Benthic deep-sea genera are usually cosmopolitan, although the species may belong within the limits of certain oceans. Geographical submarine barriers are also influential in limiting distribution. A classical example is the Wyville Thomson Ridge, which forms a barrier between the deep-sea faunas of the Atlantic and the Norwegian Sea, only 12 per cent of the faunas being common to both seas. The reason for this will be discussed further on p. 849.
Nekton, the Swimming Animals
The assemblage of animals comprising this group are provided with efficient locomotive organs enabling them to swim against currents and waves. The locomotor efforts are not only capable of being sustained for considerable length of time, but the movement is also effectively directed towards pursuit of prey, escape from enemies, and instinctive migratory journeys. Structurally, most nektonic animals are well adapted to these ends. They are typically streamlined in shape and frequently covered with slime to decrease resistance in passing through the water. The musculature, nervous system, and sense of vision are notably well developed. Among the members are adult fishes, squids, whales, dolphins, seals, and a few crustaceans. All parts of the pelagic region of the sea contain representatives of the group which, together with the plankton, make up the pelagic life of the sea. It has been noted by Hjort (1912) that the idea of a pelagic mode of life was originally associated with animal life of the ocean surface, but it applies also to the drifting and swimming life of deeper waters, since its main characteristic is its independence of the bottom. Deep-living pelagic animals are called bathypelagic. Pelagic animals are either neritic or oceanic, depending upon whether they belong to the neritic or the oceanic province. There is no well-defined line between the two.
In the nekton we find the great migratory animals which make journeys of hundreds of miles to and from their breeding grounds or roam
The spawning migrations of the European eel, Anguilla vulgaris, are perhaps of the most remarkable among fishes. The journeys involve the swimming of the adult eel over a distance of about 5000 km from European coasts to the spawning area near Bermuda and the subsequent return of the larvae to the fresh-water habitats on the coast of Europe. This will be more fully discussed in a later chapter.
The guiding instinct in these journeys appears more remarkable than that in migratory birds, for recognizable landmarks do not exist in the open sea, where the horizontal chemical-physical gradients are too weak and variable to render anything but negligible directing aids during the oceanic portion of the journey.
Among the marine mammals whales are known to travel great distances. Recovery of American harpoons embedded in blue whales killed in Barents Sea, where harpoons of such make were never used, indicate migrations from the coast of North America (Hjort, 1912). These and other whales alternately travel from low-latitude breeding grounds to the rich feeding grounds of higher latitudes.
The only invertebrates that are clearly nektonic are some of the cephalopods, especially the squids. These animals are powerful swimmers which effect rapid locomotion by spasmodically ejecting jets of water from the mantle cavity through the swimming organ known as the funnel, a tubelike structure representing a modification of the molluscan foot. Associated with this rapid locomotion the cephalopods possess highly developed eyes, and also a highly developed brain as compared with other invertebrates.
A few of the pelagic prawns may be included as nekton, although they are usually on the borderline, approaching either benthic or planktonic life. Such special groups as seals, otters, and marine snakes may for convenience be placed also in this category, although the life habits of some require a period on the immediate foreshore for the care of the young.
Biologically the nekton includes only a very few of the major animal groups, as indicated above; but the large size of individual members, their tendency to form into schools, and their commercial value as food,
Zooplankton, the Floating Animals
The benthic and nektonic groups were the first to be observed or studied by man. But as systematic investigations of the sea progressed, with the improvement of collecting methods and the use of the microscope, it became obvious that another ecological group existed, which for convenience of study should be considered distinct from the bottom-dwelling and the fast-swimming forms to which it holds such vital relationships. This group is now called the plankton, a term first used by Victor Hensen in 1887 to distinguish the vast assemblage of feebly swimming or floating organisms, both plants and animals, that drift about with little or no resistance to water movements. To the plankton belong not only by far the greatest number of marine organisms, but also those of widest dispersal.
Photomicrograph of a plankton community containing copepods (Calanus and Metridia), young euphausiids, and fish eggs.
The general plankton is divided into two large groups: Phytoplankton and Zooplankton. To the phytoplankton belong most of the diatoms, dinoflagellates, and other unicellular plants or animal-like plants that are capable of synthesizing food. These, in contrast to the consumers making up the zooplankton, are the chief producers of the primary food of the sea. They are more fully discussed in chapters XVI and XIX.
In the zooplankton are included many of the protozoa, especially tintinnids, radiolarians, and foraminifera, a large number of the small crustaceans such as copepods, ostracods, euphausiids, amphiopods; the jellyfishes and siphonophores; many worms; a number of molluscs, such as the pteropods and heteropods; and the eggs and larval stages of most of the benthic and nektonic animals of all kinds. Figures 222 and 223 are photomicrographs of typical zooplankton catches from coastal waters.
Photomicrograph of plankton dominated by the arrow worm, Sagitta, and including copepods, young euphausiids, and fish larvae.
Undoubtedly the first notice taken of the general microscopic plankton was not of the individual organisms themselves, but rather of such phenomena as discoloration of the water, associated with their swarming. These observations, of course, could only increase the mysteries of the sea, for the causes were in most instances entirely unknown. Probably one of the earliest references applying to general plankton phenomena was made by Pytheas in the fourth century B.C. During a voyage in the North Atlantic he reported that the sea became sluggish and thick like a jellyfish (Herdman, 1923). There are records where the occurrence of the color phenomenon was accompanied by considerable destruction of marine life along the coasts, such as has been witnessed on the coasts of California, Japan, and elsewhere. The terms “red-water,” “red-tide,” and “sliming” have been applied to some of these displays. In other instances, the discoloring became associated with good or bad fishing conditions, and recent investigations (Hardy et al, 1936) have, indeed, shown that there is a correlation between herring catches and color of water resulting from microorganisms (p. 907). Perhaps the most
Among the first important typically planktonic organisms to be studied in detail were the boreal copepod Calanus finmarchicus (fig. 227-c), described by Gunnerus under the name Monaculus finmarchicus in 1765, and Ceratium tripos (fig. 74-a), a dinoflagellate described by O. F. Müller in 1777. Little was accomplished, however, until about 1846, when Johannes Müller introduced the plankton net for use in extensive studies. Since then the plankton has been the subject of a vast amount of investigation.
It will be noted that the three categories, benthos, nekton, and plankton, are not sharply separated. There are not only transitory stages but also many organisms of borderline habits. Most members of the nekton and benthos are for a period properly plankton. The swimming powers of many animals put them midway between the plankton and the nekton, and many forms, for example some mysids, amphipods, cumacids, and so forth, live both on or near the bottom and are sometimes called hypoplankton. Many of the planktonic animals do swim freely and may quickly move many times their body length, although, owing to their small size, little distance is covered. The direction of swimming is frequently haphazard and intermittent, resulting in little progress. However, under certain directing stimuli such as light and gravity, the resultant movements do bring about consistent, although restricted, migrations.
Categories of animal plankton are defined according to duration of the life cycle in the pelagic state, according to size, or according to habitat.
Temporary Plankton. The planktonic eggs and larvae of the benthos and nekton make up what is known collectively as the temporary plankton (fig. 224). This temporary element, or meroplankton as it is sometimes called, is especially abundant in the neritic waters and is composed mainly of developmental stages of the invertebrates, but includes also the young of the fishes.
The following examples give the computed maximum concentrations of various invertebrate larvae taken at separate stations by means of a No. 20 plankton net towed vertically from 25 to 0 m in neritic waters of the Bering Sea during August (Johnson, 1937):
| Larvae | Number per cubic meter of water |
| Ophiopluteus. | 1,235 |
| Echinopluteus | 12,195 |
| Bipinnarian | 837 |
| Annelid | 8,130 |
| Barnacle nauplius | 694 |
| Pelecypod veliger | 17,073 |
| Gastropod veliger | 7,883 |

Characteristic larvae of the meroplankton: (a) chaetate larva of the annelid Platynereis agassizi; (b) zoea of sand crab, Emerita analoga; (c) cyphonautes larva of bryozoa; (d) tadpole larva of sessile tunicate; (e) pilidium larva of nemertean worm; (f) advanced pluteus larva of sea urchin; (g) fish egg with embryo; (h) trochophore larva of scaleworm; (i) veliger larva of snail; (j) pluteus larva of brittle star; (k) nauplius larva of barnacle; (l) cypris larva of barnacle; (m) planula larva of coelenterate; (n) medusa of hydroid.
The temporary plankton is characteristically seasonal in occurrence since it is dependent upon the spawning habits of the parental stock. But there is sufficient variation in spawning time of different species, or even continuous spawning of a single species, to provide a greater or smaller amount of temporary plankton at all seasons, even in high boreal waters where the temporary element is usually much suppressed. The length of larval period is also important in this respect, and may vary
Characteristic holoplankton protozoa: (a) foraminifera (Globigerina); (d) dinoflagellate (Gymnodinium); (c) tintinnid (Stenosomella); (d) tintinnid (Favella); (e) radiolarian (Protocystis); (f) radiolarian; (g) dinoflagellate (Noctiluca).
Characteristic holoplankton coelenterates and ctenophores: (a) comb-jelly (Pleurobrachia); (b) siphonophore (Velella); (c) jellyfish (Aglantha); (d) siphonophore (Diphyes).
Permanent Plankton. The remaining part of the plankton is made up of animals living their complete life cycle in the floating state and is called the permanent plankton or holoplankton (figs. 225–228).
The holoplankton is composed of forms representing nearly every phylum of the animal kingdom with the exception of the sponges, bryozoans,
Characteristic holoplankton crustaceans: (a) euphausiid (Euphausia); (b) ostracod (Conchoecia); copepod (Calanus); (d) amphipod (Phronemia) in empty mantle of the pelagic tunicate Salpa.
Characteristic holoplankton, miscellaneous: (a) arrow worm (Sagitta); (b) annelid (Tomopteris); (c) nemertean (Nectonemertes); (d) pteropod mollusc (Limacina); (e) tunicate (Oikopleura); (f) pteropod mollusc (Clione).
Some floating adaptations of plankton animals: (a) copepod (Aegisthus); (b) decapod (Lucifer); (c) barnacle nauplius; (d) copepod (Oithona); (e) holothurian (Pelagiothuria); (f) pelagic egg of copepod (Tortanus); (g) phyllosome larva of lobster; (h, i) copepod (Sapphirina), side and dorsal views.
All other phyla are abundantly represented in the holoplankton. However, no plankton animals play so vital a role in the economy of the sea as do the Crustacea of the phylum Arthropoda, and among these the copepods rank first in most parts of the ocean although in many instances euphausiids are of equal or greater importance as food for the larger plankton-feeding animals (p. 905). Among the higher crustaceans we should mention the decapod crustacean, Lucifer, which, though of small importance numerically, illustrates a remarkable divergence from others of the group in adjusting itself to a floating life (fig. 229-b). It is of interest to note here that in the sea, as on land, it is the arthropods that have gained the greatest diversity and numbers. In the sea the Crustacea are a counterpart of the Insecta on land.
Macro-, Micro-, and Nannoplankton. Most of the planktonic organisms are microscopic or semimicroscopic in size but there are notable exceptions, for instance, among the scyphozoan jelly fishes, some of which may attain 1 m or more in diameter, with tentacles up to 25 m long. This wide range in size has, for convenience of study, led to yet further subdivision of the plankton on the basis of relative size. Thus we may distinguish broadly between three (or more) convenient size groups. No sharp lines can be drawn between these, but usually the macroplankton is that taken with a coarse net. It includes the large forms and many small ones that can be readily seen with the unaided eye, that is, animals of about 1 mm or more in length that would be normally caught with a net of No. 00 or 000 bolting cloth. (The phytoplankton does not usually form a part of this division.) The forms between about 1 mm and 1 cm are sometimes called mesoplankton, but the term should be avoided in this sense because it is also used to designate the general plankton living in mid-depth waters below the epiplankton. The largest of the plankton forms are sometimes called megaloplankton. The microplankton, also in part called net plankton, is that which is composed of individuals below about 1 mm in size, but yet large enough to be retained by a net of No. 20 bolting cloth with a mesh aperture of about 0.076 mm. The nannoplankton (dwarf plankton) comprises many of the very small forms (about 5 to 60 μ) such as the smaller diatoms, dinoflagellates, coccolithophores, protozoans, and bacteria, which readily pass through the meshes of a new No. 20 net (fig. 90, p. 377) and must therefore be collected by centrifuging the water. Sizes below these are the ultraplankton. Lohmann (1903) demonstrated the presence of nannoplankton by using hard filter paper, and also by a unique method in which he examined the tiny forms caught in the filtering apparatus of the “house” of the appendicularian Oikopleura. The appendicularian “house” is a temporary gelatinous structure that serves as a complete investing case which protects the animal and also acts as a filtering apparatus for catching food (fig. 239). In the “house” there is a set of
Neritic and Oceanic Plankton. Many pelagic organisms, both plants and animals, are bound strictly to coastal waters while others occur normally only in offshore waters. These requirements give rise to two divisions of the plankton, based on their relative dependence on the coast.
To the neritic ecological division belong the forms which normally inhabit the waters in the coastal areas and extend only a short distance seaward, depending upon the depth and type of circulation. The neritic forms on the whole prefer relatively warm water during the growing season, with some reduction of salinity. They are usually seasonal in occurrence, especially in the northern latitudes. Vast swarms of pelagic larvae of benthic invertebrates and many fish eggs and fish larvae are characteristic of the neritic plankton. Resting stages occur in the life histories of many of the species, such as the cladocerans Podon and Evadne, and the rotifers. It must not be understood, however, that the neritic plankton is composed chiefly of temporary plankton. On the contrary, the dominant element is often the holoplankton, adults and young, which are bound to the coastal regions for some unknown reason—perhaps by nutritive, physical, or chemical bonds. The copepods loom large among these permanent plankton forms.
In discussing the plankton of the Gulf of Maine, Bigelow (1926) cites certain of the medusae as conspicuous inhabitants of neritic nature. These are the moon jelly Aurelia; the large red jellyfish Cyanea; and the small hydromedusæ Melicertum companula and Sarsia, all of which are budded from sessile stages in the shallow coastal zone. Many other medusae and also pelagic larvae of such animals as shore crabs and molluscs could be added to this list of strictly neritic forms. It is significant to note, as Bigelow has pointed out for Melicertum companula, that some of these pelagic stages are confined mainly to coastal zones because they have originated there from parental stock dependent upon the immediate coast and not because of any inability to withstand oceanic conditions. Some neritic animals may be found in oceanic waters into which they have been carried, but they are relatively or totally sterile, being unable to complete successfully all stages of the life cycle (p. 859).
The neritic forms are the greatest producers of the sea, for in the coastal waters the food materials are most readily available for plants and through these, successively, for small and large animals. Practical evidence of this relation is seen in the fact that most commercial fish are taken in coastal waters.
The oceanic division, as the name implies, includes forms that are contrasted with the coastal population, since they occur typically at some distance from the coast and over profound depths in the open sea. They constitute the so-called “blue-water” or high-oceanic population. The animals of the oceanic plankton are characteristically holoplankton types that are not dependent on the sea bottom or on the proximity of land; indeed, as a rule, they do not survive long if blown by winds or swept by currents into really neritic situations. Characteristic animals of the oceanic plankton are: Velella, which floats in vast swarms at the surface with its oblique sail projecting to catch the surface breeze; the salps; the violet snail, Janthina exigua, which in time of storm drifts to the beaches in company with Velella; many copepods of different genera, Sapphirina, Rhincalanus, Eucalanus, and others. It is not possible to distinguish sharply between the neritic and the oceanic populations, for there is much overlapping at the border line; there are also forms of relatively great ecological valence, that is, forms tolerant of a wide range of ecological conditions, and such forms are to be found indifferently in both coastal or offshore situations. These are the panthalassic types.
Special Adaptations of Animals to Planktonic Existence. In discussing the adaptations of the phytoplankton, it was pointed out that the rate of sinking of a body heavier than water depends upon the ratio of surplus weight to friction, and friction in turn is determined mainly by the surface area. The simplest way to obtain a relatively large area is to reduce the absolute size. Therefore the small size of most planktonic animals is of extreme importance in keeping them afloat; but, as indicated for the plants, special structural adaptations are also provided.
In contrast to most members of the phytoplankton, the planktonic animals usually have some power to swim. That this is highly important, especially for the larger crustacean forms, is shown in the following summary from Gardiner (1933), which gives the average time required for anesthetized Calanus finmarchicus of different lengths to sink through a column of water 250 mm deep having a temperature of 18.5°C and a salinity of 35.01 ‰:
| Length of specimen (mm) | Mean time for sinking (seconds) | Length of specimen (mm) | Mean time for sinking (seconds) |
| 2.1 | 181.3 | 3.2 | 70.3 |
| 2.3 | 110.6 | 3.4 | 58.9 |
| 2.6 | 114.9 | 3.6 | 57.9 |
| 2.8 | 106.8 | 3.9 | 43.9 |
| 3.0 | 74.3 | 4.0 | 31.0 |
The experimental data included additional lengths, and the correlation between sinking time and length of specimen, expressed as coefficient of correlation, was
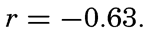
The ability to swim varies greatly with different animals, but even very feeble swimming, when favorably directed as a response to gravity or to light, must work to great advantage in keeping the organism within the water stratum having tolerable living conditions. The ciliates depend largely on ciliary action as do also the ctenophores, the trochophores, and other similar larvae. It is significant to note that the pelagic young of bottom-dwelling forms almost invariabley possess a great development of cilia or a greater length of spines and bristles in greater profusion than occurs in the adults. Euphausiids and at least the larger copepods keep their locomotive organs (pleopods, maxillae, second antennae, and so forth) almost incessantly in motion for feeding, respiration, and swimming, and appear to depend rather little on special suspensory organs. The chaetognaths, or arrow worms, all species but one of which are planktonic, depend mainly upon swimming, for which they are rather well adapted by development of fins and longitudinal muscles. But many of the plankton animals that can swim are also especially adapted to resist sinking when they are in a state of rest. Here the means of adaptation are mostly along the lines of increased length of appendages, of spines or bristles, or of dorsoventral flattening of the body (fig. 229, p. 818).
The radiolaria and pelagic foraminifera develop long spines and irregular shapes, a method not unlike that employed by some diatoms, and the size of some species of radiolaria may be much decreased in the warmer surface water. In Challengeria, for example, certain of the smaller species averaging about 0.11 to 0.16 mm live in the less viscous surface waters of 50 to 400 m depth, whereas the larger species averaging from 0.35 to 0.58 mm live in the colder viscous waters of 1500 to 5000 m depth. Between these depths the average size of different species ranges from 0.26 to 0.28 mm. The chief method of flotation for many of the copepods is found in the increased length of appendages and the spines or bristles that grow upon them. The tropical forms show a greater development of plumose structures than do the northern species, and this is just what we should expect because of the reduced viscosity of the warmer water (see p. 857). The warm-water copepod, Sapphirina (fig. 229h and i), has no extensive development of spines of plumose structure, but it is flattened dorsoventrally in a manner that enlarges the ventral surface and gives greater water resistance while sinking. The lobster phyllosoma larva is similarly constructed and adapted to its pelagic period. The long spines, antennae, and so forth, common in
The presence of oil is a common and most effective method of reducing specific weight in pelagic eggs; it is also found in the copepods, euphausiids, radiolarians, Noctiluca, and others. In the copepod Calanus finmarchicus there is a well-defined hydrostatic organ filled with oil; this consists of a very thin sinus lying in the mid-dorsal axis of the body. The oil also apparently functions as a food reserve since it varies greatly in quantity, and its quantity is perhaps indicative of past living conditions.
Among the siphonophores, pneumatic floats serve as a hydrostatic apparatus. Physalia and Velella are good examples of this type of adjustment and, in addition to the floats, possess sails that extend above the water surface to enlist the aid of the wind in giving more rapid transportation.
Finally, it should be noted that the water content of many animals of the plankton community is very high, being in excess of 95 per cent in some jellyfish. The jelly-like transparency of many plankton animals, for instance the salps, the leptocephalus eel larvae, the pelagic annelid Tomopteris, the ctenophores, the heteropods, the chaetognaths, the copepods Eucalanus and Haloptilus, and many others attest to the high water content of their bodies. The maintenance of this high water content is facilitated because the body fluids are isotonic with sea water. The skeletons (when present) of planktonic animals are remarkably thin in contrast to many related benthic forms. Some of the typical means of flotation are illustrated in fig. 229.
For a fuller discussion of the planktonic adaptations, the reader is referred especially to Steuer (1910).
RELATIONS TO PHYSICAL-CHEMICAL PROPERTIES OF THE ENVIRONMENT
A study of the influence of environmental factors on the lives of marine animals encounters numerous difficulties not met with in the study of plants. The fundamental factor of nutrition is more clearly recognized in plants than in animals, for we know rather well the simple elements that are utilized by plants in the synthesis of their carbohydrates and proteins, and several of these elements are now readily measured quantitatively. The means by which the elements are conveyed to the very limited euphotic zone of the sea where plants may grow can also be determined approximately by hydrographic surveys. The quantity of light needed for plants to balance photosynthesis and respiration is measurable. Under favorable conditions the rate of production in unicellular plants, especially diatoms, is extremely rapid, thus offering a good index to the operation of environmental factors. In most animal
The duration of life of the individual animal is on the whole relatively long, and frequently the development is very complex with separate stages, each with habits and needs of its own (p. 318). The various degrees or methods of locomotion are highly important in the adjustment to the conditions of life. All these variations make it necessary in biological studies to consider not only the separate species but also the whole life cycle of the individuals from the egg to the spawning adult. This will become increasingly obvious as we consider in the following pages the influences of the various factors.
In studying conditions of the natural environment it is not possible to isolate completely for discussion the separate factors, since these factors do not in nature operate separately on the population but rather directly or indirectly in groups. We shall discuss the subject, however, under separate headings in order to emphasize outstanding features, at the same time feeling free to introduce correlated features. These headings are (a) light, (b) salinity, (c) temperature, (d) ocean currents, (e) oxygen.
Light
Of all the environmental factors, light is perhaps the most readily isolated of all, for its momentary influence on temperature is small and therefore of small importance in influencing circulation or density of the water. Its direct effect on chemical reactions in the sea is concerned largely with metabolism of the organisms, as in photosynthesis and pigmentation. Light is also a factor showing very frequent and marked fluctuations in the upper layers of the sea.
To animals, light has its greatest significance indirectly, as a source of energy for the photosynthetic processes of plants upon which all animals are wholly dependent for their nourishment. Aside from this, animal life may exist without solar light, as is witnessed by the presence of animals in the abyssal depths. Nevertheless, light or absence of light has been one of the most potent factors in the molding of structural development and in the adaptations of most marine animals. Light is also a great factor in the movement of animals.
Light and Color. The variegated colors, bandings, mottlings, and so forth, of many marine fishes living among the fronds and stipes of sea-weeds is a well-known phenomenon to anyone familiar with the sea. Likewise, various shades and patterns of gray and black are common, for instance, among tide-pool sculpins and the littoral flatfish of sandy or muddy bottoms. Many littoral crustaceans living upon seaweeds
In more recent publications Sumner (1934, 1939, 1940) has reviewed his own and other investigations pertaining to mechanisms of color changes and quantitative effects of visual stimuli on pigmentation, especially in fishes. The mechanisms that bring about these changes in color or shade are associated with the chromatophores or pigment cells, the contents of which are either activated directly by intensity of incident light or mediated through the eyes and nervous system in response to color or to albedo (proportion of incident light reflected) of the background. The pigments of the chromatophores produce degrees of shade or color by the dispersion or concentration of the pigment within the irregularly shaped chromatophore cell. A display of greater or smaller amounts of the pigment results, either evenly over the whole surface of the body or irregularly in patches, the resultant effect depending upon the degree of dispersion or concentration of pigment and upon the amount of pigment involved.
In the above we have referred mainly to a method of color change that is concerned only with rearrangement of the pigments already present. Such changes are usually quite rapid and may even occur within a few seconds, as is witnessed by reactions of the cephalopods in which color intensity may quickly shift from pale gray to a rich chocolate as the animal passes over a lighter or a darker substratum. Here light appears to be the stimulus activating the changes but, in addition, nervous reactions related to feeding or presence of enemies may also produce the temporary color changes in cephalopods.
A second type of color change involves gradual change in the quantity of pigment or in the number of chromatophores present. Experiments by Sumner and Doudoroff (Sumner, 1940) showed that during a period of about two months the amount of the pigment melanin produced in the guppy (Lebistes reticulatus) was nearly independent of the intensity of the light but was dependent upon the albedo of the background. The amount of melanin (or the number of melanophores) was found to be
Much might be written pertaining to protective coloration of animals, its physiology, evolution, and purpose, but ecologically the greatest significance that can be attached to the ability, possessed by some animals, to respond to their background by closely matching their own color with it, is the protection they must thereby gain in relation to their organic environment. It has been shown experimentally (Sumner, 1935) that certain fishes (Gambusia) adapted to blend with their background have a greater likelihood of survival from attack by predators than do fishes of the same type that are in contrast with the background. If we may trust our own visual sense as an index, we know that only the closest scrutiny can reveal the presence of some animals made practically invisible by the cloak of blending color or shade.
In what has been said, we have considered only littoral animals that live on or near a more or less illuminated background of solids, either the substratum or larger plants. There is, however, a great array of animals not normally provided with such a background. In the pelagic habitat, for example, the “background” is the surrounding water, and in the abyssal-benthic division the background is entirely devoid of solar light. In the pelagic division the aqueous surroundings have all degrees of light intensity, from sunlight at the surface to absolute darkness in the great depths. The quality of light is also different at different depths, since water does not absorb all light rays uniformly, but the Michael Sars Expedition found that in southern waters even the most penetrating rays failed to affect photographic plates exposed for two hours at a depth of 1700 m (p. 83).
It is of special biological interest to note that at a depth of 500 m the rays detected are not entirely diffused by the water but are directed so that shadows, however faint, should result. The dorsal side of an animal even at this depth is more exposed to light than the ventral or lateral sides and this may exert an influence, along with the force of gravity, in the orientation of the animals. To animals living at shallow depths the direction of light appears to be of great significance and most fishes of these zones are notably darker above than underneath. Investigators concerned with the effect of light on pigmentation have expressed the opinion that the shade assumed by an animal is chiefly determined by the ratio between the light from overhead and the light reflected by
Just how this principle of reaction to light would operate to affect the fishes and other animals in the open sea has not been shown, but in the zone where there is still considerable light there must be a difference in the light intensity from above and below. It appears that the above principle is best applied to conditions where the water is shallow and the background a well-defined reflecting surface with various values for the albedo. Be this as it may, there is still much evidence, especially from the findings of the Michael Sars Expedition in the North Atlantic, to show that there is a very real, though not satisfactorily explained, correlation between the light entering the sea and the color of the animals at various levels of light penetration.
The uniform dark pigmentation of fishes in the lightless depths, as contrasted with the ventral-dorsal differentiation of those inhabiting the lighted zone, indicates that the direction of light is significant in the distribution of pigment. But just why abyssal fishes do not become blanched in the absence of light as do cave fishes has not been satisfactorily explained.
It is generally known by mariners and fishermen that the animals living at or near the surface of the sea, especially in lower latitudes, are commonly blue in color. Such common fishes as the flying fish, mackerel, bonita, tuna, and others have backs of blue or blue-green. Some invertebrates, for example the siphonophore Velella and the pelagic molluscs Janthina exigua and Glacucus eucharis, are among the larger and better known, while copepod species of Pontellopsis, Anomalocera, and Corycaeus are frequent among the microscopic forms.
The blue and green colors are indeed striking characteristics of the surface open-sea life but it must not be concluded that all oceanic animals are blue or even predominantly so with respect to numbers. In many of the smaller forms, copepods and other crustaceans, pale red is a very common color, which like blue may occur as faintest tints in relatively hyaline forms. Hyaline or colorless animals (sometimes with the digestive tract or other parts colored) are as characteristic of the open sea as are the blue, or even more so, from near the surface to moderate depths (up to 200 to 300 m or deeper). Among these hyaline forms may be mentioned the salps Salpa and Doliolum; the arrow or glass worms Sagitta; the pelagic heteropod molluscs Pterotrachea and Atlanta; the Ctenophora or comb jellies; the copepods Eucalanus and Haloptilus; and many fish
larvae. The list could be extended almost indefinitely. The crystal clear aspect of many of these animals must make them practically indistinguishable to predators. Yet if this is a protective adaptation, we are left with the need of explaining why many species of these hyaline forms are so rare in comparison with others of the same type of animals that are more conspicuous owing to presence of color. As examples we may mention the hyaline versus the opaque or colored copepods. The latter are far more abundant as a rule. Perhaps the protective feature is coupled with a low rate of fecundity; or in plankton forms the unselective mode of feeding by predators may be yet another explanation since the hyalinity would be of little survival value.
At depths of about 300 to 500 m the silvery fishes, Argyropelecus (fig. 231-a), Chauliodus, and others, form a conspicuous though small part of the fauna, and there is a marked increase in reddish and dark-colored animals: dark fishes such as Cyclothone; many red crustaceans, wholly or partly colored, including, for example, the red prawn Acanthephyra, and numerous copepods such as Getanus, Metridia, Pleuromamma, and Euchaeta. The red Sagitta macrocephala and Eukronia fowleri of these depths are in contrast with colorless chaetognaths taken at higher levels. Other dark colors occur, including dark violet pteropods (Peraciles diversa) black or dark violet fishes (Gonostoma spp.), and brown medusae (Atolla).
In the deeper lightless waters, brilliant red, scarlet, or red-violet prawns (Acanthephyra spp.) persist, but the fishes are all black, black-violet, or brownish.
The depths at which these characteristically colored animals appear are not the same in all parts of the world. In waters of higher latitude the species of intermediate depths are nearer the surface than in tropical seas. Forms occurring at about 200 to 500 m in the higher latitudes, between about 67° and 50°N, will be found near 750 m at the latitude 33°N (Hjort, 1912). This difference indicates strongly a correlation with the degree of submarine illumination, for the upper limit of the dark pigmented forms agrees with the relative depths of light penetration at these latitudes. Further evidence is gleaned from the fact that in related species or varieties the darker and more heavily pigmented ones come from the greater depths. For example, among the fishes the light-colored Cyclothone signata has its lower limit near the upper limit of the black C. microdon. This is indicated by the following hauls taken at three depths by the Michael Sars at about 35°N.
| Depth (m) | Light-colored C. signata, individuals | Dark-colored C. microdon, individuals |
|---|---|---|
| 500 | 1240 | 214 (small) |
| 1000 | 82 | 448 |
| 1500 | 22 | 322 |
A similar vertical distribution was found for certain other forms of life. The deep-sea medusa Atolla bairdi has four varieties based on the degree of pigmentation. They range from a variety with pigment only in the stomach to the deepest dwelling variety with quite general pigmentation.
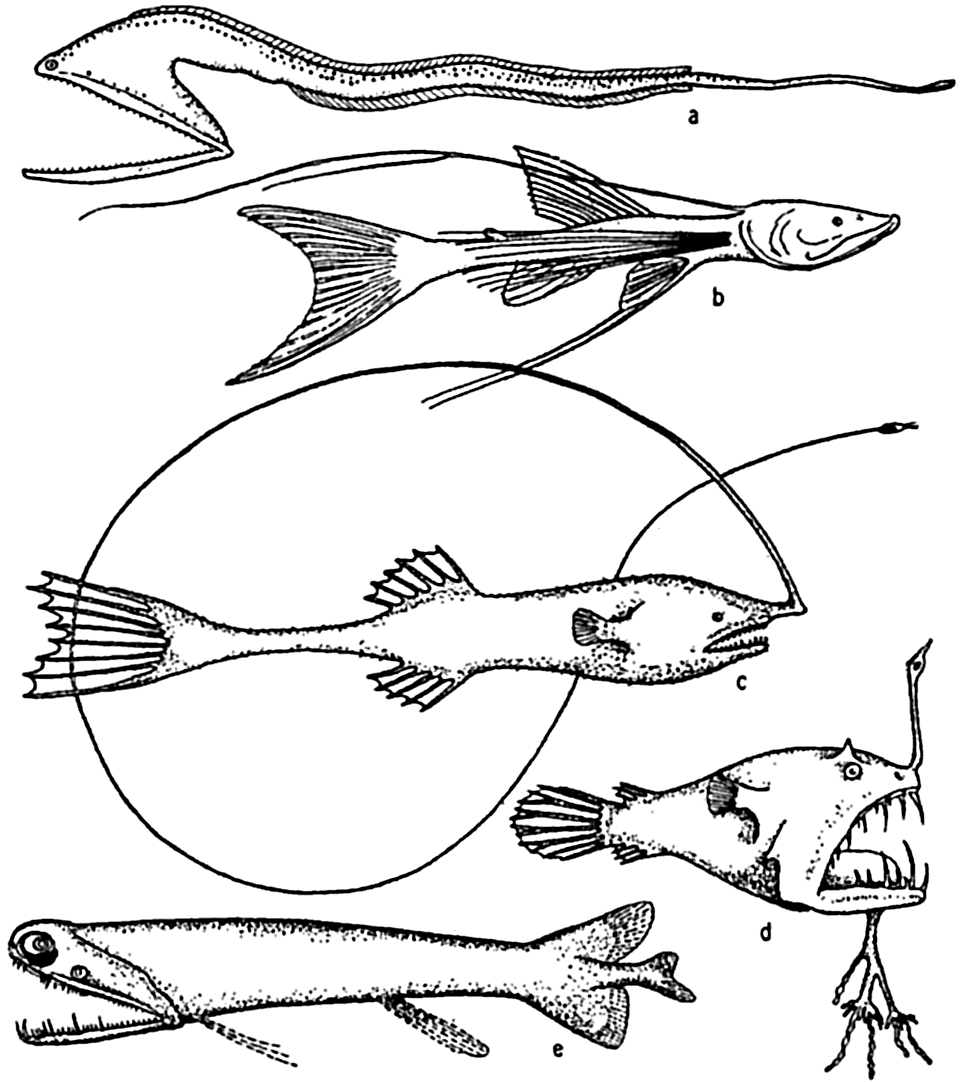
Deep-sea fishes: (a) Macropharynx longicaudatus (after Brauer), length 15.1 cm, from 3500 m depth; (b) Bathypterois longicauda (after Günther), length 7.6 cm, from 550 m depth; (c) Gigantactis macronema (after Regan), length 13.3 cm, from 2500 m depth; (d) Linophryne macrodon (after Regan), length 5.3 cm, from 1500 m depth; (e) Malacostus indicus (after Brauer), length, 8 cm, from 914–2500 m depth.
The red rays in the spectrum are quickly absorbed by the surface waters, hence, the animals below the surface live in a green, blue-green, or lightless world. In the abyssal regions it is indeed difficult to imagine what survival value any color can have, but near the surface, for example, the fishes with blue or green backs and silvery or light ventral sides are rendered thereby less conspicuous both from above and below, and the darker colors of fishes in dimly lighted depths also seem appropriate. In daylight red is a conspicuous color, but in the sea a red object appears quite black at a distance of only a few meters owing to the rapidity with which red rays are absorbed by water; and at depths below the penetration
Light and Structural Adaptations. That the quantity or quality of light has a marked influence on the coloration of marine animals inhabiting different depths of the sea seems beyond all reasonable doubt, but the influence of deep twilight or absence of light has indirectly placed a more remarkable stamp on structure than on color. This is manifest by the strange and weird anatomical adaptations, especially of many abyssal fishes.
These adaptations are concerned with structural modifications fitting the animals better to survive in faintest light or in utter and perpetual darkness. They are mainly along three lines: (1) tactile structures, (2) food-procuring contrivances, (3) light production.
Reference to publications dealing with abyssal fishes (Günther, 1887, Brauer, 1906, Murray and Hjort, 1912, Regan, 1932) will illustrate how characteristic are modifications along these lines. Development of tactile devices is an important feature in numerous instances and is well illustrated in Macropharynx longicaudatus, several species of Bathypterois, Gigantactis macronema, Linophryne macrodon, and other deep-sea angler fishes (fig. 230). These sensory structures may, as indicated in the figures, involve modification of the whole body whereby it is elongated and ends in a disproportionately long threadlike tail as in Macropharynx; or, in the more conventional bodies, the fin-rays may grow to a length several times that of the body; or tactile threads of various types may grow directly from the head. The prawns of deep water also possess extremely long tactile antennae, some of which may be twelve times the length of the body as in Aristaeus aristaeopsis.
The food-procuring contrivances of deep-sea fishes consist commonly of an extraordinarily immense mouth in proportion to the body size. The stomach and abdominal wall may be so elastic that it is possible for some of these fishes, Cheasmodus or Melanocetus for example, to swallow other fishes three times their own size and many times their own weight. Many of the deep-sea fishes are provided with formidable teeth, attesting to their carnivorous nature. As if this were not enough, some species of deep-sea angler fishes possess a tactile organ, the illicum, useful as rod and line, and provided with a terminal luminous lure, which in some cases may even be armed with hooks, as is the case with Lasiognathus (Regan, 1926; fig. 231-b). These angling processes may be four times as long as the fish, as in Gigantactics macronema (fig. 230-c). In food habit these fish must be mainly piscivorous. The possession of these unusual devices is correlated with the scarcity of food in the deep-sea pelagic
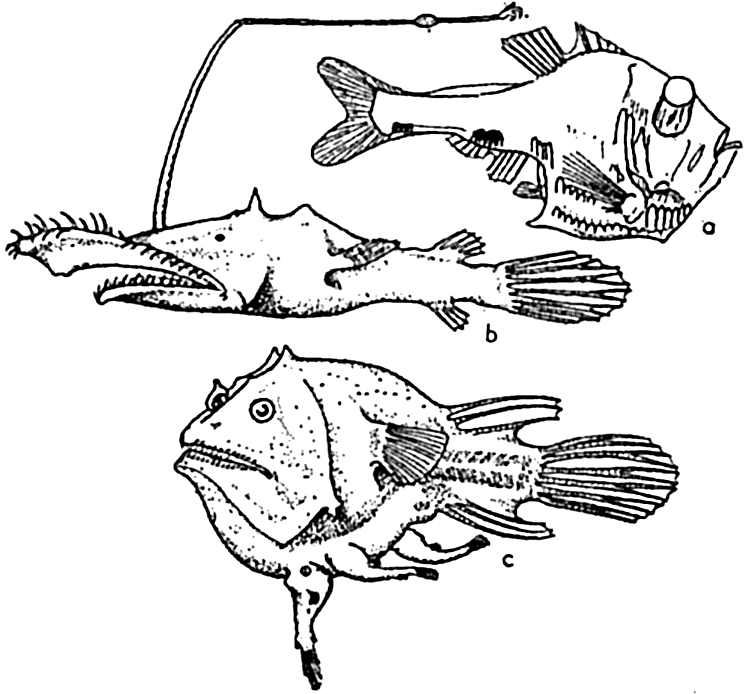
Deep-sea fishes: (a) Argyropelecus hemigymnus (after Hjort), length 3.5 cm, from 300 m depth; (b) Lasiognathus saccostoma (after Regan), length 7.5 cm, from 2000 m depth; (c) Edriolychnus schmidti (after Regan), length 7 cm, from 2000 m depth.
We have but little information regarding the depth at which fishes and other animals can see, but for purposes of comparison the question may be raised as to the depth at which light is still perceptible to the human eye. The human eye appears to respond to an intensity of light about 10−10 times that of bright sunlight, the greatest sensitivity at low intensities lying in the green at wave length .503 μ. One can easily find the depth at which light is still perceptible by making use of the absorption coefficients at .503 μ which have been found for the different types of water (p. 84). These depths, based on Utterback's data (1936), are entered to the left in table 97, and to the right in the same table are entered corresponding values which Clarke has computed from his observations. In the clearest oceanic water light should still be perceptible at a depth of 700 m, whereas in average oceanic water the corresponding depth would be 300 m, and in turbid coastal water 60 m. The values agree well with those of Clarke (1936), who finds that in the Sargasso Sea light is perceptible down to 430 m, whereas in Woods Hole Harbor light could not be perceived below a depth of 75 m if the waters were that deep. Clarke compares his results with Beebe's observations from the bathysphere, according to which complete darkness for the human eye was reached at a depth of between 520 and 580 m. Helland-Hansen's observations indicate that even at these depths light is directed, wherefore weak shadows will be present. According to the experiments by Grundfest (1932), the sunfish Lepomis can see at illumination as low as that
| Type of water (from Utterback's data) | Depth (m) | Region (from Clarke) | Depth (m) |
|---|---|---|---|
| Pure sea water. | 1530 | ||
| Clearest | 700 | Sargasso Sea | 430 |
| Oceanic water Average | 300 | Deep basin, Gulf of Maine | 230 |
| Turbid | 158 | Georges Bank | 180 |
| Clearest | 115 | Off Gray Head | 130 |
| Coastal water Average | 80 | Woods Hole Harbor | 75 |
| Turbid | 57 |
In a world of much reduced light or absolute darkness, it is to be expected that the organs of vision will be among those modified, either towards ends resulting in better utilization of the faint rays of solar or biological light that may be present, or in diminution or entire loss through disuse. Both of these modifications have occurred, even in forms that are closely related. The former has been accomplished in some instances by enlargement of the eyes to receive better the faint rays of light, and by increase of visual cones and loss of the rods in the retina. The cones are the functional cells for dim light. Reduced light appears also to have led in some instances, in both fish and cuttlefishes, to the development of “telescopic” eyes, that is, large-lensed eyes that protrude from the sockets as in Argyropelecus (fig. 231-a), indicating binocular vision. This type of adaptation is not an isolated one but is said to occur in five orders and several suborders of fishes.
The conditions of light in the deep sea have not invariably led to a convergent evolution providing more efficient eyes according to the above modifications; many animals, especially the bathypelagic fishes (but also crustaceans, at least one species, and a squid), have evolved species that are blind or have degenerate eyes, apparently atrophied from disuse.
Bioluminescence. In the biological world, heat and motion are common expressions of energy but electricity and light are also produced, especially by marine animals. Bioluminescence, popularly spoken of as “phosphorescence” because of an earlier belief that it was caused by the element phosphorus, is primarily a phenomenon of the sea. It is not exclusively confined to the sea, to be sure, but is overwhelmingly more abundant there than anywhere else. No light is known to be produced by fresh-water animals with the exception of one aquatic glowworm, and in terrestrial organisms the production of light is relatively rare. In the sea, the power to emit light is not confined to any particular taxonomic group of animals but is so generally distributed that most major animal groups are involved, from the protozoans to the vertebrates. Many marine bacteria also are luminescent.
The number of animal species capable of emitting light runs into many thousands, distributed among such groups as the radiolarians, dinoflagellates, hydroids, jellyfishes, alcyonarians, ctenophores, bryozoans, polychaete worms, brittle stars, many crustaceans (including ostracods, copepods, schizopods, and decapods), gastropods, bivalves, cephalopods, protochordates, and true fishes. Harvey (1920, 1940) should be consulted for a fuller discussion of these. It is highly probable that many groups not now known to be luminescent will prove to be so as our information becomes more complete. Only recently the nemerteans have been reported to have members that luminesce. Light producers are found in all marine communities from the surface of the sea to abyssal depths. As far as surface display is concerned, luminescence is more common in tropical than in northern latitudes, although it may be very striking in boreal waters during the warmer seasons. But this is associated in part with the fact that many luminescent organisms of the surface, especially the dinoflagellates, are mainly thermophiles, requiring
The light rays produced by organisms are wholly within the range of human vision and may at times be sufficiently brilliant to make the crests of breaking waves, the wake of a ship, or other mechanically agitated water glow with a general greenish light of sufficient intensity to enable one to read. This general phenomenon wherein the water itself appears to glow is caused by innumerable microscopic organisms, mainly dinoflagellates of various types, such as Ceratium or Noctiluca (fig. 225-g). Scattered throughout the glowing water are the larger, brighter points of flashing light emitted by jellyfish, copepods, euphausiids, annelids, or other larger forms.
In many of the luminescent organisms the light results from luminous slime secreted over parts of the body or thrown out as a glowing cloud about the animal, as in the case of the squid Heteroteuthis, which produces this secretion in a gland corresponding to the ink sac of better known squids. Many of the fishes and crustaceans possess very highly specialized luminous organs which in some cases are under nervous control. These organs are provided with light-producing cells, reflector, pigment layer, and lens. It has been observed (Macdonald, 1927) that six specimens of the crustacean Meganyctiphanes norvegica in a two-liter jar voluntarily emitted sufficient light for reading news print.
Only in relatively few instances can we perceive a usefulness of the light to the organism producing it. In dinoflagellates, bacteria, jellyfish, hydroids, and so forth, there appears to be no possible utility; but in the higher forms, particularly those with specialized light organs capable of flashing under nervous control and arranged in definite patterns and even specific colors, utility seems clear. Light can have meaning in these instances only if eyes are developed to see it. In this respect it is significant to note, as has been pointed out by Hjort (1912), that pelagic fishes living above 500 m have both well-developed eyes and luminous organs, while in the bathypelagic forms below 500 m both types of organs are diminished. An apparent anomaly then occurs at the bottom, where the eyes of the fishes are well developed but luminous organs are scarce
Confronted with the information which we now have on the distribution of organisms with eyes and on the highly complicated structures for light production (Brauer, 1906), we cannot but believe that luminosity is of specific use to many animals, although in many forms such as bacteria and protozoans its inception may have been only a secondary physiological manifestation.
The biochemical activities involved in bioluminescence are only in part understood. It is a highly efficient process since the light is practically without heat and is entirely within the spectral region of human vision, there being no rays of infrared or ultraviolet. The light is produced by oxidation of a substance, probably a simple protein known as luciferin, that is produced by the living cells but that may function even though separated from the cells. However, before light can be produced by union with oxygen it is necessary that another substance, luciferase, be present as a catalyst to accelerate the oxidation.
It has been suggested (Pierantoni, 1918) that wherever light is produced the actual agents are bacteria living symbiotically with the animals, but there is evidence that this is not universally true (Harvey, 1920).
Bioluminescence has been discussed at some length because, in commanding the attention of ecologists, morphologists, physiologists, bacteriologists, chemists, and physicists alike, it is representative of the problems of marine biology.
Vertical Migrations. Light is a significant factor in the behavior of animals both pelagic and littoral. It is therefore an especially important factor in the local or restricted (as opposed to geographic) distribution of animals. In the intertidal zone most animals are found in shaded situations, in crevices, or on the under sides of rocks or ledges. Much caution must be exercised, however, in attributing this type of distribution
The correlation of animal movements with light is best studied in the pelagic division of the ocean and we shall limit our discussion mainly to the animals of this environment. Numerous investigations of the vertical distribution of plankton organisms of the open sea have shown that many, if not most, of the pelagic forms make daily journeys from deeper water to the surface at the approach of darkness and begin returning to deeper water at or before the break of dawn. This rhythmic movement is known as diurnal migration. See Kikuchi (1930) for a review of various factors that have been considered as motivating forces. The range of depth covered and the time of movement vary with different species of animals. Those forms capable of moving vertically through several hundred meters of depth, whether in diurnal or irregular movements, are the eurybathic animals with a wide range of tolerance to rather rapid changes in pressure. Since the range of temperature may be considerable they may also be eurythermic.
A great amount of investigation has been carried on with reference particularly to diurnal migrations of pelagic copepods and chaetognaths, and these may be considered as typical of much of the plankton community and its movements.
The population does not accumulate and move in a compact body; rather, it shows a more or less continuous but uneven vertical distribution that sometimes extends over two or three hundred meters in depth. The greatest number of individuals will be found concentrated at a level where conditions are optimum with respect to light in relation to other factors. That portion of the population found at given distances below or above the optimum may consist of individuals of uniform age or sex (Russell, 1927, Gardiner, 1933, Nicholls, 1933). In one investigation (Nicholls, 1933) of a mixed population of Calanus finmarchicus, the adult females exhibited diurnal migrations to a greater degree than other members of the population. The following data will serve to illustrate the general nature of migrations in that species (fig. 232):
It will be seen that at 4:00 p.m. on January 24th the females were massed between 30 and 80 meters. The sun set at 4:27 p.m. and by 7:00 p.m. most of these females had moved into the upper 30 meters of water. Throughout
― 837 ―the investigation a small proportion remained in the deeper water irrespective of the migration of the bulk. By 10:00 p.m. the accumulation in the upper layers was more marked, but by 1:00 a.m. the descent had begun and females were evenly distributed from the surface down to 80 meters.At 4:00 a.m. they were concentrated between 30 and 60 meters with none at the surface. By 7:00 a.m. they were found between 30 and 80 meters. The sun rose at 8:37 a.m. and by 10:00 a.m. the upper layers were quite deserted; most were found between 60 and 80 meters, but a large proportion was distributed below 80 meters, and 4:00 p.m. on the 26th saw a return to the condition in which they were found at that time on 25th.
The more even distribution at 1:00 a.m. is interpreted as indicating the beginning of descent following complete removal of the stimulus of diffused light, but this scattering or descent apparently does not always occur until return of light at dawn (cf. Metridia, fig. 233; Clarke, 1933).
Diurnal migrations of adult female, Calanus finmarchicus (from Nicholls).
Not only do different species react differently, but different stages of development, and the sexes also, have their own characteristic behavior with respect to diurnal response associated with light. A further complication is encountered in that the degree of response is also seasonal, indicating changes in physiological state (Russell, 1928). Species of Acartia give some indication of a diurnal physiological state which causes migrations even in the absence of light (Esterly, 1917).
Since an animal is constantly subjected to various and simultaneous stimuli, some of fluctuating intensity, the nature of the movement will depend upon the combination at any one time, and it is not always clear which is the dominating stimulus.
In attempts to analyze these daily migratory habits several views have been expressed. It is agreed that light is the chief motivating factor, but we do not know whether it operates by virtue of its absolute magnitude of intensity or by change in intensity (Clarke, 1933, Johnson, 1938). Also it is not yet clear whether light evokes response directly or only indirectly through its modification of response to such factors as gravity, temperature, and food. The chief directional stimuli that plankton animals can receive are gravity and light, but the response to these may be modified by temperature, salinity, hunger for food, and so forth.
Gravity is an invariable factor constantly in operation, a force of momentous importance in the life of planktonic organisms. If it is not favorably overcome within water layers offering tolerable living conditions for the organisms it must result in their ultimate destruction in lower water layers or on the bottom. Some of the means employed to minimize this rate of sinking by wholly or relatively passive forms have been discussed elsewhere (p. 821). It must be emphasized that swimming upwards (negative geotropism) is of extreme importance, even to such weakly motile animals as copepods. But as observations have shown that plankton organisms have a twenty-four-hour cycle in which upward and downward migrations occur, it has been suggested that the intensity of light may be the agency affecting a change in the sign of geotropism (Esterly, 1917, 1919, Clarke, 1934). Thus in bright light the reaction to gravity is positive and the animals not only sink but may actually swim downward. In the comparative darkness of greater depths the effect of light becomes progressively less compelling and a threshold is finally reached, as is shown by a maximum density of animals at some depth. At midday this maximum will be found at its greatest depth. A reduction in light intensity with the approach of evening reverses the geotropism and the population spreads upward even to the surface. However, on approaching the surface, the population may sometimes encounter a sharp gradient of temperature, the thermocline, that may supply a sufficiently strong stimulus to dominate the field of stimuli and prevent further ascent toward the surface. Likewise a sharp thermocline limits the downward distribution of some surface forms. Observations in the Gulf of Maine show that the maximum number of Metridia lucens generally ascends to the thermocline, which has a gradient of about 7°C in 10 m, but does not pass through it (fig. 233); and Centropages typicus, which inhabits the warm-water stratum from 10 to 20 m, does not in general go below the thermocline into water of 8° to 5°C (Clarke, 1933).

Diurnal migrations of the adult female copepod, Metridia lucens. The changes in light intensity are indicated by lines representing the depth at which 1000 microwatts, 100 microwatts, and so forth, occurred (from Clarke).
Since most of the microplankton and diatoms upon which larger plankton forms subsist are produced in the euphotic layer, it has also been suggested that upward migrations may be made in search of food when light intensities are not so great as to be prohibitive (Worthington, 1931).
The phenomenon of diurnal migrations is not confined to animals living relatively near the surface. Sergastid prawns, for example, have their maximum abundance between 0 and 200 m at night and between 600 and 800 m during the day (Welsh, Chace, and Nunnemacher, 1937). We learned earlier that light is directional even at these depths and could conceivably be the directing force in very light-sensitive forms, as these must be. Dark-colored deep-water fishes were taken by the Michael Sars at the surface during the dark hours, whereas during the day they occurred only in the depths of much reduced light. The whole problem of vertical migrations is complex; and although we know that extensive vertical migrations occur with recurrent external conditions, yet they are variable in extent with respect to place and season, and need much additional investigation.
Other vertical migrations are discernible as general seasonal movements of certain populations. These movements are associated with critical periods, breeding for example, in the life cycle of the species involved rather than with light, and are best discussed elsewhere (p. 322). Since reactions related to spawning may be more or less spasmodic and contrary to the regularly observed reactions, so that extensive swarms may be found at the surface even during the daytime, they must be kept in mind in the interpretation of vertical movements.
Salinity
The character of the population of the sea is unique largely because of conditions inherent in the vast extent and depth of the marine environment, such as uniformity over vast areas; but the chief single factor which makes marine life in general what it is results from the salt content of the water.
It has already been mentioned that a close osmotic balance exists between sea water and the body fluids of the marine invertebrate organisms, and that this precludes the need of impervious teguments or special expenditure of energy in maintaining the body fluids at the proper concentration (chapter VIII). However, the marine invertebrates are usually poikilosmotic only within rather narrow limits and the concentration of salts is not the same everywhere in the sea, but in numerous instances the gradients are sharp and great fluctuations may occur in restricted coastal regions. Yet all conceivable habitats are occupied by a greater or smaller number of animals suited to the circumstances, even under very extreme fluctuations; this dispersion gives rise to a classification of animals as well as plants into two large groups, depending upon their tolerance to changes in salinity.
1. Stenohaline animals are those which are sensitive to relatively small changes in salinity. The animals of this group are especially characteristic of deep water and of the open sea, where over vast areas the
2. Euryhaline animals are those having a great degree of tolerance to wide ranges of salinity. They are naturally characteristic inhabitants of the coastal regions and of estuaries. However, owing to their tolerance, they are also frequently found far from shore as scattered specimens in the domain of more stenohaline forms. Apparently other factors related to the open sea prevent their successful propagation to a point of numerical dominance. The degree of euryhalinity varies greatly in different species. Intertidal animals, because of their periodic exposure to direct rains or runoff from land, are subject to considerable fluctuations in salinity, but when low tide is combined with unusually heavy rains the result may be lethal to much of the life on exposed flats and in small pools. Much damage may occur to oyster beds during excessively rainy seasons even though the adults may survive; major fluctuations in salinity in the Fal Estuary are held responsible for the failure of one fifth of the ripe females to spawn properly (Orton, 1937). Corals cannot live where rivers cause a persistent and great fall in salinity, although some reduction can be tolerated; the damaging effect of rivers may result in part from sedimentation. Vaughan (1919) reports that corals living in the tropics are tolerant to a 20 per cent reduction in the salinity of the water of theri normal environment. An extreme case of euryhalinity occurs in the harpacticoid copepod Tigriopus, which inhabits small pools usually reached only by the spray of breaking waves and therefore subject to great evaporation with attendant concentration of salts, or at other times to great dilution from rains. The calanoid Pseudodiaptomus euryhalinus is yet another copepod subjected to salinity ranges varying at least from 1.8 to 68.4 ‰. It normally inhabits small coastal lagoons or ponds along the southern California coast and from them it sometimes finds its way into the sea; these ponds are periodically diluted or concentrated (Johnson, 1939a). In these instances the animals have not sought the salinity in which they live by reaction to a gradient. They simply tolerate the salinity and their optimum concentration is not known. Completely tolerant forms are exemplified in the salmon and the eel, each of which spends a part of its life successively in marine and fresh-water environments.
In a study of the distribution and biology of animals we see that within the sea the salinity influences the character or type of animals that will be present in any region rather than the rate of reproduction or the total amount of animal organic material produced. However, the
Pelagic organisms, such as radiolarians that secrete silica, find their optimum living conditions in waters of somewhat lower salinity than that of the open oceans, and this provides a suggestion as to the condition of the Pre-Cambrian ocean when, judging from Pre-Cambrian rocks (Murray, 1895), radiolarians were apparently more abundant than now.
The relation between the salinity of the water and the prevailing faunas has been an invaluable aid to the study of paleogeography, and has led to an interpretation and understanding not only of the geographic arrangement of ancient seas, but also of the degree of salinity that must have prevailed when the fossilized animals inhabited the area. Conclusions can be drawn because many of these fossils are represented in present-day faunas by identical or closely related species in communities whose natural salinity demands can be ascertained. For example, it has been estimated by Ekman (1935) that during the Littorina stage the central and innermost parts of the Baltic Sea were about 5 ‰ more saline than at the present time. This is proved by a study of the then inner limits of distribution of certain molluscs. Littorina litorea, the common shore snail, formerly lived as far north as Sundsvall (62°20′N),
Size and Salinity. Among euryhaline animals, individuals living in reduced salinities frequently have a smaller maximum size than do those of the same species inhabiting more saline waters. This may indicate that the greater dilution is inimical and that the animals, although able to survive and perhaps even to reproduce, are living near the lower limit of their range of euryhalinity, and that only a slightly greater deviation from the optimum would cause death. On the other hand, the reduced size may result directly from failure of sufficient food supply of a type normally dependent upon higher salinity. This is to say that the organisms serving as the animal's food must be adapted to live in the same biotope or in one sufficiently near to enable it to drift in with water movements. Whatever the cause may be, it should be noted here that it is a strange and unexplained fact that with few exceptions marine animals from groups with fresh-water representatives are larger than the fresh-water relatives and usually the size difference is enormous. In planktonic forms this may be due in part to reduced viscosity of fresh water, but for the population as a whole the matter of food supply or rate of metabolism needs to be considered. Respiration is more difficult in fresh than in sea water. To this burden imposed by the environment is also added the necessity for fresh-water forms to expend special energy in overcoming the effects of the hypotonic surrounding medium and in maintaining a proper osmotic equilibrium. The fresh-water animals doubtless have suffered many vicissitudes not experienced in the more stable marine environment, but the effect of this is unknown.
To return again to the ecological significance of varying salinity in the sea, passive offshore plankton organisms, such as eggs and larvae having a specific gravity very near that of the water in which they float, are likely to lose their buoyancy, sink to the bottom, and be destroyed when they are swept by wind and currents into the less dense dilute waters near shore or at river outlets (Johnstone, 1908). In a study of the distribution of haddock eggs Walford (1938) concluded that the eggs tend to remain afloat in water of the same density as that in which they were fertilized. When forced into water of a different density, however, they are able at least within narrow limits to adopt a new specific gravity to conform with the water in which they drift. In the presence of
Much experimentation has been conducted relative to the specific biological effect or function of the various ions in sea water. It will not be possible here to give an adequate review of this important subject, which can be found discussed at length in special articles and texts in physiology and physiological chemistry. The function of salts in sea water is obviously not restricted to the maintenance of a favorable osmotic pressure with the body fluids, for many forms, notably fishes, are not isotonic with sea water in this respect. Waters of inland salt lakes may have a favorable osmotic pressure (resulting from concentration of various salts) for marine organisms, but other essential salts are wanting and the waters will therefore not support marine life. Even such forms as the shore isopod Ligia, which avoids being submerged in the sea, from whence it appears to be in process of migration, is unable to live unless its gills are moistened with sea water in order that it may acquire the essential salts and water useful in its respiration (Barnes, 1932).
Temperature
Temperature is a factor of prime importance in the marine environment because of its action (1) directly upon the physiological processes of the animals, especially upon the rate of metabolism and the reproductive cycle, and (2) indirectly through its influence on other environmental factors such as gases in solution, viscosity of the water, and density distribution with all its important hydrographic implications, discussed elsewhere.
An extensive literature has been built up pertaining to the effect of temperature on biological phenomena in the sea. This results first of all from the general recognition of the eminent importance of this factor and also from the fact that it is the most readily and accurately measured of the factors. This combination of circumstances may tend to give undue weight to the significance of temperature in relation to factors such as season, exchange or movement of water, and so forth, of which the temperature is only an index, and to factors such as density or viscosity which are functions of temperature (pp. 56 and 69). Nevertheless the abundant proof of its effects on life in the sea either directly or indirectly warrants a rather extensive review.
The range of temperature in the sea varies from about −3°C to 42°C, depending on season and locality, but in the open ocean the maximum temperature does not exceed 30°C. This range is small when
It should be remembered, however, that in the cold-blooded or poikilothermic animals living in an aquatic environment all changes of temperature of the external medium are accompanied (because of the high conductivity of water) by an immediate change in the internal temperature of the body. The regulatory mechanisms developed in many terrestrial forms are wanting and vital processes must consequently be affected accordingly. It is therefore not surprising that within the narrow temperature range found in the sea there are temperature barriers segregating faunas into rather well-defined geographical regions of submarine climatic conditions that are controlled not only by latitude but also by depth of water and general circulation.
Animals are commonly divided into two large groups with reference to their tolerance to temperature range, namely stenothermic and eurythermic animals. But, as with other classifications, there are many intergradations between the typically stenothermic and the typically eurythermic forms and the degree of tolerance may also vary with the stage in the life history of the individual. Nevertheless, the classification is sufficiently distinctive to characterize vast numbers of species and therefore faunas in general.
Within the temperature limits tolerated by an animal there are three fundamental temperatures. These are the optimum, the maximum, and the minimum. The optimum temperature for any given species is not readily defined, since it is evidently not the same for all stages and functions of life, as is indicated in reproductive cycles associated with season. The maximum and minimum refer to the upper and lower limits of thermal tolerance. They also vary with the stage of the life cycle and the past thermal history of the individual. It is generally thought that the optimum temperature lies nearer the maximum than the minimum, but recent studies on fishes indicate that this is not always so (Doudoroff, 1942).
In areas with severe winters the intertidal animals are likely to be relatively few in number owing to winter destruction by freezing or to abrasion of beaches by ice. Wholesale destruction sometimes occurs in milder regions during unusually cold winter periods. In a special investigation on the mortality among intertidal animals of Danish waters during an unusually severe and protracted winter period in which ice formed on the beach and sand froze to a depth of 15 cm, Blegvad (1929) found a very marked destruction of animals. The percentage of animals killed in the area studied is as follows: Mytilus edulis, 100 per cent; Littorina litorea, 100 per cent; Cardium edule, 80 per cent; Nereis diversicolor, 70 per cent; Arenicola marina, 95 per cent; Mya arenaria, 80 per cent; Macoma baltica, 33 per cent.
The optimum may be at the same or at a very different temperature for different species. Hence there are both cold-limited (phychrophile) and warmth-limited (thermophile) stenothermic forms, and as a result we find animals that are strictly endemic to cold- or warm-water areas of the ocean, as the case may be.
Geographic Distribution. It has been pointed out (Ekman, 1935) that early zoogeographers drew putative boundaries for littoral faunas based on climatic and hydrographic conditions. Rather little was known about the actual distribution limits of large numbers of species and faunal groups, but climatic boundaries had been discovered and the faunal areas were arranged according to these without their natural boundaries having been determined by empirical study. Zoogeographic boundaries must be determined in the final analysis by the actual distribution of the animals, but the marked importance of climate is shown by the fact that the early boundaries, drawn in the main speculatively, have been proved empirically to be well founded; which is to say that temperature is one of the most significant factors in the development of marine faunas.
Where temperature gradients are not well defined, the faunal zones do not have sharp boundaries either but merge one into the other with wide transition zones. The conditions in the Northeast Atlantic and the Northeast Pacific are considered especially illustrative of this. Along the east Atlantic coast, faunal boundaries are difficult to establish and a study of the isotherms of the North Atlantic reveals that the lines diverge toward the east and converge toward the west (charts II and III). For example, 36 per cent of the species of fishes found north of the Arctic Circle off Norway are found also in the Mediterranean. In the Northeast Pacific similar conditions are encountered, which are related to the divergence of isotherms on approaching the American continent. Here, however, the seasonal range in temperature is relatively small and upwelling along the coasts of North and South America keeps the coastal water cool to unusually low latitudes. The fauna of north temperate character has an extensive spread from the Bering Sea to Lower California, its closest affinities being with the Arctic rather than with the Tropical fauna. Among the arctic-temperate animals may be mentioned the genera Pandalus, Oregonia, Henricia. It must be noted also that in the east Atlantic boreal region the seasonal variations in water temperature are large in the coastal zone, having a range of 10° to 12°C off the coast of Norway and 10° to 15°C in the North Sea. These conditions tend to obliterate faunal boundaries for reasons discussed below.
Temperature and Reproduction. We have learned that there are many animals which are eurythermic while others are stenothermic, and that the stenothermic forms may be either warm stenothermic or cold stenothermic; that is, their optimum condition is at high or at low temperatures,
The very mixed fauna of the European boreal region is believed to be accounted for partly by these adjustments to suitable spawning season, for in these waters the seasonal range of temperature is sufficient to allow for northern and southern vegetative eurythermic forms to find periods suitable for stenothermic reproduction in the same area.
Results of examination of different species of oysters illustrate the variations in the critical spawning temperatures of marine animals. For both economic and scientific reasons, these animals have been studied in great detail by Trevor Kincaid, W. R. Coe, and others mentioned below, and the following minimum spawning temperatures have been established with considerable certainty (review by Hopkins, 1937):
| Ostrea virginica 20°C (exceptionally at temperatures as low as 17°C or slightly less; Loosanoff, 1939) |
| O. gigas 22–25°C (Galtsoff, 1930; Elsey, 1934) |
| O. edulis 15–16°C (Orton, 1920) |
| O. lurida 14–16°C (Hopkins, 1937) |
Although the above temperatures may be considered threshold temperatures, they can operate as determining factors only when other external and internal conditions are also within the favorable range. For example, the gonads must have reached the proper degree of development, which is itself a function of temperature and nourishment; the pH must be favorable, about 8.2 for Ostrea virginica (Prytherch, 1929); the presence of spermatozoa in the water may be necessary; and other uncertain factors also are involved (Galtsoff, 1930, 1938). The temperatures given above represent findings relative to the initiation of female spawning. Once begun it may continue at higher temperatures.
A good deal of evidence, both observational and experimental, shows that the distribution of many marine animals is dependent upon the above type of adjustments of critical reproductive periods within rather narrow temperature ranges. Orton (1920) concluded that:
A review of all the information collected bearing on the influence of temperature changes on breeding leads one to the conclusion that a temperature stimulus of some kind is the normal impulse for inducing sexual activity in marine animals assuming normal biological conditions. In marine invertebrates, at least, the impression is gathered that normal salinity variations within the habitat of the species have little effect on breeding. Since temperature is known to be of paramount importance in controlling distribution, it would seem that its influence on breeding is one of the ways in which the controlling effect is exerted.
Figure 234 and table 98, from an investigation by Runnström (1927), will serve to illustrate the relation between temperature and reproduction and larval survival of littoral marine fauna, of Arctic-boreal, boreal, and Mediterranean-boreal types of animals in boreal waters.
Vegetative distribution, especially of pelagic forms, may extend to areas beyond the limits set by the reproductive stenothermy; but such areas must be restocked regularly by adults or juveniles drifting in from favorable outside areas. This extended distribution is known as sterile distribution, and though the failure to reproduce in these extended areas may result from external environmental factors other than temperature, temperature seems nevertheless to be the major cause. It has been found, for instance, in the Bay of Fundy, that some species of fishes with floating eggs and such forms as the medusa Aglantha, the amphipod Parathemisto, the arrow worm Sagitta elegans, and still other forms either fail to reproduce at all or have very restricted success in reproduction although spawnings may occur (Huntsman and Reid, 1921, Fish and Johnson, 1937). The bulk of these animals must therefore be recruited seasonally by means of waters flowing in from the Gulf of Maine.
In the Gulf of Maine, Bigelow (1926) found that Sagitta serratodentata is a common constituent of the plankton. It thrives in these waters in the juvenile and adult stages, growing to a size greater than in its normal breeding habitat, but it is unable to breed in the Gulf because of the cold water. In the inner parts of the Gulf it succumbs during the winter and must be replenished each year by a new supply coming in with mixed water from the neighboring Gulf Stream. Its normal distribution is in waters above about 15°C.
Temperature and reproduction. Lines above temperature series indicate the temperature range within which normal development takes place for each of the three faunal groups included. The lines below the temperature series give the temperature range for the regions indicated.
| Fauna | Animal | Jan. | Feb. | Mar. | Apr. | May | June | July | Aug. | Sept. | Oct. | Nov. | Dec. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Arctic-boreal | Strongylocentrotus drobachiensis | + | + | + | |||||||||
| Cucumaria frondosa | + | + | + | ||||||||||
| Dentronotus frondosus. | + | + | |||||||||||
| Boreal | Pleuronectes platessa. | + | + | + | |||||||||
| Mytilus edulis. | + | + | + | + | |||||||||
| Echinus esculentus. | + | + | + | + | + | ||||||||
| Asterias rubens | + | + | + | + | |||||||||
| Mediterraneanboreal | Psammechinus miliaris | + | + | + | + | + | |||||||
| Echinocyamus pusillus | + | + | + | + | |||||||||
| Echinocardium flavescens | + | + | + | + | + | ||||||||
| Echinocardium cordatum | + | + | + | + | |||||||||
| Ciona intestinalis | + | + | + | + | + | + |
The tropical and subtropical copepod Eucalanus elongatus is carried far north with the Gulf Stream, but only adult or submature specimens appear to survive in the gradually cooling waters approaching the higher latitudes (Farran, 1911, With, 1915).
One of the most striking instances of the effectiveness of temperature differences as a barrier to distribution of benthic animals in the open deep sea is shown by a study of the fauna on the two sides of the Wyville Thomson Ridge (Murray and Hjort, 1912). Over this ridge, covered by water to a depth of about 500 m and connecting the Shetland and Faeroe Islands, the Gulf Stream water flows into the cold Norwegian Sea (p. 652). At the top of the ridge temperatures on both sides are only moderately different, but bottom temperatures of 4°C are found at a depth of 1500 m on the south or Atlantic slope while on the northern slope in the Norwegian Sea the temperature is 4°C at about 600 m, 0°C at 850 m, and −0.41°C in the bottom waters. An analysis of the fauna of each side showed that only 48 species and varieties, or about 11 per cent of a total of 433 enumerated by Murray, are common to both sides.
Bipolarity. It has long been known that the faunas of the cold waters of the north and south latitudes contain many elements in common. The animals or animal groups that form these elements may be wanting in the intervening tropical region. A break in the continuity of distribution of a species or higher division is called discontinuous distribution; when it occurs in a meridional direction so that the animals involved are absent from the tropical belt, the phenomenon is known as bipolar distribution or bipolarity. According to the older concept, only the arctic and antarctic regions are involved, but more recent usage includes the temperate zones also, and bipolar animals need not necessarily be polar. This is bipolarity of relationship and may be defined as a bipolar distribution in which animals of higher latitudes are more closely related taxonomically to each other than to those of lower latitudes. There is also bipolarity of phenomena such as are associated with mass vernal production of diatoms, for example, or with production of great numbers of individuals but of relatively few species.
Associated with bipolarity of relationship is the phenomenon of tropical submergence. Stenothermic animals that require cold water can of course find this by seeking greater depths; if they are sufficiently euryhaline and eurybathic, northern littoral or surface pelagic animals may form a continuous distribution from high northern to high southern latitudes by living in deep water in that part of their meridional range
Examples of bipolarity are found in the gephyrean Priapulus caudatus of the Northern Hemisphere and a subspecies in the Southern Hemisphere. The pteropods Limacina helicina and Clione limacina of the north have related forms in the Southern Hemisphere. Other examples are the ascidian Didemnum albidum, and the shark Lamna cornubica. Bipolarity is not confined to species; the counterparts may be genera or families, in which cases bipolarity seems to be of older standing.
Since we are interested here mainly in showing the influence of temperature on distribution as illustrated by bipolarity, it is not proposed to discuss fully the means by which bipolarity was established. Two chief hypotheses have been advanced, the first holding that bipolar animals are relics of a previously cosmopolitan fauna, the tropical portion of which is now extinct; the second hypothesis holds that animals have migrated through cold deep water. A third hypothesis involves parallel development of the bipolar forms. It has been pointed out that the first two hypotheses do not conflict but are only different interpretations of the same idea, which we must accept under any circumstances if we consider the subject from the viewpoint of the history of development, to wit, that today's discontinuity emerged from yesterday's continuity. For one species the discontinuous distribution may have developed according to one hypothesis and for another species according to another; therefore each case must be studied independently.
Recently, through the purposeful efforts of man, a bipolarity has apparently been established in the Pacific salmon Oncorhynchus. The native distribution of this fish is confined mainly to the temperate waters of the North Pacific, but extends also into colder waters of the adjacent northern seas. Foreign transplantation of species of this genus has been successful in South Island, New Zealand, and at the southern tip of Chile. Many attempts to establish these migratory fish in the intervening areas of the tropical region between the native range and the new locations have met with failure. A study of the limiting environmental factors (Davidson and Hutchinson, 1938) shows that the temperature conditions at the newly established localities are comparable to those at the southern
The effect of temperature differences on animals influences the vertical as well as the horizontal distribution. This was illustrated by the tropical submergence of forms which, showing a continuous meridional distribution, inhabit both high southern and high northern latitudes.
In arctic waters, where the range of temperature between deep and shallow water is small compared with differences between shallow and deep water of lower latitudes, the demarcations between littoral and deep-water fauna are less clearly defined. Examples of this are the sea star Hymenaster pellucidus and the pycnogonid Nymphon robustum, each of which occurs in the Norwegian Sea at depths of 2000 m, while near Spitsbergen the former occurs at 27 m and the latter thrives at 6 m. It appears from these and many other instances that temperature and not depth is the controlling factor. In a study of recent foraminifera in ocean sediments extending from lagoonal conditions to a depth of 2540 m, Natland (1933) found that the vertical distribution of the animals was arranged in five zones, each with certain key species correlated with submarine temperatures. A complementary study showed the same type of zonation of the same species in fossil-bearing geological strata of outcrops and oil-well borings in the same general region, thus providing a means of arriving at the probable temperature and perhaps, therefore, also the depth of water and other conditions that prevailed when these strata were formed as sediments on the bottom of the sea. In other words, this zonation is illustrative of the fact that dissimilar fossil faunas may have been contemporaneous but may also have lived under different environmental conditions with respect to temperature.
Pelagic animals also show a degree of bathymetric stratification which may be associated with the temperature distribution in the sea. In this connection it is difficult, however, to isolate the effect of temperature from that of light or to find out whether the temperature exercises a direct or an indirect influence. Indirectly it may act through its influence on viscosity, or it may change the reactions of the animals to gravity or to light, that is, change the sign of tropism with respect to these factors. Even in the phenomenon of tropical submergence we must not fail to be aware of the fact that light, owing to the great intensity of the tropical sun, may possibly force some animals, especially pelagic animals, to seek greater depths.
In the discussion of diurnal migrations we noted that the sharp temperature gradient frequently encountered at the thermocline deters some of the deeper migrants from coming to the surface or some of those living normally near the surface from venturing below into markedly colder water (p. 838). Bigelow and Sears (1939) indicate that, aside from
Species of the fish genus Cyclothone descend to greater depths in southern than in northern waters. Among crustaceans the larger individuals of the pelagic prawn Acanthephyra purpurea occur at a depth of 500 to 750 m in the northern section traversed by the Michael Sars. In the lower latitudes these were found most abundant at 1000 m.
Metabolism. The optimum temperature for life activity is considered to be nearer the maximum than the minimum limit, for which reason a small rise in temperature from the optimum is more likely to be disastrous to cold-blooded animals than is a greater lowering (see p. 844). The latter will result in a marked slowing up of vital processes, but if not extreme may actually lead to an extension of the individual's life by inducing a period of quiescence when other factors, especially food supply, are at a minimum. This life extension may be illustrated by such forms as Calanus finmarchicus and C. hyperboreus, which during the winter months sink to, or seek, deeper water (200 to 300 m in some areas) and reduce their migratory activities (Gran, 1902, Sömme, 1934). Experimental tests have also indicated that Calanus grows and moults into successively older stages less rapidly at a temperature of 3°C than at temperatures of 6°C and 9°C, but survival is definitely better at the lowest temperature (Clarke and Bonnet, 1939).
The rate of metabolism (measured by oxygen consumption and production of carbon dioxide) of all poikilothermic organisms is very much increased with rise of temperature. According to van't Hoff's rule the increase is two to three times for each 10°C rise in temperature within favorable limits. Hence, it serves as one of the factors in the rapid and abundant spring production in boreal regions. During the winter when food supply is at a minimum in boreal waters, Calanus finmarchicus, for example, in copepodid stage V is found to sink to deep water, as already mentioned, where the temperatures are uniformly low and metabolism is accordingly slowed up. Here the animals may remain more or less quiescent until the return of spring, when they approach the surface, assume the adult state, and spawn in the upper water layers at a time when food has again become abundant. Among the coastal forms, the daphnids Podon and Evadne survive the low winter temperatures as resistant resting eggs. Rotifers and perhaps other coastal animals may do likewise, and are therefore able to appear suddenly in abundance in the spring plankton when vernal warming has taken place.
Numerous experiments have shown that oxygen consumption increases directly with rise in temperature. For a typical planktonic animal,
Calcium Precipitation. Temperature influences to a marked degree the rate at which calcium carbonate can be precipitated by animals in the formation of skeletal parts, shells, and spicules. The chemical reactions involved are not clearly understood, but they proceed more rapidly at high than at low temperatures; hence organisms that utilize calcium compounds in their supporting or protective skeletal structures are notably abundant in warm tropical waters, for in this environment shells can be grown faster and heavier than in the cold waters of higher latitudes or the deeper water layers where calcium precipitation is accomplished under great difficulty (Murray, 1895). Among the littoral life we need mention only (1) the marvelous coral faunas which have developed extensive reefs of great geologic importance and which have a wide north-south range in the western sections of the oceans but a narrower range in the eastern sections where the range of warm water is also narrowed, and (2) the beautiful and varied molluscan shells, including the giant clam Tridacna gigas, which may grow to a length of 1.5 m and a weight of 250 kg (551 lb). Conspicuous among the warm-water pelagic animals are the shelled foraminifera and pteropods.
Calcium-precipitating organisms are present in all seas, but their numbers are much reduced in the fauna of the cold polar seas and the shells of those present are relatively more weakly constructed. Some cold-water pteropods construct no shell, living naked, as some species of the beautiful and large Clione. Limacina helicina of Arctic waters does possess a shell but the animal is reduced in size and its shell is very thin. Among the foraminifera, a group apparently very sensitive to temperature conditions, the calcareous-shelled species are replaced in cold northern waters by the arenaceous types, which build shells of sand, fragments of shells, spicules, and so forth, cemented together with noncalcareous cement. Arenaceous types are also characteristic of deep-water foraminifera. In very deep water, therefore water of low temperatures, the skeletons of benthic animals are notably thin and fragile, as exemplified
This restricted production of calcareous structures in deep-sea animals can hardly result from a lack of lime for many poorly calcified forms are found where the bottom deposits consist of globigerina ooze which has resulted from precipitation of pelagic foraminifera living in the upper layers. Low temperature is apparently a major cause of the limited production of calcareous structures although the great hydrostatic pressure in deep water may be of importance because it is believed to increase the solubility of calcium carbonate (Buch and Gripenberg, 1932). The absence of violent water movement or even moderately fast flow in the deep sea may also be responsible for the small deposition of calcium by sessile organisms, and the absence of strong motion makes it possible, on the other hand, for many of the fragile-shelled and weak organisms to survive where otherwise they could not exist.
The effect of temperature on biological deposition of calcium carbonate provides a key to the interpretation of temperature conditions and water depths that must have prevailed at periods when certain geological strata of marine origin were laid down in the distant past. The present slight deposition of lime in cold polar regions, as contrasted with what must have occurred when ancient coral reefs were constructed there in Paleozoic times, leads to the theory that these ancient seas must have had a temperature of about 15° to 18°C (Murray, 1895).
Coral-reef formation is a most striking example of marine biological activity, which has attracted wide attention of both laymen and scientists. The coral reefs do not result from spectacular outbursts of activity such as occur among pelagic forms, but rather from the persistent accumulation of calcareous deposits which remain long after the cessation of the biological activity which produced them.
These great structures are outstanding features of the tropical seas. However, since the process of reef formation is a result of biological precipitation of calcium from sea water by corals, the rate of deposition is thermally controlled, as with other organisms. The inequalities of temperature distribution along the continental margins of the tropical
The organisms entering into reef formation are of several types, including chiefly the stony or madreporarian corals, but associated with these are also a number of other calcium-depositing coelenterates such as the Millepora. Very important are the foraminifera and a number of calcareous coralline algae known as the nullipores, of which the red Lithothamneon and the green alga Halimeda are examples. The nullipores in particular contribute vastly to reef formation. In some reefs corals play only a subordinate role.
The reef-producing corals can flourish only in water above about 20°C and are therefore confined to the shallow water of tropical seas. Although conditions are unfavorable for growth below a depth of 50 to 60 m, the slopes of reefs are known to extend to great depths. Also, through examination of material brought up from deep borings (340 m, 1114 ft) within the reefs it is shown that the structure of coral reefs extends to depths far greater than are tolerated by the living animals or plants that enter into the formation of the reefs. Obviously, if the coral fragments occurring at the base of the reefs were laid down in situ, the water level must have been at one time near the level of the base. This implies that the sea bottom on which the reef rests was once at a higher level, or that the sea surface was lower than we now know it.
The subject of reef formation from geological and biological viewpoints has been dealt with in an extensive literature to which the interested reader is referred (see especially Davis, 1928, and Gardiner, 1931). For our purpose it will suffice to state here that the theories which have been advanced largely involve changes in sea level with respect to the substratum on which the coral-building organisms initiated their growth. Some theories assume a sinking of the earth's crust, others a rise in sea level, or a combination of both. Without entering into details on these theories, we shall point out that here is illustrated a problem of the sea the interpretation of which is directly dependent upon an understanding of the organisms involved, for any theory advanced must take into account the biological requirements of the reef-building organisms, which comprise warm, relatively shallow, clear, saline water.
Temperature and Size. There is much evidence, from direct observation of populations obtained from various waters, to indicate that frequently cold-water animals grow to a larger size than do similar animals in warm water. A few examples will suffice to illustrate this point.
The warm-water epiplankton populations of copepods, the most characteristic of plankton animals, stand in striking contrast to the cold-water populations because of the apparently greater success of the larger species in the cold waters. A fair number of small species of such genera as Oithona, Oncea, Pseudocalanus, and others, of size ranging from about 0.5 to 1.5 mm, do live in cold northern waters and, conversely, a number of large forms, for instance, Eucalanus elongatus (8.0 mm) and Rhincalanus cornutus (3.4 mm) are found in warm waters; however, the warm-water populations are especially characterized by a large number of small species whereas the populations of arctic and boreal waters are mainly composed of great numbers of individuals of a few species, for example, Calanus hyperboreus (10 mm), C. finmarchicus (5.4 mm), C. cristatus (9.3 mm), Eucalanus bungii (8.0 mm). The deep cold waters of lower latitudes are also populated by large forms comparable in size to northern species. The numbers of individuals are, however, relatively fewer.
This tendency to larger size in colder waters is noticeable in related species and even in individuals of the same species. Jespersen (1939) reports that Calanus finmarchicus in Greenland waters forms two size groups, the larger being found particularly in waters of low temperature and the smaller-sized population in warmer surface layers of pronouncedly Atlantic waters. Steuer (1933) found a three-modal curve for body size of three varieties of Pleuromamma taken in the Benguela stream. A dwarf variety (P. minima) occurred in the uppermost, warmest water, a medium-sized race (P. piseki) in the middle layer, and a giant race (P. maxima) in the lower and coldest layer at about 600 m. Steuer has shown also that individuals of the copepods Acartia negligens and A. danae become smaller in transition from the Canary Current to the warm Guinea Stream. Similarly A. danae is larger in the South Equatorial Current, which is mixed with cold water of the Benguela Current.
Some radiolaria, especially the Challengeridae, have been shown to increase in size progressively with depth. In the genus Challengeria eight species can be grouped into three size categories: 0.11 to 0.16 mm, three species; 0.215 to 0.28 mm, three species; and 0.35 to 0.58 mm, two species. These categories correspond to depths of 50 to 400 m, 400 to 1500 m, and 1500 to 5000 m, respectively. Thermal influence on the size of pelagic protozoans is well illustrated also by the ciliates Tintinnoinea collected by the Agassiz Expedition. An analysis of the dimensions of loricae of 1000 individuals of a single species (Tintinnus tenue) of these animals showed that those taken in the Peruvian Current stations with surface temperatures of 19° to 23°C, were predominantly larger than those taken elsewhere at stations with temperatures of 24° to 28°C (Kofoid, 1930).
The effect of this factor on size is indicated also in the plankton fishes. Investigations of the Michael Sars showed that the small deep-sea fishes
Two explanations have been given to account for the increased size of cold-water planktonic forms.
(1) The increased density and viscosity of cold waters enables large forms to keep afloat more successfully in cold than in warm water (p. 822). The matter of overcoming the constant action of gravity is of paramount importance to weakly swimming animals like the smaller crustaceans, as well as to the passively floating radiolaria and many other forms. A size commensurate with viscosity and swimming power is one of the means of overcoming this ever-present tendency to sink. Just how important viscosity may be for delicately adjusted forms is suggested by the fact that the value of the viscosity at 50 m in the Norwegian Sea corresponds to that at 800 m farther south in the Atlantic (Murray and Hjort, 1912).
(2) Lowered temperatures lengthen the time required for poikilothermic animals to reach sexual maturity. Hence, in cold-water forms the delay permits a longer growing period with resultant larger size at maturity. It has been shown that the oxygen consumption of certain nonlocomotory warm-water benthic species is higher than that of related cold-water species with which they were experimentally compared, and this difference in metabolism may have a bearing on the question (Fox, 1936).
The more rapid attainment of sexual maturity in warm-water animals has certain important implications in that it permits a more rapid succession of generations in waters of tropical and subtropical regions. To illustrate this we may refer again to the oyster, Ostrea virginica. In a study of the sexual phases of large numbers of these bivalve molluscs, Coe (1938) found that
From Cape Cod to the Chesapeake Bay, most of the young oysters may be expected to spawn at the age of one year. North of Cape Cod the first spawning is stated to occur more often at the end of the second year, as is the case with some individuals in certain years south of Cape Cod. On the coast of North Carolina and in the Gulf of Mexico, well-nourished individuals of the early set spawn toward the end of their first summer, when only three to four months of age, while those of the later set do not become mature until the following spring.
An increased rate of reproduction is also common in other animals. The more rapid turnover of generations and the more nearly optimum living conditions of lower latitudes, with relative absence of drastic seasonal changes associated with temperature conditions, apparently lead to production of a greater number of species of most animal groups and to
Ocean Currents
If the waters of the oceans were not kept in vigorous circulation by the various forces discussed elsewhere, they could support only a small fraction of the marine life that actually now exists. First of all, the amount of primary food produced by plants would be so curtailed by exhaustion of the essential nutrients in the euphotic zone that only a few animals could find nourishment. The slow diffusion of gases and toxic wastes that could take place would set shallow vertical limits of distribution to all forms of life except certain anaerobic bacteria. The northern and southern boundaries of faunal zones dependent on temperature or light would coincide with parallels of latitude.
But the ocean waters are not stagnant. Vertical circulation extending to great depths occurs, and greater or smaller masses of water flow continuously in systems extending in diverse directions over vast areas, irrespective of latitude. Far to the north along western continental shores in the Northern Hemisphere the currents convey heat that has been stored in the waters during their passage through warm, tropical regions. Similarly, along the eastern continental shores cold water masses are carried to the south by currents of arctic or subarctic origin, causing isotherms to streak obliquely across the oceans in a general northeasterly direction. Systems of similar character and magnitude exist in the Southern Hemisphere (Charts II and III).
Water movements provide a means of transportation for organisms which, when combined with temperature and other factors, may control the limits of propagative and sterile distribution of both pelagic and benthic life. The character of the fauna and flora is thus governed by the nature of the currents—namely, their origin, direction of flow, magnitude, coldness or warmth, degree of salinity or density, and their character as regards other attributes such as relative richness in nutrients.
We have just reviewed some of the influences of temperature on animal life. Some of these influences are inseparable from ocean currents, for temperature is usually an index of flow. With this in mind, we shall now endeavor to examine more closely some features wherein water movements are of far-reaching biological significance.
Significance of Currents in Dispersal and Maintenance of Populations. Perhaps the most obvious importance of currents on marine life results from its direct influence on dispersal. It has already been pointed out (p. 315) that nearly all benthic animals in the littoral zone possess free-swimming or floating eggs and larvae. The significance attached to this type of life history in any given species must be that it provides a means of taking advantage of water movements to bring
about and maintain as wide distribution as possible, so that all environmental facies favorable to the life requirements of the adult both for spawning and vegetative growth can be inhabited. During this dispersal, countless thousands of larvae are carried into areas where they are unable to live or where at desertion of the pelagic life the sessile stages find conditions unsuitable with respect to depth of water, substratum, chemical-physical character of the water, or such other factors as food and enemies. This, however, is the price paid for the widest possible distribution.
Vast numbers of young are accordingly produced by each individual in order to overcome the hazards of the temporary pelagic existence (see p. 316). By far the largest number of larvae of benthic forms are eaten by predacious animals or succumb as a result of settling in inimical environments at the time of metamorphosis and desertion of the pelagic habit. That great numbers, however, do find favorable settlement is witnessed by extensive populations of benthic animals. Certain areas may be quite suitable to maintain a population but this population may be unable to restock to any appreciable extent from its own spawning, owing to the prevailing currents carrying the eggs and larvae completely away from the area and into other situations where settlement may or may not occur. These areas cannot be considered as areas of sterile distribution for reproduction does take place and larvae can survive, but because of circumstances associated with currents the areas must be regularly restocked by incoming larvae from elsewhere. Most benthic populations, perhaps, experience to some degree such renewal of stock by larvae produced elsewhere, and in turn they contribute their own larvae to restock other areas. Oscillating currents related to tides within a bay or fjord function to reduce loss of larvae and to maintain a degree of independence for its population.
When the larvae of benthic forms have survived to settle in a favorable habitat, the new stage of life is still dependent upon currents to maintain tolerable living conditions with respect to aeration, dispersal of toxic wastes, and supply of planktonic food. To coastal animal communities where the temporary plankton element is conspicuous, coastal circulation resulting from more or less local conditions such as tides and winds is of especial importance; but we shall see that larger and more permanent current systems also affect the lives of members of the temporary plankton and their adult stages.
As illustrative of the role of currents in the life of coastal benthic animals we refer to the study of Emerita analoga (Johnson, 1939b), the sand crab which in the benthic state inhabits sandy beaches in the intertidal zone. The female incubates the eggs, which remain attached to body appendages until the first zoeal larval stage. Then the larvae are freed to seek food and to face the regular hazards of enemies and possibly
The distance to which these or other temporary larvae can be transported depends of course upon the speed of the currents, the adaptability of the larvae, and especially upon the normal length of pelagic larval existence. In Emerita the larval stage is of long duration, being a matter of about four to five months and resulting in transport seaward at least 200 miles and doubtless much greater distances in coastwise currents. In the oyster the larval stage is shorter, being only about two to four weeks, depending upon temperatures. Yet oysters are known to extend their range of distribution at least 30 miles in one season through drift of the pelagic larval stage (Elsey and Quayle, 1939).
The dispersal of larval stages of Emerita analoga and other littoral crustacean larvae. Figures within the squares indicate the number and zoeal stages of Emerita; the symbol + followed by a number indicates the number of unidentified crab larvae. The character of the currents is indicated by the lines with arrows. (From Johnson.)
The great stretch of open water between the west coast of Central America and the easternmost Polynesian Islands is considered an effective
The depth at which passive eggs of the temporary plankton are carried by water currents depends to a great extent on their specific gravity in relation to that of the waters wherein they were spawned or to which they may rise (Walford, 1938). It was found (Thompson and Van Cleve, 1936) that halibut eggs occur in the denser waters some distance offshore at the outer edge of the spawning banks in depths of 100 to 200 m, though occasionally at only 40 m and at other times as deep as 935 m. The eggs were completely absent in shallower net hauls near the surface in waters with a low salinity and low specific gravity. From these facts it appears that they drift with the slowly moving deep currents. The newly hatched halibut larvae are found outside the continental shelf and at depths over 200 m. As the larvae develop, however, they rise to the upper layers until at the age of three to five months all of them are found at depths of 100 m or less. With the rise to the surface they are carried by inshore currents into shallow Alaskan bays, where they are found on the bottom. The cycle requires about six or seven months for completion. In the southern range of the northern halibut the powers of recuperation of the overfished stock are apparently less than in the stock of the Alaskan area, owing to a more unfavorable dispersal of the pelagic eggs by offshore or southward-moving currents in the southern area (Thompson, 1936).
Perhaps the best known example of transoceanic transportation of organisms is found in the investigations of Johannes Schmidt (1925a), dealing with the life history of the European eel Anguilla vulgaris. Full-grown and submature eels inhabit fresh-water streams and lakes, but upon approach of complete sexual maturity in autumn they desert these waters and disappear into the sea to spawn. The destination of the eels during these spawning journeys was for centuries one of the deepest mysteries of the sea. The young, recently metamorphosed eels, known as elvers, (about 6 or 7 cm long) have long been known to occur in the European coastal waters where in spring they enter fresh water in great numbers, but it was not known where in the sea they had originated. Strange theories were advanced; for example, Pliny and Aristotle believed they arose from mud of the sea bottom. Only in the last few decades have these mysteries been solved. Not until 1896 was it shown (Grassi, 1896) that a strange ribbonlike little fish, considered since 1856 as a separate species called Leptocephalus brevirostris, was in reality an eel developmental stage which through metamorphosis becomes the elver.
With this information at hand Johannes Schmidt in 1904 began investigations which extended over many years, involving examination
The American eel Anguilla rostrata breeds in the same or adjacent waters. Its life history requires only two years of larval life, for although the bulk of larvae migrate for a period in the same current as the European larvae, upon nearing the North American coast they become segregated from the European larvae, which are destined to continue slowly onward to the east.
The animals belonging to the permanent plankton may also be transported by currents over great distances, and this is particularly true with respect to the main oceanic currents. If the courses be sufficiently long or circular, the animals will successfully propagate while en route. Successful propagation is indicated when all stages of development of a given species are found in the transporting waters. Usually, however, the waters change their character as regards temperature, salinity, and so forth, or they may merge with other waters and lose their identity entirely or in part. In this case many of the animals that are being transported may die. Some of the hardier species frequently survive for some time and may even spawn, but the young are unable to withstand the environment unnatural to them (see p. 863). In this event the plankton catches will show only adult or submature stages, sometimes eggs and a few early stages, but few if any of the intermediate ones. Restocking must then take place regularly or periodically in successive invasions from the outside. The presence of these exotic animals is living evidence of the source of the water, provided the normal habitat of the species is known. Gulf Stream species are classical examples of planktonic animals that appear as visitors in localities where they do not normally breed. Illustrative of this are certain salps and the tropical copepod Rhincalanus nasutus occurring off the coast of Norway. Other examples are found in the northern penetration of R. nasutus and also
On the west Atlantic coast a number of Gulf Stream forms are swept by offshoots of the main current into the Gulf of Maine. They may survive there for varying periods of time, although the temperature and salinity are much reduced by mixture with coastal waters. Bigelow (1926), by a study of plankton catches, has determined the point of entrance of these immigrant forms and has traced their course after entering the Gulf and mingling with the endemic plankton community. They enter the Gulf at three levels and show varying degrees of success in establishing themselves, depending upon their species and adaptability. It is found, for example, that Sagitta serratodentata is a very hardy warmwater visitor that survives long enough to complete a good portion of the large counterclockwise gyral within the Gulf, and it may even grow to a larger size than in its native Gulf Stream habitat, although it cannot reproduce with sufficient success to establish itself as endemic. Adults may live for a time in waters with temperatures as low even as 3.9°C but do not survive the winter in the invaded area. Redfield and Beale (1940) have verified Bigelow's conclusion (1926) that this species does not reproduce in the Gulf of Maine. Because of this sterile distribution the animals are known as terminal immigrants. Their periodic occurrence depends upon periodic changes in the flow of outside water into the area. Sagitta maxima enters the Gulf in the deep layers and becomes dispersed in the deeper part where salinity is highest. Rhincalanus cornutus and R. nasutus are also stray tropical and oceanic visitors in the Gulf.
Arctic forms are also found in the Gulf of Maine, giving evidence of the penetration of the southward-flowing cold Nova Scotian water past Cape Sable into the Gulf. Among these cold-water strays are included Calanus hyperboreus, the pteropod Limacina helicina, and the appendicularian Oikopleura vanhoffeni.
The pattern of horizontal flow is a determining factor not only in the widespread dispersal of exotic plankton elements from their centers of production, but also in maintaining an endemic population. The effect of oscillating tidal currents with a minimum residual flow was mentioned above as contributing to the maintenance of an endemic stock in restricted areas. Many partially landlocked bays maintain a characteristic population through such action. The semiclosed lochs of the Clyde Sea area, for example, have proved favorable regions for scientific study of local population cycles without too great an exchange with biological elements produced elsewhere and carried into the lochs (p. 903). But certain types of nontidal current systems are also effective in supporting a self-sustaining population of specific forms. Such are the eddies of
The growth of population in a mass of water assumed to move along the course indicated in inset. Ordinate: volume of zooplankton in cubic centimeters per square meter of sea surface; abscissa, time in months. The black bars indicate the volumes caught at the selected stations. The position of these stations and the month of collection are indicated on the inserted chart. (From Redfield.)
Damas (1905) and Sömme (1934) have discussed the importance of such currents in maintaining a breeding stock for pelagic populations in the Norwegian Sea. The Gulf of Maine on the American coast offers an excellent example of the biological effect of this type of circulation. Redfield (1941), carrying forward the earlier analyses of Bigelow and of Huntsman, concludes that the great cyclonic eddy of the basin of the Gulf is a vital factor in maintaining sufficient breeding stock to perpetuate an endemic calanoid population (Calanus finmarchicus and related forms) in that area and also to contribute to other neighboring waters. The regular recurrence of a closed eddy during the summer provides a tolerably uniform environment permitting the endemic species to complete their whole life cycle from egg to spawning adult while being swept involuntarily along in the moving mass of surface water wherein the bulk of the animals occur. Figure 236, from Redfield, shows how the shift of population center was followed in its drift around the Gulf. In chapter IX we learned that the rate of breeding of C. finmarchicus permits of two or three generations in a year. The rate of flow of water within the Gulf is about seven miles per day and requires about three months to make the complete circuit, thus allowing considerable time for development. In early winter there is an indraft of relatively barren water from the northeast, and also during this time the center of the endemic population is being forced gradually to the southwest, but in
A cyclic circulation resulting in a flow of water around an island may also lead to maintenance of an endemic stock. A good example depicting this is the investigation of the drift of eggs and larvae of gadoid fishes around Iceland (Schmidt, 1909). Hydrographic investigations show a clockwise current which flows around the island at a speed just sufficient to transport the developing eggs and larvae passively from the spawning ground, located on the south and west coasts, to the north and east coasts where the advanced larvae seek the bottom to continue growing after their coastwise journey of several hundred miles in the plankton. The motility of the older fish is also a factor in maintaining the local stock, but any circuit of this nature must be a particularly significant factor in maintaining an endemic population of benthic life and of the general plankton as well.
Finally, the biological implications resulting from a difference in rate of flow of surface and subsurface water masses in any given area should be mentioned. Planktonic animals that inhabit deep water and that perform no vertical migrations must cross into other water masses less frequently than those making vertical diurnal migrations. Periodically the latter will become segregated horizontally from the former when their journey takes them into waters with different rates of flow. Different stages of development or even the sexes may experience some degree of segregation from this cause, since it is known that the adults and juveniles, as well as the sexes of some species, do not all migrate at the same rate (p. 837). Hardy (1935) has shown how vertical migrations and the dynamics of distribution may function to segregate phytoplankton and zooplankton swarms (p. 900).
Certain areas of slowly moving water at depths of 300 m or more are held responsible for the maintenance of a stationary winter population of Calanus finmarchicus in the Norwegian Sea (Sömme, 1934). If these animals were to winter in the surface waters instead of descending to greater depths, they would become dispersed by the more rapid surface currents and thus dilute the breeding stock for spring production.
Indicator Species. From what has been said of the far-reaching biological influences of water movements, it becomes obvious that the intelligent interpretations in any marine ecological investigation must be based in part on data which provide a reliable picture of ocean currents both locally and in general. Descriptions of current systems and discussions of methods for observing or computing currents are given elsewhere,
We have seen that many animals are carried passively by currents into areas other than those in which they normally live and breed. If now we consider the problem conversely, these exotic forms whose developmental history, habits, and source are known become invaluable indicators of the source of the currents or water masses in which they are found.
A review of the voluminous literature bearing upon this subject is best obtained in recent special publications (Russell 1935a, 1935b, 1939). As examples of indicators we need here only refer back to the forms used in illustrating the dispersal of animals by currents. It must be born in mind that for most reliable use of indicator species the following pre-requisites are necessary:
Exact identification of the species or varieties of organisms involved must be possible.
Their propagative and sterile distribution must be satisfactorily known.
The morphological stages of development in the life history must be known for the species or must be deducible from what is known of the group to which they belong. In this connection the time and depth at which spawning occurs and the duration of the various stages are important. Passive eggs and larvae may be adjusted in specific gravity to heavy or light water layers and therefore transported mainly in layers of corresponding density (p. 861).
It should be known to what extent ecological adjustment can be made by migrations into deeper or shallower water in the extended geographical distribution. For example, Calanus hyperboreus and Parathemisto oblivia, arctic species, may live in deep cold water in lower latitudes and by vertical migration may appear also in surface layers (Gran, 1902).
A clear distinction must be made between animals brought in from outside geographical areas and those of biological groups that develop locally when conditions simulate those of the outside geographical area, especially with respect to temperature (see p. 793).
Associations of organisms transported from a common center of distribution are of more value than occasional strays. Such associations may be expected to be found especially among the euryhaline-stenohaline neritic forms occurring in offshore situations, indicating seaward drift of coastal waters. Pelagic larvae of intertidal benthic species may be of special value if the duration of the various larval stages is sufficiently well known to supply information not only on distance of drift but also
― 867 ―on the time involved (fig. 235). These larvae thus serve as myriads of tiny drift bottles released along the coast.
Species Development. Indirectly, currents must have played an important role in the development of species. Through the ages, the currents have persisted in the dispersal of marine animals and many euryhaline and eurythermic species have become cosmopolitan. However, distributional limits are usually much more narrow for most animals since the scattering effect of currents must constantly work in opposition to the limiting effects of other factors and in particular to those of temperature, salinity, and light. It appears that the persistent pressing by currents of both the holo- and meroplanktonic forms into regions deviating from the optimal living conditions has had profound effects on the character of the fauna established in the more adverse regions. The less tolerant species are eliminated and certain genetic strains adapted to the more selective conditions are developed. It is generally believed that species-producing centers occur in the temperate or warm stable waters of the tropical belt. Strongly indicative of this is the correlation between temperature and the number of species of Tintinnoinea (Kofoid, 1930). Of the 705 known species of the suborder, 8 are restricted to fresh water, 59 to the Arctic seas, 42 to the Antarctic, and 515 to the warm temperate and tropical oceans. Though the polar faunas are not so fully known as the tropical, the ratio of cold- to warm-water species appears to be one to five.
Not merely species but many genera and even higher systematic groups are confined entirely, or nearly so, to the tropical region (Ekman, 1935). From these rich centers temperate and cold-water species have seemingly evolved through the process of selection at border regions where conditions become farther and farther removed from the optimum for stenothermic warm-water forms. The more rigorous living conditions of bordering areas have allowed only relatively few species to become established compared to the abundant fauna of tropical waters. This relation is brought out also for certain of the higher pelagic animals in table 99, adapted with modifications from a summary of the better-known holoplanktonic groups which was compiled from various specialists by Russell (1935b). The numbers given are not to be considered final, for it is certain that many species have not yet been recorded or are not included, but they are sufficiently complete to illustrate the preponderance of species in warm areas and to indicate other relative features to which reference will be made later.
The greater number of planktonic species in the antarctic region than in the arctic may be associated with the far greater area of confluence between the warm and cold waters in the Southern Hemisphere but, in addition, the general oceanic currents of the Atlantic appear to play a part, especially for the cold-water copepods (Russell, 1935b).
Cold-water species evolving outward from warm-water surface species may do so by dispersal either in a northerly or southerly direction, and also by submergence into the deep cold water of the tropics where deepwater genera and species are formed. The deep-water current system in the Atlantic (p. 747) favors the carrying of these deep-water forms, as well as those of the Arctic, toward the antarctic surface region (p. 620). That the antarctic and subantarctic copepod population has a closer connection with deep-sea genera is shown by the fact that in the Antarctic and Subantarctic 18 species belong to deep-sea genera (that is, genera in which 50 per cent or more of the species in a genus may be regarded as belonging to the deep sea), as opposed to only 3 species belonging to deep-sea genera in the Arctic and in boreal waters. Species that are bipolar-epiplanktonic (p. 850) are representatives mainly of surface genera (that is, genera in which less than 50 per cent of the species in a genus can be regarded as deep-sea species). Judged by these standards, 5 species of bipolar-epiplanktonic copepods are among surface genera and only 1 species from deep-sea genera. The extent to which bipolar-epiplanktonic species can develop apparently depends largely on the ability of northern cold-water species to withstand tropical submergence.
| Animals | Arctic | Arctic-Boreal and Boreal | Antarctic | Subantarctic | Bipolar-epiplanktonic | Cosmopolitan | Warm water | Deep sea | Total | |
|---|---|---|---|---|---|---|---|---|---|---|
( ) = Bipolar subarctic and subantarctic. | ||||||||||
| Coelenterata | ||||||||||
| Trachy- and Narcomedusae | 4 | 10 | 3 | 6 | 90 | 21 | 134 | |||
| Siphonophora: Calycophorae. | 2 | 1 | 64 | 5 | 72 | |||||
| Physophorae. | 1? | 2 | 29 | 2 | 34 | |||||
| Ctenophora. | 1 | 2 | 2 | 1 | 2 | 69? | 3 | 80? | ||
| Nemertea | 52 | 52 | ||||||||
| Polychaeta | ||||||||||
| Tomopteridae | 1? | 4 | 1 | 38 | ? | 44 | ||||
| Chaetognatha. | 2 | 2 | 2 | 18 | 6 | 30 | ||||
| CRUSTACEA | ||||||||||
| Cladocera. | 1 | (3) | 3 | 7 | ||||||
| Copepoda. | 7 | 10 | 32 | 5 | 1(5) | 10 | 489 | 195 | 754 | |
| Amphipoda | ||||||||||
| Hyperiidea | 2 | 10 | 2 | 250 | 28 | 292 | ||||
| Gammaridea. | 7 | 20 | 17 | 44 | ||||||
| Euphausiacea | 6 | 2 | 7 | (1) | 46 | 23 | 85 | |||
| Mollusca | ||||||||||
| Pteropoda | ||||||||||
| Thecosomata. | 2 | 1(1)? | 44 | 3 | 51 | |||||
| Gymnosomata | 1 | 2 | (1)? | 37 | ? | 41 | ||||
| Heteropoda. | 90 | 90 | ||||||||
| Tunicata | ||||||||||
| Appendicularia. | 2 | 1 | 6 | 1 | 48 | 3 | 61 | |||
| Thaliacea | ||||||||||
| Doliolidae | 1? | 11 | 12 | |||||||
| Salpidae | 1 | 24 | 25 | |||||||
| Pyrosomidae. | 8 | 8 | ||||||||
| Total | 23 | 35 | 71 | 19 | 17 | 15 | 1378 | 358 | 1916 | |
The greater number of species in the antarctic region over the arctic is also evidenced by littoral benthic life. But here the reason seems to be an historic one and not a matter of pelagic larvae or adults being transported thence by currents, for the Antarctic Continent is an isolated one and an extraordinarily large endemic population exists on its shores. Whatever the reason may be, it is of interest to note that, though warm or temperate waters appear favorable to species development, yet paradoxically the Antarctic possesses a littoral fauna richer in species than the Arctic shores of the Northern Hemisphere although the antarctic environment is colder than the arctic.
Oxygen
Oxygen is indispensable to the maintenance of the life processes of all organisms. It is available for normal metabolic activities of nearly all organisms only when it is in solution in a free state. A very few forms, notably the anaerobic bacteria, are able to carry on intermolecular respiration whereby the oxygen bound in the complex molecule of organic substance is made available as a source of energy. Therefore, biologically, free oxygen is comparable to carbon dioxide in being one of the two most important dissolved gases in the sea.
There are about 200 ml of oxygen in a liter of air as opposed to a maximum of about 9 ml in a liter of sea water. This is a great boon to air-breathing life, but with this advantage go also some disadvantages resulting from the need of maintaining moist respiratory surfaces in a desiccating environment. Aquatic and atmospheric respiration are similar in that the oxygen requires water as a respiratory medium; but in the former it should be noted that the oxygen-laden water is typically passed freely over the surface of relatively exposed respiratory organs or surfaces. Hence, although the concentration of oxygen reaching the respiratory surface is small, there is some compensation in its being rapidly replenished with complete flushing and aeration of the surfaces.
More oxygen can be dissolved in fresh water than in sea water, which should be advantageous to fresh-water animals; but, on the other hand,
The rate of metabolism is roughly doubled by a 10° increase in temperature. Therefore, during winter or in deep cold water, owing to the decreased rate of metabolism, much less food is required for repair following this slowing up of the katabolic processes. This reduced requirement must have an important bearing on the survival of many forms during winter when little food is being produced by the plants. The amount of oxygen used is somewhat different for different marine animals.
The order of magnitude of oxygen consumption in milliliters per gram of wet weight per hour within a temperature range of 17° to 25°C for various groups of marine invertebrates is as follows (averages from data of Fox, 1936, and compilations of Heilbrunn, 1937): Protozoa (Colpidium) 2.0; Coelenterates (jellyfish and ctenophores) 0.005; Echinoderms (various) 0.026; Annelids (various) 0.017; Crustacea (shrimps) 0.181.
For various marine bacteria the rate of oxygen consumption is very high compared to the above figures, being of the order of about 110 ml/g/hr at 22°C and depending upon nutrient conditions (ZoBell, 1940).
The great differences in the amounts of oxygen used per gram of wet weight are related to the great diversity in the water content of the living organisms. For example, low values found in coelenterates are correlated with the small percentage of solid organic material. Norris (in Hyman, 1940), for instance, found that the organic matter constituted only 0.85 per cent of the jellyfish Aequorea. The stage of development of some animals is also a factor in the rate of respiration. At 10°C Stage V of Calanus finmarchicus was shown to consume 0.25 ml of oxygen per thousand individuals per hour while adult females consumed 0.40 ml of oxygen per thousand individuals per hour (Marshall, Nicholls, and Orr, 1935). In recalculating the data of these investigators so as to present the oxygen consumption per hour in relation to weight in grams—using the average dry weight 27.35 mg/100 individuals of Stage V (Marshall, Nicholls, and Orr, 1935, p. 805), and considering the dry weight at 25 per cent of wet weight as Heilbrunn has done in his compilations—we arrive at an oxygen consumption of 0.228 ml/g/hr. If these figures present an accurate picture, we must assume that the metabolic rate of copepods is relatively high compared to other invertebrates, but this is in keeping with their very active lives. The figures arrived at for oxygen consumption by this species at Woods Hole are even considerably higher, namely 0.896 ml/g/hr at 15.5°C (see below). These values are higher than the ones found for certain marine fishes (Wells, 1935), the maximum oxygen consumption for Fundulus at 16°C being 0.220 ml/g/hr and for Girella at 20°C 0.242 ml/g/hr.
The concentration of oxygen in the sea is not only very much less per unit volume than in the air but there is also very much greater irregularity in its distribution and in some instances very sharp gradients may exist. The range of oxygen may be from 0 to 6.4 ml/l over a depth range of only 10 m, and in such rather isolated instances as in stagnant fjords the oxygen deficiencies are markedly reflected in the fauna.
The physical factors involved in the concentration, renewal, and distribution of oxygen in the sea are discussed elsewhere, and from these we note that on the whole the ocean, even in abyssal depths, is well supplied with oxygen for aquatic breathing organisms. We may therefore consider that oxygen is not, as a rule, a determining factor in the distribution and movements of most marine life. However, the irregularities in oxygen content and distribution referred to above are none the less highly important and, in many restricted instances, the low supply of oxygen and the hydrogen sulphide associated with this condition exclude all but anaerobic organisms on or near the bottom. Under these circumstances there may be not only an exclusion of animal life but a wholesale destruction of aerobic forms living at higher levels when temporary disturbances resulting from storms or surface cooling cause an upward displacement of these poorly aerated waters. This is witnessed periodically in certain Norwegian “threshold fjords” where a shallow sill prevents free water exchange with the sea and where summer heating and influx of fresh water have established a strong stratification of the water (pp. 147 and 802).
The Black Sea, with a maximum depth of 2104 m, being isolated from free circulation with the Mediterranean by the Bosporus Ridge, which extends upward to a depth of about 40 m, is illustrative of a condition where a more permanent biological climax has been reached. This high ridge precludes all opportunity of renewal of bottom water by oxygen-laden water from an outside source, and the accumulation of fresh water together with thermal conditions in the upper layers preclude any very deep aeration through convection currents. Decomposition of the rich organic material accumulating on the bottom from the productive surface layers has used up all of the free oxygen so that hydrogen sulphide extends upward from the bottom forming a layer of toxic water over 1800 m thick so that the lower limit of animal life is about 130 to 190 m (fig. 237). Only anaerobic bacteria can exist in the deeper portion of this environment, which constitutes about five times the volume of the upper portion capable of being inhabited by other organisms. These rigorous conditions, coupled with a reduced salinity, have led to an impoverished fauna with elimination of stenohaline and stenothermic species.
Very little is known regarding the relationship that exists between the oxygen-deficient or minimum layer (pp. 686–728) characteristic of
A section through the Black Sea to show hydrographic and biological conditions. (Modified from Nikitin.)
Schmidt (1925b) found that at a depth of 300 m in the Gulf of Panama, where there was only a 2 per cent oxygen saturation of water, plankton was about ten times more abundant than at the same depth in the Caribbean Sea with a saturation of 50 per cent. Oxygen determinations given in per cent may be misleading since they are a function of temperature and do not necessarily show the respiratory value associated with diminished metabolic rate in cold waters. The oxygen requirements of typically deep-sea plankton animals have apparently not been investigated.
Bibliography
“American Association for the Advancement of Science” . 1939. The migration and conservation of salmon.A.A.A.S. Pub.no. 8, F. R. Moulton, ed., 106 pp., 1939.
Barnes, T. C.1932. “Salt requirements and space orientation of the littoral isopod Ligia in Bermuda.” Biol. Bull., v. 63, p. 496–504, 1932.
Bigelow, Henry B.1926. “Plankton of the offshore waters of the Gulf of Maine.” U. S. Bur. Fisheries, v. 40, (for 1924), pt. 2, 509 pp., 1926.
Bigelow, H. B., and M. Sears. 1939. “Studies of the waters of the continental shelf, Cape Cod to Chesapeake Bay” . Museum Comp. Zool., Mem., v. 54, p. 189–378, 1939.
Blegvad, H.1929. “Mortality among animals of the littoral region in ice winters.” Danish Biol. Sta., Repts., v. 35, p. 51–62, 1929.
Bogorov, B. G.1932. “Materials on the biology of the copepods of Barents and the White Seas.” U.S.S.R., State Oceanogr. Institute, Bull.no. 4, English summary, p. 14–16, Moscow, 1932.
Brauer, A.1906. “Die Tiefsee-Fische.” Deutsche Tiefsee-Exped. Valdivia, Wiss. Erg., v. 15, Teil I, 432 pp., 1906.
Buch, K., and S. Gripenberg. 1932. “Über den Einfluss des Wasserdruckes auf pH und Kohlensäuregleichgewicht im grosseren Meerestiefen.” Conseil Perm. Internat. p. l’Explor. de la Mer, Jour. du Conseil, v. 7, p. 233–245, 1932.
Clarke, G. L.1933. “Diurnal migration of plankton in the Gulf of Maine and its correlation with changes in submarine irradiation.” Biol. Bull., v. 65, p. 402–436, 1933.
Clarke, G. L.1934. “Factors affecting vertical distribution of copepods.” Ecological Monographs, v. 4, p. 530–540, 1934.
Clarke, G. L.1936. “On the depth at which fish can see.” Ecology, v. 17, p. 452–456, 1936.
Clarke, G. L., and D. D. Bonnet. 1939. “The influence of temperature on the survival, growth, and respiration of Calanus finmarchicus.” Biol. Bull., v. 76, p. 371–383, 1939.
Coe, W. R.1938. “Primary sexual phases in the oviparous oyster (Ostrea virginica).” Biol. Bull., v. 74, p. 64–75, 1938.
Damas, D.1905. “Notes biologiques sur les copepodes de la mer Norvégienne.” Conseil Perm. Internat. p. l’Explor. de la Mer, Pub. de circonstance, no. 22, 23 pp., 1905.
Davidson, F. A., and Samuel Hutchinson. 1938. “The geographic distribution and environmental limitations of the Pacific salmon (Genus Oncorhynchus).” U. S. Bur. Fisheries, Bull., v. 48, p. 667–692, 1938.
Davis, W. M.1928. “The coral reef problem.” Amer. Geogr. Soc., Spec. Pub. 9, 596 pp., 1928. New York.
Doudoroff, Peter. 1942. “The resistance, reactions, and acclimatization of some marine fishes to changes of temperature.” Biol. Bull., v. 83.
Ekman, Sven. 1935. “Tiergeographie des Meeres.” Akad. Verlagsgesellsch. M. B. H., Leipzig, 542 pp., 1935.
Elsey, C. R.1934. “The Japanese oyster in Canadian Pacific waters.” Fifth Pacific Sci. Congr., Canada, 1933, Proc., v. 5, p. 4121–4127, 1934.
Elsey, C. R., and D. B. Quayle. 1939. “Distribution of oyster larvae from the 1936 spawning in Ladysmith Harbour.” Pacific Biol. Sta., Nanaimo, B. C., Progress Repts., no. 40, p. 8–10, 1939. Fisheries Research Bd., Canada.
Esterly, C. O.1917. The occurrence of a rhythm in the geotropism of two species of plankton copepods when certain recurring external conditions are absent.Univ. California Pub. in Zool., v. 16, p. 393–400, 1917.
Esterly, C. O.1919. Reactions of various plankton animals with reference to their diurnal migrations. Univ. California Pub. in Zool., v. 19, p. 1–83, 1919.
Farran, G. P.1911. “Resumé des observations sur le plankton. 2. Copepoda.” Conseil Perm. Internat. p. l'Explor. de la Mer, Bull. Trimestriel, p. 81–105, 1911.
Fish, C. J., and M. W. Johnson. 1937. “The biology of the zooplankton population in the Bay of Fundy and Gulf of Maine with special reference to production and distribution.” Biol. Board of Canada, Jour., v. 3, p. 189–322, 1937.
Fox, H. Munro. 1936. “The activity and metabolism of poikilothermal animals in different latitudes. 1.” Zool. Soc. London, Proc., p. 945–955, 1936.
Galtsoff, P. S.1930. “The role of chemical stimulation in the spawning reactions of Ostrea virginica and Ostrea gigas.” Nat. Acad. Sci., Proc., v. 16, p. 555–559, 1930.
Galtsoff, P. S.1938. “Physiology of reproduction of Ostrea virginica. 1. Spawning reactions of the female and male.” Biol. Bull., v. 74, p. 461–486, 1938.
Gardiner, A. C.1933. “Vertical distribution in Calanus finmarchicus.” Marine Biol. Assn. U. K., Jour., v. 18, p. 575–610, 1933.
Gardiner, J. Stanley. 1931. Coral reefs and atolls.London, Macmillan, 181 pp., 1931.
Gran, H. H.1902. “Das Plankton des Norwegischen Nordmeeres.” Rept. on Norwegian Fishery and Marine Investigation, v. 2, no. 5, 222 pp., 1902.
Grassi, B.1896. “The reproduction and metamorphosis of the common eel (Anguilla vulgaris).” Roy. Soc. London, Proc., v. 60, p. 260–271, 1896.
Grundfest, H.1932. “The sensibility of the sun-fish, Lepomis, to monochromatic radiation of low intensities” . Jour. Gen. Physiol., v. 15, p. 307–328, 1932.
Günther, A.1887. “Report on the deep-sea fishes collected by H.M.S. Challenger during the years 1873–1876.” Challenger Repts., v. 22, p. 1–335, 1887.
Hardy, A. C.1935. “The plankton of the South Georgia whaling grounds and adjacent waters 1926–1927, pt. 5., The plankton community, the whale fisheries, and the hypothesis of animal exclusion.” Discovery Repts., v. 11, p. 273–370, 1935.
Hardy, A. C., C. E. Lucas, G. T. D. Henderson, and J. H. Fraser. 1936. “The ecological relations between the herring and the plankton investigated with the plankton indicator.” Marine Biol. Assn. U. K., Jour., v. 21, p. 147–291, 1936.
Harvey, E. N.1920. “The nature of animal light.” Monographs on Exper. Biology.Philadelphia and London, Lippincott, 172 pp., 1920.
Harvey, E. N.1940. Living light.Princeton Univ. Press, 328 pp., 1940.
Heilbrunn, L. V.1937. An outline of general physiology.Philadelphia and London, W. B. Saunders Co., 603 pp., 1937.
Herdman, W. A.1923. The founders of oceanography.London, Edward Arnold & Co., 340 pp., 1923.
Hjort, J.1912. General biology. In Depths of the Ocean, by Murray and Hjort.London, Macmillan, 821 pp., 1912.
Hopkins, A. E.1937. “Experimental observations on spawning, larval development, and setting in the Olympia oyster, Ostrea lurida.” U. S. Bur. Fisheries, Bull., v. 48, p. 439–503, 1937.
Huntsman, A. G., and M. E. Reid. 1921. “The success of reproduction in Sagitta elegans in the Bay of Fundy and the Gulf of St. Lawrence.” Roy. Can. Inst., Trans., v. 13, pt. 2, p. 1–13 (Can. Biol. Bd., Studies, no. 5), 1921.
Hyman, Libbie H.1940. “Observations and experiments on the physiology of Medusae.” Biol. Bull., v. 79, p. 282–296, 1940.
Jespersen, P.1939. “Investigations on the copepod fauna in east Greenland waters.” Medd. om Grönland, Bd. 119, no. 9, p. 1–116, 1939.
Johnson, Martin W.1937. “The production and distribution of zooplankton in the surface waters of Bering Sea and Bering Strait. Rept.” Oceanogr. Cruise U. S. Coast Guard CutterChelan1934–37, Pt. II (B), p. 45–82, 1937.
Johnson, Martin W.1939a. “Pseudodiaptomus (Pseudodiaptallous) euryhalinus, a new subgenus and species of Copepoda, with preliminary notes on its ecology.” Amer. Micros. Soc., Trans., v. 58, p. 349–355, 1939.
Johnson, Martin W.1939b. “The correlation of water movements and dispersal of pelagic larval stages of certain littoral animals, especially the sand crab, Emerita.” Jour. Marine Research,v. 2, p. 236–245, 1939.
Johnson, W. H.1938. “The effect of light on the vertical movements of Acartia clausi (Giesbrecht).” Biol. Bull., v. 75, p. 106–118, 1938.
Johnstone, James. 1908. Conditions of life in the sea.Cambridge Univ. Press, 332 pp., 1908.
Keeble, F. W., and F. W. Gamble. 1904. “The colour physiology of the higher Crustacea.” Roy. Soc. London, Phil. Trans., (B)v. 196, p. 295–388, 1904.
Kikuchi, Kenzo. 1930. “Diurnal migrations of plankton Crustacea.” Quart. Rev. Biol., v. 5, p. 189–206, 1930.
Kofoid, Charles A.1930. Factors in the evolution of the pelagic Ciliata, the Tintinnoinea. p. 1–39 in Contributions to Marine Biology, Western Soc. Naturalists, Stanford Univ. Press, 1930.
Lohmann, H.1903.
“Neue Untersuchungen über den Reichtum des Meeres an Plankton und über die Brauchbarkeit der verschiedenen Fangmethoden.”
Komm. z. Wissensch. Untersuch. d. Deutschen Meere in Kiel und d. Biologischen
Loosanoff, V. L.1939. Spawning of Ostrea virginica at low temperatures. Science, v. 89, p. 177–178, 1939.
Macdonald, Roderick. 1927. “Food and habits of Meganyctiphanes norvegica.” Marine Biol. Assn. U. K., Jour., v. 14, p. 753–784, 1927.
Marshall, S. M., A. G. Nicholls, and A. P. Orr. 1935. “On the biology of Calanus finmarchicus. pt. 6. Oxygen consumption in relation to environmental conditions.” Marine Biol. Assn. U. K., Jour., v. 20, p. 1–28, 1935.
Murray, John. 1895. Summary of the scientific results, obtained at the sounding, dredging and trawling stations of H.M.S. Challenger, Repts., Summary, pt. 2, p. 797–1608, 1895.
Murray, John. 1913. The ocean. London, Williams and Norgate, 256 pp., 1913.
Murray, John, and J. Hjort. 1912. Depths of the ocean.London, Macmillan, 821 pp., 1912.
Natland, Manley L.1933. “The temperature and depth-distribution of some recent and fossil foraminifera in the southern California region.” Scripps Inst. Oceanogr., Bull., v. 3, p. 225–230, 1933.
Nicholls, A. G.1933. “On the biology of Calanus finmarchicus. III. Vertical distribution and diurnal migration in the Clyde Sea area.” Marine Biol. Assn. U. K., Jour., v. 19, p. 139–164, 1933.
Nikitin, W. N.1931. “Die untere Planktongrenze und deren Verteilung im Schwarzen Meer.” Internat. Rev. d. ges. Hydrobiol. u. Hydrogr., Bd. 25, p. 102–130, 1931.
Orton, J. H.1920. “Sea-temperature, breeding and distribution in marine animals.” Marine Biol. Assn. U. K., Jour., v. 12, p. 339–366, 1920.
Orton, J. H.1937. Oyster biology and oyster culture.London, Edward Arnold & Co., 211 pp., 1937.
Pearse, A. S.1936. The migrations of animals from sea to land.Duke Univ. Press, 176 pp., 1936.
Pierantoni, Umberto. 1918. Les microörganismes physiologiques et la luminescence des animaux. Scientia, v. 23, Suppl., p. 43–53, 1918.
Prytherch, H. F.1929. “Investigation of the physical conditions controlling spawning of oysters and the occurrence, distribution, and setting of oyster larvae in Milford Harbor, Conn.” U. S. Bur. Fisheries, Bull., v. 44, p. 429–503, 1929.
Redfield, A. C.1941. “The effect of the circulation of water on the distribution of the calanoid community in the Gulf of Maine.” Biol. Bull., v. 80, p. 86–110, 1941.
Redfield, A. C., and A. Beale. 1940. “Factors determining the distribution of populations of Chaetognaths in the Gulf of Maine.” Biol. Bull., v. 79, p. 459–487, 1940.
Regan, C. Tate. 1926. “The pediculate fishes of the suborder Ceratioidea. Danish Dana Expeds.” 1920–22, Oceanogr. Repts., no. 2, 45 pp., 1926.
Regan, C. Tate. 1932. “Deep-sea angler fishes (Ceratioidea).” Dana Rept.no. 2, 113 pp., 1932.
Runnström, S.1927. “Über die Thermopathie der Fortpflanzung und Entwicklung mariner Tiere in Beziehung zu ihrer geographischen Verbreitung.” In Bergens Mus. Aarb., Naturv. rekke, no. 2, 1927.
Russell, F. S.1927. “The vertical distribution of marine macroplankton. v. The distribution of animals caught in the ring-trawl in the daytime in the Plymouth area.” Marine Biol. Assn. U. K., Jour., v. 14, p. 557–608, 1927.
Russell, F. S.1928. “The vertical distribution of macroplankton. VII. Observations on the behavior of Calanus finmarchicus.” Marine Biol. Assn. U. K., Jour., v. 15, p. 429–454, 1928.
Russell, F. S.1935a. “On the value of certain plankton animals as indicators of water movements in the English Channel and North Sea.” Marine Biol. Assn. U. K., Jour., v. 20, p. 309–332, 1935.
Russell, F. S.1935b. “A review of some aspects of zooplankton research.” Conseil Perm. Internat. p. l’Explor. de la Mer, Rapp. et Proc.-Verb., v. 95, p. 3–30, 1935.
Russell, F. S.1939. “Hydrographical and biological conditions in the North Sea as indicated by plankton organisms.” Conseil Perm. Internat. p. l’Explor. de la Mer, Jour. du Conseil, v. 14, p. 170–192, 1939.
Russell, F. S., and C. M. Younge. 1928. The seas.London, F. Warne & Co., 379 pp., 1928.
San Francisco Bay Marine Piling Committee (C. L. Hill and C. A. Kofoid, eds.). 1927. Marine borers and their relation to marine construction on the Pacific coast. Final report of the committee cooperating with the National Research Council and the American Wood-Preservers' Association. San Francisco, 357 pp., 1927.
Schmidt, Johannes. 1909. “The distribution of pelagic fry and the spawning regions of the gadoids in the North Atlantic from Iceland to Spain, based chiefly on Danish investigations.” Conseil Perm. Internat. p. l’Explor. de la Mer, Rapp. et Proc.-Verb., v. 10, pt. 4, 229 pp., 1909.
Schmidt, Johannes. 1925a. “The breeding places of the eel. Smithsonian Inst.” , Ann. Rept. for 1924, p. 279–316, 1925.
Schmidt, Johannes. 1925b. “On the contents of oxygen in the ocean on both sides of Panama.” Science, v. 61, p. 592–593, 1925.
Sömme, J. D.1934. Animal plankton of the Norwegian coast waters and the open sea. I. Production of Calanus finmarchicus (Gunner) and Calanus hyperboreus (Kröyer) in the Lofoten area. Repts. on Norwegian Fishery and Marine Invest., v. 4, no. 9, 163 pp., 1934.
Steuer, A.1910. Planktonkunde.Leipzig and Berlin, B. G. Teubner, 723 pp., 1910.
Steuer, A.1933. Bericht über die Bearbeitung der Copepodengattung Pleuromamma Giesbr. 1898 der Deutschen Tiefsee-expedition Valdivia. Thalassia (Istit. Italo-Germanico di Biol. Marina, Rovigno d’Istria), v. 1, no. 2, 48 pp., 1933.
Sumner, Francis B.1911. “The adjustment of flatfishes to various backgrounds. A study of adaptive color change.” Jour. Exper. Zool., v. 10, p. 409–506, 1911.
Sumner, Francis B.1934. Studies of the mechanism of color changes in fishes. p. 62–80 in James Johnstone Memorial Volume, Lancashire Sea Fisheries, Liverpool, England, 348 pp., 1934.
Sumner, Francis B.1935. “Studies of protective color change. III. Experiments with fishes both as predators and prey.” Nat. Acad. Sci., Proc., v. 21, p. 345–353, 1935.
Sumner, Francis B.1939. “Quantitative effects of visual stimuli upon pigmentation.” Amer. Naturalist, v. 73, p. 219–234, 1939.
Sumner, Francis B.1940. “Quantitative changes in pigmentation, resulting from visual stimuli in fishes and amphibia.” Biol. Reviews, v. 15, p. 351–375, 1940.
Thompson, W. F.1936. “Conservation of the Pacific halibut, an international experiment.” Smithsonian Inst., Ann. Rept. for 1935, p. 361–382, 1936.
Thompson, W. F., and R. Van Cleve. 1936. “Life history of the Pacific halibut. 2. Distribution and early life history.” Intenat. Fish. Comm., Rept.no. 9, p. 11–184, 1936. Seattle.
Utterback, C. L.1936. “Spectral bands of submarine solar radiation in the North Pacific and adjacent inshore waters.” Conseil Perm. Internat. p. l’Explor. de la Mer, Rapp. et Proc.-Verb., v. 101, pt. 2, no. 4, 15 pp., 1936.
Vaughan, T. Wayland. 1919. “Corals and the formation of coral reefs.” Smithsonian Inst., Rept. for 1917, p. 189–276, 1919.
Walford, Lionel A.1938. “Effect of currents on distribution and survival of the eggs and larvae of the haddock (Melanogrammus aeglefinus) on Georges Bank.” U. S. Bur. Fisheries, Bull., v. 49, Bull. no. 29, 73 pp., 1938.
Wells, Nelson A.1935. “The influence of temperature upon the respiratory metabolism of the Pacific killifish, Fundulus parvipinnis.” Physiol. Zool., v. 8, p. 196–227, 1935.
Welsh, J. H., F. A. Chace, and R. F. Nunnemacher. 1937. “The diurnal migration of deep-water animals.” Biol. Bull., v. 73, p. 185–196, 1937.
With, Carl. 1915. “Copepoda. I. Calanoida amphascandria.” Danish Ingolf Exped., v. 3, no. 4, 260 pp., 1915. Copenhagen.
Worthington, E. B.1931. “Vertical movements of freshwater macroplankton.” Internat. Revue d. ges. Hydrobiol. u. Hydrogr., Bd. 25, p. 394–436, 1931.
ZoBell, Claude E.1940. “The effect of oxygen tension on the rate of oxidation of organic matter in sea water by bacteria.” Jour. Marine Research, v. 3, p. 211–223, 1940.
XVIII. Interrelations of Marine Organisms
In the preceding chapters we have dealt at some length with the external conditions affecting the lives of organisms of the sea. Except for incidental references, the discussion has been concerned mainly with factors of the inorganic environment. But it must be borne in mind that the organisms themselves as a group form a vital portion of the environment, being a part of the whole series of factors that control the lives of the individuals. This complete aggregation of organisms of all kinds, together with their activities, constitute what is known as the organic environment. Its study is concerned with the interrelations within the whole marine populations, both plants and animals.
In the final analysis, many of the inorganic factors operate indirectly through the organic factors which they foster. To use the most general illustration, animals can be abundant only where inorganic surroundings permit an abundant growth of plants or where currents carry in food from regions so supplied.
It has been noted (p. 275) that the inanimate environment may be classified into a number of more or less sharply defined divisions or provinces. Of these, the biotope is the primary topographic unit (p. 279). In the sea it represents a portion of the marine environment in which the conditions are sufficiently uniform to foster a characteristic community of organisms. It follows that other biotopes with different sets of environmental conditions will be populated by somewhat different communities although many organisms with wide tolerance may be common to two or more communities. Because terminology used in evaluating communities is in an unsettled state the reader is referred to ecological studies dealing specifically with the subject (Petersen, 1913, Allee, 1934, Shelford, Weese, et al, 1935, Pearse, 1939).
NATURAL ASSOCIATIONS OF ORGANISMS
Depending upon their degree of intimacy, four types of associations may be recognized among organisms. The four types are: (1) association arising from similar requirements as to environment; (2) commensalism; (3) symbiosis; and (4) parasitism.
Environmental Association. Animals and plants of different species will be found associated together in ecological communities or biocoenoses provided their environmental requirements with respect to physical and chemical conditions are much the same. The food relationships or predatory habits of the members must be such that their habits do not interfere seriously with each other. Much of the food may be brought to the community incidentally by currents and other water movements, but usually a restricted food cycle is established and many carnivorous animals prey upon each other. One species may dominate numerically owing to better means of protection or greater powers of survival or proliferation.
It should be noted that in a natural community the inorganic forces function to select a general type of fauna. All species that have not become adapted to the physiographic conditions, the range of salinity or temperature, will be promptly eliminated from the community. For instance, only organisms suited to live on muddy bottoms can become established in such habitats, and the same is true of rocky shores (Ricketts and Calvin, 1939, Pearse, 1939). However, since there is a great array of animals capable of living within the extremes of chemical-physical conditions of these environments, a competition for food and space is established among the members. It is here that some of the biotic forces come into play in determining the species or groups of species that will make up any given community. It has been found that certain species live most successfully only in certain combinations of associates (Petersen, 1913). The principal characteristic animal or animals supply the name to the community; thus there may be a Venus community or a Macoma community, depending upon the importance of these bivalves and the combination of animals associated with them. Communities are also sometimes named for the habitat, for example, they may be estuarine communities, exposed rocky coast communities, or wharf-pile communities.
The forces operating to mold the character of a fauna are thus a combination of the organic and inorganic factors, but the communities are more or less unstable since the forces so acting do not remain unchanged. Changes resulting from erosion of the substratum or from the degree or character of terrigenous deposition on a shore, for example, will result in a gradual succession of communities. It is obvious also that the organisms themselves, plants and animals, both pelagic and benthic, slowly bring about fundamental changes in the nature of the bottom, its macro- and microscopic structure, even to great ocean depths. Alterations may result from (1) burrowing activities of many forms such as worms, molluscs, crustaceans, and others that live in or upon the mud and sand, grinding and intermixing the sediments to a depth of a third of a meter or more; (2) boring into and eroding such harder structures as
Commensalism. A closer association than that above discussed is commensalism. Here two organisms live together, one at least being benefited and the other neither injured nor benefited. Certain small decapods are frequently found thus associated with bivalves, living within the mantle cavity. Scaleworms (polynoids) inhabit similar positions with limpets and chitons, and are also found between the rays or in the ambulacral grooves of starfish. Certain small fishes (gobies) live in the burrows of burrowing worms and crustaceans, and many small pelagic fish seek refuge among the stinging tentacles of large jellyfish and siphonophores. According to Wilson (1932) at least 80 per cent of the copepods belonging to the suborder Notodelphyoidea with 41 genera are commensals within ascidians. Certain barnacles (Coronula) and also diatoms (Cocconeis coticola) grow upon the skin of whales. The relative abundance of this diatom on the skin of whales is correlated with the length of time the animals have been in Antarctic waters, since this diatom does not thrive in the warm waters of lower latitudes. The yellow color imparted by these organisms to the ventral surface of the whale is thus an index of the fat condition, for it is in these waters that fatting takes place (Hart, 1935). Commensalism is very common among marine animals.
Symbiosis. Another type of yet closer association is found in the relationship known as symbiosis, wherein two or more organisms live together, this usually being obligatory and mutually beneficial. As illustrative of this mode of life may be mentioned the association between certain one-celled yellow (Zooxanthella) or green (Zoochlorella) algal plants and such animals as radiolaria, sponges, corals, sea anemones, and even bivalves and echinoderms. The algal partner, which in the sea usually is one of the Zooxanthellae, may live within the cytoplasm of the single cell as in the radiolaria; or within the cells intracellularly, or within the body cavities of multicellular forms. This type of relationship is common in the sea but its significance in the economy of the sea is not
It is probable that the algae symbiotic with such tropical planktonic animals as the Radiolaria represent an important flora which compensates in part for the scarcity of the free phytoplankton diatoms generally reported from high seas of tropical waters where the plant nutrients are low in the surface waters (Hardy, 1936).
Parasitism. In this type of close association one organism lives at the expense of another, known as its host. There are large numbers of both external and internal parasites in the sea. Even the diatoms do not escape; Chaetoceros, for instance, is host to Paulsenella, an unarmored dinoflagellate. Among the temporary planktonic parasites are unarmored dinoflagellates, many copepods, and the cercaria larvae of the flukes.
NUTRITIONAL RELATIONSHIPS
In the sea, as in the terrestrial environment, the prime relationship between organisms is that associated with nutrition, and, indeed, the relationships leading to the above classification of associations are, in the final analysis, nutritional.
Other relationships are expressed in associations for protection and, within species, for reasons of propagative or social instincts. But the association for protection is only a reaction against rapacious enemies seeking food and is therefore part of a nutritional relationship between predator and prey.
Allen (1934) has reviewed pertinent literature dealing with the microscopic plants as the primary food of the sea. In the sea as on land the nutritional relationships result in a food cycle of producers and consumers in which solar energy and the regeneration of inorganic nutrients utilized by plants in photosynthesis form vital links. But the relation
The Significance of Micro-plants
It has been shown that sea water possesses in solution all of the necessary inorganic elements, phosphorus, nitrogen, iron, and so on, for the manufacture of plant substance with the aid of light. In other words, the sea as a whole possesses the potentialities of sustaining such autotrophic organisms as are capable of capitalizing upon this tremendous supply of nutrient material held in solution. Although the sea offers these possibilities to plant growth, at the same time it also sets up certain serious physical difficulties and barriers by reason of the magnitude, depth, and fluidity of the oceans. We know that it is only the merest rim of the sea that has sufficient light and, at the same time, suitable substratum for attached and other bottom-living plants, and that in the open sea plant life is restricted by the factor of illumination to only the upper few meters represented by the euphotic zone. This relative restriction of living space makes it of vital importance to plants that they overcome or minimize materially the effect of gravity that might lead to their destruction below the euphotic zone. This serious challenge of the pelagic environment has been successfully met by the plants, and the method by which it has been conquered has determined largely also the kind of animal life that the sea can support.
In order that the vast stretches of the ocean may be populated and its nutrient resources used by plants beyond a depth of about 40 m, special types of plants adapted to a floating existence have evolved. To accomplish a pelagic habit, two methods appear to be open. (1) The development of buoyant forms with air bladders or similar features to keep them at the surface. This is the means evolved by the macroscopic alga Sargassum. This method, however, is subject to serious handicaps and can hardly be considered a successful one; moreover, although plants of this nature float in large masses and reproduce vegetatively in restricted places such as the Sargasso Sea, yet their natural home is along the shore attached to rocks from which they have been torn. Such buoyant plants can extract nutrients only from a shallow layer at the immediate surface and unless maintained in large eddies of relatively quiet water, they are subject to being rapidly driven by the wind and currents into coastal areas, there to be destroyed by stranding and by beating of the surf. The contribution of organic material by such plants is relatively small. (2) The really successful method by which plants have been able to
The Significance of Micro-animals
One may ask what influence this type of development of the plants has had on the animal population of the sea. Along what lines has the animal economy evolved to exploit this vast supply of microscopic plant food in the sea? A plant population consisting mainly of scattered individuals that are microscopic in size must impose certain restrictions and requirements upon the animal grazers that depend upon it for nourishment. It is significant that in the sea the chief grazers, representing the main bulk of the zooplankton, are also microscopic or semimicroscopic in size and vast in numbers. Foremost among the grazers of the pelagic region are placed the copepods, the diet of which has been shown by direct analysis to consist mainly of diatoms, dinoflagellates, and other micro-plants, but many other small herbivores, especially protozoans, euphausiids, and larval stages of larger invertebrates also graze directly upon the phytoplankton.
Through all the tiny grazers of the sea nature accomplishes two important ends: first, complete utilization of even the minutest particles of primary food; and, second, transformation of the organic material of these plants into animal substance of size sufficiently large to be caught and utilized by carnivorous forms. The large number of carnivorous animals that occur in the sea is abundant evidence that the numbers of microscopic grazers must indeed be great (p. 896). Much economy would result if the larger animals could feed directly upon the plants in the manner of the large terrestrial animals, but the nature of the environment prohibits the growth of large plants except in a narrow fringe along shore and, except for a small amount in the eel grasses, no seeds with concentrated nutriments are produced as on land for immediate use or as a store to be drawn upon during periods of low vegetative growth. It is true that some fishes, particularly the herrings, feed to some extent directly upon minute plants, especially during their larval stages (Lebour, 1924a), and an exceptional few, such as the menhaden with their notably fine filtering apparatus, feed partly on diatoms and dinoflagellates throughout life (Bigelow, 1926).
In our concept of plant-animal relations, the plants are to be looked upon chiefly as autotrophic organisms capable of converting inorganic material to organic material, thus making it available to animals as particulate food. Lohmann found in the Bay of Kiel that for every multicellular animal there were one thousand protozoan and seven thousand protophytan forms. It is extremely difficult to obtain reliable measurements of the relative volume of plant and animal substance in the sea, but, since only through the endothermic process of photosynthesis can the solar energy be bound and become available for the building of animal substance, it is obvious that the mass of plant material produced must be greater over a long period of time than the mass of animal material. It appears that even at periods of only moderate production the very rapid rate of reproduction in unicellular plants is sufficient to maintain the zooplankton population, even though the bulk of plants actually present at any moment may be less than that of the animals. It should be emphasized that the rapidity of reproduction of the nanno- and microplankton is as important as the bulk present in the water as food at any given time. Lohmann calculated that even though the mass of plants may fall below that of animals in the Bay of Kiel, yet plant production usually exceeds animal consumption during the summer months. The excess may be 29 mm3/100 l of sea water. During winter both production and consumption fall off, but during midwinter, January and February, there is a production deficiency of −0.8 mm3/100 l of sea water.
It must be pointed out that some of the organic material produced by plants is lost to the animals through solution in the sea water; the content of dissolved organic matter in the sea runs as high as six or more milligrams per liter of sea water (up to three milligrams of carbon per liter; p. 250). This represents much more organic material in the sea in solution than exists there as particulate food at any one time, and any organisms that are capable of reclaiming this dissolved organic material have an important role in the economy of the sea. Bacteria doubtless serve this purpose (p. 911), but other saprophytic forms may also play a part. Some dinoflagellates are believed to be saprophytic, but their utilization of dissolved organic matter from the water in such dilute concentrations has not been demonstrated. Attention has already been called to certain “olive-green cells” regularly collected in deep water from the South Atlantic by the Meteor. These have a maximum distribution below the euphotic zone and Hentschel (1936) believes them to live heterotrophically. If this is true, they are important in reclaiming dissolved organic matter and building it into bodies of suitable size for use by filter-feeding animals at mid-depths.
In the following analysis of food relationships our purpose is not so much to learn the habits of individual animals, though to do so is extremely important and indispensable in understanding the biology of
In studying the food relationships of the marine organisms, it is perhaps most convenient for our purpose to group the animals according to the kind or source of food upon which they subsist and according to general methods of feeding, remembering at the same time that the feeding habits of many are unknown and that many have habits not clearly confined to any one of these categories but overlapping more or less into others. The larval and adult stages may also differ both in food required and in the method of procuring it. The first two groups given below are based on the source and kind of food used and, incidentally, on the method of feeding. The last two groups are based mainly on methods of feeding, but this feature itself results largely from the nature of the food.
Plankton and Filter Feeders
Under this heading are included the forms that feed upon microscopic or semimicroscopic organisms and suspended detritus floating or swimming freely in the water. It is here that the uniqueness of the food cycle of the aquatic environment is most clearly manifest. It is not practicable to segregate strictly the true plankton feeders as a group from the feeders on finely divided, suspended organic detritus because most plankton feeders include detritus in their diet, owing in part to the method of gathering food. They may also be designated as “suspension feeders,” after Hirsch. Many of the plankton feeders may be called filter feeders because of the method in which they collect their food. Most of them are provided with some type of screening device through which the water is passed while the small organisms are retained as food. A few examples will serve as illustrations.
In filter-feeding copepods, Calanus finmarchicus for example, the head appendages known as the second maxillae are provided with a number of curved setae or spines each covered by numerous fine hairlike processes. The appendages are paired and together form the main part of a filtering net or chamber just posterior to the mouth. The head appendages lying between the first antennae and the second maxillae,
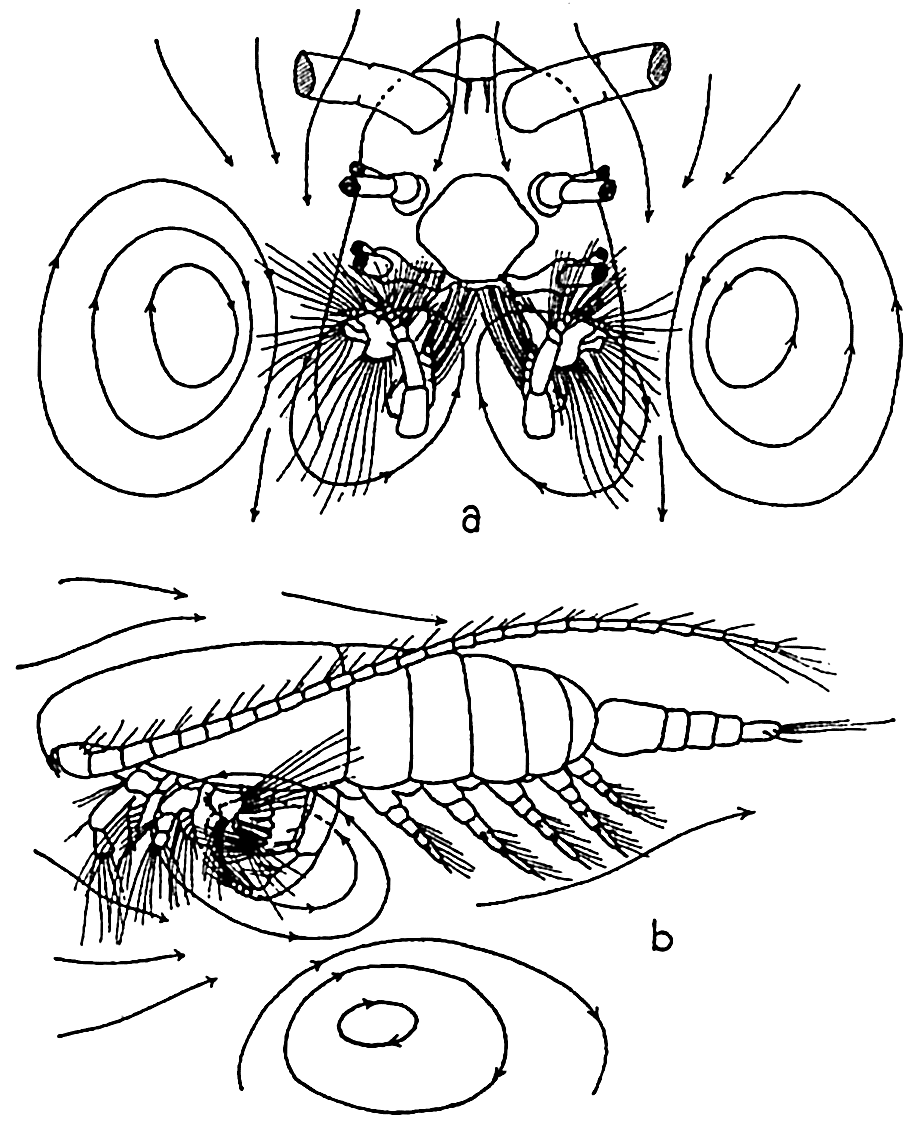
The filter-feeding apparatus of Calanus finmarchicus: (a) ventral view, anterior portion of animal, distal parts of first and second antennae and mandibles removed; (b) lateral view of entire animal. The lines with arrows indicate the vortices set up. (According to Cannon.)
The great abundance of euphausiid crustaceans makes them highly important plankton feeders because they share largely with the copepods the distinction of being grazers upon diatoms and, owing to their habit of living in large swarms below the euphotic zone, they must be of great significance in intercepting and utilizing the slowly sinking plant material produced above in the lighted zone. Euphausiids are known to be quite omnivorous, feeding on a wide variety of floating material, plants, animals, and detritus. This they comb out of the water with their long thoracic limbs which together form a basket through which water is pumped by the swimming legs (Bigelow, 1926, Lebour, 1924b).
The pelagic tunicate Oikopleura is a most remarkable type of filter feeder. Its food consists of the minutest of drifting organisms, the nannoplankton such as coccolithophores, bacteria, small diatoms and dinoflagellates, and other minute forms, which are filtered from the water by means of gratings in the animal's temporary vestments or “houses.” This portion of the plankton may constitute as much as a third or more of the total mass of plankton at some seasons and localities. The house of Oikopleura, in which it lives while drifting about in the plankton (fig. 239), is a gelationous investing structure secreted by the animal. Water is drawn into the house through funnel-like structures guarded by a set of fine mesh gratings (outer filter) capable of excluding organisms of size greater than about 0.127 mm × 0.0345 mm. In the house the water circulates through another set of filters (inner filter) that retain organisms about 0.030 mm in diameter. The water is circulated by undulatory movements of the animal's “tail” and is expelled through a second opening in the house, thus propelling the house through the water. The extremely fine material collected on the inner filter is drawn into the animal's mouth by means of ciliar action. After a few hours the screening devices become clogged and the animal then escapes from the structure through a third separate opening (exit). Having freed itself from the old useless vestment, it secretes a new one with all the complicated structures for gathering the type of food upon which it is dependent.
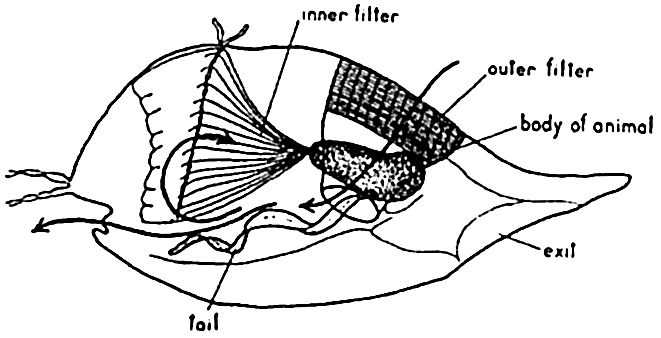
The filter-feeding apparatus of Oikopleura.
There are also many plankton filter feeders among the sedentary or burrowing animals. Indeed, the permanently attached forms so characteristic of the marine fauna (and by comparison so conspicuously wanting in land fauna) can exist as such only because the water carries to them sufficient nourishment in the form of suspended particulate food,
A familiar example of the filter-feeding habit is that of the simple sponge, wherein flagellated cells lining internal cavities propel the water into the sponge by way of the numerous incurrent pores covering the surface of the body. After passing through the more or less complicated canal system, the water is then expelled through a common opening, the osculum, but enroute the individual flagellated cells select out the fine particles of food carried by the water.
Many plankton feeders may be better classified as preying animals, although in some respects they combine this habit with filter feeding. Any attempt to distinguish between such categories is based largely on the relative degree of selectivity exercised in feeding. Few animals are wholly indiscriminate in feeding, and even filter feeders exercise some degree of selection, either by a mechanical segregation of size dependent upon apertures of the screening apparatus, as in Oikopleura or sponges, or by rejecting through ciliary or other action certain particles unpalatable for chemical or physical reasons.
We have mentioned copepods chiefly as herbivorous plankton filter feeders but not all copepods feed upon diatoms and other phytoplankton organisms. The free-living types like Tortanus and Candace that may be considered largely carnivorous and rapacious have very strongly built mouth appendages for catching and holding their prey.
Jellyfishes and ctenophores are highly predaceous in habit, feeding voraciously upon other plankton animals that drift within their reach. The former paralyzes its prey by means of batteries of nettle cells which cover the tentacles. The latter (Pleurobrachia) when in swarms are very destructive to large numbers of other small organisms, of which they sweep the waters quite clean. The prey is entangled in the trailing tentacles which are provided with sticky adhesive cells. In his study of food relationships in the Gulf of Maine, Bigelow states that “of all the members of the plankton, the most destructive to smaller or weaker animals are the several coelenterates, and especially the ctenophore genus Pleurobrachia, a pirate to which no living creature small enough for it to capture and swallow comes amiss.”
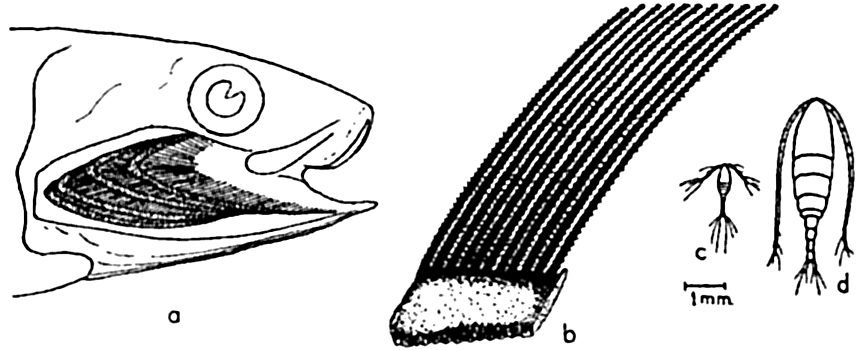
The filter-feeding apparatus of the California sardine: (a) gill cover and gills removed to show one side of branchial sieve formed by gill rakers; (b) enlarged camera lucida drawing of section of branchial sieve; (c) Oithona plumifera, a small copepod drawn to the same scale as (b); d, Calanus finmarchicus, a medium-sized copepod drawn to same scale as (b). Compare with fig. 90, p. 377.
The formidable jaws of the arrow worm Sagitta attest that it is also a highly rapacious plankton feeder; being able to snatch individual organisms like Calanus and larval fish despite the fact that it possesses only light-sensitive “eye spots” instead of true eyes (fig. 228a).
Among smaller important plankton forms, mention should also be made of the tintinnids, radiolarians, foraminifera, Noctiluca, and other planktonic Protozoa that engulf such small organisms as chance carries within their reah. These are plankton feeders but not filter feeders. That some may exercise a degree of selective feeding is indicated by the tintinnids, some of which are found regularly to contain only the shells of silicoflagellates, while others select certain coccolithophores, the coccoliths or armor of which they use in building their shells.
Among the more or less obvious preying plankton feeders may be placed many fishes, notably herring, mackerel, sardines, and others of this type (p. 896) which either select out individual animals of the plankton or filter quite indiscriminately by the aid of the gill rakers, which form a net through which water entering the mouth must pass in its course over the gills and out under the gill coverings (fig. 240). The fineness of the net or branchial sieves formed by the gill rakers varies with different types of fishes, and in unclogged condition determines the minimum size of the planktonic organisms that can be sieved out for food. Even the menhaden, Brevoortia tyrannus, with a notably fine branchial sieve, is unable to retain organisms as minute as coccolithophores and small diatoms and infusoria. In the herring the sieve is much coarser, and though these fish are known to select out organisms individually the gill rakers must assist materially in retaining many of the smaller Crustacea. The stomach of a single herring has been found to contain more than 60,000 copepods. It should be noted that though much of plankton feeding may appear indiscriminate, yet a good deal of selection does occur, since swarms of specific prey may be selected and followed, as is evidenced in the herring and in the filter-feeding whalebone whales. The plankton-feeding fishes are swift swimmers but the usefulness of this ability must be in large measure to escape their enemies, the typical large predators (see below), although most plankton feeders do in part also prey upon other smaller fishes.
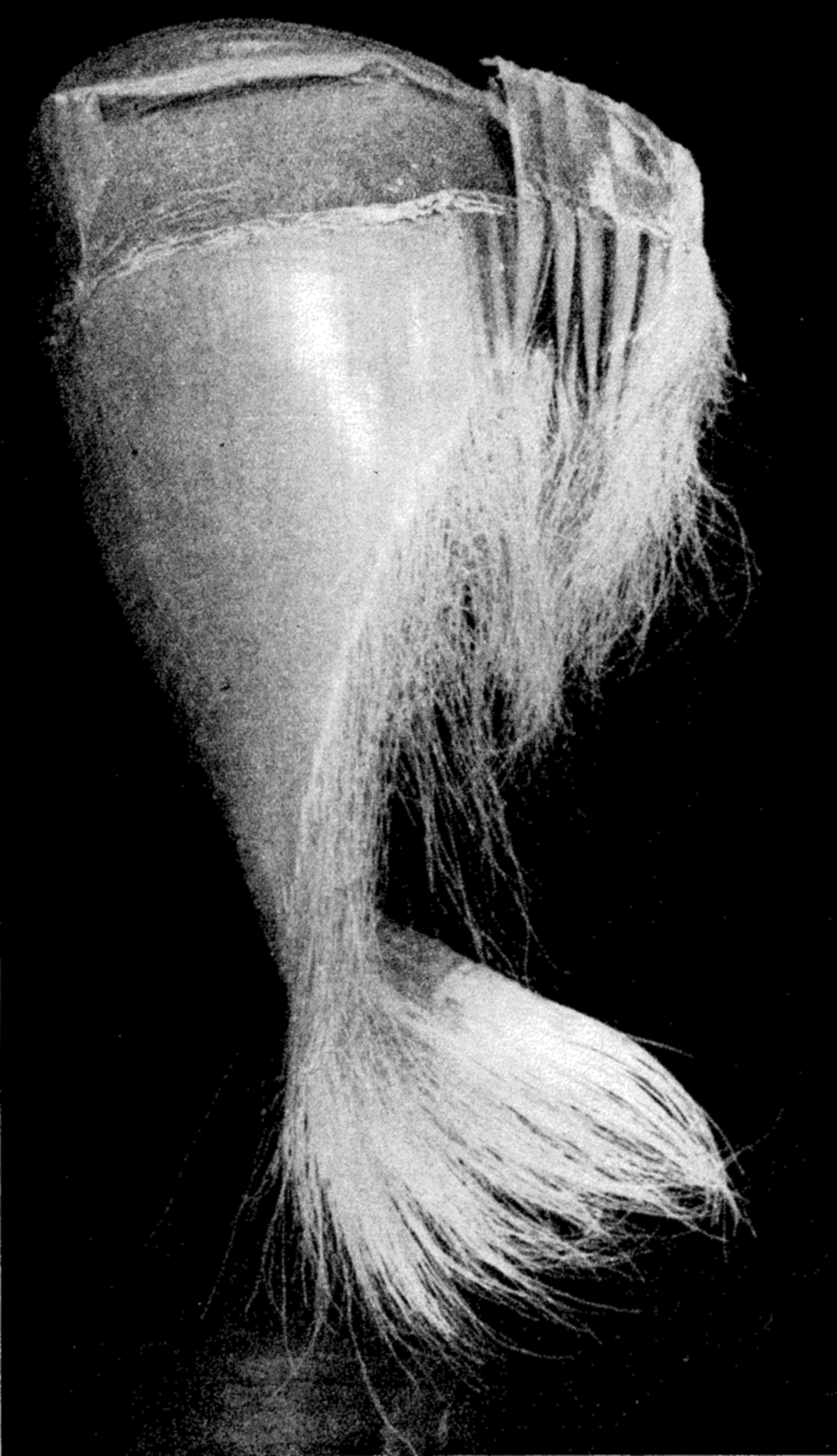
A portion of the frayed baleen plates forming the filter-feeding apparatus of the whalebone whale.
It is a strange fact that the largest animals, that is, certain of the whales, are plankton feeders, living upon great masses of very small animals. These are the Mystacoceti or whalebone whales, of which the blue whale or sulphur bottom, the largest of all living animals, is an example (fig. 76 a, p. 314). In the mouth of this type of whale are suspended the closely set plates of whalebone (fig. 241) through the frayed ends of which water is passed while the planktonic euphausiids, copepods, pteropods, and so forth, which make up the principal diet, are filtered out. Whales are most abundant in waters rich in planktonic life and, as indicated in fig. 244, p. 904, their numbers may be correlated with the abundance of planktonic food of their preference.
Numerous other examples could be given from diverse animal groups to illustrate the manner in which nature exploits the supply of microscopic but vastly numerous and scattered particulate food floating freely in the water. Any considerable fluctuations in the abundance or distribution of the planktonic food must quickly affect the plankton feeders and, in due time of course, other types of feeders as well.
More will be said later (p. 901) about general problems involving filter feeding, production, and population density.
Detritus Feeders and Scavengers
We have learned that much of the organic material produced in the pelagic zone is precipitated to the bottom in the form of living or dead bodies of the planktonic and nektonic organisms and their excreta. Added to this is detrital material resulting from disintegration of benthic plants and animals and also from influx of terrestrial material. In
The organic material available in this mixture on the bottom is fed upon by bacteria and other microorganisms such as Protozoa, nematodes, and rotifers, and the whole mixture in turn is consumed by larger detritus feeders. Bottom organic detritus is sometimes considered the main source of nourishment for most benthic invertebrates. In a survey of Danish waters Blegvad (1914) concluded that of 90 or more species of invertebrates investigated, 69 (the most common animals) were some form of detritus eaters, while 5 were herbivorous and carnivorous and 16 were purely carnivorous. In the strictest sense only those organisms subsisting solely on detrital organic remains are detritus feeders, but it is not practicable in a general survey to draw the line so closely. So in a broader sense, we see that some detritus feeders may be nourished in part by living organisms and are not necessarily entirely scavengers in habit. In the littoral zone, especially in the eulittoral zone, part of the detrital mixture consists of photosynthetic organisms such as littoral diatoms growing naturally on the bottom and thus contributing to the organic material available in the detritus.
The concentration of detritus feeders is, of course, dependent upon the extent of production of plants and nonscavenger animals. Where this production is great, there also the scavengers must be numerous. With increasing depth, the detrital food on the bottom becomes less. The plant material diminishes until in the great depths not even sinking pelagic plants produced in the euphotic zone above ever reach the bottom, being disintegrated through bacterial action or autolysis, or eaten and converted into bodies of animals. Such mid-depth and abyssal pelagic animals serve as links in a series of changes that convey sufficient organic material, as animal detritus, from the euphotic zone downward to the bottom to support at least a sparse benthic population of detritus-feeders, and the animals that in turn live upon them. It is hardly conceivable that any plant material as such ever reaches the bottom to enrich the detritus of abyssal depths. The rate of sinking of Chaetoceros diatoms in still water is only about 1 m in 4 3/4 hours. Plankton animals such as salps sink at the rate of 4000 m in 2 days 7 hours (Hesse, Allee, and Schmidt, 1937). The low temperature of great depths is important in delaying bacterial action, thus allowing more time for sinking before complete disintegration takes place, while the rate of sinking must
Various types of animals may be mentioned as detritus feeders. Their habits of feeding are varied and may combine several methods. Such burrowing worms as the lugworm Arenicola and others, and the protochordate Balanoglossus, swallow the mud indiscriminately in the process of digging and are nourished by whatever digestible material may be present in the mud and sand.
The clam Macoma nasuta, lying buried in the mud and sand of shallow water, extends its long inhalant siphon to suck up slime that has accumulated on the surface of the mud. The digestible material thus taken in is entangled in mucus and propelled by cilia to the labial palps and the mouth. The bivalves Nacula and Yoldia gather detrital material by directly extending the unusually long labial palps to pick up the food.
Among the echinoderm detrital feeders the sea cucumbers, illustrated by Stichopus, suck up large quantities of mud and detritus that has come to rest on the bottom. It has been calculated (Crozier, 1918) that in certain shallow coastal areas of Bermuda, these animals pass 6 or 7 kg (dry weight) of mud per square meter per year through their digestive tracts; in a certain enclosed area of 1.7 mi2 the mud eaten annually may be from 500 to 1000 tons. The stomach fluids are somewhat acid and may dissolve calcium carbonate. Feeding of this type is important in the biological “working over” of bottom deposits. The sea urchins, Strongylocentrotus spp., also subsist on plant and animal detritus. The mud-dwelling brittle star lies buried below the surface of the mud with several arms extended out over the surface in contact with the top slime which they collect and carry to the mouth.
Mud-dwelling tube worms collect the nutrient-rich detritus by means of extended cirri along which food material can be carried in ciliated grooves. Detritus feeders living in the mud also have their quota of filter and mucus feeders, although the material consumed doubtless also consists of typical planktonic organisms as well as suspended organic detritus stirred off the immediate bottom by currents or, in some instances, purposely stirred into suspension by the animals, for example, by Callianassa and other Crustacea.
The echiuroid worm Urechis, which inhabits U-shaped burrows in muddy sand, has a remarkable method of obtaining food through a combination of mucus secretion and filtration. Mucous glands at the anterior end of the worm secrete a funnel-shaped mass of mucus 5 to 20 cm long lining the upper end of the burrow in front of the animal. The broad end of the funnel fits against the walls of the burrow, while the narrow end fits as a snug collar around the anterior end of the animal. Water is then forcibly pumped through the burrow from front to back and in its passage through the mucous tube small particles of detritus,
An interesting method of detrital feeding is shown by the sand crab Emerita, which inhabits wave-washed sandy beaches especially in tropical and subtropical waters. Living in sand burrows in the lower part of the intertidal region, the animals face seaward while their long feathery antennae protrude from the sand to intercept fine detrital material that is washed out with the receding waves.
Littoral Browsers
In the littoral zone where large quantities of attached benthic plants are produced, many herbivorous or omnivorous animals also are found that feed directly upon the growing plants and are therefore to be considered a complement to the small but numerous planktonic grazers and the plant detrital feeders so vital in converting plants into animal substance. The large benthic algae have their greatest significance as a source of animal food in the temperate and boreal regions (p. 293).
Numbered among these littoral algal grazers are many gastropods, crabs, shrimps, and amphipod and isopod crustaceans. The devices used in mincing the plants consist of horny rasplike radulae in the gastropods, and claws, pinchers, and mandibles of heavy chitin in the crustaceans. A number of fishes, for example the rudder fish (Kyphosus) and the butterfly fish (Chaetodon) as well as other reef and littoral fishes, also browse on the attached algae.
It is not feasible to separate sharply the browsers from the detritus feeders and scavengers, since they perhaps all feed more or less indiscriminately upon growing plants or upon living or dead fragments, some of which may be washed far to sea. Indeed, most plants are eaten after they have become detached from their moorings and while in the process of breaking up mechanically or through decay. This was also the conclusion of Hewatt (1937) in special observations on food relations of intertidal animals at Monterey Bay. Petersen (1918) reports that eel grass is utilized mainly as detritus and that it may either be spread over the bottom or carried as fine particles in the water.
The relation of marine wood-boring organisms to their food supply constitutes an unusual one in the sea and may be arbitrarily mentioned under this presnent heading.
Much organic material is washed or blown into the sea from land which incidentally becomes available as food for marine life. Few instances can be cited wherein typical organisms of the sea are directly dependent upon organic products from the land. Such dependence is
Preying Animals
On the whole, it is animals of this type that are best known to the layman, for they are usually relatively large and their feeding habits tend towards the spectacular. We have already had occasion to mention a few of the preying animals such as the jellyfish, arrow worm, certain copepods, plankton-feeding fishes, and whalebone whales because of their role in utilizing the food offered by the micro- and macroplankton. The fishes and whales of this type were considered, in part, also as filter feeders.
Fast-swimming predators, among which are the surface fishes tuna, barracuda, and salmon, are provided with well-developed eyes and efficient teeth to aid in capture of their prey, which consists largely of plankton-feeding fishes. It should be noted here that such plankton-feeding fishes as the herring, sardine, menhaden, mackerel, anchovy, and alewife are fishes of exceptionally great abundance and are eagerly sought as food by the larger preying animals of the pelagic region. Some idea of their numbers may be gleaned from the fact that over 500,000 tons of sardines have been taken in in one year from California waters alone (Scofield, 1937), and the menhaden yield of the east American coast may reach 400,000 tons in a year (Tressler, 1923). Such fishes must therefore stand as an important link between the animal plankton and the larger piscine predators unprovided with direct means of gaining sustenance from the small planktonic life. High in this complex food pyramid are also the toothed whales and other marine mammals.
The pelagic fishes of great depths are also predators but they are of relatively small size, usually ranging upward to only a few centimeters. This small size may well be correlated with the scarcity of food at these depths. The diminutive sizes not only represent a conservation of organic material in growth, but also, owing to the increased ratio of
Among the nonplankton-feeding predator mammals of the sea are the toothed whales, for example the sperm whale (fig. 76b, p. 314), which is provided with teeth only in the lower jaw and which dives to great depths for its favorite food the squids, including the giant squid, the largest of all invertebrates. Other cetacean predators are the killer whales, porpoises, and dolphins, animals adapted to swimming with incredible speed and provided with teeth in both upper and lower jaws. To these must be added the seals, the sea lions, and the walruses. The first two catch their prey (fish and crustaceans) with very well-developed but ordinary teeth, while the last are specialized with long tusks with which to dig shellfish from the bottom.
Many benthic animals are predaceous, living upon each other and upon other bottom animals already discussed as users of detrital and finely divided food occurring on the bottom. The list includes many bottom-living fish called “bottom feeders” or “ground fish.” The best known among these are the plaice, flounders, halibut, croakers, cods, and rays which live on the crustaceans, shellfish, worms, and coelenterates of the bottom community.
Sea stars are notably voracious feeders on bivalve molluscs, a single specimen having been known to devour five or six clams in a day. Predaceous snails, distinguished by their long siphons, are also enemies of bivalves and other molluscs, drilling a neat hole through the shell and eating the soft contents.
The interrelations of the organisms of the sea are diagrammatically summarized in fig. 242. The volumes indicated are not based on computations and should be considered as being only very roughly proportional
The marine bacteria are a vital link in the nutritional relationships of all marine organisms, but it is more convenient to discuss these later under a special heading (p. 908).
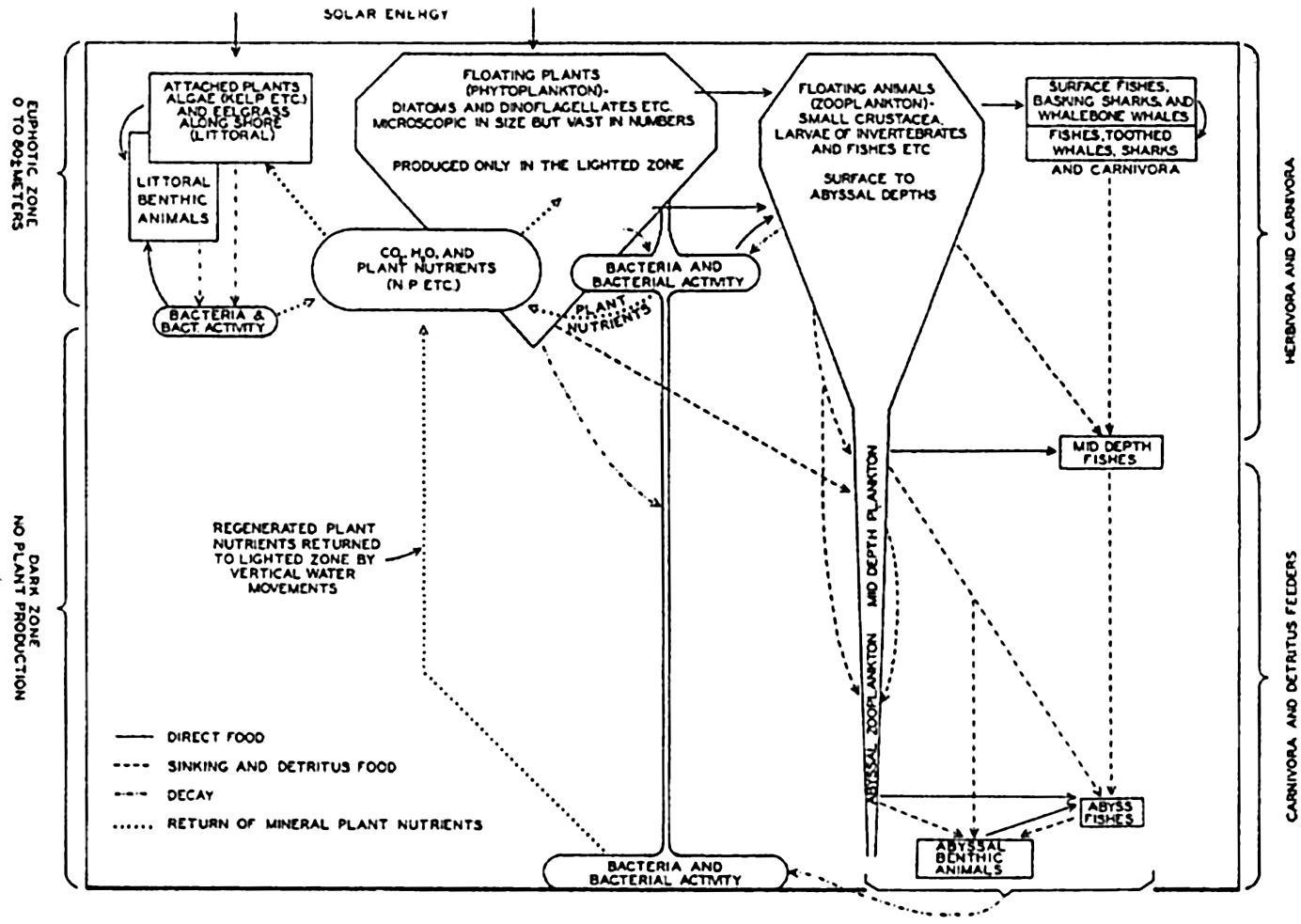
The main features of the interrelations of marine organisms.
BIOLOGICAL FACTORS INFLUENCING MOVEMENTS AND CONCENTRATION OF ORGANISMS
From what has just been said concerning the interrelations of organisms, it is obvious that in a study of the combination of factors controlling the whole or a given portion of the population it is necessary to consider seriously not only physical and chemical factors but also biological factors that have direct bearing on the lives of the individuals of the population. These factors are associated chiefly with feeding but there may be other less obvious influences. We have already alluded to the abundance of plant production in the coastal waters and to the inanimate factors making for high productivity. The direct corollary is the abundant animal life of the coastal regions as opposed to the more sparse population of the waters far from shore.
Phytoplankton—Zooplankton
In attempting to evaluate the importance of the ecological relationships of natural biological groups in the sea as a whole, we are forced to
Organisms making up the plankton are usually short-lived, particularly the photosynthetic organisms since these are notably sensitive to changes in the physical-chemical living conditions. Seasonal and sometimes interseasonal periods prevail, therefore, when but little phytoplankton can be found; but, at least in temperate regions, a vernal production followed by subsidiary increases of phytoplankton can be depended upon each year. This vernal production of phytoplankton must be considered as an event of great significance, for it comes at a time coinciding with abundant production of pelagic larvae, especially of invertebrates, that feed upon it (see below). Any factor, whether it be in reference to phytoplankton food or to inorganic living conditions, that hampers the success of these swarms of larvae will function immediately to the disadvantage of higher plankton feeders that utilize the larvae directly or the adult population resulting therefrom. Studies have indicated that among these feeders may be placed many commercial fishes, especially the young, but also the adults. Any degree of failure of the spawning or development of larvae of the permanent plankton (of which copepods may be considered typical) must also be reflected only a few weeks later in the adult stock available in any area, for the adults are short-lived and apparently die after the spring and summer propagative periods and therefore depend upon the success of these broods to maintain the adult stock at a high numerical level. Copepods, we know, feed upon the phytoplankton and in turn constitute an important item in the diet of many fishes. Assuming that phytoplankton production may be correlated with abundance of light, an example of the far-reaching effect of phytoplankton production on the mackerel is offered in a study by Allen (1909), which shows a direct correlation between the abundance of fish caught during May and the total hours of sunshine for the preceding February and March, over a period of seven years (fig. 243). Official figures for the mackerel fisheries as a whole show a marked drop in 1906, and Bullen (1909) has shown a
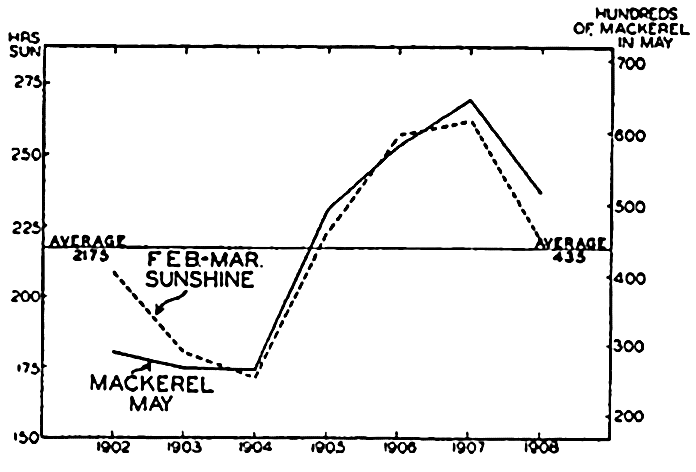
Correlation between sunshine and the abundance of mackerel. (From Allen).
Many investigators have observed that during the growing season when diatoms occur in abundance there frequently appears to be a scarcity of zooplankton. A combination of causes doubtless operates to produce this effect. Two main hypotheses have been advanced in explanation of the phenomenon of inverse relations. The least complicated explanation is found in the hypothesis of grazing (Harvey, 1934), which holds that diatom numbers are controlled through consumption by animals. The alternate hypothesis is that of animal exclusion, advanced by Hardy (Hardy and Gunther, 1935; Hardy 1936).
Animal Exclusion. According to this view, which involves a consideration of the regular vertical diurnal migrations of the zooplankton, certain of the animals during a part of the day swim upward into the layer of water where diatoms are being produced. The duration of their sojourn in the upper layer is inversely related to the concentration of the phytoplankton. Thus they are excluded vertically for a considerable period of time when diatom production has resulted in a dense swarm of diatoms. It should be noted that this exclusion is primarily a vertical one; nevertheless it may result in lateral exclusion when there is a difference in the speed or direction of flow of the upper euphotic layer and of the deeper layer into which the animals have descended and in which, when the diatoms are very abundant, they may spend a disproportionately long time. A lateral displacement may therefore be more or less complete and the greatest concentration of animals will finally occur in areas where diatoms are relatively scarce. The implications of this hypothesis on the habit of diurnal migrations should be noted (p. 836).
As evidence in support of this hypothesis, it was found during the Discovery investigations in the Antarctic that the greatest concentration of zooplankton occurs in areas low in phytoplankton content and relatively high in phosphate content, which indicated that phytoplankton production had been low for some time. Correlated with this disparity was the fact that blue and fin whales, which are known to seek out and feed upon zooplankton, were present in greatest numbers in the areas rich in phosphates. Some support is also given through experiments which indicate that some animals are more strongly negatively phototropic in the presence of many diatoms (Lucas, 1936). Plankton animals exhibiting the most pronounced activity in diurnal vertical migrations are the ones most likely to be excluded according to the hypothesis. Young stages are believed to show less tendency to exclusion. In the hypothesis of animal exclusion, which is considered as a tentative one, the emphasis is placed on the inimical effect (presumably chemical) of plants on the animals.
Grazing. The concept in this hypothesis shifts the emphasis to the effect of the grazing zooplankton as a control of phytoplankton production. That grazing is a highly important factor in the control of phytoplankton is given much support by various investigators (Harvey et al, 1935, Fuller, 1937).
According to this point of view, large phytoplankton and zooplankton populations cannot exist simultaneously in the same area for long, since the extensive grazing by the zooplankton prevents the phytoplankton from building up or maintaining dense growth. As a result of investigations of Harvey et al (1935) it is indicated that in general “a change in diatom population is brought about by a change in one or both of two opposing factors—the rate of growth of the diatoms (depending upon illumination and probably on concentration of nutrient salts) and the rate at which the diatoms are eaten (depending upon the number and kind of herbivorous animals).” Therefore, in any area a dense phytoplankton population is the result of optimum growing conditions combined with a relative scarcity of grazing animals, the yield of plant cells having been greater per unit time than the consumption by animals plus the loss that may result through other causes. Since dense plant growth is favored in the absence of grazers it appears as if the animals have been excluded because they avoid a dense diatom population. Evidence of grazing is found in the fact that phytoplankton may “disappear” when nutrients and other growing conditions are good.
In this connection it is significant to note that computations indicate that during maximum grazing plankton animals may consume somewhat less than half their own weight per day. The copepod Eurytemora hirundoides is said to eat as many as 120,000 small diatoms (Nitzschia closterium) in a day (Harvey et al, 1935). Lohmann (1908), in an exhaustive study of plankton at Kiel, assumed that each metazoan animal requires a daily ration of one tenth its own volume. A 30 per cent daily increase in plants was assumed to take place, and only this much could then be removed without reducing the initial plant stock by overgrazing. As stated elsewhere (p. 885), calculations on this basis showed a plant deficiency during the seasons of low plant production. As a matter of fact, the rate of increase in numbers of plants cannot be so simply stated. It varies greatly and so also does the rate of feeding in grazing animals, and widely different combinations of plants and grazers must occur.
Evidence has been brought to indicate that some plankton filter-feeding animals, that is, copepods and mysids, filter the water at a rather constant rate regardless of the concentration of the microscopic particulate food that is present (Lucas, 1936, Fuller and Clarke, 1936, Fuller, 1937, Fleming, 1939). Other factors, such as light, temperature, and size of particles, function to vary the filtering rate (Fuller, 1937). This
| Time in days | Population (cells per liter) | ||
|---|---|---|---|
| Grazing element doubled | Grazing element increased fivefold | ||
| 0 | 1,000,000 | 1,000,000 | |
| 1 | 487,000 | 62,000 | |
| 2 | 237,000 | 3,900 | |
| 3 | 106,000 | 240 | |
| 4 | 56,000 | 15 | |
| 5 | 27,000 | <1 | |
When plants have been reduced through grazing or when conditions for growth of the plants become less favorable and the division rate diminishes to a point where production of new cells is less than the number consumed by the grazers, animals again dominate the field. The progressively diminishing efficiency in catching plants as they become scarce is important to the survival of the diatoms since as a result there is likely always to be some “seed” left in the water. It is important to note that observations taken at fixed places, in areas where an exchange of water masses occurs, may show an apparent succession of phyto- and zooplankton populations. However, under such conditions no true alternation has occurred but only an apparent one owing to the exchange of water within the area under observation. Investigations of food relations in the plankton can, of course, be most reliably carried on in bodies of water such as bays or other closed systems that are sufficiently isolated to experience little or no influence from inflow or outflow from adjacent waters and therefore support an endemic self-contained population. In open coastal areas where much exchange of water occurs, the details
Some investigations do, nevertheless, show a clear relation between phytoplankton increases and the dependent plankton animals. For example, in Loch Striven, a semienclosed area, Marshall, Nicholls, and Orr (1934) were able to correlate directly three main successful broods of Calanus finmarchicus with diatom increases in (1) March-April, (2) May, and (3) July and August-September, the main spawning having occurred in February-March, May, and July. A fourth period of spawning occurred but was abortive owing to scarcity of food for the early stages of development. There were also indications that a storage of fat can take place during periods of plentiful phytoplankton.
Nielsen (1937) found that in the open coastal waters of Iceland the phytoplankton maximum occurred in May. In these waters the zooplankton was poor and was represented mainly by juvenile individuals, while at the same time in the protected fjords, where diatom maximum came a month earlier, there was an abundance of animal plankton with numerous full-grown individuals.
Mention should here be made of the mutually beneficial relationship derived by the phytoplankton and the zooplankton through an exchange of oxygen and carbon dioxide in solution. We know that during photosynthesis by the plants much oxygen is produced in the waters of the euphotic zone. It is not clear, however, to what extent this means of aeration is a necessary supplement to that which results from diffusion at the contact zone with the atmosphere. In isolated quiet waters it must be an important item. Waters of great depths have a sufficient supply of dissolved oxygen to support their characteristic types of animal life and this must have been transported directly from the surface or euphotic zone through diffusion and the action of water currents. It is probable, however, that a greater rate of metabolism in the more abundant animals of shallower depths, where temperatures are higher and food more abundant, sets up a requirement which could not readily be met by diffusion of oxygen from the surface alone. Plankton animals do occur in the oxygen minimum layer below the euphotic zone of the Pacific, and in the Gulf of California they are found at mid-depth layers where oxygen is near zero. The numbers of animals in the oxygen minimum layer are nevertheless small, and this may have resulted in part from the low oxygen content in the absence of photosynthesis or rapid diffusion from better aerated waters.
Plants in the lighted zone must derive some benefit through the carbon dioxide produced by animals living in the same waters; but here also the significance of this source, though certainly not negligible, has not been established.
The interrelations of the plankton animals have not been studied in such detail as those between the plants and animals. That many of them are carnivorous or omnivorous has been mentioned, and among these the medusae and ctenophores are notably influential in sweeping the waters clean of other planktonic animals upon which they feed (p. 890).
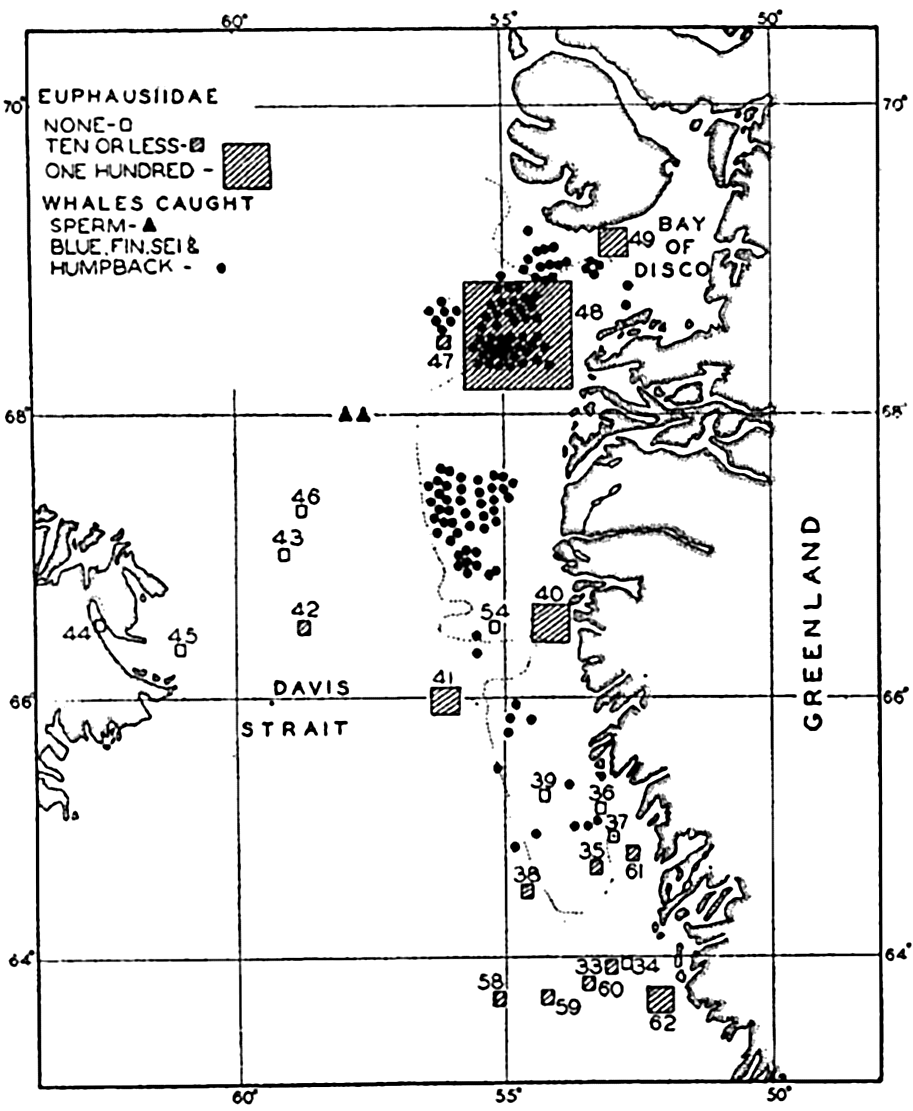
Correlation of the catches of whales with abundance of euphausiids in Davis Strait. (After Hjort and Ruud.)
Nekton
The migrations and concentrations of nektonic animals are governed largely by two biologic factors, reproduction and search of food. Mention need only be made of such truly phenomenal alternating wanderings as are witnessed in the salmon and the eel. Many other fishes also migrate, although the reasons for the migration of some of them have not been ascertained even in a general way. As a matter of fact, even in the
Among the great wanderers of the seas are the marine mammals. The habits of the Alaskan fur seal in returning to the Bering Sea to breed are widely known, and some whales migrate regularly to warm waters for breeding and between breeding times to the feeding grounds of the polar regions for food.
It will be realized from the above that any study of migratory animals and their habits as related to these biologic factors is complicated to the extent to which breeding and feeding grounds do not coincide.
It is well known among whalers and scientists that blue, fin, sei, and humpback whales feed wholly or partly upon planktonic life. Scientific investigations carried on in cooperation with whaling companies have shown, as might be expected, that the occurrence of plankton-feeding whales is correlated with the distribution of the planktonic life upon which they are known to subsist. In Davis Strait it was shown by Hjort and Ruud (1929) that young euphausiid crustaceans (the young are considered to reflect numbers of old specimens not so readily caught with vertically hauled nets) had their maximum concentration over certain coastal banks, and it is precisely in these waters that the maximum numbers of whales also occurred (fig. 244). The euphausiids tend to collect in swarms during breeding and the appearance of blue whales coincides with the periods of spawning of the dominant species in the region. Sperm whales, which feed largely on squids and not directly on plankton, are found to be present farther offshore, as indicated in the figure. The same authors compare the numbers of sei whales (Balaneoptera borealis) with the concentration of Calanus finmarchicus during the same period from the coastal banks. Figure 245 shows a striking correlation in the abundance of these animals, with the increase in Calanus preceding somewhat the appearance of the whales. Data also
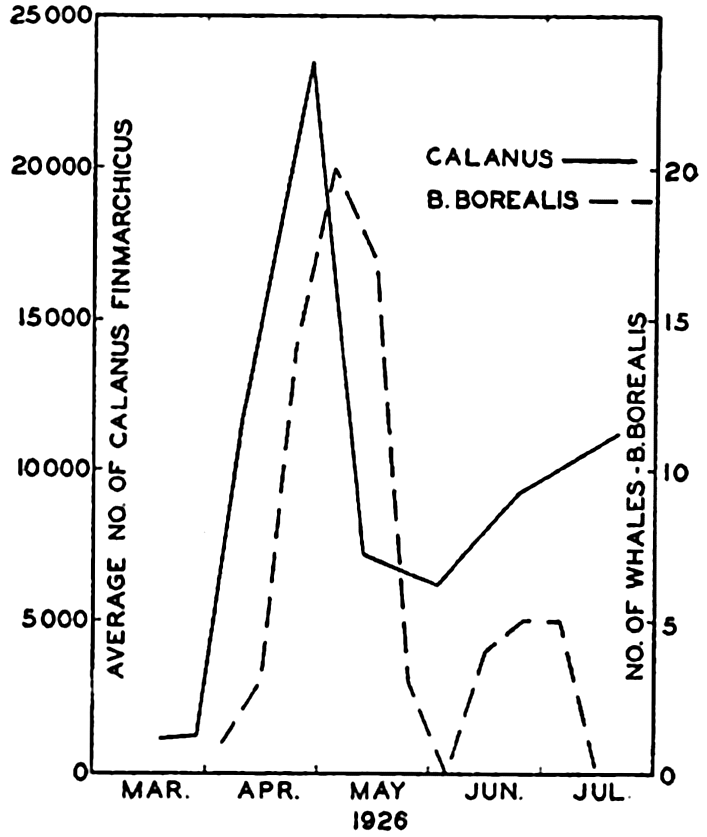
Correlation of the catch of sei whales (Balaneoptera borealis) with the number of copepods. (After Ruud.)
Investigations by the Discovery likewise showed a positive correlation between distribution of blue and fin whales and abundance of zooplankton, especially with their favorite food Euphausia superba (Mackintosh. 1934, Hardy and Gunther, 1935).
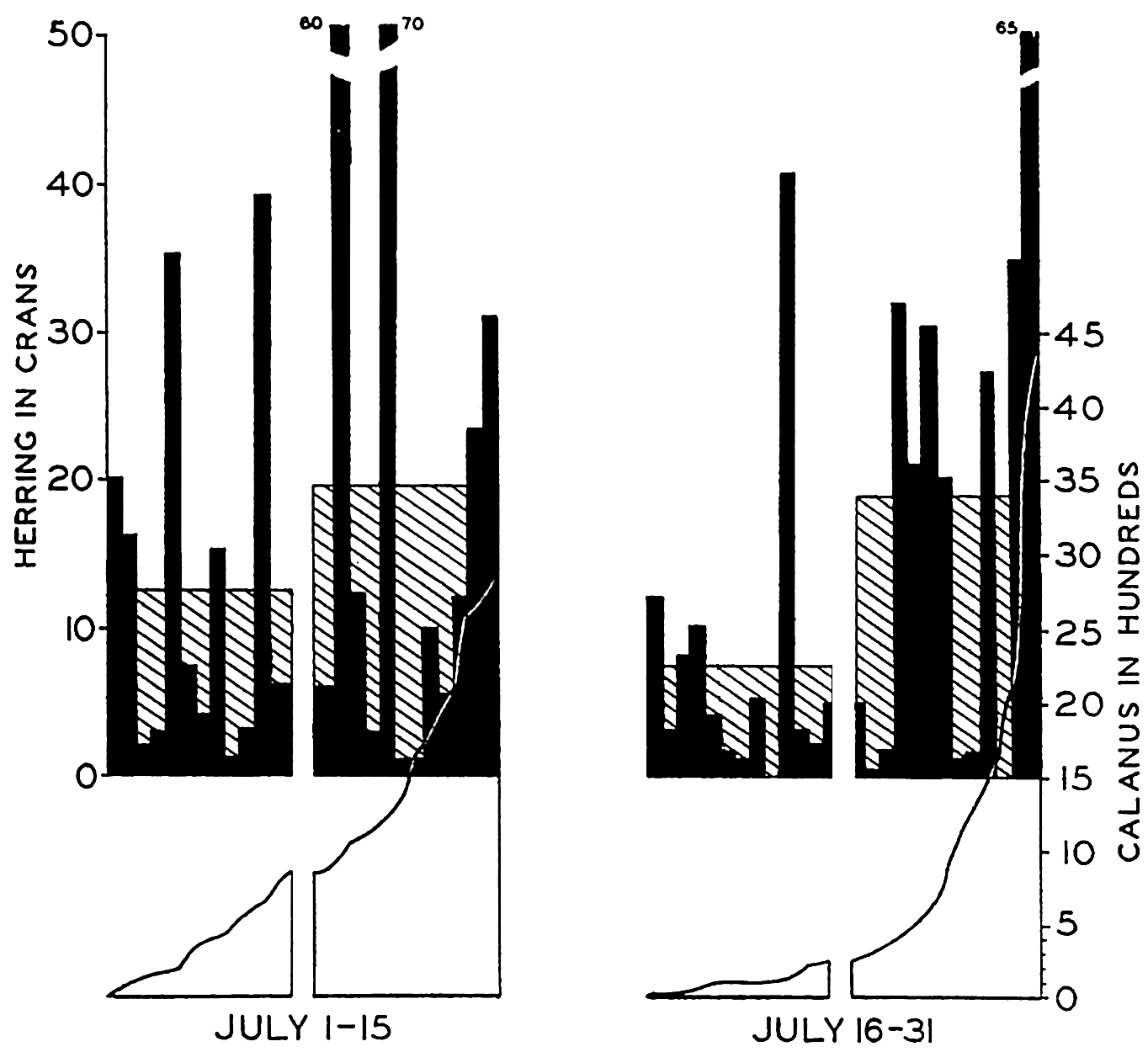
Histograms showing (in black) the individual catches of herring in half-monthly periods arranged in each period from left to right in the order of ascending values of Calanus in the associated plankton samples. The average catches of herring are shown as shaded histograms. The left half of each series represents catches in the poorer, and the right half in the richer Calanus water as indicated in the graph for associated Calanus values. (From Lucas.)
Numerous other examples might be given showing the concentration of whalebone whales in coastal areas rich in plankton food, and their instinctive migrations into these waters at the swarming season of such forms as euphausiids is truly phenomenal. One is impressed with the efficiency of the metabolism of some of the large animals which feed upon the animal plankton. For instance, at birth the blue whales are about 7 m long and weigh about 2000 kg (4400 lb), and at weaning, seven
Among the pelagic fishes the best material illustrative of correlation with plankton comes from studies of the herring. It has long been believed that the movements and concentrations of these fish are associated with the relative concentrations of the zooplankton upon which they feed. Hardy, Lucas, Henderson, and Fraser (1936) have recently investigated the plankton by means of the plankton indicator (a quick-sampling device) and, in correlating the numbers of Calanus copepods of the plankton with the amount of herring caught by fishermen in the same areas, they have shown in most instances that the greatest number of adult herring are caught in Calanus-rich waters. Theoretically the gains derived through fishing exclusively in Calanus-rich waters may be as high as 21 per cent. In Fig. 246, from Lucas, is shown the general trend of the relation that exists when the Calanus series are arranged in ascending order of numbers and each half of the series compared with the average catch of herring for the period.
A negative correlation is found between heavy phytoplankton and herring. North Sea fishermen have observed this in practice, and designate the heavily diatom-populated waters as “weedy water” or “stinking water” and consider it a bad omen to fishing.
Benthos
Among the benthic organisms the animate factors of the environment are manifest not only in predacity and competition for food but also in competition for favorable space for attachment or burrowing. The competition for space is most obvious in sessile forms such as barnacles and mussels of the intertidal zone, where overcrowding must lead to elimination as growth proceeds, and many pelagic larvae of sessile forms perish by failure to find attachment at all. A foremost problem in oyster culture is the curtailment of oyster production that results in beds in which the slipper shell Crepidula is a serious competitor with the oyster for food and space. In English waters as much as twenty tons of Crepidula have been removed from certain beds daily, and some beds there and elsewhere have been completely abandoned for culture because of this pest.
Many good examples of the influence of biological factors on the benthic populations are also offered by studies of other pests on oyster beds (Orton, 1937). Among these we may mention the common drill Urosalpinx cinerea, which may destroy 50 per cent of the young oysters settling on a bed. In Australia whole beds have been destroyed in a few days by yet another predator, the mangrove crab Scylla serrata. The extent to which sea stars are a factor in reducing the yield of oysters in Long Island Sound is indicated by reports that as much as 500,000 bushels are annually killed by these pests in that small area alone (Galtsoff and Loosanoff, 1939).
In the above, attention has been directed to the effect of predacity on the prey, but we may shift the emphasis and consider an instance wherein the predator is the object of economic interest.
According to quantitative investigations of benthic invertebrates with reference to their utilization as food for the bottom-feeding plaice, it has been calculated by Blegvad (1930) that over an area of 3445 square miles in the Kattegat there is produced, as a minimal figure, about 230,000 tons of “first-class” plaice food. (The food is considered first-class when it is of a type available to young as well as adult animals, and second-class when it can be eaten only by the grown animals.) This amount of food is believed sufficient to produce 12,800 tons of plaice. Animals known to compete for the food of the plaice take about one tenth of the total.
These few examples selected from a field of study intensively pursued for economic reasons are doubtless illustrative also of similar biological aspects that enter into the control of any population in the sea (see also fig. 249, p. 937).
MARINE BACTERIA AND THEIR ROLE IN THE BIOLOGICAL AND CHEMICAL CYCLES IN THE SEA
Because of the specific role of bacteria in the nutritional cycle of the sea, it is fitting at this point to consider in some detail the general biology and activities of these microorganisms.
Although the existence of marine bacteria has long been recognized and was early verified even in depths of over 1000 m in the Gulf of Naples (Russell, 1892), yet it is only in recent years that the study of bacteria in the metabolism of the sea has gotten well under way. For a synoptic review of works especially relevant to the development of the subject the student is referred to Benecke (1933).
Structure and Reproduction
Bacteria are unicellular organisms although some of them form chains or groups of cells. Morphologically there are the following three forms:
In their structure and activities they form a rather well-defined group of organisms, although some possess animal characteristics, especially in chemical composition, while others approach more nearly the plants, particularly the blue-green algae, with which they share the characteristic of having scattered nuclear material. Some authors consider them as occupying an intermediate position between the plants and animals (Jordan, 1931). A distinct plant characteristic is the ability of some to synthesize such complex substances as amino acids with only ammonia as a source of nitrogen. It is important to note that none possess chlorophyll, nor are their cell walls composed of cellulose. For convenience, however, they are all placed with the plants; but owing to the absence of chlorophyll in their structure they must be regarded as fungi, and since their common method of multiplication is by simple fission, they are named fission fungi or Schizomycetes.
Structurally, the marine bacteria are represented mostly by motile rods and various types of vibrios or comma-shaped forms, and there are fewer spore-formers in the sea than on land (Waksman, 1934). About 70 per cent of marine bacteria are colored as opposed to 15 per cent of the terrestrial forms.
Characteristically, bacteria are the smallest of all organisms, some measuring only 0.0005 mm in diameter. This extreme minuteness has a profound bearing on the activities of bacteria and also introduces very special problems and difficulties in the technique of collecting and in the estimation of actual numbers and mass.
Characteristic also of bacteria is their rapid rate of reproduction. This is accomplished by vegetative cell division. It may again be emphasized here that in nearly all instances where swarms of organisms—bacteria, diatoms, dinoflagellates—occur in such large numbers that the water is discolored by the accumulation of their bodies, the method of reproduction has been one of binary fission. Assuming an uninterrupted physiological state and optimum growing conditions, the accumulation of individuals can be extremely rapid since the increase is by geometric progression. The rate of division of bacteria may be as frequent as once every twenty or thirty minutes. Hence, biologically, there is a tremendous potentiality to build up an excessively large mass. However, large masses do not accumulate because of natural checks which hold the tendency to mass production within bounds. Among such checks may be mentioned availability of food supply, formation of toxic metabolic products, physical-chemical conditions of the water, nature of substratum, and consumption by other organisms. An understanding of these checks or controlling factors is one of the ends sought in the study of marine bacteriology, for such an understanding provides an explanation
Associated with bacterial reproduction is the faculty of spore formation, whereby the individual bacterium of certain species is enabled to withstand adverse conditions while remaining in a state of quiescence for long periods of time. How significant this faculty is in the marine environment, where physical and chemical conditions are relatively uniform, at least with respect to the open water, is not clear. Viable bacteria have been taken from strata of marine mud where they must have remained buried for thousands of years (p. 920). However, the functions of these buried forms as effective transformers in the water or immediate bottom have apparently ceased, and the likelihood of their revival in the sea bottom is remote. Those not too deeply buried may serve to some extent as food for burrowing detritus-feeding animals.
Bacterial Modes of Life
For our immediate study of the relationship of bacteria to other organisms and to the chemical cycles of the sea, it is necessary to take into consideration the vital implications of their activities as a part of the dynamic energy cycle within the marine population of which they are a part. The investigations of marine bacteria are therefore concerned chiefly with their physiological processes as applied to the sea and its chemical and biological problems. Their indispensable function in the economy of the sea is primarily one concerned with transformation of organized substances and not with accumulation or storage of organic matter.
In order to understand better the activities of bacteria, it is necessary to distinguish between certain of the different modes of life. These are concerned especially with the source of nutrition and the oxygen supply.
Autotrophic Bacteria. These resemble green plants in their ability to build carbohydrates and proteins out of the simple substances carbon dioxide and inorganic salts. Some of these, known as photosynthetic, possess coloring material, or bacteriochlorin, and use radiant energy in building up protoplasm, while others, known as chemosynthetic, derive their energy from the oxidation of various inorganic compounds such as H2S, S, or NH4.
The amount of organic material synthesized in the sea by bacteria is small when compared to that produced by the chlorophyll-bearing plants. It is not fully known to what extent the chemosynthetic forms contribute to organic material on the sea bottom where depths are so great that there is insufficient light for photosynthesis, but the concentration of benthic animals suggests correlation mainly with the pelagic and benthic algae as the source of primary food and not with the bacteria.
However, autotrophic purple sulphur bacteria have been on several occasions reported as being so abundant in isolated inshore situations as to impart a red tint to the water, to the surface of algae, or to the bottom (Benecke, 1933).
Heterotrophic Bacteria. These obtain their energy by the oxidation of organic compounds. Hence they live as saprophytes or parasites. Most bacteria of the sea are of this type.
We have learned that in the cycle of organic material in the sea it falls to the phytoplankton, in particular, but also to other algae to synthesize organic substance from such inorganic raw materials as carbon dioxide, nitrates, phosphates, and others. But the store of certain of these materials may be exhausted in the euphotic layer and become bound as part of the substance of organisms. However, over a long period of time organisms die at the same rate as they are born, and thus a continuous return of the raw material is possible if a transforming agency is provided. Such an agency exists in the heterotrophic bacteria, whose enormous task is to perpetuate this phase of the cycle through mineralization of organic matter. Animals take part in the general cycle, but owing to the fact that as a group they are neither producers nor transformers (in the sense that plants and bacteria are), a reduced cycle could go on without them; indeed, considerable quantities of plants must at times by-pass the animals and be directly reduced to inorganic state by bacteria (fig. 248, p. 926). The interposition of animals no doubt functions to smooth out the cycle so that bacterial activity goes on at a more even rate throughout the year. There appears to be no evidence that the number or kind of bacteria show any marked seasonal cycles (Lloyd, 1930, ZoBell, 1938). During seasons of plant production, rapidly growing animals incorporate large quantities of plant substance into their own structure and, owing to the longer life cycles of many animals, much of this material may become more gradually available to bacteria at periods of minimum plant production. Illustrative of this is Lohmann's study of the cycle of plankton organisms over the whole year at Kiel. According to his observations the plants for the year averaged 56 per cent of the volume of the total pxsankton However, it was found that from December to February plants formed scarcely a third of the total plankton. At Plymouth the winter production of plants is set at about one fourth of the summer rate. These rates apply only to calculations based on given diatom populations during twenty-four hour periods of production during these seasons and may vary with other species and conditions (Harvey et al, 1935).
Utilization of Dissolved Organic Matter. In discussing the chemistry of the sea, it was pointed out (p. 248) that an appreciable quantity of organic matter is present in solution in sea water. The concentrations per unit volume of water are very much smaller than those
It was believed by Pütter (1907) that many marine animals are able to absorb dissolved organic matter through their gills and integuments and may thus obtain a portion of their food through utilization of the organic matter in solution in the sea. There is little evidence that other forms than bacteria make any considerable use of this supply of nutriment (Krogh, 1934b, Bond, 1933).
According to some authorities the low concentration and uniform distribution of dissolved organic matter in the sea may result from the action of heterotrophic bacteria. Sea water may be looked upon as a dilute culture medium in which the upper limit of concentration of dissolved organic substance is a threshold value maintained by the bacteria at a level below 10 mg/l. In apparent contradiction it must be mentioned that this may appear too dilute for bacterial growth, since for some non-marine bacteria 10 mg/l of different carbon compounds is the minimum concentration in which successful growth occurs (Stephenson, 1939). This may also be true for marine bacteria suspended free in the water. But when the bacteria and other organic material are adsorbed to solid surfaces a greater efficiency in utilization of dilute organic matter is possible, and growth occurs although concentrations may be much lower than 10 mg/l.
Experimentally it has been shown by ZoBell and Anderson (1936a) that in normal filtered sea water bacteria may flourish but do so best when grown in receptacles providing the greatest solid surface area per unit volume of sea water. Increased surfaces were obtained by introducing sterile beads, siliceous sand, and so forth. Increasing the ratio of solid surface to water leads to increased bacterial activity only when the nutrient medium is of low concentration such as that prevailing in the sea. It is explained that the increased surfaces offer places for attachment of greater numbers of periphytic bacteria (that is, those which grow attached to solid surfaces). Clean glass microscope slides submerged in the sea also quickly show a concentration of bacteria following adsorption of organic food and provision of solid surface.
The efficiency of the activities of periphytic bacteria is believed to be enhanced owing to adsorption of organic matter to solid surfaces and to the reduction of diffusion at the immediate surfaces of bodies and within the interstices at the tangent of the bacterial cell and the solid surfaces. Thus these micro-volumes serve as concentrating foci for bacterial
In nature the solid surfaces are provided by all types of particulate matter, animate or inanimate, on the bottom, in the plankton, and on the nekton.
Oxygen Relations. It is convenient to classify the bacteria further on the basis of their different oxygen requirements or tolerances. There are obligate aerobes which use free oxygen, obligate anaerobes which function in the total absence of free oxygen, facultative forms which may live in either type of environment, and microaerophiles which require a reduction of free oxygen but not to the point of anaerobic conditions. Most marine bacteria are said to be of this type.
Bacterial Chemical Transformations. To facilitate study of the cycle of substances in the sea, it is necessary further to classify the marine bacteria into several convenient general groups, namely nitrifying, denitrifying, nitrogen fixing, sulphur, and iron bacteria, and so on, based upon their metabolic activities in the transformation of these substances. To describe these groups is to describe the role of bacteria in the chemical and biological cycles of the sea.
The Nitrogen Cycle
The main features of the nitrogen cycle must be considered because of the outstanding importance of nitrogen to all forms of life and because of the great general interest it holds in illustrating the successive ecological implications with respect to bacteria.
It has been pointed out (chapter VI) that nitrogen exists in the sea in combination with other elements, for example, in ammonia (NH3), and as oxides of nitrogen in nitrite ion (NO2), and nitrate ion (NO3). Nitrogen enters into the composition of all living things. It is one of the building blocks (nutrients) used by plants in forming the complex protein molecules of their bodies from which animals must derive their nitrogen. However, not all forms of nitrogen can be used by plants, hence the complex nitrogenous compounds found in both plants and animals must, upon death of the organisms, be decomposed, along with their products of excretion, to chemically simpler compounds utilizable by the plants. This decomposition, we know, is accomplished mainly by the activity of proteolytic bacteria.
The process of decomposition involves a series of steps in which specifically different bacteria are concerned. The early stages of the transformations are not fully known, but amino acids result and the nitrogen compounds—ammonia, nitrites and nitrates—are a part of this process. It is these inorganic compounds and also, to some extent, the amino acids that can be used directly by the plants for their supply of nitrogen.
The main store of nitrogen in the sea has been considered elsewhere (pp. 181 and 242). We need to be concerned here only with the main features of the chemical circulation of this element as activated by organisms including the plants, animals, and bacteria living within the sea. We may begin with the large and complex protein molecule of plant or animal tissue which is broken down into more simple products containing nitrogen. The cycle is composed of six transitions known as ammonification, nitrification, nitrogen assimilation, denitrification, and nitrogen fixation.
Ammonification. It is well known that ammonia is a product associated with decay of organic material. There are a number of stages and different products involved in this simplification of the molecule, among which products are the amino acids, considered present in the sea only by inference (Cooper, 1937). The bacterial process of deaminization results in splitting off the NH2 group in the amino acids, and there are many types of bacteria in the sea which are endowed with the ability to carry on this process. In weak solutions the ammonia may be intercepted at this point and the nitrogen assimilated directly by diatoms, as is known to occur also with higher plants. ZoBell (1935) and Cooper (1937) review the literature, in which there is much evidence that ammonia nitrogen constitutes one of the important sources of nitrogen utilized by unicellular algae. Ammonia is present usually only in small quantities and its distribution and concentration appear to indicate the place and intensity of organic decomposition (Redfield and Keys, 1938).
Nitrification. It was formerly suggested by some investigators that the sea water must derive its nitrates through drainage from land or through electrical discharges and photochemical processes. The nitrifying bacteria occurring near shore were thought to have washed in from land and not to live normally in the sea. In more recent years investigations have concluded from bacteriological and chemical studies that this type of bacteria is also beyond doubt truly marine. Carey (1938) summarizes briefly the development of our knowledge of these microorganisms in the sea.
The complete process of nitrification includes the formation of nitrates from ammonia and nitrites (NH3 → NO2 → NO3). The organisms responsible for converting the ammonia to nitrite are called Nitrosomonas and Nitrosococcus. They may live in the absence of organic material, obtaining their carbon through assimilation of carbon dioxide and their energy to carry on life processes through the oxidation of ammonia to nitrites. Investigations by Carey indicate that this takes place mainly in two regions, on or near the bottom in coastal areas and in the water in association with plankton at moderate depths, though some nitrites may also be formed at mid-depths. Oxidation of ammonia to nitrite may also occur photochemically (p. 256).
Following the conversion to nitrites, another group of bacteria oxidizes the nitrites to nitrates. The source of carbon for the nitrateformers is apparently also the carbon dioxide, and the energy is derived through oxidation of nitrities.
Nitrogen Assimilation. The process of nitrogen assimilation is primarily a function of the plants, the phytoplankton and benthic algae, but bacteria also assimilate nitrogen. Nitrogenous nutrients such as amino acids, ammonia, nitrates, or nitrites are the available sources of the nitrogen used by the plants in building up the amino-nitrogen of the protoplasm. It is not clear which of the last three mineralized compounds are preferred by phytoplankton as a source of nitrogen, but field observations provide evidence that they may be used simultaneously. During periods of low plant production the process of nitrification results in the storage of nitrogen as nitrates, and subsequent outbursts of diatoms then draw heavily upon this supply. After assimilation these plants may die and be dissociated directly by bacteria, or what is perhaps the most usual occurrence, they may be eaten by animals which require organic nitrogen from the plants directly or indirectly. In any event, a return to the inorganic nitrogen compounds is eventually effected by the bacteria, although animals preying directly upon each other may keep the organic nitrogen within their own cycle for some time. However, due to constant losses, this cycle cannot be self-perpetuating, and there must therefore be a large group of herbivorous animals to serve as food for the carnivorous forms.
Nitrate Reduction and Denitrification. The nitrogen cycle in the sea is more involved than is indicated by the above discussion. Gran (1901) and later Baur (1902) showed that denitrifying bacteria also exist in the sea. These denitrifiers and nitrate-reducers produce the effect just opposite to nitrification. Accordingly, nitrates are reduced to nitrites by splitting off a part of the oxygen, and other bacteria, the true denitrifiers, may carry the process even further with complete reduction of the nitrites and evolution of free nitrogen (NO3 → NO2 → N2). This last step, which is apparently not of great importance in the sea, constitutes a loss to the cycle in the sea unless the elementary nitrogen can be reclaimed by nitrogen-fixing bacteria (see below). The relatively uniform distribution of dissolved nitrogen in the sea also suggests that true denitrifiers and nitrogen fixers are not important in the general economy of the sea (Hamm and Thompson, 1941).
It has been held that the process of reduction of nitrates and nitrites by bacteria is characteristic of an environment lacking or poor in oxygen. Under these anaerobic conditions and in the presence of organic matter the bacteria find their source of needed oxygen in the molecules of these compounds. Rather little is known about the extent of denitrification in the sea, but since most sea waters have at least a small supply of
Nitrogen Fixation. In the terrestrial environment, the fixation of free nitrogen by bacteria is an important factor. To what extent similar nitrogen fixation occurs in the sea through the activity of bacteria is not well known. However, nitrogen fixers are reported from coastal areas, some in symbiosis with algae, and the extent to which they function in fixing free nitrogen depends upon environmental conditions involving the amount of available nitrogen compounds at their disposal, since nitrogen fixation is not an obligatory process (Benecke, 1933).
Phosphorus, Carbon, and Sulphur Cycles
Though they are allotted relatively less space for discussion, it is not intended to minimize the importance of bacterial activity in the transformation of these elements.
Phosphorus is another of the important plant nutrients which has a biologically activated cycle involving alternation of organic and inorganic phases. Whereas carbon dioxide is always present in sufficient quantity for the needs of marine plants, the phosphorus, like the nitrogen, may be depleted to the extent of interfering with the fullest growth. In laboratory experiments phosphate is apparently quickly regenerated by bacteria and other agencies following the death of plants and animals. In studies on stored sea water, Renn (1937) and Waksman et al (1938) found that phosphates are assimilated by bacteria in the growth of their cell substance but that bacterial competition with diatoms for this element is not serious under these conditions, since upon death and autolysis of the bacteria the phosphates are returned in a few days in mineralized form. When a supply of decomposing diatoms is at hand, the phosphates are regenerated from these more rapidly than they are consumed by the bacteria. Under these experimental conditions, approximately two thirds of the total phosphorus present in the diatoms was liberated within 132 hours through bacterial activities. Cooper (1935) found a more rapid regeneration of phosphates from animal plankton than from diatoms.
It must be emphasized, however, that these quick regenerations of phosphates in laboratory experiments are at variance with findings relative to the rate of regeneration in the sea, where renewal in the water is much slower, requiring three to four months (p. 260).
The complex carbon compounds built up by marine plants and animals are decomposed through bacterial action with the formation of carbon dioxide. This formation supplements the carbon dioxide that is produced through respiration by all other organisms and helps maintain the
Sulphur is one of the essential constituents of living matter, and its compounds, like those of other elements of protoplasm, are acted upon by bacteria. Transformations wrought by bacteria in the chemical compounds of sulphur may have far-reaching effects on the associated plant and animal populations and also upon chemical and geological phenomena. First, it may be mentioned that plants utilize a small quantity of sulphur in their metabolism; the compound used, namely sulphate, is produced by chemical or biological oxidation. Second, in the decomposition of organic compounds containing sulphur, hydrogen sulphide is produced as a disintegration product which, when present in large quantities, is inimical to plant and animal life. The odor of hydrogen sulphide is frequently noticeable at low tide in the organically rich muds of protected bays and in muds brought up from deeper water.
This hydrogen sulphide may be formed by splitting off the H2S group of the protein molecule or through a process of reduction of the proteins by heterotrophic bacteria. The inorganic compounds of sulphur, such as sulphates and sulphites, may also be reduced to hydrogen sulphide by heterotrophic bacteria under anaerobic conditions in the presence of organic material. Hence it is important to note that through intramolecular respiration oxidation of organic matter can continue even though all free oxygen has been removed. In areas with little or no circulation of water near the bottom and with an accumulation of organic detritus these heterotrophs as well as true sulphur bacteria abound, but the hydrogen sulphide evolved inhibits any other forms of life. In the Black Sea hydrogen sulphide is found from 180 m to the bottom; and from a depth of 300 m to 1500 m it increases from 1.48 cm3/l to 6.17 cm3/l (fig. 237, p. 872, Nikitin, 1931). Other classical examples are found in the oyster pools of threshold fjords (p. 802).
Not all bacteria that are involved in the sulphur cycle produce hydrogen sulphide. The metabolic requirements of the true sulphur bacteria produce the opposite effect through the process of oxidation. During the assimilation of carbon dioxide by autotrophic sulphur bacteria in the presence of free oxygen, the hydrogen sulphide is oxidized according to the following chemical equation:
In some types of bacteria, including many purple bacteria, the sulphur is deposited as reserve material within the bacterial cell. The nitrogen needed is obtained from ammonium salts.
Bacteria and Bottom Deposits
Only brief mention can be made of the activities of bacteria in the processes of sedimentation on the ocean bottom. Further consideration
The activities of the various types of bacteria that occur in great abundance in the bottom sediments are believed to have a significant role in determining the character of the bottom deposits and the diagenesis of rock strata. Some of the results of chemical transformations wrought by these microorganisms are:
Formation of humus, a very stable organic end product of decomposition with a characteristic carbon-nitrogen ratio varying from 8:1 to 12:1 (Jensen, 1914).
Calcium precipitation in the presence of calcium salts and high pH.
It is believed by some investigators—Drew (1914), Bavendamm (1932), and others reviewed by Benecke—that bacteria in the sea are important agents in the precipitation of calcium carbonate in marine sediments and may therefore be of special geological importance. Many bacteria are known experimentally to produce an alkaline reaction in the presence of calcium and organic material, yielding ammonia. Such organisms may encrust themselves with areolas of calcium carbonate. The extent to which this type of precipitation can occur is still a moot question. Lipman (1929) was of the opinion that in the sea there can be no calcium precipitation because sea water does not contain sufficient concentration of calcium, but the general opinion seems to be that under certain natural conditions bacterial precipitation of calcium can and does occur in the sea, especially in bays in the tropics where there is an abundance of organic material.
Iron and manganese may be precipitated by bacteria that form sheaths of compounds of these metals (Harder, 1919). For example, they obtain energy from the oxidation of the soluble ferrous bicarbonate using the carbon dioxide liberated and precipitating ferric hydroxide.
Distribution of Bacteria in the Sea
The greatest numbers of marine bacteria have been found in the coastal waters where the greatest abundance of plant and animal life is also produced. In vertical distribution we find two main centers, on the bottom a few millimeters below the mud-water interface, and in the pelagic zone attached to the floating plants and animals and other particulate matter (fig. 247). Reference to table 100, from ZoBell and Anderson (1936b), will illustrate typical vertical distribution off the California coast. It should be noted that even though one center of distribution is in the pelagic zone, associated with the plankton, the existence of bacteria is apparently not truly planktonic but sessile upon organisms, and must therefore also closely coincide vertically and horizontally with the maximum distribution of these organisms.
It has been indicated by Carey and Waksman (1934) and others that bacteria are also present in relatively small numbers in the water even to a depth of 5000 m, and to that extent must be considered planktonic. But since the favorite habitat is one of attachment, it is not possible at present to know how normal the true planktonic existence is. Many individuals may be there through accident and be able to survive and multiply only to the degree that they are capable of utilizing the dilute organic matter that is in solution in the water. The advantages of a periphytic habit were discussed elsewhere (p. 912). A planktonic distribution must, however, be of great significance in the dispersal of these microorganisms.
The vertical distribution of bacteria in the sea.
The greatest density by far of bacterial populations is found on the bottom, where as many as 420,000,000 cells per gram of wet mud may occur (ZoBell and Anderson, 1936b). Such dense populations are possible mainly because in a thin layer representing an interface between mud and water there is concentrated a large portion of the organic detritus, dead bodies of plants and animals, which is constantly sinking and forming an abundant rich food supply for bacteria as well as for bottom-dwelling animals which compete with them. Most bacteria occur in the first few millimeters of bottom ooze and there is a gradual diminution of numbers with the increasing thickness of the bottom deposits. Viable
In fig. 247 is shown the vertical distribution of bacteria and its relation to the diatom population. It will be noted that the large bacterial population of the pelagic region coincides roughly with the vertical range of floating plants and animals. This apparently results from the periphytic habit of many bacteria. The plankton organisms—diatoms, copepods, and so forth—living most abundantly in the euphotic zone, serve as surfaces for attachment and offer a favorable environment for multiplication (p. 912). The presence of a large periphytic bacterial population in the plankton results in prompt bacterial decomposition of large quantities of dead organisms before they have sunk to great depths; thus a large portion of mineralized plant nutrients is regenerated within or only a little below the euphotic zone.
| Sample | Depth (m) | Number of bacteria | ||
|---|---|---|---|---|
| Water | 1 | 147 | 344 | 261 |
| Water | 10 | 238 | 400 | 360 |
| Water | 20 | 292 | 528 | 395 |
| Water | 50 | 86 | 620 | 208 |
| Water | 100 | 14 | 17 | 53 |
| Water | 200 | 3 | 2 | 0 |
| Water | 500 | 2 | 0 | 0 |
| Sediment | Bottom | 2,170,000 | 768,000 | 16,200,000 |
| E. W. Scripps Station No. | 32A1 | 32B2 | 33A3 | |
| Water depth | 704 m | 610 m | 1287 m | |
Bibliography
Allee, W. C.1934. “Concerning the organization of marine coastal communities” . Ecological Monographs, v. 4, p. 541–554, 1934.
Allen, E. J.1909. “Mackerel and sunshine” . Marine Biol. Assn. U. K., Jour., v. 8, p. 394–406, 1909.
Allen, W. E.1934. “The primary food supply of the sea” . Quart. Rev. Biol., v. 9, p. 161–180, 1934.
Bauer, E.1902. “Ueber zweid enitrificirende Bakterien aus der Ostsee” . Komm. z. Wissensch. Untersuch. der Deutschen Meere in Kiel und d. Biologischen Anstalt auf Helgoland. Wissensch. Meeresuntersuch., N. F., Abt. Kiel, Bd. VI. p. 11–21, 1902.
Bavendamm, W.1932. “Die microbiologische Kalkfällung in der tropischen See” . Archiv. f. Mikrobiol., v. 3, p. 205–276, 1932.
Benecke, W.1933. “Bacteriologie des Meeres” . In Abderhalden's Handbuch d. Biol. Arbeitsmethoden, v. 9, p. 717–854, 1933.
Bigelow, H. B.1925. “Plankton of the offshore waters of the Gulf of Maine” . U. S. Bur. Fisheries, Bull., v. 40 (for 1924), pt. 2, 509 pp., 1925.
Blegvad, H.1914. “Food and conditions of nourishment among the communities of invertebrate animals found on or in the sea bottom of Danish waters” . Danish Biol. Sta., Repts., v. 22, p. 41–78, 1914.
Blegvad, H.1930. “Quantitative investigation of bottom invertebrates in the Kattegat with special reference to the plaice food” . Danish Biol. Sta., Repts., v. 36, p. 3–55, 1930.
Bond, R. M.1933. “A contribution to the study of the natural food-cycle in aquatic environment” . Bingham Oceanogr. Coll., Bull., v. 4, art. 4, 89 pp., 1933.
Boynton, L. C., and R. C. Miller. 1927. “The occurrence of a cellulase in the shipworm” . Jour. Biol. Chem., v. 75, p. 613–618, 1927.
Braarud, T., and A. Klem. 1931. “Hydrographical and chemical investigations in the coastal waters off Möre and in the Romsdalsfjord” . Hvalrådets Skrifter, no. 1, 88 pp., 1931.
Bullen, G. E.1909. “Plankton studies in relation to western mackerel fishery” . Marine Biol. Assn. U. K., Jour., v. 8, p. 269–302, 1909.
California, Div. Fish and Game. 1937. “California's sardine catch” . Fish Bull. no. 49, p. 11–15, 1937.
Cannon, H. G.1928. “On the feeding mechanism of the copepods, Calanus finmarchicus, and Diaptomus gracilis.” British Jour. Exper. Biol., v. 6, p. 131–144, 1928.
Carey, C. L.1938. “The occurrence and distribution of nitrifying bacteria in the sea” . Jour. Marine Research, v. 1, p. 291–304, 1938.
Carey, C. L., and S. A. Waksman. 1934. “The presence of nitrifying bacteria in deep seas” . Science, v. 79, p. 349–350, 1934.
Cooper, L. H. N.1935. “The rate of liberation of phosphate in sea water by the breakdown of plankton organisms” . Marine Biol. Assn. U. K., Jour., v. 20, p. 197–200, 1935.
Cooper, L. H. N.1937. “The nitrogen cycle in the sea” . Marine Biol. Assn. U. K., Jour., v. 22, p. 183–204, 1937.
Crozier, W. J.1918. “The amount of bottom material ingested by holothurians (Stichopus)” . Jour. Exper. Zool., v. 26, p. 379–389, 1918.
Drew, G. H.1914. “On the precipitation of calcium carbonate in the sea by marine bacteia and on the action of denitrifying bacteria in tropical and temperate seas” . Carnegie Inst. Washington, Pub. no. 182, p. 7–45, 1914.
Fisher, W. K., and G. E. MacGinitie. 1928. “Natural history of an echiuroid worm” . Ann. Mag. Nat. Hist., ser. 10, p. 204–213, 1928.
Fleming, Richard H.1939. “The control of diatom populations by grazing. Conseil Perm” . Internat. p. l'Explor. de la Mer, Jour. du Conseil, v. 14, no. 2, p. 210–227, 1939.
Fox, D. L., (ed.). 1936. “The habitat and food of the California sea mussel” . Scripps Inst. Oceanogr., Bull., v. 4, p. 1–64, 1936.
Fuller, J. L.1937. “Feeding rate of Calanus finmarchicus in relation to environmental conditons” . Biol. Bull., v. 72, p. 233–246, 1937.
Fuller, J. L., and G. L. Clarke. 1936. “Further experiments on the feeding of Calanus finmarchicus” . Biol. Bull., v. 70, p. 308–320, 1936.
Galtsoff, P. S., and V. L. Loosanoff. 1939. “Natural history and method of controlling the starfish (Asterias forbesi Desor)” . U. S. Bur. Fisheries, Bull., v. 49, p. 75–132, 1939.
Gran, H. H.1901. “Studien über Meeresebakterien” . Bergens Mus. Aarbog, no. 10, p. 1–23, 1901.
Hamm, Randall E., and T. G. Thompson. 1941. “Dissolved nitrogen in the sea water of the Northeast Pacific with notes on the total carbon dioxide and the dissolved oxygen” . Jour. Marine Research, v. 4, p. 11–27, 1941.
Harder, E. C.1919. “Iron–depositing bacteria and their geologic relations” . U. S. Geol. Surv., Prof. Paper, no. 113, 89 pp., 1919.
Hardy, A. C.1936. “Plankton ecology and the hypothesis of animal exclusion” . Linn. Soc. London, Proc., 148th Session, p. 64–70, 1936.
Hardy, A. C., and E. R. Gunther. 1935. “The plankton of the South Georgia whaling grounds and adjacent waters, 1926–1927” . Discovery Repts., v. 11, p. 1–456, 1935.
Hardy, A. C., C. E. Lucas, G. T. D. Henderson, and J. H. Fraser. 1936. “The ecological relations between the herring and the plankton investigated with the plankton indicator” . Marine Biol. Assn. U. K., Jour., v. 21, p. 147–291, 1936.
Hart, T. J.1935. “On the diatoms of the skin film of whales, and their possible bearing on problems of whale movements” . Discovery Repts., v. 10, p. 249–282, 1935.
Harvey, H. W.1934. “Annual variation of planktonic vegetation, 1933” . Marine Biol. Assn. U. K., Jour., v. 19, p. 775–792, 1934.
Harvey, H. W., L. H. N. Cooper, M. V. Lebour, and F. S. Russell. 1935. “Plankton production and its control” . Marine Biol. Assn. U. K., Jour., v. 20, p. 407–442, 1935.
Hentschel, E.1936. “Allgemeine Biologie des Südatlantischen Ozeans” . Deutsche Atlantische Exped. Meteor, 1925–1927, Wiss. Erg., Bd. 11, 343 pp., 1936.
Hesse, R., W. C. Allee, and K. P. Schmidt. 1937. Ecological animal geography. New York, John Wiley & Sons, 597 pp., 1937.
Hewatt, Willis G.1937. “Ecological studies on selected marine intertidal communities of Monterey Bay, California” . Amer. Midland Naturalist, v. 18, p. 161–206, 1937.
Hjort, Johan, and Johan T. Ruud. 1929. “Whaling and fishing in the North Atlantic” . Conseil Perm. Internat. p. l'Explor. de la Mer, Rapp. et Proc.-Verb., v. 56, no. 1, 123 pp., 1929.
Jensen, P. B.1914. “Studies concerning the organic matter of the sea bottom” . Danish Biol. Sta., Repts., v. 22, p. 1–39, 1914.
Jordan, E. O.1931. Textbook of general bacteriology. Philadelphia and London, W. B. Saunders, 819 pp., 1931.
Krogh, August. 1934a. “Physiology of the blue whale” . Nature, v. 133, p. 635–637, 1934.
Krogh, August. 1934b. “Conditions of life at great depths in the ocean” . Ecological Monographs, v. 4, p. 430–439, 1934.
Lebour, Marie V.1924a. “The food of young herring” . Marine Biol. Assn. U. K., Jour., v. 13, p. 325–330, 1924.
Lebour, Marie V.1924b. “The Euphausiidae in the neighborhood of Plymouth” . II. Nyctiphanes couchii and Meganyctiphanes norvegica. Marine Biol. Assn. U. K., Jour., v. 13, p. 810–847, 1924.
Lipman, Charles B.1929. “Further study on marine bacteria with reference to the Drew hypothesis on CaCO3 precipitation in the sea” . Carnegie Inst.
Lloyd, Blodwen. 1930. “Bacteria of the Clyde Sea area: a quantitative investigation” . Marine Biol. Assn. U. K., Jour., v. 16, p. 879–907, 1930.
Lohmann, H.1908. “Untersuchungen zur Feststellung des vollständigen Gehaltes des Meeres an Plankton” . Komm. z. Wissensch. Untersuch. d. Deutschen Meere in Kiel und d. Biologischen Anstalt auf Helgoland. Wissensch. Meeresuntersuch., N.F., Abt. Kiel, Bd. 10, p. 131–370, 1908.
Lucas, C. E.1936. “On certain interrelations between phytoplankton and zooplankton under experimental conditions” . Conseil Perm. Internat. p. l'Explor. de la Mer, Jour. du Conseil, v. 11, p. 343–362, 1936.
MacGinitie, G. E.1939. “The methods of feeding of tunicates” . Biol. Bull, v. 77, p. 443–447, 1939.
Mackintosh, N. A.1934. “Distribution of the macroplankton in the Atlantic sector of the Antarctic” . Discovery Repts., v. 9, p. 65–160, 1934.
Marshall, S. M., A. G. Nicholls, and A. P. Orr. 1934. “On the biology of Calanus finmarchicus. V. Seasonal distribution, size, weight and chemical composition in Loch Striven in 1933 and their relation to phytoplankton” . Marine Biol. Assn. U. K., Jour., v. 19, p. 793–828, 1934.
Nielsen, S. E.1937. “On the relation between the quantities of phytoplankton and zooplankton in the sea” . Conseil Perm. Internat. p. l'Explor. de la Mer. Jour. du Conseil, v. 12, p. 147–154, 1937.
Nikitin, W. N.1931. “Die untere Planktongrenze und deren Verteilung im Schwarzen Meer” . Internat. Rev. d. ges. Hydrobiol. u. Hydrogr., Bd. 25, p. 102–130, 1931.
Orton, J. H.1937. Oyster biology and oyster culture. London, Edward Arnold & Co., 211 pp., 1937.
Parr, A. E.1934. “Report on experimental use of a triangular trawl for bathypelagic collecting. With an account of the fishes obtained and a revision of the family Cetomimidae” . Bingham Oceanogr. Coll., Bull., v. 4, art. 6, 59 pp., 1934.
Pearse, A. S.1939. Animal ecology. New York, McGraw-Hill Book Co., 642 pp., 1939.
Petersen, C. G. J.1913. “Valuation of the sea. II. The animal communities of the sea bottom and their importance for marine zoogeography” . Danish Biol. Sta., Repts., v. 21, p. 1–44, 1913.
Petersen, C. G. J.1918. “The sea bottom and its production of fish food” . Danish Biol. Sta., Repts., v. 25, 62 pp., 1918.
Pütter, A.1907. “Der Stoffhaushalt des Meeres” . Zeitschr. f. allg. Physiol., v. 7, p. 321–368, 1907.
Redfield, A. C., and A. B. Keys. 1938. “The distribution of ammonia in waters of the Gulf of Maine” . Biol. Bull., v. 74, p. 83–92, 1938.
Renn, C. E.1937. “Bacteria and the phosphorus cycle in the sea” . Biol. Bull., v. 72, p. 190–195, 1937.
Ricketts, E. F., and J. Calvin. 1939. Between Pacific tides. Stanford Univ. Press, 320 pp., 1939.
Rittenberg, Sydney C.1940. “Bacteriological analysis of some long cores of marine sediments” . Jour. Marine Research, v. 3, p. 191–201, 1940.
Russell, H. L.1892. “Untersuchungen über in Golf von Neapel lebende Bacterien. Zeitschr” . Hyg. Infk., Bd. 11, p. 165–206, 1892.
Scofield, W. L.See: California, Div. Fish and Game.
Seiwell, H. R., and G. E. Seiwell. 1938. “The sinking of decomposing plankton in sea water and its relationship to oxygen consumption and phosphorus liberation” . Amer. Philos. Soc., Proc., v. 78, p. 465–481, 1938.
Shelford, V. E., A. O. Weese, et al.1935. Some marine biotic communities of the Pacific coast of North America. Ecological Monographs, v. 5, p. 251–354, 1935.
Stephenson, M.1939. Bacterial metabolism. New York, Longmans, Green & Co., 2nd ed., 391 pp., 1939.
Tressler, Donald K.1923. Marine products of commerce. New York, Chemical Catalog Co., 762 pp., 1923.
Vaughan, T. Wayland. 1930. The oceanographic point of view. p. 40–56 in Contributions to marine biology. Stanford Univ. Press, 277 pp., 1930.
Waksman, S. A.1934. “The role of bacteria in the cycle of life in the sea” . Scientific Monthly, v. 38, p. 35–49, 1934.
Waksman, S. A., M. Hotchkiss, C. Carey, and Y. Hardman. 1938. “Decomposition of nitrogenous substances in sea water by bacteria” . Jour. Bact., v. 35, p. 477–486, 1938.
Wilson, C. B.1932. “Copepods of the Woods Hole region, Massachusetts” . U. S. Nat. Mus., Bull. 158, 623 pp., 1932.
Yonge, C. M.1928. “Feeding mechanisms in the invertebrates” . Biol. Reviews. v. 3, p. 21–76, 1928.
Yonge, C. M.1931. “Digestive processes in marine invertebrates and fishes” . Conseil Perm. Internat. p. l'Explor. de la Mer, Jour. du Conseil, v. 6, p. 175–212, 1931.
Yonge, C. M.1936. “Mode of life, feeding, digestion, and symbiosis with Zooxanthellae in the Tridacnidae” . Great Barrier Reef Exped. 1928–29, Repts., v. 1, p. 283–321, 1936.
Yonge, C. M.1940. “Observations on the biology of coral reefs” . Sixth Pacific Sci. Congr., California, 1939, Proc., v. 3, p. 605–613, 1940.
ZoBell, Claude E.1935. “The assimilation of ammonium nitrogen by Nitzschia closterium and other marine phytoplankton” . Nat. Acad. Sci., Proc., v. 21, p. 517–522, 1935.
ZoBell, Claude E.1938. “Studies on the bacterial flora of marine bottom sediments” . Jour. Sedimentary Petrol., v. 8, p. 10–18, 1938.
ZoBell, Claude E., and D. Q. Anderson. 1936a. “Observations on the multiplication of bacteria in different volumes of stored sea water and the influence of oxygen tension and solid surfaces” . Biol. Bull., v. 71, p. 324–342, 1936.
ZoBell, Claude E., and D. Q. Anderson. 1936b. “Vertical distribution of bacteria in marine sediments” . Amer. Assn. Petrol. Geol., Bull., v. 20, p. 258–269, 1936.
XIX. Organic Production in the Sea
In the previous chapters dealing with the marine organisms in relation to the factors of the inorganic and organic environment, we have had many occasions to refer directly to plant or animal production in the sea. Indeed, most biological studies relating to controlling factors lead to and are essential to an elucidation of the problem of quantitative and qualitative production of plants or animals in the sea. Studies pertaining to production in the sea are of vital interest to several marine sciences, particularly to the chemical, biological, or geological, because of their bearing on the extent, time, and spatial distribution of organic and certain inorganic constituents of the water and of the bottom.
The gross production (primary production) in the sea can be defined as the amount of organic material which by the activity of organisms in unit time is synthesized in a unit volume of water (production per unit volume), or in unit time is synthesized from inorganic substances in a water column of unit area cross section and extending from the sea surface to the bottom (production per unit area). The amount of organic material can be expressed as carbon, and thus, the production per unit volume can be reported as grams of carbon per cubic meter per day and the production per unit area as grams of carbon per square meter per day (daily gross crop). Productivity of the sea, on the other hand, can be defined as the capacity to produce, and is commonly used as a qualitative term for indicating the fertility of any ocean region.
The term production is also frequently applied in a more limited sense, namely, to denote the product, that is, the amount produced, of any given group of organisms in the sea. The terms plant production, phytoplankton production, zooplankton production, and commercial production are thus employed. The plants are the only organisms in the sea which can synthesize organic matter from inorganic substances in significant quantities. The plant production, therefore, nearly equals the gross production minus the amount of organic matter that is oxidized by the plants themselves and the amount that is secreted by the organisms. Where the depth to the bottom is too great to permit the existence
It is necessary to distinguish sharply between production and population. Population is the amount of organisms per unit volume or unit area as given by weight (grams of carbon, dry weight, or wet weight) or by number present at any given time. The populations can therefore be ascertained by a single survey, but in order to determine the production at least two surveys must be made at different times, and the processes must be known by which organic matter is built up or destroyed in the time intervals between the surveys.
The cycle of organic matter in the sea.
If we consider the cycle of life in the sea, as represented in its simplest form in figure 248, we note that it is made up of two alternating phases, the inorganic and the organic, the latter being split into two parts by the plants and animals. Theoretically it should be possible to measure the amount of organic material produced by measuring the amount of material going through either the organic or inorganic portion of the cycle. Both methods are used, but both are beset with a number of difficulties, as will be noted below. Since the pioneering work of Hensen (1887), much progress has been made toward numerical values of the production of the sea, yet the best that can be claimed for these at present is that they are rough approximations only.
Phytoplankton Production
Data on phytoplankton production may be obtained by direct census or pigment analysis of the phytoplankton population, or through chemical analysis of the water in which it has grown.
Direct Census. Any sample of the population is only a measure of the standing crop, that is, the density of individuals or total volume or weight present at the moment and place of sampling. The common method of phytoplankton population analysis consists of centrifuging or filtering a known volume of water and counting directly under the microscope the number of cells of species making up the population thus concentrated. The population is then reported in numbers of cells of the various species prevailing per liter or per cubic meter of the water.
This method is essential to detailed analysis of the constituents of the phytoplankton communities and for arriving at an understanding of the factors operative in controlling the production of the different ecological types. To illustrate this it is necessary only to recall the plankton diatom types of Cleve (see p. 791) or to consider the divergence of requirements of the two main synthesizing groups, namely the diatoms and dinoflagellates. When the capacity of diatoms to continue a lively rate of organic production drops with increasing temperatures or diminution of essential nutrients, this drop is often in part compensated for by a flare of production by the warmth-loving dinoflagellates, which by reason of their low nutrient requirements and their motility may be able to utilize the nutrients below the lower threshold for spring diatoms (see p. 385).
It is, however, extremely difficult to arrive at accurate estimates of volumes or weights of organic matter through plankton counts alone, since diatom and dinoflagellate species and even individuals of the same species vary greatly in size and organic content and an appreciable portion of the diatoms is inorganic material forming the siliceous shells. Measurements of volume are sometimes made by centrifuging or allowing the plankton catch to settle in graduate cylinders and noting the volume of the precipitated material in milliliters. This method, however, does not serve to separate plant from animal material and the widely different types of organisms with respect to radiating spines and fluid content prevent comparable compactness in settling, with the result that the volume readings represent relative values which give only the major differences. This objection is partly overcome by measuring the total catches in terms of the number of milliliters of fluid which they displace. This is accomplished by noting the fluid volume before and after filtering out all of the organisms. It is not possible however, completely to drain
Plant Pigments and other Plankton Equivalents. In view of the fact that the direct plankton measurements are inadequate for arriving at figures of total vegetative organic matter in the standing crop or the total production for a given period of time, attempts are made to use chemical analysis of the essential plant nutrients that have been consumed from the water by the plants in their production.
In order to estimate the organic content of a standing crop of phytoplankton, Harvey (1934) has described an adaptation of the method of Kreps and Verjbinskaya (1930) whereby the yellow-green pigment present in the plants filtered from a known volume of water is extracted by acetone and the pigment thus obtained in a known volume of acetone solution is determined colorimetrically with an arbitrary standard of 25 mg of potassium chromate and 430 mg of nickel sulphate dissolved in 1 : 1 of water. One milliliter of the standard solution is equivalent to one “pigment unit” of chlorophyll. This pigment unit amounts to 0.88 ± .01 μg (1 μg = 0.001 mg) of chlorophyll (Riley, 1938) or the equivalent of 3.3 × 10−3 mg of organic carbon. The total organic carbon content can then be calculated for the volume of water filtered. For more direct comparison with plankton counts it is also computed that, in the English Channel, one pigment unit is equal to 4000 diatoms of “average cell contents.” Additional plankton equivalents are summarized in table 101, compiled by Fleming (1940).
In this table the “wet plankton” is defined by Atkins (1923) according to whom 1520 mg of wet plankton contains one milligram of phosphorus. This definition, however, is not based on analyses of phytoplankton but of seaweed and may be subject to revision. The equivalents of dry plankton, settling volumes, and displacement volumes are based on observations by Moberg and by M. W. Johnson (unpublished material). The equivalents of carbon, nitrogen, and phosphorus are based on the experimental results that the ratios C:N:P = 41:7.2:1 by weight. If other ratios are introduced, the equivalents must be altered correspondingly. The oxygen equivalent is obtained by assuming that the oxidation of one atom of carbon requires two atoms of oxygen, but Gilson (1937) suggests that the oxygen equivalent should be 20 per cent greater because allowance should be made for the oxygen consumed in oxidizing ammonia to nitrate.
So far, we have dealt with population only. To arrive at the total production of diatoms, for example, for a given unit of time it is necessary to have a series of samples over an interval of time so that calculations can be made on the basis of differences between the standing crops at each sampling. The average reproductive rate of diatoms constituting the population, the rate at which they are regularly eaten by the animal plankton (cf. p. 901), and perhaps also the rate at which they sink below the euphotic zone are factors for which corrections must be made in the final calculations. An example from Lohmann's observations (1908) at Kiel will illustrate the procedure. Lohmann calculated that the daily plant increment was 30 per cent of the standing crop, that the protozoan animals consume daily one half their own weight in plants, and that the metazoan animals (copepods and other forms above the protozoa) consume daily one tenth their own weight. The daily phytoplankton production would then amount to the 30 per cent increase assigned to the rate of production, but if this increase be exactly the same as the day's ration required by the volume of animals present per cubic meter of water for the day, the standing crop of diatoms would show no increase for the day.
| Carbon (1 mg) | Nitrogen (1 mg) | Phosphorus (1 mg) | Plant pigment (1 unit) | Wet plankton (1 mg) | Dry plankton (1 mg) | Settling volume (1 ml) | Displacement volume (1 ml) | Oxygen equivalent (1 ml) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Carbon (mg) | 1 | 5.7 | 41 | 3.3 × 10−3 | 0.027 | 0.44 | 1.4 | 5.6 | 0.536 | |
| Nitrogen (mg) | 0.18 | 1 | 7.2 | 0.58 × 10−3 | 0.0047 | 0.0765 | 0.24 | 1.0 | 0.097 | |
| Phosphorus (mg) | 0.024 | 0.14 | 1 | 0:08 × 10−3 | 0.00066 | 0.011 | 0.034 | 0.14 | 0.013 | |
| Plant pigment (units) | 305 | 1740 | 12,500 | 1 | 8.25 | 133 | 412 | 1690 | 163 | |
| Wet plankton (mg) | 37 | 211 | 1,520 | 122 × 10−3 | 1 | 16 | 50 | 203 | 20 | |
| Dry plankton (mg) | 2.3 | 13.1 | 94 | 7.5 × 10−3 | 0.06 | 1 | 3.1 | 12.7 | 1.2 | |
| Settling volume (ml) | 0.7 | 4.2 | 30.2 | 2.4 × 10−3 | 0.02 | 0.32 | 1 | 4.1 | 0.4 | |
| Displacement volume (ml) | 0.18 | 1.0 | 7.4 | 0.59 × 10−3 | 0.005 | 0.08 | 0.25 | 1 | 0.1 | |
| Oxygen equivalent (ml) | 1.9 | 10.6 | 76 | 6.1 × 10−3 | 0.05 | 0.8 | 2.5 | 10.2 | 1 |
As stated elsewhere, Lohmann arrived at figures indicating a plant production of 10 mm3/m3 during February, the month of minimum plant production. But though the animals were few during the same period their food requirement was 18 mm3/m3. This left a daily deficiency of 8 mm3/m3 in food production for the month. The standing crop must therefore have been on a decline due to grazing, provided the animals at that season actually consumed the normal ration calculated for that month. On the other hand, most months showed a considerable surplus in production of plant material per cubic meter of water over that of consumption by animals. In August, the month of highest production, this surplus amounted to 290 mm3/m3. During that month the animals were also numerous and required a daily supply of food equal to 60 mm3/m3. Therefore the daily total organic material produced in August must have been 290 + 60, or 350 mm3/m3.
It should be noted here, however, that the production and consumption rates are not so simply estimated as assumed in these calculations. The rate of diatom division is not constant as here indicated, but may vary within wide limits between individuals or species, depending upon nutritional and physical factors which vary greatly over the year. Gran (1929) estimated that Ceratium spp. during the summer may have a daily increase of 30 per cent whereas some diatoms, for example Chaetoceros curvisetum, under favorable conditions may increase over 350 per cent daily. Thus during the period of maximum volumes of plants the conditions for rapid multiplication must have been more pronounced than during the periods represented by minimum volumes. With regard to consumption by animals, recent information indicates that the grazing animals apparently do not eat a fixed ration daily in relation to their weight, but instead during periods of high phytoplankton production eat much more than they can digest. This undoubtedly applies to filter feeders, which consume amounts of plants proportional to the concentration of the plants in suspension during the time of filtering. The
Plant-nutrient Consumption as an Index of Organic Production. Changes in the concentrations of the essential plant nutrients coincident with plant growth are highly useful as indexes of production. Redfield, Cooper, and others have demonstrated the existence of a rather constant ratio between the elements carbon, nitrogen, and phosphorus in the organic content of mixed plankton (p. 768). The ratios C:N:P = 41:7.2:1 by weight, or 106:16:1 by atoms, are also in close agreement with the proportions of these elements in sea water (p. 236). Therefore a measurement of the drop in any one of these elements in the mineralized state in the sea water could reasonably be supposed to indicate an equivalent incorporation into organic material during synthesis of carbohydrates or proteins. The assimilation of CO2 and its effect on pH was used as an index by Moore in estimating the organic production in the Irish Sea (p. 768) and it has subsequently been used elsewhere in conjunction with other chemical changes associated with plant growth. When CO2 utilization is used as an index, the respiration of animals and the tendency for CO2 of the water to be in equilibrium with that in the air must be taken into consideration.
During winter in the higher latitudes there is a maximum accumulation of phosphate in the water. This, when returned to the euphotic zone, is the available supply for the following spring growth of plants. In chapter XVI we noted that in some areas a vigorous consumption by plants may lead to a depletion of this nutrient during the growing season. In such an event the area has yielded its maximum production until further regeneration has taken place or further renewal has occurred, for instance by currents from subsurface nutrient-rich layers or by influx from elsewhere. There is considerable variation from year to year in the amount of phosphate that has been drawn upon by the plants and this must be a reflection of the variability in the capacity of plants to use the supply available because of other environmental factors either inorganic or organic which promote or retard the use of the nutrient. In a review of phosphate records covering fourteen years of observations in the English Channel, Cooper (1938) found that the percentage consumption of the total inorganic phosphate of the water column fluctuates between 49 per cent and 81 per cent for the spring productive period and between 63 per cent and 93 per cent for the entire period between the winter maximum and the summer minimum of phosphate. He points out that by April, on an average, one half of the phosphate supply
In connection with phosphate regeneration it should be pointed out here that when a higher concentration of phosphate occurs in isolated areas below the euphotic zone than occurs in the waters forming the regular source supply of phosphate to the euphotic layer, such phenomena must indicate that the excess phosphate has been regenerated in situ. The high phosphate values reflect a high organic production in the immediate overlying waters or in the surface layers of the region from which the phosphate-rich water spreads out. In these instances the growing organisms have served to entrap the phosphate in their bodies which subsequently sink and decay at intermediate depths, thus leading to high concentrations of this substance in these layers. As illustrative of this cycle, see fig. 45, p. 239. Such areas also show low oxygen content as a result of oxidation of organic material.
As a complementary study to phosphate utilization Harvey et al (1935) made analysis of the phosphorus compounds of the planktonic organisms. They found only a fraction of the phosphate removed from the water to be present in the plankton population, and concluded that much of the organic phosphorus compounds passes through the animals undigested and is then dissolved in the water until it is later regenerated to inorganic state.
The utilization of nitrate by the growing phytoplankton also gives an index of seasonal production. The various steps in the regeneration (see p. 913) are believed to retard the process so that nitrate accumulation during winter is especially pronounced in the northern latitudes, where well-defined growing seasons occur. However, since it is only the nitrogen that plants require from this compound, they can acquire this nitrogen from ammonia, and perhaps also from amino acids. Ammonia
Oxygen Production and Consumption as an Index of Organic Production. The plants obtain carbon for carbohydrate synthesis from the CO2 in the water according to the equation
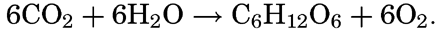
In the experiment to which we have referred (table 93, p. 777), the exposed plankton association was a mixture of phyto- and zooplankton. The respiration of both plants and animals is therefore included, and this explains the high observed values of the respiration. Observations on pure cultures of phytoplankton organisms indicate that the ratio of respiration to maximum photosynthesis is usually less than 10 per cent. In a pure culture of Nitzschia closterium (Barker, 1935a) this ratio was 8 per cent; in a pure culture of a species of Peridinium (Barker, 1935b) it varied from 7 per cent to 14 per cent; in another culture of Nitzschia closterium (Clarke, 1936) it was less than 1 per cent; and in an apparently pure culture of Coscinodiscus excentricus (Jenkin, 1937) it varied from 3 per cent to 12 per cent.
In these instances the phytoplankton production would nearly equal the gross production, but the values were obtained under conditions when photosynthesis was rapid. On an average for a whole year the ratio of
The efficiency of the gross production, that is, the fraction of the energy penetrating the sea surface which is utilized in photosynthetic activity, is, in Long Island Sound, 0.55 to 0.82 per cent (Riley, 1941).
In nature, the oxygen accumulates in the layers of organic production and thus its fluctuations in time and space give a measure of the intensity of phytoplankton outbursts. It can provide only minimal values because the exact quantity of oxygen produced is obscured by the respiratory activities of animals and bacteria, and in case of surface supersaturation some oxygen is given off to the atmosphere.
Associated with the above is the problem of estimating the production of organic material by a study of the oxygen consumed in the eventual oxidation of the material below the water layers in which it was produced. This association necessitates a consideration of the oxygen used in the oxidation of the carbon and in converting ammonia to nitrates, but the hydrography of the area must be such that the water layer in which oxygen consumption is being measured can be definitely referred to the euphotic layer in which the production of organic material is supposed to have occurred some time previously. As yet no method has been developed by which the amount of oxygen consumed can be determined directly, but indirectly it can be found if it is assumed that in the subsurface layer the distribution of oxygen is stationary (p. 161). On this assumption the amount of oxygen which in unit time is brought into a given volume by processes of diffusion and advection must equal the amount which in the same time is consumed in the same volume. The replenishment of oxygen by diffusion and advection can be determined if sufficient hydrographic data are available (for example, Seiwell, 1935, Sverdrup and Fleming, 1941), and so far our knowledge of oxygen consumption in the subsurface layers is derived from such computations only.
In closing this brief review of the various indices of organic production in the sea, it may be stated that the most reliable figures are, doubtless, to be obtained by a combination of the various methods, both biological and chemical, in order to provide corroborative evidence.
Zooplankton Production
An approach to the problems of organic production of the sea is possible through a study of zooplankton production, since the animals of this group are in general the chief grazers and must fluctuate with the supply of their food (cf. p. 899). They are vastly more numerous and regularly distributed than the predatory animals and any fluctuations in population numbers are not influenced by fishing.
That the production of zooplankton is indeed large may be seen from Redfield's analysis (1941) of the standing calanoid population of the Gulf of Maine. The average monthly catch for all sections of the Gulf was about 40 ml of water-free plankton per square meter of surface. The highest monthly value, 90 ml, was obtained in September and the lowest value, about 10 ml, was obtained in May. Water-free or dry plankton volumes were obtained by filtering the water from the animals. This allows them to become more compact than when measuring the volume by precipitation in fluid. The latter method gave volumes usually about 4.9 times greater.
On the basis of the above water-free values the standing crop for the whole Gulf would be some four million tons. The crop increased by about 80 ml of water-free plankton per square meter between May and September, which is a net gain of about eight million tons. In the English Channel the maximum standing crop for zooplankton in 1934 was calculated (Harvey et al, 1935) at about 40 mm3 per 100 liters. Considering the depth at 100 m, this would be about 40 ml/m2 of surface, or the average annual value found for the Gulf of Maine. If the zooplankton production is to be considered a measure of the phytoplankton production, many factors tending to vary the volume of zooplankton in relation to the plants have to be taken into account. We enumerate the four following:
(1) Much of the zooplankton is consumed by predatory plankton feeders that live regularly in the area of production or that enter it as invaders from less productive areas. The extent of such consumption is not known, but we know, for instance, that rich herring hauls are correlated with abundant Calanus, and that plankton-feeding whales also seek out productive waters such as those of the Antarctic and of northern coastal banks that are rich in their favorite food (p. 905). It has been estimated that on an area 8,000,000 km2 there may be as many as 300,000 whales. The food required by these animals alone must be enormous. They may grow to a length of nearly 28 m and a weight of 80 tons in about two years. Their resting metabolism requires 38 l of oxygen per minute (p. 907). The energy required for this rapid growth and katabolic processes must make notable inroads on the animal plankton.
(2) Many of the plankton animals eat more plants than they can use in their metabolic processes and thus pass through the digestive tract much undigested material during periods of high plant production. This waste makes it impossible to assign a fixed value to the amount of food that animals of a given weight should consume per day to grow and repair breaking-down processes within certain temperature ranges. If a figure for consumption is to be obtained for filter-feeding forms it would
(3) Few plankton animals are strictly plant eaters, but instead have a mixed diet of plants and animals or of detritus arising from both, while yet others are wholly carnivorous. The direct relationship of the zooplankton production to the phytoplankton as a source of energy is in this way obscured and separated in time.
(4) Finally, much of the phytoplankton production is not consumed by planktonic animals but instead sinks to the bottom to serve as food for benthic animals or dies and becomes food directly for the bacteria without the intervention of animals at all.
Commercial Production
Studies may be concerned primarily with the amount of organic material represented in tons per year of fish over certain fishing grounds, the poundage yield of oysters on cultivated beds, or the season's yield in barrels of oil from whales. These are evaluations of commercially important yields and though they do have a direct relation to the total organic production in certain sections of the sea, yet they are too far removed from the original source of synthesis of organic material to give anything more than a very general picture of production of the sea; for we do not know the ratio between the volume of fish, and so forth, and the volume of plants which, through various animal transformations, have supplied the food for growth and other vital energy-consuming processes of these and the intermediary animals. The yield of commercially sought animals is also subject to change through the influence of man and may therefore not give a true value representing their place in the balance of nature. Nevertheless, in semiclosed areas it is possible to arrive at figures which illustrate in a broad way the relationship in production of plants and herbivorous and carnivorous animals. Petersen (1918) has made certain calculations of the quantitative food relations of important animals in coastal waters where eelgrass, Zostera, furnishes the main source of primary food. This relationship is diagrammatically shown in fig. 249, from his report. As a working hypothesis he has assumed that each unit of weight of herbivorous animal substance requires ten units of plant substance in its formation, and each unit of weight of carnivorous organism feeding directly upon herbivorous forms requires ten units of the latter, hence one hundred plant units are needed to produce each unit of a carnivorous animal such as is represented by the plaice, for instance. But many carnivorous forms such as the cod feed only upon carnivorous animals, as shown by the radiating arrows in the figure, and this habit entails another similar loss as the length of the chain of transformers is increased, with the result that it has required a thousand units weight of Zostera to produce one unit weight of cod or
From these calculations, which can give only rough approximations, we can at least obtain some perception of the vast quantity of plant substance involved in production of a small amount of carnivorous animal tissue, and in the light of this the world's production of fish, which is in the neighborhood of 13 million tons annually, takes on a new significance. Failure in production in the initial link of the food chain must be recorded in the series of sequences leading up to the predators of highest rank.
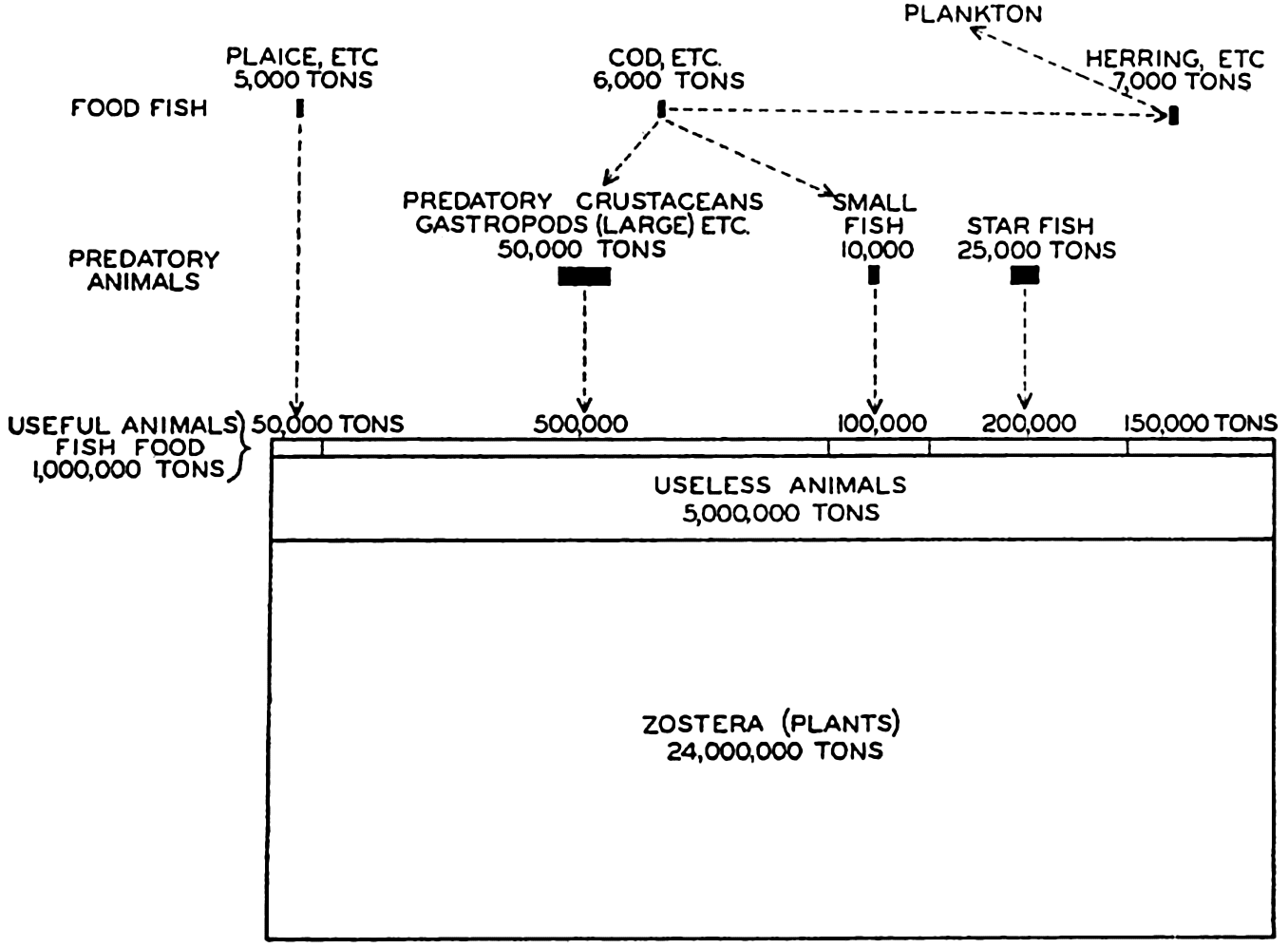
Quantitative food relations of certain animals dependent on Zostera for the primary food. (After Petersen.)
The Production in Different Regions
It is very well known that some regions of the oceans give evidence of being on the whole more productive than others. Locally also, considerable variation exists in different coastal areas. We have already learned what some of the underlying reasons may be. Precise quantitative data on initial organic production are scanty and diverse as far as the methods of estimating and the period of time involved are concerned. In table 102, which is taken mainly from Riley (1941), some estimates are given from separate areas which will serve to illustrate the best available figures, in terms of grams of carbon per square meter or per cubic meter, on the order of magnitude of phytoplankton production.
| Location | Production | Method | Authority | |||
|---|---|---|---|---|---|---|
| Carbon (g/m2/yr) | ||||||
| Long Island Sound | 600–1000 | |||||
| Western Atlantic, 23°–38°N | 530 | Gross production—O2 production in experimental bottles | ||||
| Western Atlantic, 38°–41°N | 320 | |||||
| Dry Tortugas | 60–430 | Riley, 1938, 1939, present paper | ||||
| Experimental observations | 400–700 | Phytoplankton production—O2 production | ||||
| Long Island Sound | 440–875 | P consumption | ||||
| 100–200 | N consumption | |||||
| 95–190 | Chlorophyll production | |||||
| Western Atlantic, 23°–41°N | 140–365 | N consumption | ||||
| Dry Tortugas | 27 | P consumption | ||||
| 5 | Plant pigment production | |||||
| Western Atlantic 3°–13°N | 278 | Oxygen consumption | Seiwell, 1935 | |||
| Off southern California | 215–430 | Sverdrup and Fleming, 1941 | ||||
| Long Island Sound | 384 | Increase in oxygen—experimental | Riley | |||
| 84 | P consumption | Atkins, 1923 | ||||
| 98 | Changes in CO2 | |||||
| Observations on natural environment | 60 | Changes in O2 | ||||
| English Channel | 70 | Changes in P | ||||
| 88 | Changes in N | Cooper, 1938 | ||||
| 7 | Changes in Si | |||||
| 5 | Changes in Ca | |||||
| Barents Sea | 170–330 | P consumption | Kreps and Verjbinskaya, 1930 | |||
| Long Island Sound | 138–350 | P consumption | Riley | |||
| Carbon (g/m3/day) | ||||||
| Norwegian coast | 0.14 | Gran, 1927 | ||||
| Short-period experimental observations | Scottish coast | 0.16 | Marshall and Orr, 1930 | |||
| Dry Tortugas | 0.07 | |||||
| Western Atlantic, 23°–41°N | 0.01–0.12 | Gross production—O2 production in experimental bottles at the surface | Riley | |||
| Western Atlantic—George's Bank | 0–0.88 | |||||
| Long Island Sound | 0.02–0.41 | |||||
| Scripps Istitution pier | 0.01–0.15 | Sargent, manuscript |
Large seasonal variations in the nutrient elements have been observed in coastal areas in temperate latitudes where there are marked variations in the physical, chemical, and biological factors during the year. In the English Channel, which is only about 100 m deep, conditions are such that complete mixing from the surface to the bottom takes place in the winter months. Even during the summer this condition prevails for short periods, consequently the entire water column may be depleted of nutrients. In the Gulf of Maine a similar mixing occurs during the winter months and near Friday Harbor strong tidal currents and irregular topography contribute to intense vertical mixing throughout the year.
For these and other reasons (such as the proximity to land) the annual variations in the plankton population and in the distribution of the nutrient elements characteristic of these individual localities can not be applied to other regions or to the open sea without a careful consideration of the different factors which may be involved. In areas such as the English Channel, where the nutrients are more or less completely removed from the water column during the summer, it is quite probable that the amount of production is related to the store of nutrient elements present at the beginning of the vegetative season. In localities where there are vertical gradients in the nutrient concentrations, diffusion and turbulence will carry a certain amount into the euphotic zone. Such processes are so effective in certain areas, for instance near Friday Harbor, that plant development does not deplete the nutrients to a point where the amounts present can affect the rate of growth. In these areas other factors must limit the organic production (p. 769). In table 103 are given, for a number of localities, the approximate averages for the contents of nitrate, phosphate and silicate in the upper 25 m at the times
| Locality | Latitude | NO3-N | PO4-P | SiO3-Si | |||
|---|---|---|---|---|---|---|---|
| Max. | Min. | Max. | Min. | Max. | Min. | ||
* Surface values only. | |||||||
| English Channel | 50°N | 7. | 0 | 0.55 | 0 | 4. | 0 |
| Friday Harbor[*] | 48°N | 25. | 15. | 2. | 1. | 57. | 42. |
| Gulf of Maine | 43°N | 12. | 2. | 1. | 0.2 | ||
| South Georgia | 54°S | 1.7 | 0.9 | 30. | 5. | ||
| Barents Sea | 73°N | 12.5 | 1. | 0.63 | 0 | ||
In order to estimate the rate of production in areas where there is no marked seasonal change in the distribution of nutrients, it is necessary to take into account the supply of these materials which will result from diffusion. Even in localities where there is a marked seasonal change, estimates of production based on the removal of nutrients during the vegetative season must be corrected for this process or a layer of sufficient thickness to eliminate this factor must be used when calculating the total amount of any element removed from the water column. The latter method has been used at a number of localities to estimate the differences in the amounts of the nutrient elements in the water column at the times of winter maxima and summer minima. From these data, the net utilization in grams per square meter column of NO3-N, PO4-P and SiO3-Si during the vegetative season have been obtained. The values are given in table 104. The net removal of nitrate and phosphate in the Barents Sea and around South Georgia is about twice as great as the utilization in the English Channel and in the Gulf of Maine. The great difference between the silicate utilization in the English Channel and around South Georgia is of interest in connection with the deposition of siliceous sediments. Estimates of seasonal production based on data of this kind are minimal because they include no consideration of the effects of regeneration, that is, that the elements may pass through the biological cycle more than once during the season. Kreps and Verjbinskaya (1932) estimate that, in the Barents Sea, production, calculated from the phosphate utilization, should be increased by about one third to correct for the concurrent regeneration.
| Locality | Length of water column (m) | NO3-N | PO4-P | SiO3-Si |
|---|---|---|---|---|
| English Channel | 75 | 6.6 | 1.1 | 7.4 |
| Gulf of Maine | 100 | 7.0 | 1.2 | |
| South Georgia | 100 | 1.9 | 70.0 | |
| Barents Sea | 200 | 11.0 | 1.9 |
Many observations indicate a higher rate of organic production in the high latitudes than in the tropics. This possibility is brought out clearly in fig. 250, from the Meteor observations, where the standing population in the Antarctic is about tenfold that in the tropical regions. The greater standing crop in high latitudes may not indicate a greater annual production because in high latitudes the production is concentrated into a few months of vigorous and spectacular growth with return of sunshine or following nutrient replenishment over the winter, whereas in the lower latitudes the growth may proceed at a slower but more continuous rate as nutrients become available.
The marked cycle of meteorological events characteristic of temperate and high latitudes leads to a number of associated phenomena vital in determining the periodicity and extent of organic production in these latitudes. The decrease of sunlight inhibits or diminishes growth during the darkest winter months and the low winter surface temperatures give rise to active convection currents effecting an abundant annual renewal of essential plant nutrients in the euphotic layer. In the Gulf of Maine these currents reach a depth of 100 m, and in shallower areas the whole column of water with its store of nutrients is involved in the mixing. Spring and summer conditions bring about a stabilization which, together with an ample supply of solar energy, provides the conditions essential for a vigorous though short period of production. Reference to the discussion of hydrographic conditions in the Antarctic will show that in that region the ascent of deep water near the Antarctic Continent brings to the surface waters an excessively rich supply of nutrients which, in moving toward the Antarctic Convergence (fig. 164, p. 620), give rise to a great flare of diatom production during the Antarctic spring and summer when sunshine is ample and the upper water layers have become stabilized through melting of northward-drifting ice (Hart, 1934). So great is the
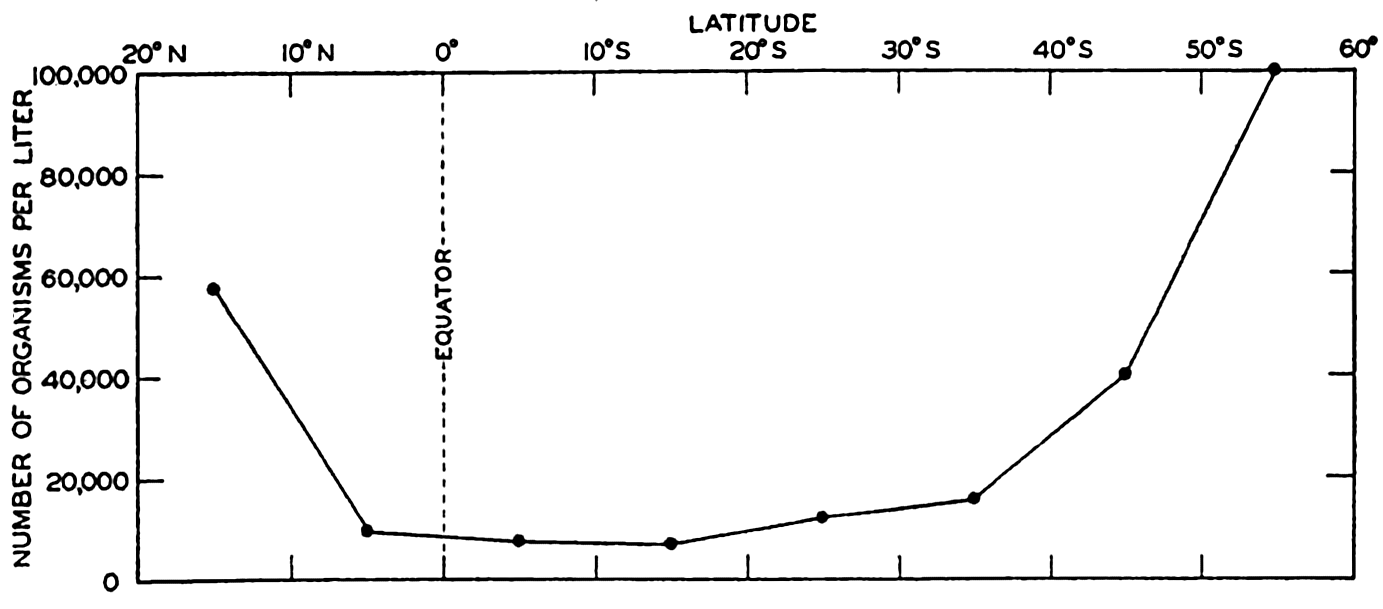
The quantity of total plankton organisms in the upper 50 m of high- and low-latitude waters of the South Atlantic.
That plankton production is indeed great in the Antarctic in spite of the short season is proven by the invasion of large numbers of feeding whales which migrate each year to these waters to fatten on the rich supply of available food there. The bottom fauna of these areas is also unusually rich, as was found by the Challenger and other expeditions. That diatom production is perhaps even greater than its animal utilization during the maximum growing period is suggested by the accumulation of the broad band of diatomaceous ooze so characteristic of the bottom deposits encircling the Antarctic Continent (fig. 253, p. 975). Hart has pointed out, however, that the types of diatoms found in these oozes belong largely to species which go unaltered through the digestive tracts of animals.
As to production in lower latitudes we can say that in general the open sea is relatively sterile (figs. 214 and 216, pp. 784 and 786). Examinations of figs. 217 and 218, pp. 787 and 788, will show why this must be so, for the supply of nutrients lies below the euphotic zone and the strong and persistent thermal stratification of the water within this zone precludes any complete or rapid renewal of nutrients in the upper layers despite the greater thickness of the euphotic layer in tropical or subtropical regions. In coastal areas with upwelling or in offshore regions of divergence, the situation is quite different. As an example of the former we have already mentioned the west African coast (p. 786). We may consider also the Peru Current, which in the tropical and subtropical regions brings to the surface an abundant continuous supply of nutrients that provide fertilization for heavy phytoplankton production, near the coast mainly but also in some sections in almost undiminished intensity to a distance of 320 km seaward (Gunther, 1936). The great production of this oceanic system is manifest in the tremendous quantities of marine birds in this area. Some idea of the magnitude of production can be had from Schott's report (1932) that on one small island of the Chinchas group there are estimated to be some five or six million marine birds, such as cormorants, pelicans, and gannets, which daily remove at least 1000 tons of small fish from the surrounding water. The great Peruvian
In comparing the great productivity of the Peru Current with that of the Antarctic, it must be borne in mind that the latter system is one of very great geographic extent while the former, like other highly productive areas in lower latitudes, is more localized and to that degree of less general significance in the economy of the region as a whole. The greater fisheries of the north and north temperate regions are in themselves indicative of great organic production and they have profoundly influenced the settlement of coastal areas by man.
It should be mentioned that the question of relative production in high and low latitudes is still an open question. Some evidence points to a greater production in the latter than has been indicated by the various oceanographic expeditions whose data have been concerned mainly with the open sea. An example of subtropical production in a restricted area is offered by the investigations of the Great Barrier Reef Expedition.
In using the zooplankton as an index of productivity, Russell (1934) concluded that the Great Barrier Reef lagoon was somewhat richer in numbers of plankton animals than all but one of five representative stations in the North Sea and the English Channel. Over two years the monthly average at these northern stations was 2815 animals per vertical haul with a 50-cm net, while a one-year investigation with a similar net, used in the same fashion in the Barrier Reef lagoon, showed the number of animals to be 5684 per haul. Usually copepods made up 70 per cent or more of the animals. In tropical regions copepods are usually less than 1 mm in length, while in the north the most abundant species are over 1.5 mm in length. When allowance is made for this small size and for a supposedly more rapid rate of metabolism for the tropical species, the conclusion is that the two areas are about equal in production of zooplankton. The phytoplankton was always scanty in the Barrier Reef lagoon, however, and this appears to be of special interest in indicating that the area was supporting its maximal zooplankton population and that, because of the even rate of phytoplankton production, no surplus of plants was being produced as it is in higher latitudes during the height of the growing season. This equilibrium is of significance also in the study of sedimentation, for it is in the high latitudes that the diatom oozes are found.
Recent studies indicate a need to consider more closely the significance of the vastly deeper euphotic zone of the tropical seas. In one investigation (Riley, 1939) it was found, for example, that in stations of latitude about 40°N plant pigments were most abundant at the surface, the maximum depth of occurrence being 100 m, whereas at tropical and subtropical stations the pigments were most abundant at 100 m and at depths of 300 to 400 m.
Many investigations have indicated a lower production of phytoplankton and zooplankton in the oceanic waters than in the neritic waters. The blueness of the waters of the open sea, as indicated in fig. 214, p. 784, is correlated with this fact. This difference is what one would expect, since the ease of nutrient renewal both by water circulation and by runoff from land is all in favor of the coastal regions. The offshore regions are favored, however, by a greater transparency of the water owing to the absence of suspended particles of terrigenous origin.
In neritic areas, the diatoms form resting spores that are believed to be important in quickly “seeding” the waters when favorable conditions return. The oceanic flora depends upon survival of sporeless individuals to initiate the crop. This may at times result in a scarcity of suitable species to take advantage of the return of favorable conditions (see p. 770), but a limited nutrient supply is doubtless the main reason for low oceanic production.
Bibliography
Atkins, W. R. G.1923. “The hydrogen ion concentration of sea water in its relation to photosynthetic changes. Part II” . Marine Biol. Assn. U. K., Jour., v. 13, p. 93–118, 1923.
Barker, H. A.1935a. “Photosynthesis in diatoms” . Archiv f. Mikrobiol., Bd. 6, p. 141–156, 1935.
Barker, H. A.1935b. “The culture and physiology of the marine dinoflagellates” . Archiv f. Mikrobiol., Bd. 6, p. 157–181, 1935.
Clarke, G. L.1936. “Light penetration in the western North Atlantic and its application to biological problems” . Conseil Perm. Internat. p. l'Explor. de la Mer, Rapp. et Proc.-Verb., v. 101, pt. 2, no. 3, 14 pp., 1936.
Cooper, L. H. N.1938. “Phosphate in the English Channel, 1933–38, with a comparison with earlier years, 1916 and 1923–32” . Marine Biol. Assn. U. K., Jour., v. 23, p. 181–195, 1938.
Fleming, Richard H.1940. “Composition of plankton and units for reporting populations and production” . Sixth Pacific Sci. Congr., Calif., 1939, Proc., v. 3, p. 535–540, 1940.
Föyn, B. R.1929. “Investigation of the phytoplankton at Lofoten. Norske Vidensk” . Akad. i Oslo, Skrifter, I Math.-Naturv. Klasse, no. 10, p. 5–71, 1929.
Gilson, H. C.1937. “The nitrogen cycle” . John Murray Exped., 1933–34, Sci. Repts., v. 2, no. 2, p. 21–81, 1937.
Gran, H. H.1927. “The production of plankton in the coastal waters off Bergen, March-April 1922. Rept” . Norwegian Fishery and Marine Invest., v. 3, no. 8, 74 pp., 1927.
Gran, H. H.1929. “Investigation of production of plankton outside the Romsdalfjord 1926–1927” . Conseil Perm. Internat. p. l'Explor. de la Mer, Rapp. et Proc.-Verb., v. 56, no. 6, 112 pp., 1929.
Gunther, E. R.1936. “A report on the oceanographical investigations in the Peru coastal current” . Discovery Repts., v. 13, p. 107–275, 1936.
Hart, T. J.1934. “On the phytoplankton of the southwest Atlantic and the Bellingshausen Sea, 1929–1931” . Discovery Repts., v. 8, p. 1–268, 1934.
Harvey, H. W.1934. “Measurement of phytoplankton population” . Marine Biol. Assn. U. K., Jour., v. 19, p. 761–773, 1934.
Harvey, H. W., L. H. N. Cooper, M. V. Lebour, and F. S. Russell. 1935. “Plankton production and its control” . Marine Biol. Assn. U. K., Jour., v. 20, p. 407–442, 1935.
Hensen, Victor. 1887. Über die Bestimmung des Planktons oder des im Meere treibenden Materials an Pflanzen und Tieren. Komm. z. Wissensch. Untersuch. d. Deutschen Meere in Kiel, Bericht 5, 107 pp., Tables, Appendix, 1887.
Jenkin, P. M.1937. “Oxygen production by the diatom Coscinodiscus excentricus Ehr. in relation to submarine illumination in the English Channel” . Marine Biol. Assn. U. K., Jour., v. 22, p. 301–343, 1937.
Kreps, E., and N. Verjbinskaya. 1930. “Seasonal changes in the phosphate and nitrate content and in hydrogen-ion concentration in the Barents Sea” . Conseil Perm. Internat. p. l'Explor. de la Mer, Jour. du Conseil, v. 5, p. 326–346, 1930.
Lohmann, Hans. 1908. Untersuchung zur Feststellung des vollständigen Gehaltes des Meeres an Plankton. Komm. z. Wissensch. Untersuch. d. Deutschen Meere in Kiel und d. Biologischen Anstalt auf Helgoland, Wissensch. Meeresuntersuch., N.F., Abt. Kiel, Bd. 10, p. 131–370, 1908.
Marshall, S. M., and A. P. Orr. 1927. “The relation of the plankton to some chemical and physical factors in the Clyde Sea area” . Marine Biol. Assn. U. K., Jour., v. 14, p. 837–868, 1927.
Marshall, S. M., and A. P. Orr. 1930. “A study of the spring diatom increase in Loch Striven” . Marine Biol. Assn. U. K., Jour., v. 16, p. 853–878, 1930.
Petersen, C. G. J.1918. “The sea bottom and its production of fish food” . Danish Biol. Sta., Repts., v. 25, no. 7, 62 pp., 1918.
Redfield, A. C.1934. On proportions of organic derivatives in sea water and their relation to the composition of plankton. p. 176–192 in James Johnstone Memorial Volume, Lancashire Sea Fisheries, Liverpool, 348 pp., 1934.
Redfield, A. C.1941. “The effect of the circulation of water on the distribution of the calanoid community in the Gulf of Maine” . Biol. Bull., v. 80, p. 86–110, 1941.
Riley, G. A.1938. “The measurement of phytoplankton” . Internat. Rev. d. ges. Hydrobiol. u. Hydrogr., Bd. 36, p. 371–373, 1938.
Riley, G. A.1939. “Plankton studies. II. The western North Atlantic, May–June 1939” . Jour. Marine Research, v. 2, p. 145–162, 1939.
Riley, G. A.1941. “Plankton studies. III. Long Island Sound. Bingham Oceanogr” . Collection, Bull., v. 7, art. 3, 93 pp., 1941.
Russell, F. S.1934. “The zooplankton. III. A comparison of abundance of zooplankton in the Barrier Reef Lagoon with that of some regions in northern European waters” . Great Barrier Reef Exped., 1928–29, Sci. Repts., v. 2, p. 176–201, 1934.
Schott, G.1932. The Humboldt Current in relation to land and sea conditions on the Peruvian coast. Geography, v. 17, p. 87–98, 1932. Manchester.
Seiwell, H. R.1935. The distribution of oxygen in the western basin of the North Atlantic. Papers in Physical Oceanogr. and Meteorol., v. 3, no. 1, 86 pp., 1935.
Sverdrup, H. U., and R. H. Fleming. 1941. “The waters off the coast of southern California, March to July, 1937” . Scripps Inst. Oceanogr., Bull., v. 4, no. 10, p. 261–378, 1941.
XX. Marine Sedimentation
INTRODUCTION
The sea floor, being the place of accumulation of solid detrital material of inorganic or organic origin, is virtually covered with unconsolidated sediments; therefore, the study of materials found on the sea bottom falls largely within the field of sedimentation, and the methods of investigation employed are those used in this branch of geology. Twenhofel (1926) has defined sedimentation as
… including that portion of the metamorphic cycle from the separation of the particles from the parent rock, no matter what its origin or constitution, to and including their consolidation into another rock. Sedimentation thus involves a consideration of the sources from which the sediments are derived; the methods of transportation from the places of origin to those of deposition; the chemical and other changes taking place in the sediments from the times of their production to their ultimate consolidation; the climatic and other environmental conditions prevailing at the places of origin, over the regions through which transportation takes place, and in the places of deposition; the structures developed in connection with deposition and consolidation; and the horizontal and vertical variations of the sediments.
Marine sedimentation is therefore concerned with a wide range of problems, some of which are more or less unique to the sea, while others are of more general character. This discussion will deal with the first group and particular emphasis will be placed upon the “oceanographic” aspects of marine sediments. The methods of studying the character and composition of marine deposits are common to all types of sediments and, since readily available sources are cited in the text, will not be described here.
The importance of investigations in marine sedimentation is obvious when it is realized that most of the rocks exposed at the surface of the earth are sedimentary deposits laid down under the sea. In order to interpret the past history of the earth from these structures, it is necessary to determine the character of the material now being deposited in different environments. As the consolidated sediments generally contain fossils, it is of equal importance to determine the biological associations under different conditions and the character of the organic materials that may
A by-product of such studies as those mentioned above, but nevertheless of the greatest importance, is the knowledge gained concerning the history of the earth and phases of geochemistry and geology. In order to reconstruct the geological history of the earth, it is essential to obtain information on the rate of sedimentation in the oceans and to determine, either directly or indirectly, the total thickness, and hence the amount, of sediments which have been deposited in the sea. Recent research has shown that the sediments found in the deep waters of the North Atlantic are stratified, and, as stratification is related to variations in the source of material and transportational agencies, many possibilities are suggested for obtaining a better understanding of the past history of the earth. The geochemist is concerned with the chemical composition of the sediments, as they differ from the original source rocks and thus show a redistribution of the various elements, and the geologist is interested in the rate of sedimentation, as crustal movements may result from the changed distribution of mass.
In addition, many problems concerning marine sediments are of immediate significance to other phases of oceanography. To name but a few examples, the biologist is interested in the associations of organisms found in different environments on the sea bottom and the remains which may be preserved in the sediments. The occurrence of certain types of organisms has actually been deduced from their skeletal remains in the sediments before they were found living in the sea. Furthermore, the sea bottom is a zone of active breakdown of much of the detrital organic matter sinking to the bottom. From a study of the mechanisms controlling the transportation of sedimentary material it is hoped that the character of the sediments may actually be used as a measure of the water movements over the bottom.
The development of the study of marine sediments has been rapid. Sir John Murray is credited with the first intensive investigations, and his report on the Challenger material (Murray and Renard, 1891) set the pattern for many later investigations. His work was largely descriptive, identifying the various constituents and considering the source of the material. More recently, as newer methods of study—microscopical, chemical, and physical—have been developed, the character of the investigations has changed. The X-ray technique has made possible the identification of the fine-grained crystalline material which had earlier been classified as “amorphous” because it could not be recognized under the microscope. The question of precipitation and solution of calcium
CONSTITUENTS OF MARINE SEDIMENTS
Since any solid material denser than sea water and relatively insoluble may fall to the sea floor, a wide variety of substances from many sources contributes to the sediments and may be considered under six headings: (1) detrital material, largely of immediate terrigenous origin, (2) products of subaerial and submarine volcanism, (3) skeletal remains of organisms and organic matter, (4) inorganic precipitates from sea water, (5) products of chemical transformation taking place in the sea, and (6) extraterrestrial materials.
Terrigenous Material. Two processes are involved in the break-down of terrigenous rocks of either igneous or sedimentary types. These are disintegration and decomposition. Disintegration is the mechanical breakdown of the rock into smaller fragments and does not necessarily involve any change in the composition of the material. Decomposition involves chemical changes in the rock substances which are brought about by the action of water and air. Certain of the constituents are more soluble or more readily attacked and, hence, pass into solution and are carried away. The processes of weathering depend upon the character of the rock and the many aspects of the climatic conditions. Weathering depends upon the amount of rock surface exposed and, therefore, to a large degree upon the amount of disintegration which will increase the exposed rock surface (Twenhofel, 1932, 1939).
The smaller the rock fragments the more likely they are to be carried to the sea, but actually those found in the sea vary from large boulders to particles of colloidal dimensions, so small that they cannot be identified under the microscope by the ordinary petrographic methods. The material found in the marine sediments varies from easily recognizable, chemically unaltered minerals, that is, the products of disintegration, to fine material which has undergone great changes in physical characteristics and chemical composition. In the first group belong the primary minerals, quartz, mica, feldspar, pyroxenes and amphiboles, and the heavy minerals. At the other extreme are the ultimate products of
Products of Volcanism. Two types of volcanism must be considered, namely, subaerial and submarine. In both, essentially the same kinds of material may be ejected; but in the first case the volcanic ejecta will be subjected to mechanical and chemical weathering before reaching the sea. Volcanic material may be first deposited on the land and later transported to the sea by the action of running water, but the lighter and more finely divided fragments may be carried over the sea by the air. As a result of transport by winds, volcanic material may be deposited in relatively large amounts over a considerable area and, in fact, ash from single eruptions is thought to have encircled the whole world. Furthermore, pumice will float in the water for some time. Volcanic material may frequently be recognized by its physical or chemical characteristics, but it is virtually impossible to determine the percentage of highly altered material which may have arisen from this source. The following types of unaltered material may occur: lava fragments, volcanic glass, pumice, and mineral grains. The greatest amounts of volcanic material are found near areas of volcanic activity and may give rise to a characteristic type of sediment. Certain parts of the sea floor are apparently covered with basaltic lava flows of relatively recent origin, either bare or covered with a thin veneer of sediments. Submarine volcanism is probably rather common and in some localities sufficient material has accumulated to reach the sea surface and give rise to volcanic oceanic islands. Further details of oceanic bottom topography will undoubtedly show tremendous numbers of such “mountains” which do not reach the sea surface.
Remains of Organisms. The hard skeletal structures of marine organisms are important constituents of marine sediments and certain types of deposits are almost entirely composed of the calcareous (calcium and magnesium carbonate) or siliceous (hydrated silica) remains of organisms. The skeletal structures are subject to mechanical disintegration and chemical transformation, the latter generally related to solution. In marine sediments calcareous or siliceous material may exist as easily recognizable complete specimens, broken pieces still identifiable, or at the other extreme, as a mass of small crystalline fragments of uncertain origin. The calcareous type of skeletal structures may be conveniently divided into two groups, plant and animal, and the
Calcareous structures of animal origin are in general more abundant than those of plants. Many floating forms contribute to the sediments, but foraminifera are most important and deposits containing large proportions of them are known as globigerina oozes or muds. The shells of planktonic mollusks, chiefly pteropods, are also abundant in certain regions. Pelagic animals also contribute to the sediments although never to the degree that the planktonic forms do. The more resistant bony structures of fish and marine mammals are sometimes found, particularly the teeth of sharks and fish and the earbones of whales.
The benthic animals, especially those living in relatively shallow water, contribute a great deal of the calcareous material in the sediments. This is particularly true in the lower latitudes and in regions where there is little or no supply of terrigenous debris. In these cases the bottom material may be almost entirely calcareous and the remains of various groups of bottom-living animals may be represented, namely: foraminifera, corals, worms, bryozoans, brachiopods, mollusks, echinoderms, arthropods, and vertebrates.
Siliceous skeletal materials do not form so important a constitutent of sediments as calcareous structures, but in certain localities they occur in such quantities that the deposits are known by the predominant type, for example, diatom and radiolarian ooze. The only forms of plant life secreting silica are the microscopic diatoms, which grow only within the euphotic layer either as free floating planktonic forms or in shallow water as benthic organisms. Diatoms are most abundant in high latitudes and in nearshore areas where upwelling or mixing is operative, and in such localities the frustules of certain of the forms may accumulate on the bottom so that the deposits are largely made up of them. Silica is also secreted by a group of protozoa, namely the radiolarians, whose
In many ways the most important contribution of marine organisms is not the hard skeletal structures which may be preserved in the sediments, but the decomposable organic matter which is continually falling from above. Below the compensation depth (p. 779) the benthic animals and bacteria are dependent upon this supply of food from above. It may consist of entire plants or animals, faecal material, and fragments of partially decomposed organisms. In both the latter categories it may be expected that it represents the more resistant types of organic materials originally forming a part of the living organisms. This is particularly true of chitin-, cellulose-, or ligninlike substances which form part of the skeletal structures. The detrital organic matter contains carbon, hydrogen, oxygen, nitrogen, sulphur, phosphorus, and probably many other elements. The activity of the bacteria and bottom-living animals, particularly the mud-eaters, destroys much of this material and returns the constituent elements to solution in inorganic form. Marine sediments contain from virtually zero to about 18 per cent organic matter, the amount present depending upon a number of factors which will be discussed later. The deepest parts of core samples and even fossilbearing sedimentary rocks show the presence of organic matter, so that organic matter must be considered as a definite source of sedimentary material. An added interest to the problem of the supply and preservation of organic matter is that it is the source of petroleum formed from marine sediments. Although it has been implied that all the decomposable organic matter is of immediate marine origin, in certain localities such as in the Baltic Sea it is thought that a considerable proportion may be of terrigenous origin, representing the soil humus carried in by rivers.
Inorganic Precipitates. Inorganic precipitates are formed when the solubility product of some substance is exceeded. The immediate products of organic activity are excluded although the conditions necessary for precipitation of some substances may result from metabolic processes. Supersaturation may be induced by physical agencies such as temperature changes, it may be associated with the removal of carbon dioxide where photosynthesis occurs, or it may be related to changes in hydrogen-ion concentration or oxidation-reduction potential brought about by the organisms. In addition, precipitation may result from evaporation in isolated lagoons and seas.
Inorganic precipitates are never abundant in marine sediments but they may form conspicuous and diagnostically important components.
It is difficult to draw the boundaries between inorganic precipitates and those which are the direct result of biological activity and those materials which are considered to arise from the modification of minerals. Twenhofel (1939) has avoided this difficulty by considering them all as products of “chemical deposition.”
Products of Chemical Transformation. In this category are placed those substances which are formed by the interaction of sea water and solid particles. The interaction may be between the solid material and “normal” sea water or the reaction may be restricted to the interstitial water of the sediments where modified properties may exist (p. 995). It is difficult to designate many definite materials formed in this way, but undoubtedly such interactions occur, particularly when fresh unweathered materials of volcanic origin are brought in contact with sea water. Most detrital material carried to the sea has been subject to subaerial weathering, which is a continuous leaching process. In the sea the environment is much more uniform and, hence, an equilibrium may readily be established. Little is known concerning the processes of submarine breakdown of either terrigenous or volcanic material. Among those substances which may be the result of or involved in such transformations are glauconite, phosphorite, feldspar (Twenhofel, 1939), phillipsite, and the clay minerals.
Extraterrestrial Materials. In those marine sediments which accumulate at extremely slow rates, such as red clay, small black magnetic spherules and brown crystalline spherules are found. These are extremely rare and never form an appreciable part of the sediment. They were first discovered and described by Murray and Renard (1891). The black spherules are composed of iron or iron alloy and have diameters of about 0.2 mm. The brown type resemble the chondrite variety of meteorite and contain silicon. They commonly have a metallic luster and striated surface, and average about 0.5 mm in diameter.
TRANSPORTATION OF SEDIMENTARY DEBRIS
Transportation of Sediment to the Sea
Twenhofel (1932, 1939) discusses the following agencies which transport material to the sea:
Rivers and streams carrying both particulate and dissolved material.
Rainwash, slumping along river banks and sea coasts, and large scale landslides.
Shoreline erosion by waves.
Glaciers and sea ice carrying rock fragments.
Biological activity which may also increase the transport by other agencies.
Winds, which pick up large amounts of fine-grained debris from barren arid areas.
Volcanic activity, which may discharge large amounts of finegrained dust into the atomosphere.
Materials transported by the first three agencies are brought into the sea near the coast lines and the bulk is deposited near the coast, whereas material transported by the last four agencies may be carried to great distances from land before dropping to the sea bottom, and may therefore contribute significantly to the deep-sea deposits. These latter agencies will be discussed more fully.
Transportation by Ice. The transportation of sedimentary debris by ice has been and still is extremely important in high latitudes. Glaciers carry large amounts of material which they erode from the land surface, and in so doing, modify the general topography. Glaciation during the ice age has left its smark on many areas now below sea level. Certain submarine topographical features, particularly around north-western Europe and northeastern America, are attributed to glaciation. By the time of the ultimate retreat of the ice such quantities of debris had been deposited that the transportation by glaciers has placed its stamp on the character of the sediments in many localities in high latitudes.
Contemporary glacier ice carries large amounts of sediment to the sea. Such material is characterized by a great range in size, varying from enormous boulders to the finest material formed by mechanical abrasion. The character of the debris will depend on the nature of the rock formations over which the glacier passes. Icebergs carry with them the enclosed rock material and, since they may float thousands of miles before melting, this material may be deposited at great distances from its source, and pebbles and boulders may be found in otherwise pelagic deposits far from land (Murray and Hjort, 1912; Bramlette and Bradley, 1940).
Sea ice, that is, ice formed in the sea, also plays a relatively important role in the transportation of sedimentary material. This is particularly true in the Arctic seas, where in large areas of shallow water the ice may freeze to the bottom in winter. When thawing commences, the melting takes place at the surface of the ice, which will tend to rise due to its buoyancy. In this way the enclosed sedimentary material may be lifted off the bottom and, as the ice breaks up, may be transported to other localities where it will be released when the ice melts. The sea ice will tend to carry the unsorted material, including shells or other remains of organisms, from shallow water into deeper water, and will therefore give rise to anomalous accumulations of remains of organisms and organic material (Twenhofel, 1939).
Organic Rafting. A less significant amount of debris may be transported in the sea by the agency of buoyant organic material of both terrigenous and marine origin. Trees and clumps of vegetation eroded during floods or by wave action may float great distances in the sea before decomposition releases the load of imbedded rock material or until the vegetation becomes waterlogged and sinks. Leaves, branches, and even entire terrigenous plant forms are sometimes found in marine deposits far from land. Marine algae with holdfasts may be torn loose and float away, carrying rock fragments which may be deposited in deeper water (Emery and Tschudy, 1941). Benthic animals may contribute to transportation, particularly by loosening and overturning the material on the sea bottom. Man has become an agency of transportation in the sea and the effects of his activities are not uncommon in certain localities. Cinders and ash from coal-burning vessels are sometimes found in samples taken along steamer routes, as well as other refuse of such a character that it may be preserved in the sediments. Near shore, particularly in harbors, material is moved by dredging activities and, indirectly, by the construction of piers and breakwaters.
Transportation by the Atmosphere. In the dispersal of terrigenous material the atmosphere undoubtedly plays an extremely important part. The materials that are carried by the winds over the sea consist mainly of volcanic dust ejected directly into the air and of the particles that are swept up by the wind from the land surface. Wind erosion of the land is most effective in localities where high wind velocities occur and where the ground is not covered by a protective blanket of vegetation. Such areas are found in the high mountains and in desert regions and in semiarid regions where there is large-scale agricultural activity. The activities of man contribute also to the air-borne debris in many other ways which can be readily called to mind. Practically any type of organic or inorganic material may be carried by the winds if it is small enough.
Transportation of solid particles by the air is comparable to that in water, which will be discussed below. In general, the lowest wind velocities are found near the ground and material swept up from the ground must be lifted to considerable altitudes if it is to be carried over long distances. The material ejected by volcanoes is thrown directly to great altitudes where high velocities prevail and will therefore, in general, be transported for greater distances than dust which is picked up from the land surface. Consequently, volcanic material which has been at least partially air-borne is world-wide in its distribution, although in the vicinity of centers of volcanic activity it will be much more abundant and of somewhat coarser texture.
Air-brone terrigenous dust is an important contributor to marine sediments where the prevailing winds are offshore and where they have a suitable source of material. In general there will be a progressive decrease in size of the air-borne material as the distance from the source is increased, because the larger particles drop out first. Extremely fine material which may remain in suspension almost indefinitely is precipitated by rainfall or snow. The actual dispersal of sedimentary material originally air-borne may be extended by transportation in the water itself. Little is known concerning the rate of supply of air-borne terrigenous material to various localities, but data given by Twenhofel (1939) suggest that it may be relatively great.
In certain localities the amount of material transported in the air over the sea is sometimes sufficient to form dust clouds. For one such region off the west coast of Africa, Radczewski (1939) has summarized the existing knowledge of the effects of the aeolian material on the formation of the deep-sea sediments in this area. According to him the following types of grains could be identified in the dust collected from the air west of the African coast: quartz, feldspar, mica, organic siliceous remains, calcite, aggregates of small particles, and other unidentifiable material. In this locality calcite, aggregates, mica, and quartz are the most abundant. All of these materials may fall to the sea bottom, where they will be mixed with the water-borne debris and the remains of marine organisms. In sediment samples it is impossible to discriminate between the air- and water-borne material except in the case of a certain amount of the quartz grains. These are the so-called “desert quartz” grains coated with reddish iron oxides, and are characteristically aeolian material. Although the percentage of desert quartz in the original air-borne dust is not known, Radczewski determined their ratio to the total number of quartz fragments in a number of samples collected by the Meteor. These are referred to as “desert quartz numbers” and are used as indices of the proportions of aeolian material in the different samples. In general, the amount decreases away from the coast and the size of the characteristic quarz grains diminishes with increasing distance from the shore.
The size of the air-borne particles in deep-sea sediments averages less than 15 microns but larger fragments are quite abundant near the coast. Technical difficulties make it impossible to distinguish aeolian material smaller than about 5 microns.
Transportation of Sediment in the Sea
Settling Velocity. Sedimentary debris which has been transported to the sea settles through the water and is at the same time carried laterally by currents of different types. The settling velocity of a sedimentary particle depends upon its specific gravity, size, and shape, and upon the specific gravity and viscosity of the water. Before considering the settling velocity of particles in the sea it is necessary to examine the simplest case, where it is assumed that only spheres are involved. The classical equation for the settling velocity of a sphere is that developed by Stokes:
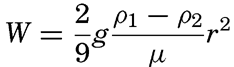
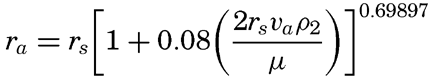
| Diameter | Settling velocity | Time to fall 10 cm | Settling velocity (m/day) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mm | Microns | Stokes’ law | Wadell | Days | Hours | Minutes | Seconds | ||
| Boulder | |||||||||
| 256 | 256,000 | ||||||||
| Cobble | |||||||||
| 64 | 64,000 | ||||||||
| Pebble | |||||||||
| 4 | 4,000 | ||||||||
| Granule | |||||||||
| 2 | 2,000 | ||||||||
| Very coarse sand | |||||||||
| 1 | 1,000 | (89.2 cm/sec) | 16.0 cm/sec | 0.6 | |||||
| Coarse sand | |||||||||
| 1/2 | 500 | (22.3 cm/sec | 7.7 cm/sec | 1.2 | |||||
| Medium sand | |||||||||
| 1/4 | 250 | (5.58 cm/sec) | 3.4 cm/sec | 2.7 | |||||
| Fine sand | |||||||||
| 1/8 | 125 | (1.39 cm/sec) | 1.2 cm/sec | 8.3 | 1040 | ||||
| Very fine sand | |||||||||
| 1/16 | 62.5 | 3482 microns/sec | 29 | 301 | |||||
| 1/32 | 31.2 | 870 | 1 | 55 | 75.2 | ||||
| 1/64 | 15.6 | 218 | 7 | 40 | 18.8 | ||||
| Silt | 1/128 | 7.8 | 54.4 | 30 | 38 | 4.7 | |||
| 1/256 | 3.9 | 13.6 | 2 | 2 | 32 | 1.2 | |||
| 1/512 | 1.95 | 3.4 | 8 | 10 | 0.3 | ||||
| 1/1024 | 0.98 | 0.85 | 1 | 8 | 41 | 0.074 | |||
| Clay | 1/2048 | 0.49 | 0.21 | 5 | 10 | 42 | 0.018 | ||
| 1/4096 | 0.25 | 0.052 | 21 | 18 | 50 | 0.004 | |||
| 1/8192 | 0.12 | 0.013 | 87 | 3 | 19 | 0.001 | |||
When mechanical analyses are made (see p. 969), the size-grade composition of a sediment is determined by sieving and by determining the settling velocity of the smaller particles. In such an analysis it is customary to employ certain physical and chemical methods for separating the individual particles which in the original sample may be cemented together or held somewhat more loosely by electrostatic or physical forces. This is particularly true of the clay and colloid material which is said to be coagulated or flocculated. Although the coarser material larger than about 15 microns may not be flocculated and will therefore settle with approximately the computed velocity, this is not true for the finer particles. Little is known concerning the state of aggregation of the clay and the colloid particles that are in suspension in the sea; however, studies by Gripenberg (1934) have shown that fine-grained material when mixed with sea water tends to flocculate into units which settle with velocity equivalent to those of quartz spheres between about 5 and 15 microns in diameter, that is, they settle between 1 m and 20 m per day. The flocculation is related to the composition of the clay minerals, particularly with respect to the exchangeable bases (p. 988) and also to the salt concentration of the water. It is probable that the flocculation is much retarded when the suspension of particles is extremely dilute. Studies of clay minerals have shown that the coagulation tends to increase the size of the units, hence to increase their settling velocity, but at the same time the coagulated particles carry with them a certain amount of the water, which reduces their effective density and therefore tends to slow them down.
A certain amount of this extremely fine-grained material may be formed in the sea, but probably most of it comes from the land, where the agencies of mechanical and chemical weathering are much more effective. If this material did not find its way to the sea floor it is obvious that the oceans would ultimately become turbid with suspended particles. Measurements of the penetration of light in the sea show that finely suspended material is present everywhere in the surface layer of the sea (p. 88), but it does not seem reasonable that the average turbidity of the water is changing. Therefore, the rate of supply of material must equal the rate of deposition. Some of the problems of submarine geology are to determine the rate of deposition, the quantity of sedimentary
Transportation of Settling Particles by Ocean Currents. The effective settling velocities of sedimentary particles probably range from less than one meter per day to many thousand meters per day. Coarse material which is brought to the sea near shore or which is released from icebergs or remains of plants at great distances from the coast will sink so fast that it is immediately deposited, but fine material with small settling velocities may be carried for considerable distances by currents. A particle 4 microns in diameter settles at a rate of about one meter per day (table 105), hence, may be carried about for many years before reaching the bottom. Such fine material may be introduced by rivers, may arise from wave action in shallow water, or may be derived from the remains of planktonic organisms. The distance to which particles can be carried depends upon their settling velocity, the velocity of the current, and in some instances upon the turbulence associated with the motion. The turbulence will lead to high values of the vertical diffusion (p. 93). This great diffusion will have no effect on the settling of very small particles if they are distributed in such a manner that the net vertical transport by diffusion is zero but, depending upon the change of concentration and the change of eddy diffusion with depth, the diffusion may lead to a net upward or downward transport of particles which may decrease or increase downward transport by settling. So far, no data are available for examination of these conditions.
Another important characteristic of the ocean currents is the presence of horizontal eddies which lead to large-scale horizontal mixing, which can be expressed as horizontal diffusion (p. 92). The horizontal diffusion is of importance near coasts where fine material is brought into the sea by rivers, wave action, wind, or other agencies. In coastal waters the great supply of fine material leads to a high concentration of suspended particles which by horizontal diffusion may be carried to considerable distances from the coast. In a steady state the amount of suspended material transported away from the coast by diffusion through a vertical plane parallel to the coast must equal the amount supplied to the water between the coast and the vertical plane minus what is deposited on the bottom inside of the vertical plane. On the basis of such considerations, Revelle and Shepard (1939) have shown how the finer material may be carried away from shore by the large-scale horizontal eddies which occur off the southern California coast. They introduced a settling velocity of 15 m per day which they consider to be that of “thoroughly coagulated suspensions.”
Transportation of Particles along the Sea Bottom. Material that settles toward the bottom is by no means always permanently
Mud flows represent movement of unconsolidated material that has accumulated on a slope and are not necessarily associated with any movement of the overlying water. Owing to instability or to a stimulus such as may be caused by seismic activity, the material begins to slide down the slope. There is some evidence that mud flows are relatively common on steep slopes and it has been suggested that they are of importance as an agency which removes accumulated sediments from submarine canyons. They are most likely to occur in areas where sediments are accumulating rapidly on relatively steep slopes, hence they may occur on the continental slope and on insular slopes. The angle of repose of unconsolidated marine sediments is not known. It is thought that mud flows can take place where the slope is only about one degree, but this does not imply that slopes of greater angle are always devoid of unconsolidated material.
Transportation by mud flows tends to break down stratification that may have developed in the deposit, and may result in the accumulation of rather coarse and unsorted material in deep water. Furthermore, mud flows may carry organisms and their skeletal remains into environments where they could not have developed, thereby leading to complications in interpretation of the environmental conditions from the study of the organic constituents of a deposit. There is very little direct evidence of the occurrence of mud flows in the seas, consequently it is as yet impossible to determine their importance as transporting agencies. The status of present knowledge is discussed by Twenhofel (1939).
In rivers the motion of individual particles along the bottom is described as sliding, rolling, and saltation (Hjulström, 1939). Sliding does not often take place, but rolling and saltation (which is a jumping motion) are common forms of transportation. Nothing is known about the extent to which such transportation takes place along the sea bottom, but certain indications can be obtained by application of results of river
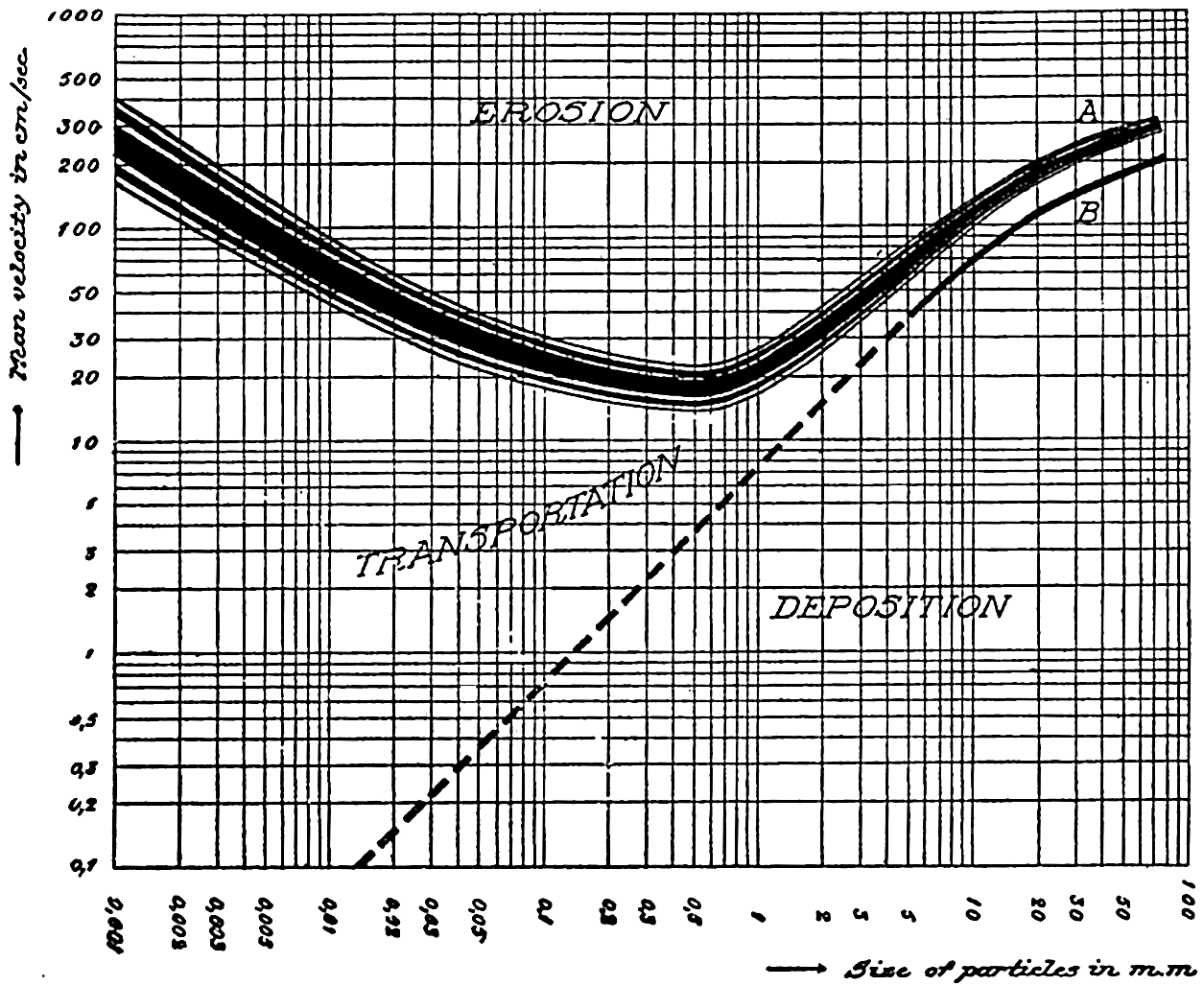
Relationship between average current velocity in a river and sediments of uniform texture showing velocities necessary for erosion, transportation, or deposition. (From Hjulström, 1939, in Recent Marine Sediments, edited by Parker D. Trask and published by the American Association of Petroleum Geologists, Tulsa, Oklahoma.)
Applying these results from rivers to the problem of transportation along the sea bottom by sliding, rolling, and saltation, it must be borne in mind that in fig. 251 the velocity represents the average velocity across a transverse profile of a river and that the velocity at the bottom is smaller. It may perhaps be assumed that the “average velocities” correspond to those occurring a few meters above the sea bottom. Taking into account the fact that high velocities near the sea bottom are common in shallow water only, it can be considered probable that eroding velocities and transportation along the bottom of coarser material, say, particles with diameters greater than 2 to 3 mm, occur only in shallow water, but that in regions of deep currents similar transportation of fine sand and silty sand may occur at depths of several thousand meters. Sediment collections made by the E. W. Scripps off the coast of California and in the Gulf of California appear to bear out such contentions except where coarse material has been found in the bottom of submarine canyons and on banks. The latter occurrence may be related to former emergence.
It should be added that on a slope alternating currents will lead to net downward transport of sediments because gravity will facilitate a downward and counteract an upward transport.
Transportation of particles in suspension near the bottom is often considered together with sliding, rolling, and saltation because the transition from one form to another is probably a gradual one. The essential difference is that material in suspension can be carried in a short time over much longer distances.
Nothing is known as to the amount or character of material in suspension near the bottom under varying conditions, but an approach to the problem can be made by application of results from laboratory studies on the characteristics of turbulent flow. Such results have been applied to the problem of transportation in rivers (Rouse, 1938), but certain modifications are necessary when dealing with transportation near the sea bottom. The basic concept is that where turbulence exists a current can carry a load of suspended particles that is determined by the condition that the downward transport by settling must equal the upward transport by eddy diffusion. The downward transport by settling equals WS where W is the settling velocity and S is the concentration of suspended particles expressed as mass per unit volume of water. The upwards transport by eddy diffusion equals 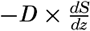 (see p. 116) where D is the coefficient of eddy diffusion and dS/dz is the concentration gradient (z is measured positive upwards). The concentration of suspended particles is therefore determined by the equation
(see p. 116) where D is the coefficient of eddy diffusion and dS/dz is the concentration gradient (z is measured positive upwards). The concentration of suspended particles is therefore determined by the equation
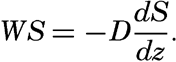
If the stability of the stratification is very small it may be assumed that near the bottom the eddy diffusion equals the kinematic eddy viscosity, that is, D = A/ρ where A is the dynamic eddy viscosity (p. 483). When dealing with currents near the sea bottom it can furthermore be assumed that in the lowest layers of the water the shearing stress is independent of the distance from the bottom and equals the stress against the bottom. This stress is (p. 479)
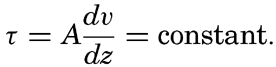
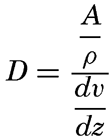
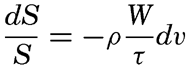
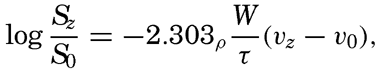
In order to make use of this general formula, specific assumptions must be made as to the variation of the eddy viscosity with increasing distance from the bottom and as to the value of the velocity at the bottom, z0. Before doing so it is necessary, however, to point out one principal difficulty that is encountered when attacking the problem in this manner, namely, that the theoretical approach leads only to relative values of the concentration of particles in suspension and not to absolute values. Actually, the mechanism which brings the particles into suspension is not clearly understood. It appears that if laminar flow exists along the bottom, that is, if the bottom is hydrodynamically smooth (p. 479), no forces are present which can thrust particles upwards. Upward thrusts probably occur only if the turbulence reaches to the very bottom, as is the case if the bottom is hydrodynamically rough. Where laminar flow is found over a smooth bottom, the velocity is always zero at the bottom and the stress exerted on the bottom varies in time only if the velocity gradient in the laminar boundary layer varies. If, on the other
Some idea as to the size or the equivalent diameter of particles in suspension can be obtained by assuming that the bottom is hydrodynamically rough. In this case (p. 479),
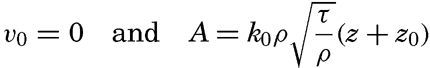
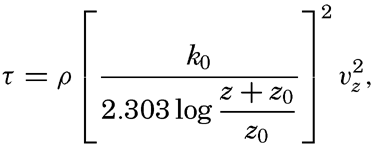
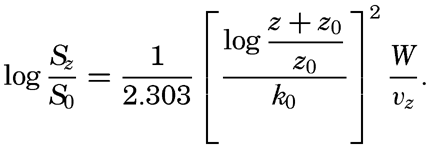
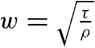 , is introduced the formula takes the simpler form
, is introduced the formula takes the simpler form
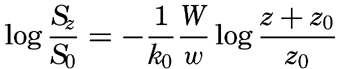
If these results are applicable to conditions near the sea bottom, one should expect that (1) very fine sand, silt, and clay can be present in suspension near the bottom, (2) the size of the particles in suspension depends upon the velocity of the current near the bottom and the roughness of the bottom, (3) the greater the velocity and the greater the roughness the larger are the suspended particles, and (4) the coarseness of the suspended material decreases rapidly with increasing distance from the bottom, provided that material of different particle sizes is present on the bottom.
In shallow water, currents of all types can bring particles into suspension. The periodic currents such as tidal currents and currents associated with seiches (p. 538) or tsunamis (p. 544) are probably the strongest; but besides these, permanent currents reaching to the bottom may exist which will carry the suspended material away. The smaller particles can then accumulate only where the deposition is greater than the transportation. This may be the case in shallow areas to which the supply of fine material is great, for example, the Mississippi Delta, or in depressions out of which no fine material is transported, for example those off the coast of southern California (fig. 264, p. 1025), or in landlocked fjords.
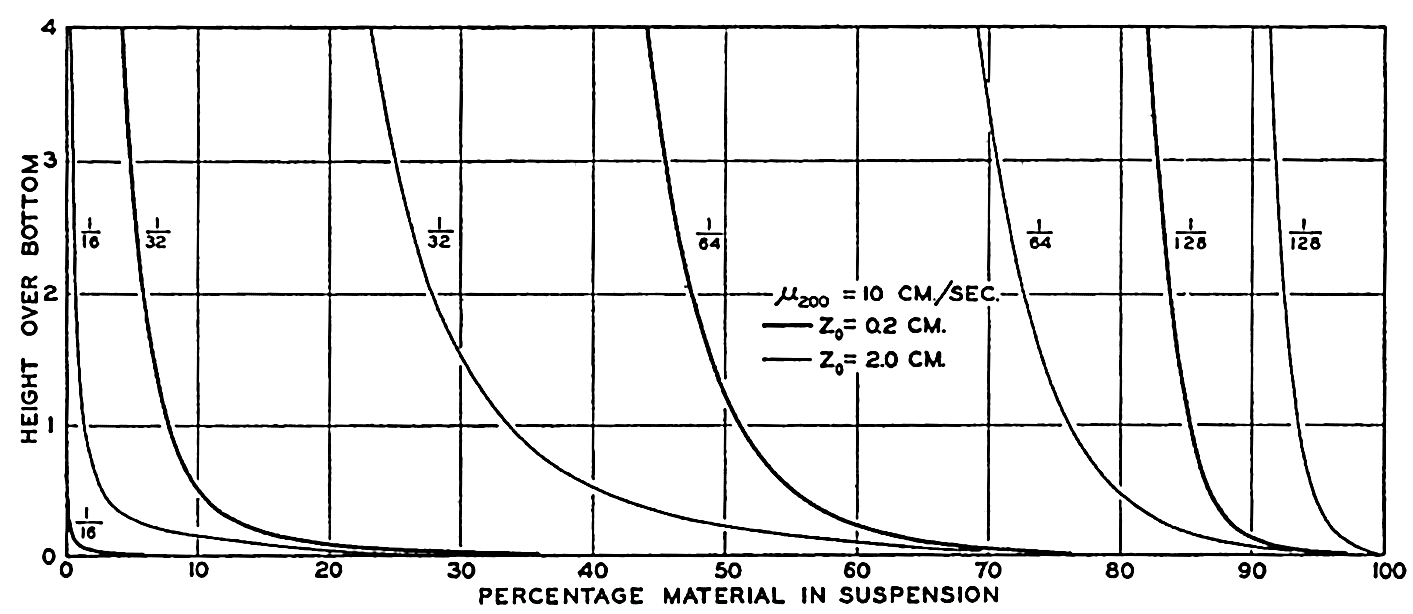
Theoretical distribution of particles of indicated diameters (1/16 to 1/128 mm) over the bottom when the velocity at 2 m above the bottom is 10 cm/sec and the roughness length is 0.2 cm and 2.0 cm.
In deep water, tidal currents are weak, but currents associated with internal waves (p. 590) may have appreciable velocities near the bottom. The permanent currents are very weak but no matter how weak they are they will transport material, which can accumulate, therefore, only where the permanent currents practically vanish, that is, in the deeper parts of ocean basins. A mechanism thus exists which will tend to sweep all finer material away from submarine ridges and peaks and will lead to accumulation of this material in the ocean basins regardless of
Effects of Transportation. The effects of transportation by the various agencies outlined above can be considered from two points of view. One can examine what happens to the shape, size, and composition of individual particles during transportation in the sea, or one can examine the net effect of transporting agencies upon the distribution of sediments. As in other aspects of sedimentation, it is impossible to do more than indicate the general character of the effects because they have not yet been studied sufficiently to afford any quantitative data. Furthermore, the physical or chemical characteristics which may be used as indices of the magnitude of transformation have not been generally applied to the study of marine sediments although the methods have been developed (Krumbein and Pettijohn, 1938).
The effects of transportation upon individual particles may modify their size, shape, and composition. In some cases the size may be increased by, say, the precipitation of calcium carbonate, but in general, transportation will tend to reduce the dimensions of solid material. Such breakdown may be the result of mechanical or chemical processes and generally both will be active. Impact or abrasion may lead to mechanical disintegration and solution, or interaction of the dissolved substances with the solid particles may tend to a reduction in size. These processes may influence not only the size of the particles but also their shape. Fracturing will reduce the size and give rise to angular fragments, whereas abrasion will generally tend to round off the sharp edges and corners. A distinction is drawn between the sphericity of particles, that is, their approach to true spherical form, and the roundness which is a measure of the smoothing away of edges and corners.
The size and shape of individual particles are not only indicative of the character of the transporting agencies and source of material but will also determine many of the properties of the sediment, for example the water content and cohesive properties of the material when wet and when dry and, for larger particles, the character of the orientation and hence the bedding of the individual grains.
The composition of the particles may be affected by the wearing away of the softer or less cohesive material by mechanical agencies or by the solution of the more soluble or more readily attacked portions by chemical processes. Such changes may be determined by examination under the petrographic microscope or by certain chemical or physical tests.
If we consider the relative effectiveness of various transporting agencies in affecting the size, shape, and composition of sedimentary material it is obvious that mechanical breakdown is most likely to occur in material moved over the sea bottom by rolling and saltation. Mechanical wear will be most rapid where particles are thrown together violently and repeatedly. In the sea such conditions are found in shallow water, where currents are strong and where the wave action extends to the bottom. The extent to which chemical weathering may act in the sea is not known, but because of the high surface: volume ratio it is undoubtedly effective on small particles and will be a function of the time of exposure rather than the character of the transporting agency. The progressive change in the character of material transported by a given agency depends upon the character of the source material, the changes in competency of the transporting agency, and the material itself and that forming the sea bottom. This general statement applies only to transportation in the water by saltation or rolling over the sea floor, as in all other agencies one or more of the variables are eliminated.
The characteristics of wind-borne material will be largely determined before it reaches the sea and are therefore outside the problem under consideration. The same is generally true of river-borne debris. Discussions of the processes of transformation associated with transportation are given by Twenhofel (1932, 1939) and Russell (1939), and the methods of determining the properties of individual grains are given by Krumbein and Pettijohn (1938).
MASS PROPERTIES OF MARINE SEDIMENTS
The mass properties of sediments are the summation of those of the component grains. Because of the variety in size and composition of the ultimate particles, the mass properties are not clear-cut and in some cases statistical methods must be used to express them. Three of the mass properties, namely, color, texture, and composition, are used for the classification of marine sediments. The advantages of such a system are that preliminary examination in the field, by visual examination and from the feel of the sample when rubbed between the fingers, enables an experienced observer to classify the sample correctly. Besides being useful to designate the type of sediment, these properties give certain indications as to the source of the constituent material (particularly the grains large enough to be recognized with a hand lens), the effective transporting agencies, and the conditions in situ.
Color of Marine Sediments. The color of a recent marine sediment depends upon the following factors: (1) whether the sample is wet or dry, (2) the primary color of the larger grains, (3) the state of division (size) of the constituent particles, (4) the state of oxidation or reduction of the iron, and (5) the amount of decomposable organic matter.
Because the color may be affected by the moisture content and the oxidation-reduction potential may be modified by bacterial activity after the sample is collected, the color should be noted soon after the material has been obtained. In order to eliminate as far as possible the subjective element in judging color when an accurate estimate is desirable, a standard color chart such as that prepared by Ridgway (1912) should be employed.
The color of the individual grains is particularly important in sediments containing a relatively large proportion of material coarser than silt. Finely divided material may have an “apparent” color which depends upon the state of division. In many ways the oxidation-reduction potential in the sediment is probably the most important factor controlling the color. When conditions are such that the potential is oxidizing for iron, reddish or brown oxides are formed. This is the condition which will normally prevail in the presence of free oxygen. When there is a relatively abundant supply of organic material, bacterial activity may use up all the available oxygen and establish highly reducing conditions. If hydrogen sulphide is produced, black iron sulphides may be formed. Intermediate stages in the oxidation or reduction of the iron may possibly produce the greenish and bluish colors characteristic of many near-shore deposits. Although the state of oxidation or reduction of the iron has been considered as the most important factor in determining the color, particularly of fine-grained sediments, the problem is not yet solved, as the sediments tend to retain their color even when treated in various ways in the laboratory.
Marine sediments vary from white through gray to black, with the addition of various amounts of yellow, red, blue, or combinations of these colors. White sediments and, in general, those of light colors are relatively coarse-grained and composed of quartz or limestone. The grays may be due to the presence of black minerals or authigenic iron and manganese grains. Black deposits are typical of stagnant conditions that may prevail in basins, fjords, and other isolated environments.
Coarse-grained sediments will generally show the color of the constituent grains. As the greatest part of the sea floor is covered with fine-grained sediments, it is of interest to note the character of the material brought to the sea. River-borne debris is generally yellow, red, or brown, and in areas where the deposition is rapid, as off the mouths of large rivers, the sediments are essentially the same color as the source material and are often referred to as red muds. Along most coasts where the deposits are predominantly terrigenous, the sediments are generally green or olive green. Hence, there seems to be some change in the color of the terrigenous material that is probably associated with the oxidation-reduction potential in the environment of deposition. Further offshore the greenish or bluish muds pass gradually into the
Both the absolute and the relative rates of deposition of decomposable organic matter and of organic skeletal structures and inorganic debris may be important in determining the color of a deposit. It is a characteristic property of many terrigenous deposits that the upper few millimeters are of a browner tint than the underlying material. This may be due to the fact that the supply of oxygen is much greater at the surface and that the oxidation-reduction potential is not as low as it is in the buried material. Lamination or stratification of the sediments in core samples may frequently be recognized by color differences. Such structures can generally be confirmed by studies of the texture or of the organic-matter content. The darker bands usually contain more organic matter.
The organic-matter content of marine sediments varies from essentially zero to more than 15 per cent. Samples containing large quantities may actually be darkened by the presence of the black or brownish organic detritus. Fox and Anderson (1941) have shown that organic pigments can be extracted from certain terrigenous muds.
Color is therefore a useful character in classifying marine sediments because it tells something of the source of the material, particularly of the coarse-grained portions, and of the conditions of deposition. If the depth and distance from shore are known, certain conclusions may be drawn as to the relative and absolute rates of deposition of decomposable organic matter and of the inert constituents and as to the oxidation-reduction potential prevailing in the sediments.
Texture of Marine Sediments. Depending upon their texture, marine sediments may be subdivided into gravels, sands, silts, muds, clays, or intermediate types (p. 972). The proportions of larger grains may be estimated visually or judged by rubbing the material between the fingers. An experienced observer is able to classify a sample in this way very easily. When an accurate knowledge of the particle-size distribution is required, laboratory tests must be made by methods such as those described by Krumbein and Pettijohn (1938) and by Gripenberg (1939b).
The particles in a marine sediment may cover a wide range in size. In general, there are no sharp limits to the sizes of the constituent grains, and as a result it is necessary to employ certain conventionalized methods for the discussion or for the graphical presentation of data of this type. In practice, it is impossible to determine the size of each individual grain
The data on size-grade distribution may be graphed in various ways. The two most common forms are histograms and cumulative curves. Because of the range in particle size usually encountered and for other reasons, it is convenient to plot histograms and cumulative curves showing the percentage weight frequency against the logarithm of the equivalent diameter. In figs. 254 and 255 (pp. 980, 981), comparable data are represented in these two ways. By convention, the smaller grade sizes are always on the right-hand side of the diagram. The heights of the columns in the histograms show the weight frequency or percentage represented by the individual size grades. The cumulative curve is obtained by successive addition of the material in the different grades and shows directly the percentage by weight of material greater or less than any designated size.
Krumbein and Pettijohn (1938) and Krumbein (1939) have discussed the statistical significance of size-grade distribution data. Certain values which can be obtained directly from the cumulative curve for an individual sample are commonly used to characterize the general size and the sorting of the sediment. These are:
The median diameter (M2) which represents the diameter which in the individual sample has 50 per cent by weight of material of smaller and larger equivalent diameters.
The first (Q1) and third (Q3) quartile diameters. The first quartile diameter has 25 per cent smaller and 75 per cent larger diameter and the third quartile has 75 per cent smaller and 25 per cent larger. The difference in the quartile diameters indicates the range covered by the middle 50 per cent of the material, but tells nothing of the coarser and finer quarters.
The sorting coefficient (S0) is a measure of the degree of sorting and is defined as
The value of S0 will approach unity as the material becomes more uniform in size. Trask (1932) found that values of S0 less than 2.5 indicated well-sorted material with about 3.0 as the average for marine sediments.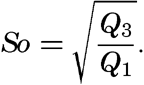 ― 971 ―When S0 is greater than 4.5, the sediment is considered to be poorly sorted.
― 971 ―When S0 is greater than 4.5, the sediment is considered to be poorly sorted.The asymmetry of the distribution about the median is designated as the skewness (Sk). The skewness may be defined as
When the size-frequency distribution curve is symmetrical the value of Sk is unity, but the values may range from less than unity to larger figures which indicate that the distribution is skewed either towards the finer or the coarser sizes.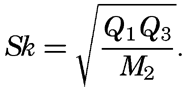
The statistical expressions given above are those recommended by Krumbein and Pettijohn (1938) and may differ from somewhat similar terms employed by other workers.
It will be seen that the median and the first and third quartile diameters and the sorting coefficient and the skewness are introduced in order to obtain simple figures to express certain features of the size-grade distribution. It is unfortunate that these expressions do not take into account the coarse and fine material lying beyond the limits of the first and third quartiles. This drawback is particularly applicable as concerns the coarser material, which may be diagnostic as to the effective transporting agencies. The finer material is not of such interest as it is more cosmopolitan in its distribution.
Composition of Marine Sediments. The composition of a sediment may be presented in various ways and a wide variety of techniques may be employed to determine it. In general, “composition” is used to indicate one of the mass properties, it may be the size-grade distribution discussed above, the chemical composition, or the percentage of different types of organic remains or minerals. On the other hand, interest may be centered upon some fraction of the sample, such as the heavy minerals or the decomposable organic matter, or upon some single chemical element. The composition is of interest because it is a way of determining the sources of the various constituents and the proportions in which they are present. Furthermore, it offers a means of determining the effects of chemical weathering and of identifying authigenic minerals.
In the field the composition of the larger grains may be determined by visual examination which may tell whether they are predominantly organic and if so, of what type, or whether they are minerals of volcanic, terrigenous, or authigenic nature. From such observations, in combination with the color and texture, the sediment may be classified. In the laboratory, examination under the microscope makes it possible to identify many more of the grains down to sizes of approximately two microns. Below this grade it is necessary to employ chemical analyses, X-ray analyses, or some other method to determine the character and
Complete chemical analyses are difficult and are rarely carried out. Much more frequently, determinations of one or more diagnostic elements are made, for example, of calcium carbonate, or organic nitrogen as a measure of the organic matter.
CLASSIFICATION OF RECENT MARINE SEDIMENTS
Marine deposits are subdivided into two major groups, termed pelagic and terrigenous. The pelagic deposits are those found in deep water far from shore and may be predominantly either organic or inorganic in origin. Pelagic deposits are light-colored, reddish or brown, fine-grained and, generally, they contain some skeletal remains of plankton organisms. Benthic forms are generally rare. The inorganic deposits are referred to as red clay and the organic deposits as oozes. The terrigenous deposits are found near shore and generally contain at least some coarse material of terrigenous origin. They cover a wide range in depth and a great variation in color, texture, and composition. They are known as sands, silts, muds, or intergrading types, depending upon their texture. Although they may have median diameters as small as certain pelagic deposits, the terms clay and ooze are never applied to terrigenous deposits. Nearshore sediments may contain remains of plankton forms but, in addition, skeletons of benthic organisms may be relatively abundant. In certain regions the deposits may be almost entirely made up of the fragments of certain calcareous benthic forms.
Pelagic deposits are classified in the following way:
Inorganic deposits. Those which contain less than 30 per cent of organic remains are known as red clay.
Organic deposits. Those which contain more than 30 per cent of material of organic origin are known as oozes. This class is further subdivided into:
Calcareous oozes. These contain more than 30 per cent calcium carbonate, which represents the skeletal material of various plankton animals and plants. The calcareous oozes may be further divided into three types, depending upon a characteristic type of organism present in the sediment, namely:
Globigerina ooze, in which the calcium carbonate is in the tests of pelagic foraminifera.
Pteropod ooze, containing conspicuous shells of pelagic molluscs.
Coccolith ooze, containing large numbers of coccoliths and rhabdoliths that form the protective structures of the minute Coccolithophoridae.
― 973 ―Siliceous oozes. These are pelagic deposits which contain a large percentage of siliceous skeletal material produced by planktonic plants and animals. The siliceous oozes are subdivided into two types on the basis of the predominance of the forms represented, namely,
Diatom ooze, containing large amounts of diatom frustules, hence, produced by plankton plants.
Radiolarian ooze, containing large proportions of radiolarian skeletons formed by these plankton animals.
The classification of terrigenous deposits is not so satisfactory as that of the pelagic sediments. A number of systems have been suggested, but the character of the deposits depends so much upon local conditions that no one system has very wide application. Relative to the pelagic deposits, terrigenous sediments cover a small percentage of the sea floor, and since they show a wide range in properties within a relatively short distance from the coast the occurrence of transitional types is more of a problem. As pointed out in the discussion of mass properties, color, texture, and composition form the basis of the classification. Hence it is desirable to indicate the terms applied to terrigenous deposits rather than set up any definite outline of classification.
The color of terrigenous deposits may range from white to black with the addition of blue, yellow, or red, or mixtures of these. In general, sediments of the shelves and slopes are dark in color, ranging from green or brown to blue. The color depends so much on the local environment that it may vary a great deal in a relatively short distance over the bottom, or with depth in the deposit.
Terrigenous deposits are generally coarser than those found in the deep sea, although certain exceptions do occur. The texture will depend not only upon the effective transporting agency but also upon the character of the source material. The following terms have been suggested by Revelle (personal communication) to designate the texture of terrigenous deposits:
Sand. More than 80 per cent of the material coarser than 62 microns in diameter.
Silty sand. Between 50 per cent and 80 per cent coarser than 62 microns.
Sandy silt. More than 50 per cent coarser than 5 microns and more than 20 per cent coarser than 62 microns.
Silty mud. More than 50 per cent coarser than 5 microns and less than 20 per cent coarser than 62 microns.
Clayey mud. Less than 50 per cent coarser than 5 microns.
By definition (p. 957) the sands may be subdivided into very coarse (2000–1000 microns), coarse (1000–500 microns), medium (500–250 microns), fine (250–125 microns), and very fine (125–62 microns). If all the material is within the limits of 62 and 4 microns the term silt may be used. It will be noted that the term mud was not listed in table 105, since it is restricted to terrigenous sediments containing particles with a wide range in size.
The composition is concerned with the character and, hence, with the source of the constituent materials. On this basis terrigenous sediments may be divided into organic and inorganic types. The terms foraminiferal, coral, diatomaceous, or other specific terms may be applied when a single type of organic remains is prominent in the sediment, and if no one form is conspicuous the general terms calcareous or siliceous may be used with the understanding that they indicate material of organic origin. Predominantly inorganic types of sediments may be expected to be related to the character of the material supplied to any area, and in this case no special term need be applied. However, the presence of mineral grains of certain types or sizes may make it desirable to add a term indicating either the source or mode of transportation. Thus, glacial may be used for sediments containing material deposited by glaciers and icebergs, volcanic when there is a large amount of pumice, volcanic ash, and glass in the deposit. Mica is sometimes a readily recognized constituent and if it is abundant the term micaceous may be introduced. In certain areas authigenic glauconite is sufficiently abundant to warrant use of the term glauconitic.
When following the above system of terminology a trinomial nomenclature may be used to describe terrigenous deposits. For example, a sediment from near a continental coast may be a green diatomaceous silty mud, or one from the shelf of an oceanic island may be a gray calcareous sand.
DISTRIBUTION OF PELAGIC SEDIMENTS
General Features of Distribution. Figure 253 shows the distribution of the various types of pelagic sediments. The representation is generalized partly to avoid confusion and partly because of the incomplete knowledge as to the types of sediments found in many parts of the oceans. Any such presentations of the distribution of pelagic sediments are modified versions of maps originally prepared by Sir John Murray and his associates. Further investigations have changed the boundaries but have not materially affected the general picture. The figure has been prepared from the most recent sources available. The distribution of sediments in the Indian Ocean is based on a map by W. Schott (1939a), that in the Pacific Ocean is from W. Schott in G. Schott (1935), with some revisions based on Revelle's studies of the samples collected by the Carnegie (Revelle, 1936). The data for the Atlantic have been drawn from a number of sources, since no comprehensive map has been prepared for many years. The Meteor material has been described by Correns (1937 and 1939) and Pratje (1939a). Thorp's report (1931) on the sediments of the Caribbean and the western North Atlantic was used for those areas, and Pratje's data (1939b) for the South Atlantic were supplemented by those of Neaverson (1934) for the Discovery samples. The distribution in the North Atlantic is from Murray (Murray and Hjort, 1912).
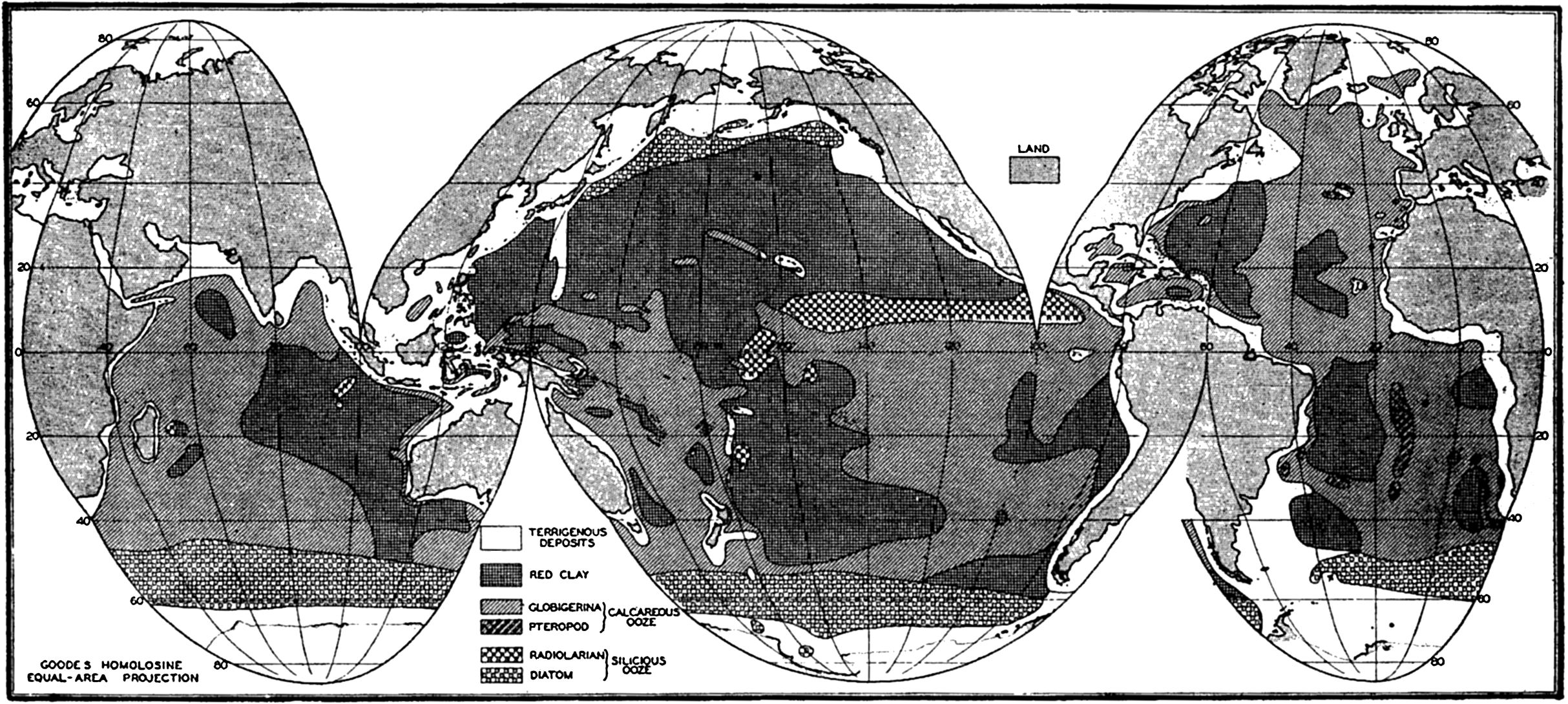
Distribution of the various types of pelagic sediments.
One type of shading has been used for all of the calcareous sediments and another for the siliceous sediments. Unless the symbol P is shown to indicate that the area is covered with pteropod ooze, it is to be understood that the calcareous sediment is globigerina ooze. The siliceous organic sediments are indicated as D for diatom ooze and R for radiolarian ooze. The unshaded areas of the oceans and seas are covered with terrigenous sediments.
Various features of the distribution of pelagic sediments should be pointed out:
Pelagic sediments are restricted to the large ocean basins.
Red clay and globigerina ooze are the predominant types of deposits.
Diatom oozes are restricted to a virtually continuous belt around Antarctica and a band across the North Pacific Ocean.
Radiolarian ooze is almost entirely limited to the Pacific Ocean, where it covers a wide band in the equatorial region.
Pteropod ooze occurs in significant amounts only in the Atlantic Ocean.
The width of the area of terrigenous sediments depends upon a number of factors such as the depth and the supply of material, but it should be noted that in general it is more extensive in high latitudes. The North Polar Basin and the seas adjacent to the northern Pacific and Atlantic Oceans are covered with terrigenous sediments. As will be shown later, the terrigenous sediments of lower latitudes are largely composed of calcareous remains of benthic organisms in contrast to those of higher latitudes, which are chiefly made up of mineral fragments.
Although no depth contours are shown in fig. 253, comparison with chart I will show that the distribution of red clay and calcareous oozes is restricted to those portions of the ocean floor with moderate or great depths.
The boundaries between different types of sediments are not distinct, since one form will graduate into another with interfingering where the topography is irregular. However, a glance at the figure will show that the marginal belts are small compared to the tremendous areas
― 977 ―of readily classified sediments, and it is for this reason that the system of classification can be considered valid.
Area of Ocean Bottom Covered by Pelagic Sediments. In table 106 are given the areas covered by the different types of pelagic sediments. The values were obtained from fig. 253. Pelagic sediments cover 268.1 × 106 km2 of the earth's surface, that is, 74.3 per cent of the sea bottom. The calcareous oozes (47.7 per cent), notably globigerina ooze, are the most extensive, with red clay (38.1 per cent) next in importance among the pelagic deposits. Siliceous oozes cover only 14.2 per cent of the total area.
| Atlantic Ocean | Pacific Ocean | Indian Ocean | Total | |||||
|---|---|---|---|---|---|---|---|---|
| Area | % | Area | % | Area | % | Area | % | |
| Calcareous oozes: | ||||||||
| Globigerina | 40.1 | 51.9 | 34.4 | |||||
| Pteropod | 1.5 | |||||||
| Total | 41.6 | 67.5 | 51.9 | 36.2 | 34.4 | 54.3 | 127.9 | 47.7 |
| Siliceous oozes: | ||||||||
| Diatom | 4.1 | 14.4 | 12.6 | |||||
| Radiolarian | 6.6 | 0.3 | ||||||
| Total | 4.1 | 6.7 | 21.0 | 14.7 | 12.9 | 20.4 | 38.0 | 14.2 |
| Red clay | 15.9 | 25.3 | 70.3 | 49.1 | 16.0 | 25.3 | 102.2 | 38.1 |
| 61.6 | 100.0 | 143.2 | 100.0 | 63.3 | 100.0 | 268.1 | 100.0 | |
The percentages of the total area of pelagic sediments in the three oceans covered by the major types of sediments are as follows:
| Sediment | Indian Ocean | Pacific Ocean | Atlantic Ocean |
|---|---|---|---|
| Calcareous oozes | 54.3 | 36.2 | 67.5 |
| Siliceous oozes | 20.4 | 14.7 | 6.7 |
| Red clay | 25.3 | 49.1 | 25.8 |
| 100.0 | 100.0 | 100.0 |
It will be seen that calcareous deposits predominate in the Indian and the Atlantic Oceans, but that in the Pacific Ocean, which is somewhat deeper, red clay is the most extensive. Of the total areas covered by the three major types of sediments the percentage distribution in the three oceans is as follows:
| Sediment | Calcareous oozes | Siliceous oozes | Red clay |
|---|---|---|---|
| Indian Ocean | 26.9 | 33.9 | 15.7 |
| Pacific Ocean | 40.6 | 55.3 | 68.7 |
| Atlantic Ocean | 32.5 | 10.8 | 15.6 |
| 100.0 | 100.0 | 100.0 |
The Pacific Ocean, because of its great size, contains the largest percentage of all of the three types and actually over 50 per cent of the siliceous oozes and red clay.
Depth Range of Pelagic Sediments. Depth is generally considered as one of the factors controlling the distribution of the different types of marine sediments. According to Murray's classification, deep-sea sediments are restricted to depths greater than about 200 m, and in general pelagic sediments are found only at considerably greater depths. Although there is some difference in the depth distribution in the three oceans, data are not comparable, and the following values for globigerina and pteropod oozes and red clay are from Murray and Chumley (1924), representing the results of studies made on 1426 samples from the Atlantic Ocean. The values for diatom and radiolarian oozes are from Andrée (1920).
| Sediment | Samples | Depth (m) | ||
|---|---|---|---|---|
| Minimum | Maximum | Average | ||
| Globigerina ooze | 772 | 777 | 6006 | 3612 |
| Pteropod ooze | 40 | 713 | 3519 | 2072 |
| Diatom ooze | 28 | 1097 | 5733 | 3900 |
| Radiolarian ooze | 9 | 4298 | 8184 | 5292 |
| Red clay | 126 | 4060 | 8282 | 5407 |
Although the ranges overlap, indicating that factors other than depth control the distribution of pelagic sediments, it can be seen that radiolarian ooze and red clay are characteristic of depths greater than 4000 m, whereas the calcareous sediments and diatom oozes are generally restricted to the lesser depths.
MASS PROPERTIES OF DEEP-SEA SEDIMENTS
Color of Deep-sea Sediments. The significance of color has been considered above, and in the system of classification it was pointed out that pelagic deposits are characterized by light colors or red or brown
The colors of the various types of pelagic sediments are as follows:
Globigerina ooze. Milky white, rose, yellow, or brown. Near land it may be dirty white, gray, or blue.
Pteropod ooze. White to light brown with reddish, pink, or yellow tinge.
Diatom ooze. Yellowish, straw, or cream colored. Dirty white when dry. Darker near land.
Radiolarian ooze. Red, chocolate brown, or straw colored.
Red clay. In North Atlantic, brick red, but in South Pacific and Indian Oceans, chocolate brown. Graduates into “blue” near shore.
As pointed out in the section on classification, the color of terrigenous deposits is extremely variable. Murray and his co-workers established various types of terrigenous sediments to which the names “blue,” “green,” and “red” muds were applied. Unfortunately, the color was not the only factor which placed a given sample within one of these groups, therefore the anomalous situation developed that a green- or brown-colored mud would be classified as a “blue mud.”
Texture of Deep-sea Sediments. The texture of pelagic sediments varies a great deal, depending largely upon the proportions of organic remains. Pteropod and globigerina oozes, containing little or no fine material, which occur on topographic highs actually are sands if texture alone is considered. At the other extreme are the fine-grained clays. It is convenient, as in the discussion of color, to consider the textural properties of the three extreme types of pelagic sediments, namely, red clay, diatom ooze high in organic remains, and globigerina ooze largely made up of foraminiferal skeletons. Intermediate types representing organic oozes diluted with clay will of course fall within the limits described by these extreme types. Coarse-grained mineral fragments are never abundant except under special circumstances.
The following data have been selected as examples. The average of five globigerina oozes from the Pacific Ocean collected by the Carnegie were analyzed by the pipette method by Revelle (1936). These samples
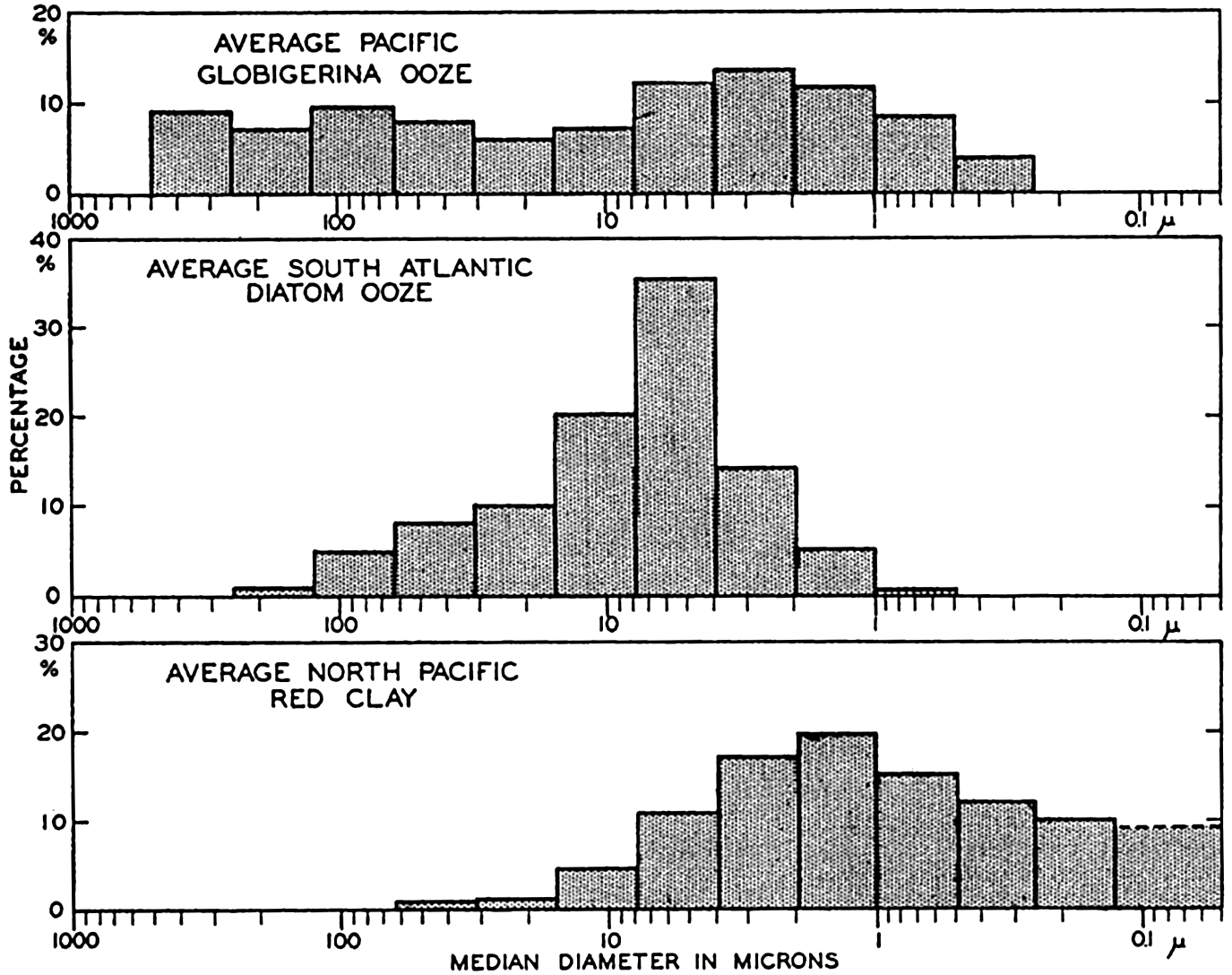
Distribution of particle size (equivalent diameter) in pelagic sediments represented by histograms (same data as in fig. 255).
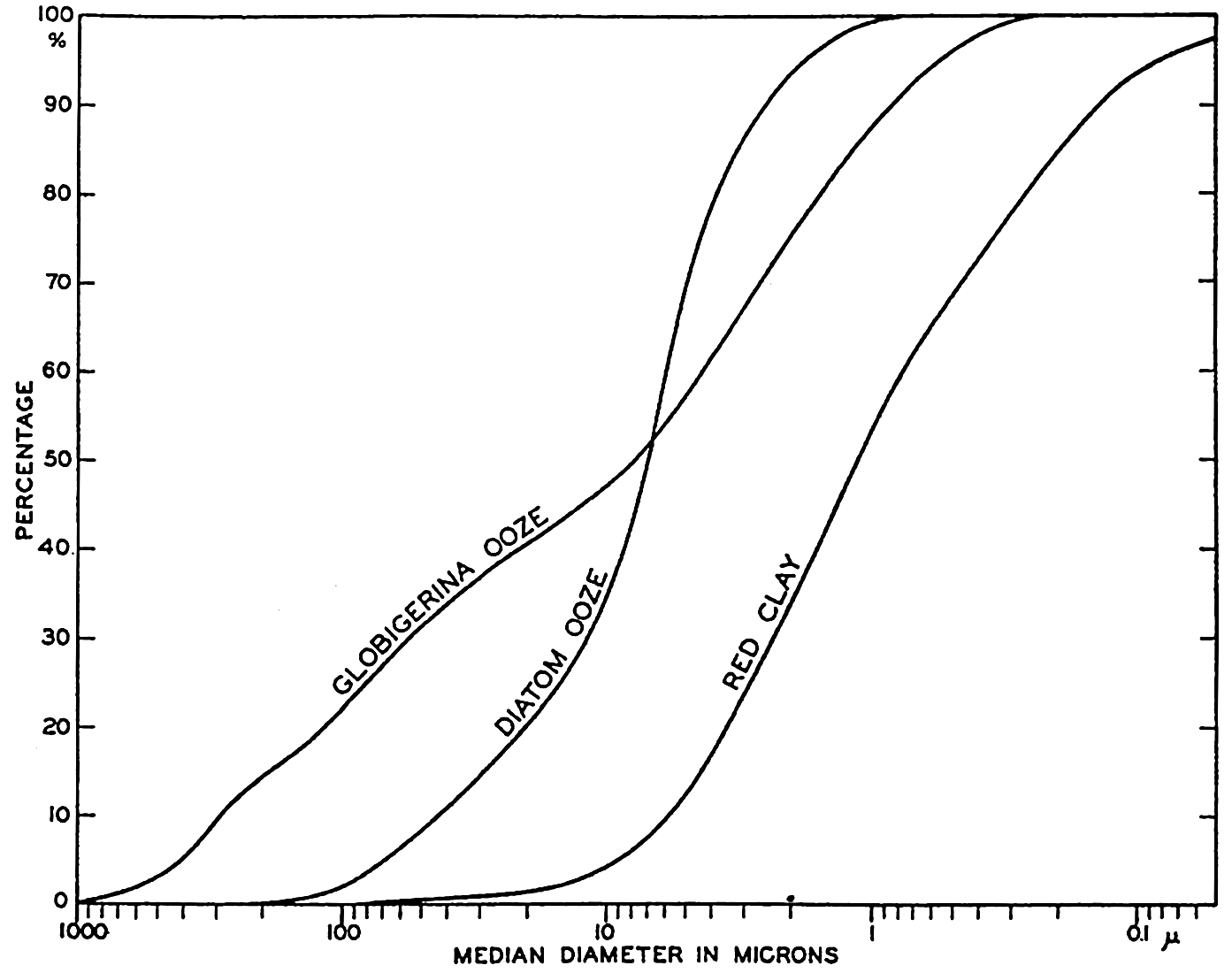
Distribution of particle size (equivalent diameter) in pelagic sediments represented by histograms (same data as in fig. 254).
| Sediment | Sand % | Silt % | Clay % | M2 μ | Q1 μ | Q3 μ | So | Sk |
|---|---|---|---|---|---|---|---|---|
| Globigerina ooze | 28.7 | 33.5 | 37.8 | 7.8 | 2.0 | 82.0 | 6.4 | 4.58 |
| Diatom ooze | 6.0 | 88.0 | 6.0 | 7.0 | 4.4 | 15.0 | 1.85 | 3.63 |
| Red clay | 0.0 | 17.3 | 82.7 | 1.1 | 0.35 | 2.8 | 2.83 | 0.94 |
The median diameter for the globigerina ooze does not represent the size of the complete tests which would mostly have diameters greater than 62.5 microns. It will be noted that the histogram shows several maxima. The histograms of globigerina oozes show two maxima characteristically, one in the coarser grades which corresponds to the relatively complete tests, and another in the fine grades. Revelle (1936) has shown that corresponding maxima are found in the CaCO3 content of the different size grades. The maximum in the small grades is due to the presence of small crystals of CaCO3 (calcite) which are believed to arise from the mechanical disintegration of the foraminiferal tests. Correns (1939) considers that the fine-grained calcareous particles result from the destruction of the albuminoid (pseudochitin) cement which binds together the carbonate crystals in the shells. More than 50 per cent of the material finer than 2 microns may be calcareous. The data for the diatom ooze show that the bulk of the material is in the silt grades with the largest fraction between 7.8 and 3.9 microns. Because of their shape and structure, radiolarian and diatom frustules will have equivalent diameters smaller than their true dimensions. Revelle (1936) shows in photomicrographs many entire radiolarians of dimensions larger than 250 microns, and the material between 250 and 125 microns is almost entirely composed of diatom frustules and smaller radiolarians.
From the foregoing discussion it may be seen that the pelagic deposits contain material of diameters ranging from a millimeter or more down to the clay fraction with diameters chiefly less than one micron. Excluding the more or less exotic volcanic material and such rare constituents as manganese nodules, sharks’ teeth, and so forth, it is obvious that the coarser fractions of true pelagic deposits are entirely composed of skeletal remains, whereas at the other extreme there is the inorganic clay fraction. The size-grade composition of a given sample may fall anywhere between these extremes and have only one maximum or several maxima, depending upon the character of the source materials and the relative proportions in which they are deposited.
Physical Composition of Deep-sea Sediments. The character of the grains larger than about two microns can generally be determined by microscopic examination. The organic remains can be identified, and with the aid of the microscope and various techniques of the petrographer the mineral grains may also be recognized. The fine material, such as that predominating in red clays, cannot be studied in this way because of the small size of the individual particles. For many years this material was considered as “amorphous,” but the development of X-ray methods for determining crystal structure and the application of various physical and chemical tests have established the identity of the clay minerals.
In the examination of sediment samples the mechanical analysis is usually made first and various convenient size grades are separated.
Organic constitutents in deep-sea sediments comprise remains of virtually every type of marine organisms possessing hard skeletal structures. The various oozes may consist almost entirely of the remains of one type of planktonic organisms; on the other hand virtually all types of organisms may be found in any one sample, although the total may not make up more than a small percentage of the deposit. The latter situation may prevail in red clays. Foraminifera, both planktonic and benthic, have been studied most extensively, and the species encountered and their distribution are fairly well known. Much less information is available concerning the species of diatoms, radiolarians, and other forms encountered in marine deposits. In many reports on the physical composition of marine sediments no attempt has been made to classify the organic remains beyond reporting the percentages of calcareous and siliceous structures. Revelle (1936) has tabulated the general organic constituents in 1156 pelagic sediment samples studied by Sir John Murray and his associates. These data are given in table 108, taken from Revelle. In it are shown the maximum, minimum, and average percentages of calcium carbonate, planktonic and benthic foraminifera, other calcareous remains, siliceous remains, and the mineral grains of diameters greater and less than 0.05 mm (50 microns) in the various types of pelagic sediments. If the extreme cases are selected, as in the case of the texture, it may be seen that red clays may contain 100 per cent of minerals less than 0.05 mm, whereas calcareous oozes may contain more than 98 per cent of calcareous remains, and siliceous oozes 90 per cent of siliceous remains. However, most samples represent mixtures of two or more of these basic types of constituents in variable proportions. The average percentage of various organic and inorganic materials can be obtained from table 108.
Calcareous structures are in general more abundant than siliceous organic remains. The various groups of pelagic and benthic organisms which may contribute to the sediments have been listed elsewhere (p. 950). Both planktonic and benthic foraminifera are found in marine sediments. Cushman (1928) lists 25 species of planktonic foraminifera. Revelle found 23 species in the deposits of the Pacific Ocean, Throp (1931) 19 species in the deposits of the western North Atlantic, and W. Schott (in Correns et al, 1937) 21 species in the Equatorial Atlantic.
| Physical composition | Red clay (%) | Radiolarian ooze (%) | Diatom ooze (%) | Globigerina ooze (%) | Pteropod ooze (%) | ||||
|---|---|---|---|---|---|---|---|---|---|
| (C) | (M) | (C) | (C) | (V) | (C) | (M) | (M) | ||
a Only in two exceptional cases; the usual maximum is not more than 5 per cent. | |||||||||
b Only in one exceptional case. | |||||||||
c Includes finely divided remains of siliceous organisms. | |||||||||
| CaCO3 | Maximum | 28.8 | 29.0 | 20.0 | 36.3 | 24.0 | 96.8 | 97.2 | 98.5 |
| Minimum | 0 | 0 | tr | 2.0 | 0 | 80.2 | 30.0 | 44.8 | |
| Average | 6.7 | 10.4 | 4.0 | 23.0 | 2.7 | 64.5 | 64.7 | 73.9 | |
| Planktonic foraminifera | Maximum | 27.0 | predominant part of CaCO3 | 80.0 | 95.0 | 75.0 | |||
| Minimum | 0 | 25.0 | 15.0 | 15.0 | |||||
| Average | 4.77 | 8.8 | 3.1 | 3.1 | 53.1 | 58.9 | 34.7 | ||
| Benthic foraminifera | Maximum | 3.0 | 10.0 | 10.0 | |||||
| Minimum | 0 | present | 0 | tr | |||||
| Average | 0.6 | 0.6 | .1 | 1.6 | 2.1 | 2.1 | 3.6 | ||
| Other calcareous remains | Maximum | 6.3 | 31.8 | 26.0 | 57.0 | ||||
| Minimum | 0 | present | 1.2 | tr | 15.8 | ||||
| Average | 1.3 | 1.0 | .8 | 3.2 | 9.2 | 3.7 | 35.5 | ||
| Siliceous remains | Maximum | 5.0 | 80.0 | 60.0 | 90.0 | 10.0 | 15.0[a] | 20.0 | |
| Minimum | 0 | 30.0 | 20.0 | 40.0 | 4.0 | tr | tr | ||
| Average | 2.4 | 0.7 | 54.4 | 41.0 | 73.1 | 1.6 | 1.7 | 1.9 | |
| Texture of mineral particles | |||||||||
| >.05 mm, diameter | Maximum | 20.0 | 60.0[b] | 5.0 | 25.0 | 40.0 | 50.0[b] | 50.0[b] | 20.0 |
| Minimum | 1.0 | tr | 1.0 | 3.0 | 1.0 | 1.0 | tr | tr | |
| Average | 5.6 | 2.4 | 1.7 | 15.6 | 8.4 | 5.3 | 5.1 | 4.7 | |
| <.05 mm, diameter | Maximum | 100.0 | 67.0[c] | 27.9[c] | 34.0 | 66.6 | 69.3 | 41.8 | |
| Minimum | 31.0 | 17.0[c] | 12.5[c] | 9.0 | 1.2 | 1.2 | tr | ||
| Average | 85.4 | 86.5 | 39.9[c] | 20.4[c] | 15.8 | 30.6 | 28.5 | 19.6 | |
| Number of samples averaged | 70 | 126 | 9 | 5 | 16 | 118 | 772 | 40 | |
According to the studies of W. Schott (1937) the benthic foraminifera constitute less than 1 per cent of the total number of foraminifera in about 50 per cent of the samples examined. In very few cases do they exceed 25 per cent of the total number of tests. The highest percentages occur in samples of intermediate CaCO3 content. This is in agreement with Revelle (1936), who found the greatest number of species in samples of intermediate carbonate content.
W. Schott (1937) has introduced the “foraminiferal number” as a measure of the abundance of relatively entire tests. He found that most of the unbroken tests were in the size grade between 2 to 0.2 mm diameter. By count he determined that 1 g of this material contained 23,300 tests. The foraminiferal number is then obtained by multiplying the fraction of the material in this size grade, less the percentage of material other than foraminiferal tests, by 23,300. From this it can be seen that a sample composed entirely of foraminifera in this grade would have a foraminiferal number of 23,300. The highest value obtained by Schott was 12,700. Much of the calcium carbonate is present as smaller tests or as broken fragments, hence the foraminiferal number is not directly proportional to the CaCO3. The relationship obtained by Schott is shown in fig. 256. Correns (1939) has suggested that the term globigerina ooze be restricted to samples with foraminiferal numbers greater than 6000, which would indicate that at least one quarter of the sediment consisted of unbroken foraminiferal tests in the size grade of diameter between 2 and 0.2 mm. As can be seen from fig. 256, such samples would contain more than 60 per cent CaCO3.
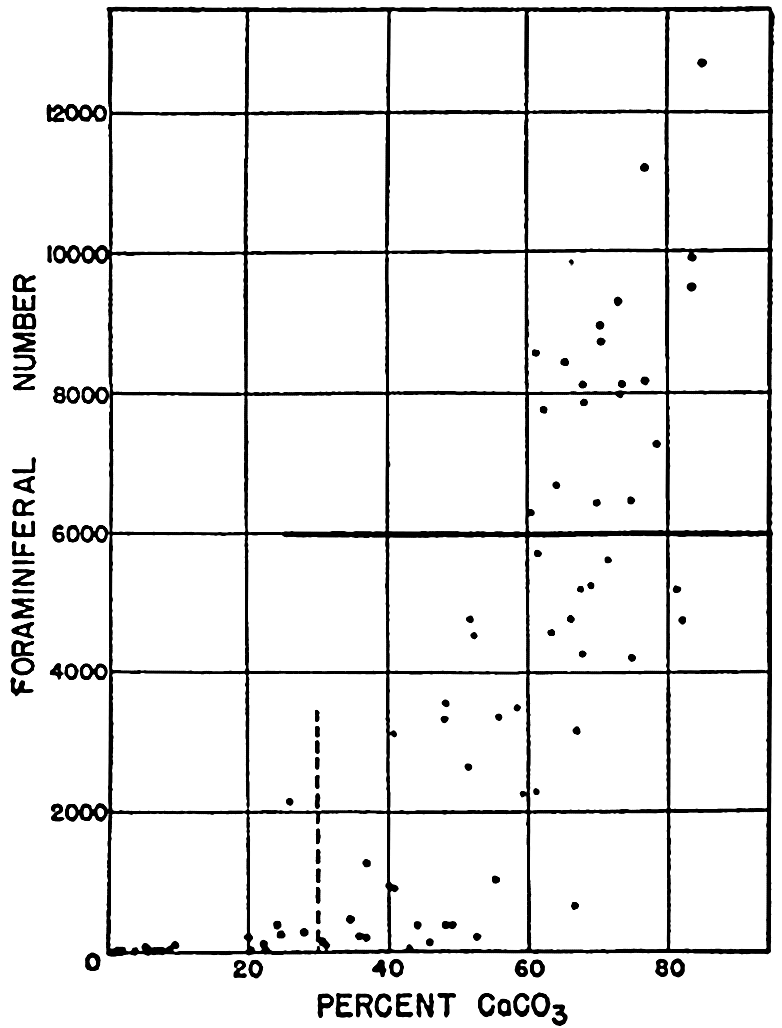
Relation of the foraminiferal number to the calcium carbonate content in sediments from the Equatorial Atlantic Ocean. (From Correns, 1939, in Recent Marine Sediments, edited by Parker D. Trask, and published by the American Association of Petroleum Geologists, Tulsa, Oklahoma.)
Because of their relatively large size, pteropods and heteropods are conspicuous constituents of certain calcareous oozes from the shallower depths in tropical latitudes. However, they never constitute more than
Calcareous remains of other types of pelagic and benthic animals may be found in pelagic deposits but they are never abundant. Echinoderms, annelids, ostracods, and polyzoa are among the benthic forms commonly present.
Calcareous structures of plant origin are among the important constituents of the pelagic deposits. Fragments of the larger calcareous algae (Lithothamnion and Corallina) are often found near land, and in the open ocean the remains of the microscopic Coccolithophoridae may be very abundant, particularly in the tropical and subtropical parts of the Atlantic Ocean. These pelagic forms are so delicate that the entire skeletons are rarely found but, instead, only the tiny plates of which they are built up. The oval plates called coccoliths and the rod-shaped fragments called rhabdoliths, which arise from the coccosphere and the rhabdosphere, may constitute as much as 74 per cent of the material between 10 and 2 microns in diameter and may form about 15 per cent of the material of finer grades. According to Correns (1939), the calcareous plant remains never form more than 13 per cent of the entire sample.
The inorganic constituents in deep-sea sediments are shown in table 109 (Revelle, 1936), giving the frequency with which the principal minerals were reported by Murray and his co-workers in the various types of pelagic deposits. These records are based on examination of the material larger than 0.05 mm and do not include the smaller particles referred to by Murray as “fine washings.” Table 108 gives the maximum, minimum, and average content of “minerals” and “fine washings” in the various types of deposits and, as can be seen from the average values, the larger grains rarely represent more than a small percentage of a pelagic sediment. Coarse terrigenous material must be rare except in regions where ice or the atmosphere are effective, because of the lack of adequate transporting agencies. Volcanic material, except pumice which will float for some time and the fine dust which may be air-borne, will also be restricted to areas of volcanic activity. The authigenic materials, on the other hand, are not directly dependent upon transporting agencies but are related to the environment prevailing in and over the sediment.
Although means have been available for many years for the identification of mineral grains, it is only recently that it has been possible to obtain any adequate idea as to the character of the fine material. Murray considered it as amorphous, that is, noncrystalline, and from the available data decided that red clays and the clay fraction of all pelagic deposits were formed on the sea bottom by the decomposition of volcanic material. It was also suggested that a certain “insoluble” fraction of calcareous and siliceous skeletons might contribute to this fraction of the deposit.
| Percent of samples analyzed in which sustance is recorded | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Principal inorganic constituents | Red clay (%) | Radiolarian ooze (%) | Diatom ooze (%) | Globigerina ooze (%) | Pteropod ooze (%) | ||||
| (C) | (M) | (C) | (C) | (V) | (C) | (M) | (M) | ||
a Always listed as hornblende, except for one reference to glaucophane, in a blue mud, and to actinolite, in a globigerina ooze. | |||||||||
b Includes all references to monoclinic feldspar. | |||||||||
c Includes all references to triclinic feldspar. | |||||||||
d Includes three references to green mica in blue and green muds. | |||||||||
e Includes one reference to bronsite in globigerina ooze. | |||||||||
f Does not include clay minerals, iron hydroxides, or colloidal silica. | |||||||||
g May be allogenic in part. | |||||||||
| 1. Allogenic minerals | |||||||||
| Amphibole[a] | 44 | 19 | 10 | 100 | 60 | 50 | 36 | 60 | |
| Chlorite | |||||||||
| Epidote | 3 | ||||||||
| Feldspar, undifferentiated | 76 | 19 | 90 | 60 | 90 | 73 | 38 | 50 | |
| orthoclase[b] | 40 | X | |||||||
| sanidine | 10 | 18 | 10 | ||||||
| plagioclase[c] | 29 | 80 | 20 | 10 | |||||
| Garnet | 1 | 20 | X | ||||||
| Magnetite | 89 | 23 | 100 | 80 | 29 | 40 | |||
| Mica, undifferentiated | 27 | 40 | 10 | 40 | 6 | 26 | 64 | 70 | |
| white mica | |||||||||
| black mica[d] | 10 | 20 | |||||||
| Olivine | 7 | 40 | 16 | 10 | |||||
| Pyroxene, undifferentiated | X | ||||||||
| enstatite | X | ||||||||
| hypersthene[e] | |||||||||
| augite | 61 | 13 | 30 | 40 | 12 | 70 | 12 | 40 | |
| Quartz | 30 | 58 | 80 | 80 | 42 | 68 | 70 | ||
| Tourmaline | 4 | 20 | X | ||||||
| Zircon | 4 | 20 | X | ||||||
| 2. Authigenic minerals[f] | |||||||||
| Analcite | 10 | ||||||||
| Glauconite | 9[g] | 14[g] | 20 | 6 | 11 | 13 | |||
| Manganese grains, nodules | 79 | 43 | 70 | 31 | 6 | ||||
| Palagonite | 31 | 9 | 40 | 20 | 8 | 30 | 40 | ||
| Phillipsite | 14 | 40 | X | ||||||
| Phosphate | X | ||||||||
| 3. Rock fragments, etc. | |||||||||
| Crystalline, sedimentary | 7 | 60 | 12 | 9 | |||||
| Volcanic, glass | 64 | 23 | 70 | 80 | 70 | 60 | 65 | ||
| lapilli, scoria | 16 | 10 | 20 | ||||||
| pumice | 49 | 8 | 20 | 40 | 30 | 40 | 30 | ||
| rock fragments | |||||||||
| 4. Magnetite, other (cosmic) | |||||||||
| spherules | 11 | 30 | X | ||||||
The development of X-ray methods for determining the crystal structure has opened up a new field in the study of fine-grained material and the application of this technique (Revelle, 1936, Mehmel 1939) has shown that the fine clayey material is largely crystalline. Methods of identification based on X-ray spectroscopy (Mehmel, 1939) and upon certain physical and chemical tests such as the temperature-dehydration characteristics and the base-exchange capacity have made it possible to identify many of the constituents of the clay fraction. The general problems in this field have been reviewed by Grim (1939) and Kelley (1939). Revelle (1936) and Correns et al (1937) have shown the presence of quartz, calcite, and other minerals, as well as a group of substances generally known as “clay minerals” in the fine fraction of marine sediments.
Clay minerals have the following characteristic properties. Within any group there is a range in chemical composition due to isomorphous replacement. They generally contain a large amount of water partly bound as water of crystallization and partly by surface and interlattice adsorption. The platelike crystal units are mechanically weak and easily broken down and may be ruptured by the process of dispersion. Many of the clay minerals possess the property of base-exchange. In base-exchange, cations in a solution may enter the crystal structure and replace a stoichiometric equivalent of another ion which passes into the solution. For this reason it is possible to have hydrogen, sodium, potassium, calcium, and other clays, where these elements are the replaceable cations. The physical properties of such clays depend upon the replaceable cation or cations. For example, sodium clays are sticky, impermeable, and readily dispersed, whereas calcium clays are relatively granular, porous, and difficult to disperse.
The replaceable cations can be arranged in a series with decreasing replacing power:
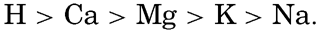
Grim (1939) considers that there are three important groups of clay minerals as well as certain miscellaneous types that do not belong to the major groups. Under natural conditions mixtures of clay minerals usually occur.
Kaolinite Group. The chief member is kaolinite which has the formula (OH)8Al4Si4O10. Other rarer forms also belong in this group.
Montmorillonite Group. The clay mineral of this name has the formula (OH)4Al4Si8O20(xH2O). The others in this group are beidellite, nontronite, and saponite. Magnesium is usually found in montmorillonite; in beidellite the SiO2:Al2O3 molecular ratio is 3 instead of 2; in nontronite, iron replaces some of the aluminum and in saponite, magnesium replaces some of the aluminum.
Illite Group. This group has the general formula
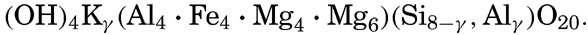
Miscellaneous Clay Minerals. In this category are placed halloysite [(OH)8Al4Si4O10] and hydrated halloysite [(OH)16Al4Si4O6]. The noncrystalline mutual solutions of silica, alumina, and water, that may also contain some bases and for which the term allophane has been proposed, are placed in this group.
The data on the physical and chemical properties of clay minerals have been assembled by Grim (1939). The base-exchange capacity, expressed as milliequivalents per 100 g, is greatest for montmorillonite (60 to 100), intermediate for illite (20 to 40), and least for kaolinite (3 to 15). Little or nothing is known about the other types.
The clay minerals are known to result from the weathering of rocks under the action of water and its dissolved substances, particulary carbon dioxide. Plants and the products of organic decomposition also contribute to the breakdown of the rock fragments. The evidence now available indicates that the character of the residual minerals depends more upon the conditions or environment of weathering than upon the type of rock attacked.
The investigations of Mehmel on the Meteor samples and of Revelle on the Carnegie samples have shown the presence of a variety of clay minerals. The sediments of the Equatorial Atlantic contained kaolinite, montmorillonite, and hydrated halloysite, and a muscovitelike clay. Revelle obtained essentially the same results, and in addition found that certain deposits of the South Pacific contained appreciable amounts of noncrystalline siliceous material. From this evidence it would appear that at least part of the clay fractions are not formed on the sea bottom but represent the products of subaerial weathering carried into the sea
There is no sharp change in mineralogical composition or properties in passing from known terrigenous deposits to the pelagic deposits.
There is no progressive change in the mineralogical constituents with depth in cores from pelagic deposits. If submarine weathering was active, changes with time should occur which would be reflected in the cores.
The variety of fine-grained minerals indicate a number of sources, as would be found in terrigenous debris.
As stated elsewhere (p. 958), fine-grained material, particularly in dilute suspensions, is not necessarily flocculated by mixing with sea water, hence can be transported for great distances in the sea.
Although the present evidence does not preclude the formation of some clay minerals from volcanic debris on the sea bottom, there is considerable evidence which indicates that much of the clay fraction found in marine deposits, both nearshore and pelagic, is of terrigenous origin. The detection of this finely divided material in the water and the determination of its distribution in the ocean waters will be the conclusive argument in deciding upon the source of the red clay and the nonorganic fraction of the pelagic oozes.
Many of the clay minerals in the sediments possess the property of base-exchange. The question of whether or not any exchange takes place when terrigenous clays come in contact with sea water is unsettled. Kelley and Liebig (1934) found that clay minerals treated with sea water attained an equilibrium in which magnesium formed the principle replaceable base, followed by sodium, calcium, and potassium. In the sea water the order of abundance of these cations is sodium, magnesium, calcium, and potassium (p. 176). The high proportion of magnesium in the clays is due to its high replacing power, while sodium takes second place because of its abundance in the water. Revelle (1936) found that the base-exchange capacity of three clay samples was relatively high (27, 34, and 39 milliequivalents per 100 g) and that the size fractions less than 1.5 microns had even higher values. In the two cases reported these were 53 and 58 milliequivalents per 100 g. Magnesium was the most abundant replaceable cation. In the whole samples, the ions were in the order magnesium, calcium, sodium, potassium, but in the material of diameters less than 1.5 microns the sodium exceeded the calcium.
It should be pointed out that leaching with pure water or treatment with any salt solution, such as those used as dispersing agents, will tend to bring about certain changes in the exchangeable cations in the clay minerals. Hence, chemical analyses or studies of the base-exchange properties must be made on unwashed samples of the sediments.
Chemical Composition of Pelagic Sediments. As pointed out above, the composition of pelagic deposits covers a wide range and no two specimens will ever be identical in physical or chemical composition. Therefore it is desirable to turn our attention once more to the three extreme types of material commonly found in pelagic deposits, namely, calcareous remains, siliceous skeletal structures, and the fine clay material.
In table 48 (p. 231) are given examples of the chemical composition of various types of skeletal structures. Revelle (1936) analyzed foraminiferal tests carefully separated from five samples of globigerina ooze. The maximum, minimum, and average amounts of the various determined constituents are given in table 110. The average CaCO3 content is 96.2 per cent. According to Revelle the high iron content may be due to changes occurring after deposition. The composition of the siliceous skeletal material may be taken to be hydrated silica (SiO2xH2O). Hence, the organic constituents will yield two extreme types of deposits which may be either virtually all CaCO3 or all SiO2. Traces of many other elements are undoubtedly represented, and there are many minor anomalies in the composition of skeletal material. For example, among the Radiolaria there are forms that secrete strontium carbonate and others that have skeletons of complex silicates, but these will not materially affect the general picture.
| Constituents | Maximum | Minimum | Average |
|---|---|---|---|
* Only two determinations. | |||
| SiO2 | 0.72 | 0.08 | 0.47 |
| Al2O3[*] | 1.35 | 0.22 | 0.78 |
| FeO,Fe2O3 | 1.68 | 0.51 | 1.08 |
| MgO | 0.16 | 0.10 | 0.13 |
| CaO | 54.52 | 53.12 | 53.82 |
| CO2 | 43.10 | 41.69 | 42.37 |
| Ignition loss[*] | 0.87 | 0.78 | 0.72 |
| 99.47 | |||
When considering the composition of the fine-grained clay material the question arises as to whether or not it is possible to consider a single type of composition or whether there are a number of varieties. The available data indicate that the first approach is a valid one. In table 111 are given three analyses of “pure” red clays. These have been adjusted to a basis as being free from salt, decomposable organic matter, calcium carbonate, and water. The analysis by Steiger (Clarke, 1924) was made on a composite sample prepared by Sir John Murray from
| Constituents | Composite of 51 samples (Steiger) | Average of 10 Pacific Ocean samples (Revelle) | Atlantic Ocean sample (Correns) | Average of igneous rocks (Clarke, 1924) |
|---|---|---|---|---|
| SiO2 | 54.48 | 55.95 | 53.27 | 59.14 |
| TiO2 | 0.98 | 0.83 | 0.98 | 1.05 |
| Al2O3 | 15.94 | 18.48 | 23.74 | 15.34 |
| Cr2O3 | 0.012 | 0.055 | ||
| Fe2O3 | 8.66 | 8.16 | 2.65 | 3.08 |
| FeO | 0.84 | 3.39 | 3.80 | |
| Ni,CoO | 0.039 | 0.025 | ||
| MnO | 0.31 | 0.124 | ||
| MnO2 | 1.21 | 0.83 | ||
| MgO | 3.31 | 2.95 | 0.38 | 3.49 |
| CaO | 1.96 | 0.45 | 2.48 | 5.08 |
| SrO | 0.056 | 0.022 | ||
| BaO | 0.20 | 0.06 | 0.055 | |
| K2O | 2.85 | 3.35 | 2.36 | 3.13 |
| Na2O | 2.05 | 1.32 | 2.27 | 3.84 |
| V2O3 | 0.035 | 0.026 | ||
| As2O3 | 0.001 | tr. | ||
| MoO3 | tr. | |||
| P2O5 | 0.30 | 0.18 | 0.02 | 0.30 |
| CuO | 0.24 | 0.015 | ||
| PbO | 0.008 | 0.002 | ||
| ZnO | 0.005 | 0.005 | ||
| ZrO | 0.14 | 0.04 | ||
| H2O | 7.04 | 7.30 | 8.15 | 1.15 |
| Total % | 100.00 | 100.00 | 100.00 | 99.77 |
| Total Fe as Fe2O3 | 9.59 | 8.16 | 6.18 | 7.31 |
| Total Mn as MnO2 | 1.21 | 0.83 | 0.38 | 0.15 |
THE ENVIRONMENT OF DEPOSITION
Samples of sedimentary rocks can be stored for years without altering their properties, but this is not true of samples of recent sediments, in which marked changes may take place after collection, particularly if they are allowed to dry out. These changes are chiefly associated with activity of organisms and the loss of water. Organic processes subsequent to collection of samples will generally not follow the pattern existing on the sea floor because of the changed environment. Increased bacterial activity will tend to modify the organic-matter content, the oxidation-reduction conditions, and the pH. The loss of water by evaportation may change the textural characteristics of the sediment, since sediments which have been dried do not disperse as completely as fresh samples (Correns, et al, 1937). Furthermore, the changing salt concentration of the interstitial water which will accompany evaporation may result in base-exchange and precipitation of salts.
The temperature prevailing in marine sediments can be closely estimated from that of the water immediately adjacent to the bottom and depends upon depth, latitude, season, and circulation, and in basins upon the surrounding topography. The temperature probably has its greatest effect through its influence upon the character and activities of the organisms living in or on the sediment. Hydrostatic pressure, which is a function of depth, is of no significance and has no effect either upon the organisms or upon the water content or porosity of the sediment. The water content can be considered an important characteristic that is part of the environment of the sediments on the sea floor. The water content, which must be determined on carefully preserved samples, is commonly reported as the weight per cent of the sediment. However, if reported as volume per cent (assuming a mean grain density of 2.6), it is an expression of the porosity. Trask (1932) discussed the water content of sediments and Krumbein and Pettijohn (1938) have given many references to studies of the porosity of sedimentary rocks. The porosity, hence the water content, depends upon the texture, shape, and sorting of the particles in the sediment. Furthermore, the compaction must be taken into account. Recently deposited material has a greater pore space and water content than that which has “aged” or which has had additional material deposited on top, that is, has been subjected to pressure. In fine-grained material, particularly the clays and the so-called colloid fraction, the effect of surface adsorption must be considered. Trask fractionated a marine sediment into a number of size grades and determined the water content of the freshly settled material (table 112). He found that the water content increases rapidly in materials smaller than about 20 microns in diameter. After standing or after the superposition of additional material the water content decreases
Water content and median diameter in core samples of terrigenous sediments obtained off the California coast. Heavy vertical lines indicate portions of the cores examined.
| Size group, microns | Water content, volume per cent |
|---|---|
| 250–500 | 45.0 |
| 125–250 | 45.4 |
| 64–125 | 46.9 |
| 16- 64 | 51.6 |
| 4- 16 | 66.2 |
| 1- 4 | 85.8 |
| <1 | 98.2 |
The permeability of a sediment, which is a measure of the ability of water to circulate through it, is related to the porosity. Although of undoubted importance in determining the chemical conditions and hence
Many chemical and biological processes are dependent upon the water content and the permeability, that is, upon the amount of interstitial water present and upon the rate at which water circulates through the sediment and exchanges with the overlying water. Where very little exchange with the overlying water takes place, depletion of the oxygen and the establishment of reducing conditions may occur. These conditions are inimical to the persistence of animal life, hence below the superficial layers there may be virtual exclusion of all living organisms except bacteria. The thickness of the superficial layer within which there is some exchange of water will depend upon the texture of the sediment, the rate of sedimentation, water movements, the oxygen content of the overlying water, and the activities of burrowing organisms.
The salinity of the interstitial water, which is determined by that of the overlying water, is probably not very important, although it may influence such processes as the solution or precipitation of calcium carbonate. Changes in the chemical composition of the dissolved materials are chiefly related to biological processes, although base-exchange with clay minerals, the formation of authigenic minerals, and the adsorption of ions on colloidal particles may play some part. Organic activity will lead to the consumption of dissolved oxygen and the formation of carbon dioxide which will tend to lower the pH of the interstitial water and favor the solution of calcium carbonate. If the oxygen is completely removed, anaerobic decomposition will lead to the formation of hydrogen sulphide from organic matter. Marine anaerobic bacteria are also capable of attacking the sulphate present in the water and of using the oxygen in the sulphate ion in their metabolic processes. This process also leads to the formation of hydrogen sulphide. The extent to which organic and inorganic processes within marine sediments may modify the composition of the interstitial water is not yet established, although scattered evidence indicates that they may be quite appreciable. The destruction of organic matter on the sea bottom also involves the nitrogen, and it is possible that a considerable amount of inorganic forms of this element are produced on the sea bottom. Under reducing conditions this must be ammonia, but within the superficial layers the ammonia may be further oxidized to nitrite or nitrate.
Many general statements have been made concerning the depletion of dissolved oxygen and the establishment of reducing conditions in marine sediments, but relatively little is known concerning the oxidation-reduction potentials prevailing in marine deposits (ZoBell, 1939). Although the state of oxidation of the iron and such other elements as manganese, sulphur, and nitrogen may be determined by the prevailing potential, it should be remembered that the reducing conditions are
In the overlying water in the presence of free oxygen, Eh potentials (p. 211) slightly higher than 0.0 volt are found (ZoBell, 1939). The Eh of sediments of the California coast has been found to range in general between —0.12 and —0.58 volt, but in certain areas of slow deposition slightly positive values may prevail. In general, the oxidation-reduction potential decreases (the negative values increase) with increasing depth in the sediment. The zone of most rapid change is within the topmost few centimeters. According to Hewitt (1937), aerobes tolerate an Eh between +0.4 and —0.2 volt; therefore the conditions beneath the uppermost few centimeters are not favorable for aerobic forms. The presence of “aerobes” at lower potentials indicates that they are either facultative anaerobes or that they are in a more or less dormant condition. The rapid decrease in numbers with depth in the cores is shown in table 113. Anaerobes are therefore responsible for the extremely low potentials found in marine sediments. These potentials sometimes exceed that of the hydrogen electrode, which, in neutral solution (pH = 7), has an Eh —0.421 volt. It will be seen from table 113 that the anaerobes also decrease in number with depth in the core, although the relative change is not as great as for the aerobes.
| Depth of strata (cm) | Anaerobes per gram | Aerobes per gram | Ratio of anaerobes to aerobes | Oxygen absorbed (mg/g) | Oxidation-reduction potential, Eh, volts |
|---|---|---|---|---|---|
| 0- 3 | 1,160,000 | 74,000,000 | 1:64 | 2.8 | -0.12 |
| 4- 6 | 14,000 | 314,000 | 1:21 | 1.3 | -0.29 |
| 14–16 | 8,900 | 56,000 | 1:6 | 0.6 | -0.37 |
| 24–26 | 3,100 | 10,400 | 1:3 | 0.7 | -0.32 |
| 44–46 | 5,700 | 28,100 | 1:5 | 0.3 | -0.37 |
| 66–68 | 2,300 | 4,200 | 1:2 | 0.4 | -0.34 |
Although the Eh decreases with depth in the sediment, the reducing capacity usually decreases. The reducing capacity can be determined on freshly collected samples by measuring the oxygen absorbed after the addition of mercuric chloride to kill living organisms and to inactivate
Benthic organisms, with or without skeletal structures, are involved in a number of sedimentation processes. Besides destroying organic matter, the larger benthic forms may ingest the sediment, causing mechanical abrasion of the solid particles and acceleration of the solution of such material as calcium carbonate. The turning over of the superficial layers by mud-eating and burrowing organisms tends to destroy laminations and to aid in the interchange of the water in the sediment with the overlying water. Characteristic constituents of many terrigenous deposits are faecal pellets of benthic animals (Moore, 1939). Faecal pellets have been considered as important in the formation of glauconite (Takahashi, 1939). The characteristic distribution of different forms of benthic organisms has received considerable attention both from marine biologists and from paleontologists, and their findings cannot be discussed here. In the sections on marine biology many references to this problem will be found.
CALCIUM CARBONATE
Factors Which Determine Accumulation and Deposition of Calcareous Material
Interest in geological problems concerning the conditions which led to the formation of limestones has greatly stimulated the study of the calcium carbonate content of marine deposits, because most calcareous formations were recognized as having a marine origin although in certain cases no fossil remains of marine organisms could be identified. Questions therefore arose regarding the environmental factors which determine the carbonate content of sediments laid down in different regions and regarding the possibility of inorganic precipitation of calcium carbonate in the sea. As the calcareous material in marine deposits is predominantly composed of skeletal structures of plants and animals, the marine biologist is directly concerned with the problem of the formation of such sediments. The precipitated carbonates are formed from materials in
The terms “calcareous” and “calcium carbonate” are not strictly synonymous. According to analyses (p. 231 and p. 991), calcareous skeletal structures contain variable proportions of other substances, such as magnesium carbonate. However, the percentage of materials other than calcium carbonate is generally small and for this reason is commonly neglected. Most of the calcium carbonate found in marine deposits is in the crystalline form known as calcite, whereas the calcareous structures of live organisms apparently contain at least some in the form of aragonite. Whether or not there is a selective solution of the aragonite or whether there is a transformation of aragonite to calcite after the death of the organisms is not known. As was pointed out in the discussion of globigerina ooze, much of the fine material is composed of minute calcite crystals which apparently arise from the mechanical disintegration of the foraminiferal skeletons and are not due to any process of reprecipitation. Finely divided calcium carbonate is found on certain shallow banks in low latitudes, such as the Bahama Banks. This is in the form of aragonite and is thought to have been precipitated directly from sea water without the immediate participation of organic agencies (Vaughan, 1924, Smith, 1940). The presence of small amounts of authigenic dolomite, that is, the form of carbonate containing equal proportions of calcium and magnesium, has been reported by Correns (1937, 1939) for the pelagic deposits of the Equatorial Atlantic. No satisfactory explanation has yet been advanced to account for the existence of calcium carbonate in the form of aragonite under one set of conditions and as calcite under another.
The precipitation or solution of calcium carbonate is controlled by the degree of saturation of the water under a given set of conditions. Although the conditions which favor either precipitation or solution of calcium carbonate are known, it is impossible to state definitely for a given set of conditions whether the water is saturated with calcium carbonate or whether precipitation or solution may take place. The supply of calcium carbonate by rivers is relatively large and therefore it is reasonable to assume that conditions closely approaching saturation must prevail.
In most discussions of calcareous sediments the emphasis is placed upon the percentage of calcium carbonate rather than upon the character
In chapter VI (p. 207) it was shown that conditions favorable for the precipitation of calcium carbonate are most likely to occur in water having high temperature and high salinity and where the activity of plants has reduced the carbon dioxide content of the water. Such conditions are found in low latitudes over shallow bottoms, but apparently in a few localities only does such precipitation occur. Smith (1940) has described the precipitation of aragonite that occurs on the Bahama Banks (see also Vaughan, 1924) and has pointed out that there the process is facilitated by seeding with the minute aragonite crystals stirred up from the bottom.
Precipitation through organic agencies does not require that the sea water be saturated with calcium carbonate. However, deposits high in calcareous skeletal structures are generally restricted to areas where the physical-chemical environment is such that the ionic product [Ca++] X [CO3−] is large (see p. 205). The photosynthetic activity of plants, which removes carbon dioxide from solution and hence tends to increase the concentration of CO3−ions, offers a simple mechanism for
Transportation is of less importance to the distribution of calcareous material than to that of certain other constituents of the sediments. The benthic forms are large and can be moved only by the action of waves or extremely strong currents. However, wave action, boring organisms, and organisms which feed on the bottom mud tend to break down the larger fragments and, in this way, coral sands and muds are formed. Such a breakdown may favor a certain amount of solution. Agencies of lateral transportation are not very important even for those pelagic forms which live in the upper layers, since their skeletons sink quite rapidly and are not transported far from the region of development.
The potential supply of calcareous material to the bottom is dependent upon the production of calcareous forms either in the plankton of the overlying water or among the benthic organisms. However, a certain amount of solution may take place after the death of the organism and may occur either while settling through the water or on the sea bottom. Whether or not solution will take place depends upon the physical-chemical conditions prevailing in the water but, as the exact value for the solubility product is as yet unknown, it is impossible to state whether or not the waters of the oceans are saturated with calcium carbonate. Earlier studies lay particular emphasis upon the solution which takes place while the calcareous material is settling through the water. Examinations of the vertical distribution of calcium and alkalinity in the Pacific and Atlantic Oceans show that usually the lowest values are found in the surface layer where a certain amount of precipitation, probably through organic agencies, has taken place. Within this surface layer the concentrations are approximately the same in both the Atlantic and the Pacific Oceans, but at greater depths the existing data indicate that the waters of the Pacific contain somewhat more calcium and have a higher alkalinity: chlorosity ratio than those of the Atlantic. The larger values in the Pacific can probably be correlated with the lower oxygen content of the intermediate and deep water. The consumption of oxygen at subsurface levels is accompanied by an increase in the total carbon dioxide and therefore tends to favor the solution of any calcareous material which may settle through the water. However, it should be remembered that the consumption of oxygen, hence the production of carbon dioxide in deeper waters, is independent of the supply of calcium carbonate settling from above. Therefore we may expect that in certain localities the subsurface waters are undersaturated, whereas in other areas where there has been an adequate supply of calcareous material the deeper waters may be completely saturated with calcium carbonate.
Calcareous material on the sea bottom is exposed to the water, and if the water is undersaturated must pass into solution. In the presence of calcareous material there must be a zone within which the water is saturated with calcium carbonate and additional solution can take place only when this water is replaced by currents or by eddy diffusion. The rate at which calcium carbonate can be dissolved therefore depends upon the character of the flow and the gradients which are established and which for a given set of conditions cannot exceed a certain upper limit. If the rate of supply of calcium carbonate is greater than the rate at which the dissolved material can be carried away there will be a net gain in the amount of calcareous material and, consequently, accumulation will take place. If the supply is less than the rate at which it can be dissolved there will be no accumulation of calcareous material although considerable amounts may fall to the sea bottom in that locality. Besides the solution which may take place if the overlying waters are undersaturated, the production of carbon dioxide on the sea bottom, a result of the decomposition of organic matter, will favor the solution of calcareous material. Even if the overlying water is saturated with calcium carbonate this process will lead to a certain amount of solution. The number of benthic organisms is largely determined by the supply of decomposable organic matter and, in addition to the production of carbon dioxide, their activities in burrowing and as mud eaters will favor the breakdown of calcareous material. Extensive observations by Wattenberg in the Atlantic Ocean show a characteristic increase in the alkalinity: chlorosity ratio immediately over the bottom, which indicates a certain amount of solution of calcareous material. Furthermore, Wattenberg's data show a decrease in the dissolved oxygen content immediately adjacent to the bottom, indicating active production of carbon dioxide.
Calcium carbonate is most likely to dissolve in water which has come from high latitudes and in which the carbon dioxide content has been increased by oxidative processes. Water from high latitudes fills the great ocean basins below depths of a thousand meters or more. In some parts of the South Atlantic Ocean there is a fairly well-defined northward flow of water immediately over the bottom and, according to the results of the Meteor expedition, such areas are poor in calcium carbonate. As the water moves toward the Equator it undoubtedly takes up more calcium carbonate and can therefore dissolve less and less, for which reason alone we may expect to find calcareous sediments in low latitudes. In areas of large organic production where there is an abundant supply of organic matter to the sea floor, as along coasts where there is upwelling, and in areas of diverging currents and active winter mixing in high latitudes, we may expect to find sediments rather low in calcium carbonate because of the large amount of solution which can take place on the bottom.
The Distribution of Calcium Carbonate
The distribution of calcium carbonate in pelagic deposits has already been discussed in some detail. In fig. 258 the percentage of calcium carbonate in the superficial layers of the sediments is shown without regard to the type of deposit or to the depth. This map, which is based on that of Trask (1937), shows only the 10 per cent and 50 per cent contours. However, as pointed out before, the transition from sediments low in carbonate to those high in calcareous material usually occurs in a relatively short distance. The 30 per cent contour which limits the pelagic calcareous deposits from the red clay and siliceous types is shown in fig. 253. Trask's map has been revised to take into account more recent data, from Schott (1939a) for the Indian Ocean, Revelle (1936) for the Pacific Ocean, and Correns et al (1937) and Pratje (1939) for the Atlantic Ocean. Figure 258 shows that sediments containing more than 50 per cent calcium carbonate are restricted to latitudes lower than 50 degrees except in the North Atlantic, where calcareous sediments extend considerably further north. A comparison of figs. 253 and 258 shows that there is no abrupt change in calcium carbonate content with distance from shore that would correspond to the transition from terrigenous to pelagic deposits. The sediments near shore and in enclosed areas are by definition described as “terrigenous,” but as can be seen from fig. 258 no such demarcation exists in the distribution of calcium carbonate. Off most continental coasts within low latitudes there is an increase in calcium carbonate content with increasing distance from the coast. This is particularly marked in regions where there is a transport of cold water from high latitudes and upwelling, as off the west coast of South America. Furthermore, in regions where there is an abundant supply of inorganic material as along coasts of heavy rainfall and off the mouths of rivers, the carbonate content is generally low. One of the striking features of the carbonate distribution is the very low values found in the North Pacific. A possible explanation for this anomalous distribution will be discussed below. It will also be noted that the carbonate content of the deeper parts of the ocean basins is generally low.
Trask (1937) has studied the distribution of the percentage of calcium carbonate in marine sediments to determine the relationships between surface temperature, surface salinity, depth, distance from shore, and the calcium carbonate content of the underlying sediments. This statistical study showed a positive correlation between the carbonate content and the salinity of the overlying surface water. When salinities were less than 34 ‰ the carbonate content was generally less than 5 per cent, whereas in regions where the surface salinity exceeded 36 ‰ the calcium carbonate was generally greater than 50 per cent. The calcium carbonate content also increased with increasing surface temperature but decreased with depth in deeper water. In general, nearshore sediments have considerably smaller contents of calcium carbonate than the pelagic deposits although this relation will not necessarily hold in low latitudes. The correlation obtained by Trask between the carbonate content of the sediments and certain conditions in the surface layers indicates the importance of the potential supply of calcareous material. Surface conditions are, in general, no indication of those which prevail at lower levels and which would determine whether or not the calcareous material would redissolve while sinking or after reaching the bottom. That is, the agreement which Trask obtained between the carbonate content of the sediments and the temperature and salinity conditions in the surface waters merely emphasizes the fact that calcareous deposits will accumulate in areas where the conditions favor the development of carbonate-secreting organisms.
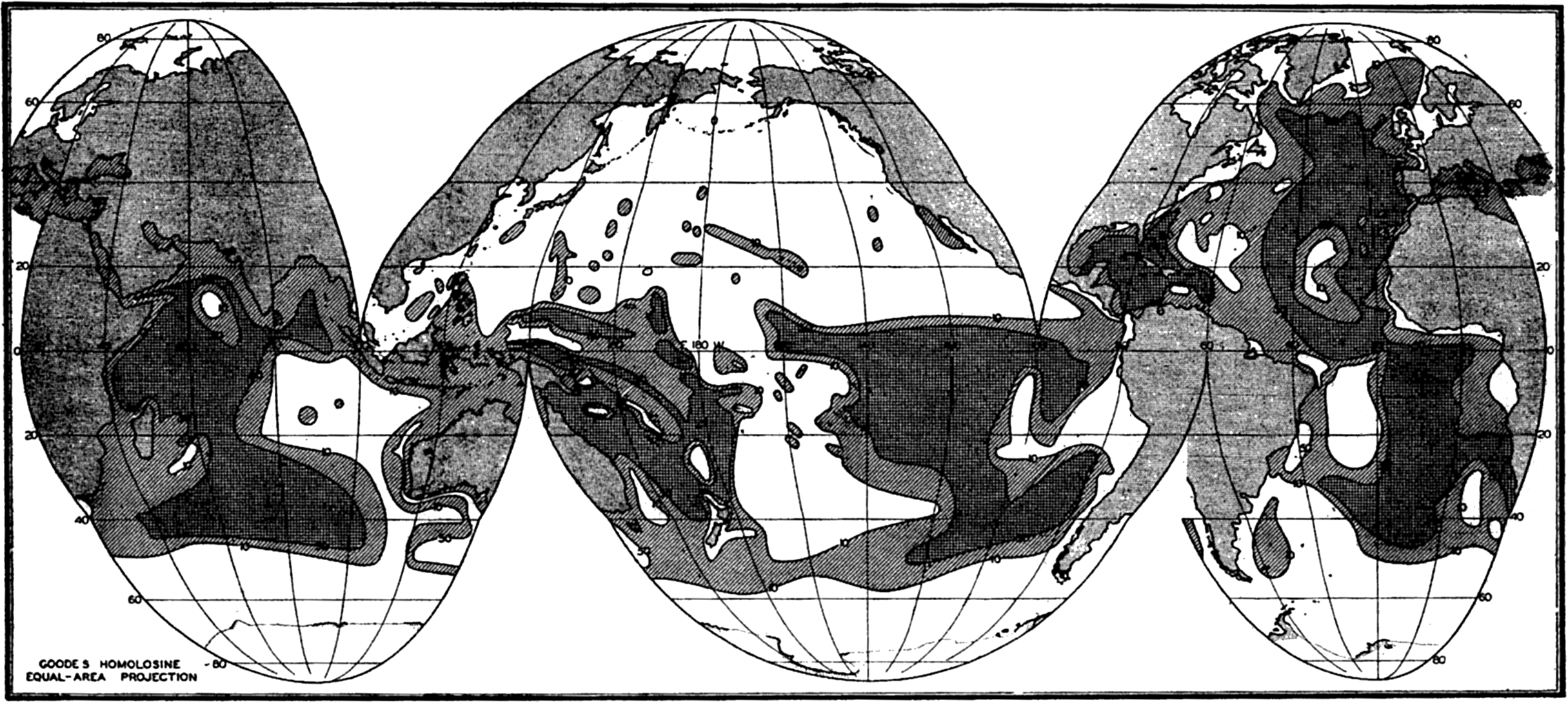
Percentage of calcium carbonate in marine sediments. (Modified from Trask, 1937.)
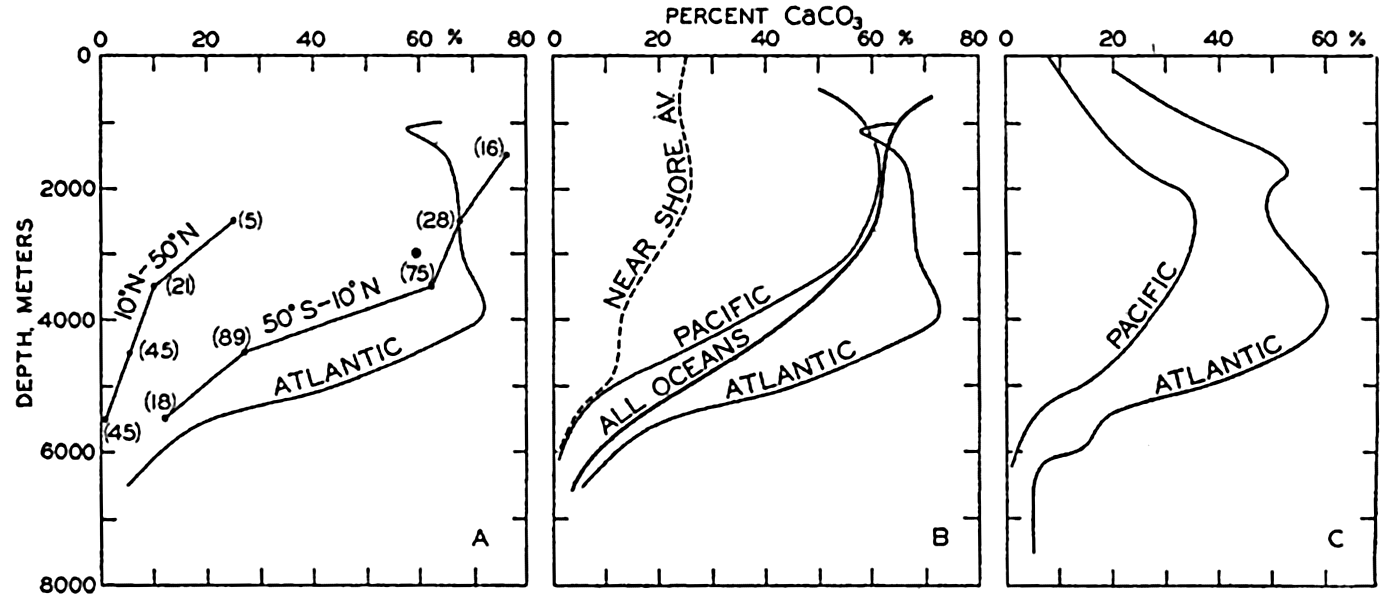
Percentage of calcium carbonate in marine sediments as a function of depth. (A) Averages for pelagic sediments from the North Pacific (10°N to 50°N), South Pacific (50°S–10°N), and from the Atlantic Ocean. (B) Averages for pelagic sediments from the Atlantic and Pacific Oceans and from all oceans, and the average curve for nearshore deposits. (C) Averages for all types of sediments from the Atlantic and the Pacific Ocean.
Revelle (1936) examined the distribution of calcium carbonate in the sediments of the Pacific Ocean with reference to the variations with latitude and depth. The average values arranged according to latitude and depth for the pelagic deposits are shown in table 114. The decrease in carbonate with increasing latitude, that is, decreasing surface temperatures, and the small percentages found at greater depths are readily seen. It will also be noted that the calcium carbonate content of sediments from the North Pacific is less than that of material from the corresponding range in latitude and depth from the South Pacific. The marked decrease does not take place exactly at the Equator, but apparently at about 10°N. The curves obtained when these data are averaged in two groups, one for the North Pacific between 10°N and 50°N, and
| Depth range (meters) | Latitude | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 50°–40°S | 40°–30°S | 30°–20°S | 20°–10°S | 10°S–0 | 0–10°N | 10°–20°N | 20°–30°N | 30°–40°N | 40°–50°N | |
| 0–1000 | 41.0 | |||||||||
| 1000–2000 | 94.0 | 74.4 | 75.0 | 38.4 | ||||||
| 2000–3000 | 82.0 | 74.7 | 63.5 | 65.9 | 68.0 | 57.8 | 32.5 | 18.0 | 22.0 | |
| 3000–4000 | 63.6 | 53.4 | 72.3 | 54.0 | 49.4 | 0.6 | 11.7 | 56.0 | 6.0 | |
| 4000–5000 | 37.5 | 18.8 | 17.9 | 19.9 | 47.5 | 55.9 | 17.6 | 1.9 | 1.8 | |
| >5000 | 0.0 | 16.0 | 10.7 | 24.7 | 1.0 | 0.8 | 0.6 | 0.5 | ||
The data in fig. 259A are presented to emphasize the differences between the average calcium carbonate content as a function of depth in the North and South Pacific and in the Atlantic Ocean. In fig. 259B the curve for the pelagic deposits of the Atlantic Ocean is repeated and the average for the Pacific Ocean as a whole is shown. Also included in this diagram are Trask's data for pelagic deposits which represent an average for all oceans. In addition, a curve based on Trask's average for nearshore sediments is included to show the lower calcareous content of terrigenous deposits. It is immediately noticed that the Atlantic Ocean is high in percentage of calcium carbonate compared to the Pacific. In fig. 259C are shown the vertical distribution of the percentage calcium carbonate where all samples, both terrigenous and pelagic, are combined. The data for the Pacific are from Revelle (1936) and those for the Atlantic are from Pia (1933). Unfortunately, Trask's data have not been combined to give a grand average for both nearshore and pelagic sediments. The differences between nearshore and pelagic
The extreme and the average carbonate contents of the various types of marine sediments have been given in table 108. Vaughan (1924) calculated the average calcium carbonate content of marine sediments from the Challenger values for the different types of deposits and the area covered by each type. In this way the following values were obtained:
| Average, all deposits | 32.2% CaCO3 |
| Average, pelagic deposits | 33.4% CaCO3 |
| Average, terrigenous deposits | 24.6% CaCO3 |
More complete data concerning the calcium carbonate content and the areal extent of the different types of deposits would modify these values somewhat. The data presented in fig. 259 can be used to estimate the average calcium carbonate content when the area represented by the different depth intervals is known (table 5, p. 21). Trask's figures for the calcium carbonate content of the pelagic deposits when treated in this way give an average of 37 per cent CaCO3. The data for the Pacific and the Atlantic (fig. 259B) give averages of 27 per cent and 54 per cent, respectively. When all types of sediments are combined (fig. 259C), we obtain an average of 18.8 per cent CaCO3 for the Pacific Ocean and 41 per cent for the Atlantic Ocean. The available data therefore indicate that the average calcium carbonate content of pelagic deposits is about 37 per cent and for terrigenous sediments about 25 per cent. Owing to the greater frequency of sampling in intermediate and low latitudes, the values for the terrigenous sediments may be somewhat high. The data in Clarke (1924, p. 34) indicate that the mean value for fossil-bearing shallow-water deposits is probably about one half of this, namely 12.5 per cent.
It should be pointed out that the averages given above are those for a superficial layer of the marine deposits and represent the averages for a certain thickness, regardless of the rate of deposition. The average obtained in this way, therefore, does not correspond to the ratio between the calcareous and noncalcareous material which may be carried to the sea. In order to obtain a balance sheet for the supply and deposition it is necessary to take into account the relationship between the rate of deposition and the calcium carbonate content. As shown on p. 1036, the terrigenous sediments accumulate much more rapidly than the pelagic deposits and, because of their lower calcium carbonate content, the ratio of the rates of accumulation of calcareous and non-calcareous material is 1:5.2, that is, the percentage of calcium carbonate in the total annual sedimentation is 19 per cent.
It is impossible to discuss the pattern of distribution of percentage of calcium carbonate in detail, and only a few of the major features can be considered. These are (1) the higher calcium carbonate content of the sediments of intermediate and low latitudes and the somewhat anomalous northward extension of calcareous sediments in the North Atlantic, (2) the decrease in calcium carbonate content with increasing depth in pelagic deposits, (3) the possible reasons for the difference between the carbonate content of the sediments in the Atlantic and the Pacific Oceans and between those in the North and South Pacific. Owing to the incomplete understanding of the processes involved, only the general character of the controlling agencies can be pointed out.
The contrast between the calcium carbonate content of the sediments in intermediate and low latitudes on one hand and in high latitudes on the other is undoubtedly related to the higher production of calcareous forms in low latitudes. In fact, there are virtually no calcareous planktonic forms found in high latitudes. Another factor which may contribute to the difference is that of solution of the calcium carbonate either in the water or after it has reached the bottom. As shown elsewhere, conditions favorable for the solution of calcium carbonate are characteristic of high latitudes in contrast to those in low latitudes. The relative rate of accumulation of noncalcareous material may play some part in determining the general distribution, but it is considered as secondary compared with the absolute rate of supply of calcareous material.
The decrease in the percentage of calcium carbonate with depth in pelagic deposits may be attributed to a number of factors. Possibly the most important is the effect which topography will have upon the deposition of extremely fine-grained inorganic debris. Such debris will tend to accumulate in depressions where it will be deposited more rapidly than upon topographic highs, and hence will tend to dilute the calcium carbonate. Two other factors must be considered. The first of these, namely the amount of solution during sinking, has been considered to be an important factor since the material which is deposited at great depths has to pass through a longer column of water and is therefore exposed to the solvent action for a longer period. The second factor is that of solution on the bottom. If there is a greater supply of decomposable organic material to the deep basins, the larger production of carbon dioxide may tend to dissolve more of the calcium carbonate which reaches the bottom. All of these factors may be effective in determining the decrease in the percentage of calcium carbonate with increasing depth in the open ocean.
In order to present any explanation for the difference in character between the sediments in the Atlantic and Pacific Oceans and the sediments of the North and South Pacific, it is helpful to return to the concept of the stationary distribution of properties in the water. As
It is more difficult to offer any definite reason for the difference between the North and the South Pacific. Most of the supply by rivers is actually in the North Pacific, therefore there must be a net transport of calcium across the Equator. The lower calcium carbonate content of the sediments may be due to the greater relative rate of accumulation of noncalcareous material or to the slower relative rate of deposition of calcareous material. Conditions within the water itself may also play a part. The deep-water circulation of the Pacific is such that the water flowing in from the south must ultimately turn around and flow south again (p. 752). There is a general decrease in the oxygen content and, hence, an increase in the carbon dioxide content from south to north. Therefore, conditions in the North Pacific may be more favorable for the solution of calcium carbonate both in the water and on the bottom. Further studies of the chemistry of the waters and more adequate knowledge of the solubility of calcium carbonate will make possible a more exact analysis of these various factors.
ORGANIC MATTER
Quantity and Character of Organic Matter in Marine Sediments
The term organic matter is used to designate that portion of a sediment which has arisen through organic activity and which contains carbon in any form other than carbonate. Because it is somewhat analogous to the humus fraction found in soils it may be termed “marine humus.” Sometimes the expression decomposable organic matter is used to indicate that the material may be destroyed by organisms, particularly by bacteria.
The quantity and character of organic matter in marine sediments has been studied by a number of workers whose findings have been reviewed by Trask (1932, 1939). Although the organic matter rarely forms more than a small percentage of the sediments, it has received considerable attention for the following reasons:
The organic matter settling to the sea bottom in deep water is the only source of food for benthic animals and bacteria. Hence the quantity in the sediment and, particularly, the rate of supply in any locality will have a profound effect upon the population of bottom-living organisms.
The presence of organic matter and the changes brought about by organic activity, principally bacterial, influence the physical and chemical conditions which prevail in the sediment. These in turn may affect the character of the bottom fauna and the nature of the deposit.
The burial of the organic matter implies the removal from the water of carbon, nitrogen, and possibly other elements originally in solution.
Organic matter in sedimentary formations is considered to have been the source of petroleum. This theory has stimulated most of the investigations on the organic-matter content of recent sediments, as it has been thought that they would yield results which could be applied to the study of the source beds of petroleum and in the search for new oil fields.
The organic-matter content of pelagic sediments is approximately 1 per cent. Nearshore sediments generally contain somewhat larger amounts and average about 2.5 per cent. The extreme range is from less than 0.5 to more than 10 per cent. According to Trask (1939) the sediments of the North Pacific contain from 1 to 1.5 per cent, those of the South Pacific from 0.4 to 1.0 per cent, and those of the Atlantic from 0.3 to 1.5 per cent. The high values are found in bays and estuaries, in isolated basins near shore, in fjords, and in such landlocked regions as the Black Sea, Trask (1932) summarized the data available at that time concerning the distribution of organic matter in different areas and in different types of environments. Since then Gripenberg (1934) has investigated the Baltic Sea, Ström (1936) has made detailed studies of the Norwegian fjords, and Revelle and Shepard (1939) have reported on the conditions off the coast of California. The Meteor samples from the equatorial Atlantic have been discussed by Correns (1937, 1939) and the Carnegie samples of the Pacific were studied by Revelle (1936). Wiseman and Bennett (1940) have reported on the conditions in the Arabian Sea. Trask (1939) has again summarized the existing knowledge and given many references to detailed studies.
The quantity of organic matter may be estimated in various ways. The determination of the noncalcareous carbon by either wet or dry
Little is known concerning the chemical composition of the organic matter in marine sediments. Carbon forms from 50 to 60 per cent of the material, hence the ratio of organic matter to carbon varies between 1.67 and 2.0. Trask recommends the ratio of 1.8, which corresponds to a carbon content of 56 per cent. Various factors have been shown to influence the ratio. Plant material has a somewhat higher ratio than organic matter of animal origin and under stagnant conditions the ratio is lower than average. The nitrogen content of the organic matter is also affected somewhat by the source of the material and the conditions prevailing in the sediment. The carbon: nitrogen ratio varies between 8 and 12 and averages about 10, with the extreme values found by Trask as 5.5 and 20. Wiseman and Bennett (1940) found an even greater spread in the ratios, and for this reason do not consider nitrogen as an adequate measure of the organic matter. The average recommended by Trask is 10, which implies that the organic matter contains 56 per cent carbon and 5.6 per cent nitrogen. The organic matter which accumulates on the sea bottom represents the more or less resistant fraction of plant and animal origin. Although no specific compounds have been isolated it is possible to obtain some idea as to the character of the compounds by making selective extractions and analyses. The protein content is estimated by multiplying the organic nitrogen by the conventional factor of 6.25. Extraction with a fat solvent, such as ether or carbon tetrachloride, is made to determine the fatty materials present. By subtracting the protein and ether-soluble material from the total amount of organic matter the carbohydrate fraction is determined. Tables 115 and 116 (from Trask, 1939) show the character of the organic matter in various types of organisms and in marine sediments.
| Organic-matter source | Crude protein | Ether extract | Carbohydrates | Crude fiber |
|---|---|---|---|---|
| Peridineans | 14 | 1.5 | 85? | ? |
| Diatoms | 29 | 8 | 63 | 0 |
| Copepods | 65 | 8 | 22 | 0 |
| Higher invertebrates | 70 | 10 | 20 | 0 |
| Organic matter in marine sediments | 40 | 1 | 47 | 0 |
The ultimate source of the organic matter is within the euphotic zone, either in the sea or on land. The original plant material may find its way to the sea bottom or it may have undergone transformation into animal remains or their waste products or it may have been converted into bacterial cell structure before it is deposited. Organic matter produced on land may play a relatively important role in bays and estuaries and in areas of excessive runoff and low plankton production, such as the Baltic Sea (Gripenberg, 1934). Rafts of land vegetation may be carried away from the coast and fragments of these may settle to the sea bottom. In shallow water, particularly in relativley isolated environments, such attached aquatic plants as eel grasses have been shown to be important sources of organic matter (p. 303). However, for the ocean as a whole, the supply of organic material from land and from the attached plants is relatively insignificant and of local importance only, and it is the planktonic photosynthetic organisms which are the chief source of organic matter for marine sediments.
| Organic-matter source | Percentage by weight | Ratio of organic matter to carbon | |||
|---|---|---|---|---|---|
| Carbon | Nitrogen | Hydrogen | Oxygen | ||
| Peridineans | 45 | 3 | 7 | 45 | 2.2 |
| Diatoms | 50 | 6 | 8 | 36 | 2.0 |
| Copepods | 50 | 10 | 8 | 32 | 2.0 |
| Marine sediments | 56 | 6 | 8 | 30 | 1.8 |
| Lithified sediments | 64 | 4 | 9 | 23 | 1.6 |
Since the potential supply to the bottom depends upon the production within the upper layers, there must be regional differences in the amount of organic matter in sediments related to the variations in the production. The organic material is light and sinks slowly, and it behaves in a manner similar to the finer fractions of the solid material. This resemblance is shown by the inverse relationship between the organic-matter content and the median diameter of the sediments in nearshore areas (Trask, 1932, 1939, Revelle and Shepard, 1939).
The cycle of regeneration of the elements involved in organic processes, that is, of decomposition of organic matter, has been described. It was shown that regeneration is relatively complete and that probably the greater part of the organic matter produced by the plants is mineralized before reaching the sea bottom. The amount of decomposition that will take place within the water depends upon a number of factors, such as the relation between plant production and consumption by the animals, the number and type of bacteria, and such other characteristics as the temperature of the water. The destruction of organic matter is a time-consuming process and will depend not only upon the organic activity but also upon the period during which such action can take place. For this reason the depth of water through which the organic matter may sink must be considered. The deeper the water, the longer the interval required to reach the bottom and the more likely the organic matter is to be destroyed. The presence or absence of dissolved oxygen in the water may have a profound effect upon the fate of the organic matter produced in the surface layers. In stagnant waters the destruction of organic material is not as complete as under oxidizing conditions and, hence, will tend to favor the deposition of organic matter on the sea floor. The factors that contribute to the development of stagnation are discussed elsewhere (p. 1026). One of these is the abudnant supply of organic material to the sea bottom in the absence of an adequate supply of oxygen; hence an abundant supply of organic matter tends to favor its own preservation.
Thus far, we have considered only the agencies operating within the water column. After reaching the sea bottom and even after burial, the transformation and destruction of organic matter by the bottom fauna and microorganisms is continued. The character and extent of these changes is again largely dependent upon the presence or absence of dissolved oxygen. The amount of organic matter reaching the bottom will tend to determine the number of benthic animals and microorganisms. In the absence of free oxygen only anaerobic organisms can thrive, hence the processes operative will be of a character dependent on this situation.
The relative rate of deposition of organic matter when compared with the nondecomposable material contributed to the sediment is an important factor. Although the supply of organic matter may be identical in two areas, the concentration and character of the material in the sediments may be profoundly different if there are different rates of deposition of the nondecomposable material. The latter will tend to dilute the organic matter and, furthermore, in areas of rapid deposition, burial soon after reaching the sea floor reduces the destruction by benthic animals. As emphasized elsewhere, the physical-chemical environment immediately at the surface of the sediment may be quite different from that only a few centimeters beneath. Where deposition is relatively rapid and,
From the foregoing discussion it is obvious that the environment of deposition, that is, the biological and physical-chemical conditions on and in the sediment, are probably the most important factors in determining the distribution of the organic matter. If conditions are established which are favorable to the preservation of organic matter, these will tend to be maintained.
To summarize the above generalizations, the following conditions will favor the formation of sediments rich in organic matter:
An abundant supply of organic matter.
A relatively rapid rate of accumulation of inorganic material, particulary if fine-grained.
A small supply of oxygen to the waters in contact with the sediments. The most extreme development of such conditions may be found in basins and landlocked regions where stagnation exists with the resulting exclusion of animal life.
The following factors will tend to favor the destruction of the organic matter and the formation of sediments low in organic material:
A small supply of organic matter.
Relatively slow rate of accumulation of nondecomposable material.
An abundant supply of oxygen.
With the above-mentioned points in mind, some of the differences in distribution of organic matter in oceanic sediments can be explained. The slow deposition under oxidizing conditions, characteristic of the pelagic sediments, leads to a relatively complete destruction of the organic matter, whereas in nearshore areas where deposition is rapid and in basins where stagnant conditions prevail, a much larger percentage of the organic matter may escape destruction. Furthermore, the absolute supply is probably smaller in oceanic areas than in the coastal regions where the organic production is generally greater.
Distribution of Organic Matter
Within restricted areas where the supply of organic matter to the bottom may be considered constant, it is possible to attribute local irregularities in the organic-matter content of the sediments to the effects of transporting agencies and topography. For example, in the southern California area (fig. 260) the organic content is low on the ridges and banks and high in the depressions and basins. These differences may be attributed to the more active benthic fauna that inhabit the topographic highs and the effects of currents which sweep the finely divided organic matter and the fine-grained sediments into the depressions. The latter environment favors the preservation of the organic matter.
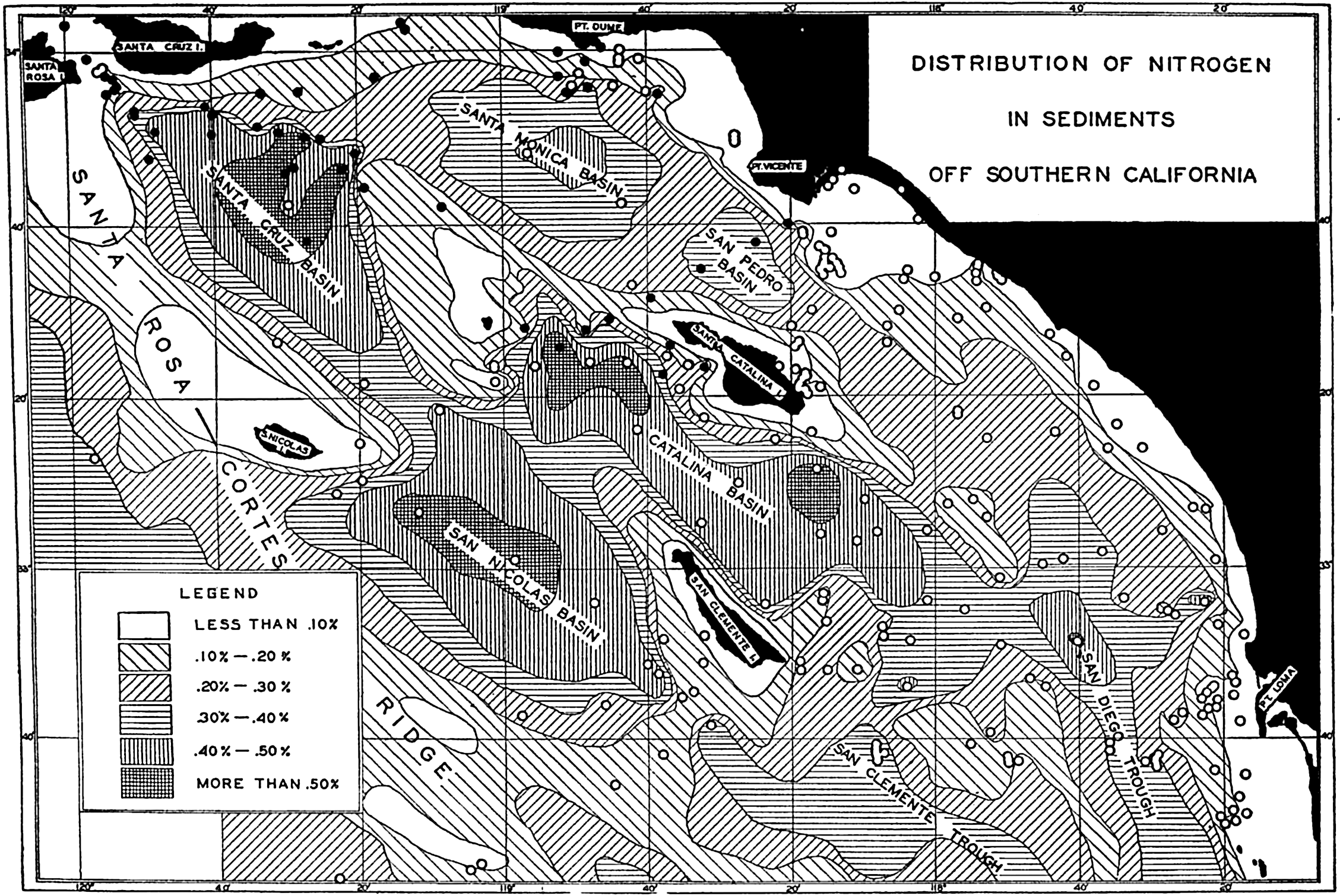
The distribution of organic nitrogen in the sediments off the southern California coast. Compare with figs. 7 and 264. (From Revelle and Shepard, 1939, in Recent Marine Sediments, edited by Parker D. Trask. American Association of Petroleum Geologists, Tulsa.)
The organic-matter content of terrigenous deposits is on the average higher than that of the pelagic deposits. According to Trask (1939), the averages are 2.5 and 1.0 per cent, respectively. As shown elsewhere (p. 1036), the rate of deposition of pelagic sediments is much less than that of terrigenous sediments, hence organic matter accumulates much more rapidly in nearshore deposits than in those of the open oceans. Trask (1939) assumed that the production of organic matter was uniform over the entire area of the oceans and attributed the more rapid accumulation in terrigenous deposits to the fact that the environment was less favorable to the destruction of organic matter on the sea bottom. However, the production cannot be assumed to be constant and the difference may be due entirely to the greater production in nearshore areas, particularly in those where upwelling and mixing are active. Until additional information is available concerning the differences in the supply of organic matter to the sea bottom it is impossible to evaluate the relative importance of supply and preservation as factors determining the organic content of the sediments. Correns (1937) attributes the higher organic content of the sediments near the African coast in the equatorial Atlantic to the larger production and, hence, greater potential supply in this region. Similarly, Wiseman and Bennett (1940) attribute the higher organic content of the nearshore sediments in the northwestern part of the Indian Ocean to the greater organic production in such areas.
Among the pelagic deposits there is less range in organic matter content. The fragmentary data available indicate that diatom oozes are the richest, followed by red clay and the calcareous oozes. Terrigenous diatomaceous deposits such as those in the Gulf of California (Revelle, personal communication) are among the richest group in their content of organic matter and may contain more than 10 per cent.
Studies of the variations in organic-matter content with depth and distance from shore generally show maxima at intermediate depths and distances. In some cases this feature is associated with basin conditions, as in the southern California area; in others it may be ascribed to the greater production or more rapid accumulation of clastic material or a combination of such factors near shore. The coarse sediments of the beach and shelf are generally low in organic matter.
Trask (1939) has summarized the organic content found in various types of shallow-water environments. These data show that shelf sediments generally contain between 2.0 and 3.0 per cent with higher values
Within the marine sediments there is generally a decrease in organic content with depth in the deposit. Correns (1937), Revelle and Shepard (1939), and Wiseman and Bennett (1940) have all reported this characteristic distribution. Within the upper 50 cm of the core as collected, the organic matter generally decreases to about two thirds of its value in the superficial layers. Irregularities in the content may usually be correlated with changes in the character of the deposit. The decrease is attributed to destruction due to bacterial activity after burial. The decrease in organic matter with depth in the sediment is accompanied by a marked decrease in the number of bacteria. Offhand, it might appear that the residual organic matter is of such a type that it cannot be attacked by bacteria. However, this is certainly not true of terrigenous sediments, and the meager data indicate that the organic matter in pelagic deposits is also subject to bacterial destruction. When brought into the laboratory, marine sediments will support large and active bacterial populations which rapidly attack the organic matter (Anderson, 1939). Under the environment prevailing in the buried sediment on the sea bottom, it is possible that biological activity has practically ceased. Nevertheless, viable bacteria are always present and if the environment is changed, say, by bringing the material into the laboratory, active growth and metabolism will result in the further alteration and oxidation of the organic matter.
The percentage of organic matter has been shown to be inversely related to the texture and it has been pointed out that the oxidation-reduction potential may be related to the organic content. Various workers have drawn attention to relationships between the organic matter and other constituents of the sediments. Correns (1937, 1939) obtained a linear relationship between organic matter and calcium carbonate and concluded that the calcareous material contained about 0.2 per cent organic matter and that the noncalcareous material contained a constant proportion of organic matter. Correns’ data also show a general relationship between the organic matter and the phosphate in the sediments. Revelle (1936), from an examination of the Carnegie
SHALLOW-WATER AND NEARSHORE SEDIMENTS
The differences between sediments found in marginal and nearshore regions and those of the open ocean can be largely attributed to the great intensity of transporting agencies in shallow water. In addition to the currents which are generally relatively strong in shallow water, the surface waves create strong disturbances and play an important role in the nearshore environment. Many of the transporting agencies effective in shallow water are subject to intermittent fluctuations that may produce stratification of the sediments. Such vertical variations in the character of the sediments as are transitory and may be destroyed by the rising tide or the next storm are lacking in deep-sea deposits, where variations in the properties of the sediments represent environmental changes with time over periods of a year to thousands of years.
Because of the stronger currents, sediments in shallow water are generally coarser and better sorted than those of the open sea. The form of the coast line and the topographic irregularities of the sea bottom have marked effects upon the supply and transportation of the sedimentary debris, leading to great local variations in the character of the sediments found in shallow water. The following discussion will apply to the sediments upon the shelf and also to those on the beach, unless specifically excepted.
Water movements associated with surface waves probably do not extend below about 100 m and it is only in very shallow water and on the beach that their motion is violent. Waves breaking on the shore are capable of transporting large amounts of sediment. During storms the coarser material is thrown high on the beach above the normal high-tide level, while at the same time the lower part of the beach is eroded and a certain amount of material carried out below low-tide level. During periods of very large waves the whole beach may undergo temporary erosion. Between storms the smaller waves return sediment from shallow water to the beach (Shepard and La Fond, 1940). Rip currents that are associated with the waves contribute to the removal of sediment from the beach (Shepard, Emery, and La Fond, 1941). In the absence of currents, waves are not effective in transporting sediment parallel to the shore unless they strike the beach obliquely or unless there is a gradient in the sediment placed in suspension by the waves.
The rise and fall of the tide once or twice each day changes the level of attack of the waves on the beach. The upper part of the beach is exposed for longer or shorter periods, depending on the elevation above mean-tide level. The beach profile and the character of the sediments are undoubtedly associated with the range in tide, but no study of this
The motion associated with semipermanent currents, internal waves, eddies, and tsunamis has been discussed elsewhere and the roles of various types of water movements in sediment transportation described (p. 959). As most currents have their greatest velocity parallel to the coast they tend to produce movement of sediment alongshore. Transportation away from shore can be produced by waves and rip currents, and can take place where there is a gradient normal to the coast in the concentration of suspended material or where the slope of the bottom is such that the gravitational component facilitates movement down the slope and away from the coast.
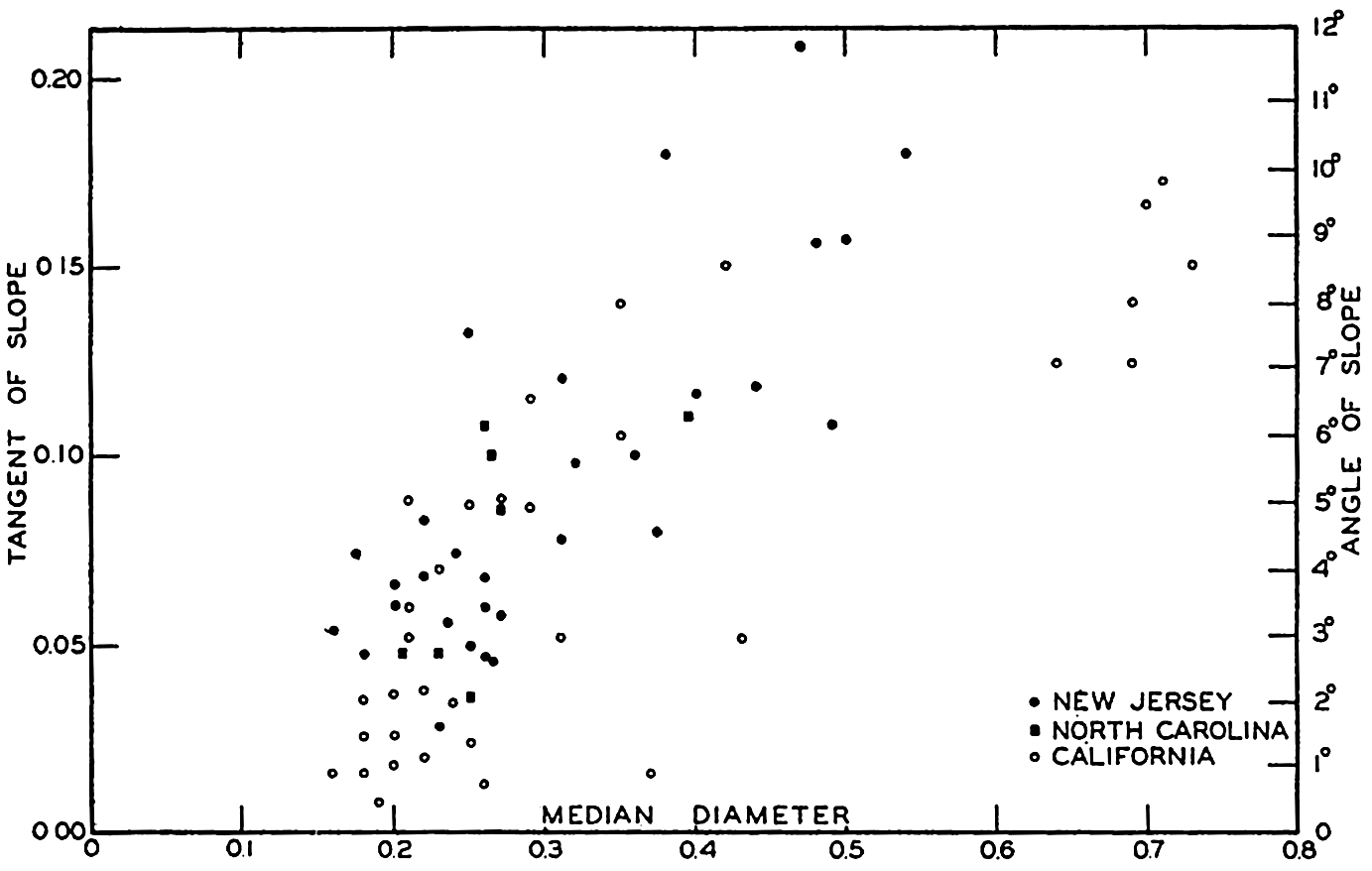
Relation between texture of sediments and slope of beaches on the east and west coasts of the United States. Median diameter in millimeters. (After data in U. S. Beach Erosion Board, 1933.)
Supply of Sedimentary Material. Beach and shelf deposits are predominantly of inorganic origin, and only in low latitudes along coasts of small runoff and around oceanic islands are the deposits high in organic calcareous debris. The nearshore zone is favorably located to receive terrigenous and volcanic material, both water-borne and carried by the atmosphere. In addition to these sources of terrigenous and volcanic material, sedimentary material is supplied by erosion of the exposed coast
The profile of the beach, the texture of the sediments, and hence, indirectly, the composition, are all closely related and are determined by such factors as the range in tide, exposure to waves and storms, and the character of the material forming the coast. The relationship between the slope of the beach and the median diameters of beach sediments on the east and west coasts of the United States is shown in fig. 261.
It is commonly stated that the inner part of the shelf represents a wave-cut terrace and that the outer extension is a wave-built platform composed of the materials carried out from the land and eroded from the shallower depths. Although wave-built terraces may be accumulating in certain localities, they are not a common feature of the continental shelf because (1) rock exposures are commonly found on the seaward edge of the shelf; (2) submarine canyons cutting across the shelf have steep and often rocky walls, even at the outer edge of the shelf; (3) the continental slope is commonly too irregular to have been produced by the accumulation of a large amount of unconsolidated material. As only the fine material is transported far out to sea, the bulk of the sediment carried away from continental coasts must accumulate either on the shelf or on the continental slope. Considerable evidence has been gathered which indicates that little or no deposition occurs on the shelf. In any coastal area in which this is true there can be no selective sorting of the material while in transit across the shelf. If there is a net accumulation, sorting may take place, leaving the coarser grains in the shallower or more exposed localities. In general, the bulk of the inorganic debris must accumulate in depressions on the shelf or immediately beyond the continental slope.
Beach and Shelf Sediments. Sediments of the beach and shelf show large vertical and lateral variations in texture. In terms of median diameters the range is from greater than 256 mm to less than 0.1 mm, namely, from boulders to fine silt. Numerous references to studies can be obtained in the symposium on Recent Marine Sediments (Trask, ed., 1939). Martens (1939) has summarized data on the textural characteristics of beach deposits from the eastern United States (table 117). These data show that the extreme range in median diameters is from 1.25 mm to 0.13 mm, but that the averages for different localities show a relatively small spread, namely, from 0.21 to 0.35 mm. The small coefficients of sorting emphasize the often stated fact that beach deposits are well sorted. The skewness values greater than unity show the predominance of the larger grades. Beach sediments on the California coast show
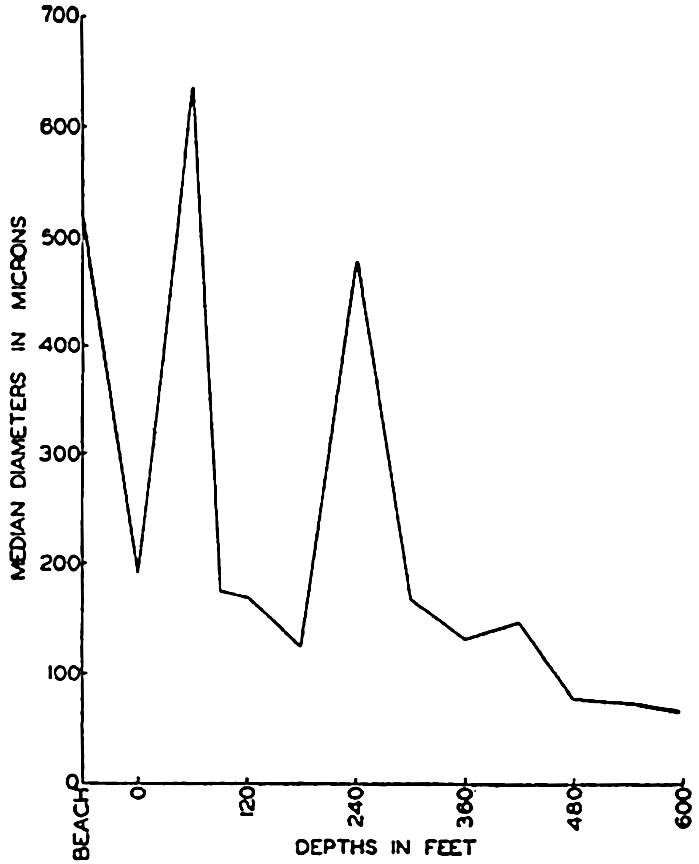
Average of median diameters of sediments from different depth zones in Santa Monica Bay, California. (From Shepard and Macdonald, 1938.)
| Region | No. of samples | Median diameter (mm) | Coefficient of sorting | Coefficient of skewness | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Max. | Min. | Average | Max. | Min. | Average | Max. | Min. | Average | ||
| South shore of Long Island | 22 | 0.48 | 0.23 | 0.35 | 1.41 | 1.16 | 1.32 | 1.15 | 0.91 | 1.01 |
| New Jersey | 37 | 0.70 | 0.15 | 0.33 | 1.53 | 1.14 | 1.27 | 1.47 | 0.88 | 1.03 |
| Del., Md., and Va. north of Chesapeake Bay | 18 | 0.54 | 0.15 | 0.30 | 1.60 | 1.13 | 1.29 | 1.08 | 0.92 | 1.01 |
| North Carolina, and Virginia south of Chesapeake Bay | 40 | 1.25 | 0.16 | 0.32 | 3.18 | 1.14 | 1.41 | 1.71 | 0.38 | 1.14 |
| South Carolina and Georgia | 9 | 0.30 | 0.16 | 0.21 | 1.54 | 1.10 | 1.31 | 1.19 | 0.96 | 1.10 |
| Florida | 19 | 0.69 | 0.13 | 0.34 | 1.76 | 1.17 | 1.42 | 1.33 | 0.86 | 1.04 |
Sediments found upon the shallower parts of the continental shelves and upon ridges and banks near shore do not differ appreciably from those found on the beach. In many localities there is a decrease in median diameter on leaving the beach, but such changes are by no means regular. This has been emphasized by Shepard and McDonald (1938) and by Revelle and Shepard (1939) for sediments on the Pacific coast, and by Stetson (1938) for sediments on the Atlantic coast of the United States. In Santa Monica Bay, California, Shepard and McDonald found a marked decrease in median diameter in shallow water within a few hundred feet of shore but no correlation between particle size and depth for the bay as a whole (fig. 262). Stetson's data from the shelf on
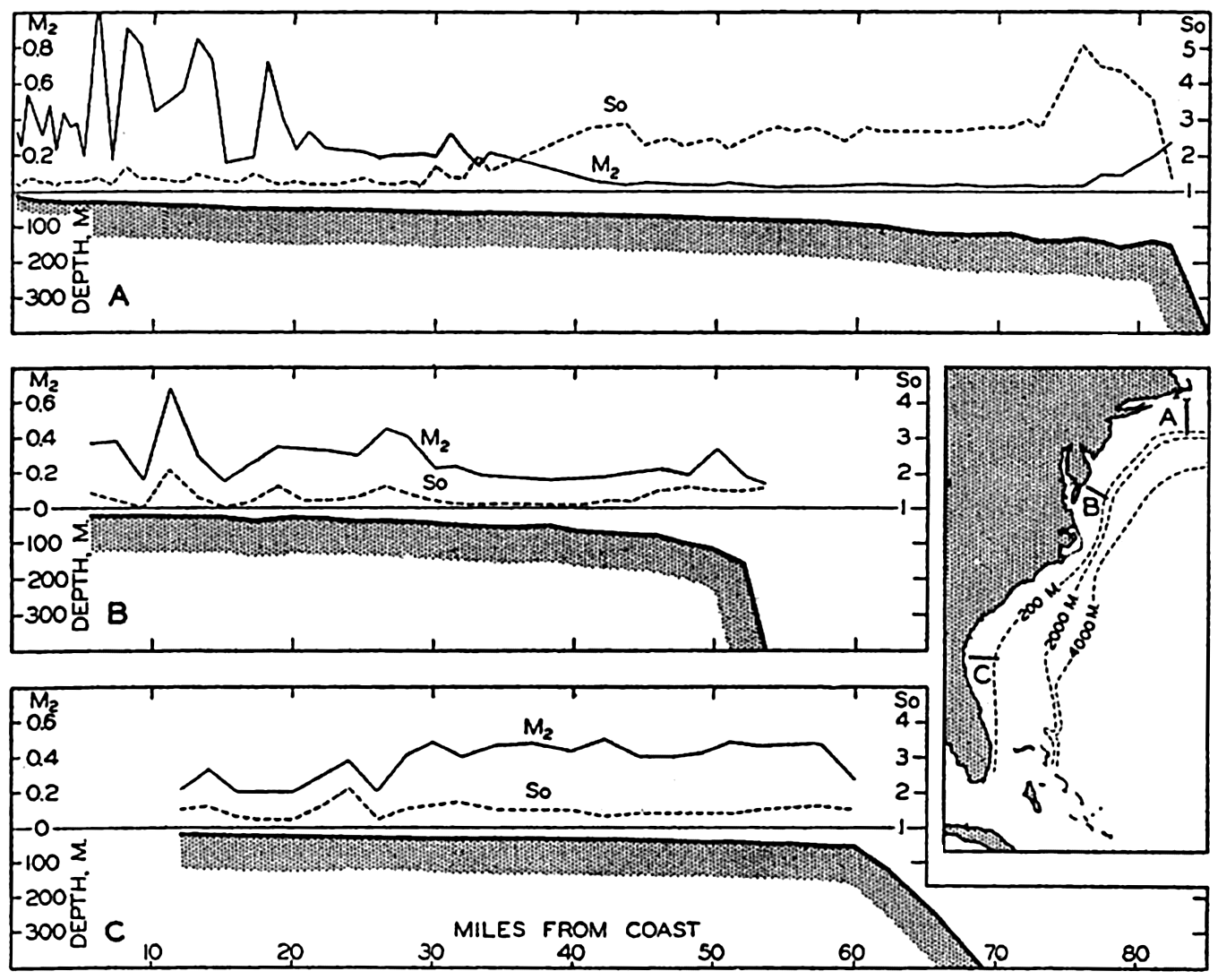
Median diameters in millimeters and sorting coefficients along representative sections off the east coast of the United States in relation to the bottom profile. (Data from Stetson, 1938.)
According to Stetson (1938, 1939) the past geological history and the supply of materials, as well as depth, are important factors in determining the character of the shelf sediments. Off the northern part of the Atlantic seaboard, where glaciation extended out beyond the present coast line, the sediments near shore are relatively fine and well-sorted sands; outside of these are coarser well-sorted sands and gravels; and succeeding these, poorly sorted silts and clays. At the edge of the shelf there is again an increase in the size of the particles. Off Maryland and New Jersey the sediments are well-sorted sands out to the break in slope, and there are no silts and clays. This is ascribed to the lack of a local supply of the finer grades. South of Cape Hatteras the relatively fine, well-sorted inorganic deposits grade into well-sorted calcareous sands
Hough (1940) has emphasized the lack of correlation between median diameter and depth for sediments in Buzzards Bay. However, he found reasonably good correlation between the median diameter and the sorting. Sediments with median diameters greater than 0.15 mm generally had sorting coefficients between 1.25 and 2.0, whereas the coefficients for the finer sediments varied between 2.0 and 3.0
The relatively coarse-grained texture of beach and shelf deposits has an indirect effect upon the composition, since only those materials occurring in relatively hard form and of sufficient size are present as “permanent” constituents of the sediments. Furthermore, as the particles are larger they are not subject to wide dispersal and, hence, are generally found relatively near their site of origin or entrance to the sea. Along irregular indented coasts where there are different types of source materials there may be marked differences in the composition of the beach sediments in adjacent bays. Where it has been possible to trace the dispersal of certain characteristic minerals (Martens, 1939) it has been found that they may travel 200 km or more along an uninterrupted coast. In the absence of relatively large supplies of inorganic material, the skeletal remains of planktonic or benthic plants and animals form a greater or less fraction of the deposit. Organic siliceous remains are never abundant, although they are cosmopolitan in distribution. In general, benthic remains are more abundant than planktonic, although on the outer part of the shelf and on isolated highs, planktonic foraminifera may form an important part of the sediment. The most common remains of benthic organisms are those of calcareous algae, mollusks, foraminifera, corals, bryozoa, annelids, echinoderms, and sponges. Siliceous diatom frustules are abundant in the sediments in some localities. The character of the inorganic fraction is influenced by the nature of the supply. Quartz is the most characteristic material with feldspar and the ferromagnesian minerals common in higher latitudes, particularly off glaciated coasts. Around volcanic islands fragments of andesitic and basaltic lavas with little or no quartz may be most common. The heavy minerals are frequently concentrated on the beaches by sorting action of the waves. The common heavy minerals are ilmenite, magnetite, garnet, zircon, monazite, and olivine (Martens, 1939).
Decomposable organic matter is generally low in the coarser deposits (p. 1016), but in the finer sediments, particularly those in basins, exceptionally high amounts are found. The low content of the sands and silts is ascribed to the fact that the organic matter is more readily attacked in such sediments and also that as the organic matter is light it is readily transported away by currents and deposited in depressions.
Beach and shallow-water sediments range from white to black with the addition of green, red, or blue. The coarser deposits are generally light in color unless in reducing environments. The finer deposits are commonly green, brown, or “blue.” Fine deposits in stagnant environments are black.
Character of the Deposits. In the foregoing discussion, emphasis has been placed on the composition of individual samples although frequent reference has been made to the variability in vertical and horizontal distribution. In fig. 263 were shown examples of the variability in the sediments off the Atlantic coast of the United States. Such differences are mostly in texture and composition, although color as related to either of these or to the environment may be very conspicuous.
Many studies of variability in the properties of beach deposits have been made in order to determine the relative importance of the numerous processes which may influence the character of such deposits. Longshore studies, such as those summarized by Martens (1939) and the detailed investigations of Schalk (1938), show marked differences in the character of the sediments. Thompson (1937) has made careful studies of the laminations which are characteristic of the coarser deposits, and Häntzschel (1939) has discussed similar features in the finer tide-flat deposits. The lateral variability can generally be related to the source localities of the constituent materials, and the relative intensity of wave and current action. The vertical laminations due to differences in texture, composition, and color are to be related to fluctuations in intensity of wave and current action associated with such periodic or random phenomena as the tides, the occurrence of storms or changing currents. Such laminations are transitory as the sediments are subject to reworking by the original causative agents. Häntzschel (1939) has pointed out that in tide flats such laminations are common although there is generally a large population of burrowing and mud-eating animals whose activities tend to destroy them. Temporary erosion and changing slopes may result in complicated internal structures in beaches. Whether or not such features exist on the shelf below tide level has not yet been determined, but as waves and currents are effective to considerable depths it is reasonable to assume that these temporary features, characteristic of the instability of the shallow-water zone, are present.
Students of sedimentary rocks lay considerable emphasis on features formed at the surface between the sediment and the overlying water or air. Such surface features are ripple marks, swash marks, rain and bubble marks, cracks, and so forth. Although common on beaches and in shallow water, it should be remembered that surface features are generally transitory and subject to erasure or changes by the next wave, high tide, or storm. It is only when exposed to the air so that the sediment is dried and thus partly consolidated that there is much likelihood
Special Nearshore Environments. The discussion thus far has been largely restricted to the character of the sediments found on the beach and shelf of the exposed coast. There are, of course, many modifications in the processes and, hence, in the character of the sediments which are associated with special local conditions. Such special localities may be placed in two major groups, (1) those environments which are transitional between marine on the one hand and fresh water, concentrated brine, or terrestrial, on the other hand, and (2) those which are more or less typically marine but where the topography introduces peculiar conditions. Of the latter group, isolated basins are the most important.
Where rivers enter the sea there is a transition from the fresh-water to the marine environment that will be reflected in the character of the fauna and the flora. Within the lower part of a river the tidal effect may be felt and certain parts of the bottom may be alternately exposed to fresh and salt water. This imposes limitations on the nature of the organisms which can develop there. In estuaries and off the mouths of large rivers there may be rapid deposition of the inorganic material carried by the rivers. Russell and Russell (1939) have reviewed the character of the sedimentation processes in the delta of the Mississippi River. The peculiar properties of these and other transitional environments, such as lagoons, have been discussed by Twenhofel (1939). Partially enclosed bays and seas will have beach and shallow-water deposits that may have properties differing to a greater or less degree from those of the open coast depending upon their size, tidal range, strength of waves, frequency of storms, and the character of the materials supplied.
Topographic features of the shelf play an important part in determining the distribution of sediments. The sediments in submarine canyons are of particular interest because of the fact that these channels may be the routes followed by large amounts of sediments which cross the shelves. Cutting as they do far into the shelf, the canyons must entrap large amounts of material in transit along the coast. In the canyon there are no known agencies of sufficient strength to raise the material again to the shelf proper. Near the canyon heads there are rapid and extensive changes in depth, indicating fill and removal. The texture of the sediments in the bottom of the canyons has been studied by Stetson (1939) and by Cohee (1938). Near the canyon heads the materials are commonly slightly finer than those on the adjacent slopes. On the other hand, pebbles and rock fragments have been found on the canyon bottoms. The coarser material may represent the more or less permanent deposit, whereas the fine materials are those being by-passed to the open sea.
Generalized map of the distribution of rock bottom and sediments off the coast of southern California. Depth contours in fathoms. (From Revelle and Shepard, 1939, in Recent Marine Sediments, P. D. Trask, ed. American Association of Petroleum Geologists, Tulsa.)
Topographically isolated basins are of particular interest because they are one of the environments in which sediments must be accumulating. Basins may be classified hydrographically, depending upon whether the inflow from the open ocean occurs at the surface or at sill depth, or conversely, whether the outflow is at the sill depth or the surface (chapter IV). Biologically and geologically the greatest distinction is between those basins which contain dissolved oxygen in the waters overlying the bottom and those which are stagnant and contain hydrogen sulphide. The latter condition may exclude animals which might otherwise inhabit the water and the bottom and which would contribute to or modify the character of the sediment.
Characteristic features of stagnant and nonstagnant basins. (From Fleming and Revelle, 1939, in Recent Marine Sediments, edited by Parker D. Trask and published by the American Association of Petroleum Geologists, Tulsa, Oklahoma.)
The texture of basin sediments is generally fine but they are poorly sorted. Studies by Revelle and Shepard (1939) in basins off the southern
Fleming and Revelle (1939) summarized Ström's data for stagnant and nonstagnant fjords (see table 118) and showed the characteristic properties of the water and the sediments in such environments (fig. 265).
ELEMENTS CONCENTRATED ON THE SEA BOTTOM AND AUTHIGENIC MINERALS
Certain elements such as calcium, carbon, silicon, iron, and manganese, carried to the sea in solution, are precipitated by organic or inorganic processes and are thereby concentrated on the sea floor. Readily recognizable minerals such as calcite and aragonite are produced in some instances, where in others the concentration is detectable only by chemical analyses which reveal the abnormal content of such elements as iron, manganese, and even the radioactive elements. The interaction of sea water and inorganic debris gives rise to certain characteristic minerals such as palagonite and phillipsite and it is probable that clay minerals are formed from the disintegration of volcanic ejecta (Bramlette and Bradley, 1940). The origin of glauconite which is a common constituent of terrigenous sediments is as yet uncertain, one theory being that it is built up from simple substances, the other that it is a product of the chemical weathering of biotite on the sea floor.
The factors affecting the deposition of calcium carbonate, both as calcite and aragonite, have been described elsewhere. Dolomite has been reported as a rare authigenic constituent of pelagic sediments by Correns (1937). Silicon in the form of dissolved silicates or as colloidal silica is one of the abundant constituents of river water. It is commonly believed that much of the silicon is immediately deposited on entering the sea by precipitation or coagulation when the river water mixes with sea water (Twenhofel, 1939, p. 373). However, there is no evidence for the presence of inorganically precipitated silica in recent marine sediments and the deposition of organic remains must be sufficient to balance the supply of dissolved and colloidal silicon compounds to the sea. The factors governing the deposition of organic siliceous remains have not been investigated thoroughly, but a relatively high content of dissolved silicates
Manganese is one of the chemical elements which is present in red clay in greater concentration than it is in igneous rocks (table 111, p. 992). In marine sediments it is chiefly present as oxides, largely manganese dioxide (MnO2), and may exist as finely divided grains, coatings over shells and inorganic material, as a cementing matrix, and in nodules and concretions. Manganese nodules, having diameters of 10 cm or more, are conspicuous constituents in dredge and trawl samples and have aroused great interest since the Challenger investigations showed their rather wide distribution. Although the nodules are characteristics of the deep-sea sediments, manganese in its other forms is commonly found also in terrigenous sediments. The manganese concretions and nodules which are found most abundantly in the South Pacific and Indian Oceans contain variable proportions of manganese dioxide, ferric oxide (limonite), and clay. The average contents of MnO2 and Fe2O3 are about 29.0 per cent and 21.5 per cent, respectively. Many individual analyses are given by Murray and Renard (1891) and by Andrée (1920). The nodules generally show laminations of different shades and textures and have a roughly concentric structure with a nucleus of pumice, volcanic glass, rock, or organic material such as a shark's tooth or an earbone of a whale.
| Characteristic | Stagnant fjords | Nonstagnant fjords |
|---|---|---|
| Amplitude of spring tides (cm) | 44 | 41 |
| Length (km) | 7 | 7 |
| Width (km) | 1.5 | 1.2 |
| Maximum depth (m) | 102 | 119 |
| Sill depth (m) | 4.2 | 10.8 |
| Surface temperature, °C | 16.3 | 16.6 |
| Bottom temperature, °C | 6.3 | 5.6 |
| Depth of isothermal layer (m) | 26 | 44 |
| Surface salinity (‰) | 19.54 | 23.10 |
| Bottom salinity (‰) | 30.07 | 33.52 |
| Density difference (surface to bottom) | .0115 | .0100 |
| Bottom H2S (ml/L) | 9.14 | |
| Bottom O2 deficit from saturation value (ml/L) | 11.74 | 5.03 |
| pH | 7.05 | 7.34 |
| P2O5 (mg/m3) | 327 | 67 |
| Organic carbon in muds, per cent | 13.0 | 9.9 |
| Thickness of black, putrid layer (cm) | >40 | ca. 20 |
Although the large nodules have aroused great interest, it is probable that they do not represent the bulk of the manganese present in most sediments. Correns (1937) in his studies of the Meteor material from the Equatorial Atlantic found that the content of manganese was conspicuously higher than in igneous rocks but he was unable to detect any manganese grains. Ten representative red clays from the Atlantic (Correns, 1939) contained an average of 1.2 per cent MnO2 on a CaCO3-free basis. The noncalcareous portion of 19 typical globigerina oozes contained 0.5 per cent MnO2. Additional data are given in table 119 (from Correns, 1939). The dark color of the red clays of the Indian and Pacific Oceans has been attributed to their manganese content, but comparison of the Carnegie data from the Pacific (Revelle, 1936) shows that the red clays of the North Pacific are lower in manganese than those of the Atlantic.
Table 111 (p. 992) shows the average of 10 North Pacific red clays to be 0.83 per cent MnO2, that is, approximately one half that of the Atlantic samples. In contrast to the samples from the Atlantic the MnO2 content is much higher in the calcareous deposits of the Pacific Ocean from which 20 samples containing more than 30 per cent CaCO3 contained on an average 5.5 per cent MnO2 when calculated on a CaCO3-free basis (Revelle, 1936). The great difference between the manganese content in the calcareous oozes of the Atlantic and the Pacific and the fact that there is no correlation with the percentage of calcium carbonate indicate that the deposition is not closely related with the accumulation of calcareous material.
There are two possible sources of the mangenese in deep-sea deposits. Murray and his associates concluded that it was a product of the submarine weathering of volcanic material. However, volcanic rocks do not contain very large amounts of manganese and in order to build up the concentrations found in red clays and in the noncalcareous fraction of globigerina oozes, it would be necessary to have large amounts of silica, aluminum, and iron leached out and redeposited elsewhere, since there is no accumulation of these substances in solution. According to Washington (1920), the average managanese content of the oceanic volcanics, expressed as MnO2, is between 0.05 and 0.18 per cent, the lower value being for the islands of the Atlantic and the higher for those of the Pacific Ocean. Consequently, a five- to tenfold concentration of manganese would be necessary if the clays were formed from this material. The manganese carried to the sea in solution forms an extremely small fraction of the dissolved solids and is rather rarely determined. According to Twenhofel (1926, p. 406) the concentration generally varies between 0.5 and 5.0 mg/L, which is greater than the amount present in sea water, namely, 0.001 to 0.01 mg/L. Murata (1939) has studied the total and exchangeable manganese content of river muds, namely, particulate material which is carried to the sea. The average total manganese in five river muds was 0.18 per cent, as MnO2, and the exchangeable manganese in these river muds was found to range from 0.03 per cent to 0.07 per cent as MnO2. From this it may be concluded that managanese is carried to the sea both in solution and as a constituent of the sedimentary debris.
| Maximum | Minimum | Percentage of calcium carbonate | All samples | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0–10 | 10–20 | 20–30 | 30–40 | 40–50 | 50–60 | 60–70 | 70–80 | 80–90 | |||||
a, percentage of total weight of sediments; b, percentage on carbonate-free basis. | |||||||||||||
The rows for the samples represent the number of samples; the other rows represent average percentage of the respective substances in the sediments. | |||||||||||||
| a | 4.00 | Trace | Samples | 14 | 2 | 9 | 6 | 12 | 10 | 18 | 11 | 6 | 88 |
| MnO2 | Average | 0.62 | 0.08 | 0.56 | 0.13 | 0.23 | 0.36 | 0.09 | 0.08 | 0.12 | 0.28 | ||
| b | 5.08 | Trace | Samples | 13 | 2 | 9 | 6 | 12 | 9 | 17 | 9 | 6 | 83 |
| Average | 0.64 | 0.12 | 0.72 | 0.20 | 0.42 | 0.81 | 0.28 | 0.47 | 0.77 | 0.51 | |||
| a | 10.69 | 0.21 | Samples | 14 | 2 | 9 | 6 | 12 | 10 | 18 | 10 | 6 | 87 |
| Fe2O3a | Average | 5.525 | 6.91 | 3.623 | 3.61 | 3.63 | 2.96 | 2.56 | 2.74 | 1.58 | 3.47 | ||
| b | 19.16 | 0.303 | Samples | 13 | 2 | 9 | 6 | 12 | 10 | 18 | 10 | 6 | 86 |
| Average | 5.71 | 8.49 | 4.71 | 5.47 | 6.61 | 6.67 | 7.32 | 10.89 | 9.82 | 7.12 | |||
| a | 1.06 | Trace | Samples | 14 | 2 | 9 | 6 | 11 | 10 | 18 | 11 | 6 | 87 |
| P2O5 | Average | 0.196 | 0.396 | 0.161 | 0.131 | 0.27 | 0.154 | 0.112 | 0.11 | 0.092 | 0.162 | ||
| b | 1.71 | Trace | Samples | 13 | 2 | 9 | 6 | 11 | 9 | 17 | 11 | 6 | 84 |
| Average | 0.257 | 0.489 | 0.21 | 0.1913 | 0.510 | 0.378 | 0.343 | 0.398 | 0.558 | 0.356 | |||
Manganese is most soluble in acid solutions when in reduced state. Hence, environments where such conditions prevail will tend to leach the manganese out of the solid material. Conversely, alkaline and oxidizing environments tend to precipitate the manganese in the very insoluble form of manganese dioxide. Whether or not bacteria or other biological agencies are directly involved in the solution or precipitation of manganese is not definitely known (ZoBell, 1939).
On reaching the sea the dissolved and exchangeable manganese is probably precipitated as finely divided MnO2 suspended in the water. If this settles in terrigenous environments where reducing conditions prevail, it again may pass into solution. The most favorable conditions for accumulation are those where the oxidation-reduction potential is relatively high as on topographic highs and in pelagic deposits where the conditions are always oxidizing, and in the presence of even slight amounts of solid CaCO3 where the pH must be relatively high. Hence, once the manganese is deposited in such an environment it is not likely to pass into solution again. This explanation does not account for the formation of the large manganese nodules which, according to Murray and Renard, may occur in clay which itself is relatively low in manganese. However, it is known that manganese accumulations tend to form on similar material, somewhat analogous to crystal growth, and possibly this may be one of the important factors. The difference in the manganese content of the sediments of the equatorial Atlantic and those of the Pacific Ocean is a problem which is yet unsolved.
Iron (table 111, p. 992) is present in red clays in concentrations somewhat greater than in the igneous rocks and terrigenous deposits, although the increase is not as marked as for manganese. As pointed out above, the manganese nodules contain a large proportion of iron oxides. Authigenic iron compounds may be found as the oxides, principally limonite and as sulphides. Table 119 contains data on the iron content of the Meteor samples, which, computed on a CaCO3-free basis, is rather erratic, and shows no correlation with the content of organic remains. The average iron content, calculated as Fe2O3, is 7.12 per cent, which, as in the case of manganese, is less than the average for the red clays. This Correns attributes to the higher iron content of the deposits of the Pacific and Indian Oceans. Examination of the Carnegie data shows that the samples with less than 30 per cent CaCO3 calculated on a CaCO3-free basis contain 7.0 per cent iron calculated as Fe2O3, whereas the calcareous deposits computed in the same way contain, on an average, 15.6 per cent
Two sources may supply iron to the marine sediments. These are: (1) the weathering of the oceanic volcanic material, which is relatively high in iron as indicated by the analyses of Washington (1920), which give about 10.8 per cent iron, calculated as Fe2O3; and (2) the considerable amounts which are carried to the sea in solution and as a constituent of the mineral debris. As the latter material may be relatively low in iron it may have a diluting effect and the dissolved iron must be the important source. Acid and reducing conditions tend to dissolve iron compounds, while alkaline and oxidizing conditions tend to precipitate the higher oxides. A mechanism somewhat similar to that described for manganese may therefore apply to the iron. The most favorable environment for the accumulation of iron oxides will be in oxidizing sediments containing calcareous material. Iron is precipitated as sulphides in stagnant environments where hydrogen sulphide is produced. Bacteria may be directly involved in the solution and precipitation of iron oxides and sulphides (Twenhofel, 1939).
Phosphorus, as P2O5, (table 111, p. 992) is found in approximately the same amounts in the red clays as in igneous rocks. However, Correns’ data (table 119) indicate that on a CaCO3-free basis there is an increase in P2O5 with the carbonate content indicating that the phosphate may form about 0.1 per cent of the calcareous skeletons. The supply of dissolved phosphate and its organic cycle in the sea have been discussed elsewhere. Apparently the regeneration of phosphorus utilized by plants is relatively complete, but it is being added to the sea as dissolved phosphate as well as a constituent of the minerals, chiefly apatite. The supply of dissolved phosphorus may be balanced by the removal in skeletal structures, some of which are extremely high in phosphorus. Furthermore, a certain amount may be deposited as a constituent of the detrital organic matter. Authigenic phosphorus compounds are not found in the pelagic deposits, but in certain nearshore localities phosphorite, Ca3(PO4)2, forms a cementing material which accumulates in nodules and crusts. These phosphate nodules are first discovered by the Challenger off the Cape of Good Hope and have subsequently been found in many coastal regions on the edge of the continental shelf and on topographic highs. Dredging off the southern California coast has shown phosphorite to be the most abundant type of rock collected.
The material collected off the coast of southern California (Deitz, et al, 1942) contained phosphorite nodules ranging in size from small oolites to
The phosphorite nodules have a characteristic smoothly rounded surface with the upper surface having a glazed unweathered appearance. Freshly broken surfaces are light brown to black and the outer surface is generally somewhat darker, owing to a thin coating of manganese oxides. Microscopic and chemical analyses show the principal mineral to be collophane. This may form virtually pure masses or act as a cement for phosphatic oolites and inorganic and organic material some of which may be more or less completely phosphatized. Most of the nodules show banding, indicating that the accumulation has been discontinuous. The calcium phosphate on the average forms about 67 per cent of the nodules, with calcium carbonate the second most abundant constituent. Sediments in the vicinity of phosphorite deposits contain approximately the same amounts as given above for pelagic deposits.
The phosphate nodules appear to be forming at the present time and several hypotheses have been advanced to explain their mode of formation (Twenhofel, 1939, Dietz et al, 1942).
Barium sulphate concretions have been found in recent marine sediments only in three widely separated localities, namely, off the west coast of Ceylon (1235 m), near the Kai Islands in the Dutch East Indies (304 m), and near Catalina Island off the coast of California (800 to 650 m). The concretions, ranging in weight from a few grams to about 1 kg, are generally of irregular shape, sometimes tubular, with concentric banding. They contain from about 60 to 82 per cent barium sulphate, which forms a cementing matrix, and contain mineral grains as well as organic remains. The bulk density of the barite concretions is high, averaging 2.70 and sometimes exceeding 3.0. Emery and Revelle (1942) examined the California material and consider that the only explanation which will account for their characteristic properties and their restricted occurrence is that the concretions are formed in the mud by the interaction of hot spring water high in barium with the sulphate present in the sea water.
The radioactive elements, particularly radium, in marine sediments have received considerable attention because of the unusually high radium content of pelagic sediments and because of the possibility of using the changes with depth in cores as a means of establishing the rates of deposition. Existing data have been assembled by the principal workers in the field, namely, Evans and Kip (1938), Evans, Kip, and Moberg (1938), Utterback and Sanderman (1938), Föyn, Karlik, Pettersson, and Rona (1939), and Urry and Piggot (1941).
The radium content of marine sediments varies between 0.1 X 10−12 g/g and values more than one hundred times as large. Low values are found in coarse-grained terrigenous deposits, whereas the high values occur in noncalcareous pelagic sediments. Bottom samples collected in the Pacific Ocean by the Carnegie were examined by Piggot and the average radium contents of the various types of sediments are given in table 120. (Revelle, manuscript.) Nearshore sediments, such as those studied by Utterback and Sanderman (1938), average about 0.3 X 10−12 g/g of radium.
The radium content of granites is about 1.6 X 10−12 g/g and that of basalts even less. The higher radium content of deep-sea marine sediments must therefore be due to a concentration taking place on the sea floor. Radium has a relatively short half-life period of about 1600 years. If radium alone were deposited on the sea floor where the rate of sedimentation is less than 1 cm in a 1000 years the amount present in the lower parts of cores, a meter or more in length, would be extremely small. Although there is generally a decrease in radium with depth, the distribution (cf. Urry and Piggot, 1941) shows that other radioactive elements which disintegrate to form radium must be deposited. Of these ionium and possibly uranium are of importance.
| Type | Number of samples | Radium g/g |
|---|---|---|
* Relatively high in siliceous organic remains. | ||
| Radiolarian ooze | 3 | 14.1 X 10−12 |
| Red clay | 7 | 8.7 |
| Globigerina ooze (siliceous[*]) | 4 | 7.2 |
| Diatom ooze | 3 | 5.0 |
| Globigerina ooze | 8 | 3.7 |
| Terrigenous mud | 2 | 2.5 |
Various mechanisms by which radium and the other radioactive elements may be concentrated in marine sediments have been suggested. Coprecipitation of radium with calcium carbonate and of uranium with iron and manganese compounds has been offered as possible mechanisms, but such hypotheses are not substantiated by the available data. Revelle (1936) pointed out the correlation between the radium and the decomposable organic matter in the Carnegie samples and suggested that organic activity might be the effective precipitating agency. Subsequently (Revelle, manuscript) he has developed this hypothesis and shown a correlation between the radium content and the organic siliceous remains
Glauconite is a green, blue, or brown hydrous silicate of potassium, magnesium, aluminum, and ferrous and ferric iron. The formula for glauconite can be written R2′O, 4(R″O,R2‴O3),10SiO2,4H2O, where R′ represents the univalent bases and R″ and R‴ the di- and trivalent bases. It is found in recent marine sediments and in many marine sedimentary rocks and it is considered to be a substance formed only in the marine environment. The distribution and properties of glauconite in both recent and fossil deposits and the various theories which have been advanced to explain its formation have been reviewed by Hadding (1932), Takahashi (1939), and Galliher (1939). Analyses given by Hadding and Takahashi show that although there is a considerable range in chemical composition there is no essential difference between the recent and the fossil material. However, as Takahashi has pointed out, the chemical composition can be varied considerably by treatment with neutral salt solutions as well as with acid and alkaline solutions. As the X-ray spectra are not materially different, it is probable that the exchange of cations is somewhat analogous to base-exchange in clay minerals.
Glauconite occurs in sediments as irregular grains between 0.1 and 1.0 mm in diameter. The surface is often polished and sometimes cracked and the grains have no definite internal structure. When present in sufficient quantity they give a greenish color to the sediment and the terms green sand and green mud were originally restricted to sediments containing glauconite. The glauconite grains often represent casts of foraminiferal shells and, in some cases, the shells are found completely filled by glauconite. Hadding has recorded glauconite present as interstitial material in porous organic and mineral substances and also as an incrustation.
Glauconite occurs in recent terrigenous sediments off continental coasts at depths ranging from a few meters down to about 2500 m. According to Galliher, it is more abundant adjacent to land areas where plutonic and metamorphic rocks are exposed. Although glauconite is found in many parts of the world it is abundant only in rather restricted localities where the environment is appropriate for its formation or accumulation, where deposition is not rapid, namely, upon the continental shelf or isolated topographic highs near the coast.
The mode of formation of glauconite is not yet definitely established. The older theories postulate the formation of an aluminosilicate gel which
RATES OF SEDIMENTATION
Methods of Determining Rates of Sedimentation. Knowledge of the rates of accumulation of sediments in the ocean is essential to an understanding of many problems both of past geological history and present sedimentation processes, but unfortunately very little is yet known about these rates. In the following discussion various indirect methods of estimation will be listed, all of which lead to values of approximately the same magnitude. The development of new means of determining the time scale, such as those based on radioactivity and magnetic measurements, may ultimately produce more reliable values. The rates of deposition are extremely small, in the open ocean of the order of less than 1 cm per 1000 years, yet, as pointed out by Kuenen (1937) and others, it is difficult to account for the supply of the tremendous mass of material which must have accumulated in the deep sea since the beginning of geological time. Questions concerning the total quantity of marine sediments, not entered upon here, have been discussed by Clarke (1924), Kuenen (1937, 1941), and Goldschmidt (1933).
Because of the extremely slow rate of deposition of deep sea sediments no adequate direct method of measurement has yet been devised. We are therefore forced to rely upon indirect methods which fall in two general groups. The stratigraphic method, widely used in the study of sedimentary, rocks, may be applied when it is possible to determine the thickness of the deposit which has accumulated in a given time interval. The supply method for estimating the rate of deposition is applicable when
The difficulty of obtaining adequate cores represents the greatest obstacle to the wide application of the stratigraphic method to recent marine sediments. Not only is it a question of obtaining cores of sufficient length but also of avoiding as far as possible the effects of what is known as “compaction” due to unsatisfactory sampling methods. Also it is often impossible to establish the time scale. To make the figures comparable to those obtained by other methods the length of core must be computed for a constant pore space (water content) or the values may be given in terms of solid material. This is important because superficial layers of sediments consist of about two thirds by volume of water. In the following discussion values are given for a “solid” layer of density 2.5, that is on a pore-free basis.
The supply method is based upon the rate of supply of sedimentary material to the sea. Such material may arise from submarine or subaerial volcanism, from erosion and transport, either in solution or in suspension, of terrestrial material, and contributions from outer space. The latter source is negligible but the magnitude of submarine volcanism is unknown. Furthermore the amount of air-borne materials, both of volcanic and terrestrial origin, has commonly been neglected, although, as shown elsewhere (p. 949 to p. 955), these may form appreciable fractions of pelagic deposits. Indirect estimates of the rate of sedimentation can best be based on the supply of river-borne dissolved material, since the amount of solid undissolved material carried to the sea by rivers is not known (Twenhofel, 1939). Rates based on the supply of dissolved material must be fairly accurate because the bulk of the elements are probably
Estimates Based on Stratigraphic Methods. The stratigraphic method has been widely applied to the study of fossil sediments, but the results obtained are very variable. Average values for sediments deposited since the Cambrian (500,000,000 years) have been derived by a study of the thickness of the column of sediments using a time scale based on radioactivity measurements. These values are (Schuchert, 1931):
| Sandstone | 68 cm/1000 years |
| Shale | 34 cm/1000 years |
| Limestone | 14 cm/1000 years |
These are for shallow water deposits where the rates of accumulation must be much greater than in the open sea.
The stratigraphic method was first applied to recent deep-sea sediments in 1913 by Braun, whose data have been re-examined by Schott (1939a). For many years it has been recognized that sediments from various parts of the deep sea are stratified. The development of more adequate coring instruments, capable of obtaining cores up to 3 m in length, has opened a new field in the study of these deposits. The interpretation of textural and other differences in these sedimentary columns in deep-sea core samples was expanded by Schott (in Correns, 1937), who examined the systematic series of samples collected by the Meteor in the Equatorial Atlantic. He found that there were characteristic differences in the pelagic foraminiferal fauna at different depths in the cores. Specifically, various warm-water forms were not found in certain zones in the column. The absence of these species was attributed to the cooler climatic conditions and possibly the modified circulation during the glacial periods. The thickness of the superficial layer, containing warm-water forms, was considered to represent the deposition during the time interval since the last glacial period, which Schott assumed to be 20,000 years. On this basis he calculated the rate of accumulation of globigerina ooze, blue mud, and red clay in the Equatorial Atlantic. Schott's values computed from the observed length in the core sample and not corrected for water content or for any distortion or compaction in sampling, are given in table 121. The average values for “blue” mud, globigerina ooze, and red clay, namely 1.78, 1.2, and 0.86 cm per 1000 years become 0.59, 0.4, and 0.29 cm per 1000 years if reduced to 1/3 to place them on a pore-free basis. The figures for globigerina ooze and diatom ooze in the southern Indian Ocean based on Braun's data are somewhat smaller. Uncorrected, the averages are 0.59 and 0.54, respectively, and if reduced to 1/3, 0.20 and 0.18 cm per 1000 years. The rate of deposition of globigerina ooze in the southern Indian Ocean is apparently about one half that in the Equatorial Atlantic.
A series of cores, obtained by means of the Piggot coring tube across the North Atlantic between the Newfoundland Banks and Ireland, have been examined (Bramlette and Bradley, 1940). In certain of these cores, ranging up to 3 m long, systematic variations in the character of the material with depth in the cores were found; that is, strata were found that contained coarse-grained material that could only have been transported to the site of deposition by floating ice. These strata were laid down during the glacial periods. Bramlette and Bradley (1940) state that in cores from the western North Atlantic the postglacial sediments are approximately 34 cm thick, which is within the range found for the Meteor samples.
| “Blue” mud | Globigerina ooze | Red clay | |
|---|---|---|---|
| Average thickness (cm) | 35.5 | 24.06 | 17.14 |
| Greatest observed thickness (cm) | 66.0 | 42.5 | 26.5 |
| Smallest observed thickness (cm) | 18.0 | 10.5 | <10.0 |
| Average rate of sedimentation (cm) per 1000 years | 1.78 | 1.2 | <0.86 |
| Greatest observed rate of sedimentation (cm) per 1000 years | 3.3 | 2.13 | 1.33 |
| Smallest observed rate of sedimentation (cm) per 1000 years | 0.9 | 0.53 | <0.5 |
| Samples used (number) | 6 | 48 | 7 |
From the foregoing it might be concluded that present-day coring techniques would show all pelagic samples to be stratified, but this is not necessarily the case. The absence of stratification within the upper few meters, the present limit of core length, may be due to a number of factors such as: more rapid local accumulation than indicated by the values given above; extensive mixing and churning of the deposit by current action, or the activities of burrowing and mud-eating benthic animals, or the absence of agencies of sufficient magnitude to modify the character of the material being deposited. The latter condition may prevail for such deposits as red clay.
The stratigraphic method has not yet been widely applied to the study of recent shallow water sediments. Moore (1931) estimated the rate of deposition in the deeper portions of the Clyde Sea from laminations which he interpreted as due to the deposition of large amounts of organic matter each spring. The laminations were between 6 and 4 mm thick, the thicker layers occurring in the upper portion of the core. The water
Estimates Based on Supply Methods. Clarke (1924) used his figures for the annual contribution of dissolved materials by rivers (p. 214) to estimate the rate of “chemical” sedimentation. He assumed that only sodium and chlorine escaped deposition by either inorganic or biological processes, and in this way found that the annual rate of chemical deposition was between 22 X 108 and 24 X 108 metric tons. If evenly spread over the entire sea floor this would form a layer of 0.25 cm/1000 years. To this must be added the particulate material of terrigenous and volcanic origin. Furthermore, it has been pointed out that nearshore deposits accumulate more rapidly than those in the open sea; therefore the value given above is too small for terrigenous deposits and too large for the deep sea sediments.
Kuenen (1937), from a consideration of the extent of erosion since the Cambrian (500,000,000 years) and the supply from terrestrial volcanoes, has estimated that the combined chemical and detrital deposition in the deep sea has been at a rate of about 0.33 cm/1000 years, a value approximately the same as those given above. Since then, Kuenen (1941) has revised his figures and reduced them to 0.1 cm/1000 years for red clay and to 0.2 cm/1000 years for globigerina ooze.
Two estimates have been made on the basis of organic deposition. Murray (Murray and Hjort, 1912) estimated the rate of deposition of globigerina ooze as 2.5 cm/10 years. This highly erroneous value was based on the study of the Atlantic submarine telegraph cables which were found to be “covered” in a period of 10 years. Actually they undoutedly settled into the ooze when laid. Computed in the units given above, this would be about 100 cm of solid material per 1000 years. Lohman estimated the rate at which coccoliths might accumulate on the sea floor from his studies of the production of the planktonic calcareous
Revelle and Shepard (1939) have used the supply method for estimating the rate of deposition in the basins of the southern California region. Their value, based on the rate of erosion of the local watersheds and the relative areas of erosion and deposition, is approximately 25 cm/1000 years.
The further development of the methods outlined above and the introduction of new techniques will undoubtedly tend to modify the values for the rates of deposition, but it does not seem probable that they will affect the order of magnitude of those for the deep sea. Large local variations in the rate of deposition of terrigenous depositions must be expected but the scattered evidence indicates that they accumulate at a rate of the order of 10 cm of solid material per 1000 years.
SUMMARY OF FACTORS DETERMINING CHARACTER OF MARINE SEDIMENTS
It has been repeatedly emphasized that the factors controlling the character of the sediment in a given locality are numberous and complicated, and it is both instructive and valuable to see to what extent it is possible to predict the characteristics of the sediment which may occur under a given set of conditions. The number of variables necessary to formulate such a prediction indicates the large number of factors which must be taken into account. The prediction of the mass properties of a sediment for a given set of conditions not only illustrates that we have some understanding of the processes of marine sedimentation but that the procedure may be reversed and certain of the important environmental factors deduced from the properties of a given sediment sample. This is of obvious value to the student of sedimentary deposits both recent and fossil, and is also instructive to the oceanographer concerned with aspects of the sea other than the sediments.
It is difficult to designate those properties of a sediment which are most “important.” The relative importance may vary with the individual interest of the worker, and what in one instance may be a minor constituent of a sediment may in another locality be the most abundant or conspicuous type of material. Glauconite in an example of such a substance. As a basis for the following discussion, those mass properties used to classify and name marine sediments will be considered, namely color, physical composition, and texture.
The environmental factors most important in determining the characteristics of marine sediments may be grouped under three main headings: (1) the general topography and depth of the site of deposition, (2) the relation of the site of deposition to sources of inorganic material, and (3) the physical and chemical conditions in the water column overlying
Topography has its more profound influence upon the textural characteristics of the sediments, and the topography surrounding a given site is usually more important than the absolute depth. Topographic highs are subject to the sweeping action of waves and currents and, hence, are either covered by relatively coarse material or lacking in unconsolidated material. Fine-grained material is always absent in shallow water except on the continental shelf, where it is being by-passed to deeper water. Conversely, depressions and basins generally contain fine-grained material but in addition may receive some coarse material swept off the shelf and highs, or supplied by pelagic or benthic organisms. The slopes where active deposition is taking place are generally covered with poorly sorted sediments. The rate of sedimentation is small on isolated topographic highs and in the major ocean basins and is relatively great on and immediately below the slopes and in nearshore basins. In those areas where the bottom is sinking, accumulation may be rapid on the shelves, otherwise it is negligible. The effect of topography and depth on texture is related to the fact that the strongest water movements, hence the ability to move particles, occur near the surface, particularly at those depths where wave action is effective. Isolated highs at all depths are affected by the sweeping action which is a combination of current motion and the force of gravity which tends to pull the material down slopes.
Indirectly topography may affect the composition where two or more types of materials have their greatest abundance in different size grades. In this case the material having the coarser texture will be concentrated on areas subjected to the stronger transporting agency, with the resulting increased relative concentration of the substance of finer texture elsewhere. This factor may account for the abundance of such materials as glauconite, phosphorite, and these materials mixed with organic remains on certain areas of the shelves, particularly on topographic highs. It has also been advanced as a possible reason for the lower calcium carbonate content of the sediments in the bottom of the major ocean basins where the finest inorganic debris accumulates.
The physical composition of a sediment sample reflects the relative rates of supply of the various types of material. These constituents fall into two major groups, namely, the organic skeletal structures and the inorganic material that may be of terrigenous or volcanic origin. The amount of inorganic material being deposited at a given locality depends upon the relation of that site to the sources of supply. Off the mouths of large rivers and near regions of active volcanism there are relatively large amounts of coarse-grained clastic material. On the other hand, in the open ocean, far removed from the source of such material, the inorganic
After the inorganic material has reached the sea the effect of transporting agencies must be considered. Because of the decreasing intensity of wave action with depth, there is a tendency for the coarser materials to accumulate near the source, whereas the finer materials are transported for great distances. The character of the inorganic material and the texture of the material in a sediment at a given locality can therefore be predicted with some accuracy if we know the depth and topography of the site of deposition and the character of the source. The relative abundance of such material in a sediment of course depends upon the relative rate of deposition of organic material.
The supply of inorganic material is limited to the coast lines and to regions of submarine volcanism and there are of course regions of the sea which are thousands of miles from any such source. This is not so true
The physical-chemical conditions surrounding topographic highs are generally rather similar to those in the surrounding water at approximately the same depth. This statement does not apply, however, to isolated depressions where basin conditions may prevail. In such regions (p. 1026) the physical-chemical conditions may be very different from those at a comparable depth in the open sea in adjacent regions. The most striking contrasts are found in such stagnant basins as the Black Sea and the Norwegian fjords. Sediments accumulating in basins have certain characteristic features which may be used to identify them.
A prediction of the character of a sediment may therefore be made if the following variables are established: topography surrounding the site of deposition, the depth, the relationship to the sources of inorganic material, and the physical-chemical conditions in the overlying water. Conversely, if the character of a sediment is known it is possible to recognize the more important factors of the environment of deposition.
Bibliography
Anderson, D. Q.1939. “Distribution of organic matter in marine sediments and its availability to further decomposition” . Jour. Marine Research, v. 2, p. 225–235, 1939.
Andrée, K.1920. “Geologie des Meeresbodens” . Bd. II. Bodenbeschaffenheit, Nutzbare Materialien am Meeresboden. Leipzig, Gebrüder Borntraeger, 689 pp., 1920.
Bramlette, M. N., and W. H. Bradley. 1940. “Geology and biology of North Atlantic deep-sea cores” . Part 1. Lithology and geologic interpretations. U. S. Geol. Survey, Prof. Paper 196-A, 34 pp., 1940.
Cayeux, Lucien. 1931. “Introduction à l'étude pétrographique des roches sédimentaires” . Paris, Ministére des Travaux Publics, Texte, 524 pp., Atlas, 56 pls., 1931.
Clarke, Frank W.1924. “The data of geochemistry” . U. S. Geol. Survey, Bull. 770, 841 pp., 1924.
Cohee, George V.1938. “Sediments of the submarine canyons off the California coast” . Jour. Sedimentary Petrology, v. 8, p. 19–33, 1938.
Collet, Léon W.1908. “Les dépôts marins” . Paris, Octave Doin, Éditeur, 325 pp., 1908.
Cornish, Vaughan. 1934. Ocean waves and kindred geophysical phenomena. London, Cambridge Univ. Press, 164 pp., 1934.
Correns, Carl W.1939. Pelagic sediments of the North Atlantic Ocean. p. 373–395 in Trask (ed.), Recent marine sediments, 1939.
Correns, Carl W. et al. 1937. “Die Sedimente des äquatorialne Atlantischen Ozeans. Deutsche Atlantische Exped” . Meteor1925–1927, Wiss. Erg., Bd. III, 3. Teil, 298 pp., 1937.
Cushman, Joseph A.1928. “Foraminifera: their classification and economic use” . Cushman Lab. Foram. Research, Spec. Publ. no. 1, Sharon, Mass., 401 pp., 1928.
Dietz, R. S., K. O. Emery, and F. P. Shepard. 1942. “Phosphorite deposits on the sea floor off southern California” . Geol. Soc. Amer., Bull., v. 53, p. 815–848, 1942.
Emery, K. O., and Roger Revelle. 1942. “Barite concretions from the ocean floor” . Geol. Soc. Amer. (in press).
Emery, K. O., and R. H. Tschudy. 1941. “Transportation of rock by kelp” . Geol. Soc. Amer., Bull., v. 52, p. 855–862, 1941.
Evans, Robley D., and A. F. Kip. 1938. “The radium content of marine sediments from the East Indies, the Philippines, and Japan, and of the Mesozoic fossil clays of the East Indies” . Amer. Jour. Sci., v. 36, p. 321–336, 1938.
Evans, Robley D., A. F. Kip, and E. G. Moberg. 1938. “The radium and radon content of Pacific Ocean water, life, and sediments” . Amer. Jour. Sci., v. 36, p. 241–259, 1938.
Fleming, Richard H., and Roger Revelle. 1939. Physical processes in the ocean. p. 48–141 in Trask (ed.), Recent marine sediments, 1939.
Fox, Denis L., and L. J. Anderson. 1941. “Pigments from marine muds” . Nat. Acad. Sci., Proc., v. 27, p. 333–336, 1941.
Föyn, Ernst, B. Karlik, H. Pettersson, and E. Rona. 1939. “The radioactivity of seawater” . Oceanografiska Inst. Göteborg (Göteborgs K. Vetensk … Handlingar, 5, Ser. B), Meddelanden, N.S., 44 pp., 1939.
Galliher, E. Wayne. 1933. “The sulfur cycle in sediments” . Jour. Sedimentary Petrol., v. 3, p. 51–63, 1933.
Galliher, E. Wayne. 1935a. “Glauconite genesis” . Geol. Soc. Amer., Bull., v. 46, p. 1351–1366, 1935.
Galliher, E. Wayne. 1935b. “Geology of glauconite” . Amer. Assn. Petrol. Geol., Bull., v. 19, p. 1569–1601, 1935.
Galliher, E. Wayne. 1939. Biotite-glauconite transformation and associated minerals. p. 513–515 in Trask (ed.), Recent marine sediments, 1939.
Goldschmidt, V. M.1933. “Grundlagen der quantitativen Geochemie” . Fortschritte d. Mineral., Kristal., und Petrographie, v. 17, p. 112–156, 1933.
Grim, Ralph E.1939. Properites of clay. p. 466–495 in Trask (ed.), Recent marine sediments, 1939.
Gripenberg, Stina. 1934. “A study of the sediments of the North Baltic and adjoining seas” . Fennia 60, No. 3, 231 pp., Helsingfors, 1934.
Gripenberg, Stina. 1939a. Sediments of the Baltic sea. p. 298–321 in Trask (ed.), Recent marine sediments, 1939.
Gripenberg, Stina. 1939b. Mechanical analysis. p. 532–557 in Trask (ed.), Recent marine sediments, 1939.
Hadding, Assar. 1932. “The pre-quaternary sedimentary rocks of Sweden” . IV. Glauconite and glauconitic rocks. Lunds Geol. Mineralogiska Institution, Medd. Nr. 51, 175 pp., 1932. Lund.
Häntzschel, Walter. 1939. Tidal flat deposits (Wattenschlick). p. 195–206 in Trask (ed.), Recent marine sediments, 1939.
Hewitt, L. F.1937. Oxidation-reduction potentials in bacteriology and biochemistry. 4th ed. London Country Council, no. 3200, 101 pp., 1937.
Hjulström, Filip. 1939. Transportation of detritus by moving water. p. 5–31 in Trask (ed.), Recent marine sediments, 1939.
Hough, J. L.1940. “Sediments of Buzzards Bay, Massachusetts” . Jour. Sedimentary Petrol, v. 10, p. 19–32, 1940.
Johnson, Douglas W.1919. Shore processes and shoreline development. New York, John Wiley and Sons, 584 pp., 1919.
Kelley, W. P.1939. Base exchange in relation to sediments. p. 454–465 in Trask (ed.), Recent marine sediments, 1939.
Kelley, W. P., and G. F. Liebig, Jr.1934. “Base exchange in relation to composition of clay with special reference to effect of sea water” . Amer. Assn. Petrol. Geol., Bull., v. 18, p. 358–367, 1934.
Krumbein, W. C.1939. Graphic presentation and statistical analysis of sedimentary data. p. 558–591 in Trask (ed.), Recent marine sediments, 1939.
Krumbein, W. C., and F. J. Pettijohn. 1938. Manual of sedimentary petrography. New York, D. Appleton-Century Co., 549 pp., 1938.
Kuenen, Ph. H.1937. “On the total amount of sedimentation in the deep sea” . Amer. Jour. Sci., v. 34, p. 457–468, 1937.
Kuenen, Ph. H.1941. “Geochemical calculations concerning the total mass of sediments in the earth” . Amer. Jour. Sci., v. 39, p. 161–190, 1941.
Martens, James H. C.1939. Beaches. p. 207–218 in Trask (ed.), Recent marine sediments, 1939.
Mehmel, Martin. 1939. Application of X-ray methods to the investigation of recent sediments. p. 616–630 in Trask (ed.), Recent marine sediments, 1939.
Moore, Hilary B.1931. “The muds of the Clyde Sea area. III. Chemical and physical conditions; rate and nature of sedimentation; and fauna” . Marine Biol. Assn. U. K., Jour., v. 17, p. 325–358, 1931.
Moore, Hilary B.1939. Faecal pellets in relation to marine deposits. p. 516–524 in Trask (ed.), Recent marine sediments, 1939.
Murata, K. J.1939. “Exchangeable manganese in river and ocean muds” . Amer. Jour. Sci., v. 37, p. 725–735, 1939.
Murray, Sir John, and James Chumley. 1924. “The deep-sea deposits of the Atlantic Ocean” . Royal Soc. Edinburgh, Trans., v. 54, pt. 1, 252 pp., 1924.
Murray, Sir John, and J. Hjort. 1912. The depths of the ocean. London, Macmillan, 821 pp., 1912.
Murray, Sir John, and E. Philippi. 1908. “Die Grundproben der Deutschen Tiefsee Expedition” . Deutsche Tiefsee-Exped. Valdivia 1898–1899, Wiss. Erg., Bd. 10, p. 77–206, 1908.
Murray, John, and A. F. Renard. 1891. “Report on deep-sea deposits based on the specimens collected during the voyage of H.M.S. Challenger in the years 1872 to 1876” . Challenger Repts., 525 pp., 1891.
Neaverson, E.1934. “The sea-floor deposits. I. General characteristics and distribution” . Discovery Repts., v. 9, p. 297–349, 1934.
Pia, Julius, 1933. “Die rezenten Kalksteine” . Zeitschr. f. Kristallographie, Mineral. u. Petrogr., Abt. B, Ergänzungsband, 420 pp., 1933. Leipzig.
Prandtl, L.1932. “Meteorologische Anwendungen der Strömungslehre” . Beiträge z. Physik d. freien Atmosphäre, Bd. 19, Leipzig, 1932.
Pratje, Otto. 1939a. “Sediments of South Atlantic Ocean” . Amer. Assn. Petrol. Geol., Bull., v. 23, p. 1666–1672, 1939.
Pratje, Otto. 1939b. “Die Sedimente des Südatlantischen Ozeans” . 2. Lief. Die Untersuchungsergebnisse nach Stationen geordnet. Deutsche Atlantische Exped.Meteor1925–1927, Wiss. Erg., Bd. III, 2. Teil, 2. Lief., p. 57–171, 1939.
Radczewski, O. E.1939. Eolian deposits in marine sediments. p. 496–502 in Trask (ed.), Recent marine sediments, 1939.
Revelle, Roger. 1936. “Marine bottom samples collected in the Pacific Ocean by the Carnegie on its seventh cruise” . Dissertation submitted in partial satisfaction of the requirements for the degree of doctor of philosophy in oceanography, Univ. of Calif., 317 ms. pp., 1936. (In Press, Carnegie Inst. Washington, Dept. Terr. Magnetism.)
Revelle, Roger, and F. P. Shepard. 1939. Sediments off the California coast. p. 245–282 in Trask (ed.), Recent marine sediments, 1939.
Ridgway, Robert. 1912. Color standards and color nomenclature. Washington, D. C., publ'd by the author, 43 pp., 53 colored pls., 1912.
Rouse, Hunter. 1938. Fluid mechanics for hydraulic engineers. New York, McGraw-Hill Book Co., 422 pp., 1938.
Russell, R. Dana. 1939. Effects of transportation on sedimentary particles. p. 32–47 in Trask (ed.), Recent marine sediments, 1939.
Russell, Richard J., and R. Dana Russell. 1939. Mississippi river delta sedimentation. p. 153–177 in Trask (ed., Recent marine sediments, 1939.
Schalk, Marshall. 1938. “A textural study of the outer beach of Cape Cod, Massachusetts” . Jour. Sedimentary Petrol., v. 8, p. 41–54, 1938.
Schott, Gerhard. 1935. “Geographie des Indischen und Stillen Ozeans” . Deutsche Seewarte, Hamburg, 413 pp., 1935.
Schott, Wolfgang. 1937. Die Foraminiferen in dem äquatorialen Teil des Atlantischen Ozeans. p. 43–134 in Correns et al, 1937, which see above.
Schott, Wolfgang. 1939a. Deep-sea sediments of the Indian Ocean. p. 396–408 in Trask (ed.), Recent marine sediments, 1939.
Schott, Wolfgang. 1939b. Rate of sedimentation of recent deep-sea sediments. p. 409–415 in Trask (ed.), Recent marine sediments, 1939.
Schuchert, Charles. 1931. “Geochronology, or The age of the earth on the basis of sediments and life” . p. 10–64 in Physics of the earth, v. 4, Age of the earth. Nat. Research Council, Bull.no. 80, 1931.
Shepard, Francis P., and E. C. La Fond. 1940. “Sand movements along the Scripps Institution pier” . Amer. Jour. Sci., v. 38, p. 272–285, 1940.
Shepard, Francis P., and G. A. MacDonald. 1938. “Sediments of Santa Monica Bay, California” . Amer. Assn. Petrol. Geol., v. 22, p. 201–216, 1938.
Shepard, Francis P., K. O. Emery, and E. C. La Fond. 1941. “Rip currents: a process of geological importance” . Jour. Geol., v. 49, p. 337–369, 1941.
Smith, C. L.1940. “The Great Bahama Bank. II. Calcium carbonate precipitation” . Jour. Marine Research, v. 3, p. 171–189, 1940.
Stetson, Henry C.1938. The sediments of the continental shelf off the eastern coast of the United States. Papers in Physical Oceangr. and Meteorol., v. 4, no. 4, 48 pp., 1938.
Stetson, Henry C.1939. Summary of sedimentary conditions on the continental shelf off the east coast of the United States. p. 230–244 in Trask (ed.), Recent marine sediments, 1939.
Ström, Kaare M.1936. “Landlocked waters. Hydrography and bottom deposits in badly-ventilated Norwegian fjords with remarks upon sedimentation under anaërobic conditions” . Norske Vidensk. Akad. i Oslo, Skirfter, I. Mat.-Naturv. Klasse, no. 7, 85 pp., 1936.
Ström, Kaare M.1939. Landlocked waters and the deposition of black muds. p. 356–372 in Trask (ed.), Recent marine sediments, 1939.
Sverdrup, H. U., and Staff. 1941. “Research in physical oceanography and submarine geology at the Scripps Institution of Oceanography during April, 1940, to April, 1941” . Amer. Geophys. Un., Trans., p. 490–494, 1941.
Takahashi, Jun-ichi. 1939. Synopsis of glauconitization. p. 503–512 in Trask (ed.), Recent marine sediments, 1939.
Thompson, Warren O.1937. “Original structures of beaches, bars, and dunes” . Geol. Soc. Amer., Bull., v. 48, p. 723–752, 1937.
Throp, Eldon M.1931. “Descriptions of deep-sea bottom samples from the western North Atlantic and the Caribbean Sea” . Scripps Inst. Oceanogr., Bull., v. 3, p. 1–31, 1931.
Trask, Parker D.1932. “Origin and environment of source sediments of petroleum” . Houston, Amer. Petrol. Inst., Gulf Publ. Co., 323 pp., 1932.
Trask, Parker D.1937. “Relation of salinity to the calcium carbonate content of marine sediments” . U. S. Geol. Survey, Prof. Paper 186, p. 273–299, 1937.
Trask, Parker D.1939. Organic content of recent marine sediments. p. 428–453 in Trask (ed.), Recent marine sediments, 1939.
Trask, Parker D. (ed.)1939. “Recent marine sediments” . Tulsa, Amer. Assn. Petrol. Geol., 736 pp., 1939.
Twenhofel, William H.1926. “Treatise on sedimentation” . Baltimore, Williams and Wilkins Co., 661 pp., 1926.
Twenhofel, William H.1932. Treatise on sedimentation. 2nd ed., completely revised. Baltimore, Williams and Wilkins Co., 926 pp., 1932.
Twenhofel, William H.1939. Principles of sedimentation. New York, McGraw-Hill Book Co., 610 pp., 1939.
U. S. Beach Erosion Board. 1933. Interim report. Washington, D. C., U. S. Army, Office of Chief of Engineers, mimeographed, 1933.
Urry, W. D., and C. S. Piggot. 1942. “Radioactivity of ocean sediments. V. Concentration of the radio-elements and their significance in red clay” . Amer. Jour. Sci., v. 240, p. 93–103, 1942.
Utterback, C. L., and L. A. Sanderman. 1938. “Radium content of some inshore bottom samples in the Pacific Northwest” . Jour. Marine Research, v. 1, p. 187–191, 1938.
Vaughan, T. Wayland. 1924. “Oceanography in its relation to other earth sciences” . Washington Acad. Sci., v. 14, p. 307–333, 1924.
Washington, Henry S.1920. “The chemistry of the earth's crust” . Franklin Inst., Jour., v. 190, p. 757–815, 1920.
Wiseman, John D. H., and H. Bennett. 1940. “The distribution of organic carbon and nitrogen in sediments from the Arabian Sea” . John Murray Exped. 1933–34, Sci. Results, v. 3, p. 193–221, 1940.
ZoBell, Claude E.n 1939. Occurrence and activity of bacteria in marine sediments. p. 416–427 in Trask (ed.), Recent marine sediments, 1939.
ZoBell, Claude E., and D. Q. Anderson. 1936. “Vertical distribution of bacteria in marine sediments” . Amer. Assn. Petrol. Geol., Bull., v. 20, p. 258–269, 1936.
Tables for Computing Geopotential Distances between Isobaric Surfaces
Contents
| TABLE I. | Specific volume of sea water of salinity 35 ‰ and temperature O°C, and at stated pressure, α35,0,p exprwsed in cm2/g or m3/ton. (From Bjerknes and Sandstrilm, 1910.) |
| TABLE II. | Geopotential distances from the sea surface to stated isobaric surfaces in sea water of salinity 35 ‰ and temperature O°C, D35,0,p, expressed in dynamic meters. (From Bjerknes and Sandström, 1910, expanded by ms. data.) |
| TABLE III. | 105Δs,ϑ as function of σ. (From Sverdrup, 1933.) |
| TABLE IVa. | 105Δs,p as function of salinity and pressure. (From Sverdrup, 1933.) |
| TABLE IVb. | 105Δs,p as function of salinity and pressure. (From Sverdrup, 1933.) |
| TABLE Va. | 105Δϑ,p as function of temperature and pressure. (From Sverdrup, 1933.) |
| TABLE Vb. | 105Δϑ,p as function of temperature and pressure. (From Sverdrup, 1933.) |
Symbols and Definitions
α35,0,p: Specific volume of sea water of salinity 35 ‰ and temperature O°C, and at pressure p.
δ: Anomaly of specific volume of sea water of salinity S and temperature ϑ and at pressure p (see p. 58):
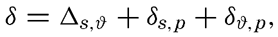
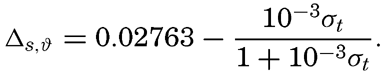
(Dl − D2)s: Standard geopotential distance between the isobaric surfaces p1 and p2 (equation XII, 6, p. 408):
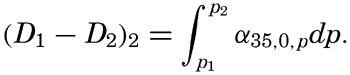
ΔD: Anomaly of the geopotential distance between the isobaric surfaces p1 and p2 (equation XII, 7, p. 409):
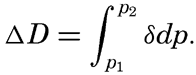
Explanation
If σt has been computed by means of Knudsen's or other tables, the specific volume anomaly, δ, can be found from tables III, IV, and V. If numerous computations are to be made, special tables should be prepared with closer intervals of the arguments. In order to facilitate such preparation and in order to avoid accumulation of errors, the terms have been tabulated with one more decimal place than warranted by the accuracy of the temperature and salinity observations.
When the specific volume anomalies have been found, the geopotential anomalies can be computed by numerical integration (table 61, p. 411).
Bibliography
Bjerknes, V., and J. W. Sandström. 1910. “Dynamic meteorology and hydrography” . Pt. I, Statics. Carnegie Inst. Washington, Pub. no. 88, 146 pp. + tables. 1910.
Knudsen, Martin. 1901. Hydrographical tables. Copenhagen. G. E. C. Gad. 63 pp. 1901.
Sverdrup, H. U.1933. Vereinfachtes Verfahren zur Berechnung der Druckund Massenverteilung im Meere. Geofysiske Publikasjoner, v. 10, no. 1, 9 pp. 1933. Oslo.
| Pressure (decibars) | 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.97264 | 0.97219 | 0.97174 | 0.97129 | 0.97084 | 0.97040 | 0.96995 | 0.96951 | 0.96907 | 0.96863 |
| 1000 | 0.96819 | 0.96775 | 0.96732 | 0.96688 | 0.96645 | 0.96602 | 0.96559 | 0.96516 | 0.96473 | 0.96430 |
| 2000 | 0.96388 | 0.96345 | 0.96303 | 0.96261 | 0.96219 | 0.96177 | 0.96136 | 0.96094 | 0.96053 | 0.96011 |
| 3000 | 0.95970 | 0.95929 | 0.95888 | 0.95848 | 0.95807 | 0.95766 | 0.95726 | 0.95686 | 0.95646 | 0.95606 |
| 4000 | 0.95566 | 0.95526 | 0.95486 | 0.95447 | 0.95407 | 0.95368 | 0.95329 | 0.95289 | 0.95251 | 0.95212 |
| 5000 | 0.95173 | 0.95134 | 0.95096 | 0.95057 | 0.95019 | 0.94981 | 0.94943 | 0.94905 | 0.94867 | 0.94829 |
| 6000 | 0.94791 | 0.94754 | 0.94717 | 0.94679 | 0.94642 | 0.94605 | 0.94568 | 0.94531 | 0.94494 | 0.94457 |
| 7000 | 0.94421 | 0.94384 | 0.94348 | 0.94312 | 0.94275 | 0.94239 | 0.94203 | 0.94167 | 0.94132 | 0.94096 |
| 8000 | 0.94060 | 0.94025 | 0.93989 | 0.93954 | 0.93919 | 0.93883 | 0.93848 | 0.93813 | 0.93778 | 0.93744 |
| 9000 | 0.93709 | 0.93674 | 0.93640 | 0.93605 | 0.93571 | 0.93537 | 0.93503 | 0.93469 | 0.93434 | 0.93401 |
| p (decibars) | D35,0,p (dynamic meters) | p (decibars) | D35,0,p (dynamic meters) |
|---|---|---|---|
| 10 | 9.7262 | 1200 | 1163.9534 |
| 20 | 19.4520 | 1400 | 1357.3295 |
| 30 | 29.1773 | 1600 | 1550.5327 |
| 40 | 38.9021 | 1800 | 1743.5639 |
| 50 | 48.6265 | 2000 | 1936.4246 |
| 75 | 72.9356 | 2500 | 2417.8360 |
| 100 | 97. 2417 | 3000 | 2898.2041 |
| 150 | 145.8457 | 3500 | 3377.5445 |
| 200 | 194.4382 | 4000 | 3855.8733 |
| 300 | 291.5898 | 4500 | 4333. 2053 |
| 400 | 388.6965 | 5000 | 4809.5559 |
| 500 | 485.7584 | 6000 | 5759.3685 |
| 600 | 582.7759 | 8000 | 7647.8173 |
| 800 | 776.6777 | 10000 | 9522.0255 |
| 1000 | 970.4032 |
| σt | .00 | 01 | 0.2 | .03 | .04 | .05 | .06 | .07 | .08 | .09 | .10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 23.0 | .487.8 | 486.8 | 485.9 | 484.9 | 484.0 | 483.0 | 482.0 | 481.1 | 480.1 | 479.2 | 478.2 |
| .1 | 478.2 | 477.2 | 476.3 | 475.4 | 474.4 | 473.4 | 472.5 | 471.6 | 470.6 | 469.6 | 468.7 |
| .2 | 468.7 | 467.7 | 466.8 | 465.8 | 464.9 | 463.9 | 462.9 | 462.0 | 461.0 | 460.1 | 459.1 |
| .3 | 459.1 | 458.1 | 457.2 | 456.3 | 455.3 | 454.3 | 453.4 | 452.5 | 451.5 | 450.5 | 449.6 |
| .4 | 449.6 | 448.6 | 447.7 | 446.7 | 445.8 | 444.8 | 443.8 | 442.9 | 441.9 | 441.0 | 440.0 |
| .5 | 440.0 | 439.0 | 438.1 | 437.2 | 436.2 | 435.2 | 434.3 | 433.4 | 432.4 | 431.4 | 430.5 |
| .6 | 430.5 | 429.5 | 428.6 | 427.6 | 426.7 | 425.7 | 424.7 | 423.8 | 422.8 | 421.9 | 420.9 |
| .7 | 420.9 | 419.9 | 419.0 | 418.1 | 417.1 | 416.1 | 415:2 | 414.3 | 413.3 | 412.3 | 411.4 |
| .8 | 411.4 | 410.4 | 409.5 | 408.5 | 407.6 | 406:6 | 405.6 | 404.7 | 403.7 | 402.8 | 401.8 |
| .9 | 401.8 | 400.8 | 399.9 | 398.9 | 398.0 | 397.0 | 396.0 | 395.1 | 394.1 | 393.2 | 392.2 |
| 24.0 | 392.2 | 391.2 | 390.3 | 389.4 | 388.4 | 387.4 | 386.5 | 385.6 | 384.6 | 383.6 | 382.7 |
| .1 | 382.7 | 381.7 | 380.8 | 379.9 | 378.9 | 377.9 | 377.0 | 376.1 | 375.1 | 374.1 | 373.2 |
| .2 | 373.2 | 372.2 | 371.3 | 370.3 | 369.4 | 368.4 | 367.4 | 366.5 | 365.5 | 364.6 | 363.6 |
| .3 | 363.6 | 362.6 | 361.7 | 360.8 | 359.8 | 358.8 | 357.9 | 357.0 | 356.0 | 355.0 | 354.1 |
| .4 | 354.1 | 353.1 | 352.2 | 351.3 | 350.3 | 349.3 | 348.4 | 347.5 | 346.5 | 345.5 | 344.6 |
| .5 | 344.6 | 343.6 | 342.7 | 341.8 | 340.8 | 339.8 | 338.9 | 338.0 | 337.0 | 336.0 | 335.1 |
| .6 | 335.1 | 334.1 | 333.2 | 332.2 | 331.3 | 330.3 | 329.3 | 328.4 | 327.4 | 326.5 | 325.5 |
| .7 | 325.5 | 324.5 | 323.6 | 322.7 | 321.7 | 320.7 | 319.8 | 318.9 | 317.9 | 316.9 | 316.0 |
| .8 | 316.0 | 315.0 | 314.1 | 313.2 | 312.2 | 311.2 | 310.3 | 309.4 | 308.4 | 307.4 | 306.5 |
| .9 | 306.5 | 305.5 | 304.6 | 303.7 | 302.7 | 301.7 | 300.8 | 299.9 | 298.9 | 297.9 | 297.0 |
| 25.0 | 297.0 | 296.0 | 295.1 | 294.1 | 293.2 | 292.2 | 291.2 | 290.3 | 289.3 | 288.4 | 287.4 |
| .1 | 287.4 | 286.4 | 285.5 | 284.6 | 283.6 | 282.6 | 281.7 | 280.8 | 279.8 | 278.8 | 277.9 |
| .2 | 277.9 | 276.9 | 276.0 | 275.1 | 274.1 | 273.1 | 272.2 | 271.3 | 270.3 | 269.3 | 268.4 |
| .3 | 268.4 | 267.4 | 266.5 | 265.6 | 264.6 | 263.6 | 262.7 | 261.8 | 260.8 | 259.8 | 258.9 |
| .4 | 258.9 | 257.9 | 257.0 | 256.1 | 255.1 | 254.1 | 253.2 | 252.3 | 251.3 | 250.3 | 249.4 |
| .5 | 249.4 | 248.4 | 247.5 | 246.6 | 245.6 | 244.6 | 243.7 | 242.8 | 241.8 | 240.8 | 239.9 |
| .6 | 239.9 | 238.9 | 238.0 | 237.1 | 236.1 | 235.1 | 234.2 | 233.3 | 232.3 | 231.3 | 230.4 |
| .7 | 230.4 | 229.4 | 228.5 | 227.6 | 226.6 | 225.6 | 224.7 | 223.8 | 222.8 | 221.8 | 220.9 |
| .8 | 220.9 | 219.9 | 219.0 | 218.1 | 217.1 | 216.1 | 215.2 | 214.3 | 213.3 | 212.3 | 211.4 |
| .9 | 211.4 | 210.4 | 209.5 | 208.6 | 207.6 | 208.6 | 205.7 | 204.8 | 203.8 | 202.8 | 201.9 |
| 26.0 | 201.9 | 200.9 | 200.0 | 199.1 | 198.1 | 197.1 | 196.2 | 195.3 | 194.3 | 193.3 | 192.4 |
| .1 | 192.4 | 191.4 | 190.5 | 189.6 | 188.6 | 187.6 | 186.7 | 185.8 | 184.8 | 183.8 | 182.9 |
| .2 | 182.9 | 181.9 | 181.0 | 180.1 | 179.1 | 178.1 | 177.2 | 176.3 | 175.3 | 174.3 | 173.4 |
| .3 | 173.4 | 172.4 | 171.5 | 170.6 | 169.6 | 168.6 | 167.6 | 166.8 | 165.8 | 164.8 | 163.9 |
| .4 | 163.9 | 162.9 | 162.0 | 161.1 | 160.1 | 159.1 | 158.2 | 157.3 | 156.3 | 155.3 | 154.4 |
| .5 | 154.4 | 153.5 | 152.5 | 151.6 | 150.6 | 149.7 | 148.7 | 147.8 | 146.8 | 145.9 | 144.9 |
| .6 | 144.9 | 144.0 | 143.0 | 142.1 | 141.1 | 140.2 | 139.2 | 138.3 | 137.3 | 136.4 | 135.4 |
| .7 | 135.4 | 134.5 | 133.5 | 132.6 | 131.6 | 130.7 | 129.7 | 128.8 | 127.8 | 126.9 | 125.9 |
| .8 | 125.9 | 125.0 | 124.0 | 123.1 | 122.1 | 121.2 | 120.3 | 119.3 | 118.4 | 117.4 | 116.5 |
| .9 | 116.5 | 115.5 | 114.6 | 113.6 | 112.7 | 111.7 | 110.8 | 109.8 | 108.9 | 107.9 | 107.0 |
| 27.0 | 107.0 | 106.0 | 105.1 | 104.1 | 103.2 | 102.2 | 101.3 | 100.3 | 99.4 | 98.4 | 97.5 |
| .1 | 97.5 | 96.6 | 95.6 | 94.7 | 93.7 | 92.8 | 91.8 | 90.9 | 89.9 | 89.0 | 88.0 |
| .2 | 88.0 | 87.1 | 86.1 | 85.2 | 84.2 | 83.3 | 82.3 | 81.4 | 80.4 | 79.5 | 78.5 |
| .3 | 78.5 | 77.6 | 76.6 | 75.7 | 74.8 | 73.8 | 72.9 | 71.9 | 71.0 | 70.0 | 69.1 |
| .4 | 69.1 | 68.1 | 67.2 | 66.8 | 65.3 | 64.3 | 63.4 | 62.4 | 61.5 | 60.5 | 59.6 |
| .5 | 59.6 | 58.7 | 57.7 | 56.8 | 55.8 | 54.9 | 53.9 | 53.0 | 52.0 | 51.1 | 50.1 |
| .6 | 50.1 | 49.2 | 48.2 | 47.3 | 46.3 | 45.4 | 44.5 | 43.5 | 42.6 | 41.6 | 40.7 |
| .7 | 40.7 | 39.7 | 38.8 | 37.8 | 36.9 | 35.9 | 35.0 | 34.0 | 33.1 | 32.1 | 31.2 |
| .8 | 31.2 | 30.2 | 29.3 | 28.3 | 27.4 | 26.4 | 25.5 | 24.6 | 23.6 | 22.7 | 21.7 |
| .9 | 21.7 | 20.8 | 19.8 | 18.9 | 17.9 | 17.0 | 16.0 | 15.1 | 14.1 | 13.2 | 12.3 |
| 28.0 | 12.3 | 11.3 | 10.4 | 9.4 | 8.5 | 7.5 | 6.6 | 5.6 | 4.7 | 3.7 |
| Pressure (decibars) | Salinity ‰ | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | |
| 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 100 | −0.8 | −0.6 | −0.5 | −0.3 | −0.2 | 0.0 | 0.2 | 0.3 | 0.4 | 0.6 | 0.7 |
| 200 | −1.5 | −1.2 | −0.9 | −0.6 | −0.3 | 0.0 | 0.3 | 0.6 | 0.9 | 1.2 | 1.5 |
| 300 | −2.3 | −1.8 | −1.4 | −0.9 | −0.5 | 0.0 | 0.5 | 0.9 | 1.3 | 1.8 | 2.2 |
| 400 | −3.0 | −2.4 | −1.8 | −1.2 | −0.6 | 0.0 | 0.6 | 1.2 | 1.8 | 2.4 | 3.0 |
| 500 | −3.8 | −3.0 | −2.3 | −1.5 | −0.8 | 0.0 | 0.8 | 1.5 | 2.2 | 3.0 | 3.7 |
| 600 | −4.5 | −3.6 | −2.7 | −1.8 | −0.9 | 0.0 | 0.9 | 1.8 | 2.6 | 3.6 | 4.4 |
| 700 | −5.3 | −4.2 | −3.2 | −2.1 | −1.1 | 0.0 | 1.1 | 2.1 | 3.1 | 4.2 | 5.1 |
| 800 | −6.0 | −4.8 | −3.6 | −2,4 | −1.2 | 0.0 | 1.2 | 2.3 | 3.5 | 4.7 | 5.9 |
| 900 | −6.8 | −5.4 | −4.1 | −2.7 | −1.4 | 0.0 | 1.4 | 2.6 | 4.0 | 5.3 | 6.6 |
| 1000 | −7.5 | −6.0 | −4.5 | −3.0 | −1.5 | 0.0 | 1.5 | 2.9 | 4.4 | 5.9 | 7.3 |
| 1100 | −3.3 | −1.7 | 0.0 | 1.7 | 3.2 | 4.8 | 6.5 | 8.0 | |||
| 1200 | −3.6 | −1.8 | 0.0 | 1.8 | 3.5 | 5.2 | 7.0 | 8.7 | |||
| 1300 | −3.9 | −1.9 | 0.0 | 1.9 | 3.8 | 5.7 | 7.6 | 9.4 | |||
| 1400 | −4.1 | −2.1 | 0.0 | 2.1 | 4.1 | 6.1 | 8.1 | 10.1 | |||
| 1500 | −4.4 | −2.2 | 0.0 | 2.2 | 4.4 | 6.5 | 8.7 | 10.8 | |||
| 1600 | −4.7 | −2.3 | 0.0 | 2.3 | 4.7 | 6.9 | 9.3 | 11.5 | |||
| 1700 | −4.9 | −2.5 | 0.0 | 2.5 | 4.9 | 7.3 | 9.8 | 12.2 | |||
| 1800 | −5.2 | −2.6 | 0.0 | 2.6 | 5.2 | 7.8 | 10.9 | 12.9 | |||
| 1900 | −5.5 | −2.7 | 0.0 | 2.7 | 5.5 | 8.2 | 10.9 | 13.6 | |||
| 2000 | −5.8 | −2.9 | 0.0 | 2.9 | 5.8 | 8.6 | 11.5 | 14.3 | |||
| 2500 | −7.2 | −3.6 | 0.0 | 3.6 | 7.1 | 10.7 | 14.2 | 17.7 | |||
| 3000 | −8.5 | −4.3 | 0.0 | 4.2 | 8.5 | 12.7 | 16.8 | 21.0 | |||
| 3500 | −9.9 | −4.9 | 0.0 | 4.9 | 9.7 | 14.6 | 19.4 | 24.2 | |||
| 4000 | −11.1 | −5.6 | 0.0 | 5.5 | 11.0 | 16.5 | 22.0 | 27.4 | |||
| Pressure (decibars) | Salinity ‰ | ||||
|---|---|---|---|---|---|
| 34.4 | 34.6 | 34.8 | 35.0 | 35.2 | |
| 2000 | −1.7 | −1.2 | −0.6 | 0.0 | 0.6 |
| 2500 | −2.2 | −1.4 | −0.7. | 0.0 | 0.7 |
| 3000 | −2.6 | −1.7 | −0.9 | 0.0 | 0.8 |
| 3500 | −2.9 | −2.0 | −1.0 | 0.0 | 1.1 |
| 4000 | −3.4 | −2.2 | −1.1 | 0.0 | 1.1 |
| 4500 | −3.7 | −2.5 | −1.2 | 0.0 | |
| 5000 | −4.1 | −2.7 | −1.4 | 0.0 | |
| 5500 | −4.4 | −3.0 | −1.5 | 0.0 | |
| 6000 | −4.8 | −3.2 | −1.6 | 0.0 | |
| 6500 | −5.1 | −3.4 | −1.7 | 0.0 | |
| 7000 | −5.5 | −3.6 | −1.8 | 0.0 | |
| 7500 | −5.8 | −3.8 | −1.9 | 0.0 | |
| 8000 | −6.1 | −4.1 | −2.0 | 0.0 | |
| 8500 | −6.4 | −4.3 | −2.1 | 0.0 | |
| 9000 | −6.7 | −4.5 | −2.2 | 0.0 | |
| 9500 | −7.0 | −4.6 | −2.3 | 0.0 | |
| 10000 | −7.3 | −4.8 | −2.4 | 0.0 | |
| Pressure (decibars) | Temperature °C | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | 20 | 25 | 30 | |
| 0. | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 100 | −0.6 | −0.3 | 0.0 | 0.3 | 0.5 | 0.7 | 1.0 | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 | 2.2 | 2.9 | 3.5 | 3.9 | 4.2 |
| 200 | −1.1 | −0.6 | 0.0 | 0.6 | 1.1 | 1.5 | 2.0 | 2.4 | 2.8 | 3.2 | 3.5 | 3.9 | 4.3 | 5.8 | 7.0 | 7.8 | 8.4 |
| 300 | −1.7 | 0.9 | 0.0 | 0.8 | 1.6 | 2.3 | 3.0 | 3.7 | 4.3 | 4.8 | 5.4 | 5.9 | 6.5 | 8.8 | 10.4 | 11.6 | 12.5 |
| 400 | −2.2 | −1.1 | 0.0 | 1.1 | 2.1 | 3.0 | 4.0 | 4.9 | 5.7 | 6.4 | 7.2 | 7.9 | 8.6 | 11.7 | 13.9 | 15.5 | 16.7 |
| 500 | −2.8 | −1.4 | 0.0 | 1.4 | 2.6 | 3.8 | 5.0 | 6.1 | 7.1 | 8.0 | 9.0 | 9.9 | 10.8 | 14.6 | 17.4 | 19.4 | 20.9 |
| 600 | −3.3 | −1.7 | 0.0 | 1.6 | 3.1 | 4.6 | 6.0 | 7.3 | 8.5 | 9.7 | 10.8 | 11.9 | 12.9 | 17.4 | 20.8 | 23.2 | 24.9 |
| 700 | −3.9 | −2.0 | 0.0 | 1.9 | 3.7 | 5.3 | 6.9 | 8.4 | 9.8 | 11.2 | 12.5 | 13.8 | 15.0 | 20.2 | 24.1 | 27.0 | 29.0 |
| 800 | −4.4 | −2.2 | 0.0 | 2.1 | 4.2 | 6.1 | 7.9 | 9.6 | 11.2 | 12.8 | 14.3 | 15.7 | 17.1 | 23.1 | 27.5 | 30.7 | 33.0 |
| 900 | −5.0 | −2.5 | 0.0 | 2.4 | 4.7 | 6.8 | 8.8 | 10.7 | 12.6 | 14.3 | 16.0 | 17.6 | 19.2 | 25.9 | 30.8 | 34.5 | 37.1 |
| 1000 | −5.5 | −2.8 | 0.0 | 2.7 | 5.3 | 7.6 | 9.8 | 11.9 | 14.0 | 15.9 | 17.7 | 19.5 | 21.3 | 28.7 | 34.2 | 38.3 | 41.1 |
| 1100 | −6.0 | −3.1 | 0.0 | 3.0 | 5.8 | 8.3 | 10.7 | 13.0 | 15.3 | 17.4 | 19.4 | 21.4 | 23.3 | 31.4 | 37.5 | ||
| 1200 | −6.5 | −3.3 | 0.0 | 3.2 | 6.3 | 9.1 | 11.6 | 14.1 | 16.6 | 18.9 | 21.1 | 23.3 | 25.4 | 34.1 | 40.7 | ||
| 1300 | −7.1 | −3.6 | 0.0 | 3.5 | 6.8 | 9.8 | 12.6 | 15.3 | 17.9 | 20.4 | 22.8 | 25.1 | 27.4 | 36.9 | 44.0 | ||
| 1400 | −7.6 | −3.8 | 0.0 | 3.7 | 7.3 | 10.6 | 13.5 | 16.4 | 19.4 | 21.9 | 24.5 | 27.0 | 29.5 | 39.6 | 47.2 | ||
| 1500 | −8.1 | −4.1 | 0.0 | 4.0 | 7.8 | 11.3 | 14.4 | 17.5 | 20.5 | 23.4 | 26.2 | 28.9 | 31.5 | 42.3 | 50.5 | ||
| 1600 | −8.6 | −4.3 | 0.0 | 4.2 | 8.2 | 12.0 | 15.4 | 18.6 | 21.8 | 24.9 | 27.8 | 30.7 | 33.5 | 44.9 | 53.6 | ||
| 1700 | −9.1 | −4.6 | 0.0 | 4.5 | 8.7 | 12.7 | 16.3 | 19.7 | 23.1 | 26.3 | 29.5 | 32.5 | 35.4 | 47.6 | 56.8 | ||
| 1800 | −9.6 | −4.8 | 0.0 | 4.7 | 9.2 | 13.4 | 17.2 | 20.8 | 24.3 | 27.8 | 31.1 | 34.3 | 37.4 | 50.2 | 59.9 | ||
| 1900 | −10.1 | −5.1 | 0.0 | 5.0 | 9.7 | 14.1 | 18.1 | 21.9 | 25.6 | 29.2 | 32.7 | 36.1 | 39.3 | 52.9 | 63.1 | ||
| 2000 | −10.6 | −5.3 | 0.0 | 5.2 | 10.1 | 14.7 | 19.0 | 23.0 | 26.9 | 30.7 | 34.4 | 37.9 | 41.3 | 55.5 | 66.2 | ||
| 2500 | −13.1 | −6.5 | 0.0 | 6.3 | 12.3 | 18.1 | 23.4 | 28.3 | 33.1 | 37.7 | 42.2 | 46.6 | 50.7 | 68.2 | |||
| 3000 | −15.4 | −7.6 | 0.0 | 7.4 | 14.4 | 21.2 | 27.6 | 33.4 | 39.1 | 44.6 | 49.9 | 55.0 | 59.8 | 80.4 | |||
| 3500 | −17.7 | −8.7 | 0.0 | 8.4 | 16.4 | 24.2 | 31.5 | 38.3 | 44.9 | 51.2 | 57.3 | 63.1 | 68.6 | 92.2 | |||
| 4000 | −19.9 | −9.9 | 0.0 | 9.5 | 18.4 | 27.0 | 35.2 | 43.0 | 50.5 | 57.6 | 64.4 | 70.9 | 77.1 | ||||
| Pressure (decibars) | Temperature °C | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −1.0 | −0.5 | 0.0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | |
| 2000 | −5.3 | −2.6 | 0.0 | 2.6 | 5.2 | 7.7 | 10.1 | 12.4 | 14.7 | 16.9 | 19.0 | 21.0 | 23.0 |
| 2500 | −6.5 | −3.2 | 0.0 | 3.2 | 6.3 | 9.3 | 12.3 | 15.2 | 18.1 | 20.8 | 23.4 | 25.9 | 28.3 |
| 3000 | −7.6 | −3.7 | 0.0 | 3.7 | 7.4 | 11.0 | 14.4 | 17.8 | 21.2 | 24.5 | 27.6 | 30.6 | 33.4 |
| 3500 | −8.7 | −4.3 | 0.0 | 4.2 | 8.4 | 12.5 | 16.4 | 20.3 | 24.2 | 28.0 | 31.7 | ||
| 4000 | −9.9 | −4.9 | 0.0 | 4.8 | 9.5 | 14.0 | 18.4 | 22.7 | 27.0 | 31.3 | 35.6 | ||
| 4500 | −11.0 | −5.4 | 0.0 | 5.3 | 10.4 | 15.4 | 20.3 | 25.0 | 29.6 | ||||
| 5000 | −12.0 | −5.9 | 0.0 | 5.7 | 11.2 | 16.7 | 22.1 | 27.2 | 32.1 | ||||
| 5500 | −13.0 | −6.4 | 0.0 | 6.1 | 12.1 | 18.0 | 23.9 | ||||||
| 6000 | −13.9 | −6.9 | 0.0 | 6.5 | 12.9 | 19.3 | 25.6 | ||||||
| 6500 | −14.8 | −7.3 | 0.0 | 6.9 | 13.7 | 20.5 | 27.3 | ||||||
| 7000 | −15.7 | −7.8 | 0.0 | 7.4 | 14.6 | 21.7 | 28.9 | ||||||
| 7500 | −16.6 | −8.2 | 0.0 | 7.8 | 15.4 | 23.0 | 30.5 | ||||||
| 8000 | −17.4 | −8.6 | 0.0 | 8.2 | 16.1 | 24.1 | 32.0 | ||||||
| 8500 | −18.2 | −9.0 | 0.0 | 8.6 | 17.0 | 25.3 | 33.5 | ||||||
| 9000 | −18.9 | −9.3 | 0.0 | 9.0 | 17.8 | 26.4 | 34.9 | ||||||
| 9500 | −19.6 | −9.7 | 0.0 | 9.4 | 18.6 | 27.5 | 36.2 | ||||||
| 10000 | −20.3 | −10.0 | 0.0 | 9.8 | 19.4 | 28.6 | 37.5 | ||||||
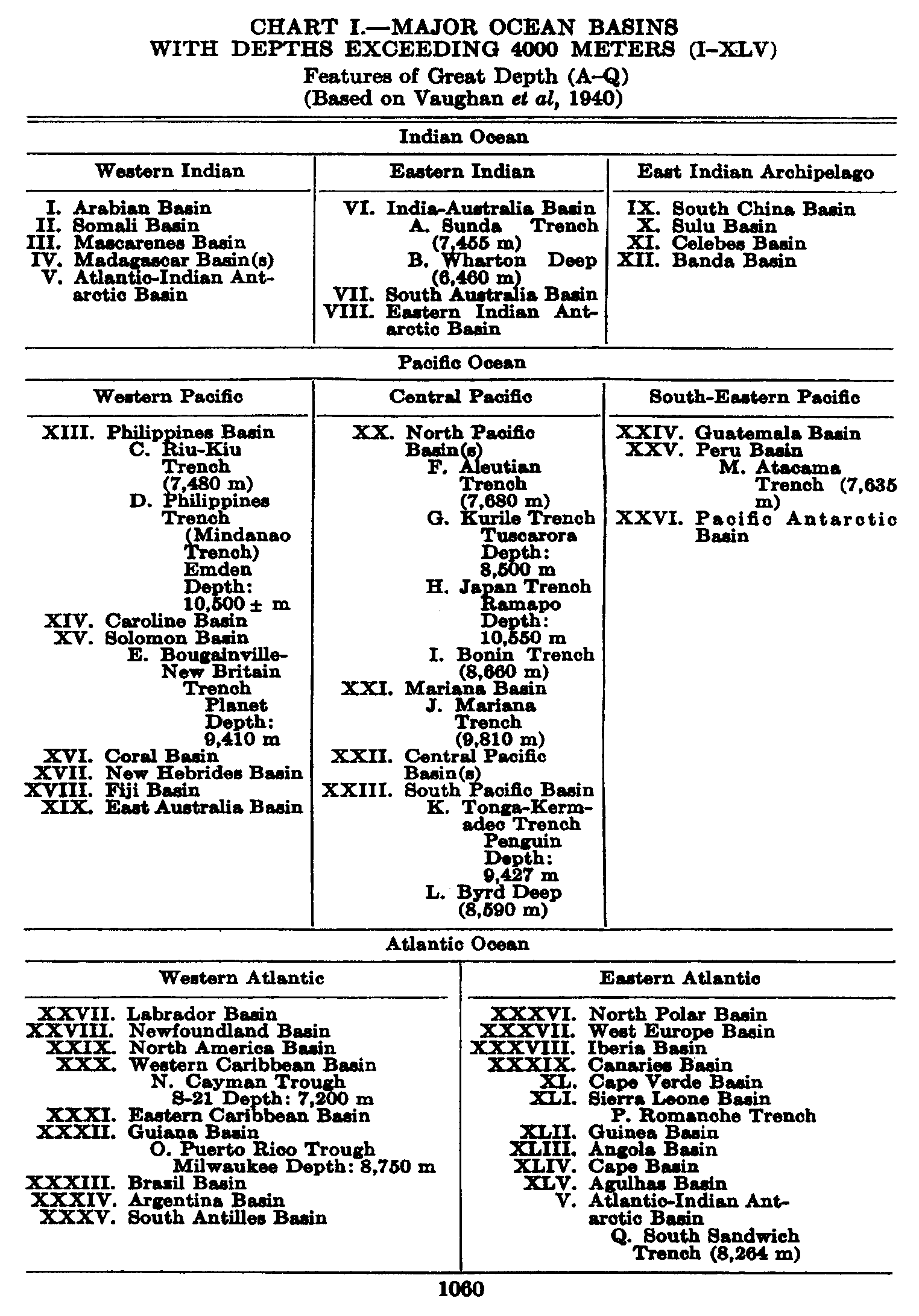
Subject Index
A
Absorption coefficients for dissolved gases, 190, 191, 202
Absorption of radiation (see Radiation)
Abyssal-benthic zone, 277
animals of, 805–810
Accessory growth factors, 769
Adaptations to planktonic existence, 764–766, 821–823
Adiabatic temperature distribution, Mindanao Trench, 739
Adiabatic temperature gradient, 63, 64
Advection, definition of, 157
Agulhas Stream, 696
Air-borne material in sediments, 955
Aleutian Current, 722, 723
Algae:
benthic, distribution of, 290, 291, 293, 295, 782
blue-green, 288–290
brown, 291–294
coralline, 290, 295, 855
green, 290–291
red, 294–295
yellow-green, 295–302
Alkalinity, 195–198
distribution, 208–210
relation to calcium carkonate content, 1000, 1001
Allogenic minerals in sediments, 987
Alternation of generations:
animals, 306, 319–320
plants, 290, 292, 294
Aluminum, 182
Ammonia:
distribution in oceans, 243, 244
produced on sea bottom, 995
role in nitrogen cycle, 256, 257
seasonal variation, 252, 253
Amphidromic point, 557, 558
Anchoring, in deep sea, 361, 362
Angular velocity of earth's rotation, 433
Animal exclusion, hypothesis of, 900
Animal population, 303
diversity of, 282
ecological gropus:
benthos, 280, 800
nekton, 281, 810
zooplankton, 281, 812
synopsis of, 304–314
Animals and the environmental factors, 823–873
light, 824
color correlations, 824–830
structural correlations, 830–833
vertical migrations, 835–839
ocean currents, 858–869
dispersal by, 858
maintenance of endemic population by, 863–865
oxygen, 869
anaerobic conditions, 871
consumption of, 852, 853, 870, 873
salinity, 839–843
a selective agency, 840
euryhalinity, 840
size and, 842
stenohalinity, 839
temperature, 843–858
effect of freezing, 844
influence on calcium precipitation, 853
influence on geographic distribution, 845, 849, 851
influence on metabolism, 852
influence on reproduction, 845–849, 857
influence on size, 855–857
influence on speciation, 867–869
Annelida:
reproduction, 321
synopsis, 308
Antarctic Circumpolar Current, 613–621
Antarctic Circumpolar Water, 607, 610–611
renewal, 620
Antarctic Convergence, 139
biology of, 809, 941, 942
formation, 618
location, 606, 607
Antarctic Intermediate Water, 139, 608
formation, 619
Indian Ocean, 691, 692, 697
North Atlantic, 670, 685, 686
South Atlantic, 626, 627, 629
South Pacific, 699–701
spreading of, 139, 744, 745
Antarctic Ocean:
bottom topography, 32
currents, 613–621
oxygen distribution, 621–623
water masses, 605–613
Antilles Current, 672, 675
Aragonite, 998, 1027
Arctic Intermediate Water:
North Atlantic, 670, 685, 686
Pacific, 717, 718
formation, 722
spreading, 745
Arctic plankton, 856, 868
Argon, 189
Arsenic, 183
Arthropoda:
reproduction, 322–324
synopsis, 309
Artificial sea water, 185, 186
Ascendant, definition of, 156
Associations of organisms, 880–882
commensalism, 881
environmental associations, 880
parasitism, 882
symbiosis, 881
Atlantic Ocean (see also North Atlantic and South Atlantic):
boundaries, 11
equatorial region, 631–637
currents, 632–637
water masses, 631, 632
oxygen distribution, 210, 686, 748
tides, 581–585
Atmosphere, composition of, 189
Authigenic minerals in sediments, 1027
frequency of occurrence, 987
Auxospores, 298
B
Bacteria:
aerobic, in sediments, 212, 996
anaerobic, in sediments, 212, 996
bottom deposits, effect on, 917–918
collection and analysis of, 383
denitrifying, 257
distribution in the sea, 918–920
importance in sedimentation, 995
importance to precipitation of iron compounds, 1032
in the Black Sea, 871
modes of life, 910, 913
autotrophic, 910
heterotrophic, 911
oxygen relations, 913, 917
nitrifying, 256
occurrence in sediments, 1016
possible role in petroleum formation, 996
structure and reproduction, 908–910
used to determine organic carbon, 249–251
utilizers of dissolved organic matter, 911–913
Baffin Bay:
bottom topography, 30
water masses, 663–665
Baltic Sea, 657–658
Barite concretions, 952, 1033
Barium, 183
Barnacles, reproduction of, 324, 326
Barriers, faunal (see Zoogeography)
Base-exchange in clay minerals, 988, 990
importance to flocculation, 958
Basins, 23, 26
adjacent seas, 37, 38, 736, 738
sediments in, 1026, 1028
with inflow across the sill, 148, 149
with outflow across the sill, 147, 148
Basin water, 147
plant nutrients, 246, 1028
stagnating, 1026, 1028
Bathythermograph, 352
Bay of Fundy:
tidal currents, 569
tides, 562, 563
Beach:
deposits:
character, 1023
composition, 1022
texture, 1019–1023
relation to slope of beach, 1018, 1019
equilibrium state, 44
terminology, 43, 44
Benguela Current, 627–629
Benthic environment and its subdivisions, 275–278
Benthic organisms, importance of to texture of sediments, 997
Benthos, 280
biological factors in the concentration, 907–908
collection of, 374–375
deep-sea, 805–810
littoral, 800–805
vertical distribution of, 806–807
Bering Sea, 732, 733
Bering Strait, currents of, 665, 723
Biocycles, 274
Biological factors influencing movements and concentrations of organisms, 898–908
Bioluminescence, 300, 304, 814, 833–835
Biosphere, 274
Biotype, 279
facies of, 280
inhabitants of, 280, 879
Bipolarity, 849–850, 868
Birds dependent upon the sea, 313, 942
Bjerknes' theorem of circulation, 460–462
Black Sea, 649–651
biology of, 871–872
lamination in sediments, 1040
Body fluids:
composition, 232, 270
osmotic relationships, 269, 272
control of, 271
relation to sea water, 269
Bolting cloth, 377, 378
Boric acid, influence of on alkalinity, 198, 199
Boron, 180
Bosporus, currents of, 650
Bottom samplers, 344–347, 375
Bottom topography:
illustrated, 18, 30, 32, 34, 35
influence on currents, 466–469
large-scale features, 23, 27–30
maximum depths, 18, 19
nomenclature, 25–27
profiles, 17, 18
representation of, 16
Bottom water, formation of, 138, 139
Antarctic, 611, 612
Irminger Sea, 682, 683
Labrador Sea, 664
Mediterranean, 645, 646
Norwegian Sea, 656, 657
Bottom water, potential temperature of, 749
Bottom water of the oceans, 745–754
Boundary condition:
dynamic, 441
kinematic, 424
Boundary surface, slope of, 444
Boundary waves (see Internal waves)
Bowen ratio, 117
Brachiopoda synopsis, 308
Brandt's theory of phytoplankton growth, 768, 784
Brazil Current, 628, 629
Bromine, 179
Browsing animals, 895–896
Bryozoa synopsis, 308
Buffer action of sets water, 195, 202
ecological importance, 268
By-the-wind sailer (see Velella)
C
Calanus:
abundance correlated with herring catches, 906–907
abundance correlated with whale catches, 905
biology of, in the Gulf of Maine, 864
feeding mechanism, 886–887
oxygen consumption by, 853, 870, 873
reproduction, 322–323, 903
vertical migrations, 836–837
Calcareous material in Sediments (see also Calcium carbonate) :
organisms contributing to, 950
Calcareous oozes (see also Pelagic sediments), 972
areas covered by, 975, 977, 978
Calcite, 998, 1027
Calcium, 178, 179
deposition by animals, 304–306, 853–855
deposition by plants, 290, 301, 855
Calcium Carbonate:
factors controlling organic precipitation, 999, 1000
inorganic precipitation, 208, 998
percentage in sediments, 998–1008
as function of depth, 1004, 1005
distribution, 1002–1008
factors controlling, 1007, 1008
solubility, 205–208
solution near bottom, 1001
supply to sediments, 1000
California Current, 724–727
annual variation of temperature, 131, 132
comparison with Peru Current, 725
off Southern California, 454
Canyons:
sediments in, 1024, 1026
submarine:
character, 39–41
formation, 41, 42
Carbon, 179
cycle of, 916
in sediments, 1010, 1011
organic, 248–251
ratio to nitrogen, 1010
Carbon dioxide:
as a limiting factor, 768
as a measure of production, 768
distribution, 208–210
exchange with atmosphere, 203
importance to deposition of calcium carbonate, 1000, 1001
methods of determination, 192, 193
partial pressure, 201–203
solubility, 190, 191, 202
system, 197–202
utilization of, by plants, 768
― 1064 ―Carbonic acid, dissociation consta,nts of, 199, 204, 205
Carbon-nitrogen-phosphorus ratio, 236, 237, 931
Caribbean Sea:
bottom topography, 35
currents, 641, 642
oxygen content, 640
water masses, 638, 641
Ceratium (see Dinoflagellates)
Chaetognatha:
as indicator species, 863
reproduction, 322
synopsis, 308
“Challenger,” dredging by, 805–807, 809
Chemical transformations, importance of to sediments, 952
China Sea, 735
Chitin, 289
Chlorine, 175
Chlorine-equivalent, 52
Chlorinity, 51, 52
units for expressing, 51
Chlorosity, 52
factors, 167
Chordata, synopsis of, 312–314
Circulation:
Bjerknes' theorem, 460–462
deep water, 745–755
thermal, 507–509
thermohaline, 509–510
transverse:
Antarctic Circumpolar Current, 618–620
caused by upwelling, 501
Equatorial Countercurrent, 635, 636, 711
Gulf Stream, 676
Circulation (water movements), biological significance of, 273–274
Clay minerals, 988–990
base exchange, 988, 990
flocculation, 958, 990
groups of, 989
origin, 990
Cl-ratio, 167
Coccolith ooze, 973
Coccolithophoridae, 301
Coelenterata:
reproduction, 319–320
synopsis, 306
Collection of:
bacteria, 383
benthos, 374
nekton, 376
plankton, 376–383
Color of animals, 824–830
changes, 825–827
of deep-sea animals, 826–829
of surface oceanic animals, 827
protective, 826
Color of sediments, 967–969
continental shelf, 1023
deep-sea, 978, 979
Color of the sea, 88, 89
Color of water, biological causes of, 289, 783–784
Compensation depth, 779
in various areas, 780
Compensation point, 778
Composition of foraminiferal tests, 991
Composition of marine organisms:
average, 230
body fluids, 232
concentration of elements, 233
elements reported, 228, 229
ratios O: C: N: P, 236, 237
skeletal material, 231
Composition of river water, 214–216
Composition of sea water, 165–174
constancy, 165–168
influenced by exchange with atmosphere, 212, 213
influenced by freezing, 216–219
influenced by rivers, 213–216
tables, 166, 173, 176, 177
Composition of sediments, 971, 972
Compressibility, 68
Concentrations, 158
conservative, 158
non-conservative, 159
units for reporting, 169, 171
Conductivity :
electrical, 71, 72
thermal (see also Eddy conductivity), 60, 61
Continental shelf:
average inclination, 21
extension, 20, 21
formation, 24, 25, 1019
sediments on, 1018–1023
Continental slope, inclination of, 22
Continuity, equation of, 423–426
used for finding layer of no motion, 457
Convergence, 419, 420
caused by winds, 500–503
regions of, 139, 140
vertical motion derived from, 425
Copepoda (see also Calanus):
as food for fish, 892, 907
as food of whales, 905
as grazers, 772, 901
food of, 901
reproduction, 322, 323, 903
synopsis, 309
Coral-reefs:
formation of, 854–855
organisms of, 855
Corals:
reproduction of, 319
systematic position of, 306
“Core method,” 146
Cores of sediments:
apparatus for obtaining, 345–347
compaction, 1037
relation between water content and particle size, 994
stratification in, 1038, 1039
Coring apparatus, 345–347
Corioli's force, 433–438
importance to ocean currents, 390
importance to waves, 520
Cotidal lines, 557
charts, 563
semidiurnal tide of Atlantic Ocean, 581, 582
Crinoidea:
bathymetric distribution, 807
synopsis, 312
Ctenophora, 307, 320, 890
Current meters, 366–373
Currents (see also Circulation, Tidal currents, and Wind currents):
absolute, 455–457
accuracy of computed, 393, 394, 453–455
computation, 391, 447–452
derived from ships' logs, 427, 428
derived from tongue-like distributions, 503–507
effect of bottom friction, 499, 500
effect of bottom topography, 466–469
Antarctic Circumpolar, 616
North Atlantic, 681
North Equatorial, Atlantic, 671, 672
importance to distribution of sediments, 965, 966, 1042, 1043
in stratified water, 444–447
related to the distribution of density, 389–395, 447–451
relative, 391, 442, 447–451
representations, 428–430
slope, 442, 458
sorting of shallow water sediments by, 1017–1019
transportation of particles along bottom by, 959–966
transportation of settling particles by, 959
units used, 363
vertical convection, 510, 511
wavelike pattern in South Atlantic, 630
Cyclic salt, 213, 214
D
Davidson Current, 725
Dead water, 587
Deeps, 20
of the oceans, 29
Deep-sea anchoring, 361, 362
Deep-sea benthos, 805–810
characteristics, 807
early discoveries, 805
food of, 808
horizontal distribution, 810
Deep-sea environmental system, 275–276
Deep water (see also under specific geographic regions):
circulation, 745–755
formation, 138, 139
Denmark Strait, flow through, 652–655
Density, 56, 57
computation, 57
direct determinations, 53
general distribution, 137–140
maximum, 66, 68
Density currents, 41
Deposition of sediments (see Sedimentation), 960
Depth of frictional resistance, 396, 493
“Desert quartz” in sediments, 955
Detritus feeders and scavengers, 892–895
Development of animals (see also Life cycles):
direct, 318
indirect, 318
of deep-sea animals, 318
Diatomaceous ooze, relation of to organic production, 942
Diatom ooze (see Pelagic sediments)
Diatoms:
as primary producers, 287, 296
auxospores, 298, 763
control by grazing, 771–772, 901–902
geographical types, 791, 793
methods of flotation, 764–765
number in the open sea, 763
number of important planktonic species, 762
nutrient absorption, 782–783
nutrient requirement, 768, 782–783
on whales, 299, 881
“persistent” culture of, 780
reproduction, 297–299
resting spores, 299, 762–763
sinking, 772, 781, 893
importance of viscosity, 794
structure, 295–297
systrophe in, 779, 781
temperature requirements, 770, 792–794
tychopelagic forms in the plankton, 762
― 1066 ―Diffusion (see also Eddy diffusivity), 69
Dimensions used in mechanics, 400–402
Dinoflagellates:
distribution, 762
methods of flotation, 765–766
number of important species in the plankton, 762
nutritional requirements, 299, 385
rate of production, 790, 930
reproduction, 300
structure, 299–300
systematic position, 304
temperature requirements, 385, 762
Diurnal migrations, 836–839
Divergence, 420
caused by wind, 500–503
near Antarctic continent, 620
near the equator, 635, 711
regions of, 140
vertical motion derived from, 425
Dolomite, 952, 998, 1027
Dredge, 374, 375
Drift bottles, 364, 365
Drift of plants, 791–792
Dynamic computations, 392, 408–411
example, 4
Dynamic equilibrium, principle of, 160–163
Dynamic meter, 392, 403
E
Earth, size of, 9
Earthquake waves (see also Tsunamis), 543, 544
Earth's rotation:
angular velocity, 433
deflecting force, 390, 433–438
East Greenland Current, 659, 660
East Indian Archipelago, basins and water of 736–739
Echinodermata:
reproduction, 324, 325, 326
synopsis, 311–312
Echo sounding (see also Sonic soundings), 76
Ecological groups of animals (see Animal population)
Eddy conductivity, 92
computation from temperature observations, 135–137
Eddy conductivity of the air, 114
Eddy diffusion:
importance to transportation of sediments along bottom, 962–966
lateral, dispersal of suspended material by, 959
Eddy diffusivity, 93
effect of stability on, 476, 477
importance to tongue-like distributions, 504, 507
lateral, 92, 93
importance to sedimentation, 959
importance to tongue-like distributions, 506–507
numerical values, 483, 485
numerical values, 481, 483, 484
Eddy viscosity, 91, 473, 474
influence of stability on, 476
numerical values, 481, 482
related to lateral mixing, 474, 475
Antarctic Circumpolar Current, 621
Equatorial Countercurrent, 634
numerical values, 485
Eel grass:
as primary producer, 303, 893, 936–937
structure and reproduction, 302–303
Eels:
dispersal of larvae, 861–862
homoiosmotic condition, 271
migrations, 811
Ekman current meter, 367, 368
Ekman spiral, 493
Ekman water bottle, 354
Elasmobranchs, 312
osmotic pressure of body fluids, 271
Electric conductivity, 71, 72
Elements derived from earth's crust, 219–222
Elements present in marine organisms, 228, 229
concentration of, 233
Elements present in sea water, 174
table, 176, 177
El Niño, 704, 705
effect on fauna, 274
Emerita:
dispersal of larvae, 859–860
feeding habits, 895
Endemic populations, maintenance of, 863–865
Energy equation, 441, 486
Environment, marine:
antiquity, 281–284
characteristics, 268
classification, 275–280
extent, 274
Environmental factors (see Light, Currents, Oxygen, Salinity, and Temperature)
Equatorial Countercurrent:
Atlantic, 633–637
Indian Ocean, 696
Pacific, 709–712
Equatorial currents (see North and South Equatorial Currents)
Equiscalar curves, 155
Equiscalar surfaces, 154, 155
Equivalent diameters of sedimentary debris, 958
compared to true dimensions, 982
statistical terms derived from, 970, 971
used for classifying sediments, 957, 974
Eroding velocity of ocean currents, 961
Erosion by currents, 41, 960–962
Euphausiids:
as food of whales, 904, 906–907
reproduction, 323
synopsis, 310
Euphotic zone, 774
Eurybathic animals, 806–807
Evaporation:
annual variation, 122
average annual, 120
computation of, 119, 120
diurnal variation, 122, 124
from the Black Sea, 650
from the Mediterranean Sea, 647
in different latitudes, 120, 121
table, 123
latent heat of, 62
observations of, 119
process of, 115–119
Extraterrestrial material in sediments, 952
F
Faeroe-Shetland Channel, flow through, 652–655
Falkland Current, 628, 630
Faunal areas (see Zoogeography)
Feeding mechanisms, 886–898
Filter feeders, 377, 886–892
rate of filtering, 901–902, 930
Fishes (see also under specific fishes):
deep-sea fishes:
adaptations, 828–835, 897
food of, 896–897
dispersal of eggs and larvae, 861, 865
feeding habits, 884, 890, 892
migrations, 811
osmotic regulations, 271
reproduction, 325
synopsis, 312
visual depths, 831–833
year classes, 326–328
Floating adaptations:
in animals, 818, 821–823
in diatoms, 764–765
in dinoflagellates, 765–766
Flocculation of fine sediments, 958
Florida Current, 672, 673–675
compared with Kuroshio, 720
Fluorine, 180
Fog, advection, 118
Foraminifera:
in deep-sea sediments, 983–985
reproduction, 319
synopsis, 304–305
Foraminiferal number, 985
Foraminiferal tests, composition of, 991
Forel scale, 88
Freezing point of sea water, 65–67
Friction:
boundary, 478–481
general terms, 469, 470
simplified terms, 475
Frictional forces, 469
in presence of turbulence, 474–476
Frictional stresses (see also Wind stress), 68, 69
due to lateral turbulence, 474
Antarctic Circumpolar Current, 621
Equatorial Countercurrent, 634
importance to dynamics of ocean currents, 489
due to vertical turbulence, 471–474
Fucus, 286, 291
reproduction, 293
zone, 277
G
Geochemistry:
importance of sediments to, 947
of the ocean waters, 219–222
Geopotential, 403
anomaly, 409
topography, 404
illustrated, 454, 726
of isobaric surfaces, 412–413
Glacier ice (see Icebergs)
Glauconite, 1035, 1036
factors important to formation, 997
frequency of occurrence, 987
Globigerina ooze (see Pelagic sediments), 305
Gradient, 156
Grazers of the sea, 884–886, 901–903
Grazing as a control of diatoms, 901–902
Gulf of California, 730–732
lamination in sediments, 1040
Gulf of Mexico:
bottom topography, 35
currents, 642
oxygen content, 641
water masses, 639–642
Gulf Stream, 672, 675–680
Gulf Stream System, 672
Gulfweed (see Sargassum)
H
Halosphaera, 301, 302
Heat:
conducted through ocean bottom, 110
exchange, ocean-atmosphere, 114, 115
off Norwegian coast, 656
specific, 61, 62
transformed from kinetic energy, 110
transported by ocean currents, 99
Helium, 189
Herring, numbers correlated with copepods, 892, 906, 907
Histogram, 970, 980
Holoplankton:
characteristic types of, 816, 817
dispersal of, 862–863
numbers of species of, 868
Hydrogen-ion (seepH):
related to organisms, 268, 770
Hydrogen sulphide, 187
amounts in sea water, 189
at bottom of basins, 1028
exclusion of animals by, 871, 872
importance to precipitation of iron, 952, 1032
in Black Sea, 651, 917
in sediments, 995
Hydrometers, 53
Hypoplankton, 814
Hypsographic curve, 19
I
Ice (see Sea ice)
Icebergs:
in the Antarctic, 624, 625
in the Arctic, 667, 668
prediction of drift, 668
transporting sedimentary debris, 953, 1043
Indian Ocean:
boundaries, 11
currents, 695–697
oxygen distribution, 697, 698
water masses, 690–695
Indicator species, 791–792, 793, 847, 849, 862–863, 865–867
Individual population succession, 384
Individual time change, 157
Inertia, circle of, 437
motion in, 438, 439
Inorganic precipitates in sediments, 951, 952
Insects, 310
Insular shelf, formation of, 24
Internal waves, 586
comparison between theory and observations, 597–600
currents associated with, 588–590, 594
effect of Corioli's force, 595, 596
effect on results of dynamic computation, 601, 602
importance to mixing, 601
long, 587
observations, 591–595
short, 586
standing, 600, 601
where density varies continuously, 589–591
Interstitial water, 995
Intertidal zone, 276
animals of, 276, 840, 844
Iodine, 183
Ionic activity, 203–205
Ionic product, 205
of calcium carbonate, 205–207, 999
Irminger Current, 682
Irminger Sea, water masses of, 682, 683
Iron, 183
as a limiting factor for diatoms, 769
in red clay, 1031, 1032
precipitation of, 952, 1031, 1032
Isentropic surfaces, 415, 416
Isobaric surfaces, 390, 440
absolute topography, 456, 457
inclination, 410–412, 440
relative topography, 412, 413, 452–455
illustrated, 454, 726
Isobaths, 16
Isotopes in sea water, 47, 49
J
Japan Current (see Kuroshio)
Japan Sea, 734, 735
Jellyfish (see Medusae)
K
Kelp, 287
habitats, 287, 291, 293
structure and reproduction, 292, 293
Knot, 363
Kuroshio, 719, 720, 721
annual variation of temperature, 131, 132
eddy conductivity derived from, 136, 137
Kuroshio Countercurrent, 719
Kuroshio Extension, 719, 721, 722
Kuroshio System, 719
L
Laboratories on board ship, 339, 340
Labrador Current, 665
meeting Gulf Stream, 682
Labrador Sea:
currents, 665, 666
water masses, 663–665
Laminar boundary layer, 479
Laminar flow, 89, 470
Laminarian zone, 277
Laminations in sediments:
deep sea, 1038, 1039
shallow water, 1039–1040
Larvae (see Zooplankton, temporary)
Lateral mixing (see Eddy viscosity and Turbulence)
Law of parallel solenoids, 455
Layer of no motion, determination of, 456, 457
Level, reference, for depths, 10
Level surfaces, 390, 402
Liebig's law of the minimum, 768, 792
Life cycles of animals (see also Reproduction), 283, 319–322
field studies of, 322–323, 845–848, 862–865
Life in the sea, development of, 281–284
Light:
related to animal ecology, 824–839, 851, 899
related plant production, 774–776, 781–782
Limacina, biological studies of, 384
Limnoria, 310
food of, 896
reproduction, 317
Lithium, 182
Littoral system, 276–277
animals of, 800–805
horizontal distribution, 803–805
plants of, 286–295, 302
subdivisions, 275, 276, 286
Local change, 157
Local sequence, 384
Luminescence (see Bioluminescence)
Lunar hours, 548
M
Magnesium, 175
Mammalia:
reproduction, 326
synopsis, 313
Manganese, 184
in red clay, 1029, 1030
nodules and concretions, 952, 1028
Mechanical analysis of sediments, 958, 970
Mediterranean Sea:
bottom topography, 34
currents, 647, 648
formation of bottom water, 645
oxygen content, 648–650
plant nutrients, 245
water masses, 643–646
Mediterranean Water, spreading of, 670, 685, 686, 745
Medusae:
biological studies on, 320, 820
reproduction, 320
synopsis, 306
Meroplankton (see Zooplankton, temporary)
Messengers, 354
Meter wheel, 338
Micro-plants, significance of, 883–884
Migrations:
eel, 811, 861–862
from land to sea, 283, 302
from sea to land, 284
salmon, 811
vertical, 835–839
whales, 811, 905
Mixing length, 472
near a boundary surface, 479
Mollusca:
reproduction of, 324
synopsis of, 310–311
Momentum, transport of, 472, 473
Mucus feeding, 889, 894
Mud flows, 960
N
Nannoplankton, 819
Nansen water bottle, 353, 354
used for collecting phytoplankton, 382
Nathansohn's theory of plant nutrient distribution, 784
Nekton, 281, 810–812
biological factors in movements of, 904–907
Nemertinea, synopsis of, 307
Neon, 189
Nereocystis:
reproduction, 292
structure, 292
Neritic environmental province, 275, 279, 784
Nets, plankton, 376
catching power, 378–379
operation, 380
types, 379
Nitrate:
distribution in basins, 245
distribution in oceans, 241–243
related to deep-water circulation, 754
factors influencing distribution, 246
produced on sea bottom, 995
reduction and denitrification, 915
regeneration, 254–257
seasonal variation, 252, 253
utilization as a measure of production, 932
― 1070 ―Nitrate-nitrogen, ratio to phosphate-phosphorus, 236, 243
Nitrite:
distribution in oceans, 243
produced on sea bottom, 995
Nitrogen, 181
compounds, utilization of by plants, 768
in see water, 252–225
seasonal variation, 252
transformations, 253–255
dissolved:
amounts in sea water, 188
determination, 187
solubility, 188–191
in sediments, 1010, 1011
Nitrogen cycle, 913–916
ammonification, 914
in the sea, 255–257
nitrification, 914
nitrogen assimilation, 915
Nitrogen fixation, 916
Nitrogen-phosphorus ratio in plankton, 236, 768
Nitzschia clasterium, 296, 769
photosynthesis, 781, 933
Noctiluca, 304
reproduction, 319
Normal Water, 51
North Atlantic Current, 673, 680–683
North Atlantic Ocean:
currents, 671–686
oxygen distribution, 686
water masses, 668–671
North Equatorial Current:
Atlantic, 671
Indian Ocean, 696
Pacific, 708, 709, 718, 719
North Pacific Current, 719, 722
North Pacific Ocean:
currents, 718–728
eastern gyral, 723, 724
oxygen distribution, 728–730, 753
water masses, 712–718
North Polar Sea:
bottom topography, 30–32
currents, 661
oxygen content, 662, 663
water masses, 658, 659
North Sea:
currents, 660
water masses, 657
Norwegian Current, 659, 660
fluctuations, 655, 661, 662
Norwegian Sea:
bottom topography, 30–32
currents, 659
inflow of water, 652–656
outflow of water, 652–656
oxygen content, 662
water masses, 656, 657
Nursery areas, 315
Nutritional relationships, 882–898
micro-animals, significance of, 884–886
micro-plants, significance of, 883
O
Obelia, 306
reproduction, 320
Ocean currents, ecological relations of:
animals, 858–869
plants, 782–792
Oceanic environmental province, 275, 278
animals, 821, 827
plants, 763
Oceanographic vessels, 331–333
Oceans:
areas, 13, 15
boundaries of subdivisions, 12
mean depths, 13, 15
volumes, 13, 15
Oikopleura:
feeding mechanism, 888
systematic position, 312
Okhotsk Sea, 733
Oozes, ecological importance of, 278
Organic constituents in Sediments, 949–951, 983–986
Organic environment, 879
Organic matter:
dissolved, utilization of, 911–913
in sediments, 951
chemical composition, 1010
decrease with depth in deposit, 1016
distribution, 1013–1017
factors determining amounts, 1012–1013
quantity, 1008–1010
sources, 951, 1011
Organic production in the sea, 925–926
commercial, 936–937
cycle of organic matter in the sea, 926
in different regions, 937–944
phytoplankton, 927–934
zooplankton, 934–936
Osmotic pressure, function of salinity and temperature, 66, 67
Osmotic relationships of body fluids:
fresh-water animals, 269
marine animals, 269, 271, 839
Oxidation-reduction potential, 211, 212
importance to accumulation of iron in sediments, 1032
importance to accumulation of manganese in sediments, 1031
in sediments, 995–997
Oxygen;
as an environmental factor, 869–873, 903, 913, 917
in organic matter in sediments, 1011
production and consumption of, as index of organic production, 933–934
production by plants, 767, 777, 933
Oxygen, dissolved:
depletion in interstitial water, 995
depletion in relation to nutrient content, 237
determination, 187
relation to pH distribution, 209
solubility, 189–191
Oxygen consumption, bacterial, as a measure of organic carbon, 250
Oxygen content (see under specific geographic regions):
oceanic deep-water, 746, 748, 752–754
Oxygen distribution (see under specific geographic regions):
conditions for stationary, 161, 162
related to deep-water circulation, 754
Oyashio, 721, 733
meeting Kuroshio Extension, 722
Oysters, reproduction of, 316, 324, 846–847, 857
P
Pacific Ocean (see also North Pacific and South Pacific):
boundaries, 11
equatorial region, 706–712
currents, 708–712
oxygen content, 710, 711
phosphate, 710, 711
silicate, 710, 711
water masses, 706–708
oxygen distribution, 728–730, 753
Palagonite, 1027
frequency of occurrence, 987
Pelagic environment and its subdivisions 278
Pelagic sediments (deposits), 972
areas covered by, 977
average percentage of calcium carbonate, 1006
chemical composition, 991, 992
classification, 972–973
color, 978, 979
content of organic matter, 1015
depth range, 978
distribution, 974–978
inorganic constituents, 986–990
iron content, 992, 1030–1032
manganese content, 992, 1028–1031
minerals, 986–990
organic constituents, 983–986
phosphorus content, 992, 1032
radium content, 1034, 1035
rate of deposition, 1038, 1039
texture, 979–982
Pendulum day, 437
Permeability of sediments, 994
Persian Gulf, 690
Peru Current, 701–705
comparison with California Current, 703
organic production in, 942
Petroleum formation in marine sediments, 947, 1009
possible role of bacteria, 996
Pettersson-Nansen water bottle, 352
Phaeocystis, 301
Phillipsite, 1027
frequency of occurrence, 987
pH of sea water, 193
determination, 193, 194
distribution, 208–210
role in carbon dioxide system, 195–202
Phosphate:
as a limiting factor, 768, 788
distribution:
factors influencing, 246, 247
in basins, 245, 246
in oceans, 239–241
related to deep-water circulation, 754
in South Atlantic, 786–788
regeneration, 260–261
in isolated areas, 932
seasonal variation, 258
utilization of, by plants, 768, 931–932
Phosphate-phosphorus, ratio to nitrate-nitrogen, 236, 243
Phosphorescence (see Bioluminescence)
Phosphorite nodules, 952, 1032, 1033
Phosphorus, 182
in red clay, 1030, 1032, 1033
organic, in sea water, 257
Phosphorus cycle in the sea, 260–261, 916
Phosphorus-nitrogen ratio in plankton, 236
Photosynthesis of phytoplankton, 774
energy and illumination, 776
experiments, 777–782, 933
assimilation, 777
Photosynthesis ratio to respiration, 933
Physalia:
reproduction, 320
systematic position, 306
Phytoplankton (see also Plankton):
collection and analysis, 382–383
number of important species in, 762
photosynthesis, 774–782
relation to zooplankton, 898–904
Phytoplankton production, 923–934
factors of (see Diatoms and Dino-flagellates)
index of:
direct census, 927
oxygen production and consumption, 933–934
plant nutrient consumption, 931–933
plant pigment units, 928
Pigments extracted from mud, 969
Plankton (see also Phytoplankton and Zooplankton), 281
adaptations, 821–823
collecting methods, 376–383
equivalents, 929
macro-, micro-, and nannoplankton, 819
neritic, 820
oceanic, 821
Plankton and filter feeders, 886–892
Plant nutrients, 235
and vertical circulation of water, 782–790
convection, 790
regions of divergence and convergence, 787, 788
stabilization, 789
turbulence, 787–789
upwelling, 785–786
factors influencing distribution, 235, 236
renewal in surface layers:
Antarctic region, 620
Equatorial Countercurrent, Atlantic, 636
Equatorial Countercurrent, Pacific, 712
North Atlantic, 682
off coast of California, 725
off coast of Peru, 702
off west coast of South Africa, 628
storage in the sea, 784–785
winter maxima and summer minima, 939
Plants (see also Algae and Eel grass):
higher plants, 302–303
major producers in the sea, 287
Thallophyta, 288–302
Platyhelminthes, 307
Pleurobrachia, 307, 890
Polymerization of water, 47
Population, 162
Porosity of sediments, 993, 994
Portuguese man-of-war (see Physalia)
Potassium, 179
Potential temperature (see Temperature)
Pressure (see also Isobaric surfaces):
as an ecological factor, 273
field of, 405
internal field, 408
total field, 413
units, 55, 170
Pressure gradient, 405
Preying animals, 896–898
Primary food of the sea, 882, 883
Production (see Organic production and Phytoplankton production), 162
importance of, to organic matter in sediments, 1011, 1015
Projections, map, 10
Protozoa:
reproduction, 319
synopsis, 304–305
Pteropod ooze (see Pelagic sediments)
R
Radiation:
absorption in pure water, 80, 81
illustrated, 105, 106
absorption in sea water (see Radiation, extinction coefficients)
effective back, 111–113
extinction coefficients, 82, 84, 85
cause, 87, 88
influence of sun's altitude on, 86, 87
of total energy, 106, 107
from sun and sky, 101–104
heating due to absorption of, 108–110
long-wave, 98
measurements of extinction, 82, 83
nocturnal (see Radiation, effective back)
reflection from ice and snow, 113
reflection from sea surface, 104
scattering, 87
short-wave, 98
solar constant, 102
“surface loss,” 106
Radioacoustic ranging, 341
Radioactive elements, 184
in sediments, 1033–1035
Radiolaria:
reproduction, 319
systematic position, 305
Radiolarian ooze (see Pelagic sediments):
areas covered by, 977
color, 979
depth range, 978
distribution, 975, 976
inorganic constituents, 984, 986–988
organic constituents, 983, 986
radium content, 1034
― 1073 ―Radium, 184
in sediments, 1033–1035
Red clay (see Pelagic sediments):
areas covered by, 977
chemical composition, 991, 992
color, 979
content of organic matter, 1015
depth range, 978
distribution, 975, 976
inorganic constituents, 984, 986–988
iron content, 1030–1032
manganese content, 1029, 1030
organic constituents, 983, 984
phosphorus content, 1030, 1032, 1033
radium content, 1034
rate of sedimentation, 1039
texture, 980–982
Red Sea:
currents, 687–690
oxygen content, 688
water masses, 687, 688
Red Sea water, spreading of, 693, 695, 745
Reducing capacity, 212
in sediments, 996
Red water, 89
Refractive index, 70, 71
Relative relief, 19
Reproduction (see also Life cycles):
related to temperature, 846–849
types, 315
Reproductive distribution, 315
Resting spores in diatoms, 299
Rip currents, 537
importance to beach sediments, 1017, 1018
River water, composition of, 214–216
Rotifera, synopsis of, 307
Roughness length, 479
of sea bottom, 480
of sea surface, 491
Rubidium, 182
S
Sagitta:
as indicator species, 863
reproduction, 322
systematic position, 308
Salinity, 50
as an ecological factor, 770, 839–843
averape surface values, 123, 124
determination, 50–54
origin, 219
periodic variations at surface, 126
range in oceans, 55
units for expressing, 51, 54
Salmon:
migration, 811
transplantations, 850
Salpa, systematic position of, 312
Sardine:
feeding mechanism, 890
quantity fished, 896
Sargassum, 293, 883
reproduction, 293
Saturation coefficients for dissolved gases, 190, 191
Scalar fields, 154–156
Sea cucumbers:
consumption of detritus by, 894
reproduction, 325, 326
synopsis, 311
Sea ice:
influence of freezing on composition of sea water, 216–219
in the Antarctic, 623, 624
in the Arctic, 666, 667
amount influenced by currents, 662
physical properties, 72–74
salinity, 71, 12
transporting sedimentary debris, 954, 1043
Sea level:
ideal, 9
mean, 10, 561
slope:
along North American east coast, 677
in Caribbean Sea, 641, 678
near the equator, Atlantic, 634
near the equator, Pacific, 709
variations, 458–460
Seals, synopsis of, 313
Sea water:
artificial, 185, 186
relation to body fluid, 269
Sedimentation, 946
rate of, 1036–1041
estimated by stratigraphic method, 1038–1040
estimated by supply method, 1040–1041
Seechi disk, 82
Seiches, 538–542
importance to transportation of sediments, 965
on open coasts, 542
Settling velocity of sedimentary debris, 956–959
importance to transportation along bottom, 962–966
size-grade distribution derived from, 970
― 1074 ―Sharks (see Elasmobranchs)
Shorelines, 42–44
classification, 43
Silicate:
as a limiting factor, 769
distribution in oceans, 244–245
related to deep-water circulation, 754
factors influencing distribution, 246
seasonal variation, 261, 262
utilization by plants, 769
Siliceous material in sediments (see Diatom ooze and Radiolarian ooze):
organisms contributing to, 950
Siliceous oozes (see also Pelagic sediments), 973
areas covered by, 977, 978
Siliceous sediments:
diatoms in, 296
radiolaria in, 305
Silicoflagellates, 302
Silicon, 180
cycle in the sea, 262, 263
Sill depth, 25, 147
importance to character of basin water, 150
Caribbean Sea and Gulf of Mexico, 640
East Indian Archipelago, 736–738
of basins in adjacent seas, 37, 38, 738
Size-grade distribution in sediments, 970, 971
represented by cumulative curves, 970, 981
represented by histograms, 970, 980
statistical terms, 970, 971
Skeletal structures of marine organisms:
as constituents of sediments, 949
composition, 231
Sliming of the sea, 290, 291
Snakes, synopsis of, 313
Sodium, 175
Solar constant, 102
Solubility:
calcium carbonate, 205–208
gases, 190, 191
salts, 210–211
Solubility product, 205
Sonic soundings:
equipment, 342, 343
importance to knowledge of bottom topography, 16
Sound energy, absorption of, 78
Soundings:
available for charts of bottom topography, 14–16
methods, 342–344
Sounding velocity, 79
Sound waves:
velocity in sea water, 76, 77, 79
wave length, 77, 78
South Atlantic Ocean:
currents, 627–630
oxygen distribution, 630, 631
water masses, 625–627
South Equatorial Current:
Atlantic, 628, 633
Indian Ocean, 696
Pacific, 708, 709
South Pacific Ocean:
currents, 701–706
oxygen distribution, 728–730
water masses, 698–701
Specific heat, 61, 62
Specific humidity, 116
Specific volume, 57
anomaly, 57, 58
computation, 58
Sphere depth, mean, 19, 20
Sponges:
reproduction, 319
synopsis, 306
Stability, 416–418
influence on turbulence, 91, 92, 476
Stagnant water:
destruction of organic matter in, 1012
development, 1026
Standard depths of observation, 357
Starfish:
bathymetric distribution, 807
synopsis, 311
Stationary distribution, 157
Stationary velocity field, 423
Sterile distribution, 315, 847
Strait of Bab el Mandeb, currents of, 688–690
Strait of Gibraltar, currents of, 646–648
Stratosphere, oceanic, 141
Stream lines, 426
Strontium, 179
Strontium carbonate in radiolarians, 991
Submarine canyons (see Canyons)
Submarine geology, topics of, 22
Submarine topography (see Bottom topography)
Subtropical Convergence, 140
in Southern Oceans, 606
sinking of water in region of:
Indian Ocean, 691
North Atlantic, 670
North Pacific, 714
South Atlantic, 626
South Pacific, 700, 701
― 1075 ―Sues Canal, flow through, 688, 689
Sulphur, 178
cycle of, 917
Surface tension, 70
Suspended particles, 958
importance to extinction of radiation, 88
Suspension of sedimentary debris near bottom, 962–965
Symbiosis, 881–882
T
Temperature:
adiabatic changes, 63–65
annual variation:
at surface, 129, 130
in surface layers, 131–133
theory, 135–137
as an ecological factor, 770, 792–795, 843–858
average surface values, 127
difference, sea-surface minus air, 128, 129
diurnal variation:
at surface, 133, 134
in surface layer, 135
measurements, 347–352
potential, 64
at depths exceeding 4000 m, 747, 749
basin water, 149
bottom water, 749
Caribbean Sea, 640, 641
China Sea and Sulu Sea, 735
Gulf of Mexico, 641
Mediterranean Sea, 644
Mindanao Trench, 739
range, in oceans, 55
Temperature-salinity diagram, 142
illustrating water masses of:
all oceans, 741
equatorial region, Atlantic, 631
equatorial region, Pacific, 707
Indian Ocean, 692
North Atlantic, 669
North Pacific, 713
South Atlantic, 626
South Pacific, 699, 700
Subantarctic region, 612
used for checking data, 358
Teredo:
depredations by, 841
diet, 896
Terrigenous materials in sedments, 948, 949
Terrigenous mud, radium content of, 1034
Terrigenous sediments, 972–974
average percentage of calcium carbonate, 1006
classification, 973, 974
distribution, 972, 975, 976
rate of deposition, 1039, 1040
Texture of sediment:
beach, 1019–1022
bearing on content of organic matter, 1016
continental shelf, 1020–1022
deep sea. 979–982
Texture of sediments, 969–971
Thermal conductivity (see also Eddy conductivity), 60, 61
Thermal expansion, 60
Thermometers, 347–352
protected reversing, 349, 350
unprotected reversing, 350, 351
Thorium, 184
Tidal currents:
Atlantic Ocean, 584, 585
effect of friction, 577–580
influence of bottom topography, 567, 568
in sounds, 568, 569
rotary, 570
due to earth's rotation, 571–573
due to interference, 570
theory, 564
Tidal energy, 569
Tide-producing forces, 545–550
“Tide rips,” 716
Tides:
analysis and prediction, 564
Atlantic Ocean, 581
character, 558
cooscillating, 553
effect of Corioli's force, 555
effect of friction, 574
importance to shallow-water sediments, 1017
independent, 554
meteorological, 559
observations, 359–361
partial, 549, 558
theories, 550–552
Tintinnoinea, systematic position of, 305
Trajectories, 426
Transparency, 85
Transport, volume of, 462–465
Antarctic Circumpolar Current, 615–617
by wind currents, 498
North Atlantic, 683–685
North Pacific, 727, 728
South Atlantic, 628, 629
Transport across the equator:
Atlantic, 637, 685
Pacific, 752
Transportation of particles along bottom, 959–966
effect on shape, size, and composition, 966–967
Transportation of particles by currents, 959
Transportation of sediments to the sea, 953–956
by ice, 953
by organisms, 954
by winds, 954–955
importance to character of Sediments, 1043
Transport of heat by ocean currents, 99
Trawls: beam, otter, and ring, 375, 376
Tripping mechanism, 380
Tropical convergences, 140
Tropical submergence, 849
Troposphere, oceanic, 141
Tsunamis (see also Earthquake waves), 543
contributing to formation of submarine canyons, 42
importance to transportation of sediments, 965
Tunicates, bathymetric distribution of, 807
Turbulence (see also Eddy viscosity and Eddy diffusion), 90–93, 471
horizontal, 477, 478
importance to transportation of sediments, 960, 962–965
influence of stability on, 92, 476, 477
transport of momentum, 472, 473
U
Ulva, 286, 290
Undertow, 537
Units, fundamental, 400
Upwelling:
effect on annual variation of tempcrature, 131, 132
effect on content of plant nutrient in surface layer, 246, 247
importance to organic matter in sediments, 1044
off coast of California, 724, 725
off coast of Peru, 702, 703
off Somali coast, 696
off west coast of North Africa, 671
off west coast of South Africa, 627, 628
process, 140, 501
Urnormal-1937, 51
V
Vapor pressure over sea water, 66, 115, 116
Vector diagrams, 421
Vector fields, 418–420
Velella, 306, 320
Vertebrata, synopsis of, 312
Viscosity (see also Eddy viscosity):
dynamic, 69, 469, 470
kinematic, 470
Volcanic material in sediments, 949
transportation to sea by winds, 955
W
Wake Stream, 676
Water mass, 143
formation, 143–146
Water masses of the oceans (see also under geographic regions), 739–745
Water type, 143
Wave of translation, 537
Waves (see also Internal waves and Wind waves):
caused by earthquakes, 543
contributing to formation of sub-marine canyons, 42
characteristics, 516–521
destructive, 542
effect of Corioli's force on, 520
“tidal,” 542
Whales:
biological factors in movements, 904–905
diatoms on, 299, 881
feeding habits, 892
feeding mechanisms, 314, 891–892
food of, 273, 904–907
migrations, 811
rate of growth, 906
rate of metabolism, 935
reproduction and growth, 326
sounding of, 273
systematic position of, 314
Winches, 333–335
Wind currents, 492
Antarctic Ocean, 617
general character, 395–397
in shallow water, 496
secondary effect of, 500
transport by, 498
velocity, 494
Wind drift of ice, 623, 666
Wind factor, 494
Wind stress, 489–491
Wind waves:
breakers, 536
effect on beaches, 1017
dissipation, 536
energy, 533
forms and characteristics, 523–527
growth, 533
height, 532, 535
importance to beach sediments, 1017–1019
interference, 529
origin, 522
particle velocity, 528
short-crested, 531
Wire ropes, 335–338
Wood-boring organisms, 317, 841, 895–896
Wyville Thompson Ridge as a faunal barrier, 810, 849
X
X-ray methods in sediment studies, 947, 988
Y
Year classes, 326–328
Yellow Sea, 735
Z
Zoogeography:
barriers:
East Pacific, 803
land, 803
Wyville Thompson Ridge, 810, 849
faunal areas, 273, 799–810
Zooplankton (see also Plankton), 812–823
adaptations, 821–823
collection and analysis, 378–382
neritic and oceanic, 820–821
permanent, 816–819
production, 934–936
relation to physical-chemical environment, 823
relation to phytoplankton, 898–904
temporary, 814–815
Zostera (see Eel grass)
Index of Names
This index includes names of vessels, in italics, and names of collaborators which may not appear in the text but do appear in the bibliographies: e.g., Bjerknes et al, p. 433, which is entered in the index of names under Bjerknes, V., Bjerknes, J., Solberg, H., and Bergeron, T.
A
Agassiz, Alexander, 6, 277, 674
Agassiz expedition, 856
Albrecht, E., 81 '
Allee, W. C., 274, 280, 293, 879, 893
Allen, E. C., 195, 197, 199, 204, 205
Allen, E. J., 769, 780, 882, 899.
Allen, W. E., 382, 725, 763, 785
Altair,439, 680, 681
Anderson, D. Q., 250, 912, 918, 919, 920, 996, 1016
Anderson, L. J., 969
Andrée, K., 948, 978, 1028
Angström, Anders, 111, 112, 115
Arber, A., 302
Ardley, R. A. B., 332
Aristotle, 861
Armauer Hansen,332, 333, 362, 366, 669, 681
Aschkinass, E., 81
Atkins, W. R. G., 5, 82, 83, 85, 87, 176, 216, 768, 769, 928, 938
Atlantis,142, 238, 239, 242, 332, 362, 366, 593, 601, 669, 679, 680, 682, 746
Ault, J. P., 332
Avers, Henry G., 677
B
B.Z.N.Z.A.R. Expedition, 692, 746
Bache,674
Ball, Eric G., 194
Bangham, D. H., 180
Barker, H. A,, 385, 933
Barlow, E. W., 687
Barnes, C. A., 245, 733
Barnes, T. C., 47, 72, 843
Bartlett, J. R., 674
Bauer, L. A., 332, 915
Bavendamm, W., 918
Bayliss, W. M., 47
Beach, E. F., 183
Beale, A., 863
Beebe, W., 831
Bein, Willy, 70., 71, 168
Bencker, H., 16, 19
Benecke, W., 908, 911, 916, 918
Bennett, H., 1009, 1010, 1015, 1016
Bergeron, T., 433, 441, 460, 507
Bergmann, Ludwig, 78, 79
Bernoulli, D., 964
Bethe, A., 270
Bigelow, Henry B., 6, 7, 320, 789, 820, 847, 851, 863, 864, 884, 888, 890, 907
Birge, E. A,, 108, 381
Bjerknes, J., 433, 441, 460, 507
Bjerknes, V., 4, 55, 57, 58, 99, 400, 403, 409, 413, 415, 418, 433, 441, 460, 462, 507, 508, 509
Blake,362, 673, 674
Blegvad, H., 844, 893, 908
Bogorov, B. G., 872
Böhnecke, G., 127, 138, 239, 242, 636, 654, 670
Bond, R. M., 249, 250, 912
Bonnet, D. D., 852, 873
Boury, M., 176
Bowditch, Nathaniel, 365
Bowen, I. S., 117
Bowie, William, 458
Boynton, L. C., 896
Braarud, T., 762, 767, 768, 771, 780, 789, 793, 916
Bradley, W. H., 953, 1027, 1039
Bramlette, M. N., and W. H. Bradley, 953, 1027, 1039
Brandt, K., 6, 768, 784
Brauer, A., 829, 830, 835
Braun, 1038
Bremner, R. W., 183, 769
Brennecke, W., 609, 612, 623
British Admiralty, 79, 564, 624, 625
Brooke J. M., 15
Brooks, Charles F., 349
Brujewicz, S. W., 185, 186
Buch, Kurt, 5, 190, 191, 194, 198, 199, 200, 201, 203, 205, 854
Buchanan-Wollaston, H. J., 373
Bucher, Walter H., 22, 23, 24, 42
Bullen, G. E., 899
Bushnell,707, 714, 715, 717, 722, 723, 724, 730, 731, 733, 746, 752, 754
C
Calvin, J., 880
Campbell, A. S., 306
Campbell, M. H., 322
Cannon, H. G., 887
Carey, Cornelia L., 256, 914, 916, 919
Carnegie,209, 239, 244, 332, 633, 634, 699, 701, 707, 708, 709, 710, 711, 712, 714, 715, 717, 718, 724, 728, 729, 751, 787, 976, 979, 980, 989, 1009, 1016, 1029, 1031, 1032, 1034
Carruthers, J. N., 365
Catalyst,332
Cauchy, A., 534
Cayeux, Lucien, 948
Chace, F. A., 839
Chadwick, H. C., 768
Challenger,2, 7, 14, 133, 134, 166, 301, 349, 365, 791, 805, 807, 809, 942, 947, 984, 987, 1006, 1028, 1032
Chelan,655
Cherevichny, 30, 31
Chevallier, J., 61
Christensen, E. H., 250
Chrystal, G., 539
Chumley, James, 978, 984, 987
Clark, Frances N., 325
Clark, W. M., 194
Clarke, F. W., 213, 214, 215, 216, 231, 991, 992, 1006, 1036, 1040
Clarke, George L., 81, 82, 86, 87, 88, 104, 381, 777, 831, 832, 837, 838, 852, 873, 901, 933
Clements, F. W., 233
Cleve, P. T., 791, 793, 927
Closs, Karl, 183
Clowes, A. J., 239, 244, 245, 612, 693, 697
Coe, W. R., 307, 324, 846, 857
Cohee, George V., 1024
Colding, A., 490
Collet, Léon W., 948
Collins, J. R., 81
Cooper, L. H. N., 5, 182, 183, 210, 212, 236, 243, 248, 252, 253, 254, 256, 257, 258, 259, 260, 261, 263, 768, 771, 901, 902, 911, 914, 916, 931, 932, 935, 938
Cornish, Vaughan, 516, 519, 525, 532, 533, 534, 535, 964
Correns, Carl W., 2, 948, 976, 982, 983, 985, 986, 988, 992, 993, 998, 1002, 1009, 1015, 1016, 1027, 1029, 1030, 1031, 1032, 1038
Crozier, W. J., 894
Cummings, N. W., 53
Curtis, J. T., 782
Cushman, James A., 983
D
Dahl, Odd, 371, 372
Dakin, W. J., 269, 270, 271, 272, 772
Daly, Reginald H., 25, 41
Damas, D., 322, 864
Dana,238, 241, 242, 245, 332, 644, 645, 649, 690, 691, 692, 694, 697, 698, 699, 700, 701, 706, 707, 708, 709, 714, 728, 729, 735, 737, 746, 751, 752, 754
Danish Meteorological Institute, 667
Darwin, G. H., 545, 547, 558
Davidson, F. A., 850
Davidson, Viola, 263
Davies, W., 233
Davis, W. M., 855
Deacon, G. E. R., 239, 241, 242, 607, 608, 615, 617, 618, 619, 622, 693, 697, 751
Debye, P., 203
Defant, A., 3, 123, 135, 136, 141, 146, 159, 239, 242, 365, 430, 439, 446, 457, 460, 484, 501, 504, 505, 506, 516, 522, 531, 538, 539, 540, 541, 542, 552, 553, 554, 557, 558, 562, 563, 581, 583, 584, 585, 594, 595, 596, 607, 627, 628, 630, 632, 633, 634, 635, 636, 654, 671, 676, 680, 681, 682, 684, 711
Dentino, L., 646
Deutsche Seewarte, 564, 657
Deutschland,609, 623
Devik, O., 99, 413, 415, 418
Dickson, H. N., 134
Dietrich, Günter, 81, 456, 458, 639, 640, 641, 642, 673, 676, 677, 678, 679, 696, 697
Dietz, R. S., 182, 345, 346, 347, 1032, 1033
Discovery,239, 241, 244, 331, 332, 334, 607, 613, 622, 690, 691, 692, 693, 697, 699, 700; 702; 746, 751; 809; 900, 976
Dittmar, C. R., 5, 166, 167, 170, 171, 173
Dole, Malcolm, 49
Doodson, A. T., 542, 552
Dorsey, N. Ernest, 49, 69, 80, 199
Doudoroff, Peter, 825, 844
Drew, G. H., 918
E
E. W. Scripps,332, 362, 411, 601, 707, 726, 730, 731, 732, 746, 752, 754, 860, 962
Eggvin, J., 661
Ekman, Sven, 275, 666, 800, 803, 804, 805, 806, 807, 841, 845, 867
Ekman, V. Walfrid, 57, 61, 64, 68, 347, 354, 367, 368, 370, 396, 437, 439, 443, 455, 458, 460, 464, 466, 474, 478, 482, 490, 492, 493, 494, 495, 496, 498, 499, 500, 587, 594, 623, 672, 676, 677
Ellia, B. F., 305
Elsey, C. R., 846, 860
Emden,18
Emery, K. O., 17, 22, 25, 30, 38, 39, 42, 182, 345, 537, 954, 1017, 1032, 1033
Emmel, V. M., 187, 188, 190, 191
Ernst, Theodor, 177
Esterly, C. O., 772, 837, 838
Evans, R. D., 177, 184, 1033
Ewan, T., 81
F
Farran, G. P., 322, 849
Fearon, W. R., 228, 229
Fessenden, R. A., 2
Field, Richard M., 22, 24, 35, 208
Fish, C. J., 847
Fisher, W. K., 895
Fjeldstad, J., 3, 136, 476, 482, 484, 496, 574, 576, 578, 579, 586, 589, 590, 591, 595, 597, 598, 600
Fleming, J. A., 332
Fleming, Richard H., 48, 59, 70, 146, 150, 160, 167, 172, 174, 175, 185, 186, 205, 206, 207, 236, 244, 254, 366, 480, 482, 485, 501, 503, 567, 712, 725, 901, 902, 928, 938, 1016, 1026, 1027, 1028
Focke, Alfred B., 79
Forbes, Edward, 805
Forch, C., 50
Fowle, Frederick E., 9
Fox, C. J. J., 187, 188, 190, 191
Fox, D. L., 889, 969
Fox, H. Munro, 177, 857, 870
Föyn, Ernst, 177, 184, 768, 1033
Fram,492
Fraser, C. McLean, 6
Fraser, J. H., 813, 907
Fredholm, J., 496
Fritsch, F. E., 295, 299
Fuller, J. L., 901
Fulton, T. W., 365
G
Gaarder, T., 109, 110, 187, 780
Gail, F. W., 294, 770
Galliher, E. Wayne, 952, 1036
Galtsoff, P. S., 846, 847, 908
Gamble, F. W., 827
Gardiner, A. C., 821, 836
Gardiner, J. Stanley, 855
Gault, C. C., 185, 186
Gehrke, J., 426
General Greene,666, 669
Geological Society of America, 30
Geophysical Institute, Bergen, 4
Gerstner, F. J. von, 3, 526
Gilson, H. C., 237, 928
Gislen, T., 276
Godthaab,666
Goldschmidt, V. M., 175, 176, 182, 183, 184, 215, 219, 221, 1036
Goldseeker,592, 593
Goode, J. P., 11
Gordon, R. D., 86
Graham, H. W., 787
Gran, H. H., 6, 299, 301, 302, 322, 382, 762, 763, 765, 769, 770, 771, 780, 784, 789, 792, 793, 852, 866, 915, 930, 938
Granquist, G., 89
Grassi, B., 861
Greenberg, D. M., 195, 197, 199
Grim, Ralph E., 988, 989
Gripenberg, Stina, 178, 190, 191, 194, 195, 199, 200, 201, 205, 854, 958, 969, 1009, 1011, 1016
Gross, F., 770
Grundfest, H., 831
Gunnerus, J. E., 814
Günther, A., 829, 830
Gunther, E. R., 89, 501, 701, 702, 703, 705, 785, 829, 900, 906, 942
Gustafson, T., 438, 596
Gutenberg, Beno, 22, 544
H
Haber, F., 177
Hadding, Assar, 1035
Haendler, H. M., 182
Hamm, Randall E., 915
Hann, Julius von, 129
Häntzschel, Walter, 1023
Harder, E. C., 918
Harding, M. W., 173, 180
Hardman, Y., 916
Hardy, A. C., 377, 378, 813, 865, 882, 900, 906, 907
Harris, Rollin A., 558, 563
Hart, T. J., 881, 941, 942
Hartge, L. A., 293
Hartmann, G. K., 79
Harvey, E. N., 833, 835
Harvey, H. W., 5, 49, 181, 183, 190, 191, 194, 199, 200, 201, 205, 768, 769, 771, 772, 900, 901, 902, 911, 928, 932, 935
Haurwitz, B., 630
Heck, N. H., 77
Heilbrunn, L. V., 870
Heimdal,653, 654
Helland-Hansen, B., 4, 64, 82, 87, 109, 110, 122, 132, 142, 332, 333, 362, 417, 450, 451, 455, 460, 462, 578, 590, 592, 593, 653, 655, 657, 659, 660, 661, 673, 680, 681, 682, 831
Henderson, G. T. D., 813, 907
Henderson, L. J., 47
Hensen, Victor, 6, 378, 379, 771, 772, 812, 926
Hentschel, E., 784, 786, 787, 885
Herdmann, H. F. P., 7, 624, 813
Herrick, C. E., 187
Hesse, Richard, 274, 280, 293, 893
Hesselberg, Th., 57, 99, 413, 415, 417, 418
Hewatt, Willis C., 276, 895
Hewitt, L. F., 212, 996
Hidaka, K., 457, 524, 542, 734
Hirsch, G. C., 886
Hirsekorn, Heinz;-Günther, 70, 71, 168
Hjort, J., 6, 7, 318, 327, 354, 810, 811, 828, 830, 833, 834, 849, 857, 904, 905, 953, 976, 986, 1040
Hjulström, Filip, 960, 961
Hoerman, Hans, 177
Höglund, 782
Honda, K., 541
Hopkins, A. E., 846
Hotchkiss, M., 916
Hough, Jack, 344, 347, 1022
Houlton, H. G., 180
Howard,'A., 691
Huckel, E., 203
Hufner, G., 81
Huntsman, A. G., 847, 864
Hustedt, F., 295
Hutchinson, A. H., 262
Hutchinson, R. C., 233
Hutchinson, Samuel, 850
Hydrographical Laboratories, Copenhagen, 51
Hyman, Libbie H., 303, 870
I
Idrac, P., 372
Igelsrud, Iver, 173, 180, 211
Institut für Meereskunde, Berlin, 4
International Association of Physical
Oceanography, 4, 25, 52, 169, 170, 171, 195, 356
International Council for the Exploration
of the Sea, 1, 50, 51, 56, 83, 792
International Gulf Stream Expedition, 681
International Hydrographic Bureau, 12, 25, 27, 29, 343
International Ice Patrol, 394, 453
Iselin, C. O'D., 144, 332, 456, 638, 670, 672, 675, 676, 679, 686
Isitani, D., 541
J
Jacobs, W. C., 121, 212
Jacobsen, J. P., 51, 52, 173, 373, 451, 476, 477, 482, 484
Jahn, G., 327, 328
Jahn, Theo. L., 47
Jakhelln, A., 463, 464, 659
James, Harry R., 81, 82, 87, 88
Jeffreys, H., 3, 519, 522, 531, 533, 535, 536, 577, 964
Jenkin, P. M., 778, 781, 933
Jensen, A. J. C., 451, 893, 918
Jesperson, P., 856, 863
John Murray Expedition, 687, 688, 690
Johnson, C. A., 368
Johnson, Douglas W., 24, 42, 43, 1024
Johnson, Martin W., 317, 725, 788, 814,
Johnson, Nils G., 86
Johnson, W. H., 837
Johnston, W. R., 173, 178
Johnstone, James, 6, 17, 22, 49, 216, 768, 842
Jordan, E. O., 909
Jorgensen, Wilhelm, 84, 87
Jowett, W. G., 233
Juday, C., 108, 381, 782
K
Kalle, K., 87, 88, 89
Karlik, B., 177, 184, 1033
Kármán, Th., 472, 473, 479, 480, 964
Karsten, G., 779, 781
Keeble, F. W., 827
Kelley, W. P., 988, 990
Kelvin, Lord, 63, 555, 556, 557, 562, 571, 572
Ketchum, B., 258, 261
Keys, Ancel, 243, 249, 250, 253, 271, 914
Kiilerich, Alf B., 665, 666
Kikuchi, Kenzo, 836
Kimball, Herbert H., 102, 103, 109, 121, 122, 130
Kincaid, Trevor, 846
King, E. J., 263
Kip, A. F., 177, 184, 1033
Kirk, P. L., 173, 178
Klem, A., 916
Klugh, A. B., 782
Knapman, F. W., 173, 174, 175
Knopf, A., 213
Knudsen, Martin, 5, 50, 51, 52, 53, 56, 57, 58, 59, 60, 65, 70, 71, 83, 173, 219, 426
Koenuma, K., 132, 136, 720
Kofoid, Charles A., 6, 299, 306, 319, 766, 856, 867
Köhler, HiIding, 212
Kossinna, Erwin, 13, 15, 19, 21
Kreps, E., 794, 928, 938, 940
Krogh, August, 181, 203, 249, 250, 783, 907, 912
Krumbein, W. C., 955, 966, 967, 969, 970, 971, 993
Krümmel, Otto, 22, 49, 61, 70, 88, 127, 134, 216, 426, 494, 516, 525, 534, 535, 544, 545, 646, 733
Kuenen, Ph. H., 22, 29, 1036, 1040
KuhIbrodt, Erich, 123, 128, 133
Kullenberg, B., 438, 596
Kuwahara, Susumu, 61
Kylin, Harold, 294
L
LaFond, Eugene C., 44, 459, 525, 537, 1017
Lamb, H., 470, 471, 516, 526, 534, 537, 555, 566, 586
Landberg, S., 782
Langevin, P., 78
Laurila, E., 458, 490
Lebour, M., 324, 771, 772, 884, 888, 901, 902, 911, 932, 935
Lek, Lodewijk, 439, 594, 597, 598, 599, 600
Lewis, G. N., 203, 205
Liebig, G. F., 990
Liljequist, G., 86
Lipman, Charles B., 918
Littlehales, G. W., 14, 21, 22, 24, 29
Liverpool Tidal Institute, 3
Lloyd, Blodwen, 911
Lohmann, H., 6, 763, 772, 819, 885, 901, 911, 930, 1040
Loosanoff, V. L., 846, 908
Louisville,724
Lubimenko, V. N., 782
Lucas, C. E., 813, 900, 901, 906, 907
Lutz, F. B., 183
Lyman, John, 59, 67, 167, 172, 174, 175, 185, 186, 205, 332
M
Macallum, A. B., 270
McCance, R. A., 233
McClendon, J. F., 185, 186
MacDonald, G. A., 1020
Macdonald, Roderick, 834
McEwen, George F., 57, 58, 121, 484, 501, 725
MacGinitie, G. E., 889, 895
Mackintosh, N. A., 332, 624, 906
Mahncke, H. E., 183
Majestic,532
Malmgren, Finn, 72, 73, 74, 75, 217, 219
Marks, Graham, 184
Marmer, H. A., 516, 535, 542, 545, 561, 563, 564, 569
Marshall, S. M., 385, 772, 780, 784, 853, 870, 873, 903, 938
Martens, James H. C., 1019, 1020, 1022, 1023
Masters, M., 233
Matthews, Donald J., 49, 57, 58, 59, 62, 77
Maud,217, 219
Maurstad, H., 623
Mehmel, Martin, 988, 989
Meinesz, F. A. Vening, 529
Merian, J. R., 539
Merz, A., 650
Messina, A. R., 305
Meteor,17, 30, 129, 133, 135, 136, 209, 239, 242, 331, 332, 344, 351, 355, 362, 366, 465, 524, 527, 584, 594, 613, 615, 625, 626, 627, 628, 629, 631, 632, 637, 654, 669, 671, 682, 683, 746, 786, 885, 941, 948, 955, 976, 980, 989, 1001, 1009, 1029, 1031, 1032, 1039
Michaelis, L., 212
Michael Sars,82, 362, 376, 417, 590, 591, 592, 593, 653, 826, 827, 828, 839, 852, 856
Michell, A. G. M., 526, 527, 533
Millar, F. Graham, 120
Miller, R. C., 896
Milwaukee,19, 36
Mitchell, P. H., 196, 208
Miyake, Y., 65, 66, 67, 70
Moberg, E. G., 5, 173, 177, 178, 180, 184, 196, 197, 199, 204, 205, 209, 244, 254, 332, 785, 928, 1033
Mohn, H., 460
Möller, Lotte, 70, 7, 1, 167, 650, 693, 694, 751
Montgomery, R. B., 120, 159, 458, 459, 477, 481, 485, 489, 494, 495, 500, 503, 535, 623, 634, 636, 637, 642, 666, 673, 675, 709
Moore, B., 768, 931
Moore, Hilary B., 994, 997, 1039, 1040
Mosby, Håkon, 100, 102, 113, 120, 352, 609, 611, 612, 622, 658, 662, 663, 665, 666
Mulholland, S., 185, 186
Müller, Johannes, 6, 376, 814
Müller, O. F., 814
Munk, W. H., 601
Murata, K. J., 1029
Murray, Sir John, 2, 7, 299, 354, 805, 806, 807, 809, 830, 833, 841, 849, 853, 854, 857, 947, 948, 952, 953, 974, 976, 978, 979, 983, 984, 986, 987, 991, 1028, 1031, 1040
Myers, E., 319
N
Nansen, Fridtjof, 4, 32, 53, 352, 353, 354, 355, 366, 373, 378, 379, 382, 450, 492, 494, 592, 656, 657, 658, 659, 660, 664, 666, 673, 682
Nathansohn, A., 645, 784
Natland, Manley L., 851
Nautilus,659
Neaverson, E., 976
Nelson, E. W., 780
Neumann, Gerhard, 126, 468, 469, 485, 681
Niblack, 24, 25
Nicholls, A. G., 322, 323, 385, 836, 853, 870, 873, 903
Nielsen, J. N., 639, 644, 645, 646, 647, 648, 649
Nielsen, S. E., 903. See also Steemann Nielsen, E.
Nikitin, W. N., 872, 873, 917
Norris, E. R., 870
Nunnemacher, R. F., 839
Nynäs, Ole, 194
O
Orr, A. P., 385, 780, 784, 853, 870, 873, 903, 938
Orton, J. H., 840, 846, 847, 908
Ostenfeld, C. H., 792
Ostler, R. H., 777
Ottestad, Per, 328
P
Palmén, E., 458, 485, 489, 490, 634, 709
Pantin, C. F. A., 269, 270
Paris, 535
Parker, W. E., 333, 355
Parr, A. E., 477, 638, 639, 641, 678, 685, 897
Patton, R. S., 516, 535, 542
Pearse, A. S., 281, 870, 879, 880
Perks, J. P. H., 362
Peters, W. J., 332, 762
Petersen, C. G. Joh., 302, 375, 879, 880, 895, 936, 937
Pettersson, Hans, 53, 82, 83, 87, 177, 184, 372, 438, 782, 1033
Pettersson, O., 352, 354, 372, 438, 600
Pettijohn, F. J., 956, 966, 967, 969, 970, 971, 993
Phelps, Austin, 247
Phifer, Lyman D., 252, 257, 762, 788
Philippi, E., 984, 987
Pia, Julius, 1005
Pierantoni, Umberto, 835
Piggot, C. S., 2, 345, 1033, 1034, 1039
Pillsbury, J. E., 362, 673, 675
Pinke, F., 332, 362
Planet,690, 692, 700, 701, 739
Pliny, 861
Poisson, S. D., 534
Poole, H. H., 82, 85, 86, 87
Powell, Wilson M., 104
Prandtl, L., 472, 473, 479, 964
Pratje, Otto,, 2, 976, 980, 1002
Pratt, Henry S., 282, 303
Proudman, J., 3, 542, 552
Prytherch, H. F., 847
Puls, C., 709
Pütter, A., 249, 912
Q
Quayle, D. B., 860
R
Radczewski, O. E., 955
Raisz, Erwin, 11
Rakestraw, N. W., 5, 181, 183, 187, 188, 190, 191, 196, 208, 241, 243, 253, 254, 255, 256
Ramage, Hugh, 177
Ramalho, A., 646
Ramapo,19
Randall, Merle, 203, 205
Rappleye, H. S., 677
Rauschelbach, H., 371
Rayleigh, Lord, 87, 541
Redfield, A. C., 236, 243, 253, 258, 260, 261, 384, 863, 864, 914, 931, 935
Regan, C. Tate, 829, 830, 831
Reger, Joseph, 123, 128, 133
Reid, M. E., 847
Reith, J. F., 183
Renard, A. F., 947, 952, 984, 987, 1028, 1031
Renn, C. E., 250, 251, 254, 255, 256, 916
Revelle, Roger, 2, 48, 70, 150, 173, 178, 196, 197, 199, 200,206, 207, 208, 209, 366, 480, 482, 959, 973, 976, 979, 980, 982, 983, 984, 985, 986, 987, 988, 989, 990, 991, 992, 1002, 1004, 1005, 1009, 1011, 1014, 1015, 1016, 1020, 1025, 1026, 1027, 1028, 1029, 1033, 1034, 1040, 1041
Ricketts, E. F., 880
Ridgway, Robert, 968
Riley, G. A., 215, 928, 934, 937, 938, 943
Ringer, W. E., 216, 218
Rittenberg, Sydney C., 920
Ritter, William E., 6
Robertson, J. D., 232
Robinson, Rex J., 172, 173, 174, 175, 177, 179, 180, 181, 182, 183, 187, 195, 211, 244, 254
Rogers, C. G., 185, 232
Rona, E., 177, 184, 1033
Ross, Sir John, 805
Rossby, C.-G., 4, 456, 481, 489, 491, 494, 495, 500, 535, 623, 630, 666, 676
Rouse, Hunter, 471, 962
Rudé, G. T., 342, 343, 360
Runnstrüm, S., 847
Russell, F. S., 771, 825, 836, 837, 850, 866, 867, 901, 902, 911, 932, 935, 943
Russell, H. L., 908
Russell, R. Dana, 967, 1024
Russell, Richard J., 1024
Russell, Scott, 523, 537
Ruud, J. T., 323, 904, 905
S
Sanderman, L. A., 1033, 1034
Sandström, J. W., 57, 58, 99, 400, 403, 415, 460, 462, 508
Sargent, M. C., 938
Sars, O., 808
Sawyer, W. R., 81, 82
Schalk, Marshall, 1023
Schimper, A. F. W., 779, 781
Schmidt, Johannes, 6, 332, 861, 865, 872
Schmidt, K. P., 274, 280, 293, 893
Schmidt, Wilhelm, 91, 104, 120
Schott, G., 12, 30, 127, 130, 134, 535, 646, 647, 700, 702, 703, 704, 712, 721, 729, 734, 739, 784, 942, 974
Schott, Wolfgang, 974, 983, 985, 1002, 1038, 1039, 1041
Schreiber, E., 768, 779, 784, 415, 460, 462, 508
Schuchert, Charles, 1037, 1038
Schumacher, A., 524, 527, 671
Schureman, P., 550, 564
Scofield, W. L., 896
Scott, A., 768
Seripps Institution of Oceanography, 453, 525, 530, 724
Sears, M., 851
Sedov,658
Seiwell, G. E., 260, 894
Seiwell, H. R., 160, 162, 239, 260, 362, 376, 439, 484, 593, 601, 639, 675, 676, 894, 934, 938
Service, Jerry H., 77
Setchell, W. A., 294
Sette, O. E., 328
Shelford, V. E., 277, 879
Shepard, F. P., 2, 17, 20, 21, 22, 24, 30, 37, 38, 39, 40, 42, 43, 44, 182, 366, 525, 537, 959, 1009, 1011, 1014, 1016, 1017, 1020, 1025, 1026, 1032, 1033, 1041
Skogsberg, Tage, 131, 299, 725
Smith, C. L., 207, 208, 952, 998, 999
Smith, Edward H., 53, 460, 623, 663, 665, 666
Smith, H. P., 241, 258, 261
Smith, P. A., 17, 21, 30, 38, 39, 40, 41, 342, 343
Snellius (seeWillebrord Snellius)
Solberg, H., 433, 441, 460, 507
Sömme, J. D., 852, 864, 865
Sörensen, S. P. L., 50
Soule, Floyd M., 53, 355, 663, 665, 666, 676
Spärck, R., 109, 110
Spiess, H. C. Fritz, 332, 362
Spilhaus, Athelstan F., 348, 351, 355
Spoehr, H. A., 778
Stanbury, F. A., 781
Steemann Nielsen, E., 773, 903. See also Nielsen, S. E.
Steiger, 991, 992
Stenius, 67
Stephenson, M., 912
Sterneck, R., 3, 552, 557, 563, 582, 583
Stetson, Henry C., 2, 38, 366, 1020, 1021, 1024
Steuer, A., 6, 823, 856
Stevenson, T., 532
Stock, C. C., 194
Stocks, Theodor, 14, 17, 18, 30, 34, 35
Stokes, Sir G. G., 3, 470, 526, 586, 956, 957, 958
Strok, L. W., 176
Ström, K. M., 150, 189, 210, 246, 663, 1009, 1016, 1027, 1040
Subow, N. N., 185, 186: See also Zubov
Suda, K., 482, 484, 734
Sumner, Francis B., 825, 826, 827
Sund, Oscar, 57
Sverdrup, H. U., 57, 58, 111, 119, 121, 122, 132, 137, 146, 159, 160, 219, 371, 372, 417, 418, 453, 457, 482, 484, 485, 491, 496, 501, 503, 556, 571, 576, 577, 578, 579, 601, 612, 618, 619, 621, 622, 633, 634, 641, 658, 659, 662, 663, 666, 678, 697, 714, 725, 785, 934, 938, 1040
Swainson, O. W., 79
Swartout, J. A., 49
Swezey, Olive, 299
Syunpu Maru, 734
T
Tait, J. B., 364, 365
Takahashi, Jun-ichi, 997, 1035
Tannehill, I. R., 545
Taylor, G. I., 92, 110, 472, 475, 476, 477, 557, 577
Taylor, H. J., 173, 180
Terada, T., 541
Thomas, B. D., 54, 70, 71, 182, 245
Thompson, E. F., 687, 688, 689
Thompson, T. G., 5, 47, 48, 49, 54, 66, 67, 70, 71, 172, 173, 175, 177, 178, 179, 180, 182, 183, 184, 187, 195, 211, 245, 252, 257, 332, 733, 769, 780, 788, 915
Thompson, W. F., 6, 325, 328, 861
Thompson, Warren O., 1023
Thomsen, Helge, 241, 245, 751
Thor,644, 645, 649
Thorade, H., 159, 363, 368, 370, 371, 372, 373, 482, 494, 501, 504, 505, 516, 522, 538, 541, 580, 725
Thorp, Eldon M., 976, 983, 984
Thoulet, J., 61
Tibby, R. B., 365, 714
Tikhouskaia, Z., 782
Tilden, J. E., 293, 295
Timmermann, E., 206, 211
Titanic,668
Tourky, A. R., 180
Transehe, N. A., 623
Trask, P. D., 347, 948, 961, 970, 985, 993, 994, 996, 1002, 1003, 1004, 1005, 1006, 1009–1011, 1014, 1015, 1019, 1025, 1026
Tressler, Donald K., 896
Truitt, R. V., 317
Tschudy, R. H., 954
Twenhofel, W. H., 946, 948, 952, 953, 954, 955, 960, 967, 1024, 1027, 1029, 1032, 1033, 1037
U
Uda, M., 365, 716, 721, 734
U. S. Beach Erosion Board, 43, 44, 529; 1018
U. S. Bureau of Fisheries, 328
U. S. Coast and Geodetic Survey, 3, 14, 17, 30, 77, 79, 341, 342, 343, 360, 460, 564, 673
U. S. Coast Guard, 53, 453, 668
U. S. Hydrographic Office, 14, 29, 38
U. S. Weather Bureau, 117
Urry, W. D., 187, 1033, 1034
Usiglio, 211
Utterback, C. L., 49, 54, 70, 71, 84, 87, 88, 831, 832, 1033, 1034
V
Valdivia,766, 781, 984, 987
Van Cleve, R., 861
van Riel, P. M., 30, 692, 736, 737, 738
van Veen, Joh., 580
Vaughan, T. Wayland, 2, 7, 25, 26, 27, 28, 29, 36, 37, 38, 319, 800, 840, 882, 998, 999, 1006
Veatch, A. C., 17, 21, 30, 38, 39, 40, 41, 342, 343
Vercelli, Francesco, 105, 108, 689, 690
Verjbinskaya, N., 794, 928, 938, 940
Vinogradov, A. P., 228, 233, 235
von Brand, Theodor, 249, 254, 255, 256
W
Wadell, H., 956, 957, 958
Waksman, S. A., 250, 251, 909, 916, 919
Walford, Lionel A., 842, 861
Washington, Henry S., 1029, 1032
Wattenberg, Hermann, 5, 161, 175, 177, 180, 181, 182, 184, 190, 191, 194, 196, 199, 200, 201, 205, 206, 207, 208, 209, 210, 211, 239, 242, 484, 654, 784, 787, 1001
Webb, D. A., 173, 175, 177, 179, 228, 229
Wedderburn, E. M., 600
Weese, A. O., 879
Wegemann, G., 133, 134
Wells, Nelson A., 870
Welsh, J. H., 839
Wenner, F., 53
Werenskiold, W., 448, 464
Wheeler, W. C., 231
Whewell, W., 563
Wiese, W., 218, 219
Wilkins, Sir Hubert, 31, 667
Willebrord Snellius,18, 19, 30, 331, 332, 362, 597, 598, 599, 601, 602, 690, 692, 737, 739
William Scoresby,699, 702, 728
Willimzik, M., 429
Wilson, C. B., 881
Wilson, D. P., 317
Wilson, T. L., 184
Winsor, C. P., 381
Wirth, H. E., 47, 48, 49, 173, 178, 181, 182, 244, 254
Wiseman, John D. H., 1009, 1010, 1015, 1016
With, Carl, 849
Witting, R., 66, 370, 426
Woods Hole Oceanographic Institution, 51, 460
Worthington, E. B., 838
Wright, C. C., 173, 175
Wüst, Georg, 12, 14, 17, 18, 28, 119, 120, 121, 123, 124, 146, 161, 351, 355, 468, 489, 619, 627, 670, 674, 675, 681, 686, 688, 693, 719, 720, 739, 747, 748, 749
Y
Yonge, C. M., 825, 882, 886, 896
Yoshida, 541
Young, R. T., Jr., 86
Z
Zimmerman, E., 535
ZoBell, Claude E., 161, 250, 256, 257, 383, 384, 768, 870, 911, 912, 914, 918, 919, 920, 995, 996, 997, 1031
Zubov, N. N., 655, 658. See also Subow, N. N.
Zukriegel, J., 623
Zwicker, B. M. G., 173, 180
Fold-outs
Bottom Topography of the Oceans.
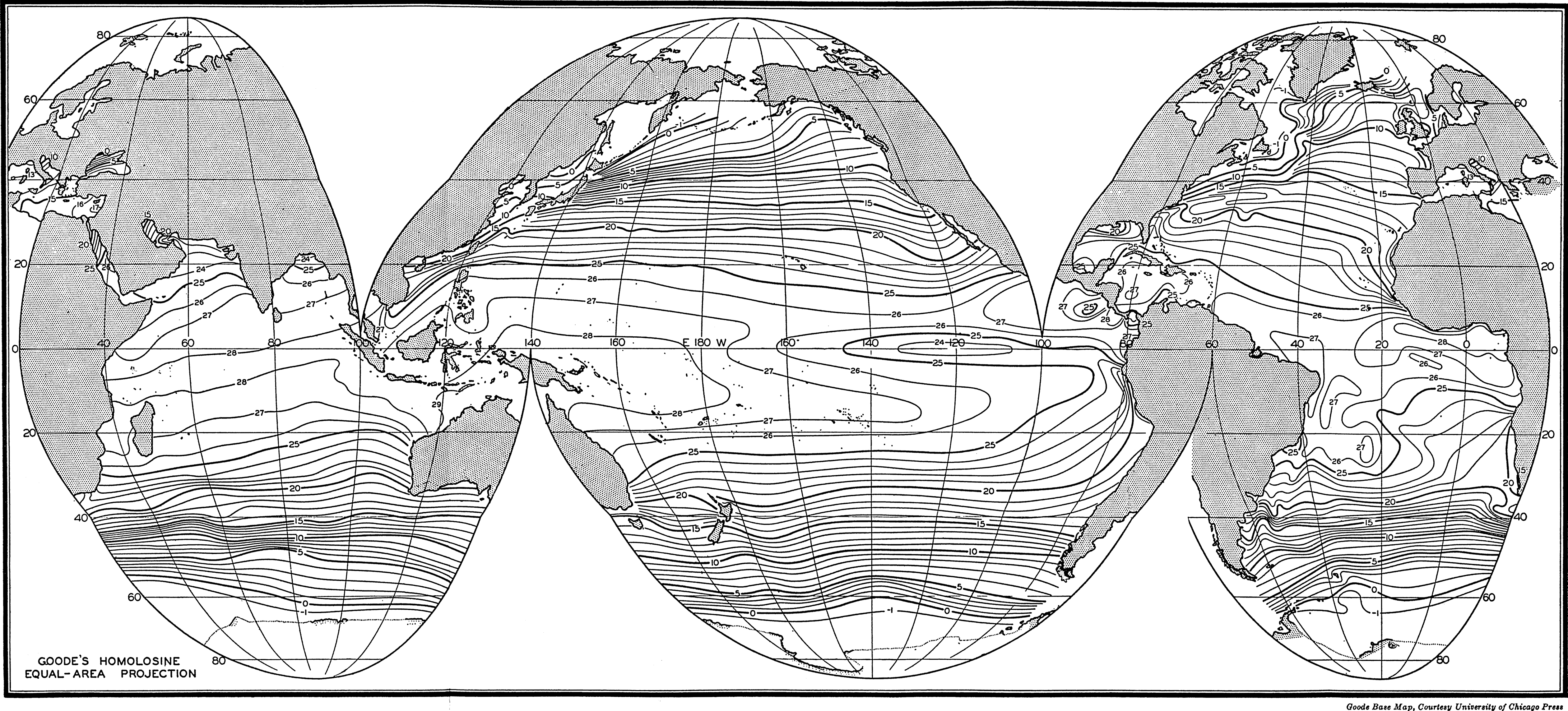
Surface temperature of the oceans in February.
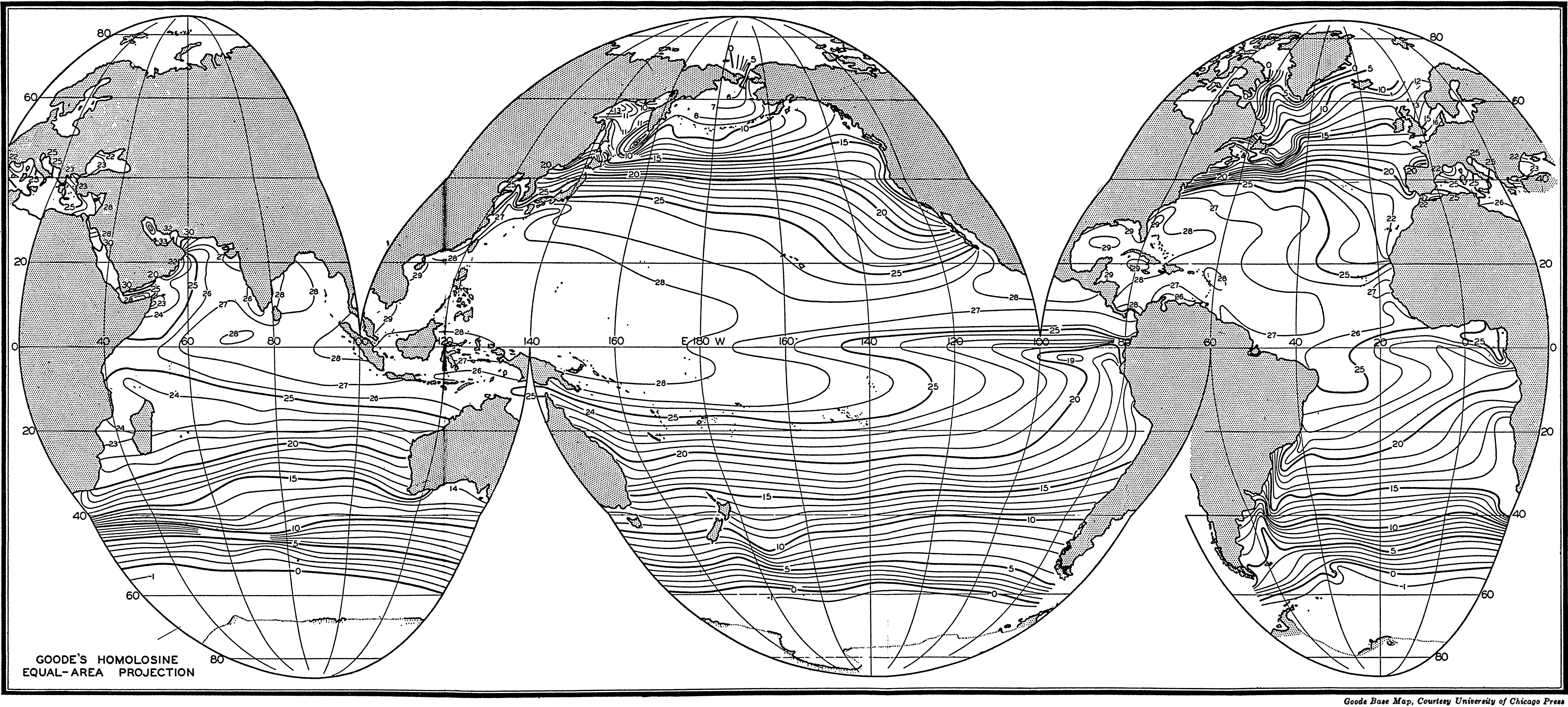
Surface temperature of the oceans in August.
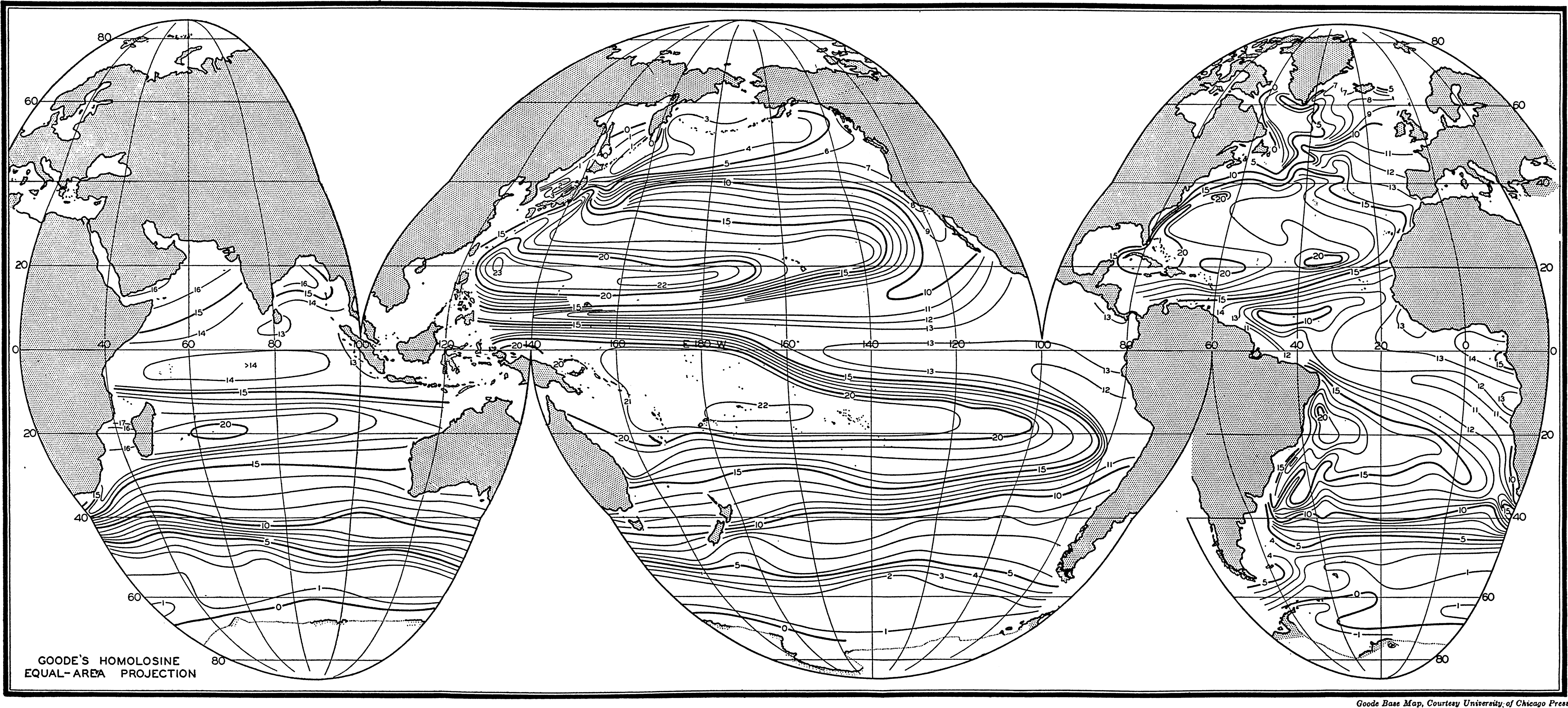
Temperature of the oceans at a depth of 200 meters.
Temperature of the oceans at a depth of 400 meters.
Surface salinity of the oceans in northern summer.
Surface currants of the oceans in February-March.
Preferred Citation: . The Oceans, Their Physics, Chemistry, and General Biology. New York: Prentice-Hall, c1942 1942. http://ark.cdlib.org/ark:/13030/kt167nb66r/