Three—
Newton's Early Dynamics:
On Uniform Circular Motion

Isaac Newton was born on 25 December 1642, in the manor house of Woolsthorpe, a very small village seven miles south of the town of Grantham. Fifty miles south of Grantham lies the university town of Cambridge, the center of Newton's university training and scholarly activities. Seventy miles south of Cambridge lies London, the location of Newton's later professional life and of his death on 27 March 1727. Newton exerted an influence, however, that extended well beyond the miles between Grantham and London and lasted much longer than the period of eighty-four years between his birth and death; his published work exerted its authority throughout the entire academic world and its influence is still felt today.

Shortly before Newton's birth, his father died, and three years later his mother married the rector of the church in a neighboring village. Newton did not live with his stepfather and mother but remained at Woolsthorpe in the care of his grandmother for nine years until his stepfather's death in 1653. Newton's mother returned to Woolsthorpe with her three children from her second marriage and, among other items, her husband's library of some two or three hundred books on theology, which may have laid the foundation for Newton's interest in theology. In addition to the books on theology, the library contained a large bound notebook of blank paper, which Newton retained and called his Waste Book . His stepfather had intended the bound notebook to serve as a repository for his theological studies but had filled only a few pages. Newton, however, filled many pages with his thoughts on a great variety of subjects, including his first work on dynamics.

Newton left his home in Woolsthorpe to enter the grammar school in Grantham at age twelve, less than two years after his mother returned home. His early mathematical training apparently did not extend beyond the

elementary rules of manipulation that were standard for the time. No evidence exists to suggest that he displayed in grammar school any of the extraordinary talent for mathematics that manifested itself shortly after he arrived at Cambridge University.

Newton, at age nineteen, entered Trinity College of Cambridge University in the summer of 1661. His first two undergraduate years were devoted to the standard scholastic curriculum of the time. His grammar school training had provided him with a firm grasp of Latin with which to begin the traditional university program of scholastic philosophy. Newton's notes on his early readings indicate that he began to work through a Latin summary of Aristotle's natural philosophy, probably under the direction of a tutor. He made notes on the sections that summarized or commented on Aristotle's Physics, On the Heavens, On Generation and Corruption , and Meteorology . He also read portions of a compendium of the main theses of Aristotelian metaphysics. This early study of the Aristotelian body of works gave him a system that organized the diversity of nature into a coherent pattern and stressed rigorous thought. Newton's Principia played a major role in the rebellion against scholasticism, but it was the scholastic system itself that initially provided him with a firm foundation from which to rebel.^[1]

Although Newton began his college training in the classical tradition, it was not long before he began to look outside the traditional curriculum, which was itself in a state of decline. Academic Aristotelianism was maintained in part by the legal mandate of a curriculum enacted by law and in part by academics with a vested interest in continuing the system that had produced them.^[2] The traditional curriculum was no longer a stimulant to intellectual vigor and by 1661 European philosophy had developed a new set of challenges. Thus, it comes as no surprise that a serious and perceptive student such as Newton never finished the Aristotelian texts he was assigned, although these early studies may have continued to influence his worldview. By 1663, the commentaries in his student notebook on the Aristotelian texts were interrupted by pages of notes devoted to the metaphysics of the contemporary French mathematician and philosopher René Descartes. He digested the work of Descartes in a way that he never had done with the work of Aristotle. He did not confine himself solely to Descartes, however. He read of the new mechanical philosophy in the works of the British physicist and chemist Robert Boyle and the British philosopher Thomas Hobbes. Moreover, he read Galileo's Two New Sciences , and he familiarized himself with contemporary astronomical writings. By 1664, however, mathematics dominated his thoughts to the virtual exclusion of everything else. In the field of mathematics, Newton was almost entirely self-taught. He attended a few lectures on the subject, but it was his reading of Descartes's Geometry and other contemporary works on mathematics that proved his real classroom. In just over a year he had mastered

the entire achievement of seventeenth-century mathematical analysis and had begun to make major contributions to it himself.

Newton concerned himself early on with topics that proved to be valuable in his later study of dynamics. In particular, the topic of conic sections was to prove important in his analysis of celestial motion. He collected various methods of constructing conic sections, investigated the role of coordinate systems in simplifying such constructions, and organized his growing knowledge of analytical geometry. During this period of self-study, Newton was creating, as well as absorbing, mathematical procedures. His development of the basic mathematical techniques of his fluxional calculus, for example, reached fruition in the tract of October 1666. Although he did not apply the method of fluxions directly to his dynamics, the work provided experience in taking limits. Newton relied on this experience when he manipulated the quasi-classical geometry that he did apply to dynamics.

By 1666 Newton concluded his first creative drive into the realm of mathematics after almost a year and a half of total dedication. It is almost impossible to overstate the degree of his success. Newton began to make original contributions to the field of mathematics even in the process of taking notes on his reading as a student. Initially, his study of existing mathematics was intermingled with his creation of new mathematics. Within the first year of his mathematical activity, however, his interest in learning from others waned and he became driven by the stimulation of his own intellect. The products of this intense activity, however, remained unknown to members of the mathematical community. Even his academic mentor, Isaac Barrow, did not know the extent of Newton's progress. Newton's research in analytical geometry and calculus from 1664 to 1666, had it been known, would have placed Newton in the front ranks of contemporary mathematicians, and with the October 1666 tract on fluxions he may well have been considered the leading mathematician of all Europe.

Uniform Circular Motion:
The Polygonal Approximation

As his first wave of mathematical creativity came to a close early in 1665, other interests began to claim Newton's attention. Among them was his study of dynamics founded on the works of Galileo and Descartes. His first investigations into this subject were concerned with collisions and appear in his bound notebook, the Waste Book . The only date among the dynamical entries in the Waste Book was the marginalia, "Jan. 20th 1664" (1665 new style),^[3] which appeared in a section devoted to problems of collisions between two perfectly inelastic bodies.^[4] In this section, Newton developed and refined the concepts and axioms of motion that Descartes had set out

in 1644. In particular, Newton's statement of Descartes's concept of linear inertia originally appeared in Newton's Waste Book as follows:

Every thing doth naturally persevere in that state in which it is unlesse it bee interrupted by some externall cause, hence . . . A body once moved will always keepe the same celerity [speed ], quantity, and determination [instantaneous direction ] of its motion.^[5]

This Cartesian view that uniform rectilinear motion is the natural isolated state is crucial to Newton's dynamics, and an enlarged version of the statement appeared some twenty years later as the first law of motion in the Principia .

Newton extended the dynamics of intermittent colliding bodies to his analysis of bodies subject to a continuous force. He determined the nature of the force directed toward the center of a circle that will move the body uniformly around the circle (i.e., the solution to the direct problem of uniform circular motion). Newton envisioned a ball in uniform circular motion about a given center, and he sought information concerning the nature of the force impressed upon the ball. In a later work he demonstrated that force was directly proportional to the square of the speed and inversely proportional to the radius of the circle. In the section on uniform circular motion that first appears in the Waste Book , however, he did not explicitly obtain that result. The relationship he did obtain compared the magnitude of the change in motion produced by a sum of impulsive forces to the magnitude of the orbital motion. It is not the type of problem that would concern a contemporary physicist. Newton's analysis, however, and not the specific problem, is of interest.

In this analysis the circular path is approximated by a polygonal path of n sides (shown in fig. 3.1 as an octagon), where the number of sides of the polygon will ultimately increase without limit. The ball is envisioned to collide elastically (i.e., the speed or magnitude of the velocity does not change) with the circle or with the circumscribed polygon. At each collision, an impulsive force, directed toward the center of the circle, acts on the ball; between collisions no force acts on the ball and it moves with uniform rectilinear motion. The impulsive force acts for an extremely short time and produces a change in what Newton called the "quantity of motion in a body." He calculated the sum of the magnitudes of these changes in the quantity of motion, which he called "the force of all the reflections," and compared that sum to the quantity of motion of the body's constant orbital motion, which he called "the force of the body's motion." As the number of sides of the polygon was increased, the polygonal path approached a circular path, and the ratio of "the force of all the reflections" and "the force of the body's motion" was found to approach the value of 2p .

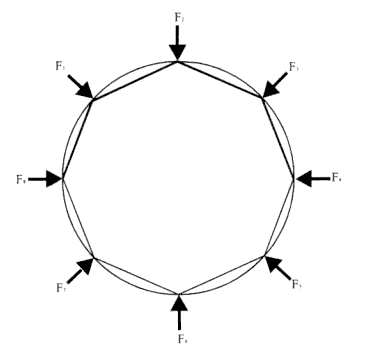
Figure 3.1
A circular path is approximated by an octagon. An impulsive force
F  acts on the body at each intersection of the circle and octagon.

To the modern eye, Newton's demonstration may seem insufficient because he did not calculate the mathematical structure of the force, directed toward the center of the circle, that is required to maintain uniform circular motion. Moreover, the modern reader will find that Newton's terminology is at variance with current usage. In modern terminology, the change in motion that Newton calculated at each collision is the magnitude of the change in the linear momentum Dmv . In the terms used in a modern textbook, this quantity Dmv is equal to the product of the force F and the small time of collision dt , where the product F × dt is defined as the impulse I . The magnitude of the vector linear momentum mv does not change at an elastic collision, only its direction. Hence, there is a finite change in the vector linear momentum Dmv provided by the impulsive force. There is no explicit use of such a modern vector resolution in Newton's text, but it resides implicitly in his analysis. One must not judge the value of the text from the viewpoint of modern expectations. Newton was exploring the phenomenon of uniform circular motion, and the techniques he developed in that exploration served him as a springboard for further analysis. The methods of analysis found in this early text provided a basis to continue into the more mature considerations to follow.

The text of Newton's analysis, which was written in English, is found on the first pages of the Waste Book and is dated about 1665.^[6] Because of the complicated but polished nature of the text, it has been argued that this passage may not represent Newton's first written thoughts on the subject of circular motion, even though it appears first in the book. He may have worked out the demonstration on loose sheets, revised it, and then transcribed it onto the blank first page.^[7] Newton makes an opening formal statement of the result he intends to demonstrate, and then he gives his detailed demonstration or proof of that opening statement. Below is this opening statement, simply intended to set forth the problem and solution. It will be followed by a detailed mathematical demonstration.

Uniform Circular Motion:
The Waste Book

If the ball b revolves about the center n, [then ] the force by which it endeavors from the center n would beget soe much motion in a body as there is in b in the time that the body b moves the length of [an arc equal to ] the semidiameter bn.^[8]Or the force from n in one revolution is to the force of the body's motion as :: periph : rad.

Note that, following Descartes, Newton is concerned with the "force by which it [the ball] endeavors from the center." That Cartesian outward endeavor will be identified below with the "force or pression" of the ball b upon the curve "at its reflecting." Some fifteen years later, after Newton had demonstrated the law of equal areas and had challenged the Cartesian system of mechanical vortices, the specific reference will be to the "center-seeking force" rather than to the outward endeavor. As will become clear in the detailed analysis in the next section, the "endeavor from the center" will be measured by the difference between the tangential displacement the ball would have made in the absence of the force and the displacement it does make in the presence of the force. That difference between the two displacements is itself a radial displacement, one which is produced by a radial force. The details of the analysis, however, are independent of Newton's identification of the displacement as either an outward or an inward displacement.

What the young Newton set forth in his opening statement (perhaps in not too clear a fashion) are two specific examples of the effect generated by the force required to produce uniform circular motion. He demonstrates these examples in the text that follows the opening statement.^[9] I paraphrase them as follows:

First Example . If the body traverses a circular arc of length S₁ equal to the radius (semidiameter) of the circle bn , then the "motion in a body" generated (begat) by the force of "endeavor from the center" is to the "force of the body's motion" as the arc length S₁ (= bn ) is to the radius bn (i.e., as 1 is to 1).

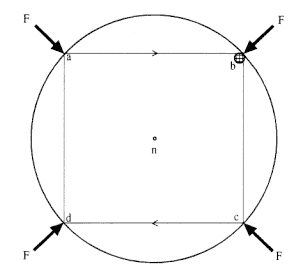
Figure 3.2
A circular path is approximated by a square path. An
impulsive force F  acts on the body at each intersection
of the circle and square.

Second Example . If the body traverses a circular arc of length S₂ equal to the circumference (one revolution) of the circle 2pbn , then the "motion in a body" generated by the force of "endeavor from the center" is to the "force of the body's motion" as S ₂ (= 2pbn ) is to the radius bn (i.e., as 2p is to 1).

In what follows, Newton considers three specific variations: first, motion along a square path inscribed in a given circle; second, motion along a general polygonal path inscribed in the same circle; and third, motion along the circular path itself. In the first example, the ratio of (A) the sum of "the force of reflections" at the four corners of the square to (B) the "force of the body's motion" along one of the sides of the square is found to be equal to the ratio of (C) the sum of the sides of the square to (D) the radius of the circumscribed circle (i.e., A / B = C / D). Then he extends the result to a general polygonal path. Finally, the number of sides of the polygon is increased without limit and the result is obtained for a smooth circular path.

Newton began his demonstration of the effect of the force required to maintain uniform circular motion by considering the motion of a body contained in a square, as shown in figure 3.2. The force is described as "the force of reflection," and the body (i.e., the "Globe b ") is envisioned to "collide" with the circle or circumscribed square at points a, b, c , and d where it is acted upon by an impulsive force F . The force on the body is supplied by the collisions of the body with the sides of the circle. Else-

where in the Waste Book , Newton discussed the uniform circular motion of a sphere as it rolls around inside a physical cylinder. The source of the force was the contact between the sphere and the wall of the cylinder.^[10] In the demonstration above, however, the circle is not explicitly described as a material body (such as the cylinder). Because the body's free motion is along the tangent line, and because the body deviates from the tangent along a chord of a concave circular arc, then there must be an inward impulsive radial force supplied by some external agency. The source of the inward radial impulse is the elastic collision of the body with the circle. The concern with the force produced by a collision is the hallmark of Cartesian dynamics, and it was perhaps natural that the young Newton began his analysis of dynamics with the interactions described. In what follows, each line of Newton's demonstration will be considered separately.

Square

[1-A] If ef = fg = gh = he = 2fa = 2fb = 2gc = 2ed. And [if ] the globe b move from a to b

See figure 3.3 for an inscribed and a circumscribed square in and around the circle given above. The body collides with the circle only in the middle of each side of the circumscribed square, and between collisions the body moves with uniform rectilinear force-free motion (i.e., inertial motion). Line [1-A] simply states that the sides of the circumscribed square (ef, fg, gh , and he ) are bisected by the points a, b, c , and d , and thus ef = 2fa , and so on.

[1-B] then 2fa : ab :: ab : fa :: force or pression of b upon fg at its reflecting : force of b's motion .

Or, 2fa / ab = ab / fa . This result may be obtained from the Pythagorean theorem applied to the right triangle afb in figure 3.3: ab ² = fa² + fb² = 2fa² , where fa = fb . Thus, 2fa² = ab² or, dividing by fa and ab , one has 2fa / ab = ab / fa , as required in the first proportion.

The second proportion requires that the ratio of the "force or pression" to the "force of motion" equals 2fa / ab (and hence = ab / fa ). The "force of motion" is proportional to the body's initial velocity, and thus in a given time it is proportional to the distance the body would travel with that initial velocity (i.e., the distance ab ). The "force or pression" is proportional to the change in velocity of the body that the impulsive force would produce, and thus in a given time it is proportional to the distance 2fa generated by that change in velocity. Implicit in this statement is Newton's understanding that the impulsive force exerted by the body b on the side of the square fg at a reflection is equal to the impulsive force exerted on the

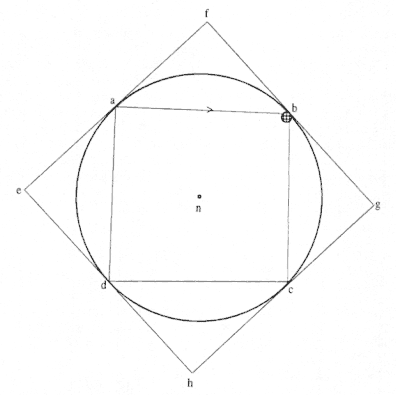
Figure 3.3
A circle with an inscribed and circumscribed square. A body rebounds at
points a, b, c , and d  and travels along the inscribed square.

body by the square (i.e., action and reaction). Newton made this relationship explicit when he reworked this example for inclusion in the Principia (see the "alternate demonstration" to follow this demonstration).

The ratio given in [1-B] entails an implicit relationship between force and displacement that is fundamental to Newton's dynamics: the force at a reflection is measured by the deviation from the rectilinear motion that the reflection produced. This relationship between force and displacement is employed in all of Newton's subsequent analyses of direct problems, but he uses it here without an explicit development. Whatever role the outward endeavor plays in Newton's thoughts about the nature of the force, here it is only the inward radial displacement, and hence the inward radial force, that is measured.

In another tract, dated 1666, Newton presented an explicit parallelogram rule for combining displacements (see fig. 3.4), and it was this rule

Figure 3.4
The parallelogram rule: the
displacement bx  combined with
the displacement by  is equivalent
to the displacement bc .

that he implicitly applied in [1-B]. The rule states that if the displacement bx from point b to point x is combined with the displacement by from point b to point y , then the net effect in a given time is the displacement bc from point b to point c , where the point c is generated by completing the parallelogram bycx (i.e., bc is the diagonal of the parallelogram formed with bx and by as two adjacent sides).^[11]

This parallelogram rule can be applied to figure 3.5, in which a point y is defined and a number of lines are added to Newton's original figure. The two displacements by and bd do not actually take place because they are virtual or imagined displacements. The two virtual displacements by and bd are combined and the resultant displacement bc is obtained:

1. The virtual displacement by , which would have been produced in a given time by the initial uniform motion the body had before the collision at point b and which, if the collision had not taken place, would have carried the body to point y .

2. The virtual displacement bd , which would have been produced by the change in motion due to the inward radial impulsive force F acting at point b and which, if there were no initial motion, would have carried the body to point d .

3. The actual displacement bc , which was the diagonal of the parallelogram bycd formed with one side as the line by and the other side as the line bd , did carry the body to point c . The parallelogram is shown in figure 3.5 as the shaded area.

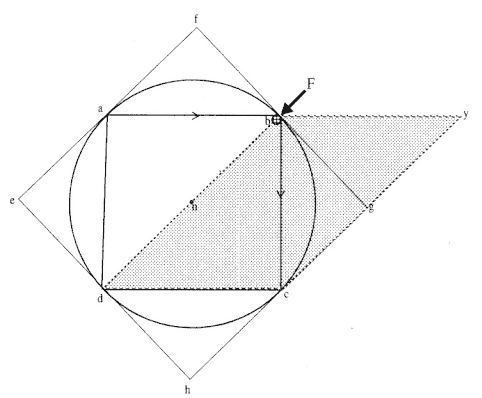
Figure 3.5
The line bc  is the diagonal of the shaded parallelogram  bycd . The line bd  is the deviation due
to the impulsive force F  acting on the body at the point  b .

The actual displacement bc can thus be viewed as the resultant of the virtual displacement by , due to the initial motion, and the virtual displacement yc (equivalent to bd ), due to the change in motion caused by the impulsive force. The line yc can be seen, for a given time, as the deviation of the body from the rectilinear path by that it would have followed if the force had not acted at point b . For a given time, the deviation yc is directly proportional to the impulsive force and thus is a measure of that force.^[12] Moreover, yc is equal to 2af . (See fig. 3.5, where yg = gc , and gc = af , and thus yc = 2gc = 2fa .) Thus, combining the statements, as Newton does without demonstration, the ratio of the "force or pression" to the "force of motion" equals the ratio of the [displacement yc to the displacement by ] which equals 2fa / ab = ab / fa .

Newton's use of the word "force" in the context of the collisions just discussed, however, is not consistent with modern usage. In contemporary terms, the impulse I is defined as the product of the force F and the time

interval dt , and this product is demonstrated to be equal to the change in momentum Dmv (magnitude and/ or direction). In these modern terms, Newton's "force of reflection" is best rendered as the "impulse" or the change in momentum produced by the impulsive force F acting over the very small time dt of the collision. Expressed in terms of the impulse I_b (= Dmv ) at point b and the initial impulse I_o (= mv ), the ratio of the "force or pression" to the "force of motion" is equal to the ratio I _b /I_o = ab / fa .^[13]

[1-C] Therefore 4ab = ab + bc + cd + da : fa :: force of reflection in one round (viz .: in b, c, d, and a) : force of b's motion .

The statement in [1-C] is an extension of [1-B] in which it was demonstrated that for a single collision the ratio of the "force or pression" to the "force of motion" is equal to the ratio of the deviation/displacement which equals yc / bc = 2af / ab = ab / fa . In [1-C] Newton summed all of the "force or pression" in one complete trip around the square (i.e., the scalar sum of the four impulses at points a, b, c , and d ), and he expressed it in ratio to the "force of motion." The ratio is now the sum of ab / fa + bc / fa + cd / fa + de / fa , or, since ab = bc = cd = de , the sum can be expressed as 4ab / fa . Thus, 4ab / fa is equal to the ratio of the "force of reflection in one round" to the "force of b 's motion" which equals SI_b /I _o , where SI_b is the sum of the four impulses exerted in "one round" and I_o is the initial impulse (i.e., I_o = mv ).

The statement in [1-C] concludes the discussion of the motion on the square. The ratio of the total "force of reflection in one round" to the "force of b 's motion" is found to be equal to the ratio of the periphery of the square (4ab ) to the radius of the circumscribed circle ( fa = bn ). In what follows, this result will be extended first to a polygon and finally to a circle.

Polygon

[2-A] By the same proceeding, if the globe b were reflected by each side of a circumscribed polygon of 6, 8, 12, 100, 1,000 sides, etc.

Or, I_b /I_o = ab / na (to be demonstrated). Now, the square path is replaced by a general polygonal path. See figure 3.6 for an example using an octagonal polygon. The deviations xb and yc are constructed parallel to the direction of the impulses I_a and I_b (arising from reflections at points a and b ), and they are thus parallel to radii na and nb , respectively. Recall that the body rebounds from the circle (or from the circumscribed polygon) at point a and continues with its speed unchanged toward point b . Point x is defined as the position the body would have reached, in the same time as it traveled to point b , if the impulsive force had not acted at point a . Because the time and the speed are the same over the distance xa and ab

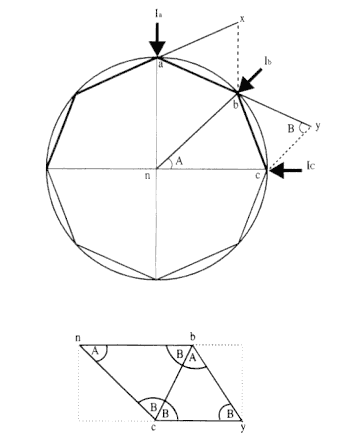
Figure 3.6
The circle is approximated by an octagonal path where the deviations
xb  and yc  are due to the impulses I_a  and I_b  at points a  and b . Note
that the triangles bnc  and  ybc  are similar (see bottom figure).

(although the directions differ), then xa = ab . Point y is related to point c in the same way: yb = bc .

Note also that triangles bnc and ybc are similar. See figure 3.6 where nb is parallel to yc, nb = nc , and bc = by : thus, the apex angles A are equal, as are the base angles B , and triangles bnc and ybc are therefore similar because all the angles are equal. From that similarity, the ratio of the sides of the triangles bnc and ybc can be written as yc / bc = bc / nb . Furthermore, note that figure anbx is identical to figure bncy , and thus xb / ab = ab / na . Hence, since I _b /I_o = xb / ab , then I_b /I_o = ab / na , which is a generalized relationship for any polygon and therefore contains the relationship in [1-B] for a square (i.e., I_b /I _o = ab / fa ).

[2-B] [then ] the force of all the reflections is to the force of the body's motion as the sume of those sides to the radius of the circle about which they are circumscribed .

S (I _b )/I_o (to be calculated). This ratio is the scalar sum of all the impulses S (I_b ) required to bring the body back to its starting point (i.e., "the force of all the reflections") divided by the initial impulse I_o required to set the body into its orbital motion (i.e., "the force of the body's motion").

S (I _b )/I_o = S (ab )/na (to be demonstrated). From [2-A], I_b /I_o = ab / na , where na is the radius of the circle about which the polygon is circumscribed. Thus, summing over both ratios, the sum is given as S (I _b /I_o ) = S (ab / na ), or, since both I_o and the radius na are independent of the sum, S (I_b )/I_o = S (ab )/na , where S (ab ) is the scalar sum of all the sides of the polygon or "the sume of those sides," and na is "the radius of the circle about which they are circumscribed."

The statement in [2-B] concludes the discussion of the motion on the general polygon. The ratio of the total "force of all the reflections" in one round to the "force of b 's motion" is found to be equal to the ratio of the periphery of the polygon (Sab ) to the radius of the circumscribed circle (na ). This result is similar to that given for the square in [1-C] above and for the circle in [3-B] below.

Circle

[3-A] And so if the body were reflected by the sides of an equilateral circumscribed polygon of an infinite number of sides (i.e., the circle itself)

If the number of sides of the polygon increases without limit, then the perimeter of the circumscribed polygon, S (ab ), approaches the circumference of the circle, 2p (na ).

[3-B] [then ] the force of all the reflections is to the force of the body's motion as all those sides (i.e., by the perimeter) to the radius .

Or, S (I_b )/I _o = S (ab )/na® (circumference)/(radius) (to be demonstrated). From [2-B], the ratio of the scalar sum of the magnitudes of all the impulses in one complete revolution S (I_b ) is to the magnitude of the initial impulse required to set the body into its orbital motion I_o as the scalar sum of all the displacements S (ab ) is to the radius of the circle na . From [3-A], the sum of the sides S (ab ) approaches the circumference of the circle (2p ) (na ) as the number of sides of the polygon increases. Thus, "the force of all the reflections" S (I_b ) is to the "force of the body's motion" I_o as the circumference of the circle is to its radius, or the ratio S (I_b )/I_o = (circumference)/(radius) = (2p ) (na ) / (na ) = 2p /1. Thus, as

set forth in the opening statement, "the force from n in one revolution is to the force of the body's motion as :: periph : rad."

From the vantage point of contemporary physics, the result of this seventeenth-century text is almost trivial. The scalar sum of the changes in the linear momentum S (mv ) is given by the product of the constant magnitude of the circular force F = mv ² / r and the period of revolution T = 2pr /v (i.e., S (mv )/mv = FT / mv = (mv² / r ) (2pr /v )/mv = 2p ), as Newton demonstrated above.^[14] Nevertheless, the polygonal approximation, which is central to this analysis, is a useful and important method as demonstrated. It was employed by Newton in his later dynamics to demonstrate Kepler's law of equal areas.

An Alternate Demonstration

Newton reworked this example as an alternate demonstration in the scholium of Proposition 4 in the 1687 Principia , and there he did obtain the nature of the force directly.^[15] His motivation for resurrecting this pre-1665 demonstration appears to stem from his desire to establish that he developed his method before Robert Hooke's suggestions in 1674. Proposition 4 demonstrates that the force directed toward the center of a circle required to maintain uniform circular motion is "as the squares of the arcs described in the same time divided by the radii of the circles." The scholium to the proposition offers the following variant demonstration in which the polygonal approximation is employed to obtain the nature of the force directly:

[A] The preceding [statements] can also be demonstrated in this way. In any circle let a polygon of any number of sides be described. And if a body, in moving at a given velocity along the sides of the polygon, is reflected from the circle at each angle of the polygon, [then] the force with which it impinges on the circle at each reflection will be as its velocity. And thus the sum of the forces in a given time will be as that velocity and number of reflections conjointly .

The critical assumption is that the impulsive force F at a collision is proportional to the velocity v . Newton does not attempt to defend the statement in the 1684 revision, nor is it true for a single collision. As demonstrated above, it is necessary to discuss the interactions in terms of the impulse I_b , which is defined as the product of the force F and the time of collision dt . In statement [2-A] in the pre-1665 version above, a generalized relationship I _b /I_o = ab / na is demonstrated for any polygon, where ab is a leg of the given polygon, na is the radius of the circle, and I_o is mv . The impulse I_b is equal to [(ab / na )m ] v . Thus, it is the impulse I , and not

the force F , that is proportional to the velocity v . The sum of the impulses over a given time T is SI = NI and is proportional to Nv , where N is the number of collisions in that given time.

[B] that is, (if the species of the polygon is given) as the [product of the] length described in that given time and that length divided by the radius of the circle: that is, as the square of that length divided by the radius .

The total length L traveled in a given time T is proportional to the velocity v and hence to the impulse I . The number of collisions N in the length L is equal to L / l , where l is the length of one of the sides of the given polygon. That length l is proportional to the radius of the circle R and thus the number of collisions is proportional to L / R . Thus, the sum of the impulses is proportional to Nv , and since N µL / R and v µL , the sum of the impulse is proportional to L² / R .

[C] Thus, if the polygon, with its sides diminished infinitely, coincides with the circle, then the sum of the forces in a given time will be as the square of the arc in a given time is divided by the radius .

Now, as the sides of the polygon diminish infinitely, the sum of the impulses over a given time T is SI = SFdt = F Sdt = FT , where Sdt = T and the force is now continuous. From [B], SI is proportional to L² / R , and since T is given, then it is correct to say that the force F is proportional to L² / R . Since the length L becomes equal to the arc of the circle as the polygon approximates the circle, then the continuous force F is proportional to "the square of the arc in a given time divided by the radius."

[D] This is the [centrifugal] force by which the body urges the circle, and equal to this is the opposite force by which the circle continuously repels the body toward the center .

The early statement of the problem was framed in terms of the force exerted by the body on the circle during the collisions. Newton now makes explicit the relationship that was left implicit: the forces are equal and opposite. In the first corollary to this proposition Newton notes that the arc is proportional to the velocity and hence the force is proportional to the squares of the velocities divided by the radius of the circle. Thus, the polygonal technique can be extended to obtain the nature of the force. (It is of interest to note that in the first edition of the Principia the word "centrifugal" is not explicitly used in the statement, but it is inserted into all the later editions.) Another technique, however, proved to be even more useful in solving direct problems: the parabolic approximation. Its roots also lie in Newton's early work and are carried forward into his mature dynamics.

Uniform Circular Motion:
The Parabolic Approximation

The text to be discussed below was written by Newton sometime before 1669, and it explicitly demonstrates that the force necessary to provide uniform circular motion is proportional to the square of the speed and inversely proportional to the radius (i.e., F = (m )v² / r ). It is an important text because it demonstrates that Newton used the parabolic approximation technique before 1669. It also gives evidence of the early influence of Descartes's writing upon Newton. More important, however, is the evidence of Newton's dynamic technique of analysis that is independent of—but obscured in part by—the Cartesian terminology used to express it. Newton will continue to employ the parabolic approximation throughout his mature dynamics.

Figure 3.7 is a comparison of the diagram on the left, which accompanied Newton's tract on uniform circular motion, with the diagram on the right, which accompanied the tract from the Waste Book discussed above. The obvious difference is that the circular path is no longer approximated by a polygon. In the previous tract, the distance bx is related to the impulse produced by the collision at point a , and the effects are summed as the number of sides of the polygon are increased. Finally, the limit is considered as the number of sides tends to infinity and the polygon tends to the circle. In the new text, the analysis begins with the consideration of the limit as the point D shrinks back to the point A . In that limit, the force that produces the displacement DB is assumed to be constant in both magnitude and direction. Galileo has demonstrated that such a constant force is directly proportional to the displacement and inversely proportional to the square of the time. The challenge therefore is to express that time in terms of meaningful parameters of the uniform circular motion. In this pre-1669 tract, Newton employs the property that the radius of the circle sweeps out equal angles in equal times plus a single proposition from Euclid to demonstrate that the magnitude of the force is proportional to the square of the period of uniform motion and inversely proportional to the diameter of the circle. In his post-1679 work on nonuniform motion, he will also invoke an initial limiting condition in which the force is assumed to be proportional to the deviation from the tangent and inversely proportional to the square of the time (i.e., the parabolic approximation). By this later period, however, Newton has demonstrated that the radius of any centripetal force sweeps out equal areas in equal times. This result plus an assortment of mathematical propositions and relationships enables him to solve a variety of direct problems, such as determining the force required for elliptical and spiral motions for various centers of force.

The use of the term "parabolic" to describe the approximation employed

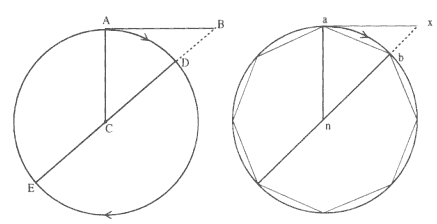
Figure 3.7
A comparison of the diagram employed in the parabolic approximation (left) with
the diagram employed in the polygonal approximation (right).

in this 1669 tract stands in contrast to the term "polygonal" used to describe the approximation in the 1665 tract. In the 1665 tract the choice of terms came from the polygonal path. In the 1669 tract the choice of terms comes from Galileo's demonstration that the combination of uniform rectilinear motion and uniformly accelerated rectilinear motion gives rise to a parabolic path. Thus, the element of the circle in the vicinity of the point A can be approximated by an element of a parabola, where the initial projection velocity is the tangential velocity at A and the constant acceleration is given by the approximately constant radial force. No explicit use is made of the properties of a parabola, but the term "parabolic" represents what is implicit in the approximation. Then, from the constant radial acceleration the force is given as directly proportional to the displacement and inversely proportional to the square of the time. This parabolic approximation is carried from this early solution into all of Newton's later work.^[16]

It is instructive to consider the outline of Newton's solution in this early tract before looking at the details. From the parabolic approximation the force is assumed to be proportional to the displacement DB and inversely proportional to the square of the time t required to traverse the arc AB . In order to render that relationship in more meaningful terms, Newton's first step is to express the displacement DB and the time t in terms of the diameter DE of the circle and the period T of the uniform motion. In the second step, he calculates the distance X that the body would move in the time T under the influence of the same constant force that produced DB in time t . For a given force, therefore, X / BD = T² / t² . (See fig. 3.8.) Moreover, because the radius sweeps out equal angles in equal times, the times

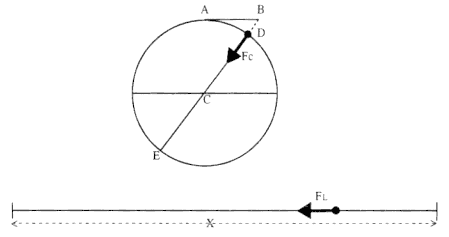
Figure 3.8
Under the action of a constant linear force  F_L  equal in magnitude to the centripetal
force F_C , a body travels the linear distance  X  in a time T  equal to the period of the
circular motion.

are proportional to the arcs (i.e., T / t = circumference / arc AD ). Calling upon a proposition from Euclid and noting that in the limit the arc DA approaches the tangent BA and the line BE approaches the diameter DE , Newton demonstrates that the distance X is proportional to the diameter of the circle DE . In the third and final step, Newton simply notes that the force is therefore proportional to the diameter and inversely proportional to the square of the period (i.e., FµX / T² µDE / T² ) or what is equivalent, F = kv² / r . In what follows, I discuss in detail Newton's derivation of this result.

The paper containing this alternate solution to the problem of uniform circular motion was written some time before 1669. It is not in the Waste Book but it survives in another collection of Newton's early writings. Most of the paper is concerned with numerical calculations of the endeavor of the moon from the earth and of the earth from the sun. In the opening section, however, Newton derives the nature of the force in order to make these calculations. The following is an English translation of a portion of the Latin text taken from the manuscript here called On Circular Motion .^[17] I have imposed the steps, which I summarized in the previous paragraph, upon Newton's solution in the following.

On Circular Motion

Step 1 . It is Newton's intent to express the displacement DB and the time t in terms of the diameter DE of the circle and the period T of the uniform motion.

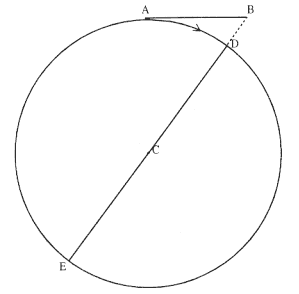
Figure 3.9
A body travels uniformly along the circular path  ADE . The
radial displacement DB  is the deviation of the circular arc
AD  from the tangential line  AB .

[1-A] The endeavor of body A, rotating on circle AD toward D, from the center [C] is as great as would carry it away from the circumference to the distance DB in the time AD (which I set to be most minute); inasmuch as it would reach that distance in that time if only it could move freely in tangent AB with no impediment to the endeavor .

See figure 3.9. As noted in chapter 2, two possible readings can be made of this statement. The first identifies the "endeavor from the center" as that which would produce the radial displacement from point D to point B along the extension of the diameter of the circle. In that reading the "impediment to the endeavor" prohibits the outward radial displacement DB and the body travels along the circular arc AD . An alternate reading identifies the "endeavor from the center" as that which produces the linear displacement from point A to point B along the tangent. In that reading the "impediment to the endeavor" prohibits the tangential displacement AB and again the body travels along the circular arc AD . In either case it is the displacement DB that measures the "impediment," be it an outward endeavor or an inward centripetal force. From the full text of this early work, it is clear that Newton intends the first reading (i.e., that expressed by Descartes). In a later version of this solution, produced after 1679, Newton intends the second reading.

[1-B] Now since this endeavor, provided it were acting in a straight line in the manner of gravity, would impel bodies through spaces that would be as the squares of the times ,

In [1-A], the time to travel the arc AD is "set to be most minute." In that limit of vanishingly small time the force is assumed to be constant in both magnitude and direction "in the manner of gravity." As Galileo has demonstrated, the displacement under a constant force is "as the square of the time."

[1-C] In order to find out through how much space in the time of one revolution ADEA they would impel [the bodies], I look for a line [X] that is to BD as is the square of the circumference ADEA to AD² .

Or, X / BD = T² / t² = ADEA² / AD ² . The line X is the distance that the body would travel under a constant force in a time T equal to the period of circular motion. Since the period T is proportional to the circumference of the circle ADEA (i.e., equal angles in equal times), then the distance X is proportional to the "square of the circumference ADEA ." From [1-B], we understand that just as the distance X is proportional to the square of the time T² so the distance BD is proportional to the square of the time t (i.e., the arc AD² ). Thus, the relationship, as given by Newton, is X / BD = T² / t ² = ADEA² / AD² .

Step 2 . Newton now calculates the distance X that the body would move in the time T under the influence of the same constant force that produced DB in time t .

[2-A] To be sure there is BE : BA :: BA : BD (by 3 Elem.).

Or, BE / BA = BA / BD . This relationship is demonstrated by reference to Proposition 36 of Book 3 of Euclid's Elements , a particular Euclidian proposition that Newton employs on a number of occasions, often without a specific reference as given here (i.e., "by 3 Elem ."). Figure 3.10 displays the results of Euclid's demonstration: the ratio of the line BE (the diameter plus the deviation) to the line BA (the tangent) equals the ratio of the line BA (the tangent) to the line BD (the deviation). Thus, one has BE : BA :: BA : BD or BE / BA = BA / BD .

[2-B] Or since the difference between BE and DE, as also between BA and DA, is supposed infinitely small, I substitute one for the other in turn and there emerges DE : DA :: DA : DB.

Or, DE / DA = DA / DB . In the limit as the point D approaches A (see fig. 3.11), the extended line BE approaches the diameter DE (i.e., BE®DE ), and the tangent BA approaches the arc DA (i.e., BA ®DA ). From [2-A], BE / BA = BA / BD . Substituting DE for BE and DA for BA , that ratio becomes DE / DA = DA / DB , as required here in [2-B], or in its equivalent form DA² = (DE ) (DB ), as required next in [2-C].

[2-C] Finally by making DA² (or DE × DB) : ADEA² :: DB : ADEA² / DE,

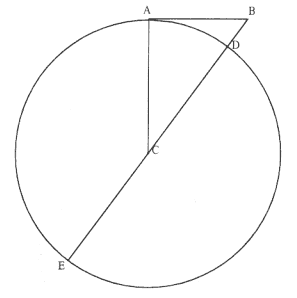
Figure 3.10
Based on Proposition 36 of Book 3 of Euclid's  Elements:
BE : BA :: BA : BD  or otherwise  BE / BA = BA / BD .

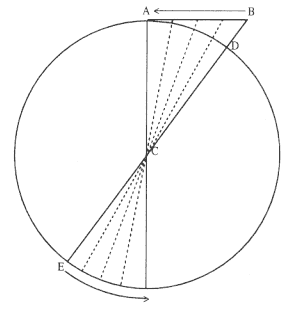
Figure 3.11
As the point D  approaches the point A , the line BE
approaches the diameter DE  and the tangent BA
approaches the arc DA .

From [2-B], DA² = (DE ) (DB ). Divide both sides by ADEA² and obtain DA² / (ADEA² ) = (DE ) (DB ) / (ADEA² ). Divide numerator and denominator of the last term by DE and obtain [DA² ]/[ADEA² ] = [DB ]/[(ADEA² ) / (DE )], as required here in [2-C]. Invert the expressions and obtain [ADEA² ]/[DA² ] = [(ADEA² ) / (DE )]/DB as required in [2-D] next.

[2-D] I obtain the line looked for (namely the third proportional in the ratio of the circumference to the diameter), through which the endeavor of receding from the center would propel a body in the time of one revolution when applied constantly in a straight line .

"The line [X ] looked for" was given in [2-A] by (X ) / (BD ) = ADEA ² / DA² . From [2-C], [ADEA² ]/[DA² ] = [(ADEA² ) / (DE )]/DB . Substituting this value of ADEA ² / DA² into the expression for (X ) / (BD ), one obtains (X ) / (BD ) = [(ADEA² ) / (DE )]/[DB ], where DE is the diameter of the circle, and ADEA is the circumference (i.e., ADEA = pDE ). Thus, X = (pDE )² / DE = p²DE , or X is proportional to DE , the diameter of the circle. Newton uses this result in the corollary that follows to demonstrate that the force, which is proportional to the displacement X , is thus proportional to the diameter of the circle, DE .

Step 3 . Newton now notes that the force is therefore proportional to the diameter and inversely proportional to the square of the period (i.e., F µX /T ²µDE /T² ) or what is equivalent, F = kv² / r .

The text then continues with a numerical calculation of the force of gravity at the equator for an object rotating on the surface of the earth and compares that value to the much larger value given for the "virtue of gravity." The difference between the two values explains why objects do not fly off the rotating earth. Following that discussion, Newton's manuscript contains the following corollary, which relates directly to the functional form of the force necessary to maintain uniform circular motion:

Corollary. Hence the endeavors from the centers in diverse circles are as the diameters divided by the squares of the times of revolution

From the parabolic approximation, the force is inversely proportional to the square of the time and directly proportional to the displacement. Recall that X was the linear distance traveled in a time equal to the period of revolution T under a constant inward radial linear force equal in magnitude to the endeavor of receding from the center. Therefore, the magnitude of the force is inversely proportional to the square of the time T and directly proportional to X and, hence, by [2-D] above, to the diameter DE . Thus, as Newton expresses it, the ratios of "endeavors from the centers in diverse circles as" the ratios (DE₁ /T₁² ) / (DE₂ /T₂² ).

[Corollary] or as the diameters multiplied by the [squares of the] number of revolutions made in any same time .

The number of revolutions N made in any time is proportional to the frequency and hence inversely proportional to the period T (i.e., T ₁ / T₂ = N₂ /N ₁ or X₁ / X₂ = (DE₁N ₁² ) / (DE₂N ₂² ). This proportionality can also be expressed as the square of the tangential speed divided by the diameter (or radius), because the period T is equal to the circumference (and hence p times the diameter D ) divided by the tangential speed v . Thus, D /T² = D /(D /v )² = v² / D or the result obtained independently by the Dutch mathematician Christiaan Huygens for the force required to maintain uniform circular motion.^[18]

Newton's later dynamics will continue to employ the parabolic approximation used in this early solution, but he will no longer employ the Cartesian terminology of the outward endeavor nor will he see the displacement as an outward radial element. His shift in perspective is dramatic, but it does not require a change in the parabolic approximation. Newton's demonstration of Kepler's law of equal areas will enable him to extend the technique to noncircular and nonuniform orbits; the number and complexity of the mathematical relationships Newton will use to carry solutions to their conclusion will increase; but the underlying parabolic approximation will remain unchanged.

Elliptical Motion:
The Circular Approximation

The two techniques for solving direct problems discussed above, the polygonal approximation and the parabolic approximation, do not exhaust the techniques found in Newton's early papers on dynamics. The Waste Book also contains a brief statement concerning elliptical motion. In it, Newton states that the force required to maintain elliptical motion can be found from the circle of curvature. In his early work on mathematics, Newton had developed the concept of curvature as a measure of the bending or "crookednesse" of a curve, and in the Waste Book he suggested that it could be employed in the analysis of elliptical motion. Newton did not provide any details in this early commentary of how he intended to implement curvature to obtain the force, but it appeared in his later work as an alternate technique for solving direct problems. The following English text is from the Waste Book and was written in late 1664 or early 1665.^[19]

Elliptical Motion

If the body b moved in an Ellipsis then its force in each point (if its motion in that point bee given ) may bee found by a tangent circle of Equall crookednesse with that point of the Ellipsis .^[20]

Among his early original contributions to mathematics, Newton developed a measure for the "crookednesse" or "curvature" of curved figures.

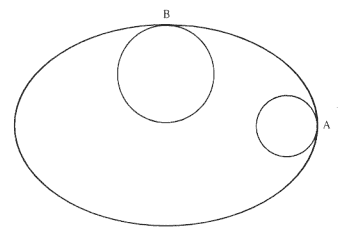
Figure 3.12
Where the ellipse curves most rapidly ( A ) the circle of curvature
is small. Where the ellipse curves most slowly ( B ) the circle of
curvature is large.

Curvature is a measure of the rate of change of the angle of inclination of the tangent line with respect to the arc length of the curve. In more descriptive terms, the curvature measures the rate of "bending" of the curve at a point. If the curve is a circle, then rate of bending is uniform (i.e., the radius of curvature is everywhere equal to the fixed radius of the circle). If the curve is not a circle, then the rate of bending changes from point to point on the curve. A useful method of measuring the bending of a general curve at a point is to give the curvature of the circle that best approximates the curve at that point, as seen in the ellipse in figure 3.12. Where the ellipse curves most rapidly, the circle of curvature is small and where it curves most slowly, the circle of curvature is large. The circle that represents the best approximation to the curvature—sometimes called the osculating circle—has the same first and second derivatives as the curve at the given point. A circle has constant uniform curvature, an equiangular spiral has curvature that changes uniformly, and conics have curvature that changes systematically but not uniformly. As early as December of 1664 Newton had roughed out a method for finding the center of curvature in an ellipse.^[21]

Newton eventually applied curvature as a measure of force and thus applied the dynamics of uniform circular motion to the more complicated problem of elliptical motion. In what I have elected to call the "circular approximation," an elemental arc of a general curve is approximated by an elemental arc of its circle of curvature. Newton employed the circular approximation to solve a number of problems, including that of elliptical motion. The first preserved record of such an analysis occurs in a solution

that Newton sent to the British philosopher John Locke in 1690. He may have produced a first draft of that solution as early as 1684, however. This technique also appeared as an alternate solution in the revised editions of the Principia . Newton's cryptic statement on elliptical motion, however, indicates that as early as 1665 he had thought of using the circle of curvature and uniform circular motion to analyze motion in an elliptical path. Michael Nauenberg has suggested that Newton may have used this curvature method to obtain numerical and analytical solutions, perhaps as early as 1665. No examples of such calculations have ever been found, however.^[22]

Conclusion

The Waste Book and Newton's other early papers contain many examples of his analysis of problems in dynamics, but the three solutions considered in this chapter are representative of his initial techniques. Before 1669, Newton had set out the three major methods of dynamical analysis that he employed in his more mature dynamics after 1679. First, the polygonal approximation that he developed in 1665 to determine the nature of circular motion in the Waste Book , he later used in his demonstration of the generalized nature of Kepler's law of uniform area following 1679. Second, the parabolic approximation that he developed before 1669 in the tract On Circular Motion , he later used in his general theorem for solving direct problems in the 1684 tract On Motion . Finally, the circular approximation that he alluded to in his statement of late 1664 or early 1665, may have been used to obtain solutions now lost. In any event he employed it in 1690 (or perhaps as early as 1684) as an alternate type of solution for direct problems. All of these techniques were unique to Newton but had their roots in the work of Galileo and Descartes. Newton began with the idealized rectilinear kinematics of Galileo and the terrestrial collisional dynamics of Descartes and from them fashioned three techniques of solving the problems of celestial motions. It is important to remember this dynamic simplicity amid the mathematical complexity of Newton's presentation.

To proceed further with the solution of the Kepler problem of elliptical orbits, one must obtain an expression for noncircular motion that relates the time in orbit to the spatial parameters. The expression that served for the special case of uniform circular motion was obtained from the property of equal angles in equal time and by the relationship between the period and the circumference. Following his correspondence with Robert Hooke in 1679, Newton demonstrated that for any force directed toward a given center the radius from the center to the general orbit sweeps out equal areas in equal times. That demonstration, it has been argued, finally

prompted Newton to question and to renounce Decartes's theory of a mechanical celestial vortex as a source of gravitational force. Following his early analysis of uniform circular motion discussed in this chapter, however, Newton appears not to have actively pursued a solution for the direct Kepler problem, other than the reference to the use of curvature. For the next decade, from 1669 to 1679, he was preoccupied with subjects other than dynamics. Thoughts mathematical, optical, theological, and alchemical concerned him, and his interest in the dynamics of the motion of bodies, both terrestrial and celestial, lay fallow until 1679, when he was prompted by correspondence from Robert Hooke to reflect once again upon the nature of the force required to maintain elliptical orbits.