PART 2
MORE EXACT SCIENCES

5
Late Enlightenment Meteorology

By Theodore S. Feldman

Meteorology in the 18th century meant more than observation and prediction of the weather. The complex and manifold processes occurring in the atmosphere brought it into contact with a large range of topics of natural philosophy—topics differently arranged than they are today, their boundaries less distinct and far more fluid. Meteorology naturally overlapped much of pneumatics, or the study of gases. The pneumatical parts of meteorology included the expansion of air with pressure and heat, evaporation and precipitation, latent heat, the behavior of aqueous vapor in air, and the closely related problems of the production of steam in both air and the vacuum. In the last decades of the century the discoveries of the chemical components of air and water led meteorologists to pneumatic chemistry and the chemical constitution of the atmosphere.

Meteorology also shared topics with electricity and magnetism. Atmospheric electricity, including lightning and the electricity of the air and clouds in fair and stormy weather, was a popular topic and the electrometer a familiar instrument of weather observation. Terrestrial magnetism belonged to meteorology at this time, and, especially in the last third of the 18th century, meteorologists improved the magnetic compass and discovered regularities in the magnetic variation.

These topics, coming from pneumatics, heat, electricity, and magnetism, belonged to natural philosophy or physics proper; a second grouping of subjects—including mechanics, geometrical optics, acoustics, and surveying and cartography—made up applied or "mixed" mathematics, as it was called.^[1] Meteorology had much in common with these as well. Barometry had its 17th-century beginnings in hydrostatics, which was part of mechanics. In the late 18th century, when the barometer became useful for the measurement of heights, it was taken up by surveyors. Atmospheric refraction, rainbows, haloes, the color of the sky, and the diminution of light through the atmosphere brought meteorology into contact with geometrical optics and the new science of photometry. Mixed mathematics gave these parts of meteorology a mathematical content throughout the 18th century.

Finally, meteorology was involved with parts of the life sciences, especially agriculture, medicine, and plant and human geography. The influence of the weather on agriculture and human health involved meteorologists in the numerous projects of agricultural and medical reform of the last third of the century. Botanists such as Linnæus and Willdenow began to consider the role of climate in the geographical distribution of plants. Montesquieu's discussion of the role of climate in human geography is well known.^[2]

[1] Applied mathematics was distinct from natural philosophy for most of the 18th century and was quantitative, where most of natural philosophy was descriptive and nonquantitative. As has been shown in several studies, quantification in physics in part reflected an alteration in the relation between these two fields. See J.L. Heilbron, Electricity in the 17th and 18th centuries. A study of early modern physics (Berkeley: University of California Press, 1979), 1–19. Theodore S. Feldman, "Applied mathematics and the quantification of experimental physics: The case of barometric hypsometry," Historical studies in the physical sciences, 15 (1985), 127–97, 128, lists further studies. The present chapter will not be concerned with this aspect of quantification.

[2] For pneumatical meteorology, see Feldman, The history of meteorology, 1750–1800. A study in the quantification of experimental physics (Ph.D. dissertation, University of California, Berkeley, 1983; DAI 45/03-A, 922), section I, and W. Knowles Middleton, "Chemistry and meteorology, 1700–1825," Annals of science, 20 (1964), 125–41. For atmospheric electricity, see Heilbron, Electricity. For earth magnetism, see D.H. Hall, History of the earth sciences during the scientific and industrial revolutions (Amsterdam, New York: Elsevier Scientific Pub. Co., 1976). For barometry, see Feldman, "Applied mathematics." For plant geography, see Adolf Engler, Die Entwicklung der Pflanzengeographie in den letzten hundert Jahren und weitere Aufgaben derselben (Berlin: W.H. Kuhl, 1899). For Montesquieu and other studies of the role of climate in human geography, see Clarence J. Glacken, Traces on the Rhodian shore. Nature and culture in western thought from ancient times to the end of the eighteenth century (Berkeley: University of California Press, 1967), chap. 12.

Meteorology not only overlapped these areas of natural philosophy; it enriched them. This was especially true in physics. Both the law of uniform expansion of air with heat and Dalton's law of partial pressures grew out of or were closely connected to meteorological investigations.^[3] Capital discoveries in electricity in the mid-18th century were the electrical nature of lightning and the phenomenon of electrostatic induction, which derived in part from the study of the electricity of clouds.^[4] A prize question on the magnetic compass led to Coulomb's discovery of the law of magnetic attraction.^[5] More important than these, meteorologists made substantial contributions to the design in the 1770s and 1780s of the first precise instruments of physics. These instruments and an emphasis on systematic measurement—which together may be called "exact experimental physics"—were crucial aspects of quantification in late 18th-century natural philosophy. They generated reliable quantitative data that could be used as a foundation for mathematical laws.^[6]

This chapter treats quantification in one part of meteorology: weather observation and climatology. The term "climatology" is something of an anachronism; it and its cognates are not to be found in the 18th century but made their appearance in the first years of the 19th.^[7] For convenience "climatology" is used—sparingly—to

[3] Students of barometric hypsometry—the barometric measurement of heights—investigated the expansion of air with heat in the 1770s. See Feldman, "Applied mathematics," 175–6. The law of partial pressures for mixtures of air and water vapor was discovered in the context of hygrometry in the 1770s and 1780s. Cf. Feldman, The history of meteorology , chap. 4.

[4] For discussion of induction, see Heilbron, Electricity , 374.

[5] Heilbron, Electricity , 469.

[6] For discussions of exact experimental physics, see Feldman, "Applied mathematics," 151–2, 164–77, and "The history of meteorology"; Heilbron, Electricity , 75–83; Maurice Daumas, "Precision measurement and physical and chemical research in the 18th century," in Alistair C. Crombie, ed., Scientific change (New York: Basic Books, 1963), 418-30.

[7] For example, W.A. Lampadius, Systematischer Grundriss der Atmosphärologie (Freiburg: Craz und Gerlach, 1806), chap. 4, "Climatologie"; and Leopold von Buch, "Klimatologische Betrachtungen über die Westküste Norwegens," Annalen der Physik, 25 (1807), 318–32.

denote the analysis of observations for weather patterns. In climatology the organizational imperative—the need for coordinated observations carried out in different locations according to a common plan—meant that strong meteorological institutions were a prerequisite for quantification. So was exact experimental physics. The two appeared almost simultaneously after 1770. In order to clarify their roles, this chapter begins with an overview of weather observation and climatology prior to 1770, then turns to quantification in the two decades 1770–90.

Weather Observation and Climatology Prior to 1770

From the invention of meteorological instruments in the middle of the 17th century, natural philosophers recognized that little could be won from individual weather diaries or registers; instead, organized groups of observers were needed. As G.A. Hamberger, Christian Wolff's mentor at the University of Jena, put it:^[8]

It is not enough to examine the state of the air in our own location, but we must direct our attention to the surrounding regions. This may best be done if well-informed persons throughout several provinces and neighboring kingdoms record [weather observations] simultaneously. . . . If many ephemerides of this type, from various locations, are published and compared, they will throw great light on [weather] phenomena.

Short-lived organizations or networks of weather observers had been set up around the middle of the 17th century by Périer, Pascal's brother-in-law; by Robert Hooke at the Royal Society of London; and by Ferdinand II of Tuscany, patron of the Accademia del Cimento in Florence.^[9] Little came of their efforts and interest in

[8] G.A. Hamberger, De barometris (1701), quoted in Gustav Hellman, Repertorium der deutschen Meteorologie (Leipzig: W. Engelmann, 1883), 884. As the title of the work suggests, Hamberger was discussing barometric observations in particular.

[9] Hellman, "Die Entwicklung der meteorologischen Beobachtungen bis zum Ende des 18. Jahrhunderts," Preussische Akademie der Wissenschaften, Physischmathematische Klasse, Abhandlungen , 1927, 9; W. Knowles Middleton, A history of the thermometer and its use in meteorology (Baltimore: Johns Hopkins Press, 1966), 30–2; H. Howard Frisinger, The history of meteorology: To 1800 (New York: Science History Publications, 1977), 101–2.

coordinated weather observation declined from about 1660 to the end of the century.

In the early years of the 18th century as few as three or four natural philosophers in all of Europe culled weather observations from newspapers and magazines and from reports of correspondents. After 1715 more energy is evident: at Breslau the physician Johann Kanold published in his quarterly Breslauer Sammlung observations he compiled from a dozen locations across Europe.^[10] In 1723 the Philosophical transactions of the Royal Society of London carried James Jurin's "Invitatio ad observationes meteorologicas."^[11] In it Jurin, the Society's secretary, laid out a plan for daily readings of barometer, thermometer, wind strength and direction, precipitation, and the state of the sky. Some fifteen observers, from Bengal and St. Petersburg to Cambridge, Massachusetts, responded with weather diaries, which William Derham, a Fellow of the Society and author of works on physicotheology, edited for the Philosophical transactions. This labor made Derham the most prolific meteorologist of the first third of the century.

Although Kanold and Jurin had ambitious hopes for their networks, the results fell short of expectations. Observers had difficulties in obtaining instruments. For example, Derham located few observations of the hard winter of 1709–10 made with instruments.^[12] There seem to have been no instruments in the American colonies prior to 1716, when the physician Cadwallader Colden began observing in New York; as late as 1727 neither barometer nor thermometer was to be found in the Boston area, where Isaac Greenwood, first Hollis Professor of Mathematics and Natural Philosophy at Harvard, served as Jurin's delegate on the weather watch.^[13] A number of Jurin's

[10] Sammlung von Nature- und Medicin- wie auch hierzu gehörigen Kunst- wie Literatur-Geschichten , Breslau, 1717–30.

[11] James Jurin, "Invitatio ad observationes meteorologicas communi consilio instituendas," PT, 32:2 (1722–3), 422–7.

[12] William Derham, "History of the great frost in the last winter 1708 and 1708–9," PT, 26 (1708–9), 454–78.

[13] Derham, "An abstract of the meteorological diaries communicated to the Royal Society," PT, 37 (1731–2), 261–79, on 267; J.H. Cassedy, "Meteorology and medicine in colonial America: Beginnings of an experimental approach," Journal of the history of medicine, 24 (1969), 193–204, on 197–9; Brooke Hindle, The pursuit of science in revolutionary America, 1735–1789 (Chapel Hill: University of North Carolina Press, 1956), 88.

volunteers observed without instruments, as did most of Kanold's—instruments seem to have come late and few to central and eastern Europe, where about half of Kanold's observers were stationed.^[14] A late 18th-century meteorologist at Prague reported that meteorological instruments first appeared in Bohemia in 1750 and were still rare two decades later.^[15]

Even when instruments were available, their measurements were nearly useless unless the instruments were comparable—that is, unless instrument scales were interconvertible. Comparability of barometric observations posed no difficulty in principle, since the length of a mercury column serves as a natural scale for atmospheric pressure—though the variety of national and even regional units of length confused matters considerably. But the variety of scales for the thermometer greatly diminished the usefulness of temperature readings. Although Jurin attempted to secure comparable observations by asking his volunteers to specify the scale and make of their thermometers, many failed to do so. Derham found reducing their data "a matter so perplexed and difficult, as not to answer the great trouble of it."^[16]

Lack of precision and reliability posed further problems. Instruments neither rendered accurate readings, nor could they be depended upon to render the same reading twice in identical situations. Precision and reliability, in fact, did not trouble early 18th-century natural philosophers.^[17] Imperfect instruments generated much confusion and waste—as late as 1750 measurements made with

[14] Jurin distributed thermometers to his observers (as had Hooke and Ferdinand II), but they were frequently lost or broken during transit. Cf. Louise Diehl Patterson, "Thermometers of the Royal Society, 1663–1768," American journal of physics, 19 (1951), 523–35; "The Royal Society's standard thermometer, 1663–1709," Isis, 44 (1953), 51–63; also J.L. Heilbron, Physics at the Royal Society during Newton's presidency (Los Angeles: William Andrews Clark Memorial Library, 1983), 105–6.

[15] Anton Strnad, "Meteorologische Beobachtungen auf das jahr 1775," Privatgesellschaft zur Aufnahme der Mathematik, der vaterlandischen Geschichte, und der Naturgeschichte, Prague, Abhandlungen, 2 (1775), 392–9.

[16] Derham, "An abstract of the meteorological diaries communicated to the Royal Society," PT, 38 (1733–4), 101–9, 334–44, and 458–70, on 464.

[17] However, see Heilbron, Electricity, 81.

inaccurate barometers led eminent natural philosophers to question Boyle's law.^[18] As for weather observation, "how many observations have we lost," lamented one late 18th-century meteorologist, "through the imperfection and uncertainty of Mr. Hauksbee's thermometer!"^[19] This was just the thermometer Jurin used and supplied to his network.

Observers were scarcely more reliable than their instruments. The discipline of recording daily temperature, pressure, humidity, winds, and cloud cover over a period of years did not come easily. As Derham put it, "these investigations require not only industry and inclination, but also leisure and means and opportunity, which you seldom find together."^[20] Rather than follow Jurin's instructions, several of his informants simply submitted registers they had completed in earlier years. Under these circumstances, a consistent collection of observations was unlikely. The labor of reducing the registers delayed publication, making matters worse. In 1732 and 1733, when the project had almost ended, Derham published comparisons of the weather of 1707 at Upminster and Coventry, the weather of 1715–22 at Upminster and Cambridge, New England, and the weather of 1724 in Lund and St. Petersburg.^[21] Analyses of the project's last registers, which had been submitted in 1734, did not appear until 1742.

Imprecision and unreliability of instruments, lack of agreement among scales, indiscipline in observation and inconsistency of published collections—all these factors limited the achievements of early 18th-century climatology. A thoroughgoing quantitative treatment was not possible. Instead, meteorologists described the weather and summarized observations by calculating monthly and annual means of temperature and pressure and amounts of rainfall. They aimed, as

[18] Feldman, "Applied mathematics," 137–8.

[19] Jan van Swinden, Dissertation sur la comparaison des thermomètres (Amsterdam, 1778), ix. Van Swinden was one of the chief meteorologists of the latter part of the century.

[20] Quoted in Heilbron, Physics at the Royal Society , 108.

[21] Derham, "An abstract of the meteorological diaries," PT (1731–2) and (1733–4).

Derham put it, to give "a just notion of the state of every month . . . and that which was most observable in it."^[22] Even when good quantitative data were available, they did not exploit it. From Jurin's observer at the Academy of Sciences in St. Petersburg Derham received records of the temperature, pressure, winds, and general state of the weather taken three times daily during 1724 and 1725. He felt, however, that the "observations (although very curious and useful), yet being too long, would be tedious to read at the Society's meetings."^[23] What sort of quantitative treatment could there be when, as was the practice at scientific academies, Derham read his reports at the Society's weekly meetings?

Besides describing the weather, meteorologists also drew comparisons among the locations reporting to them. Derham, for example, compared the mean annual rainfall of half a dozen European towns.^[24] Comparisons aimed particularly at coincidences in weather patterns at different locations, that is, at Meteorologica parallela .^[25] Derham repeatedly pointed out agreements among prevailing winds and storms at the towns he was comparing, as well as parallel barometric motions, which were striking. When temperature observations were not comparable, as between Zurich and Upminster, he could still see that the maxima and minima of the two series—that is, warm and cold spells—coincided. "Yea, oftentimes any remarkable weather (especially if of somewhat long continuance) affecteth one as well as the other place."^[26] During one month the weather at Zurich "constantly preceded ours here [at Upminster] by about five or more days." Pieter van Musschenbroek, who among his other services to natural philosophy sponsored a network of half a dozen Dutch observers, observed a similar parallelism: "when the south-east wind blows, it arises half a day sooner at Middelbourg than at Utrecht."^[27]

[22] Derham, "An abstract of the meteorological diaries" (1733–4), 105.

[23] Derham, ibid., 101–2.

[24] Derham, "A prospect of the weather," PT, 24 (1704–5), 1877–81.

[25] David Algöwer, Meteorologica parallela (Frankfurt and Leipzig, 1714), cited in Hellman, Repertorium , 880–1.

[26] Derham, "Tables of the barometrical altitudes at Zurich in Switzerland in the year 1708," PT, 26 (1708–9), 332–66, on 333.

[27] Musschenbroek, Essai de physique , 2 vols. (Leyden: Chez S. Luchtmans, 1739), 895ff.; Derham, "An abstract of the meteorological diaries," PT (1731–2).

These coincidences resulted, of course, from the fact that single weather systems cover large parts of Europe. But only one or two meteorologists understood this before the 19th century. Derham saw this much: that "the weather in both places was influenced by the same causes, whether the Alpine hills and the cold, or the influx of the moon and other heavenly bodies, or any other cause."^[28]

Meteorologica parallela were one type of correlation sought by early 18th-century meteorologists. The "weather rule" was another. Meteorologists hoped to discern patterns in their data that would allow them to predict the weather. Thus Kanold expected his collection to provide a "historical-theoretical attempt to predict one storm from another." Derham derived a number of rules from the observations of Jurin's network: "a cold summer is commonly a wet one"; "western clouds bring much wind"; "the falling of the quicksilver in dark and cloudy weather betokeneth rain; but the rain is always preceded by fair weather."^[29] These and other "superstitious calendar-prognostications"^[30] had long been common in almanacs and popular tradition. Meteorologists hoped to place them on a scientific footing.

These weather rules, meteorological parallela, and general descriptions and comparisons of the weather reflect an approach to the natural world that has been well characterized by Michel Foucault. In his study of 18th-century medical practice he wrote, "Disease is perceived fundamentally in a space of projection without depth, of coincidence without development." Disease appears in the "space" of the human body as in a space without character, flat; the different locations in this space do not affect the disease, so that for example dyspepsia in the lower abdomen, breathlessness in the chest, and epilepsy in the head represent the same disease.^[31] Just so, meteorologists perceived the space of the earth's surface as characterless. We

[28] Derham, ibid., PT (1733–4), 342.

[29] Derham, ibid., PT (1731–2), 265, 267, and (1733–4), 101–2, 105. John Locke also hoped to extract weather rules from collections of observations. See Locke, "A register of the weather for the year 1692," PT, 24 (1704–5), 1917–37; Kanold, Sammlung von Natur- und Medicin- wie auch hierzu gehörigen Kunst- wie Literatur-Geschichten .

[30] Algöwer, Meteorological parallela , "so abergläubischen Calender-Prognosticis."

[31] Michel Foucault, Birth of the clinic (New York: Vintage Books, 1975), 6, 10.

would see the space between Lund and St. Petersburg as a land (and water) mass of great extent, with a richly varied topography (and depth, embracing currents, varying temperatures, varying proximity to land masses, etc.), affecting the weather across its entire compass. For Derham and his colleagues this space might as well not exist. The weather is either the same or different at Lund and St. Petersburg; Derham could compare the weather at Upminster and Coventry, or at Upminster and Cambridge, New England, as easily. So characterless, or "flat," was his perception of space that Derham could call the Alps "hills" and say that the same causes influenced the weather at Zurich, in their midst, and at Upminster, hundreds of miles away in the plains of his island nation.

Just as space, of itself, did not affect the weather, so "there is no process of evolution in which duration [i.e., time] introduces new events of itself."^[32] The weather rule, which correlates weather events at succeeding times with no sense of the creative role played by those times, exemplifies this approach. "Western clouds bring much wind," but we have no sense of the connecting skein of time, of the intervening process.

All this represents a lack of synthetic vision, which appears also in meteorologists' failure to describe the climates of places. They calculated mean temperatures and pressures, found days of monthly and annual extremes, and counted the number of days of rainfall. They did not, however, synthesize this information into a characterization of climate. To borrow once more from Foucault, their calculations named the "visible" aspects of the weather, but they did not penetrate to the hidden coherence among these aspects, that constitutes climate.^[33]

Nor did they integrate the collection of places they studied into a the notion of a region—so that, a fortiori, they did not discuss regional climates.^[34] (Two groups did discuss regions and their

[32] Foucault, Birth of the clinic , 12.

[33] Foucault, The order of things (New York: Vintage Books, 1973), 132.

[34] Malcolm Nicholson has pointed out that 18th-century botany and plant geography similarly lacked the concept of regionality. See Malcolm Nicholson, "Alexander von Humboldt, Humboldtian science and the origins of the study of vegetation," History of science, 25 (1987), 167–94.

climates: plant and human geographers, mentioned above, and mathematicians who calculated the effects of the sun's heat on different parts of the earth. They belonged to traditions distinct from meteorology; neither group drew on the weather observations considered here.) Climatology, then, existed in neither deed nor word in the early 18th century; what meteorologists gathered was a natural history–a collection of descriptions of the weather here and there, at this time and another. Given the piecemeal character of their data, it would have been difficult for them to proceed otherwise.

Weather Observation and Climatology, 1770–1790

Between the time of Jurin's and Kanold's networks in the 1720s and 1730s and the last third of the century, interest in meteorology fell off.^[35] The wars of the mid-18th century disrupted cooperative efforts and undoubtedly discouraged individual observations as well.

Around 1770 the situation changed abruptly. No meteorological treatise of Europe-wide reputation had appeared for more than a century.^[36] Between 1770 and 1790, however, half a dozen authors in as many countries published treatises of international renown and substantial papers populated the journals;^[37] meteorology was

[35] Hellmann, Repertorium , 978, 986. Hellmann provided data on numbers of individual observers only for the Germans.

[36] See Hellmann, "Entwicklungsgeschichte des meteorologischen Lehrbuches," in Hellmann, Beiträge zur Geschichte der Meteorologie, 6 , Veröffentlichungen des Königlichen Preussischen Meteorologischen Instituts, 296 (Berlin, 1917), 1–133, on 52.

[37] Important treatises of the period include Jean André Deluc, Recherches sur les modifications de l'atmosphère, 2 vols. (Geneva: J.A. De Luc, 1772) and Idées sur la météorologie, 2 vols. (London: T. Spilsbury, 1786); Louis Cotte, Traité de météorologie (Paris: Imprimerie Royale, 1774) and Mémoires sur la météorologie, 2 vols. (Paris: Imprimerie Royale, 1788); Horace Bénédict de Saussure, Essais sur l'hygrométrie (Neuchâtel: Chez S. Fauche père et fils, 1783); van Swinden, Dissertation sur la comparaison des thermomètres ; Giuseppe Toaldo, La meteorologica applicata all'agricultura (Venice: G. Storti, 1775). Hellmann documented a sharp rise around 1770 in numbers of meteorological publications and of observing stations in Germany. The number of publications more than doubled from the 1760s to the 1770s and increased by a further 25 percent in the 1780s. The number of "station-years" of observations doubled twice in the two decades. Hellmann, Repertorium , 978, 986.

"zealously pursued throughout almost the whole of Europe."^[38] Organized meteorology prospered. Throughout France, Great Britain, and the United States, economic, agricultural, and patriotic societies sponsored programs of meteorological observation and research. In France a national network of observers was established in 1778 under the auspices of the Société royale de médicine, while the Societas meteorologica palatina at Mannheim constructed an international network whose work was not surpassed for three-quarters of a century. Contemporaries spoke of meteorology as "a new science."^[39] Ludwig Kämtz, the chief authority on meteorology during the first half of the 19th century, agreed. It was in the last half of the 18th century, he wrote, that "this part of physics first began to be treated scientifically."^[40]

Interest in meteorology derived from a number of sources, of which two particularly affected weather observation and climatology. One was the application of meteorology to agriculture and public health. Prior to the advent of bacteriological theories of disease in the late 19th century, physicians followed the ancient Hippocratic doctrine that climate, topography, and living conditions—in short, the environment—are among the chief causes of disease. The particular content of the doctrine varied. In the original Hippocratic treatise "On airs, waters, and places" the seasons influence the balance of humors in the body by virtue of what was called the "constitution" of the air: the constitution of summer being hot and dry; of autumn, cold and dry; of winter, cold and wet; and of spring, a balanced mixture of all four qualities. These constitutions favor certain groups of diseases; an abnormal season or sudden changes in the weather also cause outbreaks of disease. Winds (airs) blowing from different directions, the orientation of towns (places) facing the winds, and the towns' water supplies (waters) similarly affect disease patterns. These

[38] Jean Sénébier, "Sur les moyens qu'on pourrait employer pour perfectionner la météorologie," Journal de physique, 27 (1785), 300–15, on 301.

[39] "Sur le froid de 1776," Académie royale des sciences, Paris, Histoire , 1776, 1–14, on 9; quoted by David Cassidy, "Meteorology in Mannheim: The Mannheim Meteorological Society, 1780–1795," Sudhoffs Archiv, 69 (1985), 8–25, on 8.

[40] Ludwig Kämtz, Lehrbuch der Meteorologie , 3 vols. (Halle: Gebauer, 1831–6), 1 , viii.

groups or patterns of disease attacking a population were termed the epidemic constitution.^[41]

While abandoning the theory of humors, the 17th and 18th centuries retained the notion that airs, waters, and places influence the epidemic constitution. The same four qualities—hot, cold, wet, and dry—were now held to act mechanically on the body; the air might also contain disease-causing effluvial exhalations from the interior or surface of the earth. Such theories led numerous physicians to keep weather observations in the expectation of correlating weather patterns with diseases. A typical mid18th-century product was Paul Malouin's annual "Histoire des maladies épidémiques, observées à Paris, en même temps que les différentes températures de l'air," which offered qualitative descriptions of each month's weather and epidemic diseases.^[42] Agriculture enjoyed nothing like the corpus of theory relating the weather to disease, but agriculturalists hoped that regular observations would succeed in correlating the weather with the success of crops. The most prominent midcentury effort of this type was Duhamel du Monceau's "Observations botanico-météorologiques," which for forty years presented annual tables of weather observations and general remarks on crops and public health.^[43] Duhamel's and Malouin's series became important models for later efforts.

This genre of medical and agricultural climatology became institutionalized in the last third of the century as European states increasingly intervened in matters of public welfare. Contemporaries referred to interventionist measures as "police"; "public administration" would be a modern synonym. Medical and agricultural police needed information on the environment, diet, hygiene, and living conditions of the populace, on agriculture, and on outbreaks of disease.^[44] Dozens of state and private institutions arose to fill these

[41] Genevieve Miller, "'Airs, waters and places' in history," Journal of the history of medicine, 17 (1962), 129–40; Frederick Sargent II, Hippocratic heritage: A history of ideas about weather and human health (New York: Pergamon Press, 1982).

[42] Académie royale des sciences, Paris, Mémoires , 1746–54.

[43] Ibid., 1741–81.

[44] George Rosen, "Cameralism and the concept of medical police," and "Mercantilism and health policy in eighteenth-century French thought," From medical police to social medicine: Essays on the history of health care (New York: Science History Publications, 1974), 120–41, 211–9, resp.; see André Bourde, Agronomie et agronomes en France au XVIII siècle , 3 vols. (Paris: S.E.V.P.E.N., 1967), 3 , 1533ff., for a discussion of agricultural police in late 18th-century France; L.J. Jordanova, "Earth science and environmental medicine: The synthesis of the late Enlightenment," in L.J. Jordanova and Roy Porter, eds., Images of the earth (Chalfont-St. Giles: British Society for the History of Science, 1979), 119–46, esp. 136; Caroline Hannaway, "Discussion," in Abraham Lilienfeld et al., eds., Times, places, and persons, aspects of the history of epidemiology , supplement to the Bulletin of the history of medicine (Baltimore: Johns Hopkins University Press, 1980), 39–42, on 40; Jean-Pierre Peter, "Disease and the sick at the end of the eighteenth century," in Robert Forster and Orest Ranum, eds., Biology of man in history , transl. Elborg Forster and Patricia M. Ranum (Baltimore: Johns Hopkins University Press, 1975), 103–5.

needs. Climatology became an essential component of their programs. So strong, in fact, was the link between climatology and medicine in France during the 18th century that the French term "température" retained its ancient medical significance: it meant not the degree of heat but the "temperament" or constitution of the atmosphere.^[45]

The second stimulus to climatology was exact experimental physics. A call for reform of instruments was sounded by the Genevan meteorologist Jean-André Deluc in 1772, in his Recherches sur les modifications de l'atmosphère , which included extensive historical and critical surveys of barometers and thermometers and his own design for a portable barometer, accurate to between one-eighth and one-sixteenth of a line.^[46] Deluc discussed problems of parallax in taking readings and the proper point of the meniscus from which to read the mercury column. He demonstrated the importance of boiling the mercury in the barometer tube, a procedure that multiplied the accuracy of the instrument by a factor of 10. He showed how to use the barometer and thermometer in extensive, systematic measurement, taking all possible precautions to avoid disturbing factors. In order to establish a barometric rule for heights (i.e., a formula relating barometric pressure to altitude), he took over 400 measurements of temperature and pressure at fifteen stations on a mountain near Geneva, using great care in the exposure of the instruments and correcting for the effect of heat on both the barometer and the

[45] Note the title of Malouin's memoirs, "Histoire des maladies épidémiques . . . en même temps que les différentes températures de l'air." See also the usage of the term by Turgot and Cotte and in medical topographies, as discussed below.

[46] Deluc, Recherches . A line is 1/12 inch.

column of air whose height he was measuring. Later he made eighty-seven observations atop Geneva's cathedral. Such methods were a great novelty, and the Recherches were hailed as "a revolution in this part of physics."^[47]

The revolution spread quickly. Within a few years Jesse Ramsden, the great English instrument-maker, was constructing barometers accurate to 1/500 or 1/1,000 inch.^[48] With them two surveyor-mathematicians, William Roy and George Shuckburgh, measured mountain heights to within 0.2 and 0.7 percent, adopting Deluc's methods and his rule for heights.^[49] Hygrometry—the science of measuring humidity—presented greater difficulties than barometry and thermometry, but in the 1770s and 1780s Deluc and Horace Bénédict de Saussure designed reliable, reasonably accurate, and in de Saussure's case, comparable hygrometers. By the 1790s Alessandro Volta was measuring saturation quantities of water vapor and aqueous vapor pressures to within 4.5 percent.^[50] Around the same time he and other electricians devised sensitive electrometers, although they were not sure just what their instruments measured.^[51] Everyone knows about the adoption of exact instruments and methods in chemistry in France.^[52]

These methods transformed experimentation from a descriptive art to a quantitative science. They provided the kind of numerical data that both inspired and confirmed mathematical laws. With their emphasis on discipline, rationalization, and standardization, they were closely related to the bureaucratic impulse of the late Enlightenment.^[53]

[47] Cotte, Traité , xii.

[48] Liverpool Papers, British Library, Shuckburgh in Add. MS. 38,481, ff. 1v–4r, Roy Papers, Public Record Office, Kew, MS. WO30/119, f. 26v.

[49] Feldman, "Applied mathematics," 178.

[50] Feldman, The history of meteorology , 106, 71–2.

[51] Heilbron, Electricity, 451.

[52] French chemists relied on instruments made by compatriots—Alexis Megnié and Nicolas Fortin, among others. Their instruments were of a precision comparable to Ramsden's. Cf. Daumas, "Precision measurement."

[53] Charles Gillispie has pointed out that quantification in the late Enlightenment often meant standardization, rationalization, and a "spirit of accountancy." Science and polity in France at the end of the old regime (Princeton: Princeton University Press, 1980), esp. chap. 1, sect. 6 and p. 65.

The two reform movements—exact experimental physics and medical and agricultural reform—offered solutions to the most pressing problems of observation and climatology. Instruments were generally more reliable and accurate. Exact experimenters stressed careful specification of their make and scales. Together with the general adoption of the Fahrenheit and Réaumur scales after midcentury, this meant that the readings of different instruments could be reliably compared. The emphasis on discipline in measurement meant that observers would now read their instruments several times daily instead of the single reading common earlier in the century. (Jurin had requested one daily reading by his observers.) They would keep their weather diaries over a period of years rather than submit an out-of-date register covering a single year or less. Bureaucrats in medical and agricultural police were anxious to recruit these observers into their programs and, especially in France, had the means to enforce a proper "labor discipline." A coherent collection of weather observations became possible, and with it a quantitative climatology. A survey of late 18th-century meteorological institutions will show just where and to what degree all these possibilities were realized.

The Smaller Societies

In the German states a number of agricultural, economic, and patriotic societies took up meteorology.^[54] Their emphasis on a friendly, amateurish atmosphere and a preponderance of bureaucrats among their membership^[55] did not favor rigorous observation. Typically they published occasional weather observations, made with or without instruments, and reports of unusual or hard weather and its effects on crops and public health. The Gesellschaft der Naturforschenden Freunde at Berlin was one of the more active groups. Over two decades (1775–95) the society published some twenty reports of unusual weather, accounts of fog, snow, northern lights,

[54] Henry Lowood gives an excellent account of the more than 200 such societies in Patriotism, profit, and the promotion of science in the German Enlightenment: the economic and scientific societies, 1760–1815 (Ph.D. dissertation, University of California, Berkeley, 1987; DAI 49/06-A, 1563).

[55] Ibid., 39, 76.

and the like, as well as descriptions of improved meteorological instruments. These were brief, elementary discussions. A paper of 1787 used rainfall measurements made in Berlin in the 1730s to find monthly precipitation, numbers of rainy days, and the average precipitation on rainy days of each month.^[56] Another contributor described a lightning rod that doubled as an electroscope for atmospheric electricity. He used the apparatus intermittently: "I had no opportunity to observe during the whole of 1791; there were few storms, and [they occurred] at inconvenient times."^[57] The use of data half a century old and a casual attitude toward observation suggest that exact experimental physics had not penetrated the Gesellschaft der Naturforschenden Freunde.

Several German societies organized meteorological networks. In Silesia Ignaz Felbiger, abbot of the Monastery of Our Lady at Sagan, established a network under the auspices of the Patriotische Gesellschaft at Breslau. Felbiger's own enthusiasm for meteorology yielded papers on lightning rods, on the art of weather observation, and on the cold winters of 1783–5,^[58] and prompted him to correspond frequently with Johann Heinrich Lambert, who advised him about organizing observers.^[59] Felbiger saw the project as a second but better Breslauer Sammlung : "with the help of mathematics the necessary instruments and methods of observation have attained a far higher level of perfection since [Kanold's] time; without this exactness and precision it is impossible to compare observations."^[60] Felbiger was ambitious: his observers were to record the temperature in Fahrenheit degrees and tenths; the barometer in Paris inches, lines, and tenths; weather conditions and cloud cover; quantity of rain; wind direction and strength; humidity, by means of Lambert's new hygrometer; optical phenomena such as rainbows and haloes; and the phase of the moon. These specifications, which

[56] Rosenthal, "Bestimmung des Ganges des Niederschalges zu Berlin," Gesellschaft der Naturforschenden Freunde, Berlin, Beobachtungen, 7 (1787), 484–9.

[57] J.P. Pelisson, ibid., 398–407.

[58] Hellmann, Repertorium , 126.

[59] Lambert's considerable contributions to meteorology are discussed in Feldman, "Applied mathematics" and The history of meteorology .

[60] Patriotische Gesellschaft, Breslau, Ökonomische Nachrichten, 1 (1773), 2.

would have been impossible a decade earlier, reflect Felbiger's reading of Deluc's newly published Recherches .^[61] Felbiger also stipulated standard times of observation—soon after dawn, midday (1–4 p.m.), and evening (around 10 p.m.)—and he provided scales for cloud cover, fog, rain, wind, and snow. He had set his sights too high, however. The few observers responding submitted only occasional contributions and several did not use instruments.^[62] An invitation to cooperative weather observation from Prague's patriotic society to "all Bohemian patriots" met with even less success: the organizer found himself alone in supplying the society's journal with observations.^[63]

Western European projects achieved better results than did those in central and eastern parts. In France the Société royale d'agriculture de Paris, founded in 1761, had lapsed into inactivity by the 1770s. It was revived in 1785 by a drought and by the growing urgency of agricultural reform. The Intendant of Paris, under whose jurisdiction the Society fell, appointed the energetic Auguste Broussonet as its permanent secretary, and the Academy began publishing Mémoires , holding public meetings, awarding prizes—in short, adopting the demeanor of a learned academy of the Enlightenment.^[64] Between 1785 and its demise in 1793, the Society published in its Mémoires eight sets of "Observations géorgico-météorologiques," elicited by questionnaires distributed by the local authorities, and a paper on the cold winter of 1789. The observations, more georgical than meteorological, included detailed topographical descriptions, general monthly accounts of weather, descriptions of the effect of weather on crops and animals, harvest quantities, and grain prices.^[65]

[61] Ibid., 79.

[62] For example, Kretzschmer, "Wetterbeobachtungen in Braunau, 1778," Ökonomische Nachrichten , 6 (1778) and Freytag, "Einfluss der Witterung," ibid., 113–4, 180–1, 220–2.

[63] Strnad, "Meteorologische Beobachtungen," 397–9.

[64] Gillispie, Science and polity , 370–1, 375–6.

[65] De Courset (le Baron), "Observations géorgico-météorologiques faites dans le Boulonnais," Société royale d'agriculture, Paris Mémoires , 1786–8; Gallot, "Observations géorgico-météorologiques," ibid., 1787.

The mix of topics illustrates nicely the affinities between meteorology and agriculture.

Bern's Ökonomische Gesellschaft, which included among its members Albrecht von Haller, Daniel Bernoulli, and the important instrument-maker Michel du Crest, organized on a more ambitious scale. Since 1760 the Gesellschaft had published "Observations rurales" from seven towns and villages of the Canton. The observations included qualitative descriptions of the weather and its medical and agricultural effects; tables of monthly rainfall; degree summations of heat and cold at morning, noon, and night; and extremes of temperature and pressure. (Degree summations are sums of temperature readings taken over a given period. They indicate the total amount of heat available to plants and are a characteristic innovation of late 18th-century climatology, with its interest in agricultural applications.) In 1763 the Society resolved "to establish meteorological observers in at least six different places in the Canton, and to supply them with exact instruments." The network was part of a plan to collect information on topography, climate, and disease (i.e., on "airs, waters, and places") and on agricultural and industrial resources. It lasted a decade before submissions petered out.^[66]

The Big Projects

These smaller societies lacked personnel and resources for significant meteorological research. The great projects of the late Enlightenment were carried out by institutions that enjoyed generous funding and the full support of the state: the Societas meteorologica palatina and the Société royale de médecine. The Royal Society of London, whose connection with the state was more tenuous, provides an interesting counterpoint.

The Royal Society had maintained its interest in meteorology after the end of Jurin's group, publishing about 150 meteorological papers between 1750 and 1770.^[67] Most of these were brief notices of spells

[66] Ökonomische Gesellschaft, Bern, Mémoires , 1763–72; quotation is in Mémoires , 1763, xvii; cf. Lowood, Patriotism , 202–3.

[67] Feldman, The history of meteorology , 213–4.

of unusual or hard weather or of rainbows, haloes, and other optical phenomena, submitted by provincial correspondents. Typical were "Observations of the late severe cold weather" of the winter of 1753–4 and "Concerning a very cold day, and another very hot day" in 1748—observations of at most a few days' weather, reporting only its temperature and general character and using outdated instruments.^[68] Between 1750 and 1770 brief reports like these outnumbered meteorological registers (weather diaries covering a longer period) by almost two to one.

The contrast with the two decades after 1770 is striking. Between 1770 and 1790 registers and theoretical and experimental papers on meteorology outnumber brief, descriptive reports by eight to five. Several registers covered five or six years' weather; one spanned ten times as much. Contributors used instruments from the best artisans—Nairne and Ramsden, for example—and took care to describe their construction, calibration, and exposure.^[69] Several contributors were on assignment for the East India or Hudson's Bay Companies and observed the weather at their employers' and the Royal Society's request. The arrangement reflects the kind of relations the Society enjoyed with semigovernmental commercial and exploring ventures.^[70] The Society published their registers and those of provincial English correspondents in full.

In 1774 the Royal Society began keeping its own register of observations. Henry Cavendish submitted the Society's instruments to an

[68] William Arderon, in PT, 48 (1753–4), 249–50, and Henry Miles, in PT, 46 (1749–50), 208–13, resp.

[69] The six-decade register is Thomas Barker, "Register of the barometer, thermometer, and rain at Lyndon," PT, 61–88 (1771–98); the first year included a register of rainfall from 1736 to 1771. William Roxburgh, "A meteorological diary kept at Fort St. George in the East Indies," PT, 68 (1778), and 80 (1790), observed at three fixed times daily with a Nairne thermometer and Ramsden barometer.

[70] The best known example involving meteorology is reported in Thomas Hutchins, "An account of the success of some attempts to freeze quicksilver, at Albany Fort in Hudson's Bay," PT , 1776, 174–81, and Thomas Hutchins and Charles Blagden, "Experiments for ascertaining the point of mercurial congelation," ibid., 1783, 303–70; Roxburgh at Fort St. George provides another example. See also "Weather observations from Nain and Okak at Labrador," "Meteorological journal kept at Port Jackson in New South Wales," and others, Royal Society of London, Meteorological Archives, mss. 143, 146, etc.

exhaustive exact experimental investigation prior to the institution of twice-daily observations, which continued until 1843.^[71] The registers, printed in full in the Philosophical transactions , included readings of exterior and interior thermometers, barometers, hygrometers, and instruments to measure wind, magnetic variation and dip, and rainfall. Together with the contributions of the Society's correspondents, they constituted a far more extensive, detailed, and reliable source of data than had been available earlier in the century. The Society's registers were analyzed by its secretary Samuel Horsley, who calculated monthly mean, extreme, and mean morning and evening temperatures, extreme and mean pressures, the number of days on which the wind blew from each of the sixteen points of the compass, and the proportional rainfall in each month and season of the year.

Horsley also tested for the influence of winds and of the moon on the barometer. The moon was supposed to affect the weather by causing atmospheric tides; because its motions were periodic, a long enough series of observations might reveal correlations that would enable meteorologists to predict the weather. The theory ("so improbable, so destitute of all foundation," wrote Horsley) was eventually discredited, although adherents could be found well into the 19th century. As for the influence of wind direction on the barometer, this hypothesis contributed in the 19th century to the theories of wind rotation of H.W. Dove and others. Counting mean monthly barometer heights and corresponding directions of monthly prevailing winds, Horsley found a correlation: the barometer stood higher in months with winds in the semicircle WSW-W-N-NE; W and NE winds accompanied the greatest mean heights, and in seven months out of twelve the highest barometer reading occurred during a NE wind. Horsley must have been surprised when his count of the number of changes in the weather occurring within three days of the moon's syzygies and quadratures supported the hypothesis of lunar influence. He remarked only that the observations had not continued long enough to draw a firm conclusion.^[72]

[71] Henry Cavendish, "An account of the meteorological instruments used at the Royal Society's house," PT, 66 (1776), 375–401; Cavendish, The scientific papers , vol. 2, Chemical and dynamical (Cambridge: The University Press, 1921), 53.

[72] Samuel Horsley, "An abridged state of the weather at London in the year 1774," PT, 65 (1775), 167–93.

While Horsley was calculating, an epidemic—or, more properly, an epizootic—of cattle plague was raging through France. The quarantine and slaughter of thousands of infected cattle became necessary. Anne-Robert Turgot, Louis XVI's minister of finance, encountered bitter resistance from the peasantry; faulty communications between the central authorities and physicians in the provinces further inhibited effective action. In order to direct and enforce the necessary measures, Turgot called forth a Commission de médecine aux maladies epidémiques et epizootiques in 1776. It received letters patent in 1778 as the Société royale de médecine.^[73]

The Society was charged with the medical police of France, formerly the responsibility of the intendants. Working through them, it centralized public health policy in a single state agency staffed by trained physicians. Its duties were varied: to regulate the distribution of patent medicines and mineral waters; deploy a network of provincial physicians to gather information on public health and the environment; establish sanitary measures and regulations; advise provincial physicians on the prevention and treatment of epidemics; and, in cases of epidemic outbreaks, coordinate and enforce appropriate measures.^[74] The Society also took on all the attributes of a learned academy: titles of membership signed by its president and secretary, medals, prize questions, éloges , and a journal whose title, Histoire de la Société royale de médecine, avec les mémoires de médecine et de physique médicale, echoed that of its elder sister, the Paris Academy of Sciences.

Two aspects of the Society's operations concerned climatology. The first was the construction of "a medical and topographical map of all of France," toward which physicians "of all the cities of the realm" would contribute memoirs "on the nature of their climate (de aere, acquis, et locis ), and on the temperament of those who live

[73] Gillispie, Science and polity , 24–33; Jean-Paul Desaive et al., Médecins, climat et épidémies à la fin du XVIII siècle (Paris: Mouton, 1972), 9; Caroline Hannaway, "The Société Royale de Médecine and epidemics in the Ancien Régime," Bulletin of the history of medecine, 46 (1972), 257–73, on 259ff.

[74] Gillispie, Science and polity , 219ff. and 226ff.; Hannaway, "The Société Royale de Médecine," 258ff.; Desaive et al., Médecins, climat et épidémies , 11–2.

there."^[75] The best of these medical topographies, as they were called, won annual prizes from the Society. They might cover nearly 100 pages of text with complete environmental and geographical descriptions of the author's region, including climate and topography, economy, hygiene, and endemic diseases.^[76] By the outbreak of the Revolution, 226 topographies had been collected.^[77]

The Society's network of provincial physicians also carried out a grand program of meteorological observation. Already in 1775, in the midst of the epidemic, Turgot had tested the waters by distributing questionnaires via the provincial intendants, asking physicians in their jursidictions for "the temperature and the [epidemic] constitution of the years 1772, 1773, 1774, and 1775."^[78] The resulting medicometeorological correspondence was continued by the Commission for Epidemics. After 1778, the authors of this correspondence became the Society of Medicine's network of observers.^[79]

The direction of the network was undertaken by Louis Cotte, Oratorian priest and France's foremost meteorologist. Just a few years earlier Cotte had published the first textbook of meteorology based on observations—that is, the first to include many observations at all and to derive its discussions of the weather from them.^[80] Cotte was especially interested in agricultural applications of meteorology. He had originally planned his Traité de météorologie as an extension of Duhamel's "botanico-meteorological" investigations; it is agriculture, he wrote, "which I have had principally in view in this work." He included medicometeorology as well, excerpting Malouin's

[75] Société royale de médecine, Paris (SRM), Histoire , 1776, xiv; ibid., 1782–3, 6–7.

[76] For example, de Brieude, "Topographie médicale de la Haute-Auvergne," SRM, Mémoires , 1782–3, 257–340.

[77] Hannaway, "The Société Royale de Médecine," 267.

[78] Ibid., 3; "Questions à faire aux médecines," France. Académie nationale de médecine, Archives, SRM Carton 189, dossier 13, number 16.

[79] France. Académie nationale de médecine, Archives, SRM Carton 172, dossiers 1–22 cf. Gillispie, Science and polity , 33, 202–3.

[80] Cotte, Traité de météorologie . Cf. Gustav Hellmann, "Entwicklungsgeschichte des meteorologischen Lehrbuchs," in Hellmann, Beiträge zur Geschichte der Meteorologie, 3 (Berlin, 1922), 1–14, on 1.

memoirs extensively. The goal of meteorology, he believed, is "the perfection of the sciences of agriculture and medicine."^[81]

In the Royal Society of Medicine, Cotte had observers to pursue that goal. The requirements he imposed upon them were, in the words of one modern meteorologist, "very strict," and, in the judgment of another, comparable to mid19th-century standards.^[82] "It is necessary first of all," Cotte warned, "to have good instruments." A Réaumur mercury thermometer was to be calibrated if possible against the Society's standard; the barometer, calibrated "with the greatest exactitude," should be equipped with a vernier and readable to an accuracy of tenths or twelfths of a line. The Society would recommend reliable artisans on request. Cotte specified the proper exposure for the instruments and set fixed times for observation.^[83] "Great exactitude and a spirit of order—these are the principal requirements of the physicist who devotes himself to these sorts of observations."^[84] These words might serve as a motto for late-Enlightenment physical science.

Cotte complained more than once that his observers' instruments were not comparable, that observers were not providing "an exact description" of their instruments, that the instruments were "defective. . .supplied by travelling barometer-peddlers." But he had to admire his observers' zeal.^[85] By 1785, 150 provincial physicians were participating in the project; about 50 of them observed for more than a decade.^[86] Modern climatologists agree that the Society's observers were the elite of the medical profession—otherwise they could not have followed Cotte's instructions at all. They generated a great mass of observations over the whole of France—the largest collection, most likely, prior to the foundation of national meteorological bureaus in the mid19th century. From these observations

[81] Cotte to Macquer, 25 Aug 1768, France. Bibliothèque nationale, ms. Fr. 12305, ff. 209–11; Cotte, Traité de météorologie , ix, xvii.

[82] Desaive et al., Médecins, climat et épidémies , 90; J.A. Kington, "A late eighteenth-century source of weather data," Weather, 25 (1970), 169–75.

[83] SRM, Histoire , 1776, xi–xiv.

[84] Cotte, Traité de météorologie , 517.

[85] SRM, Histoire , 1777–8, 104; ibid., 1782–3, 245–6; ibid., 1784–5, 204.

[86] Ibid., 203; Peter, "Disease and the sick," 85, 87.

meteorologists have been able to reconstruct the climate of France in the last years of the Old Regime.^[87]

Cotte did not publish these observations in full; "Tables are not pleasant for the reader," he said, echoing Derham across a half-century.^[88] Instead he published monthly summaries of the weather at each reporting location, including its "temperature" in terms of the Hippocratic categories cold and wet, cold and dry, warm and wet, and warm and dry, along with the usual means, extremes, and descriptions of diseases. Although the summaries resembled those of Derham's time, they were more plentiful and more consistent. Cotte arranged them in great tables (tables were not to be dispensed with entirely) that amounted to the first descriptions of the climate of a nation based on detailed, regular observations.

Cotte's tables represented a collection of data dense enough over a sufficient area to reveal something of the importance of space for the weather. "These extreme temperatures take place," he said, "at the same time over a very great extent of country."^[89] This remark, made early in the Society's career, sounds like one of Derham's coincidences, only it covers more ground. A few years later Cotte wrote that the tables showed clearly "the influence of great variations of the atmosphere over a very great extent of country on the thermometer, and principally on the barometer."^[90] These isolated suggestions mark the limit of Cotte's insight. He did not draw from the tables a description of the climate of France. Moreover, the tables' monthly means and extremes could not reveal the density of the weather in time. Because Cotte did not publish the full record of observations, his observers' efforts were of as little use to other meteorologists as they seem to have been to himself. They lay hidden in the Society's archives until climatologists began to explore them around the middle of the present century.

[87] Desaive et al., Médecins, climat et épidémies , 40–2, 97. O. Muller, ibid., has submitted the Society's observations to correlation analysis. Many, especially those of Paris and the Ile de France, show a correlation coefficient of 0.8 and higher.

[88] Cotte, Traité de météorologie , 517.

[89] "Temperature" here is taken in a broad sense to include barometric pressure, rains, storms, and drought. SRM, Histoire , 1777, 105.

[90] SRM, Histoire , 1780, 261.

The Societas meteorologica palatina has enjoyed greater fame than its French sister, in part because it was an international organization whose members were the chief scientific institutions of Europe (more on this below). More significantly, the Palatine Society published the full record of its members' observations, which were excellent and became a valuable resource for 19th-century meteorologists.^[91] The Society was a product of a late 18th-century enlightened state, the principality of the Palatinate or Kurpfalz. Cultural life flourished there under the patronage of the Elector Karl Theodor, who was keen on science and its contribution to his subjects' welfare.^[92] Mannheim, Karl Theodor's capital, was one of Germany's centers of culture; the Elector lavished on it an Akademie der Wissenschaften, a Deutsche Gesellschaft, and a Deutsches Theater, and brought Gotthold Ephraim Lessing, Friedrich Gottlieb Klopstock, and Wolfgang Amadeus Mozart to write and play for him. He furnished an astronomical observatory with English instruments, then the best in the world, and directed his court chaplain and ecclesiastical councillor, Johann Jakob Hemmer, to assemble a cabinet de physique and offer lectures and demonstrations.^[93] In the 1770s Hemmer investigated the electricity of flames, of dew, and of the atmosphere, and he was largely responsible for the erection of lightning rods throughout the Elector's extensive realm. His book on the subject went through two editions. Many German rulers bought it for distribution in their principalities.^[94]

The idea for a Palatine meteorological society may have come from neighboring Baden. There, in 1778, the Karlsruhe professor of mathematics and physics Johann Böckmann founded the Badische

[91] For example, H.W. Brandes derived the first synoptic analysis of European weather in 1823 from the Society's record for the year 1783. See Brandes, Beiträge zur Witterungskunde (Leipzig, 1820).

[92] Hellmann, Repertorium , 896.

[93] David Cassidy, "Meteorology in Mannheim," 12; Hellmann, Repertorium , 193.

[94] J.J. Hemmer, Anleitung, Wetterleiter an allen Gattungen von Gebäuden auf die sicherste Art anzulegen (Mannheim, 1786, 1788). Cited by Adolf Kistner, Die Pflege der Naturwissenschaften in Mannheim zur Zeit Karl Theodors (Mannheim: Selbstverlag des mannheimer Altertumsverein, 1930), 87; Cassidy, "Meteorology in Mannheim," 14–5.

Witterungsanstalt, a network of sixteen observers within the margravate.^[95] The project failed for lack of funds, but it probably inspired Hemmer, who hired Böckmann's instrument-maker and placed his own plans before the Elector.^[96] Karl Theodor, who himself kept a weather diary, approved, and in 1780 the Societas meteorologica palatina received its charter as a three-member "Meteorologische Klasse" in the Mannheim Akademie der Wissenschaften. Hemmer, the Society's secretary, recruited observers, oversaw the construction of instruments for them, and edited the annual Ephemerides meteorologicae .

The Society's work was a model of exact experimental method. Hemmer followed Deluc closely in specifications for instruments. "We shall always search for ways to make observations more exact," he declared, "both for the sake of agriculture and for our health." Tubes of barometers and thermometers were to be exactly cylindrical, carefully cleaned, and filled with pure, boiled mercury, and the scales carefully prepared and exactly measured. Barometers were to be read to tenths of a line with the vernier against the cusp of the meniscus and thermometers to tenths of a degree. Care was to be taken to prevent disturbances from the observer's breath or candle. Observers could use their own instruments if they met these standards. Hemmer nonetheless dispatched to each of them a packet of instruments "whose comparability has been assured, sparing no expense": a barometer with correcting thermometer (the thermometer to correct for the effect of heat on the barometer), two thermometers (for exposure in sun and shade), and a hygrometer of Deluc's design (using a goose-feather quill that expanded with humidity). Selected observers received a magnetic declination compass as well. Hemmer also asked participants to observe wind direction and strength, cloud cover, precipitation and evaporation, river level, lunar phase, and medical and agricultural conditions. Hours of observation were set at 7 a.m., 2 p.m., and 9 p.m.; Hemmer supplied scales for wind

[95] J.L. Böckmann, Beiträge zur neuesten Geschichte der Witterungslehre (Karlsruhe, 1781), cited in Hellmann, Repertorium , 889.

[96] Kistner, Die Pflege der Naturwissenschaften , 96–8; Cassidy, "Meteorology in Mannheim," 17–8.

strength and cloud cover and symbols for precipitation and other "meteors."^[97]

Along with these exacting specifications went a new strategy of recruitment. In order to secure continuity in observations, Hemmer invited scientific institutions rather than individuals to participate; each institution would appoint one of its members to observe. No fewer than thirty-seven academies, universities, and monasteries in Europe and America responded, and Hemmer soon had an international network staffed by the world's capable workers. Their registers—reliable, uniform, and, in a number of cases, extending over a decade—appeared in extenso in the Society's Ephemerides . This was a "princely plan of operations," in the words of the 19th-century meteorologist John Daniell,^[98] carried out at princely expense: 1,500 gulden annually for the Ephemerides alone, or about a third more than the salary of a senior member of France's Académie royale des sciences.^[99] The resulting collection, wrote Daniell, "contain[ed] more data for a correct history of the weather than all other works on the same subject taken together."^[100] Such was the stature of the Palatine Society that its hours of observation—the so-called "Mannheim hours"—and the "Mannheim cloud cover and wind scales" were widely adopted and remained in use for more than a century.

Several of Hemmer's observers carried out extensive climatological analyses of their own weather records. Typical was the contribution of Nicholas de Béguelin of the Academy of Sciences in Berlin. He reported monthly maxima and minima for the thermometer and barometer, their monthly ranges, and annual and monthly means; the same for morning and evening thermometrical observations, together with maximum diurnal range; for the hygrometer and magnetic needle monthly mean morning, afternoon, and evening values, the mean of all three, and monthly extremes and extreme ranges; and monthly

[97] Societas meteorological palatina, Ephemerides meteorologicae, 1 (1781), 21, 7–14. See Hellmann, Repertorium , 898.

[98] John Daniell, Meteorological essays , 3d ed., 2 vols. (1845), 305.

[99] Cassidy, "Meteorology in Mannheim," 19; for salaries, see Heilbron, Electricity , 117, 122.

[100] Daniell, Meteorological essays , 305.

frequencies for each direction and degree of wind strength and for each degree of cloud cover, all according to Hemmer's scales.^[101] Participants contributed a wealth of other material, which Hemmer published indiscriminately: ten years' tidal observations from Padua, hourly barometric measurements over an entire month, hourly observations of magnetic declination from 6 a.m. to 10 p.m., Hemmer's own measurements of atmospheric electricity, and van Swinden's collection of temperature observations taken four and five times daily in nine Belgian towns during a cold spell in December 1783. From analyses of contributors' registers, Hemmer's assistant Karl König published tables like Cotte's but far more complete. A single table for each reporting location presented monthly summaries. A "general table" of all locations showed annual extremes, means, and ranges; extremes of monthly means for barometer, thermometer, and declination-needle; annual rainfall and prevailing winds; monthly sums of degrees of heat; and frequencies of wind strength and direction, "meteors," and cloud cover.

Although the collection was something of a miscellany, the observations and analyses were more consistent and rigorous than anything earlier in the century. In them we can see the first hints of a discipline of climatology: a standard and consistent practice in the gathering and analysis of weather data. This practice is reflected in the emergence of a standard set of climatological variables calculated by meteorologists such as Béguelin, König, and Horsley. Their work marks the beginning of a quantitative climatology.

The new climatology provided some definitive answers to old questions. Van Swinden, in an independent investigation, and two contributors to the Society's Ephemerides examined barometric observations taken five, six, and eighteen times daily over a year or more. They refuted the hypothesis of lunar influence but confirmed the diurnal variation, a daily fluctuation of the barometer that several earlier meteorologists thought they saw in their data.^[102] These analyses

[101] Ephemerides , 1784, appendix, 3–6.

[102] Van Swinden, Mémoire sur les observations météorologiques faites à Franeker pendant le courant de l'année MDCCLXXIX (Amsterdam: M.M. Rey, 1780), 34; Joh. Jac. Planer, "Observatio oscillationis mercurii," Ephemerides , 1783, 250–7; Vincent Chiminiello, "De diurna nocturnaque oscillatione barometri," ibid., 1784, 230–4.

exploited the density of observations in time . The coverage of observations in space led meteorologists to a greater appreciation of its role in the weather. They could now trace the paths of weather events from one end of Europe to the other: the cold wave of the winter of 1775–6, for example, and the famous hailstorm of 13 July 1788, which by destroying crops across the most fertile regions of France contributed significantly to the trouble preceding the Revolution.^[103] And they arrived at a clear statement of the spatial extent and of the motion of barometric variation. "Anyone who carefully examines and compares the barometric observations in volume I of the meteorological Ephemerides ," proclaimed Coelestin Steiglehner, "cannot fail to conclude that oscillations longer than one day extend over many places of diverse longitude and latitude."

From observations at London, Regensburg, and St. Petersburg, Steiglehner determined that a barometric minimum occurring around Christmas 1775 had traveled from west to east, striking each town in succession. Further analysis of data from London, Regensburg, St. Gotthard, Buda, Mannheim, and Vienna confirmed the rule "early in the west, late in the east."^[104] F.X. Epp had drawn a similar conclusion from the observations of the network of twenty-four Bavarian observers he directed. The Churbayrische Akademie der Wissenschaften, a sister society to the Mannheim Academy after Karl Theodor inherited Bavaria in 1777,^[105] established the network in the same year that the Palatine Society was chartered. From parallel barometric motions recorded by his observers Epp concluded that the causes of barometric variation extend over wide regions, perhaps over

[103] Van Swinden, Observations sur le froid rigoreux du mois de janvier, MDCCLXXVI (Amsterdam: M.M. Rey, 1779), 5–6; Cotte, in the "Feuille météorologique" of the Journal de france , cited in Buissart, "Mémoire sur l'orage du treize juillet, 1788," France. Académie nationale de médecine, SRM carton 141, dossier 40. On effects of the hailstorm, see Robert D. Harris, Necker and the revolution of 1789 (Lanham, Maryland: University Press of America, 1986), 273; Michel Vovelle, The fall of the French monarchy 1787–1782 , transl. Susan Burke (Cambridge: Cambridge University Press, 1984), 86.

[104] Coelestin Steiglehner, "Excerpta ex dissertatione: atmosphaerae pressio varia," Ephemerides , 444–57.

[105] See James E. McClellan III, Science reorganized. Scientific societies in the eighteenth century (New York: Columbia University Press, 1985), 118.

hemispheres. He confirmed this conclusion by examining one month's barometric variations in five European towns, the data for which he found in the Palatine Society's Ephemerides.^[106]

Finally, a few meteorologists began to synthesize descriptions of regional climates from observations. The Society of Medicine's medical topography project aimed at a "medical and topographical map of all of France." Van Swinden planned to determine the climate of Frisia from his own observations, and from others' observations throughout Holland he began to construct a picture of its provincial climates.^[107] Epp expected from his collection "a more exact knowledge of [Bavaria's] climate" and of the "physical character of the land."^[108] If the stations were properly distributed the observations would yield information on local climates as well.^[109] None of these projects, however, was completed.

Conclusion

The French revolutionary period brought a precipitous decline to meteorology. The correspondence of the Société royale de médecine ceased with the onset of the Revolution in 1789; along with all the Old Regime academies the Society was suppressed in 1793.^[110] The Palatine Society, already in decline after the death of Hemmer in 1790, collapsed in 1795 when the French army crossed the Rhine, occupied Mannheim, and closed the Academy of Sciences.^[111] In Germany the number of stations observing the weather dropped during the 1790s to a third of its peak value in the previous decade.^[112]

[106] Akademie der Wissenschaften, Munich, Ephemerides, 1 (1781), 14; ibid., 2 (1782), 39–43.

[107] Van Swinden, Observations sur le froid rigoreux , 134–5.

[108] Akademie der Wissenschaften, Munich, Ephemerides, 1 (1781), 4–5.

[109] Akademie der Wissenschaften, Munich, Anzeige an das Publikum, von den Gegenstände der Witterungslehre, und von der Art und Weise die Witterung zu beobachten (Munich, 1781).

[110] Busquet, "Les origines de l'Académie de médecine," Société française d'histoire de la médecine, Bulletin, 20 , (1926), 391–6; Cotte to Thouret, Montmorenci, 9 thermidor an 4 (1796), France. Académie nationale de médecine, Archives, SRM carton 197, dossier 3, number 3.

[111] Cassidy, "Meteorology in Mannheim," 19–20.

[112] Hellmann, Repertorium , 985.

Meteorological contributions to the Royal Society of London's Philosophical transactions had already diminished in the second half of the 1780s.

No doubt other factors besides the physical disruption of war and revolution contributed to the decline. Politics distracted natural philosophers; van Swinden, for example, became involved in administrative and educational reform. When in 1800 Cotte requested some earlier observations from him, van Swinden wrote in regret of "the oblivion to which I have consigned them, regretting all the while that so much research produced so few useful results."^[113] His remarks suggest a further reason for the loss of interest in meteorology. Meteorologists like Cotte had promised "to prove the usefulness of meteorological observation to those who deride [it]."^[114] Nothing positive seemed to have come from the expenditure of so much effort on what many considered a tedious and trivial activity.

The program of late Enlightenment climatology had failed. Meteorology had not brought "the perfection of the sciences of agriculture and medicine." No useful correlations had been discovered between the weather and agriculture or disease, and correlations like the lunar influence that might lead to predictive rules remained in doubt. "All attempts at rules governing the weather have been in vain," remarked the astronomer Bode.^[115] There were a number of causes for this failure. The meteorological projects of the late Enlightenment still confronted some of the limitations of the earlier decades of the century. Instruments had neared perfection but remained unavailable in the more remote French provinces and German states. Rigorous standards had been established for observers but were not always followed outside scientific centers. Institutional arrangements were weak in many areas; this was especially true in central and eastern Europe, where projects suffered from the small size and political fragmentation of the German states. And editors of

[113] Van Swinden, "Lettres sur les grands hivers," Journal de physique, 50 (1800), 277–96, on 277–8.

[114] Cotte, Traité de météorologie , 248.

[115] Rudolf Wolf, Biographien zur Kulturgeschichte der Schweiz , 4 vols. (Zurich: Orell, Füssli & Co., 1858–62), 1 , 451.

meteorological ephemerides retained the practice of publishing summaries rather than the full record of observations, to the frustration of generations of meteorologists.

Cotte and his colleagues no doubt believed that they might have reached some of their goals if the Revolution had not interrupted them.^[116] They were mistaken. Their search for correlations between weather patterns and agriculture and disease belonged to the "classical" episteme , as Foucault called it, the episteme of natural history and nosology.^[117] Meteorologists working within this episteme associated the weather with diseases and agriculture according to superficial correlations, without penetrating to the interior forces that govern their interactions. But climatology (parallel with the rest of Western knowledge, if Foucault was right) was moving in the last decades of the 18th century away from this approach toward the perception of these interior relations.

It was approaching this goal through quantification. Quantification here did not include mathematical theories of the weather. Other parts of meteorology did develop mathematical theories. In hygrometry, thanks to a new hygrometer and the techniques of exact experimentation, de Saussure and others announced Dalton's law of partial pressures for the special case of aqueous vapor: the total pressure of moist air at a given temperature is the sum of the pressures of its components, water vapor and dry air. From this elementary arithmetical relation de Saussure calculated the relative weights of dry and saturated air, using nothing more complicated than simple proportions.^[118] More sophisticated mathematical laws were worked out in the 1790s governing the relation of vapor pressure to temperature.^[119] In barometry Lambert, working in the tradition of mixed mathematics, had applied the integral calculus to the variation of air pressure with height in the 1760s.^[120] Studies of the distribution of

[116] This appears from Cotte's papers and his correspondence with van Swinden during the 1790s. See, for example, Cotte, ms. preface to Nouveaux mémoires sur la météorologie (1810), Laon, France. Bibliothèque municipale, ms. 568^[2] .

[117] Foucault, Order of things .

[118] See Feldman, The history of meteorology , sect. I, chap. 4.

[119] Ibid., chap. 7.

[120] Feldman, "Applied mathematics," 145–9.

heat over the earth employed trigonometry to calculate the effect of the sun's heat in different latitudes.^[121] All these results lay in areas of contact of meteorology with the numerous disciplines discussed in the introduction to this chapter. Except for one or two isolated examples,^[122] meteorology proper—the study of weather phenomena such as rain and snow, winds, and storms, as well as climatology—lacked any mathematical theory until well into the nineteenth century.

In climatology quantification meant precise instruments and a rigorous discipline of observation. The example of the Société royale de médecine shows how closely tied this discipline was with the bureaucratizing impulse of enlightened absolutism. Once observations were collected, meteorologists analyzed them using the most elementary statistical techniques: counting (the number of days of rainfall, the number of days on which the wind blew from different quarters), taking averages and ratios (means of temperature, pressure, etc., the proportion of rain falling in each season, the proportion of changes in the weather occurring within three days of the moon's syzygies and quadratures), and establishing correlations (between the weather and diseases, among the weather at different locations and times, the weather rule). It is no accident that a discipline so close to public health and administration should rely on statistical techniques.

Limited as it was, this type of quantification pushed climatology to the verge of a new existence. The "discipline" of regular observation and intensive calculation led toward the "discipline" of climatology: the practice of deriving a standard set of variables representing the typical weather of a location. By enforcing a finer coverage in time and space, this discipline led meteorologists' perception (or "gaze," as Foucault called it) toward the creative functions of time and space in weather and climate.

[121] For example, Tobias Mayer, "A more accurate definition of the variations of a thermometer," in Eric G. Forbes, ed., transl., Tobias Mayer's Opera inedita (New York: American Elsevier Pub. Co., 1971), 53–61.

[122] For example, James Hutton, "The theory of rain," Royal Society of Edinburgh, Transactions, 1 (1788), 41–86. The mathematics involved here in elementary.

Even so, there is a tremendous gap between the climatology of the late Enlightenment and that of the early years of the 19th century. The most impressive result of late 18th-century climatology, the diurnal barometric variation, remained a correlation. The discovery of the great extent of barometric variation did not capture the full role of space in modifying weather and climate. Steiglehner's "early in the west, late in the east" still sounds like a weather rule.

The climatology of the first years of the 19th century looks vastly different. Alexander von Humboldt may stand as a representative of the new point of view. Humboldt's isotherms (lines of equal temperature), presented in an essay of 1817, are syntheses of mean annual temperatures across the globe, which present immediately to the eye the role of space in the development of climate.^[123] In the same essay Humboldt speaks naturally and comfortably of the climates of the different regions of the earth; develops comparisons among the climates of eastern and western shores of continents and among coastal, continental, and island climates; and arrives at the notion of a "climatic system"—a region in which the different factors of climate vary in a continuous manner, so that in specifying for example the mean annual temperature one has fixed by implication the range of other climatic factors such as winter and summer temperature. Foucault argued that between 1775 and 1795 naturalists found the key to the new episteme —the notion of organic structure, in the case of biology—but still applied it to the old task of classification.^[124] During the same decades exact experimental physics had provided the key to an appreciation of the role of space and time in climate and the weather, but meteorologists still applied that key to the search for correlations. A mature climatology awaited the age of Humboldt.

[123] Alexander von Humboldt, "Sur les lignes isothermes et la distribution de la chaleur sur le globe," Société d'Arcueil, Mémoires, 3 (1817), 462–602.

[124] Foucault, Order of things , 226ff.

6
Accuracy, Rhetoric, and Technology: The Paris-Greenwich Triangulation, 1784–88

By Sven Widmalm

In the 18th century the technology and the scope of surveying were radically transformed. There emerged a national cartography based on comprehensive triangulation measurements and a scientific discipline, geodesy, which made use of these measurements. France was in the van: Jean-Dominique Cassini, his son, grandson, and great grandson—each of whom in turn became director of the Paris Observatory—had charge of a triangulation that, in the 1730s, developed into a national survey. The influence of the Cassini methods and style had started to spread to other nations by 1750. At first, large triangulations were employed mainly to measure arcs of meridians, providing points of reference for mapmaking and also empirical material for constructing theories of the shape of the earth. Full-fledged national surveys followed, first in Denmark, next in Great Britain.

The "Trigonometrical Survey" of Britain, known since the 1820s as the "Ordnance Survey," was founded in 1791, partly as a consequence of a geodetic measurement led by Major General William Roy and by Jacques Dominique Cassini in the mid1780s in order to connect the observatories of Greenwich and Paris. The work of Roy, which will be the main subject of this chapter, was at the time

considered unsurpassed in its technical refinement and accuracy, and it supplied the model for future British geodetical surveying. The chapter begins with an overview of the development of geodesy and cartography in the 18th century and ends with a discussion of the militarization of large-scale surveying all over Europe. The story is symptomatic of a general tendency around 1800 to amass quantified data for civilian as well as military planning and control.

Geodesy and Cartography in the 18th Century

In Cassini de Thury's influential book on the measurement of the Paris meridian, published in 1744, questions relating to the shape of the earth and to the "geometrical description of the kingdom" were treated separately.^[1] The division existed only on paper. These fields had developed side by side, ever since Jean Picard surveyed a degree of the Paris meridian in the years 1668–70. Picard's triangulation prepared for a national cartographic venture, desired by Jean Baptiste Colbert; it also produced data for calculating the size of the earth, if not its shape. Throughout the 18th century, most advanced geodetical measurements had to do with mapping projects.

Cassini de Thury and Europe

The French survey was begun in 1683 and, after frequent lengthy intermissions, produced in 1718 its first major accomplishment, the triangulation of over seven degrees of a meridian line through Paris. Operations resumed after political support for the project was regained in 1730. Prompted by Pierre Louis Moreau de Maupertuis' measurement of an arc of meridian in Scandinavia in 1736–7, members of the Paris Academy of Sciences resurveyed the Paris meridian.^[2] The Cassinis had claimed that their measurements showed

[1] César François Cassini de Thury, La meridienne de l'Observatoire royale de Paris (Paris: H.L. Guerin & J. Guerin, 1744), 26, quote, and Relation des deux voyages faits en Allemagne par ordre du roi (Paris, 1765), 1–2: "le seul moyen de perfectionner la géographie, étoit de suivre pour la description d'un pays la même méthode que l'on avoit employée pour la détermination de la figure de la terre."

[2] Josef W. Konvitz, Cartography in France 1660–1848 (Chicago: University of Chicago Press, 1987), 3–13.

the earth to have an oblong shape. But Maupertuis' result suggested otherwise; the remeasurement of the Paris meridian and a survey of an arc of meridian in South America made between 1735 and 1744 confirmed that the earth has an oblate shape. Thus measurements outside of France served to calibrate the geodetic work in France. The triangulation of the whole of France now went ahead, under the direction of César-François Cassini de Thury (third in the astronomer dynasty), although it was Nicolas-Louise Lacaille who did most of the fieldwork.^[3] Between 1739 and 1744 almost 800 triangles, from Dunkerque to Perpignan, were measured, along with nineteen bases. The triangles, printed on eighteen sheets, provided a "geometrical skeleton" rather than a map. This was considered to be sufficient for their intended users, namely, engineers involved in public construction works.^[4]

In the 1750s several projects were begun or completed in Europe to complement the measurements sponsored by the French in France, Lapland, and Peru. A leading promoter of these projects was the Jesuit Roger Boscovich, who obtained the support of the pope to measure an arc of meridian between Rome and Rimini. The survey, which ran from 1750 to 1752, had the dual purpose of adding to knowledge of the shape of the earth and updating maps of the papal state. A copy of the "toise of Peru," borrowed from Paris, allowed comparison of Boscovich's geodesy with French results. Boscovich persuaded the king of Sardinia, Carlo Emanuele III, to sponsor a measurement in Piedmont, which Giovanni Battista Beccaria, a Scolopian priest and professor of physics at the University of Turin, carried out between 1760 and 1764. Beccaria's result did not confirm the oblate shape deduced by the French and so contributed to debate about gravitational irregularities and the reliability of geodesy.^[5] This

[3] Charles C. Gillispie, Science and polity in France at the end of the Old Regime (Princeton: Princeton University Press, 1980), 113–5; Lloyd A. Brown, The story of maps ([1949] New York: Dover, 1977), 252.

[4] Konvitz, Cartography in France , 15–28.

[5] Antonio Marussi, "Italian pioneers in the physics of the universe. III: Geodesy," Cahiers d'histoire mondiale, 7:2 (1963), 473–5; Elizabeth Hill, "Roger Boscovich: A biographical essay," in Lancelot Law Whyte, ed., Roger Joseph Boscovich: Studies of his life and work on the 250th anniversary of his birth (London: George Allen and Unwin, 1961), 42–6.

was true also of the first measurement of an arc of meridian in North America, for which Boscovich was also in some measure responsible. It was carried out between 1764 and 1768 by Jeremiah Dixon and Charles Mason.

Another Jesuit, Father Joseph Liesganig, director of the Observatory at the University of Vienna, began his survey of an arc of meridian between Vienna and Brün in 1759. Maria Theresa ordered this measurement following suggestions from Boscovich, and probably also from Cassini de Thury, who worked on a triangulation to connect the Paris meridian with Vienna, one purpose of which was to correct the military maps of France's ally, Austria. Cassini de Thury participated in Liesganig's work, which was calibrated with his own by means of a copy of the toise of Peru. In 1762 Maria Theresa authorized an extension of this arc and provided Liesganig with instruments and engineers from the military academy in Vienna.^[6]

Boscovich and others, including Bouguer, had supposed that irregularities in the earth's mass distribution drew plumb bobs from the perpendicular and introduced serious error into geodetic measurements. His view was widely accepted by the 1770s. In 1775 Etienne Bonnot de Condillac made public a severe critique of existing geodetic investigations, and, in agreement with d'Alembert and later also Laplace, he judged that the different measurements of arcs of meridian were too contradictory to demonstrate that the earth has a regular ellipsoid shape. In particular, measurements in France and in Piedmont around the same degree of latitude did not agree. In Condillac's view measurements should conform to theory or else theory should be modified.^[7]

[6] Cassini de Thury, Relation des deux voyages , 3–4; Ernst Bernleithner, "Oesterreichs Kartographie zur Zeit des Grafen Ferraris," La cartographie au XVIIIe siècle et l'oeuvre du comte de Ferraris (1726–1814) , Collection histoire pro civitate, no. 54 (1978), 139–42; Johannes Dörflinger, Österreichichsche Karten des 18. Jahrhunderts (Vienna: Österreichische Akademie der Wissenschaften, 1984), 61–2.

[7] Volker Bialas, Erdgestalt, Kosmologie und Weltanschaung: Die Geschichte der Geodäsie als Teil der Kulturgeschichte der Menschheit (Stuttgart: Konrad Wittwer, 1982), 158–9, 166–7, 181–7; Condillac, Cours d'étude pour l'instruction du prince du Parme, III: De l'art de raisonner (1775; Deux-Ponts: [Bodoni], 1782), 217, 275–8. Laplace later changed his mind and advocated the view that the earth is a true ellipsoid. Pierre Simon Laplace, Oeuvres , 7 vols. (Paris: Imprimerie Royale), 5 (1846), 14–6 (text of 1823).

The conflict that Condillac and others pointed out may be characterized as one of quantification versus geometric simplicity. Possessing only a few measurements of meridianal arcs and a theoretical model authorized by the Principia , scientists could maintain that the earth had a regular shape. By the 1780s, however, it had become possible to be a Newtonian and still entertain novel shapes for the earth. The Newtonian theory flowed from the hypothesis that the earth had once been in a fluid state. With the decreasing interest in hypotheses about first causes, which characterized the late 18th-century instrumentalist attitude to science, one could choose any curve that fit the data.^[8] The work of William Roy offers an example.

Meanwhile, Cassini de Thury had created the first nationwide topographical map based on extensive triangulations. A team of draftsmen and engineers worked on the project between 1750 and its conclusion thirty-nine years later under Cassini de Thury's son, Jacques Dominique.^[9] French geodesy had a lasting influence on European cartography. As early as 1736–7, when Maupertuis visited "Lapland," the Swedish Surveying Office made an inspired but, as it happened, premature attempt to appropriate the new technology for the benefit of Swedish cartography. In Denmark, the Scientific Society of Copenhagen was commissioned to carry out a national triangulation on the French model in 1762. The Austrian military surveys by Joseph Jean Ferraris in the 1770s drew on Cassini's example in the choice of scale (1:86,400) and in the triangulation methods. Other European states and Russia did not introduce large-scale triangulations until the early 19th century.^[10]

In sum, French cartography and geodesy led European practices in both field and office. Meridianal arcs were triangulated as backbones for exact cartography; geodesists computed distances in terms of the

[8] J.L. Heilbron, Electricity in the 17th and 18th centuries: A study of early modern physics (Berkeley: University of California Press, 1979), 71–3.

[9] Gillispie, Science and polity , 480–1; Konvitz, Cartography in France , 16–21.

[10] J. Svärdson, "Lantmäteriteknik," Svenska lantmäteriet 1628–1928, 1 (Stockholm, 1928), 223; Asger Lomholt, Det Kongelige Danske Videnskabernes Selskab, 1742–1942: Samlingar til Selskabets historie, 4 (Copenhagen: E. Munksgaard, 1961), 90–104; Bernleithner, "Oesterreichs Kartographie," 132–8; Brown, Story of maps , 270.

Peruvian toise, and draftsmen used the scale of the Cassini maps, sometimes even when cartographic methods remained traditional, as in Henri Mallet's maps of Switzerland.^[11] This calibration and standardization owed much to Cassini de Thury. He envisaged a Europe geometricized to a uniform scale; to this end he extended the French triangulation to Flanders and to Austria, and tried unsuccessfully to win support for a similar extension into Italy.^[12]

Britain kept outside the sphere of Cassini de Thury's influence until 1783. Then, about a month after the end of the American war of independence, he proposed to the British government that a triangular connection should be made between London and Paris. The resulting measurement became the starting point for the Ordnance Survey, a cartographic venture undertaken by military engineers.

British Military and Scientific Engineers

British military cartography before the Ordnance Survey was poorly developed. The only important surveys outside England had been conducted in response to emergencies, like the measurements in Scotland as part of the pacification of the Highlands after the 1745 rebellion. The young draftsman William Roy led the fieldwork of the Scottish survey and later became director of the whole operation.^[13] After completing the work in 1755, he joined the corps of engineers under the Board of Ordnance and became a lieutenant in the army. Throughout his career Roy held double ranks in the engineers and in the army, the latter always being the higher.^[14] This elevated him to a higher social as well as military position than that of mere engineers, who did not acquire military rank before 1757. The status of the mere engineers rose in the 1770s, partly as a result of a new policy of

[11] M.-A. Borgeaud, "Cartographie genevoise de XVIe au XIXe siècle," Archives internationales d'histoire des sciences , no. 6 (1949), 363–74.

[12] Marussi, "Italian pioneers," 475.

[13] J.B. Harley and Yolande O'Donaghue, "Introductory notes," in The old series Ordnance Survey maps of England and Wales, 1 (Lynpne Castle: Harry Margary, 1975), xi; R.A. Skelton, "The military survey of Scotland 1747–1755," The Scottish geographical magazine, 83:1 (1967), 1–15.

[14] R.A. Gardiner, "William Roy, surveyor and antiquary," The geographical journal, 143 (1977), 441–50, on 443–4.

the Board of Ordnance that required cadets in the corps of engineers to have had some formal technical education; the requirement functioned as a social filter, favoring sons of army officers. At the same time the American war gave rise to a greater recognition of the importance of cartographic skills and to the acceptance of engineers as staff officers.^[15] By the 1780s the engineers had achieved the same social status as army officers.

Because of their specialist abilities, members of the corps of engineers (and of the artillery) saw themselves as a part of the scientific community. Some achieved membership in the Royal Society. They figured among the opposition during the so-called dissensions of 1783–4, when Sir Joseph Banks, who had been president of the Society since 1778, was attacked by practically or mathematically oriented Fellows for favoring antiquarianism and natural history—that is, "gentlemen's science."^[16] Banks' forces managed to defeat their opposition. It might therefore come as a surprise that the Banksians in the Royal Society, not the mathematical practitioners, effected the cooperation with Cassini de Thury.^[17] The key figure in their mobilization was William Roy, who belonged

[15] Douglas W. Marshall, The British military engineers 1741–1783: A study of organization, social origin, and cartography (Ph.D. dissertation, University of Michigan, Ann Arbor, 1976), 1–7, 119–24, 130, 317, 343–4.

[16] David Philip Miller, The Royal Society of London 1800–1855: A study in the cultural politics of scientific organization (Ph.D. dissertation, University of Pennsylvania, 1981), 6–14, 36–104, 115, 120, 135; W.A. Seymour, ed., A history of the Ordnance Survey (Folkestone: William Dawson, 1980), 3, 29, 67; Charles Richard Weld, A history of the Royal Society , 3 (London: J.W. Parker, 1848), 151–70; Hector C. Cameron, Sir Joseph Banks (Sydney: Angus and Robertson, 1966), 128–34; Henry Lyons, The Royal Society 1660–1940 (Cambridge: Cambridge University Press, 1944), 202–5, 211–4, 342. There is no evidence that Banks suppressed mathematically oriented science in the Philosophical transactions .

[17] These Banksians on the triangulation included Charles Blagden, Henry Cavendisch, John Lloyd, and John Smeaton, as well as Roy; all were members of the Royal Society Club, a center of Banksian sympathies. Letters of Blagden to Banks, 1783–4, as listed in W.R. Dawson, ed., The Banks letters: A calendar of the manuscript correspondence of Sir Joseph Banks (London: British Museum, 1958), 61–2, 64–5; Archibald Geike, Annals of the Royal Society Club (London: Macmillan, 1917), 174–5; Seymour, A history of the Ordnance Survey , 134.

socially and intellectually to both the Banksian and the mathematical camps.^[18]

In the 1760s Roy had settled in London and had become a Fellow of the Royal Society and a firm friend of Joseph Banks. Roy's strong interest in antiquities resulted in a major work on Roman Britain, published after his death; thus he qualified as a member of the "Banksian Learned Empire." By the early 1780s, Roy had also established a scientific reputation through painstaking work in the field of barometric hypsometry. As a major-general in the army and a lieutenant-colonel in the corps of engineers, he was an influential proponent of a national military survey, the realization of which was his main objective in the Paris-Greenwich triangulation.^[19]

The Paris-Greenwich Triangulation

In his mémoire submitted to the British government in October 1783, Cassini de Thury argued that a triangulation between Greenwich and Paris would give the relative position of the two observatories with more certainty than celestial observations at Greenwich had done.^[20] The mémoire made its way to the Royal Society, whose president arranged for his friend William Roy to lead the British part of the project. George III granted the Royal Society money to order a theodolite from Jesse Ramsden and the Board of Ordnance supported the project with manpower, both soldiers to undertake the manual work and officers to oversee it. The measurement required cooperation not only between the French and the

[18] Seymour, A history of the Ordnance Survey , 5–6; Yolande O'Donaghue, William Roy, 1726–1790: Pioneer of the Ordnance Survey (London: British Museum, 1977); Gardiner, "William Roy," 441–2; Theodore S. Feldman, "Applied mathematics and the quantification of experimental physics: The example of barometric hypsometry," Historical studies in the physical sciences, 15:2 (1985), 127–97, esp. 156–77.

[19] Gardiner, "William Roy," 446–7. Cf. H.B. Carter, Sir Joseph Banks (London: British Museum [Natural History], 1988).

[20] Nevil Maskelyne, "Concerning the latitude and longitude of the Royal Observatory at Greenwich; with remarks on a memorial of the late M. Cassini de Thury," PT, 77 (1787), 151–87, on 151–2. The mémoire is also printed in Charles Arden-Close, The early years of the Ordnance Survey ([1926] Newton Abbot: David and Charles, 1969), 13.

British but also between military officers and "scientists."^[21] In 1784 Roy supervised the measurement of a baseline on the outskirts of London, and three years later he led the survey from London to Dover and the cross-channel triangulation. The French part was carried out by Jacques Dominique Cassini (whose father had died in 1784), Pierre François Méchain, and Adrien-Marie Legendre.^[22] In 1788 Roy completed the survey between London and Dover. He published two elaborate reports in the Philosophical transactions , which included no fewer than sixteen finely engraved plates.^[23] In 1791 the duke of Richmond, Master General of Ordnance, decided that Roy's work should be continued under military direction. He bought a copy of the Royal Society's theodolite from Ramsden and engaged the civilian mathematician Isaac Dalby as the first employee of the Trigonometrical Survey. Dalby had participated in the triangulation of 1787–8 and was highly praised by Roy, who died in 1790.^[24] The employment of Dalby ensured continuity between Roy's work and its military sequel. The connection between the survey and the Royal Society continued until 1803, when the last report appeared in the Philosophical transactions .

It may be that Banks responded to Cassini de Thury's overture because it carried an implicit criticism of the astronomers of Greenwich. The Astronomer Royal Nevil Maskelyne belonged to the rebel camp within the Royal Society. One charge leveled against Banks during the "dissensions" was that he cared more for social status than for scientific ability; but by promoting the triangulation he showed himself to be a "very worthy President of the Royal Society,

[21] Although the term "scientist" was not in use in the 1780s, its functional equivalent, "scientific person," was. See Edward Williams, William Mudge, and Isaac Dalby, "An account of the Trigonometrical Survey carried on in the years 1791, 1792, 1793, and 1794," PT , 85 (1795), 432.

[22] Seymour, History of the Ordnance Survey , 15–7.

[23] William Roy, "An account of the measurement of a base on Hounslow Heath," PT , 75 (1785), 365–480; "An account of the trigonometrical operation whereby the distance between the meridians of the Royal Observatories of Greenwich and Paris has been determined," PT, 80 (1790), 111–270.

[24] Seymour, History of the Ordnance Survey , 21–2; Roy, "An account of the trigonometrical operation," 118–9. Dalby did practical as well as mathematical work. Ibid., 155.

ever zealous in the cause of science."^[25] Further, by turning the triangulation into an event of social significance, by bringing George III and other members of the highest stratum of society to visit the site of the baseline measurement, Banks also proved that patronage did pay off. Unlike his predecessor John Pringle, Banks was on good terms with the king, who financed a large part of the operation.

The Longitude of Greenwich and the Shape of the Earth

Jacques Dominique Cassini wrote in 1791 that the "sole aim" of the triangulation had been to ascertain the longitudinal difference between the observatories of Paris and Greenwich.^[26] On the other side, Roy had asserted in 1787 that the "chief and ultimate goal has always been considered of a still more important nature, namely, the laying the foundation of a general survey of the British Islands."^[27] But there is nothing to indicate that Roy had official support for such a scheme at this stage. Although he wished to create a national survey, the measurement he was actually conducting had a specific purpose within a scientific context.^[28] This purpose he had to defend. Consequently Roy accepted the French criticism depicting positional astronomy—or anyway British astronomy—as less accurate than geodesy. The fact that the expensive and time-consuming triangulation went forward without the cooperation of the astronomer at Greenwich suggests the strength of Roy's position within the Royal Society.

The disagreement between Roy and Maskelyne was ventilated in two papers published in 1787. Maskelyne wrote a belated reply to Cassini de Thury's mémoire ; Roy, annoyed at the delay, threatened

[25] Maskelyne, "Concerning the latitude and longitude," 151–2; Roy, "An account of the measurement of a base," 425, quote.

[26] Jacques Dominique Cassini, Pierre François Méchain, and Adrien-Marie Legendre, Exposé des opérations faites en France en 1787 pour la jonction des observatoires de Paris et de Greenwich (Paris, [1791]), 65.

[27] William Roy, "An account of the mode proposed to be followed in determining the relative situations of the royal observatories of Greenwich and Paris," PT , 77 (1787), 188–226, on 188.

[28] Seymour, History of the Ordnance Survey , 21–2. George III insisted that the financial support he gave go for "the science of astronomy"; Harley and O'Donoghue, "Introductory notes," xxi.

to publicize Maskelyne's idleness in the Philosophical transactions —thereby demonstrating that he had the official support of the Royal Society, whereas Maskelyne did not.^[29] Roy accentuated the criticism of British astronomy by adding to the uncertainty of eleven seconds of time in longitude between Greenwich and Paris, which Cassini de Thury had pointed out, an uncertainty of three seconds between Oxford and Greenwich. Geodetic methods would narrow the margin of error; Roy considered them "infallible," since they could always be controlled by verifying the bases. The planned triangulation would give a value for the longitudinal difference "sufficiently near the truth, and. . .probably considerably nearer than it will be brought for many years to come, by a mean of the best observations of the heavenly bodies."^[30]

Roy probably did not know that in 1785 Maskelyne had equipped his assistant Joseph Lindley with a number of watches and sent him on a secret "chronometer run" to Paris, to determine the time difference between the capitals. Lindley's result (9 minutes 20 seconds) verified Maskelyne's astronomically deduced value, published in 1787, which was later found to agree with the result of Roy's triangulation.^[31] Roy avoided admitting this embarrassing consistency, which he had earlier denied, by misquoting Maskelyne's data. In his final report he simply plucked from Maskelyne's paper a number about 10 seconds larger than the figure on which the astronomer finally settled, and claimed it as the astronomically deduced value.^[32] He thus demonstrated the superior accuracy of the geodetic method.

[29] William Roy to Nevil Maskelyne, 11 Dec 1786 (RS, DM.4.14). A copy of this letter is in PRO, O.S.3/4. Cf. Roy, "An account of the mode proposed," 213; Eric G. Forbes, "The geodetic link between the Greenwich and Paris observatories in 1787," Vistas in astronomy, 28 (1985), 173–81, on 174. Maskelyne complained that he had not been shown the mémoire until a year after preparations for the triangulation had begun. See Maskelyne, "Concerning the latitude and longitude," 153.

[30] Roy, "An account of the mode proposed," 213–4.

[31] Eric G. Forbes, Greenwich Observatory . Vol. 1: Origins and early history (1635–1835) (London: Taylor and Francis, 1975), 149–50, and "The geodetic link," 174; Maskelyne, "Concerning the latitude and longitude," 183–6; Roy, "An account of the trigonometrical operation," 231.

[32] Roy, ibid., 231. Roy's maneuvers to protect himself from the suspicion of deliberately misquoting Maskelyne are sufficiently transparent. Cf. Roy to Maskelyne, 11 Dec 1786 (PRO, O.S.3/4).

The question of the earth's shape came in as an important scientific side issue in the determination of longitude differences. Roy had developed a new technique for geodetic investigation, which involved astronomical observations of a kind different from those usually associated with longitude determinations. Nevertheless, as Isaac Dalby was to point out, it constituted perhaps the weakest link in Roy's geodetic work. By taking the angles between three mutually remote stations and at the same time observing the angles between the stations and the polestar, Roy calculated the longitudinal differences between pairs of stations by spherical trigonometry. The relationship between these differences and the distance on the ground gave a value for the length of a degree of longitude at a particular latitude. Polestar observations made at only a few stations furnished the basis for calculation of the longitude difference of the whole chain of triangles. Roy calculated the latitudes of the stations in relation to that of Greenwich from a spheroidal model of the earth devised by Pierre Bouguer.^[33]

To justify use of this spheroid, Roy computed the lengths of the arc between Greenwich and Perpignan (the southern extremity of the Paris meridian) on ten different hypotheses about the shape of the earth. In the model Roy favored, the lengths of degrees of latitude increased with the fourth power of the sine of the latitude. One of the models he rejected was an ellipsoid based on data from the six earlier arc measurements Roy thought most consistent. To achieve consistency, however, he had had to take a mean between the arcs of Cassini in France and Liesganig in Austria, since comparison between them gave an "absurd" result—that is, an oblong earth.^[34] Roy combined the six arcs into fifteen pairs and calculated the flattening for each. ("Flattening" is defined as the ratio of the equatorial axis to the difference between the equatorial and polar axes.) Values ranged from 100 to 850, but Roy did not present the extremes: he exhibited only the mean flattening of 190, well within

[33] Roy, "An account of the mode proposed," 216–20, and "An account of the trigonometrical operation," 200, 225–7.

[34] Roy, "An account of the mode proposed," 206–8.

the limits of what was considered reasonable.^[35] The same was true of the other six ellipsoids in Roy's table, resulting from other combinations of measurements or from hypothetical premises, and of the two spheroids as well.

Roy nonetheless proffered Bouguer's spheroid as the most probable alternative because, unlike the other hypotheses, it gave values sometimes above and sometimes below the lengths of the measured arcs: "a never failing proof" that it was "exceedingly near the truth."^[36] Roy hid the wide discrepancies that actually existed between different measurements behind the reassuring surface of averages. Mathematical analysis of error was then only in its infancy. Roy employed another, more visual technique for comparing the different solutions to the problem of the shape of the earth. He presented the results on the different hypotheses in tabular form so that the reader could judge, "by simple inspection only, which of the theories agrees best with actual measurement." He also gave the lengths of degrees of meridians, parallels, and oblique great circles according to Bouguer's spheroid—not only for the portion of the earth covered by his own triangulation, but for the whole earth, so that others could use these figures until, in the distant future, the shape of the earth would "ultimately" become known. Meanwhile, Roy thought, the spheroid would furnish data of "general utility."^[37]

Dalby disagreed with the use of Bouguer's spheroid and with Roy's method of finding differences in longitude. He criticized the method as too sensitive to observational errors. An error of one second of arc in the angles between the stations and the meridian would cause an error of six seconds in the longitude difference between Greenwich and Dunkerque.^[38] Roy had said that he

[35] The usual magnitude of the flattening ranged between 170 and 540—the values suggested by Maupertuis and Christian Huygens, respectively.

[36] Roy, "An account of the mode proposed," 210–1. In early mathematical analysis of observational error by Boscovich and Laplace, this condition usually came with another: that the sum of the absolute values of the errors should be minimized. See Stephen M. Stigler, The history of statistics: Measurement of uncertainty before 1900 (Cambridge, Mass.: Belknap Press, 1986), 11–61, esp. 47, 51.

[37] Roy, "An account of the mode proposed," 201, 222.

[38] Isaac Dalby, "The longitudes of Dunkirk and Paris from Greenwich, deduced from the triangular measurement in 1787, 1788, supposing the earth to be an ellipsoid," PT, 81 (1791), 236–45, on 237, and "Remarks on Major-General Roy's account of the trigonometrical operation," PT, 80 (1790), 593–614, on 607–8. Roy's method for obtaining longitudes is described in Roy, "An account of the trigonometrical operation," 206–25.

determined the longitude difference "by the instrument itself," meaning that the extreme accuracy of the theodolite guaranteed the precision of the result. Dalby challenged this assertion and rejected Roy's spheroid in favor of his own ellipsoid shape, with the flattening of 229 predicted by Newton.^[39]

As we know, the ellipsoid shape depended only on theories of gravity and mechanics and on the assumption that the earth had once been fluid. The theoretical implications of Bouguer's spheroid, on the other hand, are unclear, and probably they did not matter very much to Roy. He adopted it because it gave a good fit to existing measurements. Ramsden, not Newton, was the arbiter of exact geodesy; the theodolite could make errors "totally vanish." Dalby had no special interest in defending the elaborate technology adopted by Roy, and consequently he was happy to accept Maskelyne's value for the longitude difference between Paris and Greenwich as support for the result of the measurement in which he himself had participated.^[40] In modern terms, Roy's attitude was instrumentalist, whereas Dalby's might be called realist. Condillac, who advocated a strict empiricism, criticized both. Condillac's view eventually won out. When the concept later to be christened the geoid was developed in Germany in the early 19th century, irregularities in the earth's mass distribution ceased to be regarded as anomalies and became instead constitutive of the "real" shape of the earth.

Instruments of Competition

The technology for making accurate angular measurements under field conditions was highly refined in the second half of the 18th century, when the quality and quantity of instrument-making rose dramatically, especially in Britain. An expanding market for navigational equipment, intensified surveying, and escalating scientific

[39] Roy, "An account of the mode proposed," 219; Dalby, "The longitudes of Dunkirk and Paris," 327–8.

[40] Roy, "An account of the mode proposed," 219, quote; Dalby, "The longitudes of Dunkirk and Paris," 245.

demands for accuracy all pushed development. The accuracy of angular measurements increased from about 2 seconds to about 0.5 seconds, verniers and microscopes for reading off the scales became common equipment, and the achromatic lens and the dividing engine set new standards for precision.^[41]

The level of accuracy of surveying technology was raised significantly through the Paris-Greenwich triangulation, which for a while turned the coast of the English Channel into an arena for technological rivalry between Britain and France. The competitive spirit no doubt helped both the French and the British parties to gain financial support from their respective monarchs. George III financed the Ramsden theodolite, and Louis XVI paid for a repeating circle by Etienne Lenoir. William Roy wrote that "The honour of the nation is concerned in having at least as good a map of this as there is of any other country."^[42] Governments and the military knew that geodesy yielded accurate maps that could facilitate the exercise of political power and the waging of war. The French astronomers were directed not from the Académie des sciences but from Versailles. Cassini was to report on everything concerning the operations to the minister De Breteuil in Paris, who acted as intermediary with the court. Cassini and Méchain were instructed to undertake a little industrial espionage while in London for the triangulation, paying special attention to the telescopes of Herschel and the instruments of Dollond and Ramsden.^[43] They were also to try to talk Ramsden into

[41] Maurice Daumas, Scientific instruments of the seventeenth and eighteenth centuries and their makers (London: Batsford, 1972), 53–5, 153–6, 176, 189–204; Allan Chapman, "The accuracy of angular measuring instruments used in astronomy between 1500 and 1800," Journal for the history of astronomy, 14 (1983), 133–7; Willem D. Hackman, "Instrumentation in the theory and practice of science: Scientific instruments as evidence and as an aid to discovery," Istituto e museo di storia della scienza di Firenze, Annali, 10 (1985), 103–6.

[42] Breteuil to J.D. Cassini, 9 Jun 1787 (BOP, D5–7); Roy, "An account of the trigonometrical operation," 162–3. Cf. Daumas, Scientific instruments , 184.

[43] Breteuil to J.D. Cassini, 9 Jun and 30 Aug 1787 (BOP, D5–7). Cf. J.D. Cassini, "De la jonction des observatoires de Paris & de Greenwich, & précis des travaux géographiques exécutés en France qui y ont donné lieu," Académie des Sciences, Paris, Mémoires , 1788 (1791), 706–54, esp. 714–7.

joining the staff at the Paris observatory or taking French apprentices.^[44]

The French repeating circle (fig. 6.1) and the British theodolite (figs. 6.2, 6.3) were vastly improved versions of older instruments. They soon replaced the quadrant as the preferred instrument in large surveys. They also represented two attitudes to precision measurement that henceforth would prevail. The theodolite represented the very best in British instrument-making.^[45] The circle was also well constructed, and in that sense signified a breakthrough for French instrument-making. Equally important, however, its accuracy depended on a new principle—a method of averaging errors mechanically—which paralleled the theoretical notions of error under way in the 1780s and fully developed after 1800.^[46]

Everybody involved in the Paris-Greenwich triangulation recognized that it set new standards for surveying. Elaborate descriptions of the new instruments were published, although, in the case of the theodolite, not all the details, which (as Roy indelicately put it) would have been "a disgusting labour." Cassini and his coworkers expatiated on the merits of their repeating circle in their book on the triangulation.^[47] The circle made possible high precision by repeating the angular observations an arbitrary number of times over the whole of its limb, so that irregularities in its construction would eventually even out. The circle offered advantages of cost and size over the theodolite: it weighed only about 20 pounds; the British instrument, over 200 pounds. The cross-channel triangulation (fig. 6.4) served as an important check on the accuracy of the French method; Cassini wrote that the information about the relative merits of the circle and the theodolite would perhaps be its most interesting result. Triangles

[44] Konvitz, Cartography in France , 27.

[45] Cassini called the theodolite the "chef-d'oeuvre du plus habile Artiste qu'il y ait en Europe." Cassini, Méchain, and Legendre, Exposé des opérations faites en France , 58. Cf. Daumas, Scientific instruments , 129, 174, 186–7.

[46] Gillispie suggests a direct connection between Legendre's work on the theory of the repeating circle and his development of the method of least squares. Gillispie, Science and polity , 127.

[47] Roy, "An account of the trigonometrical operation," 135–6; Cassini, Méchain, and Legendre, Exposé des opérations faites en France , 23–7.

were closed to within a few seconds using either the circle or the theodolite.^[48] The measurement therefore served as a kind of calibration as well as demonstration of the new instruments. The size and cost of the theodolite had at least one advantage. Roy argued that it would be a great waste not to use it for a national survey toward a good map of Britain, on which, as he put it, the country's honor depended.

The Rhetoric of Accuracy

The Paris-Greenwich triangulation increased the efficiency and reliability of surveying. At the same time the praises and promises of accuracy that surrounded it served as rhetorical devices, upholding the close relationship between scientific and technological applications of precision measurement. William Roy's accomplishment depended on his command of both the rhetorical and technological resources of accuracy.

The eminent metrologist Jean André Deluc had stated: "We are obliged to take up with probability in Nature in so many respects, that it is perhaps of more importance to us to investigate the physical rules of probability than to attend to its mathematical rules upon hypotheses." Deluc advocated that research be directed toward precision measurement rather than mathematical analysis of error, and he predicted that "we shall be led to seek for exactness in every thing."^[49] Roy, who knew Deluc's work well, acted on this metrological precept. He treated every measurement with extreme care, but as an isolated event, and he did not take the accumulation of possible errors into account even when estimates of the precision of individual measurements might have been made. Like his contemporaries, Roy did not think in terms of significant figures; for example, he might add figures with five and two decimals, and give the sum to four.^[50]

[48] Cassini, Méchain, and Legendre, Exposé des opérations faites en France , 57–65. Cf. J.D. Cassini, "De la jonction des observatoires," 713.

[49] Jean André Deluc, "An essay on pyrometry and aerometry, and on physical measures in general," PT, 68 (1778), 493, 545–6. Cf. Feldman, "Applied mathematics and the quantification of experimental physics," 150–6.

[50] Roy, "An account of the measurement of a base," 401–2, 441–61, 476–8. Roy wrote: "The hypotenuse length of the base, as measured by 1369.925521 glass rods of twenty feet each + 4.31 feet. . .has been shewn to be 27402.8204." This figure was rounded off to one decimal, because "the most accurate measurement imaginable is still more liable to err in excess than in defect." Ibid., 478. Cf. Seymour, A history of the Ordnance Survey , 35.

In fact, he loved decimals, which abound in his writings far beyond practical, but perhaps within rhetorical, efficacy.^[51]

In Britain the rhetoric of accuracy extended to the prestige of the instrument-maker. Unlike their French colleagues, British instrument-makers could be highly respected members of the scientific community. Jesse Ramsden became a Fellow of the Royal Society (FRS) in 1786 and won the Copley medal in 1795. Ramsden's name was synonymous with accurate measurement, and his instruments assured the quality of the British triangulation.^[52] The implicit reasoning went like this: because Ramsden was such an "ingenious artist" (although "dilatory"), his instruments were "rendered extremely perfect," hence the measurements showed a "wonderful degree of accuracy."^[53] Most of the devices manufactured for Roy existed in one copy only; not even specialist readers were likely to get their hands on a Ramsden theodolite, but had to be convinced of its excellence verbally. Besides the theodolite, Ramsden constructed a surveying chain "which would measure distances much more accurately than anything of that kind had ever done before," a pyrometer "of such accurate construction that it seems not easy to improve it," and other smaller instruments. Furthermore, Ramsden himself sometimes took part in especially important measurements; he was called upon for advice during the Paris-Greenwich triangulation and later in the Ordnance Survey.^[54]

The commendation of Ramsden's achievements, like the long rows of decimals and the frequent references in the work of Maskelyne,

[51] Cf. Heilbron, Electricity in the 17th and 18th centuries , 76, 83; see Theodore S. Feldman, chap. 5 in this volume.

[52] Daumas, Scientific instruments , 102–6, 241–3; E.G.R. Taylor, The mathematical practitioners of Hanoverian England, 1714–1840 (Cambridge: Cambridge University Press, 1966), 43; Gillispie, Science and polity , 113; R.S. Webster, s.v. "Ramsden, Jesse," DSB, 11 , 285.

[53] Roy, "An account of the mode proposed," 189, and "An account of the trigonometrical operation," 136, 149.

[54] Roy, "An account of the measurement of a base," 394, 402, 416–7, 435, 462; Williams, Mudge, and Dalby, "An account of the Trigonometrical Survey," 432, 435, 438.

Cassini, and Roy to measurements made to "the last exactness" or to "mathematical exactness," may be considered the rhetoric of exact science.^[55] This rhetoric papered over a serious rift between Roy and Ramsden, which is worth uncovering for its illumination of underlying social realities. Roy criticized Ramsden severely for his dilatoriness in the draft of the last report on the project. Most of the complaints did not reach print because Ramsden filed countercomplaints with the Royal Society and Roy's death allowed some freedom with his text. Ramsden's complaint gives an unusual glimpse of the working relationship between a scientist and an instrument-maker during the late 18th century. He claimed the credit for the high precision achieved in the triangulation, and was sorry that Roy—a gentleman —treated him with such disrespect: it was not "consistent with common sense, that a Tradesman or Mechanic, should suffer his professional character in particular to be publicly traduced in so respectable a place as at [a] meeting of the Royal Society."^[56] Ramsden could get no satisfaction from Banks (who threatened to defend Roy's position "with every drop of my blood") and therefore appealed directly to the Council.^[57]

Ramsden asserted that Roy was not a competent judge of the technological aspect of the work; that he, Ramsden, had decided what kind of instrument should be made for the triangulation; that he, Ramsden, had written the description of the theodolite for the Philosophical transactions ; that he had constructed every single piece of apparatus used in the measurements; and that Roy had not given him full credit. He claimed further that Banks and Roy had granted him a free hand to construct a theodolite that was "superior in point of accuracy to any thing of whatever radius yet made,"^[58] and

[55] Maskelyne, "Concerning the latitude and longitude," 186, "the last exactness"; Roy, "An account of the trigonometrical operation," 165, "mathematical exactness." Cf. Roy, ibid., 149, 154, 166, 244, 161; and Cassini, Méchain, and Legendre, Exposé des opérations faites en France , 23, 34, 58–9.

[56] Seymour, A history of the Ordnance Survey , 17; Roy to Banks, 3 May 1790, The Banks letters , 721; Jesse Ramsden to the Council of the Royal Society, 30 May 1790 (RS, MM.3.30).

[57] Banks to Roy, 30 Jan 1790, The Banks letters , 720–1.

[58] Jesse Ramsden to the Council of the Royal Society, 30 May 1790 (RS, MM 3.30); cf. RS, MM.DM.4.44, an unsigned statement by Ramsden about his technical work for Roy. Roy did indeed fail to give Ramsden credit for the technical description of the theodolite; he mentioned Ramsden's name only a few times, one of them libelously, in his last report. See Roy, "An account of the trigonometrical operation," 135–60.

complained when the innovations took time to perfect. These complaints showed that Roy did not understand the character of precision technology.

If we credit any of this, Roy's dependence on Ramsden's abilities was even closer than the official reports suggested. It does seem clear that Roy controlled the successful achievement of his goal—to make a measurement and create a technology of unprecedented accuracy—not so much by mastery of the necessary technique or technology, but rather by command of the social situation through his influence in the Royal Society and in the Ordnance. Roy could purchase Ramsden's and Dalby's know-how and employ them to write the difficult technological and mathematical passages in his reports. Like Ramsden, Dalby complained that Roy could not judge his work competently, and he had to append a long list of corrections to Roy's final paper in 1790.^[59]

The rhetoric of accuracy that helped to cover up those disputes was meant to inspire faith in a vast and costly undertaking like a national survey.^[60] When Roy invited the citizens of London to confirm the accuracy of his measurements by stepping out on their rooftops and sighting the angles between buildings that had been used as triangulation stations, the cartographic entrepreneur was speaking.^[61] When the state or the public supported the geodetic and cartographic sciences, they were offered accuracy in return for their money. When they were promised "absolute" or "mathematical" accuracy, they no doubt expected new and superior technology.

[59] Roy, "An account of the trigonometrical operation," 118–9, 193; Blagden to Banks, 31 Aug, and 23 and 26 Sep 1790, The Banks letters , 76–7; Dalby, "Remarks on Major-General Roy's account."

[60] In September 1783 Roy wrote to Banks that the government would probably grant a sum of £ 1000 toward the triangulation, "if they are assured that it shall be frugally and faithfully applyed to the above, or any other scientific operation." Roy to Banks, 28 Sep 1783 (RS, DM.4.4).

[61] Roy, "An account of the trigonometrical operation," 258–9.

Accuracy and Technology

Another of Roy's rhetorical devices was his repeated use of the word "truth" in describing the intended goal of exact measurement.^[62] The quest for "truth" meant a quest for accuracy; and in surveying it covered all the steps of the operation, not just the final result. Since everything had to be superior to previous surveys, everything had to be new . Because of their novelty, the methods and instruments had to be meticulously described so that the public could affirm their value.^[63] Hence the many pages of technical description and numerous plates that made Roy's reports a résumé of the state of the art of trigonometrical surveying. Delambre's account of the methods used in the metric survey would play the same part ten years later.^[64]

The high precision of Roy's work made it possible to calibrate simpler and more convenient methods. His measurement of the baseline on Hounslow Heath is a case in point. At first Roy used the traditional wooden rods as measuring sticks. He rejected these because their contraction and expansion varied erratically with humidity, and replaced them with glass tubes, whose lengths depended only on the temperature in a way accurately determinable by Ramsden's pyrometer.^[65] Roy knew about the properties of glass from his work with the barometer: the use of glass tubes for the baseline measurement was an imaginative piece of technology transfer from barometry to geodesy.^[66] Roy used the glass tubes to control

[62] Roy, "An account of the mode proposed," 214, "sufficiently near the truth," 219, "differ very little from the truth"; cf. Roy, "An account of the trigonometrical operation," 128–9, 186, 230–1, 247.

[63] Roy, "An account of the trigonometrical operation," 247; Roy, "An account of the measurement of a base," 406, 461. Cf. A.W. Richeson, English land measuring to 1800 (London: Cambridge, Mass.: MIT Press, 1966), 180–1.

[64] J.-B.-J. Delambre, Rapport historique sur les progrès des sciences mathématiques depuis 1789, et sur leur état actuel (Paris: Imprimerie Press, 1810), 66.

[65] Roy, "An account of the measurement of a base," 434–5, 461–6. Cf. Seymour, A history of the Ordnance Survey , 34.

[66] Roy, "An account of the measurement of a base," 435. Roy's papers at the Public Record Office contain several documents relating to investigations of the behavior of rods and tubes of glass at different temperatures (PRO, O.S.3/3). Cf. Feldman, "Applied mathematics and the quantification of experimental physics," 172–4.

measurements with a surveyor's chain, also from Ramsden's workshop. The chain did well, and since it was easier to handle than glass tubes or metal bars, Roy recommended it for surveying. The chain would be good enough for the national survey, for which, as Roy put it, "there would not be any necessity for that wonderful exactness" requisite in the Paris-Greenwich triangulation.^[67] Thus "scientific" exactness became a benchmark in the creation of a solid and efficient surveying technology.

Simplifications of surveying practices were not an accidental spinoff from scientific work: Roy had identified the development of more efficient surveying techniques as an explicit goal of the triangulation.^[68] Cassini de Thury had likewise pointed out that instruments had to be simplified and made portable in order to make practical the technology of surveying.^[69] The repeating circle accomplished both objectives. The British theodolite did not meet the needs of the ordinary surveyor, but was practical in an organization that could maintain a work force to transport it, erect solid stations, operate cranes, and so forth. In short, British technology was serviceable in a military organization.

The Militarization of Cartography

In 1762, in the course of extending the French triangulation into Austria, Cassini de Thury and the Heidelberg professor Christian Mayer measured a baseline in an unusual location. They used the alley, almost three leagues long, leading up to the new observatory in the main building of the Palatine Elector Karl Theodor's summer residence, situated between Mannheim and Heidelberg. Karl Theodor was delighted: "the position of the new base and [that] of the

[67] Roy, "An account of the measurement of a base," 394, 449–50; Roy, "An account of the trigonometrical operation," 268.

[68] Roy, "On the advantages that are likely to rise from the operations on Hounslow Heath" (RS, DM.4.6).

[69] Cassini de Thury, Relation des deux voyages , 1–2.

observatory were two monuments that should coincide."^[70] The base was a monument to the scientific patronage of the creator of the Mannheim Academy of Sciences and to Cassini's knack for fraternizing with nobility and royalty. It symbolized the union of political power and science, so important in the fields of geodesy and cartography at this time and in the next century when national cartography in Europe was militarized. With the technology of triangulation, the geometrical grid—formerly present only in the mind, on maps, or in architecture—was imposed on the landscape itself. Geodetic surveying quantified geographical information, which became atomized and readily presentable in tabular form. This kind of extensive, yet compressed, knowledge was an attractive resource for centralized governmental and military planning. In the terminology of Michel Foucault, the Ordnance Survey and similar organizations brought an expansion of military surveillance from the limited disciplinary units of the garrison and the fortress to the full physical extent of a nation.^[71]

The social ascent of engineers and artillery men was a major ingredient in the genesis of national triangulation as a military operation in Britain, where it first occurred. The new strategy of the Revolutionary and Napoleonic wars also promoted the fusion of military and national cartography. Larger and more mobile armies now appeared, and the battle conquered the siege as the decisive element in war. That made every place a potential theater of war and created a demand for knowledge of the whole geography, making comprehensive and accurate cartography an essential preparation for warfare.^[72]

[70] Ibid., xxiii, xxxiii, 94–5; Adolf Kistner, Die Pflege der Naturwissenschaften in Mannheim zur Zeit Karl Theodors (Mannheim: Selbstverlag des mannheimer Altertumsverein, 1930), 52–3.

[71] Michel Foucault, Discipline and punish: The birth of the prison (Harmondsworth: Penguin Books, 1977), 184–9, 195–203.

[72] William H. McNeill, The pursuit of power: Technology, armed forces, and society since A.D. 1000 (Oxford: Basil Blackwell, 1982), 161–3, 170–1; Richard A. Preston and Sydney F. Wise, Men in arms: A history of warfare and its interrelationships with Western society , 4th ed. (New York and London: Holt, Rinehart and Winston, 1979), 133–48, 173–80; Alfred Vagts, A history of militarism: Civilian and military , 2d rev. ed. (London: Hollis & Carter, 1959; 1st. edn. 1938), 58, 75–91, 114; N.H. Gibbs, "Armed forces and the art of war," The new Cambridge modern history (Cambridge: Cambridge University Press, 1965), 10 , 62–9, 74–5; Henning Eichberg, "Geometrie als Barocke Verhaltensnorm: Fortification und Exerzitien," Zeitschrift für Historische Forschung, 1 (1977), 40–50.

In Britain, fortifications were not a major part of the defense system, which relied mainly on the navy. When William Roy proposed in 1766 that a "General Military Map of England" be drawn on the French model, he pointed out that should an enemy reach the British Isles, engagement would necessarily take place in the field, about which detailed geographical knowledge would be required.^[73] In the 1780s the question as to whether Britain should embark on a program of extensive fortification brought heated debate.^[74] The Duke of Richmond advocated defense works for the docks of Plymouth and Portsmouth; he was supported by Pitt, and vehemently opposed by others, who carried Parliament in 1786 by one vote. Richmond's opponents argued that large fortifications would lead to an "unconstitutional" militarization of British society.^[75] Thousands of men living in barracks would foster and spread a militarism, which might become a stronghold for royalist and other anti-Parliament sympathies. The agitation included some jibes at engineers:^[76]

If this Military projector [Richmond] was not checked in his career, none could know what consequences might ensue. A Master General, with his Committee of Engineers, like the Laputan philosophers in their flying island might hover over the kingdom in an Ordnance balloon, descend in a moment, and seize on any man's house and domain. . ., draw out their scales and compasses, or sketch out their works. The country Gentlemen would find their terraces converted into bastions, their slopes into glacis,

[73] George III, The correspondence of King George the Third, from 1760 to December 1784 , John Fortescue, ed. (London: Macmillan and Co., 1927), 1 , 328–9.

[74] [James Glenie], A short essay on the modes of defence best adopted to the situation and circumstances of this island , 2d ed. (London, 1785); [Charles Lennox, Duke of Richmond] An answer to "A short essay. . ." (London, 1785); [James Glenie], A reply to the answer to a short essay . . . (London, 1785), and Observations on the Duke of Richmond's extensive plans of fortification (London, 1794). Cf. Alison Gilbert Olson, The radical Duke: Career and correspondence of Charles Lennox third Duke of Richmond (London: Oxford University Press, 1961), 81–6.

[75] An authentic account of the Debates in the House of Commons, on Monday, February 27, and Tuesday, February 28, 1786, on the proposed Plan for Fortifications, by His Grace the Duke of Richmond (London, 1786), 1–2, 20, 34, 56–7.

[76] An authentic account , 48.

their pleasure grounds into horn works and crown works to which they have hitherto borne an irreconcilable aversion.

Richmond returned from his defeat five years later with a new, subtler, and more successful scheme for militarization: the Ordnance Survey. In the words of one of Richmond's critics, the survey would provide essential information to "a resistance, which is not confined to particular spots, but is capable of operating every where."^[77] It also provided the British public with detailed information about their land: in 1801 the first one-inch map, of Kent, was published.

The work of Roy and of the Ordnance Survey won acclaim outside of Britain as a model of scientific accuracy, for example in India, where military surveying using Roy's methods began in 1802.^[78] It was above all the French who exported geodetically founded military cartography to the rest of Europe, by force as well as by example. Napoleonic military cartography was founded on the methods developed by Delambre and Méchain during the metric survey of 1792–8, and therefore also on the French experiences during the Paris-Greenwich triangulation. Delambre's formulas and Lenoir's repeating circle came to dominate French military cartography, and by 1810 "an army of astronomers armed with chronometers, telescopes, and sextants" had invaded Europe.^[79]

[77] [Glenie], A short essay , 30–1.

[78] Clements R. Markham, A Memoir on the Indian Surveys (London, 1878; reprinted Amsterdam: Meridian, 1968), 60–6; [Franz Xaver von Zach], "Ost-Indische Gradmessung, der Länge und Breite," Monatliche Correspondenz zur Beförderung der Erd- und Himmelskunde, 12 (1805), 485–94. Roy's measurement was praised by Delambre, for example, although at the Dépôt de la Guerre it appeared "dégénère en science purement spéculative." J.-B.-J. Delambre, Grandeur et figure de la terre (Paris: Gauthier-Villars, 1912), 334–9; Delambre, Rapport historique , 74–5; "Des opérations géodesiques de détail," Mémorial topographique et militaire , an XI (1803), 1–56, 126.

[79] Delambre, Rapport historique , 77–8 ("une armée d'astronomes munis de chronomètres, de lunettes et de sextans"). General Nicolas Sanson, director of the Dépôt de la Guerre , prescribed the use of the repeating circle as well as the use of Delambre's mathematical methods. See Berthaud, Les ingénieurs géographes , 307; review of Sanson's "Instruction sur la disposition et la tenue des régistres de calculs géodesiques," Monatliche Correspondenz zur Beförderung der Erd- und Himmelskunde, 11 (1805), 49–66; Delambre, Rapport historique , 66. Cf. J.L. Heilbron, chap. 7 in this volume.

The French government had taken control of cartography in 1793 by expropriating the Cassini map; a quarter century later, it initiated a new survey, supervised by the general staff. The map of the Étatmajor (published 1833–81) deployed information and expertise assembled in the French army after more than a decade of military cartographic expansion.^[80] In 1801 Napoleon had started local Topographical Bureaus to extend the Carte de Cassini to the areas conquered by the French army; soon bureaus existed in Hanover, the Rhineland, Bavaria, Switzerland, Savoy, and Italy.^[81]

Austria set up similar services in 1806, and the Netherlands followed suit in 1816.^[82] In the same year, in response to its experience of French warfare, Russia founded a military cartographic organization that was to become the largest in Europe.^[83] The leader of the Franco-Italian Topographical Corps in Milano, the Swede Gustaf Wilhelm Tibell, founded a similar corps in Sweden in 1805, which made use of the technology imported from France for the remeasurement of Maupertuis' arc of meridian in Lapland in 1801–3.^[84] We see in Sweden the same interplay between military cartography and science-related geodesy that occurred earlier in Britain, and which recurred in Hanover in 1821–5 when a military survey took over Carl Friedrich Gauss' measurements.^[85]

Major Johann Jacob Baeyer, of the Prussian Army, was co-leader on Friedrich Wilhelm Bessel's famous survey of East Prussia in 1831–6; and Friedrich Georg Wilhelm Struve and general C. de

[80] Konvitz, Cartography in France , 59–61.

[81] Henri Marie Auguste Berthaut, Les ingénieurs géographes militaires 1624–1831: Étude historique (Paris: Service Géographique de l'Armée, 1902), 1 , 239–40, 305–431.

[82] See the collection La cartographie au XVIIIe siècle ; Frans Depuydt, "The large scale mapping of Belgium, 1800–1850," Imago mundi, 27 (1975), 21–4; Brown, The story of maps , 274–5.

[83] George M. Wheeler, Report upon the Third International Geographic Congress and Exhibition at Venice, Italy, 1881, accompanied by data concerning the principal government land and marine surveys of the world (Washington, D.C.: Government Printing Office, 1885), 365–79.

[84] Ulla Ehrensvärd, "Fortifikationsofficeren som kartograf," in Bertil Runnberg, ed., Fortifikationen 350 år, 1635–1985 (Stockholm: Fortifikationskåren, 1986), 115–9.

[85] W. Grossmann, "Gauss' geodätische Tätigkeit im Rahmen zeitgenössischer Arbeiten," Zeitschrift für Vermessungswesen, 80 (1955), 371–84.

Tenner found what they called "the problem of their lives" in their measurement of a meridian of more than 25° (1816–55).^[86] Baeyer subsequently founded the Europäische Gradmessung , which met seventeen times between 1864 and 1912; it brought together astronomers, military cartographers, and civilian administrators to coordinate and promote geodetic measurements all over continental Europe.^[87] The twenty national cartographic organizations that existed in Europe and its colonies in 1885 were all under military direction.^[88] The cartographic situation paralleled the use of military manpower, technology, and administrative expertise in the construction of railroads and canals and in the development of mechanized industrial production.^[89]

As the store of geodetic data increased, the notion of a regular shape of the earth came into general doubt. The long-disputed ellipsoid had been put out of court by Delambre and Méchain, whose demonstration that meridians are irregular was corroborated by the Ordnance Survey in 1803.^[90] As more surveys comparable in

[86] Friedrich Wilhelm Bessel, Gradmessung in Ostpreussen und ihre Verbindung mit Preussischen und Russischen Dreiecksketten (Berlin, 1838), iv, ix–x; Friedrich Georg Wilhelm Struve, Arc du méridien de 25 × 20' entre le Danube et la Mer Glaciale (St. Petersburg, 1860), 1 , xv ("problème de leur vie").

[87] Of those participating in the meeting in 1867, twenty-four were directors of observatories or academics, eleven were military officers, and five were civilian administrators. See C. Bruhns, W. Foerster, and A. Hirsch, eds., Bericht über die Verhandlung der vom 30. September bis 7. October 1867 zu Berlin abgehaltenen allgemeinen Conferenz der Europäischen Gradmessung (Berlin, 1868), 3–4. Bialas, Erdgestalt , 242–6.

[88] Brown, The story of maps , 280–1.

[89] See, e.g., Merritt Roe Smith, "Introduction," in Merritt Roe Smith, ed., Military enterprise and technological change: Perspectives on the American experience (Cambridge, Mass.: The MIT Press, 1985), 1–37; and Barton C. Hacker and Sally L. Hacker, "Military institutions and the labor process: Noneconomic sources of technological change, women's subordination, and the organization of work," Technology and culture, 24:4 (1987), 743–75. Cf. Svante Lindqvist's and Robin Rider's contributions in this volume (chaps. 10 and 4, resp.).

[90] For example, see the report of the international commission that investigated the metric survey. Jan Hendrik van Swinden, "Rapport sur la mesure de la méridienne de France, et les résultats qui en ont été déduits pour déterminer les bases du nouveau systéme métrique," Institut national des sciences et arts, Mémoires , Sciences mathématiques et physiques, 2 (an VII), 47, 49–52. Several contributions from the heated debate concerning the British meridian are reprinted in Olinthus Gregory, Dissertations and letters. . .tending either to impugn or defend the Trigonometrical Survey of England and Wales (London, 1815). Delambre defended the British results; see Delambre, Grandeur et figure , 363–72.

magnitude to Delambre's and Méchain's were carried out and interconnected, the ellipsoid came to be viewed as a convenient fiction. The notion of the geoid, developed by Friedrich Wilhelm Bessel and Gauss around 1830 but not christened thus until 1873, became the preferred theoretical tool to describe the physical shape of the earth (or rather of the geopotential surface).^[91] The shape of the geoid could not be predicted; it had to be measured, over and over again, whenever instrumental improvements promised refinements. Increased data caused geometrical simplicity to give way to dynamic complexity, which could be managed only by the systematic work of well organized institutions like the military.

[91] Irene Fischer, "The figure of the earth—changes in concepts," Geophysical surveys, 2:1 (1975), 3–54, esp. 20–8; Bialas, Erdgestalt , 234–5.

7
The Measure of Enlightenment

By J.L. Heilbron

The quantifying spirit united with the purposes of the Enlightenment and the Revolution to produce the metric system of weights and measures. This exemplar of 18th-century rationalism was directed against the foggy and feudal metrology of the Ancien Régime; supported by the rhetoric of the philosophes ; realized through the politics of scientific societies and revolutionary tribunals; and resisted by the common man in whose interest the reformers, philosophes , scientists, and revolutionaries claimed to act.

The Plight of the People

Cain's Legacy

God may have made the world according to weight and measure, but it was Cain who invented weights and measures, and thus—we have this from Flavius Josephus—"converted the innocent simplicity in which man had lived into a miserable existence dominated by fraud and deceit."^[1] The existence of French men and women around 1790 was made miserable by, among other things, 700 or 800 differently named measures and untold units of the same name but different sizes. A "pinte" in Paris came to 0.93 liter; in Saint-Denis, to 1.46; in Seine-en-Montagne, to 1.99; in Précy-sous-Thil, to 3.33. The aune, a unit of length, was still more prolific: Paris had three,

[1] Josephus, Jewish antiquities , cited by Witold Kula, Measures and men (Princeton: Princeton University Press, 1986), 3.

each for a different sort of cloth; Rouen had two; and France as a whole no fewer than seventeen, all in common use and all different, the smallest amounting to just under 300 lignes, royal measure, the largest to almost 600.^[2]

France possessed nonuniform measures in law as well as by custom. Their multiplicity went with other relics of the feudal system, which maintained arbitrary rents and duties usually to the disadvantage of the peasant. A landlord wanted his bushels of grain or hogsheads of beer in the biggest measures in use in the neighborhood, and he preferred to sell according to the smallest. Nor were all seigneurs above enlarging the vessel in which they collected their rents; and since in many cases they possessed the only exemplars of their patrimonial bushel, no one could be certain that it did not grow in time. But one suspected. A frequent complaint in the cahiers , or notebooks of desiderata brought by representatives of the people to the meeting of the Estates General in 1789, was that "the nobles' measure waxes larger year by year." These same representatives castigated the oppressive confusion of customary measures as barbaric, ridiculous, obscurantist, gothic, and revolting, and demanded an end to them, and the establishment of a system of unchanging and verifiable weights and measures throughout the country, or at least throughout their region. Many urged that the King's measure, the royal foot, be made the law of the land.^[3]

Sharpers and crooks whose practices were not sanctioned by ancient rights and wrongs and middlemen acting in analogy to money changers opposed the rationalization that menaced their livelihood. In 1747, shortly after returning to Paris with the vision acquired while measuring a piece of a meridian in Peru, Charles-

[2] Georges Bouchard, Un Organisateur de la victoire. Prieur de la Côte-d'Or membre du Comité de salut publique (Paris: R. Clavreuil, 1946), 286; Charles Maurice de Talleyrand-Périgord, Proposition faite à l'Assemblée nationale, sur les poids et les mesures (Paris: Impr. nationale, 1790), in John Riggs Miller, Speeches in the House of Commons upon the equalization of the weights and measures of Great Britain. . .together with two letters from the Bishop of Autun (London: J. Debrett, 1790) 60–3.

[3] Kula, Measures and men , 164–226, esp. 191–6, 230, 236; Beatrice Fry Hyslop, French nationalism in 1789, according to the general cahiers (New York: Octagon, 1968), vii, 56.

Marie de La Condamine identified and condemned this special interest, which he proposed to abolish with the confusions that engendered it. His accusation echoed in France for decades and eventually bounced across the Channel. We read in the cahiers from Orléans that multitudinous measures "expose[d] people daily to swindlers" and in the records of Parliament that John Riggs Miller, an obscure and verbose M.P., declared that they had but one purpose, "the perplexing of all dealings, and the benefitting knaves and cheats."^[4]

Reformers laid down several requirements for a new system of weights and measures. It should not rest on an arbitrary unit, especially not on a king's foot; it must not offer enticements to cheaters; and it had to be easily reproduceable were its exemplars lost. Further, it had to be rational, so as to recommend itself to all nations, and become universal. The measuring stick used by La Condamine and his colleagues, the "toise de Pérou," had attained some currency in France and in a few other countries, and the units used in Paris also had more than local authority. It would not do to impose them, however, as Talleyrand wrote Miller, since they had not been derived from nature or constructed "with the ceremony necessary to settle once and for all the opinion of all enlightened nations." Last and also first, the reformed system had to be simple, or, as Miller preferred to say, "on a level with the lowest and humblest capacity." It must not require "skill in calculation beyond what. . .the inferior orders of men commonly possess"; everyone should be able to confirm for himself the correctness of all transactions of interest to him, "the meanest intellect. . .on a par with the most dexterous."^[5]

This last paragraph contains many buzz-words of the Englightenment.^[6] The replacement of the arbitrary and the capricious, of the

[4] Charles-Marie de La Condamine, "Nouveau projet d'une mesure invariable, propre à servir de mesure commune à toutes les nations," MAS , 1747, 489-514, on 492–5; Kula, Measures and men , 209; Miller, in Thomas C. Hansard, Parliamentary history , 28, col. 322, and Miller, Speeches , 18.

[5] Talleyrand, Proposition , in Miller, Speeches , 68–9; Miller, ibid., 16, 35, and in Hansard, 28, col. 321.

[6] Cf. Maurice Crosland, "'Nature' and measurement in eighteenth century France," Studies on Voltaire and the eighteenth century, 87 (1972), 277–309, on 297.

feudal and historical, by the natural is the message of all the philosophes from Montesquieu to Condorcet. The natural coincides with the rational and the universal: when people cast aside customary belief and established abuse, they can reach agreements that all others, guided by their own reason, will accept. This reason is not the property of a few great intellects; the truth is accessible to all, or at least to every man. Everyone has the right to know, and to recognize, the truth. Any system that claims universal assent must be universally intelligible.

Mathematics and the Rights of Man

From the most remote times philosophers have taken number as the exemplar of the intelligible. Once one has grasped a principle in geometry, it was said, not even God Himself could understand it better, although, to be sure, He might know more theorems. Calculating people think for themselves; they despise the unintelligible, capricious, unfounded, authoritarian, and feudal as infringements on their thoughts and actions. In brief, mathematics is a science for free people. Or, to say the truth as the 18th century saw it, for free men. Newton's doctor, Sir John Arbuthnot, praised mathematics for giving "a manly vigour to the mind"; a tonic Newton took to such good effect that he mastered all "the noble and manly sciences" and became "the greatest man that ever liv'd."^[7] All this will help to construe the remark made by the representatives of the revolutionary government in 1799, on accepting the prototypes of the meter, liter, and kilogram. The metric measurers, they said, reaching for their highest compliment, had carried through their work "with the confidence of a male and republican spirit."^[8]

If mathematics is male, Europe grew increasingly manly during the 18th century. When Samuel Pepys became clerk of the king's ships in

[7] Quoted from, respectively, John Arbuthnot, Miscellaneous works , 2 vols. (Glasgow: J. Carlisle, 1751), 1, 9, 36, and James Jurin, in Royal Society of London, Philosophical transactions, 34 (1727), dedicatory epistle to Martin Folkes.

[8] P.L.C. Baudin, 4 messidor an VII (19 June 1799), in P.F.A. Méchain and J.B.J. Delambre, Base du système métrique decimal, ou Mesure de l'arc du méridien compris entre les parallèles de Dunkerque et Barcelone , 3 vols. (Paris: Baudoin, 1806–10), 3, 650.

1660, he had to recruit his strength (he was then 27) and repair his education (which was excellent) by learning the multiplication table. In the resulting fit of machismo , he forced his wife to learn arithmetic.^[9] Most of learned Europe in the 17th century was "innumerate," if by analogy to "literacy" we take "numeracy" to mean familiarity with numbers. During the 18th century the requirements of government bureaucracies, commerce, colonization, mining, rational agriculture, forest management, the military, and so on, brought dramatic increases in numeracy. Before 1750 Poor Richard enjoins us in rhymes to go early to bed to secure health, wealth, and wisdom; just after 1800 a book called The young man's guide delivers the same message by multiplication. If you stay up to eleven o'clock every night, the Guide admonishes, in fifty years you will uselessly expend $182.50 on candles.^[10]

Perhaps the most significant sign of this burgeoning rudimentary numeracy was the multiplication of tables of numerical equivalence. A good survey of the tables in use in commerce has yet to be made; but there is no doubt that their number increased dramatically after the Seven Years' War. They came in several sorts: conversions of weights, measures, and moneys; total cost of goods, tabulated by size and unit cost; tables of interest and annuities; agricultural yields; and so on. It did not require great prowess at mathematics to use these compilations; rather, a degree of numeracy comparable to the literacy of one who could read but not write. The spread of the metric system depended on this widespread rudimentary numeracy, and raised its level.

These tables were required not only because of the number and uncertain equivalence of feudal weights and measures, but also, and

[9] Samuel Pepys, Diary , ed. Robert Latham and William Matthews, 11 vols. (Berkeley: University of California Press, 1970–83), 3, 134, quoted by Patricia Cline Cohen, A calculating people. The spread of numeracy in early America (Chicago: University of Chicago Press, 1982), 26; Helen M. Wallis, "Geographie is better than Divinitie: Maps, globes, and geography in the days of Samuel Pepys," in Norman J.W. Thrower, ed., The compleat platt-maker. Essays on chart, map, and globemaking in England in the seventeenth and eighteenth centuries (Berkeley: University of California Press, 1978), 1–43, on 2, 6. Cf. Pepys, Diary , 3, 131, 135, 137.

[10] Cohen, Calculating people , 110–3.

perhaps primarily, because the arbitrary multiples and submultiples of the various units made computation burdensome and complex. Calculation of the price of a piece of cloth 2 yards 1 foot 4 inches square at 3 pence 2 farthings the square foot was a sufficient challenge. To change it into aunes, pieds, livres, and deniers, and to proceed to a problem in bushels and cubic king's feet, would have puzzled Archimedes. According to the Paris Academy, referring to the situation in 1790, people at ease with money computations could not handle weights and measures. "In the present state of affairs, a man who can calculate with sous and deniers cannot calculate with toises, pieds, pouces, and lignes, with livres, onces, gros and grains."^[11]

The Paris Academy and many other scientific reformers supposed that by dividing the new standards and the revised coinage decimally they would eliminate the need for specialist computers. The decimal was not free from arbitrariness; but its simplicity and convenience could not be gainsaid, at least by practiced calculators, and, as the Academy observed, although not universal it is as natural as the human hand.^[12] Only the hand of the learned had so far employed decimal arithmetic, and by no means universally, as Lavoisier pointed out in his Elements of chemistry , when urging his colleagues to state weights in decimal parts of whatever units they used. This natural arithmetic, "previously locked up in the domain of the sciences," was precisely what the reformers thought they sought. "Those who knew little will know everything; others will hurry to forget what they no longer need to know; all will accept as a true benefit a method of calculation that will save them time, study, and chances for error."^[13]

Prieur de la Côte d'Or, a former military engineer who served on the all-powerful Committee of Public Safety (Comité du salut public), expected the decimal calculus to be the technical language of Utopia.

[11] Charles Borda, J.L. Lagrange, A.L. Lavoisier, Matthieu Tillet, and M.J.A.N. Caritat, marquis de Condorcet, "Rapport" (27 Oct 1790), HAS , 1788, 1–6, on 5.

[12] Ibid., 6; cf. Crosland, "'Nature' and measurement," 299.

[13] France, Commission temporaire des poids et mesures republicaines, Instruction abrégée sur les mesures deduites de la grandeur de la terre, uniformes pour toute le République, et sur les calculs relatifs à leur division décimale (Paris: Impr. nationale exécutive du Louvre, an II), xvii, 171a; Antoine Laurent Lavoisier, Elements of chemistry (Edinburgh: William Creech, 1790), 295–6.

"How happy we will be not to be forced to consult anyone about our prosperity, property, expenses, and drink, and to have nothing to do any more with people who often seek only to profit from our ignorance."^[14] The connection between democracy and the decimal was made plain and explicit by Condorcet during the first year of the Revolution. Decimalization, he said, fit perfectly with the political program and mandate of the National Assembly. "It [the Assembly] wants to insure that in the future all citizens can be self-sufficient in all calculations related to their interests; without which they can be neither really equal in rights. . .nor really free."^[15] Long after the promulgation of the metric system, Laplace advised Napoleon that its chief advantage as understood by its creators was not the destruction of feudal metrology but the division by tens.^[16]

Republican zeal is not easy to curb, and the decimalization of everything measured or metered figured among the excesses of the French Revolution. The Paris academicians demonstrated solidarity with the regime by dividing a right angle into 100 revolutionary degrees, and each such degree into 100 minutes; and they found much pleasant recreation in recomputing the trigonometrical functions in what Jean-Baptiste Joseph Delambre, the most assiduous of the metric measurers, later extolled as "the vastest [calculation] that had ever been done, or even conceived." The innovation neither saved the Academy nor suppressed the reckoning of the Babylonians, with which it still coexists in France. A less enduring initiative, the revolutionary calendar, which came into operation retrospectively on the day of the autumnal equinox of 1792, divided the year into twelve parts of thirty days each, grouped in ten-day blocks. The five

[14] C.A. Prieur, Instruction sur le calcul décimal, appliqué principalement au nouveau système des poids et mesures (Paris: Impr. de la République, germinal an III [1795]), 4–5; cf. Miller, Speeches , 39.

[15] Condorcet, Mémoires sur les monnoies (Paris, 1790), 3–4, quoted in Ruth Inez Champagne, The role of five eighteenth-century French mathematicians in the development of the metric system (Ph.D. dissertation, Columbia University, New York, 1979), 60.

[16] Text of 7 May 1811, in G. Bigourdan, Le système métrique des poids et mesures. Son établissment et sa propagation graduelle (Paris: Gauthier-Villars, 1901), 193.

or six additional days required to make up the year were intercalated as necessary.^[17]

The unsystematic concession to lunar motions represented by the numbers 12 and 3 in the divisions of the revolutionary year was offset by a revolutionary day of ten "hours," each containing 100 "minutes" and 10,000 "seconds." Several clocks ticking 10,000 "seconds" a day were made, but most clock makers and watchers preferred to divide their time in the manner of the servile peoples of Europe. On 18 germinal an III (7 April 1795), the revolutionary government suspended republican time sine die on the official ground that it was of interest only to scientists. The calendar survived longer, until 1 January 1806, when Napoleon put an end to it.^[18]

The cost of conversion to decimal units was borne by the people whose lives the system was intended to ease. In computing prices of old goods in the new currency, sellers naturally rounded up to their advantage. The common man as naturally opposed the change. So did the common woman. According to a squib of 1791, the prostitutes of the Palais Royal, whose rates had been recomputed, complained that the 100 sols they now received for their services devalued their charms, "which opinion had previously reckoned at an écu and six livres," by a sixth.^[19] It is not easy to anticipate the effects of reform.

Another conflict between geometry and system arose in the naming of the decimal divisions of the meter. In 1792 the Academy discussed the relative advantages of system (in which divisions would be

[17] Exposition abrégée du nouveau systême des poids et mesures, d'après le mètre définitif (Avignon: Seguin, an X), 13–4; J.B.J. Delambre, Rapport historique sur les progrès des sciences mathématiques depuis 1789, et sur leur état actuel (Paris: Impr. impériale, 1810), 8; L. Rondonneau, Concordance des calendriers républicain et grégorien , 6th ed. (Paris: Rondonneau and Decle, 1812), v–vii; Georges Villain, "Etude sur le calendrier républicain," La Révolution française , 7 (1884), 451–9, 535–53 and 8 (1885), 623–56, 740–58, 830–54, 883–8.

[18] France, Commission temporaire des poids et mesures républicains, Instruction , 33–4, and Avis (Paris: Impr. de la République, frimaire an IV [1795]), 8; Bouchard, Prieur , 308–10; Thomas Bugge, Science in France in the revolutionary era , ed. M.P. Crosland (Cambridge, Mass.: MIT Press, 1969), 203–4; Rondonneau, Concordance , xii–xiv; Villain, "Calendrier républicain," 885–8.

[19] Bouchard, Prieur , 310–1.

designated by the prefixes "deci-," "centi-," "milli-," and the only multiple would be "milliaire") and familiarity (in which submultiples of the meter would have common names, like "palme" and "doigt"), and plumped for the familiar. They erred in calculating revolutionary zeal. The Committee on Public Instruction (Comité d'instruction publique) preferred a clean sweep and adopted the systematic names. This occurred on 1 August 1793, on the eve of the suppression of the Academy.^[20] One of the Academy's successors in metric matters explained that "it is almost impossible to reason correctly without a language aptly made."^[21]

The language did not please the people. Classicists objected that the prefixes (enriched by "déca-," "hecta-," and "kilo-") violated the grammar of ancient languages, while the uneducated could make no sense of them at all. "These names," declared a delegate to the Convention, "novel and unintelligible to the large majority of our citizens, are not necessary for the maintenance of the Republic."^[22] He did not know what he had escaped. Prieur de la Côte d'Or, who had taken an active part in the reform of weights and measures from the onset of the Revolution, had names of his own, derived, he said, from ancient languages and Low Breton. The irrationality of the Convention did not extend to adopting "kilicymbe," "myriadore," "ladedix," "pèzeprime," "centicadil," or "decidol," and Prieur, bending to the political wind in 1795, drew up what became the definitive metric names. The many centicadils of bitterness he then swallowed and decidols of crow he then ate were to damage the work of the metric reformers.^[23] All concerned might have spared themselves the trouble. For decades the people stubbornly opposed decimalized units and their jabberwocky names.

[20] HAS , 1789, 1–18 (text of 1792); Bigourdan, Système métrique , 78–82.

[21] France, Agence temporaire des poids et measures, Aux citoyens redacteurs de la feuille du Cultivateur, en réponse à des objections contre la nomenclature nouvelle, inserées dans le No. 38 de ce journal (Paris: Impr. de la République, thermidor an III [1795]), 10.

[22] Bigourdan, Système métrique , 82 (text of 11 Aug 1795).

[23] Bouchard, Prieur , 297–9; J.B.J. Delambre, Grandeur et figure de la terre , ed. G. Bigourdan (Paris: Gauthier-Villars, 1912), 212.

The Program of the Academy

Professional Imperatives

By 1789 the French had made three measurements of arcs along the meridian passing through Paris. The earliest, made by Jean Picard between 1668 and 1670, on an arc of about 1°20', gave a value for the length of a degree of latitude near Paris that differed by less than three parts in ten thousand from what the metric measurers later obtained with much greater labor and much better instruments.^[24] The second arc, extending over 8°30' from Dunkirk to Perpignan and completed under Jacques Cassini in 1718, authorized a new Atlantic coastline that brought some French towns a hundred or more kilometers East of their previous positions. Louis XV lost more land to his cartographers than his successors have to the Germans. The measurements were not accurate enough, however, to settle the much agitated question of the shape of the earth. In the 1730s, the Paris Academy sent out its expeditions to Peru and to Lapland to measure arcs far enough apart to reveal the departure of the earth's profile from perfect sphericity. Their results, which confirmed Newton's conclusion that mechanics required the equatorial axis to exceed the polar, agreed with the third measurement along the Paris meridian, made during 1739 and 1740 by the Abbé Nicolas-Louis de Lacaille.^[25]

As the general shape of the earth came into view, its finer features loomed ever larger in academic minds. Lacaille contributed another data point by measuring an arc at the Cape of Good Hope. The Pope, the Austrian-Hungarian Empress, and the King of Sardinia commissioned surveys of meridians traversing their domains, with the consequence, as one of the surveyors put it, that the more the earth

[24] Jean Picard, Mesure de la terre (Paris: Impr. royale, 1671); republished in MAS , 1666–99, 7, 133–90, and in P.L. Moreau de Maupertuis et al., Degré du méridien entre Paris et Amiens déterminé par la mesure de M. Picard (Paris: Martin, Coignar, and Guerin, 1740), 1–106. Picard gives 57,060 toises (fathoms) per degree, which was nominally 15 toises off the definitive value. In fact, the difference came to about 30 toises when Picard's measurements were corrected for refraction and a small error in his baseline; see Méchain and Delambre, Base, 1 , 7–8.

[25] Delambre, Grandeur , 63–72.

was measured, the more uncertain its shape became.^[26] The British then ran an arc through Greenwich, to serve as the backbone for a military map of Scotland. The Paris academicians looked upon it rather as an opportunity to improve geodesy, and in 1783 they proposed a linking of the Paris and Greenwich observatories by triangles based on the meridians already determined. The proposal had a sporting side. The linking would pit the small repeating circle then recently invented by Charles Borda, a prominent academician and a former naval officer, against the large theodolite built by the world's leading instrument-maker, Jesse Ramsden, for the triangulations in England.^[27]

Jean Dominique Cassini (Cassini IV), who took nominal charge of the French party, retrospectively threw down the challenge: "we dared to flatter ourselves that we had on our side an instrument that yielded nothing to the English in point of precision." The showdown took place in the late summer of 1787. The British turned their great theodolite toward Calais; the French aimed their delicate circle at Dover. The British took their single observations quickly; the French multiplied their repetitions slowly. The season grew late. Fog descended. The weather did not remit long enough to permit the full circle of French measurements, and the contest between the repeater and the theodolite ended indecisively.^[28] As Delambre wrote much later, however, "a more important occasion soon presented itself to demonstrate the advantages of the new instrument."^[29]

[26] R.J. Boscovich and Christoph Maire, Voyage astronomique et géographique dans l'Etat de l'Eglise: Entrepris par l'ordre at sous les auspices du pape Benôit XIV (Paris: Tilliard, 1770), 492, cited in Djordje Nikolic, "Roger Boskovic et la géodésie moderne," Archives internationales d'histoire des sciences, 14 (1961), 315–35, on 315.

[27] Jean Mascart, La vie et les travaux du chevalier Jean-Charles de Borda (1733–1799) (Lyon: A. Rey; Paris: A. Picard, 1919), 370–1, 381–3, 488–9, 501–2. Cf. S. Widmalm, chap. 6 in this volume.

[28] J.D. Cassini, "De la jonction des observatoires de Paris et de Greenwich, et précis des travaux géographiques exécutés en France, qui y ont donné lieu," MAS , 1788, 706–17, on 710–3.

[29] J.B.J. Delambre, Histoire de l'astronomie au dix-huitième siècle (Paris: Bachelier, 1827), 758.

Institutional Considerations

In exchange for their salaries, status, and grants for special projects like geodetic surveys, the Paris academicians acted as technical advisers to the Crown. Their advice tended to be conservative and elitist, especially in respect of unsolicited proposals from inventors asking for state subventions or monopolies for their novelties. Experience confirmed what arrogance had suspected: most of the proposals were worthless and most of the proposers ignorant. The Academy suggested that artisans might be licensed, but only after passing an examination in geometry and other useful arts. During the Revolution, the Academy faced the hostility directed at all enclaves of privilege and the special anger of frustrated inventors, manufacturers, and would-be scientists who had suffered at its hands.^[30]

Well into 1790 the Academy held its meetings, read papers, and planned projects as usual. Some academicians favored the new regime, but few wished it to further; almost all lamented the disturbances that kept them from their work. Many recognized, however, that they would have to reorganize their company in keeping with the new style, especially after the establishment in 1791 of a patent law that took from them their chief public service.^[31] As a partial offset, academicians became increasingly involved in government technical projects. Of these, the most important, "repeatedly paraded as a prime example of science's potential value to the nation and a concrete instance of the Academy's proper function in society," was the reform of weights and measures.^[32]

[30] C.C. Gillispie, Science and polity in France at the end of the ancien régime (Princeton: Princeton University Press, 1980), 97–9, 461–3; Roger Hahn, The anatomy of a scientific institution. The Paris Academy of sciences, 1666–1803 (Berkeley: University of California Press, 1971), 118–21; Gillispie, "The Encyclopédie and the Jacobin philosophy of science: A study in ideas and consequences," in Marshall Clagett, ed., Critical problems in history of science (Madison: University of Wisconsin Press, 1959), 255–89, on 257, 268–74.

[31] C.P. Molard, Description des machines et procédés spécifiés dans les brevets d'invention, de perfectionnement et d'importation, dont la dureé est expiré (Paris: Huzard, 1811), 7–27; Hahn, Anatomy , 186–9; Henry Guerlac, Essays and papers in the history of modern science (Baltimore: Johns Hopkins University Press, 1977), 467–8.

[32] Hahn, Anatomy , 162–3.

A month after the storming of the Bastille, academician Jean Baptiste Le Roy, physicist, mathematician, and one-time clockmaker, suggested that the Academy propose to the National Assembly a dissolution of the over-rich metrological heritage of the Republic. The proposal, probably drawn up by the Academy's secretary, the marquis de Condorcet, and certainly presented to the Assembly by Talleyrand, set aside all existing units in favor of the length of a pendulum that beat seconds at the 45th parallel of latitude, which passes just north of Bordeaux. Talleyrand proposed further that the British be invited to join in the determination and in promoting the result, "so that all nations might adopt it."^[33]

On 8 May 1790 the Assembly considered the Talleyrand or Academy proposal together with several others to the same effect, notably one by Prieur, who expressly opposed using an arc of the meridian as a basis. "Besides the magnitude of the fundamental operation required, the difficulty of verifying it, and the impossibility of doing so daily, it is not easy to decide how exact the method might be." Here Prieur spoke as a military engineer familiar with surveying practice and with the lingering uncertainties over the earlier measurements of arcs. The same considerations caused Thomas Jefferson to give up his project of taking a decimal part of Cassini's degree as the basis of a new American unit: "the various trials to measure various portions of [meridians], have been of such various result, as to show there is no dependence on that operation for certainty."^[34]

The seconds pendulum had been proposed as a standard-setter for over a century. The pioneer geodecists preferred it: Picard, in 1671, proposed defining the pied as a third, and the toise as twice, the length of the seconds pendulum at a convenient place; Jacques Cassini observed that all domestic measures could usefully be referred to

[33] Hahn, Anatomy , 163–4; Bigourdan, Système métrique , 14–5; Talleyrand in Miller, Speeches , 59.

[34] Bouchard, Prieur , 287–90; William David Pattison, Beginnings of the American rectangular land survey system, 1784–1800 (Chicago: University of Chicago Press, 1957), 48–9, after Jefferson, Papers , ed. Julian P. Boyd et al. (Princeton: Princeton University Press, 1950+), 7, 25, 150–60; Bigourdan, Système métrique , 10.

such a unit, and even all European measures, since the length of a seconds pendulum is about the same throughout the Continent; La Condamine proposed international cooperation and a pendulum regulated at the equator, as determined by himself and "the hands of nature"; and Turgot, as controller of finance under Louis XVI, almost initiated a nationwide reform based on the seconds pendulum at 45°.^[35] Just before the Revolution, Gaspar de Prony, who would play an important part in the metrication of France, declared the pendulum to be the ultimate arbiter of length; and after the promulgation of the meter, a compiler of dictionaries, no doubt lifting from his predecessors, held that "the length of the simple pendulum, an invariable quantity always easy to recover, seemed given by nature to serve as a measure in all countries."^[36] The British had also considered the advantages of Cassini's suggestion, and of calibrating their yard by the pendulum, in order that "all future generations [may] obtain similar measures of length, capacity, and weight, and thereby render it altogether needless to cut them on stone, or to engrave them on brass, to perpetuate their existence."^[37]

Miller was about to introduce proposals for the reform of English weights and measures based on the pendulum when a letter from Talleyrand inviting Britain to join France in finding the length of a seconds pendulum came to hand. The plan was simple, and a natural successor to the linking of the observatories of Paris and Greenwich, "which all Europe would take as a guarantor of rigorous exactitude."^[38] While Parliament pondered the opportunity, the Revolution became too hot for Anglo-Saxon reformers, and the Paris Academy removed the rationale for collaboration by deciding not to take the

[35] Bigourdan, Système métrique , 6–11; Jacques Cassini, De la grandeur et de la figure de la terre (Paris: Impr. royale, 1720), 250; La Condamine, "Nouveau project," 501–5, 511; Charles Henry, Correspondance inédite de Turgot et Condorcet (Paris: Charavay, 1883), xxv, 234–5.

[36] Gaspar de Prony, "Discours préliminaire," in William Roy, Description des moyens employés pour mesurer la base de Hounslow-Heath (Paris: Didot, 1787), xvi-xvii; Lunier, Dictionnaire des sciences et des arts , 3 vols. (Paris: Normant and Nicolle, 1806), 2, 615, s.v. "mesure."

[37] John Whitehurst, "An attempt toward obtaining invariable measures," in The works (London: W. Bent, 1792), iii (text of 1787); Miller, Speeches , 44.

[38] Talleyrand in Miller, Speeches , 71.

pendulum as primary. Its decision seemed odd to many.^[39] The rationale must be sought, not in the requirements of measurement, but in the circumstances into which the Revolution propelled the Academy.

The National Assembly accepted Talleyrand's proposal and sent it and a question about the most useful division of weights, measures, and monies to the Academy, which referred both matters to a committee composed of Borda, Lagrange, Lavoisier, Tillet, and Condorcet. The committee reported on 27 October 1790 that everything should be decimal.^[40] It then handed what remained of its charge to a committee consisting of Borda, Lagrange, Laplace, Monge, and Condorect. On 19 March 1791 these geometers reported that the pendulum was the poorer of the two universal and natural units they could imagine. They plumped instead for a piece of the Paris meridian and yet another measurement of it.

Their objections to the pendulum suggest a hidden agenda. In obtaining a length from pendulum beats, they wrote, a unit of time, which has nothing to do with distance, must be invoked; and this unit, the 86,400th part of a day, had the additional blemishes of being both arbitrary and nondecimal. "It is much more natural, in fact, to refer distances from one place to another [the academicians were thinking of a standard for cartography, not for commerce] to a quarter of a terrestrial circle rather than to the length of a pendulum." The committee did appreciate the greater convenience of the pendulum standard, for which they provided: the Academy would undertake to determine the length of a seconds pendulum at the Paris Observatory, to serve as a secondary reference, the primary to be one ten-millionth of the distance from pole to equator.^[41]

[39] Hansard, 28 , cols. 315–17; Miller, Speeches , 43–4; George Evelyn Shuckburgh, "An account of some endeavors to ascertain a standard of weight and measure," Royal Society of London, Philosophical transactions, 88 (1798), 133–82, on 165–6.

[40] Borda, Lagrange, Lavoisier, et al., "Rapport," 1–6; Méchain and Delambre, Base, 1 , 14; Bigourdan, Système métrique , 16.

[41] Charles Borda, J.L. Lagrange, and Gaspard Monge, "Rapport. . .sur la systême général des poids et mesures," HAS , 1789, 1–18, on 1–6 (decimalization), 7–16 (arc over pendulum). Cf. Bigourdan, Système métrique , 17–8; Méchain and Delambre, Base, 1 , 14–9.

Although the ambition of the academicians did not extend to measuring the full quarter meridian, it opened a task sufficiently large. Borda's committee proposed to redo the arc from Dunkirk to Perpignan and to extend it to Barcelona, to obtain latitudes astronomically, to lay out new baselines, to observe the pendulum, to determine the weight of an exactly measured volume of distilled water at the temperature of melting ice, and to compare all the old units in use in France with the new standards. They saw no advantage in British cooperation: "we have excluded from our advice every arbitrary determination, we have used only the common property of all nations. . . .In a word, if the memory of all our work disappeared and only the results remained, they would disclose nothing to show what nation conceived the idea and carried it through."^[42] The Academy as a whole did not readily accept the recommendations of its committee of interested mathematicians: some objected that the arc had received enough attention; others, that the pendulum was easier. In the end, however, the Academy endorsed the recommendations and sent them to the National Assembly.^[43]

The speciousness of the argument that the choice of Borda's committee was the most satisfactory and least arbitrary stands forth from their anticipation of the charge that enlightened people everywhere might not regard a section of the meridian through Paris and lying almost entirely within France as a unit dictated by nature. They argued: the section should extend equal distances on either side of the 45th parallel because there the seconds pendulum and the size of a degree have their mean values; it is a mere coincidence that the 45th parallel runs through France. But all meridians are bisected at 45°. Why take one through Paris? Because only there do meridians have arcs bisected at 45° that terminate at either end at sea level and that are short enough to measure. "There is nothing here that can give the slightest pretext for the reproach that we wished to assert any sort of dominance." Or, as Laplace put the point in a lecture in 1795, "had savants from all countries come together to fix the

[42] Borda, Lagrange, and Monge, "Rapport," 13–6, 19.

[43] Bigourdan, Système métrique , 19–21.

universal measure, they would not have made a different choice."^[44] This flim-flam was perfectly clear to Jefferson: "The element of measure adopted by the National Assembly excludes, ipso facto , every nation on earth from a communion of measurement with them; for they acknowledge themselves, that a due portion for admeasurement for a meridian crossing the forty-fifth degree of latitude, and terminating at both ends at the same level, can be found in no other country on earth but theirs."^[45]

Jean-Baptiste Biot wrote in 1803, when surveying the progress of science since the Revolution: "if the reasons that the Academy presented to the Constituent Assembly were not altogether the true ones, that is because the sciences also have their politics: sometimes to serve men one must resolve to deceive them." Biot gave as the hidden agenda the Academy's wish to settle the shape of the earth once and for all.^[46] According to Delambre, Borda convinced his committee to opt for the arc because his circle, as suggested by the Paris-Greenwich measurement of 1787, made possible a determination of the meridian far more accurate than Lacaille's. This consideration left a trace in the committee's report to the Academy in March 1791. Today's instruments, it said, are so good that future improvements would not sensibly change the length of the meter that they determine; "or at least the length of time separating us from an age when everyday transactions would require and could attain such a precision is so great in comparison with the life of a man as to amount to infinity itself."^[47]

[44] Borda, Lagrange, and Monge, "Rapport," 15–6; Bigourdan, Système métrique , 56; Laplace, Oeuvres complètes, 14 (Paris: Gauthier-Villars, 1912), 141, 145 (quote).

[45] Jefferson to William Short, 28 July 1791, quoted by C. Doris Hellmann, "Jefferson's efforts towards decimalization of United States weights and measures," Isis, 16 (1931), 266–314, on 286. The academicians' grantsmanship has succeeded with some historians: Léon Bassot, "Notice historique sur la fondation du système métrique," in France, Bureau des Longitudes, Annuaire , 1901, D. 1–43, on 2, 16; C.C. Gillispie, "Laplace," in Dictionary of scientific biography, 15 (New York: Scribners, 1978), 273–403, on 334–5.

[46] Jean Baptiste Biot, Essai sur l'histoire générale des sciences pendant la révolution française (Paris: Duprat and Fuchs, 1803), 355–6. Cf. Adrien-Marie Legendre, "Suite du calcul des triangles qui servent à déterminer la différence de longitude entre l'Observatoire de Paris et celui de Greenwhich," MAS , 1788, 747–54, on 753.

[47] Delambre, Rapport 5; Crosland, in Bugge, Science , 20; Borda, Lagrange, and Monge, "Rapport," 15.

To these objectives—the old scientific imperative and the desire to vindicate and promote French instrumentation—should be added the social and strategic concerns of forging bonds with the new state. The metric project had high priority since the abolition of feudal rights had raised the gathering of rents and taxes in kind to a new level of confusion and litigation.^[48] During the several years the project would last, the Academy could expect to enjoy strong government support and a useful flow of cash. On 8 August 1791 some 100,000 livres, more than the Academy's annual state subvention, was placed at its disposal; estimates of the entire cost of the project ran from 300,000 livres into the millions; and one can scarcely criticize the Academy if it saw in this commitment a pledge on the part of the government to see it through troublous political times.^[49]

The Labor of Academicians

Pit and Pendulum

The National Assembly approved the Academy's revised proposal on 30 March 1791. The Academy immediately divided its work among five commissions: triangulations and latitude determinations (Cassini IV, Méchain, Legendre), baselines (Meusnier, Monge), pendulum of Paris (Borda, Coulomb), weight of water (Lavoisier, Haüy), and comparison of old and new measures (Tillet, Brisson, Vandermonde).^[50] The whole enterprise was to be directed by Borda, Condorcet, Lagrange, and Lavoisier. Soon death and disinclination reduced this extraordinary mobilization of the brains of France. All geodetic work fell to Delambre and Pierre-Francois-André Méchain, an excellent compulsive astronomer; Borda and Cassini took on the pendulum, and Lavoisier the water. The first year went by making instruments. Only one Borda circle, that of 1787, existed in 1791;

[48] Kula, Measures and men , 236–7, 243.

[49] Hahn, Anatomy , 163–4, 253; Adrien Favre, Les orgines du système métrique (Paris: PUF, 1931), 121–30; Bigourdan, Système métrique , 32.

[50] Bigourdan, Système métrique , 22–6.

two more, readable to 3 or 4 seconds of arc, were ready in the summer of 1792, when Méchain set out for Spain and Delambre started north. The instrument answered its advertisements: although difficult to use in a cramped church tower, its precision with enough repetitions was, in Delambre's words, "nearly incredible."^[51]

Great accuracy was also achieved in the pendulum experiments, which took place during the summer of 1792 in a pit in the Paris observatory. The general technique, by no means original with the metric project, was to observe coincidences between a swing of a simple pendulum of length L and that of a clock that accurately beat seconds. Let t ₁ be the clock time when both pendulums move through the midpoint of their swing together, and let t₂ be the time of the next coincidence. In the interval Dt = t₂ - t ₁ , therefore, the number of swings of the two pendulums differs by one and the half period of the simple pendulum is T = Dt / (Dt ± 2). Thence the length of the seconds pendulum L_s can be deduced from the formula T ² :1 = L:L_s . If Dt is large, L_s can be obtained very accurately.

Borda designed the apparatus, which was made by Etienne Lenoir, who also supplied the repeating circles. The pendulum bob hung from a 12-foot steel cord suspended from a knife-edge mounted on a subterranean wall in the Paris Observatory. Borda and Cassini observed coincidences through a telescope pointed perpendicularly to the wall. The largest departure from the mean of the twenty coincidences they recorded was one part in 100,000. They corrected their computed L_s for the dependence of the period on the amplitude of the swing, on temperature, on air pressure, on the flexure of the support and the steel cord, on the moment of inertia of the bob, and on much else. The result: L_s = 440.5593 lines of the toise used in the expedition to Peru.^[52] "Thus," wrote the Commissioners who presided over the metric project in 1794, "the pendulum can be considered the depository of the unit of measure, or even a method of

[51] Méchain and Delambre, Base, 1 , 20, 23, 43–4, 97–9; Delambre, Rapport , 6.

[52] Borda and J.D. Cassini, in Méchain and Delambre, Base, 3 , 337–401, and in C.J.E. Wolf, ed., Mémoires sur la pendule, précédés d'une bibliographie , 2 vols. (Paris: Gauthier-Villars, 1899–91), 1 , 17–64.

measuring the earth; and nothing is more suited to instill admiration of physics and geometry than seeing an undertaking that would appear to require travel from one end of the world to the other with great machines reduced to a very simple experiment done in one place with an instrument of modest dimensions."^[53] That would have made an inexpensive as well as a reasonable standard. Lenoir's bill for the circles, the rules, the water apparatus, and the pendulum was just over 34,000 livres. The Academy then estimated—this is from a progress report of 2 May 1792–that the total project would cost 300,000 livres.^[54]

Roughing It

When Méchain and Delambre set out in the summer of 1792, the Revolution had become, in Delambre's words, "truly frightening." Méchain's instruments perplexed the southern peasants, who jailed him as a counter-revolutionary. Officials who understood numbers eventually procured his release. He decided that he would be safer in Spain, and so began his mapping there, with great efficiency until an injury compelled him to break off early in 1793. By the time he had recovered and completed the arc in Spain, with an immaculate determination of the latitude of the southern terminus at Montjouy, the Spanish government had closed the border to Frenchmen. Méchain passed his enforced leisure by observing stars in Barcelona, also with exquisite accuracy; but, to complete his misfortunes, the difference in latitude between Montjouy and Barcelona, as deduced from the stars, came out 3.24 seconds greater than the difference Méchain had calculated from measurements made on the ground.^[55] These miserable three seconds tormented Méchain for the rest of his life: he thought that Borda's circle permitted perfection and he blamed himself for blundering. Méchain had measured his angles as exactly as Borda's circle allowed. The discrepancy of 3 seconds—about the angular width of a penny observed at a distance of 450 miles—arose from

[53] France, Comm. temp., Instruction , 29–30.

[54] Bigourdan, Système métrique , 22.

[55] Méchain and Delambre, Base, 1 , 52–6; Delambre, Histoire , 759–60.

unevenness in the terrain, which dragged Méchain's plumb bobs off the vertical.^[56]

While Méchain stagnated in Barcelona, Delambre had one unpleasant adventure after another in the north of France. Anticlerical peasants had knocked down many of the church towers that had served his predecessors; when he hung lanterns as substitute sights, he was suspected of signaling to the enemy. (France had been at war with most of Europe since April 1792.) Once, having been detained by local patriots, he tried to explain his mission in an impromptu lecture on geodesy. To no avail. He was packed off to a higher jurisdiction, in Saint Denis. The square teemed with volunteers waiting to go to the front, who did not have the prerequisites for the crash course in triangulation they forced him to give. "Evening came on. . . . The audience was very large: the front rows heard without understanding; those behind heard less and saw nothing. They grew impatient, and grumbled; some proposed one of those quick means [of dealing with suspect people] then so much in vogue." Were it not for a quick-witted official, who rushed Delambre into protective custody, the arc might have ended in Saint-Denis.

The National Assembly found time while busy transforming France into a Republic, which it declared on 22 September 1792, to issue an order for Delambre's release.^[57] That did not signify a regard for academicians. On 8 August 1793 the National Assembly closed the Academy along with other unrepublican corporations. The suppression came only a week after the Assembly had given cause for reassurance to those who expected that the Academy's labors on measures in the national interest would protect it. That first week in August the Assembly had affirmed the decimal system and the meridianal definition of the meter, ordered the continuation of the work, and decreed that the Academy provide for the manufacture,

[56] Méchain and Delambre, Base, 2 , vii-ix, 617–20, 624–6, 630; Delambre, Histoire , 760–7.

[57] Méchain and Delambre, Base, 1 , 23–34, 41–4; Vulfran Warmé, Eloge historique de M. Delambre (Amiens: Caron-Duquenne, 1824), 15–16; Henri Marie Auguste Berthaut, La carte de France, 1750–1898 , 2 vols. (Paris: Service géographique, 1898–99), 1 , 121–2; Méchain and Delambre, Base, 1 , 32–4.

distribution, and explanation of provisional meters for general use while it prosecuted its measurements. This provisional meter was defined as a ten-millionth of ninety times the average degree in France as determined by Lacaille, or 443.444 lines of the Peruvian toise. It differed from the definitive meter by about a quarter of a millimeter.

It is not advisable to assign an important job to a specialized government agency one week and to abolish the agency the next. The Assembly therefore immediately accepted the recommendation of the Committee of Public Safety that—because its work would erase the last vestiges of feudal divisions—the Academy's commission on weights and measures should be reestablished, with the same personnel, as an independent temporary commission (Commission temporaire des poids et mesures républicains). It consisted of Borda, Brisson, Cassini, Coulomb, Delambre, Haüy, Lagrange, Laplace, Lavoisier, Méchain, Monge, and Vandermonde.

The Academy's confidence in metrology as an anchor against political storms thus received partial justification. The job of overseeing the making and distribution of the provisional standards brought another large and pressing public responsibility to the academic rump and an important cash flow. The minimum cost of the standards, as estimated by Lenoir and others, would be some 200,000 livres. This minimum provided for copper standards for the geographical departments into which the Revolution had divided the old provinces and for iron standards for the prefectures. The Assembly preferred to avoid this whiff of discrimination and voted an additional 60,000 livres or so to make all the standards of copper except for the platinum prototypes.^[58] The temporary commission expected the copper standards to be accurate to around one part in 100,000 for the meter and the grave (kilogram) and one part in 10,000 for the pinte (liter).^[59]

[58] Bigourdan, Système métrique , 30–5; Champagne, Role , 102–3; Bouchard, Prieur , 293; Bugge, Science , 206–7; Charles Cappelli, Rapports métriques (Turin: Felix Buzan, an X), 7; C. Doris Hellman, "Legendre and the French reform of weights and measures," Osiris, 1 (1936), 314–39, on 322–3.

[59] Bigourdan, Système métrique , 36–40.

The arrangements of August and September proved provisional in more ways than one. Lavoisier was arrested on 28 November 1793; the temporary commission requested his release as necessary to its work; the Committee on Public Safety of the Convention (into which the Assembly had transformed itself on declaring a republic) refused, and, for good measure, purged the temporary commission of Borda, Brisson, Coulomb, Delambre, and Laplace, who had not, in its opinion, shown a proper hatred for kings. The rejection of the appeal for Lavoisier and the order for the purge were drawn up by Prieur, who thus revenged himself on academicians who had opposed his political views and metrological proposals. When news of the purge, which was made public on 23 December 1793, reached Delambre, he was shivering from cold on the top of a signal tower 64 feet tall that he had erected near Orléans in the service of the people. On his return to Paris, a revolutionary committee studied his manuscripts without making much of them and pounced on a diploma from the Royal Society, which bore the arms of George III. Delambre found it prudent to disappear.^[60]

What remained of the temporary commission did little more than print explanations of the new system and revolutionary rhetoric. "Soon [our] vision will no longer be affronted by those old weights and measures that still tell of the odious remains of times and things sullied by tyrants. . . . Every child will know [the system]; and it will help diminish inequality among men."^[61] There is no reason to put off enjoyment of the great benefit; the provisional meter will be perfectly satisfactory for commerce; the definitive will only serve to make the whole operation "more worthy of the powerful and enlightened nation that has undertaken it." Neither the rhetoric nor the practical business of furnishing provisional metersticks long protected the pitiful rump commission. In the spring of 1794, it requested 50,000 livres to pay its artisans; Prieur arranged to give 10,000 and to terminate its existence.^[62]

[60] Méchain and Delambre, Base, 1 , 46–52.

[61] Bigourdan, Système métrique , 55–6 (address to the Convention, 19 Jan 1794).

[62] France, Comm. temp., Instruction , xv-xvi; Bouchard, Prieur , 295–6, 299–301, 461–4; George Sarton et al., "Documents nouveaux concernant Lagrange," Revue d'histoire des sciences, 3 (1950), 110–32, on 127.

A Military Connection

Delambre believed, probably correctly, that the Committee on Public Safety and many members of the Convention wished to kill the meridian measurement and declare the provisional meter definitive.^[63] At this point a powerful advocate of geodesy came to the rescue: General E.N. de Calon, formerly of the Royal Geographical Engineers (Ingénieurs géographes), which had been suppressed in 1791. Meanwhile Calon had become a deputy and a Jacobin; his rampant republicanism perhaps may be traced to unfulfilled ambition and a sense of injury suffered in the late 1770s, when, though an officer of twenty years' standing, he had been ordered to do survey work usually assigned to his juniors.^[64] He was a numerary as well as a passionate man. His few recorded statements in the Convention and the Jacobin Club of Paris were precise and numerical, as in the following complete discourse: "A vehicle drawn by six horses has just been stopped at Neuf-Brisach; it contains a ton of gold and of white and black uniforms."^[65]

The suppression of his former corps presented Calon with a vacuum in which to fulfill his ambition. With the corps went the map department of the Dépôt de la Guerre, the headquarters and storehouse of military cartography. The temporary organization put in its place could not handle the flood of maps, and Calon, who became head of the Dépôt in April 1793, managed to recapture most of its archives. He then purged the place of suspect employees installed by his aristocratic predecessor. To repopulate the Dépôt, Calon set up a school there in astronomy, geography, engineering, history, languages, and engraving; and to staff the school and get on with his major mission, providing maps of the front and of captured territories to the Army, he tried to attach to his service all the unoccupied savants he could find. At its height in the autumn of 1796, Calon's

[63] Bigourdan, Système métrique , 50–81.

[64] Henri Marie Auguste Berthaut, Les ingénieurs géographes militaires, 1624–1831 , 2 vols. (Paris: Service géographique, 1902), 1, 43–6, 66, 102–3, 122–3.

[65] F.-A. Aulard, La Société des Jacobins. Recueil des documents pour l'histoire du Club des Jacobins de Paris , 6 vols. (Paris: Jouaust and Noblet, 1889–97), 3 , 161, 522, 679.

cartographical program, printing establishment, and school ran at an annual cost of 300,000 livres. His expansiveness caused inefficiencies and inspired jealousies, and by the spring of 1797 he and his empire had fallen.^[66]

Among the academicians Calon recalled to government service were Méchain, who had managed to get himself to Genoa in September 1794, after a narrow escape from corsairs, and Delambre. It was agreed, probably early in 1795, that they would triangulate the new departments and that, to prepare as firm a base as possible for the work, they would resume the measurement of the meridian. Then at the zenith of his influence, Calon persuaded the Committee on Public Safety to grant 220,000 livres for map-making, half for extending the Cassinis' Carte de France into the Rhineland and half for finishing the meridian between the Loire and the Pyrenees.^[67] This largesse, given on 13 May, fit well with proposals Prieur had made in March for the prompt completion of the metric project.^[68] Prieur recommended setting up a temporary agency (Agence temporaire des poids et mesures) to push through the manufacture of provisional standards and to oversee their deployment. He estimated that much could be done for 500,000 livres. He had to request another 500,000 livres the following September. Meanwhile the Army lent a hand by collecting old metal, chiefly church bells and discarded measures, to serve materially and symbolically as raw ingredients for metric measures.^[69]

Prieur's program became law on 7 April 1795. It provide for using the "provisional" meter in everyday transactions even after the definitive platinum prototype came into existence; confirmed the basic names, meter, liter, and gram; and ordered resumption of the measurement of the arc. It established a triumvirate under the Commission of Public Instruction to oversee the manufacture, distribution, and explanation of the provisional standards, using machines

[66] Berthaut, Ingénieurs, 1 , 126–7, 130–2, 135–50.

[67] Delambre, Histoire , 756–62; Méchain and Delambre, Base, 1 , 57–8; Berthaut, Ingénieurs, 1 , 162–4.

[68] Bigourdan, Système métrique , 61.

[69] Kula, Measures and men , 244.

wherever possible, "so as to combine facility and swiftness with precision, and consequently to allow citizens to buy the new measures at a reasonable price"; and it specifically ordered the new agency to provide graphic representations of conversions requiring no calculations by users.^[70] Later that month the scientific side of operations was entrusted to academic survivors of earlier commissions: Borda and Brisson were to bring int he exemplar of the copper provisional meter within a "décade" (ten days); Méchain and Delambre, to do their thing; Delambre, Laplace, and Prony, to fix a baseline near Paris; Borda, Haüy, and Prony, to determine the standard of weight; and Berthollet, Monge, and Vandermonde, to oversee the preparation of the platinum to be used in the definitive primary standards.^[71]

Matters being thus composed, Delambre left Paris on 28 June 1795 in the capacity of "astronomer of the Dépôt de la Guerre" to resume his observations at Orléans. He had the usual trouble finding intact steeples, and the cost of erecting signals quickly depleted his cash. No one wished to accept the assignats (government IOUs) he carried; and once again Calon tided him over. Three years of republican rule had not made peasants less suspicious and superstitious. They now tore down Delambre's signals on the theory that they attracted storms.

Méchain had his hardships, too, as he crawled north across the mountains toward their rendezvous in Rodez. In one place, on a high outcrop only twelve feet wide, surrounded by precipices, he sat for days waiting for the clouds to lift long enough to work the Borda circle. He arrived within signaling distance of Rodez around 1 September 1797, shortly after Delambre had completed his part of the work. There they stopped. Méchain would not accept Delambre's help and could not go on. "In this cruel situation," he wrote his collaborator, "I prefer to stay in this terrible exile, far from what I most cherish in the world; I will sacrifice everything, give up everything,

[70] France, Convention nationale, Loi relative aux poids et mesures [18 Germinal an III] (Paris: Impr. de la République, [1795]), 4–7; Bigourdan, Système métrique , 67–70. Cf. Hellman, "Legendre," 324–7; Bouchard, Prieur , 306–7. The agency consisted of François Gattey, A.M. Legendre, and C.E. Cocquebert.

[71] Méchain and Delambre, Base, 1 , 58–64; Bigourdan, Système métrique , 71–7.

rather than return without finishing my part of the job." Delambre felt that he could not insist and Méchain finished the arc the following September.^[72]

After concluding his triangles at Rodez, Delambre joined Laplace at Melun to fix the ends of the baseline near Paris. Borda had devised special rulers for the purpose, which were not ready until the spring of 1798. Their employment was extremely tedious. Delambre could make only about ninety lengths (about 360 m) a day; it took thirty-three days to cover the entire distance of 6075.90 toise. In the summer he redid the Perpignan baseline. That took six or seven weeks. Earlier surveyors had done it in twelve hours. The length of the Perpignan base as calculated from the length of the Melun base and the triangles differed from the measurement on the ground by less than a foot. On 1 brumaire 1798 an VI (22 October 1798), everything required to calculate the length of the arc from Dunkirk to Barcelona was in hand. Méchain and Delambre returned to Paris, where an international committee had assembled to examine, approve, advertise, and propagate their results.^[73]

The Response of the People

The Academy of Sciences resumed its existence late in 1795 as the principal part of the new Institut de France, a government monopoly of the most learned new republicans. On 4 April 1796, the Institut took over the metric project through a commission composed of the reborn academicians Berthollet, Borda, Brisson, Coulomb, Delambre, Haüy, Laplace, Legendre, Méchain, Monge, and Prony. They had developed skill in the political as well as the technical aspects of their charge. Laplace proposed the convening of an international body of savants to check and accept the prototypes of the new units. "You realize [Laplace wrote Delambre] that all this is only a formality, to

[72] Berthaut, Ingénieurs, 1 , 165; Bigourdan, Système métrique , 135–45; Méchain and Delambre, Base, 1 , 66–80; Méchain to Delambre, 20 brumaire an VI (22 October 1797), ibid., 83.

[73] Méchain and Delambre, Base, 1 , 84–90; Delambre, Rapport , 6, 53–4; Berthaut, Carte, 1 , 123–4.

enable them to consider the system on their own, to do away with national envy, and to make them adopt the measures." Borda opposed the meeting; Napoleon supported it; the Directory ordered it.^[74] The irrepressible Talleyrand, now minister of foreign affairs, issued the invitations, and had the satisfaction this time of omitting Britain altogether.

The international committee of experts convened appropriately in a military setting, in the Dépôt de la Marine, on 28 November 1798, having waited in Paris for a few months for Delambre and Méchain to remeasure a baseline. These patient experts represented client states and friendly powers, to wit: the Bavarian, Cisalpine, Helvetian, Ligurian, and Roman Republics, and Denmark, Sardinia, Spain, and Tuscany. The meeting divided into three working committees, one to control the weight of the kilogram, a second to compare the scales used in the work with the old toise, and the third—composed of four members calculating independently—to deduce the length of the meter from the cornucopia of measurements made by Méchain and Delambre. Their calculations fixed the definitive meter over-precisely at 443.295936 lignes of the toise de Peru taken at 17.6°C, some 0.144 lignes shorter than the provisional meter by then distributed throughout France. (The difference was meaningless for commerce, since it amounted to one foot in a kilometer.) Independent observers had nothing but praise for Borda's circle and for the care with which the units of volume and weight were deduced from the meter and the density of water.^[75]

The Danish delegate retained enough independence to observe that although Méchain and Delambre had been as precise as was humanly possible, "it cannot be assumed that the determination of the meter is so absolutely and completely borrowed from nature that there is no doubt at all about its final accuracy." No echo of this

[74] Hellman, "Legendre," 333–5; Crosland, in Bugge, Science , 197; Laplace to Delambre, 29 Jan 1798, in Yves Laissus, "Deux lettres de Laplace," Revue d'histoire des sciences, 14 (1961), 285–96, on 287–8.

[75] Crosland, in Bugge, Science , 197–200; Bugge, ibid., 205–11; Méchain and Delambre, Base, 1 , 92–4. Praise for the circle: Bugge, Science , 204; Delambre, Rapport , 232–3, quoting F.X. von Zach.

discordant and irrelevant observation was heard in the speeches on 22 June 1799, when the joint committees formally presented the prototype standards to the people. In accepting them, the president of the upper legislative body, the Conseil des anciens, observed that it was a work of genius to have found an inviolable base of measurement in nature; "that, citizens, is the immortal service that the National Institute has rendered to the French Republic, or rather, the benefit that it offers to the entire human race."^[76] It remained only to convince the race to accept the benefit.

Resistance

The experts returned to their countries encouraged to propagate the metric system at home for the improvement of commerce and the tightening of ties to France. The sort of pressure they were under appears from a hint earlier given by the Convention's Committee of Public Instruction to a newly liberated territory. The Committee pointed to the great "advantage it would be to the union just established between the French and Batavian republics to spread the system of uniform and decimal measures beyond French territory." The Cisalpine Republic, consisting of Lombardy and Emilia-Romagna, also felt the pressure early.^[77] Annexed territory, such as the Département du Mont-Tonnerre carved out of the Rhineland, felt a heavier hand. By a decree of 18 June 1801, the Département would be obliged to use the metric system exclusively; all old weights and measures found in shops and all meter sticks on which former units of length were indicated would be confiscated.^[78]

In friendly but not subject territory the system was recommended for its combination of abstract science and practical utility. "We [in the Kingdom of Sardinia] are obliged to the nation that has

[76] Bugge, Science , 204, and in Crosland, "'Nature' and measurement," 305–8; P.C.L. Baudin, "Réponse," in Méchain and Delambre, Base, 3 , 652. The president of the lower legislative body, the Conseil des cinq cents, spoke similarly; ibid., 3 , 649.

[77] Quoted by Laissus, "Deux lettres," 288.

[78] Tables de comparaison entre les mesures anciennes en usage dans le Département du Mont-Tonnerre et les nouvelles mesures républicaines (Mayence: Pfeipfer, an X), xxxii.

sustained with unexampled courage the most terrible political upheavals for having put forth, in the very midst of a frightful tumult, the most abstract speculations of mathematicians as a rule for every-day transactions." "Nature and not France brings [the new measures] to us [Spaniards]. Let us accept them following our natural ally with whom we have so many commercial relations. . . .It behooves Spain [because it helped Méchain] to set other nations the example of adopting these units."^[79]

None of this cajoling or commanding had much immediate effect. Even in France, where the new units were to oust the old in land transactions on 1 vendémiaire an X (23 September 1801), the people declined to benefit from the republican measures created ostensibly in their interest.^[80] One of the orators at the presentation of the prototypes in July 1799 had imagined the satisfaction a peasant would feel in computing his holdings in square meters. "The field that supports my children is such and such a fraction of the globe. In that proportion I am a co-owner of the world."^[81] In practice the peasant and his surveyor, builder, and draper refused to give up their toise sticks. So brutish a rejection of the natural and the rational perplexed the savants. "There is no respect in which the reform of weights and measures has not been advantageous," declared the president of the Agricultural Society of Paris (Société d'agriculture de Paris) in 1809, "and, consequently, if reason always was listened to, the success of the reform would have been complete."^[82]

Alas, the meter had only complicated ordinary life. Artisans brought home their measures in familiar units and sat up all night converting them into meters, and into a crowd of irrelevant decimals, in order to write estimates and contracts in the obligatory figures.

[79] Capelli, Rapports , 5; Gabriel Ciscár, Memoria elemental sobre les nuevos pesos y medidas decimales fundados en la naturaleza (Madrid: Imprenta real, 1800), on 33–4.

[80] François Gattey, Eléments du nouveau systême métrique, suivis des Tables de rapports des anciennes mesures agraires avec les nouvelles (Paris: Bailey and Rondonneau, an X), 65. Cf. Bugge, Science , 205, and Maurice Crosland, "The congress on definitive metric standards, 1798–1799: The first international scientific congress?" Isis , 60 (1969), 226–31, on 229–31.

[81] Quoted by Crosland, "'Nature' and measurement," 285.

[82] L. C[hessiron], "Mesures," in Nouveau cours complet d'agriculture théorique et pratique, 8 (Paris: Delerville, 1809), 291–314, on 299–300.

Why did they not measure in meters to begin with and enjoy "the happy effects of the most useful of the gifts that scientists have been able to make to society"?^[83] Because they were creatures of habit, vain, traditional, pious, ignorant, and ungrateful.^[84] And also canny and suspicious. According to a British metrologist, who had it from a French merchant, consumers opposed the new units on the theory that they would be an advantage to shopkeepers, and shopkeepers opposed them for fear that consumers would be able to figure out true costs. The government hoped that a play with words would overcome suspicion. On 4 November 1800, it allowed the use of old words for multiples of the new measures, for example, "toise" for "two meters," "pinte métrique" for "litre," and so on. The reformers thought the concession damaging and absurd: if the people could use Greek words like "chirurgien" and "apothécaire," why not "kilogramme"?^[85]

Because the people did not like change and cared nothing for system. So stubborn and irrational were they that in 1812 the imperial government sacrificed the jewel of the reform, the key to democracy, that is, reckoning by tens. Two laws, of 12 February and 28 March of that year, indicate the state of affairs. The first ordered that the official system be taught in all schools throughout the empire, that it alone be used in public administration, markets, and commercial transactions. The second destroyed the official system by introducing "common measures" ("mesures usuelles") divided by twos and threes: a toise of 2 meters divided into 6 pieds; an aune of 1.2 meters divisible into halves, quarters, eighths, and sixteenths, and also into thirds, sixths, and twelfths; and similarly for weights and coins. Our British metrologist enjoyed the spectacle: "Thus, after twenty years of

[83] Ibid., 292.

[84] Concocted from compliments in ibid.; Méchain and Delambre, Base, 3 , 651 (text of 1799); Ciscár, Memoria , 38–9; Jean Guillaume Garnier, Traité d'arithmétique , 4th edn. (Paris: Houdin, 1818), 281.

[85] P. Kelly, Metrology; or, an exposition of weights and measures, chiefly those of Great Britain and France (London: Lockington et al., 1816), 25–6; Gattey, Eléments , 9–10; Chessiron, "Mesures," 296. The convenience of halves and doubles of the fundamental units was widely urged as an advantage of the reform, e.g., in Journal de physique, 47 (messidor an VI [1798]), 59, 60.

trouble, mystery, and litigation, no advances are made, except that of having one common standard."^[86] Otherwise confusion had only been compounded: the puzzled citizen had the provisional meter of 1795, the definitive of 1799, the compromised names of 1801, the common system of 1812, and, unofficially and omnipresent, the ancient units of the Kings of France. It is easy to change governments, not hard to reform currency, but almost impossible to alter the most common weights and measures. "Nothing has a greater tendency to grow worse, or more obstinately resists improvement." One took the long view. "This new metric system, all of whose parts fit together so simply, will no doubt triumph in the end over the obstacles that habit still opposes to its general adoption," so reads a text of 1820, "especially if it continues to be obligatory."^[87]

Spread

A gauge of the rate of penetration of the new units is the pattern of their use in books requiring specification of units, like atlases, compendia of architectural drawings, and manuals of surveying, building, and engineering. Although such works employing old units exclusively were published into the 19th century,^[88] the common pattern up to around 1815 was to present measurements and calculations in both meters and toises and their multiples. A good indication for the early years is the collection of architectural designs awarded prizes by the Institut de France and other government bodies between 1795 and 1803. Forty of these designs have units: three use toises only, two use meters only, and the balance uses both. Before 1800 toises have priority when both scales are present; after

[86] Kelly, Metrology , xiii; ibid., 27–30, for text of the laws of 1812.

[87] Respectively, Kelly, Metrology , xvi, and Louis Puissant, Traité de topographie, d'arpentage et de nivellement , 2nd edn. (Paris: Courcier, 1820), 245 (1820).

[88] See, for example, Charles-François Viel, De la construction des édifices publics sans l'emploi du fer (Paris: Perronneau, 1803); L. Ducrest, Vues nouvelles sur les courans d'eau, la navigation intérieure et la marine (Paris: Perronneau, 1803); Molard, Description , 1; J.Ch. Krafft, Recueil d'architecture civile (Paris: Bance ainé et al., 1812); Bernard Forest de Belidor, La science des ingénieurs, dans la conduite des travaux de fortification et d'architecture civile , ed. C.L.M.H. Navier (Paris: Firmin Didot, 1813).

1800, meters.^[89] A collection of plans for large structures published in 1823 shows a very considerable change: of seventy-six plates with scales, two have toises only, eleven have both, and sixty-three meters only; and the old measures occur exclusively in one section of the collection, on stone bridges.^[90] The obvious extrapolation does not hold, however; a set of 105 house plans published in 1843 under the promising title Paris moderne suggests that builders of private dwellings then still preferred to express themselves in the measures of the old regime. About 30 percent of the plans use toises only; another 30 percent, meters only; and 40 percent, both. All the plans are dated, the earliest to 1815; the strongest showing of the toise against the meter occurs not at the beginning, but in the period 1835–9. The meter takes over after 1840, the year in which the metric system at last became obligatory in France.^[91]

Up-to-date technical manuals show the same equivocation as architectural drawings. An authoritative indicator is the huge treatise on the building arts (four volumes in five of text, three of plates) published between 1805 and 1816 by Jean-Baptiste Rondelet, chief architect of the church of Sainte-Geneviève and architectural consultant to the government. Rodelet's plates strongly favor the old measures; his text appears to be the work of a schizophrenic. The earliest volume (1805) uses pieds, pouces, and lignes and also metric units, sometimes converted but often not, in tables and in calculations; at one point it gives dimensions in meters and computes in toises.^[92] In the volumes published in 1812, Rondelet usually proffers all dimensions in both the old and new style, but without the advantage of decimal notation: for example, "31 pieds 3/7 (10 mètres 209 millimètres)."

[89] Projets d'architecture et autres productions de cet art qui ont merité les grands prix accordés par l'Académie, par l'Institut national de France, et par des Jury du choix des artistes ou de gouvernment (Paris: Detourelle, 1806).

[90] Louis Bruyère, Etudes relatives à l'art des constructions (Paris: Bance ainé et al., 1823).

[91] Louis Marie Normand and G.E. Lemmonier and Paris moderne, ou choix de maisons de campagne et constructions rurales des environs de Paris , 3 vols. (Liège: d'Avanzo, 1843), and several other editions; Bouchard, Prieur , 313. The obligation was laid down in a law of 4 July 1837; it took effect on 1 January 1840.

[92] Jean Baptiste Rondelet, Traité théorique et pratique de l'art de bâtir (Paris: chez l'auteur, 1805–16), 3, 57, 66–7, 83 ff., 102, 164, 179–83, 269 ff., 388–96.

His preference for the old appears from his way of obtaining specific gravity, which he understands as the weight in grams of a cubic centimeter of a substance. He measures the weight of a sample, in air and in water, in onces and gros, deduces the weight of a cubic pied, and converts to the metric system. The preference for the old units persists into the last volumes, published in 1816. Then—after 1,839 pages of schizophrenic computations, the last of which provides the cost of old bricks in old money—Rondelet introduces some "notions about metric measures."^[93] It is instructive that this instruction precedes a recomputation of costs in metric measures and decimalized currency. The relative ease of such computations was the great benefit that the reformers had advertised.

From about 1810 many technical manuals by professors and government officials used metric measures exclusively. For example, the professor of mathematics at the Ecole impériale militaire, Louis Puissant, and Pierre Pommiés, professor at the Lycée Napoléon, both influential teachers of surveying and geodesy, used meters exclusively and without explanation in many textbooks beginning in 1807.^[94] Jean-Nicholas Hachette, professor at the Ecole polytechnique, brought the metric system into the preface of his textbook on machines, without comment, as the only satisfactory way "to express their effect in numbers." The chemist Jean-Antoine Chaptal, one-time minister of the interior and long-time educational reformer, naturally used nothing but modern measures in his survey of the state of French industry after the fall of Napoleon. Still there are hints of backsliding where least expected. The official surveyors of France might have worked exclusively in meters and understood the higher geodesy; but the local land measurer often enough made do with old units and little geometry into the reign of Louis Philippe. A manual for such measurers, "especially people who have not studied geometry," was published in 1833 by an inspector of the cadastral survey. It contains an explanation of the metric system, an injunction

[93] Ibid., 1 , 99, 101–2, 158–60; 4 , 583–604, 609–44.

[94] Puissant, Traité de topographie , 139, 154, and Michel Pommiés, Manuel de l'ingénieur du cadastre (Paris: Impr. impériale, 1808), 166–9, illustrate the type.

to use it, and tables for the easy conversion of old local measures into meters, "and vice versa."^[95]

As it spread, the metric system did help to realize the reformers' ambition to improve the numeracy of Europeans. In the Ancien Régime, despite its baroque abundance of metrological units, most people had need only for a single system; during the Empire, because of the government's policy of driving the meter home, more and more citizens had to learn how to convert one set of measures into another. If the first advance of European "Rechenhaftigkeit"—"the inclination, habit, and ability to resolve the world into numbers and to bring these numbers together into an artificial system of income and outgo"—may be likened to literacy in one language, the domestication of the metric system made reckoners bilingual.^[96]

The early treatises on metric calculations propagated not only decimal arithmetic, including the concept of place, but also the idea of significant figures and the operation of rounding off. An Exposition abrégée du nouveau système , published in the provinces in 1802 or 1803, may stand for the genre. It explains that the many decimals generated during conversion are artifacts of multiplication and division, and demands that they be dropped from the final answer.^[97] Rounding off, says Rondelet, in his belated account of metric computations, is essential to the new system. Rounding off might in practice mean only rounding up, as readers of an Arithmétique pratique of 1800, which recommends changing 0.7411440 to 0.75, learned to do; a practice that would favor shopkeepers, who could round up each of their many small transactions.^[98] Even arithmetic may have its social bias. The utility of metric conversions in teaching numeracy

[95] J.A. Chaptal, De l'industrie Françoise , 2 vols. (Paris: Renouard, 1819); A. Lefevre, Guide practique et mémoratif de l'arpenteur, particulièrement destiné aux personnes qui n'ont point étudié la géométrie (Paris: Bachelier, 1833), i-vi, 15–21.

[96] Quote from Werner Sombart, Der Bourgeois. Zur Geistesgeschichte des modernen Wirtschaftsmenschen (Munich: Duncker and Humblot, 1913), 164.

[97] Exposition abrégée , 23–4, 29–30. See also the contemporary Tables de comparaison , xiv–xxix; Capelli, Rapports , 49–57.

[98] Rondelet, Traité, 4:2 (1816), 610–3; Adrien Poittier, Arithmétique pratique et démontrée, pour réduire les anciennes mesures en nouvelles (Paris: Bernard and Moutardier, nivôse an VIII), 146–52. Gattey, Eléments , 32–3, rounds up only if the part dropped is >> 0.5 of the last figure kept.

appears further from popular textbooks of arithmetic that use such computations as exercises. This practice persisted long after the universal adoption of the metric system in France.^[99]

According to the president of the Paris Agricultural Society, the great majority of people who could read and write in 1810 knew nothing more of arithmetic than addition and subtraction. He had a prescription for correcting this innumeracy and a vision of the happy consequences. "If decimal calculations could be introduced into primary schools along with the use of the new measures, not only would the housewife be able to make all the computations she requires, but also the worker could measure without difficulty and, by adding the use of the rule and compass for tracing geometrical figures,he would be able to draw all his plans himself, and the farmer would have no problem with surveying."^[100] This grand project has been realized in large measure. The male academic and quantitative spirit of the late Enlightenment found a fertile if capricious partner in La belle Marianne , the spirit of revolutionary France.

[99] See, for example S.F. Lacroix, Traité élémentaire d'arithmétique, à l'usage de l'Ecole centrale des quatres nations , 2d edn. (Paris: Courcier, 1805), 115–46; Garnier, Traité, 1 , 263–75, 281–93; and, for the later period, A. Thinon, Leçons sur le système métrique et sur les applications usuelles de l'arithmétique (Paris: Dezobry and Magdelleine, 1860), 131.

[100] Chessiron, "Mesures," 8 , 293.

Fig. 1.1
Besides the strict mathematical method, which was intended only
for the learned reader, Wolff also used the physicotheological method 
for a popular audience. According to the latter method, everything in 
nature must be both perfect and useful. Demonstrating or proving 
this thesis became a rationale for 18th-century natural history. The 
scientist should look for "greatness in small things" (maxima in minimis), 
which phrase served as the motto for Friedrich Christian Lesser's 
Insectotheology (Frankfurt, 1740). The study of nature reveals the
infinite diligence of the wasps and the ants, the beauty and strange 
development of the butterfly, the artfulness of the spider, the utility of the 
silkworm—these and other features of nature provided inspiration 
for 18th-century research and speculation.

Fig. 1
Albrecht von Haller called Linnæus "the second Adam." He appears in this role
in a vignette for the eleventh edition of Systema naturae (ed. Lange, Haller, 1760). As
 Adam, Linnæus is sitting naked, naming all the animals (cf. Genesis 2:19). Paradise is 
crowded with animals and plants, monkeys climbing the trees, whales swimming in 
the sea; everything is at peace. The fall is yet to come. The figure in the middle is Diana 
polymammae, symbol of Nature and its generative force. Linnæus—with "his" flower
 Linnea borealis at his feet—is urging numbers and names, Numeros et nomina, 
from Diana. He is Nature's bookkeeper.

Fig. 2
This instructive vignette, from Charles Bonnet, Oeuvres d'histoire naturelle, 4 
(Neufchâtel, 1781), depicts man at the top of the scale of nature. As man belongs 
to both the material and the spiritual world, he keeps hishead in the clouds. On 
lower steps of the scale follow the monkey, the lion and the dog, the eagle, fish,
lizards, corals, and so on. Everything in nature is thus to be understood 
both in hierarchy and in continuity.

Fig. 3
In private lectures Linnæus discussed the possibility of arranging 
natural orders linearly. With so many uncertainties in establishing these 
orders and with so many more plants still to discover, however, such an 
arrangement must wait. This map, believed to be based on a drawing by
Linnæus, shows continuity between some groups, as well as gaps requiring 
more knowledge: Linnæus, Praelectiones in ordines naturales plantarum, 
ed. P.D. Gieseke (Hamburg, 1792), facing p. 623.

Fig. 3.1
Illustration of the Linnæan sexual system, from William Withering, A botanical arrangement 
of all the vegetables growing in Great Britain (1776). See chapter 3, page 77.

Fig. 3.2
Linnæus' classification of botanists, from his Bibliotheca 
botanica (1736). See chapter 3, page 79.

Fig. 3.3
René Just Haüy's geometrical forms of crystals, from his Tableau comparatif des résultats
de la cristallographie et de l'analyse chimique relativement à la classification des
 minéraux (1809). See chapter 3, page 92.

Fig. 3.4
Classification of nervous disorders showing orders, genera, species, and 
varieties, from Philippe Pinel, Nosographie philosohique, 6th ed. (1818). 
See chapter 3, page 99.

Fig. 3.5
Illustration of curves classified by Gabriel Cramer in his Introduction 
à l'analyse des lignes courbes algébriques (1750). See chapter 3, page 102.

Fig. 3.6
Portion of Jean Nicolas Pierre Hachette's classification of simple machines, from 
his Traité élémentaire des machines (1811). See chapter 3, page 106.

Fig. 6.1
The repeating circle, from Jacques Cassini, Pierre François Méchain, and 
Adrien-Marie Legendre, Exposé des opérations faites en France [1791]. By 
courtesy, National Land Survey (Lantmäteriverket), Gävle.

Fig. 6.2
According to William Roy, "It is a brass circle, three feet in diameter, 
and may be called a theodolet [theodolite], rendered exremely perfect." 
From Roy's "Account of the trigonometrical operation" in the 
Philosophical transactions for 1790.

Fig. 6.3
The theodolite was used with a portable scaffold and crane in the high-tech military surveying 
operations of the late 18th century. From Roy's "Account of the trigonometrical operation" (1790).

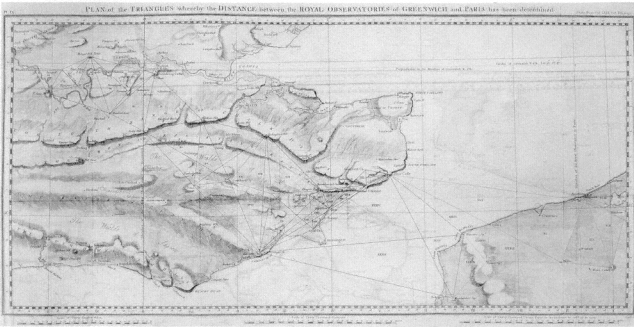
Fig. 6.4
The cross-channel connection, from Roy's "Account of the trigonometrical operation" (1790).

Fig. 8.1
The close connection between economics, technology, and chemistry in 
"die ganze Historie vom Kiess," from F.J. Henckel, Pyrotologia (1725). Instruments
in the small buildings illustrate the role of chemistry in the production
of sulfur, vitriol, and arsenic from pyrites.

Fig. 8.2
Ädelfors mine in Sweden as seen in 1767 by G. Jars. From his Voyages métallurgiques, 2 (1780).

Fig. 10.1
Tabular display of experiments in charcoal-burning in Dalecarlia, from 
Carl David af Uhr, Berättelse om kolnings-försök  åren 1811, 1812 och 1813.

Fig. 10.2
Illustrations for Zacharias Plantin's studies of the volume of rhombic sledges of charcoal, 
from the  Kungl. Vetenskapsakademiens Handlingar  for 1778 and 1784.

Fig. 10.3
Systematic display of data from Johann Eric Norberg's study (1772–3) of human muscle power,
from the Kungl. Vetenskapsakademiens Handlingar for 1799.

Fig. 11.1
Georg Hartig's 200-year plan for the Jägerthal forest district, from his Neue Instructionen (1819). 
By courtesy, Department of Special Collections, Yale University.

Fig. 11.2
Transformation of the Colditz forest district after 100 years of managements 
according to Cotta's ideal scheme. From Heske, German forestry. 
By courtesy, Stanford University Libraries.