12.3.6—
Enzymes as Control Elements
Until the discovery of feedback inhibition in 1956 enzymes were considered as biological catalysts and most enzymologists were concerned with the properties of the active site. When it became apparent that enzyme activity was under the control of specific metabolites, which were structurally unlike the active site, it became necessary to postulate a control site to which metabolites could bind and modulate the activity of the enzyme. Recognizing the lack of structural similarity between the substrate and the effector the term allosteric site was introduced (Monod, Changeux & Jacob, 1963). Subsequently Monod, Wyman and Changeux (1965) noted that many regulatory enzymes with specific allosteric sites exhibit cooperative-type kinetics and they developed a concerted transition hypothesis to explain the observed kinetics. Many workers assume that any enzyme showing sigmoidal kinetics is an allosteric enzyme and some workers imply that the mechanism of activation of all allosteric enzymes follows the mechanism postulated by Monod et al., (1965). The purist may object but the original precise definition has been replaced by a broader but less precise usage.
12.3.6.1—
Allosteric Enzymes
Before 1956, the kinetics of numerous enzymes were shown to follow the rate law of Michaelis and Menten giving a hyperbolic plot of v against S . An examination of enzymes which were known to be subject to feedback regulation showed that in some cases the relationship between v and S was sigmoid. In other cases the addition of a feedback inhibitor led to a change from a hyperbolic to a sigmoid relationship.
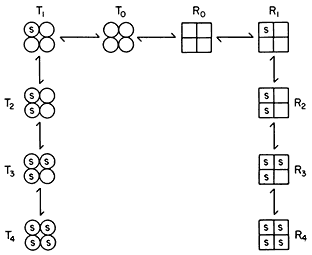
Figure 12.7
Illustration of the Monod model of an allosteric enzyme.
Monod et al., (1965) proposed a simple model to account for the observed kinetics in which they took account of the observation that allosteric enzymes are composed of subunits. They assumed that the protein subunits were arranged in such a way that they occupy equivalent positions so that the enzyme must have at least one axis of symmetry. They further assumed two interconvertible states—R and T—each maintaining the symmetry principle. A simple illustration of the model is given in Fig. 12.7 based on the symbols used by Koshland (1970). The reader is referred to the original article by Monod et al., (1965) for the derivation of the rate law. However a consideration of the illustration leads to a basic understanding of the underlying causes of sigmoid kinetics. Two types of allosteric behaviour may be distinguished—one the variable K system in which the two states of the enzyme have different affinities for the substrate, the other, the variable V system in which the R state is catalytically more active (Fig. 12.8).
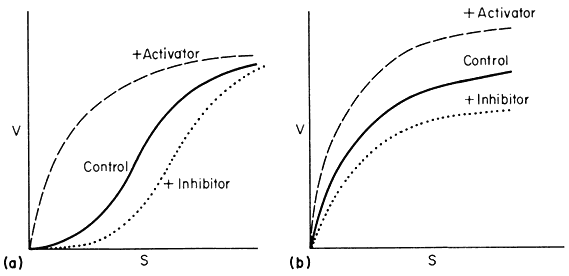
Figure 12.8
Relationship between v and s.
(A) a variable K system; (B) a variable V system.
Variable K Systems
In the variable K system, the R form is assumed to have a higher affinity for S than the T form of the enzyme. If in the absence of ligands, the equilibrium favours the T form then increasing concentrations of S will shift the equilibrium towards the R state giving sigmoid v against S plots. Another way of looking at this situation is to imagine that the interconversion of the R and T forms can be blocked and the enzyme isolated as the R or T form. The T form would give a normal Michaelis-Menten curve with a high Km(T ) and the R form would also give a Michaelis-Menten curve but with a low Km(R ) . Allowing R and T to be interconvertible allows Km to vary.
If an activator binds preferentially to the R state it will tend to put the enzyme entirely in the R state and so remove the sigmoidicity of the v against S plot. Similarly if an inhibitor binds preferentially to the T form it will increase the sigmoidicity.
Variable V Systems
In the variable V system the R form is assumed to be catalytically more active than the T form though both forms have the same affinity for the substrate so that the v/S plot is hyperbolic in the presence or absence of activators and inhibitors. An activator is assumed to have a greater affinity for the R form than for the T form whilst the reverse holds for an inhibitor.
12.3.6.2—
Alternative Models for Allosteric Enzymes
This superficial consideration of the Monod model concentrates on only one aspect of the model–the two configurational states. This limited aspect gives a qualitative explanation of' sigmoid kinetics described by the equation:
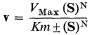
where N = 2.
To explain higher order reactions the Monod model includes some highly restrictive assumptions which produce mathematical simplicity but are nevertheless based on the fundamental properties of protein structure.
An alternative model proposed by Koshland (1970) assumes an induced fit so that the protein subunit undergoes a conformational change when it binds a ligand. A simple sequential model may be illustrated:

This simple model is not a necessary part of the induced fit model (which in fact suggests a diversity of forms of association between enzyme and ligand—25 for a tetrameric protein). Nevertheless it simplifies the mathematical treatment and in many cases provides a close fit to experimental values.
12.3.6.3—
Kinetic Constants for Allosteric Enzymes
When an electronic engineer constructs a control circuit he needs to know the characteristics of the components—the amplification factor, grid bias, etc. Similarly if we wish to understand the control of a system we need to know the characteristics of its components, that is, the kinetic constants of the enzymes. Clearly a variable K system cannot be defined by a Km value nevertheless the same operation value can be used, that is the concentration of substrate producing half maximum velocity which is in this case designated S0.5 . More generally the term (X0.5 ) is used to designate the ligand concentration at half saturation.
The constant N is operationally the order of the reaction, its physical meaning may relate to the number of substrate binding sites on the enzyme or to the degree of cooperativity of binding. Whatever the meaning of N it can be estimated by means of a Hill plot (Fig. 12.9). Another kinetic term, Rs is the ratio between the 90% and 10% saturation values. Rs will be 81 for all curves following Michaelis-Menten kinetics and less than 81 for cases of positive cooperativity–a few cases of negative cooperativity are known and these give Rs values greater than 81.
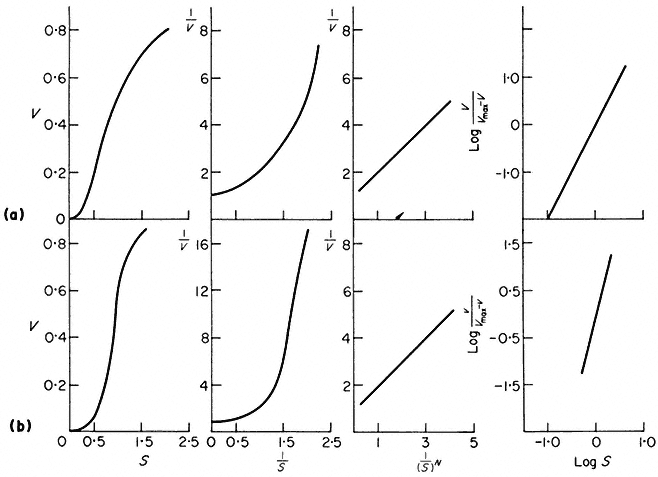
Figure 12.9
Kinetic data for an enzyme with variable 'K' properties.
The curves are drawn assuming
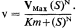
Valve characteristics define the properties of the valve but do not determine the function of the valve–the function of the valve is determined by the circuit in which it operates, in one circuit it may function as a cathode follower, in another as an amplifier. Similarly, the kinetic constants of a control enzyme do not determine its role in metabolic organization. The properties of an enzyme in a metabolic pathway are modified by its association with other enzymes. The study of control in metabolic pathways relates enzymology to physiology and illustrates the somewhat unfashionable view that the whole is more than the sum of the parts.